Artykuł w ciągu ostatnich 24 godzin czytało  1 Czytelników
Uwagi i recenzje podręcznika  przesyłać na adres wydawnictwa: wydawnictwo@chodor-projekt.net lub leszek.chodor@chodor-pojekt.pl

Podręcznik Imperfekcyjna metoda projektowania konstrukcji [ → Spis treści ]

Rozdział 1 :  WPROWADZENIE

Część1-1 : Pojęcia wstępne

Nawigacja: ⊗ ⇒ [ 1-2: Krótki przegląd metod wyboczeniowych i imperfekcyjnych ]

Do wszystkich typów konstrukcji (stalowe, żelbetowe, drewniane, murowe) stosuje się wspólną metodologię projektowania konstrukcji na płaszczyźnie metody imperfekcyjnej. Uproszczone metody z wykorzystaniem współczynników wyboczeniowych (redukcyjnych) są historyczne i nie są już zalecane w projektowaniu profesjonalnym. Podręcznik powstał na bazie praktyki projektowej wspomaganej metodami komputerowymi, a przede wszystkim po kilkunastoletniej już obserwacji wielu ważnych obiektów budowlanych zrealizowanych na podstawie projektów autora z zastosowaniem bezpośredniej (standardowej) metody imperfekcyjnej. (2)

W tym rozdziale wprowadzającym do podręcznika od razu pokazano, że niezawodność konstrukcji budowlanych można w prosty sposób wyznaczyć z dwuparametrowego rozkładu Gumbela. W tym celu opracowano oryginalny model stochastyczny mnożnika obciążeń $\Lambda= F_{lim}/F_E$, spójny ze stosowanymi w dalszej części pracy losowymi rozkładami ekstremalnymi, a będący uogólnieniem modeli Kiureghian  (1978) [1] oraz Grigoriu-Turkstry (1978) [2]. Parametry  losowego ilorazu $F_{lim}/F_E$ dla ustalonej chwili czasu sprowadzono do parametrów zastępczej  zmiennej losowej o rozkładzie normalnym, przy czym parametry normalnego rozkładu obciążeń  $F_E$ w danej chwili czasu  przyjmowano na podstawie danych normowych  [3] z zastosowaniem danych pracy Ellingwood i in. [4] oraz Barlett i in (2003) [5]) .Parametry rozkładu Gumbela nośności krytycznej na podstawie pracy Bjorhove (1972) [6]; parametry nośności plastycznej i na podstawie prac Augusti-Casciati i Chodor-Kłosowska (2014) [7]

Cel i zakres podręcznika

Artykuł jest pierwszą częścią podręcznika Imperfekcyjna metoda projektowania konstrukcji, w którym zaprezentowano podstawy metody imperfekcyjnej w odmianach geometrycznych i alternatywnych imperfekcji oraz równoważnych, fikcyjnych obciążeń. Na podstawie wieloletniej praktyki projektowej oraz wielu symulacji numerycznych pokazano praktyczny i prosty algorytm inżynierski obliczania i projektowania rzeczywistych konstrukcji obarczonych imperfekcjami z uwzględnieniem nieliniowych efektów geometrycznych oraz wielorakich form niestateczności prętów:  vwyboczenia giętnego, skrętnego, i bocznego – zwichrzenia.

Zamieszczono liczne  przykłady rachunkow dla szeregu rodzajów konstrukcji. Przykłady wykonano współczesnym programem obliczeniowym Consteel [8], w którym zaimplementowano uogólniony element prętowy- cienkościenny element Własowa [9] o siedmiu stopniach swobody (z paczeniem i bimomentem jako dodatkowym przemieszczeniem i siłą przekrojową).

Prezentowany w konkluzji podręcznika algorytm jest uogólnieniem alternatywnej, imperfekcyjnej metody geometrycznej wdrożonej przez  [10] i szczegółowo przedstawionej w pracy [11] oraz kolejnych. Alternatywna metoda imperfekcyjna jest zalecana do stosowania przez współczesne normy do projektowania konstrukcji w tym [12], a polega na założeniu kształtu imperfekcji w formie przeskalowanej, pierwszej  sprężystej postaci wyboczenia. Taka zintegrowana imperfekcja opisuje zarówno imperfekcje łukowe jak i przechyłowe.

Badania nad metodą imperfekcyjną prowadzone w podręczniku zmierzają w kierunku opisu następujących fundamentalnych problemów:

1.  Zaprezentowanie metody analizy konstrukcji, umożliwiającej zautomatyzowany proces obliczeń, uwzględniający wielorakie, sprzężone formy utraty stateczności i korelacje między nimi – bez stosowania skomplikowanego systemu normowych współczynników redukcyjnych (wyboczeniowych) przypisanych do wyodrębnianych form utraty stateczności, wraz z systemem współczynników korelacji form wyboczenia wydzielonych elementów,

2. Opisanie imperfekcji kształtem zniszczenia granicznego, wyznaczonym z warunku sprężystej niestateczności oraz zniszczenia plastycznego lub uogólnionych przegubów w konstrukcjach żelbetowych, zespolonych drewnianych i murowych.

3. Opisanie losowego charakteru imperfekcji i probabilistycznej alternatywy typów imperfekcji, a także mechanizmów zniszczenia konstrukcji: wyboczenia sprężystego i utworzenia mechanizmu plastycznego.

4. Zdefiniowanie klas wrażliwości konstrukcji i elementów konstrukcyjnych na lokalne (łukowe) imperfekcje geometryczne, których uwzględnienie w modelu konstrukcji i kombinacjach jest utrudnione.

Do rozwiązania postawionych zagadnień uogólniono imperfekcyjną metodę alternatywną poprzez wyznaczenie strzałki imperfekcji sprężysto-plastycznych. Prezentowane uogólnienie polega na ogarnięciu tą metodą:

1) wszystkich form utraty stateczności, możliwych do ujawnienia w numerycznym modelu konstrukcji,

2) traktowaniu imperfekcji, jako „losowej sumy” imperfekcji przeskalowanej z postaci sprężystej utraty stateczności systemu oraz stowarzyszonej z postacią utraty nośności plastycznej. Losowe imperfekcje opisano rozkładem Gumbela maksimów, a alternatywę typów imperfekcji oraz mechanizmów zniszczenia potraktowano, jako losowe zdarzenie łączne niezależnych losowo zdarzeń brzegowych.

W prezentowanej metodzie – sprężystej postaci utraty stateczności systemu – nie traktuje się jako ortodoksyjnego wzorca zintegrowanych (łącznie globalnych -przechyłowych  i lokalnych- łukowych ) imperfekcji systemu. W to miejsce wprowadza się podejście sprężysto-plastyczne i dodatkowo „rozmyte” na skutek losowego charakteru tych zjawisk, to znaczy podejście rzeczywiste, generalnie prowadzące do zwiększenia nośności systemu, ale w szczególnych przypadkach ujawniające niedobory nośności w stosunku do metod dotychczas stosowanych.

Metodę imperfekcyjną projektowania konstrukcji przedstawiono na przykładzie prętowych konstrukcji stalowych, żelbetowych, zespolonych, drewnianych i murowych. Nie analizowano konstrukcji powłokowych [13] , płytowych [14] , blachownic  [15] i innych specjalnych. Konstrukcje te powinny być przedmiotem odrębnych monografii, choć ogólne zasady przedstawione w tym podręczniku wymagają tylko drobnych modyfikacji. Rozważono sytuacje, które nie zawierają wpływów pożaru oraz zmęczenia.

Uwagi wstępne o imperfekcjach konstrukcji

Wszystkie systemy konstrukcyjne są obarczone losowymi imperfekcjami i nie da się tego uniknąć.

Wstępne niedoskonałości (imperfekcje) konstrukcji, takie jak wstępne wygięcia i naprężenia resztkowe, są jednym z głównych powodów nieliniowego zachowania systemów i elementów konstrukcyjnych oraz mają znaczny wpływ na wytrzymałość i stateczność całego systemu. Imperfekcje mogą być szkodliwe lub korzystne zależnie od kształtu i wielkości odchyłek od kształtu idealnego. (np. [16] ), choć najczęściej istotnie zmniejszają wytrzymałość konstrukcji (np. [17]).

Metody projektowania konstrukcji z imperfekcjami

W celu uwzględnienia wpływu imperfekcji na pracę konstrukcji stosowane jest wiele podejść, które można zakwalifikować do jednego z dwóch rodzajów:
1. WM – metody wyboczeniowe (historyczne), polegające na redukcji sztywności konstrukcji poprzez zastosowanie systemu współczynników wyboczeniowych. Zredukowane nośności elementów odnosi się do sił przekrojowych, uzyskanych z analizy 1 rzędu konstrukcji nominalnej (bez imperfekcji).
2. IM – metody imperfekcyjne (współczesne), polegające na amplifikowaniu sił przekrojowych, które odnosi się do nominalnej wytrzymałości przekrojów (a nie elementów). Amplifikacja sił następuje podczas nieliniowych geometrycznie obliczeń na konstrukcji z wymuszonymi geometrycznymi imperfekcjami systemowymi.

W metodach wyboczeniowych WM imperfekcje są uwzględniane w sposób pośredni poprzez współczynniki redukcyjne (wyboczeniowe), specyfikowane mieszanymi metodami eksperymentalno-analitycznymi. Funkcjonuje skomplikowany system kilkunastu współczynników wyboczeniowych i współczynników korelacji form wyboczenia. Metody wyboczeniowe prowadzą do akceptowanych przez inżynierów wyników przybliżonych,

W metodach imperfekcyjnych IM niedoskonałości systemowe są uwzględniane w sposób bezpośredni poprzez wymuszenie fikcyjnych imperfekcji geometrycznych lub obciążenie systemu fikcyjnymi siłami równoważnymi imperfekcjom geometrycznym. Odmiany metod imperfekcyjnych wynikają ze sposobu wyznaczania fikcyjnych wymuszeń imperfekcjami, w tym ze sposobu szacowania amplitudy imperfekcji geometrycznych. Metody imperfekcyjne są w zasadzie wolne od skomplikowanego systemu współczynników wyboczeniowych, a jednocześnie prowadzą do dokładniejszych wyników i z reguły bardziej ekonomicznych projektów, co jest szczególnie ważne w erze energooszczędności i zrównoważonego rozwoju oraz projektowania.

Metody Imperfekcyjne IM wymagają przeprowadzenia analizy geometrycznie nieliniowej (GNA) drugiego lub wyższego rzędu dla całego przestrzennego modelu konstrukcji. Analiza GNA będzie skuteczna, jeśli konstrukcja zostanie wytrącona z położenia równowagi prostej (przedbifurkacyjnej) do położenia równowagi odkształconej. W celu wytrącenia konstrukcji z położenia nominalnego obciąża się ją niewielkimi fikcyjnymi siłami poziomymi lub bezpośrednio wymusza zmianę geometria układu o niewielkie odchylenia od położenia nominalnego. Te niewielkie odchylenia geometryczne, to właśnie imperfekcje systemowe, a siły fikcyjne uzyskuje się poprzez zamianę kinematycznych warunków brzegowych na statyczne warunki brzegowe, co jest możliwe zgodnie z podstawowymi zasadami teorii sprężystości i plastyczności (np [18] ).

Współczesna praktyka projektowania i metody imperfekcyjne są nierozerwalnie związane z rozwojem procedur numerycznych, a szczególnie z implementacją nowoczesnych teorii i metod obliczeń statycznych oraz wymiarowania elementów, których zastosowanie w tradycyjnych sposobach projektowania byłoby żmudne, a często wręcz niemożliwe.

Metody imperfekcyjne stały się dostępne do powszechnego stosowania w związku z zaimplementowaniem stosownych metod i sposobów postępowania w szeregu inżynierskich programach obliczeniowych, a przede wszystkim: Consteel+csJoint [8] , RFEM, RSTAB [19] , SAP2000 [20] , SCIA [21] ,  Sofistik [22].

Wraz z rozwojem inżynierskich programów obliczeniowych coraz szerzej zaczyna być stosowane podejście ogólne OM, polegające na wyznaczeniu jednego współczynnika wyboczeniowego dla całego systemu na podstawie smukłości całego systemu, a nie dla wydzielonych prętów. Autor, nie poleca do stosowania praktycznego również tej metody, mimo że jest nareszcie zgodna z teoretycznymi podstawami teorii konstrukcji, a przez to znacznie dokładniejsza od klasycznych metod wyboczeniowych stosowanych dla wyodrębnionych prętów. W podręczniku polecane są metody imperfekcyjne IM, przede wszystkim  w wersji uogólnionej metody alternatywnej UAIM. 

Fundamentalne zasady metody imperfekcyjnej są wspólne dla podstawowych rodzajów konstrukcji budowlanych: stalowych PN-EN 1993 (2006)  [12], zespolonych PN-EN 1994 (2008) [23], betonowych, żelbetowych i sprężonych  PN-EN 1992 (2008) [24], aluminiowych PN-EN 1999 (2010) [25], mostów stalowych PN-EN 1993-2 (2010) [26], drewnianych PN-EN 1995 (2010) [27], murowych [28]. Normy wymieniono w kolejności publikowania.  W normie  projektowania konstrukcji stalowych (2006) sformułowano oryginalną wersję metod imperfekcyjnych. Wersję tę udoskonalano w kolejnych normach, a w szczególności do projektowania konstrukcji zespolonych (2008), żelbetowych (2008) i aluminiowych (2010), a także mostów stalowych (2010). Najbardziej zaawansowane metody zawarto w tej ostatniej normie. Mniej istotne są zasady podane w normach do projektowania konstrukcji drewnianych (2010) i murowych (2013), gdzie obliczenia drugiego rzędu potraktowano marginalnie.

Z analizy postanowień  różnych normach wynika, że da się sformułować wspólne zasady, a normy późniejsze podają ulepszone zasady w stosunku do normy stalowej. W niniejszym podręczniku usystematyzowano wiedzę w tym zakresie,  podano zasady uogólnione, wspólne dla wszystkich rodzajów konstrukcji, a w konsekwencji zaproponowano uproszczenie zasad projektowania konstrukcji stalowych, w szczególności poprzez ograniczenie liczby krzywych wyboczeniowych (klas imperfekcji łukowych) do jednej istotnej na akceptowalnym poziomie ufności.

Z praktyki projektowej wynika, metody imperfekcyjne stanowią tak istotny przełom dla teorii i praktyki projektowania konstrukcji, że są wprowadzane do praktyki z ostrożnością, a wręcz oporem. Nadal powszechnie stosowana jest metoda współczynników wyboczeniowych, w której stosuje się pół-empiryczne formuły projektowe.

Autor od kilkunastu lat,  jeszcze przed wejściem w życie norm Eurokod, w licznych, ważnych projektach konstrukcji stalowych, żelbetowych i zespolonych zrealizowanych w Polsce i Europie,  stosował  metodę wymiarowania prezentowaną w pracy, a mianowicie metodę imperfekcyjną, polegająca na obciążeniu konstrukcji siłami równoważnymi od imperfekcji i prowadzeniu nieliniowej geometrycznie analizy statycznej, a następnie wymiarowaniu elementów w modelu przestrzennym konstrukcji, bez wydzielania prętów oraz bez stosowania współczynników wyboczeniowych (redukcyjnych). O poprawności metody świadczy to, że konstrukcje są użytkowane bezawaryjnie od wielu lat, a o skuteczności metody świadczy to, że konstrukcje zostały zaprojektowane tak optymalnie, że nie przynosiły efektów wielokrotne próby ich zoptymalizowania przez niezależnych ekspertów.

Imperfekcje krytyczne (najgorsze)

Ważnym zagadnieniem praktycznym jest wyznaczenie takiego kształtu imperfekcji, który będzie najbardziej zmniejszał nośność graniczną $\Lambda_{lim}$.

Zwykle przyjmuje się propozycję Chladny (1958,1974) [29], [10]  i późniejszą  Brendel-Ramm (1980) [30], by  za krytyczny kształt imperfekcji zwany również najgorszym (ang. „worst”) uznać pierwszą postać wyboczenia, czyli imperfekcje wynikające z przeskalowania krytycznego wektora własnego konstrukcji. Takie podejście jest zgodne z pierwszą pracą na temat współczynnika wyboczeniowego Ayrton i Perry (1886) [31], ale przede wszytskim radykalnie redukuje koszty analizy probabilistycznej imperfekcji dla założonych właściwości probabilistycznych, przedstawione m.in w pracach: Elishakoff (1988) [32]; Lindberg (1988) [33] czy Kirkpatrick i Holmes (1989) [34], choć może być stosowane wyłącznie do geometrycznych imperfekcji systemowych.

Ikeda iMurota (1990, 1991) [35],  [36], [37] przedstawili ścisłą matematycznie teorię umożliwiającą wyznaczyć układ i wielkości imperfekcji krytycznych nie tylko niedoskonałości (geometrii konstrukcji (ułożenia węzłów w przestrzenie), ale również ścieżkę i układ obciążenia w czasie i przestrzeni, długości  skręcenia elementów, własności mechaniczne przekrojów itd.  W swoich pracach potwierdzili poprawność założenia o tym, że imperfekcje krytyczne ustroju sprężystego można prognozować na podstawie wektora własnego uzyskanego w analizie LBA. Na rys. 1 zilustrowano to na przykładzie mało wyniosłej kopuły prętowej w której obserwuje się utratę stateczności wskutek przeskoku węzła..

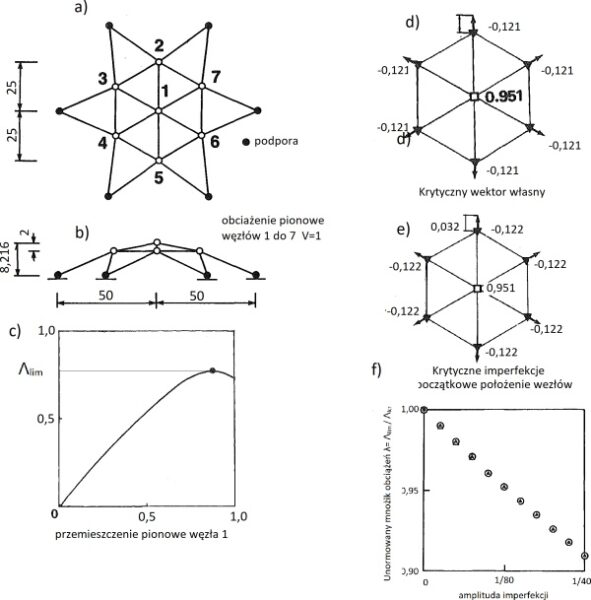
Rys.1. Imperfekcje krytyczne na przykładzie małowyniosłej kopuły [36] – złożono z fragmentów Fig.1- 7

Z porównania krytycznego (pierwszego) wektora własnego (rys.1d) z krytyczną imperfekcja (rys.1 e) stwierdzamy, że różnice praktycznie nie występują. Z rys.1. f) wynika natomiast, że imperfekcje zmniejszają nośność graniczną kopuły tym bardziej im są większe.

Tym samym hipotezę o treści ” W ustroju idealnie sprężystym z pojedynczym punktem granicznym, krytyczne (najgorsze) imperfekcje mają kształt podobny do pierwszego (najniższej) postaci wyboczenia systemu”  potwierdzono teoretycznie i jest ona podstawą analizy systemów idealnie sprężystych bez konieczności probabilistycznego badania losowych kształtów imperfekcji geometrycznych.   Ta szybka metoda dotyczy jednak wyłącznie kształtu sprężystej imperfekcji krytycznej a nie amplitudy tej imperfekcji.

Pytanie o tym jaka jest amplituda krytycznych imperfekcji sprężystych nadal pozostaje otwarte.
Z rysunku 1 f) wynika, że obniżenie nośności granicznej systemu zwiększa się wraz ze wzrostem amplitudy imperfekcji.
W pracy Ohsaki (2002) [38] pokazano, że krytyczna imperfekcja w systemie ze statecznym puntem bifurkacji – niewielka niedoskonałość może być gorsza niż duża niedoskonałość.

Wyznaczenie imperfekcji krytycznych dla konstrukcji sprężysto-plastycznej nie było poddane szczególnej analizie ze względu na wielokrotnie złożony problem.
Od VIII wieku do dzisiaj trwają na przykład dyskusje o „paradoksie  plastycznego wyboczenia”, np:  [39], czyli dyskusje o tym, która z dwóch teorii plastyczności : teorię sprężysto-plastycznych odkształceń Hencky-Iljusina (Hencky,(1924) [40] czy też teorię płynięcia  Hiil (1950) [41] – należy stosować przy analizie wyboczenia konstrukcji sprężysto-plastycznych. Badania  eksperymentalne  dają bowiem wyniki bliższe jednej lub drugiej teorii w zależności od rodzaju konstrukcji (np. słup z profilu, czy powłoka z blachy), a także rodzaju materiału , z którego jest wykonana (np stal , czy stop aluminium).

Mnożnik obciążenia miarą nośności konstrukcji

Rozważmy dowolną konstrukcję poddaną dowolnemu zewnętrznemu obciążeniu (siły skupione, rozłożone, termiczne, wymuszenia geometryczne),  w konfiguracji $F$.

Obciążenie konstrukcji w rozważanej chwili wynosi $\Lambda \cdot F$, gdzie $\Lambda$ jest mnożnikiem przez który należy przemnożyć każdą skladową konfiguracji $F$.
Mnożnik obciążenia będziemy oznaczać dużą literą $\Lambda$. W normie [12] mnożnik obciążenia jest oznaczany mała literą $\alpha$, a mnożnik obciążenia krytycznego przez $\alpha_{cr} .
Zmieniamy to oznaczenie na dużą literę w celu podkreślenia znaczenia pojęcia i wyróżniania go w tekście. Obie wielkości są tożsame $\Lambda_{cr}=\alpha_{cr}$

Załóżmy, że podczas zwiększania wartości obciążenia, działającego na konstrukcję proporcjonalnie do mnożnika $\Lambda$ – pod obciążeniem $ F_R=Λ_R \cdot F_E$ nastąpi utrata stabilności konstrukcji na skutek przekroczenia dowolnego stanu granicznego, czyli wystąpienia:

• M1={cr}: utraty stateczności  konstrukcji w dowolnej formie ( wyboczenie, zwichrzenie, dystorsja , itd), w taki sposób, że będzie to prowadziło do załamania konstrukcji lub jej części. W tym sensie nie jest  utratą stateczności miejscowe wyboczenie, jeśli konstrukcja nadal będzie pełniła rolę nośną (np płyty w stanie nośności pokrytycznej),
  przy mnożniku $\Lambda_{M,1}=\Lambda_{cr}$
• M2={pl}: mechanizmu plastycznego wskutek utworzenia się wystarczającej liczby przegubów plastycznych w konstrukcja wykonanej z materiału idealnie sztywno-plastycznego, lub przegubów uogólnionych w konstrukcji wykonanej z materiału złożonego (np. żelbetu),
  przy mnożniku $\Lambda_{M, 2}=\Lambda_{pl}$
• M3={brit}: zniszczenie konstrukcji w innej formie (np. kruche pękanie, pełzanie , itd),
  przy mnożniku $\Lambda_{M, 3}$
• M4={SLS}: przekroczenie uznanych za dopuszczalne przemieszczeń, ugięć, drgań, zarysowań itd
  przy mnożniku $\Lambda_{M, 4}$

Mnożnik obciążenia w stanie granicznym $\Lambda_{M,k}$ integruje w sobie zarówno własności własne konstrukcji (sztywności)  jak i kompletnego obciążenia działającego na konstrukcję (wymuszenia).

Jako miarę nośności konstrukcji ze względu na stan graniczny $M_k \quad (k=1, 2,\ldots, n)$ przyjmujemy mnożnik $\Lambda_{M,k}$.
Określenie:  „Nośność konstrukcji ze względu na stan graniczny $M_k$ wynosi $\Lambda_{M,k}$” oznacza, że konstrukcja niszczy się ze wzgledu na stan $M_k$ pod obciążeniem $\Lambda_{M,k}$” razy większym od obciążenia bieżącego (odnieisienia)

Mnożnik obciążenia przypisany do mechanizmu zniszczenia $M_k \quad (k=1, 2,\ldots, n)$ definiuje się następująco

$$\begin{equation} \Lambda_{M,k} = \cfrac{F_{M,k}} {F_E} \label {1}  \end{equation}$$

gdzie:
$F_E$ – konfiguracja obciążenia zewnętrznego (wzorzec odniesienia)
$F_{M,k }$ – konfiguracja obciążeń k-ta skalowana z konfiguracji odniesienia, przy zaistnieniu której realizuje się mechanizm $M_k$.

Zwróćmy uwagę, że mnożnik obciążenia ($\ref{1}$) jest zdefiniowany dla określonej konstrukcji, identyfikowanej $N$ mechanizmami zniszczenia $M_k, (k=1, \ldots, N)$, które jej dotyczą i stowarzyszonymi z tymi mechanizmami mnożnikami granicznymi $ \Lambda_{M,k} $ , ale także określona konfiguracja obciążenia zewnętrznego $F_E$

W niniejszym podręczniku ograniczono się do analizy mechanizmów zniszczenia $M_1=\{cr\} \text { oraz } M_2=\{pl\}$, co zasadniczo odnosi się do konstrukcji wykonanych z materiału sprężysto-plastycznego (metali), choć mechanizm {pl} jest z powodzeniem uogólniany na konstrukcje wykonane z innych materiałów poprzez  wprowadzenie  pojęcia uogólnionych przegubów (linii załomów)  lub linii pękania.

Nośność krytyczna i graniczna idealnie sprężysta

Nośność krytyczna $\Lambda_{cr}$

Mnożnik obciążenia krytycznego

$$\begin{equation} \Lambda_{cr} \label {2} \end{equation}$$

uzyskiwany w klasycznej analizie LBA jest taką wartością obciążenia konstrukcji przy której element, część lub całość konstrukcji traci stateczność w sensie matematycznym.  $\Lambda_{cr}$ należy traktować jako przypadek szczególny mnożnika obciążenia granicznego $\Lambda_{lim}$, ovserwowany w konstrukcji bez imperfekcji. Położenia sprężystego punktu granicznego nie da się wyznaczyć w klasycznej analizie LBA. Imperfekcje systemu i jego elementów powodują, że idealne zachowanie konstrukcji sprężystej opisywane klasycznym modelem wyboczeniowym, LBA ( Linear Bifurcation Analysis), w którym definiuje się nośność krytyczną $\Lambda_{cr}$ nie jest spotykane w rzeczywistych konstrukcjach. Pręt rzeczywisty nie ulegnie „czystemu” wyboczeniu, bo od początku pracy jest zginany, więc właściwa dla niego jest analiza geometrycznie nieliniowa, a dla słabo lub średnio nieliniowych konstrukcji, stanowiących większość układów inżynierskich – analiza drugiego rzędu.

Nośność graniczna idealnie sprężysta  $\Lambda_{lim}$

Dla konstrukcji sprężystej obarczonej imperfekcjami  geometrycznymi ( i ew. materiałowymi) definiuje się sprężystą nośność graniczną

$$\begin{equation} \Lambda_{lim} \label {3} \end{equation}$$

Na rys. 2 pokazano różnice pomiędzy nośnością krytyczną systemu idealnego (bez imperfekcji) $\Lambda_{cr}$, a nośnością graniczną $\Lambda_{lim}$ na nieliniowej gałęzi  pobifurkacyjnej ścieżki równowagi konstrukcji idealnie sprężystej .

Rys. 2 Konstrukcja idealna – nośność krytyczna; konstrukcja z imperfekcjami – nośność graniczna dla czterech przypadków ścieżek równowagi konstrukcji: a) z  punktem granicznym, b) z asymetrycznym punktem bifurkacji, c) z niestatecznym, asymetrycznym punktem bifurkacji, d) z e statecznym, symetrycznym punktem bifurkacji (na podstawie [42] )

Nośność plastyczna i sprężysto-plastyczna

Nośność  plastyczna $\Lambda_{pl}$

Nośność graniczna idealnie plastyczna

$$\begin{equation} \Lambda_{pl} \label {4} \end{equation}$$

jest wyznaczana w ramach klasycznej teorii nośności granicznej dla konstrukcji wykonanej z materiału sztywno-plastycznego.

Graniczny, plastyczny schemat konstrukcji zostanie osiągnięty po ukształtowaniu się ostatniego przegubu plastycznego potrzebnego do uruchomienia mechanizmu plastycznego. Ponieważ w rzeczywistości przeguby plastyczne w stanie granicznym formują się jednocześnie [43] , więc nie trzeba uwzględniać form utraty stateczności w schematach poprzedzających. Obliczenia iteracyjne są potrzebne wyłącznie do opisu stanu granicznego w procesie pushover [44] .

Nośność graniczna sprężysto-plastyczna

Rozróżnienie nośności krytycznej $\Lambda_{cr}$ , granicznej -sprężystej $\Lambda_{lim}$ i plastycznej $\Lambda_{pl}$ omówiono w artykule Nośność graniczna, a nośność krytyczna i plastyczna.

Interakcja nośności sprężystej $\Lambda_{R}$ oraz plastycznej definiuje nośność graniczną $\Lambda_{R}$, którą można oszacować z prostej formuły Rankine-Merchant [45]  – formuły  sumowania odwrotności nośności:

$$\begin{equation}  \cfrac{1}{\Lambda_R}= \cfrac{1}{\Lambda_{lim}} + \cfrac{1}{\Lambda_{pl }} \label {5} \end{equation}$$

$\Lambda_R$  jest nośnością graniczną systemu konstrukcyjnego otrzymaną z warunku interakcji nośności krytycznej  $\Lambda_{cr}$ ($\ref{2}$) i nośności plastycznej $\Lambda_{pl}$ ($\ref{4}$).

Nośność krytyczna  $\Lambda_{cr}$ jest osiągnięta, gdy konstrukcja, jej fragment lub element traci stateczność sprężystą w sensie metody LBA.

Opisany wyżej model stanowi podstawowe założenie uogólnionej metody stosowanej w pracy.

Założenie jest  zgodne z szerokimi badaniami [46] i innych (np. [47] , [48] ). W pracach tych pokazano, że w sytuacjach rzeczywistych, „czyste” postacie wyboczenia sprężystego praktycznie nie realizują się lub realizują na statystycznie nieistotnym poziomie nawet przy współczynniku niezawodności budynków i budowli β>3 .
Można to wykazać również teoretycznie po zastosowaniu podstawowych twierdzeń metody funkcji ważności, stosowanej w losowych symulacjach Monte Carlo, np. [49] , [50].
To samo można wykazać stosując podejście [51] , a nie [52], to znaczy podejście niesprężyste, opisujące rzeczywistą utratę stateczności.

Nośność losowa  i niezawodność konstrukcji

Stochastyczny model mnożnika obciążenia konstrukcji

Na rys. 3 pokazano model  mnożnika obciążenia konstrukcji (w skrócie obciążenia) jako procesu stochastycznego rozciągnięto w okresie użytkowania konstrukcji $T$.

Rys.3. Model mnożnika obciążeń $\Lambda$

Granicę pomiędzy stanami bezpiecznymi i niebezpiecznym i wyznacza linia
$$\begin{equation} \Lambda = 1 \label {6}  \end{equation}$$

$\Lambda_{M,k}=1$, przedstawiona linią czerwoną na rys. 2. Konstrukcja jest bezpieczna jeśli w okresie eksploatacji  zachowano warunek:
$$\begin{equation} \Lambda > 1 \label {7}  \end{equation}$$

Nośność konstrukcji  $\Lambda_R$ jest takim mnożnikiem  obciążenia zewnętrznego, przy którym w okresie użytkowania konstrukcji $T=\sum T_i$ nie zrealizuje się  żaden z mechanizmów zniszczenia  $M_1, M_2 ,\ldots M_k , \ldots \quad k=(1, \ldots N)$ , gdzie N jest liczbą mechanizmów zniszczenia. Nośność konstrukcji można zapisać następująco:
$$\begin{equation} \Lambda_R = \Lambda: \forall_{t < T}  \{ \overline{M_1} \cup  \overline{M_k} \, \ldots , \}  \quad  k=(1, \ldots, N) \label {8}  \end{equation}$$

Niezawodność konstrukcji jest prawdopodobieństwem zdarzenia, polegającego na tym że w okresie użytkowania konstrukcji $T$ nie zrealizuje się  żaden z mechanizmów zniszczenia  $ M_k \, , k=(1,N)$, co można zapisać krótko

$$\begin{equation} p_R = Pr \{  \min_{0<t\le T} \Lambda_R(t)  > 1 \}  \label {9}  \end{equation}$$

Prawdopodobieństwo zniszczenia jest dopełnieniem ($\ref{9}$) , czyli

$$\begin{equation} p_f = 1- p_R = Pr  \{ \max_{0<t\le T} \Lambda_R(t) \le 1 \} \label {10}  \end{equation}$$

Opis stochastycznego mnożnika obciążenia

Stochastyczny model obciążeń został opracowany przy współpracv z Prof. Wiesławem Dziubdzielą, autorem m.in prac [53] , [54].

Proces stochastyczny obciążenia $\Lambda(t), \quad t > 0 $ j (mnożnika obciążenia stowarzyszonego z danym mechanizmem zniszczenia $\Lambda = \Lambda_{M,k}$) zgodnie z założeniami klasycznymi Borges i  Castanheta (1971) [55],  generowano przez dwa ciągi zmiennych losowych (rys.2):

• ciąg obciążeń $\Lambda_1, \, \Lambda_2 \, \ldots, \, \Lambda_n,$
• ciąg okresów trwania obciążeń
• $\tau_1, \, \tau_2, \, \ldots, \, \tau_n,$

gdzie: i=(1, \ldots n), n – liczba  odcinków czasu na który podzielono okres użytkowania $T$.

Proces stochastyczny obciążenia $\Lambda(t) $ można opisać formułą:

$$\begin{equation}  \Lambda(t) =\Lambda_n \quad , \tau_{n-1}  \le t < \tau_n  , \quad n=1,2,\ldots \label {11}  \end{equation}$$

gdzie: $\tau_0 =0 \, , \, \tau_n= T_1+T_2 + \ldots +T_n , \quad n=1,2, \dots$.

Stochastyczny ciąg mnożników  obciążeń

Zakładamy , że ciąg $\Lambda_1, \Lambda_2, \ldots$ jest ciągiem Gausssa-Markowa (zob. [56], to znaczy:

$$\begin{equation}  \Lambda_1 = \sigma \cdot N_1+m \\ \Lambda_{n+1}=\rho \cdot \Lambda_n + \sigma \cdot \sqrt{1-\rho^2} \cdot N_{n+1} + (1-\rho) \cdot m , \quad n=1,2 \ldots \label {12}  \end{equation}$$

gdzie:

$N_1,N_2,\ldots$ jest ciągiem niezależnych zmiennych losowych o jednakowym rozkładzie Gaussa  z wartością oczekiwaną $E [ N_n] =0$ i wariancją $Var [ N_n ]=1$

$ – \infty < m < \infty $,   $ \sigma > 0 $ ,  $ -1 < \rho <1$ – liczby rzeczywiste.

Ponieważ zachodzi:

$$\begin{equation}  E [ \Lambda_1 ]  = \sigma \cdot E [ N_1 ] + m = m, \\ E [ \Lambda_{n+1}] =\rho \cdot E [ \Lambda_n]  + \sigma \cdot \sqrt{1-\rho^2} \cdot  E [ N_{n+1} ] + (1- \rho) \cdot m = m , \quad  n=1,2, \ldots \label {13}  \end{equation}$$

$$\begin{equation}  Var [ \Lambda_{n+1} ] = \rho^2 \cdot Var [ \Lambda_n ] + \sigma^2  \left ( 1-\rho^2 \right ) \cdot Var [ \Lambda_{n+1} ] = \rho^2 \cdot \sigma^2 + \sigma^2  \cdot (1- \rho^2) = \sigma ^2 ,  \quad n= 1, 2, \ldots \label {14}  \end{equation}$$

więc  ciąg obciążeń jest stacjonarnym ciągiem Gaussa z:

wartością oczekiwaną

$$\begin{equation}  E [ \Lambda_n] = m  \label {15}  \end{equation}$$

wariancją

$$\begin{equation}  Var [ \Lambda_n ] = \sigma^2 >0  , \quad n \ge 1 \label {16}  \end{equation}$$

współczynnikiem  korelacji zmiennych $\Lambda_1$ i $\Lambda_n$:

$$\begin{equation} \rho(n) =\cfrac {Cov [ \Lambda_1 , \Lambda_n ]} {{\sqrt{Var [ \Lambda_1]  \cdot Var [\Lambda_n}] }}= \cfrac {1}{\sigma^2} \left ( E [ \Lambda_1 \cdot \Lambda_n ] – m^2 \right), \quad n=2,3 ,\ldots  \label {17} \end{equation}$$

Mamy ponadto

$$\begin{equation} E [ \Lambda_1 \cdot \Lambda_n ] = E \left [ ( \sigma \cdot N_1 +m) \cdot ( \rho \cdot \Lambda_n + \sigma \cdot \sqrt{1-\rho^2} N_{n+1} + (1-\rho) \cdot m \right ]  \\= \sigma \rho \cdot E[ N_1 \Lambda_n] + m^2 \cdot \rho +(1-\rho) \cdot m^2 = \sigma \cdot \rho \cdot E[N_1 \Lambda_n] + m^2 \label {18} \end{equation}$$

Ponieważ:

$$\begin{equation} E [ N_1 \cdot \Lambda_2 ] = E \left [ N_1 \cdot [ \rho \cdot ( \sigma \cdot N_1 +m)+\sigma \cdot \sqrt{1- \rho^2} \cdot N_2 +(1-\rho) \cdot m ]  \right ] = \rho \cdot \sigma \cdot E[N_1^2] =\rho \cdot \sigma \label {19} \end{equation}$$

$$\begin{equation} E [ N_1 \cdot \Lambda_3 ] = E \left [ N_1 \cdot [ \rho \cdot \Lambda_2 =\sigma \cdot \sqrt{1-\rho^2}\cdot N_3 +(1-\rho) \cdot m \right ] = \rho \cdot E[N_1 \cdot \Lambda_2] =\rho^2 \cdot \sigma \label {20} \end{equation}$$

$\ldots \ldots \ldots$

$$\begin{equation} E [ N_1 \cdot \Lambda_n ] = \rho^{n-1} \cdot \sigma \label {21} \end{equation}$$

więc

$$\begin{equation} \rho(n) =\cfrac{1}{\sigma^2}\cdot \left( \sigma \cdot \rho \cdot \rho^{n-1} \cdot \sigma + m^2 -m^2\right) = \rho^n , \quad n=2,3, \ldots, \quad | \rho | < 1 \label {22} \end{equation}$$

Parametry rozkładu: średnia $m$ i odchylenie standardowe $]\sigma$ rzeczywistego procesu w okresie $T_i$ zależy od długości okresu uśredniania. Tym problemem zajmujemy się w dodatku B Dyskretyzacja losowo odkształcalnej konstrukcji.

W dalszej części zakładamy, że okres $T$ jest podzielony na „n” równych odcinków o długości jednego roku, to znaczy $ T_i=1 rok$, , (i=1, \dots , n). Z danych statystycznych pomirów rzeczywistego procesu ( np. obciazenia wiatrem) będziemy pobierać średnie i odchylenia standardowe roczne (ang. „annual”).

Stochastyczny ciąg okresów mnożników obciążeń

Zakładamy, że ciąg okresów obciążeń $T_1$, $T_2$, \ldots , $T_n$ ,\ldots$ jest ciągiem niezależnych zmiennych losowych o jednakowym rozkładzie wykładniczym z:

wartością oczekiwaną  $0 < E [T_n ]=1/\nu < \infty $,

to znaczy dystrybuanty zmiennych losowych $T_n$ są postaci

$$\begin{equation}  \begin{cases}
0, & t \le 0 \\
1-e^{-\nu t}, & t>0 \label {23} \end{cases} \end{equation}$$

Zatem ciąg chwil zmian obciążeń $\{ \tau , \quad n \ge 0 \}$  jest procesem Poissona o intensywności $\nu$.

Jeżeli w rozważanym modelu procesu obciążeń $\Lambda(t)$ przyjmiemy $\rho=0$, to otrzymamy często rozważany proces Poissona fal kwadratowych (Poisson Square Wave Process, przyjęty w pracy [57].

Asymptotyczna aproksymacja  niezawodności konstrukcji

Niezawodność konstrukcji ($\ref{9}$) jest prawdopodobieństwem tego, że w okresie eksploatacji konstrukcji $[0,T]$ , mnożnik obciążenia $\Lambda(t)$ zawsze będzie większy od 1, czyli

$$\begin{equation} p_R =1- Pr \{ max( \Lambda_1, \Lambda_2, \ldots, \Lambda_n ) <1 \} \label {24} \end{equation}$$

Jeśli T jest duże, rzędu okresu projektowego budowli  T= 50 lat (czyli tyle ile wynosi projektowy okres użytkowy zwykłych konstrukcji budowlanych), to można zastosować aproksymację asymptotyczne stosowane w teorii wartości ekstremalnych (p. dodatek Teoria losowych wartości ekstremalnych).

Jak pokazaliśmy – ciąg obciążeń $ \Lambda_1, \Lambda_2, \ldots $ jest stacjonarnym ciągiem Gausa  dla którego $E [ \Lambda_n ] = m $ ($\ref{15}$) , $ Var [ \Lambda_n ]=\sigma^2$ ($\ref{16}$) oraz  $ \rho(n)= \rho^n$  ($\ref{22}$).

Ponieważ

$$\begin{equation} \lim_{n \to \infty} = \rho(n) \cdot \ln {(n)} =0  \label {25} \end{equation}$$

to , korzystając ze znanego wyniku S.M. Bermana ( np. [58] -Theorem 3.81, [59] – Theorem 8.8 , mamy dla każdego $x$

$$\begin{equation} \lim_{n \to \infty} =  Pr \{ max ( \Lambda_1 , \Lambda_)2, \ldots, \Lambda_n) < \sigma \cdot b_n \cdot x + \sigma \cdot a_n  +m \} = \exp{(-e^{-x})}  \label {26} \end{equation}$$

gdzie

$$\begin{equation}  a_n = {1}{b_n} -\cdot {1}{6} b_n \cdot \left ( \ln { [ \ln{(n)}] } + \ln{(4\cdot \pi)} \right) \label {27} \end{equation}$$

$$\begin{equation}  b_n = [ 2 \cdot \ln{(n)} ]^{-1/2} , \quad n=1,2,\ldots \label {28} \end{equation}$$

W celu ustalenia  aproksymacji niezawodności ($\ref{24}$) dla dużych T, wprowadzamy najpierw odwzorowanie chwili obciążenia $\tau_n$ na numer ciągu $\nu(T)$ zalezny od przedziału czasu obciążenia:

$$\begin{equation} \nu(T) = inf \{n: \tau_n \} \label {29} \end{equation}$$

Ponieważ

$$\begin{equation} E[T_n ] =\cfrac{1}{\nu} < \infty \label {30} \end{equation}$$

to z prawa wielkich liczb wynika, że z prawdopodobieństwem 1

$$\begin{equation} \cfrac{\nu(T)}{T} \to \cfrac{1}{\nu} \text { gdy} T \to \infty \label {31} \end{equation}$$

Zatem maksimum $ M_T= \max _{0< t \le T} \Lambda(t)$  może być aproksymowane przez [56] :

$$\begin{equation} M_{\nu(T)} = \max { ( \Lambda_1, \Lambda_2, \ldots, \Lambda_{\nu(T)} ) } \label {32} \end{equation}$$

a to z kolei przez

$$\begin{equation} M_{ \left[ \frac{T}{\nu} \right]} = \max {(\Lambda_1, \Lambda_2, \ldots, \Lambda_{ \left[ \frac{T}{\nu} \right]} ) } \label {33} \end{equation}$$

gdzie symbol [ x ] oznacza cześć całkowitą liczby x (czyli jest funkcją entier ).

Z zależności ($\ref{26}$)otrzymujemy kolejno:

$$\begin{equation} \lim \limits _{T \to \infty}  Pr \{ M_{ \left[ \frac{T}{\nu} \right]} <\sigma \cdot b_ { \left[ \frac{T}{\nu} \right]} \cdot x  + \sigma \cdot a_{ \left[ \frac{T}{\nu} \right]}+m \} = exp \left (  -e^{-x}\right )  , \quad  – \infty < x < \infty \label{34} \end{equation}$$

$$\begin{equation} \lim \limits _{T \to \infty}  Pr \{ M_T <\sigma \cdot b_ { \left[ \frac{T}{\nu} \right]} \cdot x  + \sigma \cdot a_{ \left[ \frac{T}{\nu} \right]}+m \} = exp \left (  -e^{-x}\right )  , \quad  – \infty < x < \infty \label{35} \end{equation}$$

Dla dużego T otrzymaliśmy więc aproksymację

$$\begin{equation} Pr \{ M_T <\sigma \cdot b_ { \left[ \frac{T}{\nu} \right]} \cdot x  + \sigma \cdot a_{ \left[ \frac{T}{\nu} \right]}+m \} \approx  \exp {\left (-e^{-x} \right) } , \quad  – \infty < x < \infty \label{36} \end{equation}$$

a stąd otrzymujemy aproksymację prawdopodobieństwa nie przekroczenia  poziomu $u$ przez proces mnożnika obciążenia ( w skrócie obciążenia), czyli prawdopodobieństwo zniszczenia ($\ref{10}$) w dużym okresie $T$:

$$\begin{equation} p_f ( u,T) = Pr \{ M_T <u \}= \exp{ \left [-\exp{ \left (-\cfrac {u-\sigma \cdot a_{ \left[ \frac{T}{\nu} \right]}+m}{\sigma \cdot b_{ \left[ \frac{T}{\nu} \right]}}\right) } \right] } \label {37} \end{equation}$$

gdzie stałe $b_n>0$ i $ a_n$ dane są wzorami ($\ref{27}$), ($\ref{28}$)

Dla poziomu $u=1$ otrzymujemy zawodność w sytuacji przedstawionej na rys.2 i granicy bezpieczeństwa opisanej formułą ($\ref{6}$).  Dla innych ustalanych arbitralnie poziomów $u$  (np ($\ref{62}$) korzystamy z tych samych formuł. W ten sposób możemy przeliczyć poziom bezpieczeństwa $u$ na prawdopodobieństwo zniszczenia p_f i dalej na współczynnik Hasofera-Linda  $\beta_R$, stanowiący współczesną miarę niezawodności konstrukcji budowlanych  wg normy  [3].

Niezawodność systemu ($\ref{9}$) wynosi oczywiście $p_R=1- p_f$.

Mnożnik obciążenia – zmienną losową w rozkładzie Gumbela

Uzyskany wynik wskazuje, że zawodność systemu konstrukcyjnego opisuje dwuparametrowy rozkład maksimów Gumbela (rozkładu podwójnie wykładniczego), który jest zaliczony do uogólnionych rozkładów wartości maksymalnych GEV.  Estymację parametrów rozkładu można dokonać w sposób pokazany w dodatku Teoria losowych wartości ekstremalnych.  Występującą tam zmienną standaryzowaną $\xi$ oraz dwa parametry rozkładu parametr położenia $\alpha$ oraz parametr skali  $\beta$ w drodze porównania symboli zastosowanych w Dodatku oraz w formule ($\ref{37}$) można zapisać w postaci

$$\begin{equation} \xi=\cfrac{u- \alpha}{\beta} \\ \alpha= \sigma \cdot a_{ \left[ \frac{T}{\nu} \right]}- m ;\quad \\ \beta = \sigma \cdot b_{ \left[ \frac{T}{\nu} \right]} \label {38} \end{equation}$$

Sposób estymacji parametrów statystycznego rozkładu „obciążenia” w celu oszacowania niezawodności $p_R$ – pokazano w prostym przykładzie  Niezawodność sprężysto-plastyczna ramy portalowej.

Rozkład statystyczny obciążenia odniesienia $F_E$

Oddziaływania na konstrukcję przyjmuje się zgodnie regułą (3-1.1).
Ten format jest powszechnie uznawany ze względu na prostotę i został przyjęty przez wiele norm, w tym: normę europejską CEB (1976) [60], Comité Euro-International du Béton, Paris, France.)), ECS (1994) [61], amerykańskie ASCE (1986) [62] i ASCE (2000)  [63], kanadyjską NBCC (1995) [64],  autralijską SAA (1985) [65]  i inne.

Ten też format przyjmiemy do wyznaczania kon figuracji odniesienia $F_E$ mnożnika obciążeń $\Lambda$. Statystyczne parametry tych obciążeń składano z różniących się parametrów obciążeń stałych zmiennych użytkowych oraz klimatycznych : śniegiem i wiatrem. Te parametry przyjęto za pracą   Barlett i in (2003 [66]).

Rozkłady statystyczne obciążenia charakteryzowano dwoma  parametrami stosunkiem wartości średniej do nominalnej $Bias$ oraz współczynnikiem zmienności $CoV$ :

$$\begin{equation}  Bias =\cfrac{ \mu_X}{nom_X} \\ Cov= \cfrac{\sigma_X }{\mu_X}\label {39} \end{equation}$$

gdzie:
$X$ – typ obciążenia (G, Q, W,S) = (ciężar własny, obciążenie użytkowe, oddziaływanie wiatru, obciążenie śniegiem),
$ \mu_X$ – wartość oczekiwana (średnia) zmiennej X ,
$\cfrac{\sigma_X$ – odchylenie standardowe (średniokwadratowe )  zmiennej X,
$nom_X$ – wartość nominalna obciążenia – charakterystyczna wg normy dla okresu powrotu właściwego dla danego typu konstrukcji.

Rozkład statystyczny ciężaru własnego

W tab.1. zestawiono parametry: wartość średnią $\mu_G= Bias*(nom)$ oraz współczynnik zmienności $CoV_G$ ciężaru własnego G konstrukcji żelbetowych, metalowych i innych. Ciężar własny ma rozkład normalny $N(\mu_G, \sigma_G)$

Tab.1 Parametry statystyczne rozkładu ciężaru własnego $G_j$ [4] – Appendix B, C,D.

Rozkład statystyczny obciążeń użytkowych stropów

Parametry statystyczne obciążenia użytkowego stropów i innych powierzchni zależy od wielkości powierzchni na które są przyłożone. Na  rys.4 pokazano współczynnik zmienności obciążenia użytkowego stropu w budynku mieszkalnym lub użyteczności publicznej wg [66]).

Rys. 4  Obciążenia użytkowego stropów w okresie 15 lat : a) współczynnik Bias, b) współczynniki Cov[66])

Efekty obciążenia (w belkach, słupach i wg Allen (1975)  [67] nie znajdują zastosowania w naszych analizach, bowiem efekty (siły przekrojowe) będą wyznaczane w odrębnej procedurze).

Rozkład obciążenia użytkowego w długim czasie ma rozkład ekstremalny I typu (Gumbela). W określonej chwili (doraźnie) lub w okresie roku  przyjmujemy jako  rozkład normalny ze wskazanymi parametrami dla okresu 15 lat.

Rozkład statystyczny doraźnego obciążenia wiatrem oraz śniegiem

Rozkład statystyczny obciążenia wiatrem w czasie przyjmuje się najczęściej jako ekstremalny rozkład maksimów I rodzaju , czyli rozkład Gumbela  a snieg wg rozkładu Weibula maksiumów (p. przykład w dodatku B),

W tab. 2 podano wartości parametrów rozkładów obciązeń proponowane w pracy [4]

Tab.2 Parametry statystyczne rozkładu ciężaru własnego $G_j$ [4] – Tab 3.1.

Inne typy obciążeń (np. sejsmiczne, termiczne) pomija się.

Rozkład statystyczny  wartości własnej

Rozkład statystyczny  krytycznego mnożnika obciążenia $\Lambda_{cr}$ wyznaczymy za pracą Bijak, Chodor (1988) [68].

Równanie stateczności systemu zapiszemy w postaci

$$\begin{equation} \left( [K] – \Lambda_{cr} \cdot [K]^g \right) \cdot ||w||=0  \label {40} \end{equation}$$

gdzie:
$[K]$ i $[K]^g$ są losowymi macierzami sztywności , odpowiednio liniową i geometryczną,
||w|| – wektor własny, opisujący kształt konstrukcji po wyboczeniu

Przyjmijmy, że losowe własności systemu są zestawione w wektor losowy $||X|| =||X_1, X_2, \dots , X_m||$, gdzie $m$ – liczba zmiennych losowych charakteryzujących system. Później pokażemy, że możemy je zredukować do liczebności niezależnych jednostek losowych w systemie [M, K,S,C,]-[Metr, Kilogram, Sekunda, Celsjusz].

Po przemnożeniu obu stron ($\ref{40}$) przez wektor własny transponowany $||w||^T$, formalnym przeróżniczkowaniu po wektorze współrzędnej $X_i$ wektora [X] i uwzględnieniu zerowych wartości oczekiwanych, otrzymamy wyrażenie na wrażliwość (czułość) mnożnika krytycznego $\Lambda_{cr}$ na losowe zmiany współrzędnej wektora współrzędnej $X_i$

$$\begin{equation} \cfrac{\partial \Lambda_{cr}}{\partial X_i}= \cfrac{||w||^T \left [ \cfrac{\partial [K]}{\partial X_i} – \Lambda_{cr} \cfrac{d[K]^g}{d X_i}\right] ||w|| }{ ||w||^T [K]^g ||w||}  \label {41} \end{equation}$$

W przypadku zagadnienia dynamiki

$$\begin{equation} \left( [K] – \omega^2 \cdot [B] \right) \cdot ||w||=0  \label {42} \end{equation}$$

gdzie: $\omega$ – częstotliwość drgań własnych, a $[B[$ macierz bezwładności (mas)

analogicznie do  ($\ref{41}$) wrażliwość na zmiany parametru losowego przyjmie postać [69]

$$\begin{equation} \cfrac{ \partial \omega}{\partial X_i }= \cfrac{ ||w||^T  \left [ \cfrac{\partial [K]}{\partial X_i}  -\omega^2 \cfrac{\partial [B] }{\partial X_i}\right ] ||w|| }{2 \cdot \omega \cdot ||w||^T [B] ||w||} \label {43} \end{equation}$$

Macierze $[K]^g]$ oraz $[B]$ zależą  od sił węzłowych  $||P||_e$.

Smukłość i współczynnik amplifikacji

Tradycyjną analizą, stosowaną w projektowaniu konstrukcji wrażliwych na efekty niestateczności jest analiza wyboczeniowa. W podejściu inżynierskim jest ona realizowana z użyciem współczynników wyboczeniowych (najczęściej wyboczenia giętnego lub bocznego – zwichrzenia). Istotę współczynnika wyboczeniowego $\chi$ dobrze oddaje jego nazwa angielska reduction factor, czyli współczynnik redukcyjny, bo określa on redukcję (zmniejszenie) nośności elementu $F_{Rb}$  w stosunku do nośności przekroju  sprawczego tego elementu$F_R$.

$$\begin{equation}  \chi=\cfrac{F_{Rb}}{F_R} \label {44} \end{equation}$$

Współczynnik ($\ref{44}$) uwzględnia efekty niestateczności elementu (wyboczenie giętne lub skrętne lub giętno-skrętne, w tym zwichrzenie) i jest nieliniową funkcją smukłości elementu,. Przekrój sprawczy jest przekrojem elementu, który decyduje o jego nośności i jest nazywany również przekrojem wymiarującym lub krytycznym. Tego ostatniego określenia nie używamy, bo słowo „krytyczny” rezerwujemy dla zjawiska utraty stateczności, a ogólniej stabilności.

Smukłość elementu

W przepisach normowych Eurokod wprowadzono  definicję smukłości względnej pręta, jako pierwiastek ze stosunku nośności przekroju do nośności krytycznej elementu. Definicja ta w zapisie obejmującym kilka przypadków wyboczenia (*=_, ,LT, T, TF) i klas przekrojów (•= 1, 2, 3, 4) jest następująca:

$$\begin{equation}  \overline \lambda_* =\sqrt{\cfrac{F_{R•}}{F_{cr*}}} \label {45} \end{equation}$$

gdzie:
indeks przypadków wyboczenia:  _ (spacja) – wyboczenie giętne, LT- zwichrzenie (wyboczenie boczne), T- wyboczenie skrętne, TF – wyboczenie giętno-skrętne
indeks klasy przekroju: 1,2,3,4, które omówiono w artykule Klasy przekroju stalowego. Przekroje żelbetowe oraz zespolone (a także drewniane) rozpatruje się analogicznie jak przekroje stalowe klasy 3 (metodami teorii sprężystości), ale z uwzględnieniem nieliniowego zachowania betonu oraz wpływu czasu i pełzania na wytrzymałość drewna.
$F_{R•}$ – nośność sprężysta (po uplastycznieniu lub utracie wytrzymałości tylko jednego punktu przekroju) – mierzona siłą przekrojową F (siłą osiową N, lub momentem zginającym M, lub momentem skręcającym T, lub bimomentem Bω, itd.), odpowiednia dla klasy przekroju (•=1,2,3,4), na przykład: $N_{R,1,2,3} = A \cdot f_y$, $N_{R4}= A_{eff} \cdot  f_y$; $M_R= W_y \cdot f_y$ , itd.
$F_{cr*}$ – nośność krytyczna elementu przy niestateczności typu *.
Dla przypadku wyboczenia giętnego (*=_)  smukłość ($\ref{45}$) wyraża się formułą

$$\begin{equation}  \overline \lambda =\sqrt{\cfrac{N_{R}}{N_{cr}}} \label {46} \end{equation}$$

gdzie  nośność przekroju na ściskanie  $N_R=A \cdot f_y$ , ( A- pole przekroju, $f_y$ – wytrzymałość materiału – granica plastyczności dla stali), a $N_{cr}$ jest siłą krytyczną (Eulera), przy której element traci stateczność i wybacza się.
Dla przypadku  wyboczenia bocznego (zwichrzenia) (*=LT):

$$\begin{equation}  \overline \lambda_{LT} =\sqrt{\cfrac{M_{R}}{M_{cr}}} \label {47} \end{equation}$$

gdzie nośność przekroju na zginanie $M_{R}=W\cdot f_y$, ( W – wskaźnik wytrzymałości przekroju, f_y jak wyżej), a $M_{cr}$ jest zginającym momentem krytycznym (Własowa), przy której element traci stateczności przez utratę płaskiej postaci zginania (zwichrzenie).
Osiowa siła krytyczna $N_{cr}$ nazywana często siłą  Eulera $N_E$  jest obliczana ze wzoru:

$$\begin{equation}  N_{cr}= \cfrac{\pi^2 \cdot EI} {L^2_{cr}} \label {48} \end{equation}$$

Moment krytyczny $M_{cr}$ wyraża się bardziej złożonymi zależnościami i w praktyce wyznacza numerycznie, np. z zastosowaniem programu  LTBEAM [70] .

Siła krytyczna ($\ref{58}$) opisuje wyboczenie giętne idealnie prostego pręta o długości L i momencie bezwładności przekroju I, ściskanego czystą siłą osiową N. Pręt wykonany jest z materiału idealnie sprężystego o module Younga E. Wartość obciążenia osiowego pręta ($\ref{58}$) pierwiastkiem równania różniczkowego pręta zginanego i ściskanego, które uzyskał Euler już w XVIII w. i oznacza siłę, przy której następuje bifurkacja (rozdwojenie) stanu równowagi pręta, to znaczy punkt na ścieżce równowagi. w którym pręt może przeskoczyć ze stanu równowagi prostoliniowej do stanu równowagi krzywoliniowej. Takie zjawisko nazwano wyboczeniem.

Długość wyboczeniowa $L_{cr}$ jest nazywana długością Eulera $L_E$ i w praktyce wyznacza się ją z zależności:

$$\begin{equation}  L_{cr}= \mu \cdot L \label {49} \end{equation}$$

gdzie:
$\mu$ – współczynnik długości wyboczeniowej,
L- długość teoretyczna pręta.

Wprowadzenie wzoru Eulera ($\ref{58}$) do formuły ($\ref{46}$) umożliwia otrzymanie klasycznej, powszechnie stosowanej również dzisiaj, postaci wyrażenia na smukłość względną $ \overline \lambda$ pręta ściskanego o smukłości bezwzględnej  $\lambda$ ( [12]-(6.50):

$$\begin{equation}  \overline \lambda = \cfrac {\lambda} {\lambda_1}  \label {50} \end{equation}$$

gdzie:
bezwzględna smukłość pręta

$$\begin{equation}  \lambda = \cfrac{L_{cr}}{i} \cdot k_•  \label {51} \end{equation}$$

smukłość porównawcza (dla elementu stalowego)

$$\begin{equation}  \lambda_1=\pi \sqrt{\cfrac{E}{f_y}}=93,9\cdot \varepsilon \label {52} \end{equation}$$

gdzie współczynnik klasy przekroju  $k_•$ =1 dla przekroju klasy (•=1,2 i 3) oraz  $k_•=\sqrt{\cfrac {A_{eff}} {8}}$ dla przekroju klasy (• = 4) oraz współczynnik materiałowy

$$\begin{equation} \varepsilon= \sqrt{\cfrac{235}{f_y}} \label {53} \end{equation}$$

jest specyficzny dla konstrukcji stalowych.
Dla elementów żelbetowych, zespolonych i drewnianych wyrażenia ($\ref{52}$) i ($\ref{53}$) wymagają modyfikacji w sposób pokazany w dalszej części podręcznika.
Długość wyboczeniowa $L_{cr}$ wg ($\ref{59}$) jest nazywana często (np. w konstrukcjach żelbetowych) długością efektywną i oznaczana symbolem $l_0$.

W tym miejscu najczęściej prezentuje się kilka podstawowych schematów statycznych prętów i podaje dla nich współczynniki długości wyboczeniowej (rys.5). Nie powinniśmy tego robić, bo może to  wprowadzić wiele zamieszania, na przykład przez doprowadzenie do przekonania, że maksymalna wartość współczynnika μ wynosi 2 (jak dla wspornika). Jest to szkodliwa informacja, bowiem faktycznie współczynnik długości wyboczeniowej μ  pręta może być znacznie większy od 2 i przyjąć wartości z przedziału:

$$\begin{equation}  0,5 \le \mu \le \infty   \label {54} \end{equation}$$

gdzie:
$\mu=0,5$ odpowiada schematowi pręta obustronnie idealnie utwierdzonego (o nieskończonych sztywnościach podpór w tym zamocowania) (rys.5 d),
$\mu=1,0 $ opowiada prętowi podpartemu nieprzesuwnie i idealnie przegubowo na obu końcach (rys.5a),
$\mu=\infty$ dotyczy pręta obustronnie sprężyście podpartego w podporach o zerowych sztywnościach (czyli pręta swobodnie zawieszonego w przestrzeni) (rys.5g).

Rys.5 Bazowe postacie wyboczenia Bazowe postacie wyboczenia [24]– rys 5.7

Następnie należy stwierdzić, ze rzeczywiste pręty ściskane (słupy) nie są idealne:
1) oś pręta nie jest prosta ze względu na imperfekcje geometryczne osi pręta,
2) przekrój pręta i parametry materiałowe nie są stałe po długości, ze względu na niedoskonałości hutnicze, wpływające na charakterystyki przekroju,
3) siła ściskająca nie jest idealnie stała po długości pręta, ale co ważniejsze ze względu na wstępne mimośrody przyłożenia do głowicy słupa – pręt w zasadzie od początku pracy jest obciążony dodatkowymi momentami zginającymi.
W rzeczywistości nigdy nie będziemy mieli do czynienia z „czystym” ściskaniem, ale ze zginaniem ze ściskaniem, a do analizy takiego zagadnienia właściwe są metody co najmniej drugiego rzędu

Współczynnik amplifikacji

Wzór Eulera ($\ref{58}$) nie powinien być bezkrytycznie stosowany w odniesieniu do pręta rzeczywistego – jest bowiem słuszny wyłącznie dla innego jakościowo przypadku – dla ściskanego pręta idealnego. Wzór ten ma natomiast duże znaczenie poznawcze, w szczególności jako ważący przykład w teorii katastrof  [71] oraz w opisie zjawiska wyboczenia i utraty stateczności układów idealnych w naukach podstawowych: matematyce, fizyce i mechanice.

Rozważmy dowolną konstrukcję poddana dowolnemu (siły skupione, rozłożone, termiczne, wymuszenia geometryczne), zewnętrznemu obciążeniu w konfiguracji obliczeniowej $F_{Ed}$. Załóżmy, że podczas zwiększania wartości obciążenia proporcjonalnie do mnożnika $\Lambda$ – pod obciążeniem $F_{cr}=Λ_{cr} \cdot F_{Ed}$ nastąpi utrata stateczności konstrukcji.  Zgodnie z  klasyczną teoria Ayrton-Perry – przemieszczenia i siły przekrojowe  II rzędu można uzyskać poprzez przemnożenie wielkości I rzędu przez współczynnik amplifikacji (wzmocnienia)

$$\begin{equation}  a_\Lambda= \cfrac {44}{1-\cfrac{44}{\Lambda_{cr}}}  \label {55} \end{equation}$$

gdzie

$$\begin{equation}  \Lambda_{cr}= \cfrac {F_{cr}}{F_{Ed}} \label {56} \end{equation}$$

a obciążenie krytyczne  jest obciążeniem Eulera, równym dla prostego pręta sile Eulera $F_{cr}=N_{cr}$  ($\ref{58}$) obliczonej dla $L_{cr}=L$ .

 Przy zbliżaniu się do stanu krytycznego mamy;

$$\begin{equation}  \lim \limits _{F_{Ed}\to F_{cr}} \, a_\Lambda = \infty \label {57} \end{equation}$$

Przez analogię w innych stanach granicznych, będą definiowane odpowiednie mnożniki obciążenia, uznawane za nośność konstrukcji zgodnie z przyjętym kryterium stanu granicznego. Przykładowo w granicznym stanie plastycznym na skutek utworzenia wystarczającej liczby przegubów plastycznych uruchamia się mechanizm plastyczny pod obciążeniem z mnożnikiem

$$\begin{equation}  \Lambda_{pl}= \cfrac {F_{pl}}{F_{Ed}} \label {58} \end{equation}$$

Klasyfikacja teorii II rzędu

W podręczniku [72] przedstawiono klasyfikację metod drugiego rzędu na tle licznych przykładów obliczeń wykonanych programem S3D [73] , który wykorzystuje teorię dużych przemieszczeń i obrotów z uwzględnieniem przestrzennego zginania i skręcania. S3D jest oprogramowaniem badawczym na Uczelni i nie jest komercyjnie dostępny.
Autorzy pokazują, że nie ma jednej teorii II rzędu, a jej kategorie  należy ustalać wg kryterium  ujętych   efektów II rzędu i opisywanych  zjawisk. Proponują następujące kategorie teorii drugiego rzędu:

Kategorie teorii II rzędu

Kategorie 1 do 3  zdefiniowane w ramach klasycznej teorii  II rzędu  dla prętów krępych (niewrażliwych na skręcanie skrępowane):

• kategoria 1 : zagadnienie zginania jednoosiowego z siła normalną (wyboczenie giętne)
  Teoria zupełnie nieodpowiednia do praktycznych zadań inżynierskich, bowiem zwichrzenie jest obecne nie tylko w konstrukcjach metalowych, ale także żelbetowych i drewnianych,
• kategoria 2 :   zagadnienie zginania dwuosiowego z siła normalną (dwuosiowe wyboczenie giętne)
  Teoria nieodpowiednie do zagadnienia ściskania ze skręcaniem , w szczególności skrępowanym, czyli w istocie też wyłączona z praktycznych zastosowań inżynierskich,
• kategoria 3 : zagadnienie zginania dwuosiowego z siła normalną i skręcaniem (dwuosiowe wyboczenie giętne i skrętne )
  Teoria nieodpowiednia do zagadnienia  skręcania skrępowanego, czyli zwichrzenia i nie powinna być wyłączona z zastosowań inżynierskich

Kategorie  3P : kat 3 z Paczeniem ( w oryginale 3W : kat. 3 mit Wolbrakrafttorsion)  i 3PS: kat 3 ze Skręcaniem od Paczenia (w oryginale 3WS: kat 3. mit Sekundare Schubformungen)
Teorie są zdefiniowane w ramach teorii II rzędu dla prętów cienkościennych ( wrażliwych  na skręcanie skrępowane i paczenie przekroju) i mogą być stosowane do praktycznych inżynierskich zagadnień konstrukcji wrażliwych na utratę stateczności giętne, skretnej i giętno-skrętnej ( w tym zwichrzenia)

• kategoria  3P : zagadnienie skręcania prętów z przekrojem bez oporu skręcania:
  $k=\cfrac {G\cdot I_T} {E \cdot I_{ \omega} } = 0 $
  $ \to \kappa = \cfrac {44}{1+k} =1$, gdzie
  $ I_T$ – moment bezwładności czystego skręcania (Saint Venanta), G – moduł Kirchoffa,
  $I_{\omega}$ – wycinkowy moment bezwładności, E – moduł Younga,
• kategoria 3PS :  zagadnienie wyboczenia skrętnego prętów  o przekroju z charakterystyką $\kappa < 1$.
  W ramach tej teorii można analizować zjawisko wyboczenia giętno skrętnego (w tym zwichrzenia) zgodnie z teorią Własowa.

Teorie wyższych rzędów (III rząd i wyżej) powinny być stosowane dla konstrukcji cięgnowych i membranowych, co zapewniają specjalizowane programy, np. Abaqus [74] lub Sofistik [75] i in.

Dodatkowo w pracy [72] zamieszczono wyniki testów innego programu badawczego. Natomiast w opracowaniu [76]   przeprowadzono testy dla programu komercyjnego Consteel.  Z testów wynika, że jeśli program KSTAB zalicza się do dokładnych, to program Consteel należy zaliczyć do kategorii wyższej o rząd.

Zadania do testowania oprogramowania inżynierskiego

Przedstawiony w Tab.1 zestaw testów z  pracy [72] jest obecnie  uznany za zadania wzorcowe (ang. benchmark) do testowania oprogramowania stosowanego do analizy konstrukcji wg teorii drugiego rzędu, która jest nieodłączną częścią metod imperfekcyjnych.

Tab. 1. Zadania Benchmark do testowania oprogramowania drugiego rzędu [72]
(opracowano na podstawie  [76] )

Z dotychczas wykonanych  testów  wynika, że większość zadań inżynierskich można wiarygodnie analizować w ramach teorii II rzędu kategorii 3PS, ale zadania typu 2 (niesymetryczna kratownica Misesa na podporach sprężystych) oraz typu 5 (układ tensegrity) i typu 7 (zwichrzenie z siła normalną – cięgnami zamocowanymi w osi belki) a także typu 10 ( niestateczność przy bardzo dużych ugięciach) – wiarygodna jest wyłącznie teoria dużych przemieszczeń i obrotów.  W tym przypadku należy stosować programy naukowe, np. ABAQUS [74] .

We współczesnej praktyce projektowej, szczególnie konstrukcji metalowych stosuje się powszechnie pręty cienkościenne, których teoria sformułowana przez Własowa [9] jest uogólnieniem teorii prętów o przekroju krępym, a na jej gruncie można wyjaśnić i opisać zjawisko zwichrzenia i wyboczenia giętno-skrętnego.  Pręty cienkościenne nazywane uogólnionymi są podatne na paczenie  i występują w nich  dodatkowe siły przekrojowe: bimoment $B_{\omega}$ oraz  moment giętno-skrętny $T_{ \omega }$.

Dla praktyki inżynierskiej interesująca jest teoria dopiero kategorii 3PS, która jest już implementowana do współczesnych programów MES, w tym w stosowanym w niniejszym podręczniku programie [8].

Wrażliwość konstrukcji na nieliniowości, rząd teorii i imperfekcje

Wrażliwość konstrukcji na nieliniowości geometryczne objawia się tym, że rezultaty uzyskane według teorii liniowej są obarczone zbyt dużymi błędami. Dla konstrukcji wrażliwych na nieliniowości należy stosować teorię nieliniową. Poniżej pokażemy, że można wskazać proste, kryterium wrażliwości na nieliniowości, dotyczące każdej konstrukcji- nawet pręta rozciąganego. Rząd teorii nieliniowej oznacza stopień aproksymacji odkształceń (lub przemieszczeń) nieliniowych poprzez ich rozwinięcie w potęgowy szereg Taylora podług potęg tych odkształceń.

Imperfekcje są pojęciem niezależnym od wrażliwości konstrukcji na nieliniowości i rząd teorii. Ponieważ jednak analiza imperfekcyjna jest nieodłącznie związana z teorią przynajmniej drugiego rzędu, więc można przyjąć, że konstrukcje wrażliwe na efekty drugiego rzędu są wrażliwe na imperfekcje i odwrotnie.

Teoria I rzędu i wyższych. Kryterium wrażliwości „5% odkształceń”

Teoria I rzędu jest przybliżeniem zagadnienia brzegowego mechaniki konstrukcji dla małych odkształceń i przemieszczeń.

Uniwersalnym kryterium wrażliwości konstrukcji na nieliniowości jest kryterium 5% odkształceń, które można sformułować następująco:

Jeśli w dowolnym miejscu konstrukcji odkształcenia liniowe I rzędu $\varepsilon$ przekraczają 5% , to konstrukcja jest wrażliwa na nieliniowości geometryczne – powinna być analizowana teorią co najmniej II rzędu. 

Kryterium dotyczy w istocie odkształceń plastycznych i zostało oryginalnie sformułowane w obszarze technologii obróbki metali, np. [77]. ale też było wielokrotnie potwierdzane  dla różnych konstrukcji budowlanych (np. [78] i in. W niniejszym podręczniku kryterium 5% pokazano na przykładach pręta rozciąganego i pręta ściskanego z imperfekcjami.

Warto zwrócić uwagę, że kryterium 5% dotyczy odkształceń, a nie przemieszczeń, a także to, że może obowiązywać również konstrukcji żelbetowych , mimo, że odkształcenie w betonie jest ograniczane do 3,5%. Dzieje się tak , że zgodnie z normą [24]– tab. C.1 dopuszcza się odkształcenie charakterystyczne stali klasy B $\varepsilon_{uk}>5$%, a klasy C powyżej $\varepsilon_{uk}>57,5 $% ,  a graniczne odkształcenie obliczeniowe  stali zbrojeniowej wynoszą $\varepsilon_{ud}=0,9 \cdot  \varepsilon_{uk}$.

Z przykładu pręta ściskanego z imperfekcjami. wynika również, że odkształcenia preta z imperfekcjami przekraczają umowną granicę spręzystości (plastycznoąci) już dla obciążenia  $F=50$% $F_{cr}$, to znaczy klasyczna teoria wyboczeniowa [52]  nie jest właściwa, co potwierdza tezę podręcznika, że metody wyboczeniowe można uznać tylko za historyczne.

Stabilność konstrukcji

Warunek stabilności konstrukcji jest prosty

$$ \begin{equation} \Lambda_{cr} >1  \label {59} \end{equation}$$

i dotyczy globalnego mnożnika obciążeń, to znaczy uzyskanego dla całego systemu konstrukcyjnego, a nie wydzielonego pręta. Oczywiście z  globalnego warunku ($\ref{59}$) wynika, że stabilność będzie zachowana dla każdego fragmentu konstrukcji w tym dla każdego wydzielonego pręta.

Warunek ($\ref{59}$) obejmuje tylko te formy niestateczności, które są uwzględnione w analizowanym modelu matematycznym. Na przykład w klasycznym modelu, złożonym z prętów o sześciu stopniach swobody – nie będzie uwzględnione zwichrzenie prętów. W celu uwzględnienia tej formy niestateczności należy analizować pręty Własowa. Niestateczność lokalna płyt będzie uwzględniona dopiero po zamianie ścianek prętów na panele płytowe.

Kryterium „10x globalna nośność krytyczna”

Wrażliwość na efekty drugiego rzędu, jest stopniem przyrostu odpowiednich sił wewnętrznych lub momentów, lub jakąkolwiek innej zmiany zachowania się konstrukcji w wyniku deformacji. Wrażliwość ta może być oceniona poprzez zbadanie mnożnika obciążenia krytycznego ($\ref{57}$). W normie do projektowania konstrukcji stalowych [12], kl. 5.2.1(3), wzór (5.1) kryterium  wrażliwości konstrukcji na efekty drugiego rzędu zdefiniowano poprzez graniczny mnożnik krytyczny (nośność krytyczną)  $\Lambda_{cre, lim}$, w taki sposób, że  jeśli dla analizowanej konstrukcji globalnie zachodzi:

$$ \begin{equation} \Lambda_{cr} < \Lambda_{cr,lim} \label {60} \end{equation}$$

to należy stosować analizę drugiego rzędu.

Krytyczny mnożnik $ (\ref{59} $)  odniesiono do obciążeń obliczeniowych $\Lambda_{cr} = \cfrac{F_{cr}}{F_{Ed}}$,, więc mówi on o tym ile razy konfiguracja obciążenia $F$ może przekroczyć obciążenia obliczeniowe $F_{Ed}$, by nie nastąpiła jeszcze utrata sprężystej stateczności całej konstrukcji, jej fragmentu lub dowolnego elementu (np panelu płytowego lub pręta).

Wartość graniczna nośności krytycznej) $ \Lambda_{cr,lim}$ wynosi:

$$ \begin{equation} \Lambda_{cr,lim} = \begin {cases}
10, \quad \text{w przypadku analizy sprężystej} \\
15 \quad  \text { w przypadku analizy plastycznej}
\end {cases}
\label {61} \end{equation} $$

Wyższa wartość $\Lambda_{cr,lim}$ ($\ref{61}$) w przypadku analizy plastycznej jest uzasadniona tym, że zachowanie się konstrukcji oraz jej stan graniczny mogą być silnie uwarunkowane nieliniowymi właściwościami materiału (np. gdy w ramie tworzą się przeguby plastyczne i dochodzi do redystrybucji momentów, lub gdy w ramie występują węzły podatne powodujące znaczący nieliniowy wzrost odkształceń).

Z praktyki projektowej wynika, że konstrukcje stalowe o nośności krytycznej większej od  ($\ref{61}$) są wyjątkowe i wówczas najczęściej mamy do czynienia z nieoptymalnym ich zaprojektowaniem.

Dla stwierdzenia poprawnego zaprojektowania konstrukcji analizowanego modelu wystarczy spełnienie kryterium stabilności ($\ref{59} $), Jeśli model konstrukcji nie jest obarczony imperfekcjami , to stwierdzenie stabilności dotyczy konstrukcji idealnej. W tym przypadku

Kryterium ($\ref{59} $) można stosować dla innych niż stalowe konstrukcji (żelbetowe, zespolone, drewniane, murowe). W szczególności dla konstrukcji żelbetowych kryterium to powinno być stosowane równoważnie do „kryterium „10%”. Należy zwrócić uwagę, że analiza LBA wykorzystuje inny algorytm numeryczny od analizy II rzędu ( rozwiązanie problemu własnego i odwracanie macierzy sztywności układu konstrukcyjnego),ale programy w których zaimplementowano analizę LBA wyposażono również w algorytmy II rzędu.

Z praktyki projektowej wynika że:
1) większość konstrukcji inżynierskich (stalowe, zespolone) i dużą część konstrukcji żelbetowych należy analizować metodami drugiego rzędu,
2) w przypadku ograniczenia się do analiz pierwszego rzędu, należy uzasadnić, że spełniony jest warunek $\Lambda_{cr} \ge \Lambda_{cr,lim}$. Warunku tego nie trzeba sprawdzać, jeśli analiza jest „od razu” II rzędu. W przypadku niestabilności konstrukcji należy jednak przeprowadzić analizę LBA, w celu oceny problemu i zidentyfikowania tych miejsc konstrukcji, które są krytyczne dla stabilności.
3) kryterium wrażliwości na efekty drugiego rzędu nie należy traktować jako nakazu projektowania tak stabilnych konstrukcji, bo wystarczy  spełnienie warunku  stabilności ($\ref{62}$).

4) analizę LBA zaleca się przeprowadzić dla każdej konstrukcji z przewodnim celem innym od wyrażonego kryterium ($\ref{59}$), a mianowicie  jako element  optymalizacji konstrukcji , polegającej na zidentyfikowania krytycznych, lokalnych miejsc konstrukcji, których usztywnienie niewielkim kosztem może doprowadzić do wielokrotnego zwiększenia wskaźnika stabilności $\Lambda_{cr}. Jest to podstawowy sposób optymalizacji konstrukcji obok sposobu polegającego na tym, że w konstrukcjach statycznie niewyznaczalnych istotne zmniejszenie ciężaru całej konstrukcji można uzyskać poprzez zwiększenie sztywności kliku dominujących elementów i w ten sposób odciążenie (i zmniejszenie ciężaru)  innych słabszych elementów , ale występujących w większej liczbie. W większości współczesnych konstrukcji stosowanie strategii wymiarowania wyodrębnionych elementów jest zawodne z punktu widzenia uzyskania optymalnej konstrukcji

Kryterium ($\ref {61}$) pozwala zakwalifikować konstrukcje do wrażliwych jeszcze przed wykonaniem obliczeń drugiego rzędu na podstawie pomocniczej, quasiliniowej analizy LBA .
Zwracamy uwagę, że czysta analiza wyboczeniowa LBA polega na wyznaczeniu mnożnika krytycznego konfiguracji obciążeń idealnego systemu konstrukcyjnego i może być  traktowana jedynie jako pomocnicza analiza, służąca do rozpoznania wrażliwości konstrukcji i jej niestatecznych miejsc , ale nie może zastąpić metod imperfekcyjnych stosowanych do sprawdzenia stateczności i wytrzymałości poszczególnych przekrojów konstrukcji.

Wrażliwość konstrukcji na imperfekcje

Każda konstrukcja, która zgodnie z kryterium ($\ref{59} $), jest niewrażliwa na efekty drugiego rzędu jest również niewrażliwa na imperfekcje. Z praktyki projektowej wynika, że bardzo stabilne są już konstrukcje dla których 

$$ \begin{equation} \Lambda_{cr} > 3  \label {62} \end{equation}$$

Wymóg przeprowadzenia analizy II rzędu w celu uwzględnienia imperfekcji konstrukcji pociąga za sobą, wniosek, że w konstrukcji  niewrażliwej na efekty drugiego rzędu można pominąć imperfekcje. Kryterium wrażliwości ($\ref{59}$) jest warunkowane statecznością najsłabszego ogniwa zawartego w konstrukcji i wszystkich tych form niestateczności, które są uwzględniane w modelu. Dotyczy więc zarówno imperfekcji globalnych (przechyłowych) jak i lokalnych (łukowych) w konstrukcjach prętowych, a stąd wynika, że w klasycznej metodzie wyboczeniowej dla konstrukcji niewrażliwych na imperefekcje można by nie stosować współczynników wyboczeniowych ( w tym zwichrzenia , jeśli w modelu zastosowano elementy Własowa).

Podatność konstrukcji na nieliniowe efekty geometryczne oraz na imperfekcje może być kontrolowana przez projektanta w drodze doboru rodzaju systemu, prawidłowego układu elementów i poprzez dobór sztywności poszczególnych elementów. Najważniejszy przy tym jest system powiązań elementów między sobą oraz wyposażenie układu we właściwie ulokowane elementy usztywniające (stężenia, żebra, rdzenie itd).

Kryterium „10% poprawności konstrukcji”

Sformułowanie kryterium 10%

Na podstawie analizy wielu projektów (ostatni rozdział podręcznika sformułujemy kryterium 10%  jako kryterium poprawności projektu konstrukcji

Poprawność projektu konstrukcji ocenia się według kryterium 10%, zgodnie, z którym projekt jest uznany za wykonany prawidłowo, jeśli sprawcze efekty (przemieszczenia lub naprężenia, które decydują o niezawodności obiektu) ocenione wg teorii geometrycznie nieliniowej są większe, co najwyżej o 10% od efektów tej samej konstrukcji, wyznaczonych wg teorii 1. rzędu. Jeśli wpływ efektów nieliniowych jest większy, to prawdopodobnie projekt zawiera wady, najczęściej wskutek niewystarczającego stężenia układami usztywniającymi. W takim przypadku proste zwiększanie przekrojów i elementów krytycznych nie daje zadowalających rezultatów, a prowadzi do nieuzasadnionego zwiększenia zużycia materiału na konstrukcję.

Sformułowane wyżej kryterium 10%  łączy się pośrednio z warunkiem, dotyczącym dopuszczalności stosowania analizy I rzędu w projektowaniu konstrukcji żelbetowych

.Nazwa kryterium „10%” wywodzi się z wymogu dla analizy sprężystej, a podczas prowadzenia  analizie plastycznej można poprzestać man obliczeniach pierwszego rzędu wówczas, gdy mnożnik obciążenia krytycznego  nie przekracza $100/15=6,7$%

Procedura sprawdzania kryterium 10%

W celu weryfikacji poprawności projektu z kryterium 10% wrażliwości konstrukcji należy przeprowadzić testowe obliczenia nieliniowe wstępnego modelu całej konstrukcji i obserwować zbieżność procesu iteracji do rozwiązania stabilnego. Brak zbieżności lub wolna zbieżność oznacza wady projektu, najczęściej braki w układach stężeń lub innych usztywniających, albo nieprawidłowe stosunki sztywności elementów – w systemie elementów, występują elementy zbyt sztywne, np. zbyt krótkie, lub za wiotkie. Po takim sygnale inżynier lokalizuje problem, a w tym celu bada pole odkształceń konstrukcji w stanie liniowym lub w stanie krytycznym (wg teorii LBA – liniowej analizy wyboczeniowej.  poprawić go i przystąpić do kolejnego testu nieliniowego.

Dopiero po uzyskaniu modelu konstrukcji poprawnego z punktu widzenia wrażliwości na efekty nieliniowe, można przystąpić do wymiarowania poszczególnych elementów, w tym do doboru zbrojenia betonu.

Należy podkreślić, że kryterium „10%” nie jest bezwzględnie obowiązujące, bo może doprowadzić do zablokowania stosowania innowacyjnych rozwiązań konstrukcyjnych. W przypadku wdrażania takich konstrukcji należy przeprowadzić  bardziej wnikliwą analizę najczęściej wspomaganą badaniami eksperymentalnymi.

Przykłady

Kryterium 5% odkształceń dla pręta rozciąganego]

Rozpatrzmy odkształcenia skończone pręta rozciąganego lub krępego pręta ściskanego (bez wyboczenia). Przykładem takich prętów są pręty zbrojeniowe w konstrukcjach żelbetowych.

Dane:

długość początkowa pręta  $L_0$
długość końcowa (po rozciągnięciu $L_1$
siła rozciągająca (ściskająca $F$

Odkształcenie (względne skrócenie) pręta można zapisać w postaci

$$\begin{equation}  \varepsilon= \cfrac{\Delta L}{L_0} = \cfrac{L_1-L_0}{L_0} \to \cfrac{L_1}{L_0} = \varepsilon+1 \label {63} \end{equation}$$

Rzeczywiste odkształcenia $e$ są skończone i zgodnie z definicją wynoszą:

$$\begin{equation}  e= \int \limits_{L_0}^L \cfrac{dL}{L} = \ln{\cfrac{L_1}{L_0}}= \ln{( \varepsilon+1)} \label {64} \end{equation}$$

Ścisłe wyrażenie na odkształcenie można rozłożyć w szereg  MacLaurina względem $\varepsilon$:

$$\begin{equation}  e \approx \varepsilon – \cfrac{\varepsilon^2}{45}+ \cfrac{\varepsilon^3}{46} – \cfrac{\varepsilon^4}{57} +(\ldots) \label {65} \end{equation}$$

Obcięcie szeregu dla członów przy danej potędze $\varepsilon$ daje rząd teorii.

W  Tab.2 zestawiono porównanie wartości odkształceń skończonych ($\ref{64}$) (kol. 1) z klasycznymi odkształceniami ($\ref{63}$) dla  wartości odkształceń uzyskanych według teorii I rzędu od 1 do 10%. W kolumnie (2) podano błąd oszacowania. Dopuszczalną granicę błędu 2,5% przekroczono dla $\varepsilon=5%$.  Oszacowania II rzędu są już akceptowalne.

Tab. 2 Dokładność aproksymacji skończonych  odkształceń logarytmicznych

Kryterium 5% odkształceń dla pręta ściskanego z imperfekcją

Dane:
długość pręta $L$
imperfekcja łukowa $e_0$, ($n_L=L/e_0$
siła ściskająca pręt $F$

Siła ściskająca  pręt wstępnie wygięty zwiększa przemieszczenia poziomego belki  w sposób pokazany na rys.6

Rys. 6 Przemieszczenie poziome Δ(dx) przekroju belki wywołane jej ugięciem w(x)

Ugięcie odcinka dx belki-słupa powoduje przemieszczenie punktów końcowych do położenia dx’, a odkształcenie skrócenia od ugięcia pręta wynosi

$$\begin{equation} \varepsilon (x) =\cfrac{\Delta(dx)}{dx} =\cfrac{dx-dx’ }{dx} =\cfrac{ dx- \sqrt{(dx)^2-(\frac {d} {dx} dx)^2}}{dx} = 1-\sqrt{1-(w’)^2} \label {66} \end{equation}$$

Załóżmy, że wygięcie wstępne pręta (imperfekcja łukowa ) ma kształt

$$ \begin{equation} w_0(x)=e_0 \sin{\pi x/L} \label {67}\end{equation}$$

Na skutek ściskania siłą $F$  pręt zostanie dogięty do stanu

$$ \begin{equation} w(x)= a_\Lambda \cdot w_0(x) \label {68}\end{equation}$$

gdzie współczynnik amplifikacji $(\ref{55}$) jest stałą zadania.

Po podstawieniu  funkcji ugięcia ($\ref{68}$) do wyrażenie na odkształcenie $\varepsilon (x)$ i przecałkowaniu po długości pręta, otrzymujemy odkształcenie skrócenia pręta ściskanego z imperfekcją łukową ($\ref{69}$).:

$$ \begin{equation} \varepsilon= \cfrac{\Delta L}{L} = \int \limits_0^L 1- \sqrt{1- C _\Lambda  \cos^2{( \pi  x/L) }} = 1- \cfrac{E (C_\Lambda) }{\pi}   \label {69}\end{equation}$$

gdzie:
E() – całka eliptyczna pierwszego rodzaju. Całka eliptyczna jest i łatwa do wyznaczenia w programach inżynierskich – np w programie Mathematica E()=EllipticE().

Rozwiązanie jest  dopuszczalne dla

$C_\Lambda= \left( \cfrac{ \pi \cdot a_\Lambda} {n_L} \right ) ^2 < 1 $,  to znaczy dla $a_\Lambda < n_L/ \pi$, gdzie  $n_L=L/e_0 $ , czyli $\Lambda_{cr} > \cfrac{44}{1-1/(n_l/ \pi)}$

Dla zalecanych imperfekcji $n_L>150$,  mamy  $\Lambda_{cr} > 1,02$, to znaczy rozwiązanie jest dopuszczalne  w każdej konstrukcji spotykanej w praktyce.

Po rozwinięciu wyrażenia ($\ref{69}$) w szereg MacLaurina podług wytężenia pręta mierzonego zmienną $C_\Lambda$ , mamy:

$$ \begin{equation} \varepsilon \approx \cfrac{C_\Lambda}{57}+\cfrac{3 \cdot C_\Lambda ^2}{69} +\cfrac{5 \cdot C_\Lambda ^3}{256}+\cfrac{175 \cdot C_\Lambda ^4}{16384} \label {70}\end{equation}$$

W tab.Tab.3 porównano aproksymacje odkształcenia w pręcie ściskanym z imperfekcją łukową. Aproksymacja wg teorii I rzędu jest słaba dla obciążenia pręta bliskiego stanowi granicznemu ($F> 0,96 F_{cr}$). i wówczas odkształcenie skrócenia pręta  przekracza 5%.  Aproksymacja II rzędu daje zadawalające wyniki i nie byłyby już potrzebne aproksymacje wyższych rzędów. Tabelę sporządzono dla imperfekcji $n_L=200$.  Można pokazać, że dla mniejszych wartości $n_L$ granica istotnej nieliniowości przesunie się w kierunku mniejszych obciążeń.

Tab. 3 Dokładność aproksymacji odkształceń pręta ściskanego z imperfekcjami

Niezawodność sprężysto-plastyczna ramy portalowej

Przykład w edycji

Oszacować nośność i niezawodność  ramy portalowej pokazanej na rys. 7 .

Rys.7. Rama portalowa do przykładu

Rama jest zaprojektowana na okres $T= 50 lat$

Imperfekcje geometryczne przechyłowe i łukowe ramy przyjąć zgodnie z normą do -projektowania konstrukcji stalowych [12].

Niezawodność sprężysta ramy portalowej

Niezawodność sprężysta konstrukcji jest niezawodnością z warunku  nie przekroczenia mnożnika $\Lambda_{cr}$

Mnożnik  $\Lambda_{cr}$ wyznaczono programem Consteel dla schematu pokazanego na rys. 8.   Z analizy LBA otrzymano

$\Lambda_{cr}= 5,62$.

Rys. 8 Widok ramy z prohramu Consteel

Niezawodność plastyczna ramy portalowej (ze względu na ($\Lambda_{pl}$)

Niezawodność spręzżysta ramy portlowej, czyli ze względu utratę stateczności sprężystej – ze względu na $\Lambda_{cr}$

Niezawodność sprężysto plastyczna (alternatywa niezawodności sprężystej oraz plastycznej)

⊗ ⇒ [ Krótki przegląd metod wyboczeniowych i imperfekcyjnych ]

Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2017-2020), Imperfekcyjna metoda  projektowania konstrukcji, Encyklopedia  πWiki, Wydawnictwo Chodor-Projekt, [ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]

Historia edycji:
Wersja 1.0 (2019-04-07) – pierwsza wersja artykułu
Wersja 2.0 (2019-05-26) – podzielono na artykuły internetowe i zaopatrzono w połączenia odnośnikami
Wersja 2.1 (2019-06-22) – dodano rozdział dotyczące kryteriów stabilności oraz wrażliwości na efekty II rzędu i imperfekcje
Wersja 3.0 (2020-12-07) – dodano rozdział dotycząc imperfekcji krytycznych oraz rozdział „Stochastyczny model mnożnika obciążenia”

 Literatura

1. Der Kiuereghian A., (1978), Second-moment combination of stochastic loads, Journal of the Structural Divison, Vol 104, No ST 10, pp.1551-1567
2. Grigoriu M., Turkstra C., (1`978), Structural safety indices  for repeated loads, Journal of the Engineering Mechanics Divison, Vol 104, No EM 4, pp. 829-844
3. PN-EN 1990:2004/NA:2010, Podstawy projektowania konstrukcji
4. Ellingwood, B.R., Galambos, T.V., MacGregor, J.G., Cornell, C.A., (1980), Development of a probability based load criterion for American National Standard A58. NBS Special Publication 577, National Bureau of Standards, U.S. Department of Commerce, Washington, D.C.
5. Bartlett F.M., Hong H.P., Zhou W., (2003), Load factor calibration for the proposed 2005 Edition of the National Building Code of Canada:Statistics of loads and load effects, Can. J. Civ. Eng. 30: 429–439 (2003
6. Bjorhovde R., (1972), Deterministic and probabilistic approaches to the strength of steel columns, Ph.D. dissertation, Fritz Laboratory Reports. Paper 1933 [ http://preserve.lehigh.edu/engr-civil-environmental-fritz-lab-reports/1933 ]
7. Chodor L., Kłosowska J., (2014), Dobór elementów struktury konstrukcyjnej z warunku ustalonej niezawodności, mierzonej wskaźnikiem niezawodności β. Przykład liczbowy dla ramy statycznie niewyznaczalnej, ArchsWiki [ https://chodor-projekt.net/wp-content/uploads/2017/04/Dob%C3%B3r-element%C3%B3w-struktury-konstrukcyjnej-z-warunku-ustalonej-niezawodno%C5%9Bci-rama-portalowa.pdf]
8. Consteel Software, (2020), ConSteel Manual, [ https://consteelsoftware.com/downloads/]
9. Vlasov, V. Z. (1959). Tonkostiennyje uprugije stierzni | Thin-Walled Elastic Beams. PWF-ML | Israel Program for Scientific Translations
10. Chladny E. (1974), Vzper pruzne podopretych tlacenych prutov (Buckling of elastically supported compressed members). Habilitation thesis
11. Chladny E., Stujberova M. (2013). Frames with unique global and local imperfection in the shape of the elastic buckling mode.Part 1. Stahlbau, 82(8), p. 609–617
12. PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
13. PN-EN 1993-1-6:2010, Eurokod 3: Projektowanie konstrukcji stalowych, Część 1-6: Wytrzymałość i stateczność konstrukcji powłokowych
14. PN-EN 1993-1-7 + AC+Ap1:2007, Eurokod 3: Projektowanie konstrukcji stalowych , Część 1-7: Konstrukcje płytowe
15. PN-EN 1993-1-5:2008, Eurokod 3: Projektowanie konstrukcji stalowych. Część 1-5: Blachownice
16. Kim S. E., Lee D. H. (2002). Second-order distributed plasticity analysis of space steel frames. Journal of Engineering Mechanics, 24, p. 735–744
17. Rossow E. C., Barley G. B., Lee, S. L. (1967). Eccentrically Loaded Steel Columns with Initial Curvature, Journal of Structural Division, ASCE, 93(ST2), p. 339–358
18. Piechnik S. (2007), Mechanika techniczna ciała stałego. Wydawnictwo Politechniki Krakowskiej
19. Dlubal Software, (2019), RFEM, RSTAB Oprogramowanie do analizy statyczno-wytrzymałościowej (Version 8-18-01) [Computer software], [https://www.dlubal.com/pl ]
20. Computer and Structures Inc. (2019). SAP2000. Structural Software for Analysis and Design (Version 21),. [ https://www.csiamerica.com/products/sap2000 ]
21. SCIA, A Nemetschek Company, (2018), Structural An alysis and Design with SCIA Enginee (Version 18). [ https://www.scia.net/en ]
22. Sofistik, (2018). Sofistik. Imperfection Concept. Sofistik Tutorials 2018, Tutorials for Stel Design. Imperfection Concept, [ /www.sofistik.de/documentation/2018/en/tutorials/steel-design/imperfection/imperfection.html ]
23. PN-EN 1994-1-1+Ap1+AC:2008, Eurokod 4, Projektowanie zespolonych konstrukcji stalowo-betonowych, Część 1-1: Reguły ogólne i reguły dla budynków
24. PN-EN 1992-1-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
25. PN-EN 1999-1-1:2010, Eurokod 9: Projektowanie konstrukcji aluminiowych, Część 1-1: Reguły ogólne
26. PN-EN 1993-2:2010, Projektowanie konstrukcji stalowych, Część 2: Mosty stalowe
27. PN-EN 1995-1-1+A2+NA+07E :2010, Eurokod 5: Projektowanie konstrukcji drewnianych, Część 1-1: Postanowienia ogólne – Reguły ogólne i reguły dotyczące budynków
28. PN-EN 1996-1-1+A1+Ap1,2:2013, Eurokod 6: Projektowanie konstrukcji murowych , Część 1-1: Reguły ogólne dla zbrojonych i niezbrojonych konstrukcji murowych
29. Chladny E. (1958), Nosnosť tlačených pásov otvorených mostov (Buckling resistance of compressed chords of open truss bridges), PhD thesis
30. Brendel, B., and Ramm, E. (1980). „Linear and nonlinear stability analysis of cylindrical shells, Comp. Struct., 12(4), 549-558
31. Ayrton W. E., Perry J. (1886), On Struts. The Engineer, p. 464–513
32. Elishakoff, I. (1988). „Stochastic simulation of an initial imperfection data bank for isotropic shells with general imperfections.” Buckling of structures, Studies in applied mechanics, Elishakoff I. et al., eds., 19, Elsevier, Amsterdam, the Netherlands, 195-209
33. Lindberg, H. E. (1988), Random imperfections for dynamic pulse buckling, J. Engrg. Mech., ASCE, 114(7) 1144-1165
34. Kirkpatrick, S. W., and Holmes, B. S. (1989). „Effect of initial imperfections on dynamic buckling of shells.” J. Engrg. Mech., ASCE, 115(5), 1075-1093
35. Ikeda K., Murota, K. (1990), Critical initial imperfection of structures,  Int. J. Solids Struct., 26(8), 865-886
36. Ikeda K., Murota K., Computation of Critical initial imperfection of truss structures, J. Engn. Mech, Vol 116 (10),pp. 2101- 2117
37. Ikeda K, Murota K., (1991) Random initial imperfections of structures, Int. J. Solids Structures, Vol.  28, (8), pp. 1021-1099
38. Ohsaki, Critical Minor Imperfection corresponding to stable bifurcation
39. Shamass R (2020) Plastic Buckling Paradox: An UpdatedReview, Computational Methods in Structural Engineering, a section of the journal Frontiers in Built Environment, 6:35. doi: 10.3389/fbuil.2020.00035
40. Hencky, H. Z. (1924), Theorie Plastischer Deformationen und der hierdurch im Material hervorgerufenen Nachspannungen. Z. Angew. Math. Mech. 4, 323–334.
41. Hill, R. (1950). The Mathematical Theory of Plasticity. New York, NY: OxfordUniversity Press Inc
42. Ikeda K, Murota K., (1991) Random initial imperfections od structures, Int. J. Solids Structures, Vol.  28, (8), pp. 1021-1099
43. Chodor L. (1986), Losowa nośność ustrojów zginanych z uwzględnieniem sił stycznych (Praca doktorska PRE 68/86). Instytut Budownictwa Politechniki Wrocławskiej, [https://chodor-projekt.net/wp-content/uploads/PIPress/Artykuly/1986-Chodor-Dissertation-Wroclaw.pdf ]
44. Chodor L., Podstawka, R. (2009), Analiza pushover oraz przeguby i załomy nieliniowe w konstrukcjach żelbetowych. Problemy Naukowo-Badawcze Budownictwa, 215–220, [ https://chodor-projekt.net/wp-content/uploads/PIPress/Artykuly/2009-Chodor-Podstawka-Pushover-Krynica.pdf ]
45. Merchant W, (1954), The Failure Loads of Rigidly Jointed Frameworks as Influenced by Stability, The Structural Engineer,  32(7), p. 185–190
46. Godoy L. A. (1998), Stresses and pressures in thin-walled structures with damage and imperfections. Thin Walled Structures, 32, 181–206
47. Babcock C. D. (1974), Experiments in shell buckling, In: Thin Shell Structures, Theo-ry, Experiment, and Design. Prentice-Hall, Englewood Cliffs
48. Elishakoff I., Arbocz J. (1985). Reliability of axially compressed cylindrical shells with general nonsymmetric imperfections. Journal of Applied Mechanics, 1985(52), 122–128
49. Chodor L. (2015). Szybka metoda Monte Carlo, Encyklopedia Inżyniera i Architekta πPiWiki, [ https://chodor-projekt.net/encyclopedia/szybka-metoda-monte-carlo/ ]
50. Rolski T. (2013). Symulacje stochastyczne i teoria Monte Carlo, Wykład, Instytut Matematyczny, Uniwersytet Wrocławski, [ http://www.math.uni.wroc.pl/~rolski/Downloads/sym.pdf ]
51. Shanley F. (1947), Inelastic column theory. Journal of the Aeronautical Sciences, 14(5), p. 261–268
52. Ayrton W. E., Perry J. (1886), On Struts, The Engineer, p. 464–513
53. Dziubdziela W., (1975), Rozkłady graniczne ekstremalnych statystyk pozycyjnych, Roczniki Polskiego Towarzystwa Matematycznego, Seria III: Matematyka Stosowana IX (1977) 45-70
54. Dziubdziela W., Kopociński B., (1979), Oszacowania niezawodności systemów, Mat. Stos., 15,s.61-73
55. Ferry Borges, J., Castanhetta M., (1971) Structural Safety. Laborato´rio Nacional de Engenharia Civil, Lisbon, Portugal
56. Rootzén H., (1989), Maxima and excedances of stationary Markov chains , Advances in Applied Probability, 20, pp. 371-390
57. Der Kiureghian A., (1978), Second-moment combination of stochastic loads, Journal of the Structural Divison, Vol 104, No ST 10, pp.1551-1567
58. Galambos J., (1978), The Asymptotic Theory of Extreme Orfer Statistics, Wiley and Sons
59. Castello E., (1970), Extreme Value Theory in Engineering, Academic Press Inc.
60. CEB, (1976), Common unified rules of different types of construction and material. Vol. 1. Bulletin d’Information No. 116-E
61. European Committee for Standardization. 1994. ENV 1991-1: 1994 Eurocode 1: basis of design and actions on structures – Part 1: basis of design. European Committee for Standardization, Brussels, Belgium
62. AISC, (1986), Specification for structural steel buildings – load and resistance factor design. American Institute of Steel Construction , Chicago, Ill
63. ASCE, (2000), Minimum design loads for buildings and other structures (ASCE7-98). American Society of Civil Engineers, Reston, Va.
64. NBCC, (1995), National Building Code of Canada. Institute for Researchin Construction, National Research Council of Canada,Ottawa, Ont
65. Standards Association of Australia. 1985. Guidelines for conversion to limit states codes, Committee BD16 — Loading ofStructures. Standards Association of Australia, Canberra, Australia
66. Bartlett F.M., Hong H.P., Zhou W., (2003), Load factor calibration for the proposed 2005 Edition of the National Building Code of Canada:Statistics of loads and load effects, Can. J. Civ. Eng. 30: 429–439 (2003
67. Allen, D.E., (1975), Limit states design — a probabilistic study. Canadian Journal of Civil Engineering, 2: 36–49
68. Bijak, Chodor (1988), Stateczność systemów złożonych z prętów cienkościennych  w ujęciu stochastycznej metody elementów skończonych [ https://chodor-projekt.net/wp-content/uploads/PIPress/Artykuly/1988-BijakChodor-Stability-Cedzyna.pdf ]
69. Chodor L., (1988), Stochastyczna metoda elementów skończonych w zagadnieniach  losowej mechaniki konstrukcji,  Materiały XXXIV Konferencji  Naukowej PZITB i KN PAN Krynica’88, Tom I, str. 151-156 [https://chodor-projekt.net/wp-content/uploads/PIPress/Artykuly/1988-Chodor-SFEM-Krynica.pdf ]
70. CTICM, (2013), LTBeamN, [ https://www.cticm.com/logiciel/ltbeamn/ ]
71. Thom R., Giorello G., Morini S.,Duda R. (1991). Parabole i katastrofy: rozmowy o matematyce, nauce i filozofii z Giulio Giorello i Simoną Morinii. Państwowy Instytut Wydawniczy, Warszawa
72. Lumpe G., Gensichen V. (2014), Evaluierung der linearen und nichtlinearen Stabstatik in Theorie und Software: Prüfbeispiele, Fehlerursachen, genaue Theorie. Ernst
73. Lumpe G. (2011). S3D, Program badawczy. Prętowa teoria dużych przemieszczeń i obrotów (5.09.2011) [Computer software].
74. Simulia (2014). Abaqus 6.13 Documentation
75. Sofistik (2018), SofistikTutorials 2018, Tutorials for Stel Design. Imperfection Con-cept, [ /www.sofistik.de/documentation/2018/en/tutorials/steel-design/imperfection/imperfection.html ]
76. Machowiak, A. (2018). Klasyfikacja i zakres zastosowania Teorii II. rz. Obliczenia wykonane w ConSteel 11 SP3, [Raport Constell], STRENCO
77. Wusatowski Z. (1955). Właściwe sposoby określania odkształceń plastycznych. Zeszyty Naukowe Politechniki Śląskiej, Mechanika (4), s. 3–21
78. Skotny Ł. (2018), Kiedy można zignorować nieliniowość geometryczną? Enterfea, [ https://enterfea.com/kiedy-mozna-zignorowac-nieliniowosc-geometryczna/ ]

________________________________