Chodor L., Belki żelbetowe,, Encyklopedia πWiki, www.chodor-projekt.net,
13 lipca 2018 – 9 czerwca 2020 – ( publikacja kompletna)
01-02-2025 rewizja po dużej awarii portalu>
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Arkusz LCżelbet zawiera oryginalny kod – © wszelkie prawa zastrzeżone.
Artykuł w ciągu ostatnich 24 godzin czytało 20 Czytelników
Część S
Belki żelbetowe. Ścinanie i skręcanie
Nawigacja: [ R: Rysy i ugięcia ] ⇐ ⊗ ⇒ [ W: Wprowadzenie]
Przekroje betonowe w odróżnieniu od stalowych są bardzo wrażliwe na ścinanie, które jest nieodłącznie związane ze zginaniem. Zbrojenie na ścinanie wykonuje się w formie zamkniętych strzemion, najczęściej pionowych. Rzadziej od strzemion pionowych stosuje się odgięte pręty zbrojenia podłużnego, przy czym nośność samych strzemion musi zapewnić przynajmniej 50% nośności całego zbrojenia. Naprężenia poprzeczne (styczne) wywołane są także skręcaniem przekroju momentem skręcania $T$ (od słowa Torsion), a w oznaczeniach mechaniki $M_x$, tzn. momentem sił działającym wokół osi pręta x. Naprężenia od skręcania są rozłożone w przekroju zgodnie teorią prętów cienkościennych (p. skręcanie belki zelbetowej).
Wprowadzenie
Mechanizm zniszczenia belek przez ścinanie
Na rys.1 pokazano mechanizm ścinania obserwowany w belkach żelbetowych. Belka niszczy się na skutek powstania ukośnych rys., które są scalane przeciętym zbrojeniem podłużnym (siły $X_i$ oraz skierowane poprzecznie siły $Y_i$, nazywane siłami klockującymi, które mogą być przejęte przez zbrojenie pionowe w formie strzemion. Problemem podstawowym w mechanizmie zniszczenia jest wyznaczenie kąta pochylenia rys.
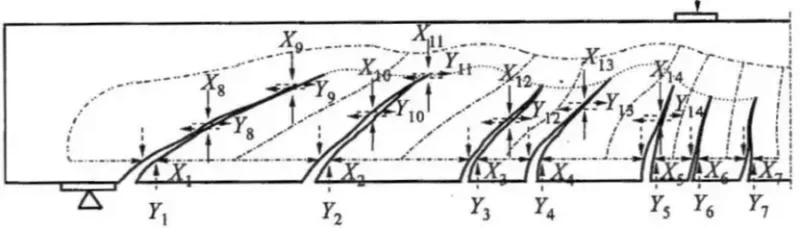
Rys.S-1. Mechanizm ścinania belki żelbetowej [1](zmodyfikowany)
Rysy powstają poprzecznie do trajektorii naprężeń głównych rozciągających, które dla belki wolnopodpartej, obciążonej równomiernie, pokazano na rys.2.
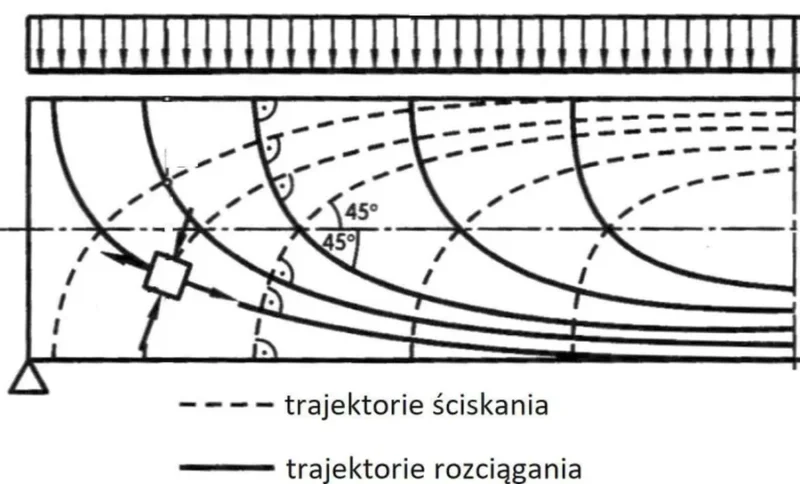
Rys.S-2 Przykład trajektorii naprężeń głównych w belce [2], rys. 7 .7
Siły i naprężenia poprzeczne
W zagadnieniu ścinania przekrojów żelbetowych posługuje się pojęciem obliczeniowych, poprzecznych sił przekrojowych $V_{Ed}$ i nośności przekroju $V_{Rd}$ lub naprężeń stycznych $v_{Ed}$ i wytrzymałości przekroju na ścinanie $v_{Rd}$:
$$\begin{equation} v_{Ed}=\cfrac {V_{Ed}}{A_v} \quad ; \quad v_{Rd}=\cfrac {V_{Rd}}{A_v} \label{1} \end{equation}$$
gdzie pole przekroju ścinania $A_v= b_w \cdot z $.
Przy zastosowaniu zapisu w naprężeniach, a nie siłach uzyskuje się prostsze formuły i w niniejszym artykule stosuje się zapis w naprężeniach, $v$, a siły uzyskuje się z zależności $V=v\cdot A_v$
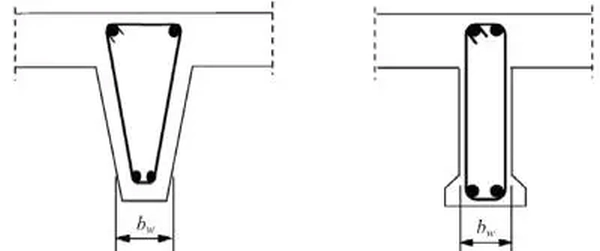
Ramię sił wewnętrznych, występujące w (W-11) przyjmuje się w $(\ref{1})$ jako $z=0,9 \cdot d_l$, gdzie $d_l$ jest wysokością użyteczną przekroju dla zbrojenia rozciąganego (dolnego) $d_l=h-a_l$, $b_w$ szerokością efektywną przekroju na ścinanie (rys. S-1)
Rys.S-3 Szerokość przekroju ścinanego [3], rys.6.5 dolny
Oznaczenia stosowane w rozdziale
$\alpha$ – kąt nachylenia zestawu zbrojenia na ścinanie (krzyżulców lub prętów ukośnych) do osi belki- dodatni przy pochyleniu zbrojenia w lewo (lewoskrętny), (rys. S-5 i S-7)
$\alpha_{cw}$ – współczynnik naprężeń dla ściskanego krzyżulca betonowego zależny od stopnia ściskania przekroju $n_{cp}$ wyznaczany z zależności ($\ref{2}$) [3], wzór (6.11a,b,c N):
$$\begin{equation} \alpha_{cw}= \begin{cases}
1,0 , & \text { dla } n_{cp}=0 \\
1+n_{cp}, & \text { dla } 0 < n_{cp} \le 0,25 \\
1,25 , & \text { dla } 0,25 < n_{cp} \le 0,5 \\
2,5\cdot ( 1 -n_{cp} ), & \text { dla } 0,5< n_{cp} \le 1,0 \\
\end{cases} \label{2} \end{equation}$$
$ \nu_1= \nu$ – współczynnik redukcji naprężeń w betonie zarysowanym przy ścinaniu [3], wzór (6.6N):
$$\begin{equation} \nu_1= \nu= 0,6 \cdot (1-\cfrac {f_{ck}} {250} ) \label{3} \end{equation}$$
$n_{cp}$ – stopień ściskania przekroju betonowego (np sprężeniem pręta betonowego) wg zależności
$$\begin{equation} n_{cp}= \cfrac{\sigma_{cp}}{f_{cd}} \label{4} \end{equation}$$
$\sigma_{cp}$ – naprężenia od ściskania przekroju betonowego [3], klauzula 6.2.3 (3),Uwaga 3:
$$\begin{equation}\sigma_{cp}=\dfrac{N_{Ed}}{A_c} \le 0,2 f_{cd} \label{5} \end{equation}$$
gdzie:
$A_c$ – pole przekroju betonu,
$N_{Ed}$ wartość przekrojowej siły ściskająćej bez znaku
$\Theta$ – kąt nachylenia do osi belki ściskanego krzyżulca betonowego równoważącego się w zbrojeniu na ścinanie , czyli pochylonego w prawo, (rys. S-5), ustęp kąt nachylenia krzyżulca, wzór ($\ref{21}$) dla prostego ścinania i ($\ref{37}$) dla ścinania ze skręcaniem
$\Theta_f$ – kąt nachylenia krzyżulca betonowego przy ścinaniu podlużnym ($\ref{25}$) i ($\ref{26}$)
$b_w$ – szerokość strefy rozciąganej belki. Dla przekrojów teowych jest grubością środnika (rys. S-1), a w belce o przekroju prostokątnym $b_w=b$ ,
$z$ – ramię sił podłużnych: ściskających $F_{cd}$ oraz rozciągających $F_{td}$ , które w przekrojach bez działania siły osiowej, przyjmuje się $z=0,9d$,
$A_v=z \cdot b_w$ efektywne pole przekroju betonu ścinanego,
$A_{sw}$ pole przekroju zbrojenia na ścinanie,
$s_l$ rozstaw podłużny zestawów zbrojenia na ścinanie ( ramion strzemion lub prętów odgiętych)
$f_{ywd}$ – obliczeniowa wytrzymałość ścinanego zbrojenia na rozciąganie (obliczeniowa granica plastyczności stali zbrojenia na ścinanie (strzemion). Zwykle przyjmuje się strzemiona z takiej samej stali jak zbrojenie glówne i wówczas $f_{ywd} = f_{yd}$
$V_{Ed}$ , $v_{Ed}$ obliczeniowa przekrojowa siła ścinająca i naprężenie od ścinania wywołane obciążeniem zewnętrznym
$V_{Rdc}$ , $v_{Rdc}$ obliczeniowa nośność na ścinanie elementu bez zbrojenia na ścinanie – mierzone siłą lub naprężeniem odpowiednio ($\ref{13}$)
$V_{Rd,max}$, $v_{Rd,max}$ maksymalna siła poprzeczna lub naprężenia które mogą być przeniesione przez element – siła ta jest ograniczona przez zrniażdżenie ściskanych krzyżulców betonowych ($\ref{17}$)
$V_{ccd}$ – obliczeniowa wartość siły poprzecznej w pasie ściskanym w przypadku gdy pas ściskany jest nachylony, (rys. S-2)
$V_{td}$ – obliczeniowa wartość siły poprzecznej składowej siły w zbrojeniu rozciąganym. w przypadku, gdy pas rozciągany jest nachylony.(rys. S-2)
Minimalne zbrojenie poprzeczne na ścinanie
W tych miejscach elementu, w których obliczeniowe naprężenia styczne $v_{Ed}$ wywołane obciążeniami zewnętrznymi spełniają warunek
$$\begin{equation} v_{Ed} \le v_{Rd,c} \label{6} \end{equation}$$
zbrojenie na ścinanie nie jest wymagane, ale w takim przypadku w belkach należy zastosować zbrojenie minimalne na ścinanie, służące do wiązania zbrojenia podłużnego, o polu przekroju spełniającym warunek stopnia zbrojenia [3], wzór (9.4) :
$$\begin{equation} \rho_w=\cfrac{A_{sw}}{s_lb_w sin \alpha} \ge \rho_{w,min}\label{7} \end{equation}$$
gdzie:
$A_{sw}$ jest polem przekroju pojedynczego zestawu zbrojenia na ścinanie (np. dwóch strzemion , jeśli zastosowano podwójne),
$ s_l$- rozstaw zestawów zbrojenia po długości pręta.
$\alpha$ – kąta nachylenia zestawu zbrojenia do poziomu.
Minimalny stopień zbrojenia wyznacza się z zależności [3],wzór (9.5N)
$$\begin{equation} \rho_{w,min} =0,08 \cdot \sqrt{f_{ck}} /f_{yk} \label{8} \end{equation}$$
Poprzeczne zbrojenie minimalne należy stosować na całej długości belki i zagęszczać w obszarach nie spełniających warunku $(\ref{6})$. Minimalne zbrojenie na ścinanie nie jest wymagane w płytach (pełnych, z żebrami lub kanałami), w których możliwa jest poprzeczna redystrybucja obciążeń. lub mniej ważnych belkach (np nadproża o rozpiętości mniejszej niż 2 m) , które nie wpływają w istotny sposób na ogólną nośność i stateczność konstrukcji.
Maksymalny rozstaw zbrojenia na ścinanie
Maksymalny rozstaw zbrojenia jest unormowany niezależnie od wymogu minimalnego pola przekroju zestawu zbrojenia $(\ref{7})$ i wynosi [3], (9.8N):
$$\begin{equation} s_{l,max}= k_l \cdot d \cdot (1+ctg \alpha) \le 600 \label{9} \end{equation}$$
gdzie $k_l$ jest współczynnikiem zależnym od rodzaju zbrojenia i wynosi: 0,75 dla zestawów zbrojenia lub dla strzemion; 0,6 dla prętów odgiętych
Z wymagań dotyczących minimalnego zbrojenia poprzecznego wynika, że podłużny rozstaw zestawów powinien spełniać warunek:
$$\begin{equation} s_l \le 12,5 \cdot \cfrac{A_{sw}\cdot f_y}{b_w sin \alpha \cdot \sqrt{f_{ck}}} \label{10} \end{equation}$$
Warunek ten powinien być spełniony na całej długości elementu. Dla najczęściej stosowanego żelbetu C30/37-B500 i strzemion pionowych mamy stąd
$$\begin{equation} s_l \le 1141 \cdot \cfrac{A_{sw}}{b_w } \label{11} \end{equation}$$
Minimalny rozstaw zbrojenia na ścinanie
Nie normuje się minimalnego rozstawu zbrojenia na ścinanie. Nie należy jednak rozstawu strzemion dobierać zbyt małego ze względów technologicznych (zagęszczenie betonu) i ekonomicznych. Zalecamy aby minimalny rozstaw zbrojenia nie był mniejszy niż połowa szerokości przekroju (b/2) i 100 mm.
Wytrzymałość przekroju nie zbrojonego na ścinanie
Nośność na ścinanie elementu betonowego $V_{Rd}$ ogólnie o zbieżnym przekroju, kącie pochylenia $\alpha_c$ do poziomu nachylenia górnego (ściskanego) i kącie $\alpha_t$ pochylenia dolnego (rozciąganego) zbrojenia oblicza się jako sumę [3], wzór (6.1):
$$\begin{equation} V_{Rd} = V_{Rd,c} +V_{ccd}+V_{td} \label{12} \end{equation}$$
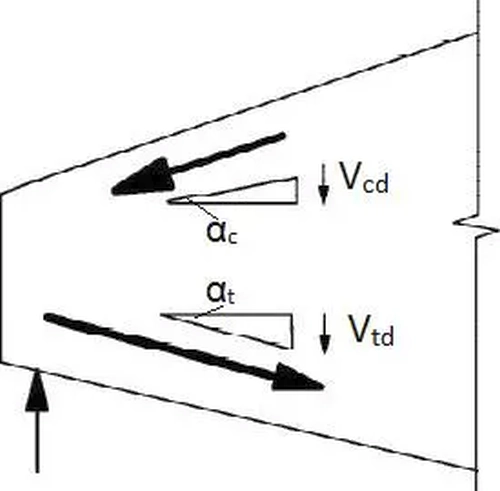
Rys. 4 Składowe siły poprzecznej w przekroju zbieżnym [3], rys.6.2
Wytrzymałość przekroju nie zbrojonego na ścinanie $v_{Rd,c}$ (mierzoną naprężeniami) można wyznaczyć z zależności [3], wzory (6.2a), (6.2b)
$$\begin{equation} v_{Rd,c}=\max{ \left \{ C_{Rd,c} \cdot k \cdot (100 \cdot \rho_l \cdot f_{ck})^{1/3} \, ; \, \nu_{min} \right \} }+ k_1 \cdot \sigma_{cp} \label{13} \end{equation}$$
gdzie obliczeniowy współczynnik korelacji pomiędzy wytrzymałością na ścinanie i ściskanie wynosi
$C_{Rd,c}=C_{Rk,c}/\gamma_c = 0,18/1,4=0,129$
$k=1+\sqrt{200/d} \le 2,0$, gdzie d- wysokość użyteczna przekroju w mm,
$\nu_{min}= 0,035 \cdot k^{3/2} \cdot {f_{ck}}^{1/2}$,
$k_1=0,15 $.
Stopień zbrojenia na zginanie (i ew. rozciąganie) $\rho_l=\dfrac{A_{sl}}{b_w d}\le 0,02$, wyznacza się z pola przekroju zbrojenia rozciąganego $A_{sl}$ , które sięga na odległość nie mniejszą niż $l_{bd}+d$ poza rozważany przekrój, gdzie $l_{bd}$ jest wymagana długością zakotwienia rozciąganego pręta zbrojeniowego. Warunek uwzględnienia zbrojenia podłużnego do stopnia zbrojenia jest klasyczny jak dla zbrojenia na zginanie i został zilustrowany na rys. S-3 na przykładzie belki lub płyty zginanej.
Rys. 5. Określenie pola przekroju zbrojenia As do wyznaczenia stopnia zbrojenia przekroju na zginanie. l_{bd } – wymagana długość zakotwienia pręta [3], rys. 6.3
W przypadku różnych stopni zbrojenia w dwóch prostopadłych kierunkach wyznacza się średnią geometryczną
$$\begin{equation}\rho_l=\sqrt{\rho_{ly}\cdot \rho_{lz}} \label {14} \end{equation}$$
W tab. S-1 zestawiono wytrzymałości betonu na ścinanie $v_{Rdc}$ $(\ref{13})$ dla najczęściej stosowanego betonu C30/37 .
Tab. 1 Wytrzymałość na ścinanie $v_{Rd,c}$ [MPa] $(\ref{13})$ betonu C30/37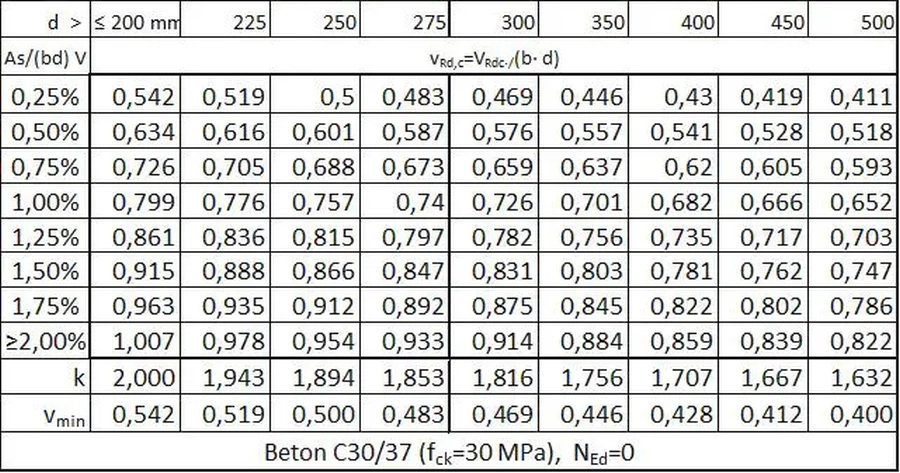
W przypadku belek wykonanych z innych betonów wytrzymałość odczytaną z tab. S-1 należy przemnożyć przez współczynnik korekcyjny $k_v$ z tab. S-2
Tab. S-2 Współczynnik korekcyjny dla wytrzymałości betonu na ścinanie wg tab. S-1 
Strefy zbrojenia na ścinanie
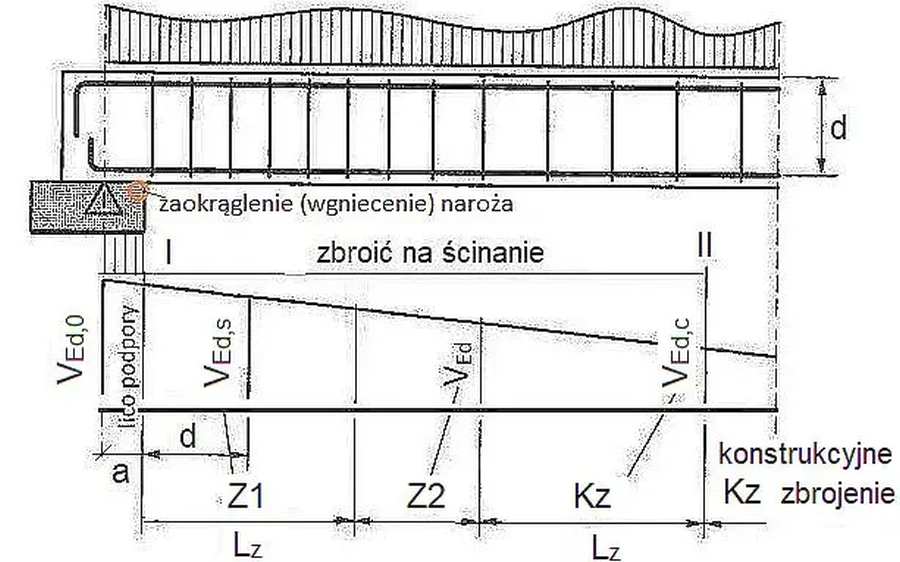
Przekroje poprzeczne ścinane siłami $V_{Ed}$ , takimi że nie jest spełniony warunek $(\ref{6})$ powinny być zbrojone wkładkami stalowymi na odcinku odcinek belki I-II, pokazanym na na rys. S-4 Na tym odcinku wydzielono trzy strefy: A,B,C na których różnicuje się zbrojenie poprzeczne.
Zbrojenie na ścinanie rozpoczyna się w licu podpory, które jest wyznaczane na siłę poprzeczną w licu. Z obliczeń statycznych najczęściej znana jest siła nad podporą $V_{Ed,0}$. Siła poprzeczna w licu podpory zależy przede wszystkim od kinematyki – obrotu na podporze (rys. S-4). Lepszym miernikiem obrotu na podporze jest moment zginający, którego redukcję nad podporą (ścięcie „ząbka”) można oszacować analogicznie do innych typów konstrukcji na $\Delta M=\cfrac{V\cdot a }{11}$ (patrz artykuł Hale i dźwigary blachownicowe ). Ponieważ siła poprzeczna jest pochodną momentu zginającego, więc zmniejszenie siły poprzecznej wyniesie $ \Delta V=\cfrac{ \Delta M}{a}= \cfrac{V}{11}$, Przyjmiemy, że w licu podpory działa siła poprzeczna $V_{Ed,lico} \cdot(1-(1/8)/2,0 = 0,94 V_{Ed,c}$ , gdzie 2,0 jest współczynnikiem bezpieczeństwa, czyli:
$$\begin{equation}V_{lico} = 0,94 \cdot V_{Ed,c} \label {15} \end{equation}$$
Jeśli w licu podpory warunek $(\ref{6}$) nie jest spełniony , to wyznacza się zbrojenie na ścinanie:
a) najpierw w strefie Z1 o długości $L_z$ na siłe $V_{Ed,s}$ – minimalną siłę poprzeczną na odcinku o długości d od lica podpory. Często na tym poprzestaje się i wyznaczone zbrojenie rozkłada na całym odcinku I-II, ale jeśli odcinek I-II jest długi, to w celu zoptymalizowania ilości stali różnicuje się zbrojenie w strefach Z2 i Kz, w taki sposób, że
b) w strefie Kz o długości $L_z$ daje się minimalne zbrojenie na ścinanie (czyli konstrukcyjne na siłę $ V_{Rd,c}$
c) w pozostałej strefie Z2 na minimalną siłę $V_{Ed}$ na tym odcinku.
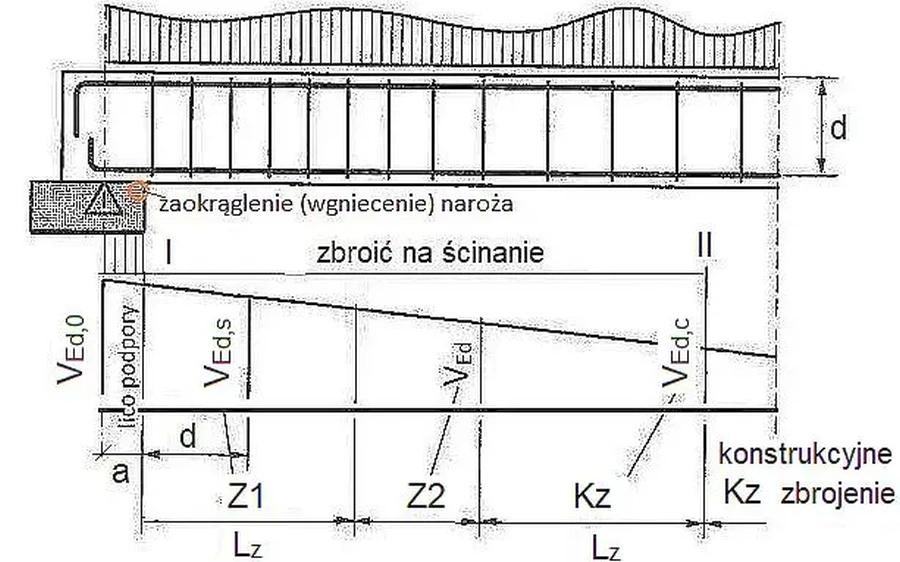
Rys 6. Strefy zbrojenia elementu żelbetowego(opracowano z wykorzystaniem fragmentów rysunku [4]
Długość strefy zbrojenia $L_z$ dobiera się po wyznaczeniu kąta nachylenia krzyżulca betonowego
$$\begin{equation} L_z=z \cdot ctg \Theta \label {16} \end{equation}$$
w którym z=0,9 d – ramię sił wewnętrznych, występujące w $(\ref{1}) $ (d- wysokość użyteczna przekroju), a kąt nachylenia krzyżulca betonowego $\Theta$ wyznaczono w rozdziale: kąt nachylenia krzyżulca betonowego
Ścinanie poprzeczne (pionowe) belek
W normie [3] wprowadzono metodę wyznaczania nośności przekroju na zginanie z uwzględnieniem działania krzyżulca betonowego nachylonego pod kątem $\Theta$. Kąt nachylenia krzyżulca betonowego zmienia się w zależności od siły ścinającej stosowane w sposób pokazany na rys.S-5.
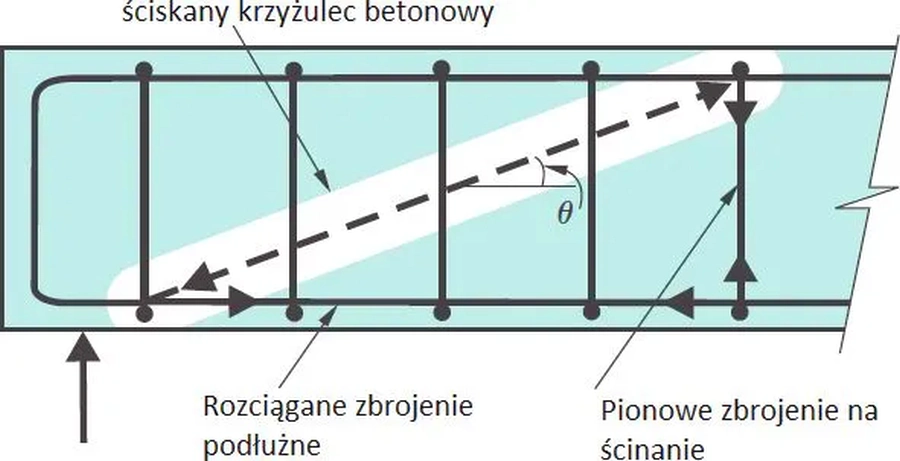
Rys. 7. Ściskany krzyżulec betonowy tworzony podczas ścinania belki [5], fig 4
Maksymalna wytrzymałość betonu na ścinanie ( krzyżulca betonowego) $v_{Rd,max}$ na podstawie [3] ,wzór (6.14) wynosi
$$\begin{equation} v_{Rd,max} = \alpha_{cw} \cdot \nu_1 \cdot f_{cd} \cdot \cfrac { ctg \Theta + ctg \alpha } {1+ctg^2 \Theta} \label {17} \end{equation}$$
gdzie: $\nu_1$ wg ($\ref{3}$) ; $\alpha_{cw}$ wg $(\ref{2}$) ; $\Theta$ w kolejnym ustępie ;
W elementach z pionowym zbrojeniem na ścinanie zależność ta upraszcza się do postaci:
$$\begin{equation} v_{Rd,max} = \cfrac{ \alpha_{cw} \cdot \nu_1 \cdot f_{cd}}{ctg \Theta +tg \Theta} \label {18} \end{equation}$$
W przekrojach, w których stopień ściskania $n_{cp}=0$ , czyli zgodnie z ($\ref{2}$) $\alpha_{cw}=1,0$ i w takich, których krzyżulec betonowy tworzy się pod możliwe najmniejszym kątem $\Theta$ (czyli $ctg \Theta = 2,0 \quad , $tg \theta \Theta =0,5 ) z ($\ref{18}$) , otrzymujemy:
$$\begin{equation} v_{Rd,max} = \cfrac{ 1,0 \cdot \nu_1 \cdot f_{cd}}{2,0 +0,5} = 0,4 \cdot \nu \cdot f_{cd}\label {18A} \end{equation}$$
Zgodnie z uwagą pod formułą (6.53) [6] maksymalną wytrzymałość krzyżulca betonowego o wartości $(/ref{18A}$) należy przyjąc dla ścinania przez przebicie w obszarze przylegającym do słupa ( dla obwodu kontrolnego $u_0$).
Kąt nachylenia krzyżulca betonowego
Doświadczenia pokazują, że kąt nachylenia krzyżulca betonowego $\Theta$ (rys.S-5) może przyjmować wartości z dość dużego zakresu, a mianowicie (wg oryginalnej normy EC2)
$$\begin{equation}1,0 \le ctg \Theta \le 2,5 \label{19} \end{equation}$$
W polskim załączniku krajowym do normy [3] zalecono nieco mniejszy zakres, a mianowicie:
$$\begin{equation}1,0 \le ctg \Theta \le 2,0 \label{20} \end{equation}$$
czyli $26,7^o \le \Theta \le 45^o$.
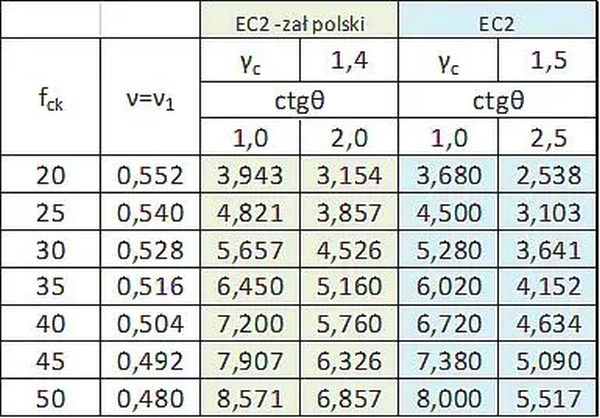
Maksymalne wytrzymałości betonu belki na ścinanie dla skrajnych wartości kąta $\Theta$ zestawiono w tab. S-3. Najkorzystniejsze jest nachylenie krzyżulca betonowego pod kątem $45^o$ ($ctg \Theta=1$,), a dla $ctg \Theta=2,5$ nachylenie jest najmniej korzystne.
Tab. S-3 Maksymalna nośność betonu na ścinanie $v_{Rd,max}$ [MPa] $( \ref{17})$ przy zastosowaniu pionowego zbrojenia na ścinanie
w zależności od kąta nachylenia krzyżulca betonowego
W praktyce konkretną wartość $\Theta$ wyznacza się w algorytmie przedstawionym na rys. S-6. lub bezpośrednio z zależności ($\ref{21}$).
W tradycyjnie stosowanym algorytmie – pierwszym kroku wyznacza się nośność krzyżulca betonowego z zależności ($\ref{17}$) dla większej z wartości skrajnych $ctg \Theta$, czyli 2,5 wg Eurokodu lub 2,0 wg polskiego załącznika. Tak wyznaczoną nośność porównuje się z naprężeniem ścinającym $v_{Ed}$ i dalej postępuje zgodnie z pokazanym algorytmem.
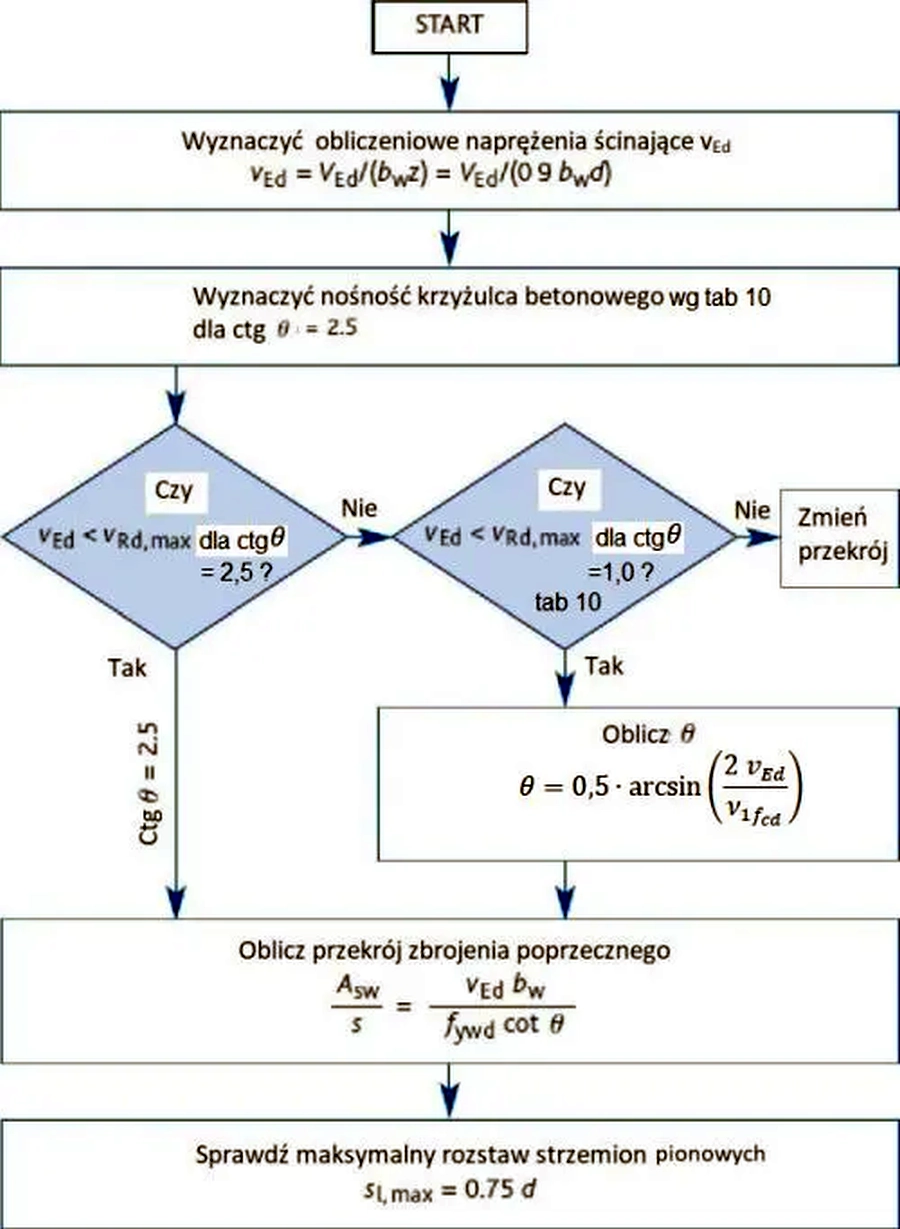
Rys. S-8 Schemat blokowy projektowania przekroju strzemion pionowych ( (Bond A. J., Brooker O., Harris A. J., Harrison C., Moss R. M., Narayanan R. S. (2006). How to Design Concrete Structures using Eurocode 2 (A Cement and Concrete Industry Publication). The Concrete Centree)) dostosowane do polskiej normy)
Dla najczęstszego przypadku pionowych strzemion – po zastosowaniu tożsamości trygonometrycznych [ $ ctg \Theta + tg \Theta = 1/ (sin \Theta \cdot cos \Theta) = 2 / sin(2 \Theta)$ ] – równanie ($\ref{17}$) = ($\ref{1}$) prowadzi do formuły
$$\begin{equation} \Theta = 1/2 \cdot arcsin \left ( \cfrac{ 2 \cdot v_{Ed}}{ \nu_1 \cdot \alpha_{cw} \cdot f_{cd}} \right ) \quad \text { ale } 26,7^o \le \Theta \le 45^o\quad \label{21} \end{equation}$$
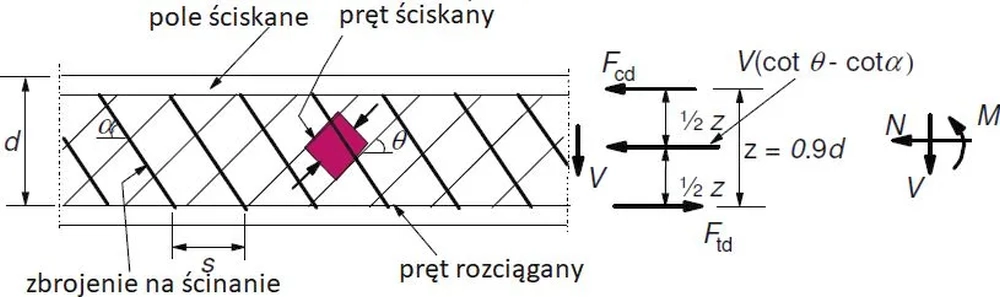
Rys. 9. Model kratownicowy ścinania belki żelbetowej [3], rys. 6.5 górny
Przekrój zbrojenia poprzecznego i nośność przekroju zbrojonego
Dla znanego kąta nachylenia krzyżulca betonowego $ \Theta$ potrzebny przekrój zbrojenia poprzecznego $A_{sw}$ rozmieszczony na długości $s_l$ (rozstawie zestawów) wynosi
$$\begin{equation} \cfrac{A_{sw}}{s_l}= \cfrac{v_{Ed}\cdot b_w}{f_{ywd} \cdot ctg \Theta} \label{22} \end{equation}$$
Wytrzymałość zbrojenia na ścinanie $v_{Rd,s}$ (strzemion lub prętów odgiętych nachylonych pod kątem $\alpha$ do osi belki ( dodatni przy pochyleniu zbrojenia w lewo (lewoskrętny) – na podstawie [3], wzór (6.13) wynosi
$$\begin{equation} v_{Rd,s} = \cfrac {A_{sw}} {s_l \cdot b_w} \cdot f_{ywd} \cdot (ctg \Theta + ctg \alpha) \cdot \sin\alpha \label{23} \end{equation}$$
Wytrzymałość przekroju zbrojonego na ścinanie jest mniejszą z wartości $( \ref{17})$ , $(\ref{23})$
$$\begin{equation} v_{Rd} = \min { \left \{ v_{Rd,s} \, ; \, v_{Rd,max} \,\right \} } \label{24} \end{equation}$$
Ścinanie podłużne (między środnikiem i półkami)
Ścinanie podłużne występuje na skutek działania sił rozwarstwiających płytę od żebra. Na rys. S-8 przedstawiono wycinek $\Delta x$ płyty z żebrem. Na końcu A-A siły ściskające płytę (od zginania) wynoszą $F_d$, a na końcu przeciwnym $F_d + \Delta F_d$. Różnica tych sił wywołuje siły rozwarstwiające, które ścinają przekrój podłużny płyty i zbrojenie $A_{sf}$.
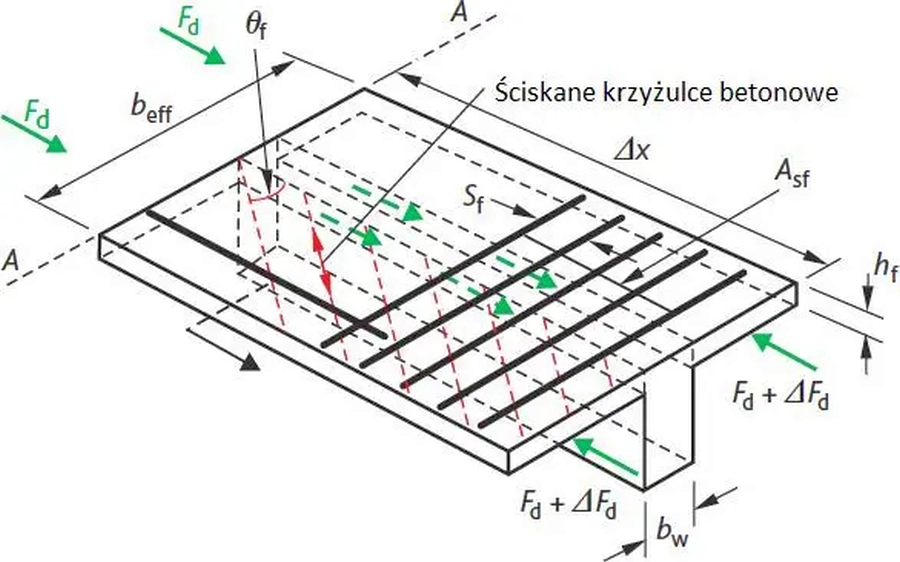
Rys. 10 Ścinanie podłużne przekroju teowego (Bond A. J., Brooker O., Harris A. J., Harrison C., Moss R. M., Narayanan R. S. (2006). How to Design Concrete Structures using Eurocode 2 (A Cement and Concrete Industry Publication). The Concrete Centree)), fig 13
nia wykazują, że kąt nachylenia krzyżulca betonowego $\Theta_f$ zależy od tego, czy półka (płyta) jest ściskana , czy rozciągana.
Jeżeli półka jest ściskana, to przyjmuje się
$$\begin{equation}1,0 \le ctg \Theta_f \le 2,0 \label{25} \end{equation}$$
Jeżeli półka jest rozciągana , to przyjmuje się
$$\begin{equation}1,0 \le ctg \Theta_f \le 1,25 \label{26} \end{equation}$$
Mechanizm zmiażdżenia ściskanych krzyżulców betonowych w półce prowadzi do warunku granicznego [3], wzór (6.22)
$$\begin{equation} v_{Ed} \le \nu \cdot f_{cd} \cdot sin \Theta_f \cdot cos \Theta_f \label{27} \end{equation}$$
przy czym zachodzi tożsamość trygonometryczna: $(sin \Theta_f \cdot cos \Theta_f) = \cfrac {ctg \Theta_f}{1+ ctg^2 \Theta_f}$.
Zbrojenie poprzeczne na jednostkę długości wyznacza sie z zależności
$$\begin{equation} \cfrac{A_{sf}}{s_f} > \cfrac{v_{Ed} \cdot h_f}{f_{yd} \cdot ctg \Theta_f} \label{28} \end{equation}$$
Wyznaczenie zbrojenia $A_{sf}$ przeprowadza się według schematu, który pokazano na rys. S-9.
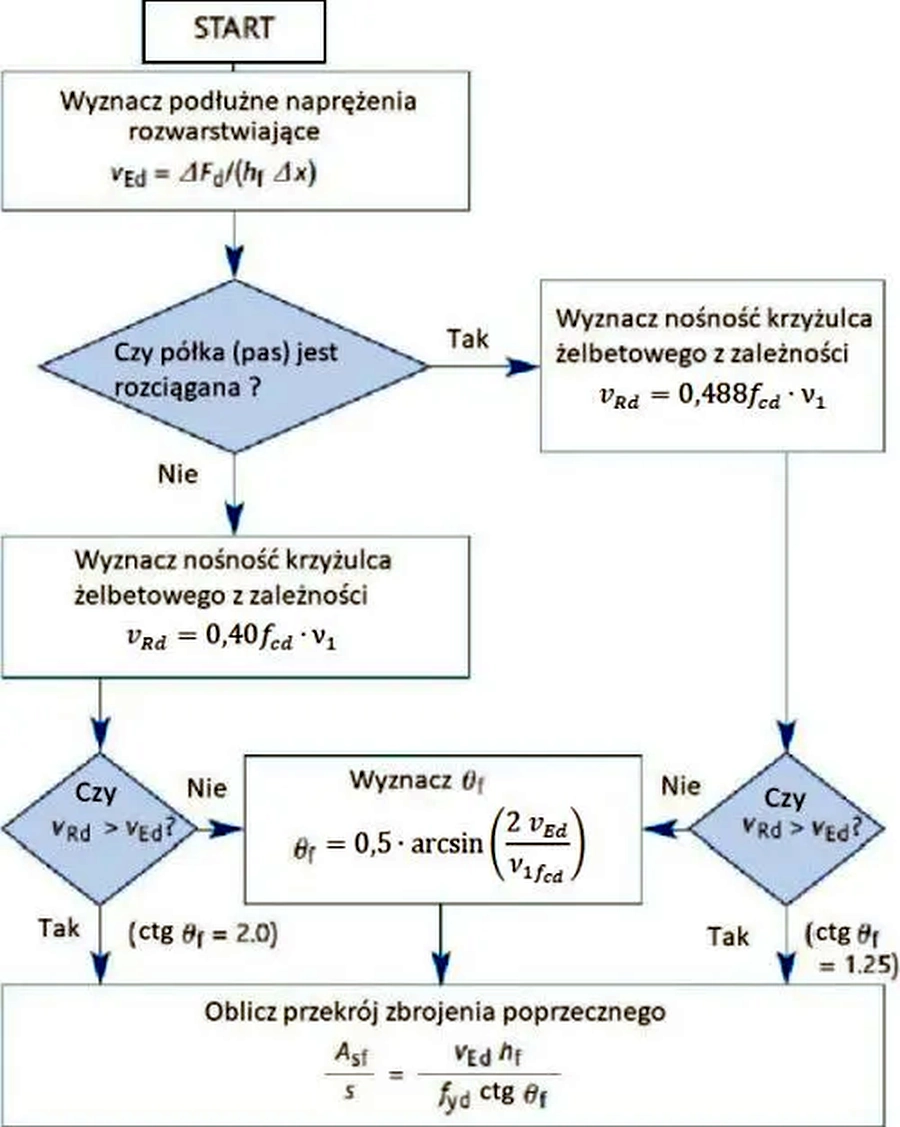
Rys. 11 Schemat blokowy do wyznaczania zbrojenia $A_{sf}$ na siły rozwarstwiające (Bond A. J., Brooker O., Harris A. J., Harrison C., Moss R. M., Narayanan R. S. (2006). How to Design Concrete Structures using Eurocode 2 (A Cement and Concrete Industry Publication). The Concrete Centree)), dostosowane do polskiej normy)
Przykłady numeryczne projektowania zbrojenia na ścinanie podłużne podano w artykule dotyczącym płyt żelbetowych.
Ścinanie przez przebicie
Ścinanie przez przebicie przedstawiono w artykule Przebicie płyty żelbetowej.
Ścinanie elementu wyodrębnionego z konstrukcji
Zbrojenie na ścinanie wyodrębnionego elementu konstrukcji w większości przypadków z wystarczająca dla praktyki dokładnością można wyznaczyć na elemencie zastępczym.
W szczególnych sytuacjach, przede wszystkim przy działaniu znacznych sił skupionych w przęśle rozkład sił poprzecznych należy przyjmować z obliczeń statycznych najczęściej prowadzonych metodą MES.
Element zastępczy
Rozpatrzmy wyodrębnioną z konstrukcji belkę zastępczą pokazaną na rys. R-9 , w której siły poprzeczne rozłożone są podług zależności
$$\begin{equation} V_{Ed} (\xi) = \cfrac{\Delta M_{Ed}}{L} + q_{z,Ed} \cdot (1/2-\xi) \label{29} \end{equation}$$
gdzie:
$\Delta M=M_L-M_0$ – różnica momentów podporowych
$\xi=x/L \in (o,,L )$ – względna rzędna liczona od lewej podpory
$q_{z,Ed} = \cfrac{6}{L^2} \left[ 2\cdot (M_{max} \pm M_w – (M_0 +M_L) \right ]$ – równomiernie rozłożone obciążenie zastępcze wg zależności (R-64).
Zakres zbrojenia minimalnego II-II
Z ($\ref{1}$) wyznaczamy naprężenia $v_{Ed}(\xi)$ i po porównaniu wartości bezwzględnej z $v_{R,dc}$ ($\ref{13}$) otrzymamy granicę II strefy zbrojenia poprzecznego (rys. S-4):
$$\begin{equation} \xi_{II} = \cfrac{1}{6}+\cfrac{1}{q_{z,Ed}}\cdot \left( \cfrac{\Delta M_{Ed}}{L} \pm A_v \cdot v_{Rd,c} \right) \label{30} \end{equation}$$
W ogólnym przypadku, rzędne wykresu naprężeń poprzecznych są znane z metody MES w dyskretnych punktach.
W tym przypadku, idąc od miejsca największych sił najpierw poszukujemy dyskretnego punktu o rzędnej ,$\xi_k$ w którym warunek ($\ref{6}$) już jest spełniony ($v_{Ed,k} <v_{Rd,c}$ . Biorąc poprzedni punkt $\xi_{(k-1)}$ z siłą $v_{Ed, (k-1)} > v_{Rd,c}$ z interpolacji liniowej uzyskujemy teoretyczną rzędną $\xi_{II}$
$$\begin{equation} \xi_{II} = \xi_{(k-1)} +\cfrac{v_{Rd,c} -v_{Ed,(k-1)}}{v_{Ed,k} -v_{Ed,(k-1)}} \cdot (\xi_{k}-\xi_{(k-1)}) \label{31} \end{equation}$$
Punkt teoretyczny $(\ref{29})$ lub $(\ref{31})$ przesuwamy w kierunku podpory o odcinek $L_z= z \cdot ctg \Theta= 0,9 \cdot d_l \cdot ctg \Theta$, ale nie dalej niż $L_z$ od podpory.
Skręcanie belki żelbetowej
Skręcanie pręta żelbetowego jest rozpatrywane w analogii do skręcania prętów cienkościennych. W celu uzyskania informacji wstępnych na ten temat odsyłam do artykułów:
- Skrecanie swobodne (czyste, nieskrępowane, Saint-Venanta) przekrojów prostokątnych, Skręcanie pręta o przekroju prostokątnym, oraz zagadnień:
- Skręcanie nieswobodne (skrępowane)
- Skręcanie pręta o przekroju zamkniętym .
- Pręty wielogałęziowe, quasi-zamknięte.
- Pręty cienkościenne
Model skręcania pręta żelbetowego
Model kratownicowy
Skręcanie w konstrukcjach żelbetowych występuje w przypadku pionowego obciążenia mimośrodowego pręta (belki) lub podłączenia do żebra płyty tylko z jednej strony (np w belkach – żebrach skrajnych przęseł) i w każdym innym przypadku, gdy z rozwiązań układu statycznego w pręcie powstaje moment skręcający $M_x$ wokół osi pręta x . Moment ten w konstrukcjach żelbetowych jest oznaczany przez $T$ od słowa angielskiego Torsion.
Na rys. S-10 pokazano użyteczny model kratownicowy skręcania pręta żelbetowego
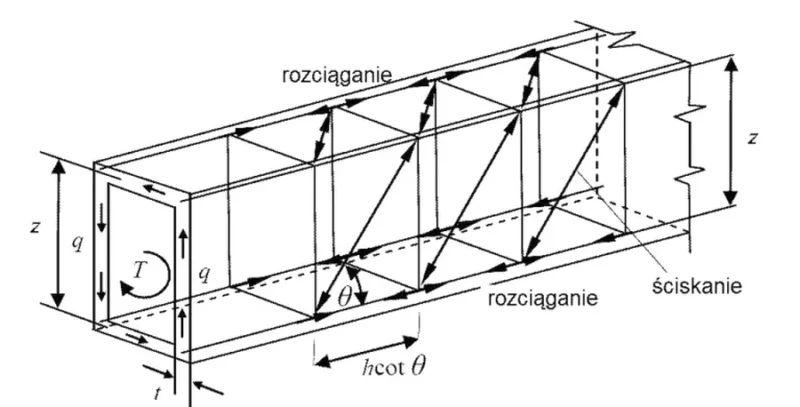
Rys 12. Model kratownicowy skręcania pręta żelbetowego zmodyfikowany rysunek z [7]
Model pokazany na rys S-9 jest zastępczym modelem kratownicowym cienkościennego pręta o przekroju zamkniętym. o wysokości $z$ i grubości ścianki $t$. W modelu tym pasy górny i dolny to zbrojenie podłużne pręta, ramki poprzeczne (słupki), to strzemiona stalowe, a krzyżulce nachylone pod kątem $\Theta$ to krzyżulce betonowe zobrazowane na rys S-4.
Zgodnie z klauzulą 6.3.1(3) [3] nośność przekroju na skręcanie można obliczyć na podstawie zastępczego cienkościennego przekroju zamkniętego, w którym zapewnia się zamknięty przepływ strumienia naprężeń stycznych $q$ tak jak pokazano na przekroju czołowym modelu kratownicowego rys. S-9. Zgodnie z ta klauzulą normową złożone kształty jak teowniki można podzielić na szereg podprzekrojów (elementów) i każdy z nich modelować zastępczym przekrojem cienkościennym, a całkowita nośność na skręcanie jest sumą nośności elementów.
Zdaniem autora jest to zbyt daleko idące uproszczenie, bowiem przekroje takie są przekrojami cienkościennymi otwartymi dla których teoria skręcania jest inna od przyjętej w normie. Przekroje takie wymagają dokładniejszej analizy. Dotyczy to w szczególności przekrojów teowych lub żeber ze współpracującymi pasmami płyt.
Uwaga: Teoria i przykład przedstawiony w opracowaniu [8] jest błędny z powodu pominięcia wyznaczenia kąta $\Theta$ i przyjęcia go arbitralnie o wartości najkorzystniejszej, więc po stronie niebezpiecznej dla konstrukcji.
Kształt strzemion na skręcanie
Na rys. S-11 pokazano zalecane kształty zamkniętych strzemion na skręcanie . W niżej opisanym algorytmie wyznacza sie potrzebne pole jednego ramienia strzemiona. W języku zbrojenia na ścinanie poprzeczne odpowiada to zbrojeniu 1-ciętemu, ro znaczy typowe zbrojenie 2-cięte należy dać o podwójnym przekroju.
Naprężenia ścinające od skręcania
Dla pręta żelbetowego o przekroju rozpatrywanym wraz z otworami, czyli też rury, z polem powierzchni $A$ oraz z obwodem zewnętrznego konturu $u$ wyznacza się efektywną grubość $t_{ef}$ ścianki z zależności (p. rys S-14):
$$\begin{equation} t_{ef} = \cfrac{A}{u} \label{32} \end{equation}$$
Następnie wyznacza się pole przekroju zawarte wewnątrz linii środkowej ścianek oraz obwód $u_k$ wokół pola $A_k$
Dla przekroju prostokątnego bxh mamy:
$$\begin{equation} t_{ef}= \cfrac{b \cdot h }{2 \cdot (b+h)} \quad ; \quad A_k=(b-t_{ef}) \cdot (h-t_{ef}) \quad ; \quad u_k=2 \cdot ( b- t_ef +h-t_{ef}) = 2\cdot (b+h – 2\cdot t_{ef}) \label{33} \end{equation}$$
Naprężenia ścinające w ściance zastępczej przekroju poddanego działaniu wyłącznie momentu skręcającemu $T_{Ed}$ można obliczyć ze wzoru znanego dla pręta cienkościennego o przekroju zamkniętym:
$$\begin{equation} v_{T, Ed} =\cfrac{T_{Ed}} {2 A_k \cdot t_{ef}} \label{34} \end{equation}$$
gdzie zewnętrzny moment skręcający $T_{Ed}$ w w artykule był oznaczany jako $M_v$ , a w mechanice oznacza się jako $M_x$. Pole przekroju $A_k$ zamknięte liniami środkowymi oznaczało się natomiast $\Omega$ .
Strumień naprężeń stycznych $q$ pokazany na rys. S-10 wynosi
$$\begin{equation} q= v_{T} \cdot t_{ef} \label{35} \end{equation}$$
Siła ścinająca i-tą ściankę o długości $z_i$ wynosi
$$\begin{equation} V_i= q \cdot z_i \label{36} \end{equation}$$
Kąt nachylenia krzyżulca betonowego przy jednoczesnym ścinaniu i skręcaniu
Praktycznie w każdym przekroju belki ( i ogólnie pręta) działają siły poprzeczne $V$ , a jeśli przekrój jest dodatkowo skręcany momentem $T$, to oba łącznie wywołują siły poprzeczne, które często mogą być przeniesione przez sam beton reprezentowany przez krzyżulce betonowe nachylone pod kątem $\Theta$ ($\ref{25}$), ($\ref{26}$).
W przypadku jednoczesnego ścinania i skręcania formuła ($\ref{21}$) na kąt nachylenia krzyżulca betonowego jest uogólniana w ten sposób, że naprężenia styczne od sił zewnętrznych podstawia się jako sumę naprężeń od ścinania i skręcania:
$$\begin{equation} \Theta = 1/2 \cdot arcsin \left ( \cfrac{ 2 (\cdot v_{V,Ed}+v_{T,Ed})}{ \nu_1 \cdot \alpha_{cw} \cdot f_{cd}} \right ) \quad \text{ale} \quad 26,7^o \le \Theta \le 45^o\quad \label{37} \end{equation}$$
Kryterium wytrzymałości krzyżulca betonowego
Nośność ścinanego i skręcanego elementu żelbetowego jest limitowana nośnością krzyżulców betonowych. Interakcję ścinania i skręcania przyjmuje się jako liniową zgodnie z zależnością:
$$\begin{equation} \cfrac{T_{Ed}}{ T_{Rd,max}} +\cfrac{V_{Ed}} {V_{Rd,max}} \le 1 \label{38} \end{equation}$$
Nośność krzyżulca betonowego na ścinanie wynosi:
- dla ścinania siła poprzeczną
$V_{Rd,max}$ wg $(\ref{17})$ lub $(\ref{18})$
- dla ścinania momentem skręcającym
$$\begin{equation} T_{Rd,max}=2\cdot \nu \cdot \alpha_{cw} \cdot f_{cd} \cdot A_k \cdot t_{ef} \cdot sin \Theta \cdot cos \Theta \label{39} \end{equation}$$
gdzie $T_{Ed}$, $V_{Ed}$ – obliczeniowe siły przekrojowe – moment skręcający i siła poprzeczna uzyskane z rozwiązania mechaniki budowli.
Sprawdzenie wytrzymałości przekroju betonowego (bez zbrojenia)
W przekrojach pełnych, w przybliżeniu bliskich prostokątnym zbrojenie minimalne uznaje się za wystarczające, gdy spełnione jest równanie interakcji
$$\begin{equation} \cfrac{T_{Ed}}{ T_{Rd,c}} +\cfrac{V_{Ed}} {V_{Rd,c}} \le 1 \label{40} \end{equation}$$
gdzie:
nośność nie zbrojonego przekroju betonowego na skręcanie (moment skręcający rysujący) wyznacza się z
($\ref{34}$) dla $v_{T, Ed} =f_{ct,d}$ , czyli z zależności:
$$\begin{equation} T_{Rd,c}= 2 \cdot A_k \cdot t_{ef} \cdot f_{ct,d} \label{41} \end{equation}$$
Nośność na ścinanie wyznacza się standardowo z formuły ($\ref{13}$) po przemnożeniu przez pole przekroju beton belki $A_v =b\cdot h$
$$\begin{equation} V_{Rd,c}= v_{Rd,c} \cdot b \cdot h \label{42} \end{equation}$$
Zbrojenie przekroju skręcanego
Minimalne zbrojenie
Zbrojenie minimalne belek skręcanych opowiada zbrojeniu minimalnemu belek zginanych, określonemu w rozdziale Belki. Kształtowanie .
Zbrojenie prętami podłużnymi
Sumaryczne pole przekroju prętów podłużnych $\sum A_{sl}$ od skręcania (zmiany paczenia (deplanacji) przekroju po długości pręta) można wyznaczyć z zależności:
$$\begin{equation} \sum A_{sl} = \cfrac{T_{Ed} \cdot ctg \Theta \cdot u_k }{2 \cdot A_k \cdot f_{yd}} \label{43} \end{equation}$$
Zbrojenie podłużne $\sum A_{sl}$ należy rozmieścić tak by w każdym narożu dać przynajmniej jeden pręt, a pozostałe pręty ułożyć wzdłuż boków tak, by odległość pomiędzy prętami nie przekraczała 350 mm.
W pasach ściskanych zbrojenie podłużne można zmniejszyć w proporcji do występujących sił ściskających. W pasach rozciąganych należy dodać do zbrojenia wynikającego ze zginania lub rozciągania.
Oznacza to , że:
- zbrojenie podłużne na skręcanie w strefie rozciąganej elementu musi być zbrojeniem dodatkowym w stosunku do obliczonego na moment zginający
- zbrojenie podłużne w strefie ściskanej (od zginania) nie wymaga uzupełnienia o pręty podłużne obliczeń na skręcanie, gdy naprężenia od skręcania są mniejsze od naprężeń ściskających od zginania
Zbrojenie podłużne normalnie rozmieszczone wzdłuż długości boków $z_i$ dla niedużych przekrojów można skupić na końcach boków.
Zbrojenie poprzeczne (strzemionami)
Zbrojenie poprzeczne na skręcanie wyznacza się z ogólnej formuły ($\ref{22}$) po podstawieniu naprężeń z wyrażenia ($\ref{34}$) i uwzględnieniu, że $b_w=t_{ef}$. Potrzebne zbrojenie poprzeczne na skręcanie wynosi:
$$\begin{equation} \cfrac{A_{sw,T}}{s_{l.T}} \ge \cfrac {T_{Ed} } {2 \cdot A_k \cdot f_{ywd} \cdot ctg \Theta } \label{44} \end{equation}$$
Odległości pomiędzy zbrojeniem na ścinanie powinny spełniać warunek [3], kl.9,2,3(4):
$$\begin{equation} s_{l,T} \le min \{ u_k / 8 \, ; \, b \, ; \, h \} \label{45} \end{equation}$$
Przykłady
Przykład S-1 [Małe ścinanie]
(Bond A. J., Brooker O., Harris A. J., Harrison C., Moss R. M., Narayanan R. S. (2006). How to Design Concrete Structures using Eurocode 2 (A Cement and Concrete Industry Publication). The Concrete Centree))), Lecture 3/24
Wyznaczyć zbrojenie poprzeczne belki ścinanej siłą poprzeczną $V_{Ed}$=705 kN.
Belka o przekroju hxb=1000×450 wykonana z betonu C30/37- B500:
$f_{ck}=30 \, MPa$, $f_{cd}=30/1,4= 21,4$ MPa
($f_{yk}=500 \, MPa,$ $f_{yd} =500/1,15=435 \, MPa$.
Otulenie osiowe zbrojenia dolnego a=66 mm, wysokość efektywna przekroju $d=1000-66=934 \, mm$
Naprężenia ścinające
$(\ref {1})$$\to $ $v_{Ed} = \cfrac{V_{Ed}} {b_w \cdot 0,9 \cdot d}= \cfrac{705}{450 \cdot 0,9 \cdot 934} \cdot 10^3= 1,68 \, MPa$
Z tab S-3 odczytujemy dla betonu C30/37:
$v_{Rd,max} (ctg \Theta=2,0)= 4,526 \, MPa$,
$\nu_1=0,528$
Korzystamy z algorytmu przedstawionego na rys. S-6
$v_{Rd, max} = 4,526 \, > \, 1,68 \, MPa \to ctg \Theta=2,0$.
Sprawdzenie z zależności ($\ref{21}$) :
$ \Theta = 1/2 \cdot arcsin \cfrac{ 2 \cdot 1,68}{ 0,528 \cdot 1,0 \cdot 21,4}=8,6^o < 26,7^o \to$ $\Theta= 26,7^o \to ctg \Theta = 2 $
Przekrój zbrojenia poprzecznego
$(\ref{22})$ $\to$ Potrzebne jednostkowe zbrojenie $\left (A_{sw}/s_l \right ) = \cfrac {1,68 \cdot 450 }{435 \cdot 2,0} = 0,869 \, mm^2/mm$
Przyjęto strzemiona Ø 10, 4-cięte: $A_{sw} = 4 \cdot \cfrac{ \pi \cdot 10^2}{4}= 314 \, mm^2 $
Wymagany rozstaw dla znanego pola przekroju z przekształcenia zależności ($\ref{22}$):
$s_l \le \cfrac{314}{0,869} = 361 \, mm \to $, przyjęto $s_l = 350 \, mm$
Sprawdzenie maksymalnego rozstawu zbrojenia poprzecznego
$(\ref {9}) \to $ $ s_{l,max}= 0,75 \cdot 934= 700 \, > 350 \, mm$
$(\ref{10}) \to $ $ s_{l,max}=12,5 \cdot \cfrac{314\cdot 500}{450 \cdot \sqrt{32}}=796 \, > 350 \, mm$
Sprawdzenie z zależności $(\ref{11})$ $\to$ $s_{l,max} = 1141\cdot 314/ 450 =796 \, mm$
Przykład S-2 [Większe ścinanie ]
(Bond A. J., Brooker O., Harris A. J., Harrison C., Moss R. M., Narayanan R. S. (2006). How to Design Concrete Structures using Eurocode 2 (A Cement and Concrete Industry Publication). The Concrete Centree)), Lecture 3/31
Wyznaczyć zbrojenie poprzeczne dla belki ścinanej
siłą poprzeczną $V_{Ed}$=312,5 kN,
przekroju hxb=550×140 ,
wykonanej z C30/37-B500
Zastosować strzemiona pionowe $\alpha=90^0$
Otulenie osiowe zbrojenia dolnego a=50 mm,
wysokość efektywna przekroju $d=550-50=500 \, mm$
Z tab. S-3 odczytujemy dla betonu C30/37:
$v_{Rd,max} (ctg \Theta=2,0)= 4,526 \, MPa$;
$v_{Rd,max} (ctg \Theta=1,0)= 5,657 \, MPa$ ,
$\nu_1=0,528 $,
$f_{cd}=30/1,4= 21,4 \, MPa$
$(\ref{1}) \to $ $v_{Ed} = \cfrac{312,5}{140 \cdot 0,9 \cdot 500} \cdot 10^3= 4,96 \, MPa$
Korzystamy z algorytmu przedstawionego na rys. S-6
Zachodzi $ 4,53\, < \, v_{Ed}=4,96 \, < \, 5,66 \, MPa \to $ należy wyznaczyć $\Theta$.
Kąt nachylenia krzyżulca betonowego
$(\ref{21}) \to$ $ \Theta= 1/2 \cdot arcsin (2\cdot 4,96 / (0,528 \cdot 1,0 \cdot 21,4 )=0,5358 \,rad=30,7^o \to ctg \Theta= 1,684 $
Przekrój zbrojenia poprzecznego
$(\ref{22})$ $\to$ Potrzebne jednostkowe zbrojenie $\left (A_{sw}/s_l \right ) = \cfrac {4,96 \cdot 140} {500 \cdot 1,684}= 0,825 \, mm^2/mm$
Przyjęto strzemiona Ø 10, 2-cięte: $A_{sw} = 2 \cdot \cfrac{ \pi \cdot 10^2} {4} = 157 \, mm^2$
$(\ref{22})$ $\to$ Rozstaw strzemion $s_l \le \cfrac{157}{0,825} = 190 \, mm \to $, przyjęto $s_l = 190 \, mm$
Sprawdzenie maksymalnego rozstawu zbrojenia poprzecznego
$(\ref {9}) \to $ $ s_{l,max}= 0,75 \cdot 500= 375 \, > 190 \, mm$
$(\ref{11})$ $\to$ $s_{l,max} = 1141\cdot 157/ 140 =1280 \, mm$
Strzemiona w rozstawie $s_l=190 \, mm $ należy ułożyć od lica podpory na długości $l_w= z \cdot ctg \Theta= 0,9 \cdot 500 \cdot 1,684= 758 \,mm$, Przyjęto $l_w= 4 \cdot 190= 760 \, mm$.
Na pozostałej części belki strzemiona można rozstawić w odległości $l < 0,75 \cdot 500=375 \, mm$. Przyjęto $l= 2 \cdot 190= 380 \, mm$
Przykład S-3 [Zbrojenie strzemionami i prętami odgiętymi ]
[9], Przykład.16.6
Swobodnie podparta belka teowa o rozpiętości l_{ef}=3×1,2=6 m, o przekroju 300x 450 (d) jest obciążona obliczeniowymi siłami skupionymi P=550 kN (rys. S-11), wykonana z C25/30- B500 $ (f_y= 500/1,15=435 \, MPa$).
Teoretyczna reakcja w ścianie wynosi $V=550 \, kN$. moment zginający w licu ściany $M_{Rd,lico}= 550\cdot 0,15= 82,5 \, kNm$, a pod siłą skupioną $M_{Ed,P}= 550\cdot 1,2= 660 \, kNm$
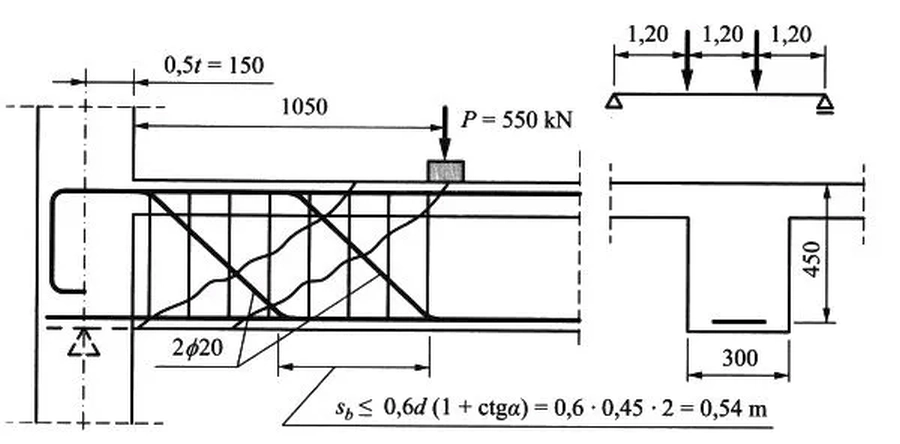
Rys. 14 Ilustracja do przykładu [9]
Siła poprzeczna na podporze $V_{Ed}=550 \, kN$
Rozważono dwa warianty zbrojenia poprzecznego:
a) tylko strzemiona pionowe,
b) hybrydowe złożone ze strzemion pionowych i prętów odgiętych
W przypadku zastosowania zbrojenia hybrydowego nośność prętów odgiętych i nośność strzemion sumuje się, ale strzemiona muszą zapewnić przynajmniej 50% wymaganej nośności.
W wariancie a):
Korzystamy z algorytmu przedstawionego na rys. S-6
$(\ref {1}) \to $ $v_{Ed} = \cfrac{550}{300 \cdot 0,9 \cdot 450} \cdot 10^3= 4,53 \, MPa$
Z tab. S-3 odczytujemy dla betonu C25/30:
$f_{cd}=25/1,4= 17,9 \, MPa$,
$\nu_1=0,540$,
$v_{Rd,max}(ctg \Theta=2,0)= 3,857 \, MPa$,
$v_{Rd,max} (ctg \Theta=1,0)= 4,821 \, MPa$
Zachodzi $ 3,857 \, < \, v_{Ed}=4,53 \, < \, 4,821 \, MPa \to $ należy wyznaczyć $\Theta$.
Kąt nachylenia krzyżulca betonowego
$(\ref {22}) \to $ $ \Theta= 0,5 \cdot arcsin (2\cdot 4,53/(0,540\cdot 17,9 )=0,6074 \, rad= 34,8^o \to ctg \Theta= 1,438 $
W pracy [9]), Przykład 16.6 – inną metodą uzyskano $ctg \Theta= 1,432 $
Przyjęto strzemiona Ø 8 czterocięte $A_{sw}= \cfrac{4 \pi\cdot 8^2}{8}=201 \, mm^2$
$(\ref{22})$ $\to$ Rozstaw strzemion $ s_l \le \cfrac {201 \cdot 435} {4,53 \cdot 300} \cdot 1,438= 93 < 100 \, mm $
Ponieważ wymagany rozstaw strzemion jest zbyt mały, więc podjęto decyzję o zastosowaniu zbrojenia hybrydowego , również prętami odgiętymi (wariant b).
W celu zwiększenia rozstawu między strzemionami, przedział przypodporowy dodatkowo zbrojono prętami odgiętymi. Nośność przekroju jest sumą nośności prętów odgiętych oraz strzemion.
Ze względów konstrukcyjnych zastosowano dwa pręty odgięte Ø 16 pod kątem $\alpha=45^o$
$A_{sw}= 2 \cdot \cfrac{\pi \cdot 1,6 ^2}{4}=4,02 \, cm^2$
$(\ref {23})$ $\to $ nośność prętów odgiętych $ v_{Rd,s} = \cfrac {4,02} {1} \cdot 435 \cdot (ctg \, 34,8^0 + ctg \, 45^0) \cdot \sin \, 45^o \cdot 10^{-1} = 300,5 \, kN$
Do przeniesienia przez strzemiona pozostaje $ V_{Ed} = 550-300 ,5 =245,5 \, kN < 0,5 \cdot 550 =275 \, kN \to V_{Ed}=275 \, kN$
Dla takiej siły naprężenia styczne wynoszą: $v_{Ed} = \cfrac{275}{300 \cdot 0,9 \cdot 450} \cdot 10^3= 2,26 \, MPa \, < \, 3,33 \, MPa$ $\to ctg \Theta= 2,0$
Wymagany rozstaw $ s \le \cfrac {201 \cdot 435} {2,26 \cdot 300} \cdot 2,0= 258 \, mm $
Przykład S-4 [Zbrojenie profilem stalowym ]
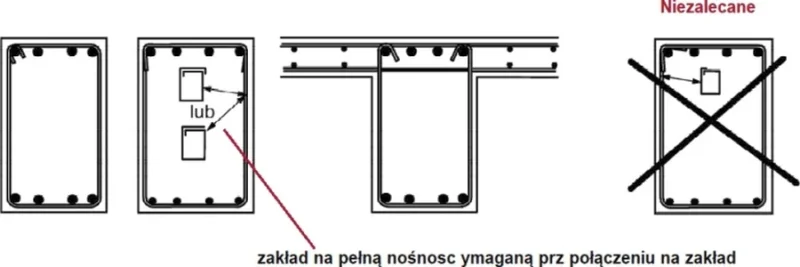
Dla belki przedstawionej w przykładzie S-3 zamiast prętów odgiętych zastosować zbrojenie profilem stalowym zastosowaniem rozwiązania z rys. S-13 ze strzemionami otwartymi spawanymi do środnika profilu dwuteowego (zgodnie z [10], rys. 6.10, Typ.2
Dane ogólne
Przyjęto stal konstrukcyjną S355 o wytrzymałości obliczeniowej :
na rozciąganie $f_y=355 \, MPa$
na ścinanie $f_{yv}= \cfrac{f_y}{\sqrt{7} \cdot \gamma_{M0}}= \cfrac{355}{\sqrt{7} \cdot 1,0}= 205,0 \, MPa$
(współczynnik materiałowy $\gamma_{M0}=1,0$)
Ścinanie i zginanie dwuteownika stalowego
Potrzebne pole przekroju środnika do przeniesienia całkowitej siły $V_{Ed}= 550 \, kN$
$A_v \ge \cfrac{550}{205}\cdot 10^1= 26,8 cm^2$
Przyjęto HEA 260 :
$A_v= 28,7 \, cm^2$
$W_{y,pl}= 919,7 \, cm^3$
Sprawdzenie, czy dwuteownik może przenieść całkowity moment zginający na odcinku przypodporowym
Nośność dwuteownika na zginanie
$M_R=355 \cdot 919,7 *10^(-3) = 326, 5 < M_{Ed,P} =660 kNm \to$ HEA 260 nie przeniesie sam momentu zginającego pod siłą skupioną, a jedynie do rzędnej $x= 326,5/550=0,6 \,m
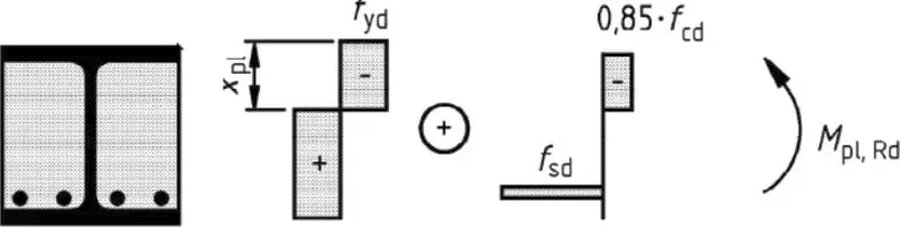
Współpraca strzemion i zbrojenia sztywnego
Zgodnie z [[10] rozdział całkowitej siły ścinającej $V_{Ed}$ na część przypadającą na profil stalowy $V_{a,Ed}$i część przypadającą na beton otaczający środnik $V_{c,Ed}$ przyjmuje się w takim samym stosunku jak udział przekroju stalowego i żelbetu obetonowania środnika w nośności na zginanie M_{pl,Rd}.
W tym przykładzie rozdział przyjmujemy zgodnie z rys. S-14
Nośność przekroju stalowego wynosi
$M_{a,Rd}= 326, 5 \, kNm$
Nośność żelbetu obetonowania środnika liczona jak dla przekroju prostokątnego żelbetowego 300x 250 (wysokość) – C30/37 -B 500 zbrojonego dołem $4 \Phi 16$ (obliczona w odrębnym zadaniu wynosi
$M_{c,Rd}= 119,,5 \, kNm$
Stosunek nośności wynosi $k_{R,ac}= \cfrac{119,5}{326,5} = 0,37$
Strzemiona powinny przenieść siłę poprzeczną $V_{c,Ed}=0,37 \cdot 550 = 203,5 \, kN$
Dla takiej siły naprężenia styczne wynoszą: $v_{Ed} = \cfrac{203,5}{300 \cdot 0,9 \cdot 250} \cdot 10^3= 3,01 \, MPa \, < \, 3,33 \, MPa$ $\to ctg \Theta= 2,0$
Przyjęto strzemiona Ø 10 dwucięte $A_{sw}= \cfrac{2 \pi \cdot10^2}{8}=113 \, mm^2$
Wymagany rozstaw $ s_l \le \cfrac {113 \cdot 435} {3,01 \cdot 300} \cdot 2,0= 157 \, mm $ Przyjęto s=150 mm
Łączniki zespolenia
Zespolenie przekroju stalowego z żelbetem uzyskano poprzez zastosowanie łączników typu Nelson.
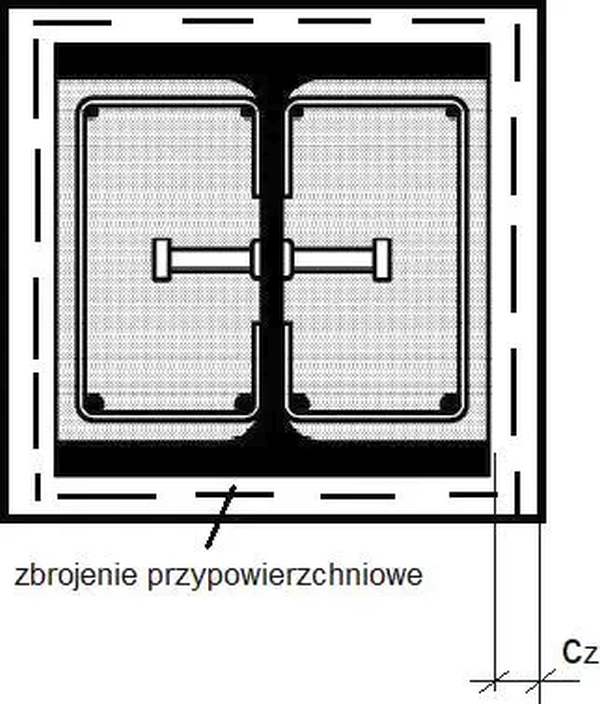
Otulenie profilu oraz zbrojenie przypowierzchniowe
Otulenie profilu powinno spełniać wymogi pożarowe zgodnie z normą [11].
Uzyskane otulenie boczne $c_z= 20 \, mm$ spełnione są wymagania dla R30 Dla innych klas odporności ogniowej należy poszerzyć belkę: dla R180 – o 60 mm (tak aby $c_z= 50 \, mm$
Zastosowano zbrojenie przypowierzchniowe zgodnie [3], Zał. J.
Uwaga o optymalności rozwiązań
Współczesne rozwiązania konstrukcyjne belek szczególnie leżącą na nich płytą stropową zmierzają współcześnie w kierunku stosowania konstrukcji zespolonych zamiast czystych rozwiązań żelbetowych zarówno w warunkach dużego zginania jak ścinania. Rozwiązania zespolone są o ok 20 do 40% bardziej optymalne. W przykładzie S-4 wskazano na mniej istotny aspekt zagadnienia – ścinanie przekroju zespolonego, a największe korzyści uzyskano by po włączeniu profilu stalowego do zginania belki. Nie jest to jednak przedmiotem przykładów w niniejszym artykule.
Przykład S-5 [ Skręcanie i ścinanie prostokątnego pręta żelbetowego ]
Przykład na podstawie [12]
Belka żelbetowa wykonana z betonu C30/37- B500
o przekroju prostokątnym 600×400
zbrojona na zginanie prętami przekroju 4#25 ($A_sl=19,63 \, cm^2$
Otulenie zbrojenia $c_l =50 \, mm$; otulenie osiowe $a_l =50+25/2= 62,5 \, mm$
Efektywna wysokość przekroju $d=d_l=600-62,5 =$ 537 mm
Ramię sił do obliczeń ścinania $z=0,9 \cdot 537 =$ 483 mm
Przekrój krytyczny belki jest poddany działaniu sił:
moment skręcający $T_{Ed}=55 \, kNm$ ,
siła poprzeczna $V_{Ed}=225 \, kN$
Dane materiałowe
Beton C30/37 $\to$ tab. W-1
$f_{ck} = 30 \, MPa$,
$f_{cd}= 21,4 \, MPa$ ($\gamma_c=1,4$),
$ f_{ctm}=2,9 \, MPa$ ;
(W-1) $ f_{ctd}=0,7 \cdot 2,9 / 1,4 = 1,45 \, MPa$
Stal zbrojeniowa B500 $\to$ tab. W-2
$f_{yk} = 500 \, MPa$ ,
$f_{yd}= 435 \, MPa$ ($\gamma_a=1,15$)
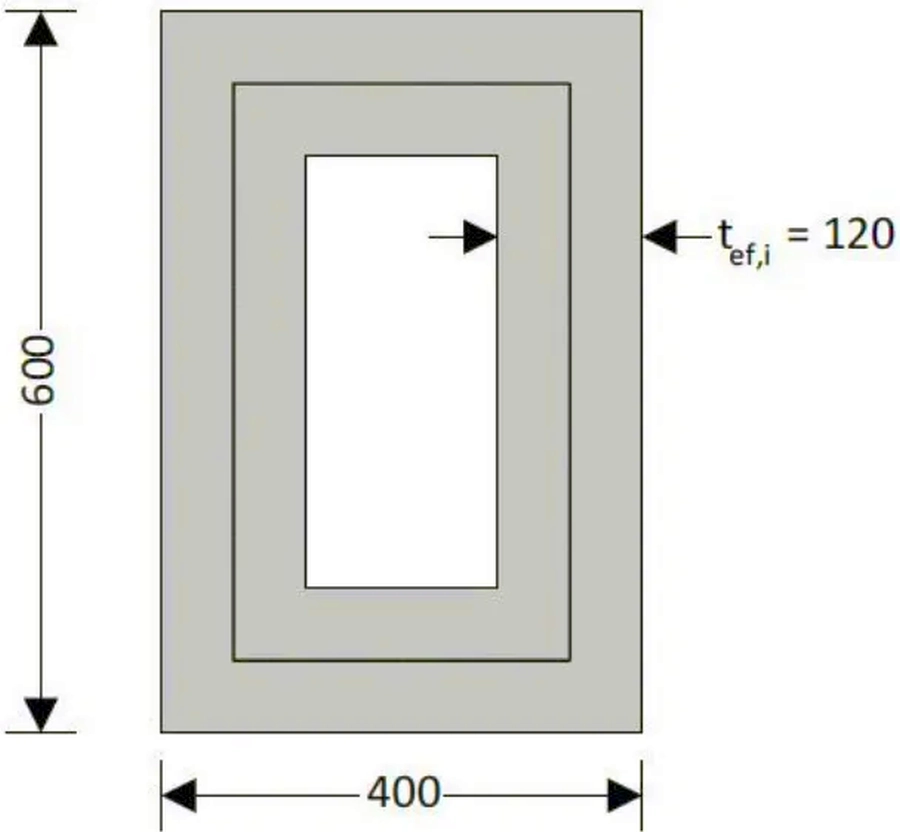
Przekrój zastępczy i grubość efektywna ścianki (rys. S-15)
Powierzchnia pola przekroju $A=60 \cdot 40 =2400 \, cm^2$
Obwód przekroju $u=2 \cdot (60+40)= 200 \, cm$
($\ref{32}$) $ \to$ Efektywna grubość ścianki przekroju $ t_{ef}= \cfrac{2400}{200}= 12 \, cm = 120 \, mm$
Parametry przekroju zastępczego na skręcanie:
$(\ref{33})$ $\to$ $A_k=(40-12) \cdot (60-12)= 1344 \, cm^2 $ ;
$u_k= 2 \cdot (400+600 – 2 \cdot 120)= 1520\, mm$
Naprężenia ścinające
Od siły poprzecznej ($\ref{1}) \to $ $v_{V,Ed} = \cfrac{225} {40 \cdot48,3} \cdot 10^1= 1,162 \, MPa$
Od momentu skręcającego $(\ref{34})$ $\to$ $v_{T,Ed} =\cfrac{55} {2 \cdot 1344 \cdot 12} \cdot 10^3 = 1,705 \, MPa$
Nośność na ścinanie
Współczynnik redukcji naprężeń
($\ref{19}$) $\to$ $\nu_1= 0,6 \cdot (1- \cfrac {31}{250}) =0,528 $
Współczynnik ściskanego krzyżulca betonowego ($\ref{20}$) $ \to \alpha_{cw}=1,0$ (dla stopnia ściskania przekroju $n_{cp}=0$),
Kąt nachylenia krzyżulca betonowego
($\ref{39})$ $ \to \Theta = 1/2 \cdot arcsin \left ( \cfrac{ 2 \cdot (1,162+1,705)} { 0,528 \cdot 1,0 \cdot 21,4 } \right )=15,2^o ( \le 45^o \, , > 26,7 ^o) \to $ przyjęto $\Theta= 26,7 ^o \to $ $ctg \Theta =2$
Nośność na ścinanie przy skręcaniu
($\ref{43}$) $\to T_{Rd,max}=2 \cdot 0,528 \cdot 1,0 \cdot 21, 4 \cdot 1344 \cdot 12 \cdot sin 26,7 \cdot cos 26,7 \cdot 10^{-3}=146,3 \, kNm$
Nośność na ścinanie przez siłę poprzeczną
($\ref{18}$) $\to$ $v_{Rd,max} = \cfrac{ 1,0 \cdot 0,528 \cdot 21,4}{ 2 +1/2} = 4,52 \, MPa$
($\ref{1}$) $\to V_{Rd,max} = 4,52 \cdot 40 \cdot 48,3 \cdot 10^{-1} = 873,2 \, kN$
Warunek wytrzymałości krzyżulca betonowego
($\ref{41}$) $\to \cfrac{55}{ 146,3} +\cfrac{225} {873,2} = 0,376 + 0,258= 0,634 \le 1$
OK: przekrój betonowy (szalunek) jest odpowiedni
Sprawdzenie wytrzymałości samego betonu na skręcanie i ścinanie
Nośność przekroju na skręcanie bez zbrojenia na skręcanie
($\ref{41}$) $ \to T_{Rd,c}= 2 \cdot 1344 \cdot 12 \cdot 1,45 \cdot 10^{-3}= 46,8 \,kNm$
Nośność przekroju na ścinanie
pod ($\ref{13}$) $\to C_{Rd,c}= 0,129$,
$k= 1+\sqrt{200/d_l} \le 2,0 = 1 + \sqrt{200/537 } =1,61 $,
$\nu_{min}= 0,035 \cdot 1,61^{3/2} \cdot 30^{1/2}= 0,392 \, MPa$,
$k_1 = 0,15$,
$\rho_l= min \{ 19,63 / (53,7 \cdot 40) \quad ; \quad 0,02 \}=0,009$
Nośność na ścinanie przekroju zbrojonego podłużnie na zginanie
($\ref{41}$) i ($\ref{13}$) $\to v_{Rd,c}= max \{ 0,129 \cdot 1,61 \cdot (100 \cdot 0,009 \cdot 30,0)^{1/3} \, ; \, 0,392 \} + 0,0588 \cdot 0 = 0,623 \, MPa $
$V_{Rd,c}= v_{Rdc} \cdot d \cdot b = 0,623 \cdot 53,75 \cdot 40 \cdot 10^{-1} = 133,9 \, kN$
Warunek nośności przekroju nie zbrojonego na skręcanie
($\ref{40}$) $\to \cfrac{55}{ 46,8} +\cfrac{225} {133,9} = 1,175 + 1,680= 2,86 \, > 1 \to $ przekrój wymaga zbrojenia na skręcanie
Zbrojenie poprzeczne na skręcanie
Wymagane poprzeczne zbrojenie na skręcanie (jedno ramię strzemiona) na długość jednostkową belki
($\ref{44}$) $ \to \left( \cfrac{A_{sw,T}}{s_{l.T}} \right) = \cfrac {55} {2 \cdot 1344 \cdot 435 \cdot 2,0 } \cdot 10^5=2,35 \, mm^2/mm $
Przyjęto strzemiona Ø 8 zamknięte (2-cięte) o przekroju jednego ramienia: $A_{sw1} = \cfrac{ \pi \cdot 8^2}{4}= 5,02 \, mm^2 $
Rozstaw strzemion na skręcanie
($\ref{45}$) $\to s_{l,T} \le min \{ 1520/8 \, ; \, 400 \,; 600 \} = 190 \, mm \to $ przyjęto $s_{l,T}= 190 \, mm$
Zbrojenie na ścinanie
Naprężenie ścinające od siły poprzecznej obliczono wyżej $v_{Ed}= v_{V,Ed} = 1,162 \, MPa$
Kat nachylenia krzyżulca betonowego $\Theta$ przyjmuje się taki sam jak dla skręcania, czyli
$ \Theta = 15,2^o ( \le 45^o \, , > 26,7 ^o) \to $ $\Theta= 26,7 ^o \to $ $ctg \Theta =2$
Przekrój zbrojenia poprzecznego na ścinanie
$(\ref{22})$ $\to$ Potrzebne jednostkowe zbrojenie $\left (A_{sw}/s_l \right ) = \cfrac {1,162 \cdot 400 }{435 \cdot 2,0} = 0,534 \, mm^2/mm $
Przyjęto strzemiona Ø 12, 2-cięte: $A_{sw} = 2 \cdot \cfrac{ \pi \cdot 12^2}{4}= 226 \, mm^2 $
$(\ref{22})$ $\to$ Rozstaw strzemion $s_l \, < 226/ 0,534 =423 \, mm \to$ przyjęto $s= 300 \, mm$
Sprawdzenie maksymalnego rozstawu zbrojenia poprzecznego
$(\ref {9}) \to $ $ s_{l,max}= 0,75\cdot 537 \cdot (1+0) = 403 \, > 300 \, mm$
$(\ref{11}) \to $ $ s_{l,max}=1141 \cdot 226 / 400=645 \, > 300 \, mm$
Strzemiona w rozstawie $s_l=300 \, mm $ należy ułożyć od lica podpory na długości $l_w= z \cdot ctg \Theta= 483 \cdot 2 = 966 \,mm$, Przyjęto $l_w= 4 \cdot 300= 1200 \, mm$.
Na pozostałej części belki strzemiona można rozstawić w odległości $l < 0,75 \cdot 537=403 \, mm$. Przyjęto $l= 400 \, mm$
Zbrojenie na ścinanie i skręcanie
Zbrojenie wymagane na skręcanie i ścinanie należy stosować łącznie, to znaczy:
1) strzemiona 2-cięte Ø 12 należy ułożyć na długości 1200 mm od lica podpory w rozstawie 300 mm
2) strzemiona 2-cięte Ø 12 poza strefami przypodporowymi 1200 mm ułożyć w rozstawie 400 mm
3) na całej długości belki (dokładniej na długości działania momentu skręcającego $T= 55 \, kNm$ ) dodatkowo dać strzemiona Ø 8 co 190 mmLiteratura
- Pyrak S. (2012), Konstrukcje z betonu (VII, Tom 5). WSiP
- Knauff M. i in., (2006), Podstawy projektowania konstrukcji żelbetowych i sprężonych: według Eurokodu 2. Dolnośląskie Wydawnictwo Edukacyjne
- PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- Knauff M., Golubińska, A.., Knyziak P. (2015). Przykłady obliczania konstrukcji żelbetowych. Budynek ze stropami płytowo-żebrowymi. Zeszyt 1. PWN
- Bond A. J., Brooker O., Harris A. J., Harrison C., Moss R. M., Narayanan R. S. (2006). How to Design Concrete Structures using Eurocode 2 (A Cement and Concrete Industry Publication). The Concrete Centree
- PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- Dahlgren A., Svenson L., (2013) Guidelines and Rules for Detailing of Reinforcement in Concrete Structures, Master Thesis, Chalmers University of Technolody, Göteborg, Sweden, fig. 6.4. [ https://publications.lib.chalmers.se/records/fulltext/188834/188834.pdf ]
- Okoński R., (2020) Skręcanie w konstrukcjach żelbetowych, Niezależny Portal Budowlany, [ https://www.statyka.info/skrecanie-w-konstrukcjach-zelbetowych/]
- Knauff M., Golubińska A., Knyziak P. (2014). Tablice i wzory do projektowania konstrukcji żelbetowych z przykładami obliczeń, Wydanie drugie. PWN
- PN-EN 1994-1-1+Ap1+AC:2008, Eurokod 4, Projektowanie zespolonych konstrukcji stalowo-betonowych, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1994-1-2:2008, Eurokod 4, Projektowanie zespolonych konstrukcji stalowo-betonowych- Część 1-2: Reguły ogólne. Projektowanie z uwagi na warunki pożarowe
- Ubani Obinna, (2021), Worked Example. Design of RC beams for torsion )EN 1992-1:2004) [ https://structville.com/2021/01/worked-example-design-of-rc-beams-for-torsion-en-1992-12004.html ]
________________________________