Chodor L., Belki żelbetowe,, Encyklopedia πWiki, www.chodor-projekt.net,
13 lipca 2018 – 9 czerwca 2020 – ( publikacja kompletna)
07-02-2025 rewizja po dużej awarii portalu
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Arkusz LCżelbet zawiera oryginalny kod – © wszelkie prawa zastrzeżone.
Artykuł w ciągu ostatnich 24 godzin czytało 26 Czytelników
Część K
Kształtowanie
Nawigacja: [ W: Wprowadzenie ] ⇐ ⊗ ⇒ [ Z: Zginanie ]
Belki obok płyt są najczęściej stosowanymi elementami konstrukcji żelbetowych. Klasyczna definicja belki – w przypadku konstrukcji żelbetowych jest osłabiona i obejmuje również stosunkowo krótkie pręty długości $L \approx 3h$.
Elementy krępe (dla $L\le 3h$) są nazywane belkami-ścianami i należy je analizować jako tarcze – nie są bowiem spełnione podstawowe założenia teorii belkowej ( w tym założenie Bernoulliego o płaskich przekrojach i założenie o małych naprężeniach stycznych), co w wyniku uniemożliwia stosowanie wzorów belkowych oraz wnioskowania dotyczącego położenia osi obojętnej przekroju oraz rozkładu naprężeń po wysokości belki-ściany. Może się zdarzyć, że w poziomej osi symetrii belki-ściany naprężenia normalne będą największe, choć zgodnie z teorią belkową powinny być zerowe. W takich przypadkach zaleca się stosowanie metody kratownicowej (modele S-T wg [1].
Belki są zginanymi poprzecznie elementami konstrukcyjnymi. W praktyce jednak zginanie przekroju jest stowarzyszone z działaniem siły osiowej- ściskającej lub rozciągająca, a elementy są belkami-słupami. Rozróżnienia między belką a słupem w istocie zależy od zjawisk niestateczności : w belce zwichrzenia, a w słupie wyboczenia. Zginanie i siły osiowe są przenoszone w belce poprzez zbrojenie podłużne. Ścinanie natomiast przez zbrojenie poprzeczne : strzemiona oraz pręty odgięte. W przypadku skręcania daje się dodatkowe zbrojenie podłużne wynikające z paczenia przekroju i potrzebne do przeniesienia dodatkowych sił podłużnych wywołanych tym odkształceniem ( w mechanice prętów cienkościennych siły przekrojowe stowarzyszone z paczeniem nazywa się bimomentem).
System konstrukcyjny, a belka żelbetowa
W konstrukcjach żelbetowych siły przekrojowe powszechnie uzyskuje się z rozwiązania systemu konstrukcyjnego złożonego z klasycznych prętów (Bernoulliego), przy czym zawsze zaleca się zastosowanie teorii 2-rzędu, to znaczy uwzględnianie wpływu przemieszczeń na siły przekrojowe. Teoria 2-rzędu jest zaimplementowana praktycznie we wszystkich współczesnych programach. Ograniczenie do klasycznej teorii 1-rzędu powinno być uzasadnione- należy wykazać, że w prętach występują małe siły ściskające $N$ , to znaczy takie, które nie mają istotnego wpływu na stateczność systemu konstrukcyjnego, oraz nie generują momentów zginających drugiego rzędu $M_{II}= N\cdot e$, gdzie $e$ jest wygięciem pręta.
Jeśli system konstrukcyjny będzie obciążony poziomymi siłami od imperfekcji, to elementy prętowe, w tym belki (i słupy) można wymiarować bez wyznaczania długości wyboczeniowej oraz współczynników wyboczeniowych elementów ściskanych lub zginanych (zjawisko zwichrzenia belek). Do tego celu konstrukcję żelbetową wystarczy obciążyć poziomo siłami (równoważnymi od imperfekcji, poprzez stowarzyszenie do każdego obciążenia pionowego $Q_V$ – obciążeń poziomych $Q_H$ w kierunkach obu osi poziomych:
$$\begin{equation} Q_{Hx}=Q_{Hy}= \cfrac{Q_V}{200} \label {1} \end{equation}$$
Symbol $Q_V$ oznacza obciążenie grawitacyjne (pionowe) zarówno powierzchniowe, liniowe jak i skupione- obejmuje więc również ciężar własny $G$.
W każdym przypadku konstrukcje żelbetowe znamienne są tym, że istotne jest w nich ścinanie elementów i przekrojów. Siły przekrojowe w belkach należałoby więc wyznaczać zgodnie z teorią Timoschenko, którą krótko opisano w artykule Belka Timoschenko na sprężystym podłożu. Niestety algorytm uwzględniania sztywności ścinania zwykle nie jest obecny w inżynierskich programach komputerowych. Dlatego w praktyce projektowej siły przekrojowe w konstrukcji żelbetowej wyznacza się z użyciem klasycznych elementów prętowych. W przypadku elementów skręcanych (np. skrzynki mostów) lub trzonów budynków wysokich stosuje się analogię teorii prętów cienkościennych (p. artykuł Pręty cienkościenne i artykuły związane)
W niniejszym opracowaniu zakładamy, że z rozwiązania statyki znane są siły przekrojowe (N, M, Q)=(siła osiowa, moment zginający, siła poprzeczna) w przekrojach belki. Na podstawie sił w konkretnym przekroju można dobrać wymagane zbrojenie w tym punkcie belki, a na podstawie rozkładu sił po długości belki można skonstruować zbrojenie całego elementu. W normie [1] przedstawiono reguły projektowania belek żelbetowych w następujących klauzulach:
klauzula kl. 6.1. – nośność na zginanie z siłą podłużną; kl. 9.2.1.1 (1), wzór (9.1.N) – minimalne zbrojenie ; kl. 9.2.1.1 (3) – maksymalne zbrojenie; kl. 6.2.2.(1), wzór (6.2a), (6.2b) – nośność na ścinanie; kl. 6.3.2 (6), (6.3.1) – interakcja ścinania i skręcania. Wymienione zasady stanowią komplet reguł projektowych, umożliwiających zaprojektowanie belki zginanej, ściskanej, ścinanej i skręcanej.
Ponadto norma podaje szereg zasad konstruowania zbrojenia, które są spójne z regułami projektowymi, ale są adresowane raczej do autorów rysunków warsztatowych, czyli wykonawców i ich technologów, a nie do projektantów: kl. 8 – konstruowanie zbrojenia; kl. 9.2 , 9.3 oraz 9.4 – konstruowanie belek i płyt pełnych oraz płaskich.
Geometria belek żelbetowych
Projektowanie geometrii belek żelbetowych wynika z warunków funkcjonalno-architektonicznych oraz prostych zasad optymalnego doboru wymiarów szalunkowych i jest praktycznie niezależnie od zbrojenia belek. Na etapie doboru zbrojenia, w szczególnych przypadkach konieczna jest korekta szalunków (zbrojenie. Często jednak w takich sytuacjach korekt dokonuje się bez zwiększania szalunków poprzez wstawienie zbrojenia sztywnego, to znaczy skonstruowanie przekroju zespolonego betonowo-stalowego.
Przekroje belek i długość obliczeniowa
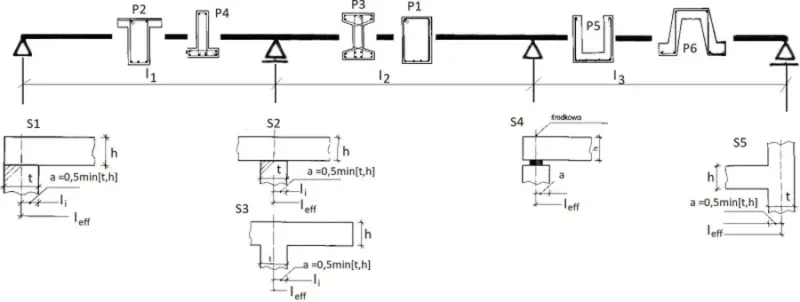
Na rys. K-1 pokazano schemat belki wieloprzęsłowej o teoretycznych długościach przęseł $l_1, l_2, l_3$. Przy oznaczeniu długości belki w świetle murów $l_i$, długość obliczeniową $l_{ef}$ zgodnie z [1] można wyznaczyć z zależności
$$\begin{equation} l_{ef}=l_i+a_l+a_r \label{2}\end{equation}$$
gdzie: $a_l$ i $a_r$ są odległościami od lica muru odpowiednio lewej i prawej podpory przęsła do obliczeniowej osi podpory $a=\min {\{ t/2 \quad ; \quad h/2 \}}$ (h- wysokość płyty, t-szerokość podpory (ściany lub słupa). W przypadku podpory środkowej z łożyskiem przyjmuje się os podpory obliczeniowej w osi teoretycznej systemu. Łożysko powoduje wycentrowanie reakcji, a w pozostałych przypadkach położenie reakcji przesuwa się w głąb ściany lub słupa.
Oparcie belek na słupach realizuje się najczęściej poprzez podcięcie słupa lub na krótkim wsporniku w sposób pokazany w artykule Słupy żelbetowe.
Belki żelbetowe mają najczęściej przekrój prostokątny P1, teowy P2, dwuteowy P3 lub rzadziej przekroje o innych kształtach (P4, P5, P6).
Belki najczęściej występują w układach płytowo -słupowych lub są stosowane jako odrębne elementy. Na rys. K-2 pokazano typowy układ płytowo-belkowo-słupowy, w którym zastosowano dwa poziomy belek: podciągi B1 oraz żebra B2. Belki wraz ze współpracującą częścią płyty nazywane są T-belkami.
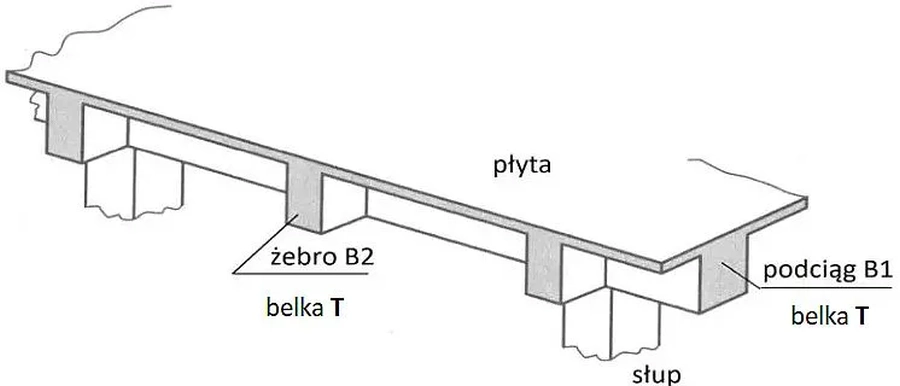
Rys. 2. Strop płytowo-belkowo-słupowy. Belki: B1 (podciąg) i B2 (żebra) (opracowano na podstawie [2], rys.4-28a)
Wysokość belki $h$
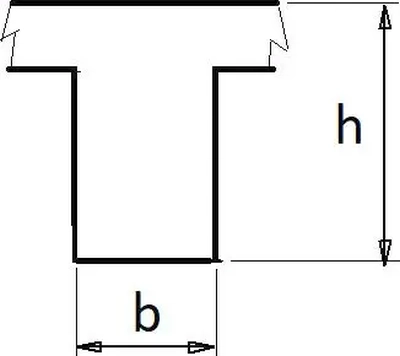
Najważniejszym parametrem belki jest jej wysokość $h$, którą należy liczyć wraz z grubością podpieranej płyty (rys. K-3).
Wymiary belek zależą w ogólności od: rozpiętości, sposobu podparcia, obciążenia, warunków pożarowych oraz środowiskowych (wymaganego otulenia zbrojenia).
Wstępnie (na etapie koncepcji) wysokość belki h przyjmuje się jako część jej długości $l$:
$$\begin{equation} h \approx \dfrac{l}{n_h} \ge 250 \text{ mm, co 50 mm } \label {3} \end{equation}$$
gdzie $n_h=10 \div 20$
przy czym w przypadku braku dokładniejszych informacji przyjmuje się $n_h=20$.
Znajomość dodatkowych cech konstrukcji pozwala na dokładniejsze przyjęcie podzielnika $n_h$ ( [1],tab.7.4.N oraz praktyka)
$$ \begin{equation} n_h= \begin {cases}
10 \div 12, & \textrm { podciagi silnie obciazone} \\
12 \div 15, & \textrm { podciagi slabo obciazone} \\
12 \div 18, & \text { zebra silnie obciazone} \\
14 \div 20, & \text { belki i płyty swobodnie podparte} \\
17 \div 24, & \text { stropy bezbelkowe (plaskie) na słupach } \\
18 \div 20, & \text { belki dachowe i inne słabo obciazone} \\
18 \div 26, & \text { skrajne przesła belek lub plyt ciąglych} \\
20 \div 30, & \text { wewnetrzne przesla belek lub plyt ciaglych} \\
\end {cases} \label{4} \end{equation}$$
Dla wsporników długość $l$ zwiększa się dwukrotnie.
Większe dzielniki $n_h$ dotyczą elementów słabo ściskanych ( stopień zbrojenia $\rho$=0,5%), a mniejsze elementów silnie ściskanych ($\rho$=1,5%).
Szerokość belki $b$
Szerokość belki $b$ przyjmuje się w zależności od wysokości $h$ w granicach:
$$\begin{equation} b \approx \dfrac{h}{2 \div 2,5 } \ge 150 \text{ mm, co 50 mm } \label {5} \end{equation}$$
Wstępny dobór zbrojenia przekroju
Oszacowanie sił przekrojowych
W obliczeniach wstępnych, koncepcyjnych – momenty zginające przekrój belki wyznacza się z szacunkowych formuł analitycznych bez uruchomiania programu komputerowego.
Miarodajny moment zginający $M_y$ w belce o długości obliczeniowej $l_{ef}$ i obciążonej w płaszczyźnie zginania równomiernie rozłożonym obciążeniem $Q_z$ można wstępnie oszacować z formuły
$$\begin{equation} M_y=\dfrac{Q_z \cdot l_{ef}^2}{n_M} \label {6} \end{equation}$$
gdzie $n_M=8 \div 12$ zależnie od schematu statycznego belki (1P – belka jednoprzęsłowa, 2P – belka dwuprzęsłowa, 3P- belka trójprzęsłowa):
$$\begin{equation} n_M= \begin {cases}
8, & \text {moment przęsłowy 1P lub moment podporowy 2P} \\
10, & \text { moment utwierdzenia 1P sprężyście zamocowanej i moment podporowy 3P} \\
12, & \text { moment podporowy 1P utwierdzono-utwierdzonej i szacunkowo przęsłowy 3P}
\end {cases} \label{7}\end{equation}$$
Koncepcyjny dobór zbrojenia
Koncepcyjny wstępny dobór zbrojenia przekroju można dokonać praktycznie bez wykonywania żmudnych obliczeń.
W przypadku przekroju symetrycznie podwójnie zbrojonego $A_{su}=A_{sl}$, nośność przekroju o wysokości h i otuleniu osiowym prętów $a$ wynosi
$$\begin{equation} M_{Rd}=\Sigma A_s \cdot f_{yd} \cdot (h-2a)\label {8} \end{equation}$$
Mamy stąd oszacowanie pola przekroju sumy zbrojenia górnego i dolnego $\Sigma A_s=A_{su}+A_{sl}$ :
$$\begin{equation} \Sigma A_s \approx \dfrac {M_y} {f_{yd} \cdot (h-2a)} \label {9} \end{equation}$$
czyli dla szczególnego przypadku ściśle symetrycznego zbrojenia.
$$\begin{equation} A_{su}=A_{sl} \approx \dfrac {M_y} { f_{yd} \cdot 2 (h-2a)} \label {10} \end{equation}$$
W oszacowaniach $(\ref{9})$ i $(\ref{10})$ nie występują parametry betonu, ani też informacje o kształcie przekroju. To znaczy formuły te są ważne dla każdego betonu i przekroju o dowolnym kształcie.
W przypadku przekroju zbrojonego pojedynczo możemy stosować analogiczne oszacowanie z warunku
$$\begin{equation} A_s \approx \dfrac{M_y} {f_{yd} \cdot z } \label {11} \end{equation}$$
gdzie
z – jest ramieniem sił wewnętrznych $z=\zeta d$
d – użyteczna wysokość przekroju $d=h-a$
$\zeta=[1 \, ; \, 0,5]$ – parametr zależny od udziału betonu w przenoszeniu momentu zginającego. W wymiarowaniu wstępnym można przyjąć $\zeta=0,85 \approx 0,9 $.
W projektowaniu wstępnym możemy stosować tablice. Obszerne tablice do wymiarowania zginanych elementów żelbetowych zawiera praca [3].
W żadnym przypadku nie można poprzestać na wymiarowaniu wstępnym. Jest ono wymagane jedynie po to, by zbudować model konstrukcji, przeznaczony do analizy w programie komputerowym, gdzie dokonuje się iteracyjnej korekty zbrojenia z warunku spełnienia stanów granicznych nośności (w stanie zarysowanym betonu) i użytkowalności, ale także optymalności z warunku kosztów całej konstrukcji.
Może się okazać, że optymalizacja elementu po elemencie nie daje rozwiązania optymalnego dla całej konstrukcji statycznie niewyznaczalnej – opłaca się przewymiarować kilka elementów, by odciążyć pozostałą część konstrukcji. We współczesnych programach obliczeniowych iteracje dokonywane są w krótkim czasie i sprawnie, co powoduje, że nie opłaca się poświęcać zbyt wiele czasu na projektowanie wstępne – zbrojenie elementów „podawane” do programu należy dobrać z grubsza.
W projektowaniu koncepcyjnym pomija się dobór zbrojenia na ścinanie, oprócz doboru grubości płyt w stropach belko-płytowych lub fundamentowych ze względu na ścinanie przy przebiciu – artykuł Przebicie płyty żelbetowej.
Kształtowanie układu zbrojenia w przekroju
Otulenie zbrojenia
Otulenie pręta $c_{nom}$ (rys. K-4) powinno zapewniać przyczepność i dobre zagęszczenie betonu, ochronę przed korozją zbrojenia oraz temperaturą w warunkach pożarowych. Wymagane otulenie zbrojenia belek podlega ogólnym wymogom dla elementów żelbetowych.
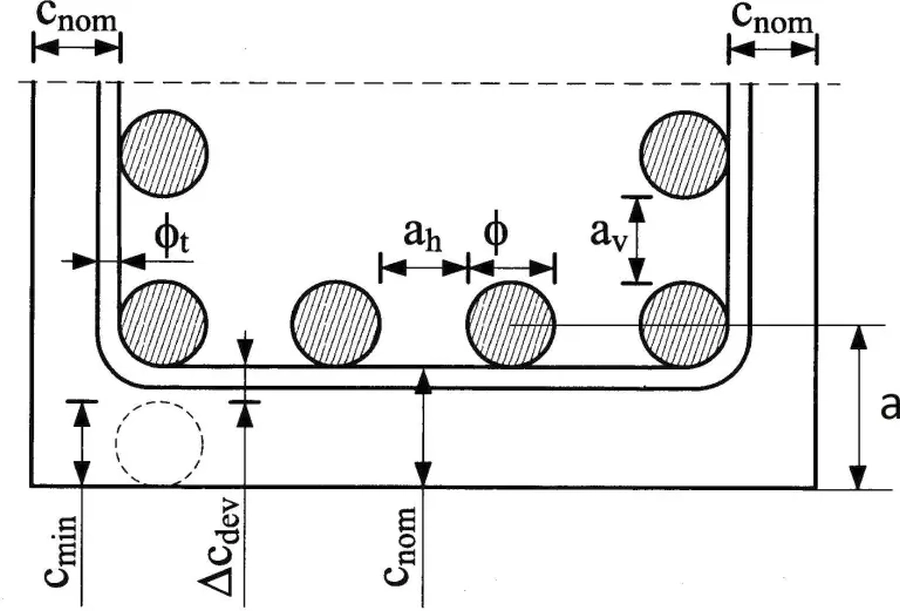
Rys. 4 Otulenie oraz odstępy prętów (zmodyfikowany rysunek [3],rys.3.1)
Wstępnie można przyjmować otulenie $c_{nom}$ (odległość od krawędzi belki do pobocznicy zbrojenia) dla założonej średnicy zbrojenia $\Phi$ z formuły
$$\begin{equation} c \approx \max { \{ \Phi \, ; \, \Delta c_{dur} \, ; \, 10 \} } + 10 \, mm \label{12} \\
\\ c_{nom}= c+ \Phi_s\end{equation}$$
gdzie $ \Delta c_{dur}$ jest otuleniem wymaganym ze względu na klasę ekspozycji.Dla typowych konstrukcji w klasie wykonania S4 i okresie użytkowania 50 lat dla najczęściej występujących klas ekspozycji możemy przyjąć
$\Delta c_{dur}$= 25 mm (XC2/XC3), 30 mm (XC4), 35 mm (XD1/XS1), 40 mm (XD2/XS2), 45 mm (XD3/XS3).
Dodatek „+ 10 mm ” w $(\ref{12})$ jest dodatkiem na odchyłki w obliczeniach $\Delta c_{dev}$. Zaleca się przyjmować $\Delta c_{dev}=10 \, mm.$, ale wartość tą można zmniejszyć (lub zwiększyć):
- gdy stosowany jest system zapewnienia jakości wykonywania elementów, polegający na pomiarach otulenia zbrojenia, to $ 5, \, mm < \Delta c_{dev} \le 10 mm$,
- gdy do wykonania pomiarów stosowane jest bardzo dokładne urządzenie pomiarowe nieklasyfikujące elementów niespełniających wymagań otulenia (np. produkcja prefabrykatów), to $ 0\, mm < \Delta c_{dev} \le 10\, mm$.
Oznacza to, że w przypadku stosowania prefabrykatów można zaoszczędzić na wymiarach elementów 5 do 10 mm z każdej strony (powierzchni).
Średnica strzemion $\Phi_s$ często jest pomijana w projektach wstępnych.
W warunkach pożarowych otulenie definiuje się jako
$$\begin{equation} a=c_{nom} +\Phi/2 \label {13} \end{equation}$$
Również w obliczeniach stosuje się otulenie osiowe $a$.
Na przykład dla minimalnej średnicy zbrojenia głównego w belkach $\Phi=10$ mm, i minimalnej średnicy strzemion $\Phi_s= 6 \, mm$ ; elementów konstrukcyjnych instalowanych wewnątrz zwykłych pomieszczeń (klasa ekspozycji XC2), mamy
$c= \max { \{ 10 \, ; \, 25 \, ; \, 10 \}} + 10 \, mm =35 \, mm$
$c_{nom} = 35+6 = 41 \, mm$
$a = 41+ 10/2=46 \, mm$
Odstępy między prętami
Odstęp z warunku technologicznego (zagęszczenia mieszanki betonowej )
Odstępy między prętami w warstwie $a_h$ oraz odstępy między warstwami $a_v$ (rys. K-4) powinny spełniać warunek
$$\begin{equation} a_{h,v} \ge \max { \{ \Phi \, ; \, 20 mm \, ; \, d_g +5 mm \}} \label {14} \end{equation}$$
gdzie $\Phi$ – maksymalna średnica prętów zbrojenia w warstwie lub warstwach, a $d_g$ – wymiar ziarna kruszywa betonu.
Wymaganie $(\ref{14} )$ w strefie zakładu prętów (na długości zakładu pręty można układać na styk). Jeżeli pręty rozmieszcza się w kilku warstwach, to w celu dostępu urządzeń wibracyjnych do zagęszczania betonu – należy je rozmieszczać jeden nad drugim, a nie mijankowo .
Odstęp między prętami głównymi z warunków konstrukcyjnych
Pręty podłużne należy umieszczać w miejscach zmian kierunku prętów poprzecznych: strzemion i wkładek tupu U. Z tego warunku wynika wymóg umieszczania prętów podłużnych co najmniej w narożach przekroju.
W celu zapewnienia prawidłowej współpracy betonu z prętami przypowierzchniowymi na obwodzie pręta lub innego elementu wymaga się, by rozstaw pomiędzy prętami nie był większy zasadniczo od
$a= 300 \, mm$ ,
a w szczególnych przypadkach maksymalnie nie większy od
$a= 350 \, mm$ .
Na danej ściance pręty należy rozmieszczać w miarę równomiernie, czyli na przykład .gdy rozstaw pomiędzy prętami narożnymi (na ściance pionowej lub poziomej) wynosi
$a= 1000\, mm$, to należy dać min dwa pręty pośrednie w rozstawie $a=1000/3=333 \, mm$
$a=1100 \, mm$ to należy dać min trzy pręty pośrednie w rozstawie $a=1100/4 =275 \, mm$
Zbrojenie przypowierzchniowe przy zbrojeniu głównym o dużej średnicy
Jeżelibrojenie główne jest wykonane z: prętów o średnicy większej niż 32 mm lub wiązek prętów o średnicy zastępczej większej niż 32 mm, zgodnie z [1] -zał J. 1. – należy zastosować zbrojenie przypowierzchniowe, zapobiegające odłupywaniu się betonu.
Zbrojenie przypowierzchniowe powinno mieć postać siatki lub składać się z prętów o małej średnicy i powinno być umieszczone na zewnątrz strzemion, jak na rys K-5.
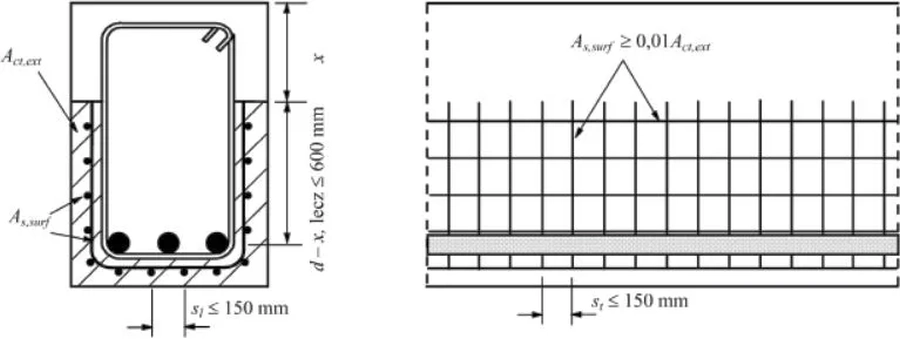
Rys. 5 Zbrojenie przypowierzchniowe [1] – rys. J.1 (x– wysokośc strefy ściskanej betonu w stanie granicznym nośności)
Analogiczne siatki zaleca się zakłądać przy wzmacnianiu i naprawie elementów żelbetowych polegającej na uzupełnianie betonu otulenia w tym w celu doporowadzenia do zgodności z aktualnymi wymogami konstrukcji pochodzących z okresu obowiązywania łagodniejszym kryteriów.
Wymagania pożarowe oraz ograniczenia stopnia zbrojenia przekroju
Wymagania pożarowe
Już na wstępie projektowania belki należy uwzględnić wymogi pożarowe. W normie [4] określono minimalne szerokości belek i otulenia zbrojenia ze względu na wymaganą odporność ogniową elementu. Klasy odporności ogniowej Rx zdefiniowano w artykule Odporność ogniowa konstrukcji budynku.
W tab.K-1 podano minimalne szerokości belek swobodnie podpartych lub ciągłych w zależności od wymaganej klasy odporności ogniowej belki. Szerokość belki jest skorelowana z otuleniem zbrojenia $a$, liczonym jako odległość osi zbrojenia od krawędzi belki. Ze względów pożarowych- przy większym otuleniu można stosować mniejsze belki, a belki ciągłe są bardziej korzystne od swobodnie podpartych.
Tab.K-1. Minimalne wymiary belek w zależności od odporności ogniowej
(wg [4], tab.5.5 , 5.6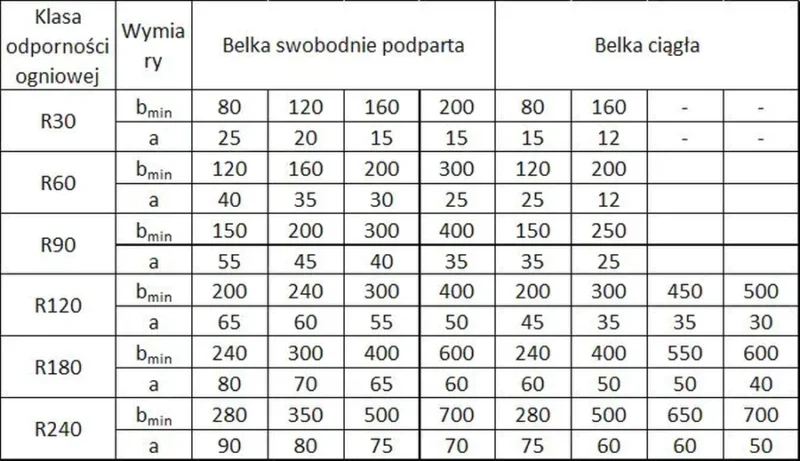
Minimalne zbrojenie belki (oraz płyty)
Minimalne pole zbrojenia podłużnego ze względu na kruche zniszczenie betonu
Pole przekroju podłużnego zbrojenia rozciąganego w przekroju belki lub płyty żelbetowej nie powinno być mniejsze niż $A_{s,min,britle}$, a jeśli jest mniejsze, to taki przekrój należy rozpatrywać jako niezbrojony. Minimalne zbrojenie zasadniczo wynosi:
$$\begin{equation} A_{s,min,britle}=ρ_{min,b} \cdot b_t \cdot d \label {15} \end{equation}$$
$$ \begin{equation} ρ_{min,b}= \ max { \{ 0,0013 \, ; \,0,26 f_{ctm}/f_{yk} \} }\label {16} \end{equation}$$
gdzie:
d – wysokość użyteczna przekroju (wysokość przekroju pomniejszona o osiowe otulenie zbrojenia ściskanego- górnego),
$b_t$ – średnia szerokość strefy rozciąganej. W belkach teowych z półką w strefie ściskanej bierze się pod uwagę tylko szerokość środnika.
$f_{ctm}$ – średnia wytrzymałość betonu na rozciąganie.
Minimalny stopień zbrojenia rozciąganego $ρ_{min,b}$ dla betonów zbrojonych stalą B500 podano w tab. W-1.
Zbrojenie minimalne $A_{s,min,britle}$, ma zapewnić, że nie nastąpi kruche zniszczenie betonu, to znaczy nagłe zniszczenie betonu, nie poprzedzone wyraźnie rosnącymi ugięciami. i widocznym rysowaniem betonu.
W elementach drugorzędnych, jeśli można zaakceptować pewne ryzyko kruchego zniszczenia, zbrojenie minimalne $A_{s,min}$ można przyjąć jako 120% zbrojenia wymaganego ze względu na stan graniczny ULS (nośności), to znaczy element zbroimy na 120% zbrojenia obliczeniowego. Zdaniem autora dotyczy to w szczególności płyt fundamentowych, spoczywających na podłożu gruntowym, w miejscach, gdzie przekroje rozciągane są skrępowane odporem i tarciem gruntu , czyli przekrojów przęsłowych płyt i ław fundamentowych. Przekroje podporowe takich płyt najczęściej należy zbroić ze względu na przebicie, które omówiono w artykule „Przebicie płyty żelbetowej„.
Wyprowadzenie formuły normowej i ogólny warunek na minimalne zbrojenie
Interpretacja wymogu minimalnego zbrojenia elementu żelbetowego nastręcza trudności ponieważ w literaturze przedmiotu nie powszechnie nie zajmuje się problemom. Dopiero Johansson (2012) w prezentacji (Johansson (2012), Armeringsutformning i betongkonstruktioner. PowerPoint presentation from study day at Reinertsen Sverige AB, Göteborg, Sweden, 2012-11-15. )) podjął próbę wyjaśnienia podstaw wymogu normowego ($\ref{15}$). Na rys. K-6 pokazano analizowany model: dwie fazy pracy przekroju prostokątnego: a) stan graniczny spękany, b) stan sprężysty niespękany tuż przed stanem krytycznym – zainicjowaniem pękania przekroju.
Zjawisko kruchego pękania betonu można uniknąć, jeśli zostanie zapewnione, że nośność graniczna przekroju mierzona momentem zginającym $M_{Rd}$ w fazie graniczne III będzie większa od nośności przekroju niespękanego $M_{cr}$ ( w fazie sprężystej I – ), czyli gdy spełniony będzie warunek
$$\begin{equation} M_{Rd} \ge M_{cr}\label {17} \end{equation}$$
gdzie:
$M_{Rd} = f_{yd}\cdot A_s\cdot z$ – rys. rys K-6a – nośnosć w fazie III granicznej
$M_{cr} =W_{el}\cdot f_{ctm}$ – rys K-6b nośność krytyczna w fazie I sprężystej tuż przed zarysowaniem dolnuych włókien przekroju,
skąd pole przekroju zbrojenia zapewnijące brak kruchego zniszczenia betonu
$$\begin{equation} A_s \ge \cfrac{W_{el}}{z}\cdot \cfrac{f_{ctm}}{f_{yd}} \label {18} \end{equation}$$
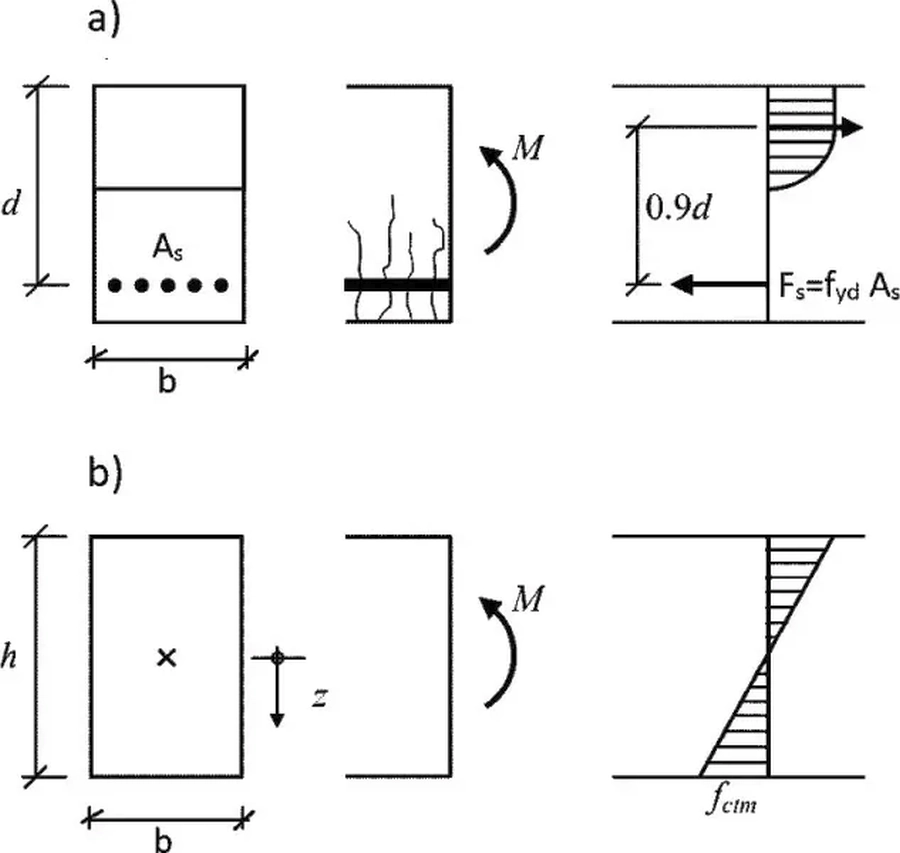
Rys. 6 Ilustracja do wyprowadzenia warunku na minimalne zbrojenie belki [5], Fig 4.6, 4.7
Przy wyprowadzeniu wzoru normowego ($\ref{16})^2$ (druga część warunku ) przyjęto dwa założenia upraszczające:
- $z \approx 0,9 \cdot d$ ( uproszczenie przyjmowane w obliczeniach wstępnych ($\ref{11}$))
- $d \approx 0,9 h$
Przy tych uproszczeniach mamy:
$M_{Rd} = f_{yd}\cdot A_s\cdot 0,9 d$,
$W_{el}= \cfrac{b \cdot h^2}{6}= \cfrac{b \cdot d*2}{6 \cdot 0,9^2}$,
$M_{cr} = f_{ctm} \cdot \cfrac{b \cdot d^2}{6 \cdot 0,9^2}$
Uwzględniając jeszcze, że $f_{yd}= \cfrac{f_{yk}}{\gamma_s} \cfrac{f_{yk}}{1,15}$, otrzymujemy ostatecznie $ A_s \ge \cfrac{f_{ctm}}{f_{yk}} \cdot\cfrac {1,15 \cdot bd}{6 \cdot 0,9^3} = 0,26 \cdot \cfrac{f_{ctm}}{f_{yk}}\cdot bd$, co odpowiada wymaganiom normowym dotyczącym minimalnego zbrojenia ($\ref{16}^2$) .
Warunek normowy ($\ref{16})^2$ na minimalne zbrojeni belki lub płyty wyprowadzono dla przekroju prostokątnego o szerokości $b$ i przy upraszczających założeniach odnośnie wysokości efektywnej przekroju oraz ramienia sił. Takie oszacowania normowe dają wyniki po bezpiecznej stronie, ale w szeregu ;przypadkach zbyt konserwatywne.
W celu dokładniejszego oszacowania minimalnego zbrojenia należy stosować formułę ($\ref{18}$), wynikającą z ogólnego i dokładnego warunku kruchego zniszczenia betonu ($\ref{17}$). Należy przy tym wskazać, że ramię sił (wewnętrzne ramię dźwigni) zależy od obciążenie przekroju i stanowi element rozwiązania zadania zbrojenia przekroju, opisanego w artykule Belki żelbetowe. Zginanie, Wyznaczenie zbrojenia z warunku nośności poprzedza sprawdzenie warunku zbrojenia minimalnego.
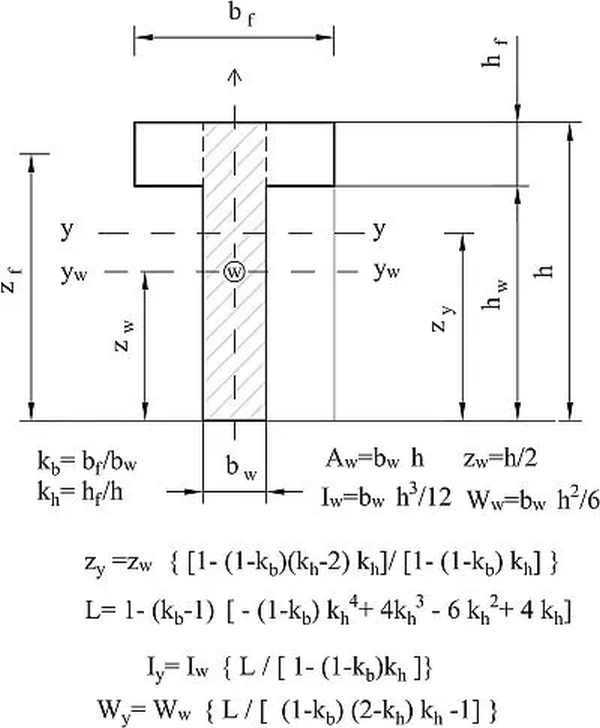
Przykładowo dla często spotykanego przekroju teowego charakterystyki geometryczne przekroju, w tym $W_{el}$ dolnego włókna belki „l” podano na rys. K-7 Przyjmując, że ramię sił $ z \approx z_f$ z równania ($\ref{18}$) otrzymamy
$$\begin{equation} A_s \ge \cfrac{b_w \cdot h} {3} \cdot \cfrac{L}{(2-k_h)\cdot [1- (1- k_b)(2-k_h) k_h} \cdot \cfrac{f_{ctm}}{f_{yd}} \label {19} \end{equation}$$
Współczynniki $k_h= h_f/ h$ , $k_b=b_f/ b_w $ oraz licznik ułamka $L$ zależą od stosunków wymiarowych przekroju (p. rys. K-6a), więc zbrojenie minimalne zależy od wymiarów całego przekroju, a nie tylko od $b_f$ oraz $d$. Na przykład dla przekroju teowego, będącego rzefmiotem przykładu rachunkowego otrzymamy $A_s \ge 0,272 \cdot b_w \cdot h \cfrac{f_{ctm}}{f_{yd}}$.
Przyjmując jak w przykładzie, że $z= 0,9832\cdot 357= 352 \, mm$ odpowiadający stopień zbrojenia sprowadzonego będzie wynosił $0,272 \cdot 400/352= 0,31$, czyli jest o $ 0,31/0,26-1=19$ % większy od wyznaczonego wg formuły normowej ($\ref{16}^2 $). Różnica jest znaczna i może być wykorzystana w opracowaniach eksperckich do optymalizacji zbrojenia minimalnego (w tym konkretnym przypadku decydujący jest warunek 0,13% ($\ref{16}^1 $ ) i optymalizajii nie można przeprowadzić, autor spotyka się z wieloma przypadkami rozwiązań. które są kwestionowwane ze względu na rzekomą niezgodnosć z warunkiem minimalnego zbrojenia).
Minimalne pole zbrojenia ze względu na zarysowanie
Ustala się również minimalne zbrojenie $A_{s,min,crack}$ ze względu na zarysowanie w strefie rozciąganej:
$$\begin{equation} A_{s,min,crack} = k_c \cdot k \cdot \cdot A_{ct} \cdot \cfrac{f_{ct,ef} }{σ_{s,lim}} \label {20} \end{equation}$$
Średnia wytrzymałość betonu na rozciąganie w chwili spodziewanego zarysowania $f_{ct,ef}$ przyjmuje się zwykle jako $f_{ctm}$ (p. tab. W-1.). Jeśli beton jest młodszy niż 28 dni, należy przyjąć zależny od czasu dojrzewania $f_{ctm} (t)$.
Pole rozciąganej strefy betonu $A_{ct}$ w chwili poprzedzającej zarysowanie wynosi:
- przy rozciąganiu osiowym $A_{ct}=A_c$ (pole całego przekroju betonu),
- przy zginaniu $A_{ct} \approx A_c/2$ (pole betonu powyżej osi obojętnej).
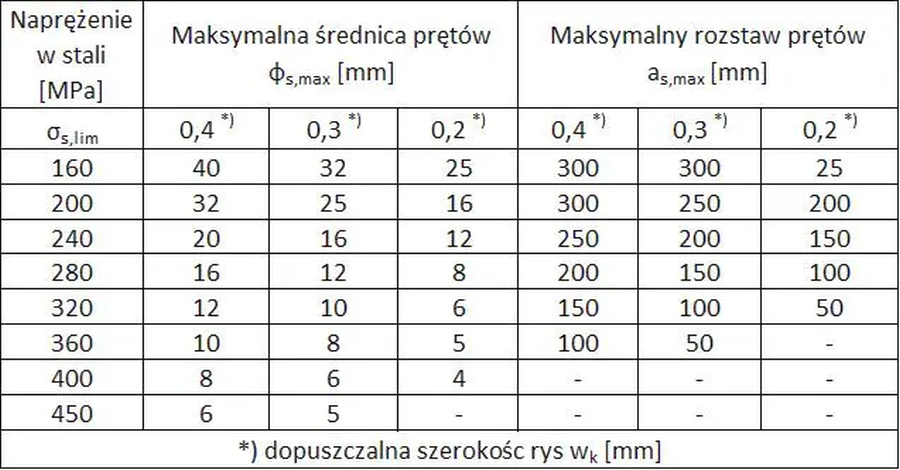
Naprężenia $σ_{s,lim}$ w zbrojeniu rozciąganym tuż po zarysowaniu można przyjmować równe $f_{yd}$, ale jeżeli wymaga się nieprzekroczenia granicznej szerokości rysy , to naprężenia można przyjmować wg tab. K-2, odpowiednio dla największej średnicy pręta lub maksymalnego rozstawu.
Tab.2. Ograniczenia rys – maksymalna średnica prętów $\Phi{s,max}$ i rozstaw prętów $a_{s,max}$ (wg [3],tab. 2.8)
Współczynnik $c$ uwzględnia rozkład naprężeń w przekroju w chwili poprzedzającej zarysowanie oraz wielkość ramienia sił wewnętrznych dla fazy II, i wynosi:
- przy rozciąganiu osiowym $k_c$=1,
- przy czystym zginaniu lub zginaniu z udziałem siły osiowej
a) dla przekrojów prostokątnych i środników belek teowych i skrzynkowych $k_c=0,4 \cdot \left( 1− \cfrac{\sigma_c}{η⋅h/h^∗⋅f_{ct,ef}} \right) \le 1$,
b) dla półek przekrojów teowych i skrzynkowych $k_c = 0,9 \cdot \cfrac{F_{cr}}{A_{ct} \cdot f_{ct,ef}} \ge 0,5 $.
Współczynnik k uwzględnia wpływ nierównomiernych naprężeń samorównoważących się w ustroju, prowadzących do zmniejszenia sił od odkształceń wymuszonych:
- k= 1,0 dla środników oraz dla półek krótszych od 300 mm,
- k=0,65 dla środników oraz dla półek większych od 800 mm.
- wartości pośrednie należy interpolować.
Współczynnik $η$ uwzględnia wpływ znaku siły podłużnej $N_{Ed}$ na rozkład naprężeń:
- $η=1,5$ dla siły dodatniej (ściskającej),
- $η=1,0$ dla siły rozciągającej.
Naprężenie $\sigma_c$ jest średnim naprężeniem w betonie w rozpatrywanej części przekroju $\sigma_c =N_{Ed}/(bh)$, gdzie $N_{Ed}$ – obliczeniowa siła podłużna, działająca na rozpatrywaną część przekroju, dodatnia – ściskająca.
Siła $F_{cr}$ jest bezwzględną wartością siły osiowej w półce bezpośrednio przez zarysowaniem, wywołanym przez moment rysujący, obliczony przy założeniu, że wytrzymałość na rozciąganie wynosi $f_{ct,ef}$.
Zastępcza wysokość przekroju $h^∗ = h$ dla $h <1,0m$ lub $h^*=1,0$ m dla $h \ge 1,0 \,m$
Spełnienie wymogu normowego ($ \ref {20}$) jest warunkiem wstępnym do wyznaczania rozwarcia rys metodami normowymi przedstawionym i w artykule Rysy i ugięcia żelbetu Wyrażenia podane w tym artykule opierają się na założeniu, że pękanie jest ustabilizowane, czyli że dalsze pęknięcia nie są już możliwe, bo krępuje je pozostała część przekroju elementu [6].
Minimalne zbrojenie na zarysowanie jest zależne od betonowego obszaru $A_{ct}$, definiowanemu jako powierzchnia betonu poddana rozciąganiu tuż przed pęknięciem. W przypadku wysokich elementów (takich jak ściany lub wysokie belki) taka definicja może prowadzić do zawyżenia powierzchni $A_{ct}$, co skutkuje nieracjonalnie dużą ilością zbrojenia (np. Johansson (2013), PhD in Concrete Structures, Reinertsen Sverige AB, Göteborg, Sweden, Spring 2013.)). Według [7],obszar betonu w równaniu ($\ref{20}$) powinien być zdefiniowany jako efektywna powierzchnia betonu zgodnie z rys. K-6b, co prowadzi do racjonalnego ustalenia minimalnego zbrojenia.
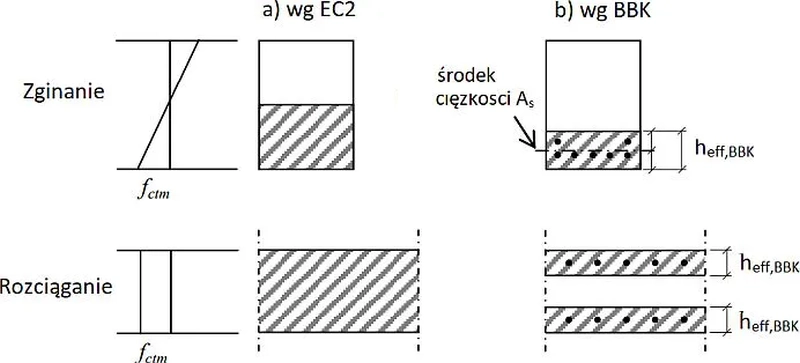
Rys. 8 Porównanie strefy rozciąganej dla minimalnego zbrojenia wg EC2 i BBK [6]
$h_{eff,BBK}= 150 \, mm$.
Należy podkreślić, że kontrolę pęknięć jest sensowna jedynie w grubych elementach. Ponadto w regionach, które są pozostawione bez zbrojenia istnieje ryzyko
Należy podkreślić, że kontrolę pęknięć jest sensowna jedynie w grubych elementach. Ponadto w regionach, które są pozostawione bez zbrojenia istnieje ryzyko powstania pojedynczych szerokich pęknięć [5],. Dlatego zmniejszenie strefy rozciąganej zalecanej przez EC2 należy stosować ostrożnie I każdorazowo poprzedzić indywidualną analizą i uzasadnić. Zdaniem autora szerokość efektywną strefy ściskanej $h_{eff}$ można stosować do wysokości elementu $h\le 800 \, mm$,
bo do takiej wysokości potwierdzono to eksperymentalnie [7]. Natomiast dla większej wysokości elementu efektywną wysokość strefy rozciąganej można dobierać proporcjonalnie do zwiększania się wysokości elementu $h$ z formuły
$h_{eff}= 150+(h/2-400)$
Minimalny stopień zbrojenia na ścinanie
Minimalny stopień zbrojenia na ścinanie wynosi
$$\begin{equation} \rho_{min,w} = 0,08 \cdot \cfrac{\sqrt{f_{ck}}}{f_{yk}}\label {21} \end{equation}$$
Analizę formuły ($\ref{21}$) przedstawiiono w artykule Rysy i ugięcia żelbetu.
Maksymalne zbrojenie podłużne belki lub płyty
Poza miejscami zakładów pole przekroju zbrojenia rozciąganego lub ściskanego nie powinno być większe niż $A_{s,max}$:
$$\begin{equation} A_{s,max} = 0,04 \cdot A_c \label {22} \end{equation}$$
gdzie $A_c$ -pole przekroju betonowego, na przykład w przypadku przekroju prostokątnego o wysokości h i szerokości b – $A_c=bh$. Projektanci często przyjmują się $A_c=bd$. Zdaniem autora artykułu ograniczenie dotyczy sumy zbrojenia przekroju $\Sigma A_s$ i powinno odnosić się do całego przekroju betonu, choć może dotyczyć wyraźnie wyodrębnianych części przekroju, np. środnika w belkach teowych i wówczas trzeba brać odpowiednie pole zbrojenia i betonu w tej części.
W miejscach zakładów zbrojenia ilość maksymalna w belkach i płytach może być 2x większa niż $(\ref {22})$ i wynosić $A_{s,max}=0,08 \cdot A_c$.
W literaturze spotyka się interpretacje , wiążące wymóg maksymalnego stopnia zbrojenia ($\ref {22}$) z zapewnieniem plastycznej pracy belki w stanie bliskim granicznego. Taka interpretacja nie jest jednak prawidłowa. W pracy [5], Ch.. 4.3.2. przeprowadzono analizy, wskazujące ponad wszelką wątpliwość, że nie istnieje bezpośredni związek pomiędzy maksymalną ilością zbrojenia a ciągliwością Górna granica zbrojenia podłużnego ($\ref{22}$) zalecane w normie jest podane z innych powodów niż zapewnienie wystarczającej plastyczności elementu.
Autor uważa, że prawdopodoną przyczyną wprowadzenia wymogu ($\ref {22}$) są względy ekonomiczne, czyli wskazanie, że przy nadmiernym stopniu zbrojenia należy zwiększyć wymiary elementu (przekrój betonu).
Kształtowanie zbrojenia po długości belki
Siły przekrojowe w prętach , w tym w belkach zmieniają się po długości, więc istotną rolę odgrywa optymalne dostosowanie układu zbrojenia do obwiedni momentów zginających M, sił osiowych N oraz sił poprzecznych. W każdym przekroju powinny być spełnione warunki minimalnego i maksymalnego stopnia zbrojenia.
Zbrojenie dostrajane do obwiedni sił
Na rys. K-9 przedstawiono zasadę układania prętów zbrojeniowych przez dostrojenie do obwiedni sił przekrojowych.
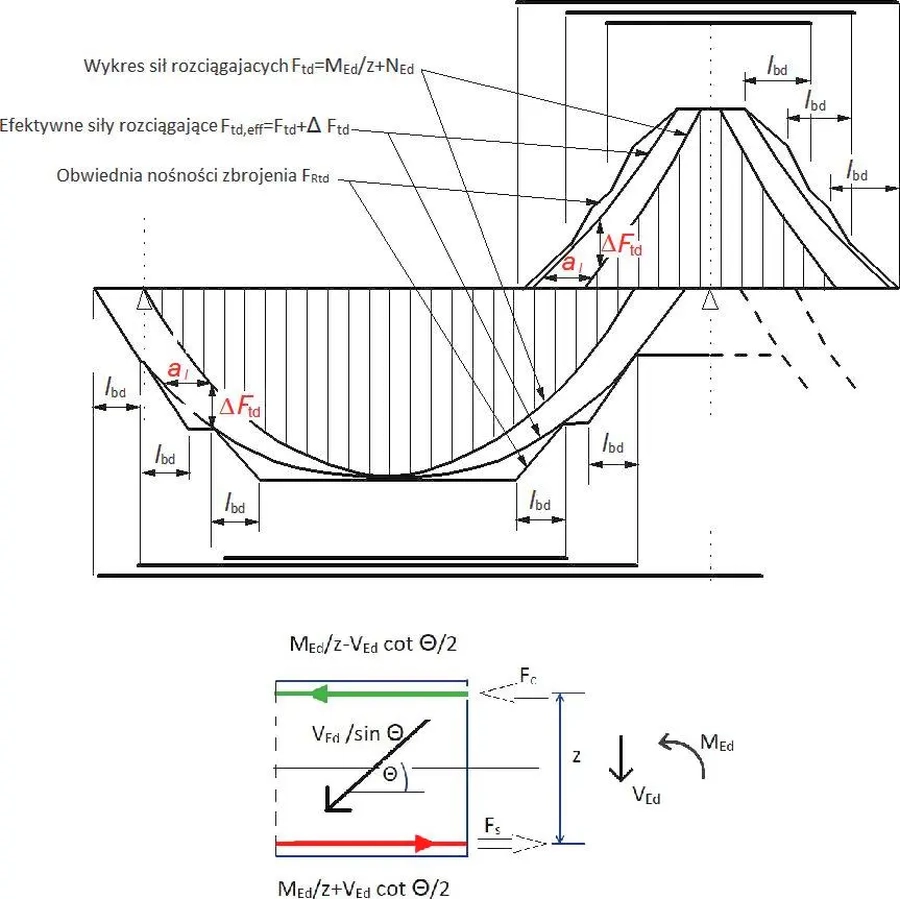
Rys. K-9. Dostrajanie układu prętów do obwiedni sił przekrojowych(opracowano na podstawie [1], rys.9.2)
Moment zginający przekrój $M_{Ed}$ jest zastąpiony parą sił w betonie $F_c$ i w stali rozciąganej $F_s$ na ramieniu z – stąd $F_s=M_{Ed}/z$.
Natomiast przydzielenie całej siły osiowej $N_{Ed}$ do pręta rozciąganego jest bardzo grubym szacunkiem, który zajdzie w sytuacji, gdy siła w betonie $F_c$ zaniknie na skutek jej pomniejszenia przynależnym rozciąganiem. Wówczas w stali będzie działała siła $F_s$=$N_{Ed}- F_{Rc}$, gdzie $F_Rc$ jest nośnością betonu na ściskanie. W celu dokładniejszego rozdziału siły $N_{Ed}$ pomiędzy $F_s$ i $F_c$ należy uwzględnić odkształcalność betonu i stali, zgodnie z zasadami podanymi w poniższych rozdziałach. Zalecenie normowe, zobrazowane na rys. K-9 dotyczy najniekorzystniejszego przypadku dla rozciągającej siły $N_{Ed}$, co jest wystarczającym przybliżeniem dla belek poddanych przeważającemu zginaniu.
Zgodnie z metodą kratownicową zilustrowaną na rys. S-5 siłę poprzeczną $V_{Ed}$ przenosi krzyżulec betonowy ( rys S-4 ) ułożony pod kątem $21,8^o \le \Theta \le 45|^o$,wydzielony rysami ukośnymi . Na skutek zarysowania siły w pręcie rozciąganym i w betonie zwiększą się o połowę składowej poziomej w krzyżulcu betonowym $V_{Ed}\cdot ctg \Theta$, czyli $\Delta F_{td}= V_{Ed} \cdot ctg \Theta$, a w przypadku prętów odgiętych lub strzemion nachylonych pod kątem $\alpha$ mamy [1],wzór (6.18):
$$\begin{equation} \Delta F_{td}= 0,5 \cdot V_{Ed} \cdot (ctg \Theta- ctg \alpha ) \label{23} \end{equation}$$
W elementach, które nie wymagają zbrojenia na ścinanie wpływ siły poprzecznej można estymować rozsuwając wykres momentów o odległość $a_l=d$ , przyjmując:
$$\begin{equation} a_l= 0,5 \cdot z \cdot V_{Ed} \cdot (ctg \Theta- ctg \alpha ) \label{24} \end{equation}$$
Naprężenia styczne od skręcania przekroju momentem skręcającym $T_{Ed}$ również spowodują zwiększenie sił osiowych w zbrojeniu zgodnie z formułą normową [1], wzór(6.28), którą na gruncie teorii prętów cienkościennych można uogólnić na inne niż zamknięte przekroje prętów.
Rysunki warsztatowe żelbetu nie są Projektem
Na rys. K-10 pokazano przykładowe ułożenie zbrojenia w belce z rys. K-9. Rysunek warsztatowy K-10 jest wykonany w historycznej konwencji – poszczególne figury zbrojeniowe zostały szczegółowo zobrazowane, a współcześnie w dobie automatyzacji procesów wytwórczych – należy stosować kody kształtów prętów zgodnie zasadą przedstawioną w artykule Standard rysunku warsztatowego konstrukcji żelbetowej.
Rysunki warsztatowe konstrukcji żelbetowej typu K-10 opracowuje Wykonawca jako wstępny etap swoich robót budowlanych i uzgadnia z Projektantem pod względem zgodności z Projektem, czyli projektem budowlanym i technicznym.
Właściwy projekt konstrukcji żelbetowej nie obejmuje rysunków warsztatowych (roboczych). Elementami projektu właściwego jest ustalenie (opracowanie):
-
- schematu i kształtu elementu konstrukcyjnego; materiałów (klasy ekspozycji oraz parametrów w tym klasy betonu , jeśli nie wynikają jednoznacznie z klasy ekspozycji);
- klasy stali oraz wyznaczenie zbrojenia teoretycznego i przedmiaru robót zbrojarskich; Przedmiar robót zbrojarskich wykonywany jest metodą szacunkową z jawnym wykazaniem dodatków na : zakłady, kotwienia, ewentualne zróżnicowanie zbrojenia przez Wykonawcę oraz inne sytuacje zależne od specyficznego sposobu wykonywania prefabrykatów. Projektant nie powinien narzucać Wykonawcy sposobu wykonania zbrojenia, jeśli nie wynika to z uzasadnionych wymogów projektowych.
- specyfikacji technicznej wykonania i odbioru konstrukcji żelbetowych. Przedmiary robót betonowych i zbrojarskich oraz wymagania specyfikacji powinny łącznie umożliwić przedstawienie przez oferentów Wykonawców ceny za wykonanie robót. Cena robót powinna uwzględnić opracowanie rysunków roboczych )zbrojeniowych wraz ze szczegółowym wykazem zbrojenia.
- sposobu włączenie elementu konstrukcyjnego w system konstrukcyjny wraz opracowaniem wymiarów funkcjonalnych i dopuszczalnych tolerancji.
- wybranych, trudniejszych detali konstrukcji i zbrojenia.
Opracowane detale powinny obrazować specyficzne wymagania projektowe, które nie są powszechnie znane – nie wynikają z ogólnie dostępnych norm, podręczników i sztuki budowlanej.
W projekcie zakłada się bowiem, że roboty budowlane wykona profesjonalny wykonawca wobec którego można stosować podwyższony miernik należytej staranności wynikający z art. 355 § 2 kc. Należytą staranność w zakresie prowadzonej przez działalności określa się przy uwzględnieniu zawodowego charakteru tej działalności. Z zawodowego charakteru działalności wykonawcy (który powinien legitymować się certyfikatem jakości), pracującego pod nadzorem Kierownika budowy (legitymującego się uprawnieniami budowlanymi(, wynika, wprost że wykonawca spełni wszystkie wymogi projektu oraz normy PN-EN 13670 [8] oraz wymagania norm związanych, a także zasady sztuki budowlanej w swoim fachu .Zakłada się również, że wykonawca dysponuje profesjonalnym biurem przygotowania produkcji, które opracuje rysunki warsztatowe elementów żelbetowych. W polskiej rzeczywistości wykonawca najczęściej zleca wykonanie rysunków warsztatowych (zbrojeniowych) dla pracowni zewnętrznej. Taką pracownię traktuje się jako podwykonawcę Wykonawcy do robót kreślarskich, a nie jako projektanta. Projektant nie ma obowiązku opracowywania rysunków zbrojeniowych.
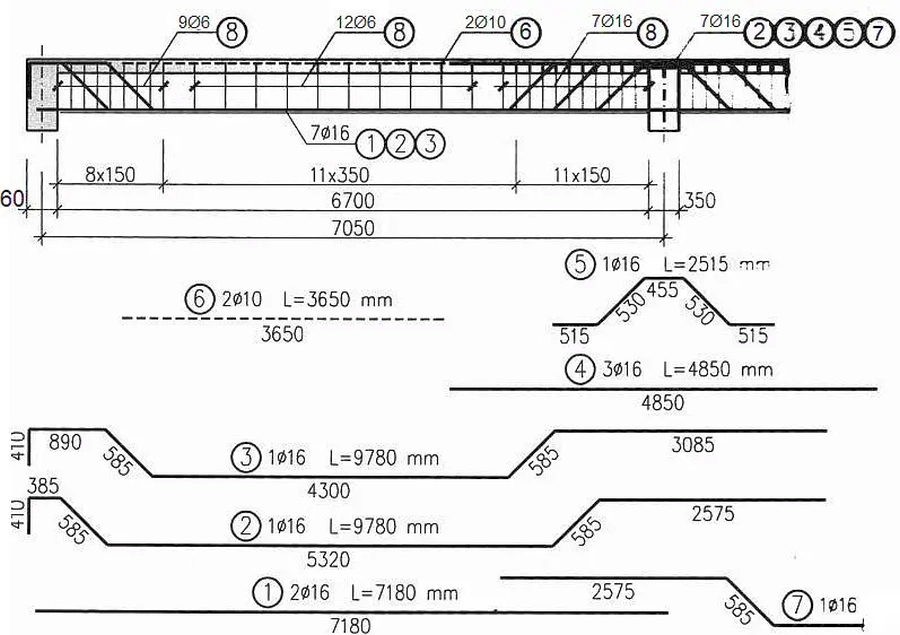
Rys. 10 Przykład rysunku warsztatowego zbrojenia belki w historycznej formie ( bez kodów kształtów zbrojeniowych) [9]
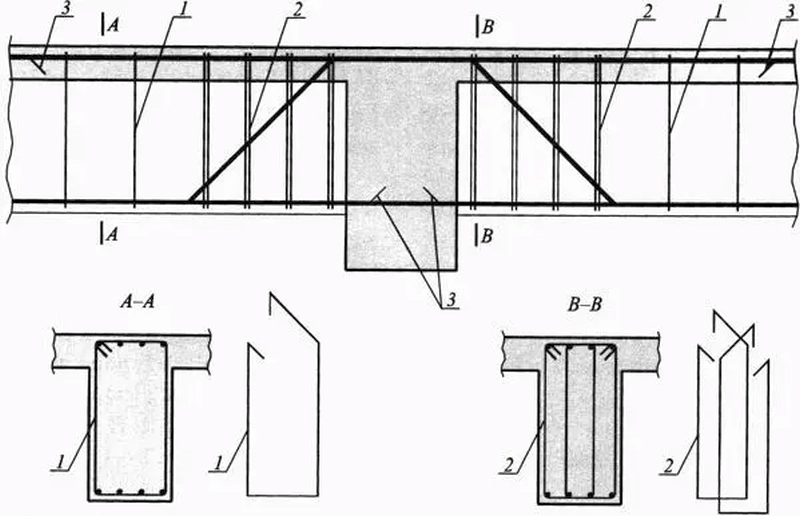
Rys. 11. Zbrojenie poprzeczne belki z rys. 8: strzemiona:1- pojedyncze, 2- podwójne. [9] rys. 1.5
W Polsce nadal jednak, niezmiennie od lat sześćdziesiątych XX wieku, w których zarówno Inwestor jak i Wykonawca oraz Projektant byli podmiotami państwowymi, a projektant oprócz właściwych prac projektowych wykonywał rysunki robocze, bo był traktowany jako służebny wobec Wykonawcy. Obecny, europejski ustrój budowlany wprowadził podział ról, kompetencji oraz prac. Profesjonalny Wykonawca powinien dysponować swoim biurem technologicznym, które w miarę potrzeb opracuje rysunki robocze, dostosowane do technologii stosowanej przez Wykonawcę. Tak opracowane rysunki warsztatowe bezwzględnie należy wykonać zgodnie z projektem budowlanym i wykonawczym a projekt właściwy nie powinien zawierać zbyt wielu detali (przede wszystkim typowych), tak by nie ograniczać Wykonawcy do określonej technologii (np. do łączenia prętów na zakład zamiast na łączniki mechaniczne, systemu szalowania itp).
Ze względu na utrzymanie na rynku polskim wielu biur technologicznych, trudniących się kreśleniem rysunków roboczych za niewielkie ceny- Polska stała się regionem Europy, do którego trafiają zlecenia na rysunki robocze od Wykonawców zagranicznych : z Niemiec, Belgii, Holandii, Wielkiej Brytanii itd, Ze względu na pracochłonność rysunków roboczych , wymagających niewielkich kompetencji – w tych krajach jest nie do pomyślenia, by wymagać takich prac od projektanta, ponieważ jego stawka godzinowa jest kilka razy wyższa od stawki kreślarza. Eksport nisko przetworzonych usług niewątpliwie nie prowadzi do rozwoju kraju.
Zagięcia prętów
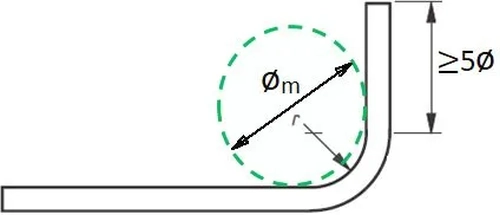
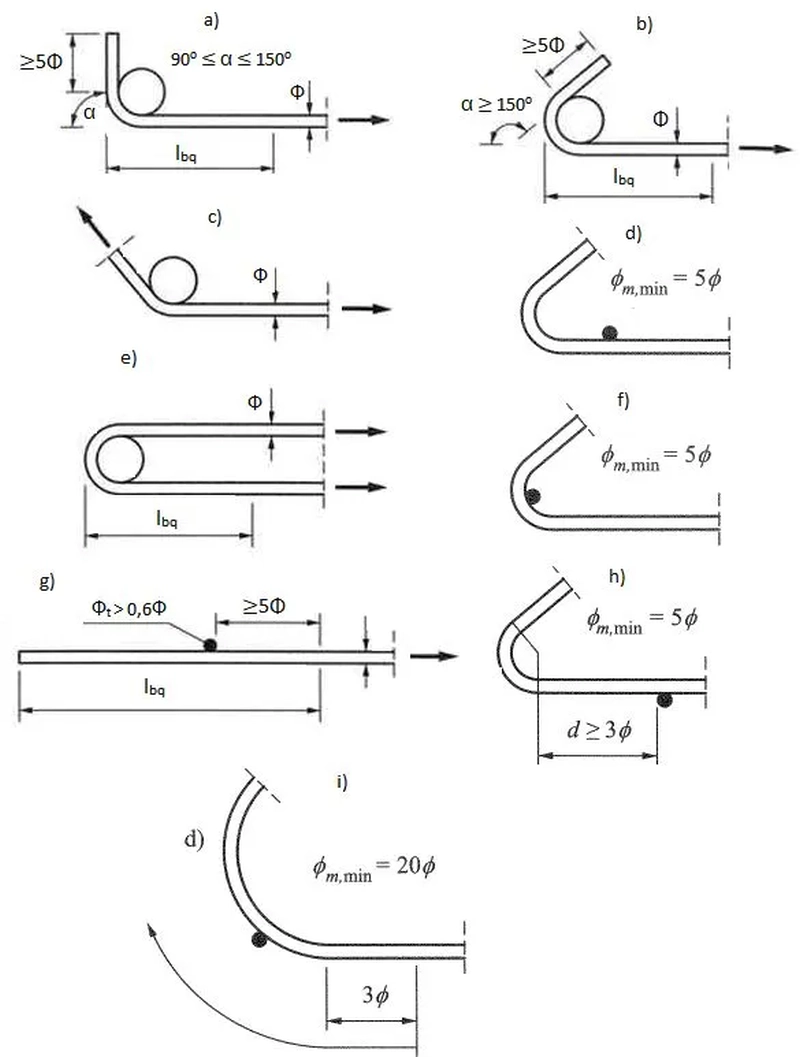
Krzywizna zagięć prętów nie może być zbyt mała. Normuje się wewnętrzną średnicę zagięcia, czyli średnicę trzpienia $\Phi_m$ na który jest nawijany pręt (rys. K-12). Minimalna średnica zaginania $\Phi_{m,min}$ wynosi
$$\begin{equation} \Phi_{m,min} = \begin {cases}
4 \Phi, & \text {jeśli $ \Phi \le$ 16 mm} \\
6 \Phi, & \text {jeśli $ \Phi$ > 16 mm }
\end {cases} \label{25} \end{equation}$$
Odcinek prosty pręta powinien być wyprowadzony poza zagięcie przynajmniej na $5\Phi$.
W przypadku zaginania pręta obok spoiny łączącej pręt poprzeczny (rys. K-13 d), f), h) średnica minimalna średnica zagięcia powinna wynosić $\Phi_{m.min}=5 \Phi$.
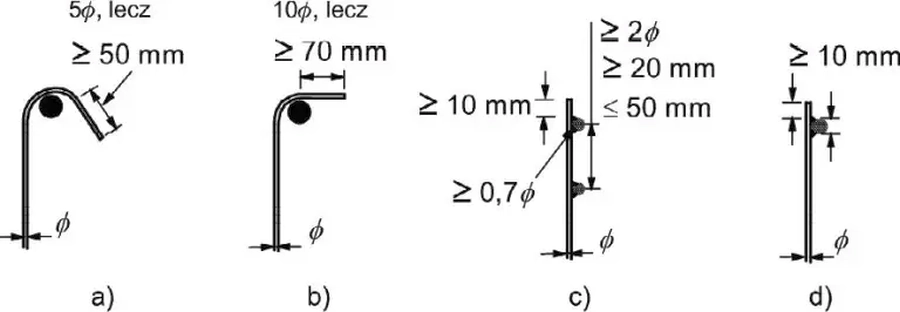
Kotwienie strzemion wymaga spełnienia warunków pokazanych na rys. K-14.
W celu uniknięcia zniszczenia betonu w zagięciu pręta wytężonego na początku zagięcia siłą $F_{bt}$ minimalna średnica zgięcia wynosi:
$$\begin{equation} \Phi_{m,min}= F_{bt} \left( \dfrac{1}{a_b}+\dfrac {1} {2 \Phi} \right) \label{26} \end{equation}$$
gdzie: $a_b$ d jest połową odległości między osiami prętów równoległych, sąsiednich zagiętych prętów, a w przypadku pręta sąsiadującego z powierzchnią elementu $a_b =\Phi/2$.
Średnica zagięcia nie musi być sprawdzana z warunku $(\ref{26})$ , jeżeli:
a) zakotwienie nie wymaga więcej niż 5 $\Phi$ prostego odcinka od zakończenia gięcia , lub
b) pręt nie jest najbliższy krawędzi i wewnątrz zagięcia jest ułożony pręt poprzeczny $\ge \Phi$.
W przypadku haków i pętli (rys. K-10 a), b),e)) należy zachować podstawowy wymiar zakotwienia $l_{bd}$.
Zakotwienie prętów zbrojeniowych
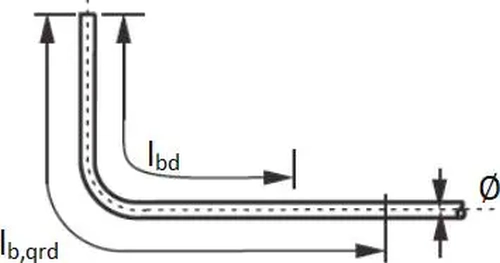
Zakotwienie pręta zbrojeniowego powinno wynosić $l_{bd}$ i zależy od długości bazowej (wymaganej) $l_{b,qrd}$ (rys. K-15) oraz zestawu współczynników $\alpha_1$ do $\alpha_5$ zgodnie z zależnością [1], kl. 8.4:
$$\begin{equation} l_0 = \alpha_1 \cdot \alpha_2 \cdot \alpha_3 \cdot \alpha_4 \cdot \alpha_5 \cdot l_{b,rqd} \ge \max { \{ 0,3 \alpha_6 l_{b,rqd}\, ; \, 10 \Phi \, ; \, 100 \, mm \}} \label{27} \end{equation}$$
przy ograniczeniu iloczynu $(\alpha_2 \cdot \alpha_3 \cdot \alpha_5) \le 0,7$
Długość bazowa zależy od średnicy pręta $\Phi$ , naprężeń w pręcie $\sigma_{sd}$ i przyczepności betonu do pręta $f_{bd}$:
$$\begin{equation} l_{b,qrd} = \Phi/4 \cdot \cfrac{\sigma_{sd}} {f_{b d}} \label{28} \end{equation}$$
Długości bazowe $l_{bd}$ dla szeregu przypadków zagięć prętów zilustrowano na rys. K-9.
Przyczepność betonu do pręta można wyznaczyć z formuły:
$$\begin{equation} f_{bd} = 2,15 \cdot \eta_1 \cdot \eta_2 \cdot f_{ctk 5 \%} / \gamma_c \label{29} \end{equation}$$
gdzie:
$\eta_1=1$ dla dobrych i $\eta_1=0,7$ dla innych warunków przyczepności w zależności o umiejscowienia pręta zbrojeniowego w elemencie ( p. informacje w kalkulatorze LCżelbet),
$\eta_2=1$ dla średnicy pręta w strefie zakładu $\Phi_z \le 32 ,\ mm$ i $\eta_2= 1,32- \Phi_z/100 )$ dla większych średnic,
$f_{ctk 5 \%}=0,7 \cdot f_{ctm}$ ($f_{ctm}= 0,3 \cdot f_{ck}^{2/3}$ wg tab. K-1)
$\gamma_c=1,4$ częściowy współczynnik bezpieczeństwa (materiałowy) dla betonu.
Górna granica przyczepności jest ograniczona wytrzymałością betonu C60/75., dla którego $f_{ctd}=4,9 \, MPa$.
W załączonym do artykułu arkuszu kalkulacyjnym (link pod Rys W-1 ) podano kryteria kwalifikacji przyczepności do dobrych warunków, a także sposób wyznaczania współczynników $\alpha_i \, i=1..,5$.
Kształtowanie zakładów prętów zbrojeniowych
Łączenie prętów zbrojeniowych na zakład jest w Polsce podstawową techniką uciąglania zbrojenia betonu. Coraz częściej zamiast łączenia prętów na zakład – stosuje się łączniki mechaniczne, opisane w artykule Systemy zbrojenia betonu. Stosowanie łączników mechanicznych wymaga precyzyjnego przygotowania końcówek prętów na warsztacie i większych umiejętności podczas scalania, ale uzyskuje się oszczędności stali (oraz energii i zmniejszenie gazów cieplarnianych) 5 do kilkunastu procent stali zbrojeniowej..
Zakład łączonych prętów powinien wynosić
$$\begin{equation} l_0 = \alpha_1 \cdot \alpha_2 \cdot \alpha_3 \cdot \alpha_4 \cdot \alpha_5 \cdot \alpha_6 \cdot l_{b,rqd} \ge \max { \{ 0,3 \cdot \alpha_6 \cdot l_{b,rqd} \, ; \, 15 \Phi \, ; \, 200 \, mm \} } \label{30} \end{equation}$$
gdzie długość bazową $l_{b,rqd}$ oraz współczynniki $\alpha_i$ (i=1,..5) są zdefiniowane w rozdziale wyżej (zakotwienie prętów).
Współczynnik $\alpha_6$ wynosi
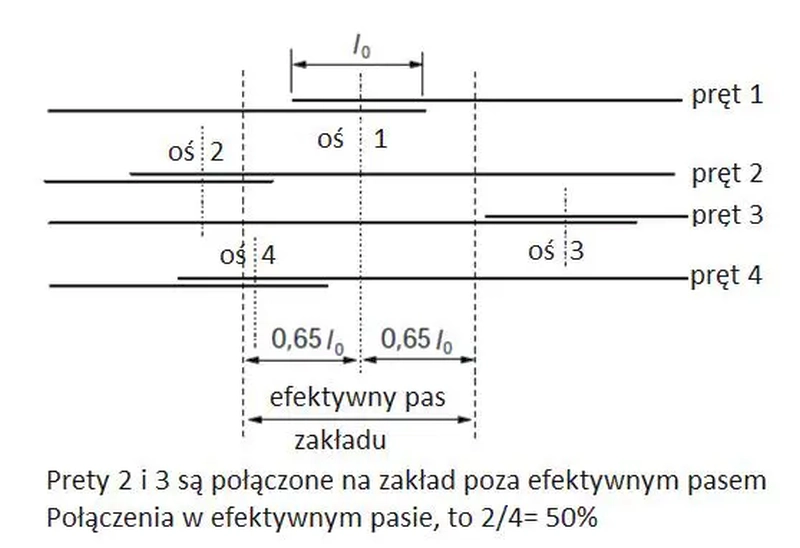
$$\begin{equation} \alpha_6 = \sqrt{\rho_1/25} \text{ , przy czym $ 1,0 \le \alpha_6 \le 1,5$} \label{31} \end{equation}$$
Współczynnik $\rho_1$ jest określany w procentach i oznacza liczbę prętów łączonych zakładami w efektywnym pasie po $0,65 l_0$ od osi przekroju, (w przykładzie na rys. K-16 pokrywającej się z osią zakładu 1) do liczby wszystkich prętów przecinających przekrój. Na rysunku pokazano przekrój z 4-roma prętami, z których tylko dwa zakłady zmieszczono w efektywnym pasie. W tym przypadku współczynnik zakładów $\rho_1$=50%, a współczynnik $\alpha_6=\sqrt{50/25}=1,4$.
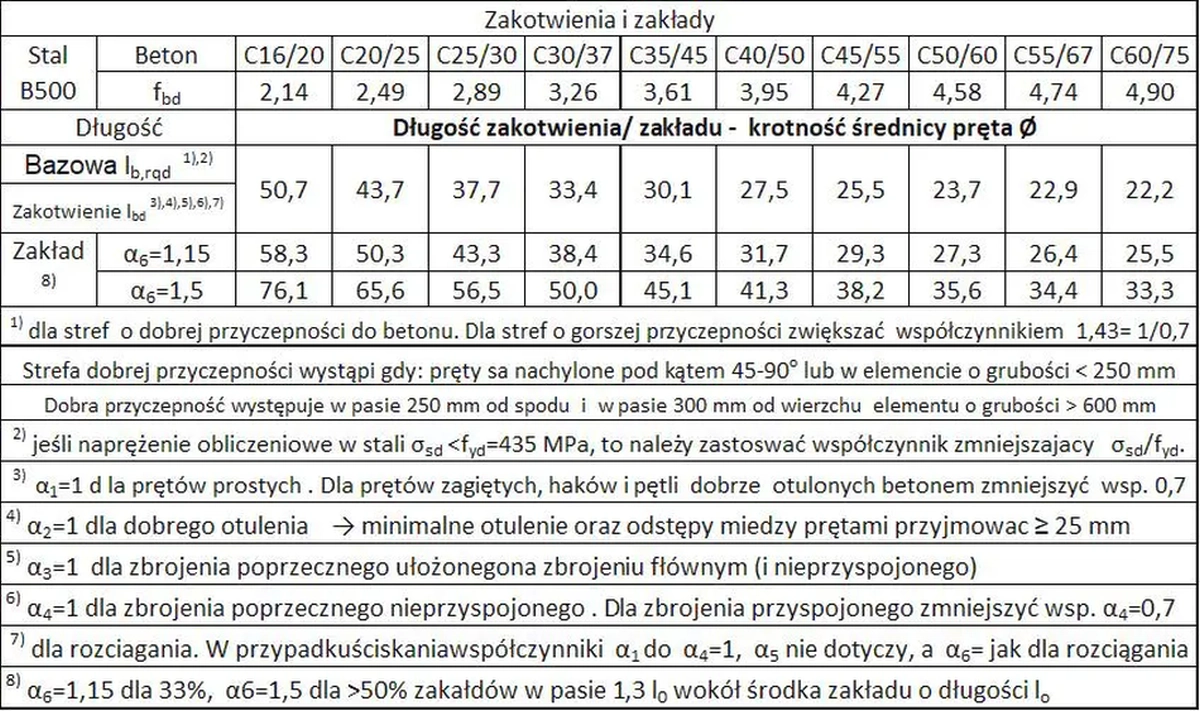
W tab. K-3. zestawiono podstawowe długości zakotwień oraz zakładów jako wielokrotność średnicy pręta ze stali B500 maksymalnie wytężonego. Dane zawarte w tej tabeli są szacunkowe.
Dokładniejsze oszacowania zakotwień oraz zakładów prętów zbrojeniowych można dokonać w arkuszu „Zakotwienia”, stanowiącym załącznik do artykułu.
Tab.K-3 Zakotwienia i zakłady prętów zbrojeniowych. Podstawowe długości
( Arkusz LCżelbet pobierzesz po kliknięciu w rys. W-1 w artykule „Belki żelbetowe” )
Kotwienie zbrojenia na podporach skrajnych
Na podporach, skrajnych gdzie moment zginający jest niewielki (lub teoretycznie zerowy) wymaga się, by doprowadzić i odpowiednio zakotwić 25% zbrojenia przęsłowego w belkach, a w płytach 50%.
Zginanie, zwichrzenie belek (wyboczenie boczne) i imperfekcje
Belki są elementami przeważająco zginanymi. Ze zginaniem nieodłącznie związane jest ścinanie, ale także utrata stateczności nazywana zwichrzeniem. Zwichrzenie może nastąpić w przypadku smukłych (wysokich) belek. Polega ono na utracie płaskiej postaci zginania,(skręceniu i wyskokowi w bok przekroju) w sposób pokazany na rys.K-17
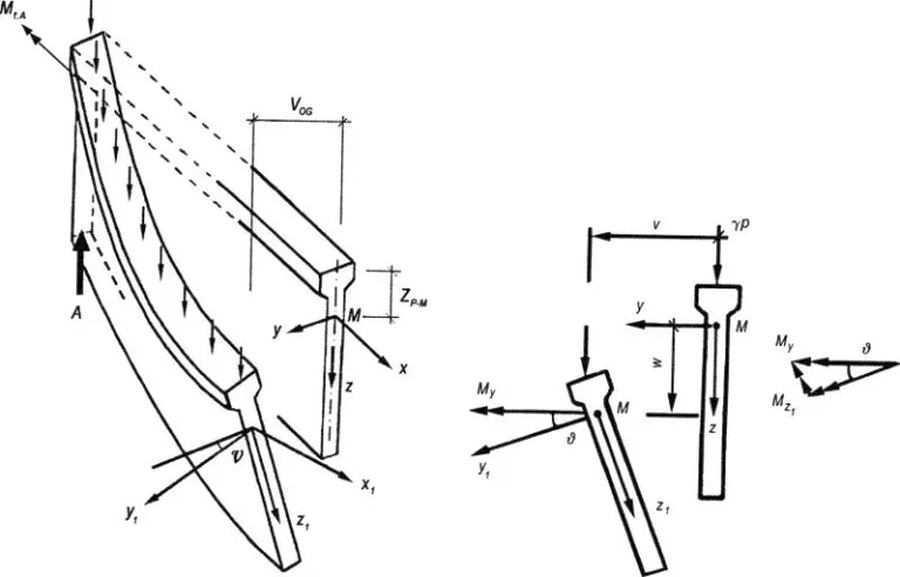
Rys. 17 Zwichrzenie smukłej belki żelbetowej [10], rys. 2.171
Zgodnie ze współczesną wiedzą i możliwościami współczesnych programów komputerowych zagadnienie zwichrzenia belek żelbetowych powinno się analizować metodą imperfekcyjną, podobnie do zagadnienia słupów.
Wstępną analizę można dokonać na podstawie zależności normowych [10], rys. 2.171 , [1], wzory (5,42a), (5.42b), gdzie wskazano, że efekty drugiego rzędu związane z niestatecznością poprzeczną można pominąć, gdy spełnione są następujące warunki:
-
- w sytuacjach trwałych
$$\begin{equation} \cfrac{l_{0t}}{b} \le 50 / (h/b)^{1/3} \quad \text { i } \quad \cfrac{h}{b}< 2,5 \label {32}\end{equation}$$
-
- w sytuacjach przejściowych
$$\begin{equation} \cfrac{l_{0t}}{b} \le 70 / (h/b)^{1/3} \quad \text { i } \quad \cfrac{h}{b}< 3,5 \label {33}\end{equation}$$
gdzie:
$l_{0t}$- długość zwichrzenia – odległość pomiędzy podporami widełkowymi (na skręcenie i boczne przesunięcie),
$b$- szerokość ściskanego pasa,
$h$ – całkowita wysokość belki w środkowej części $l_{0t}$
Jeśli szacunki powyższe nie dadzą pozytywnego rezultatu, to nie oznacza jeszcze, że belka ulegnie zwichrzeniu. W celu potwierdzenia niestateczności zaleca się przeprowadzić analizę drugiego rzędu belki obarczonej imperfekcją geometryczną – wygięciem poprzecznym $u_i= l_b /300$ , gdzie $l_b$ jest całkowitą długością belki w kompletnym schemacie statycznym i obciążeniu.
Widełkowe podparcie belek żelbetowych na słupach można uzyskać poprzez specjalne przygotowanie głowicy słupa, na przykład w sposób pokazany na rys. K-18.
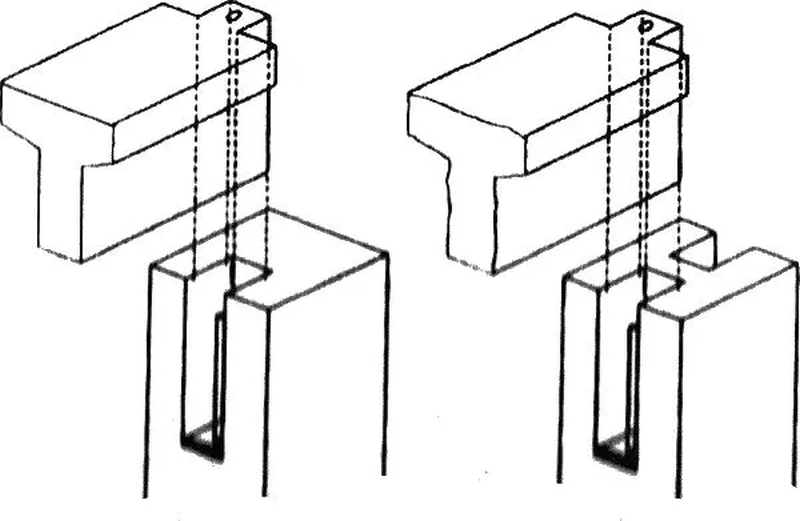
Rys. K-18 Przykład podparcia widełkowego belki na słupie [10], rys. 3.217
Przykłady rachunkowe
Przykład K-1 [ długość zakładu oraz zakotwienia prętów zbrojeniowych ]
Wyznaczyć wymaganą długość zakotwienia i zakład prętów uciąglanych dla danych:
- beton-stal C20/25-B500SP,
- element – belka,
- naprężenie w prętach $\sigma_{sly}=435 \, MPa$,
- średnica prętów Ф=16 mm,
- sposób wytężenia – rozciąganie,
- kształt prętów – inne (niż proste)
- rodzaj zakotwienia – zagięte lub hak
- warunki przyczepności – dobre,
- przyspojone pręty – nie
- ( jeśli przyspojono , to) – w narożu
– otulenie dolne $c=20 \, mm$
– otulenie boczne $c_1=25 \, mm$
r- ozstaw prętów $a=60 \, mm$), - nacisk poprzeczny $p=0 \, MPa$
- udział prętów uciąglanych – 50%
- zbrojenie prostopadle wzdłuż $l_b$ 2,51 $cm^2$
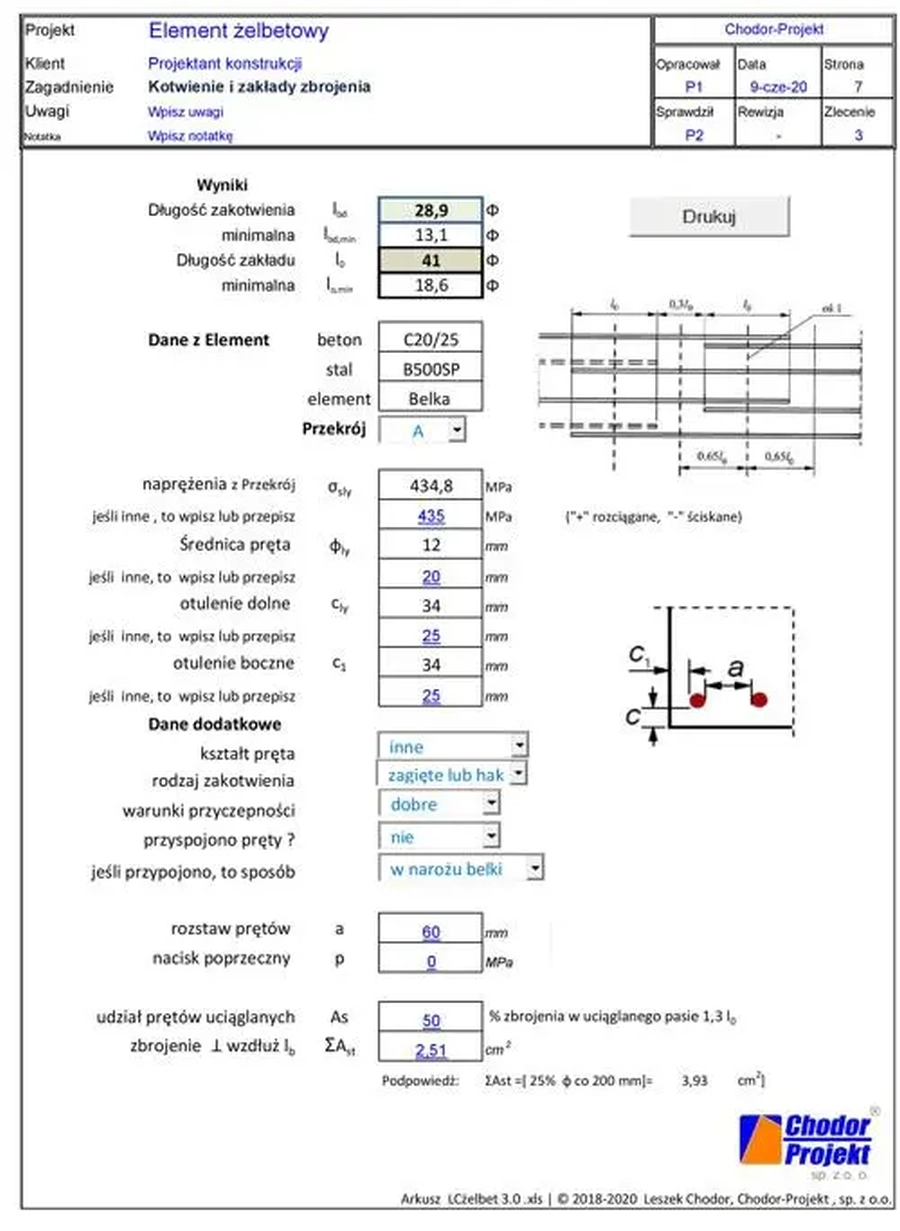
Na rys. K-19 zamieszczono odnośnik do arkusza obliczeniowego z wynikami dla przykładu obliczenia długości zakotwienia oraz zakładu prętów zbrojeniowych
W wyniku uzyskano:
długość zakotwienia $l_{bd}$ =28,9Ф
długość zakładu $l_0$=41Ф
Należy zwrócić uwagę, że w arkuszu wyniki uzyskuje się w polach poniżej słowa „Wyniki” natychmiast po wpisaniu danych poniżej, przy czym beton i stal jest pobierana z zakładki „ElementŻelbet”, (tzn należy przejść do zakładki „ElementŻelbet” tam wybrać beton, stal i rodzaj elementu powrócić do zakładki „Kotwienie”
Wartość naprężeń w pręcie $\sigma_{ sly}$ jest wpisywane w pole z czarną czcionką z zakładki „Przekrój” . Można je jednak zmienić w niższe, odblokowane dla edycji pole . Obliczenia prowadzone są dla wartości z pola edytowanego, wiec nawet dla prawidłowej podpowiedzi należy ja przepisać w pole edycyyjne. poniżej.
- PN-EN 1992-1+AC+Ap 1,2,3 :2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- Pyrak, S. (2012). Konstrukcje z betonu (VII, Vol. 5). WSiP
- Gąćkowski, R. (2013). Tablice i algorytmy do wymiarowania zginanych elementów żelbetowych. Verlag Dashöfer
- PN-EN 1992-2+AC+Ap1+Ap2:2008, Projektowanie konstrukcji z betonu, Część 1-2: Reguły ogólne. Projektowanie z uwagi na warunki pożarowe
- Dahlgren A., Svensson L., Guidelines and Rules for Detailing of Reinforcement in Concrete Structures. A Compilation and Evaluation of Ambiguities in Eurocode 2, Master’s Thesis β01γ:142, Department of Civil and Environmental Engineering, Division of Structural Engineering Concrete Structures, Chlamers Uniwersity of Technology, Göteborg, Sweden 2013
- (Boverket (2004), Boverkets handbok om betongkonstruktioner, Boverket, Byggavdelningen, Karlskrona, Sweden, 2004:9. [
http://www.boverket.se/Global/Webbokhandel/Dokument/2004/boverkets_handbok_om_betongkonstruktioner_BBK_04.pdf [2013-02-06]] - Alfredsson and Spåls (2008): Cracking Behaviour of Concrete Subjected to Restraint Forces, [PDF]. Master’s Thesis at Chalmers University of Technology, Göteborg) Sweden, 2008
- PN-EN 13670:2011, Wykonywanie konstrukcji z betonu
- Zybura, A. (Ed.). (2015). Konstrukcje żelbetowe według Eurokodu 2: atlas rysunków. Wydawnictwo Naukowe PWN
- Bachmann, H., & Steinle, A. (2011). Precast concrete structures. Ernst & Sohn : John Wiley & Sons, Inc.
________________________________