Leszek Chodor, 10 kwietnia 2020
15-02-2025 rewizja po dużej awarii portalu
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 4 Czytelników
Zagadnienie zginania belek żelbetowych jest fundamentalnym problemem rozpatrywanym w teorii żelbetu. Klasyczne rozwiązania dotyczą szczególnego zadania: przekroju pojedynczo zbrojonego, zginanego w jednym kierunku bez udziału siły osiowej. Rozwiązanie to przedstawiono w rozdziale Klasyczna_technika projektowania zbrojenia_belki. W artykule zaprezentowano metodę obciążenia zredukowanego MO* w której wprowadzono zredukowane obciążenia przekroju prostokątnego podwójnie zbrojonego lub przekroju teowego ze współpracującą płytą stropową. Stosowanie metod MU i MU* jest w zasadzie wystarczające do wstępnego projektowania przekrojów żelbetowych przez inżynierów Architektów.
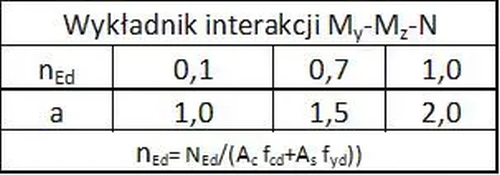
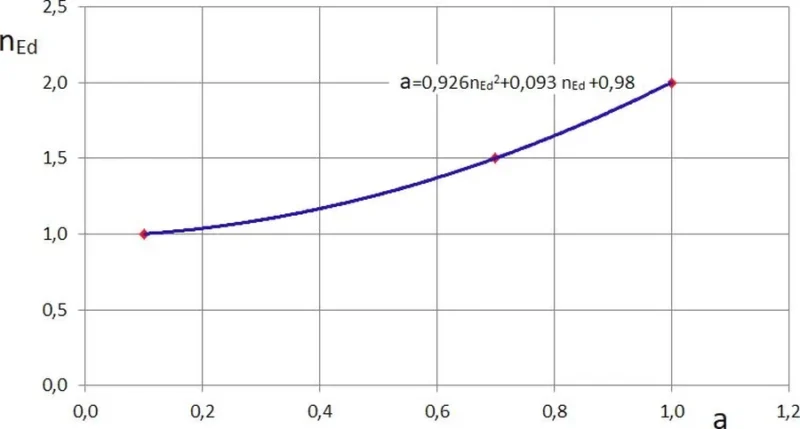
Artykuł jest kierowany do inżynierów specjalności konstrukcyjno-budowlanej i dla nich omówiono bardziej złożone zadanie zginania dwukierunkowego z udziałem siły osiowej. Zastosowano spójne podejście z zastosowaniem nieliniowego modelu żelbetu MN ($\ref{21}$) i kompleksowe porównania z modelem uproszczonym MU. Wyprowadzono nowe formuły analizy przekroju zginanego, wynikające ze znajomości współczynników (17/21) oraz (99/238) modelu MN (rys Z-1). Przeprowadzono szeroką analizę mechanizmu zniszczenie belki przez zmiażdżenie betonu przy zginaniu (Flexural Compression Failure) i wynikającego stąd wymogu zbrojenia strefy ściskanej betonu.
Artykuł w ciągu ostatnich 24 godzin czytało 4 Czytelników
Część Z Zginanie Nawigacja: [ K: Kształtowanie ] ⇐ ⊗ ⇒ [ P: Pełzanie i skurcz ]
Podstawowe oznaczenia i zależności
$\parallel \to\parallel $ symbol normalizacji (po symbolu podano zapis wyrażenia w zmiennych unormowanych),
MN – Nieliniowy- paraboliczny Model rozkładu naprężenia w przekroju ($\ref{21}$),
MU – Uproszczony -prostokątny Model rozkładu naprężenia w przekroju rys Z-2,
BZ – Beton Zwykły ( klasa max C50/60 ; $f_{ck} \le 50 \, MPa $) tab W-1,|
BWW – Beton Wysokiej Wytrzymałości ( klasa powyżej C50/60).
PZP – Pojedynczo Zbrojony Przekrój ( tylko dołem – zbrojenie rozciągane),
DZP – poDwójnie Zbrojony Przekrój (górą i dołem , górą – zbrojenie ściskane),
T, L – żelbetowy przekrój Teowy T , kątowy L
MO* -Metoda zredukowanego Obciążenia wymiarowania przekroju DZP lub T
FTF – zniszczenie belki przez zerwanie zbrojenia rozciąganego przy zginaniu (Flexural Tension Failure),
FCF – zniszczenie belki przez zmiażdżenie betonu przy zginaniu (Flexural Compression Failure),
ZM – Małe Zginanie, wystraczające tylko zbrojenie rozciągane – dołem , nie jest potrzebne zbrojenie ściskane – górą
ZS – Średnie Zginanie – wymagane zbrojenie górne – górą wystarcza tylko zbrojenie konstrukcyjne
ZD – Duże Zginanie – wymagane dodatkowe zbrojenie górne ze względu na możliwość kruchego zniszczenia betonu
$$\begin{equation} f_{cd}^{’} = \eta_c \cdot f_{cd} \quad ; \quad \eta_c= 1 – \Delta \eta \quad ; \quad \Delta \eta=\cfrac{f_{ck} -50}{200} \ge 0
\label{1}\end{equation}$$
Zgodnie z uwagą pod kl. 3.1.7(3) normy Eurokod 2 [1] – jeśli szerokość strefy ściskanej zmniejsza się w kierunku skrajnego włókna ściskanego,, to współczynnik redukcji $\eta_c$ zmniejsza się 0 10% (przemnaża przez 0,9). Dotyczy to na przykład przekroju kołowego.
$$\begin{equation} f_{yd}^{’}= \eta_s \cdot f_{yd} \quad ; \quad \eta_s=1,0 \quad ;\quad (\eta_s < 1 \text { w szczególnych, jawnie wskazanych przypadkach}).
\label{2}\end{equation}$$
Unormowane siły przekrojowe moment zginający i siła osiowa
$$\begin{equation}
\parallel \to\parallel \, m_\bullet=\cfrac {M_\bullet }{ \overline {M}} \\ \parallel \to\parallel \, n_\bullet =\cfrac{N_\bullet }{\overline N} \\ \text {gdzie czynniki normujące:} \quad \overline {M}=b d^2 f_{cd}^{’} \quad ; \quad \overline {N}=A_c \cdot f_{cd}^{’}
\label {3} \end{equation}$$
gdzie:
$\bullet$ = el – sprężysty (elastic), ult – graniczny (ultimate) ze względu na kruche zniszczenie (zmiażdżenie) betonu , Ed – obliczeniowy ( design ) od obciążeń zewnętrznych ( External ), Rd – nośność, opór ( resistans) obliczeniowy (design), itd.,
$\overline M$ – czynnik normujący moment ma wymiar nośności przekroju mierzonej momentem zginającym:
$\overline M =M_{el}/6 $, gdzie: $M_{el}= W_{el} \cdot f_{cd}^{’}$ – nośność sprężysta prostokąta bxd), $W_{el}= b \cdot d^2 / 6 $,
$\overline M =M_{pl}/4$, gdzie: $M_{pl}= W_{pl} \cdot f_{cd}^{’}$ – nośność plastyczna prostokąta bxd , $W_{pl}= b \cdot d^2 /4$,
$\overline N= A_c \cdot f_{cd}^{’}$ – nośność betonu (bez zbrojenie) na ściskanie,
$A_c=b\cdot d $ – efektywne pole przekroju betonu ($\ref{5}$),
$d$ – efektywna wysokość przekroju ($\ref{4}$),
$b$ szerokość przekroju; w sensie ścisłym dla dla belki prostokątnej,
$b= b_w$ lub pasa $b= b_f$ (rys, Z-8) dla belki teowej – szerokość środnika lub pasa ; $b=D$ średnica dla belki ko przekroju kołowym
Efektywna (użyteczna) wysokość przekroju $d$ jest odległością od krawędzi ściskanej betonu do osi zbrojenia.
Dla zbrojenia dolnego (rys. Z-1)
$$\begin{equation} d= h- a_l\label {4} \end{equation}$$
gdzie:
h – wysokość przekroju betonowego,
$a_l=c_l – \Phi/2$ – osiowe otulenie zbrojenia dolnego „l”,
$c_l$ – otulenie betonem pręta o średnicy $\Phi$,
$b$ – szerokość rozpatrywanej części przekroju:
Efektywne pole przekroju betonu
$A_c= A_{c,brutto}$ – pole otulenia dolnego $A_{su}$, czyli dla przekroju prostokątnego:
$$\begin{equation} A_c= b \cdot (h- a_l) = b\cdot d \label {5} \end{equation}$$
i analogicznie dla innych typów przekrojów
Rzeczywista wysokość ściskanej bryły betonu
$$\begin{equation} x=\cfrac{x_{eff}}{\lambda} \, \\ \parallel \to\parallel \xi=\cfrac{x}{d} = \cfrac{\xi_{eff}}{\lambda}= \begin {cases}
\xi_{MN}= 119 / 99 \cdot ( 1 -\sqrt{ 1 – 594/289 \cdot \mu_{Ed} } ), & \text{ model MN }\\
\xi_{MU}=1 / \lambda \cdot (1 -\sqrt{1- 2 \cdot \mu_{Ed}}) ,& \text{ model MU}\\
\end{cases} \label{6}\end{equation}$$
Współczynnik redukcyjny wysokości strefy ściskanej
$$\begin{equation} \lambda= \lambda_0- \Delta \lambda \quad;\quad \Delta \lambda= \cfrac{f_{ck} -50}{400} \ge 0 \label {7}\end{equation}$$
gdzie podstawowy współczynnik redukcyjny wysokości strefy ściskanej:
$$\begin{equation} \lambda_0=\begin {cases}
\lambda_{MN}=17/21 \approx 0,810 , & \text { model MN}\\
\lambda_{MU}=0,8, & \text { model MU}\\
\end{cases}\label {8}\end{equation}$$
Efektywna wysokość ściskanej bryły betonu
$$\begin{equation} x_{eff}= \lambda \cdot x \\ \parallel \to\parallel \xi_{eff}=\begin {cases}
289/ 297 \cdot \left( 1- \sqrt{1- 594/289\cdot \mu_{Ed}}\right) & \text { model MN }\\
1- \sqrt{1 – 2 \cdot \mu_{Ed}}, & \text { model MU}\\
\end{cases}\label {9}\end{equation}$$
gdzie: $\mu_{Ed} = m_{Ed}$ lub $m_{Ed}^*$
Odległość środka ściskanej bryły betonu od górnej krawędzi przekroju
$$\begin{equation} x_c= \begin {cases} 99 / 238 \cdot x \approx 0,416 \cdot x, & \text { model MN}\\
1/2 \cdot x_{eff} \approx 0, 4 \cdot x , & \text { model MU}\\
\end{cases} \label{10}\end{equation}$$
Ramię siły w betonie względem osi zbrojenia rozciąganego
$$\begin{equation} z_c = d – x_c \, \\ \parallel \to\parallel \, \zeta_c = \begin {cases}
1- 99/238\cdot \xi= \left(1 + \sqrt{1-594/289 \cdot \mu_{Ed}}\right) /2 & \text{ MN}\\
1- \xi_{eff}/2= \left (1+ \sqrt{1- 2 \cdot \mu_{Ed}}\right) /2 ,& \text{ MU}\\
\end{cases} \label{11}\end{equation}$$
gdzie: $\mu_{Ed} = m_{Ed}$ lub $m_{Ed}^*$
Sprowadzone do stali pole przekroju betonu
$$\begin{equation} A_{c→ s \bullet} = A_c \cdot \cfrac{f_{cd}^{’}}{f_{yd}^{’}} \label {12} \end{equation}$$
gdzie:
$f_{cd}^{’}$ ($\ref{1}$), $f_{yd}^{’}$ ($\ref{2}$), $ A_c = b \cdot d$ ($\ref{5})$
$\bullet = u,l$
W przypadku różnych stali używanych w przekroju, np.: stal zbrojenia żebra – dolnego (•=l) o wytrzymałości $f_{yd,l}^{’}$ ) i stal zbrojenia pasa- górnego (•=u) o wytrzymałości $f_{yd,u}^{’}$) ) sprowadzone pole $A_{c→s•}$ wyznacza się dla każdej ze stali odrębnie i stosuje zależnie od przedmiotu obliczeń: przy wyznaczaniu nośności zbrojenia górnego $m_{su,}$ stosujemy $A_{c→su}$ przy wyznaczaniu pola przekroju zbrojenia dolnego $A_{s/l,l}$ stosujemy $A_{c→sl}.
Efektywne pole ściskanej bryły betonu
$$\begin{equation} A_{cx} = \lambda \cdot b \ \cdot x =\lambda \cdot A_c \cdot \xi = A_c \cdot \xi_{eff}\\
\parallel \to\parallel a_{cx}= \xi_{eff}
\label {13} \end{equation}$$
gdzie: $\lambda$ ($\ref{7}$)
Sprowadzone do stali pole ściskanego betonu
$$\begin{equation} A_{cx→ s\bullet} = A_{c→s\bullet} \cdot \xi_{eff} \label {14} \end{equation}$$
gdzie: $\bullet$ = najczęściej „l” (sprowadzone do zbrojenia dolnego
graniczne_parametry ściskanej_strefy_betonu_z_warunku_kruchego_zniszczenia_betonu
Kryterium kruchego zniszczenia betonu FCF (Flexural Compression Failure)
$$\begin{equation} FCF: \begin {cases}
\mu_{Ed} \le \mu_{ult} & \text { w obciążenia przekroju } \mu_{Ed} = m_{Ed} \quad lub \quad m_{Ed}^* \\
\xi \le \xi_{ult} & \text { w wysokości ściskanej strefy betonu } \\
\zeta_c \ge \zeta_{ult} & \text { w ramieniu siły w betonie } \\
\end{cases} \label{15}\end{equation}$$
Maksymalna wysokość strefy ściskanej
$$\begin{equation}\parallel \to\parallel \, \xi_{ult} = \begin {cases}
\cfrac{0,85 – 0,44}{1,25} = 0,33, & \text {BZ } \\
\cfrac{0,85 – 0,54}{k_4} = \cfrac{0,31}{k_4} & \text {BWW }
\end{cases} \label{16}\end{equation}$$
gdzie wartości współczynnika $k_4$ podano w tab.W-1.
Maksymalne obciążenie przekroju momentem zginającym (BZ)
$$\begin{equation} \parallel \to\parallel \, m_{ult} = \begin {cases}
\cfrac{119}{142} \cdot 0,33 \cdot \left (1 -\cfrac{ 99}{238} \cdot 0,33 \right) = 0,23 & \text { MN }\\
0,264 \cdot \left(1- \cfrac{0,264} {2} \right) = 0,23 , & \text { MU }\\
\end {cases} \label{17} \end{equation}$$
gdzie $0,264=0,8 \cdot 0,33$
Minimalne ramię- dźwignia siły w betonie BZ
$$\begin{equation} \parallel \to\parallel \, \zeta_{c, ult} \begin {cases}
(1 + \sqrt{1-594/289 \cdot 0,23})/2 = 0,863 & \text{ MN}\\
(1+ \sqrt{1- 2 \cdot 0,23})/2 =0,867 ,& \text{ MU}\\
\end{cases} \label{18}\end{equation}$$
Stopień zbrojenia (unormowane pole zbrojenia)
$$\begin{equation} \parallel \to\parallel \, \rho_\bullet = \begin {cases}
\rho_{A,\bullet} = \cfrac{A_{s,\bullet}}{A_{p}} & \text{ geometryczny stopień zbrojenia }\\
\rho_{F,\bullet} =\rho_{A,\bullet} \cdot \cfrac{f_{yd}^{’}}{f_{cd}^{’}}= \cfrac{\overline N_{Rd,c}}{\overline N_{Rd,s,\bullet}},& \text{ fizyczny stopień zbrojenia}\\
\end{cases} \label{19}\end{equation}$$
gdzie:
($\bullet = u, l, s$) – zbrojenie górne i dolne, suma zbrojenia podłużnego w przekroju,
$A_p= b \cdot h$ rzeczywiste pole przekroju betonu lub $A_p= b\cdot d$ – efektywne pole przekroju w zależności od kontekstu (obliczenia, przedmiar , itd)
Współczynnik redystrybucji naprężenia w przekroju (stosunek momentu po redystrybucji do momentu sprężystego):
$$\begin{equation} \delta= \cfrac{\mu_{ult}}{\mu_{el}} \label {20} \end{equation}$$
Model żelbetowego przekroju zginanego
Podstawowe założenia modelu
- Żelbetowy pręt zginany analizuje się ramach klasycznej teorii belek Bernoullego, czyli przyjmuje założenie płaskich przekrojów, czyli „przekrój płaski przed odkształceniem pozostaje płaski po odkształceniu”, z którego wnioskiem jest to, że odkształcenia włókien przekroju zmieniają się liniowo po wysokości podług zależności ($\ref{32}$).
- Pomija się naprężenia rozciągające w betonie,
- Pomija się składowe naprężenia inne niż normalne w kierunku osi belki $\sigma$, a jednoosiowe prawo Hooke’a obowiązuje dla każdego włókna belki $\sigma_w =E_w \cdot \varepsilon_w$: dla betonu „w=c” wg ($\ref{38}$) , dla stali „w=s” wg ($\ref{42}$). Moduł Younga włókien stalowych wynosi $E_s= 200 \, GPa$ Moduł Younga ściskanych włókien betonowych wynosi $E_c=27 \, do \, 45 \, MPa$ (moduł średni) zależnie od klasy betonu wg tab W-1 i w zależności od stanu konstrukcji po uwzględnieniu pełzania betonu, czyli zależy od wieku analizowanego elementu – zgodnie z zasadami z rozdziału Pełzanie i skurcz betonu
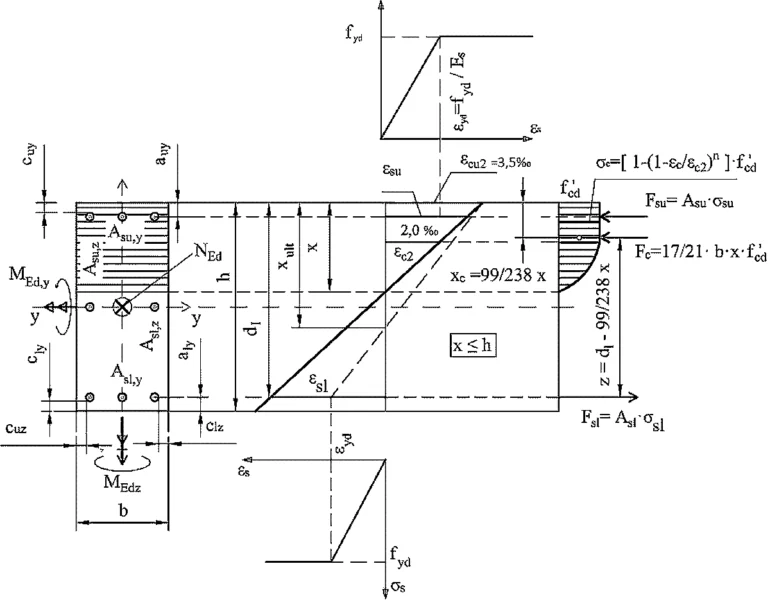
- Maksymalne odkształcenie włókna ściskanego przekroju nie może przekroczyć wartości $\varepsilon_{cu} =3,5$‰ ( $\varepsilon_{cu2}$ w modelu MN i $\varepsilon_{cu3}$ w modelu MU), (rys. Z-1 i Z-2)
- Dopuszcza się pełne uplastycznienie zbrojenia stalowego, czyli $\varepsilon_s \ge \varepsilon_{yd}= f_{yd}/E_s$, ale w ogólności naprężenia w zbrojeniu mogą być mniejsze od granicy plastyczności $\sigma_s \le f_{yd}$
- Rozkład naprężenia w części ściskanej betonu (powyżej osi obojętnej) jest paraboliczny, opisany zależnością ($\ref{23}$) – model nieliniowy MN = rys. Z-1 .
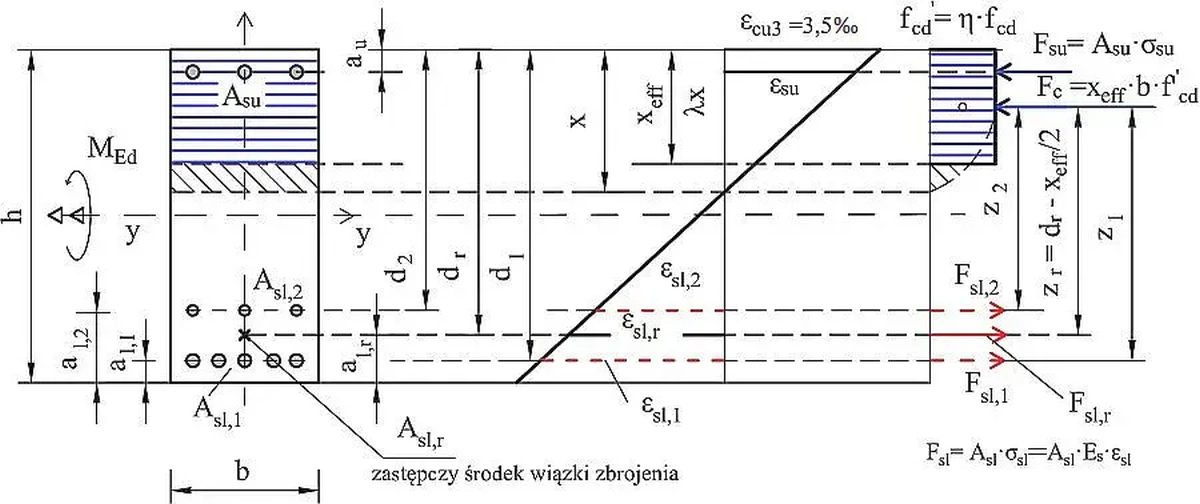
- Dopuszcza się aproksymację parabolicznego rozkładu naprężenia w strefie ściskanej przez rozkład prostokątny – model uproszczony MU (rys. Z-2 ) ze współczynnikiem redukcyjnym wysokości strefy ściskanej $\lambda_{MU}$ ($\ref{8}^2$ ).
Model nieliniowy MN
Model rozkładu naprężenia na wysokości $x$ strefy ściskanej betonu jest paraboliczny dla odkształcenia betonu $0 < \varepsilon_c \le \varepsilon_{c2} = 2,0$‰ i prostokątny dla $0 < \varepsilon_c > \varepsilon_{c2} < \varepsilon_{cu2}=3,5$‰ [1], kl. 3.1.7(1) (wykładnik potęgi $n=2$ dla betonu zwykłego BZ i n wg tab. W-1 dla betonów wysokiej wytrzymałości BWW).
Nieliniowy (paraboliczny) model betonu MN z rys. Z-1, można opisać formułami [1], wzory (3.17)-(3.18) :
$$\begin{equation}\sigma_c (z)= \begin {cases}
f_{cd}, & \text{ jeśli } \varepsilon_{c2} \le \varepsilon_c \le \varepsilon_{cu2}\\
f_{cd}\cdot \left [ 1 -\left( 1-\cfrac{\varepsilon_c}{\varepsilon_{c2}} \right)^n \right],& \text { jeśli } \varepsilon_c < \varepsilon_{c2} \\ \end{cases} \label{21}\end{equation}$$
gdzie wykładnik potęgi zgodnie z tab. W-1 (dla betonu BZ n=2), $\varepsilon_{cu2}=3,5$‰ – graniczne (maksymalne) odkształcenie betonu (dla BZ) $\varepsilon_{c2}=2$‰ – najmniejsze odkształcenie, przy którym w betonie wystąpią naprężenia $f_{cd}$ (dla BZ).
W niniejszym artykule wykładnik potęgi n da wszystkich betonów (BZ i BWW) przyjmuje się $n=2$, ale zamiast wytrzymałości $f_{cd}$ wprowadza się $f_{cd}^{’}$ ($\ref{1}$). W ten sposób również dla betonów BWW uzyskuje się wyniki akceptowane w obliczeniach inżynierskich. W zapisie ($\ref{12}$) pozostawiono jeszcze oryginalną formę wg [1], wzory (3.17)-(3.18), ale na rys Z-1 i w dalszej treści artykułu dokonano stosownych zmiany $f_{cd}$ lub $\eta \cdot f_{cd}$ na $f_{cd}^{‘}$.
Całkowanie rozkładu ($\ref{21}$) prowadzi do zależności ($\ref {14}$) na pole ściskanej bryły betonu $A_{cx}$ oraz do ($\ref{10}^1$) na odległość środka tej bryły od krawędzi górnej przekroju $x_c$.
Model uproszczony MU
Zgodnie z klauzulą [1],kl.3.1.7(3) w obliczeniach inżynierskich dopuszcza się założenia upraszczające, polegające na aproksymacji parabolicznej bryły naprężenia w modelu MN przez bryłę prostokątną MU, w sposób pokazany na rys. Z-2.
W uproszczonym modelu MU zmniejsza się wartość naprężenia w betonie do $f_{cd}^{’} = \eta f_{cd}$ i wysokość bryły naprężenia do $\lambda x$, zgodnie z wartościami zamieszczonymi w tab. W-1. W celu skrócenia zapisu formuł – zredukowana wysokość strefy ściskanej betonu jest oznaczana przez $x_{eff} = \lambda x$.
Graniczne odkształcenia betonu w modelu MU $\varepsilon_{cu3}$ są takie d\same jak modelu MU $\varepsilon_{cu2}$ i wynoszą 3,5‰. Natomiast odkształcenia betonu BZ na początku strefy prostokątnej (dla $\sigma_c =f_{cd}^{’}$) w modelu MN wynoszą $\varepsilon _{c2}$=2‰, a w modelu MU $\varepsilon _{c3}$= 1,75‰ . Dla betonów BWW stosowne wartości podano w tab. W-1.
Model MU przedstawiony na rys. Z-2 definiują formuły (3.19)-(3.22) normy [1], które opisują współczynnik $\lambda_{MU}$ ($\ref{8}^2$) , określający efektywną wysokość strefy ściskanej oraz współczynnik $\eta_c$ ($\ref{1}^2$) , określający efektywną wytrzymałość betonu.
Siły przenoszone przez beton: osiowa Fc i moment Mc
Wypadkowa bryły naprężenia w betonie $F_c$ (lub po unormowania $n_c$ ($\ref{6}$) zaprezentowana na rys. Z-1 (model MU) i rys Z-2 (model MN) wynosi
$$\begin{equation} F_c = A_{cx}\cdot f_{cd}^{’} \parallel \to\parallel n_c= a_{cx} \label{22}\end{equation}$$
gdzie $A_{c,x}, a_{cx}$ ($\ref{14}$).
Współczynnik równoważnej wysokości strefy ściskanej dla modelu nieliniowego wynosi
$\lambda_{MN}=17/21 \approx 0,810$
podczas gdy dla modelu uproszczonego i betonu zwykłego przyjmuje się $\lambda_{MU}=0.8$.
W przypadku przeważającego zginania (rys. Z-3, stan C) wysokość strefy ściskanej $x\le h$ i moment bryły naprężenia w betonie $M_c$ względem osi zbrojenia rozciąganego,- dolnego, można wyznaczyć ze standardowej zależności:
$$\begin {equation} M_c= F_c \cdot z_c, \, \parallel \to\parallel \, m_c = n_c \cdot \zeta_c \label {23} \end {equation}$$
ramię $z_c$ działania siły $F_c$ względem osi zbrojenia dolnego oblicza się z zależności ($\ref{11}$), gdzie odległość $x_c$ siły $F_c$ od górnej krawędzi przekroju zależna od modelu betonu jest opisana formułą ($\ref{10}$) i zilustrowana na rys Z-1.
W rezultacie nośność ściskanej bryły betonu $M_{Rd,c}= M_c$ ($\ref{23}$) względem osi zbrojenia dolnego -rozciąganego: można zapisać w postaci:
$$\begin{equation} M_{Rd,c} = \parallel \to\parallel m_{Rd,c} = \begin {cases}
17/21 \cdot b \cdot x \cdot f_{cd}^{’} \cdot ( d_l – 99/238 \cdot x ) \, \parallel \to\parallel \, \xi \cdot ( 17/21- 33/98 \cdot \xi ) & \text{ MN }\\
b \cdot x_{eff} \cdot f_{cd}^{’} \cdot ( d_l – x_{eff}/2 ) \, \parallel \to\parallel \, \xi_{eff} \cdot ( 1- \xi_{eff}/2 ) & \text{ MU }\\
\end{cases} \label{24}\end{equation}$$
Porównanie modelu nieliniowego MN i uproszczonego MU
Wysokość strefy ściskanej w modelu MU dla betonu zwykłego BZ wynosi $\lambda \cdot x= 0,8 \cdot x$, a w modelu MN niezależnie od rodzaju betonu $\lambda=17/21= 0.81$. Odległość siły w betonie $F_c$ od krawędzi górnej przekroju w modelu MU $x_c= x_{eff}/2= 0,5 \cdot 0,8= 0,4 \cdot x$, a w modelu MN $ x_c=99/238 = 0,416 \cdot x $. Różnice nie przekraczają kilku procent i są akceptowane w ręcznych obliczeniach inżynierskich. Różnice w zbrojeniu przekroju belki obliczone w modelu MN i MU dla trzech sytuacji projektowych przedstawiono w przykładach Z-1 do Z-3.
Graniczna parametry ściskanej strefy betonu z warunku kruchego zniszczenia betonu
Mechanizmy zniszczenia zginanego przekroju betonowego
W belce żelbetowej w stanie granicznym nośności SGN mogą wystąpić następujące mechanizmy zniszczenia:
- plastyczne zniszczenie przez rozciąganie przy zginaniu FTF (Flexural Tension Failure) polegające na zerwaniu podłużnego zbrojenia dolnego, występujące w przypadku zbyt małego zbrojenia
- kruche zniszczenie przez ściskanie przy zginaniu FCF (Flexural Compression Failure) polegające na zmiażdżeniu betonu w strefie ściskanej, występujące w przypadku zbyt dużego zbrojenia
- kombinowane zniszczenie przy zginaniu BCF (Balanced Failure), polegające na jednoczesnym wystąpieniu mechanizmów FTF i FCF w przypadku zbilansowanego zbrojenia wskutek chwilowego zachwiania równowagi, w tym przez: osłabienie spękanego betonu rozciąganego, nadmierne zwiększenie strefy ściskanej lub zastosowaniu złej jakości betonu, czyli chwilowe wystąpienie warunków sprzyjających zainicjowaniu kruchego pękaniu betonu lub uplastycznienia stali zbrojeniowej
- zniszczenie poprzez ścinanie SFM ( Shear Failure Modes) w odmianach: DTF (Diagonal Tension Failure) lub SCF (Shear Compression Failure)
Kryterium kruchego zniszczenia betonu FCF
Zmiażdżenie betonu w strefie ściskanej belki, często nazywane zniszczeniem ściskaniem przy zginaniu FCF jest mechanizmem zniszczenia kruchego, następującego nagle w sposób niesygnalizowany – rysy w strefie rozciąganej są jeszcze niewielkie, a ugięcia są niedostrzegalne. Najczęściej jest wynikiem znacznego przezbrojenia strefy rozciąganej i w konsekwencji rozrostu wysokości strefy ściskanej betonu . Wskutek tego rozpoczyna się od kruszenia betonu po stronie ściskanej, a dopiero w konsekwencji zwiększania krzywizny (uginania) płaszczyzny dolnej (rozciąganej) belki.
Ponieważ awaria wywołana mechanizmem FCF ma charakter nagły, więc nie jest to pożądana z punktu widzenia niezawodności użytkowania i diagnostyki żelbetu. W projektowaniu belek żelbetowych należy zwrócić szczególną uwagę na wyeliminowanie mechanizmu FCF. W każdym przypadku należy nadać kryterium FTF ($\ref{15}$) i wzmacniać ściskaną bryłę betonu dodatkowym zbrojeniem ściskanym. Kryterium warunku kruchego zniszczenia betonu można sformułować w wysokości strefy ściskane $\xi$ j- formuła ($\ref{15}^1$) ; obciążeniu momentem $\mu_{Ed}=m_{Ed}$ – formuła ($\ref{15}^2$) lub w ramieniu siły w betonie $\zeta_c$ – formuła ($\ref{15}^3$).
Graniczna (maksymalna) wysokość strefy ściskanej ξult, a zniszczenie kruche betonu
Wysokość strefy ściskanej betonu jest ograniczona poprzez dopuszczalną redystrybucję naprężenia w przekroju zgodnie zasadami dotyczącymi sprężystej analizy betony z ograniczoną redystrybucją. Redystrybucja naprężenia w zakresie nieliniowym dotyczy nie tylko punktów wzdłuż konstrukcji statycznie niewyznaczalnych, ale także redystrybucji naprężenia po wysokości przekroju. W przypadku redystrybucji naprężenia na wysokości przekroju również mają zastosowanie wyrażenia z klauzuli [1],kl.5.5(4), zalecanej dla analizy liniowo-sprężystej z ograniczoną redystrybucją belek lub płyt statycznie niewyznaczalnych, a mianowicie :
$$\begin{equation} \delta \ge \begin {cases}
0,44+1,25 \cdot \xi_{ult}, & \text {dla BZ} \\
0,54+k_4 \cdot \xi_{ult}., & \text {dla BWW} \\
0,7 , & \text {dla stali B lub C} \\
0,8 , & \text {dla stali A} \\
\end {cases} \label {25}\end{equation}$$
Współczynnik $k_4=\cfrac{1,25 \cdot (0,6+0,0014)}{\varepsilon_{cu}}$ dla poszczególnych betonów zestawiono w tab.W-1.
$$\begin{equation} \xi_{ult} < \begin {cases}
(\delta – 0,44)/1,25, & \text {dla BZ } \\
(\delta – 0,54)/k_4 & \text {dla BWW }
\end {cases} \label{26} \end{equation}$$
Dla powszechnie stosowanej plastycznej stali klasy B lub C – $\delta_{max}= 0,7$ (30% redystrybucji) i z równań ($\ref{26}$) otrzymano wartości ($\ref{27}$) :
$$\begin{equation} \xi_{ult,(max)} < \begin {cases}
0,208, & \text {dla BZ } \\
0,160/k_4 & \text {dla BWW } \\
\label {27} \end {cases} \end{equation}$$
W wielu polskich podręcznikach (m.in. podręcznik do technikum budowlanego [2] ; podręcznik dla studentów budownictwa [3], [4] i in.) przedstawia się odmienną interpretacje granicznej wysokości strefy ściskanej, a mianowicie taką przy której w zbrojeniu rozciąganym osiąga się granicę plastyczności. Z tego kryterium wyprowadza się formułę
$$\begin{equation} \xi_{ult,PL}= \cfrac{\varepsilon_{cu2}}{\varepsilon_{cu2} +{\varepsilon _{yd}}}\label {28} \end{equation}$$
gdzie $\varepsilon _{yd}=f_{yd}/E_s$ Na rys. Z-1 zilustrowano $x_{ult}= \xi_{ul.PL} \cdot d$ (bez indeksu PL).
Dla najczęściej stosowanej stali B500 i BZ z ($\ref{28}$) otrzymano:
$$\begin{equation} \xi_{ult,PL}= 0,617 \label {29} \end{equation}$$
Porównanie wartości $(\ref{29})$ (uzyskanej przy dopuszczeniu pełnego uplastycznienia stali) z wynikiem, ($\ref {27}$) uzyskanym dla granicznej redystrybucji naprężenia w strefie ściskanej – wskazuje, że stosowanie pierwszego, historycznego warunku ($\ref{28}$) prowadzi do znaczącego przekroczenia dopuszczalnej redystrybucji naprężenia na wysokości przekroju betonowego. Akceptacja hiper-redystrybycji dopuszcza też przypadki matematycznie nierzeczywiste (uwagi pod równaniem ($\ref{49}$)).
Przy pełnej redystrybucji naprężenia w przekroju – wysokość strefy osiągnie $\xi=0,45$, więc $\xi=0,617$ jest fizycznie niemożliwe.
Graniczna wysokość strefy ściskanej ($\ref {36}$) jest pozostałością historycznego podejścia, które jest błędne i nie powinno być nadal stosowane.
W celu ilustracji powyższego wywodu, w tab Z-1 zestawiono zależność stopnia redystrybucji $\delta$ od wysokości strefy ściskanej $\xi_{ult}$ dla betonu zwykłego BZ.
Tab. 1.Stopień redystrybucji naprężenia w betonie w funkcji granicznej wysokości strefy ściskanej z ($\ref{26}$)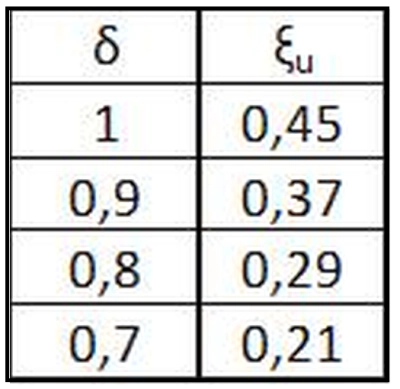
W wieku krajach, np. [5] od lat zaleca się stosowanie do wymiarowania przekrojów zginanych współczynnika redystrybucji $\delta=0,85$, Dla takiego współczynnika graniczna wysokość strefy ściskanej wyniesie $\xi_{ult}=0,33$.
Po szerokiej analizie zagadnienia kruchego zniszczenia betonu przekroju zginanego i zapewnienia odpowiedniej niezawodności zginanych przekrojów żelbetowych – w niniejszym artykule przyjęto graniczny stopień redystrybucji naprężenia w przekroju $\delta_{ult} = 0,85$, czyli: graniczną wysokość strefy ściskanej ($\ref{12}$) :
Wartości graniczne $(\ref{12})$ dotyczą rzeczywistej wysokości strefy ściskanej, a nie zredukowanej współczynnikiem $\lambda$ (efektywnej). Założenie $(\ref{12})$ o wysokości strefy ściskanej dotyczy zarówno modelu MN jak i MU.
Obciążenie graniczne (maksymalne) przekroju
Nośność graniczną bryły betonu z warunku kruchego zniszczenia uzyskano z rozwiązania $(\ref{48})$ względem $m_{Ed}$, Dla betonu zwykłego BZ, otrzymano:
$$\begin{equation} \parallel \to\parallel \, m_{ult} = \begin {cases}
\cfrac{119}{142} \cdot \xi_{ult} \cdot \left (1 -\cfrac{ 99}{238} \cdot \xi_{ult} \right) & \text { MN }\\
\xi_{ult,eff} \cdot \left(1- \cfrac{\xi_{ult,eff}}{2} \right), & \text { MU }\\
\end {cases} \label{30} \end{equation}$$
Po podstawieniu granicznej wysokości strefy ściskanej $\xi_{ult}=0,33$ ($\ref{12}$) dla betonu BZ uzyskano wartości graniczne nośności ściskanej bryły betonu ($\ref{13}$) – w modelu MU dla efektywnej granicznej wysokości $\xi_{ult,eff} =0,8\cdot 0,33= 0,264$
Dla betonów BWW $m_{ult}$ wyznacza się indywidualnie z zależności ($\ref{30}$) po podstawieniu wartości $ \xi_{ult}$ ($\ref{12}^2$) dla konkretnego betonu.
Graniczne (minimalne ) ramię- dźwignia siły w betonie
Graniczne (minimalne) ramię siły w betonie $\zeta_{c, ult}$ ($\ref{14}$) uzyskano z wyrażenia ($\ref {11}$) po podstawieniu wartości $m_{ult}$ ($\ref{13}$).
Uogólnienie granicznej wysokości strefy ściskanej
Graniczną wysokość strefy ściskanej nie może być przekroczona, po to, by zabezpieczyć beton przed kruchym pękaniem. W istocie należy ja wyznaczać z warunku granicznego gradientu (szybkości) spadku odkształceń po wysokości przekroju, jak następuje:
$$\begin{equation} \nabla \xi_{ult}= \cfrac{ \Delta \varepsilon }{ \Delta \xi_{ult}} \begin {cases}
(0,0035-0)/ 0,33 = 10,6 \text{‰}, & \text {dla BZ } \\
(0,0035-0)/ (0,34/k_4) = 10,3 /k_4 \text{‰}, & \text {dla BWW} \end {cases} \label{31} \end{equation}$$
gdzie przyrost $ \Delta \xi_{ult}$ przyjęto za $(\ref{12})$.
Powyższe uogólnienie wyjaśnia istotę granicznej wysokości strefy ściskanej jako wartości własnej betonu. Oczywiste staje się, że łączenie wysokości granicznej z wytężeniem zbrojenia nie jest właściwe.
Ponadto wyjaśniono, że graniczna wysokość strefy ściskanej dotyczy przypadku przeważającego zginania (rys. W-2c), a w przypadkach czystego lub przeważającego ściskania a także przeważającego rozciągania (rys. W-2a,b) wartości $ \nabla \xi_{ult}$ nie można przekroczyć, więc w tych przypadkach sprawdzenie warunku granicznej wysokości strefy ściskanej jest zbędne.
Równania przekroju
Zasada płaskich przekrojów
Odkształcenia podlegają zasadzie płaskich przekroi Bernoulliego , wyrażonej formułami ($\ref{32}$) wynikającymi z rys. Z-1 :
$$\begin {equation} \cfrac{\varepsilon_{sl}}{d_l-x}= \cfrac{\varepsilon_{su}}{x – d_u}=\cfrac{\varepsilon_{cu}}{x} \label {32} \end {equation}$$
gdzie: $\varepsilon_{cu}=$3,5‰ = $\varepsilon_{cu3}$ dla modelu prostokątnego MU i $\varepsilon_{cu2}$ dla modelu MN.
Z równań $(\ref{32})$ można uzyskać jawną postać odkształcenia zbrojenia górnego (u) i dolnego (l):
$$\begin {equation} \varepsilon_{sl}=\varepsilon_{cu} \cdot (d_l /x-1) \qquad \varepsilon_{su}=\varepsilon_{cu} \cdot (1 – d_u/x) \label {33} \end {equation}$$
Z zależności $(\ref{33})$ wynika, że zależnie od relacji wysokości strefy ściskanej $x$ oraz wysokości użytecznych zbrojenia zachodzą następujące przypadki wytrzymałościowe:
TT (ang. Tension-Tension) $x=0$ – przypadek dla którego odkształcenia w stali są nieokreślone. Odpowiada to jednorodnemu rozciąganiu przekroju, w którym w całym przekroju (w betonie i stali) uzyskano odkształcenia rozciągające, a przekrój podlega analizie prętów zespolonych . Takim przypadkiem nie zajęto się w niniejszym artykule – jest on przedmiotem artykułu Konstrukcje zespolone stalowo-betonowe.
CC (ang. Compresion-Compresion) $ x > d_u \, x \le d_l \to $ $\varepsilon_{su} > 0$, $\varepsilon_{sl} > 0$, oba zbrojenia są ściskane – jest to przypadek małego mimośrodu. CT (ang. Compresion-Tension) $ x > d_l \to \, \varepsilon_{su} > 0 \, , \, \varepsilon_{sl} < 0$, czyli zbrojenie górne jest ściskane, a zbrojenie dolne rozciągane – jest to przypadek dużego mimośrodu, obejmujący również klasyczne zginanie belek. Do przypadku
CT zaliczono też $ x \le d_u \to$ $\varepsilon_{su}\le 0$, $\varepsilon_{sl} > 0$, dla którego zbrojenie górne jest rozciągane, a dolne ściskane. Wystarczy analizować przekrój odwrócony o 900 . Na rys. Z3 przypadki wytrzymałościowe TT, CC, CT zestawiono w korelacji z punktami A-E na krzywej integracji zginania i ściskania przekroju żelbetowego.
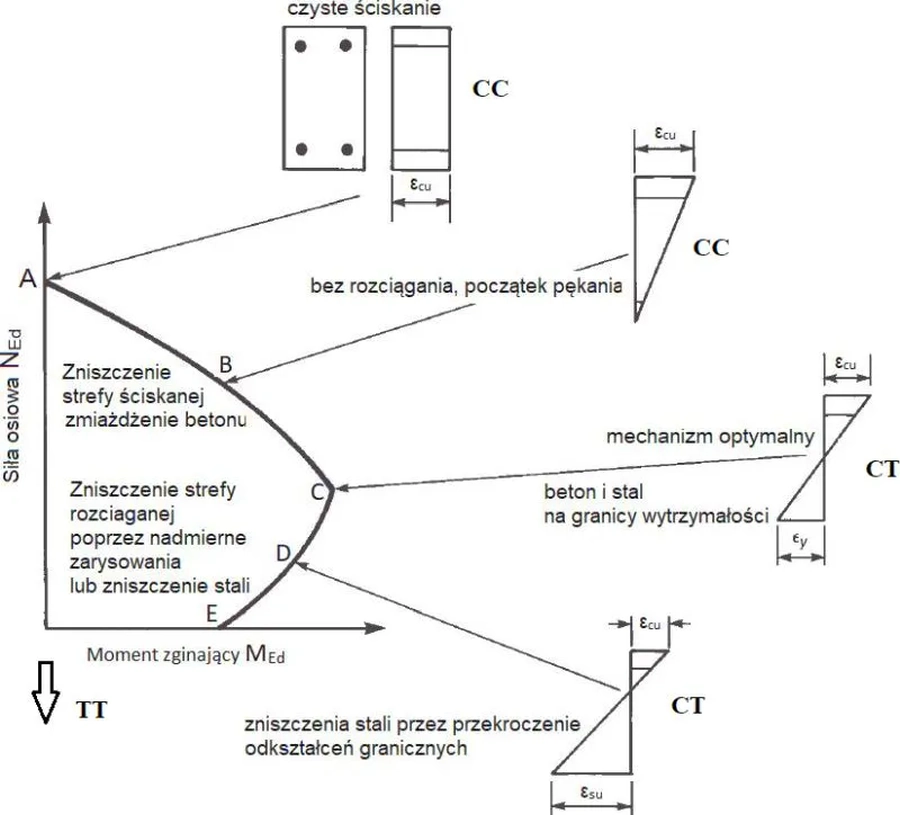
Rys. 3 Przypadki wytrzymałościowe, a interakcje sił w żelbetowym przekroju zginanym i ściskanym- na podstawie [6], Fig. 11-13
W niniejszym artkule zasadniczo zajęto się zginaniem, czyli przypadkiem wytrzymałościowym CT i to w punkcie E na rys Z-3. ($N_{Ed}=0$). Wprowadzenie do innych przypadków zawiera rozdział Dwukierunkowe zginanie_My-Mz_z udziałem N.
Warunki równowagi przekroju jednoosiowo zginanego
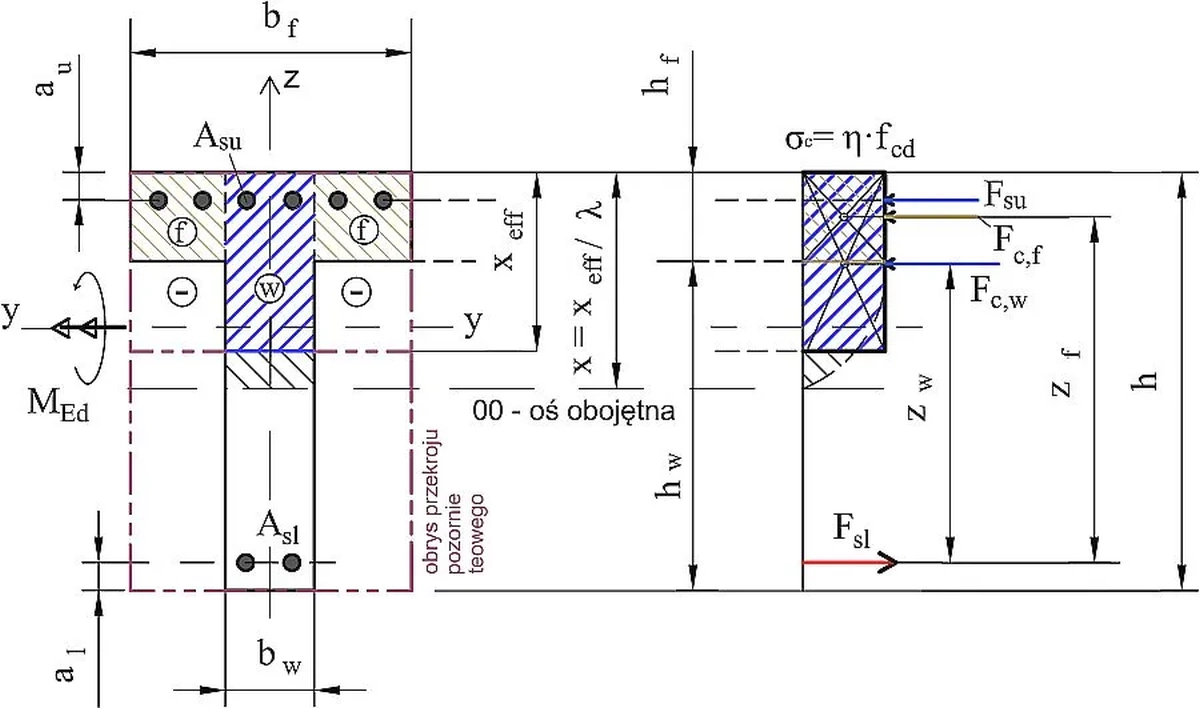
Na rys. Z-1 i Z-2 pokazano siły działające w przekroju z przyjętą konwencją znakowania sił zewnętrznych: zewnętrzny moment zginający $M_{Ed}$ jest dodatni jeśli rozciąga dolne włókna przekroju, zewnętrzna siła osiowa $N_{Ed}$ jest dodatnia, jeśli ściska przekrój. Założono też dodatnie zwroty sił wewnętrznych: siły $F_c$ i $F_{su}$ są ściskające, siła $F_{sl}$ jest rozciągająca. Jeśli z rozwiązania zadania uzyskano znaki ujemne, to będzie oznaczało, że w danej sytuacji obliczeniowej siła działa przeciwnie do założonego zwrotu.
Warunki równowagi przekroju zginanego momentem $M_{Ed} =M_y$ względem osi większej sztywności przekroju (y-y) oraz ściskanego /rozciąganego siłą osiową $N_{Ed}$ można zapisać w postaci
$$\begin{equation} \begin {cases} \Sigma X=0 \to N_{Ed} – F_c – F_{su} + F_{sl}=0\\ \Sigma M_y=0 \to M_{Ed} – M_{c,y} – F_{su} \cdot (h/2 – a_u) – F_{sl} \cdot (d_0 – a_l)=0 \end {cases} \label {34}\end{equation}$$
Ponieważ spełnione powinny być oba warunki $(\ref {34})$ jednocześnie, więc złożenie (suma) obu warunków powinna być stateczna. Po przemnożeniu pierwszego równania obustronnie przez $- h/2$ i dodaniu obu równań skonsolidowany warunek równowagi przyjmuje postać:
$$\begin{equation} R=(M_{Ed} – M_{c,y}) – (N_{Ed}+2\cdot F_{sl} – F_c)\cdot h/2 + (F_{sl} \cdot a_l+ F_{su} \cdot a_u) = 0 \label {35} \end{equation}$$
Po przekształceniach skonsolidowany warunek równowagi żelbetu można zapisać w postaci przydatnej do wyznaczania sumy zbrojenia przekroju:
$$\begin {equation} (F_{sl} +F_{su})=\cfrac {2\cdot (M_{Ed}-M_{c,y})} {d_{lu}}+ (N_{Ed}-F_c) \label {36} \end {equation}$$
gdzie:
$d_{lu}=h/2-a_u-a_l$
$F_c$ – wypadkowa bryły naprężenia w betonie ($\ref{22}$) ,
$M_{c,y}$ – moment zginający przenoszony przez beton liczony względem środka przekroju wynosi
$$\begin {equation} M_{c,y} =F_c \cdot \left( h/2 – x_c \right) \label {37} \end {equation}$$
gdzie $x_c$ ($\ref{10}$)
Prawo fizyczne betonu. Moduł materiału, a moduł górnego lub dolnego włókna belki
Prawo fizyczne betonu wiąże odkształcenia w betonie $\varepsilon_c$ z naprężeniem $\sigma_c$ i jest zapisywane w postaci analogicznej do wzoru Hooke’a dla materiału jednorodnego: $$\begin{equation}\sigma_c=E_c \cdot \varepsilon_c \label{38}\end{equation}$$
przy czym moduł odkształcalności betonu Ec(εc, t) jest w ogólności nieliniową funkcją odkształceń betonu oraz czasu $t$ i zmniejsza się istotnie wraz ze wzrostem pełzania betonu [1], Rys.3.2, a model $(\ref{38})$ jest w istocie nieliniowy. W mechanice prętów żelbetowych w normie [1] model $(\ref{38})$ aproksymowano przybliżoną, ale niezależną od czasu postacią przedstawioną na rys. Z-1 (model nieliniowy) lub na rys. Z-2 (model uproszczony).
Obliczeniowy moduł odkształcalności betonu jest modułem siecznym i jest minimalny dla włókna skrajnego (tam, gdzie odkształcenie jest maksymalne εc=εcu2 lub εcu3). Nazwano go modułem włókna górnego :
$$\begin{equation}E_{cu}=f_{cd}/\varepsilon_{cu2} \label{39}\end{equation}$$
Na przykład dla betonu C30/37 moduł włókna górnego wynosi Ecu=(30/1,4)/3,5‰=6,1 GPa. Dla porównania: średni moduł styczny dla betonu C30/37 wynosi Ecm=32 GPa, a moduł długotrwały (z uwzględnieniem pełzania) Ec,ef=Ecm/[1+φ(∞,t0)] ≈ Ecm/(1+2)=32/3=10,7 MPa.
Moduł włókna dolnego $E_{cl}$ zależy od fazy pracy przekroju, przy czym w każdej fazie obowiązuje założenie płaskich przekrojów. Z proporcji płaskiego przekroju uzyskano można wyznaczyć odkształcenie betonu na podstawie odkształcenia pręta stalowego, jak następuje:
$$\begin{equation} \varepsilon_{cl}= \varepsilon_{sl} \cdot \cfrac{h}{d_l}=\varepsilon_{sl} \cfrac{1}{1-a_l /h }\label{40}\end{equation}$$
Z prawa fizycznego ($\ref{38}$) wynika, że moduł włókna dolnego $E_{cl}$ dla $\sigma_{cl}=f_{ctm}$ wynosi
$$\begin{equation} E_{cl} =\cfrac{\sigma_{cl}} {\varepsilon_{cl}}= \cfrac {f_{ctm}}{\varepsilon_{sl}} \cdot \cfrac{1}{1-a_l /h } \label{41}\end{equation}$$
Moduły $E_{cu}$, $E_cl$ oraz $E_{cm}$ i $E_{c,ef}$ są innymi wielkościami jakościowo, bowiem $E_{cm}$ i $E_{c,ef}$ dotyczą materiału, a $E_{cu}$ i $E_{cl}$ dotyczą włókien konstrukcji.
W problemie zarysowania i ugięć (rozdział Rysy i ugięcia belek) stosuje się efektywny moduł odkształcalności $E_{c,ef}$ zależny od pełzania w czasie (rozdział Pełzanie i skurcz betonu)
Prawo fizyczne stali zbrojeniowej
Prawo fizyczne jest takie same dla zbrojenia górnego i dolnego (⊗=u,l): $$\begin{equation}\sigma_{s⊗}=E_s \cdot \varepsilon_{s⊗} \label{42}\end{equation}$$
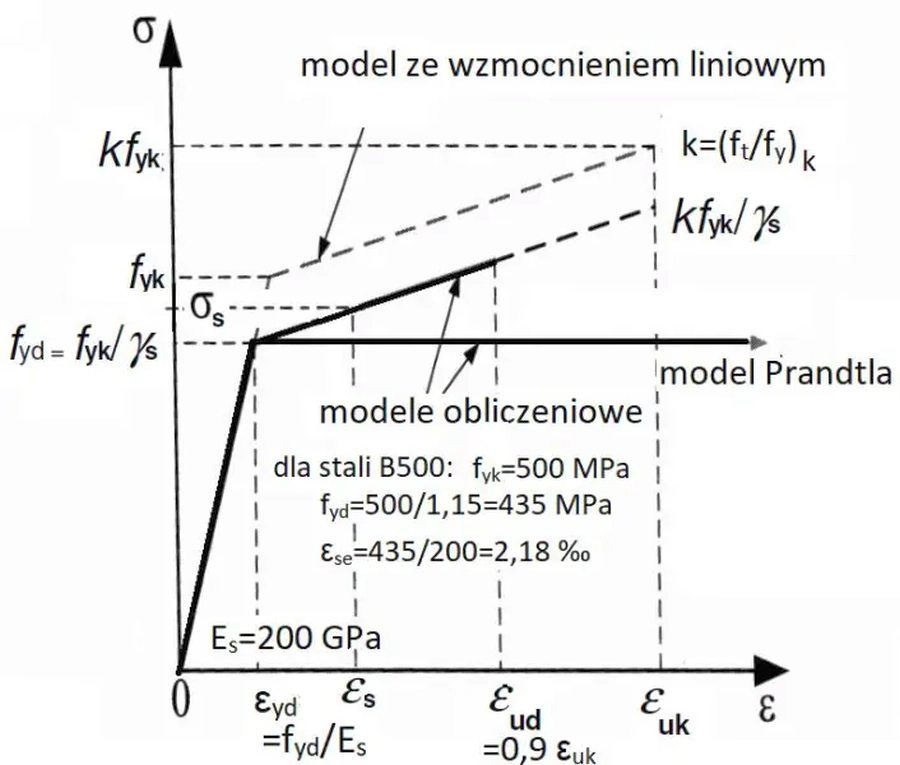
gdzie moduł Younga w zakresie sprężystym i w temperaturach $30^o C \le t \le 100^o C$ przyjmuje się $E_s=200 GPa$, a po przekroczeniu przez naprężenia granicy plastyczności $f_yd$, czyli przy odkształceniu większym $\varepsilon_{yd}=f_{yd} / E_s$ moduł odkształcalności jest modułem stycznym, zależnym od modelu stali. Dla najczęściej stosowanego modelu idealnie sprężysto-plastycznego (Prandtla) moduł styczny stali wynosi $E_s=f_yd/ \sigma_s$, gdzie $\sigma_s$ jest aktualnym naprężeniem w stali.
Stal zbrojeniowa może mieć klasę plastyczną stali ( A- mała ciągliwość , B – średnia ciągliwość . C – duża ciągliwość ), a zaleca się stosować stal klasy B lub C. Podział stali dokonuje się ze względu wartość współczynnika $k=f_t/f_y$ (= granica wytrzymałości w próbie rozciągania /granica plastyczności) oraz graniczne odkształcenia charakterystyczne $\varepsilon_{ul}$ , obserwowane przy zerwaniu próbki (przy naprężeniach $f_t$):
$$\begin{equation} \varepsilon_{uk} (f_{tk}) \in \begin {cases} [2,5 \, ; 5) \% , & \text{dla stali klasy A}\\ [5\, ; 7,5) \% , & \text{dla stali klasy B}\\ [7,5 \% , & \text{dla stali klasy C} \end {cases} \label {43} \end{equation}$$
$$\begin{equation} k=f_t/f_y \begin {cases} \ge 1,05 \% , & \text{dla stali klasy A}\\ \ge 1,08 \% , & \text{dla stali klasy B}\\ >1,15 \% ,\le 1,35 \% & \text{dla stali klasy C} \end {cases} \label {44}\end{equation}$$
W tab. W-2 zestawiono najczęściej stosowane stale zbrojeniowe.
Na rys. Z-4 pokazano modele stali przyjmowane w analizie żelbetu. Powszechnie stosuje się model idealnie sprężysto-plastyczny (model Prandtla), a w dokładniejszych analizach model ze wzmocnieniem liniowym. Pomimo tego, że współczynnik k jest niewielki dla stosowanych stali zbrojeniowych, to w modelu stali ze wzmocnieniem można uzyskać nośności nawet o 10% wyższe niż dla modelu Prandtla bez wzmocnienia.
W modelu ze wzmocnieniem liniowym naprężenia w zbrojeniu wyznacza się z zależności:
$$\begin{equation} \sigma_s = \begin {cases} E_s\cdot \varepsilon_s , & \text {dla $\varepsilon_s \le \varepsilon_{yd}$} \\ f_{yd} \cdot [ 1+k_w \cdot ( \varepsilon_s-\varepsilon_{yd})] , & \text { dla $ \varepsilon_{yd} <\varepsilon_s \le \varepsilon_{ud}$ } \\ f_{ud}=f_{uk}/1,15 , & \text{ dla $\varepsilon_s > \varepsilon_{ud}$} \end {cases} \label {45}\end{equation}$$
gdzie $\varepsilon_{yd}$ oraz $k_w$ zestawiono w tab. W-2. Graniczne obliczeniowe odkształcenie stali $\varepsilon_{ud}=0,9\cdot\varepsilon_{uk}$, przyjęto jako wartość graniczną, wynikającą z definicji rodzajów stali $(\ref{43})$.
Rozwiązanie zagadnienia jednokierunkowo zginanej belki żelbetowej
Zadanie jednokierunkowego zginania belki żelbetowej obliczeniowym momentem zginającym $M_{Ed}$ tylko w jednym kierunku ( $ M_{Ed}=M_y$ ; $N_{Ed}≡ 0$; $M_z=0$ ; $ M_T= M_x =0 $) jest podstawowym zadaniem teorii żelbetu i może być rozwiązany „w kwadraturach”.
Wynikającą z tego podejścia klasyczną technikę projektowania belki Nazwano MU lub MN zależnie od zastosowanego modelu betonu uproszczonego-prostokątnego MU ( rys. Z-2) lub nieliniowego=parabolicznego MN (rys. Z-1).
Wymaga się , by przekrój żelbetowy zginany obliczeniowym momentem zginającym pochodzącym od obciążeń zewnętrznych $M_{Ed}$ – obliczeniowa nośność przekroju $M_{Rd}$ była większa od obciążenia, co zapisuje się w postaci: (bezwzględnej) $\parallel \to\parallel$ (unormowanej):
$$\begin{equation} M_{Rd} \ge M_{Ed} \, \parallel \to\parallel \, m_{Rd} \ge m_{Ed} \label {46} \end{equation}$$
Nośność przekroju belki zależy od wysokości $x$ strefy ściskanej betonu oraz powierzchni zbrojenia dolnego (rozciąganego) $A_{sl}$ oraz górnego (ściskanego) $A_{su}$. W projektowaniu żelbetowej belki zginanej w jednym kierunku szukaną niewiadomą jest wysokość $x$ strefy ściskanej betonu, a zbrojenie belki jest funkcją tej wielkości, Belki żelbetowe są zbrojone górą i dołem (podwójnie). Najpierw rozwiązano zadanie pomocnicze: prosty problem belki zbrojonej pojedynczo. Rozwiązania tego pomocniczego zadania stanowią najważniejszy element rozwiązania belki podwójnie zbrojonej.
Przekrój PZP (pojedynczo zbrojony)
Przekrój PZP, jest zbrojony tylko dołem $A_{sl}>0$ i nie posiada zbrojenia górnego ściskanego, czyli $A_{su}=0 \to $F_{su}=0$
Nośność przekroju PZP
Nośność przekroju pojedynczo zbrojonego PZP oznaczono przez $M_{Rd,PZP}$. Nośność tą można wyznaczyć bezpośrednio z warunku równowagi momentów wokół osi zbrojenia rozciąganego jako nośność ściskanej bryły betonu $M_{Rd,c}$ ( siła w zbrojeniu $F_{sl}$ nie uczestniczy w warunku). otrzymano:
$$\begin{equation}M_{Rd,PZP} = M_{Rd,c} =M_c \label {47} \end{equation}$$
gdzie $M_c$ wg ($\ref{23}$), ($\ref{24}$)
Wysokość strefy ściskanej i ramię – mimośród siły
W staniu granicznym, czyli dla $\mu_{Ed}= m_{Rd,c}$ po rozwiązaniu równania kwadratowego ($\ref{24}$) względem wysokości strefy ściskanej $x$,$\xi$ otrzymano dwa pierwiastki
$$\begin{equation} \, \parallel \to\parallel \, \begin {cases}
\xi_{MN}(\mu_{Ed})= \cfrac{119}{99} \cdot \left ( 1 \pm \sqrt{ 1 – 594/289 \cdot \mu_{Ed} } \right) , & \text{ w modelu MN}\\
\xi_{eff,MU}(\mu_{Ed}) = 1 \pm\sqrt{1- 2 \cdot \mu_{Ed}} ,& \text{ w modelu MU}\\
\end{cases} \label{48}\end{equation}$$
gdzie: $\mu_{Ed}$ – obciążenie przekroju momentem, zależnie od sytuacji:
$\mu_{Ed} =m_{Ed}$ – obciążenie całkowite przy zbrojenia pojedynczym,
$\mu_{Ed} =m_{Ed}^*$ – obciążenie zredukowane metody MO* przy zbrojenia podwójnym DZP lub w przekrojach teowych,
Ponieważ w przypadku przeważającego zginania (rys. Z-3, stan C) wysokość strefy ściskanej $x\le h$ to pierwiastki znakiem „+” nie spełniają warunków zadania i pozostaje pierwiastek ze znakiem minus ($\ref{6}$):
Ramię siły w betonie względem osi zbrojenia rozciąganego wynosi $ z_c = d – x_c $, czyli po unormowaniu ($\ref{10}$) – ($\ref{11}$):
Wyrażenia na wysokość strefy ściskanej ($\ref{48}$) oraz dźwignię siły w betonie ($\ref{11}$) są rzeczywiste , wówczas , gdy wyrażenie podcałkowe jest dodatnie, czyli dla :
$$\begin{equation} m_{Ed}= \mu_{Ed} \le \begin {cases}
\cfrac {289}{594} = 0,487 & \text{ MN}\\
\cfrac {1}{2} = 0,5 & \text { MU }\\
\end{cases} \label{49}\end{equation}$$
Uwaga:
W formule ($\ref{48}$) podano tylko jeden z pierwiastków równania ($\ref{24}$) ze znakiem minus „-„. Drugi pierwiastek otrzymuje się przez zastąpienie znaku „-” przez „+”. Ponieważ w rozpatrywanym zadaniu zginania wysokość strefy ściskanej $x > d$, czyli ($\xi>1$), więc pierwiastek z „+” nie ma sensu fizycznego i został pominięty.
Zbrojenie rozciągane przekroju PZP
Dla znanej wysokości strefy ściskanej i momentu zginającego z warunku równowagi momentów względem wypadkowej siły w betonie $F_c$, bezpośrednio wyznaczono siłę w zbrojeniu dolnym – w punkcie wypadkowej (resulting ) (p. rys. Z-2): $F_{sl}= F_{sl,r}$ z otuleniem osiowym $a_l= a_{l,r}$, wysokością efektywną $d=d_l = d_r$ oraz ramieniem sił $z=z_r$
$$\begin{equation} F_{sl}=\cfrac{M_{Ed}}{z_c} \\ \parallel \to\parallel \, n_{sl}= \cfrac{m_{Ed}}{\zeta_c}\label {50} \end{equation}$$
gdzie $ n_{sl}=\cfrac{F_{sl}}{\overline N}$ ; $\overline N$ wg ($\ref{7}$)
a następnie teoretyczne pole przekroju zbrojenia:
$$\begin{equation} A_{sl} \ge \cfrac{M_{Ed}} {z \cdot f_{yd} } \, \parallel \to\parallel \, A_{sl} \ge \cfrac{m_{Ed}} {\zeta_c} \cdot A_{c→sl}\label {51}\end{equation}$$
gdzie pole betonu sprowadzone do stali zbrojenia dolbnego $A_{c→sl}$ ($\ref{12}$).
Przekrój DZP (podwójnie zbrojony)
Każdy przekrój żelbetowy jest podwójnie zbrojony (DZP), nawet wówczas, gdy ze względów obliczeniowych zbrojenie ściskane nie jest wymagane. Zgodnie z zasadami kształtowania belek przy górnej krawędzi belki należy dać bowiem min 2 pręty (najczęściej o średnicy jak zbrojenie dolne). Ważnym przykładem zastosowania konstrukcyjnego zbrojenia górnego jest pokazany na rys. Z-7, często spotykany przekrój teowy ukształtowany przez włączenie do współpracy z belką części płyty.
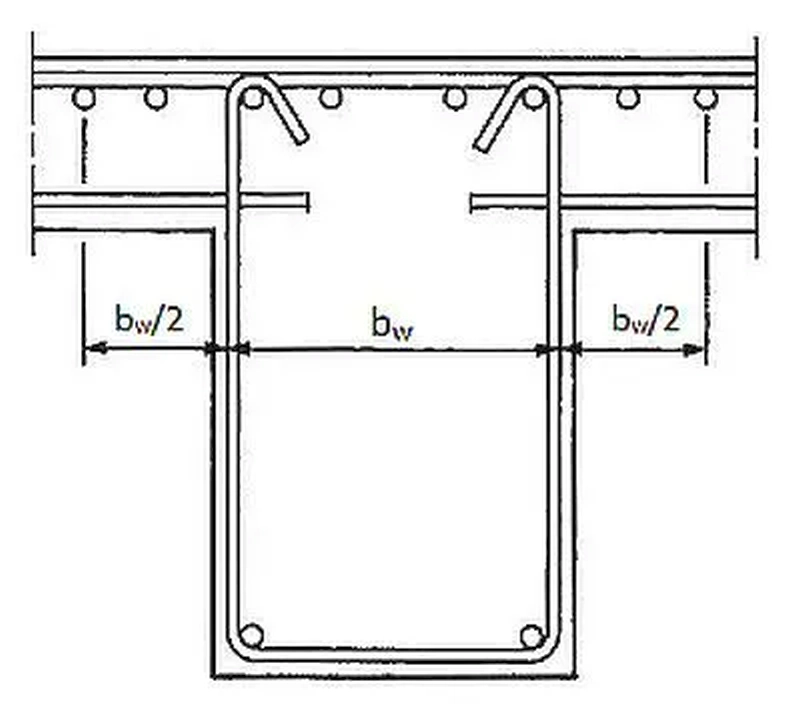
Rys.. 5 . Zalecenia zbrojenia przekroju teowego [7], Fig 5.15
Wśród inżynierów utrwalone jest stosowanie klasycznej techniki zbrojenia belki metodą MU. Technikę MO* projektowania przekroju DZP (podwójnie zbrojonego) wprowadzono w drodze modyfikacji metody MU. Do rozwiązania przekroju DZP zastosowano metodę obciążenia zredukowanego MO*. Metoda ta rozszerza metodą klasyczną projektowania przekroju PZP (pojedynczo zbrojonego) na przekrój DZP w ogólności niesymetrycznie zbrojony poprzez zastosowanie koncepcji redukcji obciążenia zewnętrznego przez nośność zbrojenia ściskanego, górnego.
Założono, że ściskane zbrojenie górne przekroju podwójnie zbrojonego DZP jest zasadniczo znane i składane jak następuje:
$$\begin{equation} A_{su} = A_{su}^{constr} + A_{su}^{add} \label {52}\end{equation}$$
gdzie:
$A_{su}^{constr}$ – zbrojenie górne , które należy zastosować z innych względów niż obliczeniowe (konstrukcyjnych). Na rys. Z-7 zbrojenie konstrukcyjne jest zbrojeniem płyty stropowej (rozdzielczym).
$A_{su}^{add}$ – zbrojenie górne , które należy dodać w przypadku, gdy nośność betonu wraz ze ściskanym zbrojeniem konstrukcyjnym jest niewystarczająca do przeniesienia obciążeń ze względu na niebezpieczeństwo kruchego pękania.
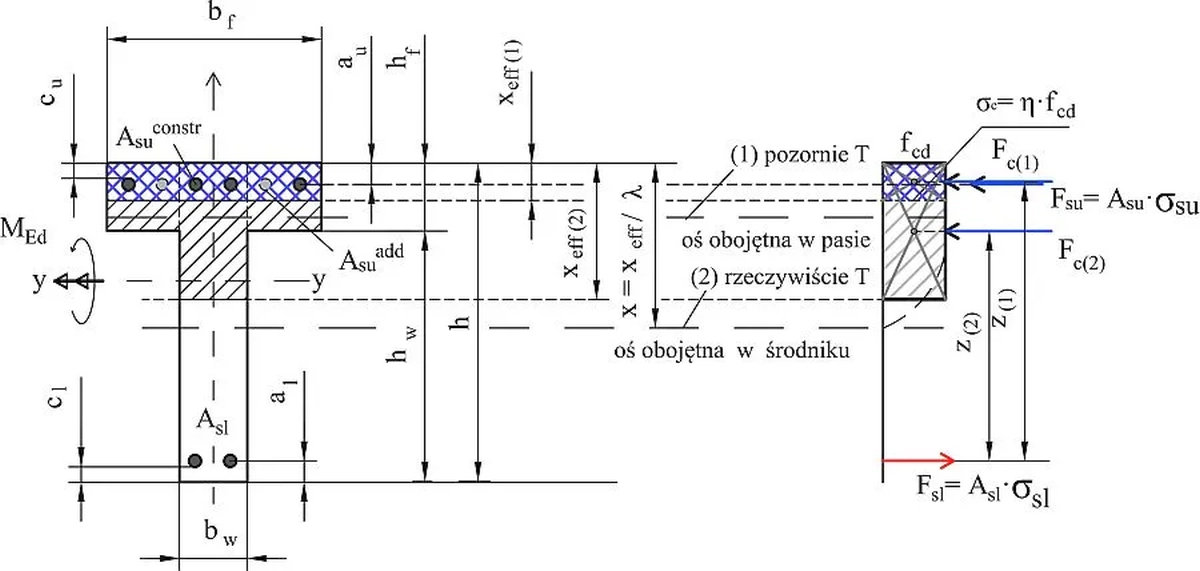
W modelu obliczeniowym, pokazanym na rys. Z-8 przyjęto, że w pasie przekroju o szerokości $b_f$ występuje zbrojenie z płyty $A_{su}^{constr}$, które często musi być jeszcze uzupełnione zbrojeniem belki $A_{su}^{add}$.
Metoda zredukowanego obciążenia MO*. Obciążenie zredukowane MEd*
Zbrojenie ułożone w strefie ściskanego betonu zwiększa nośność $M_{Rd,PZP} = M_{Rd,c}$ ($\ref{47}$) bryły ściskanej przekroju pojedynczo zbrojonego o nośność zbrojenia ściskanego $M_{Rd, su}$, do:
$$\begin{equation} M_{Rd,DZP} =M_{Rd,c} + M_{Rd,su} \, \, \parallel \to\parallel \, m_{Rd,DZP} =m_{Rd,c} + m_{Rd,su}\label {53} \end{equation}$$
gdzie moment zginający $M_{Rd,su}$ przenoszony przez zbrojenie górne jest liczony w tym samym układzie co $M_{Rd,c}$, czyli względem osi zbrojenia rozciąganego i wynosi
$$\begin{equation} M_{Rd, su} = F_{su} \cdot (d- a_u) = A_{su} \cdot f_{yd} \cdot (d-a_u) \\ \parallel \to\parallel \, m_{Rd, su}=\cfrac{ A_{su}}{A_{c→su}} \cdot (1-a_u/d) \label {54} \end{equation}$$
gdzie $A_{c→su}$ jest przekrojem betonu sprowadzonym do stali zbrojenia górnego($\ref{12}$).
W ($\ref{54}$) uwzględniono, że naprężenie w pręcie wynosi $\sigma_{cu}= E_s \cdot \varepsilon_{cu}$, czyli jest zgodne z odkształceniem niespękanego betonu, w którym pręt jest zanurzony i zawiera się w przedziale $ \varepsilon_{c2}$ =2‰ $\le \varepsilon_{su}$ < $\varepsilon_{cu2}$=3,5‰. Ponieważ stal B500 przy odkształceniu 2,5‰ jest już w pełni uplastyczniona, więc przyjęto $\sigma_{su}=f_{yd}$.
Związek ($\ref{53}$) w stanie granicznym, czyli dla $M_{Rd,DZP}=M_{Ed}$ można zapisać w postaci dogodnej do wprowadzenia metody obciążenia zredukowanego MO*:
$$\begin{equation} M_{R,dc} \ge M_{Ed}^* \\ \parallel \to\parallel \, m_{R,dc} > m_{Ed}^* \label {55} \end{equation}$$
gdzie zredukowane obciążenie przekroju wynosi:
$$\begin{equation} M_{Ed}^* = M_{Ed} -M_{Rd,su} \\ \parallel \to\parallel \, m_{Ed}^* = m_{Ed} – m_{R,d,su} \label {56} \end{equation}$$
Formułę ($\ref{55}$) uzyskano poprzez przeniesienie na stronę obciążenia składnika nośności strefy ściskanej $M_{Rd, su}$, co było możliwe dlatego, że $M_{Rd, su}$ nie jest funkcją poszukiwanej wysokości strefy ściskanej $x$. Formuła est analogiczna do standardowej ($\ref{46}$), ale zamiast obciążenia całkowitego $M_{Ed}$ występuje w niej obciążenie zredukowane $M_{Ed}^*$. Wobec tego analogiczne będą również wyrażenia na wysokość strefy ściskanej ($\ref{48}$) oraz dźwignię siły w betonie ($\ref{11}$) dla argumentu a $\mu_{Ed}=m_{Ed}^*$
Wyznaczone w ten sposób ramię-dźwignia nie jest ramieniem siły zbrojenia dolnego (odmiennie do przekroju pojedynczo zbrojonego) i nie jest przydatne do wyznaczenia zbrojenia dolnego. Właściwe ramię siły zbrojeniu dolnego $\zeta_{sl}$ opisano niżej (formułą ($\ref{61}$)). Zbrojenie dolne $A_{sl}$ należy wyznaczać z zależności ($\ref{60}$).
Kryterium dodatkowego zbrojenia ściskanego w metodzie MO*
Dodatkowe, ściskane zbrojenie górne należy stosować w celu wzmocnienia betonu w strefie ściskanej, w przypadku, gdy wysokość strefy ściskanej $\xi$ jest za duża i przekracza wartość graniczną z warunku kruchego zniszczenia betonu w tej strefie. Kryterium warunku kruchego zniszczenia betonu można sformułować w wysokości strefy ściskane $\xi$ j- formuła ($\ref{15}^1$) ; obciążeniu momentem $\mu_{Ed}=m_{Ed}$ – formuła ($\ref{15}^2$) lub w ramieniu siły w betonie $\zeta_c$ – formuła ($\ref{15}^3$).
Najbardziej dogodną postacią jest kryterium w obciążeniach ($\ref{15}^2$) sformułowana jako nadwyżka momentu obciążenie przekroju $\mu_{Ed}$ bad momentem granicznym $m_{ult}$ ($\ref{30}$), ($\ref{13}$), czyli
$$\begin{equation} \Delta m (\mu_{Ed}) = \mu_{Ed} – m_{ult} \label {57} \end{equation}$$
gdzie: $\mu_{Ed}$ – obciążenie przekroju momentem:
$\mu_{Ed} =m_{Ed}$ – obciążenie całkowite przy zbrojenia pojedynczym – w sytuacji oceny potrzeby zbrojenia ściskanego bez zbrojenia konstrukcyjnego,
$\mu_{Ed} =m_{Ed}^*$ – obciążenie zredukowane przy zbrojenia podwójnym lub w przekrojach teowych, w sytuacji ceny potrzeby dodatkowego zbrojenia ściskanego strefy z wbudowanym zbrojeniem konstrukcyjnym
Jeśli ($\Delta m \ge 0$, to nie jest wymagane dodatkowe zbrojenie strefy ściskanej $A_{su}^{add}=0$.
Jeśli ($\Delta m \le 0$, to należy strefę ściskaną dozbroić $A_{su}^{add}> 0$ wg procedury przedstawionej niżej.
Zbrojenie ściskane, górne przekroju podwójnie zbrojonego DZP w metodzie MO*
Dodatkowe zbrojenie górne $A_{su}^{add}$ dobiera się na nadwyżkę momentu zginającego $\Delta m$ ($\ref{57}$), której nie może przejąć beton ściskany wraz ze zbrojeniem konstrukcyjnym $A_{su}^{constr}$:
Dodatkowe zbrojenie górne wyznacza się z rozwiązania zależności ($\ref{54}$) względem $A_{su}$ i po zastąpieniu $m_{su}$ przez $\Delta m$:
$$\begin{equation} A_{su}^{add} = \cfrac{\Delta m}{1-a_u/d} \cdot A_{c→su} \label {58} \end{equation}$$
Całkowite zbrojenie górne $A_{su}$ przekroju podwójnie zbrojonego DZP jest sumą zbrojenia konstrukcyjnego i dodatkowego zgodnie z formułą ($\ref{52}$)
Zbrojenie rozciągane, dolne przekroju podwójnie zbrojonego DZP w metodzie MO*
Wyznaczenie wysokości strefy ściskanej bryły betonu ($\ref{50}$) poddanej zredukowanemu obciążeniu $(\mu_{Ed} = m_{Ed}^*)$ wyznaczonemu zgodnie z metodą MO* oraz ustalenie wymaganego zbrojenia górnego ($\ref{52}$) <- ($\ref{58}$) jest równoznaczne z rozwiązaniem zadania zginania (bez udziału siły osiowej) podwójnie zbrojonego przekroju betonowego. Pole przekroju zbrojenia dolnego $A_{sl}$ może być wprost wyznaczone z dowolnego warunku równowagi .($\ref{34}$).
Najprościej jest wyznaczyć zbrojenie dolne z warunku równowagi sił poziomych $\sum X$ ($\ref{34}^1$), z uwzględnieniem $N_{Ed}=0$ , które po zastosowaniu warunku wytrzymałościowego $\sigma_{sl}= F_{sl}/ A_{sl} \le f_{yd}^{’}$ można zapisać w postaci
$$\begin{equation} A_{sl} \ge \cfrac{F_{sl}}{f_{yd}^{’}} =\cfrac {F_c+F_{su}} { f_{yd}^{’}} \label {59}\end{equation}$$
skąd uzyskano
$$\begin{equation} A_{sl} \ge A_{cx→sl} + A_{su →sl} \label {60}\end{equation}$$
gdzie:
$A_{cx, sl}$ ($\ref{14}$) – pole ściskanego betonu sprowadzone do stali zbrojenia dolnego
$A_{su →sl} = A_{su} \cdot \cfrac{f_{yu}^{’}}{f_{yl}^{’}}$ pole zbrojenia górnego sprowadzone do stali zbrojenia dolnego
$A_{su}$ ($\ref{52}$) – pole przekroju zbrojenia górnego (łącznie konstrukcyjne i dodatkowe)
Wysokość strefy ściskanego betonu do wyznaczenia pola ściskanego betonu wyznaczono dla zredukowanego obciążenie ($\ref{56}$)
Ramię – mimośród siły zbrojenia dolnego
Mimośród siły w zbrojeniu dolnym $F_{sl}$ wyznaczono z zależności ($\ref{62}$) poprzez zastąpienie ramienia siły w betonie $z_c$ ramieniem – mimośrodem $z_{sl}$ siły $F_{sl}$ i rozwiązanie formuły względem $z_{sl}$
$$\begin{equation} z_{sl}=\cfrac{M_{Ed}}{F_{sl}} \, \parallel \to\parallel \, \zeta_{sl}= \cfrac{m_{Ed}}{n_{sl}}\label {61} \end{equation}$$
gdzie:
$n_{sl}=\cfrac{F_{sl}}{\overline N}=\cfrac{F_c+F{su}}{\overline N}$,
$\overline N$ wg ($\ref{7}$)
$F_c$ – siła w betonie ($\ref{24}$),
$F_{su}=F_{su} \cdot f_{yd}^{’}$ – siła w zbrojeniu górnym.
Ramiona sił $z_c$ i $z_{sl}$ będą sobie równe tylko wówczas, gdy w strefie ściskanej i w strefie rozciąganej występuje po jednej sile jak w przekroju pojedynczo zbrojonym Wówczas siłę rozciągającą zbrojenie dolne można wyznaczyć z równania ($\ref{32}$). W przypadku przekroju zbrojonego podwójnie ramię – mimośród siły rozciągającej w zbrojeniu jest średnią ważoną dźwigni sił ściskających działających w strefie ściskanej:
$$\begin{equation} z_{sl}=\cfrac{M_{Ed}}{F_{sl}} = \cfrac{M_c+M_{su}}{F_{sl}}= \cfrac{z_c \cdot F_c +z_{su} \cdot F_{su}}{F_c+F_{su}} \\ \parallel \to\parallel \, \zeta_{sl}= \cfrac{\zeta_c \cdot n_c +\zeta_{su} \cdot n_{su}}{n_c+n_{su}}\label {62} \end{equation}$$
Uwaga:
W literaturze często zaleca się, by w przypadku przekroju podwójnie zbrojenie dolne wyznaczać jak dla przekroju pojedynczo zbrojonego, a po wzmocnieniu strefy ściskanej zbrojenie górnym ściskanym – zbrojenie dolne zwiększyć o dodane zbrojenie górne. Takie podejście nie jest właściwe, bowiem amię siły w zbrojeniu dolnym $z_{sl}$ $(\zeta_{sl})$ = $z_c$ $(\zeta_c)$ dla zbrojenia podwójnego wyznaczone ze wzoru ($\ref {61}$) różni się od ramienia siły w betonie dla zbrojenia pojedynczego.
Naprężenia i siły w zbrojeniu
Dla znanej wysokości strefy ściskanej $x$ z zasady płaskich przekrojów ($\ref{32}$) oraz prawa fizycznego dla stali ($\ref{42}$) można wyznaczyć naprężenia $\sigma_{s}$ oraz siły $F_s$ w zbrojeniu o o rzeczywistym przekroju $A_s^R$
$$\begin{equation} \sigma_{s,⊗} = [ \varepsilon_{cu} \cdot (d_Ξ /x- 1)] \cdot E_s \le f_{yd^{’}} \label {63} \end{equation}$$
$$\begin{equation} F_{s,⊗}= \sigma_{s,Ξ} \cdot A_{s,Ξ}^R \label {64} \end{equation}$$
gdzie $Ξ$ = l(lower, dolne, rozciągane ) , u (unter, górne, ściskane).
Ważnym wnioskiem dla projektantów jest to, że naprężenia w prętach zbrojeniowych nie zależą wprost od przekroju zbrojenia , a tylko od stosunku wysokości użytecznej przekroju $d$ do wysokości strefy ściskanej betonu $x$: jeśli $(x=d)$ to naprężenia w zbrojeniu nie wystąpią , jeśli $x=0$, to naprężenia będą teoretycznie nieskończone. Konsekwencją zwiększania przekroju prętów będzie proporcjonalne zwiększenie sił w tych prętach.
Bezcelowe, a nawet szkodliwe jest przyjmowanie prętów o dużo większym przekroju od wymaganego – nie prowadzi to do zwiększenia bezpieczeństwa pręta, a nawet je zmniejsza na skutek wytworzenia lepszych warunków do kruchego pękania betonu – zniszczenia FCF.
Uwagi krytyczne o klasycznej technice projektowania przekrojów zginanych
- Klasyczna technika projektowania przekrojów zginanych nie uwzględnia relacji odkształceń w betonie i stali, oraz prawa fizycznego, betonu i stali, w przypadku metody NU nie są spełnione podstawowe warunki równowagi sił, na skutek pomijania zbrojenia górnego lub wyznaczania zbrojenia dolnego w przekroju podwójnie zbrojonym jak w przekroju pojedynczo zbrojonym,
- Każdy przekrój żelbetowy jest w rzeczywistości podwójnie zbrojony, co jest założeniem zmodyfikowanej metody MU*.
Przypadki ZM, ZS i ZD wymiarowania przekroju zginanego
W zależności od wielkości momentu zginającego działającego na przekrój można wyróżnić trzy przypadki wymiarowania: ZM – małe zginanie, wówczas, gdy konstrukcyjne zbrojenie górne nie powoduje zmiany zbrojenia dolnego (przykład Z-1), ZS – średnie zginanie . wówczas, gdy konstrukcyjne zbrojenie górne prowadzi do zmiany zbrojenia dolnego (przykład Z-2), ZD – duże zginanie , wówczas gdy należy stosować dodatkowe zbrojenie górne (pzykład Z-3).
Zbrojenie wielowarstwowe
W przypadku zbrojenia wielowarstwowego wiązkę (układ) zbrojenia skupia się w jeden punkt obliczeniowy środek ciężkości dolnych prętów rozciąganych (p. rys. Z-2) lub górnych ściskanych (jeśli ułożono w wielu warstwach), przy czym odległość wypadkowej siły w zbrojeniu od dolnej krawędzi belki ( efektywne otulenie osiowe) wyznacza się jako średnią ważoną otulenia osiowego warstw zbrojenia:
$$\begin{equation} a_{l,r}\approx \cfrac{ \sum A_{sl,i} \cdot a_{l,i}}{\sum A_{sl,i}} \label {65}\end{equation}$$
gdzie i – numer warstwy zbrojenia.
Dostateczność sposobu ($\ref{65}$) wynika z równowagi momentu $M_{sl}$ wywołanego siłą zastępczą $F_{sl,r}$ i wiązką sił $F_{sl,i}$ względem wypadkowej siły w betonie
$M_{sl} = F_{sl,r}\cdot z_r= \sum F_{sl,i}\cdot z_i$ Stąd po uwzględnieniu prawa fizycznego oraz zasady płaskich przekrojów $\varepsilon_{sl,i}=\varepsilon_{cu} \cdot (h- x – a_{l,i})/x$ i po przekształceniach otrzymano
$$\begin{equation} a_{l,r} = \cfrac{ \left( \sum A_{sl,i} \cdot a_{l,i} \right) -\left( \sum A_{sl,i} \cdot a_{l,i}^2 \right)/(h-x)} { \left( \sum A_{sl,i} \right) -\left( \sum A_{sl,i} \cdot a_{l,i} \right)/(h-x)} \label {66}\end{equation}$$
W pierwszym przybliżeniu ($\ref{66}$) można aproksymować przez ($\ref{65}$), ponieważ składniki ujemne sa znacznie (praktycznie o rząd) mniejsze od dodatnich. Można też, przed wyznaczeniem wysokości strefy ściskanej, przyjąć oszacowanie $ x \approx 0,2 \cdot h $.
Konstruowanie zbrojenia z wiązki prętów o mniejszej średnicy które są rozmieszczone w jednej lub kilku warstwach w strefie ekstremalnego rozciągania jest bardziej skuteczne w kontrolowaniu pęknięć i poprawie wiązania (przyczepności) od stosowania mniejszej liczny prętów o większych średnicach. W tab. K-2 podano maksymalne średnice prętów, które można stosować z warunku ograniczenia rys. W wysokich belkach, znaczna część środnika będzie rozciągana, a prawidłowo rozłożone zbrojenie rozciągane zapewnia ograniczenie rozwarcia rys na spodzie belki. Jednakże nadmierne pęknięcia mogą pojawić się wyżej – w środniku i w tych przypadkach , szczególnie w środowisku o zmiennej temperaturze i skurczu – należy stosować boczne siatki (rys. K-5).
Przekroje teowe (T i L przekrój)
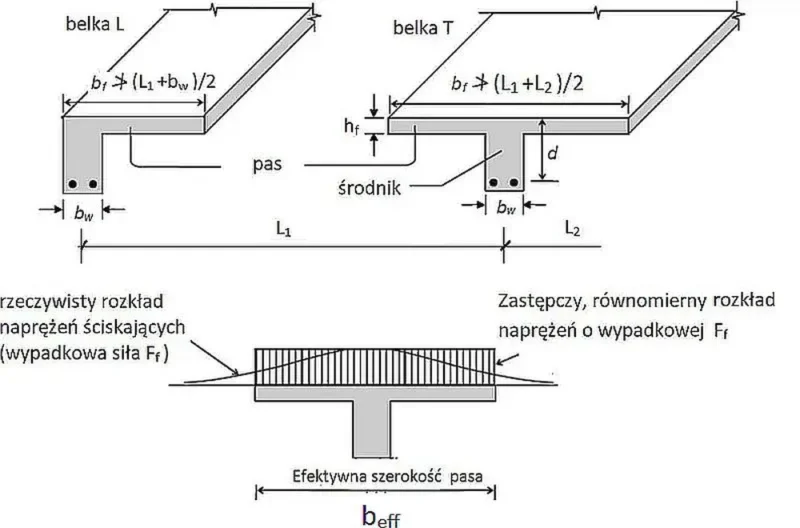
Belki (podciągi i żebra) w stropie płytowo-belkowym (rys. K-2) rozpatruje się jako teowe z górną półką utworzoną przez współpracującą część płyty. Belki o przekroju teowym (pośrednie-środkowe) lub kątowym (brzegowe- skrajne) nazywane są belkami T lub L odpowiednio. Współpracująca część płyty działa integralnie z belką – wygina się w kierunku wzdłużnym belki i jest górnym pasem belki. Część belki poniżej pasa (właściwa część belki) jest często nazywana środnikiem.
Szerokość współpracująca przekroju teowego
Zginające naprężenie ściskające we współpracującej części płyty nie jest równomierne na całej jego szerokości. Naprężenie waha się od maksimum w obszarze belki do stopniowo niższych wartości w punktach oddalonych. W celu sprowadzenia zadania do analizy w ramach klasycznej teorii zginania – zakłada się równomierny rozkład naprężenia na szerokości efektywnej (rys. Z-10).
Problem belki T sprowadzono do wyznaczenia szerokości efektywnej pasa (współpracującej części płyty). Stwierdzono, że efektywna szerokość pasa $b_{eff}$ wzrasta wraz ze wzrostem rozpiętości przęsła, szerokości belki (środnika). i grubości płyty. Zależy również od rodzaju obciążenia † (skoncentrowane, rozproszone itp.) oraz warunków podparcia (schematu statycznego). Stwierdzono na przykład że równoważna szerokość półki jest mniejsza, gdy obciążenie skupione jest przykładane w połowie rozpiętości swobodnie podpartej belki, w porównaniu z przypadkiem, gdy to samo obciążenie jest przykładane jako obciążenie równomiernie rozłożone.
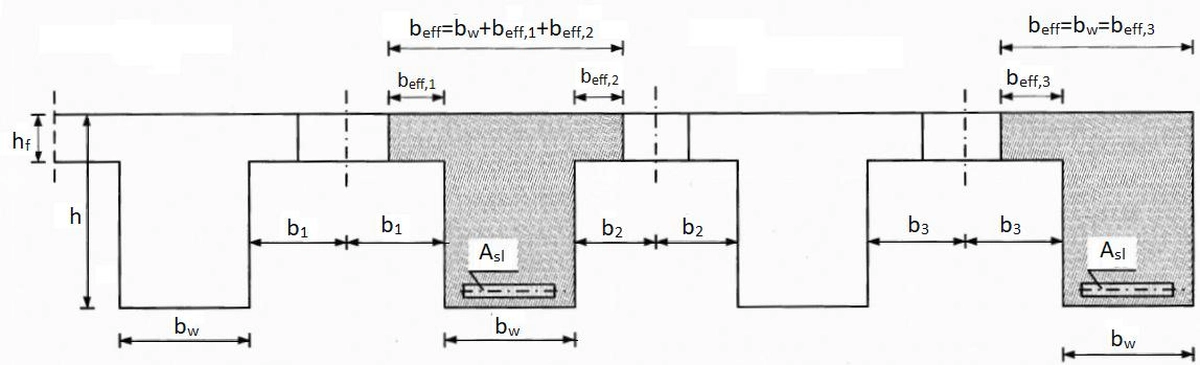
Połowa odległości w świetle przęsła z żebrem (sąsiadującym do rozpatrywanej belki wynosi rys Z-11):
$$\begin{equation} b_i= ( L_i- (b_{w,l}+ b_{w,p})/2 )/2 \, (i=1,2) \label {67} \end{equation}$$
gdzie: $b_{w,l}$, $b_{w,p}$ – szerokości żeber z lewej i prawej strony przęsła. $L_i$ – rozstawy osiowe żeber – p. też rys Z-10
Szerokość współpracująca $b_{eff,i}$ płyty z belką żebrem o szerokości $b_{w,i}$ wynosi (rys. Z-11) :
$$\begin{equation} b_{eff,i} = 0,2 \cdot b_i + 0,1\cdot L_{0,i} \le \min{ \{ b_i \, ; \, 0,2 \cdot L_{0.i} \}} \label {68} \end{equation}$$
gdzie $L_{0,i}$ jest efektywną długością zginania podłużnego belki (liczonego po długości belki poprzecznie do przekroju rys. Z-11, Efektywna długość zginania jest odległością pomiędzy punkami zerowych momentów zginających belkę i powinna być określona z wykresu momentów w systemie konstrukcyjnym.
Przybliżone wzory do oszacowania „efektywnej długości zginania belki $L_0$w zależności od obliczeniowej długości belki $L_{eff} można wstępnie przyjąć zgodnie rys. Z-12.
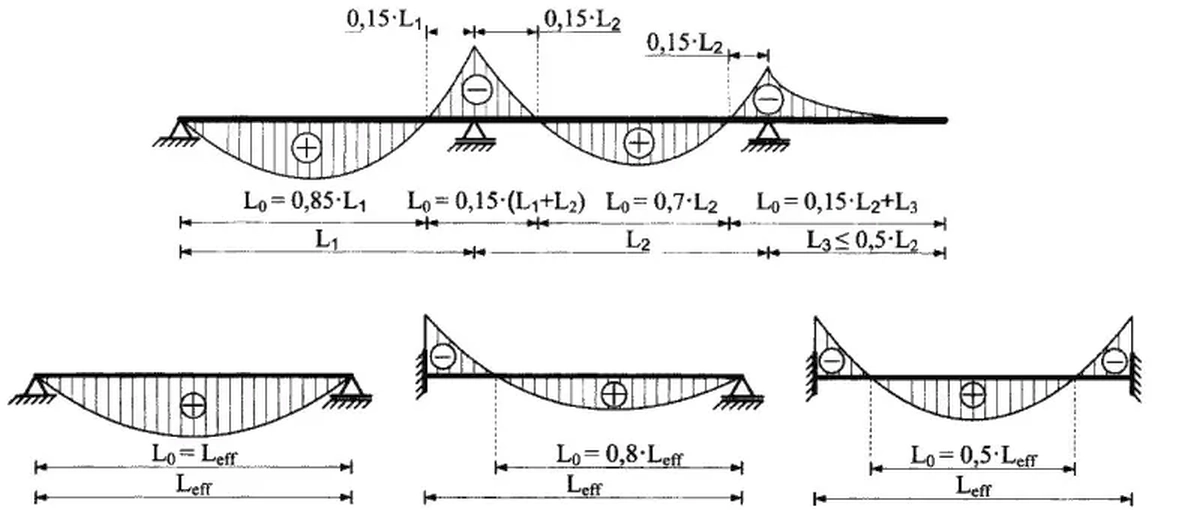
Rys. 9. Długości efektywne przęseł belek [8], rys.3.3
Szerokość półki przekroju teowego, złożonego z żebra środkowego i półki wynosi:
$$\begin{equation}b_{eff}= \begin {cases} b_{eff,1}+ b_w + b_{eff,2} \le b_1+b_w +b_2, & \text{ dla przekroju T } \\ b_{eff,1}+ b_w+ \le b_L+b_w, & \text{ dla przekroju L } \\ \end{cases} \label{69}\end{equation}$$
Przypadki obliczeniowe i położenie strefy ściskanej
Rozpatruje się dwa przypadki wytrzymałościowe przekroju teowego:
- przekrój pozornie teowy, gdy oś obojętna znajduje się w płycie (półce) – przypadek (1) na rys. Z-8. lub
- przekrój rzeczywiście teowy gdy oś obojętna znajduje się w belce (środniku) – przypadek (2) na rys. Z-8.
Wymiarowanie przekroju teowego rozpoczynamy od sprawdzenia, czy przekrój jest pozornie teowy, czyli czy zachodzi:
$$\begin{equation} x \le h_f \, \text { czyli } x_{eff} \le \lambda \cdot h_f \, \text { to przekrój jest pozornie teowy} \label {70} \end{equation}$$
Wysokość strefy ściskanej do sprawdzenia warunku ($\ref{70}$) wyznacza się z zależności ($\ref{11}$) dla belki o szerokości $b_{eff}$ ($b_f$ na rys Z-8) poddanej obciążeniu $\mu_{Ed} = m_{Ed}^{*}$ ($\ref{56}$) zredukowanemu przez znane (konstrukcyjne) zbrojenie ściskane ułożone podłużnie w płycie. Pominięcie zbrojenie konstrukcyjnego (w płtcie) $A_{su}^{constr}$ może doprowadzić do „fałszywego” zakwalifikowania przekroju do rzeczywiście teowego, podczas gdy przekrój jest pozornie teowy, co zwykle prowadzi do nieoptymalnego projektu belki.
Jeśli warunek ($\ref{70}$) jest spełniony, to przekrój pozornie teowy wymiaruje się jak prostokątny o szerokości $b_{eff}$ zgodnie zasadami podanymi w rozdziale Metoda obciążenia zredukowanego MU*. Technikę obliczeń pokazano w przykładzie Z-4 bez uwzględnienia zbrojenia górnego (płyty) oraz w przykładzie Z-5 z uwzględnieniem tego zbrojenia.
Jeśli przekrój NIE jest pozornie teowy zgodnie z warunkiem ($\ref{70}$) , to jest rzeczywiście teowy.
Przekrój rzeczywiście teowy. Uogólniona metoda MO* na przekrój T
Model przekroju rzeczywiście teowego pokazano na rys. Z-13. W belce pozornie teowej (prostokątnej o szerokości $b_{eff}$) występują nieistniejące części przekroju, oznaczone symbolem (-) na modelu. Nośność ściskanej bryły betonu belki rzeczywiście teowej M_{Rd,crz} } można obliczyć odejmując od nośności betonu belki pozornie teowej M_{Rd,cpz} nośność nieistniejących części bryły $M_{Rd,c(-)}$:
$$\begin{equation} M_{Rd,crz} =M_{Rd,cpz} – M_{Rd,c(-)} \\ \parallel \to\parallel \, m_{Rd,crz} =m_{Rd,cpz} – m_{Rd,c(-)}\label {71} \end{equation}$$
gdzie wszystkie nośności bryły betonu są liczone w tym samym układzie – względem osi zbrojenia rozciąganego, dolnego.
Z rys. Z-13 można ustalić, że nieistniejąca część przekroju (-) ma nośność : $$\begin{equation} M_{Rd, c(-)} = (b_f – b_w) \cdot (d – h_f/2- x_{eff}/2)\cdot ( x_{eff}-h_f) \cdot f_{cd}^{’} \label {72}\end{equation}$$
Ponieważ moment $M_{Rd,c(-)}$ zależy od poszukiwanej wysokości strefy ściskanej $x_{eff}$, więc nie można wprost zastosować metody MO* zredukowanego obciążenia i należy rozpatrzeć łączną nośność betonu ($\ref{71}$). Po odjęciu ($\ref{72}$) od ($\ref{48}$) otrzymano:
$$\begin{equation} M_{Rd,crz} =\left\{ \left [ (b_f- b_w) \cdot h_f \cdot \left (d- \cfrac{h_f}{2} \right) \right] +\left[ b_w \cdot x_{eff} \cdot \left (d – \cfrac {x_{eff}}{2} \right) \right ] \right\} \cdot f_{cd}^{’} \label {73} \end{equation}$$
a po unormowaniu czynnikiem normującym ($\ref{4}$), który dla przekroju teowego przyjęto w odniesieniu do szerokości środnika $b_w$ , czyli
$$\begin{equation} \overline M = b_w \cdot d ^2 \cdot f_{cd} \label {74}\end{equation}$$
otrzymano postać unormowaną nośności ($\ref{73}$) betonu przekroju rzeczywiście teowego
$$\begin{equation} \, \parallel \to \parallel \, m_{Rd,crz} = m_{Rd,cf} + m_{Rd,cw} \label {75} \end{equation}$$
Nośność skrzydeł pasa $m_{Rd,cf}$ wynosi
$$\begin{equation} \, \parallel \to\parallel \, m_{Rd,cf} = ( \cfrac{b_f}{b_w} – 1 ) \cdot χ_f \cdot ( 1– \cfrac{ χ_f}{2}) \label {76} \end{equation}$$
gdzie: $ χ_f = \cfrac{h_f}{d}$
Nośność środnika $m_{Rd,cw}$ jest określona standardową formułą ($\ref{24}$) dla środnika (przekroju prostokątnego o wymiarach $ h x b_w$ ) i jest zależna od wysokości stre4y ściskanej $x$ oraz modelu betonu
Wszystkie składniki nośności należy normować tym samym czynnikiem normującym ($\ref {74}$).
Zagadnienie przekroju rzeczywiście teowego sprowadzono do zagadnienia prostokątnego przekroju środnika o wymiarach $ h x b_w$ poddanego obciążeniu zredukowanym obciążeniem z godnie z metodą MO*
$$\begin{equation} \, \parallel \to\parallel \, m_{Ed}^* = m_{Ed} – m_{Rd,su} – m_{Rd,cf} \label {77} \end{equation}$$
Redukcję ($\ref{77}$) można przeprowadzić, ponieważ $m_{Rd,cf}$ nie zawiera pooszukiwanej niewiadomej $x$.
Dla tak zdefiniowanego obciążenia zredukowanego dobiera się dodatkowe zbrojenie górne i zbrojenie dolne jak dla przekroju podwójnie zbrojonego w procedurze: ($\ref{57}$) do ($\ref{60}$)), przy czym warunek $\ref{60}$) na dobór przekroju zbrojenia dolnego $A_{sl}$ zostaje uogólniony do postaci:
$$\begin{equation} A_{sl } \ge A_{su→sl} + A_{cf→sl} + A_{cx→sl} \label {78}\end{equation}$$
gdzie wszystkie składowe są sprowadzone do wytrzymałości stali zbrojenie dolnego:
$ A_{su→sl}= A_{su} \cdot f_{yd,u}^{’}/ f_{yd,l}^{’}$ – całkowite zbrojenie górne sprowadzone do wytrzymałości stali zbrojenia dolnego,
A_{cx→s} ($\ref{13}$) – sprowadzone do stali zbrojenia dolnego pole przekroju strefy ściskanej betonu.
A_{cf→sl}$ – sprowadzone do stali zbrojenia dolnego pole przekroju skrzydeł pasa:
$$\begin{equation} A_{cf → sl} = (b_f-b_w) \cdot h_f \cdot f_{cd}^{’} / f_{yd,l}^{’} \label {79} \end{equation}$$
Wyrażenie ($\ref{79}$) wprowadzono z uwzględnieniem tego, że naprężenie w zbrojeniu dolnym $\sigma_{sl} = f_{yd.l}^{’}$,. Odkształcenia pręta zbrojenia $ \varepsilon_{sl}= \varepsilon _{cu} \cdot ( 1/0,23-1)= 3 \cdot 3,5$ ‰ = 10,5‰ $ \gg \varepsilon _{y,dl}$ (rys. Z-4)
Uwaga:
Formuła ($\ref{75}$) jest podstawą stosowanej techniki projektowania przekrojów teowych ( podręcznik do technikum budowlanego [2] ; podręcznik dla studentów budownictwa [9]). W tych podręcznikach nośność bryły betonowej rozdziela się na dwie składowe: nośność skrzydeł pasa i nośność środnika, ale następnie na każdą z tych nośności odrębnie dobiera się zbrojenie dolne i na końcu sumuje. Takie podejście jest nieprawidłowe : różni się od przedstawionej procedury i może prowadzić do znacznego przewymiarowania zbrojenia dolnego.
Przekrój L
Zginanie przekroju L przy założeniu zachowania płaskiej postaci zginania środnika, to jest w założeniu, że oś „z”” pozostaje osią główną przekroju można analizować z wg formuły ($\ref{75}$) i stosować wynikającą z niej uogólnioną procedurę metody obciążenia zredukowanego MO* ($\ref{77}$). Założenie płaskiej postaci zginania jest bliskie rzeczywistości ze względu na utrzymywanie środnika w tym położeniu przez płytę, której częścią jest pas. Zginanie niesymetrycznego przekroju L prowadzi do zagadnienia zginania dwuosiowego ze skręcaniem, którego analiza nie jest przedmiotem niniejszego artykułu.
Przekrój kołowy
Model żelbetowego przekroju kołowego
Analizę zginania belki żelbetowej o przekroju kołowym przeprowadzono z wykorzystaniem koncepcji Di Laora (2020) [10] w której dyskretne pręty zbrojenia rozłożone na obwodzie pręta (rys. Z-4a) zastąpiono ciągłą ścianką rury o takim samym całkowitym polu przekroju stali $A_s$(rys. Z-4b). W rezultacie otrzymano stosunkowo proste zależności analityczne praktycznie bez utraty wymaganej w obliczeniach inżynierskich dokładności rozwiązania ścisłego (różnica pomiędzy proponowanym rozwiązaniem, a wynikami dokładnej numerycznej analizy w modelu MN nie przekracza 5%).
W prezentowanym podejściu zastosowano zredukowane wytrzymałości betonu i stali : $$\begin{equation} f_{cd}^{’}= \eta_c \cdot f_{cd} \, ; \, \eta_c=0,9 \label {80}\end{equation}$$
Współczynnik redukcji $\eta_c=0,9$ stosuje się zgodnie z poleceniem normy Eurokod 2 [1],uwaga pod kl. 3.1.7(3) : „Jeśli szerokość strefy ściskanej zmniejsza się w kierunku skrajnego włókna ściskanego, to wartość $\eta f_{cd}$ należy zmniejszyć o 10 %.„.
$$\begin{equation} f_{yd}^{’}= \eta_s \cdot f_{yd} \, ; \, \eta_s = 0,95 \label {81}\end{equation}$$
Współczynnik redukcji $\eta_s=0,95$ stosuje za pracą [10] się w celu skalibrowania zastępczego modelu zbrojenia ( zamiast dyskretnych prętów – ścianka rury). Model MU przekroju kołowego pokazano na rys. Z-9
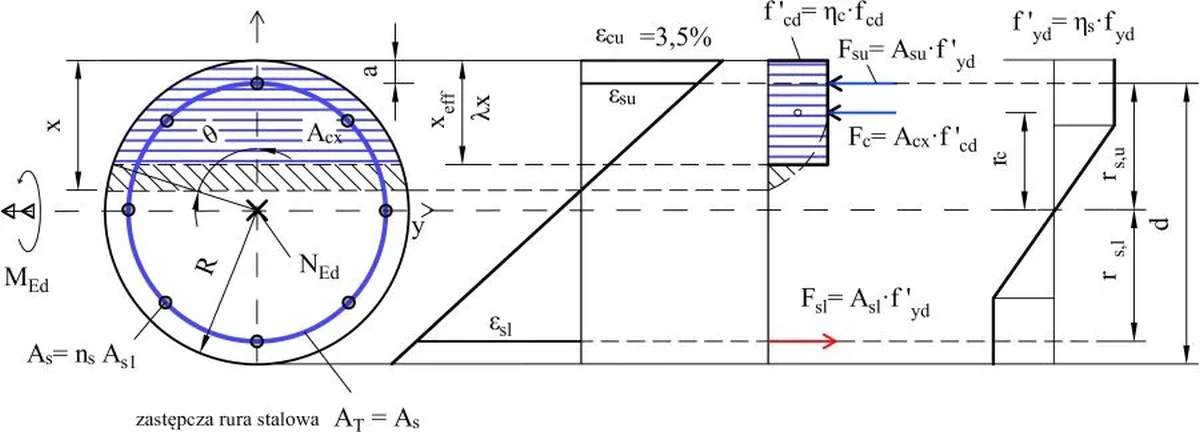
Z zależności zobrazowanych na rys. Z-9 można ustalić następujące związki geometryczne:
$$\begin{equation} \Theta = arccos \left( 1- \cfrac{x_{eff}}{R} \right) \, ; \quad A_{cx}= R^2 \,\left ( \Theta -\cfrac{sin 2\Theta}{2} \right ) \label {82}\end{equation}$$
$$\begin{equation} r_c = \cfrac{4}{3} \cdot \cfrac{sin^3 \Theta}{2\Theta – sin 2\Theta}\cdot R \, ; \quad r_{s,u}= d \cfrac{sin \Theta}{\Theta }\, ; \quad r_{s,l}= d \cfrac{sin \Theta}{\pi – \Theta }\,; \quad d = R-a \label {83}\end{equation}$$
Postawienie zadania
W zadaniu zginania (ogólnie ze ściskaniem) przekroju kołowego poszukuje się wymaganego zbrojenia przekroju $A_s$ lub stopnia zbrojenia przekroju $\rho$ ($\ref{19}$), przy czym poszukiwany jest fizyczny stopień zbrojenia całego przekroju (łączne zbrojenie obwodowe – pojęcie zbrojenia dolnego i górnego nie występuje). W ($\ref{19}^2$) taki stopień zbrojenia oznaczono symbolem $\rho_{F,s}$. W tym rozdziale będzie krótko oznaczany symbolem bez indeksów $\rho$.
Dysponujemy dwoma równaniami równowagi $\sum X=0$ oraz $\sum M=0$.
Warunek $\sum X=0$ sumy rzutów sił na oś poziomą, na podstawie rys. Z-9 ( też [10]– wzory (1),(2)), można zapisać w postaci:
$$\begin{equation} \cfrac {R^2}{2}\cdot ( 2 \Theta – sin 2 \Theta ) f_{cd}^{’} + \cfrac{ \Theta}{ \pi} \cdot A_s f_{yd}^{’} \, – \, \cfrac{ \pi – \Theta} { \pi}\cdot A_s f_{yd}^{’} =N_{Ed} \label {84} \end{equation}$$
$$\begin{equation} \parallel \to \parallel \, (2 \Theta – sin 2 \Theta) + 2 \rho \Theta – 2\rho (\pi – \Theta) = 2 \pi \cdot n_{Ed} \label {85}\end{equation}$$
gdzie obciążenie przekroju siłą osiową:
$$\begin{equation} N_{Ed} \, \parallel \to\parallel \, n_{Ed} = \cfrac{N_{Ed}}{\overline N}\label {86}\end{equation}$$
z czynnikiem normującym siłę osiową ($\ref{3}^2 $) $\overline N=\pi \cdot R^2 \cdot f_{cd}^{’}$
Warunek $\sum M=0$ sumy momentów względem osi przekroju (osi działania siły osiowej)
$$\begin{equation} M_{Rd} = M_{Ed} \, \parallel \to \parallel m_{Rd}=m_{Ed} \label {87}\end{equation}$$
z czynnikiem normującym moment ($\ref{3}^1 $) (podzielnikiem obu stron równania ($\ref{84}$)):
$$\begin{equation} \overline M =2 \pi R^3\cdot f_{cd}^{’}\label {88}\end{equation}$$
Obliczeniowa nośność przekroju na zginanie jest sumą nośności betonu $M_{Rd,c}$ oraz stali (rozciąganej i ściskanej) $M_{Rd→s}$:
$$\begin{equation} M_{Rd} = M_{Rd,c} + M_{Rd→s} \, \parallel \to\parallel \, m_{Rd}= m_{Rd,c}+ m_{Rd→s}\label {89}\end{equation}$$
Składowe nośności przekroju ($\ref{89}$) wyznaczone z zależności zobrazowanych na rys. Z-9 (też [10]– wzór (5)) wynoszą :
$$\begin{equation} M_{Rd,c} =\cfrac{2}{3} \cdot R^3 \cdot sin^3 \Theta \cdot f_{cd}^{’}\, \parallel \to\parallel \, m_{Rd,c} =\cfrac{1}{3 \pi}sin^3 \Theta \label {90}\end{equation}$$
$$\begin{equation} M_{Rd→s}= \cfrac{d}{\pi} \cdot A_s \cdot sin \Theta \cdot f_{yd}^{’} \, \parallel \to \parallel \,\ m_{Rd→s}= \cfrac{d}{ \pi R \cdot \rho } \cdot sin \Theta\label {91}\end{equation}$$
Rozwiązanie zadania zginania przekroju kołowego
Wysokość strefy ściskania dla założonego stopnia zbrojenia $\rho$ (fizycznego, całkowitego – p. wyżej) wyznaczono z warunku $\sum M$ ($\ref{86}$). W stanie granicznym dla $ m_{Rd}=m_{Ed}$, gdzie $m_{Rd}$ wg ($\ref{89}$),do ($\ref{91}$). Równanie to ma tylko jeden pierwiastek rzeczywisty
$$\begin{equation} \Theta= arcsin {\left ( \cfrac{d \cdot \rho} {W} \, – \, \cfrac{W}{ R } \right )}\label {92}\end{equation}$$
Wyróżnik $W$ wyznacza się z wyrażenia
$$\begin{equation} W= \sqrt[3]{\sqrt{(R\cdot d\cdot \rho)^3+ m_R^2} – m_R} \label {93}\end{equation}$$
gdzie $m_R= 3/2 \cdot \pi R^3 \cdot m_{Ed}$
Dla znanej wielkości strefy ściskania betonu z równania ($\ref{85}$) można wyznaczyć stopień zbrojenia przekroju. Przy zginaniu bez udziału siły osiowej $n_{Ed}=0$ zachodzi
$$\begin{equation} \rho = \cfrac{ \Theta – sin\Theta \cdot cos \Theta}{\pi – 2 \Theta } \label {94}\end{equation}$$
Rozwiązanie nieliniowego układu równań ($\ref{92}$)+($\ref{94}$) można dokonać dowolną metodą numeryczną. Zalecane jest zastosowanie podstawowego programu inżyniera – Excel z dodatkiem Solver (w wersji podstawowej Excela wtyczkę należy uaktywnić).
Zginania ze ściskaniem przekroju kołowego
Rozwiązanie zadania zginania ze ściskaniem prowadzi się posług procedury przedstawionej w poprzednim rozdziale dla niezerowej siły osiowej $n_{Ed}> 0$. W celu szybkiej oceny można użyć wykresów interakcji M-N przekroju kołowego, np. [9], tab 8.4 do 8.6.
Nośność znanego, konkretnego przekroju
Wysokość strefy ściskanej
Dla znanych sił przekrojowych $M_{Ed}$ oraz $N_{Ed}$ a także siły w zbrojeniu dolnym $F_{sl}$ oraz górnym $F_{su}$ można wyznaczyć wysokość strefy ściskanej w sposób pokazany niżej.
Podejście klasyczne
W podejściu klasycznym pole powierzchni ściskanej części przekroju betonowego o dowolnym kształcie wyznacza się z jednego warunku równowagi sumy sił na oś poziomą ($\ref{34}^1$) $\Sigma X$
$F_c= A_{cx} \cdot f_{cd} = N_{Ed} – F_{su} + F_{sl}$, skąd po podstawieniu ($\ref{36}$) i ($\ref{37}$) otrzymano wysokość strefy ściskanej przekroju:
$$\begin{equation} x= \alpha_F \cdot \cfrac{N_{Ed} -F_{su}+ F_{sl}} {b\cdot f_{cd}^{’}} \label {95}\end{equation}$$ Współczynnik $\alpha_F$ zależy od modelu betonu:
$$\begin{equation} \alpha_F= \begin {cases}
\cfrac{17}{21}= 0,81 & \text {dla modelu MN}\\
\lambda \, \text {(= 0,8 dla betonu zwykłego BZ )}& \text {dla modelu MU} \\
\end {cases} \label{96} \end{equation}$$
Podejście skonsolidowane
W podejściu skonsolidowanym warunek równowagi $(\ref{34})$ można sprowadzić do równania kwadratowego $R(x)=0$, które ma tylko jeden pierwiastek dodatni, co jest zgodne z naturą ($x>0$);. Pierwiastek ten można zapisać w postaci:
$$\begin{equation} x= \alpha_M \cdot \sqrt{ \cfrac{ (N_{Ed}+2 F_{sl})\cdot d_0 -M_{Ed}-a_l F_{sl} -a_u F_{su}} {b f_{cd}}} \label {97}\end{equation}$$
Współczynnik $\alpha_M$ zależy od modelu betonu:
$$\begin{equation} \alpha_M= \begin {cases}
\sqrt{\cfrac{98}{33}}= 1,723 & \text {dla modelu MN}\\
\cfrac{\sqrt{2}}{\lambda} \, \text {(= 1,768 dla betonu zwykłego BZ )} & \text {dla modelu MU} \\
\end {cases} \label{98} \end{equation}$$
Porównanie wysokości strefy ściskanej z podejścia klasycznego i skonsolidowanego
W szczególnym przypadku .czystego ścinania ($N_{Ed}=0$) i przekroju pojedynczo zbrojonego ($A_{su}=0$) wysokość strefy ściskanej wyznaczone z w podejściu uproszczonym i skonsolidowanym będą takie same tylko przy określonej wartości zewnętrznego momentu zginającego $M_{Ed,x}$:
$$\begin{equation} x_F ≡ x_M ⇔ M_{Ed} = M_{Ed,x} = F_{sl} \cdot \left [ d_l – \left( \tfrac{ \alpha_F}{\alpha_M} \right)^2 \cdot \cfrac{F_{sl}}{b\cdot f_{cd}}\right] \label {99}\end{equation}$$
gdzie $d_l=h – a_l$.
Oznacza to, że wysokość strefy ściskanej $x_F$ wyznaczona w podejściu uproszczonym (klasycznym) jest tylko przybliżeniem i różni się od wartości skonsolidowanej (dokładnej) tym bardziej im moment zginającym przekrój $M_{Ed}$ odbiega od wartości momentu $M_{Ed,x}$ ($\ref {99}$).
Takie same wyniki uzyskano przy momencie zginającym znacznie mniejszym od nośności przekroju $M_{Rd}$ ($\ref{92}^1$) i wynoszącym zaledwie
$M_{Ed}= M_{Rd} \, – M_{co} \, – [ (\alpha_F/\alpha_M)^2 \cdot F_{sl}/(b\cdot f_{cd})]$
Nośność przekroju żelbetowego
Nośność znanego przekroju żelbetowego ze znanym zbrojeniem dolnym $A_{sl}$ oraz górnym $A_{su}$ można wyznaczyć bezpośrednio z równań równowagi $(\ref{34})$:
$$\begin{equation} \begin {cases} M_{Rd} = M_{c,0} + F_{su} \cdot (d_0 – a_u) + F_{sl} \cdot (d_0 – a_l) \\ N_{Rd} = F_c + F_{su} – F_{sl} \end {cases} \label {100}\end{equation}$$
gdzie $F_c$ i $M_{c,0}$ dla przekroju prostokątnego i pozornie teowego wyznaczono z równania {$\ref{24}$) ; dla przekroju kołowego z równania ($\ref{89}$), a dla rzeczywiście teowego z ($\ref{75}$).
Dwukierunkowe zginanie My-Mz z udziałem N
Problem dwukierunkowego (ukośnego) zginania z udziałem siły osiowej występują praktycznie we wszystkich elementach słupowych, a w belkach najczęściej bez udziału siły osiowej.
Procedura rozwiązania problemu belki żelbetowej
W zagadnieniu zginania ze ściskaniem/rozciąganiem przekroju żelbetowego poszukuje się sześciu niewiadomych (p. rys. Z-1): $x$ – wysokość strefy ściskanej betonu, czyli pola przekroju ściskanego betonu $A_{cx}= x\cdot b$ $A_{sl}$ – pole przekroju zbrojenia dolnego (rozciąganego) $A_{su}$- pola przekroju zbrojenia górnego umieszczonego w strefie ściskanej betonu. $\sigma_{6}$, – naprężenia ściskających beton, $\sigma_{sl}$, – naprężenia w zbrojeniu dolnym, $\sigma_{su}$, – naprężenia w zbrojeniu górnym,
a do dyspozycji uzyskano tylko dwa warunki równowagi sił: $\Sigma X=0$ – stateczność sumy rzutów sił na oś poziomą X $\Sigma M_i =0$ – stateczność momentów względem dowolnej osi i = ( O, l, u) = (oś przekroju betonowego, oś dolnego zbrojenia, oś górnego zbrojenia). Wybór osi jest dowolny, ale tylko jeden z warunków ΣM jest niezależny. Trzeci warunek wynika z założenia 1 , czyli zasady płaskich przekrojów. Warunki czwarty piaty i szósty wynikają z założenia 2, czyli prawa fizycznego Hooke’a kolejno dla: betonu $(\ref{38})$, zbrojenia rozciąganego i zbrojenia ściskanego $(\ref{42})$. Siódmy warunek wynika z założenia 3, czyli $max \, \varepsilon_c = 3,5$ %.
Dodatkowo na podstawie licznych obserwacji eksperymentalnych – przyjmuje się funkcję rozkładu naprężenia po wysokości ściskanej części przekroju betonowego ($x$) podług paraboli w sposób przedstawiony w modelu MN. W tym nieliniowym modelu wypadkowa siła ściskająca beton wynosi $F_c=17/21=0,81\cdot (b\cdot x \cdot f_{cd}$) W celu uproszczenia obliczeń dopuszcza się stosowanie modelu uproszczonego MU – zastąpienie rozkładu nieliniowego – rozkładem równomiernym, ale na mniejszej wysokości – zamiast na wysokości rzeczywistej $x$ – na wysokości efektywnej $x_{eff}= \lambda \cdot x$ , gdzie $\lambda =0,8 \approx 17/21$ dla betonu zwykłego BZ.
Rozwiązanie zagadnienia belki żelbetowej zginanej i ściskanej polega na zestawieniu wskazanych wyżej zależności i rozwiązaniu utworzonego układu równań.
Układ równań rządzący zagadnieniem jest w ogólności nieliniowy i w zasadzie nie da się sformułować ogólnego rozwiązania analitycznego w „kwadraturach”. Znane rozwiązania ( np [11], [4] ) są dość skomplikowane, wielowątkowe i definiują wiele różnych przypadków projektowych dla poszczególnych układów konfiguracyjnych (stosunków sił) jednoczesnego zginania ukośnego przekroju momentem zginającym $M_{Ed,y}$ wokół osi y , momentem zginającym $M_{Ed,z}$ wokół osi z oraz ściskania/rozciągania siłą osiową $N_{Ed}$.
Równania równowagi dla dwukierunkowego zginania
W przypadku dwukierunkowego zginania przekroju momentami $M_{Ed,y}$ oraz $M_{Ed,z}$ z udziałem siły osiowej $N_Ed$ skonsolidowane równanie równowagi $(\ref {34})$ stawia aię odrębnie dla obu kierunków
$$\begin{equation} R_y=(M_{Ed,y} – M_{c0,y}) – (N_{Ed,y}+2F_{sl,y} – F_{cy}) \cdot d_{0,y} + (F_{sl,y} \cdot a_{l,y} + F_{su,y} \cdot a_{u,y}) = 0 \label {101} \end{equation}$$
$$\begin{equation} R_z=(M_{Ed,z} – M_{c0,z}) – (N_{Ed,z}+2F_{sl,z} – F_{c,z}) \cdot d_{0,z} + (F_{sl,z} \cdot a_{l,z} + F_{su,z} \cdot a_{u,z}) = 0 \label {102} \end{equation}$$
W równaniach $(\ref{104})$ , $(\ref{105})$ występują dwie dodatkowe siły $N_{Ed,y}$ i $N_{Ed,z}$, które stanowią część całkowitej siły ściskającej przekrój $N_{Ed}$ przypadającej do zginania wokół osi $y$ momentem $M_{Ed,y}$ oraz wokół osi $z$ momentem $M_{Ed,z}$ składające się na całkowitą siłę ściskającą
$$\begin{equation} N_{Ed,y}+N_{Ed,z}=N_{Ed} \label {103} \end{equation}$$
Równanie $(\ref{103})$ sprzęga dwa zagadnienia zginania jednoosiowego w jedno zagadnieniu zginania ukośnego z uwzględnieniem interakcji obu prostych zagadnień.
Nośność obliczeniową przekroju $M_{Rd} (=M_{Ed})$, $N_{Rd}(=N_{Ed})$ mierzoną czystymi siłami przekrojowymi (momentem zginającym oraz siłą osiową), odpowiadającymi konkretnym kierunkom zginania (osiom przekroju) przy już wyznaczonym zbrojenia oraz wysokości strefy ściskanej $x$ wyznaczono w sposób opisany w rozdziale Nośność przekroju betonowego.
Współdziałanie (interakcja) kilku sił redukuje nośność przekroju mierzoną czystą siłą (bez działania pozostałych). Dla przypadku jednokierunkowego zginania ze ściskaniem zależności interakcji pokazano na rys. Z-3.
W obliczeniach praktycznych zwykle przyjmuje się [6], (11-16), że składowe nośności zmniejszane są tym samym współczynnikiem redukcyjnym $k_{(M,N)}$:
$$\begin{equation} F_{Rd,(M,N)}= k_{(M,N)} \cdot \left [ M_{Rd} \, , \, N_{Rd} \right ] \label{104} \end{equation}$$
Współczynniki interakcji $k_{(M,N)}$ można wyznaczyć szacunkowo z zaleceń normy amerykańskiej w zależności od obszaru interakcji, określonej na podstawie odkształcenia zbrojenia dolnego (rozciąganego) $\varepsilon_{sl}$ [12] :
$$\begin{equation} k_{(M,N)} = \begin {cases} 0,65, & \text {dla } \varepsilon_{sl}\le \varepsilon_{sy} \\ 0,65+ (\varepsilon_{sl}-\varepsilon_{sy}) \cdot 0,29 / \varepsilon_{cu}, & \text {dla } \varepsilon_{sy} < \varepsilon_{sl} < \varepsilon_{su} \\ 0,90, & \text {dla } \varepsilon_{sl} \ge \varepsilon_{su} \end {cases} \label{105} \end{equation}$$
gdzie: $\varepsilon_{sy}=E_s / f_{yk}$ – odkształcenie plastyczne stali, $\varepsilon_{su}$ – odkształcenie graniczne stali (odpowiadające granicy wytrzymałości), $\varepsilon_{cu} =3,5$‰ ( $=\varepsilon_{cu2}$ w modelu MN ; = $\varepsilon_{cu3}$ w modelu MU) – odkształcenie graniczne betonu
W załączonym do przykładu 2 arkuszu kalkulacyjnym LCżelbet interakcja momentu zginającego oraz siły osiowej jest uwzględniana dokładnie bez potrzeby stosowania uproszczonych formuł $(\ref{106})$ z $(\ref{108})$.
Powierzchnia interakcji ukośnego zginania przekroju żelbetowego
Na rys. Z-5 pokazano powierzchnię interakcji przekroju żelbetowego zginanego ukośnie.
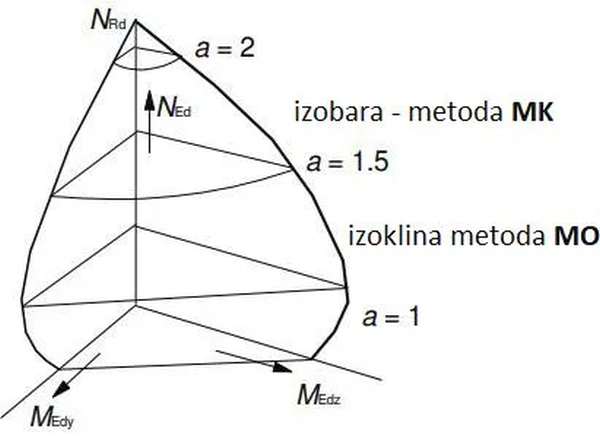
Rys. 12 Powierzchnia interakcji N-My-Mz [13]
Na powierzchni interakcji można wydzielić izobary powstałe przez przekrój powierzchni interakcji płaszczyzną prostopadłą do osi sił N (równoleżnik). Aproksymacja powstałej w ten sposób krzywej interakcji dla ustalonej siły osiowe nazywana jest Metodą Konturu (MK) i jest opisana formułą $(\ref{116} )$ stosowaną w normie europejskiej [1] .
Przekrojem pionowym na powierzchni interakcji można wydzielić izokliny, ten sposób aproksymacji nazywany jest Metodą Odwrotności (MO) ze względu na postać formuły interakcji ($\ref{116}$). Metoda odwrotności została wprowadzona do normy amerykańskiej ACI 318-05,11.
Stosowanie uproszczonych formuł interakcji ($\ref{116}$) oraz ($\ref{116}$) uzasadnione jest trudnościami rachunkowymi w ścisłym ujęciu zagadnienia, a także uzyskiwaniem bezpiecznych rozwiązań, co zostało potwierdzona wieloma badaniami eksperymentalnymi i numerycznymi. W szeregu przypadkach zyskiwane rozwiązania są jednak zbyt konserwatywne, więc nieoptymalne [14] .
Rozprzężenie zginania ukośnego
Wyznaczenie przekrojowych sił osiowych $N_{Ed,y}$ i $N_{Ed,z}$, generujących siły w zbrojeniu $F_{sl}$ oraz $F_{su}$ $(\ref{108})$ w każdym kierunku zginania jest podstawowym problemem zginania ukośnego, powalającym rozdzielić problem sprzężony na dwa problemy proste. W zadaniu rozprzężenia poszukiwano współczynników rozdziału:
$$\begin {equation} r_y=N_{Edy}/N_{Ed} \, ; \, r_z=N_{Edz}/N_{Ed} \label {106} \end {equation}$$ Z warunku $(\ref{108})$, otrzymano oczywiście $r_y+ r_z=1$
Rozprzężenie zginania ukośnego można dokonać na wiele sposobów, z których omówiono trzy:
- S – proporcjonalnej sztywności.
- R proporcjonalnej nośności,
- MO – odwrotności nośności (metoda krzywej interakcji MO).
Metoda S rozprzężenia – proporcjonalnie do sztywności
Zgodnie z podstawową zasadą rozdziału sił przekrojowych proporcjonalnie do sztywności, przyjęto rozdzielniki sił $r_y$ oraz $r_z$ w dwóch kierunkach proporcjonalnie do sztywności przekroju :
$$\begin{equation} r_y =\cfrac{s_y}{S} \, ; r_z =\cfrac{s_z}{S} \, \label{107} \end {equation} $$
gdzie:
$ S =E_{cm} \cdot ( A_c +\alpha_e \cdot \Sigma A_s) $ – sztywność osiowa całego przekroju,
$s_y =E_{cm} \cdot (A_{cy} +\alpha_e \cdot A_{sy})$,
$s_z =E_{cm} \cdot (A_{cz} +\alpha_e \cdot A_{sz})$,
$\alpha_e=E_s/E_{cm}$. – stosunek modułów sztywności stali i betonu
Przyjęto założenie że ze zbrojeniem w danym kierunku współpracuje beton proporcjonalnie do pola przekroju danego zbrojenia:
$A_{cy}/A_{cz}=A_{sy}/A_{sz}$
Przy takim założeniu stosunek współczynników rozdziału (równy stosunkowi sztywności) jest równy stosunkowi przekroju zbrojenia
$$\begin{equation} r_{yz→s}=\cfrac{r_y}{r_z} =\cfrac{s_y}{s_z} =\cfrac{ A_{sy}} {A_{sz}} \label{108}\end {equation} $$
$$\begin{equation} r_{y→s} =\cfrac{r_{yz→s}}{1+r_{yz→s}} \label{109}\end {equation} $$
Metoda R rozprzężenia – proporcjonalnie do nośności
Dla $N_{Ed} > N_{Rdx}/3$ metoda MO jest zawodna (p. niżej). W takim przypadku rozdział siły osiowej $N_{Ed}$ przeprowadzono proporcjonalnie do zbalansowanych nośności $N_{Rdy(N)}$ oraz $N_{Rdz(N)}$, uzyskanych z pomocniczego rozwiązania równań równowagi odrębnie dla każdego kierunku zginania, przy chwilowym założeniu, że przypadają na nie siły $(\ref{109})$ wyznaczone metodą S. Nośności zbalansowane są wyznaczane z pełnego układu równań problemu, więc również z uwzględnieniem rozkładu odkształceń zgodnie z geometrycznym założeniem płaskich przekrojów. W wyniku otrzymano :
$$\begin{equation} r_{y,R} =\cfrac{r_{yz,R}}{1+r_{yz,R}} \label{110} \end {equation} $$
gdzie $r_{yz,R}=\cfrac{N_{Rdy(N)}}{N_{Rdz(N)}}$
Metoda MO rozprzężenia – odwrotności nośności
Krzywą interakcji metody odwrotności MO jest określona przez trzy punkty na powierzchni interakcji (na rys Z-5) i można zapisać w postaci :
$$\begin {equation} \cfrac{1}{N_{Rd}} \approx \cfrac{1}{N_{Rdy}} + \cfrac{1}{N_{Rdz}} – \cfrac{1}{N_{Rdx}} \label {111} \end {equation}$$
gdzie: $N_{Rd} $ – Nośność przekroju mierzona siłą osiową w stanie zginania ukośnego, $N_{Rd,y}$ – nośność przekroju zginanego wokół osi y (bez ściskania i zginania wokół osi z), $N_{Rd,z}$ – nośność przekroju zginanego wokół osi z (bez ściskania i zginania wokół osi y), $N_{Rd,x}$ – nośność przekroju w stanie czystego ściskania (przy pominięciu zginania), opisana formułą $(\ref{116})$ . W stanie granicznym $N_{Rd}=N_{Ed}$ , $N_{Ed,y}=N_{Rd,y}$ i $N_{Edz}=N_{Rd,z}$, a z równania interakcji $(\ref{116})$ po uwzględnieniu definicji $(\ref{107})$ i po przekształceniach można otrzymać :
$$\begin{equation} r_y \cdot (1-r_y)=\cfrac{n_{Ed}}{1+n_{Ed}} \label {112} \end {equation}$$
gdzie: $n_{Ed}=N_{Ed}/N_{Rdx}$. Po rozwiązaniu tego równania względem $r_y$, otrzymano pierwiastek metody MO :
$$\begin{equation} r_{y,R1} =\cfrac{1}{4} \pm \sqrt{ \cfrac{1}{1+n_{Ed}}-\cfrac{4}{6}} \label{113} \end {equation}$$
Rozwiązanie powyższe ma fizyczny sens dla wyrażenia podpierwiastkowego większego od zera , czyli dla $n_{Ed}<1/3$. Oznacza to, że może być stosowane dla siły osiowej $N_{Ed}< N_{Rdx}/3$. W granicy dla $N_{Ed}=0$ uzyskano $r_{y,R1} =0$ lub 1, co odpowiada $r_{z,R1}$=1 lub 0, to znaczy zginaniu jednokierunkowemu przekroju. W przypadku $N_{Ed}= N_{Rdx}/3$, uzyskano $r_{y,R1}=r_{z,R1}=1/2$
Metoda rozprzężenia zginania ukośnego stosowana w arkuszu LCŻelbet
Omówione wyżej metody są metodami przybliżonym i i każda z nich prowadzi do innego rezultatu, przy czym najbardziej odlegle wyniki uzyskuje się w metodzie MO.
Metody S i R prowadzą do formuł $(\ref {109})$ i $(\ref{110})$ o podobnej budowie, co pozwalałoby na ich łączne rozpatrzenie. Najprostsza jest metoda S i w proponowanym algorytmie w pierwszym kroku zastosowano tę metodę w celu wyznaczenia zbalansowanych nośności przekroju, na podstawie których prowadzi się ponowny rozdział sił metodą R, który przyjmuje się za wystarczające przybliżenie rozprzężenia problemu.
Powierzchnia interakcji My-Mz-N w Eurokodzie 2
Norma do projektowania na obciążenia sejsmiczne [15] sugeruje traktowanie dwuosiowego zginania poprzez przeprowadzanie kontroli osobno w każdym kierunku, z jednoosiową wytrzymałością na zginanie zmniejszoną o 30%. Takie podejście jest zbyt konserwatywne. Dokładniejsze jest podejście prezentowane w normie podstawowej [1], kl. 5.8.9 poprzez stosowanie krzywych interakcji metodą MK (Metodą Konturu), czyli przekrojami poziomymi-izobarami powierzchni interakcji) aproksymowanych formułą [1], (5.39) :
$$\begin{equation} \Lambda_R= \left ( \cfrac{M_{Edy}}{M_{Rdy}} \right )^{\alpha_y} + \left ( \cfrac{M_{Edz}}{M_{Rdz}} \right )^{\alpha_z} \le 1 \label{114} \end{equation}$$
Momentom zginającym przekrój w dwóch kierunkach $M_{Edz}, M_{Edy}$ i odpowiadają nośności przekroju $M_{Rdz}, M_{Rdy}$ wyznaczone zgodnie z $(\ref{116})$ odrębnie dla stosownych kierunków zginania .
Normowy wykładnik powierzchni interakcji
Wykładniki interakcji w [1] przyjmuje się jednakowe dla obu kierunków $ \alpha_y= \alpha_z = a $,. Dla przekroju prostokątnego wykładnik potęgi $a$ można przyjmować zgodnie z tab. Z-2 w zależności od względnej siły osiowej $n_{Ed}=N_{Ed}/N_{Rdx}$, gdzie nośność odniesienia $N_{Rdx}$ wyznacza się z formuły:
$$\begin {equation} N_{Rdx}= A_{cx} \cdot f_{cd} + ΣA_s \cdot f_{yd} \label {115} \end {equation}$$
Tab. Z-2 Wykładnik krzywej interakcji My-Mz dla przekroju prostokątnego [1]
Dla przekroju kołowego lub eliptycznego $a=2,0$. Formułę $(\ref{116})$ zaproponował Bresler [16] , który wskazał, że a=1,15 do 1,5. W przypadku przekrojów kwadratowych zaproponował a=1,5 do 2,0. W komercyjnym programie STAAD stosuje się a=1,24 dla wszystkich kształtów przekroju.
Wartości pośrednie wykładnika interakcji należy aproksymować. Na rys. Z-6 pokazano wykres wykładnika a w funkcji względnej siły osiowej i aproksymacyjny wielomian drugiego stopnia przechodzący przez punkty z tab. Z-2
Uogólnione wykładniki powierzchni interakcji
W niniejszym artykule przyjmuje się, że wykładniki powierzchni interakcji $(\ref{116})$ są różne w zależności od kierunku zginania: $\alpha_y \neq \alpha_z$ i są wyznaczane z rys. Z-6 dla względnych sił:
$n_{Ed,•}=N_{Ed,•}/N_{Rdx}$, gdzie indeks •=y,z
to znaczy podług zależności korelacyjnej $$\begin {equation} \alpha_•=0,98 + 0,093 \cdot n_{Ed,•} + 0,926 {n_{Ed,•}}^2 \label {116} \end {equation}$$
Przykłady rachunkowe
Przykład Z-1 [Belka stropowa bez uwzględnienia współpracy płyty – przypadek ZM]
Przykład 4-1 z podręcznika [2]
Zaprojektować zbrojenie belki żelbetowej swobodnie podpartej o przekroju prostokątnym obciążonej równomiernie po długości, pokazanej na rys. Z-14 Klasa ekspozycji XC2; klasa odporności ogniowej R60; klasa konstrukcji S4.
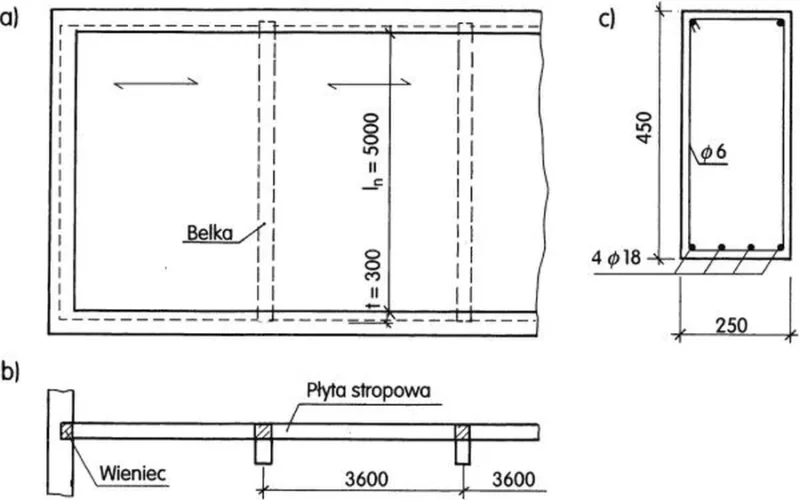
Rys. 14 Strop płytowo-belkowy: a) rzut, b) przekrój, c) belka stropowa [2], rys.4.35
Dane ogólne
Beton C20/25: ( tab. W-1) $\to$ $f_{ck}=20 \, MPa$ , $f_{ctm}=2,2 \, MPa$ , $f_{cd}=20/1,4=14,29 \, MPa$
Stal B500: (tab. W-2) $\to$ $f_{yk}= 500 , MPa$, $f_yd=500/1,15=435 \, MPa$
Długość belki w świetle murów $l_n=5,0 \, m$, Grubość muru z lewej $t_l=500 \,$mm Grubość muru z prawej $t_p=500 \,$mm
K(2) długość obliczeniowa belki $\to l_{eff} =5,0+[(300+300)/2]/1000=5,3 \, m$.
Maksymalny obliczeniowy moment przęsłowy (z obliczeń statycznych) $M_{Ed}=$ 131,5 kNm
Dobór wstępny przekroju
K(3) wysokość belki $\to h=l_{eff}/12=442$. przyjęto 450 mm
K(5) szerokość belki $\to b=h/2=450/2=225$, przyjęto 250 mm
Zbrojenie minimalne i maksymalne
- ze względu na kruche zniszczenie betonu w strefie ściskanej
K-(15) minimalny stopień zbrojenia $ρ_{min,b}= \ max { \{ 0,0013 \, ; \,0,26 \cdot 2,2 /500 \} }= 0,0013$
dokładność członu z warunku (K-18) sprawdzono po wyznaczeniu dżwigni sił poniżej
K-(16) $A_{s, min, brittle} = 0,0013 \cdot 25 \cdot 40,0=$ 1,3 cm2 - ze względu na zarysowanie belki w strefie rozciągane
K-(20) $A_{s, min, crack} = 0,4 \cdot 1,0 \cdot (25\cdot 40)/2 \cdot \cfrac {2,2}{260}= 1,7 \, cm^2$
gdzie:
$(25\cdot 40)/2$ – pole rozciąganej strefy betonu w chwili poprzedzającej zarysowanie belki zginanej (I faza – sprężysta),
c=0,4 – współczynnik uwzględniający rozkład naprężenia w przekroju w chwili poprzedzającej zarysowanie dla fazy II (przyjęto maksymalnie możliwy dla zginania),|
k =1,0 – współczynnik uwzględniający wpływ nierównomiernych naprężeń samorównoważących się (przyjęto maksymalnie możliwy),
$\sigma_{s,lim} = 260 \, MPa$ jak dla zbrojenia prętami $\Phi 18$ na podstawie tablicy K-2.
Zbrojenie minimalne
$A_{s,min}= max \{ 1,3; 1,7 \} =$ 1,7 cm2
Zbrojenie maksymalne
K-(22) $A_{s, max} = 0,04 \cdot 25 \cdot 40 cm= 40 \, cm^2$
Przyjęto wstępnie:
pręty zbrojeniowe $\Phi=18 \, mm$ : $A_{s1}=\pi \cdot 1,8^2/4 = 2,545 \, cm^2$
strzemiona o średnicy $\Phi_s= 6 \, mm$
Otulenie zbrojenia: $c_{min}=\Phi=18 \, mm$, $c_{dur}= 25 \, mm$ dla klasy ekspozycji XC2; $ \Delta c_{dev}=10 \,mm $.
K(12) $\to$ $ c= \max{ \{18\,;\,25 \} } +10= 35 \, mm$, $ c_{nom}= 35+6 = 41 \, mm$,
K(13) $\to$ $a =a_l = a_u = 41+18/2=$ 50 mm,
Wysokość użyteczna przekroju $ d=d_l =450-50=$ 400 mm
Wstępne szacunki pola przekroju zbrojenia rozciąganego
K-(10) $\to$ dla zbrojenia podwójnego (górą i dołem) $\Sigma A_s=A_{su}+A_{sl}\approx \cfrac {131,5} {435 \cdot (0,45-2\cdot 0,05)} \cdot 10^1=8,6 \, cm^2$.
co daje $4 \Phi 18$, A_s = 4\cdot 2,545 = 10,18 > 8,6 \, cm^2$
K-(11) $\to $ dla zbrojenia pojedynczego $A_{sl} \approx \cfrac{131,5} {435 \cdot 0,9 \cdot (0,45-0,05) }\cdot 10^1=8,4 \, cm^2$,
co daje $4 \Phi 18$, A_s = 4\cdot 2,545 = 10,18 > 8,4 \, cm^2$
Uwaga:
Nadwyżka zbrojenia przyjętego (rzeczywistego) nad teoretycznym wynosi 10,18/[(8,4+8,6)/2] = 1,2 (wynosi aż 20%). W celu lepszego dopasowania zbrojenia rzeczywistego do potrzeb przyjęto mniejszą średnicę prętów niż w pracy [2]– rys, Z-14. Uzasadnienie zasady „Nie przezbrajać przekroju belki żelbetowej !” podano w rozdziale Mechanizmy zniszczenia przekroju betonowego.
Przyjęto
pręty zbrojeniowe:
główne $\Phi=14 \, mm$: $A_{s1}=\pi \cdot 1,4^2/4 = 1,539 \, cm^2$
strzemiona o średnicy $\Phi_s= 6 \, mm$
Otulenie zbrojenia: $c_{min}=\Phi=14 \, mm$, $c_{dur}= 25 \, mm$ dla klasy ekspozycji XC2; $ \Delta c_{dev}=10 \,mm $.
K(12) $\to$ $ c= \max{ \{14\,;\,25 \} } +10= 35 \, mm$, $ c_{nom}= 35+6 = 41 \, mm$,
K(13) $\to$ $a =a_l = a_u = 41+14/2= 48 \approx $ 50 mm
Wysokość użyteczna przekroju $ d=d_l =450 – 50=$ 400 mm
$(\ref{12}) \to $ sprowadzone pole betonu $ A_{c, s} = 185 \cdot 40,0 \cdot \cfrac{14,29}{210}=$ 32,87 cm2
PZP (przekrój pojedynczo zbrojony)
($\ref{1} )\to$ efektywna wytrzymałość betonu $f_{cd}^{’}=1,0\cdot 14,29 = 14,29 \, MPa$
($\ref{3}^3) \to $ czynnik normujący moment $\overline M = 0,25 \cdot 0,40^2 \cdot 14,29 \cdot 10^3=572,0 \, kNm$,
($\ref{3}^1) \to $ unormowany moment zginający $m_{Ed} = \cfrac{131,5}{ 572,0}=0,229 < 0,23$,
gdzie $ (\ref{17}) \to $ $m_{ult}=0,23$ moment graniczny dla betonu zwykłego BZ
$\to$ nie trzeba dozbrajać betonu strefy ściskanej i stosować zbrojenia górnego
Nie obliczono wysokości strefy ściskanej $(\ref{6})$ , bo nie jest potrzebna przy wyznaczaniu zbrojenia przekroju pojedynczo zbrojonego
($\ref{11}$) $\to $ ramię siły betonu
$\zeta_c = \begin {cases}
(1 +\sqrt{1-594/289 \cdot 0,229}) /2 = 0,864 & \text{ MN}\\
(1+\sqrt{1- 2 \cdot 0,229}) /2 = 0,868 , & \text{ MU}\\
\end{cases}$
Różnice ramienia siły w betonie w obu modelach MN i MU są niewielkie.
$(\ref{51}) \to $ zbrojenie dolne
$A_{sl}= \begin {cases}
\cfrac{0,229}{0,864} \cdot 32,87 = 8,71 \, cm^2 & \text{ MN}\\
\cfrac{0,229}{0,868} \cdot 32,87 = 8,67 \, cm^2 & \text{ MU}\\
\end{cases}$
Różnice wymaganego zbrojenia dolnego w obu modelach MN i MU są niewielkie.
W obu modelach przyjęto: $6 \Phi 14$, $A_s = 6 \cdot 1,539= 9,23 \, cm^2 $
W przypadku prętów o średnicy $\Phi 18$ potrzeba 4 pręty o przekroju $A_s = 4 \cdot 2,545 = 10,18 \, cm^2$
Lepsze dopasowanie do potrzeb uzyskano dla prętów $\Phi 14$.
Sprawdzenia konstrukcyjne
- wymóg zbrojenia minimalnego
$ A_{sl}= 9,23 > 1,9 \, cm^2$ ( ustalono pod danymi zadania )
- wymóg zbrojenia maksymalnego (górne pręty $2 \Phi 14$)
$A_s= A_{sl}+ A_{su}$ = 9,23 + $ 2 \cdot 1,539 = 12,32 < 45 \, cm^2 $
- odstępy miedzy prętami
szerokość belki do rozmieszczenia zbrojenia
$b_{zb}=250 -2\cdot 50 = 150 \,mm $
odległości między prętami
$ a_h = b_{zb}/(m_{zb}-1) -\ Phi = 150/(6-1)- 14= 16/, mm$
K-(14) $min (a_h )= \max { \{ 14 \, ; \, 20 mm \, ; 10 +5 mm \}}= 20 \, mm$ (10 – maksymalna średnica ziarna kruszywa)
Ponieważ $a_h < min (a_h)$ to należy:
dać pręty w dwóch rzędach
lub zmniejszyć liczbę prętów w rzędzie (zwiększyć średnicę)
Optymalizację rozwiązania pozostawia się Czytelnikowi
- otulenie osiowe boczne
$a_{uz}= c_{uz}+ \Phi_s+$Phi / 2= 35+ 6+14 / 2 = 48 \approx 50 \, mm $
Przykład Z-2 [Średnie obciążenie – przypadek ZS]
Zaprojektować belkę z przykładu Z-1 na obciążenie $M_{Ed}=$ 182,8 kNm
Dane wstępne oraz wstępny dobór przekroju pozostaje bez zmian.
Powracamy do przyjętej wstępnie średnicy prętów głównych $\Phi 18$, $A_{s1}=\pi \cdot 1,8^2/4 = 2,545 \, cm^2 $
$ c_{nom}= 35+6 = 41 \, mm$,
$a =a_l = a_u = 41+18/2=$ 50 mm,
$ d=d_l =450-50=$ 400 mm
PZP (przekrój pojedynczo zbrojony)
($\ref{1} )\to$ efektywna wytrzymałość betonu $f_{cd}^{’}=1,0\cdot 14,29 = 14,29 \, MPa$
($\ref{3}^3) \to $ czynnik normujący moment $\overline M = 0,25 \cdot 0,40^2 \cdot 14,29 \cdot 10^3=572,0 \, kNm$,
($\ref{3}^1) \to $ unormowany moment zginający $m_{Ed} = \cfrac{182,8}{ 572,0}=0,320$,
$ (\ref{17}) \to $ moment graniczny dla betonu zwykłego BZ $m_{ult}=0,23$
$ (\ref{57}) \to $ $ \Delta(m_{Ed}) = 0,320 – 0,23 = + 0,09 $
Ponieważ $\Delta m> 0$, to należy zastosować zbrojenia górne, więc przekrój będzie DZP (podwójnie zbrojony)
Nie wyznacza się zbrojenia w założeniu przekroju PZP (pojedynczo zbrojonego).
DZP (przekrój podwójnie zbrojony)
Do wiązania strzemion zastosowano zbrojenie górne $2 \Phi 18$ $A_{su}^{constr} = 2\cdot 2,545 =5,09 \, cm^2$
($\ref{54}) \to$ nośność zbrojenia górnego ( tutaj konstrukcyjnego)
$m_{su}^{constr} =\cfrac{5,09}{32,87} \cdot (1 – 5, 0/40,0) = 0,135$
($\ref{56}) \to$ zredukowane obciążenie przez zbrojenie górne konstrukcyjne
$m_{Ed}^*= 0,320 – 0,135= 0,185 < m_{ult} = 0,23$
$\to$ nie trzeba dodatkowego zbrojenia górnego
$(\ref{6}) \to $ wysokość strefy ściskanej
$ \xi= \begin {cases}
119/99 \cdot (1 – \sqrt{1- 594/289 \cdot 0,185})=0,256, & \text{ MN }\\
1 / 0,8 \cdot (1 – \sqrt{1- 2 \cdot 0,185})=0,258, & \text{ MU }\\
\end{cases}$
Różnice wysokości strefy ściskanej w modelu MN i MU są niewielkie
$(\ref{13}) \to$ efektywne pole betonu ściskanego
$ a_{cx}= \begin {cases}
17/21\cdot 0,256 = 0,207 ,& \text{ MN}\\
0,8 \cdot 0,258= 0,206 ,& \text{ MU}\\
\end{cases}$
$(\ref{14}) \to$ $ A_{cx, s} = 0,207\cdot 32,87=6,80 \, cm^2 $
$(\ref{60}) \to$ $A_{sl}= 5,09 + 6,80 = 11,89 \, cm^2$
Przyjęto: $5 \Phi 18$, $A_s = 5 \cdot 2,545 = 12,73 \, cm^2 $
Stopień zbrojenia
$\sum A_s = A_{sl}+A_{su}= 12,73+ 5,09= 17,82 \, cm^2 $
$A_c= b \cdot h= 25 \cdot 45= 2 545 \, cm^2$
$\rho= 17,82/2545= 0,7 $ %
Sprawdzenia konstrukcyjne
Wykonać analogicznie do przykładu Z-1
Kalkulator LCżelbet
Dla danych z przykładu 2 przekrój zaprojektowano metodą metoda nieliniową MN z użyciem kalkulatora LCŻelbet. Poniżej, na rys Z-15 zamieszczono ekran z kalkulatora przedstawiający wyniki obliczeń 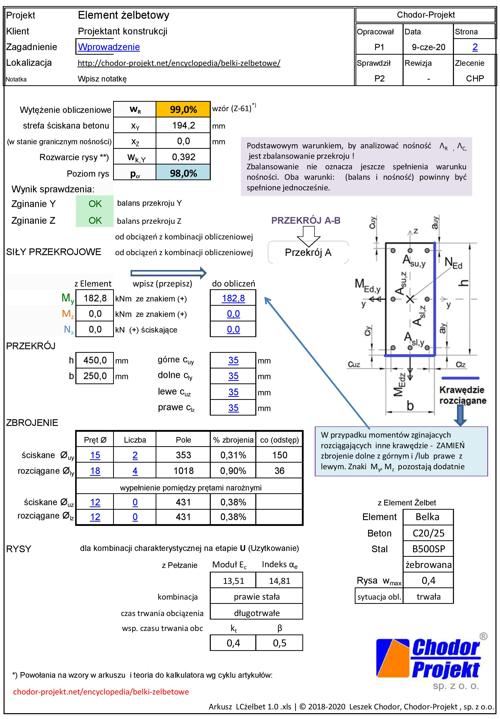
Rys Z-15 . Kalkulator LCżelbet – przykład Z-1 (kliknij , aby pobrać)
W wyniku obliczeń kalkulatorem wykazano, że zbrojenie dolne można wykonać z $4 \Phi 18$, a zbrojenie górne konstrukcyjnie $2 \Phi 16$ (wytężenie 94,7%). Jeśli zbrojenie górne jest $2 \Phi 14$, to wytężenie wynosi 98.6%, a dopiero dla $2 \Phi 12$ wytężenie jest zbyt duże.
Przykład Z-3 [Duże obciążenie – przypadek ZD]
Zaprojektować belkę z przykładu Z-1 na obciążenie $M_{Ed}=$ 271,2 kNm
Dane wstępne oraz wstępny dobór przekroju pozostaje bez zmian.
Powracamy do przyjętej wstępnie średnicy prętów głównych $\Phi 18$, $A_{s1}=\pi \cdot 1,8^2/4 = 2,545 \, cm^2 $
$ c_{nom}= 35+6 = 41 \, mm$, $a =a_l = a_u = 41+18/2=$ 50 mm, $ d=d_l =450-50=$ 400 mm
($\ref{3}) \to $ $m_{Ed} = \cfrac{271,2}{ 572,0}=$ 0,474 $> m_{ult} =0,23$,
gdzie ($\ref{17}$) $m_{ult}= 0,23
Przekrój musi być podwójnie zbrojony, więc pomija się algorytm zbrojenia przekroju PZP
DZP (przekrój podwójnie zbrojony). Procedura metody MO*
Zbrojenie górne konstrukcyjne (jak w przykładach Z-1 i Z-2)
$A_{su}= 5,09 \, cm^2$
$m_{su}^{constr}=0,135$
($\ref{56}) \to$ zredukowane obciążenie przez zbrojenie górne konstrukcyjne
$m_{Ed}^*= 0,474 – 0,135= 0,339$
$\Delta m= 0,339 – 0,23 = 0,109 > 0 $
$\to$ należy zastosować dodatkowe zbrojenie górne
($\ref{58}$) $\to $ zbrojenie górne dodatkowe
$A_{su}^{add} = \cfrac{0,109}{1-5,0/40,0} \cdot 32,87 = 4,09 \, cm^2$
$\to$ ($\ref{52}$) całkowite zbrojenie górne (konstrukcyjne + dodatkowe)
$ A_{su}= 5,09+4,09= 9,18 \, cm^2$
przyjęto $3 \Phi 18 $ , $A_{su}= 3 \cdot 2,545 = 10,18 \, cm^2$
($\ref{54}) \to $ nośność zbrojenia górnego
$m_{su}=\cfrac{10,18 }{32,87} \cdot (1-5,0/40,0) = 0,271$
($\ref{65}) \to $ obciążenie zredukowane przez całkowite zbrojenie górne całkowite
$m_{Ed}^*= 0,474 – 0,271= 0,203 < m_{ult} =0,23 $
$(\ref{6}) \to $ wysokość strefy ściskanej
$ \xi= \begin {cases}
119/99 \cdot (1 – \sqrt{1- 594/289 \cdot 0,203})=0,284 & \text{ MN }\\
1 / 0,8 \cdot (1 – \sqrt{1- 2 \cdot 0,203})=0,287, & \text{ MU }\\
\end{cases}$
$(\ref{13}) \to$ efektywne pole betonu ściskanego
$ a_{cx}= \begin {cases}
17/21 \cdot 0,284= 0,230 ,& \text{ MN}\\
0,8\cdot 0,287= 0,230 ,& \text{ MU}\\
\end{cases}$
$(\ref{14}) \to$ $ A_{cx, s} = 0,230\cdot 32,87=7,56 \, cm^2 $
$(\ref{60}) \to$ $A_{sl}= 10,18 + 7,56 = 17,74 \, cm^2$
Przyjęto: $ 7 \Phi 18$, $A_s = 7 \cdot 2,545 = 17,82 \, cm^2 $
Stopień zbrojenia
$\sum A_s = A_{sl}+A_{su}= 17,82+ 10,18= 28,0 \, cm^2 $
$A_c= b \cdot h= 25 \cdot 45= 2 545 \, cm^2$
$\rho= 28,0 /2545= 1,1 $ %
Sprawdzenia konstrukcyjne
Wykonać analogicznie do przykładu Z-1
Przykład Z-4 [ Belka pozornie teowa. Przypadek ZS, DZP (ze zbrojeniem górnym)]
Przykład 4-3 z podręcznika [2]
Zaprojektować zbrojenie belki żelbetowej teowej, pokazanej na rys. Z-16 stropu podpartego przegubowo na obwodzie i równomiernie obciążonego na powierzchni.
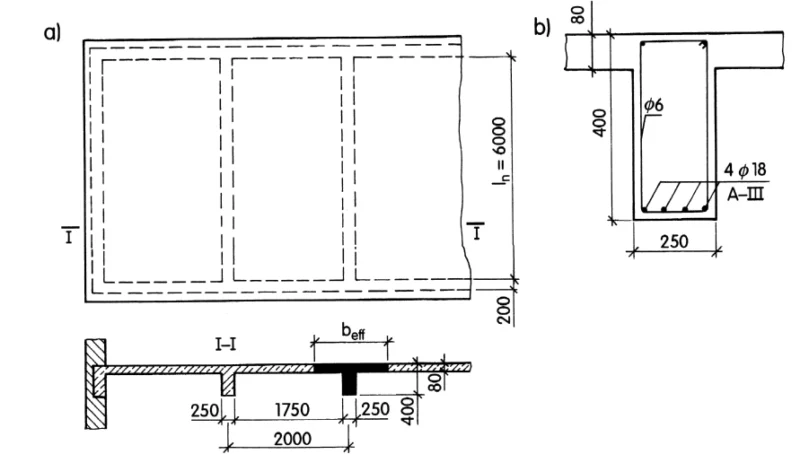
Rys. 16. Ilustracja do przykładu 2 [2], rys.4-40
Dane ogólne
Klasa ekspozycji XC1; klasa odporności ogniowej R60; klasa konstrukcji S4
Beton C20/25: ( tab. W-1) $\to$ $f_{ck}=20 \, MPa$ , $f_{ctm}=2,2 \, MPa$ , $f_{cd}=20/1,4=14,29\, MPa$
($\ref{1} )\to$ efektywna wytrzymałość betonu
$f_{cd}^{’}=1,0\cdot 14,29 = 14,29 \, MPa$
Stal (Stale obecnie nie używane – przyjęto za [2], przykłady 4.3 i 4.1 )
żebra AIII $f_{yk}= 400 \, MPa$, $f_{yd}=350 \, MPa$
płyty A I $f_{yk}= 240 \, MPa$, $f_{yd}=210 \, MPa$
Długość belki w świetle murów $l_n=6,0 \, m$, Grubość muru z lewej $t_l=200+50 =250 \,$mm ( mur – podpora szersza o 50 mm od wieńca) Grubość muru z prawej $t_p= 200+50=250 \,$mm
K(2) długość obliczeniowa belki $\to l_{eff} =6,0+[(250+250)/2]\cdot 10^{-3} =6,25 \, m$.
Maksymalny obliczeniowy moment przęsłowy $M_{Ed}=$ 110,54 kNm,
Przyjęto (wg procedury przywołanej w przykładzie Z-1) :
wysokość belki $h= 400 \, mm$
szerokość belki $b=250 \, mm$
średnica zbrojenia $\Phi= 18 \, mm$
otulina $c_{nom} \max \{ 18\,;\, 15 \} +10 = 28 \, mm$ gdzie dla XC1 $c_{dur} = 15 \, mm$ średnica strzemion $\Phi_s = 6 \, mm$
otulina osiowa $a=28 + 6 + 18/2= 43 \, mm$
wysokość użyteczna $d=d_l=400 -43 =$ 357 mm
Szerokość efektywna przekroju teowego
Szerokości żeber wokół rozpatrywanej belki
$b_{wl}= b_{wp} = 250 \, mm$
Odległośc osiowa żeber $l_z=2000 \,mm$
($\ref{67}) \to$ połowa odległości w świetle przęsła z żebrem (sąsiadującym z rozpatrywaną belką
$b_1=b_2 = ( 2000- (250+250)/2)/2= 875 \, mm$
rys Z-11 belka – żebro wolnopodarte $\to$
$L_0 = 1,0 \cdot 6250 =6250 \, mm$
($\ref{68}$) szerokości współpracujące $\to$
$b_{eff,1} = b_{eff,2} = 0,2 \cdot 875 + 0,1\cdot 6250 = 800 \, mm$
$\le \min{ \{ 875 \, ; \, 0,2 \cdot 6250} \}= 875 \, mm$
($\ref{69})\to$ szerokość półki przekroju teowego (współpracująca część płyty stropowej)
$ b_{eff}= 250 + 2\cdot 800=$ 1850 mm
$\le 2\cdot 875 + 250 = 2000$
Czy przekrój jest pozornie teowy
W pierwszym kroku założono , że przekrój jest pozornie teowy, a szerokości belki wynosi
$ b= b_{eff} = 1850 \, mm$
($\ref{3}^3) \to $ czynnik normujący moment $\overline M = 1,85 \cdot 0,357^2 \cdot 14,29 \cdot 10^3=3369,3 \, kNm$,
($\ref{3}^1) \to $ unormowany moment zginający $m_{Ed} = \cfrac{110,54}{ 3369,3} =$ 0,0328 < 0,23,
gdzie $ (\ref{17}) \to $ $m_{ult}=0,23$ moment graniczny dla betonu zwykłego BZ
$\to$ nie trzeba dozbrajać betonu w strefie ściskanej i stosować zbrojenia górnego
$(\ref{6}) \to $ względna wysokość strefy ściskanej
$ \xi= \begin {cases}
119/99 \cdot (1 – \sqrt{1- 594/289 \cdot 0,0328})= 0,0412, & \text{ MN }\\
1 / 0,8 \cdot (1 – \sqrt{1- 2 \cdot 0,0328})=0,0417, & \text{ MU }\\
\end{cases}$
$(\ref{6}) \to $ wysokość strefy ściskanej
$ x = \xi \cdot d \begin {cases}
0,0412 \cdot 357= 14,72 \, mm & \text{ MN }\\
0,0417 \cdot 357 = 14,89 \, mm & \text{ MU }\\
\end{cases}$
$x = (14,73) 14,89 < h_f = 80 \, mm$
$\to$ przekrój jest pozornie teowy
Przekrój wymiaruje się jak prostokątny DZP podwójnie zbrojony metodą MO*.
Efektywne pole betonu przekroju pozornie teowego
$A_c = 185 \cdot 35,7 = 6604,5 \, cm^2$
$(\ref{12}) \to $ sprowadzone pole betonu przekroju pozornie teowego:
do stali płyty
$ A_{c→sf} = 6604,5 \cdot \cfrac{14,29}{210}=$ 449,42 cm
do stali żebra
$ A_{c→sw} = 6604,5 \cdot \cfrac{14,29}{350}=$ 269,65 cm
W projekcie płyty [2], przykład 4.3 zastosowano zbrojenie rozdzielcze $\Phi 6$ co 24 cm, górą i dołem.
Na długości $b_{eff} = 185 \,cm$, jest $(185/24-1)= \approx 6$ prętów $\Phi 6$ w jednej warstwie. W dwóch warstwach jest 12 prętów $\Phi 6$, o przekroju
$A_{su}= 12 \cdot \pi\cdot 0,6^2/4 = 3,393 \, cm^2$.
Zbrojenie płyty (górne przekroju teowego) rozmieszczono przy górnej i dolnej powierzchni płyty, czyli średnie otulenie osiowe
$a_u=80/2 =40 \, mm$
wykonano ze stali AI – $f_{yd}^{’} = 210 \, MPa$
($\ref{53}) \to$$m_{su}=\cfrac{3,4}{449,42} \cdot (1-40/357) = 0,0067$
($\ref{56}) \to$ zredukowane obciążenie przez zbrojenie górne konstrukcyjne
$m_{Ed}^*= 0,0328 – 0,0067= 0,0261 < 0,23$,
gdzie $m_{ult}=0,23$ ($\ref {17}$)
$\to$ przekrój nie musi być dozbrajany górą.
$(\ref{6}) \to $ wysokość strefy ściskanej
$ \xi= \begin {cases}
119/99 \cdot (1 – \sqrt{1- 594/289 \cdot 0,0261}) = 0,0327, & \text{ MN }\\
1 / 0,8 \cdot (1 – \sqrt{1- 2 \cdot 0,0274}) = 0,0331, & \text{ MU }\\
\end{cases}$
$(\ref{13}) \to$ efektywne pole betonu ściskanego
$ a_{cx}= \begin {cases}
17/21\cdot 0,0327 = 0,02646 ,& \text{ MN}\\
0,8 \cdot 0,0331= 0,02645 ,& \text{ MU}\\
\end{cases}$
$(\ref{14}) \to$ sprowadzone dostali pole betonu
$ $ A_{cx→sw} =\begin {cases}
0,02646 \cdot 269,65=7,136 \, cm^2 ,& \text{ MN}\\
0,02645 \cdot 269,65=7,133 \, cm^2 ,& \text{ MU}\\
\end{cases}$
$(\ref{60}) \to$ $A_{sl}= 3,39 + 7,14 = 10,52 \, cm^2$
Przyjęto: $5 \Phi 18$, $A_s = 5 \cdot 2,545 = 12,72 \, cm^2 $
Stopień zbrojenia
$\sum A_s = A_{sl}+A_{su}= 12,72 + 3,39= 16,11 \, cm^2$
$A_c=b\cdot h= 25\cdot 40= 1000 \, cm^2$
$\rho_s= 16,11/1000= 1,61$ % w stosunku do pola przekroju żebra
Sprawdzenia konstrukcyjne
Wykonać analogicznie do przykładu Z-1
Przykład Z- 5 [Przekrój rzeczywiście teowy ze zbrojeniem górnym]
Wyznaczyć wymagane zbrojenie belki teowej z przykładu Z-4 dla zwiększonego obciążenia przekroju
$M_{Ed}=$ 750 kNm,
W pierwszym kroku założono , że przekrój jest pozornie teowy, czyli, że:
szerokości belki $ b= b_{eff} = 1850 \, mm$
czynnik normujący moment %\overline M =3369,3 \, kNm$ (wyznaczono w przykładzie Z-4), czyli:
$(\ref{3}^1) \to $ unormowany moment zginający $m_{Ed} = \cfrac{750}{3369,3} =$ 0,223 < 0,23,
gdzie $ (\ref{17}) \to $ $m_{ult}=0,23$ moment graniczny dla betonu zwykłego BZ
$\to$ nie trzeba dozbrajać betonu w strefie ściskanej i stosować zbrojenia górnego
Czy przekrój jest pozornie teowy
$(\ref{6}) \to $ względna wysokość strefy ściskanej
$ \xi= \begin {cases}
119/99 \cdot (1 – \sqrt{1- 594/289 \cdot 0,223})= 0,3168, & \text{ MN }\\
1 / 0,8 \cdot (1 – \sqrt{1- 2 \cdot 0,223})=0,3190, & \text{ MU }\\
\end{cases}$
$(\ref{6}) \to $ wysokość strefy ściskanej
$ x = \xi \cdot d \begin {cases}
0,317 \cdot 357= 113,1 \, mm , & \text{ MN }\\
0,319 \cdot 357 = 113,9 \, mm& \text{ MU }\\
\end{cases}$
Ponieważ :
$x = (113,1) 113,9 > h_f = 80 \, mm$
$\to$ przekrój jest rzeczywiście teowy
Wymiarowanie przekroju rzeczywiście teowego
($\ref{3}^3) \to $moment normujący dla przekroju rzeczywiście teowego
$\overline M = 0,25 \cdot 0,357^2 \cdot 14,29 \cdot 10^3=455,31 \, kNm$,
($\ref{3}^1) \to $ unormowany moment zginający $m_{Ed} = \cfrac{750}{ 455,18} =$ 1,6472
($\ref{5}^1) \to $ pole betonu przekroju rzeczywiście teowego (pole środnika)
$A_{cw}= d\cdot b_w= 35,7 \cdot 25= 892,5 \, cm^2$
($\ref{12}) \to$ pole betonu sprowadzone do stali
pasa
$A_{c→su}= 892,5 \cdot 14,29/210 = 60,73\, cm^2$
środnika
$A_{c→sl}= 892,5 \cdot 14,29/350 = 36,44\, cm^2$
($\ref{53}) \to$ nośność zbrojenia górnego konstrukcyjnego
$m_{su}^{constr}=3,39/60,73 \cdot (1-40/357) = 0,0496$
($\ref{76}) \to $ nośność skrzydeł pasa przekroju
$ χ_f = \cfrac{90}{357}=0,224$
$m_{Rd,cf} = ( 1850/250 – 1 ) \cdot 0,224\cdot ( 1– 0,224/2 )=1,2735 $
($\ref{77}) \to $ zredukowane obciążenie przekroju teowego
$m_{Ed}^* = 1,6472 – 0,0496 – 1,2735= 0,324 > 0,23$
$\to$ potrzebne dodatkowe zbrojenie górne
($\ref{57}) \to$
$\Delta m= 0,324 – 0,23 = 0,094$
($\ref{58}) \to$ dodatkowe zbrojenie górne – stal AIII
$A_{su}^{add} = \cfrac{0,095}{1-40/357} \cdot 36,44 = 3,86 \, cm^2$
Przyjęto 4 \Phi 12 : $A_s= 4\cdot \pi \cdot 1,2/4= 4,524 \, cm^2$
Sumaryczne pole przekroju zbrojenia górnego sprowadzone so stali zbrojenia dolnego
$A_{su} = 4,524 + 3,39\cdot 210/350 = 6,56 \, cm^2$
($\ref{53}) \to$ nośność zbrojenia górnego całkowitego
$m_{su}= 6,55/36,44 \cdot (1-40/357) = 0,1598$
($\ref{77}) \to $ zredukowane obciążenie przekroju teowego
$m_{Ed}^* = 1,6472 – 0,1598 – 1,2730= 0,2139 < 0,23$
$(\ref{6}) \to $ względna wysokość strefy ściskanej
$ \xi= \begin {cases}
119/99 \cdot (1 – \sqrt{1- 594/289 \cdot 0,2139})= 0,302, & \text{ MN }\\
1 / 0,8 \cdot (1 – \sqrt{1- 2 \cdot 0,2139})=0,304, & \text{ MU }\\
\end{cases}$
$(\ref{13}) \to$ efektywne pole betonu ściskanego
$ a_{cx}= \begin {cases}
17/21\cdot 0,302 = 0,2447,& \text{ MN}\\
0,8 \cdot 0,304= 0,2436 ,& \text{ MU}\\
\end{cases}$
$(\ref{14}) \to$ pole betonu ściskanego sprowadzone do stali zbrojenia dolnego
$ a_{cx→sl}= \begin {cases}
0,2447 \cdot 36,44 =8,915,& \text{ MN}\\
0,2436 \cdot 36,44= 8,875 ,& \text{ MU}\\
\end{cases}$
($\ref{78}) \to $ pola skrzydeł pasa sprowadzone do stali zbrojenia dolnego
$A_{cf→sl} = ( 185 – 25) \cdot 8\cdot \cfrac{14,29}{350}= 0, 523 \, cm^2 $
$(\ref{77}) \to$ pole zbrojenia dolnego – rozciąganego
$ A_{sl}= \begin {cases}
6,560 + 0,523 +8,915 = 16,0 & \text{ MN}\\
6,560+0,523+ 8,875 = 16,0 ,& \text{ MU}\\
\end{cases}$
Przyjęto: $7 \Phi 18$, $A_s = 5 \cdot 2,545 = 17, 82 \, cm^2 $
ułożone w dwóch warstwach 4+3 pręty
Stopień zbrojenia
$\sum A_s = A_{sl}+A_{su}= 17,82 + 6,56 = 24,4 \, cm^2$
$A_c=b\cdot h= 25\cdot 40= 892,5 \, cm^2$
$A_cl=b\cdot d= 25\cdot 35,7= 1000 \, cm^2$
$\rho_l= 17,82/892,5= 2,00 $ % zbrojenie dolne stosunku do efektywnego pola przekroju żebra
$\rho_c= 24,4/1000= 2,44$ % zbrojenie całkowite stosunku do pola przekroju żebra
Sprawdzenia konstrukcyjne
Wykonać analogicznie do przykładu Z-1
Przykład Z-6 [Przekrój kołowy]
Przykład tab.3,wrs 4 z artykułu [17].
Wyznaczyć zbrojenie przekroju kołowego
Dane i wynik [17]
Beton C40 wg China GB 50010: $f_{ck}= 26,8 \, MPa$, $ f_{cd}= 19,1 \, MPa$
Stal HRB 400 wg China GB 50010: $ f_{yd}= 360\, MPa$
Przekrój kołowy o promieniu $R= 250 \, mm$
otulenie osiowe prętów $a= 37, 5 \, mm$
rozmieszczenie prętów -zbrojeniowych równomiernie na obwodzie w ilości 12 sztuk ( kat miedzy prętami $30^o$)..
Przekrój poddany czystemu zginaniu
$M_{Ed}= 562,5 \, kNm$
przekrój betonu $A_c =\pi \cdot25^2= 1 963,5 \, cm^2$
W pracy [18] otrzymano (wg metody 1 z tej pracy na podstawie numerycznego całkowania rozkładu MN naprężenia w przekroju):
$A_s=96,88 \, cm^2$
($\ref{19}) \to$ stopień zbrojenia
geometryczny $ \rho_A=96,88 / 1963,5 =4,93 $ %
fizyczny $\rho_F= 4,93/100 \cdot 360/19,1 = 0,93$
Rozwiązanie nieliniowego układu równań
($\ref{92}$)+($\ref{94}$) programem Excel.
Uzyskano obraz pokazany na rys.
dalej w przebudowie – REMANENT
Przykład Z-7 [Beton wysokiej wytrzymałości BWW]
Przykłady Z-8 [Testy Benchmark arkusza LCżelbet]
Arkusz LCżelbet przetestowano na wielu przykładach, w tym publikowanych w literaturze:
- belka podwójnie zbrojona – przykład wg pracy [19] Pokazano, że stosowanie arkusza pozwala na większe o ok 17%
- nośność przekroju zbrojonego symetrycznie – przykład wg pracy [19], przykład 6.3 Uzyskano nośność 12% większą
- nośność przekroju zbrojonego symetrycznie – przykład wg pracy [1], przykład Z-13.1 Uzyskano nośność o 17% większą
- zginanie ukośne względem dwóch osi przypadek CT2 przykład wg pracy [1], przykład Z-3.6 Pokazano , że w przykładzie oryginalnym nośność zawyżono ponad dwukrotnie.
- nośność przekroju zginanego ukośnie z betonu z betonu wysokiej wytrzymałości – wg pracy [19], przykład 6.18 Pokazano, że w przykładzie oryginalnym zawyżono nośność – konieczne było boczne, uzupełniające zbrojenie rozciągane 1Ø
Powyższe testy arkusza LCŻelbet należy traktować jako testy Benchmark, obejmujące wszystkie przypadki zidentyfikowane w rozdziale Przypadki wytrzymałościowe pręta żelbetowego , które mogą wystąpić w belkach-słupach. Należy przy tym wskazać, że arkusz jest przeznaczony dla profesjonalnych inżynierów, bowiem wymaga podania danych: [ wymiary przekroju+ zbrojenie dolne+ zbrojenie górne + zbrojenie boczne ] z pewnego obszaru dla którego można znaleźć równowagę odkształceń i naprężenia. Taka równowaga nie wystąpi na przykład dla przekroju ze zbyt małym zbrojeniem, które dla danych sił wymusza nadmierne odkształcenia włókien betonu. Dopiero po znalezieniu pierwszego rozwiązania dopuszczalnego można przystąpić do optymalizacji zbrojenia. Oszczędności z użycia kalkulatora w stosunku dla klasycznych metod ręcznych lub tablicowych – mogą być nawet dwukrotne.
Literatura
- PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- Pyrak S. (2012). Konstrukcje z betonu (VII, Tom 5). WSiP
- Knauff M., Obliczanie konstrukcji żelbetowych według Eurokodu 2, PWN, Warswa 2011
- Starosolski W. (2013), Konstrukcje żelbetowe według Eurokodu 2 i norm związanych, Tom 1, Wydawnictwo Naukowe PWN, Warszawa
- MPA The Concrete Centre. (2016). Bending and Shear in Beams. Lecture 3. EC2 Webinar – Autumn, [https://www.concretecentre.com/TCC/media/TCCMediaLibrary/Presentations/Lecture-5-Slabs-and-Flat-Slabs-PHG-N-Rev13-15-Oct-16.pdf ]
- Wight, J. K., & MacGregor, J. G. (2012). Reinforced concrete: mechanics and design (6th ed). Pearson Prentice Hall
- Institution of Structural Engineers, The Institution of Civil Engineers, Manual for the design of reinforced concrete building structures to EC2, Institution of Structural Engineers, May 2022
- Gąćkowski R. (2013), Tablice i algorytmy do wymiarowania zginanych elementów żelbetowych, Verlag Dashöfer
- Knauff M., Obliczanie konstrukcji żelbetowych według Eurokodu 2, PWN, Warszawa 2011
- Di Laora R, , Galasso, C, Mylonakis G., Cosenza, E, (2020), A simple method for N-M interaction diagrams of circular reinforced concrete cross sections, Structural Concrete, 21 (1) pp. 48-55
- Knauff M., Golubińska A., Knyziak P. (2014). Tablice i wzory do projektowania konstrukcji żelbetowych z przykładami obliczeń, Wydanie drugie. PWN
- ACI 318-14 (2014), Building Code Requirements for Structural Concret
- MPA, The Concrete Centre, (2016), Columns, Lecture 8, EC2 Webinar – Autumn, [ Lecture-8-Columns-jb-9-Nov-16.pdf ]
- Di Ludovico M., Lignola G. P., Prota A., Cosenza E. (2010). Nonlinear Analysis of Cross Sections under Axial Load and Biaxial Bending. ACI Structural Journal, 107(4), 390–399
- PN-EN 1998-1:2005Eurokod 8: Projektowanie konstrukcji poddanych oddziaływaniom sejsmicznym, Część 1: Reguły ogólne, oddziaływania sejsmiczne i reguły dla budynków
- Bresler B. (1960), Design Criteria for Reinforced Concrete Columns Under Axial Load and Biaxial Loading. Journal of the American Concrete Institute, 57(5), 481–490
- Kaicheng Y.,Donghua Z., Chao S., Shuwei., JnCh. Reinforcement Calculation of Circular and Annular Cross Section, Technical Gazette 27, 6(2020), 2008-2015
- Kaicheng Y.,Donghua Z., Chao S., Shuwei J.Ch., Reinforcement Calculation of Circular and Annular Cross Section, Technical Gazette 27, 6(2020), 2008-2015
- Knauff M. i in.. (2006), Podstawy projektowania konstrukcji żelbetowych i sprężonych: według Eurokodu 2. Dolnośląskie Wydawnictwo Edukacyjne
________________________________