Wielokondygnacyjne budynki żelbetowe wykonywane są jako średniowysokie (rys.1), ale coraz częściej wypierają konstrukcję stalową w budynkach wysokich i wysokościowcach (np. rys.2). Szczególnie w wysokich budynkach istotna jest stateczność przestrzenna, a przede wszystkim skrętna, to znaczy stateczność kształtu w planie.
Spis treści
Wprowadzenie
Przykłady ukształtowania elementów budynku w celu zachowania stateczności w planie, pokazano na rys. 3, z których 3 f,g,i,j,k, l są rozwiązaniami błędnymi ze warunku stateczności przestrzennej budynku.
Rys.1 Model konstrukcji żelbetowego budynku
(Chodor, 2011)
Rys.2.Wieżowiec żelbetowy Comopolitan Twarda w Warszawie, (44 piętra i 160 m)
(Wikipedia, 2016)
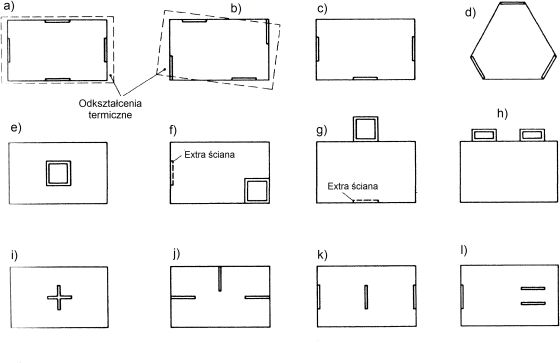
Rys.3 Kształtowanie elementów stateczności w planie budynku: a) ściany zewnętrzne – dobrze, b) możliwe skręcenia skrępowane budynku, c) konstrukcyjnie możliwe, d) plan wielokątny – dobrze, e) dobrze, jeśli trzon jest wystraczająco sztywny, f), g) źle , ponieważ extra ściana jest umieszczone niesymetrycznie, h)możliwe, ale wymaga sprawdzenia, i), j) żale – brak sztywności na skręcanie, k) mała sztywność przestrzenna w kierunku podłużnym, l) nie zalecane ze względu na nierównoimienną sztywność na skręcanie
(Bachmann, Steinle, 2011)
Wymuszenia utraty stateczności budynku
Oddziaływanie wiatru
Oddziaływanie wiatru stanowi podstawowe obciążenie zmienne budynków wysokich, przy czym istotna jest nie tylko zmienność po wysokości, ale również niesymetryczne obciążenia w planie, prowadzące do dynamicznego skręcania budynku.
Rozkład wiatru po wysokości można przyjmować zgodnie z rys. 4. Rozróżnia się dwa przypadki zależnie od stosunku wysokości $h$ do jego szerokości $b$. W każdym z nich – przy podstawie budynku do wysokości równej szerokości b przyjmuje się stałe oddziaływanie równe obciążeniu na wysokości b. W pierwszym przypadku na pozostałej powyżej, a w drugim przypadku tylko przy wierzchołku na wysokości równej $b$ przyjmuje się przyjmuje się stałe oddziaływanie równe obciążeniu na wysokości h. W odcinku pośrednim dla drugiego przypadku obciążenia stopniuje się plasterkami o grubości $h_j$. Wiatr działa na wszystkie ściany jednocześnie, tak jak pokazano na rys. 5 Dla budynku wysokiego zaleca się przyjmować współczynnik ciśnienia $C_{pe,10}$ na powierzchnię referencyjna 10 m2, a nie $C_{pe,1}$
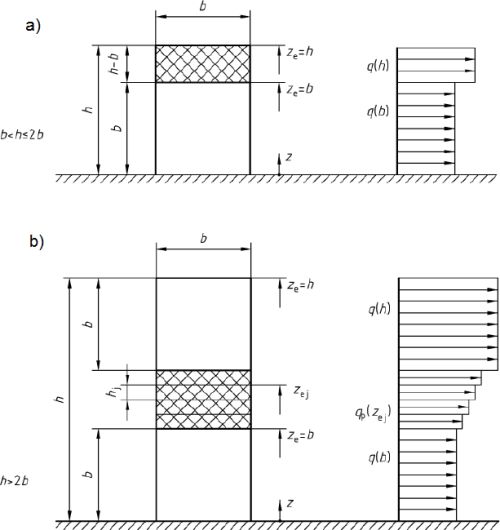
Rys.4 Oddziaływanie wiatru po wysokości budynku wysokiego: a) budynek o wysokosci h:$b<h \le 2b$, b)$h \ge 2b$ (b- szerokość ściany nawietrznej) (Schroeter, 2005) wg (PN-EN 1991-1-4, 2008)
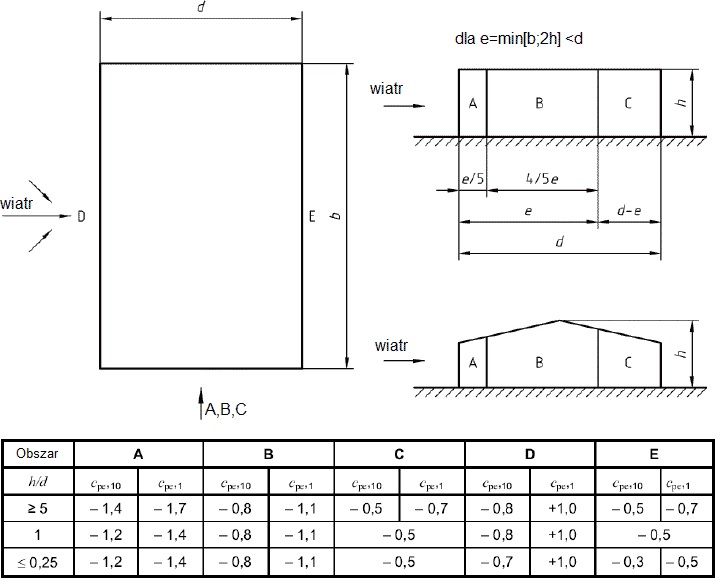
Rys.5 Oddziaływanie wiatru w planie budynku
(Schroeter, 2005) wg (PN-EN 1991-1-4, 2008)
Oddziaływania temperatury
W przypadku budynków wysokich oddziaływania temperatury są równie ważne jak działanie wiatru. Mogą one bowiem spowodować znaczne wychylenia wierzchołka budynku, co istotnie zwiększa siły w budynku liczone z uwzględnieniem efektu $P-\Delta$, a także powoduje trudności w geodezyjnym tyczeniu pionowości budynku. Zmiany termiczne następują nie tylko wraz ze zmianami pór roku, ale częściej wraz ze zmianami pór dnia i nasłonecznienia poszczególnych ścian budynku. Zmiany termiczne mogą również prowadzić do skręcania budynku, co pokazano na rys. 3b.
Dla elementów chronionych przed zmianami temperatury, jak to ma miejsce w przypadku stropów i słupów wewnętrznych w termicznie izolowanych budynkach, średnie wahania temperatur max może być w uproszczeniu przyjęty:
$\Delta T = \pm 7,5 deg$.
Specjalną uwagę należy zwrócić na działanie temperatury na zewnętrzne elementy (np płyty parkingów). Współczynnik rozszerzalności termicznej dla zwykłych konstrukcji żelbetowych mozna przyjmować o wartości
$\alpha_t = 0,8 \cdot 10^{-5} \frac {1}{deg} $.
Wpływy termiczne należy uwzględniać w sposób pokazany w normie (PN-EN 1991-1-5, 2005).
Obciążenia od imperfekcji
Obciążenia od imperfekcji, wywołane głównie niedoskonałościami systemowymi (przechyłowymi) są równie ważne jak oddziaływanie wiatru i temperatury i nie może być pominięte w analizie budynków wysokich, w tym żelbetowych.
Rys.6. Imperfekcje przechyłowe budynków wysokich
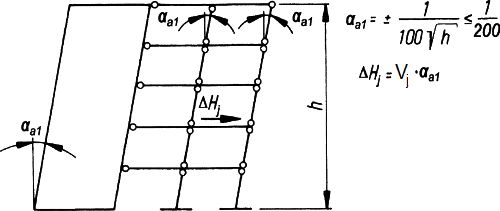
Na rys. 6 pokazano istotę problemu imperfekcji przechyłowych. Na skutek przechyłu budynku o kąt $\alpha_{a1}$ , który dla wysokich budynków należy przyjmować o wartości podstawowej
| $\alpha_1 = \frac{1}{200}$, | (1) |
Współczynnik imperfekcji można zredukować ze względu na liczbę słupów n wbudowanych na jednej kondygnacji
| $ \alpha_n= \sqrt{\frac{n+1}{2n}}$, | (2) |
Ostatecznie
| $\Delta H_j=\alpha_1 \cdot \alpha_n \cdot V_j$. | (3) |
Analogicznie jak w konstrukcjach stalowych (PN-EN 1993-1-1+A1, 2006) $V_j$ oznacza dowolne obciążenie pionowe, zarówno stałe jak zmienne, skupione jak i rozłożone. Taki sposób analizy nosi nazwę metody A ( metoda imperfekcyjna analizy konstrukcji) i został zdefiniowany w pracy .
Analiza stateczności budynku
Założenia
Analizę stateczności budynku należy prowadzić w modelu 3D konstrukcji, w którym należy prawidłowo zamodelować słupy oraz trzony usztywniające oraz ściany nośne. Zaleca się, by płyty stropowe modelować jako przepony (jako poziome tarcze: sztywne zgięciowo i odkształcalne osiowo), po to by zbędnie nie rozbudowywać rozmiaru zadania, co może prowadzić do utraty istotnych cech obiektu. Płyty stropowe zwykle analizuje się odrębnie już po zaprojektowaniu budynku w ramach rutynowych i mniej odpowiedzialnych zadań. Zleca się też, by trzony windowe, szachty instalacyjne i klatki schodowe wprowadzić do modelu jako uogólnione pręty (cienkościenne o przekroju zamkniętym)
Elementy prętowe: słupy, podciągi, trzony powinny mieć określone charakterystyki geometryczne:
- giętne i osiowe : $A$, $EI_y$, $EI_z$
- ścinania: $GA_{sy}$, $GA_{sz}$
- skręcania swobodnego: Sr. Venant $G I_T$ i Bredta $G I_b$
- skręcania skrępowanego (sztywność giętno skrętna) $EI_{\omega}$
$A_{sy}$ i $A_{sz}$ są polami przekroju ścinania: $\cfrac{1}{A_s}=\int \limits_A (\frac{\tau}{Q})^2dA$ i dla przekroju prostotkąnego wynosi $A_s=\frac{5}{6}A$ (całkowite pole przekroju).
Zagadnienie przekrojów cienkościennych omówiono w artykule Pręty cienkościenne.
Sztywność budynku i elementów
Konstrukcja nośna budynku jest złożona ze słupów, ścian i trzonów o zamkniętym , otwartym lub quasi-zamkniętym konturze, które są różnie ulokowane na planie budynku, np tak jak pokazano na rys. 7.
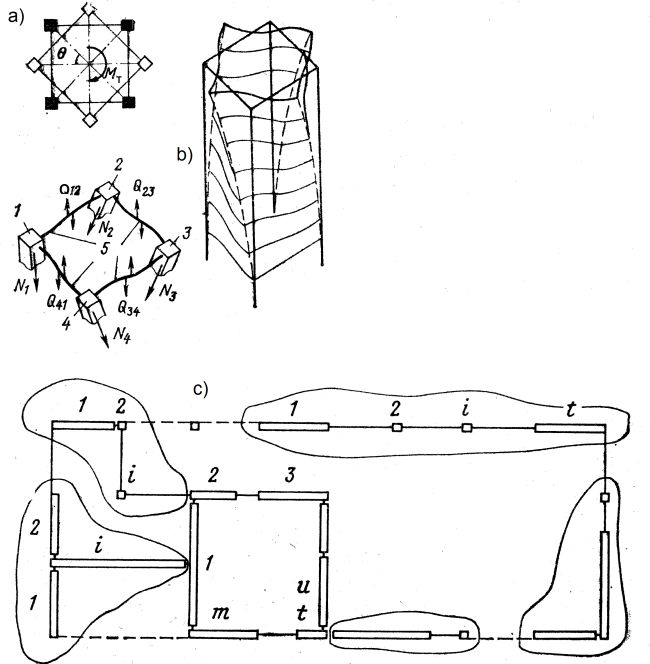
Rys.7. Układ elementów nośnych w skręcanym budynku: a)skręcanie momentem $M_T$ powoduje skręcenie o kąt $\Theta$, b) odkształcony budynek, c) plan budynku złożony z m – pionowych elementów (słupów i ścian), które układają się w kontury zamknięte lub otwarte
(Drozdov, 1977)
Ponieważ zachodzi pełna analogia pomiędzy skręcaniem pręta cienkościennego Vlasova (uogólnionego pręta) ze zginaniem pręta złożonego i pracą układu nośnego budynku (rys.7), co szczegółów pokazał (Drozdov, 1977), więc zastosujemy metodę analityczno-numeryczną, polegającą na tym, że będziemy prowadzić numeryczną analizę przestrzennego szkieletu budynku, złożonego z prętów i sztywnych tarcz stropowych. trzony zastąpimy uogólnionymi prętami, a ściany stężonymi ramami.
Rama zastępcza dla wyodrębnionej ściany
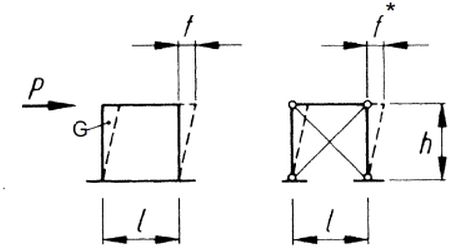
Sposób doboru sztywności zastępczej ramy przedstawiono na rys. 8.
Rys. 8 . Zastępcza rama dla wyodrębnionej ściany
Ramę zastępczą dobieramy w rozwiązaniu zadania zstępczego z warunku równości ugięć sprężystych pod poziomym obciążeniem P (dowolnym) ściany $f$ i ramy $f*$.
Wstępnie można przyjąć, że $ f=\cfrac{P\cdot h}{G \cdot l \cdot t}$,
gdzie: t – grubość ściany, G- moduł Kirchoffa żelbetu.
Ponieważ w zastępczej ramie wystąpi moduł Younga E, więc potrzebna będzie tylko znajomość zależności $E=2,4 \cdot G$.
Dobór prętów ramy zastępczej dokonać w analizach numerycznych liniowo-sprężystych I rzędu bez uwzględnienia zjawisk niestateczności.
Rama zastępcza dla ściany z otworami
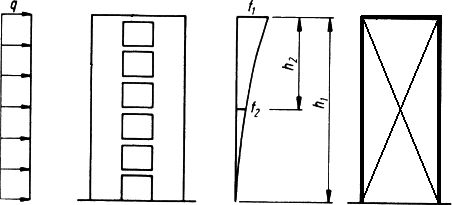
Dobór zastępczej ramy dla ściany z otworami polega na numerycznym rozwiązaniu zadania pomocniczego: dobrać pręty ramy zastępczej tak, by pod obciążeniem poziomym $q$ przemieszczenia ramy były zgodne z przemieszczeniami traczy-ściany z otworami (rys.9). Wymaga się by zgodność dotyczyła przemieszczeń $f_1$ i $f_2$ na dwóch poziomach, na przykład dla $h_1=h$ i $h_2= h/2$. Ze względu na powszechną dostępność programów obliczeniowych oraz wiele zmiennych parametrów, które można kontrolować – nie podaje się wzorów analitycznych.
Rys. 9 . Zastępcza rama dla ściany z otworami
Pręt zastępczy dla trzonu usztywniającego
Na rys. 1o przedstawiono trzy przypadki najczęściej spotykanych trzonów usztywniających budynek.
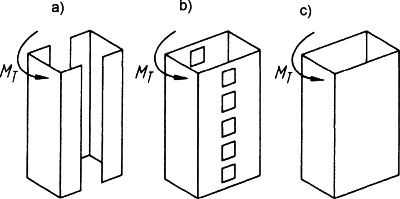
Rys.10 Trzony usztywniające: a) otwarty przekrój (dwa układy C), b) przekrój quasi-zamknięty ( z otworami), c) przekrój zamknięty
Sztywność na skręcanie wyznacza się dla przypadku obciążenia momentem skręcającym $M_T$. Najmniejszą sztywność ma przekrój otwarty rys. 10a, a największą zamknięty rys. 10c. Charakterystyki trzonu o przekroju zamkniętym można obliczyć wg zależności podanych w artykule
Skręcanie pręta o przekroju zamkniętym,
a o przekroju otwartym w artykułach:
Skręcanie swobodne pręta cienkościennego,
Skręcanie nieswobodne (skrępowane),
Współrzędna wycinkowa przekroju pręta cienkościennego.
Dla trzonu 10c, o polu zamkniętym wewnątrz linii środkowych $\Omega$ oraz długościach i grubościach ścianek $ l_i$, $t_i$ moment bezwładności czystego skręcania (Bredta) $I_v$ wynosi:
| $I_v= \cfrac {(2\Omega)^2}{\sum \limits_i \frac {l_i}{t_i}}$. | (4) |
W przypadku przekroju quasi-zamkniętego z niektórymi ściankami z otworami, należy oszacować ich grubości zastępcze $t_i^*$, prowadząc procedurę analogiczną do pokazanej na rys. 9, ale zamiast ramy zastępczej wprowadzamy ścianę zastępczą bez otworów.
Natomiast w przypadku przekroju otwartego można pominąć jego sztywność skrętną i każdą ścianę zastąpić ramą zgodnie z rys.8.
Analiza numeryczna i przykłady
Sztywność budynku, w tym jego sztywność skrętna po wprowadzeniu elementów zastępczych jest modelowana w modelu prętowym przestrzennej ramy 3D. Kontury zamknięte utworzone przez ściany w sposób pokazany na rys. 7, stanowią o sztywności przestrzennej, w tym skrętnej budynku. Nie trzeba ich analizować w sposób specjalny (np pokazany w pracy (Drozdov, 1977)), bo wprowadzenie układu ścian lub ram zastępczych (pkt 2.2.1.) do przestrzennego modelu komputerowego 3D jest wystarczające.
Uwaga o stateczności budynków wysokich
Stateczność ogólna budynków wysokich posadowionych na sprężystym podłożu omówiono w artykule Stateczność wysokich budowli. Pokazano, że w zagadnieniu można zdefiniować siłę krytyczną, po przekroczeniu, której system konstrukcyjne jest niestabilny.
Literatura
