Leszek Chodor, 5 stycznia 2019
01-02-2025 rewizja po dużej awarii portalu>
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 47 Czytelników
Płyty żelbetowe są podstawowym elementem konstrukcyjnym i są stosowane na stropy w budynkach mieszkalnych, biurowych, usługowych, użyteczności publicznej i przemysłowych. Układ konstrukcyjny płyty i jej żeber oraz podciągów powinien wynikać z siatki funkcjonalnej słupów, wymogów architektonicznych (np wymagany strop płaski bez żeber), a na końcu z warunku optymalności konstrukcyjnej – prawidłowego doboru sprzężonych parametrów: grubości płyty, wysokości belek i ilości zbrojenia. Wymogi konstrukcyjne dla płyt żelbetowych są analogiczna do wymogów dla belek żelbetowych, opisanych w artykule Belki żelbetowe. W szczególności dotyczy to obliczania zbrojenia głównego (podłużnego),, kotwienia prętów, pełzania betonu, zbrojenia minimalnego i maksymalnego.
Współcześnie ważnym typem płyt żelbetowych, stosowanym najczęściej dla płyt ułożonych na podłożu odkształcalnym (gruncie) są płyty fibrobetonowe, czyli betonowe zbrojone włóknem rozproszonym. Projektowanie płyt z fibrobetonu jest odmienne od płyt żelbetowych zbrojonych prętami stalowymi i jest opisane w Płyty ze zbrojeniem rozproszonym. Od lat tracą na znaczeniu żelbetowe konstrukcje monolityczne na rzecz konstrukcji prefabrykowanych. W zakresie budowy płyt żelbetowych i stropów w budownictwie uprzemysłowionym ważne miejsce zajmują „półprefabrykowane” płyty zespolone typu Filigran, a także płyty w pełni prefabrykowane najczęściej strunobetonowe. W budowie budynków małych stosuje się powszechnie stropy gęstożebrowe.
Konstrukcja płyty
Rozpiętość obliczeniowa płyty
Długość płyty rozpiętej nad pomieszczeniem w świetle murów $l_ś$ można wyznaczyć w sposób przyjęty dla belek żelbetowych i pokazany na rys. 1 artykułu „Belki żelbetowe-Kształtowanie„. W przypadku oparcia stropu na ścianach o grubości $t_l$ i $t_r$ z lewej i prawej strony odpowiednio (rys.1 niniejszego artykułu) rozpiętość obliczeniową płyty $l_d$ wylicza się z zależności:
$$\begin{equation} l_d=l_ś+ a_l+a_r \label{1} \end{equation}$$
gdzie: $a_l=1/2 \cdot min (h \, , t_l)$, $a_r=1/2 \cdot min (h \, , t_r )$
Układ zbrojenia płyty
W zależności od układu zbrojenia wyróżnia się płyty jedno- i dwu-kierunkowo (krzyżowo) zbrojone. Układ zbrojenia dobiera się w zależności od kształtu płyty. Dla płyty prostokątnej o bokach $l_x \times l_y$ podpartej na obwodzie, przyjmuje się:
1) przy $l_x \ge 2\cdot l_y$ – zbrojenie jednokierunkowe równoległe do boku krótszego $l_y$ – przykład na rys. 1
2) przy $l_x \approx l_y$ – zbrojenie krzyżowe, to znaczy zbrojenie nośne układane jest w obu prostopadłych kierunkach,
Na rys.1 zastosowano mieszany system zobrazowania prętów zbrojeniowych: 1) za pomocą kodów kształtów i jednocześnie 2) za pomocą pokazania figur zbrojeniowych. W przykładzie nie dostosowano się więc do podstawowej zasady rysunkowej – NIE powtarzania tych samych informacji. W praktyce NIE należy stosować takiego nadmiarowego systemu podawania informacji na rysunkach, a obowiązkowo stosować zalecany w Europie system kodów kształtów., którego zaletą jest zwiększenie czytelności rysunku żelbetu, a także typizacji prętów zbrojeniowych. Więcej informacji o systemie kodów kształtów można znaleźć w artykule Standard rysunku warsztatowego konstrukcji żelbetowych. „Wydawanie” figur zbrojeniowych dopuszcza się jedynie w przypadku braku kodu kształtu dla pręta – w tym przypadku jednak mamy najczęściej z błędem projektowo-wykonawczym i należy zastanowić się, czy nie zastosowano zbyt złożonej figury zbrojeniowej i czy nie można jej zastąpić złożeniem prostych prętów.
Rozpiętość miarodajna płyty
Zależność pomiędzy strzałką ugięcia płyty $f$ i jej rozpiętością $l$ można zapisać w postaci:
$$\begin{equation} f= \alpha \cdot l^4 \label{2} \end{equation}$$
gdzie współczynnik $\alpha$ zależy od grubości i obciążenia płyty. Dla płyt wykonanych z tego samego materiału, o takiej samej grubości i tak samo obciążonych można przyjąć, że współczynnik $\alpha = const$. Korzystając z zależności $( \ref{2})$ dla dwóch płyt „1” i „0” o różnych warunkach brzegowych lub wymiarach w planie , otrzymujemy:
$$\begin{equation} l_{ef,1}=l_{ef,0} \cdot \left( \cfrac{f_1}{f_0} \right)^{1/4} \label{3} \end{equation}$$
Długość efektywną płyty wyznaczymy z ogólnej zależności:
$$\begin{equation} l_{ef}= s \cdot l_{min} \label{4} \end{equation}$$
gdzie $l_{min}$ jest krótszym bokiem prostokątnego pola płyty, a $s$ jest współczynnikiem długości efektywnej, który poniżej został wyznaczony dla najczęściej spotykanych schematów płyt
Płyta swobodnie podparta na obwodzie
W przypadku płyty swobodnie (przegubowo podpartej na obwodzie za wzorcowa płytę „0” przyjmiemy płytę prostokątną o bardzo długim boku $l_x$ w stosunku do $l_y$, to znaczy przy stosunku boków $s=l_x/l_y=∞$ . Dla takiej płyty długością efektywną $l_{eff}$ jest krótszy bok $l_{min}$:
$$\begin{equation} l_{min}= min \{l_x\quad , l_y \} \label{5} \end{equation}$$
to znaczy współczynnik długości efektywnej $s=1$.
Dla płyt o innych stosunkach boków współczynniki długości efektywnej $s<1$ zestawiono w tab.1. Dla płyty kwadratowej współczynnik ten wynosi 0,712, a dla płyt o stosunku boków większym od 3 jest praktycznie równy 1,0. Wartości w tab.1 wyliczono na podstawie zależności $(\ref{3})$ poprzez wielokrotne rozwiązywanie płyt o różnych stosunkach boków.
Tab. 1 Współczynnik długości efektywnej płyty podpartej przegubowo na obwodzie (rys.2)![]()
Płyta oparta punktowo w narożach
Dla płyt opartych punktowo w narożach współczynnik długości efektywnej $s$ zestawiono w tab.2.
Tab. 2 Współczynnik długości efektywnej płyty podpartej punktowo w narożach![]()
Współczynnik „s” w tab.2 jest odniesiony do bardzo długiej płyty prostokątnej podpartej przegubowo na obwodzie (tab.1 ostatnia kolumna). Dla większych stosunków boków $l_x/l_y > 2$ zaleca się przyjmować $s=l_x/l_y$, czyli długością miarodajną płyty jest długość większego boku. Oznacza to, że taki przypadek dobrze będzie aproksymowany projektem belki o długości równej odległości między słupami $l_x$. Strefa podporowa wymaga analizy lokalnej ze szczególnym uwzględnieniem ścinania przez przebicie.
Płyta wieloprzęsłowa
Płyta wieloprzęsłowa podparta punktowo na słupach w węzłach jest często występującym przypadkiem. Dla płyt wieloprzęsłowych współczynnik długości efektywnej zestawiono w tab.3. Współczynnik „s” w tab. 3 jest również odniesiony do bardzo długiej płyty prostokątnej podpartej przegubowo na obwodzie (tab.1 ostatnia kolumna)
Przykład dla odczytania współczynników długości efektywnej z tab.3 podano na rys. 3.
Tab. 3 Współczynnik długości efektywnej płyty wieloprzęsłowej
Dla płyt wspornikowych długość $l_{ef} $ można przyjąć jako podwojony wysięg, czyli $s=2$.
Grubość płyty
Grubość płyty h przyjmuje się wstępnie na podstawie jej długości efektywnej $(\ref{4})$ jako część jej długości. Zaleca się
$$\begin{equation} h \approx \dfrac{l_{ef}}{41} \label {6} \end{equation}$$
Sprawdzenie tak przyjętej grubości płyty i ewentualnie jej korektę dokonuje się z warunków wytrzymałości dla stanów granicznych: nośności, ugięcia oraz ścinania przy przebiciu.
Minimalna grubość płyty jest konsekwencją technologii wykonania i wynika z warunku zmieszczenia we wnętrzu płyty krzyżującego się zbrojenia górnego i dolnego oraz wymaganego otulenia płyty oraz minimalnej odległości pomiędzy zbrojeniem, wynikającej z warunków ogólnych ( max { $20 \, mm \, ; \, ∅_{max} \, ; \, d_g+5 \, mm$ }) ($∅_{max}$ – maksymalna średnica pręta, $d_g$ – średnica największego ziarna kruszywa).
Na przykład dla zbrojenia nośnego górą i dołem ∅x=16 mm i rozdzielczego ∅y=10 mm, otulenia c=30 mm, kruszywa 0/8 – minimalna grubość płyty wynosiłaby $h=2 \cdot (16+10+30)+\max \{ 20 \,;\, 16 \, ; \, 8+5 \} = 132 \,mm$.
Minimalny i maksymalny stopień zbrojenia
Minimalny stopień zbrojenia dotyczy wszystkich stref płyty, które nie są stale ściskane. Podobnie jak w belkach zbrojenie minimalne wynika z warunku kruchego pękania betonu lub zarysowania i zostało omówione w artykule. Belki. Minimalne i maksymalne zbrojenie
Siatka podstawowa (minimalna)
Projektowanie zbrojenia płyt rozpoczyna się od doboru sitaki podstawowej, to znaczy takiego zbrojenia prętami o średnicy Φ i rozstawie $s$, które zapewnia warunki konstrukcyjne (minimalnego stopnia zbrojenia) oraz nośności i zarysowania na znacznym obszarze płyty (min 60%), a na pozostałym obszarze (obszarze spiętrzenia naprężeń) płytę należy dozbroić poprzez zagęszczenie zbrojenia lub zmianę średnicy prętów.
Minimalną średnicę pręta zbrojenia płyt monolitycznie zbrojonych przyjmuje się Φ8, a płyt prefabrykowanych ( lub Filigran) Φ6.
Pierwszym krokiem jest ustalenie minimalnej siatki z warunku minimalnego stopnia zbrojenia. Do tego celu sporządzono tab.4, w której podano wytyczne do doboru podstawowej siatki zbrojenia płyty wykonanej z najczęściej stosowanego betonu C30/37 zbrojonego prętami ze stali B500 z warunku minimalnego zbrojenia wymaganego przy kruchym pękaniu betonu. Siatkę podstawową określono przez wymaganą liczbę prętów zbrojenia $N_{min,brittle}$ na 1 m szerokości płyty dla zbrojenia o danej średnicy Φ i polu przekroju pojedynczego pręta $A_{s1}$.
Na podstawie danych z tab 4 można łatwo uzyskać maksymalny rozstaw pretów $s_{max, brittle}$ z zależności
$$\begin{equation} s_{max.brittle}= \cfrac{1}{N_{min, brtittle}-1/L_{plate}} \cdot 10^3 \, [mm] \label{7} \end{equation}$$
gdzie $L_{plate}$ w [m] jest szerokością rozpatrywanego pasa płyty na której należy umieścić wymaganą liczbę prętów $N_{min,brittle}$
Tab.4 Podstawowa siatka zbrojenia płyt o różnej grubości
minimalna liczba prętów z warunku minimalnego stopnia zbrojenia
dla żelbetu C30/37 – B500
Przykładowo dla płyty o grubości $h=180\, mm$ z otuleniem zbrojenia $c_{nom}=35 \,mm$ mamy dla prętów o średnicy $Φ8/10$ (co drugi pręt Φ8 i Φ10):
$d= 180-35-10/2= 140 \,mm$ $\to$ z wiersza tabeli „140” i kolumny ” 8/10″ tab.4 odczytujemy $N_{min,brittle} =3,77 \, szt/m$.
Maksymalny rozstaw prętów na szerokości pasa płyty $L_{plate}= 6, 0 \,m$ $(\ref{7})$ wynosi $s_{max.brittle}= \cfrac{1000}{3,77- 1/6,0}= 277 \, mm$.
Po ułożeniu prętów sprawdzamy łączne pole przekroju prętów o mieszanych średnicach na szerokości pasa płyty $s_{plate}$ i porównujemy z wymaganym zbrojeniem minimalnym $ real\, A_s \ge A_{s,min.b} \cdot s_{plate}$
Należy przy tym zwrócić uwagę na maksymalne rozstawy zbrojenia wymagane ze względów konstrukcyjnych $(\ref{8})$ i $( \ref{9})$.
Zbrojenie z warunku zarysowania sprawdza się podczas procedury doboru zbrojenia na nośność.
Krawędzie swobodne płyty i doprowadzenie zbrojenia do podpory
Zbrojenie krawędzi swobodnych
Znamienny dla płyty jest wymóg zbrojenia krawędzi swobodnych wkładkami U w sposób pokazany na rys.4, oraz dozbrajanie krawędzi z wieńcem w sposób pokazany na rys,.5.
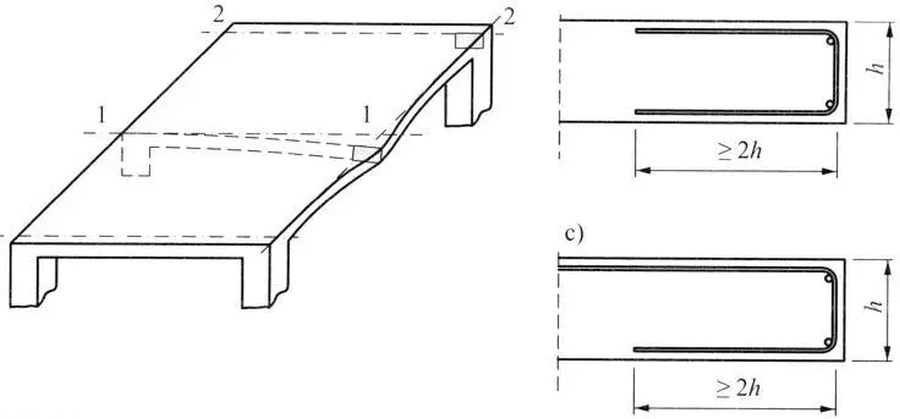
Rys. 4. Płyta żelbetowa. Zbrojenie krawędzi, wg. rys. 22.16 [1]
W przypadku zakończenia brzegu płyty wieńcem, na skutek zmiany sztywności, wystąpi niewielkie skręcanie płyty na długości ok. $0,2 \cdot l_d$. W takim przypadku do żebra należy doprowadzić min 50% przęsłowego zbrojenia i dolnego górnego kotwionego zgodnie z rys. 5.
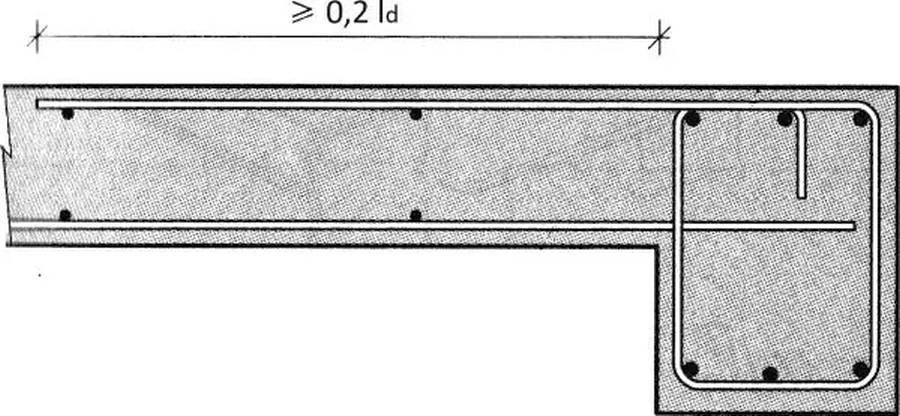
Rys. 5. Zbrojenie wieńca swobodnego brzegu płyty [2]
Wymóg doprowadzania zbrojenia do podpory
W płytach swobodnie podpartych przynajmniej 50% zbrojenia w przęśle należy doprowadzić do podpór i tam zakotwić.
Zbrojenie naroży płyty
Na rys. 6 pokazano mapy zbrojenia płyty kwadratowej opartej na przegubowo obwodzie.
W narożach płyty potrzebne jest zbrojenie zarówno dołem jak i górą. Zasięg strefy wymaganego zbrojenia góra wynosi ok 500 mm przy wymiarach płyty 6275×5675, czyli ok a/10 (a- bok płyty) . Potrzeba tego zbrojenia wynika ze skręcania płyty w narożach.
Na rys. 7 pokazano rozkład płytowych momentów skręcających $m_{41}$
Na skutek skręcania naroży płyty wymagają one dodatkowego zbrojenia. Na rys. 8 przedstawiono zbrojenie tej płyty zaprezentowane w pracy [3] . Z porównania proponowanego zbrojenia i wymaganego – należy stwierdzić, że obszar zbrojenia 8×150=1200 mm jest zbyt duży, a także to, że zbrojenie dodatkowe wymagane jest górą i dołem, a dano tylko dołem. Średnica zbrojenia powinna być ∅10.
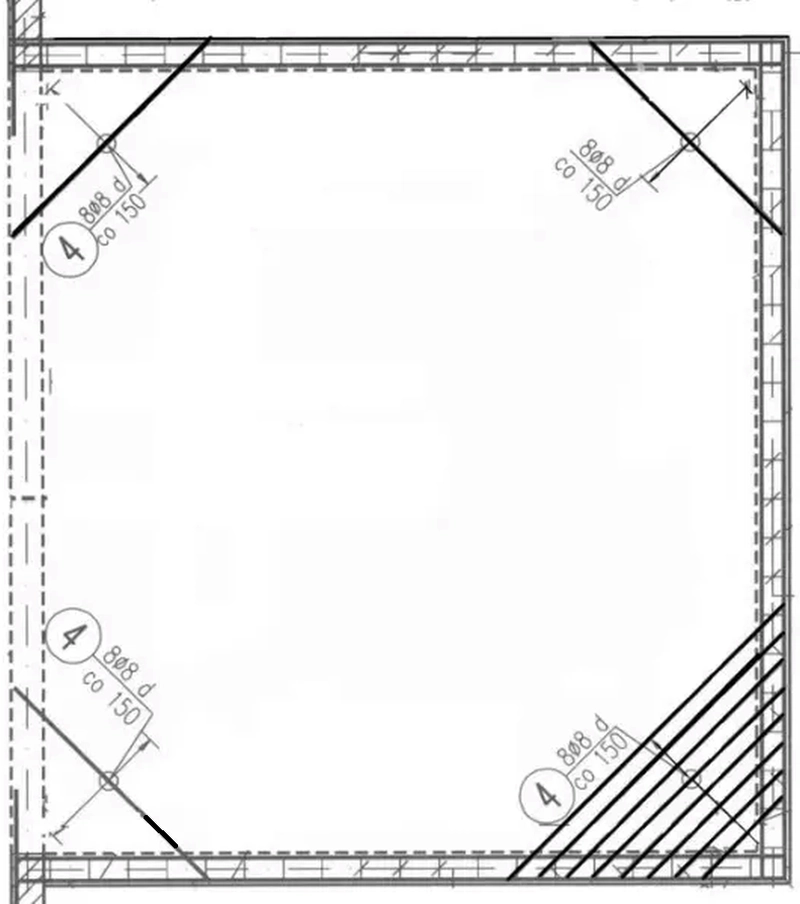
Rys. 8 Zbrojenie naroży płyty z rys. 4 [3]
Z powyższego przykładu wynika zalecenie, by naroża płyty zbroić zbrojeniem w układzie pokazanym na rys. 7, ale górą i dołem, na długości a/10+3 pręty (a-bok płyty). Stosować pręty o średnicy równej średnicy zbrojenia głównego.
Maksymalny rozstaw zbrojenia i zbrojenie rozdzielcze
W zależności od grubości płyty $h$ maksymalny rozstaw zbrojenia $s_{max}$ wynosi
- w obszarach maksymalnych momentów zginających i w takich, w których występują siły skupione:
$$\begin{equation} s_{max}=\begin {cases}
2h \quad i \quad \ge 250 \, mm, & \text {dla zbrojenie głównego (nośnego)} \\
3h \quad i \quad \ge 400 \, mm , & \text {dla zbrojenie drugorzędnego (rozdzielczego) }
\end {cases} \label{8}\end{equation}$$
- w pozostałej części płyty:
$$\begin{equation} s_{max}=\begin {cases}
3h \quad i \quad \ge 400 \, mm, & \text {dla zbrojenie głównego (nośnego)} \\
3,5h \quad i \quad \ge 450 \, mm , & \text {dla zbrojenie drugorzędnego (rozdzielczego) }
\end {cases} \label{9}\end{equation}$$
Zaleca się, by zbrojenie rozdzielcze w płytach jednokierunkowo zbrojonych nie było mniejsze niż 20% zbrojenia głównego.
Przykład zastosowania powyższych zaleceń pokazano na rys.1.
Dobór obliczeniowego zbrojenia płyty
Zagadnienie obliczeniowego doboru zbrojenia płyt żelbetowych ma pełną analolgię do zginania belek i jest szeroko omówioe w cyklu artykułów dotyczących belek żelbetowych. Podstawowym modelem pracy płyt i belek jest bowiem zginanie poprzeczne w ramach teorii Bernoulliego (załozenia płaskich przekrojów).
Również podejście do zagadnień związanych : płzanie i skurcz, rysy i ugięcia, ścinanie jest stosowane przez analogię.
Zginanie płyty
Modele żelbetu na przypadek zginania przestawiono w artykule Belki żelbetowe.Zginanie, Przedtawione tam podejscie i metody dobortu zbrojenie jest stosowane praktycznie ebz zmian róeniż do płyt żelbetowych.
Ścinanie płyty poza obszarami przebicia
W płytach typowym rozwiązaniem poza obszarami ścinania przez przebicie – jest brak zbrojenia na ścinanie, czyli taki dobór grubości płyty, który ma zapewnić, że wystarczająca jest nośność betonu nie zbrojonego na ścinanie (ale zbrojonego na zginanie) – warunek (6) w artykule „Ścinanie i skręcanie belek”. Wymagane jest natomiast zbrojenie na ścinanie żeber płyty (jeśli występują), które projektuje się tak jak zbrojenie strzemionami, prętami odgiętymi i.in. tak jak w belkach żelbetowych.
Szerokość współpracująca belki z żebrami
Płyty z żebrami często ropatruje się jak belki o przekroju teowym z pasami stanowiącymi wspólpracujące części płyty.
Ścinanie płyty przez przebicie
Nad podporami i w miejscu występowania znacznych sił skupionych (rozłożonych na małej powierzchni płyty) może wystąpić mechanizm ścięcia płyty przez przebicie i wówczas należy dodatkowo płytę zbroić zgodnie z wytycznymi zawartymi w artykule Przebicie płyty żelbetowej. [PPŻ].
Nośność płyty na ścinanie przez przebicie mierzona naprężeniem wyznacza się z zależności (23) [PPŻ], a naprężenie od zewnętrznej siły przebijającej w obwodzie kontrolnym $u_x$ z zależności (17) [PPŻ]. Położenie krytyczne obwodu kontrolnego $x_{max}$ wyznacza się w procedurze opisanej w artykule [PPŻ]. W przypadku płaskiego stropu, poza obszarem wpływ otworów można przyjąć [4] , że $x_{max} = 2\cdot d$ , gdzie $d=h-c- \Phi/2$ – wysokość efektywna przekroju płyty w przekroju krytycznym.
Wymagania pożarowe
Minimalne grubości i otulenie płyty są limitowane ze względu na wymagania pożarowe . Często są one decydujące.
W tab.5 podano minimalne grubości płyt oraz minimalne otulenia osiowe wymagane przez [5] dla wymaganych odporności ogniowych REI 30 do REI 240
Tab.5. Minimalne grubości i otulenia zbrojenia płyt żelbetowych ze względów pożarowych (opracowano na podstawie [5] )
Podane wartości pozwalają spełnić wymagania wytrzymałości R, dymoszczelności E oraz izolacyjności cieplnej i bez prowadzenia szczegółowych obliczeń. Jeśli wymaga się spełnienia wyłącznie wymagań R, co wystarcza dopełnienie wymogów normy podstawowej [6] – nie ma dodatkowych wymogów. Odległość osiowa „a”, szczególnie w płytach dwukierunkowo zbrojonych jest odległością do osi zbrojenia najbliższego powierzchni. Minimalnej grubości płyt nie należy zmniejszać poprzez wliczenie warstw wykończeniowych pod tropem, ale może ona zawierać ocieplenie zawarte pomiędzy warstwami żelbetu, a także posadzkę niepalną
W płytach ciągłych należy zapewnić wymagania zasięgu zbrojenia nad podporami jak dla belek. Ponadto należy zapewnić możliwość redystrybucji momentów zginających przynajmniej 15%. W przypadku braku możliwości redystrybucji lub braku wymaganego zbrojenia nad podporami każde przęsło należy traktować jak swobodnie podparte.
Wymogi z wiersza „W układach płytowo-słupowych” stosuje się dla płyt płaskich, w których możliwa jest redysytrybucja momentów zginających w stopniu większym od 15%. W przeciwnym przypadku należy stosować wymogi z wiersza „jednokierunkowo zbrojone”.
Jeżeli wymaga się odporności R90 lub większej, to przynajmniej 20% zbrojenia potrzebnego ( wymaganego przez normę [7] nad podporami pośrednimi w pasmach słupowych (Rys.9) w obu kierunkach, powinno być umieszczone w pasmach słupowych i rozciągać się na całej długość przęsła.
W przypadku płyt z żebrami wymogi pożarowe dotyczą również minimalnej szerokości oraz otulenia żeber zgodnie z [5].
Otwory w płycie
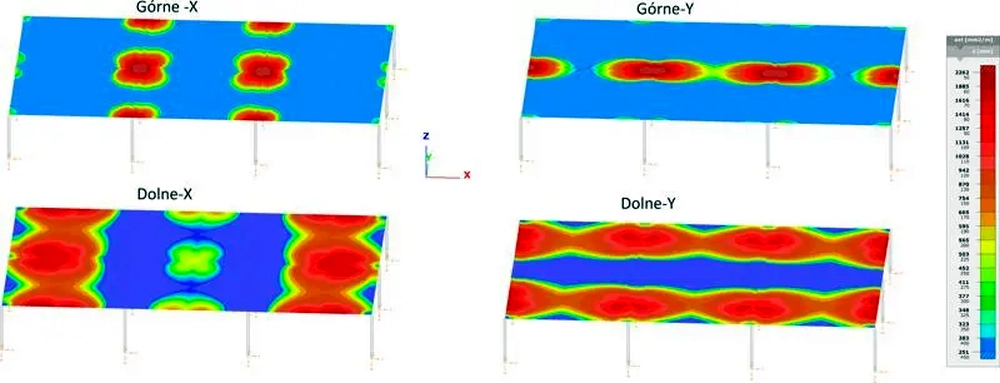
Analizy numeryczne i praktyczne zalecenia
Porównawczy model płyty bez otworów
Otwory w płycie należy uwzględnić podczas obliczeń statycznych, co będzie miało skutek w zmianie sił płytowych i rozkładzie zbrojenia głównym, ale także należy je lokalnie (obok naroży) dozbroić.
Analizę wpływu otworów na zbrojenie płyty przeprowadzimy na modelu płyty prostokątnej o wymiarach 6×9 m obciążonej równomiernie ciężarem własnym i obciążeniem powierzchniowym 5 kN/m2. Płyta jest wykonana z betonu C30/37 i zbrojona stalą B500 . Płyta na obwodzie oparta jest na ścianach o grubości 25 cm. Wstępnie do wyznaczenia rozpiętości płyty przyjęto jej grubość h=20 cm.
Rozpiętości obliczeniowe płyty $(\ref{1})$ wynoszą
$l_{dx}=9+2 \cdot 1/2 \cdot min (0,2 \, ; 0,25)=9,1 \, m$,
$l_{dy}=6+2 \cdot 1/2 \cdot min (0,2 \, ; 0,25)=6,1 \, m$,
$l_{min}=6,1 \, m$
$l_x/l_y=9/6=1,5 \to s=0,878$,
Długość efektywna
$l_{ef}=0,878 \cdot 6,1 = 5,36 \, m$
Grubość płyty
$h \approx l_{ef}/30=5,36/30= 18 \, cm$.
Płytę bez otworów oraz mapę jej zbrojenia pokazano rys. 10.
Otwór kołowy
Przeprowadzono analizę wpływu centralnego otworu kołowego o średnicy od 0,2 m do 2 m co 0,1 m. Na rys. 11 pokazano mapę zbrojenia Asy dla otworu ∅600 mm.
Tab. 6 Maksymalne zbrojenie (na brzegu otworu) strefa zwiększonego zbrojenia dla płyty z otworem kołowym
Z tab. 6 wynika, że średnica otworu w płycie nie ma tak wielkiego znaczenia. Na krawędzi otworów wymagane jest ok. 2x większe zbrojenie niż w płycie bez otworu.
Małe otwory nie wymagają zbrojenia – wystarczy umieścić na deskowaniu wkładkę styropianową czy rurę odpowiedniej średnicy. Nieduże przejście instalacyjne albo świetlik czasami można też wyciąć w gotowej płycie. Zasięg zwiększonych potrzeb zbrojenia wolno wzrasta ze zwiększającą się średnica otworu i zwykle jest nieco większy od średnicy otworu.
Otwór kwadratowy
Na rys. 12 pokazano mapę zbrojenia Asy dla otworu []600 mm.
Z porównania mapy naprężeń dla otworu okrągłego (rys.11) i kwadratowego (rys.12) wynika, że różnice nie są wielkie. Maksymalne zbrojenie $A_{sy}$ w przypadku otworu kwadratowego (11 cm2) jest nawet mniejsze od potrzebnego przy otworze okrągłym (15 cm2) i w obu przypadkach jest szacunkowo dwukrotnie większe od zbrojenia wymaganego dla płyty bez otworu. Dla większych otworów rozkład zbrojenia wokół otworu kwadratowego jest taki jak dla okrągłego.
Również w tym przypadku zalecane jest zbrojenie wokół otworu zgodnie ze wskazaniami rozwiązania podstawowego bez dozbrajania. Zaleca się jednak dozbrojenie w celu przejęcia spiętrzenia naprężeń wywołanych ostrym narożem otworu – przy każdym narożu należy dać kilka prętów ukośnych (prostopadłych do diagonali otworu ). Można przyjąć po 3. pręty ukośne o średnicy takiej jak zbrojenia główne. Dozbrojenie wokół otworu dać górą i dołem.
Szczególnie newralgiczne miejsca występują, gdy słup umieszczony jest w pobliżu otworu, ze względu na zwiększone ryzyko ścięcia płyty przez przebicie. Problemem tym zajęto się w artykule Przebicie płyty żelbetowej.
Dozbrajanie otworów. Zalecenia historyczne
Zbrojenie wokół otworów zaleca się dobierać na podstawie obliczeń indywidualnych z zamodelowanymi otworami.
Przy takiej procedurze nie jest wymagane dodatkowe dozbrojenie otworu zgodnie z klasycznymi zaleceniami (rys.13), które pochodzą z epoki obliczeń dla płyt bez otworów. Płyty obliczane w modelu z otworami są już zbrojone kompletnie i dozbrojenie wokół otworów zgodnie z zaleceniami historycznymi nie jest już wymagane. Układ dozbrojenia można jednak zaczerpnąć z rozwiązań klasycznych rys.13.
Płyty zespolone typu Filigran
Rys historyczny i przykładowa realizacja
Autorem płyt – stropów Filigran jest niemiecki inżynier i wynalazca Stefan Keller, który w roku 1954 opatentował lekkie dźwigary trójpasowe produkowane w jednej operacji (patent szwajcarski nr 335837 z dn. 8 marca 1955). [8]. Ilustrację ze zgłoszenia patentowego przedstawiono na rys. 14.
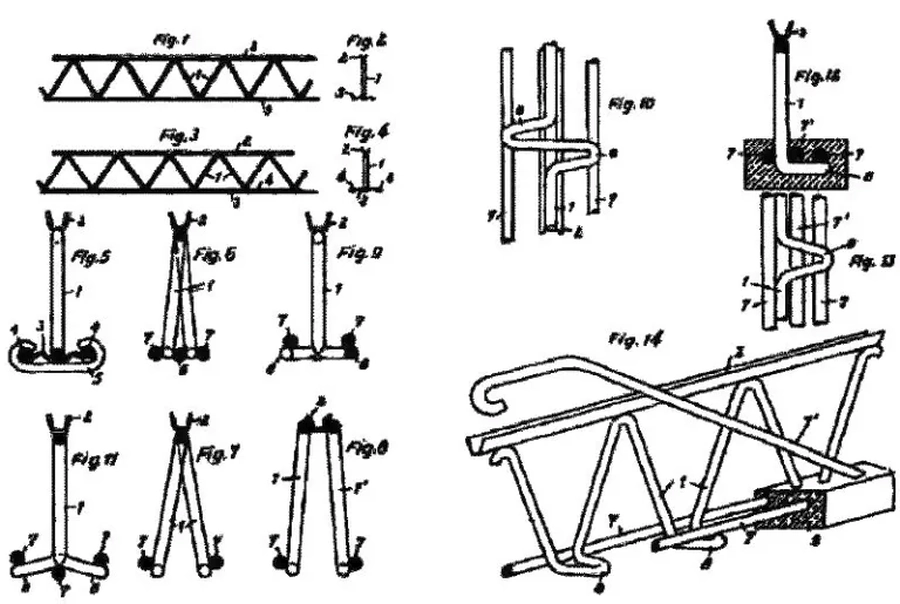
Rys.14. Patent kratownicy FIligran. Autor Keller [8]
Wynalezienie kratownicy Filigran z zastosowaniem do zabetonowania dolnych pasów w betonie było poprzedzone opatentowaniem przez Kellera w 1948 roku lekkich stalowe trójpasowych kratowych dźwigarów dachowych, nazwanymi „dźwigarami filigran” od włoskiego słowa filigraneri (oznaczającego coś bardzo delikatnego i finezyjnego).W kolejnym roku Keller rozpoczął pierwsze próby z dźwigarami kratownicowymi z obetonowaną dolną stopką, a w 1950 r. powstał pierwszy strop gęsto żebrowy z belką kratownicową i wypełnieniem w postaci ceramicznych pustaków, a niebawem zaczęto produkować stropy z pustakami betonowymi.
Wyróżnikiem stropu typu Filigran jest trójpasowa kratownica, która po wszechstronnych badaniach w tym z warunku prostoty technologicznej ( możliwości wykonania w prostej maszynie przy jak najmniejszej liczbie operacji warsztatowych) – przyjmowała kształty pokazane na rys.15.
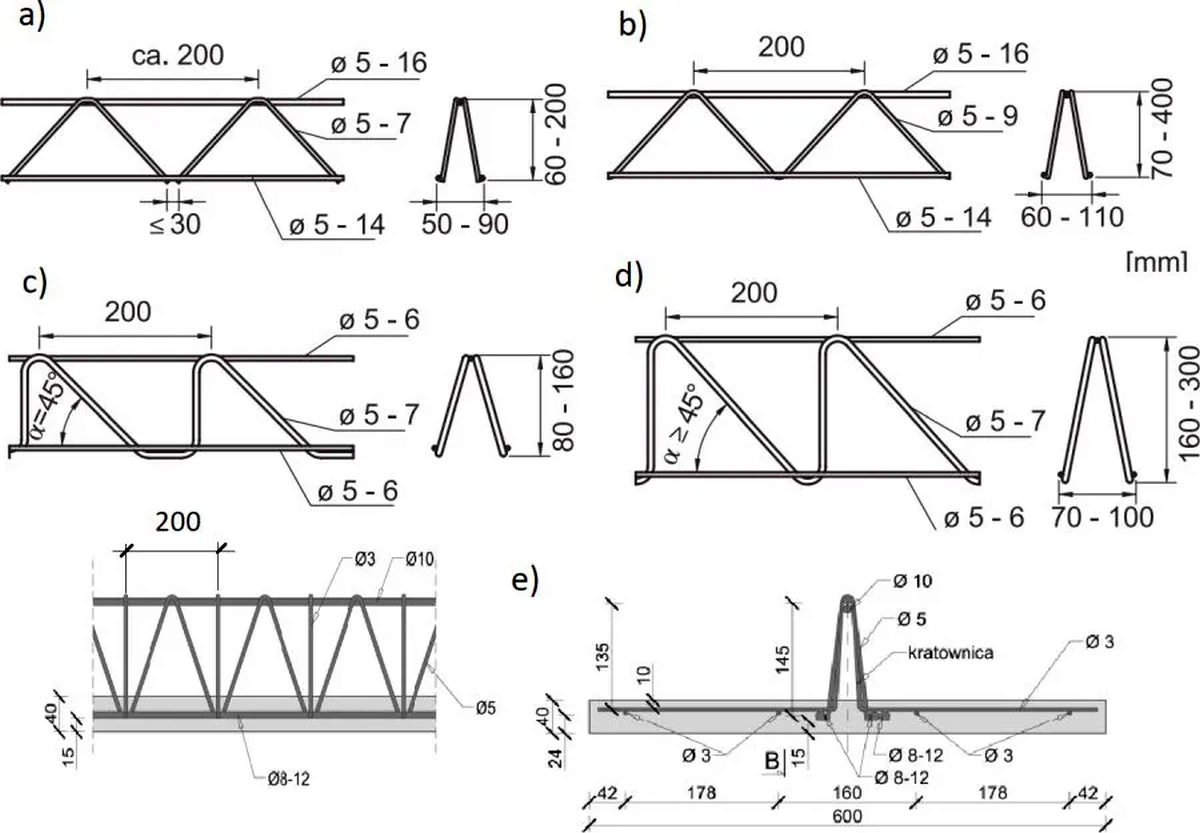
Rys.15 Ksztaltowanie kratownic Filigran: a) (2013) [9], b) (2015) [10], c) (2014) [11], d) (2014) [12], e) (2018) [13]
Powszechnie stosowany do dzisiaj strop typu Filigran ukształtował się ostatecznie na początku lat sześćdziesiątych XX wieku po badaniach Stefana Kellera, zmierzających do opracowania nowego stropu zespolonego, składającego się z dolnej warstwy – żelbetowego prefabrykatu, stanowiącego szalunek ; górnej warstwy – zbrojonego na budowie nadbetonu i łącznika zespalającego warstwy z zastosowaniem wcześniej opatentowanej kratownicy Filigran.
Budowę stropu Filigran zilustrowano dwoma fotografiami z jednej wielu realizacji: na rys.16 pokazano przygotowany do ułożenia prefabrykat – deskowanie (dolną warstwę) z wbetonowanymi w nią trójpasowymi ratowniczkami Filigran (łącznikami stropu zespolonego). Na rys, 17 pokazano etap układania zbrojenia nadbetonu (górnej warstwy) tuż przed zakryciem betonem tej warstwy

Rys.16. Prefabrykowana płyta dolna stropu typu Filigran [14]

Rys.17. Zbrojenie warstwy górnej (nadbetonu stropu typu filigran [15]
Projektowanie stropu na płycie Filigran
Przy projektowaniu stropów na płytach Filigran należy wyraźnie rozróżnić stan montażu i stan eksploatacji. Kratownica i zbrojenie prefabrykatu są projektowane na stan montażu, ale pełnią też rolę wzmacniająca w stanie eksploatacji. Dotyczy to zbrojenia płyty prefabrykatu wraz z włączonymi do zbrojenia pasami dolnymi kratownic Filigran.
W stanie montażu płyta i kratownice pracują w innym schemacie statycznym od schematu prasy w fazie eksploatacji. Są tymczasowo podparte rusztowaniem montażowym.
Faza montażu
Prefabrykat – płytę Filigran wraz z zakotwioną w niej kratownicą trójpasową. projektuje się na sytuację montażu stropu. W fazie montażu wystąpią obciążenia obciążenie od robotników i sprzętu, które przyjmuje się: $Q_u = 1,5 kN/m^2$ oraz obciążenie skupione $F_u= 1,5 kN$, a także obciążenie ciężarem nadbetonu w stanie ciekłym (przed utwardzeniem) wraz z ciężarem własnym prefabrykatu.
Podstawową zależnością do wyznaczenia potrzebnego przekroju pasów dolnych req $A_s$ kratownicy w fazie montażu jest [16]:
$$\begin{equation} req \, A_{s} = \gamma_F \cdot \cfrac{M_{E,m}}{(H_f \, – \, 10\, mm)\cdot f_y} \label{10} \end{equation}$$
gdzie:
$M_{E,m}$ – moment zginający kratownicę od obciążenia w fazie montażu,
$H_{f}$ – wysokość kratownicy Filigran (odległość osiowa pasa dolnego i górnego),
$f_y$ – granica plastyczności stali, z której wykonano kratownicę (obecnie najczęściej wykonana z prętów żebrowanych ze stali B500A ($f_y= 500 \, MPa$)
$\gamma_F = 1,75 $ globalny współczynnik bezpieczeństwa.
Zależność ($[\ref{10})$ dotyczącą pasów dolnych referuje się w tym artykule do celów projektowych : szacowania zbrojenia dolnego płyty stropu, włączonego w zbrojenie dolne stropu w fazie eksploatacji.
W fazie montażu o nośności kratownicy prawie zawsze decyduje wyboczenia pasa górnego. Dla typowych kratownic producenci sporządzili wiele tabel najczęściej dla średnicy pasa górnego od 12 mm do 16 mm i stosownego przekroju pasów dolnych. Wartości z tych tabel tylko nieznacznie odbiegają od wyznaczonych z równania ($\ref{10})$. Wiele tabel i nomogramów można znaleźć w podręczniku [17] lub w normach, na przykład DIN 488 [18].
Dobór płyty prefabrykatu wraz z kratownicami Filigran pozostaje w kompetencji producenta – to on bierze odpowiedzialność za prawidłowy przebieg montażu, w tym za dobór typu i rozstawu podpór montażowych. Projekt kratownic i prefabrykowanych płyt Filigran nie jest przedmiotem właściwego projektu stropu budowli. Narzędzia do wymiarowania płyt Filigran są powszechnie dostępne . Szczególnie użyteczny jest program firmy Filigran Trägersysteme GmbH & Co. KG. który w wersji 23.02 (aktualnej na maj 2923 ). można pobrać z ogólnodostępnej strony www FILIGRAN®.
Prefabrykaty-płyty typu filigran są produkowane na indywidualne zamówienie i według projektu wyspecjalizowanych biur inżynierskich współpracujących z producentami. Rysunki robocze stropu typu Filigran w tym układ płyt nie są elementem właściwego projektu konstrukcyjnego, ale są wykonywane we współpracy z projektantem. Projektant przekazuje producentowi informacje specyficzne dla konkretnego stropu: geometrię z ew. otworowaniem; układ elementów podpierających oraz mapy obciążeń, a szczególnie obciążenia skupione. Często zamiast mapy obciążeń projektant jako wytyczne przekazuje mapy zbrojenia wykonane analogicznie jak dla stropu monolitycznego, dla założonego zbrojenia umieszczonego w kilku warstwach, q tym zbrojenia dolnego kratownicy Filigran
Faza eksploatacji
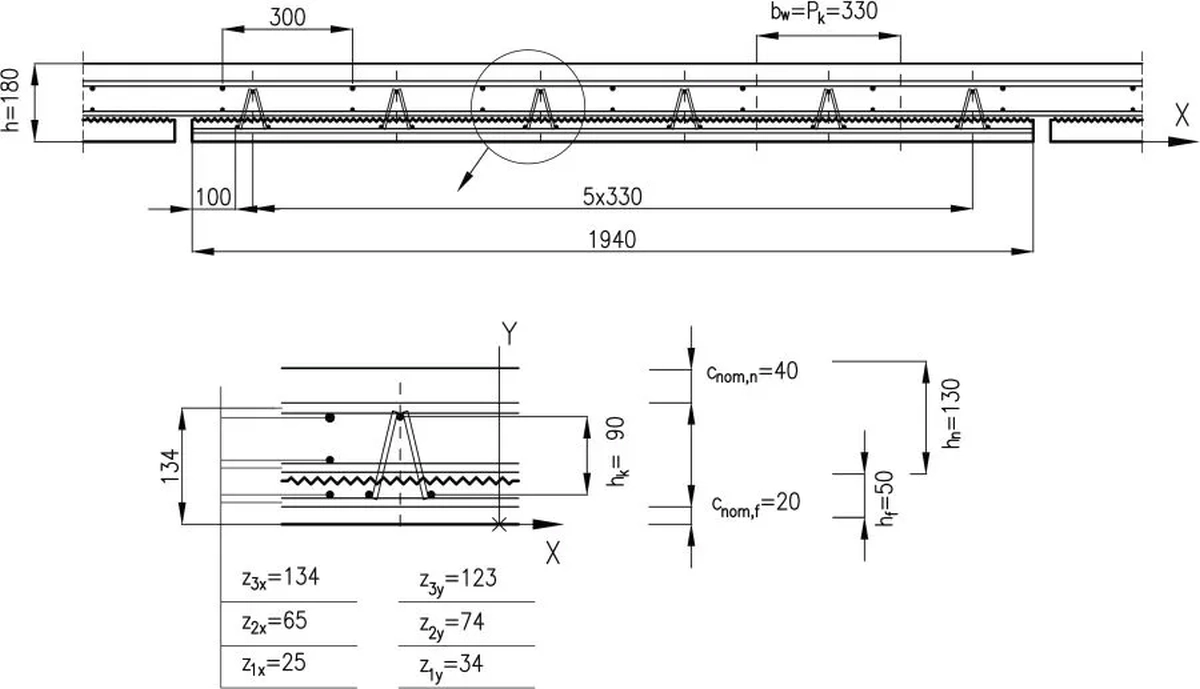
Stropy na niesprężonych płytach Filigran zwykle traktuje się jak zwykłe monolityczne stropy żelbetowe o grubości $h=h_f+h_n$, czyli równej sumie grubości prefabrykatu $h_f$ i warstwy betonu wylewanego na budowie (nadbetonu) $h_n$. Na rys.19 mamy np.: $h=180 \, mm$ ; $h_f= 50 \, mm$, $h_n=130 \, mm$.
Można przyjąć, że redystrybucja naprężeń spowodowana pełzaniem i skurczem betonu zachodzi podobnie do procesu, który zachodzi w płytach monolitycznych w statycznym układzie końcowym.
Obliczenia stropów zespolonych Filigran można wykonać metodą elementów skończonych w stanie liniowym bez uwzględniania zespolenia oraz połączeń między prefabrykatami. [19],
Właściwy projekt stropu Filigran sporządza się w schemacie pracy statycznej w stanie eksploatacji i na obciążenia docelowe, ale należy zapewnić warunki jak dla stropu izotropowego, czyli:
- zastosowanie takiej samej klasy betonu prefabrykatu i nadbetonu ( chodzi przede wszystkim o takie same moduły Younga). W przypadku różnych klas betonu klasyczne podejście wymagałoby modyfikacji, co nie jest przedmiotem niniejszego artykułu,
- zaprojektowanie połączenia zespalającego płytę prefabrykowaną oraz nadbeton umożliwiającego przeniesienie sił rozwarstwiających (p. niżej rścinanei przez ozwarstwienie ),
- ułożenia dźwigarów kratowych przy brzegach płyt porubrykowanych w odległości nie większej niz 100 mm, od fugi (rys.18a), co zabezpieczy prefabrykat przed skręcaniem naroży ( zjawisko pokazano na Rys. 7),
- ułożenie środkowej warstwy zbrojenia (dozbrojenia) w takiej odległości od zbrojenia prefabrykatu , by prześwit między nimi był mniejszy niż 50 mm [20] (rys.18b).
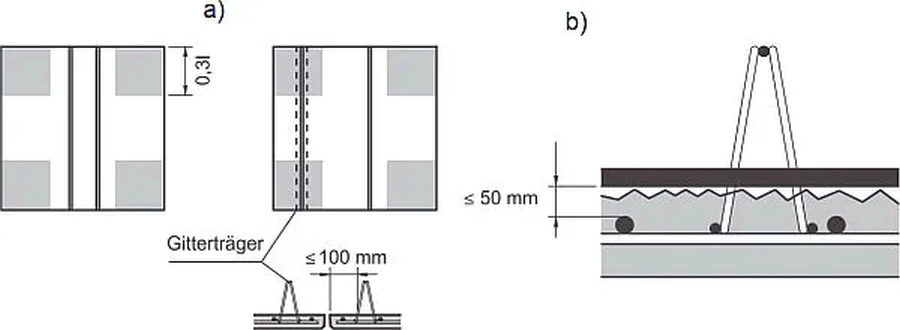
Rys. 18 Detale stropu Filigran; a) umieszenie kratownic w narozu płyt (0,3 l) obok fugi płyt: b) , ułożenie dozbrojenia dolnego na powierzchni płyty w celu traktowabnia płyty jak izotropowej [21]
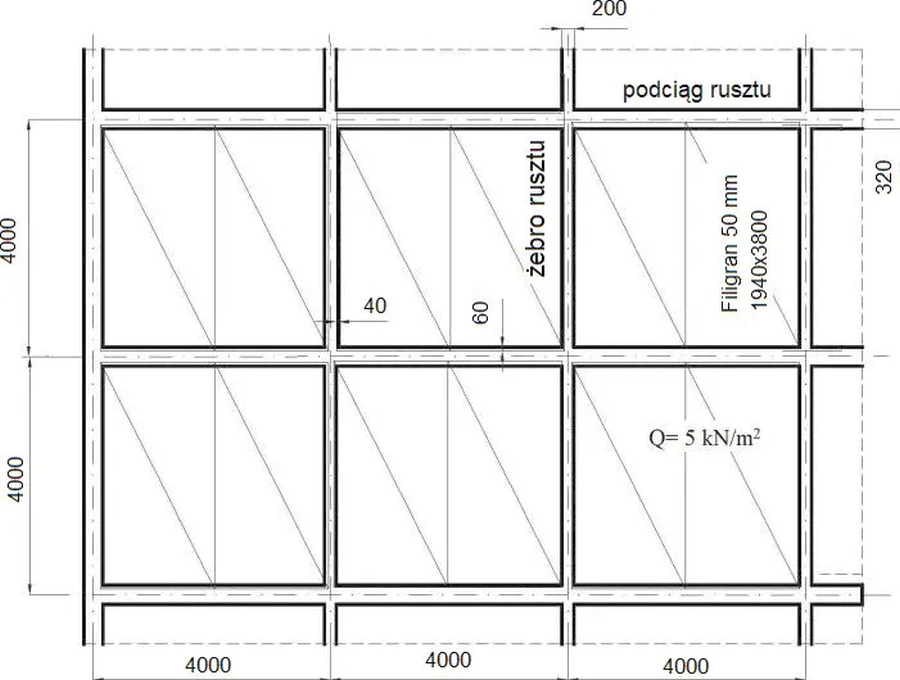
Poniżej na przykładzie zaczerpniętym z projektu [22] pokazano przykładowy układ zbrojenia stropu na płycie Filigran (rys. 19) oraz detal zespolenia płyty z podciągiem rusztu stanowiącego stałą podporę płyt Filigran układanych na wykonanym na etapie poprzedzającym rusztu złożonego ze slupów, podciągów i żeber (rys. 20).
Strop został zaprojektowany w przykładzie 2. W projekcie przewidziano, że płyty Filigran będą układane na ruszcie żelbetowym po osiągnięciu przez beton wymaganej wytrzymałości do przeniesienia ciężaru stropu z mokrym nadbetonem oraz na podporach tymczasowych (rusztowaniu) zgodnie z wytycznymi producenta. Układanie nadbetonu prowadzi się na budowie po ułożeniu płyt Filigran – zbrojenie stropu jest wplecione w trójpasowe kratownice płyt Filigran oraz startery wypuszczone z podciągów oraz żeber.
Zginanie stropu Filigran
W stanie końcowym (eksploatacji) zachowanie stropu Filigran przy zginaniu odpowiada pracy stropu monolitycznego, przy czym w obliczeniach należy uwzględnić różne otulenia górne oraz dolne, a także wielowarstwowe zbrojenie.
Otulina dolna (pod płytą filigran) – dobiera się w uzgodnieniu z producentem płyt Filigran z warunku dotrzymania odchyłki wykonawczej $\Delta c_{dev}$ oraz wymaganego otulenia zależnego od klasy ekspozycji $c_{dur}$. Najczęściej otulinę dolna wynosi $c_{nom,f}= 20\, mm$ jak dla klasy ekspozycji XC1 oraz odchyłki wykonawczej zmniejszonej do 5 mm (tak jak na rys.20). Powierzchnię dolną stropu należy zabezpieczyć izolacją lub obudową, tak by spełnić warunki ekspozycji XC1.
Otulina górna (nadbetonu) jest wyznaczana stosowanie do klasy ekspozycji powierzchni górnej stropu, np. dla XC4 – $c_{mom,n} = 40\, mm$ (tak jak na rys.20).
W ogólności płyta stropowa jest zbrojona wielowarstwowo oraz inaczej w obu kierunkach pracy płyty X i Y. Standardowo położenie zbrojenia $z_i$ od dolnej powierzchni płyty licząc, [(X,Y)=0] przyjmuje się następująco :
- w kierunku głównym X (po długości płyty):
$$\begin{equation} z_{ix}=\begin {cases}
\text{i=3: zbrojenie górne }, & z_{3x} = h – c_{nom,n} -\Phi_{3,x}/2 \\
\text{i=2: dozbrojenie środkowe na płycie Filigran }, & z_{2x} = h_f + 3/2 \Phi_{2,x} \\
\text{i=1: zbrojenie dolne w prefabrykacie }, & z_{1x}= c_{nom,f} + \Phi_{1x}/2 \\
\end {cases} \label{11}\end{equation}$$
- w kierunku Y (prętów rozdzielczych):
$$\begin{equation} z_{iy}=\begin {cases}
\text{j=3: zbrojenie górne }, & z_{3x}= h- c_{nom,n} – \Phi_{3x} – \Phi_{3y}/2 \\
\text{j=2: dozbrojenie środkowe na płycie Filigran }, & z_{2y} = h_f + 2\cdot \Phi_{2,x} + \Phi_{2y}/2 \\
\text{j=1: zbrojenie dolne rozdzielcze w prefabrykacie}, & z_{1y} = c_{nom,f} + \Phi_{1x}+\Phi_{1y}/2 \\
\end {cases} \label{12}\end{equation}$$
przy czym
$(z_{2z} -\Phi_{2x}/2 ) -(c_{nom,f} +\Phi_{1,x} + \Phi_{1y}) = (h_f – c_{nom,f} +\Phi_{2y}) \le 50 \, mm$ – patrz rys. 18b.
gdzie:
$\Phi_1,\Phi_2,\Phi_3$ – średnica pręta warstwy zbrojenia (i=1,2,3) odpowiednio ( X lub Y – kirrunek zbrojenia),
$c_{nom,f}, c_{nom,n}$ – otulenie dolne prefabrykatu Filigran oraz górne nadbetonu odpowiednio.
Zbrojenie w prefabrykacie – płycie Filigran (i, j = 1) umieszczone jest w wytwórni prefabrykatów betonowych. Dozbrojenie środkowe (i= 2) układane jest na budowie w odległości $\Phi_{2x}$ od płaszczyzny prefabrykatu ( w celu zachowania przyczepności do betonu). Dozbrojenie środkowe poprzeczne (j = 2) układane jest na budowie na zbrojeniu podłużnym (i=2). Zbrojenie górne (i, j =3) układane jest na budowie
Na rys 19 pokazano współrzędne zbrojenia $z_i$ dla projektu z przykładu 2.
Oprócz stanu granicznego nośności należy sprawdzić warunki stanu granicznego użytkowania ( szerokości rozwarcia rys i wielkości ugięcia dla obciążenia długotrwałego stałego i zmiennego).
W stropach jednokierunkowo zbrojonych przy rozpiętości powyżej 6 mb można stosować odwrotną strzałkę. Natomiast w stropach krzyżowo zbrojonych nie zaleca się stosowania strzałki odwrotnej z uwagi na konieczność konstruowania skomplikowanego układu podpór montażowych. Wielkość strzałki odwrotnej nie powinna przekraczać ugięcia od obciążeń stałych bez ścianek działowych.
Ścinanie stropu Filigran
Sprawdzenie stropu typu Filigran na ścinanie prowadzi się podług ogólnych zależności Eurokod 2 [6] syntetycznie przedstawionych w artykule Ścinanie i skręcanie belek żelbetowych [ŚSB].
Podstawowy warunek wytrzymalości na ścinanie w naprężeniach przyjmuje postać (23) [SŚB] :
$$\begin{equation} v_{Ed} \le v_{Rd} \label{13} \end{equation}$$
gdzie naprężenie $v_{Ed}$ od ścinania zewnętrzną obliczeniową siłą poprzeczną $V_{Ed}$ oblicza się z zależności (1) [SŚB]:
$$\begin{equation} v_{Ed} = \cfrac{V_{Ed}} { A_v} \label{14} \end{equation}$$
$A_v=z \cdot b_w$ efektywne pole przekroju ścinania płyty
$z= 0,9\cdot d$ – efektywne ramię sił wewnętrznych;
$d=h – c -\Phi/2 $ – efektywna wysokość przekroju w miejscu ścinania;
$h$ – grubość płyty stropu;
$c$ – otulenie pręta rozciąganego o średnicy $\Phi$ zależy od rozkładu sił w przekroju:
jeśli rozciągany pręt znajduje się w prefabrykacie ( rys 20 a, b, c), to $c=c_{nom,f} \,;\, \Phi=\Phi_f $,
jeśli rozciągany pręt jest umieszczony w nadbetonie (rys 20 d), to $c=c_{nom,n} \, ; \, \Phi=\Phi_n$,
$b_w$ szerokość analizowanego pasa płyty w zagadnieniu ścinania poprzecznego lub przez rozwarstwienie.
Zwykle przyjmuje się że czyli $b_w=P_k$ – $P_k$ podziałka stropu, czyli rozstaw kratownic ( rys. 19),
Nośność płyty na ścinanie $v_{Rd }$ wyznacza się jako minimum z nośności stowarzyszonych z możliwymi mechanizmami zniszczenie płyty przez ścinanie:
$$\begin{equation} v_{Rd} =\min { \{ v_{Rdi} \,;\, v_{Rd,max} \,;\, v_{Rd,s} \}} \label{15} \end{equation}$$
gdzie:
$v_{Rdi}$ – nośność stropu na ściananie przez rozwarstwienie w płazczyźnie styku prefabrykatu z nadbetonem;
$v_{Rd, max}$ – nośność na ścinanie poprzeczne ściskanych krzyżulców betonowych;
$v_{Rd,s}$ – nośność na ścinanie poprzeczne zbrojenia na ścinanie – tutaj krzyżulców kratownic Filigran.
Do kolekcji $(\ref{15})$ można dołączyć nośnosć stropu na ścinanie przez przbicie
Ścinanie przez rozwarstwienie
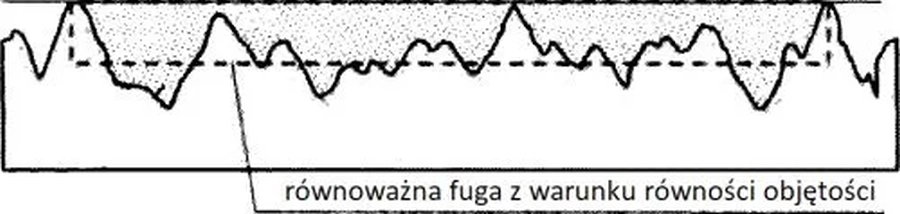
Na styku zespolenia nadbetonu i płyty Filigran mogą wystąpić dwa mechanizmy zniszczenia: a) ścięcie ukośne z częściowym przebiegiem przez złącze zespolone, b) oderwanie nadbetonu od prefabrykatu w płaszczyźnie zespolenia betonów [23]. W celu zwiększenia nośności na rozwarstwienie powierzchnię górną prefabrykatu przygotowuje się o dużej szorstkości ( przykład jak na rys. 21)
Obliczeniową nośność stropu ze względu na ścinanie przez rozwarstwienie pomiędzy prefabrykatem a nadbetonem wyznacza zgodnie z klauzulą 6.2.5 Eurokod 2 [6], wzór (6.23). dotyczącą rozwarstwienia na styku między betonami ułożonymi w różnych terminach. zależności (6.25) [24]:
$$\begin{equation} v_{Rdi} = c \cdot f_{ctd} +\mu \sigma_n +\rho \cdot f_{yd} \cdot ( 1,2 \cdot \mu \cdot sin\alpha +cos \alpha) \le 0,5 \cdot \nu \cdot f_{cd} \label{16} \end{equation}$$
gdzie:
$f_{ctd}$ , $f_{cd}$ – obliczeniowa wytrzymałość betonu na rozciąganie i ściskanie odpowiednio,
$\sigma_n$ – naprężenie normalne do powierzchni styku (dodatnie przy ściskaniu i ujemne przy rozciąganiu), ale nie większe niż $ 0,6 \cdot f_{cd}$. Naprężenie $\sigma_n$ jest wywołane przez najmniejsze obciążenie zewnętrzne powierzchni zespolenia, które działa jednocześnie z siłą ścinającą styk. Jeżeli $\sigma_n$ jest naprężeniem rozciągającym, to przyjmuje się $(c\cdot f{ctd}) =0$.
$\rho$ – współczynnik wzmocnienia zespolenia $\left (= A_s/ A_i \right)$, gdzie $A_s$ oznacza pole zbrojenia przecinającego płaszczyznę zespolenia poprawnie zakotwionego po obu stronach styku, razem ze zwykłym zbrojeniem na ścinanie (jeśli istnieje), a $A_i$ oznacza pole złącza.
$\alpha$ – kąt nachylenia ścianki wrębu, często przyjmuje się jako kąt nachylenia krzyżulca kratownicy Filigran. Przyjmuje wartości z przedziału $45^0 \le alpha \le 90^0$. Przy braku dokładniejszych danych można przyjąć $\alpha = 45^0$.
$c$ , $\mu$, $\nu$ – współczynniki zależne od szorstkości płaszczyzny zespolenia. W przypadku stropów Filigran powierzchnie przygotowuje się tak, by spełniały warunki określone w klauzuli 6.2.5 (2) normy [6] dla powierzchni z wrębami wg rys. 6.9 tej normy, czyli powierzchnię wykonuje się z wgłębieniami o głębokości $d \ge 5 \,mm $ każde o długości $\le 10 \cdot d$ i w takim samym rozstawie (np. rys.21).
Dla powierzchni wykonanej z wrębami przyjmuje się $c= 0,50$ ; $\mu=0,9$, a dla betonu zwykłej wytrzymałości ($\le C55$) $\nu=0,7$.
W przypadku powierzchni zespolenia o mniejszej szorstkości niż powierzchnia z wrębami współczynniki $c$ $, \nu$ należy przyjmować zgodnie Eurokod 2 , klauzula . 6.2.5 (2), a współczynnik $\nu$ zgodnie z klauzulą 6.2.2.(6) tej normy.
Na użytek sprawdzenia warunku ścinania przez rozwarstwienie – naprężenia $v_{Ed}$ $ (\ref{14}$) należy skorygować współczynnikiem efektywności zespolenia $\beta$ jak następuje:
$$\begin{equation} v_{Edi} = \beta \cdot v_{Ed} \label{17} \end{equation}$$
i w warunkach wytrzymalościowych stosować $v_{Edi}$.
Współczynnik $\beta$ jest stosunkiem siły rozwarstwiającej (podłużnej) $Z_F$, działającej na przekrój poprzeczny jednej z części przekroju zespolonego (nowego betonu lub prefabrykatu) do całkowitej siły podłużnej działającej w rozważanym przekroju w strefie ściskanej $\Sigma D$, albo w strefie rozciąganej$\Sigma Z$. (Warunek równowagi rzutów sił: \Sigma Z = \Sigma D). Współczynnik ten przyjmuje się zgodnie z zasadami przedstawionymi na (rys. 21):
$\beta = 1$ (rys.21a) przyjmuje się dla sytuacji w której zbrojenie rozciągane leży w całości w płycie prefabrykowanej, a strefa ściskania w nadbetonie.- taka sytuacja zachodzi dla płyty jednoprzęsłowej zbrojonej jednokierunkowo,
$\beta=0$ odpowiada sytuacji gdy prefabrykat nie przenosi sił (ani rozciągających ani ściskających) (rys.21b),
$0 \le \beta \le 1$ – prefabrykat przenosi część siły rozciągającej $Z_F$ (rys.21c) lub ściskającej $ D_F$ a pozostała część siły rozciągającej $Z_O$ lub ściskającej $D_O$ przenoszona jest przez pozostałe zbrojenie lub część przekroju betonowego. Wówczas $\beta=Z_F/(Z_F+Z_O)$ lub $\beta=D_F/(D_F+D_O)$ odpowiednio.
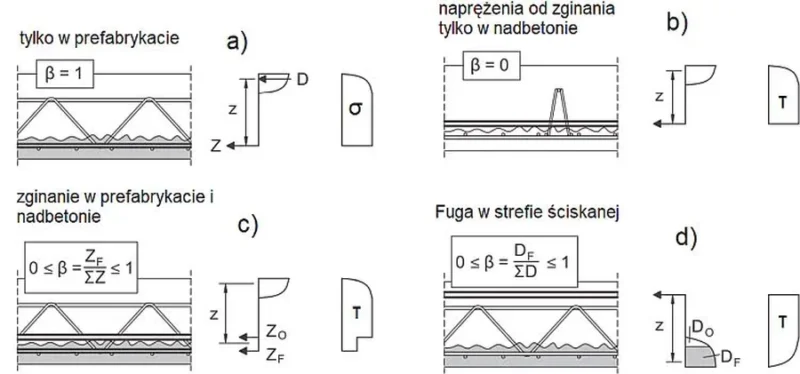
Rys. 22 Stany napreżeń w stropie Filigran. Współczynnik $\beta$ [25], zmodyfikowany rys. 72
Ponadto w zagadnieniu ścinania przez rozwarstwienie należy sprawdzić czy ramię sił wewnętrznych $z$ nie przekracza ograniczenia:
$z \le max\{ (d- 2\ cdot c_1 \, ; \, (d- c_1- 30 \, mm)\}$ ,
gdzie $c_1$ – otulina pręta położonego w strefie ściskanej: $c_1=c_n$ lub $c_1=c_f) dla sytuacji (a,b,c) lub d z rys 21 odpowiednio.
Ścinanie zbrojenia vRd,s
W płytach z zasady nie stosuje się zbrojenia na ścinanie, ale w stropach Filigran takie zbrojenie występuje zawsze w postaci krzyżulców trójpasowych kratownic nachylonych do poziomu pod kątem $\alpha$ . W trakcie ścinania system nośny zamyka się ściskanymi krzyżulcami betonowymi, które tworzą się w betonie pod kątem $\Theta$ (rys. 23).
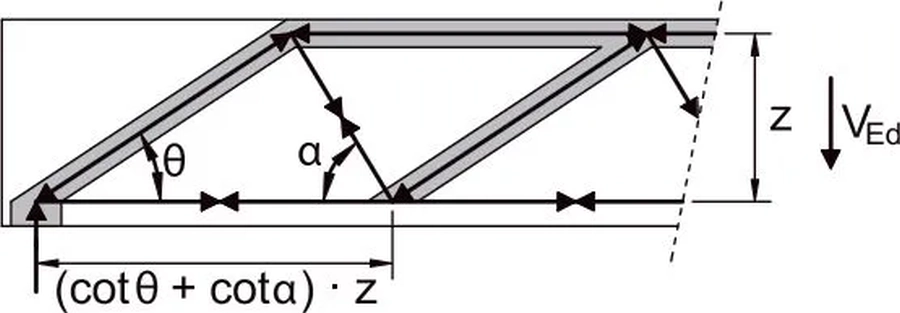
Rys. 23 Model kratownicowy do wyznaczania wytrzymałości na ścianie stropu Filigran ze zmiennym nachyleniem krzyżulca betonowego [25], rys. 70
W stropach Filigran w obszarach nie narażonych na przebicie można pominąć sprawdzanie nośności płyty bez zbrojenia na ścinanie $v_{Rd.c}$ i od razu przejść do sprawdzeniu warunku $(\ref{13}$) , zachodzi bowiem $v_{Rdc,s} \ge v_{Rd,c}$.
Nośność na ścinanie zbrojenia ( w tym przypadku krzyżulców kratownicy Filigran) wyznacza się ze wzoru (23) [SŚB].:
$$\begin{equation} v_{Rd,s} = \left(\cfrac{A_{sw}}{s _w \cdot b_w} \right) \ \cdot f_{ywd} \cdot ( ctg \Theta + ctg \alpha) \cdot sin \alpha \label{18} \end{equation}$$
Na podstawie danych producenta kratownic Filigran należy przyjąć :
$A_{sw}$ – pole przekroju zbrojenia na ścinanie, w tym przypadku pole przekroju krzyżulców kratownicy na szerokości płyty $b_w$,
$s_w$- rozstaw krzyżulców kratownicy;
$\alpha$ – kąt nachylenia krzyżulców kratownicy. Najczęściej $45^0 ≤ \alpha \le 90^0$;
$f_{ywd}$ – granicę plastyczności zbrojenia na ścinanie (krzyżulców) dla stali B500A $f_{ywd}$ = 500/1,15 = 435 \, MPa$,\
Kąt nachylenia krzyżulca betonowego $\Theta$ wyznacza się w standardowej procedurze Eurokod 2, opisanej w artykule kąt nachylenia krzyżulca betonowego
Nośność krzyżulca betonowego vRd,max
Nośność krzyżulca betonowego $v_{Rd,max}$ wyznacza się ze standardowej zależności (17) [SŚB].
Ścinanie przez przebicie
Nośność na ścinanie przez przebicie w obszarach przysłupowych lub znacznych sił skupionych sprawdza się w sposób standardowy omówiony w artykule Przebicie płyty żelbetowej [PPŻ] , przy czym specyfiką projektowania stropów Filigran na ścinania przez przebicie jest stosowanie uproszczonej formuły do wyznaczenia nośności płyty w obszarze przebicia
$$\begin{equation} v_{Rd,cs, max } = \alpha _{max} \cdot v_{Rd,c} \label{19} \end{equation}$$
gdzie:
$\alpha _{max}$ – współczynnik zwiększający nośność stropu na ścinanie przez przebicie w stosunku do nośności nie zbrojonego betonu $v_{Rd,c}$.
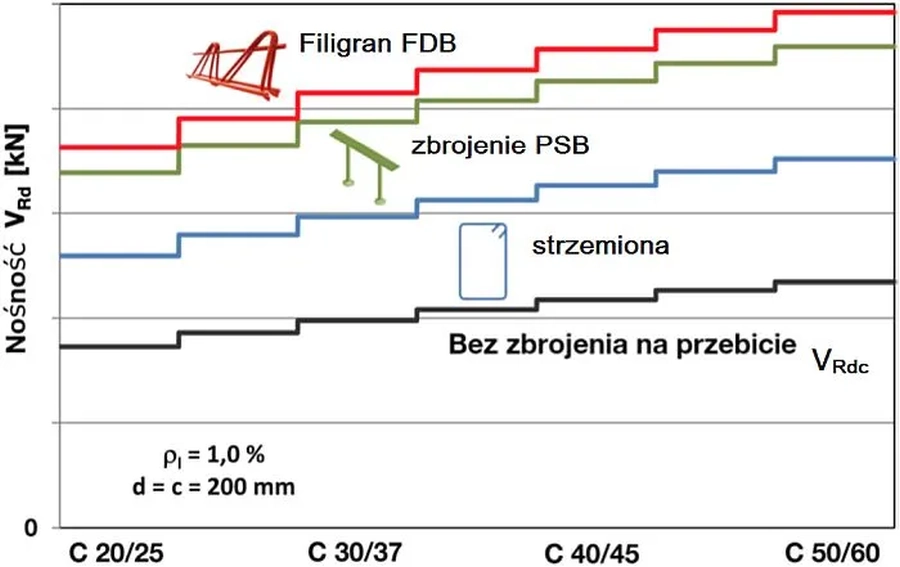
Szacuje się, że dla zbrojenia na przebicie strzemionami lub prętami odgiętymi $\alpha_{max} \approx 1,4$ . Natomiast specjalne zbrojenia systemowe (np. Filigran FDB – rys. 23 ) zwiększają nośność na przebicie dwukrotnie ($\alpha_{max} \approx 2 )$.
Nośność płyty nie zbrojonej na ścinanie przez przebicie wyznacza się w sposób standardowy z zależności (28) [PPŹ] lub (13) [ SŻB]
$$\begin{equation} v_{Rd,c}=\max{ \left \{ C_{Rd,c} \cdot k \cdot (100 \cdot \rho_l \cdot f_{ck})^{1/3} \, ; \, \nu_{min} \right \} }+ k_1 \cdot \sigma_{cp} \label{20} \end{equation}$$
-
Strop Vector
Strop Vector to w istocie odmiana stropu Filigran, opracowana w Polsce przez inż Drobiec Ł. [13].
-
Pierwsza realizacja stropu Vector, która miała miejsce w październiku 2015 r.
Modyfikacje wprowadzone do rozwiązań oryginalnych Stefan Kellera są w istocie drobne:- ograniczono asortyment szerokości poszczególnych prefabrykatów (płyt) do 600, 400 lub 200 mm, (standardowo 759, 625, 500. 440, 370. lub 330 mm)
- zmniejszono grubość płyty prefabrykatu do 40 mm, (standardowo 40, 50 , 60 mm),
- ustalono rozstawy między kratownicami Filigran na 600 mm,
- przewidziano możliwość włożenia pomiędzy kratownice Filigran wkładów styropianowych,
-
Zwiększenie chropowatości powierzchni górnej prefabrykatu betonowego przez nadanie jej wgłębień podczas przejazdu specjalnym wałkiem po dojrzewającej powierzchni betonu w podobny sposób ja w oryginalnym pomyśłe. Ograniczono możliwości projektowe poprzez ograniczenie schematów do płyt jednokierunkowo zbrojonych. Sporządzono wiele sztywnych tabel do doboru parametrów stropu. W procedurze właściwego projektowania stropu Filigran – większośc parametrów wprowadzonych w rozwiązaniach stropu Vector są zmiennymi, które projektant i tak mógł nadać może nadać zależnie od konkretnej, indywidualnej sytuacji projektowej i uzyskania z warunku optymalnego efektu techniczno-ekonomicznego.
Stropy Filigran sprężone
Sprężone płyty stropowe typu Filigran – to prefabrykowane płyty o grubości od 80 mm do 160 mm z wbetonowanym sprężonym zbrojeniem nośnym produkowane już przez wiele przedsiębiorstw w Polsce: Pekabex, Betard, Technopanel i in.
Dokumentację roboczą takich typów stropów każdorazowo opracowuje producent. Do wykonania dokumentacji roboczej stropu niezbędne są dane od projektanta: projekt budowlany w branży architektonicznej i konstrukcyjnej, mapy obciążeń stropu, wymagana ognioodporność stropu, wytyczne odnośnie przejść instalacyjnych w stropie, dane urządzeń obciążających strop i inne dane szczególne.
Stropy typu BubbleDeck

Rys.25 Przykład zastosowania technologii BubbleDeck [26]
Płyty prefabrykowane
Przedstawione wyżej stropy, w których zastosowano płyty typu Filigran można zaliczyć do częściowo prefabrykowanych stropów zespolonych. Natomiast całkowicie prefabrykowane są płyty kanałowe lub żebrowe (panwie).
Płyty kanałowe
W budownictwie mieszkaniowym chętnie stosowało się płyty kanałowe ze względu na ich zalety, a przede wszystkim szybki montaż nie wymagający stemplowania, a ponadto dobre własności akustyczne; oferta plyt dla klas ekspozycji XC1 do XC3 i dla odporności ogniowej REI60 oraz REI 120, a nawet REI 240. . Wadą płyt kanałowych jest możliwość kliszowania i w konsekwencji pękanie sufitu w miejscach styku płyt.
Płyty kanałowe oferowane są przez wielu producentów: Betard, Budmater, Consolis,. Elbet, Konbet, Pozbruk, Rooswns Beton Polska, Unimex, i innych.
Na rys. 25 pokazano przykładową budowę stropu z płyt kanałowych na prefabrykowanych ramach żelbetowych.
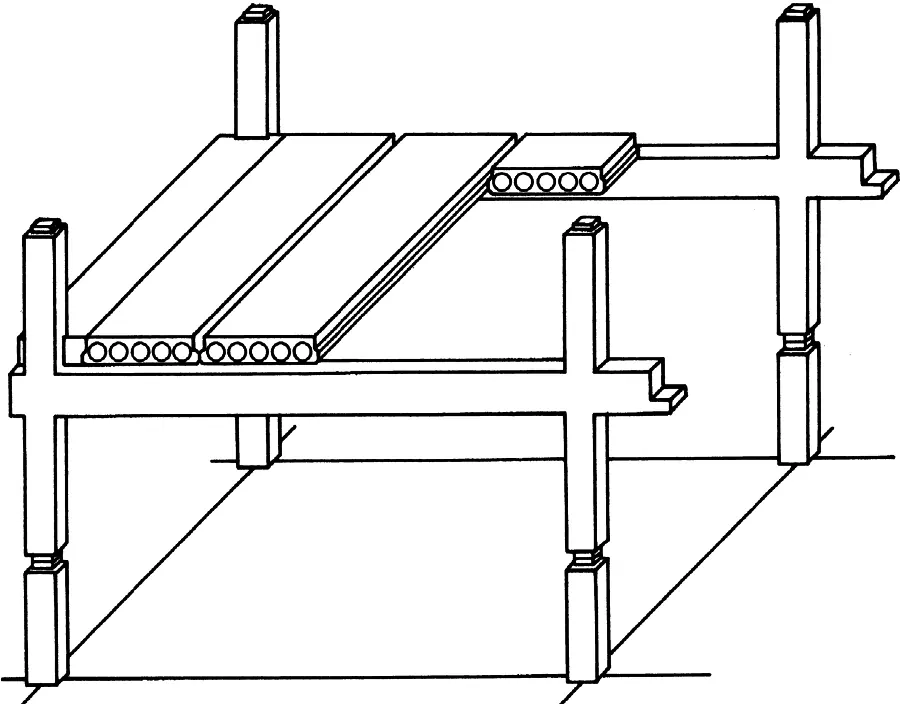
Rys. 26 Przykład układu płyt kanałowych [27]
Najchętniej stosuje się sprężone płyty kanałowe. Sztandarowym rodzajem sprężonych strunami płyt kanałowych są płyty typu HC produkcji Consolis. [28]– asortyment płyt HC zestawiono na rys. 24 a na rys. 25 przedstawiono nośność płyt HC w zależności od rozpiętości. Nośność jest mierzona zastępczym równomiernie rozłożonym charakterystycznym obciążeniem zewnętrznym w $kN/m^2$. W celu doboru płyt o większej wysokości lub wycinania otworów z nich należy posłużyć się poradnikiem [29] lub skontaktować się z biurem technicznym producenta.
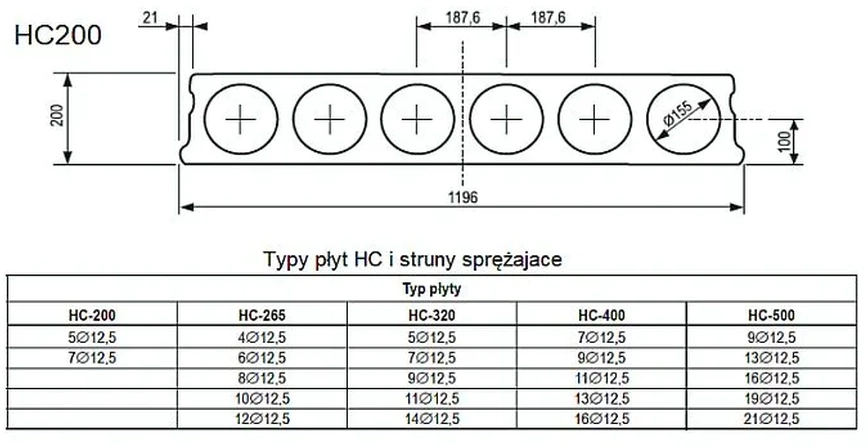
Rys.27 Typy płyt HC i struny sprężające [29]
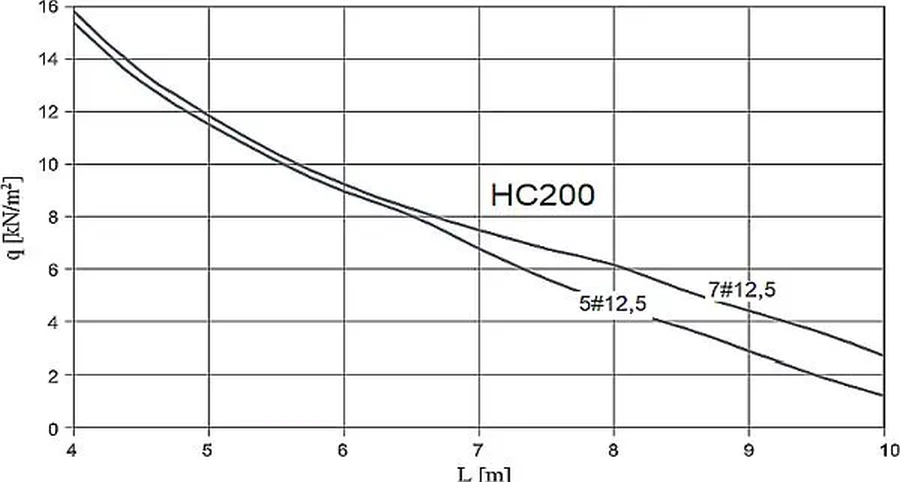
Rys.28 Nośność płyt HC200 [29]
Płyty żebrowe – korytkowe, panwiowe
Płyty korytkowe dzielą się na trzy rodzaje: obustronnie otwarte, otwarto-zamknięte i obustronnie zamknięte. Wykorzystuje się je do pokryć dachowych zwykle na garaże i do stropodachów wentylowanych domów jedno i wielorodzinnych. Do głównych zalet płyt korytkowych dachowych można zaliczyć łatwość i szybkość montażu. Płyty dachowe panwiowe (o wzmocnionych żebrach) wykorzystywane są do wykonywania pokryć dachowych i stropodachowych. Na rys. 38 pokazano przykłady produkowanych obecnie płyt korytkowych
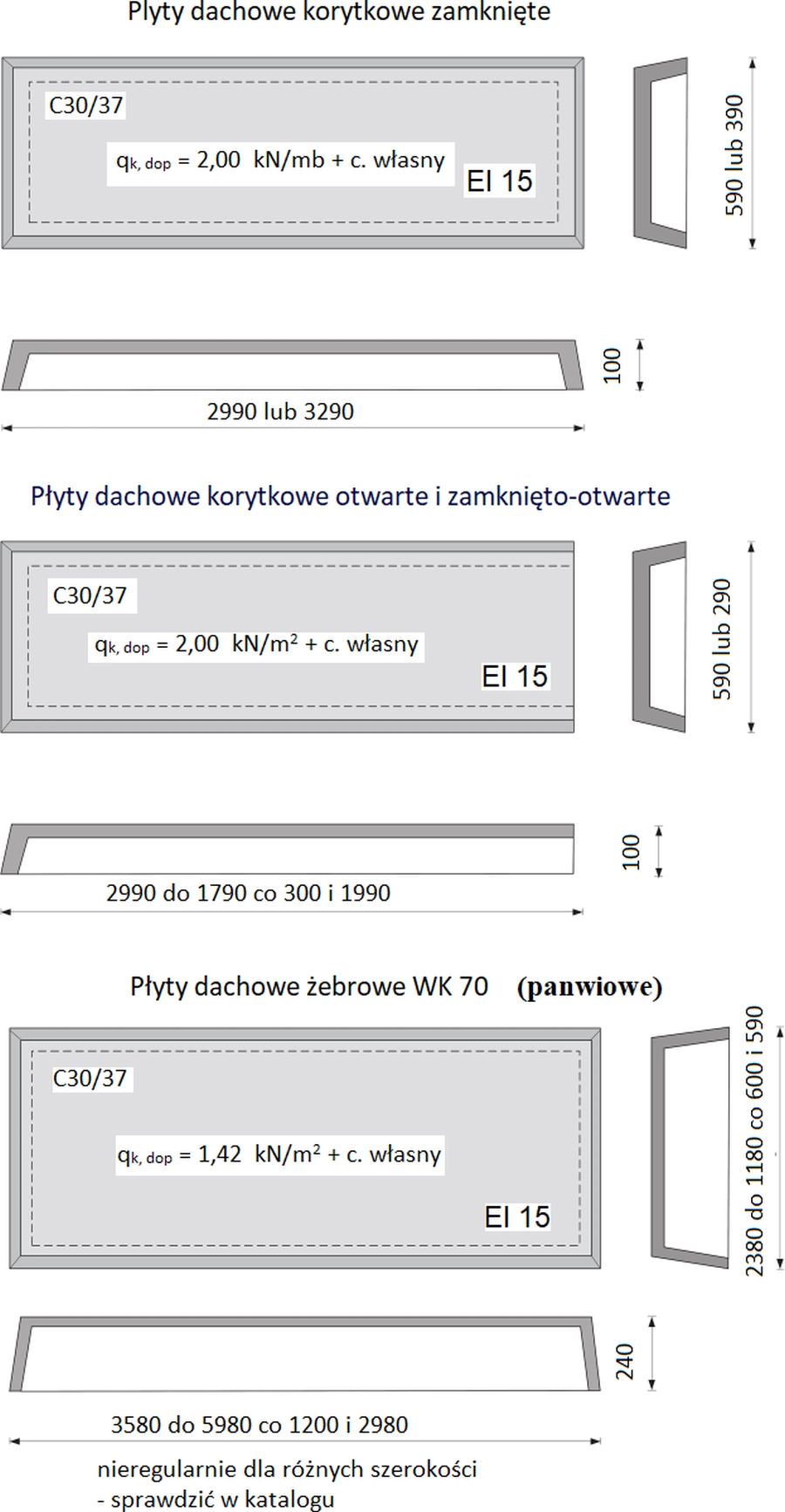
Rys 29 Płyty dachowe korytkowe – panwiowa ( opracowano na podstawie katalogu [30])
Płyty wspornikowo-żebrowe TT
Strunobetonowe płyty TT przeznaczone są do wykonywania stropów i stropodachów o dużym obciążeniu i znacznej rozpiętości. Płyty TT składają się z dwóch żeber na których opiera się zespolona z żebrami płyta stropowa(najczęściej typu Filigran). Obok przenoszenia dużych obciążeń przy znacznej rozpiętości, zaletą prefabrykowanych elementów TT jest możliwość wykonywania otworów w żebrach co pozwala na prowadzenie instalacji bezpośrednio pod płytą. wysokości trapezowych żeber przyjmuje się od 400 do 800 mm, a ich szerokość w podstawie najczęściej 120, 200 i 240 mm . Standardowa szerokość płyty wynosi 2400 mm. Długości płyt mogą sięgać 28 m.
O możliwości zastosowanie określonego typu płyty decyduje wymagana odporność ogniowa, klasa ekspozycji oraz charakter i wielkość projektowanych obciążeń przy zadanej rozpiętości. W doborze płyt należy kontaktować się z działem projektowym producenta. Płyty TT oferuje wielu producentów: Betard, Fabud WKB S.A. Gralbet, Consolis, Pekabex i inni.
Na rys.30 zaprezentowano przykładowo płytę TT o grubości żebra 120 mm produkowane przez Consolis [31].
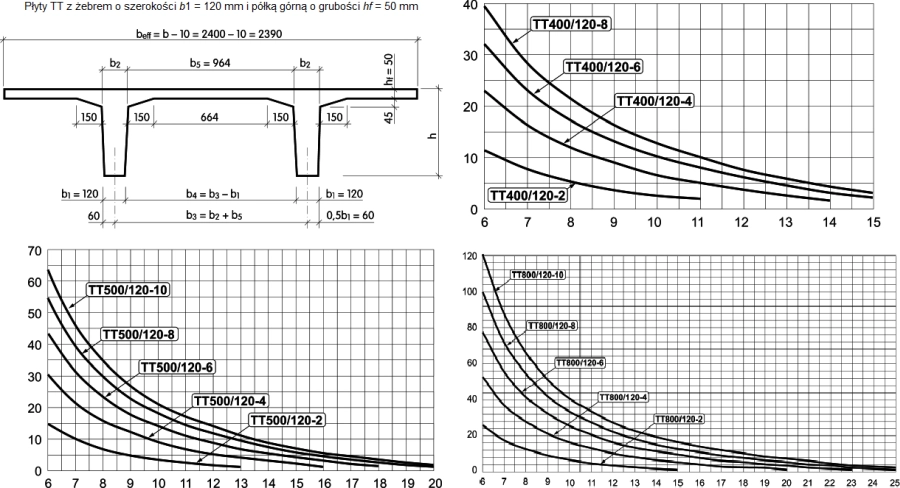
Rys. 30 Przykład płyt TT [31]
W związku z dużą różnorodnością płyt TT oraz zróżnicowaniem pomiędzy producentami projektant przed zastosowaniem powinien sprawdzić dostępność oraz parametry projektowe z katalogu producenta, (np. Betard,) lub w kontakcie z biurem technologicznym producenta.
Strop Smart
Strop Smart w istocie nie wprowadza nowych idei i – jest odmianą stropu z płyt kanałowych. Ma też podobne zalety: szybki montaż, brak nadbetonu, brak stemplowania, dobra izolacyjność dżwiękowa , duże rozpiętości ( tutaj do 10,5 m) , równa powierzchnia dolna sufitu.
Płyty (stropy) gęstożebrowe
Technologia budowy stropów gęstożebrowych jest rozpowszechniona w budownictwie domów jednorodzinnych. W tym obszarze i podobnych „detalicznych” stropy gęstożebrowe często wypierają klasyczny stropy strunobetonowe ze względu na atrakcyjną cenę oraz możliwość wykonania systemem gospodarczym z łatwo dostępnych materiałów, Pustaki stropowe posiadają stosunkowo niewielki rozmiar, a więc ograniczone są koszty transportu na budowę i na kondygnację budynku, a także możemy zrezygnować z zastosowania ciężkich sprzętów budowlanych.
Stropy gęstożebrowe występują w wielu odmianach (np. Teriva, Fert), ale zawsze składają się z gęsto rozstawionych, lekkich stalowo-betonowych lub stalowo-ceramicznych belek wypełnionych pustakami ceramicznymi lub betonowymi.
Stropy gęstożebrowe były poprzednikiem płyt typu Filigran. Strop Filigran stanowi rozwinięcie idei stropów gęsto żebrowych na większe elementy, co przyśpieszyło montaż, ale też ominęło zerzeg wad stropów gęstożebrowych: trudność wykonania stropów o skomplikowanych kształtach; podatność na klawiszowanie; niewielką izolacyjność akustyczna, a przede wszystkim ograniczenie stosowania do niewielkich obciążeń.
Spośród wielu typów stropów gętożebrowych: Klain, Ackermana, Teriva, Ytong, Porotherm czy strop) poniżej omówiono tylko jednego przedstawiciela: strop Fert. Inne typy nie są przedmiotem niniejszego artykułu.
Strop Fert
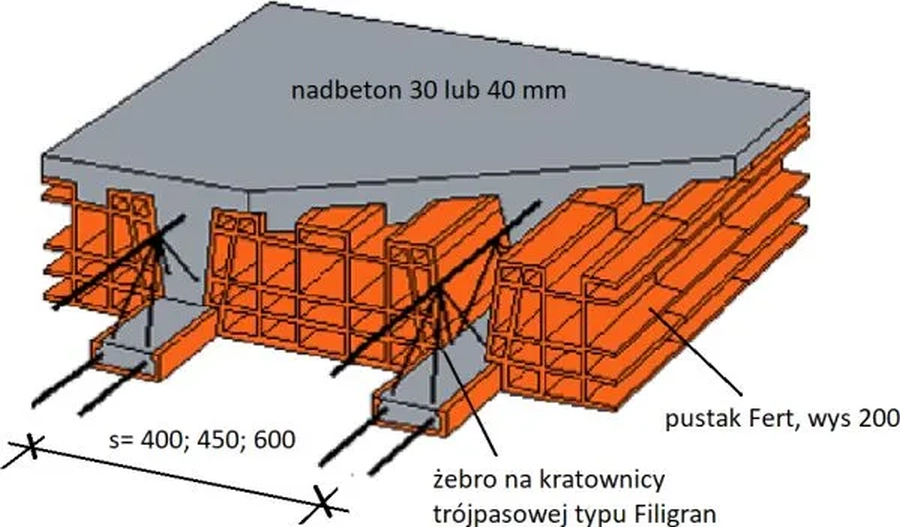
Stropy gęstożebrowe Fert wykonuje się na rozpiętość od 2,7 do 6 metrów. Na rys, 31 pokazano schemat ideowy stropu Fert.
Strop Fert może występować w trzech popularnych rodzajach: Fert 40 – jeden z popularniejszych stropów gęstożebrowych którego cechą charakterystyczną est rozstaw żeber co 400 mm wysokość pustaka 200 mm i nadbeton o grubości 3 0 mmm ; Fert 45 – rozstaw żeber wynosi 450 mm, pozostałe parametry analogicznie jak Fert 40 ; Fert 60 – rozstaw żeber wynosi 600 mm, standardowy pustak Fert o wysokości 200 mm, ale nadbeton o grubości 40 mm.
Płyty ze zbrojeniem rozproszonym (fibrobeton)
Zbrojenie rozproszone z powodzeniem zastępuje klasyczne zbrojenie wkładkami lub siatkami stalowymi. Obecnie włókna stalowe mogą być stosowane jako jedyne zbrojenie lub w połączeniu z klasycznym zbrojeniem w następujących zastosowaniach (na przykładzie Arcelor Mittal): podłogi, mieszkania, elementy konstrukcyjne, prefabrykaty, zastosowania specjalne. We wszystkich tych zastosowaniach zastosowanie włókien stalowych daje zabezpieczenie przed pękaniem skurczowym i pozwala elementowi z betonu zbrojonego włóknami stalowymi osiągnąć pełną ciągliwość, nawet jeśli zwykły beton jest kruchym materiałem.
Wytrzymałość równoważna fibrobetonu
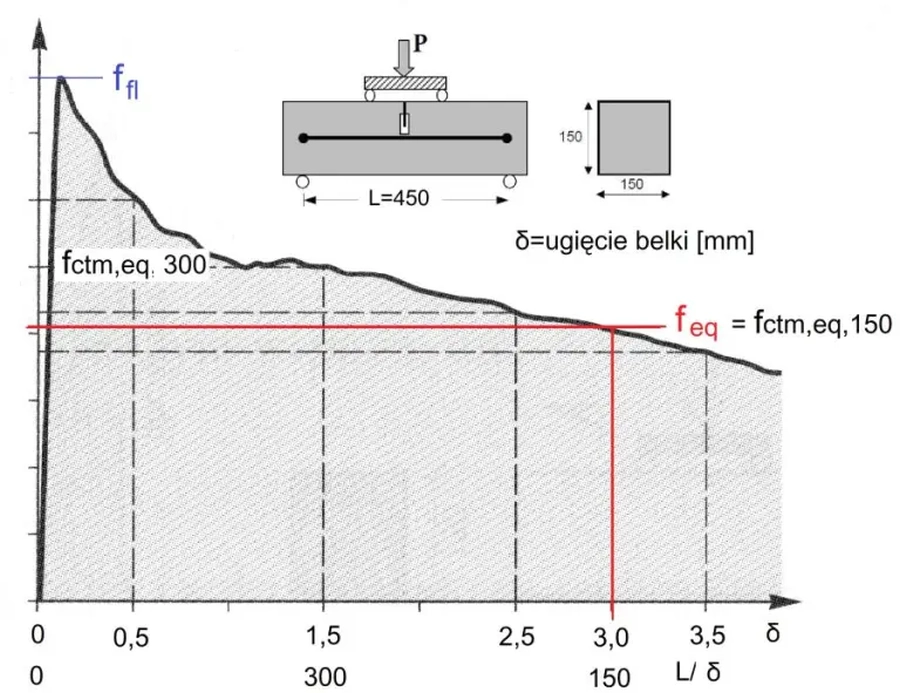
W obliczeniachwytrzymałościowych płyt i belek zbrojonym włóknem rozproszonym w szczególności posadowionych na podłożu odkształcalnym powszechnie stosuje się nowuym pojęciem kategorią wytrzymałościowej, a mianowicie wytrzymałością równoważną $f_{ctm,eq}$.
Wytrzymałość równoważną $f_{ctm,eq}$. wyznacza się w próbie wytrzymałościowej odporności na pękanie przy zginaniu belek normowych, pokazanych na rys. 32.. Podstawowo wytrzymałość równoważna $f_eq$ odpowiada obciążeniu odnotowanym przy ugięciu δ= 3,0 mm , co odpowiada L/δ=150, co zapisuje się f_{ctm,eq,150}. Czasami określa się też wytrzymałość równoważną f_{ctm,eq,300} dla poziomu ugięcia L/δ=300 . Rozpiętość belki próbnej odpowiada trzykrotnej jej wysokości. Zginanie realizuje się dwiema siłami, tak aby na 1/3 rozpiętości belki działał stały moment zginający. Podczas próby mierzy się siłę obciążającą i ugięcia belki. Miarodajne badania równoważnej wytrzymałości na zginanie wymagają wysokiej precyzji pomiaru ugięć m.in. poprzez zastosowanie zamocowania miernika ugięcia w linii wyjściowego położenia osi obojętnej belki.
Znaczący wpływ na wytrzymałość równoważną przy danej klasie betonu belki, ma zawartość włókien stalowych $W_f$, ich smukłość $l/d$ (l, d – długość i średnica włókna) oraz przyczepność do betonu (kształt haczyków), przy czym liczne badania doświadczalne potwierdzają liniową zależność dla zawartości włókien (15 do 40 )kg/m3, którą dla betonu C30/37 można zapisać w postaci [32]:
$$\begin{equation} f_{eq}= 0.73+1.027 \cdot W_f \cdot 10^{-3} \cdot (l/d) \label {21} \end{equation}$$
Zwiększanie zawartości włókien stalowych w fibrobetonie jest ograniczone technologicznie z powodu negatywnego wpływu włókien na konsystencję mieszanki betonowej. Ograniczony jest też wzrost wytrzymałości fibrobetonu wraz ze wzrostem zawartości włókien.
Znaczący wpływ na wytrzymałość równoważną na zginanie ma też klasa betonu, co jest widoczne w tab. 7 sporządzonej na podstawie badań przeprowadzonych w Belgii dla fibrobetonu z włóknami stalowymi haczykowatymi o długości l=60mm i średnicy d=0,75mm.
Tab. 7 Wpływ dozowania włókien stalowych haczykowatych l=60mm, d=0,75mm (RC-80/60-BN) na średnią wytrzymałość równoważną na zginanie $f_{eq}$ przy różnych klasach betonu [33] i średniej wytrzymałości na rozciąganie przy zginaniu $f_{fl}$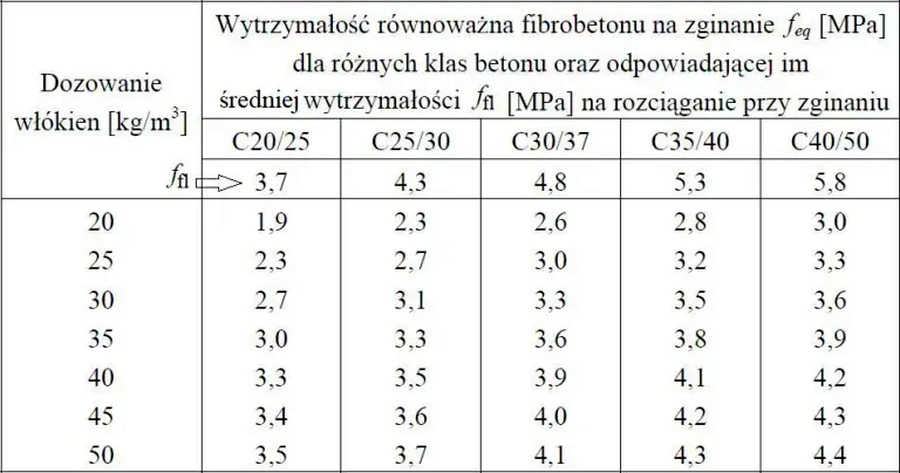
Aby ocenić efektywność zbrojenia włóknami stalowymi wytrzymałość równoważną na zginanie. porównuje się z wytrzymałością na rozciąganie przy zginaniu betonu bez włókien $f_{ctm, fl}$ ( w skrócie $f_{ctm}$) $( \ref{24})$.
Metody obliczania płyt z fibrobetonu
Klasyczna metoda sprężysta
Klasyczne programy komputerowe umożliwiają uzyskanie rozwiązania sprężystego płyty dowolnie obciążonej o dowolnych warunkach brzegowych, w tym położonych na sprężystym podłożu Winklera jedno lub dwukierunkowym. Oszacowania uzyskane z programów są znacznie dokładniejsze od analitycznych oszacowań metody Westergaarda [34]. Metodę tę należy uznać za historyczną i niezalecaną. Nie zalecane są równiż inne klasyczne metody analizy półprzestrzeni sprężystej i podłoża uwarstwionego: Boussinesqa, Odemarka, Burmistera. Zalecna jest metoda załomów plastycznych, którą szczególowo opisano w dalszej części artykułu.
Klasyczna metoda spręzysta jest punktem wyjścia do mtody linii załomów, a w szczególnosci do zdefniowania kilku pojęć wskazujących na konytnuację metod analizy płyt.
Warunek klasycznej metody sprężystej można zapisać w postaci:
$$\begin{equation} M_{Ed,el } \le M_{Rd.el} \label{22}\end{equation}$$
gdzie:
$M_{Ed,el}$ obliczeniowy, płytowy moment zginający uzyskany z rozwiązania płyty traktowanej jako liniowo sprężysta.
a nośność sprżysta $M_{Rd,el}$ płyty wynosi:
$$\begin{equation} M_{Rd,el}= W_{el} \cdot f_{ctm, fl} \label{23} \end{equation}$$
gdzie:
Wskaźnik wytrzymałości sprężystej przekroju płyty o szerokości jednostkowej, wynosi $W_{el} = \cfrac {h^2}{6} $.
Wytrzymałość betonu na rozciąganie przy zginaniu $f_{ctm, fl}$ , przyjmuje się z zależności:
$$\begin{equation} f_{ctm,fl} = f_{ctm} \cdot (1,6 -h/1000) \label{24} \end{equation}$$
$f_{ctm}$ -średnia wytrzymałość betonu na rozciąganie osiowe,
h- wysokość przekroju ( w tym przypadku grubość płyty).
Nośność sprężysta ($\ref{23}$) jest tylko częścią nośności płyty zbrojonej włóknem rozproszonym i na użytek obliczania kompozytowych płyt fibrobetnowych jest oznaczana jako nośność (-):
$$\begin{equation} M_{R(-)} = M_{Rd,el} \label{25} \end{equation}$$
Podejście sprężyste jest bardzo konserwatywne. Liczne badania doświadczalne wymienione w pracy [35] wskazują, że podejście sprężyste (także wzory Westergaarda) dają znaczne (3 do 4,5 raza) niedoszacowanie nośności płyty zbrojonej włóknami rozproszonymi, to znaczy prowadzą do nieuzasadnionego ekonomicznie znacznego przezbrojenia płyty.
Metoda plastyczna (linii załomów)
Dwukrotnie bardziej zbliżone do badań doświadczalnych wyniki można uzyskać stosując metodę nośności granicznej/plastycznej (linii załomów), o której poniżej. Zasadnicza różnica w nośności fibrobetonu i betonu bez włókien wynika z ciągliwości materiału zbrojonego włóknami, umożliwiającej powstanie przegubów plastycznych w miejscach rys i redystrybucję momentów zginających.
Metoda linii załomów w zastosowaniu do płyt fibrobetonowych
Teoria linii załomów płyt jest przedmiotem artykułu Nośność plastyczna konstrukcji . Zasady tam wyłożone stosujemy również do płyt żelbetowych.
Ograniczeniem stosowalności metody plastycznej (linii załomów) wymiarowania posadzek fibrobetonowych jest wymaganie takiej efektywności zbrojenia włóknami, aby spełniony był warunek $f_{ctm,eq}$ > 0,30 $f_{ctm, fl}$,
gdzie $f_{ctm,fl}$ jest wartością naprężenia rozciągającego odpowiadającego maksymalnej sile zginającej podczas testu z rys. 30.
Promień względnej sztywności Westergaarda oraz współczynnik $\lambda$
Za miarę sztywności płyty zbrojonej włóknem rozproszonym przyjmuje się tzw promień względnej sztywności płyty $l$ wyznaczony ze wzoru
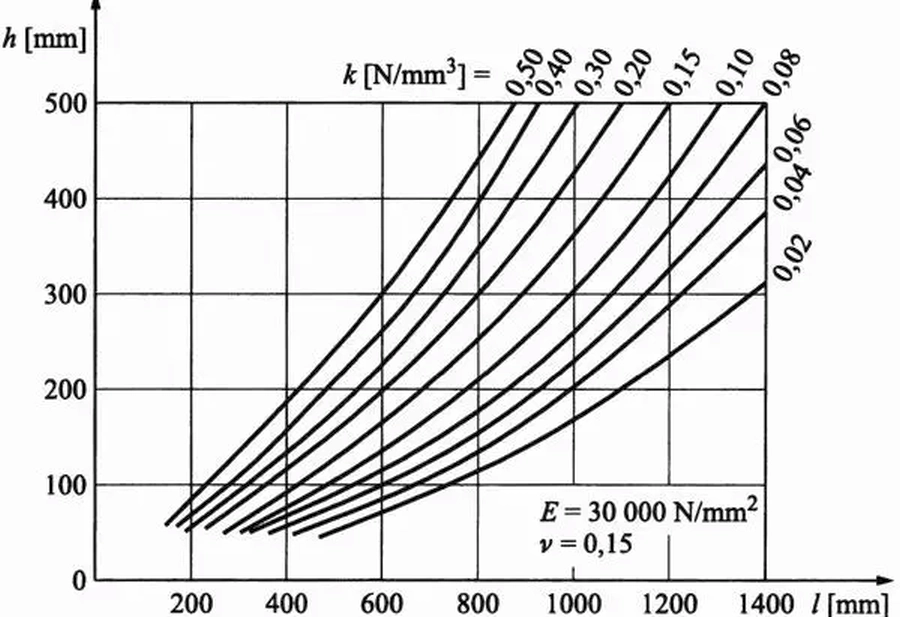
$$\begin{equation} l=\sqrt[4]{\cfrac{E_{cm} h^3}{12(1-\nu^2)k}}=k_{\nu} \cdot \sqrt[4]{\cfrac{E_{cm} h^3}{12 k}} \label {26} \end{equation}$$
gdzie:
$$\begin{equation} k_{\nu}=\cfrac {1}{\sqrt[4]{1-\nu^2}} \label {27} \end{equation}$$
Promień względnej sztywności płyty można wyznaczyć z nomogramu – rys. 31 dla sztywności podłoża $k = [ 0,02 \div 0,5 ] \, N/mm^3 \quad = [20 \div 500 ] \, kN/(m^2 mm) $. (W praktyce konstrukcyjnej współczynnik sprężystości podłoża gruntowego najczęściej podaje się w jednostkach $ kN/(m^2 \cdot mm)$
W Eurokod 2 współczynnik Poissona betonu przyjęto o wartości $\nu=0.2$ dla którego $ k_{\nu}$ ($\ref{27}$) = 1,01026.
Nomogram sporządzono dla $\nu=0,15$ dla którego $k_{\nu}=1, 0057$. Dla betonu z $\mu=0.2$, czyli wartość promienia dczytaną z nomogramu należy powiększyć mnożnikiem 1,005.
W wyrażeniach na wytężenie lub nośność płyty występuje też współczynnik $\lambda$ zdefiniowany jako
$$\begin{equation} \lambda=\sqrt[4]{\cfrac{3k}{E_{cm} h^3}}=\cfrac{k_{\nu}}{ 2 l } \label{28} \end{equation}$$
Nośność płyty fibrobetonowej nie zbrojonej prętami
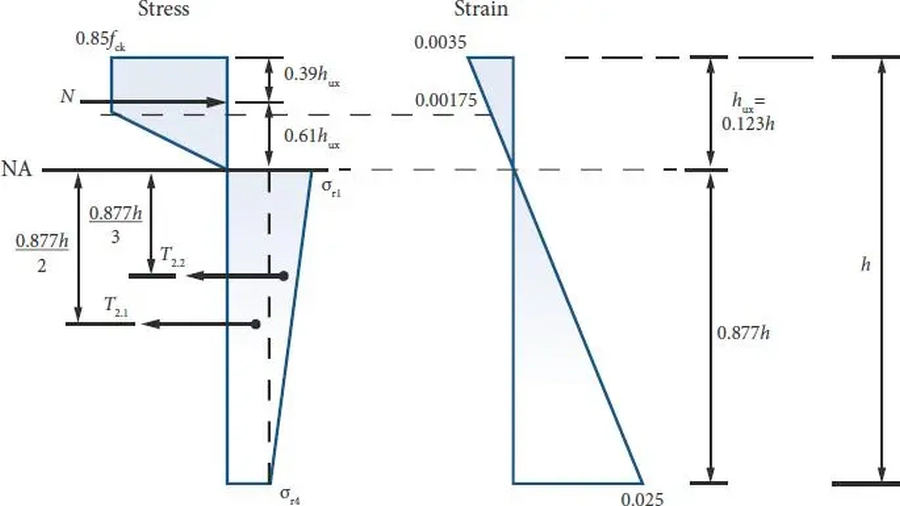
Blok naprężeń i odkształceń w przekroju płyty zbrojonej fibrobetonem bez zbrojenia prętami pokazano na rys. 34.
Nośność dolnego włókna przekroju (moment dodatni) (+) wynosi [36], rys. 6.2:
$ M_{R(+)}= h^2 \cdot (0,16 \sigma_{r1}+ 0,28 \sigma_{r4})$
gdzie:
$\sigma_{r1}=0,45 f_{ctm,eq,50}$, $f_{ctm,eq,50}$ = naprężenia w próbce przy ugięciu 0,5 mm
$\sigma_{r4}=0,37 f_{ctm,eq,350}$, $f_{ctm,eq,350}$ = naprężenia w próbce przy ugięciu 3,5 mm
Po podstawieniu wartości pośrednich otrzymamy formułę:
$$\begin{equation} M_{R(+)}= W_{el} \cdot (0,4320 \cdot f_{ctm,eq,50} + 0,6438 \cdot f_{ctm,eq,350}) \label {29} \end{equation}$$
Przy założeniu, że $f_{ctm,eq,50}=f_{ctm,eq,350}=f_{ctm,eq}$ mamy:
$$\begin{equation} M_{R(+)}= 1,076 \cdot W_{el} \cdot f_{ctm,eq} \approx W_{el} \cdot f_{ctm,eq} \label{30} \end{equation}$$
Nośność płyty fibrobetonowej zbrojonej hybrydowo (również prętami)
Nośność płyty fibrobetonowej zbrojonej hybrydowo (również prętami, kołkami lub sitakami) omówiono w opracowaniu [36]. Podano tam również nośności na ścinanie , w tym przy przebiciu.
Mechanizmy zniszczenia plastycznego płyty z fibrobetonu i nośności płyty
Rozpatruje się trzy przypadki położenia siły pokazane na rys,.35: wewnątrz płyty, na brzegu i w narożu.
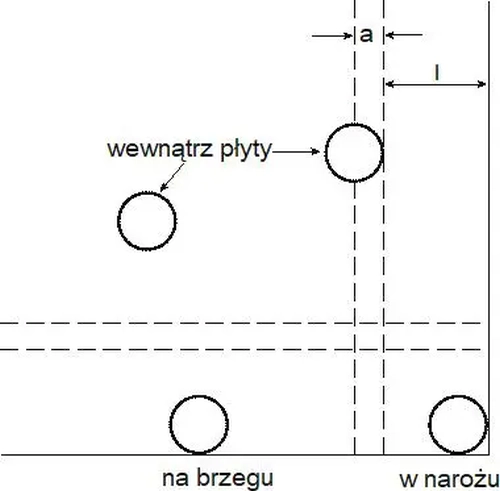
Rys. 35 Trzy przypadki położenia siły na płycie z fibrobetonu [36], rys. 7.3
Pojedyncza siła skupiona
W przypadku pojedynczej siły wewnątrz płyty mechanizmy zniszczenia plastycznego pokazano na rys.36.
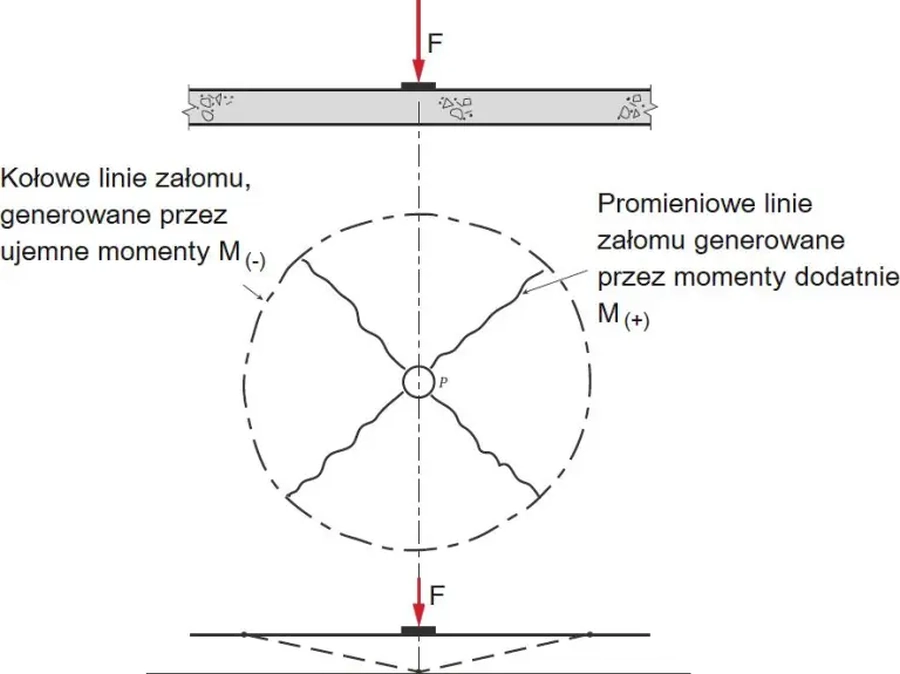
Rys. 36. Mechanizm zniszczenia płyty z fibrobetonu pod jedną siła skupioną [36], rys. 7.2.
Poniżej wprowadzono oznaczenie:
$$\begin{equation} \Sigma M_R=[ M_{(R+)}+M_{(R-)} ] \quad (\approx W_{el}\cdot(f_{ctml,fl}+f_{ctml,eq})) \label{31} \end{equation}$$
gdzie uwzględniono zależności na:
$M_{(R-)}$ nośność płyty, mierzona ujemnym (rozciągającym górne włókna płyty) momentem tak jak dla płyty bez zbrojenia – wzór $( \ref {25})$,
$M_{(R+)}$ nośność płyty, mierzona dodatnim (rozciągającym dolne włókna płyty) momentem tak jak dla płyty ze zbrojeniem rozproszonym – wzór $( \ref {29})$.
Dla pojedynczej siły (rys.34) nośność płyty $F_{R1}$ mierzona siłą obciążającą $F$ zależy od zastępczej średnicy docisku $a$ a także promienia względnej sztywności $l$ i wynosi [36]:
- dla siły wewnątrz (w) płyty nośność $F_{R1w}$:
$$\begin{equation} F_{R1w} = \begin {cases}
2 \pi \Sigma M_R, & \text {dla $a/l=0$} \\
\cfrac {4 \pi} {1- a/(3l)} \cdot \Sigma M_R , & \text {dla $a/l \ge 0,2$ }
\end {cases} \label{32} \end{equation}$$
- dla siły na krawędzi (k) lub w narożu (n) płyty (rys.16) nośność $(\ref{32})$ należy zredukować zgodnie z zależnością
$$\begin{equation} F_{R1*} =\alpha_{*} \cdot F_{R1w} \label{33}\end{equation}$$
gdzie współczynnik redukcyjny $\alpha_{*} (*=k,n)$ wynosi:
# dla siły na krawędzi (*=k) :
$$\begin{equation} \alpha_{k}= \begin {cases}
\alpha_{k0} , & \text {dla $a/l=0$} \\
\cfrac {1-a/(3l)}{1-2a/(3l)} \cdot \alpha_{k0} , & \text {dla $a/l \ge 0,2$ }
\end {cases} \label{34}\end{equation}$$
gdzie $\alpha_{k0}= \cfrac{1}{4}+\cfrac{M_{R(-)}} {\pi \cdot \Sigma M_R} $
# dla siły w narożu (*=n) płyty
$$\begin{equation} \alpha_{n}= \begin {cases}
\alpha_{n0} , & \text {dla $a/l=0$} \\
\cfrac {1-a/(3l)}{1-a/l} \cdot \alpha_{n0} , & \text {dla $a/l \ge 0,2$ }
\end {cases} \label{35} \end{equation}$$
gdzie $\alpha_{n0}= \cfrac{M_{R(-)}} {\pi \cdot \Sigma M_R} $
Dla pośrednich wartości $a/l$ można prowadzić interpolację.
Jeżeli odległość $x$ pomiędzy przyłożonymi siłami jet mniejsza od podwójnej grubości płyty h (x<2h), to przyjmuje się, że siły są zlokalizowane w tym samym miejscu.
Jeśli siła skupiona jest rozłożona w prostokącie o bokach $c_x$ x $c_y$ , to zastępczy promień przyłożenia siły $a$ wyznaczony z równości pól powierzchni przyłożenia:
$$\begin{equation} (c_x \cdot c_y)=(\pi (2a)^2/4) \to a= \sqrt {\cfrac{ c_x \cdot c_y}{ \pi} } \label{36} \end{equation}$$
Dwie siły skupione
W przypadku dwu lub czterech sił skupionych mechanizmy zniszczenia plastycznego przyjmuje się według rys. 37
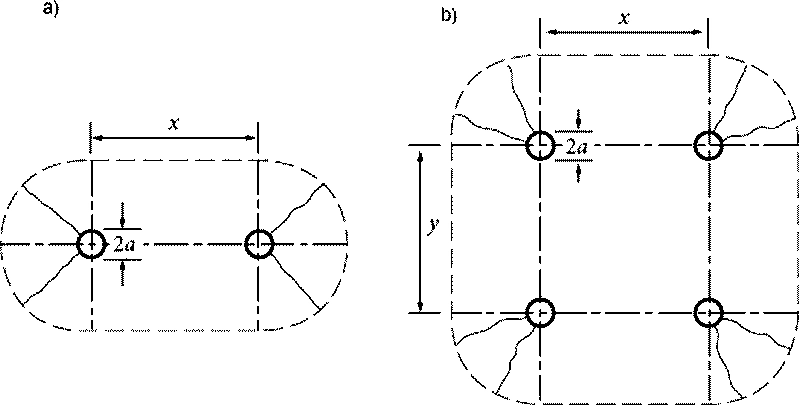
Rys. 37 Mechanizm zniszczenia dla: a) dwóch, b) czterech sił skupionych [36], rys. 7.7.
Dla dwóch sił rozstawionych w odległości $x <2h$ stosujemy podejście jak dla pojedynczej siły o zsumowanej wartości z obu sił.
Przy $x\ge 2h$ nośności wynoszą:
$$\begin{equation} F_R= \begin {cases}
\left [ 2 \pi+\cfrac{1,8 x)}{l} \right ] \cdot \Sigma M_R, & \text {dla $a/l=0$} \\
\left [ \cfrac{4 \pi}{1-a/(3l)}+\cfrac{1,8 x}{l- a/2} \right ] \cdot \Sigma M_R , & \text {dla $a/l \ge 0,2$ }
\end {cases} \label{37}\end{equation}$$
Z wyrażeń tych wynika, że przy zbliżających się siłach obciążenie graniczne zbliża się do sumy granicznych obciążeń od pojedynczych sił.
Gdy podwójna siła zbliży się do krawędzi płyty, wówczas powinna być zredukowana współczynnikiem $(\ref {34})$ , a gdy stoi w narożu płyty, współczynnikiem $(\ref {35})$.
Cztery siły skupione
Dla czterech sił rozstawionych w odległości $x $ oraz $y$ nośność jest mniejszą z wartości: 1) suma nośności czterech sił pojedynczych, 2) suma nośności dwóch sił podwójnych , lub 3):
$$\begin{equation} F_R= \begin {cases}
\left [ 2 \pi+\cfrac{1,8 (x+y)}{l} \right ] \cdot \Sigma M_R, & \text {dla $a/l=0$} \\
\left [ \cfrac{4 \pi}{1-a/(3l)}+\cfrac{1,8(x+y)}{l- a/2} \right ] \cdot \Sigma M_R , & \text {dla $a/l \ge 0,2$ }
\end {cases} \label{38} \end{equation}$$
W przypadku ustawienia dwóch sił na brzegu płyty stosuje się współczynnik redukcyjny $(\ref {34})$ jak dla pojedynczej siły.
Obciążenie równomiernie rozłożone
W przypadku obciążenia płyty nieustalonym (losowym) układem równomiernie rozłożonego obciążenia, maksymalny moment zginający w płycie jest spowodowany:
a) przez obciążenie o szerokości π / 2λ pokazane na rys. 40a dla momentu dodatniego, b) przez dwa pasma o szerokości π / λ pokazane na rys. 40b dla momentu ujemnego. Parametr $\lambda$ zdefiniowano wzorem $(\ref{28})$:
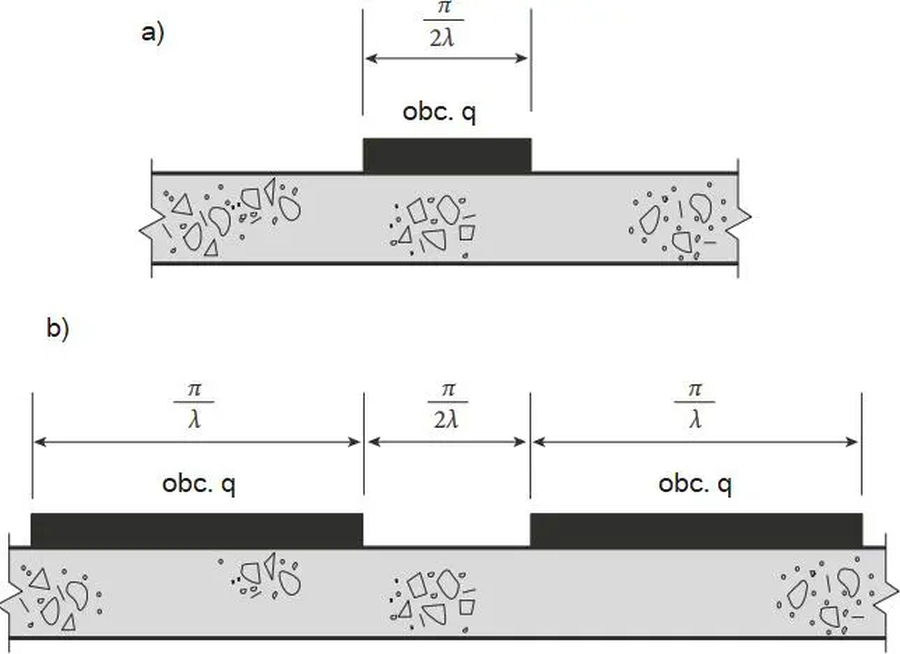
Rys. 38 Układ obciążenia równomiernego realizujący maksymalny moment: a) dodatni, b) ujemny [36], rys. 7.10
Maksymalny moment ujemny (rozciągający górne włókna) wystąpi pomiędzy pasmami obciążenia jak na rys. 40b , a nośność płyty wyniesie:
$$\begin{equation} q_R=5,95 \cdot \lambda^2 \cdot M_{R(-)} \label{39}\end{equation}$$
gdzie $M_{R(-)}$ jest nośnością płyty bez zbrojenia $(\ref {25})$.
Obciążenie liniowe
W przypadku obciążenia liniowego (np od ściany) nośność płyty fibrobetonowej wynosi
$$\begin{equation} q_R=4 \cdot \lambda\cdot M_{R(-)} \label {40} \end{equation}$$
Równanie $(\ref{40})$ ma zastosowanie do obciążeń liniowych oddalonych krawędzi płyty lub dylatacji. W przypadku gdy obciążenie liniowe znajduje się w sąsiedztwie swobodnej krawędzi, to nośność wynosi
$q_R= 3 \lambda M_{R(-)}$
zwiększając się do $q_R= 4 \lambda M_{R(-)}$, gdy obciążenie jest oddalone od krawędzi o 3 / λ. Dla dylatacji o minimalnej zdolności przenoszenia obciążenia 15%, nośność wzrasta do tej wartości już w odległości 1 / λ – patrz rys 41.
Wynika to z faktu, że w przypadku obciążenia liniowego odległego od krawędzi, zerowego momentu wystąpi w odległości około 1 / λ od obciążenia.
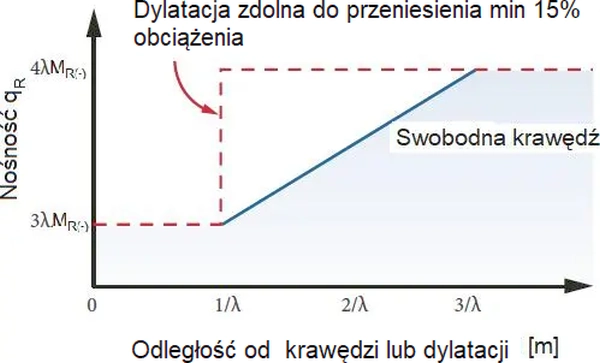
Rys. 39 Zmniejszenie nośności płyty wraz ze zbliżaniem się obciążenia do krawędzi [36], rys. 7.9
Pas przy krawędzi płyty w którym nie powinno się stawiać obciążeń ze względu zmniejszenie nośności płyty ma szerokość
$$\begin{equation} L_{pas}=3/ \lambda= \cfrac{6 l}{k_\mu } \label {41} \end{equation}$$
Wartości charakterystyczne a obliczeniowe i warunek nośności
Powyżej podano wyrażenia na wartości charakterystyczne nośności $F_k=F_R$, $q_k=q_R$
Warunek nośności
$$\begin{equation} F_{Ed} \le F_{Rd} \label {42} \end{equation}$$
odnosi się do obliczeniowych nośności, które uzyskuje się z nośności charakterystycznych przez zmniejszeniem współczynnikiem materiałowym
$F_d=\cfrac{F_k}{\gamma_c}$
przy czym dla fibrobetonu należy przyjmować $\gamma_c=1,5$
Kombinacja obciążeń
Na rys. 40 pokazano najbardziej niekorzystne ustawienie podnośnika widłowego w stosunku do regałów. Odległość H należy określić na podstawie charakterystyk geometrycznych konkretnych regałów i wózków. W przypadku braku danych można przyjąć, że H=R/2, gdzie R jest rozstawem kół podnośnika.
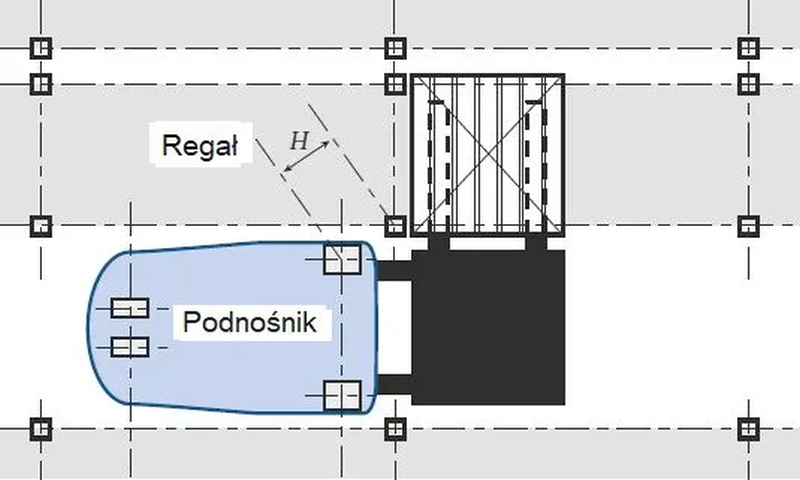
Rys. 40. Najniekorzystniejsze ustawienie obciążeń skupionych [36], rys. 7.6
Nośność w kombinacji należy określać z uwzględnieniem współczynników jednoczesności obciążeń kombinacyjnych zgodnie z [37].
Przebicie płyty fibrobetonowej
Przebicie płyty fibrobetonowej określa się zgodnie z ogólnymi zasadami opisanymi w artykule Przebicie płyty żelbetowej. Odległość obwodu krytycznego od krawędzi siły przebijającej przyjmuje się standardowo 2d, gdzie d jest efektywną wysokością przekroju. W przypadku przekroju zbrojonego tradycyjnie jest to odległości od osi zbrojenia dolnego do górnej krawędzi płyty. W przypadku zbrojenia włóknami rozproszonymi przyjmuje się
$$\begin{equation} d=0,75 h \label{43}\end{equation}$$
gdzie h- jest całkowitą grubością płyty
Dla tak określonej wysokości efektywnej przekroju maksymalna wytrzymałość betonu na ścinanie przy przebiciu $v_{Rd,max} oraz maksymalną nośność na przebicie płyty fibrobetnowej $F_{Rd,max}$
$$\begin{equation} F_{Rd,max}=v_{Rd,max} \cdot u_0 \cdot d \label {44} \end{equation}$$
gdzie $u_0$ jest obwodem wokół siły przebijającej o szerokościach efektywnych zdefiniowanych na rys. 43.
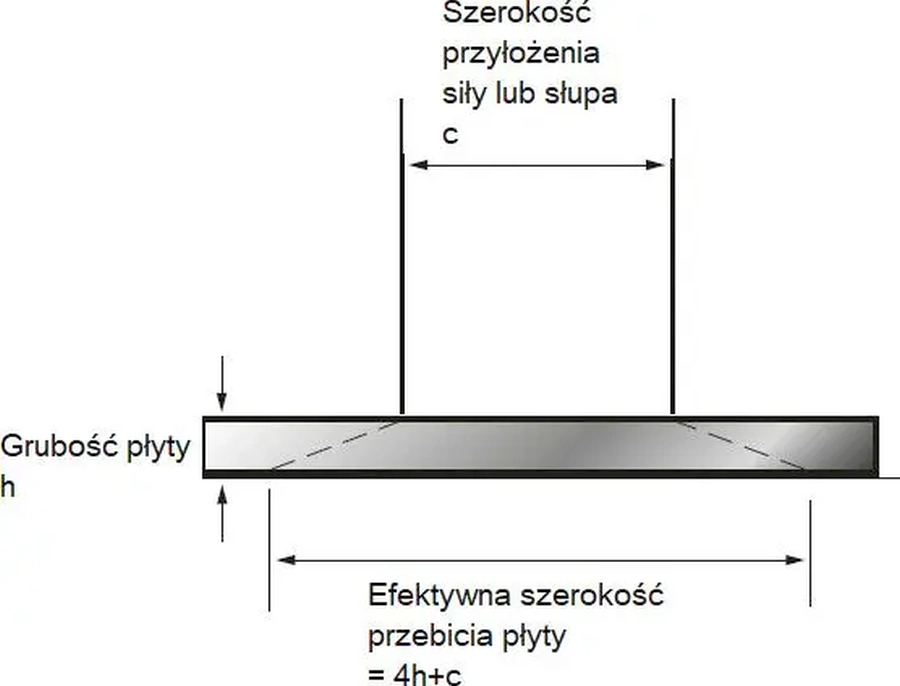
Rys. 41 Efektywna szerokość siły przebijającej fibrobeton [36], rys. 7.4
Nośność płyty fibrobetonowej na przebicie jest sumą nośności płyty betonowej nie zbrojonej na ścinanie o wytrzymałości granicznej $v_{Rd,c}$ i nośności zbrojenia rozproszonego o wytrzymałości granicznej $v_f$:
$$\begin{equation} F_{Rd,p}=(v_{Rd,c}+v_f) \cdot u_1 \cdot d \label {45} \end{equation}$$
gdzie: $v_{Rd,c} $, i długość obwodu kontrolnego $u_1$ wyznacza się standardowo zgodnie zasadami podanymi w artykule ,
a wytrzymałość zbrojenia włóknami rozproszonymi na ścinanie przy przebiciu wyznacza się z zależności
$ v_t= 0,015 \cdot ( f_{ctm,eq,50}+ f_{ctm,eq,150} + f_{ctm,eq,250} +f_{ctm,eq,350} ) \cdot d $
Ponieważ dla wytrzymałości równoważnych zachodzi:
$ f_{ctm,eq, 50} < f_{ctm,eq, 150} < f_{ctm,eq, 250} < f_{ctm,eq, 350} $, więc przy braku danych z badań włókna można przyjąć że średnią szeregu jest $f_{ctm,eq}$, a suma szeregu wynosi $4 \cdot f_{ctm,eq}$, czyli
$$\begin{equation} v_t = 0,06 \cdot f_{ctm,eq} \cdot u_1 \cdot d \label {46}\end{equation}$$
Siłę przeciwstawiającą się przebiciu (korzystną), a pochodzącą z odporu gruntu określa się zgodnie z rys. 44.
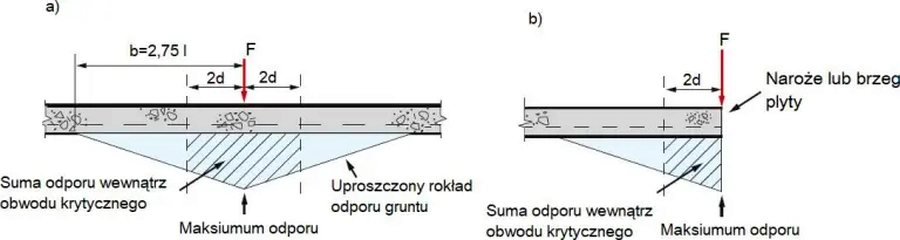
Rys. 42 Szkic do określenia odporu gruntu przy przebiciu płyty: a) wewnątrz ,b) przy brzegu [36], rys. F1-F2
W przypadku siły wewnętrznej i narożnej (odpowiednio rys.22a i rys.22b) sumaryczny odpór gruntu wynosi [36]:
$$\begin{equation} R_{odpór}= \beta \cdot (d/l)^2 \cdot F \end{equation}$$
gdzie: $\beta=1,4$ dla siły wewnętrznej i $\beta=2,4$ dla siły narożnej.
W przypadku gdy siła działa poprzez sztywny stempel (na słup o wymiarach (c_x × c_y), to całkowity ospór wgruntu wynosi [36]:
$$\begin{equation} R_{odpór, sztywny}= \beta \cdot (d/l^2) \cdot F \cdot (c_x+d_y) \label{47} \end{equation}$$
gdzie:
dla siły wewnętrznej : $\beta=0,47$ i $ d_y=$c_y$,
dla siły narożnej : $\beta=0,8$ i $ d_y=$1\cdot c_y$.
Wybrane typu zbrojenia rozproszonego
Spośród wielu typów zbrojenia rozproszonego przedstawimy dwa: DRAMIX i ArcelorMittal
Włókna Dramix
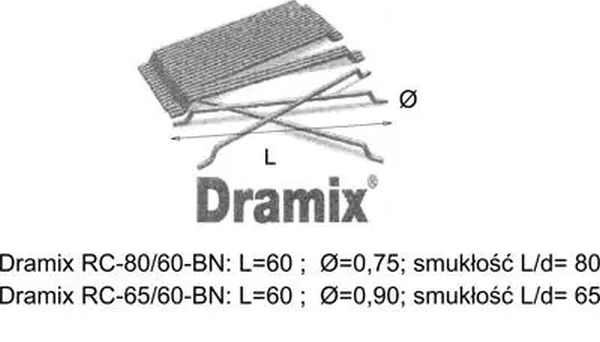
Na rys. 45 przedstawiono najczęściej stosowane rodzaje włókna typu Dramix.
W tab. 10 zestawiono własności wytrzymałościowe fibrobetonu zbrojonego włóknem Dramix 80/60. Podano wytrzymałość równoważna fibrobetonu zbrojonego włóknem RC-80/60-BN, przy czym, $f_{ctm,eq,150}$ jest średnią wytrzymałością równoważną dla ugięcia 1,5 mm, a $f_{ctm,eq,300}$ dla ugięcia próbki 3,0 mm. W taveli zasygnalizowano również podawane przez producenta włókna wytrzymałości na rozciąganie przy zginaniu $f_{ctml,fl}$ betonu klasy C20/25 do C40/45.
Tab.10 Własności wytrzymałościowe fibrobetonu zbrojonego włóknem Dramix 80/60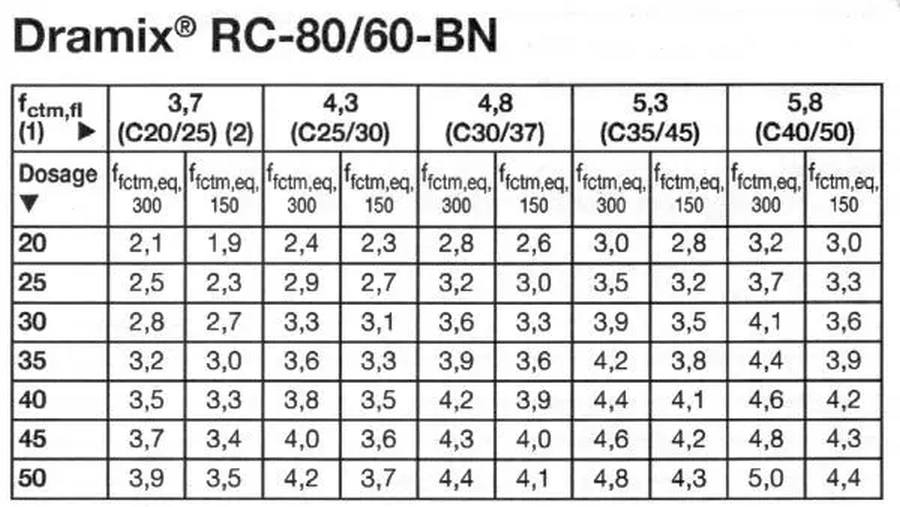
Z porównania wytrzymałości równoważnej betonu zbrojonego włókna Dramix RC- 80/60-BN (tab. 10) z badaniami prowadzonymi w Belgii (tab. 7) wynika zgodność, ale nie dotyczy to każdego włókna i w przypadku zastosowania innych rodzajów włókien należy sprawdzić wyniki badań, które powinien wyspecyfikować producent włókien.
Włókna ArcelorMIttal
Nośności fibrobetonu zbrojonego włóknami produkcji Arcelor Mittal są podawane w wartości obciążenia punktowego $q_R$ w kombinacji z ruchem kołowym 6 kN/m2. Samodzielne działanie obciążenia ciągłego równomierne rozłożonego ( nawet do wartości $Q_r= 80 kN/m^2$) nie decyduje o nośności posadzki ułożonej na poprawnie zagęszczonym podłożu gruntowym. Na rys. 44 zilustrowano przypadki wymiarujące płyty posadzek na gruncie
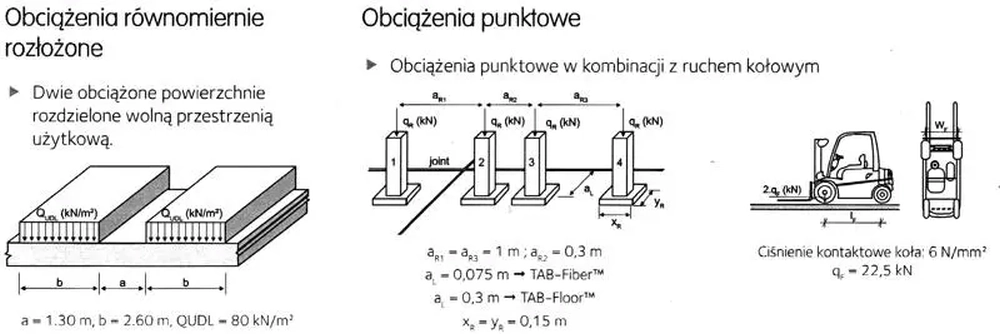
Rys. 44. Przypadki obciążeń posadzek zbrojonych włóknami rozproszonymi [38]
Dobór posadzki jest dokonywany z nomogramów pokazanych na rys. 45.
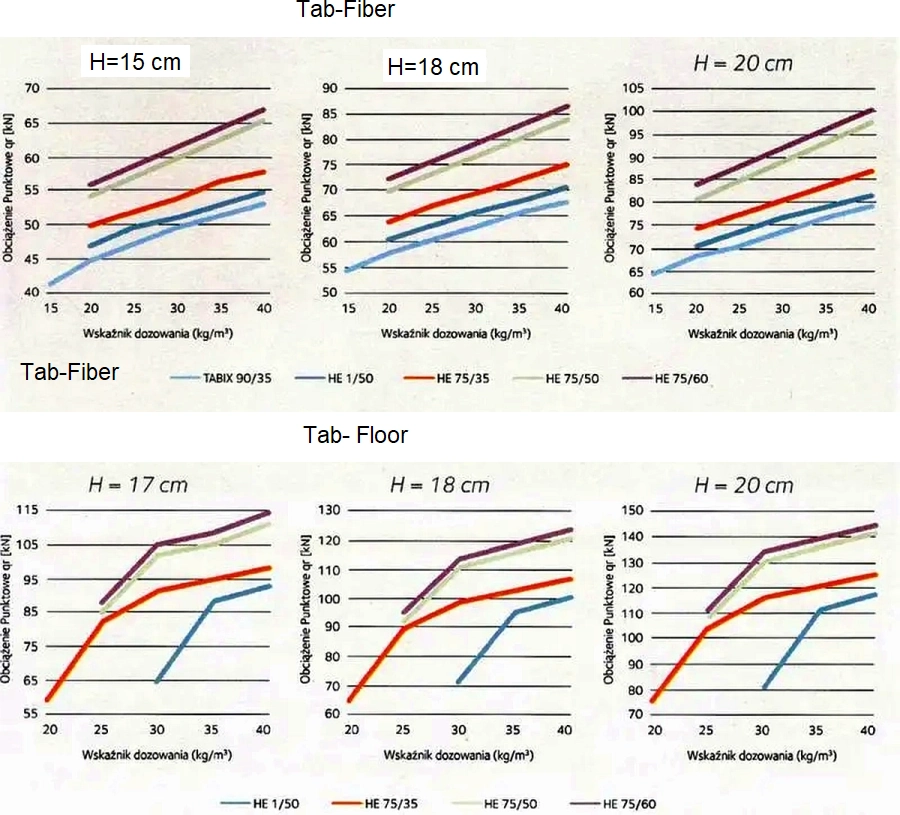
Rys.45. Nomogramy do projektowania posadzek zbrojonych włóknami ArcelorMIttal: TABIX i HE [38]
Podstawowe dwa rodzaje posadzek przemysłowych zbrojonych włóknami ArcleorMittal, to:
TAB-Fiber – posadzka nacinana: beton C25/30; odległość między nacięciami 6 m; podbudowa : kruszywo z 1x folia PV
TAB-Floor – posadzka bezspoinowa: beton C25/30; odległość między dylatacjami 30 m; podbudowa : kruszywo z 2x folia PV
Posadzki Arcelor Mittal należy ułożyć na zagęszczonym podłożu gruntowym :
stosunek modułów sprężystości E2/E1 <2,2, moduł sprężystości wtórny: E2= 100 MN/mm2
Nomogramy (rys. 45) sporządzono dla współczynnika sprężystości podłoża k=0,083 N/mm3
Płyta na podłożu sprężystym zbrojona siatką
W przypadku płyty ułożonej na podłożu odkształcalnym i zbrojonej siatką blisko dolnej powierzchni nośność płyty wynosi
$$\begin{equation} M_{R(+) siatka} = 0,95 \cdot A_s f_y \cdot d \label{48} \end{equation}$$
gdzie:
$A_s$, $f_y$ – powierzchnia i wytrzymałość stali
$d$ – efektywna wysokość płyty.
Współczynnik 0.95 jest zastosowany, ponieważ zwykle zbrojenie jest małe.
Płytę z siatką tylko blisko górnej powierzchni, należy traktować jak niezbrojoną.
Przykłady rachunkowe
Przykład 1 [ Projekt płyty stropu żelbetowego]
Zaprojektować płaski strop żelbetowy w układzie słupowo – płytowym o wymiarach:
3 pola o długości $l_x=9 \,m$ x 2 nawy o szerokości $l_y=9 \,m$
obciążony zastępczym obciążeniem równomiernym:
stałym $ G=1,5 \, kN/m^2$ (oprócz ciężaru własnego płyty),
zmiennym $Q= 3 \, kN/m^2$
i dla wymaganej wytrzymałości ogniowej REI 120
Płytę wykonano z żelbetu ( beton – stal) C30/37 – B500
Długość efektywna stropu i grubość płyty
z tab. 3 dla płyty z 2-ma nawami odczytujemy największy współczynnik długości efektywnej $s=0,962$ (dla skrajnych pól), więc
$l_{ef}=0,962 \cdot 900=866 \, cm$
Przyjęto grubość płyty
$h=866 \, cm /30=290 \, mm$
Sprawdzenie warunków pożarowych
Z tab.5 dla płyty w układzie płytowo słupowym i dla odporności ogniowej REI 120, mamy
min $h/a$=$200/35$.
Spełniony jest wymóg minimalnej grubości płyty.
Otulenie osiowe dolne i górne przyjmujemy $a_d=a_g =a= 35 \, mm$
Siatka podstawowa zbrojenia
Wysokość efektywna płyty wynosi
$h_{eff}=d= h-a= 290-35= 255 \, mm$
Z tab.4 dla żelbetu C30/37-B500 i zbrojenia o średnicy #12 odczytano
$N_{min,brittle} = (3,83+3,98)/2 = 3,91 \, szt/m (gdzie N=3,83 dla d= 250 mm, a N=3,98 dla d= 260 mm)
Przy ułożeniu prętów w pasie płyty o szerokości $s_{plate}= 4,5 \, m$ maksymalny rozstaw prętów w siatce podstawowej wynosi:
$(\ref{7}) \to$ $ s_{max.brittle}= \cfrac{1}{3,91 – 1/4,5}= 0,271 \,m = 271\, mm$
Przyjęto podstawowy rozstaw prętów zbrojeniowych #12 $s_{basic} = 250 \, mm$ (4#12- 1m).
Siatkę zbrojenia minimalnego (#12-250×250) można zastosować na całej powierzchni płyty, bowiem nad podporami, bowiem zgodnie z $(\ref{8})$ i $(\ref{9})$ spełniony jest wymóg maksymalnego rozstawu prętów również dla zbrojenia głónego w obszarach maksymalnych mometów zginajacych ( $2h= 2\cdot 290=580 \,mm i 250 \, mm)
Projekt zbrojenia płyty
Projekt zbrojenia płyty wykonano z wykorzystaniem programu obliczeniowego Consteel w.14 [39]
Na rys. 46 pokazano mapę zbrojenia płyty poddanej obciążeniu rozłożonemu na całej powierzchni. W przykładzie pominięto prezentację map zbrojenia dla schematu z obciążeniami w szachownicę (rys.47) , które należy rozpatrywać w praktycznym projektowaniu, bo daje ekstremalny rozkład sił. Wykazano, że na większości powierzchni płyty (obszary w kolorach niebieskich) wystarczy dać zbrojenie minimalne, bo obliczeniowo jest wymagane maksymalnie $ A_s=323 \, mm^2 /m$, czyli #12-350 $ > s_{basic} = 250 \, mm$. W obszarach, gdzie minimalne zbrojenie nie jest niewystraczające z warunku nośności – należy je zagęścić lub dać pręty o większej średnicy. Obszary w których wymagane jest dozbrojenie są różne dla zbrojenia górnego i dolnego i różne w kierunku X lub Y.
Układ zbrojenia i opracowanie rysunków warsztatowych należy pozostawić Wykonawcy, który powinien je przedstawić Projektantowi do uzgodnienia.
W obszarach nad słupami należy sprawdzić ścinanie przez przebicie zgodnie z zasadami przedstawionymi w artykule Przebicie płyty żelbetowej.
Przykład 2 [ Projekt stropu Filigran wieloprzęsłowego pod obciążeniem ciągłym]
Postawienie problemu
Zaprojektować strop typu Filigran, którego wycinek pokazano na rys. 48 dla podstawowych danych:
Żelbet C30/37-B500 (beton C30/37, stal B500),
Klasa konstrukcji żelnetowych S2
Klasa ekspozycji
dla powierzchni dolnej stropu XC4 $c_{dur}= 30 \, mm$ wg [40]
dla powierzchni dolnej stropu XC1, $c_{dur}= 15 \, mm$
Otulenie jak dla belek
dolna powierzchnia stropu (dół prefabrykatu):
średnica pręta zbrojenia prefabrykatu $\Phi_f = 10 \, mm$;
dodatek na odchyłkę otulenia prefabrykatu $\Delta c_{dev} = 5\, mm$
$c_{nom,f} = \max { \{ \Phi \, ; \, c_{dur} \, ; \, 10 \} } + 5 = \max { \{ 10, \, ; 15 \, ; \, 10 \} }+5=$ 20 mm;
górna powierzchnia stropu ( posadzka układana na budowie i utwardzana powierzchniowo).
średnica pręta zbrojenia $\Phi_f = 12 \, mm$;
dodatek na odchyłkę otulenia $\Delta c_{dev} = 10\, mm$
$c_{nom,n} = \max { \{ \Phi \, ; \, c_{dur} \, ; \, 10 \} } + 10 = \max { \{ 12, \, ; 30 \, ; \, 10 \} }+10 $ = 40 mm;
Wysokości płyty
h= 180 mm
Wysokość efektywna
dolna $d_d$= 180 – 20 -10/2 = 155 mm
górna $d_g$= 180 – 40 -12/2 = 134 mm
Wymiary rozpatrywanego wycinka stropu
$L_x= 3×4000=12000 \, mm$, $L_y= 2×4000=8000\, mm$,
Strop jest oparty na ruszcie żelbetowym w siatce 4×4 m. Belki główne (podciągi) mają przekrój 300x 320 (szerokośc $b_x= 320 \, mm$ , a poprzeczne żebra 300×200 (szerokosć $b_y =200 \, mm$).
Szerokość oparcia płyt FIligran na podciągach wynosi: $c_y =60 \, mm$ na podciągach ; $c_x=40 \, mm$ na żebrach.
Plyta Filigran
grubość $h_f =$ = 50 mm
szerokosć nominalna (na szerokości przęsła 2 płyty):
$b_f= (4000-200 +2\cdot 40)/2$ 1940 mm$ (wynika z siatki rusztu, szerokości żebra i podparcia płyty)
długość płyt w przęśłe:
$l_f= 4000-320 +2\cdot 60$= 3800 mm.
Uciąglenie nad podporami w sposoób pokazany na .
Obciążenia:
ciężar własny $G= 0,18\cdot 25 + 0,15 \cdot 0,6$ = 4,6 kN/m2
zewnętrzne obciążeniem (charakterystyczne) $Q_k$ = 5,0 kN/m2
współczynniki onciążeń: jak powierzchni kategorii E (pomieszczenia magazynowe),
więc współczynniki obciążeń wynoszą: $( wsp. obc. \gamma_Q$; wsp. redukcyjny $\psi_Q$)= (1,5; 1,0)$
Obciążenie obliczeniowe
$F_d = 1,35 \cdot 4,6 + 1,5 \cdot1,0 \cdot 5,0$ = 13,7 kN/m2.
System zbrojenie stropu
Zastosowano następujące średnice zbrojenia:
pręty górne układane na budowie w kierunkyu X $\Phi_{3x}= 12\, mm$,
pręty górne układane na budowie w kierunkyu Y $\Phi_{3x}= 10 \, mm$,
pręty środkowe na płycie prefabrykatu układane na budowie w kierunku X $\Phi_{2x}= 10\,mm$
pręty środkowe na płycie prefabrykatu układane na budowie w kierunku Y (rozdzielcze) $\Phi_{2y}= 8\,mm$
pręty dolne w prefabrykacie układane w wytwórni w kierunku X $\Phi_{1x}= 10 \, mm$
pręty dolne w prefabrykacie układane w wytwórni w kierunku Y (rozdzielcze) $\Phi_{1y}= 8 \, mm$
System zbrojenia płyty stropowej zaprojektowano w sposób zobrazowany na rys. 19
Warstwy zbrojenia są następujące:
w kierunku głównym X (po długości płyty) $(\ref{11}) \to$
$ z_{3x} = 180 -40 -12/2 = 134 \,mm$,
$z_{2x} = 50 + 3/2 \cdot 10= 65 \, mm$,
$ z_{1x}= 20+ 10/2 = 25 \, mm$
w kierunku Y (prętów rozdzielczych) $(\ref{12}) \to$
$z_{3y} = 180 -40 -12 – 10/2 = 123 \, mm$,
$z_{2y} = 50 + 2 \cdot 10+8/2 = 74 \, mm$
$z_{1y} = 20 + 10+ 8/2 = 34 \, mm$
Zachodzi h_f- c_{nom,f} – \Phi_{1y} = 50-20-8= 22 \le 50 \, mm$
Analiza statyczna stropu
Analizę statyczną stropu Filigran prowadzi się tak jak dla stropu żelbetowego monolitycznego.
Przykład 3 [ Projekt płyty posadzki fibrobetonowej]
Zaprojektować płytę żelbetową bezspoinową posadzki na gruncie dla danych:
podbudowa i warstwy gruntowe:
1x folia PCV
podłoże beton C8/10 – 10 cm
podbudowa kruszywo 30 cm zagęszczone do E2/E1=2,2; E2=60 MPa
piasek średni 100 cm
ił pylasty 670 cm
piasek gliniasty niżej
rozmiary pola pomiędzy słupami 24×9 m
obciążenia:
a) regały o wys. 9 m do składowania palet EUR1 800×1200 w 8-miu warstwach z podkładkami pod nóżki o wymiarach 135×119 mm. Masa jednej palety z materiałem 1000 kg,
b) zastępcze obciążeniem równomierne q=10 kN/m2,
c) wózki widłowe klasy FL5 wg klauzuli. 6.3.2.3 [41]
o wymiarach (1,80×4,60m; rozstaw kół 1,5 m; ciężar 90 kN, udźwig 60 kN; obciążenie osi 140 kN; powierzchnia docisku 0,2×0,2 mxm, współczynnik dynamiczny $\varphi=1,4$ (koła pneumatyczne)
Zestawienie obciążeń
Współczynniki obciążeń $\gamma_F$ i wsp. kombinacyjne (redukcyjne) $\psi_0$
Zgodnie z [37].:
$\gamma_F=1,5$ – dla wszystkich obciążeń zmiennych (regały wózki, obciążenie równomierne)
$\psi_0=1,0 $ regały i obciążenie równomierne (kategoria powierzchni E)
$\psi_0=0,7 $ podnośniki widłowe (kategoria powierzchni F)
Współczynnik materiałowy
$\gamma_c=1,5$
Obciążenie od nóżek regału
Obciążenie charakterystyczne
Na cztery nóżki rozstawione 800×1200 przypada: 8x 10,0= 80 kN
Na jedną nóżkę 80/4=20 kN, pole docisku (135 × 119) mm x mm
Najniekorzystniejsze jest ustawienie dwu regałów obok siebie, co daje obciążenie:
1 rząd (od ściany 75 mm) [20 kN] – 135 mm [20 kN] – (1200-135) mm – [20 kN]- 135 mm – [20 kN]
2 rząd (od 1 rzędu 800 mm) [20 kN] – 135 mm [20 kN] – (1200-135) mm – [20 kN]- 135 mm – [20 kN]
Obciążenie obliczeniowe
Siły z sąsiednich nóżek traktujemy jak jedną, czyli model obciążeń obliczeniowych
$F_{d,r} =1,5 \cdot 2 \cdot 20=60 \, kN$
pole docisku $(c_x × c_y)= (270 × 119)$ mm x mm
1-2 siła: [ 60 kN] – x= (1200+135) mm – [60 kN]
y=800 mm
3-4 siła [60 kN] – x= (1200+135) mm – [60 kN]
Obciążenie od podnośników widłowych
Obciążenie charakterystyczne
Dwie siły (koła na pierwszej osi) każda o wartości 140*1,4/2=98 kN,
Obciążenie obliczeniowe
$F_{d,p} =1,5 \cdot 98=147 \, kN$
pole docisku $(c_x × c_y)= (200 × 200)$ mm x mm
1-2 siła: [147 kN] – x=1500 mm – [147 kN]
Obciążenie równomiernie rozłożone
Obciążenie rozłożone poza regałami oraz trasami podnośników przyjęto w dwóch pasach o szerokości 800 mm każdy w rozstawie 400 mm od luźno ustawionych opakowań, ścieżek technologicznych lub innych. Maksymalna, zastępcza wartość obciążenia 10 kN/m2
$ q_d=1,5 \cdot 10=15 kN/m^2$
Obciążenie ciężarem własnym
Pomija się jako nieistotne w wymiarowaniu płyty fibrobetonowej metodą plastyczną
Współczynnik sprężystości podłoża
Współczynnik sprężystości podłoża wyznaczono zgodnie zasadami w artykule Współczynnik sprężystości podłoża
dla szacunkowego obciążenia płyty Q=10+0,2*25=15 kN/m2 (grubość płyty ok. 0,2 m) i uzyskano
$k=19,8 kN/ (m^2 mm)$
Promień względnej sztywności Westergaarda oraz pas przykrawędziowy
Przyjęto beton C20/25: (tab.1) $\to$
$E_{cm}=30 GPa = 30 000 N/mm^2$ ,
$ f_{ctm}=2,2 MPa= 2,2 kN/mm^2$
$\mu=0,2$
$(\ref {27}) \to $ $k_{\nu}=\cfrac {1}{\sqrt[4]{1-0,2^2}}=1,01026 $
$( \ref{26}) \to $ $ l=1,01026 \cdot \sqrt[4]{ \cfrac {30 000 \cdot 200^3} {12 \cdot 0,0199 }} =1011 \, mm$.
Podobną wartość, ale mniej precyzyjnie odczytamy z rys. 12.
$( \ref {41}) \to $ pas przykrawędziowy $ L_{pas} = 6 \cdot 1011 /1,01=6000 \, mm$
Dobór włókien i wytrzymałość równoważna
Przyjęto włókna DRAMIX RC-80/60-BN w ilości 30 kg/m3
Z tab. 10 $\to$
$f_{ctm,eq,50} = f_{ctm,eq,150} = 2,7 \, MPa$
$f_{ctm,eq,350} = f_{ctm,eq,300} = 2,8 \, MPa$
Nośności przekroju płyty
$(\ref{24}) \to$ $ f_{ctm,fl}=2,2 \cdot ( 1,6 – 200/1000)=3,08 MPa$
pod ($\ref{23}$) \to$ $W_{el} = \cfrac {20^2}{6}=66,67 \, cm^2/m$
($\ref{25}$) $\to$ moment ujemny (górne włókna)
$ M_{R(-)} = 66,67 \cdot 3,08 \cdot 10^{-1}=20,53 \, kNm /m$
$(\ref{29}) \to$ moment dodatni ( dolne włókna)
$M_{R(+)}= 66,67 \cdot (0,4320 \cdot 2,7 + 0,6438 \cdot 2,8 )\cdot 10^{-1}= 19,79 \, kNm/m $
Nośność linii załomu
$\Sigma M_R= 20,53+19,79=40,32 \, kNm/m$
Nośności płyty mierzone obciążeniami
dla regału siła $F_d=60 \, kN$ na powierzchni A= 270×119 mm2 :
zastępczy promień obciążenia
$a=\sqrt{\cfrac {270 \cdot 119}{\pi}}=101 mm,$
$a/l=101/1011=0,100 < 0,2$, czyli prowadzimy interpolację
$F_{R1,r} = \begin {cases}
2 \pi \cdot 40,32=253,3 \, kN , & \text {dla $a/l=0$} \\
\cfrac {4 \pi} {1- 0,2/3} \cdot 40,32=472,9 , & \text {dla $a/l = 0,2$ }
\end {cases} $
$\Delta F_{R1,r} =472,9-253,3=219,6 \, kN$
z interpolacji: $F_{R1,r}=253,3+219,6/0,2 \cdot 0,100=363,1 \, kN$
Nośność obliczeniowa
$F_{R1,r,d}=363,1/1,5=242,1 \,kN$
Mnożnik obciążenia: $\Lambda_{R1,r} =60/242,1=0,248$
dla koła podnośnika siła F=98 kN na powierzchni A=200×200 mm2
$a=\sqrt{\cfrac{200 \cdot 200}{\pi}}=113 mm,$
$a/l=112,8/1011=0,112<0,3 \to $ prowadzimy interpolację
z interpolacji: $F_{R1,p}=253,3+219,6/0,2 \cdot 0,112=376,3 \, kN$
Nośność obliczeniowa
$F_{R1,p,d}= 376,3/1,5=250,9 \,kN$
Mnożnik obciążenia: $\Lambda_{R1,p}=147/250,9= 0,586 $
$(\ref{41})$ rozstawione w odległości x
dla regału x= (1200+135)=1335 > 2h=2\cdot 200=400 mm
$F_{R2,r}= \begin {cases}
\left [ 2 \pi+\cfrac{1,8\cdot 1335)}{1011} \right ] \cdot 40,32 =349,2 \, kN , & \text {dla $a/l=0$} \\
\left [ \cfrac{4 \pi}{1- 0,2/3}+\cfrac{1,8 \cdot 1335}{1011\cdot(1-0,2/2)} \right ] \cdot 40,32=649,4 , & \text {dla $a/l=0,2$ }
\end {cases} $
$\Delta F_{R2,r}=649,4,9-349,2=300,2 \, kN$
z interpolacji: $F_{R2,r}=349,2 +300,2 /0,2 \cdot 0,100=499,2 \le 2F_{R1,r}= 2 \cdot 363,1=726,2 \, kN$
nośność obliczeniowa
$F_{R2,r,d}= 499,2/1,5=332,8 \,kN$
Mnożnik obciążenia: $\Lambda_{R2,r} =2\cdot 60/332,8=0,360 $
dla kół podnośnika $ x= 1500 \, mm$
$F_{R2,p}= \begin {cases}
\left [ 2 \pi+\cfrac{1,8\cdot 1500)}{1011} \right ] \cdot 40,32=361,0 \, kN , & \text {dla $a/l=0$} \\
\left [ \cfrac{4 \pi}{1- 0,2/3}+\cfrac{1,8 \cdot 1500}{1011\cdot(1-0,2/2)} \right ] \cdot 40,32=662,5, & \text {dla $a/l=0,2$ }
\end {cases} $
$\Delta F_{R2,p}=662,5-361,0=301,5 \, kN$
z interpolacji: $F_{R2,p} =361,0+301,5 /0,2 \cdot 0,112=529,8 \le 2 F_{R1,p}=2 \cdot 376,3=752,6 \, kN$
nośność obliczeniowa
$F_{R2,p,d}= 529,8 /1,5=353,2 \,kN$
Mnożnik obciążenia: $\Lambda_{R2,p} =2 \cdot 147/353,2 =0,832$
$(\ref{41})$ rozstawione w odległości ( x,y )
dla nóżek regału
$(x+y)=(1335+800)=2135 \, mm > 2h=2 \cdot 200=400 \, mm$
$ F_{R4,r}= \begin {cases}
\left [ 2 \pi+\cfrac{1,8 \cdot 2135 }{1011} \right ] \cdot 40,32= 406,6 \, kN, & \text {dla $a/l=0$} \\
\left [ \cfrac{4 \pi}{1-0,2/3}+\cfrac{1,8\cdot 2135 }{1011 (1-0,2/2)} \right ] \cdot 40,32=713,2 \, kN, & \text {dla $a/l \ge 0,2$ }
\end {cases} $
$\Delta F_{R4,r}= 713,2-406,6=306,6 \, kN$
z interpolacji: $F_{R4,p} =406,6+306,6 /0,2 \cdot 0,100=559,9 \le 2 F_{R1,p}=2\cdot 499,2 \, kN$
Nośność obliczeniowa
$F_{R4,r,d}= 559,9/1,5=373,3 \,kN$
Mnożnik obciążenia: $\Lambda_{R4,p} =4\cdot 60/373,3 =0,464$
współczynnik redukcji – dwie nóżki na krawędzi płyty
$\alpha_{k0}= \cfrac{1}{4}+\cfrac{20,53} {\pi \cdot 40,32}=0,412 $
$\alpha_k= \begin {cases}
0,412 , & \text {dla $a/l=0$} \\
\cfrac {1-0,2/3}{1- 2 \cdot 0,2/3} \cdot 0,412=0,380 , & \text {dla $a/l \ge 0,2$ }
\end {cases} $
$\Delta \alpha_k=0,412-0,380=0,032$
z interpolacji $\alpha_k=0,412-0,032/0,2*0,1=0,396
Mnożnik obciążenia: $\Lambda_{R4,r}^R =4 \cdot 60 / 373,3 / 0,396 =1,622$
Nośność przekroczona. Pas przykrawędziowy należy wzmocnić
Wymagany pas dozbrojenia posadzki
Szerokość pasa przykrawędziowego wymaganego do 100% nośności wynosi $L_{pas}=6000 \, mm$
Dla maksymalnego wytężenia posadzki nóżkami $W=46,4%, wymagany pas dozbrojenia:
$ L_{zbroić}=W \cdot L_{pas}=0,46,4 \cdot 6000=2784 \, mm$
Po zwieszeniu grubości płyty powyższe oszacowanie w konsekwencji ulegnie zmianie
Kombinacja obciążeń
Wobec braku danych o szerokości rozstawienia regałów rozpatrzmy sytuację obliczeniową taką, że koło podnośnika zbliży się do nóżek regału na odległość
$x= 2h=2 \cdot 200=400 mm$
W takiej sytuacji obciążenie skupione od nogi regału i od koła podnośnika można rozpatrywać jak jedną siłę skupioną:
przy wiodącym obciążeniu regałem $F_d= F_{d,r}+\psi_{0,p} \cdot F_{d,p} = 60+0,7 \cdot 147=163 \, kN$,
przy wiodącym obciążeniu podnośnikiem $F_d= F_{d,p}+\psi_{0,r} \cdot F_{d,r} = 147+1,0 \cdot 147=207 \, kN$,
Przyjmujemy , że siły są rozłożone na sumarycznej powierzchni (270+200)x(119+200)=470×319 mm x mm
$a=\sqrt{\cfrac{470 \cdot 319}{\pi}}=387 mm,$
$a / l=387/1011=0,38 $
Dla dwóch sił skupionych rozstawionych na odległość $x=R+2\cdot 2h=1500+2\cdot 400=2300 \, mm$ mamy nośność
$F_{R,komb}= \left [ \cfrac{4 \pi}{1- 0,38/3}+\cfrac{1,8 \cdot 2300}{1011\cdot(1-0,38/2)} \right ] \cdot 40,32=646,3 \, kN$
Nośność obliczeniowa
$F_{R,komb,d}=646,3/1,5=430,9 \, kN$
Mnożnik obciążenia: $\Lambda_{R2,r+p} =207/430,9 =0,48.Literatura
- Knauff, M., Golubińska, A., & Knyziak, P. (2015). Przykłady obliczania konstrukcji żelbetowych. Budynek ze stropami płytowo-żebrowymi. Zeszyt 1. PWN
- Starosolski, W. (2013). Konstrukcje żelbetowe według Eurokodu 2 i norm związanych, Tom 2 (Vol. 2). Wydawnictwo Naukowe PWN
- Zybura, A. (Ed.). (2015). Konstrukcje żelbetowe według Eurokodu 2: atlas rysunków. Wydawnictwo Naukowe PWN SA.
- Hegger, J.; Walraven, J.C.; Häusler, F.: Zum Durchstanzen von Flachdecken nach Eurocode 2. Beton- und Stahlbetonbau (2010), Heft 4, S. 206–215
- PN-EN 1992-2+AC+Ap1+Ap2: 2008 . Projektowanie konstrukcji z betonu -Część 1-2: Reguły ogólne – Projektowanie z uwagi na warunki pożarowe
- PN-EN 1992-1+AC+Ap 1,2,3: 2008. Projektowanie konstrukcji z betonu – Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1992-1+AC+Ap 1,2,3: 2008. Projektowanie konstrukcji z betonu -Część 1
- Keller, S.: Als Deckenträger verwendbarer und in einem Arbeitsgang hergestellter Gitterträger sowie Verfahren und Vorrichtung zur Herstellung dieses Gitterträgers, Schweizer Patentschrift Nr. 335837 vom 8.3.1955, Priorität: Deutschland 16.3.1954
- Deutsches Institut für Bautechnik (DIBt): Allgemeine bauaufsichtliche Zulassung Z-15.1-148 Filigran-D-Gitterträger, Filigran-DH-Gitterträger, Filigran-E-Gitterträger und Filigran-EH-Gitterträger für Balken-, Rippen- und Plattenbalkendecken mit Betonfußleisten oder Fertigplatten, 18. Dezember 2013
- Deutsches Institut für Bautechnik (DIBt): Allgemeine bauaufsichtliche Zulassung Z-15.1-147 Filigran-E-Gitterträger und Fertigplatten mit statisch mitwirkender Ortbetonschicht, 1. Januar 2015
- Deutsches Institut für Bautechnik (DIBt): Allgemeine bauaufsichtliche Zulassung Z-15.1-93 Filigran-EQ-Gitterträger für Fertigplatten mit statisch
mitwirkender Ortbetonschicht, 16. Juni 2014 - Deutsches Institut für Bautechnik (DIBt): Allgemeine bauaufsichtliche Zulassung Z-15.1-38 Kaiser-Omnia-Träger KTS für Fertigplatten mit statisch
mitwirkender Ortbetonschicht, 7. Februar 2014 - Drobiec Ł., Stropy Vector. Koncepcja, kształtowanie, obliczanie, wykonawstwo, Wydawnictwo Politechniki Śląskiej, Gliwice 2018
- kamres, Jak to jest zrobione cz.24 „Stropy poziomu -1”, 18 lipca 2013 [ Portal Roosevelta81.pl https://roosevelta81.pl/jak-to-jest-zrobione-cz-24-stropy-poziomu-1/]
- kamres, Jak to jest zrobione cz.25 „Deskowanie i betonowanie stropów, 19 lipca 2013 [ Portal Roosevelta81.pl ; https://roosevelta81.pl/jak-to-jest-zrobione-cz-25-deskowanie-i-betonowanie-stropow/
- Zelger, C.: Zulässige Schnittkräfte im Montagezustand. Gutachtliche Stellungnahme zum Filigran-D-Gitterträger mit dickem Obergurt, 20. Mai 1981
- Furche J., Bauermeister U., BetonKalender 2016, IV Elementbauweise mit Gitterträgern nach Eurocode 2, Filigran-Gitterträger, Ernst & Sohn GmbH & Co. , Germany 2015
- ] DIN 488-6:2010-01: Betonstahl – Teil 6: Übereinstimmungsnachweis. Beuth Verlag, Berlin, 2010
- Bechert, H.; Furche, J.: Bemessung von Elementdecken mit der Methode der Finite-Elemente. Betonwerk + Fertigteiltechnik (1993), Heft 5, S. 47–51.
- DIN EN 1992-1-1∕NA:2013-04: Nationaler Anhang – National festgelegte Parameter – Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken – Teil 1-1: Allgemeine Bemessungsregeln für den Hochbau. Beuth Verlag, Berlin, April 2013
- DIN EN 1992-1-1 / NA:2013-04: Nationaler Anhang – National festgelegte Parameter – Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken – Teil 1-1: Allgemeine Bemessungsregeln für den Hochbau. Beuth Verlag, Berlin, April 2014
- Chodor-Projekt, Projekt konstrukcji rozbudowy IKEA, 2023
- Schäfer, H.-G.; Schmidt-Kehle, W.: Schubdeckung und Fugenverbund bei nachträglich durch Ortbeton ergänzten Fertigplatten und Balken. Beton- und Stahlbetonbau (1995), Heft 2, S. 49–53
- PN-EN 1992-1+AC+Ap 1,2,3: 2008. Projektowanie konstrukcji z betonu -Część 1-1: Reguły ogólne i reguły dla budynków
- Furche J., Bauermeister U., BetonKalender 2016, IV Elementbauweise mit Gitterträgern nachEurocode 2, Filigran-Gitterträger, Ernst & Sohn GmbH & Co. , Germany 2015
- Górecki & Wysocki Zakład Prefabrykacji sp. z o.o., Skalmierzyce, materiały udostępnione e-mailem
- Pyrak S., Konstrukcje z betonu, WSIP, Warszawa 20021, fragment rys. 7-24
- Consolis, Strunobetonowe połyty kanałowe HC. Poradnik projektanta, Gorzkowice, 2008
- Consolis, Strunobetonowe płyty kanałowe HC. Poradnik projektanta, Gorzkowice, 2008
- Bogucin, Fabryka Domów, Katalog elementów budowlanych, Bogucin, 2015 [ http:\\www.fdbogucin.pl]
- Consolis, Strunobetonowe płyty TT, Poradnik projektanta, Gorzkowice, wrzesień 2004
- Glinicki, M. A. (2008). Wytrzymałość równoważna fibrobetonu na zginanie. Inżynier Budownictwa, styczeń 2008
- Glinicki, M. A. (2008). Wytrzymałość równoważna fibrobetonu na zginanie. Inżynier Budownictwa, styczeń 2008
- Westergaard H.M.: New formulas for stresses in concretepavements of airfields. American Society of Civil Engi-neers Transactions,113, 2340, 1948, 425-444
- Hajduk, P. (2013). Projektowanie podłóg przemysłowych. Wydawnictwo Naukowe PWN
- Concrete Industrial Ground Floors – A quide to their Design an Construction, (2003). Technical Report No 34, 4th Edition
- PN-EN 1990:2004 . Eurokod: Podstawy projektowania konstrukcji
- ArcelorMIttal. (2015). Włókna stalowe . Posadzki Przemysłowe (Distribution Solutions. Wire Solutions)
- Consteel Software. (2020). ConSteel 14 Manual. http://www.consteelsoftware.com/en/downloads/manuals-documents.
- PN-EN 10080, Stal do zbrojenia betonu — Spajalna stal zbrojeniowa — Postanowienia ogólne
- PN-EN 1991-1-1:2004. Eurokod 1: Oddziaływania na konstrukcje. Część 1-1: Oddziaływania ogólne. Ciężar objętościowy, ciężar własny, obciążenia użytkowe w budynkach,
________________________________

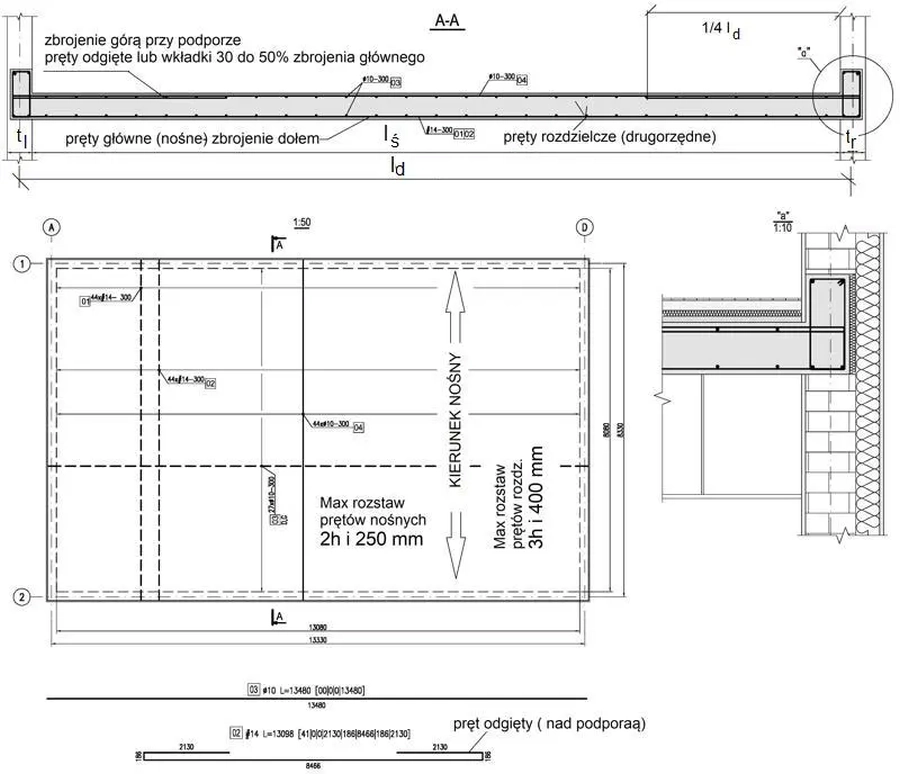
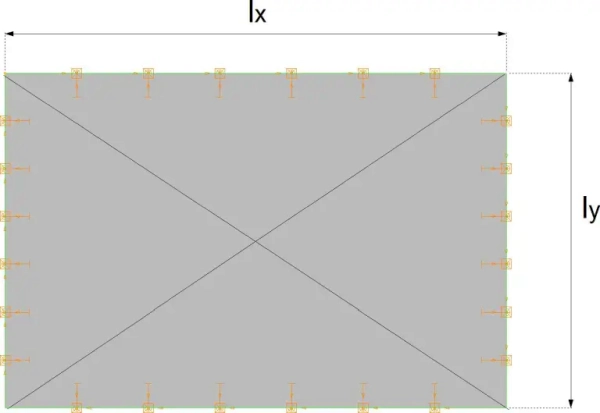
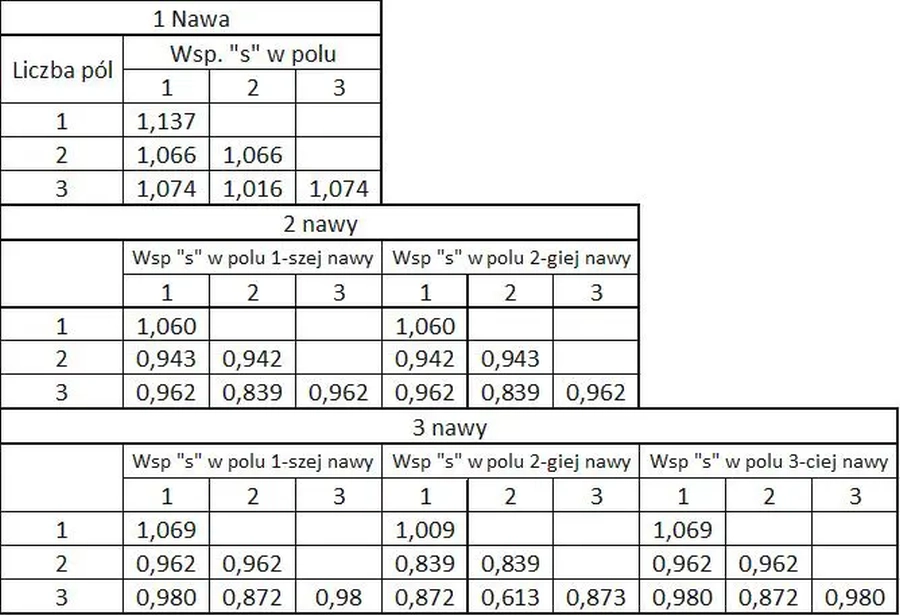
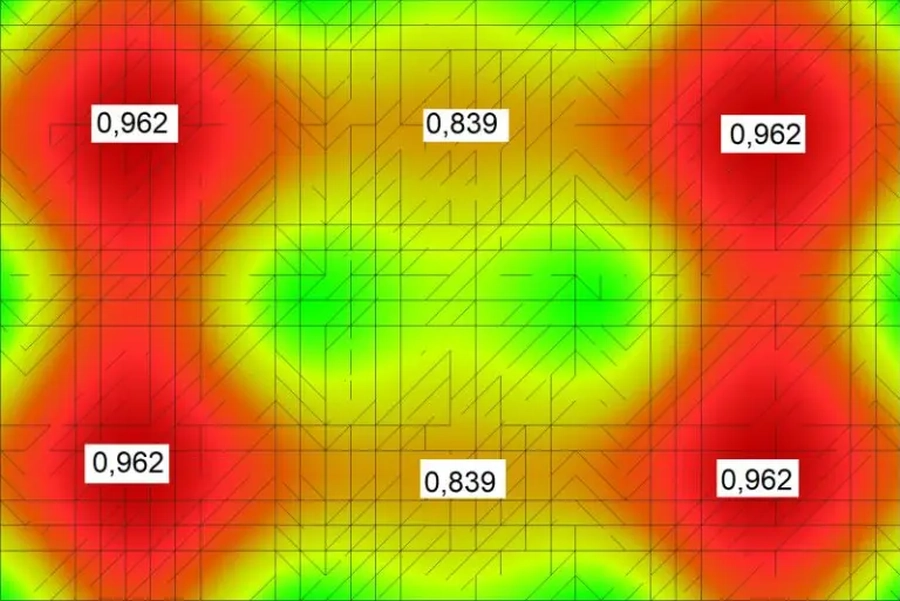
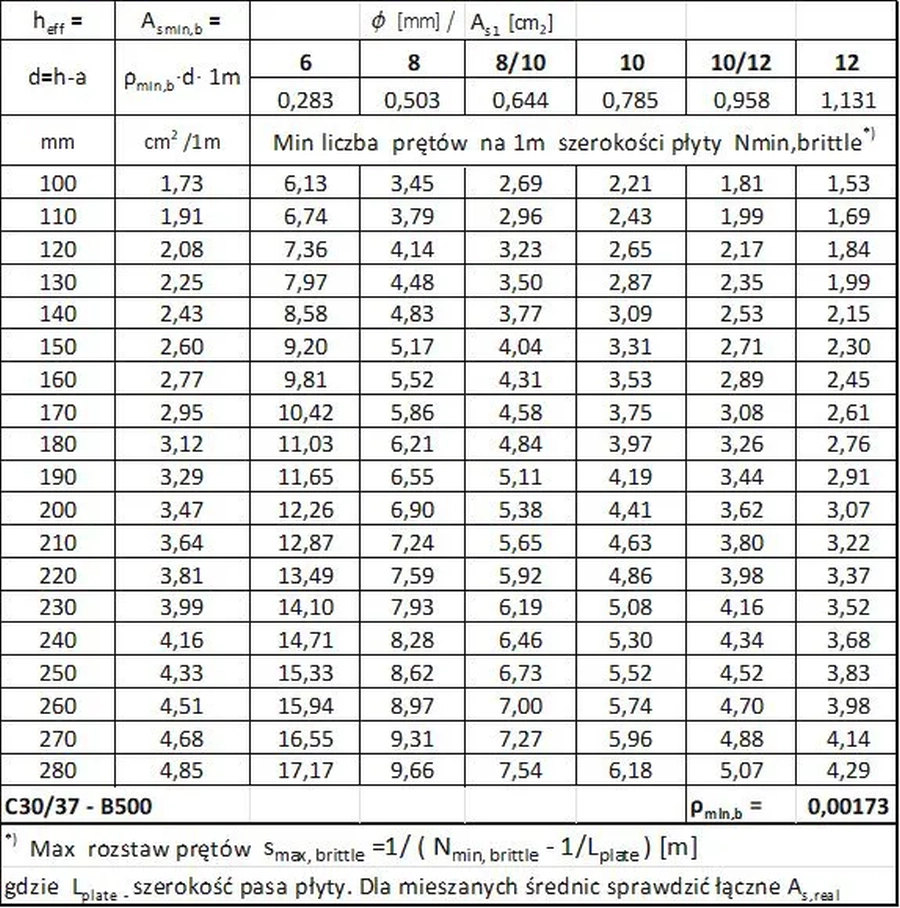

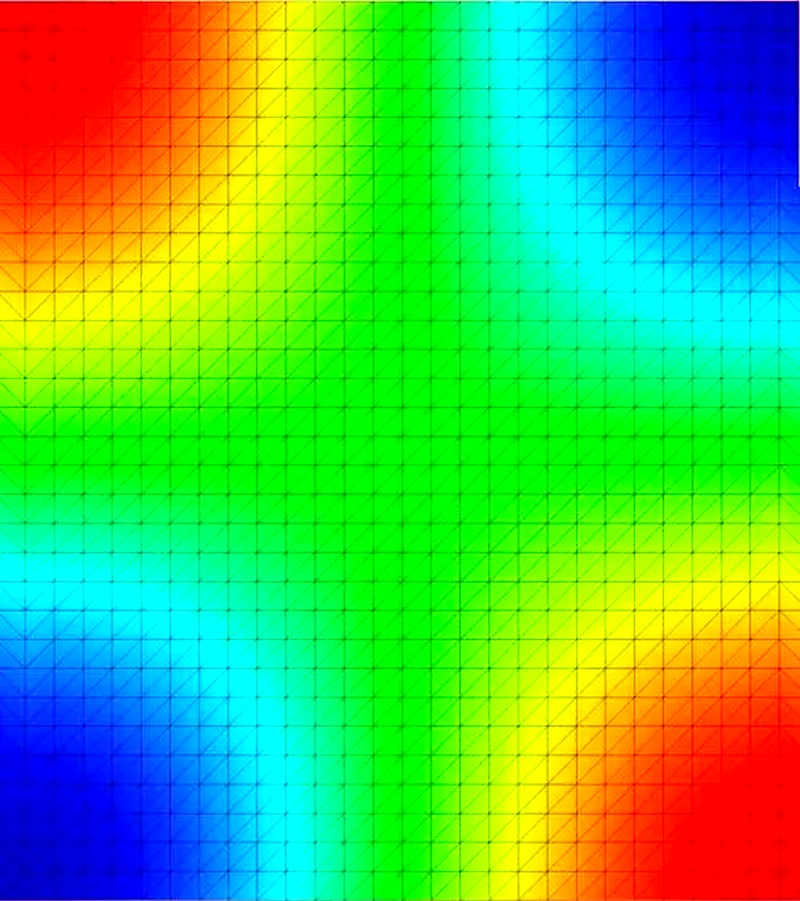
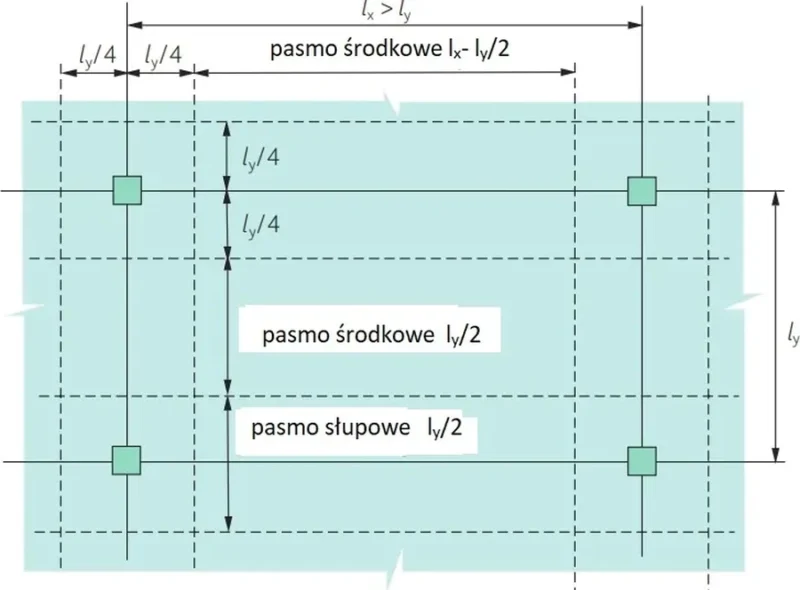
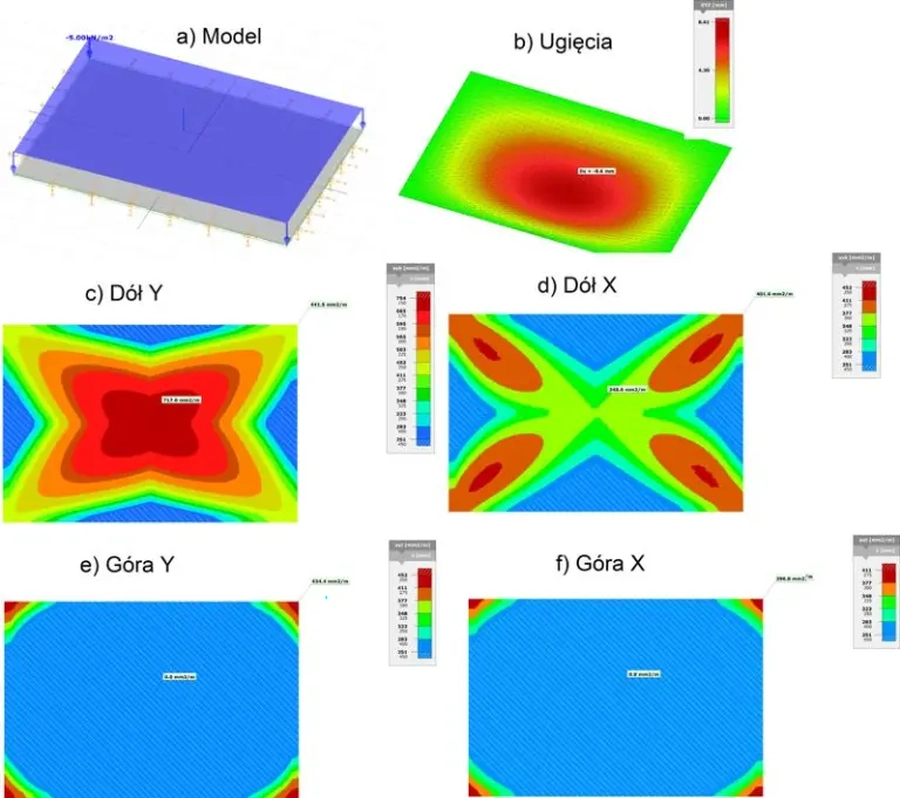
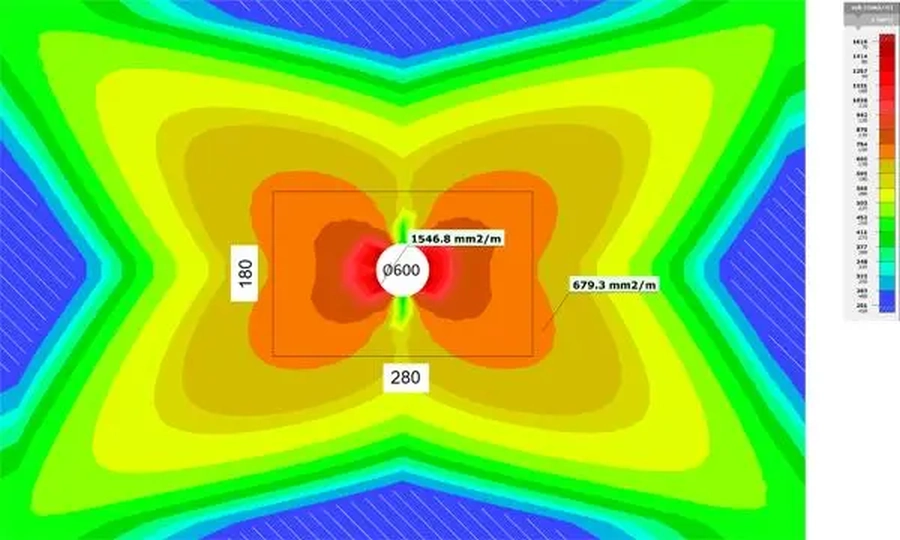
![Mapa zbrojenia płyty z otworem []600](https://chodor-projekt.net/wp-content/uploads/2019/01/rys_12_mapa-zbrojenia-plyty-z-otworem-kwadratowym-600x600-1.webp)