Drewno w konstrukcjach budowlanych

Leszek Chodor,  20 luty 2019
01-02-2025 rewizja po dużej awarii portalu
11-05-2025 wprowadzono jednolite podejście  II rzędu i formułę transformacji z sił I rzędu
22-05-2025 uporządkowano informacje o odkształcalności drewna i oddano punkt o imperfekcjach

W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co

 W ciągu ostatnich 24 godzin z artykułu korzystało  14 Czytelników

Wraz z pojawianiem się wyrobów drewnianych spełniającym warunki pożarowe (impregnacja) oraz jednorodności wytrzymałościowej  (drewno klejone) – drewno w konstrukcjach budowlanych jest coraz chętniej stosowane na odpowiedzialne elementy budowlane w zakresie znacznie przekraczającym elementy więźby dachowej. Zalety drewna, a przede wszystkim najniższa ze znanych materiałów energochłonność potrzebna do wyprodukowania, a także pozytywny odbiór przez człowieka — powoduje, że XXI wiek ma szanse stać się wiekiem drewna w architekturze i budownictwie.

Projektowanie  oraz wykonywanie budynków i konstrukcji z drewna wraz z zastosowaniem łączników metalowych jest przedmiotem zestawu norm  Eurokod 5 [1], [2],.  Normy te należy bezwzględnie stosować łącznie z Eurokod 0 i  zestawem norm obciążeniowych Eurokod 1.

Obszary zastosowań konstrukcji budowlanych w budownictwie można podzielić na [3]:

• elementy i konstrukcje tradycyjne w zastosowaniu do mało i średnio-kubaturowych obiektów, a w tym: budynki drewniane, nawiązujące do rozwiązań tradycyjnych, budynki z lekkim szkieletem drewnianym, więźby dachowe i stropodachy (stropy) na legarach drewnianych, schody drewniane i inne podobne
• budynki halowe oraz inne o specjalnym, znaczeniu, w tym przekrycia kopułowe oraz walcowe.

Największą budowlą wykonaną z drewna  jest kopuła Superior Dome w USA. Kopuła ma wysokość 44 metry (143 stopy) i  średnicę 163 m (536 stóp). Kopuła przykrywa powierzchnię  (21 000 m²). Jest to kopuła geodezyjna zbudowana z 781 daglezji i 174,6 km  jodły.  Pod kopułą zmieszczono 8 tys. miejsc siedzących przy całkowitej liczbie osób do 16 tys.   Edycja Guinness World Records z 2010 roku wymienia ją jako piątą co do wielkości kopułę i największą drewnianą kopułę na świecie [artykuł w niniejszej encyklopedii Największe kopuły z różnych materiałów.

Wprowadzono wiele ulepszonych materiałów drzewnych takich jak: płyty aglomerowane oraz klejone – MGLT, do których należą płyty i belki klejone PSL (Paralel Strand Lumber), LVL(Laminatem Veneer Lumber), OSB (Oriented Strand Board)  oraz materiałów drewnianych chemicznie modyfikowanych, aż do uzyskania kompozytów o strukturze zupełnie odmiennej od drewna tradycyjnego.

Właściwości drewna konstrukcyjnego

Rodzaje i klasy wytrzymałości drewna  konstrukcyjnego

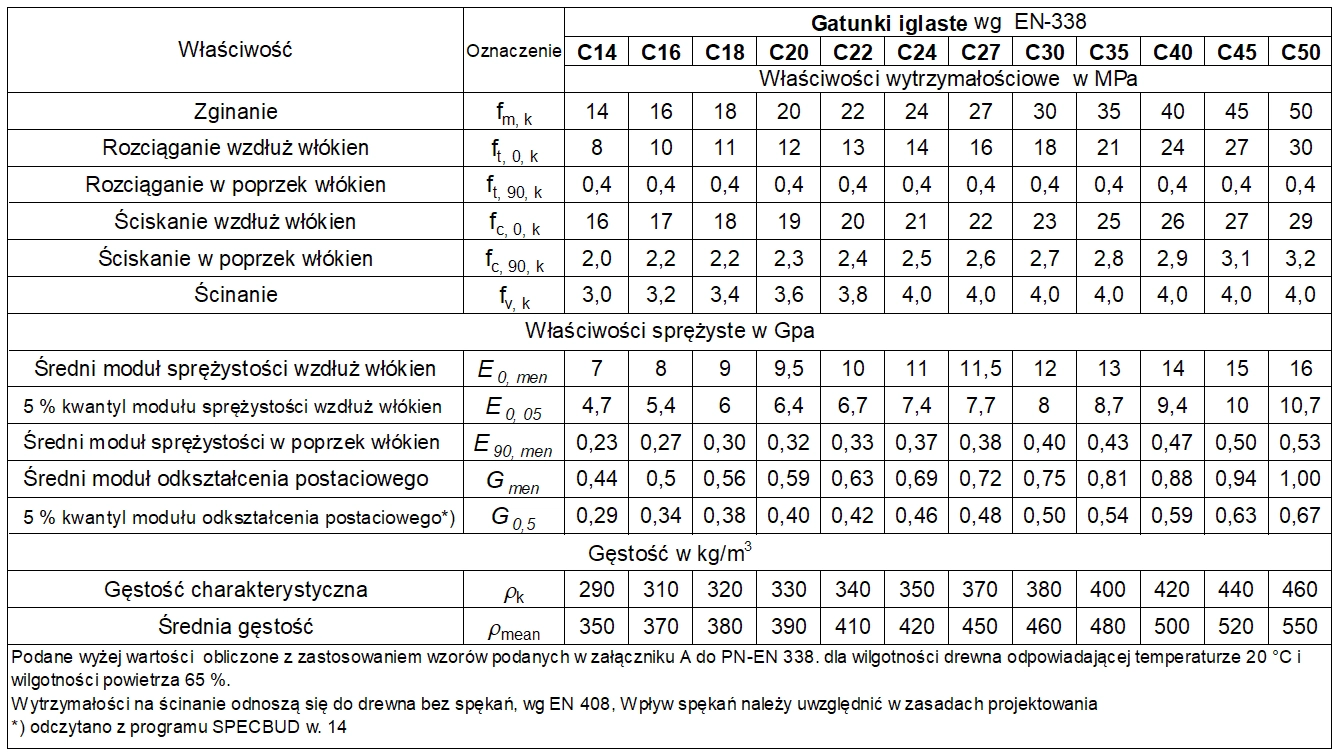
W konstrukcjach budowlanych stosuje się drewno iglaste o parametrach w tab.1 liściaste o parametrach w tab. 2  (wg [4]) . Współcześnie na elementy konstrukcyjne najczęściej stosuje się drewno klejone, o własnościach zestawionych w tab.3 [5]).

Tab.1. Klasy wytrzymałości i właściwości konstrukcyjnego drewna iglastego i topoli ( klasy C) wg [4]

Tab.2. Klasy wytrzymałości i właściwości konstrukcyjnego drewna liściastego  bez topoli ( klasy D) wg [4]

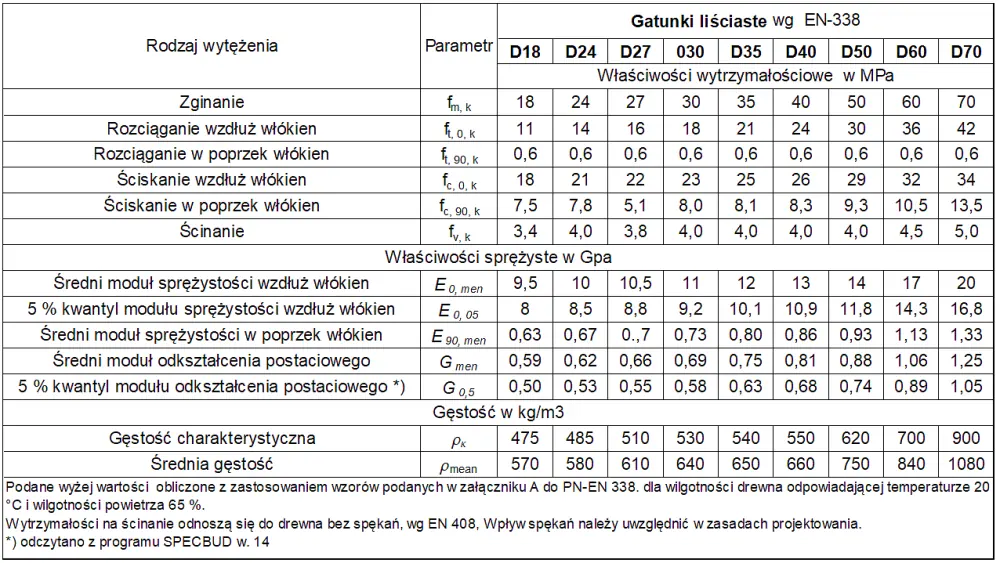
Tab.3. Klasy wytrzymałości i właściwości konstrukcyjnego drewna klejonego  (klasy GL) wg [6]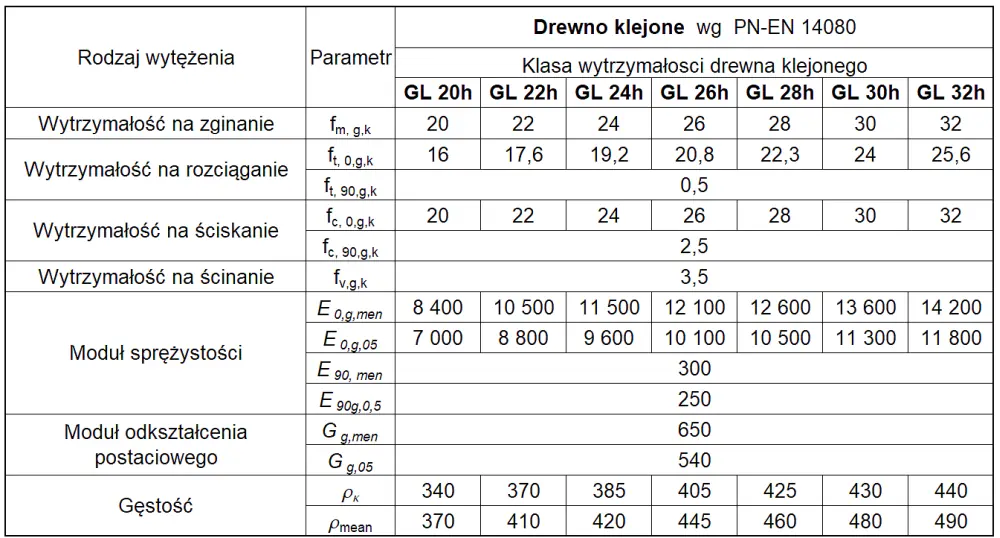

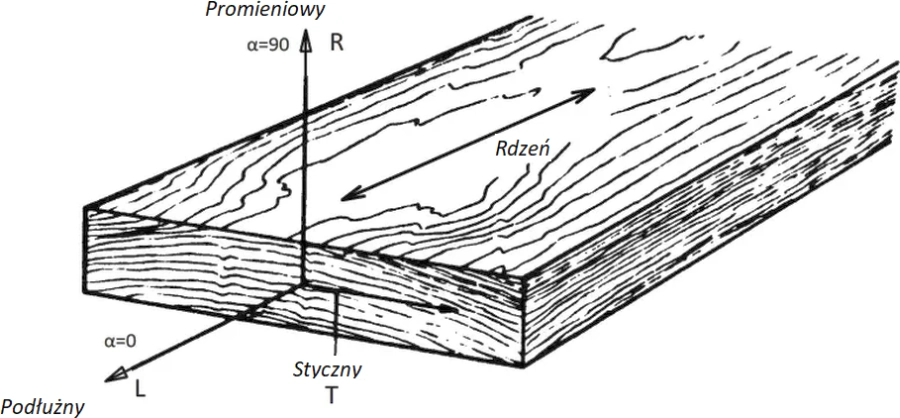
Drewno jest materiałem anizotropowym i jego własności są różne w zależności od kierunku w stosunku do kierunku rdzenia (i włókien). Główne kierunki przedstawiono na rys.1.

Rys.1. Orientacja kierunków w drewnie

W projektowaniu bardzo ważne jest, aby rozpoznać, czy drewno jest wbudowane równolegle czy prostopadle do rdzenia. W pierwszym przypadku drewno ma dobre własności mechaniczne, a w tym ostatnim przypadku wytrzymałość wynosi zwykle 1/10 wytrzymałości w kierunku podłużnym, a często bliskie zeru(rys.2).

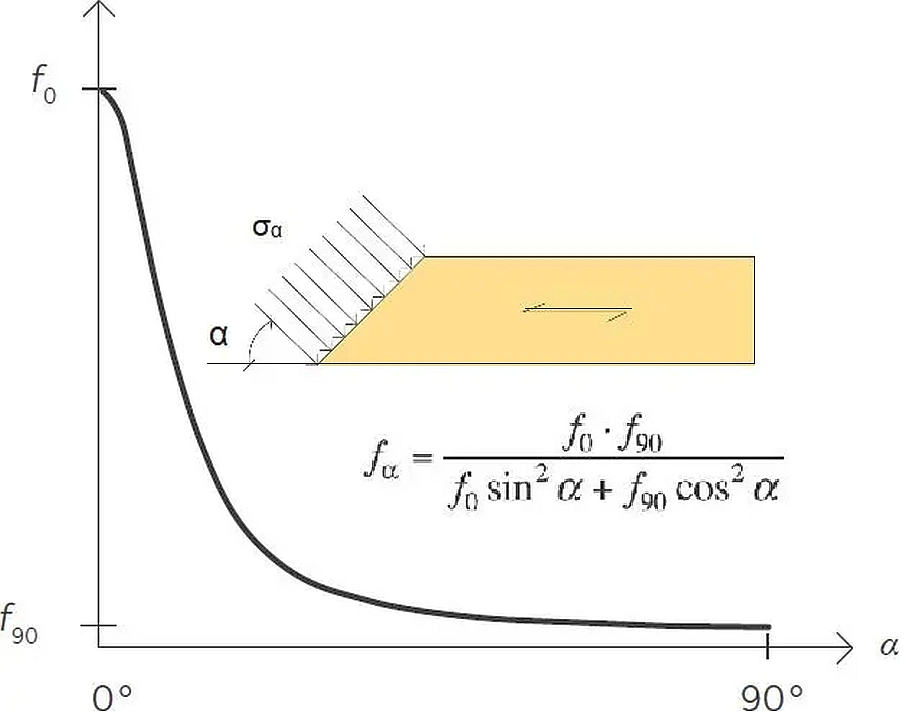
Rys.2. Zależność wytrzymałości drewna od kąta nachylenia do rdzenia [7]

Istnieje silna zależność pomiędzy wytrzymałością drewna na zginanie $f_m$ , modułem odkształcalności $E_0$ i gęstością $\rho_m$. Współczynniki korelacji statystycznej $r_{44}$  pomiędzy tymi wielkościami są następujące [8]:

$$ \begin{equation} \ r_{44}= \label{1} \begin {cases}
0,70 \div 0,65 ;  & \textrm {$X= f_m$ : Y=E} \\
0,60 \div 0,65;  & \textrm {$X= f_m$ : $Y=\rho_m$ } \\
0,60 \div 0,65 ; & \textrm {X=E  : $Y=\rho_m$ } \\
\end {cases} \end{equation} $$

Oznacza to w szczególności, iż wraz ze wzrostem gęstości drewna można oczekiwać, że jest sztywniejsze oraz bardziej wytrzymałe.

Parametry cieplne drewna

Rozszerzalność cieplna skutek zmian temperatury dla drewna w stanie użytkowym przebiega w przybliżeniu liniowo. Współczynnik rozszerzalności liniowej α_t [1/deg] szacuje się na:

$$ \begin{equation} \alpha_t = \label{2} \begin {cases}
(45 \div 60) \cdot 10^{-6}, & \textrm {styczny} \\
(25 \div 45) \cdot 10^{-6}, &\textrm { promieniowy} \\
(2,5 \div 5,0) \cdot 10^{-6}, &\textrm { wzdluż włókien} \\
\end {cases} \end{equation} $$

Drewno jest materiałem „ciepłym”, jeśli oceniać je w stosunku do żelbetu lub stali.

Współczynnik przenikania ciepła λ  [W/(mK)] w warunkach średnio-wilgotnych wynosi:

• w poprzek włókien

$$ \begin{equation} \lambda = \label{3} \begin {cases}
0,1;  & \textrm {sosna} \\
0,17;  & \textrm {jesion} \\
0,22;  & \textrm {dąb i buk} \\
\end {cases} \end{equation} $$

• wzdłuż włókien

$$ \begin{equation} \lambda [W/(mK)]= \label{4} \begin {cases}
0,3;& \textrm {sosna} \\
0,3 ; & \textrm {jesion} \\
0,4 ; & \textrm {dąb i buk} \\
\end {cases} \end{equation} $$

Jest to jednak prawie o rząd więcej od materiałów termoizolacyjnych (wełna mineralna i styropian (λ=   0,035 ÷ 0,05 W/(mK))

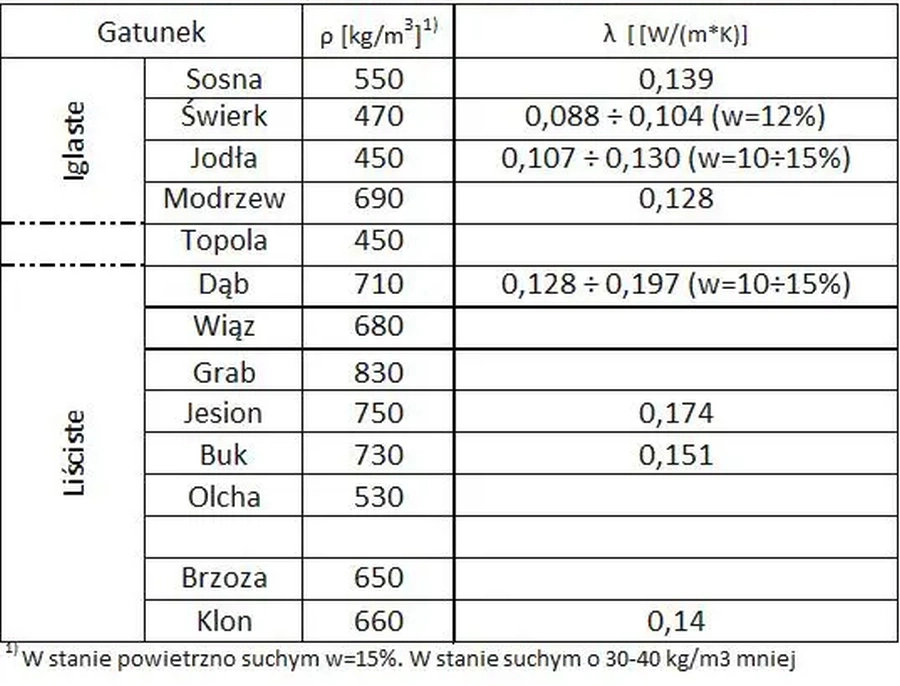
W tab.4 przedstawiono bardziej szczegółowe dane, wskazując na zależność przenikania ciepła od gęstości drewna.

Tab4 . Przenikalność ciepła dla wybranych gatunków drewna

Wilgotność drewna litego w [%] stosowanego na elementy konstrukcyjne, nie powinna przekraczać:

$$ \begin{equation} w_{max} =  \label{5} \begin {cases}
18, & \textrm {w konstrukcjach chronionych przed zawilgoceniem} \\
23, & \textrm {w konstrukcjach pracujących na  otwartym  powietrzu} \\
\end {cases} \end{equation} $$

Temperatura drewna w konstrukcjach drewnianych nie powinna przekraczać 60 „C.
W warunkach okresowego występowania temperatur wyższych nieprzekraczających 75 ^oC  zaleca się stosowanie współczynnika zmniejszającego  parametry wytrzymałościowe $k_{t,cmp}$=0,8.

Obliczeniowe własności mechaniczne drewna

Współczynniki materiałowe

Współczynniki materiałowe (częściowe współczynniki bezpieczeństwa) $\gamma_M$ dla podstawowych typów drewna konstrukcyjnego wynoszą:

$$ \begin{equation} \gamma_M =  \label{6} \begin {cases}
1,3 ; & \textrm {drewno lite} \\
1,25 ; & \textrm {drewno klejone warstwowo} \\
1,2 ; & \textrm {LVL, sklejka, plyty OSB} \\
\end {cases} \end{equation} $$

Współczynniki $\gamma_M$ dla innych typów wyrobów drzewnych podano w [1],tab. 2.3.)).

Zespół współczynników redukcyjnych

Drewno jest materiałem niejednorodnym i z tego powoduje do wyznaczenia jego własności obliczeniowych stosuje się  zespół współczynników:

• wzrostu wytrzymałości na ściskanie prostopadle do rdzenia $k_{c,90}$,
  Zwiększa wytrzymałość na ściskanie elementu w kierunku prostopadłym do rdzenia zgodnie z zaakceptowanym wzrostem obciążenia na przypadek awarii.
• zwichrzenia $k_{crit}$,
  Uwzględnia niestateczność płaskiej postaci zginania  dla belek o względnej smukłości większej od  0,75. Nie stosuje się w imperfekcyjnej metodzie projektowania,
• wyboczenia $k_{c,y}$, $ k_{c,z}$
  Uwzględnia niestateczność wyboczenia giętnego odpowiednio względem osi y i z   dla prętów osiowo ściskanych o względnej smukłości większej od  0,3. Nie stosuje się w imperfekcyjnej metodzie projektowania,
• korekcyjnego dla naprężenia prostopadłego do rdzenia w wierzchołku belki trapezowej, zakrzywionej lub ukośnej $k_{dis}$,
• Stosowany do przekrojów klejonych warstwowo lub LVL.  Koryguje wytrzymałość na rozciąganie w kierunku prostopadłym do rdzenia w strefie wierzchołkowej w przypadku belki trapezowej, zakrzywionej lub spadziste,
• skali $k_h$,
  Uwzględnia efekt skali wymiaru wysokości przekroju, mniejszego od wartości referencyjnej,
• skali $k_l$,
  Uwzględnia efekt skali wymiaru długości elementu , mniejszego od wartości referencyjnej,
• redystrybucji naprężeń przy zginaniu  dwuosiowym $k_m$,
  Uwzględnia redystrybucję naprężeń  w przekroju poddanym dwukierunkowemu zginaniu –  w przypadku przekroczenia granicy wytrzymałości nadwyżki naprężenia są przekazywane na drugi kierunek,
• systemu dystrybucji obciążenia $k_{sys}$
  Zwiększa wytrzymałość prętów w przypadku równomiernego rozdziału obciążenia  w ciągłym systemie dystrybucji,
• redukcji wytrzymałości na ścinanie ze względu na karby $k_v$,
  Uwzględnia efekt na karbu (nacięcia) na wytrzymałość elementu na ścinanie
• skali objętości dla rozciągania prostopadłe do ziarna w wierzchołku pręta trapezowego, zakrzywionego lub skośnego $k_{vol}$,
  Stosowany do przekrojów klejonych warstwowo lub LVL.  Koryguje wytrzymałość na rozciąganie w kierunku prostopadłym do rdzenia w przypadku, gdy wytężona objętość w wierzchołku belki trapezowej, zakrzywionej lub spadzistej przekracza objętość referencyjną (wzorcową)
• pełzania $k_{def}$,
  Współczynniki stosowany do odkształceń i przemieszczeń, uwzględniający ich zwiększanie się z upływem czasu (pełzanie), którego wartość zależy od typu drewna oraz jego wilgotności

Wartości obliczeniowe cech drewna

Konstrukcje drewniane są wrażliwe na wilgotność otoczenia oraz czas trwania obciążenia w stopniu większym od innych rodzajów konstrukcji (stalowych i żelbetowych). Do wyznaczenia obliczeniowych wartości cechy X (w tym wytrzymałości)  stosuje się formułę [1],(2.14))):

$$\begin{equation} X_d=k_{mod}\cdot \cfrac{X_k}{\gamma_M}  \label {7} \end{equation}$$

Wartości obliczeniowe  $X_d$ wyznacza się na podstawie wartości charakterystycznej cechy $X_k$k odczytanej z tab.1, 2 lub 3.

Współczynnik k_mod

Współczynnik $k_{mod}$  specyficzny dla konstrukcji drewnianych. W innych typach konstrukcji (żelbetowa, stalowa) czas trwania obciążenia jest skupiony we współczynnikach obciążenia $\gamma_f$ , a warunki środowiskowe we współczynnikach materiałowych $\gamma_M$. W konstrukcjach drewnianych natomiast, oprócz stosowania częściowych współczynników bezpieczeństwa $\gamma_f \, ; \, \gamma_M$ czas trwania obciążenia oraz wilgotność otoczenia uwzględnia się współczynnikiem $k_{mod}$  , który zależy od klasy użytkowania oraz od klasy trwania obciążenia.

Współczynniki $k_{mod}$ dla drewna litego, klejonego warstwowo, LVL oraz sklejki  są takie same. Zestawiono je  w tab.5

Tab.5 Współczynniki $k_{mod}$ dla drewna litego, klejonego warstwowo, LVL i sklejki

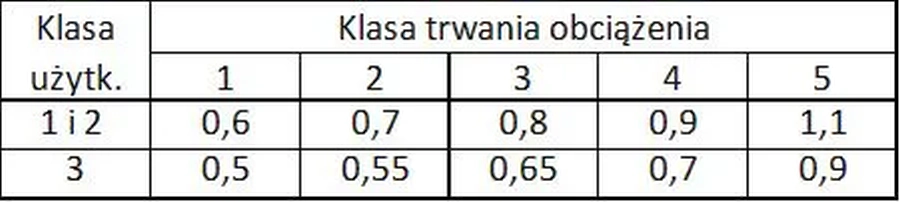Indeks klasy trwania obciążenia wg tab.7

W przypadku elementu złożonego z materiałów o dwóch klasach trwania obciążenia i odpowiadających współczynnikach $k_{mod,1}$ oraz $k_{mod,2}$, współczynnik dla elementu wyznacza się jako średnią geometryczną $k_{mod}=\sqrt {k_{mod,1} \cdot k_{mod,2}}$.

Prawidłowe przyjęcie współczynnika $k_{mod}$ jest istotne, bo w typowych sytuacjach przyjmuje wartości od 0,7 do 0,9, czyli mogące różnić się aż o (0,9/0,7) = ok 30%. O tyle można  przeszacować nośność konstrukcji drewnianej.  Często w obliczeniach profesjonalnych przyjmuje się wartość 0,9 jak dla obciążeń krótkotrwałych ( w zasadzie tylko wiatr), podczas, gdy w sprawczych kombinacjach obciążeń zasadniczą częścią obciążeń są obciążenia długotrwałe.

Zgodnie z klauzulą [1],kl. 3.1.3(2))) jeżeli kombinacja obciążeń składa się z oddziaływań należących do różnych ki as trwania obciążenia, to należy wybrać taką wartość współczynnika $k_{mod}$, która odpowiada oddziaływaniu krótszemu, np. dla kombinacji działanie trwałe i krótkotrwałe należy zastosować $k_{mod}$ odpowiadającą działaniu krótkotrwałemu. Zdaniem autora ta klauzulą jest zbyt zachowawcza, szczególnie w takich sytuacjach, gdy wkład obciążenia krótkotrwałego do wytężenia jest pomijalnie mały (np wiatr na zwykłe hale) lub kwalifikowanie śniegu jako obciążenia krótkotrwałego, podczas gdy w Polsce jest to oczywiście obciążenie średniotrwałe.  Dlatego proponujemy obiektywną zasadę polegającą na wyznaczaniu średniej ważonej według formuły:

$$\begin{equation} k_{mod} = \cfrac {  \Sigma k_{mod,i}\cdot F_i} {\Sigma F_i} \label {8} \end{equation}$$

W ostatniej kolumnie tab.7 podano propozycję szacowania udziału obciążenia F_i przypisanego do klasy trwania  obciążenia z indeksem „i”.

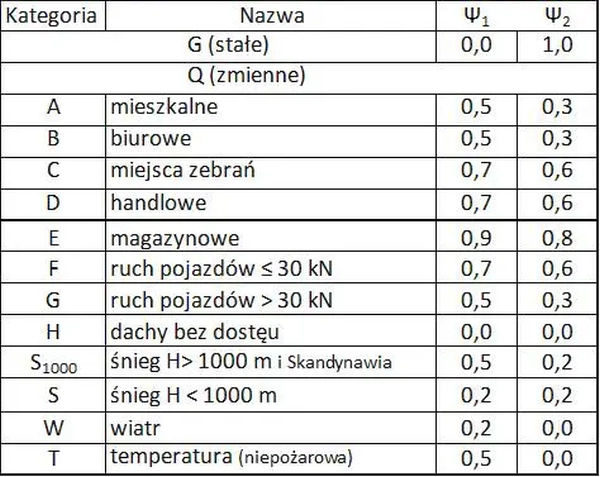
Współczynniki udziału części długotrwałej $\Psi_2$ oaz częstej $\Psi_1$ w danym obciążeniu przyjmuje się zgodnie z normą [9] – podano je  w tab. 6. Interpretacja współczynników redukcyjnych obciążeń jest przedstawiona w artykule „Kombinacje obciążeń w Eurokodach„.

Tab.6. Współczynniki udziału obciążeń  długotrwałych i  częstych

Dla płyt drewnianych ( OSB, wiórowe,  pilśniowe ) wartości współczynnika $k_{mod}$ podano w [1],tab. 3.1.)).

Przykład szacowania współczynnika $k_{mod}$ podano w przykładach rachunkowych.

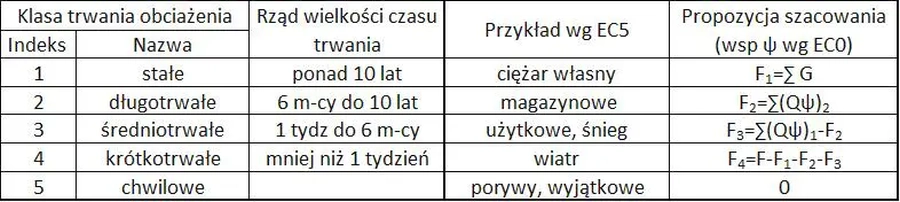
Klasy trwania obciążenia

Klasy czasu trwania obciążenia przyjmuje się wg tab.7.

Tab.7. Klasy trwania obciążenia

Klasy użytkowania

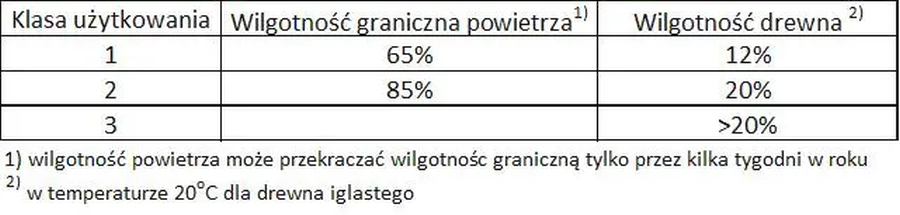
Klasy użytkowania przyjmuje się wg tab. 8.

Tab.8 Klasy użytkowania konstrukcji drewnianych

Odkształcalność drewna

Ortotropowość drewna  a  podłużne i poprzeczne  moduły odkształcalności

Odkształcalność drewna jest charakteryzowana zestawem czterech modułów : $[E, G]_0$  i $[E,G]_{90}$ – modułem odkształcalności podłużnej E (modułem Younga) oraz ,modułem odkształcalności poprzecznej (postaciowej) G (modułem Kirchoffa) w kierunku podłużnym do słoi drewna (ideks 0) oraz prostopadłym do słoi (indeks 90). W ten inżynierski sposób uwzględniono ortoropowość drewna. Rozprzężenie  stałych materiałowych w obu kierunkach pozwoliła na traktowanie drewna jako materiał izotropowy w kierunku podłużnym (rozciąganie, ściskanie, zginanie bez zwichrzenia) oraz w kierunku poprzecznym (ścinanie, skręcanie,  skrętna i giętno-skrętna utrata stateczności (w tym zwichrzenie).To z kolei umożliwiło stosowanie rozwiązań klasycznej teorii sprężystotości ciałą izotropowego (np. formuły na współczynniki wyboczenia lub moment krytyczny przy zwichrzeniu).

Czas trwania obciążenia a chwilowe i trwałe moduły odkształcalności

Odkształcalność drewna istotnie  zależy od czas trwania obciążenia i wilgotność. Te czynniki z kolei uwzględniono poprzez wprowadzenie innych modułów $[E,G]_{0 \, lub \,90}$ dla kilku  sytuacji projektowych: 

1) obliczania rozkładu sił wewnętrznych w tym sił przekrojowych –  moduły obliczeniowe:

$$\begin{equation}  E_d= \cfrac{E_{mean}}{\gamma_M} \quad ; \quad  G_d= \cfrac{G_{mean}}{\gamma_M} \label {9} \end{equation}$$

2) analizy wyboczeniowej  – 5% kwantyl modułów (moduły charakterystyczne) $E_{05}$ , $ G_{05}$ wg tab 1, 2, 3,

3) obliczania przemieszczeń chwilowych – moduły chwilowe   Younga $E_{inst}, G_{inst}$   $(\ref{9})$, przyjmowane jako średnie $E_{mean}, $G_{mean}$ z tab.1, 2 , 3, 10,

$$\begin{equation}  E_{inst}=E_{mean} \quad ; \quad G_{inst} = G_{mean}  \label {10} \end{equation}$$

4) obliczania przemieszczeń końcowych i ugięć trwałych wywołanych trwałą kombinacją obciążeń w uproszczeniu  ($G_k+\Sigma Q_k \cdot \Psi_2$)-  moduły trwałe (końcowe)

$$\begin{equation}  E_{fin}=\cfrac{E_{mean}}{1+k_{def}} \quad ; \quad  G_{fin}=\cfrac{G_{mean}}{1+k_{def}}  \quad \label  {11} \end{equation}$$

5)  specyficznym elementem konstrukcji drewnianej są połączenia, charakteryzujące się luzami, co jest specyfikowane modułem poślizgu w połączeniu  $K_{ser}$:

$$\begin{equation}  K_{ser,inst}=K_{ser} \quad ; \quad K_{ser,fin}=\cfrac{K_{ser}}{1+k_{def}} \label {12} \end{equation}$$

Współczynniki $k_{def}$ dla drewna litego, klejonego warstwowo i LVL  wynoszą dla klas użytkowania:

$$ \begin{equation} k_{def}= \label{13} \begin {cases}
0,6 , & \textrm {1 klasa użytkowania} \\
0,8 , & \textrm {2 klasa użytkowania} \\
2,0 , & \textrm {3 klasa użytkowania}
\end {cases} \end{equation} $$

Współczynniki $k_{def}$ dla innych typów wyrobów drzewnych podano w [1],tab. 3.2.)).

W klauzuli [1],kl. 2.3.2.2 (1))) zalecono moduły $X_{fin}$ do obliczania  końcowych deformacji w stanie granicznym użytkowalności (SGU) na przypadek , gdy ” konstrukcja składa się z elementów lub komponentów posiadających różne właściwości zależne od czasu„. Ostatnia część zalecenia ” konstrukcja ...) nie ma zastosowania do obliczeń systemu konstrukcyjnego metodami komputerowymi, bowiem w takich obliczeniach różnice własności elementów składowych są zawsze uwzględniane w procedurze składania sztywności systemu.

W konstrukcjach drewnianych do obliczania odkształceń przemieszczeń i ugięć trwałych pod długotrwałą kombinacją obciążeń są stosowane są moduły $X_{fin}$ ($\ref{11}$). Można wykazać, że w wyniku takich obliczeń uzyskuje się sumaryczne odkształcenia (rys. 8)

$$\begin{equation}  u_{fin}=u_{inst}+u_{crep}  = u_{inst} \cdot (1+k_{def}) \label{14} \end{equation}$$

gdzie $u_{crep}$ jest częścią ugięcia wywołaną pełzaniem konstrukcji.

Moduły odkształcalności w analizie numerycznej

W przypadku obliczeń komputerowych nie potrzeba stosować klauzuli normowej [1],kl. 2.2.3. (5))) dopuszczającej stosowanie procedury uproszczonej obliczania ugięć.

Do sprawdzania stanu granicznego nośności (SGN) to znaczy do wyznaczania sił przekrojowych nie potrzeba też stosować klauzuli [1],kl. 2.3.2.2 (2))), w której zaleca się, aby w przypadku, gdy  na na rozkład sił przekrojowych ma  rozkład sztywności elementów konstrukcji stosować moduły typu

$$\begin{equation}  X_{mean,fin}=\cfrac{X_{mean}}{1+\Psi_2 \cdot k_{def}} \label {15} \end{equation}$$

Po pierwsze w obliczeniach sił wewnętrznych ( w tym  przekrojowych w konstrukcji prętowej) obciążonej mechanicznie istotne są stosunki sztywności pomiędzy elementami, a stosowanie formuły $(\ref{15})$ nic nie zmienia w stosunkach sztywności. Po drugie współczynnik części długotrwałej obciążenia $\Psi_2$ uwzględnia się przy składaniu kombinacji obciążeń .

W przypadku obciążeń termicznych lub wymuszonych przemieszczeń (skrócenia lub wydłużenia) wartość modułu ma wpływ na wartości sił wewnętrznych (podczas transformacji wymuszeń geometrycznych na mechaniczne). W takim przypadku stosowanie większych wartości modułów, zwiększa obciążenia mechaniczne. Ponieważ w stanie granicznym nośności stosuje się obciążenia obliczeniowe, więc konsekwentnie należałoby zmniejszyć moduły odkształcalności w tym samym stosunku i zastosować moduły obliczeniowe  wg formuł [1],wzór (2.15), (2.16) ($\ref{9}$).

Współczynnik Poissona $\nu$ drewna

Tylko dwie spośród tych trzech  stałych [E,G, $\nu$ są niezależne, a każda para w pełni identyfikuje ciało sprężyste. Pomiędzy modułem Younga E, modułem Kirchoffa G i współczynnikiem Poissona $\nu$ zachodzi jednoznaczny i ścisły związek

$$\begin{equation} \nu =^{def} \cfrac{\varepsilon_R }{\varepsilon_L } =^{app} \cfrac {E}{2G}-1 \label{16} \end{equation}$$

Dla ciała izotropowego współczynnik Poissona zawiera się w granicach

$ -1 \le  \mu \le 0,5 $

i definiuje stosunek odkształceń podłużnych $\varepsilon _L$ do poprzecznych -promieniowych oznaczenia wg (rys.1)  $\varepsilon _R$

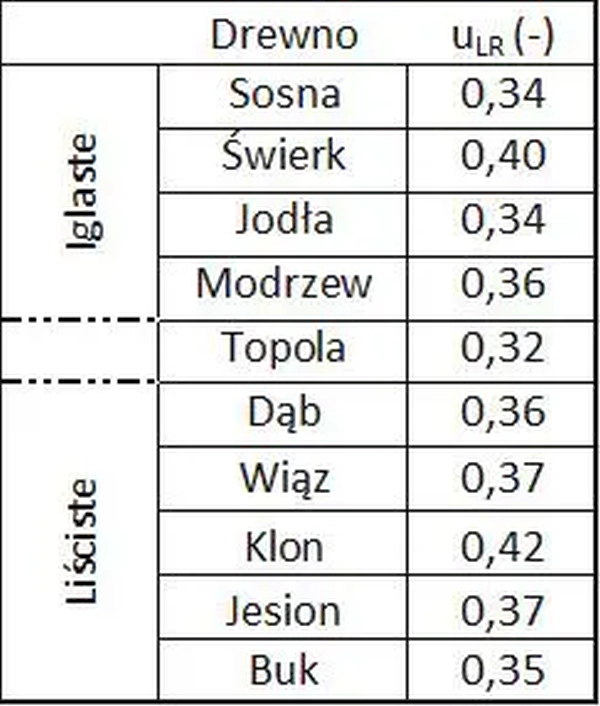
Współczynniki Poissona $\nu_{LR}$ wyznaczone eksperymentalnie z definicji (jako stosunek odkształcenia promieniowego R do podłużnego L) średnie  dla wybranych gatunków drewna przy wilgotności ok 12% podano za pracą[10] zamieszczono w tab. 11

Tab.11. Współczynniki Poissona dla drewna przy wilgotności 12% [11],tab. 4.2

W przypadku drewna (modułów wykazywanych w normach tab 1, 2, 3) zastosowanie ścisłej zależności $=^{app}$  może prowadzić do błędnego wniosku, że współczynnik Poissona drewna jest większy od 1. Jest to oczywisty fałsz, który potwierdza, że drewno jest ciałem ortotropowym, lub że wykazywane wartości modułów E i G są wyznaczane z mała dokładnością.  Zaleca się, by przy definiowaniu izotropowego materiału zastępczego w programach obliczeniowych, charakteryzowanego parą stałych [E, $\nu$], w zależności od sytuacji obliczeniowej przyjmować moduł Ypunga wg tab 1., 2 3, a współczynnik Poissona wg tab. 11.

Poślizg w złączach

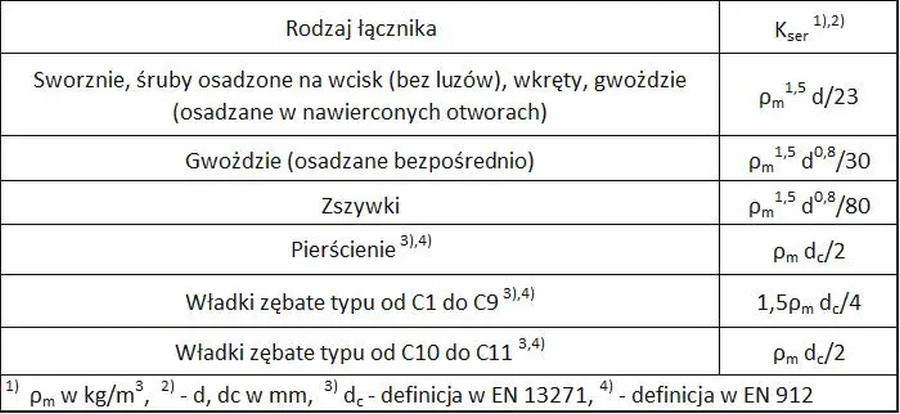
Projektując złącza na łączniki trzpieniowe należy przyjmować moduł podatności (poślizgu) $K_{ser}$ odniesiony do jednej płaszczyzny ścinania i do pojedynczego łącznika, pracującego pod obciążeniem odpowiednim dla stanu granicznego użytkowalności. Wartości $K_{ser}$  można określić na podstawie wzorów podanych w tab. 9

Tab.9. Współczynniki poślizgu w złączach $K_{ser}$ [N/mm] [1],tab.7.1.))

,Jeżeli średnie gęstości łączonych dwóch elementów na bazie drewna, mają różne wartości $\rho_{m1}$ i $\rho_{m2}$, we wzorach z tab. 10 należy przyjąć $\rho_m$ jako średnią geometryczną $\rho_m=\sqrt{\rho_{m1}\cdot \rho_{m2}}$.

W przypadku połączeń drewno-metal lub drewno-beton, do obliczeń należy określać $K_{ser}$ na podstawie $\rho_m$ elementu drewnianego, ale uzyskaną wartość przemnożyć przez 2,0.

Efekt skali w konstrukcjach drewnianych

Znany jest statystyczny efekt skali, polegający na tym, że większy obiekt (np. dłuższy pręt rozciągany) jest słabszy od obiektu mniejszego. Fizycznie tłumaczy się to tym, że w większej objętości znajdzie się więcej słabych miejsc niż w mniejszej. Można to wyjaśnić na gruncie teorii niezawodności (np. artykuł w tej encyklopedii) niezawodnościowym modelem szeregowym, który w granicy może być opisany rozkładem statystycznym Weibulla (np [12]). Z teorii niezawodności wynika, że stosunek wytrzymałości $f_{R,1}$ i $f_{R,2}$ ciała odpowiednio o objętości $V_1$ i $V_2$  podlega zależności

$$\begin{equation}  \left( \cfrac{f_{R,1}}{f_{R,2}} \right) = \left( \cfrac {V_1}{V_2} \right )^{1/p} \label {17} \end{equation}$$

gdzie p- jest współczynnikiem kształtu rozkładu Weibulla, określonym na podstawie badań doświadczalnych dla każdego konkretnego przypadku wytrzymałościowego.

W przypadku dwóch prętów drewnianych:  o przekroju $h_1 x b_1$ i długości $L_1$ – pierwszy i $h_2 x b_2 x L_2$ – drugi: objętości wynoszą $V_1=b_1 \cdot h_1 \cdot L_1$, $V_2=b_2 \cdot h_2 \cdot L_2$, a zależność  $( \ref{17} )$ można zapisać w postaci:

$$\begin{equation}  \left( \cfrac{f_{R,1}}{f_{R,2}} \right) = \left( \cfrac {b_1}{b_2} \right )^{1/p_b} \cdot \left(  \cfrac {h_1}{h_2} \right )^{1/p_h} \cdot \left( \cfrac {L_1}{L_2} \right )^{1/p_L} \label {18} \end{equation}$$

gdzie: $p_b$, $p_h$, $p_L$ są współczynnikami kształtu rozkładu dla szerokości, wysokości i długości odpowiednio.

Przy zginaniu czynnik szerokości ma pomijalny wpływ, a czynnik wysokości i długości, często łączy się wprowadza zastępczą formułę

$$\begin{equation}  \left( \cfrac{f_{R,1}}{f_{R,2}} \right) = \left( \cfrac {h_1}{h_2} \right )^{1/p_{hL}} \label {19} \end{equation}$$

Efekt skali uwzględnia się poprzez przemnożenie wartości podanych w tab. 1, 2, 3 przez współczynniki skali: wysokości $k_h$, długości $k_l$ lub objętości $k_{vol}$ w tych przypadkach, w których może mieć to istotny wpływ, zgodnie z tab. 10.

Ustalone są wielkości odniesienia $h_0$, $L_0$, $V_0$ powyżej których (dla rozmiarów większych) współczynnik skali jest mniejszy od jedności, ale ponieważ redukcja jest stosunkowo niewielka, więc jest pomijana w normie i przyjmowane są jako równe 1.
Gdy rozmiary są mniejsze niż wartość odniesienia współczynnik skali będzie większy od jedności, czyli element będzie silniejszy. W przypadku zmniejszania się rozmiaru elementu, ustawiono górny limit. 

Zestawienie formuł na współczynniki skali podano w tab. 10

Tab.10. Współczynniki  skali w projektowaniu konstrukcji drewnianych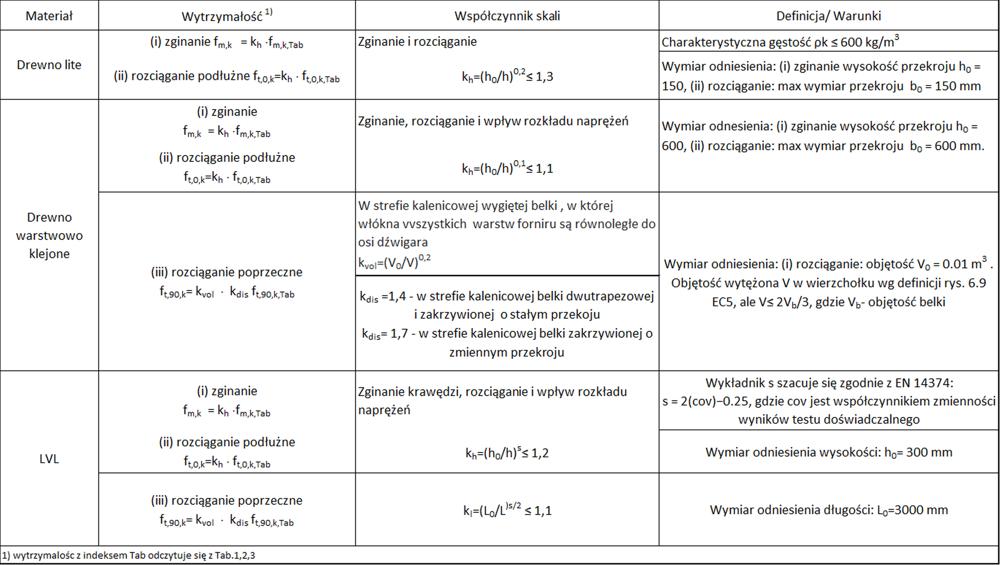

Wpływ sił poprzecznych na ugięcia

Drewno jest materiałem w, w którym istoty wpływa na przemieszczenia ma odkształcalność postaciowa.

$$\begin{equation} S_v=G \cdot A_v \label {20} \end{equation}$$

gdzie za moduł Kirchoffa G należy przyjmować wartość średnią $G_{mean}$ do obliczania przemieszczeń chwilowych i  $G_{fin}$ do obliczania przemieszczeń końcowych. Pole przekroju $A_v$ jest efektywną częścią przekroju uczestniczącą w przenoszeniu naprężeń stycznych, które ogólnie można zapisać w postaci

$$\begin{equation} A_v=\alpha_v \cdot A  \label {21} \end{equation}$$

gdzie współczynnik $\alpha_v$ zależy od kształtu przekroju i dla wybranych przekrojów wynosi:

$$ \begin{equation} \alpha_v= \label{22} \begin {cases}
2/3 , & \textrm {przekrój prostokątny} \\
A_w/A , & \textrm {$A_w$ pola środnika przekroju H lub  środników przekroju skrzynkowego} \\
\end {cases} \end{equation} $$

Do analizy konstrukcji drewnianych należałoby więc używać elementu belkowego, np w sposób opisany w artykule  Belka Timoshenko na sprężystym podłożu.

W metodzie elementów skończonych macierz sztywności jest modyfikowana współczynnikiem

$$\begin{equation} \Psi_v=\cfrac{12 EI} {GA_v \cdot l^2} \label {23} \end{equation}$$

gdzie l jest długością elementu.

który dla przekroju prostokątnego bxh wynosi

$ \Psi_v=\cfrac {E}{G} \cdot \left( \cfrac{l}{h} \right)^2$

Można pokazać, że ugięcia belki swobodnie podpartej w o długości $l$ można zapisać wzorem

$$\begin{equation}  w= w_m \cdot (1+\beta_v \cdot \Psi_v) \label{24} \end{equation}$$

gdzie $w_m$ jest ugięciem belki wywołanym momentami zginającymi ( bez uwzględnienia sztywności postaciowej), a współczynnik $\beta_v$ uwzględniający wpływ ścinania zależy od konfiguracji obciążenia belki, jak następuje:

$$ \begin{equation} \beta_v= \label{25} \begin {cases}
0,873  , & \textrm {obciążenia skupione  w 1/4 i 3/4 rozpiętości} \\
0,960  , & \textrm {obciążenie równomiernie rozłożone} \\
1,011  , & \textrm {obciążenia skupione  w 1/4 , 1/2 i 3/4 rozpiętości} \\
1,200  , & \textrm {obciążenie skupione  w środku rozpiętości (1/2 l) } \\
\end {cases} \end{equation} $$

Wzrost ugięcia na skutek odkształceń postaciowych w przypadku belki obciążonej siłą w środku rozpiętości wynosi   $1,2 \Psi_v$.  Dla konstrukcyjnego drewna iglastego dla stosunek  $ \tfrac{E}{G} \approx 16$, a w praktycznych projektach $\tfrac{h}{l} = 0,1 \div 0,05$ i wówczas ugięcie od  ścinania wyniesie  5 do  20 % ugięcia od wywołanego momentami zginającymi . To pokazuje, że w niektórych przypadkach przy projektowaniu konstrukcji drewnianych należy uwzględnić wzrost ugięcia wywołany podatnością postaciową belki.

Właściwości drewna w pożarze

Z punktu widzenia bezpieczeństwa budowli projektowanych z uwagi na warunki pożarowe jest zachowanie się drewna w pożarze.

Na rys. 3 pokazano zmniejszenie się wytrzymałości konstrukcji stalowych i drewnianych w pożarze.

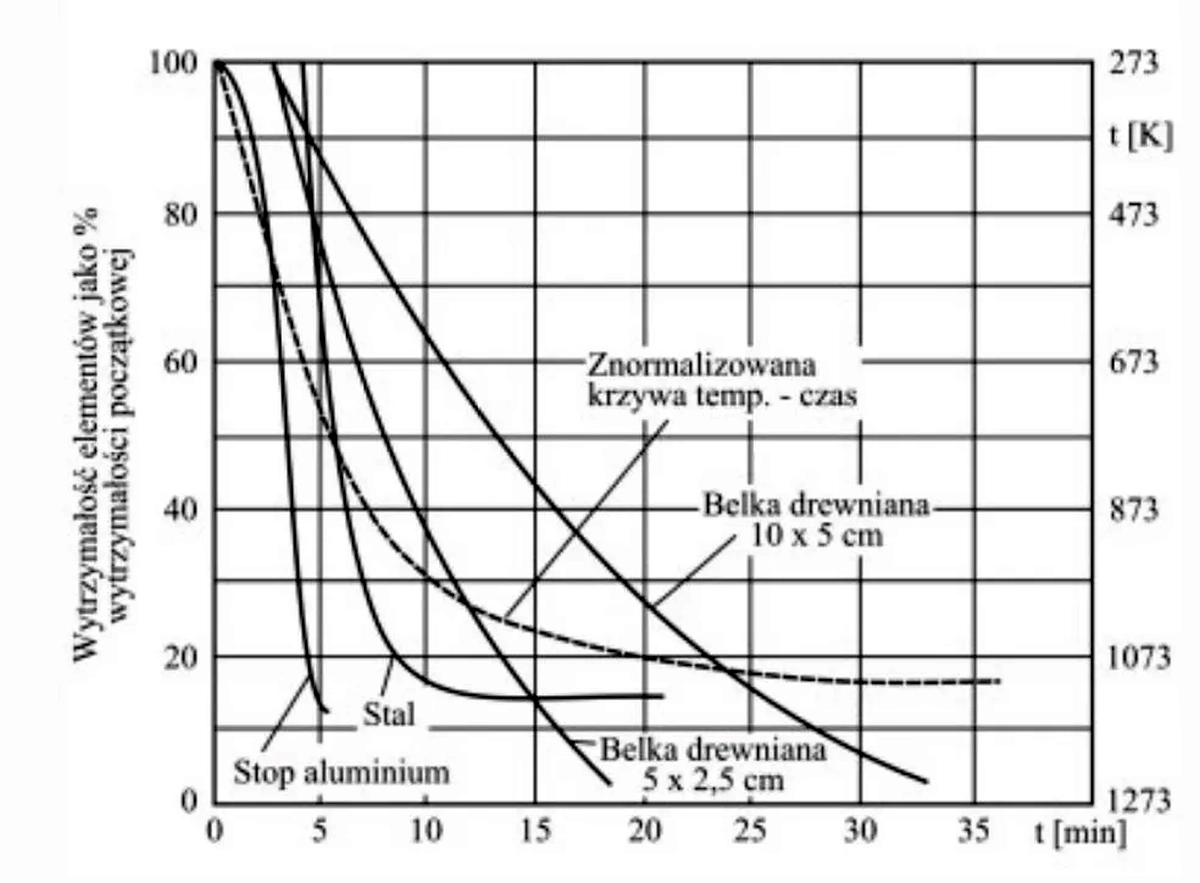
Rys.3 Konstrukcje stalowe a drewniane otoczone pożarem [13]

Z porównania zmniejszania się wytrzymałości w pożarze konstrukcji stalowych i drewnianych wynika, że znacznie lepiej w pożarze zachowuje się  drewno. Nośność konstrukcji stalowych niezabezpieczonych pożarowo przyjmuje się R15 (15 minut). Po tym czasie temperatura pożaru osiąga ok 700 ^oC , a elementy stalowe gwałtownie zaczynają się odkształcać i ich wytrzymałość wynosi tylko 14% nośności początkowej,  W tym samym czasie i temperaturze pożaru nośność belki drewnianej wynosi ok 43% nośności początkowej. Ponadto drewno podczas pożaru  wydaje dźwięki, które, zanim konstrukcja się zawali — ostrzegają przed niebezpieczeństwem, co umożliwia ewakuację osób z pomieszczeń.

W zwykłych warunkach pożar (zapalenie) drewna następuje przeważnie od źródła ognia o temperaturze 700 do 800 ^oC.

Bardziej szczegółowe informacje o projektowaniu konstrukcji drewnianych w pożarze podano w artykule Konstrukcja budowlane.

Nieliniowości geometryczne

W normie [1],rozdz.6.3)) dużo miejsca poświęcono zagadnieniom nieliniowości  geometrycznych, związanych z utratą stateczności prętów ściskanych oraz zwichrzeniem belek. Zagadnienia te przedstawiono jednak w ujęciu historycznym, podczas gdy aktualnie wymiarowanie konstrukcji dokonuje się metodą imperfekcyjną, w której zagadnienia niestateczności są równoważnie zastąpione przyłożeniem fikcyjnych obciążeń poziomych na konstrukcję, a obliczenia tak obciążonej konstrukcji dokonywane są metodami II rzędu. W tej metodzie nie potrzeba szacowania długości efektywnych $l_{ef}$ , współczynników wyboczeniowych $k_{c,y}$, $ k_{c,z}$ ani współczynnika  zwichrzenia $k_{crit}$.

Dopuszczalne odchyłki geometrii prętów drewnianych i imperfekcje przyjmowane w analizie II rzędu

Odchyłki od prostoliniowości słupów, belek i elementów ram, mierzone w połowie odległości pomiędzy podporami, w przypadku, gdy są narażone na utratę stateczności, jeśli są wykonane z drewna warstwowo klejonego lub LVL, nie powinny być większe niż 1/500 długości, a jeśli są wykonane z drewna litego, nie powinny być większe niż 1/300 długości. W większości zasad sortowania  wytrzymałościowego, niewystarczające są ograniczenia dotyczące krzywizn stosowanych materiałów i dlatego należy zwracać szczególną uwagę na prostoliniowość elementów.

Z odchyłek wykonawczych można wyprowadzić imperfekcje projektowe zgodnie zasadami artykułu Imperfekcje projektowe z odchyłek-wykonawczych

Imperfekcje przechyłowe

Podstawowa imperfekcja przechyłowa zgodnie z  [1],(5.1) powinna wynosić

$$\begin{equation} \text {co najmniej  } \Phi_0=1/200 \to n_L=200  \label {26} \end{equation}$$

czyli tak jak w przypadku konstrukcji stalowych, ale dopuszcza się przyjęcie wartości większych.

Imperfekcja podstawowa może być zredukowana współczynnikiem wysokości

$$\begin{equation} \alpha_h = \sqrt {\cfrac{5} {h}}  \label {27} \end{equation}$$

czyli o 12% więcej niż w przypadku konstrukcji stalowych.

Norma [1] nie przewiduje współczynników redukcyjnych $\alpha_m$ uwzględniających liczbę słupów $m$ na danej kondygnacji.

Imperfekcje łukowe

Imperfekcja łukowa  zgodnie z  [1],(5.2) wynosi

$$\begin{equation} \text { co najmniej  } e_0=1/400 \cdot l \to n_L=400 \label {28} \end{equation}$$

czyli są dwukrotnie mniejsze od  zalecanych dla konstrukcji stalowych  i zgodne z zaleceniami dla konstrukcji żelbetowych .

Programy do obliczeń  konstrukcji (stalowych) a konstrukcje drewniane

Zasady przyjmowania imperfekcji dla konstrukcji drewnianych nie różnią się metodycznie  od innych rodzajów konstrukcji, a różnice dotyczą tylko w wartościach impefekcji przechyłowych ($\ref{26}$) i łukowych ($\ref{28}$),  które to można w specjalizowanych programach ustalić na właściwym poziomie.  Ponieważ zaś najbardziej zaawansowane w analizach nieliniowych są programy do obliczeń konstrukcji stalowych, to zaleca się stosować programy z tej dziedziny, na przykład program Consteel, ale dla dodatkowo zdefiniowanych zastępczych elementach stalowych o własnościach przynależnych do klasy drewna, z którego są wykonane.

Zaleca się postępować według procedury:

1. zdefiniować zastępcze elementy :stalowe o własnościach przynależnych do klasy drewna odpowiednie do przeprowadzenia analizy wyboczeniowej LBA, czyli o modułach odkształcalności osiowej:
   $E_{0,05}$  w przypadku  obliczania sił przekrojowych,
   $E_{inst}, G_{inst}$   $(\ref{9})$,  $E_{fin}$ w przypadku obliczania przemieszczeń i ugięć chwilowych lub trwałych
   oraz odpowiednich dla rodzaju drewna współczynnikach Poisson
2.  zbudować model konstrukcji i obciążyć go imperfekcjami zdefiniowanymi wyżej,
3.  przeprowadzić obliczenia LBA w celu ustalenia  mnożników krytycznych , a następnie charakterystyk niestateczności bez potrzeby szacowania długości wyboczeniowych lub zwichrzenia
4.  przeprowadzić obliczenia II rzędu i odczytać siły przekrojowe w elementach drewnianych,
5. sprawdzenie wytrzymałości prętów  przeprowadzić zgodnie z formułami ustalonymi  dla elementów drewnianych ($\ref{39}$)  do ($\ref{47}$).

W pkt 1 do 6 zaprezentowanej procedury przeprowadzana jest analiza statyczna metodami wspólnymi dla elementów wykonanych z różnych materiałów, a  dla uzyskanych  sił II rzędu,  Definiowanie dokładnych wartości wytrzymałości drewna nie ejst potrzebne na tym na tym etapie. Za wytrzymałość drewna można  wytrzymałości obliczeniową odpowiednią dla zginania $f_{m,d}$.

Dopiero w pkt. 7 przeprowadza się wymiarowanie elementów drewnianych metodami specyficznymi dla nich metodami o wytrzymałościach odpowiednich do zidentyfikowanych sił przekrojowych.

Wymiarowanie konstrukcji drewnianych

Zasady ogólne

Współcześnie siły przekrojowe uzyskuje się z analizy drugiego rzędu. W analizie drugiego rzędu konstrukcji drewnianych w zakresie liniowo-sprężystym, należy przyjmować:
a) do wyznaczania sił przekrojowych i reakcji – wartości obliczeniowe bez uwzględniania czasu trwania obciążania.
b) do analizy wyboczeniowej LBA ( analizy stateczności) – 5% kwantyl modułów wg tab 1, 2, 3 ($E_{05}$, Dopuszcza się przyjmowanie jako drugiej stałe sprężystości współczynnika Poissona wg tab. 11.
(p. też rozdział Nieliniowosci_geometryczne).

W tym artykule i artykułach powiązanych przyjmujemy  że siły przekrojowe (i ogólnie wewnętrzne) uzyskano z  analizy II rzędu, a ponadto uzyskano je dla konstrukcji obciążonej imperfekcjami, co pozwala ograniczyć konieczność wyznaczania współczynników niestateczności dla elementów ściskanych bądź zginanych.

Jeśli jednak projektant analizuje konstrukcję historycznymi już metodami pierwszego rzędu (czyli bez uwzględnienia wpływu przemieszczeń na wytężenie), to :

• jeżeli na rozkład sił wewnętrznych w elementach nie ma wpływu rozkład sztywności w konstrukcji (w konstrukcjach statycznie wyznaczalnych i dodatkowo jeżeli wszystkie elementy charakteryzuje jednakowa zmienność właściwości w czasie), to w projektowaniu należy przyjmować wartości średnie, a nie obliczeniowe,.
• jeżeli elementy są złożone z materiałów o różnej zmienności właściwości w czasie, to wartości średnie właściwości należy dostosować  do czasu trwania składowej obciążenia, która wywołuje największe naprężenie w odniesieniu do wytrzymałości,  materiału,

Krótkie porównanie metod wymiarowania I i II rzędu

Wymiarowanie pręta ściskanego i zginanego metodą II rzędu przebiega według kryterium jak dla pręta rozciąganego i zginanego ($\ref{39}$), ale dla sił przekrojowych obliczonych metodą II rzędu w systemie obarczonym imperfekcjami. Tak wyliczone momenty zginające w prętach są powiększone o $\Delta M$ w stosunku do momentów zginających I rzędu $M^I$ zgodnie z formułą

$$\begin{equation}  M = M^{I}+\Delta M\label{29}\end{equation}$$

Zwiększenie momentu zginającego przekrój w systemie obciążonym imperfekcjami jest efektem działania siły ściskającej na wygięciu wstępnym pręta (imperfekcji łukowej) oraz efektem przechyłu całego systemu konstrukcyjnego (o kąt imperfekcji przechyłowej).

Z formuły ($\ref{29}$), wynika, że w przypadku pręta teoretycznie osiowo ściskanego też wystąpi moment zginający

$M = \Delta M$

W klasycznej analizie działanie „nieuchwytnego” momentu drugorzędowego $\Delta M$ jest uwzględniona ” w sposób przybliżony współczynnikiem redukcyjnym (wyboczenia). Na przykład dla pręta „osiowo ściskanego mamy :

$$\begin{equation} \sigma_{Ed} = \cfrac{N^{II}} {A} +\cfrac{\Delta M}{W} \approx  \cfrac{N^I}{A \cdot k_{stat}}\label{30}\end{equation}$$

gdzie $k_{stat}$ są współczynników niestateczności $k_{stat}= [ k_{c,y} k_{c,z}]$

Analogiczne formuły można przedstawić dla zwichrzenia belki.

Formuły wymiarowania

Siły przekrojowe

Przedstawimy formuły wymiarowania  przekroju elementu konstrukcji drewnianej obciążonego obliczeniowymi siłami przekrojowymi  $F_{Ed}$, wywołanymi obciążeniami zewnętrznymi

$$\begin{equation} F_{Ed} = \left [ N_{Ed} \,  ; \, M_{y,Ed} \,  ; \, M_{z,Ed} \,  ; \, V_{z,Ed} \,  ; \, V_{y, Ed} \,  ; \, M_{x,Ed} \right ]  \label{31}\end{equation}$$

przy czym  siła podłużna $N_{Ed}$ może być:
rozciągająca $N_t $ lub
ściskająca $N_c $ i działająca
wzdłuż włókien elementu  $N_{t,0}$, $N_{c,0}$ lub
poprzecznie do włókien $N_{t,90}$.

Momenty zginające $M_{y,Ed}$ lub  $M_{z,Ed}$ zginają przekrój odpowiednio wokół osi głównej „y” lub  „z”, gdzie
oś „y” jest główną osią centralną wokół której wskaźnik wytrzymałości przekroju $W_y$ jest największy ( $W_y > W_z$ ).

Siły poprzeczne $V_{z,Ed}$ lub  $V_{y,Ed}$ są stowarzyszone z momentami zginającymi $M_{y,Ed}$ i $M_{z,d}$ odpowiednio.
W technice oś „y” zwykle jest osią poziomą przekroju, a oś „z” osią pionową.

Moment skręcający $M{(x}$ w normie [1] jest oznaczany jako $M_{tor}$,a w mechanice najczęściej jako $M_{x}, czyli moment sił działający wokół osi pręta x.

Siły przekrojowe II rzędu z sił I rzędu

Przez lata w celu wyraźnego wskazania, że używa się sił drugiego rzędu stosowano specjalne indeksowanie sił, np $F_{Ed}^{II}$. W tym artykule takie oznaczenie już pomija się, bowiem współcześnie podstawową, domyślną metodą analizy konstrukcji jest metoda II rzędu.  Jeśli jednak projektant nie ma narzędzi do przeprowadzenia analizy II rzędu, to może oszacować siły ($\ref{31}$) na podstawie klasycznych sił  I rzędu  $F_{Ed}^I$ z formuły:

$$\begin{equation} F_{Ed} \approx \cfrac{F_{Ed}^I}{k_{stat}} \label{32}\end{equation}$$

W formule ($\ref{32}$) $k_{stat}$ współczynnik niestateczności zależnie od natury elementu i  stosownego zjawiska niestateczności przyjmuje wartości:

dla prętów ściskanych siłą $N_{c,Ed}$  ( w tym słupów)   współczynnika wyboczeniowego  $k_{c,y}$ lub  $k_{c,z}$ zależnie od płaszczyzny wyboczenia, czyli

$$\begin{equation} N_{c,Ed} \approx \cfrac { N_{c,Ed}^1}{ min { [k_{c,y} \, ; \, k_{c,z}]}} \label{33}\end{equation}$$

dla prętów zginanych siłą $M_{y,Ed}$ (w tym belek)   współczynnika zwichrzenia $ k_{crit}$,czyli

$$\begin{equation} M_{y,Ed} \approx \cfrac{M_{y,Ed}^I }{ k_{crit}} \label{34}\end{equation}$$

Dla prętów, które nie utracą stateczności ogólnej: są zabezpieczone przed niestatecznością lub są poddane rozciąganiu, ścinaniu lub znajdują się w innych stanach naprężenia, które nie mogą doprowadzić do utraty stateczności  przyjmuje się

$$\begin{equation} k_{stat}=1 \label{35}\end{equation}$$

Współczynniki niestateczności: wyboczeniowe  $k_{c,y}$ , $k_{c,z}$ i zwichrzenia $k_{crit}$ należy wyznaczyć zgodnie z [1],rozdz 6.3.

Naprężenia

Siły przekrojowe wywołują naprężenia

$$\begin{equation} \sigma_{d} = \left [ \sigma_{t,d}= \cfrac {N_{t, Ed}}{A} \vee \sigma_{c,d}= \cfrac {N_{c,Ed}}{A}  \,  ; \, \sigma_{my,d}=\cfrac {M_{y,Ed}}{W_y} \,  ; \, \sigma_{mz,d} =\cfrac {M_{z,Ed}}{W_z} \,  ; \,  \tau_{vz, d}= \cfrac {V_{y,Ed}}{A_{vy}}  \,  ; \, \tau_{vy, d}= \cfrac {V_{z,Ed}}{A_{vz}} \,  ; \,  \tau_T = \cfrac{M_T}{W_x}\right ]  \label{36}\end{equation}$$

gdzie:
$A$ – pole przekroju;
$W_y$, $W_z$  $W_x$- wskaźnik wytrzymałości na zginanie względem osi „y” i „z” odpowiednio oraz wskaźnik wytrzymałości na skręcanie $W_x =\cfrac{I_x}{t_{max}}$
$A_{v,y}$ , $A_{v,z}$ – efektywne pole przekroju ścinania wzdłuż osi „z” i „y”  odpowiednio.

Dla przekroju prostokątnego bxh: $A=b\cdot h$, $W_y=\cfrac{b \cdot h^2}{6}$, $W_z=\cfrac{h \cdot b^2}{6}$,
Efektywne pole przekroju ścinania $A_{v}$ jest zależne od kształtu przekroju, co opisano wyrażeniem $(\ref {21})$

Wskaźniki wytężenia przekroju

Wskaźniki wytężenia przekroju $\alpha_F$ w prostych stanach naprężenia  bez uwzględnienia stateczności pręta wynoszą:

$$\begin{equation} \alpha_F = \left [ \alpha_{t,0} = \cfrac {\sigma _{t,0, d}} {f_{t,0,d}} \,  ; \,   \alpha_{t,90} = \cfrac{\sigma _{t,90, d}}{f_{t,90,d}} \,  ; \, \alpha_{c,0} = \cfrac {\sigma _{c,0, d}}{f_{c,0,d} } \,  ; \,  \alpha_{my} =\cfrac {\sigma_{my,d}}{f_{m,d} } \,  ; \,  \alpha_{mz} =\cfrac {\sigma_{mz,d}}{f_{m,d} } \,  ; \,  \alpha_{vz} =\cfrac {\tau_{vz,d}}{f_{v,d}} \,  ; \,  \alpha_{vy} =\cfrac {\tau_{vy,d}}{f_{v,d}}\right ]  \label{37}\end{equation}$$

gdzie wytrzymałości obliczeniowe drewna $f_{t,0,d}$ , $f_{t,90,d}$, $f_{c,0,d}$ , $f_{m,d}$, f_{v,d} wg ($\ref{7}$) , wyznaczone z wytrzymałości charakterystycznych zestawionych w  tab.1 , 2, 3.

Wskaźnik wytężenia przekroju siłą przekrojową oznaczono przez $\alpha_F$ ponieważ takie oznaczenie przyjęto w normie do projektowania konstrukcji drewnianych w pożarze, a ona powołuje się na normę do projektowania konstrukcji drewnianych w temperaturze normalnej.
Jednakże te oznaczenie należy stosować z ostrożnością  jako specyficzny w projektowaniu konstrukcji drewnianych. W innych dziedzinach inżynierii wskaźnik wytężenia przekroju często oznacza się symbolem $\eta_F$ lub $u_F$ (od ang.  „utilization”), W teorii plastyczności i sprężystości wskaźnik wytężenia jest nazywany względną siłą przekrojową (odniesioną do nośności granicznej lub krytycznej) i oznacza się małą literą „f” odpowiadającą sile przekrojowej lub obciążeniu „F”, np. „n” – względna siła osiowa „N”, „m” -względny moment zginający  „M”, W konstrukcjach stalowych oraz w teorii projektowania metodami imperfekcyjnymi  symbol  $\alpha_{cr} > 1 $ oznacza krytyczny mnożnik obciążeń, który jest w istocie  odwrotnością stopnia wytężenia $\eta_F < 1$.

Współwystępowanie  różnych form niestateczności

W złożonym stanie naprężenia  współczynniki niestateczności $k_{stat}$ (p. ($\ref{32}$) należy używać ostrożnie, bowiem zostały wyprowadzone dla prostych przypadków wytężenia (tylko zwichrzenie lub tylko wyboczenie) i są odniesione do przekroju pręta, w którym wstąpią największe przemieszczenia podczas utraty stateczności (najczęściej przekrój w środku pręta) – zależą od schematu statycznego oraz rozkładu i rodzaju obciążenia na pręcie.  Najczęściej mamy do czynienia z taką sytuacją, w której  maksymalny wpływ wyboczenia pręta wystąpi w innym przekroju niż jego zwichrzenie i jeszcze w innym przekroju niż maksymalne naprężenia

W normie  [1] opisane  zjawisko uwzględnia się w przypadku zginania i ściskania, ale sposób uproszczony:

• wyboczenie w obu płaszczyznach jest rozdzielone do odrębnych warunków: albo $k_{c,y}$ albo $k_{c,z}$,
• współdzialanie zwichrzenia i  wyboczenia jest  opisane odrębną formułą  interakcji kwadratowej,

Na użytek opisu tych zjawisk w ramach teorii I rzędu wprowadzimy zmodyfikowane wskaźniki wytężenia pręta:

$$\begin{equation} \alpha_{F,cr} = \left [\alpha_{c, cr,y}  = \cfrac{ \alpha_{c,0}} {k_{cy}}  \,  ; \,  \alpha_{c, cr,z} = \cfrac{ \alpha_{c,0}}{k_{cz}} \,  ; \,   \alpha _{my, cr} =\cfrac{\alpha_{my}}{k_{crit}} \right]  \label{38}\end{equation}$$

Rozciąganie i zginanie

W złożonym stanie naprężenia od rozciągania siłą obliczeniową $N_{t,d}$ i od zginania ukośnego momentami obliczeniowymi $M_{y,d}$  oraz $M_{z,d}$  należy spełnić formuły interakcji liniowej [1], wzory (6.17,18))):

$$\begin{equation} \alpha_{t+my} = \alpha_{t,0} + \alpha _{my}+ k_m \cdot \alpha _{mz}\le 1\label {39} \end{equation}$$

$$\begin{equation} \alpha_{t+mz} = \alpha_{t,0} + \alpha _{mz}+ k_m \cdot \alpha _{my}\le 1\label {40} \end{equation}$$

gdzie wskaźniki  wytężenia od prostych obciążeń $\alpha_{t,0}$,  $\alpha_{my}$, $\alpha_{mz}$ wg ($\ref{37}$).

Współczynnik interakcji  $k_m$ wynosi:

$$ \begin{equation} k_m= \label{41} \begin {cases}
0,7  & \textrm {dla przekroju prostokątnego} \\
1,0  & \textrm {dla innych przekrojów} \\\end {cases} \end{equation} $$

Ściskanie i zginanie

W złożonym stanie naprężenia ściskania siłą $N_c$  zginania ukośnego momentami $M_y$  oraz $M_z$  należy spełnić warunki:

• interakcji kwadratowej [1],wzory (6.19, (6.20)- interakcja ściskania i zginania bez utraty stateczności oraz (6.35) – interakcja zwichrzenia i wyboczenia:

$$\begin{equation} \alpha_{(c+my)} = {\alpha_{c,0}}^2  + \alpha _{my}+ k_m \cdot \alpha _{mz}\le 1\label {42} \end{equation}$$

$$\begin{equation} \alpha_{(c+mz)} = {\alpha_{c,0}}^2  + \alpha _{m,z,d}+ k_m \cdot \alpha _{my}\le 1\label {43} \end{equation}$$

$$\begin{equation}  \alpha_{(m+c), cr} = {\alpha _{my, cr}}^2  + \alpha_{c, cr, z} \le 1 \label {44} \end{equation}$$

gdzie: $\alpha_{c, 0}$ wg ($\ref{37}$), a $\alpha_{my, cr}$, $\alpha_{c, cr, z}$ wg ($\ref{38}$),

W dwóch pierwszych warunkach sprawdzane jest współdziałanie zginani i ściskania przekroju bez wpływu niestateczności pręta. W trzecim warunku sprawdzana jest interakcja zwichrzenia i wyboczenia z płaszczyzny zginania (x,y)  belki- słupa  w kierunku osi z ,  to znaczy w warunku wystąpi moment zginający działający względem osi większej sztywności (najczęściej pozioma oś y) , a wyboczenie i zwichrzenie następuje po osi mniejszej sztywności (najczęściej pionowa oś z). W przypadku innego oznaczenia osi o ustalonym znaczeniu fizycznym należy dokonać korekty indeksów.

• interakcji liniowej [1],wzory (6.23), (6.24) interakcja wyboczenia i zginania pręta :

$$\begin{equation} \alpha_{(c+my),cr } = \alpha_{c,cr, y}  + \alpha _{my}+ k_m \cdot \alpha _{mz}\le 1\label {45} \end{equation}$$

$$\begin{equation} \alpha_{(c+mz),cr } = \alpha_{c,cr, z} + \alpha _{mz}+ k_m \cdot \alpha _{my}\le 1\label {46} \end{equation}$$

Wskaźniki  wytężenia od prostych obciążeń $\alpha_{my}$, $\alpha_{mz}$ wg ($\ref{37}$), a  $\alpha_{c,cr, y}$ , $\alpha_{c,cr, z}$ wg ($\ref{38}$).

Ścinanie

Ścinanie przekrojów jest nieodłącznie związane ze zginaniem. W konstrukcjach drewnianych sprawdza się warunek prosty (bez interakcji ze zginaniem):

$$\begin{equation}  \alpha_v \le 1 \label {47} \end{equation}$$

gdzie $ \alpha_v = \max { [ \alpha_{vy} \, ; \, \alpha_{vz}]} $,

a wskaźniki  wytężenia  $\alpha_{vy}$,  $\alpha_{vz}$ wg ($\ref{37}$).

Skręcanie

Skręcanie przekrojów jest przedmiotem artykułów  Na skutek skręcania przekroju momentem skręcającym $M_T$ w przekroju wystąpią obliczeniowe naprężęnia styczne $\tau_{T,d}$, które można wyznaczyć w sposób opisany w artykułach skręcanie swobodne i skręcanie nieswobodne i skręcanie pręta o przekroju prostokątnym.

Warunek wytrzymałościowy pręta drewnianego można zapisać w postaci

$$\begin{equation}  \alpha_{vx} =\cfrac{\tau_{x,d} } {k_{shape} \cdot f_{v,d}} \le 1 \label {48} \end{equation}$$

gdzie:

$\tau{x,d}$ naprężenia styczne od skręcania przekroju momentem $M_x =M_{tor}$,

$$ \begin{equation} k_{shape}= \label{49} \begin {cases}
1,2 & \textrm {dla przekroju okrągłego} \\
\min{[1+ 0,15 \cdot h/b \, ;\, 2,0] } & \textrm {dla przekroju prostokątnego} \\
\end {cases} \end{equation} $$

h, b  – dłuższy i krótszy bok przekroju odpowiednio,

$f_{v,d}$ – wytrzymałość obliczeniowa drewna na ścinanie

Jednoczesne ścinanie przekroju siłami poprzecznymi oraz momentem skręcającym  nie sumuje się algebraicznie, ale zgodnie zasadami  teorii prętów cienkościennych i przykładzie rachunkowym.

Ściskanie w poprzek włókien (docisk)

Ściskanie w poprzek włókien (docisk)  jest specyficznym przypadkiem wytrzymałościowym, w którym występuje siła powierzchniowa $F_{c,90,Ed}$ , która nie jest siła przekrojową.  Docisk do powierzchni zewnętrznej elementu drewnianego należy sprawdzać z warunku [1],(6.3)))

$$ \begin{equation} \alpha_{c, 90, d} = \cfrac { \sigma_{c,90,d}} { k_{c,90} \cdot f_{c,90,d}} \le 1 \label {50} \end{equation}$$

gdzie:
$f_{c,90,d}$ – obliczeniowa wytrzymałość na ściskanie w poprzek włókien.
$k_{c,90}$ – współczynnik uwzględniający rozkład obciążenia, możliwość powstania pęknięć oraz stopień odkształcenia przy ściskaniu,
Wartość współczynnika $k_{c,90}$ należy przyjmować za równą 1,0, z wyjątkiem przypadków:
a) podparcia w sposób ciągły (rys. 4a)  i docisku na odcinku $l \ge 2h$: $k_{c,90}=1,25$ w przypadku iglastego drewna litego ;  $k_{c,90}=1,5$ w przypadku iglastego drewna klejonego warstwowo
b) podparcia w sposób nieciągły (rys. 4b) i odległości miedzy powierzchniami docisku $l_1 \ge 2h$: $k_{c,90}=1,5$ w przypadku iglastego drewna litego ;  $k_{c,90}=1,75$ w przypadku iglastego drewna klejonego warstwowo pod warunkiem, że długość docisku $l$,  gdzie h – wysokość elementu, a l –  długość kontaktu(docisku).

Naprężenia docisku wyznacza się z zależności

$$\begin{equation}\sigma_{c,90,d} =\cfrac{F_{c,90,Ed}}{A_{ef}}\label {51} \end{equation}$$

gdzie:
$F_{c,90,d}$ – obliczeniowa, zewnętrzna siła ściskająca w poprzek włókien,
$A_{ef}$-efektywne pole docisku, które należy określać z uwzględnieniem efektywnej długości kontaktu wzdłuż włókien, biorąc pod uwagę to, że długość kontaktu $l$ jest obustronnie powiększona o 30 mm, lecz nie więcej niż a (rys.4)

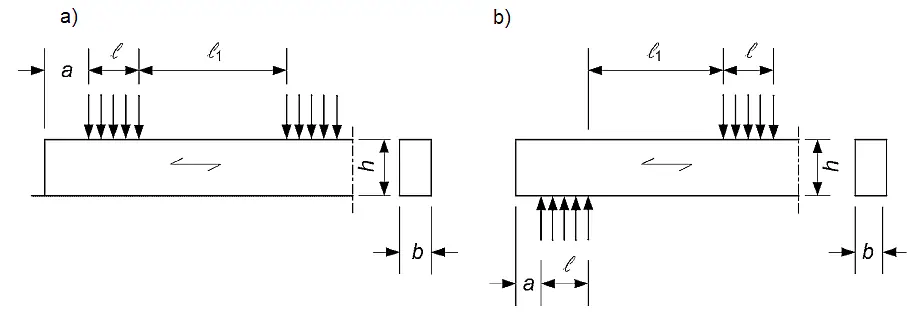
Rys.4 . Docisk do powierzchni belki: a) podpartej ciągle, v) podpartej nieciągle  (PN-EN 1995-1-1+A2+NA+07E :2010, Eurokod 5: Projektowanie konstrukcji drewnianych, Część 1-1: Postanowienia ogólne – Reguły ogólne i reguły dotyczące budynków)), rys. 6.2

Belki z otworami i podcięciami

W projektowaniu konstrukcji drewnianych ważne jest unikanie naprężeń rozciągających prostopadle na rdzenia, ponieważ nośność drewna jest bardzo niska.  Naprężenie rozciągające mogą być wywołane różnymi sytuacjami, a w szczególności w elementów zakrzywionych, w  przypadku belek z otworami lub wycięciami,lub  w złączach elementów.

Zarówno otwory, jak i wycięcia mogą znacząco zmniejszyć nośność belki i najlepiej unikać ich. Wokół otworu lub wycięcia wystąpi spiętrzenie naprężeń rozciągających, a uszkodzenie będzie  będzie kruche i nagłe, co oznacza, że ​​prawie nie będzie ostrzeżenia przed awarią tym spowodowaną.

Na rys. 5 przedstawiono rozkład naprężeń rozciągających w pobliżu wierzchołka podcięcia . Teoretycznie nieskończone naprężenia są większe od wytrzymałości.

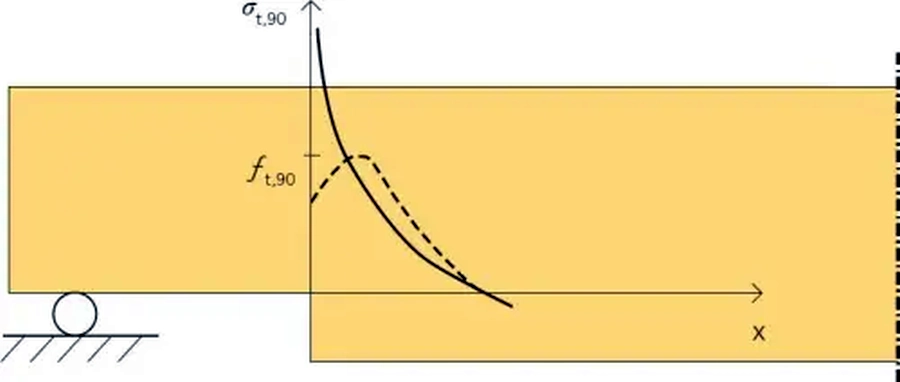
Rys.5.  Spiętrzenie naprężeń w podcięciu belki. Ciągła linia – naprężenia teoretyczne, [7],Fig. 3.7))

Otwory w belce

Dla belek z otworem w Eurokodzie nie ma formuły wytrzymałości . Jednym ze sposobów radzenia sobie z problemem jest przestrzeganie zaleceń konstrukcyjnych maksymalnego dopuszczalnego rozmiaru otworów i minimalnego promienia naroża dla wypełnienia prostokątnych otworów. Ogólnie zaleca się umieszczanie otworów w neutralnej osi belki, gdzie naprężenia styczne są największe.. Układ spotykanych otworów w belce pokazano na rys. 6. W tab. 12 zestawiono zalecenia konstrukcyjne

Tab.12 Zalecenia dla wymiarów otworów ich położenia i wyokrągleń w belkach drewnianych [14]

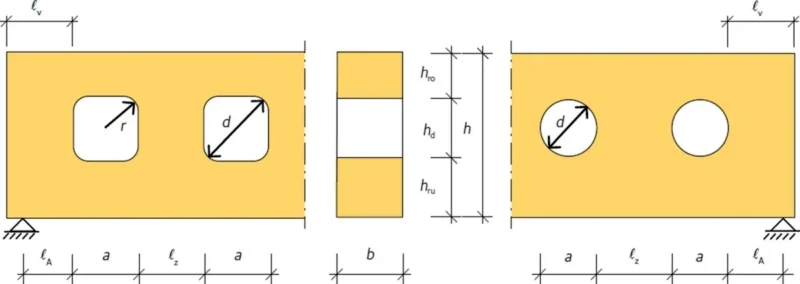
Rys.6 Otwory w belce o oznaczenia [8],Fig. 2.0))

Podcięcia na podporach

W przypadku belek o przekroju prostokątnym, w których włókna drewna są na ogół równoległe do długości elementu, naprężenia ścinające na podporze podciętej należy obliczać dla wysokości zredukowanej $h_{ef}$ (rys. 7).

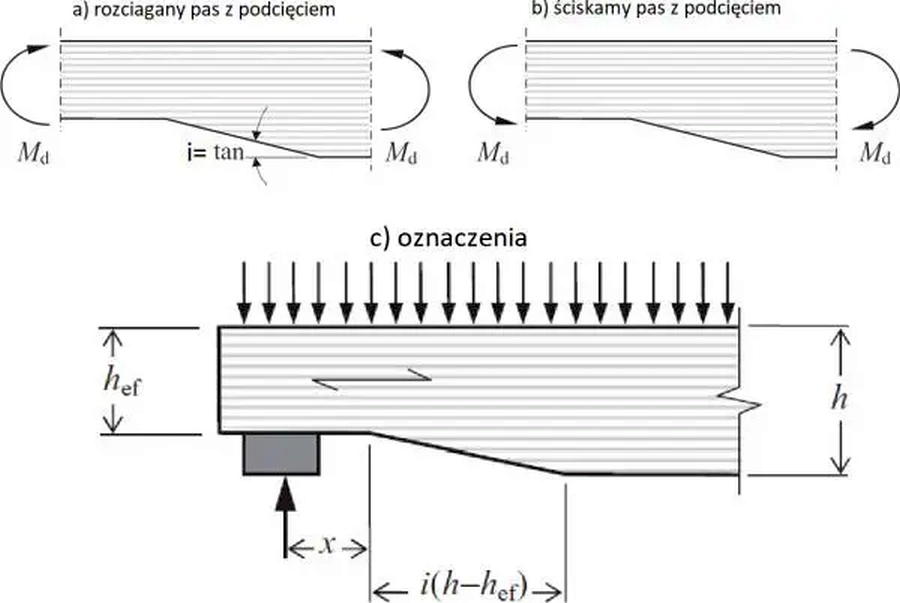
Rys.7. Podcięcie belki nad podporą [1],(6.62)))

Jeśli podcięcie nad podporą jest tak usytuowane, że na skutek zginania rozciągane są włókna dolne osłabionego przekroju (rys.7), to do wytrzymałości należy stosować współczynnik korekcyjny $k_v$ [1],(6.62))):

$$\begin{equation} k_v=\cfrac{k_n \cdot \left( 1+\cfrac{1,1\cdot i^{1,5}}{\sqrt{h}}\right )}{\sqrt{h} \cdot \left[ \sqrt{\alpha \cdot (1-\alpha)}+0,8 \tfrac{31}{h} \cdot \sqrt{1/\alpha-\alpha^2} \right ]} \label{52} \end{equation}$$

gdzie:
h w mm,
$\alpha=\tfrac {h_{ef}}{h}$
i=tangens kąta skosu podcięcia,
x-długość podcięcia, liczona od osi podpory,

$$ \begin{equation} \ k_n= \label{53} \begin {cases}
4,5  , & \textrm {dla LVL} \\
5  , & \textrm {drewno lite} \\
6,5  , & \textrm {klejone warstwowo} \\
\end {cases} \end{equation} $$

Ugięcia

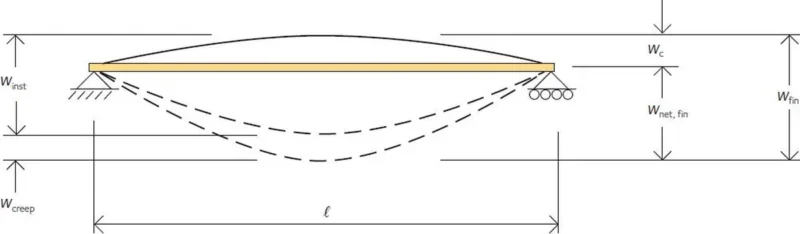
Na rys. 8 zilustrowano zależności pomiędzy:

• ugięciem  chwilowym $w_{inst}$
• ugięciem pełzania $w_{creep}$
• strzałką odwrotną $w_c$
• ugięciem końcowym $w_{fin}=w_{inst}+w_{creep}+w_c$
• ugięciem końcowym netto  $w_{net,fin}=w_{fin}-w_c=w_{inst}+w_{creep}=w_{inst}\cdot (1+k_{def})$.

Rys. 8 Oznaczenia ugięć przy sprawdzaniu SGU

[8],Fig. 7.2))

Zalecaną metodą wyznaczania ugięć jest szacowanie ich po przyjęciu stosownych modułów sprężystości oraz kombinacji obciążeń w sposób przedstawiony w rozdziale Moduły odkształcalności.

Specjalne elementy drewniane

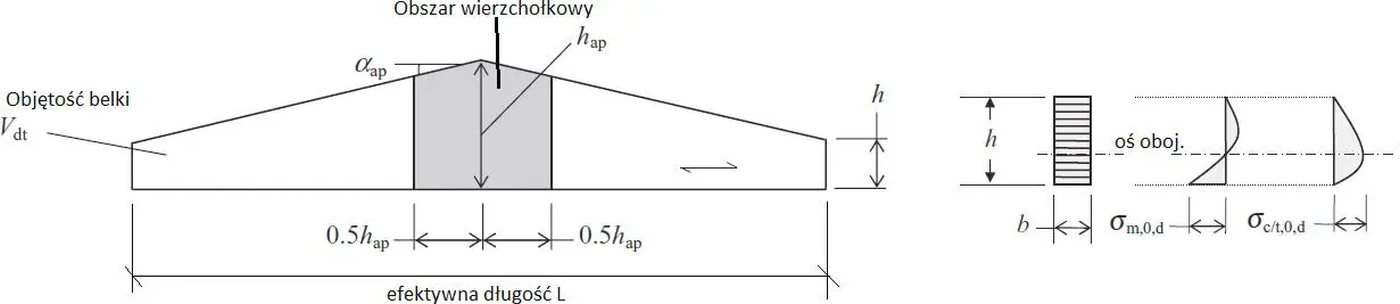
Specjalne elementy drewniane, to: dźwigary trapezowe, łuki oraz z wyokrąglonymi narożami (rys. 9).

Rys.8 Specjalne dźwigary drewniane (opracowano na podstawie [8],Fig. 3.26)))

Zagadnienie wytrzymałościowe dotyczące dźwigarów o specjalnych kształtach  jest szeroko omówione  w teorii sprężystości i konstrukcjach stalowych (np [15]).  W tym miejscu omówimy praktyczne podejście do projektowania dźwigarów drewnianych.

Dźwigary o pasie zbieżnym

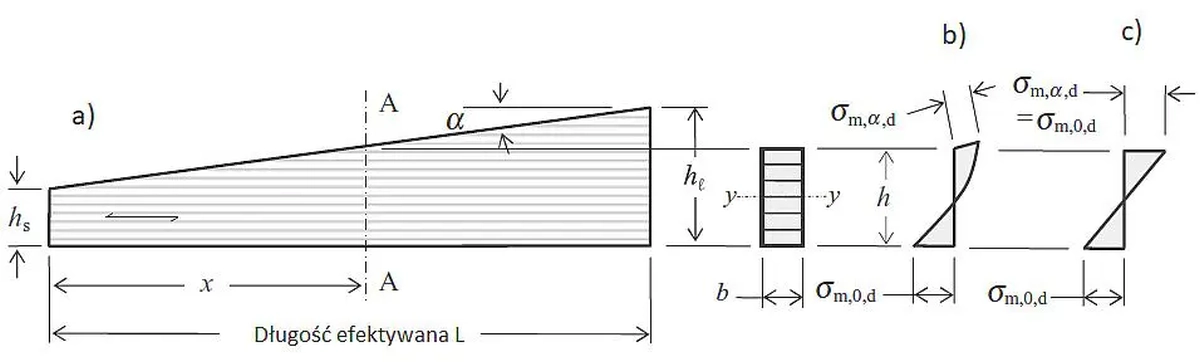
Rys.10 Dźwigar o pasie zbieżnym (jednotrapezowy): a)schemat, b) rzeczywiste naprężenia normalne , b) aproksymacja naprężeń

Na rys. 10 pokazano dżwigar o górnym pasie zbieżnym pod kątem $\alpha$ od wysokości nad podporą $h_s$ do wysokości maksymalnej $h_l$. Na rys. 10b przedstawiono rzeczywisty rozkład po wysokości  przekroju – rozkład naprężeń normalnych od zginania. Rozkład naprężeń jest nieliniowy: w dolnym włóknie wynosi $\sigma_{m,0,d}$, a w górnym nachylonym $\sigma_{m,\alpha ,d}$. Jako aproksymację tego rozkładu przyjmuje się rozkład liniowy, pokazany na rys. 10c, gdzie naprężenia na górnym i dolnym włóknie są takie same i mogą być w przybliżeniu wyznaczone ze wzoru klasycznego

$$\begin{equation} \sigma_{m,0,d}= \sigma_{m,\alpha ,d}= \cfrac {M_d} {W} \label {54} \end{equation}$$

W praktyce taka aproksymacja jest wystarczająco dokładna dla kąta nachylenia $\alpha < 10^0$.

Dla większych kątów $\alpha$ zaleca się zastosować przybliżenie [16], zgodnie z którym w dowolnym przekroju wzdłuż belki z pochyłym pasem maksymalne naprężenie równoległe do zwężającej się powierzchni w górnych włóknach i maksymalne poziome naprężenia rozciągające we włóknach dolnych można wyznaczyć z zależności:

$$\begin{equation} \sigma_{m,\alpha} = (1 – 3,7 \cdot tg^2 \alpha)   \cfrac{M} {W} \label {55} \end{equation}$$

$$\begin{equation} \sigma_{m,0} = (1 + 3,7 \cdot tg^2 \alpha)   \cfrac{M} {W} \label {56} \end{equation}$$

W belce występuje taki przekrój A-A, w którym naprężenia będą największe. Położenie tego przekroju zależy od typu obciążenia działającego na belkę w prostych przypadkach obciążeń wynosi:

$$ \begin{equation} x= \label{57} \begin {cases}
\cfrac {L}{h_l/h_s+1}  , & \textrm {dla obciążenia równomiernie rozłożonego} \\
\cfrac {L}{2} , & \textrm {dla obciążenia skupionego w środku rozpiętości, jeśli $h_l/h_s \le 3$} \\
\cfrac {L}{h_l/h_s -1 } , & \textrm {dla obciążenia skupionego w środku rozpiętości, jeśli $ h_l/h_s > 3 $}
\end {cases} \end{equation}$$

Warunek nośności belki o zbieżnym pasie:

$$\begin{equation} \sigma_{m,\alpha,d} \le k_{m,\alpha} \cdot f_{m,d} \label {58} \end{equation}$$

zawiera w sobie współczynnik korekcyjny $ k_{m,\alpha}$ obliczany z zależności

$$ \begin{equation} x= \label{59} \begin {cases}
k_{m,\alpha}=\cfrac{1} { \sqrt {  \left ( \cfrac {f_{m,d}} { 0,75 \cdot f_{v,d} } tg \alpha\right )^2 + \left( \cfrac{f_{m,d}}{f_{t,90,d}} tg^2 \alpha \right)^2}}  , & \textrm {dla rozciągajacych naprężeń pochyły  pas} \\
k_{m,\alpha}=\cfrac{1} { \sqrt {  \left ( \cfrac {f_{m,d}} { 0,75 \cdot f_{v,d} } tg \alpha\right )^2 + \left( \cfrac{f_{m,d}}{f_{c,90,d}} tg^2 \alpha \right)^2}}  , & \textrm {dla ściskajacych naprężeń pochyły  pas} \\
\end {cases} \end{equation}$$

gdzie  wytrzymałości drewna klejonego (indeks g) wynoszą

$$\begin{equation} f_{•, d} = \cfrac{ k_{mod} \cdot k_{sys}} {\gamma_M} \cdot f_{•,g,k} \label {60} \end{equation}$$

gdzie: (• = (v) lub  (t,90) lub (c,90).

W powyższych zależnościach  współczynniki redukcyjne $k_{mod}$,  k_{sys} i $\gamma_M$ są takie, jak zdefiniowano poprzednio a f_{v, g, k} , f_{t,90,g,k} i f_{c,90,g,k}, to charakterystyczne wytrzymałości na ścinanie,  rozciąganie prostopadle do rdzenia i na ściskanie prostopadle do rdzenia wg tab. 3.

Utratę stateczności belek należy rozpatrywać ogólna metoda opisaną wyżej.

Dźwigary dwutrapezowe

Pokazany na rys. 11 dźwigar dwutrapezowy. Specyficzne  okoliczności projektowania takich dźwigarów sa podobne do omówionych wyżej (dżwigary jednotrapezowe). Oprócz tego należy skontrolować stan naprężeń w strefie wierzchołkowej , biorąc pod uwagę wpływ na wytrzymałość materiału wynikającą z: naprężeń szczątkowych wywołanych procesem produkcyjnym, rozkład naprężeń i efektami objętościowymi.  Sprawdzić należy kombinacje naprężeń ścinających w strefie wierzchołkowej i naprężeń promieniowych rozciągających, prostopadłych do włókien.

Objętość obszaru wierzchołkowego jest ograniczona do  2/3 $V_b$, gdzie $V_b$ jest całkowitą objętością belki.

Rys. 11 Dźwigar dwutrapezowy

W strefie wierzchołkowej belki trapezowej rozkład naprężeń od zginania jest złożony i nieliniowy (rys.11). Normalne naprężenie poprzeczne zginania $\sigma_{c/t,0,d}$ jest maksymalne na osi obojętnej przekroju, a w skrajnych włóknach jest zerowe.

W wierzchołku belki działa moment zginający $M_{ap,d}$, który wywołuje naprężenie zginające:

$$\begin{equation} \sigma_{m,0,d}= k_l \cdot \cfrac{M_{ap,d}} {W_ap}  \label {61} \end{equation}$$

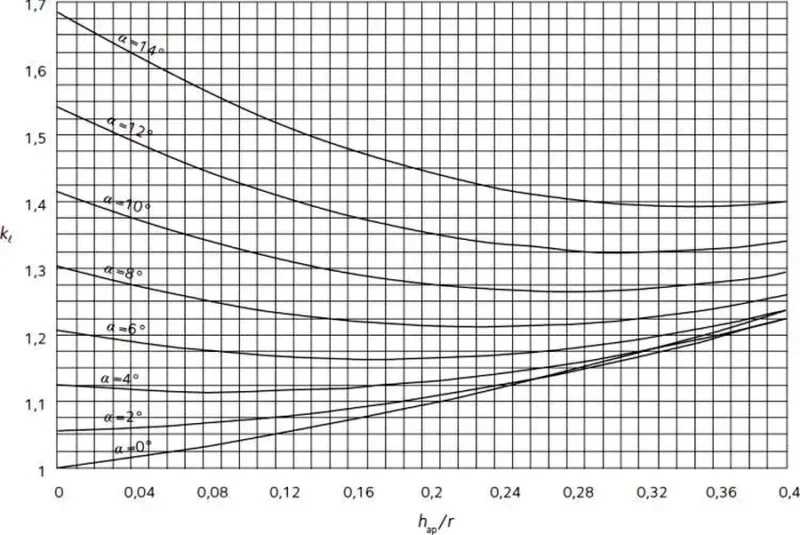
gdzie $W_{ap}=b\cdot h_{ap}^2/6$ – wskaźnik wytrzymałości przekroju w wierzchołku, a współczynnik skali $k_l$ można oszacować ze wzorów podanych w normie [1], (6.12)-(6.17), lub z rys. 11, przy czym dla dźwigara bez wyokrąglenia naroża (jak na rys. 11) przyjmuje się  promień $r=r_{in}+ h_{ap}/2$,  jak dla $r_{in}=\infty$, czyli $ h_{ap}/r=0 $.

Rys 12 Współczynnik $k_l$ dla dźwigara dwutrapezowego i belki zakrzywionej

Naprężenia poprzeczne $\sigma_{t,90,d}$ w wierzchołku można oszacować z zależności

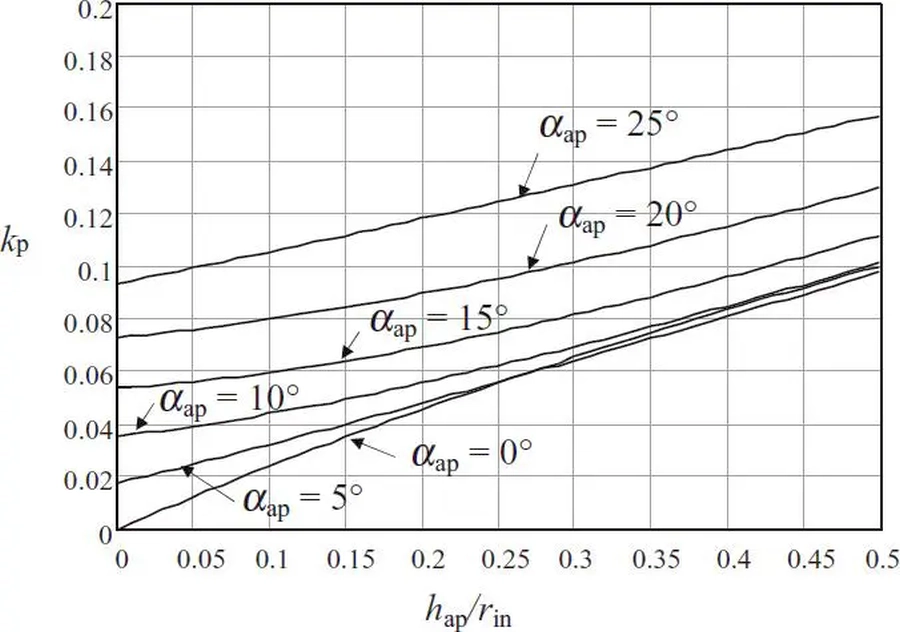
$$\begin{equation} \sigma_{t,90,d}= k_p \cdot \cfrac{M_{ap,d}} {W_ap}  \label {62} \end{equation}$$

gdzie współczynnik redukcyjny dla dżwigara dwutrapezowego  $k_p=0,2\cdot tg /alpha_{ap} $

Naprężenia normalne podłużne i poprzeczne w wierzchołku dźwigara porównuje się ze skorygowanymi  wytrzymałościami drewna:

$$\begin{equation} \sigma_{m,ap,d}= \le  k_r \cdot f_{m,d} \label {63} \end{equation}$$

$$\begin{equation} \sigma_{t,ap,90,d} \le  \sigma_{t,90,d} \le k_{dis} \left (  \cfrac{0,01}{V_{ap}}\right)^2 \cdot  f_{t,90,d} \label {64} \end{equation}$$

gdzie dla belki dwutrapezowej $k_r=1$, k{_dis}$

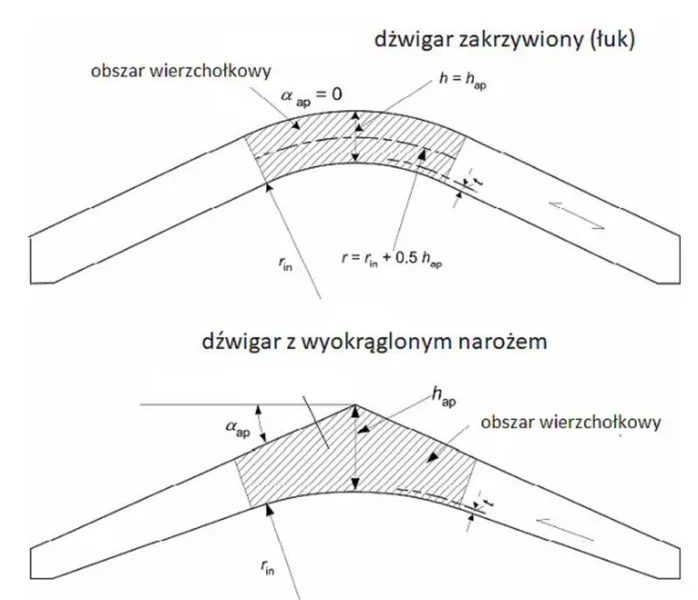
Belki zakrzywione lub z wyokrąglonym narożem

W przypadku dźwigarów zakrzywionych (łuków) lub z zakrąglonym narożem (rys.13) stosuje się również zależności z poprzedniego punktu, ale występuje w nich niezerowy $r_{in}$

Rys.13 Łuk drewniany i wyokrąglone naroże

szacuje się ze wzorów podanych w normie [1],(6.19)-(6.22))) lub z rys. 13 .

Rys.13 Współczynnik $k_p$ dla dźwigara łukowego (belki zakrzywionej) i z zakrąglonym narożem

Przykłady rachunkowe

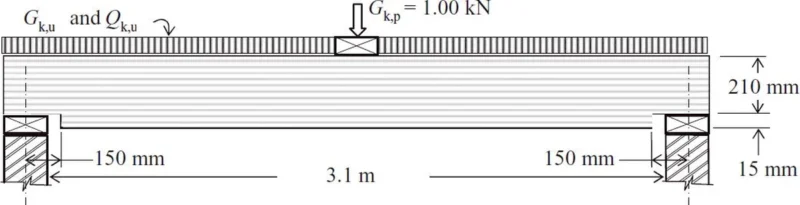
Przykład 1 [współczynnik k_mod, belka z podcięciem]

Zaprojektować belkę drewnianą o przekroju prostokątnym 225 x 63 mm, o rozpiętości l=3100 mm ( w świetle murów) wykonaną z drewna klasy C24, pokazaną na rys. 14. Belka jest na każdym końcu podparta na szerokości 85 mm.  Belka jest stężona poprzecznie przeciw zwichrzeniu i podcięta na końcach o 15 mm. Belka nie posiada podsufitki, która prowadziłaby do zaostrzenia dopuszczalnych ugięć.

Klasa użytkowania – 2

Obciążenia belki:
$G_{k,p}$ =1,00 kN – obciążenie stałe skupione w środku rozpiętości,
$G_{k,u}$ = 1,0 kN/m – obciążenie stałe (od warstw stropowych)  rozłożone po długości belki,
$Q_{k,u}$ =2,5 kN/m-obciążenie zmienne (użytkowe, kat B) rozłożone po długości belki,

Rys.15. Belka do przykładu 1

Charakterystyki geometryczne

wysokość h= 225 mm,
szerokość b= 63 mm,
długość belki w świetle $l_s$=3100 mm
szerokość podpory $l_p$=85 mm,
długość obliczeniowa belki l=3100+2*85/2=3185 mm,
wysokość podcięcia na końcach $h_p$=15 mm,
wysokość belki na podporze  $h_{ef}= 225-15=210 \,mm$,
współczynnik  $\alpha=h_{ef}/h= 210/225 = 0,93$,
długość podcięcia od osi podpory $x =150 \, mm$
nachylenie podcięcia $ i=0 $
wskaźnik wytrzymałości względem osi y-y    $W=\cfrac{63\cdot 225^2} {6}=5,32\cdot10^5\,mm^3$

Parametry drewna C24

Tab.1 $\to$
charakterystyczna wytrzymałość na zginanie   $f_{m.k} = 24 \, MPa$,
charakterystyczna wytrzymałość na ścinanie  $f_{v.k}= 4,0 \, MPa$,
charakterystyczna wytrzymałość na ściskanie poprzeczne  $f_{c.90.k}  = 2.5 \, MPa$
5% kwantyl modułu Younga wzdłuż włókien  $E_{0, 0,05}= 7.4 \, GPa$,
Średni modułu Younga wzdłuż włókien  $E_{0, mean}= 11 \, GPa$,
Średni modułu Kirchoffa wzdłuż włókien  $G_{0,mean}= 0,69 \, GPa$,
Średnia gęstość  $\rho_m = 420  \, kg/m^3$,

Współczynniki bezpieczeństwa

dla obciążeń stałych $\gamma_G=1,35$
dla obciążeń zmiennych $\gamma_G=1,5$

Tab.6 $\to$
współczynnik obciążenia długotrwałego
dla obciążeń stałych $\Psi_2 =1,0$
dla obciążenia użytkowego (kat.B) $\Psi_2=0,3$
$\ref{6}) \to$  dla litego drewna-  współczynnik materiałowy $\gamma_M=1,3$

Obciążenia wg czasu trwania

Obciążenia stałe – trwałe $\to$ tab.7 – indeks klasy obciążenia =^1, $\to$ tab 5 – $k_{m, ^1}=0,6$

#1 ciężar własny  $G_{k,g}=h\cdot b \cdot g \cdot \rho_m=0,063\cdot 0,225 \cdot 9,81 \cdot 430 \cdot 10^{-3}=0,06 \, kN/m$,

#2 obciążenie warstwami stropowymi $G_{k,u}=1,0 \, kN/m$

#3 obciążenie skupione $G_{k,p}=1,00 \, kN$

Obciążenie zmienne – średniotrwałe$\to$ tab.7 – indeks klasy obciążenia =^3$ \to$ tab 5 – $k_m^3 = 0,8$

#4 obciążenie użytkowe stropu $Q_{k,p}=2,5 \, kN/m$

Współczynnik $k_{mod}$

Ponieważ obciążenie użytkowe (kat.B) zgodnie z tab.7 jest zaliczone do średniotrwałych, więc na podstawie klauzuli [1],kl. 3.1.3(2))) należałoby przyjąć
z tab.5 $ k_{mod}=0,8$.

Na podstawie propozycji $(\ref {8})$ obliczymy teraz współczynnik $k_{mod}$ jak średnią ważoną udziałem obciążeń o różnym czasie trwania. Ponieważ obciążenia są różnej natury (rozłożone i skupione), więc ich wkład w wytężenie konstrukcji ocenimy na podstawie sprawczej (wymiarującej) siły przekrojowej, jaką w tym przypadku jest obliczeniowy moment zginający pod siłą skupioną (w środku rozpiętości belki).

Moment zginające:

$M_{ k,1}$=0,06\cdot 3,185^2/8=0,076 kNm,
$M_{k, 2}$=1,0\cdot 3,185^2/8=1,268 kNm,
$M_{k, 3}$=1,00\cdot 3,185/4=0,796 kNm,

$M_{k, 4}$=2,5\cdot 3,185^2/8=3,170 kNm,

Łącznie momenty zginające od obciążeń charakterystycznych i obliczeniowe (bez redukcji) w klasach trwania obciążenia

$M_k^1$= 0,076+1,268+0,796=2,140 \, kNm$,
$M_d^1$= 1,35 \cdot 2,140= 2,89 \, kNm$
$M_k^3$= 3,170 \, kNm$
$M_d ^3$= 1,5 \cdot 3,170=4,76 \, kNm$

Współczynniki wagowe udziału klas obciążenia zgodnie z ostatnią kolumną  tab 7:

$F = 2,89 + 4,76=7,65\, kNm$
$F_1 = \Sigma G=2,89 \, kNm$ ;  ($k_{mod,1} = 0,6$
$F_2 = \Sigma (Q \Psi_2) = 4,76 \cdot 0,3 = 1,43 \, kNm$ ;  ($k_{mod,2}=0,7$
$F_3 = \Sigma (Q \Psi_1) – F_2 = 4,76 \cdot (0,5-0,3) = 0,95 \, kNm$ ;  ($k_{mod,3}=0,8$
$F_4 = F – F_1 – F_2 – F_3 = 7,65 – 2,89 – 1,428 – 0,95=2,38 \, kNm$ ;  ($k_{mod,4}=0,9$

($ \ref{8}$) $k_{mod} = \cfrac {  2,89 \cdot 0,6 + 1,43 \cdot 0,7 + 0,95 \cdot 0,8 + 2,38 \cdot 0,9  } {7,65} = 0,74 $

Współczynniki korekcyjne

Tab. 10 dla $h>150 \to k_h=1,0$
Ponieważ belka zabezpieczona przed zwichrzeniem, $\to k_{crit}=1,0$
Współczynnik materiałowy dla podcięcia: drewno lite
$(\ref{52})  \to k_n=5,0$,

Współczynnik redukcyjny dla podcięcia $(\ref{52} ) \to$

$k_v=\cfrac{5,0 \cdot \left( 1+\cfrac{1,1\cdot 0^{1,5}}{\sqrt{225}}\right )}{\sqrt{225} \cdot \left[ \sqrt{0,93 \cdot (1-0,93)}+0,8 \tfrac{150}{225} \cdot \sqrt{1/0,93-0,93^2} \right ]}=0,68$

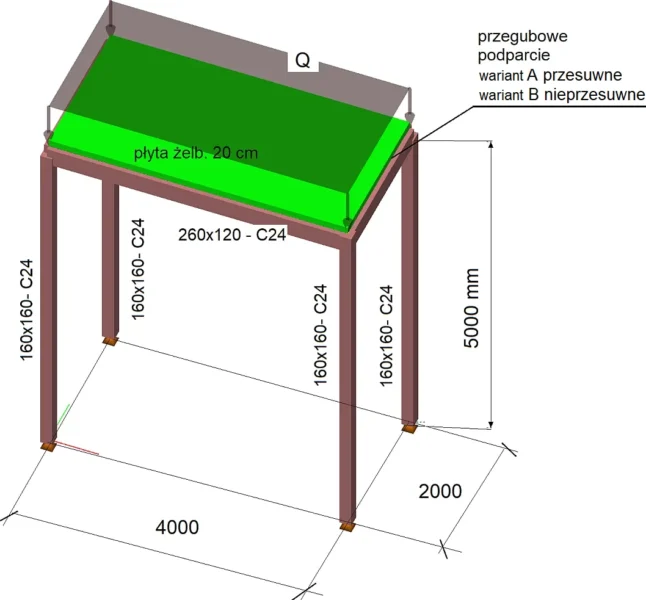
Przykład 2 [Belka i słup]

Zaprojektować pokazaną na rys, P2-1 drewnianą ramę podpierające strop żelbetowy. Zastosować teorię II rzędu z imperfekcjami i porównać z klasyczna metodą  I rzędu

Rys. P2-1 Schemat ramy drewnianej do przykładu 2

Dane

Rygiel  260×12– sosna C24 – długości 4000 i 2000 mm
Słup 160×160 – sosnaC24 = długości 5000 mm

Własności drewna C24

charakterystyczne

tab.1. $ \to$
$f_{m,k} = 24 \, MPa$,
$f_{t, 0, k} = 14 \, MPa$,
$f_{c,0, k} = 21 \, MPa$,
$f_{v, k} = 4,0 \, MPa$,
$E_{0,05} = 7, 4 \, GPa$,
$G_{0,05} = 0,46 \, GPa$,
$\rho_k= 350 \, kg/m^3$,
$\rho_m= 420 \, kg/m^3$,

obliczeniowe

tab. 8 klasa użytkowania  2
tab. 7 klasa trwania obciążenia
1 dla obciążenia $ G= 6,6 \, kN/m^2$
3 dla obciążenia $ Q=3,5 \, kN/m^2$

tab. 5 współczynnik $k_{mod}$
0,6 dla obciążenia G
0,8 dla obciążenia Q
($\ref{8}$)  $\to  k_{mod} = \cfrac {6,6 \cdot 0,6 + 3,6 \cdot 0,8}{6,6 + 3,5} = 0,7$

($\ref{6}$) drewno lite $\to \gamma_M= 1,3$

($\ref{7} \to $)
$f_{m,d} = 0,7 \cdot 24 / 1,3 = 12,9 \, MPa$,
$f_{t,0, d} = 0,7 \cdot 14 / 1,3 = 7,5\, MPa$,
$f_{c,d} = 0,7 \cdot 21/ 1,3 = 11,3  \, MPa$,
$f_{v,d} = 0,7 \cdot  4,0/ 1,3 = 2,15  \, MPa$,

Obciążenia:

charakterystyczne

posadzka i warstwy wyrównawcze 8 cm :  $ 0,08 \cdot 20 \, kN/m^3 =  1,6 \, kN/, m^2$
płyta żelbetowa 20 cm : $ 0,2 \cdot 25  \, kN/m^3 =  5 \, kN/m^2$

stałe
$G_k = 1,6+ 5= 6,6 \, kN/m^2$
ciężar własny drewna
$g_k= 350 \, kg /m^3 = 3,5 \, kN/m^3$  uwzględniane automatycznie przez program

zmienne (użytkowe)
$Q_k= 3,5o \, kN/m^3$

obliczeniowe

kombinacja (G+Qr) stałe + zmienne redukowane
$q_d = 1,35 \cdot 6,6 + 1,5\cdot 0,7 \cdot 3,5 = 12,6 \, kN/m^2$
kombinacja (Gr+Q) stałe redukowane + zmienne wiodące + pozostałe zmienne redukowane zmienne redukowane
$q_d = 1,35  \cdot 0,85 \cdot 6,6 + 1,5\cdot  \cdot 3,5 +0 = 12,8 \, kN/m^2$

Do obliczeń przyjęto Q= 12,8 \, kN/m^2 (rys. P2-1)

Imperfekcje

Przechyłowe

($\ref{26}$) $\to  \Phi_0=1/200$
($\ref{27}$) $\to \alpha_h = \sqrt {\cfrac{5} {5}}=1,0 $
$\to  \Phi_0= 1/200\cdot 1,0 = 1/200 $

Łukowe

($\ref{28}$) $\to    \text {min} \, e_0=1/400 $
W warunkach zadania ze względu na klasę sortowniczą  drewna KS średniej jakości, przyjęto
$e_0= 1/300$

Rozwiązanie statyczne

Przeprowadzono analizę statyczną układu pokazanego na rys. 2-1 wg teorii I lub II rzędu w wariantach imperfekcji: bez imperfekcji ; z imperfekcjami przechyłowymi ; z imperfekcjami łukowymi ; z obu typami imperfekcji.

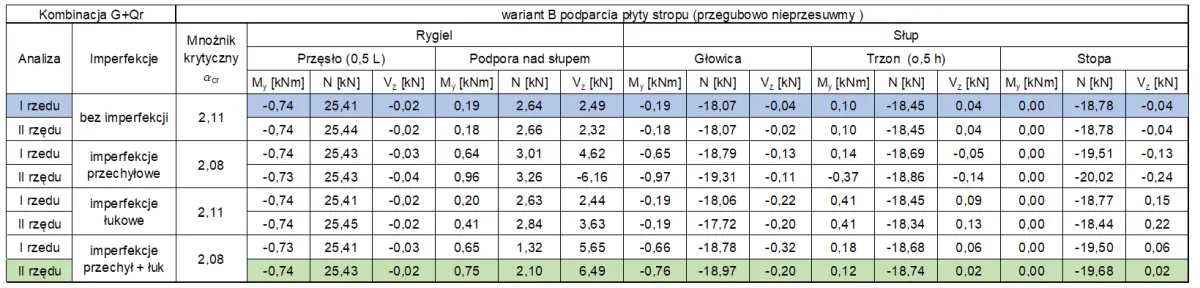
Siły przekrojowe w krytycznych przekrojach prętów zestawiono w tab.P2-1 dla wariantu B podparcia płyty. Pominięto przedstawienie wyników dla wariantu A (podparcia przegubowego nieprzesuwnego, ponieważ realizacja takiego podparcia jest trudna w praktyce. Można pokazać , że nieprzesuwność jest realizowana przez same siły tarcia pomiędzy płytą żelbetową, a ryglami drewnianymi.

Tab 2-1 Siły przekrojowe w prętach ramy z rys. P2-1 wariant podparcia B  (przegubowy nieprzesuwny)
wg teorii I lub II rzędu i z imperfekcjami systemu konstrukcyjnego

Wskutek współpracy płyty żelbetowej z ryglami drewnianymi o istotnie różnej odkształcalności (modułach Younga) obserwuje się wystąpienie w ryglu sił osiowych  (rys, P2-2) i znaczne zmniejszenie zginania (z ok 20 kNm przy zapewnieniu przesuwności rygla wobec płyty – wariant A podparcia  do ok 0,7 kNm przy podparciu przegubowym z odebraniem wzajemnej przesuwności). Ten drugi sposób oparcia jest rzeczywisty i dla wariantu B podparcia zaprojektowano ramę.

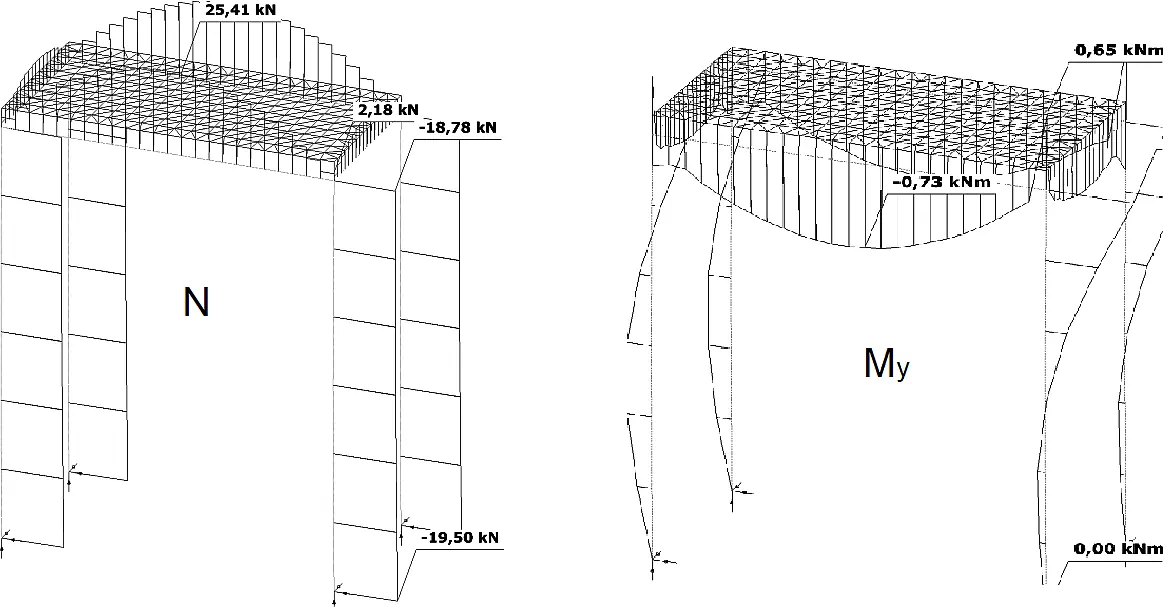
Rys_P2-2_Wykresy sil przekrojowych dla wariantu analizy II rzędu z z imperfekcjami przechyłowymi i łukowymi dla kombinacji ( Gr+Q).

Rygiel.  Wymiarowanie klasyczną metodą I rzędu

$A= 26\cdot 12 = 312 \, cm^2$,
$W_y = \cfrac{12\cdot 25^2}{6}= 1250 \, cm^3$,
$(\ref {21}) \to $ $A_v = 2/3 \cdot 912= 608 \, cm^2$

$M_{y,Ed}^I = 0,79 \, kNm$
$N_{t,Ed}^I = 25,41 \, kN$
$V_{z,Ed} = V_{z,Ed}^I = 0,02 \, kN$

belka zabezpieczona przed zwichrzeniem ($\ref{35}$)   $ \to k_{crit} = 1,0$
($\ref{34}$) $\to$  $ M_{y,Ed}= \cfrac {0,79}{1,0} = 0,79 \, kNm$

pręt rozciągany  ($\ref{35}$)   $k_{c} = 1,0$
$N_{t,Ed} =\cfrac {25,11}{1,0} = 25,11 \, kN$

Uwaga: Formułę ($\ref{34}$) zastosowano w celach poglądowych. W tym przypadku można bezpośrednio zastosować ($\ref{36}$)+($\ref{37}$)

($\ref{36}$) $\to \sigma_{d} = \left [ \sigma_{t, 0, d}= \cfrac {25,41 }{312}\cdot 10^1 = 0,8  \,  , \, \sigma_{my,d}=\cfrac {0,79}{1250} \cdot 10^3 = 0,63  ,\ ,  \,  \tau_{vy, d}= \cfrac {0,22}{608}\cdot 10^1 = 0,04 \right ] \, MPa$

($\ref{37}$) $\to \alpha_F = \left [ \alpha_{t,0} = \cfrac {0,8 } {7,5}= 0,106 \, ; \,  \alpha_{my} =\cfrac {0,63}{12,9} = 0,048 \,  ;  \alpha_{vz} =\cfrac {0,04}{2,15} = 0,018\right ]$

Rozciąganie i zginanie

($\ref{39}$) $\to$  $\alpha_{t+my} = 0,106  + 0,048+ 0 = 0,16 \le 1 \to OK $

Ścinanie

($\ref{47}$) $\to$ $alpha_{v,d} =\max { [ 0,04\, ; \, 0] } = 0,04 \le 1  \le 1 \to OK $

Słup. Wymiarowanie klasyczną metodą I rzędu

$A= 16\cdot 16 =  256 \, cm^2$,
$I_y = \cfrac{16\cdot 16^3}{12}= 5461,3\, cm^4$,
$i_y =\sqrt{5461,3 / 256} = 4,62 \, cm$
$W_y = \cfrac{16\cdot 16^2}{6}= 682,7 \, cm^3$,
$(\ref {21}) \to $ $A_v = 2/3 \cdot 256= 170,7  \, cm^2$

$l= 5000\, mm$
Długość wyboczeniowa słupa przegubowo-utwierdzonego
$\mu = 0,7$
$l_0 = 0,7 \cdot 5000 = 350 \, cm$

Siły przekrojowe, naprężenia i  wytężenie  I rzędu

($\ref{31}$), ($\ref{36}$),  ($\ref{37}$) $\to $
1 zestaw przekrój przy głowicy
$F_{Ed} = [ N_{Ed}= -18,07 \, kN  \,  ; \, M_{y,Ed}= -0,19 \, kNm \,  ; \,  V_{z,Ed}= -0,04  \. kN  ]$
$\sigma_{d} = \left [ \sigma_{c, 0}= \cfrac {18,97  }{256}\cdot 10^1 = 0,74  \,  ;  \, \sigma_{my,d}=\cfrac {0,19}{682,7} \cdot 10^3 = 0,278  \,  ;  \, \tau_{vz} = \cfrac {0,04}{170,7 } \cdot 10^1 = 0,02  \right ] \, MPa$
$ \alpha_F = \left [ \alpha_{c,0} = \cfrac {0,74} {11,3}= 0,063 \, ; \,  \alpha_{my} =\cfrac {0,278}{12,9} = 0,022 \, ; \,  \alpha_v= \cfrac{0,04}{2,25 } = 0,018 \right] $

2 zestaw przekrój w trzonie
$F_{Ed} =  [ N_{Ed}= -18,45 \, kN  \,  ; \, M_{y,Ed}= 0,10 \, kNm \,  ; \,  V_{z,Ed}= 0,04  \. kN  ]$
$\sigma_{d} = \left [ \sigma_{c, 0}= \cfrac {18,97  }{256}\cdot 10^1 = 0,74  \,  ;  \, \sigma_{my,d}=\cfrac {0,19}{682,7} \cdot 10^3 = 0,278  \,  ;  \, \tau_{vz} = \cfrac {0,04}{170,7 } \cdot 10^1 = 0,02  \right ] \, MPa$
$ \alpha_F = \left [ \alpha_{c,0} = \cfrac {0,74} {11,3}= 0,063 \, ; \,  \alpha_{my} =\cfrac {0,278}{12,9} = 0,022 \, ; \,  \alpha_v= \cfrac{0,04}{2,25 } = 0,018 \right]$

3 zestaw przekrój przy stopie
$F_{Ed} = [ N_{Ed}= -18,78 \, kN  \,  ; \, M_{y,Ed}= -0,00 \, kNm \,  ; \,  V_{z,Ed}= – 0,04  \. kN  ]$
$\sigma_{d} = \left [ \sigma_{c, 0}= \cfrac {18,97  }{256}\cdot 10^1 = 0,74  \,  ;  \, \sigma_{my,d}=\cfrac {0,19}{682,7} \cdot 10^3 = 0,278  \,  ;  \, \tau_{vz} = \cfrac {0,04}{170,7 } \cdot 10^1 = 0,02  \right ] \, MPa$
$ \alpha_F =\left  [ \alpha_{c,0} = \cfrac {0,74} {11,3}= 0,063 \, ; \,  \alpha_{my} =\cfrac {0,278}{12,9} = 0,022 \, ; \,  \alpha_v= \cfrac{0,04}{2,25 } = 0,018 \right]$

Współczynnik wyboczenia

$\lambda_y= \cfrac{l_o}{i_y}=\cfrac{250}{4,62}= 75,8 $
(6.21) [1] $ \to \lambda_{rel,y} =\cfrac{\lambda_y}{\pi} \cdot \sqrt {\cfrac{ f_{c,0, k} }{ E_{0,05} }} = \cfrac{75,8}{\pi} \sqrt{\cfrac{21}{7,4 \cdot 10^3}}= 1,285$

(6.27) [1] $ \to k_y = 0,5 \cdot [ 1+\beta_c \cdot ( \lambda_{rel,y} -0,3 ) +\lambda_{rel,y}^2 ] = 0,5 \cdot [ 1+ 0,2 \cdot  (1,285  – 0,3 ) +1,285^2] = 1,424$

(6.25) [1] $ \to k_{c,y}  = \cfrac{1}{k_y + \sqrt{k_y^2 + \lambda_{rel,y}^2}} = \cfrac{1}{1,424 + \sqrt{1,424^2 + 1,285^2}}= 0,491$

Współczynnik zwichrzenia

(tab.6.1.) [1] efektywna rozpiętość zwichrzenia belki ( jak dla belki swobodnie podpartej obciążonej równomiernie)
$\to l_{ef} =0,9 \cdot l = 0,9 \cdot 400= 360 \, cm$

(6.32) [1]
$ \to \sigma _{m,cri} =\cfrac{0,78 \cdot b^2}{h \cdot l_{ef}}\cdot E_{05}= \cfrac{0,78 \cdot 12^2}{26 \cdot 360}\cdot 7,2 \cdot  10^3 = 113,8 \, MPa$

(6.30) [1]
$\to  \lambda_{rel,m}= \sqrt{\cfrac{f_{m,k}}{\sigma_{m,crit}}} =  \sqrt{24/ 113,8} = 0,46$

(6.35) [1]
$ k_{crit,m}= \begin {cases}
1, & \text  { dla } \lambda_{rel,m} \le 0,75 \\
1,56 – 0,75 \cdot \lambda_{rel,m}   & \text  { dla } 0,75 < \lambda_{rel,m} \le 1,4 \\
\cfrac{1}{\lambda_{rel,m}^2} & \text  { dla } \lambda_{rel,m} > 1,4 \\
\end {cases}$
$ \to  k_{crit,m}=1$

Siły w przekroju krytycznym

(przekrój ulegający wyboczeniu  (trzon – 0,5 h)
tab P2-1 (pierwszy wiersz) $\to$ $M_{y,Ed}^I = 0,10  \, kNm$ , $N_{c,Ed}^I = 18,45 \, kN$
Po zastosowaniu  ($\ref{32}$) siły  przekrojowe  wynosiłyby
$M_{y,Ed}=\cfrac{0,10}{1,0} = 0,10 \, kNm$ ;  $N_{c,Ed} =\cfrac {18,45}{0,491} = 27,58 \, kN$

Dla porównania  siły II rzędu w systemie obarczonym imperfekcjami (dokładnie oszacowane) wynoszą (tab P2-1 ostatni wiersz)
$M_{y_Ed}= 0,12 $ ; $ N_{c,Ed} =18,74,58 \, kN$

Z porównania wynika, że stosowanie metody I rzędu i współczynników wyboczeniowych może prowadzić do nieuzasadnionego zwiększenia  siły ściskającej  27,58/18,74 = 1,6 razy

ściskanie i zginanie

w przekroju krytycznym ) środek trzonu słupa) wytężenie  powiększone współczynnikami niestateczności
($\ref{38}$) $\to  \alpha_{F,cr} = \left [ \alpha_{c, cr,y}  = \cfrac{ 0,063} {0,491}= 0,128  \,  ; \,  \alpha_{c, cr,z} = 0,128  \,  ; \,   \alpha _{my, cr} =\cfrac{0,022}{1,0 }= 0,022 \right]  $

($\ref{41}$) przekrój prostokątny $\to$  $ k_m = 0,7$

($\ref{42}$) $\to\alpha_{(c+my)} = 0,10^2  + 0,011+ 0,7 \cdot 0 = 0,021 \le 1 \to OK  $

($\ref{43}$) $\to \alpha_{(c+mz)} = 0,10^2  + 0+ 0,7 \cdot 0,011 = 0,018\le 1 \to OK $

($\ref{44}$) $\to \alpha_{(m+c), cr} = 0,022 ^2  + 0,128 =  0,128 \le 1 \to OK  $

($\ref{45}$) $\to  \alpha_{(c+my),cr } = 0,128  + 0 + 0,7 \cdot 0,022 = 0,143  \le  1 \to OK  $

($\ref{46}$) $\to  \alpha_{(c+mz),cr } = 0,128  + 0,022 + 0,7  \cdot 0 = 0,150 \le 1 \to OK $

Wymiarowanie metodą dokładną II rzędu

Rygiel

$M_{y,Ed} = 0,74 \, kNm$
$N_{t,Ed} = 25,43 \, kN$
$V_{z,Ed} = = 0,02 \, kN$

($\ref{36}$) $\to \sigma_{d} = \left [ \sigma_{t, 0, d}= \cfrac {25,43 }{312}\cdot 10^1 = 0,82  \,  , \, \sigma_{my,d}=\cfrac {0,74}{1250} \cdot 10^3 = 0,59  ,\ ,  \,  \tau_{vy, d}= \cfrac {0,02}{608}\cdot 10^1 = 0,0 \right ] \, MPa$

($\ref{37}$) $\to \alpha_F = \left [ \alpha_{t,0} = \cfrac {0,82 } {7,5}= 0,109 \, ; \,  \alpha_{my} =\cfrac {0,59}{12,9} = 0,046 \,  ;  \alpha_{vz} =\cfrac {0,0}{2,15} = 0,0\right ]$

Rozciąganie i zginanie
($\ref{39}$) $\to$  $\alpha_{t+my} = 0,109  + 0,046+ 0 = 0,155 \le 1 \to OK $

Słup

$M_{y,Ed} = 0,74 \, kNm$
$N_{t,Ed} = 25,43 \, kN$
$V_{z,Ed} = = 0,02 \, kN$

($\ref{36}$) $\to \sigma_{d} = \left [ \sigma_{t, 0, d}= \cfrac {25,43 }{312}\cdot 10^1 = 0,82  \,  , \, \sigma_{my,d}=\cfrac {0,74}{1250} \cdot 10^3 = 0,59  ,\ ,  \,  \tau_{vy, d}= \cfrac {0,02}{608}\cdot 10^1 = 0,0 \right ] \, MPa$

($\ref{37}$) $\to \alpha_F = \left [ \alpha_{t,0} = \cfrac {0,82 } {7,5}= 0,109 \, ; \,  \alpha_{my} =\cfrac {0,59}{12,9} = 0,046 \,  ;  \alpha_{vz} =\cfrac {0,0}{2,15} = 0,0\right ]$

Ściskanie i zginanie
($\ref{39}$) $\to \alpha_{t+my} = 0,109  + 0,046 + 0 = 0,155 \le 1 \to OK $

Z porównania procedury wymiarowania metodą klasyczną I rzędu i  metodą imperfekcyjną II rzędu, wynika, że ta druga  jest o wiele prostsza.Literatura

1. PN-EN 1995-1-1+A2+NA+07E :2010, Eurokod 5: Projektowanie konstrukcji drewnianych, Część 1-1: Postanowienia ogólne – Reguły ogólne i reguły dotyczące budynków
2. PN-EN 1995-1-2+NA+AC:2008, Projektowanie konstrukcji drewnianych, Część 1-2: Postanowienia ogólne – Projektowanie konstrukcji z uwagi na warunki pożarowe
3. Mielczarek Z. (2001). Nowoczesne konstrukcje w budownictwie ogólnym. Arkady, Warszawa
4. PN-EN 338:2016, Drewno konstrukcyjne – Klasy wytrzymałości
5. (PN-EN 14080:2013, Konstrukcje /drewniane — Drewno klejone warstwowo i drewno lite klejone warstwowo – Wymagania
6. PN-EN 14080:2013, Konstrukcje /drewniane — Drewno klejone warstwowo i drewno lite klejone warstwowo – Wymagania
7. Borgstrom, E., & Swedish Wood. (2016). Design of timber structures Structural aspects of timber construction. (Vol. 1). Swedish Forest Industries Federation
8. Borgstrom, E., & Swedish Wood. (2016). Design of timber structures Structural as-pects of timber construction. (Vol. 1). Swedish Forest Industries Federation
9. PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
10. Green, D., W., Winandy, J., E., & Kretschmann, D., E. (2010). Mechanical Properties of Wood, In: Wood Hanbook, Wood as an Engineering Material, Forest Products Laboratory
11. Green, D., W., Winandy, J., E., & Kretschmann, D., E. (2010). Mechanical Properties of Wood, In: Wood Hanbook, Wood as an Engineering Material, Forest Products Laboratory, Mdison WI, USA
12. Ditlevsen, O., & Madsen, H. O. (1996). Structural reliability methods. Wiley
13. ITB. (2017). Konstrukcjre drewniane. Zakład Badań Ogniowych Instytutu Techniki Budowlanej. [ fire @it b.pl ]
14. Danielsson H. (2008). The strength of glulam beams with holes. A Probabilistic Frac-ture Mechanics Method and Experimental Tests (Report ISRN LUTVDG/TVSM-09/3069; pp. 1–124). Division of Structural Mechanics
15. Piechnik, S. (1980). Wytrzymałość materiałów dla wydziałów budowlanych, PWN, Warszawa
16. Riberholt H. (1979). Tapered timber beams. The Proceedings of the CIB W18 Meet-ing, Paper W18/11-10-1

________________________________