Trwa remanent po dużej awarii portalu.  Przepraszam za nieczytelną część treści  do zakończenia remanentu !

Artykuł w ciągu ostatnich 24 godzin czytało 1 Czytelników
Chodor L., Belki żelbetowe,, Encyklopedia πWiki, www.chodor-projekt.net,
13 lipca 2018 – 9 czerwca 2020  – ( publikacja  kompletna)
Arkusz LCżelbet zawiera oryginalny kod – © wszelkie prawa zastrzeżone.
Leszek Chodor , E-mail lch@chodor-projekt.net ; tel. 881-949-956.

Część W
Wprowadzenie
Ze względu na obszerność artykuł podzielono na połączone rozdziały:
W Wprowadzenie (ten rozdział)
K  Kształtowanie
Z Zginanie
P Pełzanie i skurcz
R Rysy i ugięcia
S Ścinanie i skręcanie

Przedstawiono kompedium wiedzy na temat projektowania i obliczania belek żelbetowych, a także komplet arkuszy kalkulacyjnych do obliczeń  metodą nieliniową oraz porównanie z powszechnie stosowaną metodą uproszczoną. Stosowano spójną teorię żelbetu w autorskim ujęciu. Arkusz LCżelbet można pobrać poprzez kliknięcie na rys. W-1. Arkusz wymaga zainstalowania dodatku Solver w środowisku Excel.

Arkusz LCżelbet  w wersji  rys. W-1 i przykłady w niniejszym artykule – opublikowano w opcji „free”.  Arkusz ten jest długo oczekiwany przez inżynierów budownictwa – zawarto w nim komplet wymagań z norm Eurokod  z uwzględnieniem nieliniowości modelu żelbetu oraz pełzania, skurczu i zarysowań. W jednym algorytmie projektowane jest zbrojenie: belek zginanych ukośnie i ściskanych, słupów z dużym i małym mimośrodem. Przy tym w elementach ściskanych zaleca się wprowadzać do arkusza wartości sił przekrojowych z numerycznej analizy II rzędu z zastosowaniem metody nominalnej sztywności.  Autor nie ponosi odpowiedzialności za niekompetentne, stosowanie arkusza. 

W związku z licznymi problemami Użytkowników arkusz został zabezpieczony przed wprowadzaniem do niego niekontrolowanych modyfikacji. Odblokowanie do czytania formuł wpisanych w komórkach jest dostępne w wersji Premium, która może być udostępniona po uzgodnieniu telefonicznym lub e-mailowym na adres podany w nagłówku.
Uogólnienie arkusza dla innych kształtów przekrojów niż prostokątny oraz dla zbrojenia wielowarstwowego będzie wdrożony w kolejnych – komercyjnych wydaniach arkusza.

Wprowadzenie teoretyczne i wybrane przykłady rachunkowe dołączono do każdego rozdziału odrębnie, ale  podstawowym przykładem jest opisana niżej sesja w programie.

Arkusz LCżelbet

Arkusz LCŻelbet można pobrać poprzez kliknięcie w obraz rys. W-1.

Rys. W-1. Arkusz LCżelbet w.1 1. Wersja „free”

Przypadki wytrzymałościowe pręta żelbetowego

W arkuszu LCżelbet w jednym algorytmie zawarto wszystkie przypadki wytrzymałościowe pręta żelbetowego, pokazane na rys. W-2 .  Obejmuje więc belki, słupy, płyty i ściany

Rys. W-2. Przypadki wytrzymałościowe w pręcie żelbetowym

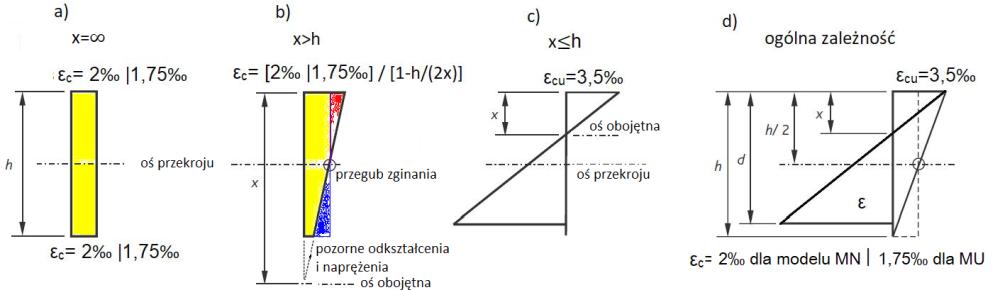
Pręty w konstrukcji są obciążone zginaniem i siłą osiową, dlatego nazywa się je belkami-słupami. W zależności od stopnia udziału zginania i ściskania można wydzielić przypadki pokazane na rys. W-2 :

a) CC_∞  (Compression-Compression ∞) – odkształcenia górnej krawędzi i dolnej są tego samego znaku, a oś obojętna przekroju znajduje się w nieskończoności .
Jest to przypadek czystego ściskania przy braku zginania. Bryłę odkształceń oznaczono kolorem żółtym. Przypadek jest czysto teoretyczny, dotyczy słupów osiowo ściskanych i należy go rozpatrywać jako przekrój zespolony betonowo-stalowy.

b) CC _x>h  – odkształcenia górnej i dolnej krawędzi  (górnego i dolnego zbrojenia) są tego samego znaku, a oś obojętna przekroju znajduje się  poza przekrojem.
Jest to przypadek czystego ściskania z dodatkiem niewielkiego zginania.  Bryłę odkształceń od zginania oznaczono kolorem czerwonym (ściskanie) i niebieskim (rozciąganie). Miejsce zerowe odkształceń (i naprężeń ) od zginania – umowny przegub oznaczono kółkiem. Naprężenia od ściskania i zginania sumują się, a  wskutek tego powstaje pozorna bryła odkształceń i naprężeń poniżej dolnej krawędzi przekroju. Oś obojętna jet również pozorna. Wysokość strefy ściskanej x>h.
Taki przypadek często nazywa się małym mimośrodem, czyli przeważającym ściskaniem i dotyczy on większości słupów rzeczywistych – jest przedmiotem artykułu Słupy żelbetowe.

c) CT (Compression-Tension) – odkształcenia górnej krawędzi jest skróceniem a dolnej wydłużeniem (zbrojenie górne ściskane, dolne rozciągane). Wysokość strefy ściskanej mieści się w przekroju x≤ h. Taki przypadek nazywa się dużym mimośrodem, czyli przeważającym zginaniem i jest przedmiotem niniejszego artykułu.

d) TT (Tension-Tension) -oba zbrojenia rozciągane – powinno być rozważane jako rozciągany przekrój zespolony.

Przedstawiono kompedium wiedzy potrzebnej do zaprojektowania belki żelbetowej, ale także najważniejsze informacje dotyczące detali zbrojeniowych, zakotwienia i uciąglania belek, które w istocie stanowią wiedzę wymaganą od technologów i kreślarzy wykonawcy, opracowujących rysunki warsztatowe i powinny uzupełniać informacje zawarte w warunkach wykonania i odbioru konstrukcji betonowych [1]..

Projektowanie właściwe nie obejmuje umiejętności wykonywania rysunków roboczych (warsztatowych) , które przyjmują formę pokazaną na rys. W-6.
Rysunki warsztatowe są opracowywane przez wykonawców i ich technologów na podstawie wytycznych Projektanta zgodnie z zasadami opisanymi w artykułach Rysunek warsztatowy a projekt wykonawczy i  Standard rysunku warsztatowego konstrukcji żelbetowej.

Projektowanie  zbrojenia przekroju żelbetowego poddanego dwukierunkowemu zginaniu $M_y$, $M_z$ oraz siły osiowej $N_x$ dla modelu MN betonu (nieliniowego-parabolicznego) oraz modelu stali SP (Prandtla – idealnie sprężysto-plastycznego) można przeprowadzić w arkuszach kalkulacyjnych, który można pobrać poprzez kliknięcie na obraz rys. K-1. W kolejnych zakładkach skoroszytu zamieszczono arkusze do projektowania zbrojenia podłużnego oraz długości zakładów i zakotwienia prętów.

Beton i stal

W tab.W-1 zestawiono parametry betonów potrzebne do analizy zagadnienia opracowane na podstawie [2], tab.3.1 i [3].

Tab. W-1. Parametry betonów [2]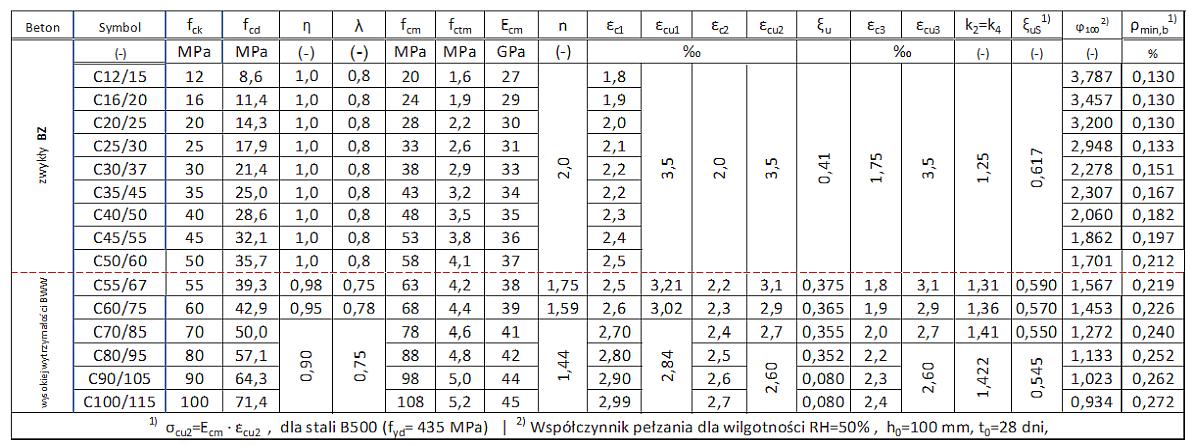W dalszej części artykułu stosuje się podział betonów na betony zwykłe (BZ) i wysokiej wytrzymałości (BWW). W tab.1 podział jest zaznaczony czerwoną linią przerywaną. Wartości współczynnika pełzania $\varphi_{100}^{2)}$ uzyskano z własnego kalkulatora.

W obliczeniach konstrukcji żelbetowych stosuje się też wytrzymałość obliczeniową betonu na rozciąganie. Uzyskuje się ją z wytrzymałości średniej na rozciąganie $f_{ctm}$ (tab W-1) . Najpierw oblicza się kwantyl 5% wytrzymałości na rozciąganie z zależności $f_{ctk,0,05} =0,7 \cdot f_{ctm}$ [4], tab.3.1) , a następnie sprowadza do wartości obliczeniowej z zastosowaniem  materiałowego współczynnika bezpieczeństwa $\gamma_c$, który w Polsce ma wartość 1,4

$$\begin{equation}  f_{ctd}=0,7 \cdot f_{ctm} / 1,4 \label {1}\end{equation}$$

W tab. W-2 zestawiono najczęściej stosowane stale zbrojeniowe.

Tab.W-2. Najczęściej stosowane stale zbrojeniowe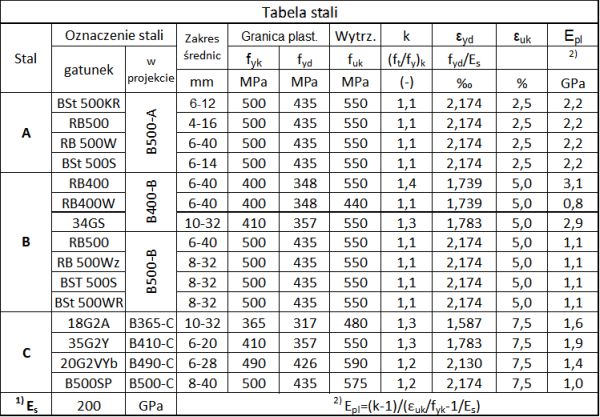

Przykład sesji w kalkulatorze LCżelbet

Sesja w kalkulatorze LCżelbet  zostanie przedstawiona na przykładzie belki z rys.W-3. Belka jest elementem stropu z przykładu Z-1, gdzie   przedstawiono więcej szczegółów i przeprowadzono dobór zbrojenia w przekroju przęsłowym A-B. W celu wstępnej prezentacji możliwości arkusza  przyjęto, że belka w przekrojach A i B ma powiększona wysokość i jest w tych przekrojach zginana  ukośnie momentami $M_y$ oraz $M_z$  i ściskana siłą $N_x$,a w rezultacie jest inaczej zbrojona, co ma swoje konsekwencje w ugięciu belki w stanie zarysowanym.

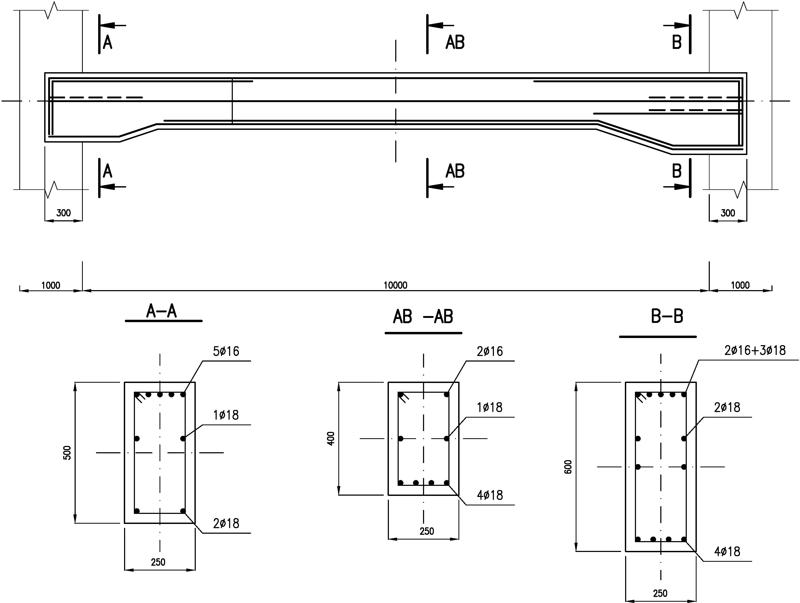
Rys.W-3 . Belka do prezentacji arkusza LCŻelbet (arkusz pobierzesz prze kliknięcie na rys.W-1)

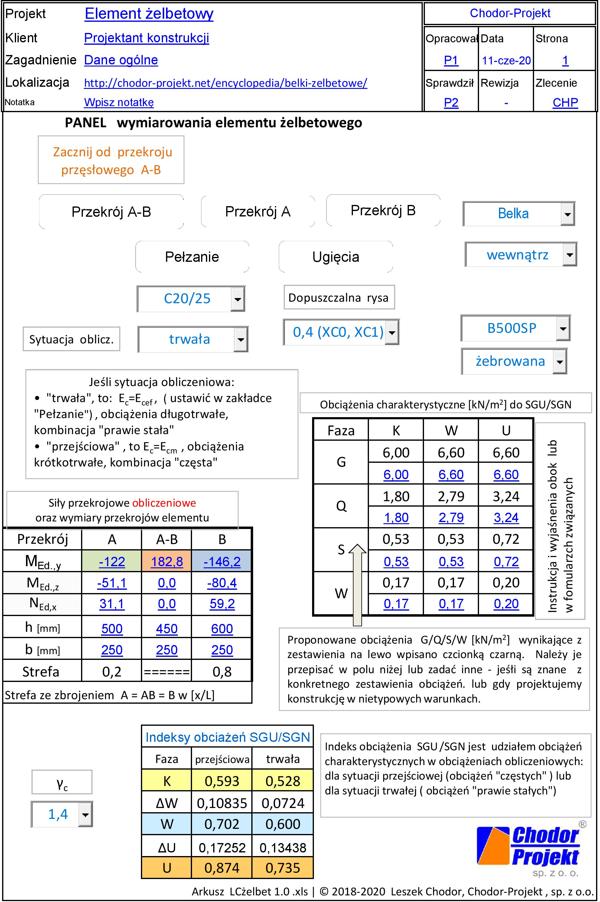
Wprowadzenie danych ogólnych

Wprowadzenie danych ogólnych należy przeprowadzić w zakładce ” ElementŻelbet”, pokazanej na rys. W-1.  Wprowadzamy dane w pola wyróżnione niebieskim kolorem.

W nagłówku strony wpisujemy:

• Nazwę projektu   (w miejsce Element żelbetowy”) – zmienna jest przenoszona na kolejne strony,
• Klient (kontrahent)  – w miejsce „Projektant konstrukcji” – przenoszone
• Zagadnienie – opis zagadnienie , które jest badane na stronie dla Projektu – może być różne na każdej stronie,
• Lokalizacja  ( w miejsce adresu strony www na której znajdziemy teorię do kalkulatora) wpisujemy  dres inwestycji lub miejsce elementu w obiekcie – przenoszone,
• Notatka – miejsce na dodatkową notatkę – przenoszone,
• Chodor-Projekt – Pole przeznaczone na nazwisko projektanta lub biura projektów – przenoszone,
• Opracował – inicjały projektanta wykonującego obliczenia – przenoszone,
• Sprawdził – inicjały osoby sprawdzającej – przenoszone,
• Data  – data pobierana z  zegara komputera – przenoszone,
• Rewizja – symbol rewizji (jeśli wystąpił) – przenoszone,
• Zlecenie – symbol zlecenia – przenoszone.

W polach wyboru wybieramy kolejno;

• klasę betonu ( np C30/37)
• sytuację obliczeniową (np trwała) – Uwaga wybór ma skutki na rodzaj obciążeń , kombinacje obciążeń charakterystycznych oraz moduł betonu, jak opisano w ramce niżej pola wyboru.
• dopuszczalną rozwartość rysy zależną od klasy ekspozycji (np 0,4 )
• klasę stali (np 18G2A (AII))
• rodzaj prętów zbrojeniowych (np żebrowana)
• rodzaj elementu (np Belka) – Uwaga wybór ma wpływ na minimalne, maksymalne zbrojenie i inne ograniczenia specyficzne dla rodzaju elementu żelbetowego,
• otoczenie (np wewnątrz pomieszczeń)

W tabeli „Siły przekrojowe obliczeniowe oraz wymiary przekrojów” podajemy dane dla trzech charakterystycznych przekrojów belki: A – podporowego lewego, A-B – przęsłowego – najczęściej tego, w którym moment zginający jest maksymalny, B – podporowego prawego.

Dane z tabeli „Obciążenia charakterystyczne do SGU/SGN” oraz Indeksy obciążeń SGU/SGN  są istotne wyłącznie przy sprawdzaniu zarysowania i ugięć. Dane  proponowane w tych tabelach czarną czcionką są tak wyspecyfikowane, że są poprawne dla większości sytuacji projektowych. W sytuacjach specyficznych można wpisać swoje dane  w tabeli „Obciążenia charakterystyczne do SGU/SGN” (pola udostępnione do edycji) lub w skróconych zestawieniach obciążeń zamieszczonych z prawej strony arkusza (pola O27:Y41), a na tej podstawie w tabeli O42:AH41  z formuł normowych wyznaczane są indeksy SGU/SGN, będące stosunkiem obciążeń charakterystycznych do obliczeniowych.

Współczynnik materiałowy dla betonu $\gamma_c=1,4$ przyjmuje się zgodnie polskim dodatkiem krajowym, a dla projektów na rynek europejski poza Polską  zmieniamy go na $1,5 $.

Przyciski panelu  służą do szybkiego przemieszczania się do innych zakładek: „Przekrój A-B” – dobór zbrojenia i sprawdzanie zarysowania dla przekroju przęsłowego „A-B” , „Przekrój A” dobór zbrojenia i sprawdzanie zarysowania dla przekroju podporowego „A” , „Przekrój B” dobór zbrojenia i sprawdzanie zarysowania dla przekroju podporowego „B” ,”Pełzanie” – wyznaczanie współczynników pełzania, „Ugięcia” – szacowanie linii ugięcia belki.

Projektowanie zbrojenia

W arkuszu można zaprojektować zbrojenie podłużne w trzech strefach belki:

• Strefa  podporowa „A”, która rozciąga się od lewego końca belki $\xi_0= x/L=0$  do  rzędnej określonej $\xi_A$ w tabeli „Siły przekrojowe”  (np.  $\xi_A =0,2$ )
• Strefa  przęsłowa „A-B”, która rozciąga się  od  $\xi_A $  do $\xi_{A-B}$ (np $\xi_{A-B}=0,8$ )
• Strefa podporowa „B”, która rozciąga się  od  $\xi_{A-B}$ do końca belki $\xi_B =1$

Projektowanie każdego z trzech przekrojów tych stref odbywa się w podobnym arkuszu w zakładkach: Przekrój „A-B”, „A”  lub „B” (patrz  niżej na umiejscowienie zakładek w Excelu)
W przypadku projektowania zbrojenia tylko w jednym przekroju symbol przekroju nie ma znaczenia.  Zaprojektowanie wszystkich przekrojów jest potrzebne wyłącznie do oszacowania ugięcia belki.
Po przejściu do jednej z tych zakładek dobierzemy zbrojenie w danej strefie belki.

Dobór zbrojenia w przekroju A-B pokazano na rys Z-10, a  w przekrojach podporowych A i B na rys. W-3.   Arkusz kalkulacyjny można pobrać przez klikniecie na rys. W-1..

Rys. W-4. Kalkulator LCżelbet . Projektowanie przekrojów A, B (pobierz prze kliknięcie  rys.1)

W bloku „Siły przekrojowe” mamy możliwość  potwierdzenia lub zmiany sił zadanych w zakładce Element Żelbet. Zwykle najpierw potwierdza się siły, a w dalszej kolejności korygujemy je, aby zaobserwować, jaka jest nośność przekroju. dla zadanego zbrojenia.

W bloku „Przekrój” przypomniano wymiary przekroju zadane w „ElementPrzekrój”. W bloku tym należy wpisać otulenie zbrojenia „c”, to znaczy otulenie krawędziowe (od brzegu betonu do krawędzi pręta)

W bloku „Zbrojenie” należy wpisać średnice i liczby prętów przy poszczególnych  krawędziach przekroju : „_ly” – dolnej, „_uy” – górnej, „_lz” – prawej, „_uz” – lewej, przy czym przy krawędziach bocznych zadaje się tylko pręty uzupełniające, położone pomiędzy zbrojeniem dolnym i górnym. Uwaga: krawędź dolna i prawa są krawędziami rozciąganymi przez momenty zginające.

Zbrojenie zadane w przykładzie pokazano na rys.2. Wyjaśnienia wymaga zadanie zbrojenia w przekroju B, w którym zbrojenie rozciągane w kierunku Y (jest to zbrojenie górne , ponieważ ten brzeg jest rozciągany ujemnym momentem zginającym) – zadano jak  5,8 ø16  , a faktycznie zastosowano zbrojenie mieszanymi średnicami 2 ø16 + 3 ø18 .

W przypadku zastosowania ze względów konstrukcyjnych mieszanych średnic (uzupełnienia zbrojenia przęsłowego) należy przeliczyć  mieszane zbrojenie na liczbę prętów o wybranej średnicy z porównania pola przekroju, czyli  dla liczby n₁ prętów o średnicy $\varnothing_1$  i n₂ prętów o średnicy $\varnothing_2$ mamy równoważną liczbę n_r prętów o średnicy $\varnothing_1$:

$$\begin{equation}  \cfrac{\pi} {4} \left( n_1 \cdot \varnothing_1^2 + n_2 \cdot \varnothing_2^2 \right) = \cfrac{\pi}{4}  \cdot n_r \cdot \varnothing_1^2  \to n_r= n_1 + n_2 \cdot \left( \cfrac{\varnothing_2}{\varnothing_1}\right)^2  \label{2} \end{equation}$$

co w naszym przypadku daje $n_r =2+ 3\cdot \left ( \cfrac{18}{16}\right) ^2 = 5,8.$.

Po ustawieniu danych jak wyżej, sprawdzamy nośność przekroju poprzez kliknięcie w przycisk „Oblicz”. Następuje automatyczne zbalansowanie przekroju, tzn wyznaczenie stanu równowagi zarówno statycznej (sił) jak i kinematycznej (odkształceń). Wyniki obliczeń umieszczane są w polach:

$w_R$ – wytężenie obliczeniowe, czyli wytężenie przekroju w złożonym stanie naprężeń (ściskanie/rozciąganie i dwukierunkowe zginanie)  w stanie granicznym nośności,
$x_Y$ – wysokość strefy ściskanej betonu po wysokości przekroju (od zginania względem osi Y),
$x_Z$ – wysokość strefy ściskanej betonu po szerokości przekroju (od zginania względem osi Z),
$w_k,Y$ [mm] – rozwarcie rysy od obciążeń charakterystycznych w zdefiniowanej sytuacji projektowej,
$p_{cr}$ – poziom rys, czyli rozwarcie rysy odniesione do wartości dopuszczalnej zdefiniowanej w zakładce „ElementŻelbet”.

Uzyskane wyniki będą wiarygodne wyłącznie wówczas, gdy nastąpi zbalansowanie przekroju, czyli w polach bloku „Wynik sprawdzenia” umieszczone będzie  „OK” . W innym przypadku należy zmienić wymiary przekroju ) (szalunku) na większe lub ograniczyć siły przekrojowe. Czasami(ale rzadka) wystarczy zwiększyć lub zmniejszyć zbrojenie. Dopiero po zbalansowaniu przekroju możemy dobierać zbrojenie tak, by zarówno stan nośności jak i zarysowania był optymalny (bliski 100%).

W bloku „Rysy” zamieszczono informacyjnie moduł betonu (w praktyce stosujemy moduł efektywny) oraz stosunek modułów betonu i stali $\alpha_e=E_s/E_{c,ef}$ stosowany do obliczania zarysowania przekroju. Zarysowanie jest wyznaczane od obciążeń charakterystycznych 'częstych”  na etapie  U – użytkowania – eksploatacji) dla parametrów ustawionych w zakładce „Pełzanie”.

W arkuszu wstępnie prowadzono obliczenia metodą klasyczną (uproszczoną). Obliczenia te są dostępne po prawej stronie arkusza doboru zbrojenia. Można na przykład porównać wysokość strefy ściskanej z obliczeń uproszczonych z wysokością strefy ściskanej  dla przekroju zbalansowanego. Różnice mogą być znaczne nawet kilkukrotne To świadczy o zawodności metod  klasycznych  i konieczności ich zastąpienia obliczeniami wykonywanymi na przykład w arkuszu LCżelbet.

Pełzanie i skurcz

W zakładce „Pelzanie” (rys.W-5) w bloku „Dane pełzania i skurczu” należy ustawić kalendarz wykonywania i eksploatacji elementu betonowego, liczony w dniach od rozpoczęcia wznoszenia elementu. czyli  wiek betonu dla kilku zdarzeń:

$t_s$ zakończenia pielęgnacji betonu- od tego dnia liczy się skurcz betonu w elemencie

$t_o1$ obciążenia montażowego. jest to dzień w którym pozwolono na częściowe obciążenie elementu – obciążeniami montażowymi zgodnie z normą [5]. Nominalnie $t_{o1}$ może wystąpić od początku budowy $t=0$, ale element do czasu uzyskania częściowej nośności jest utrzymywane w szalunkach, więc $t_{o1}>0$ i $t_{o1}< t_d$ (od dnia osiągnięcia przez beton dojrzałości = stąd pozorna nieścisłość na schemacie zamieszczonym na stronie.

$t_d$ – osiągniecie przez beton dojrzałości – nominalnie jest to 28 dni, ale w szeregu przypadków dojrzałość osiąga starszy beton

$t_k$ – zakończenie wznoszenia elementu.  W tym dniu następuje dociążenie elementu, czyli $t_k=t_{o2}$

$t_u$ – rozpoczęcie „normalnego” użytkowania elementu. W tym dniu następuje dociążenie elementu do poziomu obciążeń eksploatacyjnych, czyli $t_k=t_{o3}$

$t_\infty$ – zakończenie użytkowania podawane w latach ( w przykładzie 3 lata),
które jest automatycznie przeliczane na dni (poniżej).
W arkuszu dzień oceny pełzania i skurczu $t$ utożsamiany jest z okresem użytkowania, tzn. $t=t_\infty$.  W tym ujęciu wiek betonu może być dowolny i różnić się od projektowego okresu użytkowania zdefiniowanego  w normie [6].

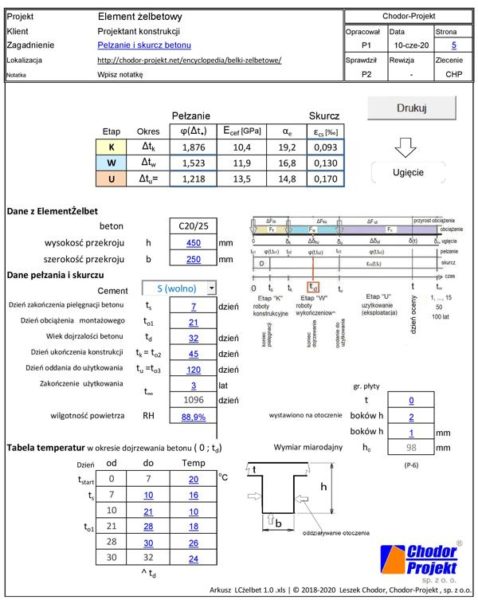
Rys. W-5 Kalkulator LCżelbet. Pełzanie i skurcz (pobierz prze kliknięcie  rys.W-1)

Oprócz tego należy wybrać rodzaj cementu zastosowany do wykonania betonu, a także wilgotność otoczenia elementu RH w % . Przy braku dokładniejszych danych dla elementu eksploatowanego wewnątrz pomieszczenia (zdefiniowano w zakładce „ElementŻelbet) można ustawić RH_{in} =50%, dla elementu eksploatowanego na zewnątrz $Rh\approx 80$%, ale wg autora w warunkach Polski ustawiać $RH_{ext} =50$%.

W przypadku dojrzewania betonu w temperaturze różnej od 20^oC, należy ustawić tabele w bloku „Tabele temperatur”

W bloku „Działanie otoczenia” należy zdefiniować liczbę boków elementu wystawionych na działanie otoczenia. Na tej podstawie wyznaczany jest miarodajny wymiar elementu $h_0$.

Ugięcia

W zakładce „Ugięcia” (rys.W-6) można wyznaczyć linię ugięcia zarysowanego, wyodrębnionego z konstrukcji elementu w kolejnych fazach wykonania i pracy.

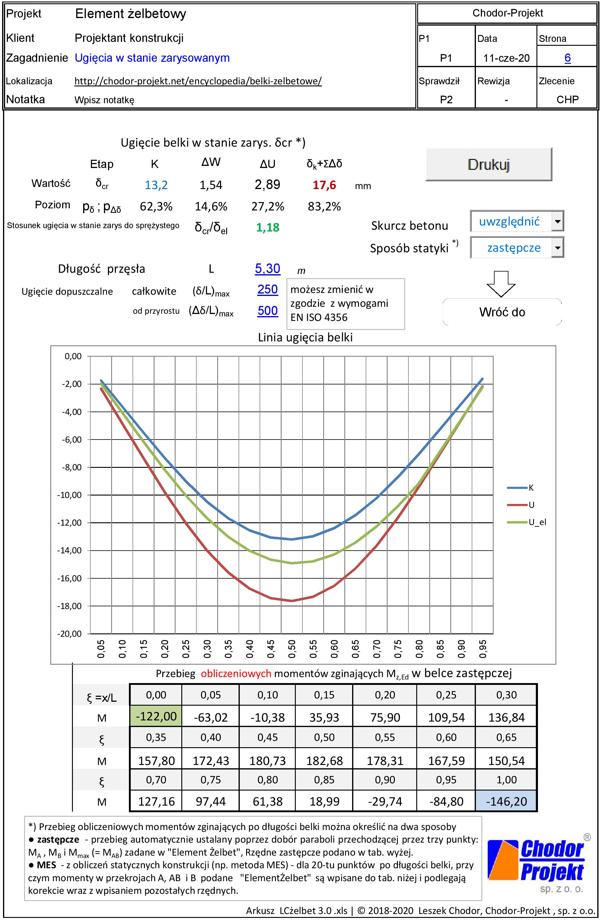
Rys.W-6 Kalkulator LCżelbet. Ugięcia.  (pobierz prze kliknięcie w rys.W-1)

Należy wybrać:

• czy uwzględnić skurcz betonu – można uwzględnić lub pominąć ugięcie elementu od skurczu betonu wyznaczonego w zakładce „Pełzanie”
• jaką metodą wyznaczane jest pole momentów w elemencie
• zastępcze: wyznaczone parabola trzeciego rzędu przez trzy zadane wcześniej punkty: momenty podporowe $M_A$ i $M_B$ oraz moment maksymalny w przęśle $M_{max,AB}
• w przypadku znajomości z obliczeń statycznych (np. metodą MES) można wybrać „MES” i w tabeli poniżej ramki wpisać 20-ścia rzędnych znanych z obliczeń.  Metoda MES jest dokładniejsza, ale wymaga poszerzonych obliczeń oraz wpisania do arkusza większej liczby danych. Powinna być stosowana w przypadku nieregularnego przebiegu momentów zginających na belce, np w przypadku  zaburzonych warunków brzegowych, obciążenia znacznymi siłami skupionymi lub innych obciążeń nieregularnych.

Ponadto należy zadać długość obliczeniową elementu  L oraz podzielniki dopuszczalnych ugięć:

• dla całkowitego ugięcia ( zwykle L/250),
• dla przyrostu ugięcia pomiędzy etapami pracy (od zwiększenia obciążenia) ( zwykle L/500).
  Proponowane ugięcia dopuszczalne można zmienić, ale tak, by były zgodne  z wymogami  EN ISO 4356.

Po wpisaniu danych automatycznie skorygowane zostaną wykresy linii ugięcia dla etapów:
K – wznoszenia konstrukcji -ugięcie stanie zarysowanym,
U – eksploatacji – ugięcie końcowe w stanie zarysowanym,
U_el  – ugięcie końcowe elementu sprężystego (jeśliby nie został zarysowany)

U góry strony umieszczone są strzałki ugięcia elementu w poszczególnych fazach pracy, a także stosunek $\delta_{cr} / \delta_{el}$  ugięcia w stanie zarysowanym $\delta_{cr}$ do ugięcia sprężystego $\delta_{el}$. Ten iloraz jest pokazany w celu szybkiego dokładniejszego oszacowania przemieszczeń elementów w stanie zarysowanym  w danej konstrukcji na podstawi wyników MES dla konstrukcji sprężystej. W przykładzie wyniki klasycznych obliczeń należy przemnożyć przez 1,95.

Ścinanie – zbrojenie poprzeczne (strzemionami)

Na rys. W-7 przedstawiono arkusz do doboru zbrojenia poprzecznego strzemionami belki

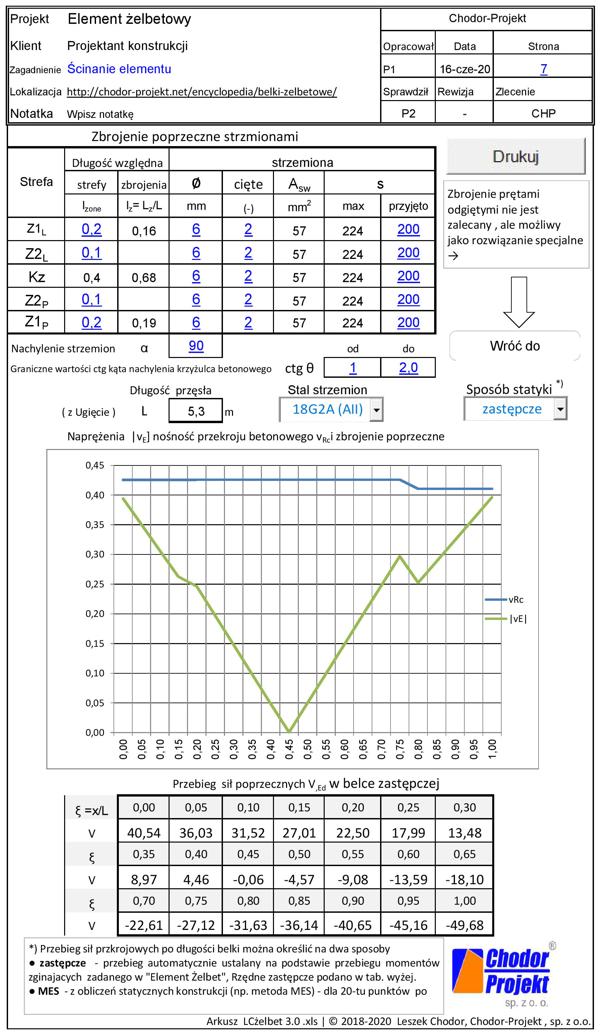
Rys.W-7 Arkusz LCżelbet. Ścinanie elementu żelbetowego  (pobierz prze kliknięcie  rys. W-1)

Sposób doboru strzemion opisany jest w instrukcji zamieszczonej po lewej stronie arkusza i  przywołanym tam artykule

Kotwienie i zakłady zbrojenia

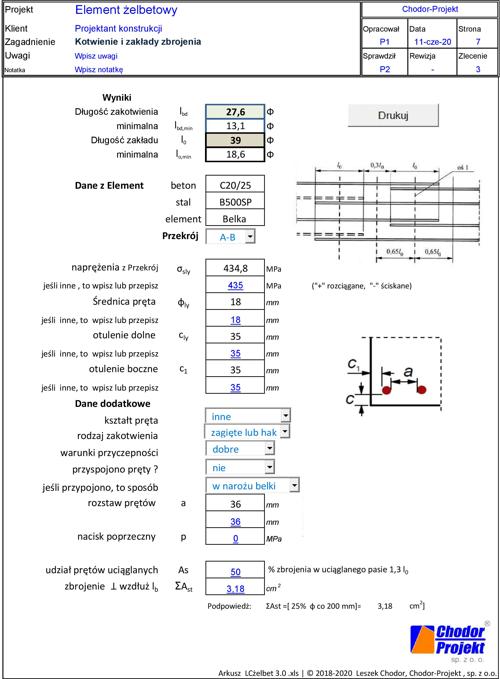
W zakładce „Kotwienie” (rys. W-8) można wyznaczyć wymagane długości zakładów oraz zakotwienia prętów zbrojeniowych w poszczególnych przekrojach elementu. Obsługa kalkulatora jest intuicyjna.

Rys.W-8 Arkusz LCżelbet. Kotwienie i zakłady (pobierz prze kliknięcie  rys. W-1)

Należy wskazać, że kalkulator dotyczy tradycyjnego łączenia prętów przez zakład i kotwienia przez przyczepność do betonu, a nie obejmuje nowoczesnych, ekonomicznych sposobów uciąglania i kotwienia prętów za pomocą łączników mechanicznych.Literatura

1. PN-EN 13670:2011, Wykonywanie konstrukcji z betonu
2. PN-EN 1992-1+AC+Ap 1,2,3 :2008, Projektowanie konstrukcji z betonu, Część 1-1:  Reguły ogólne i reguły dla budynków
3. Pędziwiatr, J. (2010). Wstęp do projektowania konstrukcji żelbetowych wg PN-EN 1992-1-1:2008. Dolnośląskie Wydawnictwo Edukacyjne
4. (PN-EN 1992-1+AC+Ap 1,2,3 :2008, Projektowanie konstrukcji z betonu, Część 1-1:  Reguły ogólne i reguły dla budynków
5. PN-EN 1991-1-6:2007, Eurokod 1: Oddziaływania na konstrukcje, Część 1-6: Oddziaływania ogólne. Oddziaływania w czasie wykonywania konstrukcji
6. PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji

________________________________

Related Baza wiedzy

• Belki żelbetowe. Zginanie
• Dylatacje budynków żelbetowych i krótkie wsporniki
• Krzywe interakcji M-N nieliniowego żelbetu
• Model żelbetu My-Mz-N
• Pełzanie i skurcz betonu
• Przebicie płyty żelbetowej (+)
• Rysy i ugięcia żelbetu (+)
• Ścinanie i skręcanie belek żelbetowych (+)