Artykuł w ciągu ostatnich 24 godzin czytało 15 Czytelników
Chodor L., Belki żelbetowe,, Encyklopedia πWiki, www.chodor-projekt.net,
13 lipca 2018 – 9 czerwca 2020  – ( publikacja  kompletna)
Arkusz LCżelbet zawiera oryginalny kod – © wszelkie prawa zastrzeżone.

Część P
Belki żelbetowe. Pełzanie i skurcz
Nawigacja: [ Z:  Zginanie ] ⇐ ⊗ ⇒  [ R: Rysy i ugięcia ]

Rozwój pełzania, skurczu, ugięć i obciążania

W celu prawidłowego uwzględnienia skurczu, pełzania i ugięć konstrukcji żelbetowych w ogólności należy prowadzić analizy na wszystkich etapach wykonawstwa konstrukcji z uwzględnieniem obciążeń, które mogą wystąpić na danym etapie z uwzględnieniem odkształceń i sił „zastanych” z poprzedniego etapu.

Pełzanie betonu ma wpływ przede wszystkim na przemieszczenia konstrukcji, w tym ugięcia belek oraz na siły przekrojowe w konstrukcjach statycznie niewyznaczalnych, w których następuje redystrybucja sił w funkcji sztywności części składowych konstrukcji. Na skutek pełzania z czasem zwiększają się odkształcenia i przemieszczenia konstrukcji – w ślad za czym idzie zwykle zmniejszanie się naprężeń w konstrukcjach statycznie niewyznaczalnych. Skurcz z kolei istotnie zwiększa siły przekrojowe w przypadku ograniczenia swobody odkształceń (skrepowania konstrukcji lub jej fragmentu). Dlatego z kolei podstawową metoda ograniczenia efektów skurczu są zabiegi technologiczne, zmierzające do zapewnienia swobody odkształceń  w początkowym okresie wykonawstwa (np betonowanie płyt w szachownicę lub naprzemiennego wykonywania przęseł belek )

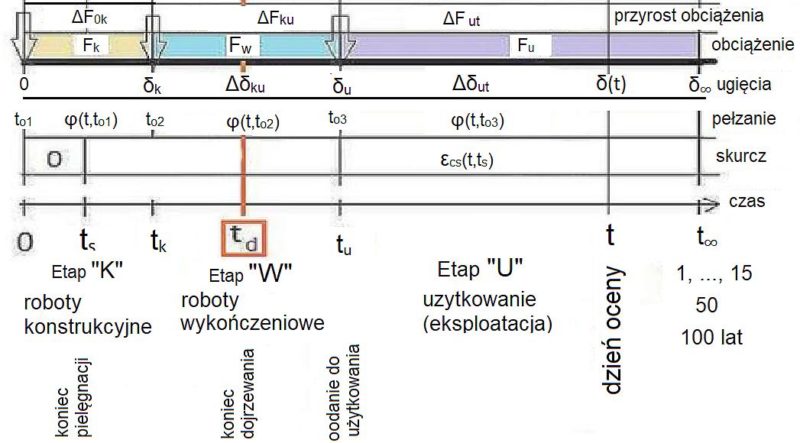
Na rys. P-1 przedstawiono schemat rozwoju pełzania , skurczu, dojrzewania i obciążenia elementu żelbetowego z uwzględnieniem korelacji czasowej zachodzenia poszczególnych zjawisk .

Rys.P-1. Rozwój pełzania, obciążani i ugięcia elementu żelbetowego

Wyróżniono następujące  etapy:
okres pielęgnacji betonu $ \{ 0, t_s \} $,
okres wznoszenia konstrukcji po pielęgnacji betonu $ \{ t_s, t_k \} $,
okres po zakończeniu wznoszenia konstrukcji, ale przed osiągnieciem przez beton wieku dojrzałości $\{t_k  , t_d \}$,
okres przed oddaniem obiektu do użytkowania, ale po dojrzałości betonu $\{t_d  , t_u \}$
okres eksploatacji (użytkowania) obiektu i elementu $\{t_d  , t_\infty \}$

Okresy pielęgnacji i wznoszenia konstrukcji oznaczono łącznie „K” ponieważ w tym okresie w przeważającym stopniu prowadzone są roboty konstrukcyjne.
Okresy wykończania budowli przed i po zakończeniu dojrzewania betonu oznaczono łącznie „W” W tym okresie w przeważającym stopniu prowadzone są roboty wykończeniowe, w tym stawianie ścian działowych i kurtynowych, wrażliwych na ugięcia stropów na których stoją
Okres od dnia oddania budowli do użytkowania aż do zakończenia eksploatacji oznaczono jako „U”.
Koniec okresu eksploatacji  oznaczono $\infty$ który oznacza projektowy okres użytkowania zgodnie z [1]   zależny od klasy konstrukcji: zwykle $\infty=50 \, lat$, ale dla konstrukcji rolniczych może wynosić  $\infty=15 \, lat$, a dla konstrukcji monumentalnych $\infty=100 \, lat$

Ocena pełzania, skurczu ugięć itd dokonywana jest w dniu „t” , który może być dowolny i znacznie mniejszy od okresu użytkowania obiektu $t_\infty$ . Może on wypaść przed lub po osiągnięciu przez beton okresu dojrzałości. Zwykle jednak element ocenia się w dniu przyłożenia obciążeń lub po zakończeniu użytkowania, czyli zwykle $ t = t_{o,k}  \text { lub  } t= t_\infty$, gdzie k – indeks obciążenia.

Zakładamy, że pielęgnacja betonu jest prowadzona zgodnie z zaleceniami  [2]. Pielęgnację rozpoczynamy  więc natychmiast po zabudowie mieszanki betonowej w konstrukcji (elemencie), a temperatura powierzchni betonu nie może być niższa niż 0°C do momentu, gdy strefa powierzchniowa osiągnie wytrzymałość minimum 5 MPa. Natomiast temperatura wnętrza betonu nie powinna być wyższa niż 70°C.
Okres pielęgnacji we wczesnym okresie dojrzewania betonu „1” $\{0,t_s\}$ zależy głownie od rodzaju cementu oraz do temperatury i wilgotności, w której pielęgnacja jest prowadzona. Pielęgnacja minimalizuje skurcz plastyczny, zapewnia odpowiednią wytrzymałość strefy powierzchniowej,  chroni przed szkodliwymi warunkami atmosferycznymi, chroni przed zamarzaniem oraz szkodliwymi drganiami, uderzeniami lub uszkodzeniami.
Czas trwania pielęgnacji powinien być jak najdłuższy, ale jest zwykle przerywany przed osiągnięciem dojrzałości betonu.
Przyjmujemy, że w okresie pielęgnacji poprawnie utrzymywane są szalunki, podpory i rusztowania montażowe., wskutek czego można go traktować jako normalny okres dojrzewania betonu bez możliwości powstawania niekontrolowanych odkształceń  i zarysowań oraz skurczu, to znaczy przyjmujemy, że okres pielęgnacji nie wpływa na skurcz i ugięcia belki, a w analizach pomijamy rysy, które mogą powstać w okresie pielęgnacji betonu, wskutek osiadania i pękania plastycznego betonu, w tym w warunkach  powstrzymywanie swobodnego osiadania zabudowanej mieszanki betonowej przez znajdujące się w niewielkiej odległości od powierzchni ziarna kruszywa grubego lub pręty zbrojeniowe.

Specjalnie wyróżniono wiek dojrzałości betonu $t_d$ ponieważ  nominalny wiek betonu w dniu obciążenia  podlega modyfikacji (wydłużeniu lub skróceniu) zależnie od temperatury otoczenia, w której beton dojrzewał. Nominalny wiek dojrzałości betonu $t_d$ (rys 1), to wiek, w którym beton osiąga wytrzymałość założoną w projekcie. Zasadniczo wynosi on 28 dni, ale przy wolnym i bardzo wolnym wzroście wytrzymałości może się wielokrotnie wydłużyć. W trakcie dojrzewania zachodzą zjawiska chemiczne wpływające na przyszłe pełzanie elementu pod obciążeniem, a zależne od temperatury w której element dojrzewa i cementu z którego wykonano beton.

Okres wznoszenia konstrukcji zwykle trwa dłużej niż okres pielęgnacji analizowanego elementu żelbetowego, ale może zakończyć się przed lub po osiągnięciu przez beton dojrzałości. Przyjmujemy, że w całym okresie wznoszenia konstrukcji od rozpoczęcia wykonywania elementu (prace szalunkowe, zbrojarskie, układanie betonu)  aż do zakończenia prac – utrzymywany jest reżim obciążeń  montażowych, w tym ochrona dojrzewającego betonu przed nasłonecznieniem, działaniem wysokich temperatur, silnego wiatru.

Obciążenie konstrukcji zmieniają  się wielokrotnie podczas budowy oraz użytkowania obiektu budowlanego. Wyróżniono trzy dni, w których następuje zmiana obciążenia konstrukcji:

• $t_{o1}$ rozpoczęcie wznoszenia konstrukcji. Konstrukcja jest stopniowo obciążana obciążeniami montażowymi. Kombinacja montażowa, zależy od fazy budowy, ale zasadniczo obejmuje ciężar własny konstrukcji , ograniczone obciążenia montażowe i klimatyczne.
  Kombinacja montażowa obciążeń $F_m$ oznacza obciążenia zgodnie z normą [3] . W szczególności przyjmujemy, że obciążenia użytkowe od robotników oraz narzędzi i sprzętu ręcznego $Q_{ca}$ nie przekroczy $1 kN/m^2$ (zgodnie z tab. 4.1. tej normy). Obciążenia ruchome $Q_{cb}$ oraz powierzchnie składowania materiałów budowlanych na stropach będą dopuszczone w projekcie, a obciążenia klimatyczne na stropodachy może wynosić maksymalnie 30% obciążenia, mogącego wystąpić podczas eksploatacji lub jest określone indywidualnie dla okresu trwania 3 dni (czyli z okresem powrotu  2 lata)  lub do 3 miesięcy (czyli z okresem powrotu 5 lat). Podstawowym obciążeniem montażowym jest ciężar własny surowej konstrukcji, ew. z wylewkami (warstwami wyrównawczymi) na płytach stropowych.
• $t_{o2}$, zakończenie wznoszenia konstrukcji nośnej i rozpoczęcie robót wykończeniowych, wśród których z punktu widzenia ugięć istotne jest postawienie ścian działowych oraz ścian kurtynowych (przeszkleń). W dniu $t_{o2} = t_k$ następuje dociążenie konstrukcji poprzez dołożenie obciążeń ściankami działowymi i  warstwami wykończeniowymi. Szczególnie istotne jest zachowanie ścianek działowych, które  w okresie eksploatacji często rysują się na skutek nadmiernych ugięć podpierającego stropu pod obciążeniami eksploatacyjnymi. Ugięcia właściwe do analizy zarysowań ścian działowych wynikają z przyrostu ugięć podpierającego stropu   w okresie $\{t_k \,, \, t_u\}$.
• $t_{o3}=t_u $. zakończenie robót wykończeniowych i oddanie obiektu do użytkowania. Przyjmujemy , że od tego dnia konstrukcja jest obciążona finalnie i zakładamy, że w tym okresie odpowiednia jest kombinacja”prawie stała” obciążeń charakterystycznych ($\ref{2}$), ujmująca ciężar ścian działowych jeszcze bez wykończeniowych warstw stropowych.  Zakładamy, że w okresie ekploatacji dział kombinacja  charakterystyczna kombinacja „częsta”. Od zakończenia wznoszenia konstrukcji do dnia oddania obiektu obiektu do użytkowania $t_u$ zwykle mija sporo czasu, poświęconego na czynności administracyjne, ale przede wszystkim związane z zasiedleniem obiektu oraz z pracami wykończeniowymi „lokatorskimi”, czyli zakładaniem tynków, podłóg itd.

Ze względu na nieliniowość zachowania konstrukcji żelbetowych w ogólności nie może być stosowana zasada superpozycji i efekt końcowy $Ef(t)$po czasie $t$ należy składać z przyrostów tego efektu $ \Delta Ef_k $ z okresów poprzedzających, to znaczy 

$$\begin{equation} Ef(t) = Ef_1 \sum \limits_k^n  \Delta Ef_k =  \label{1} \end{equation}$$

gdzie:
$Ef(t) $ efekt Ef (np ugięcie $\delta$ ) obserwowany po czasie użytkowania $t$,
$Ef1 $ efekt Ef po pierwszym okresie, w rozpatrywanym przypadku po okresie „K” wznoszenia konstrukcji $t$,
$ \Delta Ef_k $ – przyrost efektu Ef w okresie „k”, czyli w rozpatrywanym przypadku w okresie „W” oraz części lub całości okresu „U” $.
Przyrosty \Delta Ef_k $ spowodowane są przyrostami obciążeń w stosunku do etapu poprzedniego, ale też innym pełzaniem wyrażonym współczynnikiem pełzania $\varphi (t \,,\, t_{ok}$ $(\ref{18})$, czyli inną sztywnością wyrażoną efektywnym modułem odkształcalności $E_{c,ef} $(\ref{33})$.

Kombinacje charakterystyczne  w stanach granicznych użytkowalności

Stany granicznych użytkowalności, a mianowicie :  zarysowania, ugięcia , i drgania konstrukcji należy  sprawdzać  pod działaniem obciążeń w kombinacjach charakterystycznych. Ugięcia i związane z nimi pełzanie oraz skurcz betonu są zależne od czasu. Zakładamy, że w każdym okresie życia na konstrukcję działają obciążenia charakterystyczne w innej kombinacji obciążeń.

Zwykle okres użytkowania (eksploatacji) składa się z wielu podokresów, w których być może działają podobne obciążenia, ale zmieniają się warunki wilgotnościowe oraz temperatura, w której jest użytkowany element.

Formacje kombinacji charakterystycznych

Kombinacje charakterystyczne obciążeń rozpatruje się według dwóch formuł kombinacyjnych:

a) kombinacja   charakterystyczna „prawie stała” (indeks „ps”) dla nieodwracalnych stanów granicznych, np. przemieszczenia trwałe, rysy zgodnie z  [1], (6.16b)

$$\begin{equation} F_{ps} = \sum \limits_{j \ge 1}  G_{k,j } \text {„+”}  \sum \limits_{ i \ge > 1} \psi_{2,i} \cdot Q_{k,i} \label{2} \end{equation}$$

Kombinacja „prawie stała” jest jedna – wszystkie obciążenia zmienne są redukowane współczynnikiem $\psi_2$.

b) kombinacje charakterystyczne „częste ” (indeks”cz”) dla odwracalnych stanów granicznych, np. drgania, przemieszczenia sprężyste, zgodnie z  [1], (6.15b)

$$\begin{equation} F_{cz}= \sum \limits_{j \ge 1}  G_{k,j } \text {„+”} \psi_{1,1} \cdot Q_{k,1}  \text{„+”}  \sum \limits_{ i>1} \psi_{2,i} \cdot Q_{k,i} \label{3} \end{equation}$$

Kombinacji  „częstych jest tyle, ile rodzajów obciążeń zmiennych (każde z nich może być obciążeniem wiodącym „1” redukowanym współczynnikiem wartości częstej $\psi_1$ , pozostałe obciążenia zmienne są redukowane współczynnikami wartości „prawie stałej” $\psi_2$.

Indeks kombinacji SGU₁/SGN i SGU₂/SGN

Na użytek szacowania zarysowań oraz ugięć konstrukcji z wykorzystaniem pola sił przekrojowych uzyskanych dla stanu granicznego nośności SGN wprowadza się ndeksy SGU₁/SGN i SGU₂/SGN:

$$\begin{equation}  SGU_1/SGN =\cfrac{F_{cz}}{F_d} \label{4} \end{equation}$$

czyli iloraz sprawczej siły przekrojowej  $F$  z najniekorzystniejszej kombinacji charakterystycznej częstej ($\ref{3}$) do siły $F_d$ z kombinacji obliczeniowej

$$\begin{equation}  SGU_2/SGN =\cfrac{F_{ps}} {F_d} \label{5} \end{equation}$$

czyli  iloraz sprawczej siły przekrojowej  $F$  z kombinacji charakterystycznej „prawie stałej”  ($\ref{2}$) do siły $F_d$ z kombinacji obliczeniowej wg  [1] – p. również artykuł  Kombinacje obciążeń w Eurokodach.

Przekrojową siłą sprawczą
* w przypadku przeważającego zginania belek – maksymalny moment zginający $F=M$,
* w przypadku przeważającego zginania belek – maksymalna siła osiowa $F=N$,
* w ogólnej sytuacji, w tym w przypadku zginania M ze ściskaniem N, – mnożnik  sił $F= \Lambda=\cfrac{ [M,N]_{komb} }{[M,N]_{ref}}$, gdzie siły odniesienia przyjmuje się  dla współczynników obciążeń $\gamma_F$  oraz redukcyjnych $ \psi_0 , \psi_1, \psi_2$ równych 1

Skurcz i pełzanie

Pełzanie oraz skurcz betonu można oszacować wg formuł normy [4], kl. 3.1.4 . Kalkulator pełzania i skurczu uwzględniający wytyczne normowe  jest opublikowany w zakładce „Pełzanie” kalkulatora żelbetu LCżelbet (rys. W-1)  , w którym przy wyznaczaniu współczynników pełzania, skurczu oraz ugięć stosuje się podział na okresy zdefiniowane na rys. 1 i podane tam kombinacje obciążeń , wartości skurczu $\epsilon_{cs}$ oraz współczynników pełzania.$\varphi$ i wynikające stąd efektywne wartości modułu odkształcalności betonu $E_{c,ef}$ $(\ref{33})$.

Skurcz i pełzanie betonu zależą od wielkości elementu, mierzonego miarodajnym wymiarem $h_0$ wyznaczanym  z zależności [4], (B-6) :

$$\begin{equation}h_0=\dfrac{A_c}{u} \label{6} \end{equation}$$

gdzie $A_c$ jest polem powierzchni betonu elementu ( w szalunkach), a $u$ obwodem wystawionym na wysychanie (na bezpośrednie działanie atmosfery). Na przykład dla belki z ułożoną na niej płytą u=2h+b,

a także zależy od wilgotności otoczenia, w którym pracuje. Wilgotność otoczenia $RH$ zależy od wielu czynników. Można w uproszczeniu przyjąć, że średnia wilgotność powietrza zewnętrznego w regionie nadmorskim (wg PN-EN 12831:2006) wynosi 52%, a w pozostałych regionach 48%. Oczekiwana wilgotność w pomieszczeniach do pobytu ludzi wynosi 40-60%. Dlatego najczęściej przyjmuje się wilgotność RH=50%.
Poniżej w formułach ($\ref{14}$) oraz ($\ref{28}$), ($\ref{27}$)  wilgotność względną (RH) należy podstawiać w postaci liczby dziesiętnej: (RH) = (RH(%) / 100%) <1,0.

Skurcz betonu

Całkowite odkształcenie skurczowe $\varepsilon_{cs}$ składa się z dwóch składników: odkształcenia skurczowego spowodowanego wysychaniem  $\varepsilon_{cd}$ i autogenicznego (samorodnego) odkształcenia skurczowego $\varepsilon_{ca}$ [4],(3.8) :

$$\begin{equation}  \varepsilon_{cs}= \varepsilon_{cd} +\varepsilon_{ca}\label{7}\end{equation}$$

Przyjmujemy, ze pielęgnacja betonu zakończyła się w dniu $t_s$ i od tego dnia rozpoczęło się wysychanie betonu i trwa do dnia oceny $t>t_s$

Okres  wysychania betonu wynosi

$$\begin{equation}  \Delta t_s= t-t_s \label{8}\end{equation}$$

Skurcz samoistny

Skurcz  wywołany przez przyczyny wewnętrzne (autogeniczny – samoistny) zależy od wytrzymałości betonu i czasu $t_{\infty}$ w dniach po którym oceniamy skurcz zgodnie z zależnością [4], (3.11) :

$$\begin{equation}  \varepsilon_{ca} (t) = \beta_{ca}(t) \cdot \varepsilon_{ca, \infty}  \label{9}\end{equation}$$

w którym [4], (3.12),  (3.13) :

$$\begin{equation} \varepsilon_{ca, \infty} = 2,5 \cdot ( f_{ck} -10) \cdot 10^{-3} \text{[‰]} \label{10}\end{equation}$$

$$\begin{equation} \beta_{ca} (t) = 1 -exp \left ( -0,2 \sqrt{t} \right )\label{11}\end{equation}$$

Skurcz od wysychania

Skurcz  wywołany wysychaniem zaczyna się najczęściej po zakończeniu pielęgnacji betonu w dniu $t_s$ (rys P-1)  i zależy od wytrzymałości betonu oraz okresu czasu $(\Delta t_s = t-t_s)$  w dniach po którym jest oceniany, zgodnie z zależnością [4],(3.9) :

$$\begin{equation}  \varepsilon_{cd} (t) = \beta_{ds}( \Delta t_s) \cdot \varepsilon_{cd,\infty} \label{12} \end{equation}$$

w którym $\varepsilon_{cd, \infty} $ – skurcz wysychania na końcu okresu $\Delta t_s$ wg zależności:

$$\begin{equation}  \varepsilon_{cd, \infty} =\cdot k_h  \cdot \varepsilon_{cd,0} \label{13}\end{equation}$$

gdzie:
$k_h$ – współczynnik zależny od efektywnego rozmiaru elementu  zgodnie z tab P-1:

Tab.P-1. Współczynniki pomocnicze $k_h$ do szacowania skurczu $\varepsilon_{cd, \infty}$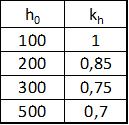

$\varepsilon_{cd,0}$ – skurcz  na początku okresu wysychania wyznaczony z zależności empirycznej [4], (B11-12)

$$\begin{equation}  \varepsilon_{cd,0}= 1,3175 \cdot (220+110 \cdot \alpha_{ds1}) \cdot  \left ( 1- (RH)^3 \right) \cdot \exp { \left (-  \alpha_{ds2} \cdot f_{cm} /10 \right ) } \cdot 10^{-3} \text{[‰]} \label{14}\end{equation}$$

Współczynniki zależne od czasu wyznacza się z zależności:

$$\begin{equation}  \beta_{ds} (t) = 1- \exp { (-0,2 \cdot \sqrt{t})} \label{15}\end{equation}$$

$$\begin{equation} \beta_{ds}(\Delta t_s) =\cfrac{\Delta t_s}{\Delta t_s + 0,04 \cdot \sqrt{h_0^3}} \label{16}\end{equation}$$

Współczynniki pomocnicze  wynoszą:

$$\begin{equation} \alpha_{ds}= \begin {cases}
\text {dla cementu klasy S} & \alpha_{ds1}= 3 , & \alpha_{ds2}=0,13\\
\text {dla cementu klasy N} & \alpha_{ds1}= 4 , & \alpha_{ds2}=0,12\\
\text {dla cementu klasy R} & \alpha_{ds1}= 6 , & \alpha_{ds2}=0,11\\
\end {cases} \label{17}\end{equation}$$

Pełzanie betonu

Istotnym czynnikiem wpływającym na zwiększanie szerokości rozwarcia rysy jest pełzanie betonu, największe tuż po ułożeniu betonu i zmniejszające się wraz z upływem czasu.

W analizie konstrukcji żelbetowych pełzanie betonu o wieku $t$  w dniu obciążenia $t_o$ uwzględnia się poprzez zastosowanie współczynnika pełzania  $\varphi (t\, , \, t_o) $,.

Wiek betonu $t$ jest czasem  od dnia ułożenia betonu $0$ do dnia $t$ oceny zjawiska. Pełzanie oceniamy zwykle pod koniec okresu użytkowania, który oznaczamy $t_\infty$ lub po prostu $\infty$, choć może zajść potrzeba oceny w dowolnym czasie $t$ życia obiektu.

Współczynnik pełzania jest stosunkiem odkształcenia konstrukcji w ocenianej chwili ( w teraźniejszości ($t$) z uwzględnieniem pełzania betonu  od dnia jego ułożenia $0$ do odkształcenia doraźnego, w dniu $t$, to znaczy odkształcenia sprężystego  (czyli bez uwzględnienia pełzania)  i zależy od szeregu czynników, a w tym wilgotności powietrza $RH$ oraz wielkości elementu żelbetowego.

Współczynnik pełzania

Współczynnik pełzania $ \varphi( t \, ,\, t_o )$  jest zależny od okresu czasu  trwania obciążenia $ \Delta t_o = t- t_o $, czyli różnicy  wieku betonu $t$ i wieku ( dnia) obciążenia $t_o$ ,  gdzie $t$  jest końcowym dniem użytkowania obiektu $t=\infty$, lub dowolnym innym dniem w życiu budowli , w którym oceniamy pełzanie, moduł odkształcalności , ugiecia itd.

W dalszym ciągu w parametrach zależnych od czasu trwania obciążenia zamiast argumentu $( t \, ,\, t_o )$ będziemy stosować krótszy zapis $(\Delta t_o )$.

Współczynnik pełzania wyznacza się z zależności [4],(B.1)

$$\begin{equation} \varphi (t,\, , \, t_o ) = \varphi (\Delta t_o ) = \beta_c (\Delta t_o ) \cdot \varphi_o (t_{o,m} ) \label{18}\end{equation}$$

Podstawowy współczynnik pełzania $\varphi_o (t_{o,m} ) $ wynosi [4], (B.2)

$$\begin{equation}  \varphi_o (  t_{o,m} ) = \beta_{fcm} \cdot \varphi_{RH} \cdot \beta_T (t_{o,m}) \label{19} \end{equation}$$

gdzie współczynnik $\beta_T (t_{o,m})$ zależy od temperatury otoczenia poprzez zmodyfikowany wiek betonu w dniu obciążenia  $t_{o,m}$ (patrz niżej) i wynosi [4], (B.5)

$$\begin{equation}  \beta_T (t_{o,m}) = \cfrac {1} {0,1 + t_{o,m} ^{0,20} } \label{20}\end{equation}$$

Współczynniki zależne od wytrzymałości betonu

Beton w zagadnieniu pełzania jest charakteryzowany średnią wytrzymałością na ściskanie

$f_{cm} = f_{ck} + 8 \, MPa $.

Na podstawie tej wytrzymałości wyznacza się :

• współczynniki  pomocnicze $\alpha _i, \, (i=1,2,3)$ :

$$\begin{equation} \alpha_{1,2} = \begin{cases}
\alpha_1= \alpha_2 =1  & \text { dla } f_{cm}\le 35 \, MPa\\
\alpha_1 =\left( \cfrac{36}{f_{cm}} \right)^{0,7} ;  \quad  \alpha_2 =\left( \cfrac{36}{f_{cm}} \right)^{0,2} , & \text { dla } f_{cm} > 35 \, MPa\\
\end{cases}
\label{21}\end{equation}$$
$$\begin{equation} \alpha_3=\sqrt{ \cfrac{36}{f_{cm}}}  \label{22}\end{equation}$$

• współczynnik $\beta_{fcm}$  [4], (B.4) :

$$\begin{equation}  \beta_{fcm}=\cfrac{16,8}{ \sqrt{f_{cm}}} \label{23}\end{equation}$$

Współczynniki zależne od wilgotności otoczenia RH

Poniżej we wzorach ($\ref{28}$), ($\ref{27}$) wilgotność (RH) jest względną wilgotnością powietrza wyrażoną jako ułamek dziesiętny, czyli (RH)= (RH%)/100%

Współczynniki zależne  od wilgotności powietrza wynoszą [4], (B.3)”], [4], (B.8) :

$$\begin{equation} \beta_{RH}= \begin{cases}
1,5\cdot \{ 1+\left (1,2 \cdot (RH) \right)^{18}\} \cdot h_0+250 \le 1500 , & \text { dla } f_{cm}\le 35 \, MPa\\
1,5\cdot \{ 1+\left ( 1,2 \cdot (RH) \right)^{18}\} \cdot h_0+250 \cdot \alpha_3 \le 1500 \cdot \alpha_3 , & \text { dla } f_{cm} > 35 \, MPa\\
\end{cases}
\label{24}\end{equation}$$

$$\begin{equation}  \varphi_{RH}=\alpha_2 \cdot \left ( 1+ \alpha_1 \cdot \cfrac{1-(RH)}{ 0,1 \cdot {h_0 }^{1/3} } \right )  \label{25}\end{equation}$$

Współczynniki zależne od wieku betonu w dniu obciążenia

Dzień obciążenia  może wypaść w okresie dojrzewania betonu lub w wieku po osiągnięciu dojrzałości.

Zmodyfikowany wiek betonu w dniu obciążenia

Jeśli w okresie dojrzewania betonu $(0, t_d)$ wystąpiły okresy dni $\Delta t_i$, w których  temperatura otoczenia $T_i$ była inna niż $20^o C $ , to w formule ($\ref{20})$ (ale tylko w tej) wiek betonu w dniu obciążenia należy zmodyfikować jako sumę ważoną zgodnie z zależnością [4], (B-10) :

$$\begin{equation} t_{o,T} = \sum \limits_{i=1}^{n}  f (T_i) \cdot \Delta t_i  \label{26} \end{equation}$$

gdzie suma obejmuje okres dojrzewania $ [ 0, t_{d,o}]$,  a $t{d,o} = t_d$, ale nie więcej niż wiek betonu w dniu obciążenia. $t_o$. To znaczy suma rozciąga się na okres dojrzewania przed dniem obciążenia.

Wagi $f(T_i)$  w sumie $(\ref{26})$ wynoszą:

$$\begin{equation} f(T_i) = \exp { \left  [  4000 \cdot \left (  1/293 -1/(273+T_i \right  )  \right ]  } \label{27} \end{equation}$$

Oznacza to, że okresy z temperaturą mniejszą od $20^0 C$ skraca się, a okresy z temperaturą większą wydłuża.

Wiek betonu w dniu obciążenia  modyfikuje się również ze względu na rodzaj cementu użyty w betonie w ten sposób, że zmodyfikowany temperaturą wiek betonu $t_{o, T}$ ($\ref{26}$) przekształca się w zmodyfikowany wiek obciążenia zgodnie z formułą [4], (B-9) :

$$\begin{equation} t_{o,m} = t_{o,,T} \cdot \left( – \cfrac{11}{2+t_{o,T}^{1,2}}+1\right)^{\alpha} \ge 0,5 \label{28} \end{equation}$$

gdzie wykładnik $\alpha$ zależy od rodzaju cementu i wynosi

$$\begin{equation} \alpha= \begin {cases}
-1, & \text {dla cementu klasy S} \\
0, & \text {dla cementu klasy N}  \\
1, &  \text {dla cementu klasy R} \\
\end {cases} \label{29}\end{equation}$$

Jeśli wiek obciążenia zmodyfikowany temperaturą $(\ref{26}$) $t_{o,k,T} > 7 $ dni, to do szacowania zmodyfikowanego  dnia obciążenie możemy stosować przybliżone zależności:

$$\begin{equation} t_{o,m} \approx t_{o,T} + \begin {cases}
– 3 ,& \text {dla cementu klasy S}\\
0,& \text {dla cementu klasy N}\\
+5, & \text {dla cementu klasy R}  \\
\end {cases} \label{30}\end{equation}$$

Współczynniki  zależne od okresu trwania obciążenia

Okres trwania obciążenia, czyli różnica między wiekiem betonu w dniu oceny ( w teraźniejszości) i wieku betonu w dniu obciążenia :

$$\begin{equation}  \Delta t_o= t- t_o \label{31}\end{equation}$$

często jest liczony dla $t=t_\infty$ lub po prostu $\infty$, czyli okresu użytkowania obiektu.

Współczynnik zależny od okresu trwania obciążenia wynosi [4], (B.7)

$$\begin{equation}\beta_{ \Delta t_o}= \left( \cfrac{ \Delta t_o} { \beta_{RH}+ \Delta t_o} \right)^{0,3} \label{32}\end{equation}$$

Poprzez współczynnik  $\beta_{ \Delta t_o}$ również współczynnik pełzania $(\ref{18})$ jest zależny od okresu trwania obciązenia

Efektywny moduł odkształcalności

W celu uproszczenia analizy wprowadza się zastępczy (długotrwały, efektywny  moduł odkształcalności betonu $E_{c,ef}$ $(\ref{33})$, a analizę prowadzi się jak dla liniowo sprężystego betonu i stali, po postawieniu $E_c = E_{c,ef}$. Moduł efektywny (zastępczy) zależy od współczynnika pełzania zgodnie z formułą  [5], (5.28) :

$$\begin{equation}  E_{c,ef}= \dfrac{E_{cm}}{1+\varphi(t, t_o )}\label{33}\end{equation}$$

w którym $\varphi(t, t_o)=\varphi(\Delta t_o)$  ($\ref{18}$)  jest współczynnikiem pełzaniem,  od dnia obciążenia betonu $t_o$ do dnia  obecnego (analizy) $t$

W tab. W-1 w celach orientacyjnych, podano wartości bazowe  współczynnika pełzania $\varphi_0$  dla wilgotności RH=50% , temperatury dojrzewania T=$20 ^o C$ , wieku obciążenia betonu $t_o = 28 \, dni$  w dniu $t= 50 \, lat + 7 \, dni$  czyli dla okresu $\Delta t_o = 50$ lat oraz dla miarodajnego wymiaru  elementu $(\ref{6}$) $h_0= 100 \, mm$. Z zależności ($\ref{33}$) można oszacować efektywny współczynnik sztywności betonu.

Efektywna sztywność belek

Efektywna sztywność przekroju betonowego uwzględniająca  zarysowanie przekroju oraz pełzanie pręta jet żmudna do ścisłego wyznaczenia. W praktyce inżynierskiej stosuje się  oszacowania, które można sprowadzić do wyrażenia na sztywność nominalną w postaci normowej [5], (5.21) , opisanej w artykule Słupy żelbetowe: sztywność :

$$\begin{equation} EI_{ef}= EI  = K_c \cdot E_{cd} \cdot I_c +K_s \cdot E_s \cdot I_s \label {34} \end{equation}$$

gdzie:

$I_c$  – moment bezwładności przekroju betonu (w normie amerykańskiej [6]   $I_g$ -„gross area” -moment bezwładności przekroju brutto)
$E_s =200 \,GPa$ – obliczeniowy modułu sprężystości zbrojenia
$l_s$  – momentem bezwładności pola przekroju zbrojenia względem środka ciężkości powierzchni betonu,
$K_c$  – współczynnik zależny od wpływów zarysowania, pełzania itd. betonu
$K_s$  – współczynnik zależny od udziału zbrojenia,
$E_{cd}=\cfrac {E_{c,m}} {\gamma_{cE}}$ – obliczeniowy moduł sprężystości betonu; współczynnik materiałowy $\gamma_{cE}$ zaleca się przyjmować o wartości 1,2, ale często przyjmuje się $\gamma_{cE}=\gamma_c=1,4$; ; $E_{cm}$ wg tab.W-1
$K_s=1,0$  dla stopnia zbrojenia przekroju $\rho=A_s/A_c >0,002$, ( czyli praktycznie dla wszystkich przekrojów ).

Zgodnie z procedurami dedykowanymi dla słupów – w przypadku siły osiowej $N_{Ed}=0$ współczynniki  $K_c= 0 $,. Taki przypadek mamy dla belek  zginanych. Prowadzi to do błędnych wyników procedur numerycznych. Dlatego postulujemy zastosowanie zalecanych przez normy wielu krajów wartości współczynnika redukcji sztywności :

$$\begin{equation} K_{ef} =\cfrac{EI_{ef}}{EI_c} \begin {cases}
0,35 & \text {wg ACI 318-11, ACI 318-14 ; LATBSDC ; CSA A 33.3-14} \\
0,5 & \text { wg PN-EN 1998-3 ; FEMA 356 ; PEER TBI } \\
0,40  & \text { wg NZS 3101 ; TS 500-2000}
\end {cases} \label{35}\end{equation}$$

W wykazie zastosowano skróty opracowań:
ACI 318-11  [6] ;
ACI 318-14 [7] ;
LATBSDC  [8] ;
CSA A23 [9] ;
PN-EN 1998-3 [10] ;
FEMA 356 [11] ;
PEER TBI [12] ;
NZS 3101, [13];
TS 500 [14] .

Istnieje prosta zależność pomiędzy $K_c$ i $K_{ef}$ (dla $E=E_{cd}$):

$$\begin{equation} K_c=  K_{ef}  – K_s \cdot \cfrac{E_s I_s}{E_{cd} I_c} \label{36} \end{equation}$$

W typowym przypadku betonu C30/37: $E_s/E_{cd}=200/(33/1,2)= 7,2$,
Dla przekroju prostokątnego bxh: $I_c=\cfrac{b h^3}{14}= A_c \cdot \cfrac{h^2}{14}$, zbrojonego symetrycznie zbrojeniem o łącznym przekroju $A_s$
$I_s= A_s \cdot \cfrac {(h-a)^2}{5} \stackrel {a=0} { = } A_s \cdot \cfrac {h^2}{5}$,

czyli $I_s/I_c \approx \rho/3$.

Dla optymalnego stopnia zbrojenia belek $\rho=A_s/A_c=0,5$% mamy

$K_c=K_{ef}- 0,012$ – z zależności ($\ref{36}$) dla belek otrzymujemy $K_c= 0,35-0,012 \approx 1/3 $

Wartość 1/3 współczynnika redukcji sztywności belek żelbetowych stosuje się powszechnie w praktyce inżynierskiej. Oznacza to, że ugięcie belki w stanie zarysowanym jest ok 3-krotnie większe od ugięcia belki sprężystej.

Problem  zjawisk krótko- i długo-trwałych w betonie

W wielu miejscach normy [4] w sposób niespójny pojawiają się pojęcia związane z czasem trwania obciążenia:

a) stany zarysowania  i ugięć wyznacza się  pod działaniem kombinacji charakterystycznych obciążeń, to znaczy takich, które są wywołane  charakterystycznymi siłami przekrojowymi. Definiuje się dwie kombinacje charakterystyczne : „prawie stałą” ($\ref{2}$) oraz „częstą” ($\ref{3}$)

b) moduł betonu $E_c$ oznacza się jako doraźny $E_{cm}$ lub efektywny $E_{c,ef}$  ($\ref{33}$), to jest  z uwzględnieniem pełzania w określonym wieku betonu

c) rysy we metodzie KO (krytycznych odkształceń) (R-28) wyznacza się z uwzględnieniem współczynnika czasu trwania obciążenia  $k_t$

d) ugięcia w stanie zarysowanym wyznacza  metodą UO się z użyciem

Przykłady rachunkowe

Przykład P-1 [ Efektywny moduł sprężystości betonu w szczególnych warunkach pełzania ]

Wyznaczyć efektywny moduł sprężystości dla belki o przekroju prostokątnym:
wymiary $h= 400 \, mm$ , $b=250 \, mm$
$(\ref{6}) \to$ $ h_0= \cfrac {250\cdot 400}{2\cdot 400+250} = 95,2 \, mm$
beton  C30/37   Tab W-1 $\to$ $f_{ck}=30 \,MPa$, $f_{cm}=38 \, MPa $, $E_{cm} = 33 \, GPa$,

w szczególnych warunkach pełzania:

• w środowisku o wilgotności $RH=88,9$%=0,889,
• o okresie użytkowania  $t_\infty = 3$  lata  $ =3 \cdot 365,25 = 1096 \, dni$  (365,25 jest średnia liczbą dni w roku z uwzględnieniem lat przestępnych).

• Obciążenie konstrukcji realizowane było w następujących dniach od początku budowy elementu licząc:

  $k=1$ – montażowe $t_{o,1} = 21$  dzień  – obciążenie charakterystyczne, wynikające z potrzeb robót budowlanych,
  $k=2$ – „prawie stałe”  $t_{o,2} = 45$ dzień – obciążenie charakterystyczne  najbardziej prawdopodobne w okresie przygotowania elementu do oddania do użytkowania.,
  $k=3$ – „częste $t_{o,3} =120$  – obciążenie charakterystyczne najbardziej prawdopodobne w okresie użytkowania

Poszczególne okresy życia  elementu i temperatury, notowane w  dzienniku budowy oraz eksploatacji  obiektu pokazano w tab. 2, w której podano ważne dla skurczu i pełzania wydarzenia z określeniem dnia  oraz pomiarów temperatur otoczenia

Tab.P-2  Kalendarium życia betonu do przykładu  P-1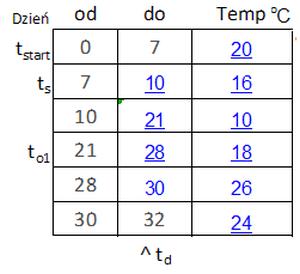

Tabela 2 obejmuje okres dojrzewania betonu, czyli od początku ułożenia $t_p= 0 \, dni $  do wieku, w którym beton osiągnął założoną wytrzymałość $t_d=32 \, dni$ (wieku dojrzałości).

Współczynniki pełzania

Współczynniki zależne od wytrzymałości betonu

$ f_{cm}= 38 >35 \, MPa$
$(\ref{21}) \to  \alpha_1 =\left( \cfrac{36}{38} \right)^{0,7}=0,944,$ ,
$\alpha_2 =\left( \cfrac{36}{38} \right)^{0,2}=0,984$
$(\ref{22}) \to  \alpha_3=\sqrt{ \cfrac {36}{38}}= 0,960$

$( \ref{23}) \to  \beta_{fcm}=\cfrac{16,8}{ \sqrt{38}}=2,725$

Współczynniki zależne od wilgotności otoczenia

$(\ref{24}) \to  \varphi_{RH}=0,984 \cdot \left ( 1+ 0,944 \cdot \cfrac{1-0,889}{ 0,1 \cdot {95,2 }^{1/3} } \right )=1,2094$
$( \ref{25}) \to   \beta_{RH}=  1,5\cdot \{ 1+( 1,2 \cdot 0,889)^{18} \} \cdot 95,2+250 \cdot 0,960 =840,29 \le 1500 \cdot 0,960 = 1440 \to \beta_{RH}=840,29$

Współczynniki zależne od wieku betonu w dniu obciążenia montażowego $k=1$

Zmodyfikowany wiek betonu w dniu obciążenia i $\beta_T$

Podokresy dojrzewania betonu zastosowane w formule ($\ref{26}$) wynoszą:
„1” :  $\Delta t_1 =7-0= 7$ dni z  temperatura  $T_1 = 20^o C$
„2” : $\Delta t_2 =10-7= 3$ dni z  temperatura  $T_2 = 16^o C$
„3” : $\Delta t_3 =21-10= 11 $ dni z  temperatura  $T_2 = 10^o C$

Wagi temperatury ($\ref{27}$) :
$f(T_1) = \exp{ \left  [  4000 \cdot \left (  1/293 -1/(273+20 \right )  \right ]}=1,0$,
$f(T_2) = \exp{ \left  [  4000 \cdot \left (  1/293 -1/(273+16 \right )  \right ] } =0,828$,
$f(T_3) = \exp{ \left  [  4000 \cdot \left (  1/293 -1/(273+10 \right )  \right ] } =0,617$,

Wiek betonu w dniu obciążenia zmodyfikowany temperaturą $( \ref{26})$:  $ t_{o,1,T} =  7 \cdot 1,0 +3 \cdot 0,828 +11 \cdot 0,617 = 16,27 $ dni

$(\ref{29}) \to$ dla betonu klasy „S” $\alpha =-1$

Zmodyfikowany wiek obciążenia betonu $( \ref{28}) \to$:   $ t_{o,m,1} = 16,27  \cdot \left( – \cfrac{11}{2+16,27 ^{1,2}}+1\right)^{-1}= 12,56  \ge 0,5 $

$(\ref{20}) \to  \beta_T (t_{o,m}) = \cfrac {1} {0,1 + 12,56 ^{0,20} } = 0,5686$

$( \ref{19}) \to \varphi_o (  t_{o,m} ) = 2,725 \cdot 1,209  \cdot 0,569= 1,874$

Współczynniki zależne od okresu trwania obciążenia

$( \ref{31}) \to \Delta_{o,1}=  t-t{o,1}= 1096 – 21 = 1075 $ dnia  (okresu  trwania obciążenia nie modyfikuje się)

$( \ref{32}) \to \beta_c (\Delta t_{o,1}) = \left( \cfrac{ 1075} { 840,29+1075} \right)^{0,3}=0,841$

Współczynnik pełzania

$( \ref{18}) \to  \varphi(\Delta t_{o,1}) =  1,874 \cdot 0,841= 1,576$

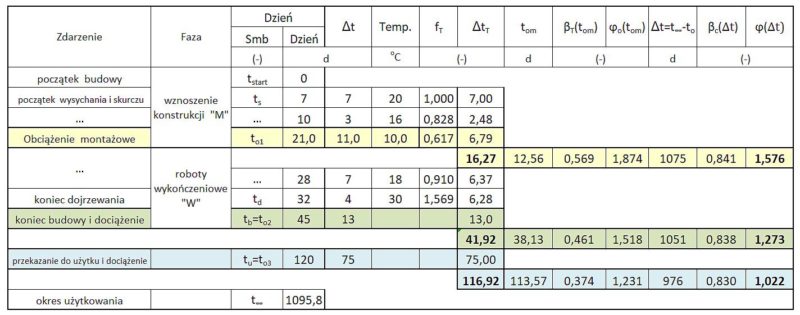
Analogicznie przebiegają obliczenia dla pozostałych dni obciążenia $k=2,3$ . Wyniki pokazano w  tab. P-3 .

Tab.P- 3 Zestawienie obliczeń współczynników pełzania do przykładu P-1

Efektywne moduły odkształcalności i indeks  modułów

dla obciążenia (k=1)
$(\ref{33} \to  E_{c,ef} = 33/(1+1,576)= 12,8\, GPa$
(R-2) $\to \alpha_e= 200/12,8= 15,6 $

Kalkulator LCżelbet

Arkusz kalkulacyjny LCżelbet z zakładką „Pełzanie” do obliczeń pełzania i skurczu betonu można pobrać przez kliknięcie na rys.1 w artykule Belki żelbetowe.

Przykład P-2 [Skurcz betonu ]

Wyznaczyć skurcz betonu dla danych z przykładu wyżej. Wysychanie betonu rozpoczęło się w $t_s=7$ dniu po rozpoczęciu budowy elementu – w tym dniu zakończono pielęgnację ocenianego elementu.

Dla czasu użytkowania $t_\infty= 3 \,lata =1096 \, dni$ , okres wysychania wynosi
$( \ref{8})  \Delta_{ts} = 1096 -7= 1089 \, dni$

Skurcz samoistny (autogeniczny)

$( \ref{10}) \to  \varepsilon_{ca,\infty} = 2,5 \cdot (30 -10) \cdot 10^{-3} = 0,05$‰

$( \ref{11}) \to \beta_{ca, \infty} = 1 – exp \left ( -0,2 \sqrt{1089} \right )= 0,9986$

$(\ref{9}) \to  \varepsilon_{ca,}(t) =0,9986  \cdot 0,5= 0,04993$ ‰

Skurcz od wysychania

Beton wykonano z zastosowaniem cementu CEM 32,5 N , czyli krótkotwardniejącego klasy „S” . Dla tej klasy cementu:

$(\ref{17}) \to \alpha_{ds1}= 3 , \quad \alpha_{ds2}=0,13$

Współczynnik $k_h$ wyznaczono z interploacji  z tab 1:

dla $h_0= 95,2 \, mm$ (z przykładu  wyżej ), mamy : $k_h=1,007$.

$(\ref{14}) \to \varepsilon_{cd,0}= 1,3175 \cdot (220+110 \cdot 3) \cdot \left ( 1- 0,883^3 \right) \cdot \exp { \left (-  0,13 \cdot 38 / 10 \right ) } \cdot 10^{-3} = 0,1315$ ‰

$(\ref{16})  \beta_{ds}(\Delta t_s) =\cfrac{1089}{1089 + 0,04 \cdot \sqrt{95,2^3}}= 0,967$

$(\ref{13}) \to \varepsilon_{cd, \infty} =0,1315  \cdot 1,007 =0,1324$ ‰

$(\ref{12}) \to  \varepsilon_{cd} (t) = 0,1324 \cdot0,967 = 0,12803$ ‰

Skurcz całkowity

$(\ref{7}) \to  \varepsilon_{cs} 0,04993 + 0,12803 =0,178$ ‰

Taką samą wartość skurczu uzyskano w kalkulatorze LCżelbet.

Przykłady P-1 i P-2 zostały sprawdzone z użyciem kalkulatora Strusoft [15] . Otrzymano zgodność wyników z zastrzeżeniem różnic wynikających z modyfikowania wieku betonu w dniu obciążenia (kalkulator Strusoft nie przewiduje takiej opcji).

 Literatura

1. PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
2. PN-EN 13670:2011: Wykonywanie konstrukcji z betonu
3. PN-EN 1991-1-6:2007, Eurokod 1: Oddziaływania na konstrukcje, Część 1-6: Od-działywania ogólne – Oddziaływania w czasie wykonywania konstrukcji
4. PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
5. PN-EN 1995-1-1+A2+NA+07E :2010, Eurokod 5: Projektowanie konstrukcji drewnianych, Część 1-1: Postanowienia ogólne – Reguły ogólne i reguły dotyczące budynków
6. ACI 318-11, (2011), Building Code Requirements for Structural Concrete and Commentary
7. ACI 318-14 (2014), Building Code Requirements for Structural Concret
8. LATBSDC 2017 Edition with 2018 Supplements, An alternative procedure for seismic analysis and Design of tall buildings located in the Los Angeles region
9. CSA A23, (2015), Concrete materials and methods of concrete construction/Test methods and standard practices for concrete
10. PN-EN 1998-1:2005, Eurokod 8: Projektowanie konstrukcji poddanych oddziaływa-niom sejsmicznym, Część 1: Reguły ogólne, oddziaływania sejsmiczne i reguły dla budynków
11. FEMA 356, (2000), Prestandard and commentary for the Seismic rehabilitation of buildings
12. PEER/ATC, (2010), Modelling and acceptance criteria for seismic design and analysis of tall buildings, PEER/ATC Report No. 72–1,  Applied Technology Council
13. NZS 3101.1+2, (2006) , Concrete structures standard
14. TS 500, (2000), Requirements for design and construction of reinforced concrete structures
15. Strusoft, (2019), Concrete creep and shrinkage calculator, [ https://concrete-creep.strusoft.com/ ]

________________________________