Niniejszy artykuł stanowi Część 5 cyklu Elementarz niezawodności konstrukcji. W całym cyklu artykułów zachowano ciągłość numeracji: wzorów i ilustracji. Numeracja rozdziałów jest odrębna dla każdej części.
Zamieszczono wybrane przykłady rachunkowe obliczenia niezawodności konstrukcji budowlanych z wykorzystaniem dyskretnych modeli niezawodnościowych mieszanych. Rozważono: rozciągany pręt żelbetowy, kratownicę statycznie wyznaczaną oraz ramę sprężysto-plastyczną w granicznym stanie plastycznym, a także inne bardziej zaawansowane zagadnienia.
Pracę opatrzono wnioskami, ważnymi dla Konstruktora i Architekta obiektów budowlanych.
Przykłady rachunkowe
Rozciągany pręt żelbetowy
Sprawdzić bezpieczeństwo rozciąganego pręta żelbetowego o długości $L=6 m$. Zbrojenie pręta zaprojektowano zgodnie z normą [1] wariantowo: A z 4-ch prętów, B z 8-miu prętów (o mniejszych średnicach). W zadaniu nie są istotne konkretne średnice prętów, ale stwierdzenie, że w każdym przypadku spełniono wymagania normowe, czyli projekt wykonano dla wymaganego przez normę [2] wskaźnika niezawodności :
$\beta_{global}=3,8 $.
Granica plastyczności prętów zbrojeniowych jest oznaczana na próbkach długości
$L_0=30 cm$
jako kwantyl 5%, czyli prawdopodobieństwo zniszczenia próbki wynosi
$p_{si}=0,95$
Rozwiązanie:
Wymagana niezawodność pręta, mierzona prawdopodobieństwem zniszczenia, wynosi:
| $p_s=\Phi(-\beta_{global})=\Phi(-3,8)=0,999927652$, | (53) |
Pręt jest zbrojony prętami w liczbie
Wariant A: $m_A=4$ ; Wariant B: $m_B=8$,
a każdy z prętów jest złożony z
$n=\dfrac {L} {L_0}=\dfrac {600}{30}=20$ elementów połączonych szeregowo.
Pręt żelbetowy jest strukturą z ogólnym rezerwowaniem, której model pokazano na rys. 98 i którą opisuje wzór (27) w artykule Złożone struktury niezawodnościowe.
Ze wzoru (27) obliczamy niezawodności systemu w poszczególnych wariantach liczby prętów:
Wariant A: $p_s=1-(1-0,95^{20})^4=0,831$
Wariant B: $p_s=1-(1-0,95^{20})^8=0,971$,
czyli w obu wariantach o kilka rzędów za małe od wymaganego (40). Przy tym zbrojenie prętami o mniejszej średnicy, ale większej liczbie w wiązce zwiększa niezawodność systemu. W przykładzie uzyskaliśmy wzrost niezawodności mierzonej prawdopodobieństwem przeżycia o ok. 17%.
W celu uzyskania wymaganej niezawodności pręta, potrzebną niezawodność elementów (odcinków zbrojenia) dla bardziej korzystnego wariantu B można wyznaczyć z równania:
$0,999927652=1-(1-p_{si}^{20})^8$.
Z rozwiązania tego równania uzyskano $p_{si}=0,982$, co daje współczynnik tolerancji ok. 2,10, a nie 1,64 jak dla normowego kwantyla 5% charakterystycznej wytrzymałości (granicy plastyczności) stali. W w celu utrzymania niezawodności pręta na poziomie (36) należałoby istotnie zwiększyć nośność prętów zbrojeniowych poprzez zwiększenie ich przekroju lub klasy stali. Wymiarowanie pręta z warunku $\beta \le 3,8$ nie jest przedmiotem niniejszego przykładu, ale prowadzone wyliczenia pokazały ważną okoliczność:
Projektowanie konstrukcji bez uwzględnienia struktury niezawodnościowej jest zawodne i to również wówczas, gdy jest prowadzone metodą stanów granicznych z częściowymi współczynnikami bezpieczeństwa.
Niestety w europejskich normach projektowania nie uwzględnia się pokazanych wyżej mechanizmów niezawodnościowych.
Kratownica statycznie wyznaczalna
Zaprojektować kratownicę pokazaną na rys. 10 , tak by jej niezawodność mierzona wskaźnikiem Hasofera-Linda wynosiła β =3,8.
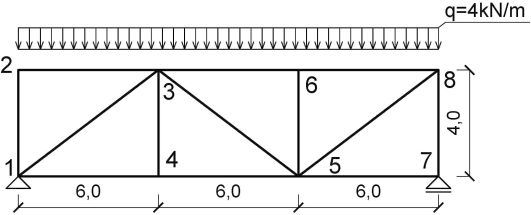
Rys.10. Schemat kratownicy statycznie wyznaczalnej – niezawodnościowy system szeregowy (do przykładu 3.2)
Rozwiązanie zadania podano w odrębnym artykule:
Sprężysto-plastyczna rama portalowa
Zaprojektować ramę pokazaną na rys. 11 , tak by jej niezawodność mierzona wskaźnikiem Hasofera-Linda wynosiła β =3,8.
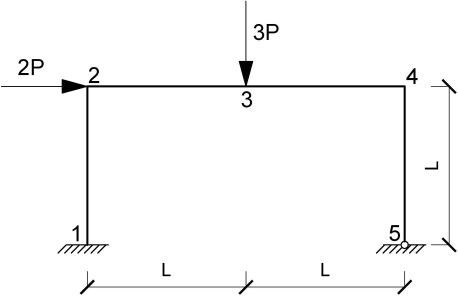
Rys.11. Schemat ramy statycznie niewyznaczalnej – niezawodnościowy system mieszany (do przykładu 3.4)
Rozwiązanie zadania podano w odrębnym artykule:
![]() [PDF] Dobór elementów złożonej struktury konstrukcyjnej z warunku wskaźnika niezawodności .
[PDF] Dobór elementów złożonej struktury konstrukcyjnej z warunku wskaźnika niezawodności .
Zastosowano klasyczne podejście teorii nośności plastycznej, a także najprostsze oszacowania granic niezawodności systemu niezawodnościowego.
Kratownica Ditlevsen-Madsen
Minimalne ścieżki i cięcia
Przykład wyznaczenia minimalnych ścieżek i cięć konstrukcji przestawimy za pracą [3]
Na rys. 12 pokazano kratownicę Ditlevsen-Madsen.
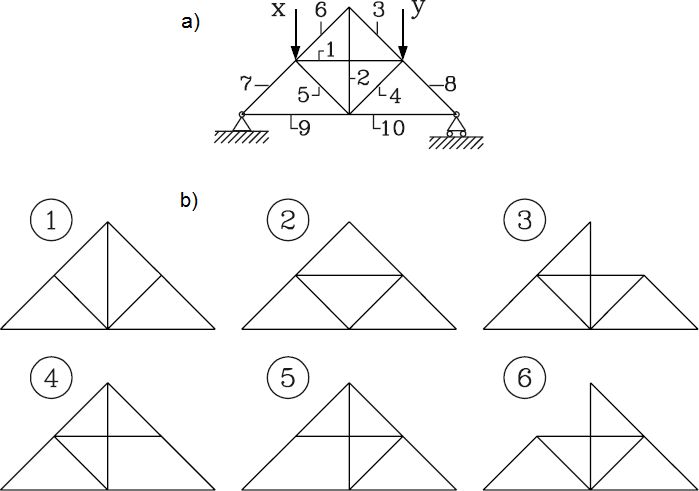
Rys.12. a) schemat kratownicy Ditlevsen-Madsen z jednym stopniem statycznej niewyznaczalności, b) sześć podstawowych kratownic – minimalnych cięć, które pozostają geometrycznie niezmienne, ale statycznie wyznaczalne [3]
Terminologia ” minimalne ścieżki ” i ” minimalne cięcia” są zapożyczone z teorii układów elektrycznych. Awaria układu odpowiada sytuacji, gdy wszystkie przyłącza są krojone na funkcjonowanie System odpowiada sytuacji, w której co najmniej jedno z połączeń pracuje.
Kratownica Ditlevsen-Madsen składa się z 10. elementów {1,2,3,4,5,6,7,8,9,10}. Kratownice podstawowe (1) do (6) uzyskano poprzez usunięcie odpowiednio pręta: 1, 2, 3, 4,5, 6, to znaczy są to wszystkie możliwe schematy geometrycznie niezmienne.
Usunięcie pręta 7,8, 9 lub 10 prowadziłoby do ustroju geometrycznie zmiennego (mechanizmu) i nie spełnia podstawowego warunku systemu konstrukcyjnego, a także wymogu dla minimalnej ścieżki elementów w konstrukcji budowlanej. Również usunięcie kolejnych prętów w schemacie (1) do (6) zamieniłoby konstrukcję budowlaną w konstrukcję mechaniczną (mechanizm, czyli system o jednym stopniu swobody).
Minimalne ścieżki
Minimalne ścieżki kratownicy Ditlevsen-Madsen, obrazują schematy (1) do (6) na rys 11. Odpowiadające zbiory elementów można zapisać następująco:
| minimalne ścieżki: $\{2, 3, 4, 5, 6, 7, 8, 9, 10\}$ $\{1, 3, 4, 5, 6, 7, 8, 9, 10\}$ $\{1, 2, 4, 5, 6, 7, 8, 9, 10\}$ $\{1, 2, 3, 5, 6, 7, 8, 9, 10\}$ $\{1, 2, 3, 4, 6, 7, 8, 9, 10\}$ $\{1, 2, 3, 4, 5, 7, 8, 9, 10\}$ |
(54) |
Każdy z tych systemów jest układem szeregowym z punktu widzenia niezawodności, zawierającym po n9-ć elementów (prętów).
Te minimalne ścieżki są pomiędzy sobą równolegle połączone z punktu widzenia niezawodności.
Minimalne cięcia
Ponieważ elementy 7,8,9, 10 występują w każdej minimalnej ścieżce, to mamy cztery minimalne cięcia po jednym elemencie w każdym zbiorze:
{7}, {8}, {9}, {10}.
Każdy z pozostałych sześciu elementów: 1 , 2 , 3 , 4 , 5, 6 występuje po pięć razy we wszystkich minimalnych ścieżkach., to znaczy , ze wszystkie pozostałe zestawy minimalnych cięć mają dwa elementy i pojawiają się w identycznych parach, a zatem istnieje $\dfrac {5 \cdot 6} {2}= 15$ minimalnych cięć z dwoma elementami, co zapiszemy następująco:
{1,2}, {1,3}, {1,4}, {1,5}, {1,6}, {2,3}, {2,4}, {2,5}, {2,6}, {3,4}, {3,5}, {3,6}, {4,5}, {4,6}, {5,6}.
Ostatecznie mamy 19. minimalnych cięć, które reprezentują system szeregowy z 19. oma elementami, z których 15. stanowi równoległe systemy z dwoma elementami. Ostatecznie mamy następujące minimalne cięcia
| minimalne cięcia: $\{7\} ,\{8\} ,\{9\} ,\{10\}, $ $\{1,2\}, \{1,3\}, \{1,4\}, \{1,5 \}, \{1,6 \}, $ $\{2,3\}, \{2,4\}, \{2,5\}, \{2,6 \}, $ $\{3,4\}, \{3,6\}, $ $\{4,5\}, \{4,6\}, $ $\{5,6\}. $ |
(55) |
Oszacowania niezawodności
Przyjmijmy dość oczywiste założenie stowarzyszenia elementów (stowarzyszenia zapasów nośności poszczególnych prętów kratownicy), a następnie przyjmijmy, że elementy mają identyczną niezawodność r :
$r_i=r (i=1,…10)$
Najbardziej zgrubne oszacowanie dla elementów stowarzyszonych , ale bez znajomości minimalnych ścieżek i cięć wyznaczamy z zależności (41)
| $(r_1 \cdot r_2 \cdot r_3 \cdot r_4 \cdot r_5 \cdot r_6\cdot r_7\cdot r_8\cdot r_9\cdot r_{10})=r^{10} \le r_s \le [1- (1-r_1)\cdot (1-r_2)\cdot (1-r_3)\cdot (1-r_4)\cdot (1-r_5)\cdot (1-r_6)\cdot (1-r_7)\cdot (1-r_8)\cdot (1-r_9)\cdot (1-r_{10})]=1- (1-r)^{10}$, | (56a) |
Jeśli uwzględniamy znajomość minimalnych ścieżek (54) oraz minimalnych cięć (55), to zgodnie z (42b), mamy:
| $ max \{r_2 r_3 r_4 r_5 r_6 r_7 r_8 r_9 r_{10} \, ; \, r_1 r_3 r_4 r_5 r_6 r_7 r_8 r_9 r_{10} \, ; \, r_1 r_2 r_4 r_5 r_6 r_7 r_8 r_9 r_{10} \, ; \, r_1 r_2 r_3 r_5 r_6 r_7 r_8 r_9 r_{10} \, ; \, r_1 r_2 r_2 r_3 r_4 r_6 r_7 r_8 r_9 r_{10} \, ; \, r_1 r_2 r_3 r_4 r_5 r_7 r_8 r_9 r_{10} \} = r^9\, \le \, r_s \, \le \,min \{ r_7+r_8+r_9+r_{10} – r_7 r_8 – r_7 r_9 – r_7 r_{10} \, ; \, ……. \}$ | (56b) |
Bikonstrukcja (sprzężone dźwigary płaskie) – metoda uogólnionej korelacji
Na prostym przykładzie zespołu kratownic płaskich K1, K2 (prawa, lewa) (rys.13) sprzężonych stężeniami T1 (górne i dolne) oraz T2 (pionowe) przeanalizujemy wpływ stężeń na niezawodności bikonstrukcji.
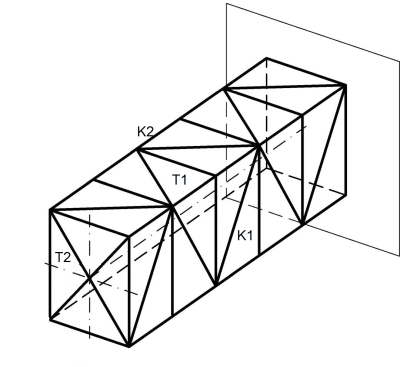
Rys.13. Bikonstrukcja: kratownice K1, K2 sprzężone stężeniami T1, T2
Analiza wpływu stężeń na nielosową nośność bikonstrukcji
Mechanizmy zniszczenia ustroju zależą o konfiguracji obciążeń. Dla dominujących obciążeń pionowych kratownice K1 i K2 są będą obciążone siłami pionowymi w węzłach pasów górnych. W przypadku rozprzężenia mechanizm zniszczenia kratownicy K1 (lub K2) pokazano na rys. 14.

Rys. 14. Mechanizm zniszczenia kratownicy K1 pod obciążeniami pionowymi (kratownica przed zniszczeniem – szara, po zniszczeniu -niebieska). Zniszczenie polega na utracie płaskiej postaci zginania
Obraz z rys. 14 uzyskano dla kratownicy o wysokości 3 m, rozpiętości 5×3=15 m, obciążonej siłami skupionymi V=23 kN w każdym węźle górnym i równoważnymi siłami poziomymi od imperfekcji H=V/100=0,23 kN i po przeprowadzeniu obliczeń 2-rzędu $P-\Delta$.
Dla prętów wykonanych z RP 200x100x5-S355 (większy wymiar rury w pionie), czyli o sztywności osiowej
| $ EA=2,1 \cdot 10^5 \cdot 28,36 \cdot 10^{-4}=5,96 \cdot 10^2 MN$ | (57) |
(moduł Younga stali $E=2,1 \cdot 10^5 MPa$ ; pole przekroju dla RP 200x100x5: $A=28,36 cm^2$)
Obliczenia wykazały, że krytycznym punktem konstrukcji jest pas dolny przy podporze, który przy uwzględnieniu zjawisk niestateczności i innych warunków normowych [4] jest pod obciążeniem porównawczym V=23 kN wytężony w 90,9 %.
Oznacza to, że obciążenie można w zwiększyć o
1/90,9%=1,100
do wartości $V=1.1 \cdot 23=25,3 kN$, by wyczerpać nośność . Graniczny mnożnik obciążenia (nośność konstrukcji ) wynosi:
| $\Lambda=1,10$, | (58) |
Przemieszczenia końca wspornika wynoszą: pionowe $\delta_z= 22 mm$, a boczne $\delta_y=18 \cdot \delta_z$ przy 100x mniejszej sile poziomej. Skrócenie pręta (od spaczenia 2- rzędu ) wynosi $\delta_x= \dfrac{\delta_z} {10}$.
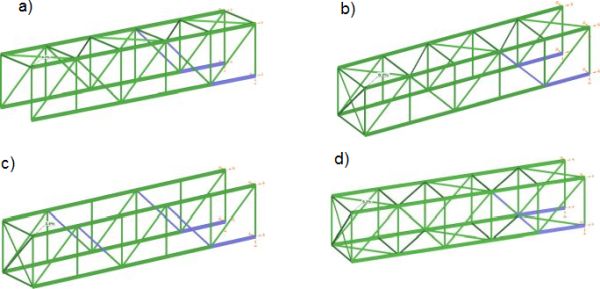
Rys. 15. Sprzężone kratownice płaskie: a) stężeniem górnym T1, b) stężeniem czołowym T2, c) stężeniami T1+T2, d) stężeniami T1+T2+T1* (stężone dolne pasy)
W tab.2 zestawiono nośności bikonstrukcji sprężonej stężeniami w układach z rys. 15.
Tab.2. Wpływ stężeń bikonstrukcji na jej nośność $\Lambda$
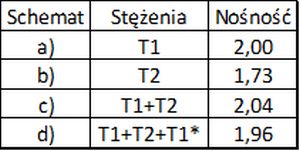
Sprzężenie pasów górnych stężeniem T1 prowadzi do wzrostu nośności $\dfrac{2,0} {1,105} = 81%$. Natomiast sprzężenie czoła stężeniem T2 o 63%, a stężeniami T1+T2 o 94%. Sprzężenie pasów dolnych jest niekorzystne z powodu nadmiernego skrępowania bikonstrukcji.
Nośność bikonstrukcji stężonej przez T1+T2 zwiększyła się dwukrotnie w stosunku do rozprzężonej kratownicy płaskiej. Należy zwrócić uwagę na to, że efekt taki uzyskano przy obciążeniu każdego węzła identyczną siłą – to znaczy sumaryczne obciążenie bikonstrukcji jest dwa razy większe od obciążenie kratownicy płaskiej.
Korelacja konstrukcyjna i współczynnik korelacji
Wprowadzimy pojęcie korelacji konstrukcyjnej, analogicznie do korelacji funkcyjnej.
Współczynnik korelacji zmiennych losowych $X$ i $Y$ o wartościach oczekiwanych $\mu_x=E X$ i $\mu_y=E Y $ oraz odchyleniach standardowych $\sigma_x=\sqrt {Var X}$ i $\sigma_y=\sqrt {Var Y}$, oraz kowariancji zmiennych $C_{xy} = Cov (X, Y) $, jest wartością oczekiwaną iloczynu standaryzowanych zmiennych [5]:
| $\rho_{xy}= \rho \{X , Y \}= E \left \{ \dfrac {X-\mu_x}{\sigma_x} \cdot \dfrac {Y-\mu_y}{\sigma_y} \right\}= \dfrac {C_{xy }} {\sigma_x \cdot \sigma_y}$ | (59) |
Współczynnik korelacji określa siłę sprzężenia zmiennych i przyjmuje wartość w przedziale
| $ -1 \le \rho_{xy}\le 1 $ | (60) |
Wartość $ \rho_{xy}=0 $oznacza brak związku (sprzężenia), a dla zmiennych rozłożonych normalnie – niezależność zmiennych. Dla $ \rho_{xy} = 1 $ sprzężenie jest silnie dodatnie, to znaczy wzrost (lub zmniejszenie) $X$ najczęściej prowadzi do wzrostu (lub zmniejszenia)$Y$. Na odwrót dla $ \rho_{xy}= – 1 $ relacja jest odwrotnie proporcjonalna.
W analizie regresji $X_2$ jest zapisywana jako suma zmiennych losowych $g_y$ i $h_y$ [5] :
| $ Y = g_y(X)+h_y(X, Y)$, | (61) |
gdzie $h_y(X, Y)$ jest poprawką.
Konstrukcyjny współczynnik korelacji będziemy obliczać bezpośrednio z definicji (59), a charakterystyki probabilistyczne szacować numerycznie na teoretycznym modelu konstrukcji. Podobne podejście można stosować do symulacji eksperymentalnych.
W erze informatyzacji konstrukcje budowlane praktycznie wyłącznie oblicza się z użyciem programów komputerowych za pomocą algorytmów numerycznych, gdzie zależności analityczne nie są potrzebne. Funkcja $\varphi(x)$ jest określona za pośrednictwem macierzy sztywności, a zagadnienia nieliniowe statycznie są rozwiązywane iteracyjnie, gdzie w każdym kroku rozwiązuje się zadanie liniowe. Statyczna liniowość nie oznacza liniowości probabilistycznej. Konstrukcje rzeczywiste są obarczone szeregiem imperfekcji geometrycznych (imperfekcje systemowe, czyli odchylenia węzłów od położenia nominalnego i imperfekcje lokalne, czyli wstępne wygięcia i skręcenia nominalnie prostych elementów prętowych i płytowych lub odchylenia od powierzchni nominalnej powłok, a także inne.
Momenty statystyczne (wartości oczekiwane, odchylenia standardowe oraz kowariancje i korelacje) losowych zmiennych wyjściowych (przemieszczenia, siły przekrojowe lub mnożnik nośności ) konstrukcji rzeczywistych wyznaczane są numerycznie. Do wyznaczenia parametrów statystycznych funkcji losowych wykorzystuje się dwie metody:ścisłą i linearyzacji, które przedstawiono w artykule Momenty funkcji zmiennych losowych. Metoda linearyzacji.
Wpływ stężeń T1 i T2 na niezawodność bikonstrukcji
Przenalizujemy wpływ stężeń T1 i T2 niezawodności bikonstrukcji, pokazanej na rys. 13. Przyjmiemy, że informacje o stężeniu o zadanym układzie geometrycznym są zintegrowane w jednej wejściowej zmiennej losowej X, którą jest sztywność osiowa pręta stężenia. Natomiast zmienną wyjściową $Y$ jest nośność konstrukcji $\Lambda$.
| $ X=EA$, $Y=\Lambda$ |
(62a,b) |
gdzie E jest modułem Younga, a A polem przekroju pręta, a $\Lambda$ jest mnożnikiem obciążenia przy którym konstrukcja przestaje spełniać warunki graniczne.
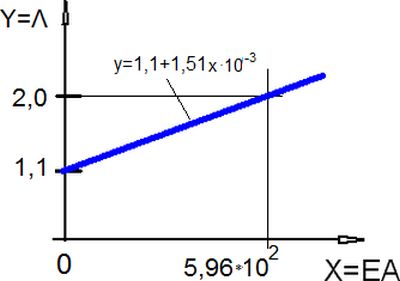
Rozważmy najpierw wpływ tylko stężeń T1. Brak stężeń [rys.13 i nośność (58)] oznacza realizację bikonstrukcji ze stężeniami o zerowej sztywność (EA=0). W przypadku występowania stężeń o sztywności nominalnej (57) realizacje nośności bikonstrukcji zestawiono w tab.2. Dla tych dwóch punktów sporządzono nielosową zależność nośności konstrukcji od sztywności stężeń T1 i pokazano ją na rys. 16.
Funkcję stanu granicznego $Y=g(X)$ w tym przypadku opisuje prosta
| $ Y=\varphi (X)=1,1+1,5 \cdot 10^{-3} X $, | (63) |
W przypadku większej liczby punktów obliczeniowych dokładność wyznaczenia zależności $EA \to \Lambda$ zwiększy się. Funkcję ciągłą w tych przypadkach zaleca się wyznaczać procedurami metody minimów kwadratów (metodami regresji) dla funkcji sklejanych z odcinków parabol. Procedura ogólna będzie przedmiotem innego opracowania. W tym przypadku wyznaczamy podstawowy tok postępowania i nie będziemy rozszerzać rozważań na okoliczności poboczne.
Parametry statystyczne zmiennej wejściowej X=EA, określimy na podstawie publikowanych wyników badań dla modułu Younga oraz pola przekroju profili stalowych [9] :
moduł Younga E: $\mu_E=2,1 10^5 MPa$; $v_E=1,5%$,
współczynnik zmienności długości ścianki: $v_l=3%$
współczynnik zmienności grubości ścianki: $v_t=2%$
pole przekroju A: $\mu_A= 28,36 cm^2$ ( z tablic producenta); $v_A= \sqrt{4( 3^2\%+2^2\%)}=3,6\%$ (cztery ścianki rury prostokątnej)
sztywność EA:
$ (57) \to $ $\mu_{EA}=5,96 \cdot 10^2 \, kN $;
$v_{EA}=\sqrt{ 1,5^2+3,6^2}=3,6 \%$;
$\sigma_x=v_{EA} \cdot \mu_{EA}= 5,96 \cdot 10^2 \cdot 3,6 \%=0,215 \cdot 10^2 =21,5\, kN $,
Powyżej wyrażenia na współczynniki zmienności funkcji otrzymano w drodze linearyzacji, w sposób analogiczny jak pokazano niżej.
W celu zaprezentowania metody, parametry statystyczne funkcji (63) wyznaczymy metodą linearyzacji, mimo, że funkcja jest liniowa i możnaby wyznaczyć je z definicji.
$\varphi(x)^{’} = \dfrac {\partial \varphi(X)}{\partial X}= 1,5 \cdot 10^{-3}$
$\sigma_y^2= [\varphi(0^{’}]^2 \cdot \sigma_x^2=(1,5 \cdot 10^{-3})^2\cdot 70,3^2=7,4 \cdot 10^{-3}$
Postępując analogicznie wyznaczamy parametry losowe funkcji wspływu stężeń T2 na nośność bikonstrukcji
Literatura
- PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
- Ditlevsen, O., & Madsen, H. O. (1996). Structural reliability methods. Wiley
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- Korn T., M. (1983), Matematyka dla pracowników naukowych i inżynierów (Tom. 1, 2), PWN, Warszawa
- Melnyk M. (1974), Principles of applied statistics. Pergamon Press
- Cox D. R., Hinkley D. V. (2000). Theoretical statistics. Chapman & Hall/CRC,
- Seber G. A. F., Lee A. J. (2003), Linear regression analysis (2nd ed). Wiley-Interscience
- Mrazik A. (1987). Teoria Spolahlivosti ocelovych konstrukcii. VEDA Vydatelstvo slovenskej akadamie VIED
________________________________