Leszek Chodor, 30 sierpnia 2021
01-02-2025 rewizja po dużej awarii portalu>
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 19 Czytelników
Podatność podłoża gruntowego ma istotny wpływ na projekt konstrukcji. We współczesnych analizach konstrukcyjnych podatność podłoża uwzględniana jest przez wprowadzenie liniowego i obrotowego współczynnika sprężystości podpór. W przypadku podpór posadowionych na gruncie (fundamentów) wymagana jest znajomość współczynnika sprężystości podłoża Ks (indeks s od soil – ang grunt), czyli współczynnika sprężystości podłoża Winklera. Poprawne wyznaczenie tego współczynnika jest zadaniem trudnym ze względu na znaczną zmienność parametrów gruntów, a w szczególności ich zagęszczenia. W artykule zaprezentowano metodologię wyznaczania liniowego modułu podłoża gruntowego $K_s$ oraz modułu podłoża na obrót ${K_s}^\varphi$ w funkcji jego modułów: sprężystości Younga E lub edometrycznego M, które są wyznaczane w badaniach gruntów in situ (metodami CPT, PLT i in.) z uwzględnieniem zagęszczenia gruntu. Stopień zgęszczenia podłoża istotnie wpływa na zmianę podatności podłoża i w rezultacie na wytrzymałość i stateczność konstrukcji. Często jednak – w przypadkach, gdy na mniej zagęszczonym podłożu budowla będzie bezpieczna i zachowane będą warunki stateczności, wytrzymałości oraz użytkowalności – nie mają uzasadnienia sztywne wytyczne dotyczące zagęszczenia podłoża.
Sztywność gruntu
Prawo fizyczne (konstytutywne) gruntu można przedstawić w postaci ścieżki równowagi pomiędzy odkształceniami osiowymi $\varepsilon$ (najczęściej pionowymi- indeks v lub z ) $ \varepsilon_1= \varepsilon_v $, a miarodajnym naprężeniem $\sigma$ (aksjatorem naprężeń $\sigma_1-\sigma_3$, czyli różnicą naprężeń głównych $\sigma_1$ ( pionowych) i $\sigma_3$ (poziomych), co pokazano na rys.1.
Sztywność gruntu jest wyznaczona nachyleniem ścieżki równowagi do poziomu, czyli stosunkiem $\Delta \sigma / \Delta \varepsilon$ Grunt jest tym sztywniejszy im to nachylenie jest większe, to znaczy wówczas, gdy do danego odkształcenia gruntu należy użyć większych naprężeń (siły).
W ten sposób jest zdefiniowany moduł Younga gruntu $E_s$ lub krótko $E$
$$\begin{equation} E_s=E \stackrel {def} {=} \cfrac{\Delta \sigma} {\Delta \varepsilon} \label{1} \end{equation}$$
gdzie:
$\Delta \varepsilon$ – przyrost miarodajnych odkształceń,
$\Delta \sigma$ – przyrost miarodajnych naprężeń,
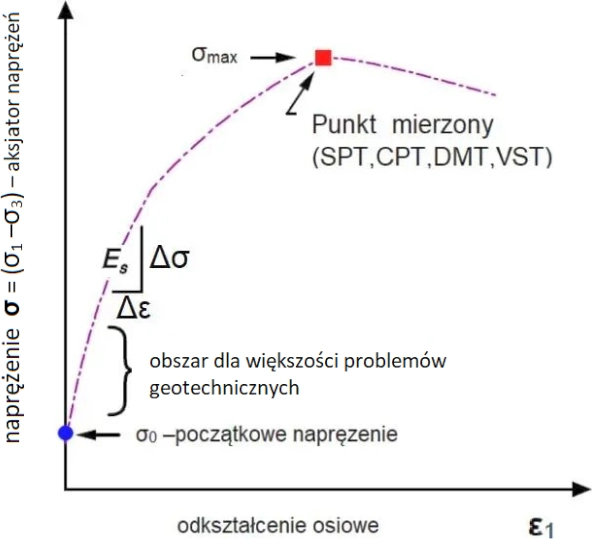
Rys.1 Prawo konstytutywne gruntu [1]: SPT, CPT,DMT, VST – metody pomiaru odkształcalności gruntu
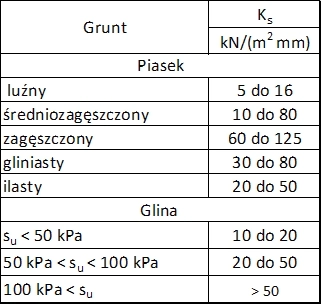
Orientacyjne zależności pomiędzy stopniem i wskaźnikiem zagęszczenia gruntu sypkiego oraz modułem odkształcalności (modułem Younga E) zamieszczono w tab.1
Tab.1. Stan zagęszczenia a moduł Younga gruntu sypkiego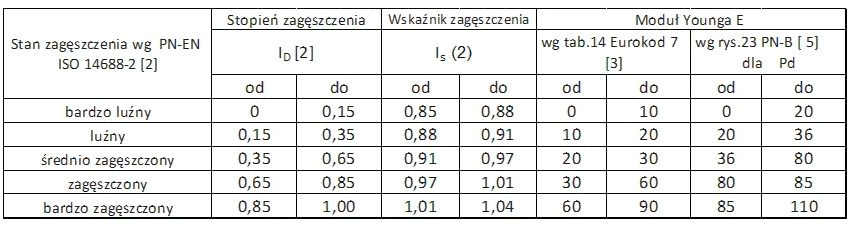
Moduły sztywności gruntu
Sztywność gruntu można mierzyć modułami:
- modułem Younga po odsączeniu $E$,
- modułem ściśliwości edometrycznej $M$,
- modułem objętościowym $K$,
- modułem ścinania (Kirchoffa) przy małych odkształceniach $G_{max}$,
- modułem reakcji podłoża $K_s$,
- modułem odporności (podłoża dróg ) $M_R$.
- Efektywne parametry sprężystości gruntu uzyskane w drodze badań polowych (in-situ) oznaczane są apostrofem (’) , np E’, M’, K’ itd.
Moduł sprężystości (Younga) E, E’
Definicję modułu Younga (modułu sprężystości) opisuje formuła ($\ref{1}$). Moduł Younga jest wyznaczany w warunkach jednoosiowego stanu naprężenia. Zgodnie z podstawowymi prawami teorii sprężystości towarzyszy mu trójosiowy stan odkształceń, to znaczy możliwe jest boczne odkształcenie badanej próbki.
Moduł Younga jest współczynnikiem proporcjonalności w klasycznym prawie Hooka. W gruntach moduł Younga wyznacza się po odsączeniu wody.
Pobieranie próbek do badania modułu Younga gruntu z definicji $(\ref{1})$ jest trudne. Dlatego najczęściej stosuje się oznaczanie in situ, w tym sondowanie CPT, SPT, pomiary dylatometrem DMT lub sondą obrotową VST i innymi. Badania te,, a w szczególności CPT można wykorzystać do oszacowania modułu w gruntach z uwzględnieniem historii obciążania stanu naprężeń i odkształceń oraz starzenie się i mineralogii gruntu.
Moduł Younga $E$ może być oszacowany z badań CPT jako efektywny moduł $E’$. Dla gruntów niespoistych $E’$ można wyznaczyć z zależności [2]:
$$\begin{equation} E’ =\alpha_E \cdot q_n \label{2} \end{equation}$$
gdzie:
$q_n$ opór stożka netto w badaniu CPT ($\ref{15}$).
Współczynnik $\alpha_E$ zależy od poziomu obciążenia,, gęstości gruntu, historii obciążenia, (historii naprężeń i odkształceń), wieku gruntu (konsolidacji, starzenia), i zawiera się w wartościach:
2 do 4 dla bardzo młodych, normalnie skonsolidowanych piasków;
4 do 10 dla starszych (> 1000 lat), normalnie skonsolidowanych piasków;
6 do 20 dla piasków prekonsolidowanych.
Dokładniejsze wartości $\alpha_E$ dla młodych, niescementowanych piasków (głównie krzemianowych) można oszacować z nomogramu rys. 15 zamieszczonego w rozdziale Korelacja z modułem Younga. Współczynnik $\alpha_E$ został określony dla $\varepsilon_v = \, 0,1$% ( w początkowym zakresie wykresu konstytucyjnego rys.1 ). Dla większych odkształceń oraz przy zwiększaniu głębokości poniżej terenu – moduł $E’$ zmniejsza się.
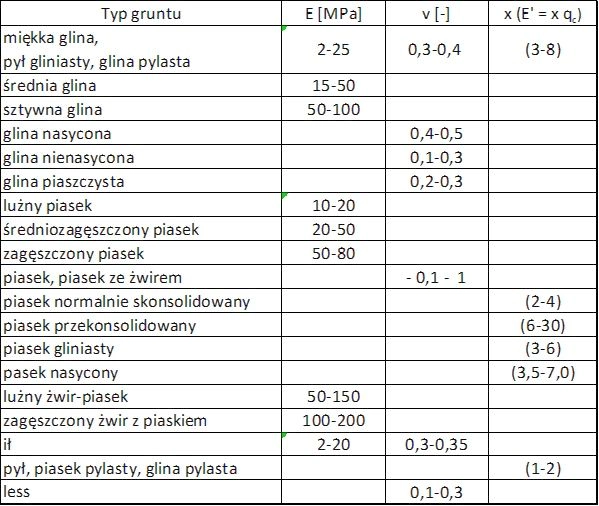
Szacunkowe wartości modułu Younga $E$ dla dużej klasy gruntów podano w tab.2, i tab.3.
Moduł ściśliwości edometrycznej M i M’
Definicję modułu edometrycznego podobnie jak modułu Yonga też opisuje formuła ($\ref{1}$), ale moduł ściśliwości edometrycznej jest mierzony w warunkach jednoosiowego stanu odkształcenia poprzez ograniczenie odkształceń bocznych przez cylinder edometru- urządzenia w którym jest mierzony edometru (stąd nazwa moduł „edometryczny’). Zgodnie z podstawowymi prawami teorii sprężystości towarzyszy mu trójosiowy stan naprężenia, to znaczy oprócz naprężęń osiowych występują napreżenia boczne – nacisk na ścianki cylindra.
Pomiędzy modułami $E$ i $M$ istnieje prosta zależność funkcyjna znana z klasycznej teorii sprężystości ciała stałego :
$$\begin{equation} E = \delta \cdot M \label{3} \end{equation}$$
$$\begin{equation} \delta= 1 -\cfrac{2 \nu^2}{1-\nu }= \cfrac{(1+\nu)\cdot (1- 2 \nu)}{1- \nu} \label{4} \end{equation}$$
gdzie $\nu$ – współczynnik Poissona gruntu. Znając E i M można z tej zależności wyznaczyć $\nu$, ale częściej z modułu edometrycznego $M$ wyznacza się moduł Younga $E$ dla znanego współczynnika Poissona gruntu $\nu$. Dlatego zależność ($\ref{3}$) przedstawiono w postaci $E=E(M, \nu)$.
Moduł M zmienia się w szerokich granicach w zależności od konsystencji gruntu spoistego (zawartości naturalnej wody) lub stanu gruntu piaszczystego i może być oszacowany z badań CPT jako efektywny moduł edometryczny $M’$ z zależności [3]:
$$\begin{equation} M’= \alpha_M \cdot q_n\label{5} \end{equation}$$
gdzie: $q_n$ jak w ($\ref{2}$).
Meigh (1987) [4] zasugerował, że
$\alpha_M =2 \quad do \quad 8$,
Mayne (2001) [5] oraz Saftner [1] wskazali ogólną wartość
$\alpha_M =5$.
Lunne i in. (1998) [6] oraz Robertson (2009) [7] podają, że:
$$ \begin{equation} \alpha_M = \begin {cases}
0,0188 \cdot \left [ 10 ^{(0.55\cdot I_c + 1.68) } \right ] , & \textrm { dla gruntów gruboziarnistych } I_c< 2,2 \\
Q_t , & \textrm { dla gruntów drobnoziarnistych } I_c \ge 2,2 \quad i \quad Q_t <14 \\
14 , & \textrm { dla gruntów drobnoziarnistych } I_c \ge 2,2 \quad i \quad Q_t \ge 14 \\
\end {cases} \label{6} \end{equation}$$
gdzie:
$I_c$ indeks zachowania gruntu CPT ($\ref{25}$),
$Q_t$ -znormalizowany opór stożka w badaniu CPT ($\ref{18}$).
Powyższe podejście wynikające z analiz 1-D można zastosować do wszystkich gruntów i jest ogólniejsze od wyznaczania $\alpha_E$ z rys. 15, ;ub z ($\ref{30}$) , bo to podejście stosuje się tylko do piasków a dla gruntów słabo zagęszczonych w przypadku lub dla obciążeń znacznie przekraczających $\sigma’_{vp}$.($\ref{51}$) należy przeprowadzić głębsze analizy
Współczynnik Poissona
Współczynnik Poissona $\nu$ jest stosunek odkształcenia poprzecznego do odkształcenia podłużnego w próbie jednoosiowego ściskania. Jeżeli w rozpatrywanym punkcie gruntu, traktowanego jako materiał izotropowy, wyróżnimy kierunek „m” i jeżeli w tym punkcie jedynie naprężenie $\sigma_m \neq 0$, zaś pozostałe składowe naprężenia są równe zero), to współczynnik Poissona:
$$\begin{equation} \nu \stackrel {def} {=} \left | \cfrac{\varepsilon_n} {\varepsilon_m} \right | \label{7} \end{equation}$$
gdzie: „n” – dowolny kierunek prostopadły do „m”
Szacunkowe wartości modułu wspólczynnika Poissona $\nu$ dla dużej klasy gruntów podano w tab.2, tab.3 oraz w tab. 5.
Moduł sprężystości objętościowej K’
Moduł sprężystości objętościowej związany jest z modułem Younga i współczynnikiem Poissona w sposób znany z klasycznej teorii sprężystości ciała stałego:
$$\begin{equation} K’=\cfrac{E’}{3 \cdot (1-2 \cdot \nu)} \label{8} \end{equation}$$
gdzie: $\nu$ -współczynnik Poissona gruntu
Moduł dylatometryczny MDMT
Moduł dylatometryczny $M_{DMT}$ oznaczany często przez $E_D$ jest oznaczany w aparacie dylatometrze płaskim Merchantego i jest związany z modułem Younga zależnością [8]:
$$\begin{equation} M_{DMT} = E_D = \cfrac{E}{1- \nu^2} \label{9} \end{equation}$$
Oznacza to, że moduł dylatometryczny jest klasycznym modułem odkształcalności płytowej $E_{plate}$ $(\ref{70})$ z teorii cienkich płyt sprężystych.
Wskazuje się [9], że oznaczanie bezpośrednich parametrów odkształceniowych gruntów za pomocą dylatometru DMT jest bardziej precyzyjne i wiarygodne od metody CPT/CPTU, a te ostatnie należy uzupełnić bezpośrednimi pomiarami wytrzymałości na ścinanie w warunkach bez drenażu w celu wyznaczenia współczynnika stożka dla potrzeb ekstrapolacji wyników z pomiarów CPTU.
Tabele szacunkowych wartości parametrów gruntów
Szacunkowe parametry gruntów sypkich i spoistych w różnym stanie zestawione w tab. 2 oraz tab. 3 . Wartości parametrów różnią się nieco lub dotyczą innych klas gruntów, a projektant dla danej sytuacji projektowej wybierze najlepiej dopasowaną wartość, pamiętając, ze są tylko orientacyjne, moduł sprężystości pod fundamentem zależy jeszcze od kształtu fundamentu (kołowy, kwadratowy, ława) oraz głębokości poniżej poziomu gruntu.
Tab. 2 Szacunkowe parametry gruntów w różnym stanie wg [10]
Tab. 3 Orientacyjne wartości modułu Younga E oraz współczynnika Poissona$\nu$ dla gruntów
wg AASHTO 2004 [11], na podstawie [12],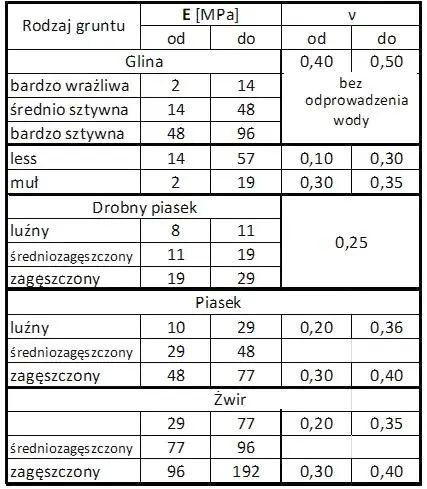
Parametry gruntów wg norm
Zależności w Eurokod 7
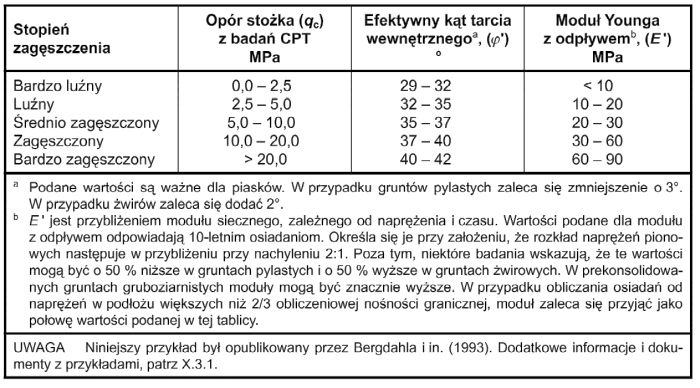
W tab. 4 podano korelacyjne zależności między stanem zagęszczenia gruntu, oporem stożka $q_C$ w badaniu CPT, katem tarcia wewnętrznego, a modułem Younga .
Tab. 4 Moduł Younga gruntu dla piasków kwarcowych z odpływem wg [13], tab D.1.
Zależności w normach PN-B
W tab. 5 podano zalecane przez PN-B-03200:1981 [14]) współczynniki Poissona i stosunki modułów E/M.
Tab.5. Współczynnik Poissona oraz relacje pomiędzy modułem Younga E i edometrycznym M dla gruntów .Klasyfikacja PN-B [14]
W normie [14] zamieszczono zależności korelacyjnych pokazane na rys. 2 dla gruntów piaszczystych na na rys. 3 dla gruntów spoistych.
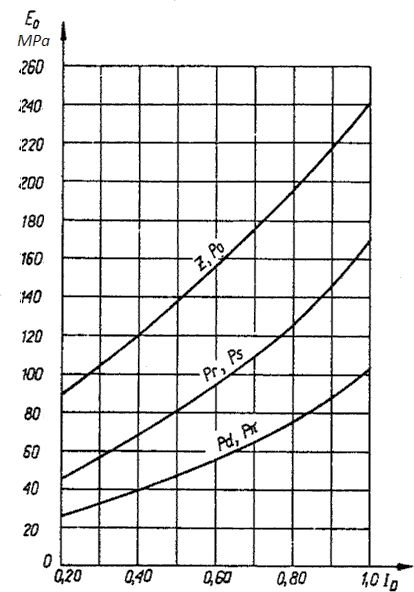
Rys 2 Zależności korelacyjne modułu początkowego $E_0$ od stopnia zagęszczenia $I_D$ dla gruntów piaszczystych [15]
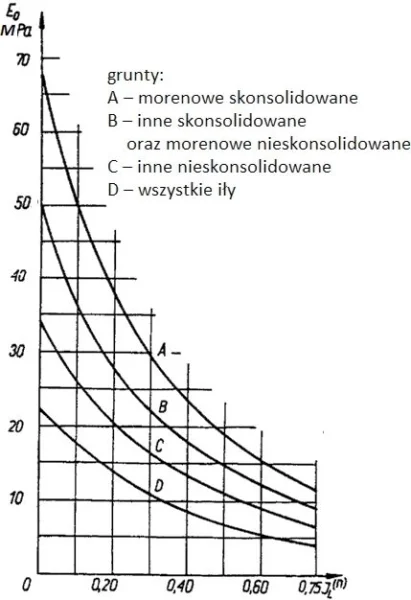
Rys.3 Zależności korelacyjne modułu początkowego $E_0$ o od stopnia zagęszczenia $I_D$ dla gruntów spoistych [14]
Moduł $E_0$ i $M_0$ w relacji ($\ref{3}$) są modułami odpowiednimi dla obciążeń pierwotnych. Przy powtórnym obliczeniu gruntu odpowiednie moduły E i M należy wyznaczyć w zależności od wskaźnika skonsolidowania $\beta$ wg tab. 5.
Zagęszczenie gruntu
Zagęszczenie gruntu w sensie ścisłym może dotyczyć gruntów sypkich (żwirów piasków itd. ), wśród których rozróżnia się stany od od luźnego do bardzo zagęszczonego. Natomiast „zagęszczenie” gruntów spoistych (glin, pyłów itd ) oznacza ich konsystencję związaną z wilgotnością naturalną (nawodnieniem), która tradycyjnie jest mierzona stopniem plastyczności.
Zagęszczenia gruntów niespoistych (sypkich, piaszczystych)
Miary zagęszczenia gruntów sypkich
Miarą zagęszczenia gruntów spoistych jest stopień zagęszczenia $I_D$ lub wskaźnik zgęszczenia $I_s$.
Wskaźnik zagęszczenia $I_s$ jest parametrem zagęszczenia gruntu uformowanego (nasypanego i ew. zagęszczonego) przez człowieka. Wyraża się on stosunkiem gęstości objętościowej badanego gruntu zagęszczonego na budowie $\rho_d$ do maksymalnej gęstości objętościowej gruntu $\rho_s$, oznaczonej w laboratorium aparatem Proctora .
$$\begin{equation} I_s =\cfrac{\rho_d}{\rho_s} \label{10} \end{equation}$$
Wskaźnik zagęszczenia $I_s$ można oznaczać zarówno dla gruntów sypkich jak i spoistych. Jego wartość najczęściej waha się między 0,95–1,00, choć zdarzają się przypadki gdy wartość ta przekracza 1,00.
Stopień zagęszczenia $I_D$ dotyczy wyłącznie rodzimych gruntów sypkich (niespoistych).
Korelacja pomiędzy miarą zagęszczenia Is a ID gruntów piaszczystych (sypkich, niespoistych)
Istnieje silna korelacja pomiędzy stopniem $I_D$ i wskaźnikiem zagęszczenia $I_S$. Zależności korelacyjne $I_D \to I_s$ wg różnych autorów podano w tab. 6
Tab. 6. Zależności korelacyjne ID ↔ Is wg różnych autorów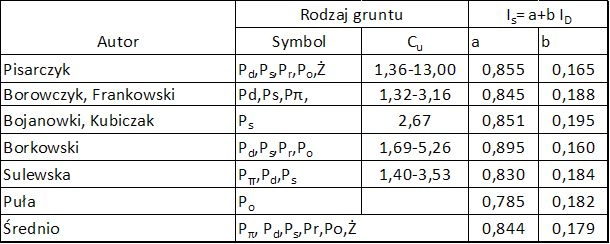
Wskaźnik różnoziarnistości $C_u$ wskazuje na możliwość stosowania formuł zarówna dla gruntów dobrze jak i źle uziarnionych.
W opracowaniu IBDiM (1998) [16] podano, że pomiędzy $I_D$ i $I_s$ zaleca się stosowanie korelacji opisanej formułą
$$\begin{equation} I_s =\cfrac{0,818}{0,958 – 0,174 \cdot I_D} \label{11} \end{equation}$$
czyli po odwróceniu
$$\begin{equation} I_D =5,506 – \cfrac{4,701}{I_s}\label{12} \end{equation}$$
Dla Is=0,97 szacowane jest ID = 0,66, (grunt zagęszczony/ średnio zagęszczony).
Jest to zgodne z odczytem z nomogramu Wiłuna (2013) [17] gdzie dla $I_s =0,97$ mamy $I_D=0,67$.
Miary konsystencji gruntów spoistych
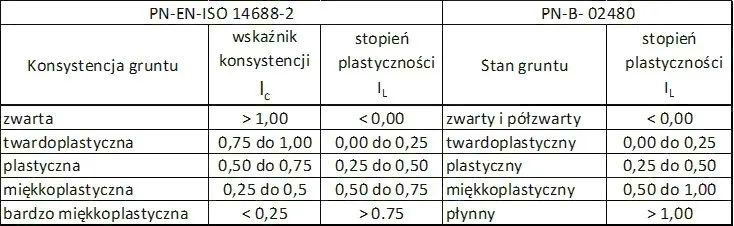
Miarą konsystencji gruntów spoistych jest wskaźnik konsystencji $I_c$ [18] zgodnie z tab. 7.
Uwaga wskaźnik konsystencji $I_c=1-I_L$ gruntu spoistego (tab. 7) ma taki sam symbol jak indeks stanu gruntu CPT ($\ref{25}$), więc wyraźnie należy wskazywać., którą wielkość analizujemy w określonej sytuacji.
Tab.7 Wskaźnik konsystencji $I_c$ i stopień plastyczności $I_L$ [18] i porównanie z normą PN-B -02480
Wymagania normowe zagęszczenia gruntów
W niniejszym artykule stosuje się oznaczenia i klasyfikację gruntów zgodnie z normami [13] , [18], [19] oraz klasyfikacji rodzajów gruntu Robertsona (2010) (Robertson, P.K., (2010), Soil behaviour type from the CPT: an update. 2nd International Symposium on one Penetration Testing, CPT’10, Huntington Beach, CA, USA)). W celach porównawczych odwoływano się do wycofanych norm polskich [14].
Wymagania dla podłoża fundamentów
Wymagania normy PN-B-06050 Gotechnika – roboty ziemne
Wskaźnik zagęszczenia gruntów podłoża, na którym mają być posadowione fundamenty konstrukcji wg [20] nie powinien być mniejszy niż Is= 0,97.
Wymagania dla budynków przez analogię „droga→fundament”
Źródło analogii „droga→fundament”
Na rys.4 pokazano wykres zależności obciążeń współczynnika redukcyjnego dla klimatycznych w rozkładzie statystycznym Gumbela o współczynniku zmienności V oraz okresowi powrotu T odniesione do obciążeń o okresie powrotu 50 lat.
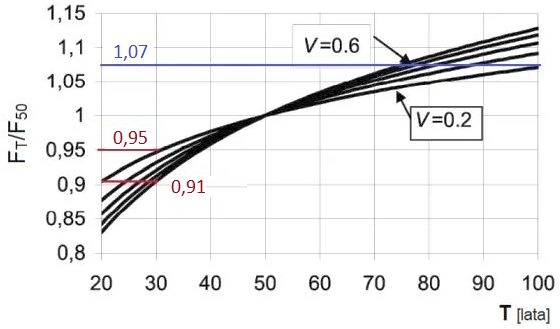
Rys. 4 Współczynnik redukcyjny obciążeń: brązowy – drogi ( współczynnik zmienności V=0,6 ; okres powrotu T=20 lub 0 lat) ; niebieski – fundamenty ( współczynnik zmienności 0,2 ; okres powrotu T=100 lat). Opracowano na podstawie [21] , rys. D.1
Wykres pochodzi z normy obciążenia śniegiem [21]. Charakter obciążenia dróg jest podobny do obciążenia śniegiem, bowiem z normy [22] wynika , że oba typy obciążeń mają podobne wartości częste ($\psi_1 = 0,5$) i prawie stałe: $\psi_2$ = 0,3 dla dróg i 0,2 dla śniegu.
W konsekwencji obciążenia obliczeniowe fundamentów są większe od obciążeń obliczeniowych drogi o takim samym obciążeniu charakterystycznym o $k=\cfrac{1,07}{0,91} = 1,18$. Przy tym obciążenie charakterystyczne powierzchni G (dróg) wg [22],tab.6.8 – wynosi $ 5 \, kN/m^2 $, a obciążenie fundamentów waha się wokół 0,2 MPa=200 kN/m2, to jest 40 x większe.
Wynika stąd, że wytyczne z rys. 6 sformułowane dla dróg w wykopie – stanowią minimalne wymagania do przygotowania podłoża pod fundamenty budynków i budowli kubaturowych.
Kategorię równoważnej konstrukcji drogi należy wyznaczać biorąc pod uwagę poziom naprężeń pod fundamentem, schemat statyczny, klasę niezawodności (konsekwencje jakie może wywołać awaria lub nadmierne przemieszczenia konstrukcji), a także rodzaj oddziaływań gruntu (statyczne, dynamiczne) oraz projektowy okres użytkowania obiektu.
Drogi są projektowane dla projektowego okresu użytkowania 20 lat lub 30 lat (drogi krajowe i autostrady) [23], a obiekty budowlane: zwykłe na T=50 lat , monumentalne i fundamenty na T=100 lat [22]. Tak więc okres projektowy użytkowania fundamentów jest zwykle 100/20 = 5 razy dłuższy niż dla dróg.
W tab. 8 zaczerpniętej z Katalogu [23] podano wymagania dotyczące parkingów, placów i dróg manewrowych, które nieodłącznie występują wokół obiektu kubaturowego.
Tab. 8 Wymogi zagęszczenia gruntów pod parkingami [23], tab. 6.2.
Stosowanie analogii „droga→fundament”
Wymogi zagęszczenia gruntu pod fundamentami nie mogą być niższe od wymogów zagęszczenia dla dróg, co prowadzi do zasad:
- Fundamenty obciążone statycznie w konstrukcjach zwykłych słabo i średnio obciążonych o schemacie statycznie niewyznaczalnym w tym posadowionych na kilku ławach lub stopach należy projektować co najmniej na kategorię KR2 ,
- .Fundamenty konstrukcji wspornikowych (nury oporowe, fundamenty pod wsporniki (kominy itp) należy projektować co najmniej na kategorię KR3.
- Fundamenty konstrukcji odpowiedzialnych i silnie obciążonych należy projektować co najmniej na kategorię KR4 , tzn. na stropie gruntu rodzimego należy wykazać Is=1,0 i $E_2 > 60 \, MPa$
- Parkingi dla samochodów osobowych ze sporadycznym parkowaniem samochodów ciężarowych należy projektować na kategorię KR2.
Dla ustalonej zastępczej kategorii KR z rys. 6 (lub rys. 7 , jeśli mamy dom czynienia z nasypami) można ustalić wymagany moduł wtórny $E_2$ oraz wskaźnik zagęszczenia gruntu $I_S$ Na przykład dla kategorii KR2 podłoże gruntowe z gruntów niespoistych powinno mieć E2> 60 MPa oraz Is > 0,97, a na powierzchni robót ziemnych należy uzyskać E2> 100 MPa oraz Is > 1,0.
Wymagania dla podłoża dróg (→fundament)
Warstwa górna (spąg) warstwy nośnej gruntu rodzimego (na rys. 5 warstwy oznaczonej kolorem żółtym) jest jednocześnie spodem konstrukcji. Spodem konstrukcji nawierzchni jest spód jej najniższej warstwy, spoczywającej na podłożu gruntowym nawierzchni lub na warstwie ulepszonego podłoża. Poziomem niwelety robót ziemnych jest: poziom górnej powierzchni gruntu nasypowego w nasypie, lub poziom górnej powierzchni gruntu rodzimego w wykopie, lub poziom górnej powierzchni warstwy ulepszonego podłoża, o ile taka warstwa występuje. Poziom niwelety robót ziemnych pokrywa się ze spodem konstrukcji podbudowy pod drogę lub fundament.
Wymagania zagęszczenia dotyczą zarówno warstwy gruntu rodzimego jak i każdej warstwy podbudowy pod fundamentem lub drogą. W Polsce do dziś stosuje się wymagania normy PN-S-02206 [24], które są odniesione do badań polowych płytą sztywną PLT (VSS) oddzielnie dla zagęszczenia gruntów w wykopach i nasypach dróg.
Wymagania zagęszczenia dla dróg w wykopie podano na rys. 6 i w tab. 9, a dla dróg w nasypie na rys. 7 i w tab. 10.
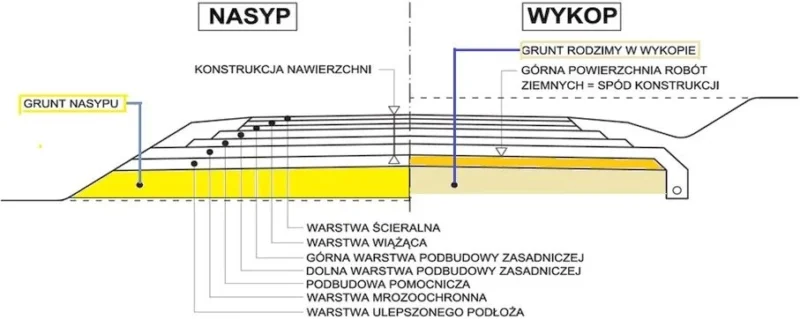
Rys. 5 Układ warstw drogi w nasypie i wykopie [23]
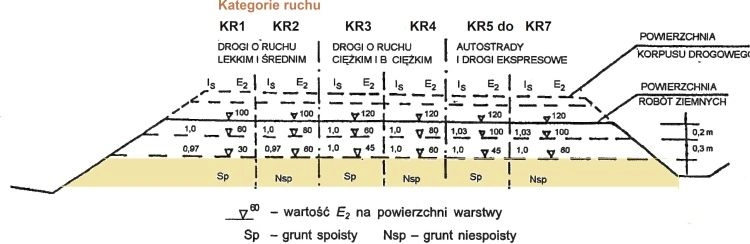
Rys. 6 Wymagania dla drogi w wykopie [24], rys. 4 – zmodyfikowany poprzez wprowadzenie aktualnych symboli kategorii ruchu
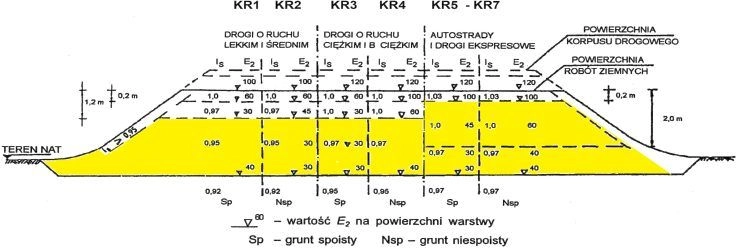
Rys. 7 Wymagania dla drogi w nasypie [25], rys. 3 – zmodyfikowany poprzez wprowadzenie aktualnych symboli kategorii ruchu
Tab. 9 Wymagania zagęszczenia wykopów [26]
Tab. 10 Wymagania zagęszczenia nasypów [26]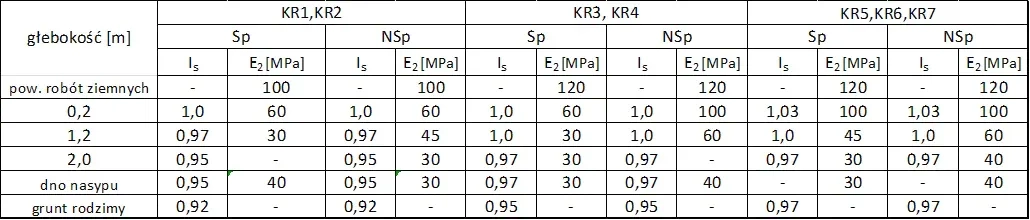
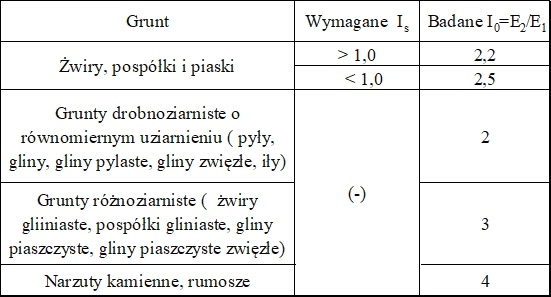
Jako zastępcze kryterium oceny wymaganego zagęszczenia gruntów, dla których trudne jest pomierzenie wskaźnika odkształcenia $I_s$ , przyjmuje się wartość wskaźnika odkształcenia $I_0$ równego stosunkowi modułów odkształcenia wtórnego $E_2$ do pierwotnego $E_1$. Wymagania zestawiono w tab.11
Tab. 11 Wskaźnik zagęszczenia $I_0$ dla wymaganego $I_s$ (opracowano na podstawie [24] )
Dla gruntów antropogenicznych wymagane I0 wyznacza się doświadczalnie, a dla gruntów ulepszonych spoiwami I0 ≤ 2,2.
Trwa remanent po dużej awarii portalu. Przepraszam za nieczytelne treści poniżej tego komunikatu aż do zakończenia remanentu !
Wymagania dla podłoża posadzek przemysłowych
Na rys. 8 pokazano przekrój przez typową podłogę przemysłową
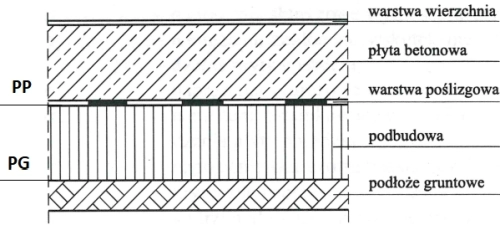
Rys.8 Typowa konstrukcja podłogi przemysłowej (Hajduk P. (2013), Projektowanie podłóg przemysłowych, PWN, Warszawa, 2013))
Wymogi odnośnie nośności i stopnia zgęszczenia gruntów i kruszyw dotyczą poziomu PG – powierzchni podłoża gruntowego (rodzimego) oraz PP – powierzchni podbudowy. Hajduk (2013) [27] podał minimalny moduł odkształcenia wtórnego $E_2$ ($\ref{27}$), który powinien być osiągnięty na obu tych poziomach w zależności od maksymalnych, oczekiwanych obciążeń punktowych $V$ podłogi. W formule ($\ref{13}$) wymogi dla $E_2$ podano w zapisie PP/PG (=podbudowa/grunt):
$$ \begin{equation} E_2 \ge \begin {cases}
80/30 , & \textrm { przy } V \le 32,5 \, kN\\
100/45 , & \textrm { przy } V \ge 60 \, kN\\
120/60, & \textrm { przy } V \ge 100 \, kN\\
150/80 , & \textrm { przy } V \ge 150 \, kN\\
180/100 , & \textrm { przy } V \ge 200 \, kN\\
\end {cases} \label{13} \end{equation}$$
przy czym zagęszczenie gruntu lub kruszywa $ I_0=E_2/ E_1 \, \le 2,5$. Z rys. 6 odczytujemy $I_s = 0,97$ (czyli $I_d= 0,67$), co jest zgodne z tab 11 ($I_s< 1,0$ ).
Zadaniem podbudowy jest nie tylko doprowadzenie do równomiernego przekazywania obciążenie a posadzki na grunt, i ciągłe podparcie płyty betonowej, ale przede wszystkim regulowanie stosunków wodnych (odprowadzanie wody spod nawierzchni), zapobieganie jej wysadzin i przełomów. Na podbudowę nie powinno stosować się wyłącznie betonu lub gruntu stabilizowanego cementem. W przypadku zastosowania warstwy ok 10 cm betonu dać warstwę min 20 cm kruszywa 0/(31-63).
Metody badania zagęszczenia gruntu
Zagęszczenie gruntu można oznaczać laboratoryjnie lub w bezpośrednich badaniach polowych („in situ” ) [13].
Do oceny podłoża gruntowego w trakcie budowy najbardziej użyteczne są badania polowe, które z kolei mogą być wykonane sondami dynamicznymi ( SPT, DP (DPL,DPM,DPH,DPSH) i in. ) lub statycznymi (CPT/CPTU, DMT,PMT, FVT, WST, PLT i in.). Wybór metod badawczych zagęszczenia i nośności gruntu stosuje w zależności od typu budowli, rodzaju gruntu oraz wymagań projektanta konstrukcji.
Metoda laboratoryjna
Badania laboratoryjne stopnia $I_D$ lub wskaźnika zagęszczenia $I_s$ gruntu sypkiego lub też stopnia plastyczności $I_L$ lub wskaźnika konsystencji $I_c$ lub wskaźnika wskaźnika zagęszczenia $I_s$ gruntu spoistego
polegają na oznaczeniu tych cech na próbkach pobranych z warstwy gruntu bez naruszenia jej struktury (czyli próbek kategorii A -najwyższej wg PN-EN ISO 22475-1 [28] oraz wg PN-B-04452 [29]. Próbki kategorii A to próbki pobierane bez naruszania struktury gruntu z zachowaną wilgotnością i porowatością, co realizuje się poprzez pobraniu próbki cylindrem o znanej objętości i przeniesieniu jej do laboratorium, gdzie oznacza się masę oraz wilgotność. Ważne jest, aby próbkę dobrze zabezpieczyć przed utratą wilgotności.
Metoda laboratoryjna jest pracochłonna i wymaga pobrania jakościowo dobrych próbek materiału o nienaruszonej strukturze i wilgotności. W gruntach sypkich zwykle nie można uzyskać nienaruszonej próbki do badań laboratoryjnych [30]. Z tych powodów w praktyce budowlanej najczęściej stosuje się badania polowe i zależności korelacyjne dla wyprowadzenia badanych cech gruntu.
Metody polowe (in situ)
Metody polowe (in situ) są najczęściej stosowanymi w budownictwie metodami badania zagęszczenia gruntu. Sondowania gruntu są penetracją podłoża gruntowego przy użyciu różnych końcówek zagłębianych przez wbijanie, wciskanie lub wkręcanie, z jednoczesnym określaniem oporów występujących przy ich pogrążaniu. Dzielą się na statyczne i dynamiczne.
W tab. 12 zestawiono za pracą Jermołowicz (2019 ) [31] najczęściej stosowane techniki badań in situ i ich przydatność do badań stanu zagęszczenia.
Tab. 12 Techniki badań in situ i ich przydatność do badań stanu zagęszczenia [31]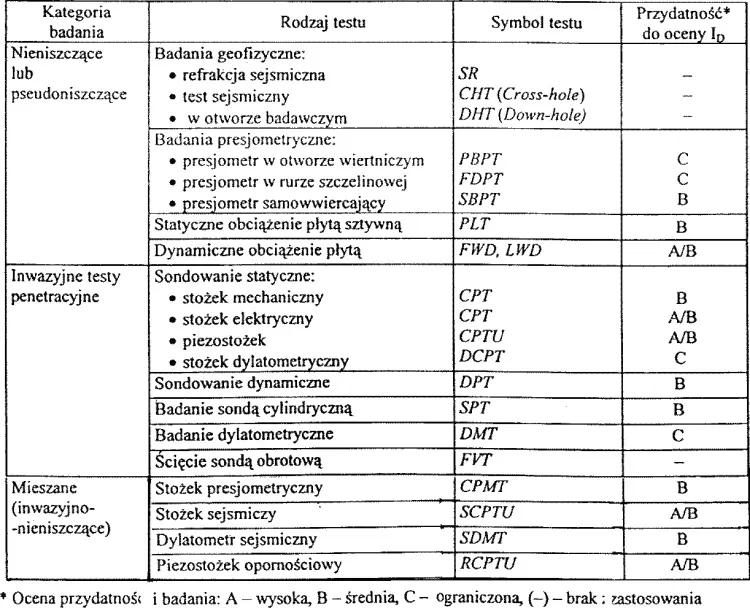
Wysoką skuteczność do badania zagęszczenia gruntu mają metody: FWD/LWD; CPT ze stożkiem elektryczny,; CPTU; SPTU oraz RCPTU. Średnią skuteczność mają: ABPT, PLT (VSS); CPT; DPT; SPT; CMPT.
Sondowania statyczne CPT / CPTU
Sondowanie statyczne CPT/CPTU to podstawowy typ badań polowych gruntu na terenie Europy. Praktycznie zupełnie wyparł klasyczne odwierty geotechniczne. Badanie polega na wciskaniu w grunt stożka elektrycznego z systemem czujników rejestrujących parametry gruntu „in situ”( w stanie pierwotnym) w sposób ciągły. Jest to jedno z niewielu badań gruntu nie zaburzających jego struktury – a więc najbardziej miarodajne [6].
Sondowanie statyczne CPTU to jedna z najnowocześniejszych metod badania gruntu na świecie. Pozwala ona bardzo precyzyjnie określić parametry gruntów. Badania nie posiada ograniczeń ze strony rodzaju badanego gruntu. Sondowania można wykonywać w gruntach sypkich, spoistych, organicznych oraz nasypowych, dzięki czemu jest uniwersalnym rodzajem badania gruntu [32]. Sonda CPT oraz CPTU różni się od siebie rodzajem wykorzystywanego stożka pomiarowego. Sondowanie CPTU pozwala na pomiar ciśnienia porowego gruntu. Analiza wyników sondowań pozwala na określenie typu gruntu w podłożu, a w przypadku sondowań CPTU również poziomu zwierciadła wody gruntowej.
Należy zwrócić uwagę, że w nowoczesnych sposobach rozpoznania gruntowego nie określa się tradycyjnej nazwy gruntu (np glina piaszczysta morenowa), a tylko charakter zachowania („Soil Behavior Type”).
Podczas sondowania statycznego CPT/CPTU rejestrowane są (rys. 9):
- $q_c= \cfrac{Q_c}{A_c}$,opór pod stożkiem gdzie: $Q_c$ siła nacisku na sondę, $ A_c$ rzutowane na poziom pole powierzchni stożka
- $f_s$ tarcie na pobocznicy stożka (na tulei ciernej o polu powierzchni $A_s$) ,
- $u$ ciśnienie porowe gruntu ( tylko w badaniu CPTU),
- $u_2$ ciśnienie wody dolne na obudowę sondy (bezpośrednio nad stożkiem)
- głębokość, prędkość penetracji oraz inklinację ( odchylenie sondy od pionu).
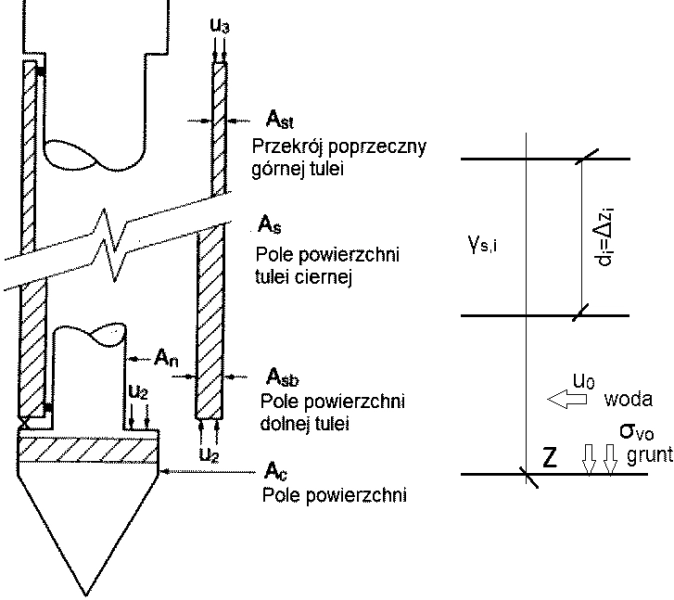
Rys. 9 Końcówka stożka i tuleja cierna [2] – fig. 20 – uzupełnione na potrzeby artykułu
Na podstawie wartości zarejestrowanych wylicza się wartości skorygowane oraz znormalizowane [2]:
- opór na stożku skorygowany przez efekt ciśnienia porowego
$$\begin{equation} q_t = q_c +u_2 \cdot (1-a_n) \quad ; \quad \text { w gruntach piaszczystych } q_t=q_c \label{14} \end{equation}$$
gdzie:
$a_n$ jest współczynnikiem powierzchni netto ustalonym podczas kalibracji laboratoryjnej sondy. Typowa wartość zawiera się między 0,70 a 0,85 [2],
- opór na stożku netto z uwzględnieniem ciśnienia „in situ”
$$\begin{equation} q_n= q_t – \sigma_{v,0} (z) \label{15} \end{equation}$$
gdzie:
$\sigma_{v,0}(z)$ pionowe ciśnienie „in-situ” , naprężenie geostatyczne w gruncie przed wykonaniem fundamentu ( na etapioe „0”) na głębokości „z” poniżej terenu.
$$\begin{equation} \sigma_{v,0} (z) = \int \limits_0^z \gamma_{s,z} \cdot dz \approx \sum_i \gamma_{s,i} \cdot d_i \label{16} \end{equation}$$
gdzie:
$\gamma_{s,z}$, $\gamma_{s,i}$ – ciężar objętościowy gruntu na głębokości „z”, warstwy „i” w stanie naturalnym bez uwzględnienia wyporu wody gruntowej, ale z uwzględnieniem ciężaru wody w porach, to znaczy w przypadku zalegania warstwy gruntu pod wodą $\gamma_{s,i} = \gamma_{sr,i} $ – ciężar gruntu nasyconego wodą, $d_i$ – grubość i-tej warstwy gruntu
Uwzględnienie ciśnienia porowego $u(z)$ wywołanego wyporem wody gruntowej prowadzi do definicji efektywnego ciśnienia „on situ”
$$\begin{equation} \sigma’_{vo}(z)= \sigma_{vo}(z) -u(z)\label{17} \end{equation}$$
Jeśli nie są prowadzone pomiary CPTU, to zwykle przyjmuje się $u(z)=u_0(z)$ – ciśnienie hydrostatyczne wody gruntowej na poziomie z
- znormalizowany opór stożka
$$\begin{equation} Q_t =\cfrac{q_n}{\sigma’_{vo}(z)} \label{18} \end{equation}$$
- bezwymiarowy znormalizowany opór stożka, skorygowany o rodzaj gruntu i poziom obciążeń Robertson (2009) [7]
$$\begin{equation} Q_{tn} = \left( \cfrac{q_n}{P_{a2}} \right) \cdot \left ( \cfrac{P_a}{\sigma’_{vo}}\right )^n \label{19} \end{equation}$$
gdzie:
$P_a$ oraz $P_{a2}$ są wartościami normalnego ciśnienie atmosferycznego (wartość odniesienia) w tych samych jednostkach jak licznik $q_n$ (dla $P_{a2}$) lub $\sigma_{vo}$ (dla $P_a$).
Normalne ciśnienie atmosferyczne wynosi 100 kPa lub 0,1 MPa i takie wartości stosuje się w ($\ref{19}$).
$n = 0.381 \cdot I_c) + 0.05 \cdot \cfrac {\sigma_{vo}}{Pa} – 0.15 \le 1,0$
wyznacza się w procedurze iteracyjnej zgodnie z algorytmem zamieszczonym w pracy [7].
Jeśli procedury iteracyjnej nie podejmuje się, to zwykle przyjmuje się $n=1$, czyli $Q_{tn}=Q_t$
- współczynnik tarcia jako stosunek tarcia na tulei $f_s$ do oporu stożka $q_t$ – oba mierzone na tej samej głębokości w gruncie
$$\begin{equation} R_f = \cfrac{f_s}{q_t} \cdot 100 \text { %} \label{20} \end{equation}$$
- znormalizowany współczynnik tarcia
$$\begin{equation} F_r =\cfrac{f_s}{q_n} \cdot 100 \text { %} \label{21} \end{equation}$$
$$\begin{equation} B_q = \cfrac{\Delta u}{q_n} \label{22} \end{equation}$$
gdzie $\Delta u=u_2- u_0$ zmierzone ciśnienie porowe $u_2$ pomniejszone o ciśnienie porowe in situ $u_0$. Ciśnienie $u_0$ jest ciśnieniem hydrostatycznym (wyporem wody gruntowej). Dla gruntu ponad wodą gruntową $u_0=0$, a pod warstwą wodonośną jest to ciężar wody w tej warstwie.
Tarcie na pobocznicy $f_s$ jest tak skalibrowane, że daje pomiar wytrzymałość gruntu na ścinanie przekształconego $s_{u(r)}$. (oznaczenie Robertson [7]) w mechanice gruntów jest oznaczana przez $c_u$.
Wroth and Wood (1978) [33] zaproponowali następującą zależność korelacyjną pomiędzy stopniem plastyczności $I_L$, a wytrzymałością na ścinanie gruntów spoistych /p>
$$\begin{equation} f_s= c_u= 0,17 \cdot \exp{(-4,6 \cdot I_L)} \, [MPa] \label{23} \end{equation}$$
Stopień plastyczności $I_L$ gruntu spoistego określa jego konsystencję zgodnie z tab. 7.
Dla gruntów piaszczystych przyjmuje się $c_u=0$, więc również $f_s = 0$, ale z pracy Robertson, Campanella (1983) [34] wynika, że tarcie na pobocznicy $f_s$ występuje w zależności od rodzaju gruntu oraz oporu na stożku $q_c$
$$\begin{equation} F_r= 0,1 \div 5 \text{ % z rys. 10 } \label{24} \end{equation}$$
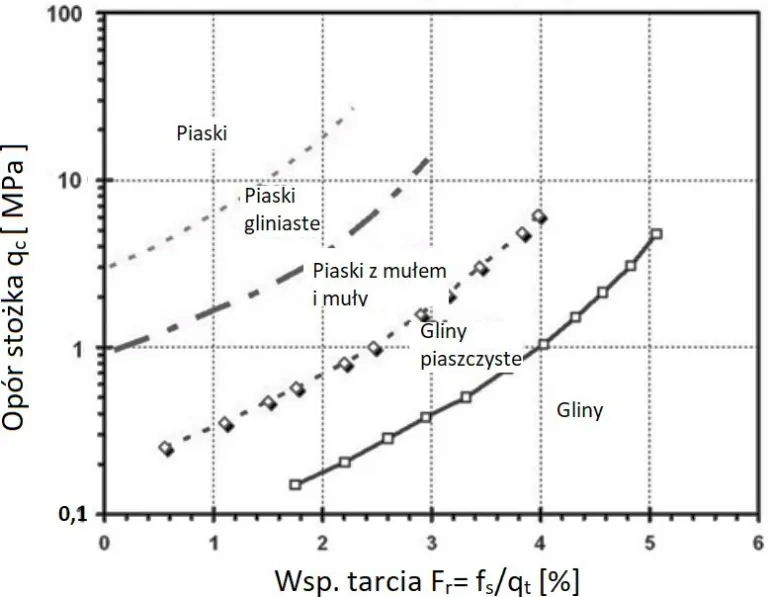
Rys. 10 Klasyfikacja gruntów Robertson-Campanella (1998) [34]
Na podstawie znormalizowanego oporu stożka $Q_t$ oraz współczynnika tarcia $R_f$ wylicza się indeks $I_c$, który jest promieniem w przybliżeniu koncentrycznych okręgów, oddzielających granice pomiędzy każdą z 9-ciu stref podziału gruntów Robertsona (rys.11).
Indeks $I_c$ można zdefiniować następująco [2]:
$$\begin{equation} I_c=\sqrt{ (3,47 – log Q_t)^2 + (1,22+log F_r)^2} \label{25} \end{equation}$$
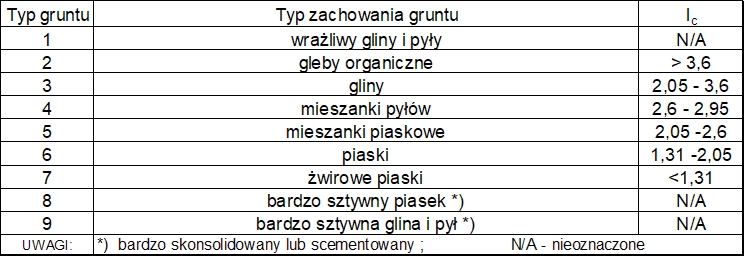
Typy gruntów przypisane do poszczególnych obszarów na rys. 11 zestawiono w tab.13
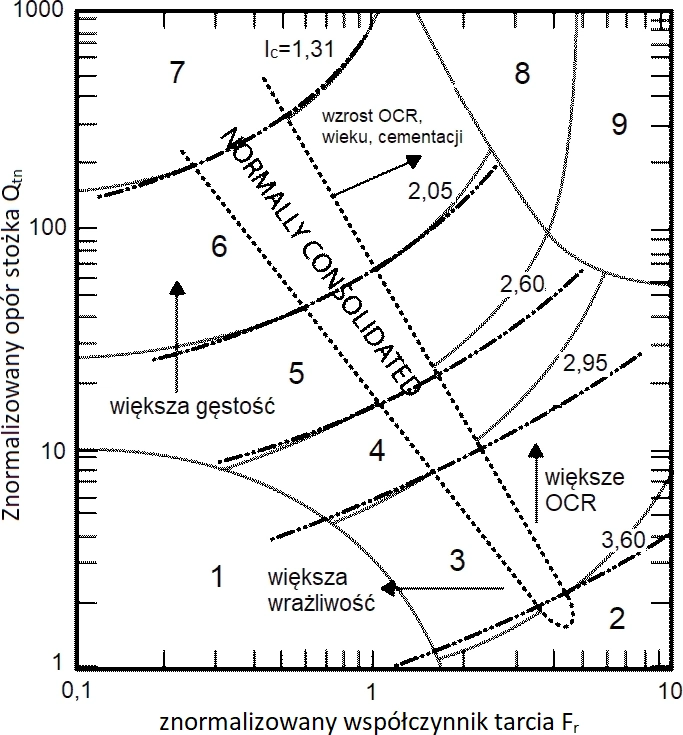
Rys. 11 Klasyfikacja gruntów Robertsona (2010) z granicami indeksu $I_c$ [35], opracowano na podstawie [2] – figure 22
Tab.13 Typy gruntów wg Robertsona [2]– dostosowane do artykułu
W tab. 14 przedstawiono klasyfikację norm amerykańskich. wynikającą z typów gruntu Robertsona .
Tab. 14 Typy gruntów Robertsona. Kryteria klasyfikacji wg ASTM [36]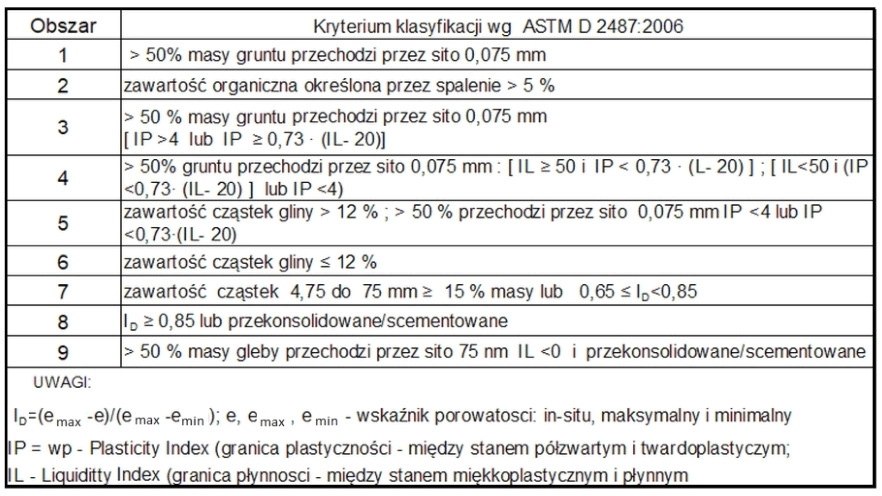
Wymagania sprzętowe dotyczące dotyczące wykonawstwa oraz dokumentowania sondowań statycznych z zastosowaniem stożka elektrycznego lub piezo-elektrycznego podano w normie [37].
Płyta statyczna PLT (VSS)
Badanie płytą sztywną PLT (VSS) jest chętnie stosowane w drogownictwie za sprawą szczegółowych, praktycznych zleceń zawartych w normie PN-S- 02206 [24]. Metoda polega na wywieraniu statycznego nacisku na badaną warstwę płytą stalową.
Najczęściej stosuje się płytę o średnicy 30cm. Moduł odkształcenia jest to iloczyn przyrostu obciążenia jednostkowego do przyrostu odkształcenia badanej warstwy w ustalonym zakresie obciążeń jednostkowych przez średnicę płyty obciążającej. Stanowi on miarę nośności badanej warstwy.
Badania in situ za pomocą aparatu VSS polega na wyznaczeniu pierwotnego modułu odkształcenia $E_1$, wtórnego modułu odkształcenia $E_2$ – tzw. modułu odkształcenia sprężystego oraz wskaźnika odkształcenia $I_0$ tzn. stosunku modułów wtórnego do pierwotnego
$$\begin{equation} I_0=\cfrac{E_2}{E_1} = \cfrac{\Delta p_2}{\Delta p_1} \cdot \cfrac{\Delta s_1}{\Delta s_2} \stackrel {\Delta p_1 =\Delta p_2} {==} \cfrac{\Delta s_1}{\Delta s_2} \label{26} \end{equation}$$
gdzie:
$E_1$ – pierwotny moduł odkształcenia [MPa],
$E_2$ – wtórny moduł odkształcenia [MPa],
$\Delta p_1$, $\Delta p_2$ – różnica obciążeń w pierwszym (1) i drugim (2) cyklu obciążenia w [MPa],
$\Delta s_1$, $\Delta s_2$ – przyrost osiadania w pierwszym (1) i drugim (2) cyklu obciążenia w [mm], odpowiadający zakresom obciążeń,
Moduł $I_0$ wyraża wiec stopień wzmocnienia gruntu po usunięciu wstępnych porów oraz wody.
Pomiar modułów prowadzony jest w dwóch cyklach obciążenia(i=1 i 2), pomiędzy którymi przeprowadza się proces odciążenia podłoża. Obciążenie odbywa się stopniami co 0,05 MPa do wymaganej wartości końcowej natomiast odciążenie realizuje się stopniami co 0,1 MPa. Zakresy obciążeń różnią się w zależności od rodzaju podłoża, a podczas badania podłoża z kruszywa nieulepszonego lub gruntu rodzimego wynoszą $ (0,05 \, do \, 0,15) \,; \, (0,15 \, do \, 0,25) \, MPa$, czyli są rzędu obciążenia gruntu przez fundament bezpośredni.
Moduły odkształcenia określa się z zależności [13]– dodatek K.2. Zgodnie z normą [38], kl. 4.11.4 (1).
$$\begin{equation} E_i= \cfrac{ \pi}{4} \cdot \cfrac {\Delta p_i}{ \Delta s_i} \cdot D \cdot (1-\nu^2), \quad (i=1,2) \label{27} \end{equation}$$
gdzie:
$D$ – średnica płyty pomiarowej i $D=300 \, mm$.
$\nu$ – współczynnik Poissona badanego podłoża. Przy braku dokładnych danych można przyjąć $\nu=0,5$ w warunkach bez odpływu w gruncie drobnoziarnistym oraz $\nu=0,3$ w gruncie gruboziarnistym.
Wyniki badania PLT mogą być wprost wykorzystane do prognozowania osiadania fundamentów bezpośrednich bez wyprowadzania parametrów gruntów, jednak efekt skali (różnicy wielkości płyty i fundamentu) może istotnie zaburzyć wyniki. Terzaghi (1955) [39] zasugerował związek między osiadaniem $s$ stopy kwadratową o boku b i płyty $s_1$ w następujący sposób:
$$\begin{equation} s= s_1 \cdot \left ( \cfrac{b+1}{2b}\right)^2 \label{28} \end{equation}$$
Wyniki uzyskane ze wzoru ($\ref{28}$) mają jednak bardzo duży rozrzut ze względu na zmienność sztywności podłoża wraz z głębokością.
W normie [13] wskazano, że bezpośredni pomiar osiadania płytą PLT można stosować w przypadku, gdy jednorodna warstwa gruntu występuje do głębokości równej dwukrotnej szerokości planowanych fundamentów bezpośrednich ( do głębokości wpływu 2B wg rys. 21). Osiadanie $s_1$ oznaczone w badaniu PLT można bezpośrednio przeliczyć na osiadania fundamentu $s$ poprzez skalę szerokości $b/b_1$ zgodnie z rys. 12.
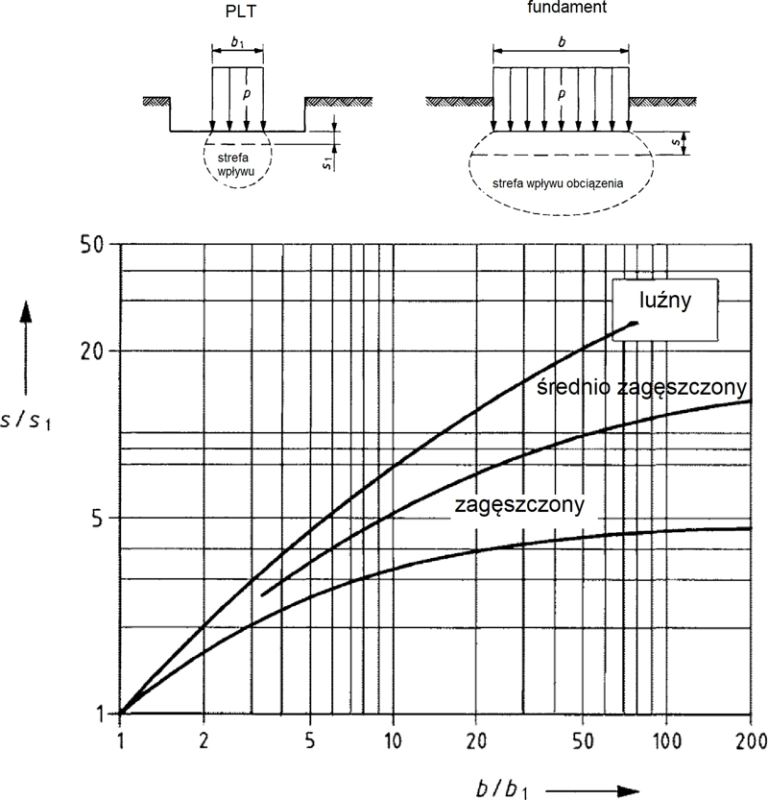
Rys. 12 Bezpośrednie oznaczanie osiadania fundamentu z badań PLT: $b/b_1$ – skala szerokości fundamentu w stosunku do średnicy $b_1$ płyty PLT; $s/s_1$ – skala osiadania fundamentu $s$ w stosunku do osiadania płyty $s_1$ na gruntach o różnym zagęszczeniu piasków [40], również [38] – rys. K2+K3
Do wyznaczenia parametrów geotechnicznych warstwy jednorodnej na potrzeby metod pośrednich (analitycznych)- warstwa poniżej płyty powinna mieć grubość równą przynajmniej dwukrotnej szerokości albo średnicy płyty.
Płyta dynamiczna DP
Płyta dynamiczna jest bardzo chętnie stosownym urządzeniem w drogownictwie, ale najbardziej kontrowersyjnym. Kontrowersje dotyczą badań korelacyjnych, które są nakazane w instrukcjach obsługi, a które powszechnie nie są wykonywane przez prowadzących badania. Na przykład w instrukcji nowoczesnego urządzenia Terratest [41] podano pouczenie: „Przeprowadzaj zawsze pomiary korelacyjne z płytą statyczną VSS”.
Ze względu na kontrowersje, wskazujące na brak wiarygodności badań płytą dynamiczną (stosowanej bez właściwej kalibracji), ale również dlatego, że w niezbyt rozległych wykopach pod fundamenty budowli najczęściej wystarczają same pomiary płytą VSS – nie zalecamy stosowanie płyty dynamicznej do badania zagęszczenia gruntu w budownictwie kubaturowym.
Częstość kontroli zagęszczenia w wykopach zgodnie z normą PN_S-02205 [24],, nie powinna być bowiem mniejsza niż 3 testy na 500 m3 objętości zasypu, lecz nie rzadziej niż 1 test co 30m długości ściany konstrukcji oraz 50 m długości wykopów dla przewodów . Natomiast dla nasypu należy wykonać minimum 1 test na 1000 m3 objętości nasypu oraz 3 testy w każdej jednorodnej warstwie nasypu, lecz nie rzadziej niż 1 test na 500 m2 jednorodnej warstwy
Stosowanie płyty dynamicznej do oznaczania zagęszczenia gruntu jest możliwe bezwzględnie PO prawidłowej kalibracji i ściśle w reżimie zgodnym z instrukcja użytkowania – zwykle prowadzi do zmniejszenia nakładu pracy na kontrolę zagęszczenia, szczególnie po zastosowaniu formuł korelacyjnych ($\ref{35}$).
Liczne korelacje wskaźnika zagęszczenia gruntu $I_s$ z modułem dynamicznym $E_{vd}$ i z powszechnie akceptowanymi jako wzorcowe badaniami płytą statyczną PLT (VSS) – są sporządzane przez producentów urządzeń do badań dynamicznych DP [42], [41], [43] i inne Należy przyjąć, że takie badania porównawcze były prowadzone przez producentów lub niezależnych od wykonawców badaczy na dobrze skalibrowanych urządzeniach.
Korelacja zagęszczenia gruntu z badaniami in-situ
Współcześnie najczęściej stosowaną metodą badań polowych gruntu jest sondowanie CPT/CPTU. Dlatego w pierwszej kolejności krótko omówimy korelację wskaźników zagęszczenia gruntu z wynikami CPT
Sondowania statyczne CPT / CPTU
Grunty sypkie (piaszczyste, niespoiste)
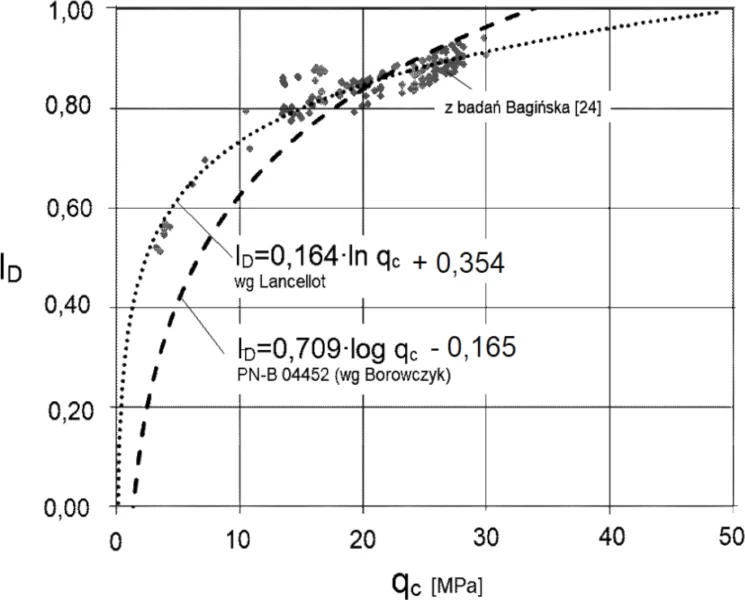
Na rys. 13 pokazano zależności korelacyjne pomiędzy badaniami sondą CPT a stopniem zagęszczenia gruntu zamieszczone w pracy [44]
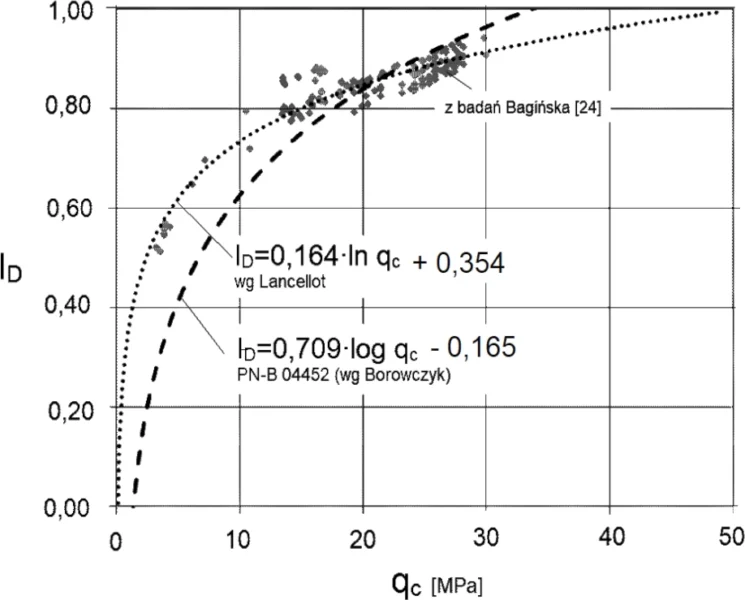
Rys. 13 Formuły korelacyjne CPT $q_c$ – stopień zagęszczenia $I_D$ dla gruntów sypkich Bagińska I., (2015)
Ocena stopnia zagęszczenia gruntu sondą dynamiczną DPH i sondą statyczną CPTU, Przegląd komunikacyjny, 3/2015, str. 6-10)) – zmodyfikowane na potrzeby artykułu.
Formuła korelacyjna Lancellota [6] w przekształconej postaci [44] oraz formuła Borowczyka [45] maja postać:
$$ \begin{equation} I_D = \begin {cases}
0,164 \cdot ln ( q_c ) + 0,354 & \textrm { wg Lancellota }\\
0,709 \cdot log ( q_c ) – 0,165 & \textrm {wg Borowczyka } \\
\end {cases} \label{29} \end{equation}$$
i są często używane po odwróceniu
$$ \begin{equation} q_c = \begin {cases}
exp \left ( \tfrac{I_D – 0,354}{0,164} \right), & \textrm { wg Lancellota } \\
10^{\tfrac{I_D+ 0,165}{0,709}}, & \textrm { wg Borowczyka} \\
\end {cases} \label{30} \end{equation}$$
Formułę Borowczyka zaleca polska norma [29] dla piasków o dowolnej ziarnistości (drobnych, grubych i średnich ). Jednak jak wynika z badań Bagnińskiej (2015) [44] dla stopni zagęszczenia $I_D<0,8$ , czyli w zakresie interesującym w budownictwie ($I_s<0,82$) znacznie lepsze dopasowanie do natury ma formułą Lancellota. Tę fomułę zalecamy do stosowania.
Grunty spoiste
Na rys. 14 zaprezentowano stosowane w Polsce korelacje pomiędzy stopniem plastyczności $I_L$ a oporem stożka $q_c$ sondy CPT w gruntach spoistych podzielonych na trzy grupy w zależności od wartości kąta tarcia wewnętrznego $\Phi$.
Korelacja z modułem Younga
Na rys. 15 przedstawiono nomogram do wyznaczania modułu Younga dla dla piasków krzemowych bez dodatku cementu zamieszczony w pracy Robertosn, Cabal (2015) [2]
Z nomogramu można odczytać współczynniki $\alpha_E$, a następnie wyznaczyć moduł Younga $E’$ z formuły $(\ref{2})$ lub po odczytaniu współczynnika $K_E$ z formuły
$$\begin{equation} E’= K_E \cdot P_a \cdot \sqrt{ \cfrac{ \sigma’_{v0}}{P_a} } \label{31} \end{equation}$$
gdzie:
$\sigma’_{v0}$ – efektywne ciśnienie gruntu jak w ($\ref{18}$),
$P_a=100 \, kPa= 0,1 \, MPa$ – normalne ciśnienie atmosferyczne (wartość odniesienia)
Współczynnik $\alpha_E$ można też wyliczyć z zależności:
$$\begin{equation} \alpha_E = 0,015 \cdot \left[ 10 ^{(0.55\cdot I_c + 1.68)} \right] \label{32} \end{equation}$$
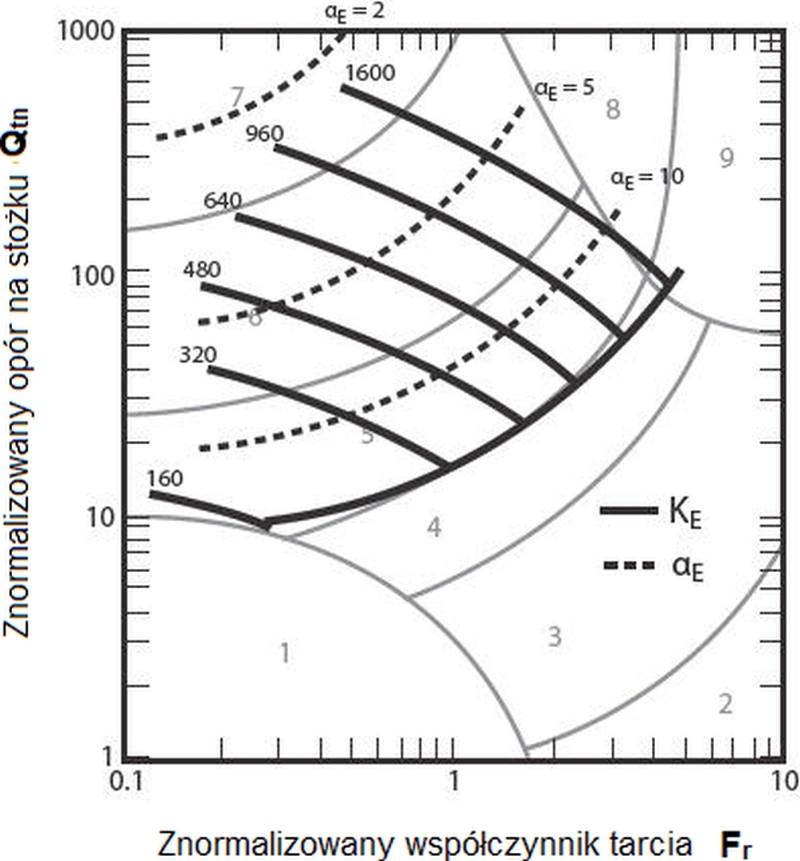
Rys. 15 Nomogram do wyznaczania modułu Younga gruntu z próby CPT Opracowano na podstawie [2] -fig 38
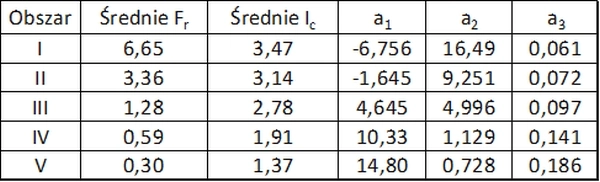
Użyteczne formuły regresji podał Melnikov i Boldyrev (2015) [47] . Formuły regresji dotyczą gruntów z obszarów I do V wg rys. 16.
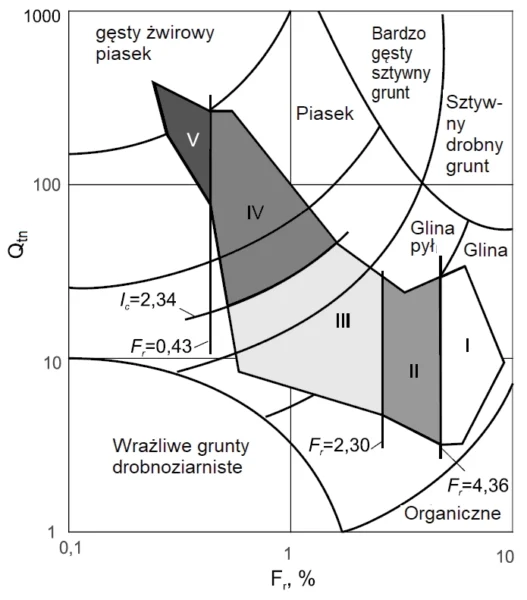
Rys. 16. Obszary regresji modułu E’ najczęściej spotykanych gruntów [47] -fig.3
Krzywe regresji mają postać
$$\begin{equation} E’ = a_1 + a_2 \cdot q_c +a_3 \cdot f_s \label{33} \end{equation}$$
gdzie współczynniki regresji $a_1$,$a_2$, $a_3$ zestawiono w tab.15
Tab.15 Współczynniki regresji $(\ref{33})$ wg [47]
Grunty polskie
Na rys. 17 zaprezentowano nomogram do wyznaczania zagęszczenia gruntów polskich na podstawie badań Wysokińskiego z zespołem (2008) [48]. W zależności od oporu stożka $q_c$ i rodzaju gruntów ( żwir do ił) można oszacować dla gruntów sypkich wskaźnik zagęszczenia $I_D$ ($\ref{10}$), a dla gruntów spoistych stopień konsystencji $I_c=1-I_L $. (tab. 7)
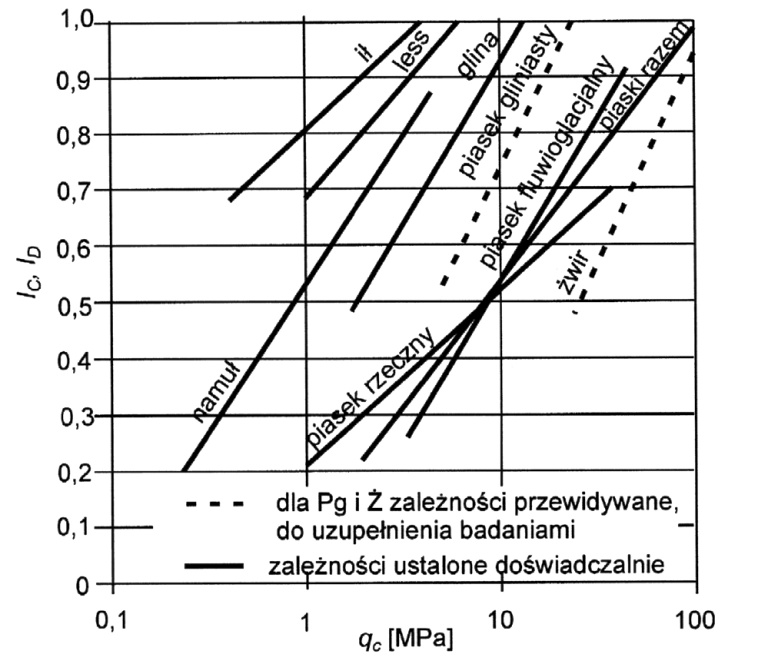
Rys. 17 Nomogram do wyznaczania stopnia zagęszczenia $I_D$ gruntów piaszczystych i wskaźnika konsystencji $I_c$ gruntów spoistych na podstawie badań CPT [49]
Wysokiński z zespołem (2008) przeprowadzili szerokie badania parametrów gruntów polskich na podstawie sondowań [48]. Na rys 18 przedstawiono nomogram do określenia modułu dylatometrycznego ($\ref{7}$) na podstawie wyników z sondowań CPT: oporu stożka $q_c$ oraz współczynnika tarcia $R_f$ ($\ref{20}$).
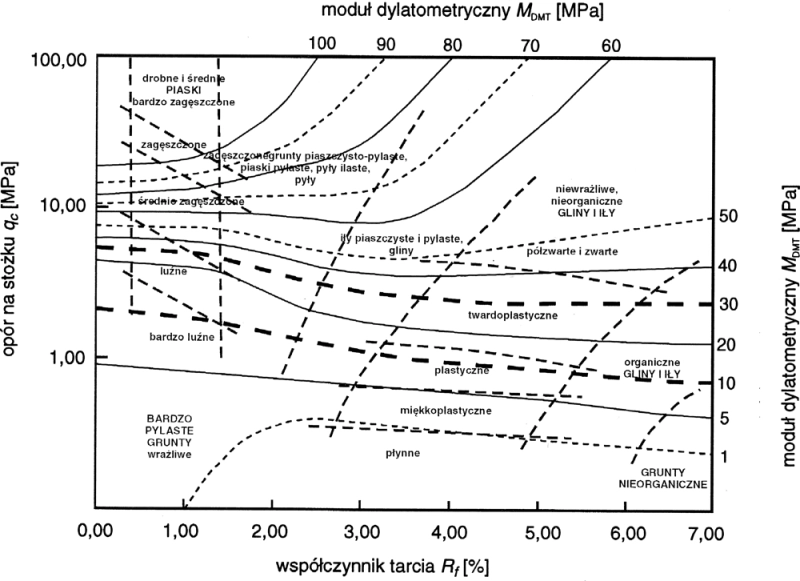
Rys. 18 Nomogram Wysokińskiego (Wysokiński L. i zespół, (2008), Projekt badawczo-rozwojowy, KBN Nr 4 T07E 047 30 Zależności regionalne parametrów geotechnicznych na podstawie sondowań , badań laboratoryjnych i pomiarów osiadań, ITB, Warszawa))
Płyta statyczna PLT
Korelacja wskaźnika zagęszczenia Is z wtórnym modułem E2
Korelacje wyników próby PLT ze wskaźnikiem $I_s$ ($\ref{8}$), a poprzez korelację ($\ref{10}$) również ze stopniem zagęszczenia $I_D$ są dokonywane z wtórnym modułem odkształcenia $E_2$, a nie ze wskaźnikiem $I_0$ ($\ref{26}$) przez co w istocie zakłada się, że proces obciążania podczas 1. cyklu próby PLT (VSS) i odciążenia (podczas wyznaczania modułu $E_1$) zlikwidował „luzy” i $E_2$ jest miarodajne do oceny zagęszczenia gruntu
W tab. 16 zestawiono tabelę korelacyjną zamieszczoną w pracy Rafalskiego (2005) [42]
Tab.16 Korelacja wskaźnika zagęszczenia $I_s$ z modułem$E_2$ z badań PLT wg [42],tab. 4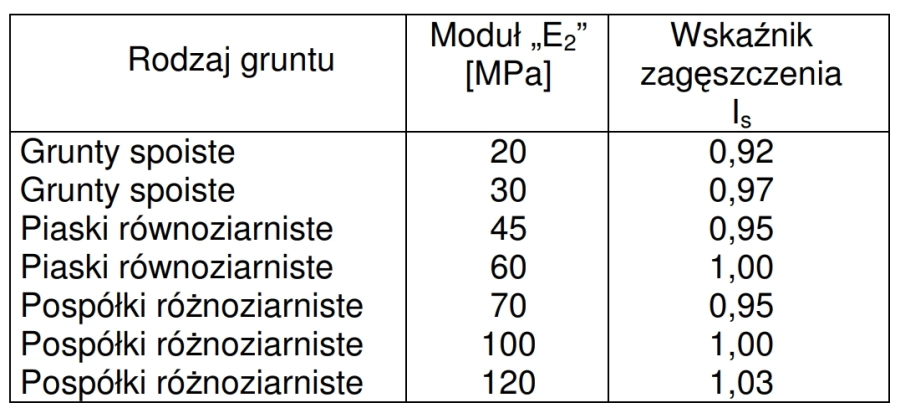
W tab.17 zestawiono zależności korelacyjne pomiędzy wskaźnikiem zagęszczenia, a modułami z badania płytą statyczną PLT oraz dynamiczną z niemieckich wytycznych ZTVE-StB 09 przywołanych w instrukcji obsługi płyty dynamicznej Terratest [41].
Tab.17 Tabela korelacji $(I_s → E_2 → E_{vd})$ =(wskaźnik zagęszczenia, moduł wtórny PLT, moduł dynamiczny DP)
wg niemieckich wytycznych ZTVE-StB 09 wg [41]
Z porównania tab.17 z tab. 16 widać, że zależności podane w pracy [42] podano za zaleceniami wytycznych niemieckich ZTVE-StB 09.
Korelacja Is z pierwotnym modułem E1
W Austrii z kolei stosuje się korelacje modułu dynamicznego $E_{vd}$ z badań lekka płytą dynamiczną DPL $E_{vd}$ do modułu pierwotnego $E_1$ z badania PLT ÖFSV (2008) [50]. Przyjmuje się że minimalna wymagana wartość, która odpowiada pierwotnemu modułowi obciążenia statycznego Ev1 może być sprawdzona płytą dynamiczną. na podstawie zależności
$$ \begin{equation} E_{vd} = \begin {cases}
10+ 6/5 E_1 & \textrm { dla sypkich przy } E_1 < 25 \, MPa\\
10+ 4/5 E_1 & \textrm { dla sypkich przy } E_1 \ge 25 \, MPa \quad \text { i wszysttkich spoistych}\\
\end {cases} \label{34} \end{equation}$$
Z zależności ($\ref{34}$) można przeliczać wymagane wartości graniczne , ale nie należy przeliczać wartości pomiarów $(E_{vd} \to E_1)$.
Formuła korelacyjna E2 → Is
Rafalski i in (2005) [51] przeprowadzili szerokie badania gruntów niespoistych w celu określenia zależności korelacyjnych pomiędzy modułem dynaikznym $E_{vd}$ z badań płytą dynamiczną DP a modułem wtórnym $E_2$ z badań płytą statyczną PLT, a także korelacji modułu dynamicznego $E_{vd}$ ze wskaźnikiem zagęszczenia $I_s$ i wykazali silną korelację liniową w postaci:
$$\begin{equation} Y = A_i \cdot X + B_i \label{35} \end{equation}$$
gdzie:
$Y=E_2$ lub $Y= I_s $,
$X=E_{vd}$ (lub w analizach autora $X=E_2$)
współczynniki kierunkowe $A_i$ oraz wyrazy wolne $B_i$ są indeksowane numerem korelowanej zależności:
(i=1) dla $E_{vd} \to E_2$,
i=2) dla $ E_{vd} \to I_s$,
(i=3) dla $ E_2 \to I_s $,
przy czym ostatnia zależność (i=3) wyspecyfikował autor artykułu poprzez złożenie współczynników dla (i=1 i 2). Współczynniki korelacyjne dla (i=1 i 2) pochodzą bezpośrednio z pracy [51].
Na przykład dla piasków grubych o dobrym uziarnieniu (ciągłym) korelacja $E_{vd} \to E_2$ jest opisana zależnością:
$E_2= 2,03 \cdot E_{vd} – 8,35$
a dla piasków drobnych o złym uziarnieniu (nieciągłym) korelacja $E_2 \to I_S$ jest opisana zależnością:
$$\begin{equation} I_s= 0,00083 \cdot E_2 + 0,94 \label{36} \end{equation}$$
Grunty niespoiste (sypkie, ziarniste) podzielono na cztery grupy: żwir, pospółka, piasek gruby, piasek średni i piasek drobny) a każdą grupę na dwie w zależności od uziarnienia : ciągłego ( możliwe zagęszczenie) i nieciągłego dla wskaźnika jednorodności uziarnienia $c_u$ wg normy [52]
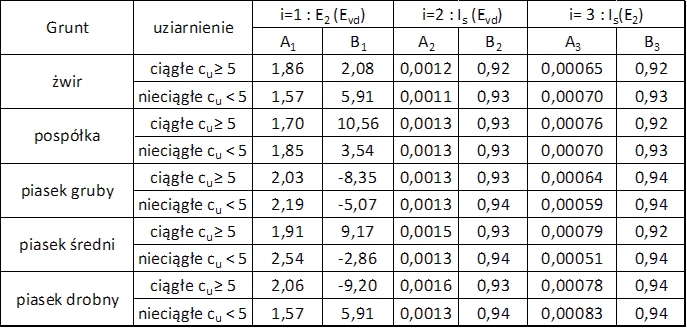
W tab. 18 zestawiono współczynniki regresji liniowej, umożliwiające na podstawie znanego wtórnego modułu statycznego $E_2$ lub modułu dynamicznego $E_{vd}$ oszacować wskaźnik zagęszczenia $I_s$ z formuły ($ \ref{35}$).
Tab.18 Współczynniki korelacji zagęszczenia gruntu sypkiego $I_s$ z badaniami płytą statyczną PLT i dynamiczną do wzoru ($\ref{35}$)
Osiadania fundamentu
Ogólna formuła
Ogólną formułę do szacowania osiadania gruntu $s$ pod liniowym fundamentem (np ławą o szerokości B) podano w [19]-wzór F.1.:
$$\begin{equation} s=\cfrac{p \cdot B \cdot f}{E_m}\label {37} \end{equation}$$
gdzie:
p – nacisk na grunt wywierany przez fundament w poziomie posadowienia
B – szerokość fundamentu liniowego
$E_m$ – wartość obliczeniowa modułu sprężystości, przyjmowana stosowanie do metody i skłądowej szacowanego osiadania
Osiadanie gruntu pod fundamentem $s$ jest sumą trzech składowych :
$s_e$ – osiadania sprężystego (natychmiastowego). Osiadanie natychmiastowe następuje po przyłożeniu obciążenia lub w okresie około 7 dni od przyłożenia . Analiza natychmiastowego osiadania jest stosowana dla wszystkich gruntów drobnoziarnistych, w tym iłów i glin o stopniu nasycenia < 90% oraz dla wszystkich gruntów gruboziarnistych o dużym współczynniku przepuszczalności (powyżej 10,2 m/s).
$s_k$ – osiadania konsolidacyjnego
$s_w$ – osiadania od wtórnej kompresji.
Każdy grunt posiada pory, wilgoć i gazy. W gruntach wilgotnych i drobnoziarnistych (o małej przepuszczalności) takich jak iły, czy gliny – osiadanie będzie trwało przez długi czas z powolnym odpływem wody i ponowną regulacją szkieletu gruntu, aż do całkowitego rozproszenia się nadciśnienia w porach. W tych gruntach większe znaczenie mają kładowe osiadania $s_k$ i $s_w$.
Osiadanie jest niestacjonarnie (zależne od czasu), co oznacza, że nie występuje natychmiast po wprowadzeniu obciążenia, lecz jest zależne od konsolidacji gruntu. Mniej ściśliwe grunty (piasek, żwir) odkształcają się szybciej, natomiast nawodnione grunty gliniaste o niskiej przepuszczalności doświadczają stopniowego odkształcenia zwanego konsolidacją. Zjawisko to jest oceniane przez teorię konsolidacji Terzaghiego. Do oszacowania tego przedłużonego osiadania stosowane są metody nieliniowe., które nie są przedmiotem niniejszego artykułu.
Współczynnik osiadania $f$, występujący w ogólnych formułach ($\ref{37}$) i ($\ref{75}$) nie jest wyspecyfikowany w normie [19] i należy go wyznaczyć zależnie od przyjętej metody szacowania osiadania $s$ w tym także od uwzględnianej składowej przemieszczenia.
Poniżej omówiono metody szacowania pierwotnego (natychmiastowego, sprężystego) osiadania $s_e$ w gruntach, które zakładają liniowy związek pomiędzy przyrostem obciążenia gruntu, a przyrostem osiadania.
Obciążenie mimośrodowe
Zwykle fundament w podstawie jest obciążony mimośrodowo, nawet w przypadku przegubowego oparcia słupa, ponieważ w tym przypadku oddziaływania poziome $[(H_B \, , (H_L]$ słupa/ ściany (indeksy oznaczają siły równoległe do B lub L odpowiednio) na skutek działania na pewnej wysokości ponad podstawą – wywołują momenty zginające $[M_B \, , M_L]$ (indeksy oznaczają zginanie wokół osi prostopadłej do boku.
W przypadku mimośrodowego ściskania Meyerhof [53] zaproponował wprowadzenie zredukowanych wymiarów podstawy fundamentu, nazywanych odpowiednio efektywną szerokością B’ i efektywną długością L ’ z następujących formuł:
$$\begin{equation} B’ = B – 2 \cdot e_B \text { i } L’ = L – 2 \cdot e_L \label {38} \end{equation}$$
gdzie:
$e_B=\cfrac{M_B}{V}$ , $e_L=\cfrac{M_L}{V}$, a V- pionowa siła obciążająca (ściskająca)
Formuła $(\ref{38}$) dotyczy fundamentu o podstawie prostokątnej. W przypadku fundamentu o podstawie kołowej zależności są bardziej złożone. W tym przypadku odsyłamy do pracy Lancelotta [54] lub [55].
Podejście wyrażone formułą ($\ref{38}$) nie jest ścisłe, ale powszechnie stosowane [56]. Podejście jest równoznaczne z zastąpieniem mimośrodowego obciążenia działającego na powierzchnię A = B L obciążeniem osiowym działającym na powierzchnię A = B’ L ’, jak pokazano na rys. 19.
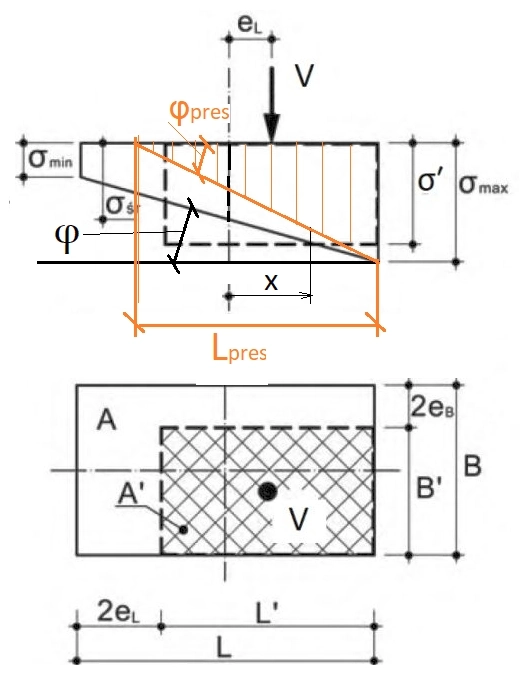
Rys. 19 Stopa fundamentowa obciążona mimośrodowo: oryginalna o podstawie A i zastępcza A [55] – Uzupełnione o obrót podstawy o kąt $\varphi$ i stan częściowego docisku do gruntu (na pomarańczowo) $L_pres$ – długość docisku
Kolorem pomarańczowym na rys. 19. zobrazowano sytuację w której fundament jest częściowo odrywany od podłoża. Powszechnie nie dopuszcza się do takiej sytuacji, co oznacza wymóg pozostawania siły V w rdzeniu przekroju., czyli:
$$\begin{equation} \cfrac{e_B}{B} \le \cfrac{1}{6} \text { ; } \cfrac{e_L}{L} \le \cfrac{1}{6} \text { ; } \left( \cfrac{e_B}{B} + \cfrac{e_L}{L} \right ) \le \cfrac{1}{6} \label {39} \end{equation}$$
Przy tak umiejscowionym obciążeniu naprężenia w narożach fundamentu oryginalnego o podstawie $A=B \cdot L$ wynoszą
$$\begin{equation} \sigma_{max/min } = \cfrac{V}{A} \cdot \left ( 1 \pm \cfrac {6\cdot e_L}{L} \pm \cfrac{6\cdot e_B}{B}\right) \label {40} \end{equation}$$
Natomiast w przypadku fundamentu o podstawiezredukowanej $A’=B’\cdot L’$ sa stałe i wynoszą
$$\begin{equation} \sigma’ = \cfrac{V}{A’} \label {41} \end{equation}$$
W najgorszym położeniu siły V – na granicy rdzenia otrzymujemy stosunek naprężęń zredukowanych do ekstremalnych [55]:
$$\begin{equation} \cfrac{\sigma’ }{\sigma_{max}} \approx 0,75 \label {42} \end{equation}$$
Zastosowanie redukcji $(\ref{38}$) prowadzi do niewielkiego zapasu bezpieczeństwa.
Osiadanie natychmiastowe se
Metody szacowania osiadania sprężystego
W zastosowaniach inżynierskich funkcjonują trzy metody szacowania osiadań sprężystych gruntu [55]:
- metoda odkształceń jednoosiowych, zwana też metodą naprężeń, nazywana też metodą modułu edometrycznego jest szeroko stosowana w Polsce, bo była polecana przez polską normę [14]. W niniejszym artykule reprezentuje ją metoda Pieczyraka.
Zgodnie z zaleceniami Eurokod 7 nadal może być stosowana, choć prostsze, a przede wszystkim lepiej dopasowane do obserwacji są metody współczynnika wpływu. - metoda odkształceń trójosiowych, lub metoda odkształceń nazywana też metodą modułu Younga. W niniejszym artykule reprezentuje ją metoda Mayne-Poulos
- metoda współczynnika wpływu. W niniejszym artykule reprezentuje ją metoda Schmertmann.
Zasada addytywności i głębokość aktywna
Wszystkie metody wymienione powyżej stosują zasadę addytywności polegającą na tym, że osiadanie całkowite fundamentu $s$ składa się z osiadania poszczególnych warstw $s_{e,i}$ [19] – klauzula F.1.zd.3
$$\begin{equation} s_e=\sum \limits_1^n s_{e,i} \label {43} \end{equation}$$
gdzie $n$ – liczba warstw gruntu które uwzględnia się przy wyznaczaniu osiadania
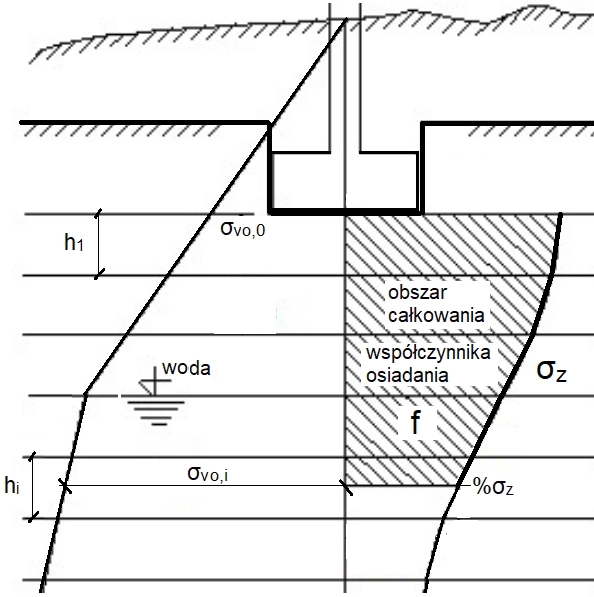
Sumowanie w $(\ref{43})$ przebiega od poziomu posadowienia do głębokości aktywnej $z_a$, poniżej której wpływ odkształcalności gruntu jest pomijalnie mały. Do ustalenia głębokości aktywnej $z_a$ najczęściej stosuje się metodę procentunaprężenia geostatycznego, zgodnie z którą głębokość aktywna reprezentowana jest głębokością pod fundamentem, gdzie naprężenia $\sigma_z$ wywołane obciążeniem fundamentu osiągną pewien procent naprężenia geostatycznego $\sigma_{v0}$ ($\ref{16}$) (rys. 20)</a:
$$\begin{equation} \sigma_{z} = x \% \sigma _{v0} \label {44} \end{equation}$$
gdzie x% =
20% wg Eurokod 7-1 [19]
30% wg PN-B [15]
Szacowanie parametrów odkształcalności gruntu
Wiarygodne oszacowanie wartości modułu sprężystości Younga $E$ lub edometrycznego $M$ oraz współczynnika Poissona $\nu$ gruntów nie jest łatwe. Wynika to głównie z trudności próbkowania, a przede wszystkim zależności modułu sprężystości od stanu naprężenia.
W szczególności przyjmowanie wartości tych parametrów na podstawie historycznych zależności podanych na rys. 2 i rys. 3 powinno być zweryfikowane badaniami polowymi. Zależności korelacyjne przedstawione w artykule: $(\ref{2}), $(\ref{4})$, $(\ref{27})$, $(\ref{33})$, $(\ref{35}) oraz z nomogramów rys.17, rys. 18 – należy stosować rozważnie po analizie problemu i uzasadnieniu wyboru.
Norma Eurokod 7 [19] – klauzula F.1- zdanie 2 nakłada obowiązek „należy stosować wartości modułów odkształcenia lub inne zależności naprężenie-odkształcenie, określone na podstawie badań laboratoryjnych i z zaleceniem kalibrowania na podstawie badań polowych„.
Wykorzystywane w metodzie Mayne-Poulos. zwiększanie się modułu Younga wraz z głębokością $k$ dokonuje się również z badań CPT po wyznaczeniu modułu $E$ na kolejnych poziomach badań,
Przede wszystkim ze względu na zgrubne oszacowanie parametrów gruntu –nie należy uważać obliczeń osiadań za dokładne ( o tym wprost stanowi norma Eurokod 7).
Zalecamy stosowanie metod współczynnika wpływu Schmertmann lub metodę Mayne-Poulos , a do szybkich szacunków metodę Pieczyraka.
Współczesne metody szacowania sprężystego osiadania gruntu
Metoda Schmertmann i in. (1978)
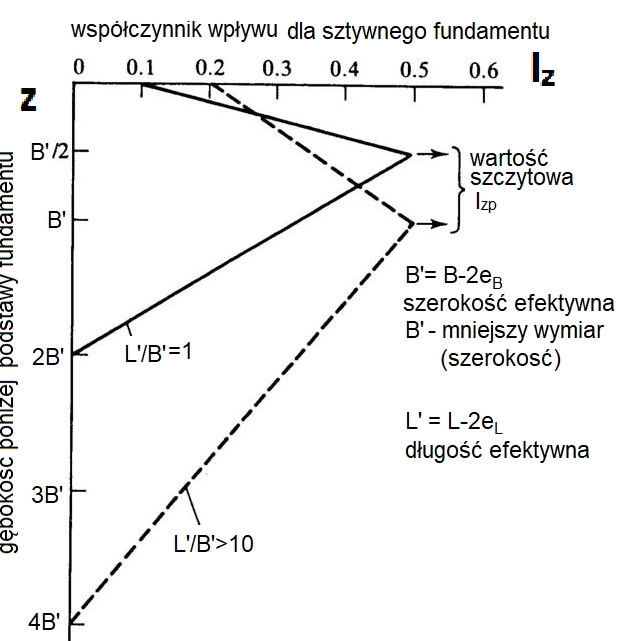
Do obliczania osiadania bezpośrednich (płytkich ) fundamentów w gruntach gruboziarnistych (niespoistuch) użyteczna jest metoda Schmertmann, (1978) [57], [58]. W metodzie wykorzystywany jest współczynnik wpływu $I_{zp}$, określający wpływ warstw w gruntu położonych poniżej podstawy fundamentu na osiadanie. Wyznacza się go z nomogramu zamieszczonego na rys. 21
Metoda Schmertmanna jest metodą półempiryczną skorelowaną z wynikami pomiarów przemieszczeń w naturze oraz analizami prowadzonymi metodą elementów skończonych na nieliniowym modelu naprężenia – odkształcenia z uwzględnieniem trójosiowego stanu odkształcenia (współczynnika Poissona ujęty we współczynniku wpływu $i_z$). Metoda ma zastosowanie do normalnie skonsolidowanych piasków Przemieszczenia mogą być znacznie mniejsze dla piasków wstępnie obciążonych lub zagęszczonych w inny sposób.
W ujęciu przestawionym w w załączniku D Eurokod 7 – cz.2 [13] osiadania fundamentu szacuje się z formuły:
$$\begin{equation} s_e = C_1 \cdot C_2 \cdot \Delta p \cdot \int \limits_0^z \left ( \cfrac {I_z}{C_3 \cdot E’} \right ) \label{45} \end{equation}$$
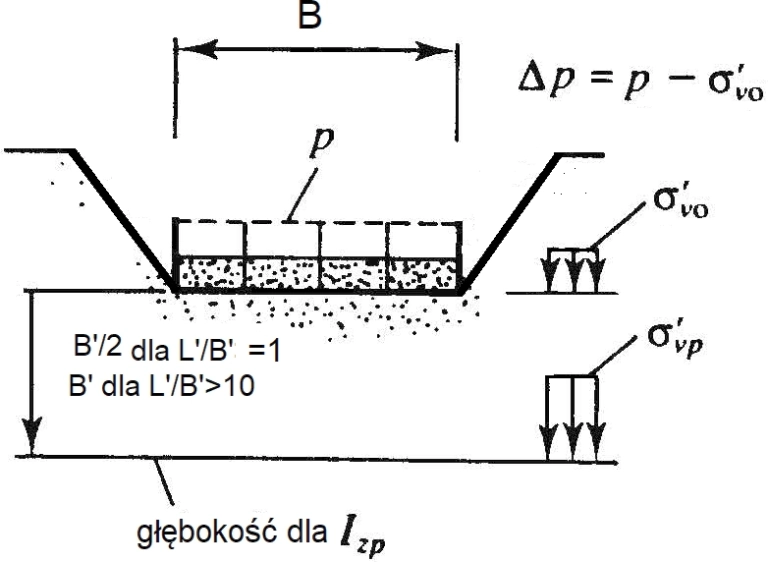
Obciążenie netto gruntu $\Delta p$ w poziomie posadowienia (patrz rys. 22) jest równomiernie rozłożonym naciskiem konstrukcji na grunt pomniejszonym o efektywne naprężenia geostatyczne w gruncie (przed wykonaniem fundamentu z uwzględnieniem wyporu wody)
$$\begin{equation} \Delta p = p- {\sigma’}_{v,0} \label{46}\end{equation}$$
Efektywne ciśnienie geostatyczne , w gruncie w poziomie posadowienia $\sigma’_{v,0}$ w sformułowaniu oryginalnym [59] przedstawiono w postaci
$$\begin{equation} \sigma’_{v,0} = \gamma_s \cdot D_f \label{47}\end{equation}$$
gdzie: $\gamma_s$ – ciężar objętościowy pierwotnego gruntu przeznaczonego do usunięcia w celu zagłebienia dundamentu do głebokości $D_f$ (poziomu posadowienia fundamentu poniżej poziomu terenu).
W przypadku różniących się warstw gruntów, występujących powyżej poziomu posadowienia efektywne ciśnienie geostatyczne wyznacza się z formuł ($\ref{16}$) i ($\ref{17}$) dla rzędnej $z = z_0 = D_f$, czyli w poziomie posadowienia, od poziomu terenu pierwotnego. licząc.
Całkę w wyrażeniu ($\ref{45}$) w praktyce aproksymuje się sumą
$$\begin{equation} s_e = \int \limits_0^z \left ( \cfrac {I_z}{C_3 \cdot E’} \right ) \approx \sum \limits_0^{z_2} \left ( \cfrac {d_{ef,i}}{C_3 \cdot E’} \right ) \label{48} \end{equation}$$
gdzie sumowanie biegnie po wszystkich warstwach gruntu o grubości $d_i$ od poziomu posadowienia, o rzędnej pionowej z=0 do poziomu $z=z_2$, na którym zanika wpływ naprężeń na osiadanie fundamentu i którą przyjmuje się w zależności od kształtu fundamentu jak następuje:
$$ \begin{equation} z_2 = \begin {cases}
2B’ & \textrm { dla stopy osiowosymetrycznej (kwadratowej lub kołowej) lub płyty L’/B’=1}\\
4B’ & \textrm { dla ławy fundamentowej L’/B>10}\\
\end {cases} \label{49} \end{equation}$$
Efektywna grubość warstwy gruntu o grubości rzeczywistej $d_i$ wynosi
$$\begin{equation} d_{ef,i} = d_i \cdot I_{z,i} \label{50} \end{equation}$$
Współczynniki poprawkowe $C_1, \,C_2, \,C_3$ wynoszą:
- ze względu na obciążenia fundamentu zagłębionego poniżej poziomu gruntu $C_1$:
$$\begin{equation} C_1= 1 -0,5 \cdot \left( \cfrac{ {\sigma’}_{v,0}}{\Delta p}\right) \label{51} \end{equation}$$
- ze względu na pękanie i obciążenia cykliczne $C_2$
$$\begin{equation} C_2= 1+0,2 \cdot log (10 \cdot T) \label{52} \end{equation}$$
gdzie: $T$ czasem w latach od przyłożenia obciążenia. Współczynnik $C_2$ jest skalibrowany tak, by przyjmował wartość 1 przy T-0,1 roku,, czyli niezwłocznie po wykonaniu fundamentu. W gruntach niespoistych i nienasyconych spoistych oraz o niskiej plastyczności, czas osiadania T można przyjmować 0,1 do 1 roku dla obciążeń statycznych. i szacowania przemieszczenia natychmiastowego , ale także konsolidacyjnego.
Dla projektowanego okres użytkowania fundamentu T=100 lat wg [22] : $C_2$ = 1,6 jest zwykle zbyt duży i w tym przypadku zaleca się prowadzenie analiz z uwzglednieniem konsolidacji.gruntu w czasie.
- ze względu na kształt fundamentu $C_3$
$$\begin{equation} C_3= 1,25 \cdot \left[ 1 +0,4 \cdot \log{\left( \cfrac{L’}{B’} \right)}\right ] \label{53} \end{equation}$$
Dla fundamentu kwadratowego (L’=B’) $C_3=1,25$, a dla fundamentu pasmowego $L’/B’= 10$ $C_3 = 1,75$.
Formułę ($\ref{53}$) w części ujętej w nawisy kwadratowe podał Terzaghi i in (1996) [60]. Natomiast współczynnik zwiększający 1,25 pochodzi z normy PN-EN 1997-2( 2009) [13]
$B’$ i $L’$ są efektywną szerokością oraz długością fundamentu wyznaczonymi z formuły ($\ref{39}$) w celu uwzględnienia mimośrodowego obciążenie fundamentu.
Współczynnik wpływu odkształcenia $I_{z,i} $ zależy od głębokości zalegania warstwy poniżej podstawy fundamentu. wg rys. 21. i zmienia się liniowo z punktem załamaniem na głębokości $z_1$ poniżej poziomu fundamentu. Głębokość załamania wynosi $z_1= B’/2$ dla fundamentu kwadratowego (ogólnie osiowo-symetrycznego $L’/B’=1)$ i $z_1= B’$ dla fundamentu pasmowego przy (L’/B/’>10). W przypadku płyty $L’, B’ \to \infty)$ i L’/B’=1.
W pracy [61] zaproponowano następujące formuły interpolacyjne do wyznaczenia punktów charakterystycznych nomogramu Schmartmann w zależności od stosunku boków fundamentu:
$$\begin{equation} \cfrac{z_1}{B’}= 0,5+0,0555 \cdot \alpha’ \le 1 \quad ; \quad \cfrac{z_2}{B’}= 2+0,222 \cdot \alpha’ \le 4 \quad ; \quad I_{z0} = 0,1+0,0111 \cdot \alpha’ \le 0,2 \label{54} \end{equation}$$
gdzie: $\alpha’= \cfrac{L’}{B’}-1 $
Wartość szczytowa współczynnika wpływu odkształcenia $I_{zp}$ wynosi
$$\begin{equation} I_{zp}=0,5+0,1 \cdot \sqrt{ \cfrac{ \Delta p }{ \sigma’_{v,p}}} \label{55} \end{equation}$$
Obciążenie brutto podstawy fundamentu przez zewnętrzną charakterystyczną siłę obciążającą $F_k$
$$\begin{equation} p=\cfrac{F_k}{B’ \cdot L’} \label{56}\end{equation}$$
Efektywne ciśnienie geostatyczne gruntu w poziomie w poziomie szczytu współczynnika wpływu wyznacza się też z formuł ($\ref{16}) i ($\ref{17}) , ale dla $z_1$, ale dla $z=z_1$
$$\begin{equation} {\sigma ’}_{v,p}= {\sigma ’}_{v,0} + \sum \limits_0^{z_1} ( \gamma’_{s.i} \cdot d_i ) \label{57}\end{equation}$$
gdzie: $\gamma’_{s,i}, \quad d_i$ – efektywny ciężar właściwy gruntu ( z uwzględnieniem wyporu wody gruntowej) oraz grubość i-tej warstwy gruntu
Dla wyznaczonych punktów charakterystycznych nomogramu można obliczyć wartość współczynnika wpływu dla rzędnej wysokości $z$ z równań linii prostych:
$$\begin{equation} I_z (z) =\begin {cases}
I_{z0} – (I_{z0}-I_{zp}) \cdot \cfrac{z}{z_1}, & \text{ dla } \quad 0 < z \le z_1 \\
I_{zp} \cdot \cfrac{z_2-z }{z_2- z_1}, & \text{dla} \quad z_1< z \le z_2 \\
\end {cases} \label{58}\end{equation}$$
Procedurę wyznaczania przemieszczenia fundamentu metodą Schmertmann pokazano na rys. 23 i w przykładzie 4 w tym artykule.
Opór stożka $q_c$ jest ustalony w każdej warstwie jako średnia oporu na grubości warstwy.
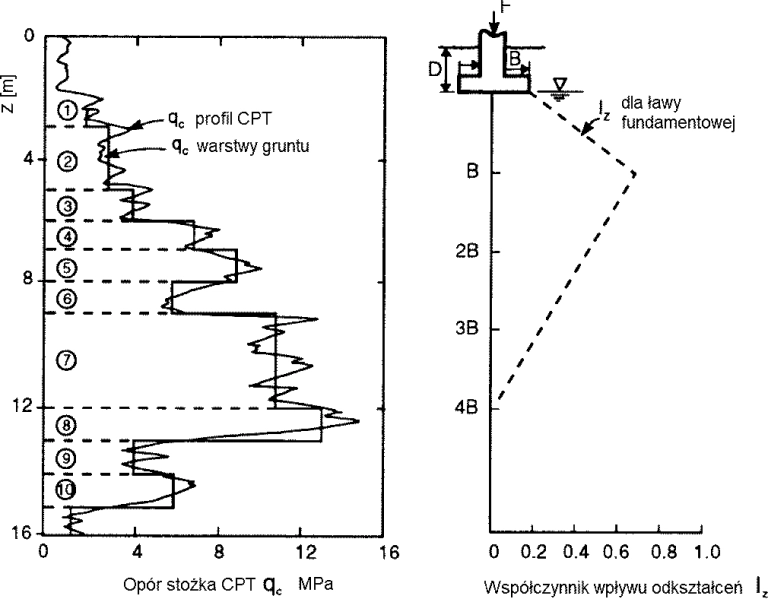
Rys. 23. Procedura wyznaczania przemieszczenia fundamentu metodą Schmertmann, (1978) [62]
W zależności od oporu stożka $q_c$ efektywny moduł Younga E’ w normie [13]:wskazano nawystępoeanie korelacj: $E’= 2,5 \cdot q_c$ dla stopy osiowosymetrycznej (kwadratowej lub kołowej) lub płyty L’/B’=1 ; $E’=3,5 \cdot q_c$ dla fundamentu pasmowego – ławy.
Należy jednak zwrócić uwagę, że korelacje te s,a już uwzględnione w mnożniku ujętym w nawiasy kwadratowe w ($\ref{53}$) ($C_3/1,25$ ). Wobec tego nie powinno się powtórnie ich stosować. Dla normalnie skonsolidowanych gruntów piaszczystych, niezależnie od kształtu fundamentu należy przyjmąc
$$ \begin{equation} E’ \approx 2,5\cdot q_c \label{59} \end{equation}$$
a dla innych gruntów wg tab.2.
Metoda Pieczyrak (1992)
Metoda Pieczyraka polega na uproszczonym całkowaniu rozkładu normalnych, pionowych naprężeń w podłożu pod środkiem rozpatrywanego fundamentu i jest odmianą metody naprężeń z zastosowaniem modułu edometrycznego.
Pieczyrak (1992) [63] przedstawił następującą formułę do szacowania osiadania gruntu:
$$\begin{equation} s=\cfrac{p \cdot B \cdot f}{M_0}\label {60} \end{equation}$$
gdzie:
p – obciążenie zastępcze na podstawę fundamentu – przyjmowane jako średni nacisk od obciążenia konstrukcji (mimośrody są uwzględniane poprzez wyznaczenie efektywnych wymiarów fundamentu zgodnie
$M_0$ – moduł edometryczny ściśliwości pierwotnej, a współczynnik osiadania $f$ w formule $(\ref{75})$ można wyznaczyć z zależności:
$$\begin{equation} f= \cfrac{\alpha}{\sqrt[4,3]{0,002 +0,021 \cdot \zeta_D} +(0,993+ 0,395 \cdot \zeta_D) \cdot \cfrac{\alpha}{\zeta_D}} \label {61} \end{equation}$$
gdzie:
$\alpha= \cfrac{L}{B}$
$\zeta_D= \cfrac{z_D}{B}$
$z_D$ – głębokość aktywna, na której zanika wpływ na osiadanie fundamentu: wg formuły $(\ref{45}$) lub zgodnie przez analogię do metody Schmertmanna (2B’ lub 4B’) lub Mayne-Poulos (max 5B’)
Metoda Mayne-Poulos (1999)
Mayne i Poulos (1999) [64] podają ulepszony wzór do obliczania sprężystego osiadania według modelu pokazanego na rys. 24. Uwzględniają sztywność fundamentu i jego zagłębienia fundamentu $D_f$. Efektywne (netto) naprężenia działające na grunt $p_i=p_0-\gamma_g \cdot z$ uwzględniają poprzez zwiększanie modułu sprężystości gruntu wraz z głębokością aż do sztywnych warstw położonych na ograniczonej głębokości.
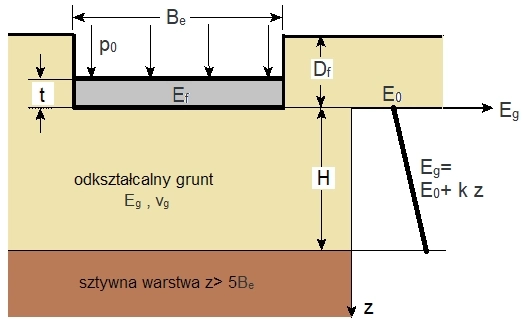
Rys. 24 Model Mayne-Poulos dio wyznaczania przemieszczeń fundamentu [64]
Formułę Mayne, Poulos można zapisać w postaci (Braja M. Das, (2011), Principles of Foundation Engineering, Seventh Edition, Cengage Learning, USA)) :
$$\begin{equation} s_e= p_0 \cdot B_e \cdot I_G \cdot I_F\cdot I_E \cdot \cfrac{1-\nu^2}{E_0}\label{62} \end{equation}$$
gdzie:
$p_0$ – równomiernie rozłożone obciążenie pod stopą fundamentu,
$B_e$ – miarodajna szerokość fundamentu
$$\begin{equation} B_e=\begin {cases}
\sqrt{ \cfrac{4 B L}{\pi}} \quad , & \text {dla fundamentu o podstawie prostokątnej BxL } \\
D \quad, & \text {dla fundamentu o podstawie kołowej średnicy D}
\end {cases} \label{63}\end{equation}$$
Gibson (1967) [65] zaproponował liniową formułę do opisu zagadnienia wzrostu modułu sprężystości gruntu $E_g$ wraz z głębokością w formie
$$\begin{equation} E_g= E_0 + k \cdot z \label{64} \end{equation}$$
gdzie:
$E_0$ – wartość modułu gruntu bezpośrednio pod podstawą fundamentu (z = 0);
$k$ – współczynnik szybkości wzrostów modułu wraz z głębokością $z$ (rys 24)
Współczynnik wzrostów modułu $k$ wyznacza się z badań gruntowych in situ (np. CPT i zależności korelacyjnych), przy czym znormalizowany współczynnik Gibsona $\beta$ przyjmuje wartości
$$\begin{equation} \beta= \cfrac{E_0}{k \cdot B_e} ;\quad \text {przy czym } 0,01 \le \beta \le 100 \label{65}\end{equation}$$
$I_G$ – współczynnik wpływu zmian modułu $E_g$ po głębokości, wyznaczany z nomogramu rys.25 dla współczynnika $\beta$ $(\ref {78})$ oraz $H/B_e$, czyli stosunku głębokości warstwy odkształcalnej $H$ do miarodajnego wymiaru fundamentu ($\ref{78}$):
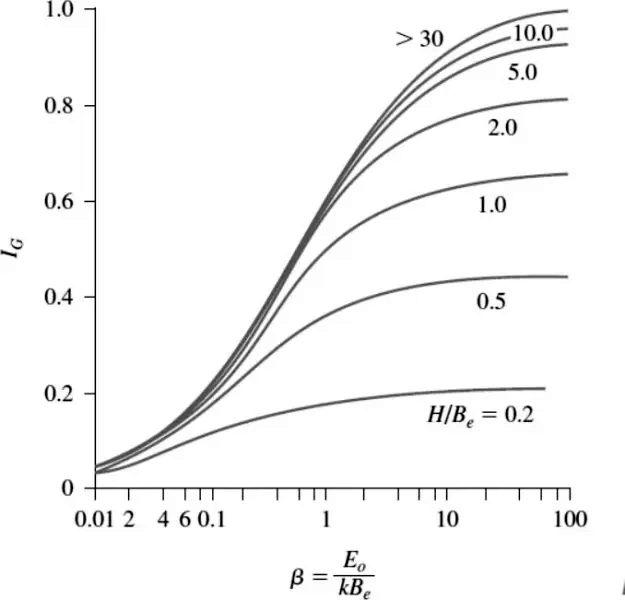
Rys. 25. Nomogram do wyznaczania współczynnika wpływu $I_G$ (Braja M. Das, (2011), Principles of Foundation Engineering, Seventh Edition, Cengage Learning, USA))
Współczynnik korekcyjny sztywności fundamentu wyznacza się z zależności:
$$\begin{equation} I_F= \cfrac{\pi}{15}+ \cfrac{1}{4,6 +10 \left( \cfrac{E_f}{E_0+ \cfrac{B_e}{2}\cdot k} \right ) \cdot \left ( \cfrac{2t}{B_e}\right)^3 } \label{66}\end{equation}$$
Współczynnik korekcyjny zagłębienia fundamentu wyznacza się z zależności:
$$\begin{equation} I_E= 1 \, – \cfrac{1}{3,5 \cdot \exp{(1,22 \cdot \nu -0,4)} \cdot \left(\cfrac{B_e}{D_f}+1,6 \right) } \label{67}\end{equation}$$
Współczynnik sprężystości (moduł) podłoża Ks
W analizach projektowych, zmierzających do ustalenia wymogów zagęszczenia podłoża pod budowle, należy uwzględnić, to, że:
a) dużą klasę konstrukcji należy posadowić na bardziej odkształcalnym podłożu, np. w warunkach sejsmicznych, na bagnach lub na morzu. Do istniejących warunków gruntowych należy dostosować schemat konstrukcji, poprzez zwiększenie jej podatności konstrukcji na obciążenia para/sejsmiczne ( skonstruowaniu przegubów wewnętrznych, łożysk sprężystych itd.). Do poprawnego zaprojektowania konstrukcji w tej klasie konieczne jest właściwe oszacowanie podatności/sztywności podłoża gruntowego.
b) dla wielu konstrukcji zagęszczenie podłoża do stopnia wskazywanego w ogólnych wytycznych może być nadmierne i nie jest wskazane, szczególnie gdy prowadzi do niejednorodności przestrzennej lub utraty wymaganej elastyczności lub porowatości podłoża i w konsekwencji do zaburzenia redystrybucji obciążeń i odporu gruntu oraz odwodnienia,
c) dla wielu innych konstrukcji zagęszczenie podłoża do stopnia wskazywanego w ogólnych wytycznych jest konieczne. Dotyczy to zwłaszcza tradycyjnych konstrukcji budowanych z materiałów kruchych (mury, beton i o tradycyjnych schematach statycznie niewyznaczalnych. Konstrukcje takie słabo znoszą niejednorodne lub nadmierne przemieszczenia podpór i wymaga dobrze zagęszczonego lub wzmocnionego podłoża, często nawet palowania.
W zależności od rodzaju konstrukcji i jej wrażliwości na osiadanie podłoża – wymogi zagęszczenia są ustalane indywidualnie przez Projektanta, który prowadzi analizy wytrzymałości i stateczności konstrukcji. Autor zaleca, by takie analizy były prowadzone przy różnym zagęszczeniu gruntu, tak by do realizacji został wybrany wariant optymalny ze względów techniczno-ekonomicznych. W praktyce występują bowiem różnorodne sytuacje zależne od indywidualnych cech konstrukcji (materiału i schematu statycznego), co decyduje o współdziałaniu z podłożem gruntowym poprzez ustalenie modułu podłoża.
Wymogi zagęszczenia gruntu do posadowienia konstrukcji należy rozpatrywać indywidulanie jako zagadnienie współdziałania konstrukcja-grunt, a posługiwanie się wyłącznie wytycznymi przepisów lub norm dotyczy w zasadzie tylko konstrukcji typowych i mało odpowiedzialnych, ( które najczęściej nie wymagają właściwego projektu indywidualnego).
Oddziaływanie zagęszczenia podłoża budowli na konstrukcję przejawia się zmianą warunków jej podparcia. We współczesnej analizie konstrukcji przyjmuje się model sprężystego podłoża Winklera, czyli takiego, w którym reakcje fundamentu są proporcjonalne do przemieszczenia fundamentu wraz ze współczynnikiem proporcjonalności (modułem ) $K_s$. Zalecane jest stosowanie modelu podłoża jednostronnego (nie przenoszącego rozciągania – odrywania od podłoża), choć w celu zoptymalizowania posadowienia należy dążyć do takiego ukształtowania fundamentu, by obciążenie działało w jego rdzeniu.
Moduł reakcji podłoża jest złożonym parametrem gruntowo-konstrukcyjnym, gdyż jego wartość zależy od sztywności podłoża i sztywności obciążonej konstrukcji oraz samego fundamentu. Moduł podłoża definiuje się jako
$$\begin{equation} K_s \stackrel {def} {=} \cfrac{F}{s} \label{68} \end{equation}$$
gdzie:
$F$- przyłożone obciążenie
$s$ wywołane przemieszczenie
Elementarne rozwiązania
Z elementarnego rozwiązania półprzestrzeni sprężystej z modułem Younga E’, obciążonej równomiernie obciążeniem $p$ na powierzchni koła o średnicy „D” wynika, że ugięcie $s$ w środku koła wyniesie [66]:
$$\begin{equation} s_e=\cfrac{ p \cdot D}{E_{plate}}[mm]\label{69} \end{equation}$$
gdzie płytowy moduł Younga $E_{plate}$ wynosi
$$\begin{equation} E_{plate} = \cfrac{E’} {1-\nu^2} \label{70} \end{equation}$$
Po podstawieniu $(\ref{69})$ do $(\ref{68})$ dla $s=s_e$ uzyskuje się moduł podłoża , który po odniesieniu do rozłożonego obciążenia $F= p$ można zapisać w postaci:
$$\begin{equation} K_{s,Ø} = \cfrac{E_{plate}}{D} [kN/(m^2\cdot mm) ] \label{71} \end{equation}$$
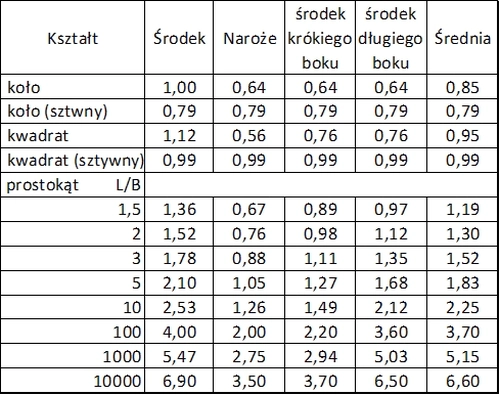
W przypadku innych od kołowego kształtów fundamentu uzyskamy inny wynik. Na przykład w przypadku fundamentu w kształcie kwadratu o boku „B” – przemieszczenie maksymalne wyniesie [66],zad. 3.58 :
$$\begin{equation} s_e=\cfrac{4}{\pi} \cdot ln(1+\sqrt{2}) \cdot \cfrac{ p \cdot B}{E_{pl} } \approx 1,122 \cdot \cfrac{ p \cdot B}{E_{plate}}\label{72} \end{equation}$$
czyli moduł podłoża przy odniesieniu do obciążenia $F=p$, wyniesie
$$\begin{equation} K_{s,□} = \cfrac {E_{plate}}{1,122 \cdot B} = K_{s,Ø}/1,122 \label{73} \end{equation}$$
Rezultat ($\ref{73}$) można uogolnć do formuły
$$\begin{equation} K_{s,F} = \cfrac {K_{s,Ø}}{C_d} \quad \text {czyli} \quad s_F= C_d \cdot s_Ø \label{74} \end{equation}$$
gdzie:
F- kształt fundamentu (kol.1 w tab. 19)
$C_d$ – współczynnik sztywności podany w tab 19.
Tab .19 Współczynniki sztywności podłoża $C_d$ w zależności od kształtu fundamentu Winterkorn, Fung (1975 [67]
Wyznaczania modułu podłoża Ks w praktyce
Formuły $(\ref{45})$ lub $(\ref{2})$ mają znaczenie tylko teoretyczne.
W praktyce moduł podłoża $K_s$ wyznacza się w ten sposób, że najpierw szacuje się osiadanie $s$ fundamentu posadowionego na uwarstwionym podłożu i następnie bezpośrednio korzysta z definicji $(\ref{69})$.
Jednostki modułu podłoża $K_s$ będą różne w zależności od rodzaju obciążenia $F$ w formule $(\ref{69})$.
Jeśli osiadanie s wyznaczono w mm, to:
- dla F w $[kN]$ (siła skupiona) jednostką będzie $[kN/mm]$
- dla F w $[kN/m]$ (obciążenie ,liniowe – np na ścianę i ławę) jednostką będzie $[(kN/m)/mm ]$
- dla F w $[kN/m^2$ (obciążenie powierzchniowe ) , to jednostką będzie $[(kN/m^2)/mm]$.Szacowania osiadania fundamentu
Po podstawieniu $(\ref{37})$ do $(\ref{69})$ otrzymujemy ogólną formułę na współczynnik sprężystości podłoża pod liniowym fundamentem o szerokości B obciążający grunt liniowo rozłożonym obciążeniem $F=p$
$$\begin{equation} K_s=\cfrac{E_m} { B \cdot f} \label {75} \end{equation}$$
gdzie $E_m$ obliczeniowy moduł gruntu zależny od metody szacowania osiadania ($\ref{37}$)
Szacunkowe wartości modułu Ks
Współczynnik reakcji podłoża nie jest parametrem gruntu, ponieważ zależy od wielkość stopy i stopień obciążenia. Często jednak szacunki wstępne są dokonywane z tabelach podanych przez Terzaghi (1955) [68], co podano w tab. 19 .
Tab. 20 Szacunkowe modułu podłoża $K_s$ dla różnych gruntów wg [68]
Moduł podłoża na obrót Ksφ
Rozważmy sytuację, w której płaska podstawa fundamentu obróci się o mały kąt $\varphi \approx tg \varphi$ (rys.23) :
$$\begin{equation} \varphi=\cfrac{\Delta s}{L} =\cfrac{1}{K_s} \cdot \cfrac{\Delta \sigma}{ L}\label {76} \end{equation}$$
gdzie:
różnica osiadań krawędziowych $ \Delta s= s_{max}-s_{min}$
różnica naprężeń krawędziowych $ \Delta \sigma= \sigma_{max}-\sigma_{min}$,
$K_s$ – moduł podłoża $(\ref{69})$
Przebieg naprężeń pod stopą można opisać zależnością
$$\begin{equation} \sigma (x) = ( K_s \cdot \varphi ) \cdot x + \sigma _{śr} \label {77} \end{equation}$$
Odpór gruntu $\sigma$ ($\ref{77}$) wywołuje:
siłę osiową $V=\int \limits_A \sigma dA=\sigma_{śr} \cdot A$
oraz moment sił :
$$\begin{equation} M= \int \limits_A \sigma \cdot x \cdot dA = ( K_s \cdot \varphi ) \int \limits_A x^2 \cdot dA =( K_s \cdot \varphi ) \cdot I_x \label {78} \end{equation}$$
gdzie $I_x=\cfrac{B\cdot L^2}{3}$ moment bezwładności przekroju względem osi x prostopadłej do boku $L$ fundamentu.
Stąd otrzymujemy definicję modułu podłoża na obrót fundamentu
$$\begin{equation} K_s^{\varphi} \stackrel {def} {=} \cfrac{M}{ \varphi} = K_s \cdot I_m \label {79} \quad [kNm/rad] \end{equation}$$
gdzie $I_m$- moment bezwładności podstawy fundamentu wokół osi obrotu ( m=x dla obrotu wokół osi równoległej do B oraz m=y dla obrotu wokół osi równoległej do L)
Należy zwracać uwagę na jednostki. Jeśli K_s jest w [ $kN/(m^2 \cdot mm$ ] a w I w [m^4}, to w celu uzyskania modułu gruntu na obrót w [kNm/rad] – wynik ($\ref{79}$) należy przemnożyć przez $10^{15}$ . Natomiast jeśli chcemy uzyskać wynik w [kNm/ deg}, to należy jeszcze uwzględnić, że $1 \, deg= \pi/180 \, rad$.
W przypadku analizy konstrukcji ze sprężystą podporą powierzchniową lub liniową – nie jest istotny moduł podłoża na obrót ($\ref{79}$) .
Przykłady
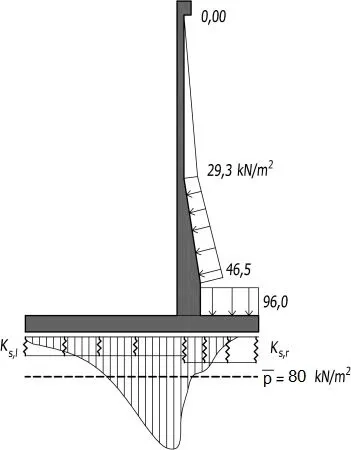
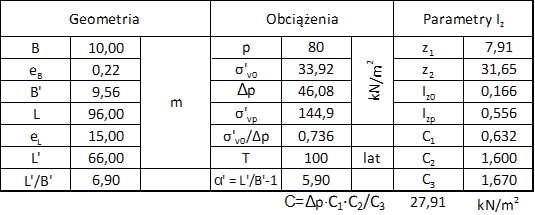
Przykład 1 [Ciśnienie geostatyczne i efektywne gruntu]
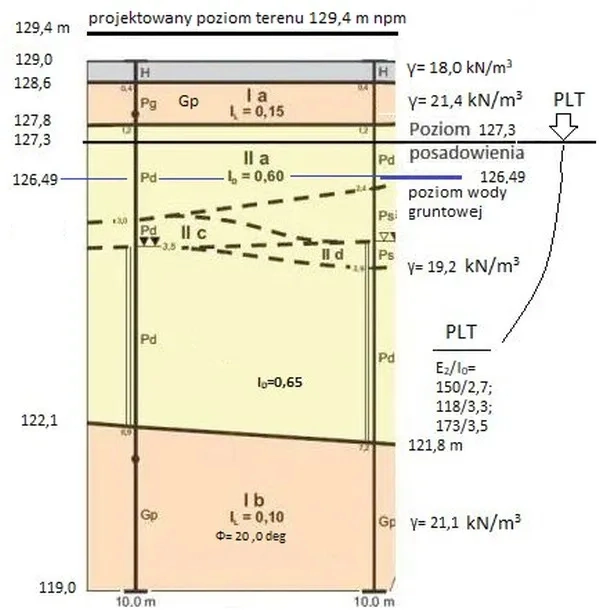
Na rys. 26 przedstawiono przekrój geotechniczny przez grunt, uzyskany w drodze klasycznych badań w miejscu przyszłego posadowienia budowli. Grunt jest uwarstwiony następująco istniejącego poziomu terenu 129,0 m npm licząc:< /p>
- gleba urodzajna (humus) do poz. 128, 6 m,
- warstwa „Ia” glina piaszczysta do poz. 127,8, stopień plastyczności $I_L=0,15$, ciężar właściwy $\gamma=21,4 \, kN/m^3$,
- warstwy ” II a -d” piasków drbnych do poz 122,1 – 122,8, stopień zagęszczenia: $I_D=0,60$ przy stropiwe warstwy do $I_D=0,65$ przy spągu wartwy, $\gamma= 19,2 \, kN/m^3$,
- warstwa „Ib” glina piaszczysta do poziomu odwiertów 119,0 m, stopień plastyczności $I_L=0,10$, kąt tarcia wewnętrznego $\Phi=20,0 \, deg$ ciężar właściwy $\gamma=21,1 \, kN/m^3$
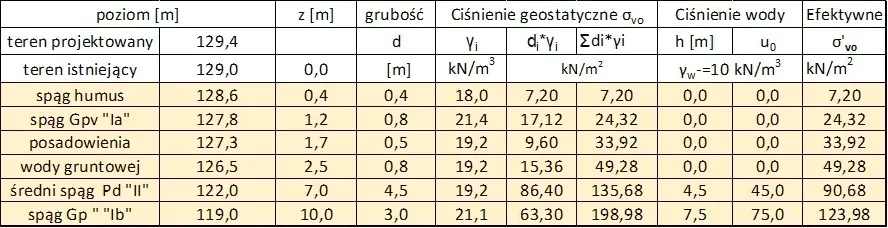
Sumowanie ciśnienia geostatyczne (przed wybudowaniem fundamentu) jest prowadzone od poziomu trenu istniejącego 129,0 m npm, czyli z warstw zaznaczonych piaskowym tłem w tab.21
Tab. 21 Ciśnienie geostatyczne i efektywne gruntudoptzykładu1
Na poziomie posadowienia ( 127,3 m npm ) ciśnienie geostatyczne gruntu wynosi na przykład:
($\ref{16}$) $\to$ $z= 129,0- 127,3= 1,7 \, m \quad \sigma_{v,0} (1,7) = 0,4 \cdot 18,0 + 0,8 \cdot 21,4 + 0,5 \cdot 19,2 = 33,92 \, kN/m^2$
Ciśnienie hydrostatyczne wody gruntowej o ciężarze objętościowym $\gamma_w= 10 kN/m^3$ na poziomie (122 m npm) nad spągiem warstwy piasku $P_d$
$z_w= 126,5-122= = 4,5 \, m \quad u_0= 10 \cdot 4,5 = 45,0 kN/m^2$
Efektywne ciśnienie gruntu na poz. 122 m
($\ref{17}$) $\to$ $\sigma’_{v0}= 33,92+ (0,8+4,5) \cdot 19,2 – 4,5 \cdot 10=135,68 – 45,0= 90,68 \, kN/m^2$
Przykład 2 [Moduł gruntu sypkiego dla znanego ID poprzez korelacje CPT]
Dla gruntów sypkich z przekroju geotechnicznego z rys. 26: nie są dostępne wyniki badań CPT. Dokonać prognozy parametrów badania CPT z korelacji ($\ref{30}$) i rys.10. i następnie oszacować moduły gruntu ze znanych korelacji do badań CPT
Prognoza parametrów badania CPT ze znanego $I_D$
Dla warstwy Pd „II” górnej wg rys. 26 poziom 127, 3 m $I_D=0,6$:
($\ref{30}$) $\to$ $ q_c= exp \left ( \tfrac{0,60 – 0,354}{0,164} \right) = 4,5 \, MPa$ (wg Lacellota ),
rys.10, $\to$ dla $q_c= 4,6 \, MPa$ i piaski $\to$ $F_r= 0,1 $%
Analogicznie przeprowadzono prognozy dla warstwy Pd „II dolnej na poziomie poziomie 122,0 m, $I_D=0,65$ i zestawiono w tab. 21
Prognoza modułu E’ na podstawie parametrów CPT
Dla warstwy Pd „II” górnej
($\ref{14}$) $\to$ $q_t=q_c =4,5 $ (piaski),
($\ref{15}$) $\to$ $q_n= 4,5 – 33,92/1000= 4,5 -0,03 = 4,5 \, MPa$,
($\ref{18}$) $\to$ $Q_t = \cfrac{4,5}{ 33,92/1000}= 132 $,
($\ref{19}$) $\to$ $ Q_{tn} = Q_t = 132 $ (n=1),
($\ref{25}$) $\to$ $I_c=\sqrt{ (3,47 – log 132)^2 +( 1,22+log 0,1)^2} = 1,38$
Klasyfikacja gruntu Robertsona
$Q_t=132$ ; $F_r=0,1$% ; $I_c= 1,38$
rys. 11 $\to$ typ 6 – piasek słabo skonsolidowany
Moduł Younga E’
($\ref{32}$) $\to$ $\alpha_E = 0,015 \cdot 10 ^{(0.55 \cdot 1,38 + 1.68)}= 4,1$
($\ref{2}$) $\to$ $ E’ =4,1 4,5 =18,4 \, MPa$
Analogicznie przeprowadzono prognozy dla warstwy Pd „II dolnej na poziomie poziomie 122,0 m, $I_D=0,65$ i zestawiono w tab. 21
Dla tej warstwy z klasyfikacja gruntu Robertsona dla $Q_t=68$ ; $F_r=0,1$% ; $I_c= 1,66$
rys. 11 $\to$ typ 6 – piasek słabo skonsolidowany
Moduł Younga E’
$E’= 35,8 \, MPa$
W tab.. 22 zestawiono wyniki obliczeń: przeliczenia parametrów klasycznych na parametry CPT oraz oszacowanie modułu Younga E’ z korelacji CPT przeprowadzone metodą Robertsona dla grunt ów sypkich (warstwa II).
Tab.22. Korelacje pomiędzy badaniami klasycznymi a CPT oraz moduł Younga E’ metodą Robertson dla piasków (wartswa „II”

Przykład 3 [Moduł gruntu spoistego dla znanego IL poprzez korelacje CPT]
Prognoza parametrów badania CPT ze znanego $I_L$
Dla warstwy Gp „Ib” wg rys. 26 poziom 119,03 m $I_L=0,1$:
rys. 14 dla kąta tarcia wewnętrznego Φ=20,0 deg (z badań klasycznych) $\to$ $q_c =10^{\tfrac{0,518 – 0,1}{0,653}}= 4,4 \, MPa$,
($\ref{23}$) $\to$ $f_s= 0,17 \cdot \exp{(-4,6 \cdot 0,1)}= 0,11 \, MPa$.
Prognoza modułu E’ na podstawie parametrów CPT
($\ref{15}$) $\to$ $q_n= 4,4 – 198,98/1000= 4,4 -0,2 = 4,2 \, MPa$,
($\ref{18}$) $\to$ $Q_t = \cfrac{4,2}{ 123,98/1000}= 34 $,
($\ref{19}$) $\to$ $ Q_{tn} = Q_t = 34$ (n=1),
($\ref{21}$) $\to$ $F_r= \cfrac{0,11}{4,2} \cdot 100= 2,6 $ %
($\ref{25}$) $\to$ $I_c=\sqrt{(3,47 – log 34)^2 +( 1,22+log 2,6)^2}= 2,57$
Klasyfikacja gruntu Robertsona
$Q_t=34$ ; $F_r=2,6$% ; $I_c= 2,57$
rys. 11 $\to$ typ 3 – glina bliska normalnej konsolidacji
Moduł Younga z korelacji ($\ref{5}$),($\ref{6}$) (poprzez $M’$ i $\alpha_M$):
($\ref{6}$) $\to$ $\alpha_M =14$ ( dla $I_c>2,2$ i $Q_t>14$),
($\ref{5}$) $\to$ $M’=14 \cdot 4,2 = 58,3 \. MPa$,
Współczynnik Poissona dla $G_p$: tab.5 ( grunt typu B) $\to$ $\nu=0,29$ ; tab. 3 $\nu=0,4$
Przyjęto $nu=0,35$
($\ref{4}$) $\to$ $\delta= \cfrac{(1+\nu)\cdot (1- 2 \nu)}{1- \nu}= \cfrac{(1+0,35)\cdot (1- 2 \cdot 0,35)}{1- 0,35} = 0,623 $
($\ref{3}$) $\to$ E’=0,623 \cdot 58,3 = 45,5 \, MPa $
Dla porównania z korelacji ($\ref{2}$) jak dla gruntów sypkich :
($\ref{32}$) $\to$ $\alpha_E = 0,015 \cdot 10 ^{(0.55 \cdot 2,54 + 1,68)}= 17,9$
($\ref{2}$) $\to$ $ E’ =17,9 \cdot 4,2 =75,2 >> 45,5 \, MPa$
Ten wynik nie jest miarodajny. Przyjęto $E’=45,5 \, MPa$
W tab.. 22 zestawiono wyniki obliczeń: przeliczenia parametrów klasycznych na parametry CPT oraz oszacowanie modułu Younga E’ z korelacji CPT przeprowadzone metodą Robertsona dla gruntu spoistego (warstwa Ib).
Tab.23. Korelacje pomiędzy badaniami klasycznymi a CPT oraz moduł Younga E’ metodą Robertson dla gliny
Przykład 4 [Osiadanie. Metoda Schmertmann]
Konstrukcję hali posadowiono na ławach fundamentowych w sposób pokazany na rys. 27 .
Prostokątne ławy pod ścianami mają wymiary w planie:
$B= 10 \, m$
$L=96 \, m$
na głębokości
$D_f = \,2,1 \, m$
Konstrukcję posadowiono na podłożu piaszczystym uwarstwionym wg rys.26.
Obciążenie gruntu fundamentem pokazano na rys. 28
Średni odpór $\overline p= 80\, kN/m^2$
z mimośrodem w kierunku szerokości ławy (uzyskanym przez całkowanie odporu):
$e_B= 0,22 \, m$,
($\ref{38}$) $\to$ $B’= 10- 2 \cdot 0,22= 9,56 \, m$,
$ e_L \approx 15 \, m$,
$L’=96 -2 \cdot 15= 66 \,m $,
$L’/B’= 66/9.56 = 6,90$,
$\alpha’= 6,90-1 = 5,9$.
Moduły sprężystości warstw gruntu
Moduły sprężystości E’ warstw gruntu wyznaczono w przykładzie 2 dla gruntów sypkich i przykładzie 3 dla gruntu spoistego:
warstwa Pd „II” górna $ E’= 18,4 /,MPa$ przy oszacowanym $q_c= 4,5 \,MPa$, czyli $x=18,4/4,5 = 4 \in (2 \div 4)$ dla piasku normalnie skonsolidowanego wg tab.2
warstwa Pd „II” dolna $ E’= 35,8 /,MPa$ przy oszacowanym $q_c= 6,1 \,MPa$, czyli $x=35,8/6,1= 5,9 \in (3,5 \div 7)$ dla piasku nasyconego wg tab.2
warstwa Gp „Ib” $E’=45,5 \, MPa$ , przy oszacowanym $q_c= 4,4 \,MPa$, czyli $x=35,5/4,4= 8 \in (3 \div 8) $ dla gliny wg tab.2
Punkty charakterystyczne nomogramu Schmartmanna
($\ref{54}$) $\to$
$\cfrac{z_1}{B’}= 0,5+0,0555 \cdot 5,9 = 0,827 \le 1$
$\cfrac{z_2}{B’}= 2+0,222 \cdot 5,9= 3.31 \le 4$
$I_{z0} = 0,1+0,0111 \cdot 5,9 = 0,166 \le 0,2$
$z_1= 0,827 \cdot 9,56= 7,91 \, m $
$z_2 = 3,31 \cdot 9,56= 31,65 \, m$
Tab. 24 Zestawienie obciążeń i punktów charakterystycznych nomogramu Schmertmann
Szczytowy współczynnik wpływu $I_{zp}$
($\ref{57}$) $\to$ ${\sigma’}_{v,0} =0,4 \cdot 18,0 + 0,8 \cdot 21,4 + 0,5 \cdot 19,2 = 33,92 \, kN/m^2$
($\ref{56}$) $\to$ $\Delta p = 80,0 -33,92 = 46,08 \, kN/m^2$
($\ref{51}$) $\to$ ${\sigma’}_{v,p} = 33,92+ 0,8\cdot 19,2 + (2,28+2,27)\cdot (19,2-10,0) +2,55 \cdot 21,1 =144,9 \, kN/m^2$
($\ref{55}$) $\to$ $I_{zp} =0,5 +0,1 \cdot \sqrt{ \cfrac{46,08}{144,9}}= 0,556$
Wspłczynniki Schmertmann
($\ref{51}$) $\to$ $C_1= 1-0,5 \cdot \cfrac{ {33,92}}{46,08}= 0,632$
$T=100$ lat
($\ref{52}$) $\to$ $C_2= 1+0,2 \cdot log (10 \cdot 100)=1,6$
($\ref{53}$) $\to$ $C_3= 1,25 \cdot ( 1 +0,4 \cdot log 6,9) = 1,67$
Osiadanie fundamentu
W tab.24 zestawiono obliczenia osiadania i współczynnika sprężystości podłoża. W kolumnach „Warstwy” podano numery warstw i ich symbolikę wprowadzoną na , rys. 26. , a w kolejnych kolumnach: poziom stropu i spągu warstwy,, rzędną z liczona od poziomu terenu przed wybudowaniem fundamentu., grubość warstwy $d$, ciężar właściwy gruntu $\gamma_s$ , ciężar właściwy wody $\gamma_w$ i ciężar efektywny $\gamma’=\gamma_s-\gamma_w$ (jeśli woda występuje w warstwie) oraz ciężar warstwy $ g=\gamma’ \cdot d$.
W bloku „współczynnik wpływu” podano efektywny moduł Younga $E’$ wyznaczony w przykładzie 2 i przykładzie 3. W kolumnie $I_z$ podano współczynniki wpływu $I_z$ na rzędnej stropu i spągu warstwy oraz w środku warstw wg wzoru ($\ref{58}$)
Na przykład w warstwie 4 dla $z= 1,7 \, i \, 2,5 \le z_1= 7,91 \, m $ mamy:
($\ref{58}$) $\to$ $ I_z (1,7) = 0,166- (0,166-0,556) \cdot \cfrac{1,7}{7,91}= 0,250$
$\to$ $ I_z (2,5) = 0,166- (0,166-0,556) \cdot \cfrac{2,5}{7,91}= 0,289$
$I_z$ na środku wartswy $(0,250+0,289)/2= 0,269$
Natomiast w warstwie 8 dla $z= 9,6 \, i \, 10,0 \ge z_1= 7,91 \le z_2 = 31,65 \, m $ mamy:
($\ref{58}$) $\to$ $ I_z (9,6) =0,556 \cdot \cfrac{31,65-9,6 }{31,65- 7,91}= 0,517$
$\to$ $ I_z (10,0) =0,556 \cdot \cfrac{31,65-9,6 }{31,65- 7,91}= 0,507$
$I_z$ na środku warstwy $(0,517+0,507)/2= 0,512$
W kolejnej kolumnie podano efektywne grubości warstw. Na przykład dla warstwy 4 , mamy
$d’=0,269\cdot 0,80= 0,215 \, m$.
W ostatniej kolumnie wyliczono składową osiadania warstwy. Na przykład dla warstwy 4 , mamy
$s_{(4)} = 0,215/ 18,4= 0,0117 \quad m/MPa$
Suma współczynników z ostatniej kolumny wynosi $\sum (d’\cdot E’) = 0,12048 \quad m/MPa$
Iloczyn mnożnika z tab. 21 $C=\delta p \cdot C_1 \cdot C-2/C_3= 46,08 \cdot 0,632 \cdot 1,600 / 1,67= 27,91 \, kN/m^2$
i suma współczynników $\sum (d’\cdot E’)$ jest osiadaniem fundamentu
($\ref{45}$( + ($\ref{48}$) $\to$ $s_e= 27,91 \cdot 0,12048 \cdot 10^{-3}= 3,48 \cdot 10^{-3} \.m= 3,48 \, mm$
Tab.24 Tabela obliczeń osiadania i modułu podłoża
Współczynnik sprężystości (moduł) podłoża
($\ref{68}$) $\to$ $K_s = \cfrac{80}{3,4 }= 23,4 \, kN/(m^2 \cdot mm)$
Przykład 5 [Metoda Mayne-Poulos]
Konstrukcja posadowiona jest za pośrednictwem stopy wg rys. 22 na glinie pylastej o parametrach (uzyskanych w badaniach in-situ):
grubość warstwy odkształcalnej (gliny pylastej) $H=3,66 \, m$,
moduł Ypunga gruntu pod podstawą fundamentu $E_0= 9700 \, kN/m^2$,
współczynnik zmian modułu po głębokości $k=600 \, (kN/m^2)/m$
współczynnik Poissona $\nu_s = 0,3$
Stopa fundamentowa ma wymiary:
$B= 1,52 \, m$,
$L=3,05 \, m$
$t= 305 \, mm$
Głębokość posadowienia
$D_f= 1,52 \, m$
Nacisk stopy w poziomie posadowienia (obciążenie gruntu):
$p_0 = 240 \, kN/m^2$ bez mimośrodów
Moduł sztywności materiału stopy
Stopa wykonana jest z betonu C30/37 i zbrojona stalą B500
Z tab W-1 ( artykuł Belki żelbetowe) mamy:
średni moduł Younga betonu $E_{cm} =33 \, GPa$
orientacyjny współczynnik pełzania $\varphi= 2,278$ (dla wilgotności RH=50%, wymiaru $h_0 = 100 \, mm$ oraz po czasie $t_0=28 \, dni$)
Do niniejszego przykładu przyjęto.
$\varphi = 3$
W innych przypadkach współczynnik pełzania należy wyznaczyć wg artykułu Współczynnik pełzania.
Efektywny moduł sprężystości betonu wyznaczono wg artykułu Efektywny moduł odkształcalności. z zależności
$E_{c,ef}= \cfrac{E_{cm}}{1+\varphi} =\cfrac{33}{1+3}= 8,3 \cdot 10^6 \, MPa$
Osiadanie fundamentu metodą Mayne-Poulos
$(\ref{78})$ $\to$ dla fundamentu o podstawie prostokątnej
$ B_e= \sqrt{ \cfrac{4\cdot 1,52 \cdot 3,05}{\pi}}= 2,43 \, m$
$(\ref{78})$ $\to$ $ \beta= \cfrac{9700}{600 \cdot 2,43}= 6,65 \ge 0,01 \, \le 100$
$H/B_e= 3,66/ 2,43 = 1,51$
rys. 27 (dla $\beta= 6,65$ i $ H/B_r=1,51$ $\to$ $I_G \approx 0,67$
$(\ref{77})$ $\to$ $I_F= \cfrac{\pi}{15}+ \cfrac{1}{4,6 +10 \left( \cfrac{8,3 \cdot 10^6}{9700 + \cfrac{2,43}{2}\cdot 600} \right ) \cdot \left ( \cfrac{2\cdot 0,305}{2,43}\right)^3 } =0,793$
$(\ref{{78})$ $\to$ $I_E=1- \cfrac{1}{ 3,5 \cdot exp (1,22 \cdot 0,3 -0,4) \cdot \left( \cfrac{2,43}{1,52}+1,6 \right) } =0,908 $
$(\ref{77})$ $\to$ $ s_e= 240 \cdot 2,48 \cdot 0,67 \cdot 0,793 \cdot 0,908 \cdot \cfrac{1-0,3^2}{6700} =0,039 \, m = 39 \, mm$
Moduł podłoża
($\ref{69}) \to$ $K_s= \cfrac{240}{75} = 6,15 \, kN/(m^2\cdot mm)$
($\ref{75}) \to$ $K_{s,L}^{\varpi}= 6,15 \cdot \cfrac{1,52 \cdot 3,05^3}{3} = 22,10 \cdot 10^3 \, kNm/rad$
Przykład 6 [Metoda Pieczyrak]
Postawienie zadania
Dla danych jak w przykładzie 5 osiadanie fundamentu wyznaczyć metodą Pieczyraka.
Moduł edometryczny
z zależności ($\ref{15}$) uzyskujemy
$M_0=E_0 \cdot \cfrac{1-\nu_s}{(1+\nu_s)(1-2\cdot \nu_s}= 6700 \cdot\cfrac{1-0,3}{(1+0,3)(1-2\cdot 0,3)}= 6700 \cdot 1,35 = 9045 \, MPa$
Współczynnik przemieszczenia
Ponieważ $H=3,66 \le 5\cdot B_e = 5\cdot 2,43= 12,15 \, m$, więc głębokość zanikania naprężeń sprawczych przyjmuje się $z_D= H= 3,66 \,m$
$\zeta_D= \cfrac{z_D}{B}= 3,66/1,52= 2,41$
$\alpha= \cfrac{3,05}{1,52}= 2,01$
$(\ref{76}$) $\to$ $f= \cfrac{2,01}{\sqrt[4,3]{0,002 +0,021 \cdot 2,41} + (0,993+ 0,395 \cdot 2,41) \cdot \cfrac{2,01}{2,41}}= 1,239$
$(\ref{75})$ $\to$ $ s= \cfrac{240 \cdot 1,52 \cdot 1,239}{9045}= 0,050 \, m = 50 \, mm$
Osiadanie uzyskane metodą P:ieczuraka ( daną metodą naprężeń) jest o 39/50= 28% większe od osiadania uzyskanego metodą Mayne-Poulous. Przyczyną są mniej dokładne założenia metody Pieczyraka, a przede wszystkim nie uwzględnienie głębokości posadowienia ( przekrycia fundamentu przed wypieraniem gruntu)
Moduł podłoża
($\ref{69}) \to$ $K_s= \cfrac{240}{58} = 4,8 \, kN/(m^2\cdot mm)$
($\ref{75}) \to$ $K_{s,L}^{\varpi}= 4,8 \cdot \cfrac{1,52 \cdot 3,05^3}{3} = 17,25 \cdot 10^3 \, kNm/rad$
Literatura
- Saftner D., (2018), Cone Penetration TestDesign Guide for State Geotechnical Engineers, Report 2018-32, Minnesota Department of Transportation Research Services & Library
- Robertson P.K., Cabal K.L., (2015), Guide to Cone Penetration Testing for Geotechnical Engineering, Gregg Drilling & Testing, Inc, 6 th Edition
- Sanglerat, G.. (1972), The Penetrometer and Soil Exploration. Elsevier Pub.,Amsterdam
- Meigh, A.C. (1987), Cone Penetration Testing: Methods and Interpretation. Butterworths, London
- Mayne, P.W., (2005), Integrated Ground Behavior: In-Situ and Lab Tests, Deformation Characteristics of Geomaterials, Vol. 2 (Proc. Lyon), Taylor& Francis, London, p. 155-177
- Lunne T., Robertson P.K., Powell J.J.M. (1997), Cone Penetration Testing in Geotechnical Practice
- Robertson, P.K., (2009), Interpretation of cone penetration tests – a unified approach., Canadian Geotechnical Journal, 46:1337-1355
- Bowles J., E., (1997), Foundation analysis and design, Fifth Edition, McGraw-Hill Companies, NY, …
- PKP, (2014) Wytyczne badań podłoża gruntowego dla potrzeb budowy i modernizacji infrastruktury kolejowej, Wydawnictwo PKP, Warszawa
- Gunaratne M., (2014), Foundation Engineering Handbook, Second Edition, CRC Press, Boca Raton,
- AASHTO (2004 with 2006 Interims). (2001), AASHTO LRFD Bridge Design Specifications. 3rd
Edition, American Association of State Highway and Transportation Officials, Washington, D.C - U.S. Department of Transportation,Federal Highway Administration, Soil and Foundation, Reference Manual – Volume I Publication No. FHWA NHI-06-088
- PN-EN 1992-2:2009. Eurokod 7. Projektowanie geotechniczne Część 2: Rozpoznanie i badanie podłoża gruntowego
- PN-B-03020:1981, Grunty budowlane – Posadowienie bezpośrednie budowli – Obliczenia statyczne i projektowanie
- (PN-B-03020:1981, Grunty budowlane – Posadowienie bezpośrednie budowli – Obliczenia statyczne i projektowanie
- Kłosiński B., Grzegorzewicz K., i. in. , (1998), Instrukcja badań podłoża gruntowego budowli drogowych i mostowych, cz. 1 i 2 , IBDiM Warszawa
- Wiłun Z., (2013), Zarys geotechniki, WKŁ, Warszawa
- PN-EN ISO 14688-2: 2018, Rozpoznanie i badania geotechniczne – Oznaczanie i klasyfikowanie gruntów — Część 2: Zasady klasyfikowania
- PN-EN 1997-1:2008 Eurokod 7 Projektowanie geotechniczne – Część 1: Zasady ogólne
- PN-B-06050/Ap:1999, Geotechnika – Roboty ziemne -Wymagania ogólne
- PN-EN 1991-3:2009, Oddziaływania na konstrukcje. Część 1-3: Obciążenia śniegiem
- PN-EN 1990, Podstawy projektowania konstrukcji
- Judycki J., zespół KDiMIID (2014), Katalog typowych konstrukcji nawierzchni podatnych i półsztywnych, Generalna Dyrekcja Dróg Krajowych i Autostrad
- PN-S-02205:1998, Drogi samochodowe. Roboty ziemne. Wymagania i badania
- PN-S-02205, Drogi samochodowe. Roboty ziemne. Wymagania i badania
- GEO24, (2004) Zbiór wymagań zagęszczenia gruntu dla budownictwa i drogownictwa [http://www.geo24.eu/wymagania%20zageszczenia%20gruntu.pdf]
- Hajduk P. (2013), Projektowanie podłóg przemysłowych, PWN, Warszawa, 2013
- PN-EN ISO 22475-1, Rozpoznanie i badania geotechniczne – Pobieranie próbek metodą wiercenia i odkrywek oraz pomiary wód gruntowych -Część 1: Techniczne zasady wykonania
- PN-B-04452: 2002 Geotechnika – Badania polowe
- Massarsch K.R., Fellenius B., H., (2014), Use of CPT for design, monitoring, and performance verification of compaction projects, 3rd International Symposium on Cone Penetration Testing, Las Vegas, Nevada, USA – 2014, p. 1187- 1200
- Jermołowicz P., (2019), Problematyka zagęszczania i stabilizacji gruntów w budownictwie. Technologie i ich skuteczność. Zasady projektowania i wykonawstwa. Materiały szkoleniowe [ https://www.opl.piib.org.pl/component/phocadownload/category/14-wszystkie-branze?download=786:problematyka-zageszczania-i-stabilizacji-gruntow-w-budownictwie-technologie-i-ich-skutecznosc-zasady-projektowania-i-wykonawstwa-21-03-2019-r ]
- Sikora Z., (2006).: Sondowanie statyczne metody i zastosowanie w geoinżynierii, Wydawnictwo Naukowo-Techniczne, Warszawa
- Wroth C.,P. , Wood D.,M., (1978) The correlation of index properties with some basic engineering properties of soils, Canadian Geotechnical Journal 15(2), pp. 137–145
- Robertson P.,K., Campanella R.G., (1983), Interpretation of cone penetration tests. Part I: Sand, Canadian Geotechnical Journal 20, pp. 718-733
- Robertson, P.K., (2010), Soil behaviour type from the CPT: an update. 2nd International Symposium on one Penetration Testing, CPT’10, Huntington Beach, CA, USA
- ASTM D2487 (2000), Standard Classification of Soils for Engineering Purposes – Unified Soil Classification System
- PN-EN ISO 22476-1:2013-03 Rozpoznanie i badania geotechniczne. Badania polowe. Część 1: Badania sondą statyczną ze stożkiem elektrycznym oraz piezo-elektrycznym
- PN-EN 1997-2:2009 Eurokod 7 Projektowanie geotechniczne – Część 2: Rozpoznanie i badania podłoża gruntowego
- Terzaghi (1955), On Coefficients of Subgrade Reaction
- Bergdahl, U., Ottosson, E., Malmborg, B.S. (1993), Plattgrundlaggning, Stockholm: AB Svensk Byggtjanst
- Terratest, Instrukcja obsługi lekkiej płyty dynamicznej do dynamicznych badań nośności „TERRATEST4000 USB“ „TERRATEST5000 BLU“
- Rafalski B (Red) (2005), Badanie i ustalanie zależności korelacyjnych dla oceny stanu zagęszczenia i nośności gruntów niespoistych płytą dynamiczną , IBDiM, Warszawa, listopad 2005
- Instrukcja obsługi sondy dynamicznej ZORN ZFG3000
- Bagińska I.,(2015) Ocena stopnia zagęszczenia gruntu sondą dynamiczną DPH i sondą statyczną CPTU, Przegląd komunikacyjny, 3/2015, str. 6-10
- Filipowicz A., Frankowski Z., Wysokiński L., (1994), Projekt normy – Podłoże gruntowe i fundamenty. Badania polowe. Sondowania. arch. ITB, arch. PKN, 1994
- Borowczyk M., Frankowski Z. (1985)., Problemy interpretacji wyników sondowań dynamicznych w gruntach niespoistych, Inżynieria i Budownictwo, nr 7-8,1985
- Melnikov A.V., Boldyrev G.G. (2015), Correlations between СPT resistance and Young modulus of soils, Soil Mechanics and Foundation Engineering , January 2015
- Wysokiński L. i zespół, (2008), Projekt badawczo-rozwojowy, KBN Nr 4 T07E 047 30 Zależności regionalne parametrów geotechnicznych na podstawie sondowań , badań laboratoryjnych i pomiarów osiadań, ITB, Warszawa
- Wysokiński L, Kotlicki W., H., Godlewski T, (2011), Projektowanie geotechniczne według Eurokodu 7. Poradnik, ITB, Warszawa
- Österreichische Forschungsgesellschaft Straße-Schiene-Verkehr F.S.V / Austriackie Stowarzyszenie Badawcze Drogi-Kolej-Transport, (2008), Austriackie przepisy kontrolne RVS 08.03.44, Wydanie z 1 marca 2008
- Rafalski B (Red) (2005a), Badanie i ustalanie zależności korelacyjnych dla oceny stanu zagęszczenia i nośności gruntów niespoistych płytą dynamiczną, Załącznik.1, IBDiM, Warszawa, listopad 2005
- PN-B-02481:1998, Geotechnika — Terminologia podstawowa, symbole literowe i jednostki miar
- Meyerhof G. G., (1951), The ultimate Bering capacity of foundations. Geotechnique, 2, 1951, 301-332
- Lancellotta R., (2009), Geotechnical Engineering. Second Edition. Taylor &Francis, London, New York) lub Pieczyraka
- Pieczyrak J. (2013), Nośność jednorodnego podłoża gruntowego, Inżynieria Morska i Geotechnika, nr 5/2013 [http://imig.pl/pliki/artykuly/2013-5/2013-5_431-441_Pieczyrak.pdf]
- Harr M. E., (1971), Foundations of Theoretical Soil Mechanics. Izdatielstvo Literatury po Stroitielstvu, Moskwa
- Schmertmann, J. H., Hartman, J. P., Brown, P. R. (1978). „Improved Strain Influence Factor Diagrams.” American Society of Civil Engineers, Journal of the Geotechnical Engineering Division, 104 (No. GT8), 1131-1135
- Schmertmann, J.H., (1978). Guidelines for cone penetration tests performance and design. Federal Highways Administration, Washington, D.C., Report FHWA-TS-78-209
- Braja M. Das, (2011), Principles of Foundation Engineering, Seventh Edition, Cengage Learning, USA
- Terzaghi K., R. Pecko B., Mesri G..,(1996), Soil Mechanics in Engineering Practice, 3rd Edn.,Wiley, New York,
- Salgado R., (2008), The Engineering of Foundations, McGraw-Hill, New York
- Schmertmann, J.H. 1978. Guidelines for cone penetration tests performance and design. Federal Highways Administration, Washington, D.C., Report FHWA-TS-78-209
- Pieczyrak J., (1992), Analiza osiadań metoda naprężeń. Inżynieria i Budownictwo, nr 8/1992. 302-304
- Mayne, P. W., and Poulos, H. G. (1999). “Approximate Displacement Influence Factors for Elastic Shallow Foundations,” Journal of Geotechnical and Geoenvironmental Engineering, ASCE, Vol. 125, No. 6, pp. 453–460.
- Gibson, R. E. (1967), Some results conceming displacements and stresses in a nonhomogeneous elastic half-space., Geotechnique, London, 17(1), 58-67
- Krzyś, Życzkowski, (1962), Sprężystość i plastyczność. Wybór zadań i przykładów, PWN, Warszawa
- Winterkorn H., F., Fung F.Y. (1975), Foundation Engineering HandbookVan Nostrand Reinhold Company
- Terzaghi (1955), On Coefficients of Subgrade Reaction
________________________________