Trwa remanent po dużej awarii portalu. Przepraszam za nieczytelną część treści do zakończenia remanentu !
Artykuł w ciągu ostatnich 24 godzin czytało 7 Czytelników
Uwagi i recenzje podręcznika przesyłać na adres wydawnictwa: wydawnictwo@chodor-projekt.net lub leszek.chodor@chodor-pojekt.pl
spis treści prodręcznika: [ Imperfekcyjna metoda projektowania konstrukcji ]
Część 1-2
Nawigacja: [ 1-1: Imperfekcyjna metoda projektowania. Wprowadzenie ] ⇐ ⊗ ⇒ [ 2-1: Imperfekcje konstrukcji i ich źródła ]
Przedstawiona w artykule klasyfikacja metod wymiarowania konstrukcji, dotyczy konstrukcji żelbetowych, stalowych, zespolonych aluminiowych, drewnianych oraz murowych i jest opracowana na podstawie norm do projektowania tych konstrukcji: [1], [2], [3], [4], [5], [6]. Na prostych przykładach zaprezentowano i porównano nowoczesne metody imperfekcyjne z klasycznymi metodami wyboczeniowymi. Do metod wyboczeniowych zaliczamy metody wywodzące się z formuły Ayrton-Perry, a do metod imperfekcyjnych metody, w których imperfekcje geometryczne stanowią bezpośrednie wymuszenia podczas analizy statycznej konstrukcji metodami II rzędu.
Klasyfikacja i cechy metod wymiarowania konstrukcji
Metody wymiarowania konstrukcji budowlanych można podzielić na dwie grupy
WM – Wyboczeniowe Metody
IM – Imperfekcyjne Metody
W każdej z tych grup w sposób odmienny uwzględnia się imperfekcje geometryczne konstrukcji i jej elementów oraz stosuje inne współczynniki materiałowe (częściowe współczynniki bezpieczeństwa)
Klasyfikacja metod wyboczeniowych i imperfekcyjnych
Na rys. 1 pokazano schemat klasyfikacyjny metod wymiarowania konstrukcji z uwzględnieniem nowoczesnych metod imperfekcyjnych. W schemacie przewidziano miejsce dla uogólnionej metody alternatywnej UAIM, to znaczy metody skalowania sprężysto-plastycznej postaci wyboczonej, która jest po raz pierwszy wprowadzona w niniejszym podręczniku.
W grupie metod wboczeniowych WM wyróżnimy odmiany:
(a) EWM – Elementarna Wyboczeniowa Metoda, w której projektowane są elementy wydzielone z całego systemu konstrukcyjnego. W odmianie tej wyróżnimy wersje:
- HWM – Historyczna Wyboczeniowa Metoda, polegająca na zmniejszeniu sztywności elementu poprzez redukcję współczynnikiem wyboczeniowym, wyznaczonym dla smukłości z długości efektywnej elementu,
- SWM – Standardowa Wyboczeniowa Metoda, polegająca na wyznaczeniu smukłości elementu na podstawie sił krytycznych wyznaczonych w pomocniczej, liniowej analizie analizie wyboczeniowej (postaci własnych) LBA (Linear Buckling Analysis),
(b) OWM – Ogólna Wyboczeniowa Metoda, w której w pierwszym etapie wyznacza się mnożnik krytyczny obciążeń dla całego systemu w pomocniczej analizie wyboczeniowej LBA. Ten etap analizy może stanowić przejście do metody UEM, lub poprzedza drugi etap metody ogólnej, w którym wyznacza się smukłość całego systemu, a na tej podstawie jeden współczynnik wyboczeniowy wspólny dla wszystkich elementów konstrukcji.
W grupie metod imperfekcyjnych IM wyróżnimy odmiany:
(a) GIM – Geometryczna Imperfekcyjna Metoda, polegająca na wymuszeniu imperfekcji geometrycznych.
W odmianie tej wyróżnimy wersje:
- SIM – Standardowa Imperfekcyjna Metoda, polegająca na bezpośrednim wymuszeniu imperfekcji przechyłowych i łukowych z amplitudami normowymi,
- AIM – Alternatywna Impefekcyjna Metoda, polegająca na wymuszeniu zintegrowanych imperfekcji systemu z alternatywą amplitudą, – skalą dla sprawczego kształtu utraty stateczności. Modyfikowanie geometrii systemu w klasycznym ujęciu metody AIM odbywa się poprzez wymuszenie alternatywnych imperfekcji geometrycznych, przeskalowanych z kształtu wyboczenia sprężystego wyodrębnionego typu (np.tylko wyboczenia giętnego lub tylko zwichrzenia),
(b) QIM – Obciążeniowa Imperfekcyjna Metoda, polegająca na obciążeniu konstrukcji siłami poziomymi równoważnymi imperfekcjom geometrycznym
(c) HIM – Hybrydowa Imperfekcyjna Metoda, w których część imperfekcji uwzględnia się obciążeniowo, a część geometrycznie, to znaczy poszczególne rodzaje systemowych imperfekcji uwzględnia się różnymi metodami.
Wprowadzona systematyka metod projektowania konstrukcji podatnych na efekty nieliniowe nie zmienia systematyki obliczeń statycznych norm dla konstrukcji powłokowych [7] oraz płytowych [8]. Systematyka ta wyróżnia:
LA – analiza liniowo sprężysta – zamiennie stosowana jest nazwa: teoria pierwszego rzędu,
LBA – analiza sprężysta bifurkacyjna – zamiennie stosowana jest nazwa analiza wyboczeniowa lub wartości własnych,
GNA – geometrycznie nieliniowa analiza sprężysta – w pracy ograniczona do teorii drugiego rzędu,
MNA – analiza fizycznie nieliniowa – w pracy stosowana najprostsza z metod fizycznie
nieliniowych, czyli metoda nośności granicznej (przegubów plastycznych)
GMNA– analiza geometrycznie i fizycznie nieliniowa,
GNIA – geometrycznie nieliniowa analiza konstrukcji z imperfekcjami,
GMNIA – geometrycznie i fizycznie nieliniowa analiza konstrukcji z imperfekcjami.
Przedstawiane w podręczniku metody należy w większości zaliczyć do GNIA, a w wersji uogólnionej metody alternatywnej UAIM do metod GMNIA.
Klasy imperfekcji w metodach wyboczeniowych i imperfekcyjnych
W tab. 1. zestawiono klasy imperfekcji prętów stalowych oraz wynikające z nich parametry ustalone w normie EC3 [2].
Tab.1. Klasy imperfekcji prętów stalowych oraz wynikające z nich:
# parametry klasy imperfekcji $\alpha$ (wg EC3,- tab 6.3., 6.4 i 6.5)
# amplitudy imperfekcji $n_L=L / e_0$ (wg EC3- tab 5.1)
W metodach wyboczeniowych klasy imperfekcji są charakteryzowane parametrem klasy imperfekcji $\alpha$, zestawionymi w wierszach (a) do (c). W metodach imperfekcyjnych – klasy imperfekcji charakteryzowane są amplitudami imperfekcji względnych $n_L=L/e_0$ ($L$ i $e_0$ są długością pręta i strzałką imperfekcji łukowej odpowiednio), które zestawiono w wierszach (d) i (e).
Zarówno parametr klasy imperfekcji $\alpha$ jak i amplituda $n_L$ zależą od pięciu klas imperfekcji ($a_0$, $a$, $b$, $c$, $d$) – kolumna (1) do (5).
Klasy imperfekcji zależą z kolei od rodzaju przekroju poprzecznego pręta i sposobu jego wytworzenia (walcowany, spawany) zgodnie z tab. 3-2.1 dla wyboczenia giętnego oraz zgodnie z tab. 3-2.2 dla przypadku zwichrzenia. Klasy imperfekcji są wspólne dla trzech typów niestateczności:
- giętnego, to jest wyboczenia Eulera – nieindeksowanego *=_,
- zwichrzenia, to jest wyboczenie bocznego Własowa, indeksowanego przez $ *=LT$ (metoda ogólna)
- zwichrzenia dwuteowników walcowanych lub ich spawanych odpowiedników, indeksowanego przez $ *=LT,szcz$ (metoda szczególna),
- ogólnego, to jest obejmującego oba wyżej wymienione typy wyboczenia, indeksowanego przez $*=op$.
Zwichrzenie jest rozdzielone na dwie kategorie, bowiem w przypadku dwuteowników walcowanych lub ich spawanych odpowiedników – zgodnie z normą [2] klasy imperfekcji nie są jednoznaczne, bo zależą od wyboru metody projektowania: ogólnej lub szczególnej zgodnie z tab. 3-2.2. Norma nie wskazuje metody polecanej i wybór zależy od decyzji projektanta, przy czym w typowych przypadkach projektowych zalecamy stosowanie metody szczególnej, bowiem uzyskuje się wówczas oszczędności: dla dwuteowników walcowanych 3 do 16% przy h/b ≤ 2,5 oraz 5 do 18% przy h/b > 2, a dla dwuteowników spawanych: 12–27% przy h/b ≤ 2 oraz 18–27% przy h/b > 2. Maksymalne przyrosty nośności uzyskuje się jednak dopiero przy stosunkowo dużych smukłościach względnych, co raczej rzadko występuje w praktyce.
Zgodnie z [2]– klauzula 5.3.4(3), gdy analiza drugiego rzędu ma uwzględniać zwichrzenie elementów zginanych, to można przyjmować imperfekcje tych elementów jako
$$\begin{equation} e_{0,LT} = k\cdot e_0 \to \quad n_{LT}=\cfrac{n_L}{k} \label {1} \end{equation}$$
gdzie $e_0$ – zastępcza wstępna imperfekcja łukowa w płaszczyźnie najmniejszej bezwładności przekroju. Uwzględnianie dodatkowych imperfekcji skrętnych na ogół nie jest wymagane. Zaleca się $k = 0,5$.
Liczba klas imperfekcji wynika z dążenia do najlepszego dopasowania teorii łukowych współczynników wyboczeniowych Ayrton-Perry do licznych wyników badań eksperymentalnych, zgromadzonych w europejskich i światowych bazach danych.
Postulat ograniczenia liczby klas imperfekcji
Zdaniem autora, do czasu wprowadzenia metod imperfekcyjnych do powszechnej praktyki – liczbę klas imperfekcji w metodach wyboczeniowych należałoby ograniczyć z pięciu do jednej lub maksymalnie dwóch Takie uproszczenie prowadzi do statystycznie nieistotnych odchyleń od bezpieczeństwa projektowanych prętów na kacptow;anym pozsiomie ufności > 90%. Zagadnieniem zjmowano się w pracach [9], )), [10]. Zmniejszenie liczby klas imperfekcji spowodowałoby natomiast znaczne uproszczenie analiz w szczególności optymalizacyjnych, zmierzających do optymalnego doboru rodzaju kształtownika.
Imperfekcje układów konstrukcyjnych są sprowadzone do imperfekcji przechyłowych, globalnych z podstawową wartością przechyłu wstępnego $ n_G = 200$ bez podziału na klasy tych imperfekcji. Nie zależą ponadto od metod wymiarowania, przy czym w wyboczeniowych metodach wymiarowania w zasadzie nie były obecne, natomiast w metodach imperfekcyjnych są przedmiotem podstawowego zainteresowania.
W niniejszej pracy przeprowadzone zostaną symulacje ograniczenia klas imperfekcji łukowych do jednej klasy $ n_L = 200$. Rozważania są kontynuacją badań przeprowadzonych w pracy Tarasa i Greinera [11], a ta dotyczącej nowej klasyfikacji klas imperfekcji dla przypadku zwichrzenia.
Współczynniki materiałowe w metodach wyboczeniowych i imperfekcyjnych
System częściowych współczynników bezpieczeństwa, opisany w artykule Imperfekcje konstrukcji, a współczynniki bezpieczeństwa – zawiera tzw. współczynniki materiałowe $\gamma_M$ uwzględniające niepewność dotyczącą właściwości materiałów, ale również odchyłek wymiarowych przekroju.
Wśród współczynników materiałowych można wyróżnić dwa, związane bezpośrednio z metodami projektowania: wyboczeniowymi lub imperfekcyjnymi:
- metody wyboczeniowe są znamienne tym, że polegają na sprawdzenia nośności elementu, która jest zredukowaną nośnością przekroju poprzez współczynniki wyboczeniowe.
Właściwym do takiej sytuacji jest współczynnik materiałowy stosowany przy sprawdzaniu stateczności elementów, $\gamma_M=\gamma_{M1} =1,1$, to znaczy
wytrzymałość materiału $f_{y,w}=\cfrac{f_y}{1,1}$
nośność przekroju $F_{Ed}= \cfrac{F_{Ek} }{1,1}$
gdzie $F_{Ed}= [ N_{Ed} , M_{y,Ed}, M_{z,Ed}, B_{Ed}]$
- metody impefekcyjne są znamienne tym, że sprawdzeniu podlega przekrój sprawczy (krytyczny) układu bez stosowania współczynników redukcyjnych. W wymiarowaniu bierze się siły przekrojowe otrzymane w analizie II rzędu konstrukcji obarczonej imperfekcjami. Właściwym do takiej sytuacji jest współczynnik materiałowy stosowany przy sprawdzaniu nośności przekroju $\gamma_M=\gamma_{M0} =1,0$, to znaczy
wytrzymałosć materiału $f_{y,i} =\cfrac{f_y}{1,0}$
nośność przekroju $F_{Ed}=\cfrac{F_{Ek}}{1,0}$
Ze względu na opisane wyżej zmniejszenie niepewności modelu – metody imperfekcyjne są o 10% mniej konserwatywne od metod wyboczeniowych i już tylko z tego powodu rachunki wykonywane metodami imperfekcyjnymi powinny dawać wyniki korzystniejsze o 10%.
Krótka charakterystyka metod wyboczeniowych
Wymiarowanie metodami wyboczeniowymi znamienne jest tym, że stosowane są współczynniki wyboczeniowe (redukcyjne). Warunek stateczności i wytrzymałości elementu obciążonego siłą ściskającą $N_{Ed}$ , momentem zginającym w płaszczyźnie potencjalnego zwichrzenia $M_{y,Ed}$, momentem zginającym z płaszyczyzny głównej $M_{z,Ed}$ przypadek oraz bimomentem $B_{Ed}$ jest zapisywany na poziomie elementu formułami typu [2]-(6.61):
$$\begin{equation} n_y + k_{yy} \cdot m_y + k_{yz} m_z + b _\omega \le 1 \\
n_z + kz_{zy} \cdot m_y + k_{zz} \cdot m_z +b_\omega \le 1 \label {2} \end{equation}$$
gdzie względne siły w elemencie wylicza się z zależności:
$$\begin{equation} n_y= \cfrac{N_{Ed}}{\chi_y \cdot N_{Rd}} \, ; \, n_z = \cfrac{N_{Ed}}{\chi_z \cdot N_{Rd}} \, ; \, m_y =\cfrac{ M_{y,Ed}}{\chi_{LT} \cdot M_{y, Rd}} \, ; \, m_z =\cfrac{ M_{z,Ed}}{ M_{z, Rd}} \, ; \, b_\omega = \cfrac{B}{B_{Rd}} \\
\label {3} \end{equation}$$
Nośności obliczeniowe przekroju $F_{Rd} =[ N_{Rd} \, ; \, M_{y,Rd} \, ; \, M_{z,Rd} \, ; \, B_{Rd} ]$ wylicza się ze standardowych wyrażeń:
$$\begin{equation} F_{Rd}=\cfrac{ W_F \cdot f_y} {\gamma_{M1}} \label {4} \end{equation}$$
gdzie:
$f_y$ – granica plastyczności stali (ogólnie wytrzymałość materiału),
$W_F = [A_•, W_•y, W_•z, W_\omega$] , gdzie (• 1,2,3,4) – klasa przekroju – geometryczne wskaźniki wytrzymałości przekroju, odpowiadające siłom $F=[N, M_y, M_z, B]$ (B jest bimomentem) i wynoszą:
$A_{1,2,3}=A$, $A_4=A_{eff}$, $W_{1,2}=W_{pl}$, $W_3=W_{el}$, $W_4=W_{eff}$.
Współczynnik materiałowy $\gamma_{M1}=1,1 $ , ponieważ sytuacja obliczeniowa dotyczy sprawdzania warunków stateczności.
W formule ($\ref{2}$) współczynniki interakcji $k_{yy}$, $k_{yz}$, $k_{zy}$, $k_{zz}$ wyznacza się metodą 1 wg [2]-Zał.A dla dowolnych przekrojów lub metodą 2 wg [2]-Zał.B dla przekrojów dwuteowych i rurowych. W załączniku do polskiej normy zaleca się stosowanie prostszej metody 2 [2]-Tab B.2, w której dla przekrojów dwuteowych współczynniki korelacji wyznacza się z zależności:
- dla przekrojów dwuteowych klasy 1 i 2 w elementach niewrażliwych na deformacje skrętne
$$\begin{equation} \begin{cases}
k_{yy}= C_{my} \cdot \min { \left \{ [ 1+ ( \overline \lambda_y – 0,2 ) \cdot n_y ] \, ; \, ( 1+0,8 \cdot n_y ) \right \} } \\
k_{yz}=0,6 \cdot k_{zz},\\
k_{zy}= 0,6 \cdot k_{yy},\\
k_{zz} = C_{mz} \cdot \min { \left \{ [ 1+( 2 \cdot \overline \lambda_z – 0,6 ) \cdot n_z ] \, ; \, ( 1+1,4 \cdot n_z ) \right \} } \\\end{cases} \label {5} \end{equation}$$
gdzie: $n_y$, $n_z$ wg ($\ref{3}$)
- dla przekrojów dwuteowych klasy 3 i 4 w elementach niewrażliwych na deformacje skrętne
$$\begin{equation} \begin{cases}
k_{yy} = C_{my} \cdot \min { \left \{ ( 1+ 0,6 \cdot \overline \lambda_y \cdot n_y ) \, ; \, ( 1+0,6 \cdot n_y ) \right \} } , & \\
k_{yz}= k_{zz}\\
k_{zy}=0,8\cdot k_{yy} \\
k_{zz}= C_{mz} \cdot \min { \left \{ ( 1+ 0,6 \cdot \overline \lambda_z \cdot n_z ) \, ; \, ( 1+ 0,6 \cdot n_z ) \right \} } \\
\end{cases} \label {6} \end{equation}$$
- dla przekrojów dwuteowych klasy 1 i 2 w elementach wrażliwych na deformacje skrętne
$$\begin{equation} \begin{cases}
k_{yy} \text { wg } (\ref{5}) & \\
k_{yz} \text { wg } (\ref{5}) & \\
k_{zy}= \min { \left \{ (0,6+\overline \lambda_z ) \, ; \, ( 1- 0,1 \cdot \overline \lambda_z \cdot n_{LT}) \right \} } , & \text {dla} \overline \lambda_z < 0,4\\
k_{zy}= \max { \left \{ ( 1- 0,1 \overline \lambda _z \cdot n_{LT} ) \, ; \, ( 1- 0,1 \cdot n_{LT}) \right \} } , & \text {dla} \overline \lambda_z \ge 0,4\\
k_{zz} \text { wg } (\ref{5})&
\end{cases} \label {7} \end{equation}$$
- dla przekrojów dwuteowych klasy 3 i 4 w elementach wrażliwych na deformacje skrętne
$$\begin{equation} \begin{cases}
k_{yy} \text { wg } (\ref{6}) & \\
k_{yz} \text { wg } (\ref{6}) & \\
k_{zy}= \max { \left \{ ( 1- 0,05 \overline \lambda _z \cdot n_{LT}) \, ; \, ( 1- 0,05 \cdot n_{LT}) \right \} } , &
k_{zz} \text { wg } (\ref{6})&
\end{cases} \label {8} \end{equation}$$
gdzie: $n_{LT} = \cfrac{n_z} {C_m -0,25}$
Współczynniki równoważnego stałego momentu $C_m$ występujących w powyższych formułach są zależne od rozkładu momentów zginających pomiędzy punktami podparcia (stężenia) elementu. Poniżej podano przykładowe formuły dla trzech często spotykanych przebiegów momentów zginających, przy znaczeniu przypadków:
[P] =prostoliniowy przebieg momentów przy ( $\psi$ -dowolne ),
[K1]= krzywoliniowy przebieg momentów od obciążenia równomiernego, przy ($\alpha_s < 0$ ; $ \psi>0$) ,
[K2]= krzywoliniowy przebieg momentów od obciążenia równomiernego, przy ($\alpha_h > 0$ ; $\psi -dowolne $):
$$\begin{equation} C_m= \begin{cases}
\max { \{ 0,6+ 0,4 \cdot \psi \, ;\, 0,4 \} } & \quad [P]\\
\max { \{0,1-0,8 \cdot \alpha_s \, ;\, 0,4 \} } & \quad [K1] \\
0,95 +0,05 \cdot \alpha_h & \quad [K2] \\
\end{cases} \label {9} \end{equation}$$
gdzie:
$\psi= M_i/M_j$ – stosunek wartości momentów utwierdzenia na końcu „i” oraz „j”, przy czym $|M_j| \le |M_i|$ oraz $-1 \le \psi \le 1$
$\alpha_s= M_s/M_h$ – stosunek momentu przęsłowego do podporowego $M_j$, przy czym $M_s$ jest przeciwnego znaku od $M_j$
$\alpha_h= M_h/M_s$ – stosunek momentu podporowego $M_h$ do przęsłowego $M_s$, przy czym oba są takiego samego znaku.
Dla innych przypadków należy skorzystać z [2]-Tab. B.3.
Elementy o przekrojach rurowych są niewrażliwe na deformacje skrętne, a współczynniki interakcji należy dla nich wyznaczać z formuł [2]-Tab B.2, które mają podobną strukturę do wyrażeń stosownych dla przekrojów dwuteowych.
Elementy dwuteowe są niewrażliwe na deformacje skrętne , jeśli są stężone przeciwskrętnie. Elementy, które nie można zaliczyć do grupy niewrażliwych, są wrażliwe na deformacje skrętne
Występujące w formule ($\ref{3}$) współczynniki wyboczenia: giętnego $\chi_y, \chi_z$ oraz zwichrzenia $\chi_{LT}$ od dziesiątków lat uzależnia się od smukłości, która po uogólnieniu jest obecnie stosowana w postaci smukłości względnej
$\overline \lambda_*$ (1-1.2)
właściwej dla rodzaju wyboczenia „*” : ( *= [_, LT, T, TF ]= [ giętne , zwichrzenie, skrętne, giętno-skrętne ] )
a współczynniki wyboczeniowe $\chi$ szacuje się podług historycznej teorii Ayrton-Perry [12] z formuł (2-3.13) do (2-3.16) lub w przypadku szczególnym dla dwuteowników walcowanych i ich spawanych odpowiedników można je wyznaczać z formuł (3-2.7).
Wprowadzenie do teorii współczynnika wyboczeniowego Ayrton-Perry podano w rozdziale Geneza metod imperfekcyjnych
W obecnie stosowanych formułach obok współczynników wyboczeniowych stosuje się system współczynników korelacji $k_{yy}$ oraz $k_{yz}$ korygujących standardowe formuły typu ($\ref{2}$) do sytuacji jednoczesnego działania ściskania $N_{Ed}$ i zginania $M_Ed,y$ oraz $M_Ed,z$ oraz korelacji zjawisk wyboczenia giętnego i zwichrzenia. System współczynników redukcyjnych: wyboczeniowych oraz korelacyjnych jest bardzo złożony i powoduje , że metody wyboczeniowe są bardzo skomplikowane oraz trudne do stosowania nawet w projektowaniu wspomaganym komputerowo. Przede wszystkim jednak metody wyboczeniowe dają tylko przybliżone wyniki i w zasadzie nie powinny być stosowane jako wzorzec do kalibrowania metod imperfekcyjnych, w tym parametrów imperfekcji – zależność powinna być odwrotna.
W praktyce inżynierskiej od lat (niemalże od zawsze) stosuje się elementarną metodę wyboczeniową HWM, w której smukłość pręta wyznaczano dla znanej długości wyboczeniowej z formuły (1-1.7). Metoda jest już historyczna, choć nadal często stosowana przez projektantów.
Metodę HWM ulepszono poprzez wyznaczanie sił krytycznych w prętach na podstawie analizy wyboczeniowej systemu prętów (całej konstrukcji) i obliczenie smukłości pręta bezpośrednio z formuły (1-1.3) bez używania wzoru Eulera (1-1.5). Ten ulepszony sposób wyznaczania smukłości pręta nazwaliśmy metodą SWM.
Zarówno w metodzie HWM jak i SWM dokonuje się rozróżnienia rodzajów niestateczności: giętnej i skrętnej ( w tym giętno-skrętnej, czyli zwichrzenia) i stosuje się odrębne współczynniki wyboczeniowe (por. formuła ($\ref{2}$). Oprócz tego do każdego elementu wydzielonego z konstrukcji przypisuje się inne współczynniki wyboczeniowe.
Metoda HWM (elementarna – historyczna)
Zalecenia normowe pozostawiają możliwość klasycznego wymiarowania pręta na podstawie długości wyboczeniowych, ale w bardzo ograniczonym zakresie. Zgodnie z [2]– kl. 5.2.2 (3) dopuszcza się sprawdzenie wytrzymałości i stateczności elementów wyłącznie poprzez indywidualne sprawdzenia stateczności elementów, przyjmując odpowiednie długości wyboczeniowe ustalone w globalnej utraty stateczności wg pkt 6.3.[2]– kl. 6.3, ale tylko w przypadkach elementarnych.
Zauważmy, że w praktyce przypadki elementarne właściwie nie występują. Przypadek elementarny będzie miał miejsce wyłącznie wówczas, gdy potrafimy wykazać w sposób nie budzący wątpliwości, że zamocowanie węzłów spełnia idealne warunki. Autor zna w zasadzie tylko jeden przypadek elementarny – słupa-wahacza, to znaczy takiego pręta ściskanego, dla którego uzasadnimy, że będzie zachowywał się jak pręt przegubowo-przegubowy (np. Rys. 1-1.2 a) lub e).
Projektant powinien przedstawić uzasadnienie dlaczego występuje przypadek elementarny. Niedopuszczalne jest przyjęcie schematu wyboczeniowego pręta wydzielonego z konstrukcji bez uzasadnienia dotyczącego przesuwności i podatności jego węzłów. Przeprowadzenie wystarczającego dowodu jest zwykle trudne i czasowo porównywalne z bezpośrednim zastosowaniem bardziej dokładnych metod, więc od razu zalecamy zastosowanie metody WEM lub OWM, a najlepiej i najłatwiej jednej z metod IM. Metody IM mogą być bowiem niemal automatycznie stosowane we współczesnych programów komputerowych, w zasadzie bez szczegółowego zgłębiania problemu przez inżyniera i prowadzenia oszacowań długości wyboczeniowych, czyli sił lub momentów krytycznych.
Długość wyboczeniową pręta $L_{cr}$ można wyznaczyć po przeprowadzeniu analizy LBA ze ścisłej zależności:
$$\begin{equation} L_{cr}=\cfrac{\pi}{k_\bullet} \cdot \sqrt{\cfrac{EI_y}{N_{cr}}} \label {10} \end{equation}$$
Długość zwichrzenia można wyliczyć z zależności:
$$\begin{equation} L_{LT}=\cfrac{\pi}{k_\bullet} \cdot \sqrt{\cfrac{ W_y}{A} \cdot \cfrac{E(I_y+I_z) }{M_{cr}}} \label {11} \end{equation}$$
gdzie:
$N_{cr}=\Lambda_{cr}\cdot N_{Ed}$, oraz $M_{cr} =\Lambda_{cr} \cdot M_{Ed} $.
$N_{Ed}$ oraz ${M_Ed}$ siła osiowa, moment zginający w pręcie, wywołane tym obciążeniem dla którego oszacowano mnożnik krytyczny $\Lambda_{cr}$,
$\Lambda_{cr}$ jest globalnym mnożnikiem obciążeń krytycznych wyznaczonym w analizie LBA,
Współczynnik klasy przekroju stalowego $k_•$ =1 dla przekroju klasy (•=1,2 i 3) oraz $k_•=\sqrt{\cfrac {A_{eff}} {A}}$ dla przekroju klasy (• = 4).
$ A, W_y, E(I_y+I_z)$ – pole przekroju, wskaźnik wytrzymałości i sztywność osiowa pręta .
Wyrażenia ($\ref{10}$) oraz ($\ref{11}$) uzyskano z porównania formuł (1-1.3)=(1-1.7) i uwzględnieniu (1-1.8) oraz (1-1.9). Długość zwichrzenia przyjęto z definicji $\lambda_{LT}=\cfrac{L_{LT}}{i_0}$, gdzie osiowy promień bezwładności $i_0=\sqrt{I_0/A}$., $I_0=I_y+I_z$.
Obie formuły maja zastosowanie przy weryfikacji długości wyboczeniowych wyznaczonych metodami przybliżonymi w tym nomonografowymi.
We współczesnych normach współczynniki wyboczeniowy: $\chi$ jest obliczany z formuły (2-3.13) wraz z pomocniczymi współczynnikami $\Phi$ (2-3.14) oraz $\Theta$ (2-3.15).
O dokładności metody HWM decyduje poprawność oszacowania długości wyboczeniowej pręta $L_{cr}$. (1-1.7). Niedokładność rzędu kilkunastu procent w oszacowaniu długości wyboczeniowej może prowadzić do kilkudziesięcioprocentowego błędu w oszacowaniu współczynnika wyboczeniowego, a to z kolei do znacznego przeszacowania lub niedoszacowania nośności pręta. To w zasadzie wyklucza metodę z praktycznego projektowania.
Metoda SWM (wydzielonych elementów ze znaną siłą krytyczną)
Podstawowa wada metody HWM, polegająca na silnej zależności jej dokładności od precyzji wyznaczenia długości wyboczeniowych jest poprawiona w ten sposób, że smukłość pręta szacuje się bezpośrednio z formuły (1-1.2) ( przy standardowym wyboczeniu giętnym z zależności (1-1.3), przy zwichrzeniu z zależności (1-1.4), ale siły krytyczne $N_{cr}$ $M_{cr}$ wyznacza się z rozwiązania zadania pomocniczego, a nie z wzorów Eulera lub Własowa. Siły te należy wyznaczyć eksperymentalnie lub w pomocniczej numerycznej analizy wyboczeniowej LBA, z której uzyskuje się globalny mnożnik obciążeń krytycznych $\Lambda_{cr}$ .s
Z rozwiązania pierwszego rzędu układu konstrukcyjnego poddanego tym samym obciążeniom dla których wyznaczono krytyczny mnożnik obciążeń wyznacza się siły przekrojowe $[N_{E}, M_{y,E}, B_{E}]^{I}$. Nie ma przy tym znaczenia czy w obu stanach obciążenia są obliczeniowe $_{Ed}$, czy charakterystyczne $_{Ek}$ i czy siły przekrojowe są obliczeniowe lub charakterystyczne. Przy większych obciążeniach mniejszy będzie mnożnik krytyczny obciążeń.
$$\begin{equation} [N_{E}, M_{y,E}, B_{E}]_{cr}= \Lambda_{cr}\cdot [N_{E}, M_{y,E}, B_{E}] \label {12} \end{equation}$$
W ogólności konstrukcja ma inne siły krytyczne w każdym przekroju i nie są one wartością własną układu, a nawet elementu w konstrukcji.
W przypadku zwichrzenia układu prętów siły krytyczne istotnie zależą od konstrukcji węzłów oraz połączeń między elementami ze względu na różne mechanizmy przenoszenia deplanacji z rygla na słup lub z belki na belkę (tzn. transformacji bimomentu). Dlatego analiza LBA wykonywana przez programy, w których nie zaimplementowano analizy węzłów jest wystarczająco dokładna tylko w prętach z zachowaniem ciągłości deplanacji . W tym zakresie poleca się sprzężenie programu do analizy systemu (np Consteel) z programem do analizy węzłów (np Idea StatiCa).
Współczynniki wyboczeniowe dla sił krytycznych wyznaczonych w zadaniu pomocniczym wyznacza się ze standardowych formuł, analogicznych do (2-3.13), a wskazanych w następujących klauzulach normowych :
- dla prętów stalowych:
ściskanych [2]-klauzula 6.3.1,
zginanych [2]-kl. 6.3.2, - dla prętów aluminiowych:
ściskanych [6]-kl. 6.3.1.2,
zginanych [6]-kl. 6.3.2.2, - dla prętów zespolonych
belek [3]-kl. 6.4,
słupów [3]-kl. 6.7, - dla prętów żelbetowych
metoda nominalne sztywności [1]-kl.5.8.7,
metoda nominlanej krzywizny [1]-kl. 5.8.8,
zwichrzenie belek [1]-kl. 5.9,
i inne klauzule - dla prętów drewnianych
wyboczenie słupów [4]-kl. 6.3.2
zwichrzenie belek [4]-kl. 6.3.3
Ten sposób podejścia nazwiemy metodą SWM ( częściowo ogólną)
Obecnie metodę SWM często używa się do wyznaczenia współczynnika zwichrzenia belki.
Moment krytyczny $M_{cr}$ wyznacza się za pomocą kalkulatora LTBeamN [13]. Kalkulator LTBeamN jest użyteczny do wyznaczania mnożnika krytycznego (momentu krytycznego) belek i słupów ciągłych złożonych z elementów ułożonych w linii prostej. Natomiast w przypadku ram (prętów łączonych pod kątem) można posłużyć się programem Consteel , w którym zaimplementowano najważniejsze topologie połączeń w narożach ram: śrubowane lub spawane z żebrami diagonalnymi lub nakładkami.
Problemem podstawowym metody SWM jest to, że oszacowanie wytężenia elementów ze wzorów ($\ref{2}$) wymaga dokonania obliczeń dla „czystych” form wyboczenia: giętnego w płaszczyźnie, giętnego z płaszczyzny oraz zwichrzenia, a jest to utrudnione w układzie elementów, ponieważ poszczególne formy są sprzężone i ich rozdzielenia można dokonać tylko w przybliżeniu poprzez wydzielanie elementu i nadawanie mu szacunkowych warunków brzegowych lub analizę różnych schematów układu z zablokowaną możliwością wyboczenia wg form, nie będących przedmiotem analizy. W rezultacie inżynierowie „uciekają” prostszego (choć mało dokładnego) oszacowania długości wyboczenia giętnego w płaszczyźnie i z płaszczyzny oraz oszacowania momentu krytycznego zwichrzenia dla wydzielonego elementu.
Problemy powyższe są rozwiązane w metodzie OWM, czyli w metodzie pełnej ogólnej, opisanej w kolejnym punkcie lub w drodze stosowania bezpośrednich metod imperfekcyjnych.
Metoda OWM (pełna ogólna)
W przypadku, gdy nie są miarodajne warunki [2]-kl.6.3.1, 6.3.2, 6.3.3, pozwalające zastosować metody WEM (HWM lub SWM) ), to sprawdzenia stateczności i wytrzymałości elementów należy prowadzić metodą OWM (zotpressInText item=”{TSFWTQGW,kl. 6.3.4.(1)}”])Metoda OWM została opisana w rozdziale normy „6.3.4 Ogólna metoda oceny stateczności elementów ze względu na zwichrzenie i wyboczenie z płaszczyzny układu”.
Ponieważ nie są znane jednoznaczne warunki miarodajności metod WEM, więc oznaczałoby to, że metodę ogólną OWM należałoby z ostrożności stosować w każdym przypadku, ale niestety nie pozwalają na to dopuszczenia metody ogólnej. Dychotomię tą rozwiązuje zastosowanie metod imperfekcyjnych IM, które stosujemy już bez ograniczeń, a nadto są one łatwiejsze do zastosowania i dokładniejsze. Oznacza to dalsze uproszczenie procesu wymiarowania oraz zbliżenie do logicznych zasad naturalnych.
Metoda OWM jest nazywana jako ogólna, choć w istocie ma ograniczenia i nie powinna być bezkrytycznie stosowana poza przypadkami określonymi w normie, czyli dla:
a) elementów pojedynczych lub złożonych o stałym lub zmiennym przekroju i różnych warunkach podparcia, lub
b) płaskich ram lub podzespołów ram złożonych z elementów poddanych ściskaniu i/lub jednokierunkowemu zginaniu w płaszczyźnie układu, przy czym zginanie ma charakter sprężysty.
Wynika stąd, że do czasu przeprowadzenia dopuszczających badań – metody ogólnej nie należy bezkrytycznie stosować do konstrukcji przestrzennych lub obciążonych przestrzennie w tym skręcaniem.
Przede wszystkim należy stwierdzić, że w warunkach stosowalności metody OWM nie stwierdzono, że dotyczy wyłącznie elementów prostoliniowych, lub takich które ulegną wyboczeniu z płaszczyzny lub zwichrzeniu. W przykładach pokażemy, że metodę można z powodzeniem stosować w odniesieniu do łuków i do elementów zabezpieczonych przez zwichrzeniem i wyboczeniem z płaszczyzny.
W metodzie OWM używany jest jeden globalny współczynnik niestateczności $\chi_{op}$ wyznaczony dla smukłości względnej $ \overline \lambda_{op}$ układu podatnego na utratę stateczności z płaszczyzny lub zwichrzenie elementów wg [2]-kl. 6.3.4 (1 do 4).
Głównym punktem metody jest analiza stateczności, która powinna obejmować zwichrzenie lub wyboczenie z płaszczyzny.
W nowoczesnych programach komputerowych (np. [14], [15]
) metoda OWM jest zaimplementowana jako podstawowa metoda sprawdzania wytrzymałości i stateczności konstrukcji.
W metodzie OWM należy przeprowadzić analizę wyboczeniową systemu (LBA) i określić krytyczny mnożnik obciążeń
- $\Lambda_{cr}$ (1-1.13) , w EC3 oznaczony jako $\alpha_{cr,op}$.
Oprócz tego należy określić graniczny (plastyczny) mnożnik obciążenia
- $\Lambda_{pl}$ (1-1.15) w EC3 oznaczony jako $\alpha_{ult,k}$
W metodzie ogólnej uznaje się, że cała konstrukcja posiada jeden mnożnik graniczny i krytyczny, co skutkuje jedną dla całej konstrukcji smukłością. Jest to zgodne z teoretyczymi postulatami teorii sprężystości
$$\begin{equation} \overline \lambda_{op}=\sqrt{\cfrac{\Lambda_{pl}} {\Lambda_{cr}}}= \sqrt{\cfrac{\alpha_{ult,k}}{ \alpha_{cr,op}}} \label {13} \end{equation}$$
W metodzie OWM wytężenie elementu jest faktycznie wytężeniem przekroju i nie trzeba poszukiwać interakcji wyboczenia, zwichrzenia, ściskania i zginania. Wskazuje to w oczywisty sposób na to, że cały zbiór współczynników korelacji stosowany w klasycznych metodach wymiarowania konstrukcji jest zbiorem nienaturalnych współczynników.
Wszystkie te współczynniki korelacyjne wraz z zespołem współczynników wyboczeniowych wyznaczanych oddzielnie dla każdego elementu i każdej postaci niestateczności okazują się niepotrzebne, bo mogą być zastąpione jednym integralnym współczynnikiem wyboczenia. W ten sposób upraszcza się proces projektowania, ale również sprowadza zasadę projektowania na zgodną z teorią , a nadto zmniejsza ryzyko pomyłek i błędów obliczeniowych oraz przewymiarowania elementów.
Głównym punktem metody jest analiza wyboczeniowa LBA, która powinna obejmować boczne wyboczenie (zwichrzenie).
Zgodnie z EC3, graniczny mnożnik obciążeń $\alpha_{ult,k}$, jest minimalnym mnożnikiem obciążeń obliczeniowych, przy którym przekrój krytyczny osiąga nośność charakterystyczną w warunkach płaskiego stanu deformacji z uwzględnieniem właściwych imperfekcji geometrycznych.
Inaczej mówiąc mnożnik graniczny jest mnożnikiem plastycznym $\Lambda_{pl}$ wyznaczonym zgodnie z teorią nośności granicznej (plastycznej), która jest przedmiotem artykułu Nośność plastyczna konstrukcji.
W przypadku konstrukcji statycznie wyznaczalnej, można wyróżnić jeden przekrój krytyczny (najbardziej wytężony), tzn. taki, który pierwszy osiągnie nośność graniczną i wówczas zgodnie z zasadą graniczny mnożnik obciążeń jest odwrotnością wytężenia $w_{ult}$ przekroju w stanie granicznym $ult
Przy pominięciu sił poprzecznych i momentów skręcających wytężenie jest określone lewą stroną wyrażenia ($\ref{2}$). Dla zginania względem większej sztywności $y$, otrzymujemy stąd formułę normową [2]-kl.6.65}:
$$\begin{equation} \cfrac{1}{\alpha_{ult,k}} = \cfrac{N_{Ed}}{N_{Rk}}+\cfrac{M_{Ed}}{M_{y,Rk}} \label {14} \end{equation}$$
W przypadku konstrukcji statycznie niewyznaczalnych, które posiadają strukturalne zapasy nośności, ze względu na jej utratę dopiero po utworzenia się kilku przegubów plastycznych, a nie tylko jednego – mnożnik należy wyznaczać w procedurze nośności granicznej (np. zgodnie z artykułem [16], przy czym nośność przegubu plastycznego należy wyznaczać z uwzględnieniem interakcji sił przekrojowych, co najmniej momentów zginających i siły osiowej (np. zgodnie z pracą. W celu uzyskania minimalnego mnożnik obciążeń należy stosować podejście statyczne.
Krytyczny mnożnik obciążeń $\alpha_{cr,op}$ jest minimalną, obliczeniową wartością własną analizy wyboczeniowej LBA rozpatrywanej części lub całości systemu z warunku niestateczności sprężystej z płaszczyzny układu. Wyboczenie całej konstrukcji z płaszczyzny układu może przybrać formę wyboczenia bocznego (zwichrzenia), giętnego z płaszczyzny lub giętno-skrętnego. W analizie wyboczeniowej sprężystego przestrzennego systemu złożonego z uogólnionych prętów Własowa, nie prowadzi się rozdzielenia poszczególnych fizycznych postaci wyboczenia, ponieważ takie rozdzielenie sprzężonych postaci niestateczności nie jest możliwe, ale też nie jest potrzebne. W takiej analizie przyjmuje się, że mnożnik jest mnożnikiem krytycznym konfiguracji obciążeń obliczeniowych, wybranym jako minimalny z wszystkich teoretycznych postaci wyboczenia (czyli jest zapewne pierwszą wartością własną).
Oszacowania mnożników $\alpha_{cr,op}$ jest możliwe praktycznie tylko metodami numerycznymi. Na rynku funkcjonuje kilka programów, umożliwiających taką analizę (np. [14], [17], dedykowane do analiz inżynierskich z zastosowaniem uogólnionego elementu prętowego (cienkościennego elementu Własowa).
Smukłość ($\ref{13}$) zależnie od stosowanej analizy przy wyznaczaniu mnożnika obciążeń jako minimalnego, zawiera w sobie korelacje wszystkich uwzględnionych form wyboczenia (wyboczenia giętnego, bocznego itd.).
Integralny (globalny) współczynnik wyboczenia $\chi_{op}$ wyznaczany jest dla smukłości ($\ref{13}$) z klasycznej zależności (2-3.13) dla (*=op), przy czym pomocnicze współczynniki wyznacza się z (2-3.14) $\Phi$ oraz (2-3.15) $\Theta$, a dla zwichrzenia po wyborze metody szczegółowej dla stalowych duteowników walcowanych i ich spawanych odpowiedników z (3-2.7)
Ponieważ parametr klasy imperfekcji $\alpha_*$ jest zależny od kierunku i formy wyboczenia, więc dla każdej z tych form inne będą współczynniki wyboczenia systemu. Zgodnie z [2]-kl. 6.3.4.(4)a – współczynnik wyboczenia systemu $\chi_{op}$ wyznacza się jako minimalną wartość ze współczynników wyboczenia giętnego i zwichrzenia.
$$\begin{equation} \chi_{op} =\min { \{ \chi_z \, ; \, \chi_{LT} \} }\label {15} \end{equation}$$
Współczynnik wyboczenia można więc wyznaczać dla bardziej niekorzystnej, czyli czyli większej wartości parametru klasy imperfekcji $ \alpha_{op} $ przyjmowanego z tab.1. Takie postępowanie jest zgodne z założeniem, że mnożnik $\alpha_{ult,k}$ został wyznaczony jako odwrotność wytężenia przekroju krytycznego zgodnie z formułą ($\ref{14}$) .
W metodzie OWM zbiór klasycznych warunków stateczności i wytrzymałości elementów systemu ($\ref {2}$) przy indywidualnych dla każdego elementu współczynnikach wyboczenia ( w tym zwichrzenia) – zostaje zastąpiony jednym warunkiem nośności stateczności i wytrzymałości całej konstrukcji w przekroju sprawczym, który nazwiemy warunkiem OWM „A”
$$\begin{equation} \cfrac {\chi_{op} \cdot \alpha_{ult,k} } { \gamma_{M1}} \ge 1 \label {16} \end{equation}$$
gdzie $\gamma_{M1}=1,1$,
Alternatywnie do reguły ($\ref{15}$) zgodnie [2]-kl. 6.3.4.(4)b – współczynnik wyboczenia można wyznaczać jako interpolowany między wartościami współczynników $\chi_z$ i $\chi_{LT}$, a formułę interpolacyjną można zapisać w postaci alternatywnego do $(\ref{17}$) warunku nośności, wynikającego z reguły szacowania $\alpha_{ult,k}$ ($\ref{14}$),
który nazwiemy warunkiem OWM „B”
$$\begin{equation} \cfrac{N_{Ed}}{\chi_z \cdot N_{Rd}}+\cfrac{M_{y,Ed}} {\chi_{LT} \cdot M_{y,Rd}} \le 1 \label {17} \end{equation}$$
Uwagi krytyczne do metod wyboczeniowych
Przedstawiona powyżej procedura metody wyboczeniowej jest skomplikowana i trudna do zastosowań, choć była wykorzystywana przez dziesiątki lat, bowiem inżynierowie musieli sobie radzić w sytuacji braku komputerów i pietrzących się trudności w wykonywaniu obliczeń nieliniowych, a nawet pseudoliniowych LBA.
W celu ogarnięcia fenomenu utraty stateczności starano się rozdzielać i nazywać poszczególne postanie niestateczności.
Faktycznie zaś typy niestateczności są sprzężone, a ich rozdział jest niepotrzebny (a nawet ściśle niemożliwy). System konstrukcyjny charakteryzuje jeden mnożnik krytyczny i rozdział tego mnożnika na poszczególne elementy również nie jest potrzebny i nie jest ściśle możliwy. Te spostrzeżenia są podstawą koncepcji ogólnej metody wyboczeniowej OWM, w której stosuje się jeden mnożnik krytyczny dla całego systemu i form niestateczności, a do całego systemu konstrukcyjnego (i każdego zawartego w nim elementu) przypisany jest jeden współczynnik wyboczeniowy.
Kolejnym krokiem do usunięcia niedoskonałości i paradoksów metod wyboczeniowych jest wyeliminowanie stosowania abstrakcyjnego parametru klasy imperfekcji $\alpha$ (tab.1) na rzecz mierzalnych imperfekcji – niedoskonałości geometrycznych konstrukcji wprowadzanych do modelu geometrycznego lub poprzez równoważne siły imperfekcji, co jest istotą metod imperfekcyjnych.
Krótka charakterystyka metod imperfekcyjnych
Metody imperfekcyjne są w istocie pojęciowo najprostszą metodą sprawdzania wytrzymałości i stateczności systemów konstrukcyjnych i ich elementów i obecnie są zgodne zaleceniami normowymi [2]-kl.5.2.2(3)a. W normach podano tylko ogólny opis metody. Niniejsza praca ma wypełnić treścią tę ogólną zasadę, tak by inżynierowie mogli ją wdrażać w praktyce projektowej i tak, by umożliwić budowę procedur i komputerowych programów wspomagających projektowanie. Całość podręcznika jest poświęcona imperfekcyjnej metodzie IM projektowania konstrukcji stalowych, żelbetowych i zespolonych ze zwróceniem uwagi na uniwersalne, wspólne cechy metody dla konstrukcji wykonanych z różnych materiałów, więc również+dla konstrukcji hybrydowych.
W odróżnieniu od metod wyboczeniowych wymiarowanie konstrukcji metodami imperfekcyjnymi odbywa się na poziomie przekroju i zamiast formuły ($\ref {2}$) lub ($\ref {17}$) stosujemy
$$\begin{equation} \cfrac{N_{Ed}}{ N_{Rd}}+ \cfrac{M_{Ed,y}}{ M_{Rd,y}} + \cfrac{M_{Ed,z}}{ M_{Rd,z}} + \cfrac{B} { B_{Rd}} \le 1 \label {18} \end{equation}$$
gdzie nośności obliczeniowe są wyznaczane są z ($\ref{3}$) dla $\gamma_M=\gamma_{M0}=1,0$ , tzn. $F_{Rd}=F_{Rk}$.
W metodach imperfekcyjnych nie stosujemy współczynników wyboczenia, ale siły przekrojowe $F_{Ed}$ są obliczane metodami drugiego rzędu w systemie za danymi imperfekcjami geometrycznymi przechyłowymi oraz łukowymi elementów.
Metoda SIM (standardowa, bezpośrednia metoda imperfekcyjna)
Standardowa metoda imperfekcyjna SIM jest w literaturze zagranicznej często nazywana metodą OIM (Overall Imperfection Method) i polega na zadaniu imperfekcji łukowych poprzez geometryczne wygięcie osi pręta w kształt sinusoidy z amplitudą określoną tab.1 oraz imperfekcji przechyłowych zależnie od typu konstrukcji (np dla konstrukcji stalowych) poprzez zmianę fizyczną zmianę geometrii systemu konstrukcyjnego z wartością wychylenia określoną w normach. Metoda jest zaimpementowana miedzy innymi w programie Consteel.
Zasadniczym elementem metody SIM jest zadanie imperfekcji geometrycznych na modelu idealnym, a to związane jest z niepewnościami:
1) wyboru kierunku sprawczych imperfekcji łukowych związanego z formą wyboczenia: wokół osi y-y (wyboczenie giętne w płaszczyźnie ), wokół osi z-z (wyboczenie giętne z płaszczyzny) czy wyboczenie giętno skrętne (przemieszczenie ze skręceniem.
Pręt jest obarczony imperfekcjami „takimi jakie są”, czyli o z góry ustalonym kształcie najczęściej zarówno w płaszczyźnie zginania wokół osi y-y jak i z-z oraz skręceniem przekroju, ale wyboczenie zajdzie tylko w jednym z tych kierunków.
Wyboczenia giętne w obu płaszczyznach są w zasadzie rozprzężone i w przypadku zabezpieczenia belki-słupa przed zwichrzeniem można zadać imperfekcje normowe w obu kierunkach, a pręt wyboczy się w kierunku słabszym
Natomiast w przypadku możliwości zwichrzenia należy zdecydować się jaką część imperfekcji zadać z płaszczyzny i jaki zastosować współczynnik k w formule ($\ref{1}$). Wzrost wytężenia pręta jest praktycznie proporcjonalny do współczynnika $k$ i oscyluje wokół wartości prawidłowej dla $k=1/2$. To znaczy jeśli nie zastosujmy redukcji imperfekcji, to uzyskamy wytężenie dwukrotnie za duże.
2) wyboru zwrotu imperfekcji łukowych (a także przechyłowych) . Ustalenie zwrotu przeciwnie do przemieszczeń wywołanych obciążeniami zewnętrznymi może spowodować wzrost nośności pręta.
Obie niepewności 1) i 2) musi rozstrzygnąć inżynier projektant na podstawie zachowania konstrukcji. Użyteczna jest analiza LBA, która powinna być wykonana jako krok wstępny w analizie metodami imperfekcyjnymi.
Metoda QIM (obciążeniowa metoda imperfekcyjna)
Metoda obciążeniowa QIM polega na zastąpieniu imperfekcji geometrycznych równorzędnymi obciążeniami, które w przypadku imperfekcji przechyłowych szacuje się z formuły (3-2.6), która zachowuje postać dla wszystkich typów konstrukcji (stalowe, żelbetowe itd). Obciążenia równoważne imperfekcjom łukowym dla przypadku pręta przegubowo-przegubowego można oszacować z formuły (3-2.7).
Metoda HIM (hybrydowa, geometryczno-obciążeniowa metoda imperfekcyjna)
Często stosuje się metodę hybrydową (mieszaną ) HIM , w której imperfekcje przechyłowe uwzględnia się metodą obciążeniową QIM, natomiast imperfekcje łukowe elementu metodą HWM na poziomie wydzielonego elementu, traktowanego jak pręt przegubowo- przegubowy, czyli jako zastępczy przypadek elementarny, dla którego długość efektywna $L_{cr}=L$.
Wydzielony element jest wymiarowany na siły drugiego rzędu, uzyskane w systemie obarczonym imperfekcjami globalnymi. Dobrze zilustrowano to w normie do projektowania konstrukcji aluminiowych, Rys. 3- 4.1b.
Metoda AIM (alternatywna metoda – skalowania sprężystej postaci własnej)
Szczególne miejsce będzie zajmowała geometryczna metoda alternatywna AIM. Alternatywna imperfekcja integruje w sobie imperfekcje właściwe dla utraty stateczności podług dowolnej formy wyboczenia: giętnego, bocznego, skrętnego, i miejscowego.
Metodę AIM opisano w artykule Alternatywne,zintegrowane imperfekcje konstrukcji, a w przykładach rachunkowych tego rozdziału powołuje się na metodologię przedstawioną w tym artykule.
Przykłady rachunkowe
Prosta belka-słup
Metody wymiarowania konstrukcji przedstawimy na przykładzie prostej belki-słupa, z rys..2. Wymiary i obciążenia belki zaczerpnięto z pracy [18], dotyczącej klasycznej metody alternatywnej AIM na przypadek zwichrzenia belki-słupa, obciążonej stałymi po długości siłami przekrojowymi.
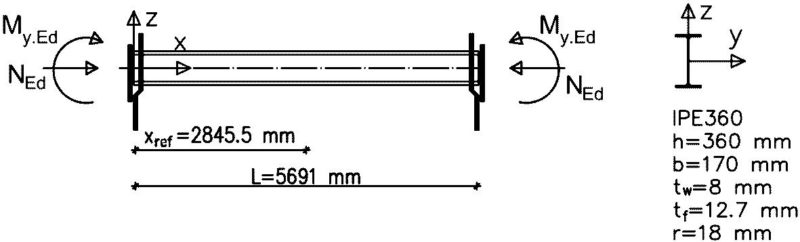
Rys.. 2 Schemat belki-słupa z przykładów 1-2 [18],
Dane:
Długość
$L=5691 \, mm$.
Siły przekrojowe stałe po dług\ości belki:
$N_{Ed}= 497,364 \, kN$,
$M_{Ed,y}= 25,436 \, kNm$.
Belka jest wykonana z kształtownika IPE 360 – S235
$f_y=235 MPa \,$, $E=210 \, GPa$
Charakterystyki geometryczne przekroju IPE 360:
$A= 72,73 \, cm^2$, $I_y= 16256,3 \, cm^4$, $I_z=1043,5 \, cm^4$, $I_\omega= 313600 \, cm^6$,
$i_y= 14,96 \, cm$, $i_z= 3,79\, cm$, $i_0=\sqrt{15,0^2+3,79^2}=15,5 \, cm$
$EA=210 \cdot 72,73 \cdot10^2= 15267330 \, kN$, $EI_y= 210 \cdot 16256,3 \cdot 10^{-2}= 34238 kNcm^2$, $EI_z=210 \cdot 1043,5 \cdot 10^{-2}= 2191,4 kNcm^2$,
$W_{y,el}= 904,63 \, cm^3$, $W_{z,el}= 122,76 \, cm^3$, $W_{\omega,el}= 2119 \, cm^5$, $W_{y,pl}= 1019 \, cm^3$, $W_{z,pl}= 184\, cm^3$, $W_{\omega,pl}= 3186 \, cm^5$,
Klasa przekroju belki przy zginaniu w płaszczyźnie i z płaszczyzny jest 1 , a przy czystym ściskaniu jest 3. W złożonym stanie obciążenia siłami $N_{Ed}$ oraz $M_Ed$ z procedury opisanej w artykule Klasy przekroju stalowego uzyskujemy informację, że klasa o przekroju jest (• =1). Dlatego odpowiednimi nośnościami przekroju są nośności plastyczne:
$N_{Rk}= 235 \cdot 72,73 \cdot 10^{-1}= 1709,2 \, kN$, $M_{y,Rk,pl}= 1019\cdot 235 \cdot 10^{-3}= 239,5 \, kNm$, $M_{z,Rk,pl} = 184\cdot 235 \cdot 10^{-3}= 43,24 \, kNm$,
Częściowy współczynnik bezpieczeństwa do wyznaczania nośności obliczeniowych z nośności charakterystycznych:
w przypadku sprawdzania stateczności elementu (metodami wyboczeniowymi) $\gamma_{M}=\gamma_{M1} =1,1$,
w przypadku sprawdzania nośności elementu z nośności przekroju na podstawie sił II rzędu (metodami imperfekcyjnymi) $\gamma_{M}=\gamma_{M0} =1,0$.
(1-1.10) $\to$ współczynnik materiałowy $\varepsilon= \sqrt{ 235 / 235}=1,0$
(1-1.9) $\to$ smukłość porównawcza $ \lambda_1=93,9 \cdot 1,0=93,9$, gdzie współczynnik klasy przekroju $k_•=1$
(2-3.16) $\to$ smukłość progowa $\overline \lambda_0 =0,2 $
Metody wyboczeniowe
Metoda HWM
Długości wyboczenia
Idealne warunki brzegowe (podparcie widełkowe obu końców belki ze swobodą deplanacji przekrojów końcowych) wskazują, że (rys. 1-1.2a):
$\to$ współczynnik długości wyboczeniowej giętnej $ \mu_y=\mu_z=1$
$\to$ współczynnik długości wyboczeniowej na zwichrzenie $\mu_{LT}=1$
(1-1.6) $\to$ długość wyboczeniowa, giętna $L_{cr} = L_{cr,y}=L_{cr,z}=1,0 \cdot 5,691=5,691 \, m$
długość wyboczeniowa, zwichrzeniowa $L_{LT}=1,0\cdot 5,691=5,691 \, m$
Sprawdzenie długości wyboczeniowych
($\ref{10}$) $\to$ $L_{cr,y }= \pi \cdot \sqrt{34157/10408,9}=5,691 \ m $ (OK)
($\ref{11}$) $\to$ $L_{LT }= \pi \cdot \sqrt{903,63/72,7\cdot 10^{-2} \cdot 36348 /182,4}=15,63 \ m > 5,91 \,m \to$ $\mu_{LT}=15,63/5,691=2,75$
Wniosek: Zawodne jest szacowanie współczynnika długości zwichrzenia na podstawie warunków brzegowych z pominięciem wyznaczenia $M_{cr}$.
Smukłości pręta
(1-1.8) $\to$
$\lambda_y= \cfrac{569,1}{14,96}\cdot 1,0=38,1$
$\lambda_z= \cfrac{569,1}{3,79}\cdot 1,0=150,2$
(1-1.7)
$\to$ $\overline \lambda_y =\cfrac{38,0} {93,9}=0,405$
$\to$ $\overline \lambda_z =\cfrac{150,21} {93,9}=1,60$
Rozpatrujemy przypadek elementarny czystego zginania i widełkowego podparcia na podporze, w którym przy zaniedbaniu sztywności skrętnej $GI_T$ w stosunku do sztywności giętnych inżynierowie często stosują podejście :
promień bezwładności osiowy $i_0=\sqrt{i_y^2+i_z^2}=\sqrt{14,96^2+3,79^2}=15,43 \, cm$
(*) smukłość zwichrzenia $\lambda_{LT}= \cfrac{569,1}{15,43}\cdot 1,0=36,88$
(**) smukłość względna $ \overline \lambda_{LT} =\cfrac{36,88}{93,9}=0,39$
W celu sprawdzenia tych oszacowań wyznaczymy moment krytyczny z zależności analitycznej, która w przypadku czystego zginania upraszcza się do postaci:
$M_{cr}= C_1 \cdot N_{cr,z} \sqrt { \left( \cfrac{L_{LT}}{L_z}\cdot \cfrac{I_\omega}{I_z} +\cfrac{ G I_T} {N_{cr,z}} \right) }= 1,0 \cdot 667,8 \cdot \sqrt{\left( \cfrac{5,691}{5,691} \cdot \cfrac{313600}{1043,5} \cdot 10^{-4} +\cfrac{ 29,84}{667,8}\right) }= 182,4 \, kNm$
(***) smukłość względna z formuły ogólnej
$ \overline \lambda_{LT} =\sqrt{ \cfrac{W_{pl,y} \cdot f_y } { M_{cr}}}=\sqrt{\cfrac{1019\cdot 235}{182,4}\cdot 10^{-3}}=1,146$
Z porównania (**) z (***) wynika, ze aproksymacja typu (*) jest błędna i nie powinna być stosowana.
Współczynniki wyboczeniowe
wyboczenie giętne w płaszczyźnie (y-y)
Tab 3-2.1 $\to$ klasa imperfekcji „b” , Tab. 1(1) $\to $ $ \alpha_y= 0,34$
(2-3.15) $\to$ parametr imperfekcji $\Theta_y=0,34 \cdot ( 0,405- 0,2)=0,0698$
(2-3.14) $\to$ współczynnik pomocniczy $\Phi_y=1/2 \cdot \left ( 1+0,068+ 0,405^2 \right )=0,617$
(2-3.13) $\to$ współczynnik wyboczenia $\chi_y=\cfrac{1}{0,617 +\sqrt{0617^2- 0,405^2}}=0,924$
wyboczenie giętne z płaszczyzny (z-z)
Tab 3-2.1 $\to$ klasa imperfekcji „c” , Tab. (1-2-1) $\to $ $ \alpha_y= 0,49$
(2-3.15) $\to$ $\Theta_z=0,49 \cdot ( 1,60- 0,2)=0,686$
(2-3.14) $\to$ $\Phi_z=1/2 \cdot \left ( 1+0,686+ 1,600^2 \right )=2,123$
(2-3.13) $\to$ $\chi_z=\cfrac{1}{2,123 +\sqrt{ 2,123^2- 1,60^2}}=0,284$
zwichrzenie (LT)
Tab 3-2.1 $\to$ klasa imperfekcji „b” , Tab.1 $\to $ $ \alpha_y= 0,34$
(2-3.15) $\to$ $\Theta_{LT}=0,34 \cdot ( 1,146- 0,2)=0,322$
(2-3.14) $\to$ $\Phi_{LT}=1/2 \cdot \left ( 1+0,322+1,146^2 \right )=1,318$
(2-3.13) $\to$ $\chi_{LT}=\cfrac{1}{1,318 +\sqrt{ 1,318^2- 1,146^2}}=0,508$
zwichrzenie – przypadek szczególny (LTszcz)
Tab 3-2.1 $\to$ klasa imperfekcji „c” , Tab.1) $\to $ $ \alpha_y= 0,49$
(2-3.15) $\to$ $\Theta_{LTszcz}=0,49 \cdot ( 1,146- 0,4)=0,366$
(2-3.14) $\to$ $\Phi_{LTszcz}=1/2 \cdot \left ( 1+0,366+ 0,75 \cdot 1,146^2 \right )=1,175$
(2-3.13) $\to$ $\chi_{LTszcz}=\cfrac{1}{1,175 +\sqrt{ 1,175^2- 0,75 \cdot 1,146^2}}=0,554$
Współczynniki iterakcji
jak dla przekroju dwuteowego klasy 1 w elemencie wrażliwym na deformacje skrętne
przypadek [R] w ($\ref{9}$) – stały moment zginający po długości elementu,
Ponieważ $M_{z,Ed}=0$, więc ograniczmy się do wyznaczenia $k_{yy}$ oraz $k_{zy}$.
($\ref{9}$) $\to$ $C_m= C_{my}=C_{mz} = C_{mLT} = 0,6+0,4 \cdot \psi =0,6+0,4 \cdot 1,0=1,0$, gdzie $\psi=1,0$
$n_y=\cfrac{N_Ed}{\chi_y \cdot N_{Rd}}= \cfrac{497,364}{ 0,924 \cdot 1553,8 }= 0,3464$
$n_z=\cfrac{N_Ed}{\chi_z \cdot N_{Rd}}= \cfrac{497,364}{ 0,284 \cdot 1553,8 }= 1,1263$
$m_y=\cfrac{25,436}{ 0,508 \cdot 217,7}= 0,230$
$m_{y, szcz}=\cfrac{25,436}{ 0,554 \cdot 217,7}= 0,211$
($\ref{5}$) $\to$
$k_{yy}=1,0 \cdot \min {\{ (1+(0,405-0,2)\cdot 0,346 \,;\, (1+0,8\cdot 0,346\}}=1,07$
dla $\overline\lambda_z = 1,600 > 0,4 \to$ ($\ref{7}$)
$k_{zy}=\min{ \{ 1- 0,1 \cdot 1,600 \cdot 1,1263 \,;\,\ 1-0,1 \cdot 1,1263/(1-0,25) \} }=0,850$
Wytężenie belki-słupa
w przypadku ogólnym w= $n_z +k_{zy}\cdot m_y= 1,126+0,850 \cdot 0,230=$ 1,322,
w przypadku szczególnym w= 1,126+0,850\cdot 0,211= 1,305.
Metoda SWM
Metoda SWM tym różni się od HWM, że siły krytyczne $N_{cr}$ oraz $M_{cr}$ szacuje się w zadaniu pomocniczym bez wydzielania pręta z systemu z użyciem programów komputerowych.
Oszacowanie sił krytycznych programem LTBeamN
Zastosowano program LTBeamN [19] krótko opisany w artykule Zginane pręty stalowe
W przypadku systemu jednoelementowego mamy przypadek elementarny, w którym powinniśmy uzyskać zgodność z wzorami Eulera i Własowa. Z obliczeń programem LTBeam uzyskano wyniki:
- przy czystym ściskaniu i wyboczeniu z płaszczyzny
$N_{cr,z}=667,75 \, kN$, to znaczy
$\Lambda_{cr,N,z}=667,75/497,364 = 1,343$. - przy czystym zginaniu
$M_{cr,LT}= 182,89 \, kNm$, to znaczy
$\Lambda_{cr,M}=182,89/25,346 = 7,212$, - przy ściskaniu siłą $N= 497,364 \, kN$ i jednoczesnym zginaniu $M=25,346 \, kNm $
mnożnik krytyczny $\Lambda_{cr,MN}=1,281$.
Mnożniki krytyczne w powyższych formułach są inne, ponieważ rozpatrywano trzy różne konfiguracje obciążeń.
Z porównania uzyskanych sił krytycznych $N_{cr,z}$ oraz $M_{cr,LT}$ z uzyskanymi analitycznie w przykładzie HWM, wynika, że uzyskano pełną zgodność. Zgodność występuje dla przypadku elementarnego systemu złożonego z jednego elementu. W praktycznych przypadkach rozbieżności mogą być znaczne głównie ze względu na przybliżone ujęcie warunków brzegowych w formułach analitycznych.
W tym prostym przykładzie sprawdzimy możliwość stosowania formuły Merchanta (1-1.13). Mamy:
$ \Lambda_{cr,MN} \approx \cfrac{1}{1/\Lambda_{cr,N} +1/\Lambda_{cr,M}} =\cfrac{1}{1/1,343+1/7,212}= 1,132$
Stosunek wyniku dokładnego i aproksymowanego wynosi 1,281/ 1,132=1,13. Oszacowanie z interakcji liniowej może być stosowane we wstępnym, koncepcyjnym projektowaniu.
Smukłości pręta
z zależności ogólnej:
(1-2.3) $\to$ $\overline \lambda_y =\sqrt{ \cfrac{1709,2}{10409}}=0,405$,
(1-2.3) $\to$ $\overline \lambda_z=\sqrt{ \cfrac{1709,2}{667,75}}=1,600$,
(1-2.4) $ \overline \lambda_{LT} = \sqrt{\cfrac{239,5}{182,89}}=1,144$
Porównując otrzymane w przykładzie smukłości ze wzoru ogólnego (metoda SWM) ze smukłościami otrzymanymi w metodzie HWM stwierdzamy zgodność. Należy jednak zważyć, że rozpatrujemy przypadek idealny: pojedynczego pręta o idealnych warunkach brzegowych. W praktyce praktycznie przypadki takie nie występują i praktycznie nigdy nie uzyskamy wystarczającej zgodności metod HWM i SWM
Dalszy tok postępowania w metodzie SWM jest analogiczny jak w metodzie HWM (przykład 1-2.1a)
Wytężenie belki-słupa
w przypadku ogólnym w=1, 228
w przypadku szczególnym w= 1,224.
Metoda OWM
Przekrój krytyczny znajduje się w dowolnym miejscu belki-słupa, w których działają siły przekrojowe:
$N_{Ed}= 497,364 \, kN$, $M_{Ed,y}= 25,436 \, kNm$
Mnożnik plastyczny wylicza się jak następuje:
($\ref{14}$) $\to$ $\cfrac{1}{\alpha_{ult,k}} = \cfrac{497,364}{1709,2}+\cfrac{25,436}{239,5}= 0,397 \to \alpha_{ult,k} = \Lambda_{pl} =\cfrac{1}{0,397}=2,518$
Krytyczny mnożnik obciążeń oszacowano w Oszacowanie sił kytycznych programem LTBeamN i wynosi on $\Lambda_{cr} = \alpha_{cr,op} =1,281$.
Smukłość układu ($\ref{13}$) $\to$ $ \overline \lambda_{op}=\sqrt{\cfrac{2,518} {1,281}}= 1,402$
wyboczenie giętne z płaszczyzny Tab 3-2.1 $\to$ klasa imperfekcji giętnej „c” $\to$ Tab. (1-21) $\to$ $\alpha_z= 0,49$
(2-3.15) $\to$ parametr imperfekcji $\Theta_z=0,49 \cdot ( 1,402- 0,2)= 0,589$
(2-3.14) $\to$ współczynnik pomocniczy $\Phi_z=1/2 \cdot \left ( 1+0,589 + 1,402^2 \right )=1,777$
(2-3.13) $\to$ współczynnik wyboczenia $\chi_z=\cfrac{1}{1,777 +\sqrt{1,777^2 – 1,402^2}}=0,349$
wyboczenie boczne (zwichrzenie) Tab.3-2.2 $\to$ klasa imperfekcji „b” $\to$ Tab. (1-2-1) $\to$ $\alpha_z= 0,34$
(2-3.15) $\to$ parametr imperfekcji $\Theta_{LT}=0,34 \cdot ( 1,402- 0,2)=0,409 $
(2-3.14) $\to$ współczynnik pomocniczy $\Phi_{LT}=1/2 \cdot \left ( 1+0,409 + 1,402^2 \right )=1,687$
(2-3.13) $\to$ współczynnik wyboczenia $\chi_{LT}=\cfrac{1}{1,687 +\sqrt{1,687^2 – 1,402^2}}=0,381$
($\ref{15}$) $\to$ $\chi_{op}= \min { \{ 0,349 \quad ; \quad 0,381 \}} =0,349$,
OWM”A” ($\ref{16}$) $\to$ $\cfrac{0,349 \cdot 2,518} {1,1}= 0,798 <1 \to w=1/0,798=1,254$,
OWM „B” ($\ref{17}$) $\to$ $\cfrac{497,364}{0,349 \cdot 1553,82}+\cfrac{25,436}{0,381 \cdot 217,72}= 0,918+0,307=1,225$
Metody imperfekcyjne
Metoda SIM
Bezpośrednie wymuszenie imperfekcji geometrycznych zrealizujemy z użyciem programu Consteel [14]
Najpierw wprowadzamy system o idealnej geometrii jak na Rys. 3
Imperfekcje łukowe
w płaszczyźnie zginania: Tab 3-2.1 $\to$ klasa imperfekcji „a” $\to$ Tab.1-2.1 $\to$ $n_{L,y}=350$ ,
Imperfekcje łukowe z płaszczyzny zginania : Tab 3-2.1 $\to$ klasa imperfekcji „b” $\to$ Tab.1-2.1 $\to$ $n_{L,z} =250$,
Imperfekcja dla zwichrzenia ($\ref{1}$) $\to$ $n_{LT}=250/0,5=500$
Imperfekcje przechyłowe
W przykładzie nie są istotne imperfekcje przechyłowe, ponieważ wychylenie głowicy pręta nie wywołuje sił przekrojowych, więc sa pominięte.
Rozwiązanie statyczne układu z imperfekcjami
Siły przekrojowe drugiego rzędu w systemie z imperfekcjami z płaszczyzny $n_{LT}=500$ i w płaszczyźnie $n_{L,y} =350$ wynoszą
$N^{II}=497,362 \, kN$,
$M^{II}_y= 37,490\, kNm$ ,
$M^{II}_z= 25,660 \, kNm$ ,
$B^{II} = 0,680 \, kNm^2$ ,
Warunek nośności belki jest warunkiem nośności przekroju z równania konserwatywnego $ref{18}$):
w= \cfrac{497,36}{1709,2} \cfrac{37,49}{239,5}+ \cfrac{25,66}{43,2}+\cfrac{0,680}{7,5} = 1,132
Metoda QIM
Dla $n_{LT}=500$ $\to$ $q_{d,z}= \cfrac{8 \cdot 497,36}{500 \cdot 5,691}= 1,398 \, kN/m$
Dla $n_{L,y}=350$ $\to$ $q_{d,y} = \cfrac{8 \cdot 497,36}{350 \cdot 5,691} =1,998 \, kN/m$
Po obciążeniu belki dodatkowym obciążeniem w osi otrzymamy:
N^{II}=497,36 \, kN$,
$M^{II}_y= 37,27 \, kNm$ ,
$M^{II}_z= 27,30 \, kNm$ ,
$B^{II} = 0,718 \, kNm^2$ ,
w= \cfrac{497,36}{1709,2} \cfrac{37,27}{239,5}+ \cfrac{27,30}{43,2}+\cfrac{0,718}{7,5} =1,154
Metoda AIM
(z przykładu Prosta belka-słup ):
$N_{Ed}= 497,364 \, kN$,
Tab.1-2.2 N_Rk}=1709,2 \, kN$
$w_N= 497,364/1709,2=0,291 \to \alpha_{ult}=\Lambda_{pl}= 1/0,291=3,44$
Mnożnik krytyczny obciążeń
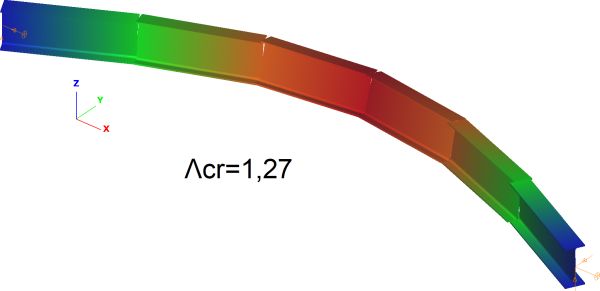
W pkt (Oszacowanie sił krytycznych programem LTBeamN ) mnożnik krytyczny obciążeń oszacowano programem LTBeam na $\Lambda_{cr}=1,281$. Postać własną oraz oszacowanie mnożnika krytycznego programem Consteel pokazano na Rys. 4.
Do obliczeń metoda AIM przyjęto mnożnik krytyczny obciążeń
$\Lambda_{cr}=1,27$
Przekrój sprawczy
Przekrój krytyczny zgodnie z definicją podaną w artykule Przekrój sprawczy znajduje się w środku rozpiętości belki, co wynika z analizy postaci wyboczonej belki (kształt zwichrzenia w postaci sinusoidy – rys. 1-2.5 ), to znaczy:
$x_m=L/2= 5691/2= 2845 \, mm$
Amplituda alternatywna
(3-8.32) $\to$ $\overline\lambda=\sqrt{\cfrac{3,44}{1,27}}=1,646$,
Tab.3-2.2 $\to$ klasa imperfekcji dla wyboczenia bocznego „b” $\to$ Tab.1 $\to$ $\alpha= 0,34$,
(2-3.15) $\to$ $\Theta =0,34 \cdot ( 1,646 – 0,2)=0,492$,
(2-3.14) $\to$ $\Phi=1/2 \cdot \left ( 1+0,492 + 1,646^2 \right )=2,10$,
(2-3.13) $\to$ $\chi=\cfrac{1}{2,10 +\sqrt{2,10^2 – 1,646^2}}=0,294$,
(3-8.25) $\to$ $e_{0k}=0,492 \cdot \cfrac{903,63}{72,7}=6,12 \,cm$,
(3-8.29) $\to$ $k_\chi =0,294 \cdot 1,646^2 = 0,797$,
(3-8.30) $\to$ $k_{\chi,d} =0,797/1,1= 0,724$,
(3-8.28) $\to$ $\gamma_{e0} =\cfrac{1-0,797}{1-0,724}=0,736$,
(3-8.26) $\to$ $e_{0d}=6,12/0,736=8,321 \,cm$,
(3-8.25) $\to$ $N_{cr}=1,27 \cdot 497,364= 631,7 \,kN$,
(3-8.21) z programu Consteel $M_{z, \eta,cr}= 30 \, kNm= 3000 \,kNcm$,
(3-8.24) $\to$ $A_m= \eta_{init,max} = 8,321 \cdot 631,7/ 3000=1,752 \, cm= 17,52 \, mm$
Amplituda alternatywna z programu Consteel
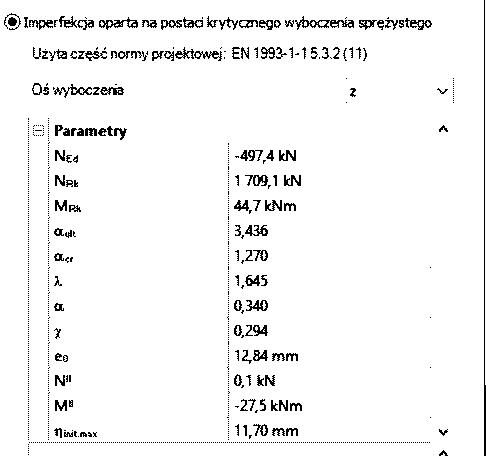
Amplitudę alternatywną oszacujemy za pomocą kalkulatora w programie Consteel, którego okienko pokazano na na rys.1-2.6. Kalkulator automatycznie wylicza amplitudę alternatywną z zależności normowej dla odczytanych z modelu wartości sił przekrojowych i nośności przekroju. W rozpatrywanym przykładzie amplituda alternatywna wynosi $\eta_{init, max}= 11,70 mm$
Dla tak wyliczonej wartości imperfekcji przeprowadzono analizę II rzędu i oszacowano wytężenie w programie Consteel i uzyskano:
w= 1,17
Wnioski z przykładu prosta belka-słup
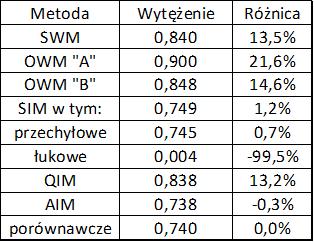
W tab. 1-2.2 porównano wyniki uzyskane w metodach wyboczeniowych i imperfekcyjnych dla elementu jednoelementowego
Tab.1-2.2 Porównanie metod wymiarowania prostej belki-słupa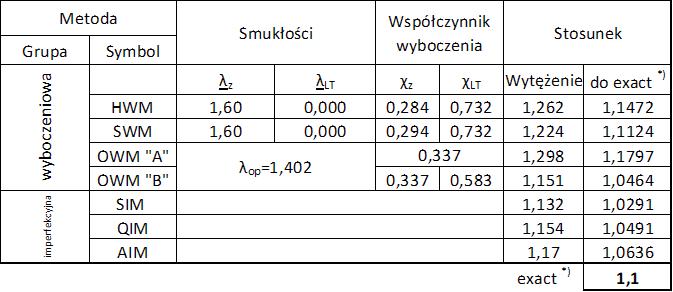
W ostatniej kolumnie wyniki porównano do wartości ścisłej wytężenie, podanej w pracy [20], a uzyskanej metodą GMNIA.
Wnioski:
- Wszystkie przedstawione metody wykazują, że nośność belki-słupa jest niewystarczająca, ale rozrzut wyników jest znaczny, co może przysparzać problemów w wyborze prawidłowej metody projektowania. Od wartości ścisłej wyraźnie odstają wyniki uzyskane metodami wyboczeniowymi: HWM, SWM oraz OWM „A”. Spośród metod wyboczeniowych tylko metoda OWM „B”, czyli metoda ogólna dla interpolowanego współczynnika wyboczenia daje wyniki podobnej klasy , co metody imperfekcyjne.
- Proste w zastosowaniu metody imperfekcyjne SIM, QIM oraz AIM dają wyniki o kilka procent wyższe od wyniku dokładnego,.
- Problemem podstawowym w metodzie bezpośredniej SIM, jest wybór kierunku i zwrotu imperfekcji.
- Metoda AIM rozwiązuje problem metody SIM, wskazując, że kierunek imperfekcji jest zgodny z podstawową postacią własną wyboczenia sprężystego w przestrzeni, wiec jej wyniki są bardziej wiarygodne. Model konstrukcji stosowany w metodzie AIM powinien obejmować te formy wyboczenia, które mogą być sprawcze- należy dbać o to, by nie pominąć krytycznej postaci wyboczenia.
W przypadku konstrukcji stalowych model obciążeniowy powinien obejmować zwichrzenie, to znaczy pręty powinny posiadać stopień swobody deplanacji. W przypadku konstrukcji żelbetowych i drewnianych najczęściej wystarcza model klasyczny prętów Bernoulliego. lub w przypadkach wątpliwych model płytowo-tarczowy . Możliwe jest też zastosowanie zastępczego materiału stalowego i zastosowanie modelu Własowa.
Rama portalowa
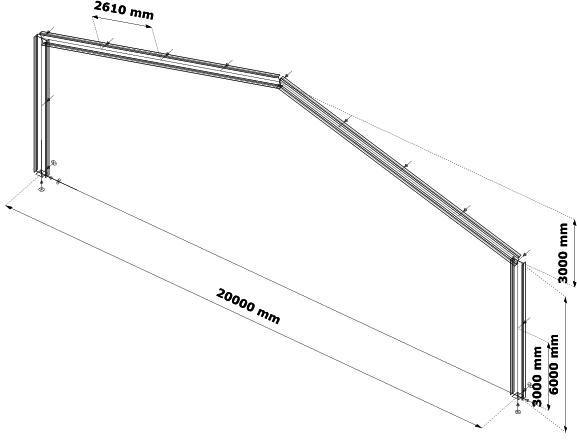
. Model geometryczny pokazano na rys. 1-2.7. Rygle ramy są obciążone pionowym obciążeniem $Q= 12 \, kN/m$
Rygiel jest odparte z płaszczyzny płatwiami w odstępach co $a=2,61 \,m$. Słupy jest poparty ryglami co $a=3,0 \,m$.
Dane
Konstrukcję wykonano ze stali S235:
$f_y = 235 \, MPa$, $E=210 \,GPa$,
smukłość progowa:
dla przypadku ogólnego $\lambda_0=0,2$
dla przypadku szczególnego $\lambda_{0,szcz}=0,4$
częściowy współczynnik bezpieczeństwa (materiałowy) przy sprawdzaniu warunków stateczności metodami wyboczeniowymi $\gamma_{M1}=1,1$
Słup wykonano z kształtownika IPE 500 o klasie przekroju 1 ocenionej dla złożonego stanu obciążenia wyznaczonego zgodnie z artykułem Klasa przekroju stalowego za pomocą programu SemiComp.
Rygiel wykonano z kształtownika IPE 450 o klasie przekroju klasa przekroju 1
Analiza LBA
Na rys. 1-2.8 pokazano postać własną ramy. Mnożnik obciążeń krytycznych wynosi $\Lambda_{cr} =5,27$
Metody wyboczeniowe
Metoda HWM
Oszacowanie długości wyboczeniowych
Na podstawie artykułu Długości wyboczeniowe prętów w systemie
Dane:
Rygiel IPE 500: $I_R=33740 \, cm^4$, $ l_R=20000 \, cm $, (zaniedbano efekt daszkowy ale także, to że długość rygla jest większa od jego rzutu)
Słupy IPE 450: $I_S=48200 \, cm^4$ , $l_S=600 \, cm$, $A= 116 \,cm^2$,
Stosunek obciążenia słupów: $m=1$.
Długość wyboczeniowa wg [21]
Rama jest układem o węzłach przesuwnych w płaszczyźnie.
Sztywność rygla $\overline K_R= 2 \cdot \cfrac{33740}{2000}=33,74 cm^3$
Sztywność słupa $\overline K_S= \cfrac{48200}{600}= 80,33 cm^3$
Sztywność zamocowania $\overline K_F= \overline K_S$ (stopa jest zamocowana)
Współczynnik podatności węzła dolnego $k_1= \cfrac{80,33}{80,33+80,33}=0,5$
Współczynnik podatności węzła górnego $k_2= \cfrac{80,33}{80,33+33,74}=0,70$
Z nomogramu rys. 9 artykułu „Ściskane pręty stalowe” po interpolacji liniowej odczytujemy $\mu=1,68$
Długość wyboczeniowa słupa $L_{cr}=1,68 \cdot 400=672 cm$.
Długość wyboczeniowa wg [22]
Współczynnik stosunku sztywności słupów i rygla wynosi $k_{S-R}=\cfrac{1}{6}\cfrac{EI_S}{EI_R} \cfrac{l_R}{l_S}=\cfrac{ 48200\cdot20,0}{6\cdot 33740\cdot 6,0}=0,794$.
Z nomogramu rys. 16 artykułu „Ściskane pręty stalowe”dla ramy ze stopami utwierdzonymi i równych sił w słupach odczytujemy $ \mu=1,48$.
Ponieważ siły w słupach są równe , współczynnik korekcyjny wynosi $\alpha_m=\sqrt{0,5(1+1)}=1$.
Ostatecznie:
współczynnik długości wyboczeniowej słupa 1: $\mu=1 \cdot 1,48=1,48$,
długość wyboczeniowa słupa 1: $L_{cr}=1,48 \cdot 600=888 cm$,
Długość wyboczeniowa metodą dokładną
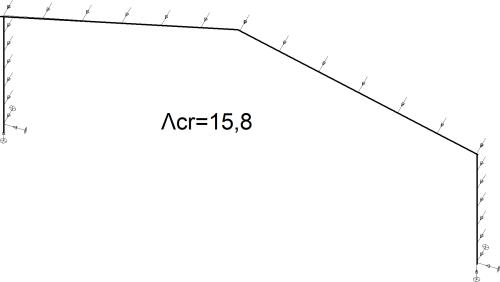
Wyniki uzyskane metodami nomogramowymi sprawdzimy metodą dokładną z zależności ($\ref{10}$) dla
$\Lambda_{cr,y}= 15,8$
$N_{Ed}= \cfrac{20\cdot 12}{2}=120 \,kN$
Sztywność giętna słupa $EI=210\cdot 48200 \cdot 10^{-2}=10122 \, kNm^2$
Mnożnik obciążenia krytycznego $\Lambda_{cr,y}$ uzyskano dla schematu z wyeliminowaniem wyboczenia z płaszczyzny ramy wg rys. 1-2.9
($\ref{10}$) $\to$ $ L_{cr}= \cfrac{\pi}{1} \cdot \sqrt{\cfrac{10122}{15,8\cdot 120}}=7,26\, m$
Błąd w oszacowaniu długości wyboczeniowej wg [23] wynosi $7,26/6,72= – 8$ %, a wg [24] $8,88,/7,26=+22$%
Tak duże różnice są niedopuszczalne w praktycznym projektowaniu, co dyskwalifikuje metodę HWM. Pomijamy dalsze obliczenia tą metodą, w tym oszacowani długości wyboczenia z płaszczyzny ramy.
Metoda SWM
Podstawowym parametrem metody SWM są mnożniki obciążeń krytycznych systemu, które zgodnie z analizą LBA i obliczeniami powyżej dla poszczególnych kierunków wyboczenia wynoszą:
$\Lambda_{cr,z} \Lambda_{cr,LT} =5,27$.
$\Lambda_{cr,y} =15,8$.
Słup IPE 500
Wyniki obliczeń pomocniczych metodą SWM dla słupa IPE 500 zestawiono w tab. 1-2-4
Tab.1-2.4 Zestawienie obliczeń metodą SWM dla słupa z przykładu 1-2.2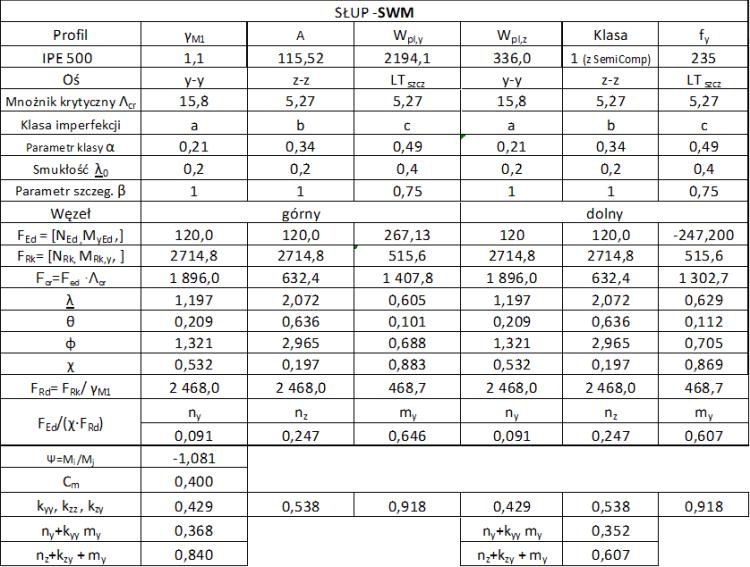
Smukłość pręta może być inna w każdym węźle przekroju, ponieważ inne mogą być siły przekrojowe. Dlatego obliczenia prowadzono dla węzła górnego (głowicy słupa) oraz dolnego (stopy).
Klasy imperfekcji ustalono na podstawie Tab 3-2.1 w przypadku wyboczenia giętnego i na podstawie tab. Tab 3-2.2 w przypadku zwichrzenia, następnie z tab. 1-2.1 ustalono parametry klasy zwichrzenia $\alpha$. W rezultacie otrzymano: $\alpha_y=0,21$, $\alpha_{z-z}=0,34$ , $\alpha_{LT, szcz} =0,49$ .
Poniżej przedstawiono wyliczenia współczynnika wyboczenia na przykładzie węzła górnego w przypadku szczególnego zwichrzenia.:
Nośności przekroju $M_{Rk}=W_{pl,y} \cdot f_y= 2194,1 \cdot 235 \cdot 10^{-3}= 515,6 \, kNm$
Moment krytyczny $M_{cr} = M_{y,Ed} \cdot \Lambda_{cr} = 267,13 \cdot 5,27= 1407,8 \, kNm$
(1-1.3) $\to$ $\overline \lambda_{LT, szcz} =\sqrt{ \cfrac{515,6}{1407,8}}=0,605$,
(2-3.15) $\to$ $\Theta_y=0,49 \cdot ( 0,605- 0,4)=0,101$
(2-3.14) $\to$ $\Phi_{LT,szcz} =1/2 \cdot ( 1+0,101+ 0,75 \cdot 0,605^2 )=0,688$
(2-3.13) $\to$ $\chi_{LT,szcz} =\cfrac{1}{0,688 +\sqrt{0,688^2 – 0,75 \cdot 0,605^2}}=0,882$
Momenty zginające na długości słupa maja przebieg prostoliniowy [P], a współczynnik stosunku momentów na końcach słupa
$\psi=\cfrac{-267,13}{247,20}=-1,081$.
($\ref{9}$) $\to$ $C_m=C_y=C_z=C_{LT}= \min{ \{ 0,6+0,4\cdot (-1,081)\, ;\, 0,4 \}} = 0,4$.
Słup jest wrażliwy na wyboczenie skrętne, więc dla klasy 1-szej przekroju:
$n_y=\cfrac{120}{(2714,8/1,1) \cdot 0532}= 0,091$,
$n_z=\cfrac{120}{(2714,8/1,1) \cdot 0197}= 0,247$,
$m_y= \cfrac{267,13}{515,6/1,1 \cdot 0,883}= 0,646$,
($\ref{8}$) $\to$ $k_{yy}=0,4 \cdot \min {\{ 1+(2,072-0,2) \cdot 0,091 \,;\, 1+0,8 \cdot 0,0,09\}}=0,429$,
($\ref{2}$) $\to$ $w_y= n_y + k_{yy}\cdot m_y= 0,091+0,429 \cdot 0,646=0,368 <1$,
$w_z= 0,840$.
Rygiel IPE 450
Wyniki obliczeń pomocniczych dla rygla IPE 450 zestawiono w tab. 1-2-5
Tab. 1-2.5 Zestawienie obliczeń metodą SWM dla słupa z przykładu 1-2.2
Obliczenia dla rygla przeprowadza się w analogiczny sposób jak dla słupa. Wytężeniem całej ramy jest wytężenie przekroju krytycznego
$w = 0,979$.
Przekrojem krytycznym jest przekrój okapowy rygla.
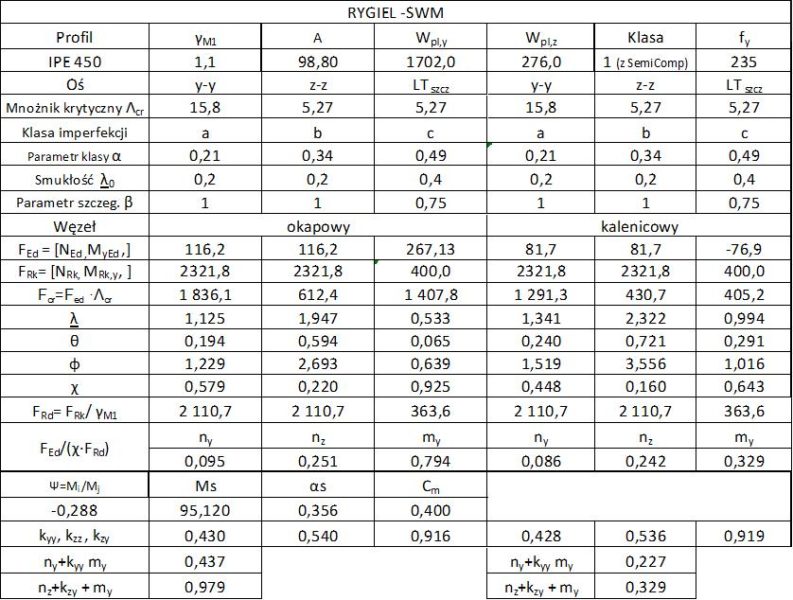
Metoda OWM
W celu określenia przekroju sprawczego (krytycznego) przeprowadzono wstępne obliczenia i wykazano, że przekrój krytyczny znajduje się węźle kalenicowym rygla, dla którego:
$N_{Ed}= 116,2 \, kN$, $M_{Ed,y}= 267,13 \, kNm$,
$N_{Rk}= 98,8 \cdot 235 \cdot 10^{-1} = 2321,8 \, kN$, $M_{y,Rk}= 1702 \cdot 235 \cdot 10^{-3} =400,0 \, kNm $
$EA= 210 \cdot 98,8\cdot 10^2=
W tab. 1-2.6 zestawiono wyniki obliczeń metodą OWM.
Tab. 1-2.6 Zestawienie obliczeń metodą OWM dla ramy z przykładu 1-2.2
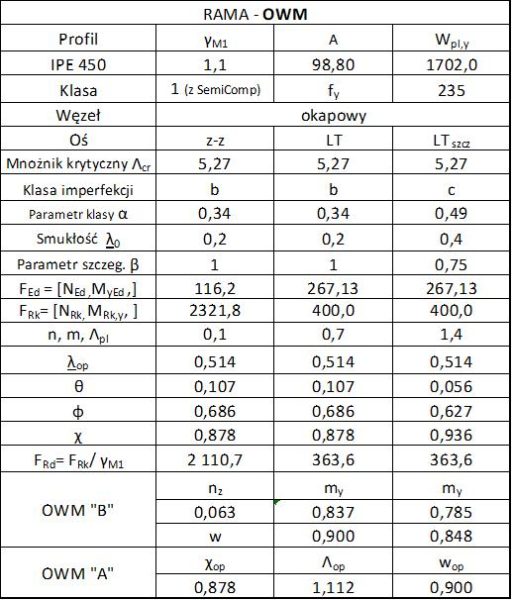
Mnożnik plastyczny wynika z wytężenia przekroju krytycznego i wynosi
($\ref{14}$) $\to$ $\cfrac{1}{\Lambda_pl } = \cfrac{116,2}{2321,8}+\cfrac{267,13}{400}= 0,718 \to \alpha_{ult,k} = \Lambda_{pl} =\cfrac{1}{0,718}= 1,393$
Analizę LBA (rys. 1-2.8) przeprowadzono z uwzględnieniem zwichrzenia i wyboczenia z płaszczyzny. Mnożnik $\Lambda_{cr}$ odpowiada podstawowej (pierwszej) postaci wyboczenia , czyli minimalny mnożnik obciążeń obliczeniowych
$\alpha_{cr, op}=\Lambda_{cr}=5,27$
($\ref{13}$) $\to$ $ \overline \lambda_{op}= \sqrt { \cfrac{1,393} {5,27}}= 0,514$
Smukłość systemu $\lambda_{op}$ dotyczy wszystkich form wyboczenia. Ponieważ jednak dla wyboczenia giętnego oraz zwichrzenia inne mogą być klasy imperfekcji , to w konsekwencji inne będą współczynniki wyboczenia.
Tab 3-2.1 $\to$ klasa imperfekcji giętnej z-z „b”, $\to$ Tab. (1-2-1) $\to$ $\alpha_z= 0,34$
(2-3.15) $\to$ $\Theta_z=0,34 \cdot ( 0,514- 0,2)=0,107$
(2-3.14) $\to$ $\Phi_z=1/2 \cdot \left ( 1+0,107 + 0,514^2 \right )=0,686$
(2-3.13) $\to$ $\chi_z=\cfrac{1}{0,686 +\sqrt{0,686^2 – 0,514^2}}=0,878$
Tab.3-2.2 $\to$ klasa imperfekcji zwichrzenia przypadek szczególny „c” $\to$ Tab. (1-2-1) $\to$ $\alpha_z= 0,49$
(2-3.15) $\to$ $\Theta_{LT,szcz}=0,49 \cdot ( 0,514- 0,4)= 0,056 $
(2-3.14) $\to$ $\Phi_{LT,szcz}=1/2 \cdot \left ( 1+0,056 + 0,75 \cdot 0,514^2 \right )=0,627$
(2-3.13) $\to$ $\chi_{LT,szcz}=\cfrac{1}{0,627 +\sqrt{0,627^2 – 0,75 \cdot 0,514^2}}=0,936$
($\ref{15}$) $to$ $\chi_{op}= \min { \{ 0,878 \quad ; \quad 0,936 \} } =0,878$.
OWM”A” ($\ref{16}$) $\to$ $\cfrac{0,878 \cdot 1,393} {1,1}= 1,112 >1 \to w=1/1,112= 0,900$,
OWM”B”
przypadek ogólny zwichrzenia:
($\ref{17}$) $\to$ $w= \cfrac{116,2} {2110,7 \cdot 0,878} +\cfrac{267,13}{363,6 \cdot 0,878}= 0,063+ 0,837= 0,900$
przypadek szczególny zwichrzenia:
($\ref{17}$) $\to$ $w= \cfrac{116,2} {2110,7 \cdot 0,878} +\cfrac{267,13}{363,6 \cdot 0,936}= 0,063+ 0,785= 0,848$
Najbardziej wiarygodnym jest wynik uzyskany metodą OWM”B” na przypadek szczególny , czyli $w=0,848$
Metody imperfekcyjne
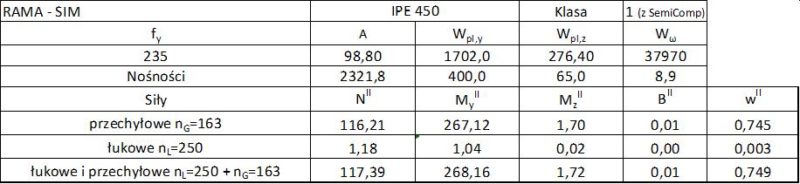
Metoda SIM
Bezpośrednie wymuszenie imperfekcji geometrycznych zrealizujemy z użyciem programu Consteel [14]
Imperfekcje łukowe w płaszczyźnie zginania
Tab 3-2.1 $\to$ klasa imperfekcji „a” , Tab.1-2.1 $\to$ $n_L=300$
Imperfekcje łukowe z płaszczyzny zginania
Tab 3-2.1 $\to$ klasa imperfekcji „b” , Tab.1-2.1 $\to$ $n_L=250$
Imperfekcje przechyłowe wg Imperfekcje geometryczne przechyłowe
(3-2.1) $\to$ $n_\Phi,0=200$
(3-2.2) $\to$ $\alpha_h= \cfrac{2}{\sqrt{6}}=0,816$
(3-2.3) $\to$ $\alpha_m= 1$
(3-2.4) $\to$ \n_\Pi = 200 \cdot 0,816 \cdot 1 =163$.
Tab. 1-2.7 Zestawienie obliczeń metodą SIM dla ramy z przykładu 1-2.2
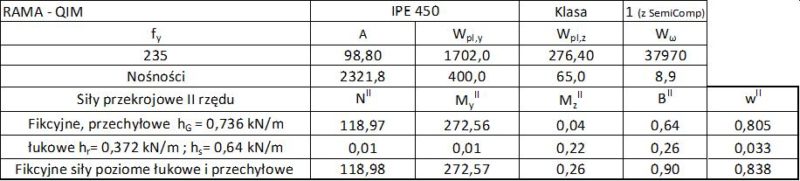
Metoda QIM
Poziome obciążenia fikcyjne równoważne imperfekcjom przechyłowym $n_G=163$:
(3-2.6) $\to$ $h_G=Q/n_G=120/163=0,736 \, kN/m$ jako dodatkowa składowa pozioma obciążenia rygla Q=12 kN.
Poziome obciążenia fikcyjne równoważne imperfekcjom łukowym $n_L=250$ z płaszczyzny zginania
rygiel $N_Ed= 116,2 \, kN$ $L=10 \, m $:
(3-2.7) $ \to$ $h_r= \cfrac {8 \cdot 116,2}{250 \cdot 10} =0,372 \, kN/m$
słup $N_Ed= 120 \, kN$ $L=6,0 \, m $:
(3-2.7) $\to$ $h_s= \cfrac{8N\cdot 120}{250 \cdot 6,0} =0,64 \, kN/m$
Tab. 1-2.8 Zestawienie obliczeń metodą QIM dla ramy z przykładu 1-2.2
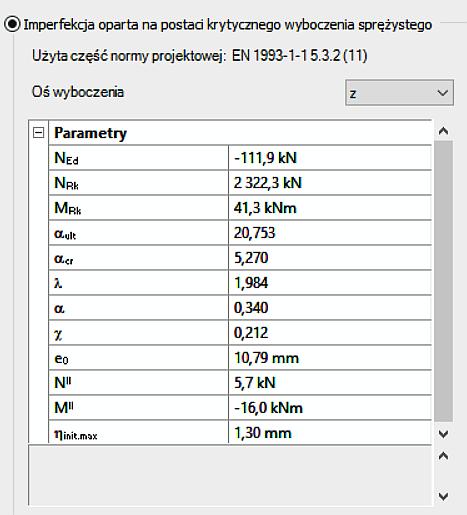
Metoda AIM
Amplitudę alternatywna wyznaczono z użyciem kalkulatora Consteel , którego okienko pokazano na rys. 1-2.10
Wytężenie przekroju krytycznego pod działaniem imperfekcji alternatywnych wyniosło w= 0,738
Wnioski z przykładu Rama portalowa
W tabeli 1-2.7 zestawiono wyniki uzyskane w przykładzie 1-2.2. Wyniki metody ogólnej OWM uzupełniono o rezultaty obliczeń w programie Consteel dla opcji $\chi_{op}= min(\chi, \chi_{LT}$ i $\chi_{op}$ interpolowane między ($\chi, \chi_{LT}$) .
Tab 1-2.9 Zestawienie wyników dla ramy z przykładu 1-2.2
Wnioski:
- Stosowanie metody wyboczeniowej w odmianie historycznej HWM, w której szacuje się długości wyboczeniowe daje błędne wyniki i stosowanie metody powinno być wykluczone z warsztatu projektanta.
- Metody wyboczeniowe SWM oraz OWM, a także obciążeniowa metoda imperfekcyjna QIM dają wyniki znacznie odbiegające ( o kilkanaście procent) od najbardziej prawdopodobnego wyniku uzyskanego metodą AIM.
- Metody imperfekcyjne SIM oraz AIM dają podobne rezultaty.
- W przykładzie ramy portalowej imperfekcje łukowe są pomijalne.
- Biorąc pod uwagę wyniki z innych przykładów zamieszczonych w podręczniku, najbliższa faktycznemu wytężeniu jest metoda alternatywna AIM w której uzyskano wytężenie 74%.
Łuk
Treść przykładu zaczerpnięto z pracy [25]
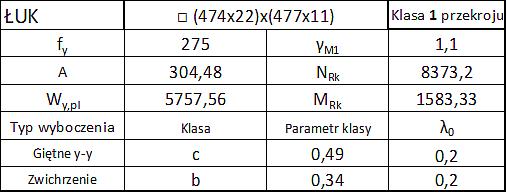
Łuk ma przekrój skrzynkowy: pasy (474×22), środniki (477×11) i jest niewrażliwy na odkształcenia skrętne. Klasa przekroju 1
Podparcie z płaszczyzny jest realizowane przez podpory (płatwie) rozstawione co 4m). Materiał S275 ($f_y=275 \, MPa$).
Zagadnienie jest rozpatrywane w płaszczyźnie łuku z utratą stateczności giętnej względem osi y-y.
Parametry przekroju łuku zestawiono w tab. 1-2.10. Nośności przekroju jak dla klasy 1:
$N_{Rk}=304,48 \cdot 275 \cdot 10^{-1}= 8373,2 \, kN$, $M_{Rk}= 5757,56 \cdot 275 \cdot 10^{-3}=158,33$
Tab.1-2.10 Parametry przekroju łuku z przykładu 1-2.3
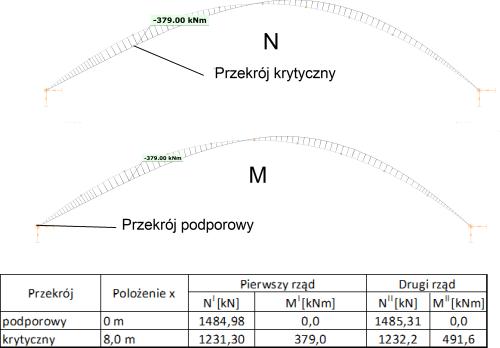
Wykresy sił przekrojowych pokazano na rys. 1-2.12
Analiza LBA
Na rys. 1-2.13 pokazano postać własną łuku uzyskaną z analizy LBA w programie Consteel. Minimalny mnożnik obciążeń krytycznych wynosi
$\Lambda_{cr}=4,33$.
Metody wyboczeniowe
Metoda HWM
Metody historycznej HWM w przykładzie nie stosuje się ponieważ jest zdyskwalifikowana do zastosowań inżynierskich.
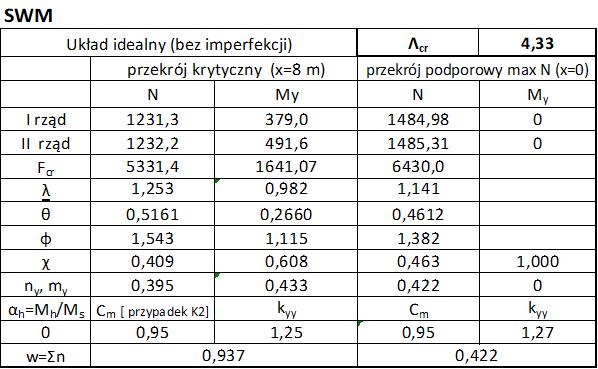
Metoda SWM
W tab. 1-2.8 zestawiono obliczenia łuku metodą SWM.
Obliczenia wykonano dla przekroju podporowego (max N) oraz przekroju krytycznego, w którym wytężenie jest największe. Mimo, że nośności przekrojów $N_{Rk}$ i $M_{Rk}$ są takie same, to smukłości pręta w tych węzłach są inne.
Tab. 1-2.8 Zestawienie obliczeń SWM dla łuku przykład 1-2.3
Współczynnik wyboczenia giętnego dla przekroju krytycznego:
($\ref{12}$) $\to$ $N_{cr} = 4,33 \cdot 1231,3 = 5331,4 \, kN$,
(1-1.3) $\to$ $\overline \lambda_y =\sqrt{ \cfrac{8373,2}{ 5331,4}}=1,253$
Tab 3-2.1 $\to$ klasa imperfekcji giętnej w płaszczyźnie „c” (przekrój skrzynkowy z grubymi spoinami) $\to$ Tab. (1-2-1) $\to$ $\alpha= 0,49$
(2-3.15) $\to$ $\Theta_y=0,49 \cdot ( 1,253- 0,2)=0, 516$
(2-3.14) $\to$ $\Phi_y=1/2 \cdot \left ( 1+0,516 + 1,253^2 \right )=1,543$
(2-3.13) $\to$ $\chi_y=\cfrac{1}{1,543 +\sqrt{1,543^2 – 1,253^2}}=0,409$
$n_y=\cfrac{1231,3}{8373,2/1,1 \cdot 0,409}=0,395$,
$m_y=\cfrac{379}{1583,33/1,1 \cdot 0,608 }=0,433$.
($\ref{9}$) $C_m=0,95+ 0,05 \cdot 0=0,95$ (przebieg momentów od obciążenia równomiernego [K2] dla $\alpha_h=0$.
($\ref{6}$) $\to$ $ k_{yy}= 0,95 \cdot \min { \{ (1+(1,253-0,2) \cdot 0,397) \, ; \, (1+0,8\cdot 0,397) \}}= 1,250$
(przekrój klasy 1 niewrażliwy na deformacje skrętne $\to k_{yy}$ jak dla przekroju dwuteowego)
Wytężenie $w=0,397+1,250 \cdot 0,433= 0,938$.
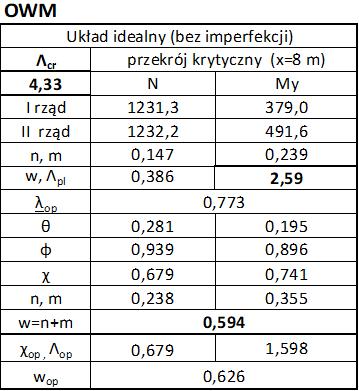
Metoda OWM
W rozpatrywanym przypadku nie są spełnione warunki klauzuli [2]-kl.6.3.4, bo układ nie wyboczy się z płaszczyzny ani nie zwichrzy. Zastosujemy jednak metodę OWM w celu porównania z innymi.
($\ref{14}$) $\to$ $\cfrac{1}{\alpha_{ult,k}} = \cfrac{1231,3}{8373,2}+\cfrac{379,0}{1583,33}= 0,147+0,239 =0,4386 \to \alpha_{ult,k} = \Lambda_{pl} =\cfrac{1}{0,386}= 2,59$
$\alpha_{cr, op}=\Lambda_{cr}=4,33$
($\ref{13}$) $\to$ $ \overline \lambda_{op}= \sqrt { \cfrac{2,59} {4,33}}= 0,773$
Tab.3-2.1 $\to$ klasa imperfekcji giętnej „c” $\to$ Tab. (1-2-1) $\to$ $\alpha_y = 0,49$
(2-3.15) $\to$ $\Theta_{y}= 0,49 \cdot ( 0,773- 0,2)=0,281 $
(2-3.14) $\to$ $\Phi_{y}=1/2 \cdot \left ( 1+ 0,281 + 0,773^2 \right )= 0,939$
(2-3.13) $\to$ $\chi_{y}=\cfrac{1}{0,939 +\sqrt{0,939^2 – 0,773^2}}=0,679$
Tab.3-2.2 $\to$ klasa imperfekcji zwichrzenia „b” $\to$ Tab. (1-2-1) $\to$ $\alpha_{LT}= 0,34$
(2-3.15) $\to$ $\Theta_{LT}= 0,34 \cdot ( 0,773- 0,2)=0,195$
(2-3.14) $\to$ $\Phi_{LT}=1/2 \cdot \left ( 1+0,195 + 0,773^2 \right )= 0,896$
(2-3.13) $\to$ $\chi_{LT}=\cfrac{1}{0,896 +\sqrt{0,896^2 – 0,773^2}}=0,741$
OWM „B” ($\ref{16}$) $\to$
$n=\cfrac{1231,3}{8373,2/1,1 \cdot 0,679}= 0,238$ $m=\cfrac{379}{1583,33/1,1\cdot 0,741}=0,355$ $=0,238+0,355=0,594$.
($\ref{15}$) $to$ $\chi_{op}= \min { \{ 0,679 \quad ; \quad 0,741 \} } =0,679$.
OWM”A” ($\ref{17}$) $\to$ $ \Lambda_{op}=\cfrac{2,59 \cdot 0,679}{1,1}= 1,598$, $w_{op}= 1/1,590= 0,626$
W tab. 1-2.9 zestawiono obliczenia metoda OWM dla łuku. Należy zwrócić uwagę, ze zamiast wyboczenia z płaszczyzny brano pod uwagę wyboczenie giętne w płaszczyźnie.
Tab. 1-2.9 Zestawienie obliczeń metodą OWM dla łuku
 Metody imperfekcyjne
Metody imperfekcyjne
Metoda SIM
Imperfekcje łuku określimy na podstawie wytycznych normowych zawartych w tab. 3-6.1 . Dla klasy imperfekcji „c” (przekrój skrzynkowy z grubymi spoinami) oraz niesymetrycznej postaci wyboczenia w płaszczyźnie mamy:
$n_L=400$ w stosunku do połowy rozpiętości łuku $l=L/2$ o strzałce wyniosłości $f$
Imperfekcje łukowe nadano w kształt sinusoidy poprzez wyliczenie współrzędnych węzłów $z$ zgodnie z zależnością
$z(x) =z_{perf} + e(x)$
gdzie współrzędne idealnego łuku parabolicznego $z_{perf}= \cfrac{f}{l}\cdot (2\cdot l-x) \cdot x $
imperfekcje $e= e_0 \cdot \sin (\pi x/l )$, gdzie amplituda imperfekcji $e_0=l/ n_L$
Współrzędne łuku idealnego i z imperfekcjami zestawiono w tab. 1-2. 10
Tab.1-2.10 Współrzędne łuku: idealnego z , imperfekcja e oraz współrzędne łuku z imperfekcją (z+e)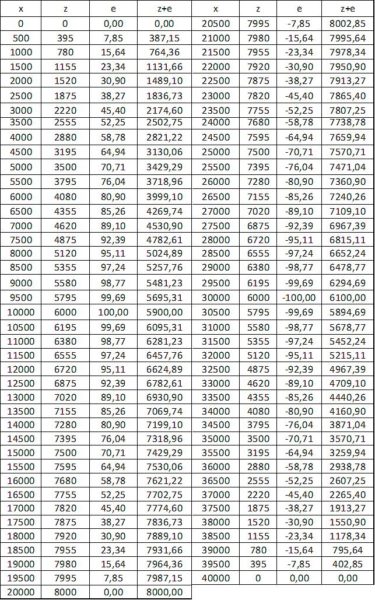
Z rozwiązania łuku z imperfekcjami o geometrii przedstawionej w tab.1-2.10. Siły siły II rzędu w przekroju krytycznym (x=8 m) wynoszą:
$N_{Ed}= 1232,2 \, kN$;
$M_{y,Ed} =491,61 \, kNm$.
$M_{z,Ed}=0 $
$B_{Ed}=0$.
Wytężenie przekroju krytycznego wynosi:
$w=\cfrac{1283,41}{8373,2}+\cfrac{658,58}{1583,33}= 0,153 + 0,416$= 0,569.
Wynik pogrubiono, ponieważ jest on najbardziej prawdopodobny przy założeniu, że w normie [2] prawidłowo określono klasy imperfekcji, a w [26] prawidłowo określono amplitudy imperfekcji łukowych łuków.
Oczywiście ograniczone zaufanie należy mieć również do parametrów klasy imperfekcji stosowanych w metodach wyboczeniowych i kilkudziesiecio-procentowa różnica między metodami nie musi wskazywać na błąd metody imperfekcyjnej
Metoda AIM
Amplitudę alternatywną wyznaczono z użyciem kalkulatora Consteel , którego okienko pokazano na rys. 1-2.14.
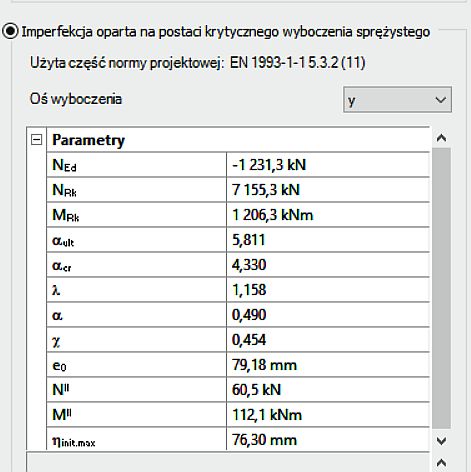
Rys.1-2.14. Obraz kalkulatora w programie Consteel do oszacowania amplitudy impefekcji alternatywnej
Wytężenie przekroju krytycznego pod działaniem imperfekcji alternatywnych wyniosło w= 0,738.
⊗ ⇒ [ Imperfekcje konstrukcji i ich źródła ]
Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2017-2020), Imperfekcyjna metoda projektowania konstrukcji, Encyklopedia πWiki, Wydawnictwo Chodor-Projekt,
[ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]
Historia edycji:
Wersja 1.0 (2019-04-07) – pierwsza wersja artykułu
Wersja 2.0 (2019-05-26) – podzielono na artykuły internetowe i zaopatrzono w połączenia odnośnikamiLiteratura
- PN-EN 1992-1-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1994-1-1+Ap1+AC :2008, Eurokod 4: Projektowanie zespolonych konstrukcji stalowo-betonowych, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1995-1-1+A2+NA+07E :2010, Eurokod 5: Projektowanie konstrukcji drewnianych – Część 1-1: Postanowienia ogólne – Reguły ogólne i reguły dotyczące budynków
- PN-EN 1996-1-1+A1+Ap1,2:2013, Eurokod 6: Projektowanie konstrukcji murowych , Część 1-1: Reguły ogólne dla zbrojonych i niezbrojonych konstrukcji murowych
- PN-EN 1999-1-1:2010, Eurokod 9: Projektowanie konstrukcji aluminiowych, Część 1-1: Reguły ogólne
- PN-EN 1993-1-6: 2010, Eurokod 3: Projektowanie konstrukcji stalowych, Część 1-6: Wytrzymałość i stateczność konstrukcji powłokowych
- PN-EN 1993-1-7 + AC+Ap1:2007, Eurokod 3: Projektowanie konstrukcji stalowych , Część 1-7: Konstrukcje płytowe
- Kala Z., (2015), Realiability analysis of the lateral torsional buckling and the ultimate limit state of stell beams with random imperfewctions, Journal of Cicil Engineering and Management, Vol. 21(7), pp. 902-911
- Kala Z., ( 2013 ), Elastic Lateral-Torsional Buckling of Simply Supported Hot-Rolled Steel I-Beams with Random Imperfections, Procedia Engineering 57 pp. 504 – 514
- Taras A., Greiner R. (2010), New design curves for lateral-torsional buckling. A Proposal based on a consistent derivation, Journal of Constructional Steel Research, 66(5), 648–663
- (Ayrton W. E. Perry J. (1886), On Struts, The Engineer, 464–513
- CTICM, (2013), LTBeamN, [ https://www.cticm.com/logiciel/ltbeamn/ [
- Consteel Software. (2019). ConSteel 13 Manual, [https://consteelsoftware.com/downloads/ ]
- Sofistik, (2018). Sofistik. Imperfection Concept. Sofistik Tutorials 2018, Tutorilas for Stel Design. Imperfection Concept, [ /www.sofistik.de/documentation/2018/en/tutorials/steel-design/imperfection/imperfection.html ]
- Chodor L. (2016), Nośność plastyczna konstrukcji, [ https://chodor-projekt.net/encyclopedia/nosnosc-plastyczna-konstrukcji/]
- Computer and Structures Inc. (2019), SAP2000., Structural Software for Analysis and Design (Version 21), [ https://www.csiamerica.com/products/sap2000 ]
- Hajdu G., Papp F., Achim R. (2017). Vollständige äquivalente Imperfektionsmethode für biege- und druckbeanspruchte Stahlträger. Stahlbau, 86(6), 483–495
- CTICM, (2013), LTBeamN, [ https://www.cticm.com/logiciel/ltbeamn/ ]
- Tankova T., Marques L., Simoes da Silva, L.,Andrade A. (2017). Development of a consistent methodology for the out- of- plane buckling resistance of prismatic beam-columns. Journal of Constructional Steel Research, 128, 839–852
- PN-90/B-03200, Konstrukcje stalowe – Obliczenia statyczne i projektowanie
- Petersen C. (2013). Stahlbau: Grundlagen der Berechnung und baulichen Ausbildung von Stahlbauten (4 Wydanie- überarb. und aktualisierte Aufl). Springer Vieweg
-
PN-90/B-03200, Konstrukcje stalowe – Obliczenia statyczne i projektowanie
- Petersen C. (2013). Stahlbau: Grundlagen der Berechnung und baulichen Ausbildung von Stahlbauten (4 Wydanie- überarb. und aktualisierte Aufl). Springer Vieweg
- Dallemule M. (2015). Equivalent imperfections in arched structures. Slovak Journal of Civil Engineering, 23(3), 9–15
- PN-EN 1993-2:2010, Projektowanie konstrukcji stalowych, Część 2: Mosty stalowe
________________________________