Stateczność ogólna wysokich budowli jest istotna przy projektowaniu takich obiektów jak: kominy, wieże, budynki wysokie, fundamenty słupów elektroenergetycznych, kolei linowych, ścian oporowych itp.
Warunek stateczności ogólnej można zapisać [1]:
| $ E_{dst.d} \le E_{stb,d}$ | (1) |
gdzie:
$ E_{dst.d}$ – obliczeniowy efekt wywolany działaniem destabilizujących obciążeń,
$ E_{stb.d}$ -obliczeniowy efekt wywołany działaniem obciążeń stabilizujących.
są iloczynem iloczyn z wartości charakterystycznych $E_j$ i częściowych współczynników bezpieczeństwa $E_d= \gamma_F \cdot E_k$ , gfzie $\gamma_F$ zestawiono w tab.1.
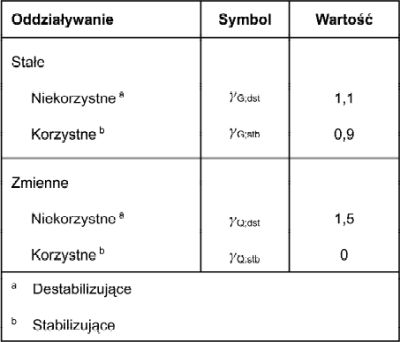
Tab.1.Współczynniki czesciowe $\gamma_F$ do oddziaływań w stanie równowagi granicznej EQU [1]
Wnormie [1] nie definiuje się globalnego współczynnika bezpieczeństwa
| $ \gamma= \dfrac {E_{stb,d}}{E_{dst.d}}$ | (2) |
choć warunek (1) można zapisać w postaci z użyciem (2) w postaci (3)
| $ \gamma\le 1$ | (3) |
W przypadku konstrukcji wysokich i stanu granicznego obrotu, efekty oddziaływań $E$ należy traktować jako momenty sił utrzymujące $M_{stb}$ i wywracające $M_{dst}$.
Wadą podejścia (1) lub (3) jest traktowanie systemu jak bryły sztywnej i nie uwzględnienie podatności układu, w szczególności sprężystości podłoża gruntowego. Tymczasem już w 1936 roku Cramer [2] rozwiązał zagadnienie stateczności wieży na podłożu sprężystym (rys.1).
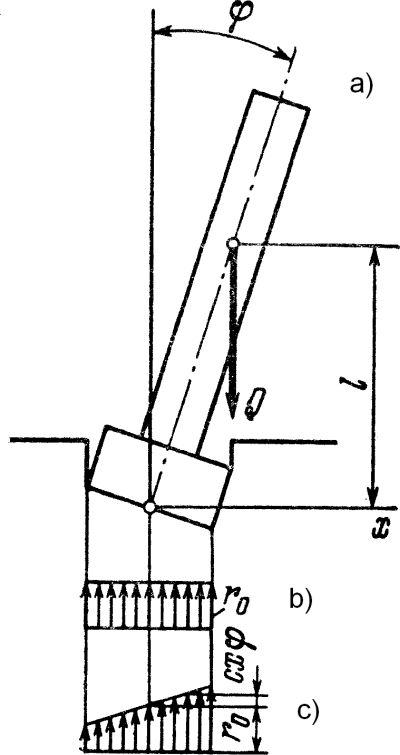
Rys.1. Stan równowagi EQU: a) schemat układu, b) reakcje podłoża w położeniu początkowym, c)reakcje podłoża w położeniu obróconym (odkształconym) [3]
Załóżmy, ze podłoże jest typu Winklera, czyli z reakcjami $r$ proporcjonalnymi do osiadania $z$ :
| $ r=-cy$ | (3) |
W nieodkształconej konfiguracji (rys1 b) zachodzi
| $ r=r_0=\dfrac{Q}{A}$ | (4a) |
gdzie $A$ – pole powierzchni fundamentu, a konfiguracji odkształconej zachodzi:
| $ r=r_0+cx\varphi$ | (4b) |
gdzie: $\varphi$ – kąt odchylenia wieży od pionu, x – odległość pozioma punktu od osi fundamentu wieży. W położeniu odkształconym spełnione jest równanie momentów względem osi fundamentu:
| $ -Ql\varphi+\int \limits_{(A)}rbx dx=0$ | (5) |
gdzie $b=b(x)$ jest szerokością stopy fundamentowej (prostopadle do płaszczyzny rysunku). Po podstawieniu (4b) do (5) i przecałkowaniu, otrzymujemy:
| $ -Ql\varphi+c\varphi I=0$ | (6) |
gdzie : I – moment bezwładności stopy względem jej osi. Warunek (6) powinien być spełniony dla dowolnych wartości Q. Jeśli $\varphi=0$, to trywialne rozwiązanie oznacza równowagę wieży w położeniu nieodkształconym. Natomiast dla $\varphi \ne 0$ siła powinna spełniać warunek:
| $ Q=Q_{cr}= \dfrac{cI}{l}$ | (7a) |
Stąd wspólczynnik stateczności (2) w stanie krytycznym wynosi:
| $ \gamma_{cr}=\dfrac{Q_{cr}}{Q}=\dfrac{cI}{Ql}$ | (7b) |
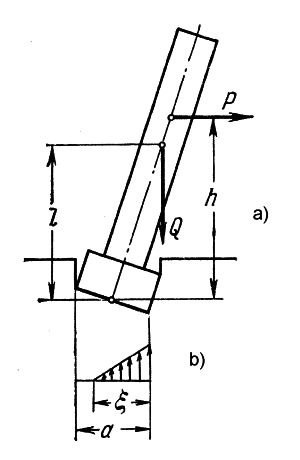
Rys.2. Stan równowagi EQU przy odrywaniu stopy: a) schemat układu, b) reakcje podłoża [3]
W przypadku odrywania stopy od podłoża należy rozważyć sytuację, pokazaną na rys.2.
Równanie równowagi dla sytuacji z rys.2 można zapisać w postaci:
| $ -Ph-Ql\varphi+c\varphi I=0$ | (8) |
przy czym przyjęto, że $\varphi \approx tg\varphi \approx \sin \varphi$ .
Z (8) otrzymujemy liniową zależność
| $ p+\dfrac{cI-Ql}{h}\varphi$ | (9) |
Zależność (9) pozostaje słuszna dopóty odpór rozkłada się tak jak pokazano na rys. 1c. Wraz ze wzrostem kąta $\varphi$ nadejdzie sytuacja pokazana na rys. 2b, w której lewa część stopy oderwie się od podłoża. Można wykazać [3], że dla stopy prostokątnej axb $(I=\dfrac {ba^3}{12})$, kąt $\varphi$ przy którym zaczyna się odrywanie stopy od gruntu, wynosi
| $ \varphi_1= \dfrac{2Q}{ca^2b}$ | (10) |
a odpowiadająca wartość siły wynosi
| $ P_1=\dfrac{Qa}{6h} \left( 1- \dfrac{Ql}{cI}\right)$ | (11) |
Przy dalszym wzroście kąta $\varphi$ moment rekacji podłoża wynosi:
| $ M_r=Q \left( \dfrac{1}{2}-\dfrac{\xi}{3}\right)$ | (12) |
gdzie $\xi$ – szerokość kontaktu podłoża ze stopą:
| $ \xi=sqrt{\dfrac{2Q}{\varphi b c}}$ | (13) |
Stąd otrzymujemy:
| $ -Ph-Ql\varphi+Q\left ( \dfrac{a}{2}-\dfrac{1}{3}\sqrt{\dfrac{2Q}{\varphi b c}}\right)=0$, | (14) |
a po wyznaczeniu siły P:
| $ P=\dfrac{Q}{h}\left( \dfrac{a}{2}-\dfrac{1}{3}\sqrt{\dfrac{2Q}{\varphi b c}}-l \varphi\right)$ | (15) |
Wykres (15) pokazano na rys. 3
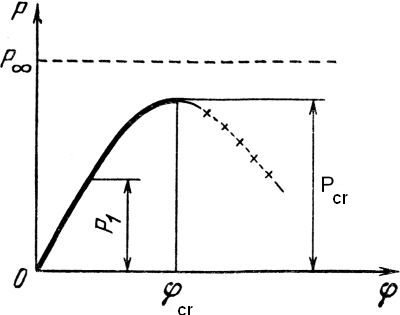
Rys.3. Krzywa stateczności wysokiej budowli na podłożu sprężystym [3]
Obciążenie krytyczne $P_{cr}$ jest maksymalnym obciążeniem, w którym stan wieży jest stabilny. Odcinek ścieżki równowagi oznaczony z krzyżykami jest niestabilny. Siłę $P_{\infty}$ wyznacza się w sytuacji, absolutnej sprężystości podłoża ze wzoru:
| $P_{\infty}= \dfrac{Qa}{2h}$ | (16) |
i wynika z (2) dla $\gamma=1$.
Maksimum krzywej zawsze jest położone poniżej (16) i jest osiągana dla kąta obrotu
| $\varphi_{cr}=\sqrt[3]{\dfrac {Q}{18bcl^2}} $ | (17) |
Odpowiada to watrości krytycznej obciązenia P:
| $P_{cr}= \dfrac{Qa}{2h} \left [ 1-\sqrt[3]{\dfrac{Ql}{cI}}\right]$ | (18) |
Z przedstawionych rozważań wynika, że warunek stanu granicznego (1) lub (3) daje niebezpieczne oszacowanie niezawodności budowli wysokiej posadowionej na sprężystym podłożu. Na przykład dla słupa, charakteryzowanego dużym $\dfrac {cI}{Ql}=8$, zastosowanie warunku (1) prowadzi do dwukrotnego zawyżenia bezpieczeństwa.
Literatura
- PN-EN 1997-1+AC+Ap1+Ap2:P2008 Projektowanie geotechniczne – Część 1: Zasady ogólne
- Cramer G. (1936), Uber eine Eigenschaft der Normalen Verteilungsfunktion,. Math. Zeitschrift, 41, 405–414
- Panovko J., G., Gubanova, I. I. (1967), Ustojčivost i kolebanija uprugich system. Sovremennyje koncepcii, paradoksy i ošibki (4th ed.), Nauka, Moskva
________________________________