Leszek Chodor, 8 kwietnia 2016
08-02-2025 rewizja po dużej awarii portalu
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 28 Czytelników
Rzeczywiste, stalowe dźwigary kratowe nazywane popularnie kratownicami w analogii do ustrojów mechanicznych w istocie nie są modelowymi kratownicami. Klasyczne metody wymiarowania prętów kratownic mogą być stosowane wyłącznie we wstępnym projektowaniu koncepcyjnym i przed zastosowaniem zweryfikowane metodami imperfekcyjnymi.
Dźwigary kratowe w systemach konstrukcyjnych
Rodzaje kratownic systemowych
Na rys. 1a pokazano systemowe rodzaje kratownic: K1 – kratownica skrajna, K2– kratownica przedskrajna, K3 – kratownica pośrednia, definiujące pola hal: skrajne Ps i przedskrajne Pp, istotne przy konstruowaniu stężeń hal.

Rys.1 Dźwigary kratowe w ustrojach hal: a) systemowe rodzaje kratownic, b) teoretyczna kratownica i jej cechy (kratownice stalowe są rzeczywiste i nie spełniają warunków kratownicy teoretycznej)
Kratownice teoretyczne, a rzeczywiste
Teoretyczne kratownice są ustrojami prętowymi:
- złożonymi z prętów idealnie prostych,
- połączonych przegubowo i
- osiowo połączonych w węzłach,
- obciążonych silami skupionymi przyłożonymi w węzłach ( rys.1b ) .
Przy spełnieniu tych założeń w prętach powstaną wyłącznie siły osiowe.
Rzeczywiste kratownice nie spełniają praktycznie żadnego z założeń kratownic: a) pręty są rzeczywiste, czyli ze wstępnymi wygięciami, b) węzły są rzeczywiste, czyli najczęściej nie przegubowe, c) pręty są często łączone w węzłach z mimośrodami, d) obciążenia są często przyłożone między węzłami (np. płatwie). W konsekwencji w prętach obok sił osiowych powstają momenty zginające. Rzeczywista kratownica nie jest więc kratownicą, a ramą.
W projektowaniu kratownic stalowych należy przestrzegać następujących zasad:
- Węzły konstruuje się maksymalnie usztywnione, czym zwiększamy niezawodność systemu konstrukcyjnego,
- połączenia węzłach staramy się konstruować bez mimośrodów. Wprowadzanie mimośrodów do węzłów dopuszcza się w przypadkach uzasadnionych prostotą technologiczną,
- obciążenia przykładamy w węzłach. Obciążenia międzywęzłowe dopuszcza się w przypadkach uzasadnionych funkcjonalnie (np. płatwie) lub prostotą technologiczną.
W przypadku spełnienia postulatu węzłów osiowych oraz obciążeń węzłowych po rozwiązaniu ustroju jako ramy możemy oczekiwać , że ustrój będzie bliski kratowemu, to znaczy momenty zginające będą małe, a nawet pomijalnie małe, to znaczy w węzłach uzyskamy przeguby logiczne, nawet w przypadku skonstruowania połączeń sztywnych.
Typy kratownic i optymalizacja
Geometria obrysu kratownicy i typy skratowania
Na rys. 2 pokazano najczęściej stosowane obrysy kratownic statycznie wyznaczalnych i systemy skratowania.
Kratownice mogą mieć obrysy:
- o pasach równoległych: a), d),
- ze słupkiem podporowym: b),e), h),
- z opuszczonym pasem dolnym k), mk), p),
- trójkątne: g), j), l), o),
- ze świetlikiem: c),
- z łukowym pasem dolnym: f),
- z wielołamanym pasem górnym – i),
- z łukowym pasem górnym: n), r),
- typu Finka: o).
Kratownice mogą mieć skratowanie:
- typu N (Pratta) – a), h), j),
- typu V ze słupkami (zmodyfikowany Warren) : b), c), d), g), l), n), p), r),
- typu V bez słupków (Warren): e), f), m),
- z drugorzędowym skratowaniem: p), r).
W kratownicach statycznie niewyznaczalnych często stosuje się skratowanie typu X, często nazywane inteligentnym. Inteligencja polega na tym, że jeden z krzyżulców jest rozciągany, a drugi ściskany w zależności od kierunku obciążenia i niezależnie od smukłości prętów element zachowuje nośność nawet po wyłączeniu pręta ściskanego na skutek utraty stateczności.
Pokazane na rys, 2 kratownice stosowane są od rozpiętości ok 9 m do ok. 36 m. Naniesione pochylenia pasów górnych są orientacyjne i należy je skorygować w zależności od zastosowanego typu pokrycia oraz wymogów funkcjonalnych.
Przy większych rozpiętościach można stosować kratownice o kształcie pokazanym na rys. 3.

Rys.3 Kratownice płaskie o dużych rozpiętościach i trójpasowa o bardzo dużej rozpiętości [1]
Wysokość konstrukcyjną (w osiach pasów) kratownic o pasach równoległych i dwuspadowych w kalenicy przyjmuje się w granicach
$$\begin{equation}H= \left ( \dfrac {L}{11} \div\dfrac {L}{15} \right) \to \dfrac {L}{13} \label{1}\end{equation}$$
przy czym największą wysokość mają kratownice jednoprzęsłowe. Natomiast w przypadku kratownic z podniesionym pasem dolnym wysokość kratownicy nad pasem może być mniejsza ze względu na działanie efektu kopułowego (daszkowego).
Wysokość słupka podporowego, np. w kratownicy 2b) powinna umożliwić bezkolizyjne skonstruowanie węzłów, co zwykle daje wymiar min 200 mm (najczęściej ok 300 mm).
Nachylenie elementów ukośnych w stosunku do pasów powinno zawierać się w przedziale od 35° do 55°, a najlepiej 45° . Orientacja elementów ukośnych powinna zapewniać, że najdłuższe elementy są poddawane rozciąganiu (elementy krótsze są poddawane ściskaniu).
Optymalizacja
Analizy optymalizacyjne dźwigarów kratowych przedstawiono w pracach [2] i [3]. Na rys. 4 pokazano zależność masy kratownic w zależności od rozpiętości i typu skratowania.

Rys. 4. Analizy optymalizacyjne kratownic [2]
Analizy optymalizacyjne prowadzono dla następujących typów skratowania: typ Warren (V) (rys.2e) , zmodyfikowany Warren (V ze słupkiem) (rys. 2b) oraz typ Prato (N) (rys 2a). Pokazano, że optymalne są wiązary o rozpiętości ok. 24 m z węzłami (płatwiami) rozstawionymi, co 1,5 m z wykratowaniem typu V ze słupkami (typ Warren ze słupkiem podpierającym ściskany pas górny). Nieco mniej ekonomiczne są wiązary z węzłami, co 3 m. Ponieważ jednak wraz ze wzrostem rozstawu płatwi rośnie zużycie stali na płatwie, więc obie cechy należy rozpatrywać jednocześnie.
Na podstawie wykresu można dobrać optymalny typ skratowania dla danej rozpiętości wiązara. Systematycznie uzyskiwano optymalną długość wiązara około 24 m. Po przekroczeniu rozpiętości 27 m następuje duży wzrost masy przekrycia i należy zastanowić nad zastosowaniem innego typu przekrycia, a w tym: rusztu, przekrycia strukturalnego, cięgnowego lub wykorzystanie efektu kopułowego. Takie rodzaje przekryć są przedmiotem wykładu „Złożone konstrukcje metalowe” opisano je w pracy [3].
Wykres z rys. 4 jest również przedmiotem analiz w artykule Hale stalowe optymalnie funkcjonalnie w którym przedstawiono analizy optymalizacyjne na tle innych elementów konstrukcyjnych hal.
Stężenia (usztywnienia) wiązarów
Kratownice są elementem systemu konstrukcyjnego, w którym jest zapewniona stateczność w każdej fazie prazy systemu . W celu zapewnienia stateczności przestrzennej kratownic stosuje się stężenia (usztywnienia): pionowe między wiązarami oraz w płaszczyźnie pasów górnych (połaciowe). Wprowadzenie do systemu usztywnień w halach przedstawiono w artykułach: Hale optymalne konstrukcyjnie oraz Stężenie hal i budowli.
Stężenia pionowe między wiązarami
Na rys.5. pokazano typowe systemy pionowych skratowań stężających pomiędzy wiązarami: a) – typu X stosowane przy odległości między wiązarami a≤ 6 m; b) – typu V stosowane przy odległości między wiązarami 6 < a< 12 m; c) – typu VV, stosowane przy rozpiętości między wiązarami a> 12 m; d) z zastrzałami do pasów dolnych wiązara zabezpieczającymi stateczność pasów dolnych na odcinkach ściskanych.

Rys. 5. Typowe systemy stężeń pionowych między kratownicami [1]
Stężenie w poziomie pasów górnych
Na rys. 6 pokazano standardowe detale mocowania do wiązarów prętów stężeń wykonanych z kątowników.

Rys.6. Detale mocowania stężeń z kątowników do wiązarów: a), b), c) – stężenia poziome połaciowe, d) stężenia pionowe międzywiązarowe [1]
Standardowo pręty stężeń, o ile nie odgrywają innej roli, wykonuje się z kątowników i konstruuje tak, by ułożone były w regularną siatkę z osiami przecinającymi się z osiami prętów wiązarów bez mimośrodów. W uzasadnionych przypadkach uproszczenia konstrukcji, dopuszcza się odstępstwo od tych zaleceń. Pręty stężeń można łączyć z konstrukcją w tym z blachami węzłowymi za pomocą jednej śruby. Stanowi to wyjątek od zasady, że „jedna śruba – żadna śruba”. Śrubę dobiera się na nośność pręta stężenia.
Dopuszczalne ugięcia kratownicy i strzałka odwrotna
Dopuszczalne ugięcie kratownicy jest przyjmowane jak dla elementu konstrukcyjnego, w której roli występuje. Wstępnie można przyjąć, że ugięcie dźwigara kratowego o rozpiętości L, wyznaczone od obciążeń charakterystycznych nie powinno przekroczyć wartości granicznych $\delta_{dop}$:
$$ \begin{equation} \delta_{dop}= \begin {cases}
L/200, & \textrm { płatwie} \\
L/250, & \textrm { dżwigar dachowy} \\
L/350, & \text { główne belki stropowe} \\
L/250, & \text { drugorzędne belki stropowe} \\
\end {cases} \label{2} \end{equation}$$
W przypadku wiązarów o rozpiętości większej od 30 m należy zaprojektować strzałkę odwrotną, którą nadaje się podczas wykonania dźwigara.
Zaleca się, by strzałka odwrotna nie przekraczała ugięć wywołanych obciążeniami stałymi oraz 50% obciążeń zmiennych i nie przekraczała L/250.
Zmianę geometrii wiązara na skutek nadania strzałki odwrotnej nie odzwierciedla się na rysunkach w projekcie budowlanym i wykonawczym, a jedynie zawiera się stosowana uwagę do zastosowania przez wykonawcę. Wykonawca decyduje czy jego rysunki warsztatowe będą zawierały modyfikacje związane z wymogiem nadania strzałki odwrotnej, czy też strzałka zostanie nadana na warsztacie przez robotników w stosunku do nominalnej geometrii, pokazanej na rysunkach.
Kształtowanie (konstruowanie) kratownic
Współczesne konstrukcje kratownicowe
Na rys. 7 zaprezentowano przykład współczesnej konstrukcji kratownicy, której pasy wykonano z profili HEA, a krzyżulce z rur kwadratowych, Kratownica charakteryzuje się prostotą konstrukcji: praktycznym brakiem blach węzłowych i przewiązek, prostymi węzłami podporowymi i montażowymi, co powoduje znaczne ograniczenie kosztów wytworzenia, co wraz ze zmniejszeniem zużycia stali w stosunku do kratownic klasycznych. Możliwość automatyzacji procesu wytwórczego sprawia, że są one konkurencyjne w stosunku do pełnościennych rygli blachownicowych
Przykładowy dźwigar kratowy ma rozpiętość 34,9 m i wysokość w kalenicy 3000 mm oraZ nad podporą 2127 mm. Pasy wiązara wykonano z dwuteowników szerokostopowych HEA, a krzyżulce z rur kwadratowych RK.. Zamieszczono ważniejsze detale projektu: a)- detal kalenicy, b)- detal okapowy, c) detal podpory przesuwnej, d) podpory nieprzesuwnej. Elementy T1 i T7 są sztywnymi stężeniami z rur łączącymi sąsiednie wiązary. zastosowanymi w celu zmniejszenia długości wyboczeniowej pasa górnego przy wyboczeniu z płaszczyzny wiązara.
Wiązar przekrycia stalowego jest dostostosowany do posadowienia na ścianach (lub słupach) żelbetowych, czyli jest elementem optymalnej konstrukcji budynków ( w tym hal), w której słupy (lub ściany)są wykonane jako żelbetowe, a dżwigary i płatwie są stalowe, o czym w artykule Hale optymalne konstrukcyjnie.
Dodatkowo na rys, 7a, pokazano detal montażowy dżwigara o długości 24 m z innego projektu. Styk montażowy umieszczono w środku rozpiętości kratownicy, bo możliwy był podział na dwa elementy wysyłkowe o długości 12 m każdy, mimo konieczności zastosowania śrub o dużej nośności ze względu na umieszczenie styku w miejscu maksymalnych sił w pasach.

Rys_7_Współczesny dźwigar kratowy [4]

Rys.7a. Połączenie montażowe kratownicy z pasami z dwuteownika HEA [5]
Podczas projektowania takich kratownic należy zwrócić uwagę na poprawny dobór wysokości konstrukcyjnej ($\ref{1}$): zbyt duża wysokość może spowodować nieuzasadnione zwiększenie masy dźwigara z powodu przyjęcia rozmiaru profilu pasa ze względów konstrukcyjnych (możliwości skonstruowania węzłów ), a nie z warunku wytężenia pasa. Zbyt mała wysokość powoduje przekroczenie dopuszczalnych ugięć ($\ref{2}$). Kratownice o konstrukcji z rys 7 są stosowane dla większych rozpiętości $L > 12 \,m$ oraz przy średnich/dużych obciążeniach. Dla mniejszych wymagań stosuje się konstrukcje odpowiednie dla płatwi, kratownice z profili giętych na zimno lub pełnościenne.
Profile prętów kratownic
Współcześnie na pasy kratownic stosuje się najczęściej walcowane dwuteowniki szerokostopowe HEA lub HEB , a na krzyżulce i słupki rury kwadratowe lub prostokątne walcowane lub gięte na zimno (np. , a jednocześnie ogranicza się maksymalnie liczbę blach węzłowych.
Wcześniej pręty kratownic wykonywano z szerokiej gamy walcowanych profili zestawionych na rys. 8 .

Rys .8 Klasyczne profile walcowane prętów kratownic [5]
Współcześnie profile z rys. 8 stosuje się najczęściej na złożone pasy oraz na słupki i krzyżulce.. Na pasy stosuje się najczęściej profile jednogałęziowe HEB, HEA, RO, RK,RP.
Dźwigary dachowe typu lekkiego (np. płatwie kratownicowe) wykonuje się z kształtowników cienkościennych profilowanych na zimno.
Dźwigary typu ciężkiego (silnie obciążone, o dużej rozpiętości) mają pręty o przekroju złożonym lub skrzynkowym, wykonanym z blach i kształtowników walcowanych.
Pasy kratownic o małej i średniej rozpiętości (do 30 m) wykonuje się najczęściej o stałym przekroju na całej długości. Różnicuje się natomiast przekrój słupków i krzyżulców, ale tak by liczba różnych przekrojów nie była zbyt duża.
Jako najmniejsze przekroje prętów stosuje się: L 45x 5 (wyjątkowo 40×4), RO 38x 3,2 ; ø 16, HEA 120. Grubość ścianki rur giętych na zimno nie powinny być mniejsze niż 3 mm ( wyjątkowo 2,5 mm).
Kształtowanie węzłów kratownic
Zasady kształtowania
Konstruowanie węzłów jest faktycznym etapem projektu kratownicy. Węzły kratownic wykonuje się, jako spawane z użyciem lub bez stosowania blach węzłowych. Współczesną zasadą jest maksymalne ograniczanie blach węzłowych.
Przy konstruowaniu węzłów kratownic należy przestrzegać zasad:
- połączenia w węźle powinny być symetryczne względem osi pręta i przenosić obciążenia nie mniejsze niż nośność pręta (węzły projektujemy na nośność pręta, a nie na siły zewnętrzne). Wymagana nośność dotyczy nie tylko zastosowanych łączników (spoiny, śruby , zgrzeiny), ale również części składowych węzła( ścianki, blachy węzłowe,
- pręty powinny mieć przekrój symetryczny względem płaszczyzny kratownicy.
- pręty powinny dochodzić jak najbliżej środków węzłów, zwłaszcza pręty ściskane,
- pręty ściskane w węźle podporowym należy doprowadzić do osi podpoi, a pręty rozciągane mogą być połączone z nimi,
- należy dożyć do jak najmniejszych wymiarów węzła, aby niepotrzebnie go nie przesztywniać,
- dążymy do wyeliminowania blach węzłowych,
- blachy węzłowe powinny być płaskie , o możliwe prostym kształcie, bez kątów ostrych i wcięć (powstawanie karbów i koncentracji naprężeń).
Pręty kratownicy powinny spełniać warunki określone w normie podstawowej [6] , a dodatkowo węzły powinny przenieść siły, które mogą wystąpić w prętach w stanie granicznym nośności.
To znaczy węzły należy projektować na nośność prętów.
Węzły podatne i niepodatne
W nawiązaniu do wyznaczania długości wyboczeniowych kratownic, omówionych w rozdziale Analogia belkowa -wprowadzimy podział na węzły niepodatne i podatne. Węzły niepodatne, to takie dla których można stosować redukcję długości wyboczeniowych, a podatne to takie, które mają sztywność bliższą przegubowi fizycznemu.
Węzłami podatnymi są takie, w których ścianka pasa wyraźnie odkształca się pod naciskiem krzyżulca, np:
- rurowe krzyżulce podłączone do o cienkiej półki rury pasa – rys. 17a i rys.13,
- pas z ceownika z nieusztywnionym środnikiem – rys.12,
- w przypadku kratownicy z kształtowników giętych na zimno, jeśliby nie zastosowano przepon cienkich półek pod krzyżulcami. (Na rys. 14 takie przepony dano i węzły są niepodatne).
Inne węzły można traktować jako niepodatne.
W taki sposób zaleca się modelować je w modelu statycznym, chyba, że przeprowadzono dokłądniejszą analizę pomocniczą.
Kratownice klasyczne
Kratownice klasyczne były i są konstruowane z profili walcowanych – rys 8 najczęściej zastosowaniem blacha węzłowych (np. rys 9).
W ubiegłych latach chętnie stosowano kratownice z prętami wykonanymi z kątowników. Na rys. 9 pokazano wybrane węzły takich kratownic.

Rys.9 Kratownica z blachami węzłowymi i prętami z kątowników [5]
Węzły podporowe
Wybrane węzły podporowe klasycznych kratownic pokazano na rys. 10. W podobny sposób należy konstruować węzły podporowe kratownic z rur i kształtowników giętych na zimno (np rys. 7).

Rys.10. Wybrane węzły podporowe kratownic: a) pręty 2L, b) 1/2I pas dolny poziomy, c) 1/2 I pas dolny pochyły [5]
Połączenia montażowe
Połączenia montażowe elementów wysyłkowych kratownic należy projektować jako śrubowe.
Elementy wysyłkowe kratownic powinny spełniać warunki wymiarowe (tak by zmieścić się w skrajni dla danego środka i trasy transportu) oraz masy (tak, by zastosowane urządzenia umożliwiły załadunek, wyładunek oraz zamontowanie elementu w konstrukcję). Zwykle decydującym są rozmiary elementu. Zwykle przyjmuje się, że elementy nie przekraczające długości 12 m , i wysokości 2,4 m są możliwe do transportu. Wynika stąd, że wszystkie dźwigary kratowe o rozpiętości większej od 12 m należy podzielić na elementy wysyłkowe i na budowie scalać za pomocą styków montażowych.
Na rys. 11 pokazano połączenia montażowe pasa górnego i pasa dolnego klasycznego wiązara.
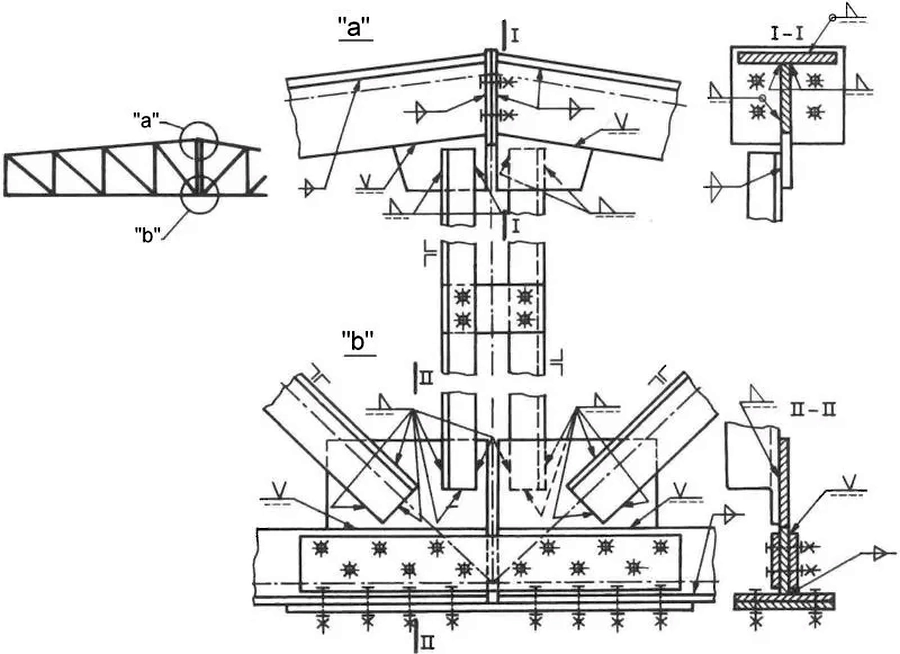
Rys.11. Połączenie montażowe kratownicy z pasami z 1/2I [5]
Węzły bez blach węzłowych
We współczesnej praktyce najczęściej stosuje się kratownice bez blach węzłowych, na przykład pokazane na rys.12 do 14. Często pasy kratownic typu (rys 12a) wykonuje się z dwuteowników szerokostopowych, np. HEA, a nie z rur (RHS) i z rurowymi krzyżulcami oraz słupkami przyciętymi powierzchniami pasów kształtowników pasowych (podobnie do rys. 7, 14a). Grubość ścianek półek kształtowników pasów pozwala ominąć kilka mechanizmów zniszczenia, które należy przeanalizować dla przypadku zastosowania pasów z cienkościennych rur (rys.16).

Rys. 12. Proste wiązary kratowe bez blach węzłowych: a) z rur kwadratowych lub prostokątnych, b) z połówek dwuteowników, c) z dwuteowników i ceowników [3]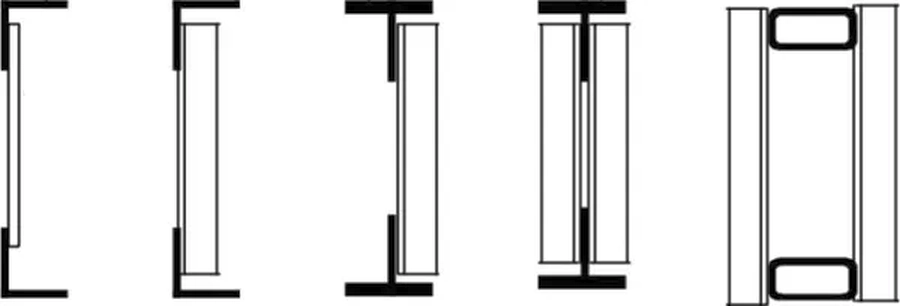
Rys.13 Wybrane kratownice bez blach węzłowych [3]Na rys. 14 b.c przedstawiono często stosowane w klasycznych kratownicach połączenie pasów wykonanych z połówek dwuteowników IB (lub IPE) ze względu na brak blach węzłowych.

Rys.14. Kratownice bez blach węzłowych: a) pas dwuteowy -krzyżulce rurowe, b) z połówek dwuteowników (rys. 8b), c) połówka dwuteownika+ kątowniki [5]

Rys.15. Kratownice bez blach węzłowych: pas ceownik, krzyżulce i słupki kątowniki obrócone [5]

Rys.16 Wybrane mechanizmy zniszczenia kratownic z rur [7]
Węzły kratownic z rur okrągłych
Przykłady węzłów kratownic z rur okrągłych przedstawiono na rys. 17 .

Rys.17. Węzły kratownicy z prętami z rur okrągłych: a) bez blach węzłowych, b) z blachami węzłowymi [5]
Kratownic z rur prostokątnych lub kwadratowych (RHS, RP…RK)
Zasady projektowania węzłów kształtowników rurowych zawiera rozdział 7 [7], a w szczególności zasady zobrazowane na rys. 22: b) z blachą pionową pomiędzy krzyżulcami, c) z blachami pionowymi obejmującymi krzyżulce, e)z żeberkiem w pasie HEA pod osią krzyżulca z rury.
Typy węzłów z rur RHS
Na rys. 18 pokazano typy węzłów i ich nazewnictwo stosowane w kratownicach z rur

Rys.18 Typy węzłów kratownic z kształtowników rurowych [7]
Nominalna grubość ścianki kształtownika rurowego nie powinna być mniejsza niż 2,5 mm, a zastosowanego na pas, nie powinna być większa od 25 mm, chyba że przewidziano specjalne środki zapobiegające pęknięciom laminarnym. Nominalna granica plastyczności nie powinna przekraczać 460 MPa, przy czym dla fy>355 MPa, obliczeniowe nośności statyczne należy redukować współczynnikiem 0,9
Spawane węzły z rur
Na rys. 19 przedstawiono sposób konstruowania węzłów pośrednich kratownic z rur RHS.

Rys.19. Węzły spawane pomiędzy krzyżulcami RHS (rurami kwadratowymi) a pasami z RHS [7]
Kąty θ między pasami i prętami skratowania, a także pomiędzy sąsiednimi prętami skratowania powinny spełniać warunek θ≥30° (wymóg normowy).
Końce prętów, które zbiegają się w węźle powinny być przygotowane w ten sposób , aby ich kształt poprzecznego pozostał nie zmieniony. Połączenia końców spłaszczonych wymagają odrębnych analiz lub badań
W węzłach z odstępem (rys 19 a,d,e) ze względu na warunki spawania odstęp miedzy prętami skratowania nie powinien być mniejszy niż suma grubości ścianek łączonych krzyżulców (t1+t2). Na rys. 20 zdefiniowano odstęp i zakładkę.

Rys.20. Definicja odstępu g i zakładki λov [7]
W węzłach zakładkowych wzajemna zakładka między prętami skratowania powinna być wystarczająca ze względu na właściwe przenoszenie sił ścinających w węźle. W każdym przypadku zakładka powinna wynosić, co najmniej 25%. Gdy pręty skratowania w węźle zakładkowym mają różne grubości i/lub różne klasy wytrzymałości, to pręt o niższej wartości (t·fyi) powinien być prętem zakrywającym.
Uzupełnieniem do rys.19 są przykłady wzmocnień węzłów kratownic z rur RHS pokazane na rys. 21.

Rys.21 Wzmocnienia węzłów RHS: a) bez wzmocnienia; b) blacha pionowa; c) blacha pozioma; d), e) – blachy ukośne [8]
Na rys. 22 pokazano sposób umieszczania blach węzłowych na pasach z rur kwadratowych, pod montaż profili ze ściankami płaskimi (np L lub C).
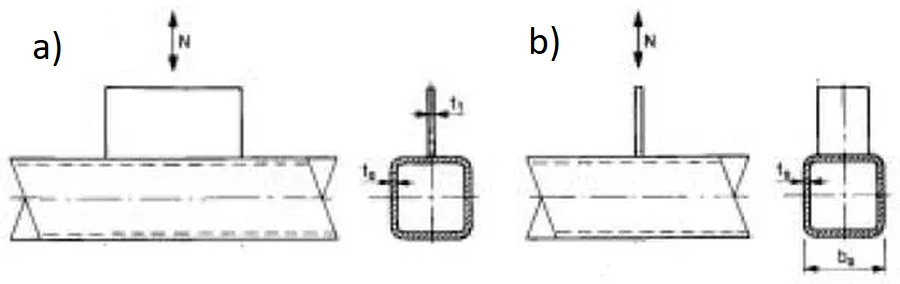
Rys.22 Blachy węzłowe pasa z RHS: a) podłużna, b) poprzeczna [8]
Śrubowe węzły z rur. Połączenia montażowe
Na rys. 23 pdo 25 przedstawiono przykłady śrubowych połączeń prętów z rur.

Rys.23. Połączenia śrubowe prętów RHS: a),b),c) – na blachę zakładkową, d), e) na blachę czołową, f) na widelec [8]

Rys.24 Połączenia zakładkowe prętów RHS: a) z nakładkami, b) na widelec [7]

Rys.25. Połączenia montażowe RHS: a) z nakładkami zewnętrznymi przypawanymi jednostronnie, b) z wspawanymi kątownikami profilowanymi na zimno, c) z wkładką spawaną z rury i skręcany śrubami przechodzącymi przez element, d) z wewnętrznymi płaskownikami wspawanymi spoiną otworową i z drugiej strony z połączeniem na śrubę, e) z nakładkami wewnętrznymi łączonymi śrubami jednostronnymi [8]
Kratownice z profili giętych na zimno
W ostatnich latach coraz częściej stosuje się kratownice skonstruowane z kształtowników giętych na zimno. Przykład takiej kratownicy pokazano na rys. 26.
Profile gięte na zimno wymagają sprawdzenia klasy przekroju. Sprawdzenie klasy przekroju omówiono w artykule Klasa przekroju stalowego [9]. Scianki ściskanych elementów prętowych powinny spełniać warunki smukłości dla przekrojów klasy 1 lub 2 .

Rys.26 Przykład kratownicy z kształtowników giętych na zimno [5]
Stosowanie kształtowników giętych na zimno prowadzi do oszczędności zużycia stali, ale zwiększa wymogi technologiczne wytwarzania , ale też projektowania dźwigarów i wymaga specjalistycznych wytwórni oraz stosowania specjalizowanego oprogramowania do projektowania (np program Consteel).
Kształtowniki gięte na zimno, które mogą być zastosowane na pręty kratownic w konstrukcjach budowlanych zaprezentowano w artykule.
Metody obliczeniowe
Projektowanie wstępne -analogowe
Klasyczna analogia belkowa
W obliczeniach wstępnych można w prosty sposób oszacować siły w kratownicy z analogii belkowej (rys.30) . Zauważmy najpierw, że kratownica jest faktycznie belką.
Dla belki zastępczej, poazanej na rys. 28 (nazywanej też globalną) przy znanym jej schemacie statycznym oraz obciążeniu. możemy wyznaczyć siły przekrojowe (moment zginający, siła poprzeczna) $= [M,V]_}belka$.
Siły te można prosto wyznaczyć dla ustroju statycznie wyznaczalnego. Na przykład dla kratownicy (belki) wolnopdpartej o rozpiętości L i obciążonej zastępczym równomiernie rozłożonym obciążeniem q, mamy
w środku rozpiętości
$$\begin{equation} M_{belka}= \cfrac{q L^2}{8} \label{8A} \end{equation}$$
nad podporą
$$\begin{equation} V_{belka}= \cfrac{q L}{2} \label{8B} \end{equation}$$
Dla ustroju statycznie niewyznaczalnego potrzebna jest znajomość sztywności EI belki. Sztywność tą wyznaczymy dla kratownicy jak dla przekroju dwupunktowego pasa górnego $A_1$ i dolnego $A_2#, oddalonych o h. Oczywiście mamy:
$$\begin{equation}I=\sum \limits _{i=1} \limits^{3} \ \ (I_i+A_i \cdot d_i^2) \label{9} \end{equation}$$
gdzie:
$A_i$ – pole przekroje pasa i-tego,
$d_i$ – odległość osi pasa i-tego od osi obojętnej przekroju.
Oś obojętna przekroju dwupunktowego jest oddalona o:
$$\begin{equation}d_2= \dfrac {A_1 \cdot h}{A_1+A_2} \\ d_1 = h-d_2 \label{10} \end{equation}$$
od osi pasa 2-giego i 1-szego odpowiednio.
Dla $A_1 = A_2$, mamy $d_1 = d_2 = h/2$ .
Ze względu na połączenie pasów skratowaniem, a nie pełnym środnikiem, należy zredukować moduł Younga E. Zredukowany moduł Ered= 160 000 MPa (zamiast E=210 000 MPa)
Z zależnosci (8), (9) i po uwzględnieniu zmniejszenia sztywności o 160/210= 0,76 oraz pomijalnie małych momentów bezwładności względem własnej osi I1, I2 , otrzymujemy:
$$\begin{equation}I_{red} =0,76 \cdot \dfrac {A_1 \cdot A_2 \cdot h^2} {A_1+A_2} \label{11} \end{equation}$$
Posługując się takim momentem bezwładności moduł Younga stali przyjmujemy o standardowej wartości E=210 000 MPa.
Kratownice w systemie zastępujemy belkami o takiej sztywności i dla ramy znajdujemy rozkład momentów zginających
Na podstawie uzyskanych momentów belkowych Mbelka i sił poprzecznych Vbelka możemy wyznaczyć siły w pasach kratownicy Np i krzyżulcach Nk z prostej zależności:
$$\begin{equation}N_p= \dfrac {M_{belka}}{h} \label{12} \end{equation}$$
$$\begin{equation}N_k= \dfrac {V_{belka}}{cos \Theta } \label{13} \end{equation}$$
Analogia belki Timoshenko
Ponieważ kratownice są dźwigarami zginanymi ze środnikiem (skratowaniem) podatnym na wpływy ścinanie, więc dokładniejszą analogią belkową jest analogia belki Timoshenko, w którym ye wpływy można uwzględnić.
Podstawy teoretyczne elementu Timoshenki podano w artykule Chodor (2013) [10] podano podstawy teoretyczne.
W tab.1 podano wyrażenia na szacowanie sztywności postaciowej skratowania, a zastosowanie metody pokazano na przykładzie 1.
Tab.1. Strzałka ugięcia prętów podatnych na ścinanie
[11],tab. 1.3

Klasyczna metoda (kratownicowa)
Klasyczna metoda projektowania („długości wyboczeniowych”) jest już metodą przestarzałą i nie stosowaną w profesjonalnym projektowaniu konstrukcyjnym, ale nadal stosowana w projektowaniu wstępnym (koncepcyjnym) i powinna być znana przez projektantów i studentów. Klasyczna metoda projektowania prętów ściskanych została szczegółowo omówiona w artykule Ściskane pręty stalowe [12], a rozciąganych w artykule Rozciągane pręty stalowe.
Metoda klasyczna polega na na wymiarowaniu pręta na występującą w nim obliczeniową siłę osiową $N_{Ed}$ z klasycznego warunku analogicznego do słupów stalowych :
$$\begin{equation}N_{Ed} \le N_{b,Rd} \label{3}\end{equation}$$
gdzie $N_{b,Rd}$ jest nośnością pręta kratownicy, wyznaczoną z zależności
$$\begin{equation} N_{b,Rd}= \chi \cdot \dfrac{A_* \cdot f_y}{\gamma_{M1}} \label{4} \end {equation}$$
Sposób obliczania pola przekroju pręta A* zależy od sposobu wytężenia i klasy przekroju:
$A_* =A_t $ ( netto, czyli z pominięciem otworów na łączniki) dla pręta rozciąganego,
$A_* =A_c $ ( brutto, czyli wraz z przekrojem wyciętym na otwory pod łączniki) dla pręta ściskanego i klasy przekroju 1,2,3,
$A_* =A_{eff}$ dla pręta ściskanego i klasy przekroju 4.
fy – granica plastyczności stali,
$\gamma_{M1}=1,0$ – współczynnik materiałowy dla elementu.
W przypadku pręta rozciąganego współczynnik wyboczeniowy $\chi=1,0$. W przypadku pręta ściskanego należy go wyznaczyć w zależności od smukłości względnej:
$$\begin{equation} \overline \lambda=\sqrt {\dfrac {A_c \cdot f_y} {N_{cr}}} = \dfrac {L{cr}}{i} \cdot \dfrac {\sqrt {A_*/A_c}}{\lambda_1} \label{5}\end {equation}$$
gdzie:
$\lambda_1= \sqrt { \dfrac {E}{f_y}}=93,9 \varepsilon$,
$\varepsilon= \sqrt { \dfrac {235}{f_y}}$ (fy [MPa]),
$ i=\sqrt {\dfrac{I}{A}}$ – promień bezwładności przekroju.
W klasycznym podejściu smukłość pręta wyznacza się na podstawie długości wyboczeniowej
$$\begin{equation}L_{cr}= \mu \cdot L \label{6} \end{equation}$$
gdzie L jest ługością teoretyczną pręta, μ – współczynnikiem długości wyboczeniowej.
Długość wyboczeniową $(\ref{Lcr})$ wyznacza się z zasad zobrazowanych na rys. 27:

Rys. 27. Długości wyboczeniowe prętów kratownicy: a) w płaszczyźnie kratownicy, b) z płaszczyzny kratownicy (opis w tekście) [5]
- Przy wyboczeniu prętów z płaszczyzny kratownicy przyjmuje się równą długości teoretycznej Lcr= 1,0 L, przy czym długość L przyjmuje się na podstawie rys.8b) jako odległość pomiędzy stężeniami bocznymi,
- Przy wyboczeniu w płaszczyźnie kratownicy Lcr=0,9 L, przy czym długość L przyjmuje się na podstawie rys, 8a) jako odległość pomiędzy węzłami kratownicy. Takie zmniejszenie długości wyboczeniowej w stosunku do długości teoretycznej możliwe jest w przypadku , gdy pasy są ciągłe, a połączenia węzłowe niepodatne (pkt. 5.3). W przypadku, gdy połączenia prętów w węzłach są podatne (lub przegubowe), to Lcr=1,0 L
- jeśli pręty skratowania zaprojektowano z kątowników, a pasy i połączenia między nimi zapewniają odpowiedni stopień zamocowania kątowników (są niepodatne), to można pomijać mimośrody konstrukcyjne, jednocześnie przyjmując smukłość względną, następująco:
przy wyboczeniu względem osi v,
$$\begin{equation}\overline \lambda_{eff}=0,35+0,7\overline \lambda_v \label{7} \end{equation}$$
przy wyboczeniu względem osi i=(y, z),
$$\begin{equation}\overline \lambda_{eff}=0,50+0,7\overline \lambda_i \label{8} \end{equation}$$
W projektowaniu profesjonalnym i do sprawdzenia poprawności wstępnego projektu kratownicy należy stosować niżej omówioną metodę imperfekcyjną.
Pręty wielogałęziowe
Pręty złożone z wielu gałęzi łączy się między sobą za pomocą przewiązek, które powinny być rozmieszczone regularnie przy nieparzystej liczbie przedziałów. Klasyczna metoda projektowania prętów wielogałęziowych w tym bliskogałęziowych, jest analogiczna do kształtowania i obliczania słupów złożonych, a ogólnie prętów (belek-słupów) obciążonych ściskaniem lub rozciąganiem i zginaniem zgodnie z normą [6].
Pręty wielogałęziowe można też projektować z wykorzystaniem belki Timoshenko, który omówiono w rozdziale.
Metoda imperfekcyjna
W pracy [3] przedstawiono założenia metody imperfekcyjnej, wymagającej przyłożenia do kratownicy obciążeń równoważnych od imperfekcji oraz przeprowadzenia obliczeń II rzędu (P-Δ).
W metodzie imperfekcyjnej nie jest potrzebne przyjmowanie długości wyboczeniowych prętów oraz wyznaczanie współczynnika wyboczeniowego w sposób pokazany w poprzednim rozdziale (klasyczna metoda), ale zgodnie z zaleceniami normy [6] należałoby uwzględniać imperfekcje łukowe ( wygięcia wstępne prętów pomiędzy węzłami).
W pracy [13]. pokazano, że po zamodelowaniu kratownicy jako ramy (sztywne połączenia w węzłach) oraz wprowadzeniu sił imperfekcji działających w każdym węźle w płaszczyźnie i z płaszczyzny – wpływ imperfekcji łukowych jest mały i pomijalny dla prętów o smukłości $\lambda=L/i \le 100 $ (L=długość teoretyczna pręta, i-minimalny promień bezwładności przekroju). Wówczas pręty wymiaruje się metodą konserwatywną, to znaczy ogranicza się do zwymiarowania dwóch przekrojów dla : $(M_{max} ,N_{odp})$ oraz $(N_{max} ,M_{odp})$, bez uwzględniania znaku sił osiowych N obliczonych zgodnie z teorią 2 rzędu.
Podejście takie jest zgodne z koncepcją Pałkowskiego (2011) [11] preferowania metody imperfekcyjnej przed klasyczną metodą współczynnika wyboczeniowego w odniesieniu do słupów (i prętów) złożonych. Zagadnienie ściskania osiowego pręta zostaje zastąpione ściskaniem mimośrodowym w ujęciu teorii II rzędu.
Przykłady rachunkowe
Przykład 1 [ Ugięcia kratownicy z analogii belkowej Timoshenki ]
Wyznaczyć strzałkę ugięcia kratownicy, pokazanej na rys. 29. Kratownica obciążona jest w węzłach siłami skupionymi P=30 kN rozstawionymi co 1,2 m , czyli obciążeniem zastępczym równomiernie rozłożonym q= 30/1,2= 25 kN/m .

Rys. 29. Przykład wyznaczania ugiecia kratownicy w analogii Timoshenko [11]
Położenie osi y, przechodzącej przez środek ciężkości przekroi złożonego zaznaczono na rysunku. Moment bezwładności przekroju kratownicy wynosi:
$I=2 \cdot (145+15,5 \cdot 63,9^2 + 59,3 + 11,5 \cdot 86,1^2) =297 492 cm^4$
Sztywność na ścinanie przekroju kratownicy wg [10] Tab.1}”] (praca Belka Timoshenko na sprężystym podłożu) (za [11],tab. 1.1.):
$S_v=EA_k \cdot sin^2\alpha \cdot cos \alpha=E \cdot 13,8 \cdot 0,7809^2 \cdot 0,6247 = 5,26 E$
Pomocniczy współczynnik k, wynosi
$k = \dfrac{EI}{S_vL^2}= \dfrac {297 492} {5,26 \cdot 1200^2 }=0,039$
Na podstawie zależności z tab. 1, wrs 6, mamy:
$\delta= \dfrac {6}{384} \cdot \dfrac {qL^4} {EI}\cdot (1+9,6 k=\dfrac {5 \cdot 0,25 \cdot 1200^4} {384 \cdot 21 000 \cdot 297492 }\cdot (1+0,6 \cdot 0,039)=1,49 cm$
Jeśliby nie uwzględnić podatności na ścinanie (k=0), otrzymalibyśmy \(\delta= 1,09 cm\), czyli o ok 30% za mało.
Rozwiązanie ścisłe ( ugięcie teoretycznej kratownicy) dałoby 1,55 cm , to znaczy w przykładzie uzyskano oszacowanie z błędem nie przekraczającym 4%.
Zmniejszenie sztywności kratownicy na skutek odkształcalności postaciowej środnika wynosi 1,09/1,55= 0,70. Jest to nieco mniej od przyjętej w klasycznej analogii wartości 0,76, ze względu na stosunkowo wysoką kratownicę o małych przekrojach krzyżulców.
Literatura
- Bogucki, W. (Ed.). (1982). Poradnik projektanta konstrukcji metalowych (1st ed., Vol. 2). Arkady
- Chodor, L., & Malik, Ł. (2014). Optymalizacja konstrukcji nośnej hali stalowej – Optimization of the supporting structure of steel hall. Short Papers, 195–198
- Chodor, L. (2016). Przekrycia hal i galerii. In XXXI Ogólnopolskie Warsztaty Pracy Projektanta Konstrukcji: Vol. I (pp. 25–202). https://chodor-projekt.net/wp-content/uploads/2016/03/Chodor_LPrzekrycia-hal-i-galerii-WPPK-2016.pdf
- Chodor-Projekt, wiązar przekrycia nad magazynem zboża, archiwum, Biura 2021
- Włodarczyk, W. (2002). Konstrukcje stalowe. Wydawnictwa Szkolne i Pedagogiczne
- PN-EN 1993-1-1+A1:2006. Eurokod 3 – Projektowanie konstrukcji stalowych – Część 1-1: Reguły ogólne i reguły dla budynków,
- PN-EN 1993-1-8 +Ap1+AC:2006. Eurokod 3 -Projektowanie konstrukcji stalowych -Część 1-8: Projektowanie węzłów,
- Matusiak, A., , Miłaczewski, K. (2003). Wytyczne obliczania elementów konstrukcji ze stalowych rur prostokątnych i kwadratowych giętych na zimno. Stalprodukt. http://www.stalprodukt-centrostal.pl/pdf/wytyczne_obliczania_elementow_konstrukcji.pdf
- Chodor, L. (2015). Klasa przekroju stalowego, πWiki-Inżynierowie i Architekci Chodor-Projekt. https://chodor-projekt.net/encyclopedia/klasy-przekrojow-stalowych/
- Chodor, L. (2013). Belka Timoshenko na sprężystym-podłożu. PiWiki – Inżynierowie i Architekci Chodor-Projekt. https://chodor-projekt.net/encyclopedia/belka-timoshenko-sprezyste-podloze/
- Pałkowski, S. (2009). Konstrukcje stalowe: wybrane zagadnienia obliczania i projektowania. Wydawnictwo Naukowe PWN
- Chodor, L. (2015). Ściskane pręty stalowe. PiWiki -Inżynierowie i Architekci Chodor-Projekt. https://chodor-projekt.net/encyclopedia/sciskane-prety-stalowe/
- Chodor, L. (2018). Metoda imperfekcyjna projektowania konstrukcji. Polskie Wydawnictwo Naukowe – w przygotowaniu
________________________________






