Leszek Chodor, 5 listopada 2014
09-02-2025 rewizja po dużej awarii portalu>
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 8 Czytelników
Konstrukcja nośna hali musi spełniać warunki geometrycznej niezmienności ustroju w przestrzeni. Zapewniają to stężenia kolejnych układów poprzecznych, w szczególności stężenia połaciowe przekrycia hali. Stężenia należy tak rozmieścić, by zapewnić stateczność oraz sztywność przestrzenną hali i tak, aby elementy stężeń nie utrudniały procesów produkcyjnych, nie zmniejszały powierzchni użytkowej, bądź innych walorów użytkowych lub architektonicznych obiektu. Nadto należy uwzględnić pomocniczy udział stężeń w procesie montażu systemu hali.
Warunki ogólne kształtowania systemu stężeń w halach
Wymogi rozmieszczania stężeń sprowadzono do wymogu ogólnej stateczności i sztywności przestrzennego systemu hali, a pomięto wymóg konstrukcyjnego rozmieszczania stężeń, niezależnie od indywidualnych potrzeb stateczności systemu konstrukcyjnego [1]. Najistotniejszą zmianą jest zdaniem autora preferowany sposób analizy konstrukcji metodą globalną: zarówno jeśli chodzi o stateczność ogólną systemu (stężenia hal) , jak i o stateczność elementów (wyboczenie , zwichrzenie prętów). W ten sposób nareszcie wyeliminowano utrzymywany od lat paradoks wymiarowania prętów (zginanych i ściskanych) z zastosowaniem długości oraz współczynników wyboczeniowych, mimo braku teoretycznego uzasadnienia sumowania naprężeń od zginania z naprężeniami od ściskania powiększonymi o współczynnik wyboczeniowy. Rozwój informatyzacji i metod obliczeniowych wyeliminował też potrzebę wyznaczania momentu krytycznego (zwichrzenia) za pomocą wzorów analitycznych, co prowadziło w przeszłości do błędów obliczeniowych i do awarii konstrukcji [1].
Analizę stateczności przestrzennej hal można dokonać wstępnie w drodze analizy zachowania się szeregu układów poprzecznych hali, myślowo przegubowo połączonych z fundamentami i z płatwiami w sposób pokazany w pracach [2] i [3]. Po myślowym przechyleniu w kierunku podłużnym hali, stwierdzimy, że taki układ „złoży” się jak plik kart.
W celu zachowania stateczności wystarczy połączyć ze sobą sąsiednie układy poprzeczne prętami dodatkowymi, zwanymi stężeniami, np. prętami T1, T3 i T4, w sposób pokazany na rys. 1 w polach skrajnych (pierwszym i ostatnim) układu podłużnego hali.
Inne pokazane na rys.1 stężenia, a to: T2, i T3 na całej długości hali, T5 i T6 – nie są zawsze potrzebne i są stosowane wyłącznie w przypadkach uzasadnionych wytrzymałością elementów lokalnych, a nie całego ustroju hali.
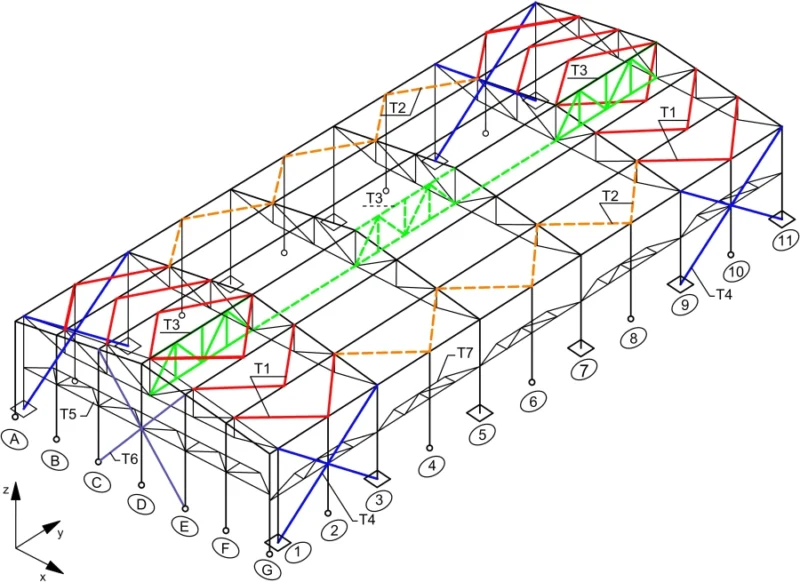
Rys.1. Klasyczny układ stężeń hal: T1 – stężenie połaciowe poprzeczne, T2 – stężenie pionowe podłużne T3 – stężenie pionowe między wiązarami, T4 – stężenie pionowe podłużne słupów, T5 – stężenie wiatrowe, ściany czołowej, podpierany, T6– Stężenie pionowe ściany szczytowej, T7 – stężenia wiatrowe ścian podłużnych
Takie uproszczone analizy we współczesnej praktyce inżynierskiej stosowania zaawansowanych narzędzi informatycznych i analizy 3D tracą sens, ponieważ warunki kształtowania stężeń powinny wynikać z analizy macierzy sztywności przestrzennego układu prętowego hali i badania osobliwości pełnej macierzy sztywności układu. Jeśli układ będzie bliski osobliwemu (bliski mechanizmowi kinematycznemu), to w wyniku uzyskamy brak możliwości jednoznacznego rozwiązania układu (wyznacznik macierzy sztywności równy zero), bądź brak zbieżności przy próbie analizy nieliniowej, bądź duże przemieszczenia poziome lub pionowe niektórych punktów konstrukcji. Każdy z tych objawów będzie świadczył o potrzebie dodania dodatkowych prętów, ścian, ram (wszystko to są stężenia), bądź o potrzebie zwiększenia sztywności istniejących prętów lub węzłów.
Istnieje wiele rozwiązań konstrukcyjnych, umożliwiających zapewnienie wymaganej stateczności i sztywności układu, a ich wachlarz nie ogranicza się do zastosowania układu stężeń pokazanego na rys. 1. Możemy zastosować: 1) dodatkowe pręty w rozmaitych konfiguracjach – stężenia prętowe, 2) dodatkowe tarcze, np. ściany lub płyty, w tym blachę dachową – stężenia tarczowe lub ścienne, 3) dodatkowe usztywnienia w węzłach – stężenia ramowe.
Optymalny układ i rodzaj stężeń należy dobierać przy dwóch należy wyznaczyć z warunku minimalizacji liczby elementów stężeń – nadmiar liczby stężeń ogranicza funkcjonalność hali i zwiększa jej złożoność konstrukcyjną, przy jednoczesnej optymalizacji kosztów zastosowania różnych rodzajów stężeń – np. zastosowanie stężeń ramowych prowadzi zwykle do większych wydatków od zastosowania stężeń prętowych. Kryterium ograniczenia liczby stężeń i uproszczenia złożoności konstrukcji można uzyskać poprzez zastosowanie stężeń ramowych lub tarczowych, ale zwykłe jest to rozwiązanie droższe od zastosowania stężeń prętowych. Zadanie optymalizacji systemu stężeń należy rozwiązać poprzez analizę porównawczą kilku wariantów, gwarantujących stateczność i sztywność układu.
Na rys. 1 liniami przerywanymi oznaczono te stężenia, które są opcjonalne i nie zawsze wymagane:
1) stężenia połaciowe podłużne T2 są wymagane w zasadzie wyłącznie w potrzebie podparcia głowic pośrednich słupków ściennych,
2) stężenia pionowe między wiązarami są wymagane w polach, w których występują stężenia połaciowe poprzeczne, a w innych polach tylko w sytuacjach szczególnych:
a) przy umiarkowanie dużych obciążeniach poziomych i/lub dynamicznych sprzęga się dżwigary w co drugim polu,
b) przy dużych obciążeniach poziomych i/lub dynamicznych stężenia T3 daje się na całej długości hali.
c) często we celu zapewnienia stateczności pasów dolnych wiązarów łączy się pasy dolne prętami po całej długości hali. Stężenia pionowe daje się w miejscach załamań opasów i nie rzadziej niż co 12 m (rys. 3f).
Stężenia hal złożonych z płaskich układów poprzecznych
Stabilność klasycznych hal złożonych z płaskich układów poprzecznych, pokazanych na rys. 3 a, f (i niestężonych ) nie jest zachowana (szczególnie w kierunku podłużnym hali) i należy wprowadzić dodatkowe elementy usztywniające (stężenia).
W celu przestrzennego usztywnienia układów poprzecznych należy połączyć ramy między sobą, najlepiej tworząc poziomą ramę w płaszczyźnie połaci dachowej oraz dodać pionowe tarcze pomiędzy układami poprzecznymi wzdłuż hali w linii ścian i/lub wewnątrz hali. Tarcze usztywniające mogą być powłokowe (np. pokrycie z blachy fałdowej, ściany żelbetowe i trzony w budynku) lub zastępcze prętowe.
Na rys. 5 pokazano klasyczny układ stężeń prętowych w halach wg [4] i zmodyfikowany w pracy [5].
Klasyczne (ale już historyczne) zasady rozmieszczania głównych typów stężeń w halach, przewidują zastosowanie:
1) w płaszczyźnie połaci dachowej obowiązkowych stężeń połaciowych poprzecznych T1, które należy dać pomiędzy polami skrajnymi lub przed skrajnymi i nie rzadziej niż co ósme pole między układami poprzecznymi;
2) w celu utworzenia bikonstrukcji układu hali w tych samych polach, w których zastosowano stężenia połaciowe poprzeczne – stężeń pionowych T4 w płaszczyźnie ścian bocznych i/lub wewnętrznych liniach słupów;
3) w przypadku zastosowania wysokich rygli dachowych, np. w postaci kratownic, w tych samych polach, w których występują stężenia połaciowe poprzeczne – w celu utworzenia bikonstrukcji dźwigarów – stężeń pionowych między wiązarami na ich wysokości T3 .
4) w przypadku dynamicznych lub miejscowych obciążeń hali – stężenia T3 należy dać jeszcze w innych polach między wiązarami, co na rys.1 zaznaczono symbolicznie, stosując linię przerywaną,
5) stosowanie stężeń połaciowych podłużnych T2 ogólnie nie jest konieczne, ale są one potrzebne, w przypadku lokalnego obciążenia głowicami ściennych słupków pośrednich, co pokazano linią przerywaną na rys. 1.
6) podobnie jak w przypadku konieczności zastosowania stężeń połaciowych podłużnych z warunku wytrzymałości lokalnych elementów (płatwi dachowych), – konieczność stosowania innych stężeń, w tym wiatrownic T5 i T7 wynika z potrzeb wytrzymałości słupków ściennych hal i nie jest bezwzględnie wymagana do zapewnienia stateczności hali. Również stężenia typu T6 są stężeniami lokalnymi (w tym przypadku konstrukcji ściany szczytowej) i zasady ich kształtowania nie są związane ze statecznością głównego układu konstrukcyjnego hali.
Należy zwrócić uwagę na to, że mimo tego, że w Eurokodach zrezygnowano ze sztywnych zasad rozmieszczania stężeń, to w polskiej praktyce inżynierskiej nadal stosowane są klasyczne układy stężeń pokazane na rys. 1. Tymczasem układy usztywniające mogą się znacznie różnić w formie lub umiejscowieniu, choć w każdym przypadku należy stosować zasadę bikonstrukcji, którą Kowal (1973) [6] zdefiniował na przykładach pokazanych na rys. 2.
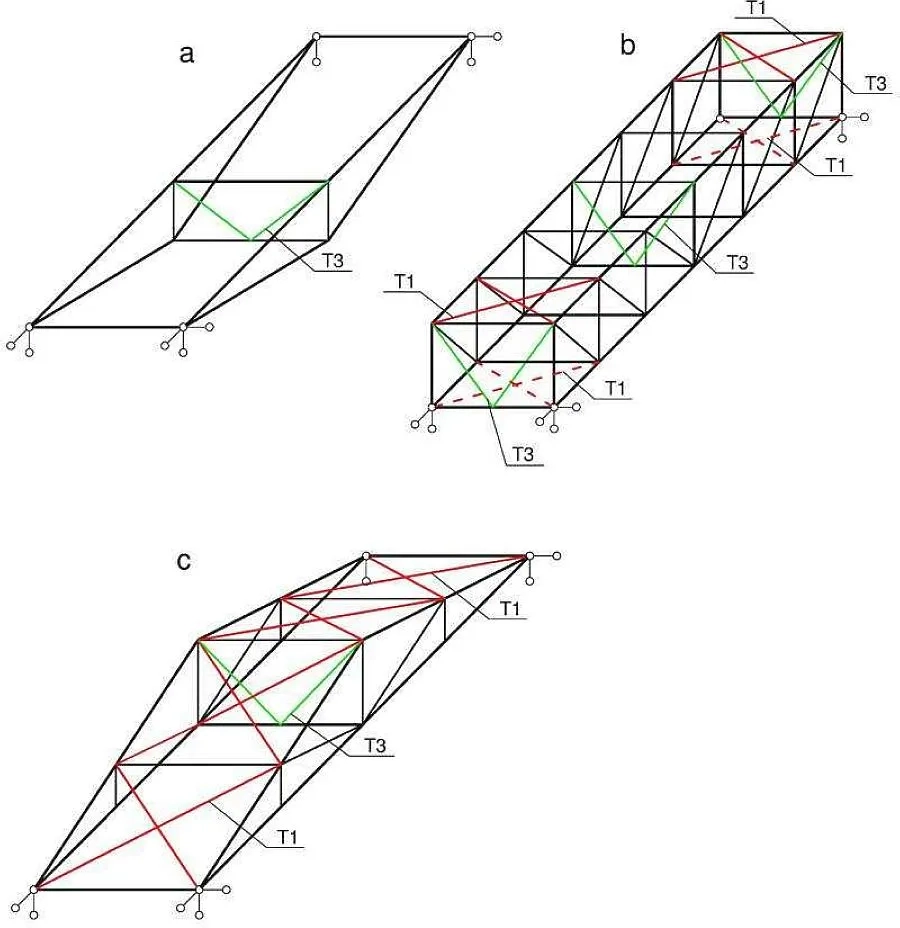
Rys.2. Przykłady bikonstrukcji, tworzących stateczny, przestrzenny układ: prętowy: a), c ) wiązary trójkątne połączone w płaszczyźnie załamania pasów, b) wiązary o pasach równoległych połączone w płaszczyznach podporowych [6]
Przekrycie jest konstrukcją nośną dla pokrycia oraz urządzeń umieszczonych na dachu oraz dla obciążęń klimatycznych (śnieg, wiatr). Spośród elementów pokazanych na rys.1. do przekrycia należą dźwigary dachowe, płatwie, a także stężenie połaciowe poprzeczne T1 i podłużne T2, oraz stężenia pionowe między wiązarami T2. Do przekrycia wliczmy również blachę dachową, płyty warstwowe lub inne prefabrykowane (np. żelbetowe, kanałowe), ułożone na płatwiach, lub bezpośrednio na wiązarach. W tym ostatnim przypadku mamy do czynienia z przekryciem bezpłatwiowym, w którym rolę płatwi pełnią płyty dachowe ( w tym blacha). W przypadku zastosowania płyt warstwowych na przekrycie, są one jednocześnie pokryciem i z reguły nie wymagają dodatkowych warstw izolacyjnych. W innych przypadkach warstwy pokrycia składają się z warstwy izolacji termicznej oraz izolacji przeciwwodnej.
Wskazuje się również, że stężenia ramowe są mniej optymalne od prętowych stosownie do generalnej zasady, że doprowadzenie do zginania prowadzi najczęściej do wzrostu kosztu konstrukcji – zasada natury: stan błonowy lepszy od stanu zgięciowego.
Zmniejszenie liczby stężeń jest możliwe przy zastosowaniu rusztów, a wyeliminowanie klasycznego systemu stężeń jest możliwe po zastosowaniu struktur prętowych.
Warunki szczegółowe kształtowania stężeń w halach
Stężenia prętowe
Na rys.3. pokazano warianty skratowań prętowych stężeń konstruowanych w przekryciach dachowych z wiązarami kratowymi z załamaniami pasa.
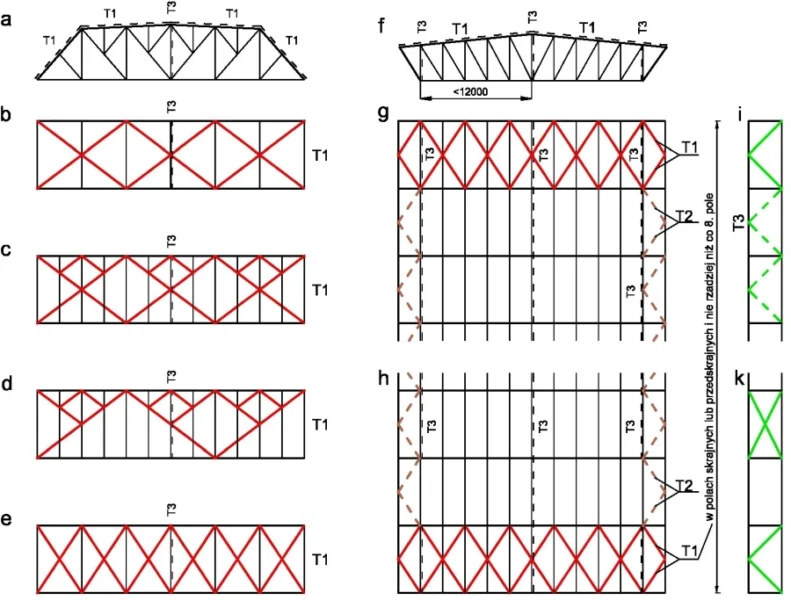
Rys.3. Systemy stężeń pokrycia dachowego: a,f wiązar z układem stężeń, b,c,d,e – stężenia połaciowe poprzeczne T1, g,h – stężenia połaciowe poprzeczne i podłużne T2, i,k – stężenia pionowe T3,[7]
Generalną zasadą, wynikającą z rozkładu sił w systemach prętów, jest zasada umieszczania pręta ukośnego pod katem ok 45 ± 15° do osi pręta podłużnego. Z tej zasady wynika dopuszczalny typ skratowania pola prostokątnego axb, gdzie a jest większym bokiem: jeśli a≈b, to niezawodnym systemem skratowania jest typ X – skratowanie na krzyż (rys 3 b, e) ; jeśli a≈2b, to stosujemy skratowanie typu V (rys. 3 c, d, g, h, i) z wierzchołkiem w połowie dłuższego boku; jeśli a>3b, to należy wprowadzić podział boku na liczbę krotności b (lub ich przybliżenie). Z zasady wynika, że na rys 2k, skratowanie typu V jest lesze od X . Przy a>3b nie powinno się stosować skratowania typu X.
Skratowanie typu X jest inteligentnym typem skratowania polegającym na tym, że ten sam pręt może być raz ściskany, a raz rozciągany zależnie od kierunku obciążenia, a po wyłączeniu z pracy elementów ściskanych (wskutek wyboczenia) ustrój nadal pozostaje stateczny. Z tego powodu każdy z prętów możemy zaprojektować o smukłości większej niż minimalna dla pręta ściskanego (λ>200).Ta własność powoduje, ze stężenie typu X jest optymalne ze względu na zużycie materiału, ale wymaga stosowania napięcia wstępnego prętów, poprzez zastosowanie nakrętek rzymskich. Taki system, zawierający pręty ‘tylko rozciągane’ jest nieliniowy strukturalnie i wymaga stosowania procedur iteracyjnych.
Stężenia ramowe
Z punktu widzenia geometrycznej zmienności systemu stężeń, w każdym przypadku układ prętów z węzłami przegubowymi można zastąpić układem prętów ramowych z połączeniami sztywnymi.
W przypadku zastosowania stężeń ramowych zamiast kratowych, zyskujemy większą swobodę funkcjonalną (np. możemy zwolnić płaszczyzny ścian w celu przejazdu lub uzyskania okien bez przecinających je prętów), ale z reguły zużycie stali jest nieco większe.
Stężenia płytowe/tarczowe
W płaszczyznach, w których należy zastosować stężenia, zamiast układu prętów możemy zastosować membrany, wykonane ze ścian lub tarcz pokrycia dachowego, albo tarcz stropowych.
Zaleca się prowadzenie analizy stężeń tarczowych w zastępczym modelu prętowym i następnie przeniesienie uzyskanych sił w prętach zastępczej kratownicy na sprawdzenie sztywności i wytrzymałości usztywnień tarczowych. Analogię kratownicową do analizy tarcz wyczerpująco omówił [8].
Blacha fałdowa jako stężenie połaciowe
Klasycznym przykładem jest zastosowanie pokrycia dachowego z blach trapezowych. W tym przypadku należy przeprowadzić analizę dopuszczalności potraktowania tarczy dachowej z blach trapezowych, jako współpracującej z prętowym szkieletem nośnym. Należy przy tym uwzględnić fazę montażową, w której blacha ułożona na dźwigarach nie jest jeszcze z nimi połączona łącznikami i nie zabezpiecza ich górnych pasów przed utratą stateczności, a także stężenia montażowe, zapewniające stateczność i prawidłowe usytuowanie dźwigarów dachowych w czasie montażu.
Unormowania w tym względzie zawiera rozdział 10.3 „Projektowanie z uwzględnieniem współpracy blach poszycia” normy [9]. Zastosowanie blachy jako stężenie pasów wiązarów płaskich w dachach bezpłatwiowych omówiono w pracy [10]. Więcej informacji zawiera ten rozdział.
Analiza pracy i siły w prętach systemu
Uwagi fundamentalne do metod analizy
W tym miejscu należy odnieść się do analizy wyboczeniowej, polegającej na wyznaczeniu wartości i wektorów własnych macierzy geometrycznej modelu mechanicznego konstrukcji. Z całą stanowczością należy przypomnieć, że wbrew powszechnemu przekonaniu – analiza wyboczeniowa nie jest analizą nieliniową. Jest procedurą quasi-nieliniową (pozornie nieliniową) i umożliwia przeprowadzenie procedury teorii katastrof, a w podejściu inżynierskim umożliwia wyznaczenie krytycznych mnożników obciążenia (w prostym przypadku sił i momentów krytycznych).
Takie podejście nazwiemy wyboczeniowym lub zachowawczym. Słowo zachowawczy jest stosowne w kontekście podejścia mającego na celu utrzymanie dotychczasowego stanu rzeczy; przywiązanego do tradycji, konserwatywnego, bez względu na znane opisy nauki i techniki, które jednoznacznie wskazują, że takie podejście w praktycznych, złożonych lub nieidealnych (imperfekcyjnych) sytuacjach – nie ma żadnego uzasadnienia teoretycznego, co zwykle powadzi do procedur niejasnych, do wielu opcji, braku ogólności, do procedur pełnych wyjątków i w konsekwencji trudniejszych do ogarnięcia i stosowania przez inżynierów praktyków. Stwierdzamy, żę we współczesnej, zinformatyzowanej praktyce projektowej, utrzymywanie takiego stanu rzeczy jest szkodliwe
Niestety konserwatywne podejście jest nadal prezentowane jako podstawowe w normach europejskich [11] poprzez zastosowanie systemu współczynników wyboczeniowych (ogólniej niestateczności: giętnej, skrętnej, dystorsyjnej, giętno-skrętnej, itd). Podejście wyboczeniowe może być w prostych przypadkach zastosowane do prętów ściskanych, prętów zginanych, w złożonym stanie naprężenia, a w nojogólniejszej i najlepszej formule zachowawczej, wyrażonej w metodzie ogólnej. Ważne ustalenia w tym względzie dokonano w normie [11] w rozdziale , dotyczącym analizy globalnej konstrukcji. Powyższe jest ściśle związane z analizą stateczności. W tym miejscu zauważmy, że podstawowa metodą sprawdzania stateczności konstrukcji i jej elementów jest analiza globalna, to znaczy taka, którą prowadzi się metodami drugiego rzędu z uwzględnieniem imperfekcji. Wyłącznie w przypadkach elementarnych (przy pełnej i precyzyjnej znajomości modelu pracy statycznej elementu, w tym stopnia utwierdzenia końców prętów) dopuszcza się indywidualne sprawdzanie stateczności elementów z zastosowaniem klasycznej metody smukłości i współczynników wyboczeniowych.
Mamy więc tak sytuację, że po raz kolejny realizuje się znana teza Feynmanna [12], że nowe teorie zwyciężają nie dlatego, że są lepsze, ale dlatego, że wymierają stare.
W wykładzie Leszka Chodor, kilkunastoletniego projektanta ważnych konstrukcji stalowych w Polsce i w Europie, przyjmujemy zasadę, którą od 25-ciu lat stosuje w swoich projektach (ta metoda imperfekcyjna w normie [11] została co prawda zaprezentowana do stosowania w praktyce, ale w istocie przesłonięto ją metodą globalna oraz klasyczną):
Konstrukcje i elementy stalowe wymiarujemy w procedurze realnej (niezachowawczej), której główne założenia są następujące:
- Projektowanie systemów i elementów konstrukcji stalowych prowadzimy metodą ogólną, na siły powstałe w konstrukcji w stanie nieliniowym geometrycznie przynajmniej rzędu II (tzn rozwinięcia macierzy sztywności minimum do wyrazy rzędu drugiego), czyli w procedurze P-Δ, w której siły przekrojowe są wyznaczone z uwzględnieniem wpływu przemieszczeń na ścieżce pobifurkacyujnej, lub przynajmniej rzędu III w elementach cięgnowych lub błonowych.
- Konstrukcję wytrącamy z idealnej ścieki równowagi i w rezultacie wprowadzamy na ścieżkę pobifurkacyjną poprzez przyłożenie zastępczych sił od imperfekcji do węzłów konstrukcji i na długości elementów obciążonych grawitacyjnie (pionowo), wynikających z losowych niedoskonałości położenia węzłów konstrukcji i osi elementów w przestrzeni,
- Elementy wytrącamy ze idealnej ścieki równowagi i w rezultacie wprowadzamy na ścieżkę pobifurkacyjną poprzez przyłożenie zastępczych sił od imperfekcji na długości: a) prostoliniowych elementów ściskanych, b) elementów zginanych z prostą płaszczyzną zginania. Te lokalne siły imperfekcji pochodzą od wstępnych wygięć pręta ściskanego pomiędzy węzłami lub lokalnych skręceń elementu zginanego , wynikających z imperfekcji osi pręta . Przyjmuje się , że te siły przykłada się dodatkowo do każdego elementu nominalnie prostoliniowego obciążonego ściskaniem w zależności od wielkości siły ściskającej.
- Stosownie do analizowanego zjawiska dobieramy rodzaj elementów skończonych, którymi modelujemy układ rzeczywisty:
- w przypadku konstrukcji nie zawierającej belek podatnych na zwichrzenie i elementów cienkościennych niepodatnych na lokalną utratę stateczności, ale tylko dla takich konstrukcji dopuszcza się stosowanie tradycyjnego modelu prętów o przekroju zwartych (elementy Bernoulliego-Eulera)
- w przypadku konstrukcji zawierającej belki, podatne na zwichrzenia, czyli w zasadzie większość belek stalowych nie zabezpieczonych przed zwichrzeniem należy stosować uogólnione elementy prętowe, czyli elementy cienkościenne (elementy Własowa)
- niestateczność miejscową ściankę przekrojów uwzględniamy na poziomie przekroju klasy 4, w sposób prezentowany przez normę lub stosujemy elementy płytowo-tarczowe do aproksymacji ścianek prętów
- Stosowanie elementów płytowo-tarczowych jest poprawne, ale z punktu widzenia inżynierskiego nie zalecane, ponieważ istotnie: a) zwiększa rozmiar zadania około 100 razy ( np w pracy [13] na przykładzie prostej ramy pokazano, że dyskretyzacja elementami belkowymi była możliwa z użyciem 60 prętów i 61 węzłów lub równoważnie z użyciem 4465 elementów płytowych i 4829 węzłów),
b) utrudnia analizę zbyt dużej liczby wyników,
c) umożliwia uzyskanie tylko mnożników obciążeń granicznych i krytycznych, a wymiarowanie należy przeprowadzić jak dla elementu prętowego.
Uznajemy, że podstawowym sposobem wymiarowania prętów stalowych jest metoda realna (drugiego rzędu, bez stosowania współczynników wyboczeniowych, zwichrzenia itd.). Metoda realna jest nieczuła na brak precyzji w przyjmowaniu długości wyboczeniowych pręta – eliminuje podstawową wadę metody klasycznej, to znaczy dużą wrażliwość na dokładność oszacowania długości wyboczeniowej pręta sprężyście zamocowanego na końcach ,pracującego w układzie przesuwnym. Wielokrotnie wskazywano na niedokładności metody klasycznej dochodzące do kilkuset procent, co w sposób oczywisty wskazywało na potrzebę wyeliminowania tej metody z praktyki inżynierskiej. W normie europejskiej jako definicję podstawową smukłości pręta wskazano co prawda formułę znaną z teorii sprężystości, a mianowicie przyjęto , że smukłość pręta należy wyznaczać z formuły:
$$\begin{equation} \overline \lambda= \sqrt{\cfrac {N_R}{N_{cr}}} \label{1}\end{equation}$$
gdzie: NR jest graniczną nośnością przekroju (zależnie od rodzaju siły i klasy przekroju), a Ncr jest nośnością krytyczną elementu . Ta definicja w praktyce działa prawidłowo dla smukłości na zwichrzenie, gdzie siłę krytyczną Mcr wyznacza się w odrębnej procedury (najczęściej z użyciem programu LTBeamN), ale już dla pręta ściskanego najczęściej Ncr przyjmuje się ze wzoru Eulera i następuje powrót do skrytykowanego szacowania współczynnika długości wyboczeniowej.
Realna analiza (II rzędu) jest jakościowo inna od metody klasycznej z szacowaniem długości wyboczeniowych prętów – jest prowadzona w procedurze nieliniowej (iteracyjnej) i umożliwia na drodze teoretycznie uzasadnionej wyznaczyć siły przekrojowe powiększone (amplifikowane) poprzez wystąpienie zjawisk wyboczeniowych. Analiza przebiega już na pobifurkacyjnej ścieżce równowagi bez badania stanów pośrednich, a zwłaszcza bez poszukiwania punktów krytycznych (wyboczeniowych lub wartości własnych macierzy sztywności).
Do tego potrzebne jest jednak wytrącenie konstrukcji lub elementu z idealnej ścieżki równowagi na ścieżkę po utracie stateczności. W tym celu konstrukcję należy obciążyć wystarczy dociążyć niewielkimi siłami wytrącającymi, utożsamianymi najczęściej z siłami poziomymi od imperfekcji. Sposób szacowania sił wytrącających omówimy poniżej.
Zastępcze siły poziome od imperfekcji w analizie systemu i stężeń
Fundamentalną metodą, którą należy sprawnie posługiwać się w analizie stężeń oraz analizie przestrzennej konstrukcji jest wyznaczanie zastępczych sił poziomych, którymi można zastąpić niedoskonałości przyłożenia sił pionowych.
Niedoskonałości geometryczne systemu były przedmiotem badań statystycznych przez wielu autorów, np przez Mrazik’a [14]. Niezaprzeczalną zaletą Eurokodu 3 jest to, że uporządkował te badania i wskazała na bezpieczne aproksymacje normowe.
Niedoskonałości (imperfekcje ) obejmują szereg odstępstw konstrukcji rzeczywistej od modelu idealnego, takich jak brak pionowości, prostoliniowości, gładkości, dopasowania, istnienie niezamierzonych mimośrodów. Imperfekcje dzielimy na globalne (systemowe) oraz lokalne (elementu). Globalne niedoskonałości mogą być uwzględnione przez wymodelowanie konstrukcji o geometrii , będącej wynikiem nałożenia niedoskonałości na geometrię idealną (oczekiwaną), albo przez przyłożenie równoważnych sił poziomych, wywołujących takie odchylenia geometryczne. Zalecane jest drugie podejście.
Siły równoważne od imperfekcji globalnych
Na rys. 3 pokazano model przyjmowany do analizy imperfekcji globalnych systemów konstrukcyjnych, polegających na pochyleniu budowli o wysokości h w kierunku poprzecznym o kąt Φ, lub pochyleniu rzędu słupów podłużnym również o kąt Φ.
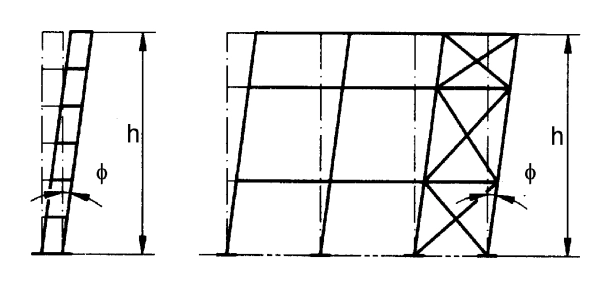
Rys 4. Imperfekcje globalne w analizie konstrukcji [11]
Podstawowa i jednocześnie największa możliwa wartość pochylenia zgodnie z normą, to
$$\begin{equation} \Delta=\phi\cdot h=\Delta_0 = \cfrac {h}{200} \label{2}\end{equation}$$
Wartość ta może być zredukowana współczynnikami redukcyjnymi αh – w zależności od wysokości budowli h oraz αm w zależności od liczby słupów m w rozpatrywanym szeregu podłużnym (bardziej ogólnie współczynnik ten powinien być obliczony dla liczby słupów stabilizowanych w kilku rzędach, a nie tylko w jednej ścianie [11]) :
$$\begin{equation} \phi=\phi_0 \cdot \alpha_h \cdot \alpha_m= \cfrac {1} {200}\cdot \alpha_h \cdot \alpha_m \label{3}\end{equation}$$
Współczynniki redukcyjne wynoszą:
$$\begin{equation} \alpha_h= \cfrac {2}{\sqrt{h}}\ \ge \frac {2}{3} \label{4}\end{equation}$$
$$\begin{equation} \alpha_m= \sqrt{ \cfrac {m+1} {2 \cdot m}} \label{5}\end{equation}$$
Współczynniki przyjmują maksymalne możliwe wartości 1,0 odpowiednio dla h= 4 m i m=1. Na przykład dla konstrukcji z rys. 1 mamy m=6 słupów nośnych w ścianie podłużnej i redukcja wynosiłaby
$$\begin{equation} \alpha_m= \sqrt{ \frac {6+1} {2 \cdot 6}}=0,76 \label{6}\end{equation}$$
Ponieważ w praktycznie spotykanych przypadkach wpływ sił imperfekcji na zwiększenie wytężenia początkowego nie jest zbyt istotny, ale spełniają one pożyteczną rolę wyprowadzenia systemu z idealnego położenia, więc w celu uproszenia procedur ignoruje się te współczynniki i w praktyce dla zwykłych przypadków przyjmuje najniekorzystniejszą wartość
$$\begin{equation} \phi=1/200 \label{7}\end{equation}$$
Jeśli zewnętrzna siłą pozioma przekracza 15% całkowitej siły pionowej, to siły od imperfekcji można pominąć.
Zamiast modyfikowania geometrii modelu, wprowadza się równoważne siły poziome HEd , wywołane imperfekcjami globalnymi, które są przyłożone do głowicy i do stopy słupa w przeciwnych kierunkach, o wartości
$$\begin{equation} H_{Ed}=\phi\cdot N_{Ed} \label{8}\end{equation}$$
gdzie: $N_{Ed}$ jest siłą osiową w słupie.
Sytuacje obliczeniowe dla systemu stężeń pionowych
System stężeń pionowych (rys.3 lub T4, T6 na rys.1) musi mieć zdolność do przeniesienia sił wywołanych obciążeniami równoważnymi HEd. Dodatkowo pręty stężeń powinny być sprawdzone na siły poziome dla dwóch wykluczających się sytuacji obliczeniowych dla każdej kondygnacji odrębnie ( w halach parterowych dla poziomu „0”):
- od obciążenia poziomego z płyty stropu (lub przekrycia rys.1),
- od imperfekcji elementów .
W obu sytuacjach , system stężeń jest sprawdzany lokalnie (powyżej i poniżęj poziomu kondygnacji )dla kombinacji obciążeń zewnętrznych i jednej opowiadających wymienionych wyżej sytuacji od imperfekcji Tylko jeden ze schematów imperfekcji należy uwzględnić w tym samym czasie.
W przypadku zastosowania kilku systemów stężeń należy dokonać rozdziału powyższych sił poziomych pomiędzy te systemy. Nie należy sprawdzać każdego systemu na wszystkie siły.
Zaleca sie bv elementy stężeń sprawdzać na siły imperfekcji bez uwzględniania stowarzyszonego ścinania, ponieważ niewielkie jest prawdopodobieństwo wystąpienia maksymalnego ścinania prętów (belek) wraz z maksymalnymi niedoskonałościami.
Obciążenie równoważne od imperfekcji lokalnych (elementu)
Na rys, 4 pokazano model do wyznaczenia równoważnego obciążenia qd elementu ściskanego siłą NEd.

Rys.4. Imperfekcje lokalne w analizie elementu [11]
Należy przyjąć, że elementy prostoliniowe mają wygięcia wstępne ze strzałką wygięcia
$$\begin{equation} e_{o,d}= \alpha_m \cdot \cfrac {L}{500} \label{9}\end{equation}$$
gdzie: L- długość elementu, αm – współczynnik wg formuły (4), w którym m oznacza liczbę prętów, które są stabilizowane. Na przykład liczba stabilizowanych płatwi w połaci hali z rys.1 wynosi m=6 , a z rys. 4, wynosi m=5 (dwie płatwie skrajne liczymy jako jedną ponieważ przenoszą dwa razy mniejsze obciążenie).
Obciążenie równoważne od imperfekcji elementu przykładamy jako równomiernie rozłożone obciążenie poprzeczne o wartości
$$\begin{equation} q_d=\sum {N_{Ed}}\cdot \cfrac {8\cdot(e_{0,d}+\delta_q)}{L^2} \label{10}\end{equation}$$
gdzie: NEd – siła osiowa działająca w stabilizowanym pręcie, e0,d – wg wzoru (7), δq– strzałka ugięcia w płaszczyźnie układu usztywniającego wywołane obciążeniami qd i ewentualnymi obciążeniami zewnętrznymi liczona według teorii I rzędu. Przy obliczeniach wg teorii II rzędu można przyjąć δq=0.
Ponieważ δq wywołane obciążeniami od imperfekcji jest małe rzędu niższego od e0,d , więc przyjmuje się, że ta składowa mimośrodu jest zerowa. W uzasadnionych przypadkach należy uwzględnić tę strzałkę ugięcia , ale wywołaną obciążeniami zewnętrznymi. W ten sposób unikamy iteracyjnego obliczania obciążeń równoważnych.
Obciążenia skupione na węzły kratownicy stężającej o rozstawie węzłów a=L/n, oblicza się ze wzoru
$$\begin{equation} Q_d=q_d \cdot a \label{11}\end{equation}$$
Źródło imperfekcji (imperfekcje, a tolerancje wykonania)
Dopuszczalne odchyłki wykonania systemów i elementów konstrukcyjnych podano w [15].
Porównując obliczeniowe mimośrody eo,d, wynikające z EC3, z granicznymi tolerancjami Δ mamy:
- dla słupów (ogólnie) : eo,d=L/(100 do 350); Δ = L/750,
- dla belek: eo,db= eod/2= L/(200 do 600); Δ = L/750,
- dla płyt: eo,d= b/200 ; Δ = b/400, (b- szerokość lub wysokość płyty),
- dla żeber eo,d= b/400 ; Δ = b/400, (b- wysokość żebra),
- dla słupa ramy: eo,db= h/200 ; Δ = b/500, (h- wysokość słupa).
Mimośrody wstępne, przyjmowane do obliczania sił imperfekcji są znacznie większe od tolerancji wykonania dla słupów i dla płyt. Dalsze informacje na ten temat zawiera artykuł Imperfekcje projektowe z odchyłek wykonawczych.
Imperfekcje, a krzywa wyboczeniowa
Zastąpienie przez analizę realną wyliczania współczynników wyboczeniowych jest uzasadnione również tym, że imperfekcje lokalne (pkt. 3.2.3) są wynikiem przyjęcia krzywych wyboczeniowych zgodnie z [11], tab. 5.1. To znaczy strzałkę e0,d można i należy przyjmować w zgodzie z krzywymi wyboczeniowymi przypisanymi do rodzaju przekroju i analizy.
Uproszczona, klasyczna analiza stężeń prętowych
Uproszczona (klasyczna) analiza stężeń prętowych polega na rozpatrzeniu uproszczonych schematów stężeń, obciążeniu ich siłami imperfekcji oraz obciążeniami od obciążeń zewnętrznych (najczęściej wiatru n ścianę szczytową) oraz od wstępnego naciągu (sprężenia) prętów stężeń, i zwymiarowaniu zgodnie z ogólnymi zasadami.
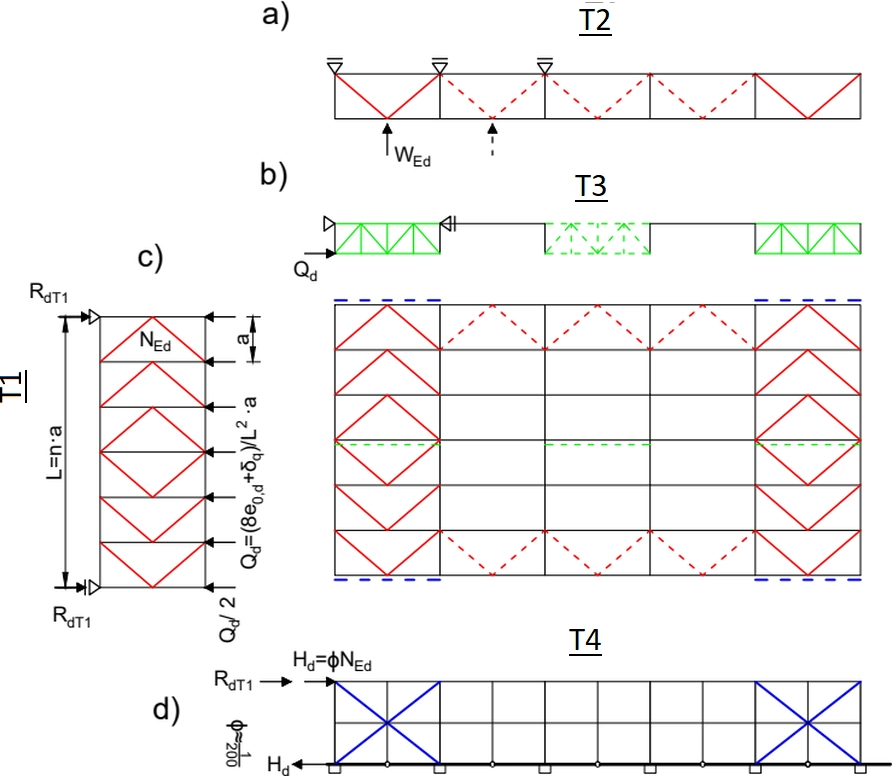
Rys.5. Zastępcze modele płaskie do analizy stężeń w halach: a) T2-połaciowe podłużne, b) T3 – pionowe między wiązarami, c) T1- połaciowe poprzeczne, d) T4 – pionowe w linii ścian bocznych
Na rys. 5 pokazano płaskie schematy zastępcze stężeń , które są przyjmowane do wymiarowania wstępnego prętów stężeń.
Stężenie połaciowe poprzeczne T1
Model stężenia połaciowego poprzecznego T1 ( rys.5c), to kratownica podparta na stężeniach pionowych w linii ścian (tężniki pionowe w modelu zastąpiono podporami), Kratownica pozioma T1 obciążona jest w węzłach siłami skupionymi (13) od stabilizowanych pasów kratownic zebranych z długości hali.
Dla przypadku pokazanego na rys.5, przy L=24 m, oraz dla obliczeniowej maksymalnej (tj. w środku rozpiętości) siły ściskającej pas kratownicy pośredniej NEd=400 kN mamy:
- liczba pasów kratownic dachowych na długości hali $m_d=4+50% \cdot2=5$ (4 pasy kratownic środkowych i 2 pasy kratownic skrajnych z obciążeniem 50%),
- suma sił w prętach pasach (prętach stabilizowanych) $\sum {N_{Ed}}=4 \cdot 400+ 2 \cdot 50% \cdot 400=2000 kN$,
- liczba stężeń połaciowych poprzecznych na długości hali, objętych rozpatrywanymi wiązarami $m_s=2$,
- na jedno stężenie przypada liczba sił destabilizujących $m=\frac {m_d}{m_s}=\frac{5}{2}=2,5 $,
- współczynnik redukcyjny ze względu na liczbę elementów stężanych (8) $\alpha_m= \sqrt{ \frac {2,5+1} {2 \cdot 2,5}}=0,84$,
- strzałka wstępnej imperfekcji łukowej (11) $ e_{o,d}= 0,84 \cdot \frac {24}{500}=0,040 m$,
- strzałka ugięcia kratownicy od obliczeniowego obciążenia równoważnego (8) δq=0, wobec obliczeń prowadzonych metodą II rzędu.
- równoważne obciążenie obliczeniowe (12) $q_d=2000 \cdot \frac {8\cdot(0,040+0)}{{24}^2} =1,11$,
- liczba pól kratownicy n=6
- odległość między węzłami kratownicy $a=\frac{L}{n}= \frac{24}{6}=4 m$,
- obciążenie węzłowe kratownicy $Q_d=1,11 \cdot 4=4,44kN$.
Siły w prętach kratownicy od obciążeń równoważnych, także innych obciążeń, wymienionych niżej, wyznaczamy metodami mechaniki budowli w schemacie statycznym pokazanym na rys. 4.
Siłę w pręcie i-tym, pochodzącą od Qd oznaczmy przez Nd,Qi. Siła ta jest siłą obliczeniową pochodzącą od obciążeń pionowych, które wywołują siły w pasach NEd, to znaczy od : obciążeń stałych, od śniegu, obciążenia użytkowego na dachu, od urządzeń technologicznych umieszczonych na dachu, od instalacji i elementów podwieszonych do przekrycia, a także od oddziaływania wiatru na połać dachową.
Ponadto siła w i-tym pręcie będzie wywołana przez:ewentualny naciąg (sprężenie) pręta (charakterystyczny naciąg oznaczymy przez Nk,si) oraz parciem wiatru na ścianę czołową (charakterystyczną siłę od wiatru oznaczymy przez Nk,wi). Stoimy na stanowisku, że ze względu na słabą korelację pomiędzy siłą obliczeniową imperfekcji Nd,Qi, a siłami Nk,wi, a także Nk,si:
1) zaniedbać problem jednoczesności działania wiatru na połać dachową i ściany czołowe (mimo, że wiatr działa jednocześnie na wszystkie przegrody budynku) i przyjąć, że $N_{d,wi}= (\gamma_f=1,5)\cdot (\psi=0,6) \cdot N_{k,wi}=0,9N_{k,wi}$,
2) oddziaływania poziome od wiatru przyjmujemy tylko na jedną ścianę czołową najbliżej położoną stężenia, uwzględniając tym fakt lokalnego wpływu działań zgodnie z zasadą Saint-Venanta
3) siłę od sprężenia traktujemy jako niekorzystną (lokalnie na pręt) ze współczynnikiem $\gamma_f \psi=1,0$, czyli $N{d,si}=1,0 \cdot N_{k,si}$.
Obliczeniową siłę w i-tym pręcie stężenia wyznaczymy poprzez sumowanie sił od wszystkich oddziaływań:
$$\begin{equation} N_{d,i}= N_{d,Qi}+N_{d,si}+N_{d,wi} \label{12}\end{equation}$$
co spełnia ideę formuł kombinacyjnych [16] opisanych w [17].
Stężenie połaciowe podłużne T2
Model stężenia połaciowego podłużnego T2 (rys.5a) oddaje sytuację, w której to stężenie jest wymagane. Dotyczy to sytuacji, w której płatwie skrajne są obciążane międzywęzłowo przez słupki pośrednie siłami od wiatru WEd . Wówczas przekrój międzywęzłowy należy podeprzeć prętami stężeń w celu uniknięcia nadmiernego zginania płatwi skrajnych (okapowych) .Siły w prętach T2 wyznacza się z warunku równowagi obciążonego węzła.
W zasadzie w innych sytuacjach stężenia połaciowe podłużne nie są wymagane, chyba że będą potrzebne z innych względów, w tym w celu poprawy stateczności poziomej przekrycia poprzez skonstruowanie poziomej ramy na obwodzie całego przekrycia z pól stężonych przez T1 i T2. W takim przypadku siły w prętach stężęń T2 należy wyznaczyć w schemacie tej poziomej ramy.
Stężenie pionowe między wiązarami T3
Potrzeba stężenia pionowego między wiązarami T3 wynika z konieczności sprzężenia dwóch sąsiednich wiązarów, w taki sposób, by w modelu rys. 5c, czyli kratownicy z pasem górnym zawieszonym na płatwiach stabilizował pas dolny.
Pas dolny jest zwykle rozciągany, ale zalecamy by siłę stabilizującą Qd wyznaczyć na przypadek ściskania pasa dolnego siłą równą jego nośności plastycznej to znaczy $N_{Rd}=f_y \cdot A$. Siła działająca na pręt podpierający, stabilizująca pręt ściskany (przyjmujemy, że również cięgno rozciągane), wynosi:
$$\begin{equation} Q_d= \cfrac {N_{Rd}}{100} \label{13}\end{equation}$$
Stężenie pionowe w linii ścian T4
Model stężenia pionowego w linii ścian bocznych pokazano na rys. 5d, na którym pokazano sytuację, w której słupy główne są utwierdzone w blokach fundamentowych, co może mieć miejsce w przypadku stężeń ramowych, to znaczy wówczas, gdy utwierdzenie w stopach jest wystarczające do przeniesienia obciążeń pokazanych na modelu. W takim przypadku nie są potrzebne stężenia prętowe, ale musimy się liczyć z powstaniem momentów utwierdzenia i zginaniem podporowych przekrojów słupów momentami zginającymi, które mogą prowadzić do zwiększenia przekrojów słupów.
Dodatkowe zginanie słupów można wyeliminować poprzez zastosowanie stężeń prętowych T4 i wprowadzeniu przegubów podporowych w miejsce utwierdzeń.
W głowicy każdego słupa działa siła pozioma Hd=1/200 NEd, gzie NEd jest siła ściskającą dany słup. Należy zwrócić uwagę, że mnożnik 1/200 może być zmniejszony zgodnie z pkt. 3.2.3 normy [1]. Często we wstępnych analizach całą ścianę obciąża się na poziomie głowicy 1-szego słupa sum sił poziomych z wszystkich słupów szeregu. Natomiast w obliczeniach numerycznych każdą siłę pionową VEd działającą na pokrycie uzupełnia się automatycznie siłami HEdx=HEdy=1/200 VEd. Oprócz siły poziomej, wywołanej imperfekcjami samych słupów na głowice słupów działa reakcja RdT1 ze stężenia połaciowego poprzecznego, określona w modelu z pkt 3.2.1 normy [1].
Analiza przestrzenna stężeń prętowych
W analizie przestrzennej nie są potrzebne uproszczone schematy przedstawione wyżej. W jednym kroku na podstawie rozwiązania przestrzennego modelu zawierającego wszystkie pręty lub tarcze stężeń i obciążonego siłami imperfekcji, wyznaczmy siły w prętach stężeń, które podlegają weryfikacji wytrzymałościowej według ogólnych zasad. Model obciąża się równoważnymi siłami imperfekcji zarówno od przechyłu słupów w sposób opisany w ostatnim akapicie pkt 3.3.4 normy [1] . jak imperfekcjami łukowymi działającymi na stężenia połaciowe poprzeczne, określonymi zgodnie z pkt. 3.3.1 [1].
Analiza stężeń tarczowych
Zasady ogólne
W płaszczyznach, w których należy zastosować stężenia, zamiast układu prętów możemy zastosować membrany, wykonane ze ścian lub tarcz pokrycia dachowego, albo tarcz stropowych.
Zaleca się prowadzenie analizy stężeń tarczowych w zastępczym modelu prętowym i następnie przeniesienie uzyskanych sił w prętach zastępczej kratownicy na sprawdzenie sztywności i wytrzymałości usztywnień tarczowych. Analogię kratownicową do analizy tarcz wyczerpująco omówił [8].
Blacha trapezowa jako stężenie dachowe
Klasycznym przykładem jest zastosowanie pokrycia dachowego z dachowych blach trapezowych. W tym przypadku należy przeprowadzić analizę dopuszczalności potraktowania tarczy dachowej, jako współpracującej z prętowym szkieletem nośnym. Należy przy tym uwzględnić fazę montażową, w której blacha ułożona na dźwigarach nie jest jeszcze z nimi połączona łącznikami nie zabezpiecza ich górnych pasów przed utratą stateczności, a także stężenia montażowe, zapewniające stateczność i prawidłowe usytuowanie dźwigarów dachowych w czasie montażu.
Unormowania w tym względzie zostały w prowadzone w rozdziale 10.3 „Projektowanie z uwzględnieniem współpracy poszycia” normy [9]. W pracy[18] omówiono sposób uwzględnienia blachy fałdowej jako usztywnienia pasów kratownic płaskich przy wyboczeniu z ich płaszczyzny.
W przypadku zastosowania blachy fałdowej również jako stężenia połaciowego poprzecznego w układzie płatwiowym dachu rozpatrzymy schemat rys. 5c, w którym zamiast prętów wykratowania mamy blachę fałdową. Pole ograniczone wiązarami i płatwiami definiuje nam panel, pokazany na rys 6. Poszycie z blachy należy traktować jako środnik przenoszący siły poprzeczne , a elementy brzegowe (płatwie lub pasy górne dźwigarów) przenoszą siły osiowe w pasach utworzonego dźwigara. Na rysunku: a=L (szerokość hali), b- rozstaw wiązarów po długości hali.
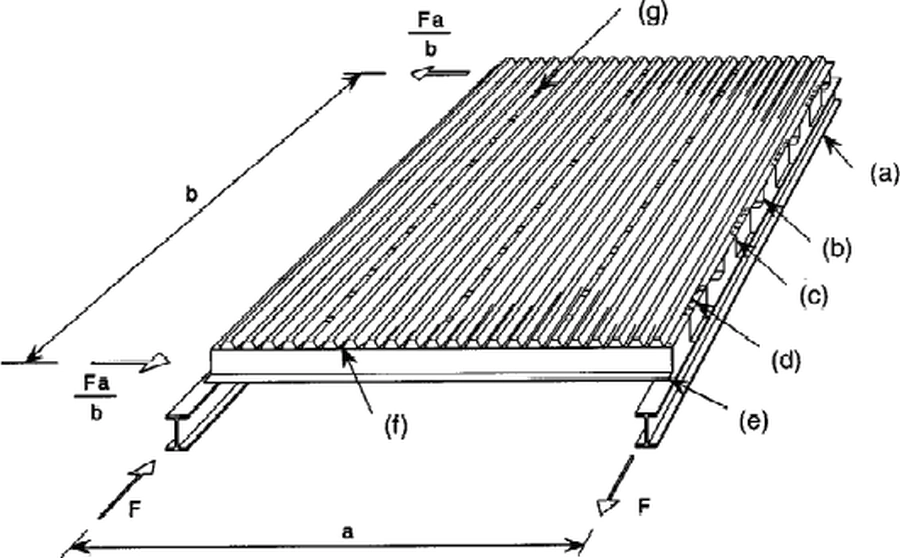
Rys.6 Pojedynczy panel i jego elementy PN-EN 1993-1-3:2008, Eurokod 3: Projektowanie konstrukcji stalowych, Część 1-3: Reguły uzupełniające dla konstrukcji z kształtowników i blach profilowanych na zimno, rys.10.14: (a) rygiel, (b,e) płatew, (c) podpórka brzegowa, (d) łączniki poszycia i podpórki brzegowej. (g)- łącznik szwu
Mogą zajść przypadki:
PP – dach płatwiowy – fałdy blachy prostopadłe do osi hali (i do płatwi). W tym przypadku siła w pasach wiązarów od obciążenia równoważnego qd (\ref{13}$) wynosi
$F=q_d \cdot \frac {L^2}{8 \cdot b}$
BP – dach bezpłatwiowy – fałdy blachy równoległe do osi hali (prostopadłe do pasów dźwigarów). W tym wypadku siła
$F=R_{dT1}=q_d \cdot \frac {L}{2}$.
Nośność tarczy dachowej na ścinanie przyjmuje się jako nośność połączenia między blachami lub połączenia blachy z elementem biegnącym wzdłuż lub poprzek rozpatrywanego panelu poszycia. Nośność łączników należy szacować zgodnie z [9], kl. 8.3..
Główną rolą blachy jest przeniesienie obciążeń prostopadłych do pokrycia (zginających). W celu zachowania tej roli jako dominującej, ogranicza się naprężenia wynikające z roli stężenia do
$25% \cdot f_{y}/\gamma_{M1}$
Tarczę dachową z blach trapezowych obowiązkowo należy wyposażyć w elementy brzegowe (obróbki blacharskie) na obwodzie tarcz dachowych oraz elementów pośrednich, a także na krawędziach swobodnych wokół otworów dachowych. W miąższości blach trapezowych często stosuje się elementy z profili giętych na zimno, mocowane nitami jednostronnymi jako „wymiany” pod lekkie urządzenia dachowe: świetliki, klapy dymowe, wentylatory itp.
Analiza stężeń w obiektach innych niż hale
W konstrukcjach innych niż hale stosuje się zasady analogiczne do przedstawionych powyżej. Przedstawione w artykule sposoby wyznaczania sił od imperfekcji są uniwersalne. Kształtowanie układu stężeń w specyficznych konstrukcjach, np. w budynkach wysokich może podlegać specyficznym wymaganiom.
Przykłady podano w przedmiotowych artykułach:
- budynki wysokie, ((Chodor, L. (2015). Budynki wysokie. πWiki – Inżynierowie i Architekci Chodor-Projekt. https://chodor-projekt.net/encyclopedia/budynki-wysokie/))
- przekrycia cięgnowe [19]
- hale wykonane z elementów cienkościennych [20]
Wyznaczanie równoważnych obciążeń
Obciążenia q równoważne wymuszeniu F wyznacza się ogólnie w drodze porównania skutków wywołanych wymuszeniem F i q.
Ogólna metoda energetyczna
W zależności od rodzaju skutków w procedurze porównawczej uzyskujemy różne wartości obciążeń porównawczych. Najlepsza i najmniej obciążona jest metoda energetyczna. W tej metodzie porównuje się pracę sił wywołanych wymuszeniem F i q. Zgodnie z podstawowym twierdzeniem Lagrange’a można porównywać wirtualną pracę sił zewnętrznych L lub wewnętrznych W, co w przypadku sprężystej analizy liniowej na jedno wychodzi.
Obciążenie równoważne wyznaczymy z porównania wirtualnej pracy siły ściskającej N $\delta W_N$ na skróceniu spowodowanego założonym kształtem wstępnego wygięcia (imperfekcji) oraz pracy równoważnego $\delta W_q$ obciążenia poprzecznego q na wygięciach pochodzących od imperfekcji:
$$\begin{equation} \delta L_N=\delta L_q \label{14}\end{equation}$$
W przypadku wymuszenia kinematycznego wstępnym wygięciem w0(x) wirtualną pracę sił siły osiowej $\delta L_N$ w pręcie o długości L, przekroju zwartym z momentem bezwładności Iy, ściskanego siłą N wyznaczymy z zależności:
$$\begin{equation} \delta L_N=\int \limits_0 \limits^L \cfrac {N}{2}\cdot {[w^{’}_{0} (x)]}^2 \cdot dx \label{15}\end{equation}$$
Wyrażenie (16) jest pracą siły N skróceniu $\Delta_w$, które zależy nieliniowo od zmian ugięcia na długości pręta i jest efektem II rzędu, przedstawionym na przykład w pracy [21].
Praca sił zewnętrznych q stałych na długości q i poprzecznych , wynosi:
$$\begin{equation} \delta L_q=q \cdot \int \limits_0 \limits^L w(x) dx \label{16}\end{equation}$$
Praca(16) i (17) zależy od kształtu wygięcia pręta. Zwykle przyjmuje się strzałkę wstępnego wygięcia $w_0 (x)$zgodnie z postacią wyboczonego pręta idealnego, którą dla pręta przegubowo-przegubowego mozna zapisać w postaci:
$$\begin{equation} w_0(x)=f_0 \cdot (1-cos kx) \label{17}\end{equation}$$
Obciążenie równoważne wyznaczymy z warunku ($\ref{14}$) po obliczeniu całek ($\ref{15}$) i (\$\ref{16}$) dla przyjętego kształtu wygięcia wstępnego ($ref{17}$).
Zwróćmy jeszcze uwagę , że obciążenie równoważne q zależy od warunków brzegowych (schematu pręta) również z tego powodu, że funkcja wygięcia wstępnego (imperfekcji) (16) jest różna dla różnych schematów nawet dla pierwszej postaci wyboczenia.
Uproszczone metody
Uproszczonym (inżynierskim) sposobem oszacowania wartości obciążeń równoważnych jest
- zrównanie przemieszczenia sprawczego wywołanego obciążeniem rzeczywistym i równoważnym.
- porównanie wybranych sił przekrojowych (najczęściej w przekroju krytycznym) dla takiego samego schematu statycznego ale z obciążeniem rzeczywistym i zastępczym (równoważnym).
Literatura
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- Biegus, A. (2003). Stalowe budynki halowe. Arkady
- Biegus, A. (2012). Projektowanie stężeń stalowych budynków halowych [Wykład]. Politechnika Wrocławska
- Biegus, A. (2012). Projektowanie stężeń stalowych budynków halowych [Wykład]. Politechnika Wrocławska. http://www.kkm.pwr.wroc.pl/KONSTRUKCJE%20METALOWE%20ELEMENTY,%20HALE,%20OBIEKTY%20-%20WYKLAD/02_A.Biegus%20-%20Projektowanie%20stezen.pdf
- Chodor L. (2015). Stężenia hal i budowli. PiWiki – Inżynierowie i Architekci Chodor-Projekt, [ https://chodor-projekt.net/encyclopedia/stezenia-hal-i-budowli/ ]
- Kowal Z. (1973). Wybrane działy z konstrukcji metalowych Część I i II (Wydanie 2), Wydawnictwo Politechniki Wrocławskiej
- Kowal, Z. (1973). Wybrane działy z konstrukcji metalowych Część I i II (IWydanie 2 ), Wydawnictwo Politechniki Wrocławskiej
- Brzoska Z. (1965). Statyka i stateczność konstrukcji prętowych cienkościennych (Wydanie drugie), PWN
- PN-EN 1993-1-3:2008, Eurokod 3: Projektowanie konstrukcji stalowych, Część 1-3: Reguły uzupełniające dla konstrukcji z kształtowników i blach profilowanych na zimno
- Biegus A. (2014). Blacha fałdowa jako usztywnienie pasów kratownic płaskich przy wyboczeniu z ich płaszczyzny. Budownictwo i Architektura, 13(3) (2014), 209–217
- PN-EN 1993-1-1+A1:2006, Eurokod 3 – Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- Feynman, R. P., Leighton, R. B., Sands, M. L., Rejmer, K., Gajewski, R., & Grynberg, M. (2014). Feynmana wykłady z fizyki.Tom 1 część 1 Mechanika. Szczególna teoria względności. Wydawnictwo Naukowe PWN
- Gulbrandsen, M., & Petersen, R. (2013). Advanced Analysis of Steel Structures. Aalborg University
- Mrazik, A. (1987). Teoria Spolahlivosti ocelovych konstrukcii. VEDA Vydatelstvo slovenskej akadamie VIED
- PN-EN 1090-2+A1:2012, Wykonanie konstrukcji stalowych i aluminiowych – Część 2: Wymagania techniczne dotyczące konstrukcji stalowych
- PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
- Chodor, L. (2015). Kombinacje obciążeń w Eurokodach. πWiki-Inżynierowie i Architekci Chodor-Projekt. https://chodor-projekt.net/encyclopedia/kombinacje-obciazen-w-eurokodach/
-
Biegus A. (2014). Blacha faldowa jako usztywnienie pasów kratownic płaskich przy wyboczeniu z ich płaszczyzny. Budownictwo i Architektura, 13(3) (2014), 209–217
- Chodor L. (2016) Przkrycia cięgnowo–membranowe, πWiki – Inżynierowie i Architekci Chodor-Projekt , https://chodor-projekt.net/encyclopedia/konstrukcje-ciegnowe/
- Chodor, L. (2015). Kształtowniki stalowe gięte na zimno. πWiki – Inżynierowie i Architekci Chodor-Projekt https://chodor-projekt.net/encyclopedia/ksztaltowniki-stalowe-giete-na-zimno/
- Piechnik, S. (1980). Wytrzymałość materiałów dla wydziałów budowlanych. PWN
________________________________




