Leszek Chodor, 26 lipca 2018 do 17 wrzesień 2024
26 lipca 2018 – wydanie pierwsze;
7 luty 2023 duże korekty;
13 marzec 2024 – dodano przykłady;
19 kwiecień 2024 dodano autorskie modele ST.
17 wrzesień 2024, drobne korekty literówek i numeracji wzorów
25 luty 2025 – dodano rozdział o dylatacjach budynków żelbetowych i połączono z artykułęm „dylatcje płyt stropowych”.
19-02-2025 rewizja po dużej awarii portalu
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 12 Czytelników
Ze względu na wpływy niemechanicznie, w tym oddziaływania temperaturowe i odsiadania gruntu, ale przede wszystkim skurcz betonu w trakcie dojrzewania, budynki żelbetowe powinny być dzielone na oddylatowane segmenty, przy maksymalnej długości segmentów zależnej od odkształcalności budynku oraz technologii wykonania robót betonowych. Ważną rolę w kształtowaniu dylatacji budynków żelbetowych zarówno prefabrykowanych jak i monolitycznych mają krótkie wsporniki słupów, belek i płyt stropowych.
Krótkie wsporniki, podcięcia belek stanowią obszary krępe konstrukcji Smukłość tych obszarów liczona jako stosunek długości L do wysokości H jest mniejsza od L/H < 4 (dla wsporników 2), co wskazuje, że są tarczami, a nie prętami i nie obowiązuje dla nich teoria belkowa. Stosowany powszechnie klasyczny mechanizm kratownicowy Mōrscha [1], jest obecnie nazywany mechanizmem ST (Strut-Tie) [2]. Nie ma jednego, ogólnego modelu ST żelbetowych wsporników – podobnie jak modelu załomów plastycznych płyt. To projektant decyduje o doborze modelu obliczeniowego, tak aby opracować projekt optymalny ze względów niezawodności i ekonomiki. Model ST nie wyjaśnia mechanizmu zarysowania elementu, dlatego oprócz zbrojenia nośnego w miejscach potencjalnie narażonych na powstawanie zarysowań, np. w narożach wklęsłych należy dodać zbrojenie konstrukcyjne przeciw zarysowaniom betonu.
Dylatacje budynków żelbetowych
Maksymalne odległości pomiędzy przerwami dylatacyjnymi budynków żelbetowych podano w tab. NA-1 normy [2] , którą zacytowano w tab.1.
Należy je traktować jako orientacyjne, a nie jako bezwzględnie obowiązujące, a decydująca jest analiza statyczno-wytrzymałościowe przestrzennego, odkształcalnego modelu budynku.
Tab.1. Odległości między dylatacjami w budynkach żelbetowych [2], tab. NA-1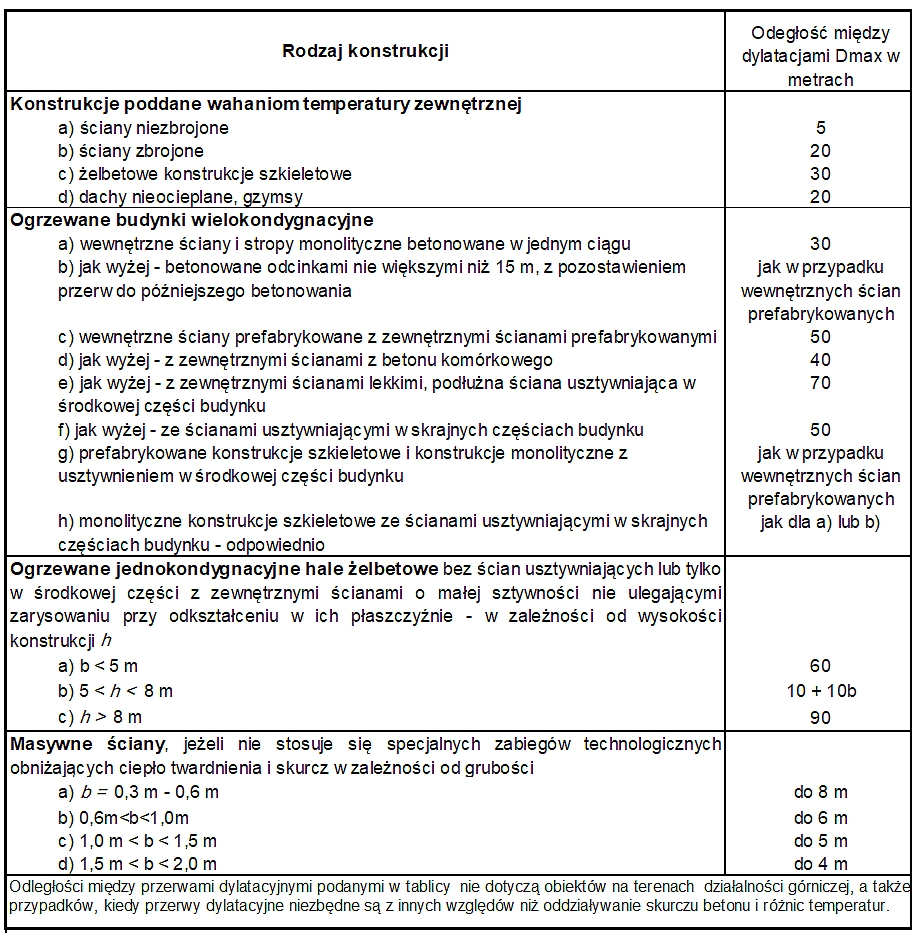
W przypadku ogrzewanych budynków wielokondygnacyjnych podstawowa długość segmentu między dylatacjami $D_{max}$ wynosi :
$$\begin{equation} D_{max} = \begin {cases}
30 \, m , & \text{ w budynkach monolitycznych, betonowanych w jednym ciągu },\\
50 \,m , & \text{ w budynkach prefabrykowanych}, \\
\end{cases} \label{1}\end{equation}$$
Budynki monolityczne betonowane odcinkami nie większymi niż 15 m z pozostawieniem przerwy do późniejszego betonowania można traktować tak jak budynki prefabrykowane.
Przerwa dylatacyjna zasadniczo powinna być skonstruowana tak, aby przechodziła przez całą szerokość i wysokość obiektu, od fundamentów po dach. W części podziemnej szczelina dylatacyjna wymaga zabezpieczenia przed zasypaniem w sposób umożliwiający nieskrępowane przemieszczenia segmentów. W części nadziemnej przerwy dylatacyjne powinny mieć osłony lub zamknięcia w postaci profili dylatacyjnych. W praktyce dylatacje budynków dzielące go fizycznie na całej wysokości w jednej płaszczyźnie i wykonane przez zdublowanie słupów lub ścian – zastępuje się równoważnym statycznie podziałem z użyciem ślizgowych podpór poziomych oraz przegubów wewnętrznych, tak by zapewnić swobodę odkształceń budynku na spodziewane wpływy niemechanicznie.
Takie ślizgowe podpory lub przeguby kształtuje się z zastosowaniem krótkich wsporników słupów lub belek lub płyt.
Długość dylatowanego segmentu, a odkształcalność budynku
Na rys.1 zilustrowano sposób wstępnej oceny długości segmentu budynku. Poszarpaną linią oznaczono potencjalne zarysowania, sygnalizujące potrzebę wykonania dylatacji. Przypadki zilustrowane na rysunku 1nie wyczerpują możliwości kształtowania usztywnień budynku. Można jednak wskazać na ogólne zasady z których wynika, ze długość segmentu D , to odległość pomiędzy usztywnieniami wewnątrz budynku lub połowa długości (lub szerokości budynku) w przypadku braku usztywnień. Wstępnie oszacowane D porównujemy z wartościami granicznymi Dmax. Przyjmuje się, że
$$\begin{equation} \text { Jeśli } D < D_{max} \to \text {dylatacje nie są wymagane }\label{2} \end{equation}$$
W przeciwnym przypadku konieczność stosowania dylatacji można rozstrzygnąć w drodze analizy numerycznej lub eksperymentalne odkształcalnego modelu całości budynku. Wstępnie można przyjąć zasady przedstawione na rys.1.
`Rys.1. Zależność długości segmentu dylatacyjnego D od rozmieszczenia usztywnień: a) budynek ze środkowym trzonem , b) budynek z trzonami w skrajnych częściach, c) budynek bez trzonu, e) budynek z narożnymi sztywnymi scianami [3]
Konstrukcja przerwy dylatacyjnej: pełna, a rzeczywista
Pełny podział pionowy wymagany jest w sytuacjach drastycznie zmiennych warunków gruntowo-wodnych i spodziewanych istotnie różnych osiadania różnych części budynku, albo też znacznie różniących się obciążeń poziomych albo innych wpływów powodujących efekty, który będzie trudno lub kosztownie przejąć przez zwiększenie wytrzymałości i stateczności budynku poprzez rozwiązania mechaniczne lub technologiczne (np. kolejność betonowania).
Budynki prefabrykowane, a monolityczne
Konstrukcje budynków prefabrykowanych mają wbudowane wiele przegubów wewnętrznych, co powoduje, że z warunku dylatacyjnego są to konstrukcje lepsze od monolitycznych. Na rys. 2 pokazano typowe schematy prefabrykowanych budynków żelbetowych.
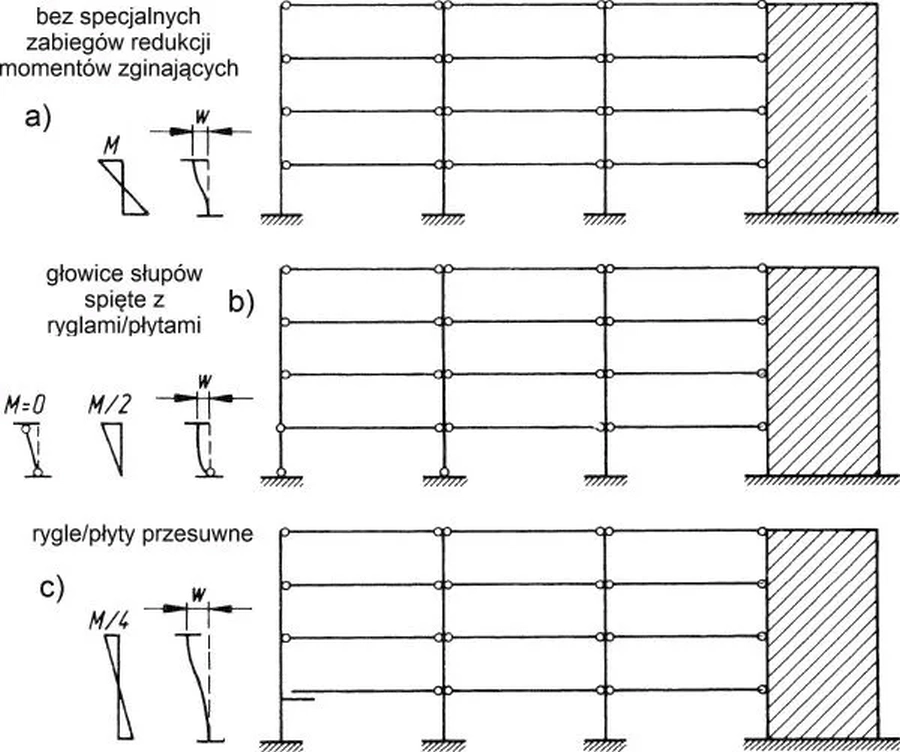
Rys.2. Schematy do zabiegów zmniejszenia odkształcalności słupów i ścian od poziomego rozporu stropów [3]
Kształtowanie przerw dylatacyjnych w budynku żelbetowym
Na rys. 3 dla zasadniczych przypadków umieszczenia trzonów usztywniających (kolumny a) do c) w wierszu 2) pokazano lokalizację dylatacji, w wierszu 3) odpowiadające schematy statyczne płyty stropowej .
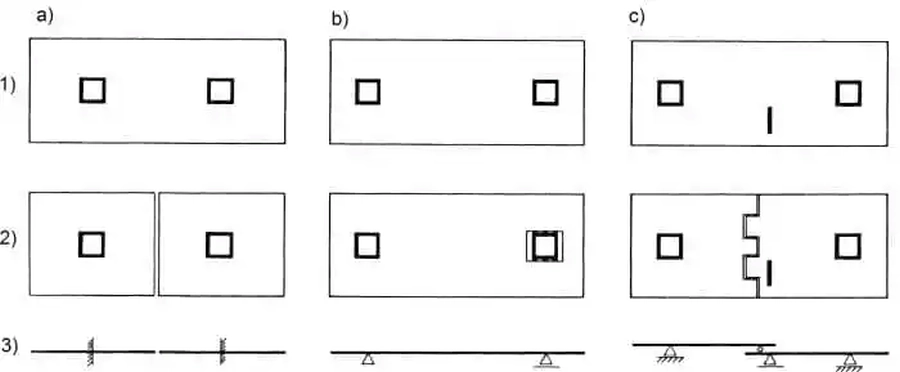
Rys.3 Zasady lokalizacji dylatacji: 1) lokalizacja trzonów budynku, 2) lokalizacja dylatacji płyty stropowej, 3) modele/schematy statyczne płyty z dylatacją; a), b) budynek z trzonami, c) dodatkowa ściana nośna
Na rys. 4 przedstawiono detale realizacji dylatacji płyt: a), b), g) w środku rozpiętości płyty bez wspornika ; c), f) e) przy/nad podporą z zastosowaniem wspornika płyty; d) na krótkim wsporniku słupa.
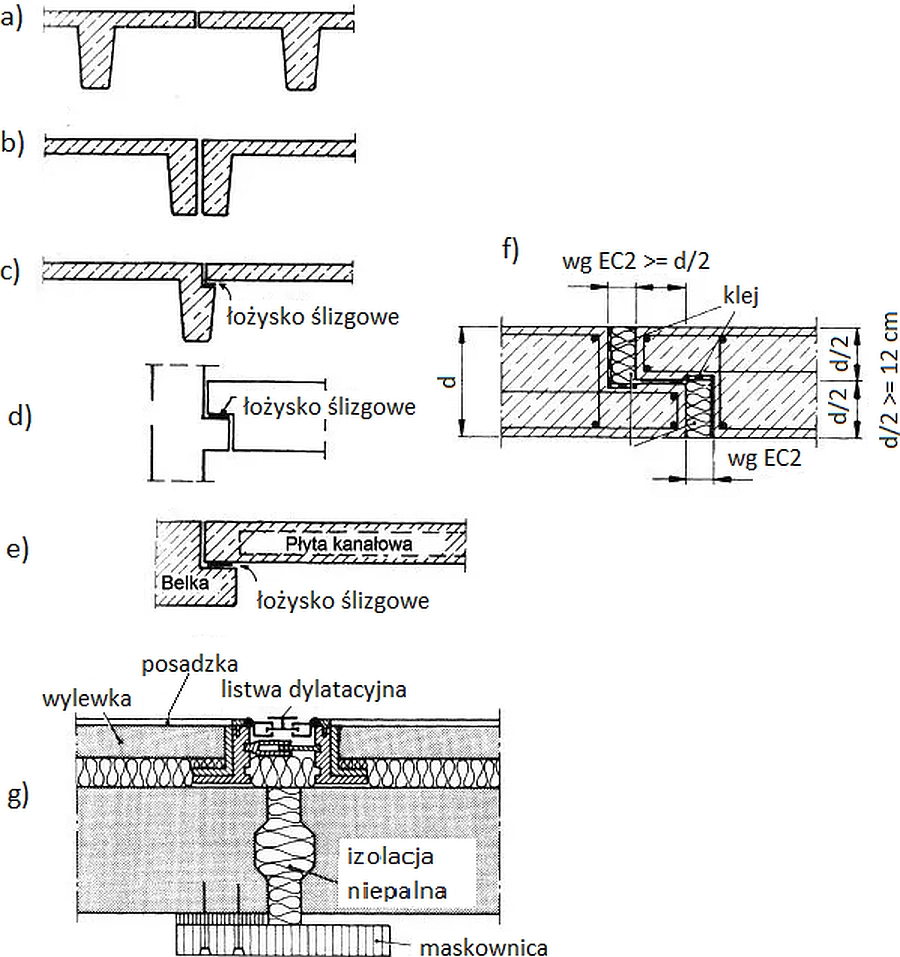
Rys.4. Dylatacje-przeguby w budynku prefabrykowanym: a), e) pomiędzy płytami żebrowymi, b) pomiędzy belką i płytą kanałową, c) element płytowy i odwrócona belka L, f) płyta na wsporniku ściany, g) połączenie płyt na „ząbek, h) dylatacja systemowa pomiędzy płatami prefabrykowanymi [3]
Przedstawione na rys. 4 rozwiązania stosowane są w budynkach prefabrykowanych. W budynkach monolitycznych w przypadku potrzeby wykonania dylatacji konstrukcyjnych stosujemy rozwiązanie c) d f), czyli przeguby przesuwne. Rozwiązania takich przegubów będą inne w przypadku oparcia rygli na słupach i przy oparciu płyt płaskich (bez żeber) na ścianach lub słupach.
Krótki wspornik słupa
Mechanizm zniszczenia i definicja
Krótki wspornik słupa (rys. 4 d) jest obszarem nieciągłości typu tarczowego Dt (p. Idea hybrydowego projektowania żelbetu), który wymaga analizy metodami innymi niż klasyczna teoria belkowa i standardowa metoda elementów skończonych z elementami skończonymi typu prętowego.

Rys.5 Mechanizm zniszczenia krótkiego wspornika żelbetowego z badań doświadczalnych [4]. (uzupełniono przez zaznaczenie na niebiesko linii krzyżulca betonowego S, linie czerwone i napisy jak w oryginale artykułu)
Na rys.5 pokazano mechanizm zniszczenia krótkiego wspornika słupa, obserwowany w badaniach eksperymentalnych [4]. Zniszczenie polegające na zmiażdżeniu betonu krzyżulca betonowego S jest podstawowym mechanizmem uszkodzenia, wymagającym analizy metodą tarczową (lub ST) . Inne mechanizmy: utrata nośności zginania lub ścięcie w przekroju przysłupowym, zerwanie zakotwienia głównego zbrojenia lub kruszenie betonu pod łożyskiem można analizować metodami standardowymi.
Przez krótki wspornik słupa żelbetowego uważa się wspornik, którego wysięg $a_c$ (liczony od lica słupa do osi obciążenia pionowego ( rys.6a) jest co najwyżej rzędu wysokości wspornika $h$ w licu słupa, a dokładniej, gdy zachodzi ( wg normy [2]):
$$\begin{equation} a_c < z_0 \, ( \approx 0,85\cdot d)\label{3} \end{equation}$$
gdzie $z_0$ jest ramieniem działania poziomej siły rozciągającej $F_{td}$ w pasie górnym liczonym od pkt 2 (na rys.13) do punktu przecięcia osi krzyżulca betonowego z licem słupa.
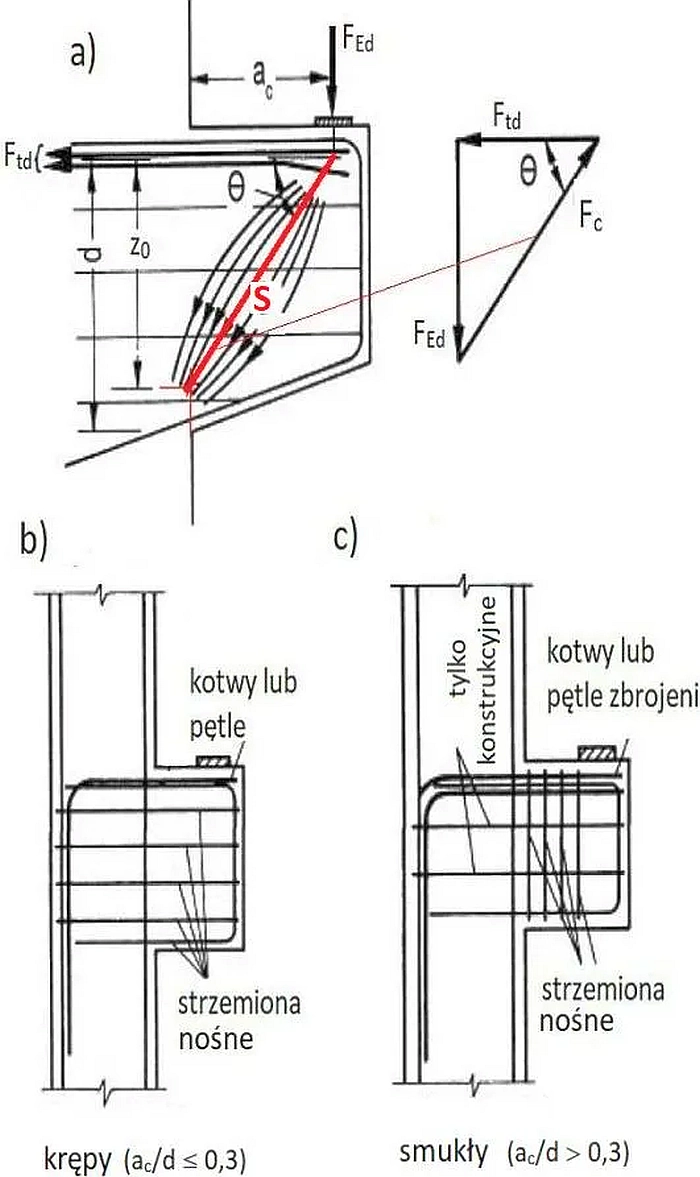
Rys.6 Krótki wspornik żelbetowy: a) mechanizm pracy , b) zbrojenie dla $ a_c/d \le 0,3$ ; c) zbrojenie dla $a_c/d > 0,3$ podział wg [5], Fig 2.152
Ramię $z_0$ można wyznaczyć dopiero po zbudowaniu modelu ST i wyznaczeniu kąta nachylenia krzyżulca betonowego $\Theta$, ale wstępnie wg [6] można przyjąć $ z_0 =0,85 \cdot d$, gdzie $d= h-a_u $ jest wysokością efektywną przekroju: h- wysokość wspornika, $a_u$ – otulenie głównego zbrojenia (górnego).
W przypadku krótkiego wspornika założenia teorii belkowej, a szczególnie płaskich przekrojów są silnie zaburzone i w konsekwencji zawodzi chętnie stosowana przez inżynierów standardowa metoda belkowa. Teoretycznie uzasadnionym modelem krótkiego wspornika jest model tarczowy, lub zastępczy, przybliżony model kratownicowy ST, a klasa „krótkich” wsporników rozciąga się na większy od określonego przez wyrażenie ($\ref{3}#) zakresu smukłości wspornika, który faktycznie wynosi
$$\begin{equation} a_c < 2 \cdot h\label{4} \end{equation}$$
Dla wsporników krótkich spełniających warunek ($\ref{4}$) nie należy stosować metody belkowej, mimo że w literaturze, np. w pracy Urban (2012) [7] można znaleźć zalecenie o dopuszczalności stosowania tej metody już od $a_c > 0,5 d$. Jednakże badania teoretyczne i eksperymentalne (np. [4]) jednoznacznie wskazują, że model belkowy może być stosowany dopiero dla smukłych wsporników ($a_c > 2d \approx 2h$).
Przestrzeganie tej zasady pozwala uniknąć błędów, które wielokrotnie prowadziły do awarii krótkich wsporników.
Geometria wspornika i warunki konstrukcyjne
Wymagane wymiary i zbrojenie wsporników zależą od wielu czynników ( stosunku i wielkości obciążeń, stosunków wymiarowych słupa i wspornika, warunków brzegowych – w tym sprężystego zamocowania wspornika w słupie oraz sztywności słupa w części nad- i pod-wspornikowej), więc formułowanie ogólnych zaleceń nie jest możliwe ani wskazane. Poniższe zalecenia należy traktować jako propozycje, a nie obowiązujące zasady.
Wysokość krótkiego wspornika
Szacunkową wysokość krótkiego wspornika przy założeniu, że naprężenie w ściskanym krzyżulcu betonowym nie przekroczy wytrzymałości betonu na ściskanie $\sigma_c < 1,0 \cdot f_{cd}$ można wyznaczyć z zależności [5], wzór(28):
$$\begin{equation} min \, d = \cfrac{3,58\cdot F_{Ed}}{f_{cd}\cdot b} \label {5}\end{equation}$$
Wysokość wspornika oszacowana z ($\ref{5}$) nie jest zależna od $a_c / h$ i ma zastosowanie dla wsporników o smukłości $a_c / h \le 1,1$ . W przypadku dłuższych wsporników $\cfrac{a_c}{h} > 1,1 $ wstępną wysokość można przyjąć jak dla belki o długości liczonej jako potrojony wysięg wspornika przed lico słupa $ L=3 \cdot a_c$.
Wysokość krótkiego wspornika powinna umożliwić prawidłowe ułożenie i zakotwienie głównego zbrojenia górnego, które jest rozciągane siłą w przybliżeniu proporcjonalną do wysokości wspornika – niewielkie zwiększenie wysokości wspornika może w prosty sposób rozwiązać problemy konstrukcyjne. Zwiększenie wysokości wspornika może też być potrzebne w celu spełnienia warunków wytrzymałościowych dla ściskanego krzyżulca betonowego i jego docisku do węzła.
Odchyłki, detale i długość oparcia
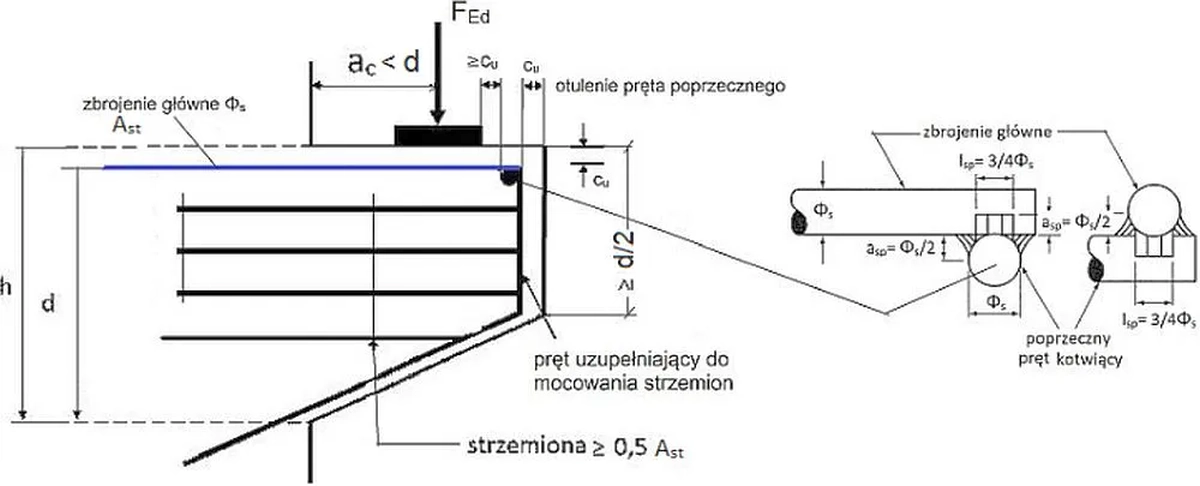
O wiele ważniejsze od dokładnego zbrojenia jest prawidłowe zaprojektowane detali wspornika. Ze względu na małe wymiary należy stosować niewielkie tolerancje i odchyłki oraz dokładną kontrolę jakości wykonania szalunku oraz zbrojenia wspornika. Potencjalne problemy byłyby całkowicie nieproporcjonalne do oszczędności w zbrojeniu lub betonie.
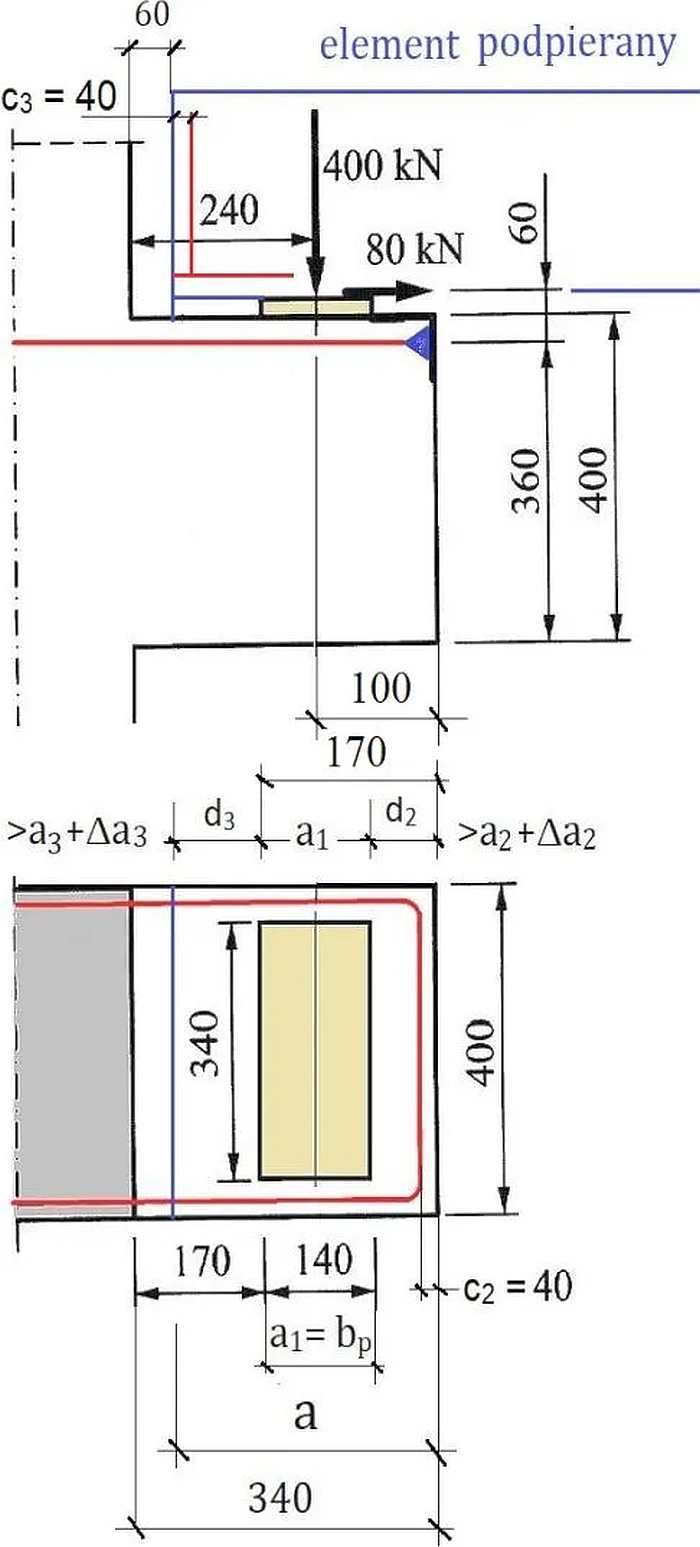
Kształtowanie zbrojenia w elementach podpieranych i podpierających należy przeprowadzić z uwzględnieniem dopuszczalnych, specyficznych dla strefy podparcia odchyłek wykonawczych. Na rys. 7 pokazano wymiary podkładki oraz odległości podpory od krawędzi będące przedmiotem unormowania [2]. Skuteczna długość podparcia zależy od odległości $d$ między krawędziami łożyska i krawędziami rozpatrywanych elementów, która wynosi:
- w elementach z pętlami poziomymi lub z końcami prętów zakotwionymi w inny sposób
$d_i = c_i+\Delta a_i$. - w elementach z prętami odgiętymi pionowo
$d_i = c_i +\Delta a_i + r_i$,
gdzie: $c_i$ otulenie betonem, $\Delta a_i$ – odchyłka określona w tabelach normy [2], tab. 10.4 i 10.5; $r_i$ – promień zagięcia.
Nominalną długość $a$ potrzebną do umieszczenia prostego podparcia można obliczyć z [2],- wzór (10.6):
$$\begin{equation} a= a_1+a_2+a_3+\sqrt{\Delta a_2^2 +\Delta a_3^2 }\label{6} \end{equation}$$
gdzie $a_1$ jest długością podparcia netto (szerokością podkładki) wyznaczoną ze względu na naprężenie na powierzchni podparcia jak następuje:
$$\begin{equation} \sigma_{Ed}= \sigma_m = \cfrac{F_{Ed}}{a_1 \cdot b_1} \le f_{Rd,max} \quad \to a_1= \cfrac{F_{Ed}}{b_1 \cdot f_{Rd}} \label{7} \end{equation}$$
ale nie mniej niż minimum według tab.1.
W niniejszym artykule często oznacza się $a_1=a=b_p$ (wg rys. 13) i $b_a= l_p$, W ogólności (dla obciążeń innych niż skupione) naprężenie $\sigma_m$ ($\ref{7}$) jest średnim naprężeniem pod podkładką
Tab.2. Minimalne wartości $a_1$, $a_2$ – rys. 7 [2], tab. 10.2 i tab. 10.3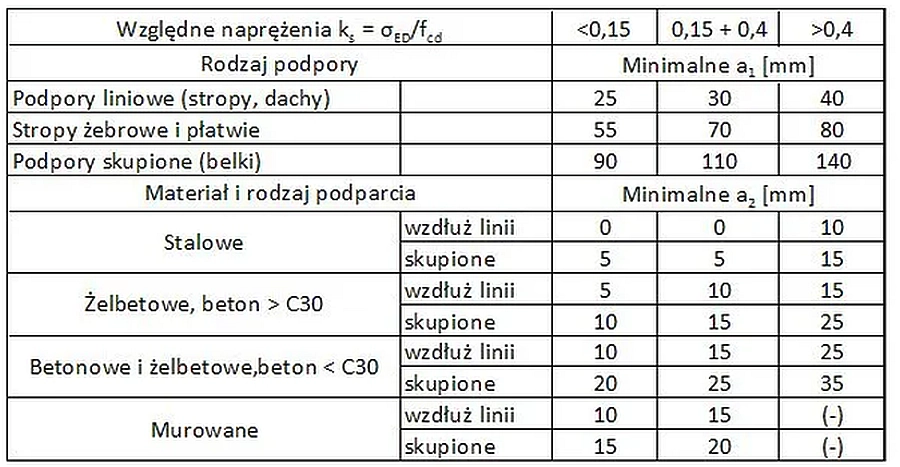
Minimalne wartości $a_3$ zależą od sposobu zbrojenia nad podpora liniową lub skupioną:
- dla prętów ciągłych nad podporami (zamocowanymi lub nie) $a_3 = 0$,
- dla prętów prostych, pętli poziomych blisko końca elementu: $a_3=5$ mm (podpora liniowa), a dla podpory skupionej 15 mm, ale nie mniej niż otulenie końca,
- dla cięgien lub prętów prostych odsłoniętych na końcu elementu: $a_3=5$ mm (podpora liniowa) lub 15 mm dla podpora skupionej,
- dla pionowych pętli zbrojenia $a_3=15$ mm (podpora liniowa), a dla podpory skupionej otulenie końca plus wewnętrzny promień zagięcia.
$\Delta a_2$ jest poprawką w mm ze względu na odchyłki odległości między elementami podpierającymi i wynosi
$$\begin{equation} \Delta a_2 = \begin {cases}
10 \le l/1200 \le 30, & \text{ dla stali lub betonu prefabrykowanego },\\
15 \le l/1200 +5 \le 40 & \text{ dla muru lub betonu układanego na budowie}, \\
\end{cases} \label{8}\end{equation}$$
gdzie $l$ – odległość w świetle między licami podpór,
$\Delta a_3$ jest poprawką w mm ze względu na odchyłki długości elementu podpieranego i wynosi
$$\begin{equation} \Delta a_3 = \cfrac{l_n}{2500} \label{9}\end{equation}$$
gdzie $l_n$ – długość elementu podpieranego w mm.
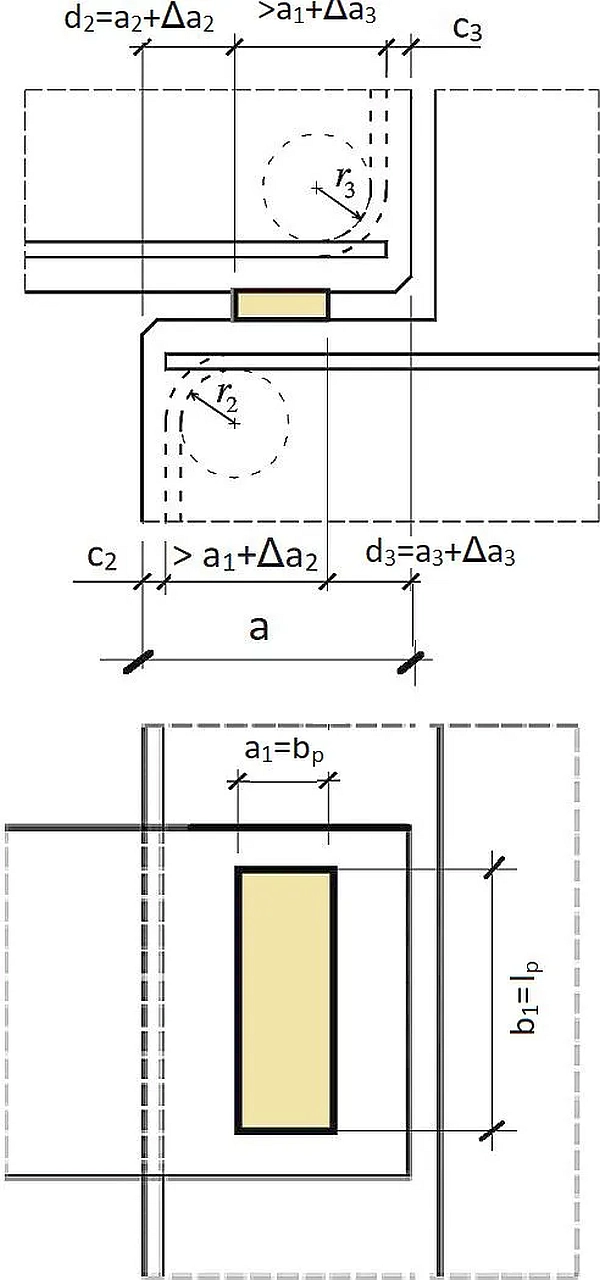
Rys.7. Wspornik żelbetowy. Odchyłki [2], rys. 10.5 i 10.6 (zmodyfikowane)
Jeżeli w celu uzyskania równomiernego nacisku na podporze podjęto kroki takie jak np. zastosowanie podkładki z zaprawy, neoprenu lub inne podobne, to za obliczeniową szerokość podpory b] można przyjąć jej szerokość rzeczywistą. W innych przypadkach, gdy nie wykonuje się dokładniejszej analizy, wartość nie powinna być większa niż 600 mm.
Ważne są sfazowania naroży wklęsłych wspornika (p. rys. 12) oraz naroży zewnętrznych (p. rys 7) w każdym przypadku, gdy nie osłaniamy ich kątownikiem lub innym kształtownikiem. Należy prawidłowe zakotwić łożyska do układu zbrojenia w zależności od sił obliczeniowych, rektyfikacji (ustawienia) łożyska na etapie montażu i podczas eksploatacji oraz przemieszczeń montażowych, termicznych itp.
Wytrzymałości betonu wspornika
Wytrzymałość obliczeniowa betonu w strefie podparcia
Jeżeli nie ma innych ustaleń, to w przypadku połączeń suchych (to znaczy takich, w których nie zastosowano warstwy materiałów takich jak zaprawy, betony lub polimery), za wytrzymałość obliczeniową betonu w strefie podparcia można przyjmować $f_{Rd} = 0,4 \cdot f_{cd}$.
We wszystkich pozostałych przypadkach:
$$\begin{equation} f_{Rd} = f_{bRd} \le 0,85 \cdot f_{cd}\label{10} \end{equation}$$
gdzie:
$f_{cd}$ jest mniejszą z wytrzymałości obliczeniowych betonów elementu podpartego i podpierającego,
$f_{bRd}$ jest wytrzymałością obliczeniową materiału warstwy wyrównującej.
Za strefę poparcia uważa się obszar betonu pod płytką podporową lub podlewką z zaprawy montażowej, itp. To znaczy wytrzymałość ($\ref{14}$) jest właściwa przy doborze powierzchni poparcia i wymiarów podkładki.
Wytrzymałość betonu na ściskanie wewnątrz wspornika
Wytrzymałość betonu na ściskanie wewnątrz wspornika, w tym w węzłach z zakotwionymi prętami rozciąganymi T (w jednym kierunku, w dwóch kierunkach – rys 8, lub bez zakotwionych prętów T lub dla samego pręta ściskanego S) wyznacza się z zależności [2], klauzula 6.5.4 (4)
$$\begin{equation} \sigma_{Rd, max} =k \cdot \nu’ \cdot f_{cd} \label{11} \end{equation}$$
gdzie:
współczynnik redukcyjny $\nu’$ uwzględnia zarysowanie strefy i wynosi wg [2], klauzula 6.5.2 (2) , wzór (6.57N)
$$\begin{equation} \nu’ =1- \cfrac{f_{ck}}{250} \label{12} \end{equation}$$
Współczynnik $k$ zależy od rodzaju węzła ( sposobu obciążenia):
$$\begin{equation} k= \begin {cases}
1,0 & \text{ w węzłach w których nie są zakotwione żadne pręty rozciągane typu T (6.60)},\\
0,85 & \text{ z zakotwionymi w węźle prętami rozciąganymi T w jednym kierunku (6.61)}, \\
0,75 & \text{ z zakotwionymi w węźle z prętami rozciąganymi T w dwóch kierunkach (6.62) – rys.3},\\
0,6, & \text{ dla pręta betonowego ściskanego T pomiędzy węzłami (6.56)},\\
\end{cases} \label{13}\end{equation}$$
W formule ($\ref{12)$) w nawiasach () podano numery wzorów w normie [2].
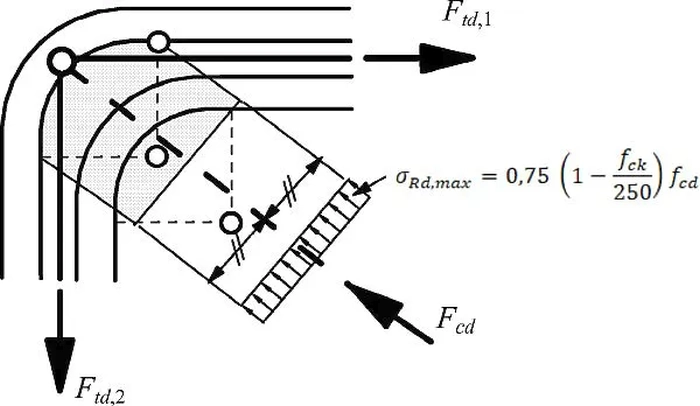
Rys.8 Węzeł typu T-T [2], rys. 6.28
Model tarczowy krótkiego wspornika
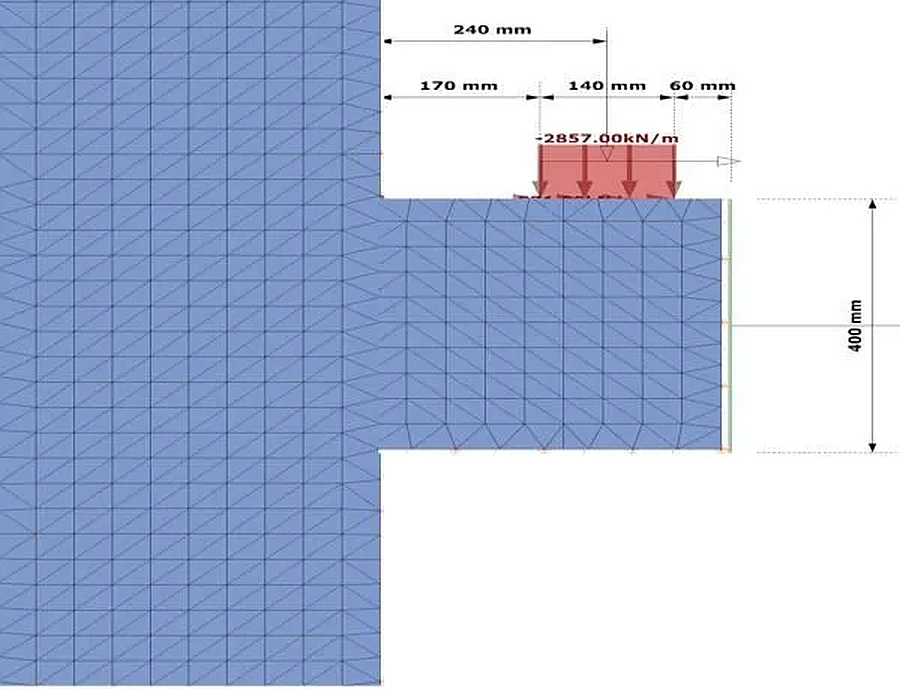
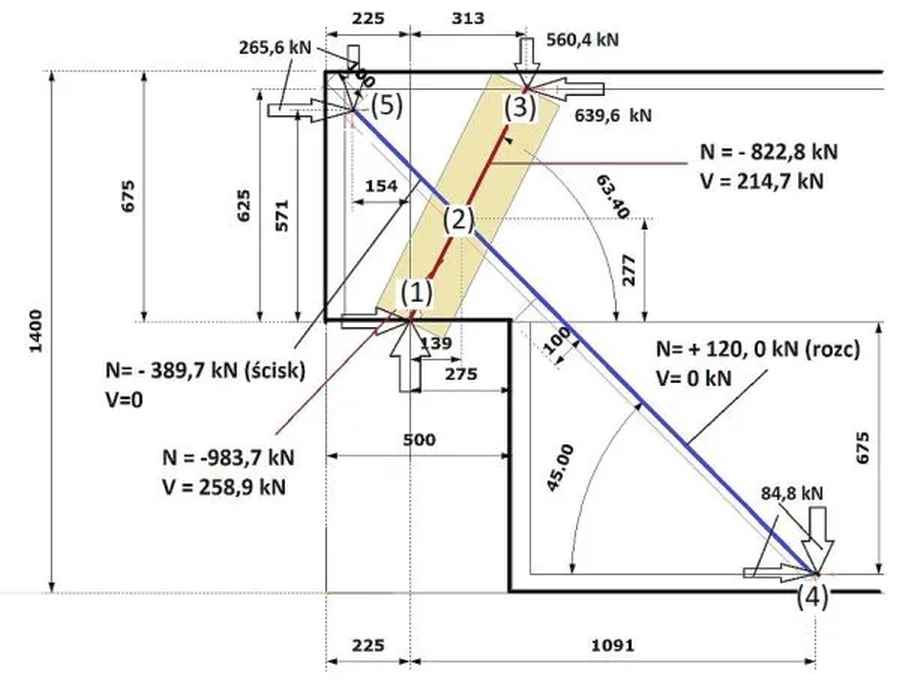
Budowę modelu tarczowego krótkiego wspornika przedstawiono na przykładzie wspornika z przykładu 21.1 z pracy [8], zobrazowanego na rys. 9.
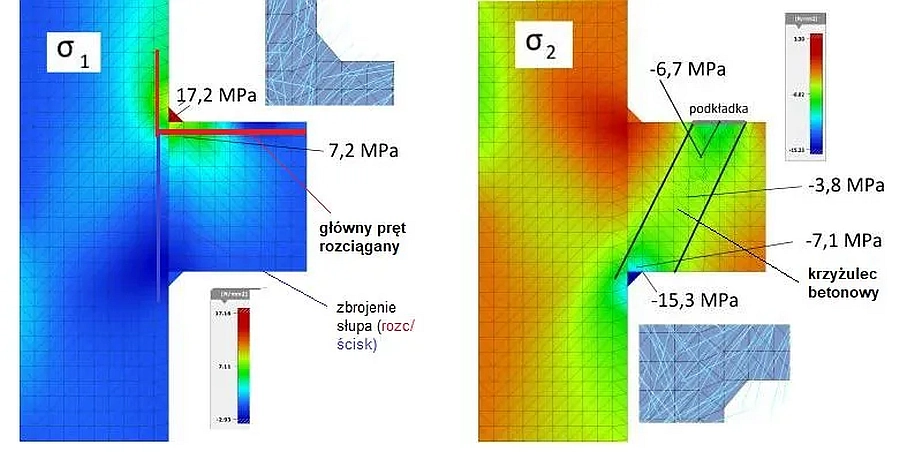
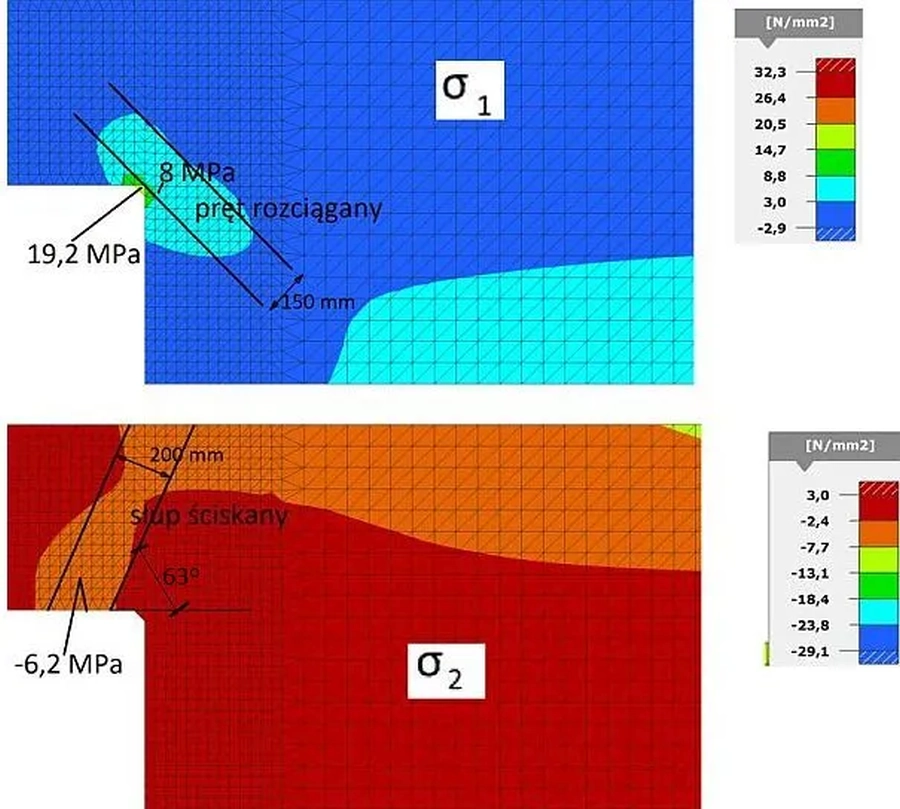
Na rys 10 pokazano modelu tarczowy krótkiego wspornika z rys. 9. Na rys. 11 przedstawiono pole naprężeń głównych: maksymalnych $\sigma_1$ oraz minimalnych $\sigma_2$ we wsporniku ze sfazowanymi narożami połączeń wspornika ze słupem. Naprężenia rozciągające są dodatnie, a ściskające ujemne.
Analiza tarczowa naprężeń minimalnych (ściskaj7cych) $\sigma_2$ jednoznacznie pokazuje ścieżkę wędrówki naprężeń od powierzchni przyłożenia obciążeń (podkładka) do słupa poprzez krzyżulec betonowy o szerokości szacunkowo takiej, jak szerokość podkładki (w przykładzie c=140 mm). Krzyżulec ten jest nachylony do poziomu pod kątem $\Theta$, spełniającym warunek ($\ref{14}$). W ten sposób zidentyfikowano tworzenie się ściskanego krzyżulca betonowego.
Przy górnej powierzchni wspornika tworzy się linia rozciągania – jest największa w pobliżu słupa i wędruje ku części słupa nad wspornikiem.
Obserwuje się jakościową zmianę przebiegu naprężeń rozciągających w słupie w stosunku do teorii belkowej, podług której krawędź zewnętrzna słupa w obszarze wspornika powinna być rozciągana, a krawędź wewnętrzna ściskana. Tymczasem oś obojętna słupa przebiega ukośnie, a rozciąganie i ściskanie krawędzi słupa zmienia się na wysokości obszaru wspornika, a ścinanie przekroju słupa jest największe na wysokości wspornika. Przy krawędzi dolnej występują naprężenia ściskające, a zbrojenie podłużne wymagane jest tylko ze względów konstrukcyjnych (do mocowanie strzemion pionowych). W narożu górnym połączenia słupa ze wspornikiem mimo sfazowania naroża nadal występuje spiętrzenie naprężeń. Z kierunku naprężeń głównych w narożu wynika, że rozwarstwiają one naroże prostopadle do przekątnej. Wobec tego można zastosować standardowe zbrojenie naroża.
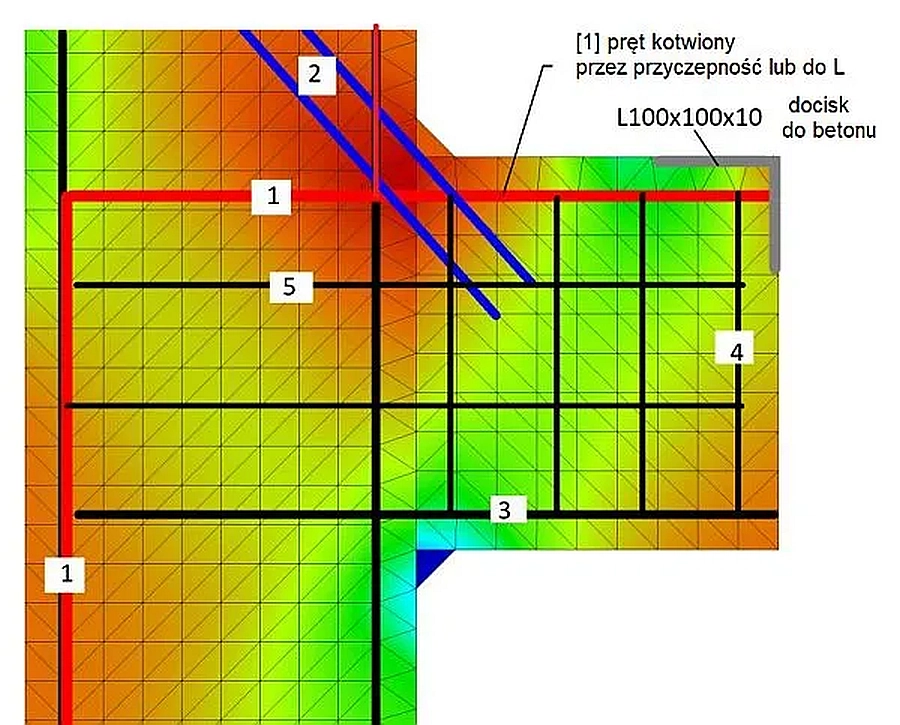
Z analizy naprężeń tarczowych (rys. 11) wynika sposób zbrojenia pokazany na rys. 12.
Dokładność oszacowania sił działających w prętach zbrojenia i krzyżulcu betonowym zależy od dokładności odczytania wartości naprężęń i szerokości ich występowania, a to wymaga dużej wprawy w analizie mapy naprężeń przy określeniu sprzężonych – do stosowania w projektach inżynierskich zaleca się stosowanie metody ST, która została zbudowana na zidentyfikowanym wyżej modelu krótkiego wspornika.
Dopuszczalny kąt nachylenia krzyżulca betonowego $\Theta$
W tradycyjnej analogii kratownicowej Mōrscha [1] przyjmowało się $\Theta=45^0$. W procedurze wymiarowania Eurokod 2 [2] – wzór (6.7N) zaleca się, by ten kąt przyjmować w granicach:
$$\begin{equation} 0,5 < ctg \, \Theta \le 1,0 \label{14} \end{equation}$$
czyli $ 45^0 \le \Theta < 63,4^0$ (wg wersji angielskiej $0,4 < ctg \,\Theta \le 1,0$ , czyli $ 45^0 \le \, \Theta < 68,2^0$).
Model ST krótkiego wspornika EC2
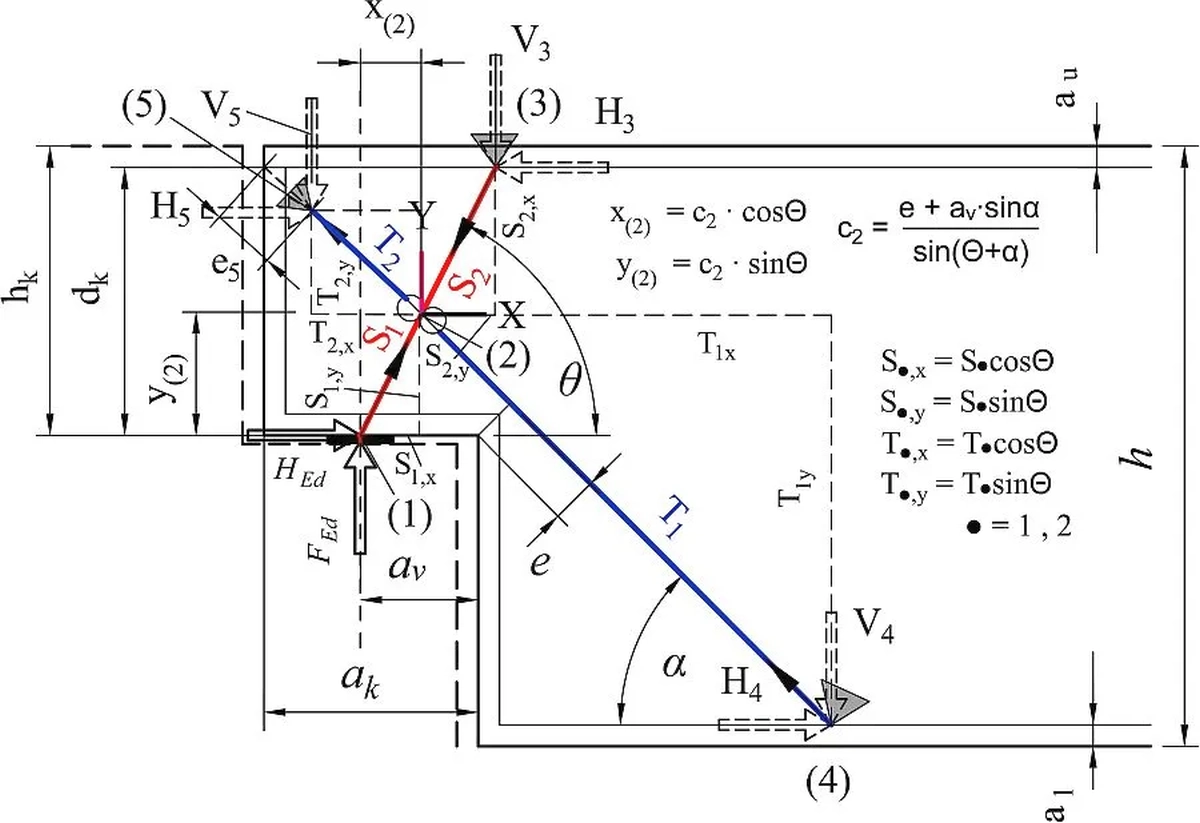
W tym rozdziale podano analityczne zależności, umożliwiające oszacowanie sił przekrojowych działających w modelu ST proponowanym w normie EC2 [2], przedstawionym na rys. 13.
Układ prętów zastępczej kratownicy ST z rys. 13 oraz schemat sił wynika z mechanizmu zniszczenia (rys. 6a) rozpoznanego w drodze badań eksperymentalnych oraz analizy tarczy (rys 7).
Model ST składa się tylko z dwóch prętów i podpory : stalowego pręta T rozciąganego S z siłą $F_{td}$ oraz żelbetowego krzyżulca S ściskanego siłą $F_c$ opartego na podporze (1) o szerokości o $x$ położonej już wewnątrz słupa. Pręt T musi być poprawnie zakotwiony w betonie na obu końcach – szczególnie istotne jest zakotwienie w węźle (2). Ścinanie międzywęzłowe przenosi beton dozbrajany strzemionami.
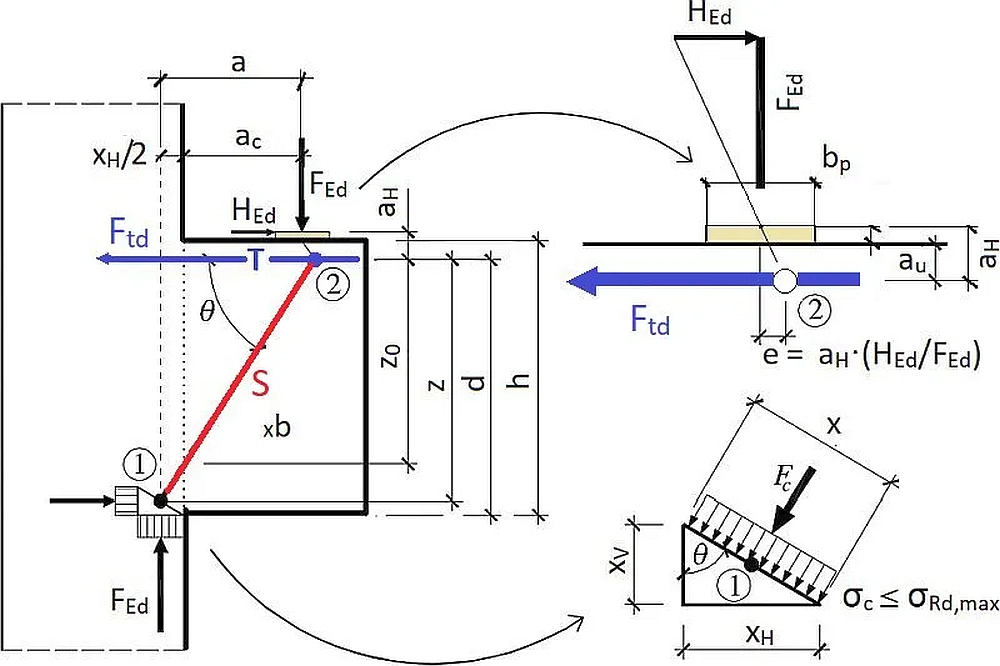
Rys.13 Model ST krótkiego wspornika EC2 [7], rys. 3.2. (z modyfikacjami)
Położenie punktu CCT (2)
Położenie punktu (2) wyznaczamy z zależności
$$\begin{equation} a_H = t_p+ a_u \quad ; \quad e= a_H \cdot \cfrac{H_{Ed}}{F_{Ed}} \label{15} \end{equation}$$
gdzie:
$t_p$ grubość podkładki podporowej
$a_u$ otulenie osiowe – odległość od powierzchni wspornika do środka ciężkości najczęściej wielowarstwowego prętów zbrojenia górnego złożonego z pętli ,
W przypadku zbrojenia ułożonego w jednej warstwie $a_u=c_u+Ø_u/2$, gdzie $c_u$ – otulenie pręta o średnicy $Ø_u$
$F_{Ed}$ – pionowa składowa obciążenia obliczeniowego,
$H_{Ed}$ – pozioma składowa obciążenia obliczeniowego (ze znakiem dodatnim – rozciągająca wspornik)
Związki położenie punktu CCC (1) oraz kąt $\Theta$
Położenie punktu (1) powszechnie (np [7], [8], [9]) wyznacza się z szerokości docisku krzyżulca betonowego $x$ i jego składowych: poziomej $x_H$ pionowej $x_V$ (rys.13) przy założeniu pozostawania punktu (1) w stanie granicznym. Z tego założeniu wyznacza się graniczną, maksymalną szerokość docisku $x$, czyli maksymalne przesuniecie punktu (1) do wnętrza słupa.
Poziomą długość docisku $x_H$ krzyżulca betonowego S ściskanego siłą $F_c$ wyznaczamy z zależności:
$$\begin{equation} x_H = \cfrac{F_{Ed}}{b \cdot \sigma_{Rd,max}} \label{16} \end{equation}$$
gdzie:
$b$ – szerokość wspornika
$ \sigma_{Rd, max}$ ($\ref{11}$) jest wytrzymałością betonu w warunkach wytężenia węzła (1), w którym nie ma zakotwionych prętów rozciąganych, więc $k=1,0$
Z rys. 13 można odczytać następujące relacje
$$\begin{equation} ctg \, \Theta= \cfrac{x_V}{x_H} = \cfrac{a}{z}\label {17} \end{equation}$$
Rozwiązanie układu równań ($\ref{17}$) względem $x_V$ można sprowadzić do równania kwadratowego (p. [7],str. 15), którego pierwiastkiem jest:
$$\begin{equation} x_V= d – \sqrt{d^2 – x_H \cdot \left[ x_H +2 \cdot ( a_c+e) \right]} \le x_{V, lim}\label{18} \end{equation}$$
gdzie nieprzekraczalną wartość $x_{V, lim}$ przyjęto za [5], Fig 2.153 (c):
$$\begin{equation} x_{V,lim} = 0,4 \cdot \nu \cdot d \label{19} \end{equation}$$
Współczynnik $\nu =0,8$ dla betonu zwykłego (≤ C50) i $\nu =1/(1-f_{ck}/250)$ dla betonu wysokiej wytrzymałości (> C50).
Jeśli wynik uzyskany z ($\ref{17}$) wykracza poza dopuszczalny przedział ($\ref{14}$) , to należy przyjąć dolna lub górną granicę przedziału odpowiednio.
Ramię siły poziomej z
Ramię sił pionowe $z$ i poziome $a$ wynosi:
$$\begin{equation} z = d-\cfrac{x_V}{4} \quad ; \quad a = a_c + \cfrac{x_H}{4} + e \label{20} \end{equation}$$
Całkowita szerokość krzyżulca betonowego $x$ wynosi:
$$\begin{equation} x=\sqrt{x_V^2 + x_H^2} \label {21} \end{equation}$$
Naprężenia ściskające $\sigma_c$ w węzłach betonu powinny spełniać warunek
$$\begin{equation} \sigma_c \le \sigma_{Rd,max} \label {22} \end{equation}$$
gdzie $\sigma_{Rd,max}$ wg ($\ref{11}$).
Siła pozioma w zbrojeniu głównym $F_{td}$
Z warunku równowagi momentów względem względem punktu (1) można wyznaczyć siłę rozciągającą zbrojenie główne $F_{td}$
$$\begin{equation}F_{td} = F_{Ed} \cdot ctg \, \Theta + H_{Ed} \cdot ( 1 + a_H/z) > 0,5 \cdot F_{Ed} \label {23} \end{equation}$$
gdzie ograniczenie minimalnej wartości siły $F_{td}$ podano za [5], Fig 2.154 Dolna granica siły rozciągającej wynosząca $0,5 \cdot F_{Ed}$ ma zastosowanie do wsporników o dużym wysiegu, a jej stosowanie w praktyce oznacza ograniczenie kąta $\Theta$ do $60^o$. Długie wsporniki pracują „belkowo” i wymagają zbrojenia głównego nie tylko w pobliżu górnej powierzchni wspornika, ale także przy powierzchni dolnej.
Jeżeli nie zastosowano łożyska ślizgowego, to należy przyjąć siłę poziomą przynajmniej o wartości $H_{Ed} = 0,2 \cdot F_{Ed}$ nawet jeśli z obliczeń statycznych wychodzi mniejsza. Jako pierwsze przybliżenie, często wystarczające w zastosowaniach inżynierskich można stosować szacunkową wartość siły rozciągającej zbrojenie główne $F_{td}$, wyznaczoną z zależności:
$$\begin{equation}F_{td} \approx 1,3 \cdot \left( F_{Ed} \cdot \cfrac{ a_c}{h} + H_{Ed}\right) \label {24} \end{equation}$$
którą uzyskano z ($\ref{23}$) przy założeniach upraszczających: $z \approx 0,85 \cdot d$ ; $d\approx 0,9 \cdot h $ ; $ a_H/z \approx 0,3$
Zakotwienie głównego zbrojenia
Główne zbrojenie rozciągane z siłą $F_{td}$ (pręt [1] na rys. 9) powinno być zakotwione na obydwu końcach. Zakotwienie w słupie (punkt TTC) dokonuje się zwykle poprzez odgięcie do zbrojenia zewnętrznego w słupie na długość zakotwienia (zwykle ok $25 Ø$, Ø – średnica pręta) liczoną od wewnętrznej krawędzi płytki podporowej. Zakotwienie we wsporniku dokonuje się metodami pokazanymi w rozdziale Kotwienie_pretow w obszarach_nieciaglosci. Jeśłi akotwienie przez przyczepność (w tym pętle poprzez poziome) nie wystarcza lub jest konstrukcyjnie trudne, to stosuje się zakotwienie spawane, (np do kątownika narożnego lub przyspojenie poprzcznych prętów zbrojeniowych. Zakotwienie pętlami pionowymi ( poprzez zagięcie pręta w dół przy krawędzi zewnętrznej wspornika – zbrojenie konturowe) jest najczęściej zawodne, bo może wystąpić zmiażdżenie betonu w zagięciu pręta pętli pionowej w węźle (2).
Krzyżulec betonowy
Przy znajomości $F_{td}$ ($\ref{23}$) oraz kąta $\Theta$ ($\ref{17}$) siłę w krzyżulcu betonowym można wyznaczyć na wiele sposobów, np z warunku rzutów na kierunek $F_c$ lub jako wypadkową sił $F_{td}$ i $F_{Ed}$:
$$\begin{equation} F_c = (F_{td} – H_{Ed}) \cdot cos \, \Theta + F_{Ed}\cdot sin \, \Theta = \sqrt{ (F_{td} – H_{Ed})^2 + F_{Ed}^2} \label{25} \end{equation}$$
lub z innych warunków np. sumy momentów względem punktu (2).
Użyteczne oszacowanie
$$\begin{equation} F_c \approx F_{Ed}\cdot \sqrt{1+\cfrac{a^2}{d^2}} \label{26} \end{equation}$$
uzyskano z ($\ref{25})^3$ po odrzuceniu wartości „małych”.
Naprężenia w krzyżulcu pomiędzy węzłami (1) i (2) powinny spełnić warunek
$$\begin{equation} \sigma_c = \cfrac{F_c}{ x \cdot b} \le \sigma_{Rd, max} \label {27} \end{equation}$$
gdzie:
$\sigma_{Rd, max}$ wyznacza się z zależności ($\ref{11}$) dla k=0,6 ( w przypadku zastosowania strzemion poziomych można przyjąć k=0,75),
x- całkowita szerokość krzyżulca wg ($\ref{21}$).
Zbrojenie na ścinanie
Zbrojenie na ścinanie musi być szczególnie starannie zaplanowane, bowiem strzemiona poziome lub pionowe zapobiegają przedwczesnemu uszkodzeniu krzyżulca betonowego, Strzemiona wspornika należy zaprojektować tak, by zabezpieczyć przed ścięciem na odcinku $s_w$ pomiędzy licem słupa, a krawędzią wewnętrzną płytki podporowej. Jeśli na odcinku $s_w$ nie można rozmieścić wymaganej liczbę strzemion pionowych, to stosuje się strzemiona poziome Strzemiona poziome są bardziej skuteczne od pionowych, bowiem są ściskane i współpracują z betonem ściskanym.
Na rys 14 przedstawiono nomogram do doboru powierzchni $A_{sw}$ strzemion pionowych lub poziomych w zależności od smukłości wspornika $\cfrac{a_c}{h}$ w funkcji siły rozwarstwiającej $V$ (przecinającej strzemiona). W zależności od kierunku strzemion siłą rozwarstwiającą jest:
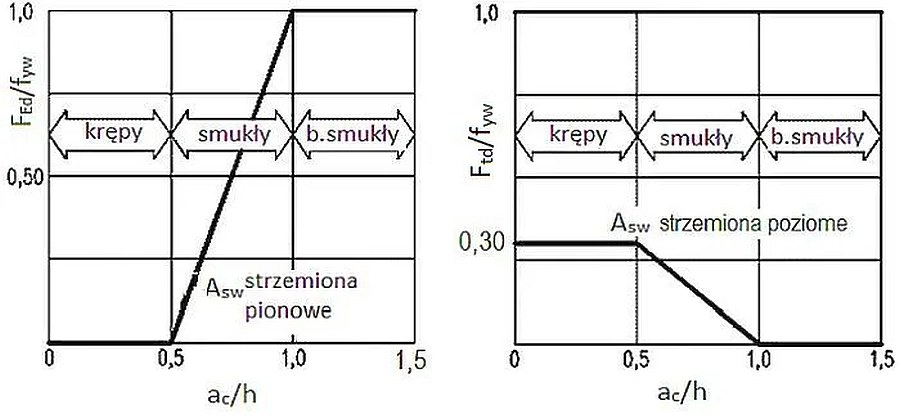
Rys. 14 Dobór strzemion w krótkim wsporniku w zależności od jego smukłości $a_c/h$ ( na rys. 2 smukłość $a_c/d \approx 0,9 \cdot a_c/h$)
W zależności od smukłości wspornika $\cfrac{a_c}{h}$ stosuje się:
- dla wsporników krępych o smukłości $\cfrac{a_c}{h}\le 0,5$
poziome strzemiona o polu przekroju
$A_{sw} = 0,3 \cdot \cfrac{F_{td}}{f_{yw}}$,
W tym przypadku nie stosuje się nośnych strzemion pionowych, a tylko strzemiona pionowe konstrukcyjne do związania zbrojenia górnego w maksymalnym rozstawie konstrukcyjnym - dla wsporników smukłych o smukłości $ 0,5 < a_c/ h\le 1,0$
pionowe strzemiona o polu przekroju
$A_{sw} = ( 0\, do \, 1 ) \cdot \cfrac{F_{Ed}}{f_{yw}}$,
i jednocześnie
poziome strzemiona o polu przekroju
$A_{sw} = ( 0,3 \, do \, 0) \cdot \cfrac{F_{td}}{f_{yw}}$, - dla wsporników bardzo smukłych o smukłości $1,0< \cfrac{a_c}{h} \le 1,5$ (wg autora do $\cfrac{a_c}{h} = 2,0$),
strzemiona pionowe lub pręty odgięte zgodnie z zasadami stosowanymi w projektowaniu belek: ścinanie poprzeczne , pionowe belek
Powyżej oznaczono $f_{yw}$ – wytrzymałość obliczeniowa stali strzemion.
Maksymalny, konstrukcyjny rozstaw strzemion poziomych lub pionowych nie przekraczał 0,35 h i 150 mm. [8].
Zalecenia podane na rys. 14 uwzględniają zwiększenie wytrzymałości betonu ścinanego na skutek obciążenia dociskiem przyłożonym do górnej powierzchni wspornika, które są przewidziane dla metody belkowej i nie należy ich stosować powtórnie.
Strzemiona są zwykle dwucięte ($n_t=2$), ale w przypadkach szczególnych można zastosować strzemiona podwójne (czterocięte) ($n_t=4$). Liczba wymaganych strzemion $n_w$ o średnicy $Ø_w$ czyli polu pręta $A_{w1}=\cfrac{\pi \cdot Ø_w^2}{6}$ wyniesie
$$\begin{equation} n_w = \cfrac{A_{sw}}{n_t \cdot A_{w1}} \label{28} \end{equation}$$
Model ST krótkiego wspornika BS8110
W podejściu EC2 kąt nachylenia krzyżulca betonowego $\Theta$ wyznaczamy z zależności ($\ref{17}$) przy dwóch przyjętych apriori założeniach: 1) krzyżulec betonowy jest dociskany do wnętrza słupa na głębokość $x_H$ , 2) węzeł (1) krzyżulca betonowego pozostaje w stanie granicznym ($\ref{16}$). Powyższe założenia nie są systematycznie potwierdzane doświadczalnie ani numerycznie.
Na rys. 1 przedstawiono na przykłąd fotografię z badań przedstawionych w pracy [4] na której linią w kolorze niebieskim (w celu odróżnienia od linii naniesionych przez autorów badań) naniesiono zaobserwowaną linię krzyżulca betonowego S. Wyraźnie widać, że przebiega on od osi obciążenia do krawędzi słupa, czyli tak jak założono w modelu ST z rys. 15.
Również analiza tarczowe przeprowadzona w artykule prowadzi do innych wniosków: 1) linia krzyżulca betonowego ma początek pod płytką podporową, okrąża naroże dolne wspornika i wnika do słupa (rys 11), 2) węzeł (1) krzyżulca betonowego nie jest w stanie granicznym – na rys 7: $\sigma_{max}= 15,3 MPa <\sigma_{R, max}= 19,86 \, MPa$ (patrz przykład 1).
Z analizy wrażliwości kata $\Theta$ opisanego funkcją ($\ref{17}$) wynika, że dokładność oszacowania jest bardzo mała z uwagi na niewielką wiarygodność oszacowania składowych szerokości docisku $x_H$ oraz $x_V$. Niewielkie różnice w oszacowaniu kąta $\Theta$ mogą prowadzić do znaczących zmian w siłach rozciągających zbrojenie, co pokazano w przykładzie 2.
Model ST krótkiego wspornika słupa przedstawiony na rys.15 prowadzi do stabilnego rozwiązania wg normy BS 810 [10].
Model wyczyszczono z nieistotnych (mieszczących się w granicach dokładności rozwiązania) mimośrodów $e$, $a_H$, $x_H/2$,. Rozwiązanie otrzymano bez przyjmowanie kwestionowanych założeń 1) i 2) modelu EC2.
W podejściu BS8110 analizuje się przekrój wspornika w licu słupa. Bryła naprężeń dociskowych ma wysokość strefy $x$, analogicznie jak w dobrze zbadanym i nie kwestionowanym, rozwiązaniu belki zginanej z uproszczonym (prostokątnym) rozkładem naprężeń. Ten model stosowany w obszarze anglosaskim dostosujemy do zasad Eurokodów.
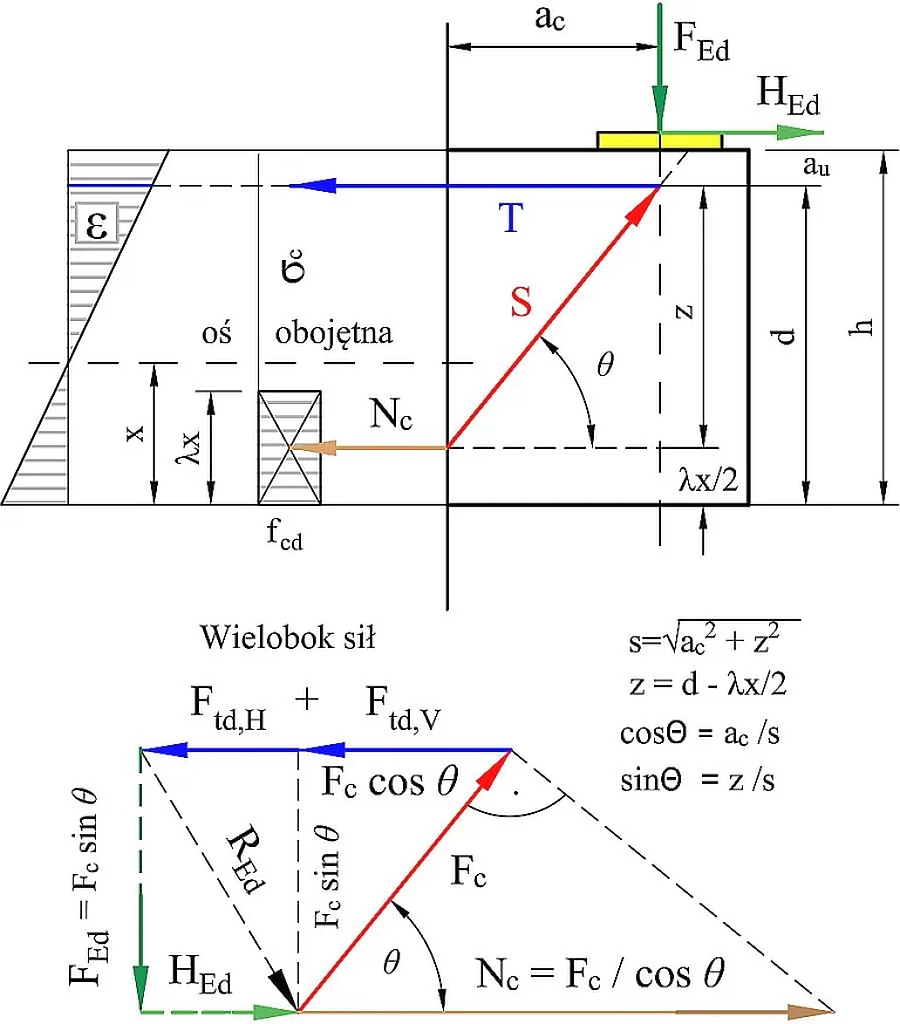
Z rys. 15 można odczytać zależności geometryczne:
$$\begin{equation} sin \, \Theta = \cfrac{z}{s} \quad ; \quad cos \, \Theta = \cfrac{a_c}{s} \quad ; \quad z = d- \cfrac{x_{eff}}{4} \quad ; \quad s = \sqrt{a_c^2 + z^2} \label {29} \end{equation}$$
gdzie:
$a_c$ – obliczeniowy wysięg wspornika
$d = h- a_h$ – wysokość efektywna przekroju zbrojonego górą z otuleniem osiowym $a_h$
$ a_h = c_l+ Ø_l /2$,
$c_l$ – otulenie pręta T o średnicy $ Ø_l $,
$ x_{eff} = \lambda \cdot x $ – zredukowana wysokość strefy ściskanej $x$,
$\lambda= 0,8 $ dla betonu zwykłego BZ
Siłę docisku do betonu $N_c$ wyznaczamy jak dla uproszczonego prostokątnego rozkładu naprężeń stosowanego w teorii zginania żelbetu:
$$\begin{equation} N_c = b \cdot x_{eff} \cdot f_{cd}\label {30} \end{equation}$$
Z wieloboku sił naniesionego na rys.15 odczytujemy, że siłę $F_{td}$ w zbrojeniu T można złożyć z siły $F_{td,H}$ wywołanej przez obciążeniem poziomym $H_{Ed}$ i z siły $F_{td,V}$ wywołanej przez obciążeniem pionowym $F_{Ed}$
$$\begin{equation} F_{td} = F_{td,H} + F_{td,V} \text { , gdzie } F_{td,H}=H_{Ed}\label {31} \end{equation}$$
Siła $N_c$ jest funkcją pionowego obciążenie $F_{Ed}$:
$$\begin{equation} F_{Ed} = N_c \cdot sin \, \Theta \cdot cos \, \Theta \label {32} \end{equation}$$
Formułę ($\ref{32}$) uzyskano ze złożenia zależności: $F_{Ed} = F_c \cdot sin \, \Theta$ i $N_c = F_c / cos \, \Theta$.
Po podstawieniu do ($\ref{32}$) zależności ($\ref{29}$), ($\ref{30}$) i po uporządkowaniu uzyskano równanie kwadratowe z jedną niewiadomą $x_{eff} =\lambda \cdot x$ czyli na wysokość strefy ściskanej $x = x_{eff}/ \lambda$ ( $\lambda=0,8$):
$$\begin{equation} (a_c^2+d^2) \, – \, d\cdot (1+k_E) \cdot x_{eff}\, + \, 1/4 \cdot (1+2\cdot k_E )\cdot x_{eff}^2 =0\label {33} \end{equation}$$
gdzie parametr $k_E$ obciążenia zewnętrznego $F_{Ed}$ wynosi
$$\begin{equation} k_E=\cfrac {a_c \cdot b\ \cdot f_{cd}} {F_{Ed}} \label {34} \end{equation}$$
Równanie ($\ref{33}$) ma dwa pierwiastki
$$\begin{equation} x_{eff} = \cfrac{ 2 d } { (1+ 2 k_E) } \cdot \left [ 1+ k_E \mp \sqrt{ k_E^2 – (a_c/d)^2 (1+ 2 k_E) } \right ] \label {35} \end{equation}$$
Po oszacowaniu wysokości docisku $x$ wyznaczamy ramię sił $z$ , długość krzyżulca betonowego $s$ i kąt $\Theta$ z zależności ($\ref{29}$),
Siłę w krzyżulcu betonowym $F_c$ z formuły odwrotnej do ($\ref{33}^1$) :
$$\begin{equation} F_c =\cfrac{F_{Ed}}{sin \, \Theta}\label {36} \end{equation}$$
Siła w pręcie T , wywołana siła pionową wynosi
$$\begin{equation} F_{td,V}= F_c \cdot cos \, \Theta = N_{Ed} \cdot ctg \, \Theta \label {37} \end{equation}$$
Całkowita siła w pręcie T opisana jest wzorem ($\ref{31}$)
Dalsze obliczenia prowadzi się w sposób opisany w rozdziałach zakotwienie zbrojenia głównego T, krzyżulec betonowy, zbrojenie na ścinanie
Zbrojenie krótkiego wspornika wg normy ACI 318-14
Na rys.16 pokazano zasady zbrojenia krótkiego wspornika opracowane na podstawie normy amerykańskiej ACI 318-14 [12], (Buildings Department of Hong Kong, Manual for Design and Detailing of Reinforced Concrete to the Code of Practice for Structural Use of Concrete 2013 September, Hong Kong, 2013)).
Porównanie rozwiązań krótkiego wspornika
Przedstawione rozwiązania krótkiego wspornika żelbetowego wg norm: europejskiej EC2 ; Hong Kong BS 8110 i amerykańskiej ACI 318-14 są tylko przykładami rozmaitych podejść do ważnego problemu konstrukcji żelbetowych.
Na rys. 17 przedstawiono porównanie zbrojenia krótkiego wspornika uzyskane z teorii prezentowanych przez:
1 Steinle (1975) [13],
2 – Hegger i in (2004) [14]),
3 – Reineck (2005) [15]),
4 – Stenzel, Fingerloos (2007)[16]. .
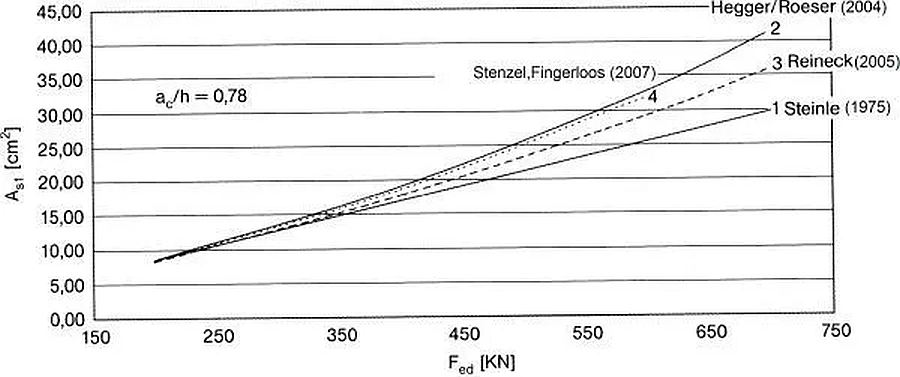
Rys.17 Wykres doboru zbrojenia krótkiego wspornika. Porównanie różnych teorii: 1 Steinle (1975) [13], 2 – Hegger i in (2004) [14]), 3 – Reineck (2005) [15]),4 – Stenzel, Fingerloos (2007)[16].
Z wykresu porównawczego można dobrać pola przekroju zbrojenia głównego rozciąganego $A_{st}$ w zależności od obliczeniowej wartości obciążenia wspornika $F_{Ed}$, przy czym smukłość wspornika wynosi $a_c/h=0,78$. Różnica między rozwiązaniami dochodzi do 30%, co nie jest różnicą znaczną w praktyce projektowej zbrojenia krótkich wsporników.
Z analizy formuły ($\ref {24}$) wynika, że wraz ze zwiększaniem się smukłości wspornika $a_c/h$ zwiększa się potrzebne zbrojenie szacunkowo podług zależności
$$\begin{equation} A_{st,1} \approx A_{st,0} \cdot \left[ \cfrac{(a_c/h)_1 + {H_{Ed}/F_{Ed}}_1}{(a_c/h)_0 + {H_{Ed}/F_{Ed}}_0}\right ] \label {38} \end{equation}$$
gdzie:
$(a_c/h)_1$ i $(a_c/h)_0 =0,78$ – smukłości wspornika docelowego i porównawczego (z rys.17) odpowiednio,
${H_{Ed}/F_{Ed}}_1$ i ${H_{Ed}/F_{Ed}}_0$ – stosunek obciążenia poziomego do pionowego wspornika docelowego i porównawczego odpowiednio.
Przy braku obciążenia poziomego przyjmuje się $ {H_{Ed}/F_{Ed}}_0 = {H_{Ed}/F_{Ed}}_1 = 0,2 $.
Podcięcie belki lub płyty
Definicja i mechanizm zniszczenia podcięcia belki
Podcięcia belek mogą mieć bardzo różny kształt, choć generalnie przyjmuje się [8], że przybliżoną metodę ST można stosować dla podcięć spełniających warunki (oznaczenia wg rys. 18) :
$$\begin{equation} l_k \le h_k \quad oraz \quad h_k = (0,3 ÷ 0,7)\cdot h\label{39} \end{equation}$$
Na rys. 18 linią falistą zaznaczono linie zniszczenia obserwowane eksperymentalnie.
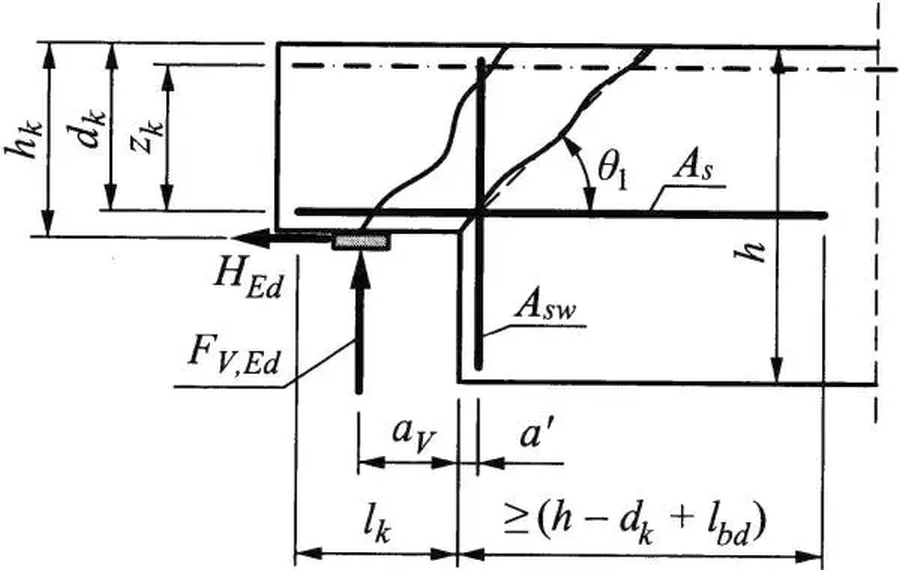
Rys.18 Wspornik (podcięcie) belki. Oznaczenia [8]– rys.21.5
Modele ST1 i ST2 wg EC2
Rygorystyczne stosowanie takiej geometrii podcięć, ograniczałoby bezzasadnie możliwości kształtowania stref podporowych belek, często wymuszonych konkretną sytuacją projektową. Z tego powodu zarówno norma [2] jak i inne wytyczne nie zawierają szczegółowych wytycznych do projektowania całej klasy podcięć. Z klauzuli 10.9.4.6. normy [2] wynika również, że nie można wskazać jednego modelu obliczeniowego ST elementu podciętego. W normie [2] wskazano dwa alternatywne modele, ale takie które można łączyć, to znaczy stosować je jednocześnie, przypisując każdemu określoną cześć obciążenia. Oba modele pokazano na rys. 18: model ST1 z pochyłym słupem betonu C oraz pionowym prętem $T_1$ , a także model ST2 z pionowym słupem betonu C i nachylonym prętem $T_1$
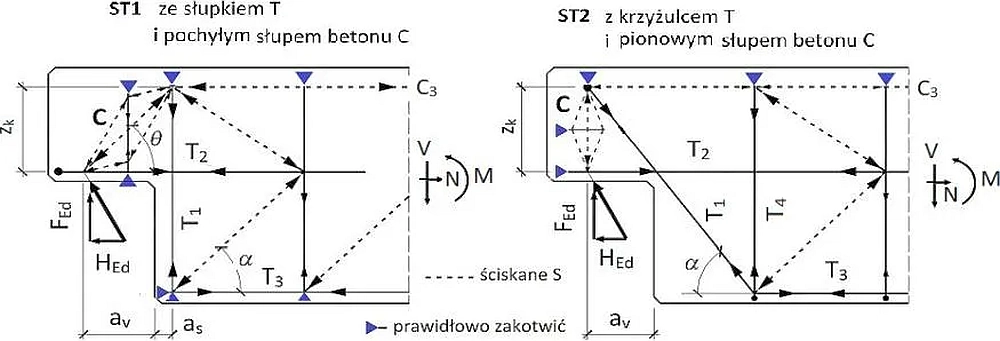
Rys.19. Modele ST podcięcia belki [2], rys. 10.4 (uzupełniony)
Warunki dodatkowe na wartości sił w prętach modelu ST1 i ST2 pokazanych na rys. 19 podaje Urban (2012) [7].
Ze względu na różnorodność kształtów krótkich wsporników i w konsekwencji różnorodność mechanizmów zniszczenia mechanizmy ST1 i ST2 mają znaczenie poglądowe i nie powinny być bezkrytycznie stosowane do każdego przypadku projektowego. To projektant decyduje o tym jaki modele wybrać i w jakim stopniu je zmieszać. Do wykonania wyboru potrzebna jest dodatkowa analiza – zalecamy budowę pomocniczego modelu tarczowego w celu rozpoznania mechanizmu zniszczenia oraz układu prętów ST dla konkretnych wymiarów, obciążenia i podparcia podcięcia, np. w sposób pokazany niżej.
Oszacowanie wysokości podciętej części belki lub płyty („ząbka”)
Minimalna wysokość efektywna „ząbka” $d_k$ (rys .13) może być oszacowana z zależności:
$$\begin{equation} min{\, d_k} \approx \cfrac {4 \cdot F_{Ed}}{b \cdot f_{cd}} \label{40} \end{equation}$$
gdzie:
$F_{Ed}$ – obliczeniową wartością reakcji pionowej ,
$b$ – szerokość belki lub jednostką długości płyty,
$ f_{cd}$ – obliczeniowa wytrzymałością betonu na ściskanie
Model tarczowy podcięcia belki
Na rys. 20 pokazano model tarczowy belki z podcięciem na którym opracowano nowy model obliczeniowy ST podcięcia belki.
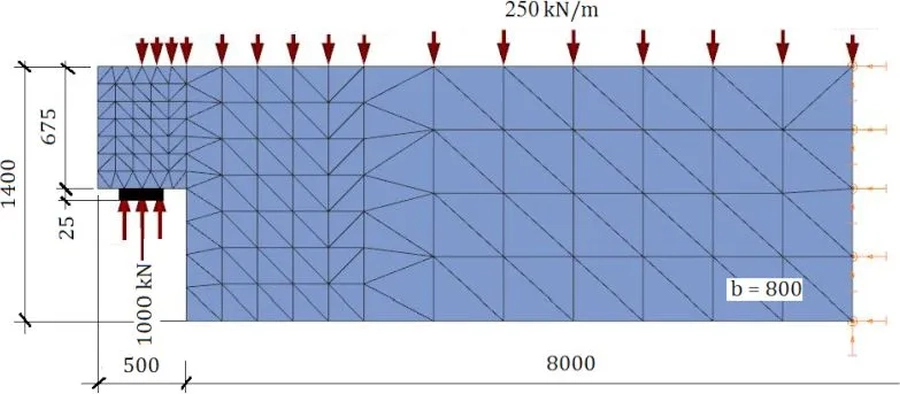
Rys. 20 Model belki-tarczy z podcięciem. Wymiary i obciążenia wg przykładu [17], Example 6.11
W modelu z rys. 20 wystąpią naprężenie główne maksymalne (rozciągające) $\sigma_1$ i minimalne (ściskające) $\sigma_2$ , których obraz przedstawiono na rys.21.
Z analizy naprężeń głównych w modelu tarczowym podcięcia wynika, że nad podporą tworzy się ściskany słup betonowy, który łączy się z ściskanym górnym obszarem belki. Rozciąganie następuje w pasie prostopadłym do wklęsłego naroża belki oraz w dolnym obszarze belki. Oś obojętna (granica pomiędzy obszarem ściskanym a rozciąganym belki jest krzywoliniowa, przesunięta w stosunku do osi belki i w ogólności nie pokrywa się z osią obojętną wynikającą z teorii belkowej.
Nowa propozycja modelu ST podcięcia belki
Na podstawie wyników analizy analizy tarczowej podcięcia z rys,20, zdefiniowano model ST pokazany na rys, 22, który jest modelem pośrednim pomiędzy ST1 i ST2 (rys.19) . Pętla P nie jest elementem modelu ST, lecz konstrukcyjnym zbrojeniem uzupełniającym.
Przy braku dokładniejszych danych dla innych przypadków projektowych zaleca się:
1) przyjmować: kąt nachylenia $\Theta$ słupka betonowego S oraz kąt nachylenia $\alpha$ pręta rozciąganego T odpowiednio jako górną i dolną granicę z zakresu określonego w normie [2] ( w nawiasie wg oryginalnej normy Eurokod ) wg zależności (\ref{41}$) i (\ref{42}$)
$$\begin{equation} ctg \, \Theta = 0,5 \, (0,4) \to \Theta \approx 63^0 (68^o) \label{41} \end{equation}$$
$$\begin{equation} ctg \, \alpha = 1,0 \, (1,0) \to \alpha \approx 45^0 (45^o) \label{42} \end{equation}$$
czyli $\Theta \approx 63^0$, $\alpha = 45 ^0$
2) umieszczać pręt T w odległości $ e \approx 2\cdot a$ od naroża wklęsłego,
3) kotwić pręt T górą jak najbliżej czoła belki w odległości min $ e_5 \approx 2\cdot a$,
gdzie $a=c + Ø/2$ – otulenie osiowe prętów zbrojeniowych
Zbrojenie dolne belki w pręcie T3 oraz zbrojenie górne C3 jest znane i jest zbrojeniem wymaganym ze względu na zginanie całej belki.
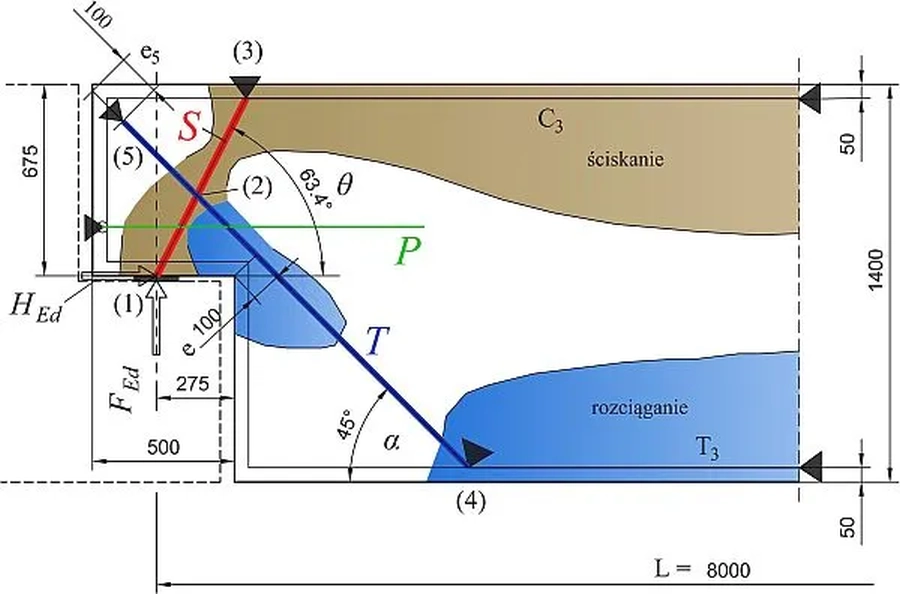
Schemat statyczny i geometria modelu ST
Na rys. 23 przedstawiono ogólną geometrię modelu ST podcięcia , który można stosować do projektowania podcięć o podobnym kształcie.
Współrzędne $(x, y)_i$ węzłów modelu (i)= 1, … 5 w układzie (X,Y) zaczepionym w punkcie (1) wynoszą:
$$\begin{equation} (x,y)_i = \begin {cases}
(1) \to (0\,;\, 0) & \text { podpora}\\
(2) \to c_2 \cdot (cos \, \Theta \, ; \, sin \, \Theta) & \text { przecięcie S-T }\\
(3) \to d_k \cdot (ctg \, \Theta\, ;\, 1) & \text { punkt docisku słupka }\\
(4) \to (a_v + h_D \cdot ctg \, \alpha +e / sin\, \alpha \, ;\, -h_D) & \text {zagięcie zbrojenia}\\
(5) \to (a_v-a_5\, ;\, a_5 \cdot tg \, \alpha + e/cos \, \alpha) & \text {zakotwienie zbrojenia}\\
\end{cases} \label{43}\end{equation}$$
gdzie:
$h_k$ wysokość podciętej części belki,
$d_k =h_k – a_u$ – efektywna wysokość podciętej części belki, $a_u$ – górne otulenie zbrojenia,
$ h_D= h – h_k – a_h$, $a_h$ dolne otulenie zbrojenia,
$ c_2= \cfrac {e+ a_v \cdot sin \, \alpha}{ sin (\alpha + \Theta)}$,
$ a_5= a_k – e_5 \cdot cos\, \alpha$ .
Długości prętów $ L_{T1} \, ;\, L_{T2} \, ;\, L_{S1} \, ;\, L_{S2} $ wyznaczono z zależności typu $L=\sqrt{(\Delta x)^2+(\Delta y)^2}$, np długość
$L_{T1} =\sqrt{ (x_4 – x_2)^2 + (y_4 – y_2)^2}$
$$\begin{equation} L_{T,S} = \begin {cases}
L_{T1} =& \left ( h_D + c_2 \cdot sin \Theta \right) /sin\alpha, & \text { zbrojenie (4)-(2) }\\
L_{T2} =& \cfrac{ a_k -a_v/2}{cos \, \alpha} +\cfrac{ e\cdot cos \, \Theta +a_v/2 \cdot sin (\alpha – \Theta) } {cos \, \alpha \cdot sin ( \alpha+ \Theta)} – e_5 & \text { zbrojenie (2)-(5) }\\
L_{S1} =& c_2, & \text {słupek betonowy (1)-(2)} \\
L_{S2} =& \sqrt{(d_k\cdot ctg \Theta – c_2 \cdot cos \,\Theta)^2 +(d_k – c_2 \cdot sin \, \Theta)^2}& \text{ słupek (2)-(3) }\\
\end{cases} \label{44}\end{equation}$$
gdzie: $c_2$ , $h_D$ i inne – jak wyżej.
Warunki równowagi
Warunki równowagi $\sum F$ systemu ST można zapisać układem równań:
$$\begin{equation} \sum F= \begin {cases}
\sum X &= H_{Ed} – H_3 +H_4 + H_5 = 0\\
\sum Y &= F_{Ed} – V_3 – V_4 – V_5 = 0 \\
\sum M_{(2)} &= V_3 \cdot S_{2.x} – H_3 \cdot S_{2,y} + F_{Ed}\cdot S_{1,x} – H_{Ed}\cdot S_{1,y} + \\
&V_4\cdot T_{1,x} – H_4 \cdot T_{1,y} – V_5\cdot T_{2,x} + H_5 \cdot T_{2.y} = 0 \\
\sum M_{(4→2)} &= V_4\cdot T_{1,x} + H_4\cdot T_{1,y} \\
\sum M_{(5→2)} &= V_5 \cdot T_{2,x} + H_4 \cdot T_{2,y}\\
\end{cases} \label{45}\end{equation}$$
gdzie rzuty poziome X i pionowe Y długości prętów wynoszą:
$S_{•,x}=L_{S•} \cdot cos \, \Theta$
$S_{•,y}=L_{S•} \cdot sin \, \Theta$
$T_{•,x}= L_{T•}\cdot cos \, \alpha$
$T_{•,y}= L_{T•}\cdot sin \, \alpha$
$• =(1, 2)$
Prawo fizyczne
Układ 5-ciu równań ($\ref{45}$) zawiera 6 niewiadomych. Dodatkowy 6-ty związek uzyskano ze związku fizycznego – nierozdzielności pręta T w punkcie (2) w postaci:
$$\begin{equation} \cfrac{N_1}{N_2}=\cfrac{L_{T1}}{L_{T2}}\label{46} \end{equation}$$
Warunek($\ref{46}$) uzyskano z porównania wydłużenia pręta T na odcinku 1=(4-2) ze skróceniem /wydłużeniem pręta na odcinku 2= (2-5). Przy założeniu długości i sił osiowych w prętach odpowiednio: $(L_{T1} ; N_1) $ i $(L_{T2} ; N_2)$ z prawa Hooke’a wydłużenia prętów wynoszą:
$\Delta L_{T1} = E_s \cfrac {N_1}{A_s}\cdot L_{T1}$,
$\Delta L_{T2} = E_s \cfrac {N_2}{A_s}\cdot L_{T2}$,
gdzie: $E_s$ – moduł Younga stali, $A_s$ – przekrój pręta zbrojeniowego (lub wiązki prętów) taki sam na obu odcinkach.
Ponieważ oba odcinki pręta oraz reakcje podpor (4) i (4) y pochylone pod tym samym katem $\alpha$ , to warunek ($\ref{46}$) można przedstawić dla rzutów długości oraz składowych reakcji jak następuje:
$$\begin{equation} T_{2,x} \cdot V_5 – T_{1,x} \cdot V_4 \quad {lub}\quad T_{2,y} \cdot H_5 – T_{1,y} \cdot H_4\label{47} \end{equation}$$
i wybrać do obliczeń jeden z nich.
Reakcje podpór
Rozwiązanie układu równań ($\ref{47}$)+ ($\ref{41}$) daje reakcje podpór $H,V$:
$$\begin{equation} H,V = \begin {cases}
H_4= & dF \cdot c_R\\
H_3 = & H_{Ed} + H_4\cdot \cfrac{\sum L_T}{L_{T2}}\\
H_5= & H_4 \cdot \cfrac{L_{T1}}{L_{T2}} \\
V_4 = & H_4 \cdot tg \, \alpha \\
V_3 = & H_3 \cdot tg \,\Theta \, -\, dF \cdot \cfrac{L_{S1}}{L_{S2} \cdot cos \, \Theta} \\
V_5 = & H_5 \cdot tg \, \alpha \\
\end{cases} \label{48}\end{equation}$$
gdzie:
$$\begin{equation} dF= F_{Ed} \cdot cos \, \Theta – H_{Ed} \cdot sin\, \Theta \label{49}\end{equation}$$
$$\begin{equation} c_R= \cfrac{\sum L_T}{\sum L_S} \cdot \cfrac{L_{T2}}{L_{S2}} \cdot \cfrac{\sin \, \alpha}{sin \, (\alpha+\Theta)}\label {50}\end{equation}$$
$\sum L_S= L_{S1}+L_{S2}$,
$\sum L_T= L_{T1}+L_{T2}$.
Pobocznie wskażemy, że rekcję $V3$ m0żna też wyznaczyć z zależności $V_3= H_{Ed}\cdot (tg\,\Theta+ tg \,\alpha) + \cfrac {dF}{cos \,\Theta} – H_3 \cdot tg \, \alpha$, którą uzyskano po przekształceniach ($\ref{48})^3$.
Siły w prętach modelu ST
Siły osiowe $N$ oraz poprzeczne $V$ w prętach S i T wynoszą
$$\begin{equation} (N , V) = \begin {cases}
N_{T1} = H_4 \cdot cos \, \alpha + V_4 \cdot sin \, \alpha & = \cfrac{ H_4 }{ cos \, \alpha }\\
N_{T2} = H_5 \cdot cos \, \alpha + V_5 \cdot sin \, \alpha & = N_{T1} \cdot \cfrac {L_{T1}}{L_{T2}}\\
N_{S1} = H_{Ed} \cdot cos \, \Theta + V_{Ed} \cdot sin \, \Theta \\
N_{S2 }= H_3 \cdot cos\,\Theta + V_3 \cdot sin \, \Theta \\
V_{T1} = H_4 \cdot sin \, \alpha – V_4 \cdot cos \, \alpha & = 0\\
V_{T2} = H_5 \cdot sin \, \alpha – V_5 \cdot cos \, \alpha & = 0\\
V_{S1} = V_{Ed}\cdot cos \, \Theta – H_{Ed}\cdot sin \, \Theta \\
V_{S2}= V_3 \cdot cos \, \Theta – H_3\cdot sin \, \Theta \\
\end{cases} \label{51}\end{equation}$$
W przykładzie 2 przedstawiono zastosowanie nowego modelu ST do projektowania zbrojenia znanego przypadku podcięcia belki.
Dyskusja założeń i wyników
- W nowej propozycji modelu ST podcięcia belki uzyskano stosunkowo proste analityczne formuły ($\ref{48}$), co było możliwe przy założeniu przegubowego podłączenia zbrojenia do węzła (2) (rys.22). W rzeczywistości pręt zbrojeniowy jest ciągły na całym odcinku (4)-(5). W przykładzie 3 przeprowadzono porównanie rozwiązania dla zbrojenia ciągłego z wynikami uzyskanymi w modelu analitycznym. Stwierdzono, że różnice są pomijalnie małe, a model analityczny można stosować również dla ciągłego pręta zbrojeniowego.
- Wyniki wskazują na jakościową zmianę wytężenia pręta T: ściskanie na odcinku powyżej krzyżulca betonowego i rozciągamy poniżej. To zjawisko jest odmienne od znanych modeli ST i wymaga potwierdzenia eksperymentalnego.
Przykłady zbrojenia podcięcia belki
Zbrojenie dla modeli ST1i ST2 wg Ec2
W projektowaniu może być stosowany model ST1 lub równoważnie ST2 z rys. 19.
Z modelu St1 wynika potrzeba stosowania zbrojenia poziomego na silę oraz zbrojenia pionowego (strzemion ) na siłę. Natomiast z modelu ST2 zbrojenie pionowe oraz poziome jest zastąpione zbrojeniem ukośnym. Nie ma potrzeby stosowania i jednego i drugiego zbrojenia. Odpowiadające detale zbrojeniowe pokazano dla przykładowego zbrojenia na rys. 24a,b.
Na rys. 25 pokazano możliwy, alternatywny wariant zbrojenia strzemionami ukośnymi.
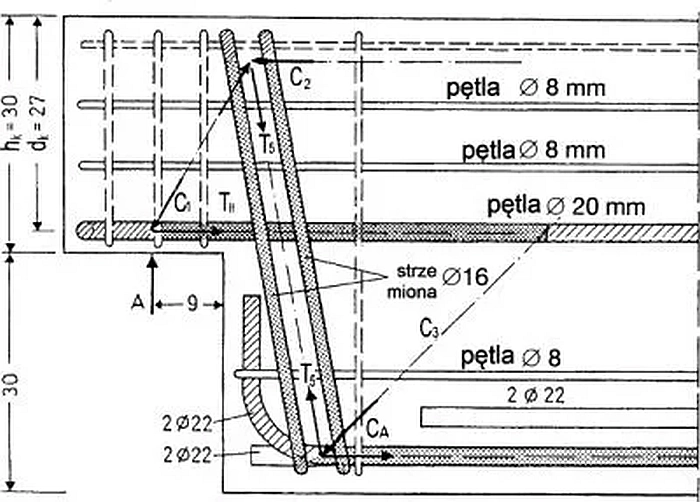
Rys.25 . Przykład zbrojenia podcięcia belki strzemionami ukośnymi [3]
Rozwiązania z rys. 25 stosuje się przy małej, możliwej długości oparcia.
Zakotwienie mechaniczne
W realizacji modelu z rys. 22 stosuje się zakotwienie pręta T w sposób pokazany na rys. 26.
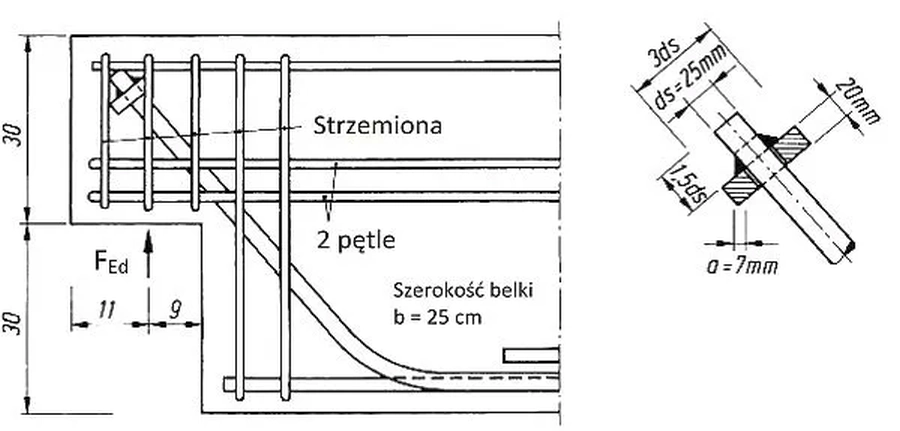
Rys. 26 Zakotwienie spawane pręta rozciąganego w narożu podciecia [5], Fig 3.17
Zakotwienie pętlami ukośnymi
Zakotwienie zbrojenia nośnego można też zrealizować za pomocą ukośnych pętli w sposób pokazany na rys. 27.
Zbrojenie sztywne dla małych wysokości podcięcia
W przypadku bardzo małych wysokości belek lub grubości płyt, lub też niewielkich długości oparcia należy stosować specjalne rozwiązania., np z zastosowaniem zbrojenia sztywnego w postaci dwuteownika stalowego (rys. 28).
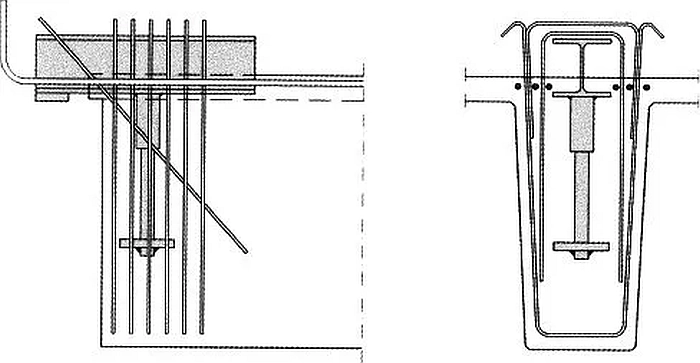
Rys. 28 Przykład zbrojenie niskiego „ząbka”[3]
Naprężenia w rozciąganej grupie różnych prętów
Siła rozciągająca zbrojenie główne krótki wspornika $F_{td}$ ($\ref{23}$)l lub ($\ref{31}$) (lub analogiczna w innych obszarach nieciągłości) jest zwykle przenoszona przez grupę (wiązkę równoległych) prętów o różnej średnicy , z których każdy powinien zostać poprawnie zakotwiony.
Załóżmy, że siła w pręcie „i” wynosi $F_{td,i}$. Siła ta jest przyjmowana przez pręt w zależności proporcjonalnie do jego sztywności w grupie (wiązce) prętów podług zależności
$$\begin{equation} F_{td, i} = F_{td}\cdot \cfrac{ A_{s,i}}{\sum \limits_{j=1}^ n A_{s,j}} =F_{td} \cdot \cfrac{Ø_i^2}{\sum \limits_{j=1}^ n Ø_j^2} \label {52}\end{equation}$$
gdzie
(j =1,…n) – numer pręta, n-liczba prętów w grupie , np. na rys 29 n=4) , $A_{s,i}$ – pole przekroju pręta „i”, $Ø_i$ – średnica pręta „i”.
Z ($\ref{52}$) wynika, że naprężenia w poszczególnych prętach są takie same:
$$\begin{equation} \sigma_{sd}=\cfrac{F_{td}} {A_s} = \sigma_{sd,i}=\cfrac{F_{td,i}}{A_{s,i}} \label {53}\end{equation}$$
gdzie $A_s =\sum \limits_{j=1}^n A_{s,j}$
Zakotwienie prętów w obszarach nieciągłości w tym w krótkich wspornikach i pocięciach
Obszary nieciągłości w tym krótkie wsporniki maja zwykle zbyt małe wymiary, by zapewnić wymaganą długość zakotwienie prętów przez przyczepność. Dlatego ważne są metody zwiększenia efektywności kotwienia pręta.
W krótkim wsporniku długość zakotwienia pręta głównego liczy się od krawędzi wewnętrznej (bliższej słupowi) płytki podporowej zgodnie z rys. 26.
Na długości zakotwienia występują trzy elementy poprawiające zakotwienie:
1) nacisk poprzeczny pod płytką podporową – uwzględniany współczynnikiem $\alpha_5$,($\ref{42}$)
2) nie przyspojone pręty poprzeczne w postaci strzemion pionowych- uwzględniane współczynnikiem $\alpha_3$ ($\ref{42}$),
3) przyspojone (przyspawane) pręty poprzeczne (oznaczone kolorem czerwonym). uwzględniany współczynnikiem $\alpha_4$ ($\ref{51}$) oraz zmniejszeniem długości $l_{b,rqd}$ ($\ref{51}$), ($\ref{52}$)
Najbardziej efektywne kotwienie mechaniczne (połączenia spawane lub śrubowe ) stosowane wówczas, gdy powyższe metody są niewystarczające.
Poniżej krótko przestawiono też zasady wymiarowania kotwienia przez przyczepność w celu przeanalizowania czynników wpływających na skuteczność zakotwienia.
Zakotwienie przez przyczepność do betonu
Obliczeniowa długość zakotwienia
Obliczeniową długość zakotwienia $l_{bd}$ przez przyczepność pręta do betonu wyznacza się z zależności [2], wzór (8.4)
$$\begin{equation} l_{bd}= \alpha_1 \cdot \alpha_2\cdot \alpha_3\cdot \alpha_4\cdot \alpha_5 \cdot l_{b,rqd}\ge l_{b, min} \label {54}\end{equation}$$
Dla prętów rozciąganych minimalna długość zakotwienia wynosi
$$\begin{equation} l_{b.min} = max \{0,3 \cdot l_{b.rqd} \,;\, 10 Ø \,;\, 100 \, mm \} \label {55}\end{equation}$$
W spółczynniki korekcyjne $\alpha_i \,(i=1,2 , … , 5)$ zależą od kształtu pręta, otulenia, ułożenia prętów poprzecznych oraz docisku do betonu
Podstawowa długość zakotwienia $l_{b,rqd}$ jest wyznaczana z zależności [2], wzór (8.3)
$$\begin{equation} l_{b,rqd}= \cfrac{Ø \cdot \sigma_{sd}}{4 \cdot f_{bd}} \label {56}\end{equation}$$
gdzie Ø – średnica pręta kotwionego,
Naprężęnia $\sigma_{sd}$ są naprężeniami w pręcie z uwzględnieniem przejmowania siły przez przez dodatkowe więzi wewnątrz betonu na długości zakotwienia
$$\begin{equation} \sigma_{sd} = \cfrac{F_{td} -F_{btd}}{A_s} \label {57}\end{equation}$$
gdzie:
$F_{td}$ – siła w pręcie kotwionym od obciążeń zewnętrznych: w krótkim wsporniku ($\ref {24}$) lub analogiczna w innych przypadkach obszarów nieciągłości,
$F_{btd}$ – siła przejmowana przez więzi wewnątrz elementu betonowego inne niż przyczepności do betonu rozłożone po długości $l_{bd}$.
Najczęściej takimi więzami są pręty poprzeczne przyspojone do pręta głównego. Dla tej sytuacji $F_{btd}$ wyznacza którą uwzględnia się z ($\ref{52}$)+($\ref{45}$).
Obliczeniowe graniczne naprężenie przyczepności $f_{bd}$ wyznaczane z zależności [2], wzór (8.2)
$$\begin{equation} f_{bd}=2,25 \cdot \eta_1 \cdot \eta_2 \label {58}\end{equation}$$
gdzie:
$\eta_1 =0,7$ – współczynnik zależny od jakości warunków przyczepności i pozycji pręta w czasie betonowania gdy warunki nie są „dobre”,
$\eta_2 =1,0$ – współczynnik zależny od średnicy pręta dla Ø < 32 mm,
Obliczeniowa wytrzymałość betonu na rozciąganie wg [2], wzór (3.16) wynosi $f_{ctd} = \cfrac{0,7 \cdot f_{ctm}}{\gamma_c}$,
gdzie średnia wytrzymałość na rozciąganie $f_{ctm}$ z tab. 3.1. [2] lub Tab.W-1 , a $\gamma_c=1,4$ współczynnik materiałowy dla betonu.
Współczynniki $\alpha_1$ oraz $\alpha_2$ są zależne od kształtu pręta i jego otulenia. Dla spotykanych w praktyce obszarów nieciągłości, które charakteryzują się niewielkimi wymiarami przy których nie stosuje się powiększonego otulenia prętów i przyjmuje się [2], tab.8.2
$$\begin{equation} \alpha_1=1 \quad oraz \quad \alpha_2=1,0 \label {59}\end{equation}$$
Przyjęcie mniejszych od 1 współczynników $\alpha_{1,2}$ możliwe jest dopiero przy otuleniu górnym, dolnym i bocznym pręta $c > 3 \cdot Ø$. Jeśli możemy zastosować tak duże otulenia, to wówczas te współczynniki należy przyjąć zgodnie z [2], rys. 8.1, 8.3), tab.3.1. Wówczas $\alpha_{1,2} \approx 0,7$.
W sytuacji korzystnego wpływu na zakotwienie przez zewnętrzny nacisk poprzeczny $p$, zamiast szacowania stosownej siły $F_{btd}$ – zmniejsza się potrzebną długość zakotwienia współczynnikiem $\alpha_5$ ($\ref{42}$).
Korzystny wpływ zbrojenia poprzecznego
Nie przyspojone zbrojenie poprzeczne
Korzystny wpływ zbrojenia poprzecznego ułożonego lub obejmującego zbrojenie główne polega na ograniczeniu przemieszczenia pręta rozciąganego ze swojej płaszczyzny. Przy braku zespojenia (przyspawania) zwiększenie efektywności jest uwzględniane współczynnikiem $\alpha_3$ wyliczanym z zależności [2], tab. 8.3
$$\begin{equation} \alpha_3= 1- K \cdot \lambda \ge 0,7 \label {60}\end{equation}$$
gdzie:
$K=0,1$ na przypadek krótkich wsporników ( i analogicznych obszarów nieciągłości), gdzie stosuje się strzemiona pionowe obejmujące pręt zbrojenia rozciąganego (p. rys. 17), a dla tego przypadku (po przekształceniu onaczenia $\lambda$ [2], tab.9.3)
$\lambda =\cfrac{\sum A_{st}}{A_s} – 0,25$
gdzie $A_s$ – pole przekroju pojedynczego pręta zbrojenia kotwionego ( o największej średnicy) , $A_{st}$ – pole przekroju zbrojenia poprzecznego (strzemion pionowych) na długości $l_{bd}$
Przyspojone zbrojenie poprzeczne
W przypadku przyspojenia zbrojenia poprzecznego – p. rys..21 ( na rys. 25 pręty przyspojone wyróżniono na czerwono) stosuje się współczynnik
$$\begin{equation} \alpha_4=0,7 \label {61}\end{equation}$$
przy czym średnica pręta przyspojonego $Ø_t \ge$ od średnicy pręta kotwionego Ø
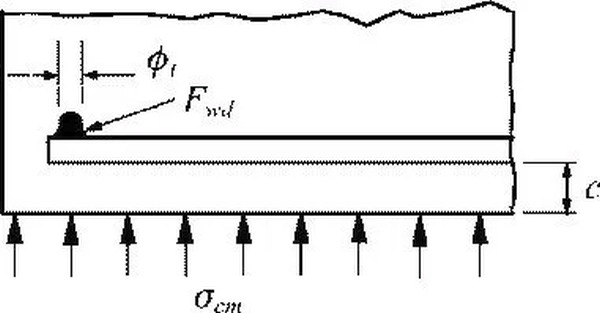
Rys. 29 Przyspojony pręt poprzeczny jako środek wspomagający zakotwienie [2], rys. 8.6
Pręt poprzeczny kotwi pręt główny siłą
$$\begin{equation} F_{btd} = F_{wd} \le F_{btd,max} \label {62}\end{equation}$$
gdzie $F_{wd}$ – nośność spoiny łączącej pręt poprzeczny z prętem kotwionym. Nośność tę można oszacować wg rys. 22 jak następuje
$$\begin{equation} F_{wd} \approx 0,5 \cdot F_{Rs} = A_s \cdot f_{yd} \label {63}\end{equation}$$
Nieprzekraczalna wartość siły kotwiącej wynosi
$$\begin{equation} F_{btd,max} \begin {cases}
16 \cdot A_s \cdot f_{cd} \cdot \cfrac{Ø_t}{Ø},& \text{ dla } Ø_t \le 12 \, mm \\
l_{td} \cdot Ø_t \cdot \sigma_{td}, & \text{ dla } 14 \le Ø_t \le 32 \, mm \\
\end{cases} \label{64}\end{equation}$$
Siłę kotwienia $F_{btd}$ ($\ref{52}$) zwiększa się współczynnikiem 1,41 przy dwóch przyspojonych prętach po tej samej stronie pręta kotwionego, jeśli są rozstawione nie rzadziej niż $3 \cdot Ø$.
W przypadku przyspojenia prętów po przeciwnych stronach pręta kotwiącego siłę kotwienia można zwiększyć dwukrotnie, o ile otulenie zewnętrznego pręta spełnia ogólne wymagania. Jeśli pręty poprzeczne mają średnicę mniejszą od 12 mm, i są rozstawione nie mniej niż na $Ø$ to nośność zakotwienia określoną wzorem ($\ref{45})^1) zwiększa się współczynnikiem 1,41.
Długość $l_{td}$ wynosi
$$\begin{equation} l_{td} =1,16 \cdot Ø_t \cdot \sqrt{\cfrac{f_{yd}}{\sigma_{td}}} \le l_t \label {65}\end{equation}$$
gdzie:
$ l_t$ jest długością pręta poprzecznego, ale nie większą niż rozstawu kotwionych prętów
Naprężęnie $\sigma_{td}$ w betonie wynosi:
$$\begin{equation} \sigma_{td} = \cfrac{f_{ctd}-\sigma_{cm}}{y}\le 3\cdot f_{cd}\label {66}\end{equation}$$
Naprężenie ściskające w betonie prostopadłe do obu prętów (wartość średnia, dodatnia przy ściskaniu),
$$\begin{equation} \sigma_{cm}=\cfrac{F_{Ed}}{l_p \cdot l_{bF}}\label {67}\end{equation}$$
gdzie:
$F_{Ed}$ obciążenie pionowe podkładki
$l_{bF}$ – przyjęta długość zakotwienia (np. na rys. 2 $l_{bF}=170-40= 130 \, mm$
$l_p$ – długość podkładki (na rys 2 $l_p=b_1= 340 \, mm$
Funkcję otulenie pręta $y$ wyznacza się następująco:
$$\begin{equation} y =0,015+0.14 \cdot e^{-0,18 \cdot x}\label {68}\end{equation}$$
gdzie otulenie względne $x$ przy otuleniu $c$ w kierunku prostopadłym dla obu prętów
$$\begin{equation} x= \cfrac{2\cdot c}{Ø_t} +1 \label {69}\end{equation}$$
Nacisk poprzeczny
Korzystny wpływ nacisku poprzecznego $p$ wzdłuż odcinka zakotwienia $l_{bd}$ uwzględnia się współczynnikiem redukcyjnym długości zakotwienia $\alpha_5$:
$$\begin{equation} \alpha_5 = 1- 0,04 \cdot p\label {70}\end{equation}$$
Nacisk poprzeczny $p$ w MPa do kotwionego pręta najczęściej szacuje się jak $\sigma_{cm}$ na rys. 21 czyli jako średni nacisk na długości zakotwienia z zależności ($\ref{52}$).
Jednoczesność czynników zakotwienia
Jednoczesność uwzględnienia czynników ograniczona jest nierównością dla współczynników długości zakotwienia:
$$\begin{equation} \alpha_2 \cdot \alpha_3 \cdot \alpha _5 \ge 0,7\label {71}\end{equation}$$
to znaczy w zasadzie nie uwzględnia się jednocześnie wpływu otulenia z nie-przyspojonymi prętami poprzecznymi i z naciskiem poprzecznym.
Zakotwienia spawane
Na rys. 23 przedstawiono najczęściej stosowane spawane zakotwienia do płytek stalowych, którymi mogą być inne stalowe profile zatopione w betonie, np. kątowniki (lub stanowiące okucie ), a nawet poprzeczne pręty zbrojeniowe.
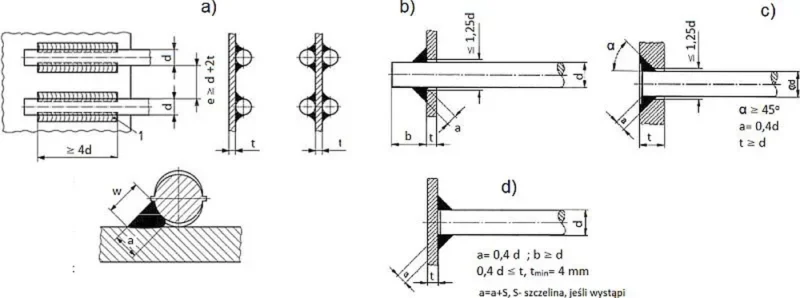
Rys. 31 Zakotwienia mechaniczne zbrojenia: a) do poziomej płytki ; do płytki prostopadłej: b) spoiną pachwinową przez otwór , c) spoiną otworową , d) spoina pachwinową bez otworu [18]
Pokazane na rys.23 zakotwienia spawane są bardzo podatne na błędy, przy czym połączenie typu 13b w którym pręt przechodzi przez płytę zapewnia pełną nośność pręta Zależnie od rodzaju stali płytki zakotwienie typu 13d (pachwinowe bez otworu) ma tylko część nośności pręta (dla połączenia z rys. 8 wyliczono niżej), a połączenie 23c ma nośność bliską nośności pręta, a połączenie ogólności wymagają indywidulanych obliczeń wg normy do projektowania węzłów w konstrukcjach stalowych [19].
Zakotwienia spawane muszą być wykonane wyłącznie na zamówienie przez spawaczy posiadających kwalifikacje zgodne z normą ISO 9606-1 (badanie spoiny pachwinowej) i po ukończeniu dodatkowego szkolenie w zakresie spawania prętów zbrojeniowych wg Ponadto wykonawca lub wytwórca musi zatrudnić osobę nadzorującą zgodnie z przepisami ISO 14731.
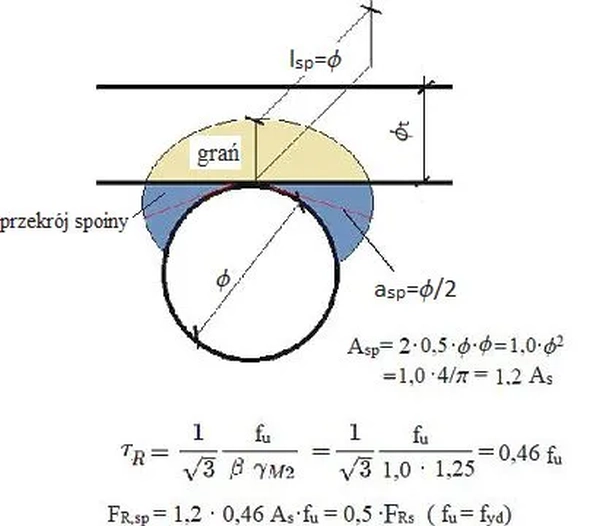
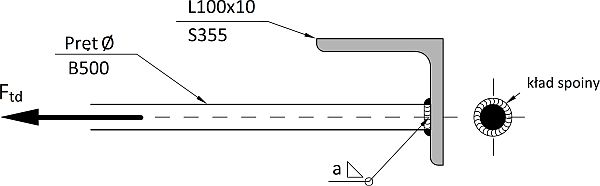
Na rys. 24 pokazano zakotwienie pręta zbrojeniowego o średnicy $d=Ø$ wykonanego ze stali B500 w kątowniku L 100x100x10 wykonanego ze stali S355.
Kład spoiny o grubości $a$ ma pole przekroju $A_{sp}= \pi/4 \cdot [ (d+2a) ^2 – d^2]= \pi \cdot (d+a)\cdot a$
Naprężenia rozciągające w spoinie wynoszą $\sigma= \cfrac{F_{td}}{A_{sp}}$. Składowe naprężeń w złożonym stanie napręzeń spoiny pachwinowej wynoszą ( artykuł Połaczenia spawane ): $\sigma_⊥ =\tau_⊥ = \sigma/ \sqrt{4}$.
Naprężenia zastępcze w spoinie $\sigma_{sp}$ powinny być mniejsze od wytrzymałości spoiny $f_{sp}$
$$\begin{equation} \sigma_{sp}= \sqrt{\sigma_⊥^2 + 3\tau_⊥^2}= \cfrac{\sqrt{4} \cdot F_{td}}{A_{sp}} \le f_{sp} \label {72} \end{equation}$$
Wytrzymałość spoiny $f_{sp}$ w połączeniu dwóch rodzajów stali jet mniejszą z nośności łączonych stali:
$f_{sp} = min [ f_{u1} / \beta_1 \, ; \, f_{u2} / \beta_2 ] / \gamma_{M2}$
gdzie:
$f_{ui}$ jest wytrzymałością łączonego materiału „i”: np. dla B500 $f_{u1} = 575 / 1,15 = 500 \, MPa$ (wg danych producenta stali zbrojeniowej), dla S355 $ f_{u2} = 490 \, MPa$ (wg normy PN-EN 1993-1);
$\beta_i$ jest współczynnikiem korelacji wg normy [19] : dla stali B500 $\beta_1 =1,0$, dla stali S355 $\beta_2=0,9$;
współczynnik materiałowy $\gamma_{M2}= 1,25$ dla połączeń spawanych wg [19].
Z warunku zrównania się nośności spoiny $F_{R,sp}= ( \sigma_{sp}=f_{sp}) \cdot A_{sp}$ z nośnością pręta $F_{R,Ø}=\pi d ^2/4 \cdot f_{yd}$, gdzie $f_{yd}=f_y/( \gamma_s(=1,15))$ jest obliczeniową granicą plastyczności pręta zbrojeniowego, uzyskujemy następujący warunek na grubość spoiny pachwinowej $a_{eq}$:
$$\begin{equation} a_{eq} = \cfrac{d}{4} \cdot \left( \sqrt{1+\sqrt{4}/k_f } \, -1 \right) \label {73}\end{equation}$$
gdzie $k_f =f_{sp}/f_{yd}$
Po podstawieniu wartości dla połączenia stali B500-S355, czyli:
$f_{sp}=\cfrac{}min \{500/1 \, ; \, 490/0,9 \}{1,25} = 400 \, MPa$,
$f_{yd}=500/1,15= 435 \, MPa$,
czyli $ k_f=400/435= 0,92$, otrzymamy
$$\begin{equation} a_{eq} = 0,296\cdot d \label {74}\end{equation}$$
Jeśli połączenie będzie wykonywane w warunkach montażowych (na budowie), wynik należy powiększyć w stosunku 0,9, czyli
$a_{eq,b }= a_{eq} / 0,9 = 0,296 /0,9 = 0,329 \cdot d \approx 0,4 d$
(patrz rys. 23d)
Jeśli ze względów konstrukcyjnych nie można zastosować spoiny o grubości $a_{eq, b}$, to pręty-startery należy spawać na warsztacie lub połączenia należy wzmocnić blachami lub pierścieniami węzłowymi.
Kotwienie za pomocą prętów poprzecznych
Kotwienie za pomocą zbrojeniowych prętów poprzecznych jest alternatywą dla połączeń spawanych omówionych wyżej. Korzystny wpływa mają nawet nie przyspawane pręty poprzeczne, ale znacznie większy przyspojone pręty poprzeczne, Te zagadnienia są przedmiotem unormowania [2], klauzula 8.6.
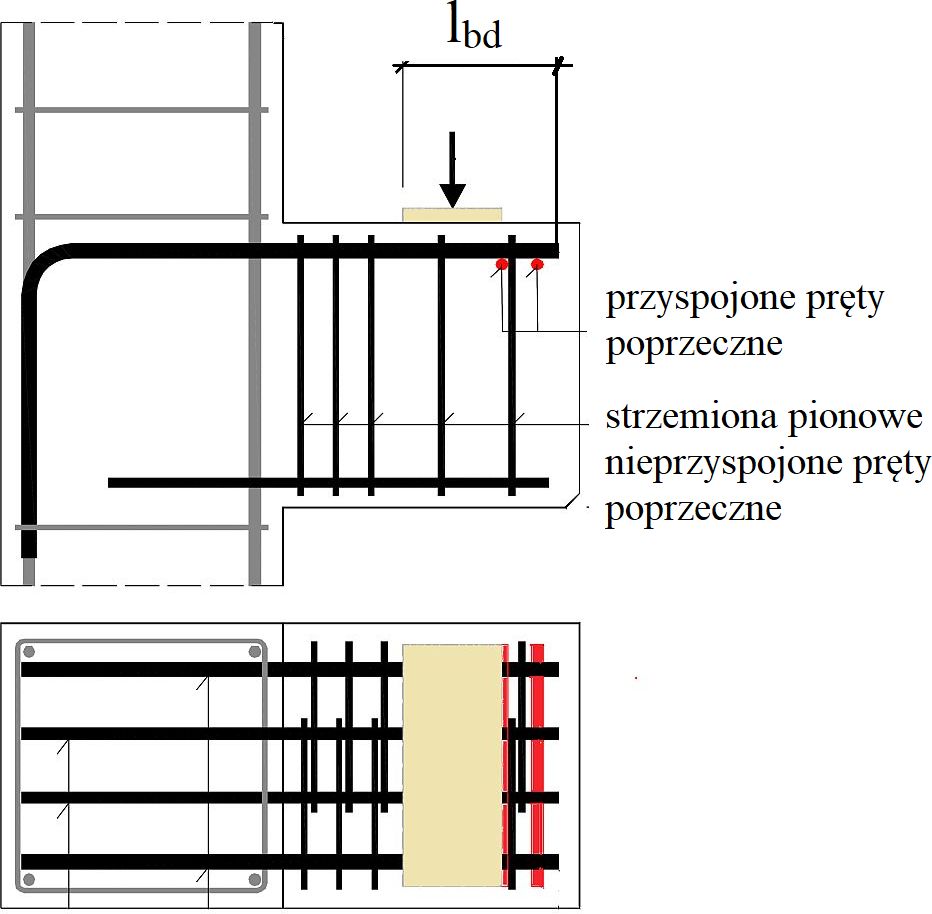
Rys. 33. Zakotwienie pręta nośnego przez przyspojone i nie przyspojone pręty poprzeczne w krótkim wsporniku [7], rys. 5.1. (zmodyfikowany)
Kotwienie za pomocą pętli
Zarówno pętle poziome jak i pionowe (często nazywane zbrojeniem konturowym) na skutek zmiany kierunku siły są gięte, a w na długości łuku dochodzi do docisku do betonu . Warunek zmiażdżenia betonu na łuku pręta należy sprawdzić, gdy zakotwienie pręta wymaga długości większej niż 5d poza końcem zagięcia,
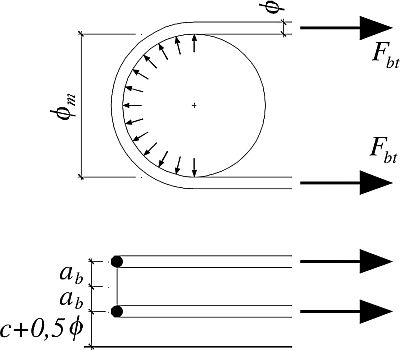
Na rys 26 pokazano mechanizm docisku na przykładzie pętli poziomych o średnicy $Ø_m$ , wykonanych z prętów o średnicy $Ø$ ułożonych w dwóch warstwach: pierwszej (od od strony powierzchni betonu) otulonej betonem o grubości $c+Ø/2$ i drugiej zw odstępie osiowym $2 a_b$
Aby uniknąć zmiażdżenia betonu wewnątrz zagięcia pręta należy tak dobrać średnicę zagięcia $Ø_m$, aby spełnić warunek
$$\begin{equation} \sigma_b= \cfrac{F_{bt}}{A_{b}} \le \sigma_{Rd,max} \label {75}\end{equation}$$
gdzie:
$\sigma_{Rd,max}$ – wytrzymałość betonu na ściskanie w węźle ($\ref{11}$)
$A_{b}=l_{b}\cdot Ø$ – powierzchnia docisku w węźle;
$l_{b} = alpha_{b} \cdot Ø_m $ ;
$\alpha_{b}$ – kąt wygięcia w radianach, np: na rys. 26 $\alpha_{b}=\pi$
Równoważnie średnicę zagięcia wyznaczyć wprost z klauzuli 8.3(3), wzór (8.1) [2]:
$$\begin{equation} Ø_{m,min} = \cfrac{F_{bt}}{f_{cd}} \cdot \left( \cfrac{3}{a_b} +\cfrac{3}{2\cdot d}\right)\label {76}\end{equation}$$
gdzie d – średnica pręta pętli.
$F_{bt}$ siła maksymalna w pręcie na początku pętli (wygięcia).
Z równowagi sił ( rys. 26 ) wynika, że siła w jednej gałęzi pętli $F_{bt}$ jest połową całkowitej siły rozciągającej warstwę.
$ a_b = \begin {cases}
c + Ø/2 , & \text{ dla pręta pierwszej warstwy (pod powierzchnią betonu)},\\
0,5 \cdot s_z & \text{ dla pręta drugiej warstwy pętli}, \\
\end{cases} $
gdzie:
$c$ -otulenie pręta o średnicy $Ø$
$s_z$ – osiowy rozstaw prętów sąsiednich warstw
Pętle mogą być ułożone pionowo (przy powierzchni czołowej wspornika) i wówczas obowiązują analogiczne zasady prawidłowego zakotwienia.
Kotwienie hybrydowe za pomocą pętli i zbrojenia konturowego
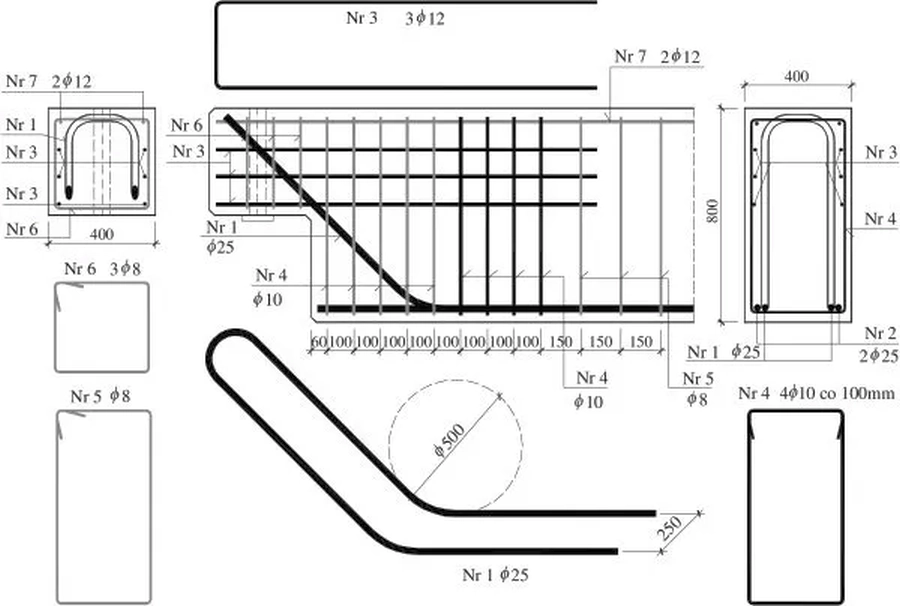
Na rys. 35 pokazano przykład zbrojenia krótkiego wspornika za pomocą pętli poziomych (Nr 1) i zbrojenia konturowego (Nr 2). Na rysunku wskazano krytyczne naroże, które powinno być sprawdzone z warunku zmiażdżenia betonu ($|ref{42}$).
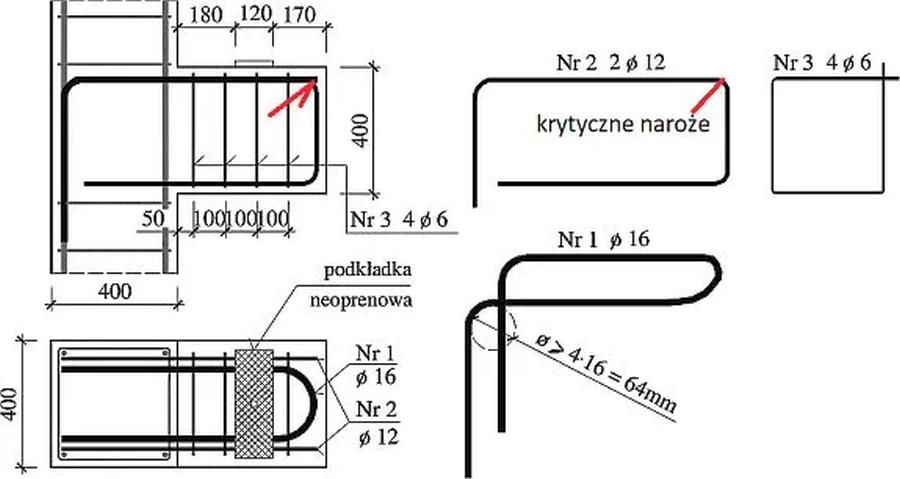
Rys.35 Przykład zbrojenia wspornika pętlami 1 i prętami konturowymi [7], rys. 2.5 (zmodyfikowany)
Rozdział całkowitej siły $F_{td}$ ($\ref{23}$) na pętle poziome i zbrojenie konturowe dokonuje się podług zależności ($\ref{52}$)
Naroże krytyczne z rys. 35 odpowiada sytuacji pokazanej na rys.4 , czyli zakotwieniu prętów rozciąganych w dwóch kierunkach dla $ F_{td1}=F_{td2}= F_{td}$.
Siła docisku do betonu jest wypadkową obu sił i wynosi $F_{cd}= \sqrt{4}\cdot F_{td}$ . Sprawdzenie wytrzymałości betonu dokonuje się zgodnie z warunkiem ($\ref{42}$), przy czym pole docisku przy normowym wyokrągleniu $Ø_M = 4 Ø$ i zagięcia pod kątem prostym $\alpha_{b}=\pi/2$ można sprowadzić do postaci
$ A_b = l_b\cdot Ø= \alpha_b \cdot Ø_m \cdot Phi = \pi/4 \cdot 4 Ø \cdot Phi =\pi Ø^2$,
a naprężenie dociskowe do postaci (dla prętów o różnych średnicach jest jednakowe):
$$\begin{equation} \sigma_{b,i}= \cfrac{\sqrt{4}\cdot F_{td,i}}{\pi \cdot Ø_i^2} \approx 0,45 \cdot \cfrac{F_{td,i}}{Ø_i^2} = 0,45 \cdot \cfrac{F_{td}}{\sum_j Ø_j^2}= \sigma_b \label {77}\end{equation}$$
Wytrzymałość betonu $\sigma_{Rd, max}$ ($\ref{11})$ należy obliczać dla k=0,75.
Podkładki elastomerowe
Łożyska ślizgowe uwidocznione na rysunkach w tekście , w tym na rys, 36 wykonuje się najczęściej jako łożyska elastomerowe, które są przedmiotem normy [20]. Łożyska elastomerowe mogą być stosowane w temperaturach -25 oC do 50 oC, czyli praktycznie w każdym zastosowaniu wewnątrz budynku,
W przypadku braku wymagań pożarowych można stosować podkładki zbrojone., a w przypadku wymaganej klasy odporności ogniowej R stosuje się podkładki niezbrojone zgodnie z wytycznymi producenta.
Typowe zastosowanie podkładki elastomerowej pokazano na rys.36 na przykładzie dylatacji w postaci łożyska ślizgowego na slupie (wsporniku) lub ścianie (pilastrze) konstrukcji .
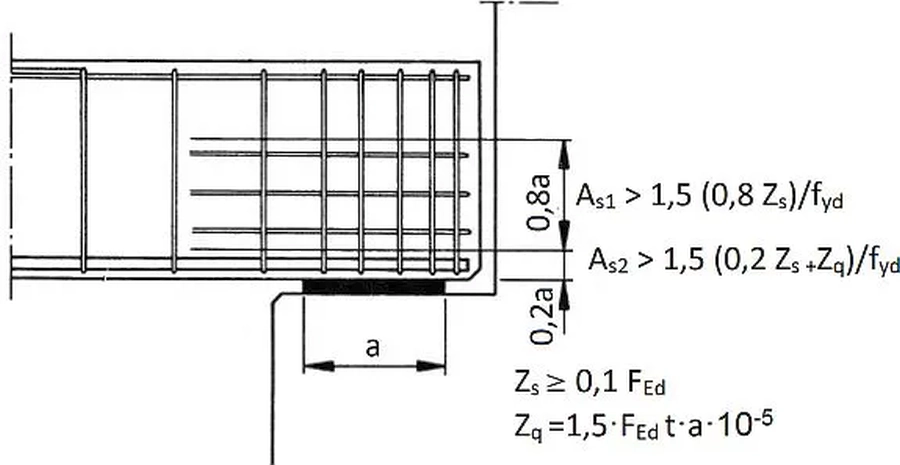
Rys.36 Zbrojenie płyty/belki na nad łożyskiem ślizgowym na wsporniku/ głowicy słupa [3]
Podkładki elastomerowe są często stosowane do posadowienia konstrukcji na krótkim wsporniku lub w podcięciu belek i są objęte normą DIN 4141, część 3 [21] i nowej normy DIN EN 1337. Łożyska elastomerowe wykonane są z kauczuku syntetycznego o dużej odporności na starzenie (handlowe nazwy: neopren, Bayprenr). Występują w wielu postaciach, zbrojonych i niezbrojonych,
Rosnąca popularność niezbrojonych łożysk elastomerowych w budownictwie wynika z małych wymiarów, trwałości i elastycznego dopasowania do podłoża oraz rzeczywistych warunków. Niezbrojone łożyska elastomerowe są znacznie tańsze niż wersje zbrojone i mają tę zaletę, że nie są ograniczone do określonych kształtów lub typów łożysk, a także mają dużą odporność ogniową (wg katalogu producenta). Mogą być dostosowane do konkretnych celów, np poprzez wycięcie otworów pod kołki lub nadanie specjalnego kształtu, bo są wycinane na wymiar z arkuszy wielkoformatowych.
Można je stosować głównie przy obciążeniach statycznych, ponieważ istnieje ryzyko pełzania przy obciążeniach dynamicznych.
Dobór wymiarów podkładki elastomerowej
Dobór podkładki należy dokonać na podstawie danych katalogowych producenta tak, by zdolna była do przeniesienia średniego docisku pionowego oraz spełniała wymagane warunki brzegowe: dopuszczała wymagany obrót oraz wymagane przesunięcia poziome wywołane obciążeniami poziomymi $H_{Ed,x}$- $H_{Ed,y}$
Wstępny dobór wymiarów podkładki elastomerowej można dokonać z warunku dopuszczalnego nacisku łożyska na powierzchnie elementów podpierającego i podpieranego ($\ref{7})$
Norma [21] dotyczy łożysk, których wymiary spełniają następujące warunki dla grubości oraz szerokości podkładki $t_p$ oraz $ b_p$
$$\begin{equation} 5 \le \cfrac{b_p}{43} \le t_p \le \cfrac{b_p}{12} \le 12 \, mm \quad ; \quad 70 \, mm \le b_p \le 200 \, mm \label {78}\end{equation}$$
Grubość $t_p$ można zmniejszyć do 4 mm, jeśli można zagwarantować mniejsze tolerancje płaskości (1,5 mm). Istotne jest, aby zapobiec bezpośredniemu kontaktowi elementów betonowych, nawet w przypadku obrotu podpory, i to jest główna zasada przy określaniu grubości. Do niewzmocnionych łożysk elastomerowych można stosować wyłącznie produkty wulkanizowane na bazie kauczuku chloroprenowego (CR).
Norma [21] określa wytrzymałość samej podkładki mierzonej naprężeniami $\sigma_m$ wg ($\ref{6})^2$ jako:
$$\begin{equation} \sigma_{Rd,m} = 1,2 \cdot G \cdot S \label {79}\end{equation}$$
gdzie:
$G$ – moduł Kirchoffa (styczny) łożyska podawany przez producenta – dla podkładek elastomerowych Betomax $G=1,5 \, MPa$
$S$ – współczynnik kształtu łożyska wyznaczany z zależności:
$$\begin{equation} S = \begin {cases}
\cfrac{b_f \cdot l_f}{2 \cdot ( b_f + l_f) \cdot t_f} & \text{ dla podkładki prostokątnej } b_f \, x \, l_f \quad ; \quad l_f \le 2 \cdot b_f \\
\cfrac{D}{4 \cdot t_f} & \text{ dla podkładki okrągłej o średnicy D}, \\
\end{cases} \label {80}\end{equation}$$
Otwory w podkładkach , np. w przypadku kołków można pominąć, jeśli nie przekraczają 10% powierzchni podkładki.
Z zależności ($\ref{46}$) dla standardowych geometrii łożysk otrzymujemy wytrzymałość podkładki $\sigma_m=$ 10. do 12 MPa. Jeśli jednak mają zastosowanie specyficzne warunki stosowania (np. dla złączy doczołowych słupów obciążonych ściskaniem), wówczas dopuszczalne są naprężenia ściskające dochodzą do 20MPa.
W przypadkach standardowych stosuje się następujące wymagania wymiarowe dla podkładek elastomerowych :
grubość podkładki $ 5 mm \le \cfrac {a}{32} \le t \le \dfrac {a}{11} \le 12 mm$
rozmiar w planie $ 70 mm \le a \le 200 mm $,
gdzie $a$ – długość łożyska. Grubość jest redukowana do 4 mm, gdzie najmniejsza tolerancja jest gwarantować $\le 1,5 mm$
Wytrzymałość konkretnych typów podkładki należy przyjmować z materiałów producenta.
Warunki przy dużych naciskach
W przypadku dużego docisku na łożysko
$\sigma \ge 0,2 f_{ck}$
minimalna długość wspornika $l$ powinna spełniać warunek (oznaczenia na rys.37.)
$$\begin{equation} l = b_L+ v_{Tr} +v_K +max \, \Delta l \label {81}\end{equation}$$
gdzie:
$ v_{( Tr\,lub \, K)} = (c_1 / 2 + d_s / 2 + c_2)_{( Tr\,lub \, K)}$ – odległości brzegów podkładki od lica belki lub płyty
$b_L$ – szerokość podkładki,
max $ \Delta l$ – największa odchyłka długości wspornika
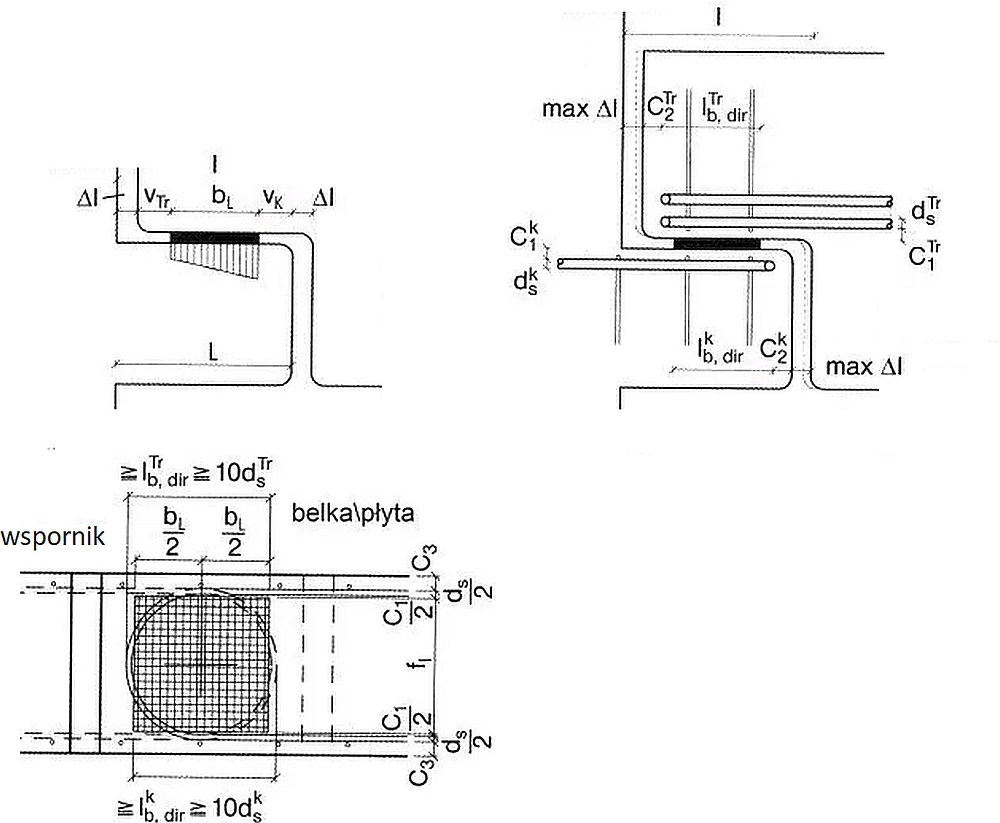
Rys.37 Minimalna długość wspornika dla dużych obciążeń $\sigma \ge 0,2 f_{ck}$ [3]
Jeżeli długość zakotwienia zbrojenia rozciąganego wspornika $l){b,dir}$ nie jest w tej sytuacji wystarczająca, należy odpowiednio zwiększyć długość łożyska, a tym samym długość wspornika. Należy pamiętać, że dopuszczalne tolerancje konstrukcyjne dotyczące umiejscowienia zbrojenia i płytki łożyskowej oraz wymiarów elementów konstrukcyjnych są w praktyce wykorzystywane mniej więcej w pełnym zakresie. Dlatego tam, gdzie (małe) wymiary są w pełni wykorzystywane, przestrzeganie wymiarów powinno być gwarantowane poprzez środki kontroli jakości. Podobnie szerokość wspornika $b_w$ to suma wymaganej szerokości podparcia $t_L$ plus dodatkowa szerokość po obu stronach:
$$\begin{equation} b_w = t_l+ c_l + d_s + 2 \cdot c_3 \label {82}\end{equation}$$
Dozbrojenie strefy podporowej
Dozbrojenie strefy podporowej elementu podpierającego i podpieranego
Strefa podporowa w elemencie podpierającym powinna zostać zostać wzmocniona zgodnie z przedstawionymi na rys.38: od lewej: przyspojonym prętem poprzecznym od dołu do pręta nośnego; pętla pętlą poziomą, zakotwieniem na długość $2s_s$ lub pętla pionową. Wymiar $r_1$ należy tak dobrać, by powierzchnia styku mogła się powiększyć bez uszkodzenia łożyska przy rozszerzeniu przez przez obciążenie pionowe i przez obrót, przemieszczeniu poziomym od obciążeń poziomych oraz oraz niedokładnego montażu łożyska. Szacunkowo $r_1=t/2 + \, 10 \, mm$.
Niezależnie od zbrojenia przypowierzchniowego należy zapewnić odpowiednie zbrojenie na rozciąganie w odpowiedniej odległości od powierzchni oraz w rozmiarze i rozłożyć odpowiednio do rozszczepiających sił rozciągających jak pokazano na rys. 36.
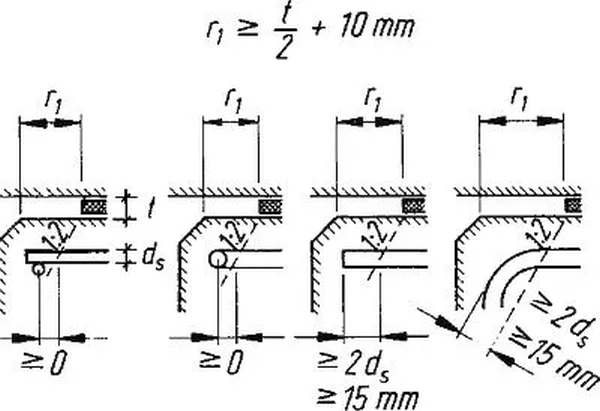
Rys.38 Wzmocnienie strefy podporowej elementu podpierającego [5]
Warunki dozbrojenia belki/płyty nad podkładką ślizgową łożyska pokazano na rys. 36.
Dylatacje z pozostawieniem przerw
Dylatowanie technologiczne polega na betonowaniu o ograniczonej długości (zwykle do 16 m) z pozostawieniem przerw do późniejszego betonowania. W pozostawionej przerwie technologicznej powinno być ułożone zbrojenie lub połączone spawaniem i zabetonowane.
Przerwy robocze w konstrukcjach można stosować:
- dla belek i podciągów w miejscach najmniejszych sił poprzecznych,
- dla słupów w płaszczyznach stropów, belek lub podciągów,
- dla płyt w linii prostopadłej do belek lub żeber, na których opiera się płyta, przy betonowaniu płyt w kierunku równoległym do podciągu dopuszcza się przerwę roboczą w środkowej części przęsła płyty, równolegle do żeber, na których wspiera się płyta.
Powierzchnia przerwy roboczej przed wznowieniem układania mieszanki betonowej powinna być starannie przygotowana do połączenia betonu stwardniałego z nowym. Czynność ta wymaga usunięcia z powierzchni stwardniałego betonu luźnych okruchów oraz warstwy szkliwa cementowego i przepłukania wodą. Po ułożeniu betonu , nalezy przeprowadzić precycyjne wibrowanie.
Uciąglanie zbrojenia w przerwie technologicznej
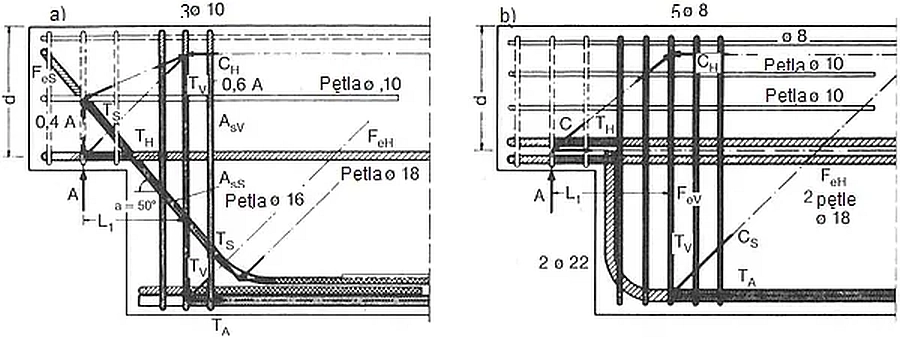
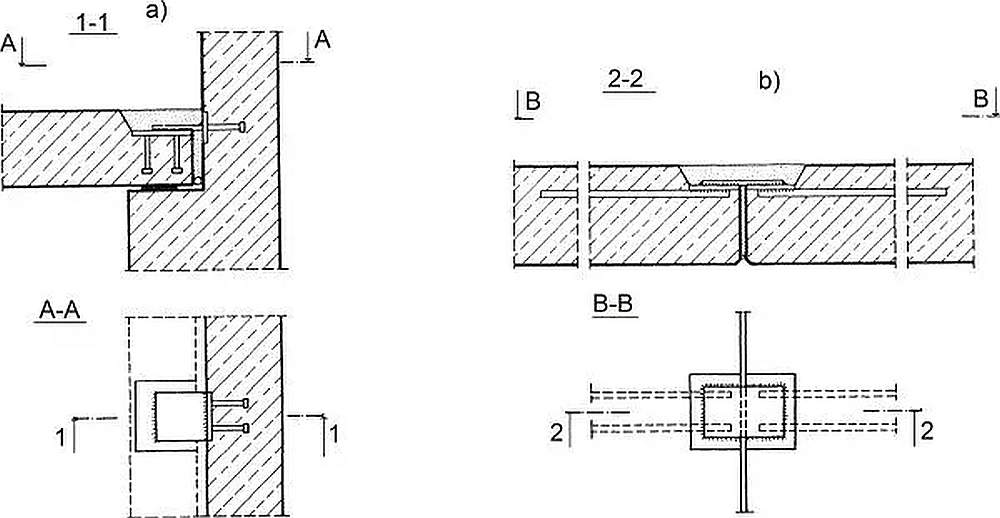
Przykłady uciąglenia zbrojenia w przerwach technologicznych pokazano na rys. 39.
Zastosowanie szalunku siatkowego
Na rys. 13 pokazano zastosowanie siatkowego szalunku traconego umożliwiającego zapewnienie ciągłości zbrojenia pomiędzy etapami betonowania, a także szorstkiej powierzchni styku gwarantującą pewne połączenie z drugą fazą betonowania.
Wzmacnianie, modernizowanie wsporników
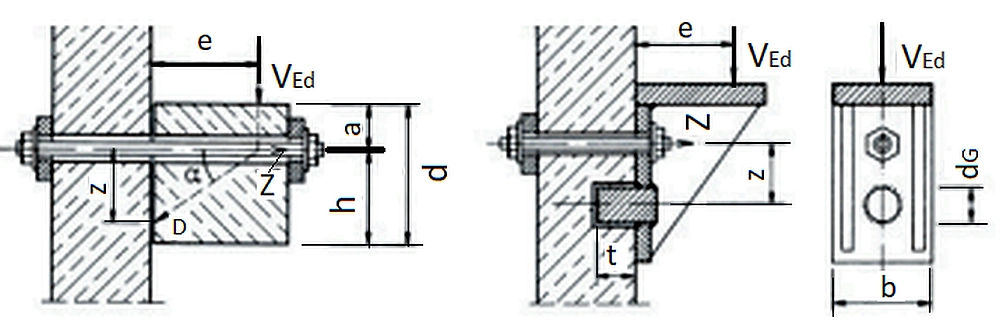
Gdy wsporniki muszą zostać zamontowane później ze względu na rodzaj zastosowanej obróbki, np. ściany wzniesionej przy użyciu szalunku ślizgowego, lub w przypadku konieczności zamontowania wsporników w czasie eksploatacji przebudowy obiektu – możliwe jest późniejsze przymocowanie wsporników, wykorzystując tarcie i działanie kołków do przenoszenia sił na przykład w sposób pokazany na rys. 41.
W tych przypadkach siły rozciągające – wyrywające wspornik ze ściany/ słupa najczęściej są przenoszone za pomocą gwintowanych mocowań, tak jak przyjęto w obu pokazanych wariantach modernizacji wspornika. Niebezpieczeństwo skręcenia wspornika w wyniku niewielkich niedokładności i rozluźnienia śrub minimalizuje się poprzez wstępne sprężenie śruby siłą rozciągającą Z, które można nadać z wykorzystaniem pras hydraulicznych, takich jak te stosowane w konstrukcjach z betonu sprężonego, jednak wygodniejsze jest użycie klucza dynamometrycznego, który jednak powoduje także skręcanie śruby, jak i jej rozciąganie.
Uogólnienie. Idea hybrydowego projektowania żelbetu
Mechanizm zniszczenia poprzez ścinanie jest niejednoznaczny przy analizie takich elementów jak: krótkie wsporniki, podcięcia belek i płyt, połączenia i przeguby i ogólnie obszary nieciągłości rozumiane jako połączenie obszarów tarczowych z belkowymi lub płytowymi. Obszary konstrukcji o mechanizmach zniszczenia, wymagających zastosowania różnych rodzaju elementów najczęściej dzieli się na elementy w sposób pokazany na rys.42:
-
- regiony typu B (od ang. Beam), czyli takie obszary, w których zachowana jest zasada płaskich przekrojów (Bernoulliego-Naviera). W takich obszarach można stosować teorię belkową,
- regiony typu D (od ang. Discontuity), czyli obszary nieciągłości (lub zaburzeń [racy belkowej) są regionami, w którym nie obowiązuje zasada Bernoulliego i nie można używać wzorów z modeli prętowych (belkowych). Obszary D wystąpią również w belkach- ścianach.
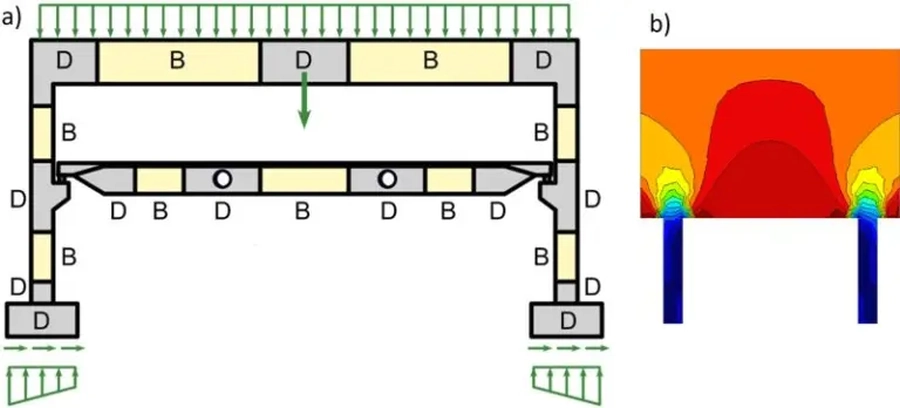
Rys.42. Obszary belkowe B oraz nieciągłości D: a) w ramie płaskiej, b) w belce ścianie (cały obszar) [22]
We współczesnej dobie informatyzacji zaleca się projektowanie hybrydowe prętowo-tarczowe, w którym można wydzielić charakterystyczne etapy:
- Etap I: konstrukcję analizujmy pod względem występowania różnych obszarów.
W pierwszej kolejności wydzielamy regiony B belek (prętów) czyli takich elementów których wymiar długości L jest większy od wysokości h
* min 8 razy (L> 8h) dla prętów stalowych ,
* min 4 razy (L> 4h) dla prętów żelbetowych,
Dla wsporników o wysięgu $w$ można przyjąć $l=2w$. - Etap II w grupie prętów stalowych wydzielmy regiony Bc prętów cienkościennych dla których grubość ścianki $\delta$ jest mniejsza nie mniej niż 8 razy od długości ścianki l ($l > 8 \delta$
- Etap III pozostałe obszary konstrukcji, to obszary D, w których możemy wydzielić
* obszary tarczowe Dt – naroża ram, krótkie wsporniki, belki z otworami w środniku,
* obszary płytowe Dp – stropy , stopy fundamentowe itd
* obszary powłokowe Dpo – płyty zagięte, pochyłe itd,
* obszary 3d – fundamenty masywne itd
Przykłady rachunkowe
Przykład 1 [ Krótki wspornik – metoda ST, EC2]
Zaprojektować zbrojenie wspornika pokazanego na rys. 4. Sprawdzić wymiary wspornika z warunku odchyłek wykonawczych oraz dobrać podkładkę elastomerową.
Dane
Zgodnie z przykładem 21.1 z pracy [8] lub przykładem 3.1. z pracy [7] mamy:
żelbet C30/37 – B500: $f_{ck}=40 \, MPa$, $f_{cd}=30/1,4 =21,43 /, MPa$, $f_{yd}= 500/1,15= 435 \, MPa$.
obciążenie: $F_{Ed} = 400 \, kN$ , $ H_{Ed} = 80 \, kN$
grubość podkładki $t_p = 20 \, mm$
otulenie osiowe górne $a_u=40 \, mm$
szerokość wspornika $b = 400 \, mm$
wysokość wspornika $h = 400 \, mm$
wysokość użyteczna $d=400-40=360\,mm$
wysięg wspornika $a_c= 240 \, mm$
Sprawdzenie wartości siły poziomej
$H_{Ed} = 80 \, kN \ge 0,2 \cdot 400 = 80 \, kN$ $\to$ OK
Wytrzymałość betonu krótkiego wspornika
Wytrzymałość w strefie podparcia
($\ref{10}$) $\to$ $f_{Rd} = 0,85 \cdot 21,.13= 18,0 \, MPa$
Wytrzymałość w węzłach wspornika
($\ref{11}$) $\to$ $ \nu’ = 1+\cfrac{32}{250}= 0,88$
($\ref{13}$) $\to$
$ k= \begin {cases}
1,0 & \text{ w węźle (1)},\\
0,85 & \text{ węźle (2)}, \\
0,6, & \text{ dla krzyżulca betonowego pomiędzy węzłami (1)-(2)},\\
\end{cases}$
($\ref{11}$) $\to$
$ \sigma_{Rd, max}= \begin {cases}
1,0 \cdot 0,88 \cdot 21,43 = 18,86 \, MPa & \text{ w węźle (1)},\\
0,85\cdot 0,88 \cdot 21,43 = 16,03 \, MPa& \text{ węźle (2)}, \\
0,75\cdot 0,88 \cdot 21,43 = 14,14 \, MPa& \text{ w narożu T-T)}, \\
0,6\cdot 0,88 \cdot 21,43 = 11,32 \, MPa & \text{ dla krzyżulca betonowego pomiędzy węzłami (1)-(2)},\\
\end{cases}$
Dobór podkładki
Wymagana powierzchnia podkładki ze względu na docisk do betonu ($\ref{14}$) , czyli wyżej wyliczone $f_{Rd}=18 \, MPa$
($\ref{7}$) $\to$ $A_p \ge \cfrac{F_{Ed}}{f_{Rd}}= \cfrac{400}{21}\cdot 10^1 = 222 \, cm^2$
$\to$ przyjęto podkładkę (rys.5) $l_p= 340 \, mm$ , $b_p = 140 \, mm$ , $A_p= 34\cdot 14= 476 \, cm^2 > 222 \, cm^2$
($\ref{7}$) $\to$ $
\sigma_m = \cfrac{400}{476}\cdot 10^1= 8,4 \, MPa$
$k_{\sigma}=\cfrac{\sigma_m}{f_{cd}}=\cfrac{8,4}{21,43}=0,39$
Tab.1. $\to$ minimalna szerokość podkładki
$\to$ $min \, a_1= 110\,,mm$ dla $k_{\sigma}=0,39$
Przyjęto $b_p = 140 > 110\, mm$ $\to$ OK
Przyjęto podkładkę elastomerową na średnie naprężenia pod podkładką $\sigma_m= 8,4 \,MPa$
niezbrojoną typu > N10 prod. np. Betomax (liczba po N oznacza wytrzymałość podkładki w MPa)
Sprawdzenie wymiarów wspornika z warunku odchyłek wykonawczych
Rys 3, Tab.1. $\to$
Minimalna odległość podkładki od krawędzi elementu podpierającego dla podpory żelbetowej ($ C \ge 30$), skupionej i dla $k_{\sigma}=0,39 \in [0,15 \, ;\, 0,40]$.
$\to$ $a_2 =15 \, mm$
Minimalna odległość $a_3$ podkładki od elementu podpieranego dla zbrojenia nad podporą dla pionowych pętli zbrojenia z otuleniem $c_3= 40 \ , mm$
i promienia wewnętrznym zagięcia $r= 80 \, mm$
$\to$ $a_3 = 40+80=120 \, mm$
Poprawka ze względu na odchyłki odległości między elementami podpierającymi
dla prefabrykowanej belki podpieranej o długości $l= 8000 \, mm$, czyli $l/1200 = 8000/1200= 7 \, mm$
($\ref {8}$) $\to$ $\Delta a_2= 8000/1200 = 7 \, mm < 10 \,mm \to Delta a_2 = 10 \, mm$
Poprawka ze względu na odchyłki długości elementu podpieranego
($\ref{9}$) $\to$ $\Delta a_3 = 8000/250= 4 \, mm$
Minimalne odległości między krawędziami łożyska i krawędziami rozpatrywanych elementów
$d_2 = c_2+\Delta a_2 = 40 +10 = 50 > 340-170-140= 30 \, mm$ (Rys 3) ,
z czego wynika, że w przypadku ogólnym zaprojektowana odległość $d_2 = 30 \, mm$ byłaby z byt mała.
Jednakże w przypadku zastosowania okucia końca wspornika przez kątownik można przyjąc , że dla prętów nośnych $c_2=10 \, mm$ i wymagana odległość $d_2=10+10 = 20 < 30\,mm . przy innym sposobie zakotwienia prętów nośnych należałoby zwiększyć długość wspornika lub dosunąć płytkę do słupa, ale tak by zachować położenie elementu podpieranego w systemie konstrukcyjnym.
$d_3 = c_3+\Delta a_3 = 40 +4 = 44 < 170-60=110 \, mm$ (Rys 3)
Minimalna długość podparcia wspornika
($\ref{6}$) $\to$ a=110+15+120+\sqrt{10^2 +4^2 }= 256 \, mm.
Wymagana nominalna długość podparcia $a=256 \, mm$ jest mniejsza od przyjętej wynoszącej (Rys 3) $ a=340-60=180 \, mm$.
Układ prętów ST i kąt pochylenia krzyżulca betonowego $\Theta$
Położenie punktu (2)
($\ref{15}$) $\to$ $ a_H=t_p+a_u = 20 +40 = 60 \, mm$ , $ e= 60 \cdot \cfrac{80}{400} = 12 \, mm$
Położenie punktu (1)
Zakładamy, że naprężenia dociskowe $\sigma_c$ na boku poziomym węzła (1) o długości $x_H$ jest równe wytrzymałości betonu w tym węźle $\sigma_{Rd, max}= 18,86 \, MPa$ (p. wyżej)
($\ref{16}$) $\to$ pozioma długość docisku $ x_H = \cfrac{400}{400 \cdot 18,86} \cdot 10^3 = 53,2 \approx 54 \, mm$
($\ref{18}$) $\to$ pionowa długość docisku $ x_V = = 360 – \sqrt{360^2 – 54 \cdot \left[ 54 +2 \cdot ( 240+12) \right]} = 44,6 \, mm$
($\ref{19}$) $\to$ $\le x_{V, lim}= 0,4 \cdot 0,88 \cdot 360= 126 \, mm$
($\ref{21}$) $\to$ całkowita szerokość krzyżulca betonowego $x= \sqrt{44,6^2 + 54^2}= 70,0 \, mm$
Ramiona siły
($\ref{14}$) $\to$ ramię pionowe $z= 360 – 44,6/2 = 337,7 \, mm$ ; ramię poziome $ a = 240 + 54/2 +12 = 279 \, mm$
Kąt pochylenia krzyżulca betonowego
($\ref{17}$) $\to$ $ ctg \, \Theta = ctg\, \cfrac{44,6}{46}= 0,826$ ; $\Theta = arcctg \, 0,826 = 50,44^o$ ; $ ctg\, \Theta = \cfrac{279}{337,7}= 0,826$
Sprawdzenie dopuszczalności: ($\ref{14}$) $\to$ $ 0,5 < ctg \,\Theta= 0,826 \le 1,0 \to$ OK
Zbrojenie główne rozciągane
($\ref{23}$) $\to$ $ F_{td} = 400 \cdot 0,826 + 80 \cdot ( 1 + 60/337,7) = 424,6 \, kN > 0,5 \cdot 400 = 200 \, kN$
($\ref {24}$) $\to$ pierwsze przybliżenie $F_{td} \approx 1,3 \cdot \left ( 400 \cdot \cfrac{ 240}{400} + 80 \right) = 416 \, kN$
Różnica pomiędzy rozwiązaniem ścisłym i oszacowaniem $(424,6 /416-1) $ =2% i jest akceptowalna w obliczeniach inżynierskich
Pole zbrojenia zbrojenia głównego
$A_s= \cfrac{424,6}{435}\cdot 1o^1 = 9,76 \, cm^2$ $ \to$ przyjęto 2Ø16+ 2Ø20
Sumaryczne pole przekroju prętów $A_s= 2\cdot \pi/4 \cdot (2^2 +1,6^2) 10,3 \, cm^2$
Zakotwienie zbrojenia głównego
Zakotwienie spawaniem do kątownika brzegowego
Grubość spoiny połączenia z rys.24 przy której połączenie będzie miało wytrzymałość pręta dla stali zbrojenia- kątownika B500-S355
($\ref{46}$) $\to$ $a_{eq} = 0,296\cdot 20 = 6 \, mm$
Dla połączenia wykonanego na budowie $a=6/0,9=7 \le 0,4\cdot min \, d =0,4\cdot 16= 7 \, mm$
Przyjęto a= 7 mm dla prętów o obu średnicach.
W przypadku zwymiarowania spoiny nie na nośność pręta, ale na siłę należy zastosować mnożnik zmniejszający w stosunku pola przekroju zbrojenia potrzebnego do przyjętego $9,76/10.3= 0,95$
czyli $a= 0,95 \cdot 7 = 7 \, mm$
Zakotwienie pętlami poziomymi
$ 2 \cdot F_{bt} = F{td}= 424,6 \, kN$
Rozdział sił na pętle $Ø20$ i $Ø16$
$\sum Ø_j^2 = 2\cdot (20^2+16^2)= 1312 \, mm^2$
$c=40 \,mm$ , otulenie osiowe $a_1=c+Ø/2 = 40+20/2= 50 \ mm$
odległość osiowa pomiędzy warstwami przyjęto $a_2= 50 \, mm$
$ F_{bt} = \begin {cases}
424,6 \cdot \cfrac{16^2}{1312}=82,9 \, kN & \text{ dla Ø16 },\\
424,6 \cdot \cfrac{20^2}{1312}=129,5 \, kN & \text{ dla Ø20 },\\
\end{cases}$
$ a_b = \begin {cases}
a_2/2 =5/2=2,5\, cm & \text{ dla Ø16 },\\
a_1 = 5 \, cm & \text{ dla Ø20 },\\
\end{cases}$
Wymagana średnica pętli ($\ref{76}$) $\to$
$ Ø_{m,min} = \begin {cases}
\cfrac{82,9}{21,43} \cdot 10^1 \left( \cfrac{3}{2,5} +\cfrac{3}{2\cdot 1,6}\right)= 27,5 \, cm & \text{ dla Ø16 },\\
\cfrac{129,5}{21,43} \cdot 10^1 \left( \cfrac{3}{7} +\cfrac{3}{2\cdot 2}\right)= 27,2 \, cm& \text{ dla Ø20 },\\
\end{cases}$
Przyjęto pętle o średnicy $Ø_m =300 \,mm$
otulenie boczne $c=(400-300)/2-20/2= 40 \, mm$
Zakotwienie przyspojonymi prętami poprzecznymi
Przyjęto dwa pręty poprzeczne $Ø 16$ umieszczone jak na rys. 25 (oznaczono na czerwono)
(rys.3) $\to$
długość podkładki $l_p= 340\, mm$
odległość osi podkładki od czoła wspornika $100 \,mm$
otulenie czołowe $c_2=50 \, mm$
fizyczna długość zakotwienia $l_{bf}=170 -40= 130 \, mm$
otulenie w kierunku prostopadłym dla obu prętów $c = 40 \, mm$
Zmienne otulenia
($\ref{46}$) $\to$ $x= \cfrac{2\cdot 40}{19}+1= 6 $
($\ref{45}$) $\to$ $ y = 0,015+0.14 \cdot e^{-0,18 \cdot 6}= 0,0625 $
Średni nacisk na długości zakotwienia
($\ref{52}$) $\to$ $\sigma_{cm}=\cfrac{F_{Ed}}{l_p \cdot l_{bf}}= \cfrac{400}{130 \cdot 340}\cdot 10^3= 7,16 \, MPa$
($\ref{51}$) $\to$ $\sigma_{td} = \cfrac{21,43 – 7,16} {0,0625} = 228,3 \, MPa > 3 \cdot 21,43 = 64,3 \, MPa$ $\to$ $\sigma_{td}= 64,3 \, MPa$
Obliczeniowa długość pręta poprzecznego
($\ref{42}$) $\to$ $l_{td} =1,16 \cdot 16 \cdot \sqrt{\cfrac{435}{64,3}} = 125,6 > l_t= 90 \, mm$ $\to$ $l_{td} = 90 \, mm$
gdzie $l_t = min \{340-2\cdot 40 \,;\, 90 \}= min \{260 \,;\, 90\} \, mm $ ; 260 mm – długość pręta poprzecznego; 90 mm – rozstaw prętów głównych
Nośność spoiny ($\ref{42}$) ; ($\ref{45}$) $\to$
$ F_{btd} = F_{wd}= \begin {cases}
\approx 0,5 \cdot \pi\cdot 1,6^2/4 \cdot 435 \cdot 10^1= 43,7 \, kN < F_{btd,,max} & \text{ dla }Ø16,\\
\approx 0,5 \cdot \pi\cdot 2,0^2/4 \cdot 435 \cdot 10^1= 63,3 \, kN < F_{btd,max} & \text{ dla }Ø20,\\
\end{cases}$
$ F_{btd,max}= \begin {cases}
90 \cdot 16 \cdot 64,3 \cdot 10^{-3} = 92,6 \, kN & \text{ dla }Ø16,\\
90 \cdot 20 \cdot 64,3 \cdot 10^{-3} = 115,7 \, kN & \text{ dla }Ø20,\\
\end{cases}$
Łącznie udział prętów poprzecznych dla $2Ø20$ + $2Ø16$:
$\sum F_{btd}=2\cdot (63,3 + 43,7) = 214,0 \, kN$
Ponieważ zastosowano dwa pręty poprzeczne w rozstawie $3Ø$ , to siłę kotwiącą zwiększa się 1,41 razy i ostatecznie
$\sum F_{btd}=q,41 \cdot 214,0 = 301,7 \, kN$
Siłą w prętach kotwionych z uwzględnieniem przyspojonych prętów poprzecznych jest znacznie zmniejszona do
$ F_{sd} 424,6 -301,7 = 122,9 \, kN$
Naprężenia w pręcie kotwionym
($\ref{52}$) $\to$ $ \cfrac{122,9}{10,3}\cdot 10 = 119,3 \, MPa$
Graniczne naprężenie przyczepności ($\ref{45}$) $\to$
$f_{bd}=2,25 \cdot 0.7 \cdot 1,0 \cdot 1,45 = 2,284 \, MPa$
Długość podstawowego zakotwienia z uwzględnieniem przyspojenia prętów ($\ref{51}$) $\to$
$ l_{b,rqd}= \begin {cases}
\cfrac{16 \cdot 119,3 \cdot 2,284}= 209 \, mm & \text{ dla }Ø16,\\
\cfrac{20 \cdot 119,3 \cdot 2,284} = 261 \, mm & \text{ dla }Ø20,\\
\end{cases}$
Współczynnik korekcyjny w sytuacji ograniczenia odkształceń przez przyspojone zbrojenie poprzeczne
($\ref{51}$) $\to$ \alpha_4=0,7 $
Potrzebna długość zakotwienia po uwzględnieniu przyspojonych prętów (tylko dla $Ø20$ jako bardziej wymagających)
($\ref{45}$) $\to$ $l_{bd} = 261 \cdot 0,7 = 183 > l_{bF} =130 \, mm$
$\to$ wymagana jest większa długość zakotwienia od możliwej do osiągniecia, więc należy uwzględnić jeszcze inne czynniki zmniejszające wymaganą długość zakotwienia.
Zakotwienie nie przyspojonymi prętami ( pionowymi strzemionami)
W rozważanym przypadku na długości zakotwienia (od wewnętrznej krawędzi płytki licząc zastosowano dwa strzemion czterocięte $Ø8$ (rys.18), czyli
$\sum A_{st}=2\cdot 4 \cdot \pi/4 \cdot 0,8^2 = 4,02 \, cm^2$
Współczynnik $\alpha_3$:
$K=0,1$
pole przekroju pojedynczego pręta o największej średnicy $A_s = \pi\cdot 2,0^2/4 = 3,14 \, cm^2$
$\lambda =\cfrac{4,02}{3,14} – 0,25= 1,03$
Współczynnik $\alpha_3$ ($\ref{42}$) $\to$
$\alpha_3= 1- 0,1 \cdot 1,03 = 0,897 > 0,7$ $\to$
Potrzebna długość zakotwienia po uwzględnieniu przyspojonych prętów poprzecznych i nie przyspojonych strzemion pionowych
($\ref{45}$) $\to$ $l_{bd} = 261 \cdot 0,7 \cdot 0,897 = 164 > l_{bF} =130 \, mm$
$\to$ wymagana jest większa długość zakotwienia od możliwej do osiągniecia, więc należy uwzględnić jeszcze inne czynniki zmniejszające wymaganą długość zakotwienia.
Wpływ nacisku poprzecznego
Nacisk poprzeczny szacujemy jako $\sigma_{cm} =7,16 \, MPa$ z zależności ($\ref{52}$) (wyliczono wyżej)
Współczynnik $\alpha_5$ ($\ref{42}$) $\to$ $\alpha_5 = 1- 0,04 \cdot 7,16= 0,72 > 0,7 $
Jednoczesność wpływu czynników
Ograniczenie współczynników korekcyjnych długość zakotwienia
($\ref{51}$) $\ to$ $ \alpha_2 \cdot \alpha_3 \cdot \alpha _5 = 1,0 \cdot 0,897 \cdot 0,72 = 0,64 < 0,7 $
Skuteczność zakotwienia przyspojonymi prętami
Długość zakotwienie wyznaczona dla przyspojonych prętów poprzecznych można zmniejszyć współczynnikiem $\alpha=0,7$, czyli
$l_{bd}= 183 \cdot 0,7 = 128 < l_{bF} =130 \, mm$ $\to$ zakotwienie jest skuteczne.
Pętle pionowe
Rozważono zastosowania zbrojenia głównego w formie pętli pionowych z normowym wyokrągleniem $4Ø$ z węzłami typu T-T (rys.3)
Rozdział sił na pręty $Ø20$ i $Ø16$ ($\ref{52}$) $\to$ ( też w przykładzie wyżej dla pętli)
$\sum Ø_j^2 = 2\cdot (20^2+16^2)= 1312 \, mm^2=13,12 \, cm^2 $
$ F_{td} = \begin {cases}
424,6 \cdot \cfrac{16^2}{1312}=82,9 \, kN & \text{ dla }Ø16,\\
424,6 \cdot \cfrac{20^2}{1312}=129,5 \, kN & \text{ dla }Ø20,\\
\end{cases}$
Naprężenia docisku do betonu w narożu dla poszczególnych prętów ($\ref{52}$) $\to$
$ \sigma_{b} \approx\begin {cases}
0,45 \cfrac{82,9}{1,6^2}\cdot 10^1 = 145,7 \gg \sigma_{Rd, max} =14,14 \, MPa & \text{ dla }Ø16,\\
0,45 \cfrac{129,5}{2,0^2}\cdot 10^1 = 145,7 \gg \sigma_{Rd, max} =14,14 \, MPa\, MPa & \text{ dla }Ø20,\\
\end{cases}$
gdzie $\sigma_{Rd, max} =14,14 \, MPa$ wyznaczono na początku przykładu z ($\ref{11}$)
lub dla każdego pręta – też z wzoru ($\ref{52}$) :
$ \sigma_b \approx 0,45 \cfrac{424,6}{13,12}\cdot 10^1 = 145,7 \, MPa \gg \sigma_{Rd, max}$
Wniosek:
Zastosowanie pętli pionowych (zbrojenia brzegowego) z promieniem wygięcia 4d doprowadzi do zmiażdżenia betonu w wygięciu pręta.
Należy zastosować inny rodzaj zakotwienia.
Krzyżulec betonowy
$(\ref{25})^1$ $\to$ $ F_c = (424,6 – 80) \cdot cos 50,44^o + 400 \cdot sin 50,44^o = 527,85 \, kN$
$(\ref{25})^2$ $\to$ $ F_c = \sqrt{ (424,6 – 80)^2 + 400^2}= 527,96 \, kN$
$(\ref{25})^3$ $\to$ $\to$ użyteczne oszacowanie $ F_c \approx 400\cdot \sqrt{1+\cfrac{279^2}{360^2}}= 506,1 \, kN$
Różnica między rozwiązaniem ścisłym i oszacowaniem $ 527,9/506-1$ = 4% jest akceptowalna w projektowaniu wstępnym (właściwym).
$(\ref{27})^2$ $\to$ naprężenia w krzyżulcu w węźle (1) – szerokość krzyżulca $x_{3}=70 \, mm$
$\sigma_c = \cfrac{527,9} { 7,0 \cdot 40,0} \cdot 10^1 = 18,85 \le 18,86 \, MPa$
Efektywne szerokości krzyżulca w węźle (2) oraz pomiędzy węzłami (1) oraz (2) muszą być nieco większe i wynoszą
pomiędzy węzłami (1)-(2) $x_{(1)-(2)}\approx \cfrac{527,9}{40 \cdot 11,32}\cdot 10^{-1+3}=116 \, mm$
w węźle (2) $x_{(2)}\approx \cfrac{527,9}{40 \cdot 16,03}\cdot 10^{-1+3}=82 \, mm$
Przykład 2 [ Krótki wspornik – metoda ST, BS8110]
Przykład 1 rozwiązać metodą ST BS8110 [11]
Dane
Z przykładu 1:
$f_{cd}=30/1,4 =21,43 /, MPa$,
$f_{yd}= 500/1,15= 435 \, MPa$.
$F_{Ed} = 400 \, kN$ ,
$ H_{Ed} = 80 \, kN$
wysięg wspornika $a_c= 240 \, mm$
wysokość wspornika $h = 400 \, mm$
otulenie osiowe górne $a_u=40 \, mm$
wysokość użyteczna $d=400-40=360\,mm$
szerokość wspornika $b = 400 \, mm$
Wysokość strefy ściskanej
Parametr $k_E$ obciążenia zewnętrznego $F_{Ed}$
($\ref{34}$) $\to$ $k_E=\cfrac {240 \cdot 400\ \cdot 21,43} {400}\cdot 10^{-3}= 5,143 $
Wysokość zredukowana docisku $x_{eff}$ ($\ref{35}$ $\to$
$ x_{eff} = \cfrac{ 2 \cdot 350} { (1+ 2 \cdot 5,143) } \cdot \left [ 1+ 5,143 \mp \sqrt{ 5,143^2 – (240/360)^2 (1+ 2\cdot 5,143) } \right ]= \{ 96,5 \,;\, 687,3 \} \, mm$
Przyjęto wartość fizycznie możliwą:
$ x_{eff}=96,5 \, mm$
czyli $x=96,5/0,8 = 120,6 \, mm$
Geometria ST
($\ref{29}$) $\to$
$z=360- 96,5/2=311,7 \, mm$
$s=\sqrt{240^2 + 311,7^2}= 393,4 \,mm $
$\Theta= arc sin (311,7/393,4)= arc sin \, 0,792 = 52,4 ^0$
Sprawdzenie dopuszczalności: ($\ref{14}$) $ \to$ $ 0,5 < ctg \,\Theta= 0,77 \le 1,0 \to$ OK
Dla porównania w przykładzie 1 uzyskano $\Theta = 50,44^o$ , czyli rozbieżność rozwiązań wynosi (52,4/50,44) -1 = 4%
Siły w prętach
($\ref{36}$) $\to$ $F_c =\cfrac{400}{sin \, 52,4^0}= 504,9 \, kN$
($\ref{37}$) $\to$ $N_{td,V} = 504,9 \cdot cos \, 52,4^0 = 400 \cdot ctg \, 52,4^0 = 308,1 \, kN$
($\ref{31}$ ) $\to$ $F_{td} =308,1 + 80 = 388,1\, kN$
Dla porównania w przykładzie 1 uzyskano $ F_{td} = 424,6 \, kN $ , czyli rozbieżność wynosi (388,1/424,6) -1 = 9%
Zbrojenie główne rozciągane
Pole zbrojenia zbrojenia głównego
$A_s= \cfrac{388,1}{435}\cdot 1o^1 = 8,92 \, cm^2$ $ \to$ przyjęto 2Ø16+ 2Ø20
Sumaryczne pole przekroju prętów $A_s= 2\cdot \pi/4 \cdot (2^2 +1,6^2) 10,3 \, cm^2$
Zakotwienie o zagięty w narożu i przyspojony pręt poprzeczny
Zastosowano zakotwienie spawaniem o zagięte pręty uzupełniające wg rys. 12.
Ten typ zakotwienia nie wymaga sprawdzenia obliczeniowego.
Przykład 3 [ Podcięcie belki -nowa metoda ST]
W przykładzie pokazano zastosowanie nowej metody projektowania podcięcia belki na przykładzie z pracy [17], Example 6.11.
Dane
rys.17 oraz rys.18 $\to$:
$h=1400 \, mm$,
$ b=800 \, mm$,
$h_k=675 \, mm$,
$a_h=a_u = 50 /mm$
$d_k= h_k-a_u = 675- 50= 625 /, mm$
$l_k=500 \, mm$,
$a_v=275 \, mm$,
długość belki $l_{eff}=8000 \, mm$,
szerokość podkładki centrującej 160 mm,
beton C25/30,
stal B450C.
Obciążenie równomiernie rozłożone na długości belki
$Q_{Ed}= 250 \, kN/m$ ,
Reakcje z obliczeń statycznych:
pionowa $F_{Ed}=250\cdot 8 /2=1000 \, kN$,
pozioma $H_{Ed}=0 $ ,
Przyjęto $H_{Ed}=0,2 \cdot F_{Ed} =0,2 \cdot 1000 = 200 \, kN$.
Dobór podkładki
Wymagana powierzchnia podkładki ze względu na docisk do betonu ($\ref{14}$) , czyli wyżej wyliczone $f_{Rd}=18 \, MPa$
($\ref{7}$) $\to$ $A_p \ge \cfrac{V_{Ed}}{f_{Rd}}= \cfrac{1000}{21}\cdot 10^1 = 554 \, cm^2$
$\to$ przyjęto podkładkę $l_p= b- 2\cdot 50 = 800-100= 700\, mm$ , $b_p = 160 \, mm$ , $A_p= 70\cdot 16= 1120 \, cm^2 > 554 \, cm^2$
($\ref{7}$) $\to$ $\sigma_{Ed}=\sigma_m= \cfrac{1000}{1120}\cdot 10^1 = 8,9 \, MPa$
$k_{\sigma}=\cfrac{\sigma_m}{f_{cd}}=\cfrac{8,9}{21,43}=0,42$
Tab.1. minimalna szerokość podkładki
$\to$ $min \, a_1= 140\,,mm$ dla $k_{\sigma}=0,42$
Przyjęto $b_p = 160 > 140\, mm$ $\to$ OK
Przyjęto podkładkę elastomerową na średnie naprężenia pod podkładką $\sigma_m= 8,9 \,MPa$
niezbrojoną typu > N10 prod. np. Betomax (liczba po N oznacza wytrzymałość podkładki w MPa)
Sprawdzenie wymiarów podcięcia z warunku odchyłek wykonawczych
Przeprowadzić analogicznie jak w przykładzie 1.
Model ST
Dla podcięcia wg rys. 18 mamy:
$\Theta = arctg \, \frac{675-50}{313}= 63,4^o$,
$\alpha= 45^0$,
$e = 2\cdot 50 = 100 \, mm$,
$e_5= 2\cdot 50 = 100 \, mm$,
$h_k=675 \, mm $,
$d_k=675=50 = 625 \, mm $,
$a_k= 500 \, mm$,
$a_v = 275 \, mm$,
$ h_D= 1400-675 -50 = 675 \, mm$,
$ c_2= \cfrac {100+ 275 \cdot sin 45^o}{ sin (45^0 +63,4^0} = 310 \, mm$,
$ a_5= 500 -100 \cdot cos45^0= 429 \, mm$.
Współrzędne punktów modelu
(\ref{43}) $\to$ współrzędne $(x, y)_i$ wg rys. 18
$ (x,y)_i = \begin {cases}
(1) \to = & (0\, ;\, 0) \\
(2) \to (310 \cdot (cos \, 63,4^0 ; \, sin \, 63,4^0 ) & = (139 \, ;\, 277) \, mm\\
(3) \to (625 \cdot (ctg \, 63,4^0 \, ;\, 1) & = (313 \, ;\, 625) \, mm \\
(4) \to (275 + 675 \cdot ctg \, 45^0 +100/sin \, 45^0 \, ;\, – 675) &= (1091 \, ; \, -675) \, mm \\
(5) \to (275 – 429 \,;\, 100 /cos, 45^0 +429 \cdot tg \, 45^0) & = ( -154 \,;\, 571 ) \, mm \\
\end{cases}$
Długości prętów modelu ST
(\ref{44}) $\to$ długości prętów modelu
$ L_{T,S}= \begin {cases}
L_{T1} = \cfrac{ 675 + 310 \cdot sin \, 63,4^0}{sin \, 45^0} =1347 \, mm \\
L_{T2} =\cfrac{500 – 275/2 }{cos \, 45^0}+\cfrac{100 \cdot cos\, 63,4^0 + 275 /2 \cdot sin (45 – 63,4)^0 } {cos\, 45^0 \cdot sin (45 + 63,4)^0} – 100 = 415 \, mm\\
L_{S1} = 310 \, mm \\
L_{S2} = \sqrt{(625 \cdot ctg \, 63,4^0 -310 \cdot cos \, 63,4^0)^2 +(625 -310 \cdot sin \, 63,4^0)^2}= 389 \, mm\\
\end{cases}$
Reakcje podpór modelu
$dF= F_{Ed} \cdot cos \, \Theta – H_{Ed} \cdot sin\, \Theta = 1000 \cdot cos 63,4^0 – 200 \cdot sin 63,4^0 = 268,9 kN$,
$\sum L_T= 1347 + 415= 1762 \, mm$
$\sum L_S= 310 + 389 = 699 \, mm$
$c_R= \cfrac {1762}{699} \cdot \cfrac{415}{389} \cdot \cfrac{cos\, 45^0}{sin (45 + 63,4)^0} = 0,3155$
(\ref{48}) $\to$
$ H,V = \begin {cases}
H_4= 268,9 \cdot 0,3155 = 84,84 \, kN \\
H_3 = 200 + 84,84 \cdot \cfrac {1762}{415} = 560,4 \, kN \\
V_3 = 560,4 \cdot tg\, 63,4^0 + 268,9 \cdot \cfrac{ 1347}{ 389} \cdot \cfrac{3}{cos\,63,4^0}= 639,6 \, kN \\
V_4 = 84,8 \cdot tg \, 45^0 = 84,84 \, kN \\
H_5= 84,8\cdot \cfrac{1347}{415}= 275, 6 \, kN\\
V_5 = 275,6 \cdot tg\, 45^0 = 275,6 \, kN \\
\end{cases}$
Siły w prętach modelu
(\ref{51}) $\to$
$(N , V) = \begin {cases}
N_{T1} = 84,84 \cdot cos \,45^0 + 84,84 \cdot sin \, 45^0 & = 120,0 \, kN = \cfrac{84,84 }{ cos \, 45^0 }= + 120,0 \, kN \\
N_{T2} = 275,6 \cdot cos \, 45^0 + 275, 6 \cdot sin \, 45^0 = 389, 8 \, kN & = 120,0 \cdot \cfrac {1347}{415}= – 389,7 \, kN\\
N_{S1} = 200 \cdot cos \, 63,4^0 + 1000 \cdot sin \, 63,4^0 = 983,7 \, kN\\
N_{S2 }= 560,4 \cdot cos\,63,4^0 + 639,6 \cdot sin \, 63,4^0 = 822,6 \, kN \\
V_{T1} = 84,84 \cdot sin \, 45^0 – 84,84 \cdot cos \, 45^0 =0 \, kN & = 0 \, kN\\
V_{T2} = 275,6 \cdot sin \, 45^0 – 275,6 \cdot cos \, 45^0 =0 \, kN & = 0 \, kN\\
V_{S1} = 1000 \cdot cos \, 63,4^0 – 200 \cdot sin \, 63,4^0 =258,9 \, kN\\
V_{S2}= 639,6 \cdot cos \, 63,4^0 – 560,4\cdot sin \, 63,4^0 = 214,7 \, kN\\
\end{cases} $
Zbrojenie główne rozciągane
Pole zbrojenia zbrojenia głównego
na odcinku (2-4) $N_t= +120 \, kN$ (rozciąganie)
na odcinku (5-2) $N_t= – 389.7 \, kN$ (ściskanie)
$A_{s, potrz} = \cfrac{389,7}{435}\cdot 1o^1 = 8,95 \, cm^2$ $ \to$ przyjęto 2Ø20+2Ø16
$A_s= 2\cdot \pi/4 \cdot (1,6^2+2^2 )= 10,3 > 8,95\, cm^2 $
Zakotwienie zbrojenia głównego
Zakotwienie spawaniem do płytki końcowej – rys .19
stal płytki S355
średnica płytki $D_p = 3\cdot 20 = 60 \,mm$
Naprężenia dociskowe do betonu
$\sigma_m= \cfrac{389,7}{\pi\cdot 6,0/4}\cdot 10^1= 11,2 \le 18,86 \, MPa$,
gdzie
($\ref{11}$) $\to$ $\sigma_{Rd,max}= 0,88 \cdot 1,0 \cdot 30/1,4 = 18,86 \, MPa$,
($\ref{12}$) $\to$ $ \nu’ = 1+\cfrac{32}{250}= 0,88$
($\ref{13}$) $\to$ $k= 1,00 \text{ pręt ściskany}$
Grubość spoiny połączenia z rys.24 przy której połączenie będzie miało wytrzymałość pręta
($\ref{46}$) $\to$ $a_{eq} = 0,296\cdot 20 = 6 \, mm$
Zakotwienie pętlami ukośnymi – rys .20
Pętle w dwóch warstwach: górą Ø20+ dołem Ø16
w odległości osiowej pomiędzy warstwami $a_2= 50 \, mm$
$\sum Ø_j^2 = 2\cdot (20^2+16^2)= 1312 \, mm^2$
$c=40 \,mm$ , otulenie osiowe $a_1=c+Ø/2 = 40+30/2= 50 \ mm$
$ F_{bt} = \begin {cases}
389.7 \cdot \cfrac{16^2}{1312}=76,0 \, kN & \text{ dla }Ø16,\\
389.7 \cdot \cfrac{20^2}{1312}=118,8 \, kN & \text{ dla }Ø20,\\
\end{cases}$
Wymagana średnica pętli ($\ref{76}$) $\to$
$ Ø_{m,min} = \begin {cases}
\cfrac{76,0}{21,43} \cdot 10^1 \left( \cfrac{3}{2,5} +\cfrac{3}{2\cdot 1,6}\right)= 25,3 \, cm & \text{ dla }Ø16,\\
\cfrac{118,8}{21,43} \cdot 10^1 \left( \cfrac{3}{5,0} +\cfrac{3}{2\cdot 2}\right)= 24,9 \, cm& \text{ dla } Ø20,\\
\end{cases}$
gdzie
$ a_b = \begin {cases}
a_2/2 =5/2=2,5\, cm & \text{ dla }Ø16,\\
a_1 = 5 \, cm & \text{ dla }Ø20,\\
\end{cases}$
Przyjęto pętle o średnicy $Ø_m =260 \,mm$
otulenie boczne $c=(400-260)/2-20/2= 60 \, mm$
Krzyżulec betonowy
$(\ref{27})^2$ $\to$ naprężenia w krzyżulcu
w węźle (1) – szerokość krzyżulca $ x= b_p = 160 \, mm$
$\sigma_c = \cfrac{983,7} { 16,0 \cdot 40,0} \cdot 10^1 = 15,36 \le 18,86 \, MPa$
w węźle (3) – szerokość krzyżulca $x=0,8\cdot 160=128 \, mm$
$\sigma_c = \cfrac{822,6} { 12,8 \cdot 40,0} \cdot 10^1 = 16,0 \le 18,86 \, MPa$
Pętle poziome
Pętle poziome stanowią zbrojenie na ścinanie krzyżulca pionową siła rozwarstwiającą
(w przybliżeniu) $V=F_{Ed}=1000 \, kN$
(dokładniej) $V=N_{S1}\cdot cos \, \Theta + V_{S1}\cdot \sin \, \Theta = 983,7 \cdot cos, 63,4 + 258,9\cdot sin \, 63,4 = 672,0 \, kN$
Potrzebne pole pętli
$A_{w, potrz} = \cfrac{1000}{435}\cdot 10^1 = 23,0 cm^2$ $ \to$ przyjęto 4 pętle o przekroju ścinanym 2 x4 =8Ø20
$A_w= 8\cdot \pi/4 \cdot 1,6^2 = 25,1 > 23,0\, cm^2 $
Strzemiona pionowe
Stosuje się strzmiona konstrukcyjne jak dla strefy przypodporowej belki w rozstawie min $s=150 \, mm$
Przykład 4 [ Podcięcie belki. Porównanie MES z modelem analitycznym ST i analiza wpływu przegubów w zbrojeniu]
W celu sprawdzenia poprawności modelu ST z rys 18 i uzyskanych formuł analitycznych – system ST rozwiązano w programie numerycznym Consteel 17 w schemaciie pokazabym na rys, 43. .
W tab.3 porównano reakcje podpór i siły w prętach w modelu analitycznym ST i numerycznym MES z przegubami i bez przegubów w węźle (2). Uzyskano zgodność rozwiązania analitycznego oraz numerycznego MES w modelu z przegubami oraz niewielkie różnice (max do 2%) dla modelu z ciągłym zbrojeniem (bez przegubów w węźle (2)).
Tab.3. Porównanie sił (w kN) w modelu analitycznym ST i numerycznym MES
z przegubami i bez przegubów w węźle (2)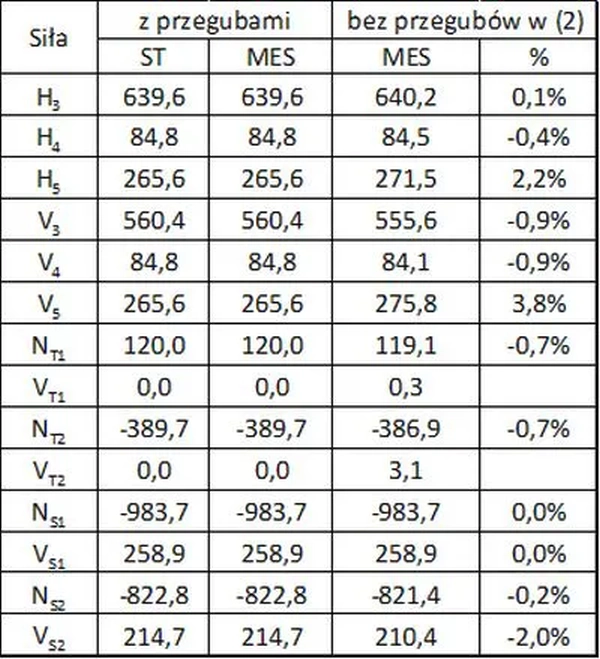
Literatura
- Mōrsch E. (1929). Der Eisenbetonbau, seine Theorie und Anwendung. Verlag K. Wittwer
- PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- Bachmann H., Steinle A. (2011), Precast concrete structures. Ernst & Sohn : John Wiley & Sons, Inc.
- Abdul-Razzaq S. K., Dawood A. A., Corbel strut and tie modeling – Experimental verification, Structures 26 (2020) 327–339
- Bachmann H., Steinle A., Precast Concrete Structures, Ernst+Sohn Berlin, 2011
- Niedenhoff Strut and Tie approach, PhD thesis, Glasgow, 1961
- Urban T., Przykłady projektowania krótkich wsporników. Zeszyt 2, Wydawnictwo Politechniki Łódzkiej, Łódź, 2012
- Knauff M., Golubińska A., Knyziak P. (2014). Tablice i wzory do projektowania konstrukcji żelbetowych z przykładami obliczeń, Wydanie drugie. PWN
- Stenzel, G; Fingerloos, F., Konstruktion und Bemessung von Details nach DIN 1045-1. Beton-Kalender, 2007, Teil 2
- Allen A.H. (1988) Reinforced Concrete Design to BS8110 Simply Explained E.& F.N. Spon London New York
- Buildings Department of Hong Kong, Manual for Design and Detailing of Reinforced Concrete to the Code of Practice for Structural Use of Concrete 2013 September, Hong Kong, 2013
- American Concrete Institute , ACI 318-14. , Building code requirements for structural concrete, Detroit 2014
- Steinle A. (1975), Zur Frage der Mindestabmessungen von Konsolen. Beton Und Stahlbeton, 6, 150–153
- Hegger J., RoeserW., Lotze, D. (2004), Kurze Verankerung langen mit Rechteckan-kern Bewerhung + Bauausfuhrung. In Beton – Kalendar 2004 (Vol. 1
- Reineck K. H. (2005). Modellirung der D-Bereiche bei Vertigteilen. In Beton Kalendar 2005 (Vol. 2, p. 241ff
- Stenzel G., Fingerloos, F. (2007), Konstruktion und Bemessung von Details nach DIN 1045-1. In Beton – Kalendar 2007 (Vol. 2
- ECP ASBL. (2008). Eurocode 2. Worked Examples (rev A 31-03-2017), European Concrete Platform. http://www.europeanconcrete.eu/publications/eurocodes
- PN-EN ISO 17660-1:2008, Spawanie -Spawanie/zgrzewanie stali zbrojeniowej – Część 1: Złącza spawane/zgrzewane nośne
- PN-EN 1993-1-8, Eurokod 3: Projektowanie konstrukcji stalowych – Część 1-8: Projektowanie węzłów
- PN-EN 1337-3:2010, Łożyska konstrukcyjne – Część 3: Łożyska elastomerowe
- DIN 4141-3:1984-09, Lager im Bauwesen; Lagerung für Hochbauten
- Navratil, J., Ševcik, P., & Michalcík, L. (2017). A solution for walls and details of con-crete structures. 24. Czech Concrete Days (2017). https://resources.ideastatica.com/Content/03_Concrete/Verifications/Articles/A_solution_for_walls_and_details_of_concrete_structures_US.pdf
________________________________