Artykuł w ciągu ostatnich 24 godzin czytało  0 Czytelników
Uwagi i recenzje podręcznika  przesyłać na adres: wydawnictwo@chodor-projekt.net lub  leszek@chodor-pojekt.pl
spis treści prodręcznika: [ Imperfekcyjna metoda projektowania konstrukcji ]

Część 2-3
Nawigacja: [2-2:  Geneza metod imperfekcyjnych ]  ⇐  ⊗   ⇒ [2:4 : Skalowanie pierwszej postaci wyboczenia ]

Formuła Ayrton-Perry (APF) [1] jest podstawą współczesnej formacji współczynników wyboczenia i zwichrzenia  mimo, że została sformowana dla prostego przypadku ściskanego osiowo pręta idealnie sprężystego, obarczonego zdeterminowaną imperfekcją w postaci łukowego wygięcia. Obecnie formułę tę uogólniono na przypadek łącznego działania wyboczenia i zwichrzenia, czym zastąpiono skomplikowany układ współczynników korelacji z normy Eurokod. 

Artykuł w opracowaniu

Uogólnienie formuły APF na zwichrzenie pręta

Podejście Eurokod

Maquoi i Janss (1991), [2] podjęli próbę uogólnienia formuły APF na przypadek zwichrzenia pręta w drodze skalibrowania formuły pierwotnej do wyników eksperymentalnych. W późniejszej wersji normy [3] zaimplementowano zmodyfikowaną wersję tej formuły w postaci przedstawionej w rozdziale postać Eurokod APF .Wyprowadzenie teoretyczne formuły APF na przypadek skręcania i zwichrzenia prętów podali Chapman  i Buhagiar (1993) [4]. 

Modyfikacja Taras-Greiner

Taras i Greiner (2010) [5]  zaproponowali zmodyfikowaną postać współczynnika zwichrzenia , która jest dokładniejsza niż wyrażenia podane w EC3 [3] i jednocześnie bardziej spójna z innymi zasadami projektowania prętów. Zmodyfikowaną  postać uzyskano w drodze kalibracji numerycznej ogólnych krzywych normowych dla belek „testowych” pokazanych na rys. 1. Kalibrację przeprowadzono metodą GMNiA (Geometrycznie i Materiałowo Nieliniowa Analiza  MES) dla belek jednoprzęsłowych zginanych równomiernie, obarczonych imperfekcją łukową $e_0 = L/1000) i wykonanych z dwuteowników europejskich, obarczonych naprężeniami resztkowymi.

Rys. 1. Przypadek „benchmark”. Założenia przyjęte w analizie GMNiA [5]– fig. 5

Krzywe teoretyczne podobne do podanych w nomie Eurokod (2-2.13) i (2-2.14) dla przypadku zwichrzenia zaproponowano w zmodyfikowanej postaci

$$\begin{equation} \chi_{LT}=\cfrac{1}{\Phi_{LT} +\sqrt{\Phi_{LT}^2 –  \overline \lambda_{LT}^2}} \quad  \le 1 \label {1} \end{equation}$$

$$\begin{equation} \Phi_{LT}= 0,5 \cdot \left ( 1+ \Theta_{Taras} + \overline \lambda_{LT}^2 \right )  \label{2}\end {equation}$$

gdzie zmodyfikowany (w stosunku do (2-2.15) parametr imperfekcji  $\Theta_{Taras}$ wynosi

$$\begin{equation} \Theta_{Taras}=\alpha_{Taras} \cdot(\overline\lambda_z -0,2) \cdot \sqrt{\cfrac{W_{y,el}}{W_{z,el}}} \cdot \cfrac{\overline \lambda ^2_{LT}} {\overline \lambda^2_z}\label{3}\end {equation}$$

W przypadku kształtowników półzwartych klasy 3 należy dodatkowo sprawdzić warunek:

$$\begin{equation} M_{Ed}< M_{Rd}= \cfrac{W_{y,el}\cdot f_y}{\gamma_{M1}}\label{4}\end {equation}$$

Zmodyfikowane w stosunku do propozycji normy [3] współczynniki klasy imperfekcji dla kształtowników walcowanych należy przyjmować następująco:

$$\begin{equation} \alpha_{Taras} = \begin {cases}
0,16 & \text { dla  } \cfrac{h}{2} \le 1,2\\
0,12 & \text { dla  } \cfrac{h}{2} > 1,2
\end{cases} \label{5} \end {equation}$$

Przypomnijmy, że według obecnej normy [3] granice pomiędzy klasami imperfekcji wyznacza stosunek wymiarów przekroju $h/b=2$, a współczynniki klasy imperfekcji wynosiły: $\alpha_{LT}=0,2$ (krzywa wyboczeniowa (a)) dla niższych przekrojów oraz  $\alpha_{LT}=0,2$ (krzywa wyboczeniowa (b)) dla wyższych przekrojów. Nadto w EC3 wprowadzono procedurę szczególn: $\alpha_{LT}=0,34$ (krzywa wyboczeniowa (a)) dla niższych przekrojów oraz $\alpha_{LT}=0,49$ (krzywa wyboczeniowa (b)) dla wyższych przekrojów. Modyfikacja Taras-Greiner nie przewiduje procedury szczególnej.

Uogólnienie formuły APF na zwichrzenie ze ściskaniem

Formuła Szalai-Papp

Warunki stosowania formuły APF  dla wyboczenia i zwichrzenia

Szalai i Papp (2010) [6] wykazali, że  uogólnienie formuły Ayrton-Perry na przypadek  belki-słupa, podlegającemu wybaczaniu w dwóch kierunkach oraz zwichrzenia – można uzyskać w prostej formie analitycznej, podobnej do znanej formuły APF  tylko wówczas, gdy  formuła amplifikacji typu (1.12) spełnia dwa warunki:
1) liniowa  Liniowość oznacza formułę amplifikacji przemieszczeniowej  typu (2.2.32)
2) spójna.. Spójność polega na tym, że dla poszczególnych form niestateczności i stowarzyszonych przemieszczeń  formuła amplifikacji ma identyczną postać.
W celu zachowania warunku liniowości i spójności formuły amplifikacji podczas oLTBiążania pręta wymagane jest, by  wstępne imperfekcje geometryczne były ułożone w kształt  zgodny z pierwszą postacią sprężystej niestateczności,  Ten warunek nazwiemy warunkiem Szalai-Papp.

W konsekwencji podczas procesu obciążania pręta sprężyste przemieszczenia drugiego rzędu będą proporcjonalne do postaci imperfekcji (czyli pierwszej postaci wyboczenia) – zmienia się tylko amplituda przemieszczeń.  Już w pracy [7] pokazano, że dla  kształtów imperfekcji innych niż pierwsza postać zwichrzenia – formuła amplifikacji staje się nieliniowa  i niespójna. W pracy [6] przeprowadzono formalny dowód powyższego warunku dla trzech przypadków historii oLTBiążenia złożonego: 1)  zmienny moment zginający przy stałym ściskaniu, 2) zmienne ściskanie przy stałym zginaniu, 3) zmienny moment zginający oraz ściskanie przy zachowaniu dla oLTBiążenia jednoparametrowego ( stały stosunek zginania  i ściskania).

Z warunku Szalai-Papp wynika, że stosunek amplitud wygięcia bocznego i skręcenia (a więc i impefekcji) jest stały. Według rozprawy doktorskiej Szalai  [8] i pracy [9] w przypadku zwichrzenia stosunek ten wynosi:

$$ \begin {equation}  i_{LT}= \cfrac{v_0}{\varphi_0} = \cfrac{M_{cr}}{N_{cr,z}}= r_0 \cdot \sqrt{\cfrac{N_{cr,x}}{N_{cr,z}}} \label {6}  \end {equation}$$

Czyste siły krytyczne  dla analizowanego pręta wzorcowego (belki swobodnie podpartej) można przedstawić w postaci:

$$ \begin {equation} M_{cr}= r_0 \cdot \sqrt{N_{cr,x} \cdot N_{cr,z}} \label {7}  \end {equation}$$

$$ \begin {equation} N_{cr,z}=\cfrac{EI_z \pi^2}{L^2} \label {8}  \end {equation}$$

$$ \begin {equation} N_{cr,x}= \cfrac{1}{r_0^2}\left( \cfrac{EI_\omega \pi^2}{L^2}  +GI_T\right) \label {9} \end {equation}$$

gdzie:  $M_{cr}$ moment zginający prowadzący do zwichrzenia; oraz  $N_{cr,z}$, $N_{cr,x}$ –  osiowe siły krytyczne  przy wyboczeniu giętnym z płaszczyzny i wyboczniu skrętnym odpowiednio

W pracy [6] współczynnik  ($\ref{6}$) na przyp[adek zwichrzenia ze ścikaniem LTB zapisano w postaci:

$$ \begin {equation} i_{LTB}=  \cfrac{v_0}{\varphi_0} =  r_0 \cdot \sqrt{ \cfrac{N_{cr,x}-N} {N_{cr,z}-N}} \label {10}  \end {equation}$$

Po wprowadzeniu  pojęcia giętno-skrętnego momentu krytycznego ze ściskaniem

$$ \begin {equation}    M_{cr,N}=r_0\cdot \sqrt{(N_{cr,z}-N)\cdot (N_{cr,x}-N)}\label {11} \end {equation}$$

w drodze algebraicznych przekształceń ($\ref{10}$) można zapisać w postaci

$$ \begin {equation} i_{LTB} = \cfrac{M_{cr,N}}{N_{cr,z}} \cdot \cfrac{1}{1-\cfrac{N}{N_{cr,x}}} = \cfrac {M_{cr,N}}{N_{cr,z}} \cdot a_{ \Lambda,x}  \label {12}  \end {equation}$$

gdzie  mnożniki krytyczne $\Lambda_{cr,x}$,  $\Lambda_{cr,x}$ oraz współczynniki amplifikacji $a_{\Lambda,x}$ oraz  $a_{\Lambda,z}$  – można wyznaczyć z zależności zależności (1-1.12),  (1-1.13) ,uogólnionych na przypadek wyboczenia skrętnego i wyboczenia z płaszczyzny :

$$ \begin {equation} \Lambda_{cr,x}=\cfrac{N_{cr,x}}{N} \quad ; \quad  a_{\Lambda,x}= \cfrac{1}{1-1/\Lambda_{cr,x}}\label {13}  \end {equation}$$

$$ \begin {equation} \Lambda_{cr,z}=\cfrac{N_{cr,z}}{N} \quad ; \quad  a_{\Lambda,z}= \cfrac{1}{1-1/\Lambda_{cr,z}}\label {14}  \end {equation}$$

Związek imperfekcji bocznej i skręcenia w sytuacji LTB

Amplitudę imperfekcji skręcenia $\varphi_0$  w sytuacji LTB  można uzyskać z amplitudy imperfekcji bocznej $v_0$  z wyrażenia uzyskanego z przekształcenia  ($\ref{12}$) do postaci

$$ \begin {equation} \varphi_0= \cfrac {v_0} {r_0 \cdot \sqrt{ (a_{\Lambda,z} – 1) / (a_{\Lambda,x}-1)} } \label {15} \end {equation}$$

Rozwiązanie problemu korelacji niestateczności podczas ściskania ze zginaniem

W drodze czysto teoretycznych rozważań Szalai i Papp przedstawili następnie  rozwiązanie fundamentalnego problemu korelacji ściskania ze zginaniem z uwzględnieniem wyboczenia giętnego oraz bocznego (zwichrzenia). Na rys.2 pokazano zastosowane oznaczenia.

Rys. 2  Model pręta w stanie zwichrzenia ( opracowano na podstawie [10] (z własnymi modyfikacjami)

Parametry problemu zwichrzenia z wyboczeniem w pracy  [6] oznaczono indeksami BC ( Buckling-Compression). W literaturze (np. [11].) stosowane są indeksy LTB (Lateral-Torsional-Buckling), co lepiej oddaje problem  i takie oznaczenie będziemy stosowali w niniejszym artykule.

Formułę APF dla problemu LTB  daje się zapisać w postaci  podobnej do  równania kwadratowego Eurokod (2-2.12) dla czystego wyboczenia.  Uogólnionienie na przypadek LTB  (formuła Szalai-Papp) ma postać:

$$ \begin {equation}  \chi_{LTB}^2 + \chi_{LTB} \cdot \left [ – \, \beta_N \, – \cfrac{1}{ \overline \lambda_{LTB}^2} \cdot  \left( 1-\Theta_{LTB} \right )  \right ] +\cfrac{1}{ \overline \lambda_{LTB}^2} \beta_N = 0 \label {16} \end {equation}$$

gdzie współczynnik redukcyjny $\chi_{LTB}$ jest uogólnionym współczynnikiem  wyboczeniowym-zwichrzenia  na przypadek zginania ze ściskaniem, który jest  zapisany  formułą ($\ref{31}$) poniżej.

Równanie ($\ref{16}$) można przedstawić w równoważnej, krótszej formie da Silva (2.2.9)

$$ \begin {equation}  ( \beta_N- \chi_{LTB}) \cdot (1-\overline \lambda_{LTB}^2 \cdot \chi_{LTB}) = \Theta_{LTB} \cdot \chi_{LTB} \label {17} \end {equation}$$

Zapis  ($\ref{17}$) jest stosowany w pracach Giżejowskiego i in, np [11].

Uogólniony parametr imperfekcji

Uogólniony w stosunku do (2-2.10)=(2-2.3) parametr imperfekcji  $\Theta_{LTB}$ wynosi:

$$ \begin {equation}  \Theta_{LTB}= v_0 \cdot \cfrac{W_y}{W_\omega} \cdot  \left [ a_{ \Lambda,z }+ \cfrac{ \varphi_0}{v_0}  \cdot a_{ \Lambda,x } \left( \cfrac{W_\omega }{W_z} – \cfrac{GI_t}{F_{cr}} \right ) \right ] \label {18}  \end {equation}$$

gdzie amplitudy imperfekcji pręta wynoszą (rys.2) :
$v_0$ –  strzałka bocznego wygięcia wstępnego
$\varphi_0$ – kąt wstępnego skręcenia.
$F_{cr}=M_{cr}$

Po podstawieniu warunku Szalai-Papp ($\ref{15}$)  do  ($\ref{18}$) otrzymamy:

$$ \begin {equation}  \Theta_{LTB}= a_{\Lambda,z} \cdot v_0 \cdot  \cfrac{W_y}{W_\omega} \cdot \left [ 1+ C_1 \cdot \cfrac{a_{\Lambda,x}}{a_{\Lambda,z}} \cdot \left( \cfrac {W_\omega}{W_z} \,- \,  C_2 \cdot GI_t/ N  \right) \right ] \label {19}  \end {equation}$$

gdzie:

$$ \begin {equation} C_1= \cfrac{1}{r_0} \cdot \sqrt{\cfrac{ (a_{\Lambda,x} -1)} {(a_{\Lambda,z} -1)}} \label {20}  \end {equation}$$

$$ \begin {equation} C_2= \cfrac{1}{r_0}  \cdot \sqrt{ \cfrac{(a_{\Lambda,x}- 1) \cdot( a_{\Lambda,z} -1)} { a_{\Lambda,x} \cdot a_{\Lambda,z}} } \label {21}  \end {equation}$$

Współczynnik imperfekcji $\Theta_{LTB}$ zależy od:

• imperfekcji bocznej $v_0$  (i skrętnej $\varphi_0$;, ale poprzez warunek Szalai-Papp)
• charakterystyk geometrycznych przekroju belki-słupa $W_z$, $W_y$, W_\omega$ oraz $I_t$ (wskaźników wytrzymałości giętnej względem osi z, y  oraz giętno- skrętnej i momentu bezwładności czystego skręcania Sant-Venanata odpowiednio;
• unormowanych (względnych) smukłości pręta $\lambda_z$, $\lambda_x$ – giętnej z płaszczyzny i skrętnej odpowiednio (pominięto klasyczne nadkreślenia);
• modułu poprzecznego (Kirchoffa) materiału $G$
• współczynników amplifikacji $a_{|Lambda,z}$ , $a_{\Lambda,x$ przy czystym wyboczeniu z płaszczyzny i skręcaniu , odpowiednio
•  wartosci siły ściskającej N

Stwierdzenie zależności $\Theta_{LTB}$ od współczynników amplifikacji i siły ściskającej oznacza, że zmienia się on wraz z narastającym obciążeniem.  Zależność smukłości pręta od wielkości obciążenia jest powszechnie znane (p. np. artykuł Pręty ściskane) . Współczynnik imperfekcjji przy zmierzaniu obciążenia do obciążenia krytycznego $a_{\Lambda ,x}->1)$  jest skończony , nie zalezy od $\varphi_0$  i wynosi

$$ \begin {equation}  \lim_{a_{\Lambda,x} \rightarrow 1} \Theta_{LTB} = a_{\Lambda,z} \cdot v_0 \cdot  \cfrac{W_y}{W_\omega}  \label {22}  \end {equation}$$

Należy podkreślić, że  parametr imperfekcji ($\ref{19}$) wyznaczono dla $F_{cr}=M_{cr}$ w równaniu ($\ref{18}$)

W celu zachowania spójności zagadnienia LTB w tym miejscu  należałoby stosować $F_{cr}= M_{cr,N}$ . Po takim podstawieniu wynik uprości się: bez mian pozostanie formuła  ($\ref{19}$) oraz $C_1$ ($\ref{20}$), ale  $C_2$ ($\ref{21}$)przyjmie postać

$$ \begin {equation} C_2= \cfrac{1}{r_0}  \cdot \sqrt{ (a_{\Lambda,x}- 1) \cdot( a_{\Lambda,z} -1) } \label {23}  \end {equation}$$

Współczynnik efektu ściskania

Współczynnik efektu ściskania $\beta_N$  został wyprowadzony  w sytuacji  równomiernego zginania siłami drugiego rzędu (pochodzącymi z rozwiązania II rzędu):  momentem $M_y^{II} $ w kierunku głównej osi przekroju, $M_z^{II}$ w kierunku słabszej osi i ściskanych stałą siłą osiową $N_x$ , a także paczonych bimomentem  $B^{II}$ .W takim stanie  naprężenia  w przekroju sprawczym  wynoszą:

$$ \begin {equation}  \sigma=\cfrac{M_y}{W_y}+ \cfrac {M_Z^{II}}{W_z}+\cfrac{B^{II}}{W_\omega}=f_y  \label {24}  \end {equation}$$

gdzie $M_Z^{II}$, ${B^{II}}$ są siłami obl;iczonymi wg teorii II rzędu: momentem zginającym z płaszczyzny oraz  bimomentem odpowiednio

Siły  drugiego rzędu od wymuszeń imperfekcji. można też oszacować w przybliżeniu z zależności:

$$ \begin {equation}    M_z^{II}=M_{z,0} \cdot a_{\Lambda,z} =N\cdot v_0\cdot a_{\Lambda,z} \label {25} \end {equation}$$

$$ \begin {equation}    B^{II}= \varphi_0\cdot a_{\Lambda,x} \cdot \left [ N\cdot r_0^2 -GI_T \cdot \left (1-\cfrac{1}{ a_{\Lambda,x}} \right )\right ]  \label {26} \end {equation}$$

Współczynnik wpływu ściskania można obliczyć z formuły

$$ \begin {equation}   \beta_N =1-n+m_z^{II}+b^{II} \label {27} \end {equation}$$

gdzie względne siły przekrojowe wynoszą:

$$ \begin {equation}  n=\cfrac{N}{N_R} \quad ; m_z^{II} == \cfrac{M_z^{II}} {M_{R,z}}  \quad;  b^{II}=\cfrac{B^{II}}{B_R}\label {28} \end {equation}$$

Siły względne są odniesione do nośności przekroju: $N_R=N_{pl}= A \cdot f_y$, $M_{R,z}=W_z\cdot f_y$, $B_R=W_\omega\cdot f_y$,
gdzie $A$ – pole przekroju, $W_z$ – wskaźnik wytrzymałości względem osi słabszej, $W_\omega$ – wycinkowy wskaźnik wytrzymałości. giętno-skrętnej

Po podstawieniu do ($\ref{27}$) zależności ($\ref{13}$), ($\ref{14}$) i ($\ref{25}$) uzyskamy:

Krzywe niestateczności LTB

W rezultacie wykazano, że zagadnieniem wyboczenia-zwichrzenia LTB rządzi formuła APF analogiczna do (2-3.13} w postaci:

$$\begin{equation} \chi_{LTB}=\cfrac{\beta_N}{\Phi_{LTB} +\sqrt{\Phi_{LTB}^2 –  \beta_N  \lambda_{LTB}^2}} \label {29} \end{equation}$$

$$\begin{equation} \Phi_{LTB} = 0,5 \cdot \left( 1+ \Theta_{LTB} +\beta _N \cdot \lambda_{LTB}^2  \right) \label {30} \end{equation}$$

gdzie parametr imperfekcji  $\Theta_{LTB}$ wg ($\ref{18}$).

Współczynnik niestateczności (redukcyjny) $\chi_{LTB}$ zależy od smukłości pręta $\lambda_{LTB}$

$$ \begin {equation}   \lambda_{LTB} =  \sqrt{\cfrac{W_y f_y}{M_{cr,N}}}\label {31} \end {equation}$$

Dla czystego zwichrzenia (N=0) zachodzi $\lambda_{LTB}=\lambda_{LT}$, a dla czystego ściskania (M=0) mamy dwa rozseparowane przypadki $\lambda_{LTB}=\lambda_y$ lub $\lambda_{LTB}=\lambda_z$. W każdym przypadku chodzi o smukłości względne, a klasyczne nadkreślenie jest pominięte.

Moment giętno-skretny ($\ref{11}$), po skorzystaniu z definicji ($\ref{13}$) i ($\ref{14}$) w postaci można uzależnić od współczynników amplifikacji (własne przedstawienie)

$$ \begin {equation}  M_{cr,N}= \cfrac{N \cdot r_0}{\sqrt{(a_{\Lambda,x}-1) \cdot (a_{\Lambda,z}-1)}} \label {32} \end {equation}$$

Przykład krzywych niestateczności LTB

Dla dwóch przypadków: czystego zwichrzenia oraz interakcji zginania i ściskania dla poziomu ściskania ($\ref{28}$) $ n=0,3$ wykresy niestateczności  profili szerokostopowych przedstawiono na rys. 3.  Krzywe sporządzono kolejno dla przekrojów:  HEM 300, HEB300, HEA300,HEAA300 (linia ciągła od grubej do cienkiej),  HEM900, HEB900, HEA900, HEAA900 (linia przerywana od grubej do cienkiej).

W przypadku  interakcji zginania i ściskania krzywe niestateczności mogą  przyjąć zupełnie inny kształt od krzywych normowych, ale w ten sposób rozwiązano zagadnienie skomplikowanych współczynników interakcji stosowanych w normie [3] – metoda 1 i 2 ;  patrz również rozdział Krótka charakterystyka metod wyboczeniowych.

Rys.3. Krzywe nistateczności dla zwichrzenia i ściskania (n=0,3) ze zwichrzeniem dla wybranych dwuteowników

Uwagi krytyczne do modelu Szalai-Papp

Współczynniki ($\ref{9}$)  i ($\ref{10}$) można przedstawić w krótkiej formie po skorzystaniu z definicji ($\ref{13}$) i ($\ref{14}$) w postaci (własne przedstawienie):

$$ \begin {equation} A_{0,Szalai}= \cfrac{v_0}{\varphi_0} =  r_0 \cdot \sqrt{ \cfrac { a_{\Lambda,z}-1) \cdot a_{\Lambda,x} } { (a_{\Lambda,x}-1) \cdot a_{\Lambda,z}} }\label {33} \end {equation}$$

$$ \begin {equation} A_{0,Szalai-Papp}= \cfrac{v_0}{\varphi_0} =  r_0 \cdot \cfrac {a_{\Lambda,x}} {a_{\Lambda,z}} \cdot \sqrt{ \cfrac { a_{\Lambda,z}-1} { a_{\Lambda,x}-1}}  \label {34} \end {equation}$$

Współczyniki  ($\ref{9}$) i ($\ref{10}$), nie są tożsame, bo ich stosunek wynosi

$$ \begin {equation} \cfrac{A_{0,Szalai-Papp}}{A_{0,Szalai}}= \sqrt{ \cfrac { a_{\Lambda,x}} { a_{\Lambda,z}} }\label {35} \end {equation}$$

Różnica nie jest praktycznie istotna, a tożsamość zajdzie w szczególnym przypadku, gdy $N_{cr,z}=N_{cr,x}$ lub ogólniej  gdy  $(N_{cr,x}-N)/(N_{cr,z}-N) = N_{cr,x} / N_{cr,z}$. Ta „niedokładność” pozwoliła  jednak na analityczne rozwiązanie problemu.

Zarówno uogólniony parameter imperfekcji $\Theta_{LTB}$ jak i współczynnik wpływu ściskania $\beta_N$ zależą od amplitud geometrycznych imperfekcji wygięcia bocznego $v_0$ i kąta skręcenia wstępnego $\varphi_0$.

Mamy tylko jedną zależność funkcyjną ($\ref{10}$) pomiędzy tymi wielkościami.  W pracy Szalai-Papp [6] nie przedstawiono procedury do wyznaczenia amplitud imperfekcji, a bez tego rozwiązania zagadnienia ma ograniczoną przydatność dla praktyki, bowiem jest niejednoznaczny

Amplituda imperfekcji bocznych i skrętnych

W pracy Tankova i in. [12]. Przyjęto mianowicie, że imperfekcje z płaszczyzny $v_0$ i skrętna $\varphi_0$ można połączyć ze zmodyfikowaną imperfekcją łukową $e_0$ zdefiniowaną w normie [3], uwzględniającą również obecność naprężeń szczątkowych podjęto próbę usunięcia niejeznoznacznosci modelu Szali-Papp.  Przyjęto, że  nomową imperfekcję projektową $e_0$ można wyrazić w postaci:

$$ \begin {equation} e_0=v_0+\varphi_0\cdot \cfrac{h}{2} \label {36}  \end {equation}$$

co zilustrowano na rys, 4.

Rys.4 związek pomiędzy imperfekcją $e_0$ oraz $v_0$ i $\varphi_0$ [12]

Autor wskzuje, że założenie  ($\ref{36}$) (rys.4) określa jedynie imperfekcję boczną  mierzoną w osi górnej półki w zależności od imperfekcji składowych.  Możłiwe są inne podejścia. Np. w pracy [13] wskazano, że z imperfekcja boczna $e_0$ daje skręcenie  wstępne $\varphi_0=e_0/h$.

Prowadzono nieliczne badania doświadczalne z jednoczesnym pomiarem imperfekcji bocznych oraz skrętnych. Na podstawie wyników badań doświadczalnych zestawionych w pracy Kalkan (2010) [14] dla serii belek żelbetowych o różnej długości $L$ i przekroju prostokątnym o różnej wysokości $h$ mierzono boczne imperfekcje $u_0$ na wysokości osi obojętnej przekroju oraz skręcenia $\varphi_0$ wokół środka przekroju. Indeks $\cfrac{\varphi_0 \cdot h}{u_0}$ .
Na podstawie tych wyników autor wykonał analizę przestawioną w tab.1, z któej wynika, że $\varphi_0= \text {(0 do 10,8)} \cdot v_0/h$, czyli średnio znacznie więcej niż założono w pracy  [12] , a nawet w pracy [13].

Tab.1. Imperfekcje boczne i skrętne z badań belek żelbetowych [14]

Obszerne badania numeryczne wpływu rozmaitych modeli imperfekcji  geometrycznych (bocznych i skrętnych) oraz wynikających z napreżeń resztkowych w przkrojach stalowych dwuteowników przeprowadzili  Boissonnade i Somja (2012) [15]. Rozpatrzyli trzy modele naprężeń resztkowych,  3 modele stali, 11-modeli globalnych imperfekcji materiałowych różnicowanych imperfekcjami $v_0$ oraz $\varphi_0$ , w tym przedstawionych na rys. 5

Rys.5 Modele imperfakcjia nalizowane w pracy [15]

Stwierdzono, że najlepsze dopasowanie do krzywych zwichrzenia normowego dają modele pokazane na rys. 6

Rys.6 Rekomendowane imperfekcje [15]

Rekomendowana  imperfekcja boczna wynosi $v_0=(11+5)=8/12000 \approx 1/1000 \cdot L$

Natomiast rekomendowana imperfekcja skrętna wynosi  $\varphi_0 =L/(2000 \cdot h) \approx \cfrac{v_0}{2\cdot h}$

Jednocześnie w pracy [15] wskazano, że imperfekcje loklane (wybrzuszenia ścianek) nie mają istotnego znaczenia i mogą być pominięte.

W dalszej części tego podręcznika przyjmujemy dla cwlów porówenawczych często przyjmujemy

$$ \begin {equation} v_0=e_0 \label {37}  \end {equation}$$

$$ \begin {equation} \varphi_0=\cfrac{v_0}{2 \cdot h} \label {38}  \end {equation}$$

gdzie: $e_0$ jest projektową imperfekcją określoną zgodnie z normami przedmiotowymi (dla danego rodzaju konstrukcji) bądź na podstawie tolerancji wykonawczych w sposób pokazany w rozdziale Imperfekcje projektowe z odchylek wykonawczych.

Badania Tankova i in

Tankova i in (2017)  [12]  zweryfikowali metodę Szalai-Papp poprzez obliczenia nośności kilku schematów belek-słupów  poddanych działaniu zginanie i ściskania, a także pronali z wieloma badaniami doświadczalnymi,obliczenimi numerycznymi GMNiA oraz formułami interakcji normy [3]. Potwierdzono  poprawność formuły Szalai-Papp ($\ref{29}$).

Do powiązania  imperfekcji bocznych $v_0$ i skrętnych  $\varphi_0$ z imperfekcją projektową $e_0$ przyjęli zależność ($\ref{36}$)  i przy tym założeniu wyprowadzili zmodyfikowane formuły na parametr imperfekcji $\Theta_{LTB}$ ($\ref{18}$) oraz współczynnik ściskania $\beta_N$  ($\ref{27}$).
Przyjęte założenie, zgodnie z analizą przedstawioną w punkcie wyżej – nie jest akceptowane, więc nie podajemy wyników uznanych za niepełne.
W celu uwzględnienia nierównomiernie rozłożonych momentów zginających po długości pręta, za propozycją Taras (2010) [16], zastosowano współczynnika normujący bezpośrednio współczynnik wyboczeniowy ($\ref{29}$).

W niniejszej pracy po krytycznej analizie, skorygowano  rozwiązania Tankova i in [12] w ten sposób, że:

1) założenie Tankova  (${36}$) , zostało zastąpione przez ($\ref{37}$)+($\ref{38}$), a w rezultacie dla równomiemego zginania pręta pozostawiono bez korekt teorię Szalai-Papp 

2) uwzględnienie nierównomiernego zginania zaproponowano poprzez normalizację momentu krytycznego ($\ref{11}$) na podstawie znanych metod aproksymacyjnych , a w ogólnym przypadku  w drodze rozwiązania  pomocniczego zadania programem LTBeamN , w którym moment krytyczny jest obliczany ściśle dla dowolnego schematu statycznego, dowolnych obciążeń oraz stężeń po długości belki.

Uzyskany z programu   LTBEamN moment krytyczny $M_{cr, LTBeam}$ może posłużyć do obliczenia współczynnika równoważnego stałego momentu $C_1$

$$ \begin {equation} C_1 =\cfrac{M_{cr, LTBeam}}{M_{cr,N} \label {39}  \end {equation}$$

Znormalizowaną (względną) smukłość $\lambda_{LTB}$ ($\ref{31}$) oblicza się z użyciem momentu krytycznego $C_1  \cdot M_{cr,N}$

Takie podejście jest uzasadnione licznymi badaniami (np. Trahair (2008) [17], które  wskazują na to, że  moment krytyczny ($\ref{7}$)uzyskany z analizy LBA  dla stałego momentu zginającego $\ref{9}$)  można korygować dla innych typów rozkładu zginania poprzez zastosowanie współczynnika $C_1$,

Do obliczeni współczynnika równomiernego momentu $C_1$ można też korzystać z aprokysmacji analitycznych. W przypadku symetrycznego schematu oLTBiążeń, współczynnik $C_1$ wyznacza się ze wzoru Bijaka (2011) [18], [19], który lepiej przybliża $M{cr}$ do rozwiązania otrzymanego z MES w porównaniu od analogicznych propozycji podanych w innych pracach, np Trahair (2008) [17]:

$$ \begin {equation} C_1= \sqrt{\cfrac{21 \cdot M_0^2}{M_0^2 +6 M_2^2 + 8 M_3^2 +6 M_1^2}} \label {40}  \end {equation}$$

gdzie: $M_0$, $M_2$, M_2$, M_3$ – wartości momentów zginających na belce M2, M3, M4 – momenty zginające odpowiednio dla x = 0, L/4, L/2, 3L/4.

Dalsza procedura wyznaczenia współczynnika redukcyjnego (niestateczności) przy zginaniu i ściskaniu jest zgodna z metodą Szalai-Papp i polega na kolejnym zastosowaniu zależności:  ($\ref{8}$) – ($\ref{9}$) – ($\ref{11}$) -($\ref{18}$) -($\ref{27}$) -($\ref{31}$) -($\ref{30}$) -($\ref{29}$).

W pracy  [12] zdefiniowano  pojęcie równowaźnej imperfekcji j$e_0$ jako wynikającej z definicji parametru imperefekcji (2-2.3):

$$ \begin {equation} e_0= \Theta \cdot \cfrac{W_z}{A} =  \end {equation}$$

gdzie $\Theta =\Theta_{LTB}$ ($

jako

przy czym dla zwichrzenia $e_0=v_0$

Formuła Szalai

Szalai (2017) [20] zaprezentował  ogólne równanie  APF rozciągnięte na dowolne przypadki obciążenia belki-słupa o przekroju symetrycznym lub niesymetrycznym.

Warunek Szalai -Papp ($\ref{10}$ przedstawiono w ogólnej postaci:

$$ \begin {equation}  i_{LTB} = \cfrac{1}{r_0} \cdot \sqrt {\cfrac{N_{cr,z} – \Lambda_{cr}\cdot N} {N_{cr,x} – \Lambda_{cr} \cdot N}} = \cfrac{N_{cr,z}}{M_{cr}} \cdot \mu \label {41}  \end {equation}$$

gdzie $\Lambda_{cr}$ globalny mnożnik krytyczny obciążeń konstrukcji (1-1.13), a $M_{cr}$ monet krytyczny dla czystego zwichrzenia ($\ref{7}$)

Współczynnik $mu$  oblicza się z zależnośći:

$$ \begin {equation}  \mu= \sqrt{\cfrac{1-\Lambda_{cr} \cdot N/N_{cr,z}}{1-\Lambda_{cr} \cdot N/N_{cr,x}}}\label {42}  \end {equation}$$

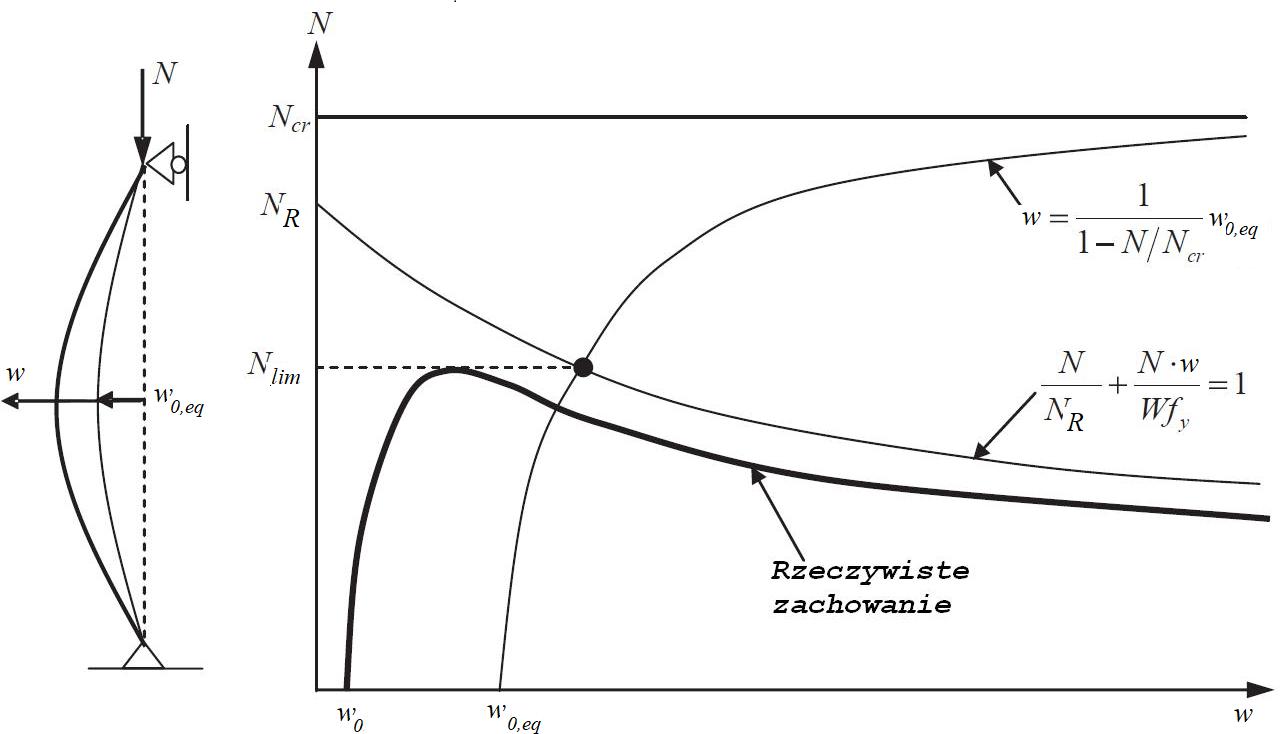
Ilustrację analizowanej sytuacji pokazano na rys. 6. , gdzie:

$N_{cr}$ – sprężyste obciążenie krytyczne pręta , przy którym zachodzi utrata stateczności w jednej z form: giętnej, skrętnej, zwichrzenia. Obciążenie krytyczne stanowi ograniczenie z góry obciążeń,
$N_R = A \cdot f_y$ – nośność na ściskanie przekroju  (bez uwzględnienia utraty stateczności pręta),
$N_{lim}= N_b$ – nośność pręta,
$v_{0,eq}$ – amplituda imperfekcji równoważnej do imperfekcji normowej $e_0$ dla przypadku złożonej utraty stateczności,

Rys. 6 Ilustracja do formuły Szalai [20]

$$ \begin {equation}  [u](x) =a_\Lambda \cdot [u]_0(x) \label {43}  \end {equation}$$

gdzie:
$[u]_0(x) $  imperfekcje geometryczne pręta: wstępne skrócenia $u_0 (x)=0$, wygięcia w kierunku poprzecznym do pręta $v_0(x)$, ugięcia $ w_0(x)$ oraz skręcenia $\varphi_0(x)$ ujęte w wektor
$ [u]_0 (x)= \left [ \begin{array}{l}
0 \\
v_0(x)\\
w_0(x)\\
\varphi_0(x)
\end{array} \right] $

$[u](x)$ całkowite przemieszczenie pręta w stanie II rzędu   złożone z imperfekcji  $[u[_0(x)$ oraz ich przyrostu wywołanego działaniem sił przekrojowych
$ [u] (x)= \left [ \begin{array}{l}
u(x) \\
v(x)\\
w(x)\\
\varphi(x)
\end{array} \right] $

Współczynnik amplifikacji $a_{\Lambda}= \cfrac{1}{1-\tfrac{1}{\Lambda_{cr}}}$ zdefiniowano w  rozdziale „Imperfekcyjna metoda. Pojęcia podstawowe”  wzór (1-1.12),

przy czym mnożnik krytyczny $\Lambda_{cr}$ należy wyznaczać w analizie LBA całego ustroju na modelu uwzględniającym wszystkie badane postacie wyboczenia, czyli wyboczenie giętne, skrętne i giętno-skrętne (zwichrzenie). Takim modelem jest uogólniony pręt Własowa, to znaczy pręt o siedmiu stopniach swobody z paczeniem jako siódmym stopniem.

Formuła ($\ref{41}$) jest uogólnieniem klasycznej formuły amplifikacji ($\ref{2-3.22}$) i jest analogicznie wyprowadzona. Całość wyprowadzenia można znaleźć w pracy [20].

Na rys. 5 pokazano ilustrację zagadnienia ściskania rzeczywistego pręta w nomenklaturze przyjętej w pracy [20] . Nośność $N_R$ jest nośnością przekroju na czyste ściskanie. Natomiast $N_{cr}$ jest nośnością pręta (Eulera). Definiuje się następujące mnożniki oLTBiążenia $N$:
krytyczny  $\Lambda_{cr}=N_{cr}/N$ (1-1.13),
graniczny (spręzysto-plastyczny) $\Lambda_{lim}=N_{lim}/N$ (1-1.16)
przekroju (nośności plastycznej $N_R=A \cdot f_y$ , $\Lambda_R=N_R/N$
Odróżnienie tego podejścia od prezentowanego w podręczniku polega na tym, że w miejsc mnożnika plastycznego konstrukcji $\Lambda_{pl}$ (1-1.15) stosuje się nośność plastyczną przekroju $\Lambda_R$.

Kierunki rozwoju zastosowania formuły APF

Słupy-belki z bocznymi stężeniami po długości

Giżejowski i Stachura [11] zaprzentowali rozszerzoną   formułę APF  Tankowej [12] na przypadek elementów, które mają po rozpiętości dyskretne utwierdzenia boczne i przeciwskrętne. Współczynnik smukłości belka-słup przy różnych kombinacjach oLTBiążenia oceniano z wykorzystaniem mnożnika oLTBiążenia sprężystego wg teorii Trahair [21].

⇒ [ Alternatywna amplituda imperfekcji ]

Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2017-2020), Imperfekcyjna metoda  projektowania konstrukcji, Encyklopedia  πWiki, Wydawnictwo Chodor-Projekt,
[ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]

Historia edycji artykułu:
Publikacja jest edytowana od roku 2017, pierwotnie jako podręcznik dla wydawnictwa PWN, Zakończenie edycji zostało przerwane na początku roku 2018 na skutek wypadku i rekonwalescencji autora podręcznika.  Obecnie cykl artykułów składający się na podręcznik jest w trakcie edycji internetowej i jest publikowany odcinkami.

(2019-04-08 do 15) wersja 1,0: wersja pierwotna
(2019-05-27) Wersja 2.0: dokonano podziału rozdziału na części w celu poprawy procesu wczytywania strony Literatura

1. Ayrton W. E., Perry J. (1886). On Struts. The Engineer, 464–513
2. Maquoi R., Janss J., (1991), EC3 design model for lateral torsional buckling resistance. In: International conference on steel and aluminium structures, Singapore, 22-24 May 1991
3. PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
4. Chapman J. C., Buhagiar D. (1993), Application of Young’s buckling equation to design against torsional buckling. Proc Instn Civ Engrs Structs and Bldgs, 99, 359–369
5. Taras A., Greiner R., (2010), New design curves for lateral-torsional buckling-Proposal based on a consistent derivation, Journal of Constructional Steel Research 66, pp.648-663
6. Szalai J, Papp F., (2010), On the theoretical background of the generalization of Ayrton–Perry type resistance formulas, Journal of Constructional Steel Research, 66 , 670–679
7. Boissonnade N, Villette M, Muzeau JP.  (2001), About amplification factors for lateral-torsional buckling and torsional buckling., In: Festschrift Richard Greiner,TU Graz; 2001.
8. Szalai J., (2005), Analysis of the resistance of steel beam-column on probabilistic basis, Ph.D. dissertation, Budapest University of Technology and Ekonomics
9. Papp F. (2016), Buckling assessment of steel members through overall imperfection method. Engineering Structures, 106, 124–136
10. Papp F. (2016). Buckling assessment of steel members through overall imperfection method. Engineering Structures, 106, 124–136, [ https://doi.org/10.1016/j.engstruct.2015.10.021 ]
11. Giżejowski M. A., Stachura Z. (2017), A consistent Ayrton-Perry approach for the flexural-torsional buckling resistance evaluation of steel i-section members,  Civil and Environmental Engineering Reports (CEER), 25 (2), 089-105
12. Tankova T., Marques L., Simoes da Silva L., Andrade A. (2017), Development of a consistent methodology for the out- of- plane buckling resistance of prismatic beam-columns. Journal of Constructional Steel Research, 128, 839–852
13. Chodor L. (2016), Przekrycia hal i galerii. W: XXXI Ogólnopolskie Warsztaty Pracy Projektanta Konstrukcji: Tom I, s. 25–202, [ https://chodor-projekt.net/wp-content/uploads/2016/03/Chodor_LPrzekrycia-hal-i-galerii-WPPK-2016.pdf ]
14. Kalkan I., (2010) Application of Southwell Method on the Analysis of Lateral Torsional Buckling Tests on Reinforced Concrete Beams, Int.J.Eng.Research & Development,Vol.2,No.1,January 2010
15. Boissonnade N.,, H. Somja H., (2012), Influence of Imperfections in FEM Modeling of Lateral Torsional Buckling, Proceedings of the Annual Stability Conference Structural Stability Research Council, Grapevine, Texas, April 18-21, 2012
16. Taras A. (2010), Contribution to the Development of Consistent Stability Design Rules for Steel Members, PhD thesis TU Graz, 2010
17. Trahair N.S., Bradford M.A., Nethercot D.A., Gardner L.: The behaviour and design of steel structures to EC3 (4th Edition), Taylor & Francis, London-New York 2008
18. Bijak R.: Moment krytyczny zwichrzenia niestężonych bisymetrycznych belek dwu-teowych podpartych widełkowo. ICMS 2011 Conference, Wrocław 2011
19. Bijak R., (2017), Giętno-skrętna utrata stateczności podpartych widełkowo i oLTBiążonych mimośrodowo słupów dwuteowych, Journal of Civil Engineering, Enviroment and Architecture (JCEEA), t. XXXIV, z. 64 (3/I/17), liipiec-wrzesień 2017, s. 461-470
20. Szalai J. (2017). Complete generalization of the Ayrton-Perry formula for beam-column buckling problems. Engineering Structures, 153, 205–223
21. Trahair N.S., (1993),  Flexural-Torsional Buckling of Structures, Boca Raton, CRC Press Inc.

________________________________