Leszek Chodor, 5 grudnia 2018
07-02-2025 rewizja po dużej awarii portalu
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co

Artykuł w ciągu ostatnich 24 godzin czytało 43 Czytelników

Słupy żelbetowe są głównym elementem konstrukcji szkieletowych lub płytowo-słupowych.

Slupy znamienne są tym, że mogą ulec  utracie stateczności – wyboczeniu, a także tym, że są wrażliwe na efekty II rzędu, czyli na wpływ przemieszczeń na siły przekrojowe. Zjawiska te są obszernie analizowane w internetowym podręczniku „Imperfekcyjna metoda projektowania„.

Konstrukcja, zawierająca słupy powinna być analizowana metodami imperfekcyjnymi na modelu całego systemu. Tradycyjnie stosowana analiza wydzielonych elementów prowadzi do skomplikowanej procedury projektowania a jednocześnie przybliżonej i jest już uznana za metodę historyczną, więc nie będziemy się nią zajmować.

Metoda imperfekcyjna jest pojęciowo prosta, choć wymaga zastosowania  programów komputerowych z analizą II rzędu. Praktycznie wszystkie współczesne programy komputerowe posiadają procedury analizy nieliniowej i drugiego rzędu, więc analizę II rzędu należy traktować jako metodę standardową, a metody I rzędu już tylko jako historyczne.

Konstrukcję jako całość należy obciążyć wymuszeniami od imperfekcji, czyli niedoskonałości geometrycznych. W praktyce oznacza to obciążenie  konstrukcji równoważnymi, fikcyjnymi siłami poziomymi, stowarzyszonymi z obciążeniami grawitacyjnymi (pionowymi). Siły przekrojowe uzyskane z rozwiązania II rzędu idealnego geometrycznie systemu konstrukcyjnego obciążonego łącznie siłami zewnętrznymi i siłami imperfekcji zawierają w sobie siły drugiego rzędu (wyboczeniowe) i w rezultacie nie jest wymagana analiza wydzielonych elementów ściskanych wg [1], kl.5.8.3. W konsekwencji problem sprowadza się w istocie do analizy przekrojów, a nie elementów.

Specyfika konstrukcji żelbetowych w istocie sprowadza się do zdefiniowania metody wyznaczenia sztywności pręta betonowo-stalowego. Standardowo stosujemy metodę nominalnej sztywności, umożliwiającą analizę sił przekrojowych i stateczności statycznie niewyznaczalnych konstrukcji żelbetowych procedurami przewidzianymi dla konstrukcji wykonanych z materiałów jednorodnych (np stali).

Kształtowanie słupów żelbetowych

Słupy żelbetowe mają najczęściej przekrój prostokątny (rys.1) lub okrągły, a w przypadkach szczególnych (np w narożach) stosuje się słupy o innym przekroju (rys. 3d). Jako słupy uważa się elementy pionowe, których stosunek boków nie jest większy niż 4 (h/b ≤4 ). Elementy o stosunku boków większych niż (h/b >4 )  uznaje się za ścianę. Ta kwalifikacja jest istotna ze względów ochrony pożarowej zgodnie z normą [2].

Ze względu na dokładność metody analizy statycznej przyjmuje się, że wysokość słupa H, traktowanego jako pręt  powinna być większa niż 3-krotny większy wymiar  przekroju poprzecznego (H/h>3). Krótsze słupy należy analizować jak tarcze.

Zaleca się, aby smukłość słupa żelbetowego, wyznaczona z klasycznej zależności  $\lambda=\cfrac{l_0}{i_c} $  nie była zbyt duża:

$$\begin{equation} \lambda \le 100 \label{1} \end{equation} $$

Długość obliczeniowa (wyboczeniowa) $l_0$  dla słupa przegubowo-przegubowego wynosi $l_0=H$. W obliczeniach wstępnych zwykle przyjmuje się  długość obliczeniową jako wysokość słupa w świetle stropów (czyli $l_0 \approx H$).

Promień bezwładności przekroju betonowego $i_c = \sqrt{ I_c/A_c}$ jest obliczany dla przekroju niezarysowanego betonu bez  uwzględnienia zbrojenia.

W przypadku przekroju prostokątnego o wymiarach (hxb) promień bezwładności wynosi  $i_c=\sqrt{ (b \cdot h^3/12)/(b \cdot h)}= h/  \sqrt{12}$  i smukłość pręta wynosi

$$\begin{equation} \lambda=\cfrac{\sqrt{12} l_0}{h}= 3,464 \cfrac{l_0}{h} \label {2}\end{equation}$$

a ograniczenie ($\ref{2}$) sprowadza się do

$$\begin{equation} \lambda_c= \cfrac{l_0}{h} \le 30 \label{3} \end{equation} $$

Warunki $(\ref{2})$ lub ($\ref{3}$) są tylko informacyjne (nie obowiązujące) i mają  na celu ograniczenia nadmiernego wpływu niestateczności słupa na jego wymiary w przypadkach nie poddanych analizie stateczności ( dla konstrukcji spełniającyh ( $ \ref{12}$)). We współczesnych konstrukcjach często potrzebne jest zastosowanie słupów o większej smukłości słupów, ale wówczas należy przeprowadzić dokładną analizę stateczności, ale też rozważyć, czy bardziej ekonomicznym rozwiązaniem nie będzie zastosowanie słupa zespolonego.

W każdym przypadku należy sprawdzić wymiary oraz  smukłość słupa żelbetowego z warunku ochrony pożarowej zgodnie z [2].

Zbrojenie podłużne

Na rys.1 zilustrowano podstawowe zasady kształtowania zbrojenia w przekroju poprzecznym słupa. Średnica zbrojenia podłużnego nie powinna być mniejsza niż 8 mm (w Polsce 6 mm). W słupach o przekroju wielokątnym w każdym narożu należy umieścić co najmniej jeden pręt. W słupach o przekroju kołowym należy stosować co najmniej 4 pręty.

Suma przekroju zbrojenia podłużnego $A_s$ powinna spełniać wymagania:

$$\begin{equation} A_s \ge 0,002 A_c  \text { oraz } \ge \cfrac{0,10 N_{Ed}}{f_y}  \text { oraz } \le  0,04 A_c \label{4} \end{equation}$$

gdzie $A_c$ – pole betonu.

Wymóg maksymalnego zbrojenia 4% może być dwukrotnie przekroczony na odcinkach, w których pręty są łączone na zakład, a także wówczas, gdy w drodze badań zostanie wykazane, że nie wpłynie to negatywnie na właściwości konstrukcyjne betonu i jego współpracę ze stalą (osiąga się pełną nośność przekroju).

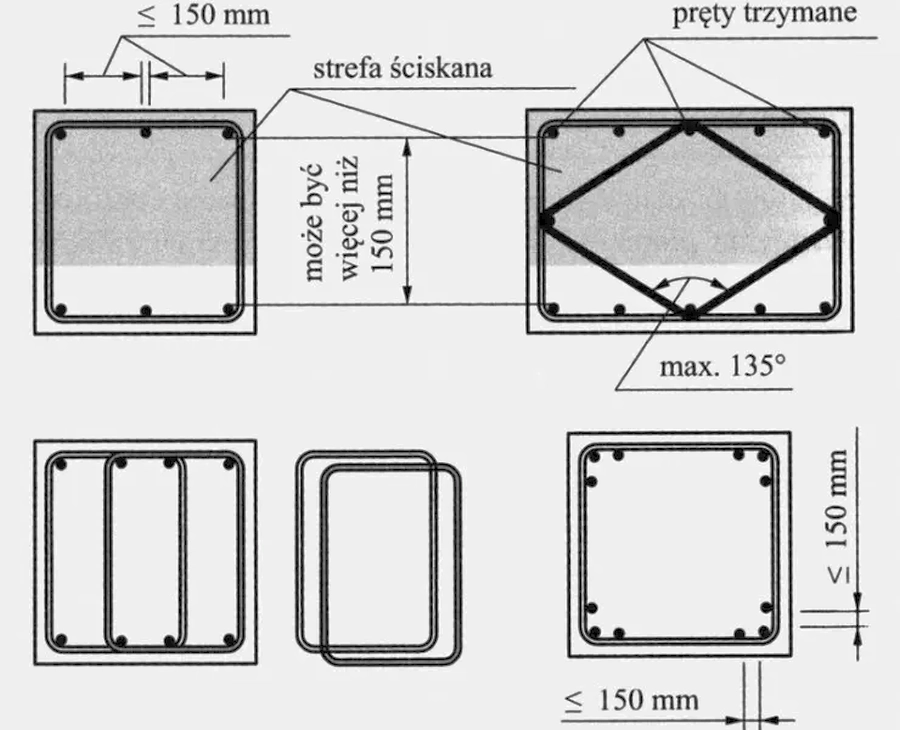
Rys.1 Kształtowanie przekroju słupa [3], rys.22.21

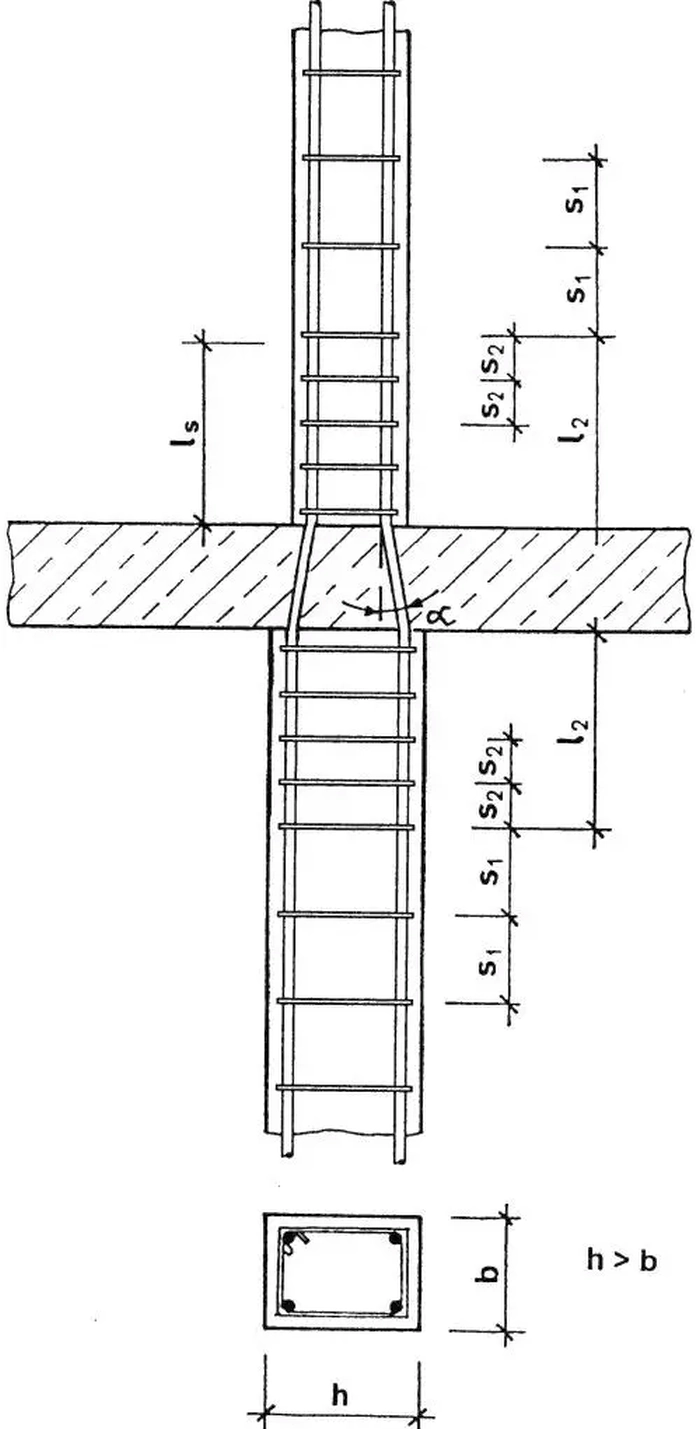
Rys.2. Rozmieszczanie strzemion w słupie (opis w tekście) [4],  rys. 13.98

Zbrojenie poprzeczne (strzemiona)

Wszystkie ściskane pręty podłużne powinny być objęte przez strzemiona, tak by każdy pręt umieszczony w narożu był trzymany w dwóch kierunkach.  W strefie ściskanej odległości między dowolnym prętem, a prętem trzymanym nie powinna przekraczać 150 mm.

Długości zakładów wyznacza się na  zasadach ogólnych przedstawionych w artykule „Belki żelbetowe” i  oblicza za pomocą zamieszczonego tam arkusza kalkulacyjnego.

Średnica zbrojenia poprzecznego ( strzemion, siatek, spiral) w słupach okrągłych nie powinna być mniejsza od 6 mm i 0,25 największej średnicy zbrojenia podłużnego.

Podstawowy rozstaw strzemion $s_1$ (rys.2) nie powinien przekraczać

• 400 mm
• długości mniejszego boku słupa
• 20 średnic zbrojenia podłużnego.

Podstawowy rozstaw strzemion  $s_1$ należy zmniejszyć do $s_2=0,6 s_1$ w przypadkach:

• powyżej i poniżej belki lub płyty na odcinkach o długości $l_2=h$ (większego boku słupa)
• na odcinkach połączenia na zakład prętów o średnicy większej niż 14 mm. Wówczas wymaga się przynajmniej trzech strzemion rozmieszczonych równomiernie na długości zakładu.

W przypadku, gdy łączone odcinki słupa nad i pod belka (płytą) nie różnią się znacznie wymiarami, to pręty podłużne można złamać w sposób pokazany na rys 2, ale kąt załamania $\alpha$ powinien spełniać warunek $tg \alpha  \le  1/6$. Ponadto w przypadku załamania prętów podłużnych należy zastosować dodatkowe strzemiona przejmujące siłę wypadkową z prętów załamanych. Siła to wynosi $H_{Ed}=N_{Ed} \cdot tg \alpha$, czyli średnica dodatkowych strzemion $Ø_s \ge tg \alpha \cdot Ø$, gdzie Ø jest średnicą zbrojenia głównego.

Jeżeli łączone odcinki słupa znacznie różnią się wymiarami, to nie należy wyginać prętów połączeniu, lecz zastosować oddzielne pręty łączące, połączone na zakład z prętami podłużnymi  lub zastosować połączenia spawane , bądź śrubowe.

Strzemiona pojedyncze (rys. 2) stosuje się tylko dla słupów o wymiarze przekroju nie przekraczającym 400 mm. W innych przypadkach stosuje się strzemiona wielokrotne (przykład rys. 3 b-d)

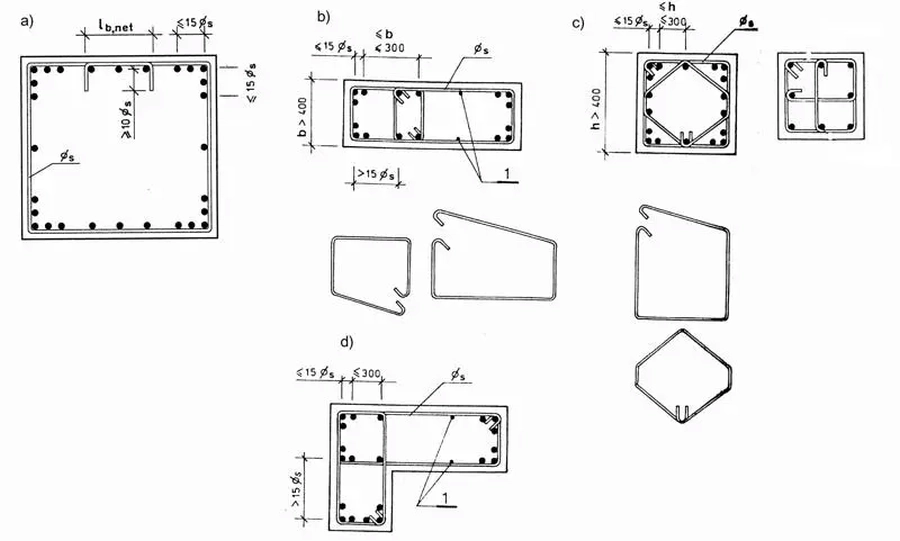
Rys.3. Szczególne przypadki zbrojenia przekroju słupa: a) słup z hakami  l_b,net, b) słup- ściana, c) podwójne strzemiona, d) słup narożny, 1– pręty montażowe (Starosolski, W. (2013). Konstrukcje żelbetowe według Eurokodu 2 i norm związanych, Tom 3, Wydawnictwo Naukowe PWN)),  rys. 13.96-97

W przypadku gdy w narożu słupa znajdują się więcej niż trzy pręty podłużne, to należy stosować strzemiona zamknięte z hakami prostopadłymi $l_{b,net}$ (rys.3a).

Przeguby. Styki czołowe elementów ściskanych

Przeguby  w tym stopy lub głowice przegubowe słupów występują najczęściej w słupach prefabrykowanych. W przypadku słupów monolitycznych często projektuje się przegubowe głowice.
Prefabrykaty ( lub powierzchnie czołowe elementów wykonywanych na budowie)   należy zawsze układać na łożyskach  lub na warstwie zaprawy montażowej. łożyska bez warstwy pośredniej (łożyska suche) są dopuszczone jedynie w przypadku niewielkiego naprężenia ściskającego w styku  wynoszącego nie więcej niż $0,4 f_{cd}$ [5], rozdział 13.18.2,  W każdym jednak przypadku należy stosować przekładkę z materiału izolacyjnego. 

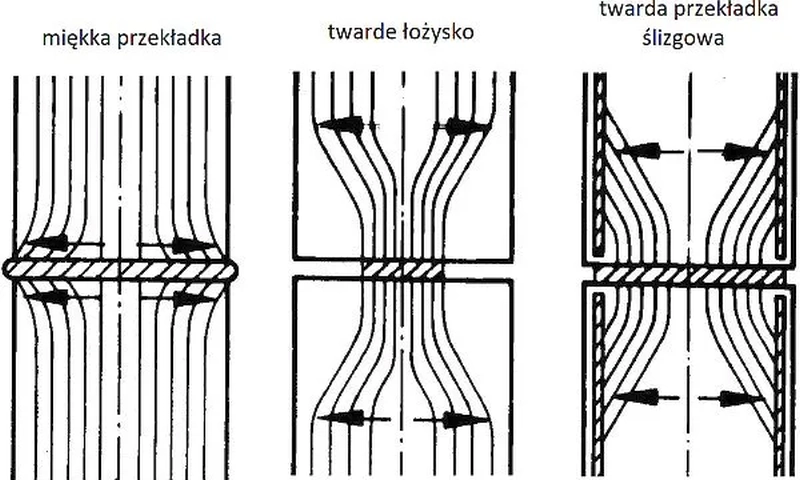
Rys 4. Przeguby w żelbecie [6], fig.3.1

Rozróżnia się przeguby z miękkimi i twardymi łożyskami. W przypadku złącze z miękkim łożyskiem (rys 4 – 1-sza z lewej) -boczne przemieszczenie materiału łączącego prowadzą do powstania sił rozciągających blisko powierzchni czołowych. Powstałe boczne naprężenia rozciągające muszą zostać przeniesione przez zbrojenie przypowierzchniowe oraz strzemiona lub poprzez okucie końca elementu .

Złącze z twardym łożyskiem jest rodzajem złącza, w którym moduł sprężystości materiału przekładki jest równy co najmniej 70% modułu sprężystości elementu dochodzącego (betonu). Złącze z twardym łożyskiem i zmniejszonym przekrojem (rys. 4 środkowy) powoduje powstawanie rozciągania bocznego w wyniku przekierowania sił z całego przekroju na przekrój zredukowany. Siły boczne musi przejąć zbrojenie strzemionami w pewnej odległości od powierzchni czołowej (zasadniczo mniejszej od wymiaru boku elementu).

Twarde łożysko nieskrępowane (rys. 4 z prawej) uzyskuje się przez zmniejszenie tarcia na powierzchniach czołowych materiału przekładki twardej (kryterium wyżej). Boczne naprężenia rozciągające spowodowane przekierowanie składowej obciążenia w pręty podłużne  są stosunkowo małe

Rozróżniamy dwa rodzaje detali połączeń doczołowych :
a) ze stalową podkładką (marką, okuciem), b) z siatkami zbrojeniowymi pod powierzchniami czołowymi. Zastosowanie blach stalowych na czołach słupów jest bardzo skutecznym sposobem zapobiegania naprężeniom bocznym. Obciążenie podłużne jest dobrze przenoszona przez zaprawę (podlewkę) lub łożysko elastomerowe, a w sąsiedztwie łożyska nie powstają naprężenia wynikające z zakotwienia końcowego zbrojenia podłużnego słupa,
b) z siatkami zbrojeniowymi pod powierzchnią czołową słupa. W tym przypadku , tylko część siły działającej na powierzchnię czołową
jest przekazywana na łożysko podporowe, co powoduje mniejsze obciążenie pionowe, ale większe poziome siły rozpychające podkładkę. Większe naprężenia poziome musza być przeniesione przez zbrojenie obwodowe (strzemiona).

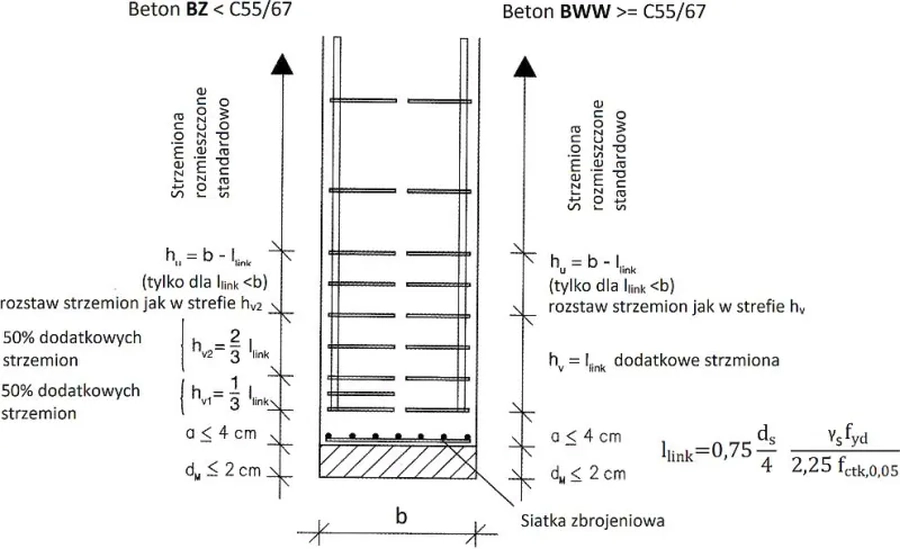
Rys.5  Zbrojenie słupa nad  przegubowym łożyskiem [7]

Na rys. 5 pokazano detal zbrojenia słupa pomad łożyskiem przegubowym [7] w wariancie b) wyżej (bez stalowego podkucia, z siatką zbrojeniową). W tym wariancie  siatka zbrojeniowa jest mieszczona centalnie w osi słupa na całej powierzchni czołowej. Siatka jest wbudowana w słup bezpośrednio bez otuliny betonowej Siatka powinna być wykonana z prętów o średnicy średnicę prętów  nie większą niż $d_s= 12 \, mm$ Zewnętrzne węzły siatki muszą być ustawione na zewnętrznych powierzchniach słupa, a miejsca przecięcia muszą być starannie zespawane. Rozstaw prętów powinien być mniejsze niż  $s_M= 50 \, mm$, a łączniki ścinane (strzemiona) powinny być rozmieszczone zgodnie z rysunkiem.
Niestandardowe siatki na czołowe ściany słupów nie są zazwyczaj łatwo dostępne i należy je przygotować indywidualnie.
Nie należy przekraczać maksymalnej dopuszczalnej grubości płyty pod łożyskiem typu butt-joins  z twardym łożyskiem  $max \, d_m= 20 \, mm$

Detal  z rys.5  należy rozpatrywać  łącznie z rys.2.
Dla najczęściej stosowanego betonu C30/37 (dla którego  f_{ck,0,05 = \, 2 MPa) i stali B500 ( dla której $\gamma_s \cdot f_{yd}= f_{yk} = 500 \, MPa)$ zachodzi:
$l_{link}=   \left( \cfrac {0,75}{4 \cdot 2,25 } =\cfrac{3}{36}\right)   \cdot d_s \cfrac {f_{yk}}{f_{ctk 0,05}} = 3/36 \cdot 500/2 \cdot d_s=  20 d_s$.

Przykładowo dla słupa 400×400 zbrojonego prętami $d_s=12 \, mm$ mamy:
(rys. 5 ) $\to$   $ l_{link}=20 \cdot 12= 240 \,mm$ , $h_u= b – l_{link}= 400-240= 160 \, mm$
(rys. 2)  $\to$  długość odcinka zagęszczenia strzemion  $l_2= h= 400 \, mm$ z rozstawem strzemion $ s_2 =0,6 \cdot \max{400 \, ; \, 20 \cdot 12 \,;\, 400 }= 240 \, mm$
W rozważanym przypadku strzemiona należy zagęścić n a odcinku (powyżej otulenia $a$ od czoła słupa licząc):
$ l_2= \max{ 160 \, ; \, 400}= 400 \, mm$
w rozstawie $ s_2= \min { \{ 240 \, ; \, 240\} }=240 \, mm$
Odcinek  $l_2$ jest podzielony na trzy strefy , gdzie długości dwóch dolnych (powyżej otulenia $a$ wynoszą
$h_{1, 2} = l_{link} / 3= 240/3= 80 \, mm$ . w każdej z tych stref umieszcza się strzemiona na granicy i połowie strefy, czyli o rozstawie $s_{link}= 80/2= 40 \, mm$
W trzeciej, najwyższej  strefie o długości
$h_3= 400- 2 \cdot 80 = 240 \, mm$ rozmieszcza się strzemiona w rozstawie $240/2=120 \, mm$

Stopy słupów żelbetowych

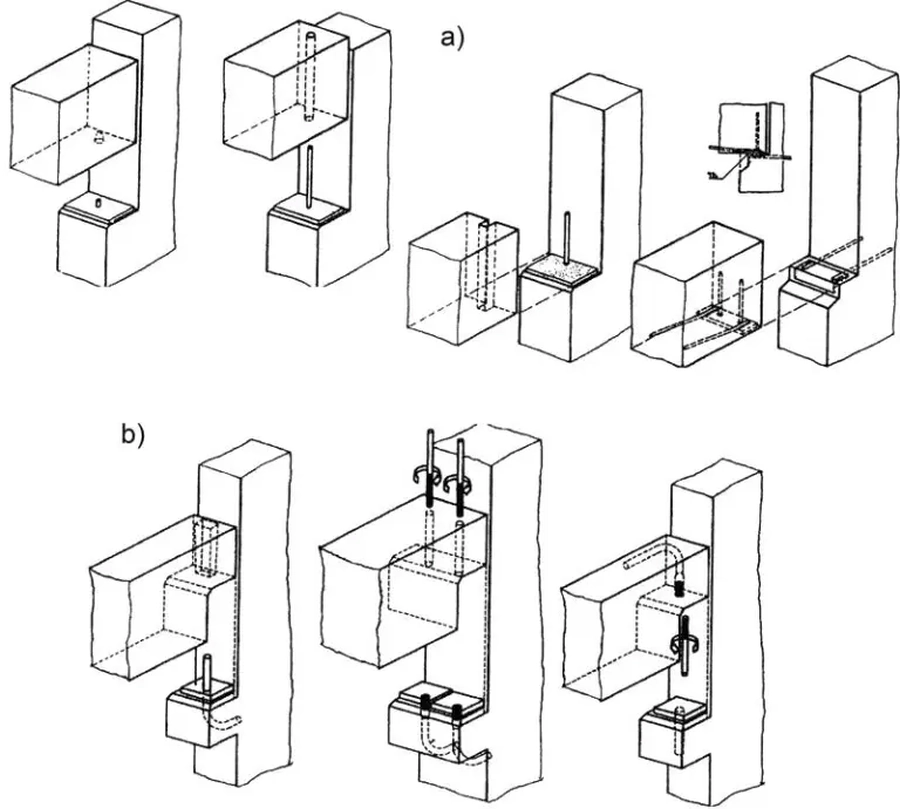
Stosowane rodzaje stóp słupów pokazano na rys. 6

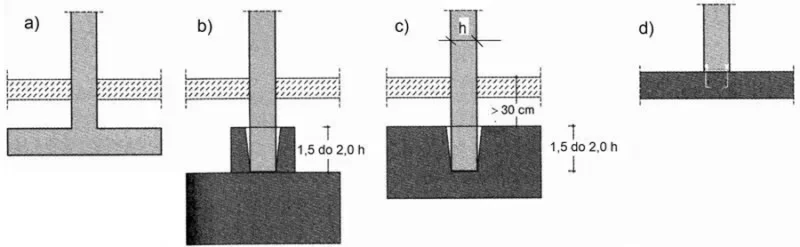
Rys.6: Stopy fundamentowe: a) monolityczna, b) kielichioowa w stopie, c) kielichowa w płycie, c) na łączniki mechaniczne [4], rys. 2.93

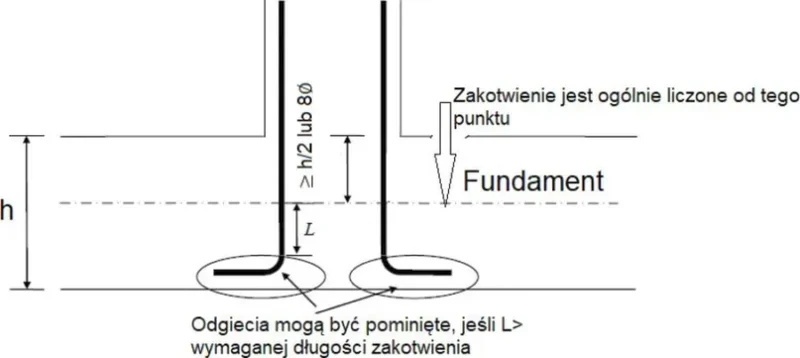
Słupy żelbetowe kotwione w fundamencie monolitycznie powinny być zakotwione na długość wynikającą z ogólnych warunków, przy czym należy zwrócić uwagę, że długość zakotwienia liczy się od środka fundamentu liczonego pomiędzy zbrojeniem górnym i dolnym. Jeśli długość zakotwienia L jest zbyt mała, to wówczas pręty należy odgiąć pod kątem 900, tak by łączna długość zakotwienia była wystarczająca (rys.7).

Rys.7. Detal zakotwienia monolitycznego słupa

W praktyce chętnie stosuje się zakotwienie słupa w stopie kielichowej, w sposób pokazany na rys. 6b i c. Przykład rysunku warsztatowego stopy kielichowej pokazano na rys. 8. Należy zwrócić uwagę, że rysunek został wykonany zgodnie z danymi zasadami rysunkowi – współczesne zasady opisane w artykule Standard rysunku warsztatowego konstrukcji żelbetowej przewidują jako zasadę stosowanie kodów kształtów oraz nie umieszczanie „drabinek” z numerami prętów i umieszczanie tych informacji w systemie linii wymiarowych.

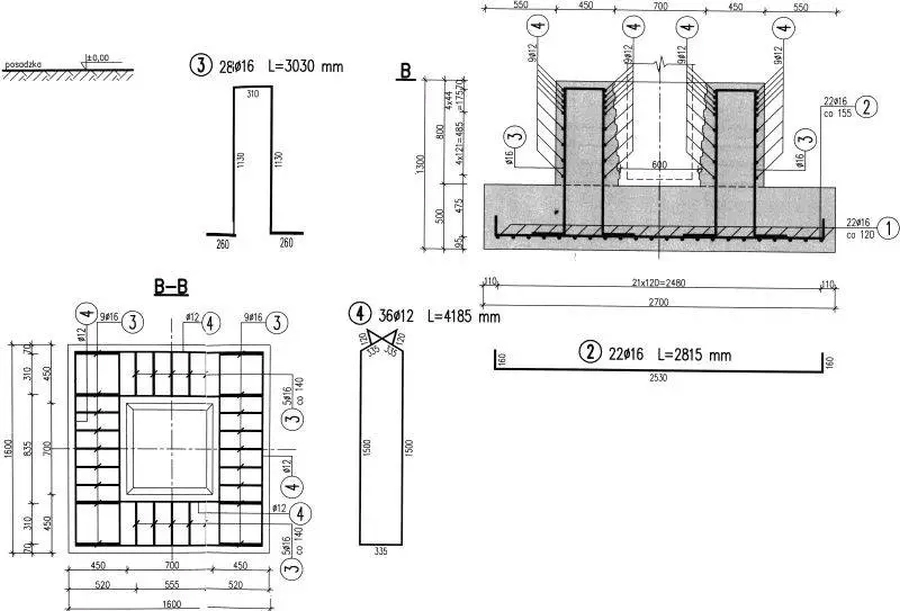
Rys.8 . Stopa kielichowa. Rysunek warsztatowy [8], rys. 10.3

Ze względów inżynierskich najciekawsze są stopy na łączniki mechaniczne z zastosowaniem śrub fundamentowych i rektyfikujących, które najczęściej są stosowane w konstrukcjach prefabrykowanych. Zwykle są to rozwiązania patentowe, np firmy Halfen- system HCC, Peikko- system HPKM (rys. 9.) i  inne. 

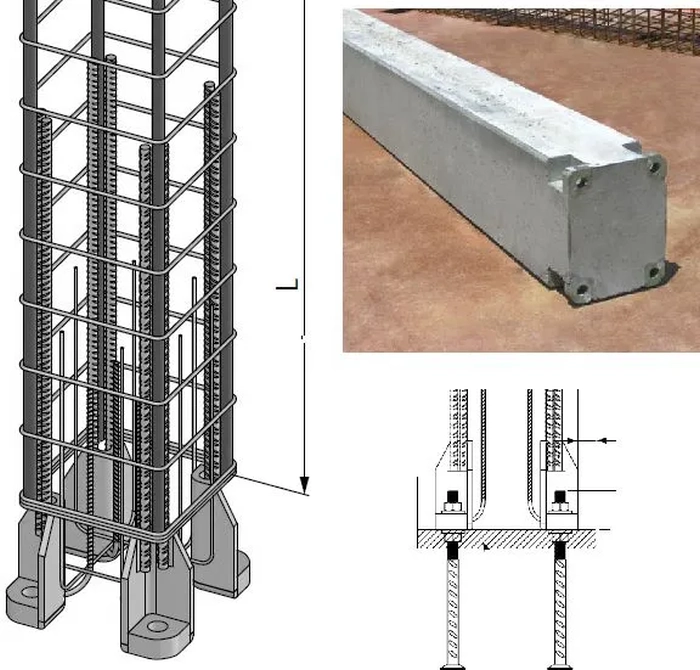
Rys. 9. Detale systemu Peikko HPKM [ wybrano z folderu reklamowego PEIKKO]

Głowice słupów żelbetowych

Głowice słupów żelbetowych są kształtowane w zależności od przebicia przez ścinanie płyty żelbetowej, co omówiono w artykule Przebicie płyty żelbetowej.

Krótkie wsporniki słupów

Krótkie wsporniki słupów żelbetowych należy analizować jako tarcze ( w płaskim stanie naprężenia, a nie wg teorii belkowej) w sposób pokazany w artykule: (…) Krótki wspornik.  Jako uproszczenie można stosować teorię ST (metodę kratownicową) w sposób pokazany w artykule Model krótkiego wspornika i przykłady zbrojenia.

Na rys. 10a pokazano przykłady oparcia belki podciętym słupie żelbetowym , a na rys. 10b  na krótkim wsporniku słupa.

Rys. 10.  Oparcie belki: a) na podciętym slupie, b) na krótkim wsporniku.

Analiza wytrzymałościowa słupów

Zasady ogólne

W ogólności konstrukcje żelbetowe są mniej wrażliwe na efekty II rzędu od smukłych konstrukcji stalowych, ale kryteria normowe [1], kl. 5.8.2 (6) pomijania efektów drugiego rzędu w konstrukcjach żelbetowych są nieostre i w istocie odwołują się same do siebie. Mianowicie w celu pominięcia efektów II rzędu należy znać stopień wpływu tych efektów. Jeśli stopień wpływu jest mniejszy od 10% to można je pomijać. Współcześnie często konstruuje się nietypowe konstrukcje dla których nie można bez obliczeń stwierdzić, że efekty II rzędu są pomijalnie małe. Dlatego bezpiecznie jest przeprowadzić analizę II rzędu w każdym przypadku, tym bardziej, że stosowanie współczesnych programów obliczeniowych uczyniło rozwiązanie tego zadania procedurą standardową i szybką.

Podobnie anachroniczne są już uproszczone metody oceny efektów II rzędu podane w [1], kl.5.8.3, a w tym:

• kryterium smukłości elementów wydzielonych [1], kl. 5.8.3.1 zastosowane nie tylko do imperfekcji łukowych, ale również do systemowych,
• oszacowanie długości efektywnych elementów wydzielonych [1], kl. 5.8.3.2 z rys. 5.7. i wzorów uproszczonych,
• ocena globalnych efektów drugiego rzędu w budynkach  [1], ,kl. 5.8.3.3.

Do współczesnych zastosowań wartościowe są natomiast zasady sformułowane do metod obliczeń konstrukcji żelbetowych  [1], kl. 5.8.5, a w szczególności metoda nominalnej sztywności, opisana w ustępie Nominalna sztywność przekroju żelbetowego., a także zasady uwzględnienia pełzania [1], kl. 5.8.4,

Metoda imperfekcyjna w konstrukcjach żelbetowych

Układy konstrukcyjne i ich elementy są obarczone odchyleniami od kształtu idealnego, zwanymi imperfekcjami i nie da się tego wyeliminować.
Imperfekcja jest wymuszeniem geometrycznym i  zasadniczo powinna być uwzględniona poprzez zmianę  geometrii konstrukcji z modelu idealnego  na system przechylony z wygiętymi elementami. Okazuje się, że żmudną zmianę systemu geometrycznego można zastąpić przez obciążenie konstrukcji idealnej przez siły równoważne od imperfekcji i przeprowadzeniu obliczeń z analizą drugiego rzędu.  Dlatego często będziemy mówili o obciążeniu konstrukcji siłami imperfekcji.

Po przeprowadzeniu obliczeń metodą imperfekcyjną nie ma potrzeby analizy wydzielonych elementów konstrukcyjnych – wystarczy zwymiarować tylko krytyczne przekroje konstrukcji.

Możemy zapomnieć więc o długościach wyboczeniowych (efektywnych), a w przypadku stosowania obliczeń z uogólnionymi elementami skończonymi (o siedmiu stopniach swobody w każdym węźle – z paczeniem jako 7-mym stopniem) możemy zapomnieć również o zwichrzeniu smukłych (wysokich) belek.

Szeroki opis metody imperfekcyjnej projektowania konstrukcji budowlanych, w rym konstrukcji żelbetowych podano w podręczniku  „Metoda imperfekcyjna projektowania konstrukcji”. Poniżej w skrócie podano wybrane informacje, specyficzne dla konstrukcji żelbetowych. W celu rozszerzenia wiedzy odsyłamy do podręcznika.

Imperfekcje geometryczne i równoważne siły imperfekcji

Imperfekcje (niedoskonałości) konstrukcji żelbetowej, stalowej, aluminiowej czy zespolonej dzieli się na (rys. 11) :

• globalne – układu   (przechyłowe)
• lokalne (elementu – łukowe, a w konstrukcjach żelbetowych również niezamierzone mimośrody).

Miarą imperfekcji globalnych jest parametr imperfekcji $\theta_i$, który reprezentuje kąt przechyłu systemu. Na rys. 11a kształt idealny konstrukcji oznaczono linia przerywaną. Po jej przechyleniu o niezmierzony kąta $\theta_i$ konstrukcja przyjmie kształt oznaczony linią ciągłą.

Parametr imperfekcji wyznacza się z zależności [1]:

$$\begin{equation} \theta_i=\theta_0 \cdot \alpha_h \cdot \alpha_m \label {5} \end{equation}$$

gdzie:
$\theta_0=1/200$ podstawowa (bazowa) wartość parametru imperfekcji,
$\alpha_h= 2/ \sqrt{h}$ przy czym $( 2/3 \le \alpha_h \le 1)$ – współczynnik redukcyjny ze względu na wysokość (długość) $h$ w m elementu lub konstrukcji,
$alpha_m=\sqrt{1/2\cdot(1+1/m)}$ – współczynnik redukcyjne ze względu na  liczbę elementów  „m” uczestniczących w przenoszeniu obciążenia imperfekcji (np. całkowitą liczbę słupów na kondygnacji)

Rys. 11: a) imperfekcje systemowe, b) momenty II rzędu, c) imperfekcje łukowe

W konstrukcjach żelbetowych stosuje się metodę imperfekcyjną z ideą przedstawioną na rys. 11, w której

a) imperfekcje układu (systemowe)  $\theta_i$ (rys. 11a) zastępuje się równoważnymi, fikcyjnymi siłami imperfekcji $H_i$

$$\begin{equation} H_i= \theta_i \cdot V  \label {6} \end{equation}$$

gdzie V jest symbolem obciążenia grawitacyjnego. Równoważne siły imperfekcji przykłada się do konstrukcji jako dodatkowe obciążenia i dla uzupełnionych wymuszeń przeprowadza się analizę II rzędu.

W praktyce polega to na stowarzyszeniu z każdym obciążeniem pionowym (skupionym lub rozłożonym) sił poziomych w dwóch kierunkach, to znaczy wektor obciążenia każdego punktu konstrukcji ma trzy składowe:  $ [H_x,H_y,V_z,]= V \cdot[ \theta_i ; \quad \theta_i ; \quad 1]$

b) Konstrukcję obciążoną jak w pkt a) poddaje się analizie drugiego rzędu. W rezultacie w każdym punkcie konstrukcji uzyskuje się siły przekrojowe drugiego rzędu: momenty zginające $M^{II}$ oraz siły osiowe $N^{II}$

c) imperfekcje łukowe $e_i = \theta_i l_0/2$  (rys. 11c) uwzględnia się jak dla elementu wydzielonego o długości efektywnej $l_0$ i zastępuje fikcyjnymi siłami imperfekcji

$$\begin{equation} q_i= \cfrac{8 N e_i}{l_o^2} = \cfrac{4N \theta_i}{l_0}\label {7} \end{equation}$$

W normie [1] imperfekcje łukowe  zastąpiono fikcyjnymi siłami skupionymi w środku długości $l_0$, które można otrzymać poprzez porównanie momentu zginającego w środku elementu wywołanego obciążeniem skupionym $M_H=H_i l_0/4$ z momentem wywołanym obciążeniem rozłożonym $M_q=q l_o^2/8$ czyli

$$\begin{equation} H_i= \cfrac{q_i \cdot l_o}{2}= 2 \theta_i N\label {8} \end{equation}$$

Powyższe oszacowania dotyczą elementów w montowanych w system w tak zwanym układzie usztywnionym.

W przypadku elementów nieusztywnionych, np wspornika analiza będzie odmienna i prowadzi do wniosku, że siła imperfekcji systemowych $(\ref {5})$ uwzględnia już imperfekcję łukową i dalsze obciążanie takich elementów nie jest potrzebne.

Oszacowanie długości efektywnej (wyboczeniowej) i smukłości pręta

Nie powinno się używać  oszacowań wynikających z rysunku 5.7 EC2, ani też z formuł (5.15) lub (5.16) tej normy, ze względu na ich zawodność w większości zastosowań praktycznych.  Wyłącznie w przypadku idealnych warunków brzegowych (przegubu lub utwierdzenia) długości wyboczeniowe są zgodne z podanymi na rys. 5.7 EC2. Problem w tym, że nigdy warunki brzegowe nie  są idealne. Nawet w przypadku pręta przegubowo-przegubowego $l_{0}<L$, a w przypadku wspornika $l_{0}>2L$.

Rozsądne oszacowanie długości efektywnej i smukłości pręta w systemie możliwe będzie dopiero po oszacowaniu mnożnika krytycznego $\Lambda_{cr} =\alpha_{cr}$, czyli takiego mnożnika konfiguracji obciążenia P,  że pod obciążeniem $\Lambda_{cr}$P  konstrukcja, jej część lub element traci stateczność.  W krytycznym stanie w elemencie (e) działa  krytyczna siła osiowa:

$$\begin{equation} N_B= \Lambda_{cr} \cdot N_{(e)} \label {10} \end{equation}$$

gdzie $N_{(e}}$ jest siła osiową wywołaną obciążeniem P.

Teraz z formuły Eulera [1], kl. (5.17)  można wyznaczyć długość efektywną (wyboczeniową) :

$$\begin{equation} l_0=\pi \sqrt{\cfrac{EI}{N_B}}\label {9} \end{equation}$$

Kryterium uwzględniania imperfekcji elementu (łukowych)

W konstrukcjach żelbetowych najczęściej mamy do czynienia z krępymi elementami i zgodnie z kryterium podanym niżej imperfekcji łukowych nie musimy uwzględniać.

Stosownie do kryterium normowego [1] – nie są wrażliwe na efekty II rzędu elementy ściskane o smukłości

$$\begin{equation} \lambda \le \lambda_{lim}\label {12} \end{equation}$$

Graniczną wartość smukłości określa się z zależności

$$\begin{equation} \lambda_{lim}=\cfrac{20 \cdot A \cdot B \cdot C}{\sqrt{n}} \label {13} \end{equation}$$

Współczynnik $ A=\cfrac{2}{1+0,2 \varphi_{ef}}$  – dla nieznanego $\varphi_{ef}$ można przyjmować o wartości A=0,7

Współczynnik $B=\sqrt{1+2 \omega}$ – dla nieznanej intensywności zbrojenia $\omega= \cfrac {A_s f_y}{A_c f_{cd}}$ można przyjmować B=1,1

Współczynnik $C=1,7 – r_m$,
gdzie $r_m=M_{01}/M_{02}$ – stosunku momentów pierwszego rzędu na końcach elementu. Przy wyznaczania stosunku momentów na końcu „01” i „02” elementu, należy je uporządkować tak, by $|M_{01}| \ge |M_{02}|$.
dla nieznanego  $r_m$ można przyjmować  C=0,7.

Sposób uwzględnienia imperfekcji łukowych

Do elementów konstrukcji żelbetowej, których smukłość nie spełnia warunku $( \ref {12})$ należy przyłożyć obciążenia międzywęzłowe zgodnie z formułą $(\ref{7})$ lub  $(\ref{8})$.

Nominalna i efektywna sztywność przekroju żelbetowego

Idea metody nominalnej sztywności polega na tym, by oszacować sztywność przekroju żelbetowego tak by w obliczeniach statycznych traktować go jako zintegrowaną sztywność przekroju jednorodnego z uwzględnieniem zarysowania oraz pełzania betonu.

Sztywność EI przekroju słupa żelbetowego zgodnie z [1] można oszacować z formuły

$$\begin{equation} EI =K_c E_{cd} I_c +K_s E_s I_s \label {14} \end{equation}$$

$I_c$  jest momentem bezwładności przekroju betonu,
$E_s$ jest obliczeniową wartością modułu sprężystości zbrojenia
$l_s$ jest momentem bezwładności pola przekroju zbrojenia względem środka ciężkości powierzchni betonu,
$K_c$ jest współczynnikiem zależnym od wpływów zarysowania, pełzania itd. betonu
$K_s$ jest współczynnikiem zależnym od udziału zbrojenia.

Obliczeniowy modułu sprężystości betonu wynosi

$$\begin{equation} E_{cd}=\cfrac {E_{c,m}} {\gamma_{cE}} \label {15} \end{equation}$$

gdzie współczynnik materiałowy $\gamma_{cE}$ zaleca się przyjmować o wartości 1,2, ale często przyjmuje się $\gamma_{cE}=\gamma_c=1,4$

Jeżeli stopień zbrojenia przekroju $\rho=A_s/A_c >0,002$, można stosować następujące współczynniki:

$$\begin{equation} K_s=1,0 \label {16} \end{equation}$$

$$\begin{equation} K_c= \cfrac{k_1 k_2}{1+\varphi_{ef}} \label {17} \end{equation}$$

Warunek stopnia zbrojenia  dotyczy w zasadzie każdego przekroju żelbetowego.

W przypadku mocno zbrojonego przekroju $\rho>$1% i tylko jako wstępne przybliżenie można stosować uproszczoną formułę $K_c=0,3/(1+0,5 \varphi_{ef})$.

Współczynnik $k_1$ zależy od klasy wytrzymałości betonu:

$$\begin{equation} k_1= \sqrt{ \cfrac{f_{ck}} {20}} \label {18} \end{equation}$$

Współczynnik $k_2$ zależy od względnej siły podłużnej $n=N_{Ed}/(A_c f_{cd})$ i smukłości słupa $\lambda$:

$$\begin{equation} k_2= min \{ n \cdot \cfrac{\lambda}{170} \, ; \, 0,2 \} \label {19} \end{equation}$$

Jeśli smukłość nie jest określona, to można przyjąć $k_2=min \{0,3 n \, ;\, 0,2 \}$.

Efektywny współczynnik pełzania $\varphi_{ef}$ oblicza się z wyrażenia:

$$\begin{equation} \varphi_{ef}= \varphi (\infty ;t_0) \cdot k_{0,qp} \label {20} \end{equation}$$

gdzie $k_{0,qp}=\cfrac{M_{0qp}} {M_{0Ed}}$ jest udziałem obciążeń prawie stałych w całkowitych obciążeniach, mierzonych momentami zginającymi:

$M_{0qp}$ jest momentem zginającym pierwszego rzędu wywołanym prawie stałą kombinacją obciążeń (SLS),

$M_{0 Ed}$ jest momentem zginającym pierwszego rzędu wywołanym obliczeniową kombinacją obciążeń (ULS).

Długotrwały współczynnik pełzania $\varphi (\infty ;t_0)$ można oszacować na podstawie tab.1 artykułu Belki żelbetowe (…) i współczynników korekcyjnych wg tab. 8 w tym artykule.

W przypadku jednoparametrowego obciążenia konstrukcji stosunek momentów zginających jest stosunkiem obciążeń prawie stałych (współczynnik redukcyjny $\psi_2$) i kombinacyjnych (współczynnik redukcyjny $\psi_0$). Dla często występującego w konstrukcjach żelbetowych stosunku obciążeń stałych (ciężaru własnego) i zmiennych 60% do 40% i dla struktury obciążeń zmiennych: 70% użytkowe (mieszkalne), 15% śnieg, 15% wiatr  mamy oszacowania:

$M_{0,qp} \sim 1,0 \cdot 0,6 + 1,0 \cdot 0,4 \cdot ( 0,3 \cdot 0,7 + 0,2 \cdot 0,15 +0,0 \cdot 0,15= 0,696$
$M_{0,Edp} \sim 1,35 \cdot 0,6+ 1,5 \cdot 0,4 \cdot ( 1,0 \cdot 0,7 + 0,5 \cdot 0,15 +0,6 \cdot 0,15= 1,329 $

$$\begin{equation}  k_{0,qp} \approx \cfrac {0,696}{1,329}=0,52 \approx 0,6 \label {21} \end{equation}$$

Często stosowanym oszacowaniem współczynnika pełzania jest  $\varphi (\infty, t_0)  \approx 2,5$. Stąd $\varphi_{ef}=2,5 \cdot 0,6= 1,5$.  Wartość ta może być stosowana w obliczeniach wstępnych i wymaga sprawdzenia dla każdego konkretnego przypadku.
Dla często stosowanego betonu C30/37 : $k_1=\sqrt{30/20}=1,22$  i dla $k_2=0,2$, mamy:

$$\begin{equation} K_c= \cfrac{1,22 \cdot 0,2}{1+1,5}=0,1 \label {22} \end{equation}$$

W konstrukcjach statycznie niewyznaczalnych należy uwzględniać niekorzystne wpływy zarysowania elementów przylegających. Dla tych elementów stosowanie powyższych wyrażeń na ogół nie jest właściwe. Częściowe zarysowanie i współpracę betonu na odcinkach między rysami można uwzględniać w sposób stosowany przy obliczaniu ugięć, ale jako uproszczenie zwykle przyjmuje, że przekroje są w pełni zarysowane, a sztywnośćnależy oprzeć na efektywnym module sprężystości betonu stosując wzór:

$$\begin{equation} E_{cd,ef}=\cfrac{E_{cd}}{1+\varphi_{ef}}\label {23} \end{equation}$$
w którym:
$E_{cd}$ jest obliczeniową wartością modułu sprężystości $(\ref {15})$,
$\varphi_{ef}$ jest efektywnym współczynnikiem pełzania $( \ref {20} )$.

Sztywność nominalną  ($\ref{14}$) w literaturze zagranicznej często  nazywa się sztywnością efektywną $K_{eff}$

$$\begin{equation} K_{eff} = EI_{eff}= k \cdot EI_c \label {24} \end{equation}$$

gdzie współczynnik redukcyjny $k=\cfrac{I_{eff}}{I_c}$ zależy od obciążenia słupa (względnej siły osiowej $n=\tfrac{N_{Ed}} {A_c \cdot f_{cd}}$ oraz stopnia zbrojenia $\rho=\tfrac{A_s}{A_c}$ co przedstawiono na rys. 12. Sztywność słupa wzrasta wraz ze wzrostem obciążenia oraz wraz ze wzrostem stopnia zbrojenia. 

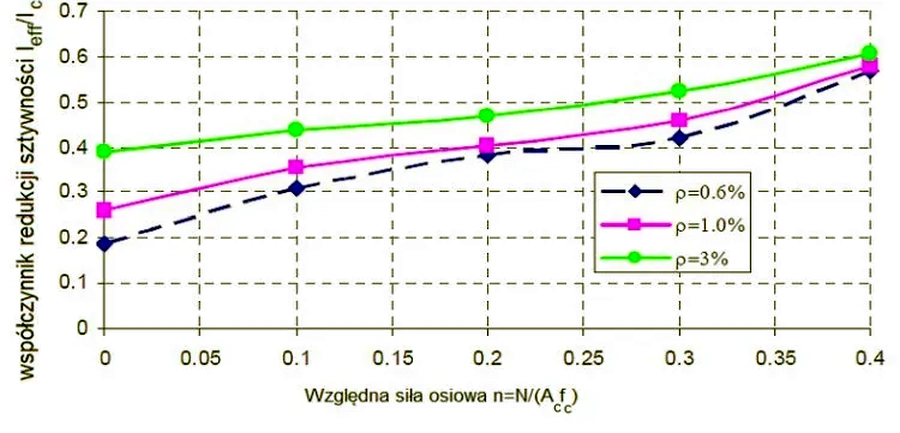
Rys. 12 Współczynnik redukcji sztywności słupa $k$ w zależności od obciążenia $n$ oraz stopnia zbrojenia $\rho$

Z rys. 12 wynika, że oszacowanie ($\ref{22}$) jest zbyt konserwatywne. Dla optymalnego zbrojenia słupa  ( stopnia zbrojenia $\rho=1$%) i obciążenia $n=0,25$ redukcja sztywności powinna wynosić $K_{eff}=0,42$.

Obliczanie zbrojenia podłużnego przekroju słupa

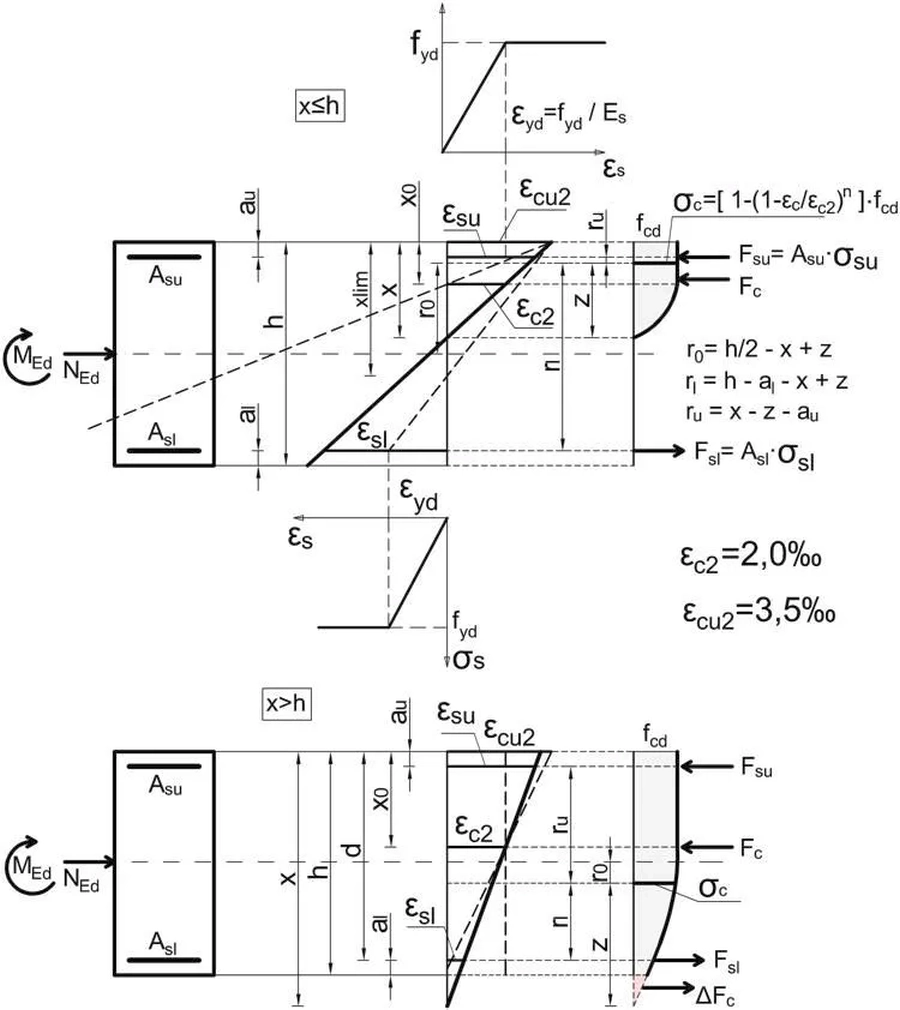
Na rys. 13 pokazano model przekroju betonowego dla dwóch przypadków wytężenia:

• • przypadek CT – duży mimośród  (górne zbrojenie ściskane, dolne rozciągane), gdzie wysokość strefy ściskanej x ≤h,
  • przypadek CC  -mały mimośród (oba zbrojenia ściskane), gdzie x>h 

Rys.13 Model przekroju żelbetowego: x < h przypadek CT, x > h przypadek CC

Przekroje ściskane i zginane z dużym mimośrodem (przypadek CT) , czyli z przeważającym zginaniem są projektowane jak przekroje belek zgodnie z zasadami podanymi a artykule Belki żelbetowe. i nie są przedmiotem niniejszego artykułu.  Przytoczymy najważniejsze wyniki analizy przypadku CT.  Wypadkowa  bryły naprężeń w betonie dla przypadku CT , ale również CC, ale liczona wraz z bryłą „pozorną” wynosi:

$$\begin{equation}F^0_c= \dfrac{18}{23}\cdot b \cdot x \cdot f_{cd} \label {25} \end{equation}$$

a moment tej bryły względem środka przekroju betonowego (na ramieniu $d_0=h/2$) wynosi:

$$\begin{equation}M^0_{c,0}= F^0_c \cdot \left (d_0- \dfrac {693} {1666} \cdot  x \right)  \label {26} \end{equation}$$

Przekroje z małym mimośrodem rodzaju CC (oba zbrojenia ściskane), charakteryzują się tym, że wysokość strefy ściskanej x>h.  W tym przypadku  pod przekrojem (na odcinku x do h) naprężenia faktycznie nie działają, a były wliczone w wyrażenia dla przypadku x<h,.  Z tego powodu wyrażenia $(\ref{25})$ i $(\ref {26})$ należy skorygować, jak następuje:

$$\begin{equation}F_c= F^0_c -F_N \cdot(21+20 \overline x) \label{27}\end{equation}$$

$$\begin{equation}M_{c,0}=M^0_{c,0} + F_N \cdot h \cdot  ( 7+8 \overline x+9 \overline x^2) \label{28}\end{equation}$$

gdzie: $\overline x=x/h$ ,  $ F_N = \dfrac{10}{192} \dfrac{(1-\overline x)^2}{\overline x^2} \cdot b \cdot h\cdot f_{cd}$.

Wyprowadzenie powyższych wzorów zamieszczono w artykule  Krzywe interakcji M-N żelbetu.

Przykłady rachunkowe

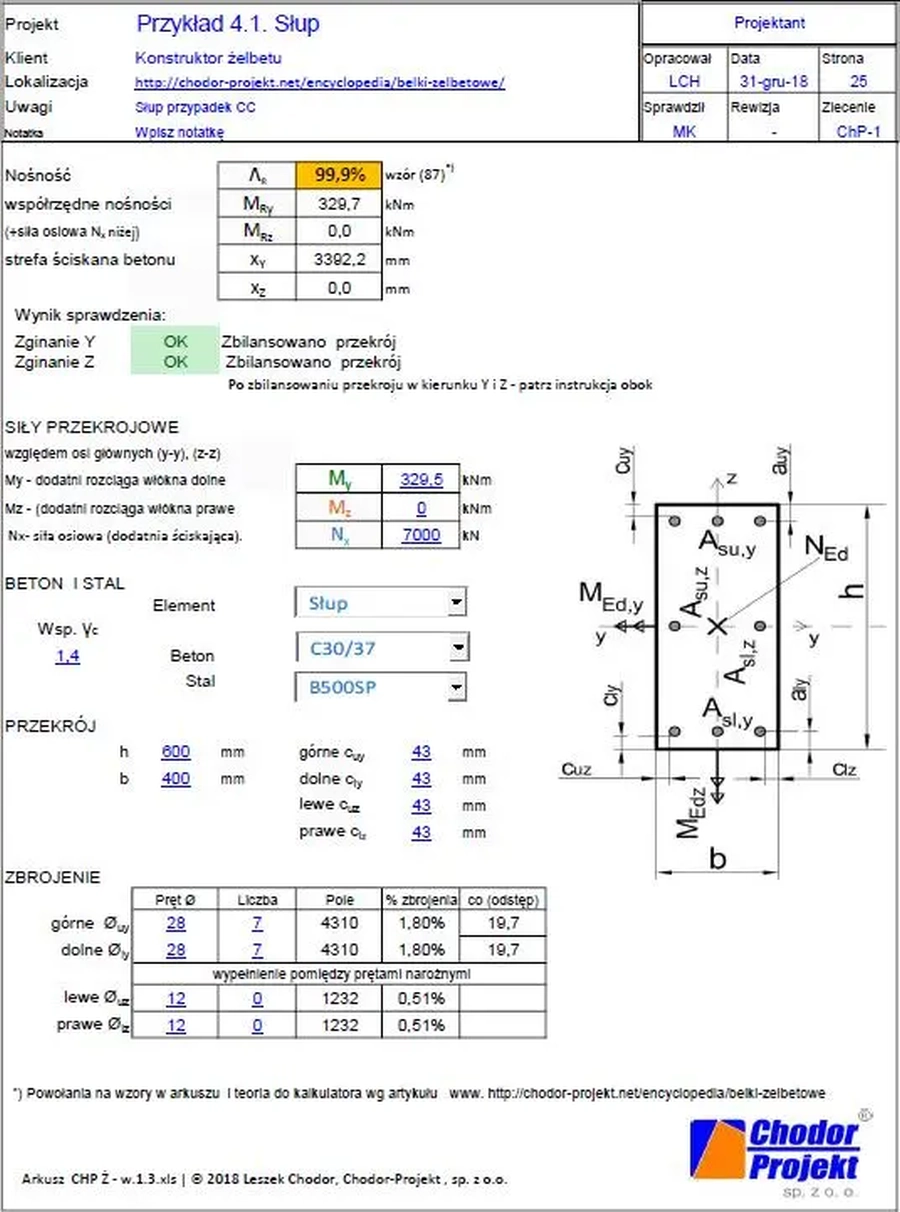
Przykład 1 [ Dobór zbrojenia w przypadku CC]

[9], Przykład 13.3

Przekrój  600×400 z betonu C30/37-B500 jest zbrojony symetrycznie $A_{sl}=A_{su}=$ 7Ø28  ( przekrój ok 43 cm²)
i obciążony siłą ściskającą $N_{Ed}=7000 \, kN$.
Otulenie osiowe zbrojenia wynosi a=55 mm.

Obliczyć nośność przekroju mierzoną momentem zginającym $M_{y}.

Wynik przykładu oryginalnego

$M_{Rdy}=241,2 \, kNm$

Zastosowanie arkusza CHP-Ż, w 1.3

Na rys. 14 pokazano wyniki zastosowania arkusza. Przypadek jest CC, bo x=3392 mm > h=600 mm. Wykorzystanie przekroju w 100% uzyskano dla $M_y=329,5 \, kN$, to znaczy 329,5/241,2=1,36 razy więcej od klasycznych obliczeń [9], Przykład 13.3.

Rys. 14. Ekran arkusza do przykładu 1 (kliknij obraz, aby pobrać)

Przykład 2 [Sztywność nominalna przekroju słupa]

Dla wspornikowego słupa, pokazanego na rys. 15 obliczyć sztywność nominalną przekroju względem osi większej sztywności y-y (oś pionowa przekroju A-A).

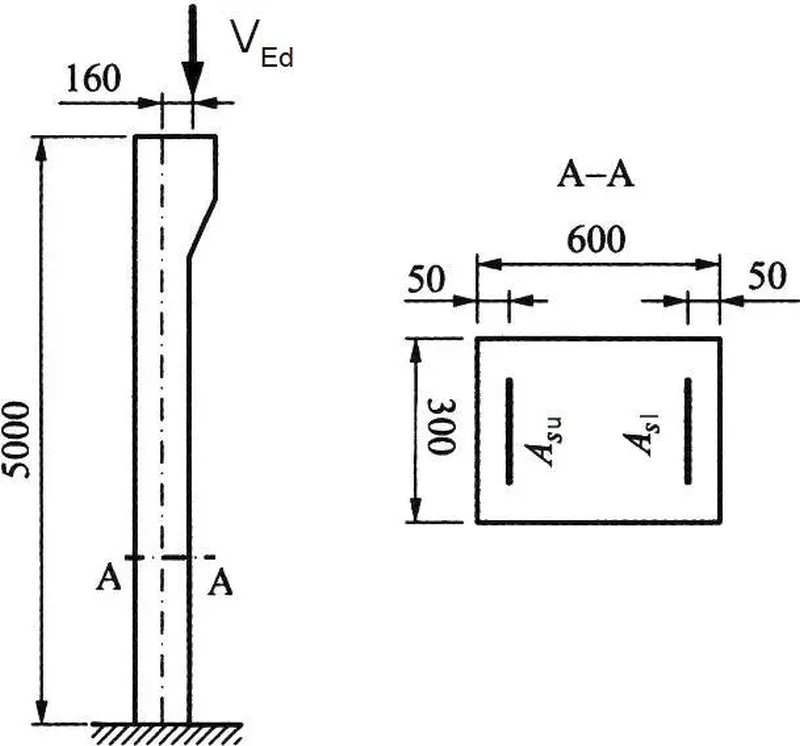
Rys.15 Słup do przykładu 2 (Knauff, M., Golubińska, A., & Kryziak, P. (2014). Tablice i wzory do projektowania konstrukcji żelbetowych z  przykładami obliczeń , Wydanie drugie., PWN)), rys.13.12

Dane podstawowe

Przekrój słupa ma wymiary 600×300 .  Słup wykonano  z betonu C25/30: $f_{cd}=25/1,4=17,86 \, MPa$ oraz zbrojono stalą B500 $f_y=500/1,15=435 \, MPa$. Zbrojenie symetryczne słupa $A{sl}= A{su}=8,84 \, cm^2$  (5∅15 górą i dołem)- pręt ∅15 tylko teoretyczny, w celu uzyskania zgodności przekroju zbrojenia z przykładem oryginalnym.
Słup jest obciążony w głowicy siłą $V_{Ed}= 1768 \, kN$ na mimośrodzie zamierzonym (bez imperfekcji) $e=16 \, cm$

Moduł Younga betonu:
sieczny  $E_{cm}= 31,5 \, GPa$
obliczeniowy  $E_{cd}=31,5/1,4=22,5 \, GPa$, (przyjęto $\gamma_{cE}=1,4$ jak w programie Consteel)

Siły przekrojowe i współczynnik udziału prawie-stały

Obliczeniowa siła osiowa w słupie (bez ciężaru własnego) $N_{Ed}=V_{Ed}=1768 \, kN$; o
obliczeniowy moment zginający pierwszego rzędu $M_{Ed}=1768 \cdot 0,16=283 \, kNm$,
Z obliczeń statycznych wynika, że maksymalny moment zginający do kombinacji prawie stałej wynosi  $M_{Ed}=190,4 \, kNm$,

Współczynnik udziału obciążeń prawie stałych $k_{0,qp}=190,4/283=0,67$.
Nośność przekroju betonowego

Względna siła osiowa $n=\cfrac{1768}{30\cdot 60 \cdot 17,86\cdot 10^{-1}}=0,555$.

Współczynnik pełzania

Z tab.1 artykułu Belki żelbetowe (…) dla betonu C25/30 bazowy współczynnik pełzania (dla $t_0=28$ dni oraz  miarodajnego wymiaru $h_0=250 mm$) wynosi

$\varphi_0=2,56$.

Z tab. 8 w artykule jw. odczytano współczynniki korekcyjne:

• dla miarodajnego wymiaru słupa $h_0=(600\cdot 300)/(2\cdot 600+300)=120 \, mm$  z interpolacji otrzymujemy $n_h=1,15-(1,15-1,04)/(200-100)\cdot (120-100)=1,13$. (obwód słupa poddany wysychaniu obejmuje dwa boki dłuższe i jeden krótszy – od tyłu do słupa dochodzi ściana i zapobiega wysychaniu).
• dla  $t_0=28 dni$ mamy $n_t=1,0$

Ostatecznie  współczynnik pełzania trwały  $\varphi( \infty, t_0)= 2,56\cdot 1,0 \cdot 1,13=2,89$.

Współczynnik pełzania efektywny $(\ref {20}) \to $ $ \varphi_{ef}= 2, 89 \cdot 0,67=1,94$.

Smukłość słupa

Długość wyboczeniowa (efektywna) słupa w czystym przypadku wspornika idealnie utwierdzonego: $l_0=2 \cdot 5,0=10,0 \, m$

Smukłość słupa  $(\ref {2}) \to $ $\lambda=3,464 \cdot 10,0/0,6=57,7$

Stopień i intensywność zbrojenia

Pole przekroju betonu $A_c=60\cdot 30=1800 \, cm^2$

Pole przekroju stali $A_s=5,84+5,84=11,68 \, cm^2$.

Stopień zbrojenia $\rho=11,68/1800=0,649 > 0,2$.%.

Intensywność zbrojenia  $\omega= \cfrac {11,68 \cdot  435}{1800 \cdot 17,86}=0,158$

Smukłość i warunek graniczny $(\ref{13})$

$ A=\cfrac{2}{1+0,2 \cdot 1,94}=0,720$,

$B=\sqrt{1+2 \cdot 0,158}=1,147$,

Moment I rzędu jest stały na wysokości słupa, więc $r_m=1$,

$C=1,7 -1,0=0,7$,

$(\ref{13}) \to$  $\cfrac{20 \cdot 0,720 \cdot 1,147 \cdot 0,7}{\sqrt{0,555}}=15,5 < 57,7 \to$ słup jest wrażliwy na efekty II rzędu

Współczynniki udziału betonu i stali

Ponieważ stopień zbrojenia 0,00649 > 0,002, więc możemy stosować wzory $(\ref{18})$ oraz $(\ref{19})$:

$k_1= \sqrt{ \cfrac{25}{20} }= 1,12$,

$k_2= min \{ 0,555 \cfrac{57,7}{170} \, ; \, 0,2 \} =0,187$.

Współczynnik udziału betonu $K_c= \cfrac {1,12 \cdot 0,187}{1+1,94}=0,071$

Współczynnik udziału stali  $ K_s=1,0 $,

Sztywność nominalna  przekroju żelbetowego

Moment bezwładności betonu $I_c=\cfrac{30\cdot 60^3}{13}=540000 \, cm^4$,

Moment bezwładności stali $I_s= 2\cdot 8,84 \cdot (60/2-5)^2= 11050\, cm^4$,

Sztywność nominalna betonu $EI_c=540000\cdot 10^{-8}  \cdot 22,5\cdot 10^6=121500 \, kN m^2$,

Sztywność nominalna stali $EI_s=11050 \cdot 10^{-8}  \cdot 200 \cdot 10^6=22100 \, kN m^2$,

Sztywność nominalna  przekroju $(\ref{14})$  $EI =0,071 \cdot 121500+1,0\cdot 22100=8627+22100=30727 \, kN m^2$,

Teoretyczna siła krytyczna ze wzoru Eulera

$N_B=N_{cr}= \pi^2 \cfrac{30727}{10,0^2}=3033 \, kN > 1768 \, kN $.

REMANENT Przykłady poniżej w rewizji

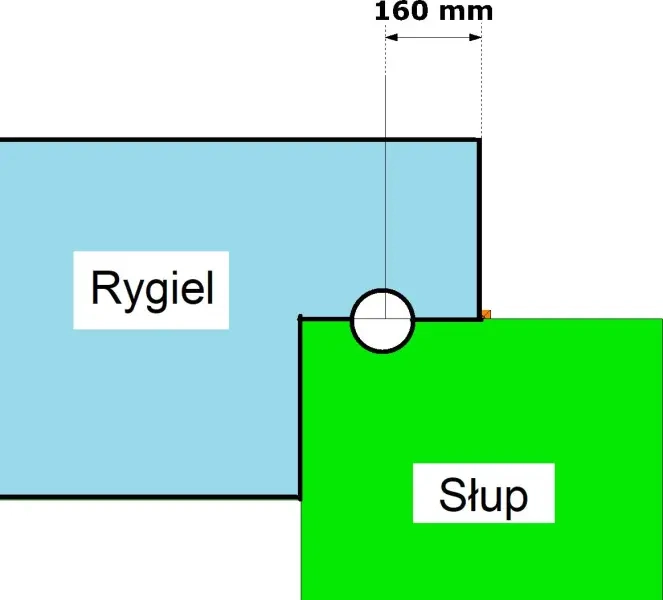
Przykład 3 [Smukłość słupa w układzie ramowym – oszacowanie numeryczne]

Dokonano oszacowania długości wyboczeniowej (efektywnej)  słupa z przykładu 1 stanowiącego element ramy portalowej, pokazany na rys. 15.  Słupy i rygiel ramy modelowano prętem betonowym zbrojonym jak w przykładzie 2 (5∅15 górą i dołem). Rama jest obciążona siłą pionową V=1768 kN na mimośrodzie 160 mm w stosunku do osi słupów. Ciężar własny rygla i słupa pominięto,

Słupy mają wysokość 5m, a rygiel rozpiętość 9 m (w osiach słupów). Oba słupy w pełni utwierdzono w fundamencie, a rygiel oparty jest na słupie poprzez podcięcie, w sposób pokazany na rys. 16

Rys.16 Węzeł rygiel-słup typu P

Najpierw przeprowadzono analizę wyboczeniową systemu z wyznaczaniem sztywności nominalnej przekroju żelbetowego dla  dla $K_c=0,071$ i $K_s=1,0$., $\varphi_{ef}= 1,94$.
Niestety nie uzyskano rozwiązania, bo proces iteracyjny był rozbieżny ze względu na zbyt dużą siłę osiową w słupach. Oznacza, to, że mnożnik krytyczny takiego systemu jest   znacznie mniejszy od jedności $\Lambda_{cr} \ll 1$, czyli siła krytyczna

$N_B \ll 1768$, to znaczy długość wyboczeniowa słupa $L_{cr} \gg 10 \, m$. Oznacza to, że błędne jest stosowanie metody wydzielonego elementu.

W obu przypadkach uzyskano takie same kształty własne ramy po wyboczeniu, a także siły osiowe w słupach ($N_{Ed}=1768 \, kN$, ale istotnie różne mnożniki krytyczne i wynikające z nich siły krytyczne $N_B$:

• dla rygla przegubowo-przegubowego P-P; $\Lambda_{cr}=1,15$ , $N_B=1,14\cdot 1768=2015,5 \, kN$,
• dla rygla utwierdzono-utwierdzonego U-U $\Lambda_{cr}=2,88$ , $N_B=2,88\cdot 1768=5091,8 \, kN$,

Z zależności $(\ref{9})$ uzyskujemy następujące długości efektywne słupa

• w przypadku  rygla P-P: $l_0=\pi \sqrt{\cfrac{14}{10}}=\pi \sqrt{ \cfrac{31577}{2015,5}}=12,43 \, m$
• w przypadku  rygla U-U: $l_0=\pi \sqrt{ \cfrac{31577}{5091,8}}=7,82 \, m$

Dla porównania przeprowadzono też obliczenia wyboczeniowe dla wspornika z przykładu 1 i uzyskano wynik identyczny jak dla rygla P-P, to znaczy długość wyboczeniowa słupa wynosi 12,43 m  (wsp. długości wyboczeniowej $\ni=12,43/5=2,49$ a nie 10 m $(\ni=2)$ jak przyjęto w przykładzie 1 na podstawie arbitralnej decyzji.

Przykład 4  [ Projekt ramy metodą imperfekcyjną ]

Metodą imperfekcyjną w odmianie równoważnych sił imperfekcji  zaprojektować słupy ramy z przykładu 3 w wariancie rygla P-P.

Równoważne siły imperfekcji systemowych

Bazowy parametr imperfekcji  $\theta_0=1/200$
Współczynnik redukcyjne ze względu na wysokość  elementu lub konstrukcji  $\alpha_h=2/\sqrt{9}=0,89 >2/3 \quad <1$
Współczynnik redukcyjny ze względu na liczbę elementów $\alpha_m=\sqrt{0,5\cdot(1+1/2)}=0,87$ (dla ramy z m=2 słupami) i $\alpha_m=1$ dla wspornika

Parametr imperfekcji  $(\ref{5})$ oraz równoważna, fikcyjna siła pozioma od imperfekcji $(\ref{5})$ przyłożona w głowicy słupa :

• dla wspornika $n_i=1/ \theta_i= 200 / (0,89\cdot 1)= 225$,  $H_i=1638/225=7,28 \, kN$
• dla ramy z ryglem U_U lub P-P: $n_i= 1/ \theta_i= 200 /(0,89\cdot 0,87)= 258$ ,  $H_i=1638/258=6,35 \, kN$

Równoważne siły imperfekcji lokalnych

Stosowane tylko dla układów usztywnionych (tutaj rama) i nie stosowane dla układów swobodnych (wspornik). Bazowy parametr imperfekcji $]theta_0=1/200$ i współczynnik redukcyjny $\alpha_h=0,89$ jak wyżej. Współczynnik redukcyjny $\alpha_m=1$. Parametr imperfekcji wynosi $n_i=1/ \theta_i= 200 / (0,89\cdot 1)= 225$

Obciążenie międzywęzłowe słupów $q_i$ $(\ref{7})$:  $q_i=  \cfrac{4\cdot 1638/225}{12,38}=2,353 \, kN/m$,

Rozwiązanie ramy metodą imperfekcyjną równoważnych obciążeń poziomych

Ramę portalową z rys. 15 dla przypadku rygla P-P obciążono siłami imperfekcji w sposób pokazany na rys. 15 w wariancie najniekorzystniejszym współdziałania obciążeń od imperfekcji systemowych oraz lokalnych .

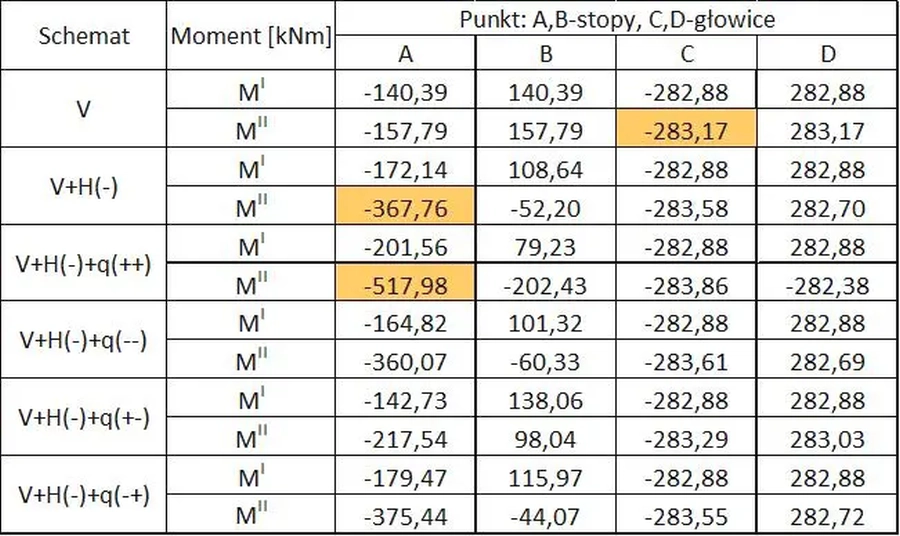
W tab.1. zestawiono momenty zginające I i II rzędu w węzłach ramy obserwowane w różnych konfiguracjach obciążeń od imperfekcji. Nie stawiano sił osiowych, ponieważ ich zmiany w w stosunku do sił pierwszego rzędu przy obciążeniu pionowym $N_{Ed}= 1680 \, kN$ w poszczególnych schematach są niewielkie.

W schemacie najniekorzystniejszym „V+H(-)+q(+/+), to jest przy łącznym działaniu sił pionowych $V=1680 \,kN$ na mimośrodach 160 mm oraz sił poziomych $H=6,35 \,kN$ stowarzyszonych z V i skierowanych przeciwnie do zwrotu osi poziomej  oraz obciążeń rozłożonych słupów g=2,35 kN/m, skierowanych zgodnie z kierunkiem osi poziomych na obu słupach, $N^{II}_{Ed} \approx= -1768$ kN w obu słupach.

Tab.1 Momenty zginające w ramie portalowej

Rama nie jest wrażliwa na efekty II rzędu. W schemacie podstawowym „V” zwiększenie maksymalnego momentu zginającego wynosi  283,17/282,88=1,001, czyli tylko 1‰.

Rama jest  mocno wrażliwa na imperfekcje:

• efekt imperfekcji systemowych na momenty zginające wynosi 367,76/283,17=1,30, czyli 30%. w stosunku do modelu bez imperfekcji
• efekt imperfekcji łukowych na momenty zginające wynosi 517,98/367,76=1,41, czyli 41% w stosunku do modelu tylko z imperfekcjami systemowymi

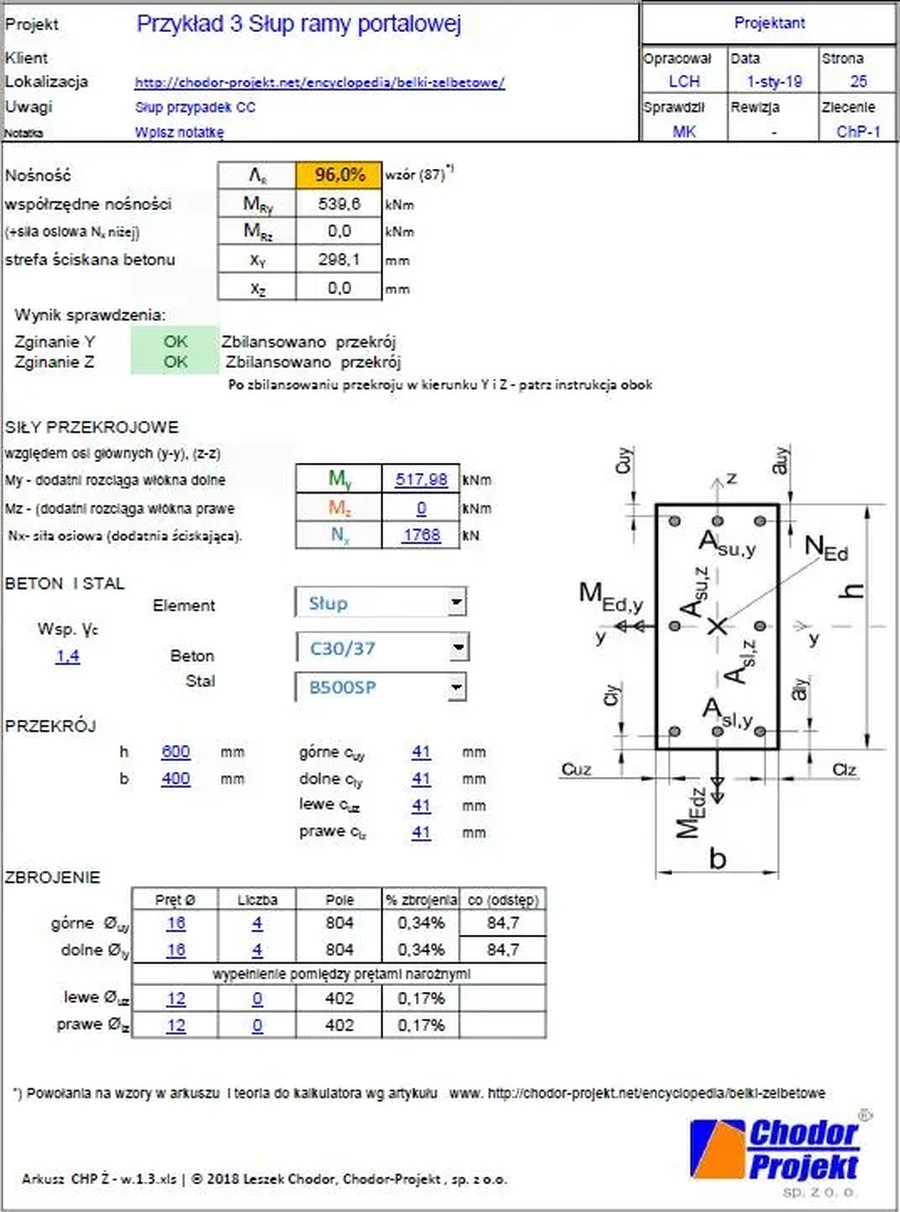
Zbrojenie podłużne słupów

Dolna cześć słupa (przekrój A lub B) : $N_{Ed}= 1768 \, kN$,  $M_{Edy}=517,98 \, kNm$
Górna cześć słupa (przekrój C lub D) : $N_{Ed}= 1768 \, kN$,  $M_{Edy}=283,86 \, kNm$

Na rys. 17  zamieszczono wyniki zbrojenia dolnej części słupa: 4∅16 (górą i dołem) . Tym samym arkuszem można dobrać zbrojenie części górnej 2∅12 (górą i dołem).

Rys.17 Ekran kalkulatora do przykładu 3 (naciśnij obraz , aby pobrać)

 Literatura

1. PN-EN 1992-1+AC+Ap 1,2,3:2008, Projektowanie konstrukcji z betonu – Część 1-1:  Reguły ogólne i reguły dla budynków
2. PN-EN 1992 1-2:2008/NA:2010, Eurokod 2: Projektowanie konstrukcji z betonu – część 1-2: Reguły ogólne – Projektowanie z uwagi na warunki pożarowe
3. Knauff, M., Golubińska, A., & Kryziak, P. (2014). Tablice i wzory do projektowania konstrukcji żelbetowych z  przykładami obliczeń , Wydanie drugie., PWN
4. Starosolski, W. (2013). Konstrukcje żelbetowe według Eurokodu 2 i norm związanych, Tom 3, Wydawnictwo Naukowe PWN
5. DIN 1045-1, Tragwerke aus Beton, Stahlbeton und Spannbeton – Teil 1: Bemessung und Konstruktion
6. Bachmann H., Steinle S., Precast Concrete Strutures, Ernst & Sohn, Berlin 2011
7. Konig G., Minnert J., Saleh H., Stumpf getsossene Fertigteilstuzen aus Noermalbeton , Beton+Fertigteil – Jahrbuch 2001, pp 110-121
8. Zybura (2015). Konstrukcje żelbetowe według Eurokodu 2: atlas rysunków, Wydawnictwo Naukowe PWN
9. Knauff, M., Golubińska, A., & Knyziak, P. (2015). Przykłady obliczania konstrukcji żelbetowych. Budynek ze stropami płytowo-żebrowymi. Zeszyt 1. PWN

________________________________