Leszek Chodor, 18 kwietnia 2016
01-02-2025 rewizja po dużej awarii portalu>
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 15 Czytelników
Słup jest podstawowym elementem prętowej konstrukcji stalowej, stosowanym głównie w konstrukcjach szkieletowych: niskich (najczęściej halach) i wysokich (najczęściej wieżowcach).
W mechanice konstrukcji slup definiuje się jako element prętowy pionowy, obciążony ściskaniem. W praktyce obie okoliczności nie są zachowane: każdy rzeczywisty slup jest obciążony nie tylko ściskaniem, ale również zginaniem i często slupy są pochyłe w sposób zamierzony. Rzeczywisty słup jest elementem belka-słup (ang beam-column) [1], rozdz 7.
Interakcja ściskania i zginania jest sprężysta lub plastyczna zależnie od klasy przekroju. Rozpatruje się dwie sytuacje: wyboczenie słupa w płaszczyźnie systemu i wyboczenie z płaszczyzny. W każdej sytuacji może następować zginanie zewnętrznymi momentami zginającymi zarówno w płaszczyźnie jak i z płaszczyzny systemu, a zwichrzenie uwzględnia się tylko dla zginania w głównej płaszczyźnie pręta. Interakcja zjawisk wyboczenia zwichrzenia i zginania jest w ogólności nieliniowa i sprzężona. W praktycznych formułach nieliniowość uwzględnia się poprzez współczynniki interakcji.
Na slupach hal opierają się dźwigary dachowe i inne urządzenia (np dźwignice) W pracach [2], [3] pokazano, że w takich konstrukcjach ekonomiczność nośnych slupów stalowych jest wątpliwa. Znacznie ekonomiczniejsze jest zastosowanie slupów żelbetowych. Elementy stalowe stosuje się w miejscach przeważającego zginania, np na słupki obudowy ściennej, które faktycznie pracują jak pionowe belki. Na słupach budynków opierają się belki stropowe.
Rodzaje słupów
- Słupy jednogałęziowe (pełnościenne) mogą być wykonane jako stalowe lub zespolone (stalowo-betonowe lub żelbetowe).
Takie słupy mogą mieć stały lub zmienny przekrój na długości. Zmienność przekroju może mieć charakter schodkowy lub ciągły (zbieżny przekrój), - Słupy wielogałęziowe, najczęściej dwugałęziowe lub trój- czterogałęziowe,
Gałęzie są łączone wykratowaniem lub przewiązkami, - Słupy o galęziach mieszanych: na części długości pełnościenne, a na części wielogałęziowe. Typowym przykładem jest słup podsuwnicowy z częścią nadsuwnicową pełnościenną i częścią podsuwnicową dwu- lub cztero-gałęziową.
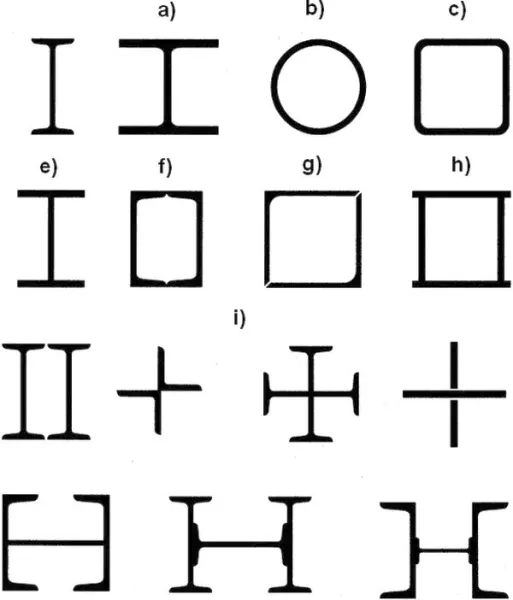
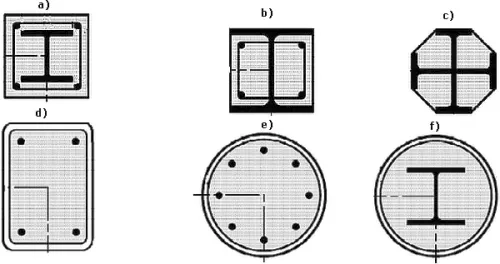
Najczęściej stosowane są słupy jednogałęziowe z profili dwuteowych: HEA, HEB, HEM (rys.1a) , HKS (rys.1e) lub rurowych: rury okrągłe RO (rys.1b), kwadratowe gięte na zimno (rys.1c), złożone z ceowników (rys.1 f), złożone z kątowników (rys. 1g) lub skrzynkowe (rys.1h), a także o przekroju złożonym z różnych profili i blach (rys. 1i).
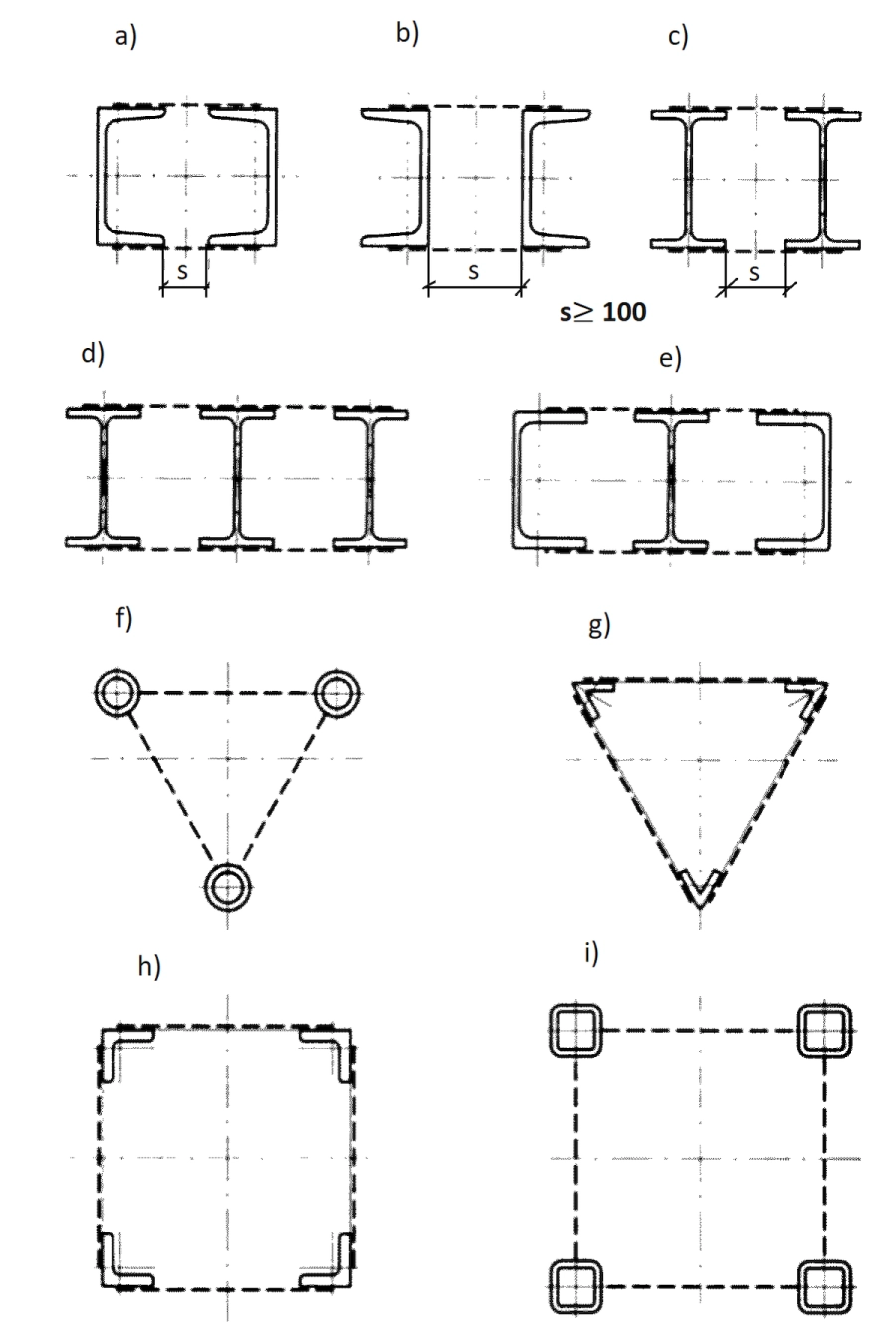
Współcześnie ze względów ekonomicznych, chętnie stosuje się słupy zespolone stalowo – betonowe: z wkładkami stalowymi giętkimi, czyli prętami zbrojeniowymi (rys. 3) lub wkładkami sztywnymi – profilami stalowymi (rys.2.). Na rys. 2 pokazano przykłady przekroi zespolonych słupów stalowo-betonowych sklasyfikowanych w normie [4], a na rys. 3 typowe przekroje słupów żelbetowych zbrojone wkładkami giętkimi stosowane w konstrukcjach żelbetowych.
Rys.2. Przekroje słupów zespolonych stalowo-betonowych [4]

Rys.3. Słupy żelbetowe o przekroju: a) prostokątnym, b) teowym, c) okrągłym, d) pierścieniowym [5]
Na rys.4 pokazano wybrane przekroje słupów wielogałęziowych.
Słupy jednogałęziowe lub wielogałęziowe mogą mieć na długości:
- stały przekrój (rys.5a,b),
- zmienny schodkowo, (rys.5 c,d,e)
- zmienny w sposób ciągły – słupy zbieżne (rys.6).
Słupy o przekroju schodkowym stosuje się w halach z transportem podpartym. Na rys 5c pokazano słup z częścią nadsuwnicowa jednogałęziową , a poddsuwnicowa dwugałęziową z przewiązkami. Na rys. 5d,e pokazano słup z częścią nadsuwnicową jednogałęziową, a podsuwnicową -dwugałęziową wykratowaną, przy czym na na rys, 5e belki podsuwnicowe występują po obu stronach słupa.
Słupy o przekroju zbieżnym stosuje się między innymi na słupy oświetleniowe, słupy wiatraków, elektroenergetyczne itp.
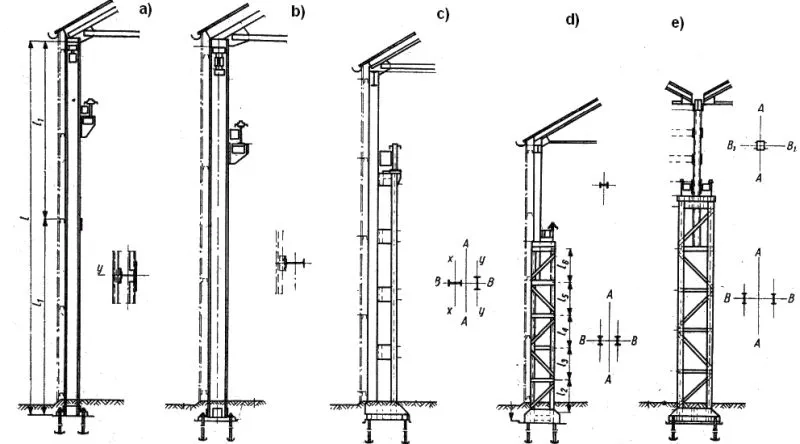
Rys.5. Słupy o przekroju na długości: a,b – stałym, c,de) – schodkowe [6]
Konstrukcja słupów
Wymiary poprzeczne słupów h (wysokość przekroju) można wstępnie dobrać na podstawie ich długości L w przedziale:
$$\begin{equation}h=\dfrac {L} {10} \div \dfrac {L} {25} \end{equation}$$
gdzie $L$- długość słupa (najczęściej wysokość hali), a $h$ – wymiar poprzeczny przekroju słupa.
W przypadku słupów podsuwnicowych (schodkowych) przy oznaczeniach naniesionych na rys. 16 (L1, h1 – długość i wysokość słupa w części podsuwnicowej; L2, h2 – długość i wysokość słupa w części nadsuwnicowej) przyjmuje się [7]:
$$\begin{equation}h_2 = \dfrac {L_2} {10} \div \dfrac {L_2} {12} \end{equation}$$
$$\begin{equation}h_1 = \dfrac {L_1+L_2} {20}\end{equation}$$
Trzon słupa
Gałęzie trzonu łupów złożonych mogą być łączone przewiązkami (rys.7) lub skratowaniem (rys.8). Zaleca się, by liczba przewiązek była nieparzysta, tak aby przewiązka nie wypadała w środku długości słupa (nie jest tam potrzebna), choć zalecenie to nie jest bezwzględne.
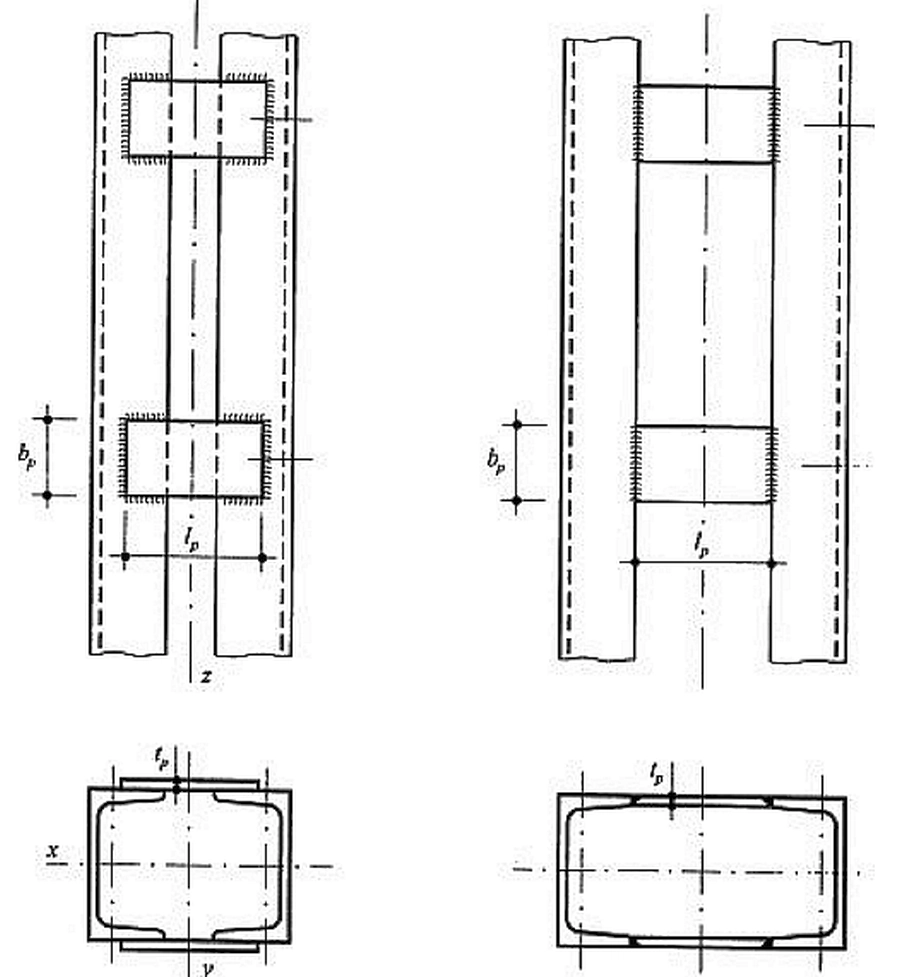
Rys.7. Gałęzie słupa połączone przewiązkami [8]
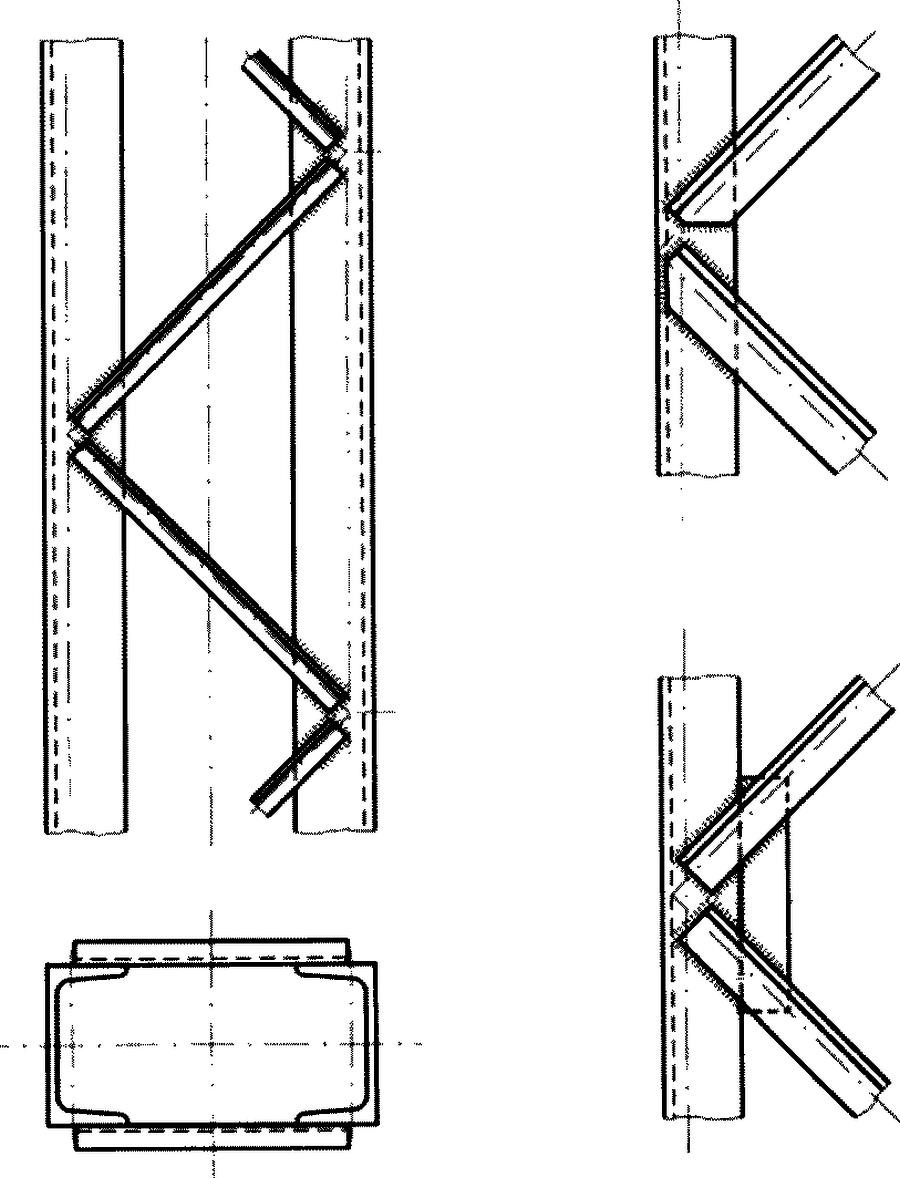
Rys.8. Gałęzie słupa połączone skratowaniem [9]
Trzony słupów wielogałęziowych można projektować i obliczać zgodnie z normą [10]. Zaleca się obliczanie trzonów słupów, przewiązek i wykratowania z analogii belki Timoshenko [11], [12] lub jako ramę (słup z przewiązkami) lub kratownicę (słup wykratowany) [13].
Głowice słupów
Głowice słupów jednogałęziowych w tym głowice części nadsuwnicowej słupa podsuwnicowego można kształtować w sposób pokazany na rys. 9. Płytkę centrującą stosuje się w przypadku dużych i średnich obciążeń. W najczęstszym przypadku małych obciążeń – płytka centrująca nie występuje. Obecnie w miejsce stalowych łożysk stosuje się łożyska elastomerowe.
Rys.9. Głowica słupa jednogałęziowego z płytką centrującą: a, b) słup dwuteowy, c,d) słup rurowy, d) płytka centrująca okrągła [14]
Wsporniki podsuwnicowe
Wsporniki podsuwnicowe występują w miejscu połączenia części nad- z pod-suwnicową słupa . Połączenie to musi mieć charakterystykę sztywną.
Na rys. 10 pokazano kilka rozwiązań konstrukcyjnych, spełniających ten warunek. Połączenia pełnościennych części słupa (rys. 11) powinno mieć wysokość nie mniejszą niż 20-30% szerokości osiowej słupa. Właściwe przenikanie elementów części nadsuwnicowej w belkę wspornika zapewniono poprzez wpuszczenie pasa części nadsuwnicowej na środnik słupa podsuwnicowego na długość ok 2x wysokość profilu i użebrowanie poziome. Belkę podsuwnicową umieszczono w osi gałęzi zewnętrzn-ej (-ych) słupa, wykonanych z dwuteowników. Całość uzupełniono użebrowaniem w miejscu występowania znacznych sił skupionych.
W przypadku części podsuwnicowej wykratowanej, połączenie części słupa można poprzez blachy obejmujące gałęzie części nadsuwnicowej ( słup z jedną belką podsuwnicową), lub poprzez zastosowanie pełnościennej belki głowicowej (przykład słupa środkowego – z dwoma belkami podsuwnicowymi).
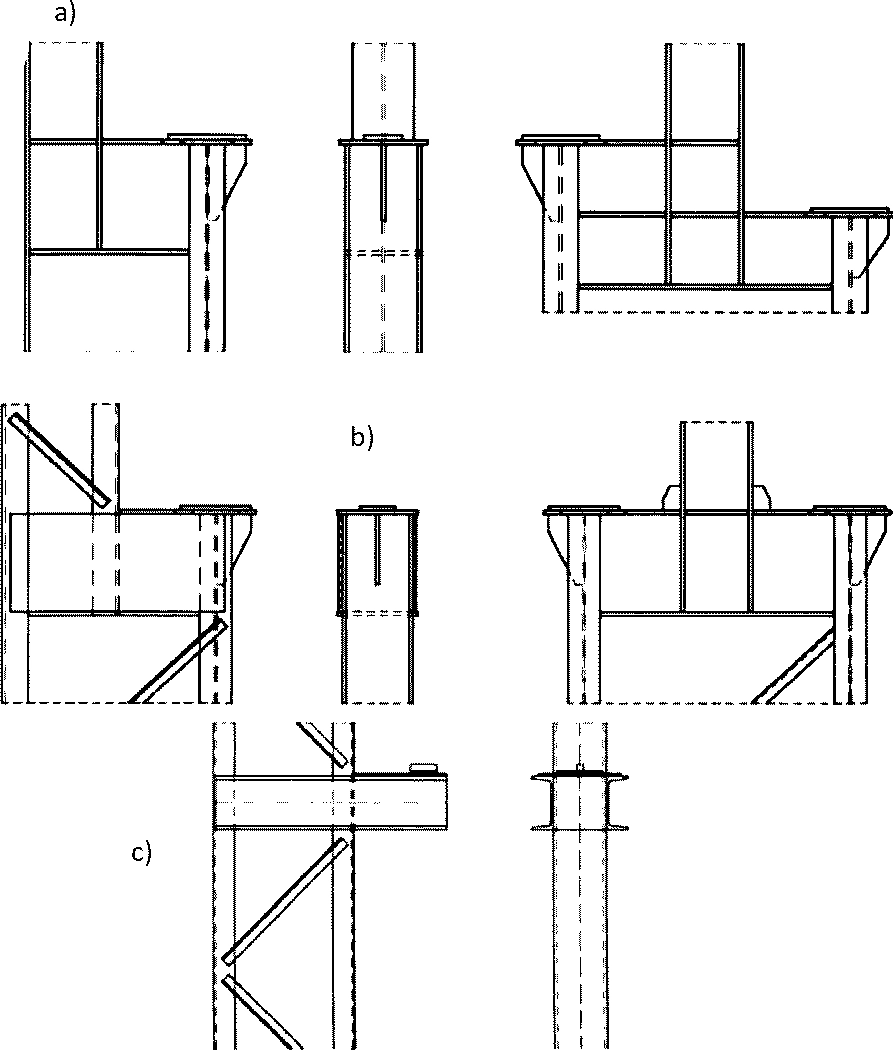
Rys.10. Wspornik podsuwnicowy słupa: a) pełnościennego, b) z częścią podsuwnicową wykratowaną, c) o stałym przekroju [15]
Stopy słupów
Typy stóp słupów
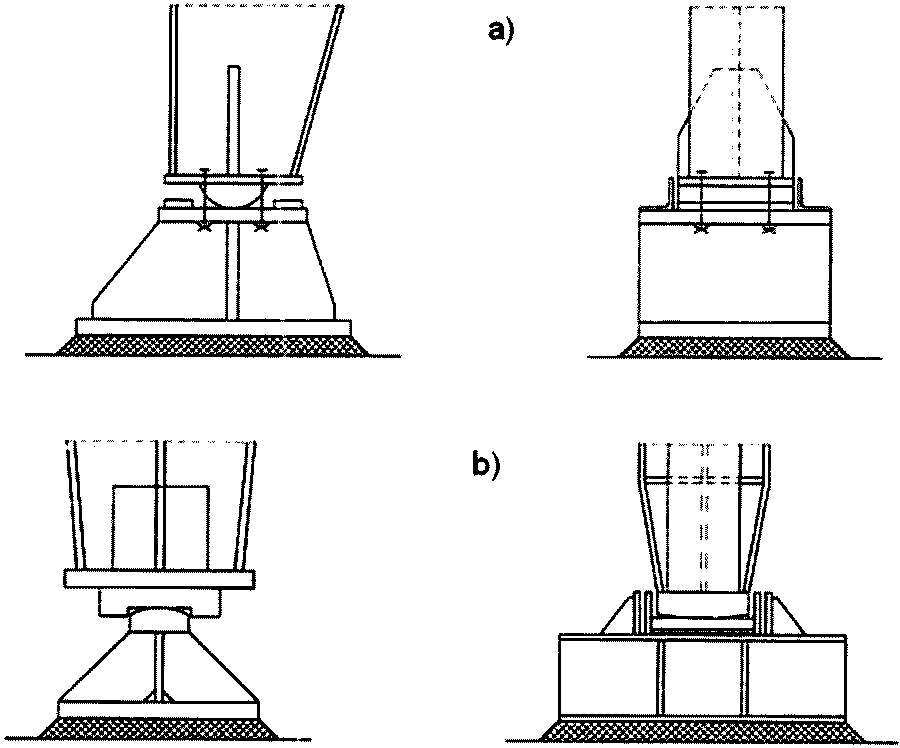
Na rys.11 przedstawiono najprostsze podstawy słupa jednogałęziowego: a) przegubową , b) utwierdzoną
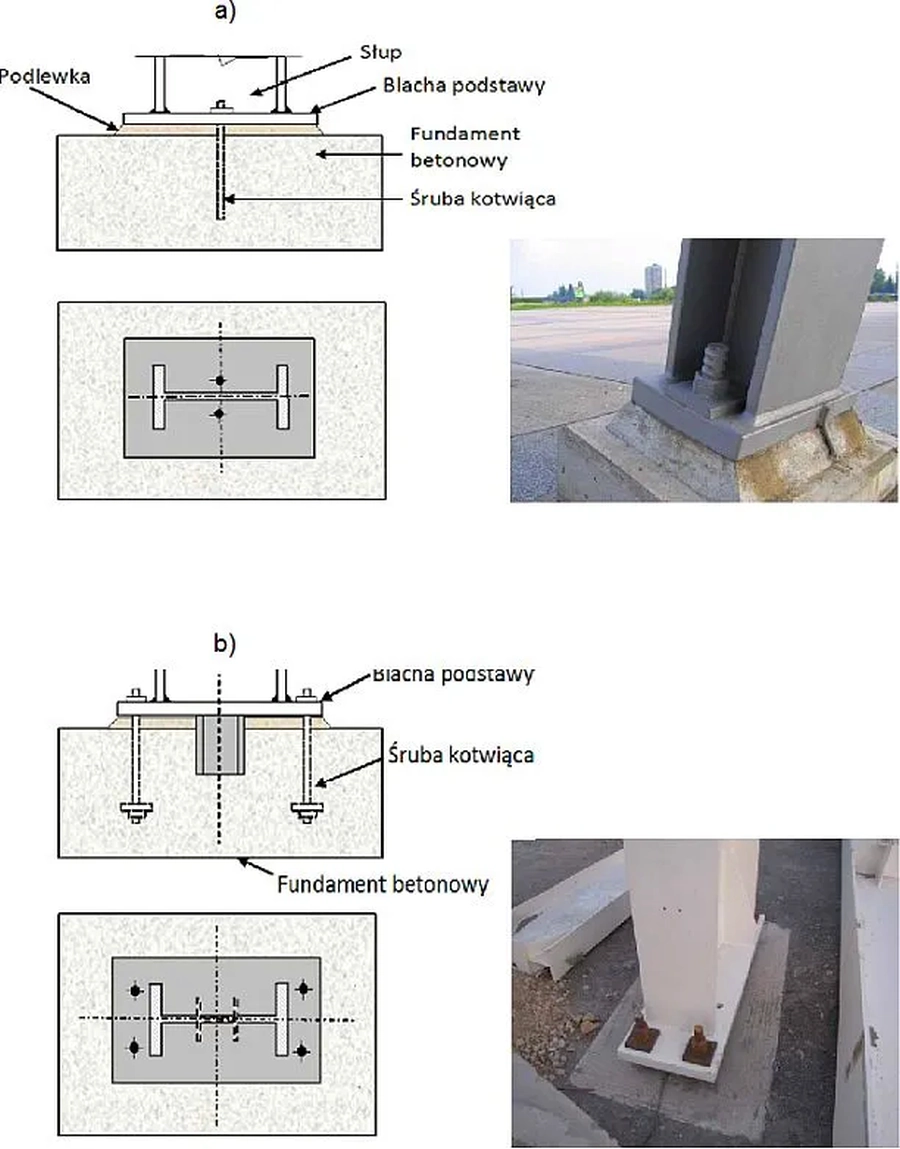
Rys.12. Proste stopy słupa stalowego: a) przegubowa, b) utwierdzona [16]
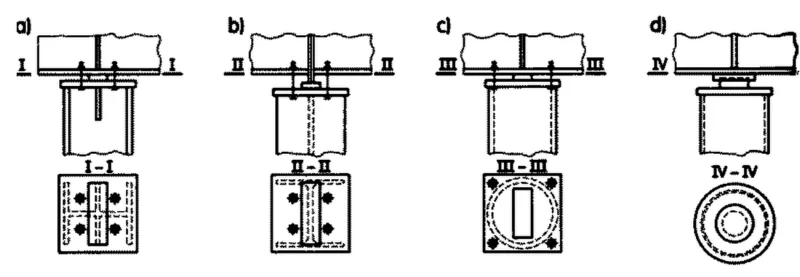
Stopy mogą być jednodzielne (rys.14a) lub dwudzielne (rys.14b), przy czym stopy dwudzielne należy traktować jako utwierdzone (integralnie), choć pojedyncze gałęzie są łączone jako przegubowe. Stopy wielodzielne są stosowane dla słupów wielogałęziowych, lub w innych przypadkach w celu zdeterminowania stref docisku.
Wybrane konstrukcje stóp przegubowych
Przegubowe połączenie słupa z fundamentem przy małych i średnich obciążeniach realizuje się bez specjalnego centrowania reakcji, w sposób pokazany na rys. 13a. W przypadku znacznych reakcji lub konieczności „wymuszenia” przegubowej podpory stosuje się bardziej rozbudowane konstrukcje, np. pokazane na rys. 13b.
Wybrane konstrukcje stóp utwierdzonych
Utwierdzenie słupa w fundamencie realizuje się poprzez takie wykonstruowanie stopy (rys.14), by przenieść podporowy moment zginający: ściskanie poprzez docisk do betonu , a rozciąganie za pomocą śrub fundamentowych.
Rys.14. Stopy utwierdzone: a) jednodzielna, b) dwudzielna [17]
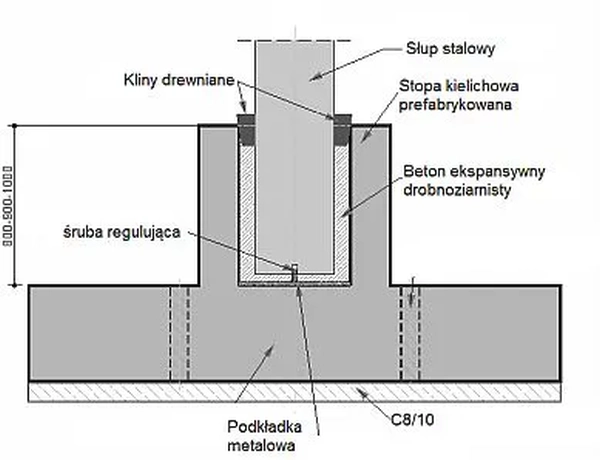
Utwierdzenie słupów stalowych, podobnie jak żelbetowych, często realizuje się za pomocą stóp kielichowych w sposób pokazany na rys.14. Stopę należy projektować zgodnie z normą [18].
Oparcie konstrukcji stalowej na słupie żelbetowym
Zgodnie z uwagą zawartą na wstępie do niniejszego artykułu słupy stalowe są obecnie coraz częściej zastępowane przez słupy żelbetowe. W takich konstrukcjach stopa słupa (słupka) konstrukcji stalowej jest umiejscowiona w głowicy słupa żelbetowego.
Na rys. 16 pokazano węzeł podporowy przekrycia rusztowego MITEX. W tym przypadku stopa słupa nośnego żelbetowego jest mocowana w fundamencie zgodnie zasadami konstrukcji żelbetowych [18], najczęściej za pośrednictwem stopy kielichowej.
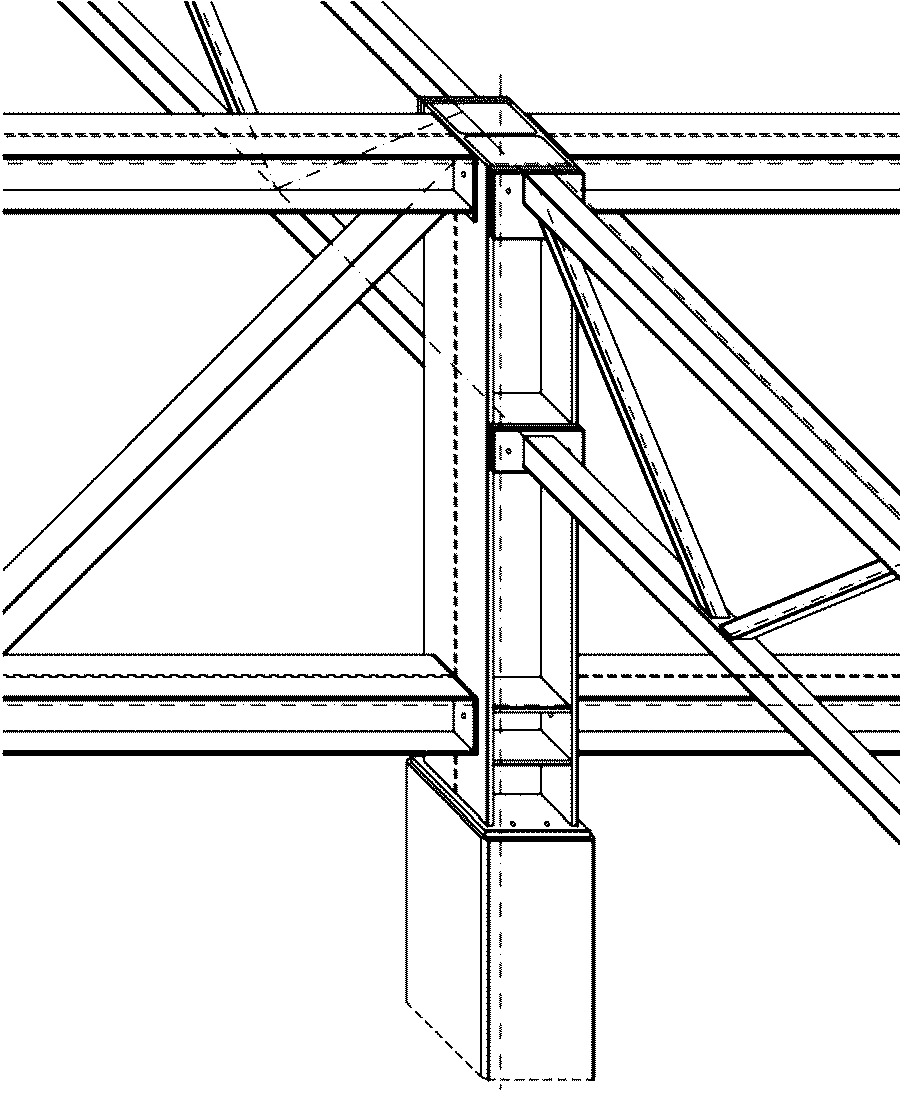
Rys. 16. Stopa słupka stalowego na głowicy słupa żelbetowego [19]
Stopy słupów podsuwnicowych
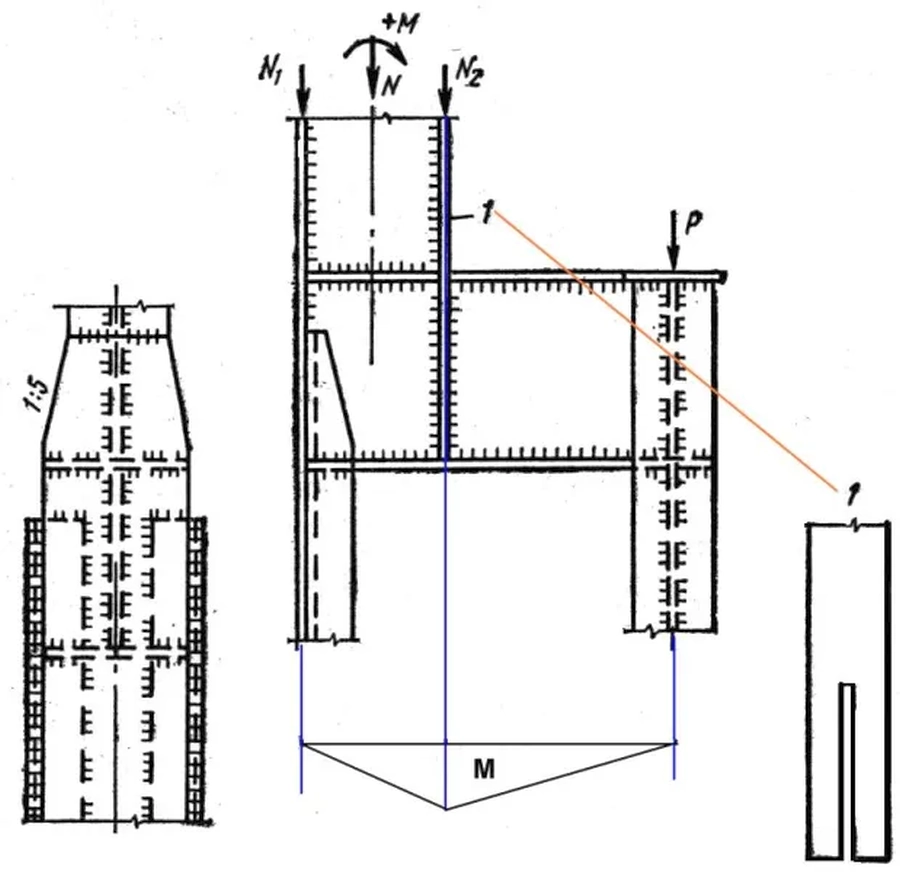
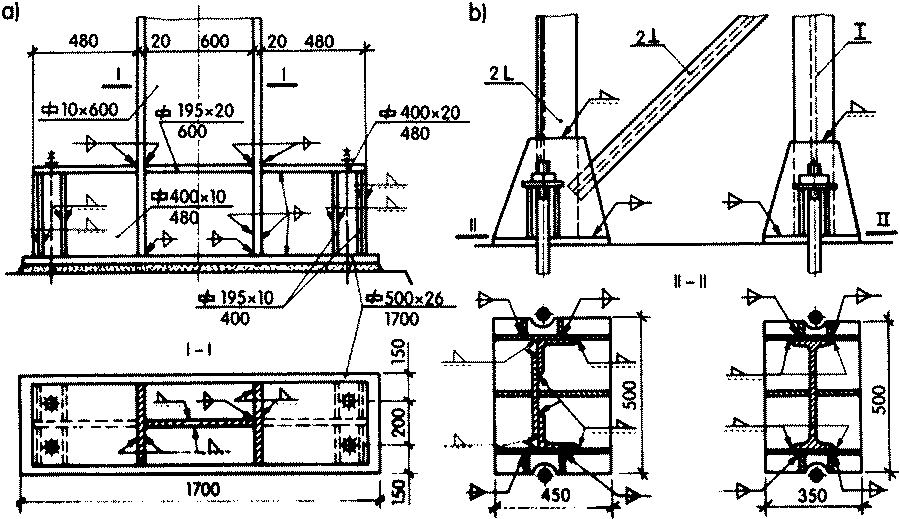
Stopy słupów podsuwnicowych są stopami utwierdzonymi i można je konstruować w sposób pokazany na rys. 12. Na rys. 17 pokazano w całości słup z częścią podsuwnicową dwugałęziową, kratową systemie Mostostal, który jest utwierdzony w fundamencie stopą dwudzielną, pełnościenną, rozdetalowaną na rys 18. Słup taki może mieć też stopę dwudzielną kratową (rys.18).
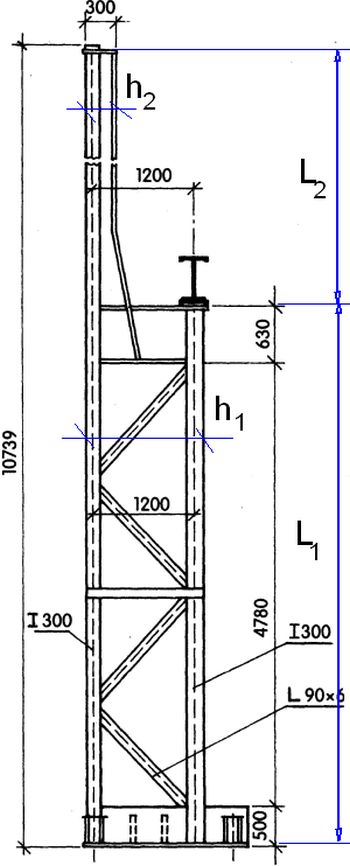
Rys. 17. Słup podsuwnicowy w systemie Mostostal (z oznaczeniami wymiarów naniesionymi na niebiesko) [17]

Rys. 18. Przykład stopy dwudzielnej, pełnościennej słupa podsuwnicowego (kolorem żółtym dodano opcjonalną podlewkę, co prowadziłoby do stopy jednodzielnej) [17]
Stopę dwudzielną, pełnościenną (z rys.16) możnaby wykonstruować w sposób pokazany na rys. 17 w opcji z podlewką wniesioną kolorem żółtym, czyli z podlewką na całej powierzchni przylegania blachy poziomej stopy. Taką stopę należałby traktować obliczeniowo jako jednodzielną.
Stopa dwudzielna charakteryzuje się tym, że siły pod każdą z gałęzi 1 lub 2 można wyznaczyć z prostej zależności:
$$\begin{equation}N_{1,2}= \dfrac {N_c} {2} \pm \dfrac {M} {h}\end{equation}$$
gdzie h- jest odległością osiową galęzi słupa – na rys. 18 jest h= 1,8 m ; Nc– siłą osiową w słupie, a M – momentem zginającym przypodporowym.
Na rys. 19 pokazano typową stopę utwierdzoną jednodzielną.

Rys. 19. Typowa utwierdzona stopa jednodzielna ze śrubami poza obrysem blachy [20]
W przypadku stopy jednodzielnej, w celu wyznaczenia sił w śrubach i docisku do betonu w stanie sprężystym należy rozwiązać zadanie nieliniowe (pkt.2.4.5.)
Wyznaczenie sił w śrubach stopy jednodzielnej w stanie sprężystym
Na rys. 20 pokazano schemat do wyznaczania sił w śrubach stopy jednodzielnej.
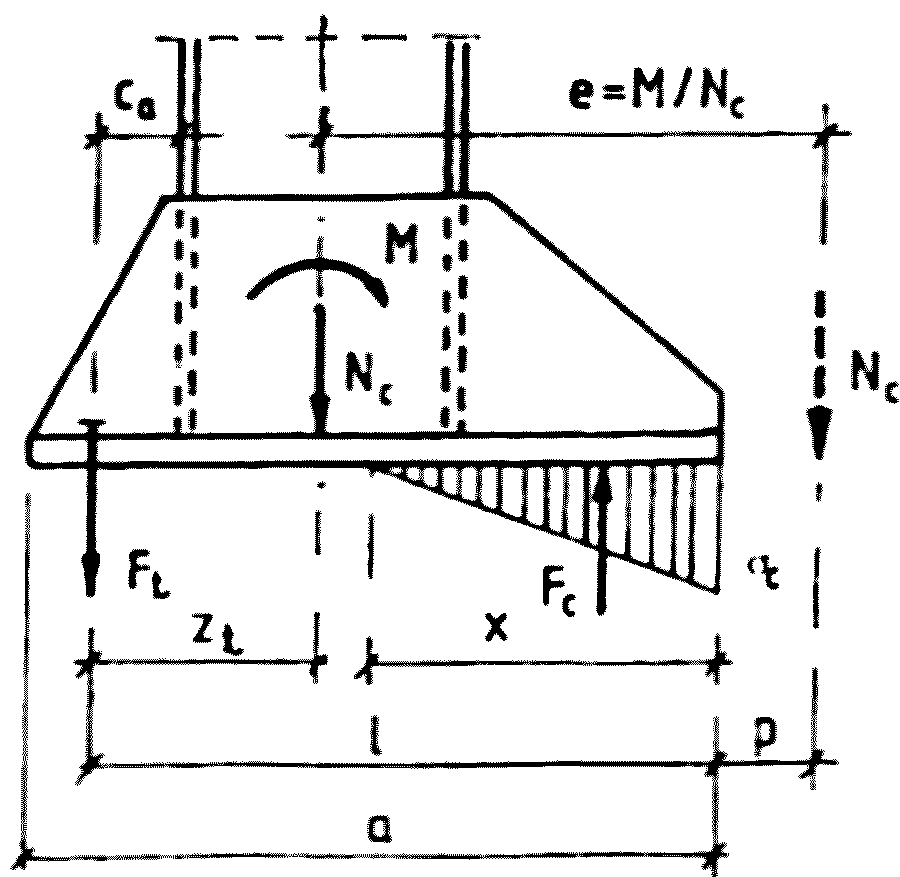
Rys. 20. Schemat rozkładu sił pod stopą słupa w stanie sprężystym [21]
Zagadnienie brzegowe przedstawione na rys. 20 ma trzy stopnie swobody (trzy niewiadome):
x- wysokość strefy docisku do betonu,
σc – naprężenia krawędziowe dociskowe,
Ft – siła rozciągająca śrubę,
Zadanie rozwiążemy zestawiając równania (b- szerokość blachy podstawy):
(a) równanie równowagi momentów ∑M (względem linii siły Fc):
$$\begin{equation} M-F_t \cdot(l-x/3)-N_c \cdot(l-z_t-x/3)=0\end{equation}$$
(b) równanie równowagi sił pionowych ∑X:
$$\begin{equation}N_c +F_t- \sigma_c \cdot x \cdot b/2 \end{equation}$$
Ponieważ zadanie jest statycznie niewyznaczalne, więc należy zdefiniować zależnosci kinematyczne i fizyczne:
c1) zasada płaskich przekrojów :
$$\begin{equation}\dfrac {\Delta_c} {x}=\dfrac {\Delta_t}{l-x}\end{equation}$$
c2) prawo Hooka
odkształcenie betonu
$$\begin{equation}\Delta_c= \dfrac {\sigma_c}{E_c}\end{equation}$$
odkształcenie śrub
$$\begin{equation}\Delta_t= \dfrac {\sigma_t}{E_s}= \dfrac{F_t}{n \cdot A_s \cdot E_s}\end{equation}$$
gdzie: Ec, Es – moduł Younga odpowiednio betonu i stali, n – liczba śrub o przekroju jednej śruby As.
Po rozwiązaniu układu równań (a,b,c) uzyskamy równanie trzeciego stopnia do wyznaczenia wysokości strefy ściskanej x:
$$\begin{equation}x^3+3px^2+k(x-l)(l+p)=0 \label{Fischer}\end{equation}$$
gdzie:
$$\begin{equation}k=\dfrac{6n A_sE_s} {bE_c}\end{equation}$$
$$\begin{equation}p=e- \dfrac {a}{2}= \dfrac {M}{N_t}\end{equation}$$
Po rozwiązaniu równania ($\ref{Fischer}$) dowolną metodą możemy wyznaczyć:
$$\begin{equation}F_t= \dfrac {N_c(p+x/3)} {l-x/3} \lt \ \ n \cdot N_{t, Rd}\end{equation}$$
gdzie Nt, Rd – nośność obliczeniowa śruby na rozciąganie, wyznaczona zgodnie z [10]:
$$\begin{equation}\sigma_c= \dfrac {2(N_c+F_t)}{xb} \lt f_{jd}\end{equation}$$
gdzie:
$f_{jd}=\alpha_{bf}\cdot \beta_j \cdot f_{cd}$
Wytrzymałość obliczeniowa betonu na docisk wyznaczona zgodnie z [18]; jeśli wytrzymałość podlewki ≥ 0,2×fcd , to przyjmuje się fjd=fcd [16].
Analiza stopy słupa zgodnie z normą europejską
Norma europejskia [22] odchodzi od analizy pracy stopy w stanie sprężystym, tak jak opisano w pkt 2.4.6 i a stosowanie zależności (5 do 7) nie jest właściwe. Projektowanie stopy należy prowadzić w stanie granicznym (plastycznym), analizując mechanizm pracy pokazany na rys.21. Wskutek odkształcalności elementów stopy. docisk do betonu następuję praktycznie w całości w niewielkiej strefie pod pasem ściskanym , a rozciąganie praktycznie w pełni przenoszą śruby.
W stanie granicznym stopa przenosi moment plastyczny Mj,Rd. Siła docisku do betonu Fc,M i rozciągania śrub FT,M, wywołana tym momentem MEd jest równa:
$$\begin{equation}F_{T,M}=F_{c,M}= \dfrac {M_{Ed}}{z}\end{equation}$$
gdzie: z=zT+zc – odległość osi śrub od wypadkowej docisku, którą można umiejscowić w osi pasa dociskanego.
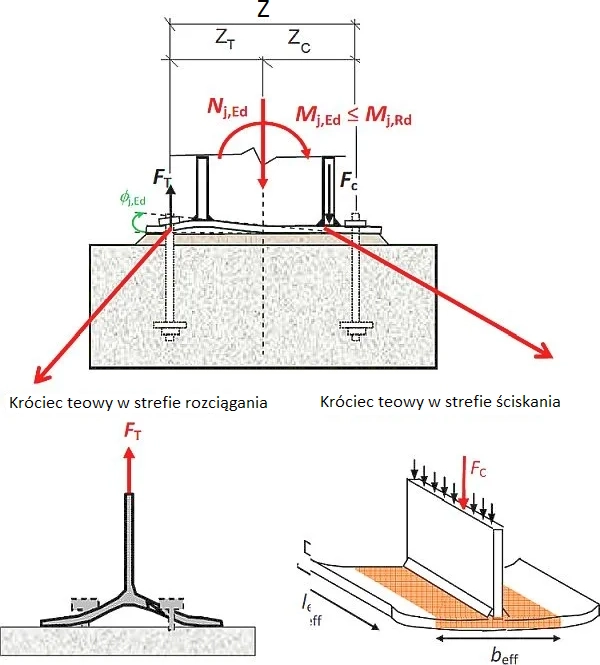
Rys.21. Mechanizm pracy stopy słupa: króćce teowe rozciągane i ściskane [23]
W ogólności należy uwzględnić podatności węzłów podporowych.
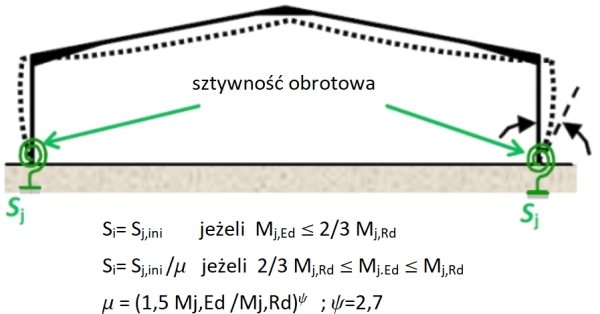
Rys. 22. Schemat statyczny układu poprzecznego hali [16]
Na rys. 22 przedstawiono ogólny schemat układu poprzecznego hali z znaczonymi sztywnościami obrotowymi stóp słupów.
Sztywności obrotowe węzłów podporowych hali w ogólności są Sj <∞ (nie są sztywne), czyli są węzłami podatnymi.
W szczególnym przypadku podstawy słupów można przyjąć jako sztywne, ale należy to uzasadnić. Takie założenie można przyjąć wyłącznie w przypadku [16],§5.2.2..5 (2):
w ramach, których układ stężeń redukuje poziomy przechył o min. 80% i w których wpływ deformacji może być pominięty, a ponadto:
gdy $\overline \lambda_0 \le 0,5 $
gdy $0,5 \le \overline \lambda_0 \le 3,93$ oraz $S_{j,ini} >7(2 \overline \lambda_0-1) \dfrac {EI_c} {L_c}$
gdy $\overline \lambda_0 \ge 3,93$ oraz $S_{j,ini} \ \ge \ 48 \dfrac {EI_c} {L_c} $
w pozostalych przypadkach, gdy $S_{j,ini} \ >\ 30 \dfrac {EI_c} {L_c}$
gdzie:
$\overline \lambda_0$ – smukłość względna słupa rozpatrywanego tak, jakby jego oba końce były przegubowe.
Lc, Ic -wysokość i moment słupa rozpatrywanej kondygnacji.
Początkowa sztywność Sj,ini została zdefiniowana na rys. 23.
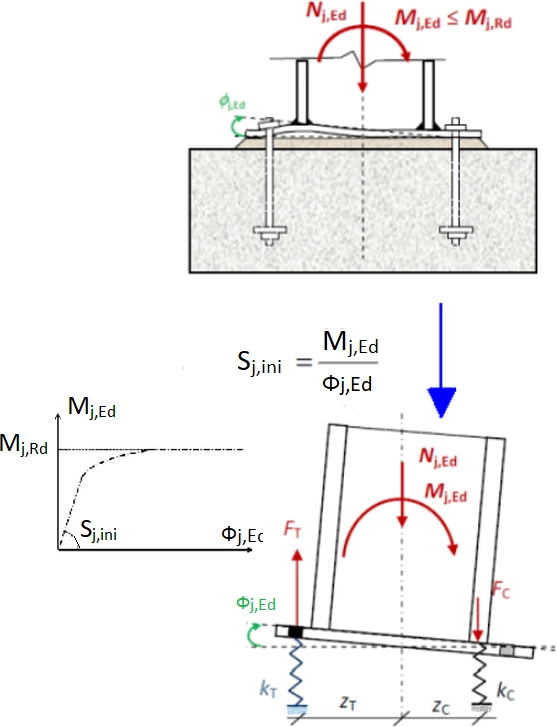
Rys. 23. Definicja początkowej sztywności obrotowej [16]
Stałe sprężystości kT i kC do wyznaczenia Sj,ini szacuje się metodą składnikową zgodnie z zależnościami tab 6.11 [16].
Sztywność początkowa zależy od wielkości mimośrodu działania sił
$$\begin{equation}e_N= \dfrac {M_{j,Ed}}{N_{Ed}}\end{equation}$$
Mogą wystąpić sytuacje przedstawione na rys. 24 i 25.
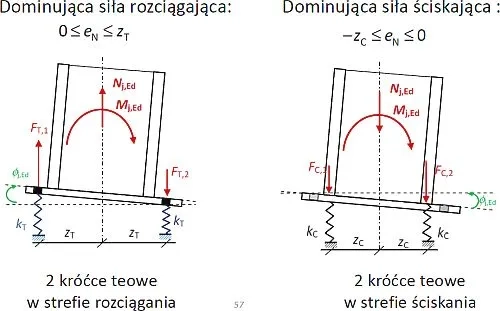
Rys. 24. Sytuacja dominującej siły rozciągającej lub ściskającej [16]

Rys. 25. Sytuacja dominującego momentu zginającego [16]
W zależności od sytuacji obliczeniowej początkową sztywność węzła podporowego można wyznaczyć z [16], tab.6.12.
Zakotwienie słupów
W przypadku zakotwienia podstawy słupa lub mniej obciążonych śrub w stopach utwierdzonych obecnie powszechnie stosuje się zakotwienie z kotew chemicznych (wklejanych) , mechanicznych (rozporowych) lub wkręcanych (typu HUS prod. HILTI) . Dalsze informacje zawiera artykuł „Technika mocowań. Nowoczesne łączniki„.
Na rys.25 pokazano rodzaje konwencjonalnych śrub fundamentowych: fajkowych, młoteczkowych oraz płytkowych.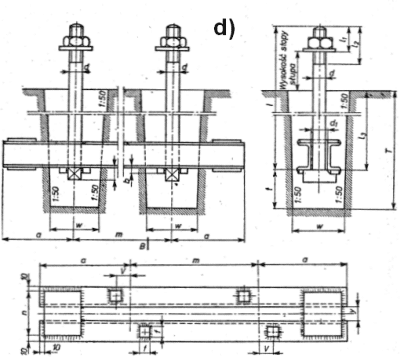
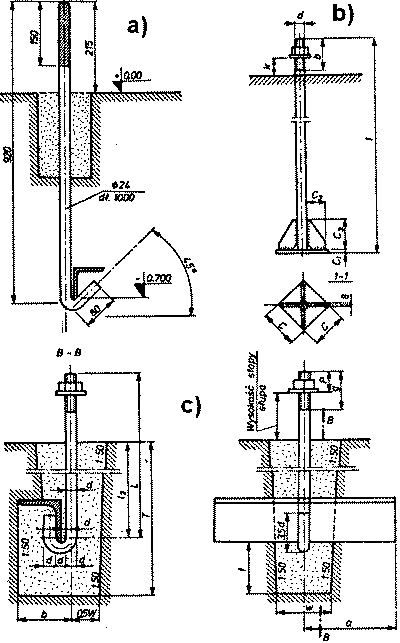
Rys. 25. Śruby fundamentowe: a,c) fajkowe, b) płytkowe, d) młoteczkowe [20]
Śruby fajkowe przy małych i średnich siłach są kotwione w betonie na przyczepność (podobnie do zbrojenia wiotkiego), a przy większych siłach stosowaną profile kotwiące, wbudowane w sposób pokazany na rys. 25a,c) oraz rys. 25-1 oraz 25-2.
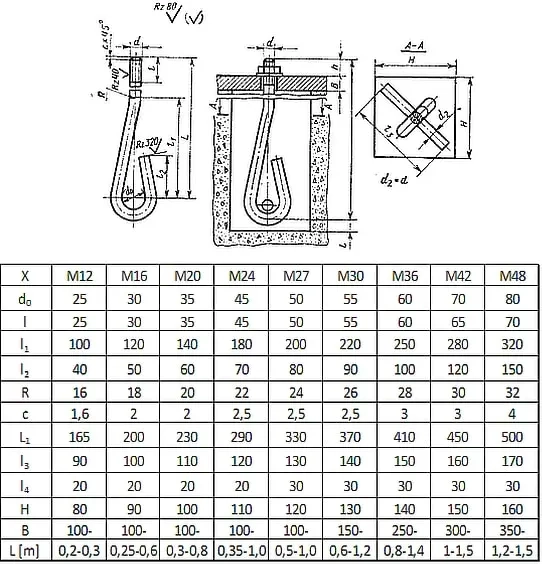
Rys. 26 Typowe zakotwienie słupa na śruby fajkowe z poprzeczką [24]
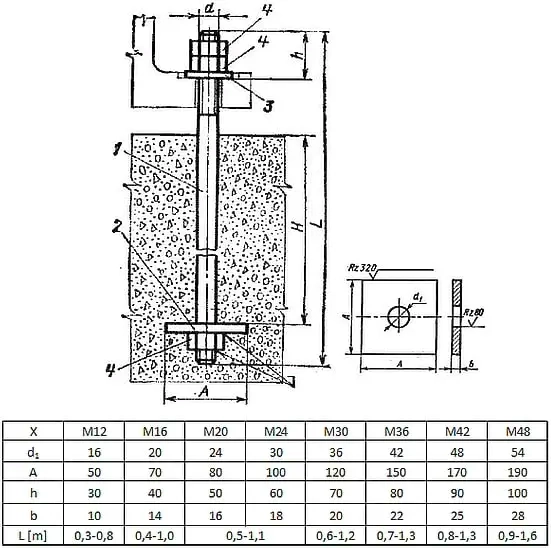
Rys.27 Typowe zakotwienie słupa na śruby fajkowe z płytką [24]
Płytki zakotwienia śrub rys. 25b) należy dobierać zgodnie z zasadami kotwienia zbrojenia w betonie, które opisano w artykule Belki żelbetowe. Kształtowanie.
Siłę rozciągającą kotew $N_R$ powiększa się 0 35% na przewidywane obciążenie wstępnego naprężenia (likwidacja luzów, itp).
Kotwy mogą być umieszczone w obrysie blachy poziomej stopy słupa ( przebijają blachę) (np. rys. 11b) lub poza obrysem blachy (np. rys. 18 ). W przypadku dużych momentów zginających zalecane jest stosowanie śrub poza obrysem i konstruowanie belek stopowych przenoszących siły z tych śrub na trzon słupa.
Przepony słupów wielogałęziowych
Trzon słupa wielogałęziowego o długości większej niż hp=5 m wymaga stosowania przepon w odległościach nie większych niż hp, które zabezpieczają kształt przekroju przekroju przed zniekształceniem. Na rys. 26 pokazano przykłady konstrukcji przepon.
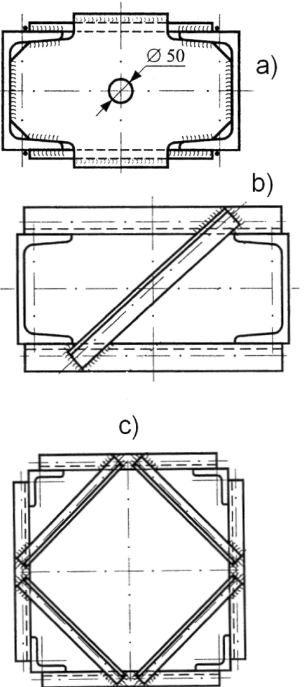
Rys. 28. Przepony słupa wielogałęziowego: a) z blachy, b, c) z prętów [25]
Analiza belek-słupów
Mechanizm zniszczenia belek- słupów
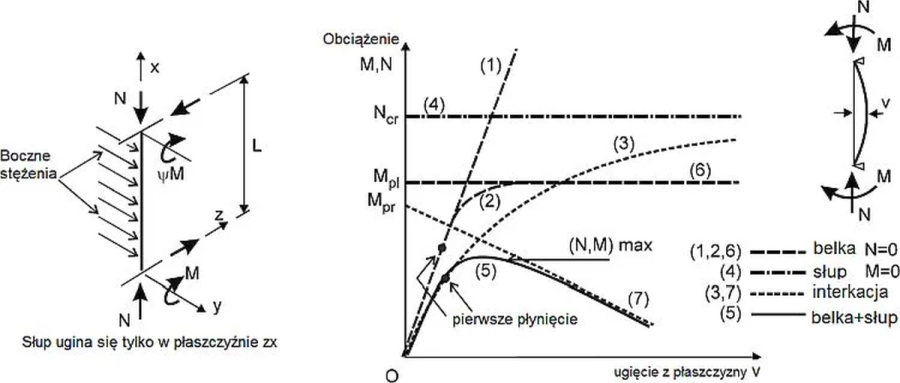
Belka-słup jest definiowana jako element poddany jednoczesnemu działaniu zginania i ściskania. W zasadzie wszystkie elementy prętowe w rzeczywistych konstrukcjach są belkami-słupami, a belka (N=0) i słup (M=0) są szczególnymi przypadkami granicznymi.
Zachowanie się belki-słupa odkształcającego się wyłącznie w płaszczyźnie systemu xz (rys.27a) pokazano na rys.27b w postaci ścieżek równowagi przemieszczenie v – obciążenie (M,N).
Prosta (1) przedstawia liniowe zachowania sprężystego pręta, a prosta (6) nośność belki sztywno-plastycznej (nośność plastyczną Mpl). Rzeczywista ścieżka równowagi będzie zawarta pod tymi prostymi. Krzywa (2) pokazuje rzeczywiste przejście belki sprężysto-plastycznej ze stanu sprężystego (1) do plastycznego (6). Prosta (4) przedstawia górne ograniczenie dla słupa, wynikające ze sprężystej siły krytycznej (Eulera) Ncr . Krzywa (3) przedstawia interakcję zginania i wyboczenie sprężystego, a prosta (7) interakcję plastyczną momentu zginającego i siły osiowej Mpr. Zależności (3) i (7) uwzględniają dodatkowe wytężenie II rzędu, spowodowane przez obciążenie osiowe N na przemieszczeniu v , czyli dodatkowy moment ΔM=N·v. Faktyczne zachowanie się słupa-belki przedstawia krzywa (5), ograniczona z góry przez (7) i (3).
Linią czerwoną oznaczono poziom maksimum (M,N) ścieżki równowagi (5). Maksimum (5) wyznacza nośność graniczną belki-słupa MR. Z rys.27 widać różnice pomiędzy nośnością krytyczną Ncr (lub Mcr) , nośnością plastyczną Mpl (lub MN), a nośnością graniczną MR. Nośność krytyczna jest wartością własną sprężystego problemu idealnego, czyli problemu quasi nieliniowego geometrycznie (nośnością na wyboczenie), nośność plastyczna jest nośnością dla problemu sztywno-plastycznego , a nośność graniczna jest maksimum na rzeczywistej ścieżce równowagi wyznaczoną z uwzględnieniem nieliniowości geometrycznych i materiałowych oraz imperfekcji elementu konstrukcyjnego.
Interakcja plastyczna (M,N) – przekrój klasy 1 i 2 [prosta (7)]
Do zrozumienia wykładu (pkt 3.2) , wymagana znajomość postawowych pojęć z inżynierskiej analizy plastyczności, które zostaly przedstawione w artykule Nośność plastyczna konstrukcji.
Nośność plastyczna Mpr (rys.11) jest momentem plastycznym Mpl przekroju pręta zredukowanym wskutek działania siły osiowej, co oznaczamy jako MN. Nośność interakcyjną możemy również zmierzyć siłą osiową NM czyli nośnością plastyczną Npl, zredukowaną wskutek działania momentu zginającego. Problem iterakcji ściskania i zginania dwuosiowego przekroju dwuteowego przedstawiono w artykule „Plastyczna interakcja ściskania i dwuosiowego zginania„.
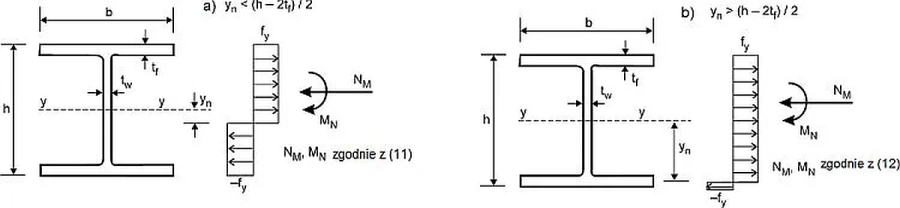
W przypadku zginania jednokierunkowego (rys.28) przekroju klasy 1 lub 2 krzywe interakcji plastycznej można zapisać w postaci:
($\ref{inter_a}, \ref {inter_b}$) dla przypadku 28a) – oś obojętna w środniku zN ≤ (h-2·tf)/2
$$\begin{equation}N_M=2 \cdot f_y \cdot t_w \cdot z_N \label{inter_a}\end{equation}$$
$$\begin{equation}M_N=f_y \cdot b \cdot t_f \cdot(h-t_f)+f_y \left [ \left ( \dfrac {h-2t_f} {2} \right )^2 – z_N^2 \right]\cdot t_w \label{inter_b}\end{equation}$$
($\ref{inter_c}, \ref {inter_d}$) dla przypadku 28b) – oś obojętna w pasie zN > (h-2·tf)/2
$$\begin{equation}N_M=f_y \cdot [ t_w \cdot (h-2t_f)+2b(t_f-h/2+z_N)] \label{inter_c}\end{equation}$$
$$\begin{equation}M_N=f_y b (h/2-z_N)(h-z_N)t_f \label{inter_d}\end{equation}$$
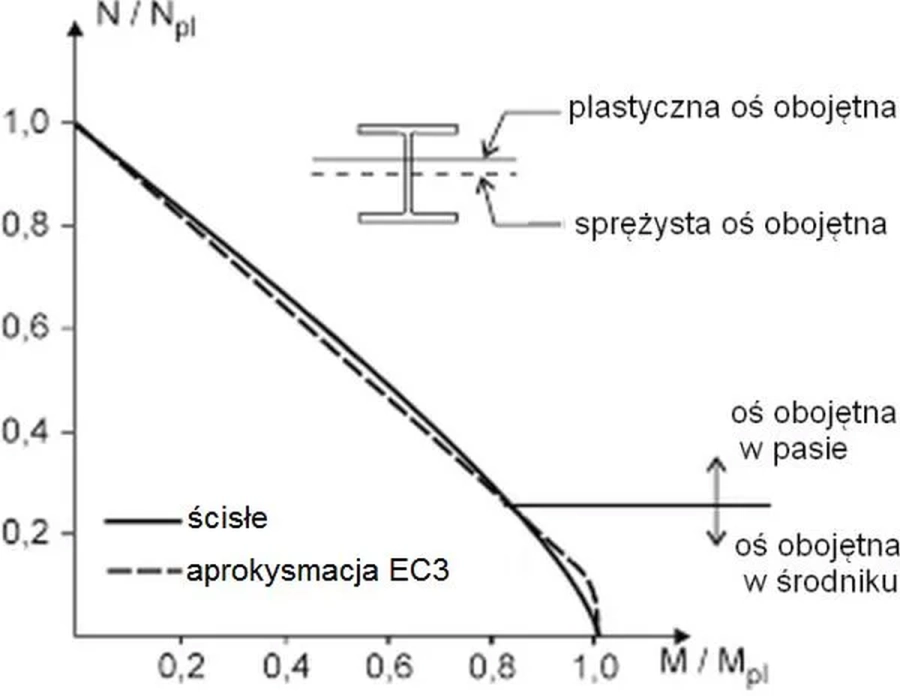
Na rys. 29 krzywe ścisłe interakcji ($\ref{inter_a}$ do $\ref{inter_d}$) porównano z aproksymacją normową [10],wzór (6.36):
$$\begin{equation}M_{Ny,Rd}=M_{pl,y}(1-n)/(1-a/2) \le M_{pl,y,Rd} \label {inter_norma}\end{equation}$$
gdzie: $n= N_{Ed}/N_{pl,Rd}$, $a= (A-2bt_f)$
Aproksymacja normowa ($\ref{inter_norma}$ ) jest dobrym przybliżeniem zależności ścisłych ($\ref{inter_a}$ do $\ref{inter_d}$). Jest opisana jedną ciągłą krzywą, co znacznie ułatwia praktyczne rachunki, w tym zastosowania numeryczne.
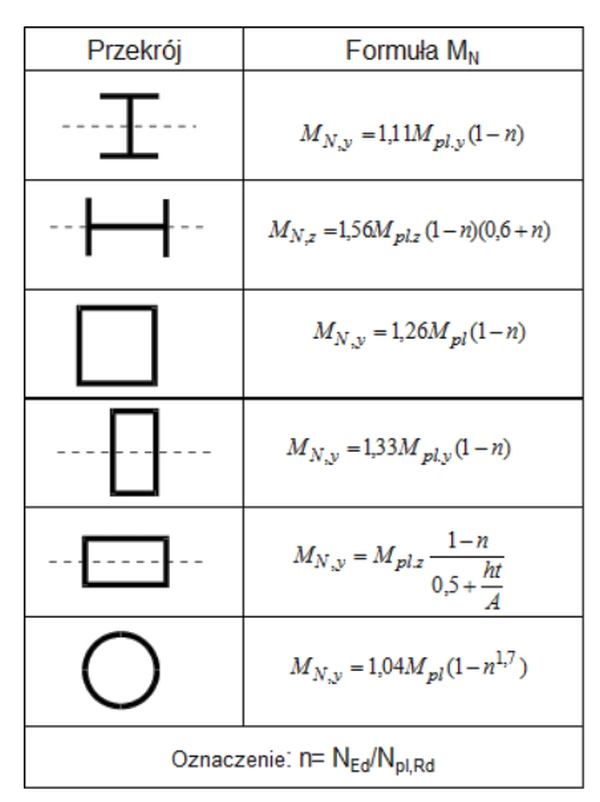
W tab.1. zestawiono krzywe interakcji plastycznej (M,N) dla najczęściej stosowanych profili słupów.
Tab.1. Wyrażenia na moment plastyczny MN zredukowany wskutek działania sily osiowej N [23]
Interakcja sprężysta
Przekrój klasy 3
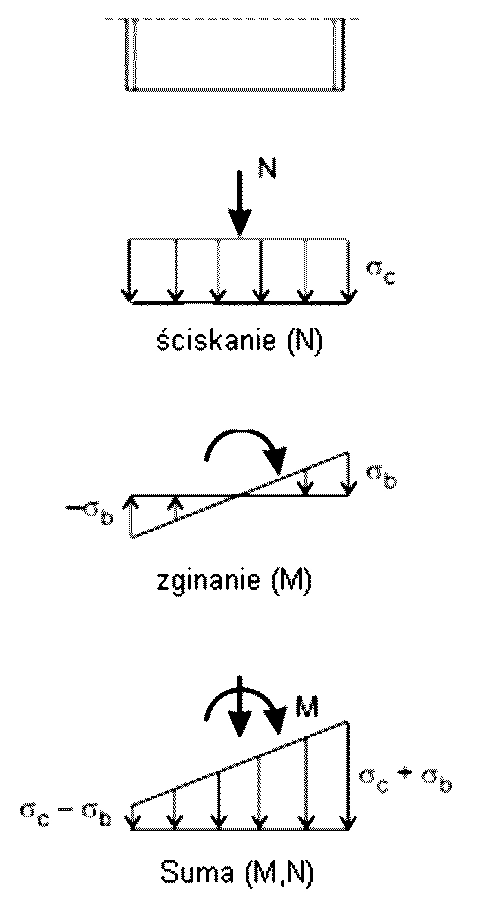
Interakcja sprężysta (M,N) podlega klasycznej superpozycji (rys.32). Graniczny stan sprężysty wystąpi, wówczas , gdy w dowolnym punkcie przekroju (maksymalne naprężenie) osiągnie granicę plastyczności, a interakcja sprężysta będzie liniowa:
$$\begin{equation}\sigma_N+\sigma_b =\dfrac {f_y} { \gamma _{M0}}\label{interakcja_el}\end{equation}$$
gdzie: $\sigma_N= \dfrac {N_{Ed}} {A}$ , $\sigma_b= \dfrac {M_{Ed}} {I} \cdot \dfrac {h} {2}$
Przekrój klasy 4 (cienkościenny)
Przekrój klasy 4 podlega interakcji sprężystej, ale charakterystyki geometryczne są obliczane przy użyciu szerokości efektywnych ściskanych ścianek ( po wyeliminowaniu tych części ścianek, które uległy utracie stateczności miejscowej) i powinien spełniać kryterium ($\ref{interakcja_el}$) dla A=Aeff i I=Ieff.
Interakcja krytyczna (M,N) – [krzywa (3)]
Do zrozumienia wykładu (pkt 3.3) , wymagana znajomość postawowych pojęć z inżynierskiej analizy plastyczności, ktróre zostaly przedstawionew w artykule Współczynnik wyboczeniowy. Geneza i mit )
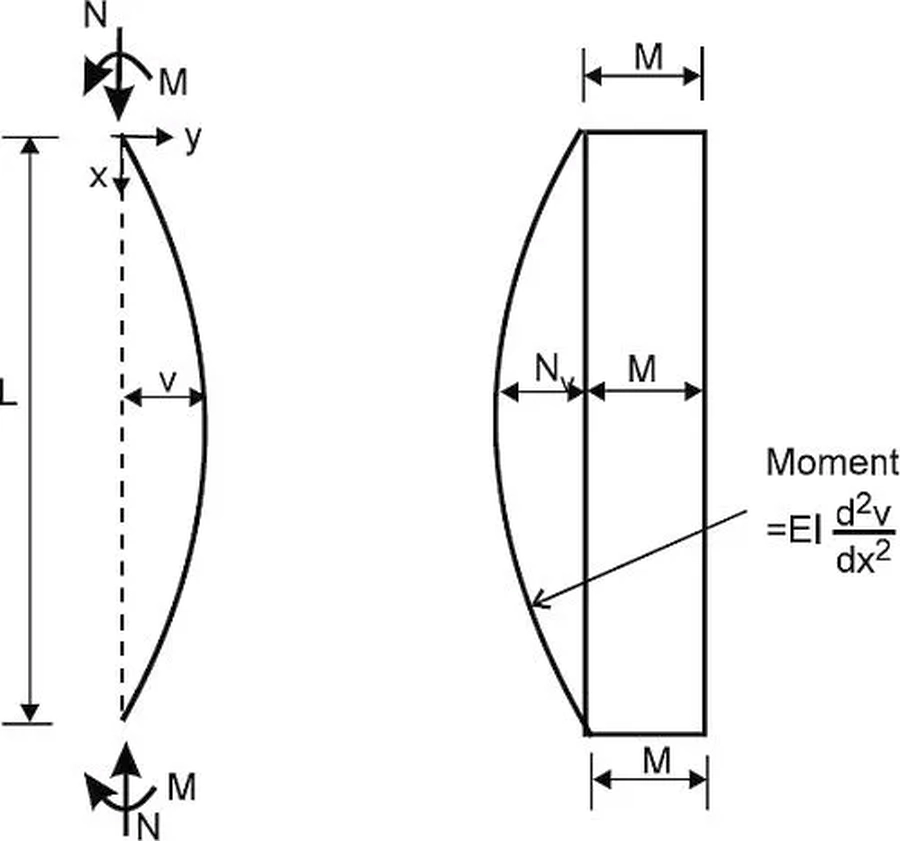
W poprzednim punkcie rozpatrzyliśmy interakcję na poziomie przekroju, teraz rozpatrzymy interakcję na poziomie elementu, pokazanego na rys. 31, czyli belki-słupa , w którym moment zginający w stanie odkształconym składa się z dwóch składników:
- momentu pierwotnego M,
- momentu drugiego rzędu ΔM= N·v.
Trahair i in. (Trahair N. S., Bradford M. A. (1988). The Behaviour and Design of Steel Structures to EC3 (2 Wydanie) )) podali wyrażenie na amplitudę wygięcia II rzędu idealnie prostego pręta w stanie sprężystym:
$$\begin{equation}v_{max}= \dfrac {M} {N} sec {\dfrac {\pi}{2}} \sqrt {\dfrac{N} {N_{cr}}-1}\label{v_max}\end{equation}$$
gdzie: $N_{cr}= \dfrac {\pi^2 \cdot EI_y} {L^2}$ jest klasyczną siła krytyczną Eulera.
Maksymalny moment zginający wynosi:
$$\begin{equation}M_{max}=M+\Delta M_{max}=M \cdot sec \dfrac {\pi}{2}\cdot \sqrt { \dfrac{N} {N_{cr}}} \label {M_max}\end{equation}$$
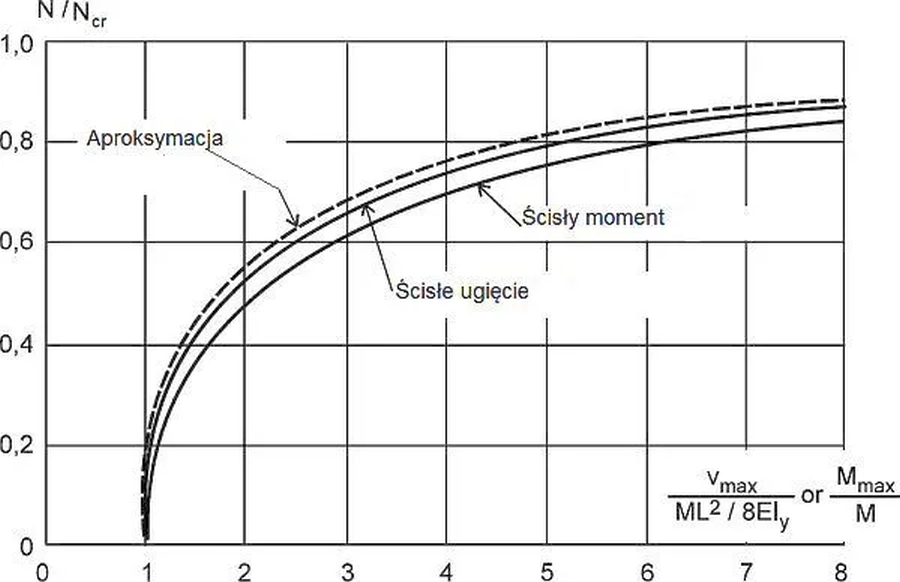
W równaniach ($\ref{v_max}$) i ($\ref {M_max}$) funkcja sec() może zostać przybliżona czynnikiem amplifikującym (zwiększającym) ugięcie pierwszego rzędu
$$\begin{equation} \dfrac {1} {1- \dfrac{N} {N_{cr}}}\end{equation}$$
co prowadzi do aproksymacji tych formuł wyrażeniami ($\ref {v_maxA}$) i ($\ref{M_maxA}$):
$$\begin{equation}v_{max}= \dfrac {M \cdot L^2} {8EI_y} \cdot \dfrac {1} {1-\dfrac{N} {N_{cr}}}\label{v_maxA}\end{equation}$$
$$\begin{equation}M_{max}= M \cdot \dfrac {1} {1-\dfrac{N} {N_{cr}}}\label{M_maxA}\end{equation}$$
w sposób pokazany na rys. 32.
Maksymalne naprężenia sprężyste w słupie-belce wynoszą:
$$\begin{equation}\sigma_{max}= \sigma _c+ \sigma_b \cdot \dfrac{M_{max}} {M}\end{equation}$$
co można zapisać w postaci:
$$\begin{equation}\dfrac {\sigma_c} {f_y}+ \dfrac {\sigma_b}{f_y \cdot\left(1-\dfrac{N}{N_{cr}}\right)}=1 \label {interakcja M-C}\end{equation}$$
Równanie ($\ref {interakcja M-C}$) można odwrócić i $\sigma_c$ i $\sigma_b$ przedstawić w funkcji naprężenia krytycznego Eulera
$$\begin{equation} \sigma_{cr}=\dfrac{N_{cr}}{A}=\dfrac{\pi^2 EI_y}{L^2 A}=\dfrac{\pi^2 E}{{\lambda_y}^2}\end{equation}$$
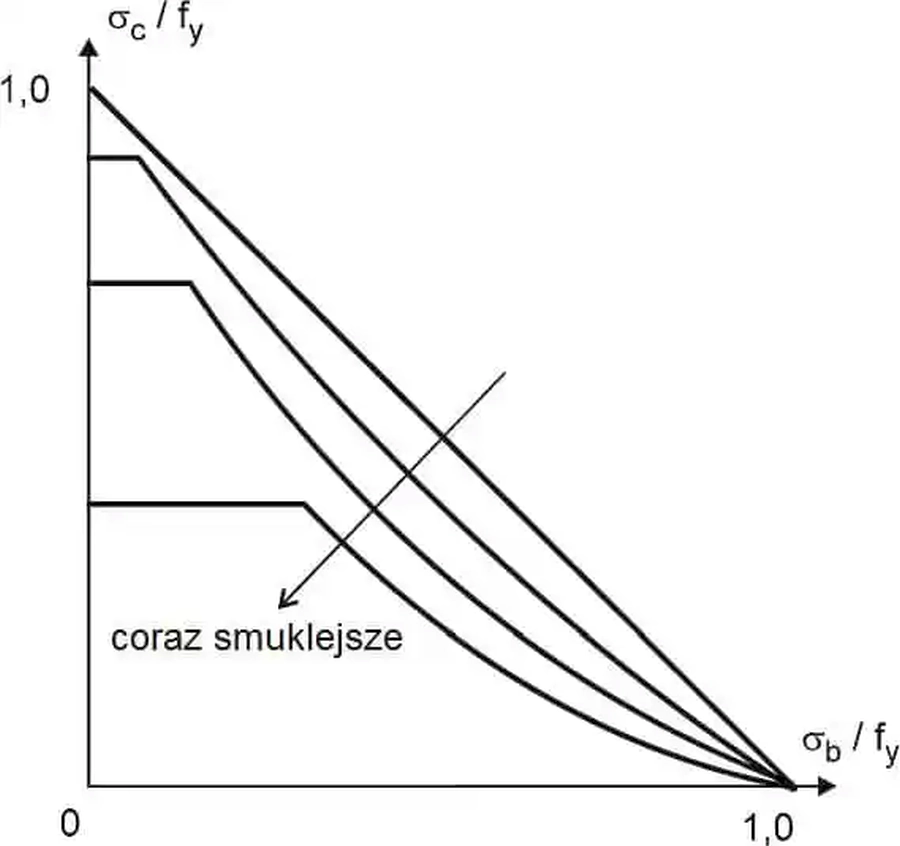
Ponieważ $\sigma_{cr}<f_y$ , więc zdążanie $\sigma_c \to f_y$ przy $\sigma_b \to 0$ powoduje, że krzywe interakcji muszą zostać zmodyfikowane przez obcięcie krzywych dla małych smukłości. Osiągnięcie naprężeń krytycznych Eulera nie jest możliwe pod czystym obciążeniem osiowym ; naprężenia te są osiągane dla dużych smukłości prętów, w zakresie praktycznie nie stosowanym.
Zmodyfikowane krzywe interakcji zginania i wyboczenia pokazano na rys. 33.
Interakcja zginania i ściskania w normach europejskich
Zależności przedstawione w poprzednich punktach, zapisane dla pręta z imperfekcjami (wstępnymi, niezamierzonymi wygięciami pręta) w przestrzeni sił przekrojowych przy uwzględnieniu ich interakcji przy jednoczesnym działaniu ściskania ze zjawiskiem wyboczenia, zginania dwukierunkowego ze zjawiskiem zwichrzenia są podstawą regulacji normowych. Poniżej najpierw omówimy zjawiska, a następnie podsumujemy je zestawieniem formuł normowych.
Element z przekrojem klasy 1 lub 2
Formuła normowa wytrzymałości elementu belki-słupa zginanego jednokierunkowo i zabezpieczonego przed zwichrzeniem jest następująca:
$$\begin{equation} \dfrac{N_{Ed}}{\chi_y \cdot A f_y} +\dfrac{k_y M_{y,Ed}}{W_{pl,y} f_y} \le 1 \label {N-My}\end{equation}$$
w której:
$\chi_y$ jest współczynnikiem wyboczeniowym słupa, wyznaczonym w stanie bezmomentowym,
$k_y$ jest współczynnikiem iterakcji, który można obliczać różnymi metodami. W normie [10] podano dwie metody: metodę 1 (załącznik A) i metodę 2 (załącznik B).
Dopuszczalne jest stosowanie innych metod od sugerowanych metod normowych 1 i 2. Poniżej podajemy formuły nas współczynniki interakcji za [23]), które były podawane we wcześniejszej wersji (2001) normy Eurocode 3, Part 1.1 :
$$\begin{equation} k_y=1-\dfrac {\mu_y N_{Ed}}{\chi_yAf_y}\le1,5 \label{k_y} \end{equation}$$
który jest współczynnikiem interakcji zmodyfikowanym czynnikiem:
$$\begin{equation}\mu_y= \overline \lambda_y \cdot (2\beta_{M_y}-4)+\dfrac {W_{pl,y}}{W_{el,y}} \label {mu_y} \le \ 0,90\end{equation}$$
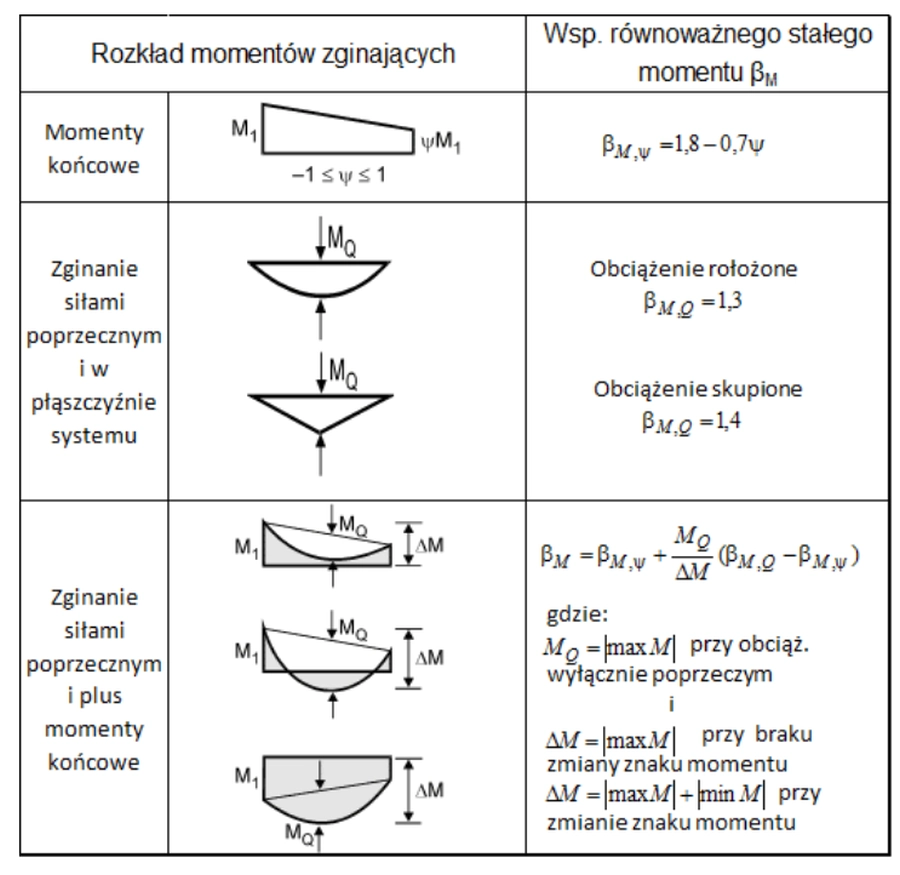
Współczynnik βMy jest współczynnikiem sprowadzającym rzeczywisty rozkład momentów zginających belkę do równoważnego, rozłożonego momentu zginającego i jest przyjmowany zgodnie z tab.2 ( dla belki stężonej w kierunku z i zginanej w kierunku y).
Tab.2. Współczynnik równoważnego stałego momentu w równaniu ($\ref{mu_y}$) [23]
Elementy z przekrojem klasy 3
Warunek nośności elementu ściskanego i zginanego z przekrojem klasy 3 jest następujący:
$$\begin{equation}\dfrac {N_{Ed}} {\chi_y \cdot Af_y}+\dfrac {k_y M_{y,Ed}} {W_{el,y} f_y }\le 1 \label{N-Mel}\end{equation}$$
Współczynnik interakcji ky można obliczyć z zależności ($\ref {k_y}$), ale dla czynnika modyfikującego
$$\begin{equation} \mu_y= \overline \lambda_y \cdot (2\beta_{M_y}-4)\ \le \ 0,90\end{equation}$$
Element z przekrojem klasy 4
Elementy klasy 4 oblicza się w stanie sprężystym, ale na skutek redukcji ścianek przekroju efektywnego, może on mieć inne położenie osi głównych, centralnych i siła ściskająca NEd może działać na mimośrodzie eNz, wywołując dodatkowe zginanie pręta momentem NEd·eEz . Formuła $(\ref{N-Mel})$ po dodaniu tego momentu daje warunek nośności
$$\begin{equation}\dfrac {N_{Ed}} {\chi_y \cdot A_{eff} \cdot f_y}+ \dfrac {k_y \cdot (M_{y,Ed}+ N_{Ed} \cdot e_{Nz})}{W_{eff,y}\cdot f_y }\le 1\end{equation}$$
gdzie:
ky – współczynnik interakcji wg ($\ref {k_y}$) i dla mnożnika modyfikującego μy wg ($\ref{mu_y}$),
Aeff – pole przekroju efektywnego,
Weff,y – wskaźnik wytrzymałości przekroju efektywnego względem osi y.
Idea współczynnika interakcji
Współczynnik interakcji ky ($\ref {k_y}$) dotyczy prostej sytuacji ściskania i jednokierunkowego zginania względem osi y. W bardziej złożonych stanach wytężenia wystąpi wiele kombinacji współczynników kij (i,j=y,x).
W każdym przypadku ich oszacowanie jest złożone, bowiem muszą ujmować wiele zjawisk. Współczynnik ky uwzględnia:
- poziom obciążenia osiowego mierzony współczynnikiem $\dfrac {N_{Ed}} {\chi_y \cdot A \cdot f_y} $
- smukłość elementu λy,
- różnicę pomiędzy plastyczną i sprężystą nośnością (stosunek Wpl /Wel – tylko dla klasy 1 i 2 )
- kształt wykresu momentów zginających
W najniekorzystniejszej kombinacji wszystkich możliwości bezpieczną wartością jest ky=1,5.
Na rys. 31 pokazano najprostszą sytuację zwiększania momentu zginającego wskutek działania siły osiowej na ugięciu (efekt P-Δ, zagadnienie II rzędu). W bardziej złożonym przypadku, gdy przebieg momentów zginających po długości pręta jest inny, to efekt amplifikacji nie jest taki prosty, bowiem moment od obciążeń poprzecznych M i dodatkowy moment Nv nie wystąpią w tym samym miejscu na długości pręta.
Na rys. 35 przedstawiono natomiast bardziej złożoną sytuację w której zachodzi amplifikacja działania siły osiowej przy zginaniu momentami przyłożonymi na końcach elementu o przeciwnych znakach dla ψ=-05. Największa amplifikacja występuje w przekroju pośrednim słupa. W ogólności maksymalne momenty pierwotne i wtórne nie muszą występować w tym samym miejscu, co należy uwzględnić w formule na współczynnik interakcji. Przedstawiona na rys. 35 sytuacja jest mniej surowa od pokazanej na rys. 31 , choć wszystkie warunki są identyczne, z wyjątkiem wartości ψ. Współczynnik interakcji zależy więc od stosunku ψ.
Dokładne określenie przebiegu momentów zginających, szczególnie podczas projektowania wstępnego może być kłopotliwe – pamiętajmy , że dla ψ=1,0 uzyskamy najmniej korzystną sytuację interakcyjną. Jeśli pierwotne momenty zginające są największe na końcach elementu, a wpływ wyboczenia jest największy w środku pręta, to należy sprawdzić nośność pręta na końcu bez wyboczenia i przekroju środkowym z wyboczeniem, ale z właściwym momentem (mniejszym od końcowego) Skojarzenie maksymalnego podporowego momentu zginającego z wyboczeniem w środku pręta mogłoby prowadzić do znacznego, nieuzasadnionego przewymiarowania pręta.
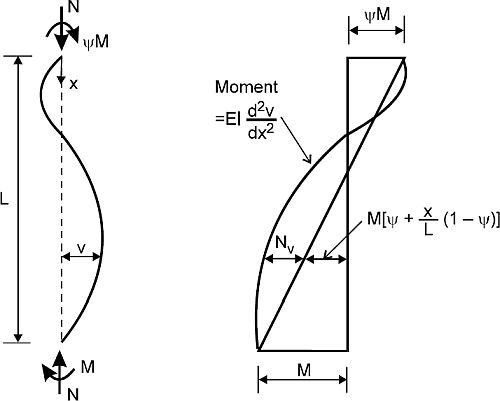
Rys.35 . Interakcja zginania i wyboczenia dla nierównomiernego momentu [23]
Teoretyczne formuły interakcji
Interakcję sprężystego wyboczenia i zwichrzenia przy działaniu siły osiowej N i momentu zginającego M w pracy[26] opisano zależnością:
$$\begin{equation}\dfrac {M^2}{i_0^2 \cdot N_{cr,z} \cdot N_{cr,o}}=\left ( 1- \dfrac {N} {N_{cr,z}}\right)\cdot \left ( 1- \dfrac {N} {N_{cr,o}}\right) \label{N-LT}\end{equation}$$
gdzie:
biegunowy promień bezwładności $i_o=\sqrt {\dfrac {I_y+I_z}{A}}$
siła krytyczna wyboczenia giętnego względem osi z (mniejszej bezwładności $N_{cr,z}=\dfrac {\pi^2 EI_z} {L^2}$
siła krytyczna wyboczenia skrętnego $N_{cr,o}=\dfrac {GI_t} {i_o^2} \cdot \left (1+\dfrac {\pi^2 EI_w} {GI_t \cdot L^2}\right )$
Równanie ($\ref{N-LT}$) opisuje wyboczenie belki przy N → 0 i wyboczenie boczne (zwichrzenie) słupa $N_{cr,z}$ lub skrętne $N_{cr,o}$ , gdy M → 0. W pierwszym przypadku krytyczna wartość M wynosi:
$$\begin{equation}M_{cr}=\dfrac {\pi}{L}\sqrt {EI_z GI_t} \cdot \sqrt{1+\dfrac { \pi^2 EI_w} { L^ 2\cdot GI_t}}\end{equation}$$
gdzie:
EIz – sztywność giętna względem osi słabszej,
GIt – sztywność skrętna,
EIw- sztywność giętno-skrętna (paczenia).
Skutek działania siły osiowej na przemieszczeniu w planie, podobnie jak wcześniej uwzględnimy współczynnikiem amplifikacji:
$$\begin{equation}\dfrac {M} {1- \dfrac{N}{N_{cr,y}}}\end{equation}$$
Równanie ($\ref{N-LT}$) możemy teraz zapisać w postaci
$$\begin{equation}\dfrac {M^2}{i_o^2 \cdot N_{cr,z} \cdot N_{cr,o}}=\left ( 1- \dfrac {N} {N_{cr,o}}\right) \cdot \left ( 1- \dfrac {N} {N_{cr,y}}\right)\cdot \left ( 1- \dfrac {N} {N_{cr,o}}\right)\end{equation}$$
Po przekształceniach formułę interakcji wyboczenia i zwichrzenia można zapisać w postaci [26]:
$$\begin{equation} \dfrac{N} {N_{cr,z}}+\dfrac {1} {1- \dfrac {N} {N_{cr,y}}\cdot \dfrac {M} {i_o \sqrt {N_{cr,z}\cdot N_{cr,o}}}}=1\end{equation}$$
lub
$$\begin{equation} \dfrac{N} {N_{cr,z}}+\dfrac {1} {1- \dfrac {N} {N_{cr,y}} }\cdot \dfrac {M} {M_{cr}}=1\end{equation}$$
Interakcja wyboczenia i zwichrzenia w normach europejskich
Formuły normowe dla przypadku wyboczenia z płaszczyzny, uogólnione na zjawisko zwichrzenia mają postać:
Element z przekrojem klasy 1 lub 2
$$\begin{equation}\dfrac {N_{Ed}} {\chi_z \cdot Af_y}+\dfrac {k_{LT} M_{y,Ed}} {\chi_{LT} W_{pl,y}f_y }\le 1\end{equation}$$
w której: $\chi_z$ – współczynnik wyboczenia z płaszczyzny zginania, $\chi_{LT}$ – wspólczynnik wyboczenia bocznego (zwichrzenia).
Współczynnik zwichrzenia oraz interakcji $k_{LT}$ można przyjąć wg [10] metoda 1 (załącznik A) lub metoda 2 (załącznik B) lub z innych technicznie uzasadnionych formuł, np. wg [23]:
$$\begin{equation}k_{LT}=1- \dfrac {\mu_{LT}M_{y,Ed}}{\chi_{LT}Af_y} \ \le 1,0\end{equation}$$
$$\begin{equation}\mu_y= 0,15 \overline \lambda_z \cdot (2\beta_{M_LT}-1) \le \ 0,90\end{equation}$$
gdzie βM,LT jest współczynnikiem równoważnego stałego momentu , który można przyjmować zgodnie z zależnościami tab.2.
Element z przekrojem klasy 3
$$\begin{equation}\dfrac {N_{Ed}} {\chi_z \cdot Af_y}+\dfrac {k_{LT} M_{y,Ed}} {\chi_{LT} W_{el,y}f_y }\le 1\end{equation}$$
Element z przekrojem klasy 4
$$\begin{equation}\dfrac {N_{Ed}} {\chi_z \cdot Af_y}+\dfrac {k_{LT} M_{y,Ed}+N_{Ed}\cdot e_{N,z}} {\chi_{LT} W_{eff,y}f_y }\le 1 \end{equation}$$
Idea współczynnika interakcji kLT
Współczynnik korelacji kLT zależy od:
- obciążenia osiowego $$\dfrac {N_{Ed}} {\chi_z \cdot A \cdot f_y} $$
- smuklość elementu λz ,
- kształt wykresu momentów zginających
Najbardziej niekorzystną wartością kLT jest 1 , co odpowiada liniowej kombinacji wyboczenia i zwichrzenia. Ogranicza to zakres efektów amplifikacji, ponieważ obciążenie NEd nie może przekroczyć χz·A·fy , która z kolei może być znacznie mniejsza niż sprężyste obciążenia krytyczne w płaszczyźnie wyboczenia Ncr,y. Jest to, oczywiście, również zabezpieczenie przed możliwością uszkodzenia płaszczyźnie poprzez nadmierne ugięcie w płaszczyźnie, przy niższym obciążeniu niż podana przez równanie (29). Może to nastąpić, na przykład w sytuacjach, w których są przewidziane różne warunki usztywnienia i/lub stężenia w płaszczyźnie XY i XZ, jak pokazano na rys. 36. W takich przypadkach powinien być traktowany przez sprawdzenie , oprócz (29), równanie w płaszczyźnie w postaci:
$$\begin{equation}\dfrac {N_{Ed}} {\chi_{min}\cdot Af_y}+\dfrac {k_{y} M_{y,Ed}} { W_{pl,y}f_y }\le 1\end{equation}$$
w którym χmin jst minimalnym współczynnikiem wyboczenia w obu płaszczyznach belki-słupa.
Rys.36 . Wyboczenie pręta w płaszczyźnie i z płaszczyzny [23]
Uogólnienie na przypadek zginania ukośnego
Pręt konstrukcji może być w ogólnym przypadku obciążony zginaniem w obu kierunkach (w płaszczyźnie XY i ZX) (rys. 37). Wykres interakcji dla takiego ogólnego przypadku pokazano na rys.38.

Rys.37 Ukośne (dwukierunkowe) zginanie belki-słupa [23]
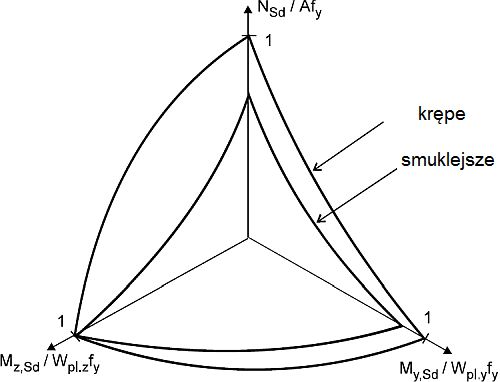
Rys. 38 Powierzchnia interakcji belki-słupa w przestrzeni [23]
Każdy punkt na i pod powierzchnią interakcji (rys.21) odpowiada bezpiecznej kombinacji obciążeń.
Formuły projektowe dla ogólnego przypadku interakcji podano w pkt. 3.7. na podstawie normy europejskiej [10]
Normowe krzywe interakcji belki-słupa
Przedstawione w poprzednich rozdziałach krzywe interakcji pręta zginanego i ściskanego z uwzględnieniem wyboczenia i zwichrzenia można aproksymować normową [10] formułą pseudoliniową:
$$\begin{equation}\sum \limits_i \ \ {\dfrac {F_{Ei}}{F_{bRi}}} \le 1 \end{equation}$$
gdzie składniki sumy pochodzą od działania zewnętrznych, obliczeniowych (indeks (Ed) sił przekrojowych: siły podłużnej NEd, momentu zginającego względem osi y (większej sztywności) My,Ed, momentu zginającego względem osi z (mniejszej sztywności) Mz,Ed i są skorygowane współczynnikami interakcji kij (ij= yy, yz, zy,zz) sił względem osi i oraz j. Rozpatrywane są dwie sytuacje: wyboczenie w planie (płaszczyźnie systemu) oraz wyboczenie z płaszczyzny i w każdej sytuacji sprzężone z nimi zjawiska.
Krzywe interakcji dla sytuacji projektowych
Y sytuacja wyboczenia względem osi Y ( w płaszczyźnie systemu ZX)
(Y1) od ściskania siłą NEd
$$\begin{equation} \dfrac {N_{Ed}} {N_{y,b,Rd}} \le 1 \end{equation}$$
$$\begin{equation}N_{y,b,Rd}=\chi_y \cdot\dfrac {N_{Rk}} {\gamma_{M1}}\end{equation}$$
χy – współczynnik wyboczeniowy w płaszczyźnie, γM1=1,0 – współczynnik materiałowy dla elementu
(Y2) od zginania w płaszczyźnie (momentem My,Ed)
$$\begin{equation}M_{y,Ed}= \chi_{LT} \cdot \dfrac {M_{y,b,Rd}} {\gamma_{M1}} \le 1\end{equation}$$
$$\begin{equation}M_{y,b,Rd}= \chi_{LT} \cdot \dfrac {M_{y,Rk}} {\gamma_{M1}}\end{equation}$$
χLT – współczynnik zwichrzenia, γM1=1,0 – współczynnik materiałowy dla elementu
(Y3) od zginania z płaszczyzny (momentem Mz,Ed)
$$\begin{equation} k_{yz} \cdot \dfrac {M_{z,Ed}+ {\Delta M_{z,Ed}}} {M_{z,b,Rd}} \le 1\end{equation}$$
$$\begin{equation}M_{z,b,Rd}= \dfrac {M_{z,Rk}} {\gamma_{M1}}\end{equation}$$
Z w sytuacji wyboczenia względem osi Z ( z płaszczyzny systemu XY)
(Z1) od ściskania siłą NEd
$$\begin{equation}\dfrac {N_{Ed}} {N_{z,b,Rd}} \le 1\end{equation}$$
$$\begin{equation}N_{z,b,Rd}=\chi_z \cdot\dfrac {N_{Rk}} {\gamma_{M1}}\end{equation}$$
χz – współczynnik wyboczeniowy w płaszczyźnie,
γM1=1,0 – współczynnik materiałowy dla elementu
(Z2) od zginania w płaszczyźnie (momentem My,Ed)
$$\begin{equation}k_{zy} \cdot \dfrac {M_{y,Ed}+ \Delta M_{y,Ed}} {M_{y,b,Rd}} \le 1\end{equation}$$
$$\begin{equation}M_{y,b,Rd}= \chi_{LT} \cdot \dfrac {M_{y,Rk}} {\gamma_{M1}}\end{equation}$$
(Z3) od zginania z płaszczyzny (momentem Mz,Ed)
$$\begin{equation}k_{zz} \cdot \dfrac {M_{z,Ed}+ {\Delta M_{z,Ed}}} {M_{z,b,Rd}} \le 1\end{equation}$$
$$\begin{equation}M_{z,b,Rd}= \dfrac {M_{z,Rk}} {\gamma_{M1}}\end{equation}$$
gdzie:
składniki ΔMy,Ed i ΔMz,Ed stosuje się wyłącznie dla przekrojów klasy 4 w przypadku, gdy efektywny przekrój ma środek ciężkości przesunięty do przekroju pierwotnego i wystąpi mimośrodowe działanie siły osiowej NEd na ewentualnych mimośrodach eN,y i\lub eN,z ,
NEd, My,Ed, Mz,Ed – wartości obliczeniowe siły ściskającej i maksymalnych momentów zginających względem osi y i zχy, χz – współczynniki wyboczenia giętnego względem osi y i z wg [10], kl. 6.3.1
χLT – współczynnik zwichrzenia wg. [10], kl. 6.3.2.
kyy, kyz, kzy, kzz – współczynniki interakcji obliczone metodą 1 (załącznik A) lub metodą 2 (załącznik 2) [10].
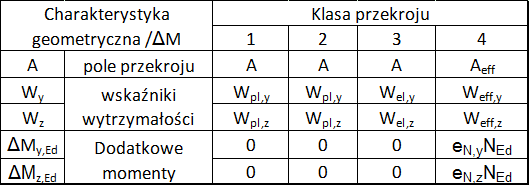
Występujące w formułach (Y) i (Z) charakterystyki geometryczne oblicza się zgodnie z tab.3 w zależności od klasy przekroju pręta,
Tab.3. Definicje Aj, Wj oraz ΔMj,Ed w zależności od klasy przekroju
Sprawdzenie przekroju
Jeśli element słup-belka został zaprojektowany z określaniem współczynników interakcji kij , to w ogólnym przypadku należy jeszcze sprawdzić, czy przekroje krytyczne elementu mają zapewnioną nośnośc w złożonym stanie naprężenia.
Dla zginania ukośnego ze ściskaniem /rozciąganiem można stosować formułę [10], wzór(6.41):
$$\begin{equation}\left(\dfrac {M_{y,Ed}}{M_{Ny,Rd}} \right)^\alpha+ \left (\dfrac {M_{z,Ed}}{M_{Nz,Rd}}\right)^\beta \le 1\end{equation}$$
gdzie wykładniki potęg zależą od kształtu przekroju poprzecznego pręta dla najczęściej stosowanych przekrojów wynoszą:
dla przekroju dwuteowego (I lub H): α=2; β=5n ≥1
dla rury okrągłej: α=β=2
dla rury prostokątnej: α=β=1,66/(1-1,33n2) ≤6
Współczynniki interakcji wg metody 1 EC3 [10]
W tab 5 i tab 6 zamieszczono wyrażenia normowe na współczynniki interakcji wg metody 1 [10].
Widoczna jest złożoność formuł i stopień ich nieliniowości. Oczywiste jest więc, że formuły interakcji (34) są nieliniowe (lub pseudoliniowe wskutek „ukrycia ” nieliniowości we współczynnikach interakcji). Ze względu na złożoność formuł wyrażenia te można uznać za użyteczne wyłącznie po opracowaniu i udostępnieniu inżynierom arkuszy lub procedur numerycznych.
Tab.5. Metoda 1: współczynniki interakcji kij
[10], tab A.1

Tab.6. Współczynniki równoważnego, stałego momentu C mi,0
[10], tab A.2

Przykłady rachunkowe
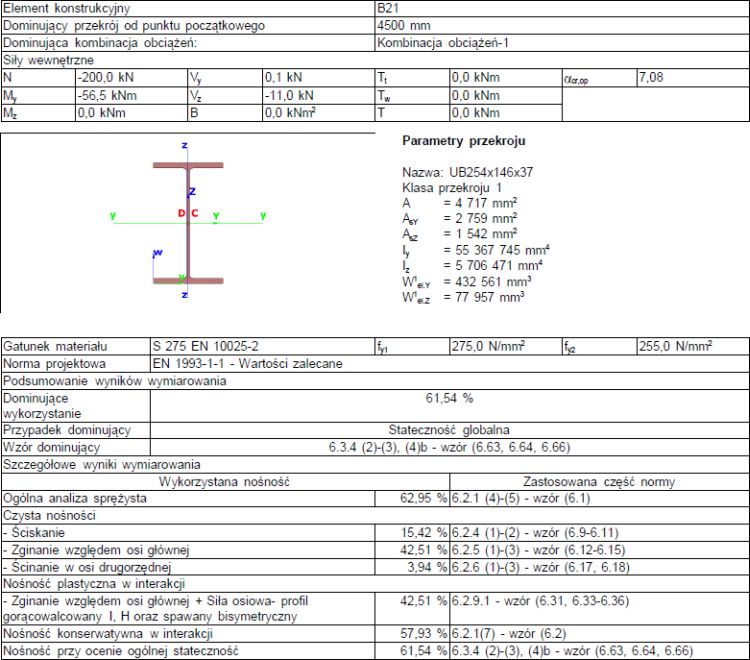
Przykłady rachunkowe słupów-belek pokazanych na rys. 39, przedstawiono w pracy [1], pkt 7.7.
Belka-słup wykonany jest z uniwersalnego profilu dwuteowego 254×146 UB 37 – S275 o charakterystykach geometrycznych zestawionych na rys. 39a.
Przykłady te zamieszczamy poniżej z porównaniem do wyników uzyskanych za pomocą współczesnego oprogramowania do projektowania konstrukcji stalowych.
Nośność w płaszczyźnie zginania (względem głównej – silniejszej osi)
Sprawdzić nośność belki-słupa, pokazanego na rys. 39b. Element jest ściskany siłą N=200 kN oraz zginany siłą V=20 kN w środku ropiętości oraz na całej długości zabezpieczony przed przemieszczeniami $\nu$ oraz obrotami $\Phi$ stężony, to zmaczy zabezpieczony przed wyboczeniem bocznym (zwichrzeniem).
Maksymalny moment zginajacy belkę w przekroju środkowym wynosi:
$ M_{y,Ed}= \dfrac{VL}{4}=\dfrac{20\cdot 9}{4}=45,0 \, kNm$.
Współczynnik materiałowy $\varepsilon=\sqrt{\dfrac{235}{275}}=0,924$. [10], tab. 5.2
Sprawdzenie nośności przekroju
Zginany przekrój walcowany jest klasy 1 przy zginaniu. W przypadku ściskania lub ściskania ze zginaniem należy sprawdzić klasę przekroju zgodnie z zasadami podanymi w artykule Klasa przekroju stalowego –[10], tab. 5.2.
Szerokość, smukłość i klasa pasa
$c_f=(146,4-6,3-2\cdot 7,7)/2=62,4 mm \,$
$\lambda_f=\dfrac{c_f}{t_f }=\dfrac{62,4}{10,9}=5,72 < 9 \cdot 0,924=8,32\to \, pas: klasa \,1 $.
Współczynnik strefy ściskanej środnika
$c_w=256,0-(2\cdot 10,9)-(2\cdot7,6)=219,0 \, mm$
$\alpha= \dfrac {h/2-(t_f+r)+ N_{Ed}/(2 t_w f_y)} {c_w}=\dfrac{256/2-(10,9+7,6)+1/2 \cdot (200 \cdot 10^3)/(6,3 \cdot 275)}{219,0}= 0,76 > 0,5$
Smukłość i klasa środnika
$\lambda_w=\dfrac{c_w}{t_w }=\dfrac{219,0}{6,3}=34,80 < \dfrac{396\varepsilon}{13\alpha-1}=41,3 \to \, $ środnik klasa 1.
Przekrój w warunkach zadania 4.1. jest klasy 1.
Nośność przekroju na zginanie jednokierunkowe (dla klasy 1,2) [10], pkt 6.2.5 (2) wzór (6.13):
$$M_{c,y, Rd}=M_{pl,Rd}= \dfrac{W_{pl} f_y}{\gamma_{M0}}= \dfrac {483\cdot 275}{1,0} \cdot 10^{-3}= 132,8 \, kNm > 45,0 \, kNm$$
Nośność przekroju na ściskanie [10],pkt 6.2.4(2), wzór (6.10)
$N_{c,Rd}=N_{pl,Rd} = \dfrac{A f_y}{\gamma_{M0}}= \dfrac{47,2 \cdot 275}{1,0}\cdot 10^{-1}=1298 ,\ kN > 200\, kN$
Sprawdzenie wytrzymałości przekroju zginanego i ściskanego dokonamy dwoma sposobami:
- Metoda prosta (liniowa interakcja – podejście konserwatywne) wg [10], kl. 6.2.1(7), wzór (6.2)
$ \dfrac{N_{Ed}}{N_{Rd}}+\dfrac{M_{y,Ed}}{M_{y,Rd}}+\dfrac{M_{z,Ed}}{M_{z,Rd}} \le 1$,
$\dfrac{200}{1298 }+\dfrac{45,0}{132,8}=0,493 \le 1 \to$ przekrój ma wystarczającą nośność.
2. Metoda dokładna (zredukowana nośność w interakcji parabolicznej) dla klasy 1 przekroju wg [10], kl. 6.2.9.1(1), wzory (6.31-6.34)
$M_{N,Rd}=M_{pl, Rd} \left[ 1- \left( \dfrac {N_{Ed}}{N_{pl,Rd}} \right)^2 \right]$,
przy czym [10], kl. 6.2.9.4. o treści: („W przypadku dwuteowników bisymetrycznych można pomijać wpływ siły podłużnej na nośność plastyczną przy zginaniu, jeśli spełnione są następujące warunki” (…) „przy zginaniu względem osi y-y”):
$N_{Ed} \le 0,25 N_{pl,Rd}$,
$\to 200 \, kN \le 0,25 \cdot 47,2 \cdot 275 /1,0 \cdot 10^{-1}=324,5 \, kN$.
$N_{Ed}\le \dfrac{0,5 h_w t_w f_y}{\gamma_{M0}}$ ,
$\to 200 kN \le [(0,5 \cdot (25,6-2\cdot 1,09)\cdot 0,63 \cdot 275]/1,0 \cdot 10^{-1}=202,9 \, kN$.
Redukcja nośności plastycznej nie jest wymagana, czyli:
$M_{N,y.Rd}=M_{pl,y,Rd}=132,8 \, kNm > 45,0 \, kNm$.
Nośność elementu na wyboczenie
Ponieważ element jest zabezpieczony przed zwichrzeniem na całej długości, więc nie trzeba sprawdzać wyboczenia bocznego belki oraz wyboczenia giętnego z płaszczyzny elementu.
Smukłość względna elementu przegubowo-przegubowego [10], wzór (6.34):
$\overline \lambda_y = \sqrt{\dfrac{A f_y}{N_{cr,y}}}=\dfrac{L_{cr,y}}{i_y}\dfrac{1}{\lambda_1}= \dfrac{900}{10,8}\dfrac{1}{93,9\cdot 0,924}=0,960$ ,
Dla profilu walcowanego $h/b>1,2$ oraz $t_f \le 40 mm$ i do wyboczenia wokół osi y-y, zastosujemy krzywą wyboczeniową „a” ($\alpha=0,21$) [10], tab. 6.1 i 6.2,
Współczynnik wyboczenia [10], kl. 6.3.1.2(1)
$\Phi=0,5[1+0,21(0,960-0,2)+0,960^2]=1,041$,
$\chi_y=\dfrac{1}{1,041+\sqrt{1,041^2-0,960^2})}=0,693$.
Nośność słupa na wyboczenie [10], pkt. 6.3.1.1(3)
$N_{b,y,Rd}=\chi_y A f_y/\gamma_{M1}=0,693\cdot 47,2 \cdot 275 /1,0 \cdot 10^{-1}=900 \, kN > 200 \, kN$
Nośność belki-słupa – Metoda uproszczona [10], Załącznik B
Współczynniki pomocnicze[10], tab. B1, B3
$\alpha_h=\dfrac{M_h}{M_s}=0,\psi=0$$ , $$C_{my}=0,90+0,1 \alpha_h =0,90$,
$C_{my} \cdot \left [ 1+( \overline \lambda_y -0,2) \dfrac{N_{Ed}}{\chi_y N_{Rk} / \gamma_{m1}} \right ]=0,90 \cdot \left [ 1+( 0,960 -0,2) \dfrac{200 \cdot 10^3}{0,693 \cdot 47,2 \cdot 10^2 \cdot 275 /1,0} \right ]=1,052$
$< C_{my} \left ( 1+0,8 \dfrac{N_{Ed}}{\chi_y N_{Rk} /\gamma_{M1}}\right)=0,90 \cdot \left( 1+0,8 \dfrac{200 \cdot 10^3}{0,693 \cdot 47,1 \cdot 10^2 \cdot 275 /1,0}\right)=1,060$,
tak, że $k_{yy}=1,052$
Warunek nośności [10], kl. 6.3.3(4):
$\dfrac{N_{Ed}}{N_{b,y,Rd}}+k_{yy}\dfrac{M_{y,Ed}}{M_{c,y,Rd}}=\dfrac{200}{900}+1,052\cdot\dfrac{45,0} {132,8}=0,222+0,356=0,579 <1$
Nośność belki-słupa – Metoda dokładna [10], Załącznik A
Parametry zadania [10],Tab. A1, A2:
$\overline \lambda_{max}=\overline \lambda_y =0,960$.
$N_{cr,y}= \dfrac{\pi^2 EI_y}{L_{cr}^2}=\pi^2 \cdot 210000 \cdot 5537 /900^2 \cdot 10^{-1}=1417 \, kN$
Ponieważ nie zajdzie zwichrzenie, to : $\overline \lambda_0=0$, $b_{LT}=0$, $C_{mLT}=1,0$.
$C_{my}=C_{my,0}=1-0,18 \dfrac{N_{Ed}}{N{cr,y}}=1-0,18 \cdot 200/1417= 0,975$,
$w_y=\dfrac{W_{pl.y}}{W_{el,y}}=483/433=1,115$,
$n_{pl}= \dfrac{N_{Ed}}{N_{Rk} /\gamma_{M1}}=\dfrac{200}{47,2 \cdot 275 \cdot 10^{-1}/1,0}=0,154$.
$C_{yy}=1+(w_y -1) \left[ \left( 2- \dfrac{1,6}{w_y} C_{my}^2 \overline \lambda _{max} – \dfrac{1,6}{w_y} C_{my}^2 \overline \lambda_{max}^2\right) n_{pl}-b_{LT}\right]=$
$=1+(1,115 -1) \left [ \left ( 2- \dfrac{1,6}{1,115}\cdot 0,975^2 \cdot 0,960 – \dfrac{1,6}{1,115} \cdot 0,975^2 \cdot 0,960^2 \right) \cdot 0,154- 0 \right]=0,990 > \dfrac{W_{el,y}}{W{pl,y}}=\dfrac{1}{1,115}=0,896$.
$\mu_y=\dfrac{1-N_{ED}/N{cr,y}}{1- \chi_y N_{ED}/N{cr,y}}=1- \dfrac{1-200/1417}{1-0,693 \cdot 200/1417}=0,952$.
$k_{yy}=C_{my}C_{mLT} \cdot \dfrac{\mu_y}{1-N_{ED}/N_{cr,y}}\cdot \dfrac{1}{C_{yy}}=0,975 \cdot 1,0 \cdot \dfrac{0,952}{1-200/1417}\cdot \dfrac{1}{0,990}=1,091 $.
Warunek nośności [10], kl. 6.3.3(4)
$\dfrac{N_{Ed}}{N_{b,y,Rd}}+k_{yy}\dfrac{M_{y,Ed}}{M_{c,y,Rd}}=\dfrac{200}{900}+1,091\cdot\dfrac{45,0} {132,8}=0,222+0,370=0,592 <1$
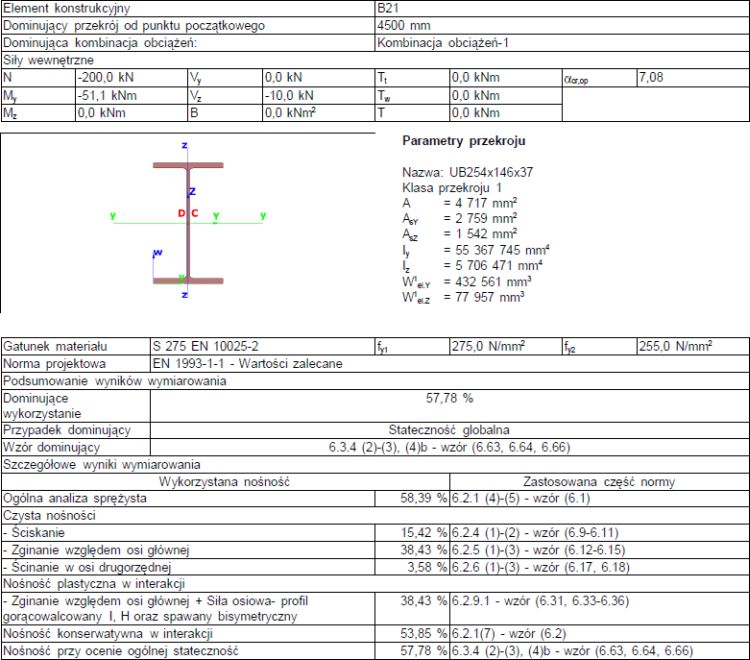
Sprawdzenie nośności elementu za pomocą programu Consteel v10
Obliczenia belki-słupa, wykonywane ręcznie z wykorzystaniem formuł normowych są bardzo uciążliwe i ze względu na swoją złożoność zawodne, a wręcz niewiarygodne.
Ten sam element sprawdzono za pomocą programu Consteel w schemacie pokazanym na rys. 40, gdzie mimośrodem „e” przyłożenia siły ściskającej modelowano imperfekcje globalne.Na rys. 43 przedsatawiono belkę słup z imperfekcjami łukowymi w kształcie jednej fali.
Przeprowadzano obliczenia II rzędu, czyli z uwzględnieniem wpływu przemieszczeń na siły przekrojowe (efekt $P-\Delta$), w kilku wariantach:
Wariant A – rys. 41 bez uwzględnienia imperfekcji,
Wariant B – rys. 42 z uwzględnieniem imperfekcji globalnych (przechyłowych L/200),
Wariant C – rys. 44 z uwzględnieniem imperfekcji lokalnych (łukowych L/200)
Wariant D – rys. 45 z jednoczesnymi imperfekcjami globalnymi i lokalnymi
W tabelach z obliczeń w programie Consteel podano wyniki:
- GE (Global Elastic) – ogólna analiza sprężysta – wzór (6.1) PN-EN: hipoteza Hubera nośności sprężystej przekroju krytycznego,
- M-NPI (Moment-Normal Plastic Interaction) – plastyczna interakcja paraboliczna zginania z siłą podłużną
- LPI (Linear Plastic Interaction)- nośność konserwatywna w interakcji -wzór (6.2) PN-EN: interakcja liniowa plastyczna sił w przekroju klasy 1 lub 2
- GS nośność przy ocenie ogólnej stateczności – (wzór 6.63,6.64,6.66) PN-EN
Wnioski:
- Sprawdzenie wg GE okazuje się się nazbyt ostrożne, ponieważ przekroje są klasy 1 i należy dopuścić uplastycznienie przekroju. Dlatego też reguły GE nie są wymiarujące w rozpatrywanym przypadku i nie będą wymiarujące w większości praktycznych przypadków elementów klasy 1 lub 2 . Wniosek jest zgodny z ostrzeżeniem normowym [10], Uwaga 6.2.1(5),
- Sprawdzenie w interakcji liniowej LPI jest konserwatywne dla przekroju, ale nie jest wymiarujące dla elementu przy uwzględnieniu niestateczności. W tym przypadku należy uwzględnić imperfekcje globalne i lokalne
- Nośność GS (Global Stability) oceniona za pomocą uogólnionego współczynnika wyboczenia dla niestateczności sprężystej z płaszczyzny układu nie jest adekwatna, ponieważ element jest zabezpieczony przed utratą stateczności z płaszczyzny, a ponadto należałoby przeprowadzić analizę wyboczeniową.
- Uwzględnienie rezerw plastycznych przekroju i jednocześnie niestateczności elementu wymaga zadania imperfekcji i ocenę nośności po przeprowadzeniu obliczeń II rzędu z warunku zginania M-NPI . Odpowiada to wariantowi D i kryterium M_N PI, które dało stopień wytężenia 50,39%
Z porównania wyników obliczeń ręcznych metodą 2 (57,9%) ; i metodą 1 (59,2%) oraz numerycznych (50,39%) , wynika, że:
wg metody 2 w obliczeniach ręcznych uzyskano $$ (1- 0,579/0,5039)$$= o 15% zawyżone wytężenie belki,
wg metody 1 w obliczeniach ręcznych uzyskano $$ (1- 0,592/0,5039)$$ = o 18%% zawyżone wytężenie belki.
Nośność względem osi słabszej
Dwuprzęsłowa belka pokazana na rys. 49c poddana jest ściskaniu siłą N=200 kN i zginana równomiernie rozłożonym obciążeniem q=3,2 kN/m. Sprawdzić nosność belki-słupa o przekroju UB 37 ułożonej środnikiem w poziomie.
Nośność przekroju
Maksymalny moment zginający $M_{z,ED}=3,2 \cdot 4,5^2/8=8,1 \, kNm$,
(ujemny podporowy moment zginający w belce dwuprzęsłowej).
Pasy są klasy 1 przy ściskaniu oraz przy złożonym obciążeniu.
Klasa środnika przy ściskaniu [10],Tab.5.2,
$\lambda_w=\dfrac{c_w}{t_w \epsilon}=(256,0-2\cdot 10,9-2\cdot 7,6)/(6,3\cdot 0,924)=37,6$
$33 < 37,6< 38 \to$ klasa 2.
Wobec tego przekrój jest klasy 2 ( najniższa klasa ścianek składowych).
Nośność przekroju na zginanie [10], kl. 6.2.5(2)
$M_{c,z,Rd}=275 \cdot 119 \cdot 10^{-3} /1,0=32,7 \, kNm > 8,1 \, kNm$ .
Sprawdzenie wytrzymałości przekroju zginanego i ściskanego:
- Metoda prosta (liniowa interakcja)
$\dfrac{8,1}{32,7}+\dfrac{200}{47,2 \cdot 275 \cdot 10^{-1}}=0,402 \le 1 \to$ przekrój ma wystarczającą nośność
2. Metoda dokładna (zredukowanej nośności w interakcji parabolicznej)
Ponieważ przekrój jest klasy 2, więc zastosowano warunek [10], kl.6.2.9.1, dla: $h_w=256-2 \cdot 10,9=234 \, mm$, $A_w=23,4\cdot 0,63=14,74 \, cm^2$
Redukcja redukcja nośności plastycznej nie jest wymagana, ponieważ :$N_{Rd}= A_w f_y/\gamma_{M0}= 14,74 \cdot 275/ 1,0\cdot 10^{-1}=405,4 \, kN > 200 \, kN$, czyli:
$M_{N,z.Rd}=M_{pl,z,Rd}=32,7\, kNm > 8,1 \, kNm \to $ przekrój ma wystarczajacą nośność.
Nośność elementu na wyboczenie
Współczynnik wyboczenia [10], tab. 6.1 i 6.2, kl. 6.3.1.2(1)
$\overline \lambda_z=\sqrt{\dfrac {Af_y}{N_{cr,z}}}=\dfrac{L_{cr,z}}{i_z}\cdot \dfrac{1}{\lambda_1}=\dfrac{450}{ (3,48)\cdot( 93,9 \cdot 0,924)}=1,490$.
Profil walcowany $h/b>1,2$ oraz $t_f \le 40 mm$, wyboczenie wokół osi z-z, $\to$ krzywa wyboczeniowa „b” ($\alpha=0,34$).
$\Phi=0,5[1+0,34(1,490-0,2)+1,490^2]=1,829$,
$\chi_z=\dfrac{1}{1,829+\sqrt{1,829^2-1,490^2})}=0,343$
Nośność słupa na wyboczenie [10]. kl. 6.3.1.1(3)
$N_{b,z, Rd}=\chi_z A f_y/\gamma_{M1}=0,346\cdot 47,2 \cdot 275 /1,0/10^{-1}=449 \, kN > 200 kN$.
Nośność belki-słupa – Metoda uproszczona
[10], tab. B3, B1
Ponieważ element jest zabezpieczony przed zwichrzeniem, więc $e_{LT}=0$,
$M_h=-8,1\, kNm$, $M_s=9\cdot 3,2 \cdot 4,5^2/128=4,56 \, kNm$. $\psi=0$,
$\alpha_s=\dfrac{M_s}{M_h}=4,56/(-8,1)=-0,563$.
$C_{mz}=0,1-0,8 \alpha_s=0,1-0,8\cdot(-0,563)=0,550 > 0,40$.
$C_{mz} \left (1+ (2\overline \lambda_z-0,6)\dfrac{N_{Ed}}{\chi_z N_{Rk}/ \gamma_{M1}}\right)= 0,550\cdot\left( 1+(2\cdot 1,490-0,6)\cdot \dfrac{200}{0,346\cdot 47,2\cdot 275 /1 \cdot 10^{-1}}\right) = 1,133$
$> C_{mz} \left( 1+1,4 \dfrac{N_{Ed}}{\chi_z \cdot N_{Rk}/\gamma_{M1}}\right)=0,550\cdot \left( 1+1,4\dfrac{200}{0,346\cdot 47,2\cdot 275/1,0\cdot 10^{-1}}\right)=0,893$
tak, że $k_{zz}=0,893$
Warunek nośności [10],kl. 6.3.3(4):
$\dfrac{N_{Ed}}{N_{b,z,Rd}}+k_{zz}\dfrac{M_{z,Ed}}{M_{c,y,Rd}}=\dfrac{200}{449}+0,893\cdot\dfrac{8,1} {32,7}=0,445+0,221=0,666 <1$
Nośność belki-słupa – Metoda dokładna
[10], tab. A1, A2
$\overline \lambda_y =0,960$, (z pkt. 4.1.2)
$\overline \lambda_{max}=\overline \lambda_z=1,490 ( pkt.4.2.2) >0,960$.
$N_{cr,z}= \dfrac{\pi^2EI_z}{L_{cr,z}^2}=\pi^2 \cdot 210000 \cdot 571 \cdot /450^2\cdot 10^{-1}=584,4 \, kN$,
$|\delta_x|=\dfrac{qL^4}{185EI_z}=\dfrac{3,2 \cdot 450^4}{185 \cdot 210000 \cdot 571}=5,9 \, mm$
$|M_{z,Ed}(x)|=8,1 \, kNm$
$C_{mz}=C_{mz,0}=1+\left( \dfrac{\pi^2EI_z |\delta_x|}{L^2 |M_{z.Ed}(x)|}-1\right)\dfrac{N_{Ed}}{N_{cr,z}}= 1+\left(\dfrac{\pi^2\cdot 210000 \cdot 571 \cdot 5,9\cdot 10^4}{4500^2\cdot 8,1\cdot 10^6}-1 \right)\cdot \dfrac{200}{584,4}=0,804$,
$w_z=\dfrac{W_{pl.z}}{W_{el,z}}=119/78=1,526 > 1,5$,
$n_{pl}= \dfrac{N_{Ed}}{N_{Rk} / \gamma_{M1}}=\dfrac{200 }{47,2 \cdot 275 /1,0\cdot 10^{-1}}=0,154$.
$C_{zz}=1+(w_z -1) \left[ \left( 2- \dfrac{1,6}{w_z} C_{mz}^2 \overline \lambda _{max} – \dfrac{1,6}{w_z} C_{mz}^2 \overline \lambda_{max}^2\right) n_{pl}-e_{LT}\right] \ge \dfrac{W_{el,z}}{W_{pl,z}}$
$C_{zz}=1+(1,5 -1) \left [ \left ( 2- \dfrac{1,6}{1,5} 0,804^2 \cdot 1,490 – \dfrac{1,6}{1,5} \cdot 0,804^2 \cdot 1,490^2 \right) \cdot 0,154- 0 \right]=0,958 \ge \dfrac{1}{1,5}=0,667$
$\mu_z=\dfrac{1-N_{Ed}/N{cr,z}}{1- \chi_z N_{Ed}/N{cr,z}}=1- \dfrac{1-200/584,4}{1-0,346 \cdot 200/584,4}=0,746$.
$k_{zz}=C_{mz} \dfrac{\mu_z}{1-N_{Ed}/N_{cr,z}}\cdot \dfrac{1}{C_{zz}}=0,804 \cdot \dfrac{0,746}{1-200/584}\cdot \dfrac{1}{0,958}=0,952 $.
Warunek nośności [10], kl. 6.3.3(4):
$\dfrac{N_{Ed}}{N_{b,z,Rd}}+k_{zz}\dfrac{M_{y,Ed}}{M_{c,y,Rd}}=\dfrac{200}{449}+0,952\cdot\dfrac{8,1} {32,7}=0,445+0,236=0,681 <1$
Sprawdzenie nośności przy zwichrzeniu
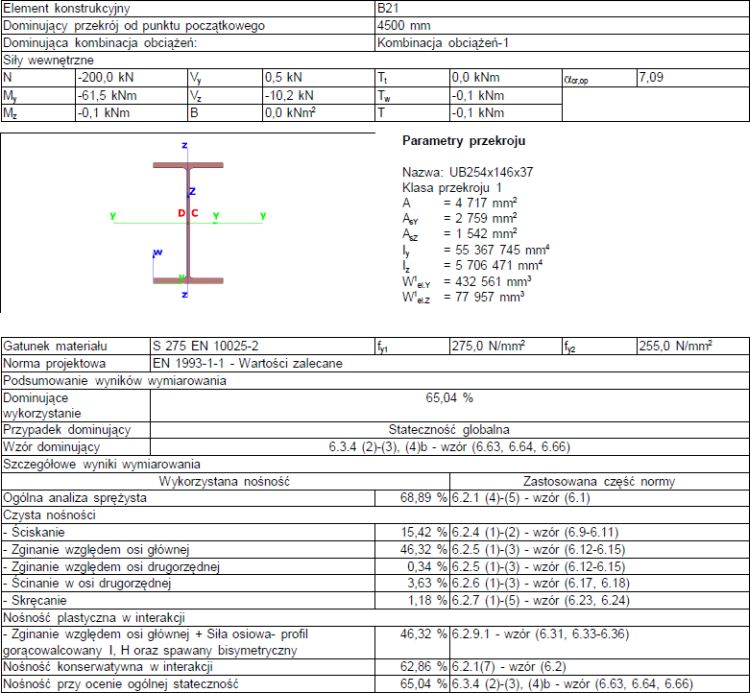
Jednoprzęsłowa belka UB 37- S275, pokazana na rys. 39d poddana jest ściskaniu siłą N=200 kN i zginana siłą V=20 kN oraz stężona bocznie i skrętnie w środku rozpiętości. Sprawdzić nośność belki-słupa.
Moment zginający $M_{y,Ed}=45,0 kNm$.
Nośność przekroju oraz zginanie belki względem osi większej sztywności bez utraty zwichrzenia sprawdzono w pkt. 4.1.
Sprawdzenie na zwichrzenie – Metoda uproszczona
Nośność belki na proste zwichrzeniem (uzyskane w odrębnym zadaniu) $M_{bRd}=121,4 \,kNm$
Nośność słupa na ściskanie (pkt. 4.1. $N_{b,y,Rd}=900 /, kN$, $k_{yy}=1,052$
Sprawdzenie nośności wg [10], kl. 6.3.3.(4)
$\dfrac{N_{Ed}}{N_{b,y,Rd}}+k_{yy}\dfrac{M_{Ed}}{M_{b,Rd}}=\dfrac{200}{900}+1,052 \dfrac{45,0}{121,4}=0,222+0,390=0,612 < 1$
Nośność elementu z płaszczyzny wg [10], wzór (6.62)
$N_{b,z,Rd}= 449 m\, kN$$, $$ \chi_z= 0,346$ , $\overline \lambda_z= \overline \lambda_{max}= 1,490$, $N_{cr,z} =584,4 \, kN$$ i $$w_z=1,5$ (pkt. 4.2).
$\psi=0$, $ C_{mLT}=0,6+0,4\psi=0,6 > 0,4 $
Współczynnik korelacji $k_{zy}$ [10], tab. B.1
$\left( 1- \dfrac{0,1\overline \lambda_z}{(C_{mLT}-0,25} \dfrac{N_{Ed}}{\chi_z N_{Ek}/\gamma_{M1}}\right)=\left( 1- \dfrac{0,1\cdot 1,490}{(0,6-0,35)} \cdot\dfrac{200}{0,346\cdot 47,2\cdot 275\cdot 10{_1}/1,0}=\right)0,810$
$\left( 1- \dfrac{0,1}{(C_{mLT}-0,25} \dfrac{N_{Ed}}{\chi_z N_{Ek}/\gamma_{M1}}\right)=\left( 1- \dfrac{0,1}{(0,6-0,25)} \cdot\dfrac{200}{0,346\cdot 47,2\cdot 275\cdot 10{_1}/1,0}=\right)0,873$,
czyli $k_{zy}=0.873$
Warunek nośności:
$\dfrac{N_{Ed}}{N_{b,z,Rd}}+k_{zy}\dfrac{M_{y,ED}}{M{b,Rd}}=\dfrac{200}{449}+0,873 \cdot \dfrac{45,0}{121,4}=0,445+0,324=0,769<1$
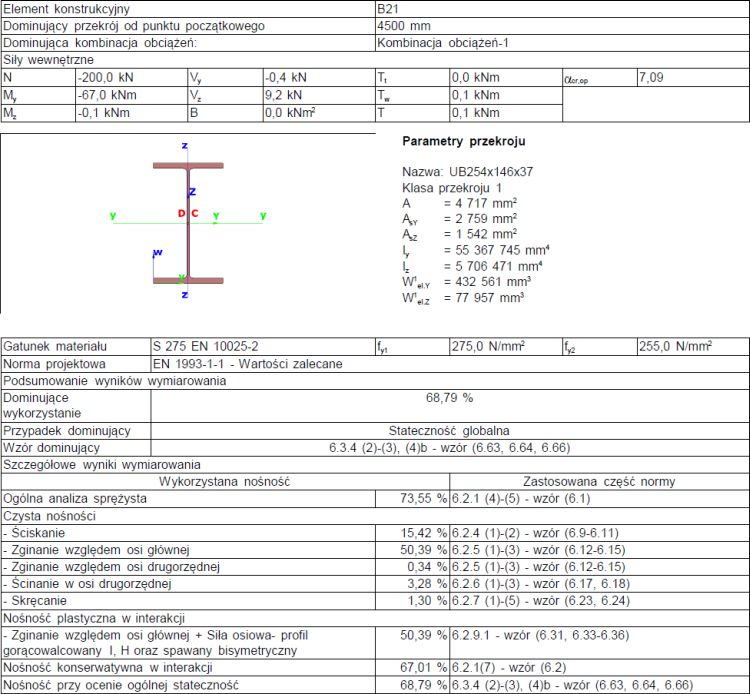
Sprawdzenie na zwichrzenie – Metoda dokładna
Boczne wyboczenie elementu jest sprawdzone w rozdz. 4.1., ale przy podejściu [10], wzór (6.61) należy sprawdzić zwichrzenie w miejsce wytrzymałości na zginanie względem głównej osi przekroju., do czego jest wymagany współczynnik interakcji $k_{yy}$.
$\overline \lambda_y=0,960$, $\overline \lambda_{max}=\overline \lambda_z=1,490$
$M_z=111,2 \, kNm$
$\overline \lambda_o=\sqrt{132,8/111,2}=1,093$,
Ponieważ przekrój jest bisymetryczny , to mamy:
$i_p=\sqrt{\dfrac{I_y+I_z}{A}}=\sqrt{\dfrac{5537+571}{47,2}}=11,38 \, cm$
$N_{cr,T}=\dfrac{1}{i_p^2} \left( GI_t+\dfrac{\pi^2EI_w}{L_{cr,T}}^2\right)=\dfrac{1}{11,38^2}\left ( 81000\cdot 15,3\cdot 10^2+ \dfrac{\pi^2 \cdot 210000\cdot 0,0857 \cdot 10^8}{450^2}\right)=1636 \,kN$,
Dla $\beta_m=0 \to C_1=1,75$
$0,2 \sqrt{C_1} \sqrt[4]{\left( 1- \dfrac{N_{Ed}}{N_{cr,z}}\right) \left( 1-\dfrac{N_{Ed}}{N_{cr,T}}\right)} =0,2 \sqrt{1,75} \sqrt[4]{\left( 1- \dfrac{200}{584,4}\right) \left( 1-\dfrac{200}{1636}\right)}=0,231 < \overline \lambda_o =1,093$ ,
$\alpha_{LT}=1=\dfrac{I_t}{I_y}=1-15,4/5537=0,997 >0 $,
$\varepsilon_y= \dfrac{M_{y,Ed}}{N_{Ed}} \dfrac{A}{W_{el,y}}=\dfrac{45 \cdot 10^4}{200 \cdot 10^3} \dfrac{47,2 \cdot 10^2}{433 \cdot 10^3}=2,453$
$N_{cr,y}=1417$ kN,
$C_{my,0}=1-0,18 \dfrac{N_{Ed}}{N_{cr,y}}=1-0,18 \cdot 200/1417=0,975$,
$C_{my}= C_{my,0}+(1-C_{my,0})\dfrac{\sqrt{\varepsilon_y}\alpha_{LT}}{1+\sqrt{\varepsilon_y}\alpha_{LT}}=0,975+(1-0,975) \dfrac{\sqrt{2,453}\cdot 0,997}{1+\sqrt{2,453}\cdot 0,997}=0,990$
Uwagi i wnioski z przykładów
Ze względu na żmudne obliczenia ręczne słupów (elementów zginanych i ściskanych), a mimo to niewystarczającą dla praktyki dokładność obliczeń – zaleca się stosowanie sprawdzonych komputerowych arkuszy, procedur i programów obliczeniowych.Literatura
- Trahair N. S., Bradford M. A. (2008). The Behaviour and Design of Steel Structures to EC3 (4 Wydanie). http://library.magistersipil.janabadra.ac.id/wp-content/uploads/2015/05/The-Behaviour-And-Design-Of-Steel-Structures-To-EC3-4th-EDITION.pdf
- Chodor, L., & Malik, Ł. (2014). Optymalizacja konstrukcji nośnej hali stalowej – Optimization of the supporting structure of steel hall. Short Papers, 195–198
- Chodor, L. (2016). Przekrycia hal i galerii. In XXXI Ogólnopolskie Warsztaty Pracy Projektanta Konstrukcji: Vol. I (pp. 25–202). https://chodor-projekt.net/wp-content/uploads/2016/03/Chodor_LPrzekrycia-hal-i-galerii-WPPK-2016.pdf
- PN-EN 1994-1-1+Ap1+AC: 2008, Eurokod 4 – Projektowanie zespolonych konstrukcji stalowo-betonowych – Część 1-1: Reguły ogólne i reguły dla budynków
- Starosolski, W. (2013). Konstrukcje żelbetowe według Eurokodu 2 i norm związanych Tom. 3, Wydawnictwo Naukowe PWN
- Bogucki, W. (Ed.). (1982). Poradnik projektanta konstrukcji metalowych (1st ed., Vol. 2). Arkady
- Tahtamyschev A. G. (1978)., Primery rascheta stalnych konstruktciy
- Rykaluk, K. (2009). Konstrukcje stalowe. Podstawy i elementy. Dolnośląskie Wydawnictwo Edukacyjne
- Rykaluk, K. (2009). Konstrukcje stalowe. Podstawy i elementy. Dolnośląskie Wydawnictwo Edukacyjne
- PN-EN 1993-1-1:2006, Eurokod 3- Projektowanie konstrukcji stalowych – Część 1-1, Reguły ogólne i reguły dla budynków
- Pałkowski, S. (2009). Konstrukcje stalowe: wybrane zagadnienia obliczania i projektowania. Wydawnictwo Naukowe PWN
- Chodor, L. (2016). Stalowe dżwigary kratowe. PiWiki – Inżynierowie i Architekci Chodor-Projekt. https://chodor-projekt.net/encyclopedia/stalowe-dzwigary-kratowe/
- Grochowska, E., & Matysiak, A. (2014). Konstrukcje stalowe ze słupami dwugałęziowymi z przewiązkami projektowane wg norm PN i EN. Przegląd Budowlany, 9/2014, 41–43
- Włodarczyk, W. (2002). Konstrukcje stalowe. Wydawnictwa Szkolne i Pedagogiczne
- Kurzawa, Z. (2012). Stalowe konstrukcje prętowe. Cz. I. Hale przemysłowe oraz obiekty użyteczności publicznej. Wydawnictwo Politechniki Poznańskiej
- SKILLS, CTICM, PIKS, Politechnika Warszawska. (2012). Podstawy słupów., http://www.piks.com.pl/wp-content/uploads/2015/05/SKILLS-M04P-Podstawy-slupow.pdf
- Włodarczyk, W. (2002). Konstrukcje stalowe. Wydawnictwa Szkolne i Pedagogiczne
- PN-EN 1992-1+AC+Ap 1,2,3:2008, Projektowanie konstrukcji z betonu -Część 1-1 Reguły ogólne i reguły dla budynków
- Chodor L. (1999). Projekt konstrukcji przekrycia Centrum Handlowego w Radomiu. Biuro Projektów Budownictwa Chodor-Projekt, sp. z o.o.; Archiwum Biura Projektów Budownictwa BPB, sp z o.o. w Kielcach
- Medwadowski, J. (Ed.). (1980). Konstrukcje metalowe i stalowe. PWN
- PN-B-03215/1998 Konstrukcje stalowe – Połączenia z fundamentami – Projektowanie i wykonanie
- PN-EN 1993-1-8 +Ap1+AC:2006, Eurokod 3 -Projektowanie konstrukcji stalowych -Część 1-8: Projektowanie węzłów
- SSEDTA (2001). Course: Eurocode 3. Lecture 14 : Beam-columns, Structural Steelwork Eurocodes Development of A Trans-national Approach
- Andrzejewski, E. (1969). Poradnik inżyniera. Mechanika. Tom II. Zagadnienia konstrukcyjne (Ed. Kocańda S,), Wydawnictwo Naukowo-Techniczne
- Rykaluk, K. (2009). Konstrukcje stalowe. Podstawy i elementy. Dolnośląskie Wydawnictwo Edukacyjne
- Chen W. F., Atsuta T. (1976). Theory of Beam-Columns (4 Wydanie , Tom 1,2 ). McGraw-Hill
________________________________