Chodor L., Belki żelbetowe,, Encyklopedia πWiki, www.chodor-projekt.net,
13 lipca 2018 – 9 czerwca 2020 – ( publikacja kompletna)
22-02-2025 rewizja po dużej awarii portalu>
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Arkusz LCżelbet zawiera oryginalny kod – © wszelkie prawa zastrzeżone.
Artykuł w ciągu ostatnich 24 godzin czytało 19 Czytelników
Część R
Belki żelbetowe. Rysy i ugięcia
Nawigacja: [ P: Pełzanie i skurcz ] ⇐ ⊗ ⇒ [ S: Ścinanie i skręcanie]
Stany graniczne użytkowalności żelbetu
Stosowane w artykule charakterystyczne okresy podczas budowy i eksploatacji elementu żelbetowego pokazano rys. R-1 Stany graniczne użytkowalności, a mianowicie: zarysowania, ugięcia , i drgania konstrukcji należy sprawdzać pod działaniem obciążeń w kombinacjach charakterystycznych. Na użytek szacowania zarysowań oraz ugięć konstrukcji z wykorzystaniem pola sił przekrojowych uzyskanych dla stanu granicznego nośności SGN wprowadza się indeksy $SGU_1/SGN$ wzór (P-4) i $SGU_2/SGN$ wzór (P-5).
Zarysowania elementu żelbetowego
W artykule Model graniczny żelbetu analizowano bryłę naprężeń rys. Z-1 w przekroju żelbetowym znajdującym się w stanie granicznym nośności. Stany graniczne użytkowalności należy analizować w poprzedzających fazach pracy w których fundamentalnym zjawiskiem jest rysowanie się przekroju, a w dłuższym okresie czasu zjawiska pełzania i skurczu betonu, przedstawione w rozdz. Pełzanie i skurcz betonu.
Graniczne (dopuszczalne) rozwarcie rys
Powstawanie rys w betonie jest podstawowym mechanizmem niszczenia betonu oraz czynnikiem, który wymusza stosowanie zbrojenia. Zarysowania powodują znaczne zmniejszenie sztywności betonu i ochrony zbrojenia przed ekspozycją środowiska, ale również mogą być nieakceptowane wizualnie. Całkowite usunięcie rys w betonie jest praktycznie niemożliwe i każda rzeczywista konstrukcja betonowa jest porysowana rysami o rozwartości $w_k$, które jednak są ograniczane do wielkości akceptowanej ze względu na ogólne wrażenie wzrokowe.
Szerokość rozwarcia rys $w_k$ jest ograniczana w sposób następujący:
$$\begin{equation} w_k \le w_{max}= \begin {cases}
0,4 \, mm, & \text {dla klasy ekspozycji XC0 i XC1 } \\
0,3 \, mm, & \text {dla XC2 do 4, XD1 do 3 oraz XS1 do 3}
\end {cases} \label{1} \end{equation}$$
Dla innych klas ekspozycji (XF, XA) graniczne szerokości rys należy ustalać indywidualnie z warunku ochrony betonu i stali przed korozją w wymaganym okresie trwałości budowli i jej elementu konstrukcyjnego.
Mechanizm rysy i fazy pracy przekroju
Zarysowania przekroju żelbetowego istotnie zależą od współpracy betonu i stali zależnej od stosunku modułów odkształcalności:
$$\begin{equation} \alpha_e= \begin {cases}
\alpha_{e,m} = E_s / E_{cm} & \text {w sytuacji doraźnej ( po 28 dniach)} \\
\alpha_{e,ef} = E_s / E_{cef} & \text { w sytuacji długotrwałej z uwzględnieniem pełzania} \\
\end {cases} \label{2} \end{equation}$$
Mechanizm powstawania rysy
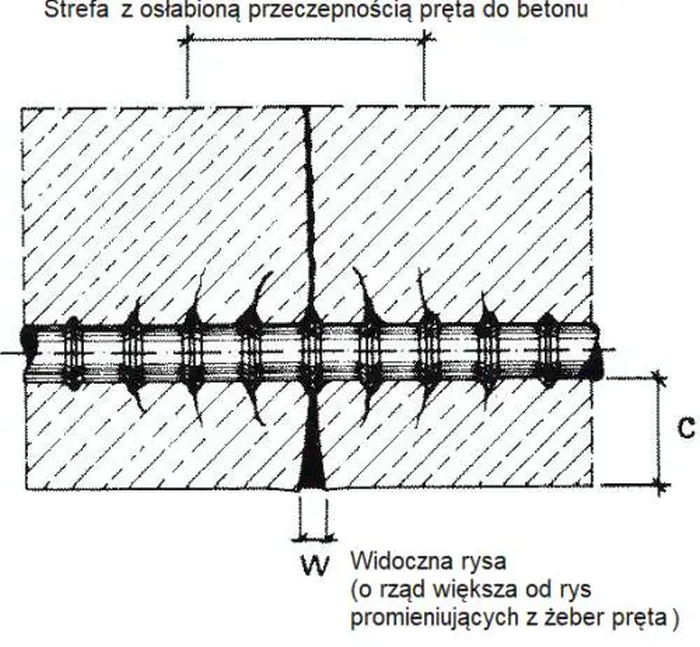
Rysy na powierzchni betonu inicjują się w sposób pokazany na rys. R-1. Model mechanizmu powstawania rysy przedstawiono na rys. R-2. Rysa powstaje na skutek różnicy pomiędzy odkształceniem stali $\varepsilon_s$ oraz betonu $\varepsilon _c$ skoncentrowanym na odcinku po $s_0$ w obie strony od potencjalnego miejsca pojawienia się rysy.
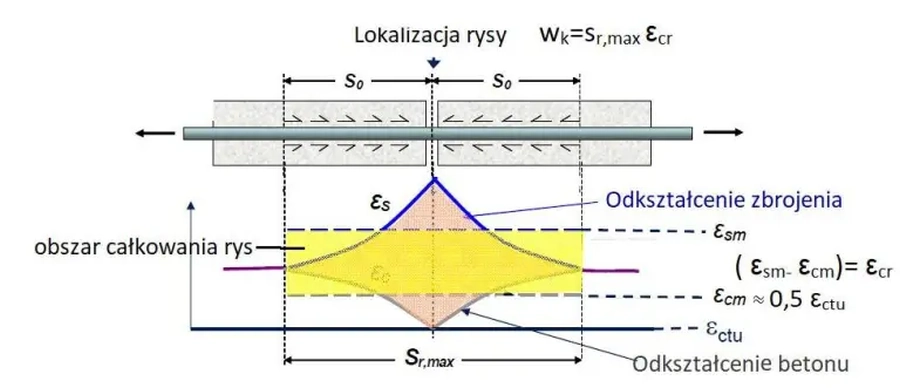
Rys. R-2. Mechanizm powstawania rysy w elemencie żelbetowym (opracowane na podstawie [1]
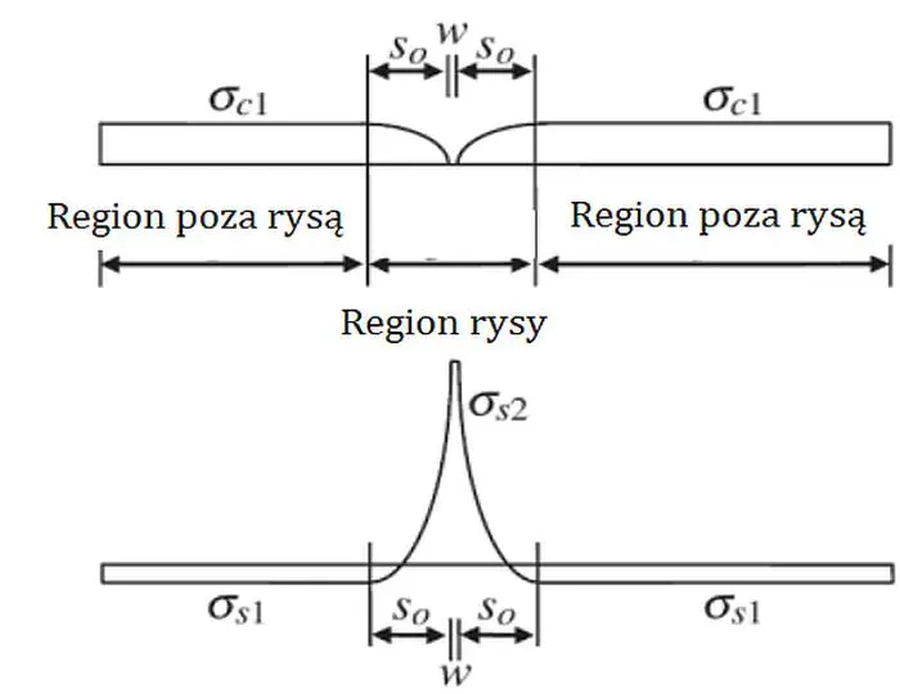
Rys. 3 Naprężenia wstali w regionie pojedynczej rysy [2]
W rezultacie układu odkształceń w obszarze rysy zobrazowanego na rys.R-2 naprężenia w betonie in stali układają się w sposób przedstawiony na rys. R-3. W tym przypadku nie ma zastosowania zasada kontinuum ciała, bowiem lokalna nieciągłość betonu w postaci rysy przenosi się na stal wskutek przyczepności betonu i w rezultacie lokalne odkształcenie i naprężenie pręta znacznie wzrasta.
Fazy pracy przekroju żelbetowego
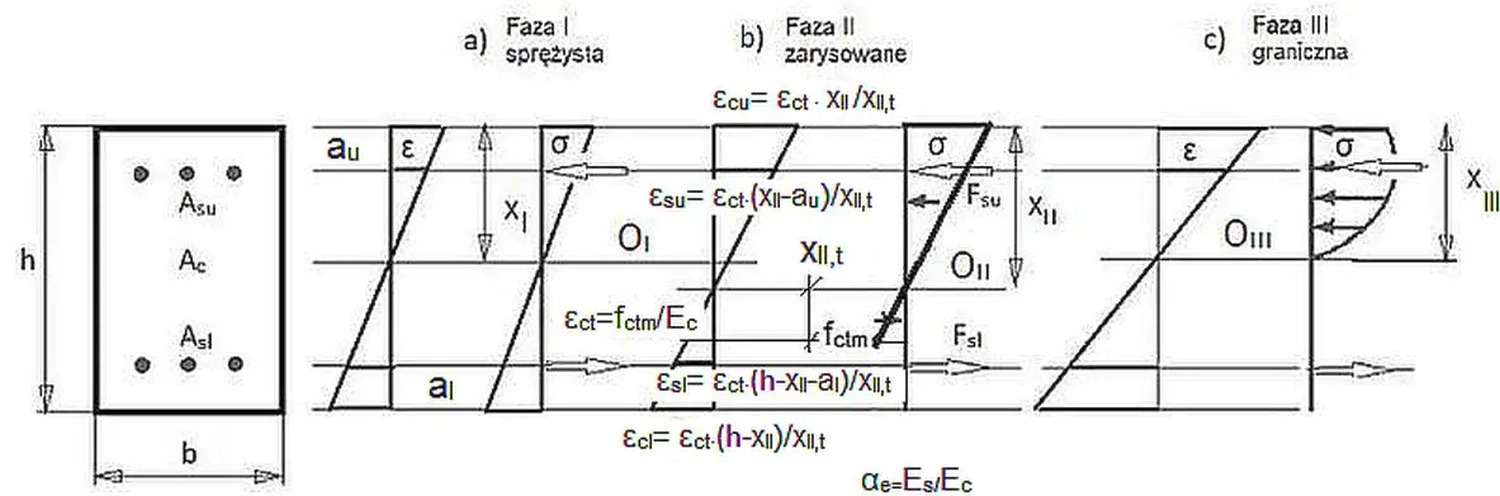
Pokazany na rys . Z-1 rozkład naprężeń w przekroju żelbetowym dotyczy stanu granicznego, który jest ostatnią fazą pracy przekroju. W fazach poprzedzających rozkład naprężeń będzie inny – silnie związany z zarysowaniem przekroju. Powstawanie rysy jest uzależnione od współpracy betonu i stali zbrojeniowej. Współpracę tę w krótkim okresie czasu można podzielić na III etapy pokazane na rys.R-4 przy czym fazę II (powstawania rys) rozbijemy na fazę IIa ( inicjacja pękania) , IIb (blokadę mechaniczną), IIc (zarysowanie). W każdej z faz obowiązuje założenie płaskich przekrojów (Z-47), (Z-48) oraz prawo fizyczne (Z-39), (Z-43).
Z zasady płaskich przekrojów dla znanego granicznego odkształcenia włókna rozciąganego w betonie $\varepsilon_{ct}=f_{ctm}/E_c$ pozostałe odkształcenia wyznaczymy z zależności:
$\varepsilon_{cu}=\varepsilon_{ct}\cdot x_{II}/x_{II,t}$,
$\varepsilon_{su}=\varepsilon_{ct}\cdot (x_{II}-a_u) / x_{II,t}$,
$\varepsilon_{sl}=\varepsilon_{ct}\cdot (h-x_{II}-a_l) / x_{II,t}$,
$\varepsilon_{cl}=\varepsilon_{ct}\cdot (h-x_{II}) / x_{II,t}$.
Jeśli natomiast znane jest odkształcenie dolnego pręta zbrojeniowego $\varepsilon_{sl}=\sigma_{sl} /E_s$, to pozostałe wyznaczymy z zależności (Z-47).
Faza I sprężysta – beton niespękany – rys. Z-4a
Na tym etapie beton przenosi rozciąganie ($\sigma_{ct}< f_{ct,m}$). Przy niskich naprężeniach w spojeniu betonu i stali (0,2 do 0,8 $f_{ct}$) nie obserwuje się pękania, a poślizg pręta jest niewielki. Zapewnione jest spojenie stali i betonu głównie przez adhezję chemiczną, a częściowo przez interakcje mikromechaniczne związane z mikroskopijną chropowatością powierzchni stali.
Rozkład naprężeń jest w przybliżeniu liniowy, zgodny z teorią belek wykonanych z materiału jednorodnego, a oś obojętna przekroju symetrycznie zbrojonego pokrywa się z osią geometryczną przekroju
Faza II – beton spękany – rys Z-4b
Fazę II (pękania betonu) podzielimy na kilka etapów , zależnie od zjawisk jakie w nich zachodzą.
Etap IIa: (inicjacja pęknieć). Naprężenie w spojeniu stali i betonu jest wyższe, a przyczepność chemiczna rozkłada się, i żebra prętów wywołują naprężenia rozciągające w betonie, co powoduje poprzeczne mikropęknięcia. Klinujący efekt promieniowy zostaje powoduje, że jeszcze nie dochodzi do rozłupywania betonu.
Etap Ib (blokada mechaniczna): Naprężenie w spojeniu jest większe niż wytrzymałość betonu na rozciąganie i wskutek działania klinującego powstają podłużne pęknięcia (zarysowania) w betonie. Jest to związane głównie ze skośnymi siłami ściskającymi wychodzące z pręta żebrowanego, które są zrównoważone przez obwodowe naprężenia rozciągające w betonie otaczającym pręt. Na tym etapie, siłę wiązania zapewnia przede wszystkim blokada mechaniczna na zbrojeniu.
Etap IIc: W elementach betonowych z gładkimi prętami etap ten następuje bezpośrednio po zerwanie wiązania z betonem. Siła jest przenoszona przez tarcie i podlega wpływowi nacisku poprzecznego, skurczu betonu i chropowatości pręta. W przypadku prętów z żebrami przy niewielkim zbrojeniu poprzecznym powstają pęknięcia podłużne przez całe otulenie, a wiązanie ma tendencję do gwałtownego zerwania. Rozerwanie otulenia nie wystąpi przy silnym zbrojeniu poprzecznym. Mechanizm przenoszenia siły zmienia się z oporu żebra na tarcie, a odporność na ścinanie staje się dominująca. W rezultacie powstaje pękniecie otulenia i pojawia się rysa.
Fazę II szczegółowo omówiono w wielu pracach, m.in. [2] oraz [3]. W niniejszym artykule poprzestaniemy na uproszczonym podejściu, w którym stan ten modeluje się rozkładem naprężeń, w którym beton nie przenosi rozciągania, a w strefie ściskania rozkład naprężeń jest trójkątny. Przyjmuje się, że odkształcenie dolnego włókna betonu $\varepsilon_{cl}=f_{ct,m}/E_c$ , gdzie moduł betonu $E_c$ jest wartością umowną i w zależności od okresu dla którego rozpatrujemy zjawisko $E_c = (E_{cm} \div E_{c,ef}$). Długotrwałe obciążenie zwiększają poślizg i redystrybucję naprężeń wiązania (prawdopodobnie z powodu pełzania). Zerwanie wiązania pod trwałymi obciążeniami, zwiększa szerokości pęknięć, rysy wydają się być bardziej równoległe. W tym przypadku stosuje się $E_c= E_{c,ef}$.
Faza III – graniczna rys. R-4c
Faza III, jest opisana modelem rys. Z-1 i jest przedmiotem analiz w rozdziale Belki żelbetowe. Zginanie .
Warunek zarysowania i sztywność przekroju w fazie I (niespękanego)
Warunek zarysowania i moment rysujący
Moment rysujący przekrój $M_{cr}$ jest to taki moment zginający, który powoduje powstanie pierwszej rysy w betonie. Pierwsza rysa powstanie na koniec pracy przekroju w fazie I (rys. R-3a), to znaczy w fazie pracy sprężystej. wówczas, gdy naprężenia na dolnej krawędzi betonu osiągną wytrzymałość na rozciąganie $f_{c,t,ef}\approx f_{ctm}$, gdzie $ f_{ctm}$ jest średnią wytrzymałością betonu na rozciąganie osiągnięta w chwili, w której – jak się oczekuje – powstaną rysy. Gdy można oczekiwać, że zarysowanie nastąpi wcześniej niż po 28 dniach, wytrzymałość $f_{c,t,ef}$ można przyjąć mniejszą $f_{c,t,ef}= f_{ctm}(t) $.
Warunek zarysowania można zapisać w postaci:
$$\begin{equation} \sigma_{cl} \ge f_{ctm} \label {3} \end{equation}$$
$$\begin{equation} M_{E,k} \ge M_{cr} \label {4} \end{equation}$$
gdzie: $M_{E,k}$ – moment zginający od charakterystycznych obciążeń zewnętrznych, działających na konstrukcję.
$$\begin{equation} M_{cr}= f_{ctm} \cdot W_{cr} \label {5} \end{equation}$$
gdzie wskaźnik wytrzymałości przekroju tuż przed zarysowaniem
$W_{cr} = I_{cr} / z_0 $ ;
$ z_0=(h -x_I) $ jest odległością włókna dolnego od osi obojętnej przekroju.
Ponieważ moment rysujący odpowiada końcowemu etapowi fazy I , to $W_{cr}=W_{I}=I_{cr}/z_0$ , przy czym $I_{cr}=I_{I}$, które wyznaczono w kolejnym punkcie.
Wysokość strefy ściskanej i moment bezwładności w fazie I
W fazie I przekrój nie jest jeszcze zarysowany, a rozkład odkształceń i naprężeń przyjmuje się w sposób zaprezentowany na rys. 4a, czyli w sposób wynikający z klasycznej teorii zginania sprężystego.
Odległość osi obojętnej od górnej krawędzi jest wysokością strefy ściskanej $x_I$. Z podstawowej zależności (e=M/A) mamy :
$$\begin{equation} x_{I} =\cfrac{ b\cdot h^2 / 2 + \alpha_e \cdot ( A_{sl} \cdot d_l \, + \, A_{su} \cdot a_u ) }{ b\cdot h + \alpha_e \cdot (A_{sl}+A_{su}) } \label {6}\end{equation}$$
Moment bezwładności przekroju niezarysowanego sprowadzony do betonu wynosi więc
$$\begin{equation} I_{I}= \cfrac{bh^3}{12} +b \cdot h \cdot (h/2 – x_I)^2 +\alpha_e \cdot \left \{ A_{sl} \cdot (d_l – x_I )^2 +A_{su} \cdot (x_I-a_u)^2) \right \} \label{7} \end{equation}$$
Często do wyznaczenia momentu rysującego pomija się wzmocnienie przekroju stalą (np. [4] ) i wówczas moment rysujący
$$\begin{equation} M_{cr}= \cfrac{b \cdot h^2}{6} \cdot f_{ctm} \label{8} \end{equation}$$
Naprężenia w stali zbrojeniowej przed zarysowaniem
Naprężenia w stali zbrojeniowej przed zarysowaniem zgodnie z klasyczną teorią zginania belek wynosiłyby
$$\begin{equation} \sigma_{s,cr} = k_t \cdot \alpha_e \cdot \cfrac{M_{cr}}{I_I } \cdot (d_l-x_I) = k_t \cdot \alpha_e \cdot f_{ctm} \cdot \cfrac{d_l- x_I} {h- x_I }\label{9} \end{equation}$$
gdzie współczynnik $k_t$ uwzględnia czas trwania obciążenia i wynosi
$$\begin{equation} k_t< \begin {cases}
0,6 & \text {dla obciążeń krótkotrwałych } \\
0,4 & \text {dla obciążeń długotrwałych } \\
\label {10} \end {cases} \end{equation}$$
W eksperymentach uzyskuje się jednak inne wartości niż określa ($\ref{9}$), co wynika z ograniczonej współpracy betonu i stali do niewielkiego obszaru betonu otaczającego pręt rozciągany, , zgodnie z formułami ($\ref{11}$) do ($\ref{13}$), a w rezultacie oszacowania naprężeń w stali zbrojeniowej przed zarysowaniem formułą ($\ref{14}$).
Przyjmuje się, bowiem że przed zarysowaniem rozciągany jest pręt betonowo- stalowy otaczający stal o wysokości $h_{c,ef}$ w sposób pokazany na rys. R-5.
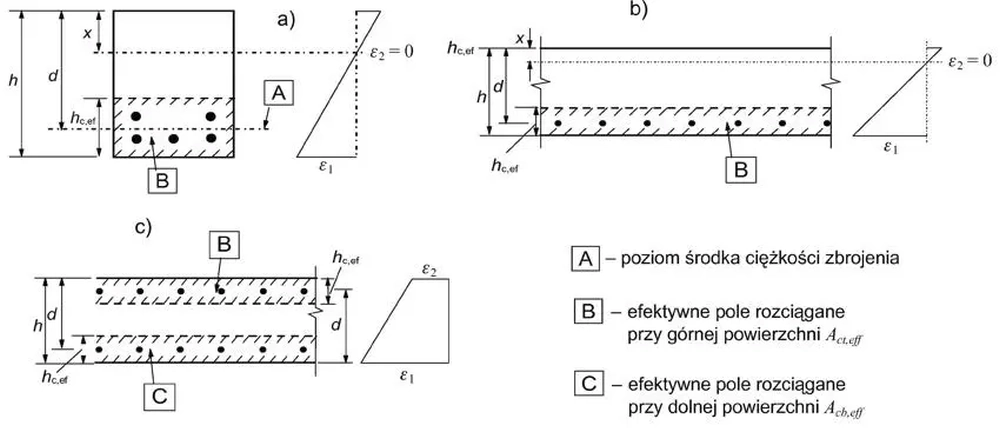
Rys. 5 Wysokość i pole efektywne uczestniczące podczas zarysowania: a) belka, b) płyta – elementy zginane, c) element rozciągany [5], Rys.7.1
Wysokość rozciąganego przekroju betonu, efektywnie współpracującego z prętem zbrojeniowym wynosi
$$\begin{equation} h_{c,ef}= \lambda_{c,ef} \cdot h \label {11}\end{equation}$$
Współczynnik efektywnej wysokości dobiera się z zależności :
$$\begin{equation} \lambda_{c,ef}= \begin {cases}
\min \left \{ \cfrac {1- \xi_{II} \cdot \delta_l}{3} \, ; \, 2,5 \cdot (1-\delta_l) \right \}, & \text { zginanie – rozciągana dolna „l” krawędź } \\
\min \left \{ 1/2 \, ; \, 2,5\cdot (1-\delta_*) \right \}, & \text { rozciąganie – dolna (*= l) i górna (*= u) krawędź} \\
\end {cases} \label{12} \end{equation}$$
gdzie:
$\xi_{II}$ wg ($\ref{18}$) – względna wysokość strefy ściskanej odniesiona do wysokości użytecznej przekroju,
$ \delta_{*} = \cfrac{d_{*}}{h}$ – względna wysokość użyteczna odniesiona do wysokości przekroju,
$d_*=h-a_*$ – użyteczna wysokość przekroju ,
$a_*= c_*+\Phi*/ 2$ – osiowe otulenie pręta,
$c_*$ – otulenie pręta do jego krawędzi,
$\Phi*$ – średnica pręta zbrojeniowego,
(* =.l . u) – indeks krawędzi dolnej (lower) i górnej(upper) przekroju
Poziom rozciągania (stopień zbrojenia rozciąganego przekroju betonu otaczającego pręty zbrojeniowe) szacujemy z formuły :
$$\begin{equation} \rho_{p,ef}= \cfrac{A_s+\xi_1^2 \cdot A_p^{’}}{ A_{c,ef}} \stackrel{A_p^{’}=0} {=} \cfrac{A_s}{A_{c,ef}} = \cfrac{ \rho_{sl} \cdot \delta_l} {\lambda_{c,ef}} \label {13} \end{equation}$$
$A_p^{’}=0$ przy braku cięgien sprężających,
$\xi_1$ – współczynnik sił przyczepności – bez znaczenia w problemie zginania bez udziału cięgien sprężających,
$A_{c,ef} =b\cdot h_{c,ef} $ jest efektywnym polem betonu rozciąganego otaczającego zbrojenie lub cięgno sprężające $A_s$,
$\rho_s=A_s/ A_c $ – stopień zbrojenia belki.
Przy braku cięgien i strun sprężających – naprężenia w zbrojeniu przed zarysowaniem szacuje się z formuły
$$\begin{equation} \sigma_{s,cr}=k_t \cdot f_{ctm }\cdot \left( \cfrac{1}{ \rho_{p,ef}}+ \alpha_e \right ) \label {14}\end{equation}$$
Sztywność przekroju w fazie II (beton spękany)
W fazie II przekrój jest w pełni zarysowany.
Wysokość górnej strefy rozciąganej
Zależność na wysokość strefy rozciąganej $x_{II,t}$, pokazanej na rys. R-5 – wyznaczymy z warunku równowagi rzutów sił na oś poziomą :
$$\begin{equation} \Sigma X = S_{cc} – S_{ct} + S_{su} – S_{sl} – N_E= 0\label{15}\end{equation}$$
gdzie $N_E$ jest przekrojową siłą osiową (od obciążeń), przy czym siła ściskająca ma znak plus, a rozciągająca minus.
Sumy sił z bryły naprężeń w betonie ściskanym $S_{cc}$, rozciąganym $S_{ct}$, pręcie stalowym górnym $S_{su}$ i dolnym $S_{sl}$ wynoszą:
$ S_{cc} = E_c\cdot(b \cdot \varepsilon_{cu} \cdot x_F)/ 2$,
$ S_{ct} = E_c \cdot ( b \cdot \varepsilon_{cl} \cdot (h-x_F)/ 2$,
$S_{su} = E_s \cdot \varepsilon_{su} \cdot A_{su}$,
$ S_{sl} = E_s \cdot \varepsilon_{sl} \cdot A_{sl}$.
Po podstawieniu wyżej zdefiniowanych zmiennych i po rozwiązaniu równania ($\ref{15}$) względem wysokości rozciąganej strefy przekroju, otrzymujemy :
$$\begin{equation} \xi_{II,t} = \sqrt{\xi_{II} +n_{E,t}^2 -2\cdot \alpha_e \cdot [(1-\delta_{u/l})\cdot \rho_{sl}-(\xi_{II}]-\delta_{u/l}) \cdot \rho_s ] } – n_{E,t} \label{16} \end{equation}$$
gdzie:
$n_{E,t} =\cfrac{N_E}{b \cdot d_l \cdot f_{ctm}}$,
względna wysokość strefy ściskanej $\xi_{II} = x_{II} /d_l$,
względna wysokość strefy rozciąganej $\xi_{II,t} = x_{II,t}/d_l$,
użyteczny stopień zbrojenia dolnego $ \rho_{sl}=A_{sl} / (b\cdot d_l)$,
użyteczny stopień zbrojenia górnego $\rho_{su}=A_{su} / (b\cdot d_l)$,
użyteczny stopień zbrojenia przekroju $\rho_s=\rho_{sl}+\rho_{su}= (A_{sl}+A_{su})/ (b\cdot d_l)$,
stosunek ramion zbrojenia górnego i dolnego $ \delta_{u/l} =a_u / d_l= \delta_u / \delta_l$,
Wysokość strefy ściskanej
W klasycznym podejściu (np. [3], [6] i in. ) zakłada się, że poniżej strefy ściskanej beton nie przenosi rozciągania, więc wysokość strefy ściskanej wyznaczymy z równania
$$\begin{equation} \xi_{II,t} = 0 \label {17}\end{equation}$$
Z rozwiązania tego równania względem $\xi_{II}$ otrzymujemy
$$\begin{equation} \xi_{II}= \sqrt{ \rho_{s,e}\cdot ( \rho_{s,e} + 2 \cdot k_{lu}) } \, – \rho_{s,e} \label {18}\end{equation}$$
gdzie wprowadzono oznaczenia:
sprowadzonego do betonu stopnia zbrojenia przekroju,
$$\begin{equation} \rho_{s,e}= \alpha_e \cdot \rho_s \label {19}\end{equation}$$
a także zmniejszającego współczynnika zbrojenia przekroju podwójnie zbrojonego, uwzględniającego mniejszy wpływ zbrojenia górnego na efektywny współczynnik zbrojenia przekroju belki :
$$\begin{equation} k_{lu}= (\rho_{sl} +\delta_{u/l} \cdot \rho_{su}) / \rho_s \label{20} \end{equation}$$
Jak wynika z zależności ($\ref{18}$) wysokość strefy ściskanej $x_{II}=\xi_{II} \cdot d_l $ , w przypadku braku betonu rozciąganego, nie zależy od wielkości sił przekrojowych.
Taki sam wynik uzyskamy z warunku równowagi momentów [7] :
$$\begin{equation} – \cfrac{b \cdot x_{II}^2}{2}+\alpha_e \cdot \{ A_{sl} \cdot (d_l- x_{II}) + A_{su} \cdot (a_u- x_{II}) \}= 0 \label{21} \end{equation}$$
Założenie o tym, że pękniecie betonu sięga aż do początku strefy ściskanej (braku strefy rozciąganej) nie jest potwierdzone badaniami doświadczalnymi ani numerycznymi. Wbrew przeciwnie z szerokich analiz numerycznych [8] wynika, że w fazie II wysokość strefy niezarysowanej wynosi ok $\xi_{II}=0,6$, co wskazywało, że istnieje obszar niezarysowanego, rozciąganego betonu. Analiza tego problemu nie jest przedmiotem niniejszego artykułu.
Moment bezwładności przekroju spękanego
Moment bezwładności przekroju w fazie II wynosi :
$$\begin{equation} I_{II}= \cfrac { b \cdot x_{II}^3}{3 } + \alpha_e \cdot \left \{ A_{sl} \cdot (d_l-x_{II} )^2+ A_{su} \cdot (x_{II}-a_u)^2 \right \} \label{22} \end{equation}$$
Naprężenia w stali zbrojeniowej po zarysowaniu
Naprężenie w rozciąganym w pręcie zbrojeniowym w przekroju o współrzędnej bieżącej osi pręta x , obciążonym momentem zginającym $M_E (x)$ obliczone przy założeniu, że przekrój jest zarysowany można oszacować z zależności
$$\begin{equation} \sigma_s (x) =\alpha_e \cdot \cfrac{M_{E,k} (x) } {I_{II}} \cdot (d_l-x_{II}) \label{23} \end{equation}$$
Zwracamy uwagę, że siły przekrojowe $M_{E,k}(x)$ należy redukować do osi obojętnej przekroju, a ponadto są one wywołane obciążeniami z kombinacji charakterystycznej.
Rozstaw rys
Maksymalny rozstawu rys $s_{r.max}$ zależy od średnicy pręta zbrojeniowego i jego otulenia oraz od szeregu czynników zgodnie z empiryczną zależnością [5],(7.11) :
$$\begin{equation} s_{r,max}=k_3 \cdot c +k_1 k_2 k_4 \dfrac{\Phi}{\rho_{p,ef}} \label {24}\end{equation}$$
w którym:
c- nominalne otulenie pręta podłużnego o średnicy $\Phi$,
$\rho_{p,ef}$ wg ($\ref{13}$).
$k_1, k_2,k_3, k_4$ – zestaw współczynników, przyjmowanych jak następuje:
$k_1$ jest współczynnikiem zależnym od przyczepności zbrojenia:
0,8 dla prętów o dobrej przyczepności
1,6 dla prętów o gładkiej powierzchni (np. pręty gładkie lub cięgna sprężające),
$k_2$ jest współczynnikiem zależnym od rozkładu odkształceń, obliczanym z zależności :
$$\begin{equation} k_2= \cfrac { \varepsilon_1+\varepsilon_2 }{ 2 \varepsilon_1} \label {25}\end{equation}$$
gdzie $\varepsilon_1$ jest większym a $\varepsilon_2$ mniejszym z odkształceń na krawędziach rozważanego przekroju, obliczonych przy założeniu. że przekrój jest zarysowany.
W przypadku elementów zginanych (belek i płyt) , czyli takich w których wysokość strefy ściskanej jest niezerowa $x>0$ przyjmuje się
$\varepsilon_2=0$ i z definicji ($\ref{25}$) mamy $k_2=0,5$.
W przypadku elementów rozciąganych:
- przy czystym rozciąganiu $\sigma_2=\sigma_1 \to k_2=1$,
- przy rozciąganiu mimośrodowego z mimośrodowym z mimosrodem $e=M_E/N_E$ przekroju prostokątnego bxh symetrycznie zbrojonego:
$\varepsilon_1= \cfrac{\sigma_N}{E_c} \cdot \left (1+6 \cdot e/h \right )$ , $\varepsilon_2= \cfrac{\sigma_N}{E_c} \cdot \left (1-6 \cdot e/h \right )$ , gdzie $\sigma_N=\cfrac{N}{A_c}$,
czyli $k_2= \cfrac { \varepsilon_1+\varepsilon_2 }{ 2 \varepsilon_1} = 1 / \left( 1+ 6 \cdot e/h \right) $,
Pozostałe współczynniki korekcyjne przyjmuje się o wartościach:
$k_3$=3,4 , $k_4$= 0,425.
Jeżeli rozstaw zbrojenia mającego przyczepność przekracza $5\cdot a$ ($a=c + \Phi/2$) , albo jeżeli w strefie rozciąganej nie ma zbrojenia z przyczepnością do betonu, to górną granicę szerokości rys nożna obliczyć, zakładając że maksymalny rozstaw rys wynosi :
$$\begin{equation} s_{r,max}= 1,3 \cdot (h – x_{II}) \label {26} \end{equation}$$
W płycie – jeżeli kąt $\Theta$ nachylenia kierunków naprężeń głównych do zbrojenia ortogonalnego przekracza $15^0$, to
$$\begin{equation} s_{r,max}=\cfrac{1}{ cos \Theta / s_{r,max,y}+ sin \Theta / s_{r,max,z} } \label {27}\end{equation}$$
w którym $s_{r,max,y}$ oraz $s_{r,max, z}$ są rozstawami rys w dwóch ortogonalnych kierunkach płyty liczonymi wg wzorów $(\ref{24})$
Rozwarcie rysy
Metody sprawdzania rys
W zwykłych sytuacjach w celu ograniczenia szerokości rys do wartości granicznych $(\ref{1})$ poprzestaje się na zastosowaniu średnic i rozstawu zbrojenia mniejszego od wartości przedstawionych w tab. R-5, a omówionych w rozdziale dotyczącym minimalnego zbrojenia belek. Metodę uproszczoną stosuje się w większości praktycznych sytuacji projektowych na etapie wstępnym – koncepcji.
Ostatecznie zaprojektowaną belkę z konkretnymi warunkami brzegowymi sprawdza się metodą ogólną opisaną niżej z zastosowaniem programów komputerowych. W kalkulatorze żelbetu LCŻelbet wdrożono obie wersje metody ogólnej :
$$\begin{equation} w_k=s_{r,max} \cdot \varepsilon_{cr} \label {28}\end{equation}$$
gdzie odkształcenie pękania $\varepsilon_{cr}$ jest różnicą odkształceń stali i betonu przy której inicjuje się pękniecie :
$$\begin{equation} \varepsilon _{cr}= \varepsilon _{sm}-\varepsilon _{cm} \label {29}\end{equation}$$
- Metoda UO [odkształceń uogólnionych] z fundamentalnej zależności normowej [5], (7.18) :
$$\begin{equation} \alpha= \alpha_I + \zeta ( \alpha_{II} – \alpha_I) \label {30}\end{equation}$$
zalecanej do prognozy uogólnionych odkształceń $\alpha$ spękanego betonu, głównie elementów zginanych
Współczynnik dystrybucji $\zeta$ szacuje się z zależności
$$\begin{equation} \zeta= 1- \beta \left( \cfrac{\sigma_{sr}}{\sigma_s} \right )^2 \label {31}\end{equation}$$
w której:
$\beta=1$ dla obciążenia krótkotrwałego; $\beta=1/2$ dla obciążeń długotrwałych i wielokrotnie powtarzanych (prawie – stałych).
Naprężenia w stali są wyznaczane w dwóch stanach :
- $\sigma_{sr}$ – naprężenie w zbrojeniu dolnym (rozciąganym), obliczone przy założeniu, że przekrój jest zarysowany obciążeniem powodującym powstanie pierwszej rysy (tzn momentem rysującym wyznaczonym w końcowym etapie fazy I)
- $\sigma_s$ – naprężenie w zbrojeniu dolnym (rozciąganym, obliczone przy założeniu, że przekrój jest w pełni zarysowany (tzn w fazie II) momentem zginającym od obciążeń charakterystycznych
Stosunek naprężeń $\cfrac {\sigma_{sr}}{\sigma_s}$ można zastąpić przez:
$M_{cr} / M_E(x)$, przy czystym zginaniu,
$N_{cr} / N_E(x) $ , przy czystym rozciąganiu,
gdzie $M_{cr}$ i $N_{cr}$ oznacza odpowiednio rysujący moment lub siłę osiową, a $M_E(x) $ oraz $N_E(x) $ siły przekrojowe działające w przekroju o współrzędnej bieżącej x.
Metoda KO [odkształceń krytycznych ] wyznaczania rozwartości rysy
Po przekształceniu wyrażenia z normy [5], (7.9) odkształcenia rysujące w betonie możemy oszacować z zależności :
$$\begin{equation} \varepsilon _{cr}= \cfrac{\Delta \sigma}{E_s} \label {32} \end{equation}$$
gdzie
$$\begin{equation} \Delta \sigma= \max { \{ \sigma_s -\sigma_{s,cr} \, ; \, 0,6 \cdot \sigma_s \} } \label {33}\end{equation}$$
w którym:
$\sigma_s$ wg ($\ref{23}$)
$\sigma_{s,cr}$ ($\ref{14}$).
Metoda UO [odkształceń uogólnionych ] wyznaczania rozwartości rysy
W metodzie odkształceń uogólnionych analizuje się odkształcenie betonu po przekroczeniu odkształcenia sprężystego $\alpha_I$ (po pojawieniu się pierwszej rysy) i osiągnięciem odkształcenia w stanie w pełni zarysowanym $\alpha_{II}$ wg formuły ($\ref{30}$), która dotyczy odkształceń uogólnionych, więc krzywizny $\psi$, przemieszczenia, obrotu, ale także szerokości rozwarcia rys $w_k$.
Na rys. R-6 zależność ($\ref{30}$) zilustrowano na przykładzie przemieszczeń prostej belki,
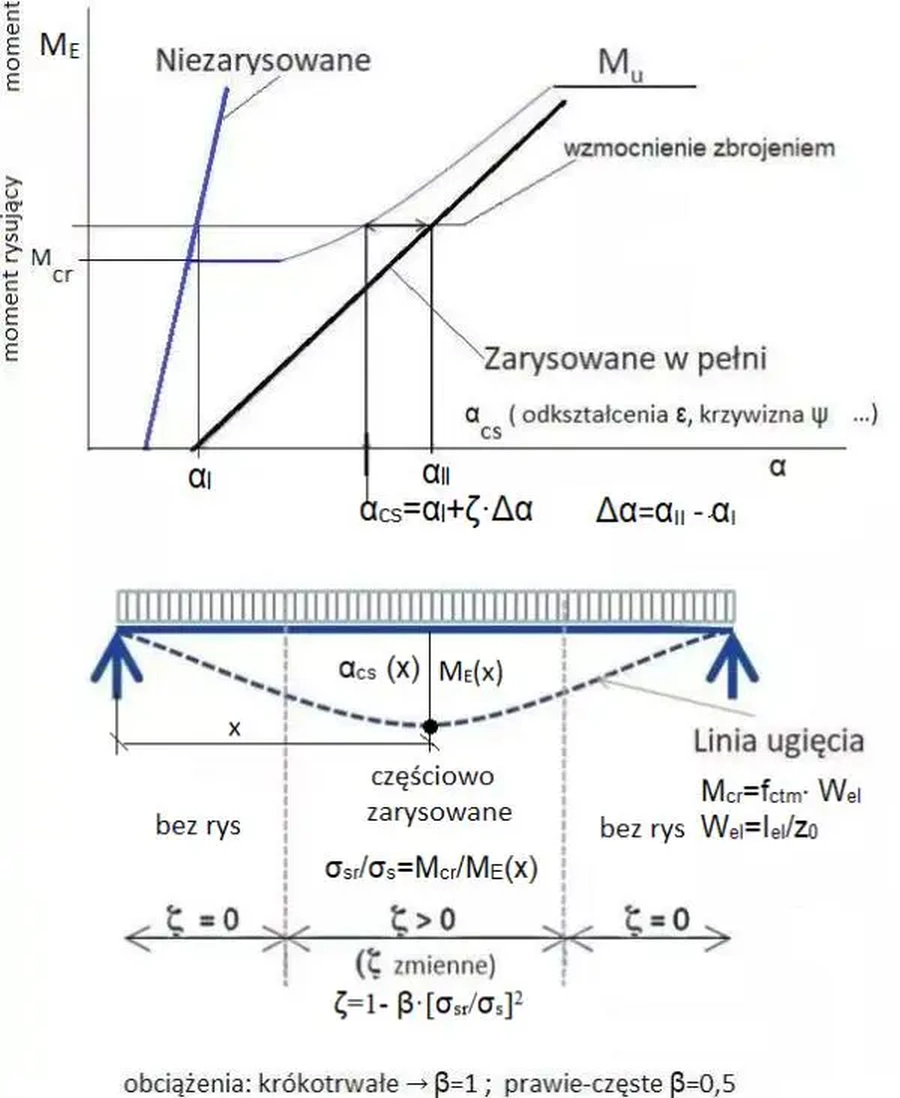
Rys. 6 Metoda odkształceń uogólnionych w elemencie żelbetowym (opracowane na podstawie [1]
$\varepsilon_s= \varepsilon_{sI}+\zeta \Delta \varepsilon_s$,
$\varepsilon_c= \varepsilon_{cI}+\zeta \Delta \varepsilon_c$,
a po odjęciu obu równań stronami i uwzględnieniu, że w fazie I występuje pełna współpraca betonu i stali ( $ \varepsilon_{sI,I}= \varepsilon_{cI,I} ) mamy :
$$\begin{equation} (\varepsilon_s-\varepsilon_c)=\zeta (\Delta \varepsilon_s- \Delta \varepsilon_c) \label {34} \end{equation}$$
Po uwzględnieniu tego, że beton zarysowany w strefie efektywnej nie przenosi rozciągania, czyli $ \varepsilon_{cl,II}=0$ i ponownie ($ \varepsilon_{sI,I} = \varepsilon_{cI,I}$) z zależności ($\ref{35}$) uzyskujemy:
$$\begin{equation} (\varepsilon_s-\varepsilon_c)=\zeta \varepsilon_{sII}=\zeta \cfrac{\sigma_s}{E_s} \label {35}\end{equation}$$
Otrzymujemy stąd wyrażenie na rozwartość rysy w postaci
$$\begin{equation} w_k=s_{r,max} \cdot \zeta \cfrac{\sigma_s}{E_s} = s_{r,max} \cdot \left [ 1 – \beta \cdot \left ( \cfrac{M_{cr}}{M_E} \right )^2 \right ] \cdot \cfrac{\sigma_s}{E_s} \label {36} \end{equation}$$
Uzyskaliśmy wyrażenie ($\ref{36}$) na szerokość rysy niezależne od parametrów betonu $f_{ctm}$ oraz $E_{c}$ (doraźnych lub efektywnych).
Ugięcia belek
Ugięcia graniczne
Odmiennie od projektowania według historycznych norm (p. artykuł Kombinacje obciążeń w Eurokodach) obecnie ( wg [9] ) fundamentalną zasadą jest to, że graniczne ugięcia konstrukcji powinny wynikać z wymagań użytkowych ustalanych z inwestorem i przyszłym użytkownikiem danej inwestycji, a nie z wymagań norm ogólnych.
W normie do projektowania konstrukcji żelbetowych [5], kl. 7.4.1. zasugerowano ugięcia graniczne, których przekroczenie może (ale nie musi) doprowadzić do utraty własności budowli ważnych ze względów konstrukcyjnych (a nie użytkowych), a do szczegółów odsyła do normy [zotpressInText item=”{BIH2F9IP . Ograniczenie dotyczy ugięć pod obciążeniami quasi-stałymi. Wartość quasi-stała oddziaływania zmiennego , wynosi ψ2 ·Qk , gdzie ψ2 jest współczynnikiem określającym stosunek części quasi-stałej (czyli takiej, dla której okres jej przekraczania stanowi znaczną część okresu odniesienia) do całkowitej wartości charakterystycznej obciążenia. Podano tylko dwa ograniczenia :
$$\begin{equation} \delta_{lim} = \begin {cases}
L/200, & \text {dla zapewnienia estetyki i ogólnej użyteczności } \\
L/500, & \text {w celu uniknięcia uszkodzenia współpracujących elementów budowli}
\end {cases} \label{37}\end{equation}$$
gdzie $L$ jest odległością pomiędzy dwoma punktami A i B konstrukcji, a $\delta$ jest strzałką ugięcia pomiędzy tymi punktami, czyli
$\delta= v_{max}- (v_A+v_B)/2$, gdzie $v_A$ i $v_B$ są przemieszczaniami pionowymi odpowiednio punktu A i B, a $v_{max}$ – maksymalnym przemieszczeniem pomiędzy tymi punktami.
Współpracującymi elementami budowli są najczęściej ściany działowe ( w tym murowane), ustawione na uginającej się płycie stropowej.
W przypadku współpracujących elementów elementów wrażliwych (np. ścian szklanych) należy zastosować specjalne ograniczenia lub dylatacje kompensacyjne, tak aby elementy wrażliwe nie zostały zmiażdżone uginającym się stropem, a limit dotyczy stropu i belek na których są postawione.
W praktyce kontrolę ugięć belek żelbetowych stosuje się przy następujących ograniczeniach:
$$\begin{equation} \delta_{lim} = \begin {cases}
L/250, & \text {max ugięcie efektywne w okresie użytkowania od kombinacji charakterystycznej”czestej”} \\
L/500, & \text {przyrost ugięcia w okresie przyrostu obciążenia od kombinacji charakterystycznej „prawie stałej }
\end {cases} \label{37a}\end{equation}$$
Sprawdzanie ugięć elementów konstrukcyjnych
Podstawowym problemem przy obliczaniu ugięć elementów i konstrukcji żelbetowych jest uwzględnienie czynników, które wpływają istotnie na zwiększenie deformacji konstrukcji żelbetowej w stosunku do odkształcenia konstrukcji sprężystej , takiej jak konstrukcja stalowa, a mianowicie:
- efekty skurczu i pełzania betonu w czasie,
- zmniejszania sztywności elementów na skutek narastającego zarysowania wraz ze wzrostem wytężenia przekroju, w sytuacji różnego zarywania przekrojów w różnych miejscach konstrukcji
Efekty skurczu i pełzania betonu uwzględnia się poprzez zastosowanie efektywnego modułu odkształcenia betonu $E_{c,ef}$ zgodnie z formułą (R-33).
Natomiast zmniejszenie sztywności żelbetu wskutek zarysowania betonu dokonuje się w sposób analogiczny do przyjętego w metodzie ogólnej szacowania rozwartości rys.
Jeśli element nie ulegnie zarysowaniu, to nie trzeba sprawdzać szerokości rys, a ugięcia oblicza się jak dla ustroju sprężystego.
W przypadku przeważającego zginania zarysowanie wystąpi, gdy moment zginający jest większy od momentu rysującego przekrój $M_{cr}$ ($\ref{5}$), Przy obciążeniu mimośrodowym wartością porównawczą do stwierdzenia okoliczności początku zarysowania przekroju jest rysująca siła osiowa $N_{cr}$
$$\begin{equation} N_{cr}= \cfrac {f_{ctm}} {e/W_I \pm 1/A_c} \label {38}\end{equation}$$
gdzie:
$e=M/N$ – mimośród siły osiowej (p. również poprzedni punkt artykułu),
$W_I=I_I/(h-x_I) $, $I_I$ ($\ref{7}$), $x_I$ ($\ref{6}$)
Znak „+” stosuje się przy rozciąganiu, „-” przy ściskaniu.
Metody sprawdzania ugięć
Stan graniczny ugięć może być sprawdzony na dwa sposoby:
1) uproszczony – wskaźnikowy – polegający na ograniczeniu stosunku rozpiętości do wysokości L/h zgodnie z [5],kl. 7.42. .
2) ogólny przez porównanie ugięcia obliczonego według [5], kl. 7.4.3. z wartością graniczną
Ze względu na złożoność /metody ogólnej do zastosowań praktycznych zaleca się sposób wskaźnikowy sprawdzania ugięć belek i płyt żelbetowych.
Metoda wskaźnikowa nie jest jednak uniwersalna, bo dotyczy zamkniętego katalogu schematów belek. Ponadto metodą wskaźnikową uzyskuje się rezultaty różniące się znacznie od rzeczywistych Na rys. R-7 porównano metodę wskaźnikową z ogólną (ścisłą) dla belki swobodnie podpartej. Błąd metody wskaźnikowej, liczony indeksem L/h jest największy dla rozpiętości belek do 6 m lub dla stosunkowo dużych obciążeń i wynosi ok 30%. W przypadku belki o rozpiętości 6 m i dla obciążeń stropów mieszkalnych Q=2,5 kN/m2 , wynosi 30/27-1 =11%. Ze względu na to, że wyniki z metody wskaźnikowej obarczone są znaczącymi błędami , to w niniejszym artykule odchodzi się od metody wskaźnikowej na rzecz metody ogólnej i obliczeń w podręcznym arkuszu obliczeniowym. Metody uproszczonej nie przedstawia się w szczegółach.
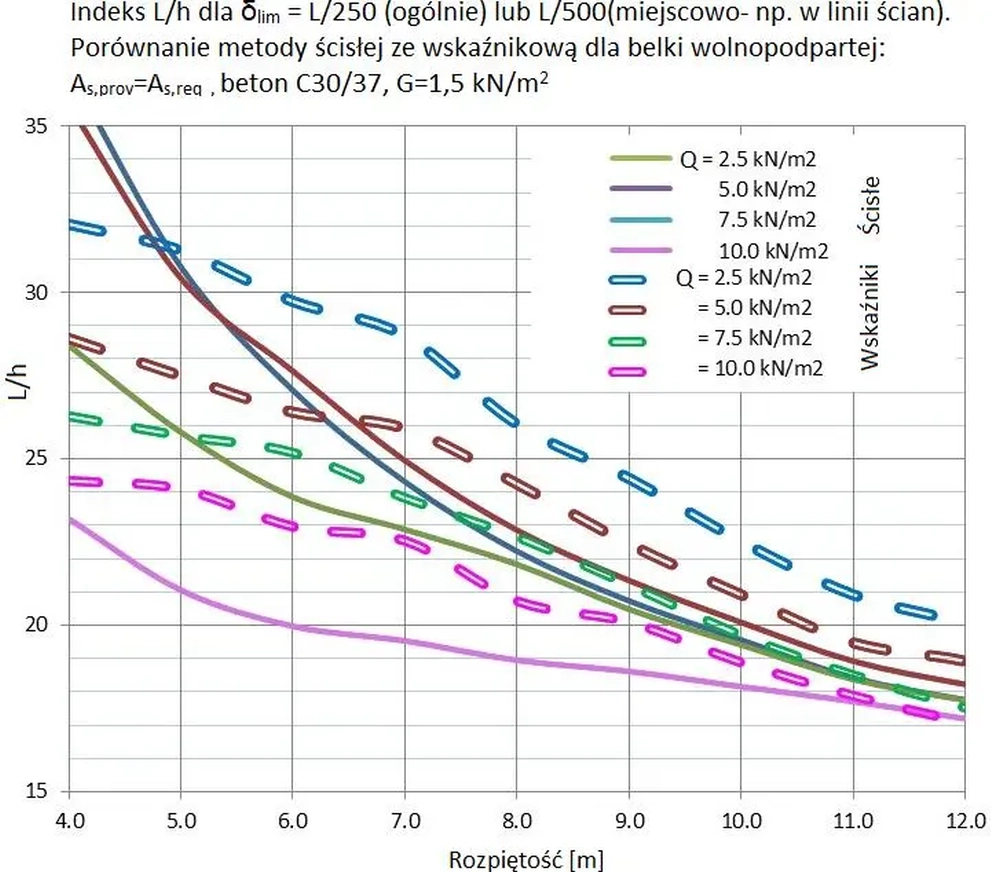
Rys. 7 Porównanie sposobu wskaźnikowego ze ścisłym dla belki wolnopodpartej (zmodyfikowane [1]
Metoda ogólna
Zastosowanie zależności ogólnej $(\ref {30})$ do szacowania krzywizny belki $\psi$ prowadzi do zależności :
$$\begin{equation} \psi=\psi_I+ \zeta \Delta \psi \label {39}\end{equation}$$
gdzie $\Delta \psi=\psi_{II}-\psi_I$
Współczynnik dystrybucji $\zeta$ szacuje się z zależności :
$$\begin{equation} \zeta= \begin {cases}
0, & \text {dla x : } M(x) \le M_{*,cr} \text { (w I fazie pracy przekroju) }\\
1- \beta \left( \cfrac{M_{*,cr}}{M(x)} \right )^2, & \text { dla x : } M(x) > M_{cr} \\
\end {cases} \label{{40}}\end{equation}$$
gdzie : $x$ jest współrzędną bieżącą belki, M(x) – moment zginający belkę w miejscu o współrzędnej $x$. $*=(u,l)$ – indeks krawędzi przekroju ( górna, dolna).
Współczynnik czasu trwania obciążenia przyjmuje się jak w ($\ref{31}$), tzn.: $\beta=1$ dla obciążenia krótkotrwałego; $\beta=1/2$ dla obciążeń długotrwałych i wielokrotnie powtarzanych (prawie – stałych).
Z elementarnych zasad wytrzymałości materiałów wiemy, że w stanie zgięciowym zachodzi zależność :
$$\begin{equation} \psi=-\cfrac{M_E}{EI} \label {41}\end{equation}$$
Krzywizna określona ścisłym wzorem $(\ref{41})$ jest zmienna po długości belki w związku ze zmiennym momentem bezwładności przekroju , powodującym rożny stopień zarysowania przekroju $I$. Przyjmuje się że moduł odkształcalności $E=E_{c,ef}$.
Na długości belki mogą wystąpić odcinki z rozciąganym włóknem górnym „u”(np nad podporami belek ciągłych )oraz z rozciąganym włóknem dolnym „l” . Odpowiadające moment y rysujące oznaczamy jako $M_{cr,u}$ i $M_{cr,l} odpowiednio$. Na odcinku z rozciąganym włóknem górnym może wystąpić część na której $|M|>M_{cr,u}$ oraz część , gdzie $|M| \le M_{cr,u}$. Na odcinku z rozciąganym włóknem dolnym może wystąpić część na której $M>M_{cr,l}$ oraz część , gdzie $M \le M_{cr,l}$
Odpowiadające sztywności przekroju wynoszą :
$$\begin{equation} EI = \begin{cases}
E\cdot I_{II,u}, & \text { jeśli } |M| >M_{cr,u} \\
E \cdot I_{I,u}, & \text { jeśli } |M| \le M_{cr,u} \\
E \cdot I_{I,l}, & \text { jeśli } M \le M_{cr,l} \\
E \cdot I_{II,l}, & \text { jeśli } M > M_{cr,l} \\
\end{cases}\label {42}\end{equation}$$
Wpływ skurczu na ugięcia belek
Do ugięć wywołanych zewnętrznymi obciążeniami dodaje się ugięcia wywołane różnicą skurczu włókien belki, spowodowanych przede wszystkim różnicami w zbrojeniu dolnym i górnym. Wygięcie belki wywołane skurczem postępuje tak, że wypukłość powstaje w kierunku silniejszego zbrojenia.
Obliczeniowo uwzględnia się to poprzez dodanie do momentu zginającego M(x) momentu $M_{cs}$ równoważnego krzywiźnie osi belki spowodowanej skurczem :
$$\begin{equation} \psi_{cs} = \varepsilon _{cs} \cdot \alpha_e \cdot \cfrac{45}{I_F}\label {43}\end{equation}$$
gdzie:
$\varepsilon_{cs}$ ( R-7) – całkowite odkształcenie od skurczu ,
$F=(I, II)$ -faza pracy rozpatrywanego przekroju,
$S_I$ , $S_{II}$ momenty statyczne zbrojenia względem osi obojętnej przekroju odpowiednio w fazie I i II.
$\alpha_e$ ($\ref{3}$)
Składając wyrażenie ($\ref{43}$) i ($\ref{41}$) uzyskujemy moment równoważny od skurczu $M_{cs}(x)$ w przekroju o współrzędnej x , :
$$\begin{equation} M_{cs,F} (x) = E_s \cdot S_F(x) \cdot \varepsilon _{cs}(x) \label {44} \end{equation}$$
$$\begin{equation} S_F= A_{xl} \cdot ( d_l -x_F) -A_{su} \cdot (x_F – a_u) = b \cdot d_l^2 \cdot [ \rho_{sl} \cdot ( 1-\xi_F ) – \rho_{su} \cdot ( \xi_F – a_u / d_l )] \label {45} \end{equation}$$
Przyjmuje się , że momenty równoważne działają na rozpatrywany element zginany w ten sposób, że przekrojowy moment zginający, M_E (x) pochodzący od obciążeń zewnętrznych jest zwiększany o moment $ M_{cs}(x)$, ($\ref{44}$), odpowiedni dla zbrojenia tego przekroju., tak że wartość momentu zginającego miarodajna do obliczania ugięcia wynosi
$$\begin{equation} M(x) =M_E(x)+M_{cs}(x) \label {46} \end{equation}$$
Obliczanie ugięcia belki z zależności różniczkowej
Przemieszczenie pionowe $w(x)$ (x – współrzędna pozioma, osi pręta) wewnątrz elementu jest związane z krzywizną $\Psi(x)=1/R(x) $ pręta zależnością różniczkową [10], (4.58) :
$$\begin{equation} \Psi= \cfrac{|w”(x)|}{[1+(w'(x))^2]^{3/2} }\label {47}\end{equation}$$
którą dla małych przemieszczeń w(x)< L/100 można zlinearyzować do postaci
$$\begin{equation} \Psi \approx |w”(x)| \label {48}\end{equation}$$
Wówczas można zapisać podstawowe równanie różniczkowe zginania pręta o sztywności giętnej $EI(x)$ wywołane przez momenty zginające M(x) w postaci:
$$\begin{equation} w”(x)=-\dfrac{M(x)}{EI(x)} \label {49}\end{equation}$$
Poprzez dwukrotne całkowanie tego wyrażenia, otrzymamy
$$\begin{equation} w =\iint \limits_0^x – \cfrac{M(x)}{EI(x)} dx +C_1x+C_2 \label {50}\end{equation}$$
gdzie $C_1$ i $C_2$ są stałymi zależnymi od warunków brzegowych na końcach elementu, a x jest bieżącą współrzędną osi pręta.
Wyznaczanie ugięcia belki żelbetowej metodą różnic skończonych
W przypadku, gdy interesuje nas ugięcie, a nie przemieszczenia wyraz ze stałą całkowania $C_2$ można pominąć. Ugięcie będzie maksymalnym przemieszczeniem $w_{max}$ na badanym odcinku [0,x].
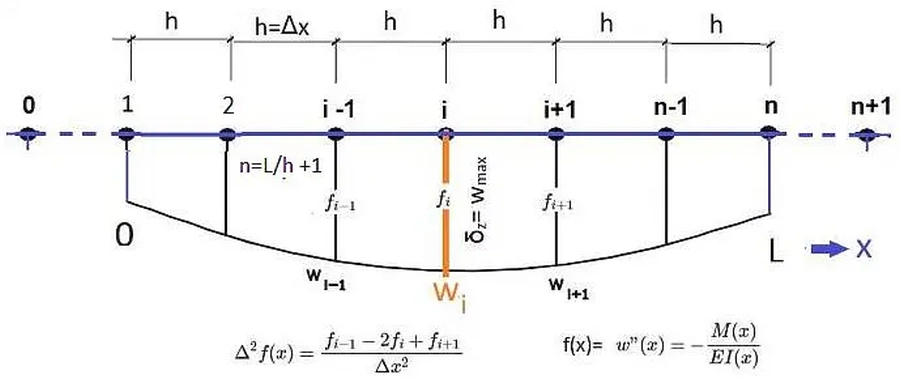
Całkowanie wyrażenia ($\ref{50}$) można przeprowadzić dowolną metodą, w tym metodą różnic skończonych, którą zaimplementowano w załączonym arkuszu kalkulacyjnym. Korzystamy z zasadniczego twierdzenia rachunku różnicowego (rys. R-8) :
$$\begin{equation} \iint_0 ^x f”(x) dx dx = \sum_{0}^{x }\Delta^2 f(x) \label {51}\end{equation}$$
$$\begin{equation}\Delta^2 f(x) = \cfrac{f_{i-1}-2 f_i +f_{i+1}}{\Delta x^2} \label {52}\end{equation}$$
Można pokazać [11] , że centralny operator różnicowy drugiego rzędu $(\ref{55})$ daje błąd aproksymacji rzędu $\Delta x^2/12$. to znaczy zmniejsza się wraz z kwadratem długości elementów $\Delta x = h $ na które zdyskretyzowano belkę.
W modelu dyskretnym wprowadzone są dwa węzły pozorne „0 ” i „n+1”. Ugięcia w tych węzłach $w_{-1}$, $w_{n+1}$ są związane z ugięciami w węzłach rzeczywistych poprzez warunki brzegowe.
$ M_0= \, – EI_1 \cfrac{ w_{0} – 2 w_1 + w_2 }{h^2} \quad \to w_{0} = \, – \, \cfrac{M_0 \cdot h^2}{EI_1} + 2 \cdot w_1- w_2 $
$M_L=\, – EI_n \cfrac{w_{n-1}-2 w_n +w_{n+1}} {h^2} \quad \to w_{n+1} =\, – \, \cfrac{M_L \cdot h^2}{EI_{n}} + 2\cdot w_n -w_{n-1}$
Powyższe dwa równania uzupełniają układ równań uzyskany z ($\ref{50}$) dla każdego z węzłów „1” do „n” . W przypadku znanych przemieszczeń na końcach elementu $w_1=w_n = 0$ wykorzystywanie powyższych warunków brzegowych jest zbędne,
Kanoniczny układ równań problemu można zapisać w postaci macierzowej .
$$\begin{equation} [A] \cdot ||w|| = ||F_r|| \label{53} \end {equation}$$
gdzie:
$||w||= | w_1, w_2 , …,w_n|$ – kolumnowy wektor przemieszczeń węzłów (1 …n),
$[A]_{n x n}$ – macierz współczynników różnicowych.
Kolumnowy wektor obciążeń różnicowych $||F_r||$ wynosi :
$$\begin{equation} ||F_r|| = – h^2/ E_c \cdot ||M / I|| \label{54} \end {equation}$$
gdzie:
$h=\Delta x$,
$||M/I|| $ – wektor ilorazów momentu zginającego i momentu bezwładności przekroju w i-tym węźle.
Moment zginający w przekroju uwzględnia skurcz betonu zgodnie z zależnością ($\ref{45} $).
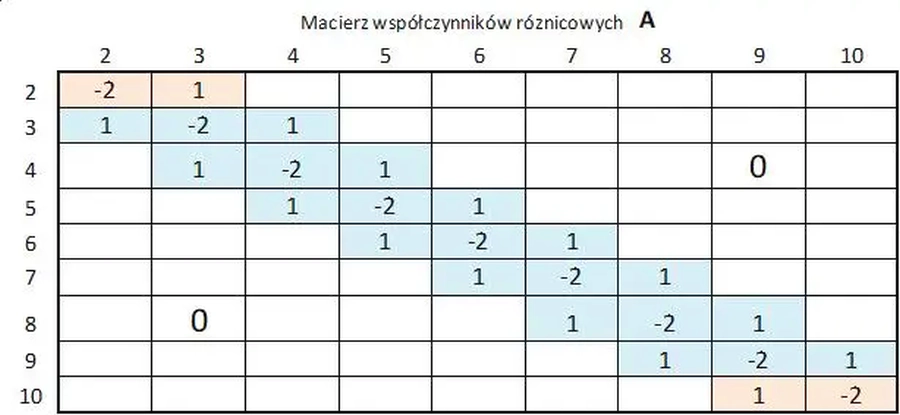
Macierz współczynników różnicowych jest niezależna od wartości obciążeń i buduje się ją z wektora współczynników $ |1, -2, 1 |$ rozmieszczanego w macierzy w prosty sposób analogiczny do pokazanego w tab. R-1 dla liczby elementów N=10, tj dla liczby węzłów n=N+1 =11 i liczby nietrywialnych równań 11-2=9. Uwzględnienie warunków brzegowych nastąpiło poprzez wykreślenie wierszy i kolumn 1 oraz n=11 (dla węzłów podporowych).
Tab. 1 Macierz współczynników różnicowych dla n=10 (dx=L/10)
Rozwiązanie równania ($\ref{52}$) możemy zapisać w postaci
$$\begin{equation} |w| = – [A]^{-1} \cdot ||F_r|| \label{55} \end {equation}$$
gdzie $A^{-1}$ -macierz odwrotna do macierzy współczynników różnicowych. Macierz $A^{-1}$ jest również niezależna od obciążenia belki oraz rozkładu jej sztywności w tym zarysowania i stła dla danej liczby węzłów. (tab. R-2 ):
Tab. 2 Odwrotna macierz współczynników różnicowych dla n=10
Ze struktury macierzy odwrotnej wynika, że największy wspływ na strzałkę ugięcia belki ma zachowanie przekrojów w węzłach środkowych.. Wiersz współczynników wpływu na strzałkę ugięcia belki (węzeł 6 ) wyróżniono na żółtym tle. Jeśli wiersz ten oznaczymy jako [A_6], to strzałka ugięcia belki wyniesie
$$\begin{equation} \delta = h^2/ E_c \cdot [ A_6 ] \cdot ||M / I|| \label{56} \end {equation}$$
Z wykorzystaniem formuły ($\ref{56}$) w szyki sposób można oszacować ugięcie belki w stanie zarysowanym. Ponieważ moment bezwładności przekroju w stanie zarysowanym stanowi ok 60% momentu bezwładności sprężystego, to szacunkowy wzrost strzałki ugięcia a na skutek zarysowania dla stałego w czasie modułu Younga wyniesie
[(0,5+1+0,5+1)+(1,5+2+2,5+2+1,5)/0,6)/(0,5+1+1,5+2+2,5+2+1,5+1+0,5] /12,5= 1,5.
W przypadku uwzględnienia modułu końcowego zamiast doraźnego różnica ta może zwiększyć się prawie dwukrotnie i przekroczyć 3. W szybkich oszacowaniach zwykle przyjmuje się, ze w celu oszacowania ugięcia końcowego belki zarysowanej na podstawie ugięcia sprężystego należy je powiększyć 3x.
Wyznaczenie ugięcia belki wyodrębnionej z konstrukcji
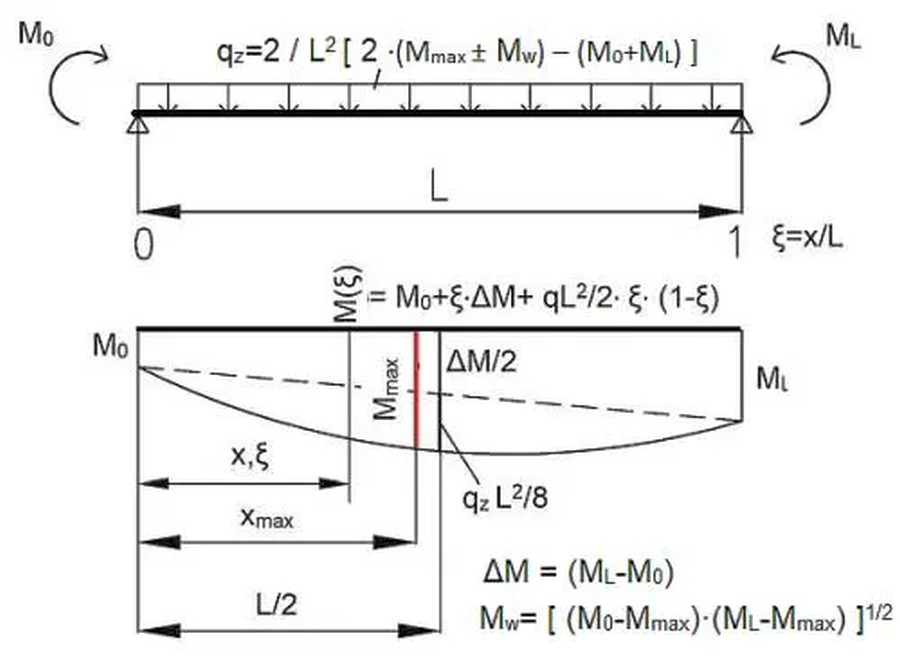
Belka wyodrębniona z konstrukcji może być przedstawiona jako belka swobodnie podparta ze skupionymi momentami zginającymi $M_0$ oraz $M_L$ przyłożonymi nad podporami, jak przedstawiono na rys. R-9.
Dowolnie przyłożone obciążenie w przęśle można zastąpić równomiernie rozłożonym obciążeniem zastępczym $q_z = \alpha_q \cdot Q / L$, gdzie $Q=\Sigma Z$ jest sumą sił pionowych przyłożonych w przęśle,. Obciążenie zastępcze można uzyskać na wiele sposobów zależnie od celu do jakiego aproksymacja ma służyć , w tym:
a) sposobu statycznego poprzez porównanie maksymalnego momentu zginającego $M_{max}$ wywołanego rzeczywistym obciążeniem i sumy na którą składają się momenty zginające wywołane obciążeniem belki zastępczej :
$$\begin{equation} \alpha_q = \cfrac{8} {Q\cdot L} \cdot [M_{max} -\Delta M( x_{max})] \label {57} \end{equation}$$
gdzie: $x_{max}$ – rzędna dla której rzeczywisty moment zginający jest maksymalny i osiąga wartość $M_{max}$.
Na przykład dla belki swobodnie podpartej obciążonej jedną siłą skupioną w środku rozpiętości:
$Q = F$ , $x_{max} = L / 2 $, $ \Delta_M = 0 $, $M_max=F \cdot L / 4 $, więc $ \alpha_q=2$
b) sposobu kinematycznego poprzez porównanie ugięcia $\delta_q$ wywołanego przez obciążenie zastępcze $q_{zast}$ z ugięciem $ \delta_F$ wywołanym obciążeniem rzeczywistym $F$, tzn
$$\begin{equation} \alpha_q \succ \delta_F =\delta_q \label {58} \end{equation}$$
Na przykład w przypadku przęsła belki o stałej po długości sztywności początkowej EI obciążonej jedną siła skupioną F w środku rozpiętości – strzałka ugięcia belki swobodnie popartej wynosi $\delta_F= \tfrac {F \cdot L^3}{48 \cdot EI}= \tfrac {Q \cdot L^4}{48 EI}$. Porównawcze ugięcie wyniesie $\delta_q= \alpha_q \cdot \tfrac{5}{384} \tfrac{q\cdot L^4}{EI}$, gdzie $q=\tfrac{Q}{L}$, czyli $\alpha_q= 384/(5\cdot 48) = 1,6$.
W przypadku przekroju żelbetowego współczynnik $\alpha_q$ będzie nieco większy, co pokazano w tab. R-3 dla belki żelbetowej obciążonej żebrami w liczbie n na długości przęsła, Ugięcia wyznaczano metoda efektywnej sztywności dla belki żelbetowej prostokątnej 30×30 cm zbrojoną Ø16 x 3 góra i doł i wykonaną z betonu C30/37 ze współczynnikiem pełzania $\varphi=2,8$ i współczynnikiem udziału betonu $K_c=0,5$.
Rozbieżności między współczynnikami oszacowanymi metodą statyczną i kinematyczną są znaczne. Metoda kinematyczna daje wyniki dokładniejsze, choć wymaga większego nakładu pracy w rozwiązanie zadania pomocniczego. Nie stanowi to jednak problemu w dobie obliczeń numerycznych.
W arkuszu LCżelbet zastosowano metodę statyczną wg wzorów zamieszczonych na rys. R-9
Tab.R-3. Szacunkowe współczynniki $\alpha_q$ dla belki żelbetowej obciążonej w przęśle „n” siłami skupionymi
Wyprowadzenie podanych zależności zaczynamy od zapisania pola momentów na belce. Reakcja lewej podpory (dla $\xi = x/L =0$ ) wynosi
$$\begin{equation} V_0 = \cfrac{M_L – M_0}{L} + \cfrac{q_z \cdot L }{2} \label{59} \end{equation}$$
Rozkład momentów zginających jest następujący:
$$\begin{equation} M(\xi) = M_0+ \Delta M \cdot \xi + \cfrac{q_z \cdot L^2}{2} \cdot \xi \cdot (1-\xi) \label {60} \end{equation}$$
gdzie $\Delta M=M_L-M_0$
Pierwsza pochodna ($\ref{60}$) wynosi
$$\begin{equation} dM(\xi)/d\xi = \cfrac{\Delta M}{L} + \cfrac{q_z \cdot L}{2} \cdot (1-2 \cdot \xi) \label {61} \end{equation}$$
Przyrównując ($\ref{61}$) do zera otrzymujemy miejsce $\xi_{max}$ ekstremalnego momentu zginającego na belce zastępczej
$$\begin{equation} \xi_{max}= \cfrac{1}{2} +\cfrac{\Delta M}{q_z \cdot L^2} \label {62} \end{equation}$$
Ekstremalny moment zginający w belce zastępczej (w miejscu $\xi_{max}$) wynosi:
$$\begin{equation} M( \xi_{max})= \cfrac{1}{2} \cdot \left[ (M_L+M_0) +\cfrac{(\Delta M)^2}{q \cdot L^2} + \cfrac{q \cdot L^2}{8} \right ] \label {63} \end{equation}$$
Porównując moment ($\ref{63}$) z ekstremalnym momentem zginającym belkę rzeczywistą $M_{max}$ i rozwiązując otrzymane równanie ze względu na $q_z$, otrzymamy dwa pierwiastki, różniące się znakiem przy $M_w$:
$$\begin{equation} q_z = \cfrac{2}{L^2} \left[ 2\cdot (M_{max} \pm M_w – (M_0 +M_L) \right ]\label {64} \end{equation}$$
gdzie $M_w = \sqrt{ [ (M_{max} -M_0) \cdot (M_{max}-M_L ] }$
Obciążenie zastępcze realizujące podobne do rzeczywistego pole momentów zginających uzyskuje się najczęściej dla znaku „+” przed średnia geometryczną $M_w$ odchyleń momentów podporowych od momentu maksymalnego $M_{max}$.
Procedura oszacowania ugięć pręta przeważająco zginanego składa się z następujących kroków:
1) dyskretyzacja belki poprzez podział na n równych elementów o długości $h$ (rys.8).
W kalkulatorze CH-P Ż zastosowano podział belki na dwadzieścia elementów o długości $h=L/20$.
2) w każdym węźle (i=1 ,… n) wyznaczany jest iloraz $f_i=M_i/ I_i$, przy czym każdorazowo wyznaczana jest sztywność przekroju w węźle z warunku ($\ref{42})$
3) rozwiązywany jest utworzony układ równań ($\ref {53}$). Ugięcie belki jest maksymalnym przemieszczeniem belki.
Metodę wyczerpująco przedstawiono w Przykład R-4 Linia ugięcia belki obciążonej odcinkowo.
Przykłady rachunkowe
Kontrola zarysowania
Przykład R-1 [Zarysowanie przekroju pojedynczo zbrojonego]
Dane wg [12], przykład 18.1 gdzie obliczenia przeprowadzono metodą KO
Obliczyć szerokość rysy w przekroju prostokątnym
wysokość $h=500 \,mm$, szerokość $b=300 \, mm$, zbrojenie jednostronne $A_{sl} = 12,57 \, cm^2$ (4 Ø 20)
otulenie $c= 40 \,mm$, $a=40+20/2=50 \, mm$, wysokość użyteczna $d_l=500-50=450 \, mm$
beton C 25/30 $\to$ tab. W-1: $f_{ck}= 25 \, MPa$, $f_{ct,ef}= f_{ctm} = 2,6 \, MPa$, $E_{cm}=31 \, GPa$
stal B490 $\to$ tab. W-2: $f_{yd}= 420 \, MPa $ , $ E_s= 200 \, GPa$
Moment zginający od kombinacji obciążeń quasi-stałej: $M_{E,k2}=124,4 \, kNm$
W obliczeniach w arkuszu LCŻelbet przyjęto $M_{Ed}=124,4 \, kNm$ i indeksy (R-1) oraz (R-2) równe jedności $SGU_1/SGN= SGU_2/SGN=1,0$ .
Przyjęto $E_c = E_{cm}=31 \, GPa$, a nie $E_{c,ef}$, to znaczy rozpatruje się przypadek doraźny, co jest niespójne z obciążeniami quasi-stałymi dla których przyjmowano współczynnik $k_t=0,4$ ($\ref{10}$),
($\ref{3}$) $\to$ $\alpha_e=200/31= 6,452$
użyteczny stopień zbrojenia dolnego $\rho_{sl}=12,57/ (30 \cdot 45)= 0,931$%
użyteczny stopień zbrojenia górnego $\rho_{su}=0$ %
użyteczny stopień zbrojenia belki $\rho_{s}=0,931+0 =0,931$%
względna wysokość użyteczna $ \delta_l= 450/500=0,9$
Obliczenie szerokości rysy metodą KO
I faza pracy
($\ref{6}) \to$ wysokość strefy ściskanej $x_{I} =\cfrac{ 30\cdot 50^2 /2 + 6,452 \cdot ( 0 + 12,57 \cdot 45 ) }{ 30\cdot 50 + 6,452 \cdot (12,57+0) }= 26,025 \, cm$
($\ref{7}) \to$ moment bezwładności przekroju w I fazie $I_I= \cfrac{ 30 \cdot 50^3}{12} + 30 \cdot 50 \cdot (50/2- 26,025)^2 + 6,452 \cdot [ 0 +12,57 \cdot (45 -26,025)^2 ] =343276,6 \, cm^4$
odległość włókna skrajnego (betonu) $z_{0,I}= h-x_I= 50 – 26,025= 23,975 \, cm$,
wskaźnik wytrzymałości w I fazie $W_I= \cfrac{ 343276,6}{23.975}=14318,11 \, cm^3$
Kryteria zarysowania przekroju:
Uwaga:
($\ref{8}) \to$ moment rysujący przy pominięciu sztywności stali $M_{cr}= ( 30\cdot 50^2)/6 \cdot 2,6 \cdot 10^{-3} = 32, 5 /, kNm$.
Oszacowanie w przykładzie jest o 37,23/32,5= 15% mniejsze od wartości z uwzględnieniem zbrojenia w sztywności przekroju.
($\ref{4}) \to$ $ M_E= 124,4 > M_{cr}= 37,23 \, kNm$,
lub alternatywnie
($\ref{5}) \to$ $ \sigma_{cl} = 124,4/ 14318,11 \cdot 10^3= 8,7 > f_{ctm}= 2,6 \, MPa$,
$\to $ przekrój ulegnie zarysowaniu.
II faza pracy
Parametry pomocnicze:
($\ref{19}) \to$ $\rho_{s,e}= 6,452 \cdot 0,00931$= 0,06007
($\ref{20}) \to$ $k_{lu}= (0,931 +0 \cdot 0) / 0,931 =1$
($\ref{18}) \to$ wysokość strefy ściskanej przy założeniu braku betonu rozciąganego $\xi_{II}= \sqrt{ 0,06007 \cdot ( 0,06007 + 2 \cdot 1) } – 0,06007= 0,291709$
$x_{II}= 0,2917109 \cdot 45 = 13,127 \, cm$
Naprężenia w zbrojeniu tuż przed pęknięciem
($\ref{12}) \to$ Współczynnik efektywnej wysokości $\lambda_{c,ef}=\min { [ 1- 0,291709 \cdot 0,9 )/3 \, ; \, 2,5 \cdot (1-0,9)] } = 0,2458$,
($\ref{11}) \to$ Wysokość efektywna betonu rozciąganego $ h_{c,ef}= 0,2458 \cdot 500 = 122,9 \, mm$
Uwaga: W pracy Knauff,… obliczono $h_{c,ef}= 123 \, mm$
($\ref{13}) \to$ Stopień zbrojenia strefy rozciąganej: $\rho_{p,ef}=\cfrac {12,57}{ 30 \cdot 12,29}= \cfrac{0,00931\cdot 0,9 }{0,2458} = 0,03409$
($\ref{14}) \to$ naprężenia w zbrojeniu tuż przed zarysowaniem : $ \sigma_{s,cr}=0,4 \cdot 2,6 \cdot \left( \cfrac{1}{ 0,03409}+ 6,452 \right )= 37,22 \, MPa$
Uwaga: w pracy Knauff,… $\sigma_{s,cr}$ oznaczono przez $\sigma_0$ i uzyskano wynik 37,7 MPa
Sprawdzenie wartości naprężeń wg formuły ($\ref{9}$) $\to$ $\sigma_{s,cr} = 0,4 \cdot 6,452 \cdot 2,6 \cdot (45- 26,026) / (50- 26,026) = 5,31 \, MPa $
Naprężenia z formuły eksperymentalnej $\ref{14}$) są znacznie większe od naprężeń teoretycznych ($\ref{9}$).
($\ref{22}) \to$ moment bezwładności przekroju w II fazie: $ I_{II}= 30 \cdot 13,127^3 / 3 + 6,452 \cdot 12,57 \cdot (45-13,127 )^2 + 0= 105010 /, cm^4$
($\ref{23}) \to$ naprężenia w pręcie zbrojeniowym po zarysowaniu przekroju:
$\sigma_s = 6,452 \cdot 124,4 / 105010 \cdot (45 – 13,127) \cdot 10^3 = 243,6 MPa$
Uwaga: w pracy Knauff,… metodą uproszczoną uzyskano $\sigma_s= 258,7 MPa$, czyli o 6% więcej.
Przyrost naprężeń w zbrojeniu
($\ref{32}) \to$ $\Delta \sigma= \max{\{ 243,6 – 37,2 \, ; \, 0,6 \cdot 243,6 \} }= 206, 4 \, MPa$
Odkształcenie pękania
($\ref{33}) \to$ Odkształcenie pękania : $ \varepsilon_{cr}=\cfrac{206,4}{200\cdot 10^3}=1,032 \cdot 10^{-3}$
Rozstaw rys
Dla danych: pręt $ \Phi=20 \, mm$, otulenie $c=40 \, mm$, $k_1=0,8$ – pręty żebrowane, $k_2=0,5$ – zginanie, $k_3$=3,4 , $k_4$= 0,425:
($\ref{24}) \to$ Rozstaw rys: $ s_{r,max}= 3,4 \cdot 40 +0,8 \cdot 0,5 \cdot 0,425 \cdot \cfrac{20}{0,0341} = 235,7 \, mm$
Uwaga: w pracy Knauff,… uzyskano wynik 237,4 mm
Rozwarcie rys
($\ref{24}) \to$ $w_k = 206,4 \cdot 1,032 \cdot 10^{-3} = 0,243 \, mm$ < $w_{max} ( \ref{1} \to)= 0,3 \, mm$
Uwaga: w pracy Knauff,… uzyskano wynik 0,262 mm
Obliczenie szerokości rysy metodą UO
Powyżej obliczono:
rozstaw rys $ s_{r,max} = 235,7 \, mm$
moment rysujący $M_{cr} =32,91 \, kNm$
naprężenie w stali $\sigma_s = 243,62 MPa$
pod ($\ref{31}) \to$ $\beta = 1/2 $ dla obciążeń prawie stałych
($\ref{36}) \to$ $w_k= 235,7 \cdot \left \{ – 1/2 \cdot \left( \cfrac{32,91}{124,4} \right)^2\right \} \cdot \cfrac {243,62}{200} \cdot 10^{-3} =0,232\, mm $
Metodą UO uzyskano szerokość rysy o 0,243/0,232=5% więcej. Taka różnica wystąpiła przy obliczeniach dwoma metodami według jednej normy . Większe różnice, ponad dwukrotne, występują pomiędzy różnymi normami narodowymi (np. [3], [13]) ).
Moduł sprężystości betonu w szczególnych warunkach pełzania
Wysokość zastępcza belki do oszacowania współczynnika pełzania $h_0= (h\cdot b/(2\cdot h +b)= 400\cdot 600/(2*600+400)= 150 \, mm$
Ponieważ belka będzie eksploatowana w szczególnych warunkach pełzania: w środowisku o wilgotności RH=88,3% i przez 5 lat, więc końcowy współczynnik pełzania należy obliczyć z ogólnych zależności. Zastosowano kalkulator CH-P, którego ekran pokazano na rys. 58. wyniku otrzymano :
$\varphi(5 lat, 28 dni) =1,476$., czyli:
(P-33) $\to$ E_{c,ef} = 33/(1+1,476)= 13,33 \, GPa$
($\ref{3}$) $\to$ $\alpha_e= \alpha_{e,ef} = 200/13,33= 15 $
Uwaga:
W warunkach normalnych $t_0=28 \, dni$ $ h_0=120 \, mm$ $\ dla C30/37 współczynnik pełzania końcowego $ \varphi( \infty, 28)=2,545$
(P-33) $\to$ $E_{c,ef} = 33/(1+2,545)= 9,31 \, GPa$ , $\alpha_e= 200/9,31= 21,5 $
Parametry pomocnicze:
$\rho_{sl}= 2714/(400\cdot 548)=0,01238$,
$\rho_{su}= 452/(400\cdot 548)=0,00206$,
$\rho_s=0,01238+0,00206 =0,01444$,
$\delta_l= 548/600= 0,9133$
$\delta_{u/l}= 46/548= 0,08394$
($\ref{19}$) $\to$ $\rho_{s,e}= 15 \cdot 0,01444$= 0,2168
($\ref{20}$) $\to$ $k_{lu}= (0,01238 +0,00206 \cdot 0,08394) /0,01444 =0,87$
Wysokość strefy ściskanej w II fazie
($\ref{18}$) $\to$ $\xi_{II}= \sqrt{ 0,2168\cdot (0,2168 + 2 \cdot 0,87) } – 0,2168= 0,4344$
$x_{II}= 0,4344 \cdot 548 = 238 \, mm$
Uwaga: W pracy [7],Example 7.3, 7.4 uzyskano $x_{II}=237,8 \, mm$ , odnosząc stopień zbrojenia przekroju do wysokości przekroju $h$, a nie do wysokości użytecznej $d_l$
Naprężenie w zbrojeniu przed zarysowaniem
($\ref{12}$) $\to$ Współczynnik efektywnej wysokości $\lambda_{c,ef}=\min { [1- 0,4344 \cdot 0,9133 )/3 \, ; \, 2,5 \cdot (1-0,9133)] }= 0,2411$,
($\ref{11}$) $\to$ Wysokość efektywna betonu rozciąganego: $ h_{c,ef}= 0,201 \cdot 600 = 120,6 \, mm$
($\ref{13}$) $\to$ Stopień zbrojenia strefy rozciąganej: $\rho_{p,ef}=\cfrac {27,14}{ 40 \cdot 12,06}= \cfrac{0,01238 \cdot 0,913 } {0,2011} = 0,0562$
($\ref{14}$) $\to$ naprężenia w zbrojeniu tuż przed zarysowaniem : $ \sigma_{s,cr}=0,6 \cdot 2,9 \cdot \left( \cfrac{1}{ 0,0562}+ 15 \right )= 57,1 \, MPa$
Moment bezwładności w fazie II i naprężenie w zbrojeniu po zarysowaniu
$(\ref{22}) \to$ $ I_{II}= \cfrac { 40 \cdot 23,8^3}{3 } + 15 \cdot \left [ 27,14 \cdot (54,8 -23,8 )^2+ 4,52 \cdot (13,58-4,6)^2 \right ]=595967 \, cm^4$
($\ref{23}$) $\to$ naprężenia w pręcie zbrojeniowym po zarysowaniu przekroju:
$\sigma_s = 15 \cdot 300 / 595967 \cdot (54,8 – 23,8) \cdot 10^3 = 234,1 MPa$
Zarysowanie przekroju
przyrost naprężeń w stali ($\ref{32}$) $\to$ $\Delta \sigma= \max{\{ 234,1 – 57,1 \, ; \, 0,6 \cdot 234,1 \} }=177 \, MPa$
odkształcenie pękania ($\ref{33}$) $\to$ : $ \varepsilon_{cr}=\cfrac{177 }{200\cdot 10^3}=0,885 \cdot 10^{-3}$,
rozstaw rys ($\ref{23}$) $\to$ $ s_{r,max}= 3,4 \cdot 40 +0,8 \cdot 0,5 \cdot 0,425 \cdot \cfrac{24}{0,0562} = 208,6 \, mm$,
rozwarcie rys ($\ref{24}$) $\to$ $w_k = 208,6 \cdot 0,885 \cdot 10^{-3} = 0,185 \, mm$ <$w_{max} \ref{1} = 0,3 \, mm$..
Obliczenie szerokości rysy kalkulatorem LCŻelbet
W kalkulatorze LCżelbet zaimplementowano opisane procedury szacowania szerokości rys. Arkusz można pobrać z rys. W-1 artykułu Belki żelbetowe.
Kontrola ugięć w stanie zarysowanym
W kalkulatorze LCżelbet zaimplementowano opisane procedury szacowania ugięć elementów żelbetowych w stanie zarysowanym . W-1 artykułu Belki żelbetowe.
Literatura
- MPA, The Concrete Centre, (2017). Crack Control and Deflection. Lecture 6. EC2 Webinar – Autumn, [ https://www.concretecentre.com/TCC/media/TCCMediaLibrary/PDF%20attachments/Lecture-6-Deflection-and-Crack-Control-cg-26-Oct-17.pdf ]
- Gilbert R. I., Ranzi G. (2011), Time-dependent behaviour of concrete structures. Spon
- Nejadi S. (2005), Time- dependent cracking and crack control in reinforced concrete structures [PhD Thesis]. University of New South Wales Sydney, Australia
- ACI 318-14 (2014), Building Code Requirements for Structural Concret
- PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- Knauff M. (2015). Obliczanie konstrukcji żelbetowych według Eurokodu 2: zasady ogólne i zasady dotyczące budynków. Wydawnictwo Naukowe PWN, Warszawa
- CH GoodChild, (2009), Worked Examples to Eurocode 2.: Volume 1. The Concrete Centre
- Kachlakev D. I., Miller T., Yim S., Chansawat K., Potisuk T. (2001). Finite Element Modeling of Reinforced Concrete Structures Strengthened with FRP Laminates,. California Polytechnic State University and Oregon State University for Oregon De-partment of Transportation
- PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
- Piechnik S. (1980). Wytrzymałość materiałów dla wydziałów budowlanych, PWN, Warszawa
- Strikwerda J. C. (2004). Finite difference schemes and partial differential equa-tions (2nd ed). Society for Industrial and Applied Mathematics.
- Knauff, M., Golubińska, A., Knyziak P. (2015). Przykłady obliczania konstrukcji żelbetowych. Budynek ze stropami płytowo-żebrowymi. Zeszyt 1. PWN.Warszawa
- Jaromska E. (2011), Obliczanie szerokości rys w zginanych elementach żelbeto-wychwg EC2:2008 i DIN 1045-1:2008. Czasopismo Techniczne, 1-B/2011(Zeszyt 3. Rok 108
________________________________