Utrata stateczności konstrukcji może zajść na skutek przeskoku z jednego położenia równowagi do innego, także położenia równowagi, ale innego od pierwotnego. Klasycznym i wzorcowym przykładem takiego układu jest kratownica Misesa. Przeskok węzła kratownicy Misesa jest dobrym przykładem teorii katastrof [1]. Oryginalnie w teorii katastrof rozpatruje się zachowanie maszyny Zimana (rys.1), która w istocie opisuje katastrofę przeskoku węzła kratownicy Misesa.
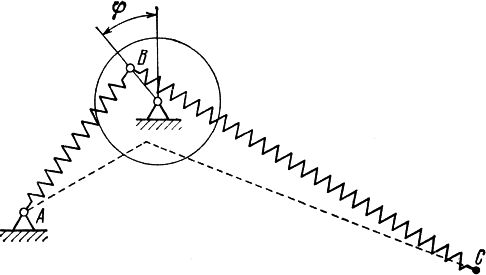
Rys.1. Maszyna Zimana. Model katastrofy w teorii katastrof [2]
Maszyna Zimana składa się z dyska, który może bez tarcia obracać się wokół swojej osi i dwóch sprężyn AB i BC z osiami zgodnymi z kątem obrotu dyska, przy czym koniec sprężyny A jest zamocowany nieprzesuwnie, podczas gdy koniec C podlega małym przemieszczeniom w płaszczyźnie ruchu. W laściwości systemu istotnie zależą od położenia punktu C. Małe zmiany położenia punbktu C są związane z małymi zmiananmi kata $\varphi$ i kierunków spreżyn. Okazuje się, że po przyjeciu przez punky C osobliwego położenia, system jakościowo zmienia swoją konfigurację – doznaje przeskoku.
Idealna kratownica Misesa (bez imperefekcji)
Analizę przeskoku węzła idealnej kratownicy Misesa dokonamy w sposób przedstawiony w pracy [2].
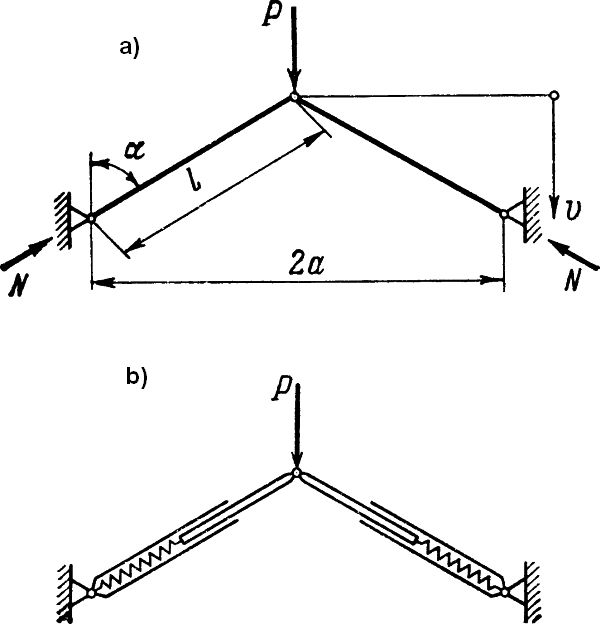
Rys.2. Kratownica Misesa a: model prętowy, b: model sprężyn [2]
Na rys.2. pokazano uproszczony model dwuprętowej konstrukcji, którą rozpatrywał Mises [3]. Uproszczenie polega na ilustracji tylko symetrycznej postaci równowagi podczas gdy Mises rozpatrywał również postać niesymetryczną. Kratownica składa się z dwóch prętów sprężystych ułożonych pod małym kątem α i obciążonych siłą P, która wywołuje w prętach siły, których wartość można uzyskać z warunku równowagi w węźle:
| $N= \dfrac{P}{2 \cdot cos \alpha}$, | (1) |
System jest statycznie niewyznaczalny, ponieważ do formuły (1) wchodzi nieznany kąt α, który zmienia się wraz z obciążeniem i będzie inny od wartości początkowej $\alpha_0$ ( od wartości w konfiguracji nieodkształconej). Skrócenie każdego pręta wynosi
| $\Delta l= \dfrac{a}{sin \alpha_0}-\dfrac{a}{sin \alpha}$, | (2) |
co wywołuje siły w prętach
| $ N= \dfrac {EA \cdot \Delta l} {l_0}= EA ( 1- \dfrac{ sin \alpha_0} {sin \alpha})$, | (3) |
Jeśli w miejsce prętów damy sprężyny (rys.1b), to sztywność EA powinna byc zastąpiona odpowiadającą sztywnością sprężyny. Porównując prawe strony (1) i (3), otrzymamy:
| $ P= 2 EA ( 1- \dfrac{ sin \alpha_0} {sin \alpha})cos \alpha$, | (4) |
Po zastąpieniu kąta α przez przez przemieszczenie $v$ i po przekształceniach, otrzymamy:
| $ P= 2 EA ( 1- \dfrac{v} {a} tg \alpha_0) \cdot \left [\dfrac {1}{ \sqrt{tg^2(\alpha_0)+(1-\dfrac{v}{a}tg \alpha_0)^2}}-cos \alpha_0 \right ]$, | (5) |
Wykres równania (5) przedstawiono na rys.3 w postaci krzywej 1-2-3-4-5-6-7-8.
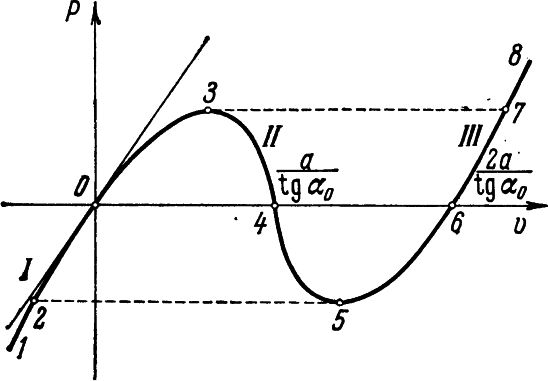
Rys.3. Ścieżka równowagi kratownicy Misesa [2]
Każdy punkt (P,υ) na krzywej jest punktem równowagi. Krzywa ma dwa ekstrema: maksimum w pkt 3 i minimum w pkt 5. Punkty te dzielą ścieżkę na trzy charakterystyczne części I, II i III. Na gałęzi I zachodzi proces obciążenia, a po osiągnięciu punktu 3 następuje przeskok węzła na gałąź III.
W procesie obciążania po przekroczeniu punktu O, tuż przed przeskokiem i tuż po przeskoku , jednej wartości obciążenia $P=P_3=P_7$ odpowiadają różne konfiguracje układu, a $P_3$ jest maksmalnym – krytycznym obciążeniem.
W procesie odciążania od punktu 8 po gałęzi III, powrotny przeskok układu z punktu 7 do 3 już nie zachodzi. PO całkowitym odciążeniu do punktu $P_6=0$ uklad nie wróci do konfiguracji początkowej. W tym punkcie odciążenia pozostaje niezerowe przemieszczenie υ≠0). Odwrotny przeskok obserwujemy dopiero PO rozpoczciu prostowania pręta z pubktu 5 do punktu 2.
Konfiguracje układu na gałęzi $II$ są niestateczne.W celu wykazania tego dokonajmy analizy energii układu. dla obciążenia $P_M$ (rys.3). Energia wewnętrzna U i zewnętrzna $W$ wynosi:
| $ U=2 \dfrac {N^2l_0}{2EA}=EAl_0 \cdot \left [ 1- cos \alpha_0 \cdot \sqrt{tg^2\alpha_0+(1- \dfrac{v}{a} tg \alpha_0)^2}) \right ]^2$,
$ W=-Pv$, |
(6) |
Całkowita energia potencjalna $\Pi=U+W$ jest pokazana na rys 4b. Ekstrema energii obserwuje się w punktach M,N i R, ale w punkcie N energia jest maksymalna, czyli punkt jest niestateczny.
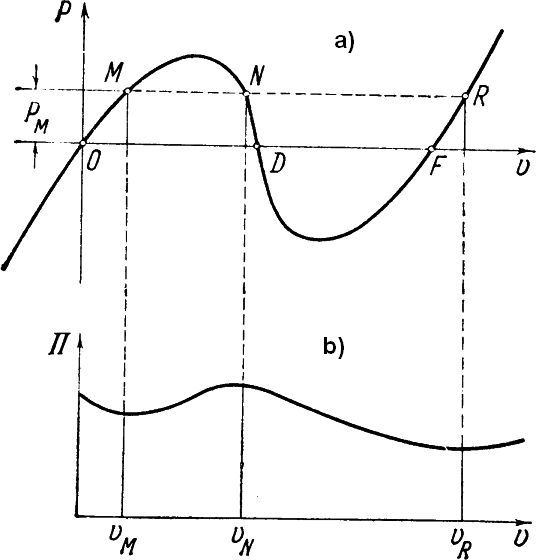
Rys.4. Kratownica Misesa: a) ścieżka równowagi, b)pełna potencjalna energia dla obciążenia $P=P_M$ [2]
Kratownica Misesa z imperfekcjami
Imperfekcje kratownicy Misesa mogą dotyczyć położenia węzłów w przestrzeni. wstępnych wygięć lub skręceń prętów albo też odchyleń parametrów przekroju prętów (charakterystyk geometrycznych lub materiałowych). Imperfekcja położenia węzła prowadzi do niewielkich zmian kąta α0 i może być zbadana z podanych wyżej zależnośći.
Wstępne wygięcia prętów
Imperfekcje geometryczne położenia węzła kratownicy Misesa mogą prowadzić do kilku charakterystycznych postaci utraty stateczności, pokazanych na rys. 5, przy czym na rys. 5a wprowadzono wygięcia wstępne tylko lewego pręta, a prawy pręt pozostaje bez niedoskonałościna, a rys. 5b niedoskonałośc są rozłożone symetrycznie (oba prety mają początkowe wygięcia).
Obciążenie krytyczne $P_{cr}$ wyznacza się poprzez badanie przemieszczenia pionowego w górnego węzła (rys.5) dla dwóch mechanizmów zniszczenia prętów: na skutek ściskania pręta (rys.3a) lub zginania pręta (rys.5b), na przykład w sposób pokazany w pracach [4], [5]).
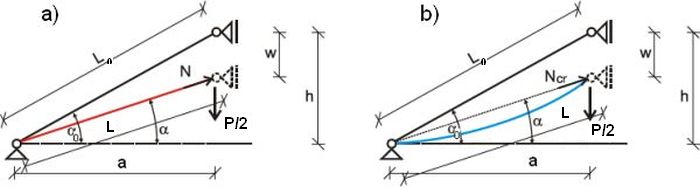
Rys.5. Mechanizmy wyboczenia kratownicy Misesa: a) ściskanie pręta, b) zginanie pręta [5])
Pierwszy przypadek (rys.5a) jest modelowany prętami z nieskończoną sztywnością na zginanie $EI=\infty$, co odbiera możliwość wyginania się prętów. Wydłużenie lub skrócenie pręta uzyskuje się z zależności:
| $\Delta L=L_0-L= \dfrac{NL_0}{EA}$, | (7) |
Z równania równowagi węzła otrzymamy:
| $P=2N sin \alpha = 2N \dfrac{h-w}{L}$, | (8) |
Z zależności (7) i (8) dla przypadku 1 (z rys. 3a) mamy równoważne obciążenie $P_1$:
| $P_1= 2EA \cdot (\dfrac{1}{L}-\dfrac {1}{L_0}) \cdot(h-w)$, | (9) |
Równanie (9) można zmodyfikować do postaci [6] :
| $P_1= \dfrac {2EA}{L_0} \cdot (h-w) \cdot \dfrac {L_0- \sqrt{L^2_0+w^2-2hw}}{\sqrt{L^2_0+w^2-2hw}}$, | (10) |
Drugi przypadek (rys.5b) jest modelowany przez zadanie prętów z dużą osiową sztywnością $EA=\infty$ i rzeczywistą sztywnością na zginanie $\dfrac{EI}{L_0}$, przez co przemieszczenia węzła $w$ wtołane jest tylko zginaniem, bez udziału ściskania.
Z rozwiązania problemu wyboczenia giętnego Eulera mamy:
| $N_{cr}=\dfrac { \pi^2EI}{L_0^2}$, | (11) |
Po zastąpieniu w równaniu (8) $N$ przez $N_{cr}$ otrzymamy,
| $P_2=2 \dfrac {\pi^2}{L_0}\cdot EI \cdot \dfrac {h-w}{L}$, | (12) |
Z porównania $P_1=P_2$, tzn. po poróenaniu formuł (10) i (12), możemy wyznaczyć krytyczne przemieszczenie $w_{cr}$:
| $w_{cr}=h- \sqrt{h^2-\pi^2 \dfrac {I}{A}\left ( 2- \dfrac {\pi ^2 I} {L_0^2 A} \right )} $, | (13) |
Po wyznaczeniu$w_{cr}$ z zależności (13), z formuł (10) i (12) otrzymamy odpowiadające obciążenia krytyczne.
Analizy wykonujemy dla konkretnych przypadków początkowej geometrii układu, profili i materiału prętów, a także wstępnych imperfekcji.
Na rys. 6 pokazano przykład kratownicy wykonanej ze stalowych prętów IPE 200 ułożonych pod kątem α0=150, obarczonych imperfekcjami łukowymi o amplitudzie L/1000.
W lewej kolumnie (rys. 6a) pokazano imperfekcje symetryczne (oba pręty z wygięciami wstępnymi), a w prawej kolumnie (rys. 6b) imperfekcje asymetryczne (tylko lewy pręt z wygięciem wstępnym) [7].
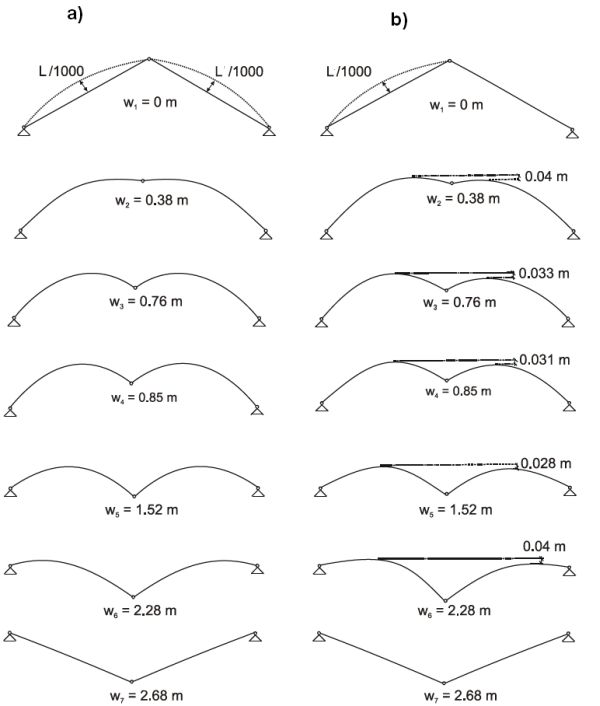
Rys.6.Postacie wyboczenia kratownicy Misesa dla imperfekcji prętów: a) symetrycznych, b) niesymetrycznych [5])
Wybrane konstrukcje z przeskokiem
Kopuła powłokowa
Kopuła z cienkościennej powłoki, pokazana na rys.7 pod wpływem powoli, ale skokowo, zwiekszającego się ciśnienia $p$ w pewnym momencie ulega „przenicowaniu”.
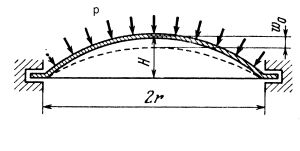
Rys.7. Model kopuły do analizy przeskoku [2]
zachowanie kopuł jest zalezne od względnej wyniosłości $\lambda=H/t$, gdzie t- grubość membrany, a $H$ strzałka wyniesienia (rys.7):
- mało wyniosłe kopuły $\lambda \le 1,5 $ nie mają skłonności do przeskoku(rys.8a),
- średnio wyniosłe kopuły $ 1,5 \le \lambda \le 3,4$ przeskakują, ale po zdjęciu obciążenia powracają do stanu początkowego (rys.8b)
- wyniosłe kopuły po przeskoku nie powracja do stanu wyjściowego (rys.8c)
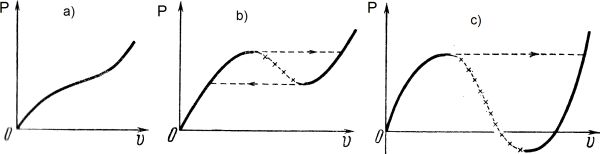
Rys.8. Charakterystyka kopuł ze względu na przeskok: a) kopuła, która nie ulega przeskokowi, b) kopuła, która po przekoku wraca do położenia początkowego, c) kopuła, która po przeskoku ma pozostające przemieszczenia [2]
System pręt-sprężyna
Rozważmy układ mechniczny pręt 1 -sprężyna 2 pokazany na rys. 9. Sprężyna 2 jest włożona do rurki w celu zabezpieczenia przed wyboczeniem. Stan równowagi pokazany na rys. 9a jest stateczny przy obciążeniu P mniejszym od obciążenia kytycznego
| $P < P_{cr}=c \cdot l$, | (14) |
gdzie c- stała sprężystości sprężymny, $l$ – długość pręta. Dla $P=P_{cr}$ stan równowagi przestaje być statecznym i system przeskokiem przechodzi w polożenie , zobrazowane na rys. 9b) do poziomego połozęmia pręta, ato położenie równowagi jest stateczne dla dowolnego obciążenia $P>0$. Oprócz tych dwóch stanów równowagi dla akzxdej wartości siły $P<P_{cr}$ możlia jest jeszcze jedna konfiguracja równowagi, pokzana na rys. 9c przy położeniu dolego przegubu w rzędnej
| $v=l \cdot \sqrt{1- \dfrac{P}{P_{cr}}}$ | (15) |
Jednakże konfiguracja 9c jest nieastateczna. Na ścieżce równowagi (rys. 9d) $P_{cr}$ określa formuła (14), a dolne obciązenie krytyczne jest róne zero.
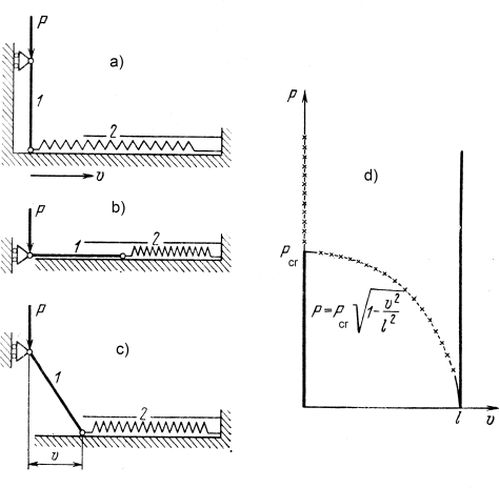
Rys.9. Przeskok układu pręt-spręzyna: a), b), c) stany równowagi przy takiej samej sile P, d) ścieżka równowagi systemu [2]
Największa osobliwość systemu objawia się tym, że przeskok jest możliwy przy obciążeniu P mniejszym od wartości krytycznej. Przykładowo, jeśli obciążenie $P=P_1<P_{cr}$, to na skutek niedoskonałości pojawia się siła pozioma $H_1$w dolnym przegubie. Jeśli przemieszczenie wywołane siłą $H_1$ spełnia nierówność:
| $v_1 <l \cdot \sqrt{1- \dfrac{P}{P_{cr}}}$ | (16) |
to pręt powróci do położenia pionowego. W przeciwnym przypadku system przeskokiem przejdzie w położenie równowagi 9b.
Sprężyna zwita
Zjawisk przeskoku obserwuje się też w zwykłej zwitej sprężynie, pokazanej na rys. 10.
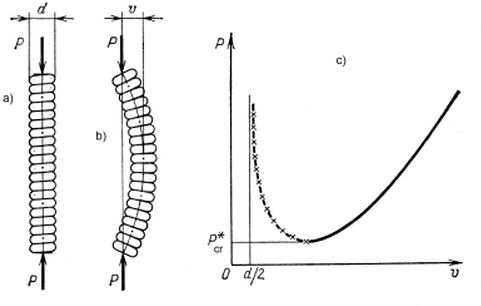
Rys.10 Zwita sprężyna: a) stan początkowy, b) po przeskoku, c) ścieżka równowagi [2]
Szczególną cechą zwitej sprężyny jest zjawisko przeskoku bez istnienia górnego ograniczenia przez obciążenie krytyczne. Do przeskoku potrzeba obciążenia większego od obciążenia $P^*_{cr}$, a ponadto tego, by sprężyna miała dostateczne wymuszenie boczne (nie mniejsze od $d/2$ – to wymuszenie wymaga przyłożenia dodatkowej siły bocznej lub imperfekcji wstępnej sprężyny.
W takim systemie przeskok wymaga przekroczenia nie „siłowej” granicy, ale przekroczenia granicy imperfekcji bocznej .
Powłoka walcowa, pionowa (puszka)
Interesujacy przypadek zjawiska przeskoku obserwuje się na zwykłych puszkach, których modelem jest walcowa pionowa powłoka (rys. 11).
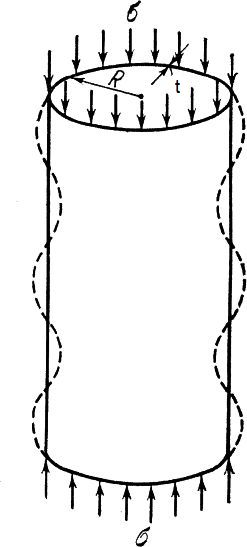
Rys.11 Osiowosymetryczna forma utraty stateczności cylindrycznej powłoki [2]
Jako pierwszy uproszczone rozwiązanie problemu stateczności cylindrycznej powłoki podano zależność w postaci formuły na naprężenia krytyczne:
| $\sigma_{cr}=\dfrac{Et}{R \sqrt{3(1-\mu^2)}} \approx 0,6 \dfrac {Et}{R}$ | (17) |
gdzie $\mu$ – współczynnik Poissona.
Karman i inni [8] pokazali, że formuła (17) nie jest potwierdzana eksperymentalnie , bo obciążenie krytyczne cienkiego cylindra jest trzy razy mniejsze. Przyczyną okazało się to, że Lorenz formułę (17) wyprowadził zgodnie z ideą Eulera w założeniu geometrycznie-liniowej idealnej powłoki (bez imperfekcji), a tymczasem zadanie jest nieliniowe o skończonych przemieszczeniach. Poprawiony wynik przedstawiono na rys. 12 w postaci ścieżek równowagi:
odskształcenie $ \varepsilon \dfrac {R}{t}$ lub $v_1=\dfrac{w_1}{t}$, gdzie: $w_1$ największe ugięcie (przemieszczenie boczne) powłoki $\to$ obciążenie $p=\sigma \cdot \dfrac{R}{Et}$.
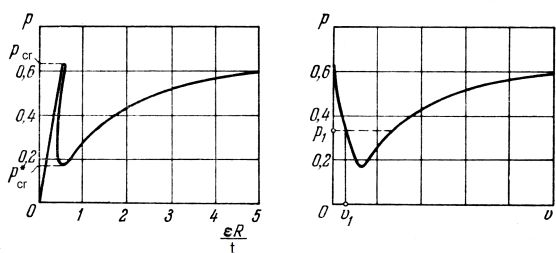
Rys.12 Ścieżki równowagi cienkiego cylindra a) w funkcji względnego skrócenia $\varepsilon R/h$, b) w funkcji wygięcia $v_1$ [2]
Dla cylindra istnieją dwie wartości krytyczne ściskjących naprężeń $p_{cr}$: jedno zgodne z rozwiązaniem Lorenza i drugie około trzykrotnie mniejsze $p^*_{cr}$. Karman zinterpretował to zaobserwowanym zjaiwskiem przeskoku na pokrytyczną ścieżkę równowagi, które zachodzi po przekroczeniu obciążenia $p^*_{cr}$. Przyczyną przeskoku okazały się imperfekcje wstępne od idealnego kształtu powłoki.
Znaczenie rozwiązania Larenza (17) dla praktyki jest niewielkie, podobnie jak rozwiązanie Eulera dla „wyboczenia” rzeczywistych prętów (p. artykuł Współczynnik wyboczeniowy. Geneza i mit).
Literatura
- Thom, R. (1972). Stabilite Structurelle et Morphogenese. Benjamin
- Panovko J., G., Gubanova, I. I. (1967), Ustojčivost i kolebanija uprugich system. Sovremennyje koncepcii, paradoksy i ošibki (4th ed.), Nauka, Moskva
- Mises, R. (1923). Uber die Stabilitatsprobleme der Elastizitatstheorie. Zeitschrift f. Angew. Math. u. Mech., 3, 406–422
- Frantik, P. (2003). Reseni vzperadla, [http://www.kitnarf.cz/publications/2003/2003.01.www_vzperadlo/2003.01.www_vzperadlo.html ]
- Kalina, M. (2015), Numerical analysis of buckling of von Mises planar truss. Transactions of the VSB -Technical University of Ostrava Civil Engineering Se-ries, 15(2
- Galambos, T. V. (Ed.). (1998), Guide to stability design criteria for metal struc-tures (5th ed). John Wiley
- Kalina, Kala, Z., Frantik, P. (2015). Elastic buckling and post-buckling of von Mises planar trusses. In N. Jendzelovsky (Ed.), Trends in statics and dynamics of constructions: selected, peer reviewed papers from the12th International Conference “New Trends in Statics and Dynamics of Buildings”, October 16-17, 2014, Bratislava, Slo-vakia. TTP, Trans Tech Publ.
- Karman, T. von, Tsien, H. S. (1941). The buckling of thin cylindrical shells under elastic compression. J Aeronaut Sci, 8, 303–312
________________________________




