Oddziaływania dynamiczne i zmęczeniowe suwnic (+)

Leszek Chodor,  7 września 2017
18-02-2025 rewizja po dużej awarii portalu>
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co

Oddziaływania a współczynnik dynamiczny

Oddziaływania dynamiczne $F_{dyn}$ w praktyce inżynierskiej są zastępowane równoważnymi oddziaływaniami statycznymi, $F_{stat}$ o takiej wartości, by efekt tego oddziaływania (odpowiedź systemu) był taki jak po zadziałaniu obciążenia dynamicznego. Stosuje się prostą zależność:

$$\begin{equation} F_{dyn}=\varphi \cdot F_{stat}  \label{1}\end{equation}$$

gdzie $\varphi$ jest współczynnikiem dynamicznym, większym od jedności (najczęściej w przedziale 1,1 do 2,0).

Dla tak ustalonych równoważnych obciążeń statycznych analizę prowadzi się w konwencjonalny sposób jak dla zadania statyki konstrukcji z pominięciem własności dynamicznych (lepkich, tłumienia itd) systemu. Z zależności ($\ref{1}$) mamy definicję współczynnika dynamicznego:

$$\begin{equation} \varphi =\cfrac {F_{dyn}} {F_{stat}} \label{2}\end{equation}$$

to znaczy współczynnik dynamiczny jest stosunkiem równoważnego oddziaływania statycznego i  ocenianego oddziaływania dynamicznego.

Opisane zależności są  fundamentalne również dla oceny oddziaływań suwnic. Podejście jest klasycznym sposobem wyznaczania oddziaływań dynamicznych w praktyce inżynierskiej w zamian za pełne analizy dynamiki konstrukcji z wykorzystaniem macierzy mas w szczególności i ich charakterystyk dynamicznych.

Specyficzne dla oddziaływań dynamicznych jest zjawisko zmęczenia materiału konstrukcji. Do sytuacji zmęczenia stosuje się równoważne obciążenia zmęczeniowe.

Współczynniki dynamiczne oddziaływania suwnicy

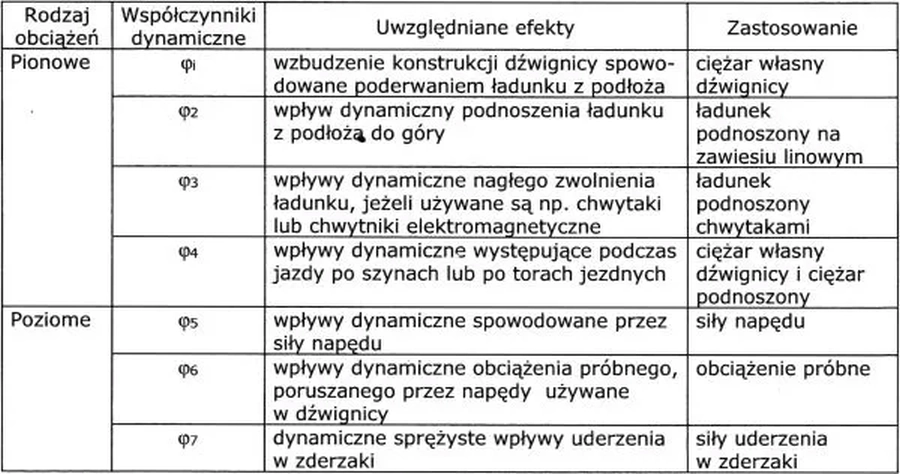
Jeżeli dostawca dźwignicy nie zaleca innych wartości współczynników dynamicznych, to do obliczenia trwałej lub przejściowej sytuacji obliczeniowej, można je ustalać na podstawie zależności normy [1] , w której  ustalono aż siedem współczynników dynamicznych w zależności od efektów działania  dynamicznego suwnicy (tab.1).

Współczynniki $\varphi_1$ do $\varphi_4$ są stosowane do określenia składowych dynamicznych obciążeń pionowych kół suwnicy. Współczynnik $\varphi_5$ jest stosowany do określania składowych dynamicznych obciążeń poziomych. Współczynnik dynamiczny $\varphi_6$ jest stosowany do określania pionowych obciążeń próbnych działających na belki podsuwnicowe. Współczynnik $\varphi_7$ jest stosowany do określenia poziomych składowych dynamicznych obciążeń wyjątkowych. Obciążenie wyjątkowe powstaje wskutek uderzeń suwnic lub wózków suwnic w zderzaki albo kolizji urządzeń chwytających z przeszkodami (siły wywołane wychyleniem). Obciążenia wyjątkowe od uderzeń są wykorzystywane do obliczania kozłów odbojowych suwnic lub wózków.

Tab.1 Współczynniki dynamiczne oddziaływania suwnic [1]

Współczynnik $\varphi_1$

Wartość współczynnika $\varphi_1$  przyjmuje się w przedziale:

$$\begin{equation} 0,9 < \varphi_1 < 1,1 \label{3}\end{equation}$$

przy czym wartość mniejszą od jedności przyjmuje się do określania stanów stateczności położenia dźwignicy, a górną 1,1 do obliczania stanu nośności belki podsuwnicowej

Współczynnik $\varphi_2$

Współczynnik $\varphi_2$ dobiera się w zależności prędkości podnoszenia $v_h$, którą podaje producent oraz w zależności klasy podnoszenia suwnicy HC1 do HC4 z zależności

$$\begin{equation} \varphi_2=\varphi_{2.min}+\beta_2 \cdot v_h \label{4}\end{equation}$$

gdzie współczynnik $\varphi_{2,min}$ oraz $\beta_2$ dobiera się wg tab.2.

Tab.2 Klasa podnoszenia suwnicy i współczynniki pomocnicze
(na podstawie [1] , [2]  i [3] )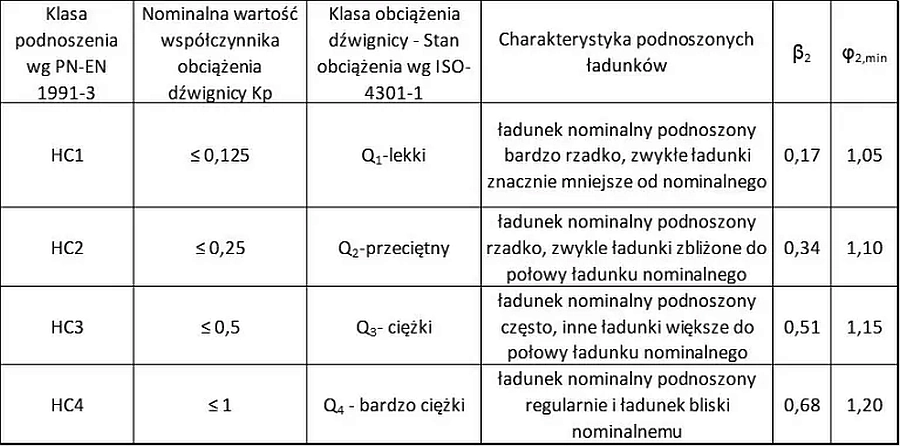

Klasa podnoszenia suwnicy uwzględnia czas pracy, częstotliwość podnoszenia ładunków i stopień wykorzystania pełnego dopuszczalnego udźwigu w okresie dnia roboczego. Obecnie niektórzy wytwórcy zagraniczni dla swoich urządzeń podają cztery grupy natężenia pracy (lekka, średnia, ciężka i bardzo ciężka), które są odpowiednikiem klas podnoszenia i są zależne od średniego czasu pracy urządzenia oraz od klasy obciążenia względnego. W tab.2. podano opisową charakterystykę podnoszenia suwnicy. Na rys.1. pokazano graficzną ilustrację klas podnoszenia HC.

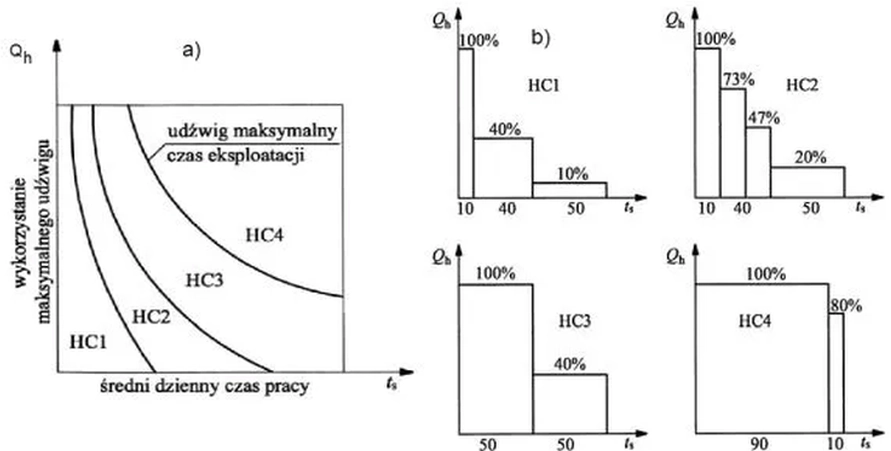
Rys.1. Klasa podnoszenia suwnicy: a) zależność klasy od czasu udźwigu maksymalnego, b) udział wykorzystania nośności suwnicy w czasie pracy ( na podstawie [4] )

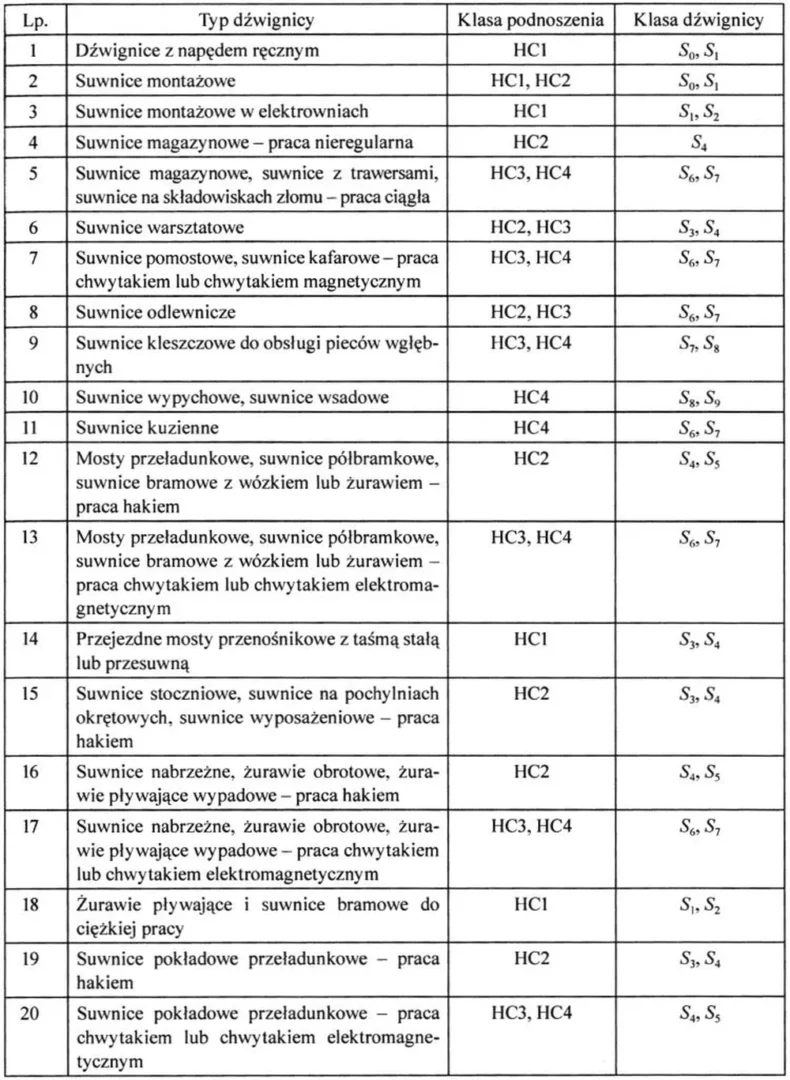
W tab.3  opisano najczęściej stosowane typy dźwignic i podano przyporządkowane do nich klasy podnoszenia HC oraz klasy historii obciążenia S0 do S9 wg [5] .

Tab.3 Typy dźwignic  i ich klasy podnoszenia HC oraz klasy historii obciążenia S
(na podstawie załacznik B [1] )

Na rys.2 zilustrowano klasę dźwignicy z warunku historii jej obciążenia .

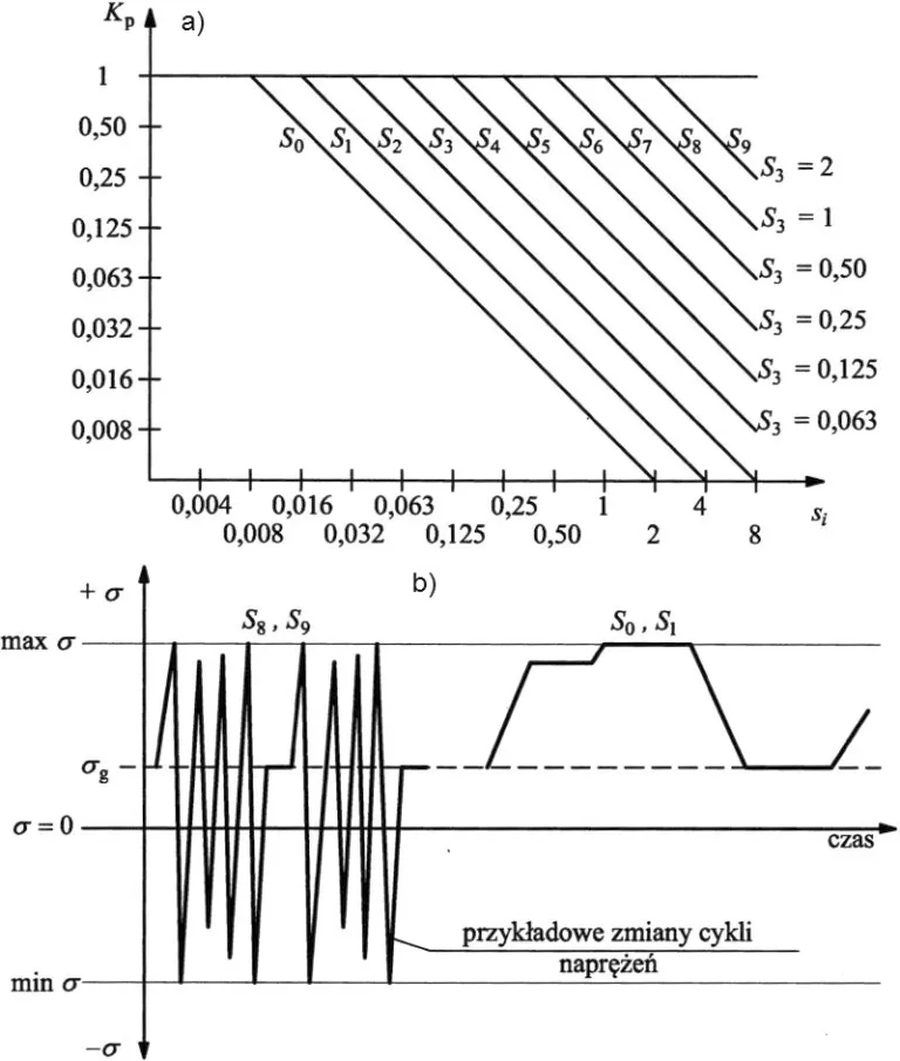
Rys.2. Klasa suwnicy w funkcji historii jej obciążenia: a) zależność współczynnika obciążenia Kp (tab.2) od stopnia wykorzystania naprężeń $s_i$ oraz klasy suwnicy $S_i$. b) wyznaczanie stopnia wykorzystania naprężeń zależnie od historii zmiany cykli naprężeń ( na podstawie [4] )

Współczynnik $\varphi_3$

Współczynnik $\varphi_3$ dobiera się w zależności stosunku masy zrzuconej lub zwolnione części $\Delta m$ podnoszonego ładunku m oraz rodzaju chwytaka do zwalniania ładunku  z zależności:

$$\begin{equation} \varphi_3=1- \cfrac {\Delta m} {m} (1+\beta_3)\label{5}\end{equation}$$

gdzie:
$\beta_3 =0,0$ dla zawiesia wiotkiego,
$\beta_3 =0,5$ dla suwnic wyposażonych w chwytaki lub inne urządzenia zwalniające powoli,
$\beta_3 =1,0$ dla suwnic wyposażonych w magnesy lub inne urządzenia szybko zwalniające.

Masa zwalniana $\Delta m$ może być równa całemu udźwigowi i wówczas $\frac {\Delta m} {m}=1$.

W przypadku, gdy nie ma możliwości gwałtownego zrzucenia ładunku,  przyjmuje się $\varphi_3=1$

Współczynnik $\varphi_4$

Współczynnik $\varphi_4=1,0$, jeśli zachowane są tolerancje dla torów podsuwnicowych podane w  [6] . W przeciwnym przypadku współczynnik ten można wyznaczyć na podstawie modelu przedstawionego w [7] .

Współczynnik $\varphi_5$

Do oceny poziomych oddziaływań należy przyjąć współczynnik dynamiczny $\varphi_5$. Współczynnik ten powinien podać Producent urządzenia, a jeśli takiej informacji nie podał, to można przyjąć:
$\varphi_5=1,0$ dla sił odśrodkowych bez istotnych zmian ich wartości podczas przejazdu,
$1,0 \le \varphi_5 < 1,5$ dla układów, w których siły zmieniają się łagodnie,
$1,5 \le \varphi_5 < 2,0$ dla układów, w których możliwe są nagłe zmiany,
$\varphi_5= 3,0$ dla napędów ze znacznymi luzami (wyeksploatowanych).

W pracy [8] wskazano, że:

• Jeżeli brak jest informacji od producenta suwnicy, a projektowany jest nowy układ suwnica-belka podsuwnicowa, to należy przyjąć $\varphi_5=$ 1,0 do 1,5 zależnie od prędkości jazdy suwnicy,
• W przypadku instalowania nowej suwnicy na starych torach, można przyjąć $\varphi_5=2,0$,
• Gdy analizuje się stare suwnice na użytkowanych torach, zaleca się wartość $\varphi_5=3,0$.

Współczynnik $\varphi_6$

Współczynnik dynamiczny $\varphi_6$ znajduje zastosowanie do obciążeń próbnych w czasie prób odbiorowych suwnic. Do statycznego  obciążenia próbnego przyjmuje się $\varphi_6=1.0$, a do dynamicznego:

$$\begin{equation} \varphi_6=\frac{1}{2}(1+\varphi_2)\label{6}\end{equation}$$

Współczynnik $\varphi_7$

Współczynnik dynamiczny $\varphi_7$ stosuje się do szacowania obciążenia wyjątkowego, spowodowanego uderzeniem suwnicy w zderzaki o charakterystyce $\xi_b$ danej przez producenta zderzaka, a wskazującej na stopień pochłaniania energii przez zderzak. Charakterystyka zderzaka, to zależność między siłą uderzenia, a przemieszczeniem zderzaka, najczęściej nieliniowa , na podstawie której określa się zmagazynowaną i pochłoniętą energię. Dla zderzaka twardego (drewno, twarda guma) $0 \le\xi_b \le 0,5$. Przy większych obciążeniach stosujemy zderzaki kolejowe, dla których często $0,5 \le\xi_b \le 1,0$.

wartość współczynnika dynamicznego $\varphi_7$ przyjmuje się:

• dla zderzaka twardego $0 \le\xi_b \le 0,5$ (np. drewno, twarda guma) $\varphi_7=1,25$,
• dla zderzaka miękkiego $0,5 \le\xi_b \le 1,0$ (np zderzaki kolejowe) $\varphi_7=1,25+0,7(\xi_b-0,5)$.

Współczynniki dynamiczne dla grup oddziaływań (przypadków obciążenia)

W celu uproszczenia analiz rozmaite obciążenia suwnicami o podobnej naturze dynamicznej są grupowane, a współczynniki dynamiczne przypisuje się do poszczególnych grup 1 do 10 , zgodnie z tab. 4. W kol. 4 tab.4 przywołano punkty normy [1], w którym analizowano daną grupę obciążeń.

Za pomocą grup obciążenia uwzględnia się jednoczesne działanie różnych składników obciążenia dźwignicami, przy czym każda z grup traktuje się jako jedno oddziaływanie charakterystyczne dźwignicy, które przyjmuje się do kombinacji obciążeń z obciążeniami nie pochodzącymi od dźwignic, w tym: obciążenie chodnika, wiatr, śnieg i inne. Oddziaływania suwnic należy analizować w 10-ciu stanach nośności pod działaniem poszczególnych grup.

Tab.4 Grupy oddziaływań suwnicy i stosowne współczynniki dynamiczne [1]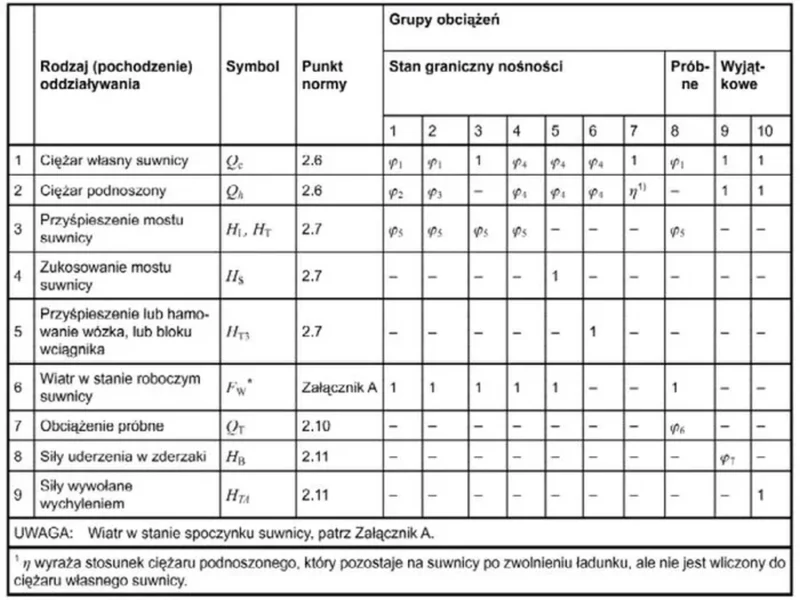

Oddziaływania suwnicy

Oddziaływania koła suwnicy na tor jezdny złożone są z trzech składowych

pionowej $F_z$,
poziomej prostopadłej do toru $F_y$,
poziomej równoległej do toru $F_x$.

Dane podstawowe

Oddziaływania suwnicy $F=[F_x, F_y, F_z]$ wyznacza się przy znajomości:

Rozpiętość mostu suwnicy L [m]
Rozstaw kół suwnicy wzdłuż toru  a [m]
Skrajne położenie haka (najbliższa odległość haka od szyny) $e_{min}$ [m]
Szerokość główki szyny $b_r$ [mm],
Prześwit między obrzeżami kół $k_k$ [mm] (jeśli elementem prowadzącym są obrzeża kół),
System kół suwnicy – zgodnie z  tab.5.  (np IFF)
Liczba par kół (osi suwnicy) n [szt]
Liczba kół napędzanych indywidualnie (pędnych) $m_w$ (najczęściej 1 lub 2)
Udźwig suwnicy $Q_{h,nom}$ [kN]
Masa suwnicy  $G_c$ [kN]
Masa wózka $G_f$ [kN]
Prędkość podnoszenia $v_h$ [m/s]

Obciążenia $F_z$ spowodowane przez dynamiczne ruchy pionowe

Obciążenia podstawowe, wywołane przez suwnicę, to przede wszystkim naciski  pionowe od ciężaru własnego części składowych suwnicy oraz od ciężaru podnoszonego. Obciążenia spowodowane przez ruchy pionowe powstają  podczas ruchu nieustalonego dźwignicy z ciężarem lub podczas podnoszenia/ opuszczania ciężaru. Są to obciążenia, które powstają na skutek przyspieszeń /opóźnienia ruchu podnoszenia, albo od pionowych uderzeń spowodowanych jazdą urządzenia po szynach.

Na rys. 3 pokazano oddziaływania pionowe kół suwnic $Q_{r, min}$ i $Q_{r, max}$ na konstrukcje wsporcze (szyny i belki podsuwnicowe). Znak sumy oznacza obciążenie łączne od wszystkich kół suwnicy znajdujących się po jednej stronie mostu suwnicy (na torze lewym lub prawym).

Nacisk minimalny koła (rys. 3a) wystąpi , gdy suwnica nie będzie obciążona ładunkiem $Q_{h,nom}$, a będą działały tylko ciężary własne: suwnicy $G_c$ i wózka $G_t$, przy czym jeśli wózek zbliży się maksymalnie do toru (na odległość $e_{min}$, to na ten tor koła będą oddziaływały siłą $Q_{r,min}$, a po przeciwnej stronie mostu (na tor 2) będzie działa siła $Q_{r,(min)}$.

Nacisk maksymalny (rys. 3b) wystąpi po dociążeniu suwnicy podwieszonym ładunkiem o wartości nominalnego udźwigu $Q_{h,nom}$.

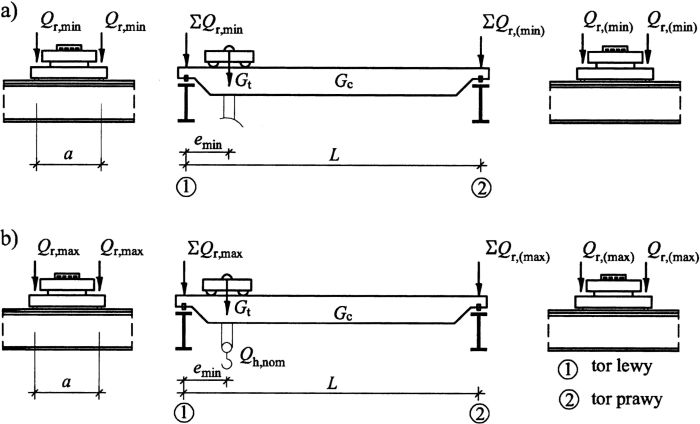
Rys.3. Oddziaływania pionowe $Q_r$ kół suwnicy: a) minimalne (suwnica bez ładunku)- od ciężaru własnego $G_c$ i ciężaru wózka $G_t$ , b) maksymalne (suwnica z ładunkiem $Q_{h,nom}$) – na podstawie [4]

Minimalne i maksymalne oddziaływania koła suwnicy wyznacza się z podstawowego równania równowagi sił w położeniu wózka suwnicy zbliżonego na odległość $e_{min}$ od toru suwnicy.

Minimalne pionowe oddziaływania kół suwnicy

Minimalne oddziaływania koła $Q_{r,min}$ wyznaczamy przy zbliżeniu się do toru wózka suwnicy nieobciążonej (rys.3a). W tym położeniu na torze przeciwnym wystąpi :minimalne uzupełniające  oddziaływanie $Q_{r,(min)}$

Dla grupy  (1 i 2) oraz  (3 do 6) charakterystyczne (ze współczynnikami dynamicznymi, ale bez współczynników obciążeń) ciężary suwnicy $Q_{c,k}$ oraz wózka $Q_{f,k}$ wyznaczamy ze współczynnikami dynamicznymi opowiednio $\varphi_1$ i $varphi_4$:

$$\begin{equation} \begin{cases} Q_{c,k}= \varphi_1 \cdot G_c \quad ;\, Q_{f,k},= \varphi_1 \cdot G_f , &  \text { dla grupy (1 i 2) }\\ Q_{c,k}= \varphi_4 \cdot G_c \quad ;\,  Q_{f,k}= \varphi_4 \cdot G_f, & \text { dla grupy (3 do 6) }\\ \end{cases} \label{7}\end{equation}$$

Oddziaływania minimalne i minimalne uzupełniające wylicza się z zależności:

$$\begin{equation} Q_{r,min}= \cfrac{Q_{c,k}- Q_{f,k}}{2\cdot n}+\cfrac{Q_{f,k}\cdot (L-e_{min})} {n\cdot L}  \label{8} \end{equation}$$

$$\begin{equation} Q_{r,(min)}= \cfrac{Q_{c,k}- Q_{f,k}}{2\cdot n}+\cfrac{Q_{f,k}\cdot  e_{min}} {n\cdot L} \label{9} \end{equation}$$

Suma oddziaływań minimalnych wynosi:

$$\begin{equation} \Sigma Q_{r,min}= \begin{cases} n \cdot Q_{r,min}, & \text { dla grupy (1 i 2) }\\ Q_{c,k}/2, & \text { dla grupy (3 do 6) }& \end{cases} \label{10} \end{equation}$$

Suma oddziaływań minimalnych uzupełniających wynosi:

$$\begin{equation} \Sigma Q_{r,(min)}= \begin{cases} n \cdot Q_{r,(min)}, & \text { dla grupy (1 i 2) } \\ Q_{c,k}/2+ Q_{f,k}, & \text { dla grupy (3 do 6) }\\ \end{cases} \label{11} \end{equation}$$

Maksymalne pionowe oddziaływania koła suwnicy

Maksymalne oddziaływanie koła suwnicy wyznaczymy dla suwnicy obciążonej przy zbliżeniu się wózka do toru.

Charakterystyczny ciężar ładunku $Q_{h,k}$ w zależności od grupy obciążeń wyznacza się dla różnych współczynników dynamicznych :

$$\begin{equation} Q_{h,k}= \begin{cases} \varphi_2 \cdot Q_{h,nom}, &  \text { dla grupy 1 } \\ \varphi_3 \cdot Q_{h,nom}, &  \text { dla grupy  2 } \\ \varphi_4 \cdot Q_{h,nom}, &  \text { dla grupy  4,5 i 6 } \\ \end{cases} \label{12}\end{equation}$$

Maksymalne oddziaływanie koła wynosi:

$$\begin{equation} Q_{r,max}=Q_{r,min}+ \cfrac {Q_{h,k} \cdot (L-e_{min})} {n \cdot L} \label{13}\end{equation}$$

Maksymalne dopełniające  (na  przeciwnym torze) oddziaływania koła suwnicy, wunosi

$$\begin{equation} Q_{r,(max)}=Q_{r,(min)}+ \cfrac { Q_{h,k} \cdot e_{min}} {n \cdot L}\label{14} \end{equation}$$

Suma oddziaływań maksymalnych wynosi:

$$\begin{equation} \Sigma Q_{r,max} =Q_{r,max} \cdot n \quad ; \quad  \Sigma Q_{r,(max)}= Q_{r,(max)} \cdot n\label {15}\end{equation}$$

Oddziaływania $F_x$ oraz $F_y$ spowodowane przez ruchy poziome

Ruchy poziome powodują powstawanie następujących obciążeń:

1. poziomych sił bocznych wywołanych jazdą (ukosowanie, znoszenie),
2. sił bezwładności związanych z ruchem nieustalonym mechanizmu jazdy, zmiany położenia ciężaru podniesionego (wysięgu). Wartość tych sił zależy od przyspieszenia/opóźnienia)  ruchu suwnicy,
3. sił odśrodkowych przy jeździe po łuku ( w niniejszym artykule przyjmuje się , że tor jazdy jest prostoliniowy i sił odśrodkowych nie analizuje się)

uderzenia w odbój (traktowane jako obciążenie wyjątkowe)

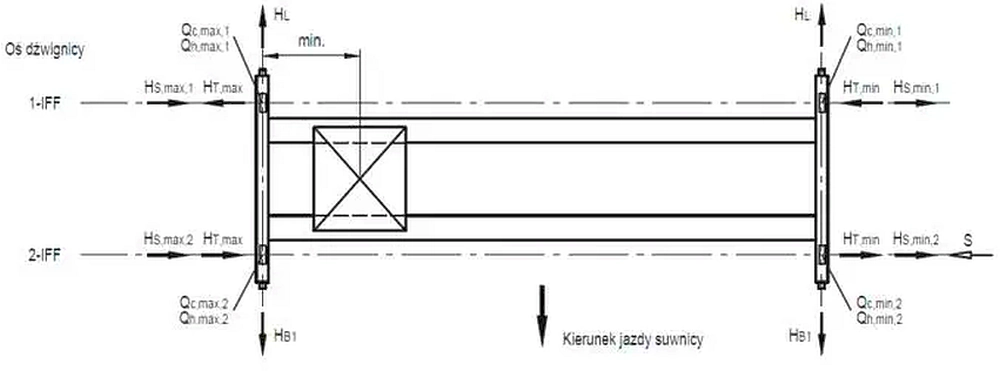
Siły spowodowane przyśpieszeniem lub hamowaniem mostu suwnicy

Siły poziome  $H_T$ prostopadłe do toru i $H_L$ równoległe do toru powinny być podane przez Producenta suwnicy. W przypadku braku tych danych można przeprowadzić oszacowania podane niżej.

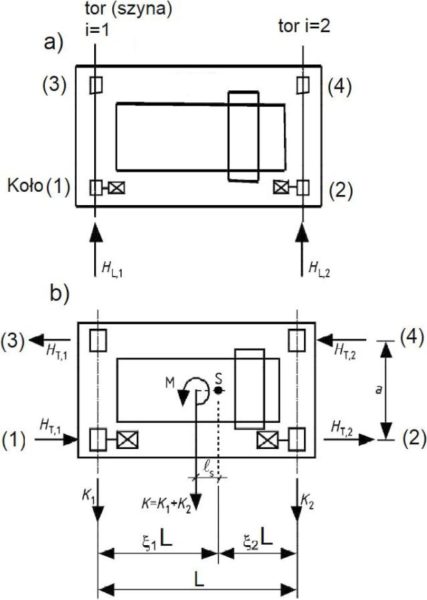
Rys.4. Siły od przyśpieszenia/hamownia mostu suwnicy: a) równoległe $H_L$, b) poprzeczne $H_T$ (indeksowane numerem  [1], rys.2.5,2.6toru)

Siła napędu K oraz oddziaływanie podłużne $H_L$

Na rys. 4a pokazano oddziaływania poziome, podłużne, które są przyłożone są do kół napędzanych do obu osi suwnicy (torów jezdnych) w postaci sił $H_{L1}$ i $H_{L2}$. Koła napędzane oznaczono numerami (1) i (2).

Wyznacza się je z zależności [1],Kl. 2.7.2(2)}

$$\begin{equation} H_{L1}=H_{L2}= \varphi_5 \cdot \cfrac{H} {n_r} \label {16} \end{equation}$$

gdzie:

$\varphi_5$ – współczynnik  dynamiczny
$n_r=2$ – liczba torów jezdnych (belek) ,
$K$ – siła napędu suwnicy.

Siła napędu K powinna być podana przez dostawcę suwnicy. Jeśli takich danych nie posiadamy, to można ją wyznaczyć z zależności [1],Kl. 2.7.3(3)} :

$$\begin{equation} K= \mu \cdot \Sigma Q^*_{r,min} \label {17}  \end{equation}$$

gdzie $\mu$ współczynnik tarcia. Dla tarcia stal-stal można przyjąć $\mu=0,2$.

Siła napędu jest przenoszona przez wszystkie napędzane koła. W przypadku napędzania jednego koła w całości przypada na to koło.

Dla suwnic bez centralnego napędu (współczesne suwnice najczęściej nie mają centralnego napędu) sumę obciążeń $\Sigma Q^*_{r,min}$, wyznacza się z zależności

$$\begin{equation}  \Sigma Q^*_{r,min}= m_w \cdot Q_{r,min} \label {18} \end{equation}$$

gdzie:
$m_w$ – liczba kół napędzanych indywidualnie  (zwykle $m_w=$ 1 lub 2).
a $Q_{r,min}$ należy przyjąć jak dla grupy obciążeń 1 lub 2.

W przypadku starszych suwnic z centralnym napędem należy przeprowadzić specjalną analizę (patrz [1],kl. 2.7.3} ).

Moment napędu M oraz oddziaływanie poprzeczne $H_T$

Moment napędu M działa w środku masy S i pochodzi od siły napędu K na mimośrodzie $l_s$:

$$\begin{equation} M= K\cdot l_s \label {19}  \end{equation}$$

Ramię siły K wynosi
$$\begin{equation} l_s= l_s= ( \xi_1-0,5)\cdot L \label{20} \end{equation}$$

Siły poziome poprzeczne do toru i=1 oraz i=2, wynoszą

$$\begin{equation}H_{T,i} = \varphi_5 \cdot \xi_{(i+1)} \cdot \cfrac{M}{a} \label {21}  \end{equation}$$

gdzie:
(i+1)=2 dla i=1 oraz (i+1)= 1 dla i=2,
$\xi_i$ wg ($\ref{24}$),
a- rozstaw kół suwnicy (po długości toru)

Przypisanie sił  $H_L$ i $H_T$ do punktów konstrukcji

Siły $H_L$ i $H_T$  przypiszemy do punków konstrukcji kół) w następujący sposób:

$$\begin{equation}  \begin{cases} F_x= \pm H_{L1} \quad ; \quad F_y= \pm H_{T1}, &  \text {koło (1)} \\ F_x= \pm H_{L2} \quad ; \quad F_y= \pm H_{T2}, &  \text {koło (2)} \\ F_x=0 \quad ; \quad F_y= \mp H_{T1}, &  \text {koło (3)} \\ F_x=0 \quad ; \quad F_y= \mp H_{T2}, &  \text {koło (4)} \\ \end{cases} \label {22}  \end{equation}$$

Znaki zależne są od  tego, czy suwnica przyspiesza cz też hamuje. Może też nastąpić zmiana kierunku jazdy i wówczas należy przenumerowąc koła: (1)=(3), (2)=(4).

Siły poziome od znoszenia suwnicy

Mechanizm ukosowania

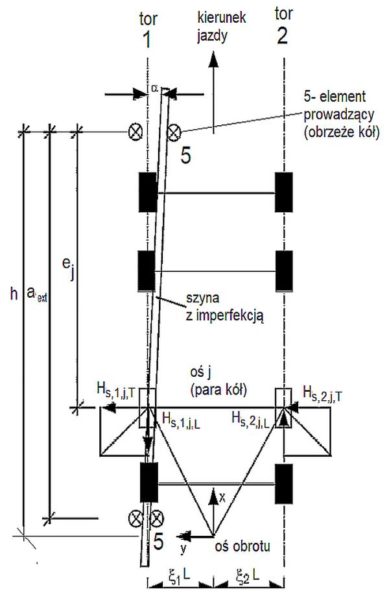
Mechanizm ukosowania przedstawiono na rys. 5 na przykładzie suwnicy poruszającej się na dwóch torach (i=1,2) z ułożonymi na nich szynami z imperfekcjami, to znaczy ze skręceniem o kąt zukosowania $\alpha$ w stosunku do idealnego, prostoliniowego toru jazdy. Mechanizm ten polega na zakleszczeniu elementów prowadzących suwnicę wokół szyny obarczonej imperfekcjami. Elementami prowadzącymi mogą być krążki prowadzące, ale najczęściej są nimi obrzeża kół. Zderzenie suwnicy z szyną następuje na pierwszym elemencie prowadzącym od czoła suwnicy patrząc. Na rys. 5 jest to przedni (górny) element 5. W mechanizmie ukosowania uczestniczy tylny (dolny) element prowadzący 5.

Rys.5. Mechanizm ukosowania suwnicy

Odległość pomiędzy przednim a tylnym elementem prowadzącym wynosi $a_{ext}$. Pomiędzy elementami prowadzącymi zmieści się  n_{ext} osi (par kół) suwnicy. W najczęściej spotykanym przypadku prowadzenia przez obrzeża kół odległość ta jest oczywiście równa rozstawowi kół $a_{ext}=a$, a liczba osi $n_{ext}$ jest równa liczbie osi $n$ suwnicy. Na rys. 5. pokazano przypadek w którym $n_{ext}=4$.

Przy skręceniu szyny o kąt $\alpha$ suwnica obróci się wokół chwilowego środka obrotu oznaczonego (x,y). Odległość pomiędzy pierwszym elementem prowadzącym , a osią obrotu wynosi $h$.

Na skutek ukosowania suwnica uderza przednim narożem siłą $S$, co generuje reakcje siłami podłużnymi $H_{S,L}$ i poprzecznymi $H_{S,T}$ na szyny w sposób pokazany na rys. 6

Należy zwrócić uwagę na różnice w układzie oddziaływań zależnie od systemu prowadzenia kół.

W przypadku prowadzenia pomiędzy rolkami (rys.6a) poprzeczne poziome reakcje $H_{S,T}$ powstają we wszystkich czterech kołach suwnicy, przy czym siły osi przedniej są przeciwnie skierowane niż na osi tylnej. W kołach tylnych działa  para sił podłużnych $H_{S,L}$, obracających suwnicę odwrotnie od skręcania siłą prowadzącą.Taki układ sił (czyli działanie na wszystkie cztery koła) jest zgodny z potocznym wyobrażeniem o mechanizmie ukosowania.

Inny mechanizm zaobserwowano w  przypadku prowadzenia w obrzeżach kół (rys. 6b). Reakcje poprzeczne powstaną tylko na kołach przednich o tym samym zwrocie, skierowanym przeciwnie do działania siły $S$.  W tym przypadku prowadzenia nie powstaną też siły podłużne.

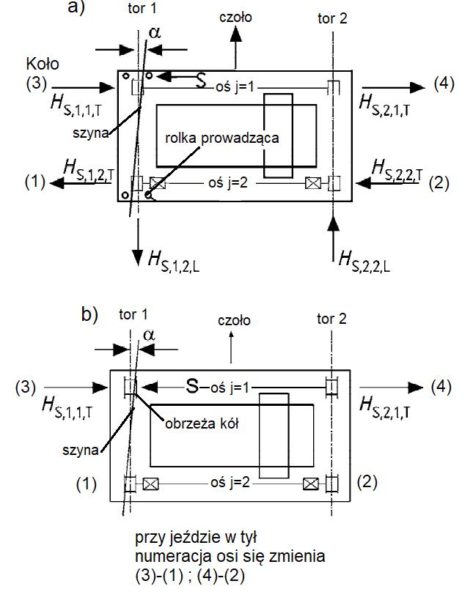
Rys. 6 Schemat działania sił podczas ukosowania suwnicy: a) przy prowadzeniu w rolkach, b) prowadzenie w obrzeżach kół

Kąt zukosowania

Kąt zukosowania $\alpha$ wyznacza się z zależności

$$\begin{equation}  \alpha=  \alpha_F +\alpha_V+ \alpha_0 = \cfrac {0,75 x + y}{a_{ext}} +0,001 \le 0,015 \, rad \label {23} \end{equation}$$

gdzie:
$\alpha_F= 0,75x / a_{ext}$ – skręcenie na skutek luzu „x”  w szczelinie między kołem a elementem prowadzącym – obrzeżem lub rolką. Luz „x”przyjmuje się zgodnie z dokumentacją koła, ale nie mniej niż:
$6,7 \, mm$ dla obrzeży kół (tzn 0,75x= 5 mm)
$13,4 \, mm$ dla rolek prowadzących (tzn 0,75x = 10 mm)
$\alpha_V=y/a_{ext}$ – skręcenie na skutek zużycia bocznego szyny i elementu prowadzącego „y”. Zużycie „y” przyjmuje się na podstawie pomiarów eksploatacyjnych , ale nie mniej niż
$y \ge 0,10 b_r$  dla obrzeży kół,
$y \ge  0,03 b_r$ dla rolek prowadzących,
Na etapie projektowania najczęściej przyjmuje się $y=15$% $b_r$ (szerokości główki szyny)

$\alpha_0=0,001$ – skręcenie wynikające z tolerancji ułożenia szyn.

$a_{ext}$ – odległość między elementami prowadzącymi.  W przypadku prowadzenia obrzeżami kół $a_{ext}=a$

Chwilowy środek obrotu suwnicy

Suwnica poruszając się w kierunku jazdy jest znoszona z chwilowym środkiem obrotu w punkcie (x,y) , położonym pomiędzy torami jezdnymi w odległości względem rozpiętości mostu) $L$ wynoszącej:

$$\begin{equation} \xi_1=\cfrac{\Sigma Q_{r,max}} {\Sigma Q_r}  \quad ; \quad \xi_2=1- \xi_1 \label {24} \end{equation}$$
odpowiednio od toru 1 i od toru 2, gdzie

$$\begin{equation} \Sigma Q_r= \Sigma Q_{r,max}+\Sigma Q_{r,(max)} \label{25} \end{equation}$$

W wyrażeniach ($\ref{24}$) oraz ($\ref{25}$) sumy oddziaływań  ($\ref{15}$) dotyczą 5 grupy obciążeń (patrz tab.4).

Siła prowadząca S

Siła prowadząca S (rys.6) wynosi [1],(2.6)}

$$\begin{equation}  S=f \cdot \lambda_{s,j} \Sigma  Q_r \label {26} \end{equation}$$

gdzie $\Sigma Q_r$ określono w ($\ref{25}$), a $\lambda_{s,j}$ w kol 2 tab. 6.

Współczynnik „niekorzystny” „f” jest wyznaczany ze wzoru

$$\begin{equation}  f=0,3 \cdot [1-exp ( -250 \cdot \alpha)] \le 0,3 \label {27} \end{equation}$$

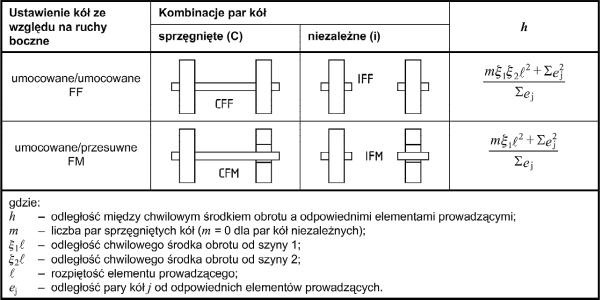
Siła prowadząca zależy od sposobu zamocowania i sprzęgnięcia kół. Stosowane są systemy CFF,CFM, IFF oraz IFM, gdzie pierwsze litery oznaczają sposób zamocowania (F- zamocowane, M- przesuwne), a dwie kolejne oznaczają sposób sprzęgnięcia (I – niezależne, C- sprzęgnięte).  W tab.5. zaprezentowano systemy kół oraz sposób wyznaczania odległości h w zależności od systemu.

Tab.5.Rodzaje systemu kół i wyznaczanie odległości h  [1],tab. 2.8}

Odległości $e_j$ $j,1,2 ,… n)$ osi kół (pary kół) od  przedniego elementu prowadzącego ( prowadnicy najbliższej do czoła suwnicy) wyznacza się następująco:

a) przednia  oś (para kół) najbliższa do czoła suwnicy jest odległa od elementu prowadzącego o $e_1$.
b) kolejne osie  (licząc w tył) są odległe są od pierwszego elementu prowadzącego o: $e_2=e_1+a$, $e_3=e_2+a$, $e_4=e_3+a$, aż do wyczerpania liczby osi $n_r$ mieszczącej się pomiędzy prowadnicami.

Dla najczęściej spotykanego przypadku suwnicy o dwóch osiach z kołami z obrzeżami mamy:

$$\begin{equation}  e_1=0  \quad ; \quad e_2=a  \label {28} \end{equation}$$

Współczynniki sił

Współczynniki sił wywołanych ukosowaniem przyjmuje się na podstawie tab. 6

Tab.6.Współczynniki sił wywołanych ukosowaniem [1],tab. 2.9}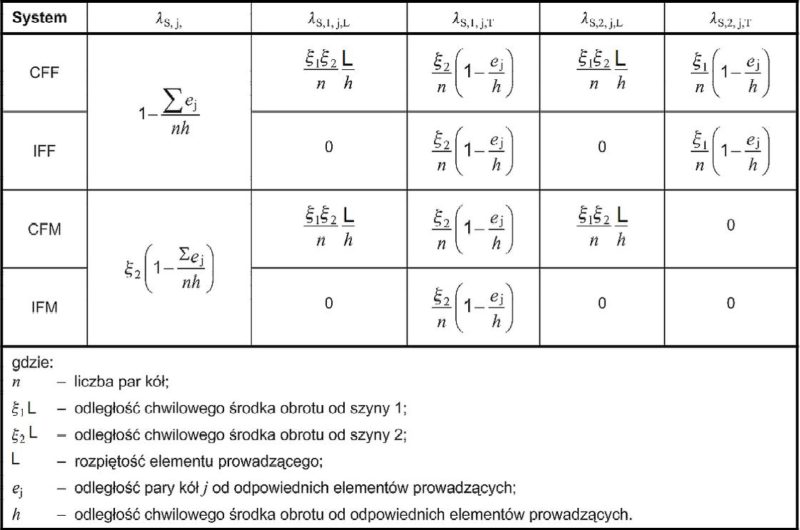

Na podstawie tab. 5  ustalamy rodzaj systemu kół. Współcześnie powszechnie stosuje się system I__, czyli koła niezależne, dla których przyjmuje się liczbę kół sprzęgniętych $m=0$. Dla $m=0$ odległość h wynosi:

$$\begin{equation}  h= \cfrac{ \Sigma e_j^2 }{\Sigma e_j} \label{29} \end{equation}$$

Dla suwnicy z dwiema osiami mamy: $h=(0^2+a^2)/(0+a)= a$, a dla suwnicy z czterema osiami $h=(0^2+a^2+(2a)^2+(3a)^2)/(0+a+2a+3a)=14/5 a$

Współczynnik siły prowadzącej $\lambda_S,j$ dla osi napędzanej „j”  wyznacza się ze wzoru

$$\begin{equation}  \lambda_S,j = \begin{cases} 1- \cfrac{\Sigma e_j }{n\cdot h}, & \text {dla systemu CFF oraz IFF}\\ \xi_2 \cdot \left ( 1- \cfrac{\Sigma e_j}{n\cdot h},\right )  & \text {dla systemu CFM oraz IFM}\\ \end{cases} \label {30}  \end{equation}$$

Dla suwnicy z najczęściej spotykanym systemem IFF i dwoma osiami n=2 mamy:
$\lambda_s,j=1-\cfrac{a}{2\cdot a}=0,5$

Współczynniki dla sił poprzecznych $H_S$ wyznacza się z formuły

$$\begin{equation} \lambda_{S,i,j,k} = \cfrac { \xi_{i+1}}{n} \cdot \left (1- \cfrac {e_j} {h} \right ) \label {31}  \end{equation}$$

gdzie:
i=(1,2) – nr koła na osi (tor, szyna)
j=(1, ..) – nr osi
k=(T,L) =(siła poprzeczna, siła podłużna).

Oddziaływania poziome $H_S$ od ukosowania

Wartości oddziaływań poziomych od ukosowania , pokazanych na rys. 6 wyznacza się ze wzorów

$$\begin{equation} H_{S,i,j,k} = f \cdot \lambda _{S,i,j,k} \cdot \Sigma H_r \label {32}  \end{equation}$$

gdzie współczynniki oddziaływań $\lambda _{S,i,j,k}$ wg ($\ref{31}$).

Siły spowodowane przyśpieszeniem lub hamowaniem wózka

Zgodnie z  [1],Kl. 2.7.5} można przyjąć, że pozioma siła poprzeczna  $H_{T3}$ spowodowana przyśpieszeniem lub opóźnieniem wózka suwnicy jest uwzględniona w sile poziomej $H_{B,2}$.

Z kolei zgodnie [1],Kl. 2.11.2} siła $H_{B,2}$ jest wywołana uderzeniem wózka lub wciągnika w zderzaki, a przy uwzględnieniu swobody wahań ładunku użytecznego wyznacza się ją z zależności:

$$\begin{equation} H_{B,2} = 0,1 \cdot  (Q_h+ Q_f )\label{33}\end{equation}$$

to znaczy 10% sumy ciężaru podnoszonego i ciężaru wózka lub wciągnika.

Jeśli warunek swobody wahań nie jest spełniony, to siłę uderzenia wózka w odbojnicę boczną należy wyznaczać zgodnie z procedurą przewidzianą dla siły uderzenia suwnicy w odbojnicę główną. Wówczas obciążenie $H_{B,2}$ traktuje się jako wyjątkowe.

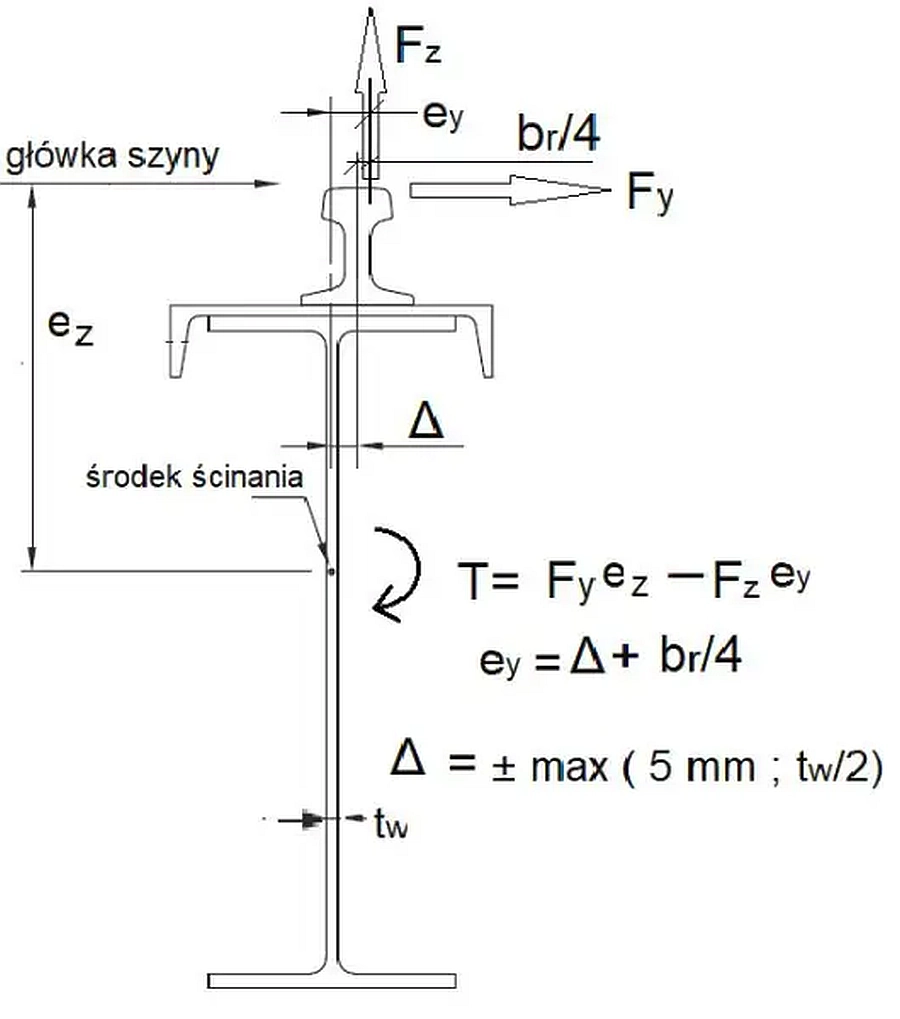
Mimośrody oddziaływań oraz momenty skręcające belkę

Obciążenia pionowe $F_z$ działają na mimośrodach przyłożenia do główki szyny $e_y$, a obciążenia poziome $F_y$ na mimośrodzie $e_z$ równym odległości od główki szyny do środka ścinania belki podsuwnicowej

$$\begin{equation} e_z=h_r+ z_{s,belka} \label{34} \end{equation}$$

gdzie:
$h_r$ – wysokość szyny,
$z_{s,belka}$- odległość od płaszczyzny zamocowania siły do środka ścinania belki podsuwnicowej. Dla przekrojów belek monosymetrycznych względem osi poziomej „y” – środek ścinania pokrywa się ze środkiem ciężkości i jest równy  połowie wysokości przekroju belki: $z_{s,belka}= h_{belka} /2$

Mimośród oddziaływań pionowych

Mimośród przyłożenia oddziaływań pionowych od kół suwnicy $e_y$ przyjmuje się w zależności od szerokości główki szyny $b_r$ o wielkości [1],kl. 2.5.2.1(2)} :

$$\begin{equation} e_r= \cfrac{b_r}{4} \label{35}\end{equation}$$

Moment skręcający belkę podsuwnicową

Na skutek mimośrodowego działania sił belka w miejscu przyłożenia koła (i) jest skręcana momentem $T_{(i)}$ (rys.6) , przy czym mimośród poizomy $e_y$ wynosi:

$$\begin{equation} e_y=\Delta+e_r \label{36}\end{equation}$$
gdzie :
$e_r$ mimośród przyłożenia siły do główki szyny wg $(\ref{35})$
$\Delta=\max{ (5 \, mm \quad; \quad t_w/2 ) }$ ( $t_w$ grubość środnika belki podsuwnicowej) ,  jest dopuszczalną tolerancją umiejscowienia szyny podsuwnicowej zgodnie z [10].

Rys.7 Moment skręcający T belkę podsuwn

Obciążenia wyjątkowe

Do obciążeń wyjątkowych suwnicy zalicza się siły uderzenia w zderzaki $H_{B1}$ spowodowane ruchem suwnicy oraz $H_{B2}$ spowodowane ruchem wózka, przy czym w przypadku swobody wahań  siłę uderzenia wózka w odbojnicę boczną można wyznaczać w sposób uproszczony .

Dla suwnic ze sztywnym prowadzeniem ładunku również siły wywołane wychyleniem. Obciążenia wyjątkowe przyjmuje się zgodnie z  [1],kl. 2.11} .

Jeżeli uwzględnia się oddziaływania wyjątkowe, to nie ma potrzeby uwzględniania równoczesnego działania
żadnego innego oddziaływania wyjątkowego. ani wiatru. ani śniegu.

Obciążenia zmęczeniowe

Obciążenia zmęczeniowe suwnicy $Q_e$ dla i-tego koła można określić jako  [1],wzór (2.16)} :

$$\begin{equation} Q_{e,i} =\varphi_{fat}\cdot \lambda \cdot Q_{max,i}\label{37}\end{equation}$$

gdzie
$Q_{max,i}$ – wartość charakterystyczna maksymalnego pionowego obciążenia od koła i,
$\lambda$ – zastępczy czynnik uszkodzeń, odniesiony do N=2,0×10⁶ cykli (czyli do trwałej wytrzymałości zmęczeniowej),
$\varphi_{fat}$- równoważny współczynnik dynamiczny powodujący uszkodzenia. Współczynnik rozróżnia się dla ciężaru własnego (i=1) i ciężaru podnoszonego (i=2) i oblicza z zależności $\varphi_{fat,i}=1/2(1+\varphi_i)$. Ponieważ wartości $\varphi_{fat}$ są różne dla ciężaru własnego i podnoszonego, więc najczęściej do obliczeń przyjmuje się wartość średnią ważoną obciążeniami:

$$\begin{equation}  \varphi_{fat}= \cfrac{ \varphi_{fat,1} \cdot Q_c+\varphi_{fat,2} \cdot Q_h} {Q_c+Q_h}= \cfrac{1}{2} \left( \cfrac{\varphi_1 \cdot Q_c +\varphi_2 \cdot Q_h} {Q_c+Q_h}\right) \label{38}\end{equation}$$

Zastępczy czynnik uszkodzeń można przyjąć na podstawie klasy Sx suwnicy zgodnie z tab .7. Załącznik B przywołany w UWAGA 2 w tej tabeli – stanowi tab. 3  w niniejszym artykule.

Tab.7. Wartości $\lambda$ według klas suwnic [1],tab. 2.12}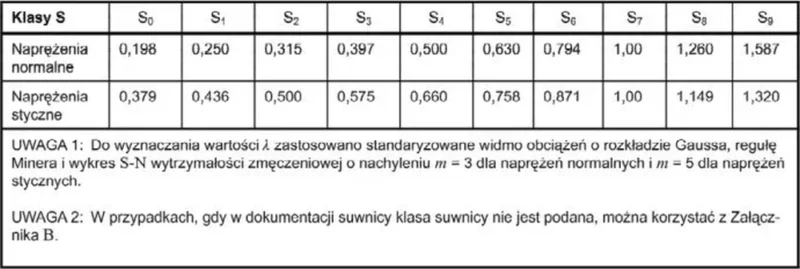

Po przeprowadzenia obliczeń dla oddziaływań dla obciążeń niezmęczeniowych, amplitudę efektów tych oddziaływań $\sigma_p$ lub $\tau_p$ w danym punkcie konstrukcji można przeliczyć na efekty zmęczeniowe przez adaptację formuły ($\ref{37}$) :

$$\begin{equation} \sigma_{E2} =\varphi_{fat}\cdot \lambda \cdot \sigma_p \label {39} \end{equation}$$

i analogicznie dla naprężeń stycznych $\tau_{E2} =\varphi_{fat}\cdot \lambda \cdot \tau_p$ lub dla naprężeń głównych.

Jeśli wyznaczono maksymalne w danym punkcie naprężenia max $[\sigma_{E2}, \tau_{E2} , \sigma_{1,E2}]$  i minimalne min $[\sigma_{E2}, \tau_{E2} , \sigma_{1,E2}]$ w trakcie przejazdu suwnicy w jednym cyklu, to ich różnica stanowi amplitudę naprężeń

$$\begin{equation} \Delta \sigma_{E2} =max \sigma_{E2} – min\sigma_{E2} \label{40} \end{equation}$$

Sprawdzenie wytrzymałości zmęczeniowej dla punktu z wyznaczona amplitudą naprężeń $\Delta \sigma_{E2}$ przeprowadza się zgodnie z normą  [11], wzór (8.2) :

$$\begin{equation} \gamma_{Ff} \cdot \Delta \sigma_{E2} \le \Delta \sigma_c  / \gamma_{Mf}\label{41}\end{equation}$$

gdzie:
$\gamma_{Ff}=1,0$ – częściowy współczynnik bezpieczeństwa dla obciążeń zmęczeniowych,
$\gamma_{Mf}=1,15$ – częściowy współczynnik bezpieczeństwa dla wytrzymałości zmęczeniowej,
$\Delta \sigma_c$ -kategoria zmęczeniowa zależna od rodzaju karbu wg [11] .

$$\begin{equation} \sigma_{E2} =\varphi_{fat}\cdot \lambda \cdot \sigma_p\label{42}\end{equation}$$

i analogicznie dla naprężeń stycznych $\tau_{E2} =\varphi_{fat}\cdot \lambda  \cdot \tau_p$ lub dla naprężeń głównych.

Obciążenia obliczeniowe

Obciążenia obliczeniowe dla suwnic  wyznacza się zgodnie z ogólnymi regułami normy Eurokod0 [12]} ,  przy czym  dla obciążeń stałych $G_s$ (ciężar suwnicy $Q_c$) i zmiennych $Q_s$ (ciężar podnoszony $Q_h$) , przyjmuje się specyficzne wartości częściowych współczynników bezpieczeństwa:

1)  w stanie SGN dla naprężeń (STR)

• dla górnej wartości amplitudy naprężeń  $\gamma_{Gs,sup}=\gamma_{Qs,sup}=1,35$,
• dla dolnej wartości amplitudy naprężeń $\gamma_{Gs,sup}=\gamma_{Qs,sup}=1,00$,

2) w stanie SGN równowagi (EQU) i  przy podniesienia podpór ciężarem własnym $G_s$

$\gamma_{Gs,sup}=1,05$, $\gamma_{Gs,inf}=0,95$ ;  $\psi_{0,Qs}=1,0$ ; $\psi_{1,Qs}=0,9$

Współczynniki redukcyjne do celów kombinacyjnych przyjmuje się następująco:

współczynnik kombinacyjny  $\psi_0=1,0$,
współczynnik wartości częstej  $\psi_1=0,9$,
współczynnik wartości prawie stałej $\psi_2$ –  stosunek oddziaływania stałego suwnicy do całkowitego oddziaływania suwnicy. W praktyce przyjmuje się  $\psi_2=0$.

Dźwignice podwieszone

W przypadku dźwignic podwieszonych oddziaływania kół na tor jezdny wyznacza się podobnie jak dla suwnic podpartych z tą różnicą, że:

1. Siły poziome od pomostowych suwnic podwieszonych przyjmuje się w poziomie styku koła z torem o wartości równej co najmniej 10% maksymalnej siły pionowej przekazywanej przez koło, bez uwzględnienia współczynnika dynamicznego, chyba że udokumentowano wartość dokładniejszą.
2. Podłużne oddziaływania poziome wciągników jednoszynowych na stacjonarne belki toru jezdnego -przy braku dokładniejszych danych- przyjmuje się równe 5%  maksymalnej siły pionowej przypadającej na koło bez współczynnika dynamicznego. Tę samą zasadę dotyczącą sił poziomych przyjmuje się w przypadku wahliwego zawieszenia belek toru jezdnego.

Siły przekrojowe od oddziaływań kół suwnicy zależą od schematu statycznego belki. Ze względu na dynamiczne działanie obciążeń oraz wielkości reakcji podporowych najczęściej stosuje się belki jednoprzęsłowe. W belkach dwuprzęsłowych reakcja na podporze jest istotnie większa (do 25%) od reakcji w belach jednoprzęsłowych, a wprowadzenie dodatkowych więzi (skrępowanie) prowadzi do powstania dodatkowych sił dynamicznych. Korzyścią stosowania belek dwuprzęsłowych jest niewątpliwie ograniczenie ugięć belek. Zdaniem autora w belach dwuprzęsłowych należy stosować  współczynnik dynamiczny $\phi_4= min 1,2$, co ogranicza zalety wieloprzęsłowych belek podsuwnicowych.

Siły przekrojowe w belkach podsuwnicowych

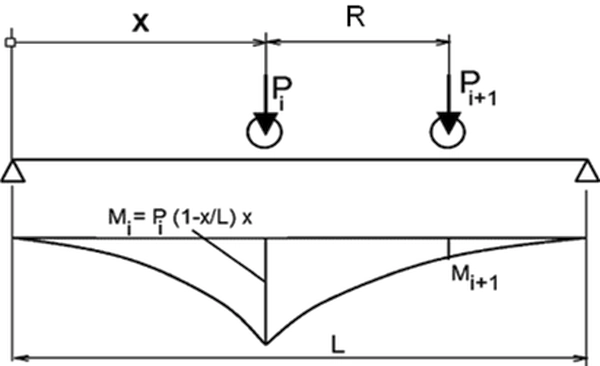
Uwagi ogólne o schemacie statycznym belek

W przypadku każdego schematu statycznego ważne jest ustawienie suwnicy wywołujące ekstremalne momenty zginające, siły poprzeczne i reakcje. Ustawienie symetryczne suwnicy zwykle nie jest miarodajne. W pliku poniżej (kliknij na obraz , aby pobrać) zamieszono arkusz do wyznaczania miarodajnej lokalizacji suwnicy o dwóch do czterech kołach lub dwóch suwnic po dwa koła na jednoprzęsłowej belce podsuwnicowej (chodzi o liczbę kół jezdnych na  jednym torze).

Rys.8 Ustawienie suwnic [kliknij , by pobrać arkusz obliczeniowy]

Można sprawdzić, że dla dwóch kół uzyskuje się wyniki zgodne z formułami analitycznymi, podanymi na przykład w pracy [8] .

Po wyznaczeniu umiejscowienia suwnicy na belce można prowadzić klasyczne obliczenia bez potrzeby wykorzystywania algorytmów dla obciążeń poruszających się.

Warunki nośności zmęczeniowej belek podsuwnicowych omówiono w artykule Zmęczenie stali konstrukcyjnej.

Przykłady rachunkowe

Przykład 1 [Oddziaływania kół suwnicy ABUS 20t]

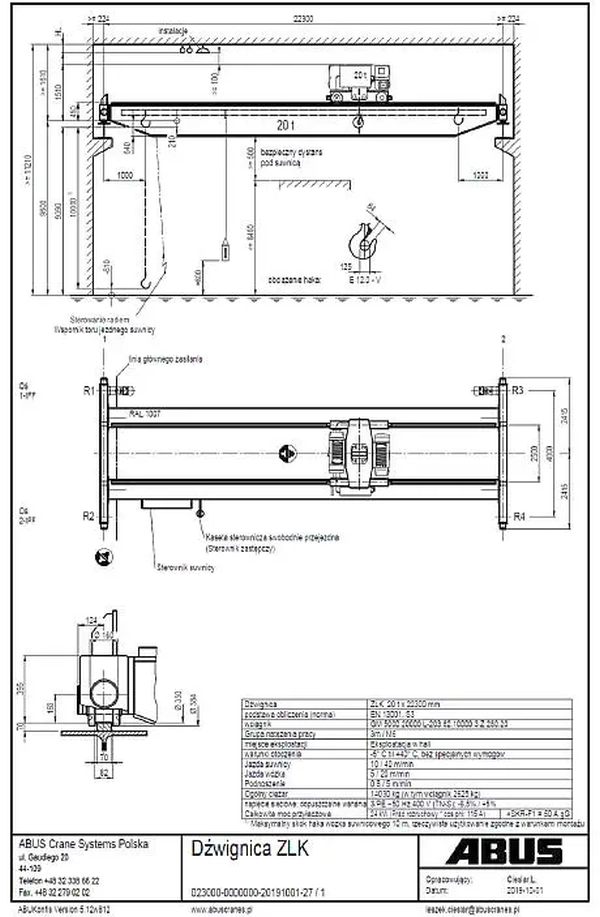
Wyznaczyć oddziaływania kół suwnicy ABUS 20t, pokazanej na rys. 9 na belkę podsuwnicową.

Dane suwnicy(karta katalogowa – rys.9 :

Rys.9 Karta katalogowa suwnicy ABUS

typ: ZLK 20t x 22300
$Q_{h,nom}=200 \, kN$
ogólny ciężar $G_c= 140,3 \, kN$, w tym wózka $G_f= 26,25 \, kN$
długość mostu L =22,3 m,
rozstaw kół a = 4 m
minimalna odległość haka $e_{min}=1,0 \, m$
system napędu IFF (koła niezależne, oba zamocowane),
liczba kół napędzanych $m_w=2$
liczba osi (torów) n= 2

grupa natężenia pracy 3m /M6
klasa suwnicy S3
prędkość:
suwnicy 10/ 40 m/min
wózka  54/20 m/min
podnoszenia $v_h = 0,8/ 5 m/min\tov_h=5/60=0,083 m/s$

W projekcie przewidziano:

• szynę dźwignicową A65:
  wysokość $h_r=75 mm$
  szerokość główki szyny $b_r=65 mm$
• koło ABUS o szerokości między obrzeżami 70 mm.

Oddziaływania podane przez Producenta

Producent podaje następujące współczynniki dynamiczne:
$\varphi_1=1,1$ (przyśpieszenie, działające na masę suwnicy, wynikające z podnoszenia i grawitacji) ,
$\varphi_2=1,1$ (bezwładność i grawitacja przy podnoszeniu bez przeszkód ładunku z podłoża),
$\varphi_3=1,0$ (bezwładność i grawitacja przy gwałtownym opuszczaniu części podnoszonego ładunku z podłoża),
$\varphi_4=1,0$ (obciążenia jazdy po nierównościach),
$\varphi_5=1,8$ (obciążenia z przyśpieszenia przez napędy jazdy suwnicy),
$\varphi_{6,dyn}=1,1$, (dynamiczne obciążenia pomiarowe),
$\varphi_{6,stat}=1,0$, (statyczne obciążenia pomiarowe),
$\varphi_7=1,25$, (obciążenia  z sił buforowych).

Rys.  10 Schemat oddziaływań suwnicy ABUS ZLK.

Producent podaje następujące wartość oddziaływań:

Pionowe od ciężaru suwnicy
$Q_{c,min,1}= 28,3 \, kN$ $Q_{c,max,1}= 39,1 \, kN$,
$Q_{c,min,2}= 28,7 \, kN$ $Q_{c,max,2}= 40,0 \, kN$
pionowe od ładunku
$Q_{h,min,1}= 4,4 \, kN$ $Q_{h,max,1}= 94,6 \, kN$,
$Q_{h,min,2}= 4,4 \, kN$ $Q_{h,max,2}= 94,6 \, kN$

Pionowe oddziaływania łączne (od ciężaru własnego i ładunku wyniosą:
$Q_{r,min,1}= 28,3+4,4=32,7 \,KN$
$Q_{r,min,2}= 28,7+4,4=33,1 \,KN$
$Q_{r,max,1}= 39,1+94,6=133,7 \, kN$
$Q_{r,max,2}= 40,0+94,6=134,6 \, kN$

Poziome poprzeczne do toru

od przyśpieszenia dźwignicy z podnoszonym ładunkiem
$H_{T,min}= 1,8 \, kN$ $Q_{T,max}= 7,3 \, kN$,

Od ukosowania suwnicy
$Q_{S,min,1}= 0 \, kN$ $H_{S,max,1}= 0 \, kN$,
$Q_{S,min,2}= 7,2 \, kN$ $H_{S,max,2}= 29,5 \, kN$

Poziome podłużne do toru
od hamowania
$H_{L}= 7,2 \, kN$
od uderzenia w odbojnicę
$H_{B,1}= 25,9 \, kN$

Oddziaływania wg [1]}

Współczynniki dynamiczne

$(\ref{3}) \to$ $\varphi_1= 1,1$

Tab.3: dla suwnicy klasy S3 , warsztatowej $\to$ klasa podnoszenia HC2
Tab.2 dla klasy HC2 $\to$: $\beta_2=0,34$, $\varphi_{2,min}=1,1$
prędkość podnoszenia $v_h$ – w danych suwnicy

($\ref{4}) \to$  $\varphi_2=1,1+0,34 \cdot 0,083= 1,13$

Nie ma możliwości gwałtownego zrzucenia ładunku (prowadzenie giętkie ładunku bez zaczepów elektromagnetycznych) $\to$ Współczynnik φ3 $\to$ $\varphi_3=1,0$

Zachowane są tolerancje dla torów podsuwnicowych $\to$ Współczynnik φ4   $\to$ $\varphi_4=1,0$,

Zgodnie z Współczynnik φ5 współczynnik $\varphi_5$ przyjmuje się o wartości podanej przez Producenta na wypadek zderzenia, czyli:
$\varphi_5=1,8$,

$(\ref{4}) \to$ $\varphi_6=\frac{1}{2}(1+1,13)= 1.07$

Zderzak twardy $\to$ Współczynnik φ7 $\to$ $\varphi_7=1,25$

W tab. 8 zestawiono wartości współczynników dynamicznych, natomiast w tab. 9 pokazano przypisanie tych współczynników do poszczególnych grup obciążeń (przypadków obciążeń oddziaływania suwnicy)

Tab.8 Zestawienie wartości współczynników dynamicznych dla przykładu 1

Tab.9 Odpowiedniość współczynników dynamicznych do grup obciążeń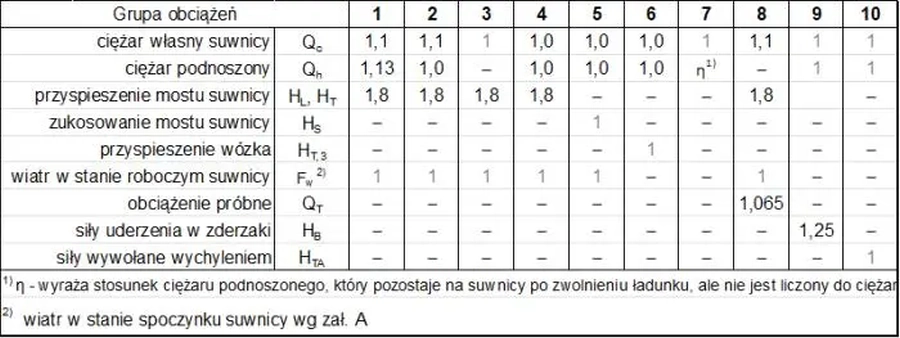

Wniosek:

Z porównania współczynników dynamicznych przyjętych zgodnie z normą ze współczynnikami podanymi przez Producenta, należy stwierdzić zgodność, choć niewielkie różnice występują dla $\varphi_2$ (1,13 zamiast 1,1 Producenta)  oraz $\varphi_6$ (1,07 zamiast 1,1 Producenta).

Minimalne oddziaływania pionowe $F_z$ (dla suwnicy bez obciążenia)

Grupa 1 i 2
$( \ref{7} )$ $\to$
$Q_{c,k}= 1,1 \cdot 140,3= 154,33 \, kN$,
$Q_{f,k}=1,1 \cdot 26,25 \cdot 1,1= 28,88 \, kN$,

$( \ref{8})$ $\to$ $Q_{r,min}= \cfrac{154,33- 28,88}{2\cdot 2}+\cfrac{28,88\cdot (22,3-1,0)} {2\cdot 22,3}= 45,15 \, kN$,
$( \ref{9})$ $\to$ $Q_{r,(min)}= \cfrac{154,33- 28,88}{2\cdot 2}+\cfrac{28,88 \cdot  1} {2\cdot 22,3}= 32,01 \, kN$,
$( \ref{10})$ $\to$ $\Sigma Q_{r,min}= 2 \cdot 45,15=90,31 \, kN$
$( \ref{11})$ $\to$ $\Sigma Q_{(r,min)} =2 \cdot 32,01 =64,02 \, kN$

Grupa 3 do 6

$( \ref{7} )$ $\to$
$Q_{c,k}=1,0 \cdot 140,3= 140,3 \, kN$,
$Q_{f,k}=1,0 \cdot 26,25 \cdot 1,1= 26,25 \, kN$,
$( \ref{8})$ $Q_{r,min}= \cfrac{140,3- 26,25}{2\cdot 2}+\cfrac{26,25 \cdot (22,3-1,0)} {2\cdot 22,3}= 41,05 \, kN$,
$( \ref{9})$ $Q_{r,(min)}= \cfrac{140,3- 26,25}{2\cdot 2}+\cfrac{26,25 \cdot  1} {2\cdot 22,3}= 29,10 \, kN$,
$( \ref{10})$ $\Sigma Q_{r,min}= 140,3/2=70,15 \, kN$
$( \ref{11})$ $\Sigma Q_{(r,min)} =140/2+26,25= =96,40 \, kN$

Maksymalne oddziaływania pionowe $F_z$ (dla suwnicy z obciążeniem)

Grupa 1:
$(\ref{12})$ $\to$ $Q_{h,k}=1,13 \cdot 200=226 \,kN$
$(\ref{13})$ $\to$ $Q_{r,max}=45,15+ \cfrac {226 \cdot (22,3-1,0)} {2 \cdot 22,3}= 153,09 \, kN$
$(\ref{14})$ $\to$ $Q_{r,(max)}=32,01+ \cfrac { 226 \cdot 1,0} {2 \cdot 22,3}= 37,08 \, kN$
$(\ref{15})$ $\to$
$\Sigma Q_{r,max}=153,09 \cdot 2 = 306,17 \, kN$
$\Sigma Q_{r,(max)}=37,08 \cdot 2 = 74,16 \, kN$

Grupa 2:
$(\ref{12})$ $\to$ $Q_{h,k}=1,0 \cdot 200=200 \, kN$
$(\ref{13})$ $\to$ $Q_{r,max}= 45,15+ \cfrac {200 \cdot (22,3-1,0)} {2 \cdot 22,3}= 140,67 \, kN$
$(\ref{14})$ $\to$ $Q_{r,(max)}= 32,01+ \cfrac { 200 \cdot 1,0} {2 \cdot 22,3}= 36,50 \, kN$
$(\ref{15})$
$\to$ $\Sigma Q_{r,max}=140,67 \cdot 2 = 281,34 \, kN$
$\to$ $\Sigma Q_{r,(max)}=42,4 \cdot 2 = 72,99 \, kN$

Grupa 4,5 i 6
$(\ref{12})$ $\to$ $Q_{h,k}=1,0 \cdot 200=200 \, kN$
$(\ref{13})$ $\to$ $Q_{r,max}=41,05+ \cfrac {200 \cdot (22,3-1,0)} {2 \cdot 22,3}= 136,56 \, kN$
$(\ref{14})$ $\to$ $Q_{r,(max)}=29,10+ \cfrac { 200 \cdot 1,0} {2 \cdot 22,3}= 33,59 \, kN$
$(\ref{15})$ $\to$
$\Sigma Q_{r,max}=136,56 \cdot 2 = 273,13 \, kN$
$\Sigma Q_{r,(max)}=33,59 \cdot 2 = 67,17 \, kN$

Wniosek:  Oddziaływania podane przez Producenta $Q_{r,min}=33,1$, Q_{r,max}=134,6} są o ok 10% mniejsze, choć nie wiadomo dla jakich grup obciążeń były wyznaczane.

Siła K i siły podłużne $H_L$

($\ref{18}$) $\to$  $\Sigma Q^*_{r,min}= 2 \cdot 45,15 =90,31 \, kN$, $(m_w=2)$
($\ref{17}$) $\to$ $K=0,2 \cdot 90,31 =18,06 \, kN$
($\ref{16}$) $\to$ $H_{L} = 1,8 \cdot  18,06 / 2=16,25 \, kN$

Producent podał $H_L=7,2 \,kN$.
Podobny wynik do podanego przez Producenta, można uzyskać jeśliby przyjąć liczbę kół napędzanych$m_w=1$

Ukosowanie suwnicy

Odległość między elementami prowadzącymi $a_{ext}= a= 4 m$

Luz w kole (między szyną a obrzeżem koła
$x= b- b_r= 70-65 = 5 \,mm$, (odległość obrzeży – szerokość główki szyny)
lecz z warunku minimum normowego przyjęto wartość bardziej niekorzystną $0,75 x = 5 \, mm$, czyli $x=6,7 \, mm$.
Zużycie boczne szyny „y”  przyjęto jako 15% szerokości główki szyny:
$y=0,15 b_r= 0,15 \cdot 65= 9,75 \,mm$

Kąt zukosowania :
$\alpha_F=\cfrac{0,75 x}{a_{ext}}=5/4000=0,00125$\alpha_V=\cfrac{y}{a_{ext}}=9,75/4000=0,00244
($\ref{16}$) $\to$   $\alpha=  0,00125+0,00244+0,001 = 0,0047 \, rad \le 0,015 \, rad$ $to$

Współczynnik „niekorzystny”
($\ref{20}$) $\to$ $f= 0,3 \cdot ( 1−\exp { (−250*0,005)} =0,2071 \le 0,3$,

Położenie chwilowego środka obrotu:
($\ref{18}$) $\to$ $\Sigma Q_r=262,4 +77,9=340,3 \, kN$
($\ref{17}$)  $\to$ $\xi_1=\cfrac{262,4}{340,3}= 0,80$ , $\xi_2=1-0,80=0,20$

Liczba kół sprzężonych
m=0 (system IFF)

odległość przedniej pary kół od elementów prowadzących
dla kół z kołnierzem:
($\ref{21}$)  $\to$ $e_1=0$
$e_2= a = 4 \, m$,

$\Sigma e_i= 0+4= 4 \, m$,
$\Sigma e_i^2=0^2+4^2= 16 \, m^2$,
($\ref{23}$)  $\to$ $h=\cfrac{ 0 \cdot 0,77\cdot 0,23 \cdot 22,3^2 + 16}{4}= 4 \, m$,

Siła prowadząca $S$
($\ref{24}$)  $\to$ $\lambda_{S,j}=1-\cfrac{4}{2\cdot 4}=0,5$
($\ref{19}$)  $\to$ $S=0,2071 \cdot 0,5 \cdot 340,3= 35,232 \, kN$

Współczynniki siły:
Tab.6 $\to$ $\lambda_{S,1,j,L}=\lambda_{S,2,j,L}=0$

Przednia para kół (j=1)
($\ref{24}$) $\to$
$\lambda_{S,1,1,T}=\cfrac{0,2}{2} \cdot \left( 1-\cfrac{0}{4} \right)= 0,100$,
$\lambda_{S,2,1,T}=\cfrac{0,8}{2} \cdot \left( 1-\cfrac{0}{4} \right)= 0,400$,

Tylna para kół (j=2)
($\ref{24}$) $\to$
$\lambda_{S,1,2,T}=\cfrac{0,8}{2}\cdot \left( 1-\cfrac{4}{4}\right)= 0$,
$\lambda_{S,2,2,T}=\cfrac{0,2}{2}\cdot \left( 1-\cfrac{4}{4}\right)= 0$,

Siły poziome od ukosowania
($\ref{25}$) $\to$
$H_{S,1,1,L}=H_{S,1,2,L}=H_{S,2,1,L}=H_{S,2,2,L}=0$

Przednia para kół (j=1)
$H_{S,1,1,T}=0,2071 \cdot 0,100\cdot 340,3=7,046 \, kN$
$H_{S,2,1,T}=0,2071 \cdot 0,400\cdot 340,3=28,186 \, kN$
Tylna para kół (j=2)
$H_{S,1,2,T}= 0$
$H_{S,2,2,T}=0$

Siły bezwładności od przyśpieszania/hamowania suwnicy

Mimośród siły napędu
($\ref{20}$) $l_s=(0,8-0,5)\cdot 22,3=6,69 \, m$
Moment napędu
($\ref{19}$) $\to$ $M=18,06 \cdot 6,69= 120,82 \, kNm$

Siły poprzeczne od bezwładności

($\ref{21}$) $\to$
$H_{T,1}= \varphi_5\cdot \xi_2\cdot M/a=1,8\cdot 0,2\cdot 120,82/4=10,87 \, kN$
$H_{T,2}= \varphi_5\cdot \xi_1\cdot M/a=1,8\cdot 0,8\cdot 120,82/4=43,50 \, kN$

Momenty skręcające belkę

Mimośród przyłożenia siły pionowej do główki szyny:
$(\ref{35}$) $\to$ $e_e=65/4= 16,25 \, mm$
Tolerancja montażu szyny na belce
$\Delta=\max{ (5 mm \quad ; \quad 10,2/2}=5,1\, mm$
Mimośród poziomy $e_y$
$(\ref{36})$ $\to$ $e_y=5,1+16,25= 21,35 \, mm=0,0214\, m$

Mimośród  pionowy $e_z$
Belka wykonana z HEB 500, więc  $h_{belka}= 500 \, mm$
$(\ref{34})$ $\to$ $e_z=  75 +500/2= 325 \, mm=0,325 \, m$

Momenty skręcające dla grupy 1 obciążeń:

oś 1, koło 1: 43,50 \cdot 0,325 – (-153,09)\cdot 0,0214= 14,138+ 3,276=17,41 kNm

Wartości momentów skręcających dla pozostałych kół i przypadków obciążeń zestawiono w tab. 10.

Zestawienie oddziaływań suwnicy

W tab. 10 zestawiono oddziaływania suwnicy w dwóch układach:

1. zestawienie obciążeń wg przypadków (grup obciążeń) , wykonane poprzez ułożenie  wyników uzyskanych wyżej.
2. zestawienie obciążeń na koła suwnicy, wykonane poprzez przypisanie oddziaływań do poszczególnych kół suwnicy w układzie $[F_x,F_y,F_z]$, co umożliwia dalej przeprowadzenie obliczeń belki podsuwnicowej oraz układu konstrukcyjnego hali.

Tab. 10 Zestawienie obciążeń dla suwnicy ABUS 20t wyznaczonych wg [1]}

Zestawienie oddziaływań według przypadków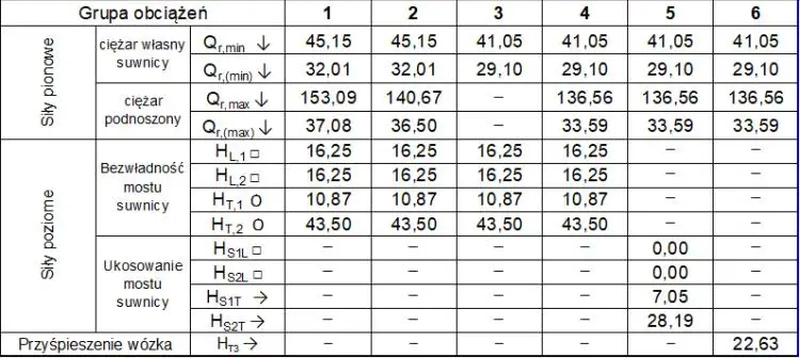

Zestawienie oddziaływań na koła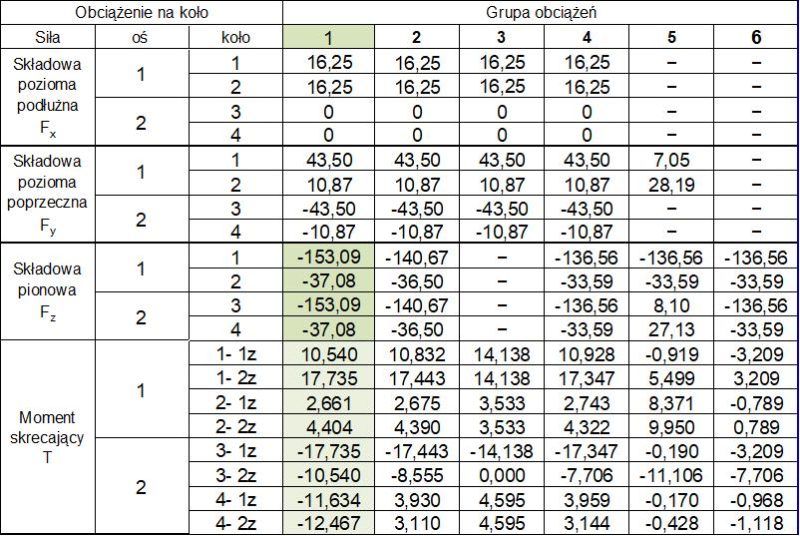

Oddziaływania suwnicy w/g kalkulatora programu Consteel

W celu sprawdzenia otrzymanych wyników , przeprowadzono obliczenia kalkulatorem wbudowanym do programu Consteel [13] i zestawiono je w tab. 11.

Tab. 11 Zestawienie oddziaływań wg Consteel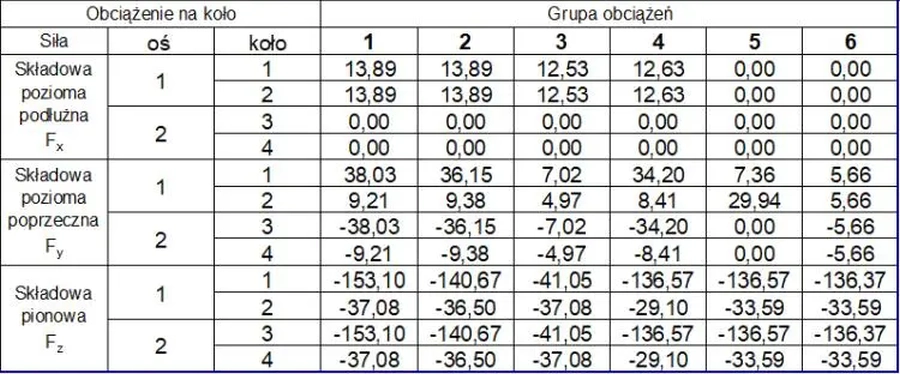

Stwierdzono dużą zgodność obliczeń ręcznych i prowadzonych przez kalkulator programu Consteel. Nieznaczne różnice dotyczą obciążeń poziomych, co jest spowodowane różnicami w przyjmowaniu luzów między szyną, a obrzeżem.

Wnioski:

1. Z analizy wyników wynika, że sprawczym przypadkiem dla obliczeń konstrukcji wsporczej suwnicy jest przypadek 1 , obserwowany dla grupy 1 obciążeń suwnicą. Ten przypadek (schemat obciążeń) jest przyjmowany do dalszych obliczeń.

Obciążenia zmęczeniowe

Zastępcze czynniki uszkodzeń zmęczeniowych
Tab.7  dla klasy S3  $\to$:
$\lambda_n=0,397$
$\lambda_s=0,575$

Współczynniki dynamiczne zmęczeniowe:
od ciężaru własnego $\varphi_{fat,1}=(1+1,1)/2=1,05$
od ciężaru podnoszonego $\varphi_{fat,1}=(1+1,13)/2=1,065$
średni $(\ref{38}$) $\to$ $\varphi_{fat}=(1+ \cfrac{1,1 \cdot 140,3}{1,13 \cdot 200} {140,3+200})/2=1,06$

Maksymalne naciski pionowe:
od koła 1 i 3 : $Q_{max,1,3}=max [153,09; 140,67; 136,56]=153,09 \, kN$,
od koła 2 i 4 : $Q_{max,2,4}=max 37,08; 36,50; 33,59)=37,08 \, kN$.

Obciążenia zmęczeniowe:
$(\ref{37}$)
od koła (1) i (3) dla  naprężeń normalnych  : $Q_{e,n ,(1,3)}= 1,06 \cdot 153,09  \cdot 0,397= 64,5 \, kN$,
od koła (1) i (3) dla naprężeń stycznych  : $Q_{e,s ,(1,3)}= 1,06 \cdot 153,09 \cdot 0,575=93,2 \, kN$

Przykład 2 [ Siły przekrojowe w belce podsuwnicowej]

W trakcie przygotowania.

Najczęściej zadawane pytania

 Literatura

1. PN-EN 1991-3: 2009, Eurokod 1: Oddziaływania na konstrukcje. Część 3: Oddziaływania wywołane dźwignicami i maszynami
2. PN-ISO 4301-1:1998, Dźwignice – Klasyfikacja – Postanowienia ogólne
3. PN-EN 13001-1:2015:2015, Dźwignice – Ogólne zasady projektowania, Część 1: Po-stanowienia ogólne i wymagania
4. Żmuda J. (2013). Konstrukcje wsporcze dźwignic. Wydawnictwo Naukowe PWN, Warszawa
5. PN-EN 13001-1:2015:2015, Dźwignice – Ogólne zasady projektowania, Część 1: Postanowienia ogólne i wymagania
6. PN-EN 1993-6+Ap1+AC:2009, Eurokod 3 – Projektowanie konstrukcji stalowych – Część 6: Konstrukcje wsporcze dźwignic
7. PN-EN 13001-2:2014, Bezpieczeństwo dźwignic – Ogólne zasady projektowania, Część 2: Obciążenia
8. Kurzawa Z., Rzeszut K., Szumigała, M. (2015). Stalowe konstrukcje prętowe. Część III Konstrukcje z łukami, elementy cienkościenne, pokrycia membranowe, elementy zespolone, belki podsuwnicowe. Wydawnictwo Politechniki Poznańskiej, Poznań
9. Sedlacek G., Schneider R., Schafer N. (2003), Design example for the aplication of Eurocode 1 Part 3: Axction induced by cranes and machinery, and Eurocode 1 Paty 6: Crane supporting structures, 2 nd Draft, [ https://estudijas.llu.lv/mod/resource/view.php?id=68497 ]
10. PN-EN 1090-2+A1:2012, Wykonanie konstrukcji stalowych i aluminiowych – Część 2: Wymagania techniczne dotyczące konstrukcji stalowych
11. PN-EN 1993-1-9:2007, Eurokod 3: Projektowanie konstrukcji stalowych, Część 1-9: Zmęczenie
12. PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
13. Consteel Software. (2020), ConSteel 14 Manual [ http://www.consteelsoftware.com/en/downloads/manuals-documents ]

________________________________