1. Zależności ścisłe dla pierwszego i drugiego momentu
1.1. Podstawowe definicje
Przyjmijmy, że losowy wektor $Y=\varphi(X)$ jest znaną, w ogólności zespoloną (z częścią nierzeczywistą) funkcją $\varphi$ zmiennej losowej X, która ma funkcję gęstości probabilistycznego rozkładu $f(X)$. Momenty losowe funkcji Y: wartość oczekiwaną $ EY=\mu_y$, wariancję $VarY$ oraz odchylenie standardowe $\sigma_y$ można oszacować ze ścisłych zależności [1]:
| $ \mu_y=EY=E \varphi(X)=\int \limits_{-\infty}^\infty \varphi(x) f(x) dx$, | (1) |
| $VarY=\sigma_y^2=E[\varphi(X)-\mu_y][\varphi(X)^*-\mu_y^*]=\int \limits_{-\infty}^\infty [\varphi(X)-\mu_y][\varphi(X)^*-\mu_y^*] f(x) dx$, | (2) |
Kowariancja wzajemna $C_{yz}=Cov(y,Z)$ dwóch losowych wektorów$Y$ i $Z$, będących funkcjami $Y=\varphi(X)$ i $Z=\psi(X)$ wektora $X$, wynosi:
| $Cov(Y,Z)==C_{yz}=E[\varphi(X)-\mu_y][\psi(X)^*-\mu_z^*]=\int \limits_{-\infty}^\infty [\varphi(X)-\mu_y][\psi(X)^*-\mu_z^*] f(x) dx$, | (3) |
W przypadku, gdy, $\psi(X) \equiv X$, to z (3) uzyskujemy wyrażenie na kowariancję $C_{xy}$ wektora $X$ i $Y$:
| $Cov(X,Y)=C_{xy}=E[X-\mu_x] [\varphi(X)^*-\mu_y^*]=\int \limits_{-\infty}^\infty [X-\mu_x][\varphi(X)^*-\mu_y^*] f(x) dx$, | (4) |
Formuły (1) do (4) dotyczą zarówno rzeczywistych lub zespolonych zmiennych skalarnych lub wektorowych. Znak (*) oznacza macierz sprzężoną zespoloną, a w przypadku macierzy rzeczywistych jest to znak transpozycji macierzy (*=T).
Współczynnik korelacji zmiennych losowych $X$ i $Y$ o wartościach oczekiwanych $\mu_x=E X$ i $\mu_y=E Y $ oraz odchyleniach standardowych $\sigma_x=\sqrt {Var X}$ i $\sigma_y=\sqrt {Var Y}$, oraz kowariancji zmiennych $C_{xy} = Cov (X, Y) $, jest wartością oczekiwaną iloczynu standaryzowanych zmiennych [2]:
| $\rho_{xy}= \rho \{X , Y \}= E \left \{ \dfrac {X-\mu_x}{\sigma_x} \cdot \dfrac {Y-\mu_y}{\sigma_y} \right\}= \dfrac {C_{xy }} {\sigma_x \cdot \sigma_y}$ | (5) |
Współczynnik korelacji określa siłę sprzężenia zmiennych i przyjmuje wartości w przedziale
| $ -1 \le \rho_{xy}\le 1 $ | (6) |
Wartość $ \rho_{xy}=0 $oznacza brak związku (sprzężenia), a dla zmiennych rozłożonych normalnie – niezależność zmiennych. Dla $ \rho_{xy} = 1 $ sprzężenie jest silnie dodatnie, to znaczy wzrost (lub zmniejszenie) $X$ najczęściej prowadzi do wzrostu (lub zmniejszenia)$Y$. Na odwrót dla $ \rho_{xy}= – 1 $ relacja jest odwrotnie proporcjonalna.
1.2.Przykłady zastosowania ścisłych formuł
1.2.1. Pole powierzchni pręta zbrojeniowego o losowej średnicy D
| $A= \varphi(R)= \pi R^2$, | (7) |
Do wyznaczenia momentów losowych funkcji (7) : wartości średniej $\mu_A$ oraz odchylenia standardowego $\sigma_A$ zastosujemy najpierw ścisłe formuły (1), (2) . Z zależności (1) mamy:
| $ \mu_A=\int \limits_{-\infty}^\infty \pi r^2 f(r)dr =\pi \dfrac{1}{\sigma_r \sqrt{2 \pi}}\int \limits_{-\infty}^\infty r^2 e^{- \dfrac{1}{2} \left( \dfrac{r-r_o}{\sigma_r}\right)^2}dr$, | (8) |
Ostatnia całka wraz z mnożnikiem $ \pi \dfrac{1}{\sigma_r \sqrt{2 \pi}}$ z definicji jest momentem drugiego rzędu losowej wielkości R, który oczywiście jest równy $r_o^2+\sigma_r^2$. Stąd otrzymujemy:
| $ \mu_A= \pi (r_o^2+\sigma_r^2)$, | (9) |
Z formuły (2) mamy:
| $VarA=\pi^2\dfrac{1}{\sigma_r \sqrt{2 \pi}}\int \limits_{-\infty}^\infty (r^2-r_o^2-\sigma_r^2)^2 \cdot e^{- \dfrac{1}{2} \left( \dfrac{r-r_o} {\sigma_r}\right)^2}dr$, | (10) |
Po obliczeniu tej całki [1], otrzymamy:
| $VarA=2 \pi^2 \sigma_r^2 (2r_o^2+ {\sigma_r}^2)$, | (11) |
1.2.2. Ugięcie wspornikowej belki Timoshenko o losowej długości L
Wyznaczymy momenty losowego ugięcie $Y$ końca wspornikowej belki Timoshenko (z uwzględnieniem sztywności postaciowej) o losowej długości $L$ i innych parametrach nielosowych, w tym o sztywności giętnej $EI$ oraz postaciowej $S_v$.
1.2.2.1. Postawienie zadania
Przemieszczenie $Y$ końca wspornika (pod siłą P) można wyznaczyć ze znanej zależności:
| $Y=\int \limits_0^L \left( \dfrac{M \overline M}{EI} + \dfrac{T \overline T}{S_v} \right ) dx$ | (12) |
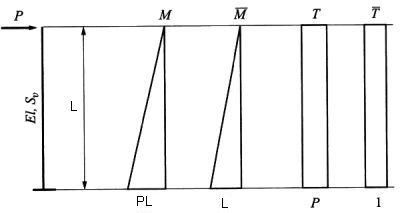Rys.1. Zginanie i ścinanie wspornika Timoshenko
Po „przemnożeniu wykresów sił”,pokazanych na rys.1. otrzymujemy formułę na ugięcie $Y$, które jest funkcją losowego argumentu $L$:
| $Y=\dfrac {PL^3}{3EI} +\dfrac{PL}{S_v}= \dfrac{P }{3 EI}( L^3+ 3 k L)$, | (13) |
gdzie współczynnik podatności na ścinanie $k = \dfrac{EI}{S_v} $.
1.2.2.2. Parametry losowej długości belki
Przyjmijmy, że losowa długość pręta X=L ma jednostajny rozkład prawdopodobieństwa z gęstością prawdopodobieństwa
$\dfrac{1}{2\cdot \Delta L}$ w przedziale $(L-\Delta L ; L+\Delta L)$, a poza tym przedziałem jest równa zero.
Rozkład ten pokazano na rys. 1. Tak przyjęty rozkład oznacza, że w przedziale możliwych wartości długości belki $L \pm \Delta L$, gdzie $\Delta L$ jest dopuszczalną tolerancją może przyjąć każdą wartość z tym samym prawdopodobieństwem
$p= Prob\{X=x\}= \dfrac{1}{2 \Delta L}$,
a kontrola jakości wyklucza wartości spoza tego przedziału.
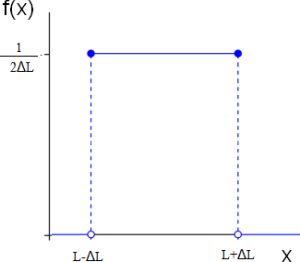Rys.1 Rozkład równomierny losowej długości belki
Z własności rozkładu jednostajnego, wynika że wartość oczekiwana długości belki wynosi
$\mu_x= \dfrac{(L-\Delta L)+(L+\Delta L)}{2}=L$,
a wariancja
$Var X= \dfrac{[(L- \Delta L)-(L+ \Delta L)]^2}{12}= \dfrac {\Delta^2 L} {3}$.
1.2.2.3. Wartość oczekiwana i odchylenie standardowe ugięcia
Wartość oczekiwana (1) ugięcia (12) wynosi:
| $\mu_y= C p \int \limits_{L- \Delta}^{L+ \Delta}\ (x^3 + 3k x) dx= C L (L^2 +\Delta^2 +3k)$, | (14) |
| $\Delta=\Delta L$, $C=\dfrac{P}{3 EI}$, $p=\dfrac{1}{2 \Delta}$ |
(15a,b,c) |
Porównując (14) z funkcją (13) widzimy zgodność zapisu dla $\Delta=0 $, to znaczy dla długości belki wykonanej bez odchyłki wymiarowej. Do porównania wrócimy jeszcze podczas omawiania metody linearyzacji.
Wariancja (2) ugięcia (12) wynosi:
| $ VarY = C^2 p \int \limits_{L- \Delta}^{L+ \Delta}(x^3 + 3k x)^2 dx = C^2 \Delta^2 \left ( 3L^4 +2L^2 \Delta^2 +3k^2 +\dfrac{6k}{5} (5 L^2 +\Delta^2) +\dfrac{\Delta^4}{7} \right) $ | (16) |
Dla długości belki wykonanej bez odchyłki wymiarowej $\Delta=0$ wariancja jest zerowa.
Kowariancja (4) ugięcia (13) z losową długością $L$wynosi:
| $ Cov _{YL}= C p \int \limits_{L- \Delta}^{L+ \Delta}(x^3 + 3k x) \cdot (x-L) dx = C \Delta^2 \left ( L^2+k+\dfrac {\Delta^2}{5} \right) $, | (17) |
| $\rho_{YL}=\dfrac{L^2+k +\dfrac{\Delta^2}{5}} {\sqrt{ (k+L^2)^2+ \dfrac {14}{105} (3k+5 L^2)\Delta^2 +\dfrac{\Delta^4}{21}}}$. | (18) |
Dla $\Delta=0$ korelacja jest pełna ($\rho_{YL}=1$).
Dla $k=0$ (dla klasycznej belki Bernoulliego) formuły (14 do 18) upraszczają się do postaci (19):
| $\mu_y= C L (L^2 +\Delta^2)$ $ VarY == C^2 \Delta^2 \left ( 3L^4 +2L^2 \Delta^2 +\dfrac{\Delta^4}{7} \right) $ $ Cov \{ Y, L \}=C \Delta^2 \left ( L^2\dfrac {\Delta^2}{5} \right) $ $\rho_{YL}=\dfrac{L^2+\dfrac{\Delta^2}{5}} {\sqrt{ L^4+ \dfrac {14}{21}\Delta^2L^2 +\dfrac{\Delta^4}{21}}}$. |
(19a-d) |
2. Metoda linearyzacji
2.1. Podstawy
Obliczanie momentów funkcji losowych ze ścisłych zależności (62, 63, 64) jest zadaniem złożonym rachunkowo, a wynik analityczny udaje się znaleźć w nielicznych przypadkach prostych funkcji oraz rozkładów probabilistycznych argumentów funkcji (przykłady 1.2. są takimi wyjątkowymi przypadkami). W celu umożliwienia oszacowania momentów złożonych funkcji, w praktyce inżynierskiej, stosuje się metodę linearyzacji, która polega na tym , że nieliniową funkcję $\varphi(x)$, zastępuje się linią prostą w punkcie najbardziej prawdopodobnym, czyli w punkcie oczekiwanym $\mu_x$ argumentu x, tak jak pokazano na rys. 16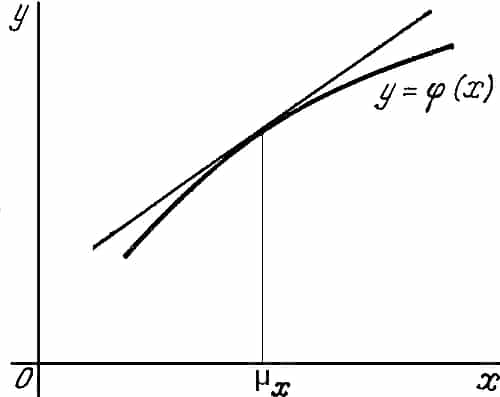
Rys.16 Linearyzacja funkcji losowej w punkcie oczekiwanym $\mu_x$ [1]
Zależność zmiennej $Y$ od $X$ zgodnie z prostą pokazaną na rys. 16 przyjmuje postać:
| $Y \approx \varphi ( \mu_x ) + \varphi^{’} (\mu_x ) (X- \mu_x )$, | (20) |
W przypadku , gdy X jest wektorem, to pochodną $\varphi^{’} (\mu_x )$ należy traktowac jako macierz wrażliwości – pochodne wszystkich współrzędnych wektora $\varphi (x )$ podług współrzędnych wektora x w punkcie $x= \mu_x$:
| $ \varphi^{’} (\mu_x ) = \left[\begin{array} {cccc} \dfrac{\partial \varphi_1} {\partial x_1} & \dfrac {\partial \varphi_1} {\partial x_2} & \ldots & \dfrac {\partial \varphi_1} {\partial x_n} \\ \ldots & \ldots & \ldots &\ldots \\ \dfrac {\partial \varphi_r} {\partial x_1} & \dfrac{\partial \varphi_r}{\partial x_2} & \ldots &\dfrac{\partial \varphi_s}{\partial x_n} \end{array} \right]_{x=\mu_x}$ | (21) |
gdzie n – rozmiar wektora $X$, r- rozmiar wektora $Y$. Do funkcji liniowej (17) możemy zastosować standardowe procedury wyznaczenia wartości oczekiwanej oraz macierzy kowariancji wektora $Y$ [1], a w rezultacie otrzymamy formuły linearyzacji probabilistycznej:
| $ \mu_y \approx \varphi ( \mu_x ) $, | (22a) |
| $ C_y \approx \varphi ^{’} ( \mu_x ) C_x \varphi ^{’} ( \mu_x )^*$, | (22b) |
gdzie $ C_x=Cov X $, $C_y=Cov Y $ są macierzami kowariancji odpowiednio wektora X i Y. W przypadku zmiennej skalarnej kowariancja staje się wariancją: $ CovX=Var X=\sigma_x^2$, gdzie $\sigma_x$ jest odchyleniem standardowym zmiennej X.
Formuły (14a, b) dotyczą zarówno rzeczywistych lub zespolonych zmiennych skalarnych lub wektorowych. Znak (*) oznacza macierz sprzężoną zespolona, a w przypadku macierzy rzeczywistych jest to znak transpozycji macierzy (*=T).
Dokładność metody linearyzacji zależy od rozproszenia losowego zmiennej wejściowej. Jeśli $ \sigma_x \ll \mu_x$. to dokładność aproksymacji jest dobra i zmniejsza się wraz ze zmniejszaniem się nieliniowości funkcji.
2.2. Przykłady metody linearyzacji i ocena dokładności
2.2.1. Pole powierzchni pręta zbrojeniowego o losowej średnicy D
Rozwiążemy zadanie z przykładu 1.2.1. metodą linearyzacji.
Pochodna cząstkowa funkcji $\varphi(x)$ (7) przy oznaczeniu $x=R$ wynosi:
| $ \varphi(x)^{’}= \dfrac {\partial \varphi(x)}{\partial x}= 2\pi r $, | (23) |
Z (22 a,b) otrzymujemy:
| $ \mu_A \approx \tilde {\mu_A}= \varphi(\mu_r)=\varphi(r_0)=\pi r_o^2 $, | (24a) |
| $ Var A \approx \tilde {VarA}= |\varphi^{’} (\mu_r)|^2 \cdot \sigma_r^2=|\varphi^{’} (r_0)|^2 \cdot \sigma_r^2=4 \pi^2 r_0^2 \sigma_r^2$, | (24b) |
Porównując oszacowania (24a,b) z wartościami ścisłymi (9), (11) , otrzymujemy:
| $ \dfrac {\mu_A} {\tilde{\mu_A}}=1+ \dfrac {\sigma_r^2} {r_o^2}$, | (25a) |
| $ \dfrac {Var A} {\tilde{Var A}}=1+\dfrac { \sigma_r^2} {2 r_o^2}$, | (25b) |
W prezentowanym przykładzie dla $\sigma_r=0,1 r_0$ błąd oszacowania średniej wynosi 1%, a wariancji 0,5% .
2.2.2. Ugięcie wspornikowej belki Timoshenko o losowej długości L
Rozwiążemy zadanie z przykładu 1.2.2. metodą linearyzacji.
Pochodna cząstkowa funkcji $Y(x)$ (12) przy oznaczeniu $x=L$ wynosi:
| $ Y(x)^{’}= \dfrac {\partial Y (x)}{\partial x}= 3C ( x^2+k)$, | (26) |
Z (22 a,b) otrzymujemy:
| $ \mu_A \approx \tilde {\mu_Y}= \varphi(\mu_x)=3C(L^2+k) $, | (27a) |
| $ Var Y \approx \tilde {VarY}= |\varphi^{’} (\mu_x)|^2 \cdot \sigma_x^2=|\varphi^{’} (L)|^2 \cdot \sigma_L^2=C^2 \Delta^4(k+L^2)^2$, | (27b) |
Porównując oszacowania (27a,b) z wartościami ścisłymi (14), (16) , otrzymujemy:
| $ \dfrac {\mu_Y} {\tilde{\mu_Y}}=1+ \dfrac {\Delta^2} {L^2+3k}$, | (28a) |
| $ \dfrac {Var Y} {\tilde{Var Y}}=1+….$, | (28b) |
W prezentowanym przykładzie dla $k=0$ (belka Bernoulliego) i dla spotykanego w praktyce $\dfrac {\Delta}{L} \approx 3 \%$ błąd oszacowania średniej i wariancji jest zaniedbywalny.
Literatura
- Pugachev V. S. (1984). Probability Theory and Mathematical Statistics for Engineers. Pergamon Press
- Korn T., M. (1983). Matematyka dla pracowników naukowych i inżynierów (Tom 1, 2). PWN, Warszawa
________________________________
