Część 2-4

Artykuł w ciągu ostatnich 24 godzin czytało  1 Czytelników
Uwagi i recenzje podręcznika  przesyłać na adres: wydawnictwo@chodor-projekt.net lub  leszek@chodor-pojekt.pl
spis treści prodręcznika: [ Imperfekcyjna metoda projektowania konstrukcji ]

Nawigacja: [2-3: Uogólnienie formuły Ayrton-Perry]  ⇐  ⊗   ⇒ [ 3-1: Imperfekcje konstrukcji, a współczynniki bezpieczeństwa ]

Powszechnie przyjmuje się, że kształt obliczeniowych imperfekcji geometrycznych jest zgodny z pierwszą postacią wyboczenia (utraty stateczności) sprężystego, idealnego systemu konstrukcyjnego. Koncepcja tej praktyki wynika z hipotezy, że najniekorzystniejsza geometria imperfekcji jest najbliższa pierwszej postaci krytycznej, ponieważ wymaga najmniejszej energii odkształcania i najkrótszą drogą prowadzi do ostatecznego zniszczenia.
Taką koncepcję zaimplementowano do normy projektowania konstrukcji stalowych [1] w klauzuli 5.3.2.(11) – wzór (5.9). Wskazano, że alternatywnie do reguł stabdardowych (klauzula 5.2.2 (3)), można przyjąć ze kształt uogólnionej, zintegrowanej imperfekcji układu odpowiada postaci wyboczenia sprężystego $\eta_{cr}$, a amplitudę tej imperfekcji można wyznaczać poprzez skalowanie pierwszej postaci wyboczenia. Od wskazania w normie metody alternatywnej, nadajemy tej metodzie nazwę AIM (Alternatywnej Metody Imperfekcyjnej).
Metoda AIM uwzględniania geometrycznych imperfekcji konstrukcji jest metodą alternatywną w stosunku do stosowania współczynników wyboczeniowych w tym  tak zwanej metody ogólnej  i staje się podstawową metodą w projektowaniu konstrukcji.

Artykuł w opracowaniu

Geneza skalowania pierwszej postaci wyboczenia

W  historycznej pracy Ayrton i Perry (1886) [2] do wprowdzenia formuły amplifikacji przyjęli kształt impwerfekcji pręta w postaci sinusoidy, czyli kształtu pierwszej postaci wyboczenia.  W kolejnych pracach, a w tym:  Hajjar (1997) (Hajjar J. F. (1997), Effective lenght and Effective length and notional load approaches for assesing frame stability : Implication for American Steel. Technical Report. Task Committee on Effective Length of the Technical  Committee on Load and Resistance Factor Design of the Technical Division of the Structural Engineering Institute of the American Society CIvil Engineers), Kim i Lee (2002) [3], Gu, Chan (2005) [4],, Mahendran (2007)  [5] i wielu innych – przyjmuje się imperfekcje w kształcie pierwszej formy wyboczenia sprężystego. W tym celu najpierw jest prowadzona klasyczna analiza LBA na idealnym modelu konstrukcji (w konfiguracji nieodkształconej i niezaburzonej imperfekcjami), a następnie odbywa się skalowanie kształtu wyboczenia otrzymanego dla pierwszej wartości krytycznej, tak, aby utworzyć początkową imperfekcję.

Metodę skalowania pierwszej postaci wyboczenia po raz pierwszy zaproponował Faltus (1955) [6].

W większości przypadków pierwsza postać wyboczenia może reprezentować kształt zniszczenia i imperfekcje zgodne z tym kształtem wspomagają zniszczenie. Jednakże są też pewne systemy, dla których postać zniszczenia różni się od pierwszej formy wyboczenia. Ponadto szerokie badania statystyczne wskazują, że rzeczywiste kształty imperfekcji prawie zawsze różnią się od krzywych wynikających ze sprężystych postaci wyboczenia, czyli w uproszczeniu od kształtu sinusoidy (np. [7] , [8] ) wskazuje się, że taka metoda nie jest wiarygodna we wszystkich przypadkach, ponieważ na poprawność modelu nie przeprowadzono niebudzącego wątpliwości dowodu. Nie pokazano, że na dającym się zaakceptować poziomie prawdopodobieństwa zniszczenia metoda skalowania pierwszej postaci wyboczenia, będzie prowadziła do poprawnego oszacowania obliczeniowej nośności konstrukcji. W pracy [9] zaproponowano, by kształt imperfekcji łukowej określać z uwzględnieniem zachowania konstrukcji w zakresie plastycznym ze względu na istotny wpływ naprężeń resztkowych i faktyczne zniszczenie plastyczne, zapoczątkowane wyboczeniem sprężystym (p. pkt 2-3.1.4). W tym ujęciu sprawczy kształt imperfekcji jest wyznaczany w trakcie rozwiązania problemu, a krytyczny kształt sprężysty jest tylko pierwszą iteracją. W istocie rozróżnia się, więc dwa pojęciowo różne rodzaje wstępnych imperfekcji konstrukcji:

• rzeczywiste, wyznaczone w drodze pomiarów
• obliczeniowe, to znaczy takie zastępcze imperfekcje nierzeczywiste, które są przyjmowane w obliczeniach, i które sprawiają, że wyznaczona nośność graniczna konstrukcji przybliża się do nośności rzeczywistej. Imperfekcje sprężyste zgodne z postacią wyboczenia mogą być wstępnym punktem startu w analizie nieliniowej, podczas której przekształcą się w inny kształt, odpowiadający mechanizmowi zniszczenia sprężysto-plastycznego.

Hipoteza Chladný

Eugen Chladný w pracy doktorskiej [10]   i habilitacyjnej [11] opracował podstawy Alternatywnej Metody Imperfekcji Geometrycznych (AIM) i w 2000 roku zaproponował tę metodę w bardziej ogólnej formie do zastosowania w normie Eurokod 3. Metoda została zaakceptowana w projekcie prEN1993-1-1 (czerwiec 2002) i wprowadzona w pkt 5.3.2 (11) do oficjalnej wersji EN1993-1-1 (2005). Rozszerzona wersja metody AIM  jest stosowana w narodowej normie słowackiej STN EN 1993-1-1 /NA (2007), a także w pkt. 5.3.2 (11) normy europejskiej do projektowania konstrukcji aluminiowych.

Metoda jest wyczerpująco opisana w pracach [12]) , [13]), [14] .

W literaturze można spotkać się z nazwą metody UGLI (Unique Global and Local Initial imperfection)  [15] lub EUGLI (Equivalent Unique Global and Local Initial imperfection”) [14]. Metoda pierwotnie opracowana na przypadek elementów o stałym przekrojów, ściskanych stałą siła osiową, jest stopniowo uogólniana na:

• elementy o zmiennym przekroju i sile osiowej po długości [15] ,
• łuki trójpunktowe (basket handle arch type) w słowackim aneksie normy ,
• klasę 4-tą przekroju elementu Brodniansky J., Rudolf Ároch R. , (2014), Unique global and local initial imperfection in the shape of the elastic buckling mode (Application of “UGLI” imperfection method for frames with class 4 cross-sections), IASS-SLTE Symposium 2014: Shells, Membranes and Spatial Structures, Brasilia, Brazil, Sep 2014,

W podejściu AIM przyjmuje się hipotezy Chladný AIM 1 i AIM 2:

AIM 1 Kształt wstępnych imperfekcji  $\eta_{ini}$ jest proporcjonalny do postaci wyboczenia sprężystego systemu $\eta_{cr}$:

$$ \begin {equation}  \eta_{ini} (x) = A_m \cdot \overline \eta_{cr} (x) \label {1}  \end {equation}$$

gdzie  $ A_m$ jest zastępczą (równoważną, alternatywną) amplitudą imperfekcji, podczas gdy $\overline \eta_{cr}(x)$ jest funkcją postaci wyboczenia elementu unormowaną w taki sposób, że jej amplituda jest jednostkowa $|\overline \eta_{cr,max}|=1$. Z wielu postaci wyboczenia systemu należy stosować najniekorzystniejszą, którą najczęściej jest pierwszą postacią wyboczenia [15] , [16] .

AIM 2 Imperfekcje alternatywne ($\ref{1}$)  opisują łącznie lokalne i globalne (zintegrowane) imperfekcje.

Wbrew temu co postulują prace [17] , [18], 35–71)) ,  przyjmujemy że jednocześnie nie wystąpią różne formy wyboczenia konstrukcji i nie należy tych postaci kombinować. Zasadę można uzasadnić w sposób niebudzący wątpliwości w języku prawdopodobieństwa zdarzeń wykluczających.

Alternatywna amplituda imperfekcji  $ A_m$ jest taką zastępczą (nierzeczywistą) amplitudą imperfekcji, która stanowi mnożnik (skalę) dla funkcji sprężystej postaci wyboczenia elementu.

Idea metody AIM

Ideę metody AIM przedstawiono na przykładzie pręta utwierdzono-przegubowego o długości L i stałych po długości charakterystykach $A, \, I_y, \, E$  , ściskanego stałą siłą osiową $N_{Ed} $ . Na Rys. 2-4.1 zilustrowano zasadnicze pojęcia metody alternatywnej w odniesieniu do м-tego przekroju sprawczego o współrzędnej $x_m$.

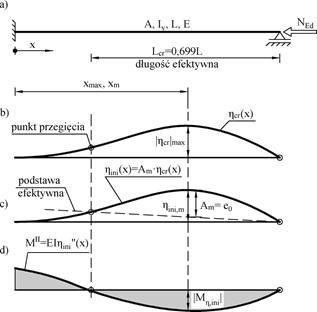
Rys. 2-4.1. Metoda alternatywna AIM: a) schemat pręta, b) postać wyboczenia , c) imperfekcje alternatywne , d) wykres momentów zginających . Linia przerywana (podstawa efektywna) łączy punkty przegięcia , czyli określa długość efektywną elementu . Imperfekcja (normowa, statystyczna) jest przyrównywana do rzędnej ugięcia w przekroju sprawczym м nad podstawą efektywną (opracowano na podstawie [16] )

Na rys. 2-4.1b wykreślono funkcję$ \overline \eta_{cr}(x)$, która jest unormowaną funkcją postaci sprawczej wyboczenia sprężystego układu (pręta lub systemu prętów). Postacią sprawczą jest podstawowa (pierwsza) postać wyboczenia, którą obserwuje się przy najmniejszym krytycznym mnożniku konfiguracji obciążenia. Inna postać wyboczenia, (ale również pierwsza) może dotyczyć innej konfiguracji obciążenia (lub innego schematu pręta, np. po utworzeniu przegubu plastycznego). Unormowanie funkcji polega na takim przeskalowaniu funkcji, by amplituda $|\eta_{cr,max}|=1$.

Na rys. 2-4.1c wykreślono funkcję , która jest alternatywną (zastępczą, równoważną) zintegrowaną (łącznie globalną i lokalną) funkcją imperfekcji układu o amplitudzie $A_m$, odmierzaną od efektywnej podstawy, którą naniesiono linią przerywaną. Podstawa efektywna łączy punkty przegięcia funkcji imperfekcji, czyli punkty zerowe momentu zginającego, odpowiadające tej linii ugięcia.

Normowa (statystycznie określona) amplituda imperfekcji $e_0$ jest amplituda $A_m$.

Na rys. 2-4.1d, wykreślono funkcję momentu zginającego, odpowiadającą kształtowi wyboczenia. Wartość bezwzględna momentu w przekroju „m” jest wartością ekstremalną. Z tego warunku wyznacza się położenie punktu sprawczego „m”.

Metoda AIM uwzględniania geometrycznych imperfekcji konstrukcji jest metodą alternatywną w stosunku do stosowania współczynników wyboczeniowych oraz tak zwanej metody ogólnej [1] i staje się podstawową metodą w projektowaniu konstrukcji.

Analiza LBA (rozwiązania problemu własnego) zaimplementowana we wszystkich pakietach numerycznych jest efektywna (mało kosztowna) i może być zastosowana do dowolnie złożonej konstrukcji. Analiza całego układu bez wydzielania elementów pozwala ujawnić wszystkie możliwe postacie wyboczenia, a w szczególności postacie globalne (przechyłowe lub przeskok) i lokalne (łukowe) w tym ich fizycznie możliwe kombinacje. W zależności od typu elementów skończonych ujawnia też rozmaite rodzaje utraty stateczności (wyboczenie giętne, boczne (zwichrzenia), skrętne, płytowe, powłokowe, itd.) oraz ich fizycznie możliwe kombinacje (interakcję). W istocie postacie i rodzaje utraty stateczności są sprzężone i nie należy dążyć do ich rozprzężenia często tylko po to, by nazwać je, a następnie zastosować uproszczone, normowe zasady interakcyjne.

Szeroka weryfikację metody skalowania pierwszej postaci wyboczenia przprowadzili Chladny i Stujberowa (2013) [19], [20].  Wykazano dobrą zgodność z innymi metody z EN 1993-1-1: 2005, 5.2.2 (3) z zastosowaniem imperfekcji zgodnie z EN 1993-1-1: 2005, 5.3.2 (3). oraz pełną zgodność  z metodą 5.2.2 (3) c) normy EN 1993-1-1: 2005  dla wyodrębionych  zwartych elementów o stałej sile osiowej na całej ich długości.

⇒ [ Imperfekcje konstrukcji, a współczynniki bezpieczeństwa ]

Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2019), Imperfekcyjna metoda  projektowania konstrukcji, Encyklopedia  πWiki, Wydawnictwo πPress, [ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]

Historia edycji artykułu:
(2019-04-08 do 15) wersja 1,0: wersja pierwotna
(2019-05-27) Wersja 2.0: dokonano podziału rozdziału na części w celu poprawy procesu wczytywania strony 

 Literatura

1. PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
2. Ayrton W. E., Perry J. (1886), On Struts. The Engineer, p. 464–513
3. Kim S. E., Lee, D. H. (2002), Second-order distributed plasticity analysis of space steel frames. Journal of Engineering Mechanics, 24, 735–744
4. Gu J. X., Chan S. L. (2005), Second-order analysis and design of steel structures allowing for member and frame imperfections. International Journal for Numerical Methods in Engineering, 62(5), 601–615
5. Mahendran M. (2007), Applications of Finite Element Analysis in Structural Engineer-ing. Proceedings. International Conference on Computer Aided Engineering, Chennai, India
6. Faltus, F., (1955), The safety of elastically supported compressed chords (in Czech: Bezpecnost tlacených pásu poddajnepodeprených). In: Stability of angle chords (in Czech: Stabilita lomených pásuv). Transactions of the Czechoslovak Academy of Sciences, Vol. 65 (1), pp. 59– 65
7. Bjerhovde R. (1972), Deterministic and probabilistic approaches to the strength of steel columns (Ph D. Dissertation No. 1933; Fritz Laboratory Reports). Lehigh University
8. Bjerhovde R., Tall, L. (1971), Maximum column strength and the multiple column curve concept (337.29; Fritz Laboratory Reports), Fritz Engineering Laboratory, Lehigh University
9. Alveranga A. R., Silveira E. A. (2009), Second-order plastic-zone analysis of steel frames- Part II effects of initial geometric imperfection and residual stress. Latin American Journal of Solids and Structures, 6(4), 323–342
10. Chladny E., (1958), Nosnosť tlačených pásov otvorených mostov (Buckling re-sistance of compressed chords of open truss bridges), PhD Thesis, SVŠT (Slovak Technical University of technology), Bratislava
11. Chladny E., (1974), Vzper pruzne podopretych tlacenych prutov (Buckling of elas-tically supported compressed members). Habilitation Thesis, Bratislava
12. Balaz I., Aroch R., Chladny E., Kmet, S., Vican J. (2007), Design of Steel Structures according o Eurocodes STN-EN 1993-1:2006 a STN-EN-1993-1-8:2007 (in Slo-vak) (1st, 2nd ed.). Slovak Chmaber of CIvil Engineers (SKS
13. Beck A. T., Doria A. S. (2008), Reliability Analysis of I-Section Steel Columns de-signed according to new Brazilian Building Codes. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 3(2
14. Sedlacek G., Eisel H., Hensen W., Kühn B., Paschen M. (2004), Leitfaden zum Fachbericht DIN 103. Stahlbrücken. Ernst & Sohn, A Wiley
15. Balaz I., Kolekova Y. (2012), Structures with UGLI imperfections (in Slovak), Pro-ceedings 18th International Conference Engineering Mechanics, pp. 61–86, Svratka – Bratislava, Czech Republic
16. Dallemule M. (2015), Equivalent imperfections in arched structures. Slovak Journal of Civil Engineering, 23(3), 9–15
17. Shayan S., Rasmussen K. J. R., Zhang, H. (2014), On the modelling of initial geo-metric imperfections of steel frames in advanced analysis. Journal of Constructional Steel Research, 98, 167–177
18. Giżejowski M. A., Szczerba R. B., Gajewski M. D., Stachura Z. (2016), Beam-Column In-Plane Resistance Based On The Concept Of Equivalent Geometric Imperfections. Archives of Civil Engineering, LXII(4 (2
19. Chladny E., Stujberova M. (2013). Frames with unique global and local imperfection in the shape of the elastic buckling mode.Part 1. Stahlbau, 82(8), 609–617
20. Chladny E., Stujberova M. (2013). Frames with unique global and local imperfection in the shape of the elastic buckling mode.Part 2 . Stahlbau, 82(9), 684–694

________________________________