Metoda Monte Carlo, to intuicyjna, odznaczająca się dużą prostotą, uniwersalna metoda , za pomocą której można rozwiązać złożone, dowolnie nieliniowe, uwikłane i sprzężone zagadnienia techniki, w tym konstrukcji budowlanych [1]. Szybka metoda Monte Carlo realizuje postulat zmniejszenia kosztowności metody, mierzonej liczbą potrzebnych cykli obliczeniowych. SMCC z powodzeniem zastępują klasyczne metody szacowania współczynnika niezawodności  konstrukcji budowlanych (SORM /FORM) i coraz częściej są realizowane w połączeniu z metodą genetyczną i warstwowania zgodnie z ideą hiperkostek łacińskich, a także szeregami Neumanna.

Wprowadzenie

Metoda Monte Carlo (MC) służy do rozwiązywania przede wszystkim zadań losowych, ale również zadań nielosowych, jak np: złożonych całek, równań różniczkowych,  równań nieliniowych, wyznaczenie ekstremum funkcji [2], [3].

Metodę MC można stosować do wszystkich tych zagadnień, w których zawodzą metody analityczne. Można do nich zaliczyć: niezawodność systemów o złożonym układzie elementów, analizę systemów o zależnych czasach pracy i awarii urządzeń  i inne  [4].

Pierwsze szerokie zastosowanie metody MC w roku 1944 przez von Neumanna umożliwiło zrozumieć fundamentalną ideę reakcji łańcuchowej, co  pozwoliło domknąć prace nad bombą atomową. Można wykazać, że metoda MC jest obecnie jedyną metodą pozwalającą na na obliczenie charakterystyk reakcji jądrowych przy dostatecznie, zbieżnych z realnymi warunkami,  ogólnych założeniach fizycznych.

Poprawność metody MC w przypadku obliczania pól lub całek można udowodnić stosując twierdzenie Picka , skąd wynika , że metoda jest słuszna dla dowolnego kształtu pola lub granic całki.

W każdym przypadku, istotą metody MC jest losowanie, rozumiane jako przypadkowy wybór, wartości zmiennych występujących w zagadnieniu. Losowanie jest dokonywane zgodnie z rozkładem statystycznym, który musi być znany.

Stosowanie metody MC jest nierozłącznie związane z rozwojem metod numerycznych oraz programami komputerowymi.
Przykładem programów do oceny niezawodności konstrukcji budowlanych z zastosowaniem prostej MC  jest zestaw programów symulacyjnych , opisany w [1], a obejmujący kilka programów:
LoadCom  do analizy kombinacji obciążeń,
M-Star do rozwiązywania algebraicznych równań nielinowych, zawierających do 30 zmiennych losowych),
AnHill do analizy zagadnień ze zmiennymi dwu- i wielo-wymiarowymi,
DamAc  do oceny wpływu historii i czasu obciążenia na odporność i niezawodność konstrukcji,
ResCom do analizy obciążeń konstrukcji.

Dokładność wyniku uzyskanego w metodzie MC jest zależna przede wszystkim od liczby losowań (sprawdzeń) oraz jakości użytego generatora liczb pseudolosowych. Dokładność metody zwykle zwiększa się wraz ze wzrostem liczby prób. Niesamowity i nieustanny wzrost mocy obliczeniowej komputerów oraz wprowadzanie nowych technologii do algorytmów numerycznych wskazuje na  to, że nieunikniony jest powrót do  stosowania metody MC i zmniejszenie znaczenia metod linearyzacji stosowanych wraz z metodami perturbacji zagadnień.

Poprawa jakości generatorów liczb losowych jest ważna, bowiem generator liczb pseudolosowych ma skończenie wiele liczb losowych w cyklu i zwiększanie liczby prób ponad liczbę losowań w cyklu nie zawsze zwiększa dokładność wyniku.

Zamiast rozwijania metod aproksymacyjnych należy skupić się nad poprawą jakości generatorów liczb pseudolosowych oraz doskonalenia metody Monte Carlo w kierunku rozwijania Szybkich Metod Monte Carlo , których klasycznym przykładem jest symulacja według funkcji ważności, próbkowanie adaptacyjnego, warstwowanie mechanizmem hipersześcianów łacińskich,  stosowanie: zmiennej kontrolnej, średniej ważonej,  obniżania krotności całki, klasycznego losowania warstwowego [2] i in..
Współcześnie rolę taką przejmują metody genetyczne (sieci neuronowe).

Ze względu na dynamiczny rozwój technik informatycznych i technologii komputerowych – autor niniejszego artykułu przewiduje, że w szybkim czasie szybka metoda Monte Carlo zastąpi stosowane obecnie, aproksymacyjne, probabilistyczne metody. a  w tym zaawansowaną metodę drugigo momentu  (Advanced Second Moment ASM) [5] która umożliwia wyznaczenie współczynnika niezawodności konstrukcji Hasofera-Linda z zachowaniem postulatu niezmienniczości [6].

Zwróćmy jeszcze uwagę, że stosowane współcześnie konstrukcje zmierzają do optymalności z warunku zużycia materiału, co powoduje że, stosuje się coraz powszechniej konstrukcje bliskie osobliwym, które są z reguły układami wysoce nieliniowymi zarówno geometrycznie jak i materiałowo, a także wrażliwych na utratę stateczności. To właśnie takie konstrukcje optymalne są szczególnie narażone na imperfekcje parametrów i ich analiza deterministyczna traci sens. W ich przypadku niestety zawodzą równiż klasyczne metody probabilistyczne. Stąd wielka waga i renesans metod Monte Carlo, stosowanych zamiennie lub łącznie z klasycznymi metodami analizy niezawodności konstrukcji (FORM/SORM)  Dlatego tak ważne jest udoskonalenie metody symulacji Monte Carlo poprzez wykorzystanie koncepcji tzw. optymalnej hiperkostki łacińskiej (ang. optimal Latin Hypercube – OLH) lub metody genetyczne.

Szybka Metoda Monte Carlo (SMMC)

Szybka metoda Monte Carlo jest odmianą prostej, ogólnej  metody MC, polegającą na zwiększeniu efektywności (szybkości) metody podstawowej, poprzez wykorzystanie  dodatkowych informacji o równaniu systemu (powierzchni granicznej) oraz o mierze, względem której wykonuje się operację (najczęściej całkowanie funkcji prawdopodobieństwa).
Algorytmy redukcji wariancji, czyli procedury pozwalające na zwiększenie precyzji estymacji, polegają na odpowiednim doborze próby (ang. sampling), tak aby zmienność wyników symulacji była jak najmniejsza. Rezultat taki można osiągnąć przez zwiększenie liczebności próby, ale często zamiast zwiększania liczebności losowań, wystarczający efekt można uzyskać korzystając z metod redukcji wariancji [7].
W klasycznej pracy [2] wskazano na kilka metod zwiększenia efektywności klasycznej metody MC poprzez zastosowanie metod:
1) metody zmiennej kontrolnej
2) metody średniej ważonej
3) metody losowania warstwowego
4) obniżenie krotności całki
5) stosowanie stochastycznych formuł kwadraturowych

3. SMMC w analizie konstrukcji budowlanych

Stocki (2010) w rozprawie habilitacyjnej [8] wskazuje, że w problemach niezawodności konstrukcji budowlanych metoda Monte Carlo jest interesującą alternatywą do standardowych metod poszukiwania punktu projektowego na powierzchni granicznej.
Omawia kilka metod pozwalających na znaczną redukcję wariancji estymatora prawdopodobieństwa awarii, co pozwala znacznie ograniczyć liczbę losowań w celu uzyskania akceptowanej dokładności obliczenia całki prawdopodobieństwa dla bardzo niezawodnych obiektów, jakimi są konstrukcje budowlane.

Metoda funkcji ważności (importance sampling)

Najważniejszą metodą redukcji wariancji MC jest metoda funkcji ważności (ang importance sampling). która jest stosowana w wielu odmianach w zależności of konkretnego problemu [9]. Metoda ta jest w istocie klasyczną metodą zmiennej kontrolnej w ujęciu ilorazu, a nie różnicy funkcji gęstości oryginalnej f(x) i tzw losującej g(x). Można pokazać, że odpowiedni wybór gęstości losującej decyduje o efektywności metody. Jeśli  g będzie proporcjonalna do f w obszarze całkowania (awarii) , to wariancja redukuje się do zera i wystarczyłoby jedno losowanie, by uzyskać wynik dokładny. Nie jest to jednak proste  i ściśle możliwe w praktycznych sytuacjach.

Liczne doświadczenia w stosowaniu metody funkcji ważności w odmianie ach uproszczonych pozwalają stwierdzić, że zwykle zadowalającą estymację można otrzymać już po wygenerowaniu od kilkuset do kilku tysięcy realizacji zmiennych. Jest to o wiele rzędów wielkości mniej niż w przypadku klasycznego Monte Carlo. Wystarczy jako gęstość losującą wybarać rozkład normalny. Wówczas oszacowanie wartości prawdopodobieństwa awarii nie jest bardzo wrażliwe na kształt obszaru awarii,a  prawdopodobieństwo, że realizacja zmiennej losowej wygenerowanej zgodnie z gęstością losującą znajdzie się w obszarze awarii wynosi około 50%. Kontrastuje to z klasyczną metodą Monte Carlo gdzie prawdopodobieństwo “trafienia” realizacji w obszar awarii było mniej więcej równe obliczanemu prawdopodobieństwu awarii [8].

Metody adaptacyjne

Ponieważ stosowanie standardowej metody funkcji ważności w szeregu przypadkach może być zawodne, bo:
* w konkretnym zagadnieniu gęstość losująca może być źle dobrana,
* powierzchnia graniczna może posiadać wiele punktów projektowych (minimów lokalnych), na przykład w przypadku rozważania kilku funkcji granicznych (mechanizmów zniszczenia)
* powierzchnie graniczne mogą mieć znaczne ujemne krzywizny,
więc stosuje się metodę adaptacyjną doboru gęstości losującej. Dobór funkcji gęstości losującej rozpoczyna się od założenia prostej funkcji gęstości, najczęściej gaussowskiej, z wartościami oczekiwanymi i wariancjami określonymi na podstawie próby o niewielkiej liczebności. Poprzez generowanie kolejnych realizacji zmiennych losowych funkcja losująca jest ciągle udoskonalana, gdyż parametry rozkładu estymuje się na podstawie coraz liczniejszej próbki. Przyjmuje się, że gęstość losująca o tak uaktualnianym położeniu oraz kształcie zbiega ostatecznie do gęstości idealnej.
Niestety, zbieżności tej nie można zagwarantować, szczególnie w przypadku złego początkowego wyboru gęstości losującej. Dlatego często stosowane są modyfikacje tej metody, polegające na tym, że funkcja gęstości losującej jest składana ze kilku funkcji gęstości z zadanymi wagami. podlegającym odrębnym optymalizacjom (adaptacjom) lub aproksymacja oryginalnej powierzchni odpowiedzi przez powierzchnie prostsze dla których można zastosować efektywne, numeryczne algorytmy optymalizacji.

Oczywiście w większości zagadnień praktycznych efektywne będą metody mieszane (hybrydowe), polegające na tym, że w trakcie symulacji losowych są jednocześnie: a) przybliżane położenie punktu projektowego,  b) uaktualniana funkcja gęstości losującej  obszarze skoncentrowanym nad punktem projektowym, c) uaktualniana aproksymacja powierzchni granicznej. W procesie adaptacyjnym należy dążyć do tego by można było zastosować optymalizacyjne metody gradientowe, znajdujące zastosowanie w przypadku różniczkowalnego wycinka powierzchni granicznej, to znaczy należy jak najszybciej ominąć punkty osobliwe powierzchni granicznej.
Punkty osobliwe często występują w konstrukcjach wrażliwych na utratę stateczności i nie wytrąconych z położenia bifurkacyjnego. Dla takich konstrukcji należy stosować specjalne metody adaptacyjne.

Metody łacińskich hiperkostek

Metoda łacińskich hiperkostek (ang . Latin Hypercube Sampling (LHS)) jest statystyczną metodą wytwarzania próbki prawdopodobnych zbiorów wartości parametrów wielowymiarowym rozkładzie prawdopodobieństwa.  Metoda pobierania próbek metodą LHS,  jest stosowana od roku 1980  po opublikowaniu pracy [10]   i opracowaniu kodów komputerowych w latach kolejnych.

Podczas pobierania próbek funkcję zmiennych, zakres każdej zmiennej jest podzielona na równie prawdopodobnych odstępach czasu. przykładowe punkty są następnie umieszczane w celu zaspokojenia wymagań łacińskich Hypercube; zauważyć, że powoduje to szereg podziałów , być taki sam dla każdej zmiennej. Należy również pamiętać, że program ten nie wymaga pobierania próbek kolejne próbki do większej liczby wymiarów (zmiennych); Niezależność ta jest jedną z głównych zalet tego systemu pobierania próbek.Kolejną zaletą jest to, że losowe próbki mogą być podjęte po jednym na raz, pamiętając, których pobrano próbki do tej pory.

Metoda LHS tym różni się od standardowych losowań, że uwzględnia wcześniej wygenerowane próbki, a ponadto należy z góry założyć ile punków próbkowania jest potrzebne. W standardowej metodzie MC próbki są generowane bez uwzględnienia wcześniej wylosowanych i nie jest znana liczba próbkowań. W metodzie LHS zapamiętywane są miejsca pobrania próbek w zapisie macierzowym (wiersz i kolumna). Optymalna hiperkostka jest generowana w metodzie ortogonalnej , w której przestrzeń  probabilistyczna jest dzielona na jednakowo prawdopodobne podprzestrzenie. Wszystkie  punkty próbkowania ortogonalnego są wybierane  jednocześnie każda podprzestrzeń jest próbkowana z tej samej gęstości.

W ten sposób próbkowanie ortogonalne zapewnia, że ​​zespół liczb losowych jest bardzo dobrym reprezentantem rzeczywistej zmienności losowej próby, podczas gdy tradycyjne (zwane ekstensywnym) jest po prostu zespołem liczb losowych bez żadnych gwarancji reprezentatywności.
Maksymalna liczba kombinacji dla łacińskiej hiperkostki  złożonej  z podziałów przy zmiennych (czyli wymiarów) można obliczyć ze wzoru:

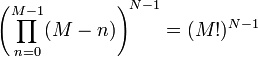
gdzie: M – liczba podziałów N-liczba zmiennych (N=2 – płaszczyzna, N=3 – przestrzeń). Przykładowo dla M=4, N=2  mamy 24 możliwych kombinacji; dla M=4, N=3 mamy 676 możliwych kombinacji(losowań)
Zwykle ten drugi sposób wystarcza do uzyskania wystarczającej ze względów praktycznych dokładności dla praktycznie częstych zagadnień, jeśli tylko spełnimy założenia generacji optymalnej hiperkostki. Dla uzyskania takiej samej dokładności w klasycznej metodzie MC zwykle potrzeba byłoby kilkaset razy więcej losowań.

Algorytmy genetyczne

Algorytmy genetyczne są stosowane w połączeniu z metodą łacińskich hiperkostek w istocie do generowania kolejnych hiperkostek w algorytmie znanym z sieci neuronowych, tzn  pozwala przewidywać następną populację na podstawie analizy łącznych zmian generowanych przez kilkadziesiąt wcześniejszych populacji  Ze względu na nieocenioną przydatność, algorytmy genetyczne w metodzie MC są przedmiotem wielu prac, np. [11].

Zastosowanie szeregu Neumanna

Do aproksymacji powierzchni granicznej stosuje się najczęściej rozwinięcie w szereg potęgowy Taylora. Wiele prac, np.: [12], [13], [14] pokazuje, że przy  optymalnym doborze parametru konwergencji i zastosowaniu algorytmu MC ,  efektywny jest rozkład w szereg Neumanna. Takie obserwacje są również renesansem pierwotnych idei opisanych na wstępie tego artykułu.

Zastosowanie twierdzenia Bayesa

Podejście Bayesa różni się fundamentalnie od istoty metody Monte Carlo, czyli podejścia częstotliwościowego  do wyznaczania prawdopodobieństwa zdarzenia z definicji i zastosowania centralnego twierdzenia granicznego. Tymczasem przypadkowość i nieprzewidywalność zjawisk  w dużej mierze związana jest z brakiem wiedzy o naturze modelu przetwarzającego zmienne wejściowe , a nie od rozrzutu tych zmiennych. Symulacja realizacji zmiennych wejściowych nie dotyka istoty rzeczy, a zwiększanie liczby symulacji nie musi prowadzić do przybliżania prawdopodobieństwa zdarzenia. Twierdzenia Bayesa (o prawdopodobieństwie warunkowym) opiera się na znacznie szerszej definicji prawdopodobieństwa od definicji częstotliwościowej.

Podejście Bayesa do wyznaczania prawdopodobieństwa zdarzenia przeżywa gwałtowny wzrost zainteresowania w niemal każdej dziedzinie [15].

Metody hybrydowe

Najbardziej efektywne jest stosowanie metod hybrydowych poprzez połączenie wymienionych wyżej metod w sposób dostosowany do konkretnego zagadnienia.

Literatura

1. Marek P., Guštar M., Anagnos T. (1995). Simulation-Based Reliability Assessment for Structural Engineers. CRC Press, Inc.
2. Jermakow S. M. (1976). Metoda Monte Carlo i zagadnienia pokrewne. PWN, Warszawa
3. Buslenko N. P., Golenko D. I., Sobol I. M., Sragowicz W. G., Szrejder J. A. (1967). Metoda Monte Carlo (I). Państwowe Wydawnictwo Naukowe, warszawa
4. Kopociński B. (1977). Zarys teorii odnowy i niezawodności. PWN, Warszawa
5. Gwóźdź M., Machowski A. (2011). Wybrane badania i obliczenia konstrukcji budow-lanych metodami probabilistycznymi. Wydawnictwo Politechniki Krakowskiej, Kraków
6. Hasofer A. M., Lind, N., C. (1974), Exact and invariant second-moment code for-mat. Journal of Engineering Mechanics Division ASCE, Vol.100(No EM1/1974), 111–121
7. Jones O., Maillardet R., Robinson A. (2009). Introduction to scientific programming and simulation using R. CRC Press
8. Stocki R. (2010). Analiza niezawodności i optymalizacja odpornościowa złożonych konstrukcji i procesów technologicznych, Praca habilitacyjna, IPPT PAN, Warszawa
9. Melchers R. E. (1992). Simulation in time-invariant and time-variant Reliability Prob-lems. In R. Rackwitz & P. Thoft-Christensen (Eds.), Reliability and Optimization of Structural Systems 91 (Vol. 76, pp. 39–82). Springer Berlin Heidel-berg. http://www.springerlink.com/index/10.1007/978-3-642-84753-0_3
10. McKay M.,D., Beckman R., J., Conover W., J., (1979), Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code, Technometrics, 21, (2), pp. 239-245
11. Stocki R., Liefvendahl M. (2006), A study on algorithms for optimization of Latin hy-percubes. Journal of Statistical Planning and Inference, 136(9), 3231–3247
12. Grigoriu M. (2012), Stochastic Systems. Uncertainty Quantification and Propagation. Springer
13. Ávila da Silva Jr. C. R., Beck A. T. (2015). New Method for efficient Monte Carlo – Neumann solution of linear stochastic systems. 40, 90–96
14. Ávila da Silva Jr. C. R., Beck A. T. (2015), Efficient bounds for the Monte Carlo – Neumann solution of stochastic thermo-elasticity problems. International Journal of Solids and Structures, 58, 136–145
15. O’Hagan A. (2006), Bayesian analysis of computer code outputs: a tutorial. Reliability Engineering and System Safety, 91, 1290–1300

________________________________