Niniejszy artykuł stanowi Część 2 cyklu Elementarz niezawodności konstrukcji. W całym cyklu artykułów zachowano ciągłość numeracji: wzorów i ilustracji. Numeracja rozdziałów jest odrębna dla każdej części.
Omówiono podstawowe struktury (systemy) z punktu widzenia niezawodności: systemy szeregowe i równoległe. Systemy szeregowe (łańcuchy) są modelem konstrukcji statycznie wyznaczalnych. Systemy równoległe (wiązki) są modelem konstrukcji statycznie niewyznaczalnych. Artykuł zilustrowano przykładami podstawowych struktur i opatrzono wnioskami ważnymi dla Konstruktora i Architekta obiektów budowlanych.
Podstawowe struktury niezawodnościowe
Podstawowe modele
Na rys. 2 pokazano schematy blokowe podstawowych struktur niezawodnościowych. Przykładem struktury szeregowej jest statycznie wyznaczalna konstrukcja (kratownica, rama, płyta , itd) . Przykładem struktury równoległej jest konstrukcja statycznie niewyznaczalna. Zarówna system szeregowy jak i równoległy (lub systemy mieszane szeregowo-równoległe) są modelami tradycyjnych systemów konstrukcyjnych, z elementami wbudowanymi na stałe (obciążonymi).
Przykładem konstrukcji z rezerwą nieobciążoną jest konstrukcja z elementami rezerwowymi włączanymi w system w przypadku awarii jakiegokolwiek innego elementu. Takie konstrukcje wymagają stałej obsługi, lecz w dobie automatycznego monitoringu i informatyzacji staną się ważną klasą systemów konstrukcyjnych.
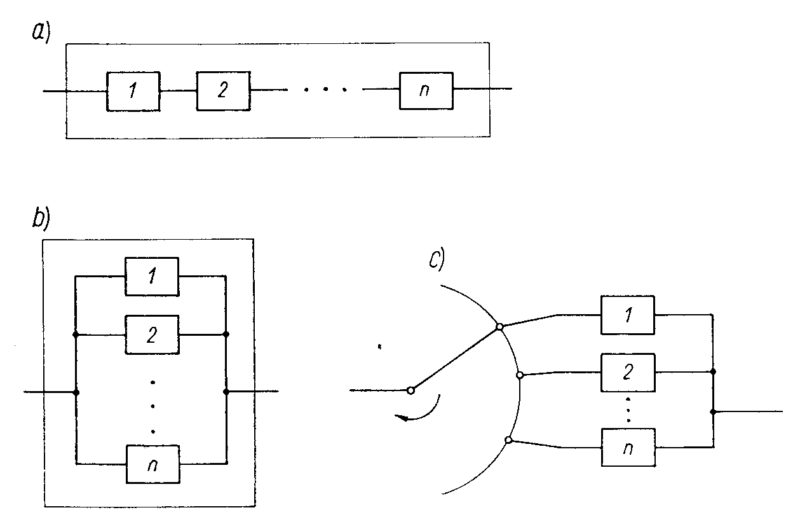
Rys.2. Podstawowe modele niezawodnościowe: a) szeregowy, b) równoległy czyli rezerwy obciążonej , c) rezerwy nieobciążonej [1]
Analizujemy systemy , w których uszkodzenia elementów $\overline \Omega_i$ są zdarzeniami wzajemnie niezależnymi. Niezależnymi są więc również zdarzenia dopełniające $ \Omega_i$.
SZEREGOWA struktura. Statystyczny efekt skali (osłabienia)
W systemie (strukturze, układzie, modelu, schemacie ) szeregowym cały system pracuje, jeśli wszystkie elementy pracują, to znaczy system szeregowy ulega awarii, jeśli choć jeden z elementów ulegnie awarii.
Przykładem konstrukcji z rezerwą nieobciążoną jest konstrukcja z elementami rezerwowymi włączanymi w system w przypadku awarii jakiegokolwiek innego elementu. Takie konstrukcje wymagają stałej obsługi, lecz w dobie automatycznego monitoringu i informatyzacji staną się ważną klasą systemów konstrukcyjnych.
W tym przypadku przy liczbie elementów $n$:
| $p_s=Prob\{ \Omega_1 \cup \Omega_2 \cup … \cup\Omega_n\}$ | (18) |
i w ślad za przyjętym założeniem o niezależności uszkodzeń elementów
| $ p_s=Prob \{ \Omega_1 \} \cdot Prob \{ \Omega_2 \} \cdot … \cdot Prob \{ \Omega_n \} $ | (19) |
czyli
| $p_s= \prod \limits_{i=1} \limits^n p_{si}$ | (20) |
Formuła (23) jest zasadą mnożenia niezawodności (prawdopodobieństw bezawaryjnej pracy ) elementów systemu szeregowego. Wyraża ona również tak zwany statystyczny efekt skali:
Im więcej elementów zawiera system szeregowy, tym mniejsza jest jego niezawodność.
Przykład rachunkowy 1:
System szeregowy składa się z $n=100$ elementów o niezawodności 90% każdy.
Niezawodność systemu będzie wynosiła $0,9^{100}=0,0000027$, to znaczy prawdopodobieństwo zniszczenia wynosi $1-0,0000027=0,9999973 \cong 1,0 $, więc zniszczenie jest prawie pewne, a przecież każdy z elementów był bardzo niezawodny.
Doświadczenie fizyczne:
Zerwanie nitki. W celu urwania nitki rozwijamy ją ze szpuli i łatwo zrywamy, ale jeśli nie można jej rozwinąć i nitka jest krótka, to trudno ją zerwać i należy użyć nożyczek lub zębów do przecięcia nitki.
Z zależności (23) wynika, że nigdy niezawodność systemu szeregowego nie jest większa od niezawodności najsłabszego elementu (ogniwa). W takim razie dla systemu szeregowego mamy:
| $ p_s \le \min \limits_i p_{si} $ | (21) |
Jeśli oznaczymy przez $p_{fi}$ prawdopodobieństwo zniszczenia i-tego elementu, to (21) możemy zapisać w postaci:
| $p_s= \prod \limits_{i=1} \limits^n (1-p_{fi})$ | (22) |
Rozkładając wielomian , będący wynikiem iloczynu (22) w szereg Newtona i odrzucając wyrazy rzędu wyższego niż liniowy (które są istotnie mniejsze o członów liniowych, bowiem bardzo małe są prawdopodobieństwa zniszczenia poszczególnych elementów budowlanych), otrzymamy oszacowanie
| $p_s \cong 1- \sum \limits_{i=1} \limits^n p_{fi} $ | (23) |
Przykład rachunkowy 2:
Wyznaczmy niezawodność elementów wymaganą do tego, by niezawodność systemu szeregowego była równa $p_s=0,999927652$ ( wymagany przez [2] indeks niezawodności $\beta=3,8$ dla klasy niezawodności RC2). System składa się z n=20 podobnych elementów (o takiej samej niezawodności).
Z formuły (22) mamy
$0,999927652=1-20 \cdot p_{fi}$, skąd wymagane jest by każdy element miał niezawodność
$p_{fi}=0,0000003619$ , czyli $p_{si}=0,9999996381 $.
W celu zachowania przez układ niezawodnosci 5 bel (5-ć dziewiątek po przecinku), wymagana jest niezawodność każdego elementu 6 bel (ponad 10-ć razy większa).
Sprawdźmy dokładność oszacowań z formuły (23):
$p_s=0,9999996381^{20}=0,999927652$,
to znaczy uzyskaliśmy wynik dokładny do 9-tego miejsca po przecinku.
Niezawodność systemu szeregowego zależy nie tylko od liczby elementów (ogniw) składowych, ale także od poziomu ich niezawodności.
Na rys. 3 pokazano zależność niezawodności systemu szeregowego $p_s$ od liczby n elementów o takiej samej niezawodności elementów $p_{si}=0,95 ; 0,98$ lub $0,99$.
Spadek niezawodności systemu wraz ze zwiększaniem się liczby elementów jest bardzo szybki, a zwiększanie niezawodności pojedynczych elementów wpływa stosunkowo mniej na zwiększenie niezawodności systemu.
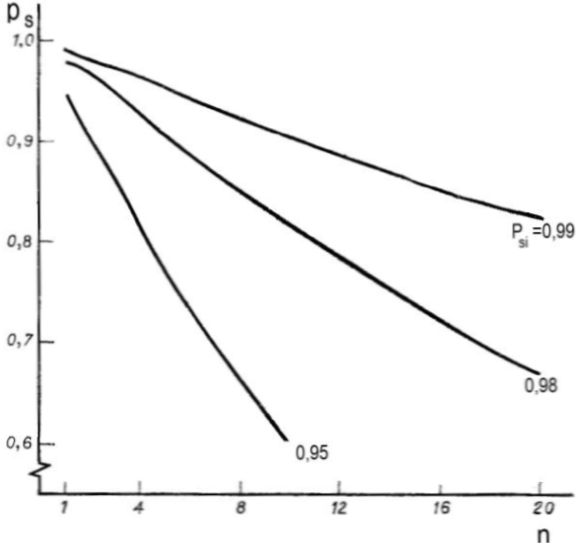
Rys.3. Niezawodność systemu szeregowego $p_s$ w funkcji liczby elementów $n$ [1]
Statystyczny efekt skali obserwowany jest zarówno w prętach, jak i w ustrojach powierzchniowych (powłoki, płyty, ściany), a także w ustrojach trójwymiarowych (bryłach). Systematycznie obserwuje się, że konstrukcja o większych rozmiarach (większej liczbie elementów skończonych) jest słabsza od konstrukcji z mniejszą liczba elementów.
- Zwiększenie niezawodności systemu szeregowego najlepiej przeprowadzić, realizując strategię :
- wyszukać najsłabszy element w systemie i zwiększyć jego nośność, więc również niezawodność
- sprawdzić nośność systemu i w przypadku niezadawalającego wyniku, przeprowadzić pkt 2 dla kolejnego elementu
- po każdym kroku starać się zmniejszyć liczbę elementów połączonych szeregowo.
W opisanej strategii uwzględniono dwa ważne wnioski z przeprowadzonych analiz: 1) o nośności i niezawodności systemu szeregowego decyduje najsłabszy element (najsłabsze ogniowo),, 2) niezawodność systemu szeregowego gwałtownie spada wraz z e zwiększającą się liczbą elementów połączonych szeregowo.
RÓWNOLEGŁA struktura. Statystyczny efekt wzmocnienia
System z elementami połączonymi równolegle (rys. 2b) nie ulegnie zniszczeniu, dopóki nie zniszczą się wszystkie elementy systemu o liczbności $m$. Niezawodność systemu $p_s$ wyznaczymy z zależności:
| $p_s = Prob \{ \overline \Omega_1 \cap \overline \Omega_2 \cap … \cap \overline \Omega_m \cap \}$ | (24) |
gdzie $\Omega_i$ oraz $\overline \Omega_i$ – są wzajemnie dopełniającymi zdarzeniami – zdarzenie oznaczone nadkreśleniem oznacza zdarzenie przeciwne i w tym przypadku zniszczenie elementu.
Jeśli zdarzenia $\Omega_i$ są wzajemnie niezależne, to również $ \overline \Omega_i $ są wzajemnie niezależne, a jeśli tak, to zachodzi:
| $p_s = 1-p_f=1-\prod \limits_{i=1} \limits ^m (1-p_{si}) $ | (25) |
Takie połączenie równoległe (elementów obciążonych – wbudowanych na stałe) jest typowe dla tradycyjnych konstrukcji budowlanych.
Na rys.4. pokazano zależność niezawodności $p_s$ systemu równoległego od liczby $m$ elementów w wiązce o takiej samej niezawodności każdego elementu $p_{si}$. Obserwujemy zwiększanie się niezawodności systemu równoległego wraz ze zwiększaniem się liczby elementów w wiązce.
Przy dużych niezawodnościach elementów ( z takimi mamy do czynienia w budownictwie) przyrost niezawodności systemu równoległego jest wolny dla liczby elementów większych od 3-ch., a przy podłączeniu czwartego elementu praktycznie nie obserwujemy zwiększenia niezawodności systemu.

Rys.4. Niezawodność systemu równoległego $p_s$w funkcji niezawodnosci elemntów $p_{si}$. Krzywe dla różnej liczby elementów $m$ [1]
Własności systemu równoległego powodują, że zwykle rozumie się go jako sposób zwiększenia niezawodności systemu poprzez zwiększenie liczby elementów połączonych równolegle. Jednakże taka cecha struktury nie zawsze skutecznie prowadzi do celu. Zwiększanie liczby elementów równoległych powyżej czterech okazuje się narzędziem mniej skutecznym i w istocie niezbyt wygodnym w stosunku do prostej wymiany jednego elementu na element o większej niezawodności.
Tym niemniej należy zauważyć, że w systemie równoległym następuje statystyczny efekt zwiększenia niezawodności systemu wraz ze zwiększającą się liczbą elementów składowych. Obserwujemy więc zjawisko przeciwne niż w systemach szeregowych.
Wynika stąd ważny wniosek dla Konstruktora konstrukcji budowlanych:
Połączenia szeregowe elementów konstrukcji (statycznie wyznaczalnych) prowadzą do istotnego zmniejszania niezawodności, natomiast połączenia równoległe elementów konstrukcji (statycznie niewyznaczalnych) prowadzą do niewielkiego zwiększenia niezawodności systemu, wraz ze zwiększaniem się liczby elementów.
Literatura
- Kapur K. C., Lamberson L. R. (1977), Reliability in engineering design. Wiley
- PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
________________________________




