Leszek Chodor, 14 maja 2016
19-02-2025 rewizja po dużej awarii portalu
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 17 Czytelników
Współczesne konstrukcje budowlane projektowane i wykonywane są tak, by osiągnąć optymalne właściwości (wytrzymałość, stabilność, tłumienie drgań, odporność ogniową, izolacyjność cieplną, trwałość, itd) w drodze połączenia zalet różnych materiałów w wybranej lokalizacji, orientacji, połączeniu i nasyceniu w konstrukcji. Uzyskuje się to poprzez budowę elementu konstrukcji z materiału kompozytowego lub łączenie elementów wykonanych z różnych materiałów poprzez zespolenie lub swobodne zestawienie. Przykładem kompozytu jest żelbet, stanowiący połączenie betonu i stali. Przykładem elementu zespolonego jest strop z płytą żelbetową na belkach stalowych z zastosowaniem łączników zespalających. Przykładem konstrukcji zestawionej z elementów wykonanych z różnych materiałów jest hala „stalowa” z przekryciem stalowym na słupach żelbetowych.
Zaprezentowano uproszczone podejście normowe [1], a także dokładniejsze numeryczne z zastosowaniem MES w ujęciu Ayoub, Filippou (2000) [2]
Wprowadzenie
Konstrukcje stalowo-betonowe wykorzystują najlepsze cechy drogiej i energochłonnej stali, tam gdzie jest potrzebna duża wytrzymałość na rozciąganie lub zginanie, i stosunkowo taniego betonu tam , gdzie jest przeważające ściskanie, gdzie potrzebne jest działanie tłumiące masy lub ognioochronne kamienia. Uzupełnieniem tych materiałów może być drewno, szkło i materiały izolacyjne. Współczesne budynki rzadko zaprojektowane są tylko z jednego materiału konstrukcyjnego, a coraz większego znaczenia nabiera łączenie różnych materiałów, a przede wszystkim stali i betonu również w elementach żelbetowych, gdzie coraz częściej stosuje się połączenia zbrojenia inne niż na przyczepność do betonu. W połączeniach elementów stalowo-betonowych ważne są połączenia suche, w tym realizowane za pomocą nowoczesnych łączników, np kotew wkręcanych, typu HUS , prod. HILTI.
Zespolenie materiałów w elemencie konstrukcyjnym może być pełne lub częściowe. Przy częściowym zespoleniu o nośności elementu decyduje odkształcalność łączników, wskutek czego na granicy warstw różnych materiałów następuje wzajemne przesunięcie. Jeśli liczba i nośność łączników zapewnia pełną współpracę, to wówczas wystąpi pełne zespolenie. Zagadnienie dobrze ilustruje podstawowe zadanie wytrzymałości materiałów, a mianowicie zadanie projektowanie złożonych belek zginanych poprzecznie.
Zespolenie
Pojęcie zespolenia
W celu zdefiniowania zespolenia rozpatrzmy zadania pomocnicze: klasyczne zadanie zginania poprzecznego belki złożonej z dwóch bali o przekroju prostokątnym bxh, zginanej siłą P (rys.1) .
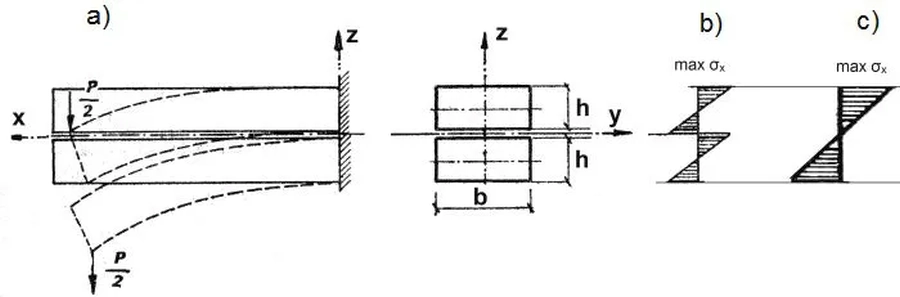
Rys. 1 Dwa bale bxh w zakresie sprężystym: a) schemat, b) swobodne, c) zespolone [3]
W przypadku, gdy bale (deski) są położone na sobie i nie są połączone, to odkształcą się tak jak pokazano na rys.1a. Skutkuje to naprężeniami pokazanymi na rys. 1b). Każdy bal przejmuje połowę siły obciążającej P/2, a maksymalne naprężenia na krawędzi każdego bala wynoszą:
$$\begin{equation} max \ \sigma= \cfrac {M} {W_{el,S}}= \cfrac {{ \frac {P} {2} \cdot l}}{ \frac {b\cdot h^2} {6}}=3 \cfrac {Pl} {bh^2} \label{1} \end{equation}$$
Jeśliby bale były ze sobą sklejone w sposób uniemożliwiający wzajemny przesuw, to rozkład naprężeń byłby taki, jaki pokazano na rys. 1c, to znaczy:
$$\begin{equation} max \ \sigma= \cfrac {M} {W_{el,Z}}= \cfrac {{ P \cdot l}}{ \frac {b\cdot (2h)^2} {6}}= \cfrac {3}{2} \cdot \cfrac {Pl} {bh^2} \label{2} \end{equation}$$
Z porównania $ ( \ref{1})$ i $ ( \ref{2})$ widać, że na skutek sklejenia bali uzyskaliśmy dwukrotne zwiększenie ich nośności w zakresie sprężystym. Pozwala to na przyjęcie mniejszych wymiarów przekroju poprzecznego.
Zjawisko zilustrowane na rys.1 i opisane zależnościami ($\ref{1})$ oraz ( $\ref{2}$) można uogólnić na inne przekroje i inne schematy statyczne. W przypadku braku zespolenia sprężysty wskaźnik wytrzymałości $ W_{el}$ belki złożonej ze swobodnie ułożonych na sobie części jest sumą wskaźników wytrzymałości:
$$\begin{equation} W_{el,S}= \sum_i W_{el,i} \label{3} \end{equation}$$
W przypadku przekroju złożonego z nieprzesuwnych (zespolonych) części sumują się momenty bezwładności zgodnie z twierdzeniem Steinera.
W przypadku zginania w zakresie plastycznym zależności ($\ref{1}$) i ( $\ref{2}$) przyjmą postać:
$$\begin{equation} max \ \sigma= \cfrac {M} {W_{pl,S}}= \cfrac {{ \frac {P} {2} \cdot l}}{ \frac {b\cdot h^2} {4}}=2 \cfrac {Pl} {bh^2} \label{4} \end{equation}$$
$$\begin{equation} max \ \sigma= \cfrac {M} {W_{pl,Z}}= \cfrac {{ P \cdot l}}{ \frac {b\cdot (2h)^2} {4}}= 1 \cdot \cfrac {Pl} {bh^2} \label{5} \end{equation}$$
i uzyskujemy podobne zwiększenie nośności przekroju zespolonego w stosunku do przekroju złożonego swobodnie.
Istota zespolenia polega na odpowiednim połączeniu leżących na sobie części elementu za pomocą łączników, którymi w powyższym przykładzie był klej. W praktyce stosuje się łączniki mechaniczne, takie jak: gwoździe, kliny, spawane spoiny i wreszcie kołki (sworznie).
W każdym przypadku łączniki te są obciążone siłą rozwarstwiającą, działającą stycznie do łączonych powierzchni ( na rys.1 poziomo w osi x) . Siła ta jest wywołana siłą poprzeczną (ścinającą) , działającą pionowo. W przypadku wspornika z rys 1 a siła poprzeczna T=P, a naprężenia rozwarstwiające w stanie sprężystym można obliczyć ze wzoru Schwedlera-Żurawskiego dla poprzecznego zginania:
$$\begin{equation} \tau(x)= \cfrac {T \cdot \overline S_y } {Iz_{y,}\cdot b} \label{6} \end{equation}$$
gdzie:
$ T = T(x)$ – siła poprzeczna w belce o współrzędnej x;
$\overline S_y$ – moment statyczny odciętej części przekroju ( w przypadku nas rys.1 połowy przekroju) względem osi obojętnej y;
$ Iz_{y}$ – moment bezwładności przekroju zespolonego Z względem osi y;
b- szerokość przekroju w miejscu zespolenia.
Jeśli w miejsce kleju zastosowane zostaną łączniki (np. kołki) w odstępie e, to łączniki powinny przenieść siłę rozwarstwiającą $T_{\tau}$, wynikającą z naprężeń ($\ref{6}$):
$$\begin{equation} T_{\tau}= b\cdot e \cdot \tau(x)= \cfrac {T(x) \cdot \overline S_y} {Iz_{y}} \cdot e \label{7} \end{equation}$$
Zasady podstawowe
Analiza przedstawiona na rys.1 dotyczy zakresu sprężystej pracy belki. Badania doświadczalne belek zespolonych stalowo-betonowych wskazują, że element zespolony osiąga nośność w zakresie plastycznym, a belka nadal ma duże zapasy nośności. Analiza sprężysta jest dokonywana tylko w szczególnych przypadkach, gdy zastosujemy łączniki podatne, co prowadzi do częściowego zespolenia, ale również wówczas metody obliczeń wykorzystują w dużym stopniu badania doświadczalne.
Badania doświadczalne [4] i inne , wykazały: że:
W belkach swobodnie podpartych występuje duża rezerwa nośności oraz duże ugięcia belek od początku uplastycznienia przekroju stalowego do osiągnięcia nośności granicznej. Jest to spowodowane wzmocnieniem stali przy odkształceniu plastycznym. Poślizg w płaszczyźnie zespolenia ma bardzo mały wpływ na nośność belki.
W belach ciągłych nośność graniczna przekroju z płytą rozciąganą jest równa momentowi plastycznemu przekroju belki stalowej i podłużnego zbrojenia płyty pod warunkiem, ze nie nastąpi utrata stateczności belki stalowej. Poślizg w płaszczyźnie zespolenia ma bardzo mały wpływ na nośność belki zarówno dodatnią jak i ujemną (moment podporowy). Obecność zbrojenia podłużnego w płycie powoduje wystąpienie siły ściskającej w belce i zwiększa ryzyko utraty jej stateczności.
Uplastycznienie przekroju jest powszechnie przyjęte jako kryterium obliczania nośności przekroju zespolonego zginanego momentem dodatnim [4].
Nośność przekroju poprzecznego belek oblicza się , przyjmując następujące założenia:
- wytrzymałość betonu na rozciąganie jest pomijalnie mała,
- obowiązuje zasada płaskich przekrojów,
- rozkład naprężeń w przekroju zgodnie z rys.2
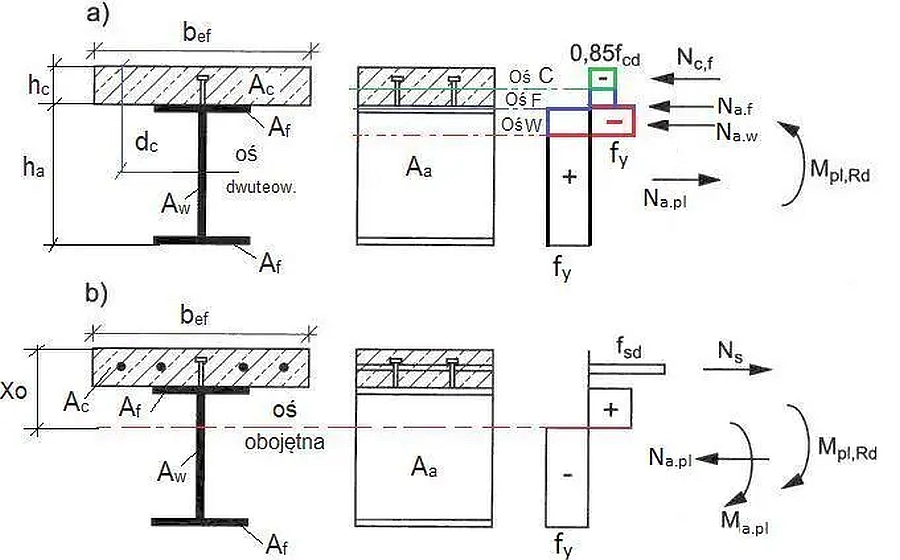
Rys.2. Rozkład naprężeń w przekroju zespolonym obciążonym: a) momentem dodatnim, b) momentem ujemnym
Wyodrębnia się dwie podstawowe postacie zniszczenia belek:
- zmiażdżenie betonu po wzmocnieniu stali przez odkształcenia plastyczne,
- zmiażdżenie betonu przed rozwinięciem znaczącego wzmocnienia stali.
W pierwszym przypadku belka jest określana jako ciągliwa, a w drugim jako krucha. Belki o przekroju ciągliwym są bardziej korzystne do konstrukcji budowlanych, ponieważ: 1) ich nośność graniczna jest zawsze większa ( nawet do 35%) od teoretycznego momentu plastycznego, 2) zniszczenie jest sygnalizowane poprzedzającymi znacznymi ugięciami, 3) odkształcenia plastyczne stali umożliwiają redystrybucję sił w belach statycznie niewyznaczalnych.
W belkach wystarczająco zabezpieczonych przed ścinaniem i poślizgiem w płaszczyźnie zespolenia, zachowanie przekroju zależy głównie od wymiarów płyty betonowej dźwigara oraz od granicy plastyczności stali i wytrzymałości betonu na ściskanie. Grubość płyty betonowej znacząco wpływa na nośność, a jej szerokość determinuje „ciągliwość” przekroju. Zwiększenie szerokości płyty umożliwia uzyskanie większego momentu wzmocnienia, ponieważ płyta może wciąż równoważyć siły w dźwigarze, gdy stal jest stopniowo wzmacniana a przez odkształcenia plastyczne.
Granica plastyczności stali ma znaczący wspływ na zachowanie się przekroju, niezależnie od geometrii płyty. Moment plastyczny wzrasta liniowo wraz ze wzrostem granicy plastyczności, ale równocześnie maleje ciągliwość przekroju. „Ciągliwość ” przekroju wzrasta jednak wraz z e wzrostem wytrzymałości betonu. Wysoka wytrzymałość betonu sprzyja powstawaniu w belce dużej krzywizny, ponieważ siła ściskająca może być przeniesiona przez cienką warstwę betonu przy wierzchu płyty. Duże krzywizny umożliwiają duże wzmocnienie dźwigara przez odkształcenia plastyczne. Jeżeli beton ma niewielką wytrzymałość , cała płyta musi przenosić się z dźwigara stalowego, a miażdżenie betonu następuje przy małej krzywiźnie [4].
Obliczenia projektowe
Sytuacje obliczeniowe
Obliczenia elementów zespolonych są prowadzone metodą stanów granicznych w sytuacjach obliczeniowych, wynikających z faz kształtowania i użytkowania konstrukcji a to:
- Faza budowy lub naprawy, ze szczególnym uwzględnieniem sytuacji, gdy beton jeszcze nie związał i całość obciążeń ma przenieść belka stalowa
- Faza eksploatacji,
- Sytuacje wyjątkowe.
Należy sprawdzić stany nośności dla wszystkich możliwych mechanizmów ( równowaga statyczna, nośność stali i żelbetu w przekroju, przekształcenie konstrukcji w mechanizm, utratę stateczności), a także stany graniczne użytkowalności (ugięcia w stanie zarysowanym betonu a także, graniczny stan zarysowania ).
Dla płyt ciągliwych (i wyłącznie dla tych) można dopuścić częściowe zespolenie i wówczas obliczenia są dokonywane również w zakresie sprężystym, co komplikuje proces projektowania. Szczególnie w takich przypadkach zalecane jest prowadzenie obliczeń z wykorzystaniem oprogramowania opisanego niżej.
Szerokość współpracująca płyty żelbetowej
Szerokość współpracującą płyty belki żelbetowej wprowadzono w celu uproszczenia obliczeń, w taki sposób, by można była przyjąć, że naprężenia ściskające $\sigma_c$ w płycie są stałe na długości $b_{ef}$, czyli z warunku $N_c=b_{ef} \cdot \sigma_c = B\cdot \sigma_{real}$, gdzie B faktyczna szerokość płyty(rys.3),
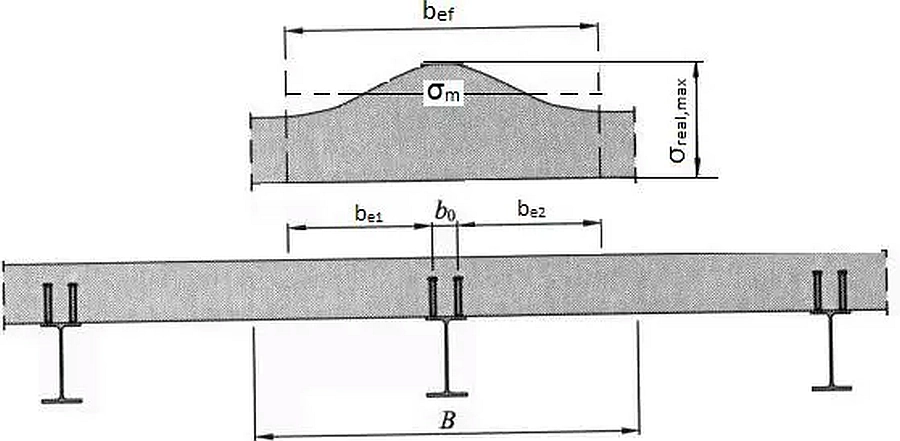
Rys. 3 Idea szerokości współpracującej $b_{ef}$ na podstawie [5] – rys. 4.2.
Szerokość współpracującą $b_{ef}$ żelbetowej płyty w praktycznych obliczeniach można oszacować z formuły
$$\begin{equation} b_{ef} = b_0 +\sum \limits_i \beta_i \cdot b_{ei} \label{8} \end{equation}$$
gdzie $b_0$ odległość miedzy środkami skrajnych ścinanych łączników po szerokości pasa ( rys.4)
$\beta_i =(0,55+0,025 \cdot L_e/ b_{ei}) \le 1,0$ – tylko na podporze skrajnej . Dla podpór pośrednich $\beta_i=1,0$
$b_{ei}$- efektywna szerokość betonowej półki z każdej strony środnika.Można ją przyjąć równą $L_i/8$., ale nie więcej niż wynosi geometryczna szerokość $b_i$.
Wartość $b_i$ może być przyjęta jako odległość od skrajnego ścinanego łącznika do punktu w połowie odległości pomiędzy środnikami sąsiednich belek mierzona w połowie grubości betonowej półki, z wyjątkiem przypadku, gdy odległość $b_i$ jest odległością od swobodnej krawędzi płyty. Długość $L_e$ jest odległością między punktami zerowych momentów zginających.
D!a typowych ciągłych zespolonych belek, kiedy obwiednia momentów pod różnymi układami obciążeń decyduje o $L_e$ oraz dla wsporników, $L_e$ może być określone jak to pokazano na rys. 4 . Rozpiętości $L_e$ z rys.4. dotyczą konstrukcji z węzłami sztywnymi.
W przypadku ram (lub belek) z węzłami podatnymi (lub przegubami Gerbera) długości te należy określić z wykresu rzeczywistych momentów zginających jako odległości między punktami zerowania się momentów.
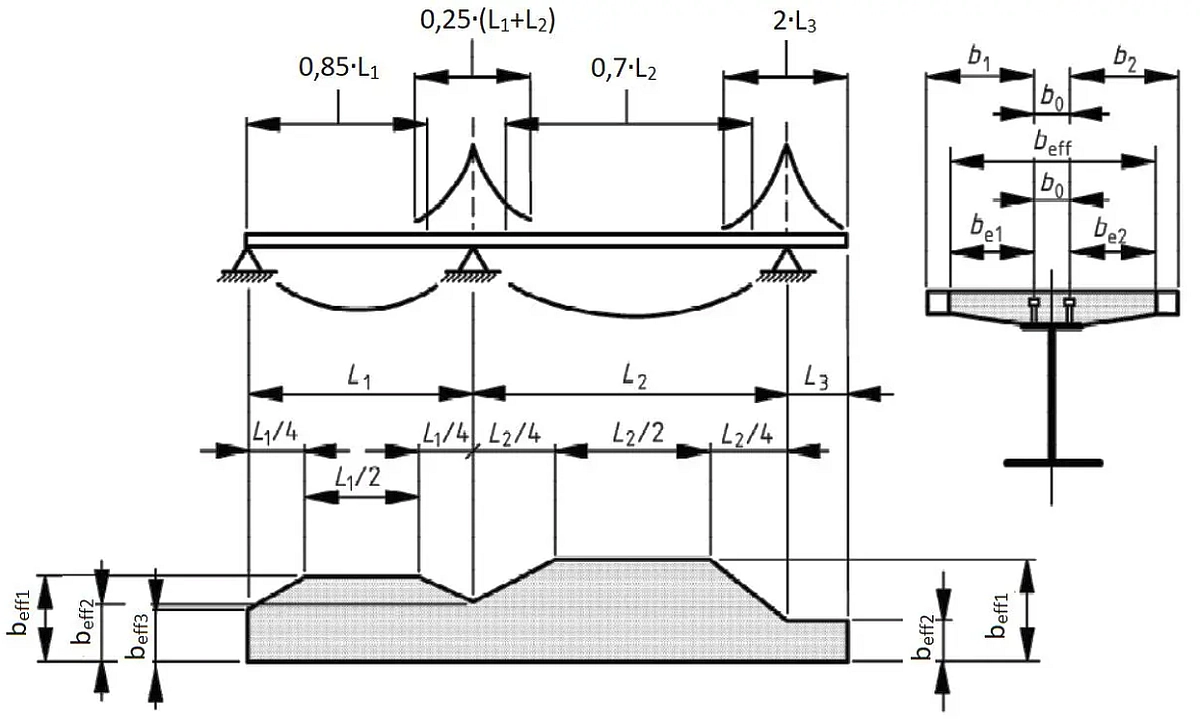
Rys.4. Równoważne rozpiętości do określenia szerokości efektywnej płyty żelbetowej w przekroju zespolonym (opracowano na podstawie [6]– rys.5.1)
Formuła ($\ref{8}$) w przypadku belki swobodnie podpartej o długości L (czyli $l_e=L$ i $b_{e1}= b_{e2} =L_e/8 \le s/2$ dla rozstawu belek $s \ge L/4$ sprowadza się do
$$\begin{equation} b_{ef} = b_0 + L/8 + L/8 \approx L/4 \label{9} \end{equation}$$
W pracy [7] pokazano , że szerokość współpracującą w stanie granicznym nośności jest większa niż wynika z uproszczonej formuły ($\ref{8}$). Przedstawiono nową definicję szerokości efektywnej w stanie granicznym w drodze analiz eksperymentalnych i w złożonym modelu MES. Pokazano również , że położenie osi obojętnej jest odmienne od wynikających z uproszczonej analizy normowej np. ($\ref{26}$).
Minimalne zbrojenie płyty żelbetowej
Zbrojenie podłużne – równoległe do belki
Zbrojenie podłużne $A_x$ na rys.9 usytuowane na szerokości efektywnej traktuje się jako integralną część przekroju zespolonego, przekrój tego zbrojenia odniesiony do przekroju płyty (stopień zbrojenia $\rho_x= A_x/A_c$ powinien spełniać warunek
$$\begin{equation} \rho_x = \begin{cases}
0,3 , & \text { % gdy płyta jest ściskana} \\
0,6 , & \text { % gdy płyta jest rozciągana} \\
\end{cases} \label{10} \end{equation}$$
Przekrój betonu płyty żelbetowej $A_c$ na długości $b_{ef}$ ujmuje również beton w bruzdach blach fałdowych równoległych do belki lub zmienną wysokość wsporników, np. mostowych. W przypadku bruzd prostopadłych do belki przekrój betonu nie obejmuje bruzd blachy. W każdym przypadku wysokość żeber płyty nie może być wiesza niż 80 mm, a grubość płyty mniejsza niż 50 mm.
Zbrojenie poprzeczne – prostopadłe do belki
Zbrojenie poprzeczne $A_y$ na rys.9 jest zbrojeniem nośnym płyty żelbetowej i powinno spełniać warunki ogólne dla zbrojenia minimalnego płyt żelbetowych zgodnie z artykułem Belki żelbetowe.
Rozwarstwienie belki zespolonej (ścinanie podłużne)
Istotą zespolenia jest uniemożliwienie poślizgu płyty betonowej w stosunku do belki stalowej. Siła rozwarstwiająca te dwa elementy konstrukcji zespolonej jest przenoszona przez łączniki zespalające (sworznie).
Klasyczne wyrażenie ($\ref{7}$) słuszne przy sprężystym zginaniu, niestety nie może być zastosowane ze względu na silnie nieliniowe zachowanie się zespolonej konstrukcji stalowo-betonowej. Na styku stali i betonu zależy od wielu czynników, takich jak: odkształcalność łączników, skurcz i pełzanie płyty betonowej. Z tych powodów stosuje się raczej metody doświadczalne, zamiast metod numerycznych nawet tych wyrafinowanych – w praktyce projektowej nie podejmuje się raczej prób dokładniejszych obliczeń dystrybucji siły rozwarstwiającej. Tam, gdzie to możliwe, łączniki są równomiernie rozmieszczone wzdłuż rozpiętość. Tam gdzie nie da się tego zrobić stosuje się metodę przybliżoną rozmieszczania równomiernego łączników ,wzdłuż każdej długości krytycznej, która jest długością przedziału między dwoma sąsiednimi krytycznymi przekrojami, czyli przekrojami, w których następuje skokowa zmiana siły poprzecznej na pręcie
Przekroje i długości rozwarstwienia
Przekrojami charakterystycznymi z punktu widzenia rozwarstwienia (krótko przekrojami rozwarstwienia), są przekroje:
- w których moment zginający osiąga ekstremum (lokalne)
- nadpodporowe
- pod siłami skupionymi
- w miejscach, w których występuje nagła zmiana przekroju pręta
- wolne końce wsporników
Powyższe dotyczy również elementów zwężających się stopniowo.
Przekroje rozwarstwienia są często nazywane w literaturze przekrojami krytycznymi, np. [4]. W każdym przekroju rozwarstwienia określamy siłę ściskającą płytę betonową $N_c$, pochodzącą od momentu zginającego jak określono niżej oraz siłę rozciągająca $N_t$ pochodzącą od obciążeń zewnętrznych. Na odcinku pomiędzy przekrojami rozwarstwienia, czyli na długości rozwarstwienia $L_{sc}$ przyrost siły ściskającej płytę wynosi $\Delta N_c= N_{c2}-N_{c1}$, gdzie $N_{C2}$ i $N_{c1}$ siła na końcu i początku długości $L_{sc}$.
Liczba łączników, które należy rozmieścić na długości $L_{sc}$wynosi
$$\begin{equation} n_s=\cfrac {\Delta N_c} {P_{Rd}} \label{11} \end{equation}$$
gdzie $P_{Rd}$ – nośność jednego łącznika wg ($\ref{12}$)
W przypadku belki swobodnie podpartej, w której maksimum momentu wystąpi w środku rozpiętości (czyli np: obciążonej równomiernie lub z siłą skupiona w środku) – długość rozwarstwienia, to połowa rozpiętości $L_{cr}=L/2$, $\Delta N_c=N_{c,max}$ – 0$ (N_{c,max}$ – siła ściskająca płytę w środku belki , a liczba łączników , które należy rozmieścić na tej długości wynosi $\cfrac{N_{cmax}}{P_{Rd}}$
Przekroje i długości rozwarstwienia $L_{sc}$ , a także rozdział łączników na poszczególne przedziały rozwarstwienia można dokonać na podstawie wykresu sił poprzecznych w sposób pokazany na rys. 5
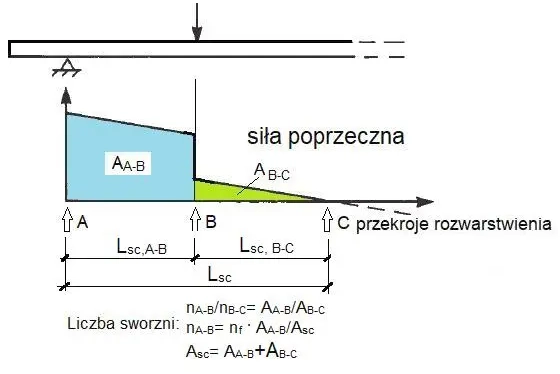
Rys. 5 Wyznaczanie przekrojów i odcinków rozwarstwieni oraz rozdział liczby sworzni na podstawie wykresu sił poprzecznych
Nośność sworznia ze względu na jego ścięcie
Nośność na ścinanie wyznacza się według wzoru [1] – kl. 6.6.3.1
$$\begin{equation} P_{Rd} = k_t \cdot \cfrac{d^2}{\gamma_v} \cdot \min { \{ 0,8 \cdot \pi / 4 \cdot f_u \, ; \, 0,29 \cdot \alpha \cdot \sqrt{f_{ck} \cdot E_{cm}}\} } \label{12} \end{equation}$$
gdzie:
$\gamma_v=1,25$ – współczynnik częściowy,
16 <d<25 mm – średnica trzpienia sworznia,
$f_u =420 \le 450 \, MPa$ – wytrzymałość na rozciąganie materiału sworznia,
$f_{ck}$ – wytrzymałość charakterystyczna betonu z uwzględnieniem pełzania (wieku betonu)
$h_{sc}$ – całkowita wysokość sworznia,
$E_{cm}$ – doraźny moduł Younga betonu
Współczynnik $\alpha$ zależy od smukłości sworznia $\lambda_{sc}= \cfrac{h_{sc}}{d}$ (stosunku wysokości sworznia do jego średnicy):
$$\begin{equation} \alpha = \begin{cases}
1,0 , & \text { dla } \lambda_{sc} \ge \\
0,2\cdot(\lambda_{sc}-1) , & \text { dla } 3 \le \lambda_{sc} < 4 \\
\end{cases} \label{13} \end{equation}$$
Współczynnik redukcyjny $k_t$ przy ułożeniu blachy prostopadle do osi belki wyznacza się z zależności [1]:
$$\begin{equation} k_t= \cfrac{0,7}{\sqrt{n_r}}\cdot \cfrac{b_p}{h_p}\cdot \left( \cfrac{h_{sc}}{h_p} -1 \right) \le k_{max} \label{14} \end{equation}$$
gdzie:
$n_r$ – liczba sworzni w jednej bruździe na skrzyżowaniu z belką (w obliczeniach nie większa od dwóch),
$h_p \le 85 \, mm$ -wysokość bruzdy blachy;
$b_p = (b_1 +b_2)/2 > h_p$ – średnia szerokość bruzdy blachy, $b_1,b_2$ – szerokość bruzdy na dole i u góry fałdy.
Maksymalna wartość współczynnika $k_t$ dla sworzni o średnicy nie przekraczającej 20 mm spawanych przez blachę o grubości $t$ [1]:
$$\begin{equation} k_{max} = \begin {cases}
1,0 & \text { dla } n_r=1 \, , \, t >1 \, mm\\
0,85 & \text { dla } n_r=1 \, , \, t \le 1 \, mm \\
0,80 & \text { dla } n_r=2 \, , \, t > 1 \, mm \\
0,75 & \text { dla } n_r=2 \, , \, t \le 1 \, mm \\
\end{cases} \label{15} \end{equation}$$
Maksymalna wartość współczynnika $k_t$ dla sworzni o średnicy 19 lub 22 mm w profilowanej blasze z otworami:
$$\begin{equation} k_{max} = \begin {cases}
0,75 & \text { dla } n_r=1\\
0,6 & \text { dla } n_r=2 \\
\end{cases} \label{16} \end{equation}$$
Stopień zespolenia
Stopień zespolenia połączenia definiuje się jako [8] , kl.6.2.1.3(3):
$$\begin{equation} \eta =\cfrac{N_c}{N_{c,f}} \label{17} \end{equation}$$
gdzie:
$N_{c,f}$ – możliwa do przeniesienia siła ściskająca w płycie betonowej przy pełnym zespoleniu $(\ref{19})$, czyli po zastosowaniu liczby łączników $n_f$
$N_c$ – faktycznie przenoszona siła ściskająca płytę betonową $(\ref{20})$ limitowana nośnością łączników w liczbie $n_s <n_f$
Stopień zespolenia można zdefiniować w sposób równoważny do $(\ref{17})$ jako
$$\begin{equation} \eta =\cfrac{n_s}{n_f} \label{18} \end{equation}$$
Siła ściskająca w płycie betonowej może przy pełnym zespoleniu osiągnąć wartość [1],rys.6.2 (rys.2a):
$$\begin{equation} N_{cf} =0,85\cdot f_{cd} \cdot A_c \label{19} \end{equation}$$
gdzie:
0,85 – współczynnik redukcyjny,
$f_{cd}$ – wytrzymałość obliczeniowa betonu na ściskanie
$A_c= b_{ef} \cdot h_z $ – pole przekroju poprzecznego poprzecznego płyty betonowej:
$h_z$ ($\ref{22}$) – grubość (zastępcza) płyty
$b_{ef}$ ($\ref{8}$)- efektywna szerokości płyty współpracującej
Siła ściskająca $(\ref{19})$ jest ograniczona przez nośność łączników na ścinanie do wartości
$$\begin{equation} N_c = \cfrac{n_s \cdot P_{Rd}}{2} \label{20} \end{equation}$$
gdzie:
$n_s$ – liczba łączników ścinanych faktycznie zastosowanych na efektywnej długości rozwarstwienia belki $L_{sc}$ (rys.5),
Liczba łączników $n_s$ nie może przekroczyć:
W układzie BP (belka prostopadła do fałd blachy): $n_s=L_{sc} /e$ gdzie e- odległość miedzy sworzniami, $L_{sc}$ – długość rozwarstwienia wg rys.5
W układzie BR (belka równoległa do fałd blachy): $n_s=n_r \cdot L_{sc}/e$ gdzie: $n_r$ – liczba sworzni w fałdzie , e – rozstaw fałd blachy trapezowej (rozstaw sworzni)
$P_{Rd}$ – nośność łącznika na ścinanie $(\ref{12})$.
Łączniki sworzniowe z łbami o całkowitej długości po przyspawaniu nie mniejszej niż 4-krotna średnica i z trzpieniem o nominalnej średnicy nie mniejszej niż 16 mm i nie większej niż 25 mm, można uznać za ciągliwe pod warunkiem następujących ograniczeń stopnia zespolenia:
$$\begin{equation} \eta_{min}= \begin {cases}
1- \left( \cfrac{355}{f_y}\right) \cdot k_e \ge 0,4,, &\text{ dla } L_e \le L_{e,max}\\
1,0 , &\text{ dla } L_e > L_{e,max}\\
\end {cases} \label{21} \end{equation}$$
Dla kształtowników stalowych z równymi półkami przyjmuje się: $k_e= 0,75- 0,03 \cdot L_e$ , $L_{e,max} = 25 \, m$,
Dla kształtowników stalowych mających pole przekroju dolnej półki równe 3-krotnemu polu przekroju górnej półki przyjmuje się: $k_e(0,3 – 0,015 \cdot L_e $ , $L_{e,max} = 20 \, m$
Długość $L_e$ jest odległością pomiędzy dwoma punktami zerowymi dodatniego momentu zginającego w metrach; dla zwykłej belki ciągłej, które można przyjąć jak na rys. 4,
Nośność w warunkach pożarowych
Analiza konstrukcji zespolonych w warunkach pożarowych może być dokonana metodami
- zaawansowana metoda obliczeniowa (z zastosowaniem MES). Metoda ta wymaga zastosowania specjalizowanych programów komputerowych i w zasadzie służy walidacji (specyfikowaniu) metod przybliżonych (dwóch pozostałych).
- prostej metody obliczeniowej dla niezabezpieczonej ogniowo blachy stalowej. Stosowane dla prostych schematów statycznych konstrukcji zespolonych
- metod tablicowych wg tablic normy [9], w której podano minimalne wymiary, obszary zbrojenia itp., w zalezności od wymaganej klasy odporności ogniowej.
Nośność przekroju zespolonego przy pełnym zespoleniu $\eta=1$
Sytuacje obliczeniowe
Nośność przekroju wyznacza się po ustaleniu położenia osi obojętnej [ C, F, W] w granicznym stanie plastycznym (lub sprężystym , jeśli nie można zastosować teorii plastycznej), co zależy od kierunku działania momentu zginającego [(„+” rozciąga dolne włókna ) lub ( „-” rozciąga górne włókna)] oraz kierunku ułożenia blachy fałdowej w stosunku do osi belki [PŁ, BP, BR].
W celu wprowadzenia spójnych formuł dla wszystkich trzech układów [PŁ, BP, BR] (rys.6) wprowadza się grubość zastępczą $h_z$ płyty betonowej:
$$\begin{equation} h_z = \begin{cases}
h_T= h_c+h_p ,& \text { w układzie PŁ } \\
h_c ,& \text{ w układzie BP } \\
h_c+\cfrac{b_1+b_2}{2} \cdot \cfrac {h_p}{e} ,& \text{ w układzie BR }\\
\end{cases} \label{22} \end{equation}$$
gdzie: $b_1,b_2,h_p, e$ odpowiednio: szerokość betonu u dołu bruzdy w blasze , szerokość betonu u góry, wysokość i rozstaw bruzd blachy trapezowej
Wysokość zastępcza bruzdy blachy wynosi (rys 6c)
$h_{pz}=h-h_z$
Rozpatruje się dwa przypadki kierunku momentu zginającego:
(+) – moment dodatni – rys.2a.
(-) – moment ujemny – rys.2b.
Mogą wystąpić trzy przypadki położenia osi obojętnej przekroju O-O o współrzędnej $x_o$ od powierzchni górnej płyty żelbetowej licząc (rys.2 i rys 7):
C (oznaczona kolorem zielonym na rys. 2a) – oś umiejscowiona w grubości płycie żelbetowej $x_o < h_z $, gdzie $h_z$ zastępcza grubość płyty betonowej zgodnie z formuła ($\ref{22}$),
F ( oznaczona kolorem niebieskim na rys. 2a) – oś umieszczona w półce dwuteownika stalowego $h_T + t_f > x_o > h_T$, gdzie: $h_T$ – całkowita wysokość blachy trapezowej, $t_f$, – grubość półki górnej dwuteownika stalowego,
W ( oznaczona kolorem czerwonym na rys. 2a,b) – oś w środniku dwuteownika stalowego $x_o > h_T+ t_f$.
Należy zwrócić uwagę, że pomiędzy belką stalową i płytą żelbetową może wystąpić wolna przestrzeń :
w przypadku BR o wysokości bruzdy blachy $h_p$,
w przypadku BP o zredukowanej wysokości bruzdy $h_{pz} =h_T – h_z$ :
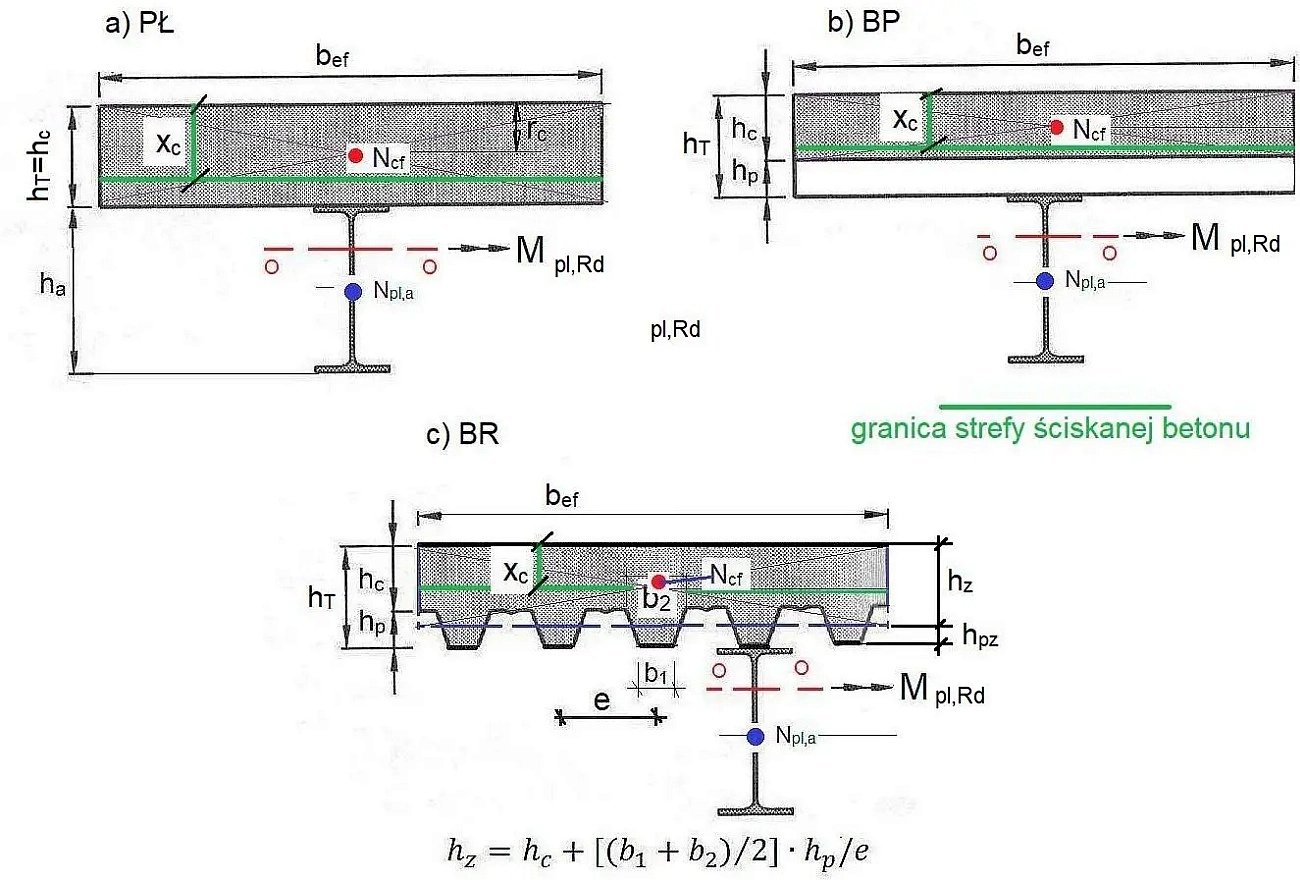
Rys.6. Układ belki: a) PŁ – płyta płaska, BP – belka prostopadła do fałd blachy, c) BR – belka równoległa do fałd blachy
(opracowano na podstawie [10]– Rys.7.9 )
Analiza statyczna przekroju zespolonego
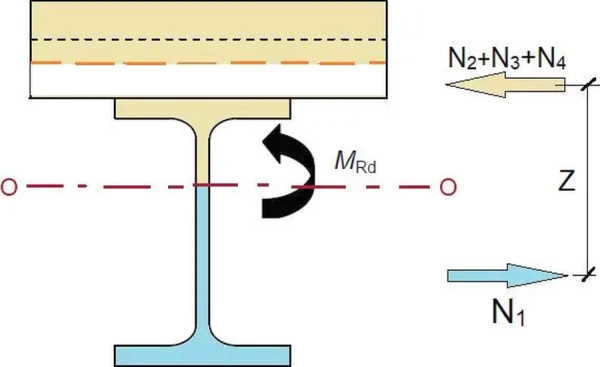
Stosujemy znakowanie sił osiowych w konwencji konstrukcji stalowych: „+” rozciąganie,”-” ściskanie.
Analiza statyczna przekroju zespolonego wynika z podstawowych zasad teorii sztywno-plastycznej i nośności plastycznej konstrukcji Nie stosuje się sprowadzonych przekrojów znanych z analizy sprężystej.
Analizę w zależności od przypadku lokalizacji osi obojętnej (rys.2) przeprowadzimy dla schematów pokazanych na rys.7. W przypadku osi F oraz W naprężenia ściskające w stali ( w pasie lub środniku) przyjmuje się $ 2\cdot f_{yd}$, co powoduje że przy stałych naprężeniach rozciągających cały przekrój stalowy $ – f_{yd}$ – w rezultacie w ściskanych częściach przekroju stalowego pozostają naprężenia $f_{yd}$.
Zgodnie z [11] współczynnik materiałowy dla stali konstrukcyjnej belki $\gamma_{M0}=1$ , więc $f_{yd}=f_y$
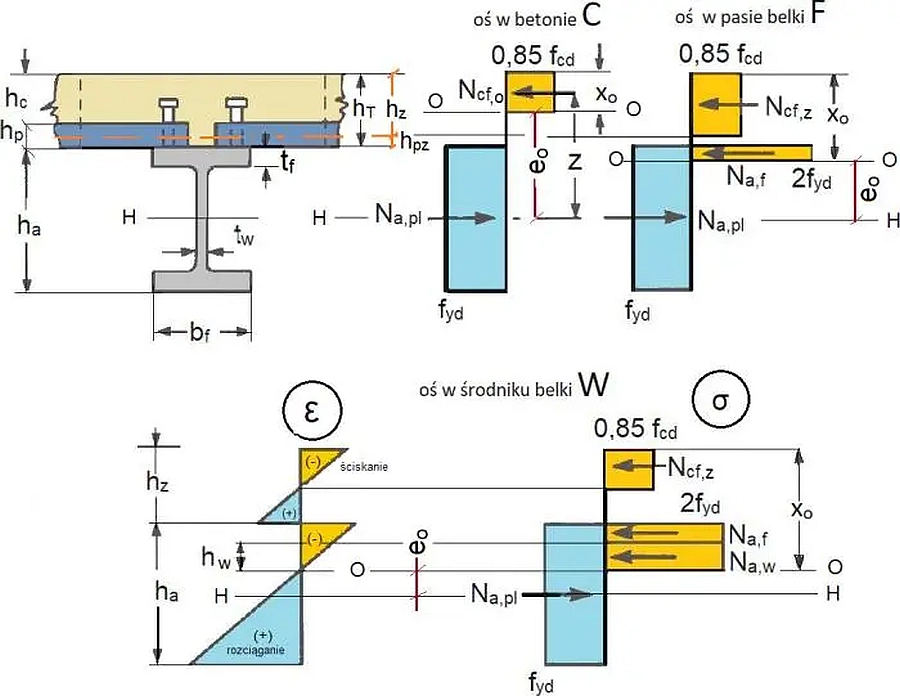
Rys.7 Model przekroju zespolonego (opracowano na podstawie [4] – Fig. 3.15)
Położenie osi obojętnej
Wprowadzamy następujące oznaczenia
$$\begin{equation} \begin{cases}
& N_1= N_{a,pl} = + A_a \cdot f_y \\
& N_2 = N_{c,f} = – 0,85 \cdot b_{ef} \cdot h_z \cdot f_{cd}\\
& N_3 = N_{a,f}= – 2 A_f \cdot f_y = 2 \cdot t_f \cdot b_f \cdot f_y\\
&N_4=N_{a,w} =- 2 A_w \cdot f_y = 2 \cdot t_w \cdot h_w \cdot f_y\\
& N_5 = N_1 – N_2 \\
&M_{pl}= M_{a,pl} =W_{pl}\cdot f_y
\end{cases} \label{23} \end{equation}$$
gdzie:
- Siła ściskająca beton: $N_{cf,o}= – 0,85 \cdot f_cd \cdot x_o$ dla przypadku osi C ; $N_{cf,z}= – 0,85 \cdot f_cd \cdot h_z$ dla przypadku osi F i W,
- Siła ściskająca pas belki: $N_{a,f}= 0$ dla osi C, $N_{a,f}= – 2 A_f \cdot f_{y} $ dla osi F i W,
gdzie pole przekroju pasa $A_f=b_f \cdot t_f$, $b_f,t_f$ – szerokość i grubość pasa belki ( z tablic wyrobów hutniczych), - Siła ściskająca środnik belki: $N_{a,w}= 0$ dla osi C i F ; $N_{a,w}= – 2 A_w \cdot f_{y}$ dla osi W,
gdzie ściskane pole przekroju środnika $A_w= t_w \cdot h_w$, $t_w$ grubość środnika (z tablic),
$h_w = x_o- h_z -t_f$ – wysokość ściskanej części środnika - Siła rozciągająca belkę stalową
$N_{a,pl} = + A_a \cdot f_y$ dla każdego przypadku ( C, F, W),
gdzie $A_a$ – całkowite pole przekroju belki dwuteowej (z tablic) - $W_{a,pl}$ – wskaźnik wytrzymałości plastycznej całego przekroju stalowego (dwuteownika)
Kryteria położenia $x_o$ osi obojętnej O-O najprościej wyznaczyć z warunku sumy rzutów sił na oś poziomą:
$$\begin{equation} N_{cf} + N_{a,f} + N_{a,w}+N_{pl,a}=0 \to N_1+ N_2+N_3 +N_4=0 \to N_5=N_3+N_4 \label {24} \end{equation}$$
Z równania ($\ref{24}$) jako wnioski z formułujemy następujące kryteria przypadków położenia osi obojętnej:
$$\begin{equation} O-O \to \begin{cases}
C: & x_o \le h_z & \text { jeśli } & (|N_1| \le |N_2|)\\
F: & x_o>h_z \text { ale } (x_o < h_z+h_{pz}+t_f),& \text { jeśli } & (|N_5| \le |N_3|)\\
W: & x_0 > h_z+h_{pz} +t_f ),& \text { jeśli } & ( |N_5| > |N_3|)\\
\end{cases} \label{25} \end{equation}$$
a także formuły na współrzędną $x_o$ osi O-O:
$$\begin{equation} x_o = \begin{cases}
\cfrac{|N_1|}{ |N_2| / h_z} ,& \text { dla osi C }\\
h_T+ \cfrac{|N_5|}{ |N_3| / t_f} ,& \text { dla osi F }\\
d_c – \cfrac{|N_2|}{|N_4|/h_w}=\cfrac{|N_2|}{2\cdot f_y \cdot t_w} ,& \text { dla osi W }\\
\end{cases} \label{26} \end{equation}$$
gdzie
$d_c = h_a / 2+h_T$ – wysokość efektywna betonu liczona do osi belki stalowej.
Współrzędna $x_0$ osi obojętnej O-O liczona jest wg rys. 2 od górnej płaszczyzny płyty betonowej. W literaturze oś obojętną przekroju zespolonego często nazywa się osią plastyczną i oznacza $x_{pl}$.
W podejściu zastosowanym w niniejszym artykule, po wprowadzeniu zastępczej grubości płyty betonowej $h_z$ formuły obliczeniowe dla układu PŁ, BP i BR są takie same i zestawione poniżej dla momentu dodatniego oraz ujemnego. W pracy [6] w układzie BR analizowane są odrębnie dwa przypadki: oś obojętna w betonie powyżej bruzdy i oś obojętna w betonie bruzdy. W ten sposób uzyskuje się wyniki dokładniejsze, ale nieistotnie z punktu widzenia praktyki projektowej.
Nośność przekroju zespolonego
Nośność przekroju zespolonego mierzona momentem zginającym $M_{Rd}$, jest zależna od osi przekroju względem której jest wyznaczana, przy czym powinna zachodzić spójność z osią względem której wyznaczane są przekrojowe siły pochodzące od obciążeń zewnętrznych $M_{Ed}$, tak by zastosować warunek nośności
$$\begin{equation} M_{Ed,s} \le M_{Rd} \label{27} \end{equation}$$,
gdzie $M_{Ed,s}$ jest momentem zginającym sprowadzonym do osi obojętnej przekroju zespolonego, to znaczy
$$\begin{equation} M_{E,d,s} = M_{E,d} \mp e_o \cdot N_{Ed} \label{28} \end{equation}$$
gdzie $e_O$ – mimośród osi – odległość między osiami O-O i H-H wg rys.6:
$$\begin{equation} e_0 = h_a/2 +h_T -x_o=d_c -x_o \label{29} \end{equation}$$
we wzorze ($\ref{25}$) siła $N_{Ed}$ze znakiem (+) rozciągająca, (-) ściskająca.
Nośność przekroju zespolonego
$$\begin{equation} M_{pl,Rd} =N_1 \cdot z \label{30} \end{equation}$$
gdzie $z$ – ramię sił wewnętrznychwg rys.8.
Siła poprzeczna ścinająca łączniki (sumowana od krawędzi górnej przekroju) wynosi:
$$\begin{equation} V_{Ed} =N_{cf} \label{31} \end{equation}$$
Nośność dla dodatniego momentu zginającego (+) ( w przęśle)
Ramię sił wewnętrznych dla poszczególnych lokalizacji osi obojętnej w formule ($\ref{30}$) wynosi:
$$\begin{equation} z = \begin{cases}
d_c- \cfrac{x_o}{2},& \text { dla osi C }\\
(h_a/2 +h_T -x_o) \, + \, N_2/N_1 \cdot (x_o-h_z/2),& \text { dla osi F }\\
(h_a+h_t-x_o – t_f )/2 +\cfrac{N_2 \cdot (x_o-h_z+h_T +t_f) +N_3 \cdot (x_o-h_T)}{2 \cdot N_1} ,& \text { dla osi W }\\
\end{cases} \label{32} \end{equation}$$
Nośność dla ujemnego momentu zginającego (-) ( nad podporą)
W sytuacji ujemnego momentu zginającego (rys2b), pomija się udział rozciąganego betonu – na rozciąganie pracuje zbrojenie płyty żelbetowej. Nie wystąpi lokalizacja C osi obojętnej w płycie żelbetowej, a formuły obliczeniowe są niezależne rodzaju płyty PŁ, BP, BR. W przekrojach z ujemnym momentem zginającym nie dopuszcza się do częściowego zespolenia (\eta <1).
W miejsce siły ściskającej ($N_{cf}$ płytę przy dodatnim momencie zginającym mamy siłę rozciągającą (rys.9).
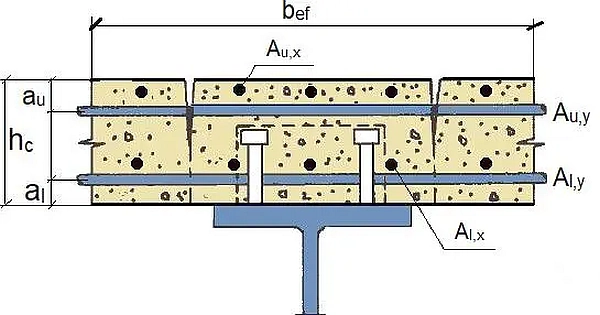
$$\begin{equation} N_{c,t} = N_{s,t} = (A_{u,x}+A_{l,x}) \cdot f_{sd} \label{33} \end{equation}$$
gdzie $f_{sd}= \cfrac{f_s}{\gamma_s}$ – $\gamma_s=1,15$ , $f_s$ – granica plastyczności stali zbrojeniowej zgodnie z tab. 2 artykułu „Belki żelbetowe”.
Na przykład dla stali zbrojeniowej B500: $f_y = 500 \, MPa$, $f_{sd}=500/1,15 =435 \, MPa.
Oznaczenia sił redefiniujemy w następujący sposób:
$$\begin{equation} \begin{cases}
& N_1= N_{a,pl} = – A_a \cdot f_y \\
& N_2 = N_{s,t} = + (A_{u,x}+A_{l,x}) \cdot f_{sd}\\
& N_3 = + 2 A_f \cdot f_y = + 2 \cdot t_f \cdot b_f \cdot f_y \text { dla W } ; \, 2 \cdot ( h_a+ h_T – x_o)\cdot b_f \cdot f_y \text { dla F } \\
& N_4 = + 2 A_w \cdot f_y = + 2 \cdot (h_a + h_T – x_o -t_f) \cdot t_w \cdot f_y \text { dla W }; \, 0 \text { dla F} \\
\end{cases} \label{34} \end{equation}$$
Równania ($\ref{24}$) przyjmuje postać:
$$\begin{equation} N_1+ N_2+N_3+N_4=0 \label{35} \end{equation}$$
skąd uzyskujemy kryteria na położenie osi obojętnej
$$\begin{equation} O-O \to \begin{cases}
F: & h_T+t_f > x_o > h_T \text { jeśli } & (N_2 \ge N_1- N_3)\\
W: & x_0 > h_T + t_f ),& \text { jeśli } & (N_2 < N_1 – N_3)\\
\end{cases} \label{36} \end{equation}$$
Położenie osi obojętnej $x_o$, liczone od dolnej krawędzi profila stalowego dla poszczególnych lokalizacji osi obojętnej w formule ($\ref{30}$) wynosi:
$$\begin{equation} x_o = \begin{cases}
h_a/2 + h_T – \cfrac{N_1-N_2 }{2\cdot t_w \cdot f_y} ,& \text { dla osi F }\\
h_a/2 + h_T – \cfrac{N_1-N_2-N_3 }{2\cdot t_w \cdot f_y}+\cfrac{h_a}{2} ,& \text { dla osi W }\\
\end{cases} \label{37} \end{equation}$$
Nośność belki zespolonej przy częściowym zespoleniu
Nośność przekroju zespolonego przy częściowym zespoleniu jest szacowany z wykorzystaniem empirycznie uzyskanej tezy postawionej już w 1965 r. w pracy [12]. Pokazano, że w przypadku zastosowania odpowiednio ciągliwych sworzni i gdy przekrój poprzeczny belki stalowej należy do klasy 1 – moment graniczny $M_{Rd}$ częściowo zespolonego przekroju belki można wyznaczyć przy wykorzystaniu sztywno-plastycznej teorii, dla zredukowanej wartości siły ściskającej w płycie betonowej, co polega na przyjęciu siły $N_c (\ref{20})$ w miejsce $N_{cf} (\ref{19})$.
Po stwierdzeniu, że nośność łączników nie jest wystarczająca do pełnego zespolenia, czyli $\eta$ $(\ref{17})$ lub $(\ref{18})$ < 1, to korzystamy ze znanych formuł $(\ref{22})$ do ($\ref{37}$), ale po zastąpieniu $N_{cf}$ przez $\eta \cdot N_{cf}$.
Analiza sprężysta belek zespolonych
Analizę sprężystą belek zespolonych należy prowadzić przy wyznaczaniu ugięć oraz nośności dla klasy 3 i 4 belki stalowej.
Współczesny sposób obliczeń konstrukcji zespolonych
Obliczenia „ręczne” utraciły na znaczeniu po wprowadzeniu na rynek przez Arcelor Mittal ogólnie dostępnej aplikacji ABC i innych. Przebieg obliczeń „ręcznych” jest przydatny wyłącznie do wytłumaczenia sposobu podejścia, co zaprezentujemy w kolejnych rozdziałach
Poniżej odnośniki do wersji instalacyjnych poszczególnych kalkulatorów i ich krótki opis. Po zainstalowaniu należy korzystać z „Pomocy” zawartej w aplikacjach.
ArcelorMittal ABC (obecnie wersja 3.51) – Belki zespolone
Program służy do projektowania stalowych i zespolonych belek. Obejmuje swym zakresem statycznie wyznaczalną belkę.
Ostatnia wersja ABC v.3.51 zawiera możliwość obliczeń w warunkach pożaru, przy zastosowaniu lub bez zastosowania ochrony przeciwpożarowej. Wprowadzono nowe rodzaje belek, wśród których możemy wymienić 3 rodzaje zespolonych belek (SFB, IFB i IFB typu B). Obliczenia mogą być również wykonywane w zwykłych warunkach, jak i w warunkach pożaru. Oprogramowanie jest w pełni zgodne z normą [1] i obecnie obowiązującymi praktykami w zakresie obliczania zespolonych belek.
ArcelorMittal ACP (obecnie wersja 1.0.2) – Zwichrzenie belek zespolonych
ArcelorMittal Construction Phase do rozwiązań zespolonych. Sprawdza zwichrzenie belek zespolonych podczas montażu.
ArcelorMittal A3C (obecnie wersja 2.98) – Słupy zespolone
Przy pomocy nowej wersji oprogramowania możliwe jest wymiarowanie słupów stalowych i kompozytowych (częściowo lub całkowicie obetonowanych) w warunkach zwykłych lub pożarowych. Zawiera bazę materiałową powłok przeciwogniowych firmy International Paint Ltd oraz możliwość sprawdzenia punktu przyłożenia obciążenia podczas sprawdzania wyboczenia giętno – skrętnego (LTB). Program jest w pełni zgodny z wymaganiami normy [1]
ArcelorMittal COP2 (obecnie wesja 1.05) Belka-słup zespolona
Wstępne projektowanie łączeń belka-słup w systemach zespolonych, zgodnie z normami z normami [13] i [1].
ArcelorMittal CoSFB (Composite Slim-Floor Beams
Oprogramowanie do obliczeń zintegrowanych belek kompozytowych (SFB, IFB) w warunkach zwykłych. Program jest w pełni zgodny z „Zulassung-SFB-Betondübel z-26.4-59”.
COFRA5 – internetowy program do projektowania zespolonych rozwiązań stropowych
Cofra5 jest oprogramowaniem służącym do obliczeń lekkich, zespolonych rozwiązań stropowych. Cofra5 ułatwia szybkie i niezawodne zaproponowanie alternatywy dla tradycyjnych konstrukcji stropów, co pozwala na ocenę wykonalności technicznej takiego rozwiązania w początkowej fazie projektu.
ArcelorMittal ACB+ (obecnie wersja 3.02) – profile ażurowe
Program służy do projektowania stropów z użyciem belek ażurowych, co pozwala na projektowanie lżejszych konstrukcji lub zwiększenie rozpiętości.
ArcelorMittal Angelina (obecnie wersja 3.02) – profile Angelina
Program ANGELINA wspiera projektowanie profili Angelina (rys.4). Program został stworzony przez CTICM (Centre Technique Industriel de la Construction Métallique – Francja).
Łączniki zespalające
Na rys. 10 pokazano najważniejsze typy łączników zespalających.
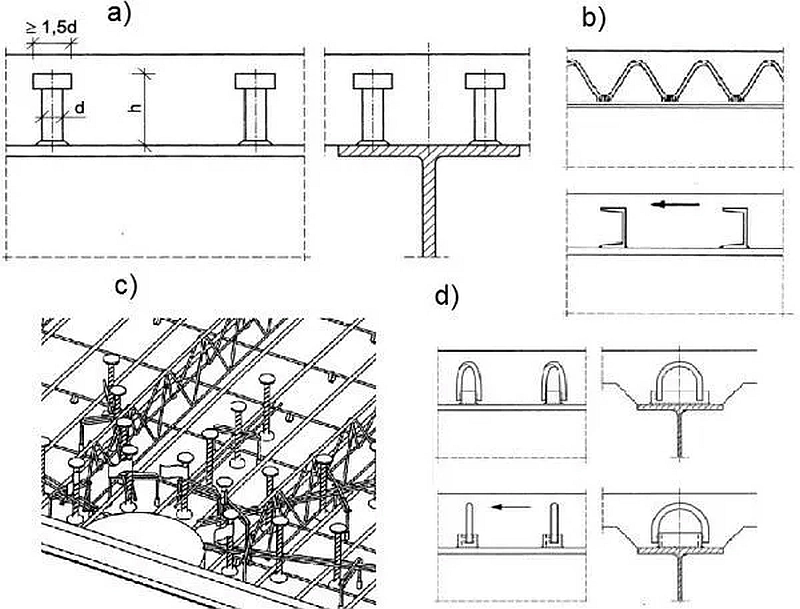
Rys. 10 Łączniki zespalające: a) typowe kołki z główką, zgrzewane lub spawane do belki stalowej, b) łączniki blokowe z kształtowników: blachy, ceowników, d) blokowe z pętlami: płaskowniki, ceowniki, c) trzpienie stalowe Schöck Bole do zespolenia betonu z betonem nad miejscem punktowym podparcia
Konstrukcje i elementy zespolone
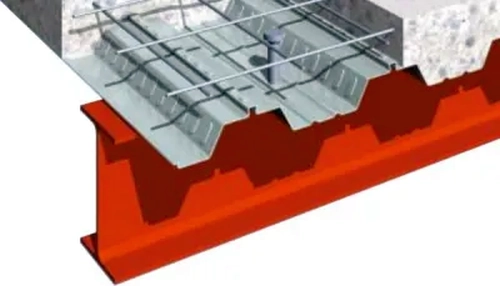
Płyty (stropy) zespolone
Stropy zespolone są najczęstszym zastosowaniem konstrukcji zespolonych.
Na rys.11 i 12 pokazano przykład stropu zespolonego na blasze fałdowej typu CofraPlus oraz CF70 , prod. Arcelor-Mittal., a na rys . 13 strop na ażurowych belkach typu Angelina z rys. 14
Słupy zespolone
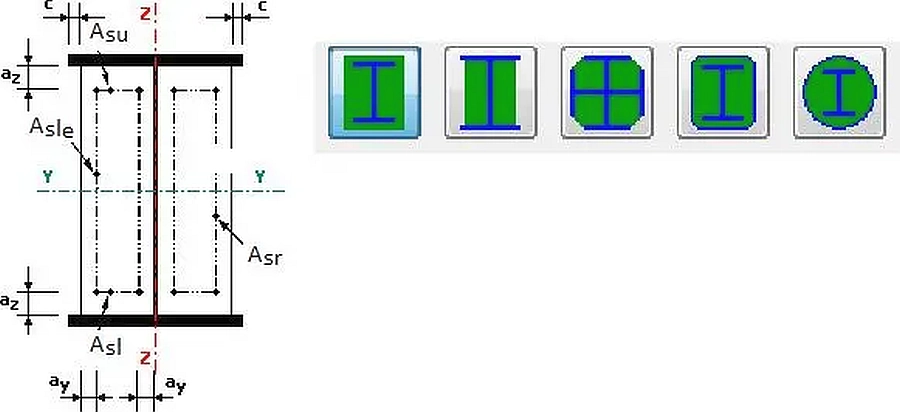
Słupy zespolone zalicza się do konstrukcji żelbetowych , ale są przedmiotem normy [1]. Na rys. 15 pokazano najczęściej stosowane przekroje słupów zespolonych i sposób ich zbrojenia na przykładzie zespolenia dwuteownika z betonem z zastosowaniem zbrojenia o przekroju $A_s$: u- górnego, l-dolnego, le-lewego i r-prawego.
Do zespolenia przekrojów słupów często stosuje się kołki oraz układa strzemiona w sposób pokazany na rys. 16.
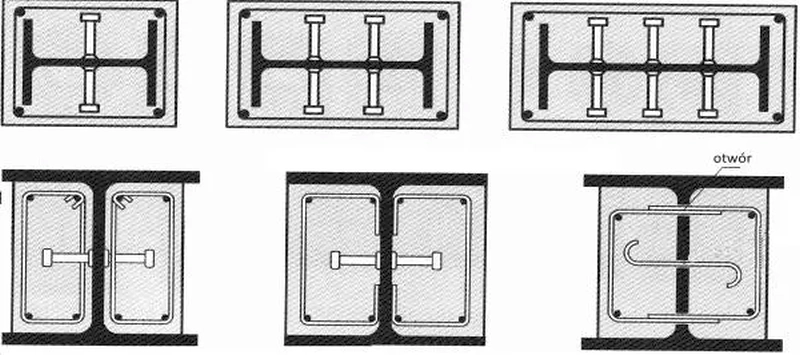
Rys. 16 Łączniki (kołki) i strzemiona w przekrojach zespolonych słupów [14]– rys. 10.46
MES w zastosowaniu do belek zespolonych
Złożone nieliniowe zachowanie belek zespolonych wymaga zaawansowanych metod Metody Elementów Skończonych, polegających na niezależnej aproksymacji sił przekrojowych oraz przemieszczeń poprzecznych czyli z zastosowaniem hybrydowej odmiany MES, na przykład wg pracy [2]
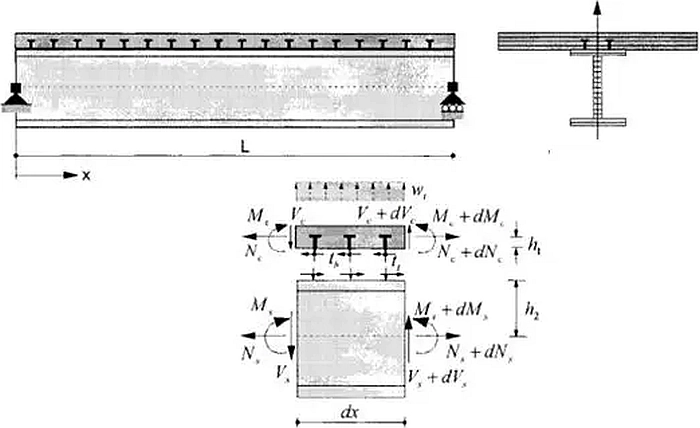
Na rys. 17 pokazano dźwigar stalowy zespolony z płytą betonową. Siły odnoszące się do betonu są oznaczone indeksem dolnym „c”, a te odnoszące się do stali indeksem dolnym „s”. Równania równowagi dla każdej składowej belki, w tym efekty poślizgu i wypiętrzenia, są wyprowadzane z podejścia Adekoli (1968) w następujący sposób
Przykłady rachunkowe
Przykład 1 [ Strop zespolony betonowo-stalowy na blasze fałdowej. Belka wolnopodparta]
Na podstawie przykładów z pracy [5]
Postawienie zadania
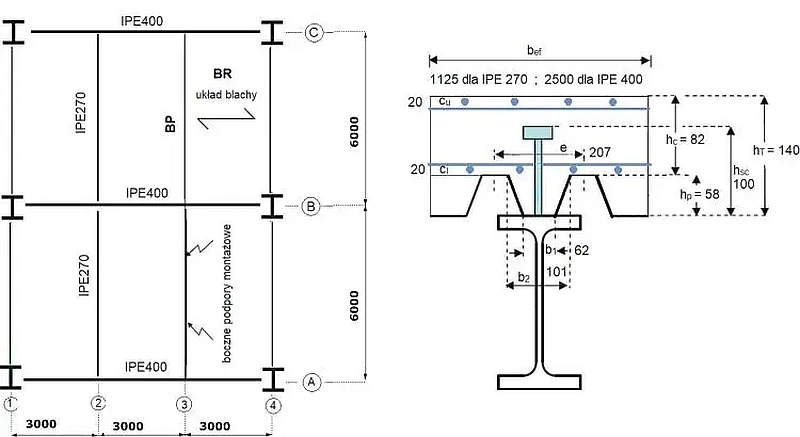
Zaprojektować strop zespolony w budynku wielokondygnacyjnym , pokazany na rys.17, gdzie rozstaw belek głównych wynosi $6 \, m$, a drugorzędnych $ 3 \, m$.
Rys.18 Belka do przykładu 1 (opracowano na podstawie[5]
Płyta żelbetowa
grubość całkowita $h_T= 140 \, mm$ (wraz z blachą fałdową)
grubość nad blachą $h_c= 82 \, mm$ zbrojona prętami ∅10 co 200 w obu kierunkach górą i dołem.
Beton C 25/30:
z Tab.1 Belki zelbetowe: $f_{ck}= 25 \, MPa$ , $f_{cd} =25/1,4 = 17,9 \, MPa$ (współczynnik materiałowy betonu $ \gamma_c=1,4$), moduł Younga doraźny $E_c= E_{cm}=31 \, GPa$
Stal zbrojeniowa B500:
współczynnik materiałowy stali zbrojeniowej $\gamma_m=1,15$
[15] B500 $to f_y=500 \, MPa$, $f_{yd}=500/1,15=434,8 \, MPa$
Blacha fałdowa Coftra Plus 60 x0,75
jest ułożona fałdami równoległe do osi belki głównej (podciągu) o rozpiętości $L= 9,00 \,m$.
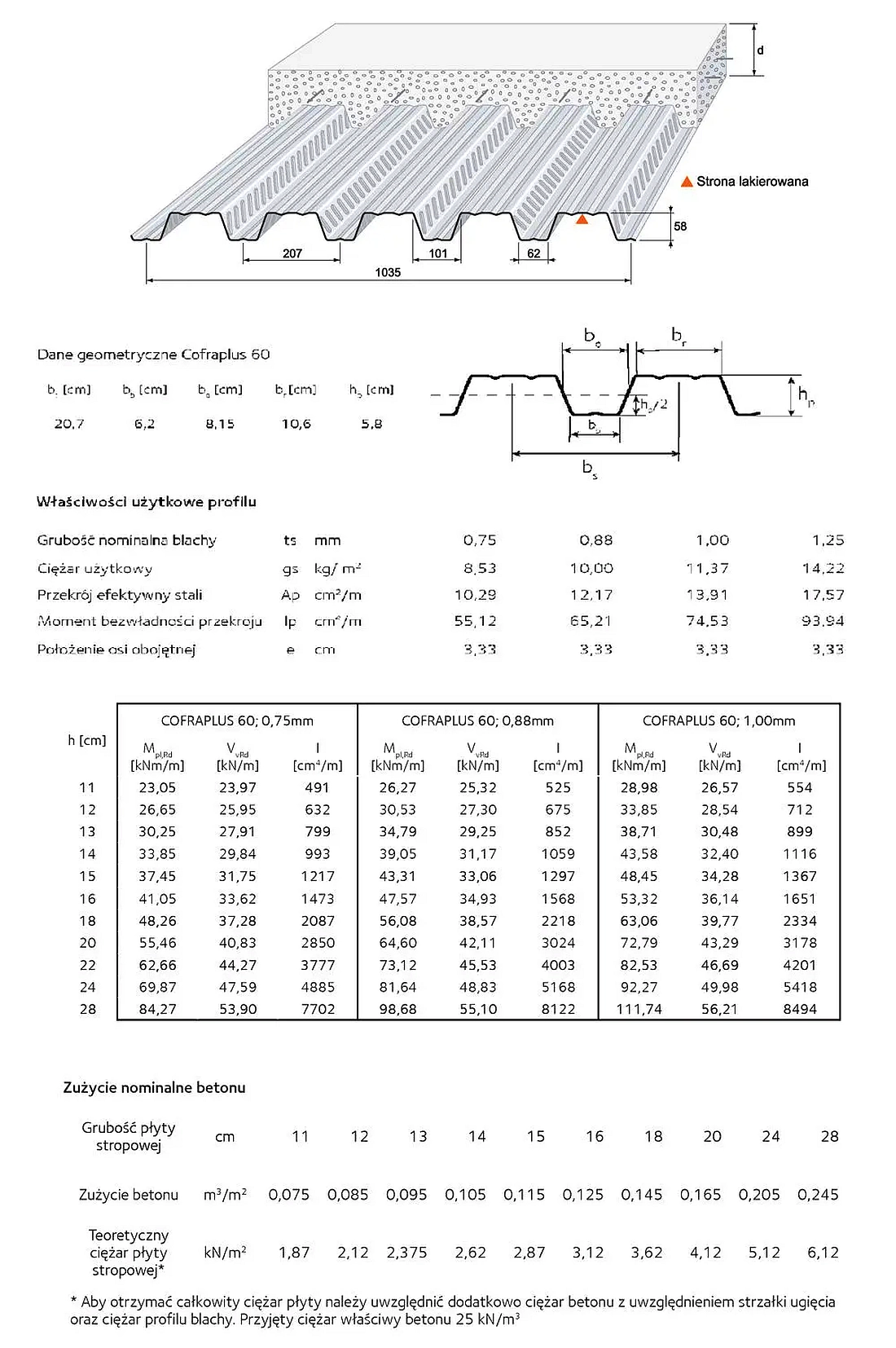
Przyjęto blachę Cofra Plus 60×0,75 ze stali S 350 GD prod Arcelor MIttal o parametrach zestawionych na rys.18, stanowiącym wyciąg z tablic producenta.
Kołki zespalające
łączniki do zespolenia – kołki Nelsona ø19 x 100 mm z łbem SD do łukowego przypawania wg PN-EN ISO 13918 ze stali czarnej 4.8 o $f_y= 340 \, MPa, f_u= 420 \,MPa$
Liczba łączników przypadająca na fałdę (bruzdę) $n_r=1$
Liczba łączników $n_f = 6000/ 207=29
Stal profilowa S355 :
współczynnik materiałowy stali profilowej $\gamma_{M0}=\gamma_{M1}= 1,0$
[11] $ \to f_y=355 \, MPa$, $f_{yd}=355/1,0=355 \, MPa$, moduł Younga stali $E_a=210 \, GPa$.
Zestawienie obciążeń
Ponieważ blacha trapezowa ma kierunek nośny do belek drugorzędnych, więc przyjęto w uproszczeniu, że obciążenia rozłożone z płyty zespolonej (stałe i użytkowe) w całości są przejmowane przez belki drugorzędne, a na podciągi w postaci sił skupionych (reakcji z belek drugorzędnych)
Obciążenia charakterystyczne
Obciążenia stałe
powierzchniowe
- Płyta betonowa: grubość (brutto)$ h_T = 14 \, cm$ , grubość średnia netto (po odliczeniu wycięć blachy fałdowej) $10,5 \, cm$ – wyznaczono na rysunku
średni ciężar betonu $g_c= 25 \cdot 0,105= 2,625 \, kN/m^2$ [ z tablic (rys.10) : $g_c= 2,62 \, kN/m^2$ ], przyjęto $g_c=2,62 \, kN/m^2$ - Blacha fałdowa CofraPlus 60 (rys.10) $g_b=0,09 \, kN/m^2$,
- Razem $g=2,62+0,09=2,71 \, kN/m^2$
liniowe na belkę drugorzędną
Cięźar własny belki drugorzędnej IPE 270 : $ g_{IPE270}= 36,1 \cdot 0,981 = 0,354 \, kN/m$
$G_b=2,71 \cdot 3 +0,354 = 8,484\, kN/m$
Reakcja skupiona na podciąg (od dwóch belek)
$V_G=8,484 \cdot 6 /2 \cdot 2 = 57,90 \, kN$
Obciążenie użytkowe
powierzchniowe
w fazie montażu
$ q_m = 1,0 \, kN/m^2$ – wg [16],
w fazie eksploatacji
obciążenie użytkowe dla powierzchni kategorii B wg [17] – tab.6.2
$q= 3,0 \, kN/m^2$
ścianki działowe o ciężarze liniowym $\le 2,0 \, kN/m$ wg [17]– kl. 6.3.1.2(8)
$q = 0,8 \, kN/m^2$
łącznie w fazie eksploatacji
$ q_u= 3,.0+0,8=3,8 \, kN/m^2$
Współczynniki redukcji:
powierzchniowy dla powierzchni obciążenia $A=6\cdot 9 = 54 \, m^2$, powierzchnia odniesienia $A_0= 10,0 \, m^2$, współczynnik kombinacyjnego dla powierzchni kat. B $\psi_0 = 0,7$,
$\alpha_A= 5/7 \cdot 0,7 +10,0/54= 0,685 <1,0$
kondygnacji – wg [17](6.2)}”] dla liczby kondygnacji nadlegających n=1
$\alpha_n=1,0 $ (liczba kondygnacji $n \le 2$.
Obciążenie użytkowe w fazie eksploatacji
$ q_u 3,8 \cdot 0,685 \cdot 1,0 = 2,61 \, kN/m^2 $
liniowe na belkę drugorzędną
$Q_b=2,61 \cdot 3 = 7,83 \, kN/m$
Reakcja skupiona na podciąg (od dwóch belek)
$V_Q=7,83 \cdot 6 /2 \cdot 2 = 46,98 \, kN$
Obciążenia klimatyczne – nie wystąpią.
Obciążenia obliczeniowe
Ponieważ obciążenia są niejednorodne ( powierzchniowe i skupione od reakcji belek drugorzędnych) , więc zgodnie z zasadami z artykułu Kombinacje obciążeń w Eurokodach) właściwe będzie wyznaczanie obliczeniowych sił przekrojowych po wyznaczeniu sił od obciążeń poszczególnej natury.
Sprawdzenie wytrzymałości blachy w fazie montażu (pod mokrym betonem) i obciążeniem użytkowym w fazie montażu
Momenty zginające od obciążeń charakterystycznych
Współczynniki jak dla belki trójprzęsłowej nad podporą przedskrajną:
przy obciążeniu G (wszystkie przęsła) $\alpha_G=0,100$
przy obciążeniu Q (dwa przesła skrajne i przedskrajne $\alpha_Q=0,117$
$M_{Gd} =0,100 \cdot 3^2 \cdot 2,71 = 2,44 \, kNm/m$
$M_{Qd} =0,117 \cdot 3^2 \cdot 1,00 = 1,05 \, kNm/m$
Momenty zginające obliczeniowe
w kombinacji z redukcja obciążeń stałych i bez redukcji wiodącego obciążenia zmiennego $M_{EI}= 0,85 \cdot 1,35\cdot 2,44 +1,5\cdot 1,05= 4,38 \, kNm/m$
w kombinacji bez redukcji obciążeń stałych i z redukcją obciążeń zmiennych $M_{EII}= 1,35 \cdot 2,44 +0,7 \cdot 1,5\cdot 1,05= 4,40 \, kNm /m$
Do obliczeń przyjęto $M_{Ed} =4,40 \, kNm/m$
Nośność blachy S 350 GD: $f_y=350 \, MPa$ , $M_{Rd}= 350 \cdot \cfrac{55,12}{8,33}/1000= 2,31 \, kNm < 4,40 \,kNm \to $ blachę należy podeprzeć montażowo na czas betonowania co $L = 3,0 \cdot \sqrt{ \cfrac{2,31}{4,40}} = 2,17 \, m$ , Przyjęto $L_{max} = 2 \,m$
Belki drugorzędne
Przyjęto IPE 270 : $g=36,1 \, kg/m$ , $ I_y =5790 \, cm^4$ , $ W_y =429 \,cm^3$, $W_{pl} = 484 \, cm^3$, $A = 45,95 \, cm^2$
Belki drugorzędne mają są belkami wolnopodpartymi o rozpiętości $L= 6 \, m$
Zginane dwuteowniki walcowane mają klasę 1 przekroju (p. artykuł Klasa przekroju stalowego ), więc osiągają nośność w stanie plastycznym.
Nośność przekroju belki
$M_{Rd,pl} = 484 \cdot 355 \cdot 10^{-3} = 171,8 \, kNm$
Zwichrzenie, współczynnik redukcyjny
Dla schematu belki wolnopodpartej widełkowo, obciążonej równomiernie otrzymano moment krytyczny wynosi $M_{cr}= 72,02 \, kNm$ . Zastosowano program LTBeamN 1.3, opisany w artykule Zginane pręty stalowe.
Współczynnik redukcyjny wyznaczono klasyczną metodą normową wg artykułu Belki stalowe dla przypadku szczególnego (dwuteowników)
smukłość $ \overline \lambda_{LT}= \sqrt {\cfrac{484 \cdot 355 \cdot 10^{-3}}{72,02}} = 1,54 $.
dwuteownik walcowany h/b>2 $\to$ krzywa zwichrzeniowa „c” $\to$ $\alpha_{LT}=0,49 $
(B-13) $\to \phi_{LT}=0,5 \left [1+0,49 ( 1,54 – 0,4) + 0,75 \cdot 1,54^2 \right] = 1,67 $,
(B-12)$\to \chi_{LT}= \cfrac {1}{ 1,67 – \sqrt {1,67^2 – 0,75 \cdot 1,54^2}} = 0,33 \le 1/ 1,54^2=0,42$
Faza montażu
Tuż po ułożeniu betonu:
obciążenie stałe $G=2,71 \cdot 3 + 0,361 = 8,491 \, kN/m$
obciążenie zmienne $Q= 3,0 \, kN/m$
kombinacja I (z redukcja obciążeń stałych i z wiodącym obciążeniem zmiennym): $F_I = 0,85 \cdot 1,35 \cdot 8,491 + 1,5 \cdot 3,0 =14,24 \, kN/m$
kombinacja II (bez redukcji obciążeń stałych, ale z redukcją obciążeń zmiennych): $F_{II} = 1,35 \cdot 8,491 + 1,5 \cdot 0,7 \cdot 3,0= 14,61 kN/m$
Do obliczeń przyjęto $F_{Ed} =14,61 \kN/m
Moment zginający i nośność belki
$M_{Ed} =14,61 \cdot 6^2/8= 65,75 > 0,33 \cdot 171,8 = 56,7 \, kNm$
Na rys. 17 wskazano, że belki IPE 270 na czas montażu będą stężone bocznie – dotyczy to wyłącznie okresu przed ułożeniem blachy fałdowej i przypawaniem kołków Nelson.
Tuż przed ułożeniem betonu belka będzie stężona blachą fałdową ułożoną poprzecznie do osi belki z użyciem kołków zespalających w sposób pokazany na rys. 17.
Można pokazać (obliczenia np programem Consteel) , że blacha fałdowa Cofra 60 mocowana w każdej fałdzie zabezpiecza belkę przed zwichrzeniem, więc współczynnik niestateczności ogólnej $\chi_{LT} =1,0$.
Faza eksploatacji
obciążenie stałe $G= 2,71 \cdot 3=8,13+0,361 = 8,491 \, kN/m$
obciążenie zmienne $Q= 2,6 \cdot 3 = 7,8 kN/m $
Obciążenia obliczeniowe
w kombinacji z redukcja obciążeń stałych i bez redukcji wiodącego obciążenia zmiennego $F_{EI}= 0,85 \cdot 1,35\cdot 8,491 +1,5 \cdot 7,8 = 21,44 \, kN/m $
w kombinacji bez redukcji obciążeń stałych i z redukcją obciążeń zmiennych $F_{EII}= 1,35 \cdot 8,491 + 0,7 \cdot 1,5 \cdot 7,8 = 19,41 \, kN/m$
Do obliczeń przyjęto $F_{Ed} =21,44 \, kN/m
Reakcja podporowa $V_{Ed} =\cfrac { 21,44 \cdot 6,0}{2} = 64,32 \, kN$
Moment zginający $M_{Ed} =\cfrac 21,44 \cdot 6,0^2}{8} = 96,48 \, kNm
Szerokość efektywna płyty żelbetowej
Średnią szerokość strefy efektywnej w przęśle wyznaczono według wzoru ($\ref{8}$) przy $\beta_i=1,0$:
$b_{ef,1} = 0 + 6,0 / 8 = 0,75 \, m$, czyli $b_{ef} = 2 × 0,75 = 1,5 m < 3,0 m
gdzie $b_0=0$ (łączniki w jednym rzędzie),
Nośność ze względu na ścinanie łączników
Dla: $n_r = 1$ , $h_p = 58 \, mm$ , $b_p= (62+101)/2 = 82 \,mm$, $h_{sc} = 100 \,mm$ , sworzni spawanych przez blachę o grubości $t<1 \, mm$
$(\ref{15}) \to k_{max} =0,75$
$(\ref{14}) \to k_t= \cfrac{0,7}{\sqrt{1}}\cdot \cfrac{82}{58}\cdot \left( \cfrac{100}{58}-1 \right) =0,717 < 0,75$,
Smukłość łączników $ \lambda_{sc}= \cfrac{100}{20}=5,3 > 4 \to $ ($\ref{13}$) $\alpha=1$
$(\ref{12}) \to P_{Rd} = 0,717 \cdot \cfrac{19^2}{1,25} \cdot \min { \{ 0,8 \cdot \pi /4 \cdot 420 \, ; \, 0,29 \cdot 1,0 \cdot \sqrt{25 \cdot 31000}\} } \cdot 10^{-3} = 52,86 \, kN$
Stopień zespolenia
Pole przekroju poprzecznego płyty betonowej:
$h_c=140 – 58 = 82 \,mm
$ $b_{ef} =1500 \,mm$,
Ponieważ strop jest w układzie BP (belka prostopadła do fałd blachy) $\to (\ref{22}$) $h_z=h_c=82 \, mm$
$A_c = b_{ef} \cdot h_z = 150 \cdot 8,2 = 1230 \, cm^2$
$(\ref{19}) \to N_{cf} =0,85 \cdot 17,9 \cdot 1230 \cdot 10^{-1}= 1871,4 \, kN$
$(\ref{20}) \to N_c =0,5 \cdot 29 \cdot 52,86 = 766,5 \,kN$
$(\ref{17}) \to \eta= 766,5/1411,6 = 0,543$
Współczynnik $\eta$ jest mniejszy niż 1,0 więc belka jest częściowo zespolona.
Minimalny stopień zespolenia dla belki o równych pasach i $L_e =6,0 m < 25 \,m$
($\ref{21}) \to \eta_{min}= 1-\left ( \cfrac{355}{355} \right) \cdot(0,75-0,04 \cdot 6,0 )= (0,48 < 0,4) < 0,543$
Sprawdzenie nośności na zginanie
Graniczny moment plastyczny w środku rozpiętości belki
($\ref{23}) \to$ wielkości pomocnicze
$ N_1= N_{a,pl} = 45,95 \cdot 355 \cdot10^{-1}=1631,2 \,kN$
$N_2 = N_{c,f} = 0,85 \cdot b_{ef} \cdot h_z \cdot f_{cd}$
$N_3 = N_{a,f}= – 2 A_f \cdot f_y = 2 \cdot t_f \cdot b_f \cdot f_y$
$N_4=N_{a,w} =- 2 A_w \cdot f_y = 2 \cdot t_w \cdot h_w \cdot f_y$
$N_5 = N_1 – N_2$
$M_{pl}= M_{a,pl} =W_{pl}\cdot f_y$
Belki główne (podciągi)
Przyjęto podciągi ( belki główne) IPE 400 (66,3 kg/m) +10% na inne (łączniki itd) $g=1,1 \cdot 0,663= 0,73 \, kN/m$
Obciążenia
Ciężar własny belki $ g= 0,73 \, kN/m$
Obciążenie rozłożone od stropu – przyjmuje się, że w całości przekazywane jest przez siły skupione – reakcje od belek drugorzędnych:
$F_G= 6,0/2 \cdot [ 3,0 \cdot ( 7,86+0,09)+0,361] = 72,6 \, kN$
w fazie montażu $F_Q= 6,0/2 \cdot 3,0 \cdot 1,0 = 9,0 \, kN$
w fazie eksploatacji $F_Q= 6,0/2 \cdot 3,0 \cdot 2,6 = 23,4 \, kN$
Przykład 2 [Zespolony podciąg z elementami pośrednimi ]
Przykład z rys. 19 pochodzi z [18]– przykład 7.3.1 , a tam z tłumaczenia wytycznych [19]
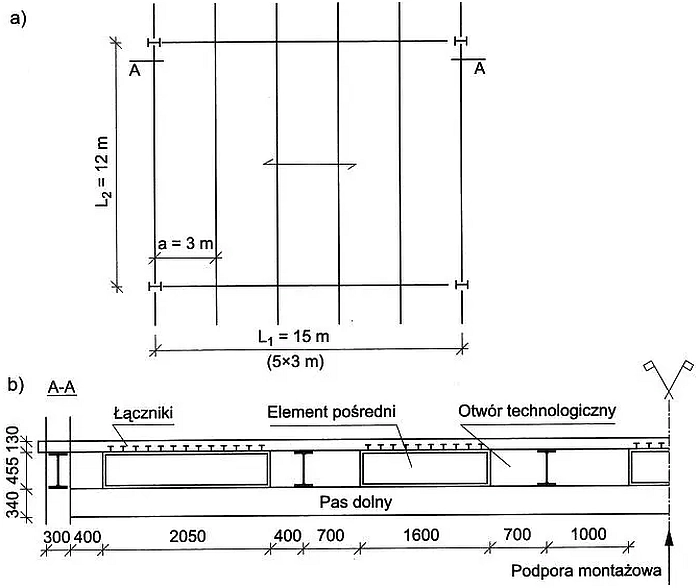
Rys.20 Schemat podciągu do przykładu 2: a) rzut stropu, b) przekrój [18],rys 7.10
Strop zaprojektowano i wykonano dla danych:
siatka słupów 12×15 m,
rozpiętość podciągu $L_1=15 \,m$,
płyta stropowa o grubości 130 mm na stalowych blachach trapezowych o wysokości $h_T= 50 \, mm$ i grubości $t_T= 1 \,mm$, fałdy równoległe do podciągu (układ BR),
beton C25/30 – z tab. W1 $\to$ $f_{cd}= 17,9 \, MPa$ ( w oryginale $f_{cd}=16,7 \, MPa$), czyli jak dla współczynnika materiałowego $\gamma_c=1,5$ – w Polsce $\gamma_c=1,5$ ),
stal konstrukcyjna S 350 $\to$ $f_y=350 \, MPa$ (w oryginale $f_{yd}= 345 \, MPa$ ),
wysokość całkowita stropu 925 mm,
łączniki sworzniowe ∅ 19×95 mm o nośności $P_{Rd}= 72 \, kN$,
Podciąg: dwuteownik walcowany z brytyjskiego programu hut UC 305x305x198,
o wymiarach:
$h_a= 340 \, mm$, $b_f= 314,5 \, mm$, $t_w = 19,1 \, mm$, $t_f= 31,4 \, mm$, $r=14,2 \, mm$
charakterystykach:
$A_a= 252 \, cm^2$, $I_y=50900 \, cm^4$, $W_{y,pl}= 3440 \, cm^3$, $A_v=70,45 \, cm^2$, $ m= 198,1 \, kg/m $.
Zestawienie obciążeń
charakterystyczne
zmienne: $Q=4 \, kN/m^2$ – użytkowe, $Q_d=1 \, kN/m^2$ – ścianki działowe, $Q_s = 0,75 \, kN/m^2$ – instalacje podwieszone, $Q_m= 0,5 \, kN/m^2$ – montażowe,
stałe: $G_p =2,3 \, kN/m^2$ – ciężar własny płyty stropowej, $Q_s= 0,4 \, kN/m^2$ – ciężar własny belek stalowych
obliczeniowe
w fazie montażu: $q_m= 1,35 \cdot (2,3+0,4) + 1,5 \cdot1,0 \cdot 0,5 = 3,65 +0,75= 4,4 \, kN/m^2$
w fazie eksploatacji: $q_u= 1,35 \cdot(2,3+0,4) +1,5 \cdot [0,7\cdot 0,75 + 0,7 \cdot (1+4)] = 3,65+ 6,04=9,7 \, kN/m^2$
Sprawdzenie nośności w fazie montażu
Schemat statyczny podciągu w fazie realizacji (montażu) jest belką dwuprzęsłową (z podporą montażową w środku rozpiętości), więc na podporą:
$M_{Ed}= \cfrac{4,4 \cdot 12 \cdot 7,5^2}{8}= 371,3 \le M_{Rd}= 3440 \cdot 350\cdot 10^{-3}= 1204 \, kNm$
Sprawdzenie nośności w fazie użytkowania
Nośność przekroju przęsłowego środkowego
Obciążenie skupione przekazywane z belek drugorzędnych
$F_d= 9,7 \cdot 3 \cdot 12/2 \cdot 2 = 349,2 \, kN$
Reakcja podciągu od sił skupionych
$V_p= 4 \cdot P /2= 2\cdot 349,2= 698,4 \, kN$
Moment zginający w środku rozpiętości od sił skupionych
$M_{Ed} = 698,4 \cdot 7,5 – 349,2 \cdot (3+12,5) – 349,2 \cdot 1,5 = 9 \cdot 349,2 = 3142,8 \, kNm$
Szerokość efektywna płyty
($\ref{9}) \to $ $b_{ef}=15/4= 3.75 \, m$.
Literatura
- PN-EN 1994-1-1+Ap1+AC (2008-12). Eurokod 4 -Projektowanie zespolonych konstrukcji stalowo-betonowych – Część 1-1: Reguły ogólne i reguły dla budynków
- Ayoub, A., & Filipou, F. (2000). Mixed formulation of nonlinear steel – concrete composite beam element. Journal of Structural Engineering, 126(3), 371–381. https://www.researchgate.net/publication/239390826_Mixed_Formulation_of_Nonlinear_Steel-Concrete_Composite_Beam_Element
- Piechnik, S. (1980). Wytrzymałość materiałów dla wydziałów budowlanych. PWN
- Johnson, R. P. (2004). Composite structures of steel and concrete: beams, slabs, columns, and frames for buildings. Blackwell Pub
- AccessSteel, Lemaire A., (2005, August). Arkusz obliczeniowy. Przykład obliczeń belki zespolonej. Przykład SX015a-PL-EU. https://www.piks.com.pl/wp-content/uploads/2015/05/SX015a-PL-EU.pdf
- Szmigiera, E., Grzeszykowski, B., & Niedośpiał, M. (2019). Projektowanie konstrukcji zespolonych stalowo-betonowych. Część 1 Elementy zginane. Wydawnictwo Nau-kowe PWN
- Nie J.-G., Tian C.-Y., Cai, C. S. (2008). Effecitve width of steel-concrete composite beam at ultimate strength state. Engineering Structures, 30, 1396–1407
- PN-EN 1994-1-1+Ap1+AC:2008, Eurokod 4, Projektowanie zespolonych konstrukcji stalowo-betonowych, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1994-1-2:2008, Eurokod 4, Projektowanie zespolonych konstrukcji stalowo-betonowych- Część 1-2: Reguły ogólne. Projektowanie z uwagi na warunki pożarowe
- Szmigiera, E., Grzeszykowski, B., & Niedośpiał, M. (2019). Projektowanie konstrukcji zespolonych stalowo-betonowych. Część 1 Elementy zginane. Wydawnictwo Naukowe PWN
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- Slutter G. C., Driscoll, G. C. (1965). Flexural strength of steel- concrete composite beams. Proc. Amer. Soc. Civ. Engrs, 91(ST2), 71–99
- PN-EN 1993-1-8 +Ap1+AC:2006, Eurokod 3 -Projektowanie konstrukcji stalowych -Część 1-8: Projektowanie węzłów
- Starosolski, W. (2013). Konstrukcje żelbetowe według Eurokodu 2 i norm związa-nych, Tom 3. Wydawnictwo Naukowe PWN
- PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1991-1-6:2007, Eurokod 1: Oddziaływania na konstrukcje. Część 1-6: Oddziaływania ogólne – Oddziaływania w czasie wykonywania konstrukcji
- PN-EN 1991-1-1:2004, Eurokod 1: Oddziaływania na konstrukcje. Część 1-1: Oddziaływania ogólne. Ciężar objętościowy, ciężar własny, obciążenia użytkowe w budynkach
- Kucharczuk, W., Labocha, S. (2008). Konstrukcje zespolone stalowo-betonowe budynków. Arkady
- Lawson R. M., & McConnel, R. E. (1993). Design of stub girders. Steel construction Institute
________________________________