W pracy przedstawiono algorytm obliczania żelbetowego przekroju mimośrodowo, dwukierunkowo zginanego i ściskanego lub rozciąganego, który jest uogólnieniem nieliniowego kalkulatora żelbetu M-N. W literaturze wzkazuje się (np Ross (1986) [1]), że wtypowym przypadku słupów dwukierunkowo zginanych zastosowanie algorytmu pozwala na oszczędności dochodzące do 30% zbrojenia.
Model żelbetowego przekroju dwuosiowo zginanego
Osie charakterystyczne
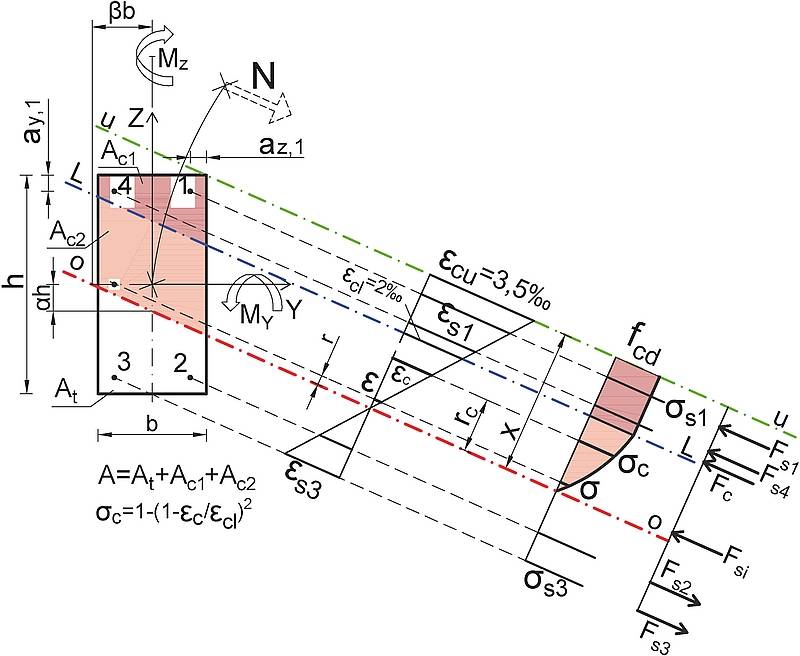
Zakładamy położenie osi obojętnej przekroju żelbetowego (przekroju zespolonego stalowo-betonowego), na której odkształcenia są zerowe. Na rys. 1 założoną oś obojętną OO oznaczono czerwoną linią kreska-kropka.
Odległość najdalej położonego ściskanego punktu betonu od osi obojętnej oznaczono przez $x$, zgodnie tradycyjnym oznaczeniem wysokości strefy ściskanej betonu, a odległość dowolnego puntu (włókna) przekroju od osi obojętnej oznaczono przez $r$. Wyróżniono, następujące charakterystyczne osie przekroju żelbetowego:
- $OO$ z odkształceniami $\varepsilon_{c}$ =0,0 ‰. Jest to oś obojętna ($\ref{odcinkowa}$),
- $LL$ z odkształceniami $\varepsilon_{cl}$ = 2,0 ‰ . Oś graniczna (limit) LL , oddziela strefę $A_{c1}$ parabolicznego przebiegu naprężeń w betonie od strefy $A_{c2}$ ze stałymi naprężeniami $\sigma_c=f_{cd}$
- $UU$ z odkształceniami $\varepsilon_{cu}$ = 3,5 ‰. Oś brzegowa (unlimit), zawiera punkty najdalej oddalone od od osi obojętnej ( na rys.1 oś UU przechodzi przez górny prawy wierzchołek przekroju).
Osie charakterystyczne są do siebie równoległe, a odległości między nimi wynoszą:
$\delta_{oo-uu}=x$ – z zalożenia,
$\dfrac{\delta_{oo-ll}}{\varepsilon_{cl}}= \dfrac{x}{\varepsilon_{cu}} \to {\delta_{oo-ll}}= \dfrac{2}{3,5} x= \dfrac{4}{7} x$ – ze stosunków odkształceń i z zasady płaskich przekrojów ($\ref{dźwignia}$).
Dźwignia punktu osi charakterystycznej wsparta na osi obojętnej wynosi:
$$\begin{equation} \overline r = \begin {cases}
\overline r_o = 0 , & \text {dla osi OO}\\
\overline r_l = 4/7, & \text {dla osi LL} \\
\overline r_u = 1 , & \text {dla osi UU}\\
\end {cases} \label{s_c}\end{equation}$$
Zasada płaskich przekrojów
Z zasady płaskich przekrojów pokazanej na rys. 1 wynika, że odkształcenie $\varepsilon$ dowolnego włókna przekroju wynosi
$$ \begin{equation} \varepsilon= \varepsilon_{cu} \cdot \overline r \label{zasada} \end{equation}$$
gdzie:
$\varepsilon_{cu}=$3,5‰ – największe (ultimate) odkształcenie włókna betonowego ( zgodnie z [2]).
.Dźwignia analizowanego włókna oparta na osi obojętnej przekroju żelbetowego O-O, wynosi
$$ \begin{equation} \overline r = \dfrac{r}{x} \label{dźwignia} \end{equation}$$
Zasada ($\ref{zasada}$) dotyczy każdego włókna przekroju: zarówno betonowego jak i stalowego.
Naprężenia w betonie i stali
Nieliniowy rozkład naprężeń w strefie ściskanej betonu zgodnie z normą [2] zapisuje się następująco:
$$\begin{equation}\sigma_c = f_{cd} \cdot \begin {cases}
1, & \text {jeśli $ \varepsilon_{cl} \le\varepsilon_c \le\varepsilon_{cu}$} \\
1- (1- \varepsilon_c/\varepsilon_{cl})^2, & \text {jeśli $\varepsilon_c <\varepsilon_{cl}$ }
\end {cases} \label{sigma_c}\end{equation}$$
Ponieważ $\dfrac {\varepsilon_{cl}}{\varepsilon_{cu}}=\dfrac {\text{2,0‰}}{\text{3,5‰}} =\dfrac{4}{7}$, to dźwignia $\dfrac{\varepsilon_{c}}{\varepsilon_{cl}}=\dfrac{ \varepsilon_{c}}{4/7 \cdot \varepsilon_{cu}}$, a po uwzględnieniu zasady ($\ref{zasada}$) mamy $\dfrac{\varepsilon_{c}}{\varepsilon_{cl}}=7/4 \cdot \overline r$, czyli:
$$\begin{equation}\sigma_c (\overline r)= f_{cd} \cdot \begin {cases}
1, & \text {jeśli $ \overline r_{ll} \le \overline r \le \overline r_{uu}$} \\
1- (1- 7/4 \cdot \overline r )^2, & \text {jeśli $\overline r < \overline r _{ll}$ }
\end {cases} \label{sigma_r}\end{equation}$$
Naprężenia w pręcie stalowym „i” , zgodnie z prawem Hooka wynoszą
$$ \begin{equation}\sigma_i=\varepsilon_i\cdot E_s \end{equation}$$
gdzie dla stali moduł odkształcalności stali zbrojeniowej $E_s$ opisują zależności (17) i (18) przedstawione w artykule Nieliniowy kalkulator żelbetu M-N.
Równanie osi obojętnej
W układzie współrzędnych głównych, centralnych osi ( Y,Z ) przekroju betonowego równanie osi obojętnej można przedstawić w postaci odcinkowej:
$$ \begin{equation}\dfrac { \overline z}{\alpha}+ \dfrac{\overline y}{\beta}=1 \label{odcinkowa} \end{equation}$$
gdzie: $\overline y = \dfrac {y}{b}$ , $\overline z = \dfrac {z}{h}$ – współrzędne względne.
Zauważmy , że na rys. 1 $\alpha$ i $\beta$ są ujemne.
Równanie ($\ref{odcinkowa}$) można zapisać w postaci kierunkowej
$$ \begin{equation} \overline z = m \cdot \overline y + t \label {kierunkowa}\end {equation}$$
gdzie współczynnik kierunkowy $m = tg \varphi_y$ jest tangensem kąta nachylenia prostej do osi współrzędnych Y , a $t$ jest współrzędną odciętą przez prostą na Y .
Dla osi obojętnej parametry prostej kierunkowej, wynoszą
$$\begin{equation} m=m_o = – \dfrac{\alpha}{\beta}\end {equation}$$
$$\begin{equation} t=t_o=\alpha\end {equation}$$
Równanie ($\ref{odcinkowa}$) można zapisać w postaci normalnej:
$$ \begin{equation} \overline y \cdot cos \varphi+\overline z \cdot sin \varphi – p=0 \label{normalna} \end {equation}$$
gdzie:
$p$ -odległość prostej od początku układu współrzędnych,
$\varphi =\varphi_z $ – kąt nachylenia prostej w stosunku do osi rzędnych Z
Zachodzą następujące zależności pomiędzy parametrami prostej w postaci odcinkowej ($\ref{odcinkowa}$) i normalnej ($\ref{normalna}$):
$cos \varphi=\alpha\cdot \mu$,
$sin \varphi=\beta\cdot \mu$
$p =\alpha \cdot\beta \cdot \mu$
Czynnik normujący $\mu$ wynosi
$$ \begin{equation} \mu=\dfrac{\epsilon_n}{\sqrt{ \alpha^2+\beta^2}}\label{normujący} \end {equation}$$
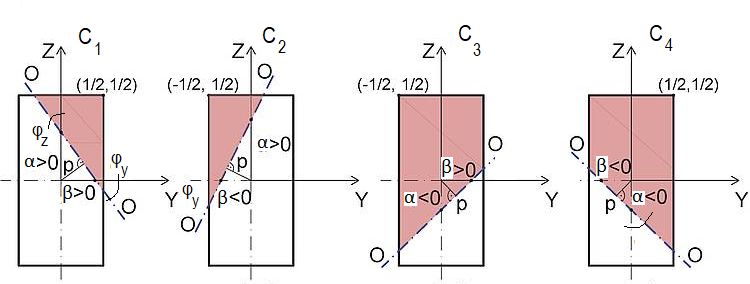
Znak czynnika normującego określamy zgodnie ze standardem [[3]: $\epsilon_n$= +1, gdy $\alpha \cdot \beta>0$ (przypadek C1 i C4) i $\epsilon_n $= -1, gdy $\alpha \cdot \beta<0$ (przypadek C2 i C3). Przypadki C1 do C4 położenia osi obojętnej zdefiniowano na rys. 2.
Równanie normalne ($\ref{normalna}$), umożliwia znakowanie odległości punktów przekroju od tej osi bez potrzeby stosowania wartości bezwzględnych, co umożliwia efektywne przeprowadzenie całkowania symbolicznego i uzyskanie zamkniętych formuł podanych w dalszej części artykułu.
Prosta $(\ref{odcinkowa})$ lub $(\ref{kierunkowa})$ przebiega powyżej początku układu(0,0) przy $t= \alpha>0$ , a poniżej przy $t= \alpha< 0$.
Równanie osi granicznej
Oś graniczna LL ( rys.1 ) jest równoległa do osi obojętnej, więc ma taki sam jak oś obojętna współczynnik kierunkowy $m$.
Równanie osi granicznej ma postać kierunkową ($\ref{kierunkowa}$) z parametrami
$$\begin{equation} m_L=m_o\end {equation}$$
$$\begin{equation} t_L=t_o+ \dfrac{2}{7}\epsilon_r (1-\alpha(2-\epsilon_n/ \beta) \label{tL}\end {equation}$$
Formułę ($\ref{tL}$) uzyskano z uwzględnieniem znaków $\epsilon_n$ w formule ($\ref{normujący}$) i $\epsilon_r$ w formule ($\ref{odległość}$), które są zależne od pokazanych na rys.2 sytuacji obliczeniowych C1 do C4 i wynoszą:
$$\begin{equation}\epsilon \to \begin {cases}
C1, & \epsilon_n= +1, \epsilon_r= +1, \\
C2, & \epsilon_n= -1, \epsilon_r= +1, \\
C3, & \epsilon_n= -1, \epsilon_r= -1, \\
C4, & \epsilon_n= +1, \epsilon_r= -1,
\end {cases} \label{epsilon}\end{equation}$$
Przypadki położenia osi obojętnej
W zależności od umiejscowienia osi obojętnej w przekroju wyróżnimy cztery przypadki, pokazane na rys.2
Najbardziej oddalony od osi obojętnej punkt przekroju jest wierzchołkiem górnym o współrzędnych U($\overline y, \overline z$)=($\epsilon_u \cdot 1/2, 1/2$), gdzie znak współrzędnej wierzchołka górnego $\epsilon_u= \epsilon_n$ ($\ref{epsilon}$).
Dźwignie i odkształcenia włókna przekroju
Odległość $r$ punktu $P(\overline y_P,\overline z_P)$ od prostej ($\ref{normalna}$) możemy wyznaczyć z podstawowych zależności planimetrii przy wykorzystania równania prostej w postaci normalnej ($\ref{normalna}$):
$$ \begin{equation} r= \epsilon _r \cdot (\overline y_P \cdot cos \varphi+\overline z_P \cdot sin \varphi – p) =\dfrac{\epsilon_r \cdot \alpha \beta \cdot (\overline z_P/ \alpha+\overline y_P / \beta – 1)}{\mu}\label{odległość} \end {equation}$$
gdzie znak $\epsilon_r$ jest dobierany zgodnie z zasadą [[3]: dodatni (+ 1), gdy punkt P i początek układu O(0,0) leżą po przeciwnych stronach danej prostej lub ujemny (-1), gdy P i O leżą po tej samej stronie danej prostej. Dla poszczególnych sytuacji obliczeniowych znaki te zestawiono w ($\ref {epsilon}$).
Odległość $x$ naroża $(\epsilon_n \cdot 1/2, 1/2)$ – najdalszego od osi obojętnej (rys.2) wynosi:
$$ \begin{equation} x= \epsilon _r \cdot ( \epsilon_n \cdot 1/2 cos \varphi+1/2 \cdot sin \varphi – p)= \dfrac{\epsilon_r \cdot \alpha \beta \cdot (1/ \alpha+\epsilon_n/ \beta – 2)}{2 \mu} \label{x} \end {equation}$$
Dźwignia dowolnego punktu przekroju wyrażona stosunkiem ($\ref{odległość}$) i ($\ref{x}$) wynosi więc:
$$ \begin{equation} \overline r (\overline y, \overline z)= \dfrac { r}{x} = 2 \cdot \dfrac{ \overline z_P / \alpha +\overline y_P /\beta -1}{ 1/\alpha + \epsilon_n /\beta -2}\label {rx} \end {equation}$$
Po podstawieniu ($\ref{rx}$) do ($\ref{zasada}$) otrzymamy odkształcenie dowolnego włókna przekroju, w tym odkształcenia pręta zbrojeniowego „i”. Znaki odkształceń określamy w ten sposób, że odkształcenie włókna znajdującego się w strefie ściskanej betonu jest dodatnie (skrócenie), a poza tą strefą jest ujemne (wydłużenie).
Siły w ściskanym betonie
Siła oporu betonu
Wypadkowa bryły naprężeń w betonie wynosi
$$\begin{equation}F_c= \int \limits _{A_c + A_t} \sigma _c \cdot dA= f_{cd}\cdot b\cdot h \cdot \left ( \int \limits _{A_{c1}} [ 1- ( 1- \varepsilon_{c}/\varepsilon_{cl} )^2] dA + \int \limits _{A_{c2}} dA \right ) \end{equation} $$
Całkę po polu $A_{c1}$ i $ A_{c2}$ obliczymy jak następuje:
$$\begin{equation}\int \limits _{A_{c1}} (…) dA = \int \limits_{-1/2}^{1/2} \left ( \int \limits _{m_o \overline y +t_o} ^{m_L \overline y +t_L} [1-(1- 7/4 \cdot \overline r)^2] d\overline z \right) d \overline y = (\epsilon_r -3) \cdot \dfrac{2 \alpha}{21}\cdot(2-1/\alpha-\epsilon_n/ \beta)\end{equation}$$
$$\begin{equation}\int \limits _{A_{c2}} (…) dA = \int \limits_{-1/2}^{1/2} d\overline y \int \limits _{m_L \overline y +t_L} ^{1/2} 1 \cdot d\overline z = (1/2-\alpha) + \dfrac{2\epsilon_r}{7}\cdot (2\alpha-1-\epsilon_n \alpha/ \beta) \end{equation}$$
Po wykonaniu stosownych przekształceń mamy:
$$\begin{equation} F_c= \left [(1-2 \alpha)\cdot \dfrac { 33 – 16 \epsilon_r}{42}+\dfrac{\alpha \epsilon_n }{21 \beta}(6 – 8 \epsilon_r) \right ] \cdot f_{cd}\cdot b\cdot h \label {Nc} \end{equation} $$
W przypadkach granicznych z formuły ($\ref{Nc}$) uzyskujemy:
- dla zginania tylko wokół osi Y (przypadek) [ $ \beta \to \infty $ ]
$$\begin{equation} \lim { {F_c}_{\{ \beta \to \infty \}}}= \dfrac { 1 – 2 \alpha} {42} \cdot (33 – 16 \epsilon_r) \cdot f_{cd}\cdot b\cdot h \label {NcY} \end{equation} $$
W tym przypadku zachoszi $\epsilon_r$ = + 1 oraz $ \alpha= (1/2-x$ ), gdzie x – wysokość strefy ściskanej i otrzymujemy wynik zgodny z klasycznym wynikiem zaprezentowanym w artykule Nieliniowy kalkulator żelbetu , a mianowicie
$N_c= \dfrac{17}{21}\cdot f_{cd}\cdot b\cdot x$
- dla zginania tylko wokół osi Z (przypadek) [ $ \alpha \to \infty $ ]
Jako jedyny przypadek w modelu prowadzi do nieoznaczoności, ponieważ w rozwiązaniu korzystano z równania kierunkowego prostej ($\ref{kierunkowa}$), które w takim przypadku daje nieoznaczone wartości rzędnych. Ten szczególny przypadek zaleca się analizować w sytuacji obróconego przekroju (tzn po obróceniu układu współrzędnych – zamianie osi Y na Z i wzajemnie). Wówczas ważne są rozwiązania podane wyżej.
Moment oporu betonu
Moment bryły naprężeń w betonie $M_c$ liczony względem osi obojętnej wynosi:
$$\begin{equation} M_c= \int \limits _{A_c + A_t} \sigma _c \cdot r_c \cdot dA= f_{cd}\cdot b\cdot h \cdot \left ( \int \limits _{A_{c1}} [ 1- ( 1- \varepsilon_{c}/\varepsilon_{cl} )^2] \cdot r_c \cdot dA + \int \limits _{A_{c2}} r_c \cdot dA \right ) \end{equation} $$
gdzie $r_c$ jest odległością włókna betonowego od osi obojętnej, którą można obliczyć z zależności ($\ref {odległość}$) ($ r_c =r(\overline y, \overline z ) $).
Całkę po polu $A_{c1}$ i $ A_{c2}$ obliczymy jak następuje:
$$\begin{equation}\int \limits _{A_{c1}} (…) dA = \int \limits_{-1/2}^{1/2} \left ( \int \limits _{m_o \overline y +t_o} ^{m_L \overline y +t_L} [1-(1- 7/4 \cdot \overline r)^2] \cdot r \cdot d\overline z \right) d \overline y = \dfrac{ \epsilon_n (\beta-2 \alpha \beta +\alpha \epsilon_n)^2 \cdot (8+3 \epsilon_r)}{147 \beta \sqrt{\alpha^2 +\beta^2}}\end{equation}$$
$$\begin{equation}\int \limits _{A_{c2}} (…) dA = \int \limits_{-1/2}^{1/2} \left ( \int \limits _{m_o \overline y +t_o} ^{m_L \overline y +t_L} r \cdot d \overline z \right) d \overline y = \dfrac{ \epsilon_r \epsilon_n \cdot [49 (\alpha^2+3(1-2 \alpha)^2 \beta^2 -48 (\beta -2 \alpha \beta- \alpha \epsilon_n)^2]}{1176 \beta \sqrt{\alpha^2 +\beta^2}}\end{equation}$$
Po wykonaniu sumowania całek i powrotu z zamiany zmiennych otrzymamy:
$$\begin{equation} M_{co}= \dfrac { f_{cd}\cdot b\cdot h }{\sqrt{\alpha^2 +\beta^2}} \cdot \left( \dfrac{\epsilon_n \epsilon_r \alpha^2 }{24 \beta}+ \dfrac{2 \alpha (1-2 \alpha) (8-9 \epsilon_r)}{147} +\dfrac{\epsilon_n (1-2\alpha)^2 \cdot (64+75 \epsilon_r) \beta }{1176}\right) \end {equation}$$Literatura
- Ross, D. A., Yen, J. R. (1986). Interactive Design of Reinforced Concrete Columns with Biaxial Bending. ACI Journal, 83(6), 988–993
- PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- Bronsztejn, I., Nikolajevic, & Semendaev, K. A. (2014). Matematyka: poradnik encyklopedyczny, PWN
________________________________