Niniejszy artykuł stanowi Część 3 cyklu Elementarz niezawodności konstrukcji. W całym cyklu artykułów zachowano ciągłość numeracji: wzorów i ilustracji. Numeracja rozdziałów jest odrębna dla każdej części.
Przedstawiono struktury mieszane złożone z punktu widzenia niezawodności: układy szeregowe połączone w wiązki oraz układy równoległe połączone w łańcuch. Większość konstrukcji budowlanych ma mieszany model niezawodnościowy. Przeprowadzono analizę ideową struktur złożonych i sformułowano wnioski ważne dla Konstruktora i Architekta obiektów budowlanych.
ZŁOŻONA struktura niezawodnościowa
W budowlanej praktyce inżynierskiej mamy najczęściej do czynienia ze złożonymi strukturami niezawodnościowymi, polegającymi na połączeniu w szereg struktur równoległych lub równoległym połączeniu łańcuchów lub też innych struktur i na dodatek z elementami wspólnymi w różnych strukturach.
Na rys. 5 pokazano model struktury z podzielonym rezerwowaniem, czyli strukturę w której systemy równoległe połączono w szereg. Przykładem takiej struktury jest konstrukcja z powielonymi układami statycznie niewyznaczalnymi. W tym przypadku prawdopodobieństwo bezawaryjnej pracy mxn elementów, każdy o niezawodności $p_{si}$ można obliczyć z zależności
| $p_{s, podzielone} = [1-(1-p_{si})^m]^n $ | (26) |
gdzie jest liczbą elementów w każdej strukturze równoległej, a
liczbą ogniw w łańcuchu.

Rys.5. Struktura z podzielonym rezerwowaniem (równoległe w szeregu) [1]
Na rys. 6 przedstawiono wykresy uzyskane z zależności (26).
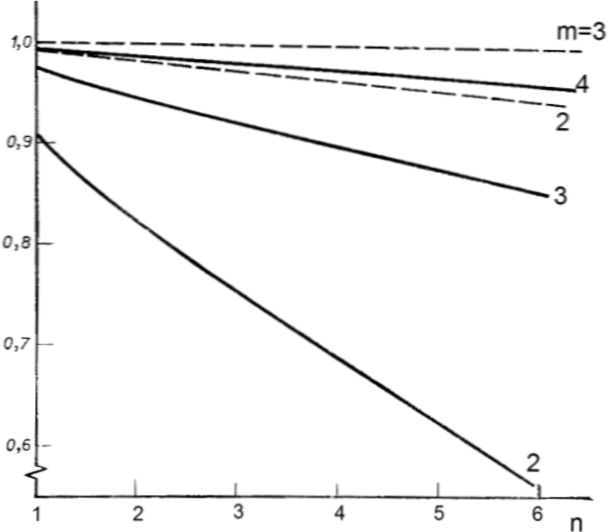
Rys.6. Podzielone rezerwowanie [1]: $n$ – liczba elementów połączonych szeregowo; $m$ – liczba równoległych połączeń ; linie przerywane dla $p_{si}=0,9$, linie ciągłe dla $p_{si}=0,7$
Na rys. 7 pokazano model struktury z ogólnym rezerwowaniem, czyli ze strukturami szeregowymi, połączonymi równolegle. W tym, przypadku niezawodność struktury można obliczyć z zależności
| $p_{s, ogolne} =1-(1-p_{si}^n)^m $ | (27) |
Na rys.8 przedstawiono zależności uzyskane z formuły (27).
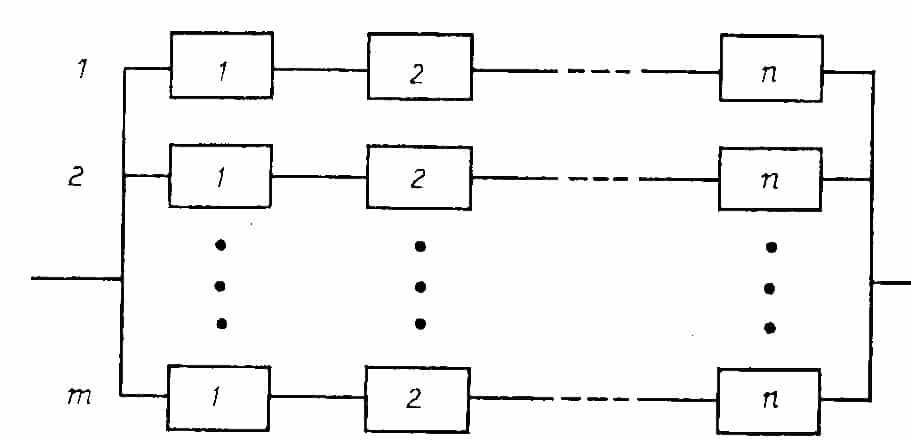
Rys.7. Struktura z ogólnym rezerwowaniem [1]
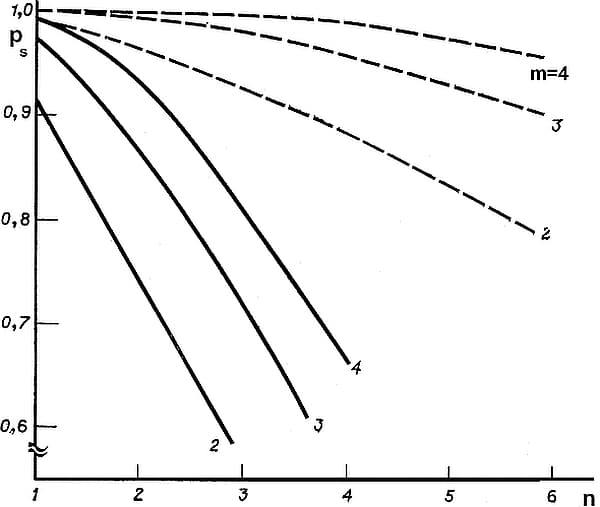
Rys.8. Ogólne rezerwowanie [1] : $n$ – liczba elementów połączonych szeregowo; $m$ – liczba równoległych połączeń ; linie przerywane dla $p_{si}=0,9$, linie ciągłe dla $p_{si}=0,7$
Zależności (26, 27) można uogólnić na przypadek, gdy struktury mają inną liczbę elementów $m$ i $n$ w sposób pokazany w pracy [1] .
Dla przypadków bardziej ogólnych połączeń zaleca się [1] rozpatrywać iteracyjnie, analizując możliwe kombinacje połączeń.
Wykresy rys. 6 i 8 pokazują , że na niezawodność systemu najbardziej wpływa liczba elementów połączonych szeregowo. Wpływ liczby połączeń równoległych jest istotny przy niewielkiej liczbie połączeń i dla $m>4$ jest praktycznie nieistotny. Wpływ liczby elementów i połączeń zmniejsza się jeśli niezawodność poszczególnych elementów jest duża, co jest charakterystyczne dla konstrukcji budowlanych.
Wprowadzenie rezerwowych elementów daje lepsze efekty od wprowadzenia rezerwowych układów.
Przykłady pokazują, że konieczne jest rozpatrywanie struktury w całości.
Projektowanie konstrukcji element po elemencie bez analizy połączeń niezawodnościowych może prowadzić do istotnego niedowymiarowania konstrukcji i wywołania katastrofy budowlanej, czego przykłady dostarczane nam są dość często.
Niezawodność konstrukcji należy rozpatrywać we wczesnym stadium projektowania, wówczas gdy wniesienie zmian nie powoduje znacznych strat, co będzie najbardziej znaczące na etapie eksploatacji.
Literatura
________________________________




