Leszek Chodor, 29 listopada 2015
14-02-2025 rewizja po dużej awarii portalu>
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 6 Czytelników
Zbiorniki powłokowe z blach cienkich stanowią ważne zastosowanie konstrukcji stalowych. Główne obszary zastosowań są związane przede wszystkim z rodzajem materiału składowanego w zbiorniku, stąd wyróżniamy: zbiorniki na ciecze, na gazy i na materiały sypkie. Najczęściej stosowane współczesne konstrukcje zbiorników zestawiono w tab.1.
Wprowadzenie
Stalowe konstrukcje powłokowe podlegają przepisom normy [1], chociaż są trzema odmiennymi rodzajami budowli, dla których opracowano przepisy szczegółowe: kominy [2], silosy [3], zbiorniki [4]. Normy Euorokod wprowadziły istotną, w stosunku do tradycyjnego ujęcia zagadnień projektowania kominów, silosów i zbiorników wspólną metodologię sprawdzania warunków wytrzymałości i stateczności w oparciu o jednolite podejście dla tych wszystkich konstrukcji powłokowych. Obszerny komentarz do obliczania i wymiarowania konstrukcji powłokowych dano w pracy [5].
Tab.1.Typy zbiorników stalowych zależnie od rodzaju dachu [5]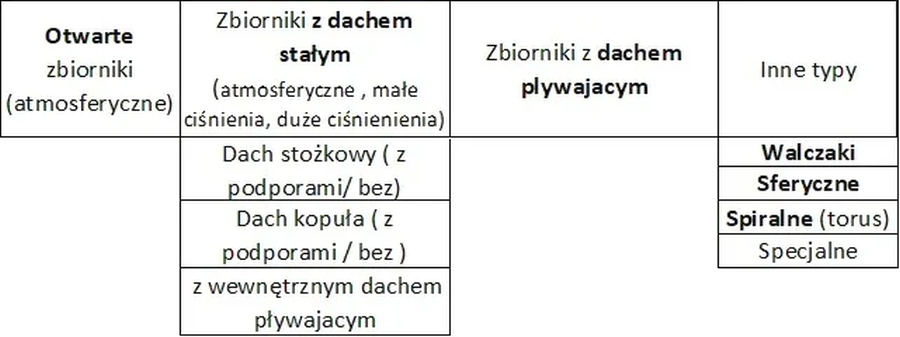
Zbiorniki stalowe były przedmiotem wielu prac, a między innymi: [6], [7], a także [8] i innych, a także przedmiotem wielu norm, a m.in. [9] i [10].
Najważniejsze konstrukcje zbiorników powłokowych, to:
- zbiorniki kuliste na gaz (rys.1),
- zbiorniki cylindryczne pionowe (rys.2),
- zbiorniki cylindryczne poziome (rys.3).
Występują jeszcze zbiorniki powłokowe o innym kształcie, jak np. zbiorniki kroplokształtne (rys.4) lub wieże ciśnień ze zbiornikiem torusem (rys.5)
Wspólną cechą zbiorników powłokowych jest zakrzywienie powłoki w taki sposób, by powłokę dostosować do pojawienia się sił błonowych (tylko rozciągających) i minimalizowanie (unikanie) zginania powłoki, które prowadziłoby do nieoptymalnego projektu ze względu na nadmierne zużycie materiału. W tym świetle zbiorniki z płaskimi ścianami nie będą optymalne, ponieważ ich wytężenie jest wywołane głównie zginaniem.
Zbiorniki powłokowe ciśnieniowe (ang thin wall pressure vessels (TWPV)) są najczęściej stosowane w przemyśle do składowania i transportu cieczy oraz gazów . Stosowane są również jako elementy pojazdów drogowych, morskich i powietrznych. Osobną grupę stanowią zbiorniki na materiały sypkie, czyli silosy – tą grupą zbiorników nie będziemy zajmować się w tym artykule.
Definicje
Przyjmuje się następujące definicje, dotyczące zbiorników walcowych:
powłoka – cienka ścianka zbiornika (inaczej: płaszcz, pobocznica, pancerz)
ogólnie – konstrukcja uformowana z cienkiej, zakrzywionej blachy
powłoka obrotowa – powłoka, która powstała przez obrót tworzącej wokół osi centralnej,
kierunek południkowy – kierunek stycznej., leżącej w płaszczyźnie pionowej,
kierunek obwodowy – kierunek stycznej., leżącej w płaszczyźnie poziomej,
zbiornik – naczynie do przechowywania produktów w stanie ciekłym lub gazowym,
smukłość powłoki walcowej o promieniu $r$ oraz grubości powłoki $t$
$$\begin{equation} \lambda_r =\cfrac{r}{t} \label {1} \end{equation}$$
gdzie $r=R-t/2$ – promień powłoki w środku grubości ścianki (promień podziałowy) – rys. 6.
W przypadku zbiorników o innych niż walcowy kształtach definicje należy odpowiednio zmodyfikować
Koncepcja i wstępne obliczenia zbiorników
Uzyskanie szybkich wyników, przydatnych w projektowaniu wstępnym jest możliwe, jeśli spełnione są następujące zasady :
- geometria i obciążenia zbiornika powinny być wyjątkowo proste i dostosowane do kształtów optymalnych (p. rys.1,2,3),
- lokalne zaburzenia geometrii i obciążeń powinny być minimalizowane i sprowadzane wyłącznie do swobodnych brzegów oraz podparcia powłoki.
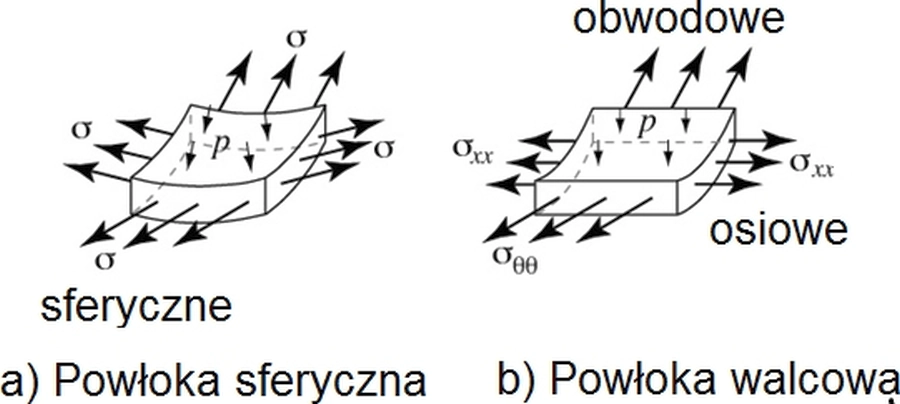
W tych warunkach ściany zbiornika powłokowego powinny pracować jak błona. Oznacza to, że na praktycznie całej powierzchni powłoka nie powinna być obciążona zginaniem, a odstępstwo od tej zasady może być dopuszczone wyłącznie lokalnie. Zachowanie powyższych zasad jest receptą na uzyskanie optymalnego projektu zbiornika powłokowego. W tym celu, zależnie od wywieranego ciśnienia należy dobierać optymalny kształt powłoki zbiornika. Sfera (rys.1) jest optymalną geometrią w przypadku równomiernego (wszechstronnego) wewnętrznego ciśnienia gazu) . Cylindryczny zbiornik (rys. 2 lub 3) jest nieco mniej efektywny z dwóch powodów: ( 1 ) na ścianie naprężenia zależą od kierunku ( 2 ) zamknięcia denne może znacznie zaburzać idealny stan membrany, co wymaga prowadzenia dodatkowych lokalnych wzmocnień. Jednak kształt cylindryczny może być bardziej wygodny do wytwarzania i transportu.
Założenia do analizy zbiorników powłokowych
Założenia w analizie zbiorników powłokowych, można sprowadzić do dwóch fundamentalnych:
1) o cienkościenności powłoki,
2) o symetrii geometrii i obciążeń.
To właśnie te założenia prowadzą do prostej teorii błonowej. Założenia teorii błonowej wraz z wynikającymi z nich wnioskami zilustrowano na rys. 6 na przykładzie zbiornika cylindrycznego o promieniu R i grubości powłoki t, z którego wzięto wycinek powłoki dx × dθ:
dla r=R (na powierzchni zewnętrznej wolnej od obciążeń w punkcie A) : σrr = τrx = τrθ =0,
dla r=R-t (na powierzchni wewnętrznej w punkcie B): nie działają naprężenia styczne, więc σrr = −p, τrx = τrθ =0,
dla r ∈ [R − t, R] (wewnątrz ścianki):
- powłoka jest cienka, więc τrx = τrθ = 0,
- σrr zmienia się od −p do zera, σrr jest dużo mniejsze od pozostałych naprężeń normalnych i w związku możemy je zaniedbać (σrr=0),
- ponieważ τrx = τxr i τrθ = τθr (symetria macierzy naprężeń), więc τxr = τθr = 0,
- ponieważ geometria i obciążenia są symetryczne i przy braku skręcania – niesymetryczne naprężenia τθx = τ\tau =0
Wnioskiem z założeń teorii błonowej jest więc stwierdzenie:
niezerowe są tylko naprężenia normalne osiowe σxx i obwodowe σθθ.
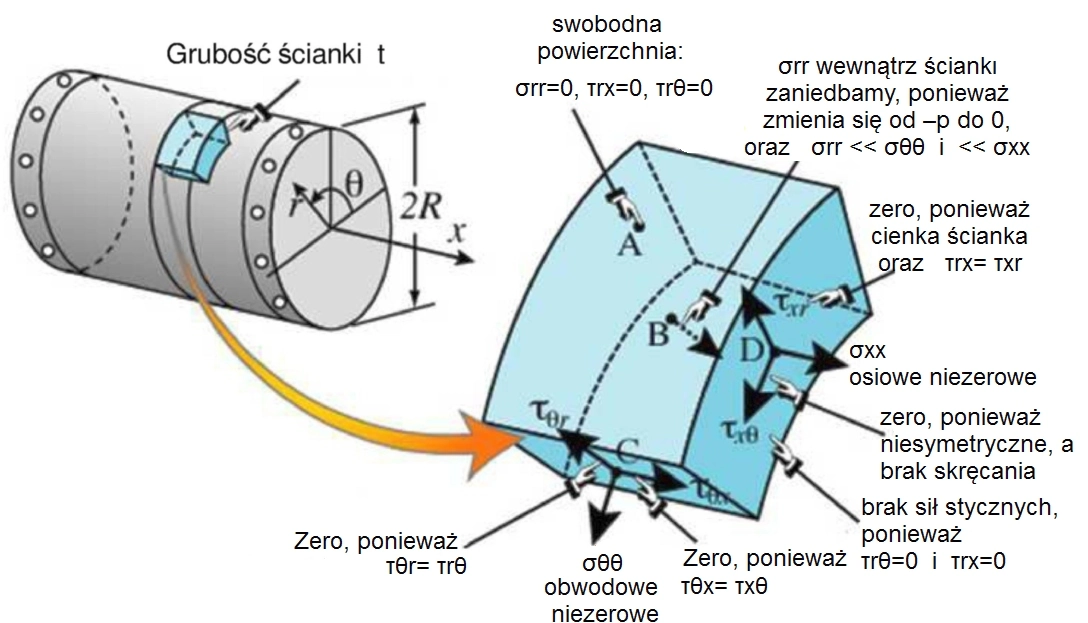
Rys.6 Powłoki cienkościenne. Założenia do analizy [11]
Zbiornik walcowy
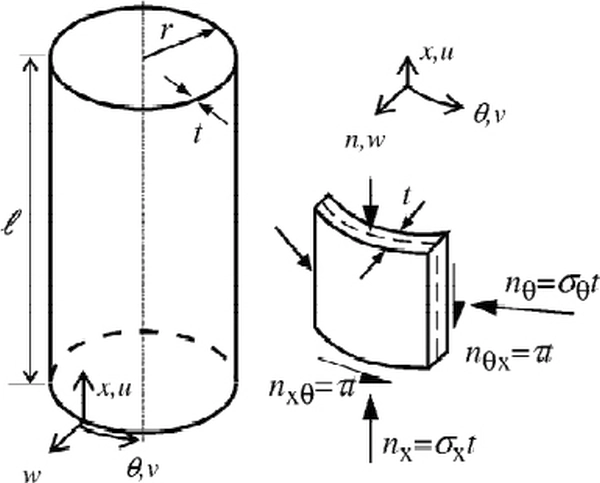
Za powłokę walcową uważamy, powłokę cylindryczną o promieniu R, grubości t, obciążoną równomiernym ciśnieniem wewnętrznym p. Rozważania prowadzimy w układzie współrzędnych walcowych ( x , r , θ ) (rys. 7a), gdzie oś x jest współrzędną liniową, θ współrzędną kątową, dodatnio skierowaną od osi y do z (lewoskrętnie).

Rys. 7 Powłoka walcowa. Naprężenia obwodowe i osiowe [11]
Niezerowe składowe naprężenia σxx and σθθ są równomiernie rozłożone wzdłuż grubości ścianki i zbiornika (z wyjątkiem zaburzeń brzegowych, opisanych niżej). Macierz naprężeń w ściance powłoki walcowej w układzie {x, θ, r } można zapisać w postaci:
$$\begin{equation} \left[\begin{array}{ccc} \sigma_{xx} & \tau_{x\Theta} & \tau_{xr} \\ \tau_{ \Theta x} & \sigma_{\Theta \Theta} & \tau_{\Theta r} \\ \tau_{rx} & \tau_{x\Theta} &\sigma_{rr} \\ \end{array} \right] =\left[\begin{array}{ccc} \sigma_{xx} & 0 & 0 \\ 0 & \sigma_{\Theta \Theta} & 0 \\ 0 & 0 & 0\\ \end{array} \right]\label{2} \end{equation}$$
W celu obliczenia tych naprężeń dla danych p, R i t, rozpatrzmy równowagę wycinka powłoki, pokazanego na rys. 7b. Otrzymamy:
$$\begin{equation} { \sigma_{\Theta \Theta} =\cfrac{pR}{t} \quad, \quad \sigma_{xx}=\cfrac{pR}{2t} =\cfrac{1}{2} \sigma_{ \Theta \Theta} } \label{3} \end{equation}$$
Stąd ostatecznie macierz naprężeń, wynosi
$$\begin{equation} \left[\begin{array}{ccc} \sigma_{xx} & 0 & 0 \\ 0 & \sigma_{\Theta \Theta} & 0 \\ 0 & 0 & 0\\ \end{array} \right]= \cfrac{pR}{2t} \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0&0 \\ \end{array} \right] \label{4} \end{equation}$$
Zbiornik sferyczny
Podobne podejście jak dla zbiornika walcowego można zastosować do zbiornika sferycznego, pokazanego na rys. 8. Rozważania prowadzimy w układzie {r, θ, φ}.
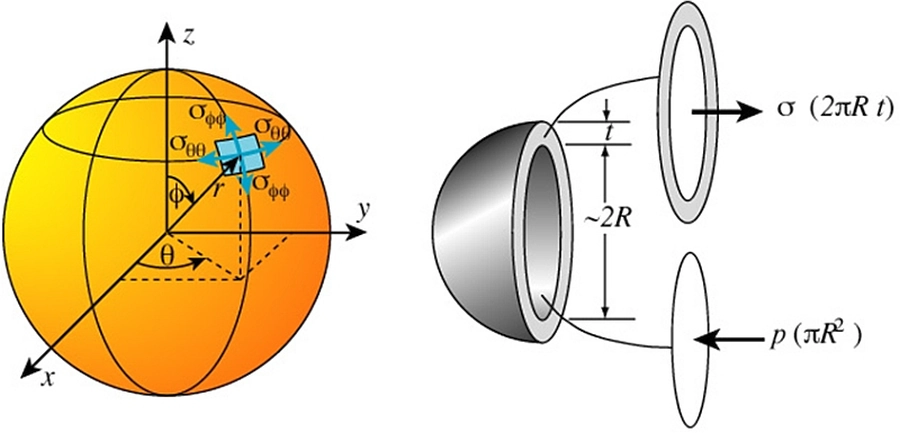
Rys. 8 Powłoka sferyczna Naprężenia sferyczne[11]
Przyjmujemy następujące założenia:
1) Wszystkie styczne naprężenia są zerowe: τrφ = τφr = 0, τrθ = τθr = τθφ = τφθ = 0.
2) Normalne naprężenia σrr zaniedbywalne w porównaniu z pozostałymi naprężeniami normalnymi.
Rozpatrując równowagę wycinka powłoki, otrzymamy:
$$\begin{equation} \sigma=\cfrac{pR}{2t} \label{5} \end{equation}$$
a w rezultacie macierz naprężeń:
$$\begin{equation} \left[\begin{array}{ccc} \sigma & 0 & 0 \\ 0 & \sigma & 0 \\ 0 & 0 & 0\\ \end{array} \right]= \cfrac{pR}{2t} \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0&0 \\ \end{array} \right] \label{6} \end{equation}$$
Uwagi do obliczeń wstępnych zbiorników powłokowych
Dla porównywalnych: promienia, grubości ścianki i wewnętrznego ciśnienia, maksymalne naprężenia normalne w zbiorniku walcowym są dwa razy większe niż w zbiorniku sferycznym. Powodem tego jest efekt zakrzywienia w obu kierunkach, co powoduje dużo korzystniejsze warunki równowagi z ciśnieniem (p. rys.9)
W przypadku zastosowani zbiorników cylindrycznych możemy jednak uzyskać bardziej efektywne wykorzystanie objętości zbiornika, a także zajętości przestrzeni przez zbiornik oraz lepszą aerodynamikę
Zwróćmy uwagę, że w przypadku rezygnacji z krzywizny powłoki w obu kierunkach, czyli dla płaskiej ścianki zbiornika otrzymujemy znacznie bardziej niekorzystne warunki. Staramy się nie projektować zbiorników z płaskimi ściankami.
Zaburzenia brzegowe
Opis zjawiska i rozwiązanie zadania
Rozważmy najpierw przypadek, w którym zbiornik jest zamknięty przez dna w sposób pokazano na rys. 10. Zarówno płaszcz jak dno powinny znajdować się w stanie błonowym, ale ze względu na to, że w płaszczu naprężenia obwodowe są dwa razy większe nie w dnie, więc różnie rozszerzają się, co wskazano przerywaną linią . Powłoka i dno nie mogą jednak odkształcać się niezależnie od siebie. W punkcie styku musi jednak zachodzić zgodność przemieszczeń, co wymusza doginanie się ścianek, tak jak pokazano na detalu „a”. Wywołane zginanie jest właśnie zaburzeniem brzegowym w stanu błonowego. Ze względu na znacznie większą różnicę odkształceń poprzecznych na styku ścianki z płaskim dnem , w tym przypadku zginanie ścianki i zaburzenia brzegowe będą również znacznie większe. Z tego powodu zamknięcia lub przekrycia walcowych zbiorników muszą być starannie zaprojektowane, przy czym należy unikać zamknięć płaskich. Większość zbiorników ciśnieniowych ma dna kopulaste (koliste) , tak by zachować w miarę gładkie przejście z powłoki w dno.

Rys.10 Zaburzenia brzegowe w powłoce zbiornika [11]
Na szczęście zaburzenia brzegowe są w praktyce ograniczone do niewielkich obszarów (są lokalne).
Na rys 11 pokazano przykładowy rozkład sił powłokowych : zginających momentów podłużnych mx oraz sił osiowych obwodowych nΘ w przypadku połączenia walcowego płaszcza z płaskim dnem .
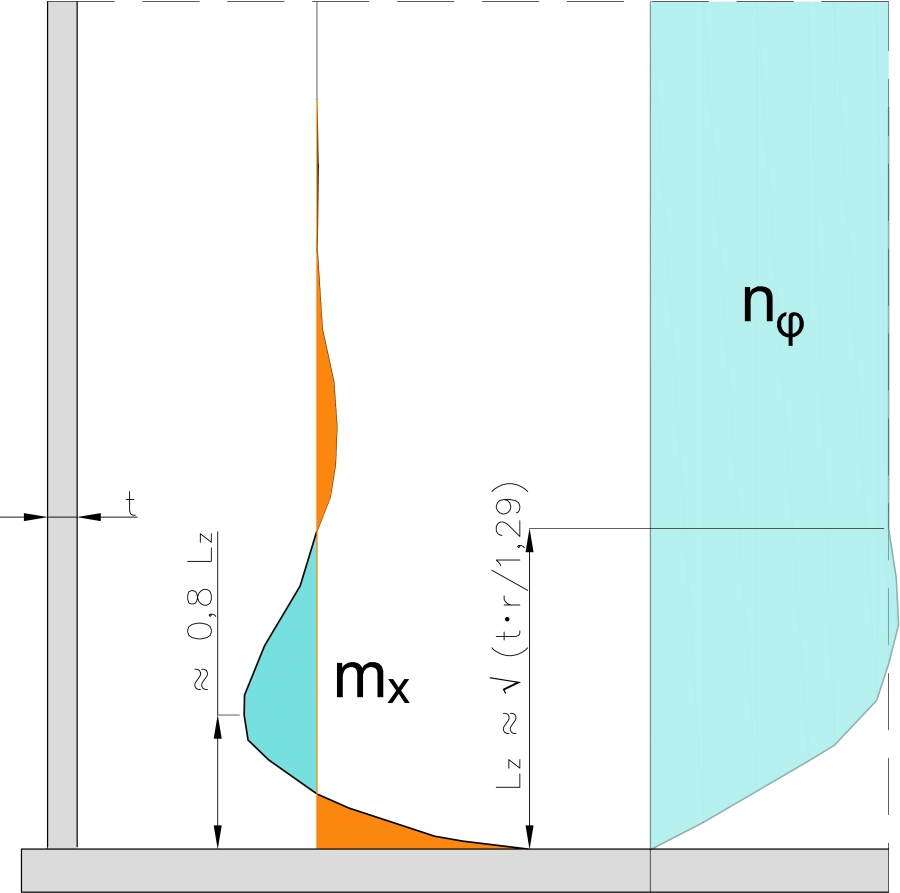
Rys.11 Zaburzenia brzegowe na styku płaszcza z dnem [6]
Zaburzenia brzegowe w tym przypadku rozciągają się szacunkowo na długości [6]:
$$\begin{equation} L_z\approx \sqrt {\dfrac {t \cdot r}{1,29}} =t \cdot \sqrt {\cfrac{ \lambda_r}{1,29}} \label{7} \end{equation}$$
gdzie smukłość powłoki $\lambda_r =r/t$ ($\ref{1}$)
Maksymalny moment zginający w płaszczu zbiornika występuje w przybliżeniu w odległości 0,8 Lz od dolnej krawędzi płaszcza.
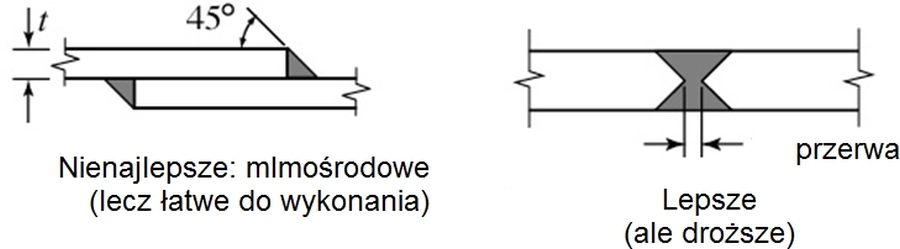
Rys.12 Jak zespawać ścianki powłoki ? [11]
Na rys. 12 pokazano inny przykład zaburzenia brzegowego, obserwowany przy skokowo zmiennej grubości powłoki , w tym przypadku przy zastosowaniu spawania blach za pomocą spoin pachwinowych zamiast czołowych.
W celu ograniczenia zaburzeń brzegowych w tym przypadku zaleca się wykonywanie łączenie powłoki płaszcza za pomocą spoin czołowych. Spawanie nakładkowe jest stosowane do łączenia pasów dna.
W ogólności rozwiązanie zadania zaburzeń brzegowych w zbiornikach w stanie sprężystym prowadzi się standardowymi metodami na gruncie teorii zgięciowej powłok.
Zaburzenia brzegowe, a projektowanie zbiorników
Można zdefiniować wiele mechanizmów zniszczenia powłok zbiorników i zazwyczaj żaden mechanizm sprawczy nie będzie polegał na wyczerpaniu nośności sprężystej, obserwowanej przy uplastycznieniu jednego punktu powłoki. Zwykle powłoka niszczy się po uruchomieniu mechanizmu plastycznego lub wskutek utraty nośności krytycznej (wyboczeniu). Mechanizm plastyczny uruchamia się dopiero po uplastycznieniu wielu punktów powłoki. Powłoki mają znaczne zapasy nośności ponad nośność sprężystą i osiągnięcie przez naprężenia zastępcze w obszarze spiętrzenia naprężeń (zaburzeń brzegowych granicy plastyczności nie jest równoznaczne z wyczerpaniem nośności przez powłokę.
Z tych powodów lokalne zaburzenia brzegowe można zignorować przy wstępnym kształtowaniu zbiorników. Generalnie powłoki, dna i dachy zbiorników projektujemy na stan błonowy, a lokalne zaburzenia brzegowe powinny być uwzględnione w drodze specjalnych zabiegów konstrukcyjnych, np. poprzez skonstruowaniu brzegowego pierścienia w dnie lub wzmocnienia otworów pod króćce.
Typy analiz i mechanizmy zniszczenia konstrukcji zbiorników
Podstawy teoretyczne analizy konstrukcji powłokowych oraz metody analizy i opis mechanizmów zniszczenia zawierają postanowienia normowe [1].
Typy analiz powłok
Zależnie od rozpatrywanego stanu granicznego stosuje się jedną lub kilka rodzajów analiz konstrukcji powłokowych:
- analizę globalną ,
- analiza według teorii błonowej,
- liniowo sprężysta analiza powłok (LA),
- liniowo sprężysta analiza bifurkacyjna (LBA),
- geometrycznie nieliniowa analiza sprężysta (GNA),
- analiza fizycznie nieliniowa (MNA),
- analiza geometrycznie i fizycznie nieliniowa (GMNA),
- geometrycznie nieliniowa analiza sprężysta z imperfekcjami (GNIA),
- analiza geometrycznie i fizycznie nieliniowa z imperfekcajmi (GMNIA).
Stany graniczne powłok
Stanami granicznymi powłok stalowych są:
- zniszczenie plastyczne (LS1),
- nieprzystosowanie plastyczne (zmęczenie niskocyklowe) (LS2),
- niestateczność (wyboczenie) (LS3),
- zmęczenie (LS4)
Pogrubieniem wyróżniono te stany graniczne, które powinny być sprawdzone praktycznie dla każdego zbiornika
Warunki brzegowe a niestateczność powłoki
Zgodnie z kl. 8.3. (1) w przypadku stanu granicznego LS3 szczególnego znaczenia nabierają warunki brzegowe determinujące przyrosty przemieszczeń podczas wyboczenia (w odróżnieniu od przemieszczeń w stanie przedwyboczeniowym). Wprowadzono następujące oznaczenia warunków brzegowych:
BC1 – brzeg utwierdzony ( sztywne przepony pośrednie lub utwierdzenie płaszcza w fundamencie)
BC2 – brzeg przegubowy ( np. w przypadku usztywnienia zbiornika górą przez dach, pierścieni pośrednich lub zakotwienia przegubowego w fundamencie),
BC3 – brzeg swobodny ( w przypadku zbiornika bez dachu)
W Załączniku A [1] podano standardowe wyrażenie uzyskane z teorii błonowej, w Załączniku B formuły nośności plastycznej powłok, wynikające z teorii nośności granicznej (plastyczne), a w Załączniku C formuły naprężeń membranowych i od zginania (analiza sprężysta). W załączniku D [1] podano szereg bardzo ważnych formuł naprężeniowych dotyczących stateczności powłok.
Imperfekcje a niestateczność powłoki
Duży wpływ na niestateczność powłoki mają imperfekcje geometryczne. typu wgnieceń.[12]. Jeśli imperfekcje wstępne (wgłębienia) $\Delta$ odniesiemy do grubości powłoki $t$ i będziemy mierzyć względnie
$$\begin{equation} \Delta_t = \cfrac{\Delta}{t} \label{8} \end{equation}$$
gdzie $\Delta$ jest odchyłką wykonawczą mierzoną w mm (rys. 13)
to zgodnie z rozważaniami Karman i Tsien (1941) [13] wraz ze wzrostem imperfekcji $Delta_t$ istotnie zmniejsza się klasyczne naprężenie krytyczne ($\ref{35}$) a współczynnik $C_{kr}$ przyjmuje wartości przedstawione w tab.2
Tab.2 Zależność współczynnika krytycznego ($\ref{35}$) od imperfekcji względnej ścianki powłoki ($\ref{6}$) (wg [12]. tab. 9.1)
Klasy wytwarzania zbiornika
Definiuje się trzy klasy wytwarzania zbiorników
$$\begin{equation} Klasa = \begin {cases}
A,& \textrm { najwyższa} \\
B,& \textrm { wysoka} \\
C,& \textrm { normalna} \\
\end {cases} \label{9} \end{equation}$$
Tolerancje wykonania zbiornika
Zbiornik wytworzony w danej klasie powinien mieć zachowane tolerancje odchyłek wykonawczych w granicach zdefiniowanych w normie PN-EN 1090-2 [14].
Dopuszczalne tolerancje dotyczące wykonania powłoki dotyczą:
- owalizacji (odstępstwa od kształtu okrągłego),
- mimośrodów (związanych z nieciągłościami powierzchni środkowej na stykach obwodowych blach),
- lokalnych wgłębień (lokalnych odchyłek prostopadłych do nominalnej powierzchni środkowej).
W stanie granicznym niestateczności powłoki LS3, szczególne znaczenie mają niedoskonałości (imperfekcje) powłoki związane z lokalnymi wgłębieniami , dlatego poniżej omawiamy je dokładniej,. W celu oceny innych tolerancji odsyłamy do normy podstawowej [14].
Tolerancje dotyczące wgłębień
Na rys. 13 pokazano definicje normowe fundamentalnych dla stateczności powłok imperfekcji geometrycznych w postaci wgnieceń południkowych (z lewej) i obwodowych ( z prawej), które wpływają na południkowe siły krytyczne zbiornika z imperfekcjami.
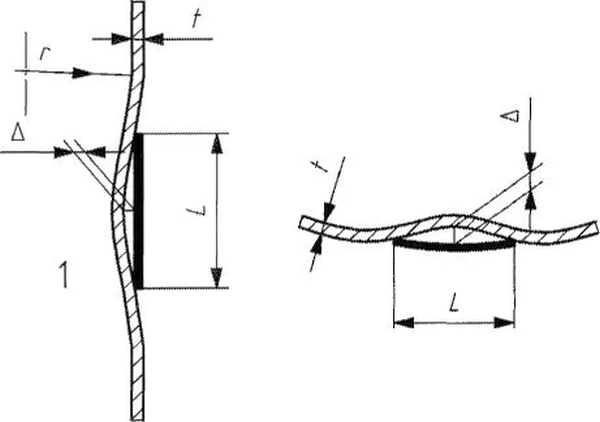
Rys.13 Definicja wgnieceń powłoki: południkowych i obowodowych wg norm [14] oraz (PN-EN 1993-1-6: 2010, Eurokod 3 – Projektowanie konstrukcji stalowych – Część 1-6: Wytrzymałość i stateczność konstrukcji powłokowych)),
Podstawową wartością długości bazowej $L$ do której odnosi się wielkości dopuszczalnych wgnieceń w obu kierunkach wynosi
$$\begin{equation} L= 4 \cdot \sqrt{r\cdot t} = 4 \cdot r \sqrt{\lambda_r} \label{10} \end{equation}$$
W kierunku obwodowym na długość bazową mamy dodatkowy warunek.
$$\begin{equation} L= 2,3 \cdot \sqrt{ h\cdot r \cdot t} = 2,3 r \cdot h \sqrt{\lambda_r} \le r \label{11} \end{equation}$$
gdzie h – wysokość segmentu powłoki
W poprzek spoin: dodatkowo L = $ 25 \cdot t < 500 mm$
Dopuszczalne odchyłki mierzone względem długości bazowej dla trzech klas dokładności wg [14] oraz [1] wynoszą:
$$\begin{equation} ±\Delta/ L = \begin {cases}
0,006 & \textrm { dla klasy A} \\
0,010 & \textrm { dla klasy B} \\
0,016 & \textrm { dla klasy C} \\
\end {cases} \label{12} \end{equation}$$
Odchyłki geometryczne powinny być utrzymane w ramach ustalonych tolerancji (kl. 4.1.3 [1])).. Na ich podstawie wyznaczane są parametry imperfekcji., istotne dla nośności powłoki.
Zbiorniki na ciecze
Znakomita większość zbiorników stalowych na ciecze jest stosowana do przechowywania produktów ropopochodnych (naftowych).
Zbiorniki na produkty naftowe
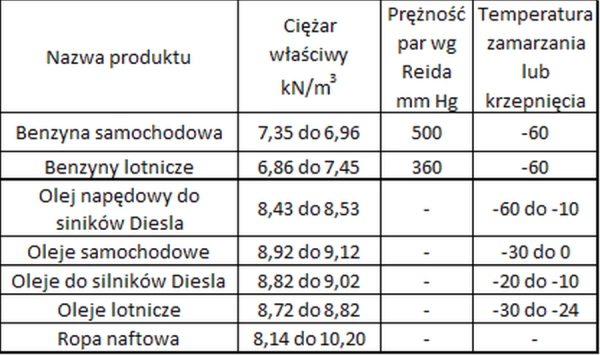
Produkty naftowe charakteryzują się łatwością parowania, co może powodować duże straty magazynowe. W tab. 3 zestawiono najczęściej składowane produkty naftowe.
Tab 3. Ogólna charakterystyka magazynowanych produktów naftowych [6]
Projektowanie baz paliw oraz zbiorników na paliwa płynne jest obarczone wieloma wymaganiami zawartymi w Rozporządzeniu Ministra Gospodarki z dnia 21 listopada 2005 r. w sprawie warunków technicznych, jakim powinny odpowiadać bazy i stacje paliw płynnych, rurociągi przesyłowe dalekosiężne służące do transportu ropy naftowej i produktów naftowych i ich usytuowanie [15].
Zbiorniki z dachami pływającymi
Ważną kategorią dachu zbiorników na ciecze jest dach pływający, który pływa bezpośrednio na produkcie. Taki sposób pracy – ze względu na wyeliminowanie przestrzeni pary ogranicza możliwość wybuchu produktu naftowego, a przede wszystkim zmniejsza straty parowania, a tym samym zanieczyszczenie powietrza. Emisja par jest możliwa tylko z obszaru uszczelniacza, a to będzie zależeć głównie od typu zastosowanego uszczelnienia. Dach pływający – ruchomy ma wiele zalet funkcjonalnych, ale jest bardziej skomplikowany i kosztowny niż dach stały.
Pływający dach jest to okrągła stalowa konstrukcja, wyposażona we wbudowane pontony, który pozwalają na unoszenie się dachu na powierzchni ciekłego produktu.
Całkowita średnica dachu jest zwykle 400 mm mniejsza niż wewnętrzna średnica zbiornika, to znaczy po obu stronach pomiędzy dachem a, a pobocznica zbiornika pozostawia się po około 200 mm.
Pływające dachy stosuje się w celu ochrony produktu wewnątrz zbiornika przed odparowaniem do atmosfery, Ze względu na kwestie ochrony środowiska, projekt uszczelnienia dachu jest jednym z głównych problemów budowy zbiorników z dachami pływającymi.
Pływający dach został wykonany już po I wojnie światowej przez Chicago Bridge & Iron Company. Po odparowaniu produktu w zbiorniku ze stałym dachem firma poniosła znaczne straty finansowe. Doprowadziło to do badań w celu opracowania dachu, który może unosić się bezpośrednio na powierzchni produktu w celu zmniejszenie strat parowania.
Zbiorniki z dachami pływającymi są bardzo szczegółowo omówione w wytycznych API (American Petrole Institute) [16]. Istnieją dwa typy pływających dachów:
- wewnętrzny pływający dach, to taki który jest umieszczony wewnątrz zbiornika z dachem stałym,
- zewnętrzny pływający dach, to taki dach, który unosi się na wierzchu produktu w otwartym zbiorniku i jest otwarty na oddziaływania atmosferyczne. Taki dach z pojedynczym pontonem pokazano na rys 14.
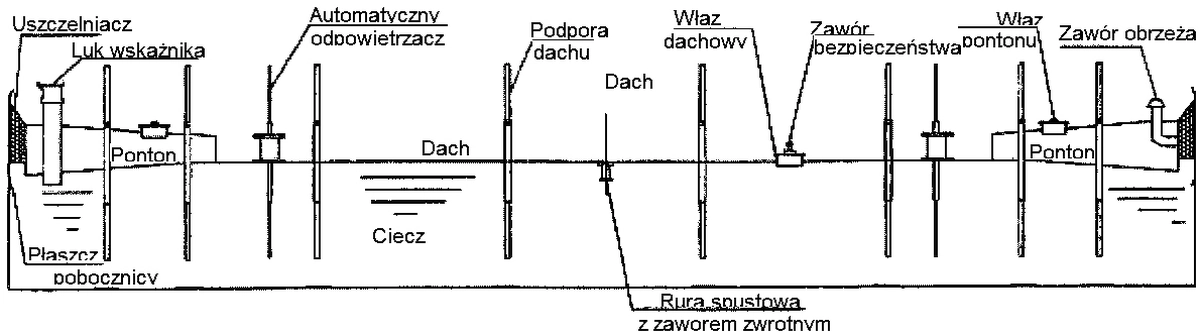
Rys. 14 Zbiornik z pojedynczym dachem pływającym [16]
W roku 1957 Wiggins[17] opatentował opatentował podwójny dach pływający, pokazany na rys. 15.
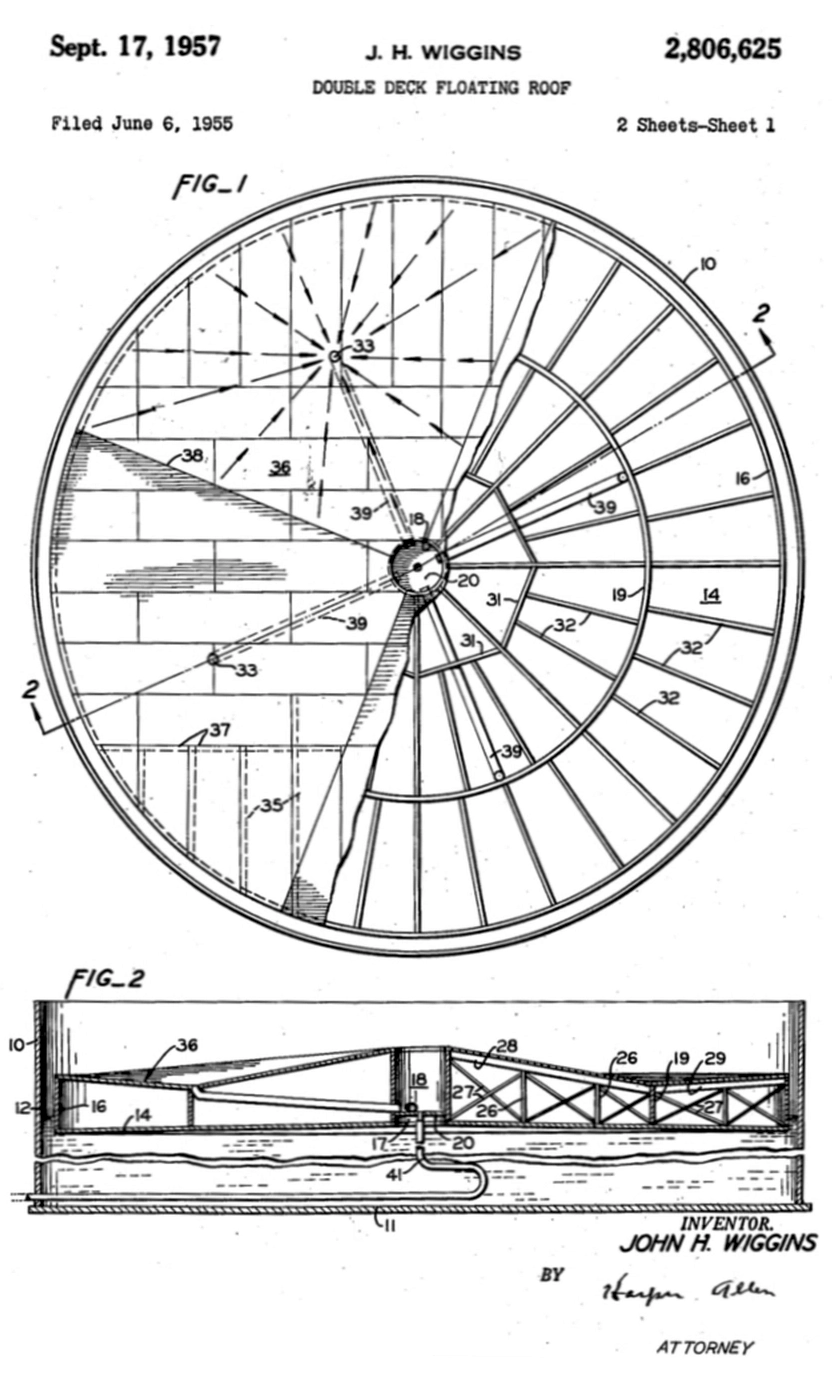
Rys.15 Patent podwójnego dachu pływającego [17]
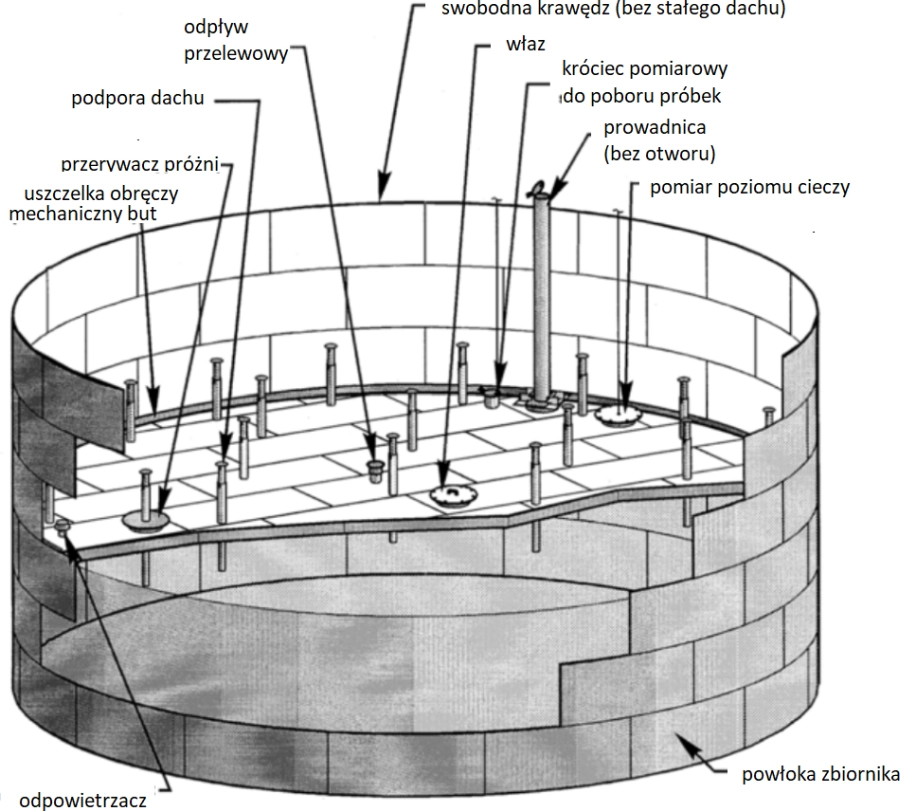
Rys.16 Zbiornik z zewnętrznym, podwójnym dachem pływającym [18]
Minimalne wymagania dla dachu pływającego pontonowego, jednopowłokowego pokazano na rys.17. [16] wymaga, by wszystkie blachy dachu miały minimalną grubość nominalnej 5 mm, a w centrum powłoki 8 mm, a pojedyncza powłoka pontonu pływającego dachu musi być zaprojektowany tak, aby być w kontakcie z płynem w czasie normalnej pracy. Konstrukcja powinna być w stanie pomieścić dach uniesiony przez opary produktu. Na przypadek awaryjny (awaria przelewu) należy zaprojektować dodatkowy ruraż do odprowadzenia wody deszczowej o objętości wynikającej ze słupa wody 250 mm.
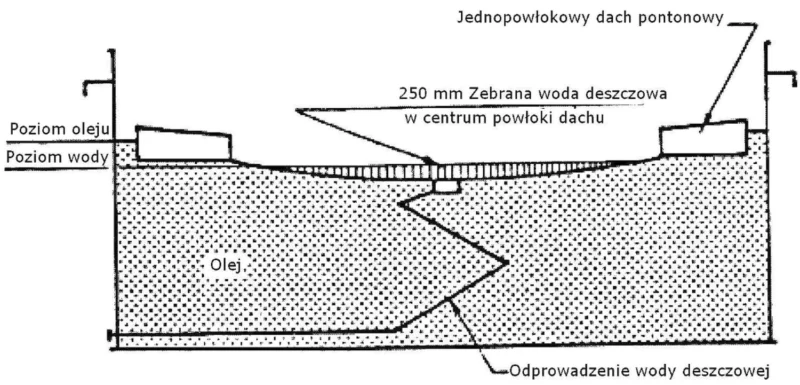
Rys.17 Minimalne wymagania dla dachu pływającego (na podstawie [16], Vol.1)
Obszerne analizy dachów pływających zawiera oprcowanie Kuan (2009) [19].
Dachy pływające są przedmiotem norm w wielu krajach, a m.in.:
- Wielka Brytania BS 2654 [20]
- Niemcy DIN 4119 – Part 1 and 2 [21]
- Francja [22]
- [16], [23]
- Normy korporacji DEP i PTS.
Procedura projektowania dachu pływającego
Praktycznie wszystkie składowe dachu pływającego objęte są ograniczonymi procedurami. Tymi składowymi są: ponton, konstrukcja nośna i poszycie dachu, akcesoria i obróbki na czas wykonawstwa i eksploatacji.
W wyborze typu dachu najistotniejszy jest typ pontonu.
Do średnicy 39 m stosujemy dach jednopowłokowy.
W przypadku większych średnic do 65 m stosujemy dachy dwupowłokowe.
Ze względu na konieczność ograniczenia odkształcalności, która rośnie nieliniowo wraz ze wzrostem średnic – dachów pływających nie stosuje się zasadniczo dla średnic powyżej 65 m. W takim przypadku stosuje się baterię zbiorników.
Wyporność dachu jednopowłokowego skupiona jest w pontonie pierścieniowym , podzielonym na komory. Centralna powłoka jest utworzona z membrany zespawanej z cienkich blach stalowych i połączonej z wewnętrzną krawędzią pontonu (pływaków).
Dach dwupowłokowy składa się z dwóch stalowych membran: górnej i dolnej oddzielonych serią obwodowych grodzi. Zewnętrzny pierścień komór jest głównym elementem wyporowym. Taki dach jest znacznie cięższy niż jednopowłokowy, ale też znacznie sztywniejszy. Powietrze zawarte pomiędzy powłokami ma działanie izolacyjne, które pomaga w zmniejszeniu energii słonecznej docierającej do produktu w czasie upałów i zapobiega stratom ciepła produktu w czasie zimy.
Na rys.18 pokazano poziomy cieczy w zbiorniku: pracy, obliczeniowe, maksymalne i minimalne .
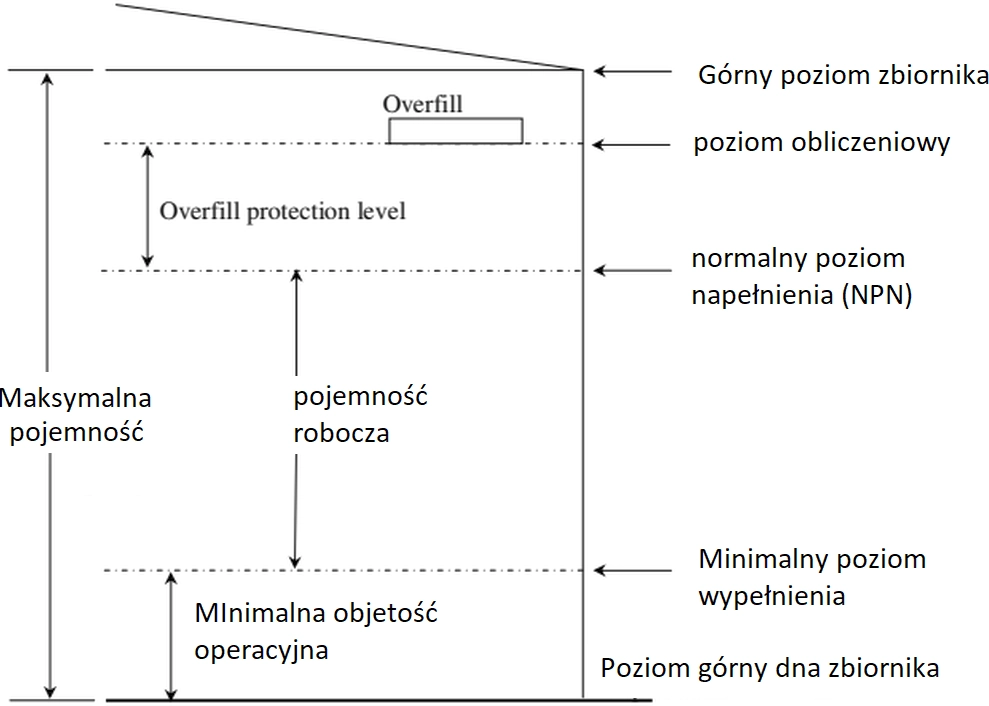
Rys. 18 Poziomy pracy i obliczeniowe [24]
Objętość cieczy w zbiorniku nie powinna w żadnym przypadku (oprócz okresu remontu) spaść poniżej poziomu minimalnego, ani też przekroczyć poziom obliczeniowy.
Wybór materiału (gatunku stali) powinien umożliwić eksploatację przez założony projektowy okres użytkowania, który zwykle przyjmuje się 30 lat.
Należy uwzględnić agresywność przechowywanych cieczy, a w tym system węglowodorów oraz CO2. W pierwszej kolejności należy wziąć pod rozwagę stal węglową jako najtańszą.
Dwutlenek węgla rozpuszcza się w wodzie i ulega dysocjacji tworząc słaby kwas węglowy, który powoduje korozjię stali węglowych. Wyższe ciśnienie cząstkowe CO2 oznacza więcej rozpuszczonego CO2, a tym samym większą szybkość korozji. Wyższe temperatury powodują wzrost szybkość korozji, ale w pewnych warunkach, około 70 do 80 °C, na powierzchni stali może tworzyć się warstwa ochronna, która zmniejsza szybkość korozji w porównaniu do niższych temperatur. Stopy odporne na korozję są stosowane w celu uniknięcia korozji na wysoką zawartość CO2, co może okazać się bardziej ekonomiczne od zastosowania stali węglowej z dużymi naddatkami na korozję i/lub inhibitora chemicznego. Obecność CO2 wskazuje, że stal węglowa będzie miała ograniczone zastosowanie, co najwyżej z naddatkiem na korozję, ale max 6 mm.
W niskich temperaturach stale ferrytyczne niestopowych ( i niskostopowe oraz ferrytyczno – austenityczne nierdzewne i stale duplex ) tracą swoją plastyczność, przez co są podatne na kruche pękanie. Aby zwiększyć odporność na kruche pękanie należy unikać karbów, kontrolować spoiny i poddawać je poddane obróbce cieplnej, np. normalizowaniu. W bardzo niskich temperaturach koniczne jest stosowanie stali drobnoziarnistych, austenitycznych i wysokoniklowych.
W normie [16] podano wykresy umożliwiające dobór gatunku stali w zależności od temperatury pracy zbiornika.
Na rys. 19 pokazano schemat dachu pływającego, a na rys. 20 przykładowy przekrój przez ponton, służący do sprawdzenia wyporu dachu pływającego.
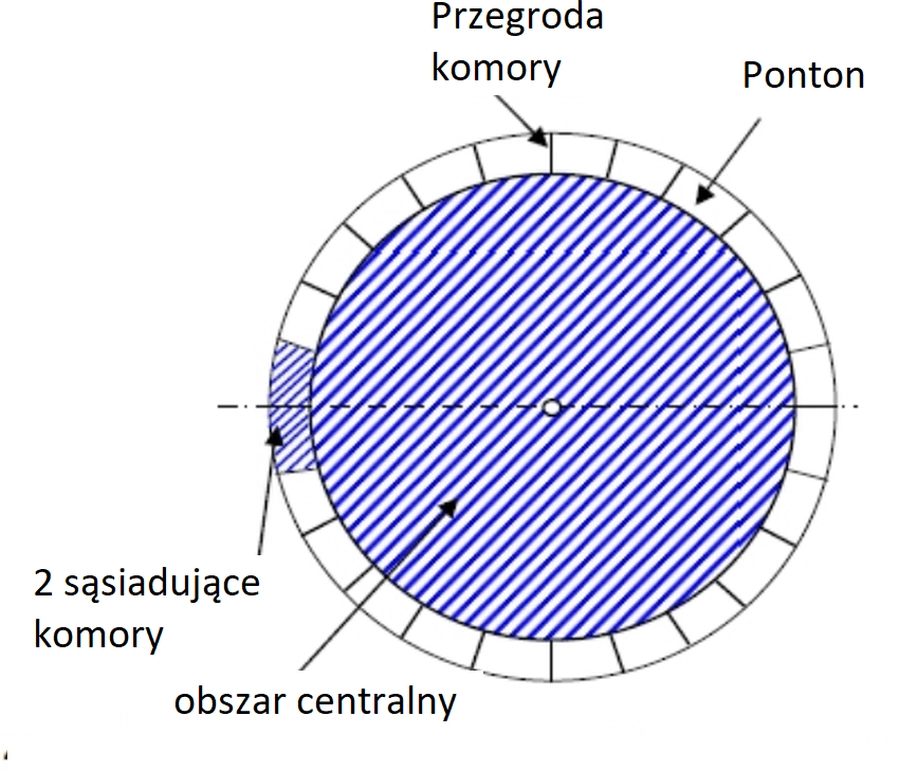
Rys.19 Schemat dachu pływającego [19]
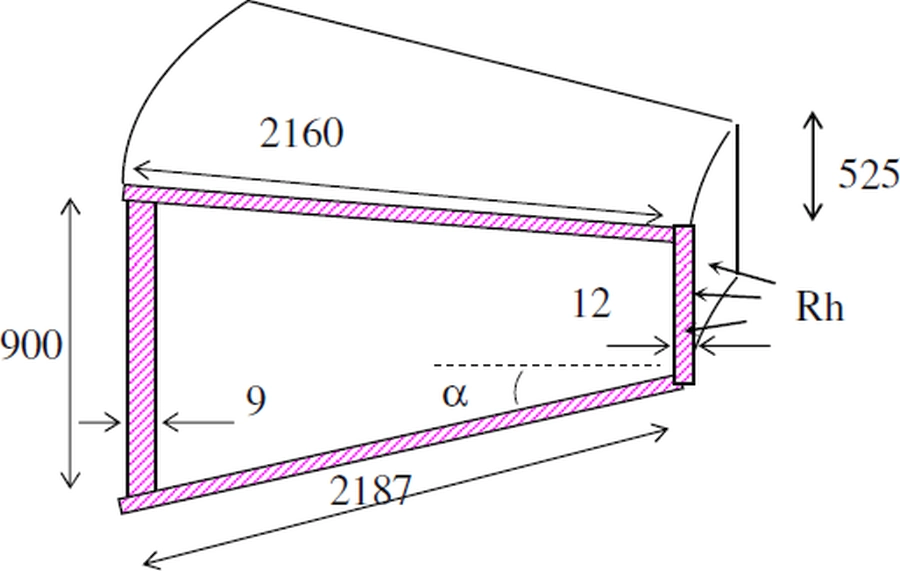
Rys.20 Przykładowy przekrój przez ponton [19]
Ważnym elementem zbiornika z dachem pływającym są akcesoria, włazy, króćce oraz wyposażenie zbiornika. W niniejszym artykule tymi problemami nie zajmujemy się i odsyłamy do innych opracowań, np: [16] i [19].
Zbiorniki na wodę
Zbiorniki kroplokształtne
Przykład zbiornika kroplokształtnego pokazano na rys. 4.
Eliminacja stanu giętnego w powłokach, o ile to możliwe ze względu na sposób obciążenia i podparcia, stanowi już pewien stopień optymalizacji projektu. Prowadzi bowiem do równomiernego przekroju powłoki , a przy dodatkowym wyrównaniu wytężenia w poszczególnych punktach powierzchni środkowej do tzw. powłok równomiernej wytrzymałości. W oparciu o najprostszy warunek wyrównania naprężeń $\sigma_\theta+\sigma_x=f_y $ kształt zbiorników kroplokształtnych wyznaczono już w roku 1918. Wykonanie takich zbiorników jest niestety dość drogie, ale uzyskuje się efekt stanu błonowego.
Cylindryczne zbiorniki poziome
Cylindryczne zbiorniki poziome (rys.3). stosuje się głównie w przemyśle chemicznym, na stacjach paliw lub do produkcji biogazu. W zbiornikach poziomych ciśnieniowych stosuje się dna wyoblone i takie zbiornika nazywa się walczakami.
Wieże ciśnień
Na wieże ciśnień chętnie stosuje się zbiorniki w formie torusa, co pokazano na rys. 5. Stosuje się również stożki, sfery itd.
Projektowanie zbiorników według Eurokod
Zasady ogólne
Zbiorniki należy projektować, wykonywać i utrzymywać zgodnie z wymaganiami normy [4] w szczególności w zakresie różnicowania niezawodności w zależności od przyjętej klasy konsekwencji zniszczenia.
Klasy konsekwencji zbiorników
CC1 – zbiorniki dla rolnictwa oraz zbiorniki na wodę,
CC2 – zbiorniki o średniej pojemności na ciecze palne lub szkodliwe dla środowiska wodnego w terenie zabudowanym,
CC3 – zbiorniki na ciecze i gazy płynne, toksyczne lub wybuchowe, lub zbiorniki o dużej pojemności palne lub szkodliwe dla środowiska wodnego w terenie zabudowanym.
Klasa konsekwencji powinna być uzgodniona pomiędzy Projektantem, Inwestorem i odpowiednimi władzami.
Naddatki korozyjne a grubość blach płaszcza
Przy sprawdzaniu nośności jako obliczeniową grubość ścianki zbiornika przyjmuje się grubość nominalną blachy, pomniejszoną o wartość maksymalnej odchyłki ujemnej oraz naddatek korozyjny.
Naddatek korozyjny jest uzależniony od właściwości przechowywanej cieczy, rodzaju stali, obróbki cieplnej oraz specjalnych środków ochrony przed korozją.. Wartość naddatków korozyjnych ustala się w projekcie.
Naddatek na korozję $\Delta_{kor}= T \cdot v_{kor} $
zależy od przewidywanego okresu eksploatacji zbiornika T oraz szacowanego postępu korozji $v_{kor}$. Oba parametry $T$ i $v_{kor}$ powinny być podane jako założenia w projekcie zbiornika.
Okres użytkowania zbiornika przyjmuje się w uzgodnieniu z klientem. Dla typowych zbiorników na wodę zwykleprzyjmuje się T=12 lat na podstawie praktyki amerykańskiej [25]. Prędkość korozji płaszcza zbiorników na wodę wykonanych ze zwykłej stali przyjmuje się zwykle $v_{kor}= 0,133 mm/ rok $. W tym przypadku naddatek na korozję będzie wynosił \Delta_{kor}=12 \cdot 0,13 = 1,6 mm $.
W normie polskiej z 1997 roku [26] podano, że okres eksploatacji zbiorników walcowych pionowych na ciecze należy przyjmować T= 50 lat.
Szybkość korozji w zbiornikach na paliwa płynne wynosi 0,04 – 0,06 mm/rok [26] ,
Oprócz naddatku na korozję należy uwzględnić naddatek na erozję ( wycieranie przez zanieczyszczenia wody lub cieczy , np zawarty w nich piasek. Łącznie stanowi to ” mechaniczne naddatki” (ang (mechanical allowances). Mechaniczne naddatki można zmniejszyć, jeśli projektuje się zabezpieczenia korozyjne powierzchni (powłoki emaliowane itp.) ochronę katodową lub inne metody bezpośredniej lub pośredniej ochrony przed korozją.
Obciążenia zbiorników
Obciążenia zbiorników przyjmuje się zgodnie z [27] przy dodatkowych zasadach według Załącznika A do [4].
Zgodnie z kl. A.2.1 (1) [4] rozpatrując warunki eksploatacji uwzględnia się ciężar przechowywanej cieczy, który może zmieniać się od zera (przy pustym zbiorniku) do wartości odpowiadającej maksymalnemu obliczeniowemu poziomowi cieczy, a zgodnie z kl. A.2.2 (1) [4] uwzględnia się minimalne i maksymalne, wartości ciśnienia wewnętrznego.
Współczynnik obciążeń $\gamma_F$ od obciążeń zmiennych cieczy w warunkach eksploatacji przyjmuje się:
$$\begin{equation} \gamma_F = \begin {cases}
1,4 & \textrm {dla cieczy toksycznych i wybuchowych}\\
1,3 & \textrm {dla cieczy palnych} \\
1,2 & \textrm { dla innych cieczy} \\
\end {cases} \label{13} \end{equation}$$
W warunkach prób lub oddziaływań wyjątkowych należy przyjmować $\gamma_F=1,0$.
Obciążenie wiatrem
W odniesieniu do okrągłych zbiorników walcowych można stosować następujące współczynniki ciśnienia wewnętrznego:
- w otwartych zbiornikach i basenach awaryjnych: $c_{pw}= -0,4$.,
- w zbiornikach wentylowanych z małymi otworami: $c_{pw}= -0,6$
Przy sprawdzaniu stanu granicznego S3 (stateczności powłoki) rzeczywiste rozkład ciśnienia wiatru (rys.21(a) można zastąpić równoważnym rozkładem równomiernym , pokazanym na rys. 21(b).
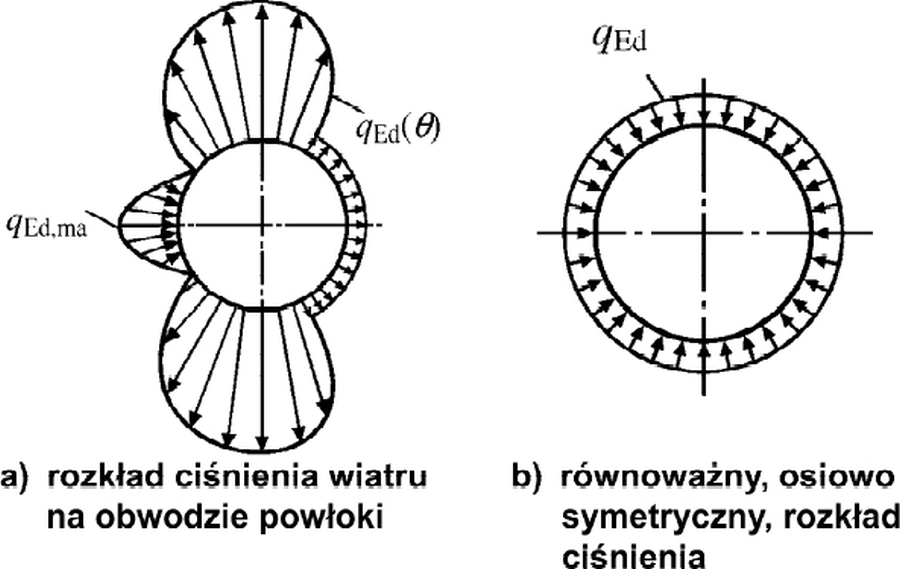
Rys. 21 Równoważne oddziaływanie wiatru na zbiornik [4]
Równoważne obciążenie wiatrem wynosi:
$$\begin{equation} w =k_w \cdot w_{max} \label{14} \end{equation}$$
gdzie $w_max$ d jest wartością maksymalną ciśnienia wiatru wgnormy [3]
Współczynnik równoważności $k_w$ wyznacza się z zależności
$$\begin{equation} k_w= \begin {cases}
\cfrac{1}{C_w} & \textrm { wg normy PN_EN 1993-4-2 } \\
0,46 \cdot \left( 1+0,1 \sqrt{\cfrac{C_\Theta \cdot \lambda_r}{\omega}} \right ), & \textrm { wg normy PN_EN 1993-1-6 } \\
\end {cases} \label{15 } \end{equation}$$
gdzie:
Cw wg [3], kl. 5.3.2.5(8).,
$C_\Theta$ wg ($\ref{41}$) lub ($\ref{42}$) w zależności od długości względnej $\omega$ ($\ref{33}$), ale przy ograniczeniu $ 0,65 \le k_w < 1,0$
W przypadku istotnych różnic miedzy wartościami $k_w$ wyznaczonymi wg normy [1] i normy [4] wartość ustala projektant. Autor zaleca stosowanie wartosci z normy [1]
Obciążenie zbiornika $p$ będzie sumą obciążenia wiatrem $w$ i ssania $q_s$ spowodowanego przewietrzaniem, podciśnieniem lub innymi zjawiskami
$$\begin{equation} p=-w -q_s \label{16} \end{equation}$$
W formule ($\ref{16}$) przy przeliczeniu na obciążenia obliczeniowe należy stosować współczynniki obciążeń przynależne naturze poszczególnych obciążeń, a w kombinacjach należy stosować współczynnik redukcyjny $\psi$ jak dla obciążenia wiatrem.
Naprężenia w powłoce od obciążenia ($\ref{16}$) wyznacza się z zależności ($\ref{18}$).
Stany graniczne zbiorników
Stany graniczne dla zbiorników zdefiniowano w normie [1].
Norma projektowania zbiorników PN-EN 1993-4-2
Projektowanie zbiorników stalowych jest objęte normą [4]. Przedmiotowa norma nie obejmuje dachów pływających oraz projektowania na warunki pożarowe.
Uproszczona metoda projektowania zbiorników
Z punktu widzenia inżynierskiego najciekawsza są uproszczone reguły projektowania zbiorników, opisane w pkt 11 [4]. Można je stosować dla zbiorników, przedstawionych na rys.22, jeśli spełnione są następujące warunki:
- jedynymi oddziaływaniami wewnątrz zbiornika jest ciśnienie cieczy i ciśnienie gazu nad lustrem cieczy,
- maksymalny obliczeniowy poziom cieczy nie przekracza górnego brzegu płaszcza zbiornika,
- nie jest wymagane uwzględnienie oddziaływań : termicznych, sejsmicznych, wyjątkowych, ani oddziaływań spowodowanych nierównomiernym osiadaniem podłoża lub podatnością połączeń,
- z wyjątkiem pasa przy pierścieniu okapowym, grubość płaszcza pasa jest nie mniejsza od pasa nadbudowanego,
- wartość obwodowych naprężeń w płaszczu zbiornika nie przekracza 435 MPa,
- w przypadku dachu sferycznego (rys.22) jego promień krzywizny wynosi od 0,8 do 1,5 średnicy zbiornika,
- w przypadku dachu stożkowego jego spadek wynosi od 1:5 przy podparciu obwodowym do 1:3 przy braku podpór wewnętrznych,
- nominalne nachylenie dna zbiornika nie przekracza 1:100
- charakterystyczne ciśnienie wewnętrzne jest nie mniejsze niż -8,5 mbar i nie większe niż 60 mbar,
- przewidywana liczba cykli obciążeń w jest wystarczająco mała, by nie zachodziło ryzyko zniszczenia zmęczeniowego.

Rys. 22 Kształt zbiornika podlegający uproszczonym regułom [4]
Wytrzymałość obliczeniową stali przyjmuje się jako
$$\begin{equation} f_{y,d}= \cfrac {f_y} {\gamma_{M0}} \label{17} \end{equation}$$
gdzie $\gamma_{M0} = 1,0$.
Płaszcz zbiornika
Naprężenia obwodowe $\sigma_{\Theta,p}$ od ciśnienia wewnętrznego $p$ nad lustrem cieczy wyznacza się ze wzoru ($\ref{2}$) dla składowej $\sigma_{\theta \theta}$, przy $R=r$, czyli
$$\begin{equation} \sigma_{\theta,p}=p \cdot \lambda_r \label{18} \end{equation}$$
gdzie:
smukłość powłoki $\lambda_r$ wg ($\ref{1}$),
$p$ wartość ciśnienia wewnętrznego
Naprężenia obwodowe od parcia hydrostatycznego cieczy wyznaczamy je ze wzoru:
$$\begin{equation} \sigma_{\theta, c}= \gamma_c \cdot H_{red,(j)}\cdot \lambda_r \label{19} \end{equation}$$
cieżar objętościowy cieczy $\gamma_c = \rho_c \cdot g $,
gdzie $\rho_c$ jest masą właściwą cieczy, a $g= 9,81 \, m/s^2$ przyśpieszeniem ziemskim.
Dla wody $ \gamma_c = \rho_c \cdot g = 1000 kg/m^3 \cdot 9,81 \cdot 10^{-3}= 9,81 \, kN/m^3$.
$H_{red,(j)}$ jest zredukowaną wysokością słupa wody j-tego pasa płaszcza (przy czym (j=1) przyjmuje się dla najwyższego pasa płaszcza. Jeśłi $H_{(j)} $ jest odległością pionową spodu j-tego pasa (cargi)od poziomu cieczy , to:
$$\begin{equation} H_{red,(j)} \begin {cases}
H_{(j)} – 300 \, mm ,& \textrm { gdy } \cfrac{H_{red,(j-1)}}{f_{ed,(j-1}} \ge \cfrac{H_{red,(j)}}{f_{ed,(j}} \\
H_{(j)} ,& \textrm { gdy } \cfrac{H_{red,(j-1)}}{f_{ed,(j-1}} < \cfrac{H_{red,(j)}}{f_{ed,(j}} \\
\end {cases} \label{20} \end{equation}$$
Jeśli sąsiednie pasy (cargi) zbiornika wykonane są z takiej samej stali, to
$$\begin{equation} H_{red,(j)} \begin {cases}
H_{(j)}- 300 \, mm ,& \textrm { gdy } H_{red, (j-1)} \ge H_{red,(j)} \\
H_{(j)} & \textrm { gdy } H_{red,(j-1)} < H_{red,(j)}\\
\end {cases} \label{21} \end{equation}$$
Warunek wytrzymałości w każdym pasie można zapisać w postaci:
$$\begin{equation} \gamma_F \cdot ( \sigma_{\theta,p}+\sigma_{ \theta,c}) \leq f_{yd}\label{22} \end{equation}$$
o ile częściowy współczynnik pbciążeń $\gamma_F$ jest taki sam dla ciśnienia cieczy i nadciścienia gazu na powierzchnia cieczy, a tak zwykle przyjmuje się.
Pierścienie usztywniające
Pierścienie wieńczące
W zbiornikach otwartych stosuje się usztywniające pierścienie wieńczące, usytuowane w pobliżu górnej krawędzi, najwyższego pasa płaszcza zbiornika. Jeśli zbiornik posiada dach stały, to dodatkowy pierścień usztywniający nie jest wymagany. Wówczas stosuje się rozwiązanie pokazane na rys. 23 z zastosowaniem pierścienia okapowego dachu.
Siła w efektywnym przekroju brzegowym powinna spełniać warunek:
$$\begin{equation} \dfrac {N_{Ed}} {A_{eff}} \leq f_{y.d} \label{23} \end{equation}$$
gdzie
$N_{Ed} = \dfrac {p{v,Ed} \cdot r^2}{2 \cdot tg\alpha}$, Aeff, α – rys. 23.
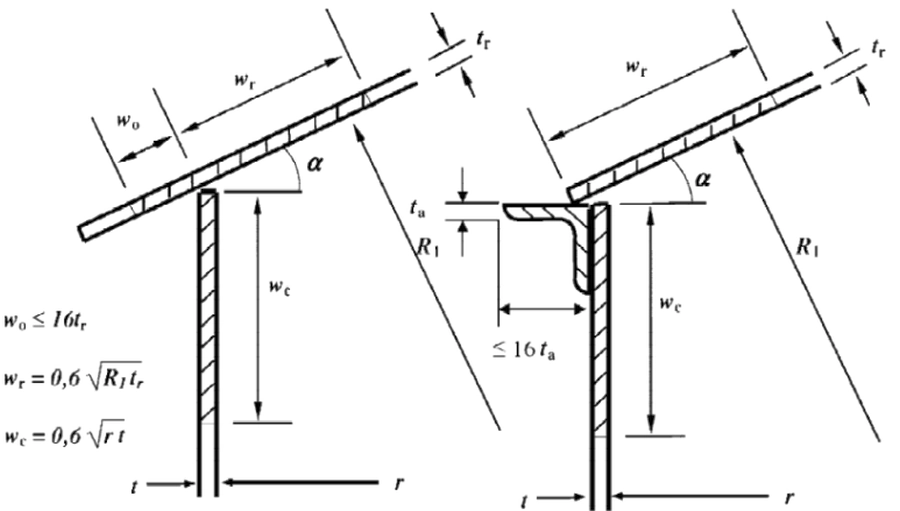
Rys. 23 Pierścień okapowy dachu [4]
Gdy odległość usztywniającego pierścienia poziomego od górnego brzegu płaszcza przekracza 600 mm , to stosuje się dodatkowy pierścień brzegowy z kątownika, spełniający warunki: L60x60x5 , gdy grubość najwyższego pasa jest mniejsza od 6 mm i 80x80x6, gdy grubość najwyższego pasa jest co najmniej 6 mm. W żadnym przypadku odległość górnej półki kątownika od brzegu blachy nie powinna przekraczać 25 mm.
Pierścienie pośrednie
W przypadkach koniecznych stosuje się pośrednie pierścienie usztywniające, zapobiegające lokalnej utracie stateczności płaszcza. Na rys. 24 pokazano rodzaje przekrojów pierścieni.
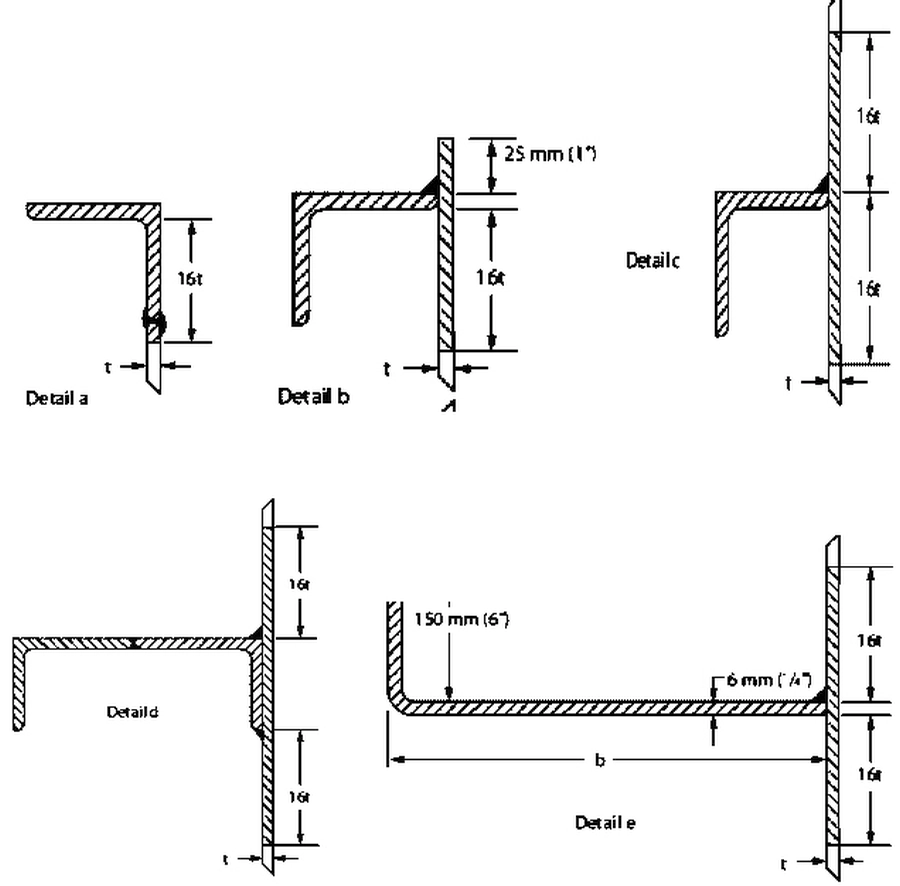
Rys.24 Typowe pierścienie usztywniające płaszcz zbiornika [16]
Wysokość odcinka powłoki, który można uznać za stateczny, bez konieczności stosowania pośrednich pierścieni usztywniających, wynosi:
$$\begin{equation} H_p=0,46 \left ( \dfrac {E} {p_{Ed}} \right)\cdot \left ( \dfrac {t_{min}} {t} \right)^{2,5}\cdot r \cdot K \label{24} \end{equation}$$
gdzie:
dla $\sigma_{x,Ed}$ rozciągającego
$$\begin{equation} K=1 \label{25} \end{equation}$$
dla $\sigma_{x,Ed}$ ściskającego
$$\begin{equation} K=\left \{ 1 – \left [ 2,67 \left ( \dfrac{\sigma_{x,Ed}} {E} \cdot \lambda_r \left ( 1+\cfrac {\lambda_r} {58} \right)^{0,72} \right )^{1,25} \right]^{0,8}\right \} \label {26} \end{equation}$$
W ($\ref{24}$) $p_{Ed}$ jest maksymalnym obliczeniowym ciśnieniem zewnętrznym, powiększonym o podciśnienie wewnętrzne, a (r/t) odpowiada miejscu w zbiorniku w którym występują podłużne naprężenia obliczeniowe σx,Ed.
Procedurę tę można prowadzić, jeśli są spełnione jednocześnie dwa warunki:
$$\begin{equation} \lambda_r \leq 200 \quad i \quad f_y \ge 1,15 E \cdot \left (\cfrac {r}{l} \right )\cdot \left (\cfrac {1}\lambda_r \right)^{1,5} \label{27} \end{equation}$$
gdzie l jest długością wyboczeniową, przyjmowaną jako wartość mniejsza od rozstawu pierścieni usztywniających, oraz
$$\begin{equation} H_E= \Sigma{h} \cdot \left( \cfrac {t_{min}} {t} \right)^{2,5} \label{28} \end{equation}$$
gdzie: tmin – grubość najcieńszego pasa, h, t – wysokość i grubość pasów do rozpatrywanego przekroju, licząc od góry zbiornika.
Jeśli zachodzi:
$$\begin{equation} H_E\leq H_p \label{29} \end{equation}$$
to stosowanie pośrednich pierścieni usztywniających nie jest wymagane.
Autor uważa, ze w warunku (11.31) podanym w normie [4] powinno być tak jak w ($\ref{49}$)- warunek 1. , czyli $\lambda_r \le 200$, a nie $\lambda_r > 200)$, bowiem dla dużych smukłości powłoki $\lambda_r$ wyrażenie traci sens ( dla większości spotykanych poziomów napreżeń przyjmuje wartości ujemne) . Na przykład dla poziomu naprężeń ściskających powłokę $\sigma_{x,Ed} = 200 \, MPa$ współczynnik $K$ będzie ujemny już dla smukłości $\lambda_r > 171$
Jeśli HE>Hp, to stosuje się regularnie rozmieszczone pierścienie w rozstawie nie większym niż Hp . Jeśli jeden pierścień pośredni okaże się niewystarczający, to powyższą procedurę można stosować oddzielnie dla poszczególnych odcinków powłoki pomiędzy już rozmieszczonymi pierścieniami.
Powyższe zasady mogą okazać się bardzo konserwatywne, szczególnie w przypadku niewysokich pasów płaszcza i wówczas zaleca się stosować postanowienia normy [1].
Jeśli grubość płaszcza do którego przymocowany jest pierścień, jest mniejsza od minimalnej, to stosuje się korektę położenia zgodnie z 11.3.2.(13) [4]
Pierścienie powinny spełniać warunki wg p-ktu (14) i (15) tej normy.
Jeśli zakotwienie dolnego brzegu blachy płaszcza, skutecznie zapobiega przemieszczeniu pionowemu, to pierścienie usztywniające można wymiarować zgodnie z [4]. Jeśli natomiast zakotwienie płaszcza nie zapobiega przemieszczeniu pionowemu, to należy ocenić stateczność zgodnie z [1].
Otwory w płaszczu zbiornika
Płaszcze w otoczeniu otworów technologicznych zwykle wymagają wzmocnienia, przy czym w strefach wysokich ciśnień (w dolnej części zbiornika) zwykle decydujące jest kryterium nośności plastycznej (LS1), natomiast w strefach niskich ciśnień (górna część powłoki zbiornika) zwykle decydujące jest kryterium stateczności (LS3).
Dla króćców małowymiarowych (o średnicy do mniejszej niż 80 mm), wzmocnienie nie jest wymagane, pod warunkiem, że grubość ścianki ze stali węglowej w miejscu króćca jest nie mniejsza niż t≥ 5,0 mm, dla do≤50, t≥5,5 mm , dla 50<do≤75 i t≥7,5 mm , dla 75<do≤80. Dla stali nierdzewnej austenityczno-ferrytycznej lub austenuitycznej grubości graniczne ścianek wynoszą odpowiednio: 3,5 ; 5,0; 6,0 mm.
Dla króćców wielkowymiarowych wymagane wzmocnienie w stanie granicznym LS1, wyznacza się metodą zmiennego przekroju. Dodatkowe pole przekroju wyznacza się ze wzoru:
$$\begin{equation} \Delta A=0,75\cdot d_o \cdot t_{rcf} \label{30} \end{equation}$$
gdzie: do– średnica otworu wyciętego w ściance powłoki, trcf – grubość ścianki powłoki nominalna (bez otworu).
Pole przekroju ΔA można wbudować na trzy sposoby lub ich kombinację:
- zastosowanie kołnierza wzmacniającego (nakładki) o średnicy dn, spełniającej warunek 1,5do≤dn≤2do. W przypadku wzmocnienia o obrysie nieokrągłym powyższy warunek odnosi się do średnicy okręgu wpisanego w obrys kołnierza,
- zastosowanie blachy grubszej powłoki rodzimej na warunkach jak powyżej,
- uwzględnienie ścianki króćca lub włazu. W tym przypadku szerokość współpracującą wyznacza się, uwzględniając grubość króćca i odległości od jego lica równe czterokrotnej grubości ścianki króćca, ale nie większe niż odległość punktów, w których grubość ta zaczyna się zmniejszać.
Na rys.25. pokazano sposoby wzmocnienia otworów wokół króćców z zastosowaniem kołnierza wzmacniającego wg pracy [28].
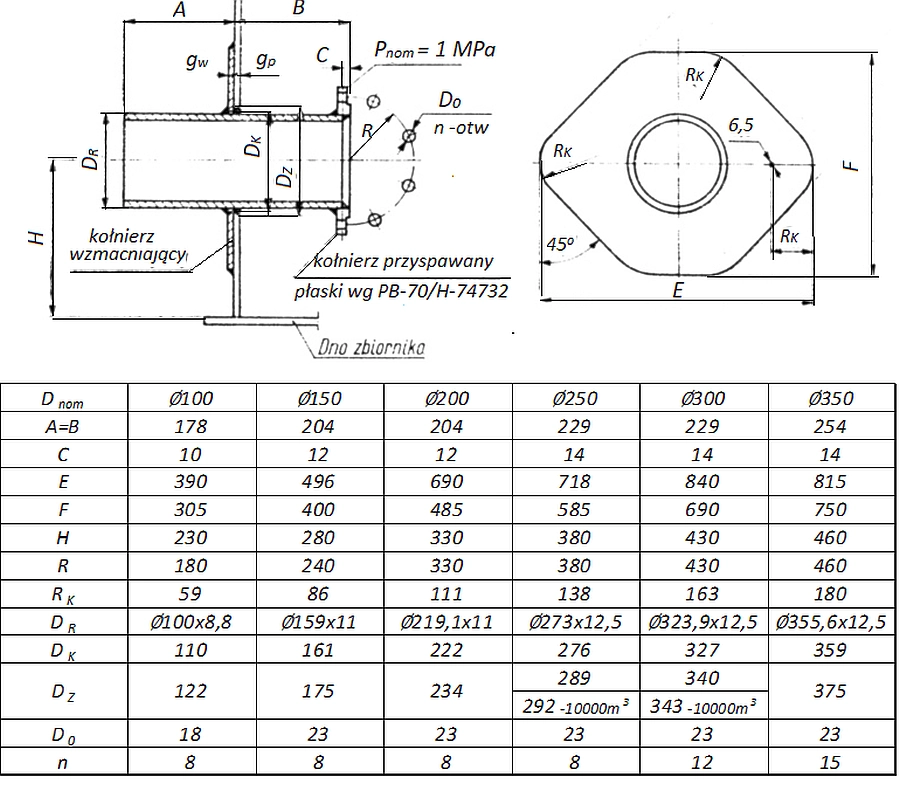
Rys.25 Kołnierze wzmacniające otwór wokół króćca w zbiorniku Bogucki W. (red.), (1982), Poradnik projektanta konstrukcji metalowych (Wydanie 1 , Tom 2), Arkady, Warszawa))
Alternatywnie do metody zmiennego przekroju wzmocnienie mona uzyskać poprzez zastosowanie wystających króćców, w sposób opisany w pkt 5.4.6.3 (5 i 6) [4].
Wzmocnienie w stanie granicznym LS3 można pomijać, jeśli spełniony jest warunek:
$$\begin{equation} \eta = \dfrac {r_o}{\sqrt{rt}} \leq \eta_{max}=0,6 \label{31} \end{equation}$$
gdzie r, t – promień i grubość powłoki w miejscu otworu o promieniu ro.
W przypadku otworu prostokątnego axb , promień zastępczy można wyznaczyć z zależności ro=(a+b)/4.
Redukcja nośności powłoki nie jest wymagana jeśli zastosowano prawidłowe wzmocnienie otworu i jeśli ro<r/3. W przeciwnym przypadku wzmocnienia należy zaprojektować za pomocą usztywnień południkowych.
Dach stały
Dach stały (rys.22) projektuje się najczęściej w samonośnej konstrukcji zgodnie z regułami klauzuli 11.2 [4]:
- konstrukcji powłokowa o złączach spawanych- kl. 11.2.1 [4],
- konstrukcji powłokowo-szkieletowa – kl. 11.2.2 [4],
- konstrukcji powłokowo-szkieletowej podpartej pośrednio na słupach – kl. 11.2.3 [4].
Grubość blach poszycia przyjmuje się nie mniejszą niż 3 mm – w przypadku stali nierdzewnych lub nie mniejszą niż 5 mm – w przypadku innych stali konstrukcyjnych. Elementy konstrukcji szkieletowej i ew. słupy wymiaruje się według normy podstawowej [29].
Układ stężeń dachu zbiornika dobiera się zgodnie z kl. 11.2.4 [4]
Jeśli średnica zbiornika z samonośnym dachem szkieletowo-powłokowym nie przekracza 60 m , a obciążenie osiowe nie odbiega zasadniczo od warunku osiowej symetrii, to w przypadku dachów sferycznych można stosować przybliżone procedury projektowania wg klauzuli 11.2.2.(6) do (10) – wzory (11.5) do (11.16) [4].
Dno zbiornika
Przy wymiarowaniu zbiornika, uwzględnia się naddatki korozyjne. Minimalne, nominalne grubości blach dna należy przyjmować dla stali węglowej: tmin=5 mm przy złączach czołowych i 6 mm przy złączach zakładkowych, a dla stali nierdzewnej odpowiednio 3 i 5 mm. W celu przeciwdziałania unoszeniu należy projektować blachy grubsze, chyba, że gwarantowany minimalny poziom cieczy zabezpiecza dno przed unoszeniem. Konstrukcję dna z blach pokazano na rys. 26.
Spoiny należy zaprojektować i wykonać szczególnie starannie zgodnie z normami [9] i [10]oraz innymi przedmiotowymi.
Blachy dna, opierające się na równoległych belkach można projektować jak belkę ciągłą w ramach teorii małych ugięć.
Dno zbiorników o średnicy większej od 12,5 m projektuje się z pierścieniem obwodowym, który pod względem wytrzymałości i udarności powinien odpowiadać materiałowi płaszcza, z którym jest połączony. Minimalna, nominalna grubość pierścienia obwodowego dna bez naddatków korozyjnych powinna być nie mniejsza niż t/3+3 ≥ 6 mm, gdzie t jest grubością stykającego się płaszcza. Przy minimalnej grubości blachy dna może utworzyć się w pierścieniu obwodowym przegub plastyczny, co jest pozytywne, bo połączenia spawane są 'odizolowane’ od cyklicznych obciążeń zmęczeniowych. Jednakże z drugiej strony należy sprawdzić unoszenie dna i w przypadku jego wystąpienia należy dno dociążyć. Blachę pierścienia obwodowego wymiaruje się w połączeniu z fundamentem i podłożem tak, by zabezpieczy nośność i stateczność posadowienia zbiornika zgodnie [30] i [31].
Szerokość wewnętrznej części pierścienia obwodowego nie powinna być mniejsza od wartości granicznej
$1,5 \cdot \sqrt { \dfrac {f_y t_a^2}{\gamma H}}\geq 500 mm$,
gdzie: ta – grubość blachy pierścienia, H-maksymalny poziom cieczy o ciężarze objętościowym γ .
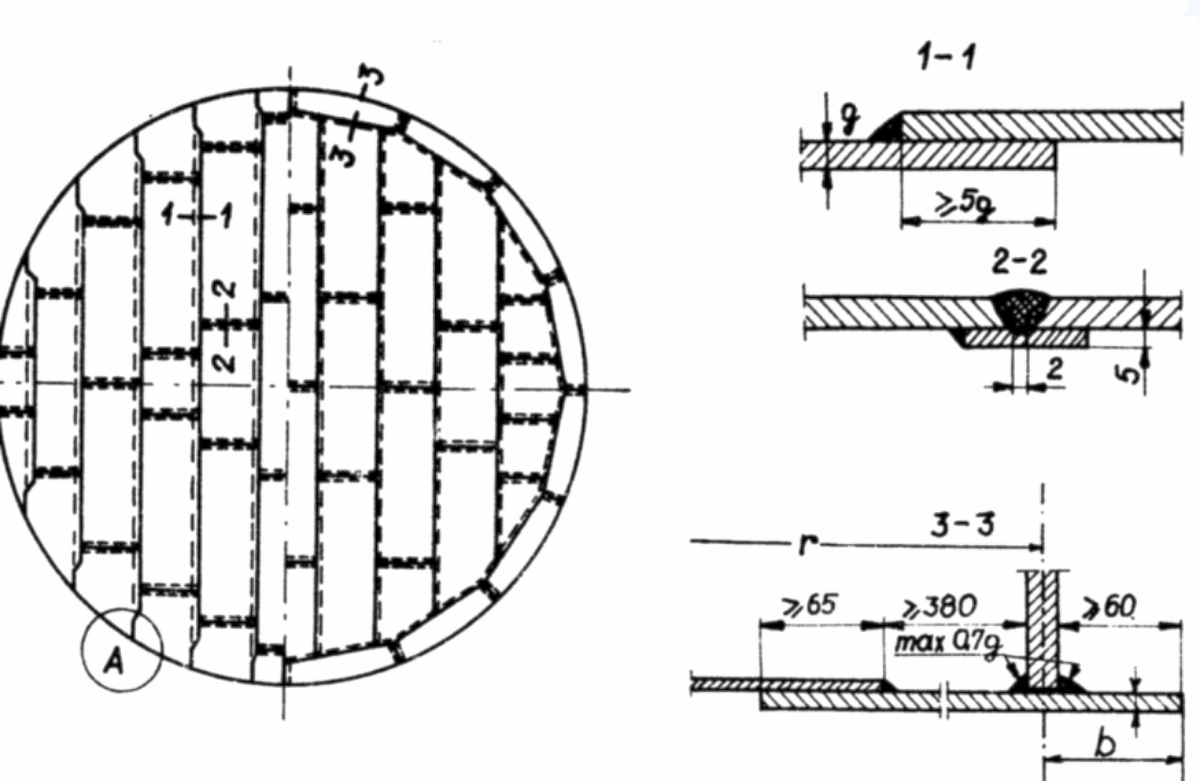
Rys.26. Konstrukcja dna zbiornika o średnicy do 12 m [6]
Złącza radialne blach dna projektuje się jako czołowe z pełnym przetopem. Wysięg podstawy na zewnątrz nie powinien być mniejszy niż 50 mm. Połączenie blachy najniższego pasa płaszcza z pierścieniem obwodowym wykonuje się za pomocą dwustronnych, ciągłych spoin pachwinowych, a grubość każdej ze spoin pachwinowych przyjmuje się równą lub większą od grubości pierścienia obwodowego lecz nie większą niż 10 mm, przy czym jeśli grubość płaszcza mniejsza niż grubość blachy pierścienia obwodowego lub blachy dna, to grubość spoin powinna wynosić: 2,0 mm dla t<5; 4,5 mm dla t= 5 i 6,0 mm dla t>5 mm.
Stateczność ogólna i zakotwienie zbiorników
Na rys. 27 pokazano schemat do sprawdzania zbiornika na wywrócenie, zakotwienie i obwałowanie zbiornika .
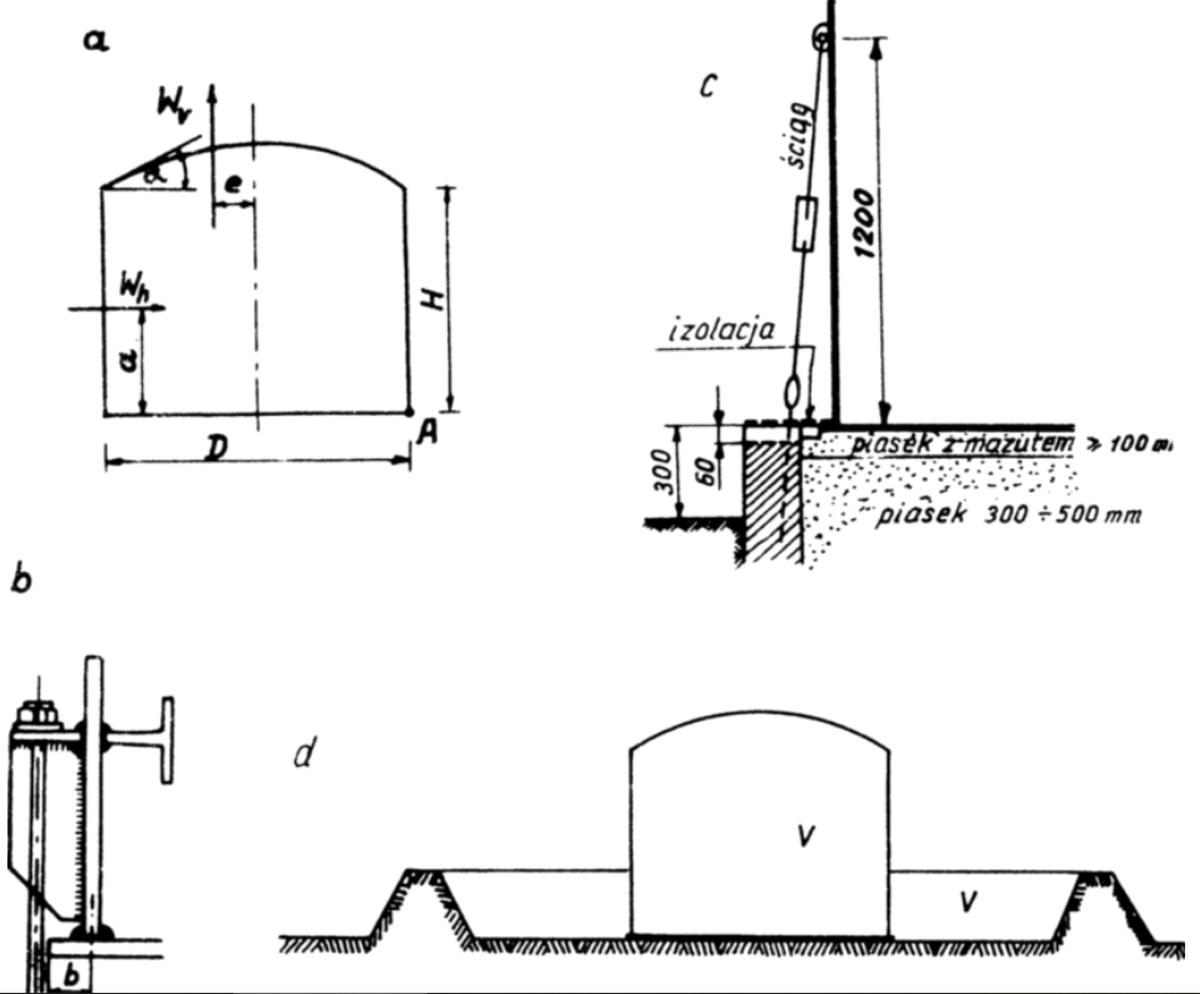
Rys. 27 Stateczność ogólna zbiornika: a – stateczność, b,c- zakotwienie, d- obwałowanie zbiornika [6]
Zakotwienie zbiorników wykonuje się, jeśli zajdzie którakolwiek z poniższych okoliczności:
- unoszeniu pustego zbiornika wskutek obliczeniowego ciśnienia wewnętrznego przeciwdziała efektywny ciężar (skorodowanej) konstrukcji dachu, płaszcza i stałych elementów wyposażenia,
- unoszeniu pustego zbiornika wskutek obliczeniowego ciśnienia wewnętrznego i oddziaływania wiatru przeciwdziała efektywny ciężar (skorodowanej) konstrukcji dachu, płaszcza i stałych elementów wyposażenia, a także resztkowej zawartości zbiornika, która zawsze występuje, zgodnie z ustaleniami między projektanta, zamawiającym i odpowiednimi władzami,
- unoszeniu pustego zbiornika wskutek oddziaływań wiatru przeciwdziała efektywny ciężar (skorodowanej) konstrukcji dachu, płaszcza i stałych elementów wyposażenia,
- unoszeniu pustego zbiornika wskutek podmycia cieczą zewnętrzną. W takiej sytuacji należy przeprowadzić odrębne analizy (obliczenia) dna zbiornika i zakotwienia.
Przy sprawdzaniu równowagi statycznej zbiornika (stanów granicznych EQU) siły wywracające od wiatru można szacować przy założeniu sztywnego konturu zbiornika. Jeśli natomiast możliwe jest lokalne unoszenie, to wymagane jest odstąpienie od tego, upraszczającego założenia i dokładniejsza analiza.
Elementy kotwiące na ogół łączy się z płaszczem, a nie tylko z pierścieniami wzmacniającymi lub brzegowymi.
Konstrukcja zakotwienia powinna umożliwiać takie ruchy zbiornika, by kompensować wahania temperatury i zmiany ciśnienia hydrostatycznego. W przypadku sztywnego zakotwienia siły kotwiące od obciążeń poziomych (wiatr, uderzenia) oblicza się według teorii powłok, a przy projektowaniu elementów zbiornika na siły kotwiące należy stosować postanowienia normy [3].
W miarę możliwości punkty zakotwienia rozmieszcza się równomiernie w jednakowych odstępach wokół obwodu zbiornika.
Metoda ogólna projektowania zbiorników
W dużej liczbie praktycznych przypadków zawodzą uproszczone procedury projektowania zbiorników stalowych. Przykładem są zbiorniki o dużej smukłości powłoki ($\ref{1}$) dla których traci sens zależność ($\ref{22}$) będąca w istocie uproszczoną metodą uwzględnienia stateczności powłoki.
W takich przypadkach należy stosować ogólne zasady projektowania powłok, pierścieni dachu oraz dna. z uwzględnieniem wszystkich form utraty stateczności.
Ponadto większość zbiorników jest eksploatowana w złożonym stanie naprężenia (ściskania obwodowego i jednoczesnego ściskania południkowego. Wówczas również wymagane jest zastosowanie metody ogólnej, a metody uproszczonej tylko do projektu wstępnego.
Metodę ogólną projektowania konstrukcji powłokowych przedstawiono w normie [1].
Smukłości względne powłoki
Smukłości względne powiązane z poszczególnymi naprężeniami składowymi są określone wzorami (8.17) [1] :
$$\begin{equation} \overline \lambda_x= \sqrt{\cfrac{f_{yk}}{ \sigma_{x,Rcr}}} ; \quad \overline \lambda_\Theta = \sqrt{\cfrac{f_{yk}}{ \sigma_{\Theta,Rcr}}}\overline ; \quad \lambda_\tau= \sqrt{\cfrac{f_{yk}/\sqrt{3}}{\tau_{x \Theta,Rcr}}} \label{32} \end{equation}$$
gdzie napreżenie krytyczne $\sigma_{x,Rcr}$, $\sigma_{\Theta,Rcr}$, $\tau_{xTheta,Rcr}$ sa zdefiniowane w kolejnym rozdziale.
Długości względne powłoki
Powłoki są klasyfikowane ze względu na długość względną $\omega$
$$\begin{equation}\omega = \cfrac {l}{\sqrt{rt}} = \cfrac{l}{r} \cdot \sqrt {\lambda_r}\label{33} \end{equation}$$
Naprężenia krytyczne idealnej powłoki
Powłoka ściskana południkowo
Dla powłoki, pokazanej na rys. 28 w normie [1] podano wyrażenie na naprężenia krytyczne południkowe w postaci ($\ref{34}$)
Rys.28 Geometria i naprężenia membranowe powłoki walcowej [1]
W zależności od długości względnej ($\ref{33}$) powłoka ściskana południkowo jest::
$$\begin{equation} Typ_x= \begin {cases}
\textrm { krótka-x} \to \omega \le 1,7 \\
\textrm { średnia-x} \to 1,7 \le \omega \le 0,5 \cdot \lambda_r \\
\textrm { długa-x } \to \omega > 0,5 \cdot \lambda_r \end {cases} \label{34} \end{equation}$$
Naprężenia krytyczne południkowe szacuje się z zależności:
$$\begin{equation} \sigma_{x,Rcr}= C_{cr} \cdot E \cdot C_X / \lambda_r \label{35} \end{equation}$$
Współczynnik $C_{cr}$ jest zgodny z klasycznym rozwiązaniem Lorenz (1908) [32] (tab2 ) i wynosi
$$\begin{equation} C_{cr}= 0,605 \label{36} \end{equation}$$
Współczynnik $C_X$ zależy od typu powłoki
$$\begin{equation} C_X = \begin {cases}
1,36- \cfrac {1,83}{\omega}+\cfrac{2,07}{\omega^2},& \textrm { dla krótka-x},\\
1,0 & \textrm { dla średni-x},\\
\max{\left[ 0,6 \, ; \, 1+\cfrac{0,2}{C_{xb}} \cdot \left (1- \cfrac{ 2\omega}{ \lambda_r} \right) \right] } &\textrm { dla długa-x }\\
\end {cases} \label{37} \end{equation}$$
Współczynnik $C_{xb}$ zależy warunków brzegowych:
$$\begin{equation} C_{xb} = \begin {cases}
6,& \textrm { dla obu brzegów utwierdzonych. (BC1-BC1) }\\
3,& \textrm { dla jednego brzegu utwierdzonego i drugiwgo przegubowego (BC1-BC2)},\\
1,& \textrm {dla obu brzegów (dolnego i górnego) przegubowych (BC2-BC2)},\\
\end {cases} \label{38} \end{equation}$$
Powłoka ściskana obwodowo
W zależności od długości względnej ($\ref{33}$) powłoka ściskana obwodowo jest::
$$\begin{equation} Typ_x= \begin {cases}
\textrm { krótka-Θ} \to \cfrac{ \omega}{C_\Theta} < 20 \\
\textrm { średnia-Θ} \to 20 \le \cfrac{ \omega}{C_\Theta} \le 1,63 \cdot \lambda_r \\
\textrm { długa-Θ} \to \cfrac{ \omega}{C_\Theta} > 1,63 \cdot \lambda_r \end {cases} \label{39} \end{equation}$$
Naprężenia krytyczne przy ściskaniu obwodowym zgodnie z zależnościami (D.23), (D.20) i (D.254) z normy [1] wyznacza się z zależności
$$\begin{equation} \sigma_{\Theta,Rcr}= \begin {cases}
0,92 \cdot E \cdot \cfrac{C_\Theta}{\omega \cdot \lambda_r}, & \textrm { dla powłok krótka-Θ } \\
0,92 \cdot E \cdot \cfrac{C_{\Theta s}}{\omega \cdot \lambda_r}, & \textrm { dla powłok średnia-Θ}\\
\cfrac{E}{ \lambda_r^2} \cdot,\left[ 0,275 +2,03 \cdot \left( \cfrac{C_\Theta}{\omega} \cdot \lambda_r \right)^4 \right ], & \textrm { dla powłok długa-Θ} \\
\end {cases} \label{40} \end{equation}$$
Współczynnik $C_\Theta $ zależy warunków brzegowych oraz długości powłoki
Dla powłok średnich i długich:
$$\begin{equation} C_\Theta = \begin {cases}
1,5 & \textrm {dla obu brzegów utwierdzonych (BC1-BC1)},\\
1,25 & \textrm { dla jednego brzegu utwierdzonego drugiego przegubowego (BC1-BC2)},\\
1,0 & \textrm { dla obu brzegów przegubowych (BC2-BC2) }\\
0,6 & \textrm { dla jednego brzegu utwierdzonego, drugiego swobodnego. (BC1-BC3) }\\
0 & \textrm { dla brzegów swobodnych (BC3-BC3) lub dla (BC3-BC2)} \\
\end {cases} \label{41} \end{equation}$$
Dla powłok krótkich:
$$\begin{equation} C_{\Theta s} = \begin {cases}
1,5 + \cfrac{34}{\omega^2} -\cfrac{5}{\omega^3}, & \textrm {dla obu brzegów utwierdzonych (BC1-BC1)},\\
1,25 + \cfrac{34}{\omega^2} -\cfrac{4}{\omega^3}, &\textrm { dla jednego brzegu utwierdzonego drugiego przegubowego (BC1-BC2)},\\
1,0 + \cfrac{3}{\omega^{1,35}}, &\textrm { dla obu brzegów przegubowych (BC2-BC2) }\\
0,6 + \cfrac{1}{\omega^2} -\cfrac{0,3}{\omega^3}, & \textrm { dla jednego brzegu utwierdzonego, drugiego swobodnego. (BC1-BC3) }\\
\end {cases} \label{42} \end{equation}$$
Powłoka ścinana
Zgodnie z klauzulą D.1.4.1. (1) [1] w przypadku powłok z brzegami BC1 (utwierdzonymi) lub BC2 (przegubowymi można stosować poniższe formuły.
W zależności od długości względnej ($\ref{33}$) powłoka ścinana obwodowo jest::
$$\begin{equation} Typ_τ= \begin {cases}
\textrm { krótka-τ } \to \omega < 10 \\
\textrm { średnia-τ} \to 10 \le \omega \le 8,7 \cdot \lambda_r \\
\textrm { długa-τ} \to \omega > 8,7 \cdot \lambda_r \end {cases} \label{43} \end{equation}$$
Naprężenia krytyczne przy ścinaniu sprężystym są określone wzorem (D.1.4.(3) [1]:
$$\begin{equation} \tau_{x \Theta, Rcr}=0,75 \cdot E \cdot C_\tau \cdot \sqrt{\cfrac{1}{\omega}}\cdot \left ( \cfrac{t}{r}\right ) \label{44} \end{equation}$$
gdzie współczynnik $C_\tau$ wynosi
$$\begin{equation} C_\tau = \begin {cases}
\sqrt{1+\cfrac{49}{\omega^2}} & \textrm {dla krótka-τ },\\
1,0 &\textrm { dla średnia-τ}, \\
\cfrac{1}{3} \cdot \sqrt{\cfrac{\omega}{\lambda_r}} & \textrm { dla długa-τ } \\
\end {cases} \label{45} \end{equation}$$
Nośność powłoki z uwzględnieniem niestateczności
Charakterystyczne naprężenia wyboczeniowe
Charakterystyczne naprężenia wyboczeniowe uzyskuje się, mnożąc charakterystyczną granicę plastyczności przez odpowiedni współczynnik wyboczenia ( współczynnik redukcyjny niestateczności) :
$$\begin{equation} \sigma_{x,Rk} =\chi_x f_{yk} \quad; \quad \sigma_{\Theta,Rk} =\chi_\Theta f_{yk} \quad; \quad \tau_{x,\Theta,Rk} =\chi_\tau f_{yk} \label{46} \end{equation}$$
Obliczeniowe naprężenia wyboczeniowe
Zgodnie z klauzulą 8.5.2(1) [1] nośność obliczeniowa (wytrzymałość wyboczeniową) rozpatruje się zależnie od naprężeń wyboczeniowych
Obliczeniowe naprężenia wyboczeniowe są określone zależnościami (8.11) [1] :
$$\begin{equation} \sigma_{x,Rd} =\sigma_{x,Rk}/\gamma_{M1} \quad ; \quad \sigma_{\Theta,Rd} =\sigma_{\Theta,Rk}/\gamma_{M1} \quad ; \quad \tau_{x,\Theta,Rd} =\tau_{x,\Theta,Rk}/\gamma_{M1}\label{47} \end{equation}$$
gdzie częściowy współczynnik $\gamma_{M1}=1,1$ ( o ile normy przedmiotowe nie stanowią inaczej)
Redukcyjne współczynniki niestateczności
Zgodnie z klauzulą 8.5.2(4) [1] redukcyjne współczynniki wyboczenia $\chi_x$, $\chi_\Theta$ $\chi_\tau$ są funkcjami smukłości względnej powłoki $\overline \lambda$, i wyznacza się z zależności:
$$\begin{equation} \chi= \begin {cases}
1 & \textrm { dla } \overline \lambda \le \overline \lambda_0\\
1- \beta \cdot \left ( \cfrac{ \overline \lambda -\overline \lambda_0 }{\overline \lambda_p -\overline \lambda_0}\right )^\eta & \textrm {dla } \overline\lambda_0 <\overline\lambda < \overline\lambda_p \\
\cfrac{\alpha}{\overline \lambda^2} & \textrm { dla } \overline \lambda_p \le \overline \lambda\\
\end {cases} \label{48} \end{equation}$$
czyli według formuł innych niż dla prętów,
gdzie:
$\alpha$ – parametr imperfekcji przy wyboczeniu sprężystym
$\beta$ mnożnik w formule interakcji pry wyboczeniu spręźysto-plastycznym
$\eta$ – wykładnik w formule interakcji pry wyboczeniu spręźysto-plastycznym
Parametery $\alpha$, $\beta$, $\eta$ zależą od kierunku wyboczenia powłoki oraz od stanu naprężenia w obu kierunkach, przy czym zgodnie z klauzulami D. 1.2.2 oraz D.1.3.2 [1] można przyjmować, że zarówno przy ściskaniu południkowym jak i obwodowym są takie same parametry $\beta$ i $\eta$ i wynoszą
$$\begin{equation} \beta=0,6 \quad ; \quad \eta=1.0 \label{49} \end{equation}$$
Ściskanie południkowe . Parametry wyboczenia
Nie jest wymagane sprawdzanie stateczności powłoki ze względu nas wyboczenie południkowe, jeśli spełniony jest warunek:
$$\begin{equation} \lambda_r \le 0,03 \cdot \sqrt{ \cfrac{E}{f_{yk}}} \label{50} \end{equation}$$
Parametr impefekcji αx przy ściskaniu południkowym
W przypadku czystego ściskania południkowego (bez napreżeń obwodowych $\sigma_\Theta=0$ współczynnik redukcyjny $\alpha_x$ ze względu na imperfekcje południkowe jest określony wzorem (D.14)[1] :
$$\begin{equation} \alpha_x= \alpha_{cr} = \cfrac{0,66} {1+1,91 \cdot \left( \Delta w_k / t \right)^{1,44}} \label{51} \end{equation}$$
gdzie $\Delta w_k $- charakterystyczna amplituda imperfekcji południkowych (D.15) [1]:
$$\begin{equation} \Delta w_k =\cfrac{t}{Q} \cdot \sqrt{ \lambda_r}\label{52} \end{equation}$$
Parametr parametr jakości wytwarzania $Q$ miarodajny przy ściskaniu południkowym zależnie od klasy wytworzenia zbiornika wynosi wg tab. D.2 [1]
$$\begin{equation} Q= \begin {cases}
40, & \textrm { dla klasy A }\\
25, & \textrm { dla klasy B }\\
18, & \textrm { dla klasy C }\\
\end {cases} \label{53} \end{equation}$$
gdzie klasy wytwarzania zdefiniowana w rozdziale pod linkiem.
Smuklość graniczna $\overline\lambda_0$ poniżej której nie trzeba sprawdzać niestateczności przy ściskaniu południkowym wynosi
$$\begin{equation} \overline \lambda_{x0} =0,2 \label{54} \end{equation}$$
W przypadku powłok długich, które spełniają warunki specjalne określone w D.1.2.1(7) [1] , smukłość graniczną $\lambda_{x0}$ można powiększyć o $0,1\cdot \sigma_{xEM} / \sigma_{xE}$, gdzie $\sigma_{xE}$ – całkowite naprężenie południkowe, a $\sigma_{xEM}$ składowa od momentu zginającego.
Ściskanie południkowe z ciśnieniem wewnętrznym
W zbiornikach z cieczą, gazem lub innymi produktami – ściskanie południkowe powłok następuje przy jednoczesnym obciążeniu ciśnieniem wewnętrznym, czyli przy rozciąganiu powłoki w kierunku obwodowym.
Zgodnie z D.1.5.2(1) [1] ocenę stateczności powłoki z udziałem ciśnienia przeprowadza się analogicznie jak w przypadku zerowego ciśnienia wewnętrznego, ale dla zmpdyfikowanego parametru imprefekcji $\alpha_{xp}$ zgodnie z D.1.5.2(1),(2), [1] :
$$\begin{equation} \alpha_{xp} = min { \{ \alpha_{xpe} \, ; \, \alpha_{xpp}\} } \label{55} \end{equation}$$
Współczynnik sprężystej stabilizacji ciśnieniowej (D.41) [1] wynosi
$$\begin{equation} \alpha_{xpe} = \alpha_x +(1-\alpha_x) \cdot \left( \cfrac{\overline p_s}{ \overline p_s +0,3/ \sqrt{\alpha_x}}\right) \label{56} \end{equation}$$
gdzie $\alpha_x$ ($ \ref{51}$) parametr imperfekcji przy czystym ściskaniu .
Współczynnik plastycznej destabilizacji ciśnieniowej wynosi:
$$\begin{equation} \alpha_{xpp} = \left( 1- \left( \cfrac{\overline p_g}{ {\lambda_x}^2} \right)^2 \right) \left [ 1- \cfrac{1}{1,12+s^{3/2}} \right] \left[ \cfrac{s^2 +1,21 \cdot \overline \lambda_x^2}{s(s+1)} \right ]\label{57} \end{equation}$$
W formułach ($\ref{56}$) i ($\ref{57}$) występują względne ciśnienia wywierane na powłokę $\overline p_s$ oraz $\overline p_g$ – odpowiednio najmniejsza i największa obliczeniowa wartość lokalnego ciśnienia wewnętrznego w rozpatrywanym punkcie powłoki występująca łącznie ze ściskaniem południkowym. Ciśnienia te normalizuje się z ciśnień bezwzględnych $p_s$ i $p_g$ odpowiednio w następujący sposób
.$$\begin{equation} \overline p_{ex} = \cfrac {p_{ex}} {\sigma_{x,Rcr}} \cdot \lambda_r \label{58} \end{equation}$$
gdzie „ex”=”s” (min) lub „g” (max) odpowiednio.
Naprężenie krytyczne $\sigma_{x,Rcr}$ wg ($\ref{35}$), a smukłośc względna $\overline \lambda_x$ wg $\ref{15A0}$).
Parametr $s$, występujący w ($\ref{54}$) oblicza się z zależności (D.45) (PN-EN 1993-1-6: 2010, Eurokod 3 – Projektowanie konstrukcji stalowych – Część 1-6: Wytrzymałość i stateczność konstrukcji powłokowych))
.$$\begin{equation} s= \cfrac{\lambda_r}{400} \label{59} \end{equation}$$
Ściskanie obwodowe. Parametry wyboczenia
Nie jest wymagane sprawdzanie stateczności powłoki ze względu nas wyboczenie obwodowe, jeśli spełniony jest warunek:
$$\begin{equation} \lambda_r \le 0,21 \cdot \sqrt{ \cfrac{E}{f_{yk}}} \label{60} \end{equation}$$
Parametr imperfekcji $\alpha_\Theta$ miarodajny przy ściskaniu obwodowym zależnie od klasy wytworzenia zbiornika wynosi wg tab. D.5 [1]
$$\begin{equation} \alpha_\Theta = \begin {cases}
0,75, & \textrm { dla klasy A }\\
0,65, & \textrm { dla klasy B }\\
0,50, & \textrm { dla klasy C }\\
\end {cases} \label{61} \end{equation}$$
gdzie klasy wytwarzania zdefiniowana w rozdziale pod linkiem.
Smuklość graniczna $\overline\lambda_0$ poniżej której nie trzeba sprawdzać niestateczności przy ściskaniu południkowym wynosi
$$\begin{equation} \overline \lambda_{\Theta 0} =0,4 \label{62} \end{equation}$$
Ścinanie. Parametry wyboczenia
Nie jest wymagane sprawdzanie stateczności powłoki ze względu nas wyboczenie wywołane ścinaniem , jeśli spełniony jest warunek:
$$\begin{equation} \lambda_r \le 0,16 \cdot \left ( \cfrac{E}{f_{yk}} \right )^{0,67} \label{63} \end{equation}$$
Współczynnik redukcyjny ze względu na imperfekcje przy ścinaniu sprężystym przyjmuje się według tab. D6 [1] zależnie od klasy jakości wytwarzania. z wartościami zgodnymi z przyjmowanymi przy ściskaniu obwodowym wg ($\ref{61}:
$$\begin{equation} \alpha_\tau=\alpha_\Theta \label{64} \end{equation}$$
Podobnie do ($\ref{62}$) przyjmuje się też smukłość graniczną:
$$\begin{equation} \overline \lambda_{\tau 0} =0,4 \label{65} \end{equation}$$
Interakcja ściskania południkowego, obwodowego i ścinania
Interakcję form stateczności ocenia się w naprężeniach wg zależności (8.19) [1]:
$$\begin{equation} \left ( \cfrac{\sigma_{xEd}}{\sigma_{x Rd}} \right)^{k+x} – k_i \cdot \left ( \cfrac{\sigma_{xEd}}{\sigma_{x Rd}} \right) \cdot \left ( \cfrac{\sigma_{\Theta Ed}}{\sigma_{\Theta Rd}} \right) + \left ( \cfrac{\sigma_{\Theta Ed}}{\sigma_{\Theta Rd}} \right)^{k_\Theta} + \left ( \cfrac{\tau_{x Theta Ed}}{\sigma_{x \Theta Rd}} \right)^k_\tau < 1 \end{equation}$$
Współczynniki k_℘ (℘=x, θ,τ, i ) wynoszą:
$$\begin{equation} k_℘= \begin {cases}
1,25+0,75 \chi_x, & \textrm { dla ℘=x }\\
1,25+0,75 \chi_\Theta, & \textrm { dla ℘=θ }\\
1,25+0,25 \chi_\tau, & \textrm { dla ℘=τ }\\
( \chi_x \cdot \chi_\Theta)^2, & \textrm { dla ℘=i }\\
\end {cases} \label{66} \end{equation}$$
Metoda numeryczna globalna LBA
Podstawowe definicje
LBA – analiza służąca wyznaczaniu wartości własnych (obciążeń krytycznych) układu oparta na teorii zginania cienkościennych powłok sprężystych o idealnej geometrii i małych ugięciach.
nośność krytyczna – nośność uzyskiwana w analizie LBA, mierzona mnożnikiem konfiguracji obciążenia przy której konstrukcja bez imperfekcji traci stateczność sprężystą. Miara nośności krytycznej jest oznaczana różnymi symbolami, a w tym:
$\Lambda_{cr}$ wg (2) artykułu Wprowadzenie do imperfekcyjnej metody projektowania – mnożnik obciążenia krytycznego,
$\alpha_{cr}$ wg normy podstawowej PN-EN-1993-1-1 [29] – mnożnik obciążenia krytycznego
$r_{cr}$ – wskaźnik sprężystej nośności krytycznej wg normy [1], zdefiniowany jako stosunek obciążenia krytycznego – najmniejszego obciążenia bifurkacyjnego lub granicznego wyznaczonego dla powłoki sprężystej o geometrii idealnej oraz przy wyidealizowanych warunkach podparcia i przyłożenia obciążenia, oraz przy założeniu izotropii materiału i braku naprężeń własnych
$r_{pl}$ – nośność plastyczna (referencyjna) . Plastyczne obciążenie graniczne wyznaczone dla powłoki z izotropowego materiału sztywno-plastycznego o geometrii idealnej i przy wyidealizowanych warunkach obciążenia i podparcia (na podstawie analizy MNA). Stosunek obciążenia granicznego z analizy MNA do obciążenia obliczeniowego.
Stan graniczny niestateczności LS3 (klauzule 8 [1].
Montaż zbiorników stalowych
Metody montażu zbiorników stalowych opisano w fundamentalnym opracowaniu z roku 1956 [33]. Przedstawione sposoby w swojej idei pozostają aktualne do dziś.
W przypadku rozmiaru zbiornika, przekraczające gabaryty możliwe do transportu w całości, zbiornik należy podzielić na elementy wysyłkowe i zbiornik składać na montażu z przetransportowanych elementów .
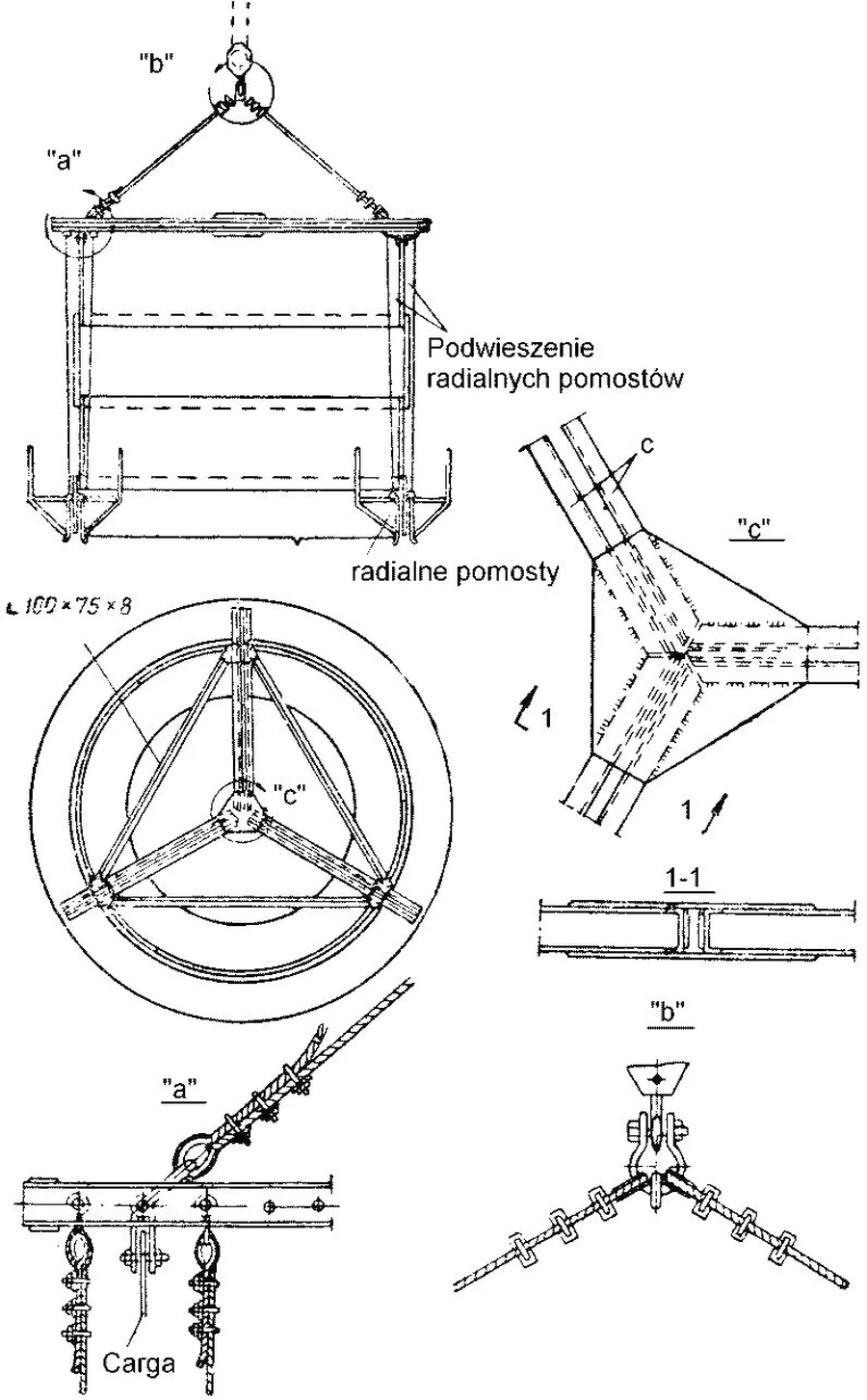
Rys.29 Montaż zbiornika poprzez podnoszenie carg za pośrednictwem trawersy [33]
W przypadku, gdy średnica zbiornika umożliwia transport odcinków pobocznicy, to stosuje się montaż z carg. Na rys. 29 przedstawiono ten sposób montażu.
Przykłady rachunkowe
Przykład 1 Powłoka zbiornika na ciecz
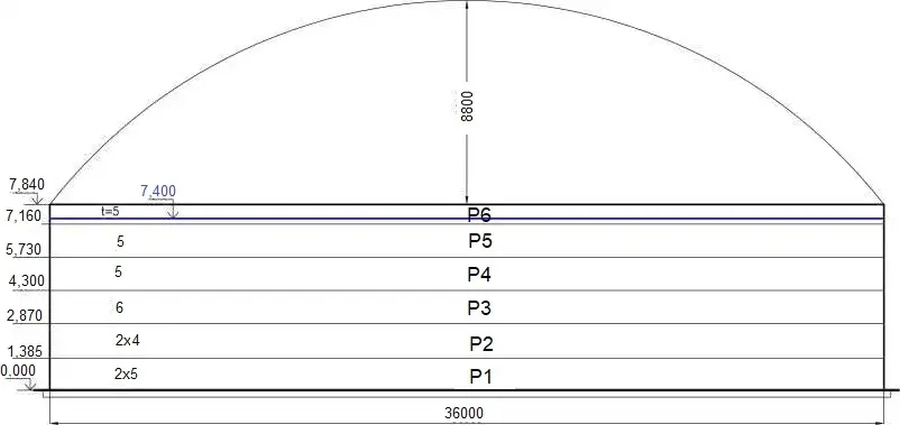
Zaprojektować zbiornik na ciecz pokazany na rys.30. Projekt dachu pozostawić do innego opracowania, a w projekcie zbiornika dach zamodelować obciążeniami i podporami sprężystymi.
Dane podstawowe
Zbiornik walcowy ma średnicę
$D_{śr} =36 \, m$ $\to$ $r = 3600/2= 18000 \, mm$
wysokość ok $h=8 m$
Zbiornik jest podzielony po wysokości na sześć pasów (paneli, carg) P1…P6
Grubości blach płaszcza wynoszą:
$t=5 \, ; \, 5\,; \, 5\,;\, 6\, ; \, 2×4=8 \,;\, 2×5=10 \, mm$
Dach zbiornika jest membranowy o zmiennym wygięciu wraz z ciśnieniem wytwarzanym podczas eksploatacji nad powierzchnią cieczy. dochodząc do strzałki wygięcia $f= 8,8 \, m$
Poziom przechowywanej cieczy w zbiorniku, to
$H_c= 7400 \,mm $
zbiornik przechowuje produkty do produkcji biogazu ( syrop lub produkty pofermentu) , więc jest zakwalifikowany do klasy konsekwencji CC1 – zbiorniki dla rolnictwa oraz zbiorniki na wodę.
Zbiornik pracuje w dwóch sytuacjach eksploatacyjnych S1 lub S2:
S1:
przechowywana ciecz o gęstości objętościowej $\rho_{S1}=1300 \, kg/m^3$
nadciśnienie w zbiorniku ponad powierzchnia cieczy $p_{S1}=0,1 \, MPa$
S2:
przechowywana ciecz o gęstości objętościowej $\rho_{S1}=1050 \, kg/m^3$
nadciśnienie/podciśnienie w zbiorniku ponad powierzchnia cieczy $p_{S1}=\pm 0,5 \, MPa$
Płaszcz wykonano ze stali S355 $\to$ $f_{yk}=f_y= 355 \, MPa$
($\ref{17}$) $\to$ $f_{yd}=355/1,0= 355 \, MPa$
Zredukowane wysokości cieczy
Ponieważ poszczególne pasy (cargi) płaszcza zbiornika są wykonane z takiej samej stali S355, to korzystamy z reguł ($\ref[20}$).
Dla pasa P6 , czyli (j=1):
$H_{(1)}= 7400-7160= 240 \, mm$
$H_{(1)} -300= 240-300 = -60 <0 \, mm$ $\to$ przyjęto $0 \, mm$
Ponieważ $H_{red,(2)= 1370 \ge 0 \to H_{red,(1) =0 \, mm$
Zredukowane wysokości ciśnienia cieczy dla pozostałych pasów wyznaczane są analogicznie.
Naprężenia obwodowe σθ od ciśnienia cieczy i gazu
Sytuacja S1
r=3600/2= 18000 \, mm
$\gamma_c= 1300 \cdot 9,81 \cdot 10^{-3} = 12,75 \, kN/m^2$
$p=0,1 \, kN/m^2$
(j=1) panel P6
$t=5 \, mm$
($\ref {1}$) $\to$ $\lambda_r= 18000/5= 3600$
($\ref{19}$) $\to$ $ \sigma_{\theta,}= ( 12,75 \cdot 0 + 0,10 ) \cdot 3600 \cdot 10^{-3}= 0,36 \, MPa$
$\ref{20}$) $\to$ $ \sigma_{\theta, d}= 1,2 \cdot 0,36 = 0,43 \approx 0,4 \, MPa$
Dla pozostałych pasów (carg) ciśnienia cieczy w sytuacji S1 wyznaczane są analogicznie
Sytuacja S2
$\gamma_c= 1050 \cdot 9,81 \cdot 10^{-3} = 10,30 \, kN/m^2$
$p= \pm 0,5 \, kN/m^2$
(j=1) panel P6
($\ref{19}$) $\to$ $ \sigma_{\theta,}= ( 10,30 \cdot 0 \pm 0,50) \cdot 3600 \cdot 10^{-3}= \pm 1,80 \, MPa$
$\ref{20}$) $\to$ $ \sigma_{\theta, d}= \pm 1,2 \cdot 1,80= \pm 2,16 \, MPa$
Dla pozostałych pasów (carg) ciśnienia cieczy w sytuacji S2 wyznaczane są analogicznie.
Literatura
- PN-EN 1993-1-6: 2010, Eurokod 3 – Projektowanie konstrukcji stalowych – Część 1-6: Wytrzymałość i stateczność konstrukcji powłokowych
- PN-EN 1993-3-2+Ap1:2008, Eurokod 3 – Projektowanie konstrukcji stalowych, Część 3-2: Wieże, maszty i kominy. Kominy
- PN-EN 1993-4-1:2009, Eurokod 3 – Projektowanie konstrukcji stalowych – Część 4-1: Silosy
- PN-EN-1993-4-2:2009, Eurokod 3 – Projektowanie konstrukcji stalowych – Część 4-2: Zbiorniki
- Rotter, J. M., Schmidt, H., European Convention for Constructional Steelwork. (2013). Buckling of steel shells: European design recommendations, [http://www.steelconstruct.com/site/index.php?process=download&id=5021&code=caf775d4657336befe56c9ea19b85a1980f9c69e ]
- Kowal, Z. (1975), Wybrane działy z konstrukcji metalowych. Część III: Zbiorniki, płyty fałdowe i warstwowe, struktury prętowe, budynki wysokie. Wydawnictwo Politechniki Wrocławskiej, Wrocław
- Ziólko, J. (1983). Zbiorniki, silosy. W: Bogucki W. (Ed.), Poradnik projektanta konstrukcji metalowych: Tom II, Arkady, Warszawa
- Ziółko, J. (1986), Zbiorniki metalowe na ciecze i gazy. Arkady, Warszawa
- PN-EN 14015:2010, Specyfikacja dotycząca projektowania i wytwarzania na miejscu zbiorników pionowych, o przekroju kołowym, z dnem płaskim naziemnych, stalowych spawanych, na ciecze o temperaturze otoczenia i wyższej
- PN-EN 14620-1:2010, Projektowanie i budowa na miejscu użytkowania pionowych, walcowych zbiorników stalowych o płaskim dnie do magazynowania oziębionych, skroplonych gazów o temperaturach roboczych pomiędzy 0 °C i -165 ° C – Część 1: Postanowienia ogólne
- Felippa, C. A. (2001). Introduction to Aerospace Structures (ASEN 3112) . Lecture 3: Thin Walled Pressure Vessels, [ http://www.colorado.edu/engineering/CAS/courses.d/Structures.d/IAST.Lect03.d/IAST.Lect03.pdf ]
- Rykaluk K., Zagadnienia stateczności konstrukcji metalowych DWE, Wrocław 2012
- Karman, T. H., Tsien, H. S. (1941). The buckling of thin cylindrical shells under axial compression. Journal of the Aeronautical Sciences, 8(8), 303-312
- PN-EN 1090-2: 2018-09, Wykonanie konstrukcji stalowych i aluminiowych – Część 2: Wymagania techniczne dotyczące konstrukcji stalowych
- Rozporządzenie Ministra Gospodarki z dnia 21 listopada 2005 r. w sprawie warunków technicznych, jakim powinny odpowiadać bazy i stacje paliw płynnych, rurociągi przesyłowe dalekosiężne służące do transportu ropy naftowej i produktów naftowych i ich usytuowanie, no. Dz.U. 2005 nr 243 poz. 2063 (2006), [ http://isap.sejm.gov.pl/Download?id=WDU20052432063&type=2 ]
- API Standard 650:2007, Welded Tanks for Oil Storage, [https://law.resource.org/pub/us/cfr/ibr/002/api.650.2007.pdf ]
- Wiggins J.H., Patent US 2806625 A. Double deck floating roof, (1957), [ http://www.google.com/patents/US2806625 ]
- Wikipedia. (2015), External floating roof tank. In wikipedia.org. [ https://en.wikipedia.org/wiki/External_floating_roof_tank ]
- Kuan S. Y., (2009). Design, Construction and Operation of the Floating Roof Tank (Dissertation ENG 4111 & ENG 4112 Research Project). Toowoomba, Australia, [ https://eprints.usq.edu.au/8503/1/Kuan_2009_Main_Project.pdf ]
- Manufacture of Vertical Storage Tanks with Buttwelded Shells for the Petroleum Industry
- Above Ground Cylindrical Flat Bottomed Storage Tanks of Metallic Materials
- Code Francais de construction des reservoirs cylindriques verticauz en acier U.C.S.I.P. et S.N.C.T.
- EEMUA Standards (The Engineering Equipments and Materials Users Association
- Kuan S. Y., (2009). Design, Construction and Operation of the Floating Roof Tank (Dissertation ENG 4111 & ENG 4112 Research Project). Toowoomba, Austral-ia, [ https://eprints.usq.edu.au/8503/1/Kuan_2009_Main_Project.pdf ]
- Babojan R., Treseder R.S., i in. (2002), NACE Corrosion Engineer’s Reference Book, 3rd Edition
- PN-B-03210: 1997, Konstrukcje stalowe. Zbiorniki walcowe pionowe na ciecze. Projektowanie i wykonawstwo
- PN-EN 1991-4:2008, Eurokod 1: Oddziaływania na konstrukcje. Część 4: Silosy i zbiorniki
- Bogucki W. (red.), (1982), Poradnik projektanta konstrukcji metalowych (Wydanie 1 , Tom 2), Arkady, Warszawa
- PN-EN 1993-1-1:2006/A1:2014, Eurokod 3: Projektowanie konstrukcji stalowych – Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1997-1+AC+Ap1+Ap2:2008, Projektowanie geotechniczne – Część 1: Zasady ogólne
- PN-EN 1997-2: 2007, Projektowanie geotechniczne – Część 2: Rozpoznanie i badanie podłoża gruntowego
- Lorenz, Z. (1908). Achsensymmetrische Verzerrungen indunwandigen Hohlzylinder. Zeitschrift des Vereines Deutscher Ingenieure, 52, 1766-1793
- Lessig, E. N., Liliev, A. F., Sokolov, A. G. (1956), Stalnyje listovyje konstrukcji. Gosudarstvennoje Izdatelstvo Literatury po Stroitelstvu i Architekture
________________________________