Leszek Chodor, 26 września 2014
15 czerwca 2025 scalenie kilku odrębnych artykułów
15 czerwca 2025 do nadal – naprawa awarii
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
W ciągu ostatnich 24 godzin z artykułu korzystało 8 Czytelników
Artykuł jest naprawiany po poważnej awarii portalu
Zagadnienie skręcania prętów jest ważnym problemem w projektowaniu konstrukcji budowlanych. Współczesne analizy wytrzymałości i stateczności systemów prowadzone są na modelach złożonych z prętów uogólnionych w stosunku do klasycznego modelu Bernoulliego. Pręt uogólniony ma dodatkowym stopień swobody węzła – paczenie (deplanację) przekroju. Uogólniona teoria belkowa Sapountzakis (2013) [1] zbudowana na dorobku kilku pokoleń inżynierów, a zapoczątkowana pracą Marguerre (1940) [2] umożliwia włączenie w proces obliczeniowy analizy wyboczenia giętno-skrętnego (w tym zwichrzenia) prętów. Analiza konstrukcji prętowych z zastosowaniem teorii zginania i skręcania skrępowanego prętów cienkościennych praktycznie w całości zastąpiła tradycyjną analizę z użyciem modelu pręta zwartego i jest stosowana w zasadzie we wszystkich nowoczesnych programach obliczeniowych (program Consteel i szereg innych).
Naprężenia, odkształcenia i przemieszczenia skręcanego pręta istotnie zależą od kształtu przekroju oraz od sposobu podparcia (warunków brzegowych ) końcowych (poprzecznych) ścianek i pośrednich przekrojów, a także od sposobu obciążenie pręta. Ścisłe rozwiązanie zagadnienia skręcania możliwe jest tylko w nielicznych przypadkach, a w zasadzie tylko dla pręta o przekroju okrągłym, ze swobodnymi ściankami poprzecznymi, obciążonymi równomiernymi obciążeniami skręcającymi o takiej samej wartości ale o przeciwnych zwrotach na obu ściankach poprzecznych. W każdym innym przypadku mamy do czynienia z rozwiązaniem przybliżonym, ale akceptowanym w praktycznym wymiarowaniu prętów
Teoria prętów cienkościennych oryginalnie sformułowana przez Własowa (1959) [3] znajduje zastosowanie w analizie nie tylko konstrukcji stalowych, ale również w analizie skręcania prętów i obiektów żelbetowych, mostów skrzynkowych lub budynków wysokich i wszędzie tam, gdzie wystąpi nieswobodne (skrępowane) skręcania prętów. W praktyce skręcanie nieswobodne występuje w każdym pręcie konstrukcji budowlanych, a skręcanie swobodne wystąpi tylko w nielicznych przypadkach, na przykład skręcania walów na łożyskach.
W prętach skręcanych swobodnie wytężenie przekrojów spowodowane jest tylko naprężeniami stycznymi, a podczas skręcania skrępowanego wystąpią również naprężenia normalne, które są spowodowane przez powstanie nieznanej w klasycznej teorii zginania prętów siłę przekrojową – bimoment $B_\omega$, stowarzyszony z deplanacją (spaczeniem) przekroju. Powstaną również dodatkowe naprężenia styczne wywołane przez działanie momentu giętno-skrętnego $M_\omega$. Rozkład naprężeń ścinających po grubości ścianki zależy od tego, czy przekrój jest otwarty, czy też zamknięty.
Współczesne programy komputerowe, szczególnie ConSteel [4], [5] pozwalają na projektowanie ram złożonych z prętów stalowych z uwzględnieniem niestateczności ogólnej dowolnego typu (wyboczenie, zwichrzenie, wyboczenie giętno-skrętne) bez potrzeby wykorzystywania skomplikowanych formuł analitycznych i normowych. W 2002 roku opublikowano do powszechnego użytku inżynierów program LTBeam [6], który umożliwiał szybkie i łatwe obliczenie momentu krytycznego belek jedno- i wieloprzęsłowych o dowolnych przekrojach bi- i mono-symetrycznych ze stężeniami bocznymi niepodatnymi lub sprężystymi założonymi na dowolnej wysokości przekroju. Od wersji LTBeamN 2.02 za pomocą programu można obliczyć siły krytyczne dla belki zginanej momentem M i ściskanej siłą N. Program został opracowany przez CTICM (Centre Technique Industriel de la Construction Metallique – France) w ramach europejskiego projektu ECSC(European Community for Steel and Coal) – Project No 7210-PR183 : „Lateral torsional buckling of steel and composite beams” – 1999-2002).
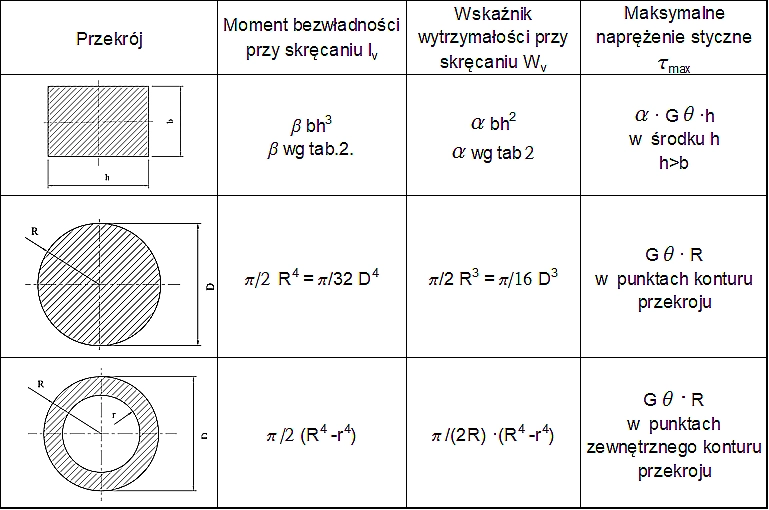
Tablice projektowe
Charakterystyki przekrojów skręcanych
Tab.1 Charakterystyki geometryczne skrętne wybranych przekrojów zwartych stosowanych w budownictwie
W przypadku swobodnego skręcania jednostkowy kąt skręcenia $\Theta$ wyznacza się z zależności ($\ref{7}$).
Tab.2 Współczynniki $\alpha$ wskaźnika wytrzymałości ($\ref{15}$) i $\beta$ momentu bezwładności ($\ref{13}$)na skręcanie dla różnych stosunków boku prostokąta (opracowano na podstawie [7] )
Tab.3. Charakterystyki geometryczne przekrojów cienkościennych. Formuły obliczeniowe wspólne dla przekrojów otwartych i zamkniętych
Tab.4. Charakterystyki geometryczne przekrojów cienkościennych. Formuły obliczeniowe dla przekrojów otwartych
Współczynnik . „k” w formule na Iv (wrs 1) uwzględnia wpływ wyokrąglę naroży kształtowników walcowanych wg tab. 0
Tab.5 Charakterystyki geometryczne przekrojów cienkościennych. Formuły obliczeniowe dla przekrojów zamkniętych
w opracowaniu
Tab.6 Charakterystyki geometryczne wybranych, zamkniętych przekrojów cienkościennych [8]
$A= \cfrac{b\cdot t_2\cdot (t_1\cdot cos 2\alpha+ t_2 \cdot cos \alpha) \cdot tg \alpha}{4 \cdot (t_1 \cdot cos \alpha + t_2)\cdot (t_1+ t_2 \cdot cos \alpha} \quad ; \quad B= \cfrac{b^3}{8} \cdot \cfrac{t_1 \cdot t_2 \cdot sin \alpha }{t_1 + t_2 \cdot cos \alpha}, \\
C= \cfrac{2 \cdot b^2 \cdot h^2 \cdot t_1 \cdot t_2}{b \cdot t_2 + h \cdot t_1} \quad ; \quad D= \cfrac{ b^2 \cdot h^2}{66}\cdot \cfrac{(b\cdot t_2 – h \cdot t_1)^2}{(b\cdot t_2 + h \cdot t_1)^2}\cdot (b\cdot t_1 + h \cdot t_2) $
Tab.7 Charakterystyki geometryczne wybranych, otwartych przekrojów cienkościennych – wg [8]
Sposób wyznaczania współrzędnych wycinkowych dla dwuteownika, ceownika i zetownika pokazano w przykładzie 1
Tab.8. Bimomenty $B_ω$, momenty giętno-skrętne $M_ω$, momenty swobodnego skręcania $M_s$ oraz kąty skręcenia $\varphi$ dla prętów cienkościennych [8], tab 1-2
Tab.9 Współczynniki korekcyjne sztywności $k$ na skręcanie kształtowników stalowych

2) Wyniki badań Foplle przedstawiono w poradniku Birger i in (1998) [7], 3) Niezgodziński (2004) [9]
Skręcanie czyste
Skręcanie czyste realizuje się podczas działania na ścianki poprzeczne (czołowe) pręta pryzmatycznego specyficznie dobranego obciążenia o gęstości $q_v = [ \, 0 \, , \, q_{vy} \, , \, q_{vz} \, ]$ (rys. 1a). Obciążenie $q_v$ można statycznie zredukować do pary momentów $M_s$ działającej w płaszczyźnie przekroju poprzecznego początkowego A i końcowego pręta (w miejscu utwierdzenia S). Obciążenie zewnętrzne parą momentów $M_s$ wywołuje moment skręcający $M_x$ w przekrojach pręta.
$M_x$ jest całkowitym momentem skręcającym przekrój wokół osi x, wyznaczonym w drodze statycznej redukcji obciążenia zewnętrznego $M_s$ do rozpatrywanego przekroju pręta w którym jest zrównoważony przez składowe siły przekrojowe: moment czystego skręcania (Saint Venanta) $M_v$ i moment giętno-skrętny $M_\omega$:
$$ \begin{equation} M_x = M_v + M_\omega \label{1} \end{equation} $$
Moment $M_v$ powstaje przy skręcaniu swobodnym, a przy skręcaniu nieswobodnym dodatkowo działa moment $M_\omega$
Można pokazać [10], że gęstość obciążenia $q_v$ ścianek czołowych pręta, prowadząca do czystego skręcania musi mieć rozkład
$$ \begin{equation} q_v =\begin {cases}
q_{vx}=0 \\
q_{vy}= \pm \Theta \cdot G \cdot\left ( \cfrac{\partial \varphi}{\partial y} – z\right ) \\
q_{vz}= \pm \Theta \cdot G \cdot\left ( \cfrac{\partial \varphi}{\partial z} +y\right ) \\
\end {cases} \label{2} \end{equation} $$
gdzie $\Theta$ jest parametrem, a funkcja $\varphi= \varphi (y,z)$ – kąt skręcenia przekroju jest funkcją harmoniczną, czyli musi spełniać warunki zagadnienia brzegowego Neumana
$$\begin {equation} \nabla \varphi^2 =0 \label {3} \end {equation}$$
i tak dobraną, że spełnia warunki równowagi (statyczne warunki równowagi) na pobocznicy oraz kinematyczne warunki brzegowe , a w tym przypadku zeruje się w punkcie utwierdzenia S (rys. 1a) .
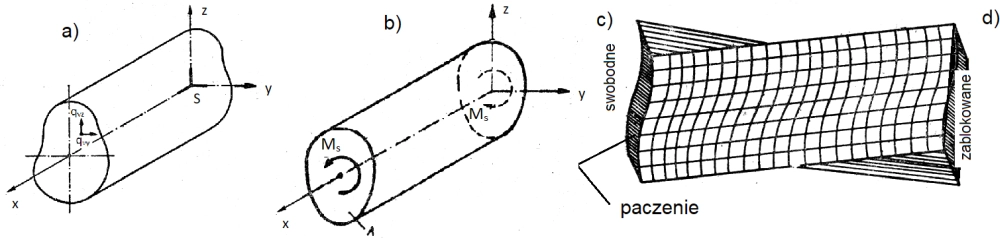
Rys.1. Skręcanie: a) czyste, b) proste, c) swobodne, d) skrępowane – nieswobodne (rysunek złożony z ilustracji z pracy [10] )
Skręcanie proste
Skręcanie proste (rys. 1b) dotyczy problemu technicznego skręcania pręta obciążonego na powierzchniach czołowych parą momentów skręcających $M_s$ (rys. 1b), czyli dowolnym (niekoniecznie spełniającym warunek ($\ref{2}$) )rozkładem obciążeń $q_v$, które jest statycznie równoważne momentowi $M_s$,
Warunek równoważności obciążenia momentami skupionymi $M_s$ oraz obciążenia realizującego czyste skręcanie ($\ref{2}$) prowadzi do zależności
$$\begin {equation} M_s = \iint_A (q_{vz} y -q_{vy} z dA = \iint_A \left [ \Theta G \left (\cfrac{\partial \varphi}{\partial z}+y \right) y – \Theta G \left (\cfrac{\partial \varphi}{\partial y}-z \right)z\right ] dA= \Theta G \iint_A \left ( \cfrac{\partial \varphi}{\partial z} y -\cfrac{\partial \varphi}{\partial y}z +y^2 +z^2 \right ) = \Theta G \cdot I_v \label{4} \end {equation}$$
gdzie wprowadzono oznaczenie definiowane jako moment bezwładności przekroju na skręcanie (Saint Vennanta).
$$\begin {equation} I_v \overset{def}{=} \Theta G \iint_A \left ( \cfrac{\partial \varphi}{\partial z} y -\cfrac{\partial \varphi}{\partial y}z +y^2 +z^2 \right ) \label{5} \end {equation}$$
Skręcanie swobodne
Przy skręcanie swobodnym pręta każdy przekrój poprzeczny może się swobodnie odkształcać w kierunku osi pręta, co wywołuje paczenie deplanację przekroju płaskiego przed obciążeniem (rys. 1c) . W praktyce oznacza to, że w przekroju występują tylko naprężenia styczne, a deplanacja na rozkład naprężeń. Taki przypadek zachodzi, gdy na końcach pręt jest obciążony równymi i przeciwnie skierowanymi momentami skręcającymi $M_s$ (rys. 1b).
Skręcanie nieswobodne
Skręcanie nieswobodne (skrępowane) to takie, w którym odebrano swobodę deplanacji przekroju (rys. 1c) i w rezultacie w pręcie oprócz naprężeń stycznych pojawiają się naprężenia normalne składające się na siłę przekrojową zwaną bimomentem.
W każdym przypadku skręcania należy zwrócić uwagę na swobodę deplanacji przekroju , bo przy jej ograniczeniu, obok naprężeń od swobodnego skręcania (Saint Venanta) szacować naprężenia od momentu giętno-skrętnego, powstających przy nieswobodnym skręcaniu.
Deplanacja przekroju pręta skręcanego
Zasada sztywnego konturu i deplanacja przekroju
Skręcanie pręta znamienne jest tym, że pręt ulega deplanacji (spaczeniu) , to znaczy przekrój płaski przed odkształceniem nie zachowuje płaskości . Zjawisko deplanacji obserwuje się w pręcie skręcanym swobodnie, co pokazano na rys. 2 , ale także w pręcie skręcanym nieswobodnie , w którym ograniczenie swobody deplanacji wywołuje nowe siły przekrojowe .
W rezultacie podczas skręcania nie jest zachowana zasada płaskich przekrojów -fundamentalna zasada stosowana w technicznej teorii zginania,. Założenie teorii zginania ” odcinek prosty i prostopadły do osi pręta przed deformacją pozostaje prosty i prostopadły po deformacji, a pręt nie doznaje odkształceń (od zginania) na linii osi przekrojów” zastępuje zasada sztywnego konturu „linie konturowa przekrojów poprzecznych pręta nie ulega odkształceniu (od skręcania), ale punktu zawarte wewnątrz konturu przemieszczają się wzdłuż osi pręta”.
Zasada sztywnego konturu jest pierwszą, podstawową hipotezą, którą postawił Własow w teorii prętów cienkościennych.
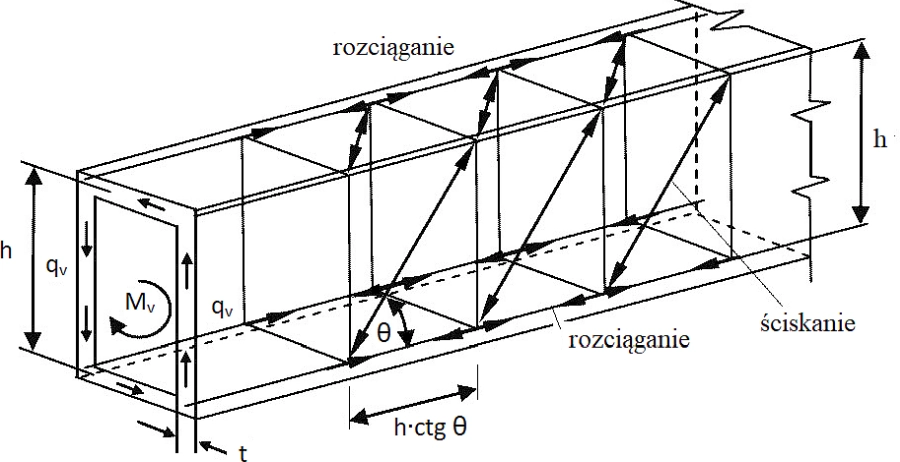
Kratowy model skręcania
Analizę napreżeń w skręcanym pręcie można przeprowadzić na kratowym modelu skręcania, pokazanym na rys.2 Model taki rozpatruje się przy analizie skręcania przekroju żelbetowego. Na rys. 3 pokazano ten model z oznaczeniem kąta nachylenia krzyżulca $\gamma$, podczas gdy w analizie konstrukcji żelbetowych kąt ten oznacza się jako $\Theta$ i utożsamia a kątem nachylenia krzyżulca betonowego tworzącego się w pręcie betonowym w granicach $ 1,0 \le ctg \Theta\le 2 $ .
Na kratowym modelu skręcania rys.3. możemy zaobserwować, że w przypadku odebrani swobody skręcania na dalszym końcu pręta w zbrojeniu podłużnym pojawia się rozciąganie w pasach górnych i dolnych, co jest objawem deplanacji przekroju (porównaj z rys.2)
Skręcanie swobodne
Ścisłe rozwiązanie zadania swobodnego skręcania w przypadku dowolnego materiału i kształtu przekroju pręta jest zaskakująco złożone, mimo, że w podstawowych podręcznika tematu zagadnienie swobodnego skręcania jest traktowane jako proste zadanie.
W 1853 roku Saint-Venant (p. np [11]) przedstawił metodę półodwrotną rozwiązania zagadnienia swobodnego skręcania izotropowych sprężystych prętów pryzmatycznych. Zaproponował metodę, w której założył postać przemieszczeń pręta z możliwością spaczenia przekroju (identycznego dla wszystkich przekrojów poprzecznych) i wyprowadził, konsekwentnie w ramach liniowej sprężystości, równania opisujące zadanie swobodnego skręcania prętów pryzmatycznych. Rozkład obciążenia zewnętrznego na końcach pręta jest identyczny z rozkładem naprężeń w każdym przekroju. Wykazał, że sposób przyłożenia statycznie równoważnego obciążenia nie jest istotny w przekrojach dostatecznie odległych od jego końców. Uogólnienie tej idei, którą nazywa się zasadą Saint-Venanta stosowaną w innych przypadkach wytrzymałościowych ciała stałego.
Na rys.2 pokazano postać odkształconą pręta o zwartym przekroju kwadratowym poddanego swobodnemu skręcaniu parą momentów skręcających $M_s$ o przeciwnych zwrotach przyłożonych do powierzchni czołowej
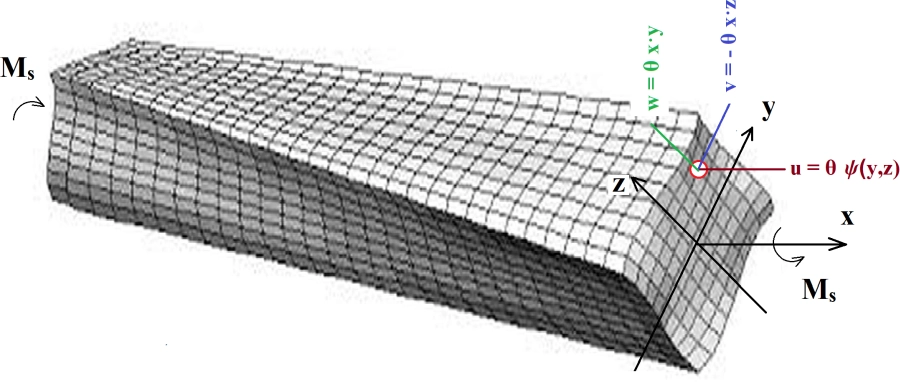
Saint Venant na podstawie wyników eksperymentów założył następujące pole przemieszczeń przekroju pręta skręcanego swobodnie ( u- przemieszczenie w kierunku osi pręta x; v- przemieszczenie wzdłuż osi y ; w-przemieszczenie pionowe wzdłuż osi z):
$$\begin {equation} u=\Theta \cdot \Phi (y,z) \quad ; \quad v= – \Theta \cdot x \cdot z \quad ; \quad w= \Theta \cdot x \cdot y \label{6} \end {equation}$$
gdzie $\Phi(y,z)$ – funkcja paczenia zależna od rodzaju przekroju. Dla przekroju okrągłego (walca) $\Phi(y,z)=1$
Jednostkowy kąt skręcenia $\Theta= \cfrac{d \varphi}{dx}$ wyznacza się z zależności
$$\begin {equation} \Theta = \cfrac{M_v}{GI_v} \label{7} \end {equation}$$
gdzie $M_v$ moment czystego skręcania Saint Venanta. Dla schematu z rys. 2 moment skręcający Saint Venanta przekrój pręta jest stały na długości pręta i równy obciążeniu zewnętrznym momentem skręcającym $ M_s $ : $M_v = M_s $
Pręt o przekroju zwartym
Z punktu widzenia praktyki istotne znaczenie ma problem czystego skręcania pręta o przekroju okrągłym oraz prostokątnym (rys.2).
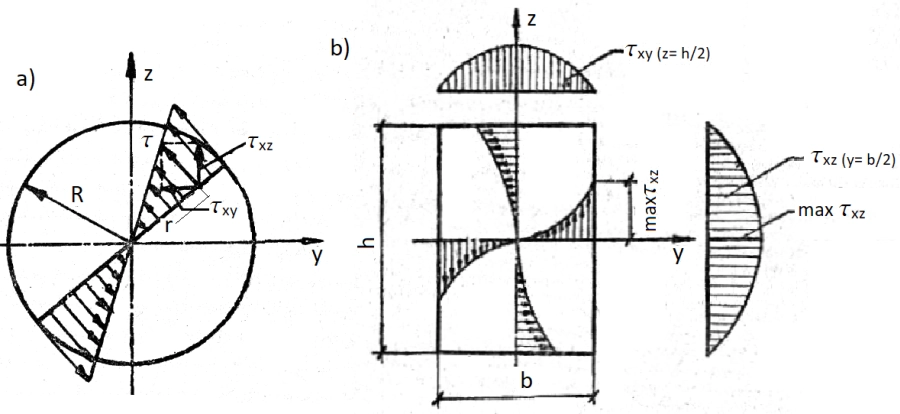
Rys.4. Naprężenia w przekroju skręcanym : s) okrągłym, b) prostokątnym [10]
Przekrój okrągły
W przypadku przekroju kołowego rozwiązaniem zagadnienia Neumanna jest funkcja
$$\begin {equation} \varphi (y,z)=0 \label{8} \end {equation}$$
W konsekwencji moment bezwładności przy skręcaniu ($\ref{5}$) wynosi
$$\begin {equation} I_v= \iint \limits_A r^2 dA= \cfrac{\pi R^4}{2}=I_0 \label{9} \end {equation}$$
Maksymalne naprężenia styczne (na obwodzie koła) wynoszą
$$\begin {equation} max \, \tau_v = \cfrac{M_v}{I_v} \cdot R \label{10} \end {equation}$$
Przekrój prostokątny
W przypadku przekroju prostokątnego o wymiarach bxh (h-wysokość) (rys. 2b) funkcja paczenia może być przedstawiona w postaci szeregu [10]:
$$\begin {equation} \varphi (y,z)=y \cdot z-\sum \limits_{i=0}^\infty \cfrac {B_n}{k_n cosh(k_n h/2}\cdot sin(k_n y) cosh (k_n z) \label{11} \end {equation}$$
gdzie
$$ \begin {equation} k_n=\cfrac { (2n+1) \pi}{b} \quad ; \quad B_n= (-1)^n \cfrac{8b}{(2b+1)^2 \pi^2} \label{12} \end {equation}$$
W konsekwencji moment bezwładności skręcania ($\ref{5}$) możemy zapisać w postaci
$$\begin {equation} I_v=\left [ \cfrac{1}{3} – \cfrac {71}{\pi^5} \cdot (h/b))^{-1} \sum \limits_{n=0}^\infty \cfrac{tgh (k_n h/2)}{(2n+1)^5}\right ] b^3 h= \beta (h/b) \cdot b^3 \cdot h \label{13} \end {equation}$$
Wyrażenie na maksymalne naprężenia styczne można zapisać w postaci:
$$\begin {equation} max \, \tau_{xz}= \cfrac{M_v} {\alpha (h/b) \cdot b^2 h} \label{14} \end {equation}$$
skąd wskaźnik wytrzymałości na skręcania
$$\begin {equation} W_v=\alpha (h/b) \cdot b^2 \cdot h \label{15} \end {equation}$$
Współczynniki $\alpha$ i $\beta$ są zależne jedynie od stosunku boków prostokąta i zestawiono je w tab.1
W literaturze podawane są jeszcze inne przybliżenia na współczynniki $\alpha$ i $\beta$. W pracy [7] i w licznych podręcznikach teorii sprężystości lub wytrzymałości materiałó w zamieszcza się przybliżone formuły:
$$\begin {equation} \beta \approx \cfrac{1}{3} \left [ 1 – \cfrac{0,63}{(h/b)} + \cfrac{0,052}{(h/b)^5 }\right ] \quad ; \quad \alpha \approx \left [ 1 – \cfrac{8}{\pi^2} + \sum \limits_{n = 1, 3, …}^\infty \cfrac{1}{ [n^2 cosh (n \pi h)/(2b)]}\right ] \label{16} \end {equation}$$
Przybliżona formuła Saint-Venanta dla sztywności skrętnej
W praktyce inżynierskiej często potrzebujemy szybkiego szacunku sztywności na skręcanie przekroju o złożonym kształcie w celu podjęcia decyzji o wprowadzeniu przekroju do projektu konstrukcji, W tym przypadku można stosować formułe podaną przez Sait-Venanta w postaci
$$\begin {equation} I_v \approx \cfrac{A^4}{40 \cdot I_0}\label{17} \end {equation}$$
gdzie:
A- pole przekroju pręta zwartego lub pole zawarte wewnątrz przekroju zamkniętego.
$I_0=I_y + I_z $ – osiowy moment bezwładności równy sumie momentów bezwładności względem osi głównych przekroju.
Formuła ($\ref{17}$) powstała po analizie wyrażenia na sztywność elipsy:
$$\begin {equation} I_v =\pi \cfrac{a^3 b^3}{a^2+b^2}\label{18} \end {equation}$$
gdzie $a$, $b$ – półosie elipsy, która ma pole przekroju $A= \pi a b$ oraz $I_o= \cfrac{\pi a b}{4}(a^2+b^2)$.
Po uwzględnieniu tego, że $4 \pi^2 \approx 40$ z ($\ref{18}$) uzyskujemy ($\ref{17}$) .
Formuła ($\ref{17}$) często jest stosowana do przybliżonego wyznaczenia sztywności na skręcanie prętów o dowolnym przekroju. Należy jednak wziąć pod uwagę, że takie przybliżenie może prowadzić do zbyt dużych błędów. Na przykład w przypadku pręta okrągłego z nacięciem błąd (zawyżenie sztywności) może osiągnąć 80% [7]
Przekrój cienkościenny
Definicja pręta cienkościennego
Pręt cienkościenny to cylindryczna lub pryzmatyczna powłoka, której trzy miarodajne wymiary są różnych rzędów: długość jest o rząd większa od szerokości (lub wysokości) przekroju, która z kolei jest o rząd większa od grubości ścianki powłoki [12]. Jak pokazuje doświadczenie, a także analiza statyczno-wytrzymałościowa oparta na hipotezach Wlasowa, pręt można uważać za cienkościenny, jeśli spełnione są warunki [3], [13], [14]:
$$\begin {equation} t \le \cfrac{l}{N_{th}} \quad ; \quad l \le \cfrac{L}{N_b}\label{19} \end {equation}$$
gdzie: $N_{th} = N_b = 10$,
$t$ – grubość ścianki, $l$ – długość ścianki , $ L$ – długość pręta.
Drugi warunek wynika z ogólnej definicji pręta (również o przekroju zwartym). Elementy o mniejszej smukłości w zasadzie powinny być analizowane jako tarcze. W technice często ten warunek osłabia się i wymaga $N_b = 8$, a w konstrukcjach żelbetowych nawet $N_b = 4$.
Przy zmniejszaniu smukłości ścianek $l/t$ lub pręta $L/l$ dokładność rozwiązania zadania jest coraz gorsza.
Pręty cienkościenne dzieli się z uwagi na geometrię przekroju na:
- otwarte, to znaczy takie, w których linia środkowa nie tworzy obwodów, czyli nigdzie nie zamyka się (np. rys. 5, 6),
- zamknięte, toznaczy takie, w których ścianka tworzy obwód zamknięty , rurę, komorę (np. rys. 7) . Przekroje zamknięte mogą być jedno- lub wielokomorowe.
- mieszane, które zawierają części otwarte i części zamknięte
- quasi-zamknięte.(rys. 9 ) i rozdział pręty wielogałęziowe oraz kratownice wielopasowe.
Przekrój otwarty
Na rys. 5 przedstawiono często stosowane w konstrukcjach stalowych .
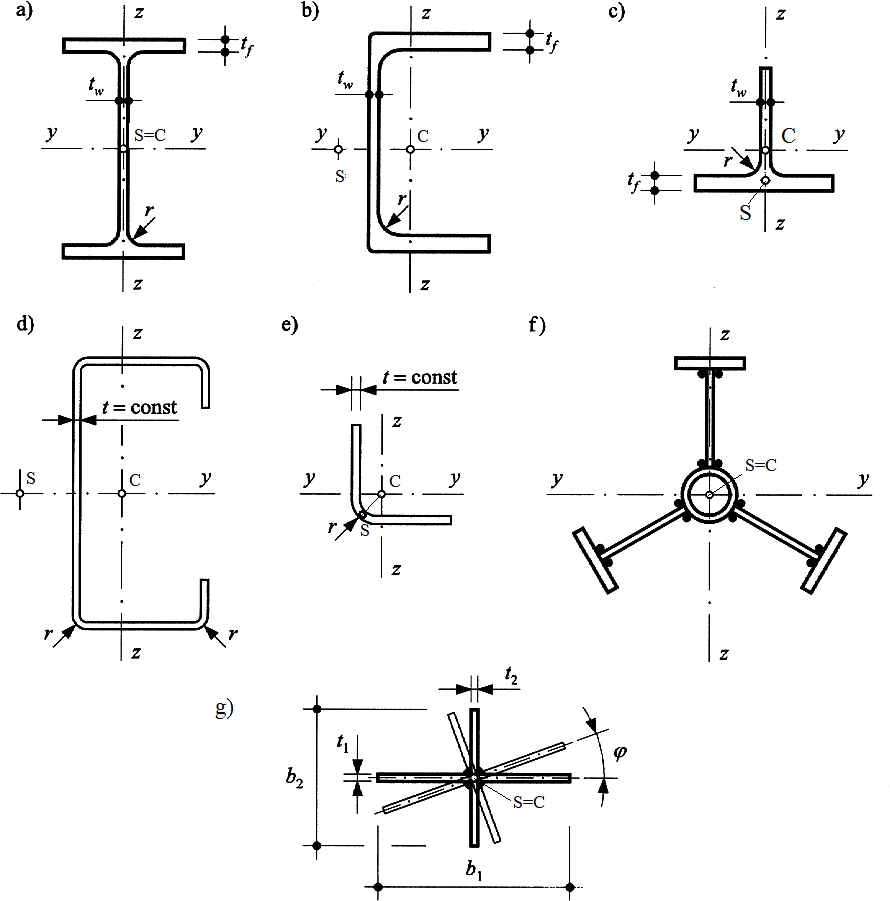
Rys.5 Przykłady przekrojów cienkościennych otwartych stosowane w konstrukcjach stalowych : a) dwuteownik walcowany, b) ceownik walcowany, c) teownik walcowany (1/2 I), d) ceownik gięty na zimno z zagiętymi pasami (C+), e) kątownik gięty na zimno, f) przekrój spawany złożony gwiaździsty , g) przekrój prosty gwiaździsty; C- środek ciężkości, S- środek zginania ( ścinania) [15]
Rozważmy przekrój poprzeczny pokazany na rys.6,, który składa się z n elementów prostokątnych o długości $l_i$ o grubości $t_i$ elementu i-tego, spełniających warunek ($\ref{27}$)..
Rys. 6 Przekrój otwarty cienkościenny złożony ze ścianek prostych [16]
Przyjmiemy następujące założenia upraszczające dotyczące otwartych profili cienkościennych [16]:
#1 jednostkowy kat skręcenia każdego elementu prostokątnego przekroju poprzecznego jest jednakowy,
#2 suma momentów skręcających poszczególne elementy Mυi jest równa momentowi skręcającemu przyłożonemu do całego profilu Mυ,
Jednostkowy kąt skręcenie występujący w ($\ref{2}$) do ($\ref{5}$) zgodnie założeniem #1 możemy napisać w postaci
$$\begin {equation} \Theta = \cfrac{M_v}{GI_v} =\cfrac{M_{vi}}{GI_{vi}} \label{20} \end {equation}$$
Moment bezwładności na skręcanie prostokąta i-tego (p. $\ref{13}$) wynosi:
$$\begin {equation} I_{v,i}=\beta_i \cdot t_i^3 \cdot l_i\label{21} \end {equation}$$
gdzie współczynnik $\beta_i$ zależy od proporcji boków prostokąta poddanego czystemu skręcaniu , dla kwadratu ($t_i =l_i$) wynosi 0,141, a dla długiego prostokąta ($ l_i / t_i >10$) wynosi 1/3 , Wytrzymałość materiałów dla wydziałów budowlanych. PWN)), dla innych wartości można je odczytać z tab.1.
Z założenia #2 mamy
$$\begin {equation} M_v=\sum \limits_{i=1}^n M_{v,i} \label{22} \end {equation}$$
skąd po podstawieniu wyrażeń na momenty skręcające z założenia #1, otrzymujemy wyrażenie na moment bezwładności czystego skręcania całego przekroju
$$\begin {equation} I_v=\sum \limits_{i=1}^n I_{v,i}=\sum \limits_{i=1}^n \beta_i \cdot t_i^3 \cdot l_i\\ \approx \cfrac{k}{3}\sum \limits_{i=1}^n t_i^3 \cdot l_i \label{23} \end {equation}$$
W oszacowaniu $I_v$ wprowadzono współczynnik korekcyjny $k$, uwzględniający zwiększenie momentu bezwładności przekroju otwartego ze względu na wyokrąglenia naroży oraz pochylenie stopek profili wg. tab.. 9.
W tab. 7 zamieszczono charakterystyki kilku otwartych przekrojów cienkościennych wg pracy [8].
W tab.4 zestawiono formuły do wyznaczania charakterystyk przekrojów cienkościennych otwartych, a w kol. 6 wrs 1 zamieszczono wyrażenie ($\ref{23}$).
Naprężenie styczne czystego skręcania w złożonym, otwartego przekroju cienkościennego wyznacza się z zależności
$$\begin {equation} max \, \tau_i = \pm \cfrac {M_v}{I_v}\cdot t_i \label{24} \end {equation}$$
przy czym minimalne i maksymalne naprężenia wystąpią na przy przeciwległych krawędziach ścianki zgodnie z rys. 6.
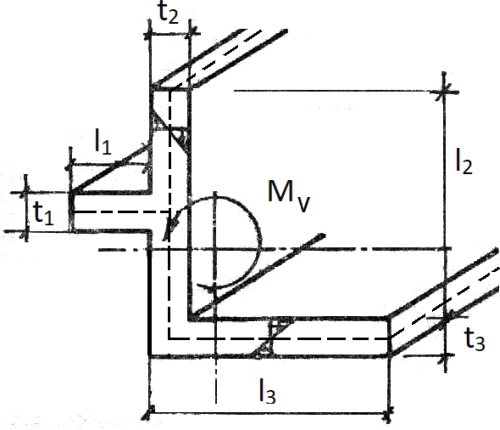
Przekrój zamknięty
Przekroje zamknięte charakteryzują się dużą odpornością na skręcanie, wielokrotnie większą od profili otwartych. W przypadku obciążenia pręta skręcaniem należy stosować profile o przekroju zamkniętym, a nie otwartym, czyli stosować rury a nie dwuteowniki.
W ściankach przekroju zamkniętego (rys.7) poddanego swobodnemu skręcaniu powstają tylko naprężenia styczne, które są równomiernie rozłożone po grubości t ścianki, czyli inaczej niż w przekroju otwartym (rys. 6), w którym zmieniają się liniowo i są zerowe w środku ścianki. Strumień naprężeń stycznych w ściance profilu zamkniętego wynosi
$$\begin {equation} q_v =\tau_v \cdot t \label{25} \end {equation}$$
i ma stałą wartość, niezależnie od współrzędnej bieżącej przekroju s, określającej położenie punktów na konturze. Strumień naprężeń stycznych ($\ref{25}$) oblicza się ze wzoru Bredta
$$\begin {equation} \tau_v = \cfrac{M_v} { \Omega \cdot t} \label{26} \end {equation}$$
gdzie $\Omega$ jest podwojonym polem powierzchni ograniczonej konturem (linią środkową ścianek) – rys.4 w ogólności wyznaczanym z formuły :
$$\begin {equation} \Omega=\cfrac {1}{2}\oint h ds \label{27} \end {equation}$$
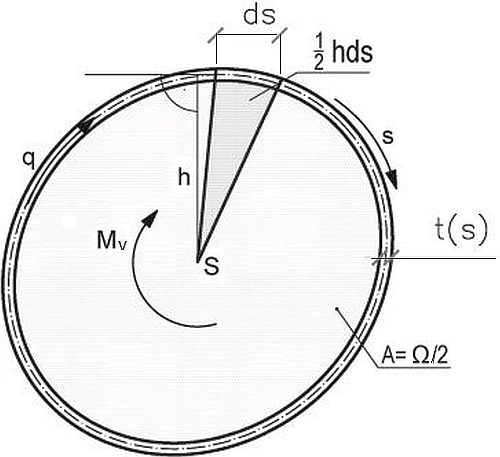
Rys.7 Przekrój zamknięty: S- środek ścinania, s -współrzędna bieżąca obwodu przekroju pręta, A- pole wewnątrz linii środkowej, Ω – podwojone pole środkowe, [17]
Moment bezwładności swobodnego skręcania zamkniętego przekroju cienkościennego $I_v$, występujący w ($\ref{23}$) wyznaczamy z zależności
$$\begin {equation} I_v = \Omega^2 \left ( \oint {\dfrac {ds} {t(s)}} \right)^{-1} = \Omega^2 \cdot \dfrac {t_0} {\overline s_0} \label{28} \end {equation}$$
gdzie:
$t_0$ – grubośc ścianki w dowolnie wybranym miejscu przekroju poprzecznego (grubość porównawcza),
$\overline s_0$ sprowadzona do $t_0$ długość obwodu przekroju:
$$\begin {equation}\overline s_0 =\oint \cfrac {t_0} {t(s)} \label{29} \end {equation}$$
Dla $t(s)=t=const$ $s_0 =s $ (s- rzeczywista długość obwodu przekroju ), moment bezwładności na skręcanie wynosi $I_v=\cfrac{t}{s}\cdot \Omega^2$,.
W tab.2 zamieszczono charakterystyki kilku zamkniętych przekrojów cienkościennych za pracą [8].
Zastępczy moduł Yonga $\overline E$ pręta cienkościennego
Piechnik (2000) [13] pokazał że analizę prętów cienkościennych należy prowadzić z zastosowaniem zastępczego modułu Younga $\overline E$ a nie modułu Younga materiału E. Zastępczy moduł Younga $ \overline {E}$ wynosi
$$\begin {equation} \overline {E} \overset {def}{=} \cfrac {E}{1 – \nu^2} \label{30} \end {equation}$$
i wiąże odkształcenia $ \varepsilon_x $ z naprężeniami $\sigma_x$ wzdłuż osi pręta
$$\begin {equation} \sigma_x = \overline E \cdot \varepsilon_x \label{31} \end {equation}$$
gdzie $\nu$ – współczynnik Poissone’a materiału pręta. Dla stali $\nu= 0,3$ i otrzymamy $\overline E = 1,01 \cdot E$, czyli jest 1% więkzy od modułu Younge’a materiału (stali).
Związki ($\ref{30}$) i ($\ref{30}$) można w prosty sposób wyprowadzić z układu uogólnionych równań Hooke’a zestawionych dla pręta cienkościennego:
$$\begin {equation} \varepsilon_x = \cfrac{1}{E} \left [ \sigma_x -+ \nu ( \sigma_s + \sigma_n \right ] \quad ; \quad \varepsilon_s = \cfrac{1}{E} \left [ \sigma_s -+ \nu ( \sigma_x + \sigma_n\right ]\label{32} \end {equation}$$
Po uwzględnieniu tego, że zgodnie z trzecią hipotezą Własowa ($\ref{35}$) $\sigma_n=0$ układ równań ($\ref{32}$) można sprowadzić do równania ($\ref{31}$) w którym wystąpi $\overline E$ ($\ref{30}$), Tą drogą otrzymujemy również związek $\sigma_s = \nu \sigma_x$
Skręcanie nieswobodne
Skręcanie nieswobodne (skrępowane) przedstawimy według technicznej teorii prętów cienkościennych Własowa (1959) [3].
W większości praktycznych przypadków deplanacja przekrojów pręta skręcanego (rys. 1c i rys.6) nie może rozwijać się swobodnie, czyli skręcanie jest nieswobodne. Przykładem skręcanie skrępowanego jest zwykłe utwierdzenie końca pręta lub specyficzny, symetryczny sposób przyłożenia momentów skręcających, wymuszający płaskość przekroju leżącego w płaszczyźnie symetrii.
W technicznej teorii nieswobodnego skręcania przyjmuje się, że słuszne są zależności wyprowadzone dla czystego skręcania. Jednostkowy kąt skręcenia $\Theta$ definiuje się podług zależności ($\ref{7}$) w funkcji położenia przekroju na osi pręta (x), proporcjonalnie do zmieniającego się po osi pręta momentu. czystego skręcania $M_v(x)$, który jest częścią cąłkowitego momentu skręcającego przekrój $M_x$ ($\ref{1}$). Przemieszczenie podłużne punków przekroju pręta są różne zależnie od położenia punktu na konturze przekroju ( rys.1c); są nazywane przemieszczeniami paczenia. i są proporcjonalne do współrzędnej wycinkowej przekroju ze współczynnikiem proporcjonalności $\Theta$, określonego w zdaniu poprzednim , wg zależności:
$$\begin {equation} u(x.y.x)=-\Theta (x) \cdot \omega \label{33} \end {equation}$$
Współrzędna wycinkowa jest specyficzną współrzędną, określającą położenie punktu $P$ (p. rys. 11 dla przekroju otwartego rys. 13 dla przekroju zamkniętego).
Rozkład przemieszczeń ($\ref{30}$) jest odejściem od klasycznego założenia Bernoulliego o płaskim przekroju na rzecz sztywnego konturu, który paczy się (deplanuje). Paczenie przekroju jest stowarzyszone z nową siła przekrojową – bimomentem.
Hipotezy teorii Własowa
Pierwsza hipoteza Własowa (sztywnego konturu)
Pierwsza hipoteza Własowa jest często nazywana hipotezą sztywnego konturu. przyjmuje się, ze przekrój poprzeczny pozostaje nieodkształcalny w swojej płaszczyźnie, to znaczy kontur przekroju w liniach środkowych po odkształceniu jest taki sam jak przed odkształceniem, to znaczy odległości między punktami na przekroju pozostają niezmienione. Powierzchnia środkowa zachowuje się tak, jakby w płaszczyżnie każdego przekroju poprzecznego, rozpostarta była sztywna tarcza oparta na liniach środkowych, idealnie jednak wiotka dla deformacji w kierunku prostopadłym do tego przekroju
Paczenie przekroju na skutek skręcania nie wpływa na kształt przekroju w jego płaszczyźnie. Faktycznie zaś takie odkształcenia powstają, a
Druga hipoteza Własowa (deplanacji)
Trzecia hipoteza Wlasowa (małych naprężeń normalnych)
W tej hipotezie zakłada się, że naprężenia normalne $\sigma_n$ do powierzchni równoległych do powierzchni środkowej sa pomijalnie małe w stosunku do dwóch pozostałych $\sigma_x$, $\sigma_n$
$$\begin {equation} \sigma_n \approx 0 \label{35} \end {equation}$$
Bimoment – nowa siła przekrojowa o dyskusyjnej naturze matematycznej
Bimoment jest nową silą przekrojową specyficzną da prętów cienkościennych proporcjonalnyądo drugiej pochodnej kąta skręcenia przekroju podług zależności. ($\ref{53}$). Bimoment jest analogiem momentu zginajacego stowarzyszoego z krzywizną pręta w zagadneiniu zginania
W tradycyjnej mechanice przyjmuje się, że bimoment jest liczbą (np. [13], [14]), której można przyporządkować nieskończenie wiele bipar (par momentów o przeciwnym zwrocie), a tymi można obciążyć pręt. W pracy [18] przedstawiono twierdzenia dotyczące algebry układów wektorów sił przyłożonych do płaskiej, sztywnej jedynie w swej płaszczyźnie, linii materialnej, to jest przy założeniu sztywnego konturu przekroju pręta cienkościennego. Rozważania prowadzono w ramach klasycznej algebry wektorów, z której można wyciągnąć wniosek , że bimoment jest liczbą (skalarem).
Autor artykułu stoi na stanowisku, że zagadnienie mechaniki prętów cienkościennych oraz algebry sił w tym bimomentu należałoby rozpatrywać w ramach ogólniejszej algebry Clifforda [19]. Zgodnie z tą teorią siła fizyczna jest trójką (skalar, wektor, biwektor), która jest nazywana pseudowektorem (qwaterionem lub auaterionem). Ta trójka obiektów posiada wszystkie cechy tradycyjnego wektora (wartość, kierunek i zwrot), skalara oraz biwekotra. Obiekty takie są analizowane w algebrze geometrycznej Clifforda [20], [21], [22], [23]. Algebra Clifforda jest szczególnie użyteczna w analizie dużych obrotów, a obecnie obserwuje się renesans jej zastosowań.
Bimoment nie jest ani skalarem , ani wektorem – jest obiektem matematycznym o nazwie quaterion (lub pseudowektor).
W podejściu technicznym bimoment często przedstawia ię jako „parą momentów” [24] (rys.8b) lub „momentem momentów”., a nigdy jako skalar, wektor lub para wektorów (moment). Na rys. 8 zilustrowano to podejście na przykładzie dwuteownika (rys. 8) , w którym bimoment $B_\omega$ przyłożony jest jako para momentów $M_{f\omega} = \cfrac{B_\omega}{h_o}$ do pasów dwuteownika, gdzie $h_o$ jest wysokością profilu w liniach środkowych pasów ($h_o=h-t_f$ .
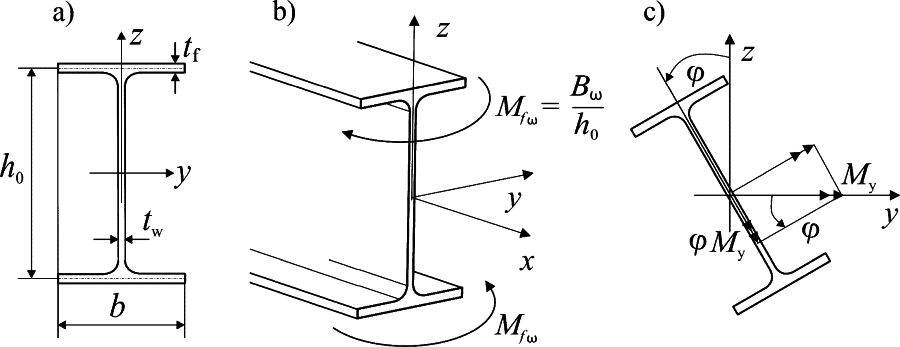
Rys.8. Modelowanie bimomentu jako pary momentów: s) przekrój pręta, b) sposób rozkładu bimomentu, c) postać skręcona dwuteownika [24]
Na rys. 8c przedstawiono dwuteownik skręcony o kąt $\varphi$ i transformację przekrojowego momentu zginającego $M_y$ do konfiguracji odkształcownej.
W niniejszym artykule nie zajmujemy się sformalizowana, matematyczną teorią bimomentów oraz z ich transformacją, a dla dalszych rozważań wystarczająca jest techniczna definicja bimomentu jako pary momentów.
Przy zginaniu nieswobodnym powstaje jeszcze jedna nowa siła przekrojowa – moment giętno-skrętny $M_\omega$ ($\ref{54}$).
Modelowanie pręta cienkościennego
Kontur przekroju cienkościennego jest sprowadzony do linii środkowych ścianek pręta, które są umieszczone w osiach ścianek a cała grubość odcinka skupia się na linii środkowej. To znaczy przekrój składa się z odcinków, o długości $l_i$ którym przypisano grubości $t_i$ Linie środkowe rys. 6 oznaczono linią przerywaną. W takim modelu przekroju cienkościennego charakterystyki geometryczne przekroju (A, Iy, Iz, itd) różnią się od wartości wyliczonych z klasycznych definicji (p. przykład 2).
Specyficznym typem podpory w analizie prętów cienkościennych jest podpora widełkowa, czyli taka w której nie jest możliwy kąt obrotu. Na rys. 9 pokazano jedną z możliwych realizacji podpory widełkowej, a obok pokazano stosowany symbol podpory i warunki brzegowe generowane przez podporę widełkową.
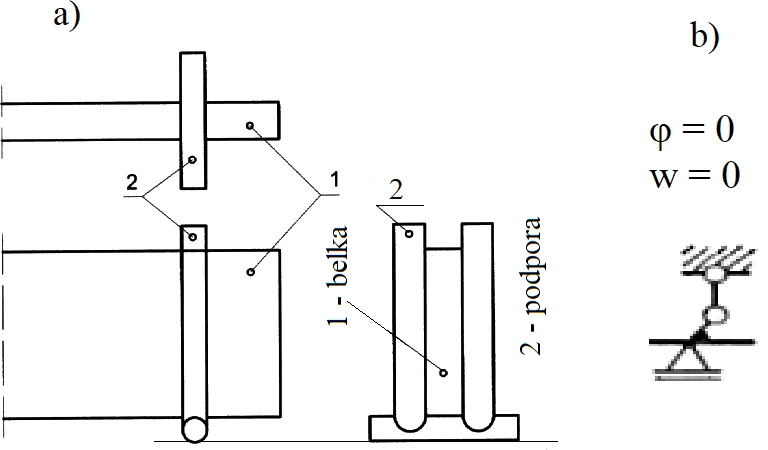
Rys. 9 Podpora widełkowa pręta cienkościennego: a ) przykład realizacji podpory, b) symbol i warunki brzegowe ( uzupełniony rys. 4.13 (Bródka J., Broniewicz N., Giżejowski M. , Kształtowniki gięte. Poradnik projektanta, PWT, Rzeszów , 2006))),
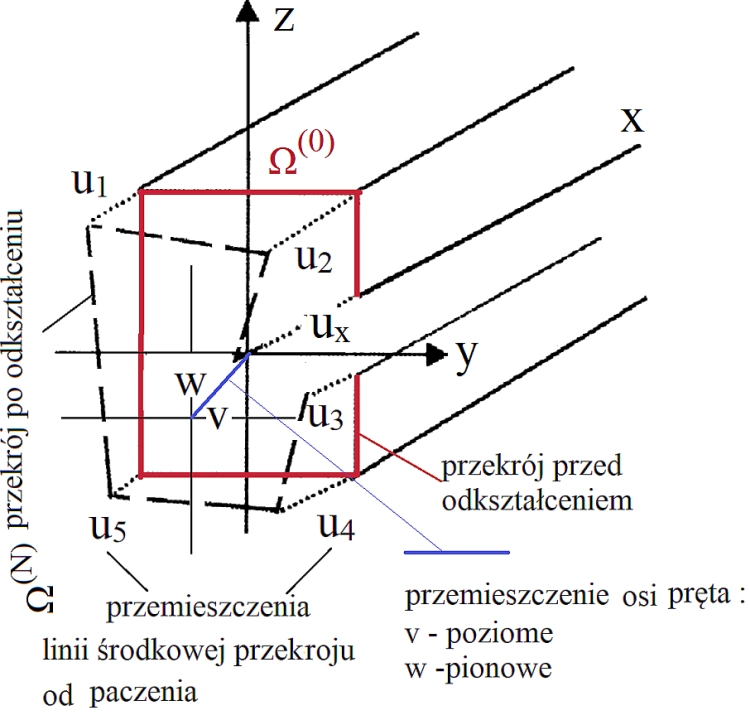
Pole przemieszczeń
Pole przemieszczeń liniowych pręta cienkościennego, opisanych formułą ($\ref{30}$), zaprezentowano na rys.10. Znamienna dla prętów cienkościennych deplanacja przekroju objawia się różnicami przemieszczeń podłużnych punktów przekroju $u_1$ do $u_5$z konfiguracji początkowej (przed odkształceniem) $\Omega^{(0)}$ do konfiguracji po odkształceniu $\Omega^{(N)}$. W celu zwiększenia czytelności na rys.9. nie wniesiono oznaczeń kątów obrotu oraz paczenia.
Przemieszczenia poprzeczne do osi pręta: pionowe $w$ oraz poziome $v$ rozpatruje się zgodnie z klasyczną teorią belki Bernoulliego.
Pole naprężeń
Naprężenia normalne
Naprężenia normalne w punkcie przekroju pręta cienkościennego $P(y^{(P)} , z^{(P)}, \omega^{(P)})$ wyznacza się z podstawowej zależności technicznej teorii prętów
$$\begin {equation} \sigma_x^{(P)} = \cfrac{N}{A} \cfrac{M_y }{I_y} z^{(P)} – \cfrac{M_z}{I_z} y^{(P)} + \cfrac{B_\omega^P }{I_\omega} \omega^{(P)} \label{36} \end {equation}$$
gdzie:
$(x, y, \omega)$- układ współrzędnych przekroju w osiach głównych centralnych (x,y) i głównego bieguna S oraz głównego punktu początkowego (B_\omega);
$N$, $M_y$, $M_z$, B_\omega$ -s siły przekrojowe : siła osiowa moment zginający względem osi y , osi z oraz bimoment
Dwa pierwsze składniki wywołane są zginaniem pręta, a trzeci składnik wywołany jest skręcaniem skrępowanym i jest specyficzny dla prętów cienkościennych
W formule ($ref\{36}$) nie uwzględniono efektów niestateczności pręta i przekroju. Efekty te sa przedmiotem innych artykułów: niestateczność przy ściskaniu , zginaniu pręta, klasie przekroju .
W przykładach pokazano technikę wyznaczania i sumowania naprężeń normalnych.
Naprężenia styczne
Naprężenia styczne wyznacza się z zależności
$$\begin {equation} \tau^{(P)} = \cfrac{V_z\cdot \overline S_y^{(P)}}{I_y \cdot t^{(P)}}+\cfrac{V_y\cdot \overline S_z^{(P)}}{I_z \cdot t^{(P)}} + \cfrac{M_\omega \cdot \overline S_\omega^{(P)} }{I_\omega \cdot t^{(P)}}+ \tau_v \label {37}\end {equation}$$
gdzie:
$V_y$, $V_z$, $M_\omega$ – siły przekrojowe : siła poprzeczna wzdłuż osi y , osi z oraz moment gięto-skrętny.
$I_y,I_z, I_\omega$ – momenty bezwładności jak w (\ref{36}$)
$ \overline S_y$, $\overline S_y$, $\overline S_\omega$ momenty statyczne odciętej części przekroju w punkcie P: giętne względem osi y,z oraz wycinkowy.
Dwa pierwsze składniki ($\ref{37}$) wywołane są ścinaniem pręta podczas zginania, trzeci składnik wywołany jest skręcaniem skrępowanym i jest specyficzny dla prętów cienkościennych.
Ostatni składnik jest wywołany skręcaniem pręta momentem Saint-Venata $M_v$ wyznacza się w odmienny sposób zależnie od stopnia zamknięcia przekroju pręta. W przypadku przekroju otwartego wyznacza się je z zależności ($\ref{24}$) , w przypadku przekroju zamkniętego z zależności ($\ref{26}$) , w przekroju quasi-zamkniętego zgodnie z procedurą opisaną w rozdziale Prety wielogaleziowe
W przykładach pokazano technikę wyznaczania i sumowania naprężeń stycznych.
Podstawowe zależności różniczkowe
Równanie skręcania nieswobodnego
Równanie skręcania pręta o przekroju cienkościennym (otwartym , zamkniętymi mieszanym), obciążonego rozłożonym wzdłuż jego osi $x$ momentem skręcającym o intensywności $m_s (x)$ ma następującą postać
$$\begin {equation} \overline E I\omega \cdot \cfrac{d^4 \varphi}{dx^4} \, – \, GI_v \cdot \cfrac{d^2 \varphi}{dx^2} = m_s (x) \label{38} \end {equation}$$
gdzie:
$\varphi(x)$ – kąt skręcenia przekroju pręta wokół osi x,
$\overline E$ zastępczy moduł Youmge’a ($\ref{30}$)
$I_\omega$ – wycinkowy moment bezwładności,
($EI\omega$ – sztywność giętno-skrętna przekroju pręta),
G- moduł Kirchoffa,
$I_v$ – moment bezwładności czystego skręcania (Saint Venanta)
($GI_v$ – sztywność skrętna przekroju pręta) ,
czyli ma postać różniczkową podobną do klasycznego równania zginania względem osi y belki Timoshenko o zwartym przekroju, sztywności giętnej $EI_y$ i sztywności na ścinanie $kGA$ obciążonej rozłożonym, i pionowymi siłami $q_z$
$EI_y \cdot d^4 w /dx^4 + kGA \cdot (\cfrac{d^2 w}{dx^2} + \cfrac{d^2ψ}{dx^2}) = q_z (x)$ , gdzie $w(x)$ jest ugięciem pręta, wywołanym obciążeniem pręta $q_z(x)$.
Ugięcie $w(x)$ belki i kąt obrotu zginania ψ(x)w punkcie belki x zależą od sztywność zginania $EI_y$ i sztywności na ścinanie $kGA$ belki ( k to współczynnik uwzględniający kształt przekroju, G – moduł Kirchhoffa, A – pole przekroju poprzecznego).
Rozwiązanie równania skręcania nieswobodnego
Równaniem stanu pręta cienkościennego jest równanie kąta skręcenia $\varphi (x,y)$. Inne zmienne stanu. w tym siły przekrojowe można wyznaczyć z formuł zależnych tylko od kąta skręcenia i jego pochodnych (patrz ($\ref{49}$), ($\ref{50}$), ($\ref{51}$)) .
Znajdziemy rozwiązanie równania ($\ref{38}$) zapisanego w postaci
$$\begin {equation} \varphi^{(iv)} (x) – \alpha^2 \varphi^{(ii)}(x) = \cfrac{m_s(x)}{EI_\omega}\label{39} \end {equation}$$
gdzie
$$\begin {equation} \alpha^2= \cfrac{GI_v}{EI_\omega} \label{40} \end {equation}$$
Rozwiązanie zwyczajnego równania różniczkowego ($\ref{39}$) jest sumą całek: ogólnej równania jednorodnego $\varphi_o (x)$ i szczególnej równania niejednorodnego.$\varphi_s (x)$
$$\begin {equation} \varphi (x)= \varphi_o (x) +\varphi_s (x) \label{41} \end {equation}$$
Zgodnie z metodą podaną przez Eulera poszukujemy rozwiązania równania jednorodnego
$$\begin {equation} \varphi^{(iii)} (x) – \alpha^2 \varphi^{(i)} (x) = 0 \label{42} \end {equation}$$
w postaci $e^{rx}$. Po podstawieniu przewidywanej postaci rozwiązania uzyskujemy następujące równanie charakterystyczne
$$\begin {equation} r^4- \alpha^2 r^2 = 0 \label{43} \end {equation}$$
które ma cztery pierwiastki
$$\begin {equation} r_1= 0 ; \quad r_2=0 ; \quad r_3=\alpha , \quad r_4 = -\alpha \label{44} \end {equation}$$
Całkę ogólną równania różniczkowego liniowego ($\ref{42}$) można zapisać więc jako kombinację liniową funkcji wykładniczych:
$$\begin {equation} A e^0 + B e^0 + C e^{\alpha x} + D e^{-\alpha x} \label{45} \end {equation}$$
Po zastąpieniu funkcji wykładniczych ich liniową kombinacją funkcji wykładniczych, zdefiniowanych jako funkcje hiperboliczne
$sinh(\alpha x) = \cfrac {e^{\alpha x}- e^{- \alpha x}}{2}$ oraz
$cosh(\alpha x) = \cfrac {e^{k\alpha }+ e^{- k \alpha}}{2}$
$$\begin {equation} \varphi_o(x) = C_1 + C_2 \cdot sinh (\alpha x) + C_3 \cdot cosh (\alpha x) +C_4 \label{46} \end {equation}$$
Całka ogólna metody parametrów początkowych
Całkę ogólną ($\ref{46}$) można przekształcić do postaci dogodnej do obliczeń metodą parametrów początkowych:
$$\begin {equation} \varphi_o(x) = C_1 + C_2 \cfrac{1}{\alpha} sinh (\alpha x) + C_3 \cfrac{1}{\alpha^2 \overline E I_\omega} \left [ 1- cosh (\alpha x) \right] + C_4 \cfrac{1}{ \alpha^3 \overline E I_\omega} \left [ \alpha x – sinh(\alpha x) \right ] \label{47} \end {equation}$$
Całka szczególna $\varphi_s(x)$ zależy od rozkładu momentów skręcających $m_s (x)$ po długości pręta i zwykle przyjmuje się ją metodą przewidywania.
Na przykład w przypadku pręta obciążonego momentem skręcającym $m_s =const$ stałym na całej długości pręta (schemat 1.3.5.7 w tab. 4) całkę szczególną można zapisać w postaci
$$\begin {equation} \varphi (x) = \cfrac{ -m_s}{\alpha^4 \overline E I_\omega} \left [ \cfrac{1}{2} (\alpha x)^2 +1 – cosh (\alpha x) \right ]\label{48} \end {equation}$$
Warunki brzegowe a stałe całkowania
Stałe całkowania $C_1, \, C_2 \, , \, C_3 , \, C_4$ w rozwiązaniu ($\ref{47}$ wyznacza się ze statycznych i kinematycznych warunków brzegowych.
W tab. 4 zapisano warunki dla najczęściej spotykanych schematów belek cienkościennych.
W innych przypadkach dobór warunków brzegowych przebiega z uwzględnieniem zasad:
- $C_1$ jest kątem obrotu $\varphi (x=0) $ na początku belki (x=0),
- $C_2$ jest pochodną kąta skręcenia $\varphi (x=0),$
- $C_3$ jest bimomentem $B_{\varphi}(x=0)$ ,
- $C_4$ jest momentem skręcającym $M_x (x=0)$
przy czym:
- przy braku obrotu $\varphi=0$ i swobodzie skręcania $M_x=0$, warunek brzegowy; $\varphi^{(iii)} – \alpha^2 \cdot \varphi^{(i)}= 0$
- dla swobodnego końca obciążonego momentem $M_s$ warunek; $ \overline E I_\omega \sim \varphi^{(iii)} – \alpha^2 \varphi^{(i)}- M_x$
- w przypadku swobodnego paczenia $B_\omega=0$, czyli $\varphi^{(ii)}=0$
- przy braku spaczenia końcowego przekroju $u=0$, czyli $\varphi^{(i)}=0$
Analizy prowadzone w pracy [13] pozwalają postawić warunki brzegowe dla bardziej złożonych przypadków z dokładnością pozwalającą uwzględniać pojedyncze więzi składających się na deplanację przekroju.
Siły przekrojowe w skręcanym pręcie cienkościennym
Skręcanie pręta cienkościennego wywołuje siły przekrojowe, które można wyznaczyć po wyznaczeniu funkcji kąta skrecenia pręta $\varphi(x)$ ($\ref{41}$) z zależności różniczkowych:
moment czystego skręcania (Saint Venanta)
$$\begin {equation} M_v(x) = GI_v \varphi ^{i} (x) \label{49} \end {equation}$$
bimoment
$$\begin {equation} B_\omega (x) = – EI_\omega \varphi ^{ii} (x) \label{50} \end {equation}$$
moment giętno- skrętny
$$\begin {equation} M_\omega (x) = – EI_\omega \varphi ^{iii} (x) \label{51} \end {equation}$$
Praktycznie w każdej sytuacji pręty skręcane są jednocześnie zginane i ścinane, Siły przekrojowe od obciążenia zginającego (poprzecznego do pręta w płaszczyżnie i z płaszczyzny zginania określa się w sposób standardowy, znany z podstawowego kursu mechaniki prętów,
Charakterystyki geometryczne przekroju cienkościennego
Przekrój cienkościenny otwarty
Współrzędna wycinkowa
Lokalny krzywoliniowy układ współrzędnych $(x,s,n)$ w dowolnym punkcie powierzchni środkowej pręta (rys. 10) definiujemy w ten sposób, że pierwszą oś układu określamy jako równoległą do osi globalnej $x$, przyjmując dla niej to samo oznaczenie (rys 5a) o wersorze $\overset{\to}{e_x}$. Druga oś $s$ jest styczna do linii środkowej, definiuje wersor $\overset {\to}{e_s}$. Oś trzecia $n$ jest wyznaczona wersorem $\overset {\to}{e_n}= \overset {\to}{e_x} \times \overset{\to}{e_s}$ Początek osi spółrzędnej łukowej $s$ przyjmujemy w ustalonym punkcie $O$ na linii środkowej, zwanym początkiem przekroju. Punkt B jest dowolnie przyjętym biegunem z którego prowadzi się promienie $\rho(s)$ do punktu bieżącego $M(s)$ i promień $ \rho (s+ds)$ do punktu bieżącego po przyroście współrzędnej łukowej s.
Obok zdefiniowanych wyżej współrzędnych w analizie prętów cienkościennych posługujemy się jeszcze współrzędną wycinkową $\omega$. Przy znajomości linii środkowej, położenia punktu początkowego (O) i bieguna (B) – współrzędna wycinkowa w sposób jednoznaczny wyznacza położenie dowolnego punktu (P). Wartość współrzędnej wycinkowej punktu (P) zależy zarówno od położenia bieguna (B) jak i punktu początkowego (O) – najczęściej punktu zerowej współrzędnej wycinkowej.
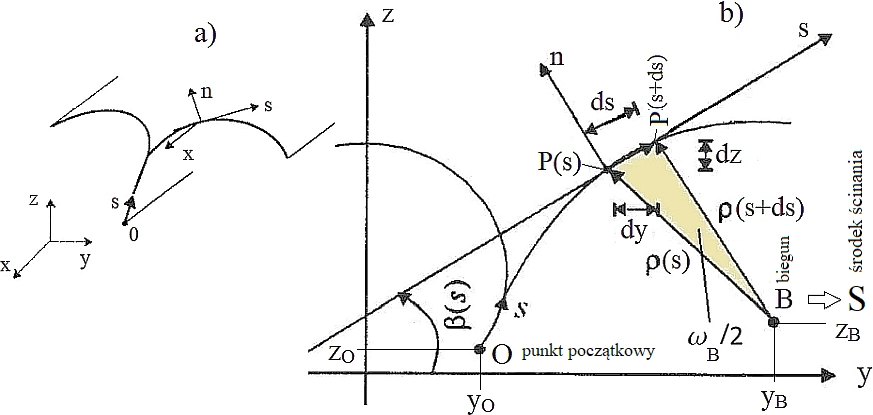
Rys. 11 Współrzędne przekroju cienkościennego otwartego (s, n, $\omega$), gdzie $\omega$ – współrzędna wycinkowa: a) układ globalny (x,y,z) i lokalny (x,n,s) współrzędnych punktu, b) współrzędna wycinkowa $\omega$ zmodyfikowane [25]
Współrzędne wersorów lokalnego układu, w dowolnym punkcie $P(s)$ odniesione do układu globalnego zapiszemy w postaci macierzy [C]:
$$ \begin{equation} [C] = \left[ \begin{array}{cc}
y^{’}(s) \vec{e_x} & z^{’}(s) \vec{e_x} \\
– z^{’}(s) \vec{e_n} & y^{’}(s) \vec{e_n}
\end{array} \right ] \label {52} \end{equation}$$
gdzie: $ y^{’}(s) = \cfrac{dy(s)}{ds}$, $z^{’}(s) =\cfrac{dz(s)}{ds}$
Na linii środkowej przekroju poprzecznego pręta przyjmiemy dowolny punkt (P) o wektorze wodzącym $\overset {\to}{\rho} (s)$ zaczepionym biegunie B o współrzędnych $B (0 \ , \, y_b \ , \, z_b)$ oraz utworzymy iloczyn skalarny, który oznaczymy przez $ [d \omega_B](s)$:
$$\begin {equation} [d \omega_B] = \vec {\rho}(s) · \vec { e_n}(s) ds \label{53} \end {equation}$$
Geometryczną interpretacją bezwzględnej wartości $ | d_\omega](s) |$ jest podwojone pole powierzchni zawartej pomiędzy promieniami wodzącymi $\overset{\to}{\rho} (s)$ i $\overset{\to}{\rho}(s+ds)$, bowiem bezwzględna wartość iloczynu skalarnego przedstawia długość rzutu wektora $\rho(s)$ na normalną do krzywej, będącego wysokością wspomnianego trójkąta.
Współrzędną wycinkową względem dowolnego bieguna (B) definiujemy jako :
$$\begin {equation} \omega_B(s) = \int \limits_0^s [ d \omega_B] (s)= \int \limits _0^s \vec{\rho}(s)\cdot \vec{e}_n ds\label{54} \end {equation}$$
Jeśli współrzędna łukowa przebiega po kilku ściankach (bokach linii środkowej), to wówczas powyższe możemy zapisać jako sumę całek
$$\begin {equation} \omega_B(s)=\int_{0}^{s}\vec{\rho}(s) \cdot \vec{ e_n} ds =\sum \limits _{{i=1}}^{j-1}\int \limits_{s_O^{’}}^{s_M^{’}} \vec{\rho}(s) \cdot \vec{e_n} ds+\int \limits_{s_0^j}^{s}\vec{\rho}(s) \cdot \vec{ e_n} ds\label{55} \end {equation}$$
gdzie: $s_O^{’}$ i $s_P^{’}$ jest wartością współrzędnej łukowej punktu i-tej krawędzi początkowego (O) i końcowego (P) na odcinku linii środkowej odpowiednio,
Bezwzględna wartość każdego i-tego składnika sumy jest równa podwojonemu polu zawartemu pomiędzy wektorem wodzącym punktu $s_O^{’}$, i-tym bokiem linii środkowej oraz wektorem wodzącym punktu $s_P^{’}$.
Zależność ($\ref{54}$) można zapisać we współrzędnych globalnych (y,z) w postaci;
$$\begin {equation} \omega_B = \int_0^s ( z – z_B) dy – (y – y_B) dz = \int_o^s (z dy – y dz) – z_B \int_0^s dy + y_B \int_0^s dz = \omega_0 (s) – z_B [y(s) – y_0 ] +y_B [z(s) -z_9] \label{56} \end {equation}$$
gdzie $(y_0 , z_0, \omega_0) $ są wspólrzędnymi środka globalnego układu.
Zapisując to samo dla dowolnego bieguna (B’) innego od (B) i odejmując stronami uzyskujemy twierdzenie o zmianie bieguna:
Jeśłi znane są współrzędne punktu dla bieguna B o współrzędnych $(y_B, z_B, \omega_B)$ w układzie głównych centralnych osi bezwładności, to współrzędną wycinkową punktu przy zmianie bieguna do punktu B’ (y(B'{, z_{B’} można wynaczyć z zależności
$$\begin {equation} \omega_{B’}(s) = \omega_B (s) – (z_{B’}-z_B ) \left [ y(s) – y_0 \right ] +(y_{B’}-y_B ) \left [ z(s)-z_0 \right ]\label{57} \end {equation}$$
Należy podreślić, że wartość współrzędnej wycinkowej zależy od wyboru bieguna (B) oraz punktu początkowego (O’).
Główne współrzędne wycinkowe wyznaczane są dla bieguna w środku zginania (B=S) oraz głównego punktu początkowego (O’=O).
Środek zginania (ścinania) (S) i główny punkt początkowy (O)
Położenie środka zginania (S) oraz głównego punktu początkowego (O) wyznacza się z układu równań wynikających z samo-równoważenia się naprężeń normalnych $\sigma_\omega = \cfrac{B_\omega^P }{I_\omega} \omega^{(P)}$ ($\ref{36} $), co prowadzi do warunków:
$$ \begin{equation} \begin {cases}
S_\omega = \int _A \omega_S dA =0\\
I_{\omega,y} = \int _A \omega_S \cdot y dA =0\\
I_{\omega,z} = \int _A \omega_S \cdot y dA =0\\
\end {cases} \label{58} \end{equation} $$
gdzie:
$S_\omega$ – wycinkowy moment statyczny
$I_{\omega,y}$ i $ I_{\omega,z}$ – wycinkowe, odśrodkowe momenty bezwładności.
Środek zginania (S) (w literaturze nazywanym również środkiem ścinania lub skręcania lub głównym biegunem wycinkowym), jest takim biegunem (B), dla którego zerują się wycinkowe momenty odśrodkowe (dewiacji) $I_{\omega,y}$, $I_{\omega,z}$, czyli z zależności ($\ref{58})^2$ i ($\ref{58})^3$. Po zastosowaniu formuły transformacji współrzędnej wycinkowej – zamiany bieguna ($\ref{57}$) do układu głównych centralnych osi bezwładności uzyskujemy praktycznie stosowane wyrażenia na współrzędne środska zginania (S) :
$$\begin {equation} y_S = y_B +\cfrac{I_{\omega^{’}_B, y}}{I_y} \label{59} \end {equation}$$
$$\begin {equation} z_S = z_B +\cfrac{I_{\omega^{’}_B, z}}{I_z} \label{60} \end {equation}$$
gdzie $\omega^{’}_B$ jest współrzędną wycinkową punktu (P) wyznaczoną z dowolnego (pomocniczego) bieguua (B) i zliczaną od dowolnego, pomocniczego punktu początkowego (O’).
Położenie głównego punku początkowego (O), określone współrzędną wycinkową $\omega_S(O)$ oblicza się po wyznaczeniu środka zginania (S) z warunku ($\ref{58})^1$ zapisanego w postaci
$$\begin {equation} \omega_S(O) = \omega_S^{’} – \cfrac{S_{\omega}^{’} }{A}\label{61} \end {equation}$$
gdzie $S_{\omega}^{’} = \int_A \omega_S^{’}$ jest wycinkowym momentem statycznym wyznaczonym względem środka zginania (S) dla współrzędnej zliczanej od dowolnego pnktu pomocniczego (O’)
Współrzędną pomocniczą $\omega_S^{’}$ względem środka zginania (S) od pomocniczego punktu początkowego (O’) najprościej wyznaczyć z ($\ref{57}$)po wuzględnieniu, że $y_0=0$, $z_0=0$:
$$\begin {equation} \omega_S^{’}(s) = \omega_B^{’} (s) – ( z_S -z_B ) \cdot y(s) + (y_S – y_B )\cdot z(s) \label{62} \end {equation}$$
gdzie $(y_s,z_s)$, $(y_B,z_B) – współrzędne środska zginania i pomcnioczego bieguna w układzie si głównych, centralnych.
Przekrój cienkościenny zamknięty
Współrzędna wycinkowa
Zamknięty przekrój cienkościenny jest niewyznaczalny w schemacie rzeczywistym i w celu wyznaczenia głównych współrzędnych wycinkowych i związanych z nimi charakterystyk należy utworzyć schemat podstawowy – przekrój otwarty) przez przecięcie przekroju w dowolnym punkcie (k) – rys. 12 .
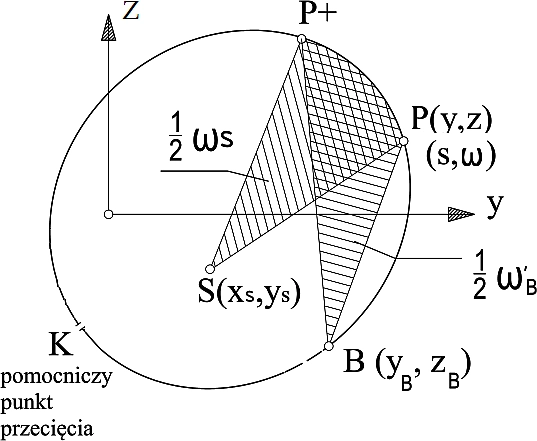
Rys. 12. Wyznaczanie głównej współrzędnej wycinkowej przekroju zamkniętego [8]
Uogólniony wycinkowy moment bezwładności dla dowolnego przekroju zamkniętego oblicza się ze wzoru
$$\begin {equation} I_{\overline \omega}=\oint \overline \omega^2 dA \label{63}\end {equation}$$
w którym $\overline \omega$ oznacza uogólnione pole wycinkowe względem środka ścinania $S$ przekroju od głównego punktu początkowego $O$.
W celu wyznaczenia ($\ref{63}$) najpierw oblicza się pomocnicze współrzędne wycinkowe $\overline \omega’_B$ w podstawowym przekroju otwartym (dla obszaru przeciętego w dowolnym punkcie (K) – rys. 13 ) względem przyjętego (tego samego) bieguna pomocniczego (B) od doolnego pomocniczego pubktu począgtkowego (O.)
Pole wycinkowe względem bieguna $B$ od dowolnego punktu początkowego O’ na konturze, oblicza się ze wzoru
$$\begin {equation} \overline \omega’_B= \omega’_B -\cfrac{\overline s}{\overline s_0} \cdot 2 \Omega \label{64}\end {equation}$$
gdzie:
$\overline s= \int \limits_0 \limits^s \dfrac {t_0} {t(s)} ds$ – sprowadzona współrzędna $s$ (długość konturu) liczona od punktu O’.
Środek zginania (ścinania)
Współrzędne środka ścinania (skręcania) (S) przekroju zamkniętego wyznacza się w układzie centralnych , głównych osi bezwładności, (y, z) z następujących wzorów:
$$\begin {equation} y_S = y_B – \cfrac{ I_{\overline \omega, y} }{I_y} \quad ; \quad z_S = z_B + \cfrac{ I_{\overline \omega, z} }{I_z} \label{65}\end {equation}$$
gdzie:
$y_B$, $z_B$ – współrzędne dowolnie przyjętego bieguna $B$, który na ogół przyjmuje się na konturze,
$I_{\overline \omega, y}= \oint \ovyerline \omega_B \cdot z \, dA $ ,
$I_{\overline \omega, z}= \oint \ovyerline \omega_B \cdot y \, dA $,
$I_y$, $I_z$ – główne momenty bezwładności przekroju poprzecznego względem głównej osi poziomej y i pionowej z odpowiednio.
Pręty o przekroju trójkątnym i inne w kształcie wieloboku foremnego, ale o stałej grubości ścianki (t=const) nie ulegają deplanacji i ich charakterystyki wycinkowe są równe zeru.
Stan naprężeń
Naprężenia
Brak swobody deplanacji wywołuje naprężenie normalne do przekroju równe
$$\begin {equation} \sigma_\omega=E \cfrac {du} {dx}=-E \frac {d^2\varphi} {dx^2} \label{66} \end {equation}$$
gdzie $E$- moduł odkształcalności podłużnej (Younga), a $\varphi$ jest kątem skręcenia przekroju. Zachodzi
Można pokazać, że naprężenia normalne $\sigma_\omega$ można wyrazić za pomocą nowej siły przekrojowej bimomentu $B_\omega$ w postaci [16]:
$$\begin {equation} \sigma_{\omega}=\cfrac {B_{\omega}}{I_{\omega}} \cdot \omega \label{67} \end {equation}$$
Moment giętno-skrętny wywołuje naprężenia styczne $\tau_\omega$ o stałej wartości po grubości ścianki, które można wyznaczyć z zależności:
$$\begin {equation} \tau_\omega= \frac {M_\omega \cdot S_\omega}{I_\omega \cdot t} \label{68} \end {equation}$$
gdzie: $S_\omega$ – wycinkowy moment statyczny przekroju, $t$ – grubość ścianki przekroju., przy czym
$$\begin {equation} M_x= M_\upsilon + M_\omega \label{69} \end {equation}$$
Naprężenie styczne od momentu czystego skręcania wyznaczamy ze wzoru[26]:
$$\begin {equation} \tau_\upsilon= \cfrac {M_\upsilon }{W_\upsilon}\label{70} \end {equation}$$
gdzie:
$$\begin {equation} W_\upsilon= \cfrac {I_\upsilon }{max \, t_i } \label{71} \end {equation}$$
jest wskaźnikiem wytrzymałości przekroju na skręcanie, równym stosunkowi momentu bezwładności na skręcanie i maksymalnej grubości ścianki.
Dla przekroju cienkościennego przekroju cienkościennego otwartego, złożonego moment bezwładności na skręcanie można oszacować z zależności ($\ref{29}$)
W przypadku przekroju zamkniętego o powierzchni $\Omega$ zamkniętej wewnątrz linii środkowych przekroju, wskaźnik wytrzymałości przekroju na skręcanie, wynosi
$$\begin {equation} W_\upsilon = 2 \cdot \Omega \cdot min \{t_i \} \label{72} \end {equation}$$
gdzie występuje minimalna grubość $t$ ścianki przekroju.
Sztywność na skręcanie przekroju zamkniętego jest wielokrotnie większa od przekroju otwartego i jest proporcjonalna do podwojonego pola zawartego wewnątrz przekroju.
Ze skręcaniem skrępowanym mamy do czynienia w przypadku skrępowania deplanacji przekroju poprzecznego pręta. W wyniku tego w przekroju powstają naprężenia normalne $\sigma_{\overline \omega}$ oraz dodatkowe naprężenia styczne $\tau_{\overline \omega}$ . Naprężenia te wyznacza się ze wzorów:
$$\begin {equation} \sigma_{\overline \omega}=\cfrac {B_{\overline \omega} \cdot \overline \omega} {I_{\overline \omega}} \label{73} \end {equation}$$
$$\begin {equation} \tau_{\overline \omega}= – \dfrac {M_{\overline \omega} \cdot \overline S_{\overline\omega} } {I_{\overline \omega} \cdot t(s)} \label{74} \end {equation}$$
gdzie:
$\overline \omega$ – główne, uogólnione pole wycinkowe (współrzędna wycinkowa przekroju);
$I_{\overline \omega}$ – uogólniony wycinkowy moment bezwładności;
$ \overline S_{\overline \omega}$ – uogólniony wycinkowy moment statyczny przekroju.
Dodatnim naprężeniom $\tau_{\overline \omega}$ odpowiada zwrot zgodny z kierunkiem dodatniego przyrostu współrzędnej s.c
W odróżnieniu od prętów o przekrojów otwartym , giętno skrętne naprężenia styczne $\tau_{\overline \omega}$ stanowią samozrównoważone układy sił i tym samym cały moment skręcający $M_v$ przenoszą naprężenia styczne swobodnego skręcania $\tau_v$.
Całkowite naprężenie styczne w dowolnym punkcie przekroju znajduje się jako sumę $\tau_v+ \tau_{\overline \omega}$.
Charakterystycznym punktem przekroju cienkościennego jest środek zginania (zwany czasami środkiem skręcania lub środkiem ścinania). Jest to punkt położony w przekroju lub poza nim, taki, że obciążenie przechodzące przez ten punkt nie powoduje skręcania pręta, a tylko jego zginanie poprzeczne. W takim przypadku słuszna pozostaje zasada płaskich przekrojów Bernulliego i pręt jest poddany zginaniu bez udziału skręcania.
Przekroje wielokomorowe
Przekroje wielokomorowe analizuje się analogicznie do przekrojów zamkniętych. Z analogii mebranowej, wynika (z dokłądnością do $ (1+ t/l \approx 1)$, że funkcja naprezęń (Prandtla) $U$ zmienia się tylko po grubości ścianki $t$.Po uwzględnieniu warunków brzegowych na funkcję Prandtla $U$ można wykazać, że zależności są prawdziwe dla wszystkich zamkniętych komór przekroju.
w opracowaniu
Technika wyznaczania charakterystyk geometrycznych przekroju cienkościennego
Stosowane procedury matematyczne
Całkowanie numeryczne iloczynu dwóch funkcji
Obliczanie charakterystyk geometrycznych przekroju cienkościennego jest w praktyce prowadzone skróconymi metodami całkowania $\int f_0^L f(x)\cdot g(x) dx$ iloczynu dwóch funkcji $f(x)$ i $g(x)$ na odcinku ścianki o długości $L$
Wyznaczanie charakterystyk dotyczy przekroju cienkościennego sprowadzonego do konturu złożonego z linii środkowych ścianek ( p. modelowanie pręta cienkościennego).
Stosuje się następujące metody całkowania, umożliwiające uzyskanie ścisłych wyników:
- metodę trapezów MT,
- metodę Simpsona MS,
- metodę Mohra-Wereszczagina MM-W
- w metodzie MT – najwyżej liniowa $g(x) = a_g \cdot x + b_g$.
- w metodzie MS – najwyżej drugiego stopnia $g(x) = a_g \cdot x^2 + b_g\cdot x +c_g$.
- w metodzie MM-W – dowolna ale taka, dla której znane jest położenie środka ciężkości (współrzędna $x_{c,g}$)
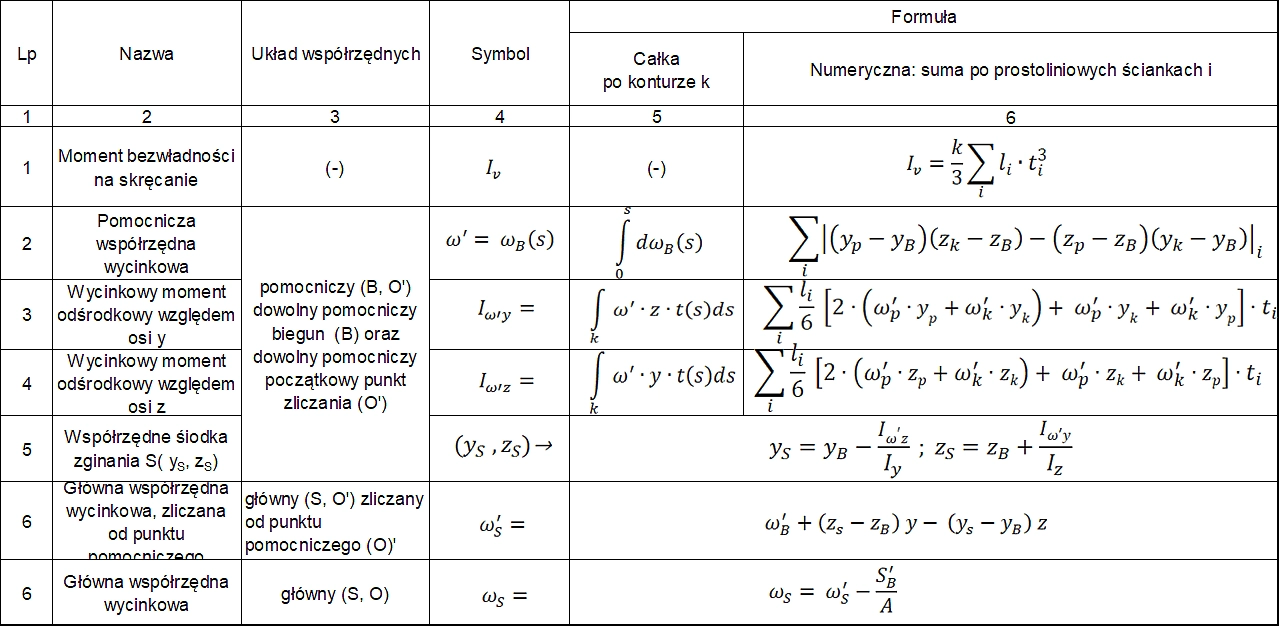
\cfrac{L}{6}\cdot \left [ 2\cdot (f_p \cdot g_p + f_k \cdot g_k ) + f_p \cdot g_k + f_k \cdot g_p \right] , & \text { dla metody MT }\\
\cfrac{L}{6}\cdot \left [ f_p \cdot g_p + 4\cdot f_s\cdot g_s + f_k \cdot g_k\right] , & \text { dla metody MS }\\
\Omega_g \cdot f(x_{c,g}) , & \text { dla metody MM-W }\\
\end {cases} \label{75} \end{equation} $$
W przypadku przekrojów złożonych z prostoliniowych ścianek wykresy współrzędnych $y$, $z$ oraz $\omega$ są liniowe i najprościej stosować metodę trapezów MT i fomułę $(\ref{75})^1$
W przypadku ścianek krzywoliniowych najczęściej stosuje się metodę MM-W.
Najprostszym przykładem zastosowania metody MM-W jest do wyznaczanie pola powierzchni przekroju z formuły
$$\begin {equation} A = \sum_i l_i \cdot t_i \cdot 1 \label{76} \end {equation}$$
Wyrażenie ($\ref{76}$) ma następującą interpretację całkowania geometrycznego MM-W:
na odcinku (ściance) „i” o długości $l_i$ ;
funkcja $ g(s) = t_i(s)$, czyli powierzchnia wykresu $\Omega_g = l_i \cdot t_i$; , a środek ciężkości wystąpi pod rzędną $x_{c,g}= l_i/2$
funkcja $f(s)≡1$ na całym odcinku $l_i$, więc: $fl_i/2)=1$.
Transformacja współrzędnych
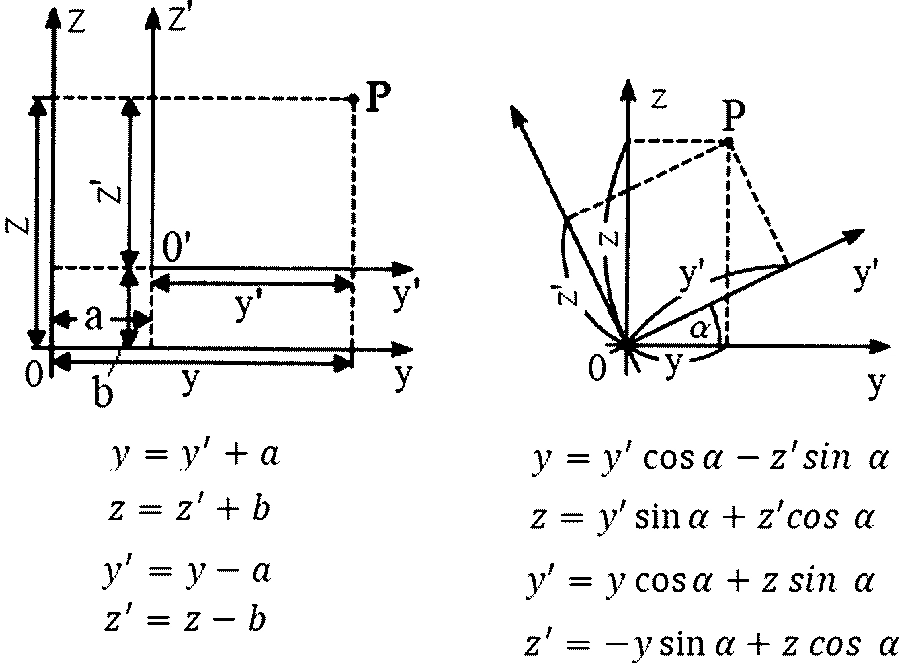
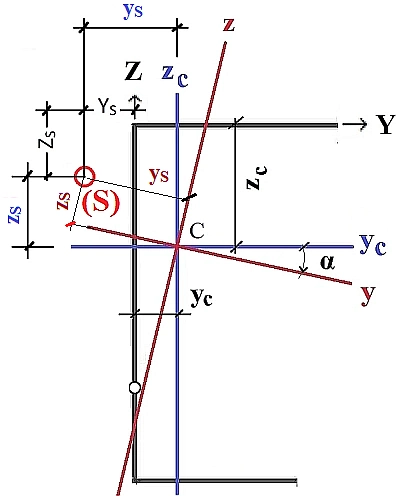
Charakterystyki geometryczne przekrojów wyznaczane są w kilku układach współrzędnych: układzie globalnym (początkowym (Y,Z), układzie centralnym $($y_c , z_c)$ (przechodzącym przez środek ciężkości , równoległym do osi globalnych lub układzie głównym (z,c) – centralnym, obróconym tak, by moment dewiacji zerował się. Operacje te podlegają matematycznym zasadom transformacji, które dla stosowanego w artykule prawoskrętnego (matematycznego ) układu współrzędnych przedstawiono na rys. 14 .
Charakterystyki wg formuł wspólnych dla otwartego i zamkniętego przekroju cienkościennego
Charakterystyki geometryczne przekroju cienkościennego wyznaczane w celu ustalenie układu osi centralnych, głównych wyznacza się zgodnie z formułami zestAwionymi w tab. 3,, kol. 7 , wrs. 1-10 i obejmują:
- pole przekroju A
- momenty statyczne przekorju $S_Y$ i $S_Z$ w układzie globalnym (Y,Z),
- współrzędne środka ciężkości przekroju (C) $(y_C, z_C)$,
- centralne momenty bezwładności w układzie globalnym (Y,Z),
- kąt nachylenia osi głównych $\alpha$
- główne centralne momenty bezwładności $I_y$, $I_z$
Charakterystyki wycinkowe dla przekroju otwartego
Charakterystyki wycinkowe dla przekroju zamkniętego
Pręty wielogałęziowe oraz kratownice wielopasowe
Pręty (kratownice) wielopasowe można przystosować do przenoszenia momentu skręcającego poprzez stosowny dobór zamykającego skratowania lub przewiązek. Przykładem skręcanych kratownic są galerie przenośnikowe, bramki nad autostradami lub słupy energetyczne. W ścianach takich kratownic powstają siły typowe dla swobodnego skręcania prętów o przekroju zamkniętym [8].
Pręty wielogałęziowe
Na rys.15 pokazano cienkościenny przekrój quasi-zamknięty oraz przykłady prętów o dwu gałęziach, które mogą być łączone skratowaniem lub przewiązkami w sposób często stosowany przy konstruowaniu dwugałęziowych slupów. Przekrój pozornie zamknięty skratowaniem lub przewiązkami można zamodelować zastępczym przekrojem cienkościennym i zastosować analogię prętową.

Rys. r5 Pręty wielogałęziowe: a) przekrój b), c) skratowany, d) z przewiązkami [8]
Sztywność przekroju na czyste skręcanie bez uwzględnienia pozornego zamknięcia wyznacza się standardowo z zależności ($\ref {23}$). Oznaczymy go jako moment bezwładności czystego skręcania przekroju otwartego
$$\begin {equation} I_{v,open} =k/3\sum_i l_i \cdot t_i^3 \label{77} \end {equation}$$
Zwiększenie sztywności przekroju na skutek zamknięcia go skratowaniem lub przewiązkami można oszacować z zależności [8]:
$$ \begin{equation} \overline I_{v,close} =\begin {cases}
\cfrac{E}{G}\left ( \cfrac{\Omega}{b} \right )^2 \cdot \ A_k \cdot \ sin^2\alpha\cos\alpha , & \text { dla skratowania typu N (bezsłupkowe) – rys. 14c }\\
\cfrac{E}{G} \left( \cfrac{\Omega}{b} \right )^2 \cdot \cfrac {A_s \cdot A_k \cdot \ sin^2\alpha \cdot cos\alpha} {A_s + A_k \ sin^3\alpha}, & \text {dla skratowania typu V – rys. 14b }\\
24 \cfrac{E}{G} \cdot \left ( \cfrac{\Omega}{b} \right )^2\cdot \cfrac{I_f}{a^2}\left ( 1+2\cfrac{b_1\cdot I_f}{a \cdot I_p}+28,8 \cdot \cfrac{E}{G} \cfrac{I_f}{ab_1 A_p} \right )^{-1} , & \text { dla przewiązek – rys. 14d }\\
\end {cases} \label{78} \end{equation} $$
gdzie:
$E, \, G$ – moduł Younga i moduł Kirchoffa materiału;
$\Omega= 2 \cdot b \cdot h$
$b, b_1$- prześwit i odległość osiowa między gałęziami pręta;
$a$- odległość osiowa między przewiązkami lub węzłami skratowania.
$A_k$, $A_s$ , $A_f$ – pole przekroju krzyżulca, słupka, gałęzi;
$I_f$- moment bezwładności giętnej pojedynczej gałęzi
Całkowity moment bezwładności czystego skręcania przekroju quasi-zamkniętego jest szacunkowo sumą powyższych części
$$\begin {equation} I_v = I_{v,open} +I_{V,close} \label{79} \end {equation}$$
Równanie różniczkowe pręta ($\ref{79}$) należy rozwiązać dla całkowitego momentu bezwładności ($\ref{79}$).
W wyniku uzyskujemy siły przekrojowe $B$, $M_\omega$ $M_v$ ($\ref{50}$) do ($\ref{52}$), przy czym należy uwzględnić, że uzyskany moment $M_v$ odpowiada swobodnemu skręcaniu pręta quasi-zamkniętego o zwiększonej sztywności w stosunku do pręta nie zamkniętego skratowaniem lub przewiązkami. W4
W celu obliczenia naprężeń stycznych swobodnego skręcania należy moment $M_v$ podzielić na część odpowiadającą przekrojowi otwartemu $M_{v,open} = $M_v \cdot \cfrac{{I_{v,open}}{I_v}$ oraz zamkniętemu $ M_{v,close}= M_v- M_{v,open}$. Dla tak obliczonych momentów można stosować wyrażenia odpowiednie dla danego typu przekroju, ro znaczy ($\ref{24}$) dla części odpowioqadajaćej przekorjowi otwartemu i wg zależnosći ($\ref{26}$) dla części odpowiadającej przekrojowi zamkniętemu.
Siły w prętach skratowań zamykających przekrój pręta (rys. 15 b,c) wyznacza się uwzględniając fakt, że są wywołane przez rozłożone obciążenie działające na ściankę o wartości
$$\begin {equation} q_v = \cfrac{I{v,close} }{I_v} \cdot \cfrac{M_v}{\Omega} \label{80} \end {equation}$$
W przypadku stężenia przewiązkami (rys. 14d) należy ponadto uwzględnić wpływ miejscowych momentów zginających
$$\begin {equation} M_1 = \cfrac{1}{4} q_v \cdot a \cdot b_1\label{81} \end {equation}$$
gdzie $g_v$ wg ($\ref{80}$).
Kratownice wielopasowe
Metoda analogii pręta cienkościennego może by stosowana do wstępnego zaprojektowania skręcanej kratownicy wielopasowej w sposób pokazany na rys. 2.
Do wstępnego wymiarowania prętów kratownic przestrzennych można pomijać zmniejszający wpływ quasi-zamknięcia pręta skratowaniem. Przy takim założeniu dla kratownicy czteropasowej lub trójpasowej pokazanych na rys. 16, kraty płaskie kratownic przestrzennych pokazanych na rys. 2 sa poddane równomiernie rozłożonemu obciążeniu zewnętrznemu Q :
$$ \begin{equation} Q=\begin {cases}
\cfrac{M_v\cdot a }{2ab}=\cfrac{M_v }{2b} , & \text { dla kraty pionowej K1 i K2 kratownicy czteropasowej }\\
\cfrac{M_v\cdot b }{2ab}=\cfrac{M_v }{2a} , & \text { dla kraty poziomej K3 i K4 kratownicy czteropasowej }\\
\cfrac{M_v }{a\cdot\sqrt{3}} , & \text { dla krat K1, K2 i K3 kratownicy trójpasowej}\\
\end {cases} \label{82} \end{equation} $$
Obciążenia poprzeczne $Q$ są przyłożone do wydzielonej kratownicy płaskiej zgodnie z przebiegiem momentu skręcającego $M_v(x) $ po długości pręta x. Siły w prętach kratownicy wyznacza się poprzez rozwiązanie kratownic płaskich pod takim obciążeniem. Należy pamiętać o sumowaniu sił w pasach od poszczególnych kratownic składowych z uwzględnieniem kierunku obciążenia Q, skąd wynika, że w szczególności, że przypadku przekroju kwadratowego a=b siły osiowe w pasach będą zerowe, a całkowity moment skręcający przenosi skratowanie ścian.
Kratownica przestrzenna, przenosząca skręcanie powinna być skratowana na wszystkich płaszczyznach bocznych oraz powinna być wyposażona w poprzeczne przepony w miejscach przyłożenia momentów (w tym w zamocowaniu) oraz nie rzadziej niż co 8-me pole kratownicy. Do wyznaczania przemieszczeń kratownicy od wpływu skręcania należy uwzględniać współczynnik $k_v <1$. Analizując kratownice w modelu zastępczym pręta w złożonym stanie obciążenia (zginanie, ścinanie, skręcanie) należy stosować element Timoshenko.
Przykłady rachunkowe
Przykłady w przygotowaniu
Przykład 1 [Współrzędne wycinkowe dla typowych przekrojów otwartych prętów stalowych; I (H) , C, Z]
Rykaluk (2012) [15].
Wyznaczyć główne współrzędne wycinkowe $\omega$, moment bezwładności na skręcanie $I_v$ oraz główny wycinkowy moment bezwładności $i_\omega$ dla dwuteownika, ceownika i zetownika.
Dwuteownik I (H)
Analizowany jest model cienkościennego przekroju ( złożony z linii środkowych ścianek). Wysokość przekroju wynosi $h$, szerokość stopki $b$, grubość stopek $t_f$, a grubość środnika $t_w$.
Przekrój jest bisymetryczny , więc środek zginania (ścinania) $S$ pokrywa się ze środkiem ciężkości $C$
Główne współrzędne wycinkowe wyznacza się z bieguna, którym jest środek zginania jako podwojone pole zakreślone przez promień wodzący, jak następuje:
punkt $P_0 \to$ $\omega_{P0}= 2\cdot h/2 \cdot 0 = 0$
punkt $2 \to $ : $\omega_2 = + 2 \cdot 1/2 \cdot h/2 \cdot b/2 = + \cfrac{b h }{4}$ (znak + , bo promień wodzący zakreślił w prawo),
punkt $1 \to $ : $\omega_1 = – 2 \cdot 1/2 \cdot h/2 \cdot b/2 = – \cfrac{b h }{4}$ (znak – , bo promień wodzący zakreślił w lewo),
analogiczne rzędne na stopce dolnej 2ynoszą $\omega= +/- bh/4$
Moment bezwładności na skręcanie
$ (\ref{23}) \to I_v = \cfrac{1}{3} \left (2 b t_f^3 + h t_w^3 \right)$
Główny wycinkowy moment bezwładności:
$I_\omega = \cfrac{b}{6} \cdot \left [ \right ] = \cfrac{h^2}{4} \cdot \cfrac{2 t_f b^3}{12}$

Rys P1-1. Współrzędne wycinkowe dla dwuteownika, ceownika i zetownika [15]
Wykresy głównych współrzędnych wycinkowym podsumowano na rys P1-1.
Przykład 2 [Różnica w wyznaczaniu momentu bezwładności przekroju wg tablic, traktowanego jako zwarty lub cienkościenny ]
Różnice w momentach bezwładności przekroju zwartego i cienkościennego pokażemy na na przykładzie dwuteownika szerokostopowego HEA,. dla którego dane z tablic przytoczono w tab. P2-1.
Tab.P2-1. Dane dwuteowników HEA z tablic hutniczych
W tab. P2-2 zestawiono charakterystyki przekroju HEA wyznaczone jak dla przekroju zwartego oraz cienkościennego.
Tab.P2-2. Charakterystyki dwuteowników HEA traktowanych jak przekrój zwarty oraz cienkościenny
Charakterystyki geometryczne jak dla przekroju zwartego wyznaczono z pominięciem wyokrągleń naroży profilu. Przykładowo pole przekroju $A_{zwarty}$ oraz moment bezwładności $I_{y, zwarty}$ wyznaczano podług formuł:
$A_{zwarty} = A_w + 2 \cdot A_f$,
$I_{y, zwarty} = \cfrac{ t_w \cdot h_w^3 }{12}+ 2 \cdot \left [ \cfrac{b \cdot t_f^3}{12} + A_f \cdot (h_c/2)^2 \right ]$
gdzie:
$A_w = h_w \cdot t_w$,
$A_f = b \cdot t_f$,
$h_w= h – 2 \cdot t_f$
$h_c= h – t_f$
Dla przekroju cienkościennego w wyrażeniach na momenty bezwładności pomijamy składniki, w których występuje grubość ścianki podniesiona do trzeciej potęgi, o to dlatego, że cała grubość odcinka skupiona jest na jego linii środkowej., a także różnicę w definicji wysokości przekroju. W rezultacie otrzymujemy
$A_{cienko} = A_w + 2 \cdot A_f$,
$I_{y, cienko} = \cfrac{ t_w \cdot h_w^3 }{12}+ 2 \cdot \left [ A_f \cdot (h_c/2)^2 \right ]$
W tab P2-2 podano współczynniki $k_y$, $k_z$, $k_v$ oraz $k_\omega$, stanowiące stosunki momentu bezwładności $I_y$, $I_z$, skręcania I_v$ oraz wycinkowego $I_\omega$ odczytane z tablic do wyliczonych jak dla przekroju cienkościennego. Współczynniki te wynoszą średnio dla wszystkich profili w typoszeregu HEA:
$k_y = 1,04 $,
$k_z = 1,00 $,
$k_v= 1,26 $
$k_\omega=1,00$
Współczynniki ujmują wpływ wyokrągleń naroży przekroju . W ta. 6 podano, że współczynnik $k_v$ uzyskany w drodze badań eksperymentalnych dla przekrojów typu HE… zawiera się w granicach (1,21 do 1,41). Rezultat wyliczony w tab.P2-2 zawiera się w podanych granicach.
Charakterystyki geometryczne dwuteownika wyliczone jak dla pręta cienkościennego różnią się od wartości dokładnych (tablicowych) w stopniu akceptowanym w obliczeniach inżynierskich.
Przykład 3 [Charakterystyki geometryczne przekroju otwartego ]
Przykład na podstawie opracowania [27]
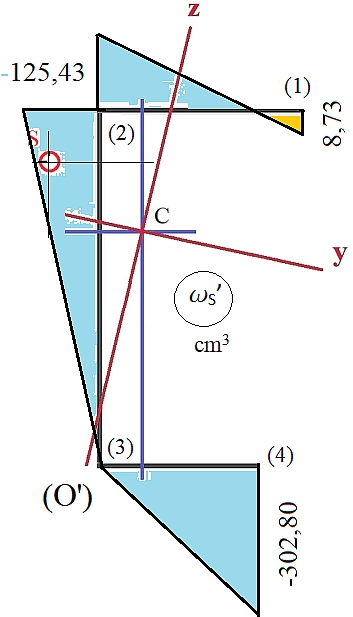
Wyznaczyć charakterystyki geometryczne $ I_y$, $I_z$, $I_v$, $I_\omega$ , oraz $\overline S_y$, $\overline S_z$, $\overline S_\omega$ odciętej części przekroju w punkcie C wg rys P2-1 . Układ globalny osi (Y,Z) jest prostopadły sdo osi pręta X i zaczepiony w lewym , górnym narożu przekroju (rys P3-1).

Rys. P3-1 Przekrój cienkościenny, otwarty wg [27]
Dane
Na rys. P3-1 przekrój w liniach środkowych ścianek oznaczono linią grubą
Węzły przekroju:
(1) $(y_1 = 20 \, ;\, z_1= 0)$ cm,
(2) $(0\, ;\, 0)$ cm,
(3) $(0\, ; , -30)$ cm,
Ścianki przekroju:
[1] =(1)-(2) $l_1= 20 \, cm$, $t_1= 2 \, cm$
[2]=(2)-(3) $l_2= 30 \, cm$, $t_2= 3 \, cm$
[3]=(3)- (4) $l_3= 13 \, cm$ $t_3= 1,3 \, cm$
Środek ciężkości, osie centralne, osie główne
Na rys. P3-2 osie centralne (przechodzące prze środek ciężkości) naniesiono liniami niebieskimi, a osie główne (osie centrale, ale nachylone pod kątem $\alpha$, względem których momenty bezładności przyjmują wartości ekstremalne, a moment dewiacji jest zerowy) oznaczono liniami bordowymi .
Pola powierzchni przekroju
$A_1$ = 20\cdot 2 = 40 \, cm^2$
$A_2$ = 30\cdot 3 = 90 \, cm^2$
$A_3$ =13\cdot 1,3 = 16,9 \, cm^2$
tab.3, kol. 7, wrs. 1 , $ \to A= 40 + 90 + 16,9 = 146,9 \, cm^2$
Współrzędne lokalnych środków ciężkości w układzie początkowym (Y, Z)
$y_1 = 20/2 = 10 \, cm$ , $ z_1 = 0 \, cm$,
$y_2 = 0 \, cm$ , $z_2 = – 30/2 = – 15 \,cm$
$y_3 = 13/2 = 6,5 \,cm $ , $ z_3 = – 30 \,cm$
Momenty statyczne w układzie (Y, Z)
tab.3, kol. 7, wrs. 2 , $ \to S_Y = 40 \cdot 0 + 90 \cdot (-15) + 16,9 \cdot (- 30)= – 1 857 \, cm^3$
tab.3, kol. 7, wrs.3 , $ \to S_Z = 40 \cdot 10 + 90 \cdot 0 + 16,9 \cdot 6,5 = 509,9 \, cm^3$
Środek ciężkości przekroju (C)
tab.3, kol. 7, wrs.4 $ \to Y_c = \cfrac{509,9}{146,9}= 3,47 \, cm$
tab.3, kol. 7, wrs.4 $ \to Z_c = \cfrac{-1 857}{146,9}= – 12,64 \, cm$
Współrzędne lokalnych środków ciężkości w układzie osi centralnych $(y_c, z_c)$
$y_{c1} = 10 – 3,47 = 6,53 \, cm$ , $ z_1 = 0 – (-12,64) = 12,64 \,cm$,
$y_{c2} = 0 – 3,47 = – 3,47 \, cm$ , $z_2 = -15 – (-12,64) = – 2,36 \,cm$
$y_{c3} = 6,5 -3,47 = 3,03 \,cm $ , $z_3 = -30 – (-12,64) = -17,36 \,cm$
Centralne momenty bezwładności
tab.3, kol. 7, wrs. 5 $\to I_{yc} = 40 \cdot 12,64 ^2 + 90 \cdot (-2,36) ^2 +16,9 \cdot (- 17,36) ^2 + \left [\cfrac{3,0 \cdot 30^3}{12}+0+0 \right ] = 18735 cm^4$,
tab.3, kol. 7, wrs. 6 $\to I_{zc} = 40 \cdot 6,53^2 + 90 \cdot ( – 3,47)^2 + 16,9 \cdot 3,03 ^2 + \left [ \cfrac{2,0 \cdot 20^3}{12} + \cfrac{1,3 \cdot 13^3}{12} + 0 \right] = 4516 \, cm^4$
tab.3, kol. 7, wrs. 7 $\to I_{yc,zc}= 40 \cdot 6,53 \cdot 12,64 + 90 \cdot (-3,47 \cdot ( – 3,47) \cdot (-2,36) +36,9 \cdot 3,03 \cdot (-17,36) = 3150 \\, cm^4$
Kąt nachylenia osi głównych
tab.3, kol. 7, wrs. 8 $\to tg (2 \alpha) = – \cfrac{ 3150}{18 735-4516}= 0,443$ $\to \alpha = 11,95^0$
$sin (11,95^o) =0,2071$
$cos (11,95^o) =0,9783$
Główne centralne momenty bezwładności
Z podstawowych zależności wytrzymałości materiałów dla przekrojów zwartych:
tab.3, kol. 7, wrs. 9 $\to I_m= \cfrac{I_{yc} + I_{zc}}{2} = \cfrac{ 18735+4516 }{2}= 11625,5\,cm^2$
tab.3, kol. 7, wrs. 9 $\to I_\Delta = \sqrt{\left( \cfrac{I_{yc} – I_{zc}}{2}\right)^2 +I_{yc,zc}^2}= \sqrt{\left( \cfrac{18735 – 4516}{2}\right)^2 +3150^2}= 7776,1 \, cm^4 $
tab.3, kol. 7, wrs. 9 $\to I_y = I_{max}=I_m+I_\Delta = 11625,5+7776,1 = 19402 \, cm^4$
tab.3, kol. 7, wrs. 10 $\to I_z = I_{min}=I_m – I_\Delta = 11625,5- 7776,1 =3849 \, cm^4$
Te same wartości uzyskano metodą mnożenia wykresów.
Współrzędne punktów przekroju w głównym układzie centralnym (y,z)
Na rys. P3-3 przedstawiono wykresy współrzędnych głównych y, z oraz współrzędnej wycinkowej względem dowolnego bieguna pomocniczego (B) oraz początkowego punktu zliczania (O). Biegun pomocniczy (B) przyjęto w górnym lewym narożu przekroju, a punku (O) w dolnym lewym narożu przekroju
Współrzędne y, z
$y_{(1)} = (20- 3,47) \cdot 0,9783 – [0-(- 12,64)] \cdot 0,2071 = 13,55 \, cm$,
$z_{(1)} = (20- 3,47) \cdot 0,2071 + [0- (-12,64)] \cdot 0,9783 =\, – 15,79 \, cm$,
$y_{(2)} = (0- 3,47) \cdot 0,9783 – [0-(- 12,64)] \cdot 0,2071 =\, – 6,01 \, cm$,
$z_{(2)} = (0- 3,47) \cdot 0,2071 + [0-(- 12,64)]\cdot 0,9783 = 11,65 \, cm$,
$y_{(3)} = (0- 3,47) \cdot 0,9783 – [30-(- 12,64)] \cdot 0,2071 = 0,20 \, cm$,
$z_{(3)} = (0- 3,47) \cdot 0,2071 + (30-12,64) \cdot 0,9783 =\, – 17,7 \, cm$,
$y_{(4)} = (13 – 3,47) \cdot 0,9783 – [30-(- 12,64)] \cdot 0,2071 =\, – 12,92 \, cm$,
$z_{(4)} = (13 – 3,47) \cdot 0,2071 + [30-(- 12,64)] \cdot 0,9783 =\, – 15,01 \, cm$,
Pomocnicze współrzędne wycinkowe $\omega’$
Biegun pomocniczy (B) przyjęto w lewym, górnym narożu profilu (2) . Pomocniczy punkt początkowy (O’) przyjęto w lewym, dolnym narożu przekroju (3).
$\omega^{’}_{(1)} =\omega_{B, (1)} = 0 \cdot 20 =0 \, cm^2$
$\omega^{’}_{(2)}= \omega{B, (2)} = 0 \cdot 0 = 0 \, cm^2$,
$\omega^{’}_{(3)}= \omega_{B.(3)}=0 \cdot 300 = 0 \, cm^2$,
$\omega^{’}_{(4)} = \omega_{B, (4)} = – 2 \cdot 1/2 \cdot 30 \cdot 13 = – 390 \, cm^2$
Moment bezwładności na skręcanie
tab.4, kol. 6, wrs. 1
$\to I_v= \cfrac{1}{3} (20 \cdot 2,0^3+ 30 \cdot 3,0^3 + 13 \cdot 1,4^3 )= 332,9 \, cm^4$
Giętne momenty bezwładności z mnożenia wykresów
tab.4, kol. 6, wrs. 3 $\to$
$I_y =\cfrac{20}{6} \left [ 2 \cdot \left ( 15,79^2 +1,65^2 \right )+ 2 \cdot 15,79 \cdot 11,65 \right ] \cdot 2,0 + \cfrac{29}{6} \left [ 2 \cdot \left ( 11,65^2 + (-17,70)^2 \right ) + 2 \cdot 11,65 \cdot (-17,70 ) \right ] \cdot 3,0 +\\ \cfrac{13}{6} \left [ 2 \cdot \left ( (-17,10)^2 + (-15,01)^2 \right ) + 2 \cdot (-17,70 ) \cdot (-15,01) \right ] \cdot 1,3 = 10402 \, cm^4$
tab.4, kol. 6, wrs. 3 $\to$
$I_y = \cfrac{20}{6} \left [ 2 \cdot \left ( 13,35^2 + (-6.01)^2 \right ) + 2 \cdot 13,35 \cdot (-6,01) \right ] \cdot 2,0 + \cfrac{29}{6} \left [ 2 \cdot \left ( (-6,01) ^2 + (0,20)^2 \right ) + 2 \cdot (-6,01) \cdot 0,20 \right ] \cdot 3,0 + \\ \cfrac{13}{6} \left [ 2 \cdot \left ( 0,20)^2 + 12,92^2 \right ) + 2 \cdot 0,20 \cdot 12,92 \right ] \cdot 1,3 = 3849 \, cm^4$
Te same wartości uzyskano metodą klasyczną (bez mnożenia wykresów), co zwykle jest mniej pracochłonne.
Wycinkowe, odśrodkowe momenty bezwładności
($\ref{58})^2$ i ($\ref{58})^3) całkowane metodą trapezów $(\ref{75})^1$:
$I_{ \omega{’},y} = \cfrac {13}{6} \cdot [ (2\cdot (13,55\cdot 0 -6,01 \cdot 0) +13,55 \cdot 0 – 6,01 \cdot 0) \cdot 2,0 + (2\cdot (- 6,01 \cdot 0 0,20 \cdot 0 ) – 6,01 \cdot 0 + 0,20 \cdot 0) \cdot 3,0 +$
$+(2\cdot 0,20 \cdot 0 + 12,92 \cdot (-390) + 0,2\cdot (-390) + 12,92 \cdot 0)\cdot 1,3 ] = – 28594 \, cm^5$
$I_{\omega{’},z} = \cfrac{13}{6}\cdot \left [ 0+0 + 2\cdot (- 17,70 \cdot 0 + (-15,01 ) \cdot (- 390) + (-17,71) \cdot (- 390) + (-15,01) \cdot 0=\right ] \cdot 1,3 = 52422 \, cm^5 $
Środek zginania (ścinania) (S) (główny biegun wycinkowy)
Na rys. P3-4 współrzędne śroska zginania (S) w różnych ukłądach współrzędnych oznaczono różnymi kolorami:
czerwonym (yS,zS) w układzie osi głównych centralnych,
niebieskim (yS,zS) w układzie osi centralnych (równoległuch do osi początkowych)
czarnym i duzymi literami (YS,ZS) w układzie osi początkowych
Współrzędne środka zginania w układzie osi głównych centralnych
($\ref{65})^1$ $\to$ yS $= − 6,01 – \cfrac{52 422}{19 402} = = −6,01 − 2,70 = −8,71 \,cm$
($\ref{65})^2 $ $ \to$ zS $= 11,65 + \cfrac{−28 594} {3 849} = 11,65 – 7,43 = 4,22 \, cm$
Współrzędne środka zginania w układzie osi centralnych równoległych do osi początkowych (Y,Z)
Współrzędne w układzie osi równoległych do osi początkowych (Y,Z) wyznacza się z zależności transformacyjnych (rys.14b):
yS = $ y_s \cdot cos (-\alpha) – z_s \cdot sin(-\alpha) = – 8,71 \cdot cos (-11,95^o) – 4,22\cdot sin(-11,95^o)= – 7,65 \, cm$
zS = $y_s \cdot sin (-\alpha) +z_s \cdot cod (-\alpha) = -8,71 \cdot sin (-11,95^o)+ 4,22\cdot cos (-11,95^o)= 5,93 \, cm$
Współrzędne środka zginania w układzie osi początkowych (Y,Z)
(rys.14a)$\to$
$Y_s= y_s + y_c = – 7,65 + 3,47 = -4,18 \, cm$
$Z_s= z_s + z_c = 5,93 – 12,64 = – 6,70 \, cm$
Pomocnicza współrzędna wycinkowa względem środka zginania
Pomocnicza współrzędna wycinkowa $\omega_S^{’}$ względem środka zginania (S) jest zliczana od pomocniczego punktu zliczania (O’)- punkt (3) przkroju, w celu wyznaczenia głónego punktu początkowego (O) i w konsekwencji głównej współrzędnej wycinkowej.
Pomocniczą współrzędną wycinkową względem środka zginania (S) wyliczymy ze współrzędnej wycinkowej względem bieguna pomocniczego (B) z zależności transformacyjnej ($\ref{62}$)
Współrzędne biegunów (S) i (B) w osiach glównych
$y_S = – 8,71 \, cm$
$z_S = 4,22 \, cm$
$y_B= y_{(2)}= – 6,01 \, cm$
$ z_B = z_{(2)} = 11,65 \, cm$
$(y_S- y_B) = (-8,71 – (-)6,01= -2,70 \, cm$
$(z_S- z_B) = (4,22 – 11,65 = – 7,43\, cm$
$ \omega_S^{’}(3) = 0 $
($\ref{62}$) $\to$
punkt (2):
$y_{(2)}= -6,01 \, cm$ ; $z_{(2)}= +11,65 \, cm$
$ \omega_S^{’}(2) = 0 -[-7,43] \cdot (-6.01) + [-2,70] \cdot (+11,65) = 13,20 $
\omega_{S,(3)} – |Y_S| \cdot l_2=0 -| – 4,18| \cdot 30 = -125,43 \, cm^3$
$\omega_S^{’} (1)= \omega_{S,(2)} +|Z_S| \cdot l_1 = -125,43 + |-6,70| \cdot 20 = 8,73 \, cm^3$
$\omega_S^{’} (4)= \omega_{S, (3)}-(l_2 -|z_S|)\cdot l_3 = 0 -(30 – |-6,71|)\cdot 13 = -302,80 \, cm^3
Wycinkowy moment statyczny
($\ref{58})^1$) całkowany metodą trapezów $(\ref{75})^1$:
$S_{\omega S}=\cfrac{8,73-125,43}{2}\cdot 20 \cdot 2 + \cfrac{-125,43+0 }{2}\cdot 30\cdot 3 +\cfrac{0-302,80}{2}\cdot 13 \cdot 1,4 = – 10 537 \, cm^4$
Współrzędna wycinkowa główna
xxxxxxxxxxxxxxxxxxxxx
Przykład 4 [ Charakterystyki geometryczne przekroju zamkniętego]
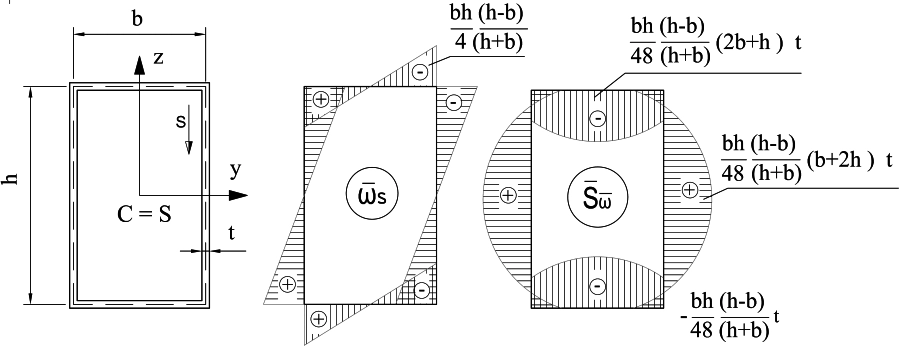
Rys.P4-1 Współrzędne wycinkowe oraz wycinkowe momenty statyczne w rurze prostokątnej [8]
Wykresy uogólnionych współrzędnych wycinkowych oraz wycinkowych momentów statycznych dla zamkniętego przekroju prostokątnego o stałej grubości ścianki $t=const$ podano na rys.7.
Dla przekroju prostokątnego o dwóch różnych grubościach ścianek (t1,t2) znajduje się wg wzoru w tabeli 1.
Przykład 5 [Siły przekrojowe w pręcie cienkościennym]
Przykład 1-2 z pracy [8]
Znaleźć kąt skręcenia i siły przekrojowe w pręcie o schemacie statycznym podanym w wrs 6. tab.4, ale dla obciążenia skupionym momentem $M_s$ przyłożonego do dowolnego miejsca po długości pręta, jak pokazano na rys. P4-1
Rys. P5-1 Schemat belki do przykładu [8]
Rozwiązanie belki znajdujemy w postaci ($\ref{47}$).
Z warunków brzegowych:
dla x=0 : $\varphi =0$ ; $B_\omega=0$ wynika wprost:
$C_1=0$ ; $C_3=0$,
a stąd kąt obrotu w przedziale (I) ($(0 \le x < a$) opisuje zależność $\varphi_I = C_2 \cfrac{1}{k sinh (kx)} +C_4 \cfrac{1}{k^3 \overline E I_\omega} [kx – sinh (kx)]$
Literatura
- Sapountzakis, E. J., Bars under Torsional Loading: A Generalized Beam Theory Approach. Review Article. ISRN Civil Engineering, 2013, pp.1–39, [ http://dx.doi.org/10.1155/2013/916581]
- Marguerre M., K., Torsion von voll-und hohlquerschnitten, Der Bauingenieur, vol. 21, pp. 317–322, 1940
- Vlasov, V. Z., Tonkostiennyje uprugije stierzni, Gos. Izd. Fiz Mat. Literat., Moskva 1959 / Thin-Walled Elastic Beams. Israel Program for Scientific Translations, Jerusalem, Israel, 1961
- STRENCO. (2016, 2019). Consteel, Oprogramowanie dla budownictwa, [http://www.strenco.pl/strenco ]
- Consteel Software. (2020), ConSteel 14 Manual , [ http://www.consteelsoftware.com/en/downloads/manuals-documents ]
- CTICM. (2013). LTBeam Software (1.011), [ http://www.cesdb.com/ltbeam.html ]
- Birger I., A., Panovko J., G., Spravochnik. Prochnost, ustojchivost, kolebania, Moschinostrojenie, Moskva 1968
- Niewiadomski Z., Wytrzymałość prętów cienkościennych – w pracy Bogucki W. (Red.), Poradnik projektanta konstrukcji metalowych: praca zbiorowa. Tom I., cz.1.1. Arkady, Warszawa), 1980
- Niezgodziński M., E., Niezgodziński T., Wzory, wykresy i tablice obliczeń wytrzymałościowych , IX Wyd. WNT 2004
- Piechnik S,. Wytrzymałość materiałów dla wydziałów budowlanych, PWN, Warszawa-Kraków 1980
- Timoshenko S., Goodier J.N.: Teoria sprężystości, Arkady, Warszawa 1962
- Birger, I. A., & Panowko, J. G.,Procnost, ustojcivost, kolebanija, Spravocnik (Vol. 1). Mosinostroejnije, 1968
- Piechnik, S. Pręty cienkościenne otwarte. Podręcznik dla studentów wyższych szkół technicznych. Wydawnictwo Politechniki Krakowskiej, Kraków 2000
- Piechnik S. Mechanika techniczna ciała stałego, Wydawnictwo Politechniki Krakowskiej, Kraków, 2007
- Rykaluk K., Zagadnienia stateczności konstrukcji metalowych, Dolnośląskie Wydawnictwo Edukacyjne , Wrocław 2012
- Piechnik S., Wytrzymałość materiałów dla wydziałów budowlanych, PWN, Warszawa-Kraków 1980
- (Niewiadomski Z., Wytrzymałość prętów cienkościennych – w pracy Bogucki W. (Red.), Poradnik projektanta konstrukcji metalowych: praca zbiorowa. Tom I., cz.1.1. Arkady, Warszawa), 1980
- Piechnik, S. (2006). Algebra of systems of forces applied to the flat material line. JTAM, 44(1), 107–125
- Clifford, W. K. (1873). Preliminary sketch of bi-quaternions. Proc. London Math. Soc., 4, 381–395
- Jancewicz, B., & Brzeski, P. (2005). Magnetic field surfaces. European Journal of Physics, 26, 617–634.
- Perwass, C. (2009). Geometric algebra with applications in engineering. Springer
- Gull, S., Lasenby, A., , Doran, C. (1993). Imaginary Numbers are not Real – the Geometric Algebra of Spacetime. Found. Phys., 23(9), 1175–1201
- Jancewicz, B. (2011). Pseudowektory. Foton, 115(Zima 2011), 31–43
- Bijak R., Chodor L., Zginanie i skręcanie dwuteowników bisymetrycznych, 61. Konferencja Naukowa KILiW PAN oraz KN PZITB Krynica 2015, 20–25 września 2015 r. Krynica-Zdrójj
- Gawłowski, S. (2006). Podejście statyczne do oceny nośności granicznej prętów cienkościennych otwartych, Praca doktorska, Politechnika Krakowska
- Brzoska Z., Statyka i stateczność konstrukcji prętowych cienkościennych, (Wyd. II, PWN, Warszawa, 1965
- Kasprzyk T., Zadanie 5- rozwiązanie przykładowe, Politechnika wrocławska KMBiIM ZWM, Wrocław maj 2021
________________________________