Leszek Chodor, 31 stycznia 2016
2023 -10-06 dodano tablice do projektowania
2024-11-30 dodano tablicę współczynników materiałowych
2024-12-18 korekta edytorska: numeracja tablic, rysunków oraz odwołań w tekście
01-02-2025 rewizja po dużej awarii portalu>
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 107 Czytelników
Połączenia śrubowe stanowią podstawowy sposób łączenia elementów konstrukcji na montażu w konstrukcjach budowlanych: stalowych, ale też żelbetowych lub drewnianych. W kompedium wiedzy zamieszczono tablice wspomagające projektowanie połączeń. Liczne przykłady rachunkowe obejmują najważniejsze zagadnienia spotykane w praktyce.
Tablice do projektowania
Nośności i sprężanie śrub
Nośności śrub
Tab.1. Własności mechaniczne oraz nośności śrub $F_{Rd}$ [kN] wg normy [1]
Siła sprężenia
Tab. 2 Siła sprężenia śrub $F_{pc}$ (c= pełne sprężenie – na 100%)
Uwaga: Siłę sprężenia śrub mierzy się momentem dokręcenia realizowanym w sposób opisany w rozdziale Metody dokręcania śrub
Współczynniki tarcia powierzchni złączy
Tab. 3. Kategorie powierzchni ciernych konstrukcji stalowych i minimalne współczynniki tarcia $\mu$ [2], tab.18
Współczynnik tarcia po powierzchni betonowej zależy od sposobu przygotowania powierzchni betonu i wynosi [3]:
$\mu=0,5$ dla powierzchni gładkiej (deskowanie drewniane/stalowe, bez deskowania),
$\mu=0,7$ dla powierzchni groszkowanej,
$\mu=0,8$ przy obróbce hydrodynamicznej betonu o wytrzymałości $f_{ck} \ge 20 \, MPa$,
$\mu=1,0$ przy obróbce hydrodynamicznej betonu o wytrzymałości $f_{ck} \ge 35 \, MPa$.
Śruby SB do połączeń niesprężanych → EN 15048 (ISO 4014/4017)
Długości oraz masy śrub SB (ISO 4014 z gwintem częściowym ; ISO 4017 z gwintem pełnym)
Tab.4. Tabela długości oraz mas śrub z gwintem:
na części długości PN-EN ISO 4014 ; na całej długości PN-EN ISO 4017 (na tle zielonym)
Długości części nagwintowanej śrub z gwintem częściowym → ISO 4014
Tab.5. Tabela długości części nagwintowanej śrub PN-EN ISO 4014 ( DIN 6914)
Dobór długości śruby prowadzić zgodnie z zasadami podanymi w stopce tab.2 i skorygować z warunku lokalizacji przekroju cięcia śruby, tak by wypadał w części nienagwintowanej śruby.
Podkładki Nord-Lock
Tab.6 Tabela grubości i masa 100 szt. podkładek Nord-Lock
W przypadku zastosowania podkładek Nord-Lock grubości $t_{pod}$ w tab,4, 5 ( lub tab.7, 8) zamienić na $T$ podane w tab.6.
Śruby do połączeń sprężanych HV i HR → EN 14399
Śruby HV → EN 14399-4
Tab. 7. Tabela połączeń śrubowych do sprężania HV klasy 10.9
Śruby HR → EN 14399-3
Tab.8. Tabela połączeń śrubowych do sprężania HR klasy 8.8. lub 10.9
Masy zestawów HV i HR
Tab.9 Tabela mas zestawów HV lub HR (wartości orientacyjne)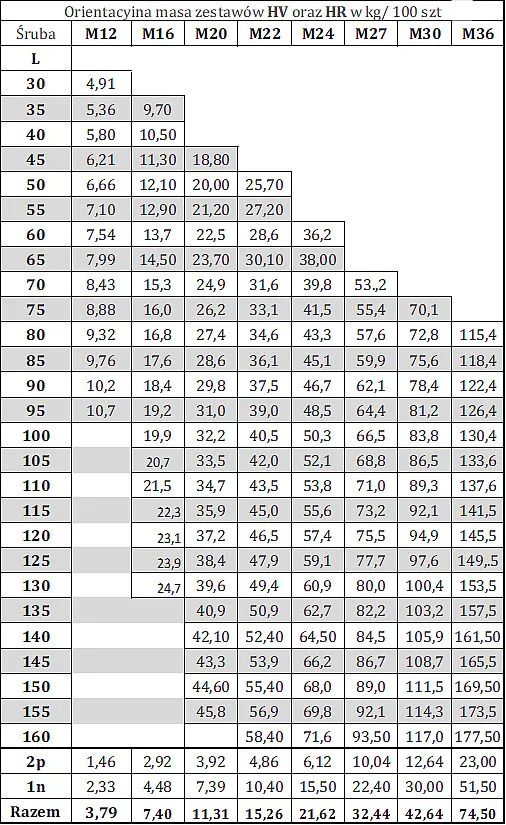
Śruby pasowane
Śruby pasowane z krótkim gwintem → PN 82341 (DIN 610)
Tab. 10 Śruby pasowane z gwintem krótkim wg PN 82341 (DIN 610)
Śruby pasowane HV do sprężania → EN 14399-3 (DIN 7999)
Tab.11. Zestawy śrubowe do sprężania ze śrubami pasowanymi HV wg DIN 7999 EN 14399-3 (DIN 7999)
Śruby pasowane → ISO 7379 maszynowe
Śruby pasowane ISO 7379 stanowią bardzo ergonomiczne i ekonomiczne elementy konstrukcyjne, szczególnie nadające się do zastosowania podczas różnego rodzaju prac montażowych. Dlatego znajdują zastosowanie nie tylko w konstrukcjach maszyn, ale też w konstrukcjach budowlanych.
Uwaga o pasowaniach i tolerancjach otworów przejściowych
Śruby pasowane są zbudowane w taki sposób, że ich odcinek gładki ma większą średnicę od odcinka gwintowanego. Przygotowywanie otworów pod te śruby odbywa się zawsze dwuetapowo: najpierw wykonywany jest otwór o mniejszej średnicy, a następnie rozwierca się go do właściwego wymiaru.
Zgodnie z normą [2], pkt 6.6.2 tolerancje średnic otworów na otwory na śruby i sworznie pasowane powinny być wykonane w klasie tolerancji H11 według ISO 286-2. Otwory w klasie tolerancji H11 mają górną odchyłkę ok 0,1 mm większą od średnicy nominalnej, np. dla średnicy 24 mm otwór rozwiercony ma wymiar : 24H11=24 +0,130 +0,0000 .
W normie PN-EN ISO 808-1 [4] pasowanie otwór/ śruba ustalono na H13/ h12, co prowadzi do luzu około 0,3 mm.
Śruby pasowane wg DIN 610 (tab.10) wykonywane są w tolerancji mieszanej (lekko ciasnej) H7/k6. Otwór w tolerancji H7 ma mniejszą górną odchyłkę od H11., np : 24H7 =24 +0,021 +0,0000 . Na rys.1 pokazano śrubę pasowaną wg ISO 7379, która jest wykonywana w pasowaniu luźnym H7/f9. Luz zależy od nominalnej średnicy otworu (i wałka) i można go wyznaczyć z tablic, np. Kalkulator tolerancji wymiarów otworu i wałka.
Dla danej śruby o określonej tolerancji – tolerancję otworu (rodzaj rozwiertaka) dobiera technolog i podaje na rysunku warsztatowym, biorąc pod uwagę parametry funkcjonalne połączenia nałożone poleceniem projektanta konstrukcji w projekcie technicznym, wytyczne norm, a także możliwości technologiczne warsztatu oraz sposób montażu. Najczęściej są stosowane tolerancje otworu H7 do H12, co skutkuje połączeniem od lekko wciskanego do umiarkowanie luźnego.
Zgodnie z klauzulą (6) do (9) pkt. 3.6.1 [1]:
-
- śruby pasowane projektuje się stosując sposoby dla śrub osadzanych w otworach normalnych,
- część gwintowana śrub pasowanych nie powinna się znajdować w płaszczyźnie ścinania.
- długość części gwintowanej śruby pasowanej w strefie docisku nie powinna przekraczać 1/3 grubości blachy (rys. 2)
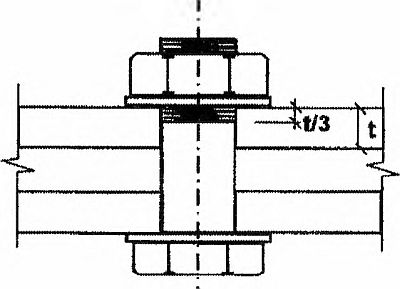
Rys.2. Ograniczenie długości nagwintowanej w pakiecie blach dla śruby pasowanej [2], rys. 4
W śrubach pasowanych według EN 14399-8 średnica nominalna trzpienia jest o 1 mm większa od średnicy nominalnej części gwintowanej
Maksymalny moment dokręcania śrub pasowanych nie jest definiowany klasą wytrzymałości materiału, lecz jest ograniczony małą powierzchnią oporową łba śruby lub podtoczeniami pomiędzy średnicami i powinien być podany przez producenta śruby z uwzględnieniem sposobu przygotowania i smarowania powierzchni gwintu.
Otwory przejściowe śrub
Tab.12 Otwory przejściowe dla klas wykonania B i C [2]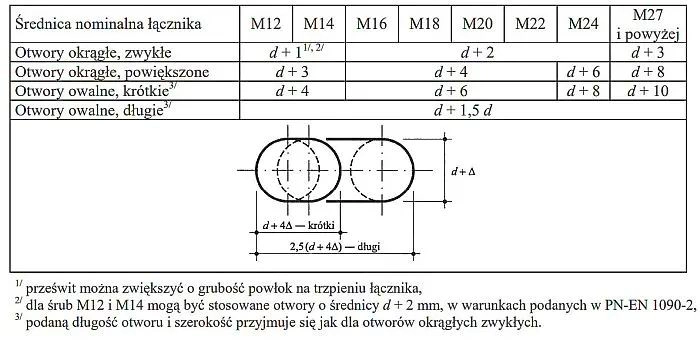
Położenie i średnice otworów w półkach kształtowników
Dwuteowniki IPN, IPE, IPE AA, IPEo, IPEv
Tab.13. Maksymalne średnice i rozstawy śrub w półkach dwuteowników [5]
Dwuteowniki HEA, HEAA, HEB, HEC, HEM
Tab. 14 Maksymalne średnice i rozstawy śrub w półkach dwuteowników szerokostopowych [5]
Ceowniki UN,UE, UPE, UAP
Tab. 15 Maksymalne średnice i rozstawy śrub w ceownikach [5]
Kątowniki równo- i nierówno-ramienne
Tab. 16 Maksymalne średnice i rozstawy śrub w kątownikach [5]
Położenie śrub a miejsca na klucz
Tab. 17. Miejsca pod klucze do śrub [6]
Śruby do betonu (kotwy wkręcane)
Śruby Fischer UltraCut FBS II
Tab. 18. Tabela geometrii i nośności śrub Fischer UltraCut FBS II na obciążenia statyczne i quasitatyczne [7]
Tabele nośności w warunkach sejsmicznych i ogniowych oraz wydłużenie śrub podano w deklaracji [7]
Producent HILTI często wprowadza nowe produkty na rynek wprowadzana, a jednocześnie zaprzestaje produkcji dotychczasowych . Obecnie wprowadzono już kotwy wkręcane HUS 4 o średnicach 10 do 16 mm i zaleca stosowanie kotew hybrydowych (wkręcanych w otwór z klejem HIT HY). Przed zastosowaniem sprawdzić dostępność u producenta lub skorzystaj z oprogramowania do doboru kotw Hilti Profis Engineering.
Kotwy wkręcane Hilti HUS 3
Tab. 19. Tabela geometrii i nośności śrub Hlti HUS3 na obciążenia statyczne i quasitatyczne [8]
Tabele nośności w warunkach sejsmicznych i ogniowych oraz wydłużenia śrub podano w deklaracji [8]
Współczynniki częściowe bezpieczeństwa γM dla połączeń śrubowych
Tab.20 Częściowe, materiałowe współczynniki bezpieczeństwa $\gamma_M$ dla połączeń śrubowych [1]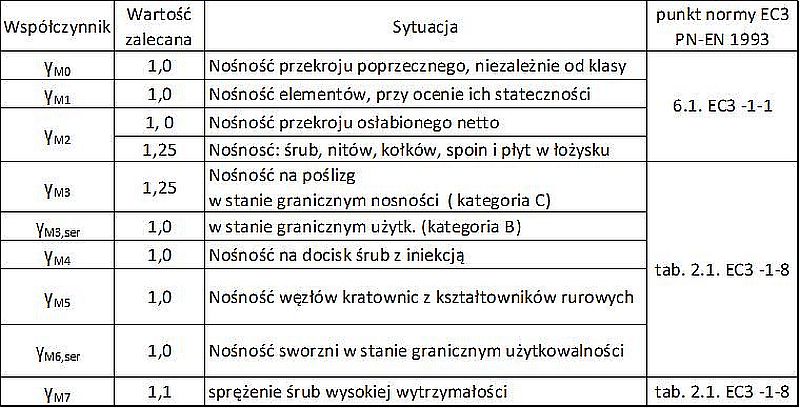
Rodzaje śrub i połączeń
Rodzaje śrub
Na rys.4 pokazano najczęściej stosowane rodzaje śrub w połączeniach elementów konstrukcji budowlanych.
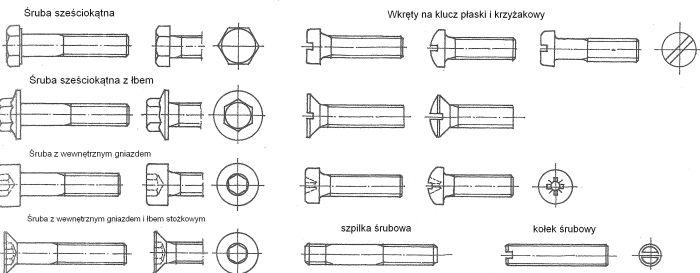
Rys. 4 Rodzaje śrub [9] rozdz.7, rys.1
Zestaw śrubowy składa się ze śruby, podkładki pod łeb, podkładki pod nakrętkę i nakrętki, co w tab. 11 pokazano na przykładzie śrub pasowanych HV (wysokiej wytrzymałości).
Do połączeń ścinanych ekonomicznie jest stosować śruby o poszerzonym trzpieniu w stosunku do średnicy gwintu. Na rys. 5 pokazano śrubę M12/14 (śruba M12 o trzpieniu D=14 mm) stosowaną chętnie w połączeniach śrubowych blach płaszcza silosów produkowanych przez Witkowitz-Envi w Ostrawie (Czechy). Śruba jest produkowana na użytek własny producenta zbiorników wg normy zakładowej [10].
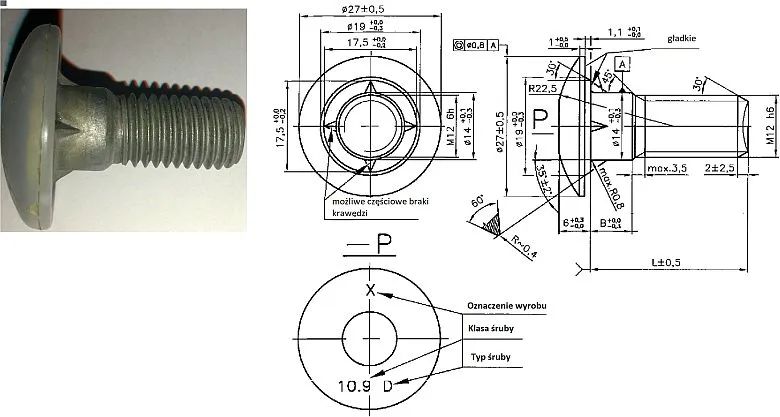
Rys.5 Śruba z powiększonym trzpieniem M12/14 [10]
Główki śrub i klucze
W tab. 21 zestawiono rodzaje główek śrub w rodzajach od A do J, stosowane dla danego rozmiaru gwintu metrycznego oraz rozmiary kluczy dla łbów sześciokątnych.
Tab. 21 Rodzaje główek (łbów) śrub i rozmiary kluczy dla śrub metrycznych z łbem sześciokątnym [11]
Dla innych typów główek niż A do D rozmiar klucza można oszacować na podstawie szerokości główki S z tab.7.
Rodzaje najczęściej stosownych kluczy pokazano na rys. 6.
Ustalanie (zabezpieczanie) nakrętek śrub
Śruby należy zabezpieczyć przed odkręceniem nakrętki. Tradycyjne sposoby ustalania nakrętek (zabezpieczania przed okręceniem) pokazano na rys. 7a-l .
Ostatnio do zabezpieczenia śrub przed poluzowaniem, chętnie stosuje się podkładki zębate, np Nord-Lock, pokazane na rys.8.
Chętnie stosowaną obecnie metodą ustalania nakrętek, szczególnie w śrubach klasy 8.8 i wyższych jest obecnie sprężanie śrub do 50% pełnego momentu sprężającego, określanego zgodnie z normą [2].
Parametry geometryczne oraz masy nakrętek Nord-Lock podano w tab.6.
Klasa śrub a własności mechaniczne
Śruby są zwykle produkowane ze stali do ulepszania cieplnego np 30H ,40H (wg. starych oznaczeń). ). Śruby klasy 9.8 wykonuje się najczęściej ze stali 30H, a 10,9 ze stali 49H po obróbce cieplnej (ulepszaniu lub hartowaniu i odpuszczaniu). Należy zwrócić uwagę, że stal konstrukcyjna S355 jest kilkukrotnie za słaba , by wykonywać z niej śruby współcześnie stosowanych klas.
W konstrukcjach budowlanych stosuje się 10 klas śrub: 4.6; 4.8; 5.6; 5.8; 6.6; 6.8; 8.8; 9.8; 10.9; 12.9
Klasy oznacza się symbolem składającym się z dwóch liczb przedzielonych kropką. Pierwsza liczba stanowi 0,01 minimalnej wymaganej wytrzymałości doraźnej na rozciąganie ($ R_m = f_{ub}$ ) stali gotowych śrub w MPa. Druga liczba stanowi 0,1 stosunku minimalnej granicy plastyczności $R_e=f_{yb}$ do minimalnej wytrzymałości doraźnej na rozciąganie materiału śrub $R_m$.
Na przykład dla śruby klasy 5.6 :
$f_{ub} = R_m = 500 \, MPa$
$f_{yb} = R_e = 0,6 \cdot 500= 300 \, MPa$
Nakrętki wykonuje się ze stali o niższej jakości niż śruby ze względu na to, iż gwint w złączu powinien zerwać się w nakrętce a nie w śrubie. Stosuje się nakrętki o klasie: 5; 6; 8; 10; 12. Symbol oznaczania nakrętki stanowi 0,01 minimalnej wymaganej wytrzymałości doraźnej na rozciąganie stali [MPa]. Do każdej klasy śrub odpowiada konkretna klasa nakrętek, co pokazano w tab.1, przypisując do klasy śruby klasę nakrętki (podano w nawiasie).
Tabela nośności śrub na rozciąganie i ścinanie
W tab.1 zestawiono własności mechaniczne śrub wraz z nośnościami obliczeniowymi na rozciąganie $F_{tRd}$ , ścinanie $F_{vRd}$ na odcinku bez gwintu i $F_{vsRd}$ na odcinku nagwintowanym śruby.
Występujące w tab.1 czynne pole $A_s$ nie należy mylić z polem rdzenia przekroju śruby (najmniejszego przekroju gwintu). Pole czynne gwintu $A_s$ jest większe d pola przekroju rdzenia o ok. 10% (p. tab.22).
$$\begin{equation} A_s= \cfrac{\pi d_s^2}{2} ,\label{1}\end{equation}$$
jest polem przekroju umownego walca o średnicy
$$\begin{equation} d_s=\cfrac{d_p+d_r}{2} \label{2}\end{equation}$$
gdzie:
$d_p$ – średnica podziałowa gwintu,
$d_r$ – średnica rdzenia gwintu
W tab.22 dokonano obliczenia pola czynnego $A_s$ na podstawie geometrii gwintów metrycznych.
Tab.22. Średnice gwintu metrycznego oraz pole czynne śruby
Definicje poszczególnych średnic rzeźby gwintu przedstawiono na rys.9. W nawiasach podano oznaczenia stosowane w mechanice maszyn: symbolem d (małe) oznaczono średnicę gwintu wewnętrznego (śruby) ; D (duże) oznacza średnicę gwintu zewnętrznego (nakrętki).
Rodzaje i kategorie połączeń śrubowych
Połączenia śrubowe dzielimy na zakładkowe (rys.10) i czołowe (rys.11).
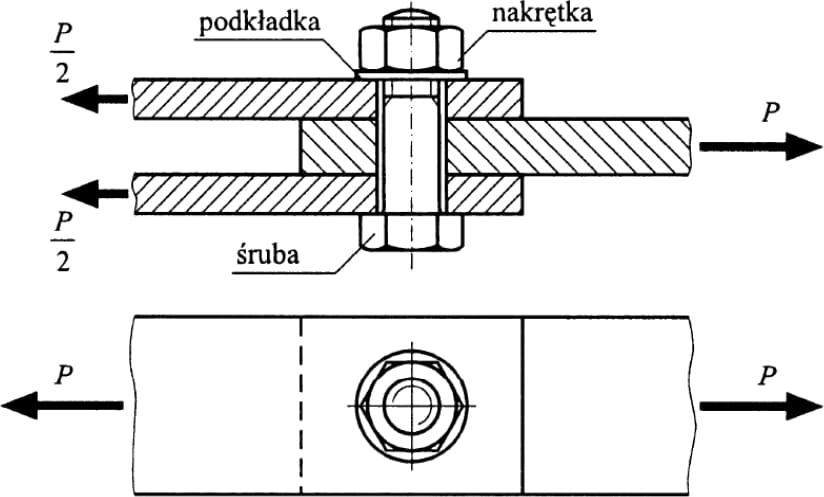
Rys.10. Zakładkowe połączenie śrubowe [12]
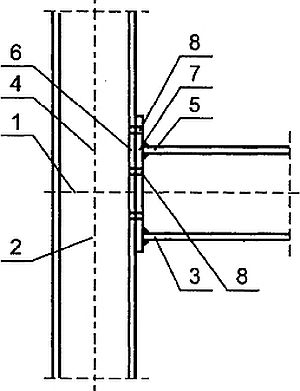
Rys.11. Czołowe połączenie śrubowe: 1- Belka, 2 – Słup, 3- Pas dolny belki, 4- słup nad belką, 5- pas górny belki, 6-pas słupa, 7- blacha czołowa, 8- śruba [12]
Połączenia zakładkowe mogą być zwykłe (rys.12a) lub cierne (rys.12b).
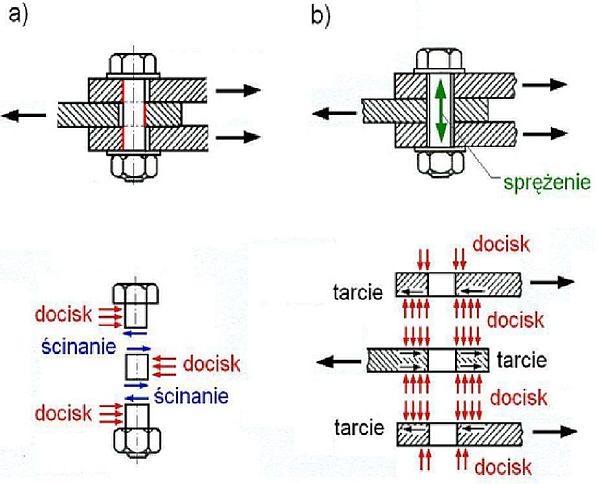
Rys.12. Połączenia zakładkowe: a) zwykłe, b) cierne [12]
Połączenia czołowe mogą być rozciągane (rys.13a), rozciągane i zginane (rys.13b), niesprężane (rys.13c) i sprężane ( rys.13d)
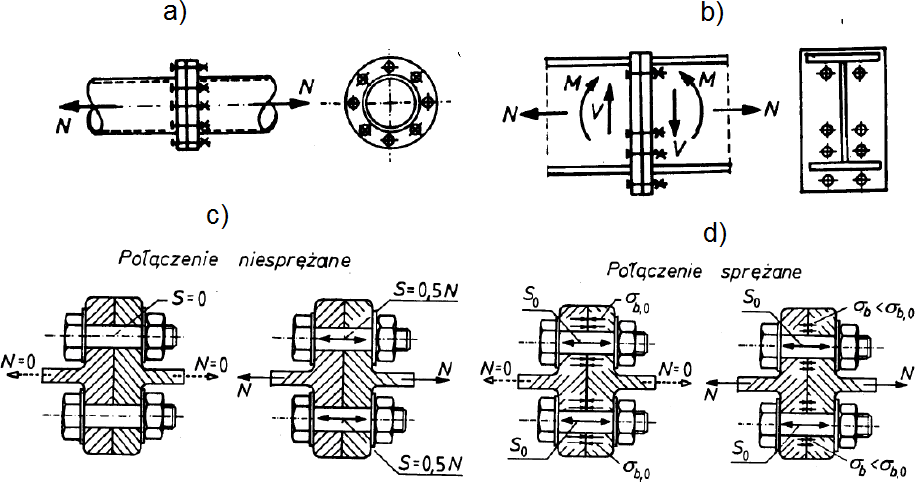
Rys.13. Połączenia czołowe: a) rozciągane , b) zginane, c) niesprężane, d) sprężane [12]
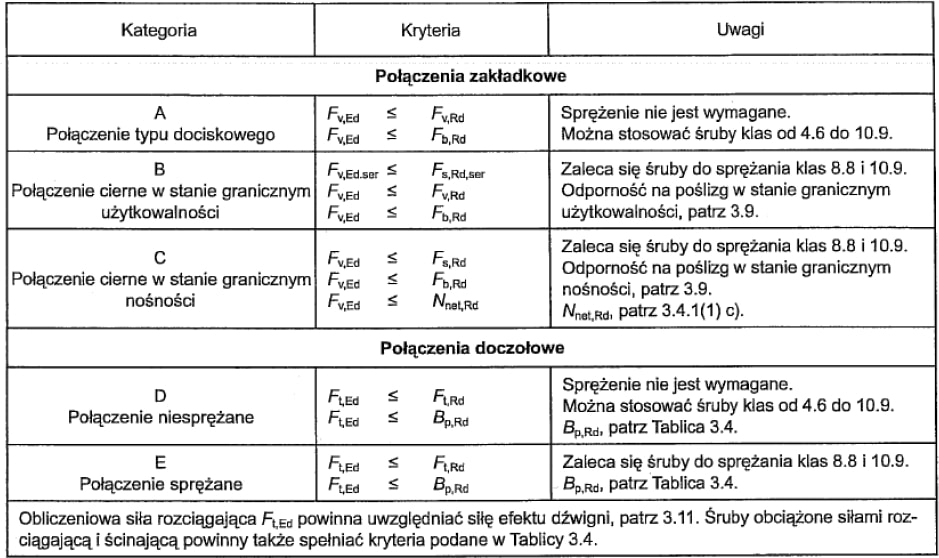
W tab.23 zestawiono kategorie połączeń śrubowych konstrukcji budowlanych.
Tab.23. Kategorie połączeń śrubowych [1]
Rozmieszczenie śrub
Wymagania normy [1]
Śruby w szeregach i rzędach należy rozmieszczać tak, by ich odległości zawierały się w granicach określonych na rys. 14.
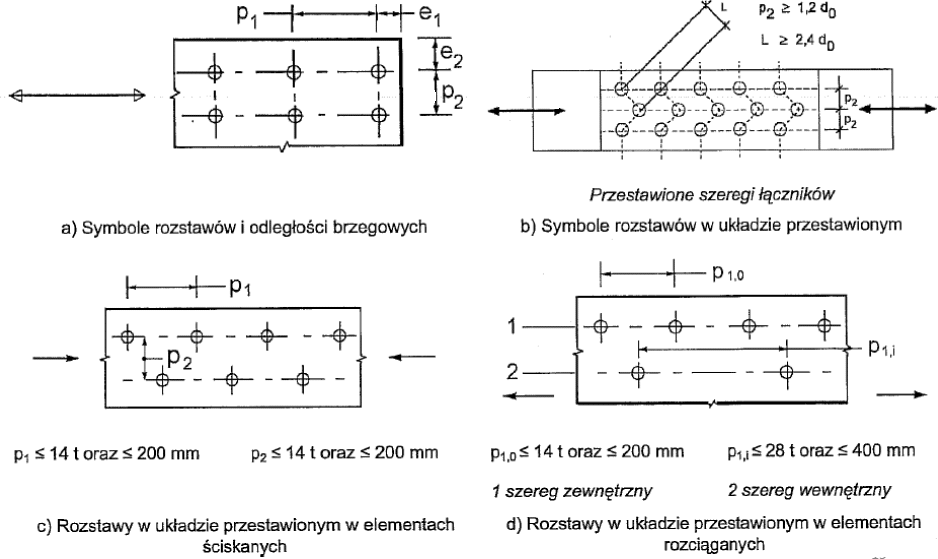
Rys.14. Rozstawy śrub [12]
W tab.24. zalecane rozstawy śrub podano tabelarycznie (oznaczenia wg rys.14)
Tab.24 Zalecane odległości śrub [1]

Uwagi: 1) Największe rozstawy oraz odległości od brzegów nie są ograniczone, z wyjątkiem przypadków: a) w elementach ściskanych blisko gałęziowych, 2) w elementach rozciąganych, aby zapobiec korozji; 2), 5) patrz [1]; 3) t – grubość cieńszej, zewnętrznej części łączonej; 4) ograniczenia wymiarów otworów owalnych podano w normach grupy 7.
Zalecenia konstrukcyjne dla wybranych profili
W tab.13 do 16 podano zalecane maksymalne średnice i rozstawy otworów w najczęściej stosowanych kształtownikach stalowych.
W tab. 17 zestawiono zalecane odległości śrub z warunku zachowania miejsca pod klucz.
Nośność śruby na rozciąganie i ścinanie
Nośność na rozciąganie
Nośność obliczeniowa śruby na rozciąganie $F_{tRd}$ wynosi
$$\begin{equation} F_{t,Rd}=\cfrac{k_2 \cdot f_{ub} \cdot A_s}{\gamma_{M2}} \label{3} \end{equation}$$
gdzie:
współczynnik $k_2=0,9$ (dla śrub z łbem wpuszczanym $k_2=0,63$ ),
$A_s$ – czynne pole przekroju śruby,
$f_{ub}$ – charakterystyczna wytrzymałość śruby wg tab.1 ($R_m$ wg starych oznaczeń)
$\gamma_{M2}=1,25 $ współczynnik materiałowy przyjmowany przy sprawdzaniu nośności połączeń.
Nośność na ścinanie w płaszczyźnie ścinania
Nośność obliczeniowa na ścinanie jednej płaszczyzny cięcia śruby wynosi
$$\begin{equation} F_{v,Rd,1}= \cfrac{\alpha_v \cdot f_{ub}\cdot A}{\gamma_{M2}} \label{4}\end{equation}$$
gdzie: A – pole przekroju śruby uczestniczące w ścinaniu:
- jeśli ścinanie następuje poza gwintem (na nienagwintowanej części śruby), to A jest polem trzpienia śruby $A=\pi \cdot d^2/4$ (d – nominalna średnica śruby).
- jeśli ścinany jest przekrój na długości nagwintowanej, to $A=A_s$, gdzie $A_s$ jest czynnym polem przekroju (polem rdzenia śruby powiększonym o ok 10%)
Współczynnik zmniejszający wynosi $\alpha_v =0,6 $ dla przypadku ścinania poza gwintem, a dla ścinania części nagwintowanej zależy od klasy śruby i wynosi: 0,6 – dla śrub klasy 4.6, 5.6, 8.8 oraz 0,5 – dla śrub klasy 4.8, 5.8, 6.8 i 10.9.
Połączenia zakładkowe
Mechanizmy zniszczenia
Na rys. 15 do rys. 18 pokazano mechanizmy zniszczenia połączeń zakładkowych: ścięcie łącznika, uplastycznienie (docisk), ścięcie lub rozerwanie blachy.
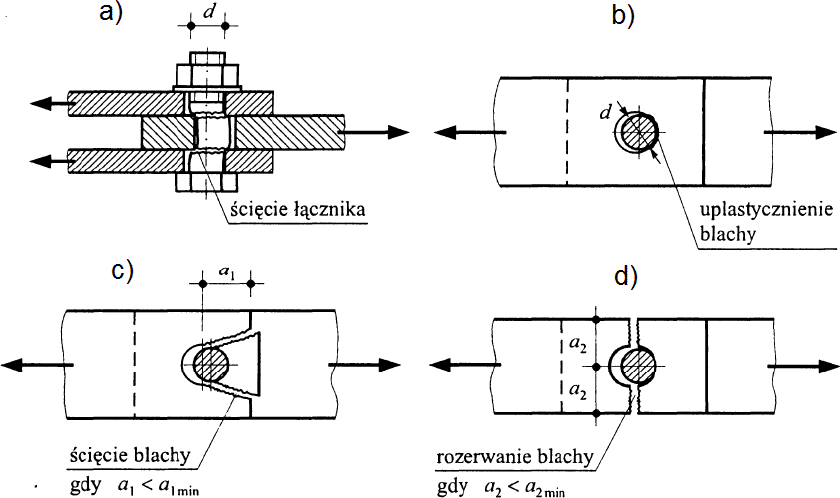
Rys. 15. Postacie zniszczenia połączeń zakładkowych: a) ścięcie łącznika, b) uplastycznienie blachy (docisk), c) ścięcie blachy, d) rozerwanie blachy [12]
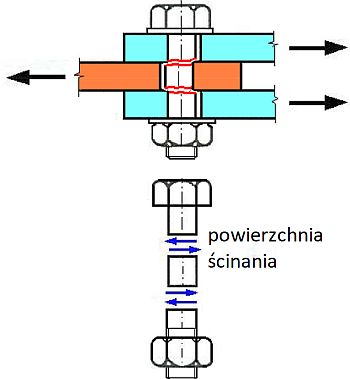
Rys.16 Śruba dwucięta [12]
Nośność śruby na ścinanie
Ścięcie łącznika zachodzi na powierzchniach ścinania, których liczba jest zależna od liczby zakładek. Na rys 15 pokazano połączenie dwucięte, a na rys. 16 połączenie czterocięte. Jeśli liczbę cięć śruby oznaczymy przez m, to nośność na ścinanie $F_{v,Rd,j} śruby wielociętej (o nr j w grupie) wynosi:
$$\begin{equation} F_{v,Rd,j}= m\cdot F_{v,Rd,1} \label{5}\end{equation}$$
gdzie nośność jednej płaszczyzny ścinania F_{v,Rd,1} wg$ (\ref{4}$)
Nośność śruby na docisk
Mechanizm docisku śruby do powierzchni blachy, pokazano na rys. 18.
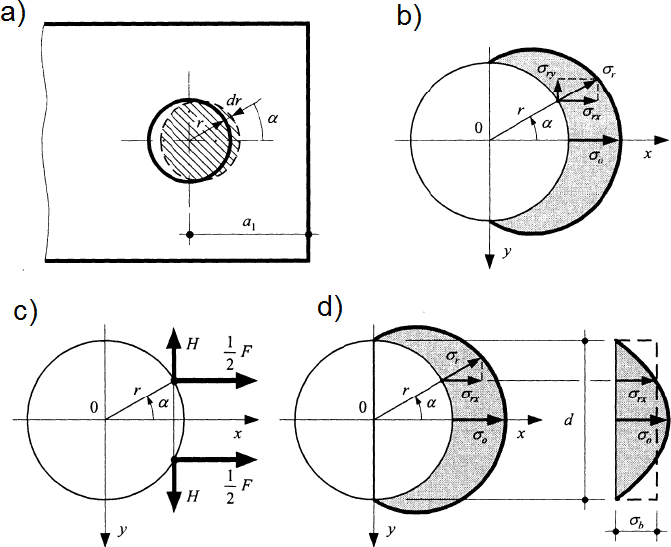
Rys.18. Nośność śruby na docisk: a) postać odkształcona, b), d) rozkład naprężeń, c) układ sił [12]
Podstawowa obliczeniowa nośność ze względu na docisk pojedynczej śruby wynosi:
$$\begin{equation} F_{b,Rd,0}= \cfrac{f_u \cdot d \cdot \sum t}{\gamma_{M2}} \label {6} \end{equation}$$
gdzie:
$d$ – średnica nominalna śruby,
∑t – suma grubości blach dociskających do śruby w kierunku obciążenia,
$\gamma_{M2}=1,25$ częściowy współczynnik bezpieczeństwa,
$f_u = \min {\{ f_{ub} \,;\, f_{us}\}}$
$f_{ub}$ granica wytrzymałości materiału śruby,
$f_{us}$ granica wytrzymałości stali łączonych blach (mniejsza , jeśli blachy wykonane są z różnych gatunków stali).
Nośność ($\ref{6}$) jest wyznaczona w założeniu, że rozkład naprężeń na powierzchni docisku jest równomierny o wartości $\sigma_b$ (rys.16) i działa na całej średnicy $d$. Ponieważ rzeczywisty rozkład naprężeń jest nieliniowy, więc wprowadza się współczynnik korygujący $ k_r$, a nośność j-rej śruby na docisk $F_{b,Rd,j}$ wyznacza z zależności
$$\begin{equation} F_{b,Rd,j} = k_{r,j} \cdot F_{b,Rd,0} \label{7} \end{equation}$$
Współczynnik korygujący $k_r$ zależy od położenia śruby w połączeniu (śruba skrajna, środkowa), od kierunku działania siły w stosunku do osi głównej linii śrub, a także od rodzaju otworu przejściowego i jest liczony jako iloczyn:
$$\begin{equation} k _r = k_o \cdot k_1 \cdot \alpha_b \label{8} \end{equation}$$
gdzie:
- współczynnik $k_o$ zależy od rodzaju otworu przejściowego wg tab 12 i dla śrub zwykłych (notka 1 pod tab. 3.4 [1] wynosi :
$$\begin{equation} k_o = \begin {cases}
1,0 & \textrm { w otworach okrągłych normalnych } \\
0,8 & \textrm { w otworach powiększonych } \\
0,6 & \textrm { w otworach owalnych, wydłużonych prostopadle do kierunku obciążenia } \\
\end {cases} \label{9} \end {equation}$$
- współczynnik $k_1$ koryguje nośność ze względu na umieszczenie śruby w kierunku prostopadłym do działania obciążenia i wynosi [1], tab 3.4
$$\begin{equation} k_1 = \begin {cases}
\min { \{ 2,8 \cdot \cfrac {e_2}{d_o} – 1,7 \, ; \, 1,4 \cdot \cfrac{p_2}{d_o}-1,7 \, ; \, 2,5 \} } & \textrm { dla śrub skrajnych} \\
\min { \{ 1,4 \cdot \cfrac {p_2}{d_o} – 1,7 \, ; \, 2,5 \} } , & \textrm { dla śrub pośrednich}
\end {cases} \label{10} \end {equation}$$
- współczynnik $ \alpha_b $ koryguje nośność ze względu na umieszczenie śruby w kierunku działania obciążenia i wynosi [1], tab 3.4:
$$\begin{equation} \alpha_b = min \{ \alpha_d \ ; \cfrac {f_{ub}}{f_u}\ ; 1,0 \} \label{11} \end{equation}$$
- współczynnik $ \alpha_d $ występujący w ($\ref{11}$) wynosi
$$\begin{equation} \alpha_d= \begin {cases}
\cfrac {e_1}{ 3 \cdot d_o}, & \textrm { dla śrub skrajnych} \\
\cfrac{p_1}{3 \cdot d_o} – \cfrac{1}{4} , & \textrm { dla śrub pośrednich}
\end {cases} \label{12} \end{equation}$$
Jeśli wyrażeniach $(\ref{10})$ lub $(\ref{12})$ nie jest określone $p_1$ lub $p_2$, to przyjmuje się wartość NaN (niezdefiniowana lub niereprezentowalna wielkość), a wyrażenie zawierające NaN jest pomijane.
W nietypowych przypadkach (skośnych krawędzi lub osi linii śrub – odległości krawędzi $e_1$ i $e_2$ oraz odległości między rzędami elementów złącznych $p_1$ i $p_2$ można określić, używając półosi w elipsie, do której krawędź blachy jest styczna, oraz półosi w elipsie, której środek znajduje się w jednym otworze i przechodzi przez drugi otwór jak pokazano na rys. 19.
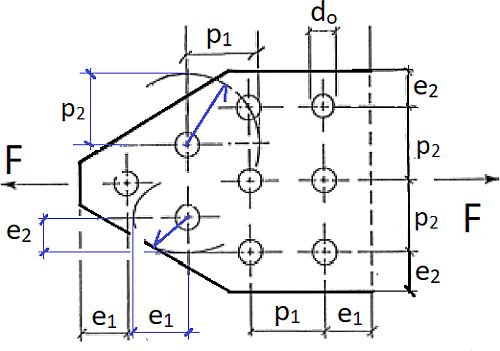
Rys.19 Odległości śrub od ukośnych krawędzi i pomiędzy ukośnymi rzędami [13]
W przypadku, gdy kierunek obciążenia śruby jest ukośny względem brzegu, to nośność na docisk można sprawdzać, rozpatrując oddzielnie poszczególne składowe obciążenia działające równolegle i prostopadle do brzegu blachy [1], notka 3 pod tab. 3.4.
Dla śrub z łbem wpuszczanym: a) nośność na docisk $F_{b,Rd}$ określa się na podstawie grubości łącznej blachy Σt zmniejszonej o połowę głębokości wpuszczenia łba, b)przy określaniu nośności na rozciąganie $F_{t,Rd}$ kąt i głębokość wpuszczenia łba powinny być zgodne z przedmiotowymi normami. W innych przypadkach nośność na rozciąganie $F_{t,Rd}$ należy odpowiednio zmodyfikować [1], notka 2 pod tab. 3.4.
Uwagi dodatkowe
[ Wybrane klauzule z pkt 3.6.1. [1] ]:
a) nośności śrub redukuje się o 15% – współczynnikiem 0,85 dla:
- śrub z gwintem nacinanym, który nie odpowiada EN 1090,
- nośności na ścinanie $F_{vRd}$ śrub M12 lub M14 klas 4.8, 5.8, 6.8, 8.8 i 10.9 w otworach przejściowych z luzem 2 mm ( pod warunkiem, że nośność obliczeniowa grupy śrub $F_{b,Rd,N}$ na docisk jest nie mniejsza od nośności grupy śrub na ścinanie $F_{vRd}$.)2.
b) w pojedynczym złączu zakładkowym z jednym szeregiem śrub, stosuje się śruby z podkładkami pod łbem i nakrętką. Nośność obliczeniową śruby na docisk $F_{b,Rd}$ w takim złączu jest ograniczona warunkiem $F_{b,Rd}\le \cfrac { 1,5 \cdot f_u \cdot d \cdot t}{\gamma_{M2}}$
c) do śrub klasy 8.8 i 10.9 w pojedynczych złączach zakładkowych na jedną śrubę lub jeden szereg śrub, stosuje się podkładki hartowane,
d) w przypadku, gdy śruby lub nity pracujące na ścinanie i docisk przechodzą przez przekładkę o grubości $t_p$ większej niż 1/3 średnicy nominalnej d, to nośność obliczeniową na ścinanie $F_{vRd,j}$ ($\ref{5}$) należy pomnożyć przez współczynnik redukcyjny $\beta_p= \cfrac{9 \cdot d}{8\cdot d+3 \cdot t_p}\le 1$
e) w przypadku połączeń dwuciętych z przekładkami po obu stronach styku, do obliczeń przyjmuje się $t_p$ równe grubości przekładki grubszej.
f) dla stali S 235 jako miarodajną wartość $f_{ur}$ można przyjmować 400 MPa.
Nośność śruby i grupy śrub
Obliczeniową nośność j-tej śruby wyznacza się jako minimum nośności ze względu na ścinanie oraz ze względu na docisk
$$\begin{equation} F_{Rd,j}= \min { \{ F_{v, Rd,j} \, ; \, F_{b, Rd,j}\}} \label{13} \end{equation}$$
gdzie: $F_{v, Rd,j}$ ($\ref{5}$), $F_{b, Rd,j}$ ($\ref{7}$)
Minimalną nośność śruby w grupie oznaczymy przez $ F_{Rd,min}$:
$$\begin{equation} F_{Rd,min}= \min {F_{Rd,j}} \label{14} \end{equation}$$
Nośność grupy N łączników $F_{Rd,N}$ można przyjmować jako [1], kl. (1), pkt 3.7.
$$\begin{equation} F_{Rd,N}= \begin {cases}
\sum \limits_{j=1}^{j=N} F_{b,Rd,j} & \textrm { jeśli dla każdej śruby j } \forall_j \, F_{v,Rd,j} > F_{b,Rd,j}\\
N \cdot F_{Rd,min} , & \textrm { w przeciwnym przypadku}
\end {cases} \label{15} \end{equation}$$
gdzie:
j – numer łącznika,
N – liczba łączników w grupie
Niesymetryczne połączenie a nośność grupy śrub
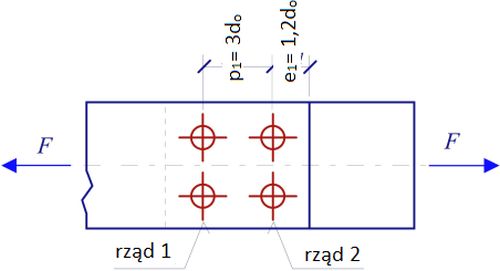
Rys. 20 Niesymetryczna grupa śrub [13]
Z wyrażenia ($\ref{15}$) wynika, że nośności śrub w grupie w ogólności nie można sumować. Wyjaśnimy to na przykładzie pokazanym na rys. 20.
Współczynnik $\alpha_d$ ($\ref{12}$) dla poszczególnych rzędów śrub wyniesie:
dla rzędu 2: $ \alpha_d= \cfrac{e_1}{3 d_o}= \cfrac{1,2 d_o}{3 d_o}=0,4$,
dla rzędu 1: $ \alpha_d= \cfrac{p_1}{3 d_o} – 0,25= \cfrac{3 d_o}{3 d_o}- 0,25 =0,75$.
Oszacowanie nośności grupy śrub można przeprowadzić dwiema metodami:
metoda 1 (sumowania bezpośredniego):
$F_{b,Rd} = \left (sum \alpha d \right ) \cfrac{2,5 d f_u}{\gamma_{M3}}= (2 \cdot 0,4 + 2 \cdot 0,75) \cdot \cfrac{2,5 d f_u}{\gamma_{M3}}= 2,3 \cfrac{2,5 d f_u}{\gamma_{M3}}
metoda 2 (minimum nośności):
$F_{b,Rd} = \left (sum \alpha d \right ) \cfrac{2,5 d f_u}{\gamma_{M3}}= (2 \cdot 0,4 + 2 \cdot 0,4) \cdot \cfrac{2,5 d f_u}{\gamma_{M3}}= 1,6 \cfrac{2,5 d f_u}{\gamma_{M3}}
Jeśli stosowana jest metoda 1, to odkształcenie w otworach rzędu 2 może być duże w stanie granicznym użytkowalności, jeśli wszystkie obciążenia są obciążeniami stałymi. Dobrą praktyką inżynierską jest tworzenie połączenia symetrycznego w celu uniknięcia niepotrzebnego plastycznego rozłożenia sił wewnętrznych. Sumowanie nośności poszczególnych śrub można stosować w przypadku sprawdzania stanu użytkowalności, a nie nośności
Jeśli istnieje potrzeba ograniczenia odkształceń, należy przeprowadzić osobne sprawdzenie stanu granicznego użytkowalności. W przypadku połączeń niesymetrycznych można uwzględnić umocnienie odkształceniowe płyt, zapewniając $F_{v,Rd}\ge 1,2 F_{b,Rd}$ [13].
Nośność grupy śrub z otworami owalnymi
Nośność śruby w otworze owalnym prostopadle do kierunku obciążenia redukuje się współczynnikiem $k_o=0,6$ ($\ref{9}$).
Współczynnik redukcji $k_o dla otworów owalnych $ wynika z wielu badań eksperymentalnych [14], [15], [16], [17].
Złącza długie
Jeśli odległość osiowa $L_j$ między skrajnymi łącznikami mierzona w kierunku obciążenia, jest większa niż 15 d, to obliczeniową nośność na ścinanie wszystkich łączników $F_{vRd,N}$ ($\ref{15}$) redukuje się współczynnikiem $\beta_{L,f}$), określonym wzorem:
$$\begin{equation} \text { jeśli } L_j> 15 \cdot d \to \beta _{L,f} = \cfrac{L_j – 15 d}{200 d} \quad lecz \quad 0,75 \ge \beta _{L,f}\le 1,00 \label{16} \end{equation}$$
Interakcja ścinania i rozciągania
Interakcja ścinania śruby siłą $F_{v,Ed}$ i jednoczesnego rozciągania siłą $F_{t,Ed}$ jest liniowa podług formuły [1], tab. 3.4., kol.5:
$$\begin{equation} \cfrac{F_{v,Ed}}{F_{v,Rd}} +\cfrac{F_{t,Ed}}{1,4 \cdot F_{t,Rd}} \le 1,00 \label{17} \end{equation}$$
gdzie :
$F_{t,Rd}$ nośność śruby na rozciąganie wg ($\ref{3}$),$F_{t,Rd}$ nośność śruby na rozciąganie wg ($\ref{3}$),
$F_{v,Rd}$ nośność śruby na ścinanie wg ($\ref{5}$).
$F_{t,Ed}$ ,$F_{v,Ed}$ – obliczeniowe siły zewnętrzne: rozciągająca i ścinająca odpowiednio.
Obserwacje eksperymentalne [18] (rys. 21) wykazały, że śruby poddane pełnemu ścinaniu mają znaczną nośność na rozciąganie. Wytrzymałość na rozciąganie jest ograniczona przez pęknięcie gwintowanej części śruby, ale zakłada się, że interakcja między ścinaniem a rozciąganiem ma miejsce w trzonie. Stwierdzono zadawalającą zgodność z normową krzywą interakcji ($\ref{17}$), choć zaproponowano dokładniejsze dopasowanie do kwadratowej krzywej regresji.
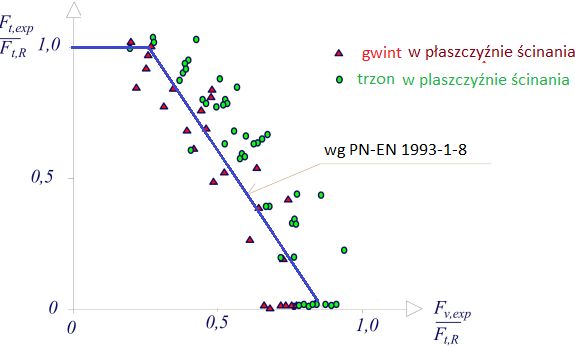
Rys. 21 Badania eksperymentalne interakcji ścinania i zginania śruby: $F_{t,exp}$, $F_{v,exp}$ – nośność na rozciąganie i ścinanie obserwowana w eksperymencie ; $F_{t,R}$ i $F_v,R}$ – nośności szacowane z formuł normowych ($\ref{3}$) i ($\ref{5}$) [18]
Wytrzymałość na ścinanie wynosi 63 do 68% wytrzymałości na rozciąganie (jeśli płaszczyzna ścinania przecina część gwintowaną) i i 75do 89%, jeśli płaszczyzna ścinania znajduje się w trzonie śruby.
Jeśli płaszczyzna ścinania przecina trzon śruby, mogą wystąpić następujące dwa tryby uszkodzenia: połączenie ścinania i rozciągania na płaszczyźnie ścinania lub alternatywnie śruba ulega uszkodzeniu głównie przez rozciąganie w części gwintowanej. W eksperymentach zaobserwowano, że wytrzymałość na ścinanie śrub wzrasta wraz ze wzrostem długości śruby. Można to wyjaśnić większym zginaniem, które rozwija się w długiej śrubie w porównaniu ze śrubą o krótkim trzonie.
Połączenia czołowe
Połączenia czołowe stosuje się najczęściej jako sprężane ( kategoria E), a czasami jako niesprężane (kategoria D).
Połączenie czołowe na śruby zwykłe , niesprężane , kategoria D
Połączenie czołowe na śruby zwykłe pokazano na rys. 13d.
W połączeniach kategorii D stosuje się stosuje się śruby od klasy 4.6 do 10.9. Połączenia tej kategorii nie powinny być stosowane przy wielokrotnie zmiennym obciążeniu rozciągającym. Mogą być one jednak używane do przenoszenia zwykłych obciążeń wiatrem.
Klasyczny, liniowo sprężysty model połączenia czołowego
W klasycznym liniowo sprężystym modelu zakłada się, że wydłużenia śrub są liniowo zależne od odległości od punktu obrotu blachy połączenia (osi pasa dolnego łączonych profili), czyli, że spełniona jest zasada płaskich przekrojów. Z tego założenia można określić stosunki sił w śrubach podług zależności:
$$\begin{equation} \cfrac {Z_i}{max Z}=\cfrac {h_i}{h} \to Z_i= max Z \cdot \cfrac {h_i}{h} \label{18} \end{equation}$$
W celu wyznaczenia sił w śrubie $Z_i$ w połączeniu pokazanym na rys. 22 porównujemy moment zewnętrzny $M_E=M+N \cdot d$
z nośnością śrub
$$\begin{equation} M_R= \sum \limits _{i=1}^n m \cdot Z_i \cdot h_i \label{19} \end{equation}$$
gdzie m jest liczbą szeregów (kolumn) śrub , n – liczbą śrub w szeregu, a $Z_i$ ramieniem działania siły (rys. 22b)
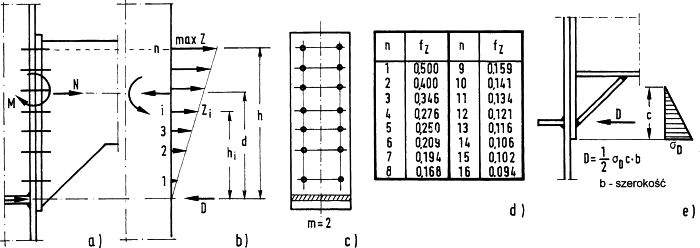
Rys.22 Szacowanie sił w śrubach połączenia zwykłego [9] str 757
Z porównania $M_E = M_R$ ($\ref{19}$) i uwzględnieniu ($\ref{18}$), otrzymamy
$$\begin{equation} max Z= \cfrac {M+Nd}{h} \cdot f_Z \label{20} \end{equation}$$
gdzie $f_Z$ jest współczynnikiem zestawionym na rys. 22d i wyliczanym z zależności:
$$\begin{equation} f_Z= \cfrac{1}{m \sum \limits_{i=1}^n {(\cfrac{h_i}{h})}^2} \label{21} \end{equation}$$
W rezultacie otrzymamy reakcję D w punkcie obrotu:
$$\begin{equation} \sum \limits_{i=1}^n m Z_i- D = N \to D= m \sum \limits_{i=1}^n Z_i- N= \cfrac{max Z}{h}m \sum \limits_{i=1}^n h_i – N \label{22} \end{equation}$$
Naprężenie dociskowe $\sigma_D$ wynoszą (p. rys. 18d):
$$\begin{equation} \sigma_D= \cfrac{2D}{c \cdot b} \label{23} \end{equation}$$
Nieliniowy, sprężysty model połączenia czołowego
Na skutek odkształcalności blach czołowych połączenia czołowego (zarówno na śruby zwykle jak i sprężane), powstaje efekt zginania blach (rys. 23), na skutek czego prostoliniowy rozkład sił w śrubach (rys. 23a) jest w rzeczywistości nieliniowy (rys. 23c). Mechanizm pracy połączenia czołowego belki ze słupem pokazano na rys. 24.
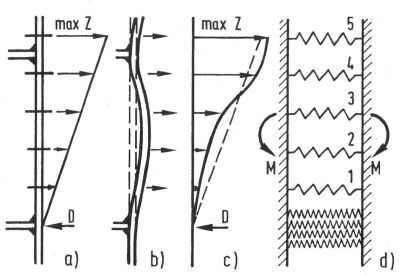
Rys. 23 Model pracy blachy czołowej połączenia: a) rozkład sił w śrubach wg rys. 22b), b) odkształcenie blachy czołowej, c) rozkład sił w śrubach rzeczywisty, d) model śrub jako sprężyn [9] str 760
 Rys. 24 Mechanizm pracy blachy czołowej połączenia czołowego: a) widok perspektywiczny R-S, b) analizowany T-króćec , c) model obliczeniowy T-króćca, d) plastyczny model zniszczenia T-króćca. [9], str 760
Rys. 24 Mechanizm pracy blachy czołowej połączenia czołowego: a) widok perspektywiczny R-S, b) analizowany T-króćec , c) model obliczeniowy T-króćca, d) plastyczny model zniszczenia T-króćca. [9], str 760
Składnikowy model połączenia czołowego w normie Eurokod 3-8
Projektowanie i obliczanie połączeń doczołowych zgodnie z normą [1] przeprowadza się metodą składnikową z uwzględnieniem sprężysto- plastycznych mechanizmów zniszczenia i odkształcalności wszystkich elementów składowych węzła a w tym: ścianek łączonych profili, blachy czołowych, śrub połączenia i innych elementów wymienionych w tab 6.1. normy [1]
Analiza węzła jest złożona i mało wiarygodna na dowód czego w artykule przedstawiono przykład rachunkowy kompletnego, ręcznego wyznaczenia nośności polączenia doczolowego kategorii_D_(niespreżanego). Wyniki uzyskane ręcznie porównano z rezultatami dostępnych arkuszy i programu obliczeniowego.
Sprężane połączenia czołowe, kategoria E
W połączeniach kategorii E stosuje się śruby do sprężania klasy 8.8 i 10.9: typu HV (tab. 7) lub HR (tab.8) zestawach klas wg tab 25 z kontrolowanym dokręcaniem wg tab 26.
Do analizy połączeń czołowych sprężanych śrubami wysokiej wytrzymałości norma [1] preferuje metodę składnikową, która jest żmudna w obliczeniach ręcznych. Prosty i użyteczny sposób wstępnego projektowania sprężonych połączeń czołowych podano w formacji dawnych norm. Połączenie dobrane zgodnie z dawną normą [19] w dalszym procesie należy bezwzględnie sprawdzić zgodnie z procedurami normy [1]., przy czym przez projekt właściwy uznajemy połączenie dobrane wstępnie i wrysowane w konstrukcję. Sprawdzenie połączenia należy traktować jako kolejną iterację projektową, prowadzącą do ulepszenia projektu właściwego.
Wymagania dotyczące zapewnienia jakości, znakowania, identyfikacji i badań przydatności wyrobów śrubowych przeznaczonych do stosowania w połączeniach sprężanych budowlanych konstrukcji stalowych, określają normy PN-EN 14399-1 [20] i PN-EN 14399-2 [21]. Do połączeń sprężanych przeznaczone są śruby i nakrętki systemu HV klasy 10.9 według PN-EN 14399-4 [22] – analogicznie do norm DIN 6914 i DIN 6915 oraz śruby i nakrętki systemu HR klasy 8.8 i 10.9 według PN-EN 14399-3 [23].
Siła sprężenia
Jeśli nie podano inaczej, to zgodnie z EN 1993-1-8 oraz PN-EN 1990-2 [2], za nominalną wartość siły sprężania $F_{pc}$ (na 100%) przyjmuje się siłę:
$$\begin{equation} F_{pc} = 0,7 \cdot f_{ub} \cdot A_s \label{24} \end{equation}$$
gdzie:
$f_{ub}$ – nominalna wytrzymałość na rozciąganie materiału śruby,
$A_s$ – pole przekroju czynnego śruby.
Odpowiednie wartości, zależne od klasy i średnicy śrub podano w tab. 2.
Ten poziom sprężania (w 100%) powinien być stosowany we wszystkich połączeniach ciernych i innych połączeniach sprężanych, chyba że ustalono niższą wartość siły sprężania. W takim przypadku należy również określić zestawy śrubowe, metodę i parametry dokręcania oraz wymagania dotyczące kontroli połączeń.
Klasy zestawów połączeń sprężanych
W tab.25 podano klasy zestawów połączeń sprężanych określone w normie PN-EN 1090-2 (PN-EN 1090-2:2018, Wykonanie konstrukcji stalowych i aluminiowych – Część 2: Wymagania techniczne dotyczące konstrukcji stalowych)).
Tab. 25 Klasy zestawów połączeń sprężanych
Przyjmuje się, że k-współczynniki podaje producent na opakowaniu zestawów śrub podczas dostawy produktu.
Najczęściej spotykanymi wartościami są :
$$\begin{equation} k-index = \begin {cases}
0,1 < k_i \le 0,16 & \textrm { dla klasy K1} \\
0,1 < k_m \le 0,23 \quad ; \quad V_K <0,1 & \textrm { dla klasy K2}
\end {cases} \label{25} \end{equation}$$
Na producentów zostało nałożone wymaganie nie tylko badań zestawów śrubowych w celu potwierdzenia cech wytrzymałościowych, ale również określania współczynnika dokręcania śrub do połączeń sprężanych w klasach K1 i K2 wg tab.25. Zaleca się by w konstrukcjach budowlanych klasy XC2 i XC3 (w zasadzie wszystkie budowlane konstrukcje nośne) stosować odpowiednio klasy K1 i K2 zestawów do połączeń sprężanych.
Oznacza to że jedynie w konstrukcjach mało odpowiedzialnych (takich jak: budynki max dwukondygnacyjne konstrukcje z profili walcowanych bez sztywnych na zaginanie styków płyt głowicowych; słupy o długości wyboczenia maximum 3m; belki o rozpiętości maksimum 5m i wysięgami do 2m; schody i poręcze w budynkach mieszkalnych ; budynki rolnicze bez regularnego ruchu osób, np. stodoły, szklarnie; ogrody zimowe w budynkach mieszkalnych; domki jednorodzinne z max 4-ma kondygnacjami) moment sprężania można określać bez znajomości współczynnika dokręcenia podanego przez producenta.
Metody dokręcenia śrub
W zależności od k-klasy zestawu sprężającego (tab. 25) norma PB-EN 1090-2 [2] przewiduje metody dokręcania: kontrolowanego momentu dokręcenia, kombinowaną HRC lub DTI, które należy stosować zgodnie z tab. 26.
Tab.26 Wybór metody dokręcania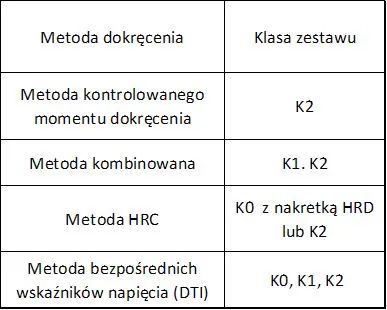
Metoda kontrolowanego momentu dokręcenia
Metoda kontrolowanego momentu dokręcenia może być stosowana dla klasy zestawu K2 (dla najbardziej odpowiedzialnych złączy). Metoda odpowiada tradycyjnym metodom dokręcania, lecz z ważnymi modyfikacjami, a przede wszystkim w związku z prowadzeniem sprężenia w dwóch etapach:
I etap – dokręcenie momentem $M_I = 0,75 \cdot M_2$ , gdzie $M_2$ z tab .25. (wiersz 3, kol. 3)
II etap – dokręcenie śrub momentem $M_{II}= 1,10 M_2 $
W celu określenia momentu pełnego dokręcenia $M_2$ producent zestawów śrubowych podaje z badań k-współczynnik $k_m$ oraz współczynnik zmienności statystycznej $V_k$.
Metoda kombinowana
Metoda kombinowana może być stosowana dla klas K1 i K2 zestawów śrub do sprężania.
Zaletą metody jest to, że w zasadzie nie trzeba znać k-współczynnika śrub stosowanych do sprężenia.
Dokręcanie metodą kombinowaną prowadzone jest w dwóch etapach:
I etap – dokręcanie kluczem dynamometrycznym na moment dokręcenia o wartości
$M_I \approx 0,75 M_i$, gdzie $M_i = M_2 \, lub\, M_1 \, lub M_{test}$;
Jeśli stosuje się $M_1$, to dla uproszczenia można przyjąć , że $ 0,75 M_1 = 0,13 \cdot F_p \cdot d $, to znaczy moment dokręcający uzyskamy na podstawie wartości sił sprężających $F_{pc}$ zestawionych w tab 2 z zależności
$M_I \approx 0,13 \cdot F_{pc} \cdot d$
Położenie nakrętki w stosunku do gwintu trzpienia śruby należy oznaczyć po zakończeniu I etapu kredką lub farbą znakującą – tak, aby obrót nakrętki w drugim etapie można było łatwo wyznaczyć.
Po dokręceniu i oznaczeniu położenia nakrętek wszystkich połączeń można przystąpić do drugiego etapu dokręcania
II etap – Dokręcanie polega na częściowym obrocie nakrętki zestawu.
Kąt dodatkowego obrotu nakrętki $\Delta \alpha$ w zależności od długości zakleszczenia $Z=\sum t$ wynosi
$$\begin{equation} \Delta \alpha = \begin {cases}
dla \quad Z< 2 d & 60^o \quad \textrm { (1/6 pełnego obrotu)} \\
dla \quad 2 d \le Z < 6 d & 90^o \quad \textrm { (1/4 pełnego obrotu)} \\
dla \quad 6 d \le Z < 10 d & 120^o \quad \textrm { (1/3 pełnego obrotu)} \\
\end {cases} \label{26} \end{equation}$$
gdzie $d$ – średnica nominalna śruby.
Metoda HRC
Stosuje się śruby z nakrętkami zrywalnymi wg normy PN-EN 14399-10 [24]
Kontroluje się wizualnie 100 % zestawów śrubowych. Jako całkowicie dokręcone traktuje się zestawy śrubowe ze ściętą (zerwaną) końcówką trzpienia. Zestaw śrubowy, w którym końcówka trzpienia nie została zerwana, uważa się za niedokręcony.
Metoda DTI
Stosuje się bezpośrednie wskaźniki napięcia wg PN-EN 14399-9 [25], które pokazują osiągnięcie w śrubie wymaganej minimalnej siły sprężenia)).
Bezpośrednie wskaźniki napięcia i związane z nimi podkładki osadza się zgodnie z Załącznikiem J [25], które pokazują osiągnięcie w śrubie wymaganej minimalnej siły sprężenia)).
Pierwszy etap dokręcania – do osiągnięcia w zestawie śrubowym stanu równomiernego „ścisłego docisku” – następuje, gdy rozpoczyna się zgniatanie wypustek podkładek DTI. Ten etap należy uzyskać we wszystkich śrubach danego połączenia przed rozpoczęciem drugiego etapu dokręcania.
Dokręcanie w drugim etapie wykonuje się według prEN 14399-9 i Załącznika J[25], które pokazują osiągnięcie w śrubie wymaganej minimalnej siły sprężenia)). Pomiary szczelin między podkładkami mogą być uśredniane przy ocenie akceptowalności dokręcenia śruby do normy .
Wyznaczanie k-współczynnika dokręcenia
Współczynnik dokręcenia K zależy od wielu czynników: geometrii gwintu, tarcia na gwincie oraz nakrętki o podkładkę, od zastosowanego środka smarującego. Na rys. 25 pokazano poglądową ilustrację tych zależności
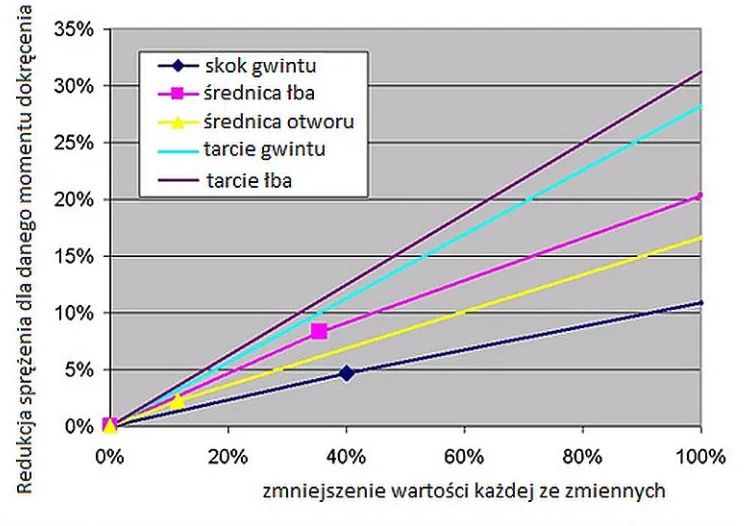
Rys.25 Efekt redukcji sprężenia przy tym samym momencie dokręcenia w zależności od zmian parametrów połączenia [26],
Z rys. 25 wynika między innymi, że podwojenie współczynnika tarcia na gwincie (przy ustaleniu pozostałych zmiennych) generuje około 28% mniejsze sprężenia śruby przy tym samym momencie dokręcenia.
W aktualnej normie, przeznaczonej dla wykonawców konstrukcji stalowych [2] uwzględniono wszywany przez wiele prac [27], [28] i in. – że tylko testy połączeń przeprowadzone w warunkach laboratoryjnych mogą określić zależność T-F (moment dokręcenia – siła sprężenia). Powszechnie uznaje się, że „tylko około 10-15% wejściowego momentu dokręcenia idzie na rozciągnięcie śruby.
Podczas dokręcania łączników gwintowanych mierzymy moment obrotowy T. Pomiar napięcia śrub F jest znacznie trudniejszy. Zależność między momentem dokręcenia T, a siłą F, powstałą w wyniku wydłużenia śruby jest najczęściej opisywana przez
$$\begin{equation} T= K \cdot d \cdot F_p \label{27} \end{equation}$$
gdzie:
K- współczynnik dokręcenia,
d – średnica śruby
$F_p$ – siła sprężenia śruby
Istnieje kilka różnych wersji formuł analitycznych na oszacowanie współczynnika „K”, a norma ISO 16047 [29] podaje następującą zależność
$$\begin{equation} K= \cfrac{1}{d} \cdot \left ( \cfrac{1}{2} \cdot \cfrac{P+ 1,154 \cdot \pi \cdot \mu_{th} \cdot d_2}{\pi – 1,154 \cdot \mu_{th} \cdot P/d_2} + \mu_b \cdot \cfrac{D_o+d_h}{2}\right ) \label{28} \end{equation}$$
gdzie parametry maszyny laboratoryjnej:
$d_2$ – średnica podziałowa gwintu,
$d_h$ – średnica otworu przelotowego.
$D_o$ – zewnętrzna średnica powierzchni nośnej (podkładki),
$P$ – skok gwintu,
$\mu_{th}$ – współczynnik tarcia na gwincie
$\mu_b$ – współczynnik tarcia pod łbem śruby.
Sprawdzanie nośności połączenia
Zaprojektowane połączenie śrubowe przyjętymi: typem, wymiarami i innymi parametrami, czyli ukształtowane metodą Steenhuis lub innymi uznanymi metodami w tym dla czołowego połączenia sprężanego metodą dawnej normy PN-90/B-03200 – należy sprawdzić metodą składnikową wg [1].
Sprawdzanie ręczne metodą składnikową jest żmudne (p. przyklad_9 Nośność polaczenia doczołowego kategorii D (niesprężanego) ) i nie jest zalecane w praktycznym projektowaniu. Dlatego do sprawdzenia nośności ukształtowanego połączenia stosujemy sprawdzone programy obliczeniowe, np.: publicznie dostępny arkusz ACoP [30] lub komercyjne oprogramowanie, np. CsJoint w pakiecie Consteel [31] lub program IDEA StatiCa Connection [32]. Użyteczne są tablice połączeń sprężanych np.: [33]. Przykład sesji w programie ACoP przedstawiono na rys. 39 do rys. 47 w przykładzie 9, a wyniki tego samego przykładu uzyskane w programie csjoint na rys. 48.
Połączenia cierne
Klasyczne połączenia cierne (kategorii C)
Nośność na poślizg połączenia ciernego
W połączeniu ciernym pokazanym na rys. 12b nośność styczna realizowana jest przez siły tarcia pomiędzy łączonymi elementami, wywołane siłami sprężenia śrub – obliczeniowa nośność połączenia na poślizg wynosi [1], tab. 3.4
$$\begin{equation} F_{s,Rd}=\cfrac{k_s \cdot n \cdot \mu}{\gamma_{M3}}\cdot F_{pc} \label{29} \end{equation}$$
gdzie:
n- liczba styków ciernych (płaszczyzn tarcia),
$\mu$ – współczynnik tarcia zależny od klasy powierzchni ciernej wg [1], tab. 3.7, wg tab.3
$\gamma_{M3}=1,25 $ – współczynnik częściowy przy obliczaniu nośności połączeń ciernych (tab.20)
$k_s$ – współczynnik zależny od rodzaju otworu przejściowego śruby wg tab.27.
Tab.27. Współczynniki $k_s$ sprawności śrub w połączeniach ciernych [1], tab. 3.6,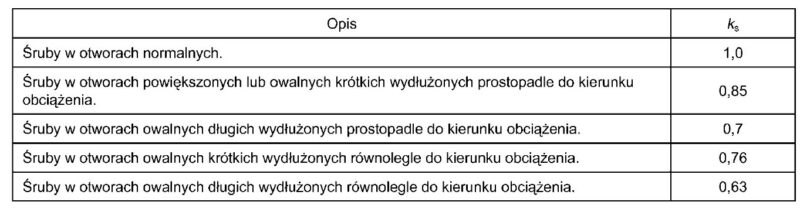
W tab.3 podano kategorie powierzchni ciernych oraz odpowiadające minimalne współczynniki tarcia dla najczęściej stosowanych powierzchni w konstrukcjach stalowych zgodnie z normą wykonawczą [2].
Połączenia cierne kategorii C sprawdza się pod kątem nośności przy obciążeniu maksymalnym. W przypadku tego typu połączeń istnieje możliwość, że niektóre śruby będą opierać się o blachy łączące w wyniku ustawienia podczas montażu (tj. śruby nie znajdują się w środku śruby otworów, ale stykają się z płytką na krawędzi otworu na śrubę). Dlatego, aby zapewnić pełne bezpieczeństwo, śruby są również sprawdzane pod kątem uszkodzeń łożysk przy maksymalnym ociążeniu.
Nominalna siła sprężenia śruby jest określana na podstawie [1],wzór (3.1) $(\ref {24})$, a jej wartości są zestawione w tab. 2. Obliczeniowa siła sprężenia $ F_{pc,d}$ w połączeniach ciernych jest nieco mniejsza i wynosi
$$\begin{equation} F_{pc,d}=\cfrac{F_{pc} }{\gamma_{M7}} \label{30} \end{equation}$$
dzie $\gamma_{M7}=1,10$ – współczynnik częściowy przy obliczaniu sił sprężających śruby o wysokiej wytrzymałości [1], kl. 2.2.(2), tab. 2.1
Przygotowanie powierzchni ciernych
W pracy [13] wskazano, że na skutek nieprawidłowego przygotowania powierzchni ciernych już przez pierwsze przez pierwsze 2-4 miesiące – może wystąpić znaczne o 25% do45%) zmniejszenie napięcia wstępnego śrub w przypadku pokrycia powierzchni ciernych standardowymi powłokami ochronnymi.
Powierzchnie przylgowe w połączeniu ciernym należy przygotować bez stosowania standardowych powłok malarskich ochronnych w połączeniach ciernych, a w przypadku konieczności zabezpieczenia antykorozyjnego należy stosować specjalne farby cierne, które nie doprowadzą do relaksacji siły sprężającej śruby, a dodatkowo zwiększą współczynnik tarcia w połączeniu zgodnie z tab. 3.
Rozciągane śruby w połączeniu ciernym
W przypadku, gdy siła zewnętrzna $F_t$ rozciąga śruby siłą $F_p$ w połączeniu ciernym, to siła wstępnego sprężenia śrub $F_{pc}$ nie zmniejsza siły rozciągającej $F-t$ [13].
Wstępne obciążenie śruby odkształca bowiem zarówno blachy, jak i śrubę. To zachowanie można uprościć do modelu pokazanego na rys. 27. Wstępne obciążenia śruby $F_p$ powoduje jej wydłużenie o $δ_b$ i jednoczesne ściśnięcie blachy o $δ_p$. Po przyłożeniu zewnętrznej siły rozciągającej $F_t$ całkowita siła w śrubie wyniesie $F_b$ przy wydłużeniu $δ_b,ext$, [34].
Zewnętrzna siła rozciągająca zostanie częściowo przejęta jako nowa, dodatkowa siła w śrubie $ΔF_b$ i częściowo doprowadzi do zmniejszenia siły, jaką złącze pierwotnie wywierało na śrubę $ΔF_j$. Wzrost siły śruby wynosi $ΔF_b$, a spadek siły docisku wynosi $ΔF_p$ wraz z odkształceniem złącza $δ_p,ext$. Linia przerywana pokazuje wpływ efektu dźwigni (podważania) na zginanie płyty. Stosunek sztywności śruby rozciąganej a blachami dociskowymi (około 1 do 4) powoduje, że pomiędzy płytami pozostaje siła kontaktowa co najmniej równa,
$$\begin{equation} F_{pc}= F_p -0,8 \cdot F_{t,Ed}\label{31} \end{equation}$$
gdzie:
$F_{t,Ed}$ zewnętrzna, obliczeniowa siła rozciągająca śruby przyłożona w zwykłych warunkach,
0,8 – współczynnik, zależny od grubości blach (rodzaju stali, liczby warstw) oraz od rodzaju śrub (klasy i średnicy). Wartość 0,8 stosuje jest ekstremalnie niekorzystny.
Zgodnie z normą [1], kl. 3.9.3 (1) w przypadkach, w których oprócz siły ścinającej, działa dodatkowo siła rozciągająca $F_{t,Ed}$, nośność obliczeniową śruby na poślizg oblicza się w taki sposób, że w miejsce siły $F_{pc}$ w wyrażeniu ($\ref{29}$) należy wstawić zmodyfikowaną siłę ($\ref{31X}$).
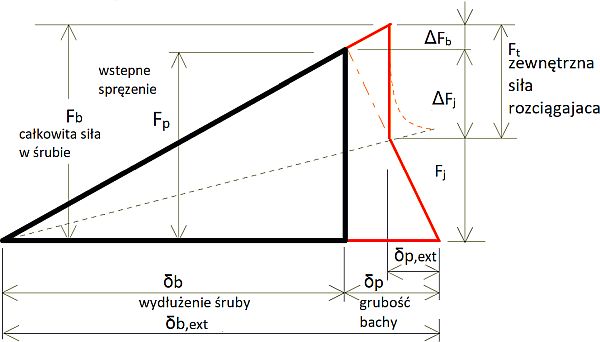
Rys.26 Wykres sił wewnętrznych w połączeniu ze śrubą naprężoną obciążoną siłami rozciągającymi [35]
W połączeniach doczołowych, w których siła docisku w strefie ściskanej równoważy siłę rozciągającą, redukcja nośności na poślizg nie jest wymagana.
Kombinacja połączenia ciernego i zaciskowego
Nowoczesne łączniki śrubowe Hilti, Fischer i in.
Ogólna metodyka oceny i projektowania łączników specjalnych wynika przede wszystkim z badań prowadzonych przez producenta, więc zależy istotnie od typu kotwy.
Obecnie technologia łączenia konstrukcji stalowych z betonem została zdominowana stosowaniem śrub do betonu (kotew wkręcanych). Kotwy wkręcane do betonu pozwalają bowiem na uzyskanie nośności zbliżonej do obciążalności kotew segmentowych, ale ich osadzanie jest dwa razy szybsze dzięki mniejszej średnicy wierconego otworu, braku konieczności czyszczenia otworu i dokręcania kotwy kluczem dynamometrycznym oraz – dzięki zminimalizowaniu kleszczenia się kotwy podczas wkręcania. Hybrydowe połączenia w technologii wkręcania z jednoczesnym wklejaniem umożliwiło dalsze zwiększenie nośności kotew przy zmniejszeniu ilości aplikowanego kleju.
Wybrane tabele do projektowania konstrukcyjnych śrub do betonu podano w rozdziale Śruby do betonu (kotwy wkręcane): w tab 15 kotwy wkręcane FBS – 2-ga generacja prod Fisher, a w tab.16 – kotwy wkręcane HUS-3-cia generacja prod. Hilti.
W tablicach wyróżniono specyficzne mechanizmy zniszczenia łączników, które zostały zdefiniowane w normie PN-EN 1992-4 [37].
1) zniszczenie stali łącznika (steel failure of fastener),
2) zniszczenie stożka betonowego (concrete cone failure),
3) wyrwanie śruby kotwiącej (pull-out failure of fastener ) – nie wymagane dla kotew wklejanych z łbem,
4) kombinowane zniszczenie stożka betonu i wyrwanie śruby ( combined pull-out and concrete failure),
5) rozłupanie betonu ( concrete splitting failure),
6) krawędziowe odłupanie betonu (concrete blow-out failure),
7) zniszczenie zbrojenia ( steel failure of renforcement),
8) zniszczenie zakotwienia zbrojenia ( anchorage failure of reinforcement).
Problematykę nowoczesnych łączników stali ( również z betonem) szerzej omówiono w artykule Technika mocowań. Nowoczesne łączniki.
Projektowanie wstępne (właściwe) połączeń śrubowych
Właściwe projektowanie połączeń śrubowych polega na wstępnym dobraniu typu połączenia śrubowego, jego wymiarów oraz parametrów wytrzymałościowych. Tak zaprojektowane połączenie śrubowe można ( i należy) następnie sprawdzić metodami dokładnymi zgodnie z zasadami normy [1] lub innymi uzasadnionymi naukowo metodami zaimplementowanym i w programach obliczeniowych , w tym ACoP [30], csJoint sJoint Consteel[31], IDEA StatiCa Connection [32].
Projektowanie właściwe polega na prawidłowym kształtowanie konstrukcji z jednoczesnym wspomaganiem się oszacowaniami nośności i odkształcalności węzła. Natomiast szczegółowe obliczenia nie są składową właściwego projektowania, a tylko sprawdzeniem poprawności ukształtowania konstrukcji i jej węzłów i są przeprowadzane w celu dokonania korekt przyjętego projektu, przy czym o klasie projektanta świadczy to, że będą to tylko drobne korekty, a nie zasadnicze zmiany we wcześniej przyjętych rozwiązaniach.
Metoda Steinhaus dla węzłów ram
Prostą metodę wstępnego (właściwego) projektowania połączeń śrubowych zaproponował Steenhuis, (1999) [38]. Metoda dotyczy połączeń belek ze słupami oraz słupów z fundamentami zestawionych w tab. 28.
Metodą Steenhuis można wstępnie dobrać główne parametry połączenia: typ połączenia A do T , wysokość przekroju przywęzłowego $r$ dla założonego typu połączenia oraz dla założonych grubości pasów $t_{fc}$ oraz rodzaju stali $f_{y,fc}$. Następnie metodami szczegółowymi można wstępnie dobrać śruby czołowego połączenia sprężanego lub inne łączniki standardowymi metodami.
Tab.28. Współczynniki sztywności $\xi$ i nośności $\zeta$ oraz ramię sił $r$ dla wybranych połączeń belek ze słupami i z podstawą [38]
W tab. 28 kolorami rozróżniono grupy typów połączeń: typ S do G na tle zielonym należy do grupy połączeń śrubowych czołowych; typ H do N na tle błękitnym należy do grupy połączeń śrubowych innych ; typ O do S na tle żółtym należy do grupy połączeń spawanych; typ T dotyczy mocowania stopy słupa do fundamentu za pośrednictwem śrub fundamentowych.
Oszacowanie sztywności i nośności złącza wynika, z jego najsłabszej części. Sztywność połączenia można oszacować z zależności
$$\begin{equation} S_{ini,j,app} = \cfrac{E \cdot r^2 \cdot t_{fc}}{\xi}\label{32} \end{equation}$$
gdzie:
$t_{fc}$ jest grubością półki słupa lub płyty podstawy,
$r$ – ramię dźwigni szacowane jako odległość między środkami półek belki (tab. 28).
Nośność połączenia mierzona momentem zginającym można oszacować z zależności
$$\begin{equation} M_{Rd,j,app} = \cfrac{ \zeta \cdot f_{y.fc} \cdot r^2 \cdot t_{fc}}{ \gamma_{M0}}\label{33} \end{equation}$$
gdzie:
$f_{y,fc}$ – granica plastyczności stali pasa półki słupa/ płyty podstawy
$\gamma_{Mo}=1,0$ – częściowy współczynnik bezpieczeństwa (materiałowy dla konstrukcji stalowej)
Współczynniki sztywności $\xi$ i nośności $\zeta$ dobiera się tab. 28.
W metodzie założono, że najsłabszym elementem jest pas słupa oraz przyjęto, że grubość blachy czołowej $t_p$ jest większa od grubości pasa ($t_p \ge t_{fc}$) ; grubość żebra środnika słupa $t_{sc} \approx t_{fb}$ ; średnica śrub jest większa niż grubość pasa słupa $d \ge t_{fc}$.
Metoda PN-90/B-03200 [19] dla sprężanych połączeń śrubowych
Ze względu na złożoność procedury składnikowej projektowania połączeń czołowych, ręczne stosowanie tej metody jest obarczone istotnymi błędami rachunkowymi (p. przykład 9 ) do wstępnego doboru śrub w sprężanym połączeniu czołowym użyteczna jest prosta metoda ze starej normy polskiej [19], w której zaprezentowano modele sprężanych połączeń zginanych: a) w stanie granicznym rozwarcia, b) w stanie granicznym rozwarcia połączeń, w których należy uwzględnić efekt dźwigni, c) w stanie granicznym zerwania śrub (rys.27).
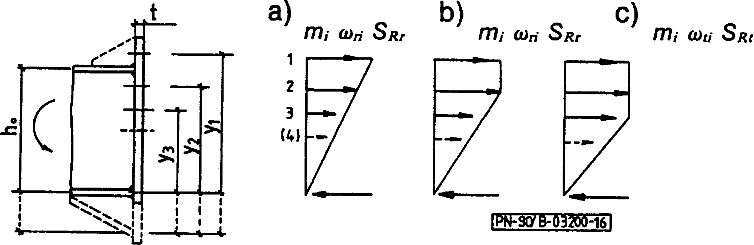
Rys.27 Modele obliczeniowe połączeń kategorii E [19], rys.16 : a) sprężysty w stanie granicznym rozwarcia, b) sprężysto-plastyczny w stanie rozwarcia (opis w tekście), c) plastyczny w stanie granicznym zerwania śrub
Z modeli obliczeniowych, pokazanych na rys.27, wynikają następujące formuły na nośność obliczeniową połączenia $ M_{Rd}$:
a) w stanie granicznym rozwarcia z rozkładu sprężystego sił (przy założeniu płaskich przekrojów):
$$\begin{equation} M_{Rd} = S_{Rt} \cdot \cfrac {1}{z_{max}} \sum _{i=p}^{p+k-1} m_i \omega_{r_i} z_i^2\label{34}\end{equation}$$
b) w stanie granicznym rozwarcia styku, w którym zachodzi wpływ tzw. efektu dźwigni na redukcję obciążenia granicznego, to znaczy efektu zwiększenia sił w śrubach na skutek sprężysto plastycznego odkształcenia blachy czołowej, który jest obserwowany przy zbyt cienkich blachach czołowych i wówczas, gdy blacha czołowa (lub jej segment) jest usztywniona wzdłuż jednej tylko krawędzi. Sprowadza się to w praktyce do przypadku wystającej blachy czołowej i 1 -szego szeregu śrub w tej części połączenia.
$$\begin{equation} M_{Rd}=S_{Rt} \cdot \left ( m_1 \omega_{r1} z_1+\cfrac{1}{z_2} \sum \limits _{i=2}^k m_i \omega_{ri} z_i^2 \right) \label{35} \end{equation}$$
c) w stanie granicznym zerwania śrub z rozkładu plastycznego na długości występowania śrub uwzględnianych w oszacowaniu
$$\begin{equation} M_{Rd}=S_{Rt} \cdot \sum \limits_{i=p}^{p+k-1} m_i \cdot \omega_{ti} \cdot z_i\label{36} \end{equation}$$
We wzorach ($\ref{34}$) do ($\ref{36}$) zastosowano następujące oznaczenia:
p=1, gdy występuje zewnętrzny szereg śrub lub p=2,
k – liczba szeregów śrub, przy czym do obliczeń przyjmuje się k ≤ 3,
SRt– nośność obliczeniowa śrub na rozciąganie,
mi– liczba śrub w i-tym szeregu,
ωti , ωri – uśrednione dla i-tego szeregu współczynniki rozdziału obciążenia, odpowiednio w stanie rozwarcia i zerwania styku. Należy je przyjmować z tab. 29,
zi – ramię działania sił w śrubach i-tego szeregu względem potencjalnej osi obrotu, przy czym w obliczeniach należy uwzględniać te śruby, dla których spełniony jest warunek zi ≥ 0,6 h0, gdzie ho jest odległością pomiędzy liniami środkowymi (osiami) zewnętrznych pasów.
W przypadku elementów dwuteowych o wysokości większej niż 400 mm lub smukłości środnika λw=hw/tw > λwgr= {140 dla stali S235 (dawna St3S); 118 dla stali S355 (dawne 18G2A) }, w stanie granicznym zamiast zi należy przyjmować zired=zi-h/6, h- jest wysokością przekroju (w krawędziach zewnętrznych pasów). W przypadku połączenia z pojedynczym pasem rozciąganym bez wzmocnienia współrzędna (ramię) zi jest odległością osi śruby od linii środkowej (osi) pasa rozciąganego.
Nośności śrub na rozciąganie SRt, występujące w formułach ($\ref{22}$) do ($\ref{29}$) , podano w tab.30.
Tab.29. Współczynnik rozdziału obciążenia w styku czołowym [19], tab.17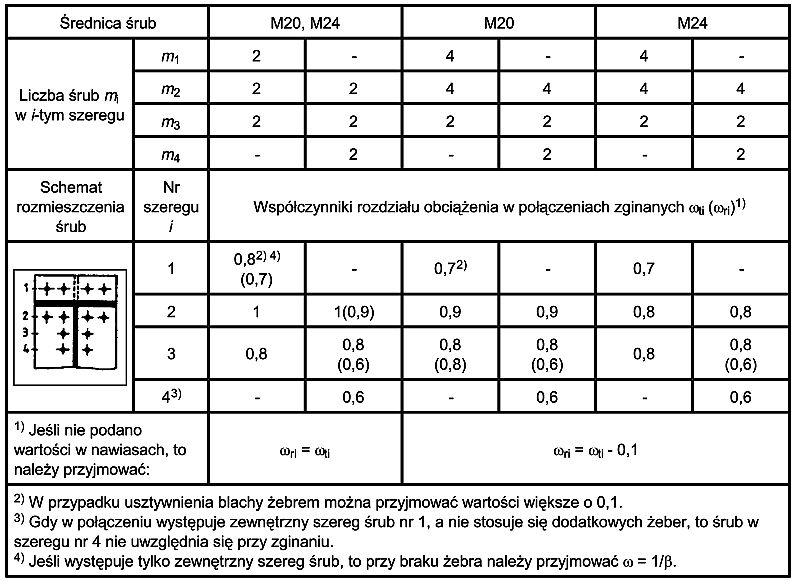
Tab.30. Nośności i własności śrub (nakrętek) [19], tab. Z2-2
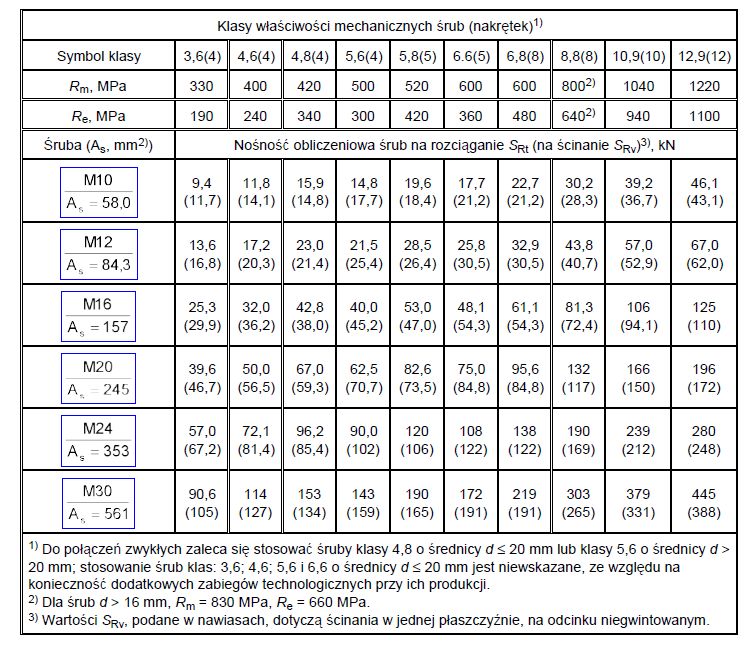
Uwaga ! : Nośności podane w tab. 30 obliczono wg formuł starej normy [19] różnią się one od nośności szacowanych według Eurokod [1] zestawionych w tab.1.
Norma PN-EN 1993-1-8 [1] podaje metody sprawdzania nośności połączeń śrubowych dla znanych sił przekrojowych działających na węzeł, które w złożonych ( statycznie niewyznaczalnych) systemach konstrukcyjnych może być trudne, bowiem siły te zależą w ogólności od rodzaju połączenia oraz od jego sztywności.
Tablice połączeń śrubowych
Z wykorzystaniem tablic na etapie projektowania właściwego w prosty sposób można dobrać połączenie śrubowe na śruby zwykłe lub sprężone, które nie wymaga już sprawdzenia nośności.
Spośród różnych, opracowanych tablic polecamy tablice niemieckie [33], znane także pod nazwą: Prüfbericht TP-12-001 vom 28.03.2013)). W przykładzie 9, na rys. 49 pokazano przykładową kartę z tablic [33] dla połączenia czołowego z tego przykładu.
Przykłady rachunkowe
Przykład 1 [Dobór długości i masy śruby ]
Dobrać śrubę w zestawie: podkładka+ śruba +podkładka +nakrętka,
to znaczy 2p+n
łączącej pakiet blach łącznej grubości
$\sum t = t_1 + t_2= 20+24 = 44 mm$
W obliczeniach wytrzymałościowych dobrano śrubę
M20
Śruba z gwintem na całej długości wg normy ISO 4017
Dla potrzebnej długości śruby
$ L_{potrz} = 44 + 1 \cdot 18 + 2 \cdot 3,0 +2 \cdot 2,5 = 73 \, mm$
gdzie: 44 mm – grubość pakietu, M=18 mm – wysokość nakrętki, $t_{pod}=3,0$ mm – grubość podkładki, P=2,5 mm – skok gwintu.
- z tab 4 podwiersz P (śruba z pełnym gwintem ), kolumny „M20” dobrano śrubę taką aby długość „L’ ( skrajna lewa kolumna) była najbliższa $ L_{potrz}$ , ale większa od niej, czyli
$L= \, 75 mm$
- Masa zestawu wynosi:
$m= ( 220+103,3)/1000 = 0,323 \, kg$
gdzie:
220 kg – masa 1000 szt śrub, odczytana z tab 4 na przecięciu kolumny M20 i wiersza 75, podwiersz C.
Uwaga w przypadku braku wartości na przecięciu – śruba nie jest dostępna i należy wybrać inną.
103,3 kg – masa 1000 szt zestawu 2p+n, odczytana ze stopki tab 4
Śruba z podkładką Nord-Lock
W przypadku zastosowania podkładki Nord-Lock przeciw odkręceniu nakrętki z tab 6. oczytano grubość podkładki $t_{pod}=T= 3, 4 \, mm$
Potrzebna długość śruby wynosi
$ L_{potrz} = 44 + 1 \cdot 18 + 3,0 +3,4 + 2 \cdot 2,5 = 73,4 \, mm$
więc:
- z tab 4
$L= \, 75 mm$
- Masa zestawu
$m= 0,323 – 17,1/1000+ 2,09/100 = 0,327\, kg$
gdzie:
0,323 kg z przykładu wyżej,
17.1/1000 – masa jednej podkładki standardowej ( stopka tab.4)
2,09/100 – masa jednej podkładki Nord-Lock (tab. 6)
Śruba z gwintem na części długości wg normy ISO 4014
Śruby na części długości są stosowane do połączeń ścinanych na odcinku bez gwintu
- W pierwszym kroku określamy długość śruby ISO 4014 – z tab. 4 dobrano śrubę z kolumny „M20” , występującą w podwierszu C (śruba z gwintem na części długości) tak aby jej długość „L’ ( w skrajnej lewej kolumnie) była najbliższa $ L_{potrz}$ (określonej jak w przykładzie wyżej), ale większa od niej :$L= \, 75 mm$
- Sprawdzamy, czy przekrój cięcia śruby wypadnie w części nienagwintowanej
długość części nagwintowanej B odczytana z tab 5 na przęcięciu kolumny M20 i wiersza „75” wynosi
$B= 31 \, mm$
Długość trzpienia bez gwintu (od łba licząc) wyniesie $L-B= 75-31= 44 \, mm$
Przekrój cięty wypadnie w odległości od łba:
$t_1 = 20 \, mm$ lub $t_2 = 24 \, mm$
i w każdym przypadku wypadnie w części nienagwintowanej -> OK.
- Masa zestawu wynosi
$m= ( 238+103,3)/1000 = 0,341 \, kg$
gdzie:
238 kg – masa 1000 szt. śrub, odczytana z tab 4 na przecięciu kolumny M20 i wiersza „75”, podwiersz C.
Uwaga w przypadku braku wartości na przecięciu – śruba nie jest dostępna i należy wybrać inną.
Śruba do sprężania HV PN-EN 14399-4
Długość zaciskowa wynosi
$Z= 44 + 2\cdot 4= 52 \, mm$
gdzie: 4= $t_{pod}$ – grubość podkładki w zestawie wg PN-EN 14399-6 ( w tab. 7 ).
Z tab. 7 w kolumnie „M20” dla długości zaciskowej $52\, mm \in [ 48 \, ;\, 53 ] mm$ , dobrano śrubę o długości
$L= 75 \, mm$
Masa zestawu odczytana z tab. 9, wynosi
$m= 26,2 + 15,62)/100 = 0,418 \, kg$
gdzie:
26,2 kg – masa 100 szt. śrub HV M20x75
15,62 kg- masa 100 szt. kompletu 2-ch podkładek + 1 nakrętka.
Śruba do sprężania HR PN-EN 14399-3
Długość zaciskowa obliczona jak wyżej wynosi
$Z= 52 \, mm$
Z tab. 8 w kolumnie „M20” i dla długości zaciskowej $52\, mm \in [ 39 \, ;\, 53 ] mm$ , dobrano śrubę o długości
$L= 75 \, mm$
Masa zestawu odczytana z tab.9, wynosi szacunkowo jak dla zestawu HV
$m= (26,2 + 15,62)/100 = 0,418 \, kg$
Przykład 2 [ Nośność rozciąganego przekroju osłabionego śrubami ]
[39],przykład 1.2
Wyznaczyć obliczeniową nośność przekroju rozciąganego. osłabionego otworami (rys. 28). Płaskownik o grubości t=10 mm wykonano ze stali S235.
Parametry wytrzymałościowe stali S235 [40], tab. 3.1:) (dla t<40 mm):
granica plastyczności fy= 235 MPa ,
granica wytrzymałości fu = 360 MPa
tab. 20 $\to$ współczynniki częściowe:
$ \gamma_{M0}=1,0$
$ \gamma_{M2}=min [1,1 \, ; \, 0,9\cdot f_u/f_y] = min[1,1 \, ; \, 0,9 \cdot 360/235 \, ] = 1,1$
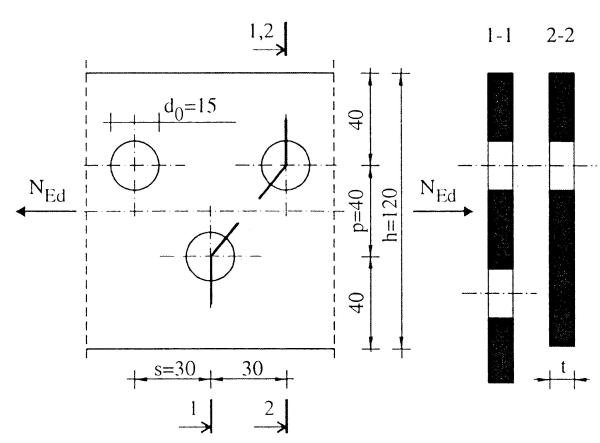
Rys.28 Rozciągany płaskownik osłabiony otworami na śruby [39], przykład 1.2.
Przekrój poprzeczny:
brutto: $A=12 \cdot 1,0=12,0 \, cm^2$,
netto [40], pkt 6.2.2.2(4)::
przekrój (1-1) $A_{net(1-1)}= A- \left ( nd_0- \sum \cfrac{s^2}{4p}\right ) t=12,0- \left( 2\cdot 1,5 – \cfrac{3,0^2}{4 \cdot 4,0} \right) 1,0= 9,56 \, cm^2$,
przekrój (2-2) $A_{net(2-2)}= 12,0 – 1,5\cdot 1,0=10,5\, cm^2$,
przekrój netto jest mniejszą z powyższych wartości: $A_{net}= \min \{9,56 ; 10,5 \}=9,56 \, cm^2$.
Nośność obliczeniowa przekroju na rozciąganie – zgodnie z [40], kl. 6.2.3.(2)b: dla elementów połączonych symetrycznie w węzłach za pośrednictwem łączników kategorii A (typu dociskowego – tab.22) obliczeniową nośność na rozciąganie wyznacza się jako nośność graniczną:
$$N_{u,Rd}=\cfrac{0,9 A_{net}\cdot f_y}{\gamma_{M2}}=\cfrac{0,9 \cdot 9,56\cdot 360}{1,1}\cdot 10^{-1}=281,6 \, kN$$
Nie może ona przekraczać nośności obliczeniowej przekroju brutto
$$N_{pl,Rd}= \cfrac {A \cdot f_y}{\gamma_{M0}}=12,0\cdot 235/1,0 \cdot 10^{-1}=282,0 \,kN $$
to znaczy ostatecznie:
$$N_{t,Rd}= \min [N_{u,Rd};N_{pl,Rd}]=[281,6; 282,0]= 281,6 \, kN$$
Przykład 3 [ Nośność zakładkowego połączenia śrubowego kategorii A ]
[39],przykład 5.1
Wyznaczyć nośność zakładkowego połączenia śrubowego kategorii A (tab.23)
śrubami M16 kl. 8.8, pokazanego na rys. 29 rozciąganego siłą podłużną $N_{Ed}=250 \, kN$, łączącego płaskownik ze stali S235.
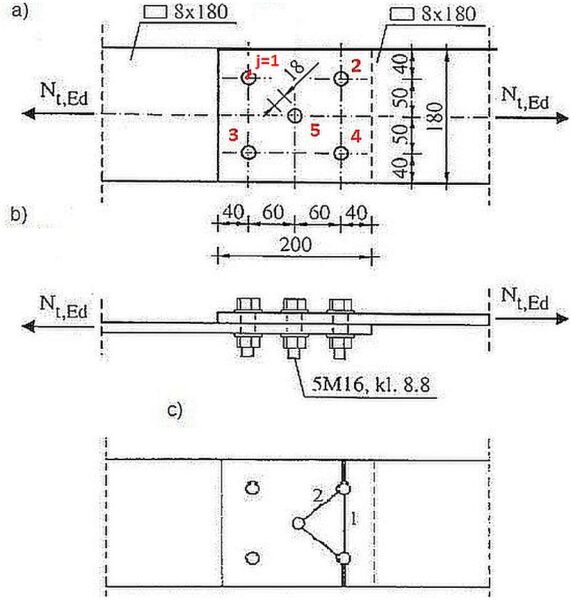
Rys.29. Szkic do przykładu rachunkowego połączenia zakładkowego [39]
tab 20 $\to$ współczynnik częściowy $\gamma_{M2}$:
= 1,1 – gdy liczona jest nośność przekroju netto,
= 1,25 – gdy liczona jest nośność śrub .
tab.1 $\to$ dla śrub M16 – 8.8:
pole przekroju śruby czynnego przy ścinaniu $A_s$=157 mm2 ,
wytrzymałość śrub na rozciąganie $f_{ub} = 800 \, MPa$,
granica plastyczności śrub $f_{yb} = 640 \,MPa$.
Dla stali S235 $f_u=360 \, MPa$
Nośność przekroju netto $N_{t,Rd}$
Pole powierzchni netto przekroju osłabionego (rys.29c)
$A_{net}=min \{ 18\cdot 0,8 -2\cdot 1,8 \cdot 0,8 \, ; \, 18 \cdot 0,8 – 0,8(3\cdot 1,8 -2 \cfrac{6,0^2}{4\cdot 5,0}\}=11,5 \, cm^2 $.
$N_{pl,Rd}=18 \cdot 0,8 \cdot 235 /1,0 \cdot 10^{-1}=338,4 \, kN$
$N_{b,Rd}= 0,9 \cdot 11,5\cdot 360/1,1 \cdot 10%^{-1}=338,7 \, kN$
$N_{t,Rd}= min \{ 338,4 ; 338,7 \}=338,4 \,kN$
Nośność śrub na ścinanie $F_{v,Rd}$
Płaszczyzna ścinania przechodzi przez gwintowaną część śruby o przekroju, więc
$A=A_s= 15,7 \, cm^2$, a dla klasy śrub 8.8. $\alpha_v =0,6$
$(\ref{4}) \to $ nośność jednej płaszczyzny ścinania śruby na ścinanie
$ F_{v,Rd,1}= 0,6 \cdot 800 \cdot 15,7 /1,25 \cdot 10^{-1}=60,2 \, kN $, co jest zgodne z wartością w tab.1. ( z dokładnością do zaokrągleń)
$(\ref{5}) \to $ nośność śruby na ścinanie
$m=1$ liczba płaszczyzn ścinania śruby,
$ F_{v,Rd,(1-5)}= 1 \cdot 60,2 = 60,2 \, kN$
(dotyczy wszystkich śrub z rys. 29a).
Nośność śrub na docisk $F_{b,Rd}$
$f_u = min \{ 800 ; 360 \}= 360 \, MPa$
$\sum t = 0,8 \, cm$,
$d= 16 \, mm$,
$d_o=18 \, mm$
$(\ref{6}) \to$ podstawowa nośność ze względu na docisk śruby
$F_{b,Rd,0}= \cfrac{360\cdot 1,6 \cdot 0,8}{1.25} \cdot 10^{-1} = 36,9 \, kN$
($\ref{9}) \to$ współczynnik korygujący dla rodzaju otworu przejściowego
$k_o=1,0 $ – otwory okrągłe normalne
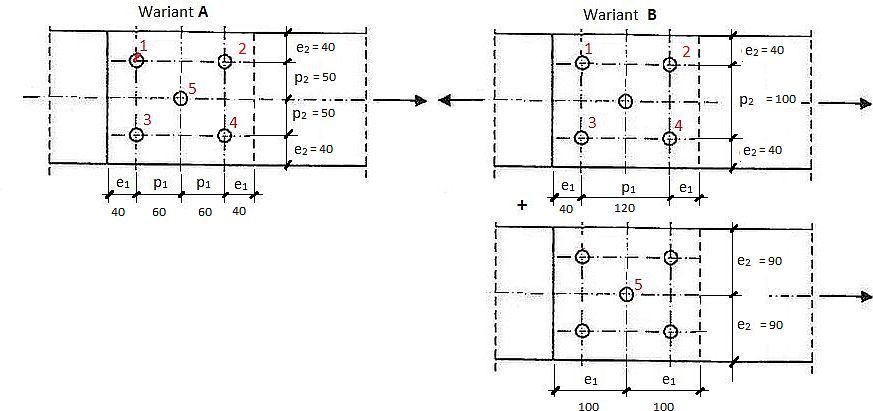
Rozważymy dwa warianty mechanizmu docisku śrub do otworów, pokazane na rys.30.
Wariant A został przyjęty w pracy [39] (skąd pochodzi przykład), w założeniu układu śrub w dwóch szykach szeregowych z włączoną śrubą 5.
Wariant B jest przyjęty w niniejszym artykule jak dla układu śrub w szyku przestawnym (rys.14 b,d )
Rys 30. Warianty mechanizmu docisku śrub: A wg [39], B – wg autora
Wariant A wg rys.30 za pracą [39]
Uwaga: wg autora artykułu wariant A nie jest właściwy, a zgodny z normą jest wariant B (niżej)
$e_1=40 mm$, $p_1=60 mm$,
$e_2=40 mm$, $p_2=50 mm$,
$(\ref{10}) \to$ wsp. korygujący $k_1$ ze względu na rozstawy śrub w kierunku prostopadłym do działania obciążenia
$k_1 = \min { \{ 2,8 \cdot \cfrac {40}{19} – 1,7 = 4,52 \, ; \, 1,4 \cdot \cfrac{50}{19} -1,7 = 2,19 \, ; \, 2,5 \} } = 2,19$,
$(\ref{12}) \to$ $ \alpha_d = \cfrac {40}{3 \cdot 18} = 0,74$,
$(\ref{11}) to$ wsp. korygujący ze względu na rozstawy śrub w kierunku działania obciążenia:
$\alpha_b= \min { \{ 0,74 \ ; \cfrac {800}{360} \, ; \, 1,0 \}}=0,74$,
$(\ref{8}) \to $ $ k _r = 1,0 \cdot 2,19 \cdot 0,74 = 1,62$,
$(\ref{7}) \to $ $F_{b,Rd,(1-5)} =1,62 \cdot 36,9 = 59,8 \, kN$,
(Przyjęto w uproszczeniu, że nośność śruby 5 jest równa nośności śrub 1 do 4).
Nośność grupy śrub
Zestawienie – wariant A :
$F_{v,Rd,(1-5)} = 60,2 \, kN$
$F_{b,Rd,(1-5)} = 59,8 \, kN$,
$(\ref{13}) \to$ $F_{Rd, (1-5) } = \min { \{ 59,8 \, ; \, 60,2\} }= 59,8 \, kN$
$(\ref{14}) \to$ $F_{Rd,min}= \min {\{60,2 \, ; \, 60,2\}}= 60,2 \, kN$
Ponieważ dla każdej śruby j=(1-5): $F_{v,Rd,j} > F_{b,Rd,j}$, to
$(\ref{15}) \to$ $ F_{Rd,N }= 59,8+ 59,8+ 59,8+ 59,8+ 59,8= 299,0 \, kN$
Warunek nośności połączenia
$F_Rd= min \{N_{r,Rd}; F_{Rd,N}\}= min \{338,4 \, ; \, 299,0\}= 299,0 kN > N_{Ed}=250 \,kN \to OK$
Wariant B wg rys.30
wg autora artykułu. Mechanizm docisku w wariancie B zgodny z zaleceniami dla przestawnego układu śrub – Rys. 14 b,d .
Rozważono dwa mechanizmy:
1) nośność śrub szeregu 1-2 (lub równoważnie szeregu 3-4), jak śrub skrajnych,
2) nośność śruby 5 jak śruby skrajnej w odrębnym szeregu
Śruby szeregów j=(1,2) i (3,4)
$e_1=40 mm$, $p_1=120 mm$,
$e_2=40 mm$, $p_2=100 mm$,
$(\ref{10}) \to$ wsp. korygujący $k_1$ ze względu na rozstawy śruby w kierunku prostopadłym do działania obciążenia
$k_1 = \min { \{ 2,8 \cdot \cfrac {40}{19} – 1,7 \= 4,52, ; \, ; 1,4 \cfrac{100}{19} -1,7=6,08 \.\; \, 2,5 \} } = 2,5$,
$(\ref{12}) \to$ $ \alpha_d = \cfrac {40}{3 \cdot 18} = 0,74$
$(\ref{11}) \to$ wsp. korygujący ze względu na rozstawy śrub w kierunku działania obciążenia:
$\alpha_b= min \{ 0,74 \ ; \cfrac {800}{360}\ ; 1,0 \}=0,74$,
$(\ref{8}) \to$ $k _r = 1,0 \cdot 2,5 \cdot 0,74 = 1,85$
$(\ref{7}) \to$ $F_{b,Rd,(1-4)} =1,85 \cdot 36,9 = 68,3 \, kN \, kN$,
Śruba w szeregu j=5
$e_1=100 mm$, ; $p_1=NaN $,
$e_2=90 mm$ ; $p_2=NaN$
$(\ref{10}) \to$ $k_1= \min { \{ 2,8 \cdot \cfrac {90}{19} – 1,7 = 12,3 \, ; \, 1,4 \cdot \cfrac{NaN}{19} – 1,7 = NaN \, ;\, 2,5 \} } = 2,5$,
$(\ref{12}) \to$ $\alpha_d = \cfrac{100}{3 \cdot 18}= 1,85 $,
$(\ref{11}) \to$ $\alpha_b= min \{ 1,85 \ ; \cfrac {800}{360} = 2,22 ; 1,0 \}=1,0$,
$(\ref{8}) \to$ $ k _r = 1,0 \cdot 2,5 \cdot 1,0 = 2,5 $
$(\ref{7}) \to$ $F_{b,Rd,5} = 2,5 \cdot 36,9 = 92,3 \, kN$,
Nośność grupy śrub
Zestawienie – wariant B:
$F_{v,Rd,(1-5)} = 60,2 \, kN$,
$F_{b,Rd,(1-4)} = 68,3 \, kN$,
$F_{b,Rd,(5)} = 92,3 \, kN$.
$(\ref{13}) \to$
$F_{Rd,(1-4)}= \min{\{ 60,2 \, ;\, 68,3\}}= 60,2 \, kN$
$F_{Rd,5} = \min{\{ 60,2 \, ; \, 92,3\}}= 60,2 \, kN$
$(\ref{14}) \to$ $F_{Rd,min}= \min {\{60,2 \, ; \, 60,2\}}= 60,2 \, kN$
Ponieważ $F_{v,Rd,(1-5)} \le F_{b, Rd, (1-4) i (5)}$ , więc
$(\ref{15}) \to$ $F_{Rd,N}= 5 \cdot 60,2= 301,1 \, kN$
Warunek nośności połączenia
$F_Rd= min \{N_{r,Rd}; F_{Rd,N}\}= min \{338,4; 301,1\}= 301,1 kN > N_{Ed}=250 \,kN \to OK$
Wniosek:
Nośność złożonej grupy śrub zależy od przyjętej struktury grupy (prosta, przestawna).
Przykład 4 [ Kątownik na jedną lub dwie śruby ]
Przykład Q&A 5.2 z pracy [13]
Przykład wyjaśnia , dlaczego wytrzymałość na rozciąganie przekroju netto kątownika za pomocą jednej śruby jest większa od połączenia niż to z dwiema śrubami ? Rozpatrywany przypadek pokazano na rys. 31.

Rys.31 Ilustracja do przykładu 8 [13]
Dane:
Kątownik L 50 × 5 – S355 ($f_u = 510 \, MPa)$
$A= 480 \, mm^2$
$e_2=25 \,mm$
$d_o= 14 \, mm$
Dla stali S355 i t< 40 mm:
fy=355 MPa ; fu=490 MPa [40],tab.3.1.,
Dla jednej śruby :
[40], kl. 6.2.3 i
[1], kl. 3.10.3 i wzór (3.11):
$A_{eff}= 2\cdot(e_2-d_o/2)\cdot t = 2\cdot(25 -14/2)\cdot 5) = 180 \, mm^2$
$N_{u,Rd} = \cfrac{A_{eff} \cdot f_u}{\gamma_{M3}}=\cfrac{180\cdot 490}{1,25} = 70568\, N$
Dla dwóch śrub:
[1], kl. 3.10.3 i wzór (3.12):
$A_{net}= A- d_o\cdot t = 480- 14\cdot 5 = 410 \, mm^2$
$A_{eff}= \beta_2 \cdot A_{net} =0,4 \cdot 410 = 164 \, mm^2$
gdzie $\beta_2=0,4$ – współczynniki redukcyjny z tab. 3.8 [1],
$N_{u,Rd} = \cfrac{A_{eff} \cdot f_u}{\gamma_{M3}}=\cfrac{164 \cdot 490}{1,25} = 64228\, N \approx$ 91% nośności L z jedną śrubą.
Liczne badania kątowników połączonych jedną i dwiema śrubami potwierdziły fakt, że nośność kątownika połączonego pojedynczą śrubą jest większa niż kątownika połączonego za pomocą dwóch lub więcej śrub. Przyczyny tego są niejasne, ale jest to możliwe ze względu na dodatkowe momenty, które są generowane w połączeniu z więcej niż jedną śrubą [13].
Przykład 5 [Połączenie belki z żebrem podciągu]
[39], przykład 5.3
Sprawdzić nośność pokazanego na rys 32, połączenia śrubowego belki z żebrem podciągu. Elementy wykonano ze stali S235, połączenie jest kategorii A (zakładkowe typu dociskowego).
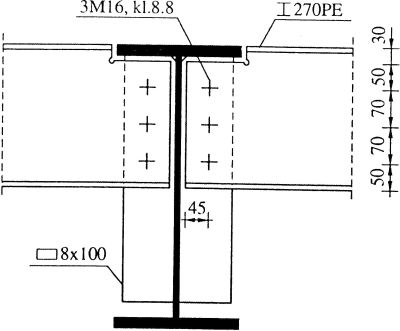
Rys.32. Połączenie śrubowe belki z podciągiem [39], przykład 5.3
Siła poprzeczna w belce na podporze
$V_{z,Ed}=100,0 \, kN$.
Parametry stali S235 – t < 40 mm:
fy=235 MPa ; fu=360 MPa [40], tab.3.1.
tab.20 $\to$ współczynniki częściowe:
γM0=1,0,
γM2=1,25.
tab.1 śruby M16- 8.8:
średnica d=16 mm , otwór d0=18 mm , pole przekroju czynnego As=161 mm2,
granica plastyczności śrub fyb=640 MPa, wytrzymałość śrub na rozciąganie fub=800 MPa.
Belka IPE 270:
wysokość $ h=270 \, mm $,
szerokość $ h=135,0 \, mm $,
grubość środnika $ t_w=6,6 \, mm $,
grubość stopki $ t_f=10,7 \, mm $,
Żebro:
wysokość żebra $ h_s=600 \,mm$,
szerokość żebra $ b_s=100 \,mm$,
grubość żebra $ t_s=8 \,mm$.
Siły w śrubach
Przy obliczaniu połączenia śrubowego, przyjmuje się, że reakcja działa w osi środnika podciągu w odległości $e$ od osi śrub.
Siła poprzeczna $V_{z,Ed}=100,0 \, kN$,
Mimośród $ e=45+ 6,6/2+ 12=60,0 mm$,
Moment $M_{Ed}=100,0\cdot 0,06=6,0 \,kNm$
$N=3$ – liczba śrub
Składowe sił w poszczególnych śrubach:
od siły poprzecznej $F_{V,Ed,j }= \cfrac{V_{Ed}}{N}=\cfrac{100,0}{3}=33,3 \, kN$,
od momentu $F_{M,Ed,j}=\cfrac{M_{Ed}\cdot r_j} {\sum \limits_j r_j^2}=\cfrac{6,0 \cdot 0,07}{2\cdot 0,07^2}=42,9 \, kN$
wypadkowa w skrajnej śrubie $F_{Ed}= \sqrt{F_{V,Ed, j }^2 +F_{M,Ed,j }^2}=\sqrt{33,3^2+42,9^2}=54,3 \, kN$
Nośność śrub na ścinanie
Płaszczyzna ścinania przechodzi przez gwintowaną część śruby , więc $ A=A_s=157 \, mm^2$, $ \alpha_v=0,6$
$F_{v,Rd,j}= \cfrac{\alpha_v f_{ub}A}{\gamma_{M2}}=\cfrac{0,6 \cdot 800 \cdot 15,7}{1,25}\cdot 10^{-1}=60,2 \, kN$
co jest zgodne z tab.1.
Nośność śrub na docisk
($\ref{9}) \to$ $ k_o= 1,0 $ (otwory przejściowe okrągłe normalne),
$\Sigma t = \min{\{8 \, ;\, 6,6\}} = 6,6 \, mm$ (grubość środnika IPE 270).
$f_u=360 \, MPa$ ( dla stali S235 – IPE270)
($\ref{6}) \to$ podstawowa nośność śruby
$F_{b,Rd,0} = \cfrac{360 \cdot 1,6 \cdot 0,66 }{1,25}\cdot 10^{-1} = 30,4 \, kN$
Śruby skrajne w szyku (pionowym)
$ e_1= 50 \, mm$ ; $p_1= 70 \, mm$.
$e_2= 45 \, mm$ ; $p_2=NaN $ .
($\ref{10}) \to$ $ k_1= min \{ 2,8\cfrac{45}{19}-1,7= 5,3 \, ; \, 1,4 \cdot \cfrac{NaN}{19} -1,7 = NaN \, ; \, 2,5 \}= 2,5$
($\ref{12}) \to$ $ \alpha_d= \cfrac{50}{3\cdot 18}= 0,93$
($\ref{11}) \to$ $ \alpha_b= min \{ 0,93 ; \cfrac{800}{360}= 2,22 ; 1,0\}= 0,93$
($\ref{8}) \to$ $ k_r=1,0 \cdot 2,5 \cdot 0,93 =2,32 $
($\ref{7}) \to$ nośność śruby j na docisk
$F_{b,Rd,j}= 2,32 \cdot 30,4 =70,7 \, kN$
Śruba pośrednia (środkowa)
$p_1= 70 \, mm$.
$p_2= NaN$
($\ref{10})\to$ $ k_1= min \{ 1,4 \cdot \cfrac{NaN}{19}- 1,7 = NaN \, ; \, 2,5 \}= 2,5$
($\ref{12}) \to$ $ \alpha_d= \cfrac{70}{3\cdot 18} – 1/4 = 1,05$
($\ref{11}) \to$ $ \alpha_b= min \{ 1,05 ; \cfrac{800}{360}= 2,22 ; 1,0\}= 1,0$
($\ref{8}) \to$ $ k_r=1,0 \cdot 2,5 \cdot 1,0 =2,5 $
($\ref{7}) \to$ nośność śruby na docisk
$F_{b,Rd,j}= 2,5 \cdot 30,4 =76,0 \, kN$.
Nośność grupy śrub
Zestawienie:
$F_{v,Rd,(wszystkie)} = 60,2 \, kN$
$F_{b,Rd,(skrajne)} = 70,8 \, kN$,
$F_{b,Rd,(środkowa)} = 76,0 \, kN$
$(\ref{13}) \to$ $F_{Rd, (wszystkie) } = \min { \{ 60,2\, ; \,70,8 \, ; \, 76,0\} }= 60,2 \, kN$
$(\ref{14}) \to$ $F_{Rd,min} = \min { \{ 60,2 }= 60,2 \, kN$
Ponieważ dla każdej śruby j=(1-5): $F_{v,Rd,j} < F_{b,Rd,j}$, to
$(\ref{15}) \to$ $ F_{Rd,N }= 3 \cdot 60,2 = 180,3 \, kN$
Warunek nośności połączenia
śruba skrajna (maksymalnie obciążona)
$F_{Rd,(skrajna)} =60,2 > F_{Ed} = 54,3 \, kN\to OK$,
grupa śrub
$F_{Rd,N }= 180,3 > V_{z,Ed} = 100,0 \, kN \to OK$.
Rozerwanie blokowe
Przekrój netto rozciągany $A_{nt}=6,6 (45,0-1/2 \cdot 18,0)=237,6 \, mm^2$,
Przekrój netto ścinany $A_{nv}=6,6 (50,0+10,0-2,5\cdot 18,0)=957 \, mm^2$,
Warunek nośności na rozerwanie blokowe $V_eff,2,Rd=\cfrac{0,5 f_u A_{nt}}{\gamma_{M2}}+\cfrac{f_y A_{nv}}{\sqrt{5} \cdot \gamma_{M0}}= (\cfrac{0,5 \cdot 360 \cdot 2,376}{1,25}+\cfrac{235 \cdot 9,57 }{\sqrt{5} \cdot 1,0}\cdot 10^{-1}=164,1 > 100 \, kN \to OK$.
Przykład 6 [Nośność połączenia kategorii C obciążonego skręcaniem]
[39], przykład 5.2
Sprawdzić nośność śrubowego połączenia kategorii C (tab.23) ciernego pokazanego na rys. 33
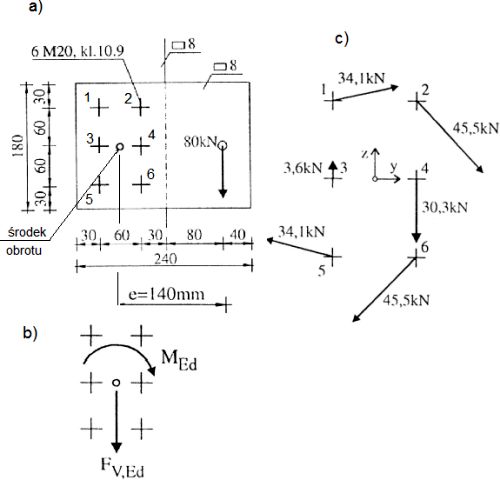
Rys.33 Śrubowe połączenie cierne. Przykład 6.3. :a) połączenie, b) układ obciążenia, c) siły działające na śruby od skręcania
Dla stali S355 i t< 40 mm:
fy=355 MPa ; fu=490 MPa [40],tab.3.1.,
tab 20 $\to$ współczynniki częściowe:
γM2=1,25 (nośność śrub na docisk),
γM3=1,25 (nośność styku na poślizg),
γM7=1,10 (sprężanie śrub wysokiej wytrzymałości)
Śruby M20 – 10.9:
tab.1 $\to$ średnica d=20 , otwór d0=22 mm, pole przekroju czynnego As=245 mm2 ,
granica plastyczności śrub fyb=900 MPa,
wytrzymałość śrub na rozciąganie fub=1000 MPa
Obliczeniowa siła sprężenia śruby
$(\ref{24}) \to$ całkowita siła sprężenia
$F_{pc} = 0,7\cdot 1000\cdot 2,45 \cdot 10^{-1} =171,5 \, kN$
co można też odczytać z tab.2 $F_{pc} =171,4 \, kN$
Siła sprężenia śruby będzie kontrolowana metodą kontrolowanego dokręcenia w złączach zakładkowych ciernych
$(\ref{29}) \to$ obliczeniowa siła sprężenia
$F_{p,cd}= \cfrac{171,5 }{1,1}=155,9 \, kN$
Obciążenie węzła
siła tnąca $V_{v,Ed}=80, 0 \, kN$,
na poszczególne śruby 1 do 6 działają takie same siły od ścinania: $F_{v,z,Ed}=\cfrac{80,0}{8}=13,3 \, kN$
moment skręcający $M_{Ed}=0,140 \cdot 80,0=11,2 \, kNm$
na poszczególne śruby od momentu skręcającego działają siły proporcjonalnie do odległości śruby $r_i$ od środka obrotu:
$F_{M,Ed,i}= \cfrac{M_{Ed} \cdot r_i}{\sum \limits_i r_i^2}$, gdzie:
$\sum \limits_i r_i^2=4\cdot(60^2+30^2)+2\cdot 30^2=19800 \, mm^2$
$r_1=r_2=r_5=r_6=\sqrt{30^2+60^2}=67,1 \, mm$.
W celu zsumowania sił w śrubach od ścinania i skręcania, wyznaczymy składową pionową i poziomą sił od skręcania:
$F_{M,y,Ed}=M_{Ed} \cfrac{z}{\sum \limits_i r_i^2}= 11,2\cdot 10^3 \cfrac{60}{19800}=33,9 \, kN$,
$F_{M,z,Ed}=M_{Ed} \cfrac{y}{\sum \limits_i r_i^2}= 11,2\cdot 10^3 \cfrac{31}{19800}=17,0 \, kN$,
Siła wypadkowa:
$F_{Ed}=\sqrt{(F_{v,Ed}+F_{M,Ed})^2+F_{M,yEd}^2}$
np w śrubie 2: $F_{Ed,2}=\sqrt{(13,3+17,0)^2+33,9^2}=45,5 \, kN$.
Wypadkowe siły w śrubach pokazano na rys. 33e.
Obliczeniowa nośność na poślizg
tab.3 $\to$ współczynnik tarcia dla powierzchni ciernej kat. B (przygotowana piaskowaniem)
$\mu = 0,4$
tab.28 $\to k_s=1,0 $ – współczynnik dla normalnego otworu przejściowego śruby
$(\ref{29}) \to$
$F_{s,Rd}=\cfrac{1,0\cdot 1,0\cdot 0,4}{1,25}\cdot 171,5=54,9 \, kN$
Warunek nośności na poślizg
$max F_{Ed}=45,5 \, kN < F_{s,Rd}=54,9 \, kN \to OK$
Przykład 7 [Połączenie cierne montażowe ]
Połączenie cierne stężenia prętowego z blachą węzłową
Przykład 4.14.3.1 [41] – zaprezentowane zgodnie z normą kanadyjską [42] i dla profili oraz śrub zgodnie z ta normą.
Poniżej pokażemy ten sam przykład dostosowany do normy Eurokod 3-8. Połączenie pokazano na rys. 34.
W tego typu połączeniach ze względu na możliwe niedokładności montażowe należy przewidzieć powiększony otwory przejściowe śrub w elementach drugorzędnych (montowanych w ostatniej kolejności). W takim przypadku bezpośrednie ścinanie śrub doprowadzi do ich zginania. Aby temu zaradzić połączenie zaprojektowano jako cierne.
Obliczeniowa siła w pręcie stężenia C130x10 (wg normy kanadyjskiej, co w przykładzie nie jest istotne) wynosi
$P_d = 100 \, kN$
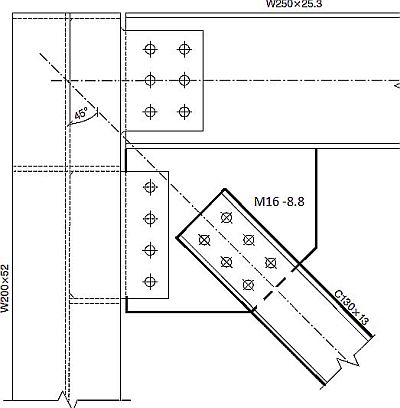
Rys.34 Połączenie cierne stężenia w naroży słup-rygiel [41] – zaprezentowane zgodnie z normą kanadyjską [42], Fig 4.90
tab.2 $(\ref{24})$\to$ siła 100% sprężenia śrub M16-8.8
$F_{pc} = 87.7 \, kN$
$(\ref{29}$) $\to$ obliczeniowa nośność połączenia na poślizg
$F_{s,Rd}=\cfrac{0,85 \cdot 6 \cdot 0,3}{1,25}\cdot 87,7 = 107,3 \ge 100,0 \, kN \to OK$
gdzie:
n=6- liczba styków ciernych (płaszczyzn tarcia) – tutaj liczba śrub,
tab.3 $\to \mu=0,3$ – współczynnik tarcia dla klasy powierzchni ciernej
$\gamma_{M3}=1,25 $
tab.30 $\to k_s=0,85$ – współczynnik dla powiększonego otworu przejściowego śruby
Przykład 8 Projektowanie wstępne (właściwe) połączenia doczołowego
Projekt wstępny dotyczy połączenia czołowego zdefiniowanwego w przykładzie 5.6 z pracy [39]
Zaprojektować wstępnie połączenie pokazane na rys. 35 śrubowego połączenia rygla ze słupem. Elementy wykonano ze stali S355, a działają w nich siły:
moment zginający w ryglu (i słupie) $ M_{j,Ed}=220 \, kNm$,
siła poprzeczna w ryglu $ V_{j,Ed}=90,0 \, kN$,
siła podłużna w ryglu $ N_j,Ed=20,0 \, kN$,
siła poprzeczna w słupie $ V_{c,Ed}=20,0 \, kN$.
Rys.35. Połączenie śrubowe rygla ze słupem [39], przykład 5.6
Dla stali S355 (t<40 mm) : $ f_y=355 \, MPa$, $ f_u= 490 \, MPa$, $E=210000 \, MPa$, $ \gamma_{M0}= 1,00$, $ \gamma_{M2} =1,25$.Współczynnik materiałowy $ \varepsilon=\sqrt{235/355}=0,81$.
Charakterystyki przekroju słupa HEB 300:
wysokość $ h_c=300 \,mm$
szerokość $ b_c=300 \, mm$,
grubość środnika $ t_{wc}=11,0 \, mm$,
grubość stopki $ t_{fc}=19,0 \,mm$,
promień zaokrąglenia $ r_c=27 mm$,
pole przekroju $ A_c=149 \, cm^2$,
moment bezwładności $ I_{yc}= 25170 \, cm^4$,
Charakterystyki przekroju rygla IPE400:
wysokość $h_r=400 \,mm$,
szerokość $b_r=180 \, mm$,
grubość środnika $t_{wr}=8,6 \, mm$,
grubość stopki $t_{fr}=13,5 \,mm$,
promień zaokrąglenia $r_r=21 mm$,
pole przekroju $A_r=84,5 \, cm^2$,
moment bezwładności $I_{yr}= 23130 \, cm^4$,
długość rygla $l_r=6,0 \, m$.
Parametry geometryczne połączenia:
Odległość śrub od środnika słupa $m=\cfrac{120-11-2\cdot 0,8\cdot 27}{2}=32,9 \, mm$,
Odległość śrub od zewnętrznego brzegu $ e=\cfrac{300-120}{2}=90 \, mm$,
Odległość śrub od końca słupa $e_1=50 mm$.
Projekt przekrojów węzła metodą Steenhuis
Typ połączenia z rys. 35 odpowiada połączeniu A z tab 28 $\to$
$\xi= 11,5$,
$\zeta= 5$.
Ramię sił mierzone jest od środka rozciąganej grupy śrub do osi pasa dolnego rygla:
$\to$ $r= h_r – t_{fr} = 400- 13,5 = 387 \, mm
grubość pasa słupa
$\to$ $ t_{fc} = 400- 13,5 = 19 \, mm
Parametry stali słupa:
moduł Younga
$E= 210 \, GPa = 210 \cdot 10^{6} \, kN/m^2$
granica plastyczności
$f_{y,fc} = 355 \, MPa$
($\ref{32} \to$ oszacowanie sztywności złącza
$S_{ini,j,app} = \cfrac{210 \cdot 387^2 \cdot 19}{11,5}\cdot 10^{-3}= 51963 kNm/rad$
($\ref{33} \to$ oszacowanie nośności złącza
$M_{Rd,j,app} = \cfrac{ 5 \cdot 355 \cdot 38,7^2 \cdot 1,9}{ 1,0}\cdot 10^{-3}= 5051 \gg M_{j,Ed} = 220 \, kNm $
$\to$ rozmiary złącza są wystarczające do zapewnienia nośności polaczenia typu A .
Projekt doczołowego połączenia sprężonego metodą PN-90/B-03200
Przykład 9 [Metoda składnikowa. Sprawdzenie nośności połączenia doczołowego kategorii D (niesprężanego)]
Metodą składnikową sprawdzić nośność połączenie doczołowego kategorii D (niesprężanego) zaprojektowanego w przykładzie 8 i pokazanego na rys. 35 i dla danych tam podanych.
Nośność środnika słupa
Nośność plastyczna panelu środnika słupa przy ścinaniu
Współczynnik materiałowy $\varepsilon=\sqrt{\cfrac{235}{355}}=0,81$,
Warunek stosowalności reguł [1], wzór (6.23)
$ \cfrac{d}{t_{wc}}=\cfrac{h_c-2(t_{fc}+r_c)}{t_{wc}}=\cfrac{300-2(19+27)}{20}=18,9 \le 69 \varepsilon=55,9$
Pole przekroju czynne przy ścinaniu słupa
$A_{vc}=A_c-2 b_{fc}t_{fc}+(t_{wc}+2r_c) t_{fc}=149-2\cdot 30\cdot 1,9+(1,1+2\cdot 2,7)\cdot 1,9=47,35 \, cm^2$,
$A_{vc}\ge \eta h_{wc} t_{wc}=1,2 \cdot (30-2\cdot 1,9)\cdot 1,1=34,58 \, cm^2$.
Nośność $V_{wp,Rd}=\cfrac{0,9f_{y,wc}A_{vc}}{\gamma_{M0}\sqrt{5}}\cdot 10^{-1}=873,4 \, kN$
Zarówno w strefie ściskanej jak i rozciąganej środnika zastosowano żebra poprzeczne. Tym samym nośność plastyczną przy ścinaniu panelu środnika można zwiększyć [1], kl. 6.2.6.1(4). W przykładzie nie stosujemy zwiększenia, bowiem nośność i tak jest wystarczająca:
Siła ścinająca panel środnika dla $z=50+200+80+120/2-14/2=383 \, mm$:
$V_{wp,Ed}=\cfrac{M_{b1,Ed}-M_{b2,Ed}}{z}-\cfrac{V_{c1,Ed}-V_{c2,Ed}}{2}=220/0,383-20/2=564,4 \, kN$
Warunek nośności $V_{wp,Rd}=873,4 \,kN \ge V_{wp, Ed}=564,4 \, kN$.
Nośność słupa przy poprzecznym ściskaniu – poziom dolnej stopki rygla
Parametr przeniesienia w przypadku węzła jednostronnego $\beta \approx 1$ [1], tab 5.4.
Współczynnik redukcyjny uwzględniający interakcję ze ścinaniem w panelu środnika słupa [1], tab 6.3.
$\omega=\omega_1=\cfrac{1}{\sqrt{1+1,3 \left( \cfrac{b_{eff,c,wc}t_{wc}}{A_{vc}}\right)^2}}$, gdzie w przypadku połączenia śrubowego z blachą czołową [1], kl. 6.2.6.2(1)
$b_{eff,c,wc}=t_{fr}+2\sqrt{2} a_f+5(t_{fc}+s)+s_p=13,5+2\sqrt{2}\cdot 10+5(19+27)+20=292 \, mm$.
Pole przekroju czynne przy ścinaniu słupa: $A_{vc}=47,35 \, cm^2$, czyli $\omega=\cfrac{1}{\sqrt{1+1,3 \left( \cfrac{29,2\cdot 1,1}{47,35}\right)^2}}=0,79$.
Nie zachodzi konieczność wyznaczania współczynnika redukcyjnego ze względu na wyboczenie miejscowe środnika słupa, ponieważ jest on usztywniony żebrami poprzecznymi, więc można przyjąć [1], 6.2.6.2(2) $k_{wc}=1,0$:
$F_{c,wc,Rd}=\cfrac{\omega k_{wc} b_{eff,c,wc} t_{wc} f_{y,wc}}{\gamma_{M0}}=\cfrac{0,79 \cdot 1,0 \cdot 29,2\cdot 1,1 \cdot 355}{1,0}\cdot 10^{-1}=900,8 \, kN$
Przy zastosowaniu żeber poprzecznych usztywniających środnik słupa, można zwiększyć nośność środnika przy poprzecznym ściskaniu [1], 6.2.6.2(5): o $F_{c,wc.Rd,add}=\cfrac {A_z f_y}{\gamma_{M0}}=\cfrac{39,2\cdot 355}{1,0}\cdot 10^{-1}=1391,6 \, kN$.
Ostatecznie nośność środnika słupa przy poprzecznym ściskaniu wynosi:
$F_{c,wc,Rd}=900,8+1391,6=2292,4 kN$.
Nośność przy poprzecznym ściskaniu stopki i środnika rygla
Wskaźnik plastyczny przekroju rygla $W_{pl}=1307,1 \, cm^3$
Nośność przy zginaniu przekroju rygla $M_{c,Rd}=\cfrac{W_{pl}f_y}{\gamma_{M0}}=\cfrac{1307,1\cdot 355}{1,0}\cdot10^{-3}=464,0 \, kNm$
Nośność przy poprzecznym ściskaniu stopki i środnika
$F_{c,dr,Rd}=\cfrac{M_{c,Rd}}{h_r-t_{fr}}=\cfrac{464,0}{0,4-0,0135}=1200,5 \, kN$
Nośność śruby na rozciąganie
$k_2=0,9$$ [1], tab. 3.4,
$F_{t,Rd}=\cfrac{k_2 f_{ub}A_s}{\gamma_{M2}}=\cfrac{0,9 \cdot 800 \cdot 2,45}{1,25}\cdot 10^{-1}=141,1 \, kN$.
Nośność pasa słupa i blachy czołowej
Przy rozpatrywaniu nośności blach czołowych połączenia stosujemy zasady teorii załomów plastycznych.
Pas słupa lokalnie zginany wskutek oddziaływań poprzecznych
Rozpatrujemy trzy szeregi śrub zgodnie z rys. 36a.
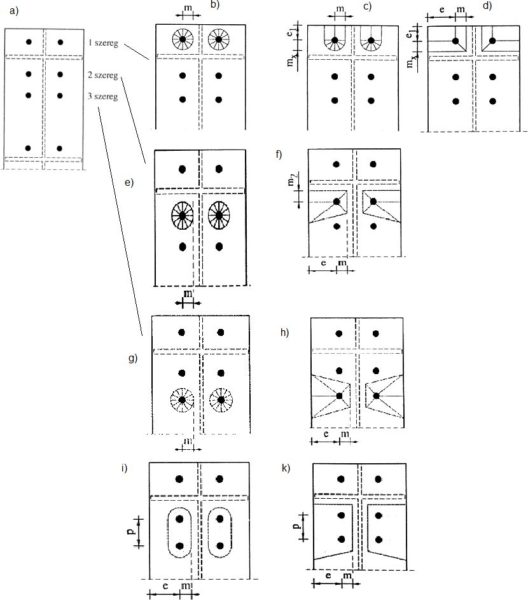
Rys.36. Mechanizmy zniszczenia pasa słupa: a) schemat, b) mechanizmy kołowe 1-szy szereg, c) mechanizmy mieszane 1-szy szereg, d) mechanizmy niekołowe 1-szy szereg, e) mechanizmy kołowe 2-gi szereg, f) mechanizmy niekołowe 2-gi szereg, g) mechanizmy kołowe 3-ci szereg, h) mechanizmy niekołowe 3-ci szereg, i) mechanizm grupowy kołowy, k) mechanizm grupowy niekołowy [39], przykład 5.6
Pierwszy szereg śrub (skrajny w pobliżu żebra) (rys. 36b-d)
Długości efektywne użebrowanego pasa słupa, gdy 1-szy szereg jest rozpatrywany indywidualnie [1],tab. 6.5,
Mechanizmy kołowe: $ l_{eff,cp,1}= min \{2\pi m = 2 \pi \cdot 32,9=206,6 \,mm \, ; \, \pi m+ 2e_1=\pi\cdot 32,9+2\cdot 50=203,3 mm \}=203,3 \, mm$,
Mechanizmy niekołowe: $\lambda_1= \cfrac{m}{m+e}=\cfrac{32,9}{32,9+90}=0,27$ [1],tab. 6.11,
$\alpha=8$ , $l_{eff,nc,1}=e_1+\alpha m – (2m+0,625e)=50+8,0 \cdot 32,9-(2\cdot 32,9+0,625\cdot 90)=191,2 \, mm$ [1],tab. 6.5,
Długość efektywna w modelu 1-szym: $ l_{eff,1,1}=l_{eff,nc,1}$, lecz $l_{eff,1,1}\le l_{eff,cp.1} \to$ $l_{eff,1,1}=191,2 \, mm$.
Długość efektywna w modelu 2-gim: $l_{eff,2,1}=l_{eff,nc,1}=191,2 \, mm$.
Obliczeniowa nośność półki króćca teowego [1],kl. 6.2.4,
$ M_{pl,1,Rd}=M_{pl,2,Rd}=\cfrac{0,25l_{eff,1} t_{fc}^2 f_y}{\gamma_{M0}}= \cfrac{0,25\cdot 19,12\cdot 1,9^2\cdot 355}{1,0}=6,13 \, kNm$
model 1: $ F_{T,1,Rd}=\cfrac{4M_{pl,1,Rd}}{m}=\cfrac{4\cdot 6,13}{0,0329}=745,3 \,kN$ [1],tab. 6.2,
model 2: $ F_{T,2,Rd}=\cfrac{2M_{pl,2,Rd}+n \sum F_{1,Rd}}{m+n}=\cfrac{2\cdot 6,13 +0,0411\cdot 2\cdot 141,1}{0,0411+0,0329}=322,4 \, kN$
$n=e=90 \, mm$, lecz $n<1,25m=1,25\cdot 32,9=41,1 \, mm$
model 3: $ F_{T,3,Rd}=\sum F_{1,Rd}=2\cdot 141,1=282,2 \, kN$
Nośność półki króćca teowego jest równa najmniejszej wartości z trzech modeli [1],pkt. 6.2.4.1(7)::
$ F_{T,fc,Rd(1)}=min \{ F_{T,1,Rd} \, ; \, F_{T,2,Rd} \, ; \, F_{T,3,Rd}\}=min \{745,3 ; 322,4 ; 282,2\}=282,2 \, kN$
Drugi szereg śrub (rys. 36e,f)
Długości efektywne użebrowanego pasa słupa, gdy 2-gi szereg rozpatrywany jest indywidualnie
Mechanizm kołowy rys. 36e: $l_{eff,cp,2}=2\pi m= 2\pi \cdot 32,9=206,6 \, mm$
Mechanizm niekołowy rys. 36f: $\lambda_1=\cfrac{m}{m+e}=\cfrac{32,9}{32,9+90}=0,27 $,
$\lambda_2=\cfrac{m_2}{m+e}=\cfrac{51}{32,9+90}=0,41$,$\alpha=8,0$, $ l_{eff.nc.2}=\alpha m =8,0 \cdot 32,9=263,2 \, mm$
Długość efektywna w modelu 1-szym: $l_{eff,1,2}=l_{eff,nc,2}$, lecz $l_{eff,1,2}\le l_{eff,cp,2} \to $ $l_{eff,1,2}=206,6 \, mm$.
Długość efektywna w modelu 2-gim: $l_{eff,2,2}=l_{eff,nc,2}=263,2 \, mm$.
Obliczeniowa nośność półki króćca teowego
$M_{pl,1,Rd}=\cfrac{0,25l_{eff,1} t_{fc}^2 f_y}{\gamma_{M0}}= \cfrac{0,25\cdot 20,66\cdot 1,9^2\cdot 355}{1,0} = 6,62 \, kNm$,
$M_{pl,2,Rd}=\cfrac{0,25l_{eff,2} t_{fc}^2 f_y}{\gamma_{M0}}= \cfrac{0,25\cdot 26,32\cdot 1,9^2\cdot 355}{1,0}= 8,43 \, kNm$
model 1: $F_{T,1,Rd}=\cfrac{4M_{pl,1,Rd}}{m}=\cfrac{4\cdot 6,62}{0,0329}=804,9 \,kN$,
model 2: $F_{T,2,Rd}=\cfrac{2M_{pl,2,Rd}+n \sum F_{1,Rd}}{m+n}=\cfrac{2\cdot 8,43 +0,0411\cdot 2\cdot 141,1}{0,0411+0,0329}=384,5 \, kN$
$n=e=90 \, mm$, lecz $n<1,25m=1,25\cdot 32,9=41,1 \, mm$
model 3: $F_{T,3,Rd}=\sum F_{1,Rd}=2\cdot 141,1=282,2 \, kN$
$F_{T,fc,Rd(2)}=min \{ F_{T,1,Rd} \, ; \, F_{T,2,Rd} \, ; \, F_{T,3,Rd}\}=min \{804,9 ; 384,5 ; 282,2\}=282,2 \, kN$.
Trzeci szereg śrub (rys. 36g,h)
Długości efektywne użebrowanego pasa słupa, gdy 3-ci szereg rozpatrywany jest indywidualnie
Mechanizm kołowy rys. 36g: $l_{eff,cp,3}=2\pi m= 2\pi \cdot 32,9=206,6 \, mm$
Mechanizm niekołowy rys. 38h: $l_{eff.nc.3}=4m+1,25c=4\cdot 32,9+1,25\cdot 90=244,1 \, mm$
Długość efektywna w modelu 1-szym: $l_{eff,1,3}=l_{eff,nc,3}$, lecz $l_{eff,1,3}\le l_{eff,cp,3} \to $ $l_{eff,1,3}=206,6 \, mm$.
Długość efektywna w modelu 2-gim: $l_{eff,2,3}=l_{eff,nc,3}=244,1 \, mm$.
Obliczeniowa nośność półki króćca teowego:
$M_{pl,1,Rd}=\cfrac{0,25l_{eff,1} t_{fc}^2 f_y}{\gamma_{M0}}= \cfrac{0,25\cdot 20,66\cdot 1,9^2\cdot 355}{1,0} =6,62 \, kNm$,
$M_{pl,2,Rd}=\cfrac{0,25l_{eff,2} t_{fc}^2 f_y}{\gamma_{M0}}= \cfrac{0,25\cdot 24,41\cdot 1,9^2\cdot 355}{1,0} =7,82 \, kNm$
Model 1:$F_{T,1-2,Rd}=\cfrac{4M_{pl,1,Rd}}{m}=\cfrac{4\cdot 6,62}{0,0329}=804,9 \,kN$,
Model 2: $F_{T,2,Rd}=\cfrac{2M_{pl,2,Rd}+n \sum F_{1,Rd}}{m+n}=\cfrac{2\cdot 7,82 +0,0411\cdot 2\cdot 141,1}{0,0411+0,0329}=368,1 \, kN$
$n=e=90 \, mm$, lecz $n<1,25m=1,25\cdot 32,9=41,1 \, mm$,
Model 3: $F_{T,3,Rd}=\sum F_{1,Rd}=2\cdot 141,1=282,2 \, kN$.
$F_{T,fc,Rd(3)}=min \{ F_{T,1,Rd} \, ; \, F_{T,2,Rd} \, ; \, F_{T,3,Rd}\}=min \{804,5 ; 368,1 ; 282,2\}=282,2 \, kN$
Drugi i trzeci szereg śrub jako grupa (rys. 36l,k )
Ze względu na to, że 1-szy i 2-gi szereg śrub są rozdzielone żebrem, to nie rozważa się 1-szego szeregu jako części grupy. Należy rozważyć 2-gi – 3-ci szereg śrub jako grupę.
Mechanizm kołowy rys. 36l: $l_{eff,cp,2,g}=\pi m+p= \pi \cdot 32,9+80=183,3 \, mm$
Mechanizm niekołowy rys. 36k: $\alpha=8,0$
$l_{eff.nc.2,g}=0,5 p +\alpha m -(2m+0,625e)=0,5\cdot 80 +8,0 \cdot 32,9- (2\cdot 32,9+0,625 \cdot 90)=181,2 \, mm$
Długości efektywne użebrowanego pasa słupa, gdy 3-ci szereg śrub rozważany jest jako część grupy szeregu śrub:
Mechanizm kołowy $l_{eff,cp,3,g}=\pi m +p=\pi \cdot 32,9 +80=183,3\, mm$,
Mechanizm niekołowy $l_{eff,nc,3,g}= 2m+0,625e+0,5p=2\cdot 32,9+0,625\cdot 90+0,5\cdot80=162,1 \, mm$,
$\sum l_{eff,cp,2-3,g}=l_{eff,cp,2,g}+l_{eff,cp,3,g}=183,3+183,3=366,6 \, mm$,
$\sum l_{eff,nc,2-3,g}=l_{eff,nc,2,g}+l_{eff,nc,3,g}=181,2+162,1=343,3 \, mm$,
Długość efektywna w modelu 1-szym $\sum l_{eff,1,2-3,g}=\sum l_{eff,2-3,g} $, lecz $\sum l_{eff,1,2-3,g} \le \sum l_{eff,cp,2-3,g} \to $ $\sum l_{eff,1,2-3,g}=343,3 \, mm$,
Długość efektywna w modelu 2-gim $ \sum l_{eff,2,2-3,g}=\sum l_{eff,nc,2-3,g}=343,3 \, mm$
Obliczeniowa nośność półki króćca teowego
$M_{pl,1,Rd}=M_{pl,2,Rd}=\cfrac{0,25 l_{eff,1} t_{fc}^2 f_y}{\gamma_{M0}}= \cfrac{0,25\cdot 34,33\cdot 1,9^2\cdot 355}{1,0} =11,0 \, kNm$,
Model 1: $F_{T,1,Rd}=\cfrac{4M_{pl,1,Rd}}{m}=\cfrac{4\cdot 11,0}{0,0329}=1337,4 \,kN$,
Model 2: $F_{T,2,Rd}=\cfrac{2M_{pl,2,Rd}+n \sum F_{1,Rd}}{m+n}=\cfrac{2\cdot 11,0 +0,0411\cdot 4\cdot 141,1}{0,0411+0,0329}=610,7 \, kN$,
$n=e=90 \, mm$, lecz $n<1,25m=1,25\cdot 32,9=41,1 \, mm$
model 3: $F_{T,3,Rd}=\sum F_{1,Rd}=4\cdot 141,1=564,4 \, kN$
$F_{T,fc,Rd(3)}=min \{ F_{T,1,Rd} \, ; \, F_{T,2,Rd} \, ; \, F_{T,3,Rd}\}=min \{1337,4 ; 610,7 ; 564,4\}=564,4 \, kN$
Parametry geometryczne połączenia
Odległości śrub od środnika rygla: $ m= \cfrac{120-t_{wr}-2\cdot 0,8\cdot a_c \sqrt{2}}{2}=\cfrac{120-8,6-2\cdot 0,8\cdot 6 \sqrt{2}}{2}=48,9 \, mm $,
Odległość śrub od zewnętrznej blachy czołowej: $e=50 \, mm$,
Odległość śrub od swobodnej górnej krawędzi blachy czołowej: $e_x=50 \, mm$
Odległość śrub od pasa rozciąganego rygla: $ m_x=50-0,8\cdot a_f \sqrt{2}=50-0,8\cdot 6 \sqrt{2}= 43,2 \, mm $,
Rozstaw szeregu śrub: $w=120 \, mm$.
Blacha czołowa przy zginaniu w strefie rozciągania
Postępujemy analogicznie do procedury szacowania nośności blachy pasa. Efekt dźwigni nie może wystąpić. Zastosowanie żebra usztywniającego powyżej pasa górnego rygla rozdzielającego śruby w szeregu, sprawia, że nie wszystkie długości efektywne blachy czołowej w przypadku 1-szego szeregu śrub podane w [1],tab.6.6 – są możliwymi mechanizmami zniszczenia.
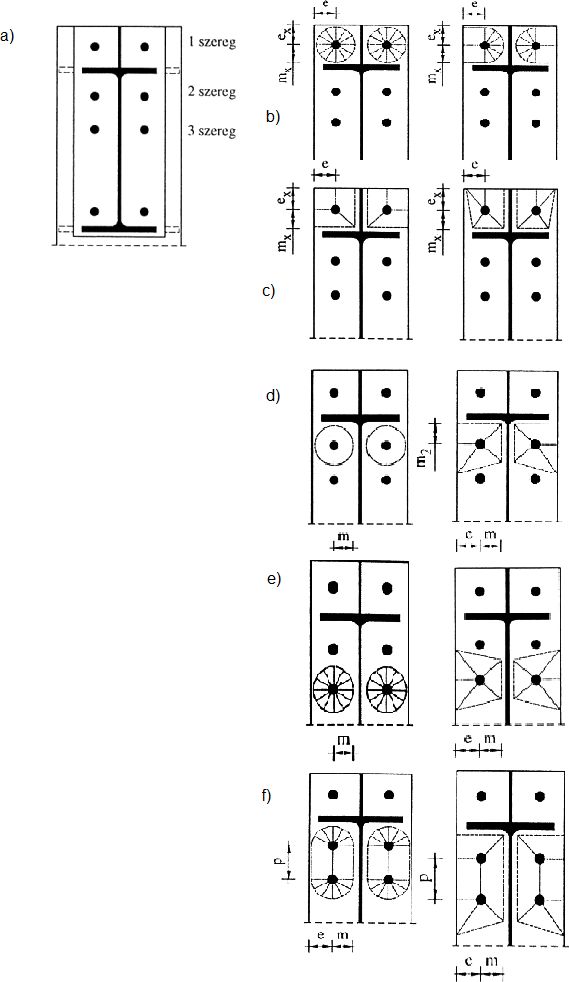
Rys.37. Mechanizmy zniszczenia blachy czołowej: a) schemat, b) mechanizmy kołowe 1-szy szereg, c) mechanizmy niekołowe 1-szy szereg, d) mechanizmy 2-gi szereg, e) mechanizmy 3-ci szereg, f) mechanizmy grupowe
Pierwszy szereg śrub (poza rozciąganym pasem rygla) ( rys. 37b,c)
Długości efektywne blachy czołowej, gdy 1-szy szereg jest rozpatrywany indywidualnie [1],tab. 6.6,
Mechanizmy kołowe: $l_{eff,cp,1}=min \{2\pi m_x=2\pi \cdot 43,2=271,3 \, mm \, ; \, \pi m_x+ 2e=\pi\cdot 43,2+2\cdot 50=235,6 mm \}=235,6 \, mm$,
Mechanizmy niekołowe: $l_{eff,nc,1}= min\{ 4 m_x+1,25 e_x=4\cdot 43,2 + 1,25\cdot 50=235,3 \, mm \, ; \, e+2m_x +0,625e_x=50+2\cdot 43,2+0,625\cdot 50=167,7 \, mm \}=167,7 \, mm$.
Długość efektywna w modelu 1-szym: $l_{eff,1,1}=l_{eff,nc,1}$, lecz $ l_{eff,1,1}\le l_{eff,cp.1} \to$ $l_{eff,1,1}=167,7 \, mm$.
Długość efektywna w modelu 2-gim: $l_{eff,2,1}=l_{eff,nc,1}=167,7 \, mm$.
Obliczeniowa nośność półki króćca teowego
$M_{pl,1,Rd}=M_{pl,2,Rd}=\cfrac{0,25l_{eff,1} t_p^2 f_y}{\gamma_{M0}}= \cfrac{0,25\cdot 16,77\cdot 2,0^2\cdot 355}{1,0} =5,95 \, kNm$
Model 1: $F_{T,1,Rd}=\cfrac{4M_{pl,1,Rd}}{m_x}=\cfrac{4\cdot 5,95}{0,0432}=550,9 \,kN$,
Model 2: $F_{T,2,Rd}=\cfrac{2M_{pl,1,Rd}+n \sum F_{t,Rd}}{m_x+n}=\cfrac{2\cdot 5,95 +0,05\cdot 2\cdot 141,1}{0,0432+0,05}=279,1 \, kN$,
$n=e=90 \, mm$, lecz $n<1,25m=1,25\cdot 32,9=41,1 \, mm$
model 3: $F_{T,3,Rd}=\sum F_{t,Rd}=2\cdot 141,1=282,2 \, kN$
$F_{T,fc,Rd(1)}=min \{ F_{T,1,Rd} \, ; \, F_{T,2,Rd} \, ; \, F_{T,3,Rd}\}=min \{550,9 ; 279,1 ; 282,2\}=279,1 \, kN$.
Drugi szereg śrub (rys. 37d)
Długości efektywne blachy czołowej, gdy 2-gi szereg rozpatrywany jest indywidualnie:
Mechanizm kołowy: $l_{eff,cp,2}=2\pi m=2\cdot \pi \cdot 48,9=307,1 \, mm$,
Mechanizm niekołowy:$\lambda_1=\cfrac{m}{m+e}=\cfrac{48,9}{48,9+50}=0,49$, $\lambda_2=\cfrac{m_2}{m+e}=\cfrac{51}{48,9+50}=0,52$, $\alpha=5,8$, $l_{eff.nc,2}=\alpha m= 5,8\cdot 48,9= 283,6\, mm$,
Długość efektywna w modelu 1-szym: $l_{eff,1,2}=l_{eff,nc,2}$, lecz $l_{eff,1,2}\le l_{eff,cp,2} \to $$l_{eff,1,2}=283,6 \, mm$,
Długość efektywna w modelu 2-gim: $l_{eff,2,2}=l_{eff,nc,2}=283,6 \, mm$.
Obliczeniowa nośność półki króćca teowego
$M_{pl,1,Rd}=M_{pl,2,Rd}=\cfrac{0,25l_{eff,1} t_p^2 f_y}{\gamma_{M0}}= \cfrac{0,25\cdot 28,36\cdot 2,0^2\cdot 355}{1,0}=10,07 \, kNm$,
Model 1: $F_{T,1,Rd}=\cfrac{4M_{pl,1,Rd}}{m}=\cfrac{4\cdot 10,07}{0,0489}=823,7 \,kN$,
Model 2: $F_{T,2,Rd}=\cfrac{2M_{pl,1,Rd}+n \sum F_{t,Rd}}{m+n}=\cfrac{2\cdot 10,07 +0,05\cdot 2\cdot 141,1}{0,0489+0,05}=346,3 \, kN$
$n=e=50 \, mm$, lecz $n<1,25m=1,25\cdot 48,9=61,1 \, mm$
Model 3: $F_{T,3,Rd}=\sum F_{t,Rd}=2\cdot 141,1=282,2 \, kN$
$F_{T,ep,Rd(3)}=min \{ F_{T,1,Rd} \, ; \, F_{T,2,Rd} \, ; \, F_{T,3,Rd}\}=min \{823,9 ; 346,3 ; 282,2\}=282,2 \, kN$
Trzeci szereg śrub (rys. 37e)
Długości efektywne użebrowanego pasa słupa, gdy 3-ci szereg śrub jest rozpatrywany indywidualnie
Mechanizm kołowy: $l_{eff,cp,3}=2\pi m= 2\pi \cdot 48,9=307,1 \, mm$
Mechanizm niekołowy: $l_{eff.nc.3}=4m+1,25e=4\cdot 48,9+1,25\cdot 90=258,1 \, mm$
Długość efektywna w modelu 1-szym: $l_{eff,1,3}=l_{eff,nc,3}$, lecz $l_{eff,1,3}\le l_{eff,cp,3} \to $ $l_{eff,1,3}=258,1 \, mm$.
Długość efektywna w modelu 2-gim: $l_{eff,2,3}=l_{eff,nc,3}=258,1 \, mm$.
Obliczeniowa nośność półki króćca teowego
$M_{pl,1,Rd}=M_{pl,2,Rd}=\cfrac{0,25l_{eff,1} t_{p}^2 f_y}{\gamma_{M0}}= \cfrac{0,25\cdot 25,81\cdot 2,0^2\cdot 355}{1,0}\cdot 10^{-3}=9,16 \, kNm$,
Model 1:$F_{T,1,Rd}=\cfrac{4M_{pl,1,Rd}}{m}=\cfrac{4\cdot 9,16}{0,0489}=749,3 \,kN$
Model 2: $F_{T,2,Rd}=\cfrac{2M_{pl,1,Rd}+n \sum F_{t,Rd}}{m+n}=\cfrac{2\cdot 9,16 +0,05\cdot 2\cdot 141,1}{0,0489+0,05}=327,9 \, kN$
$n=e=50 \, mm$, lecz $n<1,25m_x=1,25\cdot 48,9=61,1 \, mm$
Model 3: $F_{T,3,Rd}=\sum F_{t,Rd}=2\cdot 141,1=282,2 \, kN$
$F_{T,ep,Rd(1)}=min \{ F_{T,1,Rd} \, ; \, F_{T,2,Rd} \, ; \, F_{T,3,Rd}\}=min \{749,3 ; 327,9 ; 282,2\}=282,2 \, kN$
Drugi i trzeci szereg śrub jako grupa (rys. 37f)
Ze względu na to, że 1-szy i 2-gi szereg śrub są rozdzielone pasem rygla, to nie rozważa się 1-szego szeregu jako części grupy. Należy rozważyć 2-gi – 3-ci szereg śrub jako grupę.
Mechanizm kołowy: $l_{eff,cp,2,g}=\pi m+p= \pi \cdot 48,9+80=233,5 \, mm$,
Mechanizm niekołowy: $\alpha=5,8$ , $l_{eff.nc.2,g}=0,5 p +\alpha m -(2m+0,625e)=0,5\cdot 80 +5,8 \cdot 48,9-(2\cdot 48,9+0,625 \cdot 50)=194,6 \, mm$
Długości efektywne blachy czołowej, gdy 3-ci szereg śrub rozważany jest jako część grupy szeregu śrub:
Mechanizm kołowy $l_{eff,cp,3,g}=\pi m +p=\pi \cdot 48,9 +80=233,5\, mm$,
Mechanizm niekołowy $l_{eff,nc,3,g}=2m+0,625 e +0,5p=2\cdot 48,9+0,625\cdot 50+0,5\cdot 80=169,1 \, mm$,
$\sum l_{eff,cp,2-3,g}=l_{eff,cp,2,g}+l_{eff,cp,3,g}=233,5+233,5=467,0 \, mm$,
$\sum l_{eff,nc,2-3,g}=l_{eff,nc,2,g}+l_{eff,nc,3,g}=194,6+169,1=363,7 \, mm$,
Długość efektywna w modelu 1-szym $\sum l_{eff,1,2-3}=\sum l_{eff,nc2-3}$, lecz $\sum l_{eff,1,2-3} \le l_{eff,cp,2-3} \to $ $\sum l_{eff,1,2-3,g}=363,7 \, mm$,
Długość efektywna w modelu 2-gim $ \sum l_{eff,2,2-3}=\sum l_{eff,nc,2-3}=363,7 \, mm$
Obliczeniowa nośność półki króćca teowego
$M_{pl,1,Rd}=M_{pl,2,Rd}=\cfrac{0,25 \sum l_{eff,1} t_{fr}^2 f_y}{\gamma_{M0}}= \cfrac{0,25\cdot 36,37\cdot 2,0^2\cdot 355}{1,0} =12,91 \, kNm$,
Model 1: $F_{T,1,Rd}=\cfrac{4M_{pl,1,Rd}}{m}=\cfrac{4\cdot 12,91}{0,0489}=1056 \,kN$
Model 2: $F_{T,2,Rd}=\cfrac{2M_{pl,1,Rd}+n \sum F_{t,Rd}}{m+n}=\cfrac{2\cdot 12,91 +0,05\cdot 4\cdot 141,1}{0,0489+0,05}=546,4 \, kN$
$n=e=90 \, mm$, lecz $n<1,25m=1,25\cdot 48,9=61,1 \, mm$
Model 3: $F_{T,3,Rd}=\sum F_{t,Rd}=4\cdot 141,1=564,4 \, kN$
$F_{T,ep,Rd(1-2-3)}=min \{ F_{T,1,Rd} \, ; \, F_{T,2,Rd} \, ; \, F_{T,3,Rd}\}=min \{1056 ; 546,4 ; 564,4\}=564,4 \, kN$
Środnik rygla przy rozciąganiu
Szerokość efektywną środnika belki przy rozciąganiu ustala się jak w przypadku króćca teowego, odwzorowującego blachę czołową przy zginaniu, podczas rozpatrywania poszczególnych szeregów śrub i grup śrub.
Drugi szereg śrub rozpatrywany indywidualnie
$b_{eff,t,wr}= min \{ l_{eff,1,i} ; l_{eff,2,i} \}= 283, 6 \, mm$,
$F_{t,wr,Rd,(2)}=\cfrac{b_{eff,t,wr}\cdot t_{wr}\cdot f_y}{\gamma_{M0}}=\cfrac{28,36\cdot 0,86\cdot 355}{1,0}\cdot 10^{-1}=865,8 \, kN$
Trzeci szereg śrub rozpatrywany indywidualnie
$b_{eff,t,wr}= min \{l_{eff,1,i} ; l_{eff,2,i} \}= 258, 1 \, mm$,
$F_{t,wr,Rd,(3)}=\cfrac{b_{eff,t,wr}\cdot t_{wr}\cdot f_y}{\gamma_{M0}}=\cfrac{25,81\cdot 0,86\cdot 355}{1,0}\cdot 10^{-1}=788,0\, kN$
Drugi i trzeci rugi szereg śrub rozpatrywany jako grupa
$b_{eff,t,wr}= min \{ \sum l_{eff,1,2-3,g} ; \sum l_{eff,2,2-3,g} \}= 363,7 \, mm$,
$F_{t,wr,Rd,(2-3)}=\cfrac{b_{eff,t,wr}\cdot t_{wr}\cdot f_y}{\gamma_{M0}}=\cfrac{36,37\cdot 0,86\cdot 355}{1,0}\cdot 10^{-1}=1110,4\, kN$
Środnik słupa przy podany poprzecznemu rozciąganiu
W przypadku połączeń śrubowych szerokość efektywną środnika słupa przy rozciąganiu ustala się równą długości efektywnej zastępczego króćca teowego, odwzorowującego pas słupa przy rozpatrywaniu poszczególnych szeregów śrub i grup śrub.
Pierwszy szereg śrub rozpatrywany indywidualnie
$b_{eff,t,wc}= min \{ l_{eff,1,i} ; l_{eff,2,,i} \}= 191,2 \, mm$.
Parametr przeniesienia w przypadku węzła jednostronnego $\beta=1$.
Współczynnik redukcyjny uwzględniający interakcję ze ścinaniem w panelu środnika słupa $\omega=\omega_1=\cfrac{1}{\sqrt{1+1,3 \left( \cfrac {b_{eff,t,wc} t_{wc}}{A_{vc}}\right)^2}}=\cfrac{1}{\sqrt{1+1,3 \left( \cfrac{19,12 \cdot 1,1} {47,35}\right)^2}}=0,89$.
Nośność obliczeniowa $ F_{t,wc,Rd,(1)}=\cfrac{ \omega b_{eff,t,wc} t_{wc} f_y}{\gamma_{M0}}=\cfrac{0,89 \cdot 19,12 \cdot 1,1 \cdot 355}{1,0}\cdot 10^{-1}=664,5 \, kN$
Drugi szereg śrub rozpatrywany indywidualnie
$b_{eff,t,wc}= min \{ l_{eff,1,i} ; l_{eff,2,,i} \}= 206,6 \, mm$.
Parametr przeniesienia w przypadku węzła jednostronnego $\beta=1$.
Współczynnik redukcyjny uwzględniający interakcję ze ścinaniem w panelu środnika słupa: $\omega=\omega_1=\cfrac{1}{\sqrt{1+1,3 \left( \cfrac {b_{eff,t,wc} t_{wc}}{A_{vc}}\right)^2}}=\cfrac{1}{\sqrt{1+1,3 \left( \cfrac{20,66 \cdot 1,1} {47,35}\right)^2}}=0,88$.
Nośność obliczeniowa $F_{t,wc,Rd,(1)}=\cfrac{\omega b_{eff,t,wc}t_{wc} f_y}{\gamma_{M0}}=\cfrac{0,88 \cdot 20,66 \cdot 1,1 \cdot 355}{1,0}\cdot 10^{-1}=710,0 \, kN$.
Trzeci szereg śrub rozpatrywany indywidualnie
$b_{eff,t,wc}= min \{ l_{eff,1,i} ; l_{eff,2,,i} \}= 206,6 \, mm$.
Parametr przeniesienia w przypadku węzła jednostronnego $\beta=1$.
Współczynnik redukcyjny uwzględniający interakcję ze ścinaniem w panelu środnika słupa $\omega=\omega_1=\cfrac{1}{\sqrt{1+1,3 \left( \cfrac {b_{eff,t,wc} t_{wc}}{A_{vc}}\right)^2}}=\cfrac{1}{\sqrt{1+1,3 \left( \cfrac{20,66 \cdot 1,1} {47,35}\right)^2}}=0,88$.
Nośność obliczeniowa $F_{t,wc,Rd,(1)}=\cfrac{\omega b_{eff,t,wc}t_{wc} f_y}{\gamma_{M0}}=\cfrac{0,88\cdot 20,66 \cdot 1,1 \cdot 355}{1,0}\cdot 10^{-1}=710,0 \, kN$
Drugi i trzeci szereg śrub rozpatrywany jako grupa
$b_{eff,t,wc}= min \{ l_{eff,1,2-3,g} ; l_{eff,2,2-3,g} \}= 343,3 \, mm$.
Parametr przeniesienia w przypadku węzła jednostronnego $\beta=1$.
Współczynnik redukcyjny uwzględniający interakcję ze ścinaniem w panelu środnika słupa $\omega=\omega_1=\cfrac{1}{\sqrt{1+1,3 \left( \cfrac {b_{eff,t,wc} t_{wc}}{A_{vc}}\right)^2}}=\cfrac{1}{\sqrt{1+1,3 \left( \cfrac{34,33 \cdot 1,1} {47,35}\right)^2}}=0,74$.
Nośność obliczeniowa $F_{t,wc,Rd,(1)}=\cfrac{\omega b_{eff,t,wc}t_{wc} f_y}{\gamma_{M0}}=\cfrac{0,74\cdot 34,33 \cdot 1,1 \cdot 355}{1,0}\cdot 10^{-1}=992,0 \, kN$
Zastosowano żebra poprzeczne słupa więc można zwiększyć obliczeniową nośność środnika słupa [1],poz. 6.2.6.3(6):.
Pole powierzchni żebra usztywniającego środnik słupa $A_z=2\cdot b_z\cdot t_z=2\cdot 14\cdot1,4=39,2 \, cm^2$.
Przyrost nośności obliczeniowej $F_{t,wc,Rd,add}=\cfrac{A_z f_y}{\gamma_{M0}}=\cfrac{39,2 \cdot355 }{1,0}\cdot 10^{-1}=1391,6 \, kN$.
Po uwzględnieniu nośności żeber usztywniających, obliczeniowa nośność środnika słupa przy poprzecznym rozciąganiu wynosi:
1-szy szereg śrub $F_{t, wc, Rd,(1)}=664,5+1391,6=2056,1 \, kN$,
2-gi szereg śrub $F_{t, wc, Rd,(2)}=710,0+1391,6=2101,6 \, kN$,
3-gi szereg śrub $F_{t, wc, Rd,(3)}=710,0+1391,6=2101,6 \, kN$,
2-gi i 3-ci szereg śrub $F_{t, wc, Rd,(2)}=992,0+1391,6=2386,6 \, kN$.
Podsumowanie nośności poszczególnych szeregów śrub przy rozciąganiu
Pierwszy szereg śrub
Środnik słupa w strefie poprzecznego rozciagania $F_{t,wc,Rd,(1)}=2056,1 \,kN$,
Pas słupa lokalnie zginany $F_{T,fc,Rd,(1)}=282,2 \,kN$,
Blacha czołowa zginana $F_{T,ep,Rd,(1)}=279,1 \,kN$,
Nośność 1-szego szeregu śrub jest limitowana nośnością blachy czołowej i wynosi $F_{t,Rd,(1)}=279,1 \,kN$.
Redukcja ze względu na obliczeniową nośność środnika słupa przy ścinaniu.
Ponieważ $F_{t,Rd,(1)}=279,1 < \cfrac{V_{wp,Rd}}{\beta}=\cfrac {873,4}{1} \, kN \to$ redukcja nie jest wymagana.
Redukcja ze względu na obliczeniową nośność pasa i środnika belki przy ściskaniu.
Ponieważ $F_{t,Rd,(1)}=279,1 < F_{c,fr,,Rd}=1200,5 \,kN \to$ redukcja nie jest wymagana.
Redukcja ze względu na obliczeniową nośność środnika słupa przy ściskaniu.
Ponieważ $F_{t,Rd,(1)}=279,1 < F_{c,wc,,Rd}=2292,4 \,kN \to$ redukcja nie jest wymagana.
Ostatecznie nośność 1-szego szeregu śrub wynosi $F_{t,Rd,(1)}=279,1 \, kN$.
Drugi szereg śrub
Środnik słupa w strefie poprzecznego rozciągania $F_{t,wc,Rd,(1)}=2101,6 \,kN$,
Pas słupa lokalnie zginany $F_{T,fc,Rd,(1)}=282,2 \,kN$,
Blacha czołowa zginana $F_{T,ep,Rd,(1)}=282,2 \,kN$,
Nośność 2-go szeregu śrub jest limitowana nośnością blachy czołowej i wynosi $F_{t,Rd,(2)}=282,2 \,kN$.
Suma nośności szeregów 1-go i 2-giego $\sum F_{t,Rd.(1-2)}=F_{t,Rd,(1)}+F_{t,Rd,(2)}=279,1+282,2=561,3 \, kN$.
Redukcja ze względu na obliczeniową nośność środnika słupa przy ścinaniu.
Ponieważ $\sum F_{t,Rd,(1-2)}=561,3 < \cfrac{V_{wp,Rd}}{\beta}=\cfrac{873,4}{1} \to $ redukcja nie jest wymagana.
Redukcja ze względu na obliczeniową nośność pasa i środnika belki przy ściskaniu.
Ponieważ $ \sum F_{t,Rd,(1-2)}=561,3 < F_{c,fr,,Rd}=1200,5 \,kN \to $ redukcja nie jest wymagana.
Redukcja ze względu na obliczeniową nośność środnika słupa przy ściskaniu.
Ponieważ $F_{t,Rd,(1)}=279,1 < F_{c,wc,,Rd}=2292,4 \,kN \to$ redukcja nie jest wymagana.
Ostatecznie nośność 2-giego szeregu śrub wynosi $F_{t,Rd,(1)}=282,2 \, kN$.
Trzeci szereg śrub
Środnik słupa w strefie poprzecznego rozciagania $F_{t,wc,Rd,(1)}=2101,6 \,kN$,
Pas słupa lokalnie zginany $F_{T,fc,Rd,(1)}=282,2 \,kN$,
Blacha czołowa zginana $F_{T,ep,Rd,(1)}=282,2 \,kN$,
Środnik rygla w strefie rozciąganej $F_{t,ep,Rd(3)}=788,0 \, kN$.
Nośność 3-ciego szeregu śrub jest limitowana nośnością blachy czołowej przy zginaniu i wynosi $F_{t,Rd,(3)}=282,2 \,kN$.
Suma nośności szeregów 1-go , 2-giego i 3-ciego:
$\sum F_{t,Rd,(1-2-3)}=F_{t,Rd,(1)}+F_{t,Rd,(2)}+F{t,Rd,(3)}=279,1+282,2+282,2=843,5 \, kN$.
Redukcja ze względu na nośność środnika słupa przy ścinaniu.
Ponieważ $\sum F_{t,Rd,(1-2-3)}=843,5 < \cfrac{V_{wp,Rd}}{\beta}=\cfrac{873,4}{1} \,kN \to$ redukcja nie jest wymagana.
Redukcja ze względu na nośność pasa i środnika belki przy ściskaniu.
Ponieważ $\sum F_{t,Rd,(1-2-3)}=843,5 < F_{c,fr,Rd}=1200,5 \,kN \to$ redukcja nie jest wymagana.
Redukcja ze względu na nośność środnika słupa przy ściskaniu.
Ponieważ $ \sum F_{t,Rd,(1-2-3)}=843,5 < F_{b,wc,,Rd}=2292,4,kN \to$ redukcja nie jest wymagana.
Suma nośności grupy szeregów 2-go i 3-ciego:
$\sum F_{t,Rd,(2-3)}=F_{t,Rd.(2)}+F_{t,Rd,(3)}=282,2+282,2=564,4 \, kN$
Redukcja ze względu na nośność środnika słupa przy rozciąganiu, liczoną dla szeregów 2 i 3 jako grupy
Ponieważ $ \sum F_{t,Rd,(2-3)}=564,4 < F_{t,wc,,Rd,(2-3)}=2383,6 ,kN \to$ redukcja nie jest wymagana.
Redukcja ze względu na nośność pasa słupa przy zginaniu, liczonej dla szeregów 2 i 3 jako grupy
Ponieważ $ \sum F_{t,Rd,(2-3)}=564,4 = F_{T,fc,,Rd,(2-3)}=564,4 ,kN \to$ redukcja nie jest wymagana.
Redukcja ze względu na nośność blachy czołowej słupa przy zginaniu, liczonej dla szeregów 2 i 3 jako grupy
Ponieważ $ \sum F_{t,Rd,(2-3)}=564,4 > F_{T,cp,,Rd,(2-3)} > 546,4 ,kN \to$ redukcja należy zredukować nośność 3-ciego szeregu śrub.
Redukcja ze względu na nośność środnika belki przy rozciąganiu, liczonej dla szeregów 2 i 3 jako grupy
Ponieważ $ \sum F_{t,Rd,(2-3)}=564,4 < F_{t,wr,,Rd,(2-3)} > 1110,4 ,kN \to$ redukcja nie jest wymagana.
Ostatecznie nośność 3-ciego szeregu śrub po redukcji wynosi
$F_{t,Rd,(3)}=F_{T,Rd,(2-2)}-F{t,Rd,(2)}=546,4-281,2=264,2 \, kN$.
W przykładzie rozpatrywano redukcję wynikającą z [1],6.2.7.2(7) i 6.2.7.2(8):, a nie rozpatrywano redukcji wg [1],6.2.7.2(9) :, ponieważ załącznik krajowy zaleca się stosować jedynie w przypadku połączeń narażonych na oddziaływania udarowe i wibracyjne.
Zestawienie nośności poszczególnych rozciąganych szeregów śrub
Nośność węzła przy zginaniu
$M{j,Rd}=\sum h_iF_{t,Rs,(i)}=0,443\cdot 279,2 + 0,323\cdot 282,2+0,243\cdot 264,2=279,0 \, kNm$
Warunek nośności węzła przy zginaniu [1],wzór (6.23):
Ponieważ $N_{j,Ed}=20,0 kN <0,05 \cdot N_{pl,Rd}=0,05 \cfrac{A f_y}{\gamma_{M0}}=0,03 \cfrac{84,5 \cdot 355}{1,0} \cdot 10{-1}=150 \,kN \to $
$M_{j,Ed}=220 \, kN < M_{j, Rd}=279,0 \,kNm \to $ warunek nośności jest zachowany.
Nośność śrub przy ścinaniu
Do przeniesienia ścinania poprzecznego przeznaczone są śruby szeregu 4.
Nośność na ścinanie w jednej płaszczyźnie
$\alpha_v=0,6$,
$F_{v,Rd}=\cfrac{\alpha_vf_{ub} A}{\gamma_{M2}}=\cfrac{0,6\cdot 800\cdot 24,5}{1,25}\cdot 10^{-1}=94,1 \, kN$.
Nośność na docisk
$k_1=min \{ 2,8 \cfrac {e_2}{d_o}-1,7= 2.8 \cfrac{40}{31}-1,7=3,4 \, ; \, 1,4 \cfrac{w}{d_o}-1,7= 1,4 \cfrac{120}{31}-1,7=5,9 \, ; \, 2,5 \}=2,5$,
$\alpha_b=min \{ \cfrac {e_1}{3d_o}= \cfrac{50}{3\cdot22}=0,76 \, ; \, \cfrac{p_{min}}{3d_o}-\cfrac{1}{46}= \cfrac{80}{3\cdot22}-\cfrac{1}{2}=0,96 \, ; \, \cfrac{f_ub}{f_u}= \cfrac{800}{490}=1,63 \, ; \, 1,0 \}=0,76$,
$F_{b,Rd} =\cfrac {k_1 \alpha_b \cdot f_u \cdot d \cdot t_p}{\gamma_{M2}}=\cfrac{2,5 \cdot 0,76 \cdot 490\cdot 2 \cdot 2}{1,25}\cdot 10^{-1}=297,9 \, kN$
Obliczeniowa styczna nośność pojedynczej śruby $F_{Rd}=min \{F_{v,Rd} \, ;\, F_{ b,Rd}\}=min \{94,1 ; 297,9\}= 94,1 \, kN$
Sumaryczna styczna nośność śrub przeznaczonych do przeniesienia ścinania$\sum F_{v,Rd(4)}=2 \cdot 94,1=188,2 \, kN$,
Warunek nośności węzła przy ścinaniu
$V_{j,Ed}=90,0 \, kN < \sum F_{v,Rd,(4)}=188,2 \, kN$
Sztywność obrotowa połączenia
Współczynniki sztywności części podstawowych węzła
[1],tab. 6.11:
Współczynnik sztywności:
w przypadku środnika słupa w warunkach ścinania
$k_1=\infty$
w przypadku środnika słupa w strefie ściskania
$k_2=\infty$
w przypadku środnika słupa w strefie rozciągania
$k_3=\infty$
w przypadku pasa słupa zginanego w strefie rozciągania
$k_4=\cfrac{0,9 l_{eff} t_{fc}^3} {m^3}:$
1-szy szereg śrub $k_4=\cfrac{0,9\cdot 191,2\cdot 19^3}{32,9^3}=33,1 \, mm$,
2-gi szereg śrub $k_4=\cfrac{0,9\cdot 206,6\cdot 19^3}{32,9^3}=35,8 \, mm$,
3-ci szereg śrub $k_4=\cfrac{0,9\cdot 206,6\cdot 19^3}{32,9^3}=35,8 \, mm$,
w przypadku blachy czołowej zginanej w strefie rozciągania
$k_5=\cfrac{0,9 l_{eff} t_{p}^3}{m^3}:$
1-szy szereg śrub $k_5=\cfrac{0,9\cdot 167,7\cdot 20^3}{43,2^3}=15,0 \, mm$,
2-gi szereg śrub $k_5=\cfrac{0,9\cdot 283,6\cdot 20^3}{48,9^3}=35,8 \, mm$,
3-ci szereg śrub $k_5=\cfrac{0,9\cdot 258,1\cdot 20^3}{48,9^3}=15,9 \, mm$.
Współczynniki sztywności w przypadku śrub rozciąganych
grubość podkładek $t_{pod}=4 \, mm$,
grubość łba i nakrętki $k=12,85 \,mm$,
baza wydłużalności śruby $L_b=t_p+t_{fc}+2t_{pod}+1/2(2k)=20+19+2\cdot 4+1/1(2 \cdot 12,85)=59,8 \, mm$
Współczynnik sztywności
$k_{19}=\cfrac{1,6 A_s}{L_b}=\cfrac{1,6\cdot 245}{59,8}=6,5 \, mm$
Efektywne wspólczynniki sztywności [1],6..3.3.1(12):
$k_{eff}=\cfrac{1}{\sum\limits_i \cfrac{1}{k_i}}$:
1-szy szereg śrub $k_{eff,1}=\cfrac{1}{0+1/33,1+1/15,0+1/6,5}=4,0 \, mm$,
2-gi szereg śrub $k_{eff,2}=\cfrac{1}{0+1/35,8+1/17,5+1/6,5}=4,2 \, mm$,
3-ci szereg śrub $k_{eff,3}=\cfrac{1}{0+1/35,8+1/15,9+1/6,5}=4,1 \, mm$,
Zastępcze ramię dźwigni [1],6..3.3.1(3):
$z_eq=\cfrac{\sum \limits_i k_{eff,i} h_i^2}{\sum \limits_i k_{eff,i}h_i}=\cfrac{4,0\cdot 443^2+4,2\cdot 323^2+ 4,1 \cdot 243^2}{4,0\cdot 443+4,2\cdot 323+ 4,1 \cdot 243}=355,2 \, mm$
Zastępczy współczynnik sztywności [1],6..3.3.1(1):
$k_{eq}=\cfrac{\sum \limits_i k_{eff,i} h_i}{z_{eq}}=\cfrac{4,0 \cdot 443+4,2 \cdot 323+4,1 \cdot 243}{355,2}=11,6 \, mm$
Początkowa sztywność obrotowa [1],6.3.1(4)Uwaga+tab. 6.15e:
$\mu=1,0$,
$ z=h_r-0,5 t_{fr}+50-120/2=400-0,5\cdot 13,5+50-120/2=383,3 \, mm$,
$S_{j,ini}=\cfrac{Ez^2}{\mu \sum \limits_i 1/k_i}=\cfrac{210\cdot 10^3\cdot 0,3833^2}{1,0\cdot(1/\infty+1/\infty+1/11.6)}=357894 \, kNm/rad$
Sztywności graniczne [1],5.2.2.5:
$ S_{j,1}=k_b \cfrac{EI_{jr}}{L_r}=25 \cfrac{210\cdot 10^6\cdot 23130\cdot 10^{-6}}{6,0}=202388 \, kNm/rad$,
$ S_{j,3}=0,5\cfrac{EI_{jr}}{L_r}=0,5 \cfrac{210\cdot 10^6\cdot 23130\cdot 10^{-6}}{6,0}=4048 \, kNm/rad$,
Ponieważ $S_{j,ini}> S{j,1}$, więc węzeł jest sztywny.
Obliczanie połączenia z wykorzystaniem programów komputerowych
Ręczne obliczanie czołowych połączeń śrubowych, nawet na śruby niesprężane zgodnie z normą [1]: jest żmudne. Przeprowadzenia szczegółowych obliczeń nie powinno się wymagać od Projektanta, a tylko zastosowania programu lub arkusza obliczeniowegl. Poniżej przedstawiamy sesje projektowe w programie CoP [43] oraz w module csJoint Consteel[31]. Każda z nich wymagała około 5-ciu minut pracy Projektanta.
Program CoP [43]
Program Mittal ACoP version 1.0.2 jest ogólnodostępny w wersji Free. Za jego pomocą można sprawnie projektować połączenia belek, słupów i ram konstrukcji stalowych w konstrukcji zgodnie z [1]:. Mimo, że jest to uproszczona wersja (Light) programu komercyjnego, to obejmuje szeroki asortyment połączeń:
- połączenia z blachą czołową (2 śruby w jednym wierszu), w tym:
czołowe połączenie belka – słup lub belka -belka z blachą wypuszczoną (lub bez wypuszczenia) z uwzględnieniem żeber usztywniających, nakładek na środnik węzła lub nakładkami z tyłu blachy czołowej, - nakładkowe połączenie belka – słup lub belka-belka z kątownikami lub blachami nakładkowymi.
W wersji Light nie można definiować więcej niż dwóch śrub w szeregu i śrub z tulejami wciskanymi. W celu uzyskania więcej informacji zobacz stronę.
Połączenie z rys. 35 jest sklasyfikowane w programie CoP jako „Moment resistant joint, extended end plate with column web stiffeners”. Model w programie CoP pokazano na rys. 38 do rys. 44
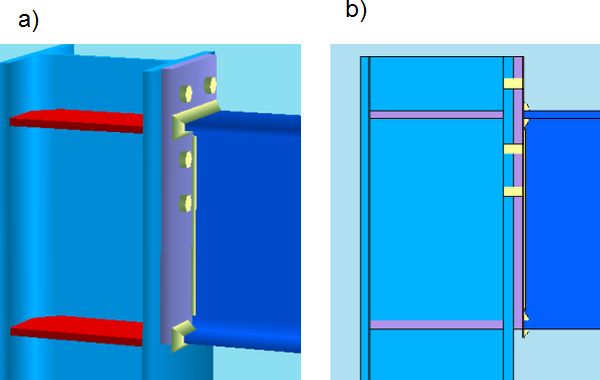
Rys.38 Model połączenia w programie CoP: [43]: a) widok 3D, b) widok z boku
W celu sprawdzenia wytrzymałości zadanego połączenia, należy wprowadzić dane pokazane na rys. 39do rys.45
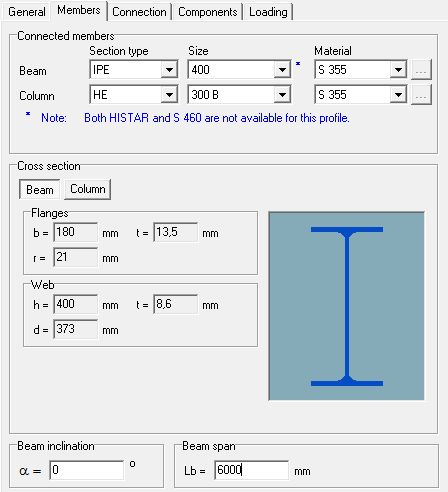
Rys.40. Przykład CoP [43]. Zakładka Members (elementy)
Po przeprowadzeniu obliczeń uzyskujemy wynik pokazany na rys. 46.
Z porównania wyników uzyskanych z programu (CoP) $M_{j,Rd}^{CoP}=251,2 \, kNm$ i obliczeń ręcznych (R) $M_{j,Rd}^{R}=279,0 \, kNm$, wynika, że nośność połączenia jest o 11% mniejsza niż obliczona ręcznie.
Jeszcze większe różnice występują w obliczeniach sztywności: w (R) połączenie zakwalifikowano jako sztywne, a w (CoP) jako odkształcalne. Na rys. 47 przedstawiono wybrane, bardziej szczegółowe wyniki.

Rys.47. Wybrane wyniki z obliczeń programem CoP [43]
Z porównania sztywności obliczonych ręcznie z obliczeniami CoP, obserwujemy istotne różnice. Sztywność początkowa $S_{j,ini}^{CoP}=77914 \, kNm/rad \ll S_{j,ini}^R=357894 \, kNm/rad$. Różnica jest znaczna – aż o rząd, co dobitnie świadczy o zawodności obliczeń ręcznych. Znaczny błąd dotyczy nośności śrub w rzędach, szczególnie w rzędzie (1) oraz (3).
Program Consteel [31]
Projektowanie połączeń czołowych zaimplementowano w module csJoint. Na rys. 48 pokazano widok 3D modelu połączenia z tego programu.
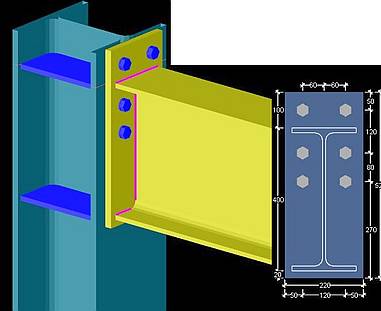
Rys. 48. Model 3D połączenia w programie Consteel moduł csJoint [31]
Po przeprowadzeniu obliczeń uzyskano nośność połączenia na zginanie, ścinanie i nośność spoin. Wyniki obliczeń zamieszczone w pliku.
Wybrane wyniki dotyczące sztywności połączenia są następujące:
Współczynnik sztywności efektywnej [1],wzór (6.30):
$k_{eff,3}= 2,14 \, mm$,
Równoważne ramię dźwigni [1],wzór (6.31)}:
$ z_{eq}= 363,16 \,mm$,
Równoważny współczynnik sztywności [1],wzór (6.9):
$k_{eq}= 6,68 \, mm $,
Sztywność początkowa z programu csJoint
$ S_{j,ini}^{csJ} = 76439,81 \, kNm/rad $,
Sztywność sieczna dla zadanego momentu:
$ S_{j,sec}^{csJ} = 38508,37 \, kNm/rad $,
Klasa sztywności: Podatny w 37,8%.
Z porównania sztywności (csJ) z (CoP) widać dużą zgodność:
sztywność początkowa $S_{j,ini}^{csJ}= 76440 /, kNm \approx S_{j,ini}^{CoP}=77914 \, kNm/rad $ (różnica 0,2%).
sztywność styczna $S_{j,sec}^{csJ}=38508 /, kNm \approx S_{j,sec}^{CoP}=38956 \, kNm/rad $ (różnica 1,1%).
Uzyskano zgodność wyników z dwóch różnych programów, ale niestety stwierdzono, że obliczenia ręczne są niewiarygodne.
Projektowanie połączenia czołowego z użyciem tablic
Na rys.49 przedstawiono kartę z katalogu Weynand i in. (2013)[33]
Nośności połączeń (Momententragfähigkeit) podano na innych kartach tych tablic i nie podajemy ich tutaj ze względu na bezprzedmiotowość dla rozpatrywanego przypadku. Z wybranej karty katalogu można odczytać, że dla połączenia belek HEA800 (nr 538) należy zastosować blachy czołowe o grubości 30 mm.

Rys. 49 Karta (Anlage) 1.151 z katalogu [33]
Przykład 10 [ Wyznaczanie momentu dokręcenia śrub sprężanych ]
Dostawca śrub wraz z dostawą przekazał następujące dane, dotyczące k-współczynników występujących w tab. 19.
$k_{max}= k_i = 0,18 $,
$k_m=0,16; \quad V_k = 0,06$
Z obliczeń wytrzymałościowych dobrano śrubę
M24- 8.8
Dla klasy 8.8 zastosowano śrubę HR wg tab.8
tab. 2 $\to $ $N_{pc}= 197,4 \, kN$
Metoda kontrolowanego momentu
Klasa zestawu K2,
Moment dokręcenia $M_2$ wg tab. 25.
$M_2= 0,16 \cdot (1+1,65\cdot 0,06) \cdot 24 \cdot 197,4 = 833 \, Nm$
I etap – dokręcenie momentem $M_I = 0,75 \cdot 833=625 \, Nm $
II etap – dokręcenie śrub momentem $M_{II}= 1,10 \cdot 833= 916 \, Nm$
Metoda kombinowana
Klasa zestawu K1 lub K2
Moment dokręcenia $M_1$ wg tab. 25
$M_1= 0,18 \cdot 24 \cdot 197,4 = 853 \, Nm$
I etap – dokręcanie kluczem dynamometrycznym na moment dokręcenia o wartości
a) $M_I \approx 0,75 \cdot M_1 = 0,75 \cdot 853 = 640 \, Nm$
lub przy braku znajomości $k_{max}$
b) $M_I = 0,13 \cdot 24 \cdot 197,4 = 616 \, Nm$
Położenie nakrętki w stosunku do gwintu trzpienia śruby oznaczono po zakończeniu I etapu.
II etap – dodatkowy obrót nakrętki o kąt
$(\ref{26}) \to \Delta \alpha = 60^o$
dla $Z=44 < 2d = 2\cdot 24= 48 \, mm $
Zagadnienia specjalne
Zagadnienie 1 [ Połączenie elementów ze stali wysokiej wytrzymałości ]Zagadnienie Q&A 2.11 z pracy [13]
Norma PN-EN 1993-1-8 [1] została zatwierdzona dla gatunków stali do S460, dlatego metoda podana w normie nie powinna być stosowana dla stali o wyższych gatunkach.
Wskazano na możliwość rozszerzenia zasad normy [1] na stal S640 (granica plastyczności $f_y=640 \, MPa$ bazując na wynikach badań eksperymentalnych przeprowadzonych przez Kouhi i Kortesmaa (1990) [44], przedstawionych na rys. 50.
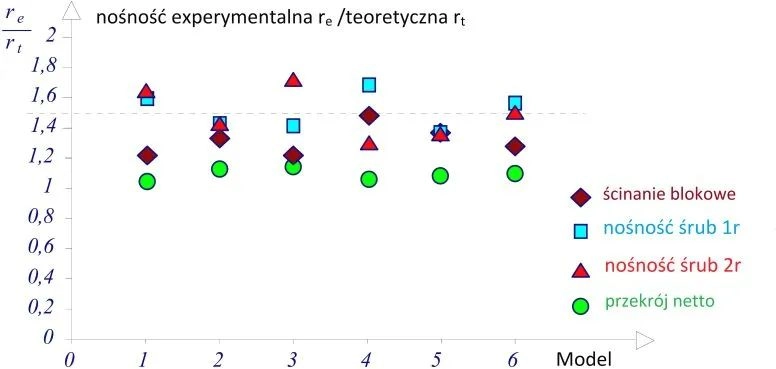
Rys.50. Wyniki testów wytrzymałościowych na połączeniach zakładkowych blach ze stali S640 [44]
Testy wytrzymałościowe wykonano na modelach z blach o grubości 3, 4, 6 i 8 mm wykonanych ze stali o granicy plastyczności $f_y= 640 \, MPa i wytrzymałości dopuszczalnej $f_u =700 \,MPa$ i łączonych śrubami lasy 10.9 na modelach: z jednym rzędem śrub (oznaczone na rys.50 jako 1r) oraz z dwoma rzędami śrub, (oznaczone jako 2r). Podczas 18-tu testów (6 modeli po trzy realizacje) stwierdzono następujące mechanizmy zniszczenia: rozerwanie blokowe, zniszczenie przekroju netto, nośność śrub (na ścinanie lub docisk)
Wyniki testów porównano z oszacowaniami nośności wg normy[1] i stwierdzono, że wszystkie wyniki są bezpieczne, co daje podstawy do stosowania reguł normowych również w odniesieniu do łączonych blach o wysokiej wytrzymałości S640.
Stwierdzono też, że odkształcenia zmierzone w testach w stanie granicznym były podobne do wielkości średnicy śruby.Literatura
- PN-EN 1993-1-8 + Ap1+ AC (2006-12). Eurokod 3 -Projektowanie konstrukcji stalowych -Część 1-8: Projektowanie węzłów
- PN-EN 1090-2:2018, Wykonanie konstrukcji stalowych i aluminiowych – Część 2: Wymagania techniczne dotyczące konstrukcji stalowych
- Hilti, Podręcznik techniki zamocowań. Technika kotwienia
- PN-EN ISO 898-1:2013-06, Własności mechaniczne części złącznych wykonanych ze stali węglowej oraz stopowej . Część 1: Śruby i śruby dwustronne o określonych klasach własności — Gwint zwykły i drobnozwojny
- Bogucki W., Żyburtowicz M. (2006), Tablice do projektowania konstrukcji stalowych, Wyd.7, Arkady
- Anuriev W.,I., Spravocnik konstruktora maszinostrojenia, Tom.1, Wydawnictwo Maszinostrojenie , Moskva 1982
- DIBt, Europäische Technische Bewertung, ETA-15/0352, 5 October 2020
- DIBt, European Technical Assessment, ETA-13/1038, 29 January 2016
- Petersen (2013). Stahlbau: Grundlagen der Berechnung und baulichen Ausbildung von Stahlbauten
- Witkowitz- Strojirienstvi, Sroub M12D-10.9 pro smaltove plechy, rys. 4/921-0484
- Kocańda S., i.in. (Red), Poradnik Inżyniera, Mechanika, T.II Zagadnienia konstrukcyjne (2009) , WNT, Warszawa
- Czepiżak (2015). Połączenia śrubowe
- Moore D.B., Wald F., (Ed) , Design of Structural Connections to Eurocode 3 – Frequently Asked Questions, Building Research Establishment Ltd, Watford, ublishing House of Czech Technical University in Prague, 2003
- Wald F., Mazura V., Moal V., Sokol Z., Experiments of bolted cover plate connections with slotted holes, CTU reports, Vol. 2, 2/2002, pp. 79-97, CUT, Praha, 2002
- [Wald F., Sokol Z., Moal M., Mazura V., Muzeau J. P.: Stiffness of cover plate connections with slotted holes, Eurosteel 2002, pp. 1007-1016, Coimbra, 2002
- Piraprez E.: Behavior of plates with slotted holes, CRIF Belgium, in Proceeding of International Conference on Steel Structures of the 2000’s, IABCE, Istanbul, 2000
- Tizani W.: The bearing capacity of plates made with long-slotted bolt holes, report, p. 58, University of Nottingham, SCI No. SCR 99002, London, 1999
- Owens G.W., Cheal D.B.: Structural Steelwork Connections, Butterworths, 1989
- PN-90/B-03200. Projektowanie konstrukcji stalowych
- PN-EN 14399-1, Zestawy śrubowe wysokiej wytrzymałości do połączeń sprężanych – Część 1: Wymagania ogólne
- PN-EN-14399-2, Zestawy śrubowe wysokiej wytrzymałości do połączeń sprężanych – Część 2: Badanie przydatności do połączeń sprężanych
- PN-EN 14399-4, Zestawy śrubowe wysokiej wytrzymałości do połączeń sprężanych — Część 4: System HV – Zestawy śruby z łbem sześciokątnym i nakrętki sześciokątnej
- PN-EN 14399-3, Zestawy śrubowe wysokiej wytrzymałości do połączeń sprężanych – Część 3: System HR – Zestawy śruby z łbem sześciokątnym i nakrętki sześciokątnej
- PN-EN 14399-10, High-strength structural bolting assemblies for preloading – Part 10: System HRC – Bolt and nut assemblies with calibrated preload
- PN-EN 14399-9, Zestawy śrubowe wysokiej wytrzymałości do połączeń sprężanych — Część 9: System HR lub HV – Zestawy śruby i nakrętki z bezpośrednim wskaźnikiem napięcia
- Medcalf J., Cof , K factor and the trouble with ISO 1404, Portal „Peak Innovations Engineering”, [ https://pieng.com/cof-k-factor-and-the-trouble-with-iso-16047/]
- Bickford J., H. (1990), An Introduction To The Design and Behavior of Bolted Joints. Marcel Dekker, Inc., NewYork
- Shigley J., E., (1977), Mechanical Engineering Design. McGraw-Hill Book Company, New York
- PN-EN ISO 16047:2007, Części złączne -Badanie zależności moment obrotowy/siła zacisku
- ArcelorMittal Connection Programme: Connection design according to ENV 1993. COP Arcelor Mittal Edition ACoP version 1.0.2, https://sections.arcelormittal.com/design_aid/design_software/EN
- Consteel Software (2021). ConSteel 15 Manual, moduł csJoint
- IDEA RS (2019). IDEA StatiCa. Engineering software. Structural design and code-check of joints, cross sections, beams and other detail
- Weynand, K., Oerder, R. (Eds.). (2013). Typisierte Anschlusse im Stahlhochbau nach DIN EN 1993-1-8. Standardised Joints in Steel Structures to DIN EN 1993-1-8 (Gesamtausg. 2013). Stahlbau
- Kulak G.L., Fisher J.W., Struik J.H.A. , Guide to design criteria for bolted and riveted joints, Second edition, J. Wiley & Sons, New York, 1974.
- Bickford J.H., An introduction to the design and behaviour of bolted joints, Third edition,Marcel Decker inc., New York 1995
- KeeSafety, Bezpieczne łączenie konstrukcji, Prospekt produktu [https://keesafety.pl/images/uploads/pl/documents/Bezpieczne_laczniki_do_konstrukcji_stalowych.pdf]
- PN-EN 1992-4, Eurokod 2: Projektowanie konstrukcji z betonu. Część 4: Projektowanie zamocowań do stosowania w betonie
- Steenhuis M.: Momentverbindungen, SG/TC10a, Stalbouwkundig Genootschap, Rotterdam 1999
- Goczek, J., Supeł, Ł., Gajdzicki, M. (2011). Przykłady obliczeń konstrukcji stalowych: Eurokod 3-1-1, Eurokod 3-1-3, Eurokod 3-1-5, Eurokod 3-1-8, Wydawnictwo Politechniki Łódzkiej
- PN-EN 1993-1-1+A1 (2006). Eurokod 3 – Projektowanie konstrukcji stalowych – Część 1-1: Reguły ogólne i reguły dla budynków
- Boracchini A., Design and Analysis of Connections in Steel Structures Fundamentals and Examples, Wilhelm Ernst & Sohn, Verlag für Architektur und technische Wissenschaften GmbH & Co, Berli, 2018
- Canadian Standards Association (CSA) (2014). Limit states design of steel structures, CSA S16-14. ON, Canada: Canadian Standards Association
- ArcelorMittal Connection Programme: Connection design according to ENV 1993. COP Arcelor Mittal Edition ACoP version 1.0.2, https://sections.arcelormittal.com/design_aid/design_software/EN
- Kouhi J., Kortesmaa M.: Strength tests on bolted connection using high-strength steels (HSS steels) as a base material, VTT Research Notes 1185, Espoo, 1990
________________________________
Portale spolecznościowe
Wyślij
Musisz się zalogować, aby móc dodać komentarz.

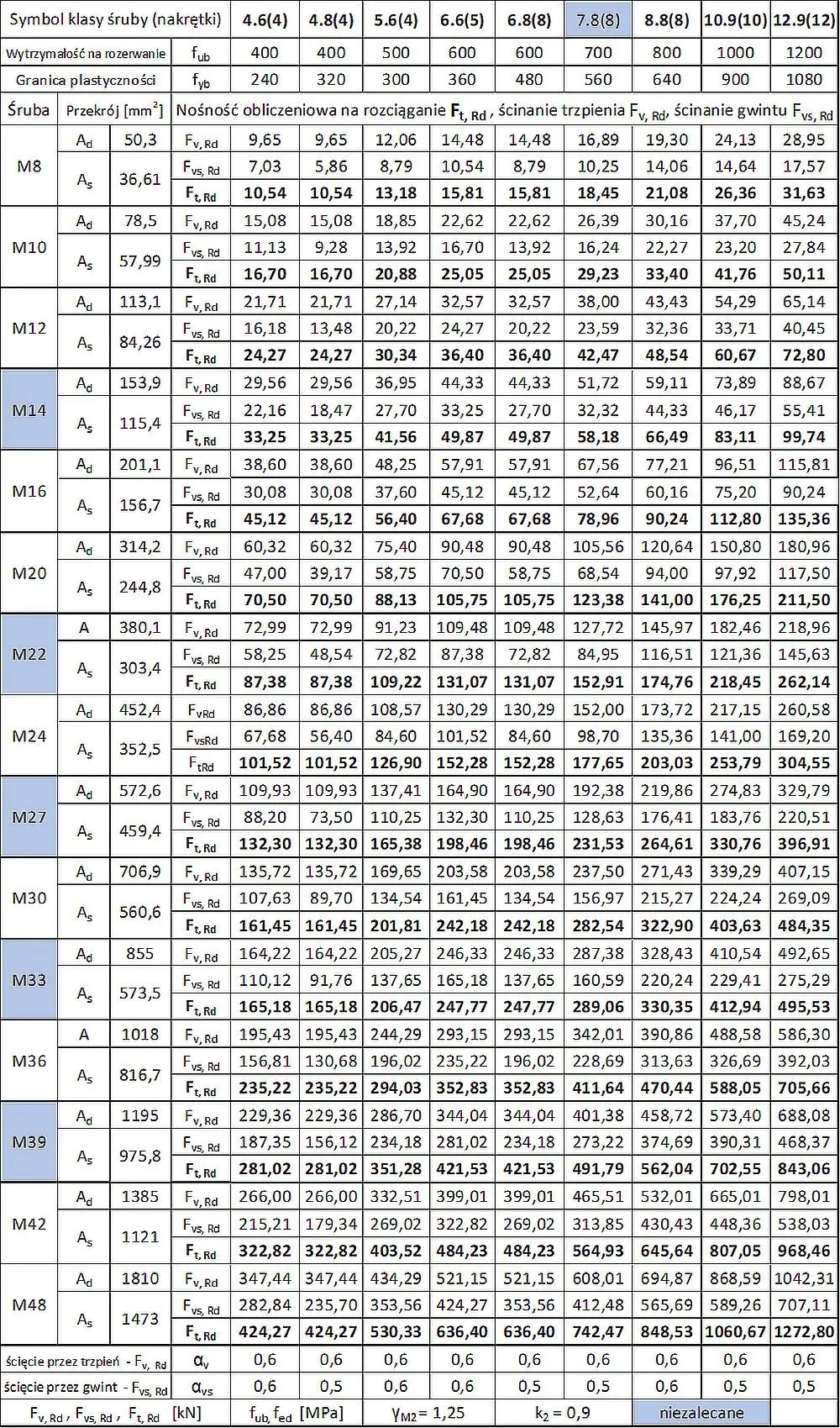

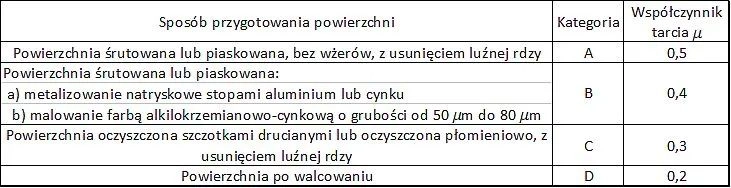
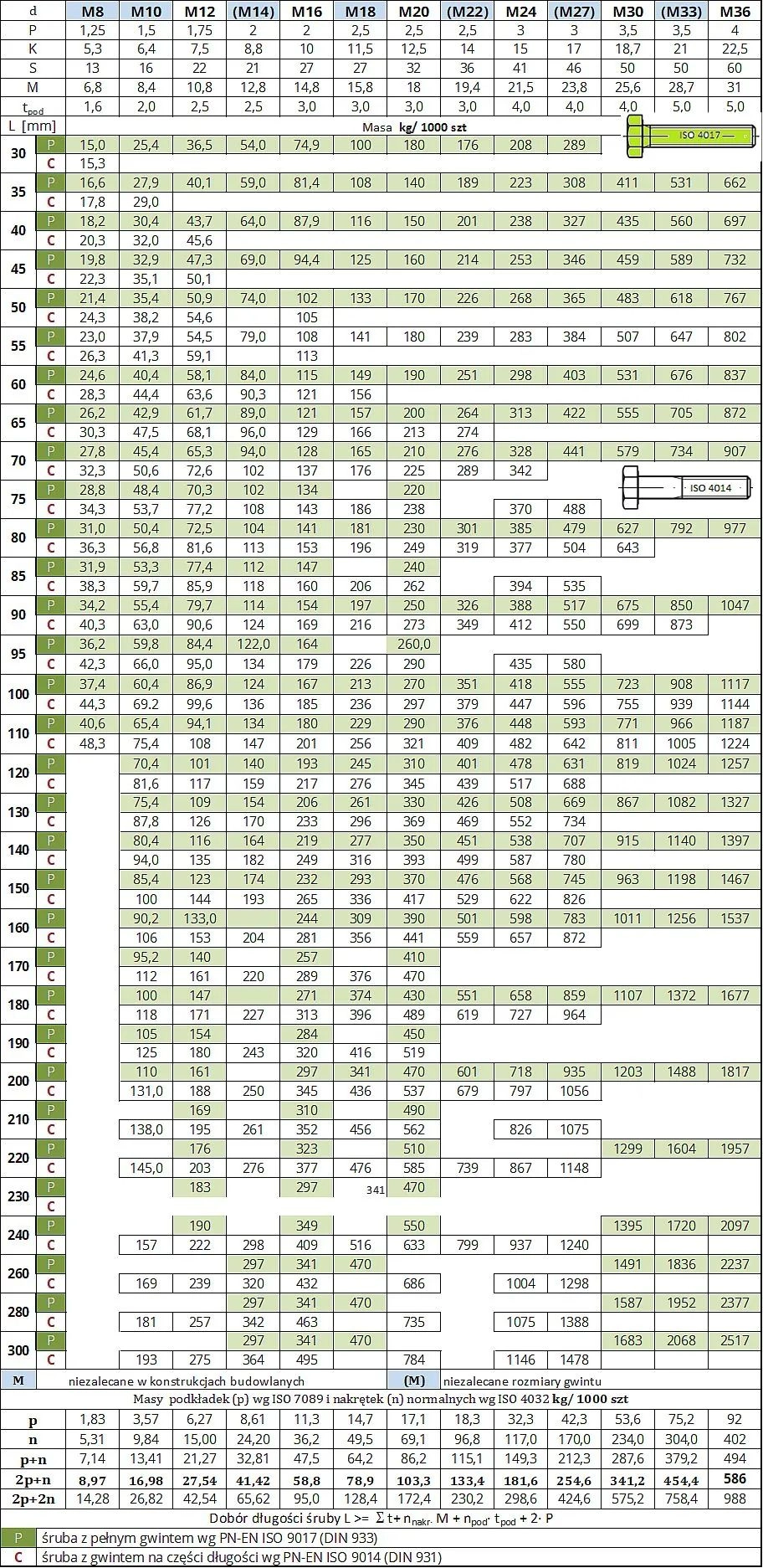
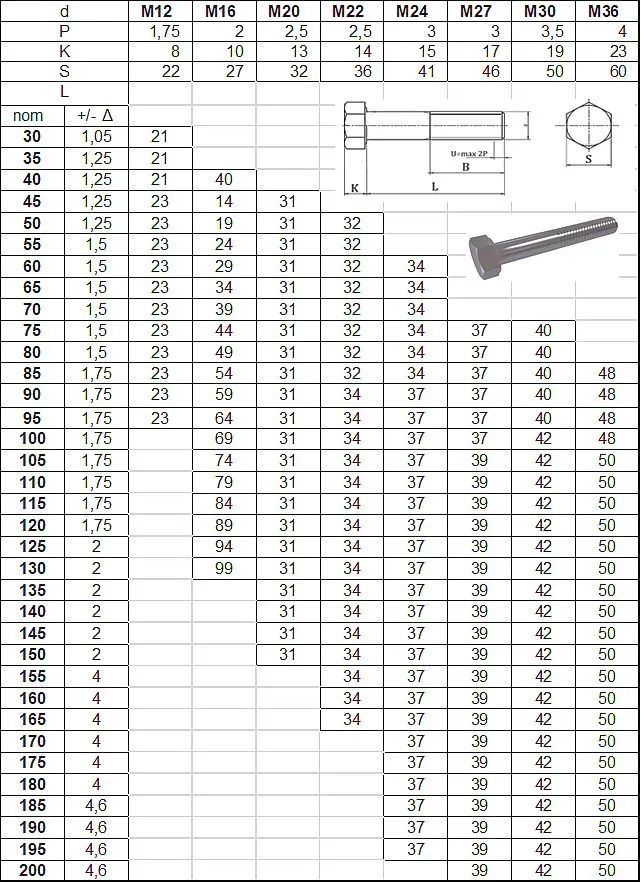
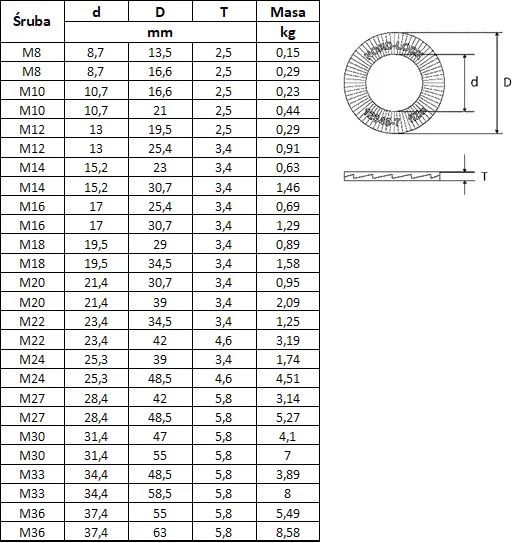
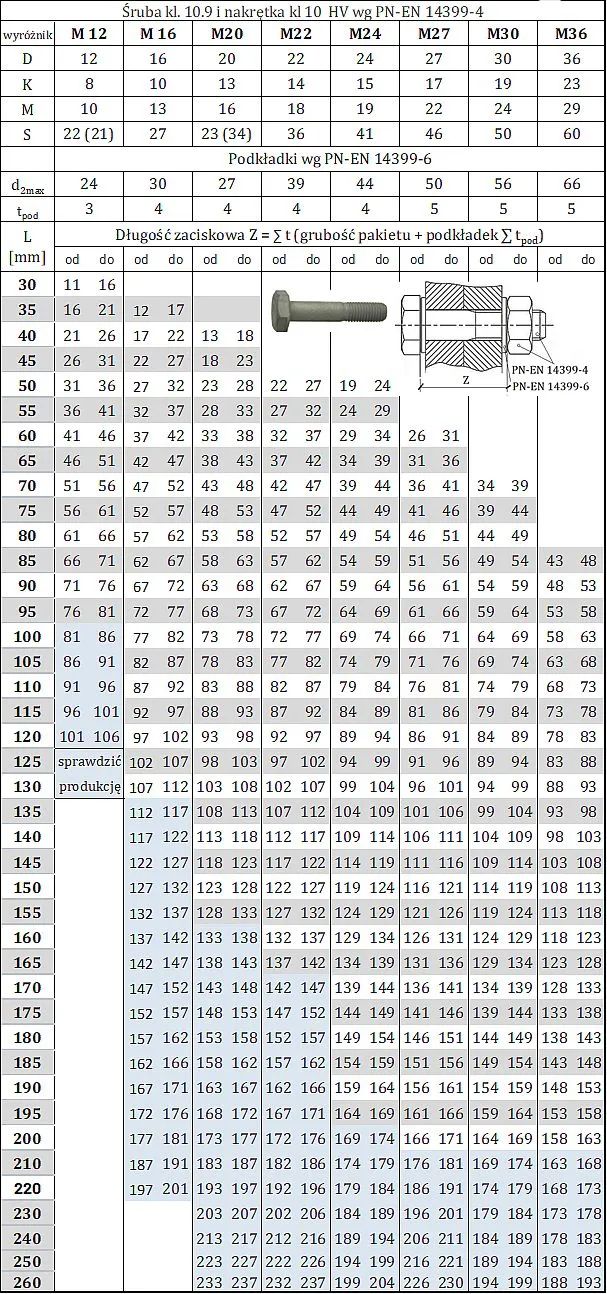
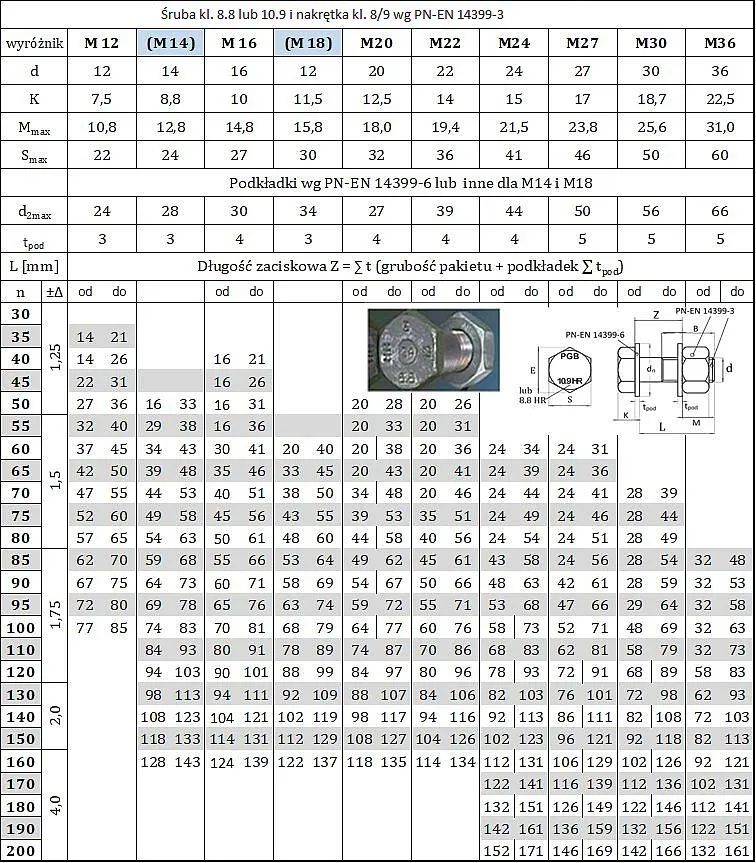
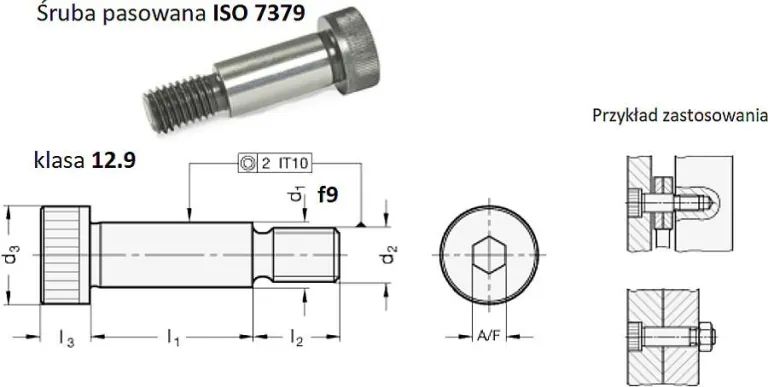
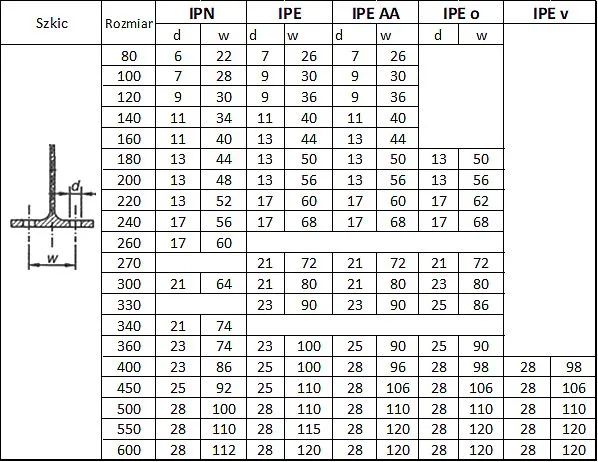
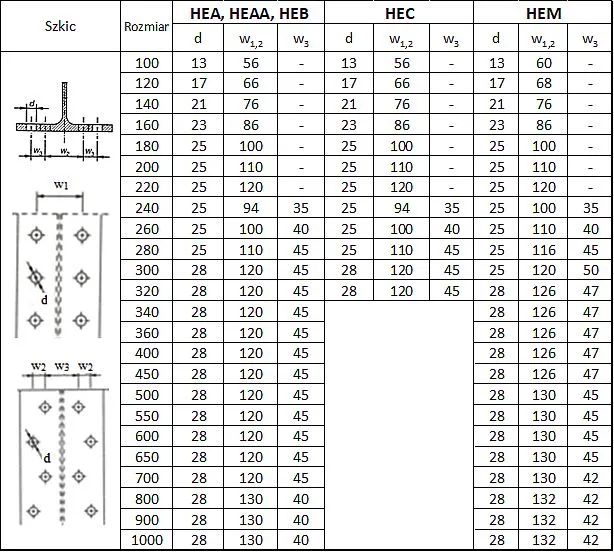
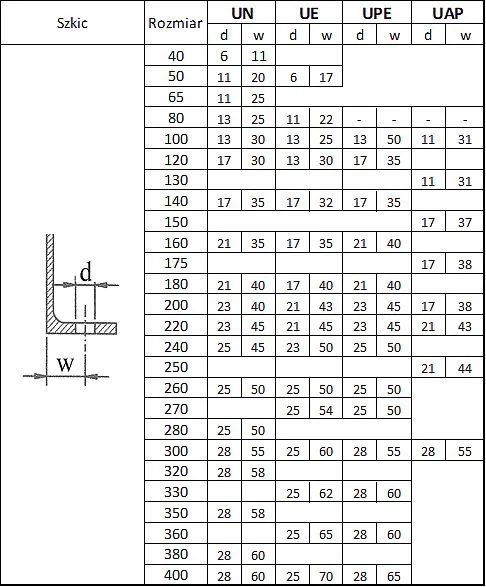
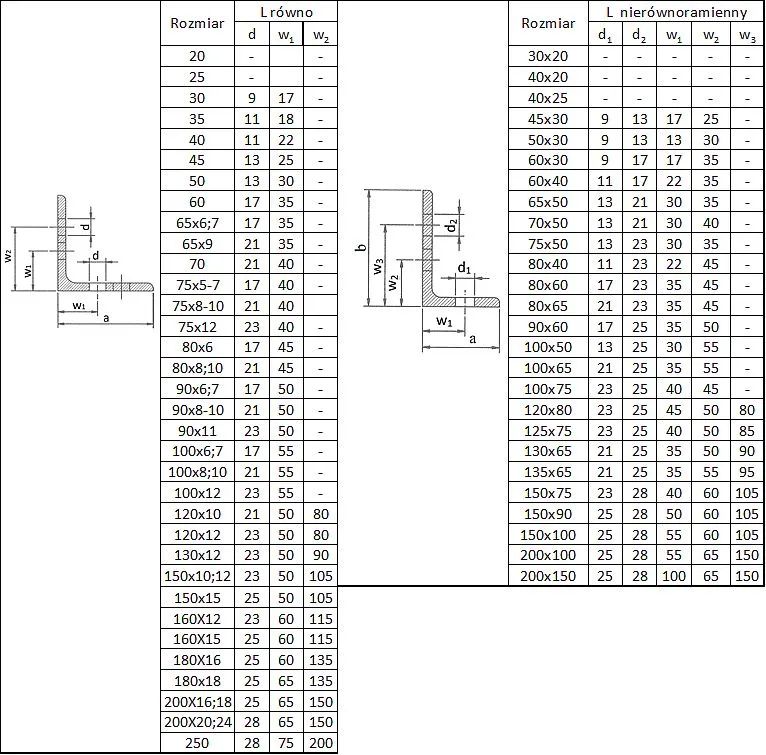
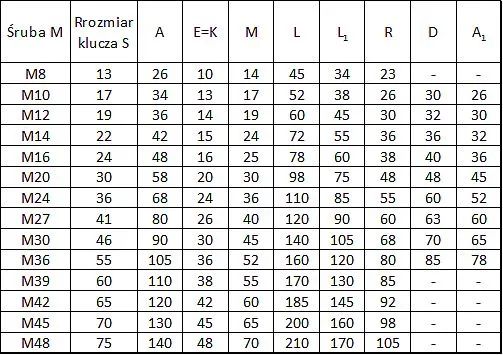
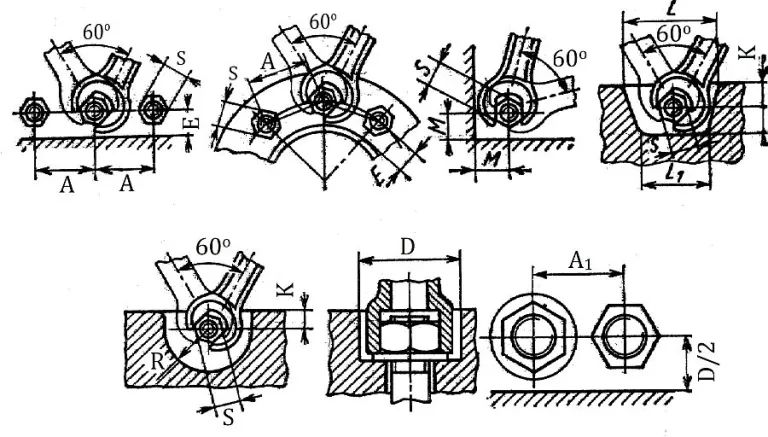
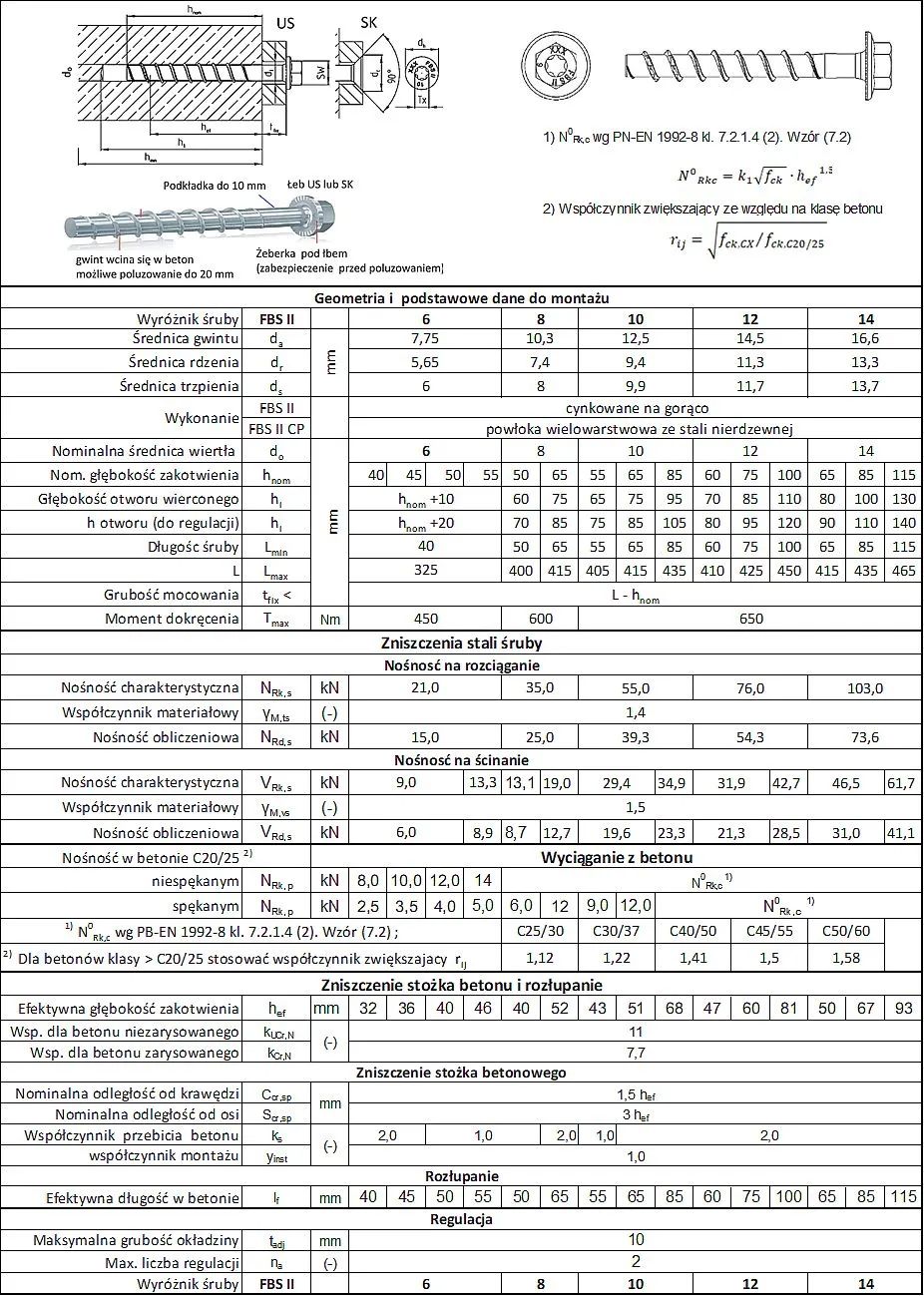
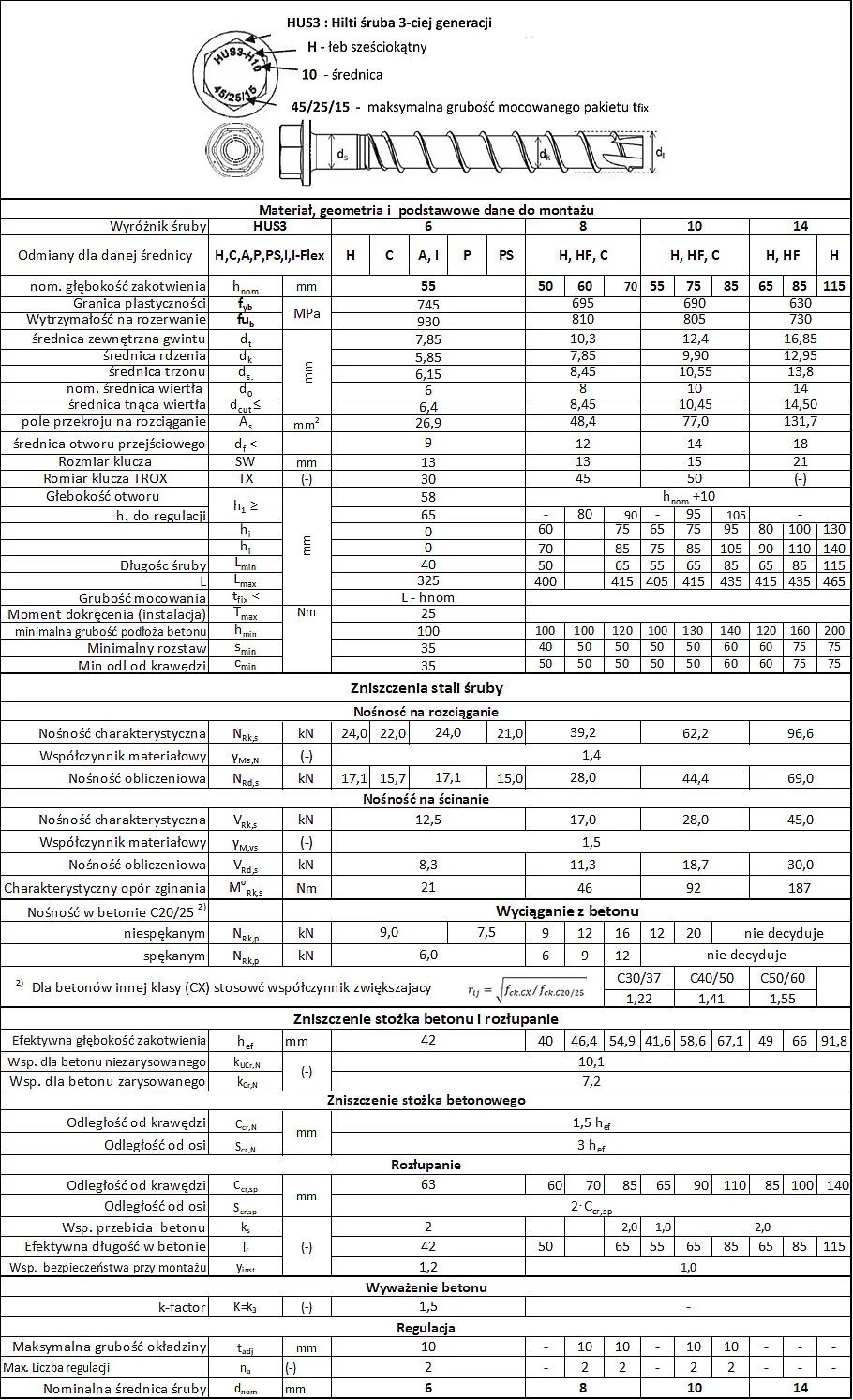
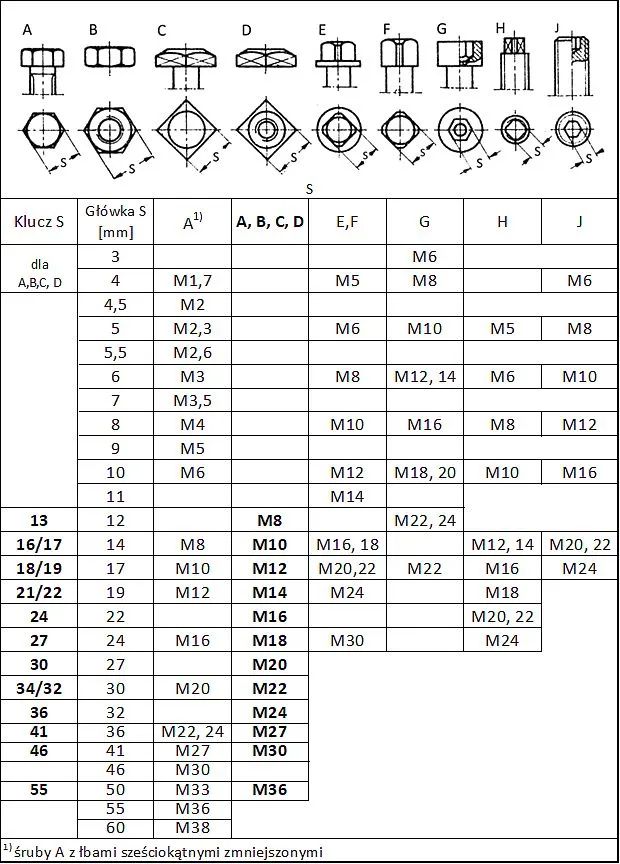
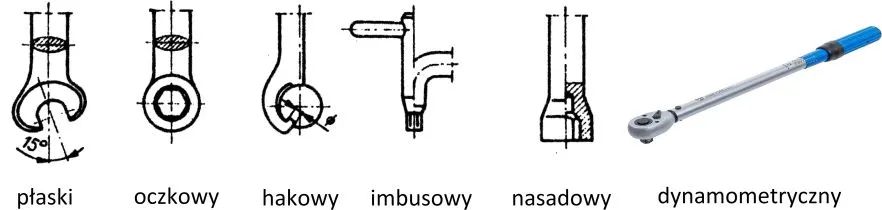
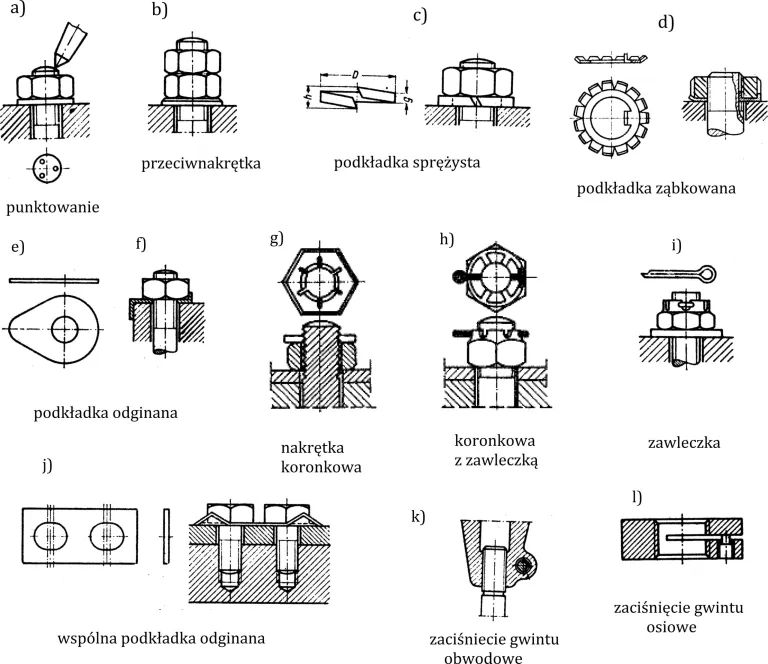

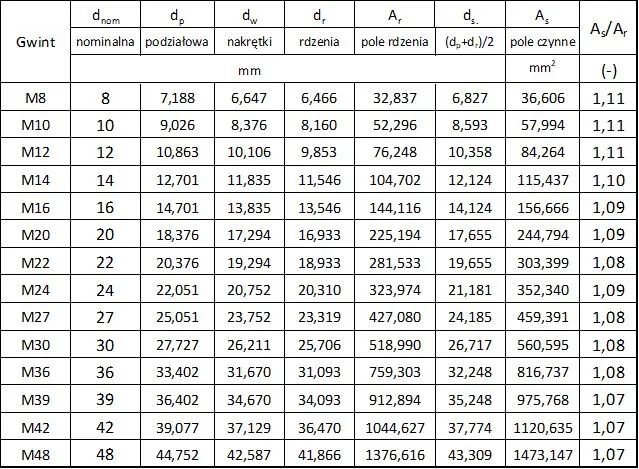
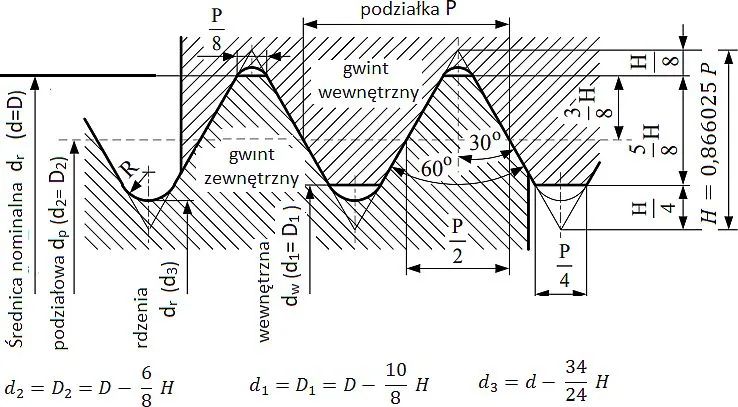
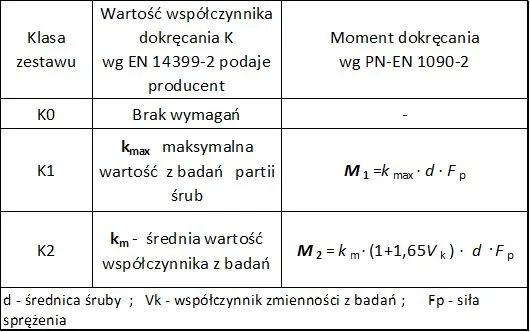
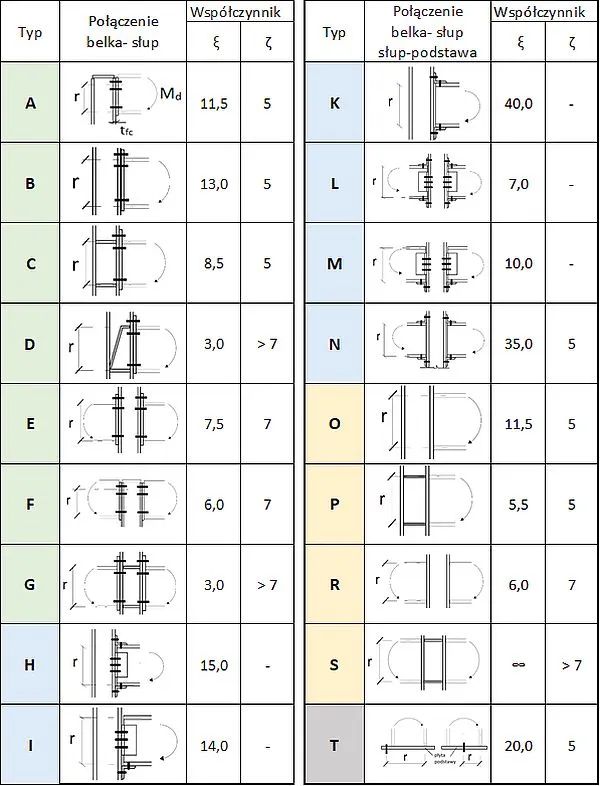
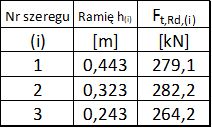




Dzień dobry,
znalazłem błąd w tabeli z nośnościami śrub (Tab 1.). Dla śruby M16 nośność Fvs,Rd jest taka sama jak Fv,Rd, a powinna być mniejsza. Przykładowo dla klasy 8.8 zamiast 77,21 powinno być 60,17 kN.
OK Dziękuję. Poprawiłem – błąd w formule Excel podczas rozszerzania tabeli ale tylko dla M16
Leszek Chodor