`Leszek Chodor, 30 kwietnia 2016
23 sierpnia do 4 września 2025 naprawa po awarii i połączenie z innymi artkułami z dziedziny
W ciągu ostatnich 24 godzin z artykułu korzystało 9 Czytelników
Współczesne podejście do projektowania konstrukcji odchodzi od klasycznych zasad liniowej sprężystości w kierunku wykorzystania zapasów nośności w stanach nadkrytycznych oraz zniszczenia plastycznego, to znaczy teorii nośności granicznej. Coraz częściej uznaje się że podstawowym sposobem analizy konstrukcji stalowych, ale też żelbetowych [1], [2] jest analiza plastyczna, a nie sprężysta.
Wyrazem tego jest wiele odniesień i dyspozycji w normie [3] i normach związanych. Dlatego podstawowym obszarem pracy i kształcenia inżyniera powinny być metody analizy plastyczne, a klasyczne metody teorii sprężystości jedynie jako pomocnicze, wstępne.
Nośność plastyczna a nośność graniczna i krytyczna
Metody analizy plastycznej prowadzą do optymalnego projektowania konstrukcji poprzez wykorzystanie rezerw plastycznych i powinny być stosowane w pierwszej kolejności. Metody teorii sprężystości można (i należy) stosować wtedy (i tylko wtedy), gdy w sposób nie budzący wątpliwości, pokażemy, że: 1) materiał nie jest w stanie osiągnąć wystarczającego stanu plastycznego, 2) przekrój elementu w przekrojach krytycznych nie ma wystarczającej swobody obrotu, umożliwiającej utworzenie przegubu plastycznego To znaczy przez domniemanie stosuje się metody plastyczne, a metody sprężyste dopiero wówczas, gdy zachodzą przesłanki, w których nie można stosować metod teorii plastyczności i nośności granicznej.
Największym ograniczeniem opisanewj wyżej kolejności stosowania metod analizy konstrukcji jest stosowane oprogramowanie inżynierskie, które wykorzystuje metody teorii sprężystości i wynikające z nich liniowe algorytmy metody elementów skończonych prowadzące so rozwiązywania liniowych układów równań. Ponieważ algorytmy teorii plastyczności prowadzą do algorytmów optymalizacji numerycznej, a nie układów równań liniowych, to wdrożenie metod plastyczności wymagałoby opracowania oprogramowania od nowa. i do utraty uniwersalności oprogramowania
Nośność graniczna konstrukcji
Na rys. 1 przedstawiono ścieżkę równowagi konstrukcji nieliniowej (linia gruba), która stanowi obwiednię ścieżek równowagi identyfikowanych podczas prostych analiz i mechanizmów zniszczenia:
- liniowe analizy sprężyste j :prosta OA (1), w której pomija się nieliniowości fizyczne i geometryczne,
- nieliniowej analizy sprężystej pęk krzywych O,C,C’,C” z różnymi formami utraty stateczności (3a), (3b), (3c) ( np. wyboczenie, zwichrzenie, przeskok węzła, utrata stateczności miejscowej), lub innymi efektami: wzmocnienie (3a), osłabienia (3c) lub pośrednimi (3b),
- nieliniowej analizy plastycznej dla różnych mechanizmów zniszczenia plastycznego (4a), (4b) (np. mechanizm belkowy, przechyłowy).
- analizy kruchej – krzywa ($\ref{39}$) .
Zauważmy, że pierwszy przegub plastyczny utworzy się przy obciążeniu Λ1 mniejszym od obciążenia krytycznego Λcr. Gdy obciążenie jest zwiększane powyżej Λ1, to ulega zmianie schemat pręta na skutek stałego obrotu w tym przegubie. dla tak zmienionego schematu pręta należałoby wyznaczyć nowe obciążenie krytyczne Λcr,1, które będzie oczywiście mniejsze od Λcr.
Ścieżki (3) uwzględniają geometryczne nieliniowości , a ścieżki (4), ($\ref{39}$) fizyczne nieliniowości konstrukcji. Maksimum na ścieżce równowagi ($\ref{40}$) – punkt F, jest graniczną nośnością konstrukcji.
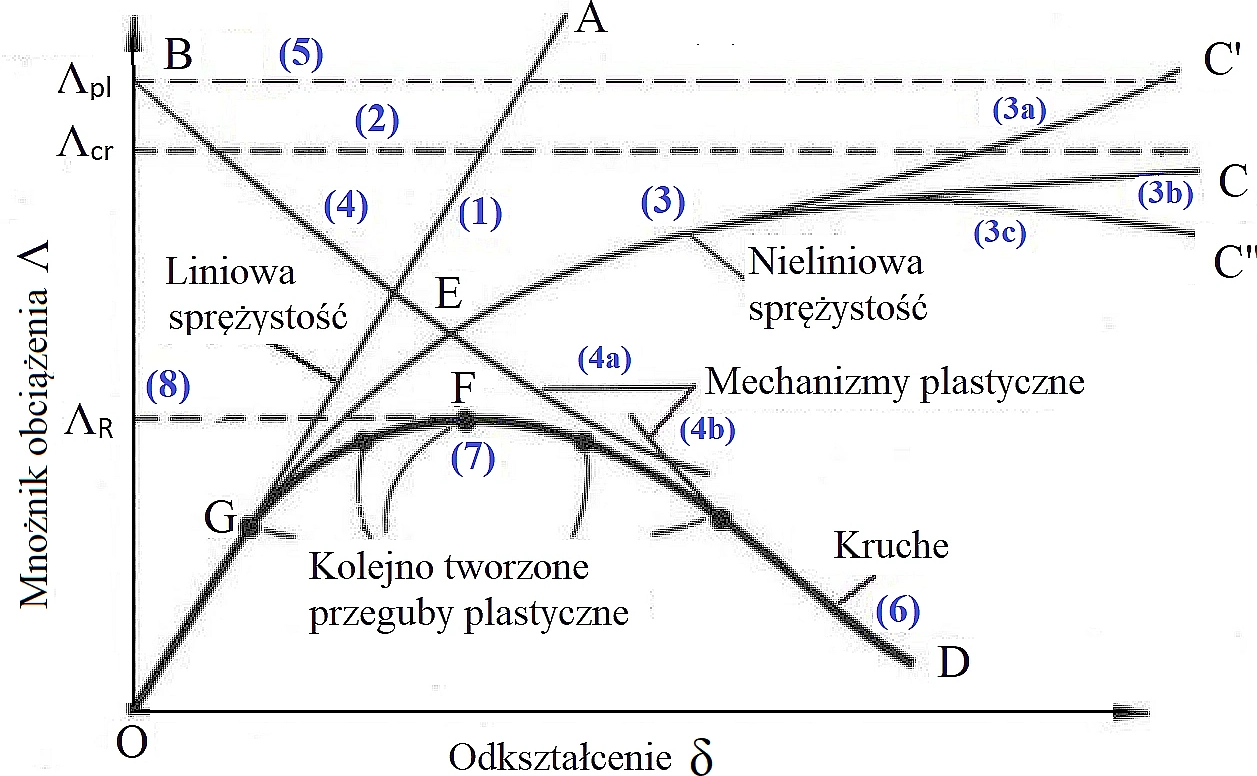
Rys.1. Ścieżki równowagi konstrukcji. Nośność (mnożnik obciążenia) w funkcji deformacji [4]
Obciążenie konstrukcji jest specyfikowane jako mnożnik obciążenia
$$\begin {equation} \Lambda \label{1} \end {equation}$$
który jest nazywany również parametrem obciążenia [4] i jest podstawą analizy jednoparametrowej, w której można zwiększać znaną konfigurację obciążenia, czyli łączne działanie wszystkich obciążeń- pionowych, poziomach, skupionych, rozłożonych itd. – proporcjonalnie do tego parametru obciążenia. Wartość mnożnika obciążenia $\Lambda$ przy której obciążenia przemnożone przez ten parametr
$$\begin {equation} P_\bullet = \Lambda_\bullet \cdot P \label{2} \end {equation}$$
wywołuje określony efekt:
1) w stanie sprężystym: przy utracie stateczności sprężystej mamy obciążenie graniczne krytyczne $\Lambda_{cr}$ (asymptota pozioma (2) na rys.1); ($\bullet=”cr”$)
2) przy uplastycznieniu choć jednego punktu w konstrukcji mamy obciążenie graniczne sprężyste $\Lambda_{el}$, ($\bullet = „el”$)
3) w stanie plastycznym przy uruchomieniu mechanizmu plastycznego, mamy obciążenie graniczne plastyczne $\Lambda_{pl}$. (asymptota pozioma ($\ref{40$) na rys.1),($\bullet=”pl”$)
Przykładowo dla modelu rys. 2b zachodzi
$$\begin {equation} M_{pl}= \Lambda_{pl}\cdot M \label{3} \end {equation}$$
Nieliniowa rzeczywista ścieżka równowagi konstrukcji oznaczona na rys. 1 literami OGFD ma maksimum w punkcie F. Obciążenie osdpowiadajaće maksimum na ścieżce róęnowagi naywa się obciążeniem granicznym
$$\begin {equation} \Lambda_R \text { : ⇐ max na ścieżce rówagi } [\Lambda – \delta ] \label{4} \end {equation}$$
gdzie:
$\Lambda$ mnożnik obciążenia ($\ref{1}$),
$\delta$ sprawcze (miarodajne ) przemieszczenie elementu lub konstrukcji.
W praktyce nośność graniczna konstrukcji sprężysto-plastycznej jest wyznaczana na podstawie znajomości nośności krytycznej $\Lambda_{cr}$, wyznaczonej w liniowej analizie wyboczeniowej LBA dla konstrukcji idealnie sprężystej oraz znajomości nośności plastyczna $\Lambda_{pl}$\, wyznaczonej dla konstrukcji sztywno-plastycznej.
Szeroko znana i wykorzystywana jest prosta formuła Rankine-Merchant [5] sumowania odwrotności nośności ( „podatności” ):
$$\begin {equation} \cfrac {1} {\Lambda_R} = \cfrac {1} {\Lambda_{pl}}+\cfrac {1} {\Lambda_{cr}} \label{5} \end {equation}$$
gdzie:
$\Lambda_R$ – nośność graniczna elementu lub konstrukcji,
$\Lambda_{pl}$ – nośność plastyczna, związana z mechanizmami plastycznego zniszczenia, wyznaczona zgodnie z teorią plastyczności I rzędu dla konstrukcji wykonanej z materiału sztywno-plastycznego
$\Lambda_{cr}$ – nośność krytyczna związana z utratą stateczności globalnej ( wyboczenie , zwichrzenie, przeskok węzła) lub miejscowej (ścianki przekroju lub płyty-tarczy, wyznaczona zgodnie z teorią LBA (Linear Buckling Analysis) dla materiału idealnie sprężystego.
Nośność $\Lambda_{pl}$ jest przedmiotem niniejszego artykułu. Nośność plastyczna, która jest ważną formą zniszczenia konstrukcji z bezpośrednim wkładem w nośność graniczną, na przykład podług uproszczonej formuły ($\ref{5}$).
Zjawiska niestateczności konstrukcji i nośność krytyczna konstrukcji jest przedmiotem innych artykułów: Geneza-metod-imperfekcyjnych i innych.
Nieliniowa ścieżka równowagi sprężysto-plastycznej konstrukcji
Nieliniowa ścieżka równowagi sprężysto-plastycznej konstrukcji wyznaczana jest iteracyjnie w procedurze sterowania przyrostem mnożnika obciążenia $\Lambda$ lub sprawczego przemieszczenia $\delta$. W trakcie analizy przyrostowej monitorowane są wartości momentów zginających oraz wyznaczane przemieszczenia sprawcze, w tym obroty w miejscach przegubów fizycznych lub plastycznych. Do czasu utworzenia pierwszego przegubu plastycznego prowadzimy klasyczną analizę sprężystą. Po utworzeniu przegubu w przekroju najbardziej wytężonym następuje skokowa zmiana ustroju konstrukcyjnego i należy powtórnie składać macierz sztywność ustroju. Dla nowego ustroju wyznaczamy kolejną gałąź ścieżki równowagi. Wskutek zmiany geometrii konstrukcji (dużych obrotów) w tworzących się przegubach plastycznych może nastąpić jakościowa zmiana pracy elementu i zjawisko $P-\delta$ innej natury od nieliniowych geometrycznie zagadnień wyboczenia sprężystego.
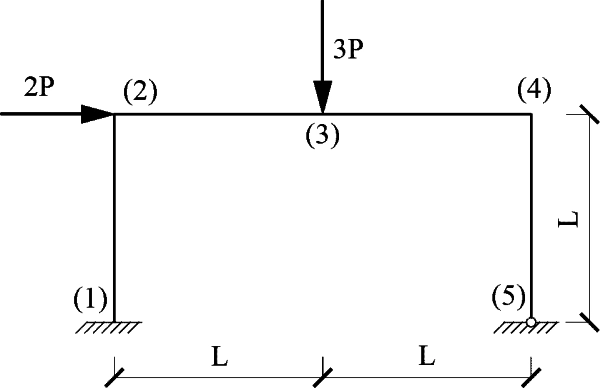
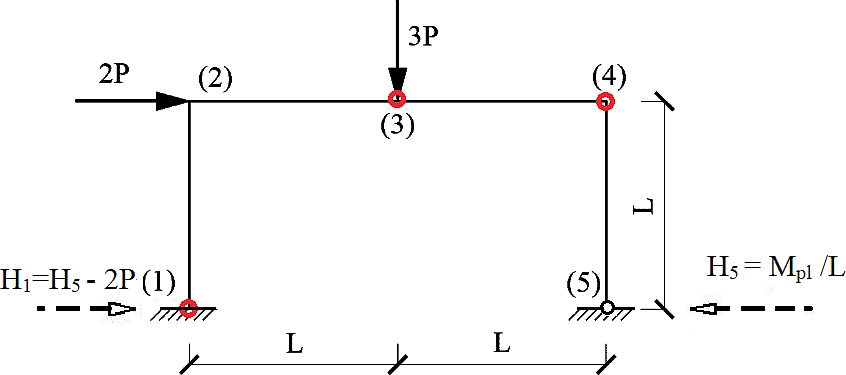
Na rys.2przedstawiono przykład ścieżki równowagi ramy portalowej , uzyskany metodą sterowania przemieszczenia ( przy zwiększających się przemieszczeniach badano zmiany parametru obciążenia $\Lambda$). Stwierdzono, że ważną cechą ramy portalowej jest obciążenia pionowe głowic słupów. W badanej konstrukcji jako pierwszy ujawnił się mechanizm belkowy z przegubem wewnętrznym, Wskutek obrotu w przegubie następuje skrócenie przęsła rygla i nachylenie słupów. To wywołuje ściskanie rygla, a dodatkowa siła ściskająca wywołuje zniszczenie w postaci wyboczenia rygla. Przykład pokazuje, że zmiana schematu statycznego podczas pracy konstrukcji ma wpływ na nośność plastyczną, w szczególności, gdy w elementach pojawią się znaczne siły ściskające. Wystąpienie jakościowo nowych sił przekrojowych zmienia również nośność plastyczną na skutek interakcji plastycznej siły osiowej i momentu zginającego.
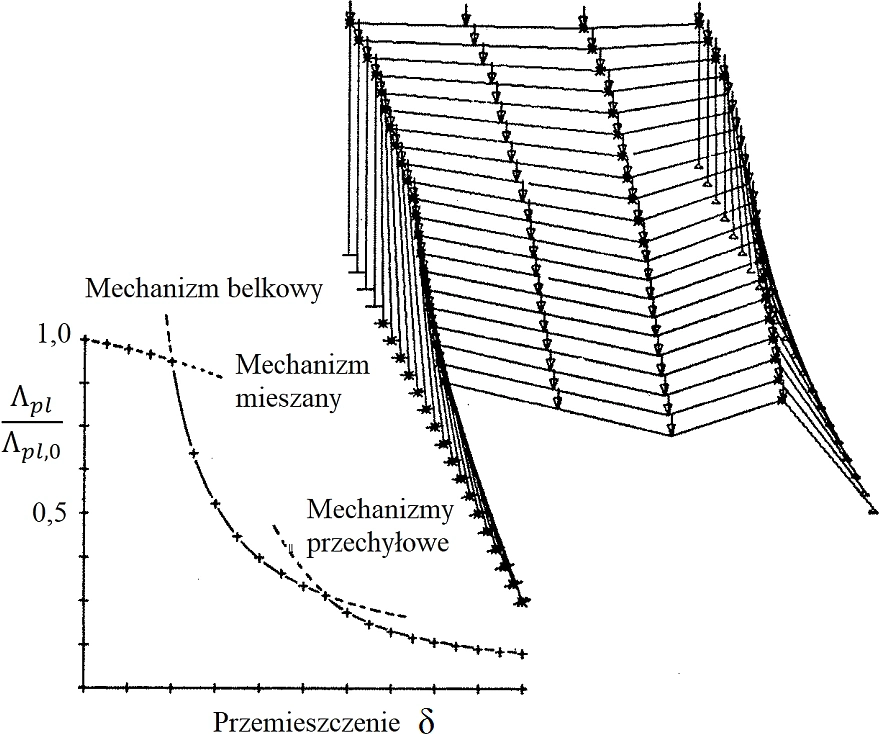
Rys.2. Przykład plastycznej ścieżki równowagi (opis w tekście) [4]
Typy analizy plastycznej
Globalna analiza plastyczna pozwala uwzględniać nieliniowe właściwości materiału przy obliczaniu skutków oddziaływań w układzie konstrukcyjnym. Do tego celu można stosować jedną z metod:
- analiza sprężysto-plastyczna, w której kolejne przekroje lub węzły osiągające nośność plastyczną traktuje się jak przeguby plastyczne (przykład na rys.2)
- nieliniowa analiza plastyczna, w której uwzględnia się rozwój stref plastycznych w elementach (tzw teoria plastyczna II rzędu)
- analiza sztywno-plastyczna, w której abstrahuje się od odkształceń sprężystych, traktując poszczególne części między przegubami jako sztywne *(teoria plastyczna I rzedu).
Stosowanie pierwszych dwóch metod wymaga odpowiedniego oprogramowania. Do obliczania belek, ram i płyt można posłużyć się trzecią metodą,, która może być stosowana ręcznie (bez specjalnego oprogramowania).
Korzyści z wykorzystania przegubów plastycznych są znaczne, szczególnie w belkach lub ramach statycznie niewyznaczalnych. Doprowadzenie do wystąpienia w takich konstrukcjach przegubu plastycznego obniża o 1 stopień statyczną niewyznaczalność ustroju, z równoczesnym zachowaniem nośności plastycznej w przegubie o wielkości ($\rewf{19}$). Pozwala to na zwiększenie obciążenia do wartości wywołującej pojawienie się kolejnego przegubu plastycznego. Stan graniczny ustroju n-krotnie statycznie niewyznaczalncgo zostanie osiągnięty, gdy wystąpi n + 1 przegubów. Wówczas ustrój zmieni się w mechanizm, osiągając nośność graniczną z uwzględnieniem rezerwy plastycznej. W celu dokładniejszego poznania zagadnień związanych ze stosowaniem teorii plastyczności można sięgnąć do szerokiej literatury przedmiotu..
Ustalanie nośności granicznej ustrojów statycznie niewyznaczalnych jest realizowane różnymi metodami. Zostaną tutaj krótko przedstawione: metoda plastycznego wyrównania momentów, zwana metodą przyrostową i metoda kinematyczna.
W metodzie przyrostowej śledzi się zachowanie konstrukcji na ścieżce równowagi oraz określa poziomy obciążenia w chwili tworzenia się kolejnych przegubów plastycznych w przekrojach elementów i w węzłach konstrukcji. Uzyskane tą drogą największe obciążenie jest obciążeniem granicznym metody statycznej (dolnym oszacowaniem).
Obciążenie graniczne uzyskane metodą kinematyczną jest górnym oszacowaniem i polega na wyszukaniu możliwych kinematycznie mechanizmów zniszczenia i na porównaniu dla każdego z nich pracy sił zewnętrznych na odpowiadających im przemieszczeniach z pracą sił przekrojowych na odpowiadających im przemieszczeniach. Z uzyskanego w ten sposób zbioru obciążeń granicznych poszczególnych mechanizmów najmniejsze obciążenie jest obciążeniem granicznym. Zastosowanie obu metod ilustrują przykłady 2 i 3 .
Przegub plastyczny i metody analizy plastycznej
Typowe ścieżka równowagi (obciążenie – moment zginający M, przemieszczenie – kąt obrotu Φ elementu lub konstrukcji sprężysto-plastycznej pokazano na rys.1.
W początkowym zakresie pracy sprężystej jest ścieżka równowagi jest liniowa. Po przekroczeniu granicznego obciążenia sprężystego $M_{el}$ ścieżka równowagi przechodzi w nieliniowa,. Po osiągnięciu przez obciążenie granicznej wartości plastycznej $M_{pl}$ ścieżka równowagi jest bliska linii poziomej (rys.1a) lub staje się linią poziomą (rys. 1b), to znaczy bez dalszego przyrostu obciążenia następuje nieograniczony wzrost przemieszczenia.
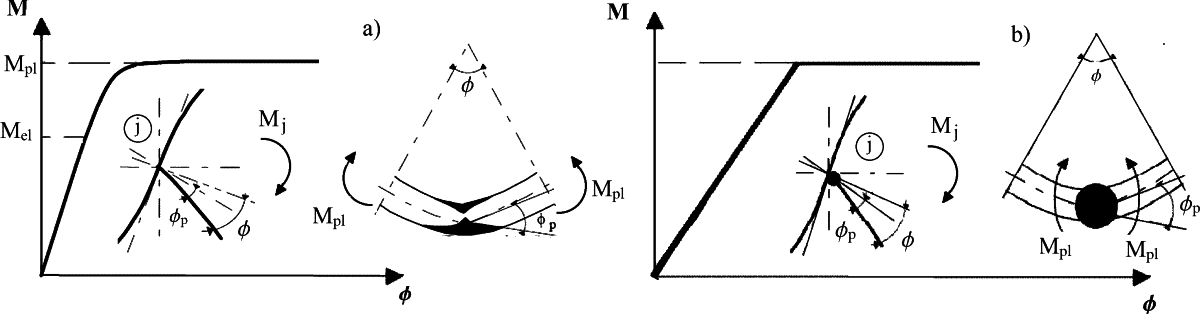
Rys. 3 Modele (M-Φ) sprężysto -plastyczne konstrukcji lub zginanego elementu (j) : a) z przegubem rozproszonym, b) z przegubem skupionym (opracowano na podstawie [6])
Po osiągnięciu przez przemieszczenie $\Phi$ granicznej wartości plastycznej $\Phi_p$ obciążenie $M$ utrzymuje się na stałym poziomie $M_{pl}$. To spostrzeżenie jest podstawą definicji przegubu plastycznego, symbolicznie przedstawionego zaczernionym kółkiem na rys. 1 b, to znaczy takiego przegubu w którym wartość siły przekrojowej jest stała, ale większa od zera i równa $M_{pl}$.
W przypadku konstrukcji żelbetowych definiuje się uogólniony przegub plastyczny w sposób pokazany na rys. 2. Przyjmuje się, że długość strefy uplastycznionej (rozproszonego przegubu) wynosi $1,2 h$, a kąt obrotu w przegubie (różnica kątów obrotu z lewej i prawej strony przegubu) wynosi $\Phi_p$.
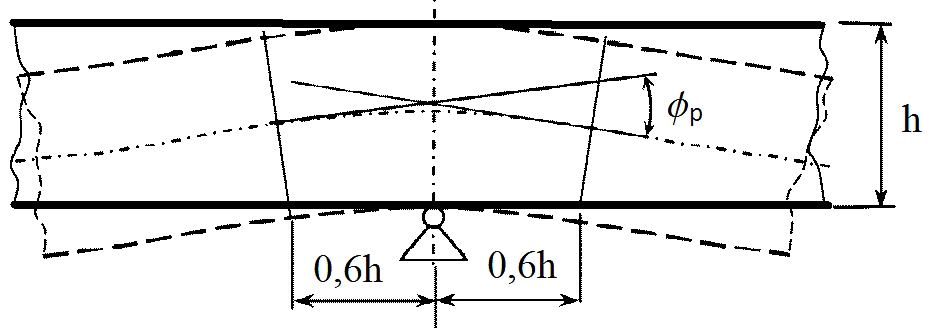
Rys. 4 Przegub plastyczny w belce lub płycie żelbetowej [7]
Przedstawiona powyżej definicja przegubu plastycznego skupionego w punkcie jest podstawą analizy sztywno-plastycznej, którą nazwiemy teorią plastyczności I rzędu i omówimy w pkt. model sztywno-plastyczny. Założenia upraszczające przyjmowane w teorii I rzędu są uzasadniane dokładniejszymi analizami teorii sprężysto-plastycznej, którą nazwiemy teorią plastyczności II rzędu i omówimy w analiza nieliniowa . W ramach teorii II rzędu analizuje sie kształt przegubów plastycznych – frontów plastycznych (pokazanych na rys. 1a) i wykazuje dopuszczalność uproszczenia przyjmowanego w teorii I rzędu o skupionych przegubach plastycznych (rys 1a), w modelu konstrukcji złożonej z prętów sprężysto-plastycznych z przegubami plastycznymi punktowymi (rys.1), przenoszącymi momenty przywęzłowe $ M_j$.
Analiza sztywno-plastyczna (I rzędu) jest klasycznie nazywana teorią nośności granicznej.np. [8], [1], a uzyskana zgodnie z tą teorią nośność konstrukcji była powszechnie nazywana nośnością graniczną. Tymczasem w świetle współczesnej nomenklatury nośność graniczna jest nośnością odpowiadającą stanowi granicznemu i jest zdefiniowana w normie [7] Wobec tego nośność graniczną wynikającą z analizy plastycznej będziemy nazywać nośnością plastyczną i oznaczać$\Lambda_{pl}$.
Mnożnik $\Lambda_{pl}$ obciążeń zewnętrznych, które wywołują choć w jednym przekroju belki statycznie wyznaczalnej moment zginający $M_{pl}$ nazywamy granicznym mnożnikiem plastycznym, a obciążenie granicznym obciążeniem plastycznym. W przypadku ustroju statycznie niewyznaczalnych pojęcie mnożnika plastycznego dotyczy przypadku, w którym liczba przekrojów, w których osiągnięty jest graniczny stan plastyczny jest tak, że powstałe przeguby plastyczne wystarczają do uruchomienia mechanizmu plastycznego W tym przypadku liczba przegubów jest większa od jednego i zwykle jest większa o 1 od stopnia statycznej niewyznaczalności ustroju.
Obciążeniem granicznym, jest mnożnik obciążenia $\Lambda_R$ odpowiadający maksimum na nieliniowej ścieżce równowagi, a przy innych obciążeniach stanowiących granicę stanu pracy przekroju, elementu lub konstrukcji zwykle pomijamy przymiotnik „graniczny”, a pozostawiamy opis efektu (np. „sprężyste”, „plastyczne”.
Analiza sprężysto-plastyczna (plastyczna II rzędu)
Przekrój belki sprężysto-plastycznej
Rozważmy przypadek prostego zginania, tzn. pręta obciążonego na końcach przeciwnie skierowanymi momentami zginającymi M, wykonanego z materiału idealnie sprężysto-plastycznego, którego model pokazano na rys. 3a). Taki model materiału nazywamy modelem idealnie spręzysto-plastycznym lub modelem Prandtla. Na rys. 3b pokazano model sprężysto-plastyczny ze wzmocnieniem, a na rys. 3c model sztywno-plastyczny ze wzmocnieniem
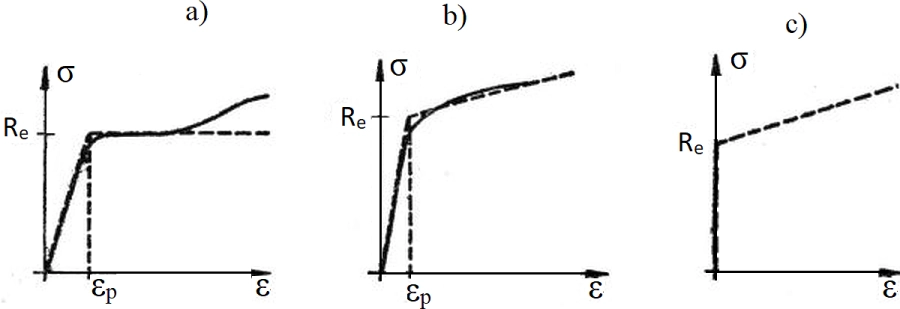
Rys. 5 Modele materiału sprężysto-plastycznego: a) idealnie sprężysto-plastyczny (Prandtla) , b) ze wzmocnieniem, c) sztywno-plastyczny ze wzmocnieniem; Re- granica sprężystości ; εp- odpowiadające odkształcenia plastyczne [9]
Można wykazać [8], że również przy plastycznym odkształceniu jednokierunkowym stan naprężenia jest możliwy tylko pod warunkiem spełnienia założenia płaskich przekrojów (założenia Bernoulliego), wyrażonego proporcją:
$$\begin {equation}\varepsilon_x= \cfrac {z} {\rho}\label{6} \end {equation}$$
gdzie: $\rho$ – promień krzywizny odkształconej osi belki, z – odległość włókna przekroju od osi obojętnej ($O_{el}$ lub $O_{pl}$). (rys. 4)
Rozkład naprężenia w przekroju sprężystym, przedstawiony na rys. 4a,b jest proporcjonalny do prostoliniowego rozkład odkształceń ($\ref{6}$), ponieważ naprężenia są związane z odkształceniami prawem fizycznym (w zakresie sprężystym prawem Hooke’a), które można zapisać w postaci :
$$\begin {equation} \sigma = E ( \varepsilon) \cdot \varepsilon \label{7} \end {equation}$$
gdzie E(ε) jest modułem odkształcenia, zależnym od wartości odkształcenia i prowadzącym w ogólności do nieliniowego rozkładu naprężenia na wysokości przekroju. Dla modelu materiału sprężysto-plastycznego ze wzmocnieniem (rys. 3b) mamy na przykład:
$$ \begin{equation} \begin {cases}
\sigma = E \cdot \varepsilon, & \text { dla } 0 < \varepsilon \le \varepsilon_p \\
\sigma – R_e = E’ \cdot ( \varepsilon – \varepsilon_p) & \text { dla } \varepsilon > \varepsilon_p \\
\end {cases} \label{8} \end{equation} $$
gdzie : E- moduł Younga; E’ współczynnik kątowy dla prostej wzmocnienia, a dla jednoosiowego rozciągania σ = σx, ε = εx,
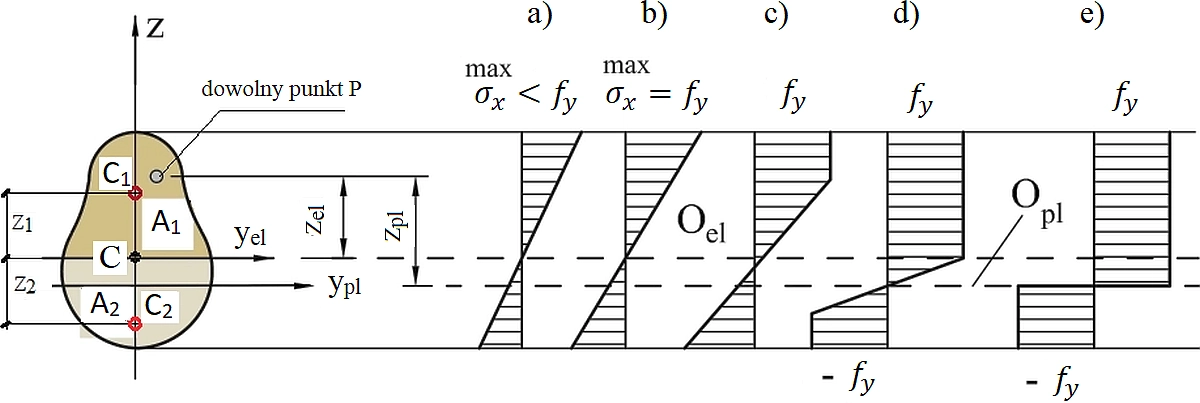
Przekroje belki, wykonanej z materiału o modelu ($\ref{7}$) podczas wzrostu obciążenia M (momentu zginającego) mogą pozostawać w stanach pokazanych na rys. 5:
a) sprężysty
b) graniczny sprężysty,
c) jednostronnie sprężysto-plastyczny,
d) dwustronnie sprężysto-plastyczny,
e) graniczny plastyczny.
Dla materiału sprężysto-plastycznego granica sprężystości $R_e$ jest równa granicy plastyczności $f_y$.
Osie obojętne sprężysta i plastyczna
Położenie osi obojętnej przekroju uplastycznionego $O_{pl}$ jest inne niż położenie sprężystej osi obojętnej $O_{el}$. Położenie osi obojętnych wyznaczymy z równań równoważności układów sił wewnętrznych i zewnętrznych:
$$ \begin{equation} \begin {cases}
N(x)=0=\iint \limits_A \sigma_x \, dA \\
M(x)= \iint \limits_A \sigma_x\cdot z \, dA
\end {cases} \label{9} \end{equation} $$
W przypadku różnych funkcji określających rozkłady naprężenia w strefie ściskanej ($z>0$) i rozciąganej $(Z<0)$ powodują, w ogólności oś obojętna nie pokrywa się z osią centralną (przechodzącą przez środek ciężkości).
Położenie osi obojętnej sprężystej
W przypadku rozkładu sprężystego (rys. 4a, b) położenie osi $O_{el}$ wyznaczymy z równań
$$ \begin{equation} \begin {cases}
0=\iint \limits _A E \cfrac {z_{el}} {\rho(x)} \, dA=\cfrac {E}{\rho(x)}\iint \limits_A z_{el} \, dA=\cfrac {E}{\rho(x)}\cdot S_{y,el} \\
M(x)=\iint \limits_A E \cfrac {z_{el}} {\rho(x)} \cdot z_{el} \, dA=\cfrac {E}{\rho(x)}\iint \limits_A z_{el}^2 \, dA
\end {cases} \label{10} \end{equation} $$
Z równania ($\ref{10})^1$ można określić położenie sprężystej osi obojętnej. Zauważmy że moment statyczny $S_{y,el}$ zeruje się, jeśli oś obojętna y jest osią ciężkości , czyli jest osią centralną. Z równania ($\ref{10})^2$, po przyjęciu definicji
$$\begin {equation} I_{y,el} = \iint \limits_A z_{el} ^2 \, dA \label{11} \end {equation}$$
otrzymamy fundamentalne związki zginania sprężystego:
$$\begin {equation}M(x)= \cfrac {E} {\rho(x)}\cdot I_{y,el} \text { , czyli } \cfrac {2} {\rho(x)} = \cfrac {M(x)}{EI_{y,el}}\label{12} \end {equation}$$
skąd
$$\begin {equation} \sigma_x= \cfrac {M(x)} {I_{y,el}} \cdot z_{el} \label{13} \end {equation}$$
Rozkład graniczny sprężysty (rys. 4b) wystąpi wówczas, gdy maksymalne naprężenia (w skrajnym najdalej oddalonym od osi obojętnej włóknie) osiągną granicę sprężystości $R_e$. W przypadku stali przyjmuje się, że granica sprężystści $R_e = f_y$ ( granica plastyczności). Stowarzyszony z takim rozkładem naprężenia moment zginający, nazywamy momentem sprężystym i oznaczamy przez $M_{el}$. Zgodnie z definicją ($\ref{12}$)
$$\begin {equation} max \ \sigma_x = f_y = \cfrac {M_{el}} {I_{y,el}}\cdot \max z_{el} = \cfrac {M_{el}} {W_{el}} \to M_{el} = f_y \cdot W_{el} \label{14} \end {equation}$$
Wartość $\Lambda_{el}$ mnożnika obciążeń zewnętrznych, wywołujących choć w jednym przekroju moment zginający $M_{el}$ nazywamy granicznym mnożnikiem sprężystym ( a obciążenie granicznym obciążeniem sprężystym).
Położenie osi obojętnej plastycznej
Dla granicznego plastycznego rozkładu naprężenia (rys. 4e) równania równości sum i momentów układów sił wewnętrznych i zewnętrznych przyjmują postać:
$$ \begin{equation} \begin {cases}
0=\iint \limits_{A_2} – f_y, dA +\iint \limits_{A_1} f_y \,dA \to A_1 = A_2 \\
M(x)=M_{pl} =\iint \limits_{A_2}( -f_y) \cdot z_{pl}, dA +\iint \limits_{A_1} f_y \cdot z_{pl} \,dA =\\
= \iint \limits_{A_2} (-f_y) z_{el}, dA +\iint \limits_{A_1} f_y \cdot z_{el} \,dA= \\
= f_y\cdot [ – S_{y} (A_2)+S_y (A_1)]=f_y \cdot [S_{y_{el}}(A_1) + S_{y_{el}}(A_1)]
\end {cases} \label{15} \end{equation} $$
Ponieważ oś $y_{el}$ jest osią centralną, więc $ – S_{y,el} (A_2) = S_{y,el} (A_1)$, czyli
$$\begin {equation} M_{pl} = S_y(A_1) – S_y (A_2) = 2 \cdot S_{y,el} (A_1)\label{16} \end {equation}$$
Przyjmując definicję
$$\begin {equation} W_{pl} = 2 \cdot S_{y,el} (A_1)\label{17} \end {equation}$$
mamy
$$\begin {equation} M_{pl}= f_y \cdot W_{pl} \label {18} \end {equation}$$
Przez analogię do stanu sprężystego charakterystykę ($\ref{17}$) nazwiemy plastycznym wskaźnikiem wytrzymałości przekroju., zaś moment ($\ref{18}$) granicznym momentem plastycznym.
Z warunku ($\ref{15})^1$ wynika, że plastyczna oś obojętna dzieli przekrój na dwie połowy $A_1 = A_2$, czyli części przekroju o powierzchni stanowiącej połowę całkowitej powierzchni.
Ponieważ oś $y_{el}$ jest osią centralną całego przekroju (przechodzącą przez środek ciężkości $C$ , więc moment statyczny przekroju względem tej osi jest zerowy $S_{yel}=0$. Oznacza to że także suma momentów statycznych części przekroju liczona względem osi centralnej jest zerowa:
$ \sum_i S_{i,el}= 0 \to A_1 \cdot z_1 – A_2 \cdot z_2 =0$
gdzie $z_1$ oraz $z_2$ są odległościami środka ciężkości $C_1$ części przekroju o powierzchni $A_1$ , oraz środka ciężkości $C_2$ części przekroju o powierzchni $A_2$ odpowiednio od środka ciężkości całego przekroju $C$.
Ponieważ $A_1=A_2 = \cfrac{A}{2}$, wiec z powyższego wynika, że dla dowolnego przekroju ( w tym niesymetrycznego) słuszna jest równość
$ y_1 = – y_2 , \to |y_1|=|y_2|$
gdzie $|y_1|$ i $|y_2|$ są o9dległościami środków ciężkości $\overline{C-C_1}$ i $\overline{C-C_2}$
Wskaźnik wytrzymałości plastycznej przekroju $W_{pl}$ jest podwojonym momentem statycznym względem osi sprężystej $y_{el}$ połowy przekroju, $A_1$ lub $A_2$. Formuła ($\ref{17}$) dotyczy zarówno przekrojów symetrycznych jak i niesymetrycznych, które są zginane względem jednej osi. W przypadku zginania względem dwóćh osi formuyły są odmienne i wyprowdzone w rozdziale
Front plastyczny
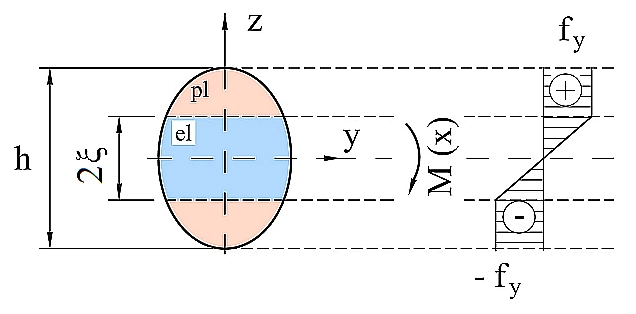
Front plastyczny w belce zginanej w zakresie sprężysto-plastycznym o bisymetrycznym przekroju, pokazanego na rys. 6 wyznaczymy z warunku równowagi momentów zginających. Z warunku zerowania siły osiowej , wynika, że oś obojętna w przypadku przekroju bisymetrycznego pokrywa się z osią centralną.
$$\begin {equation} M(x)=2 \left[ \iint \limits_{pl} \frac {Ez} {\rho(x)} z dA + \iint \limits_{el} f_y z dA \right] = 2 \cdot f_y \left[ \frac {2} {\xi} I_y^{pl}(\xi)+S_y^{el} (\xi)\right]\label{19} \end {equation}$$
Związek ($\ref{19}$) przedstawia zależność połowy wysokości ξ strefy uplastycznionej (rys.6) od wartości momentu zginającego zmiennego po długości belki M(x). Kształt frontu plastycznego zależy od rozkładu momentu zginającego na długości belki, a także od kształtu przekroju poprzecznego.
Dla najczęstszego przekroju dwuteowego i dla dwóch podstawowych przypadków obciążenia: obciążenia równomiernego oraz siłą skupioną belki swobodnie podpartej kształty frontu plastycznego pokazano na rys. 7. Na fragmentach u góry rysunku pokazano kształty frontów na etapie przejściowym przed osiągnieciem granicznego stanu plastycznego zobrazowanego na dolnych fragmentach ($\Lambda = \Lambda_{pl}$). .
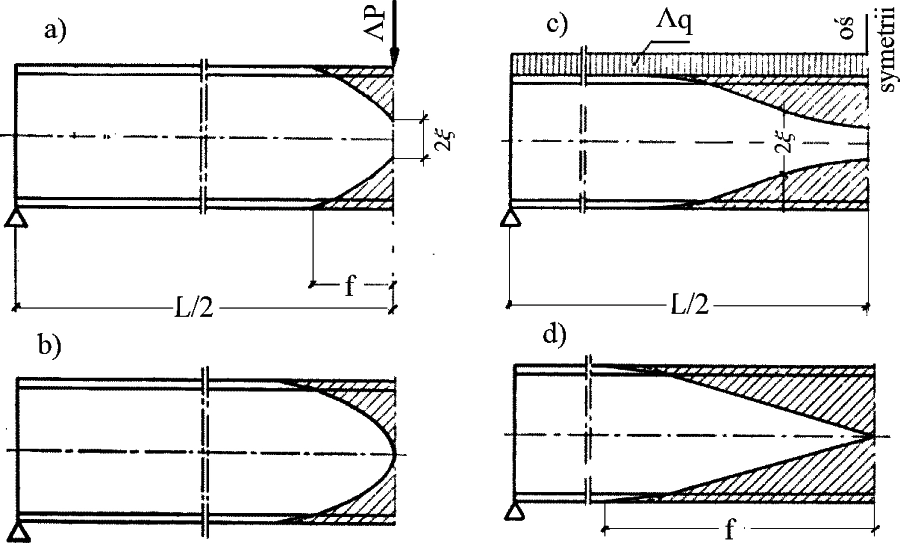
Rys 8 Kształty frontów plastycznych w belce dwuteowej pod obciążeniem: a) skupionym mniejszym od granicznego plastycznego, b) skupionym w stanie granicznym plastycznym, c) rozłożonym przed osiągnięciem granicznego stanu plastycznego, d) rozłożonym w stanie granicznym plastycznym [10]
Zasięg frontu plastycznego F= 2f w zależności od schematu wynosi [10]:
a) dla obciążenia skupionego (rys.7a)
$ f =L/2 \cdot (1-\frac {\Lambda M_{max}}{M_{pl}}) $
i w granicznym stanie plastycznym ma długość $ 2\cdot f=0,073 \cdot L$
Dla dwuteownika zachodzi $ \omega=W_{pl}/W_{el}=1,17$,
b) dla obciążenia rozłożonego (rys. 7b)
w granicznym stanie plastycznym $2\cdot f=0,190 L$ (dla $\omega =1,17$)
Z przykładu wynika, że zależnie od rodzaju obciążenia długości przegubu mogą różnić się nawet 3-krotnie.
Na rys. 8 oraz rys. 9 pokazano rzeczywiste kształty frontów plastycznych z badań eksperymentalnych opisanych w pracy [11]. Badania prowadzono dla belek o przekroju prostokątnym z użyciem elastooptyki (rys. 9) .
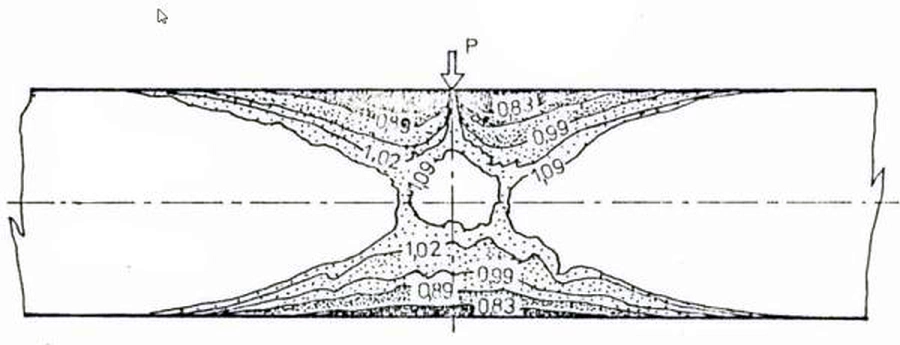
Rys.9 Rzeczywiste kształty frontu plastycznego w belce o przekroju prostokątnym [11]
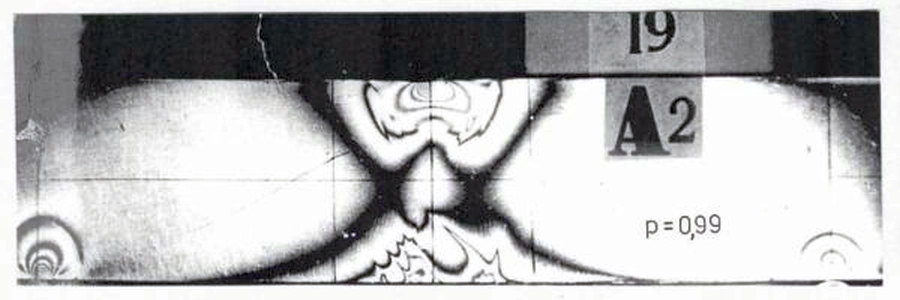
Rys.10 Obraz frontu plastycznego z badań belki H/L=4 o przekroju prostokątnym pod obciążeniem skupionym o wartości 99% teoretycznego granicznego obciążenia plastycznego [11]
Sprężysto-plastyczny model jest złożony i nie jest uniwersalny: kształt frontów plastycznych zależy od rodzaju (kształtu przekroju oraz od rozkładu sił przekrojowych na długości elementu. z tych powodów nie jest zbyt często stosowany w praktyce, ale jest podstawą sformułowania teorii nośności granicznej (modelu sztywno-plastycznego, czyli metody plastyczności I rzędu.
Proces formowania się przegubów plastycznych
W analizie sprężysto-plastycznej bada się propagację (rozrastania się) stref plastycznych w konstrukcji.
Fundamentalnym założeniem analiz jest hipoteza o sekwencyjnym (kolejnym) tworzeniu się przegubów plastycznych w konstrukcji, aż do momentu wyczerpania jej nośności plastycznej, czyli utworzenia się takiej liczby przegubów, które zmieniają układ w mechanizm plastyczny (konstrukcję geometrycznie zmienną o jednym stopniu swobody).
W pracy [11] pokazano jednak, że przeguby plastyczne tworzą się jednocześnie, jeśli tylko w procesie uplastyczniania uwzględnimy działanie sił poprzecznych (naprężenia styczne). Na rys. 9 zilustrowano proces formowania się przegubów plastycznych w belce dwuprzęsłowej, obciążonej siłami skupionymi (opis pod rysunkiem).
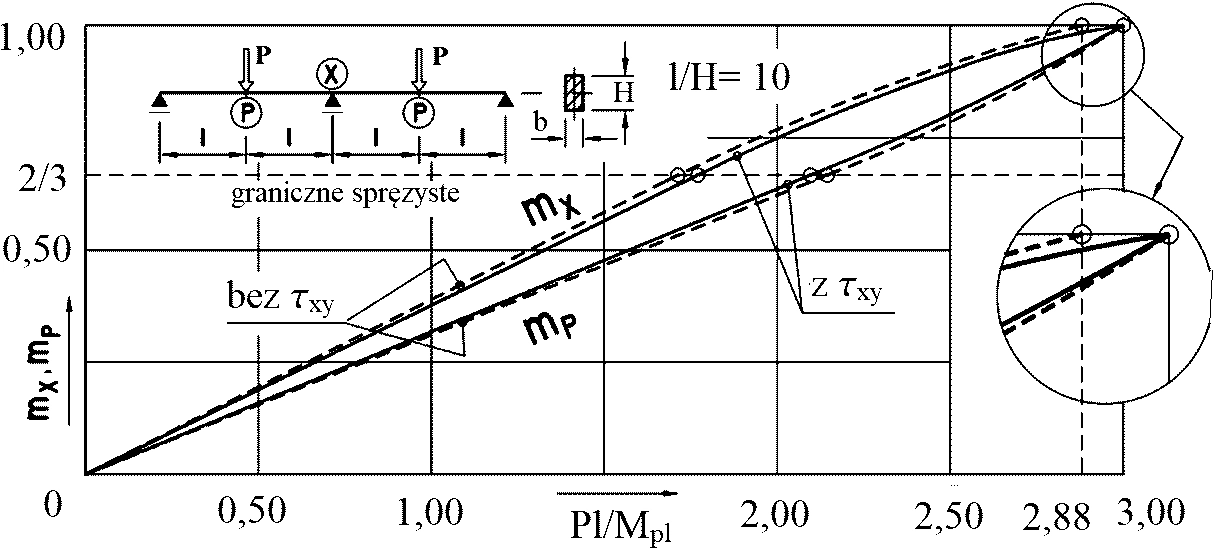
Rys.11 Proces formowania się przegubów plastycznych w belce dwuprzęsłowej l/h=10 o przekroju prostokątnym. Linia przerywana- tradycyjny proces z sekwencją tworzenia się przegubów: najpierw nad podporą X przy obciążeniu Pl/Mel=2,88, później w prześle przy obciążeniu Pl/Mel = 3,00; Linia ciągła – jednoczesność tworzenia się przegubów P i X po uwzględnieniu naprężenia stycznych τ . [11]
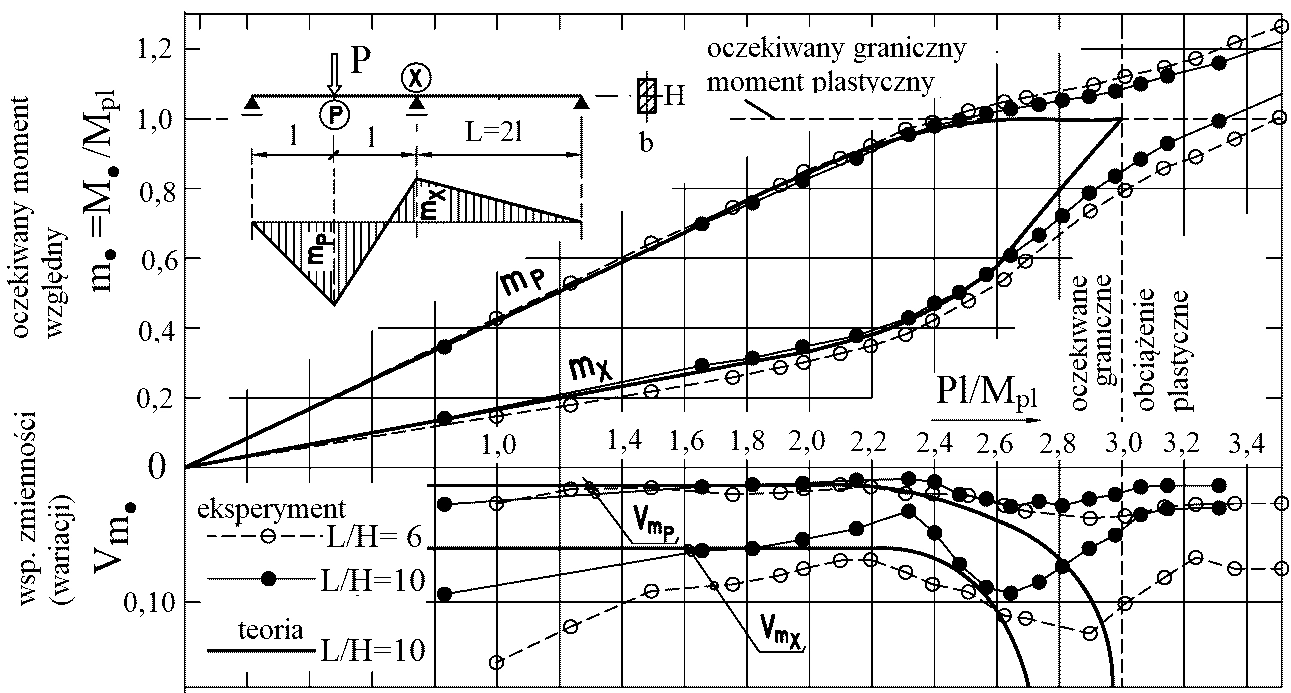
Rys.12 Porównanie teoretycznego procesu uplastyczniania belki z eksperymentem [11]
Na rys. 11 porównano teoretyczny proces tworzenia się przegubów plastycznych z uwzględnieniem naprężenia stycznych z wynikami badań doświadczalnych. Ze względu na wzmocnienie materiału rzeczywistego przeguby plastyczne tworzą się sekwencyjnie: najpierw nad podporą X, a później w przęśle. Teoretyczne spostrzeżenie jednoczesności tworzenia się przegubów plastycznych jest więc tylko teoretyczne i w świetle badań doświadczalnych nie podważa poprawności klasycznych analiz, a także rozważań prowadzonych w dalszej części niniejszego artykułu.
Przeguby plastyczne w praktyce. Graniczny kąt obrotu w przegubie plastycznym
Metody nieliniowe i metody oparte na teorii plastyczności w praktyce można stosować pod warunkiem, że kąty obrotu w przegubach plastycznych albo stopień redystrybucji momentów zginających zostaną utrzymane w przepisanych granicach.
Graniczny kat obrotu w przegubie plastycznym wyznacza się z analizy odkształceń odcinka otaczającego krytyczny przekrój. Stosując analizę sporęystą z ograniczoną redystrybucją lub analizę plastyczną należy sprawdzać, czy kąty obrotu nie przekraczają kątów granicznych.
Konstrukcje stalowe
W konstrukcjach sstalowych analizę dopuszczalności stosowania metod plastycznych określa sie poprzez badanie klasy przekroju w sposób przedstawiony w artykule klasa przekorju stalowego. Możliwość wykorzystania części zapasu nośności przekroju, wynikającego z pozasprężystego zachowania się elementu stalowego dotyczy przekrojów klasy 1 i częściowo klasy 2.
Nośnosć na zginanie $M_{Rd} =M_{pl}$ takich przkrojóe może być ustalona wg.($\ref{18}$), bo w konstrukcjach zbudowanych z prętów o przekrojach klasy 1 można zaakceptować uplastycznienie ustroju, czyli powstanie wielu przegubów plastycznych (w ustrojach statycznie niewyznaczalnych. W przypadku przekrojów klasy 2 jako dopuszczalne przyjmuje się uplastycznienie tylko jednego przekroju konstrukcji. Nie dopuszcza się stosowania metdo teorii plastyczności w przekrojach klasy 3 lub 4. Z tego wynika, że w celu optymalizacji konstrukcji statycznie niewyznaczalnych, powinno stosować się przekroju klasy 1, w których można w większym stopniu wykorzystać materiał wskutek redystrybucji momentów.
W obliczeniach statycznych elementów klasy 1. należy posłużyć się globalną analizą plastyczną. Można ją jednak stosować tylko wtedy, gdy konstrukcja w miejscach potencjalnych przegubów plastycznych ma wystarczającą zdolność do obrotu w elementach lub węzłach. Jeśli przegub plastyczny występuje w elemencie, to jego przekrój powinien być bisymetryczny lub monosymetryczny.
Wymagania konstrukcyjne dotyczące strefy przegubu plastycznego są sprecyzowane w pkt 5.6 normy [12] , a mianowicie: :
Można przyjąć, że przeguby plastyczne w elementach pełnościennych wykazują wystarczającą zdolność do obrotu, jeśli spełnione są obydwa poniższe warunki:
1) w miejscu przegubu plastycznego przekrój jest klasy 1;
2) w sytuacji, gdy siła skupiona w miejscu przegubu plastycznego przekracza 10 % nośności przekroju przy ścinaniu, środnik jest usztywniony żebrami w odległości nie większej niż h/2 od miejsca przegubu plastycznego, gdzie h – wysokość przekroju.
W przypadku projektowania plastycznego ram, ze względu na redystrybucję momentów, wymagania powyższe powinny być spełnione w każdym elemencie, w którym występują lub mogą wystąpić przeguby plastyczne w warunkach obciążeń obliczeniowych, ale w przypadku metod globalnej analizy plastycznej, które uwzględniają miarodajne rozkłady naprężeń i odkształceń w elementach oraz złożone skutki niestateczności, wymagania powyższe nie mają zastosowania.
W przypadku elementów o zmiennym przekroju powinny być spełnione warunki dodatkowe zgodnie z klauzulą 5.6 (3) normy [12], a w pobliżu przegubu plastycznego ewentualne przekroje z otworami na łączniki powinny spełniać warunek klauzuli klauzlą 5.6 (4) normy [12].
Jeśli przegub plastyczny występuje w strefie węzła, to jego odpowiednią zdolność do obrotu można zapewnić zgodnie z wymaganiami normy[13]. Można także wzmocnić węzeł tak, aby przegub powstał w przywęzłowym przekroju elementu.
W przypadku globalnej analizy sztywno-plastycznej zdolność do obrotu węzła w konstrukcji stalowej określa się zgodnie z klauzulą 6.4 [13], przy czym kryteria są różne w zależności od tego, czy węzeł jest śrubowy, czy spawany i są ograniczone do stali gatunków S235, S275 i S355 oraz do węzłów, w których obliczeniowa wartość siły podłużnej $N_{Ed}$ w dołączanym elemencie nie przekracza 5 % obliczeniowej plastycznej nośności $N_{pl,Rd}$ jego przekroju poprzecznego.
Można nie sprawdzać zdolności do obrotu węzła pod warunkiem, że obliczeniowa nośność przy zginaniu węzła $M_{Rd}$ jest co najmniej 1.2 razy większa od obliczeniowej nośności plastycznej przy zginaniu $M_{pl, Rd}$ przekroju poprzecznego dołączanego pręta. W przypadkach nieujętych w klauzuli 6.4 [13] zdolność do obrotu można wyznaczać eksperymentalnie zgodnie z procedurą podaną w Załączniku D do normy [14].
Konstrukcje żelbetowe [15]
Analiza sprężysta z ograniczoną redystrybucją (SOR)” i „analiza plastyczna (P)” dopuszczon e w normie [16] opierają się na wykorzystaniu idei przegubu plastycznego [15], rozdz. 12.3.
W uproszczeniu, kąt obrotu , który może powstać w przegubie plastycznym konstrukcji żelbetowej, zależy przede wszystkim od zasięgu strefy ściskanej. Jeżeli stopień zbrojenia w elemencie zginanym nie jest za duży, to osiągnięciu granicy sprężystości w zbrojeniu , towarzyszy zasięg strefy ściskanej mniejszy od $x_{lim}$ i odkształcenie skrajnych włókien ściskanych jest mniejsze od odkształcenia granicznego. Przy dalszym plastycznym przyroście odkształceń zbrojenia siłą w zbrojeniu pozostaje stałą, a zmiany momentu zginającego są znikome- można przyjmować, że moment pozostaje stały aż do wyczerpania nośności związanej z osiągnięciem granicznego odkształcenia betonu.
W dokładniejszej analizie zdolność do obrotu w przegubie plastycznym, trzeba rozpatrywać wpływ ciągliwości i wzmocnienia stali oraz rozkład odkształceń i naprężeń w pewnym otoczeniu krytycznego przekroju – rozpatrywanie zjawisk , które rozgrywają suę tylko w jednym przekroreju nie prowadzi do racjonalnych wniosków.
W normie [16] zakłada się, ze w uplastycznionych strefach płyt jednokierunkowo zbrojonych i belek występuje zdolność do obrotu (końcowych przekrojów względem siebie), a długość takiej strefy w przybliżeniu wynosi 1,2 wysokości przekroju (rys. 4). Jeżeli wykaże się, ze pod wpływem kombinacji obliczeniowej oddziaływań kąt obroty $\Phi$ nie przekroczy kąta obrotu plastycznego $\Phi_{pl,d}$, to można uważać, że wymagania ze względu na obrót plastyczny w stanie granicznym nośności są spełnione.
Kąt obrotu plastycznego (graniczny kąt obrotu) zależy względnej wysokości strefy ściskanej \xi=\cfrac{x_u}{d} ( $x_u$ wysokość strefy ściskanej w stanie granicznym, d- wysokość efektywna przekroju), od ciągliwości stali i od tak zwanej smukłości ścinania $\lambda =\cfrac{M_{Ed}}{V_{Ed} \cdot d}$. W normie [16] zamieszczono wykresy umożliwiające wyznaczenie granicznego kąta obrotu $\Theta_{pl,d} = \Phi_{pl,d}$, wyznaczone z analizy odkształceń odcinka otaczającego krytyczny przekrój.
Należy zwrócić uwagę, że w zagadnieniu ważną rolę odgrywa przyczepność zbrojenia do betonu i wpływ smukłości ścinania jako skutek zmian sił y w zbrojeniu podłużnym , które powstają w przypadku ukośnego zarysowania, podobnie jak przy ścinaniu.
Zamiast sprawdzania kątów obrotu można sprawdzić zastępcze kryteria, które w normie [16] zebrano w dwa zestawy:
- zestaw P (analiza plastyczna w podejściu statycznym)
Wymaganie dotyczącej ciągliwości w ramach i płytach można uznać za spełniony, gdy zachodzą trzy warunki:
* pole przekroju zbrojenia jest male na tyle, że w każdym przekroju poprzecznym $x_u / d \le o,15$ , gdy beton jest klasy wyższej niż C50/60 i $x_u / d \le o,25$ gdy beto jest klasy niższej
* stal zbrojeniowa jest klasy ciągliwości B lub C,
* stosunek momentów na podporach pośrednich do momentów w przęśle mieści się w granicach między 0,5 a 2,0. - zestaw SOR
Wymaganie dotyczącej ciągliwości w ramach i płytach można uznać za spełnione, gdy zachodzą dwa warunki (podajemy tylko dla ciągłych belek i płyt wykonanych z betonu zwykłej wytrzymałości $f_{ck} \le 500\,MPa$:
* są poddane w przeważającej mierze zginaniu,
* stosunek długości przylegających przęseł mieści się w przedziale 0,5 do 2,0
Redystrybucję momentów zginających można przeprowadzić bez jawnego sprawdzenia zdolności do obrotu w przegubach plastycznych pod warunkiem, że względna wyoskośc strefy ściskanej $\xi_u= x_u/d$ spełnia warunek
$\xi_u \le \cfrac{\delta – 0,44}{1,25}$,
gdzie $\delta$ jest stopniem redystrybucji momentu zginającego (stosunkiem momentu zginającego po redystrybucji do momentu obliczonego przy założeniu sprężystości)
i dodatkowo dla zbrojenia klasy B i klasy C $\delta \ge 0,7$. a dla zbrojenia klasy A $\delta \ge 0,8$.
Model sztywno-plastyczny (plastyczny I rzędu)
Istota modelu plastycznego I rzędu
Analiza sprężysto-plastyczna II rzędu (nieliniowa) operuje modelem konstrukcji ze skończonymi strefami uplastycznionymi. Poniżej wykażemy, że nośność plastyczna konstrukcji nie zależy od sprężystych właściwości materiału, w tym nie zależy od historii tworzenia się stref uplastycznionych i kształtów frontów plastycznych.
Do szacowania nośności plastycznej nie ma potrzeby analizy konstrukcji z materiału sprężysto-plastycznego. Nośność plastyczna
wystarczy założyć, że konstrukcja jest wykonana z materiału sztywno-plastycznego, a przeguby plastyczne są skoncentrowane (punktowe w prętach lub liniowe w płytach). W przypadku pręta model fizyczny przekroju sztywno-plastycznego w przestrzeni sił przekrojowych i stowarzyszonych przemieszczeń pokazano na rys. 12. Nośność plastyczna przekroju na rozciąganie i ściskanie oraz na zginanie wynosi
$$ \begin{equation} \begin {cases}
N_{pl,r}= f_{y,r} \cdot A, & \text { przy rozciąganiu} \\
N_{pl,c}= f_{y,c} \cdot A, & \text { przy ściskaniu} \\
M_{pl}= f_y \cdot W_{pl}, & \text { przy zginaniu} \\
\end {cases} \label{20} \end{equation} $$
gdzie: dla stali granica plastyczności przy rozciąganiu i ściskaniu jest taka sama: $f_{y,r} = f_{y,c} =f_y $, A-pole przekroju, $W_{pl}=2S_{y_el}$ – wskaźnik wytrzymałości plastycznej równy podwojonemu momentowi statycznemu połówki przekroju.
Interakcja plastyczna (przy współdziałąniu różnych prostych sił przekrojowych jest przedmiotem innych artykułów, np Interakcja plastyczna sily osiowej i dwuosiowego zginania.
W tab.1. podano wyrażenia na wskaźniki wytrzymałości plastycznej dla najczęściej stosowanych profili stalowych. W ostatniej kolumnie tabeli podano parametr $\omega\cfrac{W_{pl}}{W_{el}}$. Parametr ten wskazuje na stopień zwiększenia nośności przekroju plastycznego do nośności przekroju sprężystego. Określa on analizy plastycznej daje on stopień oszczędności, które przynosi prowadzenie analizy plastycznej zamiast sprężystej.
Tab.1 Wskaźniki wytrzymałości plastycznej i sprężystej przekroju [2]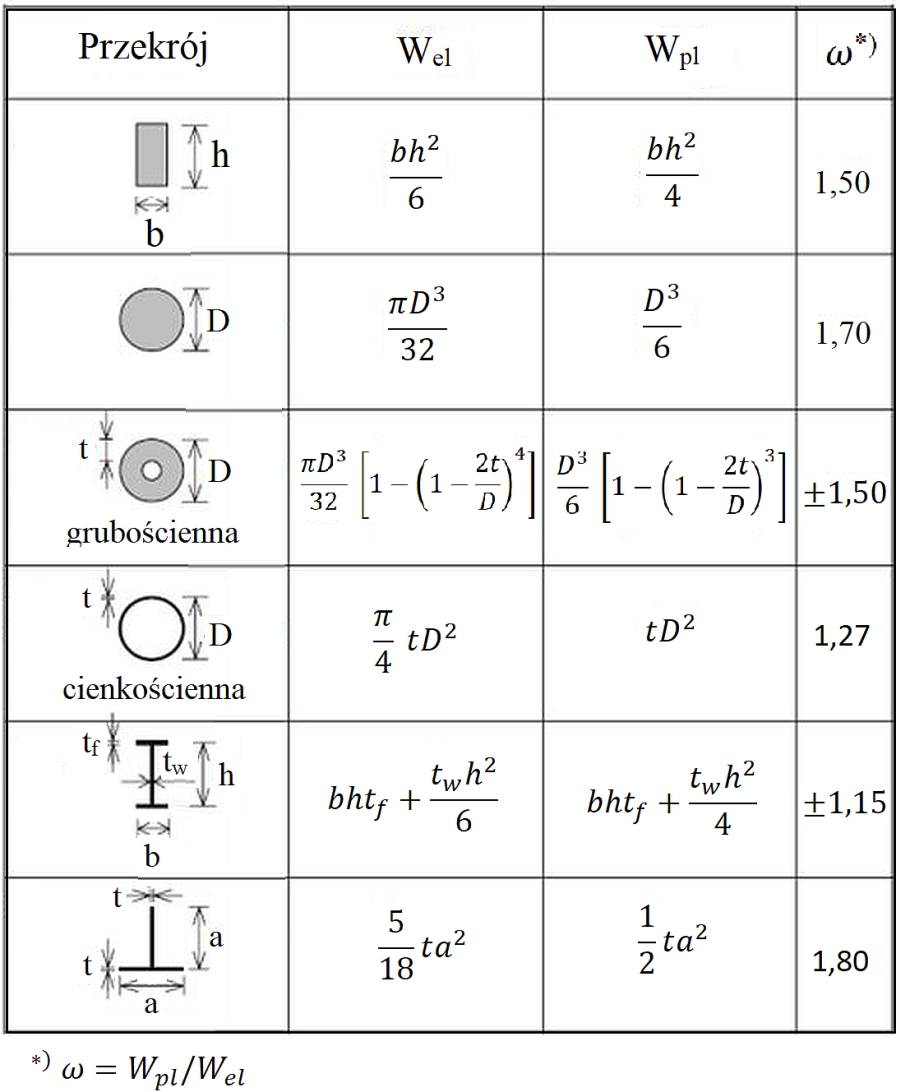 Kolejnym efektem prowadzonych analiz sztywno-plastycznych jest to, że na nośność nie wpływają samo-zrównoważone stany naprężenia od wpływu temperatury lub naprężenia resztkowe. Nośność plastyczna może zostać oszacowana od góry i od dołu na podstawie dwóch twierdzeń teorii nośności granicznej: twierdzenia kinematycznego i twierdzenia statycznego.
Kolejnym efektem prowadzonych analiz sztywno-plastycznych jest to, że na nośność nie wpływają samo-zrównoważone stany naprężenia od wpływu temperatury lub naprężenia resztkowe. Nośność plastyczna może zostać oszacowana od góry i od dołu na podstawie dwóch twierdzeń teorii nośności granicznej: twierdzenia kinematycznego i twierdzenia statycznego.
Twierdzenia ekstremalne teorii nośności plastycznej – ogólne sformułowanie
Mamy do dyspozycji dwa twierdzenia teorii nośności plastycznej:
- o oszacowaniu górnym (kinematyczne) (K),
- o oszacowaniu dolnym (statyczne) (S)
- Nośność rzeczywista zawarta jest pomiędzy oszacowaniem statycznym i kinematycznym. Jeśli oszacowanie kinematyczne będzie równe oszacowaniu statycznemu, to uzyskujemy oszacowani pełne, czyli faktyczną nośność plastyczną konstrukcji.
Umiejętne zastosowanie twierdzeń ekstremalnych, umożliwia określenie przedziału rozwiązania ścisłego, którego dokładna wartość często nie jest niezbędna a trudna do oszacowania innymi metodami.
Równanie prac wirtualnych dla ciał i ram sztywno-plastycznych
W ciałach sztywno-plastycznych odkształcenia plastyczne koncentruje się w pewnych obszarach, które w belkach zginanych nazywane są przegubami plastycznymi. Poza obszarami takiej lokalizacji odkształcenia są znacznie mniejsze. Można z wystarczającym przybliżeniem przyjąć, że konstrukcja rzeczywista posiada szereg obszarów nieodkształconych, doznających ruchu jako ciała sztywne. Taka konstrukcja jest łańcuchem ciał sztywnych, połączonych obszarami plastycznymi (przegubami lub załomami), a jej ruch możliwy jest po takim ułożeniu się brył stycznych, że zostanie utworzony mechanizm.
Fundamentalnym twierdzeniem mechaniki konstrukcji jest twierdzenie prac wirtualnych, słuszne zarówno dla ciał sprężystych jak i niesprężystych, ponieważ przy jego wyprowadzeniu nie korzysta się ze związków fizycznych. Twierdzenie prac wirtualnych w ogólnym przypadku brzmi :
Wirtualna praca $\delta L$ sił zewnętrznych $ q_{v}$, przyłożonych na powierzchni $A_u$ ciała, (na tej części powierzchni, na której są zadane kinematyczne warunki brzegowe – więzi zenęrtzne) wykonywana na przemieszczeniach wirtualnych $\delta u$ jest równa wirtualnej pracy $\delta W$ sił wewnętrznych $\sigma $ na wirtualnych odkształceniach $ \delta \varepsilon$:
$$ \begin{equation} \delta L = \iiint \limits_V \sigma \cdot \delta\varepsilon \, dV= \delta W= \iint \limits_{A_u}q_v\cdot \delta u \, dA \label{21} \end{equation} $$
gdzie $\delta$ jest symbolem przyrostu wirtualnego.
W przypadku ciała sztywno-plastycznego odkształcenia wewnętrzne koncentrują się w skończonej liczbie n- obszarów plastycznych, a poza nimi są zerowe, więc:
$$ \begin{equation} \delta W = \sum \limits_{k=1}^n M_k \cdot \, \eta_k dA \label{22} \end{equation} $$
gdzie k=(1…n) jest numerem obszaru plastycznego , $M_k$ siłą wewnętrzną działającą w obszarze k ( w tym przypadku moment zginający), a $\eta_k$ – przemieszczeniem stowarzyszonym z siłą przekrojową $M_k$( w przyapdku zginania kątem obrotu $\varphi$ w przegubie).
W ustroju ramowym, obciążonym siłami skupionymi, pokazanym na rys.13a i wykonanym z materiału sztywno-plastycznego – odkształcenia plastyczne koncentrują się w przegubach plastycznych oznaczonych zaczernionymi kółkami. Na rys. 13c w powiększeniu pokazano przegub plastyczny pod siłą skupioną P1 . W przegubie działają momenty zginające M, wywołujące kąt obrotu Φ. Moment zginający w przegubie plastycznym wynosi $M= M_{pl} $. Konfiguracja obciążenia (Pi, Pi+1) (i=1, m) wzrasta proporcjonalnie do mnożnika $\Lambda$.
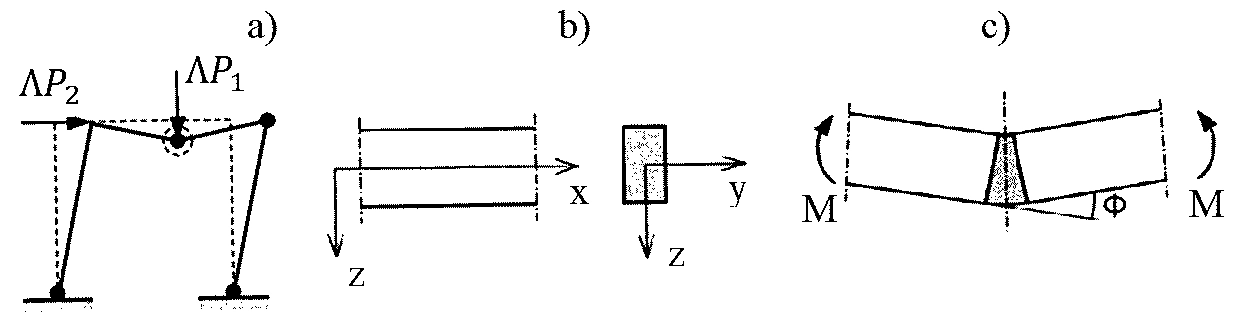
Rys.13. Moment i obrót w przegubie plastycznym: a) rama obciążona siłami P=[P1,P2] z mnożnikiem $\Lambda $, b) przekrój rygla ramy, c) przegub plastyczny w ryglu, wywołany zginaniem momentem M i stowarzyszony z nim kąt obrotu w przegubie plastycznym Φ.
W granicznym stanie plastycznym obciążenie $\Lambda P$ ukształtuje tyle przegubów plastycznych, ile jest wymaganych do przekształcenia konstrukcji w mechanizm. W tym stanie granicznym (plastycznym) równanie prac wirtualnych ($\ref{21}$) można zapisać w postaci ($\ref{23}$):
$$ \begin{equation} \delta L = \sum \limits_{k=1} \limits^n M_{pl,k} \cdot \delta \Phi_k = \delta W =\Lambda \sum \limits_{i=1} \limits^m P_i \cdot \delta u_i \label{23} \end{equation} $$
Sumowanie rozciąga się po wszystkich n-przegubach plastycznych i m-obciążeniach.
Znak wariacji $\delta$ można wyciągnąć przed znak całki i w konsekwencji pominąć. Wówczas równanie prac wirtulanych ($\ref{23}$) staje się bilansem prac $L=W$:
$$ \begin{equation} L = \sum \limits_{k=1} \limits^n M_{pl,k} \cdot \Phi_k = W =\Lambda \sum \limits_{i=1} \limits^m P_i \cdot u_i\label{24} \end{equation} $$
Dla znanych momentów w przegubach (równych $M_{pl}$ w granicznym stanie plastycznym przekroju ) i po założeniu pola przemieszczeń $(u, \Phi)$ z równania mechanizmu, z ($\ref{24}$) możemy wyznaczyć mnożnik obciążenia $\Lambda$.
Poniżej pokażemy, że :
- ze wszystkich mechanizmów „K,i” , spełniających kinematyczne warunki brzegowe – rzeczywistym może być mnożnik $\Lambda_K = min \, \Lambda_{K,i}$ , minimalny dla wszystkich mechanizmów”K,i”,
- ze wszystkich schematów „S,j”, spełniających statyczne warunki brzegowe – rzeczywistym może być mnożnik $ \Lambda_S = max \, \Lambda_{S,j} $,maksymalny dla wszystkich schmatów „S,j”,
- rzczywisty, plastyczny mnożnik obciązeń $\Lambda_{pl}$ uzykuje się tylko wówczas wskażnik statyczny i kinematyczny są równe: $\Lambda_S = \Lambda_K$
Twierdzenie kinematyczne K (o górnym oszacowaniu)
Twierdzenie K
| Konstrukcja zamienia się w mechanizm (ulega zniszczeniu), jeżeli dla kinematycznie dopuszczalnego pola przemieszczeń przyrost pracy sił zewnętrznych równy jest przyrostowi pracy sił wewnętrznych | (TK1) |
Oznacza to, że jeżeli dla zrównoważenia istniejącego obciążenia potrzebna jest zamiana konstrukcji w mechanizm, to obciążenie to jest nie mniejsze od granicznego (niszczącego). Obciążenie powodujące powstanie mechanizmu jest więc oszacowaniem od góry.
Twierdzenie K może być również sformułowane następująco:
| Dla dowolnego mechanizmu zniszczenia, obciążenia wynikające z odpowiednich równań równowagi stanowią górną wartość nośności plastycznej | (TK2) |
Mechanizm plastyczny jest to możliwy mechanizm, uruchomiony przy ograniczeniach zadanymi podporami po umieszczeniu w dowolnym miejscu konstrukcji obszarów plastycznych, tj przegubów plastycznych w przypadku prętów, załomów plastycznych w przypadku płyt i tarcz lub obszarów plastycznych w przypadku brył. Wybór lokalizacji oraz liczby obszarów plastycznych jest dowolny, czyli możliwych mechanizmów plastycznych jest nieskończenie wiele. Dla każdego uzyskamy inną wartość oszacowania nośności. Każda jednak będzie większa od nośności rzeczywistej. Spośród wielu oszacowań kinematycznych, najmniejsze z nich będzie najbliższe rzeczywistej nośności. Odpowiadający mechanizm zniszczenia będzie najbliższy rzeczywistemu mechanizmowi. Po to, by uzyskać najlepsze oszacowanie, należy starać się dobrać najbardziej prawdopodobny mechanizm zniszczenia plastycznego.
Dowód twierdzenia K podano niżej.
Równanie równowagi wspomniane w sformułowaniu (2D) twierdzenia kinematycznego formułuje się z zasady prac wirtualnych: Wirtualna praca sił zewnętrznych wykonywana na przemieszczeniach wirtualnych po uruchomieniu mechanizmu jest równa wirtualnej pracy sił przekrojowych na stowarzyszonych przemieszczeniach węzłowych.
Możliwe są dwa sposoby otrzymania końcowego schematu zniszczenia konstrukcji. Pierwszy sposób polega na wprowadzaniu kolejnych obszarów lokalizacji odkształceń (przegubów) aż do zamiany konstrukcji w mechanizm. Drugi – polega na przyjęciu obszarów lokalizacji odkształceń od razu w takiej ilości, która powoduje zamianę konstrukcji na mechanizm.
Twierdzenie statyczne S (o dolnym oszacowaniu)
Twierdzenie S
| Konstrukcja nie ulegnie zniszczeniu jeżeli dla zadanego obciążenia może być znalezione statycznie dopuszczalne pole naprężenia. | (TS1) |
Oznacza to, że jeżeli dla zadanego obciążenia można znaleźć równoważące je naprężenia, będące statycznie dopuszczalnymi, to konstrukcja znajduje się w zakresie bezpiecznej pracy, bądź co najwyżej na jego brzegu. Przeniesienie obciążenia nie implikuje przekroczenia dopuszczalnych wartości naprężenia — nośność konstrukcji jest nie mniejsza od takiego obciążenia. Jest to więc oszacowanie od dołu.
Twierdzenie S może być również sformułowane następująco:
| Dowolny, statycznie dopuszczalny stan naprężenia (nigdzie warunek plastyczności nie jest naruszony), który jest w równowadze z obciążeniem zewnętrznym zapewnia dolną granicę oszacowania nośności plastycznej | (TS2) |
Dolne oszacowanie nośności plastycznej można znaleźć dość łatwo, zważając, że:
- Dowolne, klasyczne, sprężyste rozwiązanie zapewnia dolne oszacowanie nośności plastycznej .
- Zaletą tego oszacowania jest to, że zawsze jest na bezpiecznej stronie. Jednakże wyprowadzenie takiego rozwiązanie to może być bardzo nieekonomiczne.
- Zdarza się, że poszukiwanie najlepszych dolnego oszacowania może być dokonane analitycznie lub numerycznie w jednym przebiegu, ale w większości przypadków powinna być stosowana metoda prób i błędów lub optymalizacja matematyczna.
Dowód twierdzenia S podano niżej.
Dowód twierdzeń ekstremalnych
Dowód przeprowadzimy dla pryzmatycznej prostej belki , obciążonej wyłącznie siłami skupionymi $P_i $.
Dowód twierdzenia kinematycznego K (o górnej granicy)
Przyjmijmy, że rzeczywisty mechanizm zniszczenia jest znany i realizuje się w polu przemieszczeń $u_i$ pod siłami skupionymi $P_i$ przy obrotach $\Phi_k$ w przegubach plastycznych k-tych. Rzeczywisty mnożnik obciążenia $\Lambda_{pl}$ dla nośności plastycznej może być wyznaczony z równania prac wirtualnych ($\ref{23}$), które możemy zapisać w postaci:
$$ \begin{equation} \Lambda_{pl} \sum P_i\cdot u_i=\sum M_k \cdot \Phi_k \label{25} \end{equation} $$
Wartości $M_k$ są nośnościami plastycznymi (pełnymi momentami plastycznymi) przekroju k-tego ($M_k=M_{pl,k}$) ze znakiem wynikającym ze znaku obrotu $\Phi_k$.
Arbitrarnie przyjmijmy dowolny kinematycznie dopuszczalny mechanizm zniszczenia (tzn. spełniający kinematyczne warunki brzegowe) z polem przemieszczeń $\overline u_i$ i obrotami przekrojów plastycznych $\overline \Phi_k$. Przyjęte pole przemieszczeń realizuje się przy mnożniku obciążeń $\Lambda_K$, który może być wyznaczony z równania prac wirtualnych:
$$ \begin{equation} \Lambda_K \sum P_ i\cdot \overline u_i=\sum \overline M_k \cdot \overline \Phi_k \label{26} \end{equation} $$
Wartości $\overline M_k$ są nośnościami plastycznymi przekroju k-tego $\overline (M_k= \overline M_{pl,k}$), w przegubie k-tym ze znakiem stosownie do znaku obrotu $ \overline\Phi_k$.
Ponieważ rzeczywiste rozwiązanie ($\Lambda_{pl}, M_k$) spełnia warunki równowagi, to spełnia również równanie prac wirtualnych odpowiadajace arbitralnie przyjętemu mechanizmowi realizującemu się w polu ($\overline u_i, \overline \Phi_k$). Stąd otrzymujemy:
$$ \begin{equation} \Lambda_{pl} \sum P_i\cdot \overline u_i=\sum M_k \cdot \overline \Phi_k \label{27} \end{equation} $$
Ponieważ praca $ \sum P_i \overline u_i$ w obu równaniach ($\ref{25}$) i ($\ref{26}$) jest taka sama, więc mamy:
$$ \begin{equation} \cfrac { \sum M_k \overline \Phi_k} {\Lambda_{pl}} = \cfrac { \sum \overline M_k \overline \Phi_k} { \Lambda_K} \label{28} \end{equation} $$
Ponieważ
$$ \begin{equation} \sum \overline M_k \overline \Phi_k \ge \sum M_k \overline \Phi \label{29} \end{equation} $$
więc
$$ \begin{equation} \Lambda_K \ge \Lambda_{pl}\label{30} \end{equation} $$
c.b.d.u.
Nierówność ($\ref{26}$) oczywiście zachodzi. W dowolnym przegubie k-tym obrót wirtualny $\overline \Phi_k> 0$, więc $\overline M_k=M_{pl,k}\ge M_k$ i nierówność jest prawdziwa. Jeśli $\overline \Phi_k<0$, to $\overline M_k= – M_{pl,k}\le M_k$ i nierówność też jest prawdziwa. Ponadto, jeśli nierówność jest prawdziwa dla dowolnego przegubu, to jest również prawdziwa dla sumy po przegubach.
Dowód twierdzenia statycznego S (o dolnej granicy)
Przyjmijmy, że rzeczywisty mechanizm plastyczny jest dany przez pole przemieszczeń $u_i$ i obroty $\Phi_k$ w przegubach plastycznych. Wówczas rzeczywisty mnożnik nośności plastycznej $\Lambda_{pl}$ może być wyznaczony z równania ($\ref{23}$) lub ($\ref{24}$).
Przyjmijmy teraz dowolne pole sił $\overline M$, które jest w równowadze z obciążeniem $\Lambda_S \cdot F$ i spełnia warunki plastyczności. Ponieważ równania równowagi są spełnione, to praca wirtualna dla rzeczywistego mechanizmu zniszczenia też jest spełniona:
$$ \begin{equation} \Lambda_{pl} \sum P_i \cdot u_i =\sum M_k \cdot \Phi_k \label{31} \end{equation} $$
$M_k$ jest momentem plastycznym $M_{k,pl}$ ze znakiem odpowiadającym znakowi obrotu $\Phi_k$.
Przyjmijmy arbitralnie, dowolny mechanizm z polem przemieszczeń $ \overline u_i$ i plastycznym obrotami $ \overline \Phi_k $. Przyjęte pole przemieszczeń daje mnożnik obciążenie $\Lambda_S$:
$$ \begin{equation} \Lambda_S \cdot \sum P_i\cdot \overline u_i=\sum M_k \cdot \overline \Phi_k \label{32} \end{equation} $$
Ponieważ praca $ \sum P_i \overline u_i$ w obu równaniach ($\ref{31}$) i ($\ref{32}$) jest taka sama, więc mamy:
$$ \begin{equation} \cfrac {\sum M_k \Phi_k} {\Lambda_{pl}}= \cfrac { \sum \overline M_k \Phi_k } {\Lambda_S} \label{33} \end{equation} $$
Ze związku
$$ \begin{equation} \sum \overline M_k \Phi_k \le \sum M_k \Phi_k \label{34} \end{equation} $$
wynika
$$ \begin{equation} \Lambda_S \le \Lambda_{pl}\label{35} \end{equation} $$
c.b.d.u.
Interakcja plastyczna siły osiowej i zginania
Interakcja plastyczna przy wytężeniu przekroju jednocześnie kilkoma siłami przekrojowymi jest podstawowym problemem mechaniki konstrukcji. Z problemem wyznaczenia wysokości strefy ściskanej oraz położeniem osi obojętnej w granicznym stanie plastycznym przekrojów obciążonych jednoczesnym ściskaniem i dwukierunkowym zginaniem spotykamy się już przy wyznaczeniu klasy przekroju stalowego.
Przedstawimy rozwiązania wynikające z podejścia statycznego do zadania teorii nośności granicznej (plastycznej), to znaczy uzyskane rozwiązania stanowią oszacowania rozwiązania od góry, ale są wystarczająco dokładne w praktyce inżynierskiej. W pracy [17] zaprezentowano oszacowania od dołu, wynikające z podejścia kinematycznego. Na wielu przykładach wykazano, że z podejścia statycznego najczęściej uzyskuje się rozwiązanie identyczne do rozwiązań kinematycznych, a w skrajnych przypadkach różniące się o max 1%.
Praktycznie ważny jest problem interakcji plastycznej w przekroju dwuteowym, który rozwiążemy po wstępnym przeanalizowaniu elementarnego przekroju prostokątnego.
Elementarny przekrój prostokątny
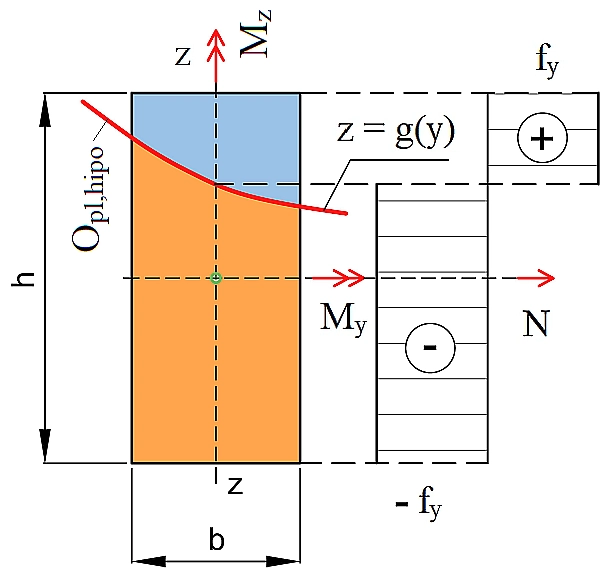
Na rys.14 pokazano przekrój prostokątny z założoną, hipotetyczną osią obojętną o równaniu z=g(y). Oś obojętna oddziela część rozciąganą przekroju (+)) od części ściskanej (-).
Rys. 14 Hipotetyczna oś obojętna g(y) przekroju prostokątnego hxb w stanie plastycznym. fy – granica plastyczności
Załóżmy, że na przekrój działa siła osiowa N oraz momenty zginające $M_y$ oraz$M_z$. Siły przekrojowe są znakowane zgodnie z zasadami mechaniki, więc są dodatnie jeśli ich wektory działają zgodnie ze zwrotem osi współrzędnych. W praktyce oznacza to, że są dodatnie, jeśli wywołują naprężenia rozciągające w pierwszym kwadrancie układu współrzędnych (y-z). Zwracamy uwagę, że w EC3 [3], przyjęto, że dodatnie są naprężenia ściskające, a nie rozciągające.
Założona na rys.14. bryła naprężeń daje następujące siły przekrojowe [18]:
$$ \begin{equation} N=- \int \limits_{-b/2}^{+b/2} 2 \cdot f_y \cdot g(y) \, dy\label{36} \quad ; \quad M_y= \int \limits_{-b/2}^{+b/2} [ \cfrac {h^2} {4}-g^2(y)] \cdot f_y \, dy \quad ; \quad M_z= \int \limits_{-b/2}^{+b/2} 2 \cdot f_y \cdot y\,\cdot g(y) \, dy \end{equation} $$
Założony stan równowagi przekroju spełnia warunki twierdzenia statycznego nośności granicznej o dolnym oszcowaniu: zadość czyni warunkom równowagi oraz nie narusza warunku plastyczności.
Twierdzenie dolnej granicy analizy granicznej stwierdza, że obciążenie obliczone na podstawie założonego stanu równowagi rozkładu naprężenia, które nie narusza warunku plastyczności, będzie mniejsze lub w najlepszym razie równe rzeczywistemu obciążeniu granicznemu lub obciążeniu niszczącemu. Rozkład naprężenia , pokazany na rys. 14 spełnia warunek plastyczności i równowagę sił przekroju prostokątnego. Powyżej hipotetycznie założonej osi obojętnej o równaniu $z=g(y)$ występuje proste rozciąganie (+), a poniżej proste ściskanie (-)
Problem poszukiwania osi obojętnej funkcji g(y), rozwiążemy w taki sposób, że znajdziemy maksymalną wartość $M_y$ możliwą przy ustalonych pozostałych siłach przekrojowych: N, $M_z$.poprzez poszukiwanie punktu stacjonarnego (ekstremum) funkcjonału
$ \int F \, dA$,
gdzie funkcjonał F ma postać :
$$ \begin{equation} F = 2 \cdot f_y \cdot \left [ 1/2 \cdot \left (\cfrac {h^2} {4}-g^2(y) \right ) – \lambda_1 \cdot y \cdot g(y)-\lambda_2 \cdot g(y)\right] \label{37} \end{equation} $$
$\lambda_1$ i $\lambda_2$ są z mnożnikami Lagrange’a, które są poszukiwanymi zadania.
Równanie Eulera stowarzyszone z funkcjonałem $\int F dA$ można zapisać w postaci
$$ \begin{equation} \cfrac{\partial F}{\partial g(y)}- \cfrac{d}{dy} \cdot \cfrac {\partial F} {\partial g^{’}(y)} =0 \label{38} \end{equation} $$
skąd wynika:
$$ \begin{equation} g(y)= – \lambda_1 \cdot y- \lambda_2 \label{39} \end{equation} $$
czyli oś obojętna w prostokącie jest linią prostą ze
współczynnikiem kierunkowym $\lambda_1 = tg\alpha$, gdzie $\alpha$ jest kątem nachylenia osi obojętnej do osi głównej y-y oraz
współczynnikiem translacyjnym $\lambda_2 = z_N $, który jest przesunięciem osi obojętnej przekroju w stosunku do osi y-y.
Po wykonaniu przypisanych całkowań siły przekrojowe można zapisać w postaci:
$$ \begin{equation} N = 2 \cdot f_y \cdot b \cdot \lambda_2 \label{40} \end{equation} $$
$$ \begin{equation} M_y = 2 \cdot f_y \cdot \left [ \cfrac {bh^2} {8}- \cfrac {\lambda_1^2}{3} \cdot \left (\cfrac {b}{2} \right)^3- \lambda_2^2 \cdot \cfrac{b}{2}\right ] \label{41} \end{equation} $$
Po wyeliminowaniu z tych równań mnożników λ1 i λ2, otrzymamy proste równanie interakcji sił przekrojowych:
$$ \begin{equation} n^2 + m_y + \cfrac {3}{4}m_z^2=1 \label{42} \end{equation} $$
ważne dla:
$$ \begin{equation} m_z \le \cfrac {2}{3}(1-n) \le m_y \label{43} \end{equation} $$
gdzie względne siły przekrojowe i nośności plastyczne i charakterystyki geometryczne przekroju prostokątnego wynoszą:
$n= N/N_{pl}$, $m_y= M_y/M_{y,pl}$, $m_z= M_z /M_{z.pl}$,
$N_{pl}= A \cdot f_y$, $M_{y,pl}=W_{y.pl}\cdot f_y $, $M_{z,pl}= W_{z,pl} \cdot f_y$ ;
$A=b \cdot h $, $W_{y.pl}= \cfrac {b \cdot h^2}{4} $, $W_{z.pl}= \cfrac{h\cdot b^2}{4} $
Przy znajomości sił przekrojowych z powyższych równań możemy wyznaczyć mnożniki Lagrange’a:
$$ \begin{equation} \lambda_1 = (tg\alpha )= \cfrac { 6 M_z} {f_y \cdot b^3} \quad ; \quad \lambda_2=(z_N)= \cfrac {N} {2 \cdot f_y \cdot b} \label {44} \end{equation} $$
co pozwala wyznaczyć położenie osi obojętnej.
W zależności od wzajemnych stosunków sił przekrojowych można ustalić, zestawione w tab.2. sytuacje o różnym układzie osi obojętnej oraz różnych równaniach interakcji.
Tab.2. Położenie osi obojętnej i krzywe interakcji n-my-mz dla przekroju prostokątnego
Przekrój dwuteowy
Postępując podobnie jak w przypadku przekroju prostokątnego można pokazać, że hipotetycznie założona oś obojętna g(y) musi być linią prostą (rys. 156b).
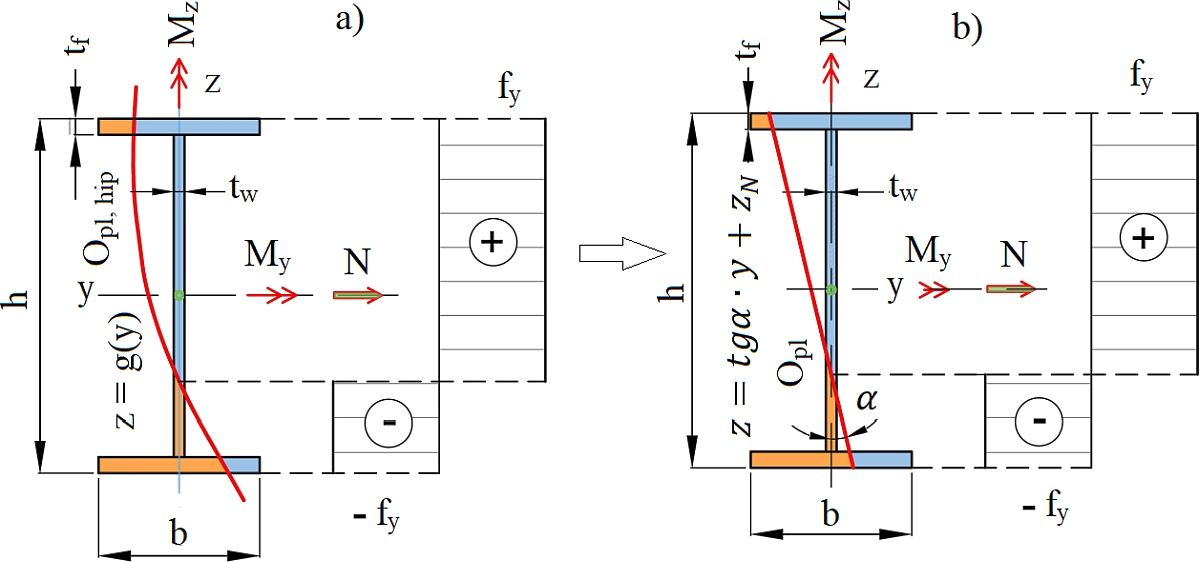
Rys.15 Plastyczna oś obojętna przekroju dwuteowego zginanego mimośrodowo i ukośnie : a) hipotetyczna, b) dopuszczalna linia prosta
Równanie możliwej plastycznej osi obojętnej można zapisać w postaci.
$$ \begin{equation} z = g(x) = – \cfrac {y}{\lambda_3} – z_N \label{46} \end{equation} $$
gdzie
$$ \begin{equation} z_N= \cfrac {\lambda_4} {\lambda_3} \label{47} \end{equation} $$
Mnożniki Lagrange’a zależą od relacji wartości sił przekrojowych. Siły te można zapisać w postaci:
$$ \begin{equation} N = f_y \cdot z_N \cdot [ 4\cdot t_f\cdot\lambda_3 +2\cdot t_w] \label{48} \end{equation} $$
$$ \begin{equation} M_y = \cfrac {4} {3} \cdot f_y \cdot [(h/2)^3-(h/2-t_f)^3] \cdot \lambda_3+f_y \cdot [(h/2-t_f)^2- z_N^2] \label{49} \end{equation} $$
$$ \begin{equation} M_z = 2 \cdot f_y \cdot \left[ b^2/4 \cdot t_f – \lambda_3^2/3 \cdot [ h^2/8 – (h/2-t_f)^3]-( \lambda_3\ \cdot z_N)^2 \cdot t_f \right] \label{50} \end{equation} $$
Po wyeliminowaniu z tych równań mnożników λ1 , λ2, λ3 i λ4 otrzymamy proste równania interakcji sił przekrojowych:
$$ \begin{equation} n=\cfrac {z_N}{A}[2 \cdot t_f \cdot \lambda_3 + t_w ] \label{51} \end{equation} $$
$$ \begin{equation} m_y=\cfrac {1}{W_{pl,y}} \left \{ \cfrac {4}{3} \left [h^3/8 – (h/2 -t_f)^3)] \cdot \lambda_3 + t_w \cdot[(h/2-t_f)^2-y_N^2] \right ]\right \} \label{52} \end{equation} $$
$$ \begin{equation} m_z=\cfrac {2}{W_{pl,z}} \left\{ [b^2/4 \cdot t_f -\cfrac {1}{3}[(h/2)^3 -(h/2 -t_f)^3)] \cdot \lambda_3^2- t_f\cdot (\lambda_3 \cdot z_N)^2 \right \} \label{53} \end{equation} $$
ważne dla:
$$ \begin{equation} 0 \le z_N \le h/2-t_f \quad i \quad \cfrac {t_w/2}{z_n+h/2-t_f} \le \lambda_3 \leq \cfrac {h/2}{d/2+z_N} \label{54} \end{equation} $$
gdzie:
względne siły przekrojowe
$n=\cfrac{N}{N_{pl}}$ , $m_y= \cfrac{M_y}{M_{y.pl}}$, $m_z= \cfrac{M_z}{M_{z.pl}}$,
nośności plastyczne przekroju dwuteowego
$N_{pl}=A \cdot f_y$ , $ M_{y,pl} = W_{y.pl}\cdot f_y$ , $ M_{z,pl}=W_{z,pl} \cdot f_y$
z charakterystykami geometrycznymi
$ A=b \cdot h$ , $ W_{y.pl}=b \cdot t_f \cdot (h-t_f)+t_w \cdot (h/2-t_f)^2$ $ W_{z.pl}=\cfrac {t_f \cdot b^2}{2}+\cfrac {t_w^2 \cdot(h-2 \cdot t_f)}{4}$
Przy znajomości sił przekrojowych z powyższych równań możemy wyznaczyć mnożniki Lagrange’a i położenie osi obojętnej.
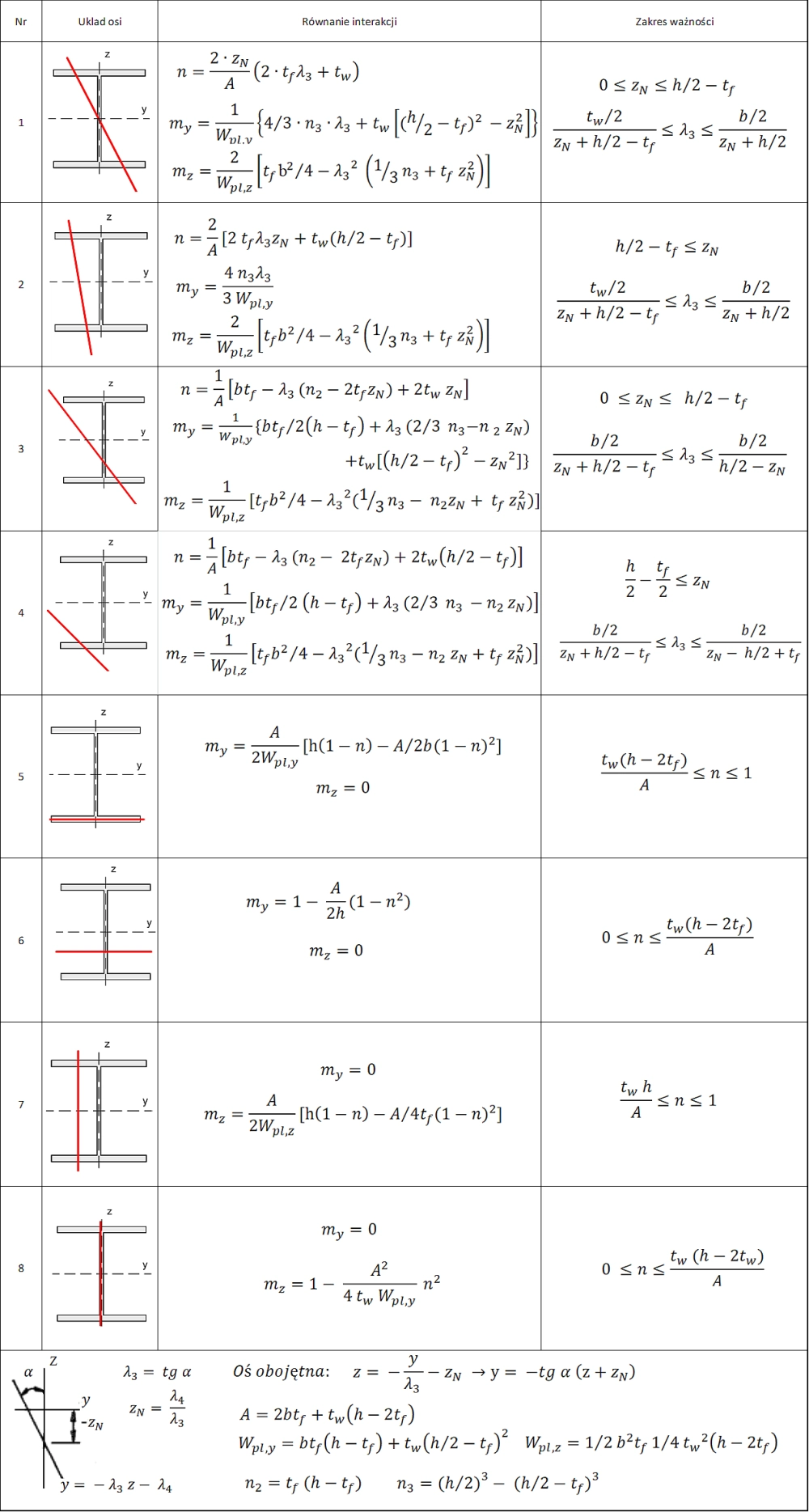
W zależności od wzajemnych stosunków sił przekrojowych można ustalić, zestawione w tab. 3 osiem sytuacji o różnym układzie osi obojętnej oraz różnych równaniach interakcji.
Parametry linii osi obojętnej: $z_N\, ; \, \alpha=arctg \lambda_3$ wyznacza się z nieliniowego układu równań interakcji, który można rozwiązać dolną metodą (np z użyciem dodatku Solver do arkusza MS Excel).
Znając wartości sił przekrojowych z tego układu równań można wyznaczyć mnożniki Lagrange’a, a następnie położenie osi obojętnej oraz równania interakcji.
Tab.3. Położenie osi obojętnej i krzywe interakcji N-My-Mz dla przekroju dwuteowego (opracowano na podstawie [17])
Przykłady
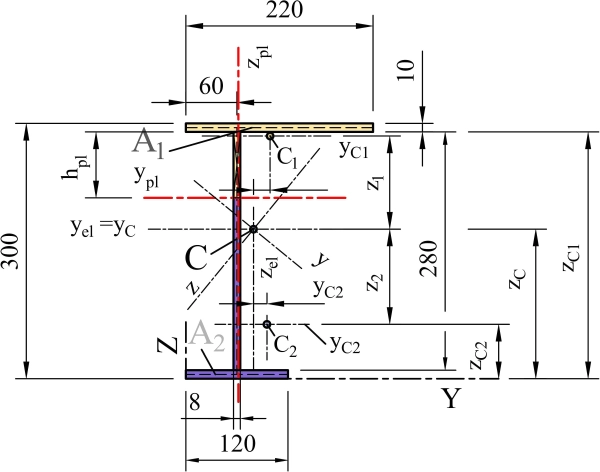
Przykład 1 [Wskaźnik plastyczny przekroju niesymetrycznego zginanego jednoosiowo]
Wyznaczyć wskaźnik plastyczny monosymetrycznego przekroju zginanego względem osi y-y, który pokazano na rys. P1-1.
Pole przekroju całego dwuteownika
$A=28\cdot 0,8 + 22 \cdot 1,0 +12 \cdot 1,0= 56,4 \, cm^2$
$(\ref{15})^1$ $\to A_1=A_2= \cfrac{56,4}{2} =28,2 \, cm^2$
Położenie osi plastycznej $y_{pl}$
$z_C= \cfrac{ 22\cdot 1,0 \cdot (28+ 1,0 + 1,0/2) + 28 \cdot 0,8 \cdot (28/2 + 1,0) +12 \cdot 1,0 \cdot 1.0/2 = 649,0 +336,0 + 6,0 = 991 } {56,4} = 17,57 \, cm$
$z_{C1} = \cfrac{ 22\cdot 1,0 \cdot (29 + 1,0/2) + 7,75 \cdot 0,8 \cdot (28+1- 7,75/2) = 649,0 + 155,8 = 804,8 } {28,2} = 28,54 \, cm$
$z_{C2} = \cfrac{ 0,8 \cdot (28- 7,75) \cdot [(28 – 7,75)/2 +1,0)] + 12 \cdot 1,0 \cdot 1,0/2 = 180,2 + 6,0 = 186,2 } {28,2} = 6,60 \, cm$
$ z_2= 17,57 – 6,60= 10,97 \, cm$
Na przykładzie potwierdzono, że $|z_1| = |z_2|$
Wskaźnik plastyczny przekroju
$S_{y1} = + 28,2 * 10,97 = 309,35 \, xm^3$
$S_{y2} = – 28,2 * 10,97 = – 309,35 \, xm^3$
($\ref{17}$) $\to W_{pl} = 2 \cdot 309,35 = 618,7 \, cm^3$
Literatura
- Meyboom J. (2003). Limit analysis of reinforced concrete slabs (1. Aufl), Zürich Vdf. Hochsch-Verlag An Der ETH
- Vrouwenvelder A. C. W. M. (2003), The plastic behaviour and the calculation of beams and frames subjected to bending [Lecture Ct 4150 ], Technical University Delft Faculty of Civil Engineering and Geosciences, [ http://homepage.tudelft.nl/p3r3s/contentsbeams.pdf ]
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- Livesley R., K. (1975), Matrix methods of structural analysis. Pergamon Press, [ http://books.google.com/books?id=tYsoAQAAMAAJ ]
- Rankine W. J. M. (1866). Useful Rules and Tables, McGraw-Hill, London
- Vellasco P., Lima L. (2012). Plastic Frame idealisation and analysis (Structural Design of Steel and Composite II) [Lecture]. Faculdade de Engenharia da UERJ, [ http://www.labciv.eng.uerj.br/pgeciv/files/4_calculo_plastico.pdf ]
- PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- Neal B. G. (1985). The plastic methods of structural analysis (3rd ed). Chapman and Hall
- Piechnik S. (1980). Wytrzymałość materiałów dla wydziałów budowlanych, PWN, Warszawa
- Mutermilch J., Olszewski E., Łubiński, M. (1954). Wymiarowanie konstrukcji metalowych. Nowe metody (I). Wydawnictwo Budownictwo i Architektura., Warszawa
- Chodor L. (1986), Losowa nośność ustrojów zginanych z uwzględnieniem sił stycznych (Praca doktorska PRE 68/86). Instytut Budownictwa Politechniki Wrocławskiej, [https://chodor-projekt.net/wp-content/uploads/PIPress/Artykuly/1986-Chodor-Dissertation-Wroclaw.pdf ]
- PN_EN-1993-1-1,Projektowanie konstrukcji stalowych. Eurokod 3: Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1993-1-8,Eurokod 3: Projektowanie konstrukcji stalowych Część 1-8: Projektowanie węzłów
- PN-EN 1990. Eurokod: Podstawy projektowania
- Knauff M., Obliczanie konstrukcji żelbetowych według Eurokodu 1, PWN, Warszawa 2013
- PN-EN-1992, Eurokod 2: Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- Santathadaporn S., Chen W.-F. (1968). Interaction Curves for sections under com-bined biaxial bending and axial force (Report No 331.3; Space Frames with Biaxial Loading in Columns). Fritz Engineering Laboratory, [ http://digital.lib.lehigh.edu/fritz/pdf/331_3.pdf ]
- Santathadaporn S., Chen W.-F. (1968). Interaction Curves for sections under com-bined biaxial bending and axial force (Report No 331.3; Space Frames with Biaxial Loading in Columns). Fritz ENgineering Laboratory, [ http://digital.lib.lehigh.edu/fritz/pdf/331_3.pdf ]
________________________________