Klasa przekroju stalowego (+)

Leszek Chodor ,  25 października 2015
06-02-2025 rewizja po dużej awarii portalu
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co

Artykuł w ciągu ostatnich 24 godzin czytało 13 Czytelników

Klasy przekroju stalowego klasyfikują odporność elementu z uwagi na utratę stateczności ścianek przekroju (miejscową utratę stateczności) oraz ze względu na możliwość obrotu w wymaganym przegubie plastycznym i z tych względów wyróżniamy cztery klasy przekrojów stalowych [1]. Generalną zasadą jest to, że klasyfikacja przekroju musi być dokonana na podstawie warunków obciążenia przekroju z uwzględnieniem łącznego działania sił przekrojowych wywołujących naprężenia normalne [N_Ed, M_yEd, M_zEd] oraz dla wszystkich kombinacji obciążeń. Zasada superpozycji nie obowiązuje. Sklasyfikowanie przekroju jest wymagane na poziomie: analizy globalnej, wyznaczania nośności elementu z uwzględnieniem stateczności, a także projektowania  przekroju.

Idea klas przekrojów stalowych

Podstawą klasyfikacji przekrojów prętów są  spostrzeżenia:

1. 1. Pręty stalowe zachowują się różnie w zależności od typu przekroju kształtownika. Różnice występują  pomiędzy prętami o takich samych integralnych charakterystykach geometrycznych [A, $I_y$,, $I_z$] w zależności od tego z jak grubych ścianek są wykonane.
   2. Najbardziej pożądanym zachowaniem prętów jest plastyczne wyczerpanie nośności wskutek ukształtowania  się takiej liczby przegubów plastycznych (przekrojów w pełni uplastycznionych), które prowadzą do pojawienia się mechanizmu plastycznego. W takim przypadku wykorzystujemy zapasy nośności pręta w stanie plastycznym i możemy zaoszczędzić na materiale pręta  ok. kilkanaście procent  lub więcej (do 30 procent po uwzględnieniu redystrybucji naprężeń w całym systemie) w stosunku do tradycyjnie stosowanej analizy w zakresie sprężystym.
   3. Niestety nie zawsze dochodzi do pełnego mechanizmu plastycznego. Analizę plastyczną możemy stosować do prętów z przekrojami krępymi ( o dużej grubości ścianek) . Są to przekroje klasy 1 lub  w części klasy 2. Jeśli nie ma warunków do uplastycznienia przekroju, to przekrój zniszczy się sprężyście i wtedy zalicza go do klasy wyższej (3-ciej lub 4-tej).
   4. Nie zawsze będziemy mogli stosować klasyczną analizę sprężystą (klasa 3), bowiem przy smukłych ściankach ( o małej grubości) przed wyczerpaniem nośności sprężystej może dojść do utraty stateczności miejscowej ścianki i należy przekrój pręta zmodyfikować poprzez wyłączenie z pracy tych części ścianek, które uległy utracie stateczności.  Taki przekrój ma klasę 4-tą.

Rys.1. Klasyfikacja przekrojów stalowych [2]

Na rys.1 opisane spostrzeżenia zilustrowano na przykładzie ścieżki równowagi (M,Θ)=(moment zginający, kat obrotu przekroju) dwuprzęsłowej belki z przekrojami różnej klasy:

1. Belka wykonana z kształtownika o przekroju krępym  (klasy 1) będzie miała ścieżkę równowagi opisaną literami ODABC i zniszczy się na skutek uruchomienia mechanizmu plastycznego, mechanizm zniszczenia zajdzie po utworzeniu dwóch przegubów plastycznych i przekrój osiągnie nośność plastyczną
   $M_{pl}=W_{pl} \cdot f_{d}$,
2. Belka wykonana z kształtownika o przekroju klasy 2 będzie miała ścieżkę równowagi opisaną literami ODAB i zniszczy się na skutek utworzenia jednego przegubu plastycznego, ale nie utworzą się w pełni kolejne przeguby ze względu na niewystarczające obroty w tych przekrojach, to znaczy nie osiągnie pełnej nośności plastycznej $M_{pl}$ , ale będzie miała nośność większą od sprężystej $M_{el}$.
3. Belka wykonana z kształtownika o przekroju klasy 3 będzie miała ścieżkę równowagi opisaną literami ODAE, i zniszczy się na skutek uplastycznienia jednego punktu przekroju, to znaczy osiągnie nośność sprężystą
   $M_{el}=W_{el}\cdot f_{d}$,
4. Belka wykonana z kształtownika o przekroju klasy 4 będzie miała ścieżkę równowagi opisaną literami ODFG,  i  zniszczy się na skutek utraty nośności przez przekrój zredukowany po wyłączeniu tych części ścianek, które utraciły stateczność, co oznacza osiągnięcie nośności efektywnej, zgodnie  teorią nośności zakrytycznej
   $M_{eff}=W_{eff} \cdot f_{d}$,

Możemy przyjąć definicje:

Klasa pierwsza – odnosi się do przekrojów które osiągają nośność plastyczną, a przeguby plastyczne mają pełną możliwość obrotu niezbędną do redystrybucji momentów zginających.

Klasa druga – są to przekroje wątpliwe, które osiągają ograniczoną nośność plastyczną, ze względu na ograniczoną możliwość obrotu w wymaganym przegubie plastycznym, przez co uniemożliwiona  jest pełna redystrybucja momentów zginających.

Klasa trzecia – przekroje tej klasy nie osiągają nośności przegubu plastycznego, ale osiągają nośność sprężystą, obserwowaną wraz z początkiem uplastycznienia dowolnego punktu w przekroju.

Ścianki elementów konstrukcyjnych o przekrojach klasy 1, 2 i 3 nie tracą stateczności miejscowej, a do przekrojów stosowana jest nazwa – przekroje krępe.

Klasa czwarta  dotyczy elementów cienkościennych osiągających nośność zakrytyczną (efektywną), która jest mniejsza niż nośność sprężysta, ze względu na utratę stateczności miejscowej przez ściankę przekroju (wybrzuszenie, zwichrowanie, itp). Przekroje klasy 4 popularnie nazywa się przekrojami smukłymi.

Na rys. 2 pokazano rozkłady naprężeń w zginanych przekrojach poszczególnych klas: rozkład plastyczny dla klasy 1 i 2, rozkład sprężysty dla klasy 3 oraz rozkład sprężysty zredukowany dla klasy 4. 

Rys.2. Nośności przekrojów stalowych jednokierunkowo zginanych, klasy przekrojów i odpowiadające rozkłady naprężeń w przekroju  [3]

Klasę przekroju ustala się w zależności od smukłości ścianek λ=c/t , tworzących przekrój oraz do stopnia ściskania ścianek (w całości lub częściowo). Na rys. 3 pokazano sposób wyznaczania wymiarów c i t ścianek przekroju.  Klasa przekroju ustalana jest zgodnie z najwyższą klasą dowolnej ścianki. W istocie powinniśmy mówić więc o klasie ścianek przekroju. Alternatywnie  określa się dwie klasy przekroju: ze względu na środnik i ze względu na pasy. 

Rys.3. Definicja szerokości c i grubości t ścianki do wyznaczania jej smukłości  [1]

Przekroje walcowane zaprojektowano tak, że w przypadku zginania przekroju ich ścianki spełniają warunki klasy 1 . Każdy zginany względem osi większej sztywności przekrój walcowany jest klasy 1 i nie potrzeba tego sprawdzać dodatkowymi rachunkami.

Dla przekrojów rozciąganych nie określa się klasy przekroju.

Procedura klasyfikowania przekroju

Klasyfikacja przekroju elementu stalowego polega na sklasyfikowaniu każdej ścianki przekroju, a klasa przekroju jest maksymalną klasę ścianek. Klasyfikacja ścianki dokonywana jest na podstawie: smukłości ścianki $\lambda=c/t$, warunków zamocowania ścianki oraz rozkładu naprężeń na jej krawędziach, co pokazano na rys.4. 

Rts.4. Idea klasyfikowania klasy przekroju przez smukłość ścianek [3])

Procedura określania klasy przekroju stalowego jest następująca:

Przez domniemanie przekrój jest klasy 1

Podstawową metodą projektowania elementów stalowych jest projektowanie w granicznym stanie plastycznym. Możliwość projektowania w innych stanach granicznych, to znaczy w granicznym stanie sprężystym, krytycznym bądź zakrytycznym MUSI być każdorazowo uzasadniona przez wykazanie że konstrukcja zniszczy się przed osiągnięciem nośności plastycznej. Oznacza to, że przez domniemanie przyjmuje się, że przekrój jest klasy 1.

Jeśli przekrój jest walcowany na gorąco i zginany (np dwuteownik bisymetryczny z rys. 5), to jest klasy 1 i kończymy procedurę. Efekty niestateczności uwzględnimy przy wymiarowaniu elementu. 

Rys.5. Dwuteownik bisymetryczny

Sprawdzenie czy przekrój jest klasy 1, 2, 3 czy 4

W przypadku przekrojów innych niż walcowane i walcowanych, ale pracujących w złożonym stanie naprężenia – sprawdzamy warunki pkt. 5.6. (Wymagania dotyczące przekrojów w analizie plastycznej) normy [1], umożliwiające kwalifikację  do klasy 1,2 i 3, to jest poprzez sprawdzenie smukłości ścianek i porównanie ich z wartościami granicznymi zestawionymi w tab. 1.

Smukłości ścianek jednoczesnemu ściskaniu i jednokierunkowym zginaniu (mimośrodowemu zginaniu) należy wyznaczać w sposób podany w rozdziale Klasa przekroju mimośrodowo ściskanego.

Tab. 1. Graniczne smukłości ścianek dwuteownika zginanego lub ściskanego (na podstawie [1]))

$$\begin{equation}\varepsilon=\sqrt{\cfrac{235}{f_y}} \label{1}\end{equation}$$

W przypadku innych przekrojów (w tym rur okrągłych i kątowników) lub inaczej wytężonych, maksymalne stosunki szerokości do grubości dla części ściskanych należy wyznaczyć zgodnie z tab 5.2  pkt 5.6. [1], w którym  podano też dodatkowe warunki, dotyczące zabezpieczenia środnika w miejscu działania znacznych sił skupionych, warunków kształtowania elementów o zmiennym przekroju lub ograniczeń w otworowaniu przekrojów uplastyczniających się.
Ważne i naukowo uzasadnione jest spostrzeżenie zawarte w normie, że przypadku stosowania metod globalnej analizy plastycznej, które uwzględniają miarodajne rozkłady naprężeń i odkształceń w elementach oraz złożone skutki niestateczności, wymagania o dodatkowych warunkach nie mają zastosowania. Globalna analiza plastyczna pozwala uwzględniać nieliniowe właściwości materiału przy obliczaniu efektów oddziaływań w układzie konstrukcyjnym. Można w tym celu stosować jedną z następujących metod: 1) analizę sprężysto-plastyczną, w której kolejne przekroje lub węzły osiągające nośność plastyczną traktuje się jak przeguby plastyczne, 2) nieliniową analizę plastyczną, w której uwzględnia się rozwój stref plastycznych w elementach, 3) analizę sztywno-plastyczną, w której abstrahuje się od odkształceń sprężystych, traktując poszczególne części między przegubami jako sztywne. Ostatnia metoda, nazywana historycznie metodą nośności granicznej [4] jest szczególnie przydatna do zastosowań inżynierskich w podejściu kinematycznym (badania plastycznych mechanizmów zniszczenia  [5], [6].

Jeśli potwierdziliśmy, że przekrój (inny niż walcowany) jest klasy 1, to kończymy procedurę. Jeśli nie potwierdziliśmy tego, to przechodzimy do kolejnego kroku, czyli sprawdzenia, czy przekrój jest klasy 3.
Jeśli przekrój (którakolwiek ze ścianek przekroju) nie spełnia warunków klasy niższej (np 1), to należy go zakwalifikować do klasy wyższej. Jeśli przekrój nie spełnia warunków dla klasy 3-ciej, to kwalifikujemy go do klasy 4-tej.

Sprawdzenie czy przekrój jest klasy 3

W celu zakwalifikowania przekroju (nie spełniającego warunków klasy 1 lub 2) do klasy 3-ciej należy sprawdzić jeszcze warunek pkt. 5.5.2 (9) [1] odnośnie wyjątkowego traktowania przekroju klasy 4 i możliwość zaklasyfikowania go do grupy przekrojów klasy 3.

W tym celu należy podwyższyć wymagania  granicznych smukłości, określonych w tab 5.2. [1] poprzez przyjęcie  powiększonego współczynnika materiałowego ε z formuły:

$$\begin{equation}\varepsilon=\sqrt{\cfrac{235}{f_y}} \cdot \sqrt{ \cfrac{f_y/\gamma_{M0}}{\sigma_{com,Ed}}} \label{2}\end{equation}$$

gdzie: $\sigma_{com.Ed}$ -największe obliczeniowe naprężenie ściskające w rozpatrywanej części, wynikające z analizy pierwszego rzędu lub, w razie konieczności, analizy drugiego rzędu. Oznacza to, że współczynnik określony pod tab.1 należy zwiększyć  o pierwiastek stopnia wytężenia części ściskanej.

Takiego wyjątkowego potraktowania przekroju nie można robić przy sprawdzaniu stateczności elementu zgodnie z  [1] , klauzula 6.3

Kwalifikowanie przekroju do klasy 4

Jeśli rozpatrywany przekrój nie spełnia warunków klasy 3, to należy go traktować jako przekrój klasy 4.

Klasa przekroju mimośrodowo zginanego

Przypadek mimośrodowego zginania (jednoczesnego ściskania i zginania) jest uogólnieniem i połączeniem przypadków prostych, czyli zginania i odrębnie ściskania, przy czym przypadki proste nie są przypadkami granicznymi mimośrodowego zginania, lecz są wzajemnie sprzężone.

W przypadku, gdy ściskająca siła przekrojowa jest duża, to  klasę przekroju można przyjmować jak dla czystego ściskania.  Jest to podejście konserwatywne, to znaczy uwzględnienie dodatkowego zginania może wykazać, ze przekrój jest klasy niższej.

Klasę przekroju ściskanego mimośrodowo sprawdza się najpierw dla czystego ściskania. Jeśli to sprawdzenie wykaże, że klasa jest 1, to nie jest potrzebne sprawdzenie dla przypadku złożonego wytężenia. W przypadku profili walcowanych taka procedura jest wystarczająca  w przeważającej liczbie przypadków praktycznych.  W  przypadku, gdy przekrój poddany czystemu ściskaniu miałby klasę 2 i wyższą, należy dokonać sprawdzenia zgodnie z zasadami podanymi niżej. 

Plastyczna interakcja zginania i ściskania oraz współczynnik α

W celu sklasyfikowania przekroju zginanego i ściskanego w stanie plastycznym potrzebne jest wyznaczenie wysokości strefy ściskanej  αc (rys. 7).

Algorytm wyznaczania współczynnika α jest zależny od kształtu przekroju.

Współczynnik α dla przekroju prostokątnego

Na rys.6 pokazano rozkład naprężeń w granicznym stanie plastycznym przekroju prostokątnego kolejno dla:  czystego zginania My≠0, czystego rozciągania  N≠0 i dla jednoczesnego zginania i rozciągania  My,N≠0.
W przypadku interakcji zginania i rozciągania  (ściskania dla ujemnej siły N) dwa warunki równowagi przekroju o szerokości b i wysokości h można zapisać w postaci:

$$\begin{equation}\sum{X:} \ N=2\cdot f_y \cdot z_N \cdot b \label {3} \end{equation}$$

$$\begin{equation}\sum {M:}\ M=M_{pl}-2 \cdot f_y \cdot z_N \cdot b \cdot z_N /2 \label {4} \end{equation}$$

skąd otrzymujemy:

$$\begin{equation}z_N= \cfrac {N} {2 \cdot f_y\cdot b }\label {5} \end{equation}$$

$$\begin{equation}M= M_{pl}- N \cdot z_N/2=M_{pl}- \cfrac {N^2} {4 \cdot f_y \cdot b} \label {6} \end{equation}$$

 i ostatecznie uzyskamy wyrażenie na współczynnik α wysokości strefy ściskanej:

$$\begin{equation}\alpha = \cfrac {1}{2}- \cfrac {z_N} {h}\label {7}  \end{equation}$$

Uzyskana formuła może być stosowana w doniesieniu do środników dwuteowników ściskanych i zginanych względem osi y-y, ale także do pasów dwuteowników zginanych względem osi z-z. Do praktycznych  obliczeń należy brać  wartości obliczeniowe sił  (N=N_Ed, M=M_Ed).

Rys. 6 Rozkład naprężeń w granicznym stanie plastycznym w przekroju prostokątnym (zmodyfikowane [3])

Współczynnik α dla środnika przekroju dwuteowego jednokierunkowo zginanego

Na rys.7 pokazano rozkład naprężeń w  przypadku jednoczesnego zginania i ściskania przekroju dwuteowego w stanie sprężystym oraz granicznym stanie plastycznym. 

Rys. 7 Rozkład naprężeń w przekroju dwuteowym (zmodyfikowane :a) siły przekorjowe, b) w stanie sprezystym, x) w  granicznym staniwe plastycznym [7]

 W tym przypadku współczynnik α można określić z zależności:

• przy ustalonej sile osiowej i przyrastaniu momentu zginającego

$$\begin{equation}z_N= \cfrac {N_{Ed}}{2 \cdot f_y \cdot t_w } \label {8} \end{equation}$$

$$\begin{equation}\alpha_w= \cfrac {1} {2}+ \cfrac {z_N}{c_w} \, \le 1  \label {9}\end{equation}$$

• przy jednoczesnym przyrastaniu momentu zginającego i siły osiowej

$$\begin{equation}\alpha_w = \cfrac {1}{2}+|e_d|\cdot \\ \cdot \left[ 1-0,5 \cdot \sqrt{( \cfrac {c_w}{e_d})^2 + \sqrt {(4 \cdot W_{pl,y,Ed} /{t_w} -c_w^2) /e_d^2}+4}\right] \label {10} \end{equation}$$

gdzie mimośród  $e_d=\cfrac{M_{y,Ed}}{N_{Ed}}$.

Analityczne rozwiązanie problemu w ogólnym przypadku, z uwzględnieniem zależności rozwiązań teorii plastyczności od kolejności przykładania i przyrastania sił jest zadaniem złożonym.  Dlatego  w praktyce zadowalamy się oszacowaniem uzyskanym dla ustalonej siły osiowej.

Współczynnik α dla przekroju dwuteowego dwukierunkowo zginanego

W przypadku przekroju ściskanego siłą NEd oraz zginanego dwukierunkowo momentami zginającymi My,Ed i Mz,Ed odpowiednio wokół osi większej sztywności y-y i mniejszej sztywności z-z, w celu wyznaczenia współczynnika α należy rozpatrzyć przypadek jednoczesnego działania wszystkich tych sił przekrojowych.  Nieprawidłowe jest podejście, w którym rozpatruje się odrębnie zginanie w kierunku osi y-y i odrębnie wokół osi z-z nawet rozdziałem siły ściskającej na dwie składowe, towarzyszące zginaniu względem stosownych osi. Należy zastosować krzywe interakcji plastycznej i wynikające z nich położenia osi obojętnej w granicznym stanie plastycznym [8].

Klasa plastyczna (1 lub 2) wewnętrznej ścianki (w tym środnika)

Środniki klasy 1 i 2 w stanie granicznym są uplastycznione , w sposób pokazany na rys.8.

Rys.8. Ścianka ściskana i zginana w stanie plastycznym: $c_w$ -wysokość środnika (ścianki wewnętrznej), α c_w-wysokość strefy ściskanej

W zależności od współczynnika wysokości strefy ściskanej $\alpha$ klasę środnika określimy z zależności w tab. 2.

Tab. 2. Klasa plastyczna ścianki wewnętrznej (środnika) zginanego i ściskanego (na podstawie [1])

Klasa plastyczna (1 lub 2) ścianki zewnętrznej (w tym pasa )

Klasę plastyczną pasa można określić z tab.3.

Tab. 3. Klasa  plastyczna ścianki zewnętrznej  (pasa) zginanego i ściskanego [1]

Sprężysta  interakcja zginania i ściskania oraz współczynnik Ψ

Współczynnik Ψ

W stanie sprężystym naprężenia normalne σ w dowolnym punkcie przekroju o współrzędnej [y,z] w układzie osi głównych, centralnych,o charakterystykach geometrycznych [A, I_y, I_z] =[pole przekroju, moment bezwładności względem osi poziomej y-y, moment bezwładności względem osi pionowej z-z] i obciążonego siłami przekrojowymi [N_Ed, M_yEd, M_zEd] =[siła osiowa, moment zginający wokół osi y, moment zginający wokół osi z] można wyznaczyć ze znanych zależności przekroju rozciąganego i dwukierunkowo zginanego  [5]:

$$\begin{equation}\sigma=\cfrac{N_{Ed}}{A}+\cfrac{M_{y,Ed}}{I_y} \cdot z+\cfrac{M_{z,Ed}}{I_z}\cdot y \label {11} \end{equation}$$

Po wyznaczeniu naprężeń normalnych σ₁ w punkcie (y₁,z₁) oraz σ₂ punkcie (y₂,z₂) ich stosunek jest poszukiwanym współczynnikiem

$$\begin{equation}\psi=\cfrac{\sigma_2}{\sigma_1} \label {12} \end{equation}$$

gdzie:
σ₂ – mniejsze brzegowe naprężenie ściskające w ściance (naprężenia rozciągające należy wstawiać do wzoru ze znakiem minus),
σ₁  –  większe brzegowe naprężenie w ściance.

Klasa sprężysta (3) wewnętrznej ścianki ( w tym środnika)

Przekroje klasy 3 w stanie granicznym są wytężone sprężyście, w sposób pokazany na rys. 9.

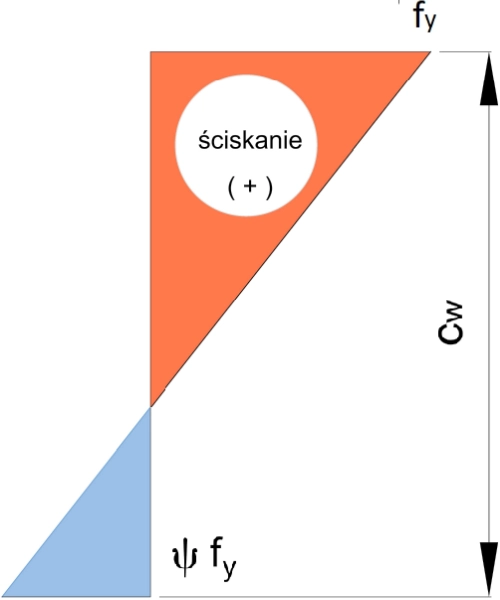
Rys.9. Przekrój sprężysty ściskany i zginany: c_w -wysokość środnika (ścianki wewnętrznej), f_y – granica plastyczności, Ψ – stosunek naprężeń krawędziowych rozciągających do ściskających

W zależności od stosunku naprężeń krawędziowych rozciągających do ściskających  Ψ ściankę zaliczymy do klasy 3 , jeśli:

dla  Ψ> -1, zachodzi:   λ_w ≤ 42·ε / (0,67+0,33·Ψ),

dla  Ψ≤ -1, zachodzi:   λ_w ≤ 62·ε (1-Ψ)·√(-Ψ).

Klasa sprężysta (3) ścianki zewnętrznej ( w tym pasa )

W przypadku pasa w dowolnej konfiguracji ściskania warunek klasy 3 można ocenić z tab 4.

Tab. 4. Klasa sprężysta ścianki  zginanej i ściskanej (na podstawie [1])

Współczynnik niestateczności miejscowej k_σ należy wyznaczać w zależności od przebiegu naprężeń w ściance i stosunku ψ=σ₂/σ₁ naprężeń minimalnych σ₂ do maksymalnych σ₁  wg tab. 5 , którą opracowano na podstawie zależności podanych w [9], tab. 4.2.

Dla ścianki ściskanej na całej długości stosunek naprężeń krawędziowych Ψ=σ₂/σ₁ jest zawsze  dodatni (i nie przekracza 1 dla równomiernego ściskania)  1> Ψ ≥ 0 .

W tym przypadku możliwy jest przebieg naprężeń po długości ścianki zewnętrznej taki , taki w którym minimalne naprężenia wystąpią na krawędzi wewnętrznej  lub zewnętrznej (rys, 10) 

Rys.10. Rozkład naprężeń w ściskanym pasie, najmniejsze naprężenia na krawędzi: a) wewnętrznej , b) zewnętrznej

Dla ścianki zginanej stosunek naprężeń krawędziowych jest ujemny  Ψ=σ₂/σ₁ <0. 

Rys.11. Rozkład naprężeń w zginanym pasie, najmniejsze naprężenia na krawędzi: a) (wewnętrznej, b) zewnętrznej

W tym przypadku możliwy jest przebieg naprężeń po długości ścianki zewnętrznej taki, w którym naprężenia maksymalne  wystąpią na krawędzi zewnętrznej lub wewnętrznej  (rys. 11).

Współczynnik niestateczności miejscowej k_σ (ψ) można obliczyć z wyrażeń, zamieszczonych w tab. 5.

Tab. 5. Współczynnik niestateczności pasów (wg [9])

Arkusz kalkulacyjny  Semi-Comp

Program SemiComp Member Design jest powszechnie dostępnym i darmowym arkuszem obliczeniowym pracującym w środowisku Excel, opracowanym przez  Institute for Steel Structures,  Graz University of Technology, Austria. Program  jest dostępny do pobrania na stronie SemiComp. Wersję 1.0.10 programu SemiComp dostępną publicznie w roku 2005 znajdziecie tutaj.

Podstawy teoretyczne przedstawiono w w finalnej wersji raportu [3] , a liczne przykłady zawarto w dokumencie  [10].

Arkusz Semi-Comp współpracuje z powszechnie dostępnym, bezpłatnym programem LTBeam do wyznaczania momentu krytycznego dowolnej belki.

Przykłady rachunkowe

Przykład 1 [Kształtownik  walcowany ma przekrój klasy 1 ? ]

Dla dwuteownika  IPE600, wykonanego ze stali S355 sprawdzić, czy jest klasy 1.

Wymiary geometryczne i charakterystyki geometryczne kształtownika odczytano z tablic profili walcowanych, obliczono smukłości środnika i półki,(tab.6).

Tab.6. Charakterystyki geometryczne IPE 600

Dla t<40 i stali S355 granica plastyczności  f_y wynosi (tab. 3.1 [1]) :
f_y=355 MPa.  ε=√(235/355)=0,81

Sprawdzenie  warunków klasy przekroju : 

środnik  λ_w/ε = 42,8/0,81 =52,8
< 72 (zginanie y-y)   → 1 klasa
> 42 (ściskanie)        → 4 klasa
(zginanie z-z)   → 1 klasa

Ostatecznie środnik ma klasę k_w=1 (tylko zginanie).
Jeśliby jednak był czysto ściskany, to miałby klasę 4.

pas  λ_f/ε = 4,2/0,81 =5,2
<9  (zginanie y-y)   → 1 klasa
> 9  (ściskanie)        → 1 klasa
> 9 (zginanie z-z)   → 1 klasa

Ostatecznie pas ma klasę k_f=1.

Ponieważ zarówno środnik jak i pas przy zginaniu względem osi y-y są klasy 1, to również przekrój jest k_A= 1, co potwierdza tezę podaną wyżej.  Sprawdzanie warunków dodatkowych pomija się.

W przypadku ściskania dwuteownik typoszeregu IPE środnik jest klasy wyższej niż 2  i dlatego na słupy najczęściej stosuje się dwuteowniki HEA i HEB, które mają lepszą klasę od IPE przy ściskaniu, ale również wymagają sprawdzenia klasy przekroju.

Przykład 2 [ Czyste ściskanie ]

Określić klasę przekroju słupa wykonanego z kształtownika HEB340 – S355.

Charakterystyki geometryczne: A= 170.9 cm2, b = 300 mm, h = 340 mm, t_f = 21,5 mm;
t_w = 12 mm, r = 27 mm, I_y = 36660 cm⁴, i_y = 14,65 cm, I_z = 9690 cm⁴, i_z = 7,53 cm.
Własności mechaniczne:  f_y = 355 MPa i  E = 210 GPa; ε=√(235/355)=0,81.

Środnik ściskany:  λ_w=[ 340-2(21,5 +27)]/12= 20,25 < 33ε=33·0,81=26,7  ⇒ k_w=  1 klasa (tab.1 ⇐ tab. 5.2 EC3-1-1),
Pas ściskany:          λ_f=[ (340-12)/2-27]/21,5= 5,4 < 9ε=9·0,81=7,3               ⇒ k_f=     1 klasa (tab.1 ⇐ tab. 5.2 EC3-1-1),

Przekrój:               ⇒   k_A=max{k_w, k_f}=max {1,1)= 1 klasa

Przykład 3 [ Ściskanie ze zginaniem jednokierunkowym (ściskanie mimośrodowe) ]

Określić klasę przekrojów belki- słupa  HEA300 – S355, pokazanej na rys. 12.

Rys.12. Belka-słup HEA 200 poddana jednoczesnemu ściskaniu i zginaniu jednoosiowemu

Obciążenie belki jest następujące:

siła ściskająca                                                    N_Ed= 500 kN,
moment zginający                                            M _y1,Ed=M _y2,Ed=200  kNm,
W każdym przekroju belki działają siły przekrojowe wykazane wyżej. Moment zginający M_yEd z zdania jest obliczeniowym (indeks d), zewnętrznym – przekrojowym (indeks E) momentem zginającym wokół osi y, stowarzyszonym z nośnością obliczeniową M_pl,yRd.

W tab. 7 zestawiono charakterystyki geometryczne przekroju, własności mechaniczne f_y, ε oraz  nośności plastyczne przekroju: N_pl,Rd , M_pl,zRd, M_pl,yRd.

Tab.7. Charakterystyki geometryczne oraz materiałowe HEA300-S355

Sprawdzenie stanu plastycznego

• Współczynnik strefy ściskanej w granicznym stanie plastycznym

W celu wyznaczenia współczynnika wysokości strefy ściskanej α ustalimy najpierw szerokość docisku z_n siły osiowej N_Ed:

$z_N=\cfrac{N_{Ed}}{2 \cdot t_w \cdot f_y}= \cfrac {500} {2 \cdot 8,5 \cdot 355}\cdot 10^3= 83 mm$

a następnie obliczymy współczynnik strefy ściskanej w sytuacji przyrastania siły osiowej:

$\alpha_w= \cfrac {1} {2}+ \cfrac {83}{208} =0,90$

Z tab.2. dla α>0,5 , otrzymujemy  dla klasy 1 smukłość graniczną
λ_w,gr=396ε/(13α-1)= 396·0,81/(13·0,90-1)=29,6
Ponieważ  λ_w,gr=29,6 > λ_w=24,5, więc środnik jest klasy 1.

W celu potwierdzenia sprawdzimy jeszcze stan sprężysty (to znaczy, czy środnik jest klasy niższej niż 3).

Uwaga: W zasadzie po stwierdzeniu klasy 1 ścianki, powinniśmy zakończyć procedurę klasyfikacji. Prowadzimy ją dalej wyłącznie w celach dydaktycznych.

Sprawdzenie stanu sprężystego

Wyznaczenie naprężeń w stanie sprężystym dokonujemy  z konwencjonalnych wzorów:

z=c_w/2= 20,8/2=10,4 cm   ⇒ $\sigma_{c_w/2}=\cfrac {500}{112,5} \cdot 10^1+\cfrac{_{200} }{18263} \cdot 10,4 \cdot 10^3=44,4+113,9=158,3 MPa$

z=-c_w/2= 20,8/2=-10,4 cm   ⇒ $\sigma_{c_w/2}=\cfrac {500}{112,5}\cdot 10^1- \cfrac{_{200} }{18263} \cdot 10,4 \cdot 10^3=44,4-113,9=-69,4 MPa$

Stosunek naprężeń krawędziowych wynosi $\psi= -69.4/158,3=-0,438.$

Ponieważ  Ψ≤ -1,więc  λ_w,gr ≤ 62·0,81 (1+0,438)·√0,438=47,8 > λ_w=24,5  ⇒  środnik jest klasy 3  lub niższej.

Klasa środnika k_w

Środnik spełnia wymagania klasy 1.
Procedurę klasyfikacji przekroju zakończono.

Klasa pasów k_f

W rozważanym przypadku zginania jednokierunkowego i siły ściskającej, pas poddany jest czystemu ściskaniu.

Z tab.1. odczytano, że:  λ_f= 8,5  < λ_f,gr=9   ⇒  pas jest klasy 1

Klasa przekroju k_A

k_A=max{k_w ; k_f}=max{1,1}= 1 .

Przekrój jest  klasy 1.

Przykład 4 [ Ściskanie ze zginaniem dwukierunkowym ]

Określić klasę  przekroju  HEA300- S355, belki- słupa  o schemacie pokazanym na rys. 13.

Rys.13. Belka-słup poddana jednoczesnemu ściskaniu i zginaniu dwukierunkowemu

Zewnętrzne siły obliczeniowe wynoszą:
siła ściskająca                                            N_Ed  = 500 kN,
moment zginający wokół osi y-y           M_yEd= 200 kNm,
moment zginający wokół osi z-z            M_zEd= 50 kNm.

Siły przekrojowe i rozkład naprężeń w przekroju w stanie plastycznym i sprężystym

Wykresy sił przekrojowych wykonano na rys. 14. Przekroje krytyczne (sprawcze) do wyznaczenia klasy przekroju belki oznaczono przez PK1 i PK2.

Rys.14. Wykresy sił przekrojowych belki-słupa z przykładu 4

Na rys.15 pokazano rozkłady naprężeń w przekrojach PK1 i PK2 w stanie plastycznym i sprężystym.

Rys.15. Rozkłady naprężeń w przekroju PK1 i PK2 w stanie sprężystym i plastycznym

Naprężenia sprężyste wyznaczono w klasyczny sposób   Na przykład naprężenia normalne w stanie sprężystym  w punkcie (y,z)=(b/2-c_f ; h/2)=( 30/2-11,88 ; 29/2)=(3,12 ; 14,5  [punkt nad początkiem wyokrąglenia pasa górnego], wynoszą:

$\sigma / f_y=\cfrac{500}{112,5}\cdot10^1+( \cfrac{_{200}}{18263} \cdot z+\cfrac{50}{6310 }\cdot {14,5}) \cdot10^3 /355= 0,519$

Klasyfikacja przekroju PK1

Środnik

λ_w=24,5  (tab.7)

A_w=24,6 cm²,

$N_{Edw}= \cfrac {24,6}{112,5}\cdot 500=109,3 kN$

$z_{Nw}= \cfrac {109,3}{2 \cdot 355 \cdot 8,5 } \cdot 10^3= 18,12 mm$

$\alpha_w= \cfrac {1} {2}+ \cfrac {36,23} {208}=0,587 \le 1$

• Sprawdzenie, czy środnik jest klasy 1 lub 2 (stan plastyczny – tab.2 , tab.5.2 EC3 arkusz 1 )

α_w =0,587>0,5, więc
smukłość zmodyfikowana  λ_w,m=λ_w·(13α_w-1)= 24,5·(13·0,587-1)=162,46 < λ_wgr=396·ε=396·0,81=320

⇒ środnik jest klasy 1.

Pas

λ_f= 8,5  (tab.7)

A_f = 112,5 – 24,6 = 87,9 cm²

$N_{Edf}= \cfrac {87,9}{112,5}\cdot 500=390,67 kN$

$z_{Nf}= \cfrac {390,67}{4 \cdot 355 \cdot 14 } \cdot 10^3= 19,65 mm$

$\alpha_f= \cfrac {1} {2}+ \cfrac {19,65} {2\cdot 118,8}=0,583 \ \le 1$

ψ_f= 0,662

Klasa 3 (stan sprężysty – tab.4 i 5, tab.5.2. EC3 arkusz 2) :

k_σ=0,57-0,21·0,662+0,07·0,662²=0,462
λ_fgr=21·ε _√k_σ=21·0,81_√0,462=11,56 > 8,5 ⇒ pas jest klasy 3 lub lepiej

Klasa 1 lub 2 (stan plastyczny – tab.3 , tab.5.2. EC3 arkusz 2) :

λ_fgr=10·ε/(α_f √α_f)=10·0,81/(0,583 ·√0,583)= 18,2 > 8,5  ⇒ pas jest klasy 2 lub lepiej

λ_fgr=9·ε/α_f √α_f=9·0,81/(0,583 ·√0,583)= 16,38 > 8,5  ⇒ pas jest klasy 1

Przekrój PK1

Przekrój PK1 jest klasy max (1;1}= 1.

Klasyfikacja przekroju PK2

Przekrój jest jednorodnie ściskany

Środnik

λ_w=24,5  < 33ε=26,7 ⇒ środnik jest klasy 1

Pas

λ_f=8,5   < 14ε = 11,3 ⇒ pas jest klasy 3 lub lepiej
>10ε=8,1     ⇒ nie jest klasy 2
>9ε=7,3)     ⇒ nie jest klasy 1

Pas jest klasy 3

 Przekrój PK2

Przekrój CS2 jest klasy max (1;3}= 3.

Klasyfikacja belki

Belka jest klasy max (1;3}= 3.

Przykład 5 [ Zastosowania programu Semi-Comp Member Design ]

Pokażemy zastosowanie arkusza Semi-Comp Member Design do wyznaczenia klasy przekroju belki z przykładu 4.

Wprowadzenie danych

Na rys. 16  pola oznaczone na błękitno w bloku Cross-Section Data oraz pola oznaczone na zielono są wybierane przez program z bazy danych po wskazaniu profilu (HEA 300) oraz klasy stali (S355).

Rys.16. Dane w arkuszu Semi-Comp dla przykładu

Siły przekrojowe w belce

Po wybraniu Calculate Force zostaną wyliczone siły przekrojowe  w belce i zobrazowane w sposób pokazany na rys. 17. 

Rys.17. Wykresy sił przekrojowych w arkuszu Semi-Comp dla przykładu 4

Klasa przekroju belki

Po wybraniu zakładki Cross Section Check uzyskamy  najważniejsze parametry oraz klasę przekroju w arkuszu pokazanym na rys 18. 

Rys.18. Sklasyfikowanie przekroju ściskanego i  ukośnie zginanego w arkuszu Semi-Comp dla przykładu 4.

Sprawdzono poprawność przeliczenia przykładu 4. Uzyskane niewielkie rozbieżności w oszacowaniu stosunków naprężeń krawędziowych z analitycznych i prezentowanych przez  arkusz Semi-Comp, nie wpływają  na  klasyfikacje klasy przekroju.

Literatura

1. PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
2. Biegus A. (2010). Projektowanie konstrukcji stalowych według Eurokodu 3. cz. 3 Wymiarowanie konstrukcji stalowych. Politechnika Wrocławska, Wydział Budownictwa Lądowego i Wodnego, Materiały dydaktyczne, Wroocław 2010
3. Greiner R., Jaspart J., Weynand P., Ziller K., Oereder R., Herbrand M. (2012), Back-ground infrormation. Design Guidlines for Cross-Section and member design accord-ing to Eurocode 3 with particular focus on semi-compact sections. Final version (March 2012) (Valorisation Ptoject No RFS2-CT-2010-00023). TU Graz Universtity, Institute for Steel Structures and Shell Structures, [ http://portal.tugraz.at/portal/page/portal/Files/i2050/pdf/Forschung/SC+_BackgroundDocumentation_March2012.pdf ]
4. Neal B. G. (1985). The plastic methods of structural analysis (3rd ed). Chapman and Hall
5. Piechnik, S. (1980). Wytrzymałość materiałów dla wydziałów budowlanych. PWN
6. Chodor L. (2013). Teoria sprężystości i plastyczności Nieliniowości fizyczne. Nieli-niowość sprężysta. Teoria nośności granicznej [Lecture-Wykład]. Wykład 6- część 2 z przedmiotu Teoria sprężystości i plastyczności , Politechnika Świętokrzyska, Kiel-ce, [ https://chodor-projekt.net/wp-content/uploads/PIPress/Wyklady/TSiP/6.2-Nieliniowosci-fizyczne-cz2.pdf ]
7. Greiner R.,Lechner a., Kettler M.,  Jaspart J-P., Weynand K., Oereder R., Dehan V. (2013), Valorisation action of plastic member capacity of semi-compact steel sections — a more economic design (SEMI-COMP+) Final report,  Directorate-General for Research and Innovation,Luxembourg: Publications Office of the European
8. Chodor L. (2015), Plastyczna interakcja ściskania i dwuosiowego zginania, Encyklopedia Inżyniera i Architekta πPiWiki, [ https://chodor-projekt.net/encyclopedia/interakcja-plastyczna-sily-osiowej-i-dwuosiowego-zginania/ ]
9. PN-EN 1993-1-5:2008, Eurokod 3: Projektowanie konstrukcji stalowych. Część 1-5: Blachownice
10. TU Graz, (2012), Worked Examples for Cross-Section and member design according to Eurocode 3 with particular focus on semi-compact sections. (Valorisation Ptoject No RFS2-CT-2010-00023). TU Graz Universtity, Institute for Steel Structures and Shell Structures,[ http://portal.tugraz.at/portal/page/portal/Files/i2050/pdf/Forschung/SC+_BackgroundDocumentation_March2012.pdf ]

________________________________