Niniejszy artykuł stanowi Część 1 cyklu Elementarz niezawodności konstrukcji.W całym cyklu artykułów zachowano ciągłość numeracji: wzorów i ilustracji. Numeracja rozdziałów jest odrębna dla każdej części.
Omówiono podstawowe pojęcia z teorii niezawodności konstrukcji potrzebne do analizy dyskretnych struktur niezawodnościowych. Przedstawiono podstawowe definicje i miary niezawodności konstrukcji dla funkcji stanu granicznego z normalnym rozkładem prawdopodobieństwa, a także numeryczne wyznaczanie wartości dystrybuant rozkładu normalnego w „ogonach rozkładu”, co jest istotne dla konstrukcji budowlanych, których niezawodność jest bardzo duża.
Wprowadzenie
Definicje i oznaczenia wielkości podstawowych
Stosować będziemy oznaczenia i definicje zgodnie z normami [1] oraz [2]:
Element konstrukcyjny – fizycznie wyróżnialna cześć konstrukcji, np. słup, belka, płyta, pal fundamentowy.
Konstrukcja – uporządkowany zespół połączonych ze sobą części, zaprojektowanych w celu przenoszenia obciążeń i zapewnienia odpowiedniej sztywności.
Ustrój konstrukcyjny – elementy nośne obiektów budowlanych oraz sposób, w jaki te elementy ze sobą współpracują.
Zgodność – spełnienie określonych wymagań.
Niezawodność – zdolność konstrukcji lub elementu konstrukcyjnego do spełnienia określonych wymagań, łącznie z uwzględnieniem projektowanego okresu użytkowania na który została zaprojektowana. Niezawodność wyraża się zwykle miarami Probabilistycznymi. Niezawodność obejmuje nośność, użytkowalność i trwałość konstrukcji.
Klasa niezawodności konstrukcji – klasa konstrukcji lub elementów konstrukcyjnych, dla których wymagany jest określony stopień niezawodności.
Oddziaływanie $F$
a) zbiór sił przyłożonych do konstrukcji (oddziaływania bezpośrednie)
b) zbiór wymuszonych odkształceń lub przyspieszeń, zasadniczo spowodowanych innymi wpływami niż wymienionymi w pkt a)
Efekt oddziaływania $E$
Efekt oddziaływań (lub oddziaływania) na element konstrukcji (np. siła wewnętrzna, moment, naprężenie, odkształcenie) lub na całą konstrukcję (np. ugięcie, obrót)
$p_f$- prawdopodobieństwo zniszczenia
$p_s$- prawdopodobieństwo przetrwania,
$Prob \{.\}$ – prawdopodobieństwo,
$g$- funkcja stanu granicznego,
$\Phi$- funkcja rozkładu prawdopodobieństwa standaryzowanego rozkładu normalnego,
$\beta$ – współczynnik niezawodności,
$\mu_x$ – wartość średnia zmiennej losowej X,
$\sigma_X$- odchylenie standardowe zmiennej losowej X,
$v_X$- współczynnik zmienności zmiennej losowej X,
$R$ – nośność,
$E$- obciążenie (efekt oddziaływania, np. siła osiowa w pręcie).
Przy oznaczeniach jak wyżej definiuje się pojęcia::
funkcja stanu granicznego
| $g=R-E$ | (1) |
prawdopodobieństwo zniszczenia
| $p_f=Prob\{g \le 0\}$ | (2) |
współczynnik niezawodności $\beta$, wynikający z równania stanu granicznego $ \mu_g-\beta \sigma_g=0 $:
| $ \beta= \dfrac {\mu_g} {\sigma_g} $ | (3) |
prawdopodobieństwo zniszczenia
| $ p_f=Prob \{ g \le \mu_g- \beta \sigma_g \} $ | (4) |
prawdopodobieństwo przeżycia (sukcesu)
| $p_s=1-p_f$ | (5) |
Dla innych rozkładów $g$ niż normalny $\beta$ jest tylko umowną miarą niezawodności.
W niniejszym artykule będziemy używać również określeń i oznaczeń jak następuje:
Metoda Probabilistyczna– oznacza, że konstrukcja została tak obliczona, aby prawdopodobieństwo zniszczenia $p_f$ nie przekroczyło granicznej wartości $p_{f,lim}$ w określonym okresie czasu:
| $p_f \le p_{f,lim}$ | (6) |
Zawodność– jest związana z przejściem stanu granicznego od stanu pożądanego do stanu niepożądanego.
System konstrukcyjny lub układ konstrukcyjny lub model konstrukcji – idealizacja ustroju konstrukcyjnego, stosowana w celu analizy, w tym przypadku analizy niezawodnościowej.
$\Omega_i$- zdarzenie, polegające na tym , że i-ty element systemu pracuje bez uszkodzenia,
$p_{si}=Prob\{ \Omega_i\}$ – prawdopodobieństwo niezawodności i-tego elementu ( bezawaryjnej pracy elementu),
$ \overline Omega_i$ – zdarzenie, polegające na tym, że i-ty element ulegnie awarii (uszkodzeniu)
$p_{fi}=Prob \{ \overline \Omega_i\}=1-p_{si} $ – prawdopodobieństwo zniszczenia (awaryjności, zawodności, usterkowości, uszkodzenia ) i-tego elementu
Odpowiadające wielkości dla całego systemu będziemy oznaczać bez indeksu : $ \Omega$,c$p_s$, $\overline \Omega$, $p_f$ .
Niezawodność elementu
Prawdopodobieństwo $ p_{fi}$ zniszczenia i-tego elementu konstrukcji (awaryjność) wynosi
| $p_{fi} =Prob \{ R_i-E_i \}=Prob\{g_i<0\}$ | (7) |
Prawdopodobieńśtwo niezawodności (krótko nazywane niezawodnością) jest jest to prawdopodobieństwo przeciwne, czyli
| $p_{si} =1- p_{fi} $. | (8) |
Niezawodność może być też mierzona współczynnikiem niezawodności $\beta$, który jest po prostu odmierany w innej skali i jest wprost przeliczalny z prawdopodobieństwa zniszczenia lub niezawodności:
| $\beta_i = \Phi^{-1} (p_{fi}) $ | (9) |
W powyższych wyrażeniach zastosowano symbole:
$R_i$ -nośność i-tego elementu,
$E_i$ -efekt oddziaływania w i-tym elemencie (obciążenie) – siła przekrojowa (siła osiowa, moment zginający, bimoment, itd)
Z Probabilistycznego punktu widzenia można przyjąć, że element ma jedną określoną postać niespełnienia niezawodności. Ustrój może mieć więcej niż jedną postać, a może także składać się z dwóch lub więcej elementów, charakteryzujących się jedną postacią niespełnienia. Zakładamy, że rozkład prawdopodobieństwa nośności ${\cal N}(\mu_{Ri},\sigma_{Ri})$ oraz obciążenia ${\cal N}(\mu_{Ei},\sigma_{Ei})$ są normalne z parametrami: wartość oczekiwana (średnia) $\mu_{Ri}$, $\mu_{Ei}$ i odchylenie standardowe $\sigma_{Ri}$, $\sigma_{Ei}$ odpowiednio. Z własności addytywności rozkładu normalnego wynika, że w sposób ścisły również liniowa funkcja stanu granicznego (margines bezpieczeństwa) ma rozkład normalny ${\cal N}(\mu_{gi},\sigma_{gi})$ z parametrami:
wartość średnia
| $\mu_{gi}=\mu_{Ri}-\mu_{Ei}$ | (10) |
odchylenie standardowe ( zgodnie z zasadą sumowania kwadratów):
| $\sigma_{gi}^2=\sigma_{Ri}^2+\sigma_{Ei}^2$ | (11) |
Normalny rozkład prawdopodobieństwa, a współczynnik niezawodności
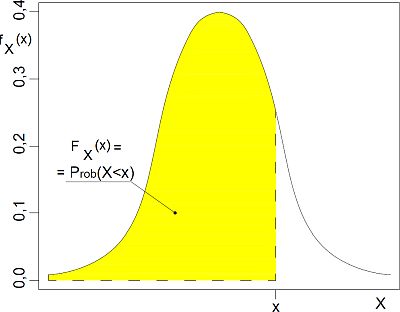
Na rys. 1 pokazano rozkład normalny zmiennej $X$. Kolorem żółtym oznaczono dystrybuantę dla wartości $x$ tej zmiennej.
| $p=Prob \{X<x\}= \Phi_X(x)= \int \limits_{-\infty} \limits^x f_X dx$ | (12) |
Dystrybuanta jest równa prawdopodobieństwu p tego , że zmienna X przyjmie wartości mniejsze od x.
Wartość $x$ zmiennej $X$ o rozkładzie $\Phi_X$ nazywamy kwantylem rzędu $p$, gdzie $0\le p<1$. Oznacza to, że kwantylem rzędu $p$ jest taka wartość $x$ zmiennej losowej $X$, że wartości mniejsze lub równe od $x$ są przyjmowane z prawdopodobieństwem co najmniej $p$, zaś wartości większe lub równe od $x$ są przyjmowane z prawdopodobieństwem co najmniej $1-p$.
Dystrybuantę rozkładu normalnego zmiennej $X$ o wartości średniej $\mu_X$ z odchyleniem standardowym $\sigma_X$ można wyznaczyć w arkuszu kakulacyjnym Excel za pomocą polecenia:
| $F_N (x)={\small ROZKL.NORMALNY} (x ; \mu_X; \sigma_X; k )$ | (13) |
gdzie: k jest parametrem o wartości k=1 w przypadku, gdy chcemy wyznaczyć dystrybuantę (rozkład skumulowany) $\Phi_X $ i o wartości k=0 , gdy wyznaczamy funkcję gęstości (rozkładzie) $f_X$ w punkcie $X=x$.
W dalszym ciągu będziemy potrzebować zarówno wartości dystrybuanty jak i funkcji gęstości rozkładu, a ponieważ wyznaczenie tych wartości w arkuszu kalkulacyjnym jest współcześnie podstawową umiejętnością , więc do techniki (13) będziemy często odwoływać się, ale już bez wskazywania na funkcję Excela. Z zależności (13) wynika , że w celu otrzymania dystrybuanty standaryzowanego rozkładu normalnego ${ \cal N }(0,1)$, tj rozkładu zmiennej losowej o wartości oczekiwanej $\mu=0$ i odchyleniu standardowym $\sigma=1$ dla wartości $x$ zmiennej $X$ należy użyć polecenia:
| $ p(0,1)= {\small ROZKL.NORMALNY } (x ; 0 ; 1; 1) $ | (14) |
W celu otrzymania wartości dystrybuanty dla dowolnego rozkładu normalnego ${ \cal N } (\mu,\sigma)$ ${ \cal N } (\mu,\sigma)$ (o danych wartościach średniej $\mu$ i odchylenia standardowego $\sigma$ ), wystarczy znajomość rozkładu standaryzowanego ${ \cal N } (0,1)$, bowiem
| Jeśli $X$ ma rozkład $ { \cal N } (\mu_X, \sigma_X)$, to $ \dfrac {X-\mu_X} {\sigma_X} $ ma rozkład standaryzowany $ { \cal N } (0, 1) $ | (15) |
Wyznaczenie dystrybuanty funkcją arkusza Excel jest bowiem wystarczająco dokładne również w zagadnieniach niezawodności budowlanych układów konstrukcyjnych, które charakteryzują się wysoką niezawodnością systemu, ale również elementów i potrzebą wyznaczania dystrybuanty w „ogonach” rozkładu prawdopodobieństwa.
Na znaczeniu straciły tablice rozkładu, dla inżynierów budownictwa, potrzebne dla zakresu dużych niezawodności.
Dla tych przypadków, w których należy przeprowadzić indywidualne obliczenia numeryczne bez możliwości wywołania funkcji arkusza Excel, na podstawie pracy [3] podajemy numeryczne formuły aproksymacyjne dystrybuanty standaryzowanego rokladu normalnego (13) :
| $\Phi(-t) \cong 1- \dfrac{1}{2} \small (+0,0498673470t + 0,0211410061t^2+0,0032776263t^3 + 0,0000380036t^4 +0,0000488906t^5+ 0,0000053830t^6)^{-16} \rm$ | (16) |
z dokładnością 1,5 10-7; dla t<0 zmienić znak.
| $\Phi(-t) \cong\sqrt {\dfrac {2}{\pi}} e^{-\dfrac{t^2}{2}} \left ( \dfrac {0,3193815} {t_z}-\dfrac{0,3565638} {t_z^2} + \dfrac{1,7814779} {t_z^3} – \dfrac{1,8212560}{t_z^4}+\dfrac{1,33027448} {t_z^5}\right ) $ | (17) |
gdzie zmienna pomocnicza ${\small t_z=1+0,2316419t }. $
Literatura
- PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
- PN-ISO 2394:2000, Ogólne zasady niezawodności konstrukcji budowlanych
- Korn T., M. (1983). Matematyka dla pracowników naukowych i inżynierów (Tom 1, 2). PWN, Warszawa
________________________________