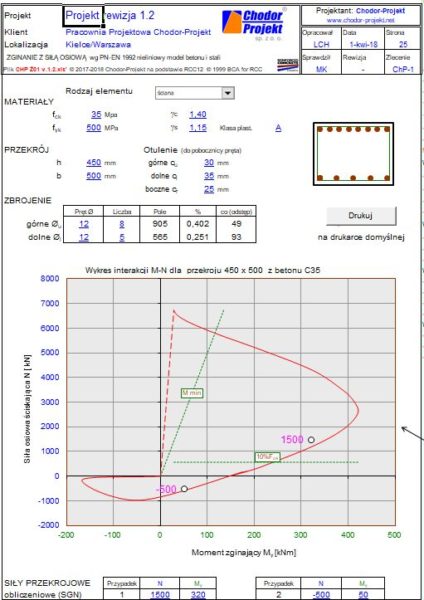
Kalkulator zbrojenia przekrojów zginanych i ściskanych lub rozciąganych, wykorzystujący nieliniowe krzywe interakcji przekroju żelbetowego  można bez opłat i rejestracji pobrać poprzez kliknięcie na rys.1. 

Opublikowano już rewelacyjny kalkulator  żelbetu umożliwiający  obliczenie zbrojenia ściskanego i zginanego przekroju prostokątnego  bez konieczności budowy krzywych interakcji. 

Rys.1. Kalkulator żelbetu M-N (CH-P Ż0.xls) rewizja 1.2 – kliknij na obraz, aby pobrać

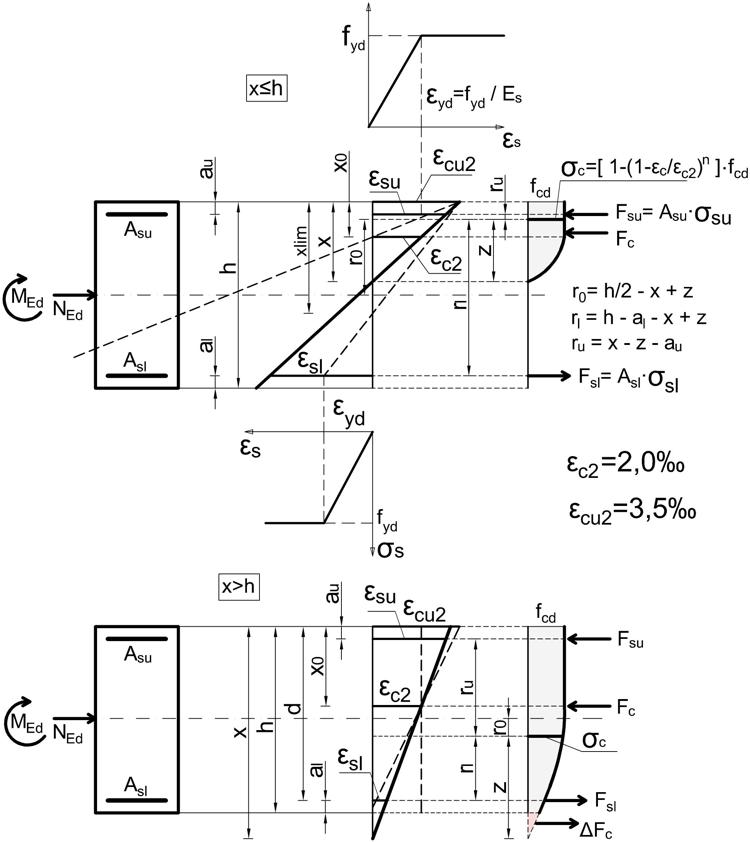
Kalkulator dotyczy  jednokierunkowo mimośrodowo ściskanego lub rozciąganego żelbetowego przekroju prostokątnego bxh zbrojonego podwójnie, pokazanego na rys. 2. Pręt żelbetowy jest nieliniowy konstrukcyjnie, ponieważ: 1) rozkład naprężeń w ściskanej strefie betonu jest nieliniowy, 2) stal zbrojenia jest materiałem sprężysto-plastycznym ze wzmocnieniem , 3) teoretyczna wysokość strefy ściskanej $x$ może przekroczyć wysokość przekroju $h$ i obejmować naprężenia pozorne. Nowy algorytm  projektowania przekroju żelbetowego opracowano z zastosowaniem nieliniowego modelu betonu [1] i modelu stali ze wzmocnieniem plastycznym [2] .  Projekty wykonane z użyciem kalkulatora, pozwalają na oszczędności  dochodzące do 30% zbrojenia, co przekracza oszczędności, które można uzyskać przy zastosowaniu standardowych procedur minimalizacji kosztu elementu żelbetowego (np. praca [3]) ).

Zaleca się, aby zestawy sił przekrojowych szacować  metodą imperfekcyjną  (teoria II rzędu z zadanymi  siłami imperfekcji) a jednocześnie pomijać współczynniki niestateczności. Wówczas obliczenia zbrojenia przekroju są zbrojeniem elementu (np słupa).

Udostępniona wersja arkusza ma chronioną treść i strukturę. Uwagi dotyczące udoskonalenia arkusza lub dostrzeżonych usterek proszę zgłaszać do autora na adres: leszek.chodor@chodor-projekt.net.

Postawienie problemu

Zagadnienie żelbetu  polega na poszukiwaniu  pięciu niewiadomych: wysokości strefy ściskanej $x$, pola zbrojenia dolnego ${A}_{sl}$ ,  górnego$A_{su}$_, a także naprężeń w stali $\sigma_{sl}$, $\sigma_{su}$ przy ograniczeniu maksymalnego odkształcenia betonu do wartości ε_cu2=3,5‰. Poszukiwane zmienne zilustrowano na rys.1. Do dyspozycji mamy tylko dwa warunki równowagi sił:  ΣX=0,  ΣM_i względem osi  „i= O, l lub u=(oś przekroju betonowego, oś dolnego zbrojenia, oś górnego zbrojenia)”. Wybór osi jest dowolny, ale tylko jeden z warunków ΣM jest niezależny. Trzeci i czwarty warunek określa fizyczne prawo dla zbrojenia górnego i dolnego. Piąty warunek jest określony przez prawo fizyczne betonu, które można zapisać w postaci:

$$\begin{equation}\sigma_c=E_c \cdot \varepsilon_c \label{s_cE}\end{equation}$$

gdzie moduł odkształcalności  E_c(ε_c, t) jest nieliniową funkcją odkształceń betonu oraz czasu $t$ i zmniejsza się istotnie wraz ze wzrostem pełzania betonu [1],Rys.3.2. .

W przypadku analizy przekrojów prętów model $(\ref{s_cE})$ można przyjąć w postaci równoważnej, niezależnej od czasu  $(\ref{s_cz})$ [1],wzory (3.17)-(3.18) :

$$\begin{equation}\sigma_c (z)= f_{cd} \cdot \begin {cases}
1, & \text {jeśli  $ \varepsilon_{c2} \le\varepsilon_c \le \varepsilon_{cu2}$} \\
1-  (1- \varepsilon_c/\varepsilon_{c2})^n, & \text {jeśli  $ \varepsilon_c <\varepsilon_{c2}$ }
\end {cases} \label{s_cz}\end{equation}$$

gdzie wykładnik modelu n=2 ,  f_cd – wytrzymałość obliczeniowa betonu na ściskanie.

Z zależności normowej $(\ref{s_cz})$, wynika, że obliczeniowy moduł odkształcalności betonu jest minimalny  dla włókna skrajnego (tam, gdzie odkształcenie ε_c=ε_cu2) i wynosi:

$$\begin{equation}E_{cu}=f_{cd}/\varepsilon_{cu2} \label{E_cu}\end{equation}$$

Moduł E_cu $(\ref{E_cu})$ zastosujemy w prezentowanym algorytmie jako parametr klasy betonu.
Na przykład dla betonu C30/37  graniczny moduł odkształcalności wynosi E_cu=(30/1,4)/3,5‰=6,1 GPa.
Dla porównania: średni moduł styczny dla  betonu C30/37 wynosi E_cm=32 GPa, a moduł długotrwały (z uwzględnieniem pełzania) E_c,eff=E_cm/[1+φ(∞,t₀)]≈E_cm/(1+2)=32/3=10,7 MPa. Pomiędzy modułami betonu E_cu, E_cm  oraz E_c,eff  w istocie nie ma związku z punktu widzenia rozpatrywanego zagadnienia.

Model obliczeniowy przekroju żelbetowego

Wypadkowa i moment naprężeń w betonie

Na rys.1. pokazano bryłę naprężeń w betonie, opisaną zależnością $(\ref{s_cz})$. Wymaga się [1], Tab.3.1. , by maksymalne odkształcenie betonu nie przekroczyło ε_cu2, a na granicy prosto-  i krzywo-liniowego  przebiegu naprężeń  odkształcenie betonu wynosi ε_c2.  W analizie   modelu z paraboliczną bryłą  naprężeń odkształcenia te wynoszą:

$$\begin{equation}  \varepsilon_{c2}=2,0 \text{%} \qquad  , \qquad \varepsilon_{cu2}=3,5 \text{%} \label{e_c2} \end{equation}$$

Rys.4 Model żelbetu

Po przekształceniu formuły $(\ref{s_cz})$ do postaci dogodnej od obliczeń numerycznych otrzymamy

$$\begin{equation}\sigma_c (z)= f_{cd} \cdot \begin {cases}
1 , & \text {jeśli  $z \ge (x-x_0) $} \\
1- [ 1- z/(x-x_0) ] ^n , & \text {jeśli  $ z < (x-x_0)$}
\end {cases} \end{equation}$$

gdzie długość wykresu prostoliniowego  x₀:

$$\begin{equation} x_0=\left (1-\varepsilon_{c2}/\varepsilon_{cu2}\right) \cdot x \end{equation}$$

Naprężenie σ_c  w odległości  „z” od osi obojętnej przekroju (od linii ε=0) działa na ramieniu:

$$\begin{equation}  r_i= d_i – x + z , \quad  (i=O,l,u) \end{equation}$$

gdzie efektywne ramię $d_i$ zależnie od osi do której jest odmierzane, wynosi:

$$\begin{equation}d_i = \begin {cases}
h/2,  & (i=O)\\
h-a_l,  & (i=l) \\
a_u,  & (i=u)
\label {signM_c} \end {cases} \end{equation}$$

uwaga ($\ref {signM_c}$):  moment o wartości $M_c=\sigma_c\cdot r_i$ jest lewoskrętny dla $i=O, l$, to znaczy ma zwrot  reakcji $M_{Rd}$ (jest przeciwny do obciążenia zewnętrznego $M_{Ed}$), a jest prawoskrętny dla $i=u$.

Rozpatrzymy  dwa przypadki wysokości strefy ściskanej, pokazane na rys.1.:
 X<h dla wysokości strefy ściskanej x ≤ h 
 X>h dla wysokości strefy ściskanej x > h

W przypadku X_<h wypadkowa bryły naprężeń w betonie wynosi

$$\begin{equation}F_c^{x<h}= b \cdot \int \limits _0^x\sigma _c \cdot dz= b \cdot f_{cd} \cdot \left( \int \limits _0^{x_0} \left \{ 1- \left [1- z/(x-x_0) \right ]^2 \right \} \cdot dz + \int \limits _{x_0}^x dz \right )= \dfrac{17}{21}\cdot b \cdot x \cdot f_{cd} \label {Nc<} \end{equation}$$

a moment tej bryły:

$$\begin{equation}M_{c,i}^{x<h}= b \cdot \int \limits _0^x\sigma _c \cdot dz= b \cdot f_{cd} \cdot \left( \int \limits _0^{x_0} \left \{ 1- \left [ 1- z/(x-x_0) \right ]^2 \right \} r_i \cdot dz + \int \limits _{x_0}^x r_i \cdot dz \right )= F_c \cdot d_i- M_c(x^2)  \label {Mc<} \end{equation}$$

gdzie $ M_c (x^2) = \dfrac {33} {98} \cdot b \cdot  x^2 \cdot f_{cd}$.

przy czym zwroty tych momentów zdefiniowano w uwadze ($\ref {signM_c}$).

Siły przekrojowe od obciążeń zewnętrznych $(N,M)_{Ed}$ uzyskuje się z rozwiązania problemu mechaniki budowli sprowadzone do osi przekroju betonowego, a w przypadku przekroju prostokątnego do osi „0”. Dlatego z punktu widzenia prezentowanego algorytmu najważniejszy jest przypadek „i=0”, czyli dla $d_i=d_0=h/2$.  W tradycyjnym podejściu często wykorzystywało się warunki dla „i=L”, co w szczególnych przypadkach prowadzi do uproszczenia formuł obliczeniowych. Takich uproszczeń nie wykorzystujemy, ze względu na brak ich ogólności.

W przypadku X_>h  na skutek tego, że pod przekrojem (na odcinku x do h) naprężenia faktycznie nie działają, a były wliczone w wyrażenia dla przypadku X_<h,  wyrażenia $(\ref{Nc<})$ i $(\ref {Mc<})$ należy skorygować:

$$\begin{equation} \begin {cases}
F_c^{x>h}= F_c^{x<h} -\Delta F_c^{x>h}\\
M_{c,i}^{x>h}=M_{c,i}^{x<h} -\Delta M_c^{x>h}
\end {cases} \label {N,Mc>}\end{equation}$$

Fragment bryły naprężeń dla z∈ [0; x-h] na rys.1. oznaczono kolorem lekko czerwonym. Daje on następujące „nadmiarowe”:  siłę Δ F_c^x>h  oraz  moment Δ M_c^x>h bryły naprężeń w betonie:

$$\begin{equation}\Delta F_c^{x>h}=b \cdot f_{cd} \cdot \int \limits _0^{x-h} \left \{ 1- \left [1- z/(x-x_0) \right ]^2 \right \} \, dz = F_N \cdot(21+20 \overline x) \label{dF_c>}\end{equation}$$

$$\begin{equation}\Delta M_{c,i}^{x>h}=b \cdot f_{cd} \cdot \int \limits_0^{x-h} \left \{ 1- \left [1-z/(x-x_0) \right ]^2 \right \} \cdot r_i \, dz= F_N\cdot h \cdot \begin {cases}
– (\, 7+8 \overline x+9 \overline x^2 \,) \text { : (i=O)}\\
[\, 7+2 \overline x – 9 \overline x^2 –  4 \overline a_l (7+5\overline x)\, ] \text { : (i=l)}\\
[ \, 21+18 \overline x + 9 \overline x^2 – 4 \overline a_u (7+5\overline x)\, ]  \text { : (i=u)}
\end {cases} \label{dM_c>}\end{equation}$$

gdzie: $\overline x=x/h$ ,  $\overline a_l=a_l/h$ , $\overline a_u=a_u/h$ , $ F_N = \dfrac{7}{192} \dfrac{(1-\overline x)^2}{\overline x^2} \cdot b \cdot h\cdot f_{cd}$.

Przypadek X_>h  w praktyce zachodzi rzadko, jednakże w celu wyznaczenia  krzywych interakcji w całym zakresie pracy pręta, korektę $(\ref{dF_c>})$,$(\ref{dM_c>})$ należy stosować.

Model stali zbrojeniowej

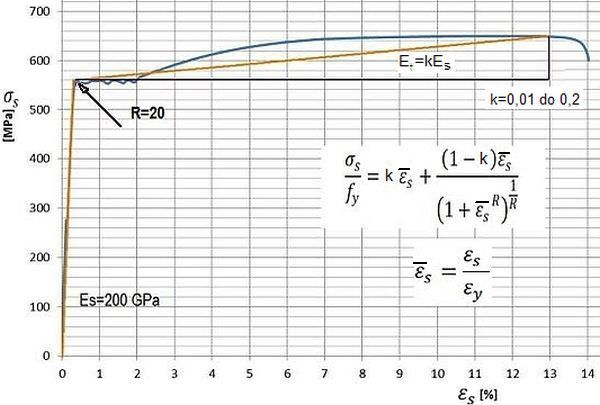
Na rys. 3 pokazano  nieliniowy model stali [2] ,  opisany formułą :

$$\begin{equation}\overline\sigma_s =k\cdot \overline\varepsilon_s + \dfrac{(1-k)\cdot {\overline\varepsilon_s}} {\left (1+{\overline\varepsilon_s}^R \right)^{1/R}}\label {s_s}\end{equation}$$

Rys.3. Model stali zbrojeniowej ( linia pomarańczowa), (wykres rzeczywisty- linia niebieska)

Sieczny moduł odkształcalności stali zdefiniujemy jako

$$\begin{equation}E_{si}=k_{si}\cdot E_s \text{ (i=l, 2)} \label {E_si}\end{equation}$$

gdzie

$$\begin{equation}k_{si} = k+\dfrac{1-k}{ \left (1+{\overline \varepsilon_s}^R \right)^{1/R}} \label{k_si} \end{equation}$$

Można przyjąć, że pręt rozciągany ($\varepsilon_{sc}>0$)  jest nieskrępowany na skutek zarysowań betonu rozciąganego.  Wobec tego naprężenie  w pręcie rozciąganym „i=t” wynosi

$$\begin{equation} \sigma_{st}= E_{sc}\cdot \varepsilon_{st} \label {s_st} \end {equation} $$.

W przypadku pręta otoczonego betonem ściskanym redukujemy naprężenia w stali ściskanej „i=c” o naprężenia w betonie, co można zapisać

$$\begin{equation} \sigma_{sc}= E_{si} \cdot \varepsilon_{sc} -\sigma_c (\varepsilon_{c}=\varepsilon_{sc}) \label {s_sc}\end {equation}$$

gdzie $\sigma_c$ wyznacza się z zależności ($\ref{s_cz}$).

W obu stanach wytężenia pręta ($\ref{s_st}$) i  ($\ref{s_sc}$)  ograniczamy odkształcenia pręta $\varepsilon_s < \varepsilon_{uk}/\gamma_s$  ($\ref{k_s}$) , co skutkuje ograniczeniem naprężeń (choć dopuszcza naprężenia w stali większe od  $f_{yd}$).

Siły w prętach zbrojenia wyznaczamy w sposób standardowy:

$$ \begin{equation} F_{si}=\sigma_{si}\cdot  A_{si} \label{N_si} \end{equation}$$

Równowaga przekroju i równanie żelbetu

Warunki równowagi przekroju

Na rys.1 pokazano siły działające w przekroju z przyjętą konwencją znakowania sił zewnętrznych:  zewnętrzny moment  zginający $M_{Ed}$ jest dodatni jeśli rozciąga dolne włókna przekroju, zewnętrzna siła osiowa$N_{Ed}$ jest dodatnia, jeśli ściska przekrój. Założono też dodatnie zwroty sił wewnętrznych: siły  $F_c$ i $F_{su}$ są ściskające, siła $F_{sl}$ jest rozciągająca. Jeśli z rozwiązania zadania uzyskamy znaki ujemne, to będzie oznaczało, że w danej sytuacji obliczeniowej siła działa przeciwnie do założonego zwrotu.

Warunki równowagi przekroju zapiszemy w postaci :

$$\begin{equation} \begin {cases}
\Sigma X        :  N_{Ed} = F_c + F_{su}  – F_{sl}\\
\Sigma M_0  :  M_{Ed} = M_{c,0} + F_{su} \cdot (d_0 – a_u) + F_{sl} \cdot (d_0 – a_l)
\end {cases} \label {R1}\end{equation}$$

Warunki równowagi  ($\ref{R1}$) można zapisać w postaci równoważnej  w drodze wyeliminowania z $\Sigma X$  kolejno F_sl lub F_su  i podstawieniu do $\Sigma M_0$:

$$\begin{equation} \begin {cases}
M_{Ed} = M_{c,0}  – (N_{Ed}- F_c) \cdot (d_0 – a_l )  + F_{su}\cdot d_s \\
M_{Ed}  = M_{c,0} +  ( N_{Ed}- F_c) \cdot (d_0 – a_u)  +F_{sl}\cdot d_s
\end {cases}  \label {R2}\end{equation}$$

gdzie $d_s=h-a_l-a_u$.

Równanie żelbetu

Po dodaniu stronami  obu równań $(\ref{R2})$ i po przekształceniach otrzymamy podstawowe równanie żelbetu:

$$\begin {equation} F_{sl} +F_{su}= \dfrac {2 (M_{Ed}-M_{c,0})} {d_s}+ (N_{Ed}-F_c) \label {Rzelbet} \end {equation}$$

Równanie żelbetu $(\ref{Rzelbet})$ zawiera ogólne informacje o modelu i w zależności od sytuacji obliczeniowej może stanowić układ równań z jednym z równań  równowagi $(\ref{R1})$ lub $(\ref{R2})$.

Równanie $x^2$

Dla przypadku X_<h po podstawieniu  wyrażeń na  $ F_c (\ref {Nc<})$  i  $ M_c  ( \ref {Mc<})$  do  równania żelbetu $(\ref{Rzelbet})$ otrzymamy równanie drugiego  stopnia ze względu na $x$:

$$\begin{equation}Ax^2+Bx+C=0 \label {X2}\end{equation}$$

gdzie:
$A=33/49$,
$B= -17/21\cdot (h+d_s)$,
$C= (C_1+C_2) /(b\cdot f_{cd})$,
$C_1= – (A_{sl}\cdot \sigma_{sl} + A_{su} \cdot \sigma_{su}) \cdot d_s$
$C_2= 2 M_{Ed}+N_{Ed}\cdot d_s$,

Założenie płaskich przekroi i przypadki wytrzymałościowe

Równanie $(\ref{X2})$ jest tylko pozornie kwadratowe, ponieważ współczynnik  C₂ zależy od σ_si, (i=l,u) , a naprężenie w stali zbrojeniowej jest funkcją odkształcenia zgodnie z $(\ref{s_s})$. Odkształcenia z kolei podlegają  zasadzie płaskich przekroi Bernoulliego , wyrażonej formułami  ($\ref{Proporcje}$) wynikającymi z  rys. 1:

$$\begin {equation} \dfrac{\varepsilon_{sl}}{d_l-x}= \dfrac{\varepsilon_{su}}{x – d_u}=\dfrac{\varepsilon_{cu2}}{x} \label {Proporcje} \end {equation}$$

Z zależność $(\ref{Proporcje})$ można uzyskać jawną postać odkształcenia zbrojenia górnego (u) i dolnego (l):

$$\begin {equation} \varepsilon_{sl}=\varepsilon_{cu2} \cdot (d_l /x-1) \qquad \varepsilon_{su}=\varepsilon_{cu2} \cdot (1 – d_u/x) \label {eslu} \end {equation}$$

Z $(\ref{eslu})$ wynika, że zależnie od relacji wysokości strefy ściskanej $x$ oraz wysokości użytecznych zbrojenia zachodzą następujące przypadki wytrzymałościowe:

T (ang. Tension)$x=0$ – przypadek dla którego odkształcenia w stali są nieokreślone. Odpowiada to jedorodnemu rozciąganiu przekroju, w którym w całym przekroju (w betonie i stali) mamy odkształcenia rozciągające, a przypadek  należy rozpatrywać w języku przekrojów zespolonych. Takim przypadkiem nie zajmujemy się w niniejszym artykule.

SE (ang. Small Eccentricity) $  x > d_u \,  x \le d_l \to $  $\varepsilon_{su} > 0$,  $\varepsilon_{sl} > 0$, oba zbrojenia są ściskane – jest to przypadek małego mimośrodu.

LE (ang. Large Eccentricity) $  x > d_l  \to $\varepsilon_{su} > 0$,  $\varepsilon_{sl} < 0$, czyli zbrojenie górne jest ściskane, a zbrojenie dolne rozciągane  – jest to przypadek dużego mimośrodu,

Do przypadku LE zaliczymy też $ x \le d_u  \to$  $\varepsilon_{su}\le 0$,  $\varepsilon_{sl} > 0$, dla którego  zbrojenie górne jest rozciągane, a dolne ściskane. Wystarczy analizować przekrój odwrócony o 90⁰ .

Przypadki X_>h  oraz   X_<h są w istocie jednym z SE lub LE.

Równanie $x^3$

Po podstawieniu do $(\ref{X2})$ formuł zasady płaskich przekroi ($\ref{Proporcje}$) oraz prawa fizycznego $\sigma_{si}=E_{si}\varepsilon_{si}$ warunek  równowagi można zapisać w  postaci równania sześciennego (zwanego równaniem $x^3$):

$$\begin{equation} Ax^3+Bx^2+Cx+D=0 \label {X3}\end{equation}$$

gdzie:
$A=33/49$,
$B= -17/21\cdot (h+d_s)$,
$C= (C_1+C_2) /(b\cdot f_{cd})$,
$C_1= – (A_{sl}\cdot n_{El} + A_{su} \cdot n_{Eu}) \cdot d_s \cdot f_{cd}$
$C_2= 2 M_{Ed}+N_{Ed}\cdot d_s$,
$D= [A_{sl}\cdot n_{El}\cdot (h-a_l) + A_{su}\cdot n_{Eu}\cdot a_u]\dfrac{d_s}{b}$

Algorytm wyznaczania nośności (interakcji) przekroju

Dwuparametrową nośność przekroju zginanego i ściskanego lub rozciąganego $(M,N)_{Rd}$  wyznaczają równania równowagi ($\ref{R1}$) po zamianie indeksów $Ed$ na $Rd$:

$$\begin{equation} \begin {cases}
N_{Rd} =  F_c + F_{su} –  F_{sl}\\
M_{Rd}= M_{c,0}+ F_{su} \cdot (d_0 – a_u) + F_{sl} \cdot (d_0 – a_l) \end{cases} \label {Interakcja} \end{equation}$$

Warunki nośności przekroju są zachowane, gdy spełniona jest nierówność

$$\begin{equation} (M,N)_{Ed} \le (M,N)_{Rd} \label{E<R} \end{equation}$$

Na rys. 3 pokazano przykład krzywych interakcji  (linie w kolorze czerwonym) i obszarów interakcji (wewnątrz obszaru objętego czerwonymi liniami) dla konkretnneg o przekroju żelbetowego. Kółkami oznaczono dwie pary sił zewnętrznych $(N,M)_{Ed}$  dla których przekrój ma wystarczającą nośność ( punkty wypadają wewnątrz obszaru interakcji).

W celu wyznaczenia krzywych interakcji , przykładowo pokazanych na rys.3 stosujemy procedurę zastosowaną w arkuszach obliczeniowych [5] , sprowadzona do następujących kroków:

1. Przyjąć przedział wysokości strefy ściskanej [$x_{min}$ ; $x_{max}$] i podzielić go na kilkadziesiąt przedziałów o szerokości $\Delta x$
2. Dla kolejnych wartości $x_i=x_{i-1}+\Delta x$ wyznaczyć kolejno:
   2.1. odkształcenia w stali ($\ref{Proporcje}$),
   2.2. naprężenia ($\ref{s_st}$), ($\ref{s_sc}$) i siły w zbrojeniu ($\ref{N_si}$),
   2.3. wypadkową ($\ref {Nc<}$) i moment ($\ref {Mc<}$) naprężeń w betonie, a jeśli $x>h$ skorygowane ($\ref {N,Mc>}$),
   2.4. nośność przekroju ($\ref {Interakcja}$),
3. Uzyskane punkty obwiedni nośności nanieść  na wykres i połączyć liniami prostymi lub funkcjami sklejanymi.

Kalkulator żelbetu

Struktura informatyczna  prezentowanego arkusza kalkulacyjnego –  rys.1. jest wzorowana na [5] (obliczenia wg normy angielskiej i uproszczonej procedury) i jest dostosowana do obliczeń wg Eurokod 2 oraz nieliniowych modeli stali oraz betonu.

Uwaga do ukośnego zginania i ściskania

Rozszerzenie zadania na ukośne (dwukierunkowe) zginanie ze ściskaniem/rozciąganiem przedstawiono w artykule Model żelbetu My-Mz-N. Rozszerzony algorytm , obejmuje praktycznie wszystkie spotykane w praktyce przypadki projektowania belek lub słupów o przekroju prostokątnym.

 Literatura

1. PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
2. Menegotto M., Pinto P., E. (1973). Method of analysis of cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under normal force and bending. [Preliminary Report IABSE]
3. Mohammad F. A., Seyan D. A. (2016). Optimum design of reinforced concrete rec-tangular columns subjected to axial compression and biaxial bending mo-ments. Athens Journal of Technology and Engineering, 3 (2
4. Filippou F., C., Popov E. P., Bertero V. V. (1983), Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints [Report EERC]. Earthquake Engi-neering Research Center, University of California, Berkeley
5. The Concrete Centre. (1999). RC Spreadsheets (1999). MPA The Concrete Center, UK London, [ http://www.concretecentre.com/Publications-Software/RC-Spreadsheets-v4B-2.aspx ]

________________________________