(2019-04-19, 30) Wersja 1.0
(2025-06-09) [Scalono artykuły dotyczące imperfekcji konstrukcji stalowych, żelbetowych, zespolonych murowych i drewnianych]
Uwagi i recenzje podręcznika przesyłać na adres leszek@chodor-pojekt.net
Artykuł w ciągu ostatnich 24 godzin czytało 4 Czytelników
Imperfekcyjna metoda projektowania. Część 3: Imperfekcje (niedoskonałości) konstrukcji budowlanych
Nawigacja: [ Geneza metod imperfekcyjnych ] ⇐ ⊗ ⇒ [ Alternatywne, zintegrowane imperfekcje konstrukcji ] ⇒ [następne R3-6] [ Imperfekcje łukowe łuków ] ⇒ [ Imperfekcje konstrukcji zespolonych i aluminiowych ]
spis treści prodręcznika: [ Imperfekcyjna metoda projektowania konstrukcji ]
Stosowanie metod imperfekcyjnych we współczesnych normach projektowych jest spójne dla podstawowych rodzajów konstrukcji: żelbetowych Eurokod 2 [1], metalowych Eurokod 3 [2], zespolonych Eurokod 4 [3], drewnianych Eurokod 5 [4], murowych Eurokod 6 [5], a także aluminiowych Eurokod 9 [6]. Wszystkie te normy zgodnie stwierdzają, że konstrukcje należy projektować według ogólnych zasad, podanych w normie podstawowej Eurokod [7]. Zasady te można uważać za spełnione, jeśli w projektowaniu zastosowano metodę stanów granicznych i częściowych współczynników bezpieczeństwa, a kombinacje obciążeń przyjęto zgodnie z tą normą oraz oddziaływania według zespołu norm Eurokod 1. Pozostałe, szczegółowe zasady projektowania konstrukcji w tym stosowanie współczynników wyboczeniowych jest zgodnie z ogólną zasadą dobrowolnego stosowania norm przez Projektanta (p. artykuł Kombinacje obciązeń w Eurokodach).
Imperfekcje konstrukcji, a współczynniki bezpieczeństwa
W miejsce stosowania współczynników wyboczeniowych można stosować bezpośrednie metod imperfekcyjne. Niezależnie od tego – do imperfekcji innych niż geometryczne (systemowe), należy stosować współczynniki bezpieczeństwa
Podstawowe założenia norm Eurokod
Postanowienia norm Eurokod zostały skonstruowane przy następujących założeniach:
1. Procesy losowe obciążeń są uwzględnione w systemie współczynników obciążeń $\gamma_F$ , stosowanym jednocześnie ze współczynnikami kombinacyjnymi (redukcyjnymi) $\psi_i (i=0,1,2)wg formuły [8]
$$ \begin{equation} F_d=”=” \sum \limits_{j \ge 1} \xi_j \cdot \gamma_{G,j} \cdot G_{k,j} „+” \gamma_P \cdot P „+” \gamma_{Q,1} \cdot Q_{k,1} \sum \limits_{i>1} \psi_j \cdot \gamma_{Q,i} \cdot Q_{k,i} \label {1} \end{equation}$$
gdzie:
$”=”$ oznacza symboliczną równość
$”+”$ uwzględnić w kombinacji
$\sum$ łączny efekt
$\xi_j$ , $ \gamma_{G,j}$ – współczynnik redukcyjny oraz współczynnik obciążeń dla j-tych charakterystycznych (indeks „k”) obciążeń stałych $G_{k,j}$
$\gamma_P$ – współczynnik obciążeń dla sił od sprężenia $P$
$\gamma_{Q,1} $ – współczynnik obciążeń dla wiodącego obciążenia zmiennego $Q_{k,1} $
$\psi_i$ , $ \gamma_{Q,i}$ -0 współczynnik redukcyjny oraz współczynnik obciążeń dla i-tych charakterystycznych (indeks „k”) obciążeń zmienych $Q_{k,i}$
Zasady stosowania reguły $\ref{2}$) omówiono w artykule Kombinacje obciążeń w Eurokodach.
2. Losowość cech materiałów (np. granicy plastyczności $f_y$ stali lub wytrzymałości betonu $f_c$) jest uwzględniona poprzez stosowanie w obliczeniach kwantyli tych losowych zmiennych, czyli wartości obliczeniowych, np. $f_{*d} =\cfrac{f_{*k}}{\gamma_M}$, gdzie – $f_{*k}$ wytrzymałość charakterystyczna, – $\gamma_M$ współczynniki materiałowe
3. Wpływ odchyłek wymiarów przekrojów jest uwzględniony w systemie materiałowych współczynników bezpieczeństwa. System materiałowych współczynników bezpieczeństwa jest zwykle rozbudowany i w zależności od konstrukcji i sytuacji obliczeniowej dotyczy i integruje w sobie rozmaite natury rozproszenia cech.
4. W systemie współczynników bezpieczeństwa nie są ujęte imperfekcje systemowe, czyli przesunięcia węzłów systemu od położenia projektowanego, a także wstępne ugięcia i skręcenia elementów (prętów, powłok i brył) wyodrębnionych z systemu konstrukcyjnego. Uwzględnienie tych zjawisk wymaga wprowadzenia do procesu projektowego metod innych niż częściowe współczynniki bezpieczeństwa. Klasycznie efekty te uwzględnia się systemem współczynników wyboczeniowych stosownym jednocześnie ze współczynnikami korelacyjnymi, ale oraz częściej w to miejsce wprowadza się imperfekcyjne metody projektowania
System współczynników bezpieczeństwa w normach Eurokod
Zależnie od specyfiki materiału , z którego wykonana jest konstrukcja – definiuje sie specyficzny zestaw częściowych współczynników bezpieczeństwa:
- w normie do projektowania konstrukcji żelbetowych [1] przyjęto następujący system współczynników bezpieczeństwa:
$\gamma_M$ – częściowy do właściwości materiału, określony z uwzględnieniem niepewności, co do samej właściwości materiału, co do odchyleń geometrycznych i co do zastosowanego modelu obliczeniowego,
$\gamma_m$ – do właściwości materiału, określony z uwzględnieniem wyłącznie niepewności właściwości materiału,
$\gamma_s$ – do stali zbrojeniowej lub sprężającej, - w normie do projektowania konstrukcji stalowych [2] i [9] mamy system współczynników bezpieczeństwa:
$\gamma_{M0} $ przy sprawdzaniu nośności przekroju poprzecznego,
$\gamma_{M1} $ przy sprawdzaniu stateczności elementów,
$\gamma_{M2} $ do właściwości śrub, nitów, sworzni, spoin, nośności na rozerwanie,
$\gamma_{M3} $ do nośności na poślizg,
$\gamma_{M4} $ do nośności na docisk śrub z iniekcją,
$\gamma_{M5} $ do nośności węzłów kratownic z kształtowników rurowych,
$\gamma_{M6 ser} $ do nośności sworzni w stanie granicznym użytkowalności,
$\gamma_{M7} $ do sprężania śrub wysokiej wytrzymałości,
$\gamma_{c} $ do betonu - w normie do projektowania konstrukcji zespolonych [3] system współczynników bezpieczeństwa obejmuje:
$\gamma_{M}$ ogólnie do właściwości materiałów, uwzględniający również niepewność geometrii i odchyłki wymiarowe,
$\gamma_{M0}$ do stali konstrukcyjnej,
$\gamma_{s}$ do zbrojenia stalowego,
$\gamma_{Mf}$ do wytrzymałości zmęczeniowej,
$\gamma_{Mfs}$ do wytrzymałości zmęczeniowej łączników ścinanych,
$\gamma_{V}$ do wytrzymałości zmęczeniowej łączników ze łbami,
$\gamma_{Vs}$ dla płyt zespolonych. - w normie do projektowania konstrukcji aluminiowych [6] przewiduje następujący system współczynników bezpieczeństwa:
$\gamma_{M1}$ dotyczący nośności przekroju bez względu na jego klasę,
$\gamma_{M1}$ stosowany przy sprawdzaniu stateczności elementu,
$\gamma_{M2}$ stosowany przy sprawdzaniu nośności przekroju ze względu na rozerwanie,
$\gamma_{Mf}$ dotyczący zmęczenia,
$\gamma_{M3}- \gamma{M7}$ stosowane do połączeń,
$\gamma_{Mw}$ do połączeń spawanych,
$\gamma_{Mp}$ do połączeń sworzniowych,
$\gamma_{Ma}$ dotyczący połączeń klejowych,
$\gamma_{Mser}$ dotyczący stanu granicznego użytkowalności, - w normie do projektowania konstrukcji drewnianych [4], mamy:
$\gamma_{M}$ do właściwości materiału, uwzględniający także niedoskonałości modelowania i odchyłki wymiarowe, - w normie do projektowania konstrukcji murowych [5], mamy:
$\gamma_{M}$ współczynnik częściowy dla właściwości materiałów, uwzględniający również niepewność modelu i odchyłki wymiarowe,
Zjawiska opisane współczynnikami wymienionymi wyżej nie powinny być dodatkowo włączane do analizy konstrukcji i nie będziemy się nimi zajmować w tej pracy.
Szczególne miejsce systemowych imperfekcji geometrycznych
Nie wszystkie imperfekcje konstrukcji da się zamknąć w częściowych współczynnikach bezpieczeństwa. Takie imperfekcje zajmują szczególne miejsce w wytycznych normalizacyjnych. Są to systemowe imperfekcje geometryczne, uwzględniające następujące zjawiska:
- odchyłki geometryczne osi lub płaszczyzn elementów od położenia oczekiwanego, wynikające z tolerancji wykonawczych, określone w normach wyrobów i normach wykonania;
- odchyłki konstrukcji, wytwórcze i montażowe , to znaczy odchylenia od zaplanowanego kształtu w tym zmiany położenia obciążeń, takich jak odchyłki pionowości, prostoliniowości, płaskości lub dopasowania oraz obecność nieuniknionych mimośrodów w węzłach nieobciążonej konstrukcji ;
- naprężenia własne w elementach stalowych.
Systemowe imperfekcje geometryczne nie zawierają imperfekcji przekrojów elementów, które są ujęte w systemie częściowych współczynników bezpieczeństwa.
Podstawowe normy zgodnie stwierdzają, że przy obliczaniu stateczności i wytrzymałości konstrukcji należy brać pod uwagę efekty drugiego rzędu, w tym naprężenia własne, imperfekcje geometryczne, miejscową niestateczność, zarysowanie, skurcz i pełzanie betonu oraz uplastycznienie stali konstrukcyjnej i zbrojenia. Konstrukcja powinna być tak zaprojektowana by zapewnić stateczność konstrukcji i wytrzymałość przekrojów w najbardziej niekorzystnych kombinacji oddziaływań w stanach granicznych nośności,. Efekty drugiego rzędu należy uwzględniać w każdym kierunku, w którym może nastąpić zniszczenie, jeśli wpływają znacząco na stateczność konstrukcji.
Jednocześnie zaleca się aby: przyjmowany w obliczeniach kształt globalnych i lokalnych imperfekcji określać na podstawie postaci wyboczenia sprężystego układu w rozpatrywanej płaszczyźnie [2]. Przewidywane imperfekcje powinny w rozpatrywanej płaszczyźnie wyboczenia w najbardziej niekorzystnych kierunkach i kształcie [3].
W badaniach [10], i innych (np. [11]) wykazano, że sprężyste postacie wyboczenia praktycznie nie realizują się w rzeczywistych konstrukcjach. Podejście zgodne z tą ideą prezentuje norma żelbetowa [1], poprzez wskazanie, że „czyste wyboczenie” nie jest stanem granicznym, który mógłby nastąpić w rzeczywistej konstrukcji, obarczonej imperfekcjami i na którą działają obciążenia poprzeczne. Tym niemniej do czasu powszechnego wdrożenia w projektowaniu procedur geometrycznie i materiałowo nieliniowych, należy przyjmować przybliżenie, poprzez przyjecie, że utrata stateczności następuje w zakresie sprężystym.
W postanowieniach norm konstrukcyjnych: żelbetowych [1], stalowych [2] , aluminiowych [6] i zespolonych [3] wprowadzono następujące typy systemowych imperfekcji geometrycznych konstrukcji:
- imperfekcje globalne przechyłowe, które oznaczamy symbolicznie (UGI) oraz stosujemy indeks G.
- imperfekcje lokalne (łukowe), które oznaczamy symbolicznie (EGI) oraz stosujemy indeks L.
Oba te typy szeregujemy w geometrycznych imperfekcjach systemowych, celem odróżnienia od innych imperfekcji geometrycznych, w tym imperfekcji charakterystyk geometrycznych przekrojów prętów i powłok, które są ujęte w materiałowych częściowych współczynnikach bezpieczeństwa.
Imperfekcje konstrukcji stalowych
W normie do projektowania konstrukcji stalowych Eurokod 3 [2] zdefiniowano oryginale zasady, stanowiące podstawę metod imperfekcyjnych. W normie tej dopuszczono jeszcze stosowanie historycznych metod wyboczeniowych, a zasady metody imperfekcyjnej były udoskonalane w normach publikowanych w kolejnych latach dla konstrukcji żelbetowych, zespolonych i aluminiowych.
Zgodnie z [2], kl.5.2.3(3), w celu uwzględnienia systemowych imperfekcji geometrycznych konstrukcji stalowych wrażliwych na efekty drugiego rzędu (w tym ram przechyłowych) można stosować uproszczoną metodę zastępczych imperfekcji geometrycznych przechyłowych i łukowych. Za dokładniejszą uznaje się metodę alternatywną, przedstawioną w dalszej części podręcznika, zgodnie z którą imperfekcje geometryczne określane są ze zintegrowanej postaci wyboczenia sprężystego. Wśród postaci wyboczenia sprężystego można wydzielić postać przechyłową lub łukową, symetryczną lub niesymetryczną, giętną lub skrętną itd., choć w ogólności jest to trudne ze względu na sprzężenie postaci wyboczenia i przy zastosowaniu współczesnych metod projektowaniu jest niepotrzebne.
Zaczniemy od przedstawienia zasad oryginalnych i w kolejnych punktach będziemy przedstawiali udoskonalenia metody, tak by w konkluzjach wskazać na syntezę zasad, które stanowią punkt wyjścia do uogólnień wprowadzanych w podręczniku.
Imperfekcje przechyłowe
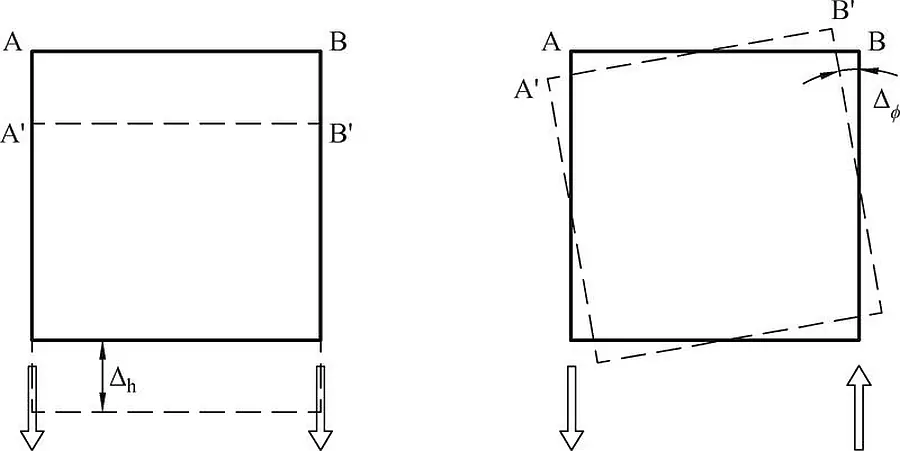
Na Rys. 1 pokazano model przyjmowany w Eurokod 3 do analizy globalnych imperfekcji systemów konstrukcyjnych. W modelu zakłada się, że na skutek niezamierzonych odchyłek, budowla o wysokości h pochyli się w kierunku poprzecznym o kąt $\Phi$ , ale też pochyli się o taki kąt w kierunku podłużnym – w płaszczyźnie rzędu słupów.
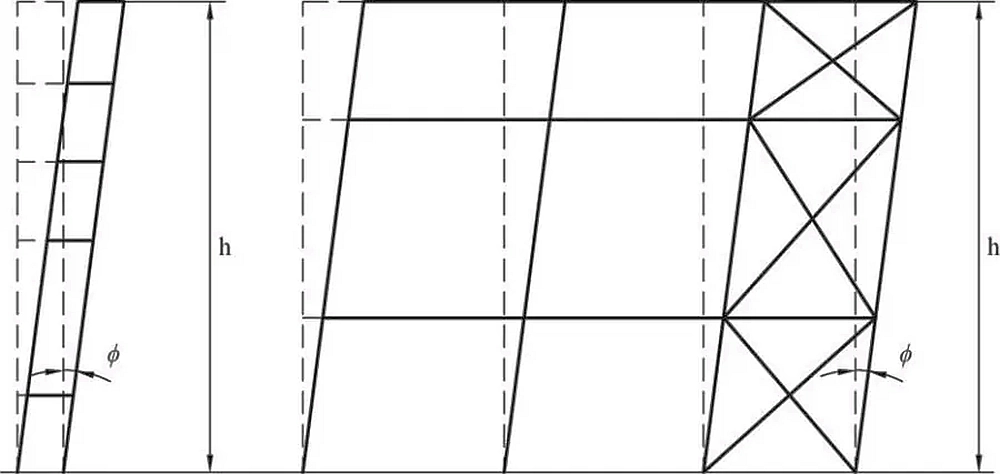
Rys.1 Imperfekcje przechyłowe UPI, [2], rys. 5.2
Podstawowa i jednocześnie największa możliwa wartość pochylenia wynosi:
$$\begin{equation}\Phi_0=\cfrac{1}{200} \to n_{\Phi,0}=200 \label {2} \end{equation}$$
Przechył ($\ref{2}$) może być zredukowany współczynnikami redukcyjnymi $\alpha_h$ oraz $\alpha_m$:
$$\begin{equation} \alpha_h = \cfrac{3}{\sqrt{h}}, \quad \text{lecz } \, 2/3 \le \alpha_h \le \, 1 \label {3} \end{equation}$$
$$\begin{equation} \alpha_m =\sqrt{\cfrac{m+1}{2m}} \label {4} \end{equation}$$
gdzie:
$h$ – wysokość budowli lub długość elementu,
$m$ – liczba słupów w rzędzie, które przenoszą obciążenie $N_{Ed}$ nie mniejsze niż 50% przeciętnego obciążenia słupa w rozpatrywanej płaszczyźnie pionowej.
Współczynnik $\alpha_m$ powinien być obliczony dla liczby słupów stabilizowanych w kilku rzędach, a nie tylko w jednej ścianie [2], kl. (5.5) , [12] . Współczynniki redukcyjne przyjmują maksymalne możliwe wartości 1,0 odpowiednio dla h= 4 metry i dla m = 1.
Zredukowany przechył wynosi
$$\begin{equation} \Phi=\Phi_0 \cdot \alpha_h \cdot \alpha_m \to n_G= n_{\Phi} =n_{\Phi,0}/ (\alpha_h \cdot\alpha_m) \label {5} \end{equation}$$
Na skutek geometrycznej imperfekcji przechyłowej na głowice i stopy słupów (Rys. 2b) i na stropy między kondygnacyjne (Rys.2a) działają równoważne siły imperfekcji
$$\begin{equation} H_{Ed} =\Phi \cdot N_{Ed} =\cfrac{N_{Ed}}{n_G}\label {6} \end{equation}$$
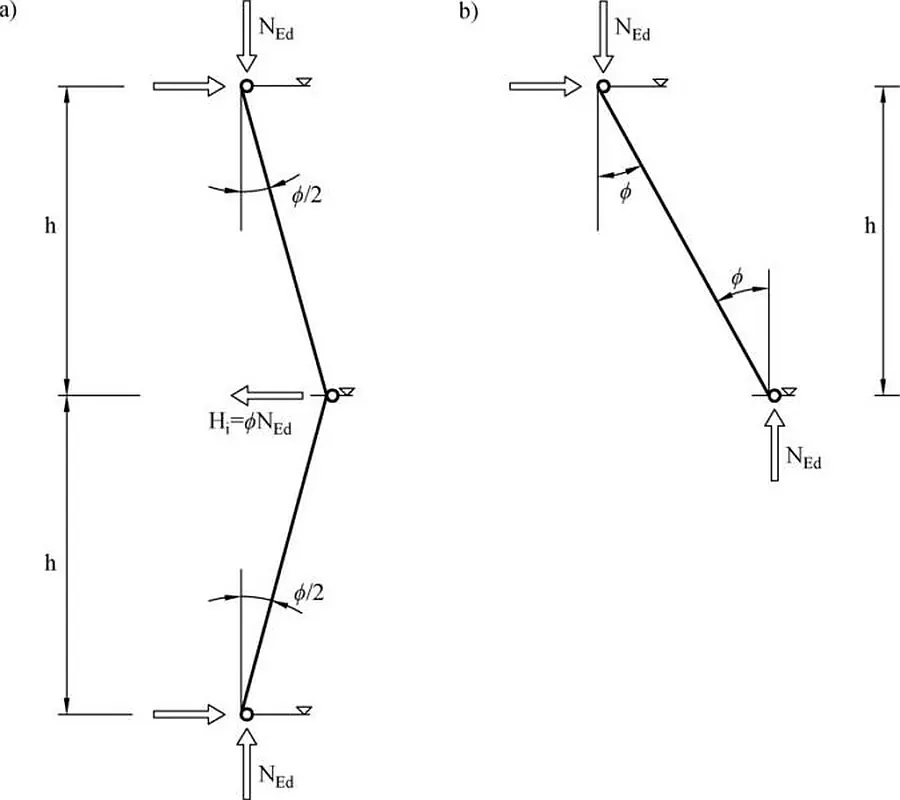
Rys. 2 Równoważne, poziome siły fikcyjne od imperfekcji przechyłowych: a) na stropy między-kondygnacyjne, b) na głowice i stopy słupów
Siła $N_{Ed}$ jest unormowaną osiową siłą przekrojową w danym słupie. Zwykle przyjmuje się, że jest to maksymalna siła ściskająca z długości słupa. W przypadkach uzasadnionych dużym wpływem sił $H_{Ed}$ na stan przemieszczeń i naprężeń, jako normę przyjmuje się średnią ważoną, proporcjonalną do odcinków długości słupa (w granicy, jako całkę po długości pręta, podzieloną przez jego długość h). Jeśli zewnętrzna siła pozioma przekracza 15% całkowitej siły pionowej, to można pominąć siły od imperfekcji ($\ref{6}$), wynikające z modelu Rys.1.
W przypadku linii słupów spiętych belką wezgłowiową do głowicy najczęściej pierwszego słupa przykłada się sumaryczną siłę od imperfekcji wszystkich słupów w szeregu $\sum H_{Ed}= \Phi \sum N_{Ed}$. Taki zabieg uogólnia się na całą kondygnację budynku wielokondygnacyjnego w przypadku baterii słupów spiętych tarczą stropową, ponieważ w praktycznie spotykanych przypadkach wpływ sił imperfekcji na zwiększenie wytężenia początkowego nie jest zbyt istotny, a siły imperfekcji spełniają pożyteczną, obliczeniową rolę, bo prowadzą do wytrącenia systemu z idealnego położenia, więc w celu uproszczenia procedur dla zwykłych przypadków przyjmuje się zwykle najniekorzystniejszą wartość ($\ref{2}$) (bez redukcji).
Przechyły $\Phi$ układu na danej wysokości układu mogą powodować zwykłą translację (Rys.3a) o odcinek $\Phi \cdot x$ (x- wysokość rozpatrywanego punktu nad poziom zerowy), albo obrót (Rys.3b ) $\Phi\cdot b/2 \cdot x/h$ (b, h – szerokość i wysokość budowli). Wartość translacji lub obrotów zmienia się po wysokości od zera (dla x=0) do maksymalnej wartości ($\ref{5}$) (dla x=h).
Zasada ($\ref{6}$) dotyczy wszystkich obciążeń grawitacyjnych, również rozłożonych (liniowych lub powierzchniowych), co można zapisać formułą:
$$\begin{equation} q_x= q_y = \Phi \cdot q_z = \cfrac{q_z}{n_G} \label {7} \end{equation}$$
Imperfekcje łukowe
Zastępcze imperfekcje łukowe elementów modelowane są wstępnym wygięciem elementu o amplitudzie (strzałce wygięcia) $e_0$ w sposób pokazany na Rys. 4b. Amplituda $e_0$ jest proporcjonalna do długości elementu oraz zależy od rodzaju prowadzonej analizy (sprężysta, plastyczna).
Klasę imperfekcji pręta stalowego , czyli typ krzywej wyboczeniowej zależy od rodzaju profilu i dobiera się z tab.1 przy wyboczeniu giętnym i z tab.2 przy wyboczeniu bocznym (zwichrzeniu).
Tab 1 Klasy imperfekcji (krzywe wyboczeniowe) wyboczenia giętnego [2], tab. 6.2.
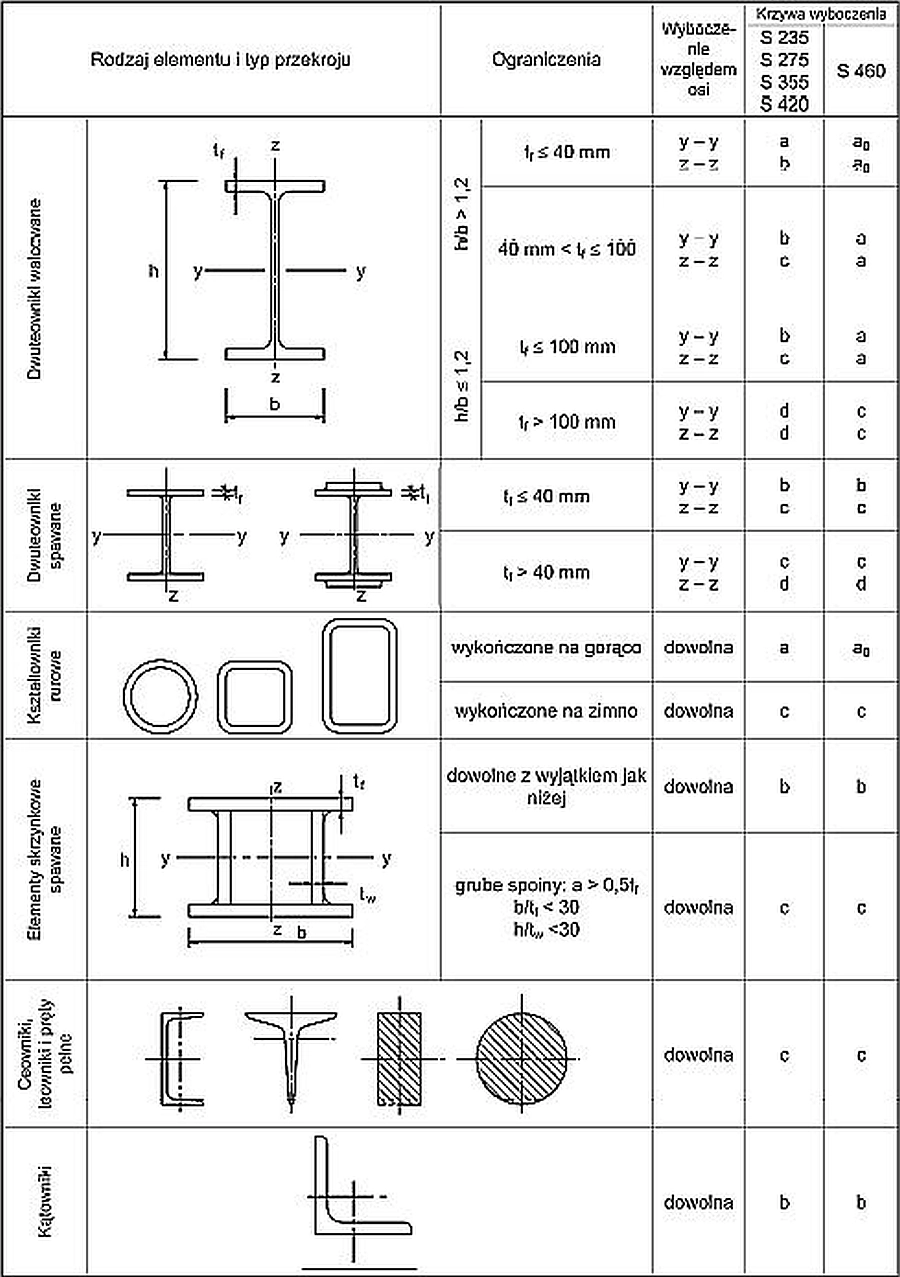
Tab. 2 Klasy imperfekcji (krzywe wyboczeniowe) przy wyboczeniu bocznym (zwichrzeniu) [2], tab 6.4 i 6.5
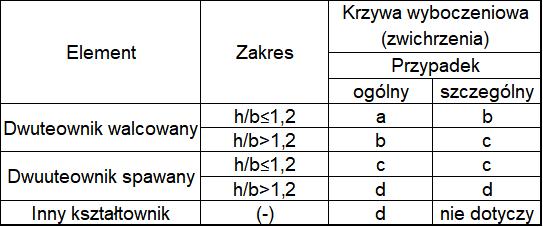
Przypadek ogólny zwichrzenia, wymieniony w tab.2 dotyczy wszystkich przekrojów zgodnie z klauzulą normową [2], kl. 6.3.2.2 . Natomiast przypadek szczególny dotyczy przekrojów dwuteowych walcowanych i ich spawanych odpowiedników zgodnie z [2], kl. 6.3.2.3 . Zastosowanie zaleceń normowych „przypadku „szczególnego” daje możliwość oszczędniejszego projektowania konstrukcji, ponieważ wartości współczynników zwichrzeniowych są większe od analogicznych wartości wyznaczanych dla przypadku ogólnego. W przypadku szczególnym współczynniki zwichrzenia wyznacza się z zależności ogólnych (2-2.13) do (2-2.15), modyfikowanych współczynnikiem $\beta=0,75$ i dla smukłości progowej $\lambda_0=0,4$.
Na podstawie klasy imperfekcji (krzywej wyboczeniowej) można dobrać wartość imperfekcji łukowej z tab.1-1.1 w zależności od typu prowadzonej analizy (sprężysta, czy plastyczna). W poprawce do polskiej wersji [13] zaleca się, by imperfekcję łukową dla wszystkich rodzajów analiz przyjmować jak dla analizy sprężystej.
Obciążenie równoważne od imperfekcji lokalnych (elementu) przyjmuje się zgodnie [2], kl. 5.3-2.2.(6) , rys.3b i zależnością:
$$\begin{equation}q_d=\cfrac{8 N_{Ed} \cdot e_0}{L^2} = \cfrac{8N_{Ed}}{n_L \cdot L} \label {8} \end{equation}\\$$
gdzie $e_0$ – obliczeniowa imperfekcja łukowa. Oznaczenie imperfekcji jest zgodne z nomenklaturą normy [6] , gdzie pominięto indeks „d”, który jest stosowany w normie [2] ( tzn. $e_0=e_{0d}$).Względną imperfekcję łukową należy przyjmować z Tab. 3-2.1. Siła jest obliczeniową siłą osiową działającą w elemencie o długości L, którą należy szacować, uwzględniając uwagi pod formułą ($\ref{6}$).
Równoważne siły imperfekcji od wstępnego skręcenia belki będą momentami skręcającymi $m_T=m_x$ równomiernie rozłożonymi po długości belki, . Postępując analogicznie do procedury szacowania równoważnych sił ($\ref{8}$), otrzymamy następujące wyrażenie na równoważne momenty skręcające od imperfekcji skrętnych:
$$\begin{equation} m_T= M_{Ed} \cdot \cfrac{8 \varphi_0}{L_T} \label {9} \end{equation}$$
gdzie: $M_{Ed}$ – obliczeniowy moment zginający, $L_T$ – efektywna długość belki, miarodajna do szacowania zwichrzenia elementu.
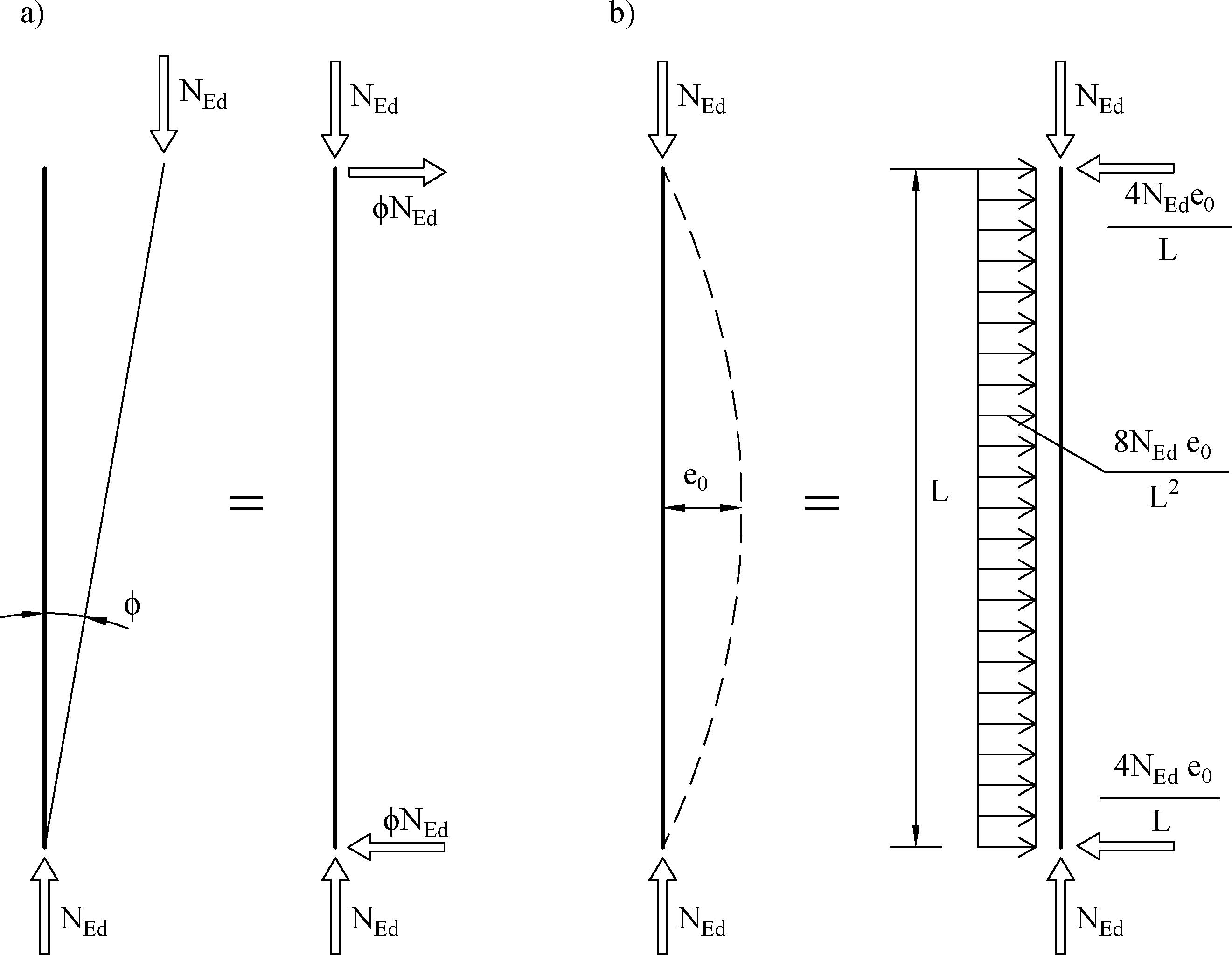
Rys. 4. Zastąpienie wstępnych imperfekcji równoważnymi siłami poziomymi : a) imperfekcje przechyłowe (globalne), b) imperfekcje łukowe (lokalne) [2], rys. 5.4.
Uwaga
W dalszej części pracy pokazano, że bezkrytyczne stosowanie fikcyjnych sił dla każdego schematu statycznego prętów zgodnie z formułą ($\ref{9}$), może prowadzić do grubych błędów. Formuła jest słuszna wyłącznie dla pręta przegubowo-przegubowego.
Równoważność imperfekcji od obciążeń i od sił przekrojowych
Fikcyjne siły imperfekcji $(\ref{6})$ są uzależnione od osiowych sił przekrojowych $N_{Rd}$ występujących w danym elemencie. Na użytek szacowania sił imperfekcji można przyjąć, że w układzie konstrukcyjnym, siły przekrojowe są proporcjonalne do mnożnika obciążeń zewnętrznych $\Lambda$ i wówczas formuła $(\ref{6})$ przyjmie równoważną postać
$$\begin{equation} H = \Phi \cdot \Lambda \cdot V \label {10} \end{equation}$$
gdzie V oznacza obciążenie grawitacyjne (pionowe) w ustalonej konfiguracji, złożone z obciążeń konstrukcji (skupionych, rozłożonych liniowo lub powierzchniowo) .
W tym ujęciu siły fikcyjne siły od imperfekcji są poziomymi obciążeniami od imperfekcji stowarzyszonymi z każdym obciążeniem grawitacyjnym, niezależnie od miejsca jego przyłożenia.
Imperfekcje konstrukcji żelbetowych
Opis imperfekcji systemowych w ujęciu Eurokod2 [1] jest spójny z opisem przedstawionym w normie Eurokod 3 z dokładnością do oznaczeń oraz pominięcia imperfekcji łukowych, a także wyraźniejszego sformułowania fundamentalnej zasady:
„Metoda MWE ( Wydzielonych Elementów) może być stosowana wyłącznie dla elementarnych przypadków, wówczas i tylko wówczas gdy w sposób wiarygodny możemy wydzielić element i określić jego długość efektywną (wyboczeniową). Ponadto może dotyczyć tylko elementów o prostym przekroju poprzecznym (prostokątny, okrągły) oraz ma zastosowanie tylko do słupów lub ścian”
Imperfekcje przechyłowe
Imperfekcja przechyłowa konstrukcji żelbetowych jest opisana wzorem (3-2.4) takim jak w normie Eurokod 3; analogiczne są również współczynniki korekcyjne $\alpha_h$ (3-2.2) i $\alpha_m$ (3-2.3) ale z innymi oznaczeniami.
W podręczniku konsekwentnie używać będziemy oznaczenia $\Phi$ zamiast $\Theta_i$, a także $h$ zamiast $l$ i
$L_{cr}$ zamiast $l_0$ (długośc wyboczeniowa, długość efektywna),
to znaczy oznaczenia stosowane w Eurokod 3 w miejsce używanych w Eurokod2 [1] .
Wartość podstawowa imperfekcji jest zgodna z ustaleniami Eurokod 3 (3-2.1) i wynosi $n_{\Phi,0}=200$.
Wpływ imperfekcji przechyłowych na wydzielone elementy można uwzględnić na dwa sposoby (rys..1):
a) poprzez zastosowanie zastępczego mimośrodu $e_i$ o wartości [1], (5.2) :
$$\begin{equation} e_i =\Phi_i/2 \cdot L_{cr} \label {11} \end{equation}$$
Dla ścian i słupów wydzielonych dopuszcza się zastosowanie współczynnika (3-2.2) $\alpha_h=1$ , czyli
$e_i=\cfrac{L_{cr}}{400} \to n_G=400$ (dla elementów o długości efektywnej równej długości teoretycznej.
Uwaga:
- W rozdziale „Zastępczy mimośród przyłożenia siły” pokazano, że zastępowanie imperfekcji łukowej przez mimośrodowe przyłożenie obciążenia w głowicy słupa jest błędne i nie powinno być stosowane. Zastępowanie imperfekcji przechyłowej przez mimośród siły ściskającej jest również błędne, ponieważ dotyczy innych obszarów mechaniki konstrukcji. Właściwy do uwzględnienia imperfekcji przechyłowych jest sposób opisany w pkt b)
- Metoda obciążeniowa IMH jest możliwa do zastosowania w celu uwzględnienia imperfekcji łukowych, choć szacunek obciążenie poprzecznego podany w [1], (5.3) dotyczy wyłącznie imperfekcji przechyłowych i nie może dotyczyć imperfekcji łukowych oraz sił przyłożonych na długości elementu (prawy rys 3.5b), a tylko przyłożonych w głowicy lub stopie słupa (w węzłach końcowych),
b) poprzez zastosowanie zastępczej siły poprzecznej $H_i$ od imperfekcji [1], (5.3) wg wzoru:
$$\begin{equation} H_i =k_i \Phi_i \cdot N \label {12} \end{equation}$$
We wzorze ($\ref{12}$) wprowadzono oznaczenia:
$\Phi_i$ imperfekcją przechyłową elementu „i” (kąt przechyłu),
$k_i$ współczynnik zależny od stopnia zamocowania końców elementu:
$k_i=1$ dla elementów nieusztywnionych (np wspornik lub z głowicą przesuwną);
$k_i=2$ dla elementów usztywnionych (np. słup z nieprzesuwnie podpartymi głowicą i stopą),
$N$ – siła osiowa działająca w elemencie.
Sposób ($\ref{12}$) (obciążeniowy) jest ogólniejszy od ($\ref{11}$) (zastępczy mimośród przyłożenia siły), bo może być zastosowany w układach statycznie wyznaczalnych i niewyznaczalnych, a fikcyjna siła od imperfekcji może być zastąpiona inną równoważną siła poprzeczną. Nie określono jednak metody wyznaczania równoważności układów sił fikcyjnych. Zdaniem autora metody a) – zastępczych mimośrodów nie powinno stosować się. Uzyskiwane wyniki są błędne, co pokażemy w przykładach w dalszej części podręcznika
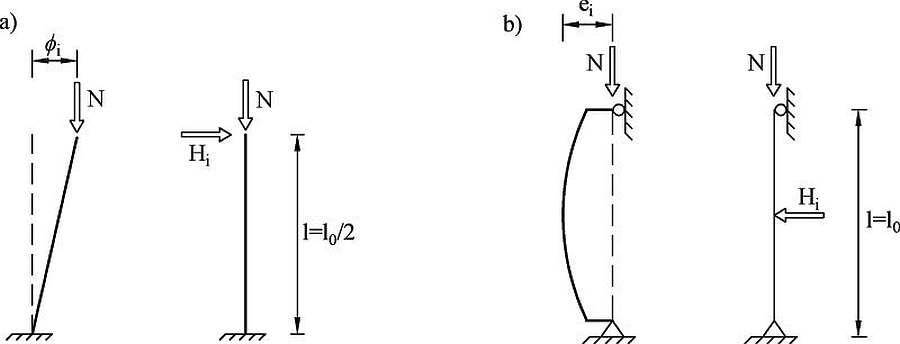
Rys. 5 Imperfekcje geometryczne konstrukcji żelbetowych działające na wydzielony element: a) w systemie nieusztywnionym, b) w systemie usztywnionym (część rys.5.1 EC2 [1])
Imperfekcje łukowe
W normie [1] w istocie nie odniesiono się do imperfekcji łukowych prętów konstrukcji żelbetowych, a pośrednie zasady (np prawy rys. 3.5 b są błędne).
W niniejszym podręczniku zaleca się , by impefekcje łukowe elementów konstrukcji żelbetowych wyznaczać na podstawie tolerancji wykonawczych. Tolerancje wykonawcze odchyłek łukowych podano w Tab. 2.2. W ostatniej kolumnie tej tabeli przedstawiono propozycję szacowania imperfekcji projektowej na podstawie tolerancji wykonawczych. Dalsze uogólnienie zaprezentowano w rozdziale 4 podręcznika ust. (4.3.6).
Sztywności żelbetu podczas obliczeń II rzędu
Przekroje żelbetowe są kompozytem betonu i prętów zbrojeniowych. Analiza ścisła powinna polegać na badaniu konstrukcji złożonej z elementów skończonych betonowych współpracujących z prętami stalowymi. Do celów analizy inżynierskiej użyteczny jest integralny model kompozytu, umożliwiających jego analizę jak przekroju jednorodnego o zastępczych charakterystykach mechanicznych, zmieniających się w procesie pracy konstrukcji w zależności od stopnia pełzania betonu, udziału betonu i stali orz innych czynników.
W normie [1] zaprezentowano dwie uproszczone metody do uwzględniania efektów drugiego rzędu w konstrukcjach żelbetowych z zastosowaniem ogólnych algorytmów mechaniki konstrukcji: metodę nominalnej sztywności (MNS) [1], kl. 5.8.7. oraz nominalnej krzywizny (MNK) [1], kl. 5.8.8.
Zaprezentujemy obie metody, choć do zastosowań praktycznych z użyciem komputera zalecamy tylko jedną z nich, a mianowicie metoda MNS. Po jej zastosowaniu analiza konstrukcji żelbetowych może być dokonana standardowymi algorytmami opracowanymi dla konstrukcji stalowych, aluminiowych i zespolonych.
Metoda nominalnej krzywizny jest przybliżoną metodą uwzględniania momentów drugiego rzędu dla prostych przypadków wydzielonych elementów żelbetowych i w tym podręczniku przedstawimy ją w skrócie w zakresie potrzebnym do przedstawienia przykładów rachunkowych w podręczniku.
Metoda nominalnej sztywności MNS
Metoda MNS umożliwia analizę elementów żelbetowych włączonych do systemów statycznie niewyznaczalnych.
Sztywność nominalną (efektywną, sprowadzoną) przekroju żelbetowego można oszacować, jako sumę sztywności betonu i zbrojenia, ważonych współczynnikami $K_c$ i $K_s$, zależnymi odpowiednio do zarysowania i pełzania betonu oraz od udziału zbrojenia [1], (5.21)
$$\begin{equation}EI=K_c \cdot E_{cd} \cdot I_c + K_s \cdot E_s \cdot I_s \label {13} \end{equation}$$
Dla stopnia zbrojenia $\rho =\cfrac{A_s}{A_c}>2$‰ można przyjąć $K_s=1$ (w praktyce stopień zbrojenia słupów spełnia podany warunek, bo jest to zbrojenie minimalne).
Współczynnik wpływu betonu
$$\begin{equation} K_c=\cfrac {k_1 \cdot k_2} {1+\varphi_{ef}} \label {14} \end{equation}$$
gdzie pomocnicze współczynniki wynoszą:
$$\begin{equation} k_1=\sqrt{\cfrac{f_{ck}}{20}}\label {15} \end{equation}$$
$$\begin{equation} k_2=\min{ \left[ \cfrac{n \cdot \lambda}{170} ; \quad 0,20\right ]} \label {16} \end{equation}$$
gdzie:
$ n=\cfrac {N_{Ed}} {N_{Rc}}$ – względna siła osiowa odniesiona do nośności betonu $N_{Rc}=A_c \cdot f_{ck}$
$\lambda=\cfrac {l_0}{i}$-smukłość elementu o długości wyboczeniowej (efektywnej) $l_0=L_{cr}$ , i – promień bezwładności przekroju niezarysowanego dla przekroju prostokątnego bxh – $i=h/\sqrt{12}$.
Niekorzystne wpływy zarysowania, czyli częściowe zarysowanie i współpracę betonu na odcinkach między rysami elementów przylegających tych elementów, można uwzględniać poprzez stosowanie efektywnego modułu sprężystości betonu zgodnie ze wzorem:
$$\begin{equation} E_{cd,eff}= \cfrac{E_{cd}}{1+\varphi_{eff}}\label {17} \end{equation}$$
w którym $E_{cd}=E_{cm}/1,2$ jest obliczeniową wartością modułu sprężystości według normy, a $\varphi_{eff}$ jest efektywnym współczynnikiem pełzania szacowanym z zależności:
$$\begin{equation} \varphi_{eff}= \varphi_0 \cdot k_{qp} \label {18} \end{equation}$$
Współczynnik pełzania $ \varphi_0 = \varphi(\infty, t_0)$ jest końcowym współczynnikiem pełzania w okresie od wieku betonu przy pierwszym obciążeniu $t_0$ (najczęściej 48 dni) do końca życia budowli ( $\infty$).
Współczynnik $ \varphi_0$ ustala się zgodnie z [1], rys. 3.1 wg zasad podanych w artykule Belki żelbetowe (tab.1 i tab 11) i zależy od klasy betonu rodzaju cementu (S,N,R) oraz efektywnego wymiaru przekroju $h_0=\cfrac {2A_c}{U}$, gdzie: $A_c$ -pole przekroju betonu (szalunku), $U$-obwód przekroju – np. dla przekroju kwadratowego $h_0 = \cfrac{h^2}{2h}=h/2$.
Często stosowaną w obliczeniach wstępnych wartością współczynnika pełzania jest
$ \varphi_0 \approx 2$.
który odpowiada sytuacji: $t_0 = 48 $ dni , cement N (normalnie twardniejącego), beton C30/37 i $h_0=400 \, mm$
Wpływ pełzania można pominąć (tzn. $\varphi_{eff}=0$), jeżeli spełnione są łącznie 3. warunki:
1) $\varphi_0 \le 2,0$;
2) $\lambda <7,5$ ;
3) $e_{N,0}=\cfrac{M_{0,Ed}}{N_{0,Ed}} > h$,
to znaczy wyłącznie dla krępych elementów z dużym mimośrodem w konfiguracji „0” (1 rzędu – bez uwzględnienia wpływu przemieszczeń na siły), w tym przy braku siły ściskającej.
Współczynnik udziału obciążeń quasi-stałych jest zdefiniowany następująco:
$k_{qp}=\cfrac{M_{0,Eqp}}{M_{0,Ed}}$,
gdzie $M_{0,d}$ obliczeniowy moment zginający w stanie granicznym nośności SGN w konfiguracji „0”, $M_{0,Eqp}$ -moment zginający od obciążeń quasi-stałych, wyznaczony jak dla stanu użytkowalności (SGU).
Współczynnik $k_{qp} jest stosunkiem momentów zginających z analizy 1 rzędu dla SGU do SGN. W praktyce dla elementów o ustalonym schemacie statycznym i konfiguracji obciążenia współczynnik ten szacuje się na podstawie obciążeń
$k_{qp}=\cfrac { G_k+\sum Q_k \cdot \psi_2 } {\max {\left \{ \gamma_G \cdot G_k+\sum \gamma_Q \cdot Q_k\cdot \psi_0 \right \} } }$
gdzie max oznacza maksymalizację mnożnika obciążeń z wszystkich kombinacji.
Na przykład w sytuacji przeważającego wpływu ciężaru własnego (żelbet w 60% niesie sam siebie) oraz pomijalnego wpływu obciążeń klimatycznych (śnieg i wiatr) dla budynku mieszkalno-biurowego ($\psi_0=0,7$ , $\psi_2=0,3$ ) mamy
$k_{qp}=\cfrac{1,0\cdot 0,6+0,3 \cdot 0,4}{1,35 \cdot 0,6+1,5\cdot 0,4}=0,7$ , czyli $\varphi_{eff}=2,0\cdot 0,7=1,4$ .
W sytuacji większego wpływu obciążeń zmiennych współczynnik zbliży się do wartości 0,5, czyli $\varphi_{eff}=2,0\cdot 0,5=1,0$.
Oszacowanie nominalnej sztywności elementu żelbetowego umożliwia zwiększenie momentu zginającego w stanie 2 rzędu współczynnikiem amplifikacji w postaci [1], kl.5.8.7.3
$$\begin{equation} M_{Ed}=M_{Ed,0} \cdot (1+a_B) \label {19} \end{equation}$$
gdzie
$$\begin{equation} a_B= \cfrac{\beta}{\tfrac{N_B}{N_{Ed}}-1}\label {20} \end{equation}$$
Siła krytyczna $N_B=N_{cr}$ (wzór (1.4) – rozdział 1) jest obliczona dla pręta o sztywności nominalnej EI i długości krytycznej (efektywnej) $L_{cr}=l_0$. Należy zwrócić uwagę, że dla $\beta=1$ zachodzi ( wzór (1.9) – rozdział 1), a ($\ref{19}$) może być zapisane w klasycznej postaci $M_{Ed} = M_{Ed,0} \cdot a_N$.
Współczynnik korelacji ściskania i zginania $\beta$ najczęściej szacuje się jak dla elementów o stałym przekroju i stałej sile podłużnej:
$$\begin{equation} \beta=\cfrac{ \pi^2}{c_0} \label {21} \end{equation}$$
gdzie współczynnik rozkładu momentu zginającego, wynosi: $c_0=8$ , gdy moment 1 rzędu jest stały wzdłuż elementu, $c_0=9,6$ , gdy ma rozkład paraboliczny), $c_0=12$, gdy ma symetryczny rozkład trójkątny). W przypadku momentu liniowo zmiennego od $M_{01}$ do $M_{02}$, przyjmuje się zastępczy stały moment $M_0= ( 0,6 \cdot M_{02}- 0,4 \cdot M_{01} \ge 0,4 M_{02}) $ i $c_0=8$ .
Podejście uproszczone ($\ref{19}$) traci na znaczeniu przy prowadzeniu analizy 2 rzędu konstrukcji żelbetowych w sposób analogiczny do obliczeń konstrukcji innych typów. W takiej analizie stosuje się nominalne (efektywne) sztywności przekroju żelbetowego ($\ref{13}$) dla dowolnej zmienności przekrojów i sił po długości pręta. Współczesny program [14] , pierwotnie opublikowany do obliczania konstrukcji stalowych, od wersji 10.0 ma możliwość analizy konstrukcji żelbetowych z płytami-ścianami oraz prętami o przekroju prostokątnym, kołowym, teowym, zbrojonych w wielu rzędach z zastosowaniem efektywnego modułu sprężystości ($\ref{17}$) (domyślnie $\varphi_{eff}=2,0$, z możliwością modyfikacji) i w procedurze doboru sztywności nominalnej ($\ref{13}$) z zastosowaniem współczynników $K_c$ i $K_s$ (domyślnie $K_c=0,5$ i $K_s=1,0$, z możliwością modyfikacji).
Metoda nominalnej krzywizny MNK
Metoda nominalne krzywizny MNK została przedstawiona w [1], kl. 5.8.8 jako metoda alternatywna do MNS w zastosowaniu do elementów wydzielonych z sytemu, czyli w zasadzie do zastosowań tradycyjnych z ery przedkomputerowej.
Przekrojowy moment zginający $M_{Ed}$ działający w elemencie wyznacza się jako sumę momentu pierwszego rzędu $M_{Ed,0}$ oraz dodatkowego momentu od efektów drugiego rzędu $M_{Ed,II}$.
Przy założeniu, że przekrojowa siła osiowa $N_{Ed}$ w elemencie jest niezerowa i prawie stała na etapach analizy, po oznaczeniu:
$e_a$ – niezmierzony mimośród zdefiniowany w $(\ref{23})$;
$e_{N,0}=\cfrac{M_{Ed,0}}{N_{Ed}}$ – mimośród od sił zewnętrznych w stanie „0” (I rzędu);
$e_{N,II}= \cfrac{\Delta M_{Ed,II}}{N_{Ed}}$ – mimośród dodatkowy od przyrostu sił zewnętrznych na przemieszczeniach (II rzędu),
otrzymujemy zasadę sumowania mimośrodów w mimośród całkowity $e_{tot}$:
$$\begin{equation} e_{tot}= e_a+ e_{N,0}+e_{N,II} \label {22} \end{equation}$$
Niezamierzony mimosród od imperfekcji systemowych $e_a$ jest powodowany przechyłem słupa i nieosiowym przyłożeniem siły i dla slupów należy go przyjmować z zależności :
$$\begin{equation} e_a= \max{ \left [ \cfrac{1}{200}\cdot L_{cr}/2; \quad \cfrac{h}{30}; \quad 20 \, mm \right] }\label {23} \end{equation}$$
gdzie
$L_{cr}=l_o$ – długość efektywna elementu,
$h$ – wysokość przekroju
Mimośród II rzędu można oszacować z formuły
$$\begin{equation} e_{N,II} = \cfrac{L_{cr}^2}{c} \cdot \left (\cfrac{1}{r} \right ) \label {24} \end{equation}$$
Współczynnik c dla elementu o stałym przekroju wynosi
$$\begin{equation} c=\pi^2 \approx 10 \label {25} \end{equation}$$
Efektywna krzywizna (1/r) wynosi
$$\begin{equation} \left (\cfrac{1}{r} \right )= \left ( \cfrac{1}{r} \right )_0 \cdot K_r \cdot K_{\varphi} \label {26} \end{equation}$$
Krzywizna 1 rzędu $(1/r)_0$ wynosi:
$$\begin{equation} \left ( \cfrac{1}{r}\right)_0 =\cfrac {\varepsilon_{yd}} {0,45 d} \label {27} \end{equation}$$
Odkształcenie plastyczne stali
$$\begin{equation} \varepsilon_{yd}=\cfrac{f_y}{E_s} \label {28} \end{equation}$$
jest wyznaczane przy naprężeniach równych granicy plastyczności $f_y$ i dla modułu stali $E_s= 200 \, GPa$.
Wysokość efektywna przekroju $d$ jest zdefiniowana standardowo $d = h – (c+∅/2) $, gdzie: $h$- wysokość przekroju, $c$ – otulenie zbrojenia o średnicy ∅
Współczynnik wpływu stopnia zbrojenia
$$\begin{equation} K_r=\cfrac{n_u-n}{n_u-n_{bal}} \label {29} \end{equation}$$
gdzie:
$$\begin{equation} n_u=1+\omega \label {30} \end{equation}$$
$$\begin{equation} \omega= \cfrac {N_{Rs}} {N_{Rc}}= \cfrac {A_s \cdot f_{yd}} {A_c \cdot f_{cd}} \label {31} \end{equation}$$
$$\begin{equation} n_{bal}=0,4 \label {32} \end{equation}$$
( $n_{bal}jest względną siłą podłużną , dla której osiąga się maksymalny moment graniczny).
Współczynnik, uwzględniający pełzanie
$$\begin{equation} K_{\varphi} =\beta \cdot\varphi_{eff} \label {33} \end{equation}$$
gdzie:
$$\begin{equation} \beta = 0,35+\cfrac{f_{ck}}{200}+\cfrac{\lambda}{150} \label {34} \end{equation}$$
$\varphi_{eff}$ – efektywny współczynnik pełzania ($\ref{18}$).
Całkowity moment zginający przekrój właściwy do jego wymiarowania wynosi
$$\begin{equation} M_{Ed}=N_{Ed} \cdot e_{tot} \label {35} \end{equation}$$
gdzie $e_{tot}$ ($\ref {22}$).
Imperfekcje konstrukcji zespolonych
Przy obliczaniu stateczności konstrukcji zespolonych zgodnie z [15] należy brać pod uwagę efekty drugiego rzędu, w tym naprężenia własne, imperfekcje geometryczne, miejscową niestateczność, zarysowanie, skurcz i pełzanie betonu oraz uplastycznienie stali konstrukcyjnej i zbrojenia. Siły wewnętrzne należy określać na podstawie analizy sprężysto-plastycznej.
Zgodnie z [15],kl. 3.2. obliczanie elementów zespolonych podatnych na imperfekcje (elementów ściskanych lub smukłych belek) należy prowadzić zgodnie z ogólnymi zasadami podanymi dla konstrukcji stalowych, a wartości podstawowych imperfekcji przechyłowych przyjmować o wartości zdefiniowanej dla konstrukcji stalowych ($\ref{2}$) do ($\ref{6}$).
Imperfekcje konstrukcji aluminiowych
Zasady Eurokod 9 przykrywają zasady Eurokod 3
Postanowienia normy Eurokod 9 [6] do projektowania konstrukcji aluminiowych są w istocie poprawioną i uogólnioną wersją postanowień normy Eurokod 3 [2] . Dlatego uznajemy, że zasady podane w normie [6] mają pierwszeństwo przed [2]
Imperfekcje przechyłowe
Globalne imperfekcje przechyłowe uwzględnia się przechyłem $\Phi$ (Rys. 3.4a) zgodnie z formułą ($\ref{2}$) również z wartością podstawową $ \Phi_0=1/200$. Imperfekcje przechyłowe można zastąpić fikcyjnymi siłami poziomymi zgodnie z Rys. 3.2a. Wstępne imperfekcje przechyłowe uwzględnia się osobno w każdym z rozpatrywanych kierunków przechyłu W przypadku wielokondygnacyjnych szkieletów słupowo-belkowych budynków siły zastępcze przykłada się na wszystkich poziomach stropów i dachu.
Przechyły konstrukcji mogą powodować translacje lub obroty przekroju budynku (Rys. 6).
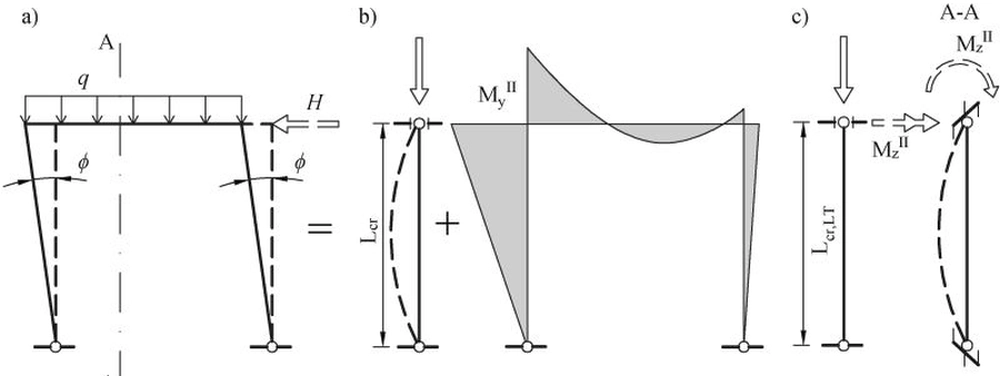
Rys. 6. Utrata stateczności ram aluminiowych: a) imperfekcje przechyłowe SGI , b) zastosowanie metody hybrydowej HIM
Ograniczenie liczby krzywych wyboczeniowych
Zgodnie z [6] lokalne imperfekcje łukowe oraz równoważne obciążenie od imperfekcji przyjmuje się zgodnie z Rys. 3.2b Wskazujemy od razu, ze zastosowanie sił fikcyjnych zgodnie z tą formułą nie zawsze jest właściwe (p. uwaga pod koniec pkt. 3.2)
Wprowadzono dwie klasy wyboczenia konstrukcji aluminiowych A i B [16],tab.3.2 , które są zależne od rodzaju stopu aluminium, ale niezależne od kształtu przekroju kształtownika W zależności od klasy wyboczenia, przyjmowane są względne strzałki imperfekcji:
- klasa A
$e_0/L= 1/300$ ($n_L=300$) w analizie sprężystej ; $e_0/L= 1/250)$ ($n_L= 250$) w analizie plastycznej, - klasa B
$e_0/L= 1/200$ ($n_L=200$) w analizie sprężystej ; $e_0/L= 1/150)$ ($n_L= 150$) w analizie plastycznej.
Przy tej okazji należy wskazać, że znaczne ograniczenie liczby krzywych wyboczeniowych również dla konstrukcji stalowych postuluje norma japońska JRA [17]. Zaleca bowiem jedną krzywą wyboczeniową położoną pomiędzy europejskim typem „b” i „c” , dla której $n_L \approx 200$ niezależnie od kształtu przekroju i typu analizy. Pokazano, że mnożenie typów krzywych wyboczeniowych nie jest statystycznie istotne, więc w praktyce nie jest potrzebne.
Postulat ograniczenia liczby krzywych wyboczeniowych konstrukcji stalowych
W niniejszej pracy stawiamy postulat, by imperfekcje łukowe konstrukcji stalowych i aluminiowych przyjmować o wartości:
$$\begin{equation} e_{0,zmod}=\cfrac {L} {200} \to n_L =200 \quad \text { dla każdego przekroju i rodzaju analizy} \label {36} \end{equation}$$
Hipoteza ($\ref{36}$) może być zweryfikowana poprzez przeprowadzenie testów statystycznych na akceptowalnym poziomie ufności, który zdaniem autora należy przyjąć o wartości 95%.
Oddziaływania poziome od imperfekcji przechyłowych na stropy i podpory budynku szkieletowego przyjmuje się zgodnie z Rys. 3.6 (analogicznie jak w konstrukcjach stalowych lub żelbetowych).
Wymóg modelowania imperfekcji łukowych
Zgodnie z [6]„] (podobnie jak [2] ) – imperfekcje łukowe generalnie mogą być pomijane (są uwzględniane przez współczynniki wyboczeniowe), ale powinny być obecne w modelu konstrukcji wrażliwych na efekty 2 rzędu, gdy co najmniej jeden węzeł końcowy elementu jest sztywny, a element jest smukły o smukłości liczonej dla pręta przegubowo-przgubowego $\overline \lambda > 0,5 \cdot\sqrt { \cfrac{A f_y}{N_{Ed}}} ( $f_y$ -granica plastyczności).
Zastosowanie metody hybrydowej
Ze względu na trudności w uwzględnieniu w modelu globalnym imperfekcji łukowych elementów oraz rozpowszechnioną metodę wyboczeniową, zaleca się, by w przypadku niepełnego uwzględnienia imperfekcji łukowych w analizie globalnej zastosować metodę HIM, zilustrowaną na Rys. 3.4b. (p. też pkt 1.3 – rozdział 1). Podobne zalecenie zawiera norma do projektowania konstrukcji stalowych [2] .
Imperfekcje skrętne
Jeśli analiza drugiego rzędu ma uwzględniać zwichrzenie elementów zginanych, to zastępcze imperfekcje tych elementów można przyjmować w płaszczyźnie najmniejszej bezwładności przekroju o strzałce równej $k e_0$, gdzie strzałka $e_0$ jest ustalona jak dla elementu ściskanego. Zaleca się $k=0,5$.
Specjalne uwzględnienie imperfekcji skrętnych na ogół nie jest konieczne, ponieważ w konsekwencji wygięcia bocznego uzyskuje się imperfekcję skrętną zgodnie z formułą (3-2.8).
Imperfekcje konstrukcji drewnianych
W niniejszym artykule przedstawia się krótki przegląd postanowień normowych dotyczącyh imperfekcji konstrukcji drewnianych i murowych. Dopuszczalne tolerancje wykonawcze tych konstrukcji przedstawiono w rozdziałach „Tolerancje konstrukcji drewnianych„, „Tolerancje konstrukcji murowych” oraz w Tab. 2.3. Sposób szacowania imperfekcji projektowych z tolerancji wykonawczych omówiono w rozdziale „Imperfekcje projektowe z odchyłek wykonawczych„.
Imperfekcje łuków oraz ram drewnianych określono w [4], kl. 5.4.4.(2)
Imperfekcje przechyłowe
Podstawowa imperfekcja przechyłowa zgodnie z [4],(5.1) powinna wynosić
$$\begin{equation} \text {co najmniej } \Phi_0=1/200 \to n_L=200 \label {37} \end{equation}$$
czyli tak jak w przypadku konstrukcji stalowych ( 3-2.1), ale dopuszcza się przyjęcie wartości większych.
Imperfekcja podstawowa może być zredukowana współczynnikiem wysokości
$$\begin{equation} \alpha_h = \sqrt {\cfrac{5} {h}} \label {38} \end{equation}$$
czyli o 12% więcej niż w przypadku konstrukcji stalowych ( 3-2.2)
Norma [4] nie przewiduje współczynników redukcyjnych $\alpha_m$ ( 3-2.3) uwzględniających liczbę słupów $m$ na danej kondygnacji.
Imperfekcje łukowe
Imperfekcja łukowa zgodnie z [4],(5.2) wynosi
$$\begin{equation} \text { co najmniej } e_0=1/400 \cdot l \to n_L=400 \label {39} \end{equation}$$
czyli są dwukrotnie mniejsze od zalecanych dla konstrukcji stalowych (3-2.1) i zgodne z zaleceniami dla konstrukcji żelbetowych (3-3.3).
Klasyczne krzywe wyboczeniowe w EC5
W klauzuli [4], kl. 5.4.4(1) i (2) (EC5) dopuszczono możliwość uwzględniania imperfekcji przechyłowych $(\ref{37})$ oraz łukowych $(\ref{39})$ prowadząc analizę liniową drugiego rzędu,
ale już w rozdz. 6, poświęconym stateczności elementów nakazuje się sprawdzać stateczność słupów i belek historyczną metodą HWEM i stosuje formułę Perry-Robertson na współczynnik wyboczeniowy pod specyficznymi symbolami:
współczynnik wyboczeniowy $k_c $ w miejsce $\chi$
smukłość względna $\lambda_{rel}$ w miejsce $ \overline \lambda$ (1.3)
parametr imperfekcji $\beta_c$ w miejsce $\alpha_*$
moduł Younga $E_{0,05}$ w miejsce $ E $ (przez domniemanie też kwantyl 95%)
itd.
Specyficzne parametry do wyznaczenia krzywych wyboczeniowych konstrukcji drewnianych wg normy EC5 są też parametry krzywych:
smukłość graniczna $\lambda_0=0,3$ ( bez oznaczenia w EC5),
parametr imperfekcji $\alpha \, (\beta_c) =$
0,2 drewno lite
0,3 drewno klejone warstwowo i LVL
Również krzywe wyboczenia bocznego (zwichrzenia) są zaczerpnięte z zależności klasycznych i można je sprowadzić do krzywych zwichrzenia podanych dla konstrukcji stalowych z zastosowaniem specyficznych parametrów.
Z przeglądu sposobu uwzględnienia wpływu przemieszczeń na siły przekrojowe konstrukcji drewnianych, wynika, że należy poszukiwać metody wprowadzenia zastępczego materiału stalowego w miejsce drewnianego, tak, aby można było skorzystać z oprogramowania dedykowanego dla konstrukcji stalowych do analiz stateczności i wyznaczania sił przekrojowych w konstrukcjach złożonych z prętów drewnianych lub hybrydowych (drewniano-stalowych). taka propozycję zawierają przykłady w rozdziale 5. podręcznika. W tym ujęciu nie jest potrzebne stosowanie krzywych wyboczeniowych i wyznaczenie sił lub momentów krytycznych elementów drewnianych.
Imperfekcje konstrukcji murowych
Ze względu na znaczne im perfekcje konstrukcji murowych uwzględnia się to przede wszystkim poprzez stosowanie stosunkowo dużych, specyficznych dla konstrukcji murowych częściowych, materiałowych współczynników bezpieczeństwa $\gamma_M$ zgodnie z tabelą zamieszczoną w [5],tab 3.6 NA2 . Wartości $\gamma_M$ dla murów w zależności od klasy wykonania i rodzaju zastosowanej zaprawy wynoszą:
dla klasy wykonania A:
1,7 gdy stosuje się zaprawę zaprojektowaną; 2,0 dla zaprawy przepisanej i 2,2 dla zaprawy dowolnej,
dla klasy wykonania B:
2,0 gdy stosuje się zaprawę zaprojektowaną; 2,2 dla zaprawy przepisanej i 2,5 dla zaprawy dowolnej.
Klasę wykonania przyjmuje się w zależności od potencjalnej dokładności wykonania muru:
klasa A wykonania robót – gdy roboty murarskie wykonuje należycie wyszkolony zespół pod nadzorem mistrza murarskiego, stosuje się zaprawy produkowane fabrycznie, a jeżeli zaprawy wytwarzane są na budowie, kontroluje się dozowanie składników, a także wytrzymałość zaprawy, a jakość robót kontroluje inspektor nadzoru inwestorskiego;
klasa B wykonania robót – gdy warunki określające klasę A nie są spełnione.
Imperfekcje przechyłowe
W normie [5],kl. 5.3(1)P i (2) wprowadzono zasadę, że należy uwzględnić imperfekcje przevchyłowe konstrukcji murowych., które określono jako przechylenie muru o kąt:
$$\begin{equation} \upsilon = \cfrac{1} { 100 \cdot \sqrt {h_{tot} } } \label {40} \end{equation}$$
gdzie $h_{tot}$ – całkowita wysokość konstrukcji w metrach
Imperfekcje łukowe
Wygięcie wstępne ściany uwzględnia się w postaci mimośrodu początkowego [5],kl. 5.5.1.1(4) :
$$\begin{equation} e_{init} =h_{ef}/450 \label {41} \end{equation}$$
gdzie $h_{ef}$ jest efektywną wysokością muru określaną zgodnie z [5],kl. 5.5.1.2 w zależności od warunków poparcia końców ściany. Dla ścian podpartych na górnym i dolnym końcu na tropach zachowawczo można przyjąć $l_{ef}=h$, gdzie $h$ 4 jest wysokością kondygnacji
Współczynniki wyboczeniowe w EC6
Oprócz wymogu uwzględnienia imperfekcji przechyłowych ($\ref{40}$) wprowadzono specyficzne współczynniki redukcyjne ( wyboczeniowe) $\Phi$ w celu uwzględnienia imperfekcji łukowych w przypadku, gdy mur jest smukły zgodnie z kryterium smukłości:
$$\begin{equation} h_{tot} \cdot \sqrt { \cfrac {N_{Ed}} { \sum EI} } \le \begin{cases}
0, 6 & \text{ dla } n \ge 4 \\
0, 3+0,1 \cdot n & \text{ dla } 1 \le n \le 4 \\
\end{cases} \label {42} \end{equation}$$
Oprócz kryterium $(\ref{42}$) wymaga się , by efektywna smukłość ścian murowych $\lambda_{ef}$ [5],kl. 5.5.1.4 oraz elementów obciążonych pionowo [5],kl. 5.5.2.1. spełniała warunek
$$\begin{equation}
\lambda_{ef}=\cfrac{h_{ef}}{t_{ef}} \le 27
\label {43} \end{equation}$$
Dla ścian murowych obciążonych przeważnie pionowo warunek nośności przyjmuje postać
$$\begin{equation} N_{Ed} \le ( N_{Rd}= \Phi \cdot t \cdot f_d ) \end{equation}$$
gdzie:
t- grubość ściany; $f_d$ wytrzymałość obliczeniowa muru.
Współczynniki redukcyjny (wyboczenia) $\Phi$, wynosi
$$\begin{equation} \Phi= 1 -2 \cfrac{e_i}{t} \label {44} \end{equation}$$
gdzie $e_i$ jest całkowitym mimośrodem siły:
$$\begin{equation} e_i=\cfrac {M_{id}}{n_{id}}+e_{he} + e_{init} \le 0,05 t \label {45} \end{equation}$$
gdzie $e_he$ jest zastępczym mimośrodem od zewnętrznych sił poziomych.
Z przedstawionych wyrażeń wynika, że metody uwzględnienia imperfekcji postulowane przez normę do projektowania konstrukcji murowych są dość zgrubnymi przybliżeniami, w których wymieszono imperfekcje systemowe $e_{init}$ z efektami działania sił zewnętrznych.
Wzór ($\ref{44}$) jest przybliżeniem rozwiązania następującego zadania:
Zadanie:
Dla ściany o grubości $t$ obciążonej siłą $N_{Ed}$ na mimośrodzie $e_i$ podać warunek wytrzymałościowy.
Ścisły warunek wytrzymałościowy dla przekroju prostokatnego o wymiarach $1xt$, czyli o przekroju $A=t$ i wskaźniku wytrzymałości $W=1\cdot t^2/6$ można zapisać w postaci
$$\begin{equation} \sigma= \cfrac {N_{Ed}} {A} + \cfrac {N_{Ed}\cdot e_i}{W} = \cfrac {N_{Ed}}{t} \cdot \left (1+ \cfrac {6 \cdot e_i }{t} \right ) \label {46} \end{equation}$$
Po przekształceniach uzyskujemy ścisłe wyrażenie na współczynnik redukcyjny $(\ref{44}$):
$$\begin{equation} \Phi= \left( 1+ \cfrac{6 \cdot e_i }{t} \right )^{-1} \label {47} \end{equation}$$
Można pokazać , że formuła przybliżona $(\ref{44}$) jest zgodna z dokładną $(\ref{47}$) tylko dla $e_i=t/3$.
W dalszej części podręcznika pokażemy, że projektowanie metodą imperfekcyjną upraszcza projektowanie również konstrukcji murowych bez potrzeby stosowania wyrażeń przybliżonych zarówno w przypadku murów ściskanych jak i zginanych wysokich belek.
Przykłady rachunkowe
Przykład 1 [Stalowa rama portalowa ]
Postawienie zadania i dane ogólne
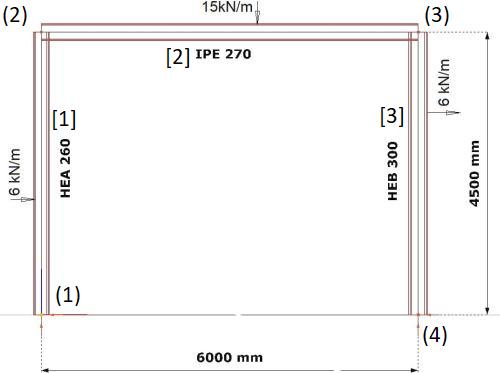
Oszacować przechyłowe oraz łukowe imperfekcje geometryczne oraz zastępcze obciążenia poziome dla ramy portalowej, pokazanej na rys.5. Rama portalowa
o rozpiętości
$L= 6 \,m$
oraz wysokości
h=4,5 \, m
wykonana jest z profili: rygiel [2] – IPE 270, słup lewy [1] – HEA 260, słup prawy [3] – HEB 300. Pręty obciążone są obciążeniami równomiernie rozłożonymi: rygiel $q_{z,[2]}= – 15 kN/m$; słupy $q_{x, [1] , [3]} = 6 \, kN/m$.
Imperfekcje geometryczne przechyłowe
Podstawowa imperfekcja przechyłowa
$( \ref{2} ) \to$ $ \Phi_0=\cfrac{1}{200} \to n_{\Phi,0}=200 $
Współczynniki redukcyjne:
wysokości $(\ref{3}) \to$ $ \alpha_h= \cfrac{3} {\sqrt{4,5}}= 0,943 \quad ( 2/3 \le 0,943 \le 1) $
liczby słupów dla $m=2$ , $(\ref{4}) \to $ $\alpha_m =\sqrt{\cfrac{2+1} {2 \cdot 2}}= 0,866$
Imperfekcja przechyłowa
$(\ref{5}) \to$ $ \Phi=1/200 \cdot 0,943 \cdot 0,866=0,00408 = 1/245$
$n_{\Phi} = \cfrac{ 200 }{0,943 \cdot 0,866}= 245$.
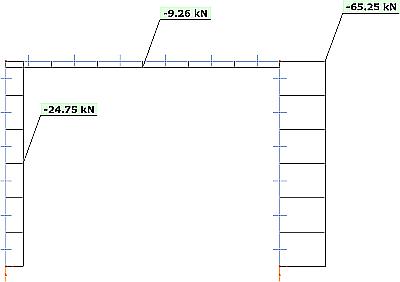
Po sporządzeniu wykresu sił przekrojowych (rys. 6) okazuje się, że:
Suma sił osiowych w słupach wynosi $\Sigma N_{Ed}=24,75+65,25=90 \, kN$, więc siła w słupie [1] $ N_{Ed, [1]} =24,75 \, kN $ < 50% $ \Sigma N_{Ed} / m = 90/2 = 45 \, kN $.
Zgodnie z zaleceniem normowym słup [1] powinno wykluczyć się z liczby słupów $m$ w wyrażeniu ($\ref{4}$), czyli :
$m=1 \to \alpha_m =\sqrt{\cfrac{1+1} {2 \cdot 1}}= 1,00 $.
$n_{\Phi} = \cfrac{ 200 }{0,943 \cdot 1,00}= 212 $.
Dalsze obliczenia w przykładzie prowadzi się dla $n_{\Phi} = 245$
Fikcyjne siły poziome od imperfekcji przechyłowych
Fikcyjne siły jako wynik sił osiowych w słupach zgodnie z ($\ref{6}$):
$H_{Ed[1]} = 24,75/245= 0,1010 kN$
$H_{Ed[2]} = 65,25/245= 0,266 kN$
$\Sigma H_{Ed}= 0,010+0,266=90/245= 0,367 \ , kN$
Zewnętrzna siła pozioma $H_{Ed[1]} =6 \cdot 4,5= 27 kN > 15 \text {% } \cdot 24,75 =3,71 \, kN; \quad \text {oraz } >15 \text {% } \cdot 65,25= 9,78 \, kN$, wiec zgodnie z zaleceniami normowymi , to można pominąć siły od imperfekcji ($\ref{6}$).
Dalsze obliczenia w przykładzie prowadzi się dla wyznaczonych wyżej sił fikcyjnych
Fikcyjne siły jako wynik obciążeń grawitacyjnych
$\Sigma V_{Ed}= 6 \cdot 15=90 \, kN$
($\ref{10}$) to \Sigma H_{Ed} = 90/245= 0,367 \ , kN$
Imperfekcje geometryczne łukowe
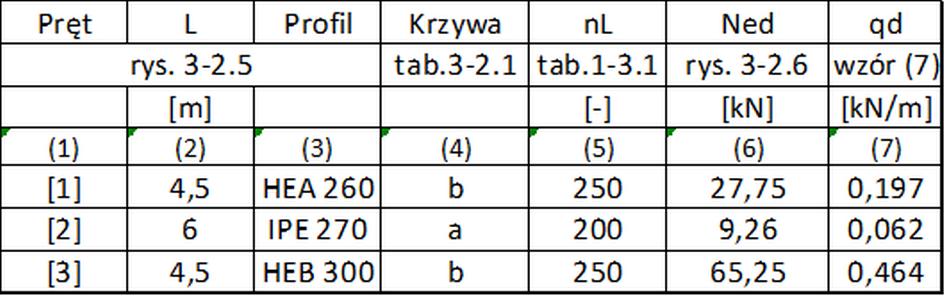
Strzałki imperfekcji łukowych przyjęto z tab 1. i tab.1-1.1 i zestawiono w tab.3-2.3
Tab. 3. Parametry geometrycznych
imperfekcji łukowych do przykładu 3-2.1.
Fikcyjne obciążenia od imperfekcji łukowych
W kolumnie (7) tab.3. podano wartości fikcyjnych obciążęń od imperfekcji łukowych $q_d$ wyliczone z formuły normowej ($\ref{9}$).
W dalszym ciągu podręcznika przeprowadzono dyskusję formuły ($\ref{9}$) i wykazano, ze obowiązuje ona wyłącznie dla prętów przegubowo-przegubowych. Pokazano metodę plastyczną i kinematyczną, umożliwiające uzyskanie poprawnych aproksymacji.
Wnioski
- Z analizy zadania w zakresie współczynnika korygującego imperfekcje przechyłowe w zależności od liczby słupów, wynika , że:
(a) wymóg ograniczenia liczby słupów uczestniczących w przenoszeniu obciążeń pionowych do celów wyliczenia współczynnika redukcyjnego $\alpha_h$, komplikuje obliczenia, bo wymaga wcześniejszego wyznaczenia rozkładu sił osiowych w słupach potencjalnie uczestniczących w przenoszeniu obciążeń pionowych,
(b) ograniczenie liczby słupów (a) prowadzi do zwiększenia imperfekcji przechyłowej konstrukcyjnego w stopniu nieistotnym statystycznie wobec niepewnej i arbitralnie przyjętej wartości imperfekcji przechyłowej.
(c) umożliwienie ograniczenia obliczeń imperfekcyjnych w przypadku, gdy zewnętrzne siły poziome przekraczają 15% obciążeń pionowych pozornie tylko upraszczaj obliczenia, bowiem sprawdzenie tego warunku wymaga wcześniejszego wyznaczenia rozkładu sił osiowych w słupach potencjalnie oraz wyznaczenie segregowanie obciążeń poziomych.
(d) z wniosku (a) i (b) wynika, że w obliczeniach praktycznych można pomijać redukcję liczby słupów $m$ z warunku ich obciążenia. „N< 50%H”.
Z wniosku (c) wynika, że w obliczeniach praktycznych można nie sprawdzać warunku „N<15%H” i procedurę wyznaczania sił imperfekcji prowadzić w każdym przypadku.
2. Zastąpienie imperfekcji przechyłowych fikcyjnymi siłami poziomymi od obciążeń grawitacyjnych jest proste i daje dokładne wyniki,
3. Zastąpienie imperfekcji łukowych fikcyjnymi siłami poziomymi od obciążeń grawitacyjnych jest złożone i nie poddaje się prostym uniwersalnym algorytmom. Zaleca się stosowanie współczesnych programów obliczeniowych, w których imperfekcje łukowe są bezpośrednio w sposób geometryczny
Przykład 2 [Żelbetowa rama portalowa – imperfekcje]
Oszacować przechyłowe oraz łukowe imperfekcje geometryczne oraz mimośrody, a także zastępcze obciążenia poziome dla ramy portalowej, pokazanej na rys. 3.5 (konstrukcja stalowa) . w wersji wykonania słupów i rygla ramy z prętów betonowych zbrojonych.
Geometria konstrukcji
Przekrój słupa $h x b = 600 x 300\,mm$:
pole przekroju $A_c=60 \cdot 30= 1800 \, cm^2$,
moment bezwładności $I_c=60^3 \cdot 30/12= 540000 \, cm^4$,
promień bezwładności $ i =\sqrt { 540000/1800}= 60/ \sqrt{12}= 17,32 \, cm$,
ciężar jednostkowy $g=25 \cdot 0,6 \cdot 0,3=4,5 \, kN/m $
Geometria układu jest taka jak w przykładzie 3.1.
Wysokość fizyczna (teoretyczna) słupa $L= 5 \, m$,
Słup hali jest usztywniony ścianami w kierunku mniejszej sztywności i nie jest usztywniony w kierunku większej i w tym kierunku pracuje jako wspornik (jest utwierdzony w stopie fundamentowej).
Długość efektywna (wyboczeniowa) wspornika $L_{cr}=l_0=2\cdot 5= 10 \, m$,
Smukłość słupa $\lambda=1000/17,32=57,7$,
Imperfekcje geometryczne przechyłowe
Takie same jak w przypadku konstrukcji stalowej są geometryczne imperfekcje przechyłowe:
(3-2.1) $\to \Phi_0=\cfrac{1}{200} \to n_{\Phi,0}=200 $
{3-2.2) $\to \alpha_h= \cfrac{3} {\sqrt{4,5}}= 0,943 $
{3-2.3) $\to \alpha_m =\sqrt{\cfrac{2+1} {2 \cdot 2}}= 0,866$
{3-2.4) $\to \Phi=1/200 \cdot 0,943 \cdot 0,866=0,00408 = 1/245$
$n_{\Phi} = \cfrac{ 200 }{0,943 \cdot 0,866}= 245$.
Przykład 3 [Porównanie metod MNS i MNK w konstrukcjach żelbetowych]
Wiarygodność i dopuszczalność oszacowań sił przekrojowych II rzędu elementów żelbetowych metodą MNS i MNK sprawdzimy na przykładzie słupa hali z [18], Przykład 13.4 .
Smukłość graniczna $\lambda_{lim}= \cfrac{ 20 \cdot 0,7 \cdot 11\cdot 0,7}{\sqrt{0,529}}=14,8$
Ponieważ $\lambda=457,7 > 14,8$, więc zgodnie z [1] $\to$ efekty II rzędu należy uwzględnić
Przechyły i mimośrody słupa
Liczba słupów uczestniczących w przechyle wynosi $m=2$,a wysokość słupa $L=5,0 \,m$, więc:
{3-2.2) $\to \alpha_h= \cfrac{3}{\sqrt{5,0}} =0,894$,
{3-2.3) \to$) $\alpha_m= \sqrt{0,5 (1+1/2)}=0,866$,
Imperfekcja przechyłowa $n_G=200/(0,866\cdot 0,894)=258$,
$\ref{11}$) $\to$ mimośród od przechyłu $e_i= \cdot (1/258) /2 \cdot 10 =0,0194 \, m =19,4 \, mm$.
Uwaga. Powyżej wyjątkowo zastosowano procedurę zastąpienia imperfekcji przechyłowej mimośrodem przyłożenia obciążenia, w celu wykazania, że jest ona błędna.
Mimośród całkowity $e_0=160+19,4= 179,4 \, mm$
Beton, zbrojenie
Beton C25/30: $f_{cd}= 25/1,4 = 17,9 \, MPa$, $E_{cm}= 31 \, GPa$, $E_{cd}= 31/1,2=25,8 \, GPa$,
Zbrojenie ze stali B500: $f_{yd}=500/1,15=435 \, MPa$, $E_z= 200 \, GPa$, $\varepsilon_{yd} =435/(2 \cdot 10^5)= 2,175$ ‰.,
Zbrojenia dołem $A_{s1}$ i górą $A_{s2}$ po $ 15 \, cm^2$, więc sumaryczne zbrojenie $(A_{s1}+A_{s2})=15+15=30 \, cm^2$,
Otulenie osiowe zbrojenia $a=c+ø/2= 50 \, mm$ . Wysokość efektywna przekroju $d= 600-50=550 \, mm$.
Siły przekrojowe i nośność przekroju
Słup jest ściskany obliczeniową siłą $ N_{Ed}= 1768 \, kN$ na mimośrodzie $e_0=160 \, mm$
Obliczeniowy moment zginający 1 rzędu w głowicy wynosi $M_{Ed,0}= 1768 \cdot 0,16=282,9 \, kNm$
Z obliczeń prowadzonych poza przykładem uzyskano informację, że moment zginający, wywołany quasi-stałą kombinacją obciążeń wynosi $ M_{0.Eqp} =190,4 \, kNm$,
zatem współczynnik udziału obciążeń quasi-stałych wynosi $k_{qp}=190,4/282,9= 0,67$.
Nośność przekroju betonowego $N_{Rc}= 1800 \cdot 17,9 \cdot 10^{-1}= 3222 \, kN$, zatem względna siła normalna $ n=1768/3222=0,55$
Nominalna sztywność słupa
W odrębnej procedurze wyznaczono współczynnik pełzania $ \varphi_0=\varphi (t_0, \infty)=2,5$.
Efektywny współczynnik pełzania ($\ref{18}$) $\varphi_{eff}= 2,5 \cdot 0,67= 1,675$.
Współczynniki pomocnicze:
$(\ref{15}) \to$ $k_1=\sqrt{\cfrac{25}{20}}= 1,12$
$(\ref{16}) \to$ $k_2= \min { \left[ \cfrac{0,55\cdot 57,7}{170}; \quad 0,20 \right ]}= 0,187$
Współczynnik wpływu betonu
$(\ref{14}) \to$ = $K_c= \cfrac{1,12 \cdot 0,187}{1+1,675}=0,0783$
Sztywność betonu – pierwszy składnik w ($\ref{13}$):
$K_c E_{cd} I_c= 0,0783 \cdot 25,83 \cdot 10^6 \cdot 540000 \cdot 10^{-8}= 10921 \, kNm^2$
Współczynnik wpływu stali $K_s=1,0$
Dla sumarycznego zbrojenia $(A_{s1}+A_{s2})= 30 \, cm^2$, moment bezwładności zbrojenia szacunkowo (tylko człon Steinera)
$I_s \approx (A_{s1}+A_{s2}) \cdot (h/2-a)^2= 30\cdot (60/2-5)^2= 18750 \, cm^4$
Sztywność stali – drugi składnik w ($\ref{13}$):
$K_s E_{s} I_s= 1,0 \cdot 200 \cdot 10^6 \cdot 18750 \cdot 10^{-8}= 37500 \, kNm^2$
Nominalna sztywność przekroju żelbetowego ($\ref{13}$) wynosi:
$EI= 10921+37500=48421 \, kNm^2$.
Moment II rzędu MNS
Siła krytyczna Eulera – wzór (1-2.5):
$N_B=N_{cr}=\cfrac{\pi^2 \cdot 48421}{10^2}=4779 \, kN$
Moment zginający 1 rzędu jest stały po wysokości słupa, więc współczynnik amplifikacji momentu:
$( \ref {21}) \to $ $\beta=\cfrac{pi^2}{9}=1,234$
Współczynnik amplifikacji
$( \ref {20}) \to$ $a_B=\cfrac{1,234}{4779/1768-1}=0,7246$,
Moment zginający amplifikowany
$( \ref {19}) \to$ $M_{Ed}= 1768 \cdot 0,1794 \cdot (1+0,7246)=547 \, kNm$.
Moment II rzędu MNK
Mimośród niezamierzony
$( \ref {23}) \to$ $ e_a=\max \left[ 1/200 \cdot 10000/2; \quad 600/30; \quad 20\right]= 25 \, mm$
Dla sumarycznego zbrojenia $\Sigma A_s=30 \, cm^2$, stosunek sztywności stali i betonu mamy:
$( \ref {30}) \to$ $n_u=1+0,405=1,405$.
$( \ref {31}) \to$ $\omega= \cfrac{30\cdot 435}{30\cdot 60 \cdot 17,9}=0,405$,
$( \ref {32}) \to$ $n_{bal}=0,4$,
Współczynnik wpływu stopnia zbrojenia
($\ref{18}$) $\varphi_{eff}= 2,5 \cdot 0,67= 1,675$ (jak wyżej),
$(\ref{29}) \to$ $ K_r=\cfrac{1,405-0,55}{1,405-0,4}=0,858$,
Współczynnik wpływu pełzania
$( \ref {34}) \to$ $\beta=0,35+25/200-57,7/150=0,090$,
$(\ref{33}) \to$ $ K_{\varphi}=1+0,090 \cdot 1,675=1,151$,
Krzywizna 1 rzędu
$(\ref{27}) \to$ $\left( \cfrac{1}{r}\right)_0=\cfrac {0,00217}{0,45 \cdot 0,55}=0,0088 \, m^{-1}$,
Krzywizna
$(\ref{26}) \to$ $\left( \cfrac{1}{r}\right)= 0,0088 \cdot 0,858 \cdot 1,151=0,0087 \, m^{-1}$
Mimośród drugiego rzędu
$(\ref{24}) \to$ $e_{N,II} = 10000^2 /10 \cdot 0,0087 =87 mm$
Całkowity mimośród
$(\ref{22}) \to$ $e_{tot}=160+25+87=272 \, mm$
Moment zginający amplifikowany
$( \ref {35}) \to$ $M_{Ed}= 1768 \cdot 0,272= 481 \, kNm$
Wnioski
- Różnice pomiędzy momentami amplifikowanymi, uzyskane metodami nominalnej sztywności oraz nominalnej krzywizny wyznaczone zgodnie z zależnościami normowymi w przykładzie 3.1 wynoszą (547/481)-1=14% .
Rożnica jest zbyt duża , by była akceptowalna w praktyce.
Można bowiem pokazać, że taka różnica w sile przekrojowej przełoży się na stosunek zbrojenia
$[4ø22+4ø24] / [(4+4)ø22]=( 33,3 \, cm^2)/ (30,4 \, cm^2)=1,10$,
czyli 10% różnicy pola przekroju zbrojenia. - W dalszej części podręcznika:
a) normowe rozwiązania przybliżone porównamy z rozwiązaniem dokładnym, uzyskanym numerycznie i pokażemy, że rzeczywiste rozwiązanie jest położone pomiędzy MNS i MNK i będzie zbieżne przy zagęszczeniu podziału słupa na elementy skończone,
b) wykażemy, że zastąpienie imperfekcji przechyłowej mimośrodem przyłożenia obciążenia doprowadziło do sytuacji, w której oba rozwiązania MNS i MNK są błędne .
Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2019), Imperfekcyjna metoda projektowania konstrukcji, Encyklopedia πWiki,
[ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]
Literatura
- PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1994-1-1+Ap1+AC :2008, Eurokod 4: Projektowanie zespolonych konstrukcji stalowo-betonowych, Część 1-1: Reguły ogólne i reguły dla budynków
- PN-EN 1995-1-1+A2+NA+07E :2010, Eurokod 5: Projektowanie konstrukcji drewnianych, Część 1-1: Postanowienia ogólne – Reguły ogólne i reguły dotyczące budynków
- PN-EN 1996-1-1+A1+Ap1,2:2023, Eurokod 6: Projektowanie konstrukcji murowych , Część 1-1: Reguły ogólne dla zbrojonych i niezbrojonych konstrukcji murowych
- PN-EN 1999-1-1:2010, Eurokod 9: Projektowanie konstrukcji aluminiowych, Część 1-1: Reguły ogólne
- PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
- PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
- PN-EN 1993-1-8 +Ap1+AC:2006, Eurokod 3 -Projektowanie konstrukcji stalowych -Część 1-8: Projektowanie węzłów
- Godoy L. A. (1998), Stresses and pressures in thin-walled structures with damage and imperfections. Thin Walled Structures, 32, 181–206
- Abel, M. (2012). P-Delta effect – Technical Knowledge Base – Computers and Struc-tures, Inc. – Technical Knowledge Base. https://wiki.csiamerica.com/display/kb/P-Delta+effect
- Ravindra M. K., Galambos T. V. (1972), Discussion of “Buckling Strength of Columns Based on Random Parameters” by B. T. K. Chung and G. C.Lee. Journal, ASCE Str. Div., 98(ST1), 215
- (PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- Consteel Software, (2019), ConSteel 13 Manual, [ https://consteelsoftware.com/downloads/ ]
- PN-EN 1994-1-1+Ap1+AC:2008, Eurokod 4, Projektowanie zespolonych konstrukcji stalowo-betonowych, Część 1-1: Reguły ogólne i reguły dla budynków
- (PN-EN 1999-1-1:2010, Eurokod 9: Projektowanie konstrukcji aluminiowych, Część 1-1: Reguły ogólne
- Fukumoto, Y. (1982). Numerical Data Bank for the Ultimate Strengths Steel Struc-tures. Der Stahlbau, 1
- Knauff, M., Golubińska, A., Knyziak P. (2015). Przykłady obliczania konstrukcji żelbetowych. Budynek ze stropami płytowo-żebrowymi. Zeszyt 1. PWN, Warszawa
________________________________