Niniejszy artykuł jest rozdziałem 2-2 podręcznika Imperfekcyjna metoda projektowania konstrukcji [ ← spis treści]
Nawigacja: [Imperfekcje i ich źródła] ⇐  ⊗  ⇒ [ Geneza metod imperfekcyjnych]

Artykuł w ciągu ostatnich 24 godzin czytało 3 Czytelników

[Imperfekcje łukowe łuków] [poprzednie] ⇐ ⊗ ⇒ [następne][ alternatywne, zintegrowane imperfekcje]

Zasady ogólne

Zasady przedstawione w poprzednich punktach rozdziału trzeciego dotyczą analizy głównego układu konstrukcyjnego, w tym elementów nośnych wydzielonych z tego układu.

Stabilność  układu nośnego jest utrzymywana przez system powiązań elementów pomiędzy sobą, oraz układy usztywniające wbudowane w układ, które w konstrukcjach prętowych nazywa się stężeniami.Szczególnie istotna rola jest układów usztywniających polega na zapewnieniu stabilności poziomej i skrętnej całej konstrukcji obarczonej imperfekcjami oraz zabezpieczeniu przed utratą stateczności ściskanych prętów i płyt  również z imperfekcjami.

Analiza oddziaływania konstrukcji na układy usztywniające jest przedstawiona w podobny sposób w normie do projektowania konstrukcji stalowych, aluminiowych, zespolonych oraz betonowych. Zbiorcze zestawienie tych zasad przedstawiono na Rys. 3-7.1

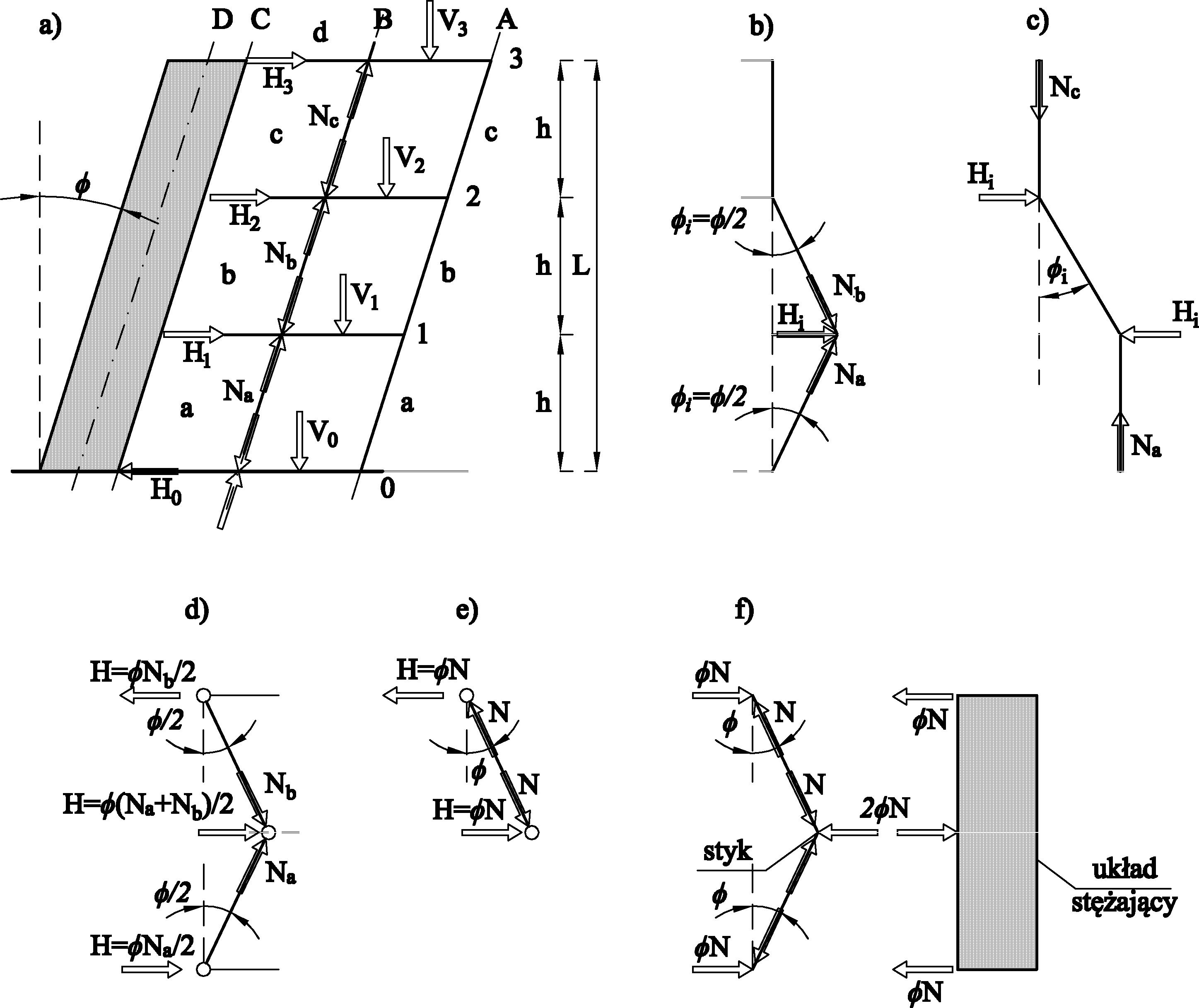
Rys.. 3.-7.1 Oddziaływania konstrukcji z imperfekcjami przechyłowymi na układy usztywniające, opracowano na podstawie rysunków w normach: a) schemat ogólny- wg rys.5.1 EC2 (norma „zelbetowa”); b), c), wg rys.5.1 EC2 ; f), g) na tarcze stropowe wg rys.5.3 EC3 (norma „stalowa”)) oraz wg rys.5.2 EC9 (norma „aluminiowa”); f) w miejscach styków słupa wg rys.5.7 EC3

Siły przekazywane na usztywnienia konstrukcji

Na schemacie rys. 3.-7.1a wyróżniono kondygnacje k=(a, b, c, d)= (parter,1,2 piętro, dach); stropy s=(0, 1, 2, 3)=(fundament,1 kondygnacja , …), oraz słupy (A, B, C, D), przy czym blok D jest trzonem usztywniającym.

Imperfekcja przechyłowa budynku $\Phi$ powoduje, że na poziomie każdego stropu obciążenia $H_i$. Obciążenie grawitacyjne (pionowe) s-tego stropu oznaczono przez $V_s$, przy czym ujmuje ono całkowite obciążenie przyłożone do stropu wraz z jego ciężarem własnym.
Obciążenia zewnętrzne  $V_s$ wywołują w słupach kondygnacji k sumaryczne siły osiowe $N_k$ , przy czym zwroty sił przywęzłowych (reakcji słupów na stropy) są przeciwnych zwrotów w głowicy i stopie słupa.

Siły w słupach kolejnych kondygnacji zwiększają się o obciążenia stropu $\Delta N=V_s$.
Ten przyrost siły w słupach obarczonych zgodną imperfekcją przechyłową $\Phi$ lub imperfekcją jednej kondygnacji $\Phi_k$ wywołuje oddziaływanie poziome na trzon usztywniający lub na tarcze stropowe pomiędzy którymi jest rozparty słup ( rys. 3-7.1 c, e) zgodnie z zależnością:

$$\begin{equation} H_s=\sin{\Phi}\cdot (N_{k-1} – N_k) \approx \Phi \cdot\Delta N_s = \Phi V_s  \label {3-9.1} \end{equation}$$

Na fundament przekazywana jest suma tych sił  $H_0=\sum \limits_{s=1}^N  H_s =\Phi \sum  \limits_{s=1}^N V_s$ (z przeciwnym zwrotem).

Nie jest do końca zrozumiałe, dlaczego w sytuacji (b, d) imperfekcję słupów przyjęto o wartości $\Phi/2$, podczas gdy w pozostałych sytuacjach, w tym (f) imperfekcja wynosi $\Phi$. Stwarza to wrażenie odmiennych sytuacji.

Zdaniem autora we wszystkich sytuacjach powinno się przyjmować imperfekcję przechyłową, będącą statystyką tolerancji wykonania. Sytuacja (b, d), tym różni się od pozostałych, że imperfekcje przechyłowe słupów dwóch sąsiednich kondygnacji są niezgodne (mają inny zwrot), ale takie same wartości  $ |\Phi_a| = |\Phi_b|=\Phi $, więc oddziaływanie na strop pośredni lub układ stężający wynosi

$$\begin{equation} H_s=\Phi\cdot (N_{k-1} – N_k) =  2 \cdot \Phi \cdot V_s  \label {3-9.2} \end{equation}$$

Dalszą analizę zagadnienia przedstawiono w rozdziale Model imperfekcji globalnych oraz Stochastyczny proces imperfekcji przechyłowych w ciągach pionowych , gdzie pokazano, że przypadek niezgodnych kierunków niezamierzonych przechyłów słupów sąsiednich kondygnacji można uwzględnić poprzez probabilistycznie uzasadnione współczynniki $\alpha_h$.

W przypadku zastosowania deterministycznej formuły normowej 3-2.2) – imperfekcja $\Phi_2$ słupa przebiegającego przez dwie kondygnacje  wynosiłaby $\Phi_2=\Phi_1/ \sqrt{2h/h}=\Phi_1 / 1,41$, gdzie $\Phi_1$ jest imperfekcją słupa jednej kondygnacji. Taki wynik jest paradoksem  i w celu jego wyeliminowania imperfekcje przychyłowe slupów należy traktować jako proces losowy, a nie deterministyczny.

W zwykłych sytuacjach należy przyjmować model ($\ref{3-9.2}$), pokazany na rys. 3.-7.1a, do którego w istocie sprowadza się teoretyczny przypadek rys. 3-7.1 b,d.

Model ($\ref{3-9.3}$) Rys. 3-7.1f. należy przyjmować przy uwzględnieniu efektów lokalnych, wywołanych losowym załamaniem słupa pomiędzy węzłami, np. w styku montażowym .Tego typu model należy traktować jako przekształcenie imperfekcji łukowych w przechyłowe (zgodnie z koncepcją przedstawioną w rozdziale Imperfekcje systemowe a efekt P-Delta ).

Z modeli przedstawionych na rys. 3-7.1, wynika, że ekstremalna lokalna siła imperfekcji potrzebna do ustabilizowania pojedynczego elementu wynosi :

$$\begin{equation} H_1=2 \Phi_N \overset{ \Phi=1/200}{=} 2\cdot 1/200 \cdot N= N/100 \label {3-9.3} \end{equation}$$

Pojedynczy pręt stężenia powinien przenieść 1/100 siły ściskającej element stabilizowany, a  w grupie m-prętów, każdy z prętów stężeń powinien przenieść  siłę [1], kl. 5.3.3(4) :

$$\begin{equation} H_L= \alpha_m \cdot N/100 \label {3-9.4} \end{equation}$$

gdzie $\alpha_m$ – współczynnik redukcyjny wg formuły (3-2.3).

W normach przedmiotu nie jest wyjaśnione, czy imperfekcję przechyłową należy ustalać dla jednej kondygnacji, czy dla dwóch, czy też dla całego budynku. W związku z różnymi współczynnikami redukcyjnymi $\alpha_h$ (3-2.2) inne będą wartości imperfekcji przechyłowej $\Phi$ (3-2.4).
W przykładach podanych podręczniku ilustrujących klasyczną metodę normową rozpatruje się odrębnie imperfekcje: jednej kondygnacji, dwóch kondygnacji oraz całego budynku.

Wpływ sztywności słupów na przejmowane siły

Bardziej znaczące od rozpatrywania działania imperfekcji na kilku kondygnacjach byłyby zabiegi konstrukcyjne, prowadzące do zmniejszenia efektu imperfekcji w slupach konstrukcji wielokondygnacyjnej poprzez konstruowanie łożysk i przegubowego oparcia na fundamencie słupów najniższej kondygnacji, szczególnie najbardziej oddalonych od trzonu usztywniającego (p. rys 3.7).

Poprzez zwiększenie zdolności słupa do odkształceń poprzecznych, istotnie można zmniejszyć momenty zginające w głowicy słupów przy podobnych imperfekcjach przechyłowych, Poprzez zwiększenie zdolności słupa do odkształceń poprzecznych, istotnie można zmniejszyć momenty zginające w głowicy słupów przy podobnych imperfekcjachprzechyłowych.

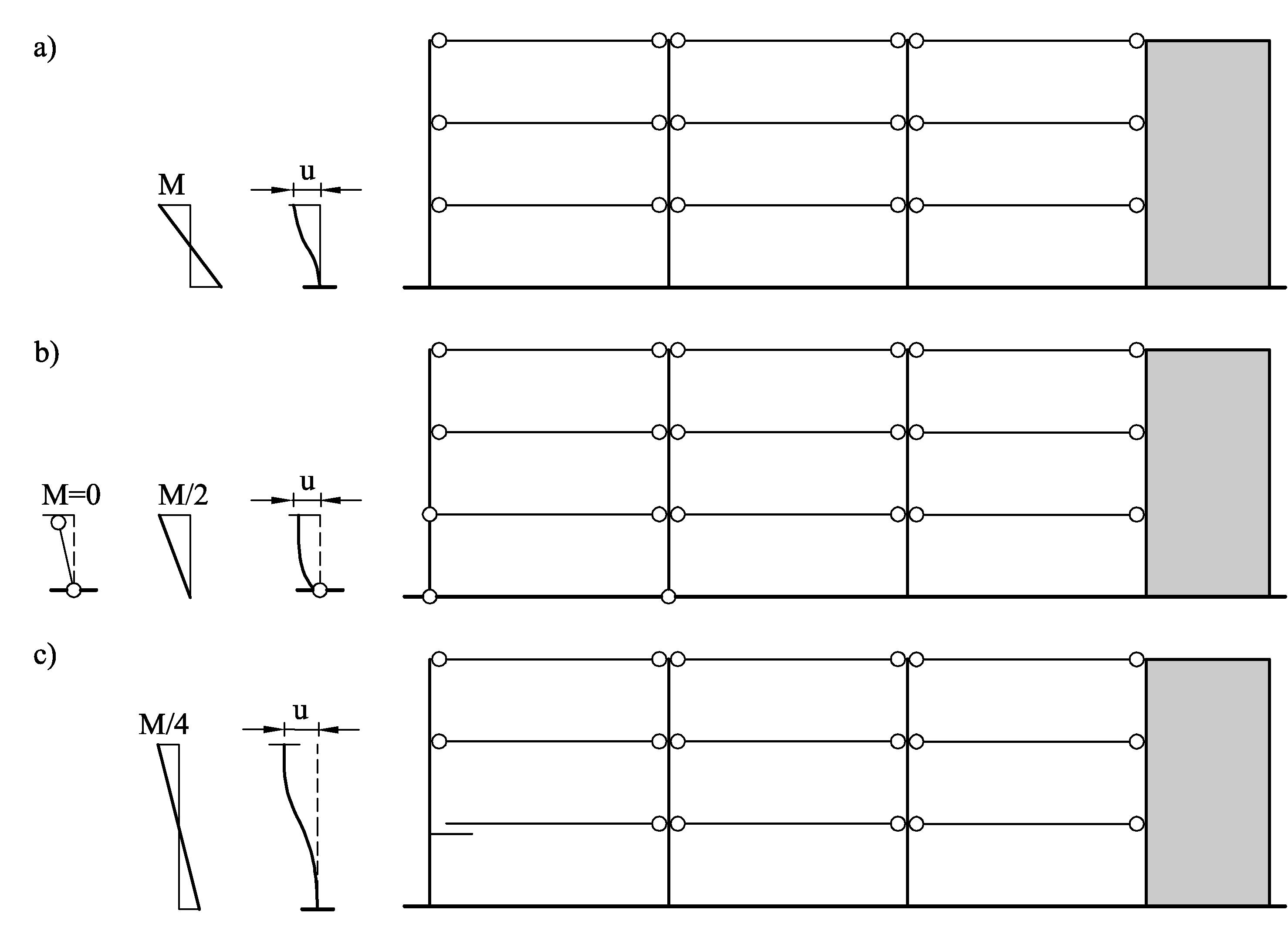
Rys. 3-7.2 Zmniejszenie momentów węzłowych w budynku przy takich samych imperfekcjach, wskutek wprowadzenia łożysk i przegubów: a) bez zmian y schematu – największy moment zginający, b) wprowadzenie przegubów w głowicy i stopie słupów skrajnych, c) wstawienie łożyska przesuwnego

(opracowano na podstawie [2] ).

Układy usztywniające konstrukcję

Stateczność budynku jest zwykle zapewniona przez trzony komunikacyjne lub pełnościenne ściany, które powinny być umieszczone w sposób zapewniający stabilność poziomą i skrętną, jak pokazano na Rys. 3-7.3. Możliwe jest zapewnienie sztywności przestrzennej budynku wyłącznie przez słupy, ale wówczas należy rozważyć uzupełnienie systemu o stężenia, analogicznie do konstrukcji stalowych (np rys. 3-7.4).

W przypadku elementów żelbetowych efekty drugiego rzędu powinny zawierać efekty zarysowania oraz pełzania betonu na sztywność elementu. W procedurach numerycznych efekty te uwzględnia się w drodze wyznaczania sztywności słupów i ściskanych ścian wg metody nominalnej sztywności zgodnie z [3], kl. 5.8.7 .

Identyfikacja układów usztywniających

Tylko w nielicznych przypadkach udaje się w sposób niebudzący wątpliwości wskazać w konstrukcji układ, który spełnia rolę układu stężającego (usztywniającego), najczęściej w drodze wykluczenia tych elementów, które są usztywniane. Zwyczajowo wskazuje się, na wybrane elementy (rys. 3-7.3). W rzeczywistości występuje współpraca wszystkich elementów konstrukcji i przy analizie przestrzennego modelu budynku, zarówno wg teorii 2 rzędu jak i 1 rzędu – taki podział nie jest potrzebny.

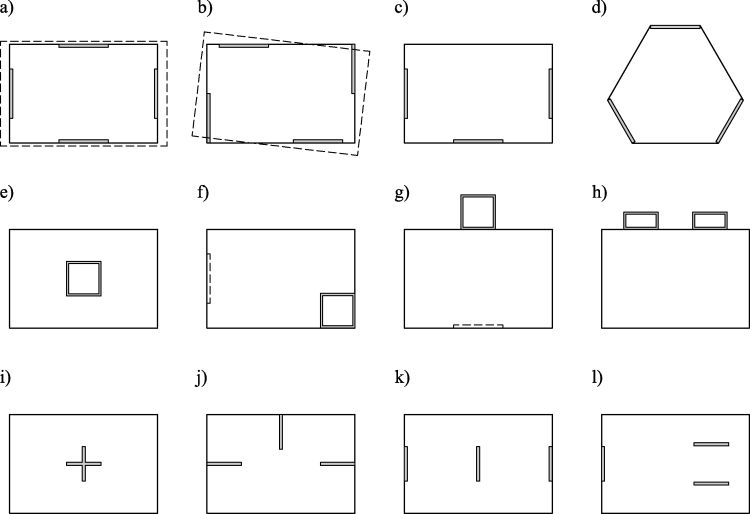
Rys. 3.-7.3.  Układy usztywniające budynek żelbetowy w planie: a, b) dobrze, – – – możliwość odkształceń termicznych, c) adekwatne konstrukcyjnie, d) dobrze, e) dobrze jeśli trzon ma odpowiednią sztywność skrętną, f ,g)___ – – – ściany dodatkowe, źle bez ściany dodatkowej, h) możliwe, ale duża nie centryczność, i) źle, j) brak sztywności na skręcanie, k) brak sztywności podłużnej, l) brak sztywności na skręcanie

(opracowano na podstawie [2] ).

Wydzielanie w konstrukcji układów usztywniających i następnie analizowanie sytuacji przedstawionych na rys. 3-7.1 może być zbyt upraszczające problem. W istocie układy stabilizujące współpracują z pozostałymi elementami systemu.

Zweryfikowanie poprawności rozmieszczenia układów usztywniających w ogólności wymaga przeprowadzenia analizy pełnego, przestrzennego modelu konstrukcji obarczonej imperfekcjami geometrycznymi. Wraz z dostępnością narzędzi komputerowych, przeprowadzenie analiz nieliniowych jest już możliwe w każdym profesjonalnym biurze projektów i powinno być kanonem projektowania zarówno konstrukcji metalowych jak i betonowych oraz innych rodzajów konstrukcji. W metodach imperfekcyjnych nie jest również potrzebne wyznaczanie długości efektywnych (wyboczeniowych) wydzielonych słupów metodami klasycznymi [3] w zależności od przesuwności głowicy i stopy słupa, czyli od sztywności elementów dochodzących. Wyznaczane są siły przekrojowe drugiego rzędu, obejmujące efekty imperfekcji oraz niestabilności systemu i elementów ściskanych. Wystarczy zwymiarować przekrój (w tym dobrać zbrojenie przekroju) na tak wyznaczone siły.

Kryterium uwzględniania efektów drugiego rzędu

Wobec braku precyzji ogólnej zasady, w myśl której efekty drugiego rzędu w konstrukcjach, a w szczególnosci w konstrukcjach żelbetowych  należy uwzględniać, jeśli ich wpływ jest większy niż 10% efektów pierwszego rzędu,

Dla konstrukcji żelbetowych wprowadzono kryterium uproszczone, które miało ułatwić ocenę wrażliwości na efekty drugiego rzędu. Zgodnie z tą zasadą  można nie sprawdzać efektów drugiego rzędu konstrukcji żelbetowej, jeśli spełniony jest warunek [3],kl. 5.18 :

$$\begin{equation} F_{VEd}= k_1 \cfrac{n_s}{n_s + 6} \cfrac{\sum E_{cd} \cdot I_c}{L^2} \label {3-9.5} \end{equation}$$

gdzie:

$F_{VEd}$  – całkowite obciążenie pionowe budynku ( przekazywanym na elementy usztywniane i usztywniające);
$k_1=0,31$ ;
$n_s$ – liczba kondygnacji budynku o całkowitej wysokości $L$ ;
$E_{cd} – obliczeniowy moduł Younga; -moment bezwładności przekroju elementów usztywniających (bierze się pod uwagę tylko niezarysowany przekrój betonu).

Stosowanie nierówności ($\ref{3-9.5}$) jest obwarowane spełnieniem kilku warunków:

1. Niestateczność przy skręcaniu nie jest decydująca, tj. konstrukcja jest dostatecznie symetryczna, globalne odkształcenia wywołane ścinaniem są pomijalne (jak w systemie usztywniającym składającym się przede wszystkim ze ścian usztywniających bez dużych otworów),
2. Elementy usztywniające są sztywno zamocowane u podstawy, tj. obroty są pomijalnie małe, sztywność elementów usztywniających wzdłuż wysokości jest stała (w rozsądnych granicach),
3. Całkowite obciążenie pionowe rośnie proporcjonalnie do liczby kondygnacji.

W załączniku [3],zał H (informacyjnym) przedstawiono dalsze kryteria, które pozwalają ocenić, czy efekty drugiego rzędu mogą być pominięte. Podano również kilka kryteriów upoważniających do pominięcia efektów drugiego rzędu dla wydzielonych słupów żelbetowych, Te ostatnie kryteria wykorzystują pojęcie długości efektywnej (wyboczeniowej) pręta ściskanego wydzielonego z całego systemu, a przecież uproszczone lub arbitralne ustalanie długości efektywnej bez przeprowadzenia analizy LBA często jest obarczone dużym błędem i nie powinno być stosowane.

Warunki upoważniające do stosowania kryterium ($\ref{3-9.5}$) są nieprecyzyjne, a warunki załącznika H w normie Eurokod 2 tracą na znaczeniu wobec powszechnej analizy modeli przestrzennych. W ogólności oznacza to, że w celu oceny wpływu efektów drugiego rzędu, należy najpierw przeprowadzić analizę II rzędu, a dopiero potem porównać efekty, choć w takim przypadku porównanie jest już zbyteczne, bowiem obliczenia nieliniowe są już wykonane,. Projekt wykonany metodą imperfekcyjną jest optymalny technicznie oraz ekonomicznie. Wynika stąd również to, że zwykła konstrukcja żelbetowa zaprojektowana prawidłowo (zgodnie z kryterium 10% wrażliwosci konstrukcji), nie powinna wymagać uwzględniania efektów drugiego rzędu. W przypadku konstrukcji inżynierskich, świadomie projektowanych, jako smukłych –  kryterium poprawności 10% nie jest odpowiednie i takie konstrukcje należy projektować w pełnym zakresie geometrycznie nieliniowym z uwzględnieniem systemowych imperfekcji geometrycznych, zgodnie z procedurami przedstawionymi w niniejszym podręczniku.

Analiza przypadków

Przypadki  poddane analizie

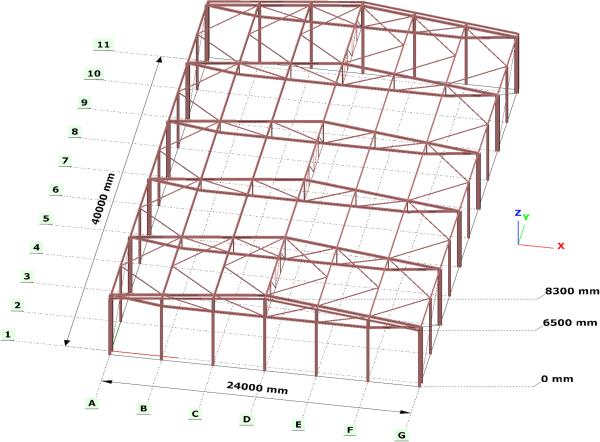
W kolejnych punktach przedstawiono podejście normowe do projektowania układów stabilizujących i porównano je ze współczesną metodą analizy nieliniowej systemu przestrzennego. Rozpatrzono kilka typowych układów konstrukcyjnych: halę stalową, pokazaną na rys. 3-7.3, budynek żelbetowy, pokazany na rys. 3-7.4 oraz most stalowo-betonowy, pokazany na rys. 3-7.5.

Rys.3-7.4. Schemat konstrukcji klasycznej hali ze stężeniami prętowymi: T1- połaciowymi poprzecznymi, T2-połaciowymi podłużnymi, T3 – pionowymi między wiązarami, T4 – pionowymi w linii ścian bocznych

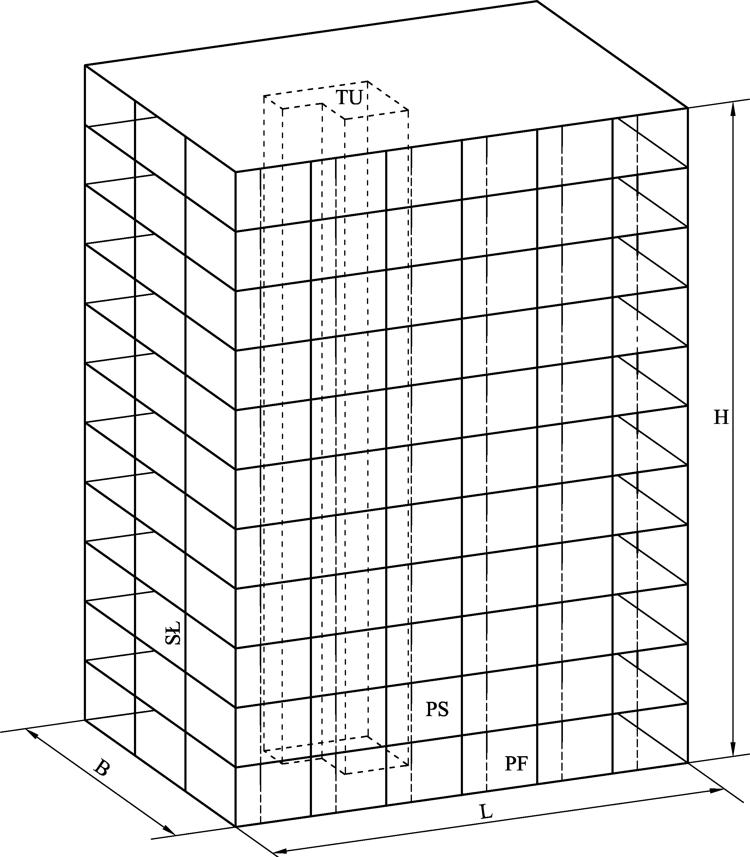
Rys. 3-7.5. Schemat żelbetowego budynku wielokondygnacyjnego z trzonem usztywniającym TU , płytą fundamentową PF oraz elementami usztywnianymi: słupami SŁ i płytami stropowymi PS (opracowanie własne)

Rys. 3-7.6. Most płytowo łukowy. Płyta jezdna żelbetowa, łuki stalowe (opracowanie własne)

W analizie układów usztywniających, zapewniających stateczność boczną elementów lub układów konstrukcyjnych (najczęściej belek lub ściskanych elementów), należy uwzględnić imperfekcje geometryczne elementów stężanych, czyli głównej konstrukcji nośnej.

Stężenia konstrukcji stalowych

W przypadku konstrukcji stalowych, klasyczne, uproszczone zasady lokalizacji systemów stężeń, zapewniających stabilność konstrukcji, dotyczą rozmieszczania stężeń prętowych lub równoważnych stężeń powłokowych (tarczowych).

W klasycznej konstrukcji stalowej, pokazanej na rys. 3-7.4. można wydzielić kilka układów spełniających określone funkcje:

• Układ poprzeczny hali [słupy, wiązar] w płaszczyźnie pionowej poprzecznej. Układ przenosi podstawowe obciążenia pionowe i obciążenie wiatrem z kierunku bocznego (parcie na jeden słup i ssanie na drugi), a także wymuszenia od imperfekcji geometrycznych w płaszczyźnie układu poprzecznego.
• Układ połaciowy [wiązary-płatwie, stężenia połaciowe T1, T2] w płaszczyźnie poziomej wraz ze stężeniami T3, sprzęgającymi wiązary w bikonstrukcje. Układ przenosi działanie wiatru na ściany szczytowe oraz niezamierzone imperfekcje geometryczne systemu w płaszczyźnie dachu w obu kierunkach. Sprzężenie sąsiednich wiązarów w bikonstrukcje, zwiększa niezawodność konstrukcji.
• Układ podłużny [słupy, wiązary stężenia międzysłupowe T4] Układ przenosi działanie wiatru na ściany szczytowe oraz niezamierzone imperfekcje geometryczne systemu w kierunku podłużnym hali
• Ściany szczytowej [ściana ze stężeniami T6] w płaszczyźnie pionowej poprzecznej. Ściana szczytowa najczęściej jest ustawiona przed skrajną ramą poprzeczną.

Każdy z tych układów odrębnie powinien być stateczny i wytrzymały na obciążenia zewnętrzne i wymuszenia spowodowane geometrycznymi imperfekcjami systemowymi.

Współcześnie obliczenia są dokonywane na modelu przestrzennym bez potrzeby wyodrębniania podukładów. Analiza wyodrębnionych układów płaskich ma jedynie tę zaletę, że umożliwia jasne rozdzielenie funkcji poszczególnych układów konstrukcyjnych i wstępne zbadanie stateczności konstrukcji. Analiza taka daje podstawowe informacje o modelowaniu równoważnych sił od imperfekcji, ale nie może zastąpić analizy na modelu [przestrzennym, bowiem jej wyniki mogą znacząco odbiegać od rzeczywistości (p. przykład 3-9-2).

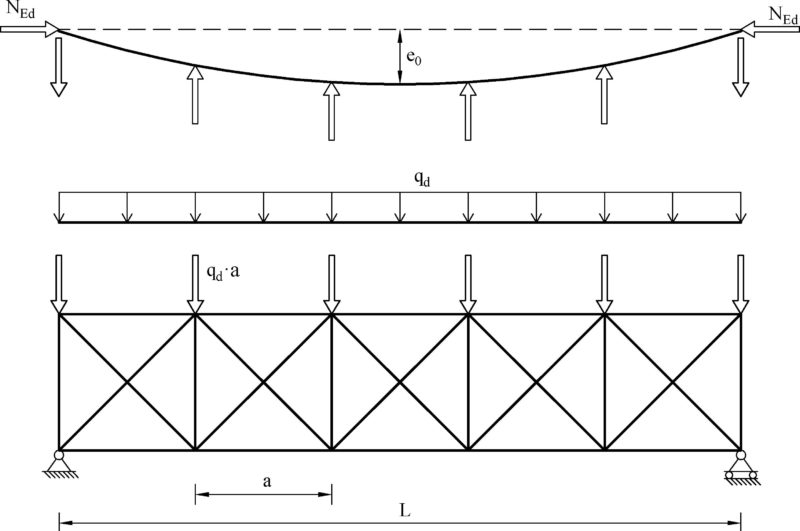
Uproszczona analiza stężeń prętowych polega na rozpatrzeniu płaskich schematów stężeń, pokazanych na rys. 3-7.7, obciążonych równoważnymi siłami imperfekcji oraz poziomymi obciążeniami zewnętrznymi (np. wiatrem na ścianę szczytową) a także siłami wstępnego naciągu (sprężenia) prętów stężeń.

Równoważne siły imperfekcji wyznacza się przy założeniu, że rygle głównych układów poprzecznych są wykonane z niezamierzonymi wygięciami, które można oszacować z formuły [1],(5.12) :

$$\begin{equation} e_0=\alpha_m \cdot \cfrac{L}{400} \quad \to n_L= \cfrac{L}{e_0} = \cfrac{500}{\alpha_m} \label {3-9.6} \end {equation}$$

gdzie:
$L$ – długość stężenia (najczęściej rozpiętość hali $L_y$,
$\alpha_m$ – współczynnik redukcyjny (3-2.3) liczony  dla m – liczby rygli stabilizowanych przez jeden układ usztywniający. Na rys. 3-7.4 i rys. 3-7.7 układem usztywniającym są dwa stężenia T1.

Liczbę rygli stabilizowanych przez jeden układ usztywniający $m$, można wyliczyć z zależności

$$\begin{equation} m=\cfrac{\sum N_{Ed}} {\sum N_{Ed,T1}} = \cfrac{m_x}{m_{T1}} \label {3-9.6a} \end {equation}$$

gdzie $N_{Ed}$ jest sumą sił ściskających wszystkie rygle, a $\sum N_{Ed,T1}$  sumą sił przypadające na jedno stężenie.

$m_{T1}$ liczba pól wypełnionych stężeniami T1.
$m_x$  jest liczba pól między układami poprzecznymi (wraz z polami stężonymi i polami skrajnymi). Dla równomiernie rozstawionych układów co $a_x$ w hali o długości $L_x$ mamy $m_x=\cfrac{L_x}{a_x}$.

Na rys 3-7.7: $m_{T1}=2$, $m_x=5$, $m= 5/2 =2,5$. Liczba  $m$ nie musi być całkowita.

Rys. 3-7.7. Zastępcze modele płaskie do analizy stężeń w halach: a) T1 połaciowe poprzeczne, b) T2 połaciowe podłużne, c) T3 pionowe między wiązarami, d) T4 pionowe w linii ścian bocznych (opracowanie własne)

Stężenie połaciowe poprzeczne T1

Imperfekcje ($\ref{3-9.5}$) i-tego dźwigara można zastąpić obciążeniem równoważnym od imperfekcji jak na Rys. 3-7.8 zgodnie z zależnością  [1],(5.13) ):

$$\begin{equation} q_{d,T1}  = \sum N_{Ed,T1} \cdot \cfrac{8 \cdot(e_0+\delta_{q,i})}{L_y^2} \overset{ \delta _{q,i}=0}{=} \cfrac{8 \cdot  \sum N_{Ed.T1}}{n_L \cdot L_y}  \label {3-9.7}\end {equation}$$

gdzie $\delta_{q,i}$ jest ugięciem stężenia uzyskanym z analizy I rzędu. Jeśli siły w ryglach otrzymano z analizy II rzędu , to przyjmuje się  $\delta_{q,i}=0$.  Współczesne obliczenia standardowo prowadzi się w analizie II rzędu,

Suma sił ściskających w ryglach, stabilizowanych przez rozpatrywane stężenie T1  dla regularnie rozłożonych po długości stężeń w liczbie $m_{T1}$ wyznaczmy z oczywistej zależności:

$$\begin{equation}  \sum N_{Ed,T1} = \cfrac{\sum N_{Ed} }{m_{T1}} \label {3-9.7a}\end {equation}$$

gdzie  $\sum N_{Ed}$ jest sumą sił ściskających wszystkie rygle, którą wyznacza się w modelu bez imperfekcji.

Rys.3-7.8. Równoważna siła stabilizująca stężenie połaciowe poprzeczne

Model stężenia połaciowego poprzecznego T1, pokazany na Rys. 3-7.6), to kratownica podparta na stężeniach pionowych w linii ścian T4 (na rysunku tężniki T4 zastąpiono podporami). Kratownica pozioma T1 obciążona jest w węzłach siłami skupionymi:

$$\begin{equation} q_{d} = Q_d \cdot a_y \label{3-9.8}\end {equation}$$

gdzie  $a_y=L-Y/n_y$ – odległość między węzłami poziomej kratownicy stężenia T1, która w pokryciu płatwiowym jest rozstawem płatwi.

Siły imperfekcji są siłami fikcyjnymi, więc można sądzić, że nie wywołują nacisku na ściany, płatwie okapowe i stężenia T4, a wywołują samozrównoważony układ sił zamknięty we wnętrzu połaci. W rezultacie w niektórych publikacjach (np. [4] ) utrzymuje się, że zerowa jest reakcja $R_{T1}$ od sił imperfekcji  stężeń T1 , przekazywana na stężenia T4.  Na gruncie geometrycznie nieliniowej teorii można jednak wykazać, że nacisk jest rzeczywisty, a z zasady Saint-Venanta [o zanikaniu zaburzeń brzegowych] wynika, nacisk rygli jest przekazywany na elementy najbliższe i stawiające najsilniejszy opór, a w tym przypadku stężenie T4 zlokalizowane w polu, w którym występują stężenia T1.

Wynika stąd zasada, że standardową lokalizacją stężenia T4 jest to pole hali, w którym dano stężenia połaciowe poprzeczne T1, a całość z tężnika połaciowego poprzecznego T1 przekazywana jest tężniki pionowe ścian podłużnych  T3 (p. również [5] ) . Reakcja od imperfekcji, wynosi

$$\begin{equation} R_{T1} = q_d \cdot  \cfrac{L_y}{2}=  \cfrac { 4 \cdot  \sum N_{Ed,T1}}{n_L} \label{3-9.9}\end {equation}$$

gdzie zgodnie z ($\ref{3-9.6}$) $n_L=\cfrac{500}{\alpha_m}$. Z tolerancji wykonawczych zgodnie z Tab. 2.1, wrs. 6 (metoda współczynnika imperfekcji) mielibyśmy  $n_L=\pm 250$ , co daje ponad dwukrotną różnicę. Z testowych symulacji dla przestrzennego modelu typowej hali (przykład 3-9-2) wynika, że żadna z tych wartości nie jest odpowiednia.

Stężenie połaciowe podłużne T2

Model stężenia połaciowego podłużnego T2 (Rys. 3-7.6) oddaje sytuację, w której stężenie jest wymagane. Dotyczy to sytuacji, w której płatwie skrajne są obciążane międzywęzłowo przez słupki pośrednie siłami od wiatru . Wówczas przekrój międzywęzłowy należy podeprzeć prętami stężeń w celu uniknięcia nadmiernego zginania płatwi skrajnych (okapowych). Siły w prętach T2 wyznacza się z warunku równowagi obciążonego węzła. W zasadzie w innych zwykłych sytuacjach stężenia połaciowe podłużne nie są wymagane, chyba, że będą potrzebne ze szczególnych względów, a przede wszystkim w celu poprawy stateczności poziomej przekrycia poprzez skonstruowanie ramy na obwodzie całego przekrycia z pól złożonych z T1 i T2 lub w celu zwiększenia niezawodności systemu (pkt 6.7). Oddziaływanie sił imperfekcji w stężeniu T2 wystąpi wówczas, gdy słupek obudowy (słupek pośredni w ścianie bocznej) będzie ściskany siłą $N_O$ (np. od ciężaru obudowy i urządzeń umieszczonych na długości słupka). W takim przypadku do jego stabilizacji wymagane jest przeniesienie przez stężenie siły poziomą przyłożonej w miejscu podparcia słupka:

$$\begin{equation} H_0=\cfrac { N_0}{n_\Phi}  \label{3-9.10}\end {equation}$$

gdzie:

$N_O $ siła ściskająca słupek obudowy w głowicy – maksymalna po słupkach,
$n_\Phi= 200$ imperfekcja przechyłowa , stanowiącą wartość podstawową (bez współczynników redukcyjnych).

Zwykle ła $$ N_O$ jest pomijalnie mała, bowiem słupki obudowy są w istocie pionowymi belkami opartymi na konstrukcji dachu z zapewnieniem przesuwu pionowego pomiędzy słupkiem a przykryciem hali. Na słupkach obudowy nie opiera się suwnic ani innych ciężkich urządzeń. Zwykle więc stężenia połaciowe podłużne nie są wymagane do przeniesienia sił imperfekcji, a tylko jako podpora pozioma dla słupów obudowy, jeśli te obciążałyby międzywęzlowo płatwie lub belki wezgłowiowe ściany bocznej hali.

Stężenie pionowe między wiązarami T3

Potrzeba zastosowania stężenia pionowego między wiązarami T3 wynika z konieczności sprzężenia dwóch sąsiednich wiązarów. W modelu Rys. 3-7.6, pokazano, że T3 jest pionową kratownicą z pasem górnym w postaci płatwi i pasem dolnym zawieszonym na pasach dolnych obu sprzęganych wiązarów. Stężenie T3 zabezpiecza kratownice główne przed niezamierzonym skręceniem płaszczyzny głównej kratownic. Wobec tego wyznaczenie sił w prętach stężenia od imperfekcji wynika z mechanizmu, w którym na stężenie działa para sił: na płatew siła $Q_d$  stabilizująca pas górny wiązara oraz równoważna siła $Q_d$ działającą na pręt dolny stężenia. Łącznie obie siły dają moment $M_d=Q_d\cdot h$ (  h -wysokość stężenia). Siłę stabilizująca pręt ściskany wyznaczymy z (3-2.3), czyli:

$$\begin{equation} Q_d= \cfrac{\alpha_m \cdot N_{Ed}}{100} \label{3-9.11}\end {equation}$$

gdzie konserwatywnie przyjmuje się $\alpha_m = 1,0$.

W opisanym mechanizmie w krzyżulcach nie powstaną żadne siły. Są one wywoływane różnicą przemieszczeń sprzężonych wiązarów i zależą od sztywności układu. Siły ($\ref{3-9.11}$) powinny być przeniesione przez płatew i pas dolny stężenia, przy czym jedna z nich jest ściskająca, a druga rozciągająca naprzemiennie w zależności od kierunku wyboczenia ściskanego pasa rygla.

Stężenie pionowe w linii słupów T4

Model stężenia pionowego T4 w linii słupów ścian bocznych pokazano na Rys. 3-7.6.

Rozważmy sytuacje, gdy stężenie w linii ścian bocznych realizowane jest poprzez pręty T4, zamontowane w tych polach hali, w których zastosowano stężenia połaciowe poprzeczne. Alternatywą jest utwierdzenie słupów głównych w blokach fundamentowych, co może mieć miejsce w przypadku stężeń ramowych, to znaczy wówczas, gdy utwierdzenie w stopach jest wystarczające do przeniesienia obciążeń pokazanych na modelu. W takim przypadku nie są potrzebne stężenia prętowe, ale musimy się liczyć z powstaniem momentów utwierdzenia i zginaniem podporowych przekrojów słupów momentami zginającymi, które mogą prowadzić do zwiększenia przekrojów słupów.  Dodatkowe zginanie słupów wyeliminowano poprzez zastosowanie stężeń prętowych T4 i wprowadzenie przegubów podporowych w miejsce utwierdzeń.

Sposób wyznaczania sił w prętach stężeń pionowych w linii słupów T4 jest standardowy, a przykład rachunkowy zamieszczono w przykładzie 3-7.1.

Przykłady rachunkowe

Przykład 3-7.1. Imperfekcje stężeń hali stalowej i siły w modelu 2D

Geometria hali

Z rysunków 3-7.3., 3-7.6:

$L_x= 40,0 \, m $  – długość hali,
$a_x= 8,0 m $ – rozstaw pomiędzy układami poprzecznymi,
$n_x=5$ – liczba pól między układami poprzecznymi.
$L_y=24,0 \, m$ – rozpiętość hali, (szerokość nawy),
$a_y =4,0 \,m$- rozstaw pomiędzy układami poprzecznymi,
$n_y= 6$- liczba pól między płatwiami,
$\alpha= 45$^o – kąt nachylenia krzyżulców stężeń,
$n_{T1}=n_{T4}=2$ – liczba pól ze stężeniami połaciowymi poprzecznymi  T1 i pionowymi ścian T4,
$h_0= 0,0 \,m$ – poziom „0” hali,
$h_p=-1,2 \, m$ – poziom zamocowania słupa w fundamencie,
$h_{okap}=7.4 \, m$  poziom okapu<
$\Delta_A= 1,2 \, m$ – wysokość attyki ponad osią wiązara (100 (1/2 profilu pasa)+300 (wysokość płatwi)+100 (blacha fałdowa)+200 (ocieplenie)+500 (attyka ponad połacią)=1200=1,2 m),
$h_{sł,c} = 7,4 +1,2 -1,2=7,4 \, m$ – średnia wysokość  słupka ściany szczytowej,
$h_{sł} = 6,5 \, m $ – wysokość słupa ściany bocznej.

Stężenia połaciowe poprzeczne T1

Współczynnik $\alpha_m$ dla stezenia T1

Rys 3-7.6  $\to$
liczba pół między układami poprzecznymi, $m_x=5$
liczba pól stężonych $m_{T1}=2$

($\ref{3-9.6a}) \to  m=\cfrac{5}{ 2 } = 2,5$

(3-2.3) $\to \alpha_m= \sqrt{\cfrac{2,5+1}{2 \cdot 2,5}}=0,837$,

Imperfekcja stężenia T1

($\ref{3-9.6})  \to n_L= \cfrac{500}{0,837} =597,4 $

Siły w pasach rygli stabilizowane stężeniem T1

Suma sił w pasach rygli (wiązarów) w całym przekryciu
Tab.3-9-1.,poz.1 $\to \sum N_{Ed}=1319,7 \, kN$ ,

Siły stabilizowane przez jedno stężenie T1 $(\ref{3-9.7b}) \to \sum N_{Ed,T1}=1319,7/ 2=659,9 \, kN$

Siły w ryglach uzyskano z rozwiązania drugiego rzędu, więc $\delta_q=0$  – komentarz pod ($\ref{3-9.7}$)

Obciążenie zastępcze od imperfekcji stężenia T1

obciążenie rozłożone $ (\ref{3-9.7})  \to q_{d,T1} =\cfrac{8 \cdot 659,9} { 597,4 \cdot 24}= 0,368 \, kN/m$

obciążenie węzłowe $(\ref{3-9.8})   \to Q_d=0,368 \cdot 4,0=1,473\, kN$,

Siły w prętach stężenia T1 od imperfekcji

Siły w prętach stężenia uzyskamy po rozwiązaniu poziomej kratownicy T1, obciążonej siłami węzłowymi

Reakcja podporowa (na jedno stężenie T4 $ ( \ref{3-9.9})  \to  R_{T1}= \cfrac {0,368 \cdot 24,0}{2}= 4 \cdot 659,9/597,4= 4,42\, kN$

Siła w krzyżulcu podporowym z warunku równowagi sił $R_{T1} – Q_d/2 = 2 K_{T1} \cdot \cos {\alpha}$:

$K_{T1}= \cfrac{4,42- 1,473/2}{2 \cos {45}}=2,60 \, kN$

Stężenia połaciowe podłużne T2

Maksymalna siłą ściskająca słupek pbudowy
Tab.3-9-1.- poz.3 $\to  N_O=22,3 \, kN$ ,

Siły imperfekcji od słupków obudowy

($\ref{3-9.10}$) $\to H_0=22,3/200=0,11 \, kN$

Z warunku równowagi sił $H_0=2 K_{T2} \cdot \cos {\alpha}$  otrzymujemy siłę w krzyżulcu stężenia podłużnego

$K_{T2}= \cfrac{0,11}{2 \cos {45}} = 0,11 \, kN$

Stężenia połaciowe podłużne T3

Siła w pasie sprzęganego wiązara Tab.3-9-1.,poz.1 $\to  N_{Ed,T3}^{II} = 328,7 \, kN$

Siła działająca na pas dolny stężenia T3   oraz
($\ref3-9.11})  $ \to Q_d= 1.0 \cdot 328,7 /100= 3,3 \, kN$

siła w płatwi oraz w pasie dolnym stężenia, $P_{T3}= Q_d =3,3 \, kN$ –

$K_{T3 }= 0$ – siła w krzyżulcu stężenia.

Stężenia pionowe między słupami T4

suma sił w stężanych słupach głównych ( w linii jednej ściany bocznej)  Tab.3-9-1.,poz.2   $\sum N_s=1260,5/2= 630,25 \, kN

(rys.3-7.6):
$\to m_x= 5 $,
$to m_{T3}=2$
$m =m_x/m_{T3}=5/2=2,5 $,
(3-2.2) $\to \alpha_h= \cfrac{2}{\sqrt{6,5}} =0,78$,
(3-2.3) $\to \alpha_m= \sqrt{\cfrac{2,5+1}{2 \cdot 2,5}}=0,837$,
(3-2.1) $\to  n_{\Phi,0}=200 $
(3-2.4) $\to n_\Phi= \cfrac{200}{0,780 \cdot 0,837}=306

(3-2.5) fFkcyjna siła pozioma na jedno stężenie T4   $\to H_{T4}= 630,25 / 306= 2,06 \, kN$

Całkowita fikcyjna siła imperfekcji działająca na jedno stężenie  T4 (na dwa stężone słupy główne)

$H=H_i+R_{T1}= 2,06+4,42 = 6,48 \, kN$

Siła w pręcie stężenia od imperfekcji (pręty tylko rozciągane – ściskany wybacza się):

$K_{T4}=6,48/cos{45}=9,16 \, kN$

Przykład 3-7.2. Siły  w stężeniach  modelu 3D

Oszacowania normowe z płaskich modeli stężeń, z przykładu 3.1.  sprawdzono na modelu przestrzennym hali Rys. 3-7.3 z imperfekcjami geometrycznymi. Imperfekcje przechyłowe zamodelowano metodą obciążeniową. Każdą siłę pionową  (grawitacyjną, skupioną lub rozłożoną, w tym ciężar własny) stowarzyszono z siłami poziomymi po osi x i y: , przy czym przyjęto stałą imperfekcję  Imperfekcje łukowe rygli nadano przez wymuszenie geometryczne . Wartości obu imperfekcji przyjęto zgodnie z wyliczonymi w przykładzie wyżej Przeprowadzono obliczenia 2 rzędu dla różnych sposobów zadawania imperfekcji, za każdym razem odczytując siły w prętach stężeń.

Geometria hali i obciążenia

Model hali z parametrami geometrycznymi jak w przykładzie 3.1 pokazano na rys. 3-7.9.

Rys.3-7.9. Przestrzenny model hali analizowany w programie Consteel w.12

Halę obciążono:

• śniegiem we wszystkich wariantach przewidzianych w normie [6] dla  miejscowości położonej na wysokości 300 m npm i dla współczynnika ekspozycji $C_e=1$ i termicznego $C_t=1$. Dach hali bez attyki i przeszkód (bez zasp śniegu),
• wiatrem we wszystkich wariantach przewidzianych w normie [7] dla czterech współczynników kierunkowych . dla dachu dwuspadowego i płaskich ścian oraz ciśnienia wewnętrznego $w_{in} =0,2 \,kN/m^2$ oraz dla bazowej prędkości wiatru $ 22\, m/s$ i III kategorii terenu,
• ciężar pokrycia $g_p$i obudowy ściennej $g_s$  $g_p= g_s =0,40 \, kN/m^2$,
• ciężar własny konstrukcji uwzględnia automatycznie program obliczeniowy,
• obciążeniem dachu kat H $q=0,4 kN/m^2$.

Uwzględniono wszystkie kombinacje obciążeń zgodnie z [8].

Siły w prętach  modelu 3D – bez imperfekcji

Siły odczytano z modelu przestrzennego 3D w programie Consteel. Siły odczytano w celu przeprowadzenia oszacowań normowych wg przykładu  3-9.2.

Siły osiowe ryglach (pasy górne wiązarów)

Suma sił średnich po długości rygli. Zebrano ze wszystkich elementów w hali
I rzedu $N_w= \sum N_{Ed}^I= 1315,5 \, kN $,
II rzedu $N_w= \sum N_{Ed}^{II} = 1319,7 \, kN $,

Siła w kalenicy wiązarów sprzęganych przez T3
$N_{Ed,T3}^{I} = 323,5 \, kN$
$N_{Ed,T3}^{II} = 328,7 kN$

Siły osiowe w słupach głównych

Suma średnich  po wysokości  12-tu słupów głównych

I rzędu $N_s \sum N_{Ed}^I1254,5 \,kN$
II rzędu  $N_s \sum N_{Ed}^{II}= 1260,5 \, kN$

Siły osiowe w słupkach obudowy

Maksymalna siła osiowa w słupkach  obudowy (słupkach ścian bocznych)

I rzędu $N_O^I = 20, 2 \, kN$
II rzędu  $N_O&{II} = 20,3 \, kN

Siły w stężeniach w modelu 3D – bez imperfekcji

T1
T2
T3
T4

Siły w stężeniach w modelu 3D  od imperfekcji  przechyłowej UPI

wymuszenie geometryczne  GIM

T1
T2
T3
T4

wymuszenie obciążeniowe  QIM

T1
T2
T3
T4

Siły w stężeniach  w modelu 3D  od imperfekcji  łukowej  EŁI

wymuszenie geometryczne  GIM
T1
T2
T3
T4

wymuszenie obciążeniowe  QIM

T1
T2
T3
T4

Siły w stężeniach  od łącznej imprefekcji przechyłowej  UPI i łukowej  EŁI

wymuszenie geometryczne  GIM
T1
T2
T3
T4

wymuszenie obciążeniowe  QIM

fikcyjne siły poziome  od przechyłu i imperfekcji łukowej

T1
T2
T3
T4

GIM – wymuszony przechył lub ugięcie łukowe
QIM  –

Wnioski z przykładu 3-7-2

1. Dla współczesnych komputerów i programów modele prętowe złożone nawet z dużej liczby prętów są bardzo prostymi modelami obliczeniowymi, zawierających pręty ze wszystkich układów pokazanych na rys. 3-7.3.
2. Model przestrzenny należy obciążyć oddziaływaniami zewnętrznymi oraz równoważnymi siłami od imperfekcji przechyłowych , a także geometrycznymi wymuszeniami łukowymi.
3. Siły w stężeniach uzyskane w modelu przestrzennym są istotnie rożne od sił oszacowanych w układach płaskich. Niezgodności są różnej wielkości i różnego znaku
4. Ponieważ wyniki uzyskane z modelu przestrzennego są znacznie bliższe rzeczywistości, więc zaleca się, by oszacowania na płaskich modelach wykorzystywać tylko do wstępnych koncepcyjnych projektów.

Przykład 3-7.3.  Imperfekcje przechyłowe płaskich usztywnień budynku żelbetowego

Oszacowano siły imperfekcji, działające w płaskim modelu usztywnień budynku wzorcowego z rys. 3-7.4 z wykorzystaniem oszacowań zestawionych na rys 3-7.1.

Na modelu przestrzennym (rys. 3-7.4) dokonano przekroju poprzecznego wzdłuż boku krótszego i uzyskano obraz pokazany na rys. 3-7.10.

Układem usztywniającym jest trzon komunikacyjny TU, a elementami usztywnianymi słupy SŁ. W przekazywaniu poziomych sił na trzon uczestniczą płyty stropowe PS. Układ od dołu zamyka płyta fundamentowa PF. Oznaczono kilka pierwszych kondygnacji „a, b, c,” oraz stropów „0, 1, 2”, a także punkty analizy:  $\Pi_1$ – oddziaływania konstrukcji na trzon usztywniający na poziomie stropu „1” oraz $\Pi_2$- oddziaływanie słupa na tarczę stropową na poziomie stropu „2”.

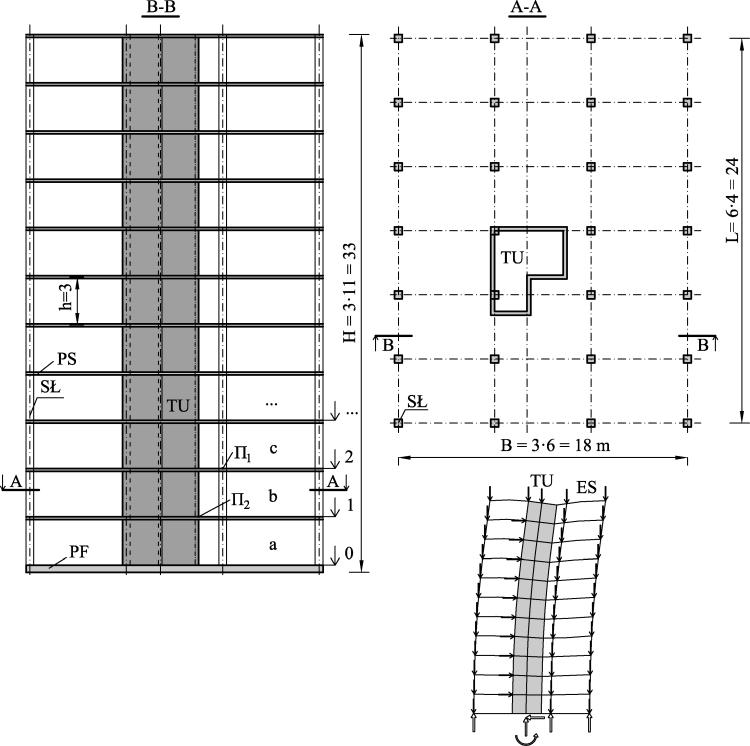
Rys. 3-7.10. Przekrój przez budynek z Rys. 3-7.4 : TU- trzon usztywniający, ES-elementy usztywniane, SŁ – słup, PF- płyta fundamentowa, PS- płyta stropowa, punkty analizy (opracowanie własne)

Zasadniczym obciążeniami budynku jest ciężar własny żelbetu i obciążenie wiatrem. W celach porównawczych wszystkie analizy prowadzono dla jednej, wybranej kombinacji obciążeń, a mianowicie dla kombinacji z redukcją obciążenia stałego i dla wiodącego obciążenia zmiennego parciem wiatru na dłuższy bok Sztywność betonu C30/37, zbrojonego stalą B500. ustalano metodą nominalnej sztywności (pkt 3.7.3.1) dla współczynnika pełzania  $\varphi_{ef},=2,0$ współczynnika wpływu betonu $K_c=0,5$i wpływu stali .$K_s=1,0$.

Geometria i obciążenia budynku

$H=33 \, m$  – wysokość,
$L=-24 \, m$ – długość,
$B= 18 \, m$ -szerokość,
$n=11$- liczba kondygnacji każda o wysokości $h=3 \,m$.
$m=28 $ – liczba słupów na kondygnacji.
$s=0,56 \, kN/m^2$ – obciążenie śniegiem ( I strefa śniegowa, teren normalny),
w (obciążenie wiatrem dla I strefa wiatrowa, teren kategorii  II,
$g_s= 2,3kN/m^2$ – ciężar warstw stropowych (bez ciężaru płyty betonowej),
$q_s =3,8 \, kN/m^2$ – obciążenie użytkowe stropu (3,0 biura + 0,8 ścianki) – nie stosowano współczynnika redukcyjnego powierzchniowego $\alpha_A$, ani kondygnacji $\alpha_n$,
Ciężar własny konstrukcji uwzględnia automatycznie program obliczeniowy.

Jedna kondygnacja – imperfekcje przechyłowe

(3-2.1) $\to \Phi_0=\cfrac{1}{200} \to n_{\Phi_0} =200$
(3-2.2) $\to \alpha_h=\cfrac{2}{\sqrt{3}}=1,15 > 1 \to \alpha_h =1,0$
(3-2.3) $\to \alpha_m= \sqrt{\cfrac{1+28}{2\cdot 28}}=0,72$
(3-2.4) $\to n_\Phi=\cfrac{200}{1,0 \cdot 0,72}=278$  ( $\Phi=1/278$)

Dwie kondygnacje – imperfekcje przechyłowe przeciwne

(3-2.1) $\to  \Phi=0 =\cfrac{1}{200} \to n_{\Phi_0} =200$
(3-2.2) $\to  \alpha_h=\cfrac{2}{\sqrt{6}}=082$
(3-2.3) $\to  \alpha_m= \sqrt{\cfrac{1+28}{2\cdot 28}}=0,72$
(3-2.4) $\to n_\Phi=\cfrac{200}{0,82 \cdot 0,72}=339$  ($\Phi=1/339$)

Cały budynek– imperfekcje przechyłowe

(3-2.1) $\to$ mperfekcja przechyłowa  $\Phi_0 =\cfrac{1}{200} \to n_{\Phi_0} =200$
(3-2.2) $\to  \alpha_h= \max{ \{ 2/3  ; \quad  \cfrac{2}{\sqrt{33}}}=0,67$
(3-2.3) $\to  \alpha_m= \sqrt{\cfrac{1+28}{2\cdot 28}}=0,72$
(3-2.4) $\to  n_\Phi=\cfrac{200}{0,67 \cdot 0,72}=415$  ($\Phi=1/415$)

Przykład 3-7.4. Przemieszczenia budynku żelbetowego z imperfekcjami przechyłowymi

W celu oceny wpływu imperfekcji i efektów nieliniowych na przemieszczenia wzorcowego budynku żelbetowego przeprowadzono analizę przemieszczeń punktu narożnego górnego stropu, oznaczonego na rys. 3-7.11

Rys. 3-7.11 Przemieszczenia górnych kondygnacji (opracowanie własne)

Imperfekcję normową określono w przykładzie 3-9.3 i wynosi ona $n_\Phi=414$.
Imperfekcje przechyłowe określone na podstawie tolerancji wykonania z tab. 2.2, kol 7 jak następuje:
dla słupa kondygnacji  $n_\Phi= \min{ \{h/30 \, ; \, 200 \} }= \min{ \{3000/30 \, ; ], 200 \} }= 100$,
dla budynku  $n_\Phi= \max{ \{ \sum h/100 \,; \, 100 \sqrt{n} \} }= \max{ \{ 33000/100 \,; \, 100 \sqrt{11} \} }=\max{ \{ 330 \,; \, 332 \} }=332$,
dla słupów sąsiedniej kondygnacji z hipotezy o zgodnym przechyle słupów $ n_{ \Phi_0}=\cfrac {1}{\Phi_0}= \min { \{200 \, ; \,100 \) } =100$
$\alpha_h=0,67$, $\alpha_m=1,0$ ,
$n_/Phi= \cfrac{100}{0,67 \cdot 1,0}=149$.

Wyniki obliczeń zestawiono w tab 3-7.1

Tab. 3-7.1 Wpływ imperfekcji przechyłowej na przemieszczenia budynku żelbetowego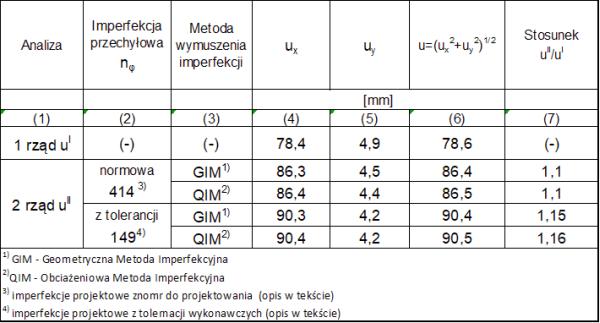

Wnioski z przykładu 3-7-4

1. Różnica przemieszczeń z rozwiązania klasycznego i 2. rzędu po wymuszeniu geometrycznej imperfekcji przechyłowej jest na granicy 10% w przypadku uwzględnienia imperfekcji normowych i większa, od 10% w przypadku zadania imperfekcji projektowych wyliczonych z tolerancji wykonawczych.
2. Z kryterium pzemieszczeniowego wynika, typowe budynki żelbetowe mogą być wrażliwe na efekty drugiego rzędu
3. Wniosek uzyskano dla typowego średniowysokiego budynku żelbetowego, które projektuje się standardowo wg teorii 1. rzędu i bez obciążenia od sił imperfekcji.
4. Można sprawdzić, że warunek ($\ref{3-9.5}$) jest spełniony Oznacza to, że uproszczony warunek ($\ref{3-9.5}$) jest zawodny i należy go stosować bardzo ostrożnie.
5. Obciążenie fikcyjnymi siłami poziomymi jest równoważne wymuszeniu geometrycznych imperfekcji przechyłowych, a jest łatwiejsze do zastosowania w konwencjonalnych programach inżynierskich, bowiem nie wymaga modyfikacji geometrii systemu.

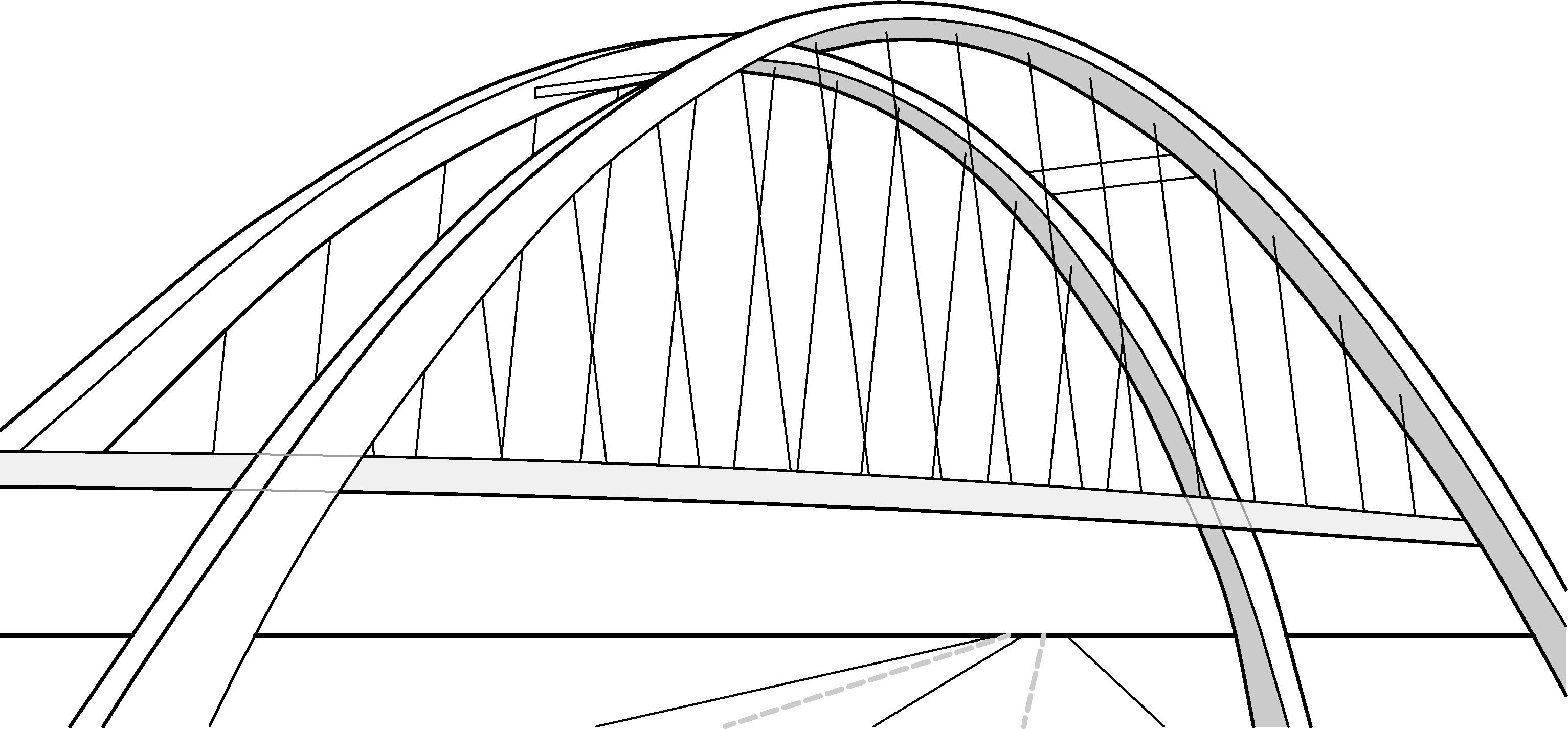
Przykład 3-7.5 Stężenia mostu łukowego

w trakcie edycji

⇒[następne][ alternatywne, zintegrowane imperfekcje]

Niniejszy artykuł jest częścią 9 rozdziału 3 podręcznika Imperfekcyjna metoda projektowania konstrukcji

Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2019), Imperfekcyjna metoda  projektowania konstrukcji, Encyklopedia  πWiki,
[ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]

Historia edycji:
(2019-04-19, 30) Wersja 1.0
(2019=06-07) zamieszczono przykład obliczania stężeń hali stalowej

Proszę społeczność Inżynierów w internecie o przesyłanie recenzji podręcznika  na adres  wydawnictwa biuro@chodor-projekt.net
Leszek ChodorLiteratura

1. PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
2. Bachmann H., Steinle A. (2011). Precast concrete structures. Ernst & Sohn : John Wiley & Sons, Inc.
3. PN-EN 1992-1+AC+Ap 1,2,3: 2008, Projektowanie konstrukcji z betonu, Część 1-1: Reguły ogólne i reguły dla budynków
4. Biegus A. (2003), Stalowe budynki halowe. Arkady, Warszawa
5. Kozłowski A. (2015). Konstrukcje stalowe. Część trzecia, Hale i wiaty. Oficyna Wydawnicza Politechniki Rzeszowskiej
6. PN-EN 1991-1-3:2006, Eurokod 1: Oddziaływania na konstrukcje, Część 1-3: Od-działywania ogólne- Obciążenie śniegiem
7. PN-EN 1991-1-4:2008, Eurokod 1. Oddziaływania na konstrukcje, Część 1-4: Oddziaływania ogólne. Oddziaływania wiatru
8. PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji

________________________________