Leszek Chodor, 18 lipca 2015
19-02-2025 rewizja po dużej awarii portalu
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 3 Czytelników
Najważniejszą częścią konstrukcyjną lekkich hal są przekrycia, które należy rozpatrywać łącznie z podporami – słupami. W artykule zajęto się optymalnym wyborem typu przekrycia oraz elementów klasycznych przekryć hal.
Artykuł „Hale stalowe optymalne funkcjonalnie” jest skróconą wersją publikacji autora (2006) [1] i stanowi wprowadzenie do optymalnego kształtowania przekryć hal i galerii poprzez wybór odpowiedniego typu konstrukcji przekrycia, które następnie będzie przedmiotem szczegółowych rozwiązań technicznych, w tym analiz statyczno-wytrzymałościowych.
Wprowadzenie
Kształtowanie, konstruowanie i obliczanie hal stalowych było przez lata wyznaczone przez stan wiedzy wyłożony w podręcznikach i opracowaniach:
(Bogucki, 1967) [2], (Krzyśpiak, 1969) [3], (Bródka, Łubiński, 1971) [4], (Kowal, 1973) [5], (Medwadowski, 1974) [6], (Biegus A. i in., 1974) [7], (Jankowiak, 1975) [8], (Krzyśpiak,1976) [9], (Bogucki, 1977) [10],
(Medwadowski, 1980) [11], (Bogucki i in., 1982) [12], (Żmuda, 1992) [13].
W ostatnich latach, w związku z „rewolucją” w normach projektowania – wraz z wejściem do praktyki polskiej norm europejskich [14] (i in.) – ukazało się wiele pozycji, dotyczących projektowania konstrukcji stalowych, obejmujących kształtowanie i obliczenia konstrukcji hal: [15], [16], [17], [18], [19], [20], [21], [22], [23].
Z przeglądu literatury wynika, że kształtowanie i konstruowanie hal i galerii w zasadzie nie uległo zmianie od lat 70-tych. Zmianie uległy zasady normowe analiz obliczeniowych systemów konstrukcyjnych i elementów hal stalowych, ale to utraciło na znaczeniu wobec przyjęcia europejskiej zasady, że stosowanie norm (oprócz norm obciążeniowych) jest dobrowolne [24]. Normy obciążeniowe są w Polsce bezwzględnie obowiązujące – zarówno co do zasady przyjmowania obliczeniowych obciążeń klimatycznych z okresem powrotu 50-lat [25], [26], jak i kombinacji obciążeń obliczeniowych z równoczesnym stosowaniem współczynników obciążeń oraz współczynników redukcyjnych [27], [28]. Niezależnie od tego stoimy na stanowisku, że analizy obliczeniowe są jedynie pomocnicze w procesie projektowania (kształtowania i konstruowania) hal stalowych i nie powinny być przedstawiane jako zagadnienia przodujące.
Rodzaje przekryć hal
Przekrycie stanowi w istocie najważniejszą cześć konstrukcji hali stalowej, zważywszy na to, że słupy hal stalowych są obecnie i powinny być powszechnie wykonywane jako żelbetowe. Jak wynika z analiz przeprowadzonych w pracy [29]również słupy podsuwnicowe powinny być wykonywane jako żelbetowe lub zespolone ze względu na zalety ekonomiczne (kilka razy tańsze od stalowych), lepsze własności tłumienie drgań, lepszą odporność pożarową oraz inne walory użytkowe, np. odporność na uderzenia i wpływy korozyjne.
Przekrycia hal jednokondygnacyjnych można podzielić na grupy w zależności od następujących cech:
- rozpiętości przekrycia (przęsła):
małe do 12 m, średnie do 36 m, duże do 100 m, bardzo duże do 200 m i więcej - rodzaju dźwigara dachowego:
kratowy lub pełnościenny, w tym ze środnikiem pofałdowanym lub pofalowanym, - kształtu osi dźwigara dachowego:
płaski – belka, krzywoliniowy ( w tym kołowy) -łuk, - wymiarowości dźwigara dachowego:
jednowymiarowy (belka lub łuk), rozpięty na powierzchni jednokrzywiznowej (sklepienie), rozpięty na powierzchni dwukrzywizowej (powłoka , kopuła), - rodzaju górnej warstwy przekrycia:
płatwiowe lub bezpłatwiowe, - spadku przekrycia:
płaskie, dwuspadowe, czterospadowe, wielospadowe, - płaszczyzn pionowych dźwigarów (kratownic):|
płaskie, ruszty kratownicowe, przekrycia przestrzenne (strukturalne), - płaszczyzn poziomych przekrycia:
jednopłaszczyznowe, kaskadowe, szedowe, złożone, - zabiegów technologicznych:
bez zabiegów, odprężenie lub sprężenie, ze strzałką wygięcia wstępnego, - podparcia przekrycia:
na słupach, na ścianach, mieszane, - doświetlenia, oddymiania lub płaszczyzn solarnoaktywnych w przekryciu:
bez świetlików lub klap dymowych, z wbudowanymi poziomymi płaszczyznami kurtynowymi (świetlikami), pionowymi ścianami kurtynowymi (boczne świetliki), z pochyłymi płaszczyznami świetlików, bądź kolektorów, złożone, - zastosowania lekkich elementów (cięgien, membran):
przekrycia membranowe, cięgnowe (najczęściej występują wspólnie), złożone z udziałem sztywnych łuków, płyt i bloków, - transportu wewnątrz hali:
bez transportu oddziałowującego na przekrycie, podparty (suwnice), podwieszony (wciągniki), - inne nie sklasyfikowane wyżej w tym kombinacje typów.
Rys historyczny
Z punktu widzenia historycznego jako pierwsze przekrycia inżynierskie, ukształtowały się kopuły oraz sklepienia i łuki. Przekrycia płaskie nie były postrzegane jako inżynierskie i w okresie rozwoju konstrukcji wykonanych z żelaza w zasadzie nie były stosowane.
Użycie nowego materiału jakim było żelazo zapoczątkowano w wyrobach z żelaza kutego oraz żeliwa. Poprzedziło to erę stali, zapoczątkowaną wraz z wdrożeniem przemysłowej technologii hutniczego wytwarzania stali, najpierw bessemerowskiej i następnie w wielkich piecach.
Przykłady pierwszych zastosowań żelaza i stali na przekrycia opisano w pracy [30]. Wskazał, że pierwsze zastosowania odnotowano w Paryżu w latach 1807 do 1811 wraz z budową żeliwnej kopuły rozpiętości 40 m nad halą targową kukurydzy, a także w roku 1820 wraz z budową żeliwnego sklepienia o rozpiętości 19 m w Wiedniu nad publiczną łaźnią Diana. Dodajmy, że niemalże w tym samym czasie w latach 1806 do 1811, w Rosji zbudowano dużą jak na ówczesne czasy kopułę z kutego żelaza nad katedrą Kazań w Sankt Petersburgu. Podczas przebudowy Paryża w 1838 r. kopuły żeliwne były szczególnie popularna we Francji. W Wielkiej Brytanii w 1815 roku rozpoczęto budowę kopuły z żelaza nad centralnym budynkiem Royal Pavilion w Brighton, a w 1828 roku, kopułą z kutego żelaza przekryto wieżę katedry w Moguncji.
Prawdziwa era żelaza w architekturze i budownictwie rozpoczęła się jednak dopiero w roku 1851 wraz z prezentacją znanego dzieła inżyniera Joseph Paxton – Pałacu Kryształowego (Crystal Palace) podczas światowej wystawy w Hyde Park w Londynie (rys.1).

Rys.1 Widok wnętrza żeliwnego sklepienia Crystal Palace [31]
Budowa przekryć stalowych hal i budynków jest nieodłącznie związana z rozwojem technologicznym produkcji stali, którą rozpoczęto produkować przemysłowo od roku 1855, w którym Henryk Bessemer wynalazł masową, konwertorową metodę produkcji stali. W konsekwencji w kolejnych latach nastąpił dynamiczny rozwój stosowani stali na konstrukcje: najpierw na amerykańskie wysokościowce. Zastosowanie stali na niskie budynki, w tym hale stało się bardziej powszechne w czasie II wojny światowej, a od lat 50-tych hale stalowe są szeroko akceptowane, głównie ze względu na swoje walory, polegające przede wszystkim na szybkiej budowie, lekkości konstrukcji, a także możliwości przekrycia dużych przestrzeni przy niewielkiej ingerencji słupów w program funkcjonalny przestrzenny hali [32].
Zakres zastosowania przekryć stalowych dużych rozpiętości, w tym silnie nieliniowych konstrukcji cięgnowych istotnie rozszerzył się wraz z ulepszaniem jakości stali i stosowaniem jej z innymi materiałami, a także wraz z dostępnością oprogramowania do projektowania wspomaganego komputerowo.
Struktura kosztów obiektu w konstrukcji stalowej
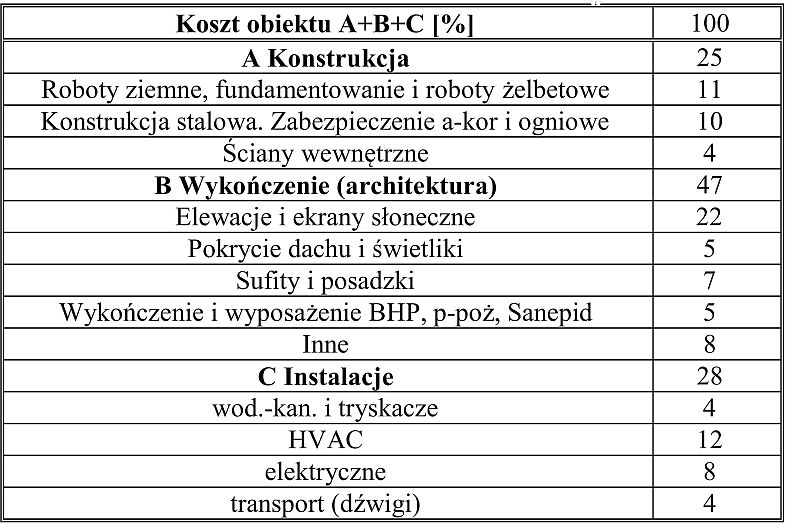
Od wielu lat sukcesywnie zmniejsza się udział kosztu konstrukcji w koszcie całego obiektu. W tab.1. pokazano współczesną strukturę kosztów obiektu w konstrukcji stalowej na przykładzie obiektów zrealizowanych w Wielkiej Brytanii [33]
Tab. 1 Struktura kosztów obiektu stalowego [33]
Udział kompletnej konstrukcji w obiekcie, to 25%, a konstrukcji stalowej zaledwie 10%. Konstrukcje żelbetowe w obiektach stalowych mają porównywalny koszt, ze względu na duże znaczenie posadzek przemysłowych oraz stosowanie słupów żelbetowych. Podobna struktura kosztów dotyczy stalowych budynków wielokondygnacyjnych, ze względu na powszechne stosowanie żelbetowych stropów.
Szacuje się, że około 50% z walcowanej na gorąco stali konstrukcyjnej jest zużywane do budowy budynków jednokondygnacyjnych, a to stanowi około 40% całkowitego zużycia stali w gospodarce. Ponadto ponad 90% jednokondygnacyjnych budynków niemieszkalnych ma konstrukcję składaną z płaskich ram stalowych, w sposób pokazany na rys.3.
Optymalny typ przekrycia hali
Pierwszą i najważniejszą analizą projektową w procesie projektowania przekryć hal i budowli jest właściwy wybór typu przekrycia. W tym artykule nie zajmujemy się zestawieniem optymalizacyjnym przekryć wykonanych z różnych materiałów, choć należy stwierdzić, że przekrycia stalowe hal są konkurencyjne nawet do przekryć drewnianych w szerokim zakresie rozpiętości, a bezkonkurencyjne dla bardzo dużych rozpiętości powyżej 60 m.
Klasyczne przekrycia hal
Wprowadzenie
W klasycznych układach konstrukcyjnych hal podstawowym elementem konstrukcyjnym jest rama poprzeczna. Rama jest podstawowym elementem nośnym na której będzie mocowana obudowa hali (dach i ściany). Najpopularniejszym i ekonomicznym sposobem jest zastosowanie serii płaskich układów, które są rozmieszczone w równych odstępach wzdłuż jednej osi, budynku, jak pokazano na rys.2. Ze względów funkcjonalnych i architektonicznych rytm (odległość pomiędzy układami poprzecznymi) jest powtarzalna, a często stosuje się ramy zewnętrzne dla podkreślenia dużego rytmu oraz dominant w hali (rys.3). Zaburzenia tego rytmu są spowodowane koniecznością dostosowania do funkcji lub innymi ważnymi powodami.

Rys. 2. Kształtowanie hali poprzez powtarzającą się płaską ramę [34]

Rys. 3. Crown Hall (architekt: Mies van der Rohe) [35]
Optymalny dobór typu rygla ram (układów poprzecznych hali)
Na rys. 4 pokazano wykres zużycia stali na typowe jednokondygnacyjne hale stalowe z ramami poprzecznymi z ryglem pełnościennym i ryglem kratownicowym [33] W układzie ram z ryglem pełnościennym i kratowym w zależności od rozpiętości ramy i dla rozstawu ram 6 lub 7,5 m. Optymalne są hale z ramami z ryglem kratownicowym o rozpiętości ok 24 m, w rozstawie co 6m.
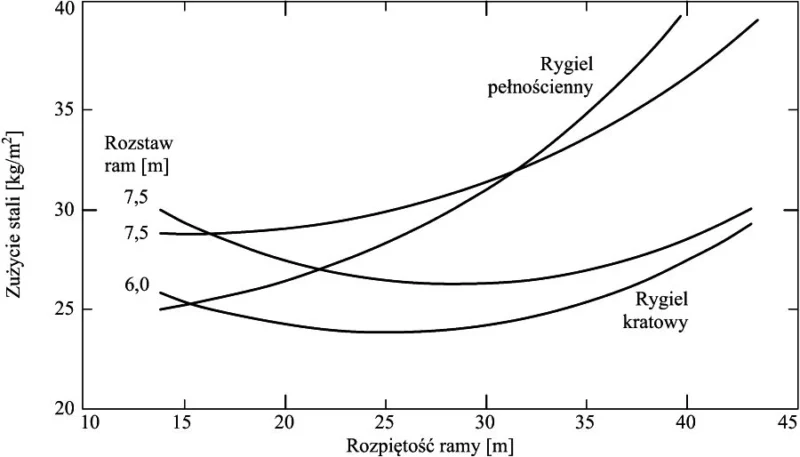
Rys. 4 Porównanie zużycia stali na hale stalowe z ryglami pełnościennymi i kratownicowymi [33]
Dobór systemu konstrukcyjnego hali jest właściwym etapem jej projektu. Analizy obliczeniowe prowadzone w trakcie projektowania są czynnościami pomocniczymi i doradczymi. Właściwe sprawdzenia stateczności i wytrzymałości układu konstrukcyjnego i jego elementów dokonuje się dopiero po zakończeniu projektu przez „obliczeniowców”, wyposażonych w odpowiednie oprogramowanie.
W klasycznych halach złożonych z układów płaskich istotny jest optymalny dobór rozpiętości ramy $L_y$ ( długości rygla ramy kratownicowego lub pełnościennego) oraz rozstawu ram $L_x$ po długości hali ( w dachu bezpłatwiowym długości płyt pokrycia lub długości płatwi w dachu płatwiowym). Podstawowe zależności pokazano na rys.1. Obie rozpiętości $L_x$ i $L_y$ są wzajemnie sprzężone: rozstaw płatwi generuje rozłożenie węzłów wiązarów, rozstaw wiązarów generuje długości płatwi. Dalsze analizy optymalizacyjne podano w rozdziałąch Kratownicowe rygle ram (rys. 7) ; Płatwie (rys.6) oraz Słupy żelbetowe , czy stalowe?
Warunek minimum kosztów
Właściwie zaprojektowana konstrukcja hali powinna spełniać optimum kosztu nie tylko inwestycyjnego, ale również kosztów eksploatacji w założonym okresie projektowym, wynoszącym zwykle 50 lat. Koszt inwestycyjny obejmuje przede wszystkim ceny materiału wraz z zabezpieczeniem antykorozyjnym i ogniowym, ale również koszty produkcji elementów, ich transportu i montażu. W przypadku standardowym, w warunkach zastosowania zwykłych technologii wykonawstwa przyjmuje się szacunkowo, że koszt hali stanowi 200% kosztów materiału wraz z zabezpieczeniami. Natomiast koszt elementów stalowych jest mało czuły na klasę stali oraz rodzaj profili i jest zwykle odnoszony do jednego kg wbudowanej konstrukcji. W 2015 roku koszt jednego kg konstrukcji wynosił średnio 6,5 zł. Można więc przyjąć w przybliżeniu, że koszt budowy hali stalowej jest proporcjonalny do masy wbudowanych elementów. Przyjmiemy, że optymalizacji będzie podlegać masa stali. Sprawa się nieco komplikuje po stwierdzeniu, że w koszcie hali stalowej porównywalny wkład ma koszt elementów żelbetowych: słupów, posadzki i fundamentów. Wobec tego w projekcie hali stalowej nie możemy zaniedbać kosztu elementów żelbetowych, a właściwie kosztów stali zbrojeniowej. Reasumując optymalizacji wstępnej powinna podlegać masa całkowita masa stali, po sprowadzeniu ceny stali zbrojeniowej do stali konstrukcyjnej
$$\begin{equation} M=M_s+M_z \cdot \frac {C_z}{C_s} \label{4}\end{equation}$$
gdzie M- masa optymalizowana, Ms,Cs ; Mz, Cz – masa i cena jednostkowa stali konstrukcyjnej i stali zbrojeniowej odpowiednio.
Procedury optymalizacji funkcji celu ($\ref{4}$) przy ograniczeniach funkcjonalnych (w tym konstrukcyjnych), wytrzymałości oraz stateczności systemu i elementów – można prowadzić standardowymi metodami, a najlepiej poprzez wykonanie wielu wariantów projektów oraz po wyborze wariantu optymalnego.
Na rys.5 pokazano porównanie kosztów wykonania 1 m2 hal w różnych wariantach wykonania (w 5-ciu przypadkach). Bezwzględne koszty robót przyjmowano wg cen z 2014 roku, ale stosunki kosztów poszczególnych wariantów sa uniwersalne (w przybliżeniu niezależne od daty budowy).
Analizowano hale jednonawowe dla ustalonej wysokości w kalenicy 7,5 m oraz nachyleniu połaci dachowej 5%, z pokryciem typu lekkiego na blasze trapezowej. Przyjęto, że dach jest kategorii H (bez dostępu z wyjątkiem zwykłego utrzymania i usług), a przekrycie obciążone instalacjami podwieszonymi 0,3 kN/m2.
Hale zbudowano z 10-ciu układów poprzecznych o rozstawie 6,0; 7,5; 9,0 lub 12,0 m. Rozpiętość nawy wynosiła: 21, 24 27 i 30 m. Porównano konstrukcje bezpłatwiowe oraz płatwiowe przy rozstawie płatwi 1,5; 3,0 lub 4,5 m. Analizowano trzy rodzaje płatwi: walcowane IPE, gięte na zimno o profilu Z oraz kratowe. Płatwie kratowe miały wysokość 60 cm dla długości 9 m oraz 80 cm dla długości 12 m oraz wykratowanie typu V. Rygle ram przyjęto jako kratowe dwutrapezowe z obniżonym pasem o zróżnicowanych parametrach: skratowanie typu V bez słupków, typu V ze słupkami i typu N. Wysokość dźwigarów h przyjęto 1,75 m dla długości L=21 m; h=2,0 m dla L=24 m; h=2,25 m dla L=27 m i h=2,50 m dla L=30 m. Słupy przyjmowane jako stalowe lub żelbetowe o wysokości ok 8,6 m w rozstawie co 7,5 m.
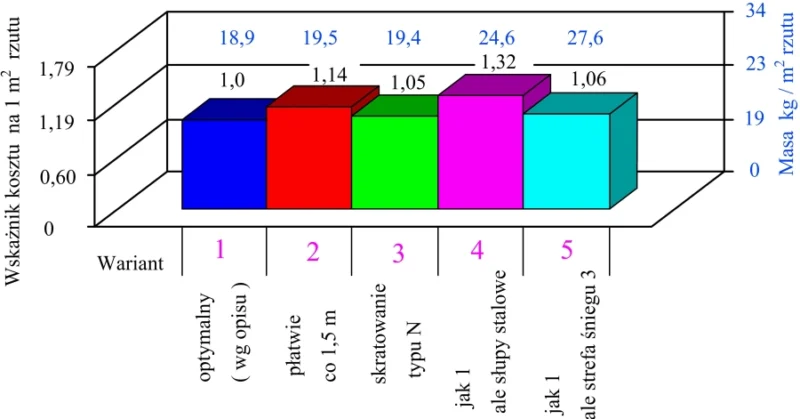
Rys.5. Koszt masa 1 m2 klasycznej hal [36]
Dla wybranych wariantów konstrukcji hal uzyskano następujące rezultaty (G- ciężar przekrycia , K- koszt łącznie ze słupami) na 1 m2 posadzkim, przy czym w cenę wliczono prefabrykację elementów żelbetowych i stalowych w wytwórni, łącznie z malowaniem antykorozyjnym i montażem konstrukcji stalowej i żelbetowej.
Wariant 1 [ najekonomiczniejszy]: G=18,8 kg/m2, K= 168,0 zł/m2
Analizy prowadzono na wzorcowej hali, która ma następujące parametry:Wymiary hali 24×67,5m , co daje powierzchnię posadzki 1620 m2,
- Rozstaw układów nośnych co 7,5 m,
- Dach bezpłatwiowy, z blachą trapezową T153-840 gr. 0,75/320,
- Dźwigar kratowy ze skratowaniem typu V ze słupkami, pasy HEA, krzyżulce i słupki rury kwadratowe,
- Słupy nośne o wysokości 8,6 m żelbetowe 30×40 cm C35/40 – B500 (17,3 cm2),
- Strefa klimatyczna 2/1 (śnieg/wiatr).
Wariant 2 [dach płatwiowy] : G=19,52 kg/m2, K= 191,3 zł/m2
Obiekt wzorcowy (jak w przypadku 1), ale przekrycie wykonane w konstrukcji płatwiowej. Płatwie LP Z/300 gr.2,5/350 w rozstawie co 1,5 m. Blacha pokrycia T55-976 gr.0,60/280 i.
Wariant 3 [ wpływ wykratowania dźwigara] : G=19,4 kg/m2, K= 176,1 zł/m2
Obiekt wzorcowy (jak w przypadku 1), ale z innym typem wykratowania dźwigara: zamiast typu V ze słupkami – typ N.
Wariant 4 [słupy stalowe] K=214,1 zł/m2
Obiekt wzorcowy (jak w przypadku 1), ale słupy stalowe zamiast żelbetowych.
Uzyskano znaczący (o 30%) wzrost ceny obiektu.
Wariant 5 [wpływ strefy obciążeń klimatycznych] K=178,1 zł/m2
Obiekt wzorcowy (jak w przypadku 1), ale w strefie klimatycznej 3/1, zamiast 2/1
Wzrost strefy powoduje wzrost ciężaru dźwigara kratowego do 8,65 kg/m2, a także wzrost wymiarów słupa żelbetowego do (30x45cm), co powoduje wzrost kosztu o 6%.
Optymalizacja pokrycia hal ( blach fałdowych)
Najistotniejszym elementem hal wpływającym na rozstaw płatwi jest rodzaj pokrycia, a w przypadku najczęściej obecnie stosowanej dachowej blachy fałdowej (trapezowej) jej nośność i ugięcia pod obciążeniem śniegiem, a w szczególności w obszarach zasp śniegu.
Optymalizacja płatwi
Na rys. 6 pokazano analizy zużycie stali na płatwie w funkcji współcześnie stosowanych typów płatwi: kratowe, gięte na zimno i walcowane IPE oraz ich rozpiętości rozstawu.
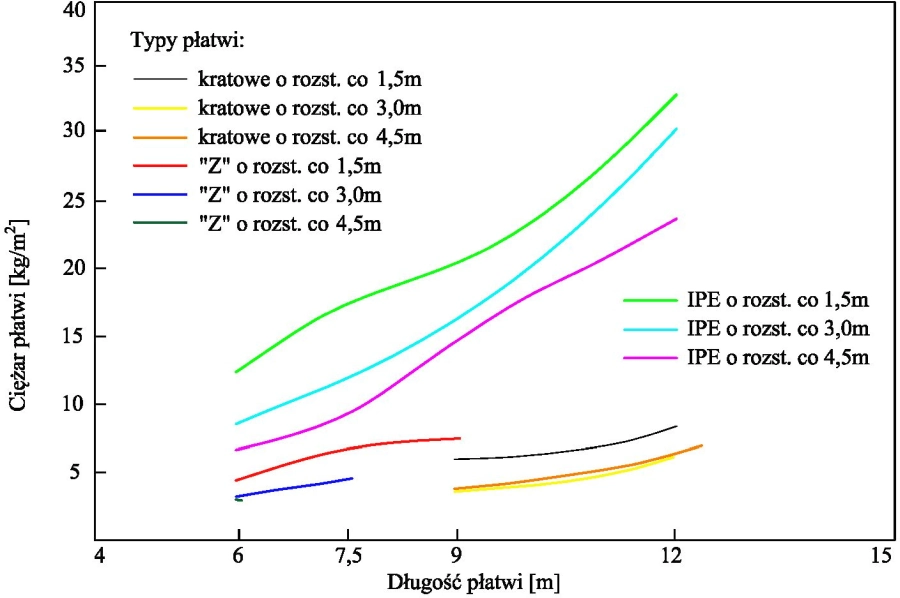
rys.6. Analizy optymalizacyjne płatwi hal [36]
Z analizy wynika, że przy rozpiętości 6 do 7,5 m optymalne jest zastosowanie płatwi giętych na zimno w rozstawie co 3 m. Przy rozpiętości 7,5 do 9 m optymalne są płatwie gięte na zimno w rozstawie co 1, 5 m. Płatwie kratowe należy stosować przy rozpiętościach 9 do 12 m. Nie jest optymalne stosowanie płatwi walcowanych IPE.
Optymalizacja kratownicowych rygli ram
Kratownicowe rygle ram (dźwigary kratownicowe) są przedmiotem artykułu w artykułu Stalowe dźwigary kratowe.
Na rys. 7 zamieszczono zależność ciężaru wiązarów w funkcji rozpiętości rygla układu poprzecznego hali i zastosowanego typu skratowania.
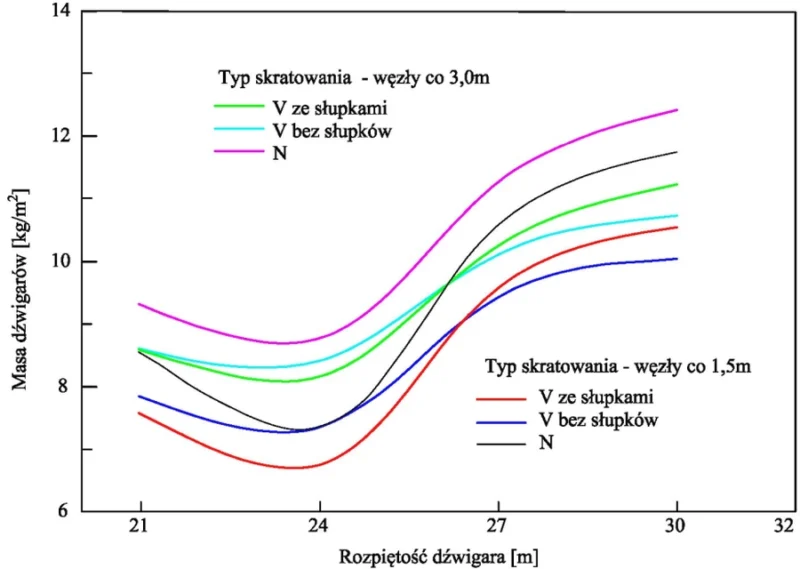
Rys.7. Analizy optymalizacyjne płaskich wiązarów kratowych hal [36]
Na podstawie wykresu można dobrać optymalny typ wykratowania dla danej rozpiętości wiązara, przy czym można przyjąć tezę, że optymalną długość swobodnie podpartego wiązara stalowego wynosi około 24 m. Po przekroczeniu rozpiętości 27 m następuje duży wzrost masy przekrycia i należy zastanowić nad zastosowaniem innego typu przekrycia, a to: zmienić warunki podparcia )utwierdzić w słupach) , zastosować ruszt, przekrycie strukturalne, przekrycia cięgnowe lub wykorzystać efektu kopułowego. Te rodzaje przekryć opisano w dalszej części opracowania.
Optymalizacja pełnościennych rygle ram
Pełnościenne rygle ram są przedmiotem artykułu Hale i dżwigary blachownicowe Podano tam zasady optymalnego kształtowania blachownic. Zakres zastosowań rygli pełnościennych w porównaniu z ryglami kratownicowymi przedstawiono na rys.4.
Optymalizacja stężeń hal
Stężenia (usztywnienia przestrzenne hal) są przedmiotem artykułu Stężenia hal i budowli.
W pracy [37] nie prowadzono analiz systemu stężeń hali. Wynika to z faktu, że w literaturze [38], [39] wskazuje się, że udział optymalnych stężeń prętowych w ciężarze przekrycia jest pomijalnie mały.
Układ stężeń powinien być optymalizowany w taki sposób, by ich liczba była jak najmniejsza, tak by zwiększyć funkcjonalność hali oraz zmniejszyć złożoność węzłów i konstrukcji. Pod tym względem od hal złożonych z płaskich układów lepsze są ruszty kratownicowe oraz przekrycia strukturalne [40].
Słupy stalowe, czy żelbetowe ?
Analizy dotyczące rodzaje materiału słupów osiowo ściskanych dają jednoznaczne wyniki (np. przypadek 4 w pkt. 6.2 oraz artykuł [40]: słupy żelbetowe są ok 4x tańsze od słupów stalowych.
Podobny wniosek można sformułować również dla mimośrodowo ściskanych i słupów podsuwnicowych, co pokazano na rys. 8 i 9.
Na rys. 8 przedstawiono analizy kosztów mimośrodowo ściskanych słupów stalowych, wykonanych z różnych materiałów w funkcji mimośrodu podporowego e=Mu/Nu (stosunek maksymalnego momentu zginającego Mu i odpowiadającej siły osiowej Nu) bez i z zastosowaniem zabezpieczeń ogniowych z warunku stanu granicznego nośności SGN (STR) Natomiast na rys.9 przedstawiono podobne analizy, ale dodatkowo z uwzględnieniem stanu granicznego użytkowalności SGU (SLS) przy ograniczeniu $ \delta_y \le \tfrac {h_c}{400}$, gdzie $ \delta_y$ – przemieszczenie poziome na wysokości połączenia części dolnej (podsuwnicowej) o długości hc z częścią górną słupa.
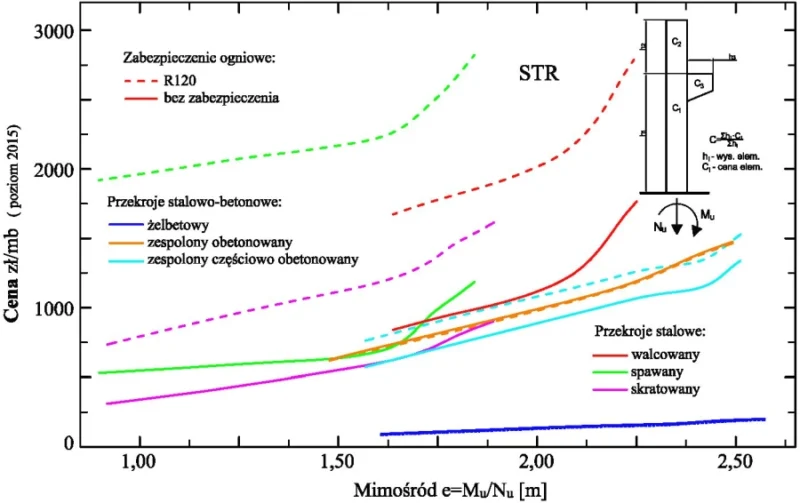
Rys. 8. Analizy kosztów słupów zginanych bez zabezpieczeń z warunku stanu granicznego STR [41]
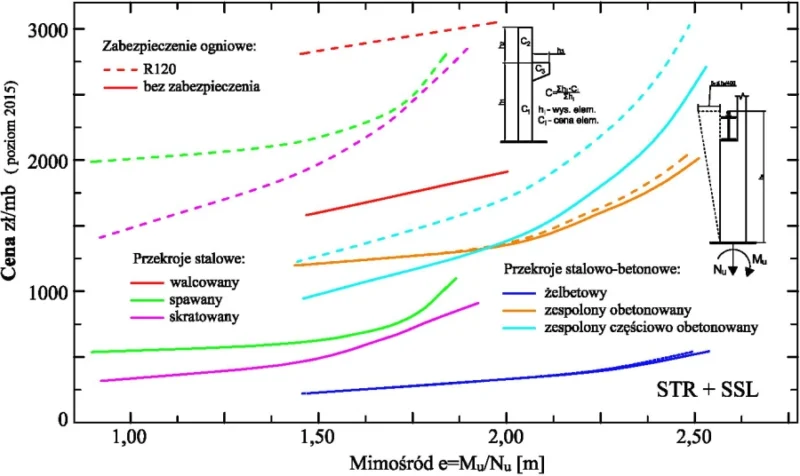
Rys. 9. Analizy kosztów słupów zginanych zabezpieczonych ogniowo z warunku stanów granicznych STR i SLS, [41]
Słupy żelbetowe są znacznie tańsze praktycznie w całym zakresie mimośrodów, czyli również przy dużym udziale zginania, ale też dla słupów osiowo ściskanych (bez udziału zginania e=0). Efekt ten powiększa się istotnie jeśli słup ma wytrzymałość ogniową.
Sprawdzanie stateczności i wytrzymałości przekrycia
Analiza tradycyjna, zgrubna – na wyodrębnionych układach płaskich
Zgrubne, tradycyjne sprawdzenie stateczności hali , wynikało z ograniczonych możliwości ręcznej techniki i ograniczeniu się do analizy wyodrębnionych płaskich układów, a mianowicie:
- układu poprzecznego hali [słupy, wiązar] w płaszczyźnie pionowej poprzecznej. Układ przenosi podstawowe obciążenia pionowe i obciążenie wiatrem z kierunku bocznego (parcie na jeden słup i ssanie na drugi),
- układu połaciowego [wiązary-płatwie, stężenia połaciowe T1, T2] w płaszczyźnie poziomej. Układ przenosi obciążenia zastępcze od imperfekcji układu w płaszczyźnie dachu i działanie wiatru na ściany szczytowe,
- układu podłużnego [słupy, wiązary stężenia międzysłupowe T4] w płaszczyźnie pionowej podłużnej. Ukłąd przenosi obciążenia zastępcze od imperfekcji działające na głowice słupów w kierunku podłużnym oraz działanie wiatru na ściany szczytowe,
- ściany podłużnej [wiązary, płatwie, stężenia pionowe między wiązarami T3] w płaszczyźnie pionowej podłużnej. Układ służy do sprężenia sąsiednich wiązarów w bikonstrukcje, przez co zwiększa niezawodność konstrukcji,
- ściany szczytowej [ściana ze stężeniami T6 ] w płaszczyźnie pionowej poprzecznej. Ściana szczytowa najczęściej jest ustawiona przed skrajną ramą poprzeczną.
Każdy z tych układów powinien być stateczny i wytrzymały na obciążenia zewnętrzne.
Takie podejście wymaga żmudnych obliczeń przybliżonych i daje wyniki, które mogą odbiegać od rzeczywistości. Ma jednak podstawową zaletę: umożliwia jasne rozdzielenie funkcji poszczególnych układów płaskich i w rezultacie zbadanie stateczności całego układu hali. Daje też podstawowe informacje o wielkości zastępczych sił od imperfekcji, potrzebnych w prowadzeniu obliczeń na modelkach przestrzennych.
Analiza współczesna – na modelu przestrzennym
Po zaprojektowaniu systemu konstrukcyjnego wymagane jest sprawdzenie numeryczne stateczności i wytrzymałości systemu i jego składowych: elementów i przekrojów. Zauważmy najpierw, że wszystkie układy konstrukcyjne pracują przestrzennie. Model konstrukcji powinien przede pozwolić na uwzględnienie wszystkich istotnych zjawisk i mechanizmów, które mogą wystąpić w sytuacjach obliczeniowych w projektowanej konstrukcji.
Na tym etapie (sprawdzenia stateczności i wytrzymałości wcześniej zaprojektowanej konstrukcji) – należy zbudować model przestrzenny 3D systemu i analizowanie go pod obciążeniami zasadniczymi oraz obciążeniami, pochodzącymi od sił imperfekcji.
Zaleca się każdą siłę pionową (skupioną lub rozłożoną) Fz stowarzyszyć ze składowymi poziomymi
$$ \begin{equation} F_x = F_z = F_y =1/200 F_z \label{6}\end{equation}$$
przy czym zastępcze siły poziome można zredukować według zasad metody opisanej w artykule Imperfekcje konstrukcji stalowych.
Podstawową i w istocie pojęciowo najprostszą metodą sprawdzania wytrzymałości i stateczności systemów konstrukcyjnych i ich elementów jest metoda globalna (ogólna), która została wprowadzona do [14], kl. 6,3,4, W przypadku, gdy sytuacja obliczeniowa nie zawiera wpływów pożaru, sprawdzenie przekrojów stalowych może być dokonane zgodnie z tą normą dla całości lub części konstrukcji.
W tym celu należy określić mnożniki obciążeń: graniczny (plastyczny) $\alpha_{ult}$ oraz krytyczny $\alpha_{cr,op}$. Oszacowanie tych mnożników należy dokonać metodami numerycznymi. Na rynku funkcjonuje kilka programów, umożliwiających taką analizę. Wymienimy tutaj program ABAQUS, ale przede wszystkim program CONSTELL, dedykowany do analiz inżynierskich z użyciem uogólnionego elementu prętowego (cienkościennego elementu Własowa), czyli w ramach obliczeń , uwzględniający formy woboczenia: giętnego, skrętnego i giętno-skrętnego(wyboczenia) elementów i systemu i konstrukcyjnego. Oszacowanie mnożnika krytycznego można przeprowadzić analizę wyboczeniową LBA. Mnożnik obciążeń $alpha_{cr,op}$ jest wartością własną analizy wyboczeniowej z uwzględnieniem wszystkich postaci wyboczenia: giętnej, zwichrzenia i giętno-skrętnej w tym dystorsyjnej. Stateczność miejscowa ścianek przekroju jest uwzględniona w nośności przekroju (klasy 4).
Dla znanych mnożników obciążeń krytycznego oraz granicznego (plastycznego) wyznacza się smukłość względną systemu z ogólnej zależności
$$\begin{equation} \overline \lambda_{op}= \sqrt{\frac {\alpha_{ult}}{\alpha_{cr,op}}}\label{5}\end{equation}$$
Współczynnik niestateczności $\chi_{op}$ jest wyznaczany ze dla smukłości względnej $\overline \lambda_{op}$ całego systemu (lub jego części).
Monitoring stanu hali
Współczesne budowle w tym wielkopowierzchniowe hale są projektowane i budowane w sposób optymalny: materiało- i energo-oszczędny w znacznie większym stopniu od hal tradycyjnych. Dlatego większego znaczenia nabiera monitoroe4ani stanu hali w trakcie jej eksploatacji. Zaleca się, by systemy monitoringu stanu bezpieczeństwa konstrukcji hali były projektowane i montowane w ramach inwestycji budowlanej.
W okresie życia obiektu konstrukcja podlega starzeniu w zmiennym środowisku zewnętrznym, a zoptymalizowana konstrukcja jest narażona na większe 6prawodpodobieństwo awarii. Montaż systemu monitoringu stanu konstrukcji jest znaczenie ekonomiczniejszy od wykonania hali odpornej na wszystkie wyjątkowe obciążęnia i w większym okresie czasu od projektowego okresu użytkowania (standardowo 50 lat dla zwykłych hal). Szczególnie dotyczy to obciążeń środowiskowych, np. obciążenie śniegiem i wiatrem lub wpływy para-sejsmiczne, a także pożarowe.
Nie jest zasadne projektowanie i budowa obiektu na bezwzględnie największe obciążenia, a obciążenia obliczeniowe są statystycznie uzasadnioną wartością mniejszą od bezwzględnie największej, która może pojawić się z małym prawdopodobieństwem. Ale może pojawić się i wtedy dojdzie do katastrofy budowlanej. Nie możemy na to pozwolić, bo koszty katastrofy również materialne mogą być wysokie. Dlatego należy rozważyć instalację ciągłego monitoringu stanu hali. Koszty inwestycyjne instalacji nie muszą być duże, a uzyskane efekty bezcenne.
Stan techniki i technologii pozwala już na instalację inteligentnego monitoringu, który w połączeniu z systemami mobilnymi i dostępem do internetu pozwalają na 24- godzinną obserwację zachowania obiektu i analizę krytycznych sygnałów o niepokojącym zachowaniu konstrukcji. Systemy takie składają się z szeregu czujników:
1) czujników odkształceń konstrukcji w miejscach krytycznych,
2) czujników pracy urządzeń,
3) czujników otwarcia klap, okien, drzwi, czujników wilgotności, temperatury , dymu.
Odpowiednio rozmieszczone czujniki wysyłają sygnały do centrali systemu (komputera). Tam są analizowane i w razie zagrożenia uruchamiane są moduły ostrzegawcze, oraz wysyłane wiadomości GSM do wyznaczonych osób o koniecznej interwencji.
Przykładowo firma Techoqu [42] oferuje system monitorowania obciążenia konstrukcji stalowych (obciążenie śniegiem), system monitorowania temperatury lub wilgotności powietrza w wyznaczonych strefach oraz system sygnalizacji otwarcia/zamknięci klap. Na rys. 1 pokazano schemat systemu monitorowania obciążenia śniegiem.
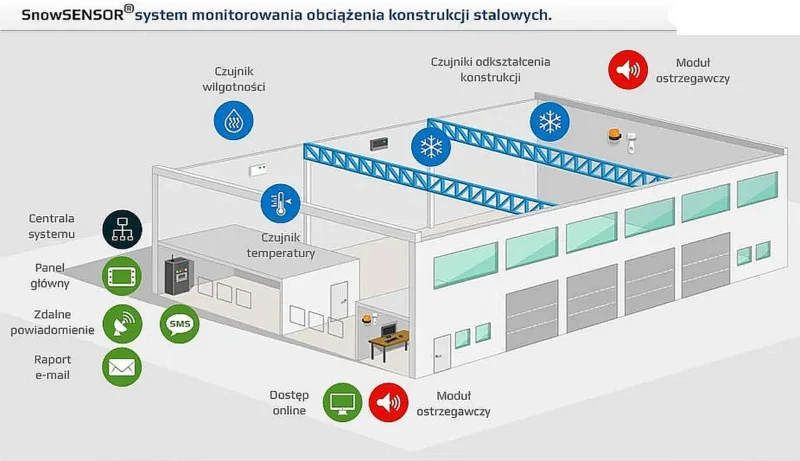
Rys. 10 Przykładowy system monitoringu stanu hali [42]
- Chodor L. (2016), Przekrycia hal i galerii, XXXI Warsztaty pracy projektanta konstrukcji. Szczyrk, 24-27 lutego 2016, s. 25-202
- Bogucki W. (1967), Budownictwo stalowe ( Wydanie, Tom 1), Arkady
- Krzyśpiak T., (1969), Budownictwo stalowe. Poradnik inżyniera i technika budowlanego, Tom 2, część 2, Arkady
- Bródka J., Łubiński M. (1971), Lekkie konstrukcje stalowe, Arkady
- Kowal Z. (1973). Wybrane działy z konstrukcji metalowych Część I i II (Wydanie 2), Wydawnictwo Politechniki Wrocławskiej
- Medwadowski J. (Ed.), (1974) Stalowe konstrukcje budowlane. Zagadnienia podstawowe. Stany graniczne: Cz.1, 2., Wydawnictwo Politechniki Łódzkiej
- Biegus A., Kowal Z., Kubica E., Rykaluk K. (1974). Hale unikatowe o dużych rozpiętościach, Prace Naukowe Instytutu Budownictwa Politechniki Wrocławskiej No. 13
- Jankowiak W. (1975). Konstrukcje metalowe, Wydawnictwo Politechniki Poznańskiej
- Krzyśpiak T. (1976), Konstrukcje stalowe hal (Wydanie 1), Arkady
- Bogucki, W. (1977). Budownictwo stalowe, Tom II (4 Wydanie), Arkady
- Medwadowski J. (Ed.). (1980). Konstrukcje metalowe i stalowe, PWN
- Bogucki, W. (Ed.). (1982). Poradnik projektanta konstrukcji metalowych (Wydanie 1, Tom 2 ), Arkady
- Żmuda J. (1992), Podstawy projektowania konstrukcji metalowych, Wydawnictwo TiT
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- Biegus, A. (2003), Stalowe budynki halowe. Arkady
- Pałkowski S. (2009). Konstrukcje stalowe: wybrane zagadnienia obliczania i projektowania. Wydawnictwo Naukowe PWN
- Giżejowski M., Ziólko (Eds.). (2010). Budownictwo ogólne, Tom 5: Stalowe konstrukcje budynków. Projektowanie według Eurokodów z przykładami obliczeń. Arkady
- Kozłowski A. (Ed.), (2010), Konstrukcje stalowe. Przykłady obliczeń według PN-EN 1993-1. Część pierwsza. Wybrane elementy i połączenia. Oficyna Wydawnicza Politechniki Rzeszowskiej
- Kurzawa Z. (2011). Stalowe konstrukcje prętowe. Cz. II. Struktury przestrzenne, przekrycia cięgnowe, maszty i wieże. Wydawnictwo Politechniki Poznańskiej
- Rykaluk K. (2012). Zagadnienia stateczności konstrukcji metalowych. Dolnośląskie Wydawnictwo Edukacyjne
- Kurzawa Z. (2012). Stalowe konstrukcje prętowe. Cz. I. Hale przemysłowe oraz obiekty użyteczności publicznej. Wydawnictwo Politechniki Poznańskiej, ((Bródka J., Broniewicz M., (2013). Projektowanie konstrukcji stalowych według Eurokodów. Podręcznik inżyniera. Polskie Wydawnictwo Techniczne 2013
- Kozłowski A. (Ed.), (2013). Konstrukcje stalowe. Przykłady obliczeń według PN-EN 1993-1. Część druga. Stropy i pomosty (III). Oficyna Wydawnicza Politechniki iRzeszowskiej
- Bródka, J., Broniewicz, M. (2013). Projektowanie konstrukcji stalowych według Eurokodów. Podręcznik inżyniera. Polskie Wydawnictwo Techniczne
- Ustawa z dnia 12 września 2002 r. o normalizacji., no. Dz.U. 2002 nr 169 poz. 1386 (2002). http://isap.sejm.gov.pl/Download?id=WDU20021691386&type=3
- PN-EN 1991-1-3:2006, Eurokod 1: Oddziaływania na konstrukcje, Część 1-3: Oddziaływania ogólne- Obciążenie śniegiem
- PN-EN 1991-1-4:2008, Eurokod 1. Oddziaływania na konstrukcje, Część 1-4: Oddziaływania ogólne. Oddziaływania wiatru
- PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
- Chodor, L. (2015). Kombinacje obciążeń w Eurokodach. PiWiki-Inżynierowie i Architekci Chodor-Projekt. https://chodor-projekt.net/encyclopedia/kombinacje-obciazen-w-eurokodach/
- Chudy, S. (2015). Optymalizacja podsuwnicowych słupów hal [Politechnika Świętokrzyska].https://chodor-projekt.net/wp-content/uploads/2015/07/https://chodor-projekt.net/wp-content/uploads/2015/07/Chudy-S.Optymalizacja-podsuwnicowych-słupow-hal-Praca-magisterska-Kielce-2015.pdf
- Makowski Z. S. (2006). Analysis, Design and Construction of Braced Barrel Vaults. Taylor&Francis, Elsevier Applied Science Publishers Ltd, Chapman & Hall Publishers
- Paxton, R. (1851). The Crystal Palace,Interior view of the Crystal Palace, 1851. [ http://images.adsttc.com/media/images/51d5/7946/b3fc/4b58/3400/0231/large_jpg/72726307.jpg?1372944709 ]
- Weston R. (2011). 100 Ideas that Changed Architecture. Lurence King Publishing Ltd.
- Davison, B., Owens, G. W., & Steel Construction Institute (Great Britain). (2005). Steel designers’ manual. Blackwell Science [ http://search.ebscohost.com/login.aspx?direct=true&scope=site&db=nlebk&db=nlabk&AN=137743 ]
- Trebilcock P., & Lawson R. M. (2004). Architectural design in steel. Spon Press
- steel-insdag.org. (2015, October 18). Trusses. Chapter 27 Teaching Material Stel-InsDag. Institute for Steel Development and Growth, [ http://www.steel-insdag.org/teachingmaterial/chapter27.pdf ]
- Chodor L., Malik Ł. (2014), Optymalizacja konstrukcji nośnej hali stalowej/ Optimization of the supporting structure of steel hall, Conference ZK2014 – Konstrukcje metalowe / Metal Structures 2-4 lipca / July 2014, Kielce-Suchedniów, Poland, Short Papers, 195-198
- Chodor L., Malik Ł. (2014), Optymalizacja konstrukcji nośnej hali stalowej/ Optimization of the supporting structure of steel hall, Conference ZK2014 – Konstrukcje metalowe / Metal Structures 2-4 lipca / July 2014, Kielce-Suchedniów, Poland, Short Papers, 195-198
- Davison B., Owens G. W., Steel Construction Institute (Great Britain). (2005). Steel designers’ manual. Blackwell Science, [http://search.ebscohost.com/login.aspx?direct=true&scope=site&db=nlebk&db=nlabk&AN=137743 ]
- Lan T. T. (2005). Space Frame Structures. In W.-F. Chen & E. M. Lui (Eds.), Handbook of Structural Engineering (2nd ed.). CRC Press
- Chodor L. (2014), Przekrycia strukturalne, Encyklopiedia PiWiki, [https://chodor-projekt.net/encyclopedia/przekrycia-strukturalne/]
- Chudy, S. (2015). Optymalizacja podsuwnicowych słupów hal [Politechnika Święto-krzyska], [ https://chodor-projekt.net/wp-content/uploads/2015/07/https://chodor-projekt.net/wp-content/uploads/2015/07/Chudy-S.Optymalizacja-podsuwnicowych-słupow-hal-Praca-magisterska-Kielce-2015.pdf ]
- Techoqu. (2016). Nadzorowanie stanu hali. Systemy inteligentnego monitoringu
________________________________