Artykuł w ciągu ostatnich 24 godzin czytało  0 Czytelników
Uwagi i recenzje podręcznika  przesyłać na adres wydawnictwa: wydawnictwo@chodor-projekt.net lub leszek.chodor@chodor-pojekt.pl

Podręcznik Imperfekcyjna metoda projektowania konstrukcji [ → Spis treści ]
Dodatek B :  Dyskretyzacja losowo odkształcalnej konstrukcji

Omówiono podstawowe zasady i twierdzenia dyskretyzacji losowo odkształcalnej konstrukcji na stochastyczne elementy skończone w zakresie potrzebnym do zrozumienia wywodów prezentowanych w podręczniku. Uśrednianie procesu stochastycznego podług okresów czasu również podlega pokazanym zasadom.

Dyskretyzacja losowo odkształcalnej konstrukcji

Konstrukcja łącznie z warunkami brzegowymi jest wektorowym polem losowym w czasoprzestrzeni. Losowe cechy konstrukcji, ale także wymuszenia i efekty tych wymuszeń są indeksowane nielosowym czasem oraz współrzędnymi przestrzennymi. Dyskretyzacja losowo odkształcalnych struktur na stochastyczne elementy skończone jest jednym z podstawowych zagadnień losowej mechaniki konstrukcji, szczególnie w stochastycznej metodzie elementów skończonych (np. [1] ). Problemem tym zajmowało się wielu autorów (m in. [2], [3], [4] , [5] i in.).

Dyskretyzacja pola losowego konstrukcji w ogólności polega zastąpieniu badania pola losowego $X(t)$ indeksowanego parametrem nielosowym t przez n-wymiarowy wektor losowy $ X=[ X_1,X_2,…, X_n ]$.

$$\begin{equation} X(t) \approx c_0(t)+ \sum \limits_{i=1}^n c_i(t) \cdot X_i \label {1}  \end{equation}$$

gdzie nielosowe współczynniki $c_i(t)$ są funkcjami nielosowego indeksu t – uogólnionego czasu, który może być również współrzędną pręta lub indeksem (etykietą, liczbą porządkową) fizycznego elementu konstrukcji. Istnieje wiele metod dyskretyzacji, ale większość z nich wykorzystuje podział obszaru konstrukcji, na którym zadane jest pole losowe, na rozłączne, przylegające podobszary, zwane stochastycznymi elementami skończonymi) w sposób podobny do stosowanego w klasycznej, deterministycznej metodzie elementów skończonych. Prowadzi to do uproszczenia implementacji, ale nakłada obowiązek uwzględnienia dodatkowych (wynikających z analizy losowej) kryteriów doboru siatki elementów, a w szczególności wielkości i zagęszczenia siatki. Kryteria deterministyczne i losowe są często przeciwstawne: w analizie deterministycznej zagęszcza się siatkę elementów w obszarze dużych gradientów naprężeń lub odkształceń, a w analizie stochastycznej zbyt małe elementy skończone prowadzą do uzyskania wyników o dużym rozproszeniu własności losowych elementów lub ze złym uwarunkowaniem numerycznym zadania w przypadku zastosowania wielu elementów o dużej korelacji własności. Efekt zwiększania losowego rozproszenia wraz ze zwiększaniem liczby elementów skończonych, jest obserwowany również wskutek deterministycznego efektu „tłumienia pasożytniczego”, czyli zmniejszanie wiarygodności wyników na skutek nawarstwiania się błędów numerycznych. W związku z tym zazwyczaj nie stosuje się tej samej siatki do dyskretyzacji pola losowego w zagadnieniu analizy stochastycznej oraz dyskretyzacji w klasycznym zadaniu MES, Podstawową techniką jest “składanie” elementów stochastycznych z kilku elementów MES.

Można dokonać następującej klasyfikacji metod dyskretyzacji pól losowych [6] :

• dyskretyzacja punktowa (ang. point discretization), w której zmienne losowesą wartościami w punktach dyskretyzowanego pola Ω, będących w charakterystycznymi punktami elementów skończonych (np. [7] ),
• metody lokalnego uśredniania (local average), w których zmienne X są ważonymi całkami pola losowego (np. [8], [9] )

$$\begin{equation} X_i = \int \limits_{\Omega^{(r)}}  \Omega \cdot w(t) d\Omega \label {2}  \end{equation}$$

• aproksymacja funkcjami kształtu, wykorzystująca znane z metody elementów skończonych funkcje kształtu oraz skończony zbiór (węzłowych) wartości pola losowego. Aproksymacja funkcjami kształtu jest szczególnym przypadkiem dyskretyzacji punktowej (np. [10] )

Stochastyczny element skończony

Przeprowadzimy dyskretyzację ciągłego procesu stochastycznego X (t) indeksowanego nielosowym parametrem t poprzez zastąpienie go ciągiem zmiennych losowych:

$$\begin{equation} X_i = \cfrac{1}{2 T_i} \int\limits_{t_i -T_i}^{t_i +T_i}  X(t) dt  , \quad (i=1,2, …) \label {3}  \end{equation}$$

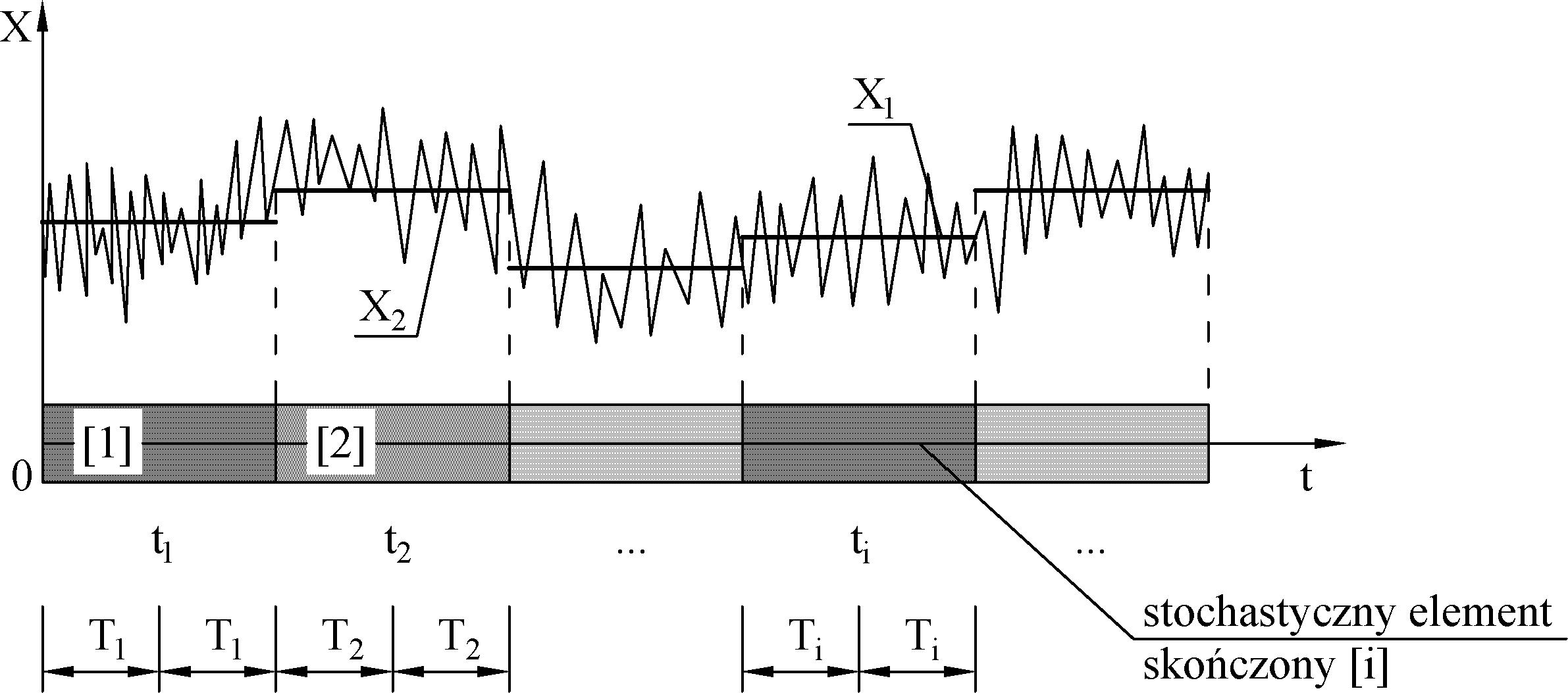
rozpiętych na długościach  elementów  o środkach  (Rys. B.1).

Rys. B.1. Realizacja zdyskretyzowanego procesu losowego

Zmienna ($\ref{3}$) zdefiniowana przez stochastyczną całką Riemanna jest lokalną średnią procesu na przedziale  $[t_i-T_i , \quad t_i+T_i ]$ , to znaczy na długości elementu $2T_i$. Ciągły parametr t (ciągły uogólniony czas) jest redukowany do dyskretnych indeksów i (dyskretnego czasu).

Element [i] jest jednowymiarowym elementem stochastycznym – wektorem cech tego elementu, np. imperfekcji geometrycznych (wstępnych wygięć lub odchyleń od pionu). Element [i] jest materialny, jeśli parametrem t jest współrzędna przestrzenna (a nie czas).

Prowadząc dyskretyzację pola losowego powinno się unikać silnego skorelowania zmiennych stanowiących efekt dyskretyzacji, to znaczy należy stosować maksymalnie duże elementy stochastyczne – grupy podobnych elementów skończonych (np. słupów) zaleca się traktować jak jeden element stochastyczny. Przed przystąpieniem do dyskretyzacji każdorazowo należy przeprowadzić analizę wstępną konstrukcji z punktu widzenia opisanego w poprzednim zdaniu.

Twierdzenia o dyskretyzacji procesu stochastycznego

W pracy [34] podano dowody trzech twierdzeń o dyskretyzacji procesu stochastycznego.

Twierdzenie 1

[o wartości oczekiwanej i kowariancji skończonego elementu procesu stochastycznego]

Niechaj $M_X(t)$, $R_{XX} (t_i, t_j)=E[X(t_i),X^T (t_j)]$ oraz $C_{XX}(t_i, t_j)=R_{XX} (t_i, t_j) – M_X(t_i) M_X^T (t_j)$  będą trendem , funkcją autokorelacji i funkcją autokowariancji procesu $X(t)$ odpowiednio. Funkcja autokowariancji jest scentrowaną funkcją kowariancji.
Jeśli zmienne losowe  $X_i$ oraz $X_j $ są lokalnymi średnimi procesu na elementach o długości $2T_i$  oraz  o długości $2T_j$,

$$\begin{equation} X_i=\cfrac{1}{2T_i}\int \limits_{t_i-T_i}^{t_i+T_i} X(t) dt , \quad  X_j=\cfrac{1}{2Tj}\int \limits_{t_j-T_j}^{t_j+T_j} X(t) dt \label {4}  \end{equation}$$

to wartość oczekiwana i kowariancja tych zmiennych losowych wynosi:

$$\begin{equation} E[X_k] \cfrac {1}{2T_k} \int\limits_{t_k -T_k}^{t_k +T_k}  X(t) dt   \label {5}  \end{equation}$$

$$\begin{equation} Cov [X_i, X_j ] = \cfrac{1}{4 T_i T_j} \int \limits_{t_i-T_i}^{t_i+T_i} \int\limits_{t_j-T_j}^{t_j+T_j} C_{XX} ( \tau_i \tau_j) d \tau_i d \tau_j \label {6}  \end{equation}$$

Wnioski:

1. Twierdzenie 1 dotyczy jednorodnych i niejednorodnych procesów $X(t)$.
2. Jeśli dla elementu $[i]$ charakterystyczny jest proces $X(t)$ , a elementu $[j]$ proces $Y(t)$, to kowariancja zmiennych powinna być obliczona z ($\ref{6}$) z użyciem funkcji wzajemnej korelacji procesów $X(r)$,i $Y(t)$

$$\begin{equation} Cov [X_i, X_j ] = \cfrac{1}{4 T_i T_j} \int \limits_{t_i-T_i}^{t_i+T_i} \int\limits_{t_j-T_j}^{t_j+T_j} C_{XY} ( \tau_i \tau_j) d \tau_i d \tau_j \label {7}  \end{equation}$$

Twierdzenie 2

[o zależności pomiędzy kowariancją i wariancjami elementów stochastycznych]

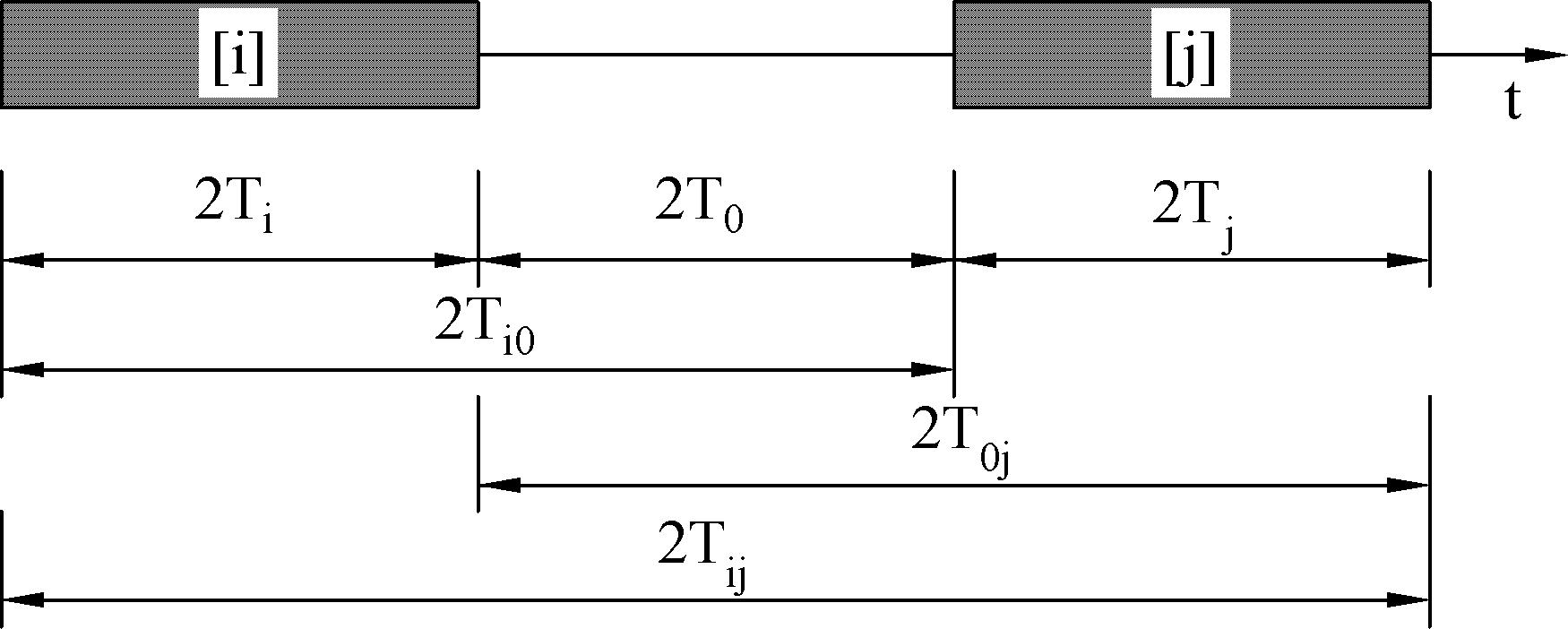
Wyznaczmy średnie ($\ref{5}$) $X_i, X_j, X_{j0}, X_{0j}, X_{ij}$ na odcinkach $2T_i, 2T_j, 2T_{i0}, 2T_{0j}, 2T_{ij}$ odpowiednio. Jeśli te odcinki są wyznaczone przez węzły elementów stochastycznych w sposób pokazany na Rys. B.2, to zachodzi:

Rys. B.2. Oznaczenia do twierdzenia 2

$$\begin{equation} Cov [X_i, X_j ] = \cfrac{1}{2 T_i T_j} \left [ T_0^2 Var[ X_0] -T_{i0}^2 Var[X_{i0}] -T_{ij}^2  Var[X_{ij}] -T_{0j}^2 Var[X_{0j}] \label {8} \right ] \end{equation}$$

Wniosek: Na podstawie Twierdzenia 2 można obliczyć kowariancję pomiędzy elementami stochastycznymi na podstawie wariancji obszarów obejmujących te elementy oraz obszar położony pomiędzy tymi elementami. Ta własność jest użyteczna przy wyznaczeniu kowariancji na podstawie danych eksperymentalnych.

Twierdzenie 3

[o kowariancji dyskretyzowanego stacjonarnego procesu stochastycznego]

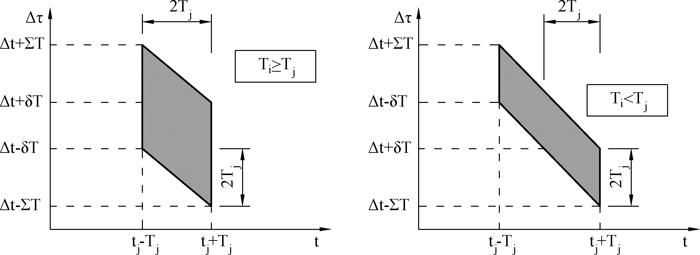
Kowariancja zmiennych $X_i$ i $X_j$ zdefiniowanych w Twierdzeniu 1 uzyskana przez uśrednienie stacjonarnego procesu po obszarze pokazanym na Rys. B.3. wynosi:

$$\begin{equation} Cov [ X_i, X_j ] = \cfrac {1}{4 T_i T_j}  \int \limits_{ \Delta \tau -\Sigma T}^{ \Delta \tau +\Sigma T} a ( \Delta \tau) \cdot C_{XX} ( \Delta \tau) \, d ( \Delta \tau)  \label {9}  \end{equation}$$

gdzie

$$\begin{equation} a ( \Delta \tau) \begin{cases}
\Sigma T- \Delta \tau & \text {jeśli  } \Delta T < \Delta \tau < \Delta t +\Delta T \\
\Sigma T- | \Delta T – \Delta t |  & \text {w pozostałych przypadkach}
\end {cases} \label {10}  \end{equation}$$

$\Delta T = |T_i-T_j | , \quad \Delta t= t_i -t_j, \quad \Sigma T =T_i+T_j$

Rys. B.3. Obszary całkowania w twierdzeniu 3

Uwagi:

1. W twierdzeniu 3 proces musi być stacjonarny, ale nie musi być ergodyczny. To twierdzenie uogólnia znany rezultat o średnim czasie stacjonarnego procesu ( [11], [12] ). Uogólnienie polega na zastosowaniu do elementów o różnej długości.
2. Zmienna $\Delta \tau$ jest odległością pomiędzy środkami elementów i zastępuje odległość pomiędzy punktami ciągłego procesu.
3. Jeśli  $i \neq j$ , to $ | \Delta t | =\Sigma T $ (Twierdzenie dotyczy kowariancji), a jeśli $i=j$ , to $ | \Delta t | =0$ (Twierdzenie dotyczy wariancji).

Wnioski:

1. 1. Jeśli dyskretyzacja stacjonarnego procesu jest prowadzona na elementach o takiej samej długości $2T_i =2T_j =2T$ , to z Twierdzenia 3 otrzymujemy:

$$\begin{equation} Cov [X_i, X_j ] = \cfrac{1} {2 T}  \int \limits_{ \Delta t- 2T}^{ \Delta t +2T} \left( 1- \cfrac{ | \Delta \tau – \Delta t | } {2T}  \right )  C ( \Delta \tau ) \, d( \Delta \tau ) \label {11} \end{equation}$$

2. W przypadku numeracji porządkowej elementów ułożonych w ciąg mamy $\Delta t = 2T \cdot (i-j) $ , gdzie $i$ oraz  $j$ są numerami porządkowymi elementów. Wariancję średniej lokalnej otrzymamy po podstawieniu  $\Delta t=0$ w ($\ref{9}$ ) i uwzględnieniu równości $C_{XX}(\Delta \tau )= C_{XX}( – \Delta \tau )$.

Zastosowanie twierdzeń o dyskretyzacji

Twierdzenia o dyskretyzacji zastosowujemy do kilku klas procesowe stochastycznych stosowanych w niniejszym podręczniku.

Dyskretyzacja procesu klasy wykładniczej

Proces klasy wykładniczej jest  szeroko stosowany do analizy zagadnień niezawodności konstrukcji budowlanych (np.  [13], [14]).

Dyskretyzujemy stacjonarny proces w jednorodnym obszarze z funkcją korelacji klasy wykładniczej

$$\begin{equation} C( \Delta \tau ) = exp \left ( -A \cdot | \Delta \tau | ^{\alpha} \right )  \label {12} \end{equation}$$

gdzie $A>0$, $( \alpha =1.2)$.  Zależność ($\ref{12}$) opisuje funkcję korelacji stacjonarnego pola losowego w szerszym sensie.

Skala fluktuacji $\Theta$ [3] tego procesu

$$\begin{equation} \Theta= \int \limits_{ – \infty}^{+ \infty} C( \Delta \tau ) d \Delta \tau=  \int \limits_0^{\infty}  exp \left ( -A \cdot | \Delta \tau | ^{\alpha} \right ) d \Delta \tau=\begin{cases} \\
– 2A & \text{  dla  }  \alpha=1 \\
\sqrt{ \cfrac{ \pi}{A}}  & \text { dla } \alpha=2
\end {cases} \label {13} \end{equation}$$

jest skończona $(\Theta < \infty $ ,więc proces może być ergodyczny (można pokazać, że tak jest faktycznie). Z formuły ($\ref{8}$) mamy

$$\begin{equation}  Cov[ X_i, X_j] = \cfrac{1}{2A T_i T_j} \int \limits_{ \Delta t -\Sigma T}^{ \Delta t +\Sigma T} a ( \Delta \tau) \cdot exp \left ( -A \cdot | \Delta \tau | ^{\alpha} \right ) d\Delta \tau \label {14} \end{equation}$$

Jeśli $\alpha=2$, to całka ($\ref{14}$) nie może być otrzymana analitycznie i całkowanie należy prowadzić numerycznie. Jeśli $\alpha=1$, to otrzymujemy:

$$\begin{equation}  Cov[ X_i, X_j] = \cfrac{1}{2A T_i T_j} [ cosh (A \cdot \Sigma T) – cosh  (A\cdot \Delta T) ] \cdot \exp {(-A \Delta T)}  \label {15} \end{equation}$$

$$\begin{equation}  Var[ X_i] = \cfrac{1}{2A^2 T_i^2} [ 2AT_i -1+ \exp {( -2AT_i )} ] \label {16} \end{equation}$$

Dyskretyzacja procesu klasy potęgowej

Zdyskretyzujmy stacjonarny proces w jednorodnym obszarze z funkcją korelacji klasy potęgowej:

$$\begin{equation} C( \Delta \tau ) = \cfrac{1}{1+A |\Delta \tau|^{\alpha}}  \label {17} \end{equation}$$

gdzie:$A>0$ ,$\alpha=1,2$ . Zależność (B.15) opisuje funkcję korelacji stacjonarnego pola losowego w szerszym sensie.

Skala fluktuacji dla tego procesu wynosi:

$$\begin{equation} \Theta = \int \limits_0^{\infty}  \cfrac{1}{1+A |\Delta \tau|^{\alpha}}  d \Delta \tau= \begin{cases} \\
\infty  & \text{  dla  }  \alpha=1 \\
\sqrt{ \cfrac{ \pi^2}{A}}  & \text { dla } \alpha=2
\end {cases} \label {18} \end{equation}$$

więc proces na pewno nie jest ergodyczny dla $\alpha=1$ i może być ergodyczny dla $\alpha=2$. Dyskretyzację przeprowadźmy przez podział osi t na elementy o takiej samej długości . Z formuły ($\ref{8}$) mamy

$$\begin{equation}  Cov[ X_i, X_j] = \cfrac{1}{2T} \int \limits_{ \Delta t -\Sigma T}^{ \Delta t +\Sigma T} \quad \cfrac{1-\cfrac { \Delta \tau – \Delta t }{2T}}{1 +\Delta | \Delta \tau |^{\alpha}} d\Delta \tau \label {19} \end{equation}$$

skąd otrzymujemy:

dla $\alpha=1$

$$\begin{equation}  Cov[ X_i, X_j] = \cfrac{1} {4 A^2 T^2} [ ( A \Delta t_1 +1) \log {(A \Delta t_1+1)} – \\
2 ( A \Delta t  +1) \log {(A \Delta t+1)} +A \Delta t_2 +1) \log {(A \Delta t_2 +1)} ]  \label {20} \end{equation}$$

$$\begin{equation}  Var[ X_i] = \cfrac{1}{2 A^2 T^2} [ (2At+1) log(2At+1) -2AT ] \label {21} \end{equation}$$

dla $\alpha=2$

$$\begin{equation}  Cov[ X_i, X_j] = \cfrac {1} {8 A T^2} \cdot \{ 2 \sqrt {A}\cdot \Delta t_1 \cdot [ arctg ( \sqrt{A}\cdot \Delta t_1) – arctg( \sqrt{A}\cdot \Delta t) ] \}+ \\
2 \sqrt{A}\cdot \Delta t_2 \cdot [ arctg ( \sqrt{A}\cdot \Delta t_2) – arctg( \sqrt{A}\cdot \Delta t) ] \} – \\
\log {(A \cdot \Delta t_1^2 +1)}+2 log{(A \cdot \Delta t^2 +1)} – log {(A \cdot \Delta t_2^2 +1)} \}   \label {22} \end{equation}$$

$$\begin{equation}  Var[ X_i] = \cfrac{1}{2 A^2 T^2} [ (2At+1) log(2At+1) -2AT ] \label {23} \end{equation}$$

Dyskretyzacja  procesu trygonometrycznego

Stochastyczny proces trygonometryczny może być traktowany jako przybliżenie dowolnej procesu przez rozwnięcie w szereg Fouriera

Proces ten jest szczególnie interesujący w zagadnieniu imperfekcji, bowiem imperfekcje łukowe elementu  najczęściej przedstawia się w postaci sinusoidy $w_0(x)= f_0 \cdot \sin {(x)} $. Pochodna szeregu Fouriera będzie procesem kątów obrotu $\varphi_0=w’_0).

Trygonometryczny proces stochastyczny $X_{[e]}$ na elemencie $[e]$ jest dany formułą:

$$\begin{equation}  X_{[e]} ( \tau ) = \sum \limits_ {i=1} ^n  [A_i \cos { \omega_i \tau } + B_i \sin { \omega_i \tau} ] \label {24} \end{equation}$$

gdzie: $A_i$  , $B_i$ są ciągiem nieskorelowanych losowych amplitud ze średnią zero: $E[ A_i A_j ]=E[A_i B_j ]=E[B_i B_j ]=E[ A_i]=E [ B_i ]=0$  oraz z jednorodną wariancją $Var[A_i]=E[A_i^2] =E[B_i^2] =\sigma_i^2$ . Częstotliwości $\omega_i$ są deterministyczne.

Trend i autokorelacja procesu ($\ref{24}$) wynosi:

$$\begin{equation}  M_{[e]} =0 ’ \qquad  R_{[e][e]} = E[ x(\tau – \Delta \tau ) X(\tau) = \sum \limits){(i)} \sigma_i^2 \cdot \cos {(\omega_i \Delta \tau ) } \label {25} \end{equation}$$

czyli proces jest stacjonarny.

Przyjmijmy, że na elemencie  $[s]$przebiega proces $X_{[s]}$ , który jest pochodną procesu ($\ref{24}$), po zadziałaniu na niego operatora liniowego  $d/dt$ (operatora pochodnej), to znaczy

$$\begin{equation}  X_{[s]} ( \tau ) =\cfrac { d X_{[e]} ( \tau – \Delta \tau )} {d \tau} = \sum \limits_ {i=1} ^n  [ – A_i \sin { \omega_i (\tau -\Delta \tau) } + B_i \cos { \omega_i (\tau -\Delta \tau) } ]  \label {26} \end{equation}$$

Wartość oczekiwana i funkcja korelacji procesów wynoszą:

$$\begin{equation}  M_{[s]} =\cfrac { d M_{[e]} ( d \tau }=0  ]  \label {27} \end{equation}$$

$$\begin{equation} R_{[e] [s]} ( \Delta\tau ) = \sum \limits_ {i=1} ^n  \omega_i \sigma_i^2 \sin { [ \omega_i ( \Delta \tau + \Delta t)] } \\
R_{[s] [s]} ( \Delta\tau ) = \sum \limits_ {i=1} ^n  \omega_i \sigma_i^2 \cos { ( \omega_i  \Delta \tau ) }
\label {28} \end{equation}$$

Ponieważ funkcje korelacji($\ref{25}$) i ($\ref{28}$) są stacjonarne, to wariancje i kowariancje pomiędzy lokalnymi średnimi można wyznaczyć z Twierdzenia 3.

Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2017-2020), Imperfekcyjna metoda  projektowania konstrukcji, Encyklopedia  πWiki, Wydawnictwo Chodor-Projekt, [ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]

Historia edycji:
(2019-04-24 do 30 )  Wersja 1.0

&nbsp;Literatura

1. Chodor, L. (1989), Algorytm szacowania losowych odpowiedzi systemów konstruk-cyjnych przy użyciu Stochastycznej Metody Elementów Skończonych, Materiały Kon-ferencji, Krynica 2915. Koferencja Naukowo-Techniczna Krynica 1989, s. 115–122
2. Wilde, P. (1981), Random Fields Discretization in Engineering Calcula-tions. Państwowe Wydawnictwo Naukowe
3. Vanmarcke, E. H. (1983), Random fields: analysis and synthesis. The MIT Press
4. Chodor L. (1991), Discretisation of Structures in the Stochastic Finite Element Meth-od, Materiały X Sc. Conf. „Computers Methods in Mechanics”,s. 70-76, Szczecin-Świnoujście
5. Stocki, R. (2010), Analiza niezawodności i optymalizacja odpornościowa złożonych konstrukcji i procesów technologicznych. IPPT PAN
6. Sudret, B., Der Kiureghian, A., (2000), Stochastic Finite Element and Reliability [A State of the Art. Technical Report]. Departament of Civil and Environmental Engi-neering, University of California
7. Der Kiureghian, A., Ke, J. B. (1988), A Structural reliability under incomplete probability information. J.Eng.Mech. ASCE, 112(10), 85–104
8. Vanmarcke, E. H., Grigoriu, M., (1983), Stochastic finite element analysis of simple beams. J.Eng.Mech. ASCE, 109(5), 1203–1205
9. Zhu, W. Q., Ren, Y. J., Wu, W. Q. (1992), Stochastic FEM Base. On Local Averages of Random Vector Fields. J. Eng. Mech. ASCE, 118(3), 496–509
10. Stocki, R., Liefvendahl, M. (2006), A study on algorithms for optimization of Latin hypercubes. Journal of Statistical Planning and Inference, 136(9), 3231–3247
11. Papoulis, A., Pillai, S. U. (2002), Probability, random variables, and stochastic pro-cesses (4th ed). McGraw-Hill
12. Bendat, J. S., Piersol, A. G. (2010), Random data: analysis and measurement procedures (4th ed). Wiley
13. Kapur K. C., Lamberson L. R. (1977), Reliability in engineering design. Wiley
14. Murzewski J. (1989), Niezawodność konstrukcji inżynierskich. Arkady, Warszawa

________________________________