Trwa remanent po dużej awarii portalu.  Przepraszam za nieczytelną część treści  do zakończenia remanentu !

W wielu zagadnieniach projektowania budowli występuje potrzeba przeprowadzenia obliczeń cieplno-wilgotnościowych przegród. Dotyczy to nie tylko budynków, co jest uregulowane w Rozporządzeniu [1], ale również budowli przemysłowych takich jak: zbiorniki do przechowywania wody i cieczy zamarzających oraz silosy do przechowywania cementu, wapna, gipsu itd. Ochrona może dotyczyć zarówno niskich lub wysokich temperatur jak i wykraplania się pary wodnej z powietrza. Szczególnie złożone są problemy pojawiąjące się  wówczas, gdy przegroda pozostaje w styku z gruntem a także  problem mostków cieplnych.

Przewodnictwo cieplne przez przegrody

Rozwiązanie klasycznego zagadnienia przewodnictwa ciepła

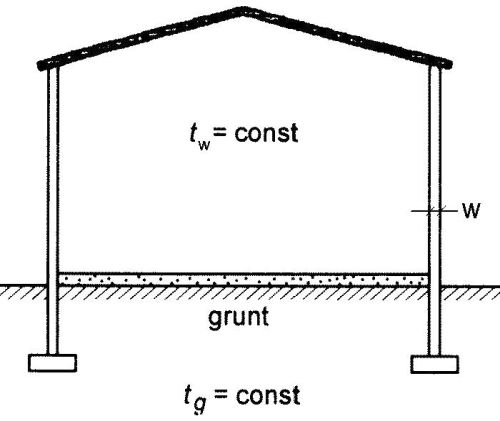
Rozwiążemy zagadnienie brzegowe jednowymiarowego, jednorodnego przepływu ciepła przez przegrodę wielowarstwową. Przegroda składa się z $n$ warstw o grubościach $d_i$  i współczynnikach przewodnictwa ciepła $\lambda_i$ , ( i =1, …n). Zakładamy, że na zewnątrz  przegrody stała temperatura  jest zadana: po lewej stronie jest $t_w$ , a po prawej $t_z$ (rys.1). Zakładamy również, że można pominąć efekty odbicia na powierzchniach zewnętrznych, a powierzchnie kontaktu między warstwami przegrody są idealne (tzn. temperatura jest na nich ciągła).

Aby określić wymianę ciepła i rozkład temperatur pomiędzy powierzchniami przegrody rozwiązujemy układ równań:

$$\begin{equation}  div \overrightarrow {q}=0 ; \quad  \overrightarrow{q}= -\overrightarrow{\lambda }\cdot grad \,  t  \label{1} \end{equation}$$

Rys.1. Schemat przewodzenia ciepła przez przegrodę

Równanie ($\ref{1}$ jest spełnione, gdy spełnione są warunki ($\ref{2}$) i  ($\ref{3}$):

$$\begin{equation} \cfrac{dq}{dx}=0 \to q=const \label{2} \end{equation}$$

$$\begin{equation} q=-\lambda \cfrac{dt}{dx} \to\\ t_{i-1}^{-} =t_{i-1}^{+} ; \quad  t_{i}^{-} =t_{i}^{+} ; \quad (i=1,2 ,..n)\\ t_0^{-}= t_w \quad ; \quad  t_n^{+} = t_z \\ \label{3} \end{equation}$$

gdzie ” + ” oznacza wartość po prawej stronie powierzchni kontaktu, a ” − ” – po lewej. Tym samym rozkład temperatury w każdej warstwie jest liniowy.

Dla temperatur na powierzchniach kontaktowych otrzymujemy:

$$\begin{equation} t_1=t_w – q\cdot \cfrac{d_1}{\lambda_1}\\ t_2=t_1 – q\cdot \cfrac{d_2}{\lambda_1}\\ t_1=t_w – q\cdot \cfrac{d_1}{\lambda_1}\\ …. \\ t_n=t_z=t_{n-1} -q\cdot \cfrac{d_n}{\lambda_n}\\ \label{4} \end{equation}$$

skąd wynika

$$\begin{equation} t_z=t_w -q \cdot \sum \limits_1^n \cfrac{d_i}{\lambda_i} =  \sum \limits_1^n R_i  \label{5} \end{equation}$$

czyli

$$\begin{equation} q = U \ \cdot  \Delta t \label{6} \end{equation}$$

gdzie wprowadzono oznaczenia:

$$\begin{equation} U=\cfrac{1}{R} \label{7} \end{equation}$$

$$\begin{equation} R=\sum \limits_1^n R_i  \label{8} \end{equation}$$

$$\begin{equation} R_i=\cfrac{d_i}{\lambda_i} \label{9} \end{equation}$$

$$\begin{equation} \Delta t = t_w – t_z  \label{10} \end{equation}$$

Temperatura wokół przegrody

Temperatura wokół przegrody wg normy konstrukcyjnej [2]

Temperatura wokół budynku jest traktowana jak obciążenie klimatyczne, a jej wartość charakterystyczna powinna być przyjmowana zgodnie z normą PN-EN 1991-1-5 [2]. Rozróżnia się temperaturę maksymalną $T_{max}$ (latem) i minimalną $T_{min}$ (zimą). Temperatury te zostały ustalone z ekstremalnego rozkładu prawdopodobieństwa  Gumbela z okresem powrotu 50 lat.

Na Rys.2. pokazano szacunkowe strefy temperatur charakterystycznych w Polsce, które zostały uzyskane z programu SPECBUD [3], który można pobrać również z tego panelu. Precyzyjne wartości dla miejscowości w Polsce na poziomie 0 m npm. można odczytać z programu.

Rys.2. Szacunkowe strefy temperatur charakterystycznych w Polsce: a) t_{min} , b) t_{max} wg normy [2]

W przypadku rozpatrywania miejsca położonego na innym niż zerowy poziomie – H metrów nad poziom morza – należy zastosować współczynniki korekcyjne:

$$\begin{equation} t(H) = \begin {cases} t_{min} -0,0035 \cdot H  & \text { dla temperatury minimalnej }\\ t_{max} -0,0053 \cdot H  & \text { dla temperatury maksymalnej} \\ \end {cases} \label{11}\end{equation}$$

Temperatura powietrza na zewnątrz przegrody  t__{out}  zależy od tego , czy przegroda jest położona powyżej terenu, czy też pod nim.
W przypadku powierzchni zewnętrznych przegród wystawionych na działanie promieni słonecznych ( położonych powyżej powierzchni terenu) temperatura powietrza zewnętrznego  latem  zależy od  współczynnika absorpcji ciepła przez powierzchnię, czyli koloru powierzchni wg zależności [2]– tab 5.2.
Dla powierzchni wystawionych na działanie słońca od strony północno-wschodniej  (Pn-Wch) – południowo-zachodniej (Pd-Zach)  dla powierzchni:
J – jasnej, lśniącej,
K – kolorowej lśniącej,
C- ciemnej,
mamy odpowiednio:

$$\begin{equation} t_{out, nadziemne, lato} = t_{max} +\begin {cases} 0 \, ^oC  & \text { dla  J : Pn-Wsch} \\ 2 \, ^oC  & \text { dla K : Pn-Wsch}\\ 4 \, ^oC  & \text { dla C : Pn-Wsch}\\ 18 \, ^oC  & \text { dla J : Pd-Zach } \\ 30 \, ^oC  & \text { dla K : Pd-Zach} \\ 42  \, ^oC  & \text { dla C : Pd-Zach} \\ \end {cases} \label{12}\end{equation}$$

Od strony północnej osiągane są zwykle najmniejsze temperatury  $t_{out, nadziemne, lato, Pn} =$  ok 50%  $t_{max}$

Temperatura powietrza zewnętrznego  zimą, przyjmuje się niezależną od obsorpcji promieni przez powierzchnię oraz od strony świata

$$\begin{equation}  t_{out, nadziemne, zima} = t_{min}  \label{13} \end{equation}$$

Temperaturę powietrza wokół podziemnych części przegród przyjmuje się dla przegród zagłębionych o H poniżej poziomu terenu [2]– tab 5.3.:

$$\begin{equation} t_{out, podziemne} = \begin {cases} -3   \, ^oC  & \text {dla  } H > 1 \, m \\ -5   \, ^oC  & \text {dla  } H < 1 \,m\\ +5   \, ^oC  & \text {dla  } H > 1 \, m \\ +8   \, ^oC  & \text {dla  } H < 1 \,m\\ \end {cases} \label{14}\end{equation}$$

Temperaturę środowiska wewnętrznego (powietrza wewnątrz pomieszczeń) przy braku danych dokładniejszych przyjmuje się  [2]– tab 5.1:

$$\begin{equation} t_{in} = \begin {cases} 20   \, ^oC  & \text { latem} \\ 25   \, ^oC  & \text { zimą } \\ \end {cases} \label{15}\end{equation}$$

Temperatura wokół przegrody wg normy ogrzewnictwa [4]

Do projektowania instalacji grzewczych zgodnie z normą PN-EN 12831 [4]

w budynkach przyjmuje się odmienną od pokazanej w poprzednim punkcie metodologię oraz wartości temperatur wokół przegród budowlanych. Na rys. 3 pokazano mapę klimatyczną Polski zgodnie z tą normą i temperatury projektowe (obliczeniowe) dla pięciu stref  termicznych.

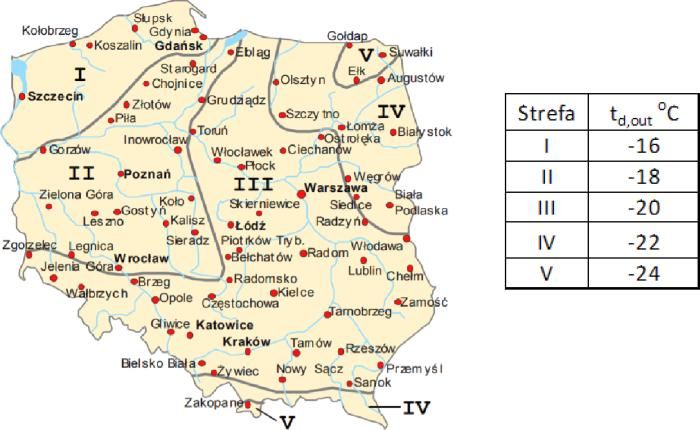
Rys.3. Szacunkowe strefy temperatur charakterystycznych w Polsce: a) t_{min} , b) t_{max} wg normy [2]

Od razu zauważamy ogromną różnice temperatur klimatycznych zgodnie z normą konstrukcyjną  [2] i instalacji grzewczych [4] . Na przykład dla kilku miast w Polsce mamy:

Szczecin:
$-16 \, ^oC$ wg [4],
$-29  \, ^oC$ wg [4] :,
z rys.2a   $-28 ÷ -30  \, ^oC$ ; średnio $-29  \, ^oC$ ,
$k_t$ = 16/29 = 0,55;

Warszawa:
$-20 \, ^oC$ wg [4],
$-29  \, ^oC$  wg [4];
$k_t$ = 20/29 = 0,69;

Suwałki:
$-24 \, ^oC$  wg [4],
$-34 \, ^oC$  wg [2] ,
$k_t$ = 24/34 = 0,71;

Zauważmy, że mapa zawarta w normie ogrzewniczej [4]  pochodzi z roku 2006 i odpowiada dokładnie podziałowi Polski przyjętemu w starej z roku 1982  „postradzieckiej” normie PN-82/B-02403 [5]. Zgodnie z normą [4] projektowa temperatura zewnętrzna jest  najniższą wartością temperatury średniej z dwóch dni, zarejestrowanej dziesięć razy w okresie min 20 lat.  Temperatura projektowa jest więc wyznaczona jako wartość szczytowa z prawdopodobieństwem przekroczenia  $p= 2 \cdot 10 /20 = 0,1$, co odpowiada okresowi powrotu $T=1/0,1 = 10 \,lat$.  W starej normie [5] nie ma niestety podanego okresu powrotu, więc nie jest jasne, czy podane tam projektowe temperatury były właściwe – przypuszczamy, że okres powrotu wynosił $T = 5 \, lat$ , bo tak zakładały ówczesne normy klimatyczne.

Przeliczenie temperatur z okresu powrotu 10 lat (czyli prawdopodobieństwa przewyższenia p= 1/10= 0,1)  na 50 lat  (czyli p=1/50=0,02)  można dokonać na podstawie współczynników stosunku $T_{min, p}/T_{min}$ zgodnie z rys.  NB.1 zamieszczonym w normie [2]. Stosunek  $T_{min, 0,1} / T_{min, 0,02}= 0,78$. Oznacza to, że  w celu uzyskania temperatury obliczeniowej (projektowej) dla potrzeb ogrzewania z temperatury charakterystycznej powinien polegać na zmniejszeniu  współczynnikiem $k_t =0,78$

Sugerujemy, by do czasu korekty map klimatycznych zawartych w normie grzewczej [4] korzystać z normy konstrukcyjnej  [2] po przemnożeniu odczytanej wartości przez współczynnik $k_t=0,78$.
Na przykład dla Warszawy mamy $t_{projektowe, zima} = -29 \cdot 0,78 = -23 ^oC$ ( a nie $-20 ^oC$).

W ten sam sposób można wyznaczyć temperatury projektowe latem, istotne przy projektowaniu klimatyzacji.

W tab. NB.2 normy [4] podano też projektowe temperatury w pomieszczeniach w budynkach $t_{in}$ . Zalecenia te przedstawiono w tab. 1 na podstawie rozporządzenia „Warunki techniczne” [6]), w którym powtórzono wymogi normowe. Wymogi te są wobec tego prawnie obowiązujące.

Tab.1. Projektowa temperatura wewnętrzna $t_{in}$ wg  § 134  [6])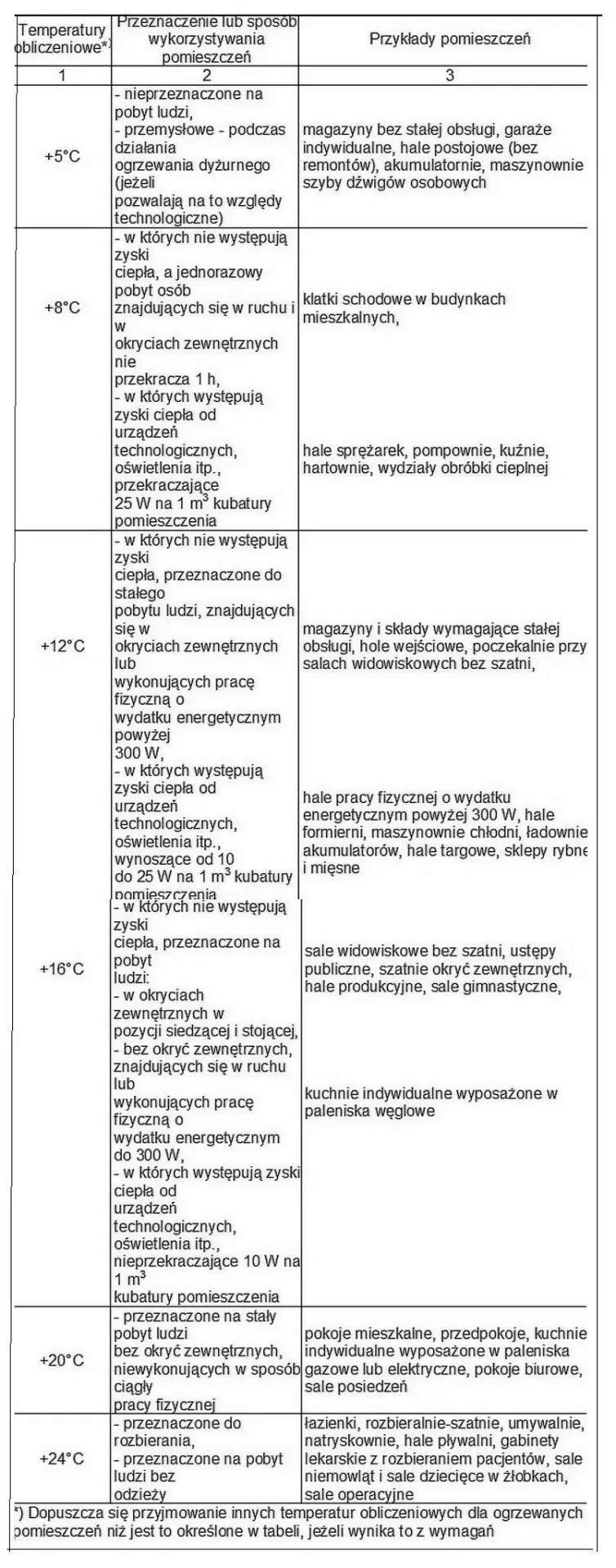

Współczynnika przenikania ciepła przez przegrody U

Ograniczenie współczynnika U dla budynków

Zgodnie z [1]– zał 2. ogranicza się od dołu współczynniki przenikalności ciepła przez przegrody wszelkich budynków z uwzględnieniem poprawek na pustki powietrzne, mostki cieplne w tym poprawki  na łączniki mechaniczne zgodnie z tab.2. :

Tab.2. Maksymalne współczynniki przewodzenia ciepła $U_{Cmax}$ [1]– zał 2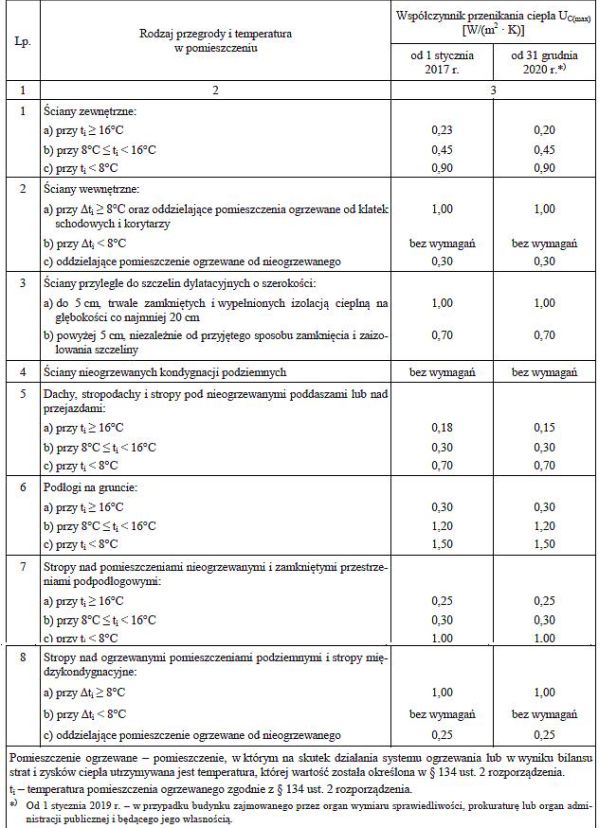

Obliczanie współczynnika przenikania ciepła U

Obliczenia współczynnika U należy przeprowadzić zgodnie z normą [7] w sposób wynikający z rozwiązania zagadnienia podstawowego przedstawionego wyżej.

Współczynnik przenikania ciepła $U_c$  $[ W/(m^2 \cdot K) ]$ ($\ref{7}$) jest odwrotnością oporu cieplnego całej przegrody  ($\ref{9}$) uzupełnionego o opory przejmowania i oddawania ciepła przez powierzchnie przegrody:

$$\begin{equation}  R_T = R_{si} + \sum \limits_1^n + R_{se} \label{16} \end{equation}$$

gdzie:

$R_{si}$ opór  przejmowania  ciepła przez przegrodę, to znaczy opór powietrza otulającego przegrodę od strony wewnętrznej „i” (na rys 1 „w”)
$R_{se}$ opór oddawania ciepła przez przegrodę, to znaczy opór powietrza otulającego przegrodę od strony zewnętrznej „e” (na rys.1 „z”)

Opory cieplne przejmowania ciepła przez przegrodę

Wartości oporów napływu i odpływu ciepła z przegród należy przyjmować zgodnie z tab.3:

Tab.3 Opory przejmowania ciepła $R_s$ $[(m^2K)/W]$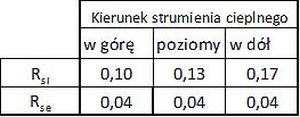

Oznaczenia (si) oraz (se) należy traktować jako oznaczenie typu powierzchni przegrody:
(si) – powierzchnia, przy której warstwa powietrza jest stabilna (nie jest omywana wiatrem lub przeciągiem)
(se) -powierzchnia, przy której warstwa powietrza pozostaje w ruchu (jest omywana wiatrem lub przeciągiem)

Oznacza to, że dla danej przegrody obie powierzchnie mogą być typu (si) – dotyczy w szczególności przegród położonych  wewnątrz budowli, lub obie powierzchnie mogą być (se) dla przegród wystawionych na zewnątrz, tak, że obie mogą być omywane wiatrem.

Opór cieplny warstwy  „i” przegrody o grubości $d_i$ i obliczeniowym współczynniku przewodzenia ciepła $\lambda_i$ wyznacza się z zależności ($\ref{9}$).

Współczynnik przewodzenia ciepła materiałów budowlanych

Współczynniki $\lambda_i$ występujące w ($\ref{9}$) należy przyjmować na podstawie tablic w których zestawiono wyniki pomiarów dokonywane przez producentów oraz niezależne instytuty ( w Polsce ITB).  Dotychczas zalecano tablice z normy PN-EN ISO 5946:1999  [8] – zał krajowy NC. Norma ta została zastąpiona normą pod tym samym numerem ale z roku 2008  [7], z której usunięto załącznik krajowy NC,  W tab. 4 podajemy wyciąg z tego załącznika obejmujący najczęściej stosowne materiały Bardziej szczegółowe tablice współczynników przewodności podano w: normie [9], w podręcznikach fizyki budowli, np. [10] oraz badaniach producentów. Wartościowe są tablice opublikowane na stronie Tablice, zebrane przez  Karolinę Kurtz. Tablice te są udostępnione również  w tym artykule Tablice_materialowe.

Tab. 4. Średnie współczynniki przewodności wybranych materiałów budowlanych
$\lambda$  w $[(m \cdot K)/W]$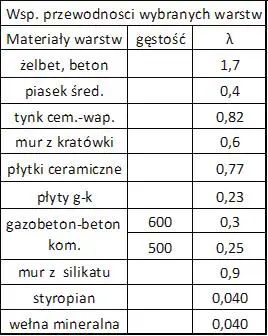 

Opór cieplny pustek powietrznych

Często przegrody budowlane mają wbudowane pustki powietrzne. W zależności od pola powierzchni otworów łączących szczelinę powietrzną ze środowiskiem zewnętrznym mogą to być warstwy powietrza:

• niewentylowane ,
• słabo wentylowane
• wentylowane

W przypadku warstw powietrza niewentylowanych opór cieplny w zależności od grubości warstwy można przyjmować z tab.5. Dla warstw o innej grubości d można stosować interpolację

.

Tab. 5 Opór  w $[(m^2K)/W]$ niewentylowanych warstw powietrza o wysokiej emisyjności powietrza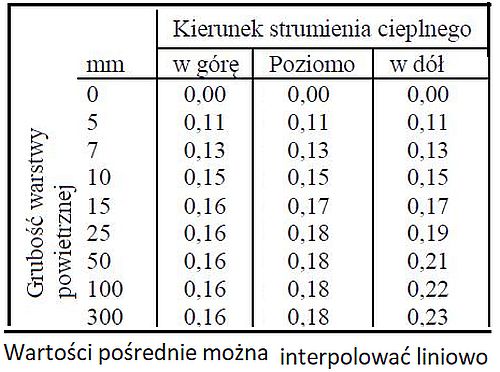

Dla warstw w pełni wentylowanych opór cieplny można pominąć, a opór przejmowania ciepła na powierzchni zewnętrznej przyjmuje się równy $R_{si}$.

W sytuacji gdy pustka jest słabo wentylowana to całkowity opór warstwy wyznaczany jest z interpolacji liniowej między wartościami dla szczeliny słabo i dobrze wentylowanej z zależności:

$$\begin{equation}  R_T = (1,5- A_v)\cdot R_{T,u} +(A_v-0,5)\cdot R_{T,v} \label{17}  \end{equation}$$

gdzie:
$A_v$ – powierzchnia otworów wentylujących w [$cm^2$]
$R_{T, u}$ – całkowity opór cieplny  z niewentylowaną warstwą powietrza
$R_{T, v}$ -całkowity opór cieplny  bez uwzględnienia warstwy powietrza

Opór cieplny warstw niejednorodnych

Gdy przegroda składa się z warstw jednorodnych i niejednorodnych cieplnie, to  jej całkowity opór wyznacza się jako średnią arytmetyczną:

$$\begin{equation}  R_T = ( {R_T}^ \prime +R_T^{\prime \prime} ) /2 \label{18}  \end{equation}$$

z kresu górnego $RT^\prime$ oporu cieplnego  obliczonego wg [7]– pkt.6.2.3,
oraz kresu dolnego $RT^{\prime \prime}$ oporu cieplnego  obliczonego wg [7]– pkt.6.2.4.

Opór cieplny przestrzeni dachowych

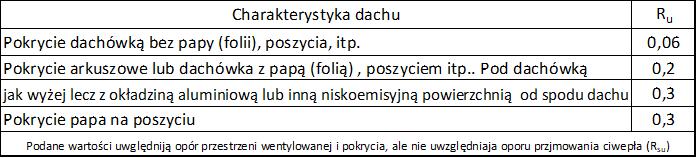
Dach stromy z płaskim izolowanym stropem przestrzeni poddasza można uznać za warstwę jednorodną cieplnie o oporze podanym w tab.6 :

Tab.6.  Opór cieplny  w $[(m^2K)/W]$ przestrzeni dachowych

Mostki cieplne

Mostek termiczny (cieplny) powstaje w wyniku naruszenia ciągłości struktury wewnętrznej przegrody w związku z występowaniem materiałów budowlanych różniących się, najczęściej znacznie, wielkością współczynników przewodności cieplnej  i może występować  w kontekście zarówno geometrii miejsca występowania mostka, jak i charakter jego oddziaływania na przegrodę lub ewentualne złącza przegród.

Występowanie mostków termicznych jest często niedostrzegane przez projektantów, architektów i konstruktorów. Tymczasem jest to zjawisko, które w istotny sposób wpływa na parametry cieplne budynku, a tym samym na jego charakterystykę energetyczną.

Zagadnienie mostków cieplnych omawiają normy [11] oraz  [12]. Oszacowanie wpływu mostka cieplnego na przenikalność cieplną przegrody powszechnie wykonuje  się metodami numerycznymi , np z wykorzystaniem programu TRISCO [13].

W niniejszym artykule problem ten tylko sygnalizujemy.  Jeśli nie są przeprowadzane dokładne obliczenia, to zalecamy, aby współczynnik przewodności każdej przegrody wyznaczony z równania ($\ref{7}$) zwiększyć o 3% do 5%,

Podłogi na gruncie

Zagadnienie przenikalności ciepła z pomieszczeń przez posadzki do gruntu  jest złożonym zagadnieniem  Do obliczeń uproszczonych  zwykle używa się metody [8]– wg załącznika  krajowego NB. Niestety nie uzyskuje się ta metodą zadawalających wyników [14].  Obecnie powszechnie stosuje się nowoczesną metody  opublikowaną w normie PN-EN ISO 13370..  Na  użytek szacunkowych obliczeń w w ogrzewnictwie opracowano uproszczoną  metodę PN-EN 12831.
Poniżej omawiamy wszystkie trzy  metody.

Metoda PN-EN-ISO 6946:1999 (NB) [8]– zał krajowy NB

Uwaga: Metoda  PN-EN ISO 6946 – zał NB nie jest aktualnie zalecana i wspierana.

Zgodnie z normą [8]– zał krajowy NB – podłogę stykającą się z gruntem dzieli się dwie strefy:
strefę I  obwodową, o szerokości 1 m przy ścianach zewnętrznych (rys.4)
strefę II – wewnętrzną – pozostała powierzchnia podłogi.

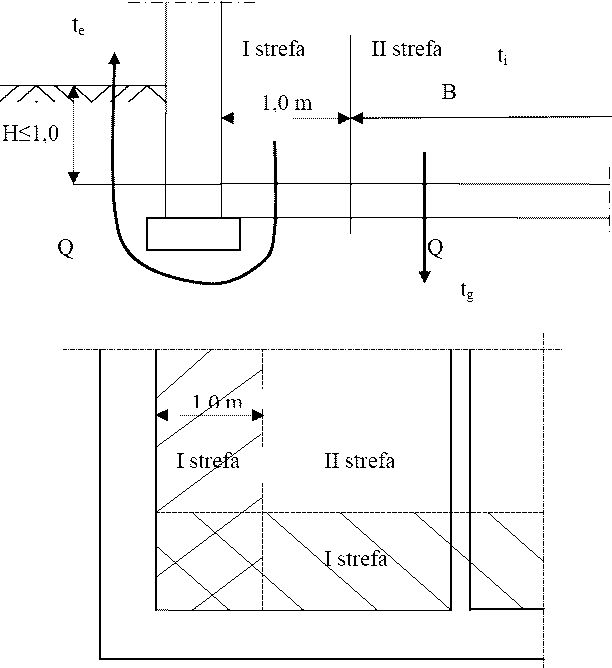
Rys.4. Podłoga na gruncie. Podział na strefy. Podział podłogi na gruncie na strefy, Oznaczenia: $t_e$ – obliczeniowa (projektowa) temperatura zewnętrzna, $t_g$ – obliczeniowa temperatura gruntu dla II strefy podłogi, $t_g = 8$ °C

Przy zagłębieniu górnej powierzchni podłogi więcej niż 1 m poniżej poziomu terenu  cała podłogę traktuje się jako strefę II.

Wartość oporu cieplnego gruntu $R_{gr}$ należy przyjmować:

w strefie I $R_{gr}=0,5 (m^2 K)/W$
w strefie II  wg tab. 7, przy czym wartość ta nie może przekraczać wartości granicznej

$$\begin{equation}  R_{g,max} =0,57 \cdot Z +0,09 \label{19}  \end{equation}$$

gdzie Z- odległość  w metrach poziomu górnego poziomu podłogi od zwierciadła wody gruntowej.:

Tab.7.  Opór cieplny gruntu przylegającego do podłogi w strefie II  [8]– Tab. NB.1

Opór cieplny przegrody posadzki na gruncie wyznacza się z zależności:

$$\begin{equation}  R_{T,gr}= R_T +R_{gr} \label{20}  \end{equation}$$

gdzie $R_T$ opór warstw posadzki wg zależności ($\ref{2}$) ,

gdzie należy przyjąć: $R_{si}= 0,17$ , $R_{se} =0$.

Opór cieplny gruntu stykającego się ze pionową ścianą przyjmuje się wg tab 8.:

Tab.8.  Opór cieplny gruntu przylegającego do ściany  [8]– Tab. NB.1

Opór ściany wraz z gruntem oblicza się wg formuły ($\ref{7}$), przy czym $R_{si}=0,13$, $R_{se}=0$.

Metoda PN-EN ISO 13370: 2008 [15]

Pole temperatury w gruncie poza budynkiem zależy praktycznie nie zależy od gradientu geotermicznego w skorupie ziemskiej, a zależy   od czynników atmosferycznych (temperatury powietrza zewnętrznego, nasłonecznienia, prędkości wiatru i pokrywy śnieżnej). W analizie przyjmuje się, że  temperatura powietrza zewnętrznego, zmienia się według  funkcji harmonicznej. z okresem niezależnym od głębokości. Amplituda wahań temperatury w gruncie zanika ekspotencjalnie (według funkcji wykładniczej) ze wzrostem głębokości. W rezultacie można wykazać (np. [14]), że na głębokości gruntu równej kilku metrom wahania dobowe i wszystkie dzienne krótkotrwałe zmiany temperatury można zaniedbać w porównaniu z wahaniami rocznymi. W praktyce na głębokości od 7 m do 10 m możemy zakładać stałą temperaturę gruntu równą wieloletniej średniej rocznej temperaturze powietrza (w Polsce środkowej przeciętnie 8 °C), podwyższonej o około 1,5 K przez promieniowanie słoneczne. Temperatura powierzchni będzie superpozycją średniej rocznej temperatury i funkcji harmonicznej o okresie 1 rok i amplitudzie rocznej.

Izotermy w gruncie przebiegają po liniach sferycznych, w sposób pokazany na rys. 5 na przykładzie  podłogi o temperaturze $20^oC$ ułożonej na gruncie według przykładu wzorcowego programu TRISCO [16].

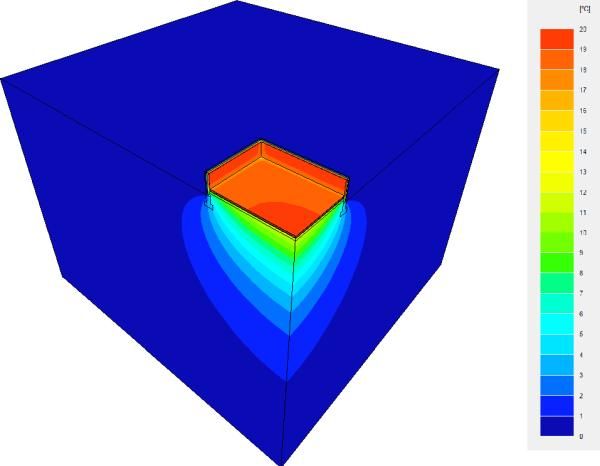
Rys. 5. Przykład rozkładu temperatur w układzie posadzka -grunt-ściana (z programu [13]

Współczynnik przenikania cieplnego przez grunt

W normie [15] została przyjęta koncepcja, aby rzeczywisty kształt podłogi na gruncie zastąpić figurą o obwodzie i polu powierzchni $A$ zgodnymi z danymi rzeczywistego rzutu podłogi. obwodowi budynku $P$ przypisujemy pas podłogi o szerokości zwanej „wymiarem charakterystycznym”, zdefiniowanej wzorem

$$\begin{equation}  B^\prime =\cfrac{A}{P/2}\label{21}  \end{equation}$$

Wielkością charakteryzującą przenikanie ciepła przez grunt w stanie ustalonym jest stacjonarny współczynnik sprzężenia cieplnego definiowany jako iloraz strumienia cieplnego przez różnicę średniej w czasie temperatury powietrza wewnętrznego i zewnętrznego. W celu uproszczenia jego wyrażania wprowadza się pojęcie „grubości równoważnej”, to jest grubości gruntu o tym samym oporze cieplnym, jak zastępowany nią opór cieplny. Wyrażenie na „grubość równoważną”  $d_t$ dla podłóg jest następujące:

$$\begin{equation}  d_t = w+ \lambda \cdot(R_{si} +R_f+R_{se}) \label{22}  \end{equation}$$

gdzie:
$w$ – grubość całkowita ściany budynku (Rys.6)
$\lambda$ – współczynnik przewodności cieplnej gruntu wg tab.9,
$R_{si}$ , $R_{se}$ – współczynniki napływu wg tab.3,
$R_f$ – opór cieplny płyty podłogi, łącznie z każdą warstwą izolacyjną, poniżej lub powyżej podłogi i każdym pokryciem podłogi.

Rys. 6. Schemat interakcji cieplnej budynku i gruntu

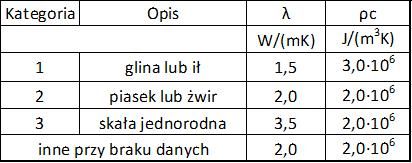
Tab. 9 Właściwości cieplne gruntów [15]– tab.1

W kol.3 tab.9 podano szacunkowe wartości współczynnika przewodzenia ciepła przez grunty, a w kol. 4 iloczyn  ρc, gdzie: : ρ – masa właściwa gruntu ( średnio  2000 kg/m³), c- ciepło właściwe niezamarzniętego gruntu  ( średnio  1000 J/(kg K ) ).

Podłoga typu „płyta na gruncie” może być:
• nieizolowana,
• równomiernie izolowana na całej powierzchni (powyżej, poniżej lub wewnątrz płyty).
W przypadku płyty izolowanej izolacja może być:
a) pozioma – rys 7a,
b) pionowa – rys. 7b.

Ponadto rozróżnia się:
c) podłogi podniesione – rys. 7 c,
d) podłogi opuszczone poniżej poziomu gruntu – rys. 7d

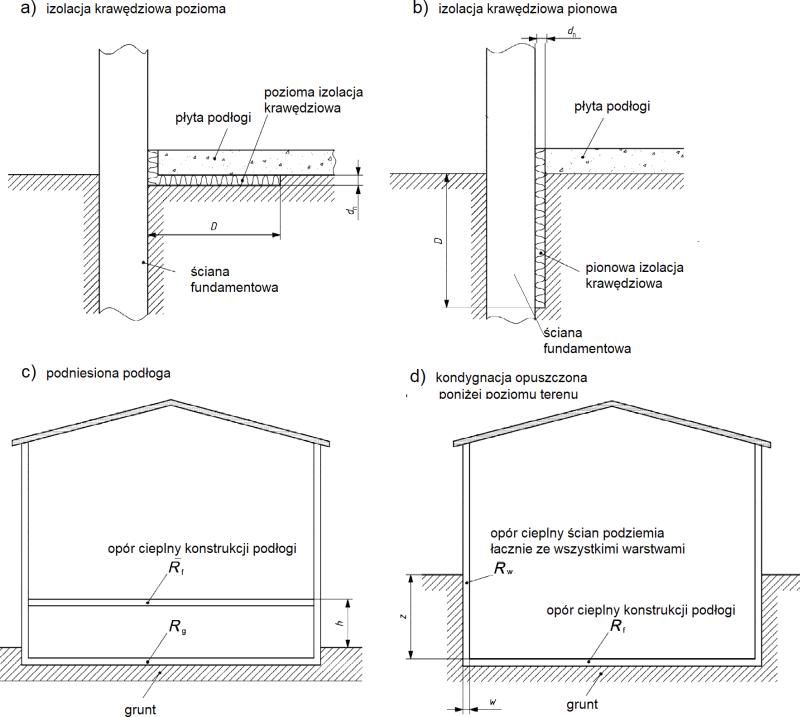
Rys. 7: Cieplna izolacja krawędziowa budynku: a) pozioma, b) pionowa, c) podniesioną podłogą, d) opuszczeniem podłogi poniżej poziomu gruntu

Podłoga z izolacją krawędziową (pionową lub poziomą)

W przypadku podłóg bez izolacji krawędziowej (rys.6)  współczynnik przenikania ciepła U wynosi

$$\begin{equation} U=U_0  \label{23}  \end{equation}$$

a w przypadku podłóg z izolacją krawędziową

$$\begin{equation} U=U_0 +\cfrac{ 2\cdot \Psi_{ge}}{B^\prime}  \label{24}  \end{equation}$$

gdzie:

$$\begin{equation} U_0 = \begin {cases} \cfrac{\lambda}{ 0,457 \cdot B^\prime + d_t} & \text {dla podłóg dobrze izolowanych:} \quad d_t \ge B^\prime \\ \cfrac{2 \lambda} {\pi B^\prime +d_t} \cdot  \ln { \left ( \cfrac{\pi  B^\prime}{d_t}+1\right)}, & \text {dla podłóg nieizolowanych i słabo izolowanych:} \quad d_t < B^\prime \\ \end {cases} \label{25}\end{equation}$$

Liniowy współczynnik przenikania ciepła związany z połączeniami  z izolacją krawędziową wyznacza się z równania:

$$\begin{equation} \Psi_{ge}=-\cfrac{ \lambda}{\pi} \cdot  \left[ \ln { \left ( \cfrac{n_{ge}\cdot D}{d_t}+1\right)} – \ln { \left ( \cfrac{n_{ge}\cdot D}{d_t+d^\prime}+1\right)} \right ] \label{26}  \end{equation}$$

gdzie

$$\begin{equation} n_{ge}=\begin {cases} 1 , & \text {dla izolacji krawędziowej poziomej}\\ 2 , & \text {dla izolacji krawędziowej pionowej}\\ \end {cases} \label{27}\end{equation}$$

W równaniach ($\ref{25}$), ($\ref{26}$):
$D$ – szerokość pionowej lub poziomej izolacji krawędziowej zgodnie z rys 3a) i b),
$d^\prime$ – dodatkowa grubość ekwiwalentna, wynikająca z izolacji krawędziowej wg zależności

$$\begin{equation}   d^\prime = R^\prime \cdot \lambda \label{28}  \end{equation}$$

$$\begin{equation}   R^\prime = R_n -\cfrac{d_n}{\lambda}\label{29}  \end{equation}$$

gdzie:
opór cieplny dodatkowej izolacji krawędziowej (lub fundamentu) w  $m^2\cdot K/W$

$$\begin{equation}   R_n = \cfrac{d_n}{ \lambda_{izolacja}} \label{30}  \end{equation}$$

$d_n$ – grubość izolacji krawędziowej (lub fundamentu) w m

Jeśli w danym detalu zastosowano kilka rodzajów izolacji krawędziowej (pionową lub poziomą, wewnętrzną lub zewnętrzną), to liniowy współczynnik przenikania ciepła  $\Psi_{ge,i}$ ($\ref{26}$) należy obliczyć dla każdej izolaacji (i=1, n) osobno , a do dalszych analiz ($\ref{24}$)  wybrać tą izolację, która daje największy redukcję przenikania ciepła, tzn:

$$\begin{equation}  \Psi_{ge} = – \max \limits_{i=1}^n { | \Psi_{ge,i}| } \label{31}  \end{equation}$$

Podłoga  podniesiona

Podłoga podniesiona  (rys. 7c) jest to podłoga zbudowana  nad gruntem, a powstała  przestrzeń  podpodłogowa  jest wentylowana grawitacyjnie (naturalnie) lub mechanicznie powietrzem zewnętrznym.  W przypadki podłogi wentylowanej naturalnie przenikalność cieplną $U$ z pomieszczenia do gruntu  można wyznaczyć  zależności

$$\begin{equation}  \cfrac{1}{U}=\cfrac{1}{U_f} +\cfrac{1}{U_g +U_x}\label{32}  \end{equation}$$

gdzie:

$U_f$  w $[W/(m^2K)]$ -współczynnik przenikania ciepła podłogi od środowiska wewnętrznego do podpodłogowej przestrzeni powietrznej. Wyznaczamy go zgodnie z normą  [7] podług ogólnej zależności  ($\ref{6}$), biorąc pod uwagę warstwy podłogi.

$U_g=U$ – współczynnik przenikania warstwy podpodłogowej. Wyznaczamy go  z zależności ($\ref{22}$)  i ($\ref{25}$) , ale:
w ($\ref{22}$)  zamieniamy  $R_f$ na $R_g$, a w ($\ref{25}$) zamieniamy $d_f$ na $d_g$ ,

gdzie: opór cieplny przestrzeni podpodłogowej zwykle $R_g=0$, gdy przestrzeń nie jest izolowana i nie traktuje się jej jako pustki powietrznej (jest z byt duża) i wobec tego z ($\ref{25}$) otrzymujemy grubość ekwiwalentną przestrzeni podpodłogowej $d_g= w+\lambda(R_{si} +R_{se}$.

Zwykle głębokość podstawy przestrzeni podpodłogowej $z$ (rys. 7d) nie przekracza 0,5 m i wówczas $U_g$ wyznaczamy z zależności ($\ref{22}$)  (po zmianie $d_f$ na $d_g$). Jeśli jednak $z>0,5$, to stosujemy zależność

$$\begin{equation}  d_t = w+ \lambda \cdot (R_{si} +R_f+R_{se}) \label{22X}  \end{equation}$$

Przenikalności od wentylacji przestrzeni podpodłogowej $U_x$obliczamy z zaleźnosci

$$\begin{equation} U_x= 2 \cdot \cfrac{h \cdot U_w}{B^\prime}+ 1450 \cdot \cfrac{\varepsilon \cdot \nu \cdot f_w}{B^\prime}\label{33}  \end{equation}$$

Metoda PN-EN 12831:2006 [4]

Ze względu na to, że szereg projektantów postrzegało trudności obliczeniowe przy stosowaniu normy [15], więc na ich użytek (projektowania instalacji grzewczych w budynkach) opracowano uproszczoną metodę wyznaczania współczynnika przenikania ciepła przez podłogę na gruncie oraz przez ścianę pomieszczenia zagłębionego w gruncie wg zasad podanych w normie [7].

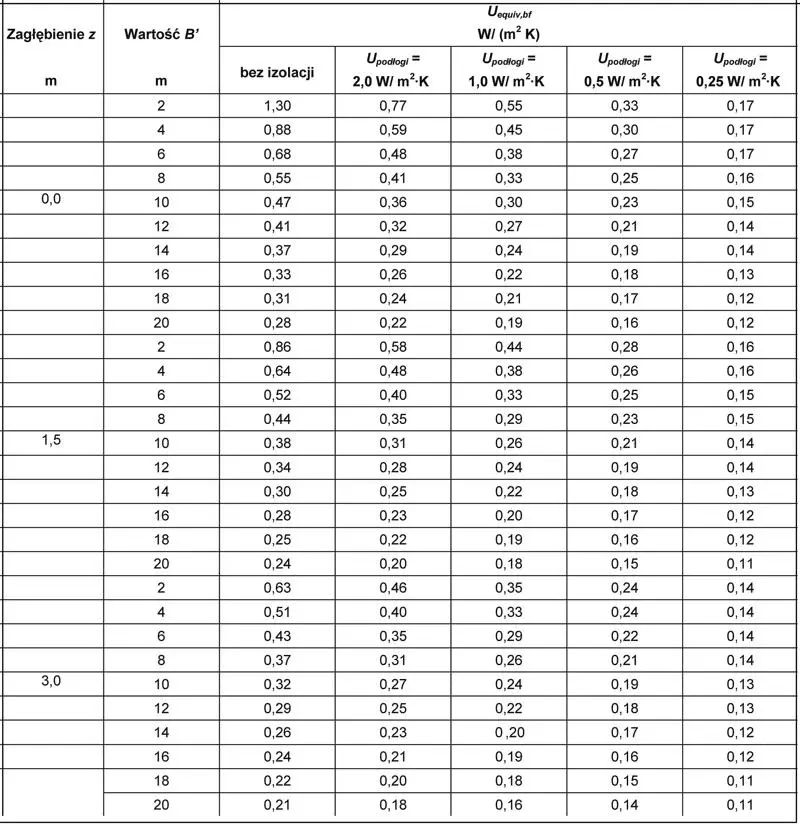
W celu obliczenia wartości U wyznacza się opór cieplny poszczególnych warstw  z uwzględnieniem oporu przejmowania ciepła od strony wewnętrznej budynku $R_{si}$, a pomijając opór przejmowania ciepła od strony gruntu, czyli przyjmując $R_{se}=0$. Na podstawie wyliczonych wartości B’ oraz U określa się wartości $U_{equiv,bf}$ przy użyciu tab.9 lub nomogramów podanych w normie [15]. Korzysta się z wartości, które są funkcją wielkości zagłębienia w terenie oraz wartości $B^\prime$ ($\ref{21}$)  i $U_{podłogi}$ w rozpatrywanym budynku. Dla wartości pośrednich $U_{equiv,bf}$ należy wyznaczyć stosując metodę interpolacji liniowej.

Tab.10 Wartości $U_{equiv,bf}$ podłogi ogrzewanego podziemia w funkcji zagłębienia poniżej poziomu terenu. i współczynnika przenikania ciepła podłogi i wartości $B^\prime$ – na podstawie normy PN-EN 12832:2002 [17]

W dobie powszechnego stosowania arkuszy kalkulacyjnych powyższa, uproszczona metoda jest coraz rzadziej stosowana.

Porównanie metod obliczania strat ciepła przez grunt

W pracy [18] przeprowadzono analizę dokładności metod obliczania strat ciepła do gruntu za pomocą:

A trójwymiarowej symulacji numerycznej zgodnie z normą PN-EN ISO 10211 [12],

B metody przybliżonej podług normy PN-EN ISO 13370 [15] i symulacją 2D mostków wg [12],

C  metody orientacyjnej wg normy normy PN-EN ISO 13370 [15] i symulacją mostków zgodnie z normą [11].

Przeprowadzono analizę podłogi na gruncie (rys 8 a) oraz podziemia nieogrzewanego (rys 8b). W obu analizowanych sytuacjach projektowych stwierdzono, że metoda szacunkowa C jest niedokładna (daje znacznie zawyżone wartości), a metoda B( przybliżona) jest mierna.

Rozkład temperatur w przegrodzie

Obliczanie rozkładu temperatury w przegrodzie powinno służyć do sprawdzenia wilgotnościowego przegród jako zadanie pomocnicze.. Wyznacza się go z zależności klasycznej  ($\ref{4}$). Strumień cieplny   q  ($\ref{6}$) zależy od różnicy ustalonych temperatur w pomieszczeniach po obu stronach przegrody ($\ref{10}$) i jest najczęściej znany z wymogów normowych .

W przypadku nieogrzewanych pomieszczeń temperatura $t_w$ nie jest znana. Wówczas  mamy do czynienia z procesem czasowym, związanym z bezwładnością cieplną obiektu, a nie tylko pomieszczenia.

Sprawdzenie kondensacji powierzchniowej

Temperatura wewnętrzna powierzchni przegrody bez mostków cieplnych liniowych

Temperaturę wewnętrzną $\vartheta_w$ na  powierzchni przegrody bez mostków cieplnych liniowych wyznacza się ze wzoru

$$\begin{equation}  \vartheta_w = t_w – U_c \cdot (t_w-t_z) \cdot R_{sw}  \label{35}  \end{equation}$$

gdzie:
$R_{sw}= 0,167 \, m^2 \cdot K/W$ – opór przejmowania ciepła przyjmowany przy sprawdzaniu minimalnej temperatury wewnętrznej powierzchni przegród nieprzezroczystych
$U_c$

Ciśnienie cząstkowe pary wodnej w pomieszczeniu

Ciśnienie cząstkowe pary wodnej w pomieszczeniu  $p_w$ zależy od wilgotności względnej  $\varphi_w$ oraz ciśnienia cząstkowego pary wodnej nasyconej dla temperatury obliczeniowej w tym pomieszczeniu  $p_n$.
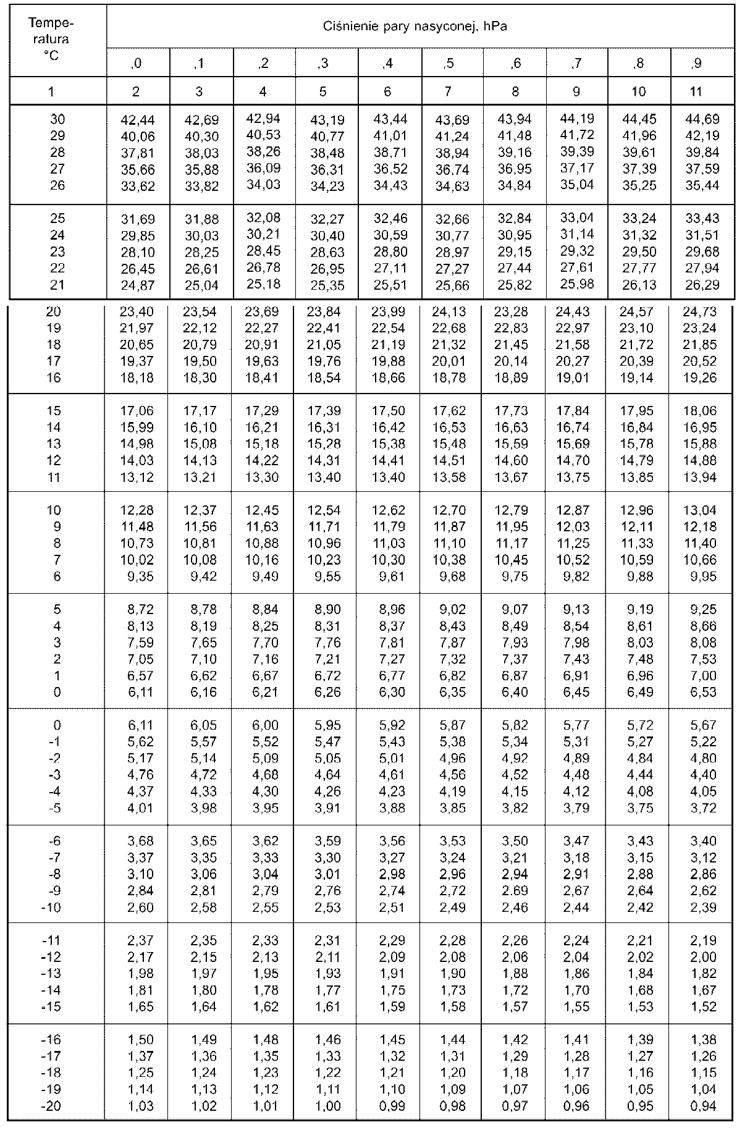
Ciśnienie cząstkowe pary wodnej nasyconej w powietrzu $p_n$ w temperaturze $t_w$ odczytuje się z tab.11. Na przykład dla  temperatury w pomieszczeniu $t_w =4 \,^oC$ odczytujemy $p_n = 8,13 \, hPa$

Ciśnienie cząstkowe pary wodnej wylicza się z zależności

$$\begin{equation}  p_w= \varphi_w \cdot p_n \label{36}  \end{equation}$$

gdzie $\varphi_w$ w ułamku dziesiętnym ( np dla 45% wstawiamy 0,45).

Jeśli z założeń technologicznych lub bilansu wilgoci nie wynikają inne wartości, to wilgotność względna w pomieszczeniach można przyjmować następująco:
$\varphi_w= 55%$ dla pomieszczeń mieszkalnych (w tym kuchnie, łazienki oraz ustępy), pokoje chorych w szpitalach, sanatoriach, pokoje dziecięce żłobkach, i przedszkolach
$\varphi_w= 45%$ dla pomieszczeń pozostałych (użyteczności publicznej i produkcyjnych) w których nie wydziela się para wodna  z otwartych zbiorników lub urządzeń technologicznych i nie stosuje się nawilżania,

Dla obliczonego ciśnienia cząsteczkowego pary $p_w$ ponownie z tab.11 odczytujemy temperaturę powietrza nasyconego $t_s$.
Na przykład dla $p_w=8,13 \cdot 0,45= 3,65 \, hPa$ mamy temperaturę nasycenia $t_s= -6,1 \,^oC$

Warunek ryzyka wykraplania (kondensacji) pary wodnej

Warunek przy którym nie nastąpi wykraplanie pary wodnej na powierzchni przegrody jest następujący:

$$\begin{equation}  \vartheta_w \ge t_s \label{37}  \end{equation}$$

gdzie:  $\vartheta_w$ ($\ref{35}$) , $t_s$ – wyżej.

Tab.11 Ciśnienie cząstkowe pary wodnej nasyconej w powietrzu $p_n$ w funkcji temperatury [8]– Tab. NA.3

Przykłady rachunkowe

Podłoga na gruncie

Dla podłogi ułożonej na gruncie (rys.6) z warstwami jak na Rys.8 wyznaczyć opór cieplny , współczynnik przenikania ciepła oraz rozkład temperatur.

Rys.8  Przykład: warstwy podłogi

Grubość ścian wynosi w=0,25\,m $.

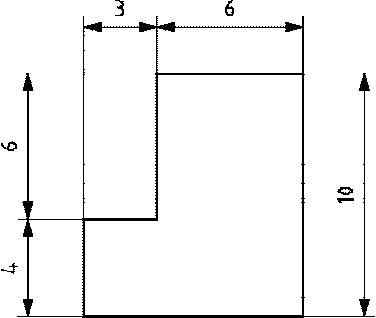
Na rys.9 pokazano plan podłogi (w rzucie z góry).
Pole powierzchni podłogi $A= 10\cdot 9 – 3\cdot 6= 72 \, m^2$
Obwód podłogi $P=10+9+4+3+6+6= 38 \, m$
Szerokość charakterystyczna:
($\ref{21}$ \toB^\prime =\cfrac{72}{38/2}=3,789 \,m$

Rys.9 Kształt podłogi z przykładu

Płyta jest ułożona na gruncie kat.1 (glina lub ił).
tab.9 $\to$  współczynnik przewodzenia ciepła przez grunt wynosi
$\lambda= 1,5 \, W/(m\cdot K)$

Opór cieplny posadzki i współczynnik przewodności cieplnej

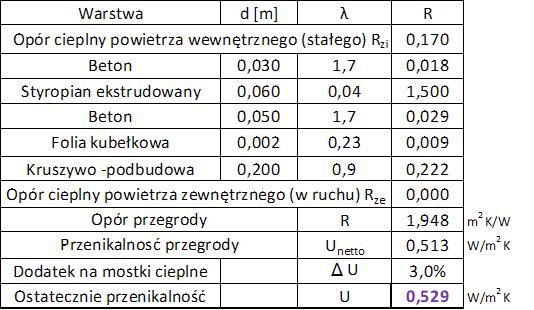
W tab. 12 zestawiono  wyniki obliczeń oporu cieplnego i przewodności cieplnej posadzki dla danych rodzajów, grubości i przewodności cieplnej warstw (kol. 1, 2 i 3).

Tab.12. Zestawienie oporów warstw posadzki z przykładu

Opory napływu ciepła na przegrodę $R_{si} =0,17$m^2\cdot K/ W$ przyjęto z tab.3  jak dla przepływu ciepła w dół przy powierzchni napływu z warstwą powietrza w bezruchu. (stałego). Natomiast opór wychodzenia ciepła z przegrody $R_{se} =0$ jak dla przegrody ułożonej na gruncie.

Opór cieplny warstw w kol ostatniej wyliczano ze wzoru ($\ref{9}$).
Na przykład dla warstwy drugiej – betonu, obliczono jak następuje $R_2= \cfrac{0,03}{1,7}=0,018 \, m^2\cdot K/ W$

Po zsumowaniu oporu cieplnego poszczególnych warstw wg wzoru ($\ref{8}$) otrzymano opór przegrody: $R=0,170+0,018+1,500+0,029+0,009+0,222+0=1,948 \, m^2\cdot K/ W$

Współczynnik przenikalności cieplnej jest odwrotnością oporu cieplnego zgodnie z formułą ($\ref{7}$) $U=1/1,948 =0,513 \,$W/(m^2 \cdot K$.
W rzeczywistości współczynnik przewodzenia ciepła przez przegrodę będzie większy ze względu na mostki cieplne w przegrodzie, wywołane przez przestrzenny układ i połączenia (w tym noraża ścian) z innymi przegrodami, łączniki, niejednorodność warstw, spoiny w murach,  i inne. Nie przeprowadzamy dokładnych obliczeń, ale powiększyliśmy go o 3% jak dla przegrody dobrej jakości zgodnie z uwagą zamieszoną w punkcie Mostki cieplne.

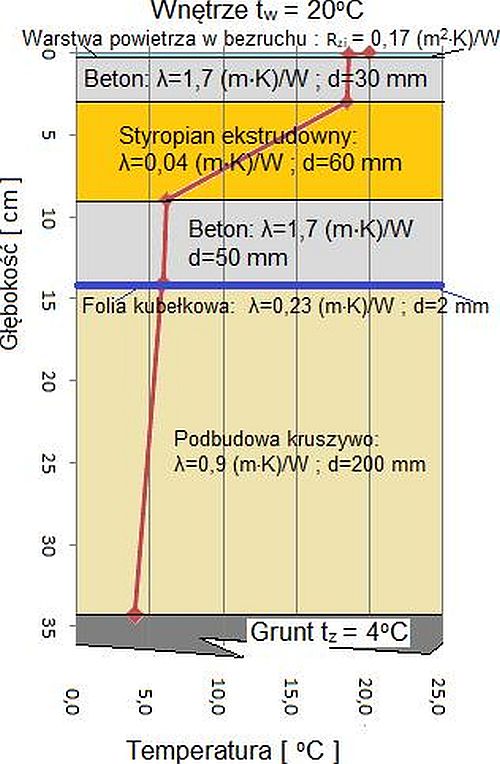
Rozkład temperatur w przegrodzie

Rozkład temperatur w przegrodzie został nakreślony czerwona linią na rys 8.
Uzyskano go zw wyrażeń ($\ref{4}$) dla strumienia cieplnego wyznaczonego ze współczynnika przenikalności cieplnej $U_{netto} = 0,513 \, W/m^2\cdot K$.(bez rozrzucania przenikalności wynikającej z mostków na poszczególne warstwy).

Temperaturę powietrza wewnątrz pomieszczenia przyjęto $t_w =20 ^oC$ jak dla pomieszczeń przeznaczonych na pobyt ludzi bez okryć zewnętrznych wg tab.1.
Temperaturę powietrza pod przegrodą (od strony gruntu) przyjęto $t_z = + 4^oC$ na podstawie indywidulanych pomiarów minimalnej temperatury pod posadzką zimą.

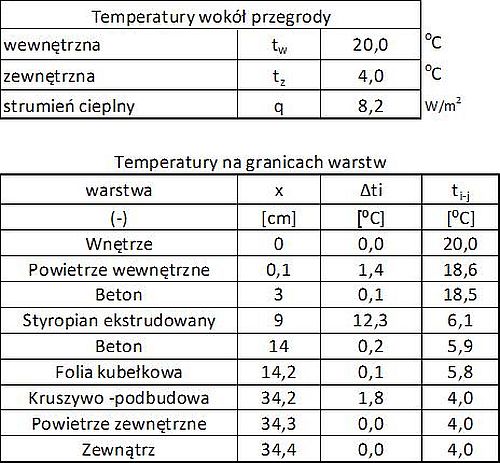
Różnica temperatur po obu stronach przegrody  ($\ref{10}$) wynosi $\Delta t = 20-4=16 \, ^oC$
Strumień ciepła  ($\ref{6}$) wynosi $q=0,513 \cdot 16= 8,2 \, W/m^2$

Temperatura we wnętrzu pomieszczenia   $20 \, ^oC$,
Temperatura na powierzchni wewnętrznej przegrody  $20-0,17 \cdot 8,2 = 18,6 \, ^oC$,
Temperatura na granicy betonu i styropianu $18,6 -0,018 \cdot 8,2 = 18,5 \, ^oC$,
Temperatura na granicy styropianu i betonu $18,5 -1,5  \cdot 8,2 = 6,1 \, ^oC$.

Zestawienie obliczeń podano w tab.13

Tab.13. Obliczenia strumienia cieplnego i rozkładu temperatur w przegrodzie

Przenikanie ciepła przez podłogę z gruntem

Maksymalny współczynnik przewodzenia ciepła $U_{Cmax}$ dla temperatury wewnątrz pomieszczenia $t_w  \ge16 ^oC \to$
$tab 2, poz. 6 $:$U_{max} = 0,3 \, W/(m^2 \cdot K)$

Wariant przy braku izolacji

przy założeniu: opór cieplny podłogi $R_f =0  \, W/(m^2\cdot K)$ wg tab.
Współczynnik napływu przy przepływie ciepła w dół wg tab.3, $R_{si}= 0,17 \, (m^2K)/W$
Współczynnik odpływu przy przepływie ciepła w dół wg tab.3, $R_{se}= 0,04 \, (m^2K)/W$
Współczynnik przewodności cieplnej gruntu$\lambda=1,5 \, W/(m\cdot K)$
Grubość ścian zewnętrznych (Rys.6) $w=0,25 \, m$

Grubość równoważna posadzki z gruntem
($\ref{22}$) $\to d_t =0,25 +1,5\cdot(0,17+ 0+ 0,04)= 0,565 \, m$

Ponieważ $d_t= 0,565 < B^\prime =3,789 \,m    \to$  podłoga jest nieizolowana (lub słabo izolowana) i:
($\ref{25}$): $U_0= \cfrac{2 \cdot 1,5} {\pi \cdot 3,789 +0,565} \cdot  \ln { \left ( \cfrac{\pi \cdot 3,789}{0,565}+1\right)}= 0,744 \, W/(m^2 \cdot K)$
($\ref{23}$): U=0,744 \, W/(m^2 \cdot K)$

Ponieważ $U= 0,744 > U_{max} = 0,3 \, W/(m^2 \cdot K) \to$ podłogę należy ocieplić.

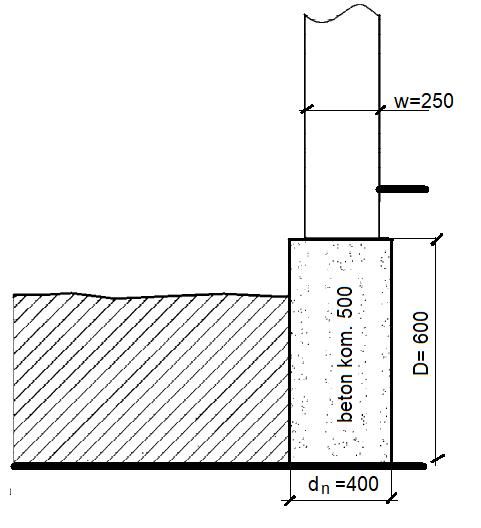
Wariant z zastosowaniem  ław z betonu komórkowego $\gamma=500 \, kg/m^3$ (rys.10)

Rozważmy wariant posadowienia  ścian na ławie wykonanej z lekkiego betonu – rys. 10. Sytuację oceniamy procedurą analogicznie do pionowej izolacji krawędziowej dla głębokości
$D=0,6 m$ i grubości $d_n=0,4 m$.
Tab. 4: dla betonu komórkowego o gęstości  $\gamma=500 \, kg/m^3$ współczynnik przewodzenia ciepła
$\lambda_{izolacja} =0,25 \, W/(m\cdot K)$

Rys.10. Posadowienie na ławie z lekkiego betonu

Opór cieplny dodatkowej izolacji krawędziowej (fundamentu):
($\ref{30}$) $\to R_n = \cfrac{0,4}{ 0,25}= 1,600  \, (m^2 K)/W$,
($\ref{29})$ $\to  R^\prime = 1,600 – \cfrac{0,4}{1,5} = 1,333 \, (m^2 K)/W$,
Dodatkowa grubość ekwiwalentna, wynikająca z izolacji krawędziowej (fundamentu)
($\ref{28}$)  $\to  d^\prime = 1,333 \cdot  1,5= 2,000 \, m$,
Liniowy współczynnik przenikania ciepła związany z izolacją krawędziową ( w tym przypadku lekkiego fundamentu):
($\ref{26}$)  $\to$
$\Psi_{ge}= – \cfrac{ 1,5}{\pi} \cdot  \left[ \ln { \left ( \cfrac{2 \cdot 0,6 }{0,565}+1\right)} – \ln { \left ( \cfrac{2 \cdot 0,6}{0,565+2,000 }+1\right)} \right ]= 0,477 \cdot (ln(3,123) – ln(1,468) = – 0,361  \, W/(m K)$,
Współczynnik przenikalności:
($\ref{24}$) $\to U=0,744 +\cfrac{ 2\cdot (-0,361)}{3,789}= 0,554 \, W/(m^2 K)$.

Ponieważ $U=0,554  > U_{max} = 0,3 \, W/(m^2 K)$,

to podłoga wymaga innego docieplenia.

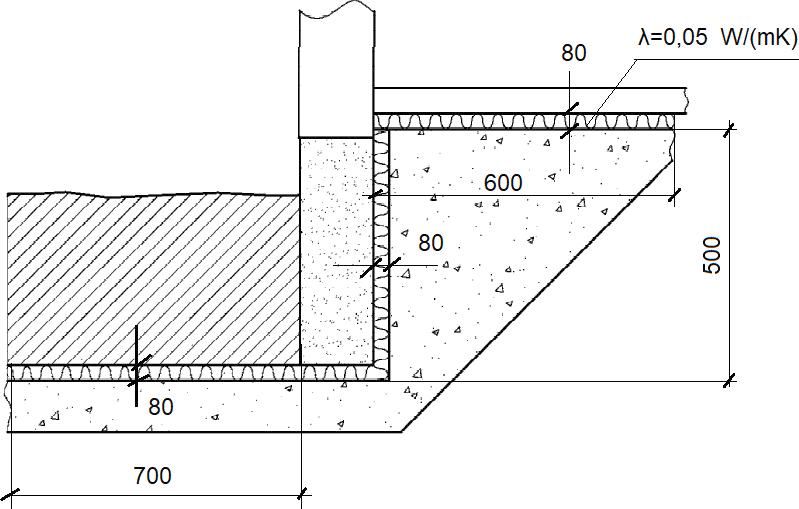
Wariant  z izolacją krawędziową – przeciwmrozową (Rys. 11)

Zastosowano:

• Izolację pionową:  grubość  $d_n=0,08 m$ ;  długość $D=0,6 m$  ; przewodność $\lambda_{izol}= 0,05 W/(m\cdot K)$
  Opór cieplny izolacji :
  ($\ref{30}$) $\to R_n = \cfrac{0,08}{ 0,05}= 1,600  \,m^2 K)/W$
  ($\ref{29}$ $\to  R^\prime = 1,600 – \cfrac{0,08}{1,5} = 1,547 \,m^2 K) /, W$
  Grubość ekwiwalentna  pionowej izolacji krawędziowej:
  ($\ref{28}$)  $\to  d^\prime = 1,547 \cdot  1,5= 2,320 \, m$,
  Liniowy współczynnik przenikania ciepła:
  ($\ref{26}$)  $\to \Psi_{ge}= – \cfrac{ 1,5}{\pi} \cdot  \left[ \ln { \left ( \cfrac{2  \cdot 0,5 }{0,565}+1\right)} – \ln { \left ( \cfrac{2 \cdot 0,5}{0,565+2,320 }+1\right)} \right ]= – 0,344  \, W/(m K)$
• Izolację poziomą :grubość  $d_n=0,08 m$ ;  długość $D=0,7 m$  ; przewodność $\lambda_{izol}= 0,05 W/(m\cdot K)$
  Opór cieplny izolacji :
  ($\ref{30}$) $\to R_n = \cfrac{0,08}{ 0,05}= 1,600  \,m^2 K)/W$
  ($\ref{29}$ $\to  R^\prime = 1,600 – \cfrac{0,08}{1,5} = 1,547 \,m^2 K) /, W$
  Grubość ekwiwalentna  pionowej izolacji krawędziowej:
  ($\ref{28}$)  $\to  d^\prime = 1,547 \cdot  1,5= 2,320 \, m$,
  Liniowy współczynnik przenikania ciepła:
  ($\ref{26}$)  $\to \Psi_{ge}= – \cfrac{ 1,5}{\pi} \cdot  \left[ \ln { \left ( \cfrac{2 \cdot 0,7 }{0,565}+1\right)} – \ln { \left ( \cfrac{1 \cdot 0,7}{0,565+2,320 }+1\right)} \right ]=  – 0,281  \, W/(m K)$

Rys. 11 Przykład izolacji krawędziowej

($\ref{31}$) $\to \Psi_{ge} = – \max {  | -0,344| \, ; \, |-0,281| } =-0,344$
czyli bardziej efektywna jest izolacja krawędziowa pionowa. Izolacji krawędziowej poziomej można nie wykonywać. Należy natomiast wykonać dodatkowe izolacje , wynikające z ochrony przed mrozem w narożach oraz innych mostków cieplnych.

Współczynnik przenikalności:
($\ref{24}$) $\to U=0,744 +\cfrac{ 2\cdot (-0,344)}{3,789}= 0,563 \, W/(m^2 K)$.

Ponieważ $U=0,563  > U_{max} = 0,3 \, W/(m^2 K)$,

to podłoga wymaga innego docieplenia.

Wariant przy  izolacji posadzki 60 mm

Opór cieplny podłogi $R_f =1,948 \, W/(m^2\cdot K)$ wg tab. 12
Współczynnik napływu przy przepływie ciepła w dół wg tab.3, $R_{si}= 0,17 \, (m^2K)/W$
Współczynnik odpływu przy przepływie ciepła w dół wg tab.3, $R_{se}= 0,04 \, (m^2K)/W$
Współczynnik przewodności cieplnej gruntu$\lambda=1,5 \, W/(m\cdot K)$
Grubość ścian zewnętrznych (Rys.6) $w=0,25 \, m$

Grubość równoważna posadzki z gruntem
($\ref{22}$) $\to d_t = 0,25 +1,5\cdot(0,17+ 1,948 + 0,04)= 3,487 \, m$

Ponieważ $d_t= 3,487 < B^\prime =3,789 \,m    \to$  podłoga jest słabo izolowana:
($\ref{25}$): $U_0= \cfrac{2 \cdot 1,5} {\pi \cdot 3,789 +0,565} \cdot  \ln { \left ( \cfrac{\pi \cdot 3,789}{0,565}+1\right)}= 0,2894 \, W/(m^2 \cdot K)$
($\ref{23}$): U=0,744 \, W/(m^2 \cdot K)$

Ponieważ $U=0,2894 \le  U_{max} = 0,3 \, W/(m^2 \cdot K) \to$ podłogę  ocieplono prawidłowo

 Literatura

1. Rozporządzenie Ministra Infrastruktury z dnia 12 kwietnia 2002 r. w sprawie warunków technicznych, jakim powinny odpowiadać budynki i ich usytuowanie, ( Dz.U. 2002 nr 75, poz.69, tekst jednolity Dz.U. 2019 poz. 1065 (z późn zmianami)
2. PN-EN 1991-1-5, Eurokod 1: Oddziaływania na konstrukcje – Część 1-5: Oddziaływania ogólne – Oddziaływania termiczne
3. SPECBUD, Mapa stref oddziaływań klimatycznych v.1.2, [ https://www.computerworld.pl/ftp/pobierz/pc/109084.html ]
4. PN-EN 12831:2006, Instalacje grzewcze w budynkach, Metoda obliczania projektowego obciążenia cieplnego
5. PN-82/B-02403, Ogrzewnictwo – Temperatury obliczeniowe zewnętrzne
6. Rozporządzenie Ministra Infrastruktury z dnia 12 kwietnia 2002 r. w sprawie warunków technicznych, jakim powinny odpowiadać budynki i ich usytuowanie, ( Dz.U. 2002 nr 75, poz.69, tekst jednolity Dz.U. 2019 poz. 1065 (z późn zmianami
7. PN-EN ISO 6946: 2008, Komponenty budowlane i elementy budynku. Opór cieplny i współczynnik przenikania ciepła. Metoda obliczania
8. PN-EN ISO 6946:1999, Komponenty budowlane i elementy budynku. Opór cieplny i współczynnik przenikania ciepła. Metoda obliczania
9. PN-EN ISO 12524:2003, Materiały i wyroby budowlane – Właściwości cieplno-wilgotnościowe. Stabelaryzowane wartości obliczeniowe
10. Pogorzelski J., A., (2003), Przewodnik po PN-EN ochrony cieplnej budynków, Wydawnictwa ITB, Warszawa
11. PN-EN ISO 14683: 2007,  Mostki cieplne w budynkach – Liniowy współczynnik przenikania ciepła –  Metody uproszczone i wartości orientacyjne
12. PN-EN ISO 10211: 2008 „Mostki cieplne w budynkach. Strumień cieplny i temperatura powierzchni. Obliczenia szczegółowe
13. Physibel, TRISCO Software, Belgia, [https://www.physibel.be/en/products/trisco]
14. Pogorzelski J., A., (2002), Straty ciepła z budynku przez grunt według PN-EN ISO 13370:2001 Wydawnictwa ITB, kwartalnik nr 3(123), Warszawa
15. PN-EN ISO 13370: 2008, Cieplne właściwości użytkowe budynków. Przenoszenia ciepła przez grunt. Metody obliczania
16. Physibel, TRISCO Software, Belgia, https://www.physibel.be/en/products/trisco]
17. Robakiewicz M., (2007), Obliczanie strat ciepła przez grunt na podstawie nowych norm, Energia i budynek 4 (4), s.29-31
18. Dylla A., Pawłowski K., Rożenek P., Analiza metody obliczania strat ciepła do gruntu z wykorzystaniem normy PN-EN ISO 14683, w: Wybrane problemy budownictwa,(Red. Sobczak-Piąstka J.), Wydawnictwa Uczelniane Uniwersytetu  Technologiczno-Przyrodniczego w Bydgoszczy, Bydgoszcz 2015

________________________________