Artykuł w ciągu ostatnich 24 godzin czytało 3 Czytelników
Uwagi i recenzje podręcznika przesyłać na adres wydawnictwa: wydawnictwo@chodor-projekt.net lub leszek.chodor@chodor-pojekt.pl
Podręcznik Imperfekcyjna metoda projektowania konstrukcji [ → Spis treści ]
Dodatek B : Teoria losowych wartosci ekstremalnych
Omówiono teorię losowych wartości ekstremalnych, w tym rozkładu Gumbela i Weibulla w zakresie potrzebnym do zrozumienia wywodów prezentowanych w podręczniku.
Rys inżynierski teorii
Teoria wartości ekstremalnych lub analiza wartości skrajnych (ang EVA) jest gałęzią statystyk dotyczących skrajnych odchyleń od mediany z rozkładów prawdopodobieństwa. Chodzi o ocenę prawdopodobieństwa zdarzenia, polegającego na tym, że w zbiorze realizacji zmiennej losowej, znajdą się obserwacje bardziej ekstremalne od notowanych wcześniej. Analiza EVA jest szeroko stosowana w wielu dziedzinach inżynierii: w hydrologii do oszacowania prawdopodobieństwa wystąpienia niezwykle dużej powodzi lub obciążenia nabrzeży, w inżynierii budowlanej w analizie obciążeń klimatycznych [1] , wytrzymałości elementów i ich systemów [2] , procesów korozji [3] lub hydrologii [4] . W ostatnich latach ważny jest obszar zastosowań w dziedzinie energetyki wiatrowej [5] , [6] . Rozkład Gumbela największych wartości, nazwany również podwójnie wykładniczym, lub rozkładem log-Weibull – jest powszechnie stosowany do wyznaczania obciążenia śniegiem lub wiatrem [7] , [8] . Rozkład Gumbela minimów został przyjęty do opisu imperfekcji przez Bj¢rhovde [9] . W każdym z tych przypadków interesuje nas probabilistyczny rozkład maksimów obciążeń i minimum wytrzymałości w procesie losowym parametryzowanym czasem albo rzędną przestrzeni.
Rozkłady ekstremalne są właściwe do opisu zdarzeń „ekstremalnych” lub „rzadkich”, to znaczy takich, które są „nadzwyczaj nieprawdopodobne”, generujących zestawy wartości o ekstremalnych odchyleniach od mediany. Opisywanie tymi rozkładami imperfekcji geometrycznych jest odpowiednie do ich natury. Pomiary lukowych imperfekcji geometrycznych nie wykazują systematyczności, ani też podobieństwa do deterministycznie najniekorzystniejszych kształtów, czyli takich, które są podobne do postaci wyboczenia sprężystego. imperfekcje geometryczne globalne (przechyłowe) oraz i ich kombinacje z imperfekcjami łukowymi również mogą być traktowane jako losowe wartości ekstremalne.
Rozkład prawdopodobieństwa statystyki porządkowej (pozycyjnej)
Realizację $\underline x =[ x_a, \, … \, x_n ]$ losowego wektora $X=[X_1 \, , … \, X_n]$ można przedstawić w postaci uporządkowanego ciągu od wartości najmniejszej do największej:
$$\begin{equation} x_{(1)} \le x_{(2)} \le … \le x_{(n)} \label {A.1} \end{equation}$$
tak, że $x{(1)}= \min{(x_1 , \, … \, , x_k.\, …\, x_n)}$ oraz $x{(n)}= \max{(x_1 , \, … \, , x_k.\, …\, x_n)}$.
Po dokonaniu wyboru z określa się nowy ciąg zmiennych losowych, stanowiący rosnący ciąg, nazywany statystyką porządkową lub ciągiem wariacyjnym z próby X:
$$\begin{equation} X_{(1)} \le … \le X_{(k)} \le … \le X_{(n)} \label {A.2} \end{equation}$$
Zmienna $X_{(k)}$ jest k-tą statystyką porządkową, a a $X_{(1)}$ i $X_{(n)}$ ekstremalnymi statystykami, odpowiednio najmniejszą i największą. Ważną charakterystyką ciągu wariacyjnego $X$ jest jego mediana, (czyli wartość środkowa), która jest równa $X_{(k+1)}$ dla nieparzystego i $(X_{(k)}+X_{(k+1)})/2$ dla n parzystego.
W niniejszej pracy przyjmujemy, że w ciągu wariacyjnym są przedstawione systemowe imperfekcje geometryczne konstrukcji. Zdarzenie $\{ X_{(k)} \le x \}$ oznacza, że nie mniej niż k-realizacji próby $X$ przyjmuje wartości nie większe od nielosowego parametru $x$ . Dystrybuanta $F_{(k)}$ k-tej statystyki porządkowej jest funkcją rozkładu dwumianowego [10] , [11] :
$$\begin{equation} F_k (x)= Pr \{ X_{(k)} \le x \} = \sum \limits_{r=k}^n { {n} \choose {k} } \cdot F^r (x) \left [ 1-F(x) \right ] ^{n-r} \label {A.3} \end{equation}$$
gdzie symbol Newtona $ {n} \choose {k}$ , r- liczba rzeczywista.
Z ($\ref{A.3}$) otrzymujemy rozkład statystyk ekstremalnych: (1)-pierwszej, czyli minimów, i (n) – ostatniej, czyli maksimów:
$$\begin{equation} F_{(1)} (x)= Pr \{X_{(1)} \le x \} = 1 – \left [ 1- F(x) \right ]^n \label {A.4} \end{equation}$$
$$\begin{equation} F_{(n)} (x)= Pr \{X_{(n)} \le x \} =F^n (x) \label {A.5} \end{equation}$$
Funkcja gęstości statystyki porządkowej , uzyskana przez różniczkowanie dystrybuanty wynosi
$$\begin{equation} f_k (x) = \cfrac{ \partial F_k (x)} {\partial x}= \cfrac{n!}{(k-1)! (n-k)!} F^{(k-1)} (x) \left [ 1-F(x) \right ]^{n-k} f_X (x) \label {A.6} \end{equation}$$
Dla dużej liczebności próby asymptotycznie dążącej do $n \to \infty$ liczba statystyk porządkowych również rośnie, a problem rozdziela się na dwa zadania: asymptotyka „średnich” elementów ciągu wariacyjnego oraz analiza wartości skrajnych (EVA). Za „średnią” ciągu wariacyjnego próby o objętości $n$ przy $n \to \infty$ uważa się statystykę $X_{(k)}$ numer której $k=k(n)$ spełnia warunek $\tfrac {k}{n} \to p$ dla $0
Ustalmy wartość $p$ i rozpatrzmy statystykę porządkową rzędu $k=[np]$. Można udowodnić [10] , że jeśli w otoczeniu punktu $x_p$ gęstość rozkładu prawdopodobieństwa $f_X(x)$ i jego pochodna są ciągłe i $f_{X(x_p)} >0 $, to przy $n \to \infty $, rozkład statystyki porządkowej rzędu $[np]$ dąży do normalnego
$ \Lambda (X_{[np]}) \sim N \left ( x_P, \tfrac{pg} {n f_X^2 (x_p)} \right )$.
Wynika stąd, że kwantyl p-tego rzędu oznaczony na próbie $X$ jest asymptotycznie nieobciążonym i efektywnym estymatorem kwantyla rozkładu teoretycznego. Oznacza to również, że „średnie” człony ciągu wariacyjnego przy dużej liczebności próby z dostatecznie gładkich rozkładów są asymptotycznie normalne. Niestety statystyki wartości skrajnych mają inne własności.
Dla skrajnych statystyk porządkowych słuszne jest twierdzenie: W próbie z absolutnie ciągłego rozkładu: statystyki $x_{(r)}$ (statystka początkowa – „mała”) i $X_{n-s+1)}$ (statystka końcowa – „duża”) dla dowolnych ustalonych $r, \, s \ge 1$ i $n \to \infty $ są asymptotycznie niezależne i zachodzi:
$$\begin{equation} \Lambda \left [ nF (X_{(r)} ) \right ] \to \Gamma (1,r) \label {A.7} \end{equation}$$
$$\begin{equation} \Lambda \left [ n \left (1-F (X_{(n-s+1)} \right) \right ] \to \Gamma (1,s) \label {A.8} \end{equation}$$
gdzie $\Gamma(a,b)$ jest rozkładem gamma o parametrach $a$ i $b$.
Standardowe programy numeryczne (np. Matlab [12] i Mathematica [13] ) są wyposażone w stosowne procedury do obliczeń gamma – funkcji oraz innych funkcji specjalnych, występujących w niniejszym artykule.
Zwróćmy uwagę, że asymptotyczne rozkłady wartości skrajnych nie są normalne. Ponadto ($\ref{A.7}$) i ($\ref{A.8}$) wskazują, że rozkład gamma dotyczy funkcji statystyk $\kappa_n =n F\left ( X_{(r)}\right) $ i $\eta_n =n F\left ( X_{(r)}\right) $, a nie samych statystyk, które są równe
$$\begin{equation} X_{(r)} =F^{-1} \left ( \cfrac{\kappa_n}{n}\right ), \quad X_{(n-s+1)} =F^{-1} \left ( \cfrac{\eta_n}{n}\right ) \label {A.9} \end{equation}$$
Zagadnienie rozkładu wartości skrajnych jest złożone i stanowi przedmiot teorii wartości ekstremalnych, rozpatrywanej oddzielnie dla wartości małych i dużych.
W celu uproszczenia zapisów dalszą analizę będziemy prowadzili na zmiennych standaryzowanych:
$$\begin{equation} Ξ =\cfrac{X – \alpha}{ \beta }\label {A.10} \end{equation}$$
Wartość $\xi$ zmiennej $ Ξ $ dla wartości argumentu x wynosi $ ξ=\tfrac {x-\alpha} { \beta} $,
Stałe normujące rozkład: parametr położenia $\alpha $ oraz parametr skali $\beta $ estymuje się na podstawie danych doświadczalnych lub innych, charakterystycznych warunków opisywanego zjawiska. Rozkłady wartości ekstremalnych mają też trzeci parametr $\gamma$ – parametr kształtu, który jest specyfikowany w miarę potrzeb. Na przykład w przypadku rozkładu Weibulla specyfikowane są parametry $\beta$ i $\gamma$ , a parametr położenia $\alpha$ wyznaczany jest ze specyfiki zagadnienia, najczęściej jako minimalna wartość badanej zmiennej losowej.
Uogólniony rozkład wartości maksymalnych GEV
Dystrybuanty ekstremalne maksimów s-tej statystyki porządkowej $Ξ_{(s)}= \cfrac { X_{(n-s+1)} -\alpha_n}{\beta_n }, \quad s >1 $ :
$$\begin{equation} \lim_\limits {n \to \infty } Pr \{ Ξ_{(s)} \le ξ \} = G_s (ξ) \label {A.11} \end{equation}$$
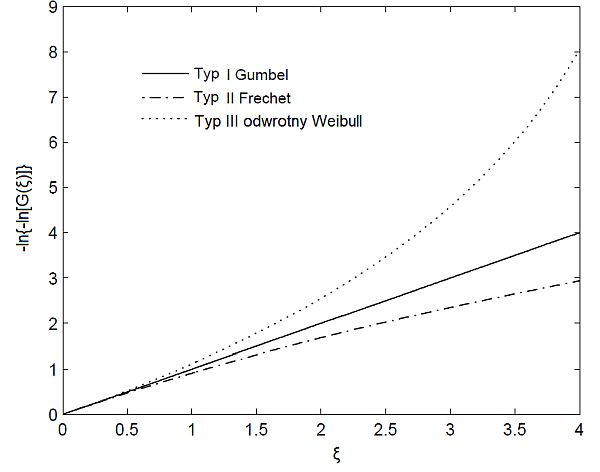
mogą przyjmować postać wyłącznie w trzech typach: I typ – Gumbela max , II typ – Frécheta i III typ – odwrotny Weibulla, które są często nazywane rozkładami Fisher-Tippett-Gniedienko.
W pracy [14] wszystkie te trzy typy rozkładów maksymalnych sprowadzono do jednej rodziny Uogólnionego Rozkładu Wartości Ekstremalnych GEV $ (\alpha, \beta, \gamma)$, przy czym w zależności od zakresu parametru kształtu $\gamma$ z rozkładu uogólnionego uzyskujemy poszczególne typy rozkładów maksymalnych :
$$\begin{equation} typ_{max} = \begin{cases}
\text { I : Gumbel max}, & \text { dla } \, \gamma=0 \quad – \infty <\xi \le \infty \\
\text { II : Frechet}, & \text { dla } \, \gamma >0 \quad \xi > \tfrac{-1}{\gamma} \\
\text { III : Weibull odwrotny}, & \text { dla } \, \gamma < 0 \quad \xi< \tfrac{-1}{\gamma} \\
\end{cases} \label {A.12} \end{equation}$$
Na rys.1. pokazano wszystkie trzy ekstremalne rozkłady wartości jako funkcję wartości zmiennej X od przekształconej dystrybuanty -ln(-ln(G(ξ))). Parametry kształtu $\gamma$ dla rozkładu Frechéta i odwrotnego rozkładu Weibulla przyjęto odpowiednio 0,2 i -0,2. Rozkład Gumbela jest linią prostą, odwrotny rozkład Weibulla jest wklęsły (ma krzywiznę w kierunku prawego punktu końcowego rozkładu), a rozkład Frechét jest wypukły i leży poniżej prostej Gumbela.
Rodzinę rozkładów GEV w zależności od parametru kształtu $\gamma$ definiuje się dystrybuantą G() i funkcją gęstości prawdopodobieństwa g() poprzez formuły [15] :
$$\begin{equation} G(ξ, \gamma) = \begin{cases}
\exp { [- \exp{ (-ξ) } ] }, & \text{ dla } \gamma=0 \\
\exp { \left [ -(1+\gamma \cdot ξ)^{ \tfrac{-1}{ \gamma} } \right ] } , & \text{ dla } \gamma \neq 0 \\
\end{cases} \label {A.13} \end{equation}$$
$$\begin{equation} g (ξ, \gamma) = \begin{cases}
\exp{(-ξ)} \cdot \exp { [- \exp{ (-ξ) } ] }, & \text{ dla } \gamma=0 \\
(1+ \gamma \cdot ξ)^{ \tfrac{-1}{ \gamma} } \cdot \exp { \left [ -(1+\gamma \cdot ξ)^{ \tfrac{-1}{ \gamma} } \right ] } , & \text{ dla } \gamma \neq 0 \\
\end{cases} \label {A.14} \end{equation}$$
Wartość oczekiwana $E[X]$, wariancja $Var[X]$, moda $Mode[X]$, mediana $Median[X]$; skośność $Skew[X]$ rozkładów GEV wynosi :
$$\begin{equation} E[X] = \begin{cases}
\alpha + C_E \cdot \beta , & \text{ dla } \gamma=0 \\
\alpha + (g_1 -1 ) \cdot \cfrac{ \beta}{\gamma} , & \text{ dla } \gamma \neq 0 \quad ; \quad \gamma <1 \\
\infty , & \text{ dla }\gamma \ge 1 \\
\end{cases} \label {A.15} \end{equation}$$
gdzie – stała $C_E= 0,577215665… $ – stała Eulera.
$$\begin{equation} Mode [X] = \begin{cases}
\alpha , & \text{ dla } \quad \gamma=0 \\
\alpha + \beta \cdot \cfrac{(1+\gamma)^{-\gamma}-1}{\gamma}, & \text{ dla } \gamma \neq 0 \\
\end{cases} \label {A.16} \end{equation}$$
$$\begin{equation} Median [X] = \begin{cases}
\alpha – \beta \cdot ln(ln2) , & \text{ dla } \quad \gamma=0 \\
\alpha +\beta \cdot \cfrac{(ln2)^{-\gamma}-1}{\gamma}, & \text{ dla } \gamma \neq 0 \\
\end{cases} \label {A.17} \end{equation}$$
$$\begin{equation} Var [X] = \begin{cases}
\cfrac{\pi^2 \beta ^2}{6} \approx 1,645 \cdot \beta^2 , & \text{ dla } \gamma=0 \\
(g_2-g_1^2) \cdot \left( \cfrac{\beta}{\gamma}\right)^2 , & \text{ dla } \gamma \neq 0 \quad ; \quad \gamma <1/2 \\
\end{cases} \label {A.18} \end{equation}$$
$$\begin{equation} Skew [X] = \begin{cases}
\cfrac{12 \sqrt{6} \zeta(3)}{\pi^3} , & \text{ dla }, \gamma=0 \\
sgn(\gamma) \cdot \cfrac{g_3 -3 g_2 g_1 +2 g_1^3}{(g_2-g_1^2)^{3/2}}, & \text{ dla } \gamma \neq 0 \quad ; \quad \gamma<1/3 \\
\end{cases} \label {A.19} \end{equation}$$
gdzie: $g_k= \Gamma(1- k \cdot \gamma), (k=1,2.3,…)$ ; $\Gamma()$ – funkcja gamma, $\zeta()$ – Zeta funkcja Riemanna.
Kwantyl p-tego rzędu jest wartością zmiennej $x_p$ , której przekroczenie zachodzi z prawdopodobieństwem p : $(Pr \left \{ X > x_p \right \} = F[x_p] =1- p $ , dla rozkładu GEV na poziomie prawdopodobieństwa p wyraża się funkcjami elementarnymi:
$$\begin{equation} x_p= G^{-1} (1-p ) \begin{cases}
\alpha \, + \beta \cdot \{ – \ln { [ – \ln { (1-p) } ] } \} , & \text { dla } \quad, \gamma \, =0 \quad ; \quad p \in (0;1) \\
\alpha \, + \cfrac{\beta}{\gamma} \cdot \{ [ – \ln{ (1- p) } ]^{ -\gamma } -1 \}, & \text { dla } ( \gamma \, >0 \quad ; p \in (0;1] ) \quad; \gamma<0 \quad ; p \in [0;1)
\end{cases} \label {A.20} \end{equation}$$
Rozkłady najmniejszych wartości
Najmniejsze wartości $X_{(r)}=-X^{’}_{(n-s+1)}$ dla szeregu wariacyjnego $ – X^{′} _{(1)} \le … \le -X^{′} _{(k)}\le – X^{′} _{(n)}$, próby $(-X_1,. .. ,-X_k, …, -X_n)$, więc rozkłady statystyki najmniejszych wartości $X_{(r)}, \quad (r \le1)$, można otrzymać przez proste przemodelowanie rozkładów największych wartości. Wystąpią również trzy typy:
Typ I min (Gumbela najmniejszych wartości)
$$\begin{equation} G^{I} _{min} (ξ) =1- exp [ -e^ξ ] \label {A.21} \end{equation}$$
Typ II min
$$\begin{equation} G^{II} _{min} (\xi) = 1- exp [ – (- \xi )^\gamma ] \label {A.22} \end{equation}$$
Typ III (Weibulla)
$$\begin{equation} G^{III} _{min} (\xi) = 1- exp [ – \xi ^\gamma ] \label {A.23} \end{equation}$$
Rozkład Gumbela najmniejszych wartości
Dystrybuanta i funkcja gęstości rozkładu Gumbela najmniejszych wartości mogą być zapisane formułami:
$$\begin{equation} F ( \xi, \alpha, \beta) = \exp { \left ( – e^{\xi} \right ) } \label {A.24} \end{equation}$$
$$\begin{equation} f ( \xi, \alpha, \beta) = \cfrac{1}{\beta} \exp { \left ( – e^\xi +\xi \right )} \label {A.25} \end{equation}$$
Modę, medianę, wariancję opisują formuły ($\ref{A.15}$) do ($\ref{A.18}$), czyli takie jak dla rozkładu Gumbela maksimów, ale wartość oczekiwana i funkcja kwantyla (tutaj p jest prawdopodobieństwem nieprzekroczenia , czyli przyjmowania wartości mniejszych) różnią się i wynoszą:
$$\begin{equation} E [X] = \alpha – C_E \cdot \beta \label {A.26} \end{equation}$$
$$\begin{equation} x_p= F^{-1} (p) = \alpha + \beta \cdot \ln { \left [ – \ln {(p)} \right]} \label {A.27} \end {equation}$$
Rozkład Weibulla
Rozkład Weibulla jest rozkładem określonym na przedziale $(\alpha, \, \infty)$ , gdzie $\alpha$ jest parametrem położenia, z kształtem określonym dwoma parametrami: skali $\beta$ oraz kształtu $\gamma$. W zależności od tych trzech parametrów rozkład Weibulla może przyjmować rozmaitą formę od unimodalnej ( z pojedynczym ekstremum lokalnym), poprzez monotoniczną i asymptotyczną. Rozkład Weibulla jest czasami określany, jako rozkład Rosin-Rammler.
Dla unormowanej zmiennej ($\ref{A.10}$) dystrybuanta F() i funkcja gęstości f() rozkładu Weibulla może być zapisana formułami:
$$\begin{equation} F ( \xi, \gamma) = 1- \exp {\left ( – \xi ^{\gamma} \right ) } \label {A.28} \end{equation}$$
$$\begin{equation} f ( \xi, \alpha, \beta, \gamma)=\cfrac{\gamma}{\beta} \cdot \xi^{(k-1)} \cdot exp \left (-\xi^\gamma \right ) \label {A.29} \end{equation}$$
Wartość oczekiwana:
$$\begin{equation} E[X] = \alpha + \beta \cdot \Gamma ( 1+ 1/ \gamma ) \label {A.30} \end{equation}$$
gdzie $\Gamma()$ – stablicowana funkcja gamma.
Mediana
$$\begin{equation} Med [X] = \alpha + \beta \cdot \ln{(2)}^{1/ \gamma} \label {A.31} \end{equation}$$
Wariancja
$$\begin{equation} Var [X] = \beta^2 [ – \Gamma (1+1 /\gamma)^2 + \Gamma (1+2 / \gamma)] \label {A.32} \end{equation}$$
Estymatory parametrów rozkładów ekstremalnych
W celu oszacowania (estymacji ) rozkładów prawdopodobieństwa na podstawie pomiarów (danych eksperymentalnych) stosuje się:
- procedury graficzne , polegające na dopasowanie krzywej (najczęściej prostej) do wyników badań metoda regresji średniokwadratowej i w taki sposób, by parametry krzywej (prostej) stanowiły poszukiwane parametry rozkładu
- procedury analityczne , polegające na porównaniu
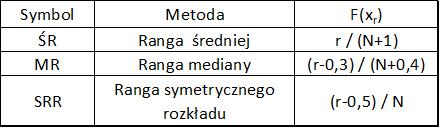
Wśród metod graficznych rozróżniamy trzy odmiany zależne od sposób szacowania dystrybuanty empirycznej na podstawie ciągu o liczebności N uporządkowanych zmiennych o numerze r , zwanym rangą.
Oszacowania $\alpha$ $\beta$ lub $\gamma$ dokonujemy na podstawie statystyki empirycznej F, określonej w tab.A.1a.:
Tab.A.1a. Metody estymacji w graficznej procedurze
Tab.1A.1b. Metody estymacji w analitycznej procedurze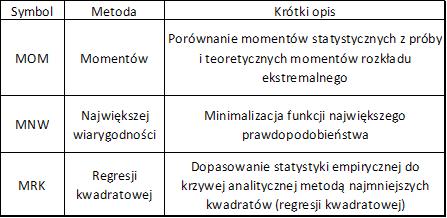
Estymatory parametrów rozkładów ekstremalnych zależą od estymatorów wartości, średniej współczynnika $m$ odchylenia standardowego $\sigma$ i współczynnika skośności $A$, które dla próby N- elementowej, wyznacza się z zależności
W tab. A.2a zestawiono estymatory parametrów ekstremalnych otrzymane metodą momentów, a w tab A2b metodą największej wiarygodności.
Tab. A.2a Estymatory parametrów rozkładów ekstremalnych metodą momentów MOM
| Typ rozkładu | Parametr położenia $\alpha $ |
Parametr skali $\beta $ |
Parametr kształtu $\gamma$ |
| (1) | (2) | (3) | (4) |
| GEV max $\gamma \neq 0$ (w tym Weibulla max) |
$m – \cfrac{\beta}{\gamma} \cdot (g_1-1)$ | $ \cfrac{\sigma \cdot | \gamma| }{\sqrt{g_2 – g_1^2}}$ | z rozwiązania równania $\cfrac{A}{sign( \gamma)}= \cfrac{g_3- 3 \cdot g_1 \cdot g_2 + 2\cdot g_1^3}{(g_2-g_1^2)^{3/2}}$ |
| GEV max ; $\gamma = 0$ (Gumbela max) |
$m – C_E \cdot \beta$ | $\cfrac{\sqrt{6}}{\pi}\cdot \sigma$ | 0 |
| Weibulla (min) | $\cfrac{m}{\Gamma(1+\sigma)}$ | $\cfrac{\Gamma(1+2\cdot \sigma)}{\Gamma^2(1+\sigma)} \approx 1+\sigma^2$ | $\cfrac{\Gamma (1+3/\gamma) \cdot \beta^3 -3\cdot \mu^W \cdot (\sigma^W)^2 -(\mu^W)^3 }{(\sigma^W)^3}$ |
| Gumbela min | $m + C_E \cdot \beta$ | $\cfrac{\sqrt{6}}{\pi}\cdot \sigma$ | 0 |
| OZNACZENIA: $C_E=0,57721$ – stała Eulera ; N- liczba pomiarów; $g_k= \Gamma(1- k \cdot \gamma), (k=1,2.3,…)$ ; $ \Gamma ()$ – funkcja gamma;Parametry z próby wartość średnia $m$, odchylenie standardowe $\sigma$, współczynnik skośności $A$: $m= \overline x=\cfrac{1}{N} \sum \limits_{i=1}^N x_i$ ; $\sigma = \sqrt { \cfrac{1}{N-1} \sum \limits_{i=1}^N (x_i-m)^2}$; $A = \cfrac{m_3}{\sigma^3}=\cfrac{1}{N \cdot \sigma^3} \cdot \sum \limits_{i=1}^N (x_i-m)^3$ Parametry rozkładu Weibulla: średnia $\mu^W$ ; odchylenie standardowe $\sigma^W$ : $\mu^W= \beta\cdot \Gamma (1+1/\gamma)$ ; $\sigma^W=\beta \cdot \sqrt{\Gamma(1+2/ \gamma)- \Gamma (1+1/ \gamma )^2}$ |
|||
Tab. A.2b Estymatory parametrów rozkładów Gumbela i Weibulla min metodą największej wiarygodności MNW
| Typ rozkładu | Parametr położenia $\alpha $ |
Parametr skali $\beta $ |
Parametr kształtu $\gamma$ |
| (1) | (5) | (6) | (7) |
| Gumbela max | $\approx – \beta \cdot \ln { \left( \cfrac{1}{N} \sum \limits_{i=1}^N e^{ – \tfrac{x_i}{\beta}}\right )}$ | $ \approx m – \cfrac{ \sum \limits _{i=1}^N x_i \cdot e^{ \tfrac{- x_i}{\beta}}}{\sum \limits _{i=1}^N e^{ \tfrac{-x_i}{\beta}}}$ | 0 |
| Gumbela min | $\approx \beta \cdot \ln { \left( \cfrac{1}{N} \sum \limits_{i=1}^N e^{ \tfrac{x_i}{\beta}}\right )}$ | $\approx m + \cfrac{ \sum \limits _{i=1}^N x_i \cdot e^{ – \tfrac{ x_i}{\beta}}}{\sum \limits _{i=1}^N e^{ – \tfrac{x_i}{\beta}}}$ | 0 |
| Weibulla (min) | $\min {x_i}$ = początek losowego okresu | $\approx \left (\cfrac{1}{N} \sum \limits_{i=1}^N \sqrt [\gamma] {x_i}\right)^{\gamma}$ | $\approx \left [ \cfrac{ \sum\limits_{i=1}^N x_i^\gamma ln (x_i) }{ \sum \limits_{i=1}^N x_i^\gamma} – \cfrac{1}{N} \sum\limits_{i=1}^N ln (x_i) \right] ^{-1} $ |
| N- liczba pomiarów; $m, \sigma, A$ – wartość średnia, odchylenia standardowe i współczynnik skośności z próby (stopka tab.A.2a) | |||
Dla rozkładu GEV max ( i dla Weibulla max – odwróconego – jeśli $\gamma<1$), parametry estymowane metodą największej wiarygodności otrzymuje się z rozwiązanie układu równań nieliniowych :
$$\begin{equation} \begin{cases}
\cfrac{1}{\beta} \cdot \sum \limits_{i=1}^N \cfrac{1+\gamma – (y_i) ^{-1 / \gamma}} {y_i} =0 \\
– \cfrac{N}{\beta} + \cfrac{1}{\beta}\cdot \sum \limits _{i=1}^N \left [ \cfrac{1+\gamma -(y_i)^{-1/\gamma} }{y_i} \xi \right ]=0 \\
– \cfrac{1}{\gamma^2} \cdot \sum \limits_{i=1}^N \left \{ \ln {( y_i )} \cdot [1+\gamma -(y_i)^ {- 1/ \gamma} ] – \cfrac{1+ \gamma -(y_i )^ {=2/ \gamma} }{y_i} \cdot \gamma \cdot \xi_i \right \} = 0\\
\end{cases} \label {A.33} \end{equation}$$
gdzie: $y_i= 1+ \gamma \cdot \xi_i $ , $\xi_i=\cfrac{x_i -\alpha} {\beta}$
Uwagi o zastosowaniu oprogramowania
Funkcja GumbelDistribution() w programach Matlab [12] i Mathematica [13] dotyczy rozkładu Gumbela dla minimalnych wartości ekstremalnych. W celu wyznaczenia wartości maksimum należy przyjąć ujemne wartości oryginalne, to jest zmienić znak argumentu oraz parametru przesunięcia lub zastosować funkcję o nazwie ExtremeValueDistribution().
Rozkład Weibulla (III typ minimów) dostarcza funkcja WeibullDistribution().
Każdy rozkład prawdopodobieństwa, w tym rozkład Gumbela można ograniczyć z góry i dołu w celu reprezentowania rozkładu wartości cenzurowanych między górną i dolną wartością (funkcja CensoredDistribution() – Mathematica], lub też można zastosować obcięcie rozkładu w celu reprezentowania rozkładu wartości obciętego między wartościami górną i dolną (funkcja, TruncatedDistribution() – Mathematica, lub też z użyciem funkcji ProductDistribution() można wyznaczyć łączny rozkład z niezależnych dystrybuant brzegowych, co jest stosowane dla łącznego rozkładu imperfekcji łukowych i przechyłowych lub imperfekcji sprężystych i plastycznych.
Przykłady rachunkowe
Przykład 1 [Rozkład Gumbela max : ciśnienie prędkości wiatru w Świnoujściu ]
Rozróżnimy wielkości, będące procesami stochastycznymi w czasie t:
prędkość wiatru $v(t)$
energię wiatru, $E(t) \sim v ^3 (t)$
ciśnienie prędkości wiatru $q(t) \sim v ^2(t)$
obciążenie wiatrem $w(t) \sim q(t)$
gdzie $\sim$ jest symbolem proporcjonalności.
Zmienne losowe $v_i, q_i, w_i, E_i $ są średnimi procesu stochastycznego na i-tym odcinku czasu (zgodnie z definicją $\Delta t= 10 \, min$) i są silnie, funkcyjnie skorelowane. Są jednak innymi zmiennymi losowymi , choć można przyjąć, że każda z nich odrębnie ma taki sam typ brzegowego rozkładu prawdopodobieństwa. Maksimum każdej z tych zmiennych w ciągach wieloletnich będzie więc podlegała rozkładowi wartości ekstremalnych. W pracy [16] zbadano dokładność dwóch rozkładów prędkości wiatru: odwrotnego Weibulla i Gumbela, Stwierdzono, że rozkład Gumbela pozwala oszacować prędkość wiatru dokładniej niż model Weibulla. Zastosujemy rozkład Gumbela największych wartości .
Obciążenie wiatrem powierzchni zewnętrznej konstrukcji wg normy [17]
Obciążenie wiatrem powierzchni zewnętrznej (indeks „e”=external) konstrukcji wyznacza się ze wzoru [17],wzór (5.1)
$$\begin{equation} w_e= q_p \cdot c_{pe} \label {A.34} \end{equation}$$
gdzie $c_{pe}$ -współczynnik ciśnienia zewnętrznego zależny od wymiarów, kształtu i ustawieniu powierzchni konstrukcji w stosunku do kierunku wiatru, przyjmowany zgodnie z rozdziałem 7 [17] dla konkretnego typu obiektu bez związku z prędkością wiatru.
Szczytowe ciśnienie prędkości wiatru $q_p$ łączy wartość średnią i chwilowe fluktuacje (turbulencje) wiatru i na wysokości $z$ ponad poziomem terenu i wyznacza się go ze wzoru [17],wzór (4.8)
$$\begin{equation} q_p= c_e(z) \cdot q_b\label {A.35} \end{equation}$$
gdzie współczynnik ekspozycji $c_e(z)$ nie zależy od prędkości wiatru.
Przekształcenie prędkości wiatru na ciśnienie
Bazowe ciśnienie prędkości wiatru $q_b$ wynosi [17],wzór (4.10)
$$\begin{equation} q_b= \cfrac {\rho}{2} \cdot v_b^2\label {A.36} \end{equation}$$
Zalecana w gęstość wiatru wynosi $\rho=1,25 \, kg/m^3 $ i jest średnią z gęstości wiatru w warunkach normalnych $1,2 \, kg/m^3$ i gęstości maksymalnej $1,3 \, kg/m^3$ dla wiatru z deszczem lub z lodem w niskich temperaturach.
Bazowa prędkość wiatru $v_b$ jest wyznaczana na podstawie podstawowej prędkości bazowej $v_{b,0}$ z zależności [17],wzór (4.1)
$$\begin{equation} v_b= c_{dir} \cdot c_{season} \cdot v_{b,0} \label {A.37} \end{equation}$$
gdzie współczynnik kierunku wiatru $c_{cdir}$ oraz sezonowy $c_{season}$ w zwykłych warunkach można przyjmować o skrajnie niekorzystnej wartości 1,0 ( zalecenia [17],kl.4.2(2P) ) to znaczy
$$\begin{equation} v_b=v_{b,0} \label {A.38} \end{equation}$$
Zgodnie z [17],kl.4.2(1P) podstawowa, bazowa prędkość wiatru $v_{b,0}$ jest wartością charakterystyczną średnich 10-cio minutowych prędkości wiatru na wysokości 10 m nad poziomem gruntu. Wartość charakterystyczna jest kwantylem rzędu p=98% ( p=1- 1/50, gdzie T=50 lat jest okresem powrotu ) rozkładu prawdopodobieństwa prędkości wiatru.
Rozkład prędkości wiatru uzyskuje się z dopasowania rozkładu teoretycznego do rozkładu empirycznego, który powstaje ze zbioru maksymalnych rocznych wartości prędkości uszeregowanych w ciągu rosnącym, gdzie indeksem jest numer roku. Tak samo, z dopasowania rozkładu teoretycznego do empirycznego otrzymamy kwantyl zmiennej losowej ciśnienia bazowego $q_b$, które jest wyznaczane z prawa fizycznego ($\ref{A.36}$) . Rozkład $q_b$ podlega również rozkładowi wartości ekstremalnych.
Współczynnik proporcjonalności (wartości szczytowej) $c_e(z) $ uzyskamy ze złożenia zależności (4.9) i (4.3) normy [17] w postaci:
$$\begin{equation} c_e(z)= [1+7 \cdot I_v(z)] \cdot [ c_r(z) \cdot c_0(z)]^2 \label {A.39} \end{equation}$$
gdzie współczynniki chropowatości terenu $c_r(z)$ i turbulencji $I_v (z)$ wynoszą [17],wzór (4.4),(4.7)
$$\begin{equation} c_r(z)= k_r \cdot ln(z / z_0) \label {A.40} \end{equation}$$
$$\begin{equation} I_v(z) = \cfrac{k_I }{c_0 (z) \cdot ln(z/z_0)} \label {A.41} \end{equation}$$
Formuły $(\ref{A.40}$) i $(\ref{A.41}$) dotyczą wysokości $z$ w granicach $z_{min} < z <\le z_{max} = 200 \, m \, npt$.
Współczynnik chropowatości terenu
$$\begin{equation} k_r = 0,19 \cdot \left( \cfrac{z_0}{z_{0,II}} \right)^{0,07}\label {A.42} \end{equation}$$
Wysokość chropowatości $z_0$ specyficzna dla danej kategorii terenu jest odniesiona do wysokości dla terenu kategorii II $z_{0,II} =0,05 \, m$
Współczynnik turbulencji $k_I$ przyjmuje się o wartości 1.
Współczynnik rzeźby terenu (orografii) uwzględnia wzrost prędkości średniej wiatru na szczycie pojedynczego wzgórza lub skarpy (ale nie na obszarach pofalowanych i górzystych) i wyznacza wg załącznika A.3. normy [17], . Współczynnik rzeźby tereny $c_0(z)=1,0$ dla terenu o małym (mniejszym od 3°) nachyleniu stoku lub klifu nawietrznego. Jako nawietrzny może być rozpatrywany teren rozciągający się na odległość równą 10 wysokościom pojedynczego wzniesienia.
Wysokość odniesienia $z_e$ najczęściej jest maksymalną wysokością konstrukcji, choć dla konstrukcji o wysokości większej od szerokości – wysokość odniesienia jest odległością od poziomu terenu do środka analizowanego plastra konstrukcji.
Parametr chropowatości terenu $k_r$, $z_0$ oraz wymiar chropowatości $z_0$ zależy od kategorii terenu.
Współczynnik rzeźby terenu $c_0(z) $ ujmuje wpływ położenia konstrukcji na skarpie, klifie lub wzgórzu i wyznacza się według procedury w załączniku A.3 normy.
W niniejszym przykładzie przyjęto założenie upraszczające, że parametry $\rho$, $k_r$, $z_e$, $z_0$, $k_I$, $c_{pe}$ są nielosowe i przyjmują wartości określone w normie [17] . Faktycznie wszystkie te zmienne są losowe i wpływają na zwiększenie rozproszenia losowego obciążenia wiatrem.
Gęstość wiatru $\rho=1,3 \, kg/m^3$ przyjęto o wartości maksymalnie możliwej, biorąc pod uwagę ekstremalne warunki pogodowe sztorm z deszczem, gradem lub śniegiem. Kategoria terenu dla Świnoujścia to „0” (tereny przybrzeżne).
W tab.A.3 przedstawiono podstawowe dane dotyczące ciśnienia prędkości wiatru w Świnoujściu dla obiektu o wysokości odniesienia $z_e =10 \, m$. Teren nadmorski, ma kategorię chropowatości „0” . Dla takiej kategorii terenu mamy [18], tab.10 : $k_r=0,156$, $z_0 =0,003 \, m$. $z_{min}= 1 \,m$.
Współczynnik rzeźby terenu dla budowli na pirsie o wysokości ok. 3 m npm przyjmuje wartość $c_0()=1,0$., a współczynnik turbulencji $k_I$ przyjmuje się o wartości 1,0.
Pomiary maksymalnych rocznych prędkości wiatru
W tab. A.4. zestawiono przekształcenie, maksymalnych rocznych z 10-cio minutowych średnich prędkości $v_b =v_{max} $, na ciśnienie prędkości wiatru $q_b$ $\ref{A.36}$). Dane prędkości $v_{max}$ przyjęto z danych historycznych ( od roku 1966 do 2003) w kolejnych 38 latach w Świnoujściu, zamieszczonych w pracy [18], rys.19 .
Przykładowo w roku 1966 pomierzono maksymalną średnią 10-cio minutową 10 m nad ziemią o wartości $V_b=v_{max} =14,2 \, m/s$. Bazowe ciśnienie prędkości wiatru wyniosło $q_{b,max} = 1,3\cdot 14,2^2/2 \cdot 10^{-3} = 0,131 \, kN/m^2$. Szczytowe ciśnienie prędkości wiatru wyniosło $q_{p,max} = 1,939 \cdot 14,2^2\cdot 10^{-3}= 0,392 \, kN/m^2$.
Tab. A.3 Maksymalne, roczne prędkości wiatru $v_{max}$ bazowe ciśnienie prędkości wiatru $q_b$
w Świnoujściu w latach 1966 do 2019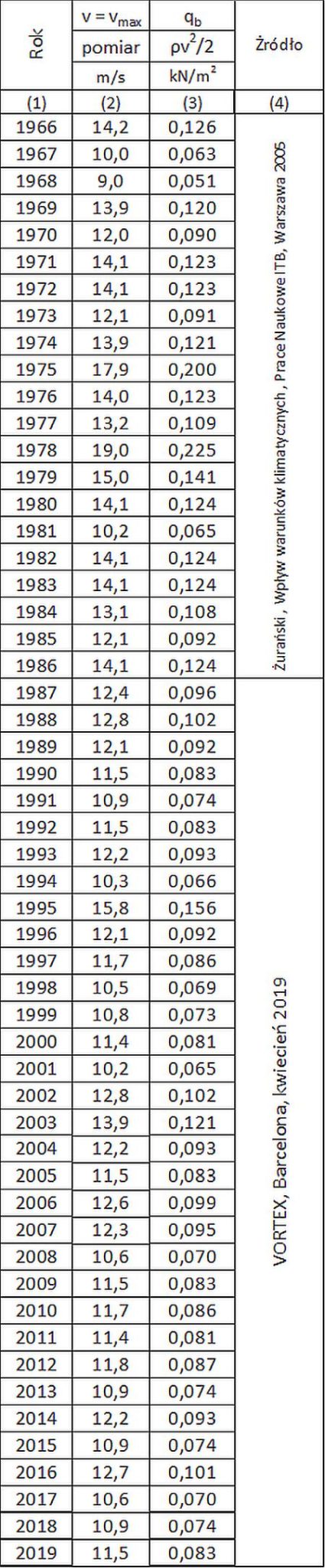

Oszacowanie parametrów rozkładu Gumbela metodą momentów MOM
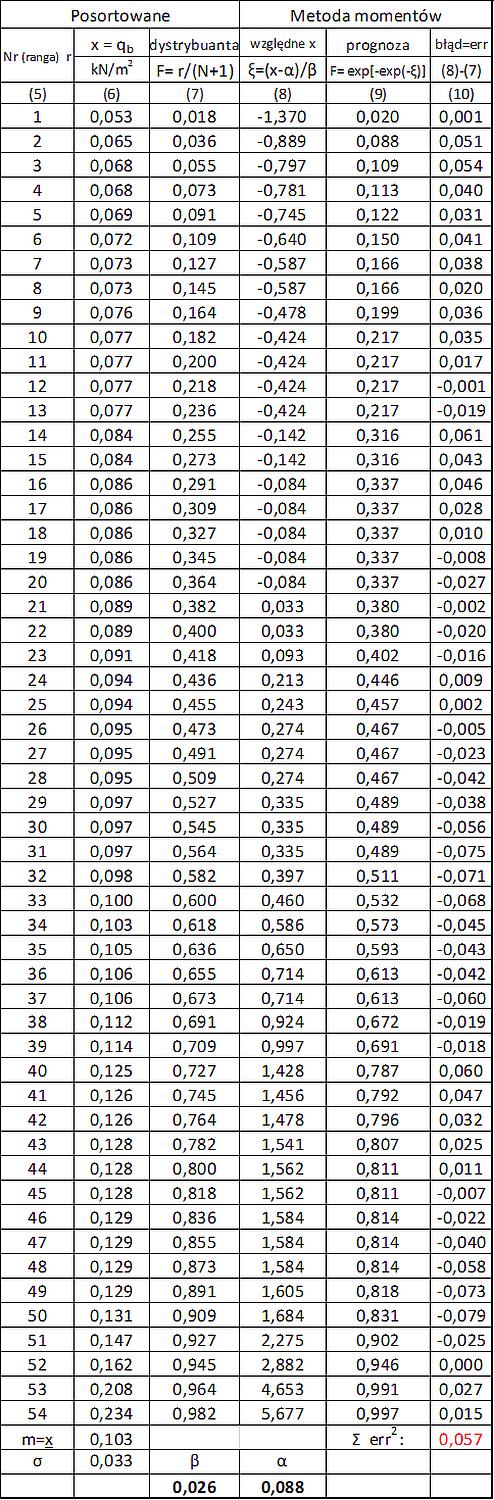
Obliczenia przeprowadzone metodą momentów zestawiono w tab.A.4.
W kolumnie (5) podano kolejny numer wyrazu (rangę) ciągu wartości szczytowego ciśnienia wiatru zestawionego w kol. (6) wartości uzyskane z posortowanvch rocznych maksimów $x= q_{p,max}$ z tab. A.3
Liczebność ciągu wynosi N=54 (jest to liczba lat pomiarów) .
W podsumowaniu kol (6) podano:
arytmetyczną średnią z pomiarów $m= \overline x =\tfrac{1}{N} \sum \limits_{i=1}^Nx_i = 0,103 kN/m^2$,
odchylenie standardowe z pomiarów $\sigma =\sqrt{ \tfrac{1}{N-1}\sum \limits_{i=1}^N (x_i-m)^2} = 0,033 kN/m^2 $.
Tab. A.4. Ciąg porządkowy i oszacowanie parametrów rozkładu Gumbela metodą momentów MOM
tab.A.2. $\to$
$\beta=\cfrac{\sqrt{6}}{\pi}\cdot \sigma = \cfrac{\sqrt{6}}{\pi}\cdot 0,033= 0,026$
$ \alpha=m – C_E \cdot \beta = 0,103 – 0,57721 \cdot 0,026=0,088$
W kol. (8) podano unormowany argument dystrybuanty, a w kol(9) prognozę dystrybuanty Gumbela dla wyznaczonych parametrów metodą MOM. W kol (10) podano błąd oszacowania err_i= kol. (8)-(7), a w podsumowaniu tej kolumny podano błąd średniokwadratowy $ \sum err^2 = 0,186$, będący miarą dobroci dopasowania rozkładu.
Oszacowanie parametrów rozkładu Gumbela metodą regresji MRK
Po dwukrotnym zlogarytmowaniu dystrybuanty Gumvela max ($\ref{A.13} \uparrow $) otrzymamy równanie $ -ln [F(\xi)]=\xi$, skąd dla danej o randze „r” i wartości dystrybuanty empirycznej $F_r=\cfrac{r}{N+1}$, otrzymujemy równanie prostej Gumbela
$$\begin{equation} \xi=\alpha +\beta \cdot y \label {A.43} \end{equation}$$
gdzie $y= -ln[ – ln(F_r)]$.
W celu określenia parametrów rozkładu Gumbela wystarczy więc poprowadzić prostą w układzie (\xi, y), a jej odsunięcie os początku układu będzie parametrem $\alpha$ ; kąt jej nachylenia parametrem $\beta$. Prostą prowadzimy metoda regresji kwadratowej.
Obliczenia metodą regresji zestawiono w tab. A.5b, będącej kontynuacja tab. A.5a. W kol. (11) zestawiono wartości „x= -ln(ln(F))”. Następnie metodą kwadratów wyznaczono liniowy trend pomiędzy wartościami $q_{p}$ (kol (6) tab. A.5a) a wartościami z kol (11) tab. A.5b. Trend ma równanie $q_p=0,099 x – 0,263$. Współczynnik kierunkowy tej prostej jest właśnie parametrem $\beta$, a wyraz wolny parametrem $\alpha$. W kol. (13) podano prognozę dystrybuanty z wzoru ($\ref{A.19}$), a w kol. (14) błąd średniokwadratowy aproksymacji $\sum err^2 = 6,384$
Tab. A.5b. Wyznaczenie parametrów rozkładu Gumbela metoda regresji
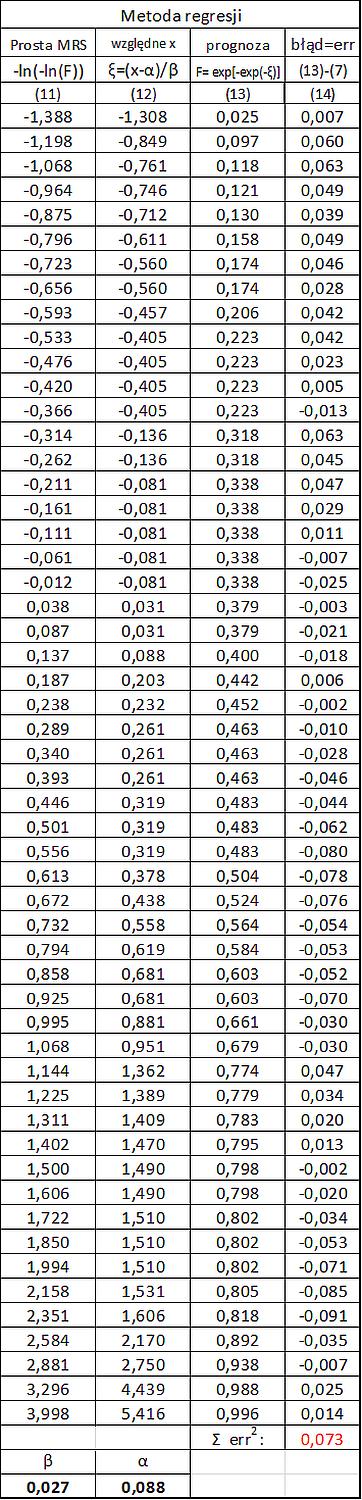
Współczynniki $\alpha$ i $\beta$ uzyskano z zastosowaniem funkcji Excel: REGLINP( kol(6) ; kol (12) ; ; )
Oszacowanie parametrów rozkładu Gumbela metodą największej wiarygodności MNW
Oszacowanie parametrów metodą MNW wymaga rozwiązania nieliniowego równania tab. A.2 [wrs „Gumbel max”, kol (5)] na parametr \beta. W tym celu można użyć dowolnej metody, na przykład dodatku Solver do arkusza kalkulacyjnego Excel.
W tym celu należy sporządzić dwie kolumny pomocnicze: (15) $ \left [ e^{ \tfrac{-x_i}{\beta}} \right ] $ oraz (16) $ \left [ x_i \cdot e^{ \tfrac{- x_i}{\beta}} \right ] $ , gdzie za $\beta$ należy wskazać dowolna komórkę, przeznaczoną do zmian, a w podsumowaniu kolumn obliczyć sumę tych wielkości.
Do innej komórki (celu zmian ) należy wpisać formułę, która będzie przyrównywana do „0”, a mianowicie
$ \left [ \beta – m + \cfrac{ \sum \limits _{i=1}^N x_i \cdot e^{ \tfrac{- x_i}{\beta}}}{\sum \limits _{i=1}^N e^{ \tfrac{-x_i}{\beta}}} \right ] $,
gdzie wskazujemy: $\beta$ – komórkę zmienianą ; m – średnia arytmetyczna z tab. A.3a, kol. (6) ; sumy kolumn $\sum …$ obliczone jak wyżej. Po uruchomieniu Solvera w komórkę $\beta$ zostanie wstawiona poszukiwana wartość. Następnie ze wzoru tab A.2 [wrs „Gumbel max”, kol. (4) – wyznaczmy parametr $\alpha$. Iteracje można też wykonać ręcznie, zmieniając wartość kolumny $\beta$ i obserwując komórkę celu zmian, czy zbliża się do „0” , aż do uzyskania żądanej dokładności.
Opisane operacje przedstawiono w tab. A.5c.
Tab. A.5c. Wyznaczenie parametrów rozkładu Gumbela metodą największej wiarygodności MNW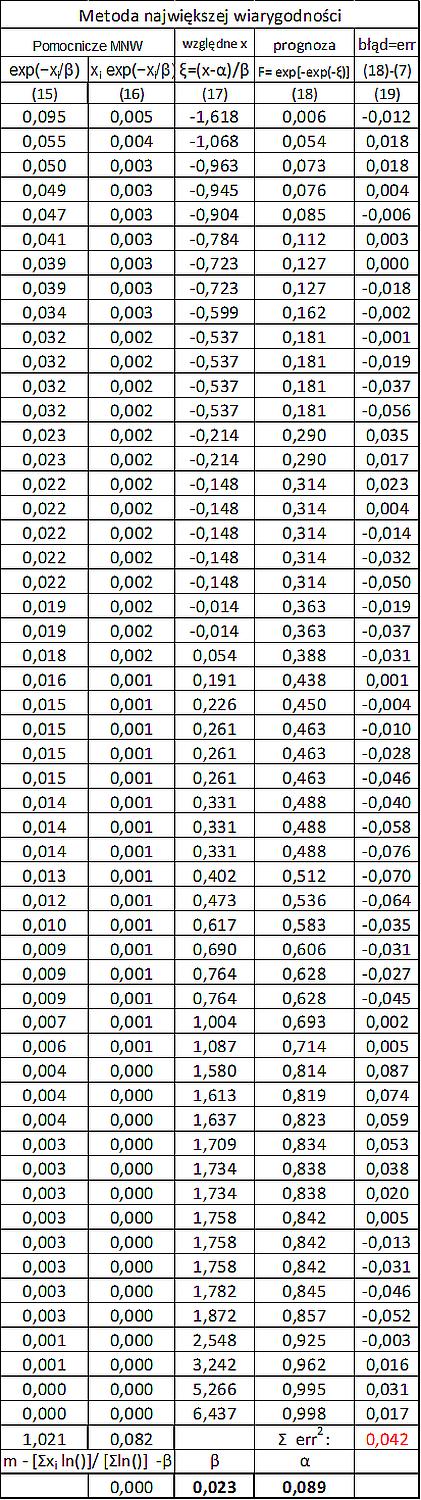
Zestawienie parametrów rozkładu Gumbela uzyskanych różnymi metodami zaprezentowano w tab. A.6.
Tab. A.6 Zestawienie parametrów rozkładu Gumbela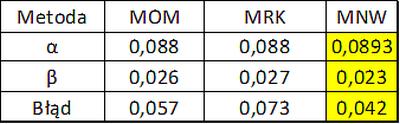
Prognozowanie charakterystycznej wartości ciśnienia wiatru w okresie powrotu T
Z ($\ref{A.23}$) oszacujemy wartość charakterystyczną szczytowego ciśnienia prędkości wiatru dla danego prawdopodobieństwa przekroczenia tego poziomu n-razy w ciągu okresu czasu T
$$\begin{equation} p=1- \cfrac{n}{T} \label {A.44} \end{equation}$$
czyli dla n=1 raz wzór ($\ref{A.23}$) przyjmie postać
$$\begin{equation} x_P = \alpha – \beta \ln { \left[ – \ln { \left ( \cfrac{1}{T} \right )} \right]} \label {A.45} \end {equation}$$
W tab. A.7 Zestawiono charakterystyczne wartości szczytowego ciśnienia wiatru $q_p$ uzyskane różnymi metodami dopasowania rozkładu Gumbela.
Tab. A.7. Zestawienie parametrów rozkładu Gumbela

Dla okresu powrotu T=50 lat szczytowe ciśnienie prędkości wiatru w Świnoujściu wynosi $q_{b,50}= 0,177 kN/m^2$, a dla okresu powrotu T=100 lat $q_{b,100}= 0,193 kN/m^2$. Taka wartość ciśnienia może być przekroczona w okresie powrotu tylko jeden raz.
Porównanie z normą [17]
Poniżej powołania wskazują na elementy normy [17] :
(rys. NA.1) $\to$ dla Świnoujścia $\to$ 2 strefie obciążenia wiatrem,
podstawowe bazowa prędkość wiatru $v_{b,0}=26 \, m/s$,
(tab.NA.2) $\to$ współczynnik kierunkowy maksymalny $c_{dir} = 1,0$,
(kl. 4.2 -UWAGA 3) $\to$ współczynnik sezonowy $c_{season}=1,0$,
(wzór 4.1) $\to$ bazowa prędkość wiatru $v_b=c_{dir}\cdot c_{season}\cdot v_{b,0}= 1,0 \cdot 1,0 \cdot 26 = 26 \, m/s$
(tab.NA.1): $\to$ podstawowe bazowe ciśnienie prędkości wiatru $q_{b,0}= 0,42 \, kN/m^2$,,
przy czym ze (wzoru 4.10) $\to$ bazowe ciśnienie wiatru $q_b= 1,25/2 \cdot 26^2 = 0,423\, kN/m^2$
Wniosek::
Z porównania teoretycznie uzasadnionej szczytowego ciśnienia prędkości wiatru
(tab A.7) $q_b^T =0,177 \, kN/m^2$ z wartością normową
$q_b^N =0,423 \, kN/m^2$
wynika, że w przypadku Świnoujścia przyjecie wartości normowej jest bardzo bezpieczne (ok. 0,423/0,177= 2,4 razy). Rozbieżności zostały wykazane przede wszystkim dlatego, że w Świnoujściu faktycznie występujące prędkości wiatru są znacznie mniejsze od przypisanych do strefy 2,
co jest związane z malejącym trendem wieloletinm związanym z zabudowywaniem terenu, co będzie postępować w przyszłości, więc trend powinien się utrzymać w przyszłości.
Szczytowe ciśnienie prędkości wiatru
dla wysokości $z = 10 m$:
(tab. NA.2) $\to$ dla terenu kat „0” $\to$ współczynnik chropowatości na wysokości z=10 m
$c_r(z)= 1,3 \cdot (z/10)^{0,11}=1,3$,
(kl. 4.3.1 – UWAGA 1) $\to$ współczynnik rzeźby terenu (orografii)$ c_0(z_e) =1,0$
(zał. A) $\to$ terenu przybrzeżny $\to$ kategoria „0”
(tab. 4.1.) $\to$ parametr chropowatości $z_0 = 0,003 \, m$,
(kl. 4.1 (1)) $\to$ współczynnik turbulencji $k_I=1,0$
(wzór 4.7) $\to$ intensywność turbulencji $I_v= \cfrac{k_I} {c_0(z) \cdot ln(z/z_0)}=\cfrac{1}{1 \cdot ln (10/0,003)}= 0,123$,
(kl. 4.5 UWAGA 2) gęstość powietrza $\rho=1,25 \, kg/m^3$,
(wzór 4.3) $\to$ średnia prędkość wiatru $v_m(z_e)=c_r (z_e)\cdot c_0(z_e) \cdot v_b = 1,3 \cdot 1,0 \cdot 26= 33,8 \, m/s$,
(wzór 4.8) $\to$ szczytowe ciśnienie wiatru $v_q (z_e) = [1+7\cdot I_v(z_e)] \cdot (1/2) \cdot \rho \cdot v_m^2(z_e) =[1+7 \cdot 0,123] \cdot (1/2) \cdot 1,25 \cdot 33,8^2 = 1328,8 \, Pa= 1,329 \, kN/m^2$
Przykład 2 [ Energia wiatru w energetyce wiatrowej ]
Energia kinetyczna powietrza przelatującego przez powierzchnię A w czasie t określa się wzorem:
$$\begin{equation} E=\cfrac{1}{2} \rho v^2 = \cfrac{1}{2} (A \cdot v \cdot t \cdot \rho) \cdot v^2 =\cfrac{1}{2} A\cdot t \cdot \rho \cdot v^3\label {A.46} \end{equation}$$
Objętość powietrza przelatującego przez powierzchnię A w czasie t wynosi $ A \cdot v \cdot t$ . Powierzchniowa gęstość mocy, czyli energia na jednostkę czasu i powierzchni, określa się wzorem
$$\begin{equation} e= \cfrac{E}{A \cdot t }= \cfrac {1}{2} \rho \cdot v^3 \label {A.47} \end{equation}$$
Moc wiatru rośnie do trzeciej potęgi z prędkością wiatru. Jednakże nie cała energia kinetyczna wiatru może zostać wykorzystana przez turbinę. Teoretycznie maksymalna efektywność turbiny może wynieść [19] $ \eta= 16/27 \approx 59,3$ %. W praktyce efektywność turbin jest niższa. W niniejszym artykule przyjęto sprawność $\eta = 30$% jako wartość nielosową.
W celu oszacowania parametrów energii ($\ref{A.47}$) można zastosować estymację do rozkładu Gumbela wg przykładu 1 lub do innego rozkładu GEV przeprowadzając analogiczną procedurę.
Niniejszy artykuł jest dodatkiem A podręcznika Imperfekcyjna metoda projektowania konstrukcji
Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2019), Imperfekcyjna metoda projektowania konstrukcji, Encyklopedia πWiki, Wydawnictwo πPress, [ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]
Historia edycji:
Publikacja jest edytowana od roku 2017, pierwotnie jako podręcznik dla wydawnictwa PWN, Zakończenie edycji zostało przerwane na początku roku 2018 na skutek wypadku i rekonwalescencji autora podręcznika. Obecnie cykl artykułów składający się na podręcznik jest w trakcie edycji internetowej i jest publikowany odcinkami po opracowaniu części rozdziału.
(2019-04-12) Dodatek A : Teoria losowych wartości ekstremalnych – Wersja 1.0 (2019-04-18)Proszę społeczność Inżynierów w internecie o przesyłanie recenzji podręcznika na moje ręce: biuro@chodor-projekt.net
Leszek Chodor
Literatura
- Żurański J. A., Sobolewski A. (2009), Obciążenie śniegiem w Polsce [Wydawnictwa Instytutu Techniki Budowlanej]. ITB
- Murzewski J. (1989), Niezawodność konstrukcji inżynierskich. Arkady
- Kapur K. C., Lamberson L. R. (1977), Reliability in engineering design. Wiley
- Katz R., W., Parlange M., B., Naveau P. (2002), Statistics of extremes in hydrolo-gy. Advanced in Water Resources, 25, 1287–1304.
- Manwell J. F., McGowan J. G., Rogers A. L. (2010), Wind Energy Explained: Theory, Design and Application (2 Ed.). Wiley
- Preś J. (2007), Zarządzanie ryzykiem pogodowym, CeDeWu
- Ravindra M. K., Galambos T. V. (1975), Load factors for wind and snow loads for use in load resistance factor design criteria (No. 62; Center for Cold-Formed Steel Structures Library). Missouri University of Science and Technology, [ https://scholarsmine.mst.edu/ccfss-library/62 ]
- Żurański J. A., Gaczek M. (2011), Oddziaływania klimatyczne na konstrukcje budow-lane według Eurokodu 1: komentarze z przykładami obliczeń / Climatic actions on building structures according to Eurocode 1 : commentary and examples of use. In-stytut Techniki Budowlanej
- Bjerhovde R. (1972), Deterministic and probabilistic approaches to the strength of steel columns (Ph D. Dissertation No. 1933; Fritz Laboratory Reports). Lehigh Uni-versity
- Ivčenko G. I., Medvedev J. I. (2015). VVedenie v matematičeskuju statistiku. Wydawnictwo DKI, Moskva
- Cox D. R., Hinkley D. V. (2000). Theoretical statistics, Chapman & Hall/CRC
- Mathworks, (2017), Matlab, Simulink. Extreme Value DIstribution, [ https://www.mathworks.com/help/stats/extreme-value-distribu-tion.html?requestedDomain=www.mathworks.com&requestedDomain=www.mathworks.com ]
- Wolfram,,MathWorld, (2019), Mathematica. Extreme Value DIstribution, [ http://mathworld.wolfram.com/ExtremeValueDistribution.html ]
- McFadden D. (1978,. Modelling the Choice of Residential Location. Transportation Research Record, 673, 72–77, [ http://onlinepubs.trb.org/Onlinepubs/trr/1978/673/673-012.pdf ]
- Reiss R., Thomas M. (1997). Statistical Analysis of Extreme Values. Birhaeuser Ver-lag
- Martin D., Zhang W., Chan J., Lindley J. (2014), A comparison of Gumbel and Weibull statistical models to estimate wind speed for wind power generation. Austral-asian Universities Power Engineering Conference (AUPEC), Perth, Australia, Pisca-taway, NY
- PN-EN 1991-1-4:2008, Eurokod 1. Oddziaływania na konstrukcje, Część 1-4: Od-działywania ogólne. Oddziaływania wiatru
- Żurański J. A. (2005), Wpływ warunków klimatycznych i terenowych na obciążenie wiatrem konstrukcji budowlanych / Influence of climatic and terrain conditions on wind loads on building structures. Wydawnictwa Instytutu Techniki Budowlanej
- Betz A. (2014), Introduction to the Theory of Flow Machines. Elsevier Science
________________________________