Rozciągane pręty stalowe

Leszek Chodor,  2 listopada 2016
11-02-2025 rewizja po dużej awarii portalu
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co

Artykuł w ciągu ostatnich 24 godzin czytało 8 Czytelników

Elementy rozciągane konstrukcji stalowych są najprostszymi elementami konstrukcyjnymi i stanowią dobre wprowadzenie do wymiarowania elementów stalowych (w innych i złożonych stanach naprężeń oraz poddanych zjawiskom niestateczności). Co prawda elementy rozciągane też mogą utracić stateczność, ale to zjawisko może być pominięte w projektowaniu inżynierskim.

Warunek nośności i stale konstrukcyjne

Warunek nośności elementu rozciąganego

Element rozciągany jest w istocie najprostszym przypadkiem elementu konstrukcyjnego, a jego wymiarowania polega na  takim wyznaczeniu  polu przekroju poprzecznego, aby przenieść przyłożoną siłę rozciągającą. Dla danej siły rozciągającej $N_{Ed}$ oraz wytrzymałości materiału  $f_y$ potrzebna powierzchnia przekroju poprzecznego A może być łatwo obliczona zależności

$$\begin {equation} A \ge \cfrac{N_{Ed}}{f_y}\label {1} \end {equation}$$

Problem jest bardziej złożony w praktyce, gdy połączenie członów elementu rozciąganego posiada mimośród (lub offset). W przypadku lin lub kabli zagadnienie nieosiowości nie jest istotne, ale wchodzą w grę inne zjawiska, jak: efekt skali, złożoność przekroju zagięcia lin w kauszach, itd. W niniejszym artykule zajmujemy się prętami wykonanymi z kształtowników walcowanych, jak pręty lite, kątowniki, dwuteowniki rury.  Elementy linowe są przedmiotem artykułu  Przekrycia cięgnowo-membranowe.

Warunek nośności elementu rozciąganego można zapisać w postaci [1], (6.5) :

$$\begin {equation} N_{Ed} \lt N_{t,Rd}\label {2} \end {equation}$$

gdzie:
$N_{Ed}$−obliczeniowa, zewnętrzna siła rozciągająca,
$N_{t,Rd}$ – obliczeniowa nośność elementu na rozciąganie.

Stale konstrukcyjne

Stal jest stopem żelaza Fe i węgla C o zawartości C do 2% z dodatkami stopowymi: niklu Ni, molibdenu Mo, aluminium Al i tytanu Ti oraz innych. Na rys. 1c dla najważniejszych metali, wchodzących w skład stali, zestawiono parametry sprężyste; moduł odkształcalności podłużnej, Younga  E, współczynnik Poissona μ oraz zależność  (E/G-2μ) do wyznaczenia modułu odkształcalności poprzecznej Kirchoffa G.
W próbie rozciągania elementu wykonanego ze stali nisjowęglowej  (np. S235) uzyskuje się wykres (ε-σ) pokazany na rys. 1b), z wyraźną półką plastyczności. W tym przypadku   można wyznaczyć górną R_eH i dolną R_eL granicę sprężystości i przyjmuje się, że granica plastyczności f_y  jest równa średniej arytmetycznej wyraźnej granicy sprężystości. Natomiast w przypadku stali stopowych (np S355), a szczególnie wysokostopowych nie obserwuje się przystanku plastycznego i za granicę plastyczności przyjmuje się  umowną granicę sprężystości dla wydłużenia ε= 0,2%, to znaczy f_y=R _{p 0,2}. Granica wytrzymałości f_u=R_m^.

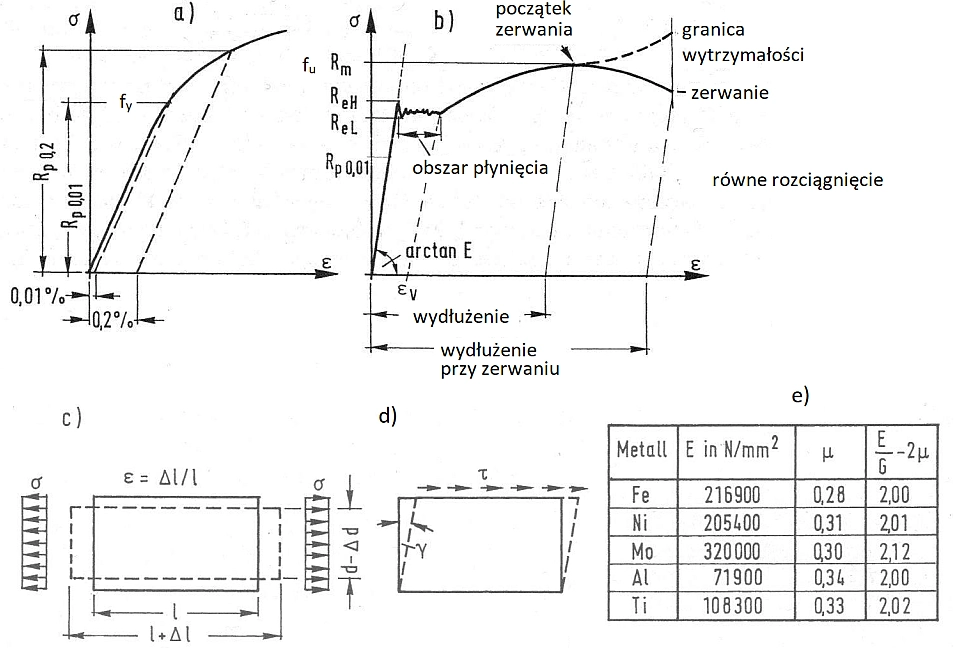
Rys.1. Element rozciągany: a) wykres rozciągania stali bez wyraźnej granicy plastycznoścći, b) wykres rozciągania stali węglowej z wyraźną granicą plkastyczności, c) wydłużenie i zwężenie pod wpływem naprężeń rozciągających, d) zmiana postaci pod wypływem naprężeń ścinających e) parametry sprężyste wybranych metali [2], Teil 1, Bild. 30, 31, 

Na rysunku 1c) pokazano, że na skutek rozciągania naprężeniami  σ=N/A element ulega wydłużeniu o ε= Δl/l, gdzie A, l są polem przekroju i długością elementu przed obciążeniem.

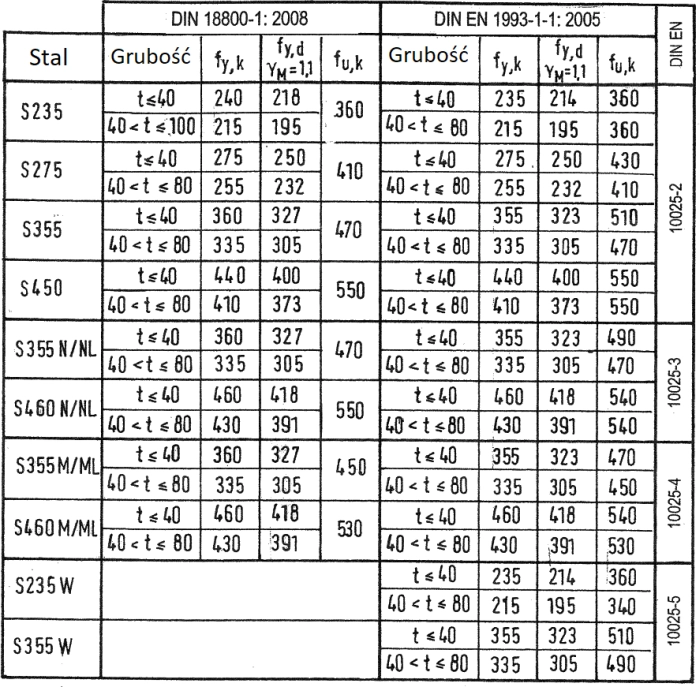
W konstrukcjach budowlanych stosuje się najczęściej stale zestawione w tab. 1. Oznaczenie stali składa się z symbolu S (ang. Steel) i liczby oznaczającej granicę plastyczności w MPa. Na przykład symbol  S235 oznacza stal konstrukcyjną o wytrzymałości (granicy plastyczności)  f_y=235MPa. Litera N oznacza normalizowanie lub walcowanie normalizujące (rodzaj obróbki cieplnej), litera M – stal walcowaną termomechanicznie, a litera L – odporność na niskie temperatury. W tab.1.  pominięto inne kwantyfikatory oznaczeń stali, np. udarność. W zależności od grubości ścianki zróżnicowana jest charakterystyczna granica plastyczności f_yk i charakterystyczna granica wytrzymałości  f_uk. W tab. 1 podano jeszcze obliczeniową granicę plastyczności f_yd wyznaczoną dla współczynnika materiałowego  $\gamma_M=1,1$.  Zależność ta jest historyczna. Obecnie przyjmuje się, że zachodzi  f_yd=f_yk, a współczynnik materiałowy γ_M stosuje się jawnie o wartości zależnej od analizowanego stanu wytężenia w następujący sposób:

$\gamma_M=\gamma_{M0}=1,0$  – przy ocenie nośności przekroju poprzecznego, niezależnie od klasy,
$\gamma_M=\gamma_{M1}=1,0$ – przy ocenie nośności elementów z uwzględnieniem ich stateczności,
$\gamma_M=\gamma_{M1}=1,25$ – przy ocenie nośności na rozerwanie przekroju z otworami.

Przy ocenie nośności węzłów należy stosować współczynniki materiałowe zgodnie z [3] .

Tab.1 Stale konstrukcyjne [2] Teil 2, Bild 3

Elementy z otworami

Rzeczywisty rozkład naprężeń w przekroju  płaskownika o szerokości b z otworem o średnicy $2r$ przedstawiono na rys.2.

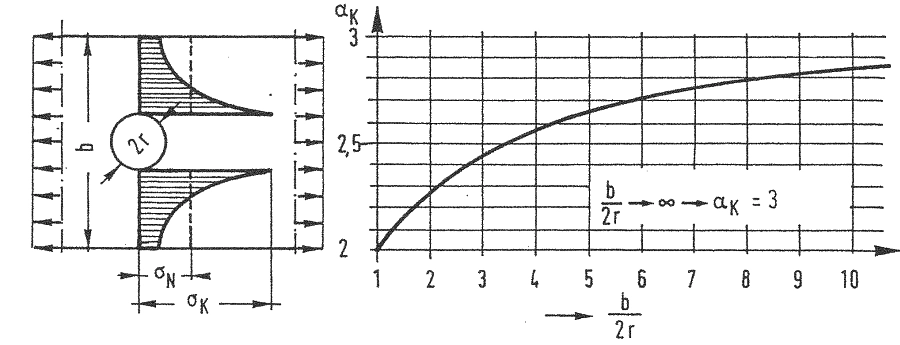
Rys. 2 Rozkład naprężeń w przekroju z otworem [2] Teil 1, Bild 54

Nieliniowy rozkład naprężeń $\sigma$ ze spiętrzeniem $\sigma_K$ na krawędzi otworu do zastosowań inżynierskich aproksymuje się równoważnym rozkładem równomiernym $\sigma_N$ w przekroju netto o szerokości $b-2r$,

Nośność elementu z otworami

Zakładamy, że naprężenia od rozciągania w przekroju elementu osłabionego otworami jest równomierne. . Otwory w elemencie możemy uwzględnić dwojako: 1) poprzez zmniejszenie przekroju elementu lub 2) zwiększenie naprężeń. W  projektowaniu konstrukcji budowlanych stosuje się metodę 1), tak jak pokazano na rys. 2, przy czym rozciągane przekroje z otworami analizowane są o polu netto, które zyskany po odjęciu od pola przekroju brutto pola przekroju otworów przejściowych na łączniki. Mimośrody w połączeniu z otworem prowadzą do drugorzędowego zginania i są zwykle pomijane.

 Nośność ($\ref{2}$) przekroju bez otworu jest nośnością plastyczną [1],(6.6)

$$\begin {equation} N_{t,Rd1}= N_{pl,Rd}= \dfrac{A \cdot f_y}{\gamma_{M0}}\label {3} \end {equation}$$

gdzie:
A – pole przekroju brutto,
$f_y$ – granica plastyczności stali,
$\gamma_{M0}=1,0$ – współczynnik materiałowy.

Dla elementów z otworami nośność jest zmniejszona poprzez redukcję pola przekroju o pole otworów. Wymagane jest też dodatkowe sprawdzenie naprężeń rozrywających, ponieważ otwory dają spiętrzenie naprężeń (p. rys. 2) i rozkład naprężeń w przekroju nie jest równomierny, co prowadzi do oszacowania nośności [1],(6.7) :

$$\begin {equation} N_{t,Rd2}=0,9 \cdot \cfrac{A_{net}\cdot f_u}{\gamma_{M2}}\label {4} \end {equation}$$

gdzie:
$A_{net}$ – pole przekroju netto,
$f_u$ – granica wytrzymałości stali,
$\gamma_{M2} = 1,25$ – współczynnik materiałowy.

Współczynnik 0,9 uwzględnia niezamierzone mimośrody i przypadkowe spiętrzenia naprężeń.

Ostatecznie nośność na rozciąganie w formule ($\ref{2}$) należy przyjąć jak mniejszą z dwóch wartości ($\ref{3}$) i ($\ref{4}$):

$$\begin {equation} N_{t,Rd}= \min{\{ N_{t,Rd1}\,;\, N_{t,Rd2}\}} \end {equation}$$

W warunku ($\ref {4}$) dozwolono, by naprężenia osiągnęły granicę wytrzymałości $f_u$, czyli by przekroczyły lokalnie granicę plastyczności. Wynika to z faktu, że awaria pręta rozciąganego z elementem złącznym powinna być opisana na poziomie odkształceń. Rozważmy na przykład pręt rozciągany o długości całkowitej $l_c$, w którym połączenie zajmuje do 5% całkowitej długości $l_p$ = 5%$l_c$. W stanie granicznym odkształcenie w obszarze połączenia jest ok 10-krotnie większe od odkształcenia poza połączeniem, ale i tak  jest znacznie mniejsze niż wydłużenie całego elementu. Zatem zniszczenie zajdzie przy nadmiernych odkształceniach całego elementu, oczywiście pod warunkiem, że wytrzymałość elementu złącznego na zerwanie  $N_{u,Rd}$  jest nie mniejsza niż wytrzymałość plastyczna $N_{pl,Rd}$ przekroju brutto. W dwóch przypadkach norma [1]  uznaje jednak za konieczne ograniczenie naprężeń w przekroju netto. Pierwszy dotyczy połączeń kategorii C, to znaczy połączeń ciernych, dla których nośność elementu  $N_{net,Rd}$ powinna być ograniczona, co wyrażono zależnością [1],(6.8) :

$$\begin {equation} N_{net,Rd}= \cfrac{A_{net} \cdot f_y}{\gamma_{M0}}\label {6} \end {equation}$$

Drugi przypadek  dotyczy elementów w których wymagane jest zdolność do odkształceń plastycznych  (np przy projektowania sejsmicznym). W takich przypadkach jest konieczne, aby zapewnić stan,w którym o nośności decyduje element brutto również w obszarze łącznika, czyli   [1],pkt 6.2.3(3) :

$$\begin {equation} N_{u,Rd} > N_{pl,Rd}\label {7} \end {equation}$$

co jest spełnione dla

$$\begin {equation} \dfrac{A_{net}}{A} \ge \dfrac{[f_u /f_y][\gamma_{M2} / \gamma_{M0}]}{0,9}\label {8} \end {equation}$$

Wyznaczanie przekroju netto

Powierzchnia netto przekroju jest powierzchnią przekroju  brutto pomniejszonego o powierzchnię  zajętą przez na otwory śrub lub  inne otwory:

$$\begin {equation} A_{net}=A- \Delta A\label {9} \end {equation}$$

gdzie łączna powierzchnia do odliczenia $\Delta A$ w dowolnym przekroju prostopadłym do osi elementu jest maksymalną sumą obszarów otworów w najniekorzystniejszym przekroju przechodzącym przez łączniki (prostopadłym, przekątnym lub zygzakowatym). Dla przypadku z rys. 3 należy przeanalizować przekroje 1-1 i 2-2 i wybrać powierzchnię mniejszą. Specjalne zasady obowiązują dla kątowników podłączonych za pośrednictwem jednej półki i analogicznie  także dla teowników.

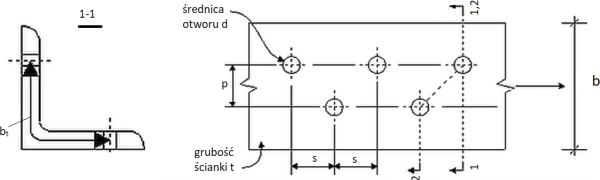
Rys.3. Wyznaczanie przekroju netto: 1-1, 2-2 : przekroje krytyczne [4]

Na rys. 3 pokazano przykład wyznaczania przekroju netto płaskownika z grupą otworów.

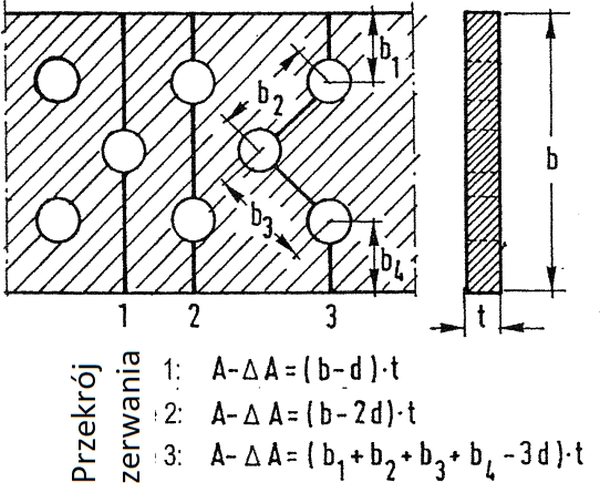
Rys.2. Przykład wyznaczania przekroju netto elementu rozciąganego [2]

Kątownik mocowany jedną półką

W przypadku przekrojów niesymetrycznych, wystąpią mimośrody (często nazywane offsetami), to znaczy przesunięcie osi środków ciężkości kształtownika i podłoża. Zagadnienie przedstawiane jest na przypadku kątownika mocowanego jedną półką (rys.4)

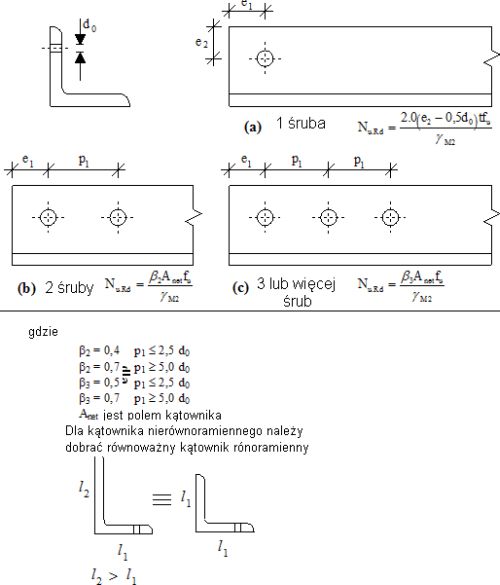
Rys. 4 Nośność przekroju kątownika [4]},rys. 3″

Dla kątowników mocowanych przez spawanie jedną półką zamiast śrub, mimośród połączenia może być przyjęty poprzez zastosowanie „sprawczej ” powierzchni przekroju, a następnie potraktowanie go jako osiowo rozciąganego. Przykłady wyznaczania sprawczego pola powierzchni przekroju pokazano na rys. 5

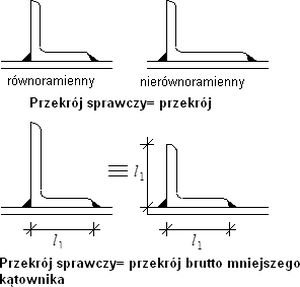
Rys.5. Przekrój sprawczy kątownika przyspawanego jedną półką [4]

Profile teowe,  i ceowniki  połączone jedną półką można  traktować analogicznie. Takie podejście może zastosowane w celu obliczenia powierzchni netto przekroju (A_net) pojedynczego odcinka teownika,  połączonego za pośrednictwem pasa lub ceownika połączonego za pośrednictwem środnika. Jako powierzchnię netto można wziąć powierzchnię przyłączonej ścianki  (części) przekroju poprzecznego oraz połowę obszaru odstających ścianek. Taka powierzchnia netto jest następnie wykorzystywana do obliczenia nośności elementu odporność przekroju netto z formuły (3b), pod warunkiem, że jest mniejsza od nośności przekroju brutto (3a).

Smukłość elementów rozciąganych i ochrona korozyjna

Elementy rozciągane pracują bardzo sprawnie przenosząc obciążenie i mają stosunkowo niewielkie przekroje w porównaniu do elementów zginanych. To sprawia, że są podatne na nadmierne ugięcia pod ciężarem własnym, a także mogą być łatwo uszkodzone podczas transportu. Z tych względów dobra praktyka ogranicza smukłość elementów głównych do $\lambda_{max}=300$ i 400 elementów drugorzędowych. Kolejnym czynnikiem, który należy uwzględnić  są duże konsekwencje ubytków korozyjnych, które są większe dla prętów rozciąganych, ponieważ korozja jest większa dla większego wytężenia (korozja naprężeniowa).

Utrata stateczności elementów rozciąganych

W ramach teorii dużych odkształceń można pokazać, że również elementy rozciągane mogą utracić stateczność.

w opracowaniu

 Literatura

1. PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
2. Petersen C. (2013), Stahlbau: Grundlagen der Berechnung und baulichen Ausbildung von Stahlbauten (4 Wydanie- überarb. und aktualisierte Aufl). Springer Vieweg
3. PN-EN 1993-1-8 +Ap1+AC:2006, Eurokod 3 -Projektowanie konstrukcji stalowych -Część 1-8: Projektowanie węzłów
4. SSEDTA, (2001), Course: Eurocode 3. Lecture 10 – Tension Members, Structural Steelwork Eurocodes Development of A Transnational Approach

________________________________