Dąży się do tego, by dwukrzywiznowe powierzchnie przekryć i elewacji budynków były składane z prostych elementów prefabrykowanych: płaskich paneli lub szkła, albo z prostoliniowych prętów. Do tego celu najlepsze są powierzchnie prostokreślne, a wśród nich paraboloida hiperboliczna i hiperboloida obrotowa jednopowłokowa. Z ich płatów tworzone są złożone powierzchnie, np nowoczesne elewacje wieżowców, pokazane na rys.1, zadaszenia z hyparaw (hiperboloidy parabolicznej), pokazano na rys. 2 i wiele innych.

Rys.1 Nowoczesne powierzchnie złożone Spiral Tower Nagoya [1]
Rys.2 Przekrycie z hypara Scotiabank Calgary
[Wikipedia]
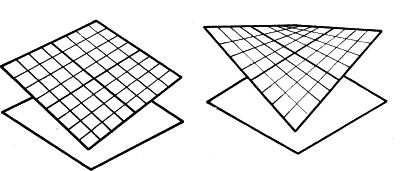
Podstawowym zadaniem jest wydzielenie płata (prefabrykatu). Na rys. 3 pokazano sposób wydzielenia płata podstawowego z powierzchni siodłowej paraboloidy hiperbolicznej. Na rys. 4 i 5 pokazano kilka wariancji składania czterech płatów podstawowych, a na rys. 5 sklejania mniejszych płatów w zwielokrotniony prefabrykat.
Rys.3 Wydzielanie płata z powierzchni siodłowej paraboloidy hiperbolicznej
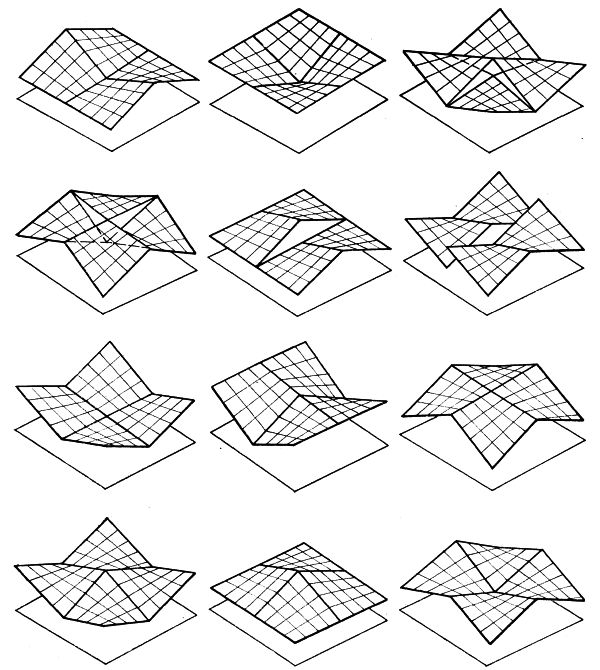
Rys.4 Przykłady prostych przekryć, sklejonych z czterech podstawowych płatów
Rys.5 Przykłady zwielokratniania płatów podstawowych
Na rys. 6 do 13 pokazano przykłady kształtowania przekryć złożonych z podstawowych płatów (płaskich).

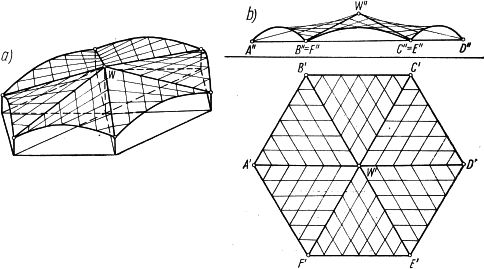
Rys.6 Dach z pionowymi swietlikami, złożony z sześciu podstawowych płatów: a) aksonometria, b) rzuty
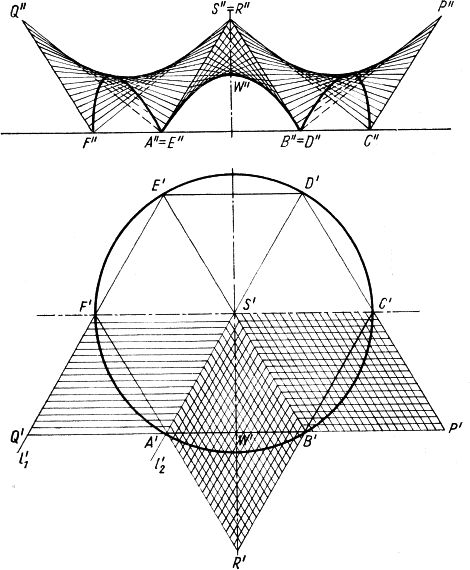
Rys.7 Przekrycie nad kołowym rzutem, złożone z sześciu jednakowych płatów podstawowych
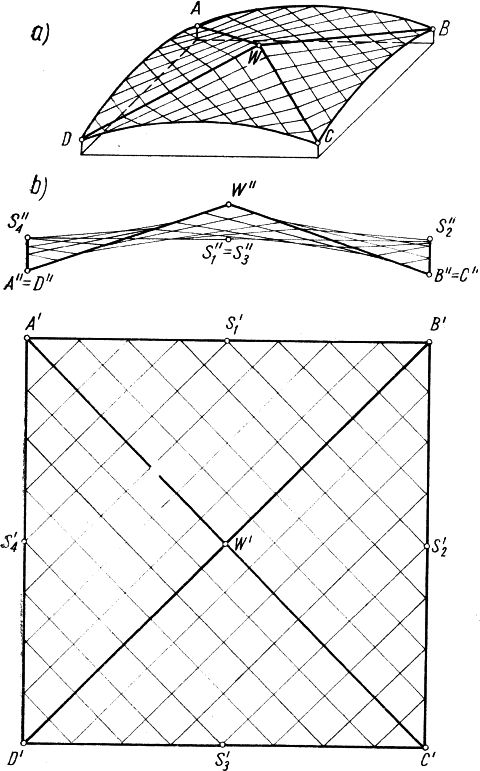
Rys.8 Przekrycie nad kwadratowym rzutem, złożone z czterech jednakowych płatów trójkątnych
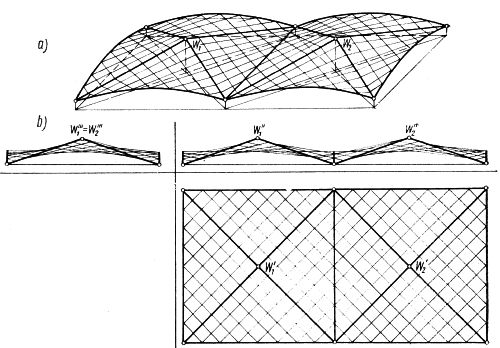
Rys.9 Przekrycie nad prostokątnym rzutem, złożone z ośmiu jednakowych płatów trójkątnych [2]
Rys.10 Przekrycie nad sześciokątnym rzutem, złożone z sześciu jednakowych płatów trójkątnych
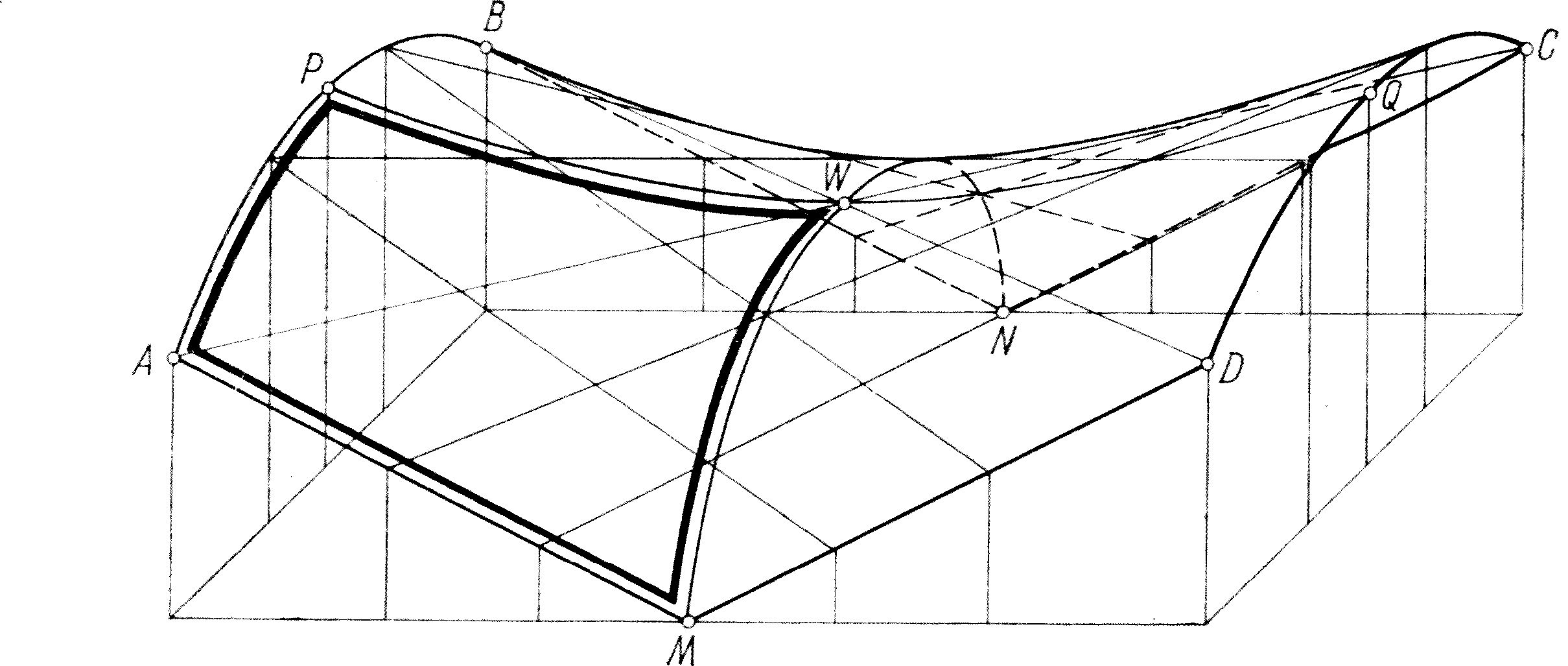
Rys.11 Płat hiperboliczny sklejony z czterech płatów podstawowych
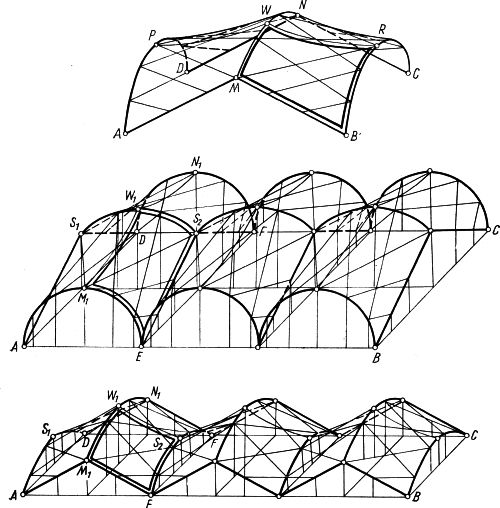
Rys.12 Trzy warianty przekryć złożonych z powtarzalnych płatów jednostkowych
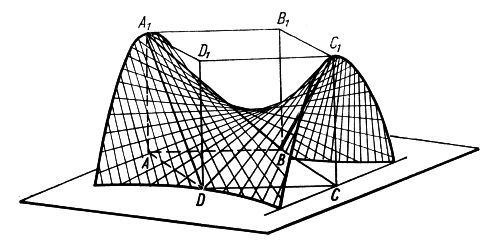
Czasami powierzchnie złożone buduje się z krzywoliniowych płatów podstawowych, wydzielanych np. w sposób pokazany na rys. 13 , 14 lub 15.
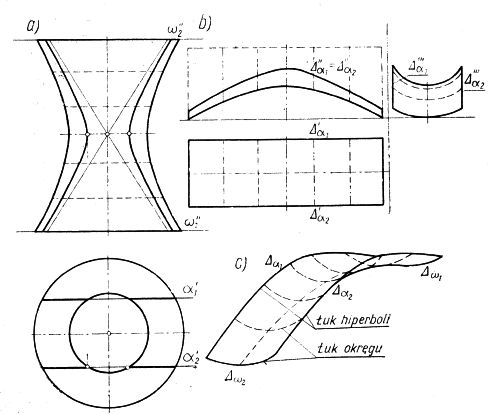
Rys.13 Wydzielenie płata z powierzchni hiperbolicznej: a) sposób wydzielenia, b) rzuty, c) aksonometria
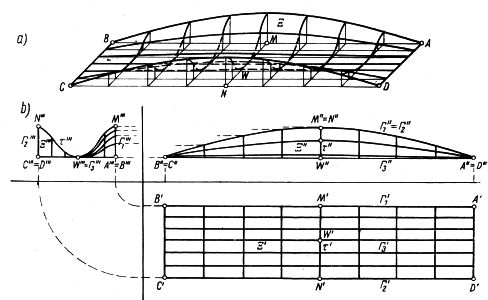
Rys.14 Wydzielenie płata z powierzchni klinowej: a) aksonometria, b) rzuty
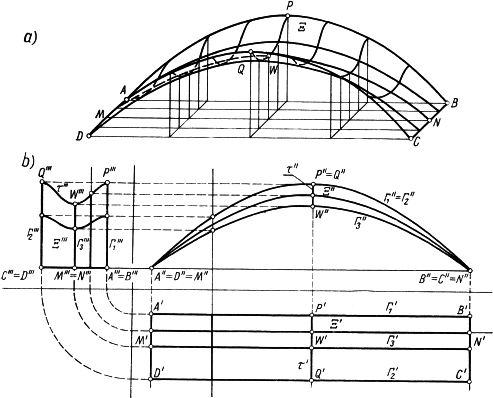
Rys.15 Wydzielenie płata z powierzchni klinowej o podwójnej krzywiźnie : a) aksonometria, b) rzuty
Rysunki 3 do 15 zaczerpnięto z pracy [2].Literatura
- Sekkei N. (2008), Mode Gakuen Spiral Towers – Nagoya, Japan, [ http://www.incredible-pictures.com/2013/05/mode-gakuen-spiral-towers-nagoya-japan.html ]
- Przewłocki S., (1969), Kształtowanie geometryczne konstrukcji powłokowych, Arkady, Warszawa
________________________________