Połączenia spawane

Leszek Chodor, 8 listopada 2016

Artykuł w ciągu ostatnich 24 godzin czytało 28 Czytelników

Połączenia spawane konstrukcji stalowych są podstawową metodą łączenia elementów na warsztacie (w wytwórni konstrukcji stalowych).

Spawalnictwo

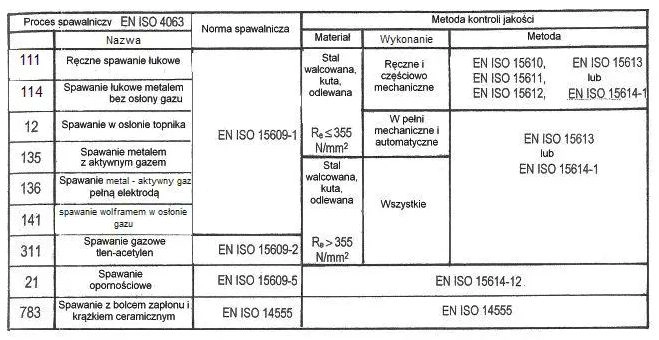
Spawalnictwo jest odrębną i ważną dziedziną konstrukcji metalowych. Spawanie polega na spajaniu metali w wysokiej temperaturze. Stosuje się metody spawania zestawione w tab.1.

Tab.1.Metody spawania [1],rozdz.6 rys.1

Na rys. 1 pokazano schemat ręcznego spawania łukowego. Na rys. 2 zilustrowano spawanie elektrodą bez osłony gazu; na rys. 3 spawanie w osłonie topnika (ang: flux, niem: pulver); na rys. 4 spawanie elektrodą wolframową, a na rys. 5 spawanie w osłonie gazów (MIG/MAG) . W tab.2 zestawiono rodzaje gazów do spawania MIG/MAG.

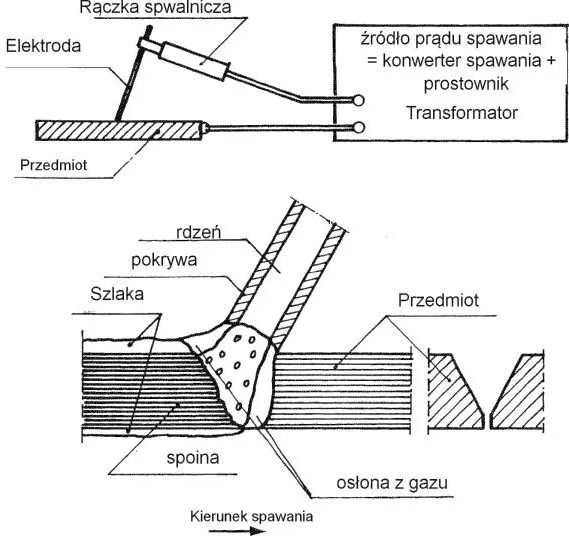
Rys.1. Spawanie łukowe, ręczne [1],rozdz.6 rys.2

Rys.2. Spawanie elektrodowe bez osłony gazu [1],rozdz.6 rys.4

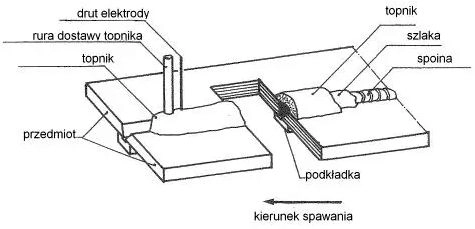
Rys.3. Spawanie elektrodowe w osłonie topnika [1],rozdz.6 rys.5

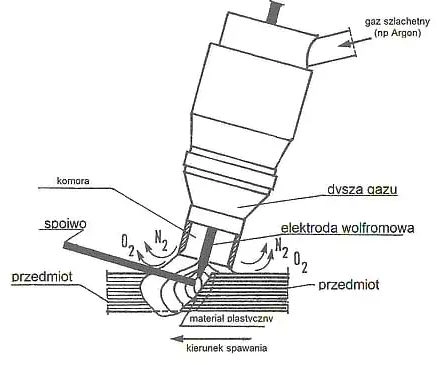
Rys. 4. Spawanie elektrodą wolframową WIG [1],rozdz.6 rys.6

Rys.5. Spawanie w osłonie gazów MIG/MAG [1],rozdz.6 rys.7

Tab.2. Rodzaje gazów stosowane w spawaniu MIG/MAG [1],rozdz.6 rys.7

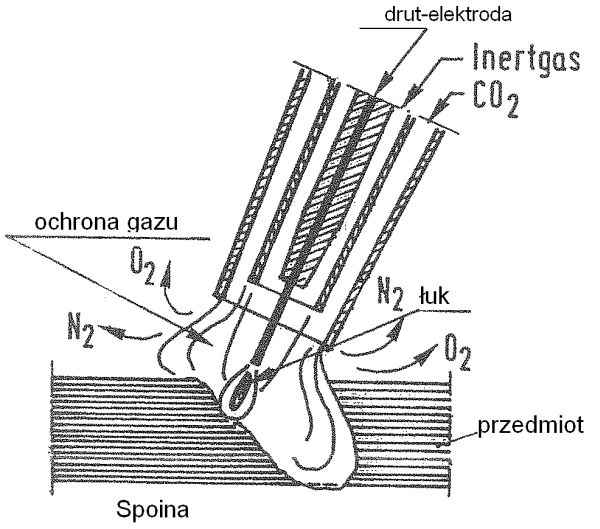
Rys.6. Spawanie w osłonie gazów MAGCI [1],rozdz.6 rys.8

Rys.7 Specjalne metody spawania: a) punktowe, b) doczołowe, c) spawanie bolców (np łaczników Nelson w belkach zespolonych) [1],rozdz.6 rys.9

Spawane krawędzie przygotowuje się do spawania poprzez ukosowanie.  Najczęściej stosowane sposoby ukosowania pokazano w tab.3

Tab.3. Ukosowanie krawędzi blach do spawania [1],rozdz.6 rys.3

Na rys. 8 pokazano wybrane zagadnienia, dotyczące złączy spawanych:

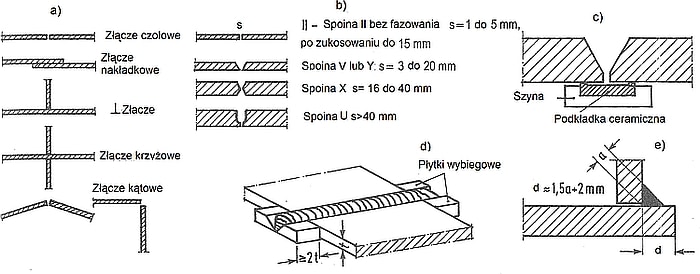
Rys. 8 Wybrane zagadnienia technologii spawania: a ) rodzaje złączy, b) szczelina spawalnicza s , c) podkładka ceramiczna, d) płytki wybiegowe, e) wysięg blachy do ułożenia spoiny [1],rozdz.6 rys.11

Spoiny

Rodzaje spoin i oznaczenia na rysunkach

Na rys. 9 pokazano rodzaje spoin , stosowane w konstrukcjach budowlanych.

Rys.9. Rodzaje i oznaczenia spoin w konstrukcjach budowlanych

W tab.4 pokazano najważniejsze oznaczenia rysunkowe spoin.

Tab.4. Oznaczenia spoin na rysunkach konstrukcyjnych [1], rozdz.6 rys. 25

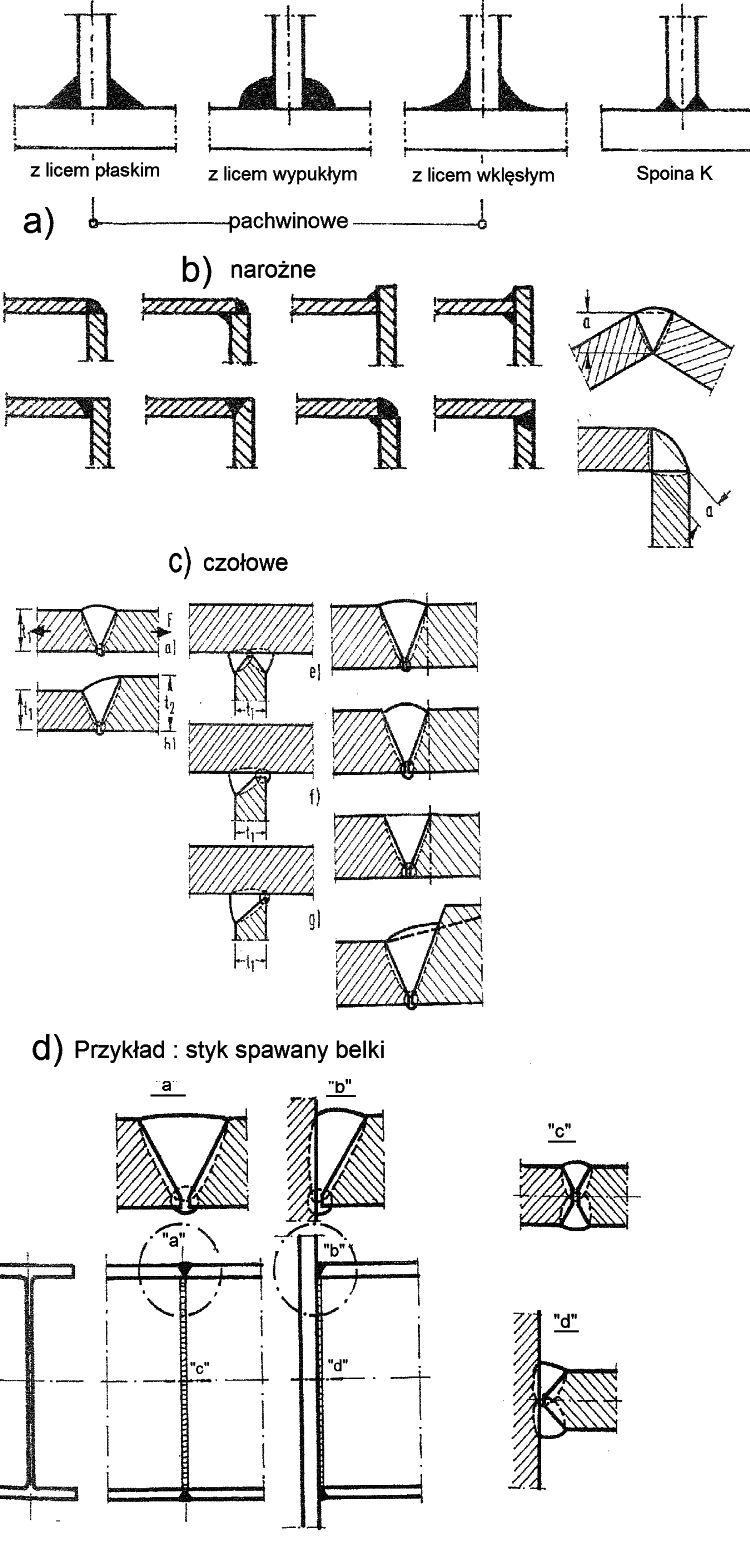
Spoiny pachwinowe

Na rys.10 przedstawiono model spoin pachwinowych w kilku przypadkach złączy: grubość obliczeniową $a$ oraz składowe  naprężeń: styczne $\tau_{||}$ i $\tau_\perp$, oraz normalne $\sigma_{||}$  i  $\sigma_\perp$ .

Rys.10 Model spoin pachwinowych: a) grubości obliczeniowe, b) naprężenia w spoinach złącza nakładkowego, c) naprężenia w spoinach pasowych, d) spoiny pasowe na różnych wysokościach profilu, e) złącze rozciągane i f) naprężenia w spoinach złącza rozciąganego [1],rozdz.6 rys.17-21

Warunki konstrukcyjne dla grubości spoiny $a$ (rys. 10a) są następujące:

$$\begin{equation} a \to \begin {cases}
& \ge 2 mm \\
&\ge \sqrt {max \, t} -0,5 \,mm \\
&\le 0,7 \cdot min \, t \\
\end {cases} \label{1} \end{equation}$$

gdzie: max t i min t – maksymalna i minimalna grubość łączonych elementów,

Formuła ($\ref{1}$) obowiązuje dla $ t \ge 3 mm$. W przypadku mniejszych grubości należy stosować postanowienia normy [2], dotyczące elementów cienkościennych.

Spoinę pachwinową uważa się za nośną, jeżeli jej długość $l$ na odcinku prostoliniowym spełnia warunek

$$\begin{equation} l \ge min \, [ \, 6a \, ;\, 30 mm] \label {2} \end{equation}$$

W ogólnym przypadku w spoinie pachwinowej mogą wystąpić następujące naprężenia (rys. 10):

• naprężenia normalne prostopadłe do przekroju spoiny $\sigma_\perp$,
• naprężenia normalne równoległe do przekroju spoiny $\sigma_\parallel$ – prostopadłe  do przekroju łączonych części – nie uczestniczące w ścinaniu spoiny i stąd nie występujące w dalszych warunkach wytrzymałościowych,
• naprężenia styczne prostopadłe do przekroju spoiny $\tau_\perp$,
• naprężenia styczne równoległe do przekroju spoiny $\tau_\parallel$,

Wytężenie spoiny pachwinowej w złożonym stanie naprężenia szacuje się ze wzoru HMH (Hubera-Misesa-Hencky):

$$\begin{equation} \sigma_w= \sqrt{\sigma_\perp^2 + 3(\tau_\perp^2+\tau_\parallel^2)} \le \sigma_{R,sp} =\dfrac{f_u}{\beta_w \gamma_{M2}}\label {3} \end{equation}$$

przy czym sprawdza się również warunek

$$\begin{equation} \sigma_\perp \le  \sigma_{R \perp} =\dfrac{0,9 f_u}{\gamma_{M2}}\label {4} \end{equation}$$

gdzie: $f_u$  granica wytrzymałości łączonej stali, $\gamma_{M2}=1,25$,

a $\beta_w$ – współczynnik korekcyjny spoiny pachwinowej zależny od rodzaju łączonej stali:

$$\begin{equation} \beta_w = \begin {cases}
0,80 & \textrm{dla stali S235} \\
0,85 & \textrm{dla stali S275} \\
0,90 & \textrm{dla stali S355} \\
1,00 & \textrm{dla stali wyższej wytrzymałosci} \\
\end {cases} \label{5} \end{equation}$$

Metoda kierunkowa ($\ref{3}$), ($\ref{4}$) jest ogólna i może być stosowana w każdym przypadku, przy czym w zależności od sposobu wytężenia spoiny naprężenia w spoinach szacuje się w odmienny sposób, ale zawsze w zgodzie ze standardowymi mechanizmami wytrzymałości materiałów.

W przypadku złącza nakładkowego (rys.10 b) naprężenia wywołane siłą rozciągającą element $F$ równoległą do spoin, wynoszą:

$$\begin{equation} \tau_\parallel=\tau_\perp= \tau_{sp}=\dfrac{F}{\sum A_{sp}}= \dfrac{F}{\sum \limits_i (a_i l_i)}\label {6} \end{equation}$$

gdzie: $a$ i $l$ – grubość i długość i-tego odcinka spoiny.

W przypadku spoin pasowych (rys. 10 c i d) łączących środnik z pasem (1) lub nakładkę pasa (2) w przekroju belki, w którym działa siła osiowa $N$ moment zginający $M$ oraz siła poprzeczna $Q$

naprężenia w spoinach wyznaczamy z zależności

$$\begin{equation} \sigma_\parallel= \sigma_{sp} \\ \tau_\parallel=\tau_{sp} \label {7} \end{equation}$$

Naprężenia (sp) wyznacza się ze standardowych formuł:

$$\begin{equation} \sigma_{sp}= \dfrac{N}{A} \pm \dfrac{M}{I}\cdot z \\  \tau_{sp}=\dfrac{Q \cdot \overline S}{I \cdot \sum a}\label {8} \end{equation}$$

gdzie:
A, I, $\overline S$ – pole przekroju, moment bezwładności i moment statyczny odciętej części przekroju,
z- odległość włókna przekroju od osi obojętnej przekroju. Na rys. 11d) dla spoiny (1) – połowa wysokości środnika, dla spoiny (2) suma połowy wysokości środnika i grubości pasa.

W przypadku połączenia rozciąganego siłą $F$ prostopadłą do spoin mamy:

$$\begin{equation} \sigma_\perp= \tau_\perp= \dfrac{\sigma_{sp}}{\sqrt{2}}\label {9} \end{equation}$$

gdzie:

$$\begin{equation} \sigma_{sp}= \dfrac{F}{\sum A_{sp}}\label {10} \end{equation}$$

Zależność  ($\ref{9}$) zachodzi, ponieważ składowe $T$ i $S$ siły $F$ wynoszą $T=S=\dfrac{F}{\sqrt{2}}$.

W przypadku dwuteownika przyspawanego do konstrukcji spoinami pachwinowymi o przekroju $A_{sp}=A_{sp,w}+A_{sp, f}$ w sposób pokazany na rys. 11 ( środnik przyspawany spoinami $A_{sp,w}$ ; pasy spawane spoinami $A_{sp,f}$) wystąpią naprężenia:

$$\begin{equation} \begin {cases}
\textrm { normalne w spoinach środnika i pasa w odległości z od osi }& \sigma_\perp =\tau_\perp= \cfrac{\sigma_{sp}}{\sqrt{2}} \\
\textrm { styczne w spoinach środnika } & \tau_\parallel=\tau_{sp}=\cfrac{Q}{\sum A_{sp,w}} \\
\end {cases} \label{11} \end{equation}$$

gdzie $\sigma_{sp}  $ wyznacza się z zależności ($\ref{8}$-1) dla $A=A_{sp}$ oraz $I=I_{sp}$ – moment bezwładności kładu spoin (B-B).

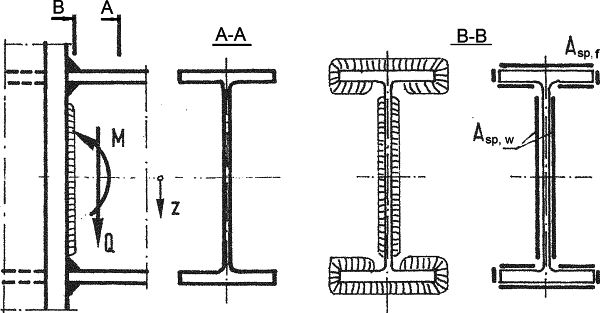
Rys. 11 Przyłączenie dwuteownika spoinami pachwinowymi [1],rozdz.6 rys.22

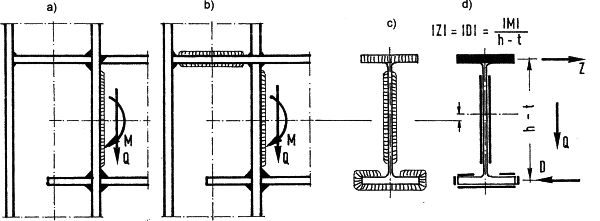
W przypadku mieszanych spoin pachwinowych i czołowych jak na rys. 12, gdzie pasy spawano spoinami czołowymi, a środnik pachwinowymi, przyjmuje się, że spoiny pachwinowe środnika przenoszą siłę ścinającą $Q$ zgodnie z ($\ref{8}$ a), a pasy są rozciągane siłą $Z$ i ściskane siłą $D$, które szacuje się z zależności podanej na rys 12 d. Sprawdzenie spoin czołowych jest prowadzone zgodnie z zasadami podanymi w kolejnym punkcie artykułu.

Rys.12 Połączenie spawane czołowo-pachwinowe

W prostych, elementarnych przypadkach  wytężenie spoin pachwinowych można stosować  uproszczone kryteria oceny nośności spoin na poziomie sił  – poprzez porównanie  jednostkowej nośności spoiny z jednostkową siłą zewnętrzną) zgodnie z historyczną metodą uproszczoną [3], pkt 4.5.3.3   oraz [2],

Wobec utraty znaczenia metody uproszczonej w artykule nie będziemy  szerzej zajmować się tą metodą.Wybrane przypadki zastosowania metody uproszczonej pokazano w przykładach rachunkowych.

Spoiny czołowe

Spoiny czołowe pokazano na rys. 9 c. Mogą one mieć krawędzie zukosowane w kształt: ||, V, X, Y, U, HN, K, w sposób zilustrowany w tab.3.

Wymiar obliczeniowy spoin czołowych należy przyjmować jako cieńszą grubość łączonego elementu:

$$\begin{equation} a = min \, t\label {12} \end{equation}$$

a pole przekroju i naprężenia w spoinie rozciąganej siłą $F$ wynoszą

$$\begin{equation} A_{sp}=a \cdot l \to \sigma_\perp=\sigma_{sp}= \dfrac{F}{A_{sp}}\label {13} \end{equation}$$

gdzie $l$ jest długością obliczeniową spoiny , w przypadku zastosowania płytek wybiegowych (rys.8d) długość $l$ jest równa szerokości przekroju, a w innych przypadkach należy ją zmniejszyć o dwa kratery (początek i koniec spawania) , czyli 2a.

W przypadku zastosowania spoin czołowych do zespawania przekroju zginanego momentem $M$ i ścinanego siłą poprzeczną $Q$ w sposób pokazany na rys 9d, naprężenia w spoinach wyznaczmy jak w przekroju rodzimym (analogicznie do 10 a,b):

$$\begin{equation} \sigma_ \perp=\sigma_{sp}= \dfrac{M}{I}\cdot z_1 \\ \tau_\parallel=\tau_{sp}=\dfrac{Q \overline S }{I \cdot t_1} \label {14} \end{equation}$$

gdzie $z_1$ oraz $t_1$ jest rzędną (odległością pionową od osi obojętnej) oraz grubością ścianki w punkcie 1 przekroju.

Nośność obliczeniową spoin czołowych o pełnym przetopie, z odpowiednim poziomem jakości wykonania, przyjmuje się równą nośności obliczeniowej słabszej z łączonych części, pod warunkiem, że będzie wykonana z odpowiedniego materiału wykazującego w próbie rozciągania spoiny minimalną granicę plastyczności i minimalną wytrzymałość na rozciąganie nie mniejszą od wartości nominalnych tych parametrów materiału rodzimego.

Oznacza to, że nie ma potrzeby sprawdzania nośności spoin czołowych zaprojektowanych na pełny przetop ,  Obecnie jako zasadę przyjmuje się projektowanie spoin czołowych na pełny przetop, a ponieważ taki wymóg jest zwykły, a nie szczególny, więc  nie opisuje się go w projekcie i na rysunkach. W przypadku dopuszczenia wykonania spoiny na niepełny przetop, powinno to być w sposób jasny opisany na rysunkach wykonawczych i w konsekwencji ujęte na rysunkach warsztatowych Wykonawcy.  W rezultacie  Wykonawca powinien spełnić wyższe wymogi jakości i odbioru spoin czołowych zgodnie z przedmiotowymi normami, kierowanymi w zasadzie wyłącznie do Wykonawcy ( [

PN-EN 1090-2+A1:2012, Wykonanie konstrukcji stalowych i aluminiowych – Część 2:  Wymagania techniczne dotyczące konstrukcji stalowych i szereg  norm z zakresu  spawalnictwa). W przypadku trudności w zapewnieniu odpowiedniego poziomu jakości wykonawstwa i materiałów dodatkowych, Wykonawca powinien zaproponować Projektantowi do zatwierdzenia rozwiązanie zamienne lub zrezygnować z przeprowadzenia prac spawalniczych.

Nośność obliczeniową spoin czołowych z niepełnym przetopem wyznacza się stosując metodę dla spoin z głębokim przetopem, ale ich grubość przyjmuje się nie większą od głębokości przetopu, jaka może być regularnie uzyskiwana.

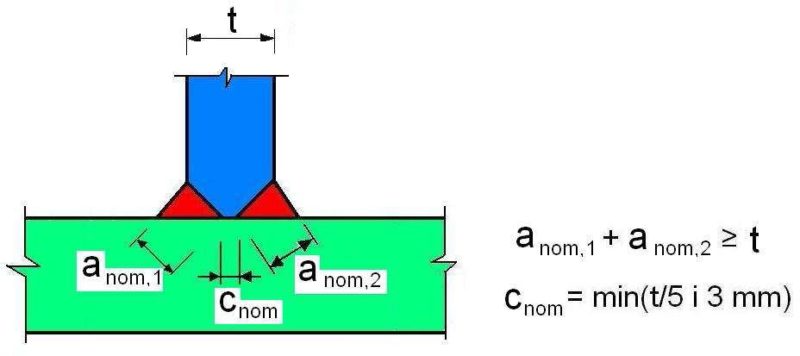
Rys.13 Spoina czołowa z niepełnym przetopem K  [4], rys. 23

Przykładowo nośność obliczeniową czołowego złącza teowego, z dwiema spoinami czołowymi z niepełnym przetopem K (rys.14)  można wyznaczyć jak w przypadku spoin czołowych z pełnym przetopem, pod warunkiem, że całkowita nominalna grubość spoiny spełnia wymagania podane na rys. 13. Jeśli nie są spełnione te wymagania, to ich grubość lub nośność ustala się jak dla spoin pachwinowych.

Spoiny obwodowe i otworowe

Rys. 14 Spoiny: a) obwodowe(otworowe wydłużone), b) otworowe  [4].rys. 4

Nośność obliczeniowa spoin pachwinowych obwodowych (wieńczących, ułożonych dookoła obwodu otworu wyciętego w jednej z blach w złączu zakładkowym – rys.14 a) określa się jak dla spoin pachwinowych.

Nośność obliczeniową spoin otworowych $F_{w,Rd}$ (rys. 14 b) określa się z wzoru

$$\begin{equation} F_{sp,Rd}=f_{ysp,d}\cdot A_{so} \label {15} \end{equation}$$

gdzie:
$f_{ysp,d}=\dfrac{f_y \sqrt{3}}{\beta_w \gamma_{M2}}$ – obliczeniowa wytrzymałość spoiny na ścinanie,
$A_{sp} $ – przekrój obliczeniowy spoiny, przyjmowany jako pole powierzchni otworu, który wypełnia spoina.

Wybrane przypadki złączy spawanych

Spoiny przerywane

Spoiny pachowinowe mogą być ułożone z przerwami miedzy nimi – jako spoiny przerywane, pokazane na rys. 15.
Spoiny czołowe wykonuje się tylko jako ciągłe.

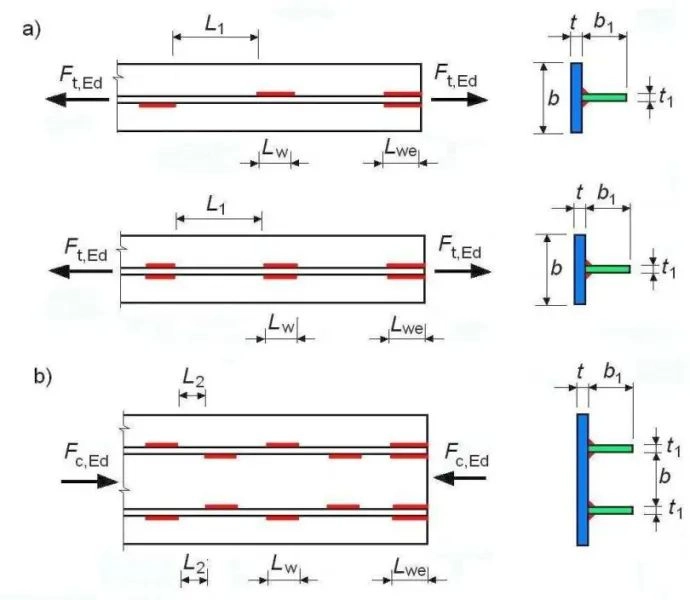
Rys. 15 Spoiny przerywwane: a) rozciągane, b) ściskane [5].rys. 16

Wymagania dotyczące przerw $L_1$ dla spoin rozciąganych oraz $L_2$ dla spoin ściskanych pomiędzy odcinkami spoin o długosci $L_w$ są następujące:

$$\begin{equation} L_i \le  \begin {cases}
min{\, [16t\, ;\, 16 t_1 \, ;\, 200] }& \textrm { dla i=1 – spoiny rozciągane}\\
min{\, [12t\, ;\, 12 t_1 \, ;\, 0,25b \,;\, 200] }& \textrm { dla i=2 – spoiny ściskane}\\
\end {cases} \label{16} \end{equation}$$

Przerwy między spoinami mierzy się jako wartość mniejszą z odległości pomiędzy końcami spoin po przeciwległych stronach i odległości pomiędzy końcami spoin po tej samej stronie. W każdym ściegu przerywanej spoiny pachwinowej jej odcinek skrajny wykonuje się zawsze na kaźdym końcu łączonych części. W elementach złożonych, w których blachy łączy się spoi/nami przerywanymi, zaleca się zastosować ciągłe spoiny pachwinowe na każdym końcu i z każdej strony blachy na długości nie mniejszej niź 3/4 szerokości węższej z łączonych blach.

Długości odcinków spoin przerywanych $L_w$ muszą spełniać warunek ($\ref{2}$)

Przyjmuje się je jako wartość mniejszą

Połączenia osiowo rozciągane

Na rys. 16 pokazano pachwinowe połączenie kątownika do blachy węzłowej w kilku wariantach ułożenia spoin.

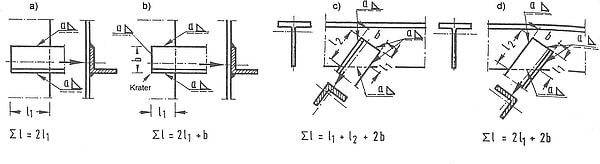
Rys.16  Połączenie osiowo rozciąganego kątownika z blachą węzłową: a) spoinami równoległymi i równych długości, b) spoinami równoległymi i poprzeczną, c) spoinami równoległymi różnych długości i jedną spoiną poprzeczną d)spoinami równoległymi różnych długości i dwoma spoinami poprzecznymi [1],rozdz.6 rys.29

W przypadku przedstawionym na rys. 17 długości spoin równoległych $l_1$ i $l_2$ należy dobierać tak, by siły w tych spoinach $F_1=\tau_{sp} A_{sp1}$ i $ F_2= \tau_{sp} A_{sp2}$ równoważyły się w sensie momentu, liczonego względem osi pręta ( rys. 16), tzn:

$$\begin{equation} F_1\cdot e_1 \cdot a_1 \cdot l_1=F_2 \cdot e_2 \cdot a_2\cdot l_2\to \dfrac{l_1 a_1}{l_2 a_2}=\dfrac{e_2}{e_1} \label {17} \end{equation}$$

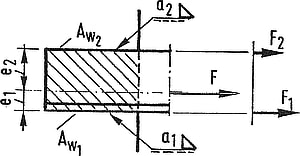
Rys.17 Długości spoin pachwinowych niesymetrycznych [1],

Spoiny pachwinowe długie

Na rys. 18 pokazano rozkład naprężeń po długości spoiny pachwinowej

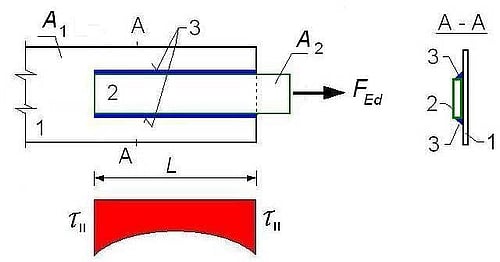
Rys.18 Rozkład naprężeń w długie spoinie pachwinowej: 1,2- łączone elementy, 3-spoina pachwinowa  [4], rys. 24

Wytężenie spoiny obliczone zgodnie z ($\ref{3}$) na początku i końcu „długiej” spoiny zwiększa się współczynnikiem $\beta_{Lw} \ge1$:

$$\begin{equation} \sigma_{sp}=\beta_{Lw} \cdot \sqrt{3}\tau_\parallel \label {19} \end{equation}$$

gdzie:

$$\begin{equation} \beta_{Lw} = \begin {cases}
1,0 & \textrm{ dla }  L \le 150 \cdot a_{sp}\\
1,2-\cfrac{0,2 \cdot L }{150 \cdot a_{sp}} \le 1,0 & \textrm{ dla }  L > 150 \cdot a_{sp}\\
&\textrm { dla spoin łączących żebra poprzeczne blachownic o L>1,7 m} \\
1,1= \cfrac{L}{18} & \textrm { przy czym } 0,6 \le \beta _{Lw} \le 1,0
\end {cases} \label{20} \end{equation}$$

Przykłady rachunkowe

Spoiny czołowe

Dane z przykładu 5,9 Goczek (2011) [6]

Sprawdzić nośność spoiny czołowej z pełnym (rys 19 a) i niepełnym przetopem (rys. 19 b).

Rys.19 Przykład 4.3. Spoina czołowa: a) z pełnym przetopem, b) z niepełnym przetopem

Elementy wykonano ze stali S235:

[7], tab. 3.1 $\to$  granica plastyczności $f_y= 235 \, MPa$ (dla $ t\le 40 \,mm$), wytrzymałość na rozciąganie  $f_u= 360 \, MPa$ (dla $ t \le 40 \,mm$).

[3]. tab. 2.1 $\to$ współczynniki częściowe: $\gamma_{M0}=1,0$ ; $\gamma_{M2}=1,25$

[3], tab. 4.1 $\to$ współczynnik korelacji dla spoin  $\beta_w=0,8$

przekrój poprzeczny płaskownika 20×160: $A=16 \cdot 2= 32 \, cm^2$.

Przypadek 1 – spoina z pełnym przetopem

[3], kl. 4.7.1(1)$\to$ nośność jak materiału rodzimego:

$F_{sp,Rd}=N_{t,Rd}=N_{pl.Rd}= \cfrac{A\cdot f_y}{\gamma_{M0}}=\cfrac{32 \cdot 235}{1,0} \cdot 10^{-1} =752,0 kN \le F_{Ed}$

Przypadek 2- spoina z niepełnym przetopem

Metoda kierunkowa [3], wzór (4.1) $\to$

Naprężenie w spoinie

$\sigma_\perp=\cfrac{F_{Ed}}{2 a l_{sp} } \, \sigma_{||}=\tau_{||}=\tau\perp=0$,

Nośność obliczeniowa spoiny

$(\ref{3}) , (\ref{4}) \to$  $ F_{sp,Rd} = min \{ \dfrac{f_u}{\beta_w \gamma_{M2}} \, ; \dfrac{0,9 f_u}{\gamma_{M2}}\} \cdot 2al_s= min \{ \dfrac{360}{0,8 \cdot 1,25} \, ; \cfrac{0,9\cdot 360}{1,25}\} \cdot 2 \cdot 6 \cdot 160= 497,7 \, kN$

Metoda uproszczona [3], pkt. 4.5.3.3

$\to$  obliczeniowa wytrzymałość spoiny na ścinanie [3], wzór (4.4)
$f_{v,sp,d}\dfrac{fu/\sqrt{3}}{\beta_w\gamma_{M2}}=\dfrac{360/\sqrt{3}}{0,8 \cdot 1,25}=208 \, MPa$

Nośność obliczeniowa spoiny  $F_{sp,Rd}=l_{sp} \cdot a\cdot f_{v,sp,d}=160 \cdot 2 \cdot 6 \cdot 208\cdot 10^{-3}=399,0 \, kN $

Wniosek:

Metodą uproszczoną uzyskano wynik  $\cfrac{399,0}{497,7}=80\% $ nośności spoiny. Metoda uproszczona prowadzi do nieefektywnych rozwiązań i powinna być stosowana wyłącznie przy projektowaniu wstępnym.

Spoiny pachwinowe zakładkowe. Przykład 1

Dane z przykładów 5,10 i 5.11, Goczek (2011) [6]

Wyznaczyć długość spoin łaczących rozciągany płaskownik (rys.20 a) oraz kątownik (rys.20 b) z blachą węzłową.

Zgodnie zasadą długość spoin należy wyznaczyć na nośność elementu rozciąganego.

Elementy wykonano ze stali S355:
[7], tab. 3.1, $\to$ granica plastyczności $f_y=355 \, MPa$, wytrzymałośc na rozciąganie $f_u=490 \, MPa$,

[3], tab. 2.1 $\to$ współczynniki częściowe $\gamma_{M0}=1,0 \, \gamma_{M2}=1,25$

[3], tab. 4.1 $\to$ współczynnik korelacji dla spoin pachwinowych $\beta_w=0.9$

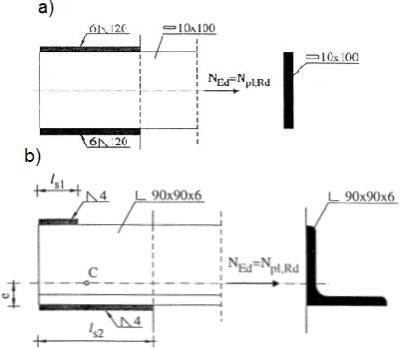
Rys.20 Połaczenie pachiwnowe: a) symetryczne , b) niesymetryczne [6], przykład 5.10, 5.11

Połączenie płaskownika 10×100

Nośność obliczeniowa płaskownika $N_{pl,Rd}=\dfrac{A\cdot f_y}{\gamma_{M0}}=\dfrac{1\cdot 10 \cdot 355}{1,0}=355 \, kN$

Naprężenia w spoinie pachwinowej  $ \tau_{||}=\cfrac{N_{pl,Rd}}{2\cdot l_{sp}\cdot a}; \quad \tau_\perp=\sigma_\perp=0$

Z warunku $\sigma_{sp}=\sqrt{\sigma_\perp^2+3(\tau_\perp^2+\tau_\parallel^2)}\le \dfrac{f_u}{\beta_2 \gamma_{M2}}$  [3], wzór. 4.1,  otrzymujemy graniczne naprężenia styczne:

$\tau_{R, ||}\le \dfrac{1}{\sqrt{3}} \dfrac{f_u}{\beta_w \gamma_{M2}}=\dfrac{1}{\sqrt{3}} \dfrac{490}{0,9 \cdot 1,25}=252 \, MPa$.

Po porównaniu z naprężeniami w spoinie, otrzymujemy warunek na potrzebną długość spoiny:

$l_{sp} > \dfrac{N_{pl,Rd}}{2a \tau_\parallel}=\dfrac{355}{2\cdot 0,6 \cdot 252}=11,8 \, cm$

Przyjęto $l_s= \, 120 \, mm $

Połączenie kątownika  L90x90x6

$ A=10,6 \, cm^2 $,
$e=24,0 \,mm $

Nośność kątownika na rozciąganie

$N_{pl,Rd}=\dfrac{10,6 \cdot 355}{1,0}=376,3 \, kN$

Potrzebna łączna długość spoin

$l_{sp1}+l_{sp2} > \dfrac{376,3}{0, 4 \cdot 252}=37,3 \, cm$

Przyjęto łączną długość spoin 380 mm

Długości spoin  różnicujemy tak, by środek ciężkości ich kładu pokrywał się z osią pręta, czyli

$\dfrac{l_{s2}}{l_{s1}}=\dfrac{b-e+a/2}{e+a/2}=\dfrac{90-24+4/2}{24+4/2}=2,62$

Stąd potrzebne długości spoin wynoszą:

$l_{sp1}=\dfrac{1}{1+2,62}\cdot 380=105 \,mm$,

$l_{sp2}=\dfrac{2,62}{1+2,62}\cdot 380=275 \, mm$.

Spoiny pachwinowe zakładkowe. Przykład 2

Na podstawie pracy Ptersen (2012) [1],rozdz.6 przykład 1

Sprawdzić nośność spoin w połączeniach pokazanych na rys. 21.

Siła rozciągająca $F=320 kN$. Elementy wykonano ze stali S235 ($f_y=235 \, MPa$, $f_u=360 \, MPa$).

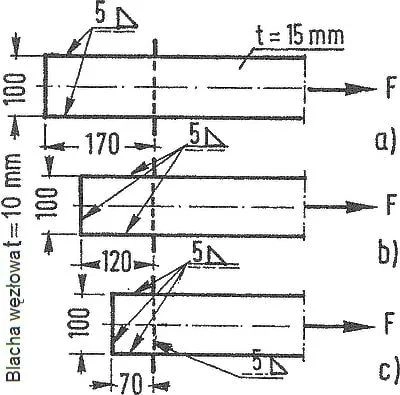
Rys.21. Przykład 1: spoiny pachwinowe [1],rozdz.6 rys.28

Sprawdzenie grubości spoin

a=5mm >min a= 2mm $\le \sqrt {max \, t}-0,5= \sqrt{16}-0,5= 3,37 mm$,
a= 5 mm < max a = 0,7 min t= $0,7 \cdot 10= 7 \, mm$.

Sprawdzenie długości spoin

l=70 mm (przypadek c) >min l= 6a= $6 \cdot 5=30 mm$ i $ 30 mm$
l=170 mm (przypadek a) < max l =150 a= $150\cdot 5= 450mm$

Sprawdzenie nośności pręta

$A=1,5 \cdot 10=15 \, cm^2 $,
$\sigma=\dfrac{320}{16}=213 \,MPa \le 235/1,0=235 \, MPa$.

Sprawdzenie nośności spoin – przypadek a)– spoiny tylko równoległe do siły F

zastępcze naprężenia graniczne  $\sigma_{sp,Rd}=\dfrac{f_u}{\beta_w \gamma_{M2}}=\dfrac{360}{0,8\cdot 1,25}=360 \, MPa$,

$A_{sp}=2\cdot 0,5 \cdot 17=17 \, cm^2$
$\tau_{||}=\dfrac{320}{18}=188,2 \, MPa$
$\sigma_{sp}=\sqrt{3}\cdot 188,2=326,0 \, MPa \le 360 \, MPa$

Sprawdzenie nośności spoin – przypadek b)– jedna spoina poprzeczna

pole spoin równoległych $A_\parallel=2\cdot 0,5 \cdot 12=12 \, cm^2$

pole spoiny poprzecznej $A_\perp=1 \cdot 0,5 \cdot 10=5 \, cm^2$

styczne naprężenia graniczne $\tau_{sp, Rd}= \dfrac{\sigma_{w,Rd}}{\sqrt{3}}=\dfrac{360}{\sqrt{3}}=207,8 \,MPa$

nośność spoin podłużnych $ F_\parallel=\tau_{w,Rd}\cdot A_\parallel=207,8 \cdot 12=249,4 \, kN$

wymagana nośność spoiny poprzecznej $F_\perp=F-F_\parallel=320-249,4= 70,6 \, kN$

wywoła napreżenie  $\sigma= \dfrac{F_\perp}{A_\perp}=\dfrac{70,6}{6}=141,2 \, MPa$

w spoinie poprzecznej wystąpią naprężenia:
$\tau_\parallel=0$,
$\tau_\perp=\sigma_\perp= \dfrac {\sigma}{\sqrt{2}}=\dfrac{141,2}{\sqrt{2}}=99,8 \, MPa$

naprężenia zastępcze w spoinie poprzecznej
$\sigma_{sp}=\sqrt{\sigma_\perp^2+ 3\tau_\perp^2}=\sqrt{99,8^2+3\cdot 99,8^2}=199,7 \,MPa \le 360 \, MPa$

Sprawdzenie nośności spoin – przypadek c)– dwie spoiny poprzeczne

pole spoin równoległych $A_\parallel=2\cdot 0,5 \cdot 7=7 \, cm^2$

pole spoin poprzecznych $A_\perp=2 \cdot 0,5 \cdot 10=10\, cm^2$

nośność spoin podłużnych $ F_\parallel=207,8 \cdot 7=145,5 \, kN$

wymagana nośność spoiny poprzecznej $F_\perp=320-145,5= 174,5 \, kN$

Naprężenia w spoinie poprzecznej:
$\sigma= \dfrac{174,5}{11}=174,5 \, MPa$
$\tau_\perp=\sigma_\perp= \dfrac{174,5}{\sqrt{2}}=123,4 \, MPa$

zastępcze  $\sigma_{sp}=\sqrt{123,4^2+3\cdot 123,4^2}=246,8 \,MPa \le 360 \, MPa$

Spoina pachwinowa w złożonym stanie naprężenia

Na podstawie pracy [1],rozdz.6 przykład 2

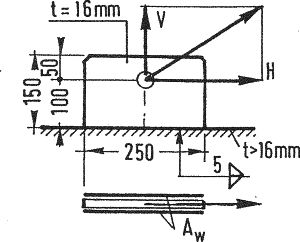
Sprawdzić nośność spoiny pachwinowej, pokazanej na rys. 22. Obciązenie: V=135 kN, H=200 kN

Rys.22 Spoina pachwinowa w złożonym stanie naprężenia

[1],rozdz.6 rys.31}"]

Sprawdzenie długości i grubości spoin

$\dfrac{l}{a}=\dfrac{250}{5}=50 \le 150\, \ge 5$

$\dfrac{a}{t}=\dfrac{5}{16}=0,31 <0,7$

Siły przekrojowe

$M=200 \cdot 10=2000 \,kNcm$,
$Q=200 \, kN$,
$N=135 \, kN$.

Charakterystyki geometryczne kładu spoin

$A_{sp}=2 \cdot 0,5 \cdot 25=25 \, cm^2$,
$W_{sp}= 2\cdot 0,5 \cdot 25^2/6= 104 \, cm^3$

Naprężenia w spoinie

$\sigma=\dfrac{135}{25}+\dfrac{2000}{104}=24,6 \, kN/cm^2$,

$\sigma_\perp=\tau_\perp=\dfrac{24,6}{\sqrt{2}}=17,4 \, kN/cm^2$,

$\tau_\parallel=\dfrac{200}{25}=8,0 \, kN/cm^2$.

$\sigma_{sp}=\sqrt{17,4^2+3(17,4^2+8,0^2)}=37,5 kN/cm^2 > \dfrac{36}{0,8\cdot 1,25}=36 \, kN/cm^2$.

Wniosek: należy przeprojektować połączenie , np. poprzez zwiększenie grubości spoiny do 6 (lub 5,5) mm.

Spoina pachwinowa pasowa

[6], przykład 5.13 

Sprawdzić nośność spoiny pasowej (łaczącej pas ze środnikiem blachownicy), pokazanej na rys. 23.
Siła poprzeczna $V_{z,Ed}= 400 \, kN$.

Stal S275: wytrzymałość na eroziąganie $f_u = 430 \, MPa$ , [7], tab. 3.1.
Współczynnik częściowy $\gamma_{M2}=1,25$  [3], tab. 2.1
Współczynnik korelacji spoin pachwinowych $\beta_w=0,85$ [3], tab. 4.1}

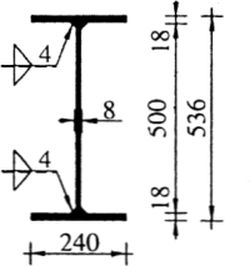
Rys.23 Przekrój blachownicy do przykładu [6], przykład 5.13

Moment bezwładności przekroju wzgledem osi y-y

$I_y=\dfrac{h^3 b_f-h_w^3(b_f-t_w}{13}=\dfrac{53,6^3 \cdot 24 -50^3(24-0,8)}{13}=66314,6 \, cm^4$.

Moment statyczny odciętej części pasa względem osi y-y

$S_{y,f}=b_f\cdot t_f\cdot (h_w+t_f)/2=24\cdot 1,8 \cdot(50+1,8)/2=1118,9 \, cm^3$

Naprężenia styczne równoległe do osi spoiny (rozwarstwiające) $\tau_{||}= \dfrac{V_{z,Rd}\cdot S_{y.f}}{I_y \sum a}= \dfrac{400 \cdot 1118,9}{66314,6 \dot 2 \cdot 0,4}=84 \, MPa$

Warunek nośności spoiny

$\tau_\parallel=84 \, MPa \le \dfrac{f_u}{\sqrt{3}\beta_2 \gamma_{M2}}=\dfrac{430}{\sqrt{3} \cdot 0.85 \cdot 1,25}=234 \, MPa$.

Połączenie spawane rygla ze słupem

[6], przykład 5.15 

Sprawdzić spoiny w połaczeniu rygla ze słupem stalowym wg rys. 24

Zgodnie z zasadą spoiny powinny być zaprojektowane na nośność, to znaczy ich nośność nie powinna być mniejsza od nośności elementów łączonych.

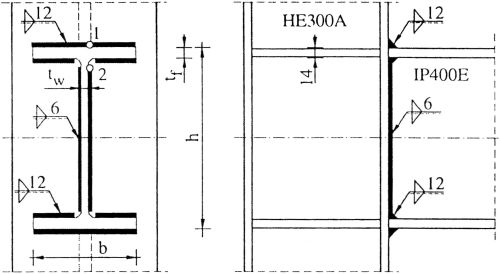
Rys.24 Połaczenie spawane rygla ze słupem [6], przykład 5.15 -1 cz.

Profil IPE 400 ma następujące charakterystyki ( z tablic):

$h=400 \, mm$, $b=180 \, mm$ , $t_f =13,5 \, mm$, $t_w =8,6 \, mm$, $r =21,0 \, mm$, $W_{pl,y} = 1307 \, cm^3$,

Charakterystyki geometryczne kładu spoin:

Pole powierzchni
$A_{sp}=2\cdot 1,2(2 \cdot 18-0,86-2\cdot 2,1)+2\cdot 0,6(40-2\cdot 2,1-2 \cdot 1,35)=114,0 \, cm^2$,

Pole powierzchni spoin pionowych
$A_{sp,w}=2\cdot 0,6(40-2\cdot 2,1-2\cdot 1,3)=39,7 \, cm^2$

Pole powierzchni spoin poziomych
$A_{sp,f}=2a_f(2b-t-w-2r)=2\cdot 1,2(2\cdot18-0,86-1\cdot 2,1)=74,3 \, cm^2$

Moment bezwładności względem osi y-y

$I_{sp,y}=\dfrac{1,2\cdot 18(40+1,2)^2}{2}+\dfrac{1,2(18-0,86-2\cdot 2,1)(40-2\cdot 1,35 -1,2)^2}{2}+\dfrac{0,6(40-2\cdot2,1-2\cdot1,35)^3}{7}=32077 \, cm^4$

Wskaźniki wytrzymałości sprężystej w punktach (1) i (2) kładu

$W_{sp,1}= \dfrac{32077}{(40+1,2)/2}=1557 \, cm^3$, $W_{sp,2}= \dfrac{32077}{(40+-2\cdot1,35-2\cdot 2,1))/2}=1938 \, cm^3$

Rozpatrzymy dwie kombinacje sił przekrojowych:

Przypadek 1: Moment zginający $M=M_{pl,Rd}$ w kombinacji z siłą poprzeczną $V=0$,
Przypadek 2: Siła poprzeczna $V=V_{pl, Rd}$ w kombinacji z momentem zginającym $M=M_{V,y,Rd}$

Przypadek 1

Dla przypadku 1  sprężysty rozkład naprężeń pokazano na rys. 25 b i c.

Moment zginający
$M+M_{pl,Rd}= \dfrac{W_{pl,y} f_y}{\gamma_{M0}}=\dfrac{1307 \cdot 355}{1,0}=464 \, kNm$

Naprężenia w pkt (1) styku rygla ze słupem:
$\sigma_1=\dfrac{M}{W_1}=\dfrac{464}{1557}= 298 \,MPa $
$\tau_1=0$.

Naprężenia te rozkładają się na składowe w spoinie (rys. 24 f):

$\sigma_\perp=\tau_\perp= \dfrac{\sigma_1}{\sqrt{2}}=\dfrac{298}{\sqrt{2}}=211 \, MPa$

$ \tau_\parallel=0$

Naprężenie zastępcze w spoinie
$\sigma_{sp}=\sqrt{\sigma_\perp^2+3(\tau_\perp^2+\tau_\parallel^2)}=\sqrt{211^2+3\cdot 211^2}=421 \,MPa $,

Warunki nośności
$\sigma_{sp} =421 MPa \le \dfrac{f_u}{\beta_w \gamma_{M2}}=\dfrac{490}{0,9\cdot 1,25}=436 \, MPa$
$ \sigma_\perp=211 MPa < \dfrac{0,9 f_u}{\gamma_{M2}}=\dfrac{0,9 \cdot 490}{1,25}=353 \, MPa$

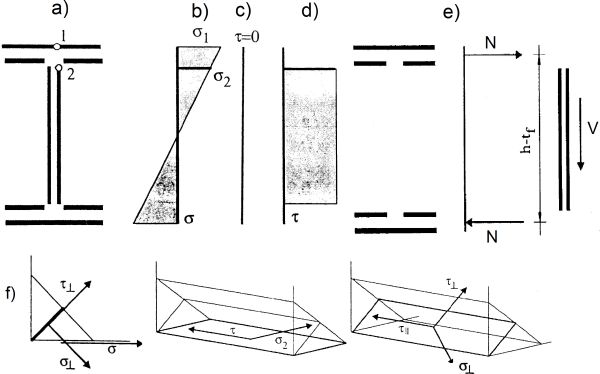
Rys.25 Rokłady naprężeń w przkroju połaczenia z przykłądu: a) kład spoin z punktami (1) i (2), b) rozkład sprężystych naprężeń normalnych, c) rozkłąd naprężeń stycznych dla V=0 , d) rozkład naprężeń stycznych dla niezerowej siły poprzecznej, e) rozkład sił w stanie plastycznym, f) oznaczenia naprężeń w spoinie [6]. przykład 5.15 – 2 cz.

Przypadek 2 – sprężyście

Dla przypadku 2  sprężysty rozkład naprężeń pokazano na rys. 25 b i d.

Pole czynne przekroju elementu przy ścinaniu
$A_v= max \{ \eta \cdot h_w \cdot t_w \, ; A-2 \cdot b \cdot t_f+(t_w+2r) t_f\}= max \{ 1,2 \cdot 37,3 \cdot 0,86 \, ;84,5 -2 \cdot 18 \cdot 1,35+(0,86+2 \cdot 2,1) 1,35\}=42,7 \, cm^2$ [7], 6.2.6(3)(a), kl. N19,

Siła poprzeczna (na nośność)
$V (=V_Ed) =V_{pl,Rd}=A_v \dfrac{f_y}{\sqrt{3} \gamma_{M0}}=42,7 \dfrac{355}{\sqrt{3}\cdot 1,0}=875,8 \,kN$

Moment zginający (na nośność)
$\rho=\left ( \dfrac{V_{Ed}}{V_{pl,Rd}}-1\right)^2=1,0$,
$M=(M_{Ed})=M_{V,y,Rd}=\left( W_{pl,y}-\dfrac{\rho \cdot A_V^2}{4\cdot t_w}\right) \dfrac{f_y}{\gamma_{M0}}=\left ( 1307 \cdot 10^{-6} – \dfrac{1,0 \cdot 42,7^2}{4 \cdot 8,6 \cdot 10^{-1}}\right)\dfrac{355 \cdot 10^3}{1,0}= 275,6 \, kNm$

Naprężenia w pkt (2) przekroju

$\sigma_2= \dfrac{M}{W_2}=\dfrac{275,6}{1938}=142 \, MPa$,
$\tau_2= \dfrac{V}{A_{w,w}}=\dfrac{875,8}{39,7}=220 \, MPa$

Naprężenia kierunkowe w spoinie

$\sigma_\perp=\tau_\perp=\dfrac{\sigma_2}{\sqrt{2}}=\dfrac{142}{\sqrt{2}}=100 \, MPa$,
$\tau_\parallel= \tau_2=220 \, MPa$

Warunki nośnosci spoiny

$\sigma_{sp}=\sqrt{100^2+3(100^2+220^2)}=432 \, MPa , \dfrac{490}{0,9 \cdot 1,25}=436 \, MPa$
$\sigma_\perp=100 \, MPa < \dfrac{0,9\cdot 490}{1,25}=353 \, MPa$

Przypadek 2 – plastycznie

Dla przypadku 2  plastyczny rozkład naprężeń pokazano na rys. 25 e.

Moment zginający przenoszą spoiny pasów, a siłę tnącą spoiny środnika . Para sił $N$ w środku ciężkości pasów wynosi

$N=\dfrac{M}{h-t_f}=\dfrac{275,6}{40-1,35}=713,1 \, kN$.

Naprężenia w  pasach: $\sigma= \dfrac{N}{A_{w,f}/2}=\dfrac{713,1}{74,3/2}=192 \, MPa$, $\tau=0$

Naprężenia w spoinie $\sigma_per=\tau_per=\dfrac{192 }{\sqrt{2}}=136 \, MPa$

Warunki nośnosci spoiny

$\sigma_w=\sqrt{136^2+3\cdot 136^2)}=272 \, MPa <\dfrac{490}{0,9 \cdot 1,25}=436 \, MPa$
$\sigma_\perp=136 \, MPa < \dfrac{0,9\cdot 490}{1,25}=353 \, MPa$

Naprężenia w środniku: $\sigma= 0 \, \tau=\dfrac{875,8}{39,7}=220 \, MPa$,

Naprężenia w spoinie $\sigma_\perp=\tau_\perp=0 $ ; $\tau_\parallel=\tau=220 \, MPa $,

Warunki nośnosci spoiny

$\sigma_w=\sqrt{3 \tau_\parallel^2}=\sqrt{3\cdot 220^2}=382 \, MPa< \dfrac{490}{0,9 \cdot 1,25}=436 \, MPa$

Uwaga: w węźle połączenia rygla ze słupem należałoby jeszcze sprawdzić warunki nośności: 1) środnika słupa z warunku ścinania, 2) środnika słupa w strefie poprzecznego ściskania, 3) środnika słupa w strefie poprzecznego rozciągania, 4) pas i środnika belki w strefie ściskanej. Takie sprawdzenia są przedstawione w innych artykułach.

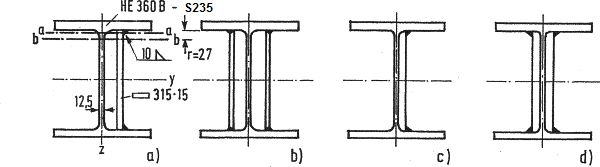
Wzmocnienie belki nakładkami na środnik

Zaprojektować  wzmocnienie belki HEB 360 -S235 obciążonej siłami : M=400 kNm, V=800 kN, pokazanej na rys. 26.

Rys.26. Wzmocnienie belki nakładkami: a), c) jednostronne, b), d) dwustronne.

Belka HEB 360 ma charakterystyki : $I_y= 43190 \, cm^4$, $W_{el,y}=2400 \, cm^3$,  $S_{1/2H}=1340 , cm^3$ (moment statyczny połówki przekroju).

Naprężenia sprężyste w przekroju przed wzmocnieniem
$\sigma=\dfrac{400}{2400}=166,67 MPa< f_y=235 \, MPa$,

$\tau=\dfrac{800 \cdot 1340}{43190 \cdot 1,25}=198,6 \, MPa > \dfrac{235}{\sqrt{3}\cdot 1,0}=135,7 \,MPa$

Środnik belki wzmocniono jednostronną nakładką  bl.15×315 (rys. 25a) . Dla wzmocnionego przekroju:

$I_y= 43190+1,5 \cdot 31,5^2/12=47097 \, cm^4$
$W_y=47097/18=2617 \, cm^3$

Przekrój a-a:
Moment statyczny odciętej części przekroju: $S_a= 30\cdot 2,25\cdot 16,88=1139 \, cm^3$

$\sigma=\dfrac{400}{2617}=152,8 \, MPa$
$\sigma_a=\dfrac{400}{47097}(18,0-2,25)=133,8 \,MPa$
$\tau_a= \dfrac{800\cdot 1139}{47097\cdot(1,15+1,5)}=71,7 \, MPa$

W spoinie a=10 mm:  $\sigma_\parallel=\sigma_a$, $\tau_\parallel=\tau_a$ są małe. Dalsze sprawdzenie pomija się.

Przekrój b-b:

$S_b=1340-1,25 (\dfrac{18-2,25-2,7}{2})^2+1,5\cdot 2,7\cdot(18-2,25-2,7/2)=1185 \, cm^3$
$\sigma_b=\dfrac{400}{47097}(18-2,25-2,7)=102,3 \, MPa$
$\tau_b= \dfrac{800\cdot 1185}{47097\cdot(1,25+1,5)}=73,2 \, MPa$
$\sigma_0=\sqrt{102,3^2 + 3 \cdot 73,2^2}=162,9 \, MPa < 235 \, MPa$

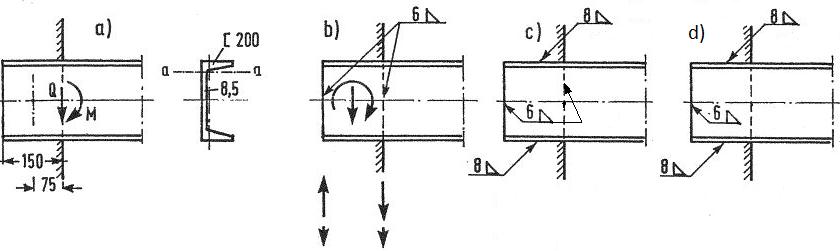
Skręcany układ spoin

Sprawdzić nośność spoin w połączeniu ceownika z blachą węzłową (rys. 27), obciążonego momentem  M=30 kNm oraz siłą poprzeczną Q=120 kN. Ceownik wykonany jest ze stali S235.

W środku zamocowania działa moment skręcający:   $M_v=30+120\cdot 0,075=39 \, kNm$  oraz siła poprzeczna: $T=Q=120 kN$

Rys,.27 Spoiny pachwinowe skręcane i ścinane

Może zajść klika przypadków wykonania połączenia:

1) ułożone są tylko pionowe spoiny (o grubości a=6 mm) – rys.27 b,

2) spoiny wystąpią na obwodzie (rys.27 c).

3) wykonane są wybrane ze wskazanych spoin, np.: obie poziome i lewa pionowa  (rys.27 d).

Przypadek 1) (tylko spoiny pionowe – rys.27 b)

Sprawdzenie warunków na grubość spoiny
$ \dfrac{a}{t}=\dfrac{7}{8,5}=0,71 \approx 0,7$

Siły pionowe od momentu skręcającego:
$ N_M=39/0,15= \pm 260 kN$

Siły pionowe od siły poprzecznej

$ N_T= 120/2=60 kN$

Maksymalna siła pionowa

$N=260+60=320 kN$

$A_{sp}=0,6(20-2\cdot 0,6)=11,28 \, cm^2$

$\tau_\parallel=320/11,28 \cdot 10^1=284 \, MPa  > \tau_{R,sp } = \dfrac{1}{\sqrt{3}} \dfrac{360}{0,8 \cdot 1,25}=208 \, MPa$.

Zastosowanie tylko spoin pionowych jest niewystarczajace. Należy ułożyć spoiny poziome.

Przypadek 2) (spoiny na obwodzie rys.27c)

Do rozwiązania zadania skręcania obwodowego układu spoin zastosujemy analogię  do swobodnego skręcania pręta cienkościennego o przekroju zamkniętym ,

to znaczy wzór Bredta do wyznaczenia strumienia naprężeń stycznych wywołanych momentem skręcającym $M_v$

$$\begin{equation} \tau_v=\dfrac{M_v} {2 \Omega \cdot t} \label {21} \end{equation}$$

gdzie

$$\begin{equation} \Omega=\dfrac {1}{2}\oint h ds\label {22} \end{equation}$$

jest polem powierzchni ograniczonej konturem, to jest linią  środkową spoin.

Pole powierzchni ograniczonej linią środkową spoin to pole prostokąta o szerokości $b_{sp}=15-0,6=14,4 \, cm $ i wysokości  $h_{sp}=20-0,8=19,2 \, cm}, czyli

$\Omega_{sp}=14,4 \cdot 19,2= 276,5 \, cm^2$.

Naprężenia styczne od skręcania w spoinie pionowej (t=0,6 \, cm$ :  $\tau_v=\dfrac{39} {2 \cdot 276,5 \cdot 0,6} \cdot 10^3 = 117 \, MPa$.

Naprężenia styczne od ścinania w spoinach równoległych do kierunku siły (w spoinach pionowych) :  $\tau_T=\dfrac{120} {2 \cdot  20 \cdot 0,6} \cdot 10^1 = 50 \, MPa$.

Sumaryczne naprężenia: $\tau_\parallel=117+50=167 \, MPa <  \tau_{R,sp } = =208 \, MPa $

Przypadek 3) (wybrane spoiny rys.27 d)

Do rozwiązania zadania skręcania otwartego układu spoin zastosujemy analogię  do swobodnego skręcanie pręta cienkościennego o przekroju otwartym,

Maksymalne Naprężenia styczne od skręcania wyznaczymy ze wzoru

$$\begin{equation} max \tau_v = \dfrac {M_v}{I_v}t \label {23} \end{equation}$$

gdzie moment bezwładności przekroju otwartego na skręcanie wyznaczamy z zalezności

$$\begin{equation} I_v= \dfrac{1}{3}\sum \limits_{i=1}^n t_i^3 l_i \label {24} \end{equation}$$

gdzie $l_i$ , i $t_i$ – długość i grubośc i-tego odcinka spoiny.

W zadaniu mamy

$ I_v= \dfrac{1}{3} \cdot (0,6^3  \cdot 20 + 2 \cdot 0,8^3 \cdot 15)=6,56 cm^4$

$ max\, \tau_v = \dfrac {39}{6,56 } \cdot 0,6 \cdot 10^3=3567 ,\ MPa \gg \tau_{R,sp }$.

Pominięcie  spoiny pionowej nie jest możliwe.Literatura

1. Petersen, C. (2013). Stahlbau: Grundlagen der Berechnung und baulichen Ausbil-dung von Stahlbauten (4 Wydanie- überarb. und aktualisierte Aufl). Springer Vieweg
2. PN-EN 1993-1-3:2008, Eurokod 3: Projektowanie konstrukcji stalowych. Część 1-3: Reguły uzupełniające dla konstrukcji z kształtowników i blach profilowanych na zimno
3. PN-EN 1993-1-8 +Ap1+AC:2006, Eurokod 3 -Projektowanie konstrukcji stalowych -Część 1-8: Projektowanie węzłów
4. Biegus, A. (2010). Projektowanie konstrukcji stalowych według Eurokodu 3. Część 5 – Połączenia spawane. Materiały dydaktyczne. Wykład: Politechnika Wrocławska, Wydział  Budownictwa Lądowego i Wodnego, Wrocław. [ http://metale.pwr.wroc.pl/files/A.Biegus-Polaczenia_Srubowe.pdf ]
5. Biegus, A. (2010). Projektowanie konstrukcji stalowych według Eurokodu 3. Część 5 – Połączenia spawane. Materiały dydaktyczne. Wykład: Politechnika Wrocławska, Wydział  Budownictwa Lądowego i Wodnego, Wrocław. [ http://metale.pwr.wroc.pl/files/A.Biegus-Polaczenia_Srubowe.pdf ]
6. Goczek J., Supeł Ł., Gajdzicki, M. (2011). Przykłady obliczeń konstrukcji stalowych: Eurokod 3-1-1, Eurokod 3-1-3, Eurokod 3-1-5, Eurokod 3-1-8. Wydawnictwo Politechniki Łódzkiej
7. PN-EN 1993-1-1+A1:2006, Eurokod 3 – Projektowanie konstrukcji stalowych – Część 1-1: Reguły ogólne i reguły dla budynków

________________________________