Elementy i połączenia podlegające znacznej liczbie zmian naprężeń należy sprawdzić oprócz zwykłych warunków nośności i użytkowalności również  wstanie granicznym zniszczenia zmęczeniowego  SGN- FAT .  Zgodnie z normą [1] możliwe są dwa podejścia:  naprężeń nominalnych lub naprężeń geometrycznych .

Metoda naprężeń nominalnych (MNN) i geometrycznych (MNG)

Metoda naprężeń geometrycznych (MNG) wymaga wyznaczenia zakresu zmienności naprężeń geometrycznych, czyli największych naprężeń w materiale rodzimym, w sąsiedztwie początku spoiny, uwzględniających  lokalny wpływ karbu konstrukcyjnego (całkowitej geometrii konstrukcji), lecz pomijających lokalny wpływ spiętrzenia spowodowany geometrią  spoiny i jej nieciągłościami. Tak wyznaczony zakres zmienności naprężeń geometrycznych porównuje się z odpowiednią dla tej metody wytrzymałością zmęczeniową, inną niż w przypadku metody naprężeń nominalnych.  MNG jest metodą nowoczesną i dokładniejszą, ale wymaga prowadzenia obliczeń MES, co jest praktycznie technicznie uzasadnione tylko w przypadku elementów maszyn i wyodrębnionych elementów konstrukcji, a staje się zbyt pracochłonne i kosztowne dla systemów konstrukcji budowlanych.

Metoda naprężeń nominalnych (MNN)  jest często nazywana metodą klasyfikacyjną. Zakres zmienności naprężeń normalnych $\Delta_{\sigma}$ lub  stycznych $\Delta \sigma $ od zmieniających się obciążeń wyznacza się dla naprężeń nominalnych, tzn przy obliczeniowym pominięciu występującego spiętrzenia naprężeń. Wartość tak wyznaczonego zakresu zmienności naprężeń porównuje się z wytrzymałością zmęczeniowa, określoną dla danego typu karbu, występującego w miejscu wyznaczenia naprężeń. Taka wytrzymałość zmęczeniowa ujmuje  w sobie wielkość spiętrzenia, rozrzut wyników badań zmęczeniowych, wpływ naprężeń własnych itp.

W metodzie MNN olbrzymią różnorodność karbów występujących w konstrukcjach  i różniących się od siebie stopniem spiętrzenia naprężeń (mimo ich geometrycznego podobieństwa) sprowadzono do tylko 14 typów dla zakresów zmienności naprężeń normalnych i do 2 typów dla zakresów zmienności naprężeń stycznych. Uproszczenie spowodowało, że w wielu przypadkach obliczeniowa wytrzymałość na zmęczenie określana jest dla ostrzejszego karbu ofd faktycznie występującego w konstrukcji. Metoda naprężeń nominalnych (MNN) jest konserwatywna, tradycyjna i może prowadzić do znacznych niedokładności , choć jest prosta i stosowana w EC3 [1].

W niniejszym artykule  zajmujemy się tylko metodą MNN.

Analiza naprężeń w karbie

Definicje podstawowe

Zmęczenie  wywoływane jest zmieniającymi się naprężeniami. Przebieg zmienności naprężeń w czasie nazywany jest widmem naprężeń.

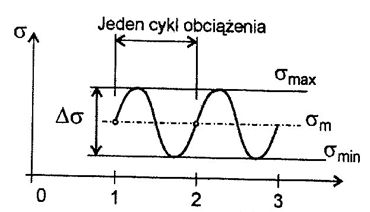
Najprostszym przykładem zmienności  naprężeń jest widmo jednorodne, czyli widmo naprężeń o stałej amplitudzie ,  które jest charakteryzowane wartościami naprężeń maksymalnych $\sigma_{max}$ oraz minimalnych $\sigma_{min}$ w poszczególnych cyklach , oraz zakresem zmienności (amplitudą). Zakres zmienności naprężeń  (normalnych  $\sigma$ oraz stycznych $\tau$ przyjmuje się jako algebraiczną różnicę maksymalnego i minimalnego naprężenia w rozpatrywanym punkcie konstrukcji, a naprężenie średni jako średnią arytmetyczną tych naprężeń (rys.1)

$$\begin{equation}  \Delta \sigma = (\sigma_{max}- \sigma _{min}) \; \hspace{1 cm}  \Delta \tau = (\tau_{max}- \tau _{min} )\end{equation}$$

$$\begin{equation}  \sigma_m =(\sigma_{max}+\sigma_{min})/2\end{equation}$$

Rys.1 Amplituda i średnia naprężeń

W przypadku elementów niespawanych lub spawanych odprężonych oraz cykli naprężeń całkowicie lub częściowo ściskających norma [1] zezwala na wyznaczenie zredukowanego zakresu zmienności naprężeń normalnych, uwzględniających tylko 60% zakresu zmienności naprężeń ściskających $\sigma_c$ i 100% naprężeń rozciągających $\sigma_t$

$$\begin{equation}  \Delta \sigma = 0,6 \cdot  \lvert \sigma_c \rvert + \vert  \sigma _t \rvert \end{equation}$$

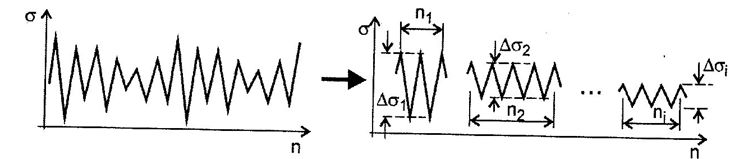
W przypadku widma o nieregularnej  zmienności naprężeń (tzw widma niejednorodnego) norma zaleca zastosowanie jednej z technik zliczania cykli w celu zamiany takiego widma na równoważny mu zbiór widm jednorodnych(rys.2).

Rys.2 Transformacja widma niejednorodnego na równoważne jednorodne

[2]

Najbardziej rozpowszechnioną metodą zliczania cyklu jest metoda „zbiornikowa”.

Metoda zbiornikowa

W metodzie zbiornikowej do zliczania cykli obciążeń bierze się reprezentatywny, powtarzalny przedział zmienności oszacowanej (lub pomierzonej) historii naprężenia. Przyjęty do analizy przedział musi powtarzać się w dłuższym okresie, a wyznacza się go między największymi wartościami naprężeń. Wykres zmienności naprężeń w takim przedziale traktuje się jak ściany zbiornika wypełnionego wodą. Procedura zliczania cykli polega na znajdowaniu najniżej położonego punktu wykresu i wyobrażeniu sobie, że otwiera się tam korek i spuszcza wodę (rys.3).

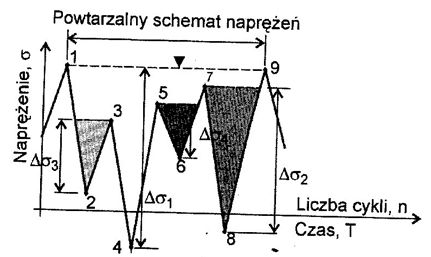
Rys.3. Zliczanie cykli metodą zbiornikową [2]

Spuszczenie wody z najniższego punktu (pkt 4 na rys wyżej) odpowiada zliczeniu jednego pełnego cyklu obciążenia o zakresie $\Delta \sigma_i$. W podobny sposób w kolejnych krokach „opróżnia się” wodę z pozostałych fragmentów zbiornika, w których jeszcze pozostała, znajdując za każdym razem najniżej położony punkt wykresu. Pozwala to na zliczenie kolejnych zakresów zmienności obciążenia $\Delta \sigma_i$, liczonych jako różnica pomiędzy obecnym poziomem spuszczanej wody, a poziomem „otwieranego” korka. Liczba cykli obciążeń n , odpowiadająca danemu zakresowi zmienności $\Delta \sigma_i$, jest liczbą „wyciągnięć korka”. Procedurę tą powtarza się, aż do całkowitego „opróżnienia” zbiornika. Najważniejszą zasadą opisanej procedury jest opróżnianie i zliczanie w pierwszej kolejności zbiorników, w których występuje największa wysokość słupa wody, czyli największy zakres naprężeń. Wyznaczając całkowitą liczbę cykli obciążeń odpowiadającą rozpatrywanemu rozpatrywanemu zakresowi naprężeń $\Delta \sigma_i$,, trzeba również uwzględnić  ile razy analizowany schemat obciążenia powtarza się podczas eksploatacji konstrukcji.

Przykład zliczania  cykli metodą zbiornikową

Mamy zarejestrowaną (lub wyznaczoną analitycznie)  historię naprężenia w elemencie pokazana na rys.4.  Pokazana sekwencja jest powtórzona  $1,1 \cdot 10^5$ razy  w całym okresie użytkowania obiektu.

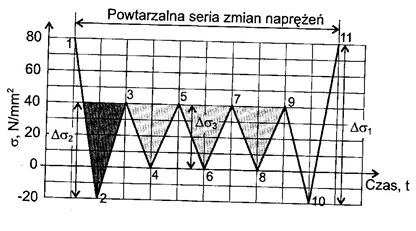
Rys.4. Przykładowe niejednorodne widmo naprężeń do metody zbionikowej [2]

Liczbami nieparzystymi ponumerowano lokalne ekstrema, natomiast parzystymi lokalne minima. Kolejne etapy otwierania „korków”:
; otwarcie korka w pkt 4 ; otwarcie korka w pkt 6 ; otwarcie korka w pkt 8.

Zliczenie cykli:
otwarcie korka w pkt 10: $\Delta \sigma_1 =80 -(-20)= 100 N/mm^2$,
otwarcie korka w pkt 2:  $\Delta \sigma_2=40 -(-20) = 60 N/mm^2$ ,
otwarcie korka w pkt 4:  $\Delta \sigma_3=40- 0= 40  N/mm^2$ ,
otwarcie korka w pkt  8:  $\Delta \sigma_3=40- 0= 40  N/mm^2$ ,
otwarcie korka w pkt 6:  $\Delta \sigma_3=40- 0= 40  N/mm^2$ ,

Zliczenie cykli :
$\Delta \sigma_1=100 N/mm^2$  – 1 cykl ,
$\Delta \sigma_2=60 N/mm^2$  – 1 cykl.
$\Delta \sigma_3=40 N/mm^2$  – 3 cykle

Liczba cykli w całej historii obciążenia:
$\Delta {\sigma_1}=100 n/mm^2$ ; $n_{E1}= 1,10 \cdot 10^5 $ ;
$\Delta {\sigma_2}=60 N/mm^2$  $n_{E2}= 1,10 \cdot 10^5$;
$\Delta {\sigma_3}=40 N/mm^2$  $n_{E3}= 3,30 \cdot 10^5$.

Wyznaczanie naprężeń w karbie w metodzie  MNN

W metodzie MNN zakres zmienności naprężeń wyznacza się  według formuł klasycznej wytrzymałości materiałów, które dla rozciąganego i zginanego poprzecznie pręta pryzmatycznego mają postać:

$$\begin{equation}   \sigma =\dfrac{N}A{}+\dfrac{M_y}{I_z} \cdot z +\dfrac{M_z}{I_y} \cdot y\end{equation}$$

$$\begin{equation}   \tau =\dfrac{V \cdot S}{I \cdot t}\end{equation}$$

gdzie siły przekrojowe wyznacza się dla obciążeń częstych oddziaływania zmiennego o wartości charakterystycznej $\Psi_1 \cdot Q_k$

W przypadku elementów belkowych uogólnionych (Własowa) należy dodać człony od bimomentu oraz od skręcania swobodnego i nieswobodnego.

Naprężeniami miarodajnym do wyznaczenia zmienności naprężeń w spoinach są naprężenia normalne

$$\begin{equation}  \sigma_{wf}=\sqrt{ {\sigma_{\perp f}}^2+ {\tau_{\perp f}}^2} \end{equation}$$

lub naprężenia ścinające $\tau_{wf}$ wzdłuż osi spoiny

$$\begin{equation}  \tau_{wf}=\tau_{||f} \end{equation}$$

Wytrzymałość zmęczeniowa

Krzywa zmęczeniowa

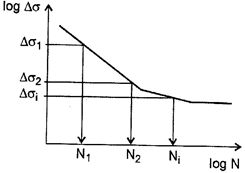
Aby określić wytrzymałość zmęczeniowa przy innej liczbie cykli naprężeń, norma [1] podaje zależność między zmiennością naprężeń, a liczbą cykli do zniszczenia w postaci zbioru krzywych, osobnych dla naprężeń normalnych   ($log \Delta \sigma_R -log N$) i dla naprężeń stycznych  ($log \Delta \tau_R -log N$). Takie krzywe często są określane mianem krzywych S-N. Przykładowy kształt jednej z krzywych dla naprężeń normalnych i stycznych pokazano na rys. 5 dla naprężeń nrmalnych i rys 6 dla naprężeń stycznych:

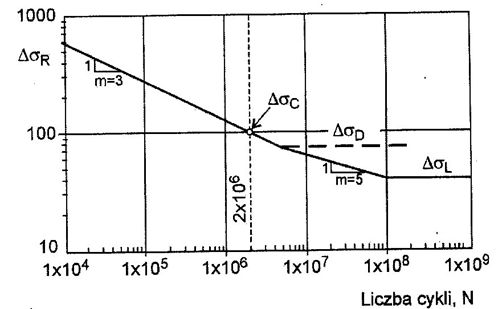
Rys.5 Krzywa zmęczeniowa dla naprężeń normalnych [1]

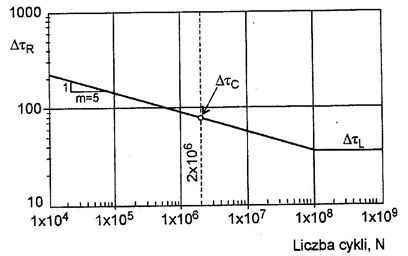
Rys 6 Krzywa zmęczeniowa dla naprężeń stycznych [1]Charakterystycznymi punktami krzywej zmęczeniowej są:

$\Delta \sigma_c$  ,  $\Delta \tau_c$  wytrzymałość zmęczeniowa normatywna  – podstawowym parametr, opisującym karb w metodzie MNN,

Jest to zakres zmienności naprężeń o stałej amplitudzie,  odpowiadający zniszczeniu przy liczbie cykli $N=2 \cdot 10^6$. Ten zakres naprężeń wyrażony w N/mm2 jest nazywany również kategorią zmęczeniową

$\Delta \sigma_d$ wytrzymałość zmęczeniowa graniczna

Jest to wartość zakresu naprężeń normalnych  przy stałej amplitudzie, dla której następuje załamanie krzywej zmęczeniowej

$\Delta \sigma_L$ wytrzymałość zmęczeniowa trwała

Jest to graniczna wartość zakresu naprężeń normalnych  przy stałej amplitudzie, poniżej której  w badaniach nie występuje nachylenie  krzywej zmęczeniowej

nachylenie krzywej zmęczeniowej  dla naprężeń normalnych ($ log  \Delta \sigma – log N$ ) (rys. 5), przyjmuje wartości:

1. dla liczby cykli do $N \le<= 5 \cdot 10^6 wynosi 1:3 ;
2. dla  liczby cykli $ 5 \cdot 10^6 < N < 10^8 wynosi 1:5.

W przypadku krzywej zmęczeniowej dla ścinania ($log \Delta \tau-log N$)  (rys.6) nachylenie odcinka prostej jest stałe w zakresie $1 \cdot 10^4 < N < 10^8$ i wynosi 1:5

Wytrzymałość zmęczeniowa

Wytrzymałość zmęczeniowa odnosząca się do naprężeń normalnych o stałej amplitudzie jest funkcją liczby cykli naprężeń, wyrażoną jako

$$\begin{equation}  \Delta\sigma_R^m \cdot N_R=\Delta\sigma_c^m \cdot 2 \cdot 10^6 \text { gdy } 1 \cdot 10^4 \le  N \le 5 \cdot 10^6 \end{equation}$$

przy czym $m=3$ , oraz

$$\begin{equation}  \Delta\sigma_D=(2/5)^{1/3} \cdot \Delta \sigma_c =0,737 \cdot \Delta \sigma_c  \text { gdy } N>5  \cdot 10^6 \end{equation}$$

W wypadku widm naprężeń niejednorodnych  (o zmiennej amplitudzie) krzywa trwałości zmęczeniowej, odnosząca się do naprężeń normalnych , opisywana jest następującymi zależnościami:

$$\begin{equation}  \text { 1) dla } 1 \cdot 10^4 \le  N \le 5 \cdot 10^6 \text { jest  : }  \Delta\sigma_R^m \cdot N_R=\Delta\sigma_c^m \cdot 2 \cdot 10^6 \text  { oraz } N=3\end{equation}$$

$$\begin{equation}  \text { 2) dla } 5 \cdot 10^6 < N \le  10^8 \text { jest  : }  \Delta\sigma_R^m \cdot N_R=\Delta\sigma_D^m \cdot 2 \cdot 10^6 \text  { oraz } N=5\end{equation}$$

$$\begin{equation} \text { 3) dla }  N > 10^8 \text { jest  : } \Delta \sigma_L =\Delta \sigma_D \cdot (5/100)^{1/7}=0,549 \Delta \sigma_D=0,549 \cdot 0,737 \Delta \sigma _c=0,405 \Delta \sigma_c  \end{equation}$$

Krzywe wytrzymałości zmęczeniowej, odnoszące się do naprężeń stycznych opisywane są podobnymi zależnościami z drobnymi zmianami wg [1].

Poziomy kontroli konstrukcji a współczynnik bezpieczeństwa $\gamma_{Mf}$

Wartość współczynnika bezpieczeństwa $\gamma_{Mf }$ zależy od poziomu kontroli konstrukcji w trakcie eksploatacji konstrukcji poddawanej zmęczeniu. oraz od konsekwencji zniszczenia,. W przypadku braku  wystarczających danych zaleca się przyjmować te współczynniki zgodnie z tab 3 , obowiązującą dla belek podsuwnicowych

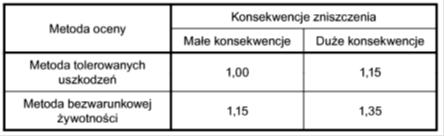
Tab.3  Wartości współczynnika bezpieczeństwa $\gamma_{Mf }$ [3] – tab.3.1.

Przy ustalaniu konsekwencji zniszczenia należy brać pod uwagę schemat konstrukcji. W przypadku schematów statycznie wyznaczalnych (belka swobodnie podparta lub zwykła kratownica) konsekwencje zniszczenia są  zwykle duże, bo lokalne pęknięcia mogą doprowadzić do zniszczenia całej konstrukcji (system szeregowy z punktu widzenia niezawodności). W takim systemie  nie dochodzi do redystrybucji naprężeń po lokalnym pęknięciu, a następuje pogłębianie się pęknięcia [3]-pkt 3.3.

Klasa konsekwencji zależy od przeznaczenia obiektu oraz projektowanego okresu eksploatacji.

Konsekwencje zniszczenia mogą być mniejsze (małe) w przypadku konstrukcji mniej ważnych, takich , których katastrofa prowadziłaby do małych strat materialnych i nie powadziłaby do strat ludzkich. Na przykład zniszczenie wolnopodpartej belki podsuwnicowej zwykle prowadzi do dużych konsekwencji zniszczenia, a zniszczenie tężnika przeciwhamownego do małych konsekwencji.

Metoda bezwarunkowej żywotności (MBŻ) będzie stosowana w sytuacji, gdy nie przewiduje się systematycznej kontroli konstrukcji podczas eksploatacji. Zakłada się mianowicie, że odpowiednią niezawodność konstrukcji można osiągnąć bez konieczności regularnych kontroli na okoliczność uszkodzeń zmęczeniowych w okresie eksploatacji

Metoda tolerowanych uszkodzeń (MTU) prowadzi do konieczności ciągłych, systematycznych obserwacji i kontroli stanu krytycznych miejsc konstrukcji.

Metodę oceny zapewnienia akceptowalnego poziomu niezawodności oraz klasę konsekwencji należy  jawni określić w  specyfikacji technicznej wykonania i odbioru konstrukcji podatnych na zmęczenie . W większości przypadków przyjmuje się metodę bezwarunkowej żywotności (MBŻ) i wówczas:

$\gamma_{Mf}=1,15$ dla konstrukcji o małych konsekwencjach zniszczenia,
$\gamma_{Mf}=1,35$ dla konstrukcji o dużych konsekwencjach zniszczenia.

Współczynnik  $\gamma_{Ff}$

Współczynnik  $\gamma_{Ff}$ jest współczynnikiem równoważnego zakresu zmienności naprężeń o stałej amplitudzie.

Jeśli nie ma specyficznych wymagań, to dla typowych konstrukcji, w tym dla belek podsuwnicowych przyjmuje się

$\gamma_{Ff}=1,0$.

Równoważne amplitudy naprężeń  $\Delta\sigma_{E2}$

Zakres (amplitudę) naprężeń $\Delta \sigma$ w danym punkcie $P$ konstrukcji, uzyskaną standardowymi metodami statyki, oznaczmy przez  $\Delta \sigma_P$.

Ze względu na rozmaite rzeczywiste widma obciążeń należy ją sprowadzić do amplitudy naprężeń, wywołanych wymuszeniami o stałej amplitudzie odniesionej do $2\cdot 10^6$ cykli. Taka amplitudę naprężeń  nazywa się równoważną, oznacza $\Delta \sigma_{E2}$ i wyznacza z ogólnej zależności

$$\begin{equation} \gamma_{Ff} \Delta \sigma_{E2}=\lambda_1 \lambda_2 \lambda_i \text{…} \lambda_n \Delta \sigma (\gamma_{Fj} Q_k) \label{SE2} \end{equation}$$

Występujące w  ($\ref{SE2}$) zmienne $\lambda_i$  są  zastępczymi czynnikami uszkodzeń, zależnymi od widma obciążeń, określanymi odrębnie dla każdego  i-tego obciążenia i są specyfikowane w normach dotyczącymi różnych konstrukcji (mosty, kominy, wieże, belki podsuwnicowe).

Dla wielu prostych konstrukcji, na które działa jednorodne widmo obciążenia, iloczyn  $\lambda_1 \lambda_2$ … można zastąpić jednym współczynnikiem równoważności  $\lambda$, szacowanym z zależnosci

$$\begin{equation} \lambda={\dfrac{N}{2 \cdot 10^6}}^{1/m} \end{equation}$$

gdzie m jest współczynnikiem nachylenia krzywek zmęczeniowej.

Wyrażenie ($\ref{SE2}$) można uzyskać z zależności [4]-(2.16), dotyczącej wymuszeń zmęczeniowych, przy założeniu, że :
1) naprężenia są proporcjonalne do obciążeń z mnożnikiem Λ,
2) naprężenia maksymalne i minimalne są  proporcjonalne do tego samego mnożnika Λ, skąd wynika, że również amplituda naprężeń jest proporcjonalna do tego samego mnożnika
Mimo to, że nie zawsze założenia proporcjonalności są spełnione, to powszechnie amplitudę równoważną wyznacza się z amplitudy $\Delta \sigma_P$ wywołanej quasistatycznymi  (po zastosowaniu współczynników dynamicznych) wymuszeniami charakterystycznymi z zależności:

$$\begin{equation} \Delta \sigma_{E2}= \lambda \cdot \Delta \sigma_P \label{P-E2} \end{equation}$$

$$\begin{equation} \Delta \tau_{E2}= \lambda \cdot \Delta \tau_P \label{T-E2} \end{equation}$$

Współczynnik równoważności widma obciążeń $\lambda$, występujący w ($ \ref{P-E2}$ )wyznacza się w zależności od rodzaju konstrukcji (belki podsuwnicowe, wieże , maszty,m mosty , itd). Na przykład w przypadku wymuszenia suwnicami można go przyjąć na podstawie klasy S w sposób pokazany w pkt. 4..1.

Karby, to typy kategorii zmęczeniowych

Znaczną różnorodność karbów, występujących w konstrukcjach zredukowano do kilkunastu kategorii. Kategorię zmęczeniową określa wytrzymałość zmęczeniowa przy liczbie cykli $N=2 \cdot 10^6$ i jest wartości liczbową przypisaną danemu karbowi (i określonemu kierunkowi naprężeń).

Kategorie zmęczeniowe $\Delta\sigma_c$ i $\Delta\tau_c$, charakteryzujące poszczególne krzywe zmęczeniowe podzielone są na następujące typy:

1. elementy bez spoin i złącza na łączniki mechaniczne
2. kształtowniki spawane
3. spoiny czołowe poprzeczne
4. dospawane blachy węzłowe i żebra
5. złącza spawane i nośne
6. kształtowniki zamknięte
7. złącza w węzłach kratownic z kształtowników zamkniętych
8. podłużnice o przekroju zamkniętym w pomostach ortotropowych
9. styki górne pasów ze środnikiem w belkach podsuwnicowych

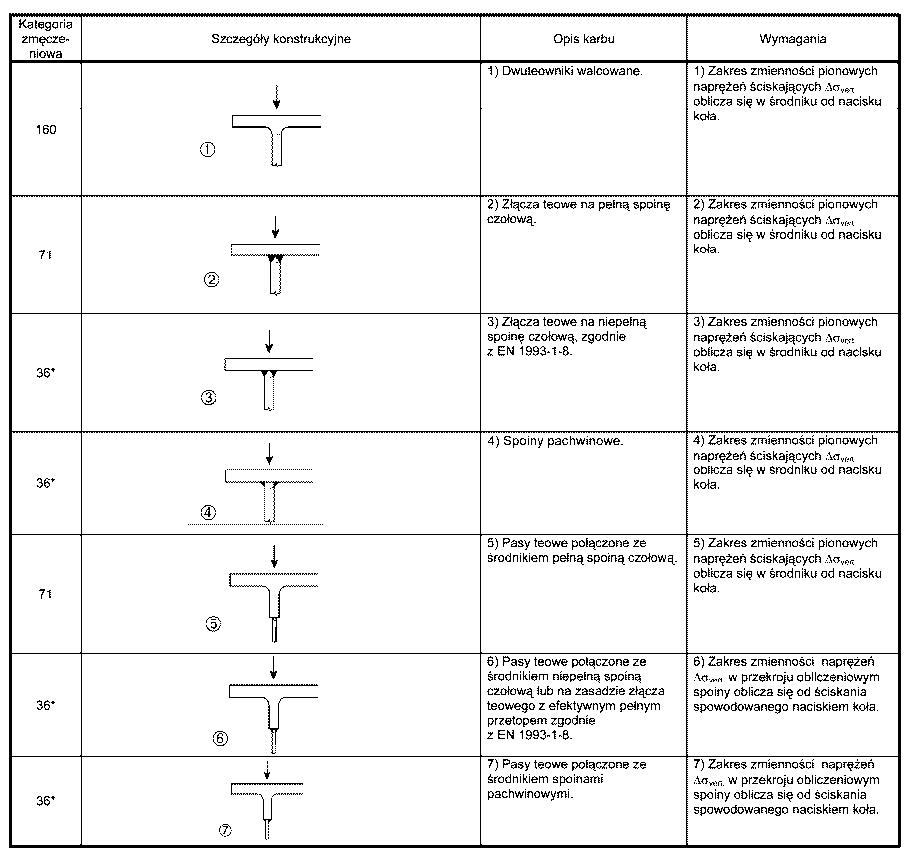
W tabeli 1  zestawiono dla przykładu kategorie zmęczeniowe styków górnych pasów ze środnikiem w belkach podsuwnicowych.

Tab.1 Kategorie zmęczeniowe  styków pasów ze środnikiem belek podsuwnicowych [1]ABUS EML 10 t

Warunki nośności zmęczeniowej

Sprawdzenie nośności zmęczeniowej polega na sprawdzeniu dwóch warunków:

1. zakresu zmienności naprężeń wywołanych obciążeniami częstymi  $\gamma_1 Q_k$ (warunek zmęczenia  niskocyklowego)
2. nośności na zmęczenie (wysokocyklowe)

Warunek zakresu zmienności naprężeń zapewnia, że konstrukcja nie ulegnie zmęczeniu w zakresie niskocyklowym (przy liczbie cykli mniejszej niż $10^4$) i można go zapisać w postaci:

$$\begin{equation} \Delta \sigma < 1,5 \cdot f_y \text { oraz } \Delta \tau < 1,5 \cdot \dfrac {f_y}{\sqrt {3}} \label {Nisko_O} \end{equation}$$

W kombinacji obciążeń $\gamma_1 Q_k$ występują charakterystyczne wartości obciążeń zmiennych $Q_k$, a $\gamma_1$  jest współczynnikiem wartości częstej oddziaływania zmiennego . Dla oddziaływań suwnic przyjmuje się $\gamma_1$=0,9$

Warunek nośności na zmęczenie  polega na sprawdzeniu amplitudy naprężeń:

a) normalnych

$$\begin{equation} \dfrac{\gamma_{Ff} \Delta \sigma_{E,2}} {\Delta \sigma_c / \gamma_Mf} \le 1,0\end{equation}$$

b)stycznych

$$\begin{equation} \dfrac{\gamma_{Ff} \Delta \tau_{E,2}} {\Delta \tau_c / \gamma_Mf} \le 1,0\end{equation}$$

Zmęczenie w warunkach złożonego stanu naprężeń

Reguła Palmgrena-Minera sumowania uszkodzeń zmęczeniowych

Jeśli widmo naprężenia nie jest jednorodne i jedna z metod zliczania cykli charakteryzuje go w postaci zbioru kilku widm jednorodnych   { $n_{Ei}$ , $ \sigma_{Ei}$ }, to ocena zmęczenia polega na wyznaczeniu sumarycznego wskaźnika uszkodzenia $D_d$  na podstawie reguły Palmgrena-Minera sumowania uszkodzeń zmęczeniowych:

$$\begin{equation} D_d= \sum \limits_i^n \dfrac{n_{Ei} }{N_{Ri}} \end{equation}$$

gdzie: $n_{Ei}$ – liczba cykli związana z zakresem zmienności w i-tym paśmie widma, $N_{Ri}$ – trwałość uzyskana na podstawie krzywej obliczeniowej $\dfrac{\Delta \sigma_c}{\gamma_{Mf}}-N_R$ dla zakresu zmienności widma, co pokazano schematycznie na rys 7:

Rys.7 Liczba cykli ,a zakres zmienności pasma widma obciążeń

Warunek nośności zmęczeniowej w przypadku stosowania formuły Palmgrena-Mirena można zapisać w postaci:

$$\begin{equation} D_d<1,0 \end{equation}$$

Warunek zmęczenia w złożonym stanie naprężeń

Naprężeniami miarodajnymi do wyznaczenia zmienności naprężeń są naprężenia normalne i styczne. W niektórych przypadkach (karby typu: elementy bez spoin i złącza na łączniki mechaniczne oraz typu kształtowniki spawane) należy wyznaczać również naprężenia zastępcze lub główne.

W przypadku naprężeń złożonych, jeśli nie podano inaczej, to należy sprawdzić warunek:

$$\begin{equation} \left( \dfrac{ \gamma_{Ff} \Delta \sigma_{E,2}} {\Delta \sigma_c / \gamma_{Mf}} \right)^3 +\left( \dfrac{ \gamma_{Ff} \Delta \tau_{E,2}} {\Delta \tau_c / \gamma_{Mf}} \right)^5 \le 1,0 \label {Warunek_zlozony} \end{equation}$$

Zmęczenie podtorza suwnic

Grupa natężenia pracy suwnicy i belki

W celu ustalenia wpływu zmęczenia na belkę podsuwnicową trzeba określić grupę natężenia pracy suwnicy  A1 do A8 lub grupę natężenia pracy belki B1 do B9. Na tej podstawie określa się rodzaj widma obciążenia suwnicy (lub belki).

Grupę natężenia pracy suwnicy określa producent dźwignicy, a w przypadku braku takich danych można ją szacunkowo przyjąć z tab.3

Tab.3 Grupy natężenia pracy suwnicy  [4]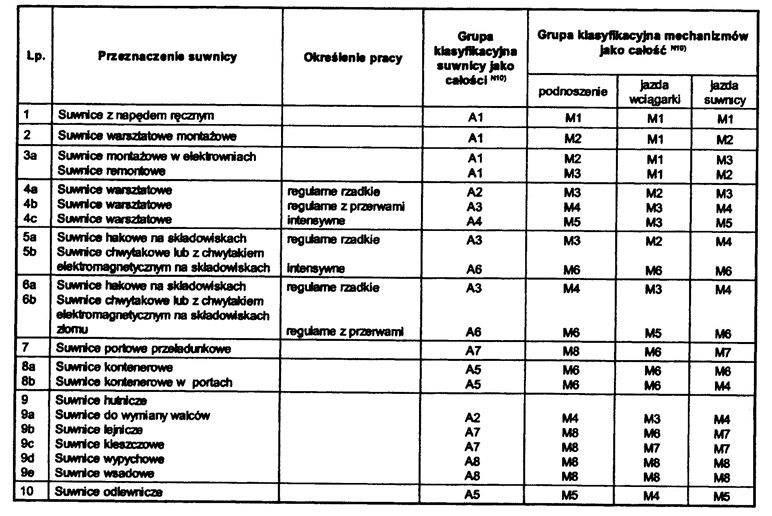

Przy braku dokładniejszych danych można przyjąć , że grupa natężenia pracy belki jest o jeden wyższa od grupy natężenia pracy suwnicy, np. A4 -> B5 .

Zmęczenie niskocyklowe

Podane wcześniej  informacje z zakresu zmęczenia konstrukcji dotyczą głównie zmęczenia wysokocyklowego (duża liczba zmian naprężeń w czasie eksploatacji elementu konstrukcji). Z tego typu zmęczeniem mamy do czynienia wtedy, gdy przekrój elementu jest obciążony urządzeniem wywołującym drgania o dużej częstości.

Suwnice należące do wyższych grup natężenia pracy (A5-A9) mogą powodować obliczeniowe zmęczenie materiału belek podsuwnicowych, przy tym zmiany naprężeń w czasie są powolne (w wybranym włóknie przekroju belki podsuwnicowej), ponieważ jazda suwnicy po belce jest stosunkowo wolna (do 80 m/min), a poza tym drgania ciężaru na haku suwnicy są tłumione masą samej suwnicy. W związku z tym zmęczenie belki podsuwnicowej może zajść juprzy małej liczbie cykli  Taki typ zmęczenia jest nazywany niskocyklowym., dla którego  teoretyczne podstawy w artykule zmęczenie niskocyklowe elemntów konstrukcji.

Praktyczne zasady uwzględniania zmęczenia niskocyklowego belek podsuwnicowych opisano w normie [1]-zał 5, a sprowadzają się one do obowiązku sprawdzenia warunku  ($\ref{Nisko_O}$):

$$\begin{equation} \Delta \sigma < 1,5 \cdot f_y \text { oraz } \Delta \tau < 1,5 \cdot \dfrac {f_y}{\sqrt {3}} \approx 0,9 f_y \label{Nisko_B} \end{equation}$$

Belki zabezpieczone przed zmęczeniem niskocyklowym po długim okresie eksploatacji mogą wejść w obszar zniszczenia wysokocyklowego.

Zmęczenie (wysokocyklowe)

Współczynnik równoważności $\lambda$

W przypadku wymuszenia dynamicznego suwnicami współczynnik równoważności $\lambda$ można go przyjąć na podstawie klasy S suwnicy zgodnie z tab .4.

Tab.4. Wartości λ według klas suwnic [4]-tab. 2.12}”]

Klasę suwnicy podaje producent, a w przypadku  braku danych wg [4]-Zał. B, który  stanowi tab. 3 w artykule.  Oddziaływania dynamiczne i zmęczeniowe suwnic. W artykule tym omówiono również zasady przyjmowania obciążeń na suwnice.

Kategoria zmęczeniowa miejsc na belce

Kategoria zmęczeniowa , dotyczy nie całej belki, ale miejsc (punktów) na belce, w których ulokowano karby konstrukcyjne najczęściej wskutek wykonania otworów na śruby lub po ułożeniu spoin , albo wskutek innych operacji technologicznych (walcowanie, cięcie itd).

Rodzaj karbu konstrukcyjnego implikuje kategorię zmęczeniową

$\Delta \sigma_c$ oraz $\Delta \tau_c$

Kategorię zmęczeniową określa się z tabel normy [1] , wyciąg z których zamieszczonopoyżej.

Zmęczenie wysokocyklowe

Założenia

Dla warunków obliczeniowych zarówno przy jednej jak dwóch suwnicach  muszą być spełnione założenia:

• co najwyżej przeciętne zagrożenie korozją,
• temperatura eksploatacji belki nie wyższa niż 150°C
• zmiany amplitudy naprężeń normalnych i tnących nie prowadzą do zmęczenia niskocyklowego (\refl{Nisko_B}).

W zależności od liczby suwnic poruszających się po belce podsuwnicowej występują zróżnicowane warunki obliczeniowe. W przypadku suwnic niezależnych uwzględnia się jedynie dwie, najbardziej niekorzystnie obciążające belkę.

Obciążenie jedną a dwoma suwnicami

Dla belek obciążonych jedną suwnicą lub dwiema sprzężonymi (zespolonymi w celu przeniesienia ciężaru większego niż udźwig jednej z nich) należy sprawdzić warunki

$$\begin{equation} max \Delta  \sigma_e \le \left( \dfrac{\Delta \sigma_R}{\gamma_f}\right)  \end{equation}$$,

$$\begin{equation} max \Delta  \tau_e \le \left( \dfrac{\Delta \tau_R}{\gamma_f}\right) \end{equation}$$,

$$\begin{equation} \left( \dfrac {\Delta \sigma_e} {\Delta \sigma_R} \right) ^3 +\left( \dfrac {\Delta \tau_e} {\Delta \tau_R} \right) ^5 \le 1,0\end{equation}$$,

gdzie wytrzymałość zmęczeniowa $\Delta \sigma_R$=$\Delta \sigma_c$ oraz $\Delta\tau_R$=$\Delta\tau_c$

Dla belek obciążonych dwiema suwnicami (niezależnymi) trzeba dodatkowo sprawdzić warunek:

$$\begin{equation} \left( \dfrac {\Delta \sigma_{e,1}} {\Delta \sigma_{R,1}} \right) ^3 +\left( \dfrac {\Delta \sigma_{e,2}} {\Delta \sigma_{R,2}} \right) ^3+\left( \dfrac {\Delta \sigma_{e1,2}} {\Delta \tau_{R 1,2}} \right) ^3 \le 1,0\end{equation}$$,

gdzie indeksy 1 i 2 dotyczą odpowiednio pierwszej i drugiej suwnicy.

W przypadku dwóch belek wytrzymałość zmęczeniowa  wynosi

$$\begin{equation}  \Delta \sigma_R=0,738 \Delta \sigma_c \left (\dfrac{5 \cdot 10^6}{N} \right )^{1/m} \ge \Delta \sigma_L \end{equation}$$

$$\begin{equation}  \Delta \tau_R=\Delta \tau_c \left (\dfrac{2 \cdot 10^6}{N} \right )^{1/m} \ge \Delta \sigma_L \end{equation}$$

gdzie m=3 , gdy $N \le 5\cdot 10^6$ i m=5 gdy $N>5\cdot 10^6$

$\Delta \sigma_c$ , $\Delta \tau_c$ – kategorie zmęczeniowe, $\Delta \sigma_L$ , $\Delta \tau_L$– wytrzymałość zmęczeniowa trwała, $\Delta \sigma_e$ , $\Delta \tau_e$– równoważny zakres zmienności naprężeń, $\gamma_f$ – częściowy współczynnik bezpieczeństwa przy zmęczeniu materiału  (1 do 1,2)

Wytrzymałość zmęczeniowa grubych elementów

Wytrzymałość zmęczeniową elementów o grubościach t > 25 mm redukuje  się według wzoru

$$\begin{equation}  \Delta \sigma_{R,red}=\Delta \sigma_R \cdot (25/t)^{1/4}\end{equation}$$Literatura

1. PN-EN 1993-1-9:2007, Eurokod 3: Projektowanie konstrukcji stalowych, Część 1-9: Zmęczenie
2. Kozłowski A. (Red.), (2010), Konstrukcje stalowe. Przykłady obliczeń według PN-EN 1993-1. Część pierwsza. Wybrane elementy i połączenia. Oficyna Wydawnicza Politechniki Rzeszowskiej
3. PN-EN 1993-6+Ap1+AC:2009, Eurokod 3 – Projektowanie konstrukcji stalowych – Część 6: Konstrukcje wsporcze dźwignic
4. PN-EN 1991-3: 2009, Eurokod 1: Oddziaływania na konstrukcje. Część 3: Oddziaływania wywołane dźwignicami i maszynami

________________________________