Kombinacje obciążeń w Eurokodach

Leszek Chodor, 16 października 2015

 W ciągu ostatnich 24 godzin z artykułu korzystało  62 Czytelników

Od 1994 r stosowanie Polskich Norm jest dobrowolne, co dramatycznie zmieniło wcześniejszą zasadę, zgodnie z którą Polskie Normy (PN) były obowiązujące do stosowania, pełniły rolę bezwzględnych przepisów i ich nieprzestrzeganie było naruszeniem prawa. Przy tym do końca 2002 roku istniała i była stosowana możliwość, nakładania przez właściwych ministrów obowiązku stosowania PN. Od 2003 roku  stosowanie PN jest już całkowicie dobrowolne, z wyjątkiem norm „obciążeniowych”, a w szczególności kombinacji obciążeń, co jest przedmiotem artykułu.

Wyjątkowo obowiązek bezwzględnego stosowania  norm Eurokod dotyczy działań wykonywanych ze środków publicznych, podlegających ustawie „prawo zamówień publicznych„.
Zdaniem części społeczności inżynierów budownictwa, obowiązek stosowania PN może być też nałożony przez inne ustawy i rozporządzenia ministrów. Zdaniem autora niniejszego artykułu takie narzucanie PN dla inwestycji innych niż publiczne (finansowane z podatków), jest niezgodne z nadrzędną Ustawą o Normalizacji oraz duchem dyrektyw Unii Europejskiej i nie powinno mieć miejsca. Zgodnie z aktem akcesyjnym Polski do Unii Europejskiej – podstawowym zadaniem  rządu i ministrów  powinna być harmonizacja polskiego systemu norm technicznych z normami i zasadami europejskimi. W tym sensie szczególną rolę w normalizacji europejskiej pełnią Europejskie normy zharmonizowane (PN-EN lub EC-Eurokody ) które wspomagają legislację w ramach tzw. Nowego Podejścia, ale zgodnie z fundamentalną zasadą ich stosowanie przez Projektanta jest całkowicie dobrowolne. To właśnie Projektant wytycza zakres i tryb stosowania norm, a także to On może nałożyć obowiązek ich stosowania na Wykonawcę i/lub Inwestora.

Inwestor ma prawo opracować swoje standardy lub założenia i zwrócić się do Projektanta o ich wdrożenie w projektowanym przedsięwzięciu. Jeśli standardy Inwestora nie są zgodne ze stosowanymi przez Projektanta zasadami i normami, to obie strony na wniosek Projektanta , obowiązane są osiągnąć konsens. Inwestor nie może zmienić warunków technicznych wprowadzonych ustawami lub rozporządzeniami,a w przypadku niezgodności standardów Inwestora z takimi warunkami, Projektant ma obowiązek przywrócić stan obowiązujący, informując o tym Inwestora w przypisanym terminie.

Szczególne znaczenie w systemie norm europejskich mają normy obciążeń konstrukcji budowlanych. W zasadzie harmonizacji przyjęto, że „normy obciążeniowe” są obowiązkowe i projektowanie konstrukcji budowlanych w Unii Europejskiej musi być prowadzone na obciążenia przewidziane normach PN-EN 1990 i 1991.

Wprowadzenie

Eurokody „obciążeniowe”  stanowią zestaw norm:

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

Eurokod 0 (EC0) zawiera istotne postanowienia, które są przedmiotem niniejszego artykułu.

Do sprawdzania stanu granicznego nośności ( symbol STR ) należy przyjmować kombinacje oddziaływań jako najmniej korzystne spośród wyznaczonych z zależności ($\ref{K1}$) i ($\ref{K2}$):

$$\begin {equation} \sum \limits_{j=1} (\gamma_{G,j}\cdot G_{k,j}) + \sum \limits_{i=1} (\gamma_{Q,i}\cdot \psi_{0,i} \cdot Q_{k,i} \label{K1})\end {equation}$$

$$\begin {equation} \sum \limits_{j=1} \, (\xi_j \cdot \gamma_{G,j}\cdot G_{k,j}) +\gamma_{Q,1}\cdot Q_{k,1}+\sum \limits_{i>1} (\gamma_{Q,i} \cdot \psi_{0,,i} \cdot Q_{k,i} )\label{K2}\end {equation}$$

gdzie:
G_k,j – j-te  charakterystyczne (indeks k) obciążenie stałe (symbol G),
Q_k,1 – 1-sze (zwane wiodącym) charakterystyczne obciążenia zmienne (symbol Q),
Q_k,i – i-te (zwane towarzyszącym) charakterystyczne obciążenia zmienne,

$\gamma_{G,j}$, $\gamma_{Q,1}$, $\gamma_{Q,i}$ – współczynniki obciążenia: stałego j-tego, zmiennego wiodącego i zmiennych towarzyszących odpowiednio,
$\xi_j$ – współczynnik redukcyjny obciążenia stałego j-tego,
$\psi_{0,1}$, $\psi_{0,i}$– współczynnik dla wartości kombinacyjnej obciążenie zmiennego (w skrócie współczynnik „kombinacyjny”), odpowiednio wiodącego i towarzyszącego. Te współczynniki w Eurokodzie oznaczane są jako $\psi_0$.

Sumowanie rozciąga się na wszystkie obciążenia stale (j) oraz na obciążenia zmienne (i), oprócz obciążenia wiodącego ($\ref{K1}$).

Formuły ($\ref{K1}$) i ($\ref{K2}$) można słownie wyrazić następująco:

Obciążenie zmienne towarzyszące muszą być możliwe fizycznie. W jednej kombinacji nie można uwzględniać jednocześnie wykluczających się obciążeń. Na przykład jeśli uwzględniamy wiatr z jednego kierunku, to nie bierzemy pod uwagę wiatru z drugiego kierunku.

Jako miarodajne należy sprawdzić następujące stany graniczne:

STR: Zniszczenie wewnętrzne lub nadmierne odkształcenia konstrukcji lub elementów konstrukcji, łącznie ze stopami fundamentowymi, palami, ścianami części podziemne, itp.,  w przypadku których decydujące znaczenie ma wytrzymałość materiału konstrukcji

EQU : Utrata równowagi statycznej konstrukcji lub jakiejkolwiek jej części, uważanej za ciało sztywne , wówczas gdy :

• małe zmiany wartości lub rozkładu w przestrzeni oddziaływań, wywołanych przez jedną przyczynę mogą być znaczące (najczęściej stan wyporu przez wodę gruntową)
• wytrzymałość materiałów konstrukcji lub podłoża na ogół jest bez znaczenia

GEO – zniszczenie lub nadmierne odkształcenie podłoża, kiedy istotne znaczenie dla nośności konstrukcji ma wytrzymałość podłoża lub skały
FAT –zniszczenie zmęczeniowe konstrukcji lub elementu konstrukcji,

W niniejszym opracowaniu zajmujemy się wyznaczaniem obciążeń kombinacyjnych ( charakterystycznych i obliczeniowych) w stanie STR, a jako poboczne również EQU oraz GEO

Stan graniczny zmęczenia FAT omówiono w artykule  Oddziaływania dynamiczne i zmęczeniowe suwnic na przykładzie oddziaływań suwnic i urządzeń.

Częściowe współczynniki bezpieczeństwa w kombinacjach obciążeń

Współczynniki obciążeń

Wartości współczynników występujących w formułach kombinacyjnych ($\ref{K1}$) oraz ($\ref{K2}$) wynoszą :

dla obciążeń stałych        $ \gamma_G =$ 1,35

dla obciążeń zmiennych  $ \gamma_Q =$ 1,5

Przy projektowania konstrukcji specjalnych powyższe wartości mogą być przykryte innymi. Na przykład dla wieży i masztów stalowych [12] oraz stalowych kominów  [13] klasy niezawodności 3 (konstrukcje w miastach) przyjmuje się  $\gamma_G=1,2$ oraz $\gamma_Q = 1,6$.

Wartości obliczeniowe oddziaływania F oznaczane są indeksem (d – design):

$$\begin {equation} F_d=\gamma_F \cdot F_{rep} \label{F_d}\end {equation}$$
(F= G lub Q) jest iloczynem wartości reprezentatywnej  $F_{rep}$ i współczynnika obciążeń $\gamma_F$.

Wartością reprezentatywną oddziaływania $F_{rep}$  może  być wartość charakterystyczna $F_k$ lub wartość towarzysząca ψ $\cdot F_k$.

Wartość charakterystyczna oddziaływania $F_k$ jest podstawową reprezentatywną wartością oddziaływania. Można ją ustalić na podstawie danych statycznych; dobiera się je w taki sposób żaby odpowiadała ona zadanemu prawdopodobieństwu nieprzekroczenia w niekorzystną stronę w trakcie  okresu czasu zwanego ”okresem odniesienia”. W okresie odniesienia uwzględnia się przewidywany okres użytkowania konstrukcji i czas trwania sytuacji obliczeniowej. Wartość charakterystyczną nazywa się zwykle wartością nominalną lub miarodajną . W ogólności nie  jest to wartość średnia, ale  kwantyl zmiennej losowej, to znaczy wartość oczekiwana powiększona (lub pomniejszona) o iloczyn współczynnika niezawodności $\beta$ i odchylenia standardowych na zadanym poziomie ufności. Zwykle w  budownictwie i architekturze przyjmuje się $\beta=3,8$, oraz „okres odniesienia”  $T= 50$ lat.

Do obliczeń należy przyjmować wartości obliczeniowe z uwzględnieniem współczynników kombinacyjnych, to jest „sumę” obciążeń z uwzględnieniem redukcji obciążeń w sytuacjach kombinacyjnych. Brak uwzględnienia redukcji współczynnikami kombinacyjnymi jest błędny i prowadzi do znacznego zawyżenia wartości oddziaływań, co jest nieakceptowalne w dobie projektowania zrównoważonego i optymalizacji wydatków energetycznych, czyli przede wszystkim materiałowych.

Podane wyżej wartości współczynników obciążeń dotyczą sytuacji, gdy obciążenie działa niekorzystnie (to znaczy wzmagają efekt E oddziaływania F ; Przykładem jest sytuacja, w której efekt E (np reakcja podpory)  jest zwiększany przez ciężar własny konstrukcji i przez oddziaływanie wiatru, bo wiatr napiera na połać z góry – wówczas oba obciążenia są niekorzystne dla efektu E i należy stosować podane wyżej współczynniki obciążeń.

Natomiast w przypadku działania korzystnego (odciążającego) należy przyjmować:

dla obciążeń stałych        $\gamma_G=$ 1,0

dla obciążeń zmiennych  $\gamma_Q =$ 0,0

Uwaga:

1. Rozpowszechniona jest opinia , że w przypadku działania korzystnego obciążenia stałego stosujemy formułę ($\ref{K2}$), ale bez redukcji obciążenia stałego, a jednocześnie wśród obciążeń zmiennych wybieramy obciążenie wiodące (bez redukcji), a pozostałe (towarzyszące) obciążenia zmienne redukujemy.
2. Powyższa zasada jest nieprawidłowa, ponieważ w warunkach rzeczywistych wartość losowego obciążenia stałego może być mniejsze od wartości nominalnej (reprezentywnej) i zastosowanie współczynnika redukcji 0,85 jest uzasadnione. Oznacza to, że również w w przypadku korzystnego obciążenia stałego formuły kombinacyjne ($\ref{K1}$) i ($\ref{K2}$) stosujemy bez modyfikacji.

W tablicy A1.2(B) [1] w wierszu dla formuły (6.10b) , czyli $(\ref{K2})$ pominięto co prawda współczynnik redukcyjny $\xi_j$ dla korzystnych obciążeń stałych, ale zdaniem autora prawidłowe jest stosowanie tego współczynnika $\xi_j$ również w tym przypadku. Przy tym na podstawie dostępnych danych  nie można odrzucić hipotezy o tym , że  $\xi_j=0,85$

Ogólną zasadą jest więc to , że działanie korzystne lub niekorzystne obciążenia oceniamy na poziomie efektów E oddziaływań F, a nie na poziomie obciążeń G, Q. To samo oddziaływanie może być bowiem niekorzystne  dla jednego efektu (np. reakcji podpory 1) , a korzystne dla innego efektu (np. dla reakcji podpory 2). 

Współczynniki redukcyjne

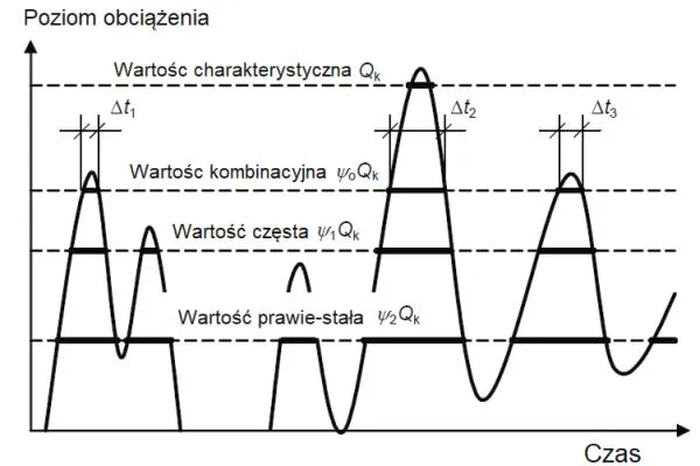
Współczynniki redukcyjne stosowane są w celu ustalenia tego poziomu obciążenia charakterystycznego traktowanego jako proces stochastyczny, którego przekroczenie w czasie użytkowania konstrukcji zajdzie ograniczoną liczbę razy. Dla przykładu na rys.1 zachodzi::

• obciążenie charakterystyczne $Q_k$  będzie przekroczone tylko jeden raz
• obciążenie kombinacyjne $\Psi_0 Q_k$ będzie przekroczone trzy razy,
• obciążenie częste  $\Psi_1 Q_k$ będzie przekroczone cztery razy,
• obciążenie prawie stałe  $\Psi_2 Q_k$ będzie przekroczone sześć razy,

Rys.1. Interpretacja redukcyjnych współczynników obciążeń

Współczynnik redukcyjny należy przyjmować o następujących wartościach:

dla obciążenie stałego _{$\xi_j$} =0,85,

a dla obciążeń zmiennych zależnie od ich natury ψ_Qi wg tab. 1.

Tab. 1. Współczynniki redukcyjne obciążeń zmiennych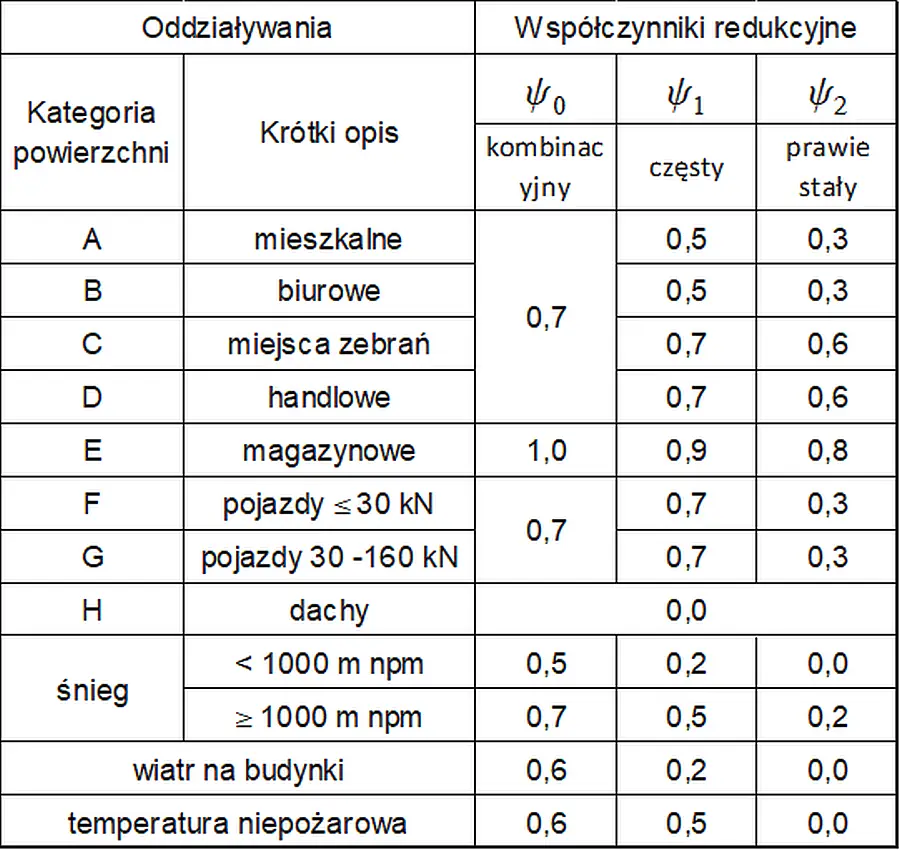

Zaleca się aby efekty oddziaływań, które ze względów fizycznych bądź z uwagi na przewidywane użytkowanie nie mogą wystąpić równocześnie, nie były uwzględniane łącznie w jednej kombinacji  (przykład: wiatr z lewej i wiatr z prawej jednocześnie – nie kombinujemy).  Wartości charakterystyczne wszystkich oddziaływań stałych, pochodzących z jednego źródła mnoży się przez $\gamma_G= 1,35$, jeżeli cały wynikający stąd efekt jest niekorzystny, a przez $\gamma_G= 1,00$ jeśli jest korzystny (przykład: wszystkie oddziaływania pochodzące od ciężaru własnego konstrukcji można uważać za pochodzące z jednego źródła; dotyczy to również przypadku, kiedy materiały są różne).

Kombinacje obciążeń klimatycznych zimą

Specyficzne reguły kombinacyjne stosuje się do obciążeń klimatycznych (temperatura, wiatr, oblodzenie) w warunkach zimowych

W zależności od temperatury powietrza obciążenia wiatrem i temperaturą przyjmuje się jak następuje:

• przy -20°C bez obciążeń zimowych i bez wiatru,
• przy -5°C ze zwykłymi obciążeniami zimowymi w kombinacji z wiatrem,
• przy +5°C z wiatrem, bez obciążeń zimowych,
  

Wymienione wyżej temperatury  zastały tak dobrane, ponieważ z badań wynika, że w mroźnym powietrzu (-20°C) jest zbyt mała wilgotność, by mógł wytwarzać się lód lub sadź. Optymalną temperaturą do tworzenia sadzi i lodu jest ok -5°C. Lód nie tworzy się w dodatnich temperaturach.

W normie [12] podano współczynniki redukcyjne (kombinacji wiatr-lód (W-L), gdy jedno z nich jest wiodące – wówczas towarzyszące redukuje się o połowę ($\psi_W=\psi_L=0,5$), co możemy zapisać regułą :

$$\begin {equation} F_d = \begin{cases}
\gamma_f \cdot (1,0 \cdot W +  0,5 \cdot L),& \text {  gdy wiatr W -wiodący} \\
\gamma_f \cdot (2,0 \cdot L +  0,5 \cdot W),& \text {  gdy lód L -wiodący}
\end {cases} \label{F_d-WL1 } \end {equation}$$

Występujące w $(\ref{F_d-WL1 }$) współczynniki obciążeń $\gamma_f$ zależą od klasy niezawodności: klasa 3 niezawodności dotyczy obiektów w miastach i konstrukcji, których konsekwencje zniszczenia mogą być bardzo poważne; klasa 2 dotyczy wszystkich obiektów, które nie są zakwalifikowane do klasy 1 lub 3 ; Klasa 1 dotyczy mało zaludnionych otwartych terenów wiejskich i obiektów o małym prawdopodobieństwie strat w ludziach.  Współczynniki obciążeń $\gamma_f$ wynoszą:

• do obciążeń stałych  $\gamma_G =  1,2; 1,1; 1,0$  – dla klasy niezawodności 3,2, i 1 odpowiednio ,
• do obciążeń zmiennych $\gamma_Q =  1,6; 1,4; 1,2 $  – dla klasy niezawodności 3,2, i 1 odpowiednio.

Zgodnie z normą do projektowania przewodów elektroenergetycznych [14]

$$\begin {equation} F_d = \begin{cases}
\gamma_f \cdot (1,0 \cdot L +  0,4 \cdot W),& \text {  gdy lód L – wiodący} \\
\gamma_f \cdot (1,0 \cdot W_{max} +  0,0 \cdot L),& \text {  gdy wiatr L – wiodący} \\
\gamma_f \cdot (0,7 \cdot W +  0,35 \cdot L ),& \text {  gdy W i L – towarzyszące} \\
\end {cases} \label{F_d-WL2 } \end {equation}$$

Oszacowanie obliczeniowych sił w konstrukcji

Podstawową zasadą wykorzystaną w przedstawionej metodzie obliczeniowej jest zasada superpozycji skutków słuszna w zakresie sprężysto-liniowej pracy konstrukcji, którą można sformułować następująco:

Gdy działa kilka przyczyn, skutek jest równy sumie skutków od pojedynczych przyczyn.

W przypadku konstrukcji nieliniowych zasada superpozycji nie działa i wyznaczanie kombinacyjnego efektu E oddziaływań kilku obciążeń należy przeprowadzić dla wielu wariantów (sytuacji obliczeniowych), a także przeprowadzić analizę dopuszczalności korzystności / niekorzystności każdego obciążenia w danej sytuacji na efekt E w badanym miejscu konstrukcji. Najpierw należy założyć, że każde obciążenie proste może  być  zarówno niekorzystne  jak i korzystne w zależności od analizowanego punktu w konstrukcji . Liczba rozszerzonych obciążeń prostych wyłącznie z tego warunku wyniesie  N=2xn, gdzie n jest liczbą obciążeń prostych. Na przykład dla zbioru obciążeń prostych: { G(stały), S(śnieg), W (wiatr) }, mamy n=3 i należy rozpatrzyć zbiór rozszerzony obciążeń prostych o liczebności N=2·3=6 : { G⁺(stały niekorzystny), G^–(stały korzystny), S+(śnieg niekorzystny), S^–(śnieg korzystny), W⁺ (wiatr niekorzystny – nie mylić z kierunkiem wiatru), W^– (wiatr korzystny – nie mylić z kierunkiem wiatru)}. Badanie korzystności/niekorzystności  obciążeń prostych przeprowadza się w kolejnych krokach standardowych numerycznych procedur analizy nieliniowej , najczęściej prowadzonych przyrostowo lub iteracyjnie (np. metodą Newtona-Raphsona). W niniejszym opracowaniu ograniczamy się do konstrukcji liniowych.

W celu wyznaczenia efektu E  (siły przekrojowej lub reakcji lub przemieszczenia, itd) konstrukcji liniowej od kilku obciążeń prostych wykonamy następujące kroki:

Krok 1:  Obciążenia proste tej samej natury (o tych samych współczynnikach obliczeniowych oraz redukcyjnych) oznaczamy kolejnymi numerami, np.:
#1 – obciążenie stałe,
#2 – obciążenie śniegiem,
#3 – obciążenie wiatrem-schemat 1,
#4  – obciążenie wiatrem-schemat 2,
#5  -obciążenie użytkowe – kat H,
#6  – obciążenie użytkowe – kat B,
# n …

Krok 2:  Wyznaczamy poszukiwaną siłę przekrojową lub reakcję X_k dla poszczególnych schematów obciążeń charakterystycznych wyznaczonych w kroku 1. Indeks (k) oznacza rekcję wywołaną obciążeniem prostym charakterystycznym.

Wyznaczamy więc kolejno  X#1k,…, X#nk.
Sposoby wyznaczania X są standardowe

Krok 3:  Wartości obliczeniowe X_d siły lub reakcji X, wyznaczamy z formuł kombinacyjnych (a): i (b): , podstawiając w miejsce G lub Q odpowiednie siły wyznaczone w kroku 2. Siły te stowarzyszone są ze współczynnikami obciążenia i współczynnikami redukcyjnymi stosownie do swej natury i rozpatrywanej sytuacji obliczeniowej.

Podsumowując:  najpierw wyznaczamy siły przekrojowe lub reakcji od obciążeń prostych charakterystycznych , a wartości kombinacyjne (zredukowane obliczeniowe) wyznaczamy, stosując współczynniki obciążeń i współczynniki redukcyjne dla wyznaczonych reakcji prostych.
W dobie Eurokodów nie wykonujemy zestawienia obciążeń obliczeniowych – poprzestajemy na zestawieniu wartości charakterystycznych.

Przykłady rachunkowe kombinacji obciążeń

Przykład 1

Uwaga:
W dobie Eurokodów wyznaczanie kombinacji obciążeń na poziomie obciążenia obiektu nie jest podejściem zalecanym i należy je stosować ostrożnie, przede wszystkim z tego względu, że na poziomie obciążeń trudno ocenić, które obciążenia są niekorzystne, a które korzystne.Najczęściej bowiem to samo obciążenie (np wiatr ssący) jest korzystny na dany efekt oddziaływania i w określonym miejscu konstrukcji (np reakcję w jednym miejscu konstrukcji), a niekorzystny na efekt oddziaływania (np moment zginający w innym miejscu konstrukcji). Dlatego, w celu manifestacji tego faktu, poniżej przekreślono takie postawienie zadania, sposób rozwiązania oraz wynik obliczeń. Podany przykład może służyć tylko do wstępnego ćwiczenia definicji obciążeń prostych oraz techniki wyznaczania wartości kombinacyjnej tych obciążeń.

Wyznaczyć obciążenia kombinacyjne działające na połać dachową budynku, przy wyznaczonych obciążeniach prostych:
Skreślenia dokonano celowo – zadanie źle postawione – powinno być postawione na poziomie efektów (sił przekrojowych), a nie obciążeń (wymuszeń).

Oddziaływania stałe:
#1 Ciężar własny konstrukcji                         0,40 kN/m²,
#2 Ciężar pokrycia dachowego                      0,35 kN/m²,

Oddziaływania zmienne
#3 Obciążenia podwieszone                            0,5 kN/m²   (przyjęte jako zmienne  elementy instalacji oraz architektury),
#4  Obciążenie użytkowe                                0,4 kN/m²  (obsługa  dachu kat. H),
#5 Śnieg                                                             0,72 kN/m²,
#6 Wiatr ssanie na połać                                  0,4 kN/m²,
#7 Wiatr parcie  na połać (otwarte bramy)   0,2 kN/m^2.

Rozwiązanie
(skreślenie celowe – rozwiązanie które nie powinno mieć miejsca)

Przyjęto następując kombinacje:

• dla działania niekorzystnego obciążenia stałego
  ($\ref{K1}$):   K1 = 1,35·(#1+ #2) +1,5·(0,7#3+ 0,0#4 + 0,5#5 + 0,6#7),
  ($\ref{K2}$):  K2 =1,35*0,85(#1+#2)+1,5*#4+1,5*(0,7#3+0,5#5+0,6#7),
        K3 =1,35*0,85(#1+#2) +1,5#5+1,5*(0,7#3+0,0#4+0,6#7), 

• dla działania korzystnego obciążenia stałego dla sytuacji obliczeniowej maksymalnego odrywania dachu – ssania wiatru
  ($\ref{K2}$): K4 = 1,0·0,85·(#1+#2)+1,5#6+0,0·(0,7#3+0,0#4+0,5#5).

Przykład 2

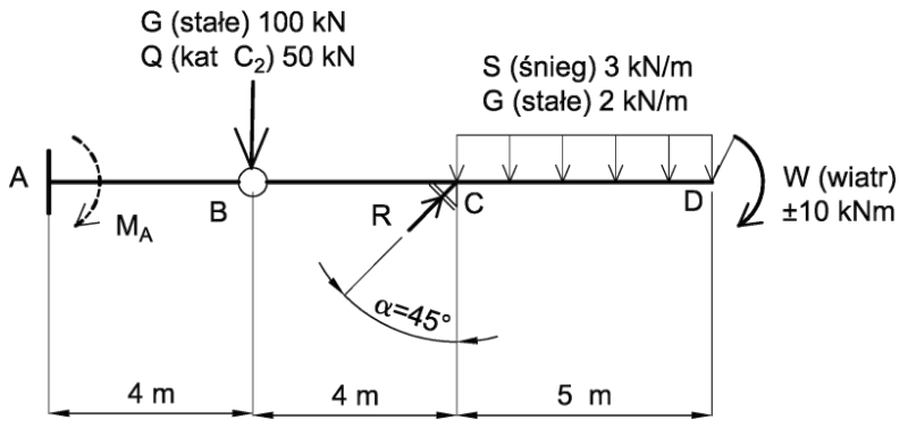
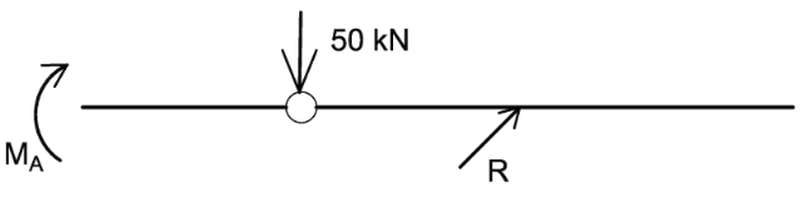
Wyznaczyć obliczeniową (kombinacyjną) reakcję M_A belki stropowej A-D w budynku biurowym ze wspornikiem balkonowym C-D , o schemacie statycznym i obciążeniu pokazanym na rys.2.

Rys.2. Schemat do przykładu 2

Rozwiązanie:

Krok 1: Definicja obciążeń prostych

Moment utwierdzenia M_A wywołany jest następującymi obciążeniami prostymi:

#1  obciążenie stałe G = [ siła skupiona 100 kN w przegubie B;  obciążenie rozłożone 2  kN/m na długości wspornika C-D ]
Uwaga: obciążenie o tej samej naturze ( w tym przypadku obciążenie stałe G), nawet jeśli działa na konstrukcję w różnych miejscach i w rozmaitych typach mechanicznych (skupione, rozłożone, itd – jest traktowane jako jedno obciążenie proste.
#2 śnieg S = 3 kN/m,
#3 obciążenie zmienne Q _{kat C2} =  50 kN.
#4 wiatr 1 (W+) = + 10 kN/m,
#5 wiatr 2 (W-) = – 10 kN/m,

Uwaga: obciążenie o jednej naturze ( w tym przypadku wiatr W), jest traktowane jako dwa obciążenia proste, bowiem należy przypuszczać, że w jednej konfiguracji będzie niekorzystne , a w drugiej korzystne , więc należy zastosować inne współczynniki obciążeń.

Krok 2: Wyznaczenie momentu  utwierdzenia  od prostych obciążeń

Przez R oznaczono reakcję podpory C nachylonej pod kątem α=45°. Rozwiązujemy belkę obciążoną TYLKO jednym obciążeniem prostym. Inne obciążenia pomijamy. Na rys. 1 zdefiniowano podporową reakcję ( symbol momentu naniesiony linią przerywaną) jako moment prawoskrętny. Poszukiwać będziemy maksymalnego i minimalnego momentu o zwrocie zdefiniowanym na rysunku ( największego i najmniejszego z uwzględnieniem znaku).

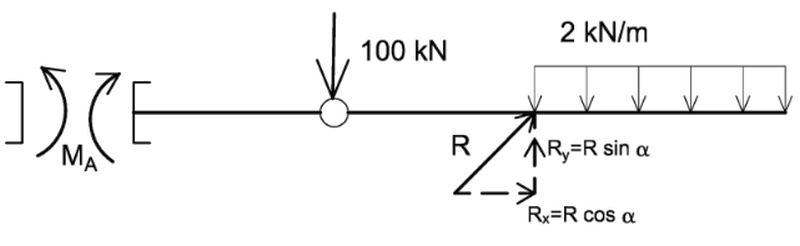
#1 : obciążenie stałe   G

Rys.2a. Schemat do przykładu 2 dla obciążenia #1= G

Podpory zastąpiliśmy siłami reakcjami. Na lewy koniec belki działa moment M_A przeciwnie skierowany do reakcji utwierdzenia.

Do wyznaczenia M_A potrzebujemy znajomości reakcji R.  Podpora jest ustawiona pod kątem α=45° i jest przesuwna, co powoduje, że kierunek reakcji R jest ustalony, a składowe pozioma R_x oraz pionowa R_y są związane ścisłymi zależnościami, pokazanymi na rysunku. Wystarczy wyznaczyć dowolną składową (R lub R_x lub R_y ). Zauważmy ponadto, że składowa R_x nie daje momentu względem osi belki. Składową nietrywialną jest R_y i tą będziemy wyznaczać. W rozważanym zadaniu pochylenie podpory nie wpływa na sposób rozwiązania.

Równania równowagi belki dają zapisujemy w postaci układu równań [(a), (b), (c), (d)]:
(a): ∑X=0 ;
(b):  ∑Y=0 ;
(c): ∑M_O=0, gdzie (O) jest dowolnym punktem na płaszczyźnie;
(d): równanie przegubu  ∑M_{C [prawa lub lewa]} =0

W rozważanym przypadku mamy:
$ (a) \to H_A + R_x=0$, gdzie  $H_A$ jest poziomą reakcją podpory A (nie zobrazowana ma szkicu, bo nie uczestniczy w zadaniu),
$ (b) \to V_A +R_y=0$, gdzie   $V_A$ jest pionową reakcją podpory  (nie zobrazowana ma szkicu, bo nie uczy w zadaniu),
(c)_(A) (suma momentów względem punktu A)  $\to M_A+100 \cdot 4- R_y \cdot 8+2 \cdot 5 \cdot(8+2,5)=0$,
(d) $\to R_y\cdot 4 – 2\cdot 5\cdot (4+2,5)=0$

Równaniem właściwym do wyznaczenia $R_y$ jest (d), to znaczy warunek, że w przegubie moment, liczony jak siła przekrojowa (suma momentów po prawej lub lewej strony przegubu) musi być zerowy, natomiast  równania (a), (b) i (c) nie są właściwe i wystarczające do wyznaczenia reakcji:

(d) $\to R_y =16,25 kN$.

Stąd moglibyśmy wyznaczyć $R=\frac {R_y}{cos \alpha}$ oraz $R_x=R sin \alpha$, lecz jest to zbyteczne, znamy już bowiem wszystkie siły z lewej strony podpory i moment podporowy obliczymy sumując momenty lewostronnie:

+ M_A+100·4-16,25·8+2·5·(8+2,5)=0 ⇒ M_A=-375 kNm.

#2  śnieg S

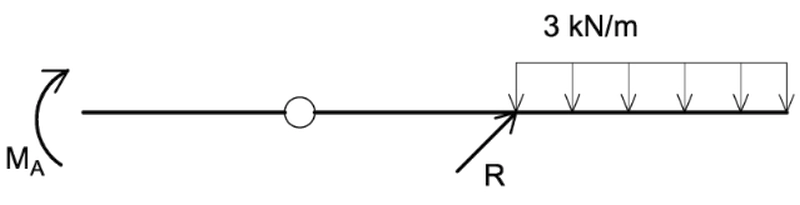
Rys,2b Schemat dla #2=S

(d): Ry·4-3 · 5 ·(4+2,5)=0 ⇒ R_y=1/4 · 3 · 5 · 6,5=24,375 kN,

+ M_A-24,75·8 – 3·5·(4+2,5)=0 ⇒ M_A=+37,5 kNm.

#3  Q _{kat C2}

Rys. 2c Schemat dla #3= Q (C2)

(d): Ry·4-=0 ⇒ R_y= 0 kN,

+ M_A+50·4=0 ⇒ M_A=-200 kNm.

#4  W+

Rys. 2d Schemat dla #4= W+

(d): R_y·4-10=0 ⇒ R_y= 2,5 kN,
+M_A-2,5·8+10=0 ⇒  M_A=10 kNm.

#5  W-

Rys. 2e Schemat dla #4= W-

(d): R_y·4-010=0 ⇒ R_y= -2,5 kN,
+M_A+2,5·8+10 ⇒  M_A=-30 kNm.

Zestawienie momentów podporowych od prostych obciążeń:

#1 (stałe G)             -375 kNm
#2 (śnieg S)           +37,5 kNm
#3 (Q_{kat C2})          -200 kNm
#4 (wiatr W+10)      +10 kNm
#5 (wiatr W-10)         -30 kNm

Krok 3:  Wyznaczenie momentu obliczeniowego (w sytuacjach kombinacyjnych)

Maksymalny moment M_A: #2, #4 – niekorzystne; #1,, #3 ,#5 – korzystne, nie uwzględniamy jednocześnie #4 i #5 (nie jest możliwe jednoczesne oddziaływanie wiatru w dwóch kierunkach)

K1  wg formuły ($\ref{K1}$) – #1 bez redukcji:
1,0·(-375)+1,5·[0,5·37,5+0,6·10]+0,0·[0,7·(-200)]=-337,9 kNm
K2  wg formuły ($\ref{K2}$) Q_{kat C2} – wiodące :
1,0·0,85·(-375)+1,5·37,5+1,5·0,6·10+0,0·[0,7·(-200)]=-253.5 kNm
K3  wg formuły ($\ref{K2}$) W+ – wiodące :
1,0·0,85·(-375)+1,5·10 1,5·0,5·37,5+0,0·[0,7·(-200)]=-275,6 kNm

M_A,d,max=max{ -337,9; -253.5; -275,6}= -253.5 kNm.

Minimalny moment M_A: #1,, #3 ,#5 – niekorzystne; #2, #4 – korzystne

K4 wg formuły ($\ref{K1}$) : #1 bez redukcji:
1,35·(-375)+1,5·[0,7·(-200)+0,6·(-30)]+0,0·[0,5·37,5]=-743,3 kNm

K5 : wg formuły ($\ref{K2}$) – #1 z redukcją; #3 – wiodące
1,35·0,85·(-375)+1,5·(-200)+1,5·[0,6·(-30)]+0,0·[0,5·37,5]=-757,3 kNm

K6 : wg formuły ($\ref{K2}$) – #1 z redukcją, #5 -wiodące
1,35·0,85·(-375)+1,5·(-30)+1,5·[0,7·(-200)]+0,0·[0,5·37,5]=-685,3 kNm

M_A,d,min=min { -743,3; -757,3; -885,3}= -757.3 kNm.

Wynik: Maksymalny, obliczeniowy  moment utwierdzenia M_A,d wynosi -253.5, a minimalny -757.3 kNm.

Przykład 3

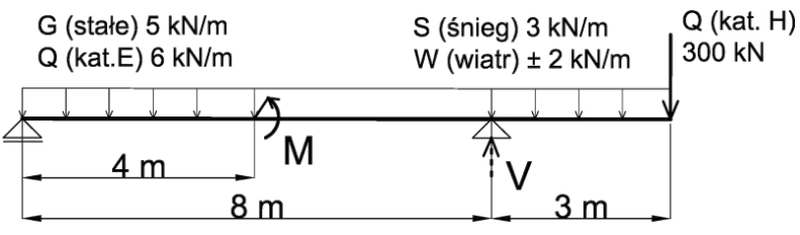
Wyznaczyć maksymalny i minimalny, obliczeniowy przekrojowy moment zginający M w  belce pokazanej na rys.3.

Rys.3. Schemat do przykładu 3

Rozwiązanie:

Krok 1: Definicja obciążeń prostych

Belka obciążona jest obciążeniami prostymi o różnej naturze, które oznaczymy następująco:
#1  obciążenie stałe G = 5 kN/m,
#2 obciążenie zmienne Q _{kat E}= 6 kN/m,
#3 obciążenie zmienne Q _{kat H}=  300 kN,
#4 śnieg S = 3 kN/m,
#5 wiatr1 W+ = + 2 kN/m,
#6 wiatr2 W-  = – 2 kN/m.

Obciążenia #2 i #3 rozróżniamy, ponieważ mają inne współczynniki redukcyjne. Obciążenia #5 i #6 rozróżniamy, ponieważ mogą mieć inne współczynniki obciążeń (działanie korzystne-niekorzystne), a ponadto mogą wystąpić winnych fizycznie możliwych sytuacjach.

Krok 2: Wyznaczenie momentu zginającego od prostych obciążeń

#1 G         :
V=1/8·5·4·2=+5 kN ,  M=V·4=5·4=+20 kNm,
#2 Q _{kat E} :
V=1/8·6·4·2=+6 kN ,  M=6·4=+24 kNm,
#3 Q _{kat H} :
V=1/8·300·11=+412,5 kN ,  M=412,5·4-300·7=-450 kNm,
#4 S     :
V=1/8·3·3·(1,5+8)=+10,7 kN ,  M=10,7·4-3·3·(1,5+4)=-6,75 kNm,
#5 W+ :
V=1/8·2·3·(1,5+8)=+7,13 kN ,  M=7,13·4-2·3·(1,5+4)=-4,5 kNm,
#6 W-  :
V=1/8·(-2)·3·(1,5+8)=-7,13 kN , M=(-7,13)·4-2·3·(1,5+4)=-61,5 kNm.

Krok 3:  Wyznaczenie momntu zginajacego w sytuacjach kombinacyjnych

Maksymalny moment zginający:

K1: kombinacja wg formuły ($\ref{K1}$): #1 i #2 działanie niekorzystne, pozostałe – działanie korzystne:
M_d= 1,35·20+1,5·1,0·24+0,0·[0,0· (-450)+ 0,5·(-6,75)+0,6·(-4,5)]=63,0 kNm

K2: kombinacja wg formuły ($\ref{K2}$):#1,#2 działanie niekorzystne, pozostałe korzystne, wiodące #2 :
M_d=0,85·1,35·20+1,5·24 0,0 + 0,0·[0,0· (-450)+ 0,5·(-6,75)+0,6·(-4,5)]=59,0 kNm

M_d,max=max{ 63,0; 59,0}=63,0 kNm.

Minimalny moment zginający
K3: korzystne działanie G, Q _{kat E}, niekorzystne pozostałe , wiodące Q _{kat H}
M_d=1,0·0,85· 20+1,5·(-450)+1,5[ 0,5·(-6,75)+0,6·(-61,5)]+ 0,0· (korzystne towarzyszące)=-718,4 kNm

M_d,min=min{ -718,4; 0}= -718,4 kNm.

Wynik: Maksymalny, obliczeniowy moment zginający  M_d wynosi +63,0, a minimalny -718.4 kNm.

Przykład 4

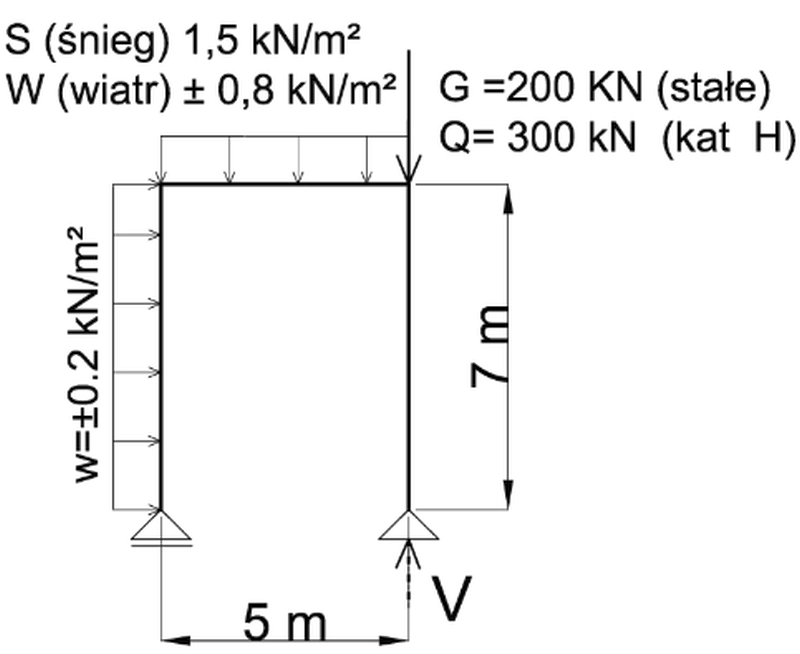
Wyznaczyć maksymalną i minimalną, obliczeniową reakcję V ramy, pokazanej na rys.4. Ramy rozstawione są co a= 2 m po długości budynku.

Rys.4. Schemat do przykładu 4

Rozwiązanie:

Krok 1: Definicja obciążeń prostych

#1 obciążenie stałe G=200 kN,
#2 obciążenie zmienne Q _{kat H} = 300 kN,
#3 śnieg S  = 1,5 kN/m² ·2m=3 kN/m,
#4 rygiel W+  =+0,8 kN/m²·2m=+1,6 kN/m,
#5 rygiel W- (-0,8 kN/m² ·2m=-1,6 kN/m),
#6 słup W+ (+0,2 kN/m² ·2m=+0,4 kN/m),
#7 słup W- (-0,2 kN/m² ·2m= – 0,4 kN/m)

Uwaga:
Wiatr może jednocześnie działać tak, że mamy kilka sytuacji obliczeniowych : 1) parcie na słup #6 + [parcie na rygiel #4 lub ssanie na rygiel #5] , lub 2) ssanie na słup #7 + [ parcie na rygiel #4 lub ssanie na rygiel #5], czyli możliwe są wszystkie kombinacje działania wiatru słup-rygiel.

Krok 2: Wyznaczenie reakcji V od prostych obciążeń

#1 (stałe)         V=+200 kN,
#2 (kat. H)      V=+300 kN,
#3 (śnieg)      V=1/5 ·3·5·2,5=+7,5 kN,
#4 (wiatr 1- rygiel parcie)  V= $\frac{}{1,6 \cdot 5}{2}=$+4,0 kN,
#5 (wiatr 1- rygiel ssanie )  V=-4,0 kN,
#6 (Wiatr 1 – słup parcie)    V= 1/5 · 0,4·7·3,5=+1,96 kN,   
#7 (Wiatr 1 – słup ssanie)    V= 1/5 · (-0,4)·7·3,5=-1,96 kN,

Krok 3:  Wyznaczenie reakcji  w sytuacjach kombinacyjnych

Maksymalna reakcja: #1, #2, #3 , (#4+#6) – niekorzystne; (#5+#7)- korzystne;  pomijamy (#4+#7), (#5+#6); wiatr działa jednocześnie i na rygiel i na słup (nie wystąpi samodzielnie #4 do #7); nie mieszamy schematów działania wiatru (nie wystąpi np (#4+#6) i (#5+#7) lub inne).

K1: Formuła ($\ref{K1}$)
V_d= 1,35·200+1,5· [0,0· 300+0,5· 7,5+0,6· (4,0+1,96)] 0,0·(korzystne) = 281,0 kN
K2: Formuła ($\ref{K2}$): #2- wiodące
V_d= 0,85·1,35·200+1,5·300+1,5·[0,5· 7,5+0,6·(4,0+1,96)]= 690,5kN
K3: Formuła ($\ref{K2}$):  #3- wiodące
V_d= 0,85·1,35·200+1,5·7,5+1,5·[0,0· 300+0,6·(4,0+1,96)]= 246,1 kN
K4: Formuła ($\ref{K2}$):  (#4+#6)- wiodące
_Vd= 0,85·1,35·200+1,5·(4,0+,96) + 1,5·[0,0· 300+0,5*7,5]= 244,1 kN

Maksymalna reakcja obliczeniowa V_{d, max}=max{281,0; 690,5;246,1 ;244,1}=690,5 kN

Minimalna reakcja: (#5+#7)- niekorzystne;  #1, #2, #3 -korzystne; ;  pomijamy (#4+#6) i inne sytuacje obciążenia wiatrem, ponieważ  wykluczają schemat niekorzystny, a nie mogą współistnieć (np. nie może być obciążony wiatrem tylko słup bez rygla).

K5: Formuła ($\ref{K1}$)
V_d= 1,00·0,85· 200+1,5· [0,6· (-4,0-1,96) ]+ 0,0·(0,0· 300+0,5· 7,5)] = 164,6 kN
K6: Formuła ($\ref{K2}$): (#5+#7)- wiodące
V_d= 1,00·0,85·200+ 1,5· [-4,0-1,96] + 0,0·(0,0· 300+0,5· 7,5) = 161,1 kN

Minimalna reakcja obliczeniowa V_{d, min}=min{164,6; 161,1}=161,1 kN

Wynik: Maksymalna, obliczeniowa reakcja  V_d wynosi +690,5, a minimalna +161,1 kN.

Kombinacje charakterystyczne

Kombinacje charakterystyczne stosuje się do oszacowania obciążeń w celu sprawdzenia stanu granicznego użytkowalności [1],  kl.  A1.4.

W stanie granicznym użytkowalności sprawdzeniu podlegają w szczególności odkształcenia i przemieszczenia poziome , ugięcia pionowe, drgania oraz zarysowania (np. w konstrukcjach żelbetowych).

Charakterystyczna formuła kombinacyjna

W kombinacjach charakterystycznych – współczynniki obciążeń są równe  1 , to znaczy $\gamma_{G,j}=1$ i $\gamma_{Q,i}=1$, więc nie występują w formułach kombinacyjnych.

Obciążenia charakterystyczne wynikają z dwóch formacji formuł kombinacyjnych

a) kombinacje   charakterystyczne  „częste ” (dla odwracalnych stanów granicznych, np. przemieszczenia rysy)  zgodnie z  [1], wzór(6.15b)

$$\begin{equation}  \sum \limits_{j \ge 1}  G_{k,j } \text {„+”}  \text{„P”}  \text {„+”}  \psi_{1,1} \cdot Q_{k,1}  \text{„+”}  \sum \limits_{ i>1} \psi_{2,i} \cdot Q_{k,i} \label{K3} \end{equation}$$

gdzie  „P” oznacza siły od sprężenia.

Kombinacji  „częstych” jest tyle, ile rodzajów obciążeń zmiennych (każde z nich może być obciążeniem wiodącym „1” redukowanym współczynnikiem wartości częstej $\psi_1$ , pozostałe obciążenia zmienne są redukowane współczynnikami wartości „prawei stałej” $\psi_2$.

b) kombinacja   charakterystyczna  „prawie stała ” (dla nieodwracalnych stanów granicznych, np. przemieszczenia rysy)  zgodnie z  [1], wzór (6.16b)

$$\begin{equation}  \sum \limits_{j \ge 1}  G_{k,j } \text {„+”}  \text{„P”}  \text {„+”}  \sum \limits_{ i \ge > 1} \psi_{2,i} \cdot Q_{k,i} \label{K3a} \end{equation}$$

Kombinacja „prawie stała” jest jedna.

W formułach ($\ref{K3}$) i ($\ref{K3a}$)występują inne niż w kombinacjach obliczeniowych współczynniki redukcyjne,  które tez są zestawione w tab.1:
$\psi_1$  – współczynnik dla wartości częstej oddziaływania zmiennego (w skrócie zwany „częsty”) ,
$\psi_2$ – współczynnik dla wartości prawie stałej obciążenie zmiennego ( w skrócie zwany „prawie stały”).

Charakterystyczną formułę kombinacyjną ($\ref{K3}$) można słownie wyrazić następująco:

Charakterystyczną formułę kombinacyjną ($\ref{K3a}$) można słownie wyrazić następująco:

Przykład wyznaczania obciążeń charakterystycznych

Wyznaczyć obciążenia charakterystyczne  działające na połać dachową budynku, przy wyznaczonych obciążeniach prostych:

Oddziaływania stałe:
#1 Ciężar własny konstrukcji                         0,40 kN/m2,
#2 Ciężar pokrycia dachowego                      0,35 kN/m2,

Oddziaływania zmienne
#3 Obciążenia podwieszone w sklepie             0,5 kN/m2   (przyjęte jako zmienne  elementy instalacji oraz architektury),
#4  Obciążenie użytkowe                                0,4 kN/m2  (obsługa  dachu kat. H),
#5 Śnieg                                                          0,72 kN/m2,
#6 Wiatr ssanie na połać                                 0,4 kN/m2,
#7 Wiatr parcie  na połać (otwarte bramy)   0,2 kN/m2.

Rozwiązanie

a) kombinacje charakterystyczne „częste”

$KC_1$ wiodące obciążenie podwieszone

$KC_1$ = (#1+ #2) + 0,7 #3+ (0,0· #4+0,2 #5 + 0,0· #7 ) = (0,40+0,35)+ 0,7· 0,5+ (0,0· 0,4+ 0,2· 0,72+ 0,0· 0,2)=1,244 kN/m2,

$KC_2$ wiodące obciążenie dachu

$KC_2$ = (#1+ #2) + 0,0 ·  #4+ (0,6 · #4 = 02 · #5+ 0,0 · #7 ) = (0,40+0,35)+ 0,0· 0,4 + ( 0,6 ·  0,5+ 0,2· 0,72+ 0,0· 0,2)=1,194 kN/m2,

$KC_3$ wiodące obciążenie śniegiem

$KC_3$ = (#1+ #2) + 0,5 ·  #5 + (06 · #3+ 0,0· #4 +0,0·  #7) = (0,40+0,35)+ 0,5· 0,72 + ( 0,6 ·  0,5+ 0,0· 0,4 + 0,0· 0,2)=1,41 kN/m2,

$KC_2$ wiodące obciążenie ssaniem wiatru

$KC_2$ = (#1+ #2) + 0,2· #6+ (0,6· #3+0,0· #4+ 0,2· #5) = (0,40+0,35) + 0,2· (-0,4) + ( 0,6· 0,5 + 0,0· 0,4+  0,2· 0,72)= 1,114 kN/m2,

$KC_2$ wiodące obciążenie parciem wiatru

$KC_2$ = (#1+ #2) + 0,2· #7+ (0,6· #3+0,0· #4+ 0,2· #5) = (0,40+0,35) + 0,2· 0,2 + ( 0,6· 0,5 + 0,0· 0,4+  0,2· 0,72)= 1,234 kN/m2,

a) kombinacje charakterystyczna „prawie stała”

$KC_3$ = (#1+ #2) + ( 0,6· #3+0,0· #4+0,0· #5 + 0,0· #7) = (0,40+0,35) + (0,6· 0,5+ 0,0· 0,4+ 0,2· 0,72+0,0 0,2)= 1,194 kN/m2,

Kombinacje w stanie równowagi EQU

W stanie granicznym równowagi EQU , np. w przypadku wyporu obiektu przez wodę gruntową do wyznaczenia wartości obliczeniowych stosuje się formule kombinacyjną ($\ref{K1}$) , to znaczy bez redukcji obciążenia stałego i z redukcją wszystkich obciążeń zmiennych

Współczynniki w formule kombinacyjnej są specyficzne i zdefiniowane w [1], tab. A1.2 oraz  [15] tab. A.1 i A.2 (Załącznik A). Zasady te syntetycznie przedstawioneo poniżej.

Wartości współczynników kombinacyjnych

Siły stabilizujące

w najczęściej występującymi przypadku stanu EQU – wyporu obiektu przez wodę gruntową, stabilizujące obciążenia są obciążeniami grawitacyjnymi  ( działają pionowo w dół) i są korzystne,

Wartości współczynników obciążeń w przypadku obciążeń korzystnych są następujące:

dla obciążeń stałych        $ \gamma_G =0,9$

dla obciążeń zmiennych  $ \gamma_Q =0,0 $

W takim przypadku nieistotne są współczynniki redukcyjne do obciążeń zmiennych.

Siły destabilizujące

Podstwowym oddziaływniem destabilizującym jest woda gruntowa działająca siłą wyposru zgodnie z prawem Archimedesa.
Przy ustalonym poziomie wody gruntowej  zastosowanie wspólczynników częściowych innych od $\gamma_G$= 1,0 jest nieuzasadnione (inny ciężar wody jest  jest nieuzasadnione fizycznie niemożliwy) – p. też klauzula 2.4.7.3.2(2) [15].

Należy natomiast uwględnić zmiany poziomu wody gruntowej (wahania sezonowe) i tę część obciażęnie wodą potraktowąć jako obciązęnie zmienne (ze współczynnikiem obciążeń $\gamma_Q=1,5$
Zmiany wypieranej objętości (zmiany wymiarów konstrukcji też byłoby nieuzasadnione, bo w konswkwencji zwiększałyby się obciążenia stabilizujące, co w bilansie działałoby w stronę niebezpieczną.

W konsekwencji w stanie wyporu wody, obciążenia destabilizujące wodą dzielimy na:
cześć stałą $ G_{H_{2O}} $ ,  czyli siły wyporu przy ustabilizowanym zwierciadle wody gruntowej
część zmienną $ Q_{H_{2O}}$, czyli siły wyporu wynikające z wahań stanu wody ponad poziom ustabilizowany.

W formule stanu granicznego EQU do sił wyporu wody $H_{2O}$ stosuje się współczynniki obciążeń :
$ \gamma_{G_{H_{2O}},dest} =1,0$
$ \gamma_{Q_{H_{2O}},dest} =1,5$

Destabilizujących obciążeń wodą nie redukuje się, *(zaróewno cześc stała jak i zmienna).

Do innych niż woda destabilizujących obciążeń stałych (lub prawie stałych) stosuje się współczynnik obciażeń

$\gamma_{G,dest} =1,1$

W przypadku braku prognoz dotyczących sezonowych zmian poziomu wody gruntowej  można w uproszczeniu do całej części stałe wyporu wody zastosować współczynnik

$ \gamma_{G_{H_{2O}},dest} =1,1$

Oznacza to szacunkowo, założenie, że  wahania $\Delta h$ poziomu ZWG przyjęto:

$Delta h = \cfrac{1,1-1 }{1,5} \cdot h \approx $ 6,7% h

Ze względu na zbyt zgrubne oszacowanie w większosći praktycznych przypadków – zaleca się postępoweanie pokazane wyzej.

W przypadku sprawdzania stateczności w stanie granicznym EQU oprócz powyższych współczynników obciążeń NIE stosuje się globalnego współczynnika pewności „n” z dawnych norm.

Przykład wyznaczania obciążeń w stanie EQU

Wyznaczyć obciążenia stabilizujące i destabilizujące w staniu EQU wyporu przez wodę gruntową budynku z częścią podziemną zanurzona poniżej zwierciadła wody gruntowej

Obciążenia stabilizujące

Oddziaływania stałe:
#1 Ciężar własny konstrukcji         1000 kN
#2 Grunt lub inne dociążenie nieprzemieszczalne           90  kN
(nie może być przemieszczony do czasu spełnienia warunku nośności w sytuacji bez j zalegania gruntu) !

Oddziaływania zmienne ( stan bez śniegu i wiatru)
#3 Grunt dociążający  przemieszczalny               120 kN
(może być usunięty w trakcie eksploatacji)

Obciążenia destabilizujące

#4 wypór wody przy ustalonym zwierciadle   800 kN
#5 wypór wody wynikający z wahań poziomu $\pm 120 $ kN

Rozwiązanie:

Obciążenie stabilizujące
$F_{stb,d}$ = 0,9· (#1+#2) + 0,0· #3= 0,9· (1000+90) + 0,0 ·120=981 kN

Obciążenie destabilizujące
$F_{dst,d}$ = 1,0·#4 + 1,5·#5= 1,0· 800 + 1,5·120=980 kN

Ponieważ

$F_{stb,d}$= 981 kN >  $F_{dst,d}$ = 980 kN, to warunek  EQU jest zachowany,

Wyjątkowe i sejsmiczne kombinacje oddziaływań

Wartości współczynników częściowych dla oddziaływań (współczynniki obciążeń) w stanach granicznych nośności w wyjątkowych i sejsmicznych sytuacjach obliczeniowych były przyjmowane równe 1,0 i formuła kombinacyjna $\ref{K3}$) zostaje rozbudowana o efekty obciążeń wyjątkowych „$A_d$”, jak następuje

$$\begin {equation} \sum \limits_{j=1} G_j + „P”+ „A_d”+( \psi_{1,1} \text { lub } \psi_{2,1} ) \cdot Q_1 + \sum \limits_{i>1} ( \psi_{2,i} \cdot Q_i) \label{K4}\end {equation}$$

gdzie:
„P” oznacza charakterystyczne siły od sprężenia.
„$A_d$” – charakterystyczne obciążenia wyjątkowe

Wybór między $\psi_{1,1}$  i $\psi_{2,1}$, a także wybór zmiennego obciążenia wiodącego $Q_1$ dokonuje się odpowiednio do miarodajnej sytuacji obliczeniowej (uderzenie, pożar, stan konstrukcji po wydarzeniu wyjątkowym). Zalecenia do wyboru zawierają normy przedmiotowe.
W praktyce formułę ($\ref{K4}$) stosuje się najczęściej w postaci ($\ref{K5}$) (bezalternatywnej), a obciążenie wiodące wybiera się z koszyka wszystkich obciążeń zmiennych i przebiega przez wszystkie  $Q_i$.

$$\begin {equation} \sum \limits_{j=1} G_j + „P”+ „A_d”+  \psi_{1,1} \cdot Q_1 + \sum \limits_{i>1} ( \psi_{2,i} \cdot Q_i) \label{K5}\end {equation}$$

Wartości współczynników redukcyjnych przyjmuje się również z tab.1.

W przypadku sytuacji sejsmicznej formuła ($\ref{K4}$) ulega drobnej korekcie, polegającej na tym, że w miejsce  obciążenia  wyjątkowego „$A_d$” wstawiamy obciążenia sejsmiczne „$A_{Ed}$”  i zmienne obciążenie wiodące redukuje się współczynnikiem $\psi_{2,1}$.

Kombinacje w stanie geotechnicznym GEO

W stanie granicznym geotechnicznym GEO, do sprawdzanie stanu granicznego elementów konstrukcji poddanych oddziaływaniom geotechnicznym (stóp fundamentowych, pali, części podziemnej ścian, itp.). dokonuje się jednym z kilku możliwych podejść, uzupełnionych w zakresie oddziaływań geotechnicznych i nośności gruntu, wyznaczonej zgodnie Eurokodem 7 [15].

W każdym podejściu, stosuje się różne kombinacje współczynników obciążeń i współczynników redukcyjnych, ale reguły kombinacyjne są standardowe ($\ref{K1}$) lub\i ($\ref{K2}$).

W niniejszym opracowaniu wskażemy jedynie na dwa najczęściej spotykane zadania, opisane niżej. Inne podejścia należy stosować zgodnie z przedmiotowymi normami

 Fundamenty budowli

Wymiarowanie fundamentów przeprowadza się zwykle na kombinacje

$$\begin {equation} \sum \limits_{j=1} (\gamma_{G,j}\cdot G_{k,j}) + \gamma_{Q_1}\cdot Q_{k, 1 } +  \sum \limits_{i>1} (\gamma_{Q,k, j}\cdot \psi_{0,i} \cdot Q_{k,i} \label{K6})\end {equation}$$.

przy czym:
$\gamma_{G,j} =1,00$,
$\gamma_{Q,j} =1,30$ (jeśli niekorzystne) ; $\gamma_{G,j} =1,00$ (jeśli korzystne)

Współczynniki przyjmuje się redukcyjne wg tab.1

Nośność konstrukcji obciążonej  geotechnicznie

Wymiarowanie konstrukcji , obciążonej geotechnicznie przeprowadza się  na zwykłe kombinacje ($\ref{K1}$) oraz ($\ref{K2}$) oraz współczynniki obciążeń i redukcyjne, przy czym oddziaływanie  geotechniczne  parciem gruntu (np na ściany części podziemnej budynku), traktuje się jako trwałe (stałe) i zalicza do obciążeń G.

Oprogramowanie

Kalkulator oddziaływań normowych EN SPECBUD

[Kliknij na obrazek – przejdziesz na stronę SPECBUD]

Inne, wybrane kalkulatory obciążeń

Kalkulator obciążeń normowych 1.
Kalkulator obciazeń.pl
Kalkulator obciązeń ComputerWorld
Kalkulatory wbudowane do programy obliczeniowych systemów konstrukcyjnych, w tym: Consteel, Ansys, Sofistic i inne.

Literatura

1. PN-EN 1990:2004, Eurokod: Podstawy projektowania konstrukcji
2. PN-EN 1991-1-1:2004, Eurokod 1: Oddziaływania na konstrukcje. Część 1-1: Oddziaływania ogólne. Ciężar objętościowy, ciężar własny, obciążenia użytkowe w budynkach
3. PN-EN 1991-1-2:2006, Eurokod 1: Oddziaływania na konstrukcje. Część 1-2: Oddziaływania ogólne. Oddziaływania na konstrukcje w warunkach pożaru
4. PN-EN 1991-1-3:2005, Eurokod 1: Oddziaływania na konstrukcje, Część 1-3: Oddziaływania ogólne- Obciążenie śniegiem
5. PN-EN 1991-1-4:2008, Eurokod 1: Oddziaływania na konstrukcje, Część 1-4: Oddziaływania ogólne. Oddziaływania wiatru
6. PN-EN 1991-1-5:2005, Eurokod 1: Oddziaływania na konstrukcje, Część 1-5: Oddziaływania ogólne. Oddziaływania termiczne
7. PN-EN 1991-1-6:2007, Eurokod 1: Oddziaływania na konstrukcje, Część 1-6: Oddziaływania ogólne. Oddziaływania w czasie wykonywania konstrukcji
8. PN-EN 1991-1-7:2008, Eurokod 1: Oddziaływania na konstrukcje, Część 1-7: Oddziaływania ogólne. Oddziaływania wyjątkowe
9. PN-EN 1991-2:2008, Eurokod 1: Oddziaływania na konstrukcje, Część 2: Obciążenia ruchome mostów
10. PN-EN 1991-3:2009, Eurokod 1: Oddziaływania na konstrukcje, Część 3: Oddziaływania wywołane dźwignicami i maszynami
11. PN-EN 1991-4:2008, Eurokod 1: Oddziaływania na konstrukcje, Część 4: Silosy i zbiorniki
12. PN-EN 1993-3-1+AC+Ap1:2008, Eurokod 3: Projektowanie konstrukcji stalowych, Część 3-1: Wieże, maszty i kominy. Wieże i maszty
13. PN-EN 1993-3-2+Ap1:2008, Eurokod 3. Projektowanie konstrukcji stalowych, Część 3-2: Wieże, maszty i kominy. Kominy
14. PN-EN 50341-3-22:2010, Elektroenergetyczne linie napowietrzne prądu przemiennego powyżej 45 kV, Część 3: Zbiór normatywnych warunków krajowych
15. PN-EN 1997-1+AC+Ap1+Ap2:2008, Projektowanie geotechniczne, Część 1: Zasady ogólne

________________________________