Artykuł w ciągu ostatnich 24 godzin czytało 4 Czytelników
Uwagi i recenzje podręcznika przesyłać na adres: wydawnictwo@chodor-projekt.net lub leszek@chodor-pojekt.pl
spis treści prodręcznika: [ Imperfekcyjna metoda projektowania konstrukcji ]
Część 2-3
Nawigacja: [2-1: Imperfekcje projektowe z odchyłek wykonawczych] ⇐ ⊗ ⇒ [ 2-3: Uogólnienie formuły Ayrton-Perry]
Geneza metod imperfekcyjnych nieodłącznie jest związana z klasyczną metodą projektowania pręta ściskanego i zginanego z użyciem współczynnika wyboczeniowego zaproponowanego już w IX wieku przez Ayrton i Perry (1886) [1] z analizy pręta ściskanego z imperfekcją łukową.
W niniejszym podręczniku uznaje się początek metod imperfekcyjnych jest związany z opublikowaniem rozwiązania Ayrton-Perry (1886). mimo że metody projektowania wywodzące się ze współczynników redukcyjnych (wyboczeniowych) są już hostoryczne. Metodami imperfekcyjnymi nazwano te metody, w których bezpośrednio zadaje się wymuszenia (obciazenia) imperfekcjami i prowadzi kompletna analizę II rzedu z pomnięciem uproszczonych reguł amplidikacji APF.
Teoria sformułowana w przez Ayrton-Perry stała się podstawą praktyki normalizacyjnej w wielu krajach. Podejście [2] jest podstawą brytyjskich norm od prawie 100 lat (w odmianie [3]) ). W pracy [4] przedstawiono wersję używaną we Francji. Teoria Ayrton-Perry jest podstawą współczesnej formacji współczynników wyboczeniowych w normie [5] i innych normach Eurokod. Teoria współczynników wyboczeniowych Ayrton-Perry jest hipotezą, wspomaganą badaniami eksperymentalnymi, w których ustala się parametr imperfekcji, wynikający z imperfekcji geometrycznych, materiałowych i naprężeń technologiczych ( walcowniczych, spawalniczyh w konstrukcjach stalowych, skurczu w konstrukcjach żelbetowych itd). Wobec tego hipotezą podlegającą weryfikacji eksperymentalnej, jest również powszechnie wykorzystywany wzór na naprężenia w pręcie zginanym momentem M i ściskanym siłą osiową N:
$$\begin {equation} \sigma= \cfrac{M}{W} + \cfrac{N}{\chi \cdot A} \label{1} \end {equation}$$
gdzie: $\chi$ – współczynnik wyboczeniowy, A- pole przekroju, W – wskaźnik wytrzymałości,
Sumowanie naprężeń normalnych od zginania oraz ściskania w sposób określony powyższą formułą należy traktować jako użyteczną, inżynierską aproksymację, umożliwiającą projektowanie konstrukcji prętowych w dobie przed-informatyzacyjnej. Obecnie, wraz z powszechnym stosowaniem obliczeń numerycznych w projektowaniu konstrukcji oraz stosowaniem nowych zaawansowanych technologii i programów obliczeniowych – era współczynnika wyboczeniowego jest schyłkowa i wchodzimy w erę metody imperfekcyjnej [6].
Klasyczna teoria Ayrton-Perry
Ayrton-Perry Formuła (APF)
W roku 1886 eksperci z dziedziny elektryczności i magnetyzmu William Ayrton i John Perry przedstawili jedną z najdłużej stosowanych teorii w wymiarowaniu konstrukcji budowlanych – teorię ściskania słupa z imperfekcjami. Na przestrzeni lat przedstawiane były rozmaite zapisy postacie tej formuły u wynikającego z niej współczynnika wyboczeniowego. Przedstawiamy kilka równoważnych postaci formuły Ayrton-Perry APF, której wyprowadzenie zaprezentowano poniżej.
Klasyczna postać APF
Teoria Perry-Robertson jest dzisiaj podstawą obliczania współczynników wyboczeniowych [6] w postaci zaprezentowanej w roku 1920 przez [2] na naprężenia w pręcie z imperfekcjami $\sigma_{imp}$, jako pierwiastek równania kwadratowego ($\ref{35}$)):
$$ \begin {equation} \sigma_{imp} =1/2 \cdot \left \{ f_y+ \sigma_{cr} (1+\Theta)-\sqrt{[f_y+ \sigma_{cr} (1+\Theta)]^2 – 4 f_y \sigma_{cr} } \right \} \label{2} \end {equation}$$
$$ \begin {equation} \Theta= e_0 \cdot \cfrac{A}{W }\label{3} \end {equation}$$
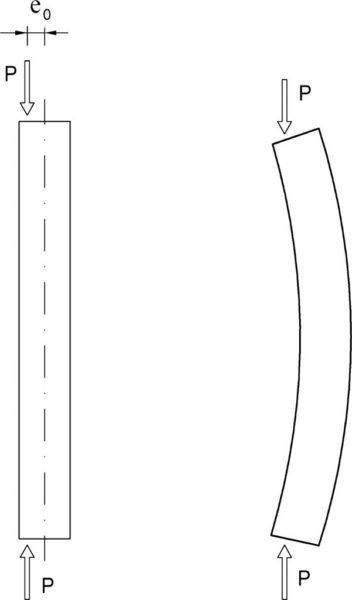
$e_0$ jest amplitudą początkowego wygięcia pręta, $A$- polem przekroju pręta, $W$ – wskaźnikiem wytrzymałości przekroju na zginanie. Formuła ($\ref{2}$) może być zapisana dla każdego kierunku wyboczenia pręta (y, z), a w każdym przypadku należy brać odpowiednie do tego kierunku wartości $e_0$ oraz $W$.
Zwarta postać APF
Po przekształceniach formalnych oryginalny zapis ($\ref {2}$) formuły APF można przedstawić w zwartej formie
$$ \begin {equation} (\sigma_{cr} -\sigma_{imp})\cdot (f_y-\sigma_{imp})=\sigma_{imp}\cdot \sigma_{cr}\cdot \Theta \label{4} \end {equation}$$
gdzie $\sigma){imp}$ – napreżenia w pręcie obarczonym impefekcjami.
Klasyczne wyrażenie na współczynnik wyboczeniowy
Definicja smukłości względnej elementu (1-1.3) może być zapisana w naprężeniach, co uzyskujemy poprzez podstawienia: $N_{cr}=\sigma_{cr} \cdot A$ oraz $N_R=f_y \cdot A$. w postaci:
$$ \begin {equation} \overline \lambda = \sqrt{\cfrac{f_y}{\sigma_{cr} }} \label{5} \end {equation}$$
Z definicji ($\ref{5}$) naprężenia krytyczne można zapisać jako:
$$ \begin {equation} \sigma_{cr}=\cfrac {f_y}{\overline \lambda^2} \label{6} \end {equation}$$
Współczynnik wyboczeniowy $\chi$ występujący w formule ($\ref{1}$) zdefiniowany w naprężeniach jest stosunkiem naprężeń w pręcie z imperfekcjami $\sigma_{imp}$ do wytrzymałości materiału $f_y$:
$$ \begin {equation} \chi = \cfrac{\sigma_{imp}}{f_y}\label{7} \end {equation}$$
Po podzieleniu obu stron ($\ref{2}$) przez granicę plastyczności $f_y$ i uwzględnieniu, ($\ref{6}$) oraz ($\ref{7}$) otrzymamy zależność współczynnika wyboczeniowego od smukłości pręta ($\ref{5}$) lub (1-1.3) w postaci
$$\begin {equation} \chi= 1/2 \cdot \left [ (1+\overline \Theta) – \sqrt{ (1+\overline \Theta)^2 – \cfrac{4}{ \overline \lambda^2} } \right ] \label {8} \end {equation}$$
gdzie wprowadzono względny parametr imperfekcji
$\overline \Theta=\cfrac{1+\Theta}{\overline \lambda^2}$
Postać da Silva APF
Formuła ($\ref{8}$)może być przekształcona do zwartej, choć uwikłanej postaci [7]
$$ \begin {equation} (1-\chi)\cdot (1- \overline \lambda^2 \cdot \chi ) =\Theta \cdot \chi \label{9} \end {equation}$$
a parametr imperfekcji ($\ref{3}$) może być zapisany w postaci
$$ \begin {equation} \Theta=\alpha \cdot (\overline \lambda -\overline \lambda_0) \label{10} \end {equation}$$
gdzie:
$\alpha$ wg Tab. (1-3-2),
$\overline \lambda_0$ wg formuły $(\ref{16}$)
skąd otrzymujemy wyrażenie na strzałkę wygięcia imperfekcji łukowej
$$ \begin {equation} e_0=\alpha \cdot (\overline \lambda -\overline \lambda_0) \cdot \cfrac{W}{A} \label{11} \end {equation}$$
Zapis współczynnika wyboczeniowego da Silva ($\ref{9}$), parametru imperfekcji ($\ref{10}$) oraz imperfekcji łukowej ($\ref{11}$) jest przydatny w opisie alternatywnej metody imperfekcyjnej AIM.
Postać Eurokod APF
Po przekształceniach ($\ref{8}$) można uzyskać standardową postać formuły APF, stosowaną współcześnie w normach Eurokod do projektowania konstrukcji budowlanych:
$$ \begin {equation} \chi^2+\chi\cdot\left[ -1-\cfrac{1}{ \overline \lambda^2}( 1-\Theta) \right ] +\cfrac{1}{ \overline \lambda^2}=0 \label{12} \end {equation}$$
Z rozwiązania równania kwadratowego ($\ref{12}$) względem współczynnika wyboczeniowego $\chi=\cfrac{N}{A\cdot f_y}$ otrzymujemy znaną formułę stosowaną w normie [5] :
$$\begin{equation} \chi_{*}=\cfrac{1}{\Phi_{*} +\sqrt{\Phi_{*}^2 – \beta \cdot \overline \lambda_{*}^2}} \quad \le \chi_{min} \label {13} \end{equation}$$
Formułę ($\ref{13}$) podano w zapisie uogólnionym na kilka rodzajów wyboczenia indeksowanych $_*$:
*= [ _= wyboczenie giętne ; LT=zwichrzenie ; $LT_{szcz}$=zwichrzenie w przypadku szczególnym ; T=wyboczenie giętno-skretne ; TF=wyboczenie giętno-skretne ].
Zwichrzenie w przypadku szczególnym dotyczy stalowych przekrojów dwuteowych walcowanych i ich spawanych odpowiedników zgodnie z [5]– kl. 6.3.2.3 .
Współczynnik pomocniczy $\Phi$ oblicza się z zależności:
$$\begin{equation} \Phi_{*}=1/2 \cdot \left ( 1+\Theta_{* }+ \beta \cdot \overline \lambda_{*}^2 \right ) \label{14}\end {equation}$$
Parametr imperfekcji ($\ref {10}$) zapisany z indeksami rodzajów wyboczenia przyjmuje podstać
$$\begin{equation} \Theta_{*}= \alpha_{*} \cdot (\overline \lambda _{*} -\overline \lambda_{*,0}) \label{15}\end {equation}$$
Wartość minimalną współczynnika wyboczenia $\chi_{min}$ oraz współczynnika modyfikacyjnego $\beta$ należy przyjmować o wartości 1,0,
a tylko w przypadku szczególnym zwichrzenia stalowych przekrojów dwuteowych walcowanych i ich spawanych odpowiedników o wartości:
$\chi_{min} = \min { \{ 1 \, ; \, 1/ \overline \lambda_{LT}^2 \} }$,
$\beta=0,75$.
Progowa smukłość $\overline \lambda_{*,0}$ , dla konstrukcji stalowych wynosi
$$ \begin {equation} \overline \lambda_{*,0} \begin {cases}
0,4, & \text {dla zwichrzenia w przypadku szczególnym}\\
0,2 , & \text {w pozostałych przypadkach} \\
\end {cases} \label{16} \end {equation}$$
W przypadku konstrukcji aluminiowych smukłość progową określa się na podstawie [8]– tab.6.6 i 6.7 .
Wyprowadzenie formuły APF
Na Rys. 2-3.1 pokazano model pręta analizowany przez Ayrton i Perry. W połowie rozpiętości pręta założono amplitudy wygięcia : początkową (imperfekcję pręta) $e_0=w_0(L/2)$, a po obciążeniu (ugięciu) $e=w(L/2)$.
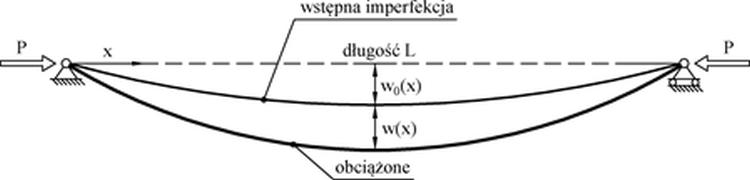
Rys. 2-3.1 Model pręta Ayrton-Perry (opracowano na podstawie [9] )
Teorię Ayrton-Perry przedstawimy w ujęciu klasycznym. Analizę problemu belki-słupa z imperfekcją łukową według teorii wyższych rzędów przedstawiono w pracach, [10] , [11] , [12] i in.
Moment zginający przekrój o współrzędnej $x$ wynosi: w stanie początkowym $M_0 (x)=P\cdot w_0 (x)$, a po obciążeniu pręta
$$ \begin {equation} M(x)=P\cdot[w_0(x)+w(x)] \label {17} \end {equation}$$
Moment zginający jest jednocześnie przeskalowaną krzywizną pręta zgodnie z zależnością:
$$ \begin {equation} M(x)=-EI \cfrac{d^2 w(x)}{dx} \label {18} \end {equation}$$
Układ równań ($\ref{17}$)+($\ref{18}$) można sprowadzić do jednego równania różniczkowego zagadnienia
$$ \begin {equation} EI w”(x) +Pw(x) = -Pw_0 (x) \label {19} \end {equation}$$
Przyjmijmy, że wygięcia wstępne są dowolną funkcją, spełniającą warunki brzegowe $w_0(0)=w_0 (L)=0$, $w_0 (L/2)=e_0$. Po rozwinięciu tej funkcji w szereg trygonometryczny Fouriera i zachowaniu pierwszego wyrazu, otrzymamy
$$ \begin {equation} w_0 (x) =e_0 \sin{\cfrac{\pi x}{L}} \label {20} \end {equation}$$
Z rozwiązania Eulera wynika, że kształt taki odpowiada pierwszej postaci wyboczonej idealnego pręta przegubowo-przegubowego. Po podstawieniu ($\ref{20}$) do ($\ref{19}$) i wprowadzeniu oznaczenia
$$ \begin {equation} \alpha^2 =\cfrac {P}{EI} \label {21} \end {equation}$$
otrzymamy równanie różniczkowe ściskania pręta z imperfekcjami:
$$ \begin {equation} w” +\alpha^2 \cdot w = -\alpha^2 \cdot e_0 \cdot \sin{ \cfrac{\pi x}{L}}\label {22} \end {equation}$$
Całką ogólną tego równania jest:
$$ \begin {equation} w_o (x) = A \sin{ \alpha x} + B \cos { \alpha x} \label {23} \end {equation}$$
$$ \begin {equation} w_{imp} (x)= C \sin{ \cfrac{\pi x}{L}} \label {24} \end {equation}$$
Po wykonaniu różniczkowania ($\ref{24}$) i podstawieniu do ($\ref{22}$), otrzymamy wyrażenie na stałą C w postaci:
$$ \begin {equation} C=\cfrac{e_0}{ (\tfrac{\pi} {\alpha L})^2-1}= \cfrac{e_0}{\tfrac{P}{P_{cr}} -1} \label {25} \end {equation}$$
gdzie uwzględniono tożsamość:
$$ \begin {equation} \left ( \cfrac{\pi} {\alpha L} \right )^2= \left (\cfrac{\pi^2 EI} {L^2} \right ) / (EI \alpha^2) =\cfrac {P_{cr}}{P} \label {26} \end {equation}$$
Siłę krytyczną $P_{cr}$ zdefiniowano w (1-1.5) (przy oznaczeniu $N_{cr}$) i jest ona obliczana dla $L_{cr}=L$. Z definicji ($\ref{21}$) mamy: $P=EI \alpha^2$ .
Zupełne rozwiązanie równania ($\ref{22}$) jest sumą całki ogólnej ($\ref{23}$) i szczególnej ($\ref {24}$) i po uwzględnieniu ($\ref{25}$), wynosi:
$$ \begin {equation} w(x)=A \sin{\alpha x}+B \cos{\alpha x}+\cfrac{e_0}{\tfrac{P_{cr}}{P}-1}\cdot \sin{\pi x/L} \label {27} \end {equation}$$
Warunki brzegowe zapiszemy w postaci:
$$ \begin {equation} w(0)=0 \to B=0 \, ; \quad w(L)=0 \to A\cdot \sin{kL}=0 \label {28} \end {equation}$$
Jeśli $A \neq 0$ , to $kL = n \pi$ i mamy zbiór rozwiązań, prowadzących do klasycznego wyniku Eulera, a kolejne obciążenia krytyczne wynoszą:
$$ \begin {equation} P_{cr,1}=\cfrac{\pi^2 EI}{L^2} \, ; \quad P_{cr,2}=\cfrac {4\pi^2 EI}{L^2} \, \quad itd \label {29} \end {equation}$$
W rozważanym przypadku interesuje nas obciążenie $P_{cr,1}$ , co zachodzi dla $A =0$ , skąd po uwzględnieniu ($\ref{20}$) otrzymujemy:
$$\begin {equation} w(x)= \cfrac { e_0 \sin {\pi x/L} } { \tfrac{P_{cr}}{P} -1}=\cfrac{w_0(x)} { \Lambda_{cr} -1} \label {30} \end {equation}$$
gdzie $\Lambda_{cr}=\cfrac{P_{cr}}{P}$ – mnożnik obciążenia krytycznego zdefiniowany w (1-1.13).
Z przekształcenia ($\ref{26}$ ) można uzyskać znane wyrażenie na całkowite ugięcie belki z imperfekcjami:
$$\begin {equation} w= w(x)+w_0 (x) = w_0 (x) \cdot \left ( 1+ \cfrac{1} { \Lambda_{cr}-1} \right )= \cfrac{w_0(x)}{1- \tfrac{1}{\Lambda_{cr}}}=a_\Lambda \cdot w_0(x) \label {31} \end {equation}$$
gdzie współczynnik amplifikacji $a_{\Lambda}= \cfrac{1}{1-\tfrac{1}{\Lambda_{cr}}}$ zdefiniowano w (1-1.12) .
Amplituda całkowitego ugięcia wynosi:
$$\begin {equation} e =a_{\Lambda} \cdot e_0 \label {32} \end {equation}$$
Ponieważ w najbardziej wytężonym (środkowym) przekroju pręta siły przekrojowe wynoszą: siła osiowa $N=P$, moment zginający $M_{max} = P \cdot e = P \cdot a_{\Lambda} \cdot e_0$, więc naprężenia w środkowym przekroju pręta wynoszą
$$\begin {equation}\sigma_{max}=\cfrac {N}{A}+ a_\Lambda \cfrac{P\cdot e_0}{W} \label {33} \end {equation}$$
Po wprowadzeniu parametru $\Theta$ ($\ref{3}$) i oznaczeniu $\sigma=N/A$, oraz $\sigma_{cr}=N_{cr}/A$ zależność ($\ref{33}$) można zapisać w postaci:
$$\begin {equation}\sigma_{max}=\sigma \cdot [ 1+ \Theta \cdot ( 1- \cfrac{\sigma}{\sigma_{cr}} ) ] \label {34} \end {equation}$$
Stąd po uporządkowaniu, w granicznym stanie plastycznym (dla $\sigma_{max}= f_y$ ) otrzymamy równanie kwadratowe ze względu na naprężenie w pręcie $\sigma$
$$\begin {equation} \sigma^2- \sigma [f_y + \sigma_{cr} (\Theta +1) ] + f_y \cdot \sigma_{cr}=0 \label {35} \end {equation}$$
Po rozwiązaniu algebraicznego równania ($\ref{35}$) jako pierwiastek $\sigma_{imp}$, czyli punkt równowagi równania kanonicznego pręta z imperfekcją, uzyskujemy formułę Ayrton-Perry ($\ref{2}$) .
Efekt P-δ
Formuła ($\ref{32}$) wyraża prawo amplifikacji ugięcia przy ściskaniu, to znaczy zwiększanie przemieszczenia poprzecznego przez ściskanie, który jest często nazywany efektem P-δ (lub P-„małe delta”).
$$\begin {equation} w(x)=a_{\Lambda} \cdot w_o(x) \label {36} \end {equation}$$
gdzie $w_0(x)$ jest ugięciem pod obciążeniem oszacowanymi wg teorii 1. rzędu, to znaczy nie musi być imperfekcją lecz ugięciem przed „zadziałaniem siły osiowej”. Zależność ($\ref {36}$) pokazano na Rys. 2-3.2b dla $ \delta =w(L/2)$
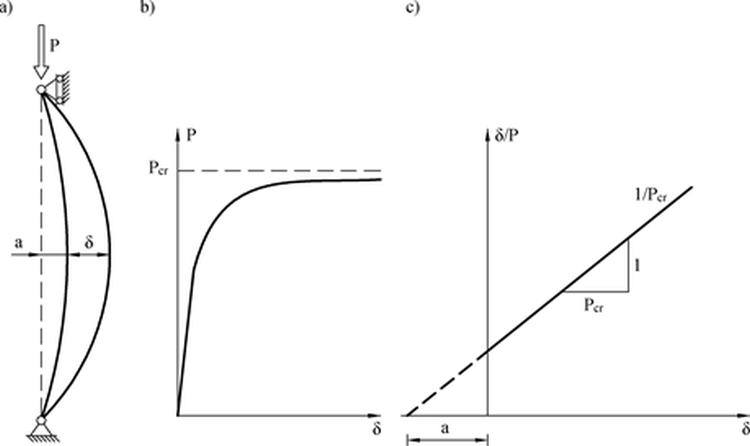
Rys. 2-3.2 Oznaczenia, b) Wykres P-δ, c) Wykres Southwella (opracowano na podstawie [9] )
Wykres Southwella
Klasyczny wykres Southwella dla pręta ściskanego – wyboczenie
Ciekawe zastosowanie ma wykres, pokazany na Rys. 2-3.2c. Przedstawia on zależność uzyskaną z ($\ref {36}$), przekształconą do postaci parametrycznej, jak następuje:
$$\begin {equation} \delta = \left [ a \cdot \left ( \cfrac{P_{cr}}{P}-1 \right) \right ] \quad \to \quad \left [\delta \left ( \cfrac{P_{cr}}{P}-1 \right) -\delta =a \right ] \quad \to \quad \left [ \left ( \cfrac{P_{cr}}{P} \right ) = \left ( \cfrac{1}{P_{cr}} \right ) \cdot \delta + \left ( \cfrac{1}{P_{cr}} \right ) \right ] \label {37} \end {equation}$$
Wykres znany, jako wykres Southwella pozwala wyznaczyć siłę krytyczną na podstawie serii pomiarów siły obciążającej pręt P i odpowiadających ugięć δ przed utratą stateczności, czyli bez doprowadzania pręta do wyboczenia.
W pracy [13] omówiono dalsze szczegóły metody Southwella w tym jej zastosowanie dla pręta ściskanego siłami na mimośrodzie i wyznaczanie imperfekcji zastępczej.
Wykres Sothwella dla belki – zwichrzenie
Wykres Southwela jest stosowany również w przypadku zwichrzenia belki (rys.2-3.2a, to znaczy nie tylko dla imperfekcji w płaszczyźnie głownej $w$ , ale rówenież dla imperfekcji bocznych $u$ oraz skrętnych $\varphi$.

Eys.2-3.2a Zwichrzenie [14]
Meck (1977) [15] pokazał, że dla wyboczenia bocznego w wykresie Southwella powinny być używane szczególne rzędne: u / P powinny być wykreślane względem φ, a φ / P powinny być wykreślane względem u.
Massey (1963) [16], zauważył , że obciążenie P na osi rzędnych należy zastąpić $P^2$ , co oznacza, że u i φ należy wykreślić odpowiednio względem $u/P^2$ i $φ/P^$2. . Zakładając, że belka nie ma początkowy kąt skręcenia (φo = 0), φ można wyeliminować Otrzymuje się równania (14) i (15) oraz jedno równanie
Formuła Robertson
[2] zaproponował, aby parametr imperfekcji w formule Perry ($\ref{2}$ ) przyjmować o wartości:
$$\begin {equation} \Theta=0,003 \lambda \label {38} \end {equation}$$
gdzie smukłość pręta $\lambda$ jest zależna od warunków brzegowych (zamocowania końców pręta.
Propozycja ($\ref{31}$) była arbitralna. W rzeczywistości parametr imperfekcji zależy od szeregu czynników, takich jak: typ przekroju (spawany, walcowany, itp.), ustawienie osi przekroju, symetrii przekroju, dokładność wytwórczych, naprężeń resztkowych, itd.
W kolejnych latach po przeprowadzeniu dużej liczby pomiarów lepsze dopasowanie do wyników uzyskiwano dla:
$$\begin {equation} \Theta=0,0003 \lambda^2 \label {39} \end {equation}$$
Formuła ($\ref {2}$) z hipotezą ($\ref{37}$) jest podstawą zastosowania współczynnika wyboczeniowego we współczesnych normach konstrukcyjnych w postaci analogicznej do pokazanej na Rys. 2-3.3, na którym pokazano przykładowo dwie krzywe wyboczeniowe Perry-Robertson, obie dla słupa ściskanego siłą , z przekrojem o takiej o nośności $P_R$ , wykonanego ze stali $ f_y=300 \, MPa$, ale dla różniących się parametrów imperfekcji: $\Theta= 0,00002 \lambda^2$ lub $\theta=0,0004 \lambda^2$ . Zwróćmy uwagę, że niewielka różnica parametru imperfekcji prowadzi do znacznych różnic między krzywymi wyboczeniowym
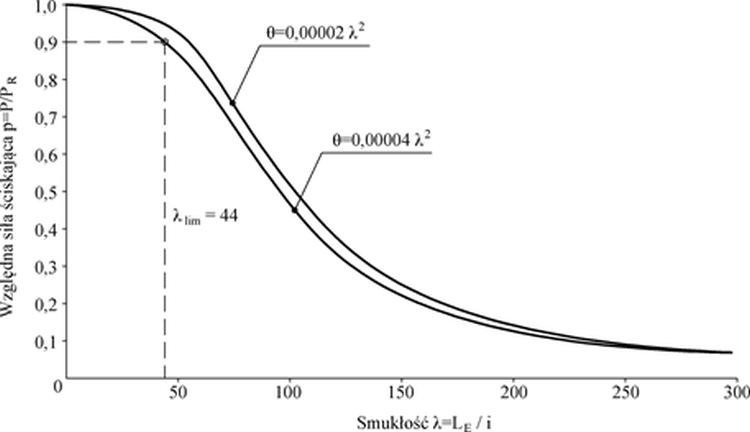
Rys. 2-3.3. Krzywe wyboczeniowe Perry-Robertson (opracowano na podstawie [9] )
Teoria Perry-Robertsona oprócz hipotecznego doboru parametru imperfekcji jest obarczona większą wadą: dotyczy prętów sprężystych, a rzeczywiste słupy mają smukłości tak małe, że nie jest słuszna dla nich teoria Eulera, a w ślad za nią również teoria Perry-Robertsona.
Doprowadzenie teorii do zgodności z pomiarami eksperymentalnymi jest możliwe poprzez mnożenie wielu krzywych wyboczeniowych zależnych od szeregu czynników. Zalecana w niniejszym podręczniku bezpośrednia metoda imperfekcyjna rozwiązuje te wieloznaczności.
Krzywe wyboczeniowe w normach światowych na tle eksperymentów
Krzywe wyboczeniowe zarówno prętów ściskanych (wyboczenie gietne) jak i belek (wyboczenie boczne – zwichrzenie) były przedmiotem licznych badań dobrej jakości, które są gromadzone w międzynarodowych bazach danych. Na Rys. 2-3.4 pokazano przykładowe wyniki badań doświadczalnych stalowych słupów (a) i belek (b), zgromadzone w japońskiej bazie danych [17] , opracowane na podstawie 447 eksperymentów na słupach oraz 418 na belkach o przekroju HE oraz IPE walcowanych i spawanych. Zaczernione kółka oznaczają eksperymentalną wartość średnią współczynnik wyboczenia giętnego lub współczynnika zwichrzenia zebranych z szerokości podstawy strzałki, czyli przedziału smukłości względnej . Rozrzut obserwowanych współczynników wynoczeniowych oznaczono słupkiem. Podstawa strzałki sięga do wartości charakterystycznej współczynnika wyboczeniowego, obliczonej jako kwantyl rozkładu normalnego , gdzie jest odchyleniem standardowym pomiarów w klasie (współczynniki zmienności współczynnika wyboczeniowego wynosiły od kilku do 15%.
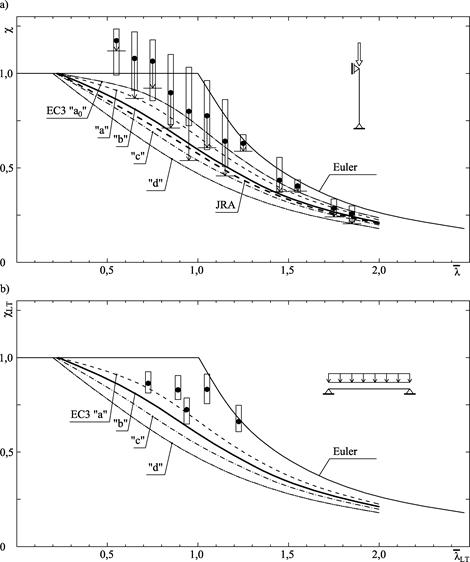
Rys. 2-3.4. Normowe krzywe wyboczeniowe na tle danych doświadczalnych: a) wyboczenie giętne słupów, b) wyboczenie boczne (zwichrzenie) belek (opracowano z wykorzystaniem danych z pracy [17] )
Na tle wyników badań wrysowano europejskie krzywe wyboczeniowe EC3 oraz japońską krzywą wyboczenia giętnego JRA. W każdym przypadku krzywe wyboczeniowe są bezpiecznym, dolnym oszacowaniem współczynnika wyboczeniowego.
Nie obserwuje się statystycznie istotnej potrzeby różnicowania na typy krzywych wyboczeniowych, a wystarczająca wydaje się być krzywa JRA położona pomiędzy europejskim typem „b” i „c”.
Na Rys. 2-3.5 porównano krzywe wyboczenia bocznego (zwichrzenia) prezentowane w innych normach światowych: amerykańskiej [18] , australijskiej oraz kanadyjskiej na tle normy europejskiej EC3 Różnice pomiędzy nimi występują szczególnie w zakresie prętów o smukłości . W tym niesprężystym obszarze pracuje większość rzeczywistych prętów. Na przykład dla różnica między normą europejską EC3 a amerykańską AISC wynosi 28%. W przypadku pręta ściskanego (wyboczenia giętnego) różnice między wytycznymi norm świata są mniejsze [19] , choć przekraczają wymaganą dokładność obliczeń wytrzymałościowych, która zwyczajowo wynosi 2%.
Z analizy zagadnienia wynika, że złożoność zjawiska utraty stateczności wymaga dokładniejszych metod od dostarczanych przez normowe formacje współczynników wyboczeniowych. Współczesne metody powinny być zgodne z fizyką zjawiska, a mniej z zaleceniami norm, które z natury rzeczy są kompromisem bezpieczeństwa, uniwersalności i prostoty wytycznych. Metoda współczynników wyboczeniowych jest obecnie zastępowana bezpośrednimi metodami imperfekcyjnymi, opisanymi w niniejszej pracy.
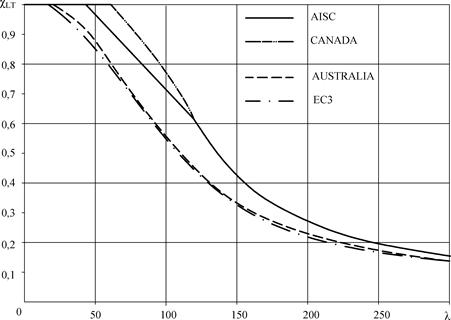
Rys.2-3.5 Porównanie normowych, światowych krzywych wyboczeniowych przy zwichrzeniu (opracowano na podstawie [19] )
Uwagi do wyboczenia pręta w konstrukcji statycznie niewyznaczalnej
Rozkład sztywności w statycznie niewyznaczalnych konstrukcjach wpływa na rozdział sił praktycznie we wszystkich rzeczywistych systemach. Dotyczy to również kratownic, które konstruuje się i współcześnie oblicza jak system prętów sztywno połączonych w węzłach.
Załóżmy, że w dowolnej, statycznie niewyznaczalnej konstrukcji pręt [e] uległ wyboczeniu podczas wzrostu obciążenia całej konstrukcji. Ponieważ wskutek wyboczenia sztywność osiowa elementu [e] zmniejsza się, to również siła przekrojowa ulega zmniejszeniu. Wobec tego nowa siła może być niewystarczającą do tego, by utrzymywać pręt w stanie wyboczenia. Taką sytuację nazwiemy „ucieczką” pręta przed wyboczeniem. W numerycznych procedurach geometrycznie nieliniowych opisane zjawisko można w prosty sposób poprawnie uwzględnić. W obliczeniach klasycznych i normowych zjawisko „ucieczki pręta przed wyboczeniem” jest pomijane. Można wykazać, że w niektórych przypadkach podejście takie jest zbyt konserwatywne (prowadzi do nieuzasadnionego przewymiarowania pręta).
Współczynnik wyboczeniowy dla pręta z imperfekcją mimośrodową
Rozważmy słup pokazany na Rys. 2-3.6 z imperfekcją mimośrodową $e_0$ przyłożenia obciążenia $P$.
Równanie różniczkowe zagadnienia można w tym przypadku zapisać w postaci:
$$\begin {equation} EI_y w” = – M(x)=- P(e_0+w) \label {40} \end {equation}$$
Rozwiązaniem tego równania jest:
$$\begin {equation} w (x) =e_0 \cdot \left ( \cos kx +\cfrac{1- \cos kL}{\sin kL} \right ) \sin kx -1 \label {41} \end {equation}$$
$$\begin {equation} \delta = w(L/2) = e_0 \cdot \left ( \cfrac { \sec{kL}}{2} -1 \right ) = e_0 \cdot \sec{ \left ( \cfrac{\pi}{2}\cdot \sqrt{\cfrac{P}{P_{cr}}} \right )} \label {42} \end {equation}$$
W środku słupa siła osiowa wynosi $N=P$. Naprężenia maksymalne wystąpią w skrajnym punkcie przekroju o współrzędnej $z_{max}$:
$$ \begin {equation} \sigma_{max} = \cfrac{N}{A}+ \cfrac{N\cdot e_0}{I_y} \cdot z_{max} = \cfrac{N}{A} \cdot \cfrac {\Theta}{ \cos { \left ( \cfrac{\pi}{2}\cdot \sqrt{\cfrac{N}{N_{cr}}} \right )}} \label {43} \end {equation}$$
gdzie parametr imperfekcji $\Theta = \cfrac{e_0 \cdot z_{max}}{I_y}$ zdefiniowano w ($\ref{3}$).
Po uwzględnieniu $N_{cr}=\overline \lambda^2 \cdot N_R$ zależność ($\ref{39}$) w granicznym stanie plastycznym, (dla $N = N_R=A\cdot f_y$) można zapisać w postaci
$$\begin {equation} \sigma_{max} = \cfrac{N}{A \cdot \chi_e } \label {44} \end {equation}$$
gdzie współczynnik wyboczeniowy $\chi_e$ dla modelu mimośrodowej imperfekcji wynosi:
$$\begin {equation} \chi_e= \cfrac {1} {\Theta} \cdot \cos { \left ( \cfrac { \pi } {2 \cdot \overline \lambda } \right )} \label {45} \end {equation}$$
gdzie $\Theta$ wg formuły ($\ref{10}$).
Porównanie współczynników wyboczeniowych z modelu łukowego i mimośrodowego
Na rys. 2-3.7 naniesiono porównanie wartości mimośrodowego współczynnika wyboczeniowego ($\ref{45}$) z wartością normową ($\ref{13}$).
Dokładność przybliżenia przez wiele lat była wystarczająca w obliczeniach inżynierskich, prowadzonych metodami „ręcznymi”. Uogólnienie zagadnienia na przypadek jednoczesnego zginania poprzecznego ( zginania z udziałem sił poprzecznych) i ściskania pręta nic nie zmieni z punktu widzenia formalizmu matematycznego, a prowadzi do jeszcze większych rozbieżności.
W dobie informatycznej jest szansa na stosowanie rozwiązań poprawnych matematycznie na gruncie teorii geometrycznie nieliniowej NLG. Obliczenia nieliniowe 2 rzędu są standardem współczesnych programów komputerowych. W ten właśnie sposób przechodzimy do przedmiotu niniejszej pracy, czyli teorii imperfekcyjnej, ideowo omówionej w pracy [6].
Wyboczeniowe teorie sprężysto-plastyczne
Zakres ważności teorii Eulera i Perry-Robertson
W 1845 roku francuski inżynier Lamarle [20] pokazał, że teoria Eulera wyboczenia prętów dotyczy przypadków, które dość rzadko występują w praktyce. Słupy rzeczywiste mają smukłość mniejszą od 100, a dla nich wzór Eulera zawodzi (Rys. 2-3.8) i wobec tego Lamarle zaproponował po prostu, aby krytyczne naprężenie rzeczywistych prętów przyjmować równe granicy plastyczności .
W ślad za pracą Lamarle, teoria Eulera była badana doświadczalnie: Bauschinger [21] przeprowadził pierwsze wiarygodne testy na słupach; Tetmajer [22] przeprowadził badania stateczności prętów o różnych przekrojach. Wszechstronny materiał został opracowany w pracy [23]. Zaproponowano empiryczny wzór liniowy do obliczenia naprężeń krytycznych. Na Rys. 2-3.7 pokazano prostą Tetmajera oraz zalecenia normowe DIN z 1952 roku.
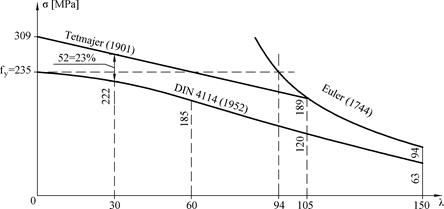
Rys. 2-3.7. Ograniczenie ważności formuły Eulera (na przykładzie stali S235) (opracowano na podstawie [24] )
Punkt przecięcia krzywej Eulera z wytrzymałością materiału $f_ty$ ma współrzędną $\lambda_{lim}=\pi \aqrt{\tfrac{E}{f_y}} i przykładowo dla stali S355 (E=210 GPa, fy=355 MPa) wynosi$\lambda_{lim}=76,4.
Hipotezy przejścia z krzywej Eulera w prostą fy
W rzeczywistości przejście z krzywej Eulera na prostą fy nie jest ostre i w obszarze „przejściowym” jest aproksymowane arbitralnie przyjętą, gładką krzywą pokazaną na Rys. 2-3.8.
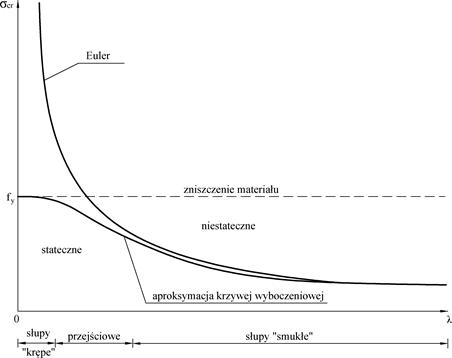
Rys. 2-3.8. Teoria Eulera jest prawdziwa tylko dla smukłych słupów (opracowano na podstawie [25] )
Klasyczne koncepcje Engesser-Karman
Do opisu sprężysto-plastycznego mimośrodowego ściskania pręta (zginania osiowego) Engesser [26] zaproponował metodę modułu stycznego, polegającą na zamianie w formułach Eulera moduł Younga przez moduł styczny $E_*=\cxfrac{e \sigma}{ e \varepsilon}, przy czym pierwotna propozycja dotyczyła całego przekroju.
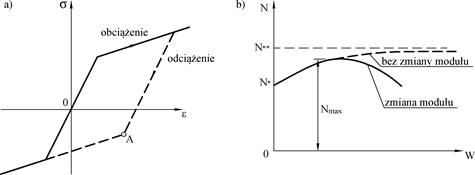
W dalszych pracach wskazano na błędne założenie, że moduł styczny dotyczy całego przekroju. Faktycznie część przekroju odciąża się i tam powinno być zachowane klasyczne prawo Hooka i zasada płaskich przekrojów (Rys. 2-3.9). [27] w miejsce $E_*$ wprowadził moduł zastępczy (zredukowany) $E_{**}= \nu E(1+\nu)$, gdzie $\nu$ – współczynnik modułu zastępczego.
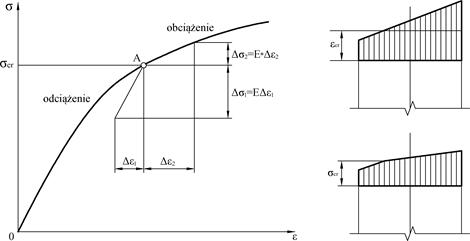
Rys. 2-3.9. Zmiana odkształceń i naprężeń wg Engessera: a) wykres σ-ε, b) zmiana odkształceń, c) zmiana naprężeń (opracowano na podstawie [28] )
Hipoteza Rankine-Merchant
Prostą formułę na krzywą „przejściową” podali Rankine i Merchant [29] . Na podstawie badań eksperymentalnych, stwierdzili, że dobrą zgodność uzyskuje się przy przyjęciu interakcji:
$$ \begin {equation} \cfrac{1}{ \sigma_{cr}}= \cfrac {1} {f_y} + \cfrac {1} { \sigma_E} \label {46} \end {equation}$$
Formuły prostego sumowania odwrotności mnożników nośności (ogólniej sztywności) analogiczne do ($\ref{3-4.1} $) są coraz częściej stosowane w rozmaitych zagadnieniach mechaniki i wytrzymałości konstrukcji.
Koncepcja Shanley
Współczesne koncepcje wyboczenia słupów pojawiły się wraz z opublikowaniem prac [30], [31], który wskazał, że przy wyprowadzeniu teorii zastępczego modułu Engessera-Karmana dokonano założeń, które nie mogą być utrzymane. W szczególności nie jest słuszne założenie, że słup pozostaje prosty podczas zwiększania siły osiowej aż do wartości siły krytycznej – dopiero po przekroczeniu, której słup wygina się. Uwzględnienie wyginania słupa od początku procesu prowadzi do mniejszych i bardziej realistycznych obciążeń krytycznych niż wynikające z klasycznej teorii modułu stycznego lub zastępczego.
(opracowano na podstawie [28] )
Na Rys. 2-3.10 pokazano analizę ścieżki równowagi pręta ściskanego siłą N, wykonanego ze sprężysto-plastycznego materiału o biliniowej charakterystyce; w jest bocznym przemieszczeniem sprawczym. Siła wynika z teorii zastępczego modułu (Engessera-Karmana) i jest asymptotą obciążenia krytycznego pręta. Siła odpowiada sile krytycznej wg teorii modułu stycznego Engessera. Na skutek zmiany modułu sprężystości w punktach przekroju podczas zmiany dociążania na odciążenie (pkt A na Rys. 2-3.10a) uzyskujemy siłę krytyczną Shanleya ( punkty na linii ciągłej Rys. 2-3.10 i Rys. 2-3.11). Siłą krytyczną pręta ściskanego osiowo nie jest ani siła , ani , dlatego, że po osiągnięciu przez obciążenie siły Engessera następuje wychylenie pręta ze stanu prostoliniowego i jest to stan stateczny, który utrzymuje się przy dalszym zwiększaniu obciążenia, a zwiększanie obciążenia prowadzi do zwiększania przemieszczenia.
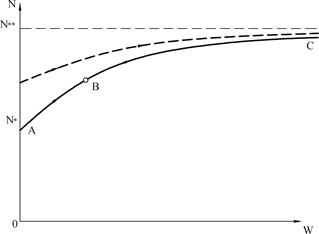
Rys. 2-3.11. Ścieżki równowagi prostego wspornika ściskanego osiowo: – najmniejsza siła, przy której możliwe jest stan równowagi wygiętego pręta (opracowano na podstawie [28] )
Koncepcja Shanleya [31] dobrze koresponduje z niezależnie ogłoszoną teorią, w której pokazano, że przyczyna szeregu niepowodzeń konstrukcyjnych oraz wielokrotnie stwierdzanych „błędów” eksperymentalnych tkwi w niedocenianiu wagi problematyki stanów pokrytycznych, to znaczy utrzymywania się statecznej ścieżki równowagi), po przekroczeniu pewnego poziomu obciążeń, który nie wyczerpuje jeszcze nośności pręta.
Teoria Shanleya pokazuje, że nie można mówić o ścisłej wartości siły krytycznej (granicznej). W zależności od okoliczności można przyjąć za siłę krytyczną obciążenie z przedziału , ale . Wskazuje również, że w problemie stateczności należy mówić o „ścieżce równowagi słupa” i zakończyć pytania o utratę stateczności i siłę krytyczną, nawet w przypadku pręta prostego, osiowo ściskanego!
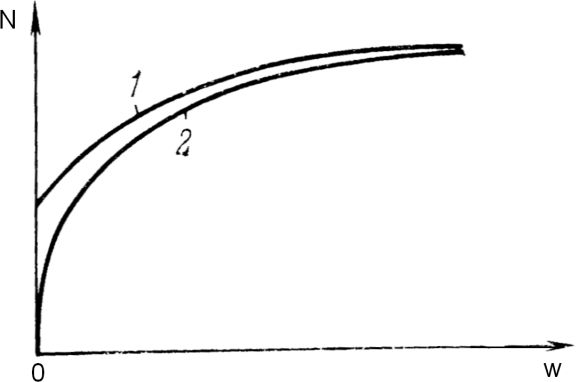
Rys.2-3-12 Ścieżki równowagi ściskanego pręta: 1 – pręt osiowo ściskany (Shanleya) , 2 – pręt mimośrodowo ściskany [28]
Wagę koncepcji Shanleya dobrze widać w zadaniu mimośrodowego ściskania, które prowadzi do rozwiązań, schematycznie przedstawionych na Rys. 2-3.12 i z których wynikają następujące wnioski:
- Powyżej krzywej Shanleya nie są możliwe stany równowagi. Krzywa Shanleya stanowi ograniczenie od góry wszystkich ścieżek równowagi prętów rzeczywistych z mimośrodami i imperfekcjami,
- Wygięcia boczne pręta rzeczywistego (mimośrodowo ściskanego lub z imperfekcjami) przebiegają od początku ścieżki równowagi, a nie od momentu osiągnięcia siły krytycznej zgodnie z teorią modułu stycznego. Poszukiwanie klasycznej siły krytycznej nie jest potrzebne przy analizie rzeczywistych prętów. Wymagana jest analiza konstrukcji obarczonej imperfekcjami wg teorii geometrycznie nieliniowej – dla systemów nie przechyłowych wystarcza analiza 2 rzędu (P-Δ). Na podstawie tej analizy uzyskujemy nośności ułożone na krzywej 2
Koncepcja Hutchinson
W pracach [32] , [33] pokazano, że w odniesieniu do plastycznej utraty stateczności konstrukcji obarczonych imperfekcjami, można stosować oszacowania asymptotyczne, uzyskiwane w duchu teorii [34] układów sprężystych.
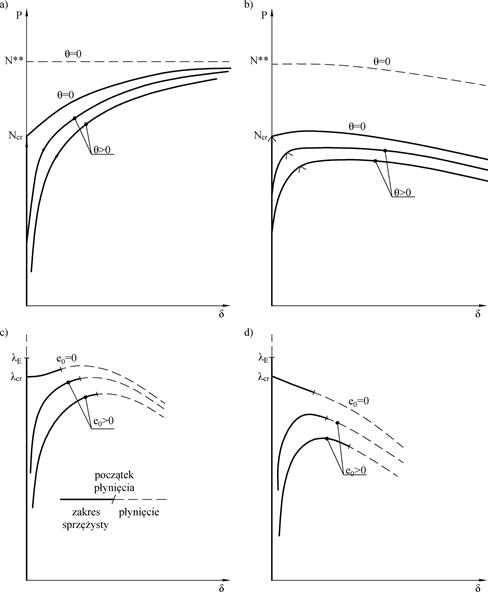
Rys. 2-3.13. Porównanie teorii Shanleya i Hutchinsona: a) klasyczny model Shanley, b), model przy dużych nieliniowościach c) teoria Hutchinsona – punkt bifurkacji symetryczny, d) teoria Hutchinsona – punkt bifurkacji niesymetryczny (opracowano na podstawie [32] )
Na Rys. 2-3.13a, b linią przerywaną oznaczono linię nośności $n^{**}$ wg teorii zredukowanego modułu, a symbolami $∧$ oznaczono punkty na ścieżce równowagi odpowiadające zapoczątkowaniu odciążenia sprężystego, Liniami ciągłymi oznaczono ścieżki równowagi $P- e$, wynikające z teorii Shanleya dla pręta bez imperfekcji ($\Theta=0$ ) i z imperfekcjami ($\Theta>0 ).
Rys. 2-3.13 c, d przedstawiono ścieżki równowagi $\lambda – e$ przy zniszczenia elementu w zakresie plastycznym na skutek utworzenie przegubów plastycznych po utracie stateczności w zakresie sprężystym, analizowane przez Hutchinsona w pracach [32] , [33] .
Zmienna jest mnożnikiem obciążenia zewnętrznego, proporcjonalnie, do którego rośnie obciążenie P. Do celów porównawczych teorii Shanley i Hutchinson można przyjąć $\lambda=N$, – $\lambda_E$ – klasyczny mnożnik obciążenia Eulera, $\lambda_{cr}$ – mnożnik obciążenia bifurkacyjnego przy symetrycznym punkcie bifurkacji (Rys. 2-3.13 c) i przy niesymetrycznym punkcie bifurkacji (Rys. 2-3.13 d). Liniami ciągłymi oznaczono fragment sprężystej ścieżki równowagi, obserwowany do momentu utworzenia przegubu plastycznego (lub przegubów), który oznaczono kreską poprzeczną na styku z plastycznym fragmentem ścieżki równowagi, (linia przerywana). Praca elementu po utworzeniu mechanizmu plastycznego następuje na silnie opadającej ścieżce równowagi, to znaczy nawet przy zmniejszającym się obciążeniu następuje przyrost przemieszczeń $e$.
Nośność graniczna, czyli maksimum ścieżki równowagi może wystąpić (zależnie od rodzaju punktu bifurkacyjnego) na sprężystej lub plastycznej części ścieżki równowagi.
Nośność graniczna jest dość dobrze przewidywana, gdy maksymalne obciążenie zachodzi bardzo blisko punktu bifurkacji sprężystej, choć amplituda postaci wyboczenia jest słabo określona. Jeśli natomiast maksymalne obciążenie znacznie przekracza obciążenie bifurkacji to dokładność oszacowania nośności gwałtownie pogarsza się.
Proces tworzenia się przegubów plastycznych konstrukcji obarczonych imperfekcjami geometrycznymi w analizie GMNIA badano w pracy [35] , gdzie pokazano, że krytyczne (prowadzące do zniszczenia plastycznego) imperfekcje geometryczne występują z udziałem naprężeń resztkowych i trwałych, wstępnych imperfekcji geometrycznych
Krzywe wyboczeniowe a dokładne rozwiązanie sprężysto-plastyczne
W pracy [36] przeprowadzono testy zależności Eurokod z wykorzystaniem programu ABAQUS i pokazano, że obliczenia prowadzone z uwzględnieniem modelu plastycznego materiału – systematycznie prowadzą do większych współczynników wyboczeniowych od analizy sprężystej, szczególnie w zakresie sprężysto-plastycznego wyboczenia dla prętów o smukłości $\overline \lambda <1$ . Różnica dochodzi do kilkudziesięciu procent. Na rys. 2-3.14 pokazano przykładowe wyniki dla prętów z rur kwadratowych KKR oraz dwuteowników szerokostopowych H.
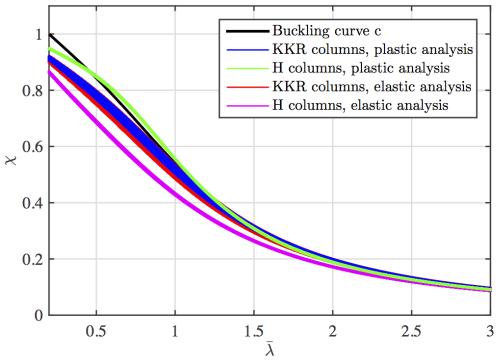
Rys.2-3.14. Porównanie współczynników wyboczeniowych ze ścisłej imperfekcyjnej analizy sprężystej i plastycznej oraz normowej krzywej wyboczeniowej „c”. [37]
Probabilistyczna podejście do stateczności konstrukcji
Już w roku 1950 Dutheil [38] wskazał na konieczność opisu stateczności słupów w języku probabilistycznym, ale efektywne rozwiązanie problemu probabilistycznego napotykało na przeszkodę związaną z brakiem zamkniętego deterministycznego opisu problemu sprężysto-plastycznej utraty stateczności [39] , a zastosowanie metody Monte-Carlo spotykało się z przeszkodą w postaci małej mocy komputerów.
Jedną z pierwszych prób probabilistycznego opisu problemu stateczności niesprężystego słupa były prace [40] , [41]) w których jako zmienne losowe traktowano styczny moduł sprężystości, co prowadziło do złożonej, wielokrotnej całki. W pracy [42] zaproponowano rozwiązanie tej całki aproksymacyjną metodą FORM (First-Order Reliability Method). Podejście sugerowane przez [38] , [43] zastosowano w pracy [44] . Przyjęto, że zmiennymi losowymi są wstępne wygięcia (imperfekcje), granica plastyczności i smukłość pręta. Wspólną cechą wspomnianych rozwiązań było założenie o losowej niezależności losowych zmiennych, co jest w ogólności nieprawdziwe.
Szerokie badania problemu prowadził Elishakoff, zarówno metodą Monte-Carlo, jak i metodami analitycznymi [45] . Szeroko stosowaną obecnie [46] , [47] ) metodą modelowania losowych modelowania imperfekcji jest metoda zbiorów rozmytych rozmyte, w której zakłada się, że zarówno kształt jak wielkość imperfekcji, jako przypadkowe.
W analizach losowych imperfekcji najczęściej (np. [48] , [49] , [50] ) tylko amplituda jest uważana za zmienną losową i to o rozkładzie normalnym lub lognormalnym, a jej przebieg na długości pręta przyjmuje się w kształcie sinusoidy. Parametry rozkładu dobiera się tak, by z prawdopodobieństwem 95% imperfekcja pozostawała w przedziale określonym tolerancją normową.
Koncepcja Bj¢rhovde
[51] przyjmuje, że losowa amplituda imperfekcji ma rozkład prawdopodobieństwa Gumbela I typu dla najmniejszych wartości (p. Załącznik A). Przyjęty rozkład ma dystrybuantę (A.33) i funkcję gęstości (A.34) ze standaryzowaną zmienną:
$ y=\cfrac{e_0 -\alpha}{\beta}$
gdzie $\alpha$ i $\beta$ są parametrami rokładu, które Bj¢rhovde wyznaczył z warunków brzegowych problemu. Przyjął mianowicie, że maksymalna dopuszczalna strzałka wstępnego wygięcia $e_{max}=e_0=L/1000$ może wystąpić z prawdopodobieństwem 2,5%, co jest zgodne z wytycznymi norm światowych [18] , co było zgodne z dawną propozycją europejską. (Obecnie Eurokod przyjmuje $e_0 \approx L/300$.
Z zależności (A.36) dla standaryzowanego rozkładu Gumbela ($\alpha= \beta= 0$) mamy kwantyl $t_{max}=0+1\cdot ln [-ln(0,025)]=1,3$, który jest poziomem tolerancji dla przekroczenia maksymalnej amplitudy imperfekcji $e_{max} = e_0$. Zatem
$$ \begin {equation} e_0=\alpha+1,3 \cdot \beta \label {47} \end {equation}$$
Ponadto przyjęto, że minimalna strzałka wstępnego wygięcia wynosi $e_{min}=0$ (dla idealnego pręta) oraz założono, że może ona nie być utrzymana z prawdopodobieństwem 1%, co odpowiada współczynnikowi tolerancji $t_{min} =ln [ -ln (1-0,01)]=-4,6 , czyli
$$ \begin {equation} e_{min}=0 =\alpha -4,6 \cdot \beta \label {48} \end {equation}$$
Z układu równań ($\ref{2-3.57}$) i ($\ref{2-3.58}$) otrzymano:
$\beta=\cfrac{e_0}{5,9}$ , $\alpha= 0,78 \cdot e_0$,
Uzyskany rozkład prawdopodobieństwa pokazano na rys. 2-3.15.
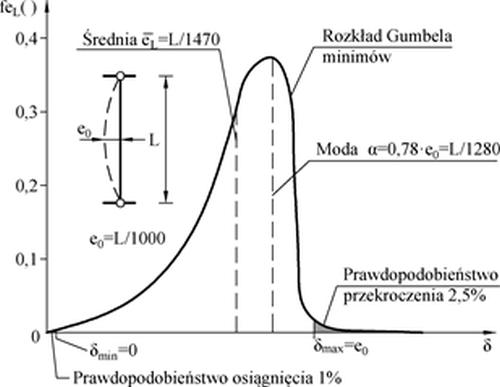
Rys. 2-3.15. Ilustracja założeń i wyników pracy [51]
Na podstawie formuł (A.35) i (A.28) wartość średnia $\overline e_0$ i odchylenie standardowe $\sigma_{e_0}$ amplitudy imperfekcji wynosi:
$$ \begin {equation} \overline e_0 = (0,78-0,5772/5,9) \cdot e_0 = 0,682 \cdot e_0= L/1470 \quad ; \quad \sigma_{e_0}= 1,283 \beta =1,283/5,9 \cdot e_0 = L/4600 \label {49} \end {equation}$$
Dla parametrów losowej amplitudy imperfekcji {$\ref{2-3.59}$) w pracy [51] sporządzono krzywe wyboczeniowe i porównano z krzywymi deterministycznymi. Oba typy krzywych są podobne, co świadczy o tym, że spośród wielu zmiennych losowych problemu ( w tym naprężeń resztkowych) imperfekcje łukowe są najbardziej znaczące. Metodą probabilistyczną uzyskano większe o kilka procent nośności krytyczne słupów.
Koncepcja Murzewskiego
Murzewski [52] , a za nim Gwóźdź [53] przedstawili interesującą, probabilistyczną interpretację współczynnika wyboczeniowego , wyznaczonego na podstawie losowej nośność granicznej $\Lambda_{lim}$ zdefiniowanej jako minimum z losowej nośności krytycznej $\Lambda_{cr}$ (wyboczenia sprężystego) oraz losowej nośności plastycznej $\Lambda_{pl}$ :
$$ \begin {equation} \min {[ \Lambda_{cr} \quad , \Lambda_{pl}]} \label {50} \end {equation}$$
Przy założeniu że zmienne losowe $\Lambda_{cr}$ i $\Lambda_{pl}$ są zmiennymi o rozkładzie Weibulla formuła ($\ref{50}$) prowadzi do następującego wyrażenia na współczynnik wyboczenia
$$ \begin {equation} \chi= \sqrt[n]{1+ \overline \lambda^{2n}} \label {51} \end {equation}$$
gdzie:
smukłość względna: $\overline \lambda=\sqrt{\cfrac{f_y}{\sigma_{cr}}}$,
wykładnik potęgi $n=1/v$, gdzie $v$ – współczynnik zmiennosci rozkładu Weibulla granicy plastyczności stali. O rozkładzie Weibulla – patrz artykuł Teoria losowych wartości ekstremal;nych.
W pracy Mlynarczyk (1986) [54] formułę sprawdzono na przykładzie interakcji mechanizmów zniszczenia blachownic stalowych z mechanizmami: uplastycznienia pasów, uplastycznienia środnika, niestatecznosći sprężystej pasa ściskanego, niestateczności sprężystej środnika, niestateczności ogólnej (zwichrzenia.
⇒ [ Uogólnienie formuły Ayrton-Perry ]
Publikacja internetowa w wersji „free” z nieograniczonym prawem cytatu – z powołaniem się na autora i źródło:
Leszek Chodor, (2017-2020), Imperfekcyjna metoda projektowania konstrukcji, Encyklopedia πWiki, Wydawnictwo Chodor-Projekt,
[ https://chodor-projekt.net/encyclopedia/imperfekcyjna-metoda-projektowania-konstrukcji/ ]
Historia edycji artykułu:
(2019-04-08 do 15) wersja 1,0: wersja pierwotna
(2019-05-27) Wersja 2.0: dokonano podziału rozdziału na części w celu poprawy procesu wczytywania strony
Literatura
- Ayrton W. E., Perry J. (1886), On Struts. The Engineer, p. 464–513
- Robertson A. (1925), The Strength of Struts, The Institution of Civil Engineers, London
- Godfrey G. B. (1962), The Allowable Stresses in Axially Loaded Steel Struts. The Struct. Engr, 40(3
- Dutheil, J. (1950). Le Flambement et le Deversement. Bulletin Bimestriel de La Societe Royale Des Ingenieurs et Des Industriels, 3
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- Chodor L. (2016), Przekrycia hal i galerii. W: XXXI Ogólnopolskie Warsztaty Pracy Projektanta Konstrukcji: Tom I, s. 25–202, [ https://chodor-projekt.net/wp-content/uploads/2016/03/Chodor_LPrzekrycia-hal-i-galerii-WPPK-2016.pdf ]
- da Silva L. S., Simoes R., Gervasio H. (2010). Design of Steel Structures: Eurocode 3: Design of Steel Structures, Part 1-1: General Rules and Rules for Buildings (ECCS Eurocode Design Manuals). ,Wiley, Ernst Sohn
- PN-EN 1999-1-1:2010, Eurokod 9: Projektowanie konstrukcji aluminiowych, Część 1-1: Reguły ogólne
- Butterworth, J. W. (2005, August). Column Buckling [Lecture], [ http://homepages.engineering.auckland.ac.nz/~jbut030/Courses/CIVIL211/Column_Buckling_Notes.pdf ]
- Frish-Fay, R. (1962). Flexible Bars , Lecturer of Civil Engineering University of New South Wales,. Butterworth & Co (Publisher) London
- Hajjar J. F. (1997), Effective lenght and Effective length and notional load approach-es for assesing frame stability : Implication for American Steel. Technical Report. Task Committee on Effective Length of the Technical Committee on Load and Re-sistance Factor Design of the Technical Division of the Structural Engineering Insti-tute of the American Society CIvil Engineers
- Shaw F. S. (1972), Virtual displacements and analysis of structures. Prentice-Hall
- Rykaluk K. (2012). Zagadnienia stateczności konstrukcji metalowych. Dolnośląskie Wydawnictwo Edukacyjne, Wrocław
- Kalkan I., (2010) , Application of Southwell Method on the Analysis of Lateral Tor-sional Buckling Tests on Reinforced Concrete Beams, Int.J.Eng.Research & Devel-opment,Vol.2,No.1,January 2010
- Meck, H. R. (1977), Experimental Evaluation of Lateral Buckling Loads, ASCE Journal of Engineering Mechanics Division, Proceedings, Vol. 103, No. 2, pp. 331-337
- Massey, C. (1963), Elastic and Inelastic Lateral Instability of I-Beams, The Engineer, Vol. 216, No. 5622, pp. 672-674
- Fukumoto, Y. (1982), Numerical Data Bank for the Ultimate Strengths Steel Structures, Der Stahlbau, 1
- ACI 318-11, (2011), Building Code Requirements for Structural Concrete and Commentary
- Galambos T. V., Surovek A. E. (2008). Structural stability of steel: Concepts and Applications for structural engineers. John Wiley & Sons, Inc., Hoboken
- Lamarle E.(1845), Memoire sur la flexion du bois, Ann. Trav. Publics de Belg., Vol. 3, pp. 1-64
- Bauschinger J. (1887). Zerknickungs-Versuche (Mitteilung an Das Heft 15, Mitteilung XVII; p. 11), Mechanische-Technologie Laboratorium, Munchen
- Tetmajer L. von. (1890). Die Gesetze der Knickungs und der Zusammeng-Esetzten Druckfestigkeit der Technisch Wichtigsten Baustoffe (Mitteilung Der Material Anstalt Auf Schweizer Polytechnikum in Zurich Heft k, 1890, Heft 8, I896.). Polytechnikum in Zurich
- Jasiński F. (1895), Noch ein Wert zu den Knickfragen. Schweizerische Bauzei-tung, 25(25), 172–175
- Herzog M. A. M. (2010), Kurze Geschichte der Baustatik und Baudynamik in der Praxis (1. Aufl), Bauwerk
- http://homepages.engineering.auckland.ac.nz/~jbut030/Courses/CIVIL211/Column_Buckling_Notes.pdf ]
- Engesser F. R. (1895), Uber Knickfragen. Schweizerische Bauzeitung, 36(4), 24–26
- Karman von T. (1910). Untersuchungen Uber Knickfestigkeit (Mitteilung Und For-schungsareiten -Arb. Geb. Ing. -Wes. Heft 81
- Panovko J., G., Gubanova, I. I. (1967), Ustojčivost i kolebnija uprugich system. Sovremennyje koncepcii, paradoksy i ošibki (4th ed.), Nauka, Moskva
- Merchant W. (1954), The Failure Loads of Rigidly Jointed Frameworks as Influenced by Stability. The Structural Engineer, 32(7), 185–190
- Shanley F. R. (1946). The Column Paradox, Journal of the Aeronautical Sciences, 13(12), 678–678
- Shanley F. (1947), Inelastic column theory. Journal of the Aeronautical Sciences, 14(5), 261–268
- Hutchinson J. W. (1974). Plastic Buckling (Vol. 14). Academic Press Inc
- Hutchinson J. W., Koiter W. T. (1971). Post buckling theory. Applied Mechanics, 24, 1353–1366
- Koiter W.T. (1945), The stabillity od elastic equilibrium, PhD Thesis, Royal Nether-lands Academy of Arts and Sciences, Amsterdam
- Alveranga A. R., Silveira E. A. (2009), Second-order plastic-zone analysis of steel frames- Part II effects of initial geometric imperfection and residual stress. Latin American Journal of Solids and Structures, 6(4), 323–342
- Henricsson A., Panarell, J. (2017). Initial bow imperfection for flexural buckling of steel members. Verification and optimisation regarding analysis of columns and beam-columns. Chalmers University of Technology. Department of Civil and Envi-ronmental Engineering.
- Henricsson A., Panarell, J. (2017). Initial bow imperfection for flexural buckling of steel members. Verification and optimisation regarding analysis of columns and beam-columns. Chalmers University of Technology. Department of Civil and Environmental Engineering
- Dutheil J. (1950), Le Flambement et le Deversement. Bulletin Bimestriel de La Socie-te Royale Des Ingenieurs et Des Industriels, 3
- Bolotin V. V. (1968). Metody statystyczne w mechanice budowli, Wydawnictwo Arka-dy, Warszawa 1968. Arkady
- Chung B. T. K., (1969), Random-Parameter Analysis of the Stability of Inelastic Structures, PhD. Dissertation. State University of New York
- Chung B. T. K., Lee, G. C. (1971), Buckling Strength of Columns Based on Random Parameters. Journal Structural DIv, ASCE, 97(ST7
- Ravindra M. K., Galambos T. V. (1972). Discussion of “Buckling Strength of Columns Based on Random Parameters” by B. T. K. Chung and G. C.Lee. Journal, ASCE Str. Div., 98(ST1), 215
- Dutheil J. (1952). The Theory of Instability through Disturbance of Equilibrium. 4th Congress of I.A.B.S.E., Cambridge
- Augusti G., Barattta A. (1971), Theorie probabiliste de la resistnce des barres com-primees. Constructiion Metallique, 2
- Elishakoff I. (2016), Probabilistic Methods in the Theory of Structures: Random Strength of Materials, Random Vibration, and Buckling. World Scientific
- (Kala Z. (2003), The influence of initial curvature of the axis upon the member ulti-mate strength. Journal of Structural Mechanics, 36(1), 3–14
- Kala Z. (2007), Stability problems of steel structures in the presence of stochastic and fuzzy uncertainty. Thin-Walled Structures, 45(10–11), 861–865
- Marek P., & Krivy V. (2006), Probabilistic reliability assessment of a steel frame ap-plying the SBRA method. 3rd ASRANet International Colloquium, Glasgow
- Omishore A. (2010), Sensitivity analysis of structures, problems and applica-tions. Proceeding 6th WSEAS International Conference on Applied and Theoretical Mechanics (MECHANICS ’10, pp. 120–125, Athens
- Omishore A., Kala Z. (2009). Reliability Analysis of Steel Structures with Imperfec-tions, Nordic Steel Construction Conference, pp. 540–545, Malmo, Sweden
- Bjerhovde R. (1972), Deterministic and probabilistic approaches to the strength of steel columns (Ph D. Dissertation No. 1933; Fritz Laboratory Reports). Lehigh University
- Murzewski J. (1976), Teoria nośności losowej konstrukcji prętowych. PWN, Warszawa
- Gwóźdź M., (1997)., Zagadnienia nośności losowej prętów metalowych. Praca doktorska, Zeszyt Naukowy 69, Politechnika Krakowska, Kraków
- Młynarczyk A., (1986), Interakcja losowych mechanizmów zniszczenia belek stalowych, Praca doktorska, Wydział Budownictwa Lądowego, Politechnika Krakowska, Kraków
________________________________