Przedstawiono rozwiązanie w przemieszczeniach pryzmatycznej, zginanej i ściskanej belki Timoshenko, spoczywającej na podłożu Winklera i na skupionych podporach sprężystych. Podłoże Winklera jest w ogólności trójparametrowe: charakteryzowane sprężystością pionową -stałą sprężystości cv(x), poziomą cH(x) i obrotową cM(x) , zmiennymi w funkcji współrzędnej belki x. Belka może posiadać więzy skupione w ogólności również sprężyste ze stałymi sprężystości [pionowa, pozioma obrotowa]=[CV, CH, CM](xk) usytuowanymi w punktach belki xk. W szczególnym przypadku, jeśli stałe sprężystości podpór przyjmą wartość C*= ∞, to podpora jest niepodatna. Wyznaczono funkcjonał Π energii potencjalnej Lagrange’a belki oraz przedstawiono kanoniczny układ równań Ritza. Pracę zilustrowano przykładem liczbowym.
Belka klasyczna Bernoulliego-Eulera
Przedstawmy najpierw rozwiązanie zadania pomocniczego dla klasycznej belki Bernoulligo-Eulera. Belka jest obciążona rozłożonym obciążeniem q(x), ściskana siłą N(x), oraz poddana działaniu obciążeń skupionych [V,H,M](xk) zlokalizowanym w punkcie o współrzędnej xk . Indeks k oznacza w zależności od kontekstu miejsce przyłożenia podpory skupionej lub obciążeń skupionych o różnej naturze.
Energia potencjalna w przemieszczeniach
Powszechnie znaną zależność na gęstość energii potencjalnej ciała sprężystego zapiszmy w postaci [1]:
| $\Phi = \frac{1}{2E} \{ \sigma_x^2 + \sigma_y^2+ \sigma_z^2 -2\nu (\sigma_x \sigma_y + \sigma_x \sigma_z +\sigma_y \sigma_z)+ 2(1+\nu)(\tau_{xy}^2+\tau_{xz}^2+ \tau_{yz}^2) \} $ | (1) |
gdzie w celu zwiększenia czytelności – zastosowano symbole klasyczne (x,y,z) ( a nie powszechnie stosowany zapis wskaźnikowy).
W przypadku zginania poprzecznego wzór ten znacznie upraszcza się. Ponieważ wpływ naprężeń σy, τxz, τyz jest pomijalnie mały, więc przyjmuje się, że różne od zera są jedynie naprężenia σx, τxy.
W podejściu klasycznym Bernoulliego-Eulera pomija się również wpływ naprężeń τxy na przemieszczenia i energię potencjalną. Wpływ naprężeń stycznych uwzględnimy w rozdziale dotyczącym belki Timoshenko.
Przy poczynionych założeniach upraszczających energia potencjalna belki zginanej wynosi:
| $\Pi_\sigma= \iiint \limits_V{\Phi \cdot dV}=\frac {1} {2E} \iiint \limits _V \sigma^2_{x} \cdot dV $ | (2) |
Energię (2) wyrazimy przez siły przekrojowe, a następnie przez przemieszczenia. Zachodzi:
| $\sigma_x= -\frac {N}{A}+ \frac {M(x)}{I_y} \cdot z $ | (3) |
gdzie: A – pole przekroju pręta, Iy – moment bezwładności przekroju względem osi głównej y, z-odległość (pionowa) punktu przekroju od osi głównej. Dalej moment bezwładności oznaczamy bez indeksu.
W przypadku przeważającego zginania przy obliczaniu minimum energii układu wpływ rozciągającej siły osiowej N jest pomijalnie mały. Wpływ siły ściskającej N uwzględniamy w dalszej części opracowania.
Całkę w równaniu (2) przekształcimy tak, by otrzymać energię w przemieszczeniach.
Ponieważ zachodzi związek pomiędzy momentem zginającym a krzywizną
| $M(x)=-EIw”(x)$ | (4) |
więc mamy:
| $\Pi_\sigma= \iiint \limits_V {\frac {1}{2E}}\left [ – \frac {EIw”(x)} {I}z \right ]^2 dV=\frac {E} {2} \iiint \limits_V [w”(x) \}^2 \cdot z^2 dV =$ $=\frac {E} {2} \int \limits _0 \limits^L [w”(x)]^2 dx \cdot \iint \limits_A z^2 dA = \frac {EI_y} {2} \int \limits_0 \limits^L [w”(x) \}^2 dx $ |
(5) |
Praca zewnętrznych sił poprzecznych
Praca zewnętrznych sił poprzecznych q(x) i momentów zginajacych m(x) rozłożonych na długości belki wynosi
| $L_q = \int \limits _0 \limits^L [q(x)w(x) +m(x) w'(x)] dx$ | (6) |
Obciążenia skupione zlokalizowane w punkcie $x_k$ możemy zapisać następująco:
| $Q_k=Q\cdot \delta(x-x_k)$ $M_k=M\cdot \delta(x-x_k)$ |
(7a,b) |
gdzie symbol Diraca : $\delta (x-x_k)$ = [ 1 dla $x=x_k$ ; 0 dla $x \ne x_k$]
Po podstawieniu (7) do (6) mamy:
| $ L_q = \int \limits_0 \limits^L [q(x)w(x) +m(x) w'(x)] dx+\sum \limits _k Q_k \cdot w(x_k) + M_k \cdot w'(x_k)$ | (8) |
Praca siły ściskającej N
Praca siły ściskającej N(x) jest wykonywana na przemieszczeniu poziomym belki, wywołanym jej ugięciem, przy tym w zagadnieniu belki pomijamy skrócenie belki pod wpływem przekrojowej siły N. W celu oszacowania tego przemieszczenia należy przeanalizować zagadnienie II rzędu zilustrowane na rys.1.
Rys.1. Przemieszczenie poziome Δ(dx) przekroju belki wywołane jej ugięciem w(x)
Analizujemy odcinek dx belki. Ugięcie powoduje przemieszczenie punktów końcowych do położenia dx’. Pozioma odległość Δ(dx) pomiędzy punktem przed i po ugięciu na której pracuje siła N wynosi:
| $ \Delta(dx)=dx=dx’=dx- \sqrt{(dx)^2-(\frac {d} {dx} dx)^2} =dx(1-\sqrt{1-(w’)^2}$ | (9) |
Po rozwinięciu w szereg MacLaurina ostatniego pierwiastka i pozostawieniu pierwszego nieliniowego wyrazu szeregu, , otrzymamy aproksymację, która jest podstawą teorii drugiego rzędu mechaniki konstrukcji:
| $ \Delta(dx) \approx dx \{ 1-(1-\frac{1}{2} {w’}^2+ \frac{1}{4} {w’}^4+…) \} \approx \frac{1}{2}\left \{ w'(x) \right \}^2$ | (10) |
W rezultacie praca siły siły podłużnej, ściskającej, wynosi:
| $ L_N = \int \limits_0 \limits^L N \cdot \Delta(dx) dx = \int \limits_0 \limits^L \frac {N}{2}[w'(x)]^2 dx$ | (11) |
Praca sił odporu
Siły odporu qz(x) są reakcją podłoża r(x) na nacisk belki. Z definicji zależą one bezpośrednio od przemieszczenia w(x) zgodnie z zależnością (12), gdzie znak (-) wynika ze zwrotu sił odporu, które są przeciwnie skierowane do ugięcia.
| $ q_z(x)=-r(x)=-c(x) \cdot w(x) $ | (12) |
Na rys. 2 pokazano odpór pionowy v podłoża o stałej sprężystości cv oraz odpór obrotowy m podłoża o stałej sprężystości cm. Analogicznie można zdefiniować odpór poziomy h podłoża o stałej sprężystości ch.
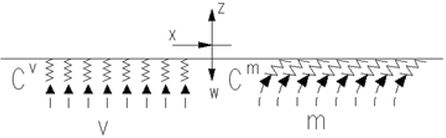
Rys.2. Siły odporu sprężystego podłoża
Reakcje V, H lub M skupionych w punkcie xk podpór sprężystych o stałych sprężystości odpowiednio CV, CH i CM otrzymamy z definicji (11) i zapisu w funkcją Diraca (7). Na przykład dla sprężystej podpory pionowej i obrotowej mamy (rys.3):
| $ q_k=-{C_k}^V \cdot w(x) \cdot \delta(x_k)$ $M_k=-{C_k}^M \cdot w^{’}(x) \cdot \delta(x_k) $ |
(13) |
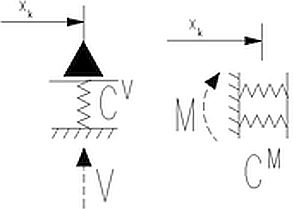Rys.3. Reakcje od podpory sprężystej pionowej i obrotowej
Nadając przyrosty przemieszczenia w nadajemy przyrosty siłom odporu. Zapisując pracę wirtualną sił odporu w postaci:
| $ \delta L_c= -\int \limits _0 \limits ^L -r(x) \delta w(x) dx= -\int \limits _0 \limits ^L c \cdot w(x) \delta w(x)dx $ | (14) |
widzimy, że nie ma możliwości wyłączenia znaku wariacji przed całkę. Będziemy to mogli zrobić dopiero wtedy, gdy ostatnią całkę zapiszemy w postaci:
| $ \delta L_c= -\int \limits _0 \limits ^L c \cdot \frac {1} {2} \delta [w^2(x)]dx= -\delta \int \limits_0 \limits^L \frac {c}{2} \cdot w^2(x)dx$ | (15) |
Teraz możemy opuścić znak wariancji (uprościć) i otrzymamy wyrażenie na pracę sił odporu podłoża sprężystego
| $ \delta L_c= \int \limits^L \limits_0 \frac {c}{2} \cdot w^2(x)dx $ | (16) |
Stosowne wyrażenia na pracę skupionych podpór sprężystych, otrzymamy z (16) po podstawieniu (12).
Funkcjonał Lagrange’a belki Bernoulliego
Ostatecznie funkcjonał Lagrange’a dla belki Bernoulliego ściskanej siłą osiową N, na podłożu sprężystym i na podporach sprężystych zapiszemy w postaci:
| $ \Pi_B = \int \limits_0\limits^L \left [ \frac {EI_y} {2} [w”(x)]^2- \frac {N(x)} {2}[w'(x)]^2 +\frac {c^v (x)}{2}[w(x)]^2-q(x)w(x) \right ] dx $ $ +\sum \limits k \left[ \frac{{C_k}^v } {2} [w(x_k)]^2+\frac{{C_k}^M} {2} [w'(x_k)]^2- V_k w(x_k)- M_kw’ (x_k) \right ] $ |
(17) |
Belka Timoshenko
Założenia i element Timoshenko
Belka Timoshenko uwzględnia korektę pierwszego rzędu teorii Bernonuliego poprzecznego zginania.. Klasyczne założenie kinematyczne jest zmienione na „ płaski przekrój pozostaje płaski, ale nie jest już prostopadły do zdeformowanej osi obojętnej belki”. Dla prostego elementu belkowego założenie to zilustrowano na rys.4.
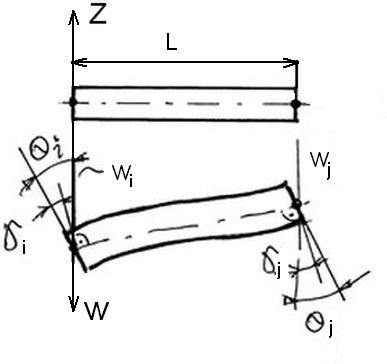
Rys.4. Dwuwęzłowy element Timoshenko [2]
Obrót przekroju poprzecznego oznaczono Q z dodatnim zwrotem od x do w. Pole przemieszczeń wynosi:
| $ u(x,z)=u(x)+z \cdot \theta \ \ \wedge \ \ w(x,z)=w(x) $ | (18) |
Zachodzi [2]:
| $ \theta =\frac {\partial w}{\partial x}- \gamma \wedge \gamma= \frac {\tau} {G}=\frac {T}{GA_z}= \frac {T}{S_v}$ | (19) |
gdzie T jest siła poprzeczną , a γ= γ(x) jest „obrotem ścinania”, uśrednionym po przekroju, G – modułem Kirchoffa, Az efektywnym polem przekroju na ścinanie, Sυ=GAz jest sztywnością postaciową (na ścinanie) przekroju belki.
Ujemny znak γ oznacza, że dodatnie siły tnące wywołują ujemny obrót ścinania (rys.5).
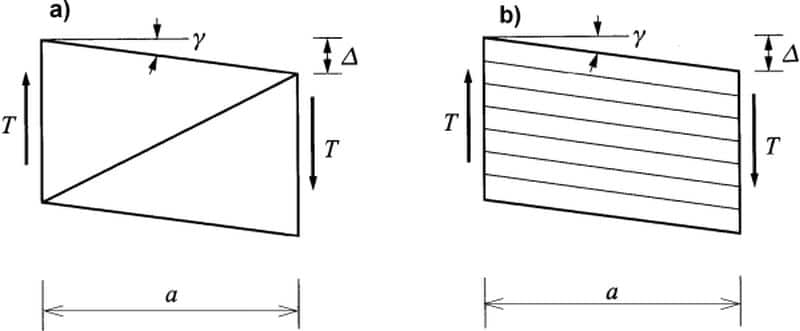
Rys. 5 Odkształcenia postaciowe elementu pręta: a) pręt rzeczywisty, b) pręt zastępczy [3]
W przypadku przekrojów złożonych (wielogałęziowych) sztywność postaciową wyznacza się na drodze porównania przemieszczeń konstrukcji rzeczywistej oraz pręta zastępczego. Dla najczęstszych przypadków prętów o pasach równoległych wyrażenia na sztywność postaciową podano w tab.1.
Tab.1. Podatność na ścinanie prętów złożonych [3]
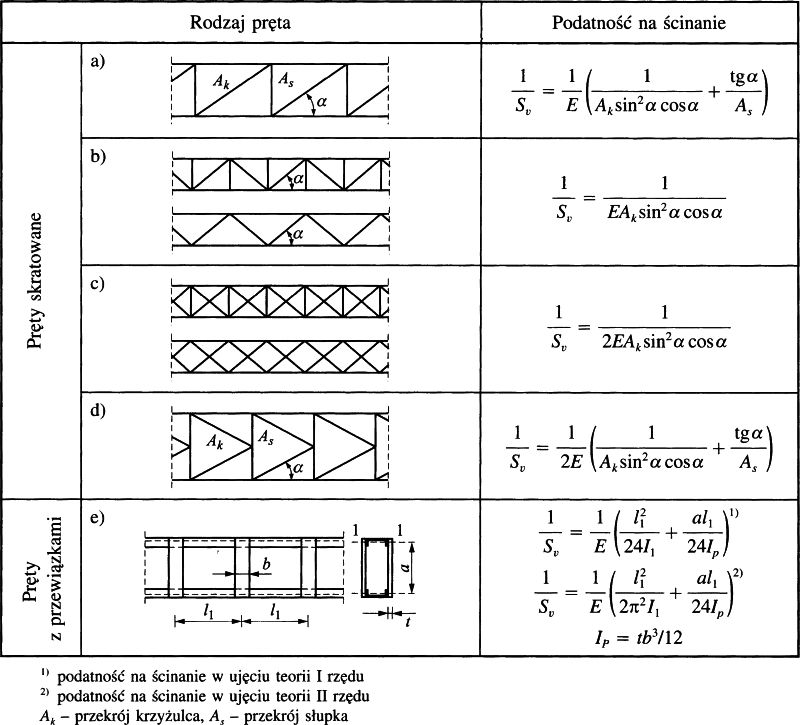
W celu stosownej modyfikacji macierzy sztywności elementu w metodzie elementów skończonych wprowadza się bezwymiarowy współczynnik, charakteryzujący „smukłość ścinania” [2]:
| $ \Psi = \frac {12EI_y} {GA_z L^2}= \frac {12EI_y} {S_vL^2}=12 \cdot k$ | (20) |
gdzie $k=EI_y/S_v L^2$ jest współczynnikiem podatności na ścinanie wprowadzonym w pracy [3].
Jeśli Ψ→0, to model Timoshenko redukuje się do klasycznego modelu Bernoulli-Eulera.
Energia potencjalna elementu Timoshenko
Energia potencjalna elementu Timoshenko wynosi:
| $ \Pi_\sigma= \frac {1}{2} \left \{ \int_0^L EI \cdot \kappa^2(x) +S_v \cdot \gamma^2(x) \right \} dx$ | (21) |
krzywizna $ \kappa =w”(x)$ . Kąt ścinania wyznaczymy z wykorzystaniem zależności różniczkowej pomiędzy siłami przekrojowymi, jak następuje:
| $ T(x)=\frac {dM(x)} {dx} \wedge M(x)=-EI_y w”(x) \to T(x)=-EI_y w^{3′}(x) \to$ $ \to \gamma(x)= \frac {T(x)}{GA_z} =-\frac {EI_y} {GA_z} w^{3′}$ |
(22) |
Stąd otrzymujemy:
| $ \Phi_{\sigma} =\frac {EI_y} {2} \int \limits_0 \limits ^L \left ( [w”(x)]^2 + \frac {EI_y} {GA_z} [w^{3′}(x)]^2 \right )dx$ | (23) |
Praca siły ściskającej i praca sił zewnętrznych
Ponieważ w pkt.1. przy wyprowadzaniu formuł na pracę siły ściskającej oraz pracę sił zewnętrznych, w tym odporu podpor sprężystych nie wykorzystywaliśmy hipotezy kinematycznej Bernoulliego, więc zależności słuszne są również dla belki Timoshenko.
Funkcjonał Lagrange’a belki Timoshenko
Ostatecznie funkcjonał Lagrange’a dla belki Timoshenko ściskanej siła osiową N , na podłożu sprężystym i na podporach sprężystych zapiszemy w postaci (24):
| $ \Pi_T = \int \limits_0\limits^L \left [ \frac {EI_y} {2} \left ( [w”(x)]^2 + \underline { \frac {EI_y} {GA_z} [w^{3′}(x)]^2 } \right ) – \frac {N(x)} {2}[w'(x)]^2 +\frac {c^v (x)}{2}[w(x)]^2-q(x)w(x) \right ] dx $ $ +\sum \limits k \left[ \frac{{C_k}^v } {2} [w(x_k)]^2+\frac{{C_k}^M} {2} [w'(x_k)]^2- V_k w(x_k)- M_kw’ (x_k) \right ] $ |
(24) |
Funkcjonał $\Pi_T$ dla belki Timoshenko różni się od potencjału belki Bernoulliego (17) jedynie składnikiem zaznaczonym podkreśleniem w formule (24).
Metoda Ritza
Minimalizacja funkcjonału Lagrange’a metodą Ritza
W metodzie Ritza poszukuje się funkcji realizującej minimum funkcjonału w klasie wielomianów:
| $ w(x)=\varphi_0+\sum \limits_{i=1} \limits ^{n} a_i \cdot \varphi_i(x)$ | (25) |
gdzie funkcje bazowe φi(x) mogą być dowolnie dobrane, ale tak, by były dopuszczalne, czyli spełniały kinematyczne warunki brzegowe.
Podstawiając (25) do (24), otrzymamy wyrażenie na $\Pi_T$ , w którym funkcjonał energii jest teraz funkcją współczynników ai. Funkcja ta osiąga minimum przy warunku:
| $ \frac {\partial \Pi_L} {\partial a_j}=0 $ , (j=1,2,…n) | (26) |
Różniczkując (24) (z aprokysmacją (25) podług $a_i$ i przyrównując pochodną do zera zgodnie z (26) po niewielkich przekształceniach otrzymamy kanoniczny układ Lagranga-Ritza dla belek:
| $ \sum \limits_{i=1} \limits^n a_i \delta_{ij}= \Delta_{ij} $ , (j=1,2,…n) | (27) |
gdzie współczynniki $\delta_{ij}$ oblicza się z wyrażeń:
| $ \delta_{ij} =\sum \limits_{i=1} \limits^n \int \limits_0 \limits ^L \left [ EI_y \left (\varphi^{„}_{i}(x) \varphi^{„}_{j}(x) + \frac {EI_y} {GA_z} \varphi^{3′}_{i}(x) \varphi^{3′}_{j}(x)\right) – \\ – N \varphi^{’}_{i}(x) \varphi^{’}_{j}(x) + c^V \varphi_{i}(x) \varphi_{j}(x)\right] dx + \sum \limits_k [C^V_k \varphi_{i}(x_k) \varphi_{j}(x_k)+C^M_k \varphi^{’}_{i}(x_k) \varphi^{’}_{j}(x_k)]$ | (28) |
a wyrazy wolne z wyrażeń:
| $ \Delta_{qj} = \int \limits_0 \limits ^L q(x) \varphi_{j}(x)dx+\sum \limits_k V_k \varphi_{j}(x_k)+\sum \limits_k M_k \varphi^{’}_{j}(x_k)$ | (29) |
Układ kanoniczny (27) wraz z wyrażeniami (28) i (29) ma analogiczną strukturę do klasycznych wyrażeń mechaniki konstrukcji w metodzie sił lub metodzie przemieszczeń. W przykładzie numerycznym 4.1. pokażemy, że zachowane są również ogólne zależności metody elementów skończonych w ujęciu klasycznym (funkcji kształtu w postaci wielomianów Ritza).
Przykład liczbowy
Rozwiązać belkę pokazaną na rys. 7 przy użyciu metody elementów skończonych. Uwzględnić wpływ sztywności ścinania na przemieszczenia i siły przekrojowe (belka Timoshenko). Belka jest kratownicą Pratt’a (z wykratowaniem typu N) – wg tab. 1 poz. a) i danych: wysokość kratownicy h=720 mm, α=45º, pasy HEA 160, krzyżulce RK 40x40x3, słupki RK 50x50x3. Wykonać wykresy linii ugięcia oraz momentów zginających.
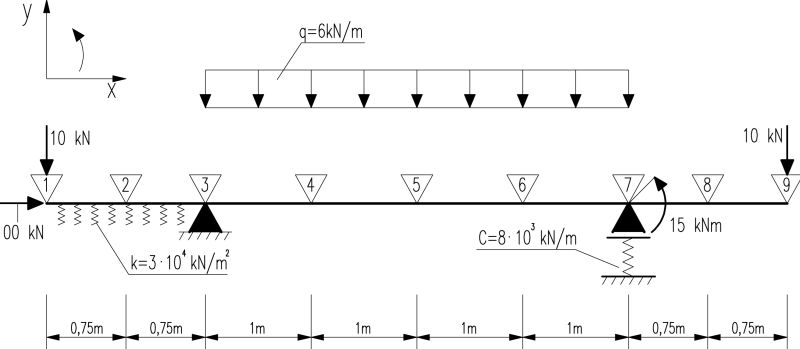
Rys. 7. Schemat belki do przykładu 4.2
Dyskretyzacja oraz sztywność belki
Przyjęto podział belki na 8. elementów skończonych. Na rys.7 węzły elementów wskzano wierzchołami trójkątów, w którego wnętrzu podano numer globalny węzła. Długości elementów (1-2), (2-3),(7-8), (8-9) wynoszą 0,75 m, a pozostałych elementów 1 m.
Belka ma stałą sztywność giętną oraz postaciową wszystkich elementów. Moment bezwładności na zginanie przekroju kratownicy, traktowanej jako belka o przekroju złożonym z pasów ( przekroju dwupunktowym) wynosi
| $ I=I_c+A_c \cdot z_c^2+I_t+A_t \cdot z_t^2= 2(1670+38,8 \cdot 36^2)=103909,6 cm^4 )$ |
gdzie dla pasów wykonanych z profilu HEA160 moment bezwładności pasa ściskanego Ic i rozciąganego It wynosi 1670 cm4 , pole przekroju Ac=At=38,8 cm2. Odległość pasa od osi obojętnej przekroju zc=zt=h/2=72/2=36 cm.
Moduł Younga stali wynosi E=210 GPa. Ponieważ w dalszej części przykładu , uwzględniamy sztywność postaciową belki, więc nie redukujemy modułu Younga przy wyznaczaniu sztywności giętnej, która wynosi:
| $ EI= 210 GPa \cdot 103909,6\ \ cm^4= 2,182 \cdot 10^5 \ \ kNm^2 $ |
Sztywność postaciową belki-kratownicy obliczono z zależności podanej w poz a) tab.1:
| $ S_v= \frac {E}{\frac {1} {A_k \cdot sin^2 \alpha \cdot cos \alpha}+ \frac {tg \alpha}{A_s}}=25233,8 kN$ |
gdzie: Ak=4,34 cm2 (krzyżulce RK40x40x3), As=5,54 cm2 (słupki RK50x50x3).
Macierze sztywności elementów
Ścisła macierz sztywności ki elementu (i) belki z uwzględnieniem ściskania przy założeniu rozdzielenia stanu zgięciowego oraz ściskania oraz bez uwzględnienia sztywności podłużnej, ale z uwzględnieniem sztywności postaciowej wynosi:
 |
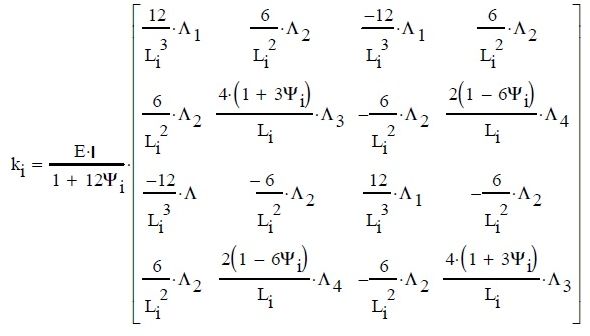(30) |
gdzie konwencjonalna macierz sztywności elementu zginanego jest zmodyfikowana ze względu na sztywność postaciową (element Timoshenko) współczynnikami Ψi (19) zgodnie z [2], a ponadto współczynnikami Λi ze względu na działanie siły ściskającej , wynikającymi ze ścisłych zależności dla nieliniowej macierzy sztywności.
Za dodatnie przyjęto przemieszczenia oraz naprężenia uogólnione (siły przekrojowe), których zwrot jest zgodny ze zwrotem kąta skierowanego (dodatniego).
Współczynniki nieliniowej macierzy sztywności, wynoszą [4]:
| $\Lambda_1= \alpha_c \Lambda_2 $ $ \Lambda_2=\frac{\alpha^3}{3 (\alpha-\alpha_c)}$ $ \Lambda_3= \frac {3}{4}\Lambda_2 +\frac {\alpha_c}{4}$ $ \Lambda_4= \frac {3}{2}\Lambda_2- \frac {\alpha_c}{2} $ |
(31) |
gdzie:
$\alpha= \frac {L} {2} \sqrt {\frac {N} {EI}} = \frac {\pi} {2} \sqrt { \frac {N} {N_{cr}}}$,
$ \alpha_c= \alpha \cdot ctg \alpha$,
$N_{cr}$ – siła krytyczna Eulera,
N jest siłą ściskającą element o długości L i sztywności EI
Po rozwinięciu nieliniowych funkcji (31) w szereg Taylora i pozostawieniu dwóch pierwszych wyrazów rozwinięcia w pobliżu α=0 , otrzymamy:
| $\Lambda_1=1- \frac {1}{10} \frac {Pl^2} {EI} $ $ \Lambda_2= 1- \frac {1}{60} \frac {Pl^2} {EI} $ $ \Lambda_3= 1- \frac {1}{30} \frac {Pl^2} {EI} $ $ \Lambda_4= 1+ \frac {1}{60} \frac {Pl^2} {EI} $ |
(32) |
Wyrażenia (32) definiują konwencjonalną macierz geometryczną elementu prętowego.
Elementy (1-2) i (2-3)
Elementy (1-2) i (2-3) mają długość l=0,75 m i są ściskane siłą N= 100 kN.
Współczynniki Λi, modyfikujące sztywność (31) lub (32) w tym przypadku wynoszą: Λi≈1,0 (i=1,2,3,4). Zwiększenie siły ściskajacej doprowadzi do sytuacji, w której nie będzie można pominąć ściskania, co nie zmniejsza ogólności rozważań.
Parametr Ψi, uwzględniający sztywność postaciową elementu (i) zdefiniowany wyrażeniem (19) wynosi:
$ \Psi_{(1-2)}= \frac {2,182 \cdot 10^5} {0,75^2 \cdot 25233,81}=15,373 $
Dla elementów (i)=(1-2) oraz (2-3) macierze sztywności są takie same: $ k^{(1-2)}=k^{(2-3)}$.
Pierwszy element tych macierzy wynosi
$ k_{1,1} ^{(1-2)}= \frac {EI} {1+12 \Psi_1} \cdot \frac {12} {L_1^3} \cdot \Lambda_1=\frac{2,182 \cdot 10^5} {1+12 \cdot 15.373} \cdot \frac{12} {0,75^2} \cdot 1,0=33462,825 $ kN/m
a pełna macierz sztywności :
$ [k]^{(1-2), (2-3)}= \small {{\left \lbrack \matrix { 33462,825 & 12548,829 & -33462,825 & 12548,829 \cr 12548,829 & 295650,171 & -12548,829 & -286242,279 \cr -33462,825 & -12548,829 & 33462,825 &-12548,829 \cr 12548,829 & -286242,279 & -12548,829 & 295650,171} \right \rbrack} } $=
$ =\left | \matrix { {[k_{11}]} & {[k_{12}]} \cr {[k_{21}]} & {[k_{22}]} } \right |$
W celu przygotowania do „sumowania MES macierz sztywności elementu składamy z czterech bloków. Bloki macierzy sztywności elementu (1-2) i (2-3) oznaczamy bez nadkreślenia np.: $[k_{11}]$. Natomiast różniące się od nich bloki macierzy innych elementów będziemy oznaczać jednym lub dwoma nadkreśleniami, $[\overline k_{11}]$ lub $[ {\overset = k }_{11}]$.
Elementy (3-4) do (6-7)
Elementy nie są ściskane P(=N)=0 → Λi =0 (i=1,2,3,4). Macierz sztywności rozpatrywanych elementów wynosi więc:
$ [k]^{(3-4)…(6-7)}=\small{ {\left \lbrack \matrix { 24992,963 & 12496,481 & -24992,963 & 12496,481 \cr 12496,481 & 224458,401 & -12496,481 & -211961,919 \cr -24992,963 & -12496,481 & 24992,963 &-12496,481 \cr 12496,481 & -211961,919 & -12496,481 & 224458,401} \right \rbrack }}$=
$ =\left | \matrix { {[\overline k_{11}]} & {[ \overline k_{12}]} \cr {[\overline k_{21}]} & {[ \overline k_{22}]} } \right |$
Elementy (7-8) i (8-9)
Macierz sztywności przy uwzględnieniu N=0 oraz długości L=L1=0,75 m , wynosi:
$ [k]^{(7-8), (8-9)}= \small {\left \lbrack \matrix { 33463,688 & 12548,883 & -33463,688 & 12548,883 \cr 12548,883 & 295652,711 & -12548,883 & -286241,049 \cr -33463,688 & -12548,883 & 33463,688 &-12548,883 \cr 12548,883 & -286241,049 & -12548,883 & 295652,711} \right \rbrack} $=
$ =\left | \matrix { {[{\overset = k }_{11}]} & {[ {\overset = k }_{12}]} \cr {[{\overset = k }_{21}]} & {[ {\overset = k }_{22}]} } \right |$
Macierz sztywności układu
Macierz sztywności układu [K] elementów ma wymiar (9×2)x(9×2)=18×18, gdzie N jest liczbą węzłów układu, a n – liczbą stopni swobody (przemieszczeń) w węźle.
Macierz tą znajdziemy drogą superpozycji – „sumowania” po elementach skończonych, według zasady:
| $ [K]=[K_{rs}]=[\sum [k_{ij}]] $ | (33) |
gdzie sumowanie dotyczy elementów zbiegających się w danym węźle, $k_{ij}$ jest podmacierzą macierzy sztywności danego elementu.
Mamy na przykład:
$ K_{11} = [k_{11}] = \small {\left \lbrack \matrix { +33462,825 & +12548,829 \cr +12548,829 & +295650,171} \right \rbrack} $
$ K_{12} = [k_{12}] = \small {\left \lbrack \matrix { -33462,825 & +12548,829 \cr -12548,829 & -286241,279} \right \rbrack} $
$K_{13}=K_{14}=K_{15}=K_{16}=0$
$ K_{22} = [k_{22}]+[k_{11}] = \small {\left \lbrack \matrix { +33462,825 & -12548,829 \cr -12548,829 & +295650,171} \right \rbrack +\left \lbrack \matrix { +33462,825 & +12548,829 \cr +12548,829 & +295650,171} \right \rbrack}$
$K_{33}=[k_{22}]+[\overline k_{11}]$, itd.
W tab.1. zestawiono zagregowaną („zsumowaną”) macierz sztywności calego układu.
Tab.1. Macierz sztywności systemu
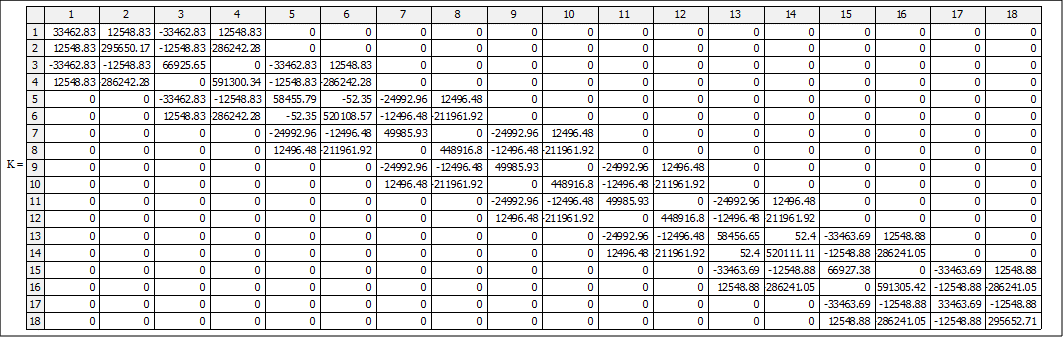
Wektor równoważników węzłowych
Dla obciążenia równomiernie rozłożonego pomiędzy węzłami obciążenie węzłowe jest równe reakcjom belki utwierdzono-utwierdzonej. W przypadku podłoża sprężystego kinematyczne warunki brzegowe zastąpiono statycznymi warunkami brzegowymi. Można wykazać [2], że równoważniki węzłowe dla elementu belki Timoshenki (i) o długości Li , spoczywającego na podłożu sprężystym o stałej sprężystości ki wynoszą:
 |
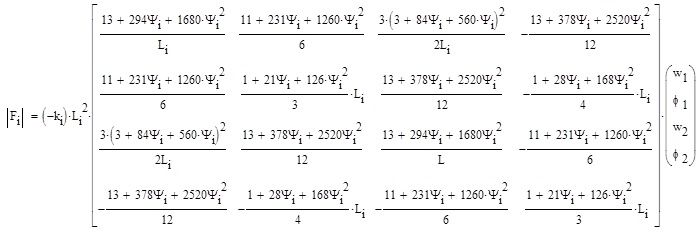(34) |
Po uwzględnieniu obciążenia międzywęzłowego q oraz reakcji od podłoża ze stałą sprężystości k – wektor równoważników węzłowych zestawiono w tab .2a i 2b
Tab. 2a Wektor równoważników węzłowych od odporu podłoża oraz od podpory sprężystej
Tab. 2b Wektor róenoważników węzłowych od obciążeń czynnych rozłożonych i skupionych
Uwaga: Funkcję kształtu przy obliczaniu wektora równoważników węzłowych elementów belki leżących na sprężystym podłożu, przyjęto jak dla elementu poddanego jedynie zginaniu, choć element ten jest również ściskany. Przybliżenie takie jest wystarczająco dokładne w obliczeniach praktycznych.
Po uwzględnieniu wartości stałych sprężystości k i C oraz obciążenia P i M oraz faktu, że q<0,P<0 (ujemne), otrzymamy wektor rónoważników węzłowych zestawiony w tab.2c.
Tab.2c. Wektor równoważników węzłowych po przeniesieniu wyrazów od sprężystych podpór
Kinematyczne warunki brzegowe. Modyfikacja macierzy sztywności
Jeśli przemieszczenia punktu węzłowego jest znane , np. wk=δ, to w celu zachowania wymiaru macierzy sztywności – kinematyczne warunki brzegowe można uwzględnić w następujący sposób: 1) przenieść iloczyny odpowiednich wyrazów macierzy sztywności i tego przemieszczenia na stronę wektora równoważników węzłowych:
| $ \overline F_r=- k_{rk} \delta +F_r$ | (35) |
a jednocześnie: 2) w wierszu macierzy , odpowiadającemu przemieszczeniu należy wyzerować wszystkie wyrazy oprócz wyrazu na głównej przekątnej, który przyjmujmy równy 1.
Jednym zdaniem do równania kanonicznego wpisujemy równość wk=δ.
W naszym przypadku wprowadzimy warunek: w3=0
Wyrazy zawierające niewiadome przemieszczenia, występujące w wektorze obciążenia przenosi się na stronę macierzy sztywności.
Po tych operacjach otrzymuje się zmodyfikowane równanie równanie kanoniczne
| $ \left \{ \overline K \right \} \cdot |u|=|\overline F| $ | (36) |
Równanie (36) dla prezentowanego przykładu podano w tab.3.
Tab.3. Zmodyfikowane równanie kanoniczne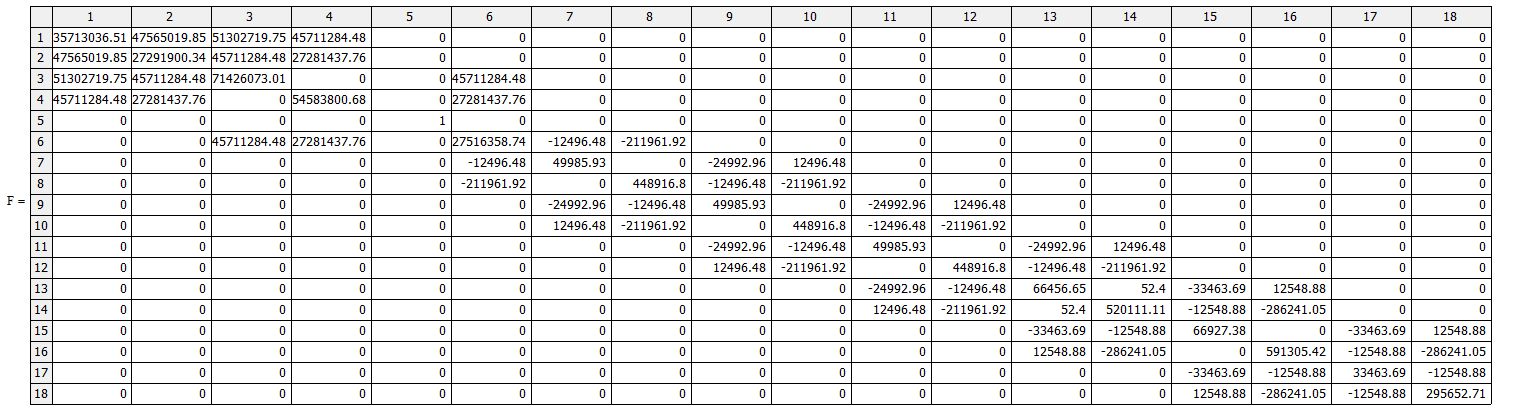
Rozwiązanie równania kanonicznego
Przemieszczenia
W wyniku rozwiązania zmodyfikowanego, kanonicznego układu równań(Tab.3), otrzymano następujące wartości przemieszczeń ($w$ [m] $\varphi $ [rad] :
$ |u| = \small {\left | \matrix { w_1= 0,00000 \cr \varphi_1 – 3,80841 \cr w_2= 0,00000 \cr \varphi_2= -3,80871 \cr w_3=0,00000 \cr \varphi_3 =-3,80964 \cr w_4=-9,21016 \cr \varphi_4 = -4,21969 \cr w_5=-1,62009 \cr \varphi_5 = -4,17215 \cr w_6= -20,65211 \cr \varphi_6=-3,94199 \cr w_7= -22,51866 \cr \varphi_7 = -3,80417 \cr w_8= -2,85051 \cr \varphi_8= -4,19084 \cr w_9= -34,68487 \cr \varphi_9= -4,31973} \right |\cdot 10^{-4} }$
Wykresy linii ugięcia pokazano na rys. 8. Wykresy uzyskano poprzez połączenie linimai prostymi wartości węzłowych lub przywęzłowych. Nie uwzględniono rzeczywistej, najczęściej nieliniowej zmienności wykresu pomiędzy węzłami. To samo dotyczy wykresu momentów zginających belkę (rys.9).
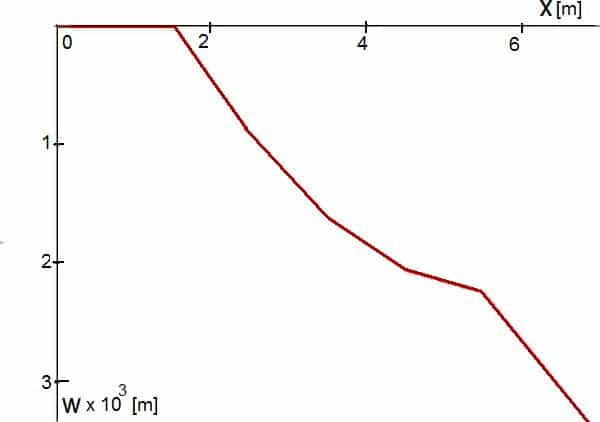
Rys. 8. Linia ugięcia belki- kratownicy z przykładu
Siły przekrojowe
Siły przekrojowe obliczono dla każdego elementu (e), wykorzystując zasadę superpozycji tzn wyznaczjać siły przywęzłowe z umy sił od znanych już przemieszczeń węzłowych i sił od bciążeń elementowych, oraz wykonujac krok odwrotny w celu okreśłenia sił od przemieszczeń, jak następuje:
|
$ |S_e|^{(e)} =|S_e|^{(e)}_{u} -|S_e|^{(e)}_{p}$ |
(37a)
|
czyli dla indeksó w numeracji lokalnej:
 |
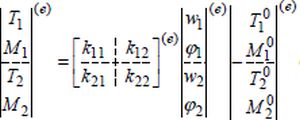(37b) |
W rezultacie uzyskamy wektory sił przywęzłowych. Postępując zgodnie z opisaną procedurą, uzyskano następujące siły przywęzłowe (T [kN], M [kNm]) dla poszczególnych elementów skończonych:
$ |S|= [T_1 | M_1 | T_2 | M_2]^{(e)}=$
$\small [ -10,000 | 0,000 | 625,91 | -7,97]^{(1-2)} $
$\small [ -625,91 | 7,97| 1455,25 | -15,94]^{(2-3)}$
$\small [ 15,99 | 15,94 | -9,99 | -2,96]^{(3-4)}$
$\small [ 9,99 | 2,96 | -3,99 | 4,03]^{(4-5)}$
$\small [ 3,99 | 4,03 | 2,02 | 5,02]^{(5-6)}$
$\small [ -2,02 | -5,02 | 8,02 | 0,00]^{(6-7)}$
$\small [ 10,00 | 15,00 | -10,00 | -7,50]^{(7-8)}$
$\small [ 10,00 | 7,50 | -10,00 | 0,00]^{(8-9)}$
Wykresy momentów zginajacych pokazano na rys. 9.
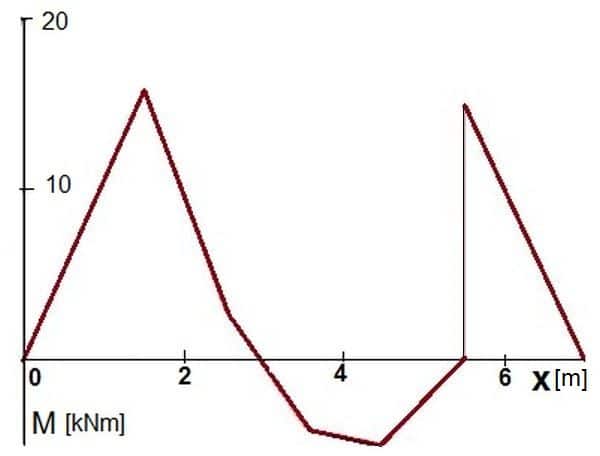Rys. 9. Wykres momentów zginających dla belki-kratownicy z przykładu
Literatura
- Piechnik, S. (1980). Wytrzymałość materiałów dla wydziałów budowlanych. PWN
- Felippa, C. A. (2001). Introduction to Finite Element (ASEN 5007) . Part 13. Lecture for Curse Fall 2001, [ http://www.colorado.edu/engineering/CAS/courses.d/Structures.d/IAST.Lect03.d/IAST.Lect03.pdf ]
- Pałkowski S., (2009), Konstrukcje stalowe: wybrane zagadnienia obliczania i projek-towania. Wydawnictwo Naukowe PWN, Warszawa
- Livesley, R. K. (1975), Matrix methods of structural analysis. Pergamon Press [http://books.google.com/books?id=tYsoAQAAMAAJ ]
________________________________
