Leszek Chodor, 2 listopada 2016
22-02-2025 rewizja po dużej awarii portalu>
W przypadku nieczytelnych treści, proszę powiadomić: leszek@chodor.co
Artykuł w ciągu ostatnich 24 godzin czytało 10 Czytelników
Podstawowymi elementami konstrukcji stalowych są belki i słupy. Belki są elementami zginanymi, a słupy ściskanymi Elementy te przed osiągnięciem pełnej nośności przekroju (plastycznej dla klasy 1-szej przekroju , lub 2-giej, sprężystej dla klasy 3-ciej lub pozakrytycznej dla klasy 4-tej) mogą utracić stateczność globalną elementu: słupy wybaczają się, a belki wichrzą i w związku z tym zasadniczo mają mniejszą nośność od przekroju pręta, z którego są wykonane.
Wprowadzenie
W artykule przedstawiono klasyczne, normowe zasady wymiarowania belek konstrukcji stalowych. Rozszerzenie tego tematu można znaleźć w artykule Współczynnik wyboczeniowy. Geneza i mit oraz w pracy [1]. Czytelnik powinien również zapoznać się z zagadnieniem nośności plastycznej elementów i konstrukcji stalowych.
Klasyczna teoria zginania belek Bernoulliego-Eulera ma bardzo ograniczone zastosowanie do belek stalowych, ponieważ przekroje belek stalowych są cienkościenne, a teoria Bernoulliego dotyczy belek o przekroju krępym. W przypadku przekrojów stalowych należy stosować uogólnioną teorię belkową (prętową) Własowa, słuszną dla przekrojów cienkościennych. W ramach teorii skręcania skrępowanego Własowa da się wyjaśni fenomen utraty stateczności belki poprzez utratę płaskiej postaci zginania, czyli zwichrzenie. Zjawiska tego nie da się wyjaśnić w ramach teorii Bernoulliego, a jest ono podstawowym zjawiskiem w konstrukcjach stalowych. Zwichrzenie belki wspornikowej o przekroju dwuteowym zginanej momentem My w płaszczyźnie z-z (względem osi y-y) zilustrowano na rys. 1
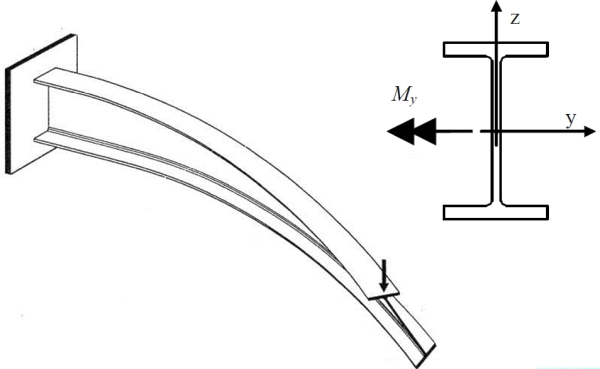
Rys. 1. Zwichrzenie dwuteowej belki wspornikowej [2]
Poniżej najpierw rozważymy belki zabezpieczone przed zwichrzeniem (rys.1), a następnie belki niestężone, podatne na zwichrzenie.
Belki stężone przeciwko zwichrzeniu
Typowe zastosowania belek stalowych
W tab.1 zestawiono podstawowe typy belek stalowych, przedział stosowanych rozpiętości oraz typowe zastosowania.
Tab. 1 Typowe rozpiętości i zastosowania belek stalowych [3], rys.2,tab.1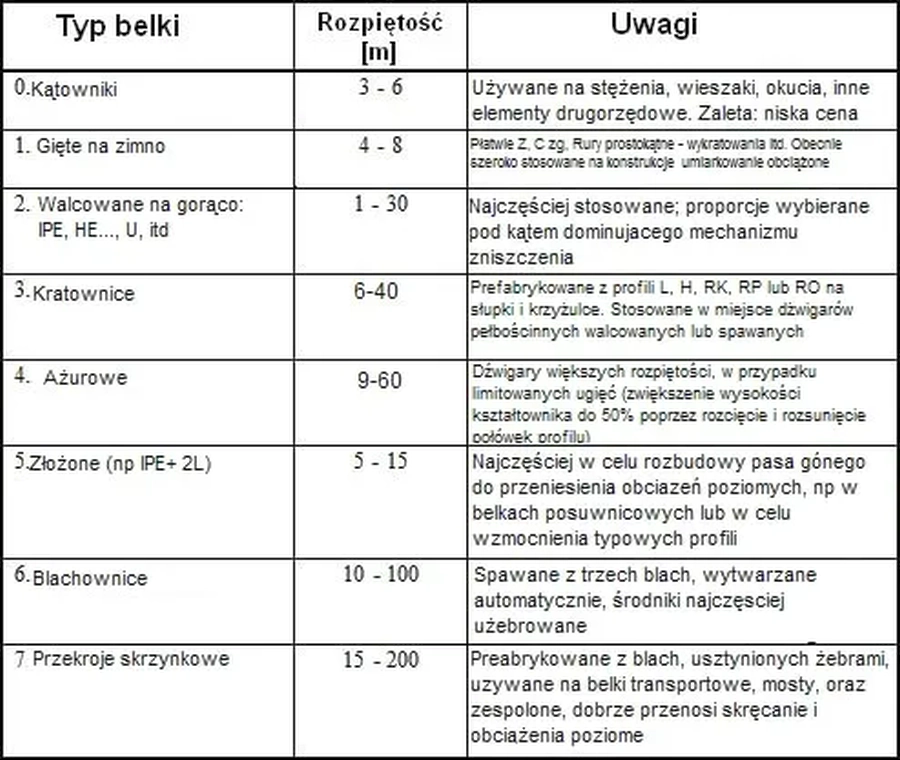
Nośność przekroju belki na zginanie
Na rys. 2 pokazano etapy pracy belki stalowej na przykładzie belki jednoprzęsłowej, obciążonej siłą skupioną F w środku rozpiętości. W pierwszym etapie sprężystej pracy belki do obciążenia $F_e$ zależność (obciążenie-przemieszczenie sprawcze – w tym przypadku strzałka ugięcia)=$(F-\delta)$, jest proporcjonalne i prostoliniowe. Wraz z uplastycznieniem 1-punktu belki (punkt najbardziej wytężony – przekrój pod siłą F w skrajnym włóknie przekroju) od punktu A na rys.1. zaczyna się etap pracy nieliniowej, sprężysto-plastycznej. Obciążenie $F_e$ wywołujące uplastycznienie pierwszego punktu jest nośnością sprężystą belki. Po przekroczeniu punktu B na wykresie nie jest możliwy wzrost obciążenia ponad $F_{pl}$ – następuje nieograniczony wzrost przemieszczenia sprawczego bez zwiększania obciążenia – belka płynie – uruchomiony został mechanizm plastyczny na skutek utworzenia przegubów plastycznych,. W belce statycznie wyznaczalnej wystarcza utworzenie jednego przegubu plastycznego – w przypadku belki jednoprzęsłowej pod siłą skupioną. Maksymalne obciążenie nazywa sie nośnością graniczną lub plastyczną belki.
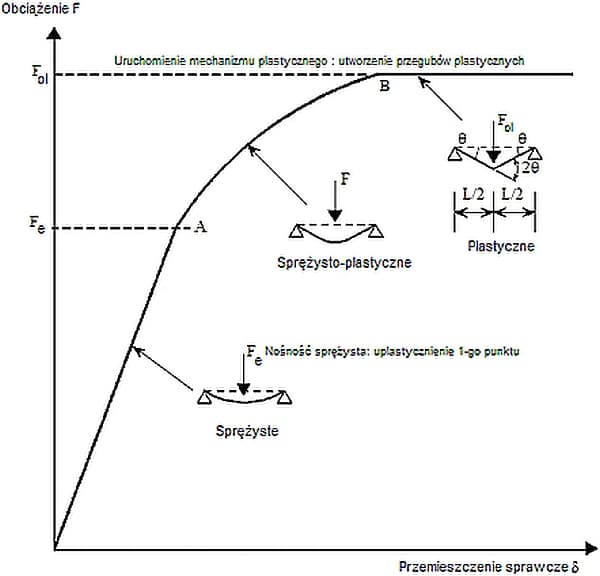
Rys. 2. Ścieżka równowagi belki jednoprzęsłowej [3]
Belki są elementami z dominującym zginaniem, a ich nośność mierzy się momentem zginającym., a nie obciążeniem. W przypadku belki zabezpieczonej przed utratą stateczności nośność belki można utożsamiać z nośnością przekroju $M_{Rd}$, obliczaną z zależności:
$$\begin{equation}M_{Rd}= \dfrac{W_y f_y}{\gamma_M}\label{1}\end{equation}$$
gdzie: wskaźnik wytrzymałości przekroju $W_y$ jest zależny od klasy przekroju:
$$\begin{equation} W_y = \begin{cases}
W_{pl,y} , & \text { dla 1,2 klasy przekroju} \\
W_{el,y} , & \text { dla 3 klasy} \\
W_{eff,y} , & \text { dla 4 klasy} \\
\end{cases} \label{2} \end{equation}$$
Współczynnik materiałowy dla klasy przekroju 1, 2 i 3 wynosi $\gamma_M=\gamma_{M0}$, a dla klasy 4: $\gamma_M=\gamma_{M1}$.
Zależność (1) jest słuszna , gdy siła ścinająca przekrój jest na tyle mała, że jej wpływ na chwilę oporu można pominąć. Norma [4]}”]ustala, że małą siła tnąca to nie więcej niż 50% nośności przekroju na ścinanie, a wówczas nośność plastyczna przekroju może być przyjmowana z ($\ref{1}$) dla wskaźnika wytrzymałości brutto.
Jeżeli pasy belki są osłabione otworami na śruby , to należy sprawdzić, czy stosunek powierzchni netto $A_{f,net}$do powierzchni brutto $A_f$ pasa nie jest tak mały, że przekrój netto będzie decydujący. Przyjmuje się, że granicznym stosunkiem jest wskaźnik przyjmowany dla elementów rozciąganych, czyli $A_{f,net}/A_f$ w pasie rozciąganym wynosi nie mniej niż 0,81 lub 0,88 dla grubości pasa t< 40 mm odpowiednio dla stali S275 i S355.
Jeśli $A_{f,net}/A_f$ jest mniejsza od tej wartości współczynnika, to przekrój pasa rozciąganego należy przyjąć jako $ A_{f,net}$. Otwory śrub w strefie ściskania (zarówno pasa jak i środnika) mogą być ignorowane, chyba że nie ejst możliwy docisk do śruby (np przy otworach owalnych).
Na rys.3 pokazano ścieżkę równowagi belki statycznie niewyznaczalnej. Utrata nośności takiej belki nie następuje po utworzeniu pierwszego przegubu plastycznego, ale dopiero po utworzeniu $N=s+1$ przegubów, gdzie $s$ jest stopniem statycznej niewyznaczalności belki. Po utworzeniu pierwszego przegubu plastycznego następuje redystrybucja naprężeń (momentów zginających) i zmiana schematu statycznego belki. W takim przypadku ważna jest możliwość plastycznego obrotu w potencjalnych przegubach, co jest możliwe dla przekroju klasy 1.
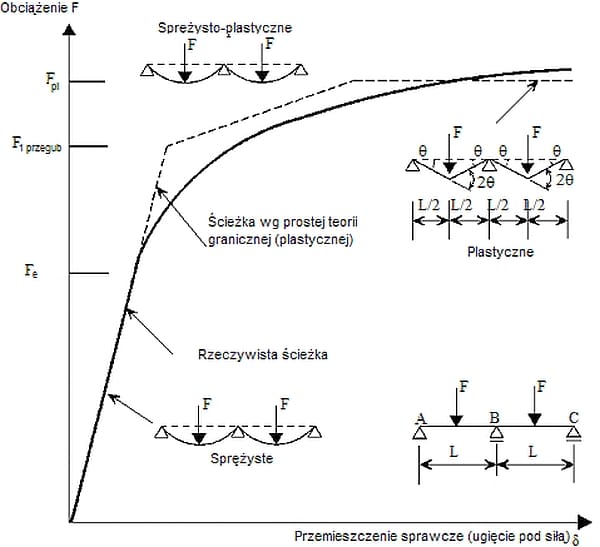
Rys. 3. Ścieżka równowagi belki dwuprzęsłowej [5], rys.2
Nośność przekroju belki na ścinanie
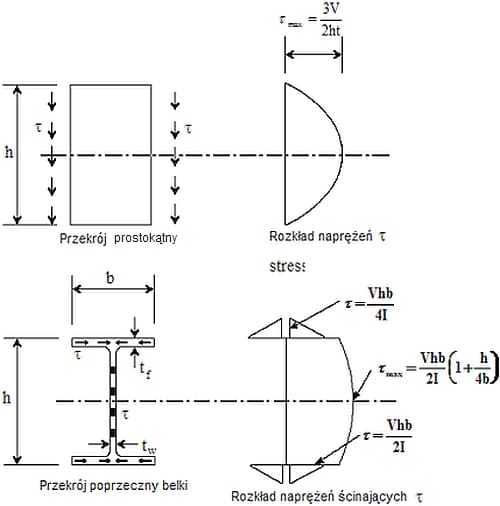
Ścinanie w belkach może być znaczące w przypadku krótkich belek z dużymi punktowymi obciążeniami. Na rys. 4 przedstawiono układ naprężeń ścinających w przekroju I w etapie sprężystej pracy belki . Praktycznie cała siła poprzeczna jest przenoszona przez środnik,a zmienność naprężenia ścinającego wzdłuż środnika jest bardzo mała, więc wystarczająco dokładne w praktycznym projektowaniu jest założenie stałych, uśrednionych naprężeń ścinających po wysokości środnika.
Z hipotezy Hubera-Misesa, wynika, ze wytrzymałość stali o granicy plastyczności $f_y$na naprężenia ścinające wynosi $f_{yv}=\dfrac{f_y}{\sqrt{3}}$. Stąd nośność przekroju na ścinanie można wyznaczyć z formuły [4], (6.18):
$$\begin{equation}V_{pl,Rd}= \dfrac{A_v \cdot f_y}{\sqrt{3} \cdot\gamma_{M0}} \label{3}\end{equation}$$
a warunek nośności belki na ścinanie przyjmuje postać [4], (6,17):
$$\begin{equation}V_{Ed} \le V_{pl,Rd} \label{4}\end{equation}$$
gdzie: $V_{Ed}$ – obliczeniowa siła poprzeczna w przekroju.
Warunek $(\ref{4})$ jest ważny dla przekrojów krępych . W przypadku smukłych ścianek należy sprawdzić wyboczenie na ścinanie. Przyjmuje się , że graniczna smukłość środnika (ścianki ścinanej) $\lambda_w =d/ t_w$ powyżej której środnik może utracić stateczność, wynosi $\lambda_w=69 \varepsilon$, tzn. 69 dla stali S235; 63,8 dla stali S275 i 56,1 dla stali S355.
Występujące w formule ($\ref{3}$) pole przekroju na ścinanie $A_v$ należy dobierać zależnie od kształtu przekroju wg tablic profili lub w przybliżeniu przyjmować, że jest to powierzhnia ścianek równoległych do działającej siły poprzecznej,
np. w przypadku dwuteownika ścinanego po osi „y” – pole przekroju środnika, a ścinanego po osi „z” – pole przekroju obu pasów
Nośność przekroju belki przy dużym ścinaniu
Jesłi siła poprzeczna przekracza 50% nośności przekroju na ścinanie, nośność przekroju poprzecznego zmniejsza się w sposób wynikający z kwadratowej formuły plastycznej interakcji zginania i ścinania:
$$\begin{equation}\left (\dfrac{\sigma}{f_y} \right)^2+ \left (\dfrac{\tau}{f_{yv}} \right)^2 \le 1 \label{5}\end{equation}$$
Formułę interakcyjną $(\ref{5})$ można przekształcić do postaci, w której redukuje się nośność przekroju mierzoną momentem zginającym w następujący sposób [4]:
$$\begin{equation}M_{v,Rd}=\left( W_{pl}-\dfrac{\rho A_v^2}{4t_w}\right) \dfrac{f_y}{\gamma_{M0}} \label{6}\end{equation}$$
gdzie współczynnik $\rho$, wynosi [4]:
$$\begin{equation}\rho=\left( \dfrac{2V_{Ed}}{V_{pl,Rd}-1}\right)^2 \label{7} \end{equation}$$
Belki niestężone
Wymiarowanie klasyczną metodą normową
Warunek nośności belki jednokierunkowo zginanej względem osi y-y można zapisać w postaci [4]
$$\begin{equation}\dfrac{M_{Ed}}{M_{b.Rd}} \le 1,0 \label{8} \end{equation}$$
gdzie: $M_{Ed}$ – obliczeniowy moment zginający , $M_{b,Rd}$- nośność na zginanie belki z warunku zwichrzenia
Nośność na zwichrzenie belek można obliczać z zależności:
$$\begin{equation}M_{b,Rd}= \dfrac{\chi_{LT} W_y f_y}{\gamma_{M1}} \label{9} \end{equation}$$
gdzie: wskaźnik wytrzymałości przekroju $W_y$ jest zależny od klasy przekroju zgodnie z zależnością ($\ref{2}$). Współczynnik materiałowy dla elementu $\gamma_M= \gamma_{M1}=1,0$.
Współczynnik zwichrzenia $\chi_{LT}$ wyznacza się w funkcji smukłości względnej $\overline \lambda_{LT}$ $(\ref{10})$ belki na zwichrzenie (indeks LT):
$$\begin{equation} \overline \lambda_{LT}=\sqrt{\dfrac{W_y \cdot f_y}{M_{cr}}} \label{10}\end{equation}$$
$$\begin{equation} \chi_{LT}= \dfrac {1}{ \phi_{LT} + \sqrt {\phi_{LT}^2 – \overline \lambda_{LT}^2}} \le 1,0 \label{11}\end{equation}$$
$$\begin{equation} \phi_{LT}=0,5 \left [1+\alpha_{LT}(\overline\lambda_{LT}-0,2) + \overline\lambda_{LT}^2 \right] \label{12}\end{equation}$$
Należy zwrócić uwagę, że w formule ($\ref{10}$) na smukłość belki w mianowniku pod pierwiastkiem występuje nośność przekroju belki $M_R=W_y \cdot f_y$ zależna od klasy przekroju zgodnie z ($\ref{2}$). Dla klasy przekroju 1: $W_y=W_{pl,y}$, a nie $W_{el,y}$ jak przyjmuje się w niektórych programach obliczeniowych i podręcznikach.
Parametr imperfekcji $\alpha_{LT}$ przyjmuje się w zależności od rodzaju krzywej zwichrzeniowej, przypisanej do kształtu przekroju, na podstawie tab.2 i tab. 3.
Tab.2. Parametry imperfekcji $\alpha_{LT}$ krzywych zwichrzenia [4]
Tab.3. Przyporządkowanie krzywych zwichrzenia [4]
Przypadek szczególny dwuteowników
W przypadku dwuteowników walcowanych i spawanych norma [4],kl. 6.3.2.3 dopuszcza stosowanie z formuł dających nieco korzystniejsze wartości od ($\ref{11}$) i ($\ref{12}$), a mianowicie:
$$\begin{equation} \chi_{LT}= \dfrac {1}{ \phi_{LT} -\sqrt {\phi_{LT}^2 – \beta \cdot \overline \lambda_{LT}^2}} \le 1,0 \text { oraz } \chi_{LT} \le 1/{\overline \lambda_{LT}^2} \label{13}\end{equation}$$
$$\begin{equation} \phi_{LT}=0,5 \left [1+\alpha_{LT}(\overline\lambda_{LT}- \overline \lambda_{LT,0}) + \beta \cdot \overline\lambda_{LT}^2 \right] \label{14}\end{equation}$$
gdzie:
$\overline \lambda_{LT,0} =0,4$ (wartość maksymalna),
$\beta = 0,75$ (wartość minimalna),
W przypadku dwuteowników walcowanych w formule ( $\ref{14}$ ) współczynnik imperfekcji $\alpha_{LT}$ przyjmuje się dla krzywej zwichrzenia innej niż w ($\ref{12}$), a mianowicie dla $ h/b \le 2 \to$ dla krzywej „b” ; dla $h/b > 2 \to $ dla krzywej „c”.
Uproszczone formuły na przypadek stężeń i w budynkach
W normie [4], kl. 6.3.2.3 podano przybliżoną metodę uwzględnienia niejednorodnego rozkładu momentów pomiędzy bocznymi stężeniami belki, a także uproszczoną metodę oceny zwichrzenia belek w budynkach. Te uproszczone, metody straciły na znaczeniu od czasu powszechnego udostępnienia dla inżynierów europejskich, programu LTBEAM do wyznaczania momentu krytycznego dowolnej belki wieloprzęsłowej o dowolnym obciążeniu i stężeniach bocznych. W artykule pomijamy omówienie historycznych już – analitycznych, przybliżonych formuł normowych, a poniżej podajemy bliższe informacje na temat stosowania programu LTBEAM.
Uwagi o perspektywach projektowania belek stalowych
W niniejszym artykule przedstawiono klasyczne normowe podejście do projektowania belek stalowych z niewielkim uogólnieniem – zaleceniem stosowania programu LTBEAM i w konsekwencji do określania smukłości zwichrzenia z formuły ogólnej $(\ref{9). Obecnie jesteśmy w przededniu „rewolucji” w metodologii projektowania konstrukcji, polegającej na tym, że stosowanie współczynników redukcyjnych (wyboczeniowych i zwichrzenia) jest zastępowane stosowaniem metod imperfekcyjnych, omówionych w cyklu artykułów Imperfekcyjna metoda projektowania. Najbliższa do powszechnego stosowania jest zaimplementowana w programie Consteel ogólna metoda imperfekcyjna [6], która jest klasyfikowana jako ogólna metoda wyboczeniowa,, czyli jest jeszcze zaliczana do metod wyboczeniowych. Metoda ta polega na stosowaniu jednego współczynnika wyboczeniowego dla całego systemu konstrukcyjnego, a nie dla każdego pręta oddzielnie, a także ujmującego wszystkie postacie niestateczności (wyboczenie gietne, skrętne i giętno-skrętne).
Przykład rachunkowy
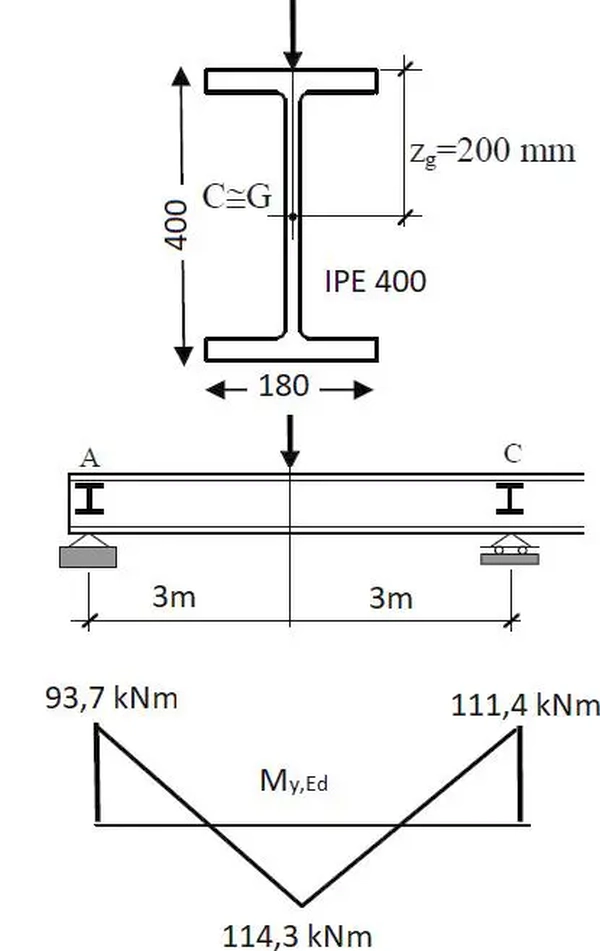
Wyznaczyć nośność podciągu stropowego w osi E, ujętego czerwona obwódką na głównym planie budowlanym – rys.2. Podciąg ma przekrój IPE 400-S355 i jest trójprzęsłowy: skrajne przęsła mają długość 6 m, a środkowe 9 m.
Geometryczne i mechaniczne charakterystyki przekroju belki:
IPE 400 -S 355:
$A$ = 84,46 cm2, $b$ = 180 mm, $h$ = 400 mm,
$t_f$ = 13.5 mm, $t_w$ = 8.6 mm, $I_y$= 23130 cm4,
$i_y$ = 16.55 cm, $I_z$ = 1318 cm4, $i_z$ = 3.95 cm,
$I_t$ = 51.08 cm4 ; $I_w$ = 490×103 cm26,
$W_{pl,y}$=1307 cm3,
$f_y$= 355 MPa , $E$ = 210 GPa.
Siły przekrojowe
Na rys.3 pokazano wykresy sił przekrojowych w podciągu ( nie występują siły osiowe)
Zwichrzenie przęsła skrajnego
Obliczeniowe siły w przęśle wynoszą:
MEd=114,3 kNm,
VEd= 75,9 kN.
Klasa przekroju
Przekrój jest klasy 1, bo jest walcowany i jednokierunkowo zginany.
Sprawdzenie nośności przekroju
Nośność na zginanie
$M_{Ed}=114,3 \ kNm$,
$(\ref{1}) \to M_{pl,Rd}= W_{pl,y}\cdot f_y / \gamma_{M0}=1307 \cdot 10^6 \cdot 355 \cdot10^3 /1.0 = 464,0 \ kNm$,
Nośność na ścinanie
$V_{Ed}=75,9 kN$,
$(\ref{3}) \to V_{pl,Rd}= \dfrac {A_v \cdot f_y} {\gamma_{M0} \sqrt{3}} = \dfrac {42,69 \cdot 10^{-4}\cdot 355 \cdot 10^3}{1,0 \cdot \sqrt{3}}=875 kN $.
$\lambda_w = \dfrac {h_w} {t_w}=\dfrac {373}{8,6}=43,4 $,
$\lambda_{w,lim}= 72 \dfrac{\varepsilon}{\eta}=72 \dfrac {0,81}{1,0}=58,3$,
Ponieważ $\lambda_w <\lambda_{w,lim}$, więc sprawdzanie nośności przekroju na ścinanie nie jest konieczne.
Interakcja zginania ścinania
$V_{Ed}=75,9 \, kN < 0,50 \cdot V_{pl,Rd}=0,50 \cdot 875,0 = 437,5 \, kN$,
więc sprawdzenie interakcji zginania i ścinania może być pominięte.
Przekrój ma wystarczającą nośność
Sprawdzenie nośności elementu (na zginanie ze zwichrzeniem)
Na rys. 4 pokazano dane do sprawdzania zwichrzenia przęsła skrajnego.
Wyznaczenie momentu krytycznego Mcr
Formuła analityczna
Przyjmując warunki podparcia w standardowy sposób (podparcie widełkowe na podporach) dla obciążenia przyłożonego do górnego pasa w środku zginania, moment krytyczny można uzyskać z następującej formuły [7]):
$$\begin{equation} M_{cr}= C_1 \cdot \cfrac{\pi^2 EI_z} {( k_z L )^2 } \left \{ \left [ \sqrt { \left( \cfrac {k_z}{k_w}\right )^2 \cfrac{I_w}{I_z} + \cfrac{(k_z L )^2 G I_T}{\pi^2 E I_z}+(C_2 z_g – C_3 z_j )^2 }\right ] – ( C_2 z_g -C_3 z_j) \right \} \label{Mcr}\end{equation}$$
Dla danych: L = 6.00 m, kz = kw = 1,0, C1 = 1,80 i C2 = 1,60 oraz zg = 200 mm, po podstawieniu do wzoru otrzymujemy:
$M_{cr}=164,7 \, kNm$
Wyrażenia analityczne na moment krytyczny są bardzo złożone, co prowadzi do częstych błędów rachunkowych, a na dodatek praktycznie każdy schemat statyczny jest opisany inną formuła , a ponadto trudno oszacować wartości i znak współczynników: kz, kw, C1, C2 oraz innych parametrów brzegowych. Nawet w przypadku, gdy zastosujemy prawidłowe formuły analityczne i dokładnie oszacujemy potrzebne współczynniki, to i tak wynik może być istotnie różny od prawidłowej wartości Mcr.
Program LTBeam
W rozpatrywanym przypadku dla sprawdzenie moment krytyczny został wyznaczony numerycznie za pomocą programu LTBeam. W tym celu należy zainstalować bezpłatny program LTBeamN (belka obciążona momentem oraz siłą ściskającą) z linków zamieszczonych na końcu artykułu po opisie programu.
Na rys. 5 pokazano postacie (mody) zwichrzenia uzyskane z wersji 1.01 tego programu.
Z programu LTBeam uzyskano wartość
$M_{cr}=175,4 \, kNm$
Jest to wartość dokładna. Różnica pomiędzy wartością uzyskaną z formuły analitycznej (mimo zachowania dużej precyzji) wynosi a aż 6,5%. Błąd w oszacowaniu nośności będzie jeszcze większy, co świadczy o małej przydatności metod analitycznych do praktycznego szacowania $M_{cr}$.
Sprawdzenie nośności belki na zwichrzenie
$ W_y = W_{pl,y}=1307 \, cm^3$ (dla klasy 1 przekroju).
$(\ref{10}$) \to$ \overline \lambda_{LT}= \sqrt {\dfrac{1307 \cdot 355 \cdot 10^{-3}}{175,6}} = 1,6 $.
Ponieważ $ h/b= 400/180=2,2 \, > \, 2$, więc krzywa zwichrzenia jest „b” (wg tab.2 ) i $\alpha_{LT}=0,34 $ ( wg tab. 3),
Po podstawieniu wartości do formuł otrzymujemy:
$(\ref{12}) \to \phi_{LT}=2,16 $,
$ (\ref{11}) \to \chi_{LT}=0,28 $,
$ (\ref{9}) \to M_{Rd}=464 \cdot 0,28 = 129,9 \, kNm$ > $M_{Ed}=114,3 \, kNm$.
Belka ma wystarczającą nośność.
Krótki opis programu LTBeamN
Za pomocą programu LTBeamN 1.0.2 można wyznaczyć mnożnik obciążenia krytycznego $\Lambda_{cr}$ Pod obciążeniem powiększonym w stosunku do mnożnika, belka ulega zwichrzeniu. $M_{cr}=\Lambda_{cr} \cdot M_{max}$, gdzie $M_{max}$ jest maksymalnym momentem zginającym wywołanym danym obciążeniem (przed powiększeniem o mnożnik αcr). Akronim LTBeamN pochodzi od angielskiego „Lateral Torsional Buckling Beam with Normal Force”. Litera N, wskazuje, że w aktualnej wersji programu belki mogą wystąpić obciążenia poprzeczne i osiowe ściskające, Odróżnia to aktualną wersję programu od wersji LTBeam udostępnianej od 2002 przez CTICM, w której nie uwzględniano siły osiowej. Ta nowa aplikacja została opracowana w języku VBNet z zaawansowanym interfejsem użytkownika, który pozwala – między innymi na analizowanie belek o zmiennej wysokości.
W programie LTBeamN belka może być złożona z elementów spójnie połączonych, o zmiennej wysokości na całej lub części długości. Element skończony jest symetryczny względem płaszczyzny zginania- możliwe jest zastosowanie dwuteowników katalogowych, lub zdefiniowanie profilu Użytkownika poprzez wskazanie wymiarów lub charakterystyk geometrycznych. Rozkład obciążeń równomiernych M i N oraz warunków stężenia bocznego może być zmieniany po długości belki w płaszczyźnie poza jej planem.
LTBeam oblicza sprężysty moment krytyczny zwichrzenia Mcr i dostarcza wiele użytecznych informacji na temat postaci zwichrzonego elementu w przypadku zróżnicowanych obciążeń i warunków podparcia. Program można zastosować w przypadku jedno i wieloprzęsłowych belek zginanych względem silniejszej osi bezwładności dla bi- i mono-symetrycznych przekrojów poprzecznych. Uwzględnia wpływ punktowych jak i ciągłych poprzecznych stężeń punktowych (sztywnych i podatnych). Obciążenia, stężenia poprzeczne mogą być przyłożone w dowolnej odległości powyżej jak i poniżej ?środka ?ścinania przekroju poprzecznego.Może być również stosowany w przypadku innych materiałów niż stal pod warunkiem wprowadzenia odpowiednich danych materiałowych.
Instalacja W celu zainstalowania oprogramowania należy rozpakować pobrane archiwum i uruchomić plik setup.exe, po uprzednim odinstalowaniu wcześniejszych wersji programu.
Poszczególne etapy definiowania belki podzielono na 4. zakładki: 1. References – wpisywanie podstawowych danych drukowanych na kartach wyników 2. Definition of Beam – definiowanie podstawowych informacji o belce: L = całkowita długość belki (łącznie wszystkie przęsła) oraz materiału, 2. Lateral Restraints – definiowanie brzegowych i pośrednich warunków podparcia, 3. Supports – definiowanie podpór 4. Loading – definiowanie obciążeń, 4. Critical Moment – wyznaczenie momentu krytycznego.
Zwraca się uwagę na fakt, że oprogramowanie LTBeamN nie służy do sprawdzania normowej nośności belki, a tylko do wyznaczenia momentu krytycznego. Jest bardzo przydatnym narzędziem do wyznaczenia momentu krytycznego, a co za tym idzie współczynnika zwichrzenia zgodnie z pkt. 2.2.
We współczesnej praktyce projektowej należy przyjąć, że posługiwanie się programem LTbeamN jest nieodzowne przez każdego inżyniera. Alternatywnie możliwe jest posługiwanie się bardziej zaawansowanymi programami, jak na przykład ConSteel. Natomiast posługiwanie się wzorami do wyznaczania momentu krytycznego belek stalowych bezwzględnie nie jest zalecane, a nawet ze względu na złożoność i częste , istotne pomyłki rachunkowe- wręcz zakazane.
Interfejs użytkownika jest dostępny w języku francuskim i angielskim. Pomoc jest dostępna tylko w języku francuskim, ale przecież działa tłumacz Google.
Pobierz oprogramowanie LTBeam v 1.0.3 z CTCIM. (strona autora programu), lub
Pobierz LTBeamN v 1.0.3 z πPortal (baza tej strony).
Po rozpakowaniu paczki i uruchomieniu pliku instalacyjnego należy postępować zgodnie z instrukcją.
Literatura
- Chodor L. (2016), Przekrycia hal i galerii. In XXXI Ogólnopolskie Warsztaty Pracy Projektanta Konstrukcji: Vol. I (pp. 25–202), [ https://chodor-projekt.net/wp-content/uploads/2016/03/Chodor_LPrzekrycia-hal-i-galerii-WPPK-2016.pdf ]
- Simoes R. (2014), Eurocodes – Design of steel buildings with worked examples. Design of Members. ECCS
- SSEDTA. (2001). Course: Eurocode 3. Lecture 11 : Restrained Beams [Lecture]. Structural Steelwork Eurocodes Development of A Trans-national Approach
- PN-EN 1993-1-1+A1:2006, Eurokod 3. Projektowanie konstrukcji stalowych, Część 1-1: Reguły ogólne i reguły dla budynków
- SSEDTA. (2001). Course: Eurocode 3. Lecture 11 : Restrained Beams [Lecture]. Structural Steelwork Eurocodes Development of A Transnational Approach
- Papp F. (2018). Global stability analysis using general method. ConsteelSoftware, [ http://www.consteelsoftware.com/en/downloads/white-papers/global-stability-analysis-using-general-method ]
- Boissonade N., Greiner R., Jaspart J. P., Lindner J. (2006). Rules for Member Stability in EN 1993-1-1: Background Documentation and Design Guidelines (Vol. 119). ECCS
________________________________